EE 42/100 Lecture 24: Latches and Flip Flops. Rev B 4/21/2010 (2:04 PM) Prof. Ali M. Niknejad
|
|
|
- Emory Hawkins
- 8 years ago
- Views:
Transcription
1 A. M. Niknejad University of California, Berkeley EE 100 / 42 Lecture 24 p. 1/20 EE 42/100 Lecture 24: Latches and Flip Flops ELECTRONICS Rev B 4/21/2010 (2:04 PM) Prof. Ali M. Niknejad University of California, Berkeley Copyright c 2010 by Ali M. Niknejad
2 A. M. Niknejad University of California, Berkeley EE 100 / 42 Lecture 24 p. 2/20 Gate Propagation Delay In a logic gate, the output does not change instantaneously when the inputs change. This delay between the output and input is caused by the finite speed of light (time it takes signals to propagate along wires). More commonly, the delay is set by the non-zero capacitance and non-zero resistance of the transistors, which means there is an RC delay associated with the gate input/output The maximum time delay from when an input changes to the output reaching its final state is known as the propagation delay, or t pd.
3 A. M. Niknejad University of California, Berkeley EE 100 / 42 Lecture 24 p. 3/20 Contamination Delay The contamination delay, tcd, is the minimum time from when an input changes until any output changes (not necessarily going to the steady value).
4 A. M. Niknejad University of California, Berkeley EE 100 / 42 Lecture 24 p. 4/20 Example Consider the multi-level digital gate shown below. Notice that for inputs A and B there is a long path from the input to the output which has to go through three gates. The longest path from the input to the output is known as the critical path, because it sets the maximum speed at which we can run a circuit. The shortest path from the input to the output is known as the short path, and it sets the contamination delay for the circuit.
5 A. M. Niknejad University of California, Berkeley EE 100 / 42 Lecture 24 p. 5/20 Glitches A B C n1 n2 Y Glitches can occur in a logic circuit if the output transitions to the wrong value but then finally settles to the correct value. The intermediate output is known as a glitch. Note that if the circuit is run sufficiently slow, determined by the propagation delay, no errors will result. But this extra transition is often unwanted (causes extra power dissipation) and may lead to problems. In this example, suppose A = 0, and B = C = 1. Next suppose B transitions from 1 0. Due to the propagation delay of the inverter, the B = 0 will initially cause both OR inputs to go to zero, which causes the output to drop to 0, but then after the B signal is inverted and applied to the AND, the output is restored. The circuit can be redesigned to avoid the glitch (homework problem?)
6 A. M. Niknejad University of California, Berkeley EE 100 / 42 Lecture 24 p. 6/20 Bistable Circuits A bistable circuit has two possible stable states. If the circuit is put into a stable state, it will remain there. The circuit has memory. If the stable state is changed (flipped there are only two states), then it will remain in the new state. Two inverters feeding back on each other, or cross coupled (inputs/outputs interchanged), form a bistable circuit. Note that when we power on the circuit we have no idea which state the bistable circuit will be in! There is also a metastable state where each output is at the midpoint. But if there is any noise or disturbance in the circuit, it will leave the metastable state.
7 A. M. Niknejad University of California, Berkeley EE 100 / 42 Lecture 24 p. 7/20 SR Latch The SR latch is essentially the same as the cross-coupled inverters, except we now have a way to set or reset it into a given state. To understand the operation, assume that we have R = 1, S = 0. Then the first NOR produces a 0 output (it only needs one 1 input to do so) and so Q = 0. But then the second NOR is fed by 0 on both inputs, so its output is 1, or Q = 1. By symmetry, if we apply R = 0 and S = 1, then Q = 1 and Q = 0. What if R = S = 1? Then both NOR gates produce a 0 output and Q = Q = 0.
8 A. M. Niknejad University of California, Berkeley EE 100 / 42 Lecture 24 p. 8/20 SR Latch Truth Table Finally, if R = S = 0, then the first NOR has an input of 0 and Q. The second NOR has an input of 0 and Q. Assume that Q = 1 so that the second NOR then produces a 0 output, which then feeds the first NOR with both 0 inputs, and the output is 1, which is the original value of Q we assumed. This state is then stable and Q = 1 is maintained and regenerated. Now if we assume Q = 0, then the second NOR is fed with 0 on both inputs, so it produces a Q = 1, which then produces a zero back on Q again (first NOR has at least one input of 1). So this state is also stable and regenerated. From this analysis, we construct the truth table of the SR latch. Note that the if R = 1(S = 0), the latch resets. If S = 1(R = 0), the latch sets. If both S = R = 0, the latch maintains its previous value. The state R = S = 1 is particularly useless and it should be avoided!
9 A. M. Niknejad University of California, Berkeley EE 100 / 42 Lecture 24 p. 9/20 D Latch The SR latch leaves something to be desired. First it requires us to avoid the bad input R = S = 1. Note that although we labeled our outputs as complementary, if we have R = S = 1 the outputs are both 0 (not complements). The D latch solves this problem by always generating complementary inputs to the SR latch. We also gate the latch so that it only changes state when the CLK is high. This is very important because we can design circuits that only change states during a positive clock cycle, and during the 0 of the clock the circuit retains its state.
10 A. M. Niknejad University of California, Berkeley EE 100 / 42 Lecture 24 p. 10/20 D Latch Truth Table The truth table for the D latch is easily constructed. When CLK = 1, we say the latch is transparent. When CLK = 0, we say the latch is opaque.
11 A. M. Niknejad University of California, Berkeley EE 100 / 42 Lecture 24 p. 11/20 D Flip Flop (FF) If we connect two latches back to back, as shown, with the clock inversion between the first and second, we obtain a flip-flop (FF). Sometimes the terms flip-flop and latch are used interchangeably, but there is a distinction. A latch is transparent during a positive clock, whereas a FF is only transparent during a brief interval during the clock transition (edge). To see why, let s analyze the circuit. When clock is low, the first latch is in transparent mode and it s sampling the input. When the clock transitions to high, the first latch goes into opaque mode and the second latch reads the last value of the input right before the clock rising edge. Hence we say the D FF is a positive edge triggered FF. You can also design a negative edge triggered FF (homework!).
12 A. M. Niknejad University of California, Berkeley EE 100 / 42 Lecture 24 p. 12/20 Registers A parallel bank of FF form a register bank. They are all clocked together and read in a word of data (or other bit widths) on the clock edge.
13 A. M. Niknejad University of California, Berkeley EE 100 / 42 Lecture 24 p. 13/20 Enabled FF Sometimes it s useful to enable a FF by adding an extra input. Then if the enable is low, the FF cannot read a new value. If enable is high, then the FF can read a value. This can be done by gating the clock with the enable signal, but gating the clock is a bad idea because it delays the clock, which means that the FF read is not perfect in sync with the clock (and perhaps the rest of the circuitry). A better solution is to MUX the input as shown.
14 A. M. Niknejad University of California, Berkeley EE 100 / 42 Lecture 24 p. 14/20 Resettable FF A reset option is very handy if we want to put our FF into a known state. The reset signal as shown is active low, which then puts a 0 into the FF. This is an synchronous reset, meaning that the FF will e reset only on the rising edge of the next clock. We can also design an asynchronous reset (homework), which means that independent of the clock the FF is reset.
15 A. M. Niknejad University of California, Berkeley EE 100 / 42 Lecture 24 p. 15/20 FF versus Latch The following timing diagram shows the difference between a latch and a FF. Note that the FF can only change on the positive edge of the clock.
16 A. M. Niknejad University of California, Berkeley EE 100 / 42 Lecture 24 p. 16/20 Finite State Machine (FSM) Inputs Combinatoral Logic Flipflop Outputs State CLK A Finite State Machine (FSM) uses latches to hold the current state of the system. At each clock cycle, the output of the FSM depends on the current input and the current state, which is encoded by the registers. Examples of FSMs: A vending machine, traffic signals, elevator controls, automatic door opener (homework),..., a CPU!
17 A. M. Niknejad University of California, Berkeley EE 100 / 42 Lecture 24 p. 17/20 State Transition Diagram Consider a light controller using a touch interface. Basically there are three four light levels, OFF, LOW, MEDIUM, and HIGH. Every time we touch the circuit, it should cycle through the states. The above state transition diagram shows the basic functionality. Each circle represents a state of the system. The arrows leaving the circle have input labels. An arrow can point back to the same state if no transition is necessary.
18 A. M. Niknejad University of California, Berkeley EE 100 / 42 Lecture 24 p. 18/20 Light Switch More Functionality Suppose that it s dark and we have a simple light sensor (lab!). Then we can add another input to the system and light up the light control so that the user can find it in the dark. Here s the new diagram. Note that we only need to turn on the light when the light is in the OFF state.
19 A. M. Niknejad University of California, Berkeley EE 100 / 42 Lecture 24 p. 19/20 State Transition Logic We need to now translate the state transition diagram into a truth table. This table has rows corresponding to the inputs and the current state, and the next state. It s a simple matter to fill this table.
20 A. M. Niknejad University of California, Berkeley EE 100 / 42 Lecture 24 p. 20/20 Circuit Realization From the state transition table, we can write Boolean expressions and design the equivalent circuits. Note that the current state will be read from a register set implemented with flip-flops.
Introduction to CMOS VLSI Design (E158) Lecture 8: Clocking of VLSI Systems
 Harris Introduction to CMOS VLSI Design (E158) Lecture 8: Clocking of VLSI Systems David Harris Harvey Mudd College David_Harris@hmc.edu Based on EE271 developed by Mark Horowitz, Stanford University MAH
Harris Introduction to CMOS VLSI Design (E158) Lecture 8: Clocking of VLSI Systems David Harris Harvey Mudd College David_Harris@hmc.edu Based on EE271 developed by Mark Horowitz, Stanford University MAH
Lecture 7: Clocking of VLSI Systems
 Lecture 7: Clocking of VLSI Systems MAH, AEN EE271 Lecture 7 1 Overview Reading Wolf 5.3 Two-Phase Clocking (good description) W&E 5.5.1, 5.5.2, 5.5.3, 5.5.4, 5.5.9, 5.5.10 - Clocking Note: The analysis
Lecture 7: Clocking of VLSI Systems MAH, AEN EE271 Lecture 7 1 Overview Reading Wolf 5.3 Two-Phase Clocking (good description) W&E 5.5.1, 5.5.2, 5.5.3, 5.5.4, 5.5.9, 5.5.10 - Clocking Note: The analysis
Lesson 12 Sequential Circuits: Flip-Flops
 Lesson 12 Sequential Circuits: Flip-Flops 1. Overview of a Synchronous Sequential Circuit We saw from last lesson that the level sensitive latches could cause instability in a sequential system. This instability
Lesson 12 Sequential Circuits: Flip-Flops 1. Overview of a Synchronous Sequential Circuit We saw from last lesson that the level sensitive latches could cause instability in a sequential system. This instability
Chapter 9 Latches, Flip-Flops, and Timers
 ETEC 23 Programmable Logic Devices Chapter 9 Latches, Flip-Flops, and Timers Shawnee State University Department of Industrial and Engineering Technologies Copyright 27 by Janna B. Gallaher Latches A temporary
ETEC 23 Programmable Logic Devices Chapter 9 Latches, Flip-Flops, and Timers Shawnee State University Department of Industrial and Engineering Technologies Copyright 27 by Janna B. Gallaher Latches A temporary
Having read this workbook you should be able to: recognise the arrangement of NAND gates used to form an S-R flip-flop.
 Objectives Having read this workbook you should be able to: recognise the arrangement of NAND gates used to form an S-R flip-flop. describe how such a flip-flop can be SET and RESET. describe the disadvantage
Objectives Having read this workbook you should be able to: recognise the arrangement of NAND gates used to form an S-R flip-flop. describe how such a flip-flop can be SET and RESET. describe the disadvantage
CS311 Lecture: Sequential Circuits
 CS311 Lecture: Sequential Circuits Last revised 8/15/2007 Objectives: 1. To introduce asynchronous and synchronous flip-flops (latches and pulsetriggered, plus asynchronous preset/clear) 2. To introduce
CS311 Lecture: Sequential Circuits Last revised 8/15/2007 Objectives: 1. To introduce asynchronous and synchronous flip-flops (latches and pulsetriggered, plus asynchronous preset/clear) 2. To introduce
Latch Timing Parameters. Flip-flop Timing Parameters. Typical Clock System. Clocking Overhead
 Clock - key to synchronous systems Topic 7 Clocking Strategies in VLSI Systems Peter Cheung Department of Electrical & Electronic Engineering Imperial College London Clocks help the design of FSM where
Clock - key to synchronous systems Topic 7 Clocking Strategies in VLSI Systems Peter Cheung Department of Electrical & Electronic Engineering Imperial College London Clocks help the design of FSM where
SEQUENTIAL CIRCUITS. Block diagram. Flip Flop. S-R Flip Flop. Block Diagram. Circuit Diagram
 SEQUENTIAL CIRCUITS http://www.tutorialspoint.com/computer_logical_organization/sequential_circuits.htm Copyright tutorialspoint.com The combinational circuit does not use any memory. Hence the previous
SEQUENTIAL CIRCUITS http://www.tutorialspoint.com/computer_logical_organization/sequential_circuits.htm Copyright tutorialspoint.com The combinational circuit does not use any memory. Hence the previous
Clocking. Figure by MIT OCW. 6.884 - Spring 2005 2/18/05 L06 Clocks 1
 ing Figure by MIT OCW. 6.884 - Spring 2005 2/18/05 L06 s 1 Why s and Storage Elements? Inputs Combinational Logic Outputs Want to reuse combinational logic from cycle to cycle 6.884 - Spring 2005 2/18/05
ing Figure by MIT OCW. 6.884 - Spring 2005 2/18/05 L06 s 1 Why s and Storage Elements? Inputs Combinational Logic Outputs Want to reuse combinational logic from cycle to cycle 6.884 - Spring 2005 2/18/05
Module 3: Floyd, Digital Fundamental
 Module 3: Lecturer : Yongsheng Gao Room : Tech - 3.25 Email : yongsheng.gao@griffith.edu.au Structure : 6 lectures 1 Tutorial Assessment: 1 Laboratory (5%) 1 Test (20%) Textbook : Floyd, Digital Fundamental
Module 3: Lecturer : Yongsheng Gao Room : Tech - 3.25 Email : yongsheng.gao@griffith.edu.au Structure : 6 lectures 1 Tutorial Assessment: 1 Laboratory (5%) 1 Test (20%) Textbook : Floyd, Digital Fundamental
Topics of Chapter 5 Sequential Machines. Memory elements. Memory element terminology. Clock terminology
 Topics of Chapter 5 Sequential Machines Memory elements Memory elements. Basics of sequential machines. Clocking issues. Two-phase clocking. Testing of combinational (Chapter 4) and sequential (Chapter
Topics of Chapter 5 Sequential Machines Memory elements Memory elements. Basics of sequential machines. Clocking issues. Two-phase clocking. Testing of combinational (Chapter 4) and sequential (Chapter
Set-Reset (SR) Latch
 et-eset () Latch Asynchronous Level sensitive cross-coupled Nor gates active high inputs (only one can be active) + + Function 0 0 0 1 0 1 eset 1 0 1 0 et 1 1 0-? 0-? Indeterminate cross-coupled Nand gates
et-eset () Latch Asynchronous Level sensitive cross-coupled Nor gates active high inputs (only one can be active) + + Function 0 0 0 1 0 1 eset 1 0 1 0 et 1 1 0-? 0-? Indeterminate cross-coupled Nand gates
Flip-Flops, Registers, Counters, and a Simple Processor
 June 8, 22 5:56 vra235_ch7 Sheet number Page number 349 black chapter 7 Flip-Flops, Registers, Counters, and a Simple Processor 7. Ng f3, h7 h6 349 June 8, 22 5:56 vra235_ch7 Sheet number 2 Page number
June 8, 22 5:56 vra235_ch7 Sheet number Page number 349 black chapter 7 Flip-Flops, Registers, Counters, and a Simple Processor 7. Ng f3, h7 h6 349 June 8, 22 5:56 vra235_ch7 Sheet number 2 Page number
A New Paradigm for Synchronous State Machine Design in Verilog
 A New Paradigm for Synchronous State Machine Design in Verilog Randy Nuss Copyright 1999 Idea Consulting Introduction Synchronous State Machines are one of the most common building blocks in modern digital
A New Paradigm for Synchronous State Machine Design in Verilog Randy Nuss Copyright 1999 Idea Consulting Introduction Synchronous State Machines are one of the most common building blocks in modern digital
Sequential Logic Design Principles.Latches and Flip-Flops
 Sequential Logic Design Principles.Latches and Flip-Flops Doru Todinca Department of Computers Politehnica University of Timisoara Outline Introduction Bistable Elements Latches and Flip-Flops S-R Latch
Sequential Logic Design Principles.Latches and Flip-Flops Doru Todinca Department of Computers Politehnica University of Timisoara Outline Introduction Bistable Elements Latches and Flip-Flops S-R Latch
Lecture 8: Synchronous Digital Systems
 Lecture 8: Synchronous Digital Systems The distinguishing feature of a synchronous digital system is that the circuit only changes in response to a system clock. For example, consider the edge triggered
Lecture 8: Synchronous Digital Systems The distinguishing feature of a synchronous digital system is that the circuit only changes in response to a system clock. For example, consider the edge triggered
Engr354: Digital Logic Circuits
 Engr354: igital Circuits Chapter 7 Sequential Elements r. Curtis Nelson Sequential Elements In this chapter you will learn about: circuits that can store information; Basic cells, latches, and flip-flops;
Engr354: igital Circuits Chapter 7 Sequential Elements r. Curtis Nelson Sequential Elements In this chapter you will learn about: circuits that can store information; Basic cells, latches, and flip-flops;
WEEK 8.1 Registers and Counters. ECE124 Digital Circuits and Systems Page 1
 WEEK 8.1 egisters and Counters ECE124 igital Circuits and Systems Page 1 Additional schematic FF symbols Active low set and reset signals. S Active high set and reset signals. S ECE124 igital Circuits
WEEK 8.1 egisters and Counters ECE124 igital Circuits and Systems Page 1 Additional schematic FF symbols Active low set and reset signals. S Active high set and reset signals. S ECE124 igital Circuits
Experiment # 9. Clock generator circuits & Counters. Eng. Waleed Y. Mousa
 Experiment # 9 Clock generator circuits & Counters Eng. Waleed Y. Mousa 1. Objectives: 1. Understanding the principles and construction of Clock generator. 2. To be familiar with clock pulse generation
Experiment # 9 Clock generator circuits & Counters Eng. Waleed Y. Mousa 1. Objectives: 1. Understanding the principles and construction of Clock generator. 2. To be familiar with clock pulse generation
Lecture 10: Sequential Circuits
 Introduction to CMOS VLSI esign Lecture 10: Sequential Circuits avid Harris Harvey Mudd College Spring 2004 Outline q Sequencing q Sequencing Element esign q Max and Min-elay q Clock Skew q Time Borrowing
Introduction to CMOS VLSI esign Lecture 10: Sequential Circuits avid Harris Harvey Mudd College Spring 2004 Outline q Sequencing q Sequencing Element esign q Max and Min-elay q Clock Skew q Time Borrowing
Lecture 11: Sequential Circuit Design
 Lecture 11: Sequential Circuit esign Outline Sequencing Sequencing Element esign Max and Min-elay Clock Skew Time Borrowing Two-Phase Clocking 2 Sequencing Combinational logic output depends on current
Lecture 11: Sequential Circuit esign Outline Sequencing Sequencing Element esign Max and Min-elay Clock Skew Time Borrowing Two-Phase Clocking 2 Sequencing Combinational logic output depends on current
To design digital counter circuits using JK-Flip-Flop. To implement counter using 74LS193 IC.
 8.1 Objectives To design digital counter circuits using JK-Flip-Flop. To implement counter using 74LS193 IC. 8.2 Introduction Circuits for counting events are frequently used in computers and other digital
8.1 Objectives To design digital counter circuits using JK-Flip-Flop. To implement counter using 74LS193 IC. 8.2 Introduction Circuits for counting events are frequently used in computers and other digital
EE552. Advanced Logic Design and Switching Theory. Metastability. Ashirwad Bahukhandi. (Ashirwad Bahukhandi) bahukhan@usc.edu
 EE552 Advanced Logic Design and Switching Theory Metastability by Ashirwad Bahukhandi (Ashirwad Bahukhandi) bahukhan@usc.edu This is an overview of what metastability is, ways of interpreting it, the issues
EE552 Advanced Logic Design and Switching Theory Metastability by Ashirwad Bahukhandi (Ashirwad Bahukhandi) bahukhan@usc.edu This is an overview of what metastability is, ways of interpreting it, the issues
Sequential Logic: Clocks, Registers, etc.
 ENEE 245: igital Circuits & Systems Lab Lab 2 : Clocks, Registers, etc. ENEE 245: igital Circuits and Systems Laboratory Lab 2 Objectives The objectives of this laboratory are the following: To design
ENEE 245: igital Circuits & Systems Lab Lab 2 : Clocks, Registers, etc. ENEE 245: igital Circuits and Systems Laboratory Lab 2 Objectives The objectives of this laboratory are the following: To design
Lecture-3 MEMORY: Development of Memory:
 Lecture-3 MEMORY: It is a storage device. It stores program data and the results. There are two kind of memories; semiconductor memories & magnetic memories. Semiconductor memories are faster, smaller,
Lecture-3 MEMORY: It is a storage device. It stores program data and the results. There are two kind of memories; semiconductor memories & magnetic memories. Semiconductor memories are faster, smaller,
Theory of Logic Circuits. Laboratory manual. Exercise 3
 Zakład Mikroinformatyki i Teorii Automatów yfrowych Theory of Logic ircuits Laboratory manual Exercise 3 Bistable devices 2008 Krzysztof yran, Piotr zekalski (edt.) 1. lassification of bistable devices
Zakład Mikroinformatyki i Teorii Automatów yfrowych Theory of Logic ircuits Laboratory manual Exercise 3 Bistable devices 2008 Krzysztof yran, Piotr zekalski (edt.) 1. lassification of bistable devices
PROGETTO DI SISTEMI ELETTRONICI DIGITALI. Digital Systems Design. Digital Circuits Advanced Topics
 PROGETTO DI SISTEMI ELETTRONICI DIGITALI Digital Systems Design Digital Circuits Advanced Topics 1 Sequential circuit and metastability 2 Sequential circuit - FSM A Sequential circuit contains: Storage
PROGETTO DI SISTEMI ELETTRONICI DIGITALI Digital Systems Design Digital Circuits Advanced Topics 1 Sequential circuit and metastability 2 Sequential circuit - FSM A Sequential circuit contains: Storage
IE1204 Digital Design F12: Asynchronous Sequential Circuits (Part 1)
 IE1204 Digital Design F12: Asynchronous Sequential Circuits (Part 1) Elena Dubrova KTH / ICT / ES dubrova@kth.se BV pp. 584-640 This lecture IE1204 Digital Design, HT14 2 Asynchronous Sequential Machines
IE1204 Digital Design F12: Asynchronous Sequential Circuits (Part 1) Elena Dubrova KTH / ICT / ES dubrova@kth.se BV pp. 584-640 This lecture IE1204 Digital Design, HT14 2 Asynchronous Sequential Machines
Sequential Circuit Design
 Sequential Circuit Design Lan-Da Van ( 倫 ), Ph. D. Department of Computer Science National Chiao Tung University Taiwan, R.O.C. Fall, 2009 ldvan@cs.nctu.edu.tw http://www.cs.nctu.edu.tw/~ldvan/ Outlines
Sequential Circuit Design Lan-Da Van ( 倫 ), Ph. D. Department of Computer Science National Chiao Tung University Taiwan, R.O.C. Fall, 2009 ldvan@cs.nctu.edu.tw http://www.cs.nctu.edu.tw/~ldvan/ Outlines
Lecture 10 Sequential Circuit Design Zhuo Feng. Z. Feng MTU EE4800 CMOS Digital IC Design & Analysis 2010
 EE4800 CMOS igital IC esign & Analysis Lecture 10 Sequential Circuit esign Zhuo Feng 10.1 Z. Feng MTU EE4800 CMOS igital IC esign & Analysis 2010 Sequencing Outline Sequencing Element esign Max and Min-elay
EE4800 CMOS igital IC esign & Analysis Lecture 10 Sequential Circuit esign Zhuo Feng 10.1 Z. Feng MTU EE4800 CMOS igital IC esign & Analysis 2010 Sequencing Outline Sequencing Element esign Max and Min-elay
Sequential Circuits. Combinational Circuits Outputs depend on the current inputs
 Principles of VLSI esign Sequential Circuits Sequential Circuits Combinational Circuits Outputs depend on the current inputs Sequential Circuits Outputs depend on current and previous inputs Requires separating
Principles of VLSI esign Sequential Circuits Sequential Circuits Combinational Circuits Outputs depend on the current inputs Sequential Circuits Outputs depend on current and previous inputs Requires separating
Counters and Decoders
 Physics 3330 Experiment #10 Fall 1999 Purpose Counters and Decoders In this experiment, you will design and construct a 4-bit ripple-through decade counter with a decimal read-out display. Such a counter
Physics 3330 Experiment #10 Fall 1999 Purpose Counters and Decoders In this experiment, you will design and construct a 4-bit ripple-through decade counter with a decimal read-out display. Such a counter
COMBINATIONAL and SEQUENTIAL LOGIC CIRCUITS Hardware implementation and software design
 PH-315 COMINATIONAL and SEUENTIAL LOGIC CIRCUITS Hardware implementation and software design A La Rosa I PURPOSE: To familiarize with combinational and sequential logic circuits Combinational circuits
PH-315 COMINATIONAL and SEUENTIAL LOGIC CIRCUITS Hardware implementation and software design A La Rosa I PURPOSE: To familiarize with combinational and sequential logic circuits Combinational circuits
NTE2053 Integrated Circuit 8 Bit MPU Compatible A/D Converter
 NTE2053 Integrated Circuit 8 Bit MPU Compatible A/D Converter Description: The NTE2053 is a CMOS 8 bit successive approximation Analog to Digital converter in a 20 Lead DIP type package which uses a differential
NTE2053 Integrated Circuit 8 Bit MPU Compatible A/D Converter Description: The NTE2053 is a CMOS 8 bit successive approximation Analog to Digital converter in a 20 Lead DIP type package which uses a differential
Digital Systems Based on Principles and Applications of Electrical Engineering/Rizzoni (McGraw Hill
 Digital Systems Based on Principles and Applications of Electrical Engineering/Rizzoni (McGraw Hill Objectives: Analyze the operation of sequential logic circuits. Understand the operation of digital counters.
Digital Systems Based on Principles and Applications of Electrical Engineering/Rizzoni (McGraw Hill Objectives: Analyze the operation of sequential logic circuits. Understand the operation of digital counters.
DIGITAL TECHNICS II. Dr. Bálint Pődör. Óbuda University, Microelectronics and Technology Institute
 DIGITAL TECHNICS II Dr. Bálint Pődör Óbuda University, Microelectronics and Technology Institute 2. LECTURE: ELEMENTARY SEUENTIAL CIRCUITS: FLIP-FLOPS 1st year BSc course 2nd (Spring) term 2012/2013 1
DIGITAL TECHNICS II Dr. Bálint Pődör Óbuda University, Microelectronics and Technology Institute 2. LECTURE: ELEMENTARY SEUENTIAL CIRCUITS: FLIP-FLOPS 1st year BSc course 2nd (Spring) term 2012/2013 1
CHAPTER 11 LATCHES AND FLIP-FLOPS
 CHAPTER 11 LATCHES AND FLIP-FLOPS This chapter in the book includes: Objectives Study Guide 11.1 Introduction 11.2 Set-Reset Latch 11.3 Gated D Latch 11.4 Edge-Triggered D Flip-Flop 11.5 S-R Flip-Flop
CHAPTER 11 LATCHES AND FLIP-FLOPS This chapter in the book includes: Objectives Study Guide 11.1 Introduction 11.2 Set-Reset Latch 11.3 Gated D Latch 11.4 Edge-Triggered D Flip-Flop 11.5 S-R Flip-Flop
Asynchronous Counters. Asynchronous Counters
 Counters and State Machine Design November 25 Asynchronous Counters ENGI 25 ELEC 24 Asynchronous Counters The term Asynchronous refers to events that do not occur at the same time With respect to counter
Counters and State Machine Design November 25 Asynchronous Counters ENGI 25 ELEC 24 Asynchronous Counters The term Asynchronous refers to events that do not occur at the same time With respect to counter
BINARY CODED DECIMAL: B.C.D.
 BINARY CODED DECIMAL: B.C.D. ANOTHER METHOD TO REPRESENT DECIMAL NUMBERS USEFUL BECAUSE MANY DIGITAL DEVICES PROCESS + DISPLAY NUMBERS IN TENS IN BCD EACH NUMBER IS DEFINED BY A BINARY CODE OF 4 BITS.
BINARY CODED DECIMAL: B.C.D. ANOTHER METHOD TO REPRESENT DECIMAL NUMBERS USEFUL BECAUSE MANY DIGITAL DEVICES PROCESS + DISPLAY NUMBERS IN TENS IN BCD EACH NUMBER IS DEFINED BY A BINARY CODE OF 4 BITS.
ETEC 2301 Programmable Logic Devices. Chapter 10 Counters. Shawnee State University Department of Industrial and Engineering Technologies
 ETEC 2301 Programmable Logic Devices Chapter 10 Counters Shawnee State University Department of Industrial and Engineering Technologies Copyright 2007 by Janna B. Gallaher Asynchronous Counter Operation
ETEC 2301 Programmable Logic Devices Chapter 10 Counters Shawnee State University Department of Industrial and Engineering Technologies Copyright 2007 by Janna B. Gallaher Asynchronous Counter Operation
ASYNCHRONOUS COUNTERS
 LB no.. SYNCHONOUS COUNTES. Introduction Counters are sequential logic circuits that counts the pulses applied at their clock input. They usually have 4 bits, delivering at the outputs the corresponding
LB no.. SYNCHONOUS COUNTES. Introduction Counters are sequential logic circuits that counts the pulses applied at their clock input. They usually have 4 bits, delivering at the outputs the corresponding
Digital Logic Design. Basics Combinational Circuits Sequential Circuits. Pu-Jen Cheng
 Digital Logic Design Basics Combinational Circuits Sequential Circuits Pu-Jen Cheng Adapted from the slides prepared by S. Dandamudi for the book, Fundamentals of Computer Organization and Design. Introduction
Digital Logic Design Basics Combinational Circuits Sequential Circuits Pu-Jen Cheng Adapted from the slides prepared by S. Dandamudi for the book, Fundamentals of Computer Organization and Design. Introduction
7. Latches and Flip-Flops
 Chapter 7 Latches and Flip-Flops Page 1 of 18 7. Latches and Flip-Flops Latches and flip-flops are the basic elements for storing information. One latch or flip-flop can store one bit of information. The
Chapter 7 Latches and Flip-Flops Page 1 of 18 7. Latches and Flip-Flops Latches and flip-flops are the basic elements for storing information. One latch or flip-flop can store one bit of information. The
Latches, the D Flip-Flop & Counter Design. ECE 152A Winter 2012
 Latches, the D Flip-Flop & Counter Design ECE 52A Winter 22 Reading Assignment Brown and Vranesic 7 Flip-Flops, Registers, Counters and a Simple Processor 7. Basic Latch 7.2 Gated SR Latch 7.2. Gated SR
Latches, the D Flip-Flop & Counter Design ECE 52A Winter 22 Reading Assignment Brown and Vranesic 7 Flip-Flops, Registers, Counters and a Simple Processor 7. Basic Latch 7.2 Gated SR Latch 7.2. Gated SR
Memory Elements. Combinational logic cannot remember
 Memory Elements Combinational logic cannot remember Output logic values are function of inputs only Feedback is needed to be able to remember a logic value Memory elements are needed in most digital logic
Memory Elements Combinational logic cannot remember Output logic values are function of inputs only Feedback is needed to be able to remember a logic value Memory elements are needed in most digital logic
L4: Sequential Building Blocks (Flip-flops, Latches and Registers)
 L4: Sequential Building Blocks (Flip-flops, Latches and Registers) Acknowledgements: Materials in this lecture are courtesy of the following sources and are used with permission. Prof. Randy Katz (Unified
L4: Sequential Building Blocks (Flip-flops, Latches and Registers) Acknowledgements: Materials in this lecture are courtesy of the following sources and are used with permission. Prof. Randy Katz (Unified
PROGETTO DI SISTEMI ELETTRONICI DIGITALI. Digital Systems Design. Digital Circuits Advanced Topics
 PROGETTO DI SISTEMI ELETTRONICI DIGITALI Digital Systems Design Digital Circuits Advanced Topics 1 Sequential circuit and metastability 2 Sequential circuit A Sequential circuit contains: Storage elements:
PROGETTO DI SISTEMI ELETTRONICI DIGITALI Digital Systems Design Digital Circuits Advanced Topics 1 Sequential circuit and metastability 2 Sequential circuit A Sequential circuit contains: Storage elements:
Chapter 2 Logic Gates and Introduction to Computer Architecture
 Chapter 2 Logic Gates and Introduction to Computer Architecture 2.1 Introduction The basic components of an Integrated Circuit (IC) is logic gates which made of transistors, in digital system there are
Chapter 2 Logic Gates and Introduction to Computer Architecture 2.1 Introduction The basic components of an Integrated Circuit (IC) is logic gates which made of transistors, in digital system there are
Layout of Multiple Cells
 Layout of Multiple Cells Beyond the primitive tier primitives add instances of primitives add additional transistors if necessary add substrate/well contacts (plugs) add additional polygons where needed
Layout of Multiple Cells Beyond the primitive tier primitives add instances of primitives add additional transistors if necessary add substrate/well contacts (plugs) add additional polygons where needed
So far we have investigated combinational logic for which the output of the logic devices/circuits depends only on the present state of the inputs.
 equential Logic o far we have investigated combinational logic for which the output of the logic devices/circuits depends only on the present state of the inputs. In sequential logic the output of the
equential Logic o far we have investigated combinational logic for which the output of the logic devices/circuits depends only on the present state of the inputs. In sequential logic the output of the
Timing Methodologies (cont d) Registers. Typical timing specifications. Synchronous System Model. Short Paths. System Clock Frequency
 Registers Timing Methodologies (cont d) Sample data using clock Hold data between clock cycles Computation (and delay) occurs between registers efinition of terms setup time: minimum time before the clocking
Registers Timing Methodologies (cont d) Sample data using clock Hold data between clock cycles Computation (and delay) occurs between registers efinition of terms setup time: minimum time before the clocking
ECE380 Digital Logic
 ECE38 igital Logic Flip-Flops, Registers and Counters: Flip-Flops r.. J. Jackson Lecture 25- Flip-flops The gated latch circuits presented are level sensitive and can change states more than once during
ECE38 igital Logic Flip-Flops, Registers and Counters: Flip-Flops r.. J. Jackson Lecture 25- Flip-flops The gated latch circuits presented are level sensitive and can change states more than once during
1. True or False? A voltage level in the range 0 to 2 volts is interpreted as a binary 1.
 File: chap04, Chapter 04 1. True or False? A voltage level in the range 0 to 2 volts is interpreted as a binary 1. 2. True or False? A gate is a device that accepts a single input signal and produces one
File: chap04, Chapter 04 1. True or False? A voltage level in the range 0 to 2 volts is interpreted as a binary 1. 2. True or False? A gate is a device that accepts a single input signal and produces one
CDA 3200 Digital Systems. Instructor: Dr. Janusz Zalewski Developed by: Dr. Dahai Guo Spring 2012
 CDA 3200 Digital Systems Instructor: Dr. Janusz Zalewski Developed by: Dr. Dahai Guo Spring 2012 Outline SR Latch D Latch Edge-Triggered D Flip-Flop (FF) S-R Flip-Flop (FF) J-K Flip-Flop (FF) T Flip-Flop
CDA 3200 Digital Systems Instructor: Dr. Janusz Zalewski Developed by: Dr. Dahai Guo Spring 2012 Outline SR Latch D Latch Edge-Triggered D Flip-Flop (FF) S-R Flip-Flop (FF) J-K Flip-Flop (FF) T Flip-Flop
RETRIEVING DATA FROM THE DDC112
 RETRIEVING DATA FROM THE by Jim Todsen This application bulletin explains how to retrieve data from the. It elaborates on the discussion given in the data sheet and provides additional information to allow
RETRIEVING DATA FROM THE by Jim Todsen This application bulletin explains how to retrieve data from the. It elaborates on the discussion given in the data sheet and provides additional information to allow
DIGITAL COUNTERS. Q B Q A = 00 initially. Q B Q A = 01 after the first clock pulse.
 DIGITAL COUNTERS http://www.tutorialspoint.com/computer_logical_organization/digital_counters.htm Copyright tutorialspoint.com Counter is a sequential circuit. A digital circuit which is used for a counting
DIGITAL COUNTERS http://www.tutorialspoint.com/computer_logical_organization/digital_counters.htm Copyright tutorialspoint.com Counter is a sequential circuit. A digital circuit which is used for a counting
Master/Slave Flip Flops
 Master/Slave Flip Flops Page 1 A Master/Slave Flip Flop ( Type) Gated latch(master) Gated latch (slave) 1 Gate Gate GATE Either: The master is loading (the master in on) or The slave is loading (the slave
Master/Slave Flip Flops Page 1 A Master/Slave Flip Flop ( Type) Gated latch(master) Gated latch (slave) 1 Gate Gate GATE Either: The master is loading (the master in on) or The slave is loading (the slave
Flip-Flops and Sequential Circuit Design. ECE 152A Winter 2012
 Flip-Flops and Sequential Circuit Design ECE 52 Winter 22 Reading ssignment Brown and Vranesic 7 Flip-Flops, Registers, Counters and a Simple Processor 7.5 T Flip-Flop 7.5. Configurable Flip-Flops 7.6
Flip-Flops and Sequential Circuit Design ECE 52 Winter 22 Reading ssignment Brown and Vranesic 7 Flip-Flops, Registers, Counters and a Simple Processor 7.5 T Flip-Flop 7.5. Configurable Flip-Flops 7.6
Flip-Flops and Sequential Circuit Design
 Flip-Flops and Sequential Circuit Design ECE 52 Winter 22 Reading ssignment Brown and Vranesic 7 Flip-Flops, Registers, Counters and a Simple Processor 7.5 T Flip-Flop 7.5. Configurable Flip-Flops 7.6
Flip-Flops and Sequential Circuit Design ECE 52 Winter 22 Reading ssignment Brown and Vranesic 7 Flip-Flops, Registers, Counters and a Simple Processor 7.5 T Flip-Flop 7.5. Configurable Flip-Flops 7.6
ENEE 244 (01**). Spring 2006. Homework 5. Due back in class on Friday, April 28.
 ENEE 244 (01**). Spring 2006 Homework 5 Due back in class on Friday, April 28. 1. Fill up the function table (truth table) for the following latch. How is this latch related to those described in the lectures
ENEE 244 (01**). Spring 2006 Homework 5 Due back in class on Friday, April 28. 1. Fill up the function table (truth table) for the following latch. How is this latch related to those described in the lectures
DIGITAL TECHNICS II. Dr. Bálint Pődör. Óbuda University, Microelectronics and Technology Institute 5. LECTURE: REGISTERS AND RELATED
 DIGITAL TECHNICS II Dr. Bálint Pődör Óbuda University, Microelectronics and Technology Institute 5. LECTURE: REGISTERS AND RELATED 2nd (Spring) term 22/23 5. LECTURE: REGISTERS. Storage registers 2. Shift
DIGITAL TECHNICS II Dr. Bálint Pődör Óbuda University, Microelectronics and Technology Institute 5. LECTURE: REGISTERS AND RELATED 2nd (Spring) term 22/23 5. LECTURE: REGISTERS. Storage registers 2. Shift
Digital Fundamentals
 igital Fundamentals with PL Programming Floyd Chapter 9 Floyd, igital Fundamentals, 10 th ed, Upper Saddle River, NJ 07458. All Rights Reserved Summary Latches (biestables) A latch is a temporary storage
igital Fundamentals with PL Programming Floyd Chapter 9 Floyd, igital Fundamentals, 10 th ed, Upper Saddle River, NJ 07458. All Rights Reserved Summary Latches (biestables) A latch is a temporary storage
CSE140: Components and Design Techniques for Digital Systems
 CE4: Components and esign Techniques for igital ystems Tajana imunic osing ources: Where we are now What we ve covered so far (Chap -5, App. A& B) Number representations Boolean algebra OP and PO Logic
CE4: Components and esign Techniques for igital ystems Tajana imunic osing ources: Where we are now What we ve covered so far (Chap -5, App. A& B) Number representations Boolean algebra OP and PO Logic
DIGITAL ELECTRONICS. Counters. By: Electrical Engineering Department
 Counters By: Electrical Engineering Department 1 Counters Upon completion of the chapter, students should be able to:.1 Understand the basic concepts of asynchronous counter and synchronous counters, and
Counters By: Electrical Engineering Department 1 Counters Upon completion of the chapter, students should be able to:.1 Understand the basic concepts of asynchronous counter and synchronous counters, and
Digital Electronics Part I Combinational and Sequential Logic. Dr. I. J. Wassell
 Digital Electronics Part I Combinational and Sequential Logic Dr. I. J. Wassell Introduction Aims To familiarise students with Combinational logic circuits Sequential logic circuits How digital logic gates
Digital Electronics Part I Combinational and Sequential Logic Dr. I. J. Wassell Introduction Aims To familiarise students with Combinational logic circuits Sequential logic circuits How digital logic gates
Cascaded Counters. Page 1 BYU
 Cascaded Counters Page 1 Mod-N Counters Generally we are interested in counters that count up to specific count values Not just powers of 2 A mod-n counter has N states Counts from 0 to N-1 then rolls
Cascaded Counters Page 1 Mod-N Counters Generally we are interested in counters that count up to specific count values Not just powers of 2 A mod-n counter has N states Counts from 0 to N-1 then rolls
Counters & Shift Registers Chapter 8 of R.P Jain
 Chapter 3 Counters & Shift Registers Chapter 8 of R.P Jain Counters & Shift Registers Counters, Syllabus Design of Modulo-N ripple counter, Up-Down counter, design of synchronous counters with and without
Chapter 3 Counters & Shift Registers Chapter 8 of R.P Jain Counters & Shift Registers Counters, Syllabus Design of Modulo-N ripple counter, Up-Down counter, design of synchronous counters with and without
Counters. Present State Next State A B A B 0 0 0 1 0 1 1 0 1 0 1 1 1 1 0 0
 ounter ounters ounters are a specific type of sequential circuit. Like registers, the state, or the flip-flop values themselves, serves as the output. The output value increases by one on each clock cycle.
ounter ounters ounters are a specific type of sequential circuit. Like registers, the state, or the flip-flop values themselves, serves as the output. The output value increases by one on each clock cycle.
Chapter 5. Sequential Logic
 Chapter 5 Sequential Logic Sequential Circuits (/2) Combinational circuits: a. contain no memory elements b. the outputs depends on the current inputs Sequential circuits: a feedback path outputs depends
Chapter 5 Sequential Logic Sequential Circuits (/2) Combinational circuits: a. contain no memory elements b. the outputs depends on the current inputs Sequential circuits: a feedback path outputs depends
DIGITAL TECHNICS II. Dr. Bálint Pődör. Óbuda University, Microelectronics and Technology Institute. 2nd (Spring) term 2012/2013
 DIGITAL TECHNICS II Dr. Bálint Pődör Óbuda University, Microelectronics and Technology Institute 4. LECTURE: COUNTERS AND RELATED 2nd (Spring) term 2012/2013 1 4. LECTURE: COUNTERS AND RELATED 1. Counters,
DIGITAL TECHNICS II Dr. Bálint Pődör Óbuda University, Microelectronics and Technology Institute 4. LECTURE: COUNTERS AND RELATED 2nd (Spring) term 2012/2013 1 4. LECTURE: COUNTERS AND RELATED 1. Counters,
(Refer Slide Time: 00:01:16 min)
 Digital Computer Organization Prof. P. K. Biswas Department of Electronic & Electrical Communication Engineering Indian Institute of Technology, Kharagpur Lecture No. # 04 CPU Design: Tirning & Control
Digital Computer Organization Prof. P. K. Biswas Department of Electronic & Electrical Communication Engineering Indian Institute of Technology, Kharagpur Lecture No. # 04 CPU Design: Tirning & Control
Digital Controller for Pedestrian Crossing and Traffic Lights
 Project Objective: - To design and simulate, a digital controller for traffic and pedestrian lights at a pedestrian crossing using Microsim Pspice The controller must be based on next-state techniques
Project Objective: - To design and simulate, a digital controller for traffic and pedestrian lights at a pedestrian crossing using Microsim Pspice The controller must be based on next-state techniques
CHAPTER 11: Flip Flops
 CHAPTER 11: Flip Flops In this chapter, you will be building the part of the circuit that controls the command sequencing. The required circuit must operate the counter and the memory chip. When the teach
CHAPTER 11: Flip Flops In this chapter, you will be building the part of the circuit that controls the command sequencing. The required circuit must operate the counter and the memory chip. When the teach
Sequential Logic. (Materials taken from: Principles of Computer Hardware by Alan Clements )
 Sequential Logic (Materials taken from: Principles of Computer Hardware by Alan Clements ) Sequential vs. Combinational Circuits Combinatorial circuits: their outputs are computed entirely from their present
Sequential Logic (Materials taken from: Principles of Computer Hardware by Alan Clements ) Sequential vs. Combinational Circuits Combinatorial circuits: their outputs are computed entirely from their present
CS 61C: Great Ideas in Computer Architecture Finite State Machines. Machine Interpreta4on
 CS 61C: Great Ideas in Computer Architecture Finite State Machines Instructors: Krste Asanovic & Vladimir Stojanovic hbp://inst.eecs.berkeley.edu/~cs61c/sp15 1 Levels of RepresentaKon/ InterpretaKon High
CS 61C: Great Ideas in Computer Architecture Finite State Machines Instructors: Krste Asanovic & Vladimir Stojanovic hbp://inst.eecs.berkeley.edu/~cs61c/sp15 1 Levels of RepresentaKon/ InterpretaKon High
CHAPTER 3 Boolean Algebra and Digital Logic
 CHAPTER 3 Boolean Algebra and Digital Logic 3.1 Introduction 121 3.2 Boolean Algebra 122 3.2.1 Boolean Expressions 123 3.2.2 Boolean Identities 124 3.2.3 Simplification of Boolean Expressions 126 3.2.4
CHAPTER 3 Boolean Algebra and Digital Logic 3.1 Introduction 121 3.2 Boolean Algebra 122 3.2.1 Boolean Expressions 123 3.2.2 Boolean Identities 124 3.2.3 Simplification of Boolean Expressions 126 3.2.4
Topics. Flip-flop-based sequential machines. Signals in flip-flop system. Flip-flop rules. Latch-based machines. Two-sided latch constraint
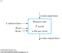
 Topics Flip-flop-based sequential machines! Clocking disciplines. Flip-flop rules! Primary inputs change after clock (φ) edge.! Primary inputs must stabilize before next clock edge.! Rules allow changes
Topics Flip-flop-based sequential machines! Clocking disciplines. Flip-flop rules! Primary inputs change after clock (φ) edge.! Primary inputs must stabilize before next clock edge.! Rules allow changes
Contents COUNTER. Unit III- Counters
 COUNTER Contents COUNTER...1 Frequency Division...2 Divide-by-2 Counter... 3 Toggle Flip-Flop...3 Frequency Division using Toggle Flip-flops...5 Truth Table for a 3-bit Asynchronous Up Counter...6 Modulo
COUNTER Contents COUNTER...1 Frequency Division...2 Divide-by-2 Counter... 3 Toggle Flip-Flop...3 Frequency Division using Toggle Flip-flops...5 Truth Table for a 3-bit Asynchronous Up Counter...6 Modulo
Wiki Lab Book. This week is practice for wiki usage during the project.
 Wiki Lab Book Use a wiki as a lab book. Wikis are excellent tools for collaborative work (i.e. where you need to efficiently share lots of information and files with multiple people). This week is practice
Wiki Lab Book Use a wiki as a lab book. Wikis are excellent tools for collaborative work (i.e. where you need to efficiently share lots of information and files with multiple people). This week is practice
DM9368 7-Segment Decoder/Driver/Latch with Constant Current Source Outputs
 DM9368 7-Segment Decoder/Driver/Latch with Constant Current Source Outputs General Description The DM9368 is a 7-segment decoder driver incorporating input latches and constant current output circuits
DM9368 7-Segment Decoder/Driver/Latch with Constant Current Source Outputs General Description The DM9368 is a 7-segment decoder driver incorporating input latches and constant current output circuits
DEPARTMENT OF INFORMATION TECHNLOGY
 DRONACHARYA GROUP OF INSTITUTIONS, GREATER NOIDA Affiliated to Mahamaya Technical University, Noida Approved by AICTE DEPARTMENT OF INFORMATION TECHNLOGY Lab Manual for Computer Organization Lab ECS-453
DRONACHARYA GROUP OF INSTITUTIONS, GREATER NOIDA Affiliated to Mahamaya Technical University, Noida Approved by AICTE DEPARTMENT OF INFORMATION TECHNLOGY Lab Manual for Computer Organization Lab ECS-453
Register File, Finite State Machines & Hardware Control Language
 Register File, Finite State Machines & Hardware Control Language Avin R. Lebeck Some slides based on those developed by Gershon Kedem, and by Randy Bryant and ave O Hallaron Compsci 04 Administrivia Homework
Register File, Finite State Machines & Hardware Control Language Avin R. Lebeck Some slides based on those developed by Gershon Kedem, and by Randy Bryant and ave O Hallaron Compsci 04 Administrivia Homework
Design Example: Counters. Design Example: Counters. 3-Bit Binary Counter. 3-Bit Binary Counter. Other useful counters:
 Design Eample: ers er: a sequential circuit that repeats a specified sequence of output upon clock pulses. A,B,C,, Z. G, O, T, E, R, P, S,!.,,,,,,,7. 7,,,,,,,.,,,,,,,,,,,. Binary counter: follows the binary
Design Eample: ers er: a sequential circuit that repeats a specified sequence of output upon clock pulses. A,B,C,, Z. G, O, T, E, R, P, S,!.,,,,,,,7. 7,,,,,,,.,,,,,,,,,,,. Binary counter: follows the binary
Combinational Logic Design Process
 Combinational Logic Design Process Create truth table from specification Generate K-maps & obtain logic equations Draw logic diagram (sharing common gates) Simulate circuit for design verification Debug
Combinational Logic Design Process Create truth table from specification Generate K-maps & obtain logic equations Draw logic diagram (sharing common gates) Simulate circuit for design verification Debug
EE 459/500 HDL Based Digital Design with Programmable Logic. Lecture 16 Timing and Clock Issues
 EE 459/500 HDL Based Digital Design with Programmable Logic Lecture 16 Timing and Clock Issues 1 Overview Sequential system timing requirements Impact of clock skew on timing Impact of clock jitter on
EE 459/500 HDL Based Digital Design with Programmable Logic Lecture 16 Timing and Clock Issues 1 Overview Sequential system timing requirements Impact of clock skew on timing Impact of clock jitter on
Admin. ECE 550: Fundamentals of Computer Systems and Engineering. Last time. VHDL: Behavioral vs Structural. Memory Elements
 Admin C 55: Fundamentals of Computer ystems and ngineering torage and Clocking eading Finish up Chapter ecitation How is it going? VHL questions/issues? Homework Homework ubmissions vis akai C 55 (Hilton):
Admin C 55: Fundamentals of Computer ystems and ngineering torage and Clocking eading Finish up Chapter ecitation How is it going? VHL questions/issues? Homework Homework ubmissions vis akai C 55 (Hilton):
Class 11: Transmission Gates, Latches
 Topics: 1. Intro 2. Transmission Gate Logic Design 3. X-Gate 2-to-1 MUX 4. X-Gate XOR 5. X-Gate 8-to-1 MUX 6. X-Gate Logic Latch 7. Voltage Drop of n-ch X-Gates 8. n-ch Pass Transistors vs. CMOS X-Gates
Topics: 1. Intro 2. Transmission Gate Logic Design 3. X-Gate 2-to-1 MUX 4. X-Gate XOR 5. X-Gate 8-to-1 MUX 6. X-Gate Logic Latch 7. Voltage Drop of n-ch X-Gates 8. n-ch Pass Transistors vs. CMOS X-Gates
Digital Logic Design Sequential circuits
 Digital Logic Design Sequential circuits Dr. Eng. Ahmed H. Madian E-mail: ahmed.madian@guc.edu.eg Dr. Eng. Rania.Swief E-mail: rania.swief@guc.edu.eg Dr. Eng. Ahmed H. Madian Registers An n-bit register
Digital Logic Design Sequential circuits Dr. Eng. Ahmed H. Madian E-mail: ahmed.madian@guc.edu.eg Dr. Eng. Rania.Swief E-mail: rania.swief@guc.edu.eg Dr. Eng. Ahmed H. Madian Registers An n-bit register
The components. E3: Digital electronics. Goals:
 E3: Digital electronics Goals: Basic understanding of logic circuits. Become familiar with the most common digital components and their use. Equipment: 1 st. LED bridge 1 st. 7-segment display. 2 st. IC
E3: Digital electronics Goals: Basic understanding of logic circuits. Become familiar with the most common digital components and their use. Equipment: 1 st. LED bridge 1 st. 7-segment display. 2 st. IC
Digital Electronics Detailed Outline
 Digital Electronics Detailed Outline Unit 1: Fundamentals of Analog and Digital Electronics (32 Total Days) Lesson 1.1: Foundations and the Board Game Counter (9 days) 1. Safety is an important concept
Digital Electronics Detailed Outline Unit 1: Fundamentals of Analog and Digital Electronics (32 Total Days) Lesson 1.1: Foundations and the Board Game Counter (9 days) 1. Safety is an important concept
Using reverse circuit execution for efficient parallel simulation of logic circuits
 Using reverse circuit execution for efficient parallel simulation of logic circuits Kalyan Perumalla *, Richard Fujimoto College of Computing, Georgia Tech, Atlanta, Georgia, USA ABSTRACT A novel technique
Using reverse circuit execution for efficient parallel simulation of logic circuits Kalyan Perumalla *, Richard Fujimoto College of Computing, Georgia Tech, Atlanta, Georgia, USA ABSTRACT A novel technique
Memory unit. 2 k words. n bits per word
 9- k address lines Read n data input lines Memory unit 2 k words n bits per word n data output lines 24 Pearson Education, Inc M Morris Mano & Charles R Kime 9-2 Memory address Binary Decimal Memory contents
9- k address lines Read n data input lines Memory unit 2 k words n bits per word n data output lines 24 Pearson Education, Inc M Morris Mano & Charles R Kime 9-2 Memory address Binary Decimal Memory contents
Electronics Merit Badge Class 3. 1/30/2014 Electronics Merit Badge Class 3 1
 Electronics Merit Badge Class 3 1/30/2014 Electronics Merit Badge Class 3 1 Decimal Base 10 In base 10, there are 10 unique digits (0-9). When writing large numbers (more that 1 digit), each column represents
Electronics Merit Badge Class 3 1/30/2014 Electronics Merit Badge Class 3 1 Decimal Base 10 In base 10, there are 10 unique digits (0-9). When writing large numbers (more that 1 digit), each column represents
Finite State Machine. RTL Hardware Design by P. Chu. Chapter 10 1
 Finite State Machine Chapter 10 1 Outline 1. Overview 2. FSM representation 3. Timing and performance of an FSM 4. Moore machine versus Mealy machine 5. VHDL description of FSMs 6. State assignment 7.
Finite State Machine Chapter 10 1 Outline 1. Overview 2. FSM representation 3. Timing and performance of an FSM 4. Moore machine versus Mealy machine 5. VHDL description of FSMs 6. State assignment 7.
Modeling Sequential Elements with Verilog. Prof. Chien-Nan Liu TEL: 03-4227151 ext:34534 Email: jimmy@ee.ncu.edu.tw. Sequential Circuit
 Modeling Sequential Elements with Verilog Prof. Chien-Nan Liu TEL: 03-4227151 ext:34534 Email: jimmy@ee.ncu.edu.tw 4-1 Sequential Circuit Outputs are functions of inputs and present states of storage elements
Modeling Sequential Elements with Verilog Prof. Chien-Nan Liu TEL: 03-4227151 ext:34534 Email: jimmy@ee.ncu.edu.tw 4-1 Sequential Circuit Outputs are functions of inputs and present states of storage elements
Upon completion of unit 1.1, students will be able to
 Upon completion of unit 1.1, students will be able to 1. Demonstrate safety of the individual, class, and overall environment of the classroom/laboratory, and understand that electricity, even at the nominal
Upon completion of unit 1.1, students will be able to 1. Demonstrate safety of the individual, class, and overall environment of the classroom/laboratory, and understand that electricity, even at the nominal
Take-Home Exercise. z y x. Erik Jonsson School of Engineering and Computer Science. The University of Texas at Dallas
 Take-Home Exercise Assume you want the counter below to count mod-6 backward. That is, it would count 0-5-4-3-2-1-0, etc. Assume it is reset on startup, and design the wiring to make the counter count
Take-Home Exercise Assume you want the counter below to count mod-6 backward. That is, it would count 0-5-4-3-2-1-0, etc. Assume it is reset on startup, and design the wiring to make the counter count
Modeling Latches and Flip-flops
 Lab Workbook Introduction Sequential circuits are digital circuits in which the output depends not only on the present input (like combinatorial circuits), but also on the past sequence of inputs. In effect,
Lab Workbook Introduction Sequential circuits are digital circuits in which the output depends not only on the present input (like combinatorial circuits), but also on the past sequence of inputs. In effect,
Decimal Number (base 10) Binary Number (base 2)
 LECTURE 5. BINARY COUNTER Before starting with counters there is some vital information that needs to be understood. The most important is the fact that since the outputs of a digital chip can only be
LECTURE 5. BINARY COUNTER Before starting with counters there is some vital information that needs to be understood. The most important is the fact that since the outputs of a digital chip can only be
