CS 4204 Computer Graphics
|
|
|
- Imogene Brooks
- 10 years ago
- Views:
Transcription
1 CS 4204 Computer Graphics 2D and 3D Transformations Doug Bowman Adapted from notes by Yong Cao Virginia Tech 1
2 Transformations What are they? changing something to something else via rules mathematics: mapping between values in a range set and domain set (function/relation) geometric: translate, rotate, scale, shear, Why are they important to graphics? moving objects on screen / in space specifying the camera s s view of a 3D scene mapping from model space to world space to camera space to screen space specifying parent/child relationships 2
3 Translation Moving an object is called a translation. We translate a point by adding to the x and y coordinates, respectively, the amount the point should be shifted in the x and y directions. We translate an object by translating each vertex in the object. t y t x x new = x old + t x ; y new = y old + t y 3
4 Scaling Changing the size of an object is called a scale. We scale an object by scaling the x and y coordinates of each vertex in the object. h old h new w old w new s x =w new /w old x new = s x x old s y =h new /h old y new = s y y old 4
5 Rotation about the origin Consider rotation about the origin by Θ degrees radius stays the same, angle increases by Θ x' = r cos (φ + θ) y' = r sin (φ + θ) x = r cos φ y = r sin φ 5
6 Rotation about the origin (cont.) From the double angle formulas: sin (A + B) = sinacosb + cosasinb cos (A+B ) = cosacosb - sinasinb Thus, x' = x cos θ y sin θ y' = x sin θ + y cos θ 6
7 Transformations as matrices Scale: x new = s x x old y new = s y y old Rotation: x 2 = x 1 cosθ - y 1 sin θ y 2 = x 1 sin θ + y 1 cos θ Translation: x new = x old + t x y new = y old + t y 7
8 Homogeneous Coordinates In order to represent a translation as a matrix multiplication operation we use 3 x 3 matrices and pad our points to become 3 x 1 matrices. This coordinate system (using three values to represent a 2D point) is called homogeneous coordinates. 8
9 Composite Transformations Suppose we wished to perform multiple transformations on a point: Remember: Matrix multiplication is associative, not commutative! Transform matrices must be pre-multiplied The first transformation you want to perform will be at the far right, just before the point 9
10 Composite Transformations - Scaling Given our three basic transformations we can create other transformations. A problem with the scale transformation is that it also moves the object being scaled. Scale a line between (2, 1) (4,1) to twice its length. Before After
11 Composite Transforms - Scaling (cont.) If we scale a line between (0,0) & (2,0) to twice its length, the left-hand endpoint does not move. Before After (0,0) is known as a fixed point for the basic scaling transformation. We can use composite transformations to create a scale transformation with different fixed points. 11
12 Fixed Point Scaling Scale by 2 with fixed point = (2,1) Translate the point (2,1) to the origin Scale by 2 Translate origin to point (2,1) Before After
13 Example of 2D transformation Rotate around an arbitrary point A: y P A x 13
14 Rotate around an arbitrary point y P A -90 P x 14
15 Rotate around an arbitrary point We know how to rotate around the origin y P A x 15
16 Rotate around an arbitrary point but that is not what we want to do! P y A -90 P x P 16
17 So what do we do? y P A x 17
18 Transform it to a known case Translate(-A x,-a y ) y P A P A x 18
19 Second step: Rotation y P Translate(-A x,-a y ) Rotate(-90) A P A P x 19
20 Final: Put everything back Translate(-A x,-a y ) y A P Rotate(-90) Translate(A x,a y ) P P A P x 20
21 Rotation about arbitrary point IMPORTANT!: Order M = T(A x,a y ) R(-90) T(-A x,-a y ) y A P P P A P x 21
22 Rotation about arbitrary point Rotation Of θ Degrees About Point (x,y) Translate (x,y) to origin Rotate Translate origin to (x,y) (x,y) (x,y) 22
23 Shears Original Data y Shear x Shear 23
24 Reflections Reflection about the y-axis Reflection about the x-axis 24
25 More Reflections Reflection about the origin Reflection about the line y=x? 25
26 Affine Transformations in 3D General form 26
27 Elementary 3D Affine Transformations Translation 27
28 Scaling Around the Origin 28
29 Shear around the origin Along x-axis 29
30 3D Rotation Various representations Decomposition into axis rotations (x-roll( x-roll, y-roll, z-roll) CCW positive assumption 30
31 Reminder: 2D rotation (z-roll) 31
32 Three axes to rotate around Z Y X 32
33 Z-roll 33
34 X-roll Cyclic indexing 34
35 Y-roll 35
36 Rigid body transformations Translations and rotations Preserve lines, angles and distances 36
37 Inversion of transformations Translation: T -1 (a,b,c) = T(-a,-b -b,-c) Rotation: R -1 (b) = R axis -1 axis(b) = -b) axis {-b Scaling: S -1 (sx,sy,sz)) = S(1/sx,1/sy,1/sz) Shearing: Sh -1 (a) = Sh(-a) 37
38 Rotation around an arbitrary axis Euler s s theorem: Any rotation or sequence of rotations around a point is equivalent to a single rotation around an axis that passes through the point. What does the matrix look like? 38
39 Rotation around an arbitrary axis Axis: u Point: P Angle: β Method: 1. Two rotations to align u with x-axis 2. Do x-roll by β 3. Undo the alignment 39
40 Derivation 1. R z (-φ)r y (θ) 2. R x (β) 3. R y (-θ)r z (φ) Altogether: R y (-θ)r z (φ)) R x (β) R z (-φ)r y (θ) We can add translation too if the axis is not through the origin 40
41 Properties of affine transformations Preservation of affine combinations of points. Preservation of lines and planes. Preservation of parallelism of lines and planes. Relative ratios are preserved Affine transformations are composed of elementary ones. 41
42 General form Rotation, Scaling, Shear Translation 42
43 Transformations as a change in coordinate system All transformations we have looked at involve transforming points in a fixed coordinate system (CS). Can also think of them as a transformation of the CS itself 43
44 Transforming the CS - examples Translate(4,4) Rotate(180 ) 44
45 Why transform the CS? Objects often defined in a natural or convenient CS (2,2) To draw objects transformed by T, we could: Transform each vertex by T, then draw Or, draw vertices in a transformed CS 45
46 Drawing in transformed CS Tell system once how to draw the object, then draw in a transformed CS to transform the object House drawn in a CS that s been translated, rotated, and scaled 46
47 Mapping between systems Given: The vertices of an object in CS 2 A transformation matrix M that transforms CS 1 to CS 2 What are the coordinates of the object s vertices in CS 1? 47
48 Mapping example Translate(4,4) P Point P is at (0,0) in the transformed CS (CS 2 ). Where is it in CS 1? Answer: (4,4) *Note: (4,4) = T 4,4 P 48
49 Mapping rule In general, if CS 1 is transformed by a matrix M to form CS 2, a point P in CS 2 is represented by MP in CS 1 49
50 Another example P Translate(4,4), then Scale(0.5, 0.5) Where is P in CS 3? (2,2) Where is P in CS 2? S 0.5,0.5 (2,2) = (1,1) Where is P in CS 1? T 4,4 (1,1) = (5,5) *Note: to go directly from CS 3 to CS 1 we can calculate T 4,4 S 0.5,0.5 (2,2) = (5,5) 50
51 General mapping rule If CS 1 is transformed consecutively by M 1, M 2,, M n to form CS n+1, then a point P in CS n+1 is represented by CS n+1 M 1 M 2 M n P in CS 1. To form the composite transformation between CSs,, you postmultiply each successive transformation matrix. 51
52 OpenGL Transformations Learn how to carry out transformations in OpenGL Rotation Translation Scaling Introduce OpenGL matrix modes Model-view Projection 52
53 OpenGL Matrices In OpenGL matrices are part of the state Multiple types Model-View (GL_MODELVIEW( GL_MODELVIEW) Projection (GL_PROJECTION( GL_PROJECTION) Texture (GL_TEXTURE( GL_TEXTURE) ) (ignore for now) Color(GL_COLOR GL_COLOR) ) (ignore for now) Single set of functions for manipulation Select which to manipulated by glmatrixmode(gl_modelview); glmatrixmode(gl_projection); 53
54 Current Transformation Matrix (CTM) Conceptually there is a 4 x 4 homogeneous coordinate matrix, the current transformation matrix (CTM) that is part of the state and is applied to all vertices that pass down the pipeline The CTM is defined in the user program and loaded into a transformation unit vertices p C CTM p'=cp vertices 54
55 CTM operations The CTM can be altered either by loading a new CTM or by postmutiplication Load an identity matrix: C I Load an arbitrary matrix: C M Load a translation matrix: C T Load a rotation matrix: C R Load a scaling matrix: C S Postmultiply by an arbitrary matrix: C CM Postmultiply by a translation matrix: C CT Postmultiply by a rotation matrix: C C R Postmultiply by a scaling matrix: C C S 55
56 Rotation about a Fixed Point Start with identity matrix: C I Move fixed point to origin: C CT Rotate: C CR Move fixed point back: C CT CT -1 Result: C = TR T 1 which is backwards. This result is a consequence of doing postmultiplications. Let s s try again. 56
57 Reversing the Order We want C = T 1 R T so we must do the operations in the following order C I C CT -1 C CR C CT Each operation corresponds to one function call in the program. Note that the last operation specified is the first executed in the program 57
58 CTM in OpenGL OpenGL has a model-view and a projection matrix in the pipeline which are concatenated together to form the CTM Can manipulate each by first setting the correct matrix mode 58
59 Rotation, Translation, Scaling Load an identity matrix: glloadidentity() Multiply on right: glrotatef(theta, vx, vy, vz) theta in degrees, (vx, vy, vz) define axis of rotation gltranslatef(dx, dy, dz) glscalef( sx, sy, sz) Each has a float (f) and double (d) format (glscaled) 59
60 Example Rotation about z axis by 30 degrees with a fixed point of (1.0, 2.0, 3.0) glmatrixmode(gl_modelview); glloadidentity(); gltranslatef(1.0, 2.0, 3.0); glrotatef(30.0, 0.0, 0.0, 1.0); gltranslatef(-1.0, -2.0, -3.0); Remember that last matrix specified in the program is the first applied 60
61 Arbitrary Matrices Can load and multiply by matrices defined in the application program glloadmatrixf(m) glmultmatrixf(m) The matrix m is a one dimension array of 16 elements which are the components of the desired 4 x 4 matrix stored by columns In glmultmatrixf, m multiplies the existing matrix on the right 61
62 Transformations in OpenGL OpenGL makes it easy to do transformations to the CS, not the object Sequence of operations: Set up a routine to draw the object in its base CS Call transformation routines to transform the CS Object drawn in transformed CS 62
63 OpenGL transformation example drawhouse(){ glbegin(gl_line_loop); glvertex2i(0,0); glvertex2i(0,2);... glend(); } drawtransformedhouse(){ } glmatrixmode(gl_modelview); gltranslatef(4.0, 4.0, 0.0); glscalef(0.5, 0.5, 1.0); drawhouse(); Draws basic house Draws transformed house 63
64 Matrix Stacks In many situations we want to save transformation matrices for use later Traversing hierarchical data structures Avoiding state changes when executing display lists OpenGL maintains stacks for each type of matrix Access present type (as set by glmatrixmode) by glpushmatrix() glpopmatrix() 64
65 OpenGL matrix stack example M 0 glloadmatrixf(m0); glpushmatrix(); glmultmatrixf(m1); glpushmatrix(); glmultmatrixf(m4); render chair2; glpopmatrix(); glpushmatrix(); glmultmatrixf(m3); render chair1; glpopmatrix(); render table; glpopmatrix(); glpushmatrix(); glmultmatrixf(m2); render rug; glpopmatrix() render room; M 1 room M 2 table rug M 3 M 4 chair1 chair2 M 0 *M 1 *M 4 M 0 *M 1 M 0 65
Computer Graphics Labs
 Computer Graphics Labs Abel J. P. Gomes LAB. 2 Department of Computer Science and Engineering University of Beira Interior Portugal 2011 Copyright 2009-2011 All rights reserved. LAB. 2 1. Learning goals
Computer Graphics Labs Abel J. P. Gomes LAB. 2 Department of Computer Science and Engineering University of Beira Interior Portugal 2011 Copyright 2009-2011 All rights reserved. LAB. 2 1. Learning goals
Given a point cloud, polygon, or sampled parametric curve, we can use transformations for several purposes:
 3 3.1 2D Given a point cloud, polygon, or sampled parametric curve, we can use transformations for several purposes: 1. Change coordinate frames (world, window, viewport, device, etc). 2. Compose objects
3 3.1 2D Given a point cloud, polygon, or sampled parametric curve, we can use transformations for several purposes: 1. Change coordinate frames (world, window, viewport, device, etc). 2. Compose objects
Lecture 3: Coordinate Systems and Transformations
 Lecture 3: Coordinate Systems and Transformations Topics: 1. Coordinate systems and frames 2. Change of frames 3. Affine transformations 4. Rotation, translation, scaling, and shear 5. Rotation about an
Lecture 3: Coordinate Systems and Transformations Topics: 1. Coordinate systems and frames 2. Change of frames 3. Affine transformations 4. Rotation, translation, scaling, and shear 5. Rotation about an
Aston University. School of Engineering & Applied Science
 CS2150 Aston University School of Engineering & Applied Science CS2150: Computer Graphics January Examinations 2010 Date: XXX Time: XXX Instructions to Candidates: 1. Answer Question ONE and any other
CS2150 Aston University School of Engineering & Applied Science CS2150: Computer Graphics January Examinations 2010 Date: XXX Time: XXX Instructions to Candidates: 1. Answer Question ONE and any other
2D Geometrical Transformations. Foley & Van Dam, Chapter 5
 2D Geometrical Transformations Fole & Van Dam, Chapter 5 2D Geometrical Transformations Translation Scaling Rotation Shear Matri notation Compositions Homogeneous coordinates 2D Geometrical Transformations
2D Geometrical Transformations Fole & Van Dam, Chapter 5 2D Geometrical Transformations Translation Scaling Rotation Shear Matri notation Compositions Homogeneous coordinates 2D Geometrical Transformations
2D Geometric Transformations
 2D Geometric Transformations (Chapter 5 in FVD) 2D Geometric Transformations Question: How do we represent a geometric object in the plane? Answer: For now, assume that objects consist of points and lines.
2D Geometric Transformations (Chapter 5 in FVD) 2D Geometric Transformations Question: How do we represent a geometric object in the plane? Answer: For now, assume that objects consist of points and lines.
Vector Notation: AB represents the vector from point A to point B on a graph. The vector can be computed by B A.
 1 Linear Transformations Prepared by: Robin Michelle King A transformation of an object is a change in position or dimension (or both) of the object. The resulting object after the transformation is called
1 Linear Transformations Prepared by: Robin Michelle King A transformation of an object is a change in position or dimension (or both) of the object. The resulting object after the transformation is called
Graphics Pipeline in a Nutshell
 Graphics Pipeline in a Nutshell How do we create a rendering such as this? CS334 Spring 2008 Design the scene (technical drawing in wireframe ) Apply perspective transformations to the scene geometry for
Graphics Pipeline in a Nutshell How do we create a rendering such as this? CS334 Spring 2008 Design the scene (technical drawing in wireframe ) Apply perspective transformations to the scene geometry for
9 MATRICES AND TRANSFORMATIONS
 9 MATRICES AND TRANSFORMATIONS Chapter 9 Matrices and Transformations Objectives After studying this chapter you should be able to handle matrix (and vector) algebra with confidence, and understand the
9 MATRICES AND TRANSFORMATIONS Chapter 9 Matrices and Transformations Objectives After studying this chapter you should be able to handle matrix (and vector) algebra with confidence, and understand the
3D Tranformations. CS 4620 Lecture 6. Cornell CS4620 Fall 2013 Lecture 6. 2013 Steve Marschner (with previous instructors James/Bala)
 3D Tranformations CS 4620 Lecture 6 1 Translation 2 Translation 2 Translation 2 Translation 2 Scaling 3 Scaling 3 Scaling 3 Scaling 3 Rotation about z axis 4 Rotation about z axis 4 Rotation about x axis
3D Tranformations CS 4620 Lecture 6 1 Translation 2 Translation 2 Translation 2 Translation 2 Scaling 3 Scaling 3 Scaling 3 Scaling 3 Rotation about z axis 4 Rotation about z axis 4 Rotation about x axis
4BA6 - Topic 4 Dr. Steven Collins. Chap. 5 3D Viewing and Projections
 4BA6 - Topic 4 Dr. Steven Collins Chap. 5 3D Viewing and Projections References Computer graphics: principles & practice, Fole, vandam, Feiner, Hughes, S-LEN 5.644 M23*;-6 (has a good appendix on linear
4BA6 - Topic 4 Dr. Steven Collins Chap. 5 3D Viewing and Projections References Computer graphics: principles & practice, Fole, vandam, Feiner, Hughes, S-LEN 5.644 M23*;-6 (has a good appendix on linear
TWO-DIMENSIONAL TRANSFORMATION
 CHAPTER 2 TWO-DIMENSIONAL TRANSFORMATION 2.1 Introduction As stated earlier, Computer Aided Design consists of three components, namely, Design (Geometric Modeling), Analysis (FEA, etc), and Visualization
CHAPTER 2 TWO-DIMENSIONAL TRANSFORMATION 2.1 Introduction As stated earlier, Computer Aided Design consists of three components, namely, Design (Geometric Modeling), Analysis (FEA, etc), and Visualization
Rotation Matrices and Homogeneous Transformations
 Rotation Matrices and Homogeneous Transformations A coordinate frame in an n-dimensional space is defined by n mutually orthogonal unit vectors. In particular, for a two-dimensional (2D) space, i.e., n
Rotation Matrices and Homogeneous Transformations A coordinate frame in an n-dimensional space is defined by n mutually orthogonal unit vectors. In particular, for a two-dimensional (2D) space, i.e., n
Geometric Transformations
 Geometric Transformations Definitions Def: f is a mapping (function) of a set A into a set B if for every element a of A there exists a unique element b of B that is paired with a; this pairing is denoted
Geometric Transformations Definitions Def: f is a mapping (function) of a set A into a set B if for every element a of A there exists a unique element b of B that is paired with a; this pairing is denoted
Transformations in the pipeline
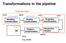 Transformations in the pipeline gltranslatef() Modeling transformation ModelView Matrix OCS WCS glulookat() VCS CCS Viewing transformation Projection transformation DCS Viewport transformation (e.g. pixels)
Transformations in the pipeline gltranslatef() Modeling transformation ModelView Matrix OCS WCS glulookat() VCS CCS Viewing transformation Projection transformation DCS Viewport transformation (e.g. pixels)
Geometric Transformation CS 211A
 Geometric Transformation CS 211A What is transformation? Moving points (x,y) moves to (x+t, y+t) Can be in any dimension 2D Image warps 3D 3D Graphics and Vision Can also be considered as a movement to
Geometric Transformation CS 211A What is transformation? Moving points (x,y) moves to (x+t, y+t) Can be in any dimension 2D Image warps 3D 3D Graphics and Vision Can also be considered as a movement to
Essential Mathematics for Computer Graphics fast
 John Vince Essential Mathematics for Computer Graphics fast Springer Contents 1. MATHEMATICS 1 Is mathematics difficult? 3 Who should read this book? 4 Aims and objectives of this book 4 Assumptions made
John Vince Essential Mathematics for Computer Graphics fast Springer Contents 1. MATHEMATICS 1 Is mathematics difficult? 3 Who should read this book? 4 Aims and objectives of this book 4 Assumptions made
Solving Simultaneous Equations and Matrices
 Solving Simultaneous Equations and Matrices The following represents a systematic investigation for the steps used to solve two simultaneous linear equations in two unknowns. The motivation for considering
Solving Simultaneous Equations and Matrices The following represents a systematic investigation for the steps used to solve two simultaneous linear equations in two unknowns. The motivation for considering
Geometry for Computer Graphics
 Computer Graphics and Visualisation Geometry for Computer Graphics Student Notes Developed by F Lin K Wyrwas J Irwin C Lilley W T Hewitt T L J Howard Computer Graphics Unit Manchester Computing Centre
Computer Graphics and Visualisation Geometry for Computer Graphics Student Notes Developed by F Lin K Wyrwas J Irwin C Lilley W T Hewitt T L J Howard Computer Graphics Unit Manchester Computing Centre
Lecture Notes. Fundamentals of Computer Graphics. Prof. Michael Langer School of Computer Science McGill University
 COMP 557 Winter 2015 Lecture Notes Fundamentals of Computer Graphics Prof. Michael Langer School of Computer Science McGill University NOTE: These lecture notes are dynamic. The initial version of the
COMP 557 Winter 2015 Lecture Notes Fundamentals of Computer Graphics Prof. Michael Langer School of Computer Science McGill University NOTE: These lecture notes are dynamic. The initial version of the
Affine Transformations
 A P P E N D I X C Affine Transformations CONTENTS C The need for geometric transformations 335 C2 Affine transformations 336 C3 Matri representation of the linear transformations 338 C4 Homogeneous coordinates
A P P E N D I X C Affine Transformations CONTENTS C The need for geometric transformations 335 C2 Affine transformations 336 C3 Matri representation of the linear transformations 338 C4 Homogeneous coordinates
Realtime 3D Computer Graphics Virtual Reality
 Realtime 3D Computer Graphics Virtual Realit Viewing and projection Classical and General Viewing Transformation Pipeline CPU Pol. DL Pixel Per Vertex Texture Raster Frag FB object ee clip normalized device
Realtime 3D Computer Graphics Virtual Realit Viewing and projection Classical and General Viewing Transformation Pipeline CPU Pol. DL Pixel Per Vertex Texture Raster Frag FB object ee clip normalized device
Vector Math Computer Graphics Scott D. Anderson
 Vector Math Computer Graphics Scott D. Anderson 1 Dot Product The notation v w means the dot product or scalar product or inner product of two vectors, v and w. In abstract mathematics, we can talk about
Vector Math Computer Graphics Scott D. Anderson 1 Dot Product The notation v w means the dot product or scalar product or inner product of two vectors, v and w. In abstract mathematics, we can talk about
Lecture L3 - Vectors, Matrices and Coordinate Transformations
 S. Widnall 16.07 Dynamics Fall 2009 Lecture notes based on J. Peraire Version 2.0 Lecture L3 - Vectors, Matrices and Coordinate Transformations By using vectors and defining appropriate operations between
S. Widnall 16.07 Dynamics Fall 2009 Lecture notes based on J. Peraire Version 2.0 Lecture L3 - Vectors, Matrices and Coordinate Transformations By using vectors and defining appropriate operations between
CS 4204 Computer Graphics
 CS 4204 Computer Graphics 3D views and projection Adapted from notes by Yong Cao 1 Overview of 3D rendering Modeling: *Define object in local coordinates *Place object in world coordinates (modeling transformation)
CS 4204 Computer Graphics 3D views and projection Adapted from notes by Yong Cao 1 Overview of 3D rendering Modeling: *Define object in local coordinates *Place object in world coordinates (modeling transformation)
Geometric Transformations
 Geometric Transformations Moving objects relative to a stationary coordinate system Common transformations: Translation Rotation Scaling Implemented using vectors and matrices Quick Review of Matrix Algebra
Geometric Transformations Moving objects relative to a stationary coordinate system Common transformations: Translation Rotation Scaling Implemented using vectors and matrices Quick Review of Matrix Algebra
Fundamentals of Computer Animation
 Fundamentals of Computer Animation Quaternions as Orientations () page 1 Visualizing a Unit Quaternion Rotation in 4D Space ( ) = w + x + y z q = Norm q + q = q q [ w, v], v = ( x, y, z) w scalar q =,
Fundamentals of Computer Animation Quaternions as Orientations () page 1 Visualizing a Unit Quaternion Rotation in 4D Space ( ) = w + x + y z q = Norm q + q = q q [ w, v], v = ( x, y, z) w scalar q =,
A vector is a directed line segment used to represent a vector quantity.
 Chapters and 6 Introduction to Vectors A vector quantity has direction and magnitude. There are many examples of vector quantities in the natural world, such as force, velocity, and acceleration. A vector
Chapters and 6 Introduction to Vectors A vector quantity has direction and magnitude. There are many examples of vector quantities in the natural world, such as force, velocity, and acceleration. A vector
3D Viewing. Chapter 7. Projections. 3D clipping. OpenGL viewing functions and clipping planes
 3D Viewing Chapter 7 Projections 3D clipping OpenGL viewing functions and clipping planes 1 Projections Parallel Perspective Coordinates are transformed along parallel lines Relative sizes are preserved
3D Viewing Chapter 7 Projections 3D clipping OpenGL viewing functions and clipping planes 1 Projections Parallel Perspective Coordinates are transformed along parallel lines Relative sizes are preserved
Android and OpenGL. Android Smartphone Programming. Matthias Keil. University of Freiburg
 Android and OpenGL Android Smartphone Programming Matthias Keil Institute for Computer Science Faculty of Engineering 16. Dezember 2013 Outline 1 OpenGL Introduction 2 Displaying Graphics 3 Interaction
Android and OpenGL Android Smartphone Programming Matthias Keil Institute for Computer Science Faculty of Engineering 16. Dezember 2013 Outline 1 OpenGL Introduction 2 Displaying Graphics 3 Interaction
521493S Computer Graphics. Exercise 2 & course schedule change
 521493S Computer Graphics Exercise 2 & course schedule change Course Schedule Change Lecture from Wednesday 31th of March is moved to Tuesday 30th of March at 16-18 in TS128 Question 2.1 Given two nonparallel,
521493S Computer Graphics Exercise 2 & course schedule change Course Schedule Change Lecture from Wednesday 31th of March is moved to Tuesday 30th of March at 16-18 in TS128 Question 2.1 Given two nonparallel,
THREE DIMENSIONAL GEOMETRY
 Chapter 8 THREE DIMENSIONAL GEOMETRY 8.1 Introduction In this chapter we present a vector algebra approach to three dimensional geometry. The aim is to present standard properties of lines and planes,
Chapter 8 THREE DIMENSIONAL GEOMETRY 8.1 Introduction In this chapter we present a vector algebra approach to three dimensional geometry. The aim is to present standard properties of lines and planes,
December 4, 2013 MATH 171 BASIC LINEAR ALGEBRA B. KITCHENS
 December 4, 2013 MATH 171 BASIC LINEAR ALGEBRA B KITCHENS The equation 1 Lines in two-dimensional space (1) 2x y = 3 describes a line in two-dimensional space The coefficients of x and y in the equation
December 4, 2013 MATH 171 BASIC LINEAR ALGEBRA B KITCHENS The equation 1 Lines in two-dimensional space (1) 2x y = 3 describes a line in two-dimensional space The coefficients of x and y in the equation
Monash University Clayton s School of Information Technology CSE3313 Computer Graphics Sample Exam Questions 2007
 Monash University Clayton s School of Information Technology CSE3313 Computer Graphics Questions 2007 INSTRUCTIONS: Answer all questions. Spend approximately 1 minute per mark. Question 1 30 Marks Total
Monash University Clayton s School of Information Technology CSE3313 Computer Graphics Questions 2007 INSTRUCTIONS: Answer all questions. Spend approximately 1 minute per mark. Question 1 30 Marks Total
Introduction to Matrices for Engineers
 Introduction to Matrices for Engineers C.T.J. Dodson, School of Mathematics, Manchester Universit 1 What is a Matrix? A matrix is a rectangular arra of elements, usuall numbers, e.g. 1 0-8 4 0-1 1 0 11
Introduction to Matrices for Engineers C.T.J. Dodson, School of Mathematics, Manchester Universit 1 What is a Matrix? A matrix is a rectangular arra of elements, usuall numbers, e.g. 1 0-8 4 0-1 1 0 11
Adding vectors We can do arithmetic with vectors. We ll start with vector addition and related operations. Suppose you have two vectors
 1 Chapter 13. VECTORS IN THREE DIMENSIONAL SPACE Let s begin with some names and notation for things: R is the set (collection) of real numbers. We write x R to mean that x is a real number. A real number
1 Chapter 13. VECTORS IN THREE DIMENSIONAL SPACE Let s begin with some names and notation for things: R is the set (collection) of real numbers. We write x R to mean that x is a real number. A real number
x1 x 2 x 3 y 1 y 2 y 3 x 1 y 2 x 2 y 1 0.
 Cross product 1 Chapter 7 Cross product We are getting ready to study integration in several variables. Until now we have been doing only differential calculus. One outcome of this study will be our ability
Cross product 1 Chapter 7 Cross product We are getting ready to study integration in several variables. Until now we have been doing only differential calculus. One outcome of this study will be our ability
CHAPTER FIVE. 5. Equations of Lines in R 3
 118 CHAPTER FIVE 5. Equations of Lines in R 3 In this chapter it is going to be very important to distinguish clearly between points and vectors. Frequently in the past the distinction has only been a
118 CHAPTER FIVE 5. Equations of Lines in R 3 In this chapter it is going to be very important to distinguish clearly between points and vectors. Frequently in the past the distinction has only been a
South Carolina College- and Career-Ready (SCCCR) Pre-Calculus
 South Carolina College- and Career-Ready (SCCCR) Pre-Calculus Key Concepts Arithmetic with Polynomials and Rational Expressions PC.AAPR.2 PC.AAPR.3 PC.AAPR.4 PC.AAPR.5 PC.AAPR.6 PC.AAPR.7 Standards Know
South Carolina College- and Career-Ready (SCCCR) Pre-Calculus Key Concepts Arithmetic with Polynomials and Rational Expressions PC.AAPR.2 PC.AAPR.3 PC.AAPR.4 PC.AAPR.5 PC.AAPR.6 PC.AAPR.7 Standards Know
Lectures notes on orthogonal matrices (with exercises) 92.222 - Linear Algebra II - Spring 2004 by D. Klain
 Lectures notes on orthogonal matrices (with exercises) 92.222 - Linear Algebra II - Spring 2004 by D. Klain 1. Orthogonal matrices and orthonormal sets An n n real-valued matrix A is said to be an orthogonal
Lectures notes on orthogonal matrices (with exercises) 92.222 - Linear Algebra II - Spring 2004 by D. Klain 1. Orthogonal matrices and orthonormal sets An n n real-valued matrix A is said to be an orthogonal
GCE Mathematics (6360) Further Pure unit 4 (MFP4) Textbook
 Version 36 klm GCE Mathematics (636) Further Pure unit 4 (MFP4) Textbook The Assessment and Qualifications Alliance (AQA) is a company limited by guarantee registered in England and Wales 364473 and a
Version 36 klm GCE Mathematics (636) Further Pure unit 4 (MFP4) Textbook The Assessment and Qualifications Alliance (AQA) is a company limited by guarantee registered in England and Wales 364473 and a
Algebra I Vocabulary Cards
 Algebra I Vocabulary Cards Table of Contents Expressions and Operations Natural Numbers Whole Numbers Integers Rational Numbers Irrational Numbers Real Numbers Absolute Value Order of Operations Expression
Algebra I Vocabulary Cards Table of Contents Expressions and Operations Natural Numbers Whole Numbers Integers Rational Numbers Irrational Numbers Real Numbers Absolute Value Order of Operations Expression
Geometric Camera Parameters
 Geometric Camera Parameters What assumptions have we made so far? -All equations we have derived for far are written in the camera reference frames. -These equations are valid only when: () all distances
Geometric Camera Parameters What assumptions have we made so far? -All equations we have derived for far are written in the camera reference frames. -These equations are valid only when: () all distances
Chapter 6. Linear Transformation. 6.1 Intro. to Linear Transformation
 Chapter 6 Linear Transformation 6 Intro to Linear Transformation Homework: Textbook, 6 Ex, 5, 9,, 5,, 7, 9,5, 55, 57, 6(a,b), 6; page 7- In this section, we discuss linear transformations 89 9 CHAPTER
Chapter 6 Linear Transformation 6 Intro to Linear Transformation Homework: Textbook, 6 Ex, 5, 9,, 5,, 7, 9,5, 55, 57, 6(a,b), 6; page 7- In this section, we discuss linear transformations 89 9 CHAPTER
CLOUD DIGITISER 2014!
 CLOUD DIGITISER 2014 Interactive measurements of point cloud sequences July 2014 Cloud Digitiser Manual 1 CLOUD DIGITISER Interactive measurement of point clouds Bill Sellers July 2014 Introduction Photogrammetric
CLOUD DIGITISER 2014 Interactive measurements of point cloud sequences July 2014 Cloud Digitiser Manual 1 CLOUD DIGITISER Interactive measurement of point clouds Bill Sellers July 2014 Introduction Photogrammetric
CSE 564: Visualization. GPU Programming (First Steps) GPU Generations. Klaus Mueller. Computer Science Department Stony Brook University
 GPU Generations CSE 564: Visualization GPU Programming (First Steps) Klaus Mueller Computer Science Department Stony Brook University For the labs, 4th generation is desirable Graphics Hardware Pipeline
GPU Generations CSE 564: Visualization GPU Programming (First Steps) Klaus Mueller Computer Science Department Stony Brook University For the labs, 4th generation is desirable Graphics Hardware Pipeline
Mathematics Notes for Class 12 chapter 10. Vector Algebra
 1 P a g e Mathematics Notes for Class 12 chapter 10. Vector Algebra A vector has direction and magnitude both but scalar has only magnitude. Magnitude of a vector a is denoted by a or a. It is non-negative
1 P a g e Mathematics Notes for Class 12 chapter 10. Vector Algebra A vector has direction and magnitude both but scalar has only magnitude. Magnitude of a vector a is denoted by a or a. It is non-negative
INTRODUCTION TO RENDERING TECHNIQUES
 INTRODUCTION TO RENDERING TECHNIQUES 22 Mar. 212 Yanir Kleiman What is 3D Graphics? Why 3D? Draw one frame at a time Model only once X 24 frames per second Color / texture only once 15, frames for a feature
INTRODUCTION TO RENDERING TECHNIQUES 22 Mar. 212 Yanir Kleiman What is 3D Graphics? Why 3D? Draw one frame at a time Model only once X 24 frames per second Color / texture only once 15, frames for a feature
Unified Lecture # 4 Vectors
 Fall 2005 Unified Lecture # 4 Vectors These notes were written by J. Peraire as a review of vectors for Dynamics 16.07. They have been adapted for Unified Engineering by R. Radovitzky. References [1] Feynmann,
Fall 2005 Unified Lecture # 4 Vectors These notes were written by J. Peraire as a review of vectors for Dynamics 16.07. They have been adapted for Unified Engineering by R. Radovitzky. References [1] Feynmann,
B4 Computational Geometry
 3CG 2006 / B4 Computational Geometry David Murray [email protected] www.robots.o.ac.uk/ dwm/courses/3cg Michaelmas 2006 3CG 2006 2 / Overview Computational geometry is concerned with the derivation
3CG 2006 / B4 Computational Geometry David Murray [email protected] www.robots.o.ac.uk/ dwm/courses/3cg Michaelmas 2006 3CG 2006 2 / Overview Computational geometry is concerned with the derivation
Exam 1 Sample Question SOLUTIONS. y = 2x
 Exam Sample Question SOLUTIONS. Eliminate the parameter to find a Cartesian equation for the curve: x e t, y e t. SOLUTION: You might look at the coordinates and notice that If you don t see it, we can
Exam Sample Question SOLUTIONS. Eliminate the parameter to find a Cartesian equation for the curve: x e t, y e t. SOLUTION: You might look at the coordinates and notice that If you don t see it, we can
We can display an object on a monitor screen in three different computer-model forms: Wireframe model Surface Model Solid model
 CHAPTER 4 CURVES 4.1 Introduction In order to understand the significance of curves, we should look into the types of model representations that are used in geometric modeling. Curves play a very significant
CHAPTER 4 CURVES 4.1 Introduction In order to understand the significance of curves, we should look into the types of model representations that are used in geometric modeling. Curves play a very significant
Math 241, Exam 1 Information.
 Math 241, Exam 1 Information. 9/24/12, LC 310, 11:15-12:05. Exam 1 will be based on: Sections 12.1-12.5, 14.1-14.3. The corresponding assigned homework problems (see http://www.math.sc.edu/ boylan/sccourses/241fa12/241.html)
Math 241, Exam 1 Information. 9/24/12, LC 310, 11:15-12:05. Exam 1 will be based on: Sections 12.1-12.5, 14.1-14.3. The corresponding assigned homework problems (see http://www.math.sc.edu/ boylan/sccourses/241fa12/241.html)
Geometry of Vectors. 1 Cartesian Coordinates. Carlo Tomasi
 Geometry of Vectors Carlo Tomasi This note explores the geometric meaning of norm, inner product, orthogonality, and projection for vectors. For vectors in three-dimensional space, we also examine the
Geometry of Vectors Carlo Tomasi This note explores the geometric meaning of norm, inner product, orthogonality, and projection for vectors. For vectors in three-dimensional space, we also examine the
Linear algebra and the geometry of quadratic equations. Similarity transformations and orthogonal matrices
 MATH 30 Differential Equations Spring 006 Linear algebra and the geometry of quadratic equations Similarity transformations and orthogonal matrices First, some things to recall from linear algebra Two
MATH 30 Differential Equations Spring 006 Linear algebra and the geometry of quadratic equations Similarity transformations and orthogonal matrices First, some things to recall from linear algebra Two
CMSC 425: Lecture 13 Animation for Games: Basics Tuesday, Mar 26, 2013
 CMSC 425: Lecture 13 Animation for Games: Basics Tuesday, Mar 26, 2013 Reading: Chapt 11 of Gregory, Game Engine Architecture. Game Animation: Most computer games revolve around characters that move around
CMSC 425: Lecture 13 Animation for Games: Basics Tuesday, Mar 26, 2013 Reading: Chapt 11 of Gregory, Game Engine Architecture. Game Animation: Most computer games revolve around characters that move around
discuss how to describe points, lines and planes in 3 space.
 Chapter 2 3 Space: lines and planes In this chapter we discuss how to describe points, lines and planes in 3 space. introduce the language of vectors. discuss various matters concerning the relative position
Chapter 2 3 Space: lines and planes In this chapter we discuss how to describe points, lines and planes in 3 space. introduce the language of vectors. discuss various matters concerning the relative position
Practice Final Math 122 Spring 12 Instructor: Jeff Lang
 Practice Final Math Spring Instructor: Jeff Lang. Find the limit of the sequence a n = ln (n 5) ln (3n + 8). A) ln ( ) 3 B) ln C) ln ( ) 3 D) does not exist. Find the limit of the sequence a n = (ln n)6
Practice Final Math Spring Instructor: Jeff Lang. Find the limit of the sequence a n = ln (n 5) ln (3n + 8). A) ln ( ) 3 B) ln C) ln ( ) 3 D) does not exist. Find the limit of the sequence a n = (ln n)6
Dear Accelerated Pre-Calculus Student:
 Dear Accelerated Pre-Calculus Student: I am very excited that you have decided to take this course in the upcoming school year! This is a fastpaced, college-preparatory mathematics course that will also
Dear Accelerated Pre-Calculus Student: I am very excited that you have decided to take this course in the upcoming school year! This is a fastpaced, college-preparatory mathematics course that will also
Vector has a magnitude and a direction. Scalar has a magnitude
 Vector has a magnitude and a direction Scalar has a magnitude Vector has a magnitude and a direction Scalar has a magnitude a brick on a table Vector has a magnitude and a direction Scalar has a magnitude
Vector has a magnitude and a direction Scalar has a magnitude Vector has a magnitude and a direction Scalar has a magnitude a brick on a table Vector has a magnitude and a direction Scalar has a magnitude
28 CHAPTER 1. VECTORS AND THE GEOMETRY OF SPACE. v x. u y v z u z v y u y u z. v y v z
 28 CHAPTER 1. VECTORS AND THE GEOMETRY OF SPACE 1.4 Cross Product 1.4.1 Definitions The cross product is the second multiplication operation between vectors we will study. The goal behind the definition
28 CHAPTER 1. VECTORS AND THE GEOMETRY OF SPACE 1.4 Cross Product 1.4.1 Definitions The cross product is the second multiplication operation between vectors we will study. The goal behind the definition
9.4. The Scalar Product. Introduction. Prerequisites. Learning Style. Learning Outcomes
 The Scalar Product 9.4 Introduction There are two kinds of multiplication involving vectors. The first is known as the scalar product or dot product. This is so-called because when the scalar product of
The Scalar Product 9.4 Introduction There are two kinds of multiplication involving vectors. The first is known as the scalar product or dot product. This is so-called because when the scalar product of
Figure 1.1 Vector A and Vector F
 CHAPTER I VECTOR QUANTITIES Quantities are anything which can be measured, and stated with number. Quantities in physics are divided into two types; scalar and vector quantities. Scalar quantities have
CHAPTER I VECTOR QUANTITIES Quantities are anything which can be measured, and stated with number. Quantities in physics are divided into two types; scalar and vector quantities. Scalar quantities have
How To Draw A Billiards Ball In Gta 3D With Texture Mapping (Gta 3) On A Computer Or 2D Or Gta 2D (Gt) On Your Computer Or Computer Or Your Computer (Or Your Computer)
 Pool Billiard An OpenGL-based billiard simulation Stefan HUBER Kamran SAFDAR Andreas SCHRÖCKER Fachbereich Computerwissenschaften Universität Salzburg June 10, 2009 S. Huber, K. Safdar, A. Schröcker: Pool
Pool Billiard An OpenGL-based billiard simulation Stefan HUBER Kamran SAFDAR Andreas SCHRÖCKER Fachbereich Computerwissenschaften Universität Salzburg June 10, 2009 S. Huber, K. Safdar, A. Schröcker: Pool
Mathematics Course 111: Algebra I Part IV: Vector Spaces
 Mathematics Course 111: Algebra I Part IV: Vector Spaces D. R. Wilkins Academic Year 1996-7 9 Vector Spaces A vector space over some field K is an algebraic structure consisting of a set V on which are
Mathematics Course 111: Algebra I Part IV: Vector Spaces D. R. Wilkins Academic Year 1996-7 9 Vector Spaces A vector space over some field K is an algebraic structure consisting of a set V on which are
http://school-maths.com Gerrit Stols
 For more info and downloads go to: http://school-maths.com Gerrit Stols Acknowledgements GeoGebra is dynamic mathematics open source (free) software for learning and teaching mathematics in schools. It
For more info and downloads go to: http://school-maths.com Gerrit Stols Acknowledgements GeoGebra is dynamic mathematics open source (free) software for learning and teaching mathematics in schools. It
Chapter 11 Equilibrium
 11.1 The First Condition of Equilibrium The first condition of equilibrium deals with the forces that cause possible translations of a body. The simplest way to define the translational equilibrium of
11.1 The First Condition of Equilibrium The first condition of equilibrium deals with the forces that cause possible translations of a body. The simplest way to define the translational equilibrium of
Solutions to Homework 10
 Solutions to Homework 1 Section 7., exercise # 1 (b,d): (b) Compute the value of R f dv, where f(x, y) = y/x and R = [1, 3] [, 4]. Solution: Since f is continuous over R, f is integrable over R. Let x
Solutions to Homework 1 Section 7., exercise # 1 (b,d): (b) Compute the value of R f dv, where f(x, y) = y/x and R = [1, 3] [, 4]. Solution: Since f is continuous over R, f is integrable over R. Let x
Connecting Transformational Geometry and Transformations of Functions
 Connecting Transformational Geometr and Transformations of Functions Introductor Statements and Assumptions Isometries are rigid transformations that preserve distance and angles and therefore shapes.
Connecting Transformational Geometr and Transformations of Functions Introductor Statements and Assumptions Isometries are rigid transformations that preserve distance and angles and therefore shapes.
13 MATH FACTS 101. 2 a = 1. 7. The elements of a vector have a graphical interpretation, which is particularly easy to see in two or three dimensions.
 3 MATH FACTS 0 3 MATH FACTS 3. Vectors 3.. Definition We use the overhead arrow to denote a column vector, i.e., a linear segment with a direction. For example, in three-space, we write a vector in terms
3 MATH FACTS 0 3 MATH FACTS 3. Vectors 3.. Definition We use the overhead arrow to denote a column vector, i.e., a linear segment with a direction. For example, in three-space, we write a vector in terms
MAT188H1S Lec0101 Burbulla
 Winter 206 Linear Transformations A linear transformation T : R m R n is a function that takes vectors in R m to vectors in R n such that and T (u + v) T (u) + T (v) T (k v) k T (v), for all vectors u
Winter 206 Linear Transformations A linear transformation T : R m R n is a function that takes vectors in R m to vectors in R n such that and T (u + v) T (u) + T (v) T (k v) k T (v), for all vectors u
Metrics on SO(3) and Inverse Kinematics
 Mathematical Foundations of Computer Graphics and Vision Metrics on SO(3) and Inverse Kinematics Luca Ballan Institute of Visual Computing Optimization on Manifolds Descent approach d is a ascent direction
Mathematical Foundations of Computer Graphics and Vision Metrics on SO(3) and Inverse Kinematics Luca Ballan Institute of Visual Computing Optimization on Manifolds Descent approach d is a ascent direction
One advantage of this algebraic approach is that we can write down
 . Vectors and the dot product A vector v in R 3 is an arrow. It has a direction and a length (aka the magnitude), but the position is not important. Given a coordinate axis, where the x-axis points out
. Vectors and the dot product A vector v in R 3 is an arrow. It has a direction and a length (aka the magnitude), but the position is not important. Given a coordinate axis, where the x-axis points out
2 Session Two - Complex Numbers and Vectors
 PH2011 Physics 2A Maths Revision - Session 2: Complex Numbers and Vectors 1 2 Session Two - Complex Numbers and Vectors 2.1 What is a Complex Number? The material on complex numbers should be familiar
PH2011 Physics 2A Maths Revision - Session 2: Complex Numbers and Vectors 1 2 Session Two - Complex Numbers and Vectors 2.1 What is a Complex Number? The material on complex numbers should be familiar
Parametric Curves. (Com S 477/577 Notes) Yan-Bin Jia. Oct 8, 2015
 Parametric Curves (Com S 477/577 Notes) Yan-Bin Jia Oct 8, 2015 1 Introduction A curve in R 2 (or R 3 ) is a differentiable function α : [a,b] R 2 (or R 3 ). The initial point is α[a] and the final point
Parametric Curves (Com S 477/577 Notes) Yan-Bin Jia Oct 8, 2015 1 Introduction A curve in R 2 (or R 3 ) is a differentiable function α : [a,b] R 2 (or R 3 ). The initial point is α[a] and the final point
Continued Fractions and the Euclidean Algorithm
 Continued Fractions and the Euclidean Algorithm Lecture notes prepared for MATH 326, Spring 997 Department of Mathematics and Statistics University at Albany William F Hammond Table of Contents Introduction
Continued Fractions and the Euclidean Algorithm Lecture notes prepared for MATH 326, Spring 997 Department of Mathematics and Statistics University at Albany William F Hammond Table of Contents Introduction
BookTOC.txt. 1. Functions, Graphs, and Models. Algebra Toolbox. Sets. The Real Numbers. Inequalities and Intervals on the Real Number Line
 College Algebra in Context with Applications for the Managerial, Life, and Social Sciences, 3rd Edition Ronald J. Harshbarger, University of South Carolina - Beaufort Lisa S. Yocco, Georgia Southern University
College Algebra in Context with Applications for the Managerial, Life, and Social Sciences, 3rd Edition Ronald J. Harshbarger, University of South Carolina - Beaufort Lisa S. Yocco, Georgia Southern University
IV. ALGEBRAIC CONCEPTS
 IV. ALGEBRAIC CONCEPTS Algebra is the language of mathematics. Much of the observable world can be characterized as having patterned regularity where a change in one quantity results in changes in other
IV. ALGEBRAIC CONCEPTS Algebra is the language of mathematics. Much of the observable world can be characterized as having patterned regularity where a change in one quantity results in changes in other
v w is orthogonal to both v and w. the three vectors v, w and v w form a right-handed set of vectors.
 3. Cross product Definition 3.1. Let v and w be two vectors in R 3. The cross product of v and w, denoted v w, is the vector defined as follows: the length of v w is the area of the parallelogram with
3. Cross product Definition 3.1. Let v and w be two vectors in R 3. The cross product of v and w, denoted v w, is the vector defined as follows: the length of v w is the area of the parallelogram with
MATH2210 Notebook 1 Fall Semester 2016/2017. 1 MATH2210 Notebook 1 3. 1.1 Solving Systems of Linear Equations... 3
 MATH0 Notebook Fall Semester 06/07 prepared by Professor Jenny Baglivo c Copyright 009 07 by Jenny A. Baglivo. All Rights Reserved. Contents MATH0 Notebook 3. Solving Systems of Linear Equations........................
MATH0 Notebook Fall Semester 06/07 prepared by Professor Jenny Baglivo c Copyright 009 07 by Jenny A. Baglivo. All Rights Reserved. Contents MATH0 Notebook 3. Solving Systems of Linear Equations........................
For example, estimate the population of the United States as 3 times 10⁸ and the
 CCSS: Mathematics The Number System CCSS: Grade 8 8.NS.A. Know that there are numbers that are not rational, and approximate them by rational numbers. 8.NS.A.1. Understand informally that every number
CCSS: Mathematics The Number System CCSS: Grade 8 8.NS.A. Know that there are numbers that are not rational, and approximate them by rational numbers. 8.NS.A.1. Understand informally that every number
Introduction to 2D and 3D Computer Graphics Mastering 2D & 3D Computer Graphics Pipelines
 Introduction to 2D and 3D Computer Graphics Mastering 2D & 3D Computer Graphics Pipelines CS447 3-1 Mastering 2D & 3D Graphics Overview of 2D & 3D Pipelines What are pipelines? What are the fundamental
Introduction to 2D and 3D Computer Graphics Mastering 2D & 3D Computer Graphics Pipelines CS447 3-1 Mastering 2D & 3D Graphics Overview of 2D & 3D Pipelines What are pipelines? What are the fundamental
Cabri Geometry Application User Guide
 Cabri Geometry Application User Guide Preview of Geometry... 2 Learning the Basics... 3 Managing File Operations... 12 Setting Application Preferences... 14 Selecting and Moving Objects... 17 Deleting
Cabri Geometry Application User Guide Preview of Geometry... 2 Learning the Basics... 3 Managing File Operations... 12 Setting Application Preferences... 14 Selecting and Moving Objects... 17 Deleting
Physics 235 Chapter 1. Chapter 1 Matrices, Vectors, and Vector Calculus
 Chapter 1 Matrices, Vectors, and Vector Calculus In this chapter, we will focus on the mathematical tools required for the course. The main concepts that will be covered are: Coordinate transformations
Chapter 1 Matrices, Vectors, and Vector Calculus In this chapter, we will focus on the mathematical tools required for the course. The main concepts that will be covered are: Coordinate transformations
Concepts in Calculus III
 Concepts in Calculus III Beta Version UNIVERSITY PRESS OF FLORIDA Florida A&M University, Tallahassee Florida Atlantic University, Boca Raton Florida Gulf Coast University, Ft. Myers Florida International
Concepts in Calculus III Beta Version UNIVERSITY PRESS OF FLORIDA Florida A&M University, Tallahassee Florida Atlantic University, Boca Raton Florida Gulf Coast University, Ft. Myers Florida International
a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a 2n x n = b 2.
 Chapter 1 LINEAR EQUATIONS 1.1 Introduction to linear equations A linear equation in n unknowns x 1, x,, x n is an equation of the form a 1 x 1 + a x + + a n x n = b, where a 1, a,..., a n, b are given
Chapter 1 LINEAR EQUATIONS 1.1 Introduction to linear equations A linear equation in n unknowns x 1, x,, x n is an equation of the form a 1 x 1 + a x + + a n x n = b, where a 1, a,..., a n, b are given
Algebra 2 Chapter 1 Vocabulary. identity - A statement that equates two equivalent expressions.
 Chapter 1 Vocabulary identity - A statement that equates two equivalent expressions. verbal model- A word equation that represents a real-life problem. algebraic expression - An expression with variables.
Chapter 1 Vocabulary identity - A statement that equates two equivalent expressions. verbal model- A word equation that represents a real-life problem. algebraic expression - An expression with variables.
3. KINEMATICS IN TWO DIMENSIONS; VECTORS.
 3. KINEMATICS IN TWO DIMENSIONS; VECTORS. Key words: Motion in Two Dimensions, Scalars, Vectors, Addition of Vectors by Graphical Methods, Tail to Tip Method, Parallelogram Method, Negative Vector, Vector
3. KINEMATICS IN TWO DIMENSIONS; VECTORS. Key words: Motion in Two Dimensions, Scalars, Vectors, Addition of Vectors by Graphical Methods, Tail to Tip Method, Parallelogram Method, Negative Vector, Vector
Content. Chapter 4 Functions 61 4.1 Basic concepts on real functions 62. Credits 11
 Content Credits 11 Chapter 1 Arithmetic Refresher 13 1.1 Algebra 14 Real Numbers 14 Real Polynomials 19 1.2 Equations in one variable 21 Linear Equations 21 Quadratic Equations 22 1.3 Exercises 28 Chapter
Content Credits 11 Chapter 1 Arithmetic Refresher 13 1.1 Algebra 14 Real Numbers 14 Real Polynomials 19 1.2 Equations in one variable 21 Linear Equations 21 Quadratic Equations 22 1.3 Exercises 28 Chapter
Conjectures. Chapter 2. Chapter 3
 Conjectures Chapter 2 C-1 Linear Pair Conjecture If two angles form a linear pair, then the measures of the angles add up to 180. (Lesson 2.5) C-2 Vertical Angles Conjecture If two angles are vertical
Conjectures Chapter 2 C-1 Linear Pair Conjecture If two angles form a linear pair, then the measures of the angles add up to 180. (Lesson 2.5) C-2 Vertical Angles Conjecture If two angles are vertical
CITY UNIVERSITY LONDON. BEng Degree in Computer Systems Engineering Part II BSc Degree in Computer Systems Engineering Part III PART 2 EXAMINATION
 No: CITY UNIVERSITY LONDON BEng Degree in Computer Systems Engineering Part II BSc Degree in Computer Systems Engineering Part III PART 2 EXAMINATION ENGINEERING MATHEMATICS 2 (resit) EX2005 Date: August
No: CITY UNIVERSITY LONDON BEng Degree in Computer Systems Engineering Part II BSc Degree in Computer Systems Engineering Part III PART 2 EXAMINATION ENGINEERING MATHEMATICS 2 (resit) EX2005 Date: August
Section 1.1. Introduction to R n
 The Calculus of Functions of Several Variables Section. Introduction to R n Calculus is the study of functional relationships and how related quantities change with each other. In your first exposure to
The Calculus of Functions of Several Variables Section. Introduction to R n Calculus is the study of functional relationships and how related quantities change with each other. In your first exposure to
The Use of Dynamic Geometry Software in the Teaching and Learning of Geometry through Transformations
 The Use of Dynamic Geometry Software in the Teaching and Learning of Geometry through Transformations Dynamic geometry technology should be used to maximize student learning in geometry. Such technology
The Use of Dynamic Geometry Software in the Teaching and Learning of Geometry through Transformations Dynamic geometry technology should be used to maximize student learning in geometry. Such technology
TRIGONOMETRY FOR ANIMATION
 TRIGONOMETRY FOR ANIMATION What is Trigonometry? Trigonometry is basically the study of triangles and the relationship of their sides and angles. For example, if you take any triangle and make one of the
TRIGONOMETRY FOR ANIMATION What is Trigonometry? Trigonometry is basically the study of triangles and the relationship of their sides and angles. For example, if you take any triangle and make one of the
Projective Geometry: A Short Introduction. Lecture Notes Edmond Boyer
 Projective Geometry: A Short Introduction Lecture Notes Edmond Boyer Contents 1 Introduction 2 11 Objective 2 12 Historical Background 3 13 Bibliography 4 2 Projective Spaces 5 21 Definitions 5 22 Properties
Projective Geometry: A Short Introduction Lecture Notes Edmond Boyer Contents 1 Introduction 2 11 Objective 2 12 Historical Background 3 13 Bibliography 4 2 Projective Spaces 5 21 Definitions 5 22 Properties
NAKURU DISTRICT SEC. SCHOOLS TRIAL EXAM 2011. Kenya Certificate of Secondary Education MATHEMATICS PAPER2 2½ HOURS
 NAME:. INDEX NO: CANDIDATE S SINGNATURE DATE:. 121 /2 MATHEMATICS ALT A. PAPER2 JULY / AUGUST 2011 2 ½ HOURS NAKURU DISTRICT SEC. SCHOOLS TRIAL EXAM 2011 INSTRUCTIONS TO CANDIDATES Kenya Certificate of
NAME:. INDEX NO: CANDIDATE S SINGNATURE DATE:. 121 /2 MATHEMATICS ALT A. PAPER2 JULY / AUGUST 2011 2 ½ HOURS NAKURU DISTRICT SEC. SCHOOLS TRIAL EXAM 2011 INSTRUCTIONS TO CANDIDATES Kenya Certificate of
A QUICK GUIDE TO THE FORMULAS OF MULTIVARIABLE CALCULUS
 A QUIK GUIDE TO THE FOMULAS OF MULTIVAIABLE ALULUS ontents 1. Analytic Geometry 2 1.1. Definition of a Vector 2 1.2. Scalar Product 2 1.3. Properties of the Scalar Product 2 1.4. Length and Unit Vectors
A QUIK GUIDE TO THE FOMULAS OF MULTIVAIABLE ALULUS ontents 1. Analytic Geometry 2 1.1. Definition of a Vector 2 1.2. Scalar Product 2 1.3. Properties of the Scalar Product 2 1.4. Length and Unit Vectors
α = u v. In other words, Orthogonal Projection
 Orthogonal Projection Given any nonzero vector v, it is possible to decompose an arbitrary vector u into a component that points in the direction of v and one that points in a direction orthogonal to v
Orthogonal Projection Given any nonzero vector v, it is possible to decompose an arbitrary vector u into a component that points in the direction of v and one that points in a direction orthogonal to v
Origins of the Unusual Space Shuttle Quaternion Definition
 47th AIAA Aerospace Sciences Meeting Including The New Horizons Forum and Aerospace Exposition 5-8 January 2009, Orlando, Florida AIAA 2009-43 Origins of the Unusual Space Shuttle Quaternion Definition
47th AIAA Aerospace Sciences Meeting Including The New Horizons Forum and Aerospace Exposition 5-8 January 2009, Orlando, Florida AIAA 2009-43 Origins of the Unusual Space Shuttle Quaternion Definition
Continuous Groups, Lie Groups, and Lie Algebras
 Chapter 7 Continuous Groups, Lie Groups, and Lie Algebras Zeno was concerned with three problems... These are the problem of the infinitesimal, the infinite, and continuity... Bertrand Russell The groups
Chapter 7 Continuous Groups, Lie Groups, and Lie Algebras Zeno was concerned with three problems... These are the problem of the infinitesimal, the infinite, and continuity... Bertrand Russell The groups
