CS 4204 Computer Graphics
|
|
|
- Phyllis Hodge
- 8 years ago
- Views:
Transcription
1 CS 4204 Computer Graphics 3D views and projection Adapted from notes by Yong Cao 1
2 Overview of 3D rendering Modeling: *Define object in local coordinates *Place object in world coordinates (modeling transformation) Viewing: Define camera parameters Find object location in camera coordinates (viewing transformation) Projection: project object to the viewplane Clipping: clip object to the view volume *Viewport transformation *Rasterization: rasterize object * Topic we ve already discussed Simple teapot demo
3 3D rendering pipeline Vertices as input Series of operations/transformations to obtain 2D vertices in screen coordinates These can then be rasterized
4 3D rendering pipeline We ve already discussed: Viewport transformation 3D modeling transformations We ll talk about remaining topics in reverse order: 3D clipping (simple extension of 2D clipping) 3D projection 3D viewing
5 Clipping: 3D Cohen-Sutherland Use 6-bit outcodes When needed, clip line segment against planes
6 Viewing and Projection Camera Analogy: 1. Set up your tripod and point the camera at the scene (viewing transformation). 2. Arrange the scene to be photographed into the desired composition (modeling transformation). 3. Choose a camera lens or adjust the zoom (projection transformation). 4. Determine how large you want the final photograph to be - for example, you might want it enlarged (viewport transformation).
7 Projection transformations
8 Introduction to Projection Transformations Mapping: f : R n R m Projection: n > m Planar Projection: Projection on a plane. R 3 R 2 or R 4 R 3 homogeneous coordinates.
9 Introduction to Projection Transformations
10 Classical Viewing Viewing requires three basic elements One or more objects A viewer with a projection surface Projectors that go from the object(s) to the projection surface Classical views are based on the relationship among these elements The viewer picks up the object and orients it how she would like to see it Each object is assumed to constructed from flat principal faces Buildings, polyhedra, manufactured objects
11 Planar Geometric Projections Standard projections project onto a plane Projectors are lines that either converge at a center of projection are parallel Such projections preserve lines but not necessarily angles Non-planar projections are needed for applications such as map construction
12 Classical Projections
13 Perspective vs Parallel Computer graphics treats all projections the same and implements them with a single pipeline Classical viewing developed different techniques for drawing each type of projection Fundamental distinction is between parallel and perspective viewing even though mathematically parallel viewing is the limit of perspective viewing
14 Perspective Projection
15 Parallel Projection
16 Taxonomy of Planar Geometric Projections
17 Examples
18 Orthographic Projection Projectors are orthogonal to projection surface
19 Multiview Orthographic Projection Projection plane parallel to principal face Usually form front, top, side views isometric front in CAD and architecture, we often display three multiviews plus isometric top side
20 Advantages and Disadvantages Preserves both distances and angles Shapes preserved Can be used for measurements Building plans Manuals Cannot see what object really looks like because many surfaces hidden from view Often we add the isometric
21 Axonometric Projections Allow projection plane to move relative to object classify by how many angles of a corner of a projected cube are the same none: trimetric two: dimetric three: isometric θ 2 θ 1 θ 3
22 Types of Axonometric Projections
23 Advantages and Disadvantages Lines are scaled (foreshortened( foreshortened) ) but can find scaling factors Lines preserved but angles are not Projection of a circle in a plane not parallel to the projection plane is an ellipse Can see three principal faces of a box-like object Some optical illusions possible Parallel lines appear to diverge Does not look real because far objects are scaled the same as near objects Used in CAD applications
24 Oblique Projection Arbitrary relationship between projectors and projection plane
25 Advantages and Disadvantages Can pick the angles to emphasize a particular face Architecture: plan oblique, elevation oblique Angles in faces parallel to projection plane are preserved while we can still see around side In physical world, cannot create with simple camera; possible with bellows camera or special lens (architectural)
26 Perspective Projection Projectors converge at center of projection Perspective projection demo
27 Vanishing Points Parallel lines (not parallel to the projection plane) on the object converge at a single point in the projection (the vanishing point) Drawing simple perspectives by hand uses these vanishing point(s) vanishing point
28 Three-Point Perspective No principal face parallel to projection plane Three vanishing points for cube
29 Two-Point Perspective On principal direction parallel to projection plane Two vanishing points for cube
30 One-Point Perspective One principal face parallel to projection plane One vanishing point for cube
31 Advantages and Disadvantages Objects further from viewer are projected smaller than the same sized objects closer to the viewer (diminution) Looks realistic Equal distances along a line are not projected into equal distances (non-uniform foreshortening) Angles preserved only in planes parallel to the projection plane More difficult to construct by hand than parallel projections (but not more difficult by computer)
32 Perspective Projections of 3-D Objects A vertex located at P in eye coordinates is projected to a certain point (x*,( y*) on the near plane, and is then mapped to the viewport on the display.
33 Perspective Projection Properties Straight lines project to straight lines. Consider the line between A and B. A projects to A and B projects to B. In between: consider the plane formed by A, B, and the origin. Since any two planes intersect in a straight line, this plane intersects the near plane in a straight line. Thus line segment AB projects to line segment A B.
34 Example: horizontal grid in perspective
35 Mathematics of a basic perspective projection Similar triangles
36 One-Point Projection in matrix form -Z Center of Projection at the origin with viewplane parallel to the x-y plane a distance d from the origin. x projected = x/(z/d) y projected = y/(z/d) +Z **Points plotted are x/w, y/w where w = z/d
Realtime 3D Computer Graphics Virtual Reality
 Realtime 3D Computer Graphics Virtual Realit Viewing and projection Classical and General Viewing Transformation Pipeline CPU Pol. DL Pixel Per Vertex Texture Raster Frag FB object ee clip normalized device
Realtime 3D Computer Graphics Virtual Realit Viewing and projection Classical and General Viewing Transformation Pipeline CPU Pol. DL Pixel Per Vertex Texture Raster Frag FB object ee clip normalized device
Basic Problem: Map a 3D object to a 2D display surface. Analogy - Taking a snapshot with a camera
 3D Viewing Basic Problem: Map a 3D object to a 2D display surface Analogy - Taking a snapshot with a camera Synthetic camera virtual camera we can move to any location & orient in any way then create a
3D Viewing Basic Problem: Map a 3D object to a 2D display surface Analogy - Taking a snapshot with a camera Synthetic camera virtual camera we can move to any location & orient in any way then create a
From 3D to 2D: Orthographic and Perspective Projection Part 1
 From 3D to 2D: Orthographic and Perspective Projection Part 1 History Geometrical Constructions Types of Projection Projection in Computer Graphics Andries van Dam September 13, 2001 3D Viewing I 1/34
From 3D to 2D: Orthographic and Perspective Projection Part 1 History Geometrical Constructions Types of Projection Projection in Computer Graphics Andries van Dam September 13, 2001 3D Viewing I 1/34
How to read Plans and Do Basic Drawings
 How to read Plans and Do Basic Drawings Workshop session W1 10.00 Site Orientation Exercise 10.10 Drawing Conventions 10.45 Can drawings Distort the Truth? 11.30 Summary + Coffee 11.45 Simple Drawing Techniques
How to read Plans and Do Basic Drawings Workshop session W1 10.00 Site Orientation Exercise 10.10 Drawing Conventions 10.45 Can drawings Distort the Truth? 11.30 Summary + Coffee 11.45 Simple Drawing Techniques
Wallingford Public Schools - HIGH SCHOOL COURSE OUTLINE
 Wallingford Public Schools - HIGH SCHOOL COURSE OUTLINE Course Title: Computer Aided Drafting & Design Course Number: 7163 Department: Career and Technical Education Grade(s): 9-12 Level(s): Academic Credit:
Wallingford Public Schools - HIGH SCHOOL COURSE OUTLINE Course Title: Computer Aided Drafting & Design Course Number: 7163 Department: Career and Technical Education Grade(s): 9-12 Level(s): Academic Credit:
4BA6 - Topic 4 Dr. Steven Collins. Chap. 5 3D Viewing and Projections
 4BA6 - Topic 4 Dr. Steven Collins Chap. 5 3D Viewing and Projections References Computer graphics: principles & practice, Fole, vandam, Feiner, Hughes, S-LEN 5.644 M23*;-6 (has a good appendix on linear
4BA6 - Topic 4 Dr. Steven Collins Chap. 5 3D Viewing and Projections References Computer graphics: principles & practice, Fole, vandam, Feiner, Hughes, S-LEN 5.644 M23*;-6 (has a good appendix on linear
Geometry for Computer Graphics
 Computer Graphics and Visualisation Geometry for Computer Graphics Student Notes Developed by F Lin K Wyrwas J Irwin C Lilley W T Hewitt T L J Howard Computer Graphics Unit Manchester Computing Centre
Computer Graphics and Visualisation Geometry for Computer Graphics Student Notes Developed by F Lin K Wyrwas J Irwin C Lilley W T Hewitt T L J Howard Computer Graphics Unit Manchester Computing Centre
3D Drawing. Single Point Perspective with Diminishing Spaces
 3D Drawing Single Point Perspective with Diminishing Spaces The following document helps describe the basic process for generating a 3D representation of a simple 2D plan. For this exercise we will be
3D Drawing Single Point Perspective with Diminishing Spaces The following document helps describe the basic process for generating a 3D representation of a simple 2D plan. For this exercise we will be
3D Viewing. Chapter 7. Projections. 3D clipping. OpenGL viewing functions and clipping planes
 3D Viewing Chapter 7 Projections 3D clipping OpenGL viewing functions and clipping planes 1 Projections Parallel Perspective Coordinates are transformed along parallel lines Relative sizes are preserved
3D Viewing Chapter 7 Projections 3D clipping OpenGL viewing functions and clipping planes 1 Projections Parallel Perspective Coordinates are transformed along parallel lines Relative sizes are preserved
Traditional Drawing Tools
 Engineering Drawing Traditional Drawing Tools DRAWING TOOLS DRAWING TOOLS 1. T-Square 2. Triangles DRAWING TOOLS HB for thick line 2H for thin line 3. Adhesive Tape 4. Pencils DRAWING TOOLS 5. Sandpaper
Engineering Drawing Traditional Drawing Tools DRAWING TOOLS DRAWING TOOLS 1. T-Square 2. Triangles DRAWING TOOLS HB for thick line 2H for thin line 3. Adhesive Tape 4. Pencils DRAWING TOOLS 5. Sandpaper
Monash University Clayton s School of Information Technology CSE3313 Computer Graphics Sample Exam Questions 2007
 Monash University Clayton s School of Information Technology CSE3313 Computer Graphics Questions 2007 INSTRUCTIONS: Answer all questions. Spend approximately 1 minute per mark. Question 1 30 Marks Total
Monash University Clayton s School of Information Technology CSE3313 Computer Graphics Questions 2007 INSTRUCTIONS: Answer all questions. Spend approximately 1 minute per mark. Question 1 30 Marks Total
Technical Drawing Specifications Resource A guide to support VCE Visual Communication Design study design 2013-17
 A guide to support VCE Visual Communication Design study design 2013-17 1 Contents INTRODUCTION The Australian Standards (AS) Key knowledge and skills THREE-DIMENSIONAL DRAWING PARALINE DRAWING Isometric
A guide to support VCE Visual Communication Design study design 2013-17 1 Contents INTRODUCTION The Australian Standards (AS) Key knowledge and skills THREE-DIMENSIONAL DRAWING PARALINE DRAWING Isometric
B2.53-R3: COMPUTER GRAPHICS. NOTE: 1. There are TWO PARTS in this Module/Paper. PART ONE contains FOUR questions and PART TWO contains FIVE questions.
 B2.53-R3: COMPUTER GRAPHICS NOTE: 1. There are TWO PARTS in this Module/Paper. PART ONE contains FOUR questions and PART TWO contains FIVE questions. 2. PART ONE is to be answered in the TEAR-OFF ANSWER
B2.53-R3: COMPUTER GRAPHICS NOTE: 1. There are TWO PARTS in this Module/Paper. PART ONE contains FOUR questions and PART TWO contains FIVE questions. 2. PART ONE is to be answered in the TEAR-OFF ANSWER
521493S Computer Graphics. Exercise 2 & course schedule change
 521493S Computer Graphics Exercise 2 & course schedule change Course Schedule Change Lecture from Wednesday 31th of March is moved to Tuesday 30th of March at 16-18 in TS128 Question 2.1 Given two nonparallel,
521493S Computer Graphics Exercise 2 & course schedule change Course Schedule Change Lecture from Wednesday 31th of March is moved to Tuesday 30th of March at 16-18 in TS128 Question 2.1 Given two nonparallel,
3D Drawing. Single Point Perspective with Diminishing Spaces
 3D Drawing Single Point Perspective with Diminishing Spaces The following document helps describe the basic process for generating a 3D representation of a simple 2D plan. For this exercise we will be
3D Drawing Single Point Perspective with Diminishing Spaces The following document helps describe the basic process for generating a 3D representation of a simple 2D plan. For this exercise we will be
An introduction to 3D draughting & solid modelling using AutoCAD
 An introduction to 3D draughting & solid modelling using AutoCAD Faculty of Technology University of Plymouth Drake Circus Plymouth PL4 8AA These notes are to be used in conjunction with the AutoCAD software
An introduction to 3D draughting & solid modelling using AutoCAD Faculty of Technology University of Plymouth Drake Circus Plymouth PL4 8AA These notes are to be used in conjunction with the AutoCAD software
Anamorphic Projection Photographic Techniques for setting up 3D Chalk Paintings
 Anamorphic Projection Photographic Techniques for setting up 3D Chalk Paintings By Wayne and Cheryl Renshaw. Although it is centuries old, the art of street painting has been going through a resurgence.
Anamorphic Projection Photographic Techniques for setting up 3D Chalk Paintings By Wayne and Cheryl Renshaw. Although it is centuries old, the art of street painting has been going through a resurgence.
Transformations in the pipeline
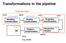 Transformations in the pipeline gltranslatef() Modeling transformation ModelView Matrix OCS WCS glulookat() VCS CCS Viewing transformation Projection transformation DCS Viewport transformation (e.g. pixels)
Transformations in the pipeline gltranslatef() Modeling transformation ModelView Matrix OCS WCS glulookat() VCS CCS Viewing transformation Projection transformation DCS Viewport transformation (e.g. pixels)
4. CAMERA ADJUSTMENTS
 4. CAMERA ADJUSTMENTS Only by the possibility of displacing lens and rear standard all advantages of a view camera are fully utilized. These displacements serve for control of perspective, positioning
4. CAMERA ADJUSTMENTS Only by the possibility of displacing lens and rear standard all advantages of a view camera are fully utilized. These displacements serve for control of perspective, positioning
A Short Introduction to Computer Graphics
 A Short Introduction to Computer Graphics Frédo Durand MIT Laboratory for Computer Science 1 Introduction Chapter I: Basics Although computer graphics is a vast field that encompasses almost any graphical
A Short Introduction to Computer Graphics Frédo Durand MIT Laboratory for Computer Science 1 Introduction Chapter I: Basics Although computer graphics is a vast field that encompasses almost any graphical
Freehand Sketching. Sections
 3 Freehand Sketching Sections 3.1 Why Freehand Sketches? 3.2 Freehand Sketching Fundamentals 3.3 Basic Freehand Sketching 3.4 Advanced Freehand Sketching Key Terms Objectives Explain why freehand sketching
3 Freehand Sketching Sections 3.1 Why Freehand Sketches? 3.2 Freehand Sketching Fundamentals 3.3 Basic Freehand Sketching 3.4 Advanced Freehand Sketching Key Terms Objectives Explain why freehand sketching
LEAVING CERT DCG SCHEME OF WORK
 2010-11 LEAVING CERT DCG SCHEME OF WORK ST OLIVER S COMMUNITY COLLEGE Mission statement The technology department aspires to provide a safe, stimulating environment where all students can develop their
2010-11 LEAVING CERT DCG SCHEME OF WORK ST OLIVER S COMMUNITY COLLEGE Mission statement The technology department aspires to provide a safe, stimulating environment where all students can develop their
How to Draw With Perspective. Created exclusively for Craftsy by Paul Heaston
 How to Draw With Perspective Created exclusively for Craftsy by Paul Heaston i TABLE OF CONTENTS 01 02 05 09 13 17 Meet the Expert One-Point Perspective: Drawing a Room Two-Point Perspective: Understanding
How to Draw With Perspective Created exclusively for Craftsy by Paul Heaston i TABLE OF CONTENTS 01 02 05 09 13 17 Meet the Expert One-Point Perspective: Drawing a Room Two-Point Perspective: Understanding
INTRODUCTION TO RENDERING TECHNIQUES
 INTRODUCTION TO RENDERING TECHNIQUES 22 Mar. 212 Yanir Kleiman What is 3D Graphics? Why 3D? Draw one frame at a time Model only once X 24 frames per second Color / texture only once 15, frames for a feature
INTRODUCTION TO RENDERING TECHNIQUES 22 Mar. 212 Yanir Kleiman What is 3D Graphics? Why 3D? Draw one frame at a time Model only once X 24 frames per second Color / texture only once 15, frames for a feature
Geometric Camera Parameters
 Geometric Camera Parameters What assumptions have we made so far? -All equations we have derived for far are written in the camera reference frames. -These equations are valid only when: () all distances
Geometric Camera Parameters What assumptions have we made so far? -All equations we have derived for far are written in the camera reference frames. -These equations are valid only when: () all distances
Introduction to Computer Graphics
 Introduction to Computer Graphics Torsten Möller TASC 8021 778-782-2215 torsten@sfu.ca www.cs.sfu.ca/~torsten Today What is computer graphics? Contents of this course Syllabus Overview of course topics
Introduction to Computer Graphics Torsten Möller TASC 8021 778-782-2215 torsten@sfu.ca www.cs.sfu.ca/~torsten Today What is computer graphics? Contents of this course Syllabus Overview of course topics
Message, Audience, Production (MAP) Framework for Teaching Media Literacy Social Studies Integration PRODUCTION
 Message, Audience, Production (MAP) Framework for Teaching Media Literacy Social Studies Integration PRODUCTION All media messages - a film or book, photograph or picture, newspaper article, news story,
Message, Audience, Production (MAP) Framework for Teaching Media Literacy Social Studies Integration PRODUCTION All media messages - a film or book, photograph or picture, newspaper article, news story,
Image Processing and Computer Graphics. Rendering Pipeline. Matthias Teschner. Computer Science Department University of Freiburg
 Image Processing and Computer Graphics Rendering Pipeline Matthias Teschner Computer Science Department University of Freiburg Outline introduction rendering pipeline vertex processing primitive processing
Image Processing and Computer Graphics Rendering Pipeline Matthias Teschner Computer Science Department University of Freiburg Outline introduction rendering pipeline vertex processing primitive processing
The Geometry of Perspective Projection
 The Geometry o Perspective Projection Pinhole camera and perspective projection - This is the simplest imaging device which, however, captures accurately the geometry o perspective projection. -Rays o
The Geometry o Perspective Projection Pinhole camera and perspective projection - This is the simplest imaging device which, however, captures accurately the geometry o perspective projection. -Rays o
TWO-DIMENSIONAL TRANSFORMATION
 CHAPTER 2 TWO-DIMENSIONAL TRANSFORMATION 2.1 Introduction As stated earlier, Computer Aided Design consists of three components, namely, Design (Geometric Modeling), Analysis (FEA, etc), and Visualization
CHAPTER 2 TWO-DIMENSIONAL TRANSFORMATION 2.1 Introduction As stated earlier, Computer Aided Design consists of three components, namely, Design (Geometric Modeling), Analysis (FEA, etc), and Visualization
Perspective and Space
 Perspective and Space Space: The element of art referring to the emptiness or area between, around, above, below, or within objects. FOREGROUND - Part of the picture plane that appears closest to the viewer
Perspective and Space Space: The element of art referring to the emptiness or area between, around, above, below, or within objects. FOREGROUND - Part of the picture plane that appears closest to the viewer
Geometric Transformation CS 211A
 Geometric Transformation CS 211A What is transformation? Moving points (x,y) moves to (x+t, y+t) Can be in any dimension 2D Image warps 3D 3D Graphics and Vision Can also be considered as a movement to
Geometric Transformation CS 211A What is transformation? Moving points (x,y) moves to (x+t, y+t) Can be in any dimension 2D Image warps 3D 3D Graphics and Vision Can also be considered as a movement to
Kankakee Community College
 Kankakee Community College Course prefix and number: DRFT 2134 Course title: AutoCAD III Semester: Fall 2014 Credit hours: 4 Lecture hours: 2.5 Lab hours: 3 Catalog description: Prerequisite: DRFT 2114,
Kankakee Community College Course prefix and number: DRFT 2134 Course title: AutoCAD III Semester: Fall 2014 Credit hours: 4 Lecture hours: 2.5 Lab hours: 3 Catalog description: Prerequisite: DRFT 2114,
Essential Mathematics for Computer Graphics fast
 John Vince Essential Mathematics for Computer Graphics fast Springer Contents 1. MATHEMATICS 1 Is mathematics difficult? 3 Who should read this book? 4 Aims and objectives of this book 4 Assumptions made
John Vince Essential Mathematics for Computer Graphics fast Springer Contents 1. MATHEMATICS 1 Is mathematics difficult? 3 Who should read this book? 4 Aims and objectives of this book 4 Assumptions made
Be visual all the time, and be verbal when labeling because explanations help clarify ideas.
 Great visual thinkers throughout history have kept records of their ideas in one form or another. (Leonardo da Vinci s sketchbooks are world famous.) Idea logs are an integral part of visual thinking and
Great visual thinkers throughout history have kept records of their ideas in one form or another. (Leonardo da Vinci s sketchbooks are world famous.) Idea logs are an integral part of visual thinking and
Geometric Optics Converging Lenses and Mirrors Physics Lab IV
 Objective Geometric Optics Converging Lenses and Mirrors Physics Lab IV In this set of lab exercises, the basic properties geometric optics concerning converging lenses and mirrors will be explored. The
Objective Geometric Optics Converging Lenses and Mirrors Physics Lab IV In this set of lab exercises, the basic properties geometric optics concerning converging lenses and mirrors will be explored. The
Activity Set 4. Trainer Guide
 Geometry and Measurement of Solid Figures Activity Set 4 Trainer Guide Mid_SGe_04_TG Copyright by the McGraw-Hill Companies McGraw-Hill Professional Development GEOMETRY AND MEASUREMENT OF SOLID FIGURES
Geometry and Measurement of Solid Figures Activity Set 4 Trainer Guide Mid_SGe_04_TG Copyright by the McGraw-Hill Companies McGraw-Hill Professional Development GEOMETRY AND MEASUREMENT OF SOLID FIGURES
Creating 2D Drawings from 3D AutoCAD Models
 Creating 2D Drawings from 3D AutoCAD Models David Piggott CrWare, LP GD205-2P This class explores the various techniques in creating 2D part and assembly drawings from 3D AutoCAD models. As part of the
Creating 2D Drawings from 3D AutoCAD Models David Piggott CrWare, LP GD205-2P This class explores the various techniques in creating 2D part and assembly drawings from 3D AutoCAD models. As part of the
Lesson Four 3D Modeling
 Lesson Four 3D Modeling In this lesson you will learn how to: Easily Rotate the UCS to model in different planes Model lines in a method similar to drawing isometrics Create 3D Router Lines Automatically
Lesson Four 3D Modeling In this lesson you will learn how to: Easily Rotate the UCS to model in different planes Model lines in a method similar to drawing isometrics Create 3D Router Lines Automatically
We can display an object on a monitor screen in three different computer-model forms: Wireframe model Surface Model Solid model
 CHAPTER 4 CURVES 4.1 Introduction In order to understand the significance of curves, we should look into the types of model representations that are used in geometric modeling. Curves play a very significant
CHAPTER 4 CURVES 4.1 Introduction In order to understand the significance of curves, we should look into the types of model representations that are used in geometric modeling. Curves play a very significant
Course Description. Spring 2004 1
 Spring 2004 1 Course Description AE4375: advanced treatment for undergrads; focus on learning and aplying CAD to engineering; CAD modeling projects. AE6380: graduate course on CAD focusing on how tools
Spring 2004 1 Course Description AE4375: advanced treatment for undergrads; focus on learning and aplying CAD to engineering; CAD modeling projects. AE6380: graduate course on CAD focusing on how tools
Introduction to 2D and 3D Computer Graphics Mastering 2D & 3D Computer Graphics Pipelines
 Introduction to 2D and 3D Computer Graphics Mastering 2D & 3D Computer Graphics Pipelines CS447 3-1 Mastering 2D & 3D Graphics Overview of 2D & 3D Pipelines What are pipelines? What are the fundamental
Introduction to 2D and 3D Computer Graphics Mastering 2D & 3D Computer Graphics Pipelines CS447 3-1 Mastering 2D & 3D Graphics Overview of 2D & 3D Pipelines What are pipelines? What are the fundamental
MA 323 Geometric Modelling Course Notes: Day 02 Model Construction Problem
 MA 323 Geometric Modelling Course Notes: Day 02 Model Construction Problem David L. Finn November 30th, 2004 In the next few days, we will introduce some of the basic problems in geometric modelling, and
MA 323 Geometric Modelling Course Notes: Day 02 Model Construction Problem David L. Finn November 30th, 2004 In the next few days, we will introduce some of the basic problems in geometric modelling, and
2.3 WINDOW-TO-VIEWPORT COORDINATE TRANSFORMATION
 2.3 WINDOW-TO-VIEWPORT COORDINATE TRANSFORMATION A world-coordinate area selected for display is called a window. An area on a display device to which a window is mapped is called a viewport. The window
2.3 WINDOW-TO-VIEWPORT COORDINATE TRANSFORMATION A world-coordinate area selected for display is called a window. An area on a display device to which a window is mapped is called a viewport. The window
Introduction to CATIA V5
 Introduction to CATIA V5 Release 16 (A Hands-On Tutorial Approach) Kirstie Plantenberg University of Detroit Mercy SDC PUBLICATIONS Schroff Development Corporation www.schroff.com www.schroff-europe.com
Introduction to CATIA V5 Release 16 (A Hands-On Tutorial Approach) Kirstie Plantenberg University of Detroit Mercy SDC PUBLICATIONS Schroff Development Corporation www.schroff.com www.schroff-europe.com
Vector Notation: AB represents the vector from point A to point B on a graph. The vector can be computed by B A.
 1 Linear Transformations Prepared by: Robin Michelle King A transformation of an object is a change in position or dimension (or both) of the object. The resulting object after the transformation is called
1 Linear Transformations Prepared by: Robin Michelle King A transformation of an object is a change in position or dimension (or both) of the object. The resulting object after the transformation is called
Three-Dimensional Figures or Space Figures. Rectangular Prism Cylinder Cone Sphere. Two-Dimensional Figures or Plane Figures
 SHAPE NAMES Three-Dimensional Figures or Space Figures Rectangular Prism Cylinder Cone Sphere Two-Dimensional Figures or Plane Figures Square Rectangle Triangle Circle Name each shape. [triangle] [cone]
SHAPE NAMES Three-Dimensional Figures or Space Figures Rectangular Prism Cylinder Cone Sphere Two-Dimensional Figures or Plane Figures Square Rectangle Triangle Circle Name each shape. [triangle] [cone]
Computer Graphics CS 543 Lecture 12 (Part 1) Curves. Prof Emmanuel Agu. Computer Science Dept. Worcester Polytechnic Institute (WPI)
 Computer Graphics CS 54 Lecture 1 (Part 1) Curves Prof Emmanuel Agu Computer Science Dept. Worcester Polytechnic Institute (WPI) So Far Dealt with straight lines and flat surfaces Real world objects include
Computer Graphics CS 54 Lecture 1 (Part 1) Curves Prof Emmanuel Agu Computer Science Dept. Worcester Polytechnic Institute (WPI) So Far Dealt with straight lines and flat surfaces Real world objects include
2: Introducing image synthesis. Some orientation how did we get here? Graphics system architecture Overview of OpenGL / GLU / GLUT
 COMP27112 Computer Graphics and Image Processing 2: Introducing image synthesis Toby.Howard@manchester.ac.uk 1 Introduction In these notes we ll cover: Some orientation how did we get here? Graphics system
COMP27112 Computer Graphics and Image Processing 2: Introducing image synthesis Toby.Howard@manchester.ac.uk 1 Introduction In these notes we ll cover: Some orientation how did we get here? Graphics system
COMPUTER GRAPHICS IMPORTANT QUESTION AND ANSWERS. Computer graphics
 Computer graphics 1. Define Computer graphics. Computer graphics remains one of the most existing and rapidly growing computer fields. Computer graphics may be defined as a pictorial representation or
Computer graphics 1. Define Computer graphics. Computer graphics remains one of the most existing and rapidly growing computer fields. Computer graphics may be defined as a pictorial representation or
Leaving Certificate. Design and Communication. (Ordinary Level and Higher Level)
 An Roinn Oideachais agus Eolaíochta Leaving Certificate Design and Communication Graphics Syllabus (Ordinary Level and Higher Level) LEAVING CERTIFICATE PROGRAMMES Aims and Principles 1. The general aim
An Roinn Oideachais agus Eolaíochta Leaving Certificate Design and Communication Graphics Syllabus (Ordinary Level and Higher Level) LEAVING CERTIFICATE PROGRAMMES Aims and Principles 1. The general aim
Canterbury Maps Quick Start - Drawing and Printing Tools
 Canterbury Maps Canterbury Maps Quick Start - Drawing and Printing Tools Quick Start Guide Standard GIS Viewer 2 Canterbury Maps Quick Start - Drawing and Printing Tools Introduction This document will
Canterbury Maps Canterbury Maps Quick Start - Drawing and Printing Tools Quick Start Guide Standard GIS Viewer 2 Canterbury Maps Quick Start - Drawing and Printing Tools Introduction This document will
A floor is a flat surface that extends in all directions. So, it models a plane. 1-1 Points, Lines, and Planes
 1-1 Points, Lines, and Planes Use the figure to name each of the following. 1. a line containing point X 5. a floor A floor is a flat surface that extends in all directions. So, it models a plane. Draw
1-1 Points, Lines, and Planes Use the figure to name each of the following. 1. a line containing point X 5. a floor A floor is a flat surface that extends in all directions. So, it models a plane. Draw
Angles that are between parallel lines, but on opposite sides of a transversal.
 GLOSSARY Appendix A Appendix A: Glossary Acute Angle An angle that measures less than 90. Acute Triangle Alternate Angles A triangle that has three acute angles. Angles that are between parallel lines,
GLOSSARY Appendix A Appendix A: Glossary Acute Angle An angle that measures less than 90. Acute Triangle Alternate Angles A triangle that has three acute angles. Angles that are between parallel lines,
Using 3D Computer Graphics Multimedia to Motivate Teachers Learning of Geometry and Pedagogy
 Using 3D Computer Graphics Multimedia to Motivate Teachers Learning of Geometry and Pedagogy Tracy Goodson-Espy Associate Professor goodsonespyt@appstate.edu Samuel L. Espy Viz Multimedia Boone, NC 28607
Using 3D Computer Graphics Multimedia to Motivate Teachers Learning of Geometry and Pedagogy Tracy Goodson-Espy Associate Professor goodsonespyt@appstate.edu Samuel L. Espy Viz Multimedia Boone, NC 28607
Adobe Illustrator CS5 Part 1: Introduction to Illustrator
 CALIFORNIA STATE UNIVERSITY, LOS ANGELES INFORMATION TECHNOLOGY SERVICES Adobe Illustrator CS5 Part 1: Introduction to Illustrator Summer 2011, Version 1.0 Table of Contents Introduction...2 Downloading
CALIFORNIA STATE UNIVERSITY, LOS ANGELES INFORMATION TECHNOLOGY SERVICES Adobe Illustrator CS5 Part 1: Introduction to Illustrator Summer 2011, Version 1.0 Table of Contents Introduction...2 Downloading
Quantifying Spatial Presence. Summary
 Quantifying Spatial Presence Cedar Riener and Dennis Proffitt Department of Psychology, University of Virginia Keywords: spatial presence, illusions, visual perception Summary The human visual system uses
Quantifying Spatial Presence Cedar Riener and Dennis Proffitt Department of Psychology, University of Virginia Keywords: spatial presence, illusions, visual perception Summary The human visual system uses
1. A student followed the given steps below to complete a construction. Which type of construction is best represented by the steps given above?
 1. A student followed the given steps below to complete a construction. Step 1: Place the compass on one endpoint of the line segment. Step 2: Extend the compass from the chosen endpoint so that the width
1. A student followed the given steps below to complete a construction. Step 1: Place the compass on one endpoint of the line segment. Step 2: Extend the compass from the chosen endpoint so that the width
First Level: 2D Fundamentals. by Randy H. Shih Oregon Institute of Technology
 AutoCAD 2008 Tutorial First Level: 2D Fundamentals by Randy H. Shih Oregon Institute of Technology MultiMedia CD by Jack Zecher Indiana University Purdue University Indianapolis SDC PUBLICATIONS Schroff
AutoCAD 2008 Tutorial First Level: 2D Fundamentals by Randy H. Shih Oregon Institute of Technology MultiMedia CD by Jack Zecher Indiana University Purdue University Indianapolis SDC PUBLICATIONS Schroff
CS 4204 Computer Graphics
 CS 4204 Computer Graphics 2D and 3D Transformations Doug Bowman Adapted from notes by Yong Cao Virginia Tech 1 Transformations What are they? changing something to something else via rules mathematics:
CS 4204 Computer Graphics 2D and 3D Transformations Doug Bowman Adapted from notes by Yong Cao Virginia Tech 1 Transformations What are they? changing something to something else via rules mathematics:
SOEM 024: Computer Aided Design. E. Rozos
 SOEM 024: Computer Aided Design E. Rozos 3D Design with AutoCAD 2002 Isometric Drawings 3D coordinates, views Wire-frame 3D modelling, extruding Primitive objects Boolean operators Terminology Boolean
SOEM 024: Computer Aided Design E. Rozos 3D Design with AutoCAD 2002 Isometric Drawings 3D coordinates, views Wire-frame 3D modelling, extruding Primitive objects Boolean operators Terminology Boolean
COMP175: Computer Graphics. Lecture 1 Introduction and Display Technologies
 COMP175: Computer Graphics Lecture 1 Introduction and Display Technologies Course mechanics Number: COMP 175-01, Fall 2009 Meetings: TR 1:30-2:45pm Instructor: Sara Su (sarasu@cs.tufts.edu) TA: Matt Menke
COMP175: Computer Graphics Lecture 1 Introduction and Display Technologies Course mechanics Number: COMP 175-01, Fall 2009 Meetings: TR 1:30-2:45pm Instructor: Sara Su (sarasu@cs.tufts.edu) TA: Matt Menke
Computer Graphics. Introduction. Computer graphics. What is computer graphics? Yung-Yu Chuang
 Introduction Computer Graphics Instructor: Yung-Yu Chuang ( 莊 永 裕 ) E-mail: c@csie.ntu.edu.tw Office: CSIE 527 Grading: a MatchMove project Computer Science ce & Information o Technolog og Yung-Yu Chuang
Introduction Computer Graphics Instructor: Yung-Yu Chuang ( 莊 永 裕 ) E-mail: c@csie.ntu.edu.tw Office: CSIE 527 Grading: a MatchMove project Computer Science ce & Information o Technolog og Yung-Yu Chuang
Solving Simultaneous Equations and Matrices
 Solving Simultaneous Equations and Matrices The following represents a systematic investigation for the steps used to solve two simultaneous linear equations in two unknowns. The motivation for considering
Solving Simultaneous Equations and Matrices The following represents a systematic investigation for the steps used to solve two simultaneous linear equations in two unknowns. The motivation for considering
Geometry and Measurement
 The student will be able to: Geometry and Measurement 1. Demonstrate an understanding of the principles of geometry and measurement and operations using measurements Use the US system of measurement for
The student will be able to: Geometry and Measurement 1. Demonstrate an understanding of the principles of geometry and measurement and operations using measurements Use the US system of measurement for
Algebra Geometry Glossary. 90 angle
 lgebra Geometry Glossary 1) acute angle an angle less than 90 acute angle 90 angle 2) acute triangle a triangle where all angles are less than 90 3) adjacent angles angles that share a common leg Example:
lgebra Geometry Glossary 1) acute angle an angle less than 90 acute angle 90 angle 2) acute triangle a triangle where all angles are less than 90 3) adjacent angles angles that share a common leg Example:
12-1 Representations of Three-Dimensional Figures
 Connect the dots on the isometric dot paper to represent the edges of the solid. Shade the tops of 12-1 Representations of Three-Dimensional Figures Use isometric dot paper to sketch each prism. 1. triangular
Connect the dots on the isometric dot paper to represent the edges of the solid. Shade the tops of 12-1 Representations of Three-Dimensional Figures Use isometric dot paper to sketch each prism. 1. triangular
CATIA for Design and Engineering. Version 5 Releases 14 & 15. David S. Kelley. Central Michigan University SDC
 CATIA for Design and Engineering ersion 5 Releases 4 & 5 David S. Kelley Central Michigan University SDC PUBLICATIONS Schroff Development Corporation www.schroff.com www.schroff-europe.com TUTORIAL Extruded
CATIA for Design and Engineering ersion 5 Releases 4 & 5 David S. Kelley Central Michigan University SDC PUBLICATIONS Schroff Development Corporation www.schroff.com www.schroff-europe.com TUTORIAL Extruded
Technical Drawing. MEC1000 Spring 2006 Instructor: David Anderson
 Technical Drawing MEC1000 Spring 2006 Instructor: David Anderson Topics Drawing Views Drawing Standards Best Practices Creating Drawings in SolidWorks Spring 2006 MEC1000 Technical Drawing - D. Anderson
Technical Drawing MEC1000 Spring 2006 Instructor: David Anderson Topics Drawing Views Drawing Standards Best Practices Creating Drawings in SolidWorks Spring 2006 MEC1000 Technical Drawing - D. Anderson
Technical Drawing. Dr. Anwar Abu-Zarifa. Dr. Anwar Abu-Zarifa. Islamic University Gaza. Industrial Engineering Department 1
 Technical Drawing الرسم الھندسي Dr. Anwar Abu-Zarifa Dr. Anwar Abu-Zarifa. Islamic University Gaza. Industrial Engineering Department 1 Office: IT Building,Room: I413 OfficeHrs: 12:00 13:00(So,Tue,We)
Technical Drawing الرسم الھندسي Dr. Anwar Abu-Zarifa Dr. Anwar Abu-Zarifa. Islamic University Gaza. Industrial Engineering Department 1 Office: IT Building,Room: I413 OfficeHrs: 12:00 13:00(So,Tue,We)
2D Geometric Transformations
 2D Geometric Transformations (Chapter 5 in FVD) 2D Geometric Transformations Question: How do we represent a geometric object in the plane? Answer: For now, assume that objects consist of points and lines.
2D Geometric Transformations (Chapter 5 in FVD) 2D Geometric Transformations Question: How do we represent a geometric object in the plane? Answer: For now, assume that objects consist of points and lines.
The Essentials of CAGD
 The Essentials of CAGD Chapter 2: Lines and Planes Gerald Farin & Dianne Hansford CRC Press, Taylor & Francis Group, An A K Peters Book www.farinhansford.com/books/essentials-cagd c 2000 Farin & Hansford
The Essentials of CAGD Chapter 2: Lines and Planes Gerald Farin & Dianne Hansford CRC Press, Taylor & Francis Group, An A K Peters Book www.farinhansford.com/books/essentials-cagd c 2000 Farin & Hansford
Raising the Roof Creating Roofs in Revit David Cohn
 David Cohn AB322-1 Roofs are one of the most complex architectural elements to model, but with Revit you can create just about any type of roof. This class will explore the best methods for creating various
David Cohn AB322-1 Roofs are one of the most complex architectural elements to model, but with Revit you can create just about any type of roof. This class will explore the best methods for creating various
Thin Lenses Drawing Ray Diagrams
 Drawing Ray Diagrams Fig. 1a Fig. 1b In this activity we explore how light refracts as it passes through a thin lens. Eyeglasses have been in use since the 13 th century. In 1610 Galileo used two lenses
Drawing Ray Diagrams Fig. 1a Fig. 1b In this activity we explore how light refracts as it passes through a thin lens. Eyeglasses have been in use since the 13 th century. In 1610 Galileo used two lenses
2D Geometrical Transformations. Foley & Van Dam, Chapter 5
 2D Geometrical Transformations Fole & Van Dam, Chapter 5 2D Geometrical Transformations Translation Scaling Rotation Shear Matri notation Compositions Homogeneous coordinates 2D Geometrical Transformations
2D Geometrical Transformations Fole & Van Dam, Chapter 5 2D Geometrical Transformations Translation Scaling Rotation Shear Matri notation Compositions Homogeneous coordinates 2D Geometrical Transformations
MATHS LEVEL DESCRIPTORS
 MATHS LEVEL DESCRIPTORS Number Level 3 Understand the place value of numbers up to thousands. Order numbers up to 9999. Round numbers to the nearest 10 or 100. Understand the number line below zero, and
MATHS LEVEL DESCRIPTORS Number Level 3 Understand the place value of numbers up to thousands. Order numbers up to 9999. Round numbers to the nearest 10 or 100. Understand the number line below zero, and
Course Title: Architectural Drawing I (Code: 3315002)
 GUJARAT TECHNOLOGICAL UNIVERSITY, AHMEDABAD, GUJARAT COURSE CURRICULUM Course Title: Architectural Drawing I (Code: 3315002) Diploma Programmes in which this course is offered Architectural Assistanship
GUJARAT TECHNOLOGICAL UNIVERSITY, AHMEDABAD, GUJARAT COURSE CURRICULUM Course Title: Architectural Drawing I (Code: 3315002) Diploma Programmes in which this course is offered Architectural Assistanship
Adobe Illustrator CS5
 What is Illustrator? Adobe Illustrator CS5 An Overview Illustrator is a vector drawing program. It is often used to draw illustrations, cartoons, diagrams, charts and logos. Unlike raster images that store
What is Illustrator? Adobe Illustrator CS5 An Overview Illustrator is a vector drawing program. It is often used to draw illustrations, cartoons, diagrams, charts and logos. Unlike raster images that store
Selecting the Best Approach to Teach 3D Modeling to Technical College Engineering
 Paper ID #12358 Selecting the Best Approach to Teach 3D Modeling to Technical College Engineering Students Dr. Farzin Heidari, Texas A&M University, Kingsville c American Society for Engineering Education,
Paper ID #12358 Selecting the Best Approach to Teach 3D Modeling to Technical College Engineering Students Dr. Farzin Heidari, Texas A&M University, Kingsville c American Society for Engineering Education,
12.5 Equations of Lines and Planes
 Instructor: Longfei Li Math 43 Lecture Notes.5 Equations of Lines and Planes What do we need to determine a line? D: a point on the line: P 0 (x 0, y 0 ) direction (slope): k 3D: a point on the line: P
Instructor: Longfei Li Math 43 Lecture Notes.5 Equations of Lines and Planes What do we need to determine a line? D: a point on the line: P 0 (x 0, y 0 ) direction (slope): k 3D: a point on the line: P
Number Sense and Operations
 Number Sense and Operations representing as they: 6.N.1 6.N.2 6.N.3 6.N.4 6.N.5 6.N.6 6.N.7 6.N.8 6.N.9 6.N.10 6.N.11 6.N.12 6.N.13. 6.N.14 6.N.15 Demonstrate an understanding of positive integer exponents
Number Sense and Operations representing as they: 6.N.1 6.N.2 6.N.3 6.N.4 6.N.5 6.N.6 6.N.7 6.N.8 6.N.9 6.N.10 6.N.11 6.N.12 6.N.13. 6.N.14 6.N.15 Demonstrate an understanding of positive integer exponents
For Environmental Health Science Students. Engineering Drawing. Wuttet Taffesse, Laikemariam Kassa. Haramaya University
 LECTURE NOTES For Environmental Health Science Students Engineering Drawing Wuttet Taffesse, Laikemariam Kassa Haramaya University In collaboration with the Ethiopia Public Health Training Initiative,
LECTURE NOTES For Environmental Health Science Students Engineering Drawing Wuttet Taffesse, Laikemariam Kassa Haramaya University In collaboration with the Ethiopia Public Health Training Initiative,
Leaving Certificate Design and Communication Graphics Syllabus. Ordinary level and Higher level
 Leaving Certificate Design and Communication Graphics Syllabus Ordinary level and Higher level For implementation in September, 2007 LEAVING CERTIFICATE DESIGN AND COMMUNICATION GRAPHICS CONTENTS Preface
Leaving Certificate Design and Communication Graphics Syllabus Ordinary level and Higher level For implementation in September, 2007 LEAVING CERTIFICATE DESIGN AND COMMUNICATION GRAPHICS CONTENTS Preface
Pro/ENGINEER Wildfire 4.0 Basic Design
 Introduction Datum features are non-solid features used during the construction of other features. The most common datum features include planes, axes, coordinate systems, and curves. Datum features do
Introduction Datum features are non-solid features used during the construction of other features. The most common datum features include planes, axes, coordinate systems, and curves. Datum features do
Engineering Graphics with AutoCAD
 Engineering Graphics with AutoCAD Overview By Prof. D. M. Kulkarni Engineering Graphics with AutoCAD http://www.phindia.com/bookdetail_forth.php?isbn=978-81-203-3783-1 Team of Authors Dr. Dhananjay M.
Engineering Graphics with AutoCAD Overview By Prof. D. M. Kulkarni Engineering Graphics with AutoCAD http://www.phindia.com/bookdetail_forth.php?isbn=978-81-203-3783-1 Team of Authors Dr. Dhananjay M.
Discovering Math: Exploring Geometry Teacher s Guide
 Teacher s Guide Grade Level: 6 8 Curriculum Focus: Mathematics Lesson Duration: Three class periods Program Description Discovering Math: Exploring Geometry From methods of geometric construction and threedimensional
Teacher s Guide Grade Level: 6 8 Curriculum Focus: Mathematics Lesson Duration: Three class periods Program Description Discovering Math: Exploring Geometry From methods of geometric construction and threedimensional
Geometry: Unit 1 Vocabulary TERM DEFINITION GEOMETRIC FIGURE. Cannot be defined by using other figures.
 Geometry: Unit 1 Vocabulary 1.1 Undefined terms Cannot be defined by using other figures. Point A specific location. It has no dimension and is represented by a dot. Line Plane A connected straight path.
Geometry: Unit 1 Vocabulary 1.1 Undefined terms Cannot be defined by using other figures. Point A specific location. It has no dimension and is represented by a dot. Line Plane A connected straight path.
SDC. Schroff Development Corporation WWW.SDCACAD.COM PUBLICATIONS. MultiMedia CD by Jack Zecher
 MultiMedia CD by Jack Zecher An audioi/visual presentation of the tutorial exercises SDC PUBLICATIONS Schroff Development Corporation WWW.SDCACAD.COM AutoCAD 2002 Tutorial 2-1 Lesson 2 Geometric Construction
MultiMedia CD by Jack Zecher An audioi/visual presentation of the tutorial exercises SDC PUBLICATIONS Schroff Development Corporation WWW.SDCACAD.COM AutoCAD 2002 Tutorial 2-1 Lesson 2 Geometric Construction
TABLE OF CONTENTS. INTRODUCTION... 5 Advance Concrete... 5 Where to find information?... 6 INSTALLATION... 7 STARTING ADVANCE CONCRETE...
 Starting Guide TABLE OF CONTENTS INTRODUCTION... 5 Advance Concrete... 5 Where to find information?... 6 INSTALLATION... 7 STARTING ADVANCE CONCRETE... 7 ADVANCE CONCRETE USER INTERFACE... 7 Other important
Starting Guide TABLE OF CONTENTS INTRODUCTION... 5 Advance Concrete... 5 Where to find information?... 6 INSTALLATION... 7 STARTING ADVANCE CONCRETE... 7 ADVANCE CONCRETE USER INTERFACE... 7 Other important
Exam 1 Sample Question SOLUTIONS. y = 2x
 Exam Sample Question SOLUTIONS. Eliminate the parameter to find a Cartesian equation for the curve: x e t, y e t. SOLUTION: You might look at the coordinates and notice that If you don t see it, we can
Exam Sample Question SOLUTIONS. Eliminate the parameter to find a Cartesian equation for the curve: x e t, y e t. SOLUTION: You might look at the coordinates and notice that If you don t see it, we can
OBJECTIVES. Computeraided. Drafting and Design. Drafting vocabulary
 This sample chapter is for review purposes only. Copyright The Goodheart-Willcox Co., Inc. All rights reserved. 50 Exploring Drafting Chapter 7 Computer-Aided Drafting and Design 5 7 Computer-Aided Drafting
This sample chapter is for review purposes only. Copyright The Goodheart-Willcox Co., Inc. All rights reserved. 50 Exploring Drafting Chapter 7 Computer-Aided Drafting and Design 5 7 Computer-Aided Drafting
CS 534: Computer Vision 3D Model-based recognition
 CS 534: Computer Vision 3D Model-based recognition Ahmed Elgammal Dept of Computer Science CS 534 3D Model-based Vision - 1 High Level Vision Object Recognition: What it means? Two main recognition tasks:!
CS 534: Computer Vision 3D Model-based recognition Ahmed Elgammal Dept of Computer Science CS 534 3D Model-based Vision - 1 High Level Vision Object Recognition: What it means? Two main recognition tasks:!
Grade 8 Mathematics Geometry: Lesson 2
 Grade 8 Mathematics Geometry: Lesson 2 Read aloud to the students the material that is printed in boldface type inside the boxes. Information in regular type inside the boxes and all information outside
Grade 8 Mathematics Geometry: Lesson 2 Read aloud to the students the material that is printed in boldface type inside the boxes. Information in regular type inside the boxes and all information outside
EXPERIMENT 6 OPTICS: FOCAL LENGTH OF A LENS
 EXPERIMENT 6 OPTICS: FOCAL LENGTH OF A LENS The following website should be accessed before coming to class. Text reference: pp189-196 Optics Bench a) For convenience of discussion we assume that the light
EXPERIMENT 6 OPTICS: FOCAL LENGTH OF A LENS The following website should be accessed before coming to class. Text reference: pp189-196 Optics Bench a) For convenience of discussion we assume that the light
Understand the Sketcher workbench of CATIA V5.
 Chapter 1 Drawing Sketches in Learning Objectives the Sketcher Workbench-I After completing this chapter you will be able to: Understand the Sketcher workbench of CATIA V5. Start a new file in the Part
Chapter 1 Drawing Sketches in Learning Objectives the Sketcher Workbench-I After completing this chapter you will be able to: Understand the Sketcher workbench of CATIA V5. Start a new file in the Part
37 Basic Geometric Shapes and Figures
 37 Basic Geometric Shapes and Figures In this section we discuss basic geometric shapes and figures such as points, lines, line segments, planes, angles, triangles, and quadrilaterals. The three pillars
37 Basic Geometric Shapes and Figures In this section we discuss basic geometric shapes and figures such as points, lines, line segments, planes, angles, triangles, and quadrilaterals. The three pillars
2. If C is the midpoint of AB and B is the midpoint of AE, can you say that the measure of AC is 1/4 the measure of AE?
 MATH 206 - Midterm Exam 2 Practice Exam Solutions 1. Show two rays in the same plane that intersect at more than one point. Rays AB and BA intersect at all points from A to B. 2. If C is the midpoint of
MATH 206 - Midterm Exam 2 Practice Exam Solutions 1. Show two rays in the same plane that intersect at more than one point. Rays AB and BA intersect at all points from A to B. 2. If C is the midpoint of
Producing 2D Documentation from 3D Models in AutoCAD
 Producing 2D Documentation from 3D Models in AutoCAD David Cohn 4D Technologies AC4689 Modeling in 3D is fine, but eventually you need to produce 2D drawings. In this class, you will learn about tools
Producing 2D Documentation from 3D Models in AutoCAD David Cohn 4D Technologies AC4689 Modeling in 3D is fine, but eventually you need to produce 2D drawings. In this class, you will learn about tools
Space Perception and Binocular Vision
 Space Perception and Binocular Vision Space Perception Monocular Cues to Three-Dimensional Space Binocular Vision and Stereopsis Combining Depth Cues 9/30/2008 1 Introduction to Space Perception Realism:
Space Perception and Binocular Vision Space Perception Monocular Cues to Three-Dimensional Space Binocular Vision and Stereopsis Combining Depth Cues 9/30/2008 1 Introduction to Space Perception Realism:
Digital Photography Composition. Kent Messamore 9/8/2013
 Digital Photography Composition Kent Messamore 9/8/2013 Photography Equipment versus Art Last week we focused on our Cameras Hopefully we have mastered the buttons and dials by now If not, it will come
Digital Photography Composition Kent Messamore 9/8/2013 Photography Equipment versus Art Last week we focused on our Cameras Hopefully we have mastered the buttons and dials by now If not, it will come
