3D Viewing. Chapter 7. Projections. 3D clipping. OpenGL viewing functions and clipping planes
|
|
|
- Dorthy Bryan
- 8 years ago
- Views:
Transcription
1 3D Viewing Chapter 7 Projections 3D clipping OpenGL viewing functions and clipping planes 1
2 Projections Parallel Perspective Coordinates are transformed along parallel lines Relative sizes are preserved Parallel lines remain parallel Projection lines converge at a point More distant objects are relatively smaller Closer to the way we actually see things 2
3 Orthogonal Projections An orthogonal projection is a parallel projection where the transformation lines are perpendicular to the view plane. Orthogonal projections are used for engineering drawings front and side elevations and plan view. Axonometric projection lets you see multiple faces of an object at once. An isometric projection has the view direction along a (1,1,1) direction of the world coordinate system. 3
4 Orthogonal Projections If the view plane is perpendicular to the z-axis, x p = y p = x y The z coordinate is used only for visibility calculations. 4
5 Clipping The view volume for an orthogonal projection is a rectangular parallelepiped with a cross-section the same size as the clipping window. This will be normalized to a cube. 5
6 Normalization The normalization transformation involves translation and scaling in all 3 directions. 2 xwmax xw min 0 0 xw max+xw min xw max xw min 2 0 xwmax xw M ortho, norm min 0 xw max+xw min xw max xw min 2 z 0 0 near +z far znear z far z near z far
7 Oblique Parallel Projections For this kind of projection, projection paths are not perpendicular to the view plane. Use two angles to specify the projection. Point (x, y, z) projects to (xp, y p, z vp ). xp = yp = x + L cos φ y + L sin φ 7
8 Oblique Parallel Projections the projection line makes an angle α with the line between the projected point and the orthogonal projection point. tan α = zvp z L An orthogonal projection has α = 90. Oblique projections correspond to a shearing transformation. Can use a projection vector to specify the projection. x 8
9 Cabinet and Cavalier Projections Typical choices for φ are 30 and 45. A cavalier projection has α = 45 A cabinet projection has tan α = 2 so α
10 Oblique Transformations The view volume is a parallelepiped. Use a shear transformation to convert this volume into a rectangular parallelepiped. 1 0 V px V V pz z px vp V pz 0 1 V py V V Moblique = pz z py vp V pz Then transform as for an orthogonal projection. This is applied after MW C, V C. Moblique, norm = M ortho,norm M oblique 10
11 Perspective Projections Parallel projections are easy but not very realistic looking. Perspective transformations are more realistic. Points are projected along lines that meet at a reference point. P 1 Projection Reference Point y view (x prp, y prp, z prp ) P 2 z view More distant objects appear relatively smaller in a perspective projection. 11
12 Transformations for Perspective Projections Use parametric equations for positions along a projection line. x = x (x x prp )u y = y (y y prp )u z = z (z z prp )u At (x, y, z), u = 0 and at (x prp, y prp, z prp ), u = 1. If the view plane is at z = zvp, then u = z vp z z prp z Then, x and y can be calculated from u. Graphics packages often restrict the projection point to either be at the origin or along the zview axis which makes the expressions for x and y simpler. 12
13 Vanishing Points In a perspective projection, parallel lines that aren t parallel to the view point converge at a vanishing point. Each direction has its own vanishing point; principal vanishing points are for lines parallel to one of the coordinate axes. Depending on the orientation of the view plane, there may be 1, 2 or 3 principal vanishing points. 13
14 View Volumes The view volume for perspective projections is an infinite pyramid formed from lines starting at the perspective reference point and going through the corners of the view plane. Adding near and far clipping planes reduces this to a frustum. 14
15 Perspective Transformations The values of xp and y p calculated earlier have coefficients that depend on z. Need to use a transformation to homogeneous coordinates of the form x p = y p = x(z prp z vp )+x prp (z vp z) z prp z y(z prp z vp )+y prp (z vp z) z prp z This converts the description to homogeneous parallel-projection coordinates. 15
16 Viewport Transformation A perspective transformation can be either symmetric or oblique. Use a shear transformation to convert an oblique perspective to a symmetric one. 16
17 OpenGL Viewing Functions Specify viewing parameters with glulookat( x0, y0, z0, xref, yref, zref, vx, vy, vx) where P 0 = (x 0, y 0, z 0 ) is the viewing origin P ref = (x ref, y ref, z ref ) is the look-at point V = (V x, v y, V z ) is the view-up vector The positive zview-axis is in the direction N = P 0 P ref Default parameters are P 0 = (x 0, y 0, z 0 ) = (0, 0, 0) P ref = (0, 0, 1) V = (0, 1, 0) 17
18 Orthogonal Projections An orthogonal projection is specified with glmatrixmode( GLPROJECTION); glortho( xwmin, xwmax, ywmin, ywmax, dnear, dfar); Default parameters are xwmin = ywmin = dnear = -1 xwmax = ywmax = dfar = 1 Note that znear is behind the viewing position. gluortho2d is equivalent to gluortho with dnear = -1.0 and dfar = 1.0. To do oblique parallel projections you need to either rotate the scene to get the effect you want or set up the matrices manually. 18
19 Field of View 19
20 Perspective Transformations For a symmetric perspective transformation, use gluperspective( theta, aspect, dnear, dfar) For a general perspective transformation, use glfrustum( xwmin, xwmax, ywmin, ywmax, dnear, dfar); 20
21 3D Clipping Algorithms Often do the clipping after normalization to make it more efficient. This also allows clipping to be done in hardware. Several algorithms Region Clipping Polygon clipping Arbitrary Clip planes 21
22 3D Region Codes Now have clipping planes instead of lines. Extend the region codes to have two extra bits. bit 6 bit 5 bit 4 bit 3 bit 2 bit 1 Far Near Top Bottom Right Left 22
23 3D Region Codes Then use the same basic rules as in the 2D algorithm for elimination and calculating intersections
24 Polygon Clipping Since most graphics packages deal with objects constructed from polygons, clipping is basically a problem of clipping polygons in 3D. Coordinate extents (bounding boxes) can be used for trivial rejection or acceptance. Then clip edges to modify and create new vertex lists. 24
25 25
26 OpenGL Clipping Planes Sometimes need to specify additional clipping planes. Use glclipplane( id, planeparameters); glenable( id); The values of id are GLCLIP_PLANE0, GL_CLIP_PLANE1 The plane parameters are given as a vector with the 4 coefficients from the equation of the plane. 26
Basic Problem: Map a 3D object to a 2D display surface. Analogy - Taking a snapshot with a camera
 3D Viewing Basic Problem: Map a 3D object to a 2D display surface Analogy - Taking a snapshot with a camera Synthetic camera virtual camera we can move to any location & orient in any way then create a
3D Viewing Basic Problem: Map a 3D object to a 2D display surface Analogy - Taking a snapshot with a camera Synthetic camera virtual camera we can move to any location & orient in any way then create a
Realtime 3D Computer Graphics Virtual Reality
 Realtime 3D Computer Graphics Virtual Realit Viewing and projection Classical and General Viewing Transformation Pipeline CPU Pol. DL Pixel Per Vertex Texture Raster Frag FB object ee clip normalized device
Realtime 3D Computer Graphics Virtual Realit Viewing and projection Classical and General Viewing Transformation Pipeline CPU Pol. DL Pixel Per Vertex Texture Raster Frag FB object ee clip normalized device
4BA6 - Topic 4 Dr. Steven Collins. Chap. 5 3D Viewing and Projections
 4BA6 - Topic 4 Dr. Steven Collins Chap. 5 3D Viewing and Projections References Computer graphics: principles & practice, Fole, vandam, Feiner, Hughes, S-LEN 5.644 M23*;-6 (has a good appendix on linear
4BA6 - Topic 4 Dr. Steven Collins Chap. 5 3D Viewing and Projections References Computer graphics: principles & practice, Fole, vandam, Feiner, Hughes, S-LEN 5.644 M23*;-6 (has a good appendix on linear
CS 4204 Computer Graphics
 CS 4204 Computer Graphics 3D views and projection Adapted from notes by Yong Cao 1 Overview of 3D rendering Modeling: *Define object in local coordinates *Place object in world coordinates (modeling transformation)
CS 4204 Computer Graphics 3D views and projection Adapted from notes by Yong Cao 1 Overview of 3D rendering Modeling: *Define object in local coordinates *Place object in world coordinates (modeling transformation)
Monash University Clayton s School of Information Technology CSE3313 Computer Graphics Sample Exam Questions 2007
 Monash University Clayton s School of Information Technology CSE3313 Computer Graphics Questions 2007 INSTRUCTIONS: Answer all questions. Spend approximately 1 minute per mark. Question 1 30 Marks Total
Monash University Clayton s School of Information Technology CSE3313 Computer Graphics Questions 2007 INSTRUCTIONS: Answer all questions. Spend approximately 1 minute per mark. Question 1 30 Marks Total
Transformations in the pipeline
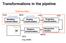 Transformations in the pipeline gltranslatef() Modeling transformation ModelView Matrix OCS WCS glulookat() VCS CCS Viewing transformation Projection transformation DCS Viewport transformation (e.g. pixels)
Transformations in the pipeline gltranslatef() Modeling transformation ModelView Matrix OCS WCS glulookat() VCS CCS Viewing transformation Projection transformation DCS Viewport transformation (e.g. pixels)
10.5. Click here for answers. Click here for solutions. EQUATIONS OF LINES AND PLANES. 3x 4y 6z 9 4, 2, 5. x y z. z 2. x 2. y 1.
 SECTION EQUATIONS OF LINES AND PLANES 1 EQUATIONS OF LINES AND PLANES A Click here for answers. S Click here for solutions. 1 Find a vector equation and parametric equations for the line passing through
SECTION EQUATIONS OF LINES AND PLANES 1 EQUATIONS OF LINES AND PLANES A Click here for answers. S Click here for solutions. 1 Find a vector equation and parametric equations for the line passing through
Geometry for Computer Graphics
 Computer Graphics and Visualisation Geometry for Computer Graphics Student Notes Developed by F Lin K Wyrwas J Irwin C Lilley W T Hewitt T L J Howard Computer Graphics Unit Manchester Computing Centre
Computer Graphics and Visualisation Geometry for Computer Graphics Student Notes Developed by F Lin K Wyrwas J Irwin C Lilley W T Hewitt T L J Howard Computer Graphics Unit Manchester Computing Centre
521493S Computer Graphics. Exercise 2 & course schedule change
 521493S Computer Graphics Exercise 2 & course schedule change Course Schedule Change Lecture from Wednesday 31th of March is moved to Tuesday 30th of March at 16-18 in TS128 Question 2.1 Given two nonparallel,
521493S Computer Graphics Exercise 2 & course schedule change Course Schedule Change Lecture from Wednesday 31th of March is moved to Tuesday 30th of March at 16-18 in TS128 Question 2.1 Given two nonparallel,
MAT 1341: REVIEW II SANGHOON BAEK
 MAT 1341: REVIEW II SANGHOON BAEK 1. Projections and Cross Product 1.1. Projections. Definition 1.1. Given a vector u, the rectangular (or perpendicular or orthogonal) components are two vectors u 1 and
MAT 1341: REVIEW II SANGHOON BAEK 1. Projections and Cross Product 1.1. Projections. Definition 1.1. Given a vector u, the rectangular (or perpendicular or orthogonal) components are two vectors u 1 and
Geometric Transformation CS 211A
 Geometric Transformation CS 211A What is transformation? Moving points (x,y) moves to (x+t, y+t) Can be in any dimension 2D Image warps 3D 3D Graphics and Vision Can also be considered as a movement to
Geometric Transformation CS 211A What is transformation? Moving points (x,y) moves to (x+t, y+t) Can be in any dimension 2D Image warps 3D 3D Graphics and Vision Can also be considered as a movement to
Math 241 Lines and Planes (Solutions) x = 3 3t. z = 1 t. x = 5 + t. z = 7 + 3t
 Math 241 Lines and Planes (Solutions) The equations for planes P 1, P 2 and P are P 1 : x 2y + z = 7 P 2 : x 4y + 5z = 6 P : (x 5) 2(y 6) + (z 7) = 0 The equations for lines L 1, L 2, L, L 4 and L 5 are
Math 241 Lines and Planes (Solutions) The equations for planes P 1, P 2 and P are P 1 : x 2y + z = 7 P 2 : x 4y + 5z = 6 P : (x 5) 2(y 6) + (z 7) = 0 The equations for lines L 1, L 2, L, L 4 and L 5 are
Image Processing and Computer Graphics. Rendering Pipeline. Matthias Teschner. Computer Science Department University of Freiburg
 Image Processing and Computer Graphics Rendering Pipeline Matthias Teschner Computer Science Department University of Freiburg Outline introduction rendering pipeline vertex processing primitive processing
Image Processing and Computer Graphics Rendering Pipeline Matthias Teschner Computer Science Department University of Freiburg Outline introduction rendering pipeline vertex processing primitive processing
Lecture 14: Section 3.3
 Lecture 14: Section 3.3 Shuanglin Shao October 23, 2013 Definition. Two nonzero vectors u and v in R n are said to be orthogonal (or perpendicular) if u v = 0. We will also agree that the zero vector in
Lecture 14: Section 3.3 Shuanglin Shao October 23, 2013 Definition. Two nonzero vectors u and v in R n are said to be orthogonal (or perpendicular) if u v = 0. We will also agree that the zero vector in
226-332 Basic CAD/CAM. CHAPTER 5: Geometric Transformation
 226-332 Basic CAD/CAM CHAPTER 5: Geometric Transformation 1 Geometric transformation is a change in geometric characteristics such as position, orientation, and size of a geometric entity (point, line,
226-332 Basic CAD/CAM CHAPTER 5: Geometric Transformation 1 Geometric transformation is a change in geometric characteristics such as position, orientation, and size of a geometric entity (point, line,
Cross product and determinants (Sect. 12.4) Two main ways to introduce the cross product
 Cross product and determinants (Sect. 12.4) Two main ways to introduce the cross product Geometrical definition Properties Expression in components. Definition in components Properties Geometrical expression.
Cross product and determinants (Sect. 12.4) Two main ways to introduce the cross product Geometrical definition Properties Expression in components. Definition in components Properties Geometrical expression.
From 3D to 2D: Orthographic and Perspective Projection Part 1
 From 3D to 2D: Orthographic and Perspective Projection Part 1 History Geometrical Constructions Types of Projection Projection in Computer Graphics Andries van Dam September 13, 2001 3D Viewing I 1/34
From 3D to 2D: Orthographic and Perspective Projection Part 1 History Geometrical Constructions Types of Projection Projection in Computer Graphics Andries van Dam September 13, 2001 3D Viewing I 1/34
Review Sheet for Test 1
 Review Sheet for Test 1 Math 261-00 2 6 2004 These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And
Review Sheet for Test 1 Math 261-00 2 6 2004 These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And
12.5 Equations of Lines and Planes
 Instructor: Longfei Li Math 43 Lecture Notes.5 Equations of Lines and Planes What do we need to determine a line? D: a point on the line: P 0 (x 0, y 0 ) direction (slope): k 3D: a point on the line: P
Instructor: Longfei Li Math 43 Lecture Notes.5 Equations of Lines and Planes What do we need to determine a line? D: a point on the line: P 0 (x 0, y 0 ) direction (slope): k 3D: a point on the line: P
Geometry of Vectors. 1 Cartesian Coordinates. Carlo Tomasi
 Geometry of Vectors Carlo Tomasi This note explores the geometric meaning of norm, inner product, orthogonality, and projection for vectors. For vectors in three-dimensional space, we also examine the
Geometry of Vectors Carlo Tomasi This note explores the geometric meaning of norm, inner product, orthogonality, and projection for vectors. For vectors in three-dimensional space, we also examine the
Fundamentals of Computer Animation
 Fundamentals of Computer Animation Quaternions as Orientations () page 1 Visualizing a Unit Quaternion Rotation in 4D Space ( ) = w + x + y z q = Norm q + q = q q [ w, v], v = ( x, y, z) w scalar q =,
Fundamentals of Computer Animation Quaternions as Orientations () page 1 Visualizing a Unit Quaternion Rotation in 4D Space ( ) = w + x + y z q = Norm q + q = q q [ w, v], v = ( x, y, z) w scalar q =,
Adding vectors We can do arithmetic with vectors. We ll start with vector addition and related operations. Suppose you have two vectors
 1 Chapter 13. VECTORS IN THREE DIMENSIONAL SPACE Let s begin with some names and notation for things: R is the set (collection) of real numbers. We write x R to mean that x is a real number. A real number
1 Chapter 13. VECTORS IN THREE DIMENSIONAL SPACE Let s begin with some names and notation for things: R is the set (collection) of real numbers. We write x R to mean that x is a real number. A real number
11.1. Objectives. Component Form of a Vector. Component Form of a Vector. Component Form of a Vector. Vectors and the Geometry of Space
 11 Vectors and the Geometry of Space 11.1 Vectors in the Plane Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. 2 Objectives! Write the component form of
11 Vectors and the Geometry of Space 11.1 Vectors in the Plane Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. 2 Objectives! Write the component form of
CS 4204 Computer Graphics
 CS 4204 Computer Graphics 2D and 3D Transformations Doug Bowman Adapted from notes by Yong Cao Virginia Tech 1 Transformations What are they? changing something to something else via rules mathematics:
CS 4204 Computer Graphics 2D and 3D Transformations Doug Bowman Adapted from notes by Yong Cao Virginia Tech 1 Transformations What are they? changing something to something else via rules mathematics:
Lecture Notes. Fundamentals of Computer Graphics. Prof. Michael Langer School of Computer Science McGill University
 COMP 557 Winter 2015 Lecture Notes Fundamentals of Computer Graphics Prof. Michael Langer School of Computer Science McGill University NOTE: These lecture notes are dynamic. The initial version of the
COMP 557 Winter 2015 Lecture Notes Fundamentals of Computer Graphics Prof. Michael Langer School of Computer Science McGill University NOTE: These lecture notes are dynamic. The initial version of the
L 2 : x = s + 1, y = s, z = 4s + 4. 3. Suppose that C has coordinates (x, y, z). Then from the vector equality AC = BD, one has
 The line L through the points A and B is parallel to the vector AB = 3, 2, and has parametric equations x = 3t + 2, y = 2t +, z = t Therefore, the intersection point of the line with the plane should satisfy:
The line L through the points A and B is parallel to the vector AB = 3, 2, and has parametric equations x = 3t + 2, y = 2t +, z = t Therefore, the intersection point of the line with the plane should satisfy:
Lines and Planes in R 3
 .3 Lines and Planes in R 3 P. Daniger Lines in R 3 We wish to represent lines in R 3. Note that a line may be described in two different ways: By specifying two points on the line. By specifying one point
.3 Lines and Planes in R 3 P. Daniger Lines in R 3 We wish to represent lines in R 3. Note that a line may be described in two different ways: By specifying two points on the line. By specifying one point
Equations Involving Lines and Planes Standard equations for lines in space
 Equations Involving Lines and Planes In this section we will collect various important formulas regarding equations of lines and planes in three dimensional space Reminder regarding notation: any quantity
Equations Involving Lines and Planes In this section we will collect various important formulas regarding equations of lines and planes in three dimensional space Reminder regarding notation: any quantity
Section 9.5: Equations of Lines and Planes
 Lines in 3D Space Section 9.5: Equations of Lines and Planes Practice HW from Stewart Textbook (not to hand in) p. 673 # 3-5 odd, 2-37 odd, 4, 47 Consider the line L through the point P = ( x, y, ) that
Lines in 3D Space Section 9.5: Equations of Lines and Planes Practice HW from Stewart Textbook (not to hand in) p. 673 # 3-5 odd, 2-37 odd, 4, 47 Consider the line L through the point P = ( x, y, ) that
Dot product and vector projections (Sect. 12.3) There are two main ways to introduce the dot product
 Dot product and vector projections (Sect. 12.3) Two definitions for the dot product. Geometric definition of dot product. Orthogonal vectors. Dot product and orthogonal projections. Properties of the dot
Dot product and vector projections (Sect. 12.3) Two definitions for the dot product. Geometric definition of dot product. Orthogonal vectors. Dot product and orthogonal projections. Properties of the dot
TWO-DIMENSIONAL TRANSFORMATION
 CHAPTER 2 TWO-DIMENSIONAL TRANSFORMATION 2.1 Introduction As stated earlier, Computer Aided Design consists of three components, namely, Design (Geometric Modeling), Analysis (FEA, etc), and Visualization
CHAPTER 2 TWO-DIMENSIONAL TRANSFORMATION 2.1 Introduction As stated earlier, Computer Aided Design consists of three components, namely, Design (Geometric Modeling), Analysis (FEA, etc), and Visualization
w = COI EYE view direction vector u = w ( 010,, ) cross product with y-axis v = w u up vector
 . w COI EYE view direction vector u w ( 00,, ) cross product with -ais v w u up vector (EQ ) Computer Animation: Algorithms and Techniques 29 up vector view vector observer center of interest 30 Computer
. w COI EYE view direction vector u w ( 00,, ) cross product with -ais v w u up vector (EQ ) Computer Animation: Algorithms and Techniques 29 up vector view vector observer center of interest 30 Computer
Aston University. School of Engineering & Applied Science
 CS2150 Aston University School of Engineering & Applied Science CS2150: Computer Graphics January Examinations 2010 Date: XXX Time: XXX Instructions to Candidates: 1. Answer Question ONE and any other
CS2150 Aston University School of Engineering & Applied Science CS2150: Computer Graphics January Examinations 2010 Date: XXX Time: XXX Instructions to Candidates: 1. Answer Question ONE and any other
2D Geometric Transformations
 2D Geometric Transformations (Chapter 5 in FVD) 2D Geometric Transformations Question: How do we represent a geometric object in the plane? Answer: For now, assume that objects consist of points and lines.
2D Geometric Transformations (Chapter 5 in FVD) 2D Geometric Transformations Question: How do we represent a geometric object in the plane? Answer: For now, assume that objects consist of points and lines.
1 Symmetries of regular polyhedra
 1230, notes 5 1 Symmetries of regular polyhedra Symmetry groups Recall: Group axioms: Suppose that (G, ) is a group and a, b, c are elements of G. Then (i) a b G (ii) (a b) c = a (b c) (iii) There is an
1230, notes 5 1 Symmetries of regular polyhedra Symmetry groups Recall: Group axioms: Suppose that (G, ) is a group and a, b, c are elements of G. Then (i) a b G (ii) (a b) c = a (b c) (iii) There is an
Lecture 3: Coordinate Systems and Transformations
 Lecture 3: Coordinate Systems and Transformations Topics: 1. Coordinate systems and frames 2. Change of frames 3. Affine transformations 4. Rotation, translation, scaling, and shear 5. Rotation about an
Lecture 3: Coordinate Systems and Transformations Topics: 1. Coordinate systems and frames 2. Change of frames 3. Affine transformations 4. Rotation, translation, scaling, and shear 5. Rotation about an
About the Tutorial. Audience. Prerequisites. Copyright & Disclaimer. Computer Graphics
 About the Tutorial To display a picture of any size on a computer screen is a difficult process. Computer graphics are used to simplify this process. Various algorithms and techniques are used to generate
About the Tutorial To display a picture of any size on a computer screen is a difficult process. Computer graphics are used to simplify this process. Various algorithms and techniques are used to generate
2.3 WINDOW-TO-VIEWPORT COORDINATE TRANSFORMATION
 2.3 WINDOW-TO-VIEWPORT COORDINATE TRANSFORMATION A world-coordinate area selected for display is called a window. An area on a display device to which a window is mapped is called a viewport. The window
2.3 WINDOW-TO-VIEWPORT COORDINATE TRANSFORMATION A world-coordinate area selected for display is called a window. An area on a display device to which a window is mapped is called a viewport. The window
Section 11.4: Equations of Lines and Planes
 Section 11.4: Equations of Lines and Planes Definition: The line containing the point ( 0, 0, 0 ) and parallel to the vector v = A, B, C has parametric equations = 0 + At, = 0 + Bt, = 0 + Ct, where t R
Section 11.4: Equations of Lines and Planes Definition: The line containing the point ( 0, 0, 0 ) and parallel to the vector v = A, B, C has parametric equations = 0 + At, = 0 + Bt, = 0 + Ct, where t R
Orthogonal Projections and Orthonormal Bases
 CS 3, HANDOUT -A, 3 November 04 (adjusted on 7 November 04) Orthogonal Projections and Orthonormal Bases (continuation of Handout 07 of 6 September 04) Definition (Orthogonality, length, unit vectors).
CS 3, HANDOUT -A, 3 November 04 (adjusted on 7 November 04) Orthogonal Projections and Orthonormal Bases (continuation of Handout 07 of 6 September 04) Definition (Orthogonality, length, unit vectors).
1 VECTOR SPACES AND SUBSPACES
 1 VECTOR SPACES AND SUBSPACES What is a vector? Many are familiar with the concept of a vector as: Something which has magnitude and direction. an ordered pair or triple. a description for quantities such
1 VECTOR SPACES AND SUBSPACES What is a vector? Many are familiar with the concept of a vector as: Something which has magnitude and direction. an ordered pair or triple. a description for quantities such
Mechanics lecture 7 Moment of a force, torque, equilibrium of a body
 G.1 EE1.el3 (EEE1023): Electronics III Mechanics lecture 7 Moment of a force, torque, equilibrium of a body Dr Philip Jackson http://www.ee.surrey.ac.uk/teaching/courses/ee1.el3/ G.2 Moments, torque and
G.1 EE1.el3 (EEE1023): Electronics III Mechanics lecture 7 Moment of a force, torque, equilibrium of a body Dr Philip Jackson http://www.ee.surrey.ac.uk/teaching/courses/ee1.el3/ G.2 Moments, torque and
Introduction to Computer Graphics
 Introduction to Computer Graphics Torsten Möller TASC 8021 778-782-2215 torsten@sfu.ca www.cs.sfu.ca/~torsten Today What is computer graphics? Contents of this course Syllabus Overview of course topics
Introduction to Computer Graphics Torsten Möller TASC 8021 778-782-2215 torsten@sfu.ca www.cs.sfu.ca/~torsten Today What is computer graphics? Contents of this course Syllabus Overview of course topics
Rotation Matrices and Homogeneous Transformations
 Rotation Matrices and Homogeneous Transformations A coordinate frame in an n-dimensional space is defined by n mutually orthogonal unit vectors. In particular, for a two-dimensional (2D) space, i.e., n
Rotation Matrices and Homogeneous Transformations A coordinate frame in an n-dimensional space is defined by n mutually orthogonal unit vectors. In particular, for a two-dimensional (2D) space, i.e., n
Understand the Sketcher workbench of CATIA V5.
 Chapter 1 Drawing Sketches in Learning Objectives the Sketcher Workbench-I After completing this chapter you will be able to: Understand the Sketcher workbench of CATIA V5. Start a new file in the Part
Chapter 1 Drawing Sketches in Learning Objectives the Sketcher Workbench-I After completing this chapter you will be able to: Understand the Sketcher workbench of CATIA V5. Start a new file in the Part
Solving Simultaneous Equations and Matrices
 Solving Simultaneous Equations and Matrices The following represents a systematic investigation for the steps used to solve two simultaneous linear equations in two unknowns. The motivation for considering
Solving Simultaneous Equations and Matrices The following represents a systematic investigation for the steps used to solve two simultaneous linear equations in two unknowns. The motivation for considering
GeoGebra. 10 lessons. Gerrit Stols
 GeoGebra in 10 lessons Gerrit Stols Acknowledgements GeoGebra is dynamic mathematics open source (free) software for learning and teaching mathematics in schools. It was developed by Markus Hohenwarter
GeoGebra in 10 lessons Gerrit Stols Acknowledgements GeoGebra is dynamic mathematics open source (free) software for learning and teaching mathematics in schools. It was developed by Markus Hohenwarter
Two vectors are equal if they have the same length and direction. They do not
 Vectors define vectors Some physical quantities, such as temperature, length, and mass, can be specified by a single number called a scalar. Other physical quantities, such as force and velocity, must
Vectors define vectors Some physical quantities, such as temperature, length, and mass, can be specified by a single number called a scalar. Other physical quantities, such as force and velocity, must
INTRODUCTION TO RENDERING TECHNIQUES
 INTRODUCTION TO RENDERING TECHNIQUES 22 Mar. 212 Yanir Kleiman What is 3D Graphics? Why 3D? Draw one frame at a time Model only once X 24 frames per second Color / texture only once 15, frames for a feature
INTRODUCTION TO RENDERING TECHNIQUES 22 Mar. 212 Yanir Kleiman What is 3D Graphics? Why 3D? Draw one frame at a time Model only once X 24 frames per second Color / texture only once 15, frames for a feature
State of Stress at Point
 State of Stress at Point Einstein Notation The basic idea of Einstein notation is that a covector and a vector can form a scalar: This is typically written as an explicit sum: According to this convention,
State of Stress at Point Einstein Notation The basic idea of Einstein notation is that a covector and a vector can form a scalar: This is typically written as an explicit sum: According to this convention,
A vector is a directed line segment used to represent a vector quantity.
 Chapters and 6 Introduction to Vectors A vector quantity has direction and magnitude. There are many examples of vector quantities in the natural world, such as force, velocity, and acceleration. A vector
Chapters and 6 Introduction to Vectors A vector quantity has direction and magnitude. There are many examples of vector quantities in the natural world, such as force, velocity, and acceleration. A vector
Name Class. Date Section. Test Form A Chapter 11. Chapter 11 Test Bank 155
 Chapter Test Bank 55 Test Form A Chapter Name Class Date Section. Find a unit vector in the direction of v if v is the vector from P,, 3 to Q,, 0. (a) 3i 3j 3k (b) i j k 3 i 3 j 3 k 3 i 3 j 3 k. Calculate
Chapter Test Bank 55 Test Form A Chapter Name Class Date Section. Find a unit vector in the direction of v if v is the vector from P,, 3 to Q,, 0. (a) 3i 3j 3k (b) i j k 3 i 3 j 3 k 3 i 3 j 3 k. Calculate
Linear algebra and the geometry of quadratic equations. Similarity transformations and orthogonal matrices
 MATH 30 Differential Equations Spring 006 Linear algebra and the geometry of quadratic equations Similarity transformations and orthogonal matrices First, some things to recall from linear algebra Two
MATH 30 Differential Equations Spring 006 Linear algebra and the geometry of quadratic equations Similarity transformations and orthogonal matrices First, some things to recall from linear algebra Two
Determine whether the following lines intersect, are parallel, or skew. L 1 : x = 6t y = 1 + 9t z = 3t. x = 1 + 2s y = 4 3s z = s
 Homework Solutions 5/20 10.5.17 Determine whether the following lines intersect, are parallel, or skew. L 1 : L 2 : x = 6t y = 1 + 9t z = 3t x = 1 + 2s y = 4 3s z = s A vector parallel to L 1 is 6, 9,
Homework Solutions 5/20 10.5.17 Determine whether the following lines intersect, are parallel, or skew. L 1 : L 2 : x = 6t y = 1 + 9t z = 3t x = 1 + 2s y = 4 3s z = s A vector parallel to L 1 is 6, 9,
H.Calculating Normal Vectors
 Appendix H H.Calculating Normal Vectors This appendix describes how to calculate normal vectors for surfaces. You need to define normals to use the OpenGL lighting facility, which is described in Chapter
Appendix H H.Calculating Normal Vectors This appendix describes how to calculate normal vectors for surfaces. You need to define normals to use the OpenGL lighting facility, which is described in Chapter
13.4 THE CROSS PRODUCT
 710 Chapter Thirteen A FUNDAMENTAL TOOL: VECTORS 62. Use the following steps and the results of Problems 59 60 to show (without trigonometry) that the geometric and algebraic definitions of the dot product
710 Chapter Thirteen A FUNDAMENTAL TOOL: VECTORS 62. Use the following steps and the results of Problems 59 60 to show (without trigonometry) that the geometric and algebraic definitions of the dot product
B2.53-R3: COMPUTER GRAPHICS. NOTE: 1. There are TWO PARTS in this Module/Paper. PART ONE contains FOUR questions and PART TWO contains FIVE questions.
 B2.53-R3: COMPUTER GRAPHICS NOTE: 1. There are TWO PARTS in this Module/Paper. PART ONE contains FOUR questions and PART TWO contains FIVE questions. 2. PART ONE is to be answered in the TEAR-OFF ANSWER
B2.53-R3: COMPUTER GRAPHICS NOTE: 1. There are TWO PARTS in this Module/Paper. PART ONE contains FOUR questions and PART TWO contains FIVE questions. 2. PART ONE is to be answered in the TEAR-OFF ANSWER
= y y 0. = z z 0. (a) Find a parametric vector equation for L. (b) Find parametric (scalar) equations for L.
 Math 21a Lines and lanes Spring, 2009 Lines in Space How can we express the equation(s) of a line through a point (x 0 ; y 0 ; z 0 ) and parallel to the vector u ha; b; ci? Many ways: as parametric (scalar)
Math 21a Lines and lanes Spring, 2009 Lines in Space How can we express the equation(s) of a line through a point (x 0 ; y 0 ; z 0 ) and parallel to the vector u ha; b; ci? Many ways: as parametric (scalar)
Exam 1 Sample Question SOLUTIONS. y = 2x
 Exam Sample Question SOLUTIONS. Eliminate the parameter to find a Cartesian equation for the curve: x e t, y e t. SOLUTION: You might look at the coordinates and notice that If you don t see it, we can
Exam Sample Question SOLUTIONS. Eliminate the parameter to find a Cartesian equation for the curve: x e t, y e t. SOLUTION: You might look at the coordinates and notice that If you don t see it, we can
FURTHER VECTORS (MEI)
 Mathematics Revision Guides Further Vectors (MEI) (column notation) Page of MK HOME TUITION Mathematics Revision Guides Level: AS / A Level - MEI OCR MEI: C FURTHER VECTORS (MEI) Version : Date: -9-7 Mathematics
Mathematics Revision Guides Further Vectors (MEI) (column notation) Page of MK HOME TUITION Mathematics Revision Guides Level: AS / A Level - MEI OCR MEI: C FURTHER VECTORS (MEI) Version : Date: -9-7 Mathematics
Math 241, Exam 1 Information.
 Math 241, Exam 1 Information. 9/24/12, LC 310, 11:15-12:05. Exam 1 will be based on: Sections 12.1-12.5, 14.1-14.3. The corresponding assigned homework problems (see http://www.math.sc.edu/ boylan/sccourses/241fa12/241.html)
Math 241, Exam 1 Information. 9/24/12, LC 310, 11:15-12:05. Exam 1 will be based on: Sections 12.1-12.5, 14.1-14.3. The corresponding assigned homework problems (see http://www.math.sc.edu/ boylan/sccourses/241fa12/241.html)
2.1 Three Dimensional Curves and Surfaces
 . Three Dimensional Curves and Surfaces.. Parametric Equation of a Line An line in two- or three-dimensional space can be uniquel specified b a point on the line and a vector parallel to the line. The
. Three Dimensional Curves and Surfaces.. Parametric Equation of a Line An line in two- or three-dimensional space can be uniquel specified b a point on the line and a vector parallel to the line. The
The Vector or Cross Product
 The Vector or ross Product 1 ppendix The Vector or ross Product We saw in ppendix that the dot product of two vectors is a scalar quantity that is a maximum when the two vectors are parallel and is zero
The Vector or ross Product 1 ppendix The Vector or ross Product We saw in ppendix that the dot product of two vectors is a scalar quantity that is a maximum when the two vectors are parallel and is zero
5. Orthogonal matrices
 L Vandenberghe EE133A (Spring 2016) 5 Orthogonal matrices matrices with orthonormal columns orthogonal matrices tall matrices with orthonormal columns complex matrices with orthonormal columns 5-1 Orthonormal
L Vandenberghe EE133A (Spring 2016) 5 Orthogonal matrices matrices with orthonormal columns orthogonal matrices tall matrices with orthonormal columns complex matrices with orthonormal columns 5-1 Orthonormal
12-1 Representations of Three-Dimensional Figures
 Connect the dots on the isometric dot paper to represent the edges of the solid. Shade the tops of 12-1 Representations of Three-Dimensional Figures Use isometric dot paper to sketch each prism. 1. triangular
Connect the dots on the isometric dot paper to represent the edges of the solid. Shade the tops of 12-1 Representations of Three-Dimensional Figures Use isometric dot paper to sketch each prism. 1. triangular
Analysis of Stresses and Strains
 Chapter 7 Analysis of Stresses and Strains 7.1 Introduction axial load = P / A torsional load in circular shaft = T / I p bending moment and shear force in beam = M y / I = V Q / I b in this chapter, we
Chapter 7 Analysis of Stresses and Strains 7.1 Introduction axial load = P / A torsional load in circular shaft = T / I p bending moment and shear force in beam = M y / I = V Q / I b in this chapter, we
We can display an object on a monitor screen in three different computer-model forms: Wireframe model Surface Model Solid model
 CHAPTER 4 CURVES 4.1 Introduction In order to understand the significance of curves, we should look into the types of model representations that are used in geometric modeling. Curves play a very significant
CHAPTER 4 CURVES 4.1 Introduction In order to understand the significance of curves, we should look into the types of model representations that are used in geometric modeling. Curves play a very significant
Geometric description of the cross product of the vectors u and v. The cross product of two vectors is a vector! u x v is perpendicular to u and v
 12.4 Cross Product Geometric description of the cross product of the vectors u and v The cross product of two vectors is a vector! u x v is perpendicular to u and v The length of u x v is uv u v sin The
12.4 Cross Product Geometric description of the cross product of the vectors u and v The cross product of two vectors is a vector! u x v is perpendicular to u and v The length of u x v is uv u v sin The
CATIA: Navigating the CATIA V5 environment. D. CHABLAT / S. CARO Damien.Chablat@irccyn.ec-nantes.fr
 CATIA: Navigating the CATIA V5 environment D. CHABLAT / S. CARO Damien.Chablat@irccyn.ec-nantes.fr Standard Screen Layout 5 4 6 7 1 2 3 8 9 10 11 12 13 14 15 D. Chablat / S. Caro -- Institut de Recherche
CATIA: Navigating the CATIA V5 environment D. CHABLAT / S. CARO Damien.Chablat@irccyn.ec-nantes.fr Standard Screen Layout 5 4 6 7 1 2 3 8 9 10 11 12 13 14 15 D. Chablat / S. Caro -- Institut de Recherche
Vector Math Computer Graphics Scott D. Anderson
 Vector Math Computer Graphics Scott D. Anderson 1 Dot Product The notation v w means the dot product or scalar product or inner product of two vectors, v and w. In abstract mathematics, we can talk about
Vector Math Computer Graphics Scott D. Anderson 1 Dot Product The notation v w means the dot product or scalar product or inner product of two vectors, v and w. In abstract mathematics, we can talk about
Chapter 17. Orthogonal Matrices and Symmetries of Space
 Chapter 17. Orthogonal Matrices and Symmetries of Space Take a random matrix, say 1 3 A = 4 5 6, 7 8 9 and compare the lengths of e 1 and Ae 1. The vector e 1 has length 1, while Ae 1 = (1, 4, 7) has length
Chapter 17. Orthogonal Matrices and Symmetries of Space Take a random matrix, say 1 3 A = 4 5 6, 7 8 9 and compare the lengths of e 1 and Ae 1. The vector e 1 has length 1, while Ae 1 = (1, 4, 7) has length
(a) We have x = 3 + 2t, y = 2 t, z = 6 so solving for t we get the symmetric equations. x 3 2. = 2 y, z = 6. t 2 2t + 1 = 0,
 Name: Solutions to Practice Final. Consider the line r(t) = 3 + t, t, 6. (a) Find symmetric equations for this line. (b) Find the point where the first line r(t) intersects the surface z = x + y. (a) We
Name: Solutions to Practice Final. Consider the line r(t) = 3 + t, t, 6. (a) Find symmetric equations for this line. (b) Find the point where the first line r(t) intersects the surface z = x + y. (a) We
B4 Computational Geometry
 3CG 2006 / B4 Computational Geometry David Murray david.murray@eng.o.ac.uk www.robots.o.ac.uk/ dwm/courses/3cg Michaelmas 2006 3CG 2006 2 / Overview Computational geometry is concerned with the derivation
3CG 2006 / B4 Computational Geometry David Murray david.murray@eng.o.ac.uk www.robots.o.ac.uk/ dwm/courses/3cg Michaelmas 2006 3CG 2006 2 / Overview Computational geometry is concerned with the derivation
How To Draw A Billiards Ball In Gta 3D With Texture Mapping (Gta 3) On A Computer Or 2D Or Gta 2D (Gt) On Your Computer Or Computer Or Your Computer (Or Your Computer)
 Pool Billiard An OpenGL-based billiard simulation Stefan HUBER Kamran SAFDAR Andreas SCHRÖCKER Fachbereich Computerwissenschaften Universität Salzburg June 10, 2009 S. Huber, K. Safdar, A. Schröcker: Pool
Pool Billiard An OpenGL-based billiard simulation Stefan HUBER Kamran SAFDAR Andreas SCHRÖCKER Fachbereich Computerwissenschaften Universität Salzburg June 10, 2009 S. Huber, K. Safdar, A. Schröcker: Pool
Solving Geometric Problems with the Rotating Calipers *
 Solving Geometric Problems with the Rotating Calipers * Godfried Toussaint School of Computer Science McGill University Montreal, Quebec, Canada ABSTRACT Shamos [1] recently showed that the diameter of
Solving Geometric Problems with the Rotating Calipers * Godfried Toussaint School of Computer Science McGill University Montreal, Quebec, Canada ABSTRACT Shamos [1] recently showed that the diameter of
Parametric Equations and the Parabola (Extension 1)
 Parametric Equations and the Parabola (Extension 1) Parametric Equations Parametric equations are a set of equations in terms of a parameter that represent a relation. Each value of the parameter, when
Parametric Equations and the Parabola (Extension 1) Parametric Equations Parametric equations are a set of equations in terms of a parameter that represent a relation. Each value of the parameter, when
Dev eloping a General Postprocessor for Multi-Axis CNC Milling Centers
 57 Dev eloping a General Postprocessor for Multi-Axis CNC Milling Centers Mihir Adivarekar 1 and Frank Liou 1 1 Missouri University of Science and Technology, liou@mst.edu ABSTRACT Most of the current
57 Dev eloping a General Postprocessor for Multi-Axis CNC Milling Centers Mihir Adivarekar 1 and Frank Liou 1 1 Missouri University of Science and Technology, liou@mst.edu ABSTRACT Most of the current
Recall the basic property of the transpose (for any A): v A t Aw = v w, v, w R n.
 ORTHOGONAL MATRICES Informally, an orthogonal n n matrix is the n-dimensional analogue of the rotation matrices R θ in R 2. When does a linear transformation of R 3 (or R n ) deserve to be called a rotation?
ORTHOGONAL MATRICES Informally, an orthogonal n n matrix is the n-dimensional analogue of the rotation matrices R θ in R 2. When does a linear transformation of R 3 (or R n ) deserve to be called a rotation?
1.(6pts) Find symmetric equations of the line L passing through the point (2, 5, 1) and perpendicular to the plane x + 3y z = 9.
 .(6pts Find symmetric equations of the line L passing through the point (, 5, and perpendicular to the plane x + 3y z = 9. (a x = y + 5 3 = z (b x (c (x = ( 5(y 3 = z + (d x (e (x + 3(y 3 (z = 9 = y 3
.(6pts Find symmetric equations of the line L passing through the point (, 5, and perpendicular to the plane x + 3y z = 9. (a x = y + 5 3 = z (b x (c (x = ( 5(y 3 = z + (d x (e (x + 3(y 3 (z = 9 = y 3
Basic controls of Rhinoceros 3D software
 lecture 2 Basic controls of Rhinoceros 3D software After the start Rhinoceros 3D software shows basic working area compound by four viewports (show model in other positions), popup menu over, palette menu
lecture 2 Basic controls of Rhinoceros 3D software After the start Rhinoceros 3D software shows basic working area compound by four viewports (show model in other positions), popup menu over, palette menu
Statistical Graphics and Visualization
 Statistical Graphics and Visualization Edward J. Wegman Daniel B. Carr Center for Computational Statistics George Mason University (c) 1992, 2001 Edward J. Wegman and Daniel B. Carr. All rights reserved.
Statistical Graphics and Visualization Edward J. Wegman Daniel B. Carr Center for Computational Statistics George Mason University (c) 1992, 2001 Edward J. Wegman and Daniel B. Carr. All rights reserved.
Section 13.5 Equations of Lines and Planes
 Section 13.5 Equations of Lines and Planes Generalizing Linear Equations One of the main aspects of single variable calculus was approximating graphs of functions by lines - specifically, tangent lines.
Section 13.5 Equations of Lines and Planes Generalizing Linear Equations One of the main aspects of single variable calculus was approximating graphs of functions by lines - specifically, tangent lines.
discuss how to describe points, lines and planes in 3 space.
 Chapter 2 3 Space: lines and planes In this chapter we discuss how to describe points, lines and planes in 3 space. introduce the language of vectors. discuss various matters concerning the relative position
Chapter 2 3 Space: lines and planes In this chapter we discuss how to describe points, lines and planes in 3 space. introduce the language of vectors. discuss various matters concerning the relative position
The Geometry of the Dot and Cross Products
 Journal of Online Mathematics and Its Applications Volume 6. June 2006. Article ID 1156 The Geometry of the Dot and Cross Products Tevian Dray Corinne A. Manogue 1 Introduction Most students first learn
Journal of Online Mathematics and Its Applications Volume 6. June 2006. Article ID 1156 The Geometry of the Dot and Cross Products Tevian Dray Corinne A. Manogue 1 Introduction Most students first learn
Angles that are between parallel lines, but on opposite sides of a transversal.
 GLOSSARY Appendix A Appendix A: Glossary Acute Angle An angle that measures less than 90. Acute Triangle Alternate Angles A triangle that has three acute angles. Angles that are between parallel lines,
GLOSSARY Appendix A Appendix A: Glossary Acute Angle An angle that measures less than 90. Acute Triangle Alternate Angles A triangle that has three acute angles. Angles that are between parallel lines,
Computer Graphics Labs
 Computer Graphics Labs Abel J. P. Gomes LAB. 2 Department of Computer Science and Engineering University of Beira Interior Portugal 2011 Copyright 2009-2011 All rights reserved. LAB. 2 1. Learning goals
Computer Graphics Labs Abel J. P. Gomes LAB. 2 Department of Computer Science and Engineering University of Beira Interior Portugal 2011 Copyright 2009-2011 All rights reserved. LAB. 2 1. Learning goals
Triangle Scan Conversion using 2D Homogeneous Coordinates
 Triangle Scan Conversion using 2D Homogeneous Coordinates Marc Olano 1 Trey Greer 2 University of North Carolina Hewlett-Packard ABSTRACT We present a new triangle scan conversion algorithm that works
Triangle Scan Conversion using 2D Homogeneous Coordinates Marc Olano 1 Trey Greer 2 University of North Carolina Hewlett-Packard ABSTRACT We present a new triangle scan conversion algorithm that works
The Geometry of the Dot and Cross Products
 The Geometry of the Dot and Cross Products Tevian Dray Department of Mathematics Oregon State University Corvallis, OR 97331 tevian@math.oregonstate.edu Corinne A. Manogue Department of Physics Oregon
The Geometry of the Dot and Cross Products Tevian Dray Department of Mathematics Oregon State University Corvallis, OR 97331 tevian@math.oregonstate.edu Corinne A. Manogue Department of Physics Oregon
MATH2210 Notebook 1 Fall Semester 2016/2017. 1 MATH2210 Notebook 1 3. 1.1 Solving Systems of Linear Equations... 3
 MATH0 Notebook Fall Semester 06/07 prepared by Professor Jenny Baglivo c Copyright 009 07 by Jenny A. Baglivo. All Rights Reserved. Contents MATH0 Notebook 3. Solving Systems of Linear Equations........................
MATH0 Notebook Fall Semester 06/07 prepared by Professor Jenny Baglivo c Copyright 009 07 by Jenny A. Baglivo. All Rights Reserved. Contents MATH0 Notebook 3. Solving Systems of Linear Equations........................
Chapter 6. Orthogonality
 6.3 Orthogonal Matrices 1 Chapter 6. Orthogonality 6.3 Orthogonal Matrices Definition 6.4. An n n matrix A is orthogonal if A T A = I. Note. We will see that the columns of an orthogonal matrix must be
6.3 Orthogonal Matrices 1 Chapter 6. Orthogonality 6.3 Orthogonal Matrices Definition 6.4. An n n matrix A is orthogonal if A T A = I. Note. We will see that the columns of an orthogonal matrix must be
Grassmann Algebra in Game Development. Eric Lengyel, PhD Terathon Software
 Grassmann Algebra in Game Development Eric Lengyel, PhD Terathon Software Math used in 3D programming Dot / cross products, scalar triple product Planes as 4D vectors Homogeneous coordinates Plücker coordinates
Grassmann Algebra in Game Development Eric Lengyel, PhD Terathon Software Math used in 3D programming Dot / cross products, scalar triple product Planes as 4D vectors Homogeneous coordinates Plücker coordinates
3. INNER PRODUCT SPACES
 . INNER PRODUCT SPACES.. Definition So far we have studied abstract vector spaces. These are a generalisation of the geometric spaces R and R. But these have more structure than just that of a vector space.
. INNER PRODUCT SPACES.. Definition So far we have studied abstract vector spaces. These are a generalisation of the geometric spaces R and R. But these have more structure than just that of a vector space.
Open Channel Flow Measurement Weirs and Flumes
 Open Channel Flow Measurement Weirs and Flumes by Harlan H. Bengtson, PhD, P.E. 1. Introduction Your Course Title Here Measuring the flow rate of water in an open channel typically involves some type of
Open Channel Flow Measurement Weirs and Flumes by Harlan H. Bengtson, PhD, P.E. 1. Introduction Your Course Title Here Measuring the flow rate of water in an open channel typically involves some type of
Intersection of a Line and a Convex. Hull of Points Cloud
 Applied Mathematical Sciences, Vol. 7, 213, no. 13, 5139-5149 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/1.12988/ams.213.37372 Intersection of a Line and a Convex Hull of Points Cloud R. P. Koptelov
Applied Mathematical Sciences, Vol. 7, 213, no. 13, 5139-5149 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/1.12988/ams.213.37372 Intersection of a Line and a Convex Hull of Points Cloud R. P. Koptelov
Pro/ENGINEER Wildfire 4.0 Basic Design
 Introduction Datum features are non-solid features used during the construction of other features. The most common datum features include planes, axes, coordinate systems, and curves. Datum features do
Introduction Datum features are non-solid features used during the construction of other features. The most common datum features include planes, axes, coordinate systems, and curves. Datum features do
3D Drawing. Single Point Perspective with Diminishing Spaces
 3D Drawing Single Point Perspective with Diminishing Spaces The following document helps describe the basic process for generating a 3D representation of a simple 2D plan. For this exercise we will be
3D Drawing Single Point Perspective with Diminishing Spaces The following document helps describe the basic process for generating a 3D representation of a simple 2D plan. For this exercise we will be
Problem set on Cross Product
 1 Calculate the vector product of a and b given that a= 2i + j + k and b = i j k (Ans 3 j - 3 k ) 2 Calculate the vector product of i - j and i + j (Ans ) 3 Find the unit vectors that are perpendicular
1 Calculate the vector product of a and b given that a= 2i + j + k and b = i j k (Ans 3 j - 3 k ) 2 Calculate the vector product of i - j and i + j (Ans ) 3 Find the unit vectors that are perpendicular
AutoCAD 2009. New Icon Quick Reference
 AutoCAD 2009 New Quick Reference Contents Chapter 1 New Quick Reference..................... 1 Toolbars................................... 1 3D Navigation Toolbar........................ 1 CAD Standards
AutoCAD 2009 New Quick Reference Contents Chapter 1 New Quick Reference..................... 1 Toolbars................................... 1 3D Navigation Toolbar........................ 1 CAD Standards
Common Core Unit Summary Grades 6 to 8
 Common Core Unit Summary Grades 6 to 8 Grade 8: Unit 1: Congruence and Similarity- 8G1-8G5 rotations reflections and translations,( RRT=congruence) understand congruence of 2 d figures after RRT Dilations
Common Core Unit Summary Grades 6 to 8 Grade 8: Unit 1: Congruence and Similarity- 8G1-8G5 rotations reflections and translations,( RRT=congruence) understand congruence of 2 d figures after RRT Dilations
Estimated Pre Calculus Pacing Timeline
 Estimated Pre Calculus Pacing Timeline 2010-2011 School Year The timeframes listed on this calendar are estimates based on a fifty-minute class period. You may need to adjust some of them from time to
Estimated Pre Calculus Pacing Timeline 2010-2011 School Year The timeframes listed on this calendar are estimates based on a fifty-minute class period. You may need to adjust some of them from time to
