6.5 Factoring Special Forms
|
|
|
- Russell King
- 10 years ago
- Views:
Transcription
1 440 CHAPTER 6. FACTORING 6.5 Factoring Special Forms In this section we revisit two special product forms that we learned in Chapter 5, the first of which was squaring a binomial. Squaring a binomial. Here are two earlier rules for squaring a binomial. 1. (a+b) 2 = a 2 +2ab+b 2 2. (a b) 2 = a 2 2ab+b 2 Perfect Square Trinomials To square a binomial such as (a+b) 2, proceed as follows: 1. Square the first term: a 2 2. Multiply the first and second term, then double: 2ab 3. Square the last term: b 2 EXAMPLE 1. Expand: (2x+3y) 2 Expand: (5a+2b) 2 Solution: Using the pattern (a+b) 2 = a 2 +2ab+b 2, we can expand (2x+3y) 2 as follows: (2x+3y) 2 = (2x) 2 +2(2x)(3y)+(3y) 2 = 4x 2 +6xy +9y 2 Answer: 25a 2 +20ab+4b 2 Note how we square the first and second terms, then produce the middle term of our answer by multiplying the first and second terms and doubling. EXAMPLE 2. Expand: (3u 2 5v 2 ) 2 Expand: (2s 3 7t) 2 Solution: Usingthepattern(a b) 2 = a 2 2ab+b 2, wecanexpand(3u 2 5v 2 ) 2 as follows: (3u 2 5v 2 ) 2 = (3u 2 ) 2 2(3u 2 )(5v 2 )+(5v 2 ) 2 = 9u 4 30u 2 v 2 +25v 4
2 Answer: 4s 6 28s 3 t+49t FACTORING SPECIAL FORMS 441 Note that the sign of the middle term is negative this time. The first and last terms are still positive because we are squaring. Once you ve squared a few binomials, it s time to do all of the work in your head. (i) Square the first term; (ii) multiply the first and second term and double the result; and (iii) square the second term. EXAMPLE 3. Expand each of the following: Expand: (5x 4 3) 2 a) (2y 3) 2 b) (4a 3b) 2 c) (x 3 +5) 2 Solution: Using the pattern (a ± b) 2 = a 2 ± 2ab + b 2, we expand each binomially mentally, writing down the answer without any intermediate steps. a) (2y 3) 2 = 4y 2 12y+9 b) (4a 3b) 2 = 16a 2 24ab+9b 2 c) (x 3 +5) 2 = x 6 +10x Answer: 25x 8 30x 4 +9 Now, because factoring is unmultiplying, it should be a simple matter to reverse the process of Example 3. EXAMPLE 4. Factor each of the following trinomials: Factor: 25x 8 30x 4 +9 a) 4y 2 12y+9 b) 16a 2 24ab+9b 2 c) x 6 +10x Solution: Because of the work already done in Example 3, it is a simple task to factor each of these trinomials. a) 4y 2 12y+9 = (2y 3) 2 b) 16a 2 24ab+9b 2 = (4a 3b) 2 c) x 6 +10x = (x 3 +5) 2 Answer: (5x 4 3) 2
3 442 CHAPTER 6. FACTORING Eachofthe trinomials in Example 4is an exampleofaperfect square trinomial. Perfect square trinomial. If a trinomial a 2 + 2ab + b 2 is the square of a binomial, as in (a+b) 2, then the trinomial is called a perfect square trinomial. So, how does one recognize a perfect square trinomial? If the first and last terms of a trinomial are perfect squares, then you should suspect that you may be dealing with a perfect square trinomial. However, you also have to have the correct middle term in order to have a perfect square trinomial. Factor: 16x 2 +72x+81 List of Squares n n EXAMPLE 5. Factor each of the following trinomials: a) 9x 2 42x+49 b) 49a 2 +70ab+25b 2 c) 4x 2 37x+9 Solution: Note that the first and last terms of each trinomial are perfect squares. a) In the trinomial 9x 2 42x+49, note that (3x) 2 = 9x 2 and 7 2 = 49. Hence, the first and last terms are perfect squares. Taking the square roots, we suspect that 9x 2 42x+49 factors as follows: 9x 2 42x+49? = (3x 7) 2 However, we must check to see if the middle term is correct. Multiply 3x and 7, then double: 2(3x)(7) = 42x. Thus, the middle term is correct and therefore 9x 2 42x+49 = (3x 7) 2. b) Inthetrinomial49a 2 +70ab+25b 2, notethat(7a) 2 = 49a 2 and(5b) 2 = 25b 2. Hence, the first and last terms are perfect squares. Taking the square roots, we suspect that 49a 2 +70ab+25b 2 factors as follows: 49a 2 +70ab+25b 2? = (7a+5b) 2 However, we must check to see if the middle term is correct. Multiply 7a and 5b, then double: 2(7a)(5b) = 70ab. Thus, the middle term is correct and therefore 49a 2 +70ab+25b 2 = (7a+5b) 2. c) In the trinomial 4x 2 37x+9, note that (2x) 2 = 4x 2 and (3) 2 = 9. Hence, the first and last terms are perfect squares. Taking the square roots, we suspect that 4x 2 37x+9 factors as follows: 4x 2 37x+9? = (2x 3) 2
4 6.5. FACTORING SPECIAL FORMS 443 However, we must check to see if the middle term is correct. Multiply 2x and 3, then double: 2(2x)(3) = 12x. However, this is not the middle term of 4x 2 37x+9, so this factorization is incorrect! We must find another way to factor this trinomial. Comparing 4x 2 37x+9 with ax 2 +bx+c, we need a pair of integers whose product is ac = 36 and whose sum is b = 37. The integer pair 1 and 36 comes to mind. Replace the middle term as a sum of like terms using this ordered pair. 4x 2 37x+9 = 4x 2 x 36x+9 37x = x 36x. = x(4x 1) 9(4x 1) Factor by grouping. = (x 9)(4x 1) Factor out 4x 1. This example clearly demonstrates how important it is to check the middle term. Answer: (4x+9) 2 Remember the first rule of factoring! The first rule of factoring. The first step to perform in any factoring problem is factor out the GCF. EXAMPLE 6. Factor each of the following trinomials: Factor: 4x 3 24x 2 36x a) 2x 3 y +12x 2 y 2 +18xy 3 b) 4x 5 +32x 4 64x 3 Solution: Remember, first factor out the GCF. a) In the trinomial 2x 3 y + 12x 2 y xy 3, we note that the GCF of 2x 3 y, 12x 2 y 2, and 18xy 3 is 2xy. We first factor out 2xy. 2x 3 y +12x 2 y 2 +18xy 3 = 2xy(x 2 +6xy +9y 2 ) We now note that the first and last terms of the resulting trinomial factor are perfect squares, so we take their square roots and factors as follows. = 2xy(x+3y) 2 Of course, the last factorization is correct only if the middle term is correct. Because 2(x)(3y) = 6xy matches the middle term of x 2 +6xy+9y 2, we do have a perfect square trinomial and our result is correct.
5 444 CHAPTER 6. FACTORING b) In the trinomial 4x 5 +32x 4 64x 3, we note that the GCF of 4x 5, 32x 4, and 64x 3 is 4x 3. We first factor out 4x 3. 4x 5 +32x 4 64x 3 = 4x 3 ( x 2 +8x 16) However, the first and third terms of x 2 +8x 16 are negative, and thus are not perfect squares. Let s begin again, this time factoring out 4x 3. 4x 5 +32x 4 64x 3 = 4x 3 (x 2 8x+16) This time the first and third terms of x 2 8x+16 are perfect squares. We take their square roots and write: = 4x 3 (x 4) 2 Again, this last factorization is correct only if the middle term is correct. Because 2(x)(4) = 8x, we do have a perfect square trinomial and our result is correct. Answer: 4x(x+3) 2 The Difference of Squares The second special product form we learned in Chapter 5 was the difference of squares. The difference of squares. Here is the difference of squares rule. (a+b)(a b) = a 2 b 2 If you are multiplying two binomials which have the exact same terms in the First positions and the exact same terms in the Last positions, but one set is separated by a plus sign while the other set is separated by a minus sign, then multiply as follows: 1. Square the first term: a 2 2. Square the second term: b 2 3. Place a minus sign between the two squares.
6 6.5. FACTORING SPECIAL FORMS 445 EXAMPLE 7. Expand each of the following: a) (3x+5)(3x 5) b) (a 3 2b 3 )(a 3 +2b 3 ) Solution: We apply the difference of squares pattern to expand each of the given problems. Expand: (4x 3y)(4x+3y) a) In (3x + 5)(3x 5), we have the exact same terms in the First and Last positions, with the first set separated by a plus sign and the second set separated by a minus sign. a) Square the first term: (3x) 2 = 9x 2 b) Square the second term: 5 2 = 25 c) Place a minus sign between the two squares. Hence: (3x+5)(3x 5) = 9x 2 25 b) In (a 3 2b 3 )(a 3 +2b 3 ), we have the exact same terms in the First and Last positions, withthefirstsetseparatedbyaminussignandthesecond set separated by a plus sign. a) Square the first term: (a 3 ) 2 = a 6 b) Square the second term: (2b 3 ) 2 = 4b 6 c) Place a minus sign between the two squares. Hence: (a 3 2b 3 )(a 3 +2b 3 ) = a 6 4b 6 Answer: 16x 2 9y 2 Because factoring is unmultiplying, is should be a simple matter to reverse the process of Example 7. EXAMPLE 8. Factor each of the following: a) 9x 2 25 b) a 6 4b 6 Solution: Because of the work already done in Example 7, it is a simple matter to factor (or unmultiply ) each of these problems. Factor: 81x 2 49 a) 9x 2 25 = (3x+5)(3x 5) b) a 6 4b 6 = (a 3 2b 3 )(a 3 +2b 3 )
7 446 CHAPTER 6. FACTORING Answer: (9x+7)(9x 7) In each case, note how we took the square roots of each term, then separated one set with a plus sign and the other with a minus sign. Because of the commutative property of multiplication, it does not matter which one you make plus and which one you make minus. Always remember the first rule of factoring. The first rule of factoring. The first step to perform in any factoring problem is factor out the GCF. Factor: 4x 4 16x 2 EXAMPLE 9. Factor: x 3 9x Solution: In x 3 9x, the GCF of x 3 and 9x is x. Factor out x. Answer: 4x 2 (x+2)(x 2) x 3 9x = x(x 2 9) Note that x 2 9 is now the difference of two perfect squares. Take the square roots of x 2 and 9, which are x and 3, then separate one set with a plus sign and the other set with a minus sign. = x(x+3)(x 3) Factoring Completely Sometimes after one pass at factoring, factors remain that can be factored further. You must continue to factor in this case. Factor: x 4 81 EXAMPLE 10. Factor: x 4 16 Solution: In x 4 16, we have the difference of two squares: (x 2 ) 2 = x 4 and 4 2 = 16. First, we take the square roots, then separate one set with a plus sign and the other set with a minus sign. x 4 16 = (x 2 +4)(x 2 4)
8 6.5. FACTORING SPECIAL FORMS 447 Notethatx 2 +4isthesum oftwosquaresanddoesnotfactorfurther. However, x 2 4 is the difference of two squares. Take the square roots, x and 2, then separate one set with a plus sign and the other set with a minus sign. Done. We cannot factor further. = (x 2 +4)(x+2)(x 2) Answer: (x 2 +9)(x+3)(x 3) Nonlinear Equations Revisited Remember, if an equation is nonlinear, the first step is to make one side equal to zero by moving all terms to one side of the equation. Once you ve completed this important first step, factor and apply the zero product property to find the solutions. EXAMPLE 11. Solve for x: 25x 2 = 169 Solve for x: 16x 2 = 121 Solution: Make one side equal to zero, factor, then apply the zero product property. 25x 2 = x = 0 Original equation. Subtract 169 from both sides. Note that we have two perfect squares separated by a minus sign. This is the difference of squares pattern. Take the square roots, making one term plus and one term minus. (5x+13)(5x 13) = 0 Use difference of squares to factor. Use the zero product property to complete the solution, setting each factor equal to zero and solving the resulting equations. 5x+13 = 0 or 5x 13 = 0 x = 13 5 x = 13 5 Hence, the solutionsof 25x 2 = 169arex = 13/5and x = 13/5. We encourage readers to check each of these solutions. Answer: 11/4, 11/4
9 448 CHAPTER 6. FACTORING Solve for x: 25x 2 = 80x 64 One can also argue that the only number whose square is zero is the number zero. Hence, one can go directly from to (7x 9) 2 = 0 7x 9 = 0. Hence, the only solution of 49x = 126x is x = 9/7. EXAMPLE 12. Solve for x: 49x = 126x Solution: Make one side equal to zero, factor, then apply the zero product property. 49x = 126x 49x 2 126x+81 = 0 Original equation. Subtract 126x from both sides. Note that the first and last terms of the trinomial are perfect squares. Hence, it make sense to try and factor as a perfect square trinomial, taking the square roots of the first and last terms. (7x 9) 2 = 0 Factor as a perfect square trinomial. Of course, be sure to check the middle term. Because 2(7x)(9) = 126x, the middle term is correct. Because (7x 9) 2 = (7x 9)(7x 9), we can use the zero product property to set each factor equal to zero and solve the resulting equations. 7x 9 = 0 or 7x 9 = 0 x = 9 7 x = 9 7 Answer: 8/5 Hence, the only solution of 49x = 126x is x = 9/7. We encourage readers to check this solution. Solve for x: 5x = x x EXAMPLE 13. Solve for x: 2x 3 +3x 2 = 50x+75 Solution: Make one side equal to zero, factor, then apply the zero product property. 2x 3 +3x 2 = 50x+75 Original equation. 2x 3 +3x 2 50x 75 = 0 Make one side zero. This is a four-term expression, so we try factoring by grouping. Factor x 2 out of the first two terms, and 25 out of the second two terms. x 2 (2x+3) 25(2x+3) = 0 Factor by grouping. (x 2 25)(2x+3) = 0 Factor out 2x+3.
10 6.5. FACTORING SPECIAL FORMS 449 Complete the factorization by using the difference of squares to factor x (x+5)(x 5)(2x+3) = 0 Use difference of squares to factor. Finally, use the zero product property. Set each factor equal to zero and solve for x. x+5 = 0 or x 5 = 0 or 2x+3 = 0 x = 5 x = 5 x = 3 2 Hence, the solutions of 2x 3 +3x 2 = 50x+75 are x = 5, x = 5, and x = 3/2. We encourage readers to check each of these solutions. Answer: 6, 6, 1/5 Let s solve another nonlinear equation, matching the algebraic and graphical solutions. EXAMPLE 14. Solve the equation x 3 = 4x, both algebraically and graphi- Solve the equation x 3 = 16x cally, then compare your answers. both algebraically and graphically, then compare Solution: Note that we have a power of x larger than one, so the equation your answers. x 3 = 4x is nonlinear. Make one side zero and factor. x 3 = 4x x 3 4x = 0 x(x 2 4) = 0 x(x+2)(x 2) = 0 Original equation. Nonlinear. Make one side zero. Factor out GCF. Apply difference of squares. Note that we now have a product of three factors that equals zero. The zero product property says that at least one of these factors must equal zero. x = 0 or x+2 = 0 or x 2 = 0 x = 2 x = 2 Hence, the solutions of x 3 = 4x are x = 0, x = 2, and x = 2. Graphical solution. Load y = x 3 and y = 4x into Y1 and Y2 in the Y= menu of your calculator. Select 6:ZStandard from the ZOOM menu to produce the graph in Figure Although the image in Figure 6.26 shows all three points of intersection, adjusting the WINDOW parameters as shown in Figure 6.27, then pressing the GRAPH button will produce a nicer view of the points of intersection, as shown in the figure on the right in Figures 6.27.
11 450 CHAPTER 6. FACTORING Figure 6.26: Sketching y = x 3 and y = 4x. Figure 6.27: Adjusting the viewing window. Use the 5:intersect tool from the CALC menu to find the three points of intersection. Press the ENTER key in response to First curve, then press ENTER again in response to Second curve, then use the left-arrow key to move your cursor close to the leftmost point of intersection and press ENTER in response to Guess. The result is shown in the first image on the left in Figure Repeat the process to find the remaining points of intersection. The results are shown in the last two images in Figure Figure 6.28: Finding the points of intersection. Thus, the graphical solutions are x = 2, x = 0, and x = 2. Reporting the solution on your homework: Duplicate the image in your calculator s viewing window on your homework page. Use a ruler to draw all lines, but freehand any curves. Label the horizontal and vertical axes with x and y, respectively (see Figure 6.29). PlaceyourWINDOWparametersattheendofeachaxis(seeFigure 6.29). Label the graph with its equation (see Figure 6.29).
12 6.5. FACTORING SPECIAL FORMS 451 Drop dashed vertical lines through each x-intercept. Shade and label the x-values of the points where the dashed vertical line crosses the x-axis. These are the solutions of the equation x 3 = 4x (see Figure 6.29). y 15 y = x 3 y = 4x Answer: 4, 0, x 15 Figure 6.29: Reporting your graphical solution on your homework. Finally, note that the graphical solutions x = 2, x = 0, and x = 2 match our algebraic solutions exactly.
13 452 CHAPTER 6. FACTORING Exercises In Exercises 1-8, expand each of the given expressions. 1. (8r 3t) 2 2. (6a+c) 2 3. (4a+7b) 2 4. (4s+t) 2 5. (s 3 9) 2 6. (w 3 +7) 2 7. (s 2 +6t 2 ) 2 8. (7u 2 2w 2 ) 2 In Exercises 9-28, factor each of the given expressions s 2 +60st+36t u 2 +24uv+16v v 2 60vw+25w b 2 42bc+9c a 4 +18a 2 b 2 +81b u 4 144u 2 w 2 +81w s 4 28s 2 t 2 +4t a 4 12a 2 c 2 +9c b 6 112b x 6 10x r r a 6 16a s 3 t 20s 2 t 2 +20st r 3 t 12r 2 t 2 +3rt a 3 c+8a 2 c 2 +2ac x 3 z 60x 2 z 2 +50xz b b 2 75b c c 2 80c 27. 5u 5 30u 4 45u z 5 36z 4 27z 3 In Exercises 29-36, expand each of the given expressions. 29. (21c+16)(21c 16) 30. (19t+7)(19t 7) 31. (5x+19z)(5x 19z) 32. (11u+5w)(11u 5w) 33. (3y 4 +23z 4 )(3y 4 23z 4 ) 34. (5x 3 +z 3 )(5x 3 z 3 ) 35. (8r 5 +19s 5 )(8r 5 19s 5 ) 36. (3u 3 +16v 3 )(3u 3 16v 3 )
14 6.5. FACTORING SPECIAL FORMS 453 In Exercises 37-60, factor each of the given expressions x b v r x 2 576y y 2 81z r 2 289s a 2 144b r 6 256t x z u 10 25w a 6 81c y 5 242y y 5 147y a 3 b 324ab b 3 c 1875bc x 3 z 1156xz u 3 v 507uv t 4 4t z 5 256z x x x x 4 1 In Exercises 61-68, factor each of the given expressions completely. 61. z 3 +z 2 9z u 3 +u 2 48u x 3 2x 2 y xy 2 +2y x 3 +2x 2 z 4xz 2 8z r 3 3r 2 t 25rt 2 +75t b 3 3b 2 c 50bc 2 +75c x 3 +x 2 32x r 3 2r 2 r+2 In Exercises 69-80, solve each of the given equations for x x 3 +7x 2 = 72x x 3 +7x 2 = 32x x 3 +5x 2 = 64x x 3 +4x 2 = 49x x = 264x x = 874x x 2 = x 2 = x 2 = x 2 = x = 608x x = 136x
15 454 CHAPTER 6. FACTORING In Exercises 81-84, perform each of the following tasks: i) Use a strictly algebraic technique to solve the given equation. ii) Use the 5:intersect utility on your graphing calculator to solve the given equation. Report the results found using graphing calculator as shown in Example x 3 = x 82. x 3 = 9x 83. 4x 3 = x 84. 9x 3 = x Answers 1. 64r 2 48rt+9t a 2 +56ab+49b 2 5. s 6 18s s 4 +12s 2 t 2 +36t 4 9. (5s+6t) (6v 5w) (a 2 +9b 2 ) (7s 2 2t 2 ) (7b 3 8) (7r 3 +8) st(s 2t) ac(2a+c) b(4b 5) u 3 (u+3) c x 2 361z y 8 529z r s (19x+23)(19x 23) 39. (4v +13)(4v 13) 41. (13x+24y)(13x 24y) 43. (23r+17s)(23r 17s) 45. (7r 3 +16t 3 )(7r 3 16t 3 ) 47. (6u 5 +5w 5 )(6u 5 5w 5 ) 49. 2y 3 (6y +11)(6y 11) 51. 4ab(19a+9b)(19a 9b) 53. 4xz(12x+17z)(12x 17z) 55. 4t 2 (12t+1)(12t 1) 57. (9x 2 +16)(3x+4)(3x 4) 59. (9x 2 +4)(3x+2)(3x 2) 61. (z +3)(z 3)(z +1) 63. (x+y)(x y)(x 2y) 65. (r+5t)(r 5t)(r 3t) 67. (x+4)(x 4)(2x+1)
16 6.5. FACTORING SPECIAL FORMS x = 6, 6, x = 8, 8, x = x = 13 4, x = 5 3, x = x = 0, 1,1 83. x = 0, 1/2,1/2
6.2 Solving Nonlinear Equations
 6.2. SOLVING NONLINEAR EQUATIONS 399 6.2 Solving Nonlinear Equations We begin by introducing a property that will be used extensively in this and future sections. The zero product property. If the product
6.2. SOLVING NONLINEAR EQUATIONS 399 6.2 Solving Nonlinear Equations We begin by introducing a property that will be used extensively in this and future sections. The zero product property. If the product
6.6 Factoring Strategy
 456 CHAPTER 6. FACTORING 6.6 Factoring Strategy When you are concentrating on factoring problems of a single type, after doing a few you tend to get into a rhythm, and the remainder of the exercises, because
456 CHAPTER 6. FACTORING 6.6 Factoring Strategy When you are concentrating on factoring problems of a single type, after doing a few you tend to get into a rhythm, and the remainder of the exercises, because
POLYNOMIALS and FACTORING
 POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
Chapter 5. Rational Expressions
 5.. Simplify Rational Expressions KYOTE Standards: CR ; CA 7 Chapter 5. Rational Expressions Definition. A rational expression is the quotient P Q of two polynomials P and Q in one or more variables, where
5.. Simplify Rational Expressions KYOTE Standards: CR ; CA 7 Chapter 5. Rational Expressions Definition. A rational expression is the quotient P Q of two polynomials P and Q in one or more variables, where
7.7 Solving Rational Equations
 Section 7.7 Solving Rational Equations 7 7.7 Solving Rational Equations When simplifying comple fractions in the previous section, we saw that multiplying both numerator and denominator by the appropriate
Section 7.7 Solving Rational Equations 7 7.7 Solving Rational Equations When simplifying comple fractions in the previous section, we saw that multiplying both numerator and denominator by the appropriate
1.3 Polynomials and Factoring
 1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
NSM100 Introduction to Algebra Chapter 5 Notes Factoring
 Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
FACTORING QUADRATICS 8.1.1 and 8.1.2
 FACTORING QUADRATICS 8.1.1 and 8.1.2 Chapter 8 introduces students to quadratic equations. These equations can be written in the form of y = ax 2 + bx + c and, when graphed, produce a curve called a parabola.
FACTORING QUADRATICS 8.1.1 and 8.1.2 Chapter 8 introduces students to quadratic equations. These equations can be written in the form of y = ax 2 + bx + c and, when graphed, produce a curve called a parabola.
6.1 Add & Subtract Polynomial Expression & Functions
 6.1 Add & Subtract Polynomial Expression & Functions Objectives 1. Know the meaning of the words term, monomial, binomial, trinomial, polynomial, degree, coefficient, like terms, polynomial funciton, quardrtic
6.1 Add & Subtract Polynomial Expression & Functions Objectives 1. Know the meaning of the words term, monomial, binomial, trinomial, polynomial, degree, coefficient, like terms, polynomial funciton, quardrtic
Factoring Quadratic Expressions
 Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
5 means to write it as a product something times something instead of a sum something plus something plus something.
 Intermediate algebra Class notes Factoring Introduction (section 6.1) Recall we factor 10 as 5. Factoring something means to think of it as a product! Factors versus terms: terms: things we are adding
Intermediate algebra Class notes Factoring Introduction (section 6.1) Recall we factor 10 as 5. Factoring something means to think of it as a product! Factors versus terms: terms: things we are adding
Tool 1. Greatest Common Factor (GCF)
 Chapter 4: Factoring Review Tool 1 Greatest Common Factor (GCF) This is a very important tool. You must try to factor out the GCF first in every problem. Some problems do not have a GCF but many do. When
Chapter 4: Factoring Review Tool 1 Greatest Common Factor (GCF) This is a very important tool. You must try to factor out the GCF first in every problem. Some problems do not have a GCF but many do. When
Chapter R.4 Factoring Polynomials
 Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c
 Tallahassee Community College 55 FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c This kind of trinomial differs from the previous kind we have factored because the coefficient of x is no longer "1".
Tallahassee Community College 55 FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c This kind of trinomial differs from the previous kind we have factored because the coefficient of x is no longer "1".
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0).
 This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
Name Intro to Algebra 2. Unit 1: Polynomials and Factoring
 Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
Factoring Polynomials
 UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
expression is written horizontally. The Last terms ((2)( 4)) because they are the last terms of the two polynomials. This is called the FOIL method.
 A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
( ) FACTORING. x In this polynomial the only variable in common to all is x.
 FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
Algebra I Vocabulary Cards
 Algebra I Vocabulary Cards Table of Contents Expressions and Operations Natural Numbers Whole Numbers Integers Rational Numbers Irrational Numbers Real Numbers Absolute Value Order of Operations Expression
Algebra I Vocabulary Cards Table of Contents Expressions and Operations Natural Numbers Whole Numbers Integers Rational Numbers Irrational Numbers Real Numbers Absolute Value Order of Operations Expression
Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder).
 Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Math 25 Activity 6: Factoring Advanced
 Instructor! Math 25 Activity 6: Factoring Advanced Last week we looked at greatest common factors and the basics of factoring out the GCF. In this second activity, we will discuss factoring more difficult
Instructor! Math 25 Activity 6: Factoring Advanced Last week we looked at greatest common factors and the basics of factoring out the GCF. In this second activity, we will discuss factoring more difficult
Factoring Polynomials
 Factoring Polynomials Factoring Factoring is the process of writing a polynomial as the product of two or more polynomials. The factors of 6x 2 x 2 are 2x + 1 and 3x 2. In this section, we will be factoring
Factoring Polynomials Factoring Factoring is the process of writing a polynomial as the product of two or more polynomials. The factors of 6x 2 x 2 are 2x + 1 and 3x 2. In this section, we will be factoring
Factoring and Applications
 Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
Factoring Flow Chart
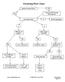 Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Unit 7 Quadratic Relations of the Form y = ax 2 + bx + c
 Unit 7 Quadratic Relations of the Form y = ax 2 + bx + c Lesson Outline BIG PICTURE Students will: manipulate algebraic expressions, as needed to understand quadratic relations; identify characteristics
Unit 7 Quadratic Relations of the Form y = ax 2 + bx + c Lesson Outline BIG PICTURE Students will: manipulate algebraic expressions, as needed to understand quadratic relations; identify characteristics
MATH 10034 Fundamental Mathematics IV
 MATH 0034 Fundamental Mathematics IV http://www.math.kent.edu/ebooks/0034/funmath4.pdf Department of Mathematical Sciences Kent State University January 2, 2009 ii Contents To the Instructor v Polynomials.
MATH 0034 Fundamental Mathematics IV http://www.math.kent.edu/ebooks/0034/funmath4.pdf Department of Mathematical Sciences Kent State University January 2, 2009 ii Contents To the Instructor v Polynomials.
A Systematic Approach to Factoring
 A Systematic Approach to Factoring Step 1 Count the number of terms. (Remember****Knowing the number of terms will allow you to eliminate unnecessary tools.) Step 2 Is there a greatest common factor? Tool
A Systematic Approach to Factoring Step 1 Count the number of terms. (Remember****Knowing the number of terms will allow you to eliminate unnecessary tools.) Step 2 Is there a greatest common factor? Tool
Operations with Algebraic Expressions: Multiplication of Polynomials
 Operations with Algebraic Expressions: Multiplication of Polynomials The product of a monomial x monomial To multiply a monomial times a monomial, multiply the coefficients and add the on powers with the
Operations with Algebraic Expressions: Multiplication of Polynomials The product of a monomial x monomial To multiply a monomial times a monomial, multiply the coefficients and add the on powers with the
Mathematics Placement
 Mathematics Placement The ACT COMPASS math test is a self-adaptive test, which potentially tests students within four different levels of math including pre-algebra, algebra, college algebra, and trigonometry.
Mathematics Placement The ACT COMPASS math test is a self-adaptive test, which potentially tests students within four different levels of math including pre-algebra, algebra, college algebra, and trigonometry.
Factoring Trinomials: The ac Method
 6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
6.3 FACTORING ax 2 bx c WITH a 1
 290 (6 14) Chapter 6 Factoring e) What is the approximate maximum revenue? f) Use the accompanying graph to estimate the price at which the revenue is zero. y Revenue (thousands of dollars) 300 200 100
290 (6 14) Chapter 6 Factoring e) What is the approximate maximum revenue? f) Use the accompanying graph to estimate the price at which the revenue is zero. y Revenue (thousands of dollars) 300 200 100
In algebra, factor by rewriting a polynomial as a product of lower-degree polynomials
 Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
Section 1. Finding Common Terms
 Worksheet 2.1 Factors of Algebraic Expressions Section 1 Finding Common Terms In worksheet 1.2 we talked about factors of whole numbers. Remember, if a b = ab then a is a factor of ab and b is a factor
Worksheet 2.1 Factors of Algebraic Expressions Section 1 Finding Common Terms In worksheet 1.2 we talked about factors of whole numbers. Remember, if a b = ab then a is a factor of ab and b is a factor
Factoring - Factoring Special Products
 6.5 Factoring - Factoring Special Products Objective: Identify and factor special products including a difference of squares, perfect squares, and sum and difference of cubes. When factoring there are
6.5 Factoring - Factoring Special Products Objective: Identify and factor special products including a difference of squares, perfect squares, and sum and difference of cubes. When factoring there are
Algebra 2 PreAP. Name Period
 Algebra 2 PreAP Name Period IMPORTANT INSTRUCTIONS FOR STUDENTS!!! We understand that students come to Algebra II with different strengths and needs. For this reason, students have options for completing
Algebra 2 PreAP Name Period IMPORTANT INSTRUCTIONS FOR STUDENTS!!! We understand that students come to Algebra II with different strengths and needs. For this reason, students have options for completing
Sect 6.1 - Greatest Common Factor and Factoring by Grouping
 Sect 6.1 - Greatest Common Factor and Factoring by Grouping Our goal in this chapter is to solve non-linear equations by breaking them down into a series of linear equations that we can solve. To do this,
Sect 6.1 - Greatest Common Factor and Factoring by Grouping Our goal in this chapter is to solve non-linear equations by breaking them down into a series of linear equations that we can solve. To do this,
FACTORING POLYNOMIALS
 296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
Factoring a Difference of Two Squares. Factoring a Difference of Two Squares
 284 (6 8) Chapter 6 Factoring 87. Tomato soup. The amount of metal S (in square inches) that it takes to make a can for tomato soup is a function of the radius r and height h: S 2 r 2 2 rh a) Rewrite this
284 (6 8) Chapter 6 Factoring 87. Tomato soup. The amount of metal S (in square inches) that it takes to make a can for tomato soup is a function of the radius r and height h: S 2 r 2 2 rh a) Rewrite this
Factoring Algebra- Chapter 8B Assignment Sheet
 Name: Factoring Algebra- Chapter 8B Assignment Sheet Date Section Learning Targets Assignment Tues 2/17 Find the prime factorization of an integer Find the greatest common factor (GCF) for a set of monomials.
Name: Factoring Algebra- Chapter 8B Assignment Sheet Date Section Learning Targets Assignment Tues 2/17 Find the prime factorization of an integer Find the greatest common factor (GCF) for a set of monomials.
Greatest Common Factor (GCF) Factoring
 Section 4 4: Greatest Common Factor (GCF) Factoring The last chapter introduced the distributive process. The distributive process takes a product of a monomial and a polynomial and changes the multiplication
Section 4 4: Greatest Common Factor (GCF) Factoring The last chapter introduced the distributive process. The distributive process takes a product of a monomial and a polynomial and changes the multiplication
Unit 7: Radical Functions & Rational Exponents
 Date Period Unit 7: Radical Functions & Rational Exponents DAY 0 TOPIC Roots and Radical Expressions Multiplying and Dividing Radical Expressions Binomial Radical Expressions Rational Exponents 4 Solving
Date Period Unit 7: Radical Functions & Rational Exponents DAY 0 TOPIC Roots and Radical Expressions Multiplying and Dividing Radical Expressions Binomial Radical Expressions Rational Exponents 4 Solving
What are the place values to the left of the decimal point and their associated powers of ten?
 The verbal answers to all of the following questions should be memorized before completion of algebra. Answers that are not memorized will hinder your ability to succeed in geometry and algebra. (Everything
The verbal answers to all of the following questions should be memorized before completion of algebra. Answers that are not memorized will hinder your ability to succeed in geometry and algebra. (Everything
5.1 FACTORING OUT COMMON FACTORS
 C H A P T E R 5 Factoring he sport of skydiving was born in the 1930s soon after the military began using parachutes as a means of deploying troops. T Today, skydiving is a popular sport around the world.
C H A P T E R 5 Factoring he sport of skydiving was born in the 1930s soon after the military began using parachutes as a means of deploying troops. T Today, skydiving is a popular sport around the world.
By reversing the rules for multiplication of binomials from Section 4.6, we get rules for factoring polynomials in certain forms.
 SECTION 5.4 Special Factoring Techniques 317 5.4 Special Factoring Techniques OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor
SECTION 5.4 Special Factoring Techniques 317 5.4 Special Factoring Techniques OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor
Unit 3: Day 2: Factoring Polynomial Expressions
 Unit 3: Day : Factoring Polynomial Expressions Minds On: 0 Action: 45 Consolidate:10 Total =75 min Learning Goals: Extend knowledge of factoring to factor cubic and quartic expressions that can be factored
Unit 3: Day : Factoring Polynomial Expressions Minds On: 0 Action: 45 Consolidate:10 Total =75 min Learning Goals: Extend knowledge of factoring to factor cubic and quartic expressions that can be factored
Factoring Polynomials
 Factoring Polynomials 4-1-2014 The opposite of multiplying polynomials is factoring. Why would you want to factor a polynomial? Let p(x) be a polynomial. p(c) = 0 is equivalent to x c dividing p(x). Recall
Factoring Polynomials 4-1-2014 The opposite of multiplying polynomials is factoring. Why would you want to factor a polynomial? Let p(x) be a polynomial. p(c) = 0 is equivalent to x c dividing p(x). Recall
Factoring Guidelines. Greatest Common Factor Two Terms Three Terms Four Terms. 2008 Shirley Radai
 Factoring Guidelines Greatest Common Factor Two Terms Three Terms Four Terms 008 Shirley Radai Greatest Common Factor 008 Shirley Radai Factoring by Finding the Greatest Common Factor Always check for
Factoring Guidelines Greatest Common Factor Two Terms Three Terms Four Terms 008 Shirley Radai Greatest Common Factor 008 Shirley Radai Factoring by Finding the Greatest Common Factor Always check for
How To Solve Factoring Problems
 05-W4801-AM1.qxd 8/19/08 8:45 PM Page 241 Factoring, Solving Equations, and Problem Solving 5 5.1 Factoring by Using the Distributive Property 5.2 Factoring the Difference of Two Squares 5.3 Factoring
05-W4801-AM1.qxd 8/19/08 8:45 PM Page 241 Factoring, Solving Equations, and Problem Solving 5 5.1 Factoring by Using the Distributive Property 5.2 Factoring the Difference of Two Squares 5.3 Factoring
Algebra 1 Chapter 08 review
 Name: Class: Date: ID: A Algebra 1 Chapter 08 review Multiple Choice Identify the choice that best completes the statement or answers the question. Simplify the difference. 1. (4w 2 4w 8) (2w 2 + 3w 6)
Name: Class: Date: ID: A Algebra 1 Chapter 08 review Multiple Choice Identify the choice that best completes the statement or answers the question. Simplify the difference. 1. (4w 2 4w 8) (2w 2 + 3w 6)
6.4 Special Factoring Rules
 6.4 Special Factoring Rules OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor a sum of cubes. By reversing the rules for multiplication
6.4 Special Factoring Rules OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor a sum of cubes. By reversing the rules for multiplication
Polynomials and Quadratics
 Polynomials and Quadratics Want to be an environmental scientist? Better be ready to get your hands dirty!.1 Controlling the Population Adding and Subtracting Polynomials............703.2 They re Multiplying
Polynomials and Quadratics Want to be an environmental scientist? Better be ready to get your hands dirty!.1 Controlling the Population Adding and Subtracting Polynomials............703.2 They re Multiplying
The Greatest Common Factor; Factoring by Grouping
 296 CHAPTER 5 Factoring and Applications 5.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
296 CHAPTER 5 Factoring and Applications 5.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
Factoring - Grouping
 6.2 Factoring - Grouping Objective: Factor polynomials with four terms using grouping. The first thing we will always do when factoring is try to factor out a GCF. This GCF is often a monomial like in
6.2 Factoring - Grouping Objective: Factor polynomials with four terms using grouping. The first thing we will always do when factoring is try to factor out a GCF. This GCF is often a monomial like in
Factoring Trinomials of the Form x 2 bx c
 4.2 Factoring Trinomials of the Form x 2 bx c 4.2 OBJECTIVES 1. Factor a trinomial of the form x 2 bx c 2. Factor a trinomial containing a common factor NOTE The process used to factor here is frequently
4.2 Factoring Trinomials of the Form x 2 bx c 4.2 OBJECTIVES 1. Factor a trinomial of the form x 2 bx c 2. Factor a trinomial containing a common factor NOTE The process used to factor here is frequently
BEGINNING ALGEBRA ACKNOWLEDMENTS
 BEGINNING ALGEBRA The Nursing Department of Labouré College requested the Department of Academic Planning and Support Services to help with mathematics preparatory materials for its Bachelor of Science
BEGINNING ALGEBRA The Nursing Department of Labouré College requested the Department of Academic Planning and Support Services to help with mathematics preparatory materials for its Bachelor of Science
SPECIAL PRODUCTS AND FACTORS
 CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
Factoring Methods. Example 1: 2x + 2 2 * x + 2 * 1 2(x + 1)
 Factoring Methods When you are trying to factor a polynomial, there are three general steps you want to follow: 1. See if there is a Greatest Common Factor 2. See if you can Factor by Grouping 3. See if
Factoring Methods When you are trying to factor a polynomial, there are three general steps you want to follow: 1. See if there is a Greatest Common Factor 2. See if you can Factor by Grouping 3. See if
Algebra Cheat Sheets
 Sheets Algebra Cheat Sheets provide you with a tool for teaching your students note-taking, problem-solving, and organizational skills in the context of algebra lessons. These sheets teach the concepts
Sheets Algebra Cheat Sheets provide you with a tool for teaching your students note-taking, problem-solving, and organizational skills in the context of algebra lessons. These sheets teach the concepts
Factoring Polynomials
 Factoring a Polynomial Expression Factoring a polynomial is expressing the polynomial as a product of two or more factors. Simply stated, it is somewhat the reverse process of multiplying. To factor polynomials,
Factoring a Polynomial Expression Factoring a polynomial is expressing the polynomial as a product of two or more factors. Simply stated, it is somewhat the reverse process of multiplying. To factor polynomials,
Using the ac Method to Factor
 4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
FACTORING ax 2 bx c. Factoring Trinomials with Leading Coefficient 1
 5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
Introduction Assignment
 PRE-CALCULUS 11 Introduction Assignment Welcome to PREC 11! This assignment will help you review some topics from a previous math course and introduce you to some of the topics that you ll be studying
PRE-CALCULUS 11 Introduction Assignment Welcome to PREC 11! This assignment will help you review some topics from a previous math course and introduce you to some of the topics that you ll be studying
MATH 90 CHAPTER 6 Name:.
 MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
Factor Polynomials Completely
 9.8 Factor Polynomials Completely Before You factored polynomials. Now You will factor polynomials completely. Why? So you can model the height of a projectile, as in Ex. 71. Key Vocabulary factor by grouping
9.8 Factor Polynomials Completely Before You factored polynomials. Now You will factor polynomials completely. Why? So you can model the height of a projectile, as in Ex. 71. Key Vocabulary factor by grouping
In this section, you will develop a method to change a quadratic equation written as a sum into its product form (also called its factored form).
 CHAPTER 8 In Chapter 4, you used a web to organize the connections you found between each of the different representations of lines. These connections enabled you to use any representation (such as a graph,
CHAPTER 8 In Chapter 4, you used a web to organize the connections you found between each of the different representations of lines. These connections enabled you to use any representation (such as a graph,
Chapter 9. Systems of Linear Equations
 Chapter 9. Systems of Linear Equations 9.1. Solve Systems of Linear Equations by Graphing KYOTE Standards: CR 21; CA 13 In this section we discuss how to solve systems of two linear equations in two variables
Chapter 9. Systems of Linear Equations 9.1. Solve Systems of Linear Equations by Graphing KYOTE Standards: CR 21; CA 13 In this section we discuss how to solve systems of two linear equations in two variables
Factors and Products
 CHAPTER 3 Factors and Products What You ll Learn use different strategies to find factors and multiples of whole numbers identify prime factors and write the prime factorization of a number find square
CHAPTER 3 Factors and Products What You ll Learn use different strategies to find factors and multiples of whole numbers identify prime factors and write the prime factorization of a number find square
MATH 102 College Algebra
 FACTORING Factoring polnomials ls is simpl the reverse process of the special product formulas. Thus, the reverse process of special product formulas will be used to factor polnomials. To factor polnomials
FACTORING Factoring polnomials ls is simpl the reverse process of the special product formulas. Thus, the reverse process of special product formulas will be used to factor polnomials. To factor polnomials
Factoring Polynomials and Solving Quadratic Equations
 Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
1.3 Algebraic Expressions
 1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
Blue Pelican Alg II First Semester
 Blue Pelican Alg II First Semester Teacher Version 1.01 Copyright 2009 by Charles E. Cook; Refugio, Tx (All rights reserved) Alg II Syllabus (First Semester) Unit 1: Solving linear equations and inequalities
Blue Pelican Alg II First Semester Teacher Version 1.01 Copyright 2009 by Charles E. Cook; Refugio, Tx (All rights reserved) Alg II Syllabus (First Semester) Unit 1: Solving linear equations and inequalities
How To Factor By Gcf In Algebra 1.5
 7-2 Factoring by GCF Warm Up Lesson Presentation Lesson Quiz Algebra 1 Warm Up Simplify. 1. 2(w + 1) 2. 3x(x 2 4) 2w + 2 3x 3 12x Find the GCF of each pair of monomials. 3. 4h 2 and 6h 2h 4. 13p and 26p
7-2 Factoring by GCF Warm Up Lesson Presentation Lesson Quiz Algebra 1 Warm Up Simplify. 1. 2(w + 1) 2. 3x(x 2 4) 2w + 2 3x 3 12x Find the GCF of each pair of monomials. 3. 4h 2 and 6h 2h 4. 13p and 26p
Factoring (pp. 1 of 4)
 Factoring (pp. 1 of 4) Algebra Review Try these items from middle school math. A) What numbers are the factors of 4? B) Write down the prime factorization of 7. C) 6 Simplify 48 using the greatest common
Factoring (pp. 1 of 4) Algebra Review Try these items from middle school math. A) What numbers are the factors of 4? B) Write down the prime factorization of 7. C) 6 Simplify 48 using the greatest common
Vocabulary Words and Definitions for Algebra
 Name: Period: Vocabulary Words and s for Algebra Absolute Value Additive Inverse Algebraic Expression Ascending Order Associative Property Axis of Symmetry Base Binomial Coefficient Combine Like Terms
Name: Period: Vocabulary Words and s for Algebra Absolute Value Additive Inverse Algebraic Expression Ascending Order Associative Property Axis of Symmetry Base Binomial Coefficient Combine Like Terms
7-6. Choosing a Factoring Model. Extension: Factoring Polynomials with More Than One Variable IN T RO DUC E T EACH. Standards for Mathematical Content
 7-6 Choosing a Factoring Model Extension: Factoring Polynomials with More Than One Variable Essential question: How can you factor polynomials with more than one variable? What is the connection between
7-6 Choosing a Factoring Model Extension: Factoring Polynomials with More Than One Variable Essential question: How can you factor polynomials with more than one variable? What is the connection between
Veterans Upward Bound Algebra I Concepts - Honors
 Veterans Upward Bound Algebra I Concepts - Honors Brenda Meery Kaitlyn Spong Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org Chapter 6. Factoring CHAPTER
Veterans Upward Bound Algebra I Concepts - Honors Brenda Meery Kaitlyn Spong Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org Chapter 6. Factoring CHAPTER
1.1 Practice Worksheet
 Math 1 MPS Instructor: Cheryl Jaeger Balm 1 1.1 Practice Worksheet 1. Write each English phrase as a mathematical expression. (a) Three less than twice a number (b) Four more than half of a number (c)
Math 1 MPS Instructor: Cheryl Jaeger Balm 1 1.1 Practice Worksheet 1. Write each English phrase as a mathematical expression. (a) Three less than twice a number (b) Four more than half of a number (c)
Answer Key for California State Standards: Algebra I
 Algebra I: Symbolic reasoning and calculations with symbols are central in algebra. Through the study of algebra, a student develops an understanding of the symbolic language of mathematics and the sciences.
Algebra I: Symbolic reasoning and calculations with symbols are central in algebra. Through the study of algebra, a student develops an understanding of the symbolic language of mathematics and the sciences.
Polynomials. Key Terms. quadratic equation parabola conjugates trinomial. polynomial coefficient degree monomial binomial GCF
 Polynomials 5 5.1 Addition and Subtraction of Polynomials and Polynomial Functions 5.2 Multiplication of Polynomials 5.3 Division of Polynomials Problem Recognition Exercises Operations on Polynomials
Polynomials 5 5.1 Addition and Subtraction of Polynomials and Polynomial Functions 5.2 Multiplication of Polynomials 5.3 Division of Polynomials Problem Recognition Exercises Operations on Polynomials
ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form
 ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form Goal Graph quadratic functions. VOCABULARY Quadratic function A function that can be written in the standard form y = ax 2 + bx+ c where a 0 Parabola
ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form Goal Graph quadratic functions. VOCABULARY Quadratic function A function that can be written in the standard form y = ax 2 + bx+ c where a 0 Parabola
BEST METHODS FOR SOLVING QUADRATIC INEQUALITIES.
 BEST METHODS FOR SOLVING QUADRATIC INEQUALITIES. I. GENERALITIES There are 3 common methods to solve quadratic inequalities. Therefore, students sometimes are confused to select the fastest and the best
BEST METHODS FOR SOLVING QUADRATIC INEQUALITIES. I. GENERALITIES There are 3 common methods to solve quadratic inequalities. Therefore, students sometimes are confused to select the fastest and the best
In the Herb Business, Part III Factoring and Quadratic Equations
 74 In the Herb Business, Part III Factoring and Quadratic Equations In the herbal medicine business, you and your partner sold 120 bottles of your best herbal medicine each week when you sold at your original
74 In the Herb Business, Part III Factoring and Quadratic Equations In the herbal medicine business, you and your partner sold 120 bottles of your best herbal medicine each week when you sold at your original
Factoring. Factoring Monomials Monomials can often be factored in more than one way.
 Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
is the degree of the polynomial and is the leading coefficient.
 Property: T. Hrubik-Vulanovic e-mail: [email protected] Content (in order sections were covered from the book): Chapter 6 Higher-Degree Polynomial Functions... 1 Section 6.1 Higher-Degree Polynomial Functions...
Property: T. Hrubik-Vulanovic e-mail: [email protected] Content (in order sections were covered from the book): Chapter 6 Higher-Degree Polynomial Functions... 1 Section 6.1 Higher-Degree Polynomial Functions...
Mathematics Curriculum
 Common Core Mathematics Curriculum Table of Contents 1 Polynomial and Quadratic Expressions, Equations, and Functions MODULE 4 Module Overview... 3 Topic A: Quadratic Expressions, Equations, Functions,
Common Core Mathematics Curriculum Table of Contents 1 Polynomial and Quadratic Expressions, Equations, and Functions MODULE 4 Module Overview... 3 Topic A: Quadratic Expressions, Equations, Functions,
15.1 Factoring Polynomials
 LESSON 15.1 Factoring Polynomials Use the structure of an expression to identify ways to rewrite it. Also A.SSE.3? ESSENTIAL QUESTION How can you use the greatest common factor to factor polynomials? EXPLORE
LESSON 15.1 Factoring Polynomials Use the structure of an expression to identify ways to rewrite it. Also A.SSE.3? ESSENTIAL QUESTION How can you use the greatest common factor to factor polynomials? EXPLORE
AIP Factoring Practice/Help
 The following pages include many problems to practice factoring skills. There are also several activities with examples to help you with factoring if you feel like you are not proficient with it. There
The following pages include many problems to practice factoring skills. There are also several activities with examples to help you with factoring if you feel like you are not proficient with it. There
8-8 Differences of Squares. Factor each polynomial. 1. x 9 SOLUTION: 2. 4a 25 SOLUTION: 3. 9m 144 SOLUTION: 4. 2p 162p SOLUTION: 5.
 Factor each polynomial. 1.x 9 SOLUTION:.a 5 SOLUTION:.9m 1 SOLUTION:.p 16p SOLUTION: 5.u 81 SOLUTION: Page 1 5.u 81 SOLUTION: 6.d f SOLUTION: 7.0r 5n SOLUTION: 8.56n c SOLUTION: Page 8.56n c SOLUTION:
Factor each polynomial. 1.x 9 SOLUTION:.a 5 SOLUTION:.9m 1 SOLUTION:.p 16p SOLUTION: 5.u 81 SOLUTION: Page 1 5.u 81 SOLUTION: 6.d f SOLUTION: 7.0r 5n SOLUTION: 8.56n c SOLUTION: Page 8.56n c SOLUTION:
Section 6.1 Factoring Expressions
 Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
SECTION 2.5: FINDING ZEROS OF POLYNOMIAL FUNCTIONS
 SECTION 2.5: FINDING ZEROS OF POLYNOMIAL FUNCTIONS Assume f ( x) is a nonconstant polynomial with real coefficients written in standard form. PART A: TECHNIQUES WE HAVE ALREADY SEEN Refer to: Notes 1.31
SECTION 2.5: FINDING ZEROS OF POLYNOMIAL FUNCTIONS Assume f ( x) is a nonconstant polynomial with real coefficients written in standard form. PART A: TECHNIQUES WE HAVE ALREADY SEEN Refer to: Notes 1.31
FACTORING OUT COMMON FACTORS
 278 (6 2) Chapter 6 Factoring 6.1 FACTORING OUT COMMON FACTORS In this section Prime Factorization of Integers Greatest Common Factor Finding the Greatest Common Factor for Monomials Factoring Out the
278 (6 2) Chapter 6 Factoring 6.1 FACTORING OUT COMMON FACTORS In this section Prime Factorization of Integers Greatest Common Factor Finding the Greatest Common Factor for Monomials Factoring Out the
CM2202: Scientific Computing and Multimedia Applications General Maths: 2. Algebra - Factorisation
 CM2202: Scientific Computing and Multimedia Applications General Maths: 2. Algebra - Factorisation Prof. David Marshall School of Computer Science & Informatics Factorisation Factorisation is a way of
CM2202: Scientific Computing and Multimedia Applications General Maths: 2. Algebra - Factorisation Prof. David Marshall School of Computer Science & Informatics Factorisation Factorisation is a way of
Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any.
 Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
Brunswick High School has reinstated a summer math curriculum for students Algebra 1, Geometry, and Algebra 2 for the 2014-2015 school year.
 Brunswick High School has reinstated a summer math curriculum for students Algebra 1, Geometry, and Algebra 2 for the 2014-2015 school year. Goal The goal of the summer math program is to help students
Brunswick High School has reinstated a summer math curriculum for students Algebra 1, Geometry, and Algebra 2 for the 2014-2015 school year. Goal The goal of the summer math program is to help students
ALGEBRA 2 CRA 2 REVIEW - Chapters 1-6 Answer Section
 ALGEBRA 2 CRA 2 REVIEW - Chapters 1-6 Answer Section MULTIPLE CHOICE 1. ANS: C 2. ANS: A 3. ANS: A OBJ: 5-3.1 Using Vertex Form SHORT ANSWER 4. ANS: (x + 6)(x 2 6x + 36) OBJ: 6-4.2 Solving Equations by
ALGEBRA 2 CRA 2 REVIEW - Chapters 1-6 Answer Section MULTIPLE CHOICE 1. ANS: C 2. ANS: A 3. ANS: A OBJ: 5-3.1 Using Vertex Form SHORT ANSWER 4. ANS: (x + 6)(x 2 6x + 36) OBJ: 6-4.2 Solving Equations by
7.1 Graphs of Quadratic Functions in Vertex Form
 7.1 Graphs of Quadratic Functions in Vertex Form Quadratic Function in Vertex Form A quadratic function in vertex form is a function that can be written in the form f (x) = a(x! h) 2 + k where a is called
7.1 Graphs of Quadratic Functions in Vertex Form Quadratic Function in Vertex Form A quadratic function in vertex form is a function that can be written in the form f (x) = a(x! h) 2 + k where a is called
