8-8 Differences of Squares. Factor each polynomial. 1. x 9 SOLUTION: 2. 4a 25 SOLUTION: 3. 9m 144 SOLUTION: 4. 2p 162p SOLUTION: 5.
|
|
|
- Mervin Terry
- 8 years ago
- Views:
Transcription
1 Factor each polynomial. 1.x 9 SOLUTION:.a 5 SOLUTION:.9m 1 SOLUTION:.p 16p SOLUTION: 5.u 81 SOLUTION: Page 1
2 5.u 81 SOLUTION: 6.d f SOLUTION: 7.0r 5n SOLUTION: 8.56n c SOLUTION: Page
3 8.56n c SOLUTION: 9.c + c c SOLUTION: 10.f f 9f + 6 SOLUTION: 11.t + t 8t SOLUTION: Page
4 11.t + t 8t SOLUTION: 1.w w 9w + 7 SOLUTION: EXTENDEDRESPONSEAfteranaccident,skidmarksmayresultfromsuddenbreaking.Theformula s = d approximates a vehicle s speed s in miles per hour given the length d in feet of the skid marks on dry concrete. 1.If skid marks on dry concrete are 5 feet long, how fast was the car traveling when the brakes were applied? SOLUTION: Page
5 EXTENDEDRESPONSEAfteranaccident,skidmarksmayresultfromsuddenbreaking.Theformula s = d approximates a vehicle s speed s in miles per hour given the length d in feet of the skid marks on dry concrete. 1.If skid marks on dry concrete are 5 feet long, how fast was the car traveling when the brakes were applied? SOLUTION: Since the speed cannot be negative, the car was traveling 6 mph when the brakes were applied. 1.If the skid marks on dry concrete are 150 feet long, how fast was the car traveling when the brakes were applied? SOLUTION: Since the speed cannot be negative, the car was traveling 60 mph when the brakes were applied. Factor each polynomial. 15.q 11 SOLUTION: Page 5
6 8-8 Differences of Squares Since the speed cannot be negative, the car was traveling 60 mph when the brakes were applied. Factor each polynomial. 15.q 11 SOLUTION: 16.r k SOLUTION: 17.6n 6 SOLUTION: 18.w 65 SOLUTION: 19.r 9t SOLUTION: Page 6
7 19.r 9t SOLUTION: 0.c d SOLUTION: 1.h 100h SOLUTION:.h 56 SOLUTION:.x x 16x + 81 SOLUTION:.x y Page 7
8 .x x 16x + 81 SOLUTION:.x y SOLUTION: 5.7h 7p SOLUTION: 6.c + c 17c 98 SOLUTION: 7.6k h 5k Page 8
9 6.c + c 17c 98 SOLUTION: 7.6k h 5k SOLUTION: 8.5a 0a SOLUTION: 9.f + f 6f 18 SOLUTION: 0.r 19r Page 9
10 9.f + f 6f 18 SOLUTION: 0.r 19r SOLUTION: 1.10q 110q SOLUTION:.xn 7x SOLUTION: 5.p r p r SOLUTION: Page 10
11 5.p r p r SOLUTION:.8c 8c SOLUTION: 5.r 5r 100r SOLUTION: 6.t 7t t + 7 SOLUTION: Page 11
12 6.t 7t t + 7 SOLUTION: 7.a 9 SOLUTION: 8.m + 9m 6m 81 SOLUTION: 9.m + SOLUTION: 0.x + x 75x 5 SOLUTION: Page 1
13 9.m + SOLUTION: 0.x + x 75x 5 SOLUTION: 1.1a + a 19a SOLUTION:.x + 6x 6x 16x SOLUTION:.15m + 1m 75m 00 SOLUTION: esolutions Manual - Powered by Cognero Page 1
14 .15m + 1m 75m 00 SOLUTION:.GEOMETRY The drawing shown is a square with a square cut out of it. a. Write an expression that represents the area of the shaded region. b. Find the dimensions of a rectangle with the same area as the shaded region in the drawing. Assume that the dimensions of the rectangle must be represented by binomials with integral coefficients. SOLUTION: a. Use the formula for the area of square A = s s to write an expression for the area of the shaded region. b. Write the area of the shaded region in factor form to find two binomial dimensions for a rectangle with the same area. The dimensions of the rectangle would be (n + 6) by (n ). 5.DECORATIONS arch decorated esolutions Manual - Powered byan Cognero with balloons was used to decorate the gym for the spring dance. The shape Page 1 of the arch can be modeled by the equation y = 0.5x +.5x, where x and y are measured in feet and the x-axis represents the floor.
15 8-8 Differences of Squares The dimensions of the rectangle would be (n + 6) by (n ). 5.DECORATIONS An arch decorated with balloons was used to decorate the gym for the spring dance. The shape of the arch can be modeled by the equation y = 0.5x +.5x, where x and y are measured in feet and the x-axis represents the floor. a. Write the expression that represents the height of the arch in factored form. b. How far apart are the two points where the arch touches the floor? c. Graph this equation on your calculator. What is the highest point of the arch? SOLUTION: a. b. Find the two places along the x-axis (the floor) where the height of the arch is 0. or Subtract the two values to find out how far apart they are: 9 0 = 9. The two points where the arch touches the floor are 9 ft. apart. c. Useagraphingcalculatortofindtheheightofthearchatitshighestpoint. [, 10] scl: by [, 10] scl: The arch is ft. high. 6.CCSS SENSE-MAKING Zelda is building a deck in her backyard. The plans for the deck show that it is to be feet by feet. Zelda wants to reduce one dimension by a number of feet and increase the other dimension by the same number of feet. If the area of the reduced deck is 51 square feet, what are the dimensions of the deck? SOLUTION: Let x be the number of feet added and subtracted to each dimension of the deck. Replace A with 51, l with + x, and w with - x. esolutions Manual - Powered by Cognero Page 15
16 [, 10] scl: by [, 10] scl: 8-8 Differences of Squares The arch is ft. high. 6.CCSS SENSE-MAKING Zelda is building a deck in her backyard. The plans for the deck show that it is to be feet by feet. Zelda wants to reduce one dimension by a number of feet and increase the other dimension by the same number of feet. If the area of the reduced deck is 51 square feet, what are the dimensions of the deck? SOLUTION: Let x be the number of feet added and subtracted to each dimension of the deck. Replace A with 51, l with + x, and w with - x. Since the amount added and subtracted to the dimensions cannot be negative, 8 feet is the amount that is added and subtracted to the dimensions. 8 = = Therefore, the dimensions of the deck are 16 feet by feet. 7.SALES The sales of a particular CD can be modeled by the equation S = 5m + 15m, where S is the number of CDs sold in thousands, and m is the number of months that it is on the market. a. In what month should the music store expect the CD to stop selling? b. In what month will CD sales peak? c. How many copies will the CD sell at its peak? SOLUTION: a. Find the values of m for which S equals 0. m =0orm = 5 esolutions Manual - Powered by Cognero The music store should expect the CD to stop selling in month 5. Page 16
17 m =0orm = 5 The music store should expect the CD to stop selling in month 5. b. Use a graphing calculator to find the maximum. [0, 10] scl: 1 by [0, 50] scl: 5 The maximum occurs at the point x =.5. So the CD sales should peak in month.5. c. The maximum on the graph is S = 156.5, where S is measured in the thousands. The peak number of copies sold is =156,50copies. Solve each equation by factoring. Confirm your answers using a graphing calculator. 8.6w = 11 SOLUTION: or The roots are and or about 1.8 and 1.8. Page 17 Confirm the roots using a graphing calculator. Let Y1 = 6w and Y = 11. Use the intersect option from the
18 c. The maximum on the graph is S = 156.5, where S is measured in the thousands. The peak number of copies sold is =156,50copies. 8-8 Differences of Squares Solve each equation by factoring. Confirm your answers using a graphing calculator. 8.6w = 11 SOLUTION: or The roots are and or about 1.8 and 1.8. Confirm the roots using a graphing calculator. Let Y1 = 6w and Y = 11. Use the intersect option from the CALC menu to find the points of intersection. Thus, the solutions are = 5x and. SOLUTION: Page 18
19 Thus, the solutions are and 8-8 Differences of Squares = 5x. SOLUTION: or The roots are and. Confirm the roots using a graphing calculator. Let Y1 = 100 and Y = 5x. Use the intersect option from the CALC menu to find the points of intersection. Thus, the solutions are and. 50.6x 1 = 0 SOLUTION: The roots are and or 0.15 and Page 19 Confirm the roots using a graphing calculator. Let Y1 = 6x 1 and Y = 0. Use the intersect option from the
20 8-8 Differences of Squares Thus, the solutions are and. 50.6x 1 = 0 SOLUTION: The roots are and or 0.15 and Confirm the roots using a graphing calculator. Let Y1 = 6x 1 and Y = 0. Use the intersect option from the CALC menu to find the points of intersection. Thus, the solutions are and. 51.y =0 SOLUTION: Page 0
21 Thus, the solutions are and. 51.y =0 SOLUTION: The roots are and or -0.75and0.75. Confirm the roots using a graphing calculator. Let Y1 = y and Y = 0. Use the intersect option from the CALC menu to find the points of intersection. Thus, the solutions are and. 5. b = 16 SOLUTION: Page 1
22 8-8 Differences of Squares Thus, the solutions are and. 5. b = 16 SOLUTION: The roots are 8and8. Confirm the roots using a graphing calculator. Let Y1 = andy = 16. Use the intersect option from the CALC menu to find the points of intersection. Thus, the solutions are 8 and x =0 SOLUTION: or Page
23 8-8 Differences of Squares Thus, the solutions are 8 and x =0 SOLUTION: or The roots are 5and5. Confirm the roots using a graphing calculator. Let Y1 = CALC menu to find the points of intersection. andy =0. Use the intersect option from the Thus, the solutions are 5 and d 81 = 0 SOLUTION: The roots are and. Page Confirm the roots using a graphing calculator. Let Y1 = 9d 81 and Y =0. Use the intersect option from the
24 8-8 Differences of Squares Thus, the solutions are 5 and d 81 = 0 SOLUTION: The roots are and. Confirm the roots using a graphing calculator. Let Y1 = 9d 81 and Y =0. Use the intersect option from the CALC menu to find the points of intersection. Thus, the solutions are and. 55.a = SOLUTION: The roots are and or and Page
25 8-8 Differences of Squares Thus, the solutions are and. 55.a = SOLUTION: The roots are and or and Confirm the roots using a graphing calculator. Let Y1 = a and Y = CALC menu to find the points of intersection.. Use the intersect option from the Thus, the solutions are and. 56.MULTIPLEREPRESENTATIONS In this problem, you will investigate perfect square trinomials. a.tabular Copy and complete the table below by factoring each polynomial. Then write the first and last terms of the given polynomials as perfect squares. Page 5
26 56.MULTIPLEREPRESENTATIONS In this problem, you will investigate perfect square trinomials. a.tabular Copy and complete the table below by factoring each polynomial. Then write the first and last 8-8 Differences of Squares terms of the given polynomials as perfect squares. b.analytical Write the middle term of each polynomial using the square roots of the perfect squares of the first and last terms. c.algebraic Write the pattern for a perfect square trinomial. d.verbal What conditions must be met for a trinomial to be classified as a perfect square trinomial? SOLUTION: a. In this trinomial, a = 9, b = and c = 16, so m + p is negative and mp is negative. Therefore, m and p must have different signs. List the factors of 9(16) or 1 with a sum of. Factors of 1 Sum 1, 1 15, 7 7, 8 51, 6 0 6, 0 8, , , 1 The correct factors are 1 and 1. In this trinomial, a =, b = 0 and c = 5, so m + p is negative and mp is negative. Therefore, m and p must have different signs. List the factors of (5) or 100 with a sum of 0. Factors of 100 1, 100, 50, 5 10, 10 Sum The correct factors are 10 and 10. Page 6
27 different signs. List the factors of (5) or 100 with a sum of 0. Factors of 100 1, Differences of Squares, 50, 5 10, 10 Sum The correct factors are 10 and 10. In this trinomial, a = 16, b = 0 and c = 9, so m + p is negative and mp is negative. Therefore, m and p must have different signs. List the factors of 16(9) or 1 with a sum of. Factors of 1 1, 1, 7, 8, 6 6, 8, 18 9, 16 1, 1 Sum The correct factors are 1 and 1. In this trinomial, a = 5, b = 0 and c =, so m + p is negative and mp is negative. Therefore, m and p must have different signs. List the factors of 5() or 100 with a sum of 0. Factors of 100 1, 100, 50, 5 10, 10 Sum esolutions Manual - Powered by Cognero The correct factors are 10 and 10. Page 7
28 Factors of 100 Sum 1, , 50 5, , 10 0 The correct factors are 10 and 10. b. See table. c. (a + b)(a + b) = a + ab + b and (a b)(a b) = a ab + b d. The first and last terms must be perfect squares and the middle term must be times the square roots of the first and last terms. 57.ERRORANALYSIS Elizabeth and Lorenzo are factoring an expression. Is either of them correct? Explain your reasoning. SOLUTION: Lorenzo is correct. Elizabeth s answer multiplies to 16x 5y. The exponent on x should be. 58.CHALLENGE Factor and simplify 9 (k + ), a difference of squares. SOLUTION: Page 8
29 8-8 Differences of Squares Elizabeth s answer multiplies to 16x 5y. The exponent on x should be. 58.CHALLENGE Factor and simplify 9 (k + ), a difference of squares. SOLUTION: Thus 9 (k + ) factor to [ + (k + )][ (k + )] and simplifies to k 6k. 59.CCSSPERSEVERANCE Factor x SOLUTION: 60.REASONING Write and factor a binomial that is the difference of two perfect squares and that has a greatest common factor of 5mk. SOLUTION: Begin with the GCF of 5mk and the difference of squares. 5mk(a b ) Distribute the GCF to obtain the binomial of 5mka 5mkb. 5mka 5mkb = 5mk(a b ) = 5mk(a b)(a + b) 61.REASONING Determine whether the following statement is true or false. Give an example or counterexample to justify your answer. All binomials that have a perfect square in each of the two terms can be factored. SOLUTION: false; The two squares cannot be added together in the binomial. For example, a + b cannot be factored. 6.OPENENDED Write a binomial in which the difference of squares pattern must be repeated to factor it completely. Then factor the binomial. SOLUTION: Ifyouplantorepeatthethefactoringtwice,youneedtofindthedifferenceoftwotermstothethpower. esolutions Manual - Powered by Cognero Page 9
30 SOLUTION: false; The two squares cannot be added together in the binomial. 8-8 Differences of Squares For example, a + b cannot be factored. 6.OPENENDED Write a binomial in which the difference of squares pattern must be repeated to factor it completely. Then factor the binomial. SOLUTION: Ifyouplantorepeatthethefactoringtwice,youneedtofindthedifferenceoftwotermstothethpower. 6.WRITINGINMATH Describe why the difference of squares pattern has no middle term with a variable. SOLUTION: When the difference of squares pattern is multiplied together using the FOIL method, the outer and inner terms are opposites of each other. When these terms are added together, the sum is zero. Consider the example. 6.One of the roots of x + 1x = is 8. What is the other root? A B C D SOLUTION: Page 0 The correct choice is B. 65.Which of the following is the sum of both solutions of the equation x + x = 5?
31 6.One of the roots of x + 1x = is 8. What is the other root? A B C D SOLUTION: The correct choice is B. 65.Which of the following is the sum of both solutions of the equation x + x = 5? F 1 G H J 1 SOLUTION: or =. The correct choice is G. esolutions Manual - Powered by Cognero are the x-intercepts of the 66.What graph of y = x + 7x + 0? Page 1
32 9 + 6 =. 8-8 Differences of Squares The correct choice is G. 66.What are the x-intercepts of the graph of y = x + 7x + 0? A, B, C, D, SOLUTION: To find the x-intercepts, find the zeros or roots of the related equation. or The correct choice is C. 67.EXTENDEDRESPONSE Two cars leave Cleveland at the same time from different parts of the city and both drive to Cincinnati. The distance in miles of the cars from the center of Cleveland can be represented by the two equations below, where t represents the time in hours. Car A: 65t + 15 Car B: 60t + 5 a. Which car is faster? Explain. b. Find an expression that models the distance between the two cars. c. How far apart are the cars after hours? SOLUTION: a. The slope represents the speed of the car. Car A has a speed of 65 mph and Car B has a speed of 60 mph. Thus, Car A is traveling at a greater speed. b. c. Substitute in for t. Page
33 or 8-8 Differences of Squares The correct choice is C. 67.EXTENDEDRESPONSE Two cars leave Cleveland at the same time from different parts of the city and both drive to Cincinnati. The distance in miles of the cars from the center of Cleveland can be represented by the two equations below, where t represents the time in hours. Car A: 65t + 15 Car B: 60t + 5 a. Which car is faster? Explain. b. Find an expression that models the distance between the two cars. c. How far apart are the cars after hours? SOLUTION: a. The slope represents the speed of the car. Car A has a speed of 65 mph and Car B has a speed of 60 mph. Thus, Car A is traveling at a greater speed. b. c. Substitute in for t. After hours,thecarsare.5milesapart. Factor each trinomial, if possible. If the trinomial cannot be factored using integers, write prime. 68.5x 17x + 1 SOLUTION: In this trinomial, a = 5, b = 17 and c = 1, so m + p is negative and mp is positive. Therefore, m and p must both be negative. List the negative factors of 5(1) or 70, and look for the pair of factors with a sum of 17. Factors of 70, 5 5, 1 7, 10 Sum The correct factors are 7 and 10. Page
34 8-8 Differences of Squares After hours,thecarsare.5milesapart. Factor each trinomial, if possible. If the trinomial cannot be factored using integers, write prime. 68.5x 17x + 1 SOLUTION: In this trinomial, a = 5, b = 17 and c = 1, so m + p is negative and mp is positive. Therefore, m and p must both be negative. List the negative factors of 5(1) or 70, and look for the pair of factors with a sum of 17. Factors of 70, 5 5, 1 7, 10 Sum The correct factors are 7 and a a + 15 SOLUTION: In this trinomial, a = 5, b = and c = 15, so m + p is negative and mp is positive. Therefore, m and p must both be negative. List the negative factors of 5(15) or 75, and look for the pair of factors with a sum of. Factors of 75, 5 5, 15 Sum 8 0 There are no factors of 75 with a sum of. So, the trinomial is prime x 0xy + 10y SOLUTION: In this trinomial, a = 10, b = 0 and c = 10, so m + p is negative and mp is positive. Therefore, m and p must both be negative. List the negative factors of 10(10) or 100, and look for the pair of factors with a sum of 0. Factors of 100, 50 5, 0 10, 10 Sum The correct factors are 10 and 10. Page
35 5, 15 0 There are no factors of 75 with a sum of. 8-8 Differences of Squares So, the trinomial is prime x 0xy + 10y SOLUTION: In this trinomial, a = 10, b = 0 and c = 10, so m + p is negative and mp is positive. Therefore, m and p must both be negative. List the negative factors of 10(10) or 100, and look for the pair of factors with a sum of 0. Factors of 100, 50 5, 0 10, 10 Sum The correct factors are 10 and 10. Solve each equation. Check your solutions. 71.n 9n = 18 SOLUTION: The roots are and 6. Check by substituting and 6 in for n in the original equation. and The solutions are and 6. Page 5
36 Solve each equation. Check your solutions. 71.n 9n = 18 SOLUTION: The roots are and 6. Check by substituting and 6 in for n in the original equation. and The solutions are and a = 7a SOLUTION: The roots are and 5. Check by substituting and 5 in for a in the original equation. and The Manual solutions are byand 5. esolutions - Powered Cognero 7.x x = 96 Page 6
37 8-8 Differences Squares The solutionsofare and a = 7a SOLUTION: The roots are and 5. Check by substituting and 5 in for a in the original equation. and The solutions are and 5. 7.x x = 96 SOLUTION: The roots are 6 and 16. Check by substituting 6 and 16 in for x in the original equation. and The solutions are 6 and 16. esolutions Manual - Powered Cognero Victoriabyand Trey 7.SAVINGS Page 7 each want to buy a scooter. In how many weeks will Victoria and Trey have saved the same amount of money, and how much will each of them have saved?
38 8-8 Differences of Squares The solutions are 6 and SAVINGS Victoria and Trey each want to buy a scooter. In how many weeks will Victoria and Trey have saved the same amount of money, and how much will each of them have saved? SOLUTION: Victoria and Trey will have saved the same amount of money at the end of week () = 0 The amount of money they will have saved is $0. Solve each inequality. Graph the solution set on a number line. 75.t SOLUTION: The solution is {t t }. 76.d +5 7 SOLUTION: The solution is {d d } k > 1 SOLUTION: Page 8
39 The solution is {d d } k > 1 SOLUTION: The solution is {k k > } < + g SOLUTION: The solution is {g g > } m SOLUTION: The solution is {m m }. 80.y > 8 + y SOLUTION: The solution is {y y > 8}. esolutions Manual - Powered Cognero Silvia isbybeginning 81.FITNESS Page 9 an exercise program that calls for 0 minutes of walking each day for the first week. Each week thereafter, she has to increase her daily walking for the week by 7 minutes. In which week will she first walk over an hour a day?
40 The solution is {y y > 8}. 81.FITNESS Silvia is beginning an exercise program that calls for 0 minutes of walking each day for the first week. Each week thereafter, she has to increase her daily walking for the week by 7 minutes. In which week will she first walk over an hour a day? SOLUTION: Silvia's time exercising can be modeled by an arithmetic sequence. 0, 7,, 1, 8, 55,... a 1 is the initial value or 0. d is the difference or 7. Substitute the values into the formula for the nth term of an arithmetic sequence: The first week in which she will walk over an hour a day is the seventh week. Find each product. 8.(x 6) SOLUTION: 8.(x )(x ) SOLUTION: 8.(x + )(x + ) SOLUTION: 85.(x 5) SOLUTION: Page 0
41 8.(x + )(x + ) SOLUTION: 85.(x 5) SOLUTION: 86.(6x 1) SOLUTION: 87.(x + 5)(x + 5) SOLUTION: Page 1
10 7, 8. 2. 6x + 30x + 36 SOLUTION: 8-9 Perfect Squares. The first term is not a perfect square. So, 6x + 30x + 36 is not a perfect square trinomial.
 Squares Determine whether each trinomial is a perfect square trinomial. Write yes or no. If so, factor it. 1.5x + 60x + 36 SOLUTION: The first term is a perfect square. 5x = (5x) The last term is a perfect
Squares Determine whether each trinomial is a perfect square trinomial. Write yes or no. If so, factor it. 1.5x + 60x + 36 SOLUTION: The first term is a perfect square. 5x = (5x) The last term is a perfect
5-3 Polynomial Functions. not in one variable because there are two variables, x. and y
 y. 5-3 Polynomial Functions State the degree and leading coefficient of each polynomial in one variable. If it is not a polynomial in one variable, explain why. 1. 11x 6 5x 5 + 4x 2 coefficient of the
y. 5-3 Polynomial Functions State the degree and leading coefficient of each polynomial in one variable. If it is not a polynomial in one variable, explain why. 1. 11x 6 5x 5 + 4x 2 coefficient of the
A.3. Polynomials and Factoring. Polynomials. What you should learn. Definition of a Polynomial in x. Why you should learn it
 Appendi A.3 Polynomials and Factoring A23 A.3 Polynomials and Factoring What you should learn Write polynomials in standard form. Add,subtract,and multiply polynomials. Use special products to multiply
Appendi A.3 Polynomials and Factoring A23 A.3 Polynomials and Factoring What you should learn Write polynomials in standard form. Add,subtract,and multiply polynomials. Use special products to multiply
1.3 Polynomials and Factoring
 1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
Factoring Polynomials
 UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
Factoring and Applications
 Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
6.3 FACTORING ax 2 bx c WITH a 1
 290 (6 14) Chapter 6 Factoring e) What is the approximate maximum revenue? f) Use the accompanying graph to estimate the price at which the revenue is zero. y Revenue (thousands of dollars) 300 200 100
290 (6 14) Chapter 6 Factoring e) What is the approximate maximum revenue? f) Use the accompanying graph to estimate the price at which the revenue is zero. y Revenue (thousands of dollars) 300 200 100
( ) FACTORING. x In this polynomial the only variable in common to all is x.
 FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
Big Bend Community College. Beginning Algebra MPC 095. Lab Notebook
 Big Bend Community College Beginning Algebra MPC 095 Lab Notebook Beginning Algebra Lab Notebook by Tyler Wallace is licensed under a Creative Commons Attribution 3.0 Unported License. Permissions beyond
Big Bend Community College Beginning Algebra MPC 095 Lab Notebook Beginning Algebra Lab Notebook by Tyler Wallace is licensed under a Creative Commons Attribution 3.0 Unported License. Permissions beyond
Algebra I. In this technological age, mathematics is more important than ever. When students
 In this technological age, mathematics is more important than ever. When students leave school, they are more and more likely to use mathematics in their work and everyday lives operating computer equipment,
In this technological age, mathematics is more important than ever. When students leave school, they are more and more likely to use mathematics in their work and everyday lives operating computer equipment,
6.1 The Greatest Common Factor; Factoring by Grouping
 386 CHAPTER 6 Factoring and Applications 6.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
386 CHAPTER 6 Factoring and Applications 6.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
MTH 092 College Algebra Essex County College Division of Mathematics Sample Review Questions 1 Created January 17, 2006
 MTH 092 College Algebra Essex County College Division of Mathematics Sample Review Questions Created January 7, 2006 Math 092, Elementary Algebra, covers the mathematical content listed below. In order
MTH 092 College Algebra Essex County College Division of Mathematics Sample Review Questions Created January 7, 2006 Math 092, Elementary Algebra, covers the mathematical content listed below. In order
Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III
 Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III Name Date Adding and Subtracting Polynomials Algebra Standard 10.0 A polynomial is a sum of one ore more monomials. Polynomial
Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III Name Date Adding and Subtracting Polynomials Algebra Standard 10.0 A polynomial is a sum of one ore more monomials. Polynomial
MATD 0390 - Intermediate Algebra Review for Pretest
 MATD 090 - Intermediate Algebra Review for Pretest. Evaluate: a) - b) - c) (-) d) 0. Evaluate: [ - ( - )]. Evaluate: - -(-7) + (-8). Evaluate: - - + [6 - ( - 9)]. Simplify: [x - (x - )] 6. Solve: -(x +
MATD 090 - Intermediate Algebra Review for Pretest. Evaluate: a) - b) - c) (-) d) 0. Evaluate: [ - ( - )]. Evaluate: - -(-7) + (-8). Evaluate: - - + [6 - ( - 9)]. Simplify: [x - (x - )] 6. Solve: -(x +
Math 0980 Chapter Objectives. Chapter 1: Introduction to Algebra: The Integers.
 Math 0980 Chapter Objectives Chapter 1: Introduction to Algebra: The Integers. 1. Identify the place value of a digit. 2. Write a number in words or digits. 3. Write positive and negative numbers used
Math 0980 Chapter Objectives Chapter 1: Introduction to Algebra: The Integers. 1. Identify the place value of a digit. 2. Write a number in words or digits. 3. Write positive and negative numbers used
SPECIAL PRODUCTS AND FACTORS
 CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
6.4 Special Factoring Rules
 6.4 Special Factoring Rules OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor a sum of cubes. By reversing the rules for multiplication
6.4 Special Factoring Rules OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor a sum of cubes. By reversing the rules for multiplication
Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any.
 Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
Answer Key for California State Standards: Algebra I
 Algebra I: Symbolic reasoning and calculations with symbols are central in algebra. Through the study of algebra, a student develops an understanding of the symbolic language of mathematics and the sciences.
Algebra I: Symbolic reasoning and calculations with symbols are central in algebra. Through the study of algebra, a student develops an understanding of the symbolic language of mathematics and the sciences.
NSM100 Introduction to Algebra Chapter 5 Notes Factoring
 Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
POLYNOMIALS and FACTORING
 POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
FACTORING OUT COMMON FACTORS
 278 (6 2) Chapter 6 Factoring 6.1 FACTORING OUT COMMON FACTORS In this section Prime Factorization of Integers Greatest Common Factor Finding the Greatest Common Factor for Monomials Factoring Out the
278 (6 2) Chapter 6 Factoring 6.1 FACTORING OUT COMMON FACTORS In this section Prime Factorization of Integers Greatest Common Factor Finding the Greatest Common Factor for Monomials Factoring Out the
What are the place values to the left of the decimal point and their associated powers of ten?
 The verbal answers to all of the following questions should be memorized before completion of algebra. Answers that are not memorized will hinder your ability to succeed in geometry and algebra. (Everything
The verbal answers to all of the following questions should be memorized before completion of algebra. Answers that are not memorized will hinder your ability to succeed in geometry and algebra. (Everything
Greatest Common Factor (GCF) Factoring
 Section 4 4: Greatest Common Factor (GCF) Factoring The last chapter introduced the distributive process. The distributive process takes a product of a monomial and a polynomial and changes the multiplication
Section 4 4: Greatest Common Factor (GCF) Factoring The last chapter introduced the distributive process. The distributive process takes a product of a monomial and a polynomial and changes the multiplication
Factoring Polynomials
 Factoring Polynomials Factoring Factoring is the process of writing a polynomial as the product of two or more polynomials. The factors of 6x 2 x 2 are 2x + 1 and 3x 2. In this section, we will be factoring
Factoring Polynomials Factoring Factoring is the process of writing a polynomial as the product of two or more polynomials. The factors of 6x 2 x 2 are 2x + 1 and 3x 2. In this section, we will be factoring
IOWA End-of-Course Assessment Programs. Released Items ALGEBRA I. Copyright 2010 by The University of Iowa.
 IOWA End-of-Course Assessment Programs Released Items Copyright 2010 by The University of Iowa. ALGEBRA I 1 Sally works as a car salesperson and earns a monthly salary of $2,000. She also earns $500 for
IOWA End-of-Course Assessment Programs Released Items Copyright 2010 by The University of Iowa. ALGEBRA I 1 Sally works as a car salesperson and earns a monthly salary of $2,000. She also earns $500 for
Algebra I Vocabulary Cards
 Algebra I Vocabulary Cards Table of Contents Expressions and Operations Natural Numbers Whole Numbers Integers Rational Numbers Irrational Numbers Real Numbers Absolute Value Order of Operations Expression
Algebra I Vocabulary Cards Table of Contents Expressions and Operations Natural Numbers Whole Numbers Integers Rational Numbers Irrational Numbers Real Numbers Absolute Value Order of Operations Expression
FACTORING ax 2 bx c WITH a 1
 296 (6 20) Chapter 6 Factoring 6.4 FACTORING a 2 b c WITH a 1 In this section The ac Method Trial and Error Factoring Completely In Section 6.3 we factored trinomials with a leading coefficient of 1. In
296 (6 20) Chapter 6 Factoring 6.4 FACTORING a 2 b c WITH a 1 In this section The ac Method Trial and Error Factoring Completely In Section 6.3 we factored trinomials with a leading coefficient of 1. In
expression is written horizontally. The Last terms ((2)( 4)) because they are the last terms of the two polynomials. This is called the FOIL method.
 A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
LAKE ELSINORE UNIFIED SCHOOL DISTRICT
 LAKE ELSINORE UNIFIED SCHOOL DISTRICT Title: PLATO Algebra 1-Semester 2 Grade Level: 10-12 Department: Mathematics Credit: 5 Prerequisite: Letter grade of F and/or N/C in Algebra 1, Semester 2 Course Description:
LAKE ELSINORE UNIFIED SCHOOL DISTRICT Title: PLATO Algebra 1-Semester 2 Grade Level: 10-12 Department: Mathematics Credit: 5 Prerequisite: Letter grade of F and/or N/C in Algebra 1, Semester 2 Course Description:
Factor Polynomials Completely
 9.8 Factor Polynomials Completely Before You factored polynomials. Now You will factor polynomials completely. Why? So you can model the height of a projectile, as in Ex. 71. Key Vocabulary factor by grouping
9.8 Factor Polynomials Completely Before You factored polynomials. Now You will factor polynomials completely. Why? So you can model the height of a projectile, as in Ex. 71. Key Vocabulary factor by grouping
MATH 90 CHAPTER 6 Name:.
 MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
1.3 Algebraic Expressions
 1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
Algebra Cheat Sheets
 Sheets Algebra Cheat Sheets provide you with a tool for teaching your students note-taking, problem-solving, and organizational skills in the context of algebra lessons. These sheets teach the concepts
Sheets Algebra Cheat Sheets provide you with a tool for teaching your students note-taking, problem-solving, and organizational skills in the context of algebra lessons. These sheets teach the concepts
Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder).
 Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Operations with Algebraic Expressions: Multiplication of Polynomials
 Operations with Algebraic Expressions: Multiplication of Polynomials The product of a monomial x monomial To multiply a monomial times a monomial, multiply the coefficients and add the on powers with the
Operations with Algebraic Expressions: Multiplication of Polynomials The product of a monomial x monomial To multiply a monomial times a monomial, multiply the coefficients and add the on powers with the
Review of Intermediate Algebra Content
 Review of Intermediate Algebra Content Table of Contents Page Factoring GCF and Trinomials of the Form + b + c... Factoring Trinomials of the Form a + b + c... Factoring Perfect Square Trinomials... 6
Review of Intermediate Algebra Content Table of Contents Page Factoring GCF and Trinomials of the Form + b + c... Factoring Trinomials of the Form a + b + c... Factoring Perfect Square Trinomials... 6
Mathematics Placement
 Mathematics Placement The ACT COMPASS math test is a self-adaptive test, which potentially tests students within four different levels of math including pre-algebra, algebra, college algebra, and trigonometry.
Mathematics Placement The ACT COMPASS math test is a self-adaptive test, which potentially tests students within four different levels of math including pre-algebra, algebra, college algebra, and trigonometry.
The majority of college students hold credit cards. According to the Nellie May
 CHAPTER 6 Factoring Polynomials 6.1 The Greatest Common Factor and Factoring by Grouping 6. Factoring Trinomials of the Form b c 6.3 Factoring Trinomials of the Form a b c and Perfect Square Trinomials
CHAPTER 6 Factoring Polynomials 6.1 The Greatest Common Factor and Factoring by Grouping 6. Factoring Trinomials of the Form b c 6.3 Factoring Trinomials of the Form a b c and Perfect Square Trinomials
MATH 60 NOTEBOOK CERTIFICATIONS
 MATH 60 NOTEBOOK CERTIFICATIONS Chapter #1: Integers and Real Numbers 1.1a 1.1b 1.2 1.3 1.4 1.8 Chapter #2: Algebraic Expressions, Linear Equations, and Applications 2.1a 2.1b 2.1c 2.2 2.3a 2.3b 2.4 2.5
MATH 60 NOTEBOOK CERTIFICATIONS Chapter #1: Integers and Real Numbers 1.1a 1.1b 1.2 1.3 1.4 1.8 Chapter #2: Algebraic Expressions, Linear Equations, and Applications 2.1a 2.1b 2.1c 2.2 2.3a 2.3b 2.4 2.5
Factoring a Difference of Two Squares. Factoring a Difference of Two Squares
 284 (6 8) Chapter 6 Factoring 87. Tomato soup. The amount of metal S (in square inches) that it takes to make a can for tomato soup is a function of the radius r and height h: S 2 r 2 2 rh a) Rewrite this
284 (6 8) Chapter 6 Factoring 87. Tomato soup. The amount of metal S (in square inches) that it takes to make a can for tomato soup is a function of the radius r and height h: S 2 r 2 2 rh a) Rewrite this
Factoring Polynomials
 Factoring Polynomials 8A Factoring Methods 8-1 Factors and Greatest Common Factors Lab Model Factoring 8-2 Factoring by GCF Lab Model Factorization of Trinomials 8-3 Factoring x 2 + bx + c 8-4 Factoring
Factoring Polynomials 8A Factoring Methods 8-1 Factors and Greatest Common Factors Lab Model Factoring 8-2 Factoring by GCF Lab Model Factorization of Trinomials 8-3 Factoring x 2 + bx + c 8-4 Factoring
SUNY ECC. ACCUPLACER Preparation Workshop. Algebra Skills
 SUNY ECC ACCUPLACER Preparation Workshop Algebra Skills Gail A. Butler Ph.D. Evaluating Algebraic Epressions Substitute the value (#) in place of the letter (variable). Follow order of operations!!! E)
SUNY ECC ACCUPLACER Preparation Workshop Algebra Skills Gail A. Butler Ph.D. Evaluating Algebraic Epressions Substitute the value (#) in place of the letter (variable). Follow order of operations!!! E)
Chapter R.4 Factoring Polynomials
 Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
Determinants can be used to solve a linear system of equations using Cramer s Rule.
 2.6.2 Cramer s Rule Determinants can be used to solve a linear system of equations using Cramer s Rule. Cramer s Rule for Two Equations in Two Variables Given the system This system has the unique solution
2.6.2 Cramer s Rule Determinants can be used to solve a linear system of equations using Cramer s Rule. Cramer s Rule for Two Equations in Two Variables Given the system This system has the unique solution
1.1 Practice Worksheet
 Math 1 MPS Instructor: Cheryl Jaeger Balm 1 1.1 Practice Worksheet 1. Write each English phrase as a mathematical expression. (a) Three less than twice a number (b) Four more than half of a number (c)
Math 1 MPS Instructor: Cheryl Jaeger Balm 1 1.1 Practice Worksheet 1. Write each English phrase as a mathematical expression. (a) Three less than twice a number (b) Four more than half of a number (c)
6.1 Add & Subtract Polynomial Expression & Functions
 6.1 Add & Subtract Polynomial Expression & Functions Objectives 1. Know the meaning of the words term, monomial, binomial, trinomial, polynomial, degree, coefficient, like terms, polynomial funciton, quardrtic
6.1 Add & Subtract Polynomial Expression & Functions Objectives 1. Know the meaning of the words term, monomial, binomial, trinomial, polynomial, degree, coefficient, like terms, polynomial funciton, quardrtic
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0).
 This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
Algebra 1 Course Title
 Algebra 1 Course Title Course- wide 1. What patterns and methods are being used? Course- wide 1. Students will be adept at solving and graphing linear and quadratic equations 2. Students will be adept
Algebra 1 Course Title Course- wide 1. What patterns and methods are being used? Course- wide 1. Students will be adept at solving and graphing linear and quadratic equations 2. Students will be adept
By reversing the rules for multiplication of binomials from Section 4.6, we get rules for factoring polynomials in certain forms.
 SECTION 5.4 Special Factoring Techniques 317 5.4 Special Factoring Techniques OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor
SECTION 5.4 Special Factoring Techniques 317 5.4 Special Factoring Techniques OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor
CRLS Mathematics Department Algebra I Curriculum Map/Pacing Guide
 Curriculum Map/Pacing Guide page 1 of 14 Quarter I start (CP & HN) 170 96 Unit 1: Number Sense and Operations 24 11 Totals Always Include 2 blocks for Review & Test Operating with Real Numbers: How are
Curriculum Map/Pacing Guide page 1 of 14 Quarter I start (CP & HN) 170 96 Unit 1: Number Sense and Operations 24 11 Totals Always Include 2 blocks for Review & Test Operating with Real Numbers: How are
Polynomials. Key Terms. quadratic equation parabola conjugates trinomial. polynomial coefficient degree monomial binomial GCF
 Polynomials 5 5.1 Addition and Subtraction of Polynomials and Polynomial Functions 5.2 Multiplication of Polynomials 5.3 Division of Polynomials Problem Recognition Exercises Operations on Polynomials
Polynomials 5 5.1 Addition and Subtraction of Polynomials and Polynomial Functions 5.2 Multiplication of Polynomials 5.3 Division of Polynomials Problem Recognition Exercises Operations on Polynomials
Vocabulary Words and Definitions for Algebra
 Name: Period: Vocabulary Words and s for Algebra Absolute Value Additive Inverse Algebraic Expression Ascending Order Associative Property Axis of Symmetry Base Binomial Coefficient Combine Like Terms
Name: Period: Vocabulary Words and s for Algebra Absolute Value Additive Inverse Algebraic Expression Ascending Order Associative Property Axis of Symmetry Base Binomial Coefficient Combine Like Terms
Indiana State Core Curriculum Standards updated 2009 Algebra I
 Indiana State Core Curriculum Standards updated 2009 Algebra I Strand Description Boardworks High School Algebra presentations Operations With Real Numbers Linear Equations and A1.1 Students simplify and
Indiana State Core Curriculum Standards updated 2009 Algebra I Strand Description Boardworks High School Algebra presentations Operations With Real Numbers Linear Equations and A1.1 Students simplify and
Factoring (pp. 1 of 4)
 Factoring (pp. 1 of 4) Algebra Review Try these items from middle school math. A) What numbers are the factors of 4? B) Write down the prime factorization of 7. C) 6 Simplify 48 using the greatest common
Factoring (pp. 1 of 4) Algebra Review Try these items from middle school math. A) What numbers are the factors of 4? B) Write down the prime factorization of 7. C) 6 Simplify 48 using the greatest common
Polynomial Equations and Factoring
 7 Polynomial Equations and Factoring 7.1 Adding and Subtracting Polynomials 7.2 Multiplying Polynomials 7.3 Special Products of Polynomials 7.4 Dividing Polynomials 7.5 Solving Polynomial Equations in
7 Polynomial Equations and Factoring 7.1 Adding and Subtracting Polynomials 7.2 Multiplying Polynomials 7.3 Special Products of Polynomials 7.4 Dividing Polynomials 7.5 Solving Polynomial Equations in
Veterans Upward Bound Algebra I Concepts - Honors
 Veterans Upward Bound Algebra I Concepts - Honors Brenda Meery Kaitlyn Spong Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org Chapter 6. Factoring CHAPTER
Veterans Upward Bound Algebra I Concepts - Honors Brenda Meery Kaitlyn Spong Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org Chapter 6. Factoring CHAPTER
SOL Warm-Up Graphing Calculator Active
 A.2a (a) Using laws of exponents to simplify monomial expressions and ratios of monomial expressions 1. Which expression is equivalent to (5x 2 )(4x 5 )? A 9x 7 B 9x 10 C 20x 7 D 20x 10 2. Which expression
A.2a (a) Using laws of exponents to simplify monomial expressions and ratios of monomial expressions 1. Which expression is equivalent to (5x 2 )(4x 5 )? A 9x 7 B 9x 10 C 20x 7 D 20x 10 2. Which expression
called and explain why it cannot be factored with algebra tiles? and explain why it cannot be factored with algebra tiles?
 Factoring Reporting Category Topic Expressions and Operations Factoring polynomials Primary SOL A.2c The student will perform operations on polynomials, including factoring completely first- and second-degree
Factoring Reporting Category Topic Expressions and Operations Factoring polynomials Primary SOL A.2c The student will perform operations on polynomials, including factoring completely first- and second-degree
Algebra 2 PreAP. Name Period
 Algebra 2 PreAP Name Period IMPORTANT INSTRUCTIONS FOR STUDENTS!!! We understand that students come to Algebra II with different strengths and needs. For this reason, students have options for completing
Algebra 2 PreAP Name Period IMPORTANT INSTRUCTIONS FOR STUDENTS!!! We understand that students come to Algebra II with different strengths and needs. For this reason, students have options for completing
EAP/GWL Rev. 1/2011 Page 1 of 5. Factoring a polynomial is the process of writing it as the product of two or more polynomial factors.
 EAP/GWL Rev. 1/2011 Page 1 of 5 Factoring a polynomial is the process of writing it as the product of two or more polynomial factors. Example: Set the factors of a polynomial equation (as opposed to an
EAP/GWL Rev. 1/2011 Page 1 of 5 Factoring a polynomial is the process of writing it as the product of two or more polynomial factors. Example: Set the factors of a polynomial equation (as opposed to an
Factoring Polynomials
 Factoring Polynomials 8A Factoring Methods 8-1 Factors and Greatest Common Factors Lab Model Factorization by GCF 8-2 Factoring by GCF Lab Model Factorization of x 2 + bx + c 8-3 Factoring x 2 + bx + c
Factoring Polynomials 8A Factoring Methods 8-1 Factors and Greatest Common Factors Lab Model Factorization by GCF 8-2 Factoring by GCF Lab Model Factorization of x 2 + bx + c 8-3 Factoring x 2 + bx + c
FACTORING POLYNOMIALS
 296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
Section 5.0A Factoring Part 1
 Section 5.0A Factoring Part 1 I. Work Together A. Multiply the following binomials into trinomials. (Write the final result in descending order, i.e., a + b + c ). ( 7)( + 5) ( + 7)( + ) ( + 7)( + 5) (
Section 5.0A Factoring Part 1 I. Work Together A. Multiply the following binomials into trinomials. (Write the final result in descending order, i.e., a + b + c ). ( 7)( + 5) ( + 7)( + ) ( + 7)( + 5) (
This unit has primarily been about quadratics, and parabolas. Answer the following questions to aid yourselves in creating your own study guide.
 COLLEGE ALGEBRA UNIT 2 WRITING ASSIGNMENT This unit has primarily been about quadratics, and parabolas. Answer the following questions to aid yourselves in creating your own study guide. 1) What is the
COLLEGE ALGEBRA UNIT 2 WRITING ASSIGNMENT This unit has primarily been about quadratics, and parabolas. Answer the following questions to aid yourselves in creating your own study guide. 1) What is the
COMPETENCY TEST SAMPLE TEST. A scientific, non-graphing calculator is required for this test. C = pd or. A = pr 2. A = 1 2 bh
 BASIC MATHEMATICS COMPETENCY TEST SAMPLE TEST 2004 A scientific, non-graphing calculator is required for this test. The following formulas may be used on this test: Circumference of a circle: C = pd or
BASIC MATHEMATICS COMPETENCY TEST SAMPLE TEST 2004 A scientific, non-graphing calculator is required for this test. The following formulas may be used on this test: Circumference of a circle: C = pd or
ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form
 ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form Goal Graph quadratic functions. VOCABULARY Quadratic function A function that can be written in the standard form y = ax 2 + bx+ c where a 0 Parabola
ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form Goal Graph quadratic functions. VOCABULARY Quadratic function A function that can be written in the standard form y = ax 2 + bx+ c where a 0 Parabola
Polynomials and Factoring
 7.6 Polynomials and Factoring Basic Terminology A term, or monomial, is defined to be a number, a variable, or a product of numbers and variables. A polynomial is a term or a finite sum or difference of
7.6 Polynomials and Factoring Basic Terminology A term, or monomial, is defined to be a number, a variable, or a product of numbers and variables. A polynomial is a term or a finite sum or difference of
8-5 Using the Distributive Property. Use the Distributive Property to factor each polynomial. 1. 21b 15a SOLUTION:
 Use the Distributive Property to factor each polynomial. 1. 1b 15a The greatest common factor in each term is 3.. 14c + c The greatest common factor in each term is c. 3. 10g h + 9gh g h The greatest common
Use the Distributive Property to factor each polynomial. 1. 1b 15a The greatest common factor in each term is 3.. 14c + c The greatest common factor in each term is c. 3. 10g h + 9gh g h The greatest common
Brunswick High School has reinstated a summer math curriculum for students Algebra 1, Geometry, and Algebra 2 for the 2014-2015 school year.
 Brunswick High School has reinstated a summer math curriculum for students Algebra 1, Geometry, and Algebra 2 for the 2014-2015 school year. Goal The goal of the summer math program is to help students
Brunswick High School has reinstated a summer math curriculum for students Algebra 1, Geometry, and Algebra 2 for the 2014-2015 school year. Goal The goal of the summer math program is to help students
Tool 1. Greatest Common Factor (GCF)
 Chapter 4: Factoring Review Tool 1 Greatest Common Factor (GCF) This is a very important tool. You must try to factor out the GCF first in every problem. Some problems do not have a GCF but many do. When
Chapter 4: Factoring Review Tool 1 Greatest Common Factor (GCF) This is a very important tool. You must try to factor out the GCF first in every problem. Some problems do not have a GCF but many do. When
Factoring Trinomials: The ac Method
 6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
Factoring Algebra- Chapter 8B Assignment Sheet
 Name: Factoring Algebra- Chapter 8B Assignment Sheet Date Section Learning Targets Assignment Tues 2/17 Find the prime factorization of an integer Find the greatest common factor (GCF) for a set of monomials.
Name: Factoring Algebra- Chapter 8B Assignment Sheet Date Section Learning Targets Assignment Tues 2/17 Find the prime factorization of an integer Find the greatest common factor (GCF) for a set of monomials.
Pre-Calculus II Factoring and Operations on Polynomials
 Factoring... 1 Polynomials...1 Addition of Polynomials... 1 Subtraction of Polynomials...1 Multiplication of Polynomials... Multiplying a monomial by a monomial... Multiplying a monomial by a polynomial...
Factoring... 1 Polynomials...1 Addition of Polynomials... 1 Subtraction of Polynomials...1 Multiplication of Polynomials... Multiplying a monomial by a monomial... Multiplying a monomial by a polynomial...
Florida Algebra 1 End-of-Course Assessment Item Bank, Polk County School District
 Benchmark: MA.912.A.2.3; Describe the concept of a function, use function notation, determine whether a given relation is a function, and link equations to functions. Also assesses MA.912.A.2.13; Solve
Benchmark: MA.912.A.2.3; Describe the concept of a function, use function notation, determine whether a given relation is a function, and link equations to functions. Also assesses MA.912.A.2.13; Solve
Factoring Polynomials and Solving Quadratic Equations
 Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
MATH 21. College Algebra 1 Lecture Notes
 MATH 21 College Algebra 1 Lecture Notes MATH 21 3.6 Factoring Review College Algebra 1 Factoring and Foiling 1. (a + b) 2 = a 2 + 2ab + b 2. 2. (a b) 2 = a 2 2ab + b 2. 3. (a + b)(a b) = a 2 b 2. 4. (a
MATH 21 College Algebra 1 Lecture Notes MATH 21 3.6 Factoring Review College Algebra 1 Factoring and Foiling 1. (a + b) 2 = a 2 + 2ab + b 2. 2. (a b) 2 = a 2 2ab + b 2. 3. (a + b)(a b) = a 2 b 2. 4. (a
AIP Factoring Practice/Help
 The following pages include many problems to practice factoring skills. There are also several activities with examples to help you with factoring if you feel like you are not proficient with it. There
The following pages include many problems to practice factoring skills. There are also several activities with examples to help you with factoring if you feel like you are not proficient with it. There
Blue Pelican Alg II First Semester
 Blue Pelican Alg II First Semester Teacher Version 1.01 Copyright 2009 by Charles E. Cook; Refugio, Tx (All rights reserved) Alg II Syllabus (First Semester) Unit 1: Solving linear equations and inequalities
Blue Pelican Alg II First Semester Teacher Version 1.01 Copyright 2009 by Charles E. Cook; Refugio, Tx (All rights reserved) Alg II Syllabus (First Semester) Unit 1: Solving linear equations and inequalities
Factoring Polynomials
 Factoring a Polynomial Expression Factoring a polynomial is expressing the polynomial as a product of two or more factors. Simply stated, it is somewhat the reverse process of multiplying. To factor polynomials,
Factoring a Polynomial Expression Factoring a polynomial is expressing the polynomial as a product of two or more factors. Simply stated, it is somewhat the reverse process of multiplying. To factor polynomials,
FACTORING ax 2 bx c. Factoring Trinomials with Leading Coefficient 1
 5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
HIBBING COMMUNITY COLLEGE COURSE OUTLINE
 HIBBING COMMUNITY COLLEGE COURSE OUTLINE COURSE NUMBER & TITLE: - Beginning Algebra CREDITS: 4 (Lec 4 / Lab 0) PREREQUISITES: MATH 0920: Fundamental Mathematics with a grade of C or better, Placement Exam,
HIBBING COMMUNITY COLLEGE COURSE OUTLINE COURSE NUMBER & TITLE: - Beginning Algebra CREDITS: 4 (Lec 4 / Lab 0) PREREQUISITES: MATH 0920: Fundamental Mathematics with a grade of C or better, Placement Exam,
When factoring, we look for greatest common factor of each term and reverse the distributive property and take out the GCF.
 Factoring: reversing the distributive property. The distributive property allows us to do the following: When factoring, we look for greatest common factor of each term and reverse the distributive property
Factoring: reversing the distributive property. The distributive property allows us to do the following: When factoring, we look for greatest common factor of each term and reverse the distributive property
Section 6.1 Factoring Expressions
 Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
Factoring Flow Chart
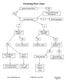 Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
PERT Mathematics Test Review
 PERT Mathematics Test Review Prof. Miguel A. Montañez ESL/Math Seminar Math Test? NO!!!!!!! I am not good at Math! I cannot graduate because of Math! I hate Math! Helpful Sites Math Dept Web Site Wolfson
PERT Mathematics Test Review Prof. Miguel A. Montañez ESL/Math Seminar Math Test? NO!!!!!!! I am not good at Math! I cannot graduate because of Math! I hate Math! Helpful Sites Math Dept Web Site Wolfson
Sect 6.7 - Solving Equations Using the Zero Product Rule
 Sect 6.7 - Solving Equations Using the Zero Product Rule 116 Concept #1: Definition of a Quadratic Equation A quadratic equation is an equation that can be written in the form ax 2 + bx + c = 0 (referred
Sect 6.7 - Solving Equations Using the Zero Product Rule 116 Concept #1: Definition of a Quadratic Equation A quadratic equation is an equation that can be written in the form ax 2 + bx + c = 0 (referred
Florida Math 0028. Correlation of the ALEKS course Florida Math 0028 to the Florida Mathematics Competencies - Upper
 Florida Math 0028 Correlation of the ALEKS course Florida Math 0028 to the Florida Mathematics Competencies - Upper Exponents & Polynomials MDECU1: Applies the order of operations to evaluate algebraic
Florida Math 0028 Correlation of the ALEKS course Florida Math 0028 to the Florida Mathematics Competencies - Upper Exponents & Polynomials MDECU1: Applies the order of operations to evaluate algebraic
Algebra EOC Practice Test #4
 Class: Date: Algebra EOC Practice Test #4 Multiple Choice Identify the choice that best completes the statement or answers the question. 1. For f(x) = 3x + 4, find f(2) and find x such that f(x) = 17.
Class: Date: Algebra EOC Practice Test #4 Multiple Choice Identify the choice that best completes the statement or answers the question. 1. For f(x) = 3x + 4, find f(2) and find x such that f(x) = 17.
FACTORING QUADRATICS 8.1.1 and 8.1.2
 FACTORING QUADRATICS 8.1.1 and 8.1.2 Chapter 8 introduces students to quadratic equations. These equations can be written in the form of y = ax 2 + bx + c and, when graphed, produce a curve called a parabola.
FACTORING QUADRATICS 8.1.1 and 8.1.2 Chapter 8 introduces students to quadratic equations. These equations can be written in the form of y = ax 2 + bx + c and, when graphed, produce a curve called a parabola.
Factoring Special Polynomials
 6.6 Factoring Special Polynomials 6.6 OBJECTIVES 1. Factor the difference of two squares 2. Factor the sum or difference of two cubes In this section, we will look at several special polynomials. These
6.6 Factoring Special Polynomials 6.6 OBJECTIVES 1. Factor the difference of two squares 2. Factor the sum or difference of two cubes In this section, we will look at several special polynomials. These
5.1 FACTORING OUT COMMON FACTORS
 C H A P T E R 5 Factoring he sport of skydiving was born in the 1930s soon after the military began using parachutes as a means of deploying troops. T Today, skydiving is a popular sport around the world.
C H A P T E R 5 Factoring he sport of skydiving was born in the 1930s soon after the military began using parachutes as a means of deploying troops. T Today, skydiving is a popular sport around the world.
Mathematics Online Instructional Materials Correlation to the 2009 Algebra I Standards of Learning and Curriculum Framework
 Provider York County School Division Course Syllabus URL http://yorkcountyschools.org/virtuallearning/coursecatalog.aspx Course Title Algebra I AB Last Updated 2010 - A.1 The student will represent verbal
Provider York County School Division Course Syllabus URL http://yorkcountyschools.org/virtuallearning/coursecatalog.aspx Course Title Algebra I AB Last Updated 2010 - A.1 The student will represent verbal
Factoring Guidelines. Greatest Common Factor Two Terms Three Terms Four Terms. 2008 Shirley Radai
 Factoring Guidelines Greatest Common Factor Two Terms Three Terms Four Terms 008 Shirley Radai Greatest Common Factor 008 Shirley Radai Factoring by Finding the Greatest Common Factor Always check for
Factoring Guidelines Greatest Common Factor Two Terms Three Terms Four Terms 008 Shirley Radai Greatest Common Factor 008 Shirley Radai Factoring by Finding the Greatest Common Factor Always check for
15.1 Factoring Polynomials
 LESSON 15.1 Factoring Polynomials Use the structure of an expression to identify ways to rewrite it. Also A.SSE.3? ESSENTIAL QUESTION How can you use the greatest common factor to factor polynomials? EXPLORE
LESSON 15.1 Factoring Polynomials Use the structure of an expression to identify ways to rewrite it. Also A.SSE.3? ESSENTIAL QUESTION How can you use the greatest common factor to factor polynomials? EXPLORE
MATH 095, College Prep Mathematics: Unit Coverage Pre-algebra topics (arithmetic skills) offered through BSE (Basic Skills Education)
 MATH 095, College Prep Mathematics: Unit Coverage Pre-algebra topics (arithmetic skills) offered through BSE (Basic Skills Education) Accurately add, subtract, multiply, and divide whole numbers, integers,
MATH 095, College Prep Mathematics: Unit Coverage Pre-algebra topics (arithmetic skills) offered through BSE (Basic Skills Education) Accurately add, subtract, multiply, and divide whole numbers, integers,
MTH 100 College Algebra Essex County College Division of Mathematics Sample Review Questions 1 Created June 6, 2011
 MTH 00 College Algebra Essex County College Division of Mathematics Sample Review Questions Created June 6, 0 Math 00, Introductory College Mathematics, covers the mathematical content listed below. In
MTH 00 College Algebra Essex County College Division of Mathematics Sample Review Questions Created June 6, 0 Math 00, Introductory College Mathematics, covers the mathematical content listed below. In
Florida Math for College Readiness
 Core Florida Math for College Readiness Florida Math for College Readiness provides a fourth-year math curriculum focused on developing the mastery of skills identified as critical to postsecondary readiness
Core Florida Math for College Readiness Florida Math for College Readiness provides a fourth-year math curriculum focused on developing the mastery of skills identified as critical to postsecondary readiness
