The Greatest Common Factor; Factoring by Grouping
|
|
|
- Allison Johns
- 8 years ago
- Views:
Transcription
1 296 CHAPTER 5 Factoring and Applications 5.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor. 3 Factor by grouping. Recall from Section 1.1 that to factor means to write a quantity as a product. That is, factoring is the opposite of multiplying. Multiplying Other factored forms of 12 are , 6 # 2 = 12 Factoring Factors Product Product Factors 3 # 4, , 12 # 1, 12 = 6 # 2 More than two factors may be used, so another factored form of 12 is 2 # 2 # 3. and OBJECTIVE 1 Find the greatest common factor of a list of terms. An integer that is a factor of two or more integers is a common factor of those integers. For example, 6 is a common factor of 18 and 24, since 6 is a factor of both 18 and 24. Other common factors of 18 and 24 are 1, 2, and 3. The greatest common factor (GCF) of a list of integers is the largest common factor of those integers. Thus, 6 is the greatest common factor of 18 and 24, since it is the largest of their common factors. NOTE Factors of a number are also divisors of the number. The greatest common factor is actually the same as the greatest common divisor. Here are some useful divisibility rules for deciding what numbers divide into a given number. A Whole Number Divisible by 2 Ends in 0, 2, 4, 6, or 8 Must Have the Following Property: 3 Sum of digits divisible by 3 4 Last two digits form a number divisible by 4 5 Ends in 0 or 5 6 Divisible by both 2 and 3 8 Last three digits form a number divisible by 8 9 Sum of digits divisible by 9 10 Ends in 0 Finding the Greatest Common Factor (GCF) Step 1 Step 2 Step 3 Step 4 Factor. Write each number in prime factored form. List common factors. List each prime number or each variable that is a factor of every term in the list. (If a prime does not appear in one of the prime factored forms, it cannot appear in the greatest common factor.) Choose least exponents. Use as exponents on the common prime factors the least exponents from the prime factored forms. Multiply the primes from Step 3. If there are no primes left after Step 3, the greatest common factor is 1.
2 SECTION 5.1 The Greatest Common Factor; Factoring by Grouping 297 EXERCISE 1 Find the greatest common factor for each list of numbers. 24, 36 54, 90, 108 (c) 15, 19, 25 EXAMPLE 1 Finding the Greatest Common Factor for Numbers Find the greatest common factor for each list of numbers. 30, = 2 # 3 # 5 45 = 3 # 3 # 5 Write the prime factored form of each number. Use each prime the least number of times it appears in all the factored forms. There is no 2 in the prime factored form of 45, so there will be no 2 in the greatest common factor. The least number of times 3 appears in all the factored forms is 1, and the least number of times 5 appears is also 1. 72, 120, = 2 # 2 # 2 # 3 # = 2 # 2 # 2 # 3 # 5 GCF = 3 1 # 5 1 = = 2 # 2 # 2 # 2 # 3 # 3 # 3 Write the prime factored form of each number. The least number of times 2 appears in all the factored forms is 3, and the least number of times 3 appears is 1. There is no 5 in the prime factored form of either 72 or 432. (c) 10, 11, = 2 # 5 11 = = 2 # 7 GCF = 2 3 # 3 1 = 24 Write the prime factored form of each number. There are no primes common to all three numbers, so the GCF is 1. The greatest common factor can also be found for a list of variable terms. For example, the terms x 4, x 5, x 6, and x 7 have x 4 as the greatest common factor because each of these terms can be written with x 4 as a factor. x 4 = 1 # x 4, x 5 = x # x 4, x 6 = x 2 # x 4, x 7 = x 3 # x 4 NOTE The exponent on a variable in the GCF is the least exponent that appears in all the common factors. ANSWERS (c) 1 EXAMPLE 2 Finding the Greatest Common Factor for Variable Terms Find the greatest common factor for each list of terms. 21m 7, 18m 6, 45m 8, 24m 5 21m 7 = 3 # 7 # m 7 18m 6 = 2 # 3 # 3 # m 6 45m 8 = 3 # 3 # 5 # m 8 24m 5 = 2 # 2 # 2 # 3 # m 5 Here, 3 is the greatest common factor of the coefficients 21, 18, 45, and 24. The least exponent on m is 5. GCF = 3m 5
3 298 CHAPTER 5 Factoring and Applications EXERCISE 2 Find the greatest common factor for each list of terms. 25k 3, 15k 2, 35k 5 m 3 n 5, m 4 n 4, m 5 n 2 x 4 y 2, x 7 y 5, x 3 x 4 y 2 = x 4 # y 7, y 15 x 7 y 5 = x 7 # y 2 There is no x in the last term, y 15, so x will not appear in x 3 y 7 = x 3 # y 5 the greatest common factor. There is a y in each term, however, and 2 is the least exponent on y. y 7 GCF = y 2 y 15 = y 15 OBJECTIVE 2 Factor out the greatest common factor. Writing a polynomial (a sum) in factored form as a product is called factoring. For example, the polynomial 3m + 12 has two terms: 3m and 12. The greatest common factor of these two terms is 3. We can write 3m + 12 so that each term is a product with 3 as one factor. 3m + 12 = 3 # m + 3 # 4 GCF = 3 = 31m + 42 Distributive property The factored form of 3m + 12 is 31m This process is called factoring out the greatest common factor. CAUTION The polynomial 3m + 12 is not in factored form when written as 3 # m + 3 # 4. Not in factored form The terms are factored, but the polynomial is not. The factored form of 3m + 12 is the product 31m In factored form EXAMPLE 3 Factoring Out the Greatest Common Factor Write in factored form by factoring out the greatest common factor. 5y y = 5y1 y2 + 5y122 GCF = 5y = 5y1 y + 22 Distributive property CHECK Multiply the factored form. ANSWERS 2. 5k 2 m 3 n 2 5y1 y + 22 = 5y1 y2 + 5y122 Distributive property = 5y y Original polynomial 20m m m 3 = 5m 3 14m m 3 12m2 + 5m GCF = 5m 3 = 5m 3 14m 2 + 2m + 32 Factor out 5m 3. CHECK 5m 3 14m 2 + 2m + 32 = 20m m m 3 Original polynomial
4 SECTION 5.1 The Greatest Common Factor; Factoring by Grouping 299 EXERCISE 3 Write in factored form by factoring out the greatest common factor. 7t 4-14t 3 8x 6-20x x 4 (c) 30m 4 n 3-42m 2 n 2 (c) x 5 + x 3 = x 3 1x x = x 3 1x Check mentally by distributing (d) 20m 7 p 2-36m 3 p 4 = 4m 3 p 2 15m 4-9p 2 2 GCF = x 3 Don t forget the 1. x 3 = 4m 3 p 2 15m 4 2-4m 3 p 2 19p 2 2 over each term inside the parentheses. GCF = 4m 3 p 2 Factor out 4m 3 p 2. CAUTION Be sure to include the 1 in a problem like Example 3(c). Check that the factored form can be multiplied out to give the original polynomial. EXERCISE 4 Write in factored form by factoring out the greatest common factor. x1x x + 22 a1t b1t EXAMPLE 4 Factoring Out the Greatest Common Factor Write in factored form by factoring out the greatest common factor. Same a1a a + 32 The binomial a + 3 is the greatest common factor. =1a + 321a + 42 x 2 1x x + 12 =1x + 121x 2-52 Factor out a + 3. Factor out x + 1. NOTE In factored forms like those in Example 4, the order of the factors does not matter because of the commutative property of multiplication. 1a + 321a + 42 can also be written 1a + 421a OBJECTIVE 3 Factor by grouping. When a polynomial has four terms, common factors can sometimes be used to factor by grouping. ANSWERS 3. 7t 3 1t x 4 12x 2-5x + 72 (c) 6m 2 n 2 15m 2 n x + 221x t a - b2 EXAMPLE 5 Factor by grouping. Factoring by Grouping 2x ax + 3a Group the first two terms and the last two terms, since the first two terms have a common factor of 2 and the last two terms have a common factor of a. 2x ax + 3a =12x ax + 3a2 = 21x a1x + 32 Factor each group. The expression is still not in factored form because it is the sum of two terms. Now, however, x + 3 is a common factor and can be factored out a21x + 32 is also correct. = 21x a1x + 32 =1x a2 x + 3 is a common factor. Factor out x + 3.
5 300 CHAPTER 5 Factoring and Applications EXERCISE 5 Factor by grouping. ab + 3a + 5b xy + 3x + 4y + 1 (c) x 3 + 5x 2-8x - 40 The final result1x a2 is in factored form because it is a product. CHECK CHECK (c) CHECK 1x a2 = 2x + ax a = 2x ax + 3a 6ax + 24x + a + 4 =16ax + 24x2 +1a + 42 = 6x1a a + 42 =1a x a x + 12 = 6ax + a + 24x + 4 = 6ax + 24x + a + 4 2x 2-10x + 3xy - 15y =12x 2-10x2 +13xy - 15y2 = 2x1x y1x - 52 =1x x + 3y2 1x x + 3y2 FOIL (Section 5.5) Rearrange terms to obtain the original polynomial. Factor each group. Remember the 1. Factor out a + 4. = 2x 2 + 3xy - 10x - 15y = 2x 2-10x + 3xy - 15y FOIL Rearrange terms to obtain the original polynomial. Factor each group. Factor out x - 5. FOIL Original polynomial (d) t 3 + 2t 2-3t - 6 =1t 3 + 2t t - 62 = t 2 1t t + 22 =1t + 221t 2 32 Check by multiplying. Be careful with signs. Write a + sign between the groups. Factor out 3 so there is a common factor, t + 2; -3(t + 2) = -3t - 6. Factor out t + 2. CAUTION Be careful with signs when grouping in a problem like Example 5(d). It is wise to check the factoring in the second step, as shown in the side comment in that example, before continuing. ANSWERS 5. 1b + 321a y x + 12 (c) 1x + 521x 2-82 Factoring a Polynomial with Four Terms by Grouping Step 1 Step 2 Step 3 Step 4 Group terms. Collect the terms into two groups so that each group has a common factor. Factor within groups. Factor out the greatest common factor from each group. Factor the entire polynomial. Factor out a common binomial factor from the results of Step 2. If necessary, rearrange terms. If Step 2 does not result in a common binomial factor, try a different grouping.
6 SECTION 5.1 The Greatest Common Factor; Factoring by Grouping 301 EXERCISE 6 Factor by grouping. 12p 2-28q - 16pq + 21p 5xy x + 2y ANSWERS 6. 13p - 4q214p x y - 32 EXAMPLE 6 Factor by grouping. Rearranging Terms before Factoring by Grouping 10x 2-12y + 15x - 8xy Factoring out the common factor of 2 from the first two terms and the common factor of x from the last two terms gives the following. CHECK This does not lead to a common factor, so we try rearranging the terms. 10x 2-12y + 15x - 8xy = 10x 2-8xy - 12y + 15x =110x 2-8xy y + 15x2 = 2x15x - 4y y + 5x2 = 2x15x - 4y x - 4y2 =15x - 4y212x x - 4y212x x 2-12y + 15x - 8xy = 10x x - 8xy - 12y = 10x 2-12y + 15x - 8xy Commutative property Factor each group. Rewrite -4y + 5x. Factor out 5x - 4y. FOIL Original polynomial 2xy y - 8x We need to rearrange these terms to get two groups that each have a common factor. Trial and error suggests the following grouping. 2xy y - 8x =12xy - 3y2 +1-8x = y12x x - 32 =12x y - 42 = 215x 2-6y2 + x115-8y2 Write a + sign between the groups. Be careful with signs. Factor each group; -412x - 32 = -8x Factor out 2x - 3. Since the quantities in parentheses in the second step must be the same, we factored out -4 rather than 4. Check by multiplying. 5.1 EXERCISES Complete solution available on the Video Resources on DVD Find the greatest common factor for each list of numbers. See Example , 20, , 30, , 24, 36, , 30, 45, , 8, , 22, 23 Find the greatest common factor for each list of terms. See Examples 1 and y, w, x 3, 40x 6, 50x z 4, 70z 8, 90z x 4 y 3, xy a 4 b 5, a 3 b m 3 n 2, 18m 5 n 4, 36m 8 n p 5 r 7, 30p 7 r 8, 50p 5 r 3
7 302 CHAPTER 5 Factoring and Applications Concept Check An expression is factored when it is written as a product, not a sum. Which of the following are not factored? 15. 2k 2 15k k 2 15k k 2 +15k k 2 + 5k2 + 1 Complete each factoring by writing each polynomial as the product of two factors m p = 3m = 6p z 9 = -4z k m 4 n a 3 b 2 = -5k = 3m 3 n1 2 = 9a 2 b y p a 2-20a = = = 10a x 2-30x 29. 8x 2 y + 12x 3 y = 15x1 2 = 4x 2 y1 2 18s 3 t st = 2st How can you check your answer when you factor a polynomial? 32. Concept Check A student factored 18x 3 y 2 + 9xy as 9xy12x 2 y2. WHAT WENT WRONG? Factor correctly. Write in factored form by factoring out the greatest common factor. See Examples 3 and x 2-4x 34. m 2-7m 35. 6t t 36. 8x 2 + 6x m 3-9m p 3-24p z z k4 + 15k x 3 + 6x b 3 + 7b y y a a w z mn m 2 n p 2 y + 38p 2 y y y 4-39y x5 + 25x4-20x p 6 q + 45p 5 q p 3 q a3z5 + 60a4z4 + 85a5z2 53. a 5 + 2a 3 b 2-3a 5 b 2 + 4a 4 b x 6 + 5x 4 y 3-6xy xy 55. c1x d1x r1x t1x m1m + 2n2 + n1m + 2n2 58. q1q + 4p2 + p1q + 4p2 59. q 2 1 p p y 2 1x x - 92 Students often have difficulty when factoring by grouping because they are not able to tell when the polynomial is completely factored. For example, 5y12x t12x - 32 Not in factored form is not in factored form, because it is the sum of two terms: 5y12x - 32 and 8t12x However, because 2x - 3 is a common factor of these two terms, the expression can now be factored. 12x y + 8t2 In factored form The factored form is a product of two factors: 2x - 3 and 5y + 8t. Concept Check Determine whether each expression is in factored form or is not in factored form. If it is not in factored form, factor it if possible t x17t r15x x x217t r x x 2 1 y y k 3 1s s Concept Check Why is it not possible to factor the expression in Exercise 65?
8 SECTION 5.1 The Greatest Common Factor; Factoring by Grouping Concept Check A student factored x 3 + 4x 2-2x - 8 as follows. x 3 + 4x 2-2x - 8 The student could not find a common factor of the two terms. WHAT WENT WRONG? Complete the factoring. Factor by grouping. See Examples 5 and 6. =1x 3 + 4x x - 82 = x 2 1x x p 2 + 4p + pq + 4q 70. m 2 + 2m + mn + 2n 71. a 2-2a + ab - 2b 72. y 2-6y + yw - 6w 73. 7z z - az - 2a 74. 5m mp - 2mr - 6pr r ry - 3xr - 2xy 76. 8s2-4st + 6sy - 3yt 77. 3a 3 + 3ab 2 + 2a 2 b + 2b x 3 + 3x 2 y + 4xy 2 + 3y a - 3b + ab x - 2y + xy m 3-4m 2 p 2-4mp + p t 3-2t 2 s 2-5ts + s y 2 + 3x + 3y + xy 84. m p + 7m + 2mp 85. 5m - 6p - 2mp y - 9x - 3xy r 2-2ty + 12ry - 3rt a 2-4bc + 16ac - 3ab 89. a a 5 b - 6b 90. b ab 3-10a RELATING CONCEPTS EXERCISES FOR INDIVIDUAL OR GROUP WORK In many cases, the choice of which pairs of terms to group when factoring by grouping can be made in different ways. To see this for Example 6, work Exercises in order. 91. Start with the polynomial from Example 6, 2xy y - 8x, and rearrange the terms as follows: 2xy - 8x - 3y What property from Section 1.7 allows this? 92. Group the first two terms and the last two terms of the rearranged polynomial in Exercise 91. Then factor each group. 93. Is your result from Exercise 92 in factored form? Explain your answer. 94. If your answer to Exercise 93 is no, factor the polynomial. Is the result the same as that shown for Example 6? PREVIEW EXERCISES Find each product. See Section x + 621x x - 321x x + 221x x1x + 521x x 2 1x 2 + 3x x 2 12x 2-4x - 92
6.1 The Greatest Common Factor; Factoring by Grouping
 386 CHAPTER 6 Factoring and Applications 6.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
386 CHAPTER 6 Factoring and Applications 6.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
By reversing the rules for multiplication of binomials from Section 4.6, we get rules for factoring polynomials in certain forms.
 SECTION 5.4 Special Factoring Techniques 317 5.4 Special Factoring Techniques OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor
SECTION 5.4 Special Factoring Techniques 317 5.4 Special Factoring Techniques OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor
FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c
 Tallahassee Community College 55 FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c This kind of trinomial differs from the previous kind we have factored because the coefficient of x is no longer "1".
Tallahassee Community College 55 FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c This kind of trinomial differs from the previous kind we have factored because the coefficient of x is no longer "1".
1.3 Polynomials and Factoring
 1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
Using the ac Method to Factor
 4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
FACTORING ax 2 bx c. Factoring Trinomials with Leading Coefficient 1
 5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
Factoring Trinomials of the Form x 2 bx c
 4.2 Factoring Trinomials of the Form x 2 bx c 4.2 OBJECTIVES 1. Factor a trinomial of the form x 2 bx c 2. Factor a trinomial containing a common factor NOTE The process used to factor here is frequently
4.2 Factoring Trinomials of the Form x 2 bx c 4.2 OBJECTIVES 1. Factor a trinomial of the form x 2 bx c 2. Factor a trinomial containing a common factor NOTE The process used to factor here is frequently
Factoring and Applications
 Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
Factoring Special Polynomials
 6.6 Factoring Special Polynomials 6.6 OBJECTIVES 1. Factor the difference of two squares 2. Factor the sum or difference of two cubes In this section, we will look at several special polynomials. These
6.6 Factoring Special Polynomials 6.6 OBJECTIVES 1. Factor the difference of two squares 2. Factor the sum or difference of two cubes In this section, we will look at several special polynomials. These
How To Factor By Gcf In Algebra 1.5
 7-2 Factoring by GCF Warm Up Lesson Presentation Lesson Quiz Algebra 1 Warm Up Simplify. 1. 2(w + 1) 2. 3x(x 2 4) 2w + 2 3x 3 12x Find the GCF of each pair of monomials. 3. 4h 2 and 6h 2h 4. 13p and 26p
7-2 Factoring by GCF Warm Up Lesson Presentation Lesson Quiz Algebra 1 Warm Up Simplify. 1. 2(w + 1) 2. 3x(x 2 4) 2w + 2 3x 3 12x Find the GCF of each pair of monomials. 3. 4h 2 and 6h 2h 4. 13p and 26p
Factoring Methods. Example 1: 2x + 2 2 * x + 2 * 1 2(x + 1)
 Factoring Methods When you are trying to factor a polynomial, there are three general steps you want to follow: 1. See if there is a Greatest Common Factor 2. See if you can Factor by Grouping 3. See if
Factoring Methods When you are trying to factor a polynomial, there are three general steps you want to follow: 1. See if there is a Greatest Common Factor 2. See if you can Factor by Grouping 3. See if
Factoring a Difference of Two Squares. Factoring a Difference of Two Squares
 284 (6 8) Chapter 6 Factoring 87. Tomato soup. The amount of metal S (in square inches) that it takes to make a can for tomato soup is a function of the radius r and height h: S 2 r 2 2 rh a) Rewrite this
284 (6 8) Chapter 6 Factoring 87. Tomato soup. The amount of metal S (in square inches) that it takes to make a can for tomato soup is a function of the radius r and height h: S 2 r 2 2 rh a) Rewrite this
Chapter R.4 Factoring Polynomials
 Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0).
 This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
Factoring (pp. 1 of 4)
 Factoring (pp. 1 of 4) Algebra Review Try these items from middle school math. A) What numbers are the factors of 4? B) Write down the prime factorization of 7. C) 6 Simplify 48 using the greatest common
Factoring (pp. 1 of 4) Algebra Review Try these items from middle school math. A) What numbers are the factors of 4? B) Write down the prime factorization of 7. C) 6 Simplify 48 using the greatest common
Factoring Polynomials
 Factoring a Polynomial Expression Factoring a polynomial is expressing the polynomial as a product of two or more factors. Simply stated, it is somewhat the reverse process of multiplying. To factor polynomials,
Factoring a Polynomial Expression Factoring a polynomial is expressing the polynomial as a product of two or more factors. Simply stated, it is somewhat the reverse process of multiplying. To factor polynomials,
FACTORING POLYNOMIALS
 296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
Math 25 Activity 6: Factoring Advanced
 Instructor! Math 25 Activity 6: Factoring Advanced Last week we looked at greatest common factors and the basics of factoring out the GCF. In this second activity, we will discuss factoring more difficult
Instructor! Math 25 Activity 6: Factoring Advanced Last week we looked at greatest common factors and the basics of factoring out the GCF. In this second activity, we will discuss factoring more difficult
Polynomials. Key Terms. quadratic equation parabola conjugates trinomial. polynomial coefficient degree monomial binomial GCF
 Polynomials 5 5.1 Addition and Subtraction of Polynomials and Polynomial Functions 5.2 Multiplication of Polynomials 5.3 Division of Polynomials Problem Recognition Exercises Operations on Polynomials
Polynomials 5 5.1 Addition and Subtraction of Polynomials and Polynomial Functions 5.2 Multiplication of Polynomials 5.3 Division of Polynomials Problem Recognition Exercises Operations on Polynomials
Factoring Trinomials: The ac Method
 6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
FACTORING OUT COMMON FACTORS
 278 (6 2) Chapter 6 Factoring 6.1 FACTORING OUT COMMON FACTORS In this section Prime Factorization of Integers Greatest Common Factor Finding the Greatest Common Factor for Monomials Factoring Out the
278 (6 2) Chapter 6 Factoring 6.1 FACTORING OUT COMMON FACTORS In this section Prime Factorization of Integers Greatest Common Factor Finding the Greatest Common Factor for Monomials Factoring Out the
expression is written horizontally. The Last terms ((2)( 4)) because they are the last terms of the two polynomials. This is called the FOIL method.
 A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
In algebra, factor by rewriting a polynomial as a product of lower-degree polynomials
 Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
Polynomials and Factoring
 7.6 Polynomials and Factoring Basic Terminology A term, or monomial, is defined to be a number, a variable, or a product of numbers and variables. A polynomial is a term or a finite sum or difference of
7.6 Polynomials and Factoring Basic Terminology A term, or monomial, is defined to be a number, a variable, or a product of numbers and variables. A polynomial is a term or a finite sum or difference of
Factoring Algebra- Chapter 8B Assignment Sheet
 Name: Factoring Algebra- Chapter 8B Assignment Sheet Date Section Learning Targets Assignment Tues 2/17 Find the prime factorization of an integer Find the greatest common factor (GCF) for a set of monomials.
Name: Factoring Algebra- Chapter 8B Assignment Sheet Date Section Learning Targets Assignment Tues 2/17 Find the prime factorization of an integer Find the greatest common factor (GCF) for a set of monomials.
Section 6.1 Factoring Expressions
 Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
Operations with Algebraic Expressions: Multiplication of Polynomials
 Operations with Algebraic Expressions: Multiplication of Polynomials The product of a monomial x monomial To multiply a monomial times a monomial, multiply the coefficients and add the on powers with the
Operations with Algebraic Expressions: Multiplication of Polynomials The product of a monomial x monomial To multiply a monomial times a monomial, multiply the coefficients and add the on powers with the
7-6. Choosing a Factoring Model. Extension: Factoring Polynomials with More Than One Variable IN T RO DUC E T EACH. Standards for Mathematical Content
 7-6 Choosing a Factoring Model Extension: Factoring Polynomials with More Than One Variable Essential question: How can you factor polynomials with more than one variable? What is the connection between
7-6 Choosing a Factoring Model Extension: Factoring Polynomials with More Than One Variable Essential question: How can you factor polynomials with more than one variable? What is the connection between
Factoring. Factoring Monomials Monomials can often be factored in more than one way.
 Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
6.4 Special Factoring Rules
 6.4 Special Factoring Rules OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor a sum of cubes. By reversing the rules for multiplication
6.4 Special Factoring Rules OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor a sum of cubes. By reversing the rules for multiplication
Factoring Polynomials
 Factoring Polynomials Factoring Factoring is the process of writing a polynomial as the product of two or more polynomials. The factors of 6x 2 x 2 are 2x + 1 and 3x 2. In this section, we will be factoring
Factoring Polynomials Factoring Factoring is the process of writing a polynomial as the product of two or more polynomials. The factors of 6x 2 x 2 are 2x + 1 and 3x 2. In this section, we will be factoring
CHAPTER 7: FACTORING POLYNOMIALS
 CHAPTER 7: FACTORING POLYNOMIALS FACTOR (noun) An of two or more quantities which form a product when multiplied together. 1 can be rewritten as 3*, where 3 and are FACTORS of 1. FACTOR (verb) - To factor
CHAPTER 7: FACTORING POLYNOMIALS FACTOR (noun) An of two or more quantities which form a product when multiplied together. 1 can be rewritten as 3*, where 3 and are FACTORS of 1. FACTOR (verb) - To factor
SPECIAL PRODUCTS AND FACTORS
 CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
Greatest Common Factor (GCF) Factoring
 Section 4 4: Greatest Common Factor (GCF) Factoring The last chapter introduced the distributive process. The distributive process takes a product of a monomial and a polynomial and changes the multiplication
Section 4 4: Greatest Common Factor (GCF) Factoring The last chapter introduced the distributive process. The distributive process takes a product of a monomial and a polynomial and changes the multiplication
5.1 FACTORING OUT COMMON FACTORS
 C H A P T E R 5 Factoring he sport of skydiving was born in the 1930s soon after the military began using parachutes as a means of deploying troops. T Today, skydiving is a popular sport around the world.
C H A P T E R 5 Factoring he sport of skydiving was born in the 1930s soon after the military began using parachutes as a means of deploying troops. T Today, skydiving is a popular sport around the world.
Factoring Quadratic Expressions
 Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
Factoring Flow Chart
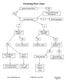 Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
15.1 Factoring Polynomials
 LESSON 15.1 Factoring Polynomials Use the structure of an expression to identify ways to rewrite it. Also A.SSE.3? ESSENTIAL QUESTION How can you use the greatest common factor to factor polynomials? EXPLORE
LESSON 15.1 Factoring Polynomials Use the structure of an expression to identify ways to rewrite it. Also A.SSE.3? ESSENTIAL QUESTION How can you use the greatest common factor to factor polynomials? EXPLORE
( ) FACTORING. x In this polynomial the only variable in common to all is x.
 FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder).
 Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
6.3 FACTORING ax 2 bx c WITH a 1
 290 (6 14) Chapter 6 Factoring e) What is the approximate maximum revenue? f) Use the accompanying graph to estimate the price at which the revenue is zero. y Revenue (thousands of dollars) 300 200 100
290 (6 14) Chapter 6 Factoring e) What is the approximate maximum revenue? f) Use the accompanying graph to estimate the price at which the revenue is zero. y Revenue (thousands of dollars) 300 200 100
Algebraic expressions are a combination of numbers and variables. Here are examples of some basic algebraic expressions.
 Page 1 of 13 Review of Linear Expressions and Equations Skills involving linear equations can be divided into the following groups: Simplifying algebraic expressions. Linear expressions. Solving linear
Page 1 of 13 Review of Linear Expressions and Equations Skills involving linear equations can be divided into the following groups: Simplifying algebraic expressions. Linear expressions. Solving linear
How To Solve Factoring Problems
 05-W4801-AM1.qxd 8/19/08 8:45 PM Page 241 Factoring, Solving Equations, and Problem Solving 5 5.1 Factoring by Using the Distributive Property 5.2 Factoring the Difference of Two Squares 5.3 Factoring
05-W4801-AM1.qxd 8/19/08 8:45 PM Page 241 Factoring, Solving Equations, and Problem Solving 5 5.1 Factoring by Using the Distributive Property 5.2 Factoring the Difference of Two Squares 5.3 Factoring
Tool 1. Greatest Common Factor (GCF)
 Chapter 4: Factoring Review Tool 1 Greatest Common Factor (GCF) This is a very important tool. You must try to factor out the GCF first in every problem. Some problems do not have a GCF but many do. When
Chapter 4: Factoring Review Tool 1 Greatest Common Factor (GCF) This is a very important tool. You must try to factor out the GCF first in every problem. Some problems do not have a GCF but many do. When
5 means to write it as a product something times something instead of a sum something plus something plus something.
 Intermediate algebra Class notes Factoring Introduction (section 6.1) Recall we factor 10 as 5. Factoring something means to think of it as a product! Factors versus terms: terms: things we are adding
Intermediate algebra Class notes Factoring Introduction (section 6.1) Recall we factor 10 as 5. Factoring something means to think of it as a product! Factors versus terms: terms: things we are adding
The majority of college students hold credit cards. According to the Nellie May
 CHAPTER 6 Factoring Polynomials 6.1 The Greatest Common Factor and Factoring by Grouping 6. Factoring Trinomials of the Form b c 6.3 Factoring Trinomials of the Form a b c and Perfect Square Trinomials
CHAPTER 6 Factoring Polynomials 6.1 The Greatest Common Factor and Factoring by Grouping 6. Factoring Trinomials of the Form b c 6.3 Factoring Trinomials of the Form a b c and Perfect Square Trinomials
Factoring Polynomials
 UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
Factoring Guidelines. Greatest Common Factor Two Terms Three Terms Four Terms. 2008 Shirley Radai
 Factoring Guidelines Greatest Common Factor Two Terms Three Terms Four Terms 008 Shirley Radai Greatest Common Factor 008 Shirley Radai Factoring by Finding the Greatest Common Factor Always check for
Factoring Guidelines Greatest Common Factor Two Terms Three Terms Four Terms 008 Shirley Radai Greatest Common Factor 008 Shirley Radai Factoring by Finding the Greatest Common Factor Always check for
Factoring - Greatest Common Factor
 6.1 Factoring - Greatest Common Factor Objective: Find the greatest common factor of a polynomial and factor it out of the expression. The opposite of multiplying polynomials together is factoring polynomials.
6.1 Factoring - Greatest Common Factor Objective: Find the greatest common factor of a polynomial and factor it out of the expression. The opposite of multiplying polynomials together is factoring polynomials.
AIP Factoring Practice/Help
 The following pages include many problems to practice factoring skills. There are also several activities with examples to help you with factoring if you feel like you are not proficient with it. There
The following pages include many problems to practice factoring skills. There are also several activities with examples to help you with factoring if you feel like you are not proficient with it. There
NSM100 Introduction to Algebra Chapter 5 Notes Factoring
 Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
Veterans Upward Bound Algebra I Concepts - Honors
 Veterans Upward Bound Algebra I Concepts - Honors Brenda Meery Kaitlyn Spong Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org Chapter 6. Factoring CHAPTER
Veterans Upward Bound Algebra I Concepts - Honors Brenda Meery Kaitlyn Spong Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org Chapter 6. Factoring CHAPTER
When factoring, we look for greatest common factor of each term and reverse the distributive property and take out the GCF.
 Factoring: reversing the distributive property. The distributive property allows us to do the following: When factoring, we look for greatest common factor of each term and reverse the distributive property
Factoring: reversing the distributive property. The distributive property allows us to do the following: When factoring, we look for greatest common factor of each term and reverse the distributive property
Factoring - Grouping
 6.2 Factoring - Grouping Objective: Factor polynomials with four terms using grouping. The first thing we will always do when factoring is try to factor out a GCF. This GCF is often a monomial like in
6.2 Factoring - Grouping Objective: Factor polynomials with four terms using grouping. The first thing we will always do when factoring is try to factor out a GCF. This GCF is often a monomial like in
Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any.
 Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
In the above, the number 19 is an example of a number because its only positive factors are one and itself.
 Math 100 Greatest Common Factor and Factoring by Grouping (Review) Factoring Definition: A factor is a number, variable, monomial, or polynomial which is multiplied by another number, variable, monomial,
Math 100 Greatest Common Factor and Factoring by Grouping (Review) Factoring Definition: A factor is a number, variable, monomial, or polynomial which is multiplied by another number, variable, monomial,
6.1 Add & Subtract Polynomial Expression & Functions
 6.1 Add & Subtract Polynomial Expression & Functions Objectives 1. Know the meaning of the words term, monomial, binomial, trinomial, polynomial, degree, coefficient, like terms, polynomial funciton, quardrtic
6.1 Add & Subtract Polynomial Expression & Functions Objectives 1. Know the meaning of the words term, monomial, binomial, trinomial, polynomial, degree, coefficient, like terms, polynomial funciton, quardrtic
6.6 Factoring Strategy
 456 CHAPTER 6. FACTORING 6.6 Factoring Strategy When you are concentrating on factoring problems of a single type, after doing a few you tend to get into a rhythm, and the remainder of the exercises, because
456 CHAPTER 6. FACTORING 6.6 Factoring Strategy When you are concentrating on factoring problems of a single type, after doing a few you tend to get into a rhythm, and the remainder of the exercises, because
Name Intro to Algebra 2. Unit 1: Polynomials and Factoring
 Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
MATH 90 CHAPTER 6 Name:.
 MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
Factoring Polynomials: Factoring by Grouping
 OpenStax-CNX module: m21901 1 Factoring Polynomials: Factoring by Grouping Wade Ellis Denny Burzynski This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 3.0
OpenStax-CNX module: m21901 1 Factoring Polynomials: Factoring by Grouping Wade Ellis Denny Burzynski This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 3.0
Factoring Polynomials
 Factoring Polynomials 4-1-2014 The opposite of multiplying polynomials is factoring. Why would you want to factor a polynomial? Let p(x) be a polynomial. p(c) = 0 is equivalent to x c dividing p(x). Recall
Factoring Polynomials 4-1-2014 The opposite of multiplying polynomials is factoring. Why would you want to factor a polynomial? Let p(x) be a polynomial. p(c) = 0 is equivalent to x c dividing p(x). Recall
Factor Polynomials Completely
 9.8 Factor Polynomials Completely Before You factored polynomials. Now You will factor polynomials completely. Why? So you can model the height of a projectile, as in Ex. 71. Key Vocabulary factor by grouping
9.8 Factor Polynomials Completely Before You factored polynomials. Now You will factor polynomials completely. Why? So you can model the height of a projectile, as in Ex. 71. Key Vocabulary factor by grouping
1.5. Factorisation. Introduction. Prerequisites. Learning Outcomes. Learning Style
 Factorisation 1.5 Introduction In Block 4 we showed the way in which brackets were removed from algebraic expressions. Factorisation, which can be considered as the reverse of this process, is dealt with
Factorisation 1.5 Introduction In Block 4 we showed the way in which brackets were removed from algebraic expressions. Factorisation, which can be considered as the reverse of this process, is dealt with
BEGINNING ALGEBRA ACKNOWLEDMENTS
 BEGINNING ALGEBRA The Nursing Department of Labouré College requested the Department of Academic Planning and Support Services to help with mathematics preparatory materials for its Bachelor of Science
BEGINNING ALGEBRA The Nursing Department of Labouré College requested the Department of Academic Planning and Support Services to help with mathematics preparatory materials for its Bachelor of Science
Algebra Cheat Sheets
 Sheets Algebra Cheat Sheets provide you with a tool for teaching your students note-taking, problem-solving, and organizational skills in the context of algebra lessons. These sheets teach the concepts
Sheets Algebra Cheat Sheets provide you with a tool for teaching your students note-taking, problem-solving, and organizational skills in the context of algebra lessons. These sheets teach the concepts
Lagrange Interpolation is a method of fitting an equation to a set of points that functions well when there are few points given.
 Polynomials (Ch.1) Study Guide by BS, JL, AZ, CC, SH, HL Lagrange Interpolation is a method of fitting an equation to a set of points that functions well when there are few points given. Sasha s method
Polynomials (Ch.1) Study Guide by BS, JL, AZ, CC, SH, HL Lagrange Interpolation is a method of fitting an equation to a set of points that functions well when there are few points given. Sasha s method
SIMPLIFYING ALGEBRAIC FRACTIONS
 Tallahassee Community College 5 SIMPLIFYING ALGEBRAIC FRACTIONS In arithmetic, you learned that a fraction is in simplest form if the Greatest Common Factor (GCF) of the numerator and the denominator is
Tallahassee Community College 5 SIMPLIFYING ALGEBRAIC FRACTIONS In arithmetic, you learned that a fraction is in simplest form if the Greatest Common Factor (GCF) of the numerator and the denominator is
1.4. Removing Brackets. Introduction. Prerequisites. Learning Outcomes. Learning Style
 Removing Brackets 1. Introduction In order to simplify an expression which contains brackets it is often necessary to rewrite the expression in an equivalent form but without any brackets. This process
Removing Brackets 1. Introduction In order to simplify an expression which contains brackets it is often necessary to rewrite the expression in an equivalent form but without any brackets. This process
Factoring A Quadratic Polynomial
 Factoring A Quadratic Polynomial If we multiply two binomials together, the result is a quadratic polynomial: This multiplication is pretty straightforward, using the distributive property of multiplication
Factoring A Quadratic Polynomial If we multiply two binomials together, the result is a quadratic polynomial: This multiplication is pretty straightforward, using the distributive property of multiplication
Factoring - Factoring Special Products
 6.5 Factoring - Factoring Special Products Objective: Identify and factor special products including a difference of squares, perfect squares, and sum and difference of cubes. When factoring there are
6.5 Factoring - Factoring Special Products Objective: Identify and factor special products including a difference of squares, perfect squares, and sum and difference of cubes. When factoring there are
FINDING THE LEAST COMMON DENOMINATOR
 0 (7 18) Chapter 7 Rational Expressions GETTING MORE INVOLVED 7. Discussion. Evaluate each expression. a) One-half of 1 b) One-third of c) One-half of x d) One-half of x 7. Exploration. Let R 6 x x 0 x
0 (7 18) Chapter 7 Rational Expressions GETTING MORE INVOLVED 7. Discussion. Evaluate each expression. a) One-half of 1 b) One-third of c) One-half of x d) One-half of x 7. Exploration. Let R 6 x x 0 x
Chapter 5. Rational Expressions
 5.. Simplify Rational Expressions KYOTE Standards: CR ; CA 7 Chapter 5. Rational Expressions Definition. A rational expression is the quotient P Q of two polynomials P and Q in one or more variables, where
5.. Simplify Rational Expressions KYOTE Standards: CR ; CA 7 Chapter 5. Rational Expressions Definition. A rational expression is the quotient P Q of two polynomials P and Q in one or more variables, where
Mathematics Placement
 Mathematics Placement The ACT COMPASS math test is a self-adaptive test, which potentially tests students within four different levels of math including pre-algebra, algebra, college algebra, and trigonometry.
Mathematics Placement The ACT COMPASS math test is a self-adaptive test, which potentially tests students within four different levels of math including pre-algebra, algebra, college algebra, and trigonometry.
Math 10C. Course: Polynomial Products and Factors. Unit of Study: Step 1: Identify the Outcomes to Address. Guiding Questions:
 Course: Unit of Study: Math 10C Polynomial Products and Factors Step 1: Identify the Outcomes to Address Guiding Questions: What do I want my students to learn? What can they currently understand and do?
Course: Unit of Study: Math 10C Polynomial Products and Factors Step 1: Identify the Outcomes to Address Guiding Questions: What do I want my students to learn? What can they currently understand and do?
Algebra I Vocabulary Cards
 Algebra I Vocabulary Cards Table of Contents Expressions and Operations Natural Numbers Whole Numbers Integers Rational Numbers Irrational Numbers Real Numbers Absolute Value Order of Operations Expression
Algebra I Vocabulary Cards Table of Contents Expressions and Operations Natural Numbers Whole Numbers Integers Rational Numbers Irrational Numbers Real Numbers Absolute Value Order of Operations Expression
Polynomial Equations and Factoring
 7 Polynomial Equations and Factoring 7.1 Adding and Subtracting Polynomials 7.2 Multiplying Polynomials 7.3 Special Products of Polynomials 7.4 Dividing Polynomials 7.5 Solving Polynomial Equations in
7 Polynomial Equations and Factoring 7.1 Adding and Subtracting Polynomials 7.2 Multiplying Polynomials 7.3 Special Products of Polynomials 7.4 Dividing Polynomials 7.5 Solving Polynomial Equations in
FACTORING ax 2 bx c WITH a 1
 296 (6 20) Chapter 6 Factoring 6.4 FACTORING a 2 b c WITH a 1 In this section The ac Method Trial and Error Factoring Completely In Section 6.3 we factored trinomials with a leading coefficient of 1. In
296 (6 20) Chapter 6 Factoring 6.4 FACTORING a 2 b c WITH a 1 In this section The ac Method Trial and Error Factoring Completely In Section 6.3 we factored trinomials with a leading coefficient of 1. In
Algebra 2 PreAP. Name Period
 Algebra 2 PreAP Name Period IMPORTANT INSTRUCTIONS FOR STUDENTS!!! We understand that students come to Algebra II with different strengths and needs. For this reason, students have options for completing
Algebra 2 PreAP Name Period IMPORTANT INSTRUCTIONS FOR STUDENTS!!! We understand that students come to Algebra II with different strengths and needs. For this reason, students have options for completing
POLYNOMIALS and FACTORING
 POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
Simplifying Algebraic Fractions
 5. Simplifying Algebraic Fractions 5. OBJECTIVES. Find the GCF for two monomials and simplify a fraction 2. Find the GCF for two polynomials and simplify a fraction Much of our work with algebraic fractions
5. Simplifying Algebraic Fractions 5. OBJECTIVES. Find the GCF for two monomials and simplify a fraction 2. Find the GCF for two polynomials and simplify a fraction Much of our work with algebraic fractions
SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS
 (Section 0.6: Polynomial, Rational, and Algebraic Expressions) 0.6.1 SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS LEARNING OBJECTIVES Be able to identify polynomial, rational, and algebraic
(Section 0.6: Polynomial, Rational, and Algebraic Expressions) 0.6.1 SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS LEARNING OBJECTIVES Be able to identify polynomial, rational, and algebraic
Academic Success Centre
 250) 960-6367 Factoring Polynomials Sometimes when we try to solve or simplify an equation or expression involving polynomials the way that it looks can hinder our progress in finding a solution. Factorization
250) 960-6367 Factoring Polynomials Sometimes when we try to solve or simplify an equation or expression involving polynomials the way that it looks can hinder our progress in finding a solution. Factorization
Sect 6.1 - Greatest Common Factor and Factoring by Grouping
 Sect 6.1 - Greatest Common Factor and Factoring by Grouping Our goal in this chapter is to solve non-linear equations by breaking them down into a series of linear equations that we can solve. To do this,
Sect 6.1 - Greatest Common Factor and Factoring by Grouping Our goal in this chapter is to solve non-linear equations by breaking them down into a series of linear equations that we can solve. To do this,
1.4. Arithmetic of Algebraic Fractions. Introduction. Prerequisites. Learning Outcomes
 Arithmetic of Algebraic Fractions 1.4 Introduction Just as one whole number divided by another is called a numerical fraction, so one algebraic expression divided by another is known as an algebraic fraction.
Arithmetic of Algebraic Fractions 1.4 Introduction Just as one whole number divided by another is called a numerical fraction, so one algebraic expression divided by another is known as an algebraic fraction.
3.1. RATIONAL EXPRESSIONS
 3.1. RATIONAL EXPRESSIONS RATIONAL NUMBERS In previous courses you have learned how to operate (do addition, subtraction, multiplication, and division) on rational numbers (fractions). Rational numbers
3.1. RATIONAL EXPRESSIONS RATIONAL NUMBERS In previous courses you have learned how to operate (do addition, subtraction, multiplication, and division) on rational numbers (fractions). Rational numbers
Radicals - Multiply and Divide Radicals
 8. Radicals - Multiply and Divide Radicals Objective: Multiply and divide radicals using the product and quotient rules of radicals. Multiplying radicals is very simple if the index on all the radicals
8. Radicals - Multiply and Divide Radicals Objective: Multiply and divide radicals using the product and quotient rules of radicals. Multiplying radicals is very simple if the index on all the radicals
EAP/GWL Rev. 1/2011 Page 1 of 5. Factoring a polynomial is the process of writing it as the product of two or more polynomial factors.
 EAP/GWL Rev. 1/2011 Page 1 of 5 Factoring a polynomial is the process of writing it as the product of two or more polynomial factors. Example: Set the factors of a polynomial equation (as opposed to an
EAP/GWL Rev. 1/2011 Page 1 of 5 Factoring a polynomial is the process of writing it as the product of two or more polynomial factors. Example: Set the factors of a polynomial equation (as opposed to an
A Systematic Approach to Factoring
 A Systematic Approach to Factoring Step 1 Count the number of terms. (Remember****Knowing the number of terms will allow you to eliminate unnecessary tools.) Step 2 Is there a greatest common factor? Tool
A Systematic Approach to Factoring Step 1 Count the number of terms. (Remember****Knowing the number of terms will allow you to eliminate unnecessary tools.) Step 2 Is there a greatest common factor? Tool
Pre-Calculus II Factoring and Operations on Polynomials
 Factoring... 1 Polynomials...1 Addition of Polynomials... 1 Subtraction of Polynomials...1 Multiplication of Polynomials... Multiplying a monomial by a monomial... Multiplying a monomial by a polynomial...
Factoring... 1 Polynomials...1 Addition of Polynomials... 1 Subtraction of Polynomials...1 Multiplication of Polynomials... Multiplying a monomial by a monomial... Multiplying a monomial by a polynomial...
SIMPLIFYING SQUARE ROOTS
 40 (8-8) Chapter 8 Powers and Roots 8. SIMPLIFYING SQUARE ROOTS In this section Using the Product Rule Rationalizing the Denominator Simplified Form of a Square Root In Section 8. you learned to simplify
40 (8-8) Chapter 8 Powers and Roots 8. SIMPLIFYING SQUARE ROOTS In this section Using the Product Rule Rationalizing the Denominator Simplified Form of a Square Root In Section 8. you learned to simplify
A. Factoring out the Greatest Common Factor.
 DETAILED SOLUTIONS AND CONCEPTS - FACTORING POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to ingrid.stewart@csn.edu. Thank you!
DETAILED SOLUTIONS AND CONCEPTS - FACTORING POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to ingrid.stewart@csn.edu. Thank you!
Determinants can be used to solve a linear system of equations using Cramer s Rule.
 2.6.2 Cramer s Rule Determinants can be used to solve a linear system of equations using Cramer s Rule. Cramer s Rule for Two Equations in Two Variables Given the system This system has the unique solution
2.6.2 Cramer s Rule Determinants can be used to solve a linear system of equations using Cramer s Rule. Cramer s Rule for Two Equations in Two Variables Given the system This system has the unique solution
x 4-1 = (x²)² - (1)² = (x² + 1) (x² - 1) = (x² + 1) (x - 1) (x + 1)
 Factoring Polynomials EXAMPLES STEP 1 : Greatest Common Factor GCF Factor out the greatest common factor. 6x³ + 12x²y = 6x² (x + 2y) 5x - 5 = 5 (x - 1) 7x² + 2y² = 1 (7x² + 2y²) 2x (x - 3) - (x - 3) =
Factoring Polynomials EXAMPLES STEP 1 : Greatest Common Factor GCF Factor out the greatest common factor. 6x³ + 12x²y = 6x² (x + 2y) 5x - 5 = 5 (x - 1) 7x² + 2y² = 1 (7x² + 2y²) 2x (x - 3) - (x - 3) =
1.3 Algebraic Expressions
 1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
Factoring Trinomials of the Form
 Section 4 6B: Factoring Trinomials of the Form A x 2 + Bx + C where A > 1 by The AC and Factor By Grouping Method Easy Trinomials: 1 x 2 + Bx + C The last section covered the topic of factoring second
Section 4 6B: Factoring Trinomials of the Form A x 2 + Bx + C where A > 1 by The AC and Factor By Grouping Method Easy Trinomials: 1 x 2 + Bx + C The last section covered the topic of factoring second
MATH 10034 Fundamental Mathematics IV
 MATH 0034 Fundamental Mathematics IV http://www.math.kent.edu/ebooks/0034/funmath4.pdf Department of Mathematical Sciences Kent State University January 2, 2009 ii Contents To the Instructor v Polynomials.
MATH 0034 Fundamental Mathematics IV http://www.math.kent.edu/ebooks/0034/funmath4.pdf Department of Mathematical Sciences Kent State University January 2, 2009 ii Contents To the Instructor v Polynomials.
6.5 Factoring Special Forms
 440 CHAPTER 6. FACTORING 6.5 Factoring Special Forms In this section we revisit two special product forms that we learned in Chapter 5, the first of which was squaring a binomial. Squaring a binomial.
440 CHAPTER 6. FACTORING 6.5 Factoring Special Forms In this section we revisit two special product forms that we learned in Chapter 5, the first of which was squaring a binomial. Squaring a binomial.
