Factoring Trinomials of the Form x 2 bx c
|
|
|
- Shana Hamilton
- 7 years ago
- Views:
Transcription
1 4.2 Factoring Trinomials of the Form x 2 bx c 4.2 OBJECTIVES 1. Factor a trinomial of the form x 2 bx c 2. Factor a trinomial containing a common factor NOTE The process used to factor here is frequently called the trial-and-error method. You ll see the reason for the name as you work through this section. You learned how to find the product of any two binomials by using the FOIL method in Section 3.4. Because factoring is the reverse of multiplication, we now want to use that pattern to find the factors of certain trinomials. Recall that to multiply two binomials, we have (x 2)(x 3) x 2 5x 6 The product The sum of The product of the first the products of the last terms (x x). of the outer terms (2 3). and inner terms (3x and 2x). CAUTION Not every trinomial can be written as the product of two binomials. Suppose now that you are given x 2 5x 6 and want to find its factors. First, you know that the factors of a trinomial may be two binomials. So write x 2 5x 6 ( )( ) Because the first term of the trinomial is x 2, the first terms of the binomial factors must be x and x. We now have x 2 5x 6 (x )(x ) The product of the last terms must be 6. Because 6 is positive, the factors must have like signs. Here are the possibilities: ( 1)( 6) ( 2)( 3) This means that the possible factors of the trinomial are (x 1)(x 6) (x 2)(x 3) (x 1)(x 6) (x 2)(x 3) How do we tell which is the correct pair? From the FOIL pattern we know that the sum of the outer and inner products must equal the middle term of the trinomial, in this case 5x. This is the crucial step! (x 1)(x 6) 7x (x 2)(x 3) 5x (x 1)(x 6) 7x (x 2)(x 3) 5x The correct middle term! 331
2 332 CHAPTER 4 FACTORING So we know that the correct factorization is x 2 5x 6 (x 2)(x 3) Are there any clues so far that will make this process quicker? Yes, there is an important one that you may have spotted. We started with a trinomial that had a positive middle term and a positive last term. The negative pairs of factors for 6 led to negative middle terms. So you don t need to bother with the negative factors if the middle term and the last term of the trinomial are both positive. Example 1 Factoring a Trinomial (a) Factor x 2 9x 8. Because the middle term and the last term of the trinomial are both positive, consider only the positive factors of 8, that is, or NOTE If you are wondering why we didn t list (x 8)(x 1) as a possibility, remember that multiplication is commutative. The order doesn t matter! (x 1)(x 8) 9x (x 2)(x 4) 6x Because the first pair gives the correct middle term, x 2 9x 8 (x 1)(x 8) (b) Factor x 2 12x 20. NOTE The factors for 20 are (x 1)(x 20) 21x (x 2)(x 10) 12x (x 4)(x 5) 9x So x 2 12x 20 (x 2)(x 10) CHECK YOURSELF 1 Factor. (a) x 2 6x 5 (b) x 2 10x 16
3 FACTORING TRINOMIALS OF THE FORM X 2 bx c SECTION Let s look at some examples in which the middle term of the trinomial is negative but the first and last terms are still positive. Consider Positive Positive x 2 11x 18 Negative Because we want a negative middle term ( 11x), we use two negative factors for 18. Recall that the product of two negative numbers is positive. Example 2 Factoring a Trinomial (a) Factor x 2 11x 18. NOTE The negative factors of 18 are 18 ( 1)( 18) ( 2)( 9) ( 3)( 6) (x 1)(x 18) 19x (x 2)(x 9) 11x (x 3)(x 6) 9x So x 2 11x 18 (x 2)(x 9) (b) Factor x 2 13x 12. NOTE The negative factors of 12 are 12 ( 1)( 12) ( 2)( 6) ( 3)( 4) (x 1)(x 12) 13x (x 2)(x 6) 8x (x 3)(x 4) 7x So x 2 13x 12 (x 1)(x 12) A few more clues: We have listed all the possible factors in the above examples. It really isn t necessary. Just work until you find the right pair. Also, with practice much of this work can be done mentally. CHECK YOURSELF 2 Factor. (a) x 2 10x 9 (b) x 2 10x 21
4 334 CHAPTER 4 FACTORING Let s look now at the process of factoring a trinomial whose last term is negative. For instance, to factor x 2 2x 15, we can start as before: x 2 2x 15 (x?)(x?) Note that the product of the last terms must be negative ( 15 here). So we must choose factors that have different signs. What are our choices for the factors of 15? 15 (1)( 15) ( 1)(15) (3)( 5) ( 3)(5) This means that the possible factors and the resulting middle terms are NOTE Another clue: Some students prefer to look at the list of numerical factors rather than looking at the actual algebraic factors. Here you want the pair whose sum is 2, the coefficient of the middle term of the trinomial. That pair is 3 and 5, which leads us to the correct factors. (x 1)(x 15) 14x (x 1)(x 15) 14x (x 3)(x 5) 2x (x 3)(x 5) 2x So x 2 2x 15 (x 3)(x 5). Let s work through some examples in which the constant term is negative. NOTE You may be able to pick the factors directly from this list. You want the pair whose sum is 5 (the coefficient of the middle term). Example 3 Factoring a Trinomial (a) Factor x 2 5x 6. First, list the factors of 6. Of course, one factor will be positive, and one will be negative. 6 (1)( 6) ( 1)(6) (2)( 3) ( 2)(3) For the trinomial, then, we have (x 1)(x 6) 5x (x 1)(x 6) 5x (x 2)(x 3) x (x 2)(x 3) x So x 2 5x 6 (x 1)(x 6).
5 FACTORING TRINOMIALS OF THE FORM X 2 bx c SECTION (b) Factor x 2 8xy 9y 2. The process is similar if two variables are involved in the trinomial you are to factor. Start with x 2 8xy 9y 2 (x?)(x?). 9y 2 ( y)(9y) ( y)( 9y) (3y)( 3y) The product of the last terms must be 9y 2. (x y)(x 9y) 8xy (x y)(x 9y) 8xy (x 3y)(x 3y) 0 So x 2 8xy 9y 2 (x y)(x 9y). CHECK YOURSELF 3 Factor. (a) x 2 7x 30 (b) x 2 3xy 10y 2 As was pointed out in the last section, any time that we have a common factor, that factor should be removed before we try any other factoring technique. Consider the following example. Example 4 Factoring a Trinomial (a) Factor 3x 2 21x 18. 3x 2 21x 18 3(x 2 7x 6) Remove the common factor of 3. We now factor the remaining trinomial. For x 2 7x 6: CAUTION A common mistake is to forget to write the 3 that was factored out as the first step. (x 2)(x 3) 5x (x 1)(x 6) 7x So 3x 2 21x 18 3(x 1)(x 6). (b) Factor 2x 3 16x 2 40x. 2x 3 16x 2 40x 2x(x 2 8x 20) Remove the common factor of 2x. The correct middle term
6 336 CHAPTER 4 FACTORING To factor the remaining trinomial, which is x 2 8x 20, we have NOTE Once we have found the desired middle term, there is no need to continue. (x 4)(x 5) x (x 5)(x 4) x (x 10)(x 2) 8x (x 2)(x 10) 8x The correct middle term So 2x 3 16x 2 40x 2x(x 2)(x 10). CHECK YOURSELF 4 Factor. (a) 3x 2 3x 36 (b) 4x 3 24x 2 32x One further comment: Have you wondered if all trinomials are factorable? Look at the trinomial x 2 2x 6 The only possible factors are (x 1)(x 6) and (x 2)(x 3). Neither pair is correct (you should check the middle terms), and so this trinomial does not have factors with integer coefficients. Of course, there are many others. CHECK YOURSELF ANSWERS 1. (a) (x 1)(x 5); (b) (x 2)(x 8) 2. (a) (x 9)(x 1); (b) (x 3)(x 7) 3. (a) (x 10)(x 3); (b) (x 2y)(x 5y) 4. (a) 3(x 4)(x 3); (b) 4x(x 2)(x 4)
7 Name 4.2 Exercises Section Date Complete each of the following statements. 1. x 2 8x 15 (x 3)( ) 2. y 2 3y 18 (y 6)( ) 3. m 2 8m 12 (m 2)( ) 4. x 2 10x 24 (x 6)( ) ANSWERS p 2 8p 20 ( p 2)( ) 6. a 2 9a 36 (a 12)( ) x 2 16x 64 (x 8)( ) 8. w 2 12w 45 (w 3)( ) x 2 7xy 10y 2 (x 2y)( ) 10. a 2 18ab 81b 2 (a 9b)( ) Factor each of the following trinomials. 11. x 2 8x x 2 11x x 2 11x y 2 y s 2 13s b 2 14b a 2 2a x 2 17x x 2 8x x 2 7x m 2 3m a 2 10a
8 ANSWERS x 2 6x x 2 11x x 2 14x s 2 4s p 2 10p x 2 11x x 2 5x a 2 2a c 2 19c t 2 4t n 2 5n x 2 16x x 2 7xy 10y x 2 8xy 12y a 2 ab 42b m 2 8mn 16n x 2 13xy 40y r 2 9rs 36s b 2 6ab 9a x 2 3xy 10y x 2 2xy 8y u 2 6uv 55v m 2 10mn n m 2 16mn n 2 338
9 ANSWERS Factor each of the following trinomials completely. Factor out the greatest common factor first a 2 3a c 2 2c r 3 7r 2 18r 50. m 3 5m 2 14m x 3 20x 2 48x 52. 3p 3 48p 2 108p x 2 y 9xy 2 36y s 4 20s 3 t 96s 2 t m 3 29m 2 n 120mn a 3 52a 2 b 96ab Find a positive value for k for which each of the following can be factored x 2 kx x 2 kx x 2 kx x 2 kx x 2 kx x 2 kx x 2 3x k 64. x 2 5x k 65. x 2 2x k 66. x 2 x k a. b. c. Multiply. Getting Ready for Section 4.3 [Section 3.3] (a) (2x 1)(2x 3) (b) (3a 1)(a 4) (c) (x 4)(2x 3) (d) (2w 11)(w 2) (e) (y 5)(2y 9) (f) (2x 1)(x 12) (g) (p 9)(2p 5) (h) (3a 5)(2a 4) d. e. f. g. h. 339
10 Answers 1. x 5 3. m 6 5. p x 8 9. x 5y 11. (x 3)(x 5) 13. (x 4)(x 7) 15. (s 10)(s 3) 17. (a 8)(a 6) 19. (x 1)(x 7) 21. (m 7)(m 4) 23. (x 10)(x 4) 25. (x 7)(x 7) 27. ( p 12)( p 2) 29. (x 11)(x 6) 31. (c 4)(c 15) 33. (n 10)(n 5) 35. (x 2y)(x 5y) 37. (a 7b)(a 6b) 39. (x 5y)(x 8y) 41. (b 3a)(b 3a) 43. (x 4y)(x 2y) 45. (5m n)(5m n) 47. 3(a 7)(a 6) 49. r(r 9)(r 2) 51. 2x(x 12)(x 2) 53. y(x 12y)(x 3y) 55. m(m 5n)(m 24n) or , 10, or , 8, 15, 24,... a. 4x 2 4x 3 b. 3a 2 11a 4 c. 2x 2 11x 12 d. 2w 2 7w 22 e. 2y 2 19y 45 f. 2x 2 23x 12 g. 2p 2 23p 45 h. 6a 2 2a
Using the ac Method to Factor
 4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
Factoring. Factoring Monomials Monomials can often be factored in more than one way.
 Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
Factoring Special Polynomials
 6.6 Factoring Special Polynomials 6.6 OBJECTIVES 1. Factor the difference of two squares 2. Factor the sum or difference of two cubes In this section, we will look at several special polynomials. These
6.6 Factoring Special Polynomials 6.6 OBJECTIVES 1. Factor the difference of two squares 2. Factor the sum or difference of two cubes In this section, we will look at several special polynomials. These
FACTORING ax 2 bx c. Factoring Trinomials with Leading Coefficient 1
 5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
Operations with Algebraic Expressions: Multiplication of Polynomials
 Operations with Algebraic Expressions: Multiplication of Polynomials The product of a monomial x monomial To multiply a monomial times a monomial, multiply the coefficients and add the on powers with the
Operations with Algebraic Expressions: Multiplication of Polynomials The product of a monomial x monomial To multiply a monomial times a monomial, multiply the coefficients and add the on powers with the
Factoring Quadratic Expressions
 Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
Factoring Trinomials: The ac Method
 6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c
 Tallahassee Community College 55 FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c This kind of trinomial differs from the previous kind we have factored because the coefficient of x is no longer "1".
Tallahassee Community College 55 FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c This kind of trinomial differs from the previous kind we have factored because the coefficient of x is no longer "1".
The Greatest Common Factor; Factoring by Grouping
 296 CHAPTER 5 Factoring and Applications 5.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
296 CHAPTER 5 Factoring and Applications 5.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
1.3 Polynomials and Factoring
 1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
Math 25 Activity 6: Factoring Advanced
 Instructor! Math 25 Activity 6: Factoring Advanced Last week we looked at greatest common factors and the basics of factoring out the GCF. In this second activity, we will discuss factoring more difficult
Instructor! Math 25 Activity 6: Factoring Advanced Last week we looked at greatest common factors and the basics of factoring out the GCF. In this second activity, we will discuss factoring more difficult
expression is written horizontally. The Last terms ((2)( 4)) because they are the last terms of the two polynomials. This is called the FOIL method.
 A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
6.4 Special Factoring Rules
 6.4 Special Factoring Rules OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor a sum of cubes. By reversing the rules for multiplication
6.4 Special Factoring Rules OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor a sum of cubes. By reversing the rules for multiplication
Tool 1. Greatest Common Factor (GCF)
 Chapter 4: Factoring Review Tool 1 Greatest Common Factor (GCF) This is a very important tool. You must try to factor out the GCF first in every problem. Some problems do not have a GCF but many do. When
Chapter 4: Factoring Review Tool 1 Greatest Common Factor (GCF) This is a very important tool. You must try to factor out the GCF first in every problem. Some problems do not have a GCF but many do. When
Chapter R.4 Factoring Polynomials
 Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
By reversing the rules for multiplication of binomials from Section 4.6, we get rules for factoring polynomials in certain forms.
 SECTION 5.4 Special Factoring Techniques 317 5.4 Special Factoring Techniques OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor
SECTION 5.4 Special Factoring Techniques 317 5.4 Special Factoring Techniques OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor
NSM100 Introduction to Algebra Chapter 5 Notes Factoring
 Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
How To Factor By Gcf In Algebra 1.5
 7-2 Factoring by GCF Warm Up Lesson Presentation Lesson Quiz Algebra 1 Warm Up Simplify. 1. 2(w + 1) 2. 3x(x 2 4) 2w + 2 3x 3 12x Find the GCF of each pair of monomials. 3. 4h 2 and 6h 2h 4. 13p and 26p
7-2 Factoring by GCF Warm Up Lesson Presentation Lesson Quiz Algebra 1 Warm Up Simplify. 1. 2(w + 1) 2. 3x(x 2 4) 2w + 2 3x 3 12x Find the GCF of each pair of monomials. 3. 4h 2 and 6h 2h 4. 13p and 26p
Factoring Flow Chart
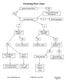 Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Factoring Algebra- Chapter 8B Assignment Sheet
 Name: Factoring Algebra- Chapter 8B Assignment Sheet Date Section Learning Targets Assignment Tues 2/17 Find the prime factorization of an integer Find the greatest common factor (GCF) for a set of monomials.
Name: Factoring Algebra- Chapter 8B Assignment Sheet Date Section Learning Targets Assignment Tues 2/17 Find the prime factorization of an integer Find the greatest common factor (GCF) for a set of monomials.
6.1 The Greatest Common Factor; Factoring by Grouping
 386 CHAPTER 6 Factoring and Applications 6.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
386 CHAPTER 6 Factoring and Applications 6.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
7-6. Choosing a Factoring Model. Extension: Factoring Polynomials with More Than One Variable IN T RO DUC E T EACH. Standards for Mathematical Content
 7-6 Choosing a Factoring Model Extension: Factoring Polynomials with More Than One Variable Essential question: How can you factor polynomials with more than one variable? What is the connection between
7-6 Choosing a Factoring Model Extension: Factoring Polynomials with More Than One Variable Essential question: How can you factor polynomials with more than one variable? What is the connection between
Factoring Polynomials
 Factoring Polynomials Factoring Factoring is the process of writing a polynomial as the product of two or more polynomials. The factors of 6x 2 x 2 are 2x + 1 and 3x 2. In this section, we will be factoring
Factoring Polynomials Factoring Factoring is the process of writing a polynomial as the product of two or more polynomials. The factors of 6x 2 x 2 are 2x + 1 and 3x 2. In this section, we will be factoring
Polynomial Expression
 DETAILED SOLUTIONS AND CONCEPTS - POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to ingrid.stewart@csn.edu. Thank you! PLEASE NOTE
DETAILED SOLUTIONS AND CONCEPTS - POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to ingrid.stewart@csn.edu. Thank you! PLEASE NOTE
POLYNOMIALS and FACTORING
 POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
AIP Factoring Practice/Help
 The following pages include many problems to practice factoring skills. There are also several activities with examples to help you with factoring if you feel like you are not proficient with it. There
The following pages include many problems to practice factoring skills. There are also several activities with examples to help you with factoring if you feel like you are not proficient with it. There
In algebra, factor by rewriting a polynomial as a product of lower-degree polynomials
 Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
SPECIAL PRODUCTS AND FACTORS
 CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
Factoring Methods. Example 1: 2x + 2 2 * x + 2 * 1 2(x + 1)
 Factoring Methods When you are trying to factor a polynomial, there are three general steps you want to follow: 1. See if there is a Greatest Common Factor 2. See if you can Factor by Grouping 3. See if
Factoring Methods When you are trying to factor a polynomial, there are three general steps you want to follow: 1. See if there is a Greatest Common Factor 2. See if you can Factor by Grouping 3. See if
MATH 90 CHAPTER 6 Name:.
 MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
The majority of college students hold credit cards. According to the Nellie May
 CHAPTER 6 Factoring Polynomials 6.1 The Greatest Common Factor and Factoring by Grouping 6. Factoring Trinomials of the Form b c 6.3 Factoring Trinomials of the Form a b c and Perfect Square Trinomials
CHAPTER 6 Factoring Polynomials 6.1 The Greatest Common Factor and Factoring by Grouping 6. Factoring Trinomials of the Form b c 6.3 Factoring Trinomials of the Form a b c and Perfect Square Trinomials
Factoring and Applications
 Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0).
 This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
FACTORING POLYNOMIALS
 296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
( ) FACTORING. x In this polynomial the only variable in common to all is x.
 FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder).
 Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
5 means to write it as a product something times something instead of a sum something plus something plus something.
 Intermediate algebra Class notes Factoring Introduction (section 6.1) Recall we factor 10 as 5. Factoring something means to think of it as a product! Factors versus terms: terms: things we are adding
Intermediate algebra Class notes Factoring Introduction (section 6.1) Recall we factor 10 as 5. Factoring something means to think of it as a product! Factors versus terms: terms: things we are adding
MATH 10034 Fundamental Mathematics IV
 MATH 0034 Fundamental Mathematics IV http://www.math.kent.edu/ebooks/0034/funmath4.pdf Department of Mathematical Sciences Kent State University January 2, 2009 ii Contents To the Instructor v Polynomials.
MATH 0034 Fundamental Mathematics IV http://www.math.kent.edu/ebooks/0034/funmath4.pdf Department of Mathematical Sciences Kent State University January 2, 2009 ii Contents To the Instructor v Polynomials.
A. Factoring out the Greatest Common Factor.
 DETAILED SOLUTIONS AND CONCEPTS - FACTORING POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to ingrid.stewart@csn.edu. Thank you!
DETAILED SOLUTIONS AND CONCEPTS - FACTORING POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to ingrid.stewart@csn.edu. Thank you!
Factoring Guidelines. Greatest Common Factor Two Terms Three Terms Four Terms. 2008 Shirley Radai
 Factoring Guidelines Greatest Common Factor Two Terms Three Terms Four Terms 008 Shirley Radai Greatest Common Factor 008 Shirley Radai Factoring by Finding the Greatest Common Factor Always check for
Factoring Guidelines Greatest Common Factor Two Terms Three Terms Four Terms 008 Shirley Radai Greatest Common Factor 008 Shirley Radai Factoring by Finding the Greatest Common Factor Always check for
6.3 FACTORING ax 2 bx c WITH a 1
 290 (6 14) Chapter 6 Factoring e) What is the approximate maximum revenue? f) Use the accompanying graph to estimate the price at which the revenue is zero. y Revenue (thousands of dollars) 300 200 100
290 (6 14) Chapter 6 Factoring e) What is the approximate maximum revenue? f) Use the accompanying graph to estimate the price at which the revenue is zero. y Revenue (thousands of dollars) 300 200 100
Academic Success Centre
 250) 960-6367 Factoring Polynomials Sometimes when we try to solve or simplify an equation or expression involving polynomials the way that it looks can hinder our progress in finding a solution. Factorization
250) 960-6367 Factoring Polynomials Sometimes when we try to solve or simplify an equation or expression involving polynomials the way that it looks can hinder our progress in finding a solution. Factorization
Greatest Common Factor (GCF) Factoring
 Section 4 4: Greatest Common Factor (GCF) Factoring The last chapter introduced the distributive process. The distributive process takes a product of a monomial and a polynomial and changes the multiplication
Section 4 4: Greatest Common Factor (GCF) Factoring The last chapter introduced the distributive process. The distributive process takes a product of a monomial and a polynomial and changes the multiplication
Name Intro to Algebra 2. Unit 1: Polynomials and Factoring
 Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
How To Solve Factoring Problems
 05-W4801-AM1.qxd 8/19/08 8:45 PM Page 241 Factoring, Solving Equations, and Problem Solving 5 5.1 Factoring by Using the Distributive Property 5.2 Factoring the Difference of Two Squares 5.3 Factoring
05-W4801-AM1.qxd 8/19/08 8:45 PM Page 241 Factoring, Solving Equations, and Problem Solving 5 5.1 Factoring by Using the Distributive Property 5.2 Factoring the Difference of Two Squares 5.3 Factoring
Algebra 2 PreAP. Name Period
 Algebra 2 PreAP Name Period IMPORTANT INSTRUCTIONS FOR STUDENTS!!! We understand that students come to Algebra II with different strengths and needs. For this reason, students have options for completing
Algebra 2 PreAP Name Period IMPORTANT INSTRUCTIONS FOR STUDENTS!!! We understand that students come to Algebra II with different strengths and needs. For this reason, students have options for completing
Factoring - Grouping
 6.2 Factoring - Grouping Objective: Factor polynomials with four terms using grouping. The first thing we will always do when factoring is try to factor out a GCF. This GCF is often a monomial like in
6.2 Factoring - Grouping Objective: Factor polynomials with four terms using grouping. The first thing we will always do when factoring is try to factor out a GCF. This GCF is often a monomial like in
Negative Integer Exponents
 7.7 Negative Integer Exponents 7.7 OBJECTIVES. Define the zero exponent 2. Use the definition of a negative exponent to simplify an expression 3. Use the properties of exponents to simplify expressions
7.7 Negative Integer Exponents 7.7 OBJECTIVES. Define the zero exponent 2. Use the definition of a negative exponent to simplify an expression 3. Use the properties of exponents to simplify expressions
1.4. Arithmetic of Algebraic Fractions. Introduction. Prerequisites. Learning Outcomes
 Arithmetic of Algebraic Fractions 1.4 Introduction Just as one whole number divided by another is called a numerical fraction, so one algebraic expression divided by another is known as an algebraic fraction.
Arithmetic of Algebraic Fractions 1.4 Introduction Just as one whole number divided by another is called a numerical fraction, so one algebraic expression divided by another is known as an algebraic fraction.
Factoring Polynomials
 Factoring a Polynomial Expression Factoring a polynomial is expressing the polynomial as a product of two or more factors. Simply stated, it is somewhat the reverse process of multiplying. To factor polynomials,
Factoring a Polynomial Expression Factoring a polynomial is expressing the polynomial as a product of two or more factors. Simply stated, it is somewhat the reverse process of multiplying. To factor polynomials,
CHAPTER 7: FACTORING POLYNOMIALS
 CHAPTER 7: FACTORING POLYNOMIALS FACTOR (noun) An of two or more quantities which form a product when multiplied together. 1 can be rewritten as 3*, where 3 and are FACTORS of 1. FACTOR (verb) - To factor
CHAPTER 7: FACTORING POLYNOMIALS FACTOR (noun) An of two or more quantities which form a product when multiplied together. 1 can be rewritten as 3*, where 3 and are FACTORS of 1. FACTOR (verb) - To factor
Factoring a Difference of Two Squares. Factoring a Difference of Two Squares
 284 (6 8) Chapter 6 Factoring 87. Tomato soup. The amount of metal S (in square inches) that it takes to make a can for tomato soup is a function of the radius r and height h: S 2 r 2 2 rh a) Rewrite this
284 (6 8) Chapter 6 Factoring 87. Tomato soup. The amount of metal S (in square inches) that it takes to make a can for tomato soup is a function of the radius r and height h: S 2 r 2 2 rh a) Rewrite this
Polynomials. Key Terms. quadratic equation parabola conjugates trinomial. polynomial coefficient degree monomial binomial GCF
 Polynomials 5 5.1 Addition and Subtraction of Polynomials and Polynomial Functions 5.2 Multiplication of Polynomials 5.3 Division of Polynomials Problem Recognition Exercises Operations on Polynomials
Polynomials 5 5.1 Addition and Subtraction of Polynomials and Polynomial Functions 5.2 Multiplication of Polynomials 5.3 Division of Polynomials Problem Recognition Exercises Operations on Polynomials
x 4-1 = (x²)² - (1)² = (x² + 1) (x² - 1) = (x² + 1) (x - 1) (x + 1)
 Factoring Polynomials EXAMPLES STEP 1 : Greatest Common Factor GCF Factor out the greatest common factor. 6x³ + 12x²y = 6x² (x + 2y) 5x - 5 = 5 (x - 1) 7x² + 2y² = 1 (7x² + 2y²) 2x (x - 3) - (x - 3) =
Factoring Polynomials EXAMPLES STEP 1 : Greatest Common Factor GCF Factor out the greatest common factor. 6x³ + 12x²y = 6x² (x + 2y) 5x - 5 = 5 (x - 1) 7x² + 2y² = 1 (7x² + 2y²) 2x (x - 3) - (x - 3) =
Factoring Polynomials
 UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
Polynomials and Factoring
 7.6 Polynomials and Factoring Basic Terminology A term, or monomial, is defined to be a number, a variable, or a product of numbers and variables. A polynomial is a term or a finite sum or difference of
7.6 Polynomials and Factoring Basic Terminology A term, or monomial, is defined to be a number, a variable, or a product of numbers and variables. A polynomial is a term or a finite sum or difference of
Simplifying Algebraic Fractions
 5. Simplifying Algebraic Fractions 5. OBJECTIVES. Find the GCF for two monomials and simplify a fraction 2. Find the GCF for two polynomials and simplify a fraction Much of our work with algebraic fractions
5. Simplifying Algebraic Fractions 5. OBJECTIVES. Find the GCF for two monomials and simplify a fraction 2. Find the GCF for two polynomials and simplify a fraction Much of our work with algebraic fractions
Click on the links below to jump directly to the relevant section
 Click on the links below to jump directly to the relevant section What is algebra? Operations with algebraic terms Mathematical properties of real numbers Order of operations What is Algebra? Algebra is
Click on the links below to jump directly to the relevant section What is algebra? Operations with algebraic terms Mathematical properties of real numbers Order of operations What is Algebra? Algebra is
Factor Polynomials Completely
 9.8 Factor Polynomials Completely Before You factored polynomials. Now You will factor polynomials completely. Why? So you can model the height of a projectile, as in Ex. 71. Key Vocabulary factor by grouping
9.8 Factor Polynomials Completely Before You factored polynomials. Now You will factor polynomials completely. Why? So you can model the height of a projectile, as in Ex. 71. Key Vocabulary factor by grouping
Factoring Polynomials and Solving Quadratic Equations
 Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
5.1 FACTORING OUT COMMON FACTORS
 C H A P T E R 5 Factoring he sport of skydiving was born in the 1930s soon after the military began using parachutes as a means of deploying troops. T Today, skydiving is a popular sport around the world.
C H A P T E R 5 Factoring he sport of skydiving was born in the 1930s soon after the military began using parachutes as a means of deploying troops. T Today, skydiving is a popular sport around the world.
15.1 Factoring Polynomials
 LESSON 15.1 Factoring Polynomials Use the structure of an expression to identify ways to rewrite it. Also A.SSE.3? ESSENTIAL QUESTION How can you use the greatest common factor to factor polynomials? EXPLORE
LESSON 15.1 Factoring Polynomials Use the structure of an expression to identify ways to rewrite it. Also A.SSE.3? ESSENTIAL QUESTION How can you use the greatest common factor to factor polynomials? EXPLORE
Chapter 5. Rational Expressions
 5.. Simplify Rational Expressions KYOTE Standards: CR ; CA 7 Chapter 5. Rational Expressions Definition. A rational expression is the quotient P Q of two polynomials P and Q in one or more variables, where
5.. Simplify Rational Expressions KYOTE Standards: CR ; CA 7 Chapter 5. Rational Expressions Definition. A rational expression is the quotient P Q of two polynomials P and Q in one or more variables, where
Polynomial Equations and Factoring
 7 Polynomial Equations and Factoring 7.1 Adding and Subtracting Polynomials 7.2 Multiplying Polynomials 7.3 Special Products of Polynomials 7.4 Dividing Polynomials 7.5 Solving Polynomial Equations in
7 Polynomial Equations and Factoring 7.1 Adding and Subtracting Polynomials 7.2 Multiplying Polynomials 7.3 Special Products of Polynomials 7.4 Dividing Polynomials 7.5 Solving Polynomial Equations in
Factoring (pp. 1 of 4)
 Factoring (pp. 1 of 4) Algebra Review Try these items from middle school math. A) What numbers are the factors of 4? B) Write down the prime factorization of 7. C) 6 Simplify 48 using the greatest common
Factoring (pp. 1 of 4) Algebra Review Try these items from middle school math. A) What numbers are the factors of 4? B) Write down the prime factorization of 7. C) 6 Simplify 48 using the greatest common
FACTORING OUT COMMON FACTORS
 278 (6 2) Chapter 6 Factoring 6.1 FACTORING OUT COMMON FACTORS In this section Prime Factorization of Integers Greatest Common Factor Finding the Greatest Common Factor for Monomials Factoring Out the
278 (6 2) Chapter 6 Factoring 6.1 FACTORING OUT COMMON FACTORS In this section Prime Factorization of Integers Greatest Common Factor Finding the Greatest Common Factor for Monomials Factoring Out the
6.6 Factoring Strategy
 456 CHAPTER 6. FACTORING 6.6 Factoring Strategy When you are concentrating on factoring problems of a single type, after doing a few you tend to get into a rhythm, and the remainder of the exercises, because
456 CHAPTER 6. FACTORING 6.6 Factoring Strategy When you are concentrating on factoring problems of a single type, after doing a few you tend to get into a rhythm, and the remainder of the exercises, because
Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any.
 Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
Section 6.1 Factoring Expressions
 Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
Mathematics Placement
 Mathematics Placement The ACT COMPASS math test is a self-adaptive test, which potentially tests students within four different levels of math including pre-algebra, algebra, college algebra, and trigonometry.
Mathematics Placement The ACT COMPASS math test is a self-adaptive test, which potentially tests students within four different levels of math including pre-algebra, algebra, college algebra, and trigonometry.
SUNY ECC. ACCUPLACER Preparation Workshop. Algebra Skills
 SUNY ECC ACCUPLACER Preparation Workshop Algebra Skills Gail A. Butler Ph.D. Evaluating Algebraic Epressions Substitute the value (#) in place of the letter (variable). Follow order of operations!!! E)
SUNY ECC ACCUPLACER Preparation Workshop Algebra Skills Gail A. Butler Ph.D. Evaluating Algebraic Epressions Substitute the value (#) in place of the letter (variable). Follow order of operations!!! E)
1.3 Algebraic Expressions
 1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III
 Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III Name Date Adding and Subtracting Polynomials Algebra Standard 10.0 A polynomial is a sum of one ore more monomials. Polynomial
Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III Name Date Adding and Subtracting Polynomials Algebra Standard 10.0 A polynomial is a sum of one ore more monomials. Polynomial
Algebra 1 Chapter 08 review
 Name: Class: Date: ID: A Algebra 1 Chapter 08 review Multiple Choice Identify the choice that best completes the statement or answers the question. Simplify the difference. 1. (4w 2 4w 8) (2w 2 + 3w 6)
Name: Class: Date: ID: A Algebra 1 Chapter 08 review Multiple Choice Identify the choice that best completes the statement or answers the question. Simplify the difference. 1. (4w 2 4w 8) (2w 2 + 3w 6)
1.5. Factorisation. Introduction. Prerequisites. Learning Outcomes. Learning Style
 Factorisation 1.5 Introduction In Block 4 we showed the way in which brackets were removed from algebraic expressions. Factorisation, which can be considered as the reverse of this process, is dealt with
Factorisation 1.5 Introduction In Block 4 we showed the way in which brackets were removed from algebraic expressions. Factorisation, which can be considered as the reverse of this process, is dealt with
CAHSEE on Target UC Davis, School and University Partnerships
 UC Davis, School and University Partnerships CAHSEE on Target Mathematics Curriculum Published by The University of California, Davis, School/University Partnerships Program 006 Director Sarah R. Martinez,
UC Davis, School and University Partnerships CAHSEE on Target Mathematics Curriculum Published by The University of California, Davis, School/University Partnerships Program 006 Director Sarah R. Martinez,
0.8 Rational Expressions and Equations
 96 Prerequisites 0.8 Rational Expressions and Equations We now turn our attention to rational expressions - that is, algebraic fractions - and equations which contain them. The reader is encouraged to
96 Prerequisites 0.8 Rational Expressions and Equations We now turn our attention to rational expressions - that is, algebraic fractions - and equations which contain them. The reader is encouraged to
4.4 Factoring ax 2 + bx + c
 4.4 Factoring ax 2 + bx + c From the last section, we now know a trinomial should factor as two binomials. With this in mind, we need to look at how to factor a trinomial when the leading coefficient is
4.4 Factoring ax 2 + bx + c From the last section, we now know a trinomial should factor as two binomials. With this in mind, we need to look at how to factor a trinomial when the leading coefficient is
Multiplying and Dividing Radicals
 9.4 Multiplying and Dividing Radicals 9.4 OBJECTIVES 1. Multiply and divide expressions involving numeric radicals 2. Multiply and divide expressions involving algebraic radicals In Section 9.2 we stated
9.4 Multiplying and Dividing Radicals 9.4 OBJECTIVES 1. Multiply and divide expressions involving numeric radicals 2. Multiply and divide expressions involving algebraic radicals In Section 9.2 we stated
Factoring - Factoring Special Products
 6.5 Factoring - Factoring Special Products Objective: Identify and factor special products including a difference of squares, perfect squares, and sum and difference of cubes. When factoring there are
6.5 Factoring - Factoring Special Products Objective: Identify and factor special products including a difference of squares, perfect squares, and sum and difference of cubes. When factoring there are
Math 10C. Course: Polynomial Products and Factors. Unit of Study: Step 1: Identify the Outcomes to Address. Guiding Questions:
 Course: Unit of Study: Math 10C Polynomial Products and Factors Step 1: Identify the Outcomes to Address Guiding Questions: What do I want my students to learn? What can they currently understand and do?
Course: Unit of Study: Math 10C Polynomial Products and Factors Step 1: Identify the Outcomes to Address Guiding Questions: What do I want my students to learn? What can they currently understand and do?
Factoring. Factoring Polynomial Equations. Special Factoring Patterns. Factoring. Special Factoring Patterns. Special Factoring Patterns
 Factoring Factoring Polynomial Equations Ms. Laster Earlier, you learned to factor several types of quadratic expressions: General trinomial - 2x 2-5x-12 = (2x + 3)(x - 4) Perfect Square Trinomial - x
Factoring Factoring Polynomial Equations Ms. Laster Earlier, you learned to factor several types of quadratic expressions: General trinomial - 2x 2-5x-12 = (2x + 3)(x - 4) Perfect Square Trinomial - x
Chapter 3 Section 6 Lesson Polynomials
 Chapter Section 6 Lesson Polynomials Introduction This lesson introduces polynomials and like terms. As we learned earlier, a monomial is a constant, a variable, or the product of constants and variables.
Chapter Section 6 Lesson Polynomials Introduction This lesson introduces polynomials and like terms. As we learned earlier, a monomial is a constant, a variable, or the product of constants and variables.
Factoring Trinomials using Algebra Tiles Student Activity
 Factoring Trinomials using Algebra Tiles Student Activity Materials: Algebra Tiles (student set) Worksheet: Factoring Trinomials using Algebra Tiles Algebra Tiles: Each algebra tile kits should contain
Factoring Trinomials using Algebra Tiles Student Activity Materials: Algebra Tiles (student set) Worksheet: Factoring Trinomials using Algebra Tiles Algebra Tiles: Each algebra tile kits should contain
Solving Quadratic Equations by Factoring
 4.7 Solving Quadratic Equations by Factoring 4.7 OBJECTIVE 1. Solve quadratic equations by factoring The factoring techniques you have learned provide us with tools for solving equations that can be written
4.7 Solving Quadratic Equations by Factoring 4.7 OBJECTIVE 1. Solve quadratic equations by factoring The factoring techniques you have learned provide us with tools for solving equations that can be written
SIMPLIFYING ALGEBRAIC FRACTIONS
 Tallahassee Community College 5 SIMPLIFYING ALGEBRAIC FRACTIONS In arithmetic, you learned that a fraction is in simplest form if the Greatest Common Factor (GCF) of the numerator and the denominator is
Tallahassee Community College 5 SIMPLIFYING ALGEBRAIC FRACTIONS In arithmetic, you learned that a fraction is in simplest form if the Greatest Common Factor (GCF) of the numerator and the denominator is
Pre-Calculus II Factoring and Operations on Polynomials
 Factoring... 1 Polynomials...1 Addition of Polynomials... 1 Subtraction of Polynomials...1 Multiplication of Polynomials... Multiplying a monomial by a monomial... Multiplying a monomial by a polynomial...
Factoring... 1 Polynomials...1 Addition of Polynomials... 1 Subtraction of Polynomials...1 Multiplication of Polynomials... Multiplying a monomial by a monomial... Multiplying a monomial by a polynomial...
Year 9 set 1 Mathematics notes, to accompany the 9H book.
 Part 1: Year 9 set 1 Mathematics notes, to accompany the 9H book. equations 1. (p.1), 1.6 (p. 44), 4.6 (p.196) sequences 3. (p.115) Pupils use the Elmwood Press Essential Maths book by David Raymer (9H
Part 1: Year 9 set 1 Mathematics notes, to accompany the 9H book. equations 1. (p.1), 1.6 (p. 44), 4.6 (p.196) sequences 3. (p.115) Pupils use the Elmwood Press Essential Maths book by David Raymer (9H
Factoring Polynomials
 Factoring Polynomials 4-1-2014 The opposite of multiplying polynomials is factoring. Why would you want to factor a polynomial? Let p(x) be a polynomial. p(c) = 0 is equivalent to x c dividing p(x). Recall
Factoring Polynomials 4-1-2014 The opposite of multiplying polynomials is factoring. Why would you want to factor a polynomial? Let p(x) be a polynomial. p(c) = 0 is equivalent to x c dividing p(x). Recall
3.1. RATIONAL EXPRESSIONS
 3.1. RATIONAL EXPRESSIONS RATIONAL NUMBERS In previous courses you have learned how to operate (do addition, subtraction, multiplication, and division) on rational numbers (fractions). Rational numbers
3.1. RATIONAL EXPRESSIONS RATIONAL NUMBERS In previous courses you have learned how to operate (do addition, subtraction, multiplication, and division) on rational numbers (fractions). Rational numbers
How To Fator
 CHAPTER hapter 4 > Make the Connetion 4 INTRODUCTION Developing seret odes is big business beause of the widespread use of omputers and the Internet. Corporations all over the world sell enryption systems
CHAPTER hapter 4 > Make the Connetion 4 INTRODUCTION Developing seret odes is big business beause of the widespread use of omputers and the Internet. Corporations all over the world sell enryption systems
Radicals - Multiply and Divide Radicals
 8. Radicals - Multiply and Divide Radicals Objective: Multiply and divide radicals using the product and quotient rules of radicals. Multiplying radicals is very simple if the index on all the radicals
8. Radicals - Multiply and Divide Radicals Objective: Multiply and divide radicals using the product and quotient rules of radicals. Multiplying radicals is very simple if the index on all the radicals
Section 5.0A Factoring Part 1
 Section 5.0A Factoring Part 1 I. Work Together A. Multiply the following binomials into trinomials. (Write the final result in descending order, i.e., a + b + c ). ( 7)( + 5) ( + 7)( + ) ( + 7)( + 5) (
Section 5.0A Factoring Part 1 I. Work Together A. Multiply the following binomials into trinomials. (Write the final result in descending order, i.e., a + b + c ). ( 7)( + 5) ( + 7)( + ) ( + 7)( + 5) (
When factoring, we look for greatest common factor of each term and reverse the distributive property and take out the GCF.
 Factoring: reversing the distributive property. The distributive property allows us to do the following: When factoring, we look for greatest common factor of each term and reverse the distributive property
Factoring: reversing the distributive property. The distributive property allows us to do the following: When factoring, we look for greatest common factor of each term and reverse the distributive property
6.1 Add & Subtract Polynomial Expression & Functions
 6.1 Add & Subtract Polynomial Expression & Functions Objectives 1. Know the meaning of the words term, monomial, binomial, trinomial, polynomial, degree, coefficient, like terms, polynomial funciton, quardrtic
6.1 Add & Subtract Polynomial Expression & Functions Objectives 1. Know the meaning of the words term, monomial, binomial, trinomial, polynomial, degree, coefficient, like terms, polynomial funciton, quardrtic
COLLEGE ALGEBRA. Paul Dawkins
 COLLEGE ALGEBRA Paul Dawkins Table of Contents Preface... iii Outline... iv Preliminaries... Introduction... Integer Exponents... Rational Exponents... 9 Real Exponents...5 Radicals...6 Polynomials...5
COLLEGE ALGEBRA Paul Dawkins Table of Contents Preface... iii Outline... iv Preliminaries... Introduction... Integer Exponents... Rational Exponents... 9 Real Exponents...5 Radicals...6 Polynomials...5
Factoring ax 2 + bx + c - Teacher Notes
 Southern Nevada Regional Professi onal D evel opment Program VOLUME 1, ISSUE 8 MAY 009 A N ewsletter from the Sec ondary Mathematic s Team Factoring ax + bx + c - Teacher Notes Here we look at sample teacher
Southern Nevada Regional Professi onal D evel opment Program VOLUME 1, ISSUE 8 MAY 009 A N ewsletter from the Sec ondary Mathematic s Team Factoring ax + bx + c - Teacher Notes Here we look at sample teacher
#6 Opener Solutions. Move one more spot to your right. Introduce yourself if needed.
 1. Sit anywhere in the concentric circles. Do not move the desks. 2. Take out chapter 6, HW/notes #1-#5, a pencil, a red pen, and your calculator. 3. Work on opener #6 with the person sitting across from
1. Sit anywhere in the concentric circles. Do not move the desks. 2. Take out chapter 6, HW/notes #1-#5, a pencil, a red pen, and your calculator. 3. Work on opener #6 with the person sitting across from
