Factoring. Factoring Monomials Monomials can often be factored in more than one way.
|
|
|
- Justina Holmes
- 10 years ago
- Views:
Transcription
1 Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example, if we multiply 5x 2 by 2y, we get 10x 2 y. So 5x 2 and 2y can be said to be factors of 10x 2 y they are terms that when multiplied together produce 10x 2 y. Factoring rewrites an expression as terms that are multiplied. Let s look at different ways of factoring. Factoring Monomials Monomials can often be factored in more than one way. Example 1 : Factor 27x 3 Possible factors are: 3x 2 9x or 9x 2 3x or 27x x 2 or 27 x 3 All of these will produce 27x 3 when multiplied etc. Factoring Out a Common Factor When we multiplied a polynomial by a monomial, we used the distributive law: A(B + C) = AB + AC. For example: 2x(x 2 + 3x 5) = 2x x 2 + 2x 3x - 2x 5 = 2x 3 + 6x 2 10x Since every term of (x 2 + 3x 5) was multiplied by the same thing (2x), 2x is called a common factor of the expression 2x 3 + 6x 2 10x and can be taken back out to express the polynomial as a product. The first question to ask when faced with factoring a polynomial is Are there any common factors? Then take out the largest common factor you can find. Example 2: Factor 18x x x 2 Step 1: Do all the terms in the polynomial have the same variable 18x x x 2 (like x or y)? If yes, factor each term in the expression so that one of the factors in each term is the variable with the lowest power 18x 3 x x x x 2 attached to it. Then take out this common factor. x 2 (18x x + 81) what s left is still added together Step 2: Do the numbers in the expression have a common factor? This may take some trial and error, so if it s not obvious, start dividing the numbers by something small, (18) (45) (81) like 2 or 3 or 5, until they are completely factored. x 2 (2 9 x x + 9 9) Department of Mathematics, Sinclair Community College, Dayton, OH 1
2 If the same factor appears in all of the terms, it is a common factor and can be taken out. 9x 2 (2x 3 + 5x + 9) This expression cannot be factored any further. Factoring by Grouping Sometimes the common factor is a polynomial. Don t let this throw you! No matter how complex an expression may be, if the same expression is a factor (a multiplier) in all of the terms in the polynomial, then factor it out. For example, we know we can factor out the common term x from the expression x 2 + x and create the product x(x + 1). What about: x(x + 1) + 5(x + 1)? The term (x+1) is a factor of each term of the expression and is therefore a common factor. When we factor it out, we get: (x+1)(x+5). what s left is still added together If you have a polynomial with no factors common to all the terms, try grouping the terms in a way that will let you factor each group. Then you might end up actually creating a factor common to both groups. Here s how it works. Example 3: Factor by grouping 6x 3 3x 2 + 2xy y Step 1. There are no factors common to all the terms. 6x 3 3x 2 + 2xy y Group the first two terms together and the last two terms together. (6x 3 3x 2 ) + (2xy y) Step 2. Factor each group separately. Take out the (2x 3x 2 3x 2 ) + (2x y y) common variable with the lowest power and any common numerical factors. 3x 2 (2x-1) + y(2x-1) Step 3. Now look again for common factors. You ve created a new common factor: (2x-1)! 3x 2 (2x-1) + y(2x-1) Step 4. Factor out the common polynomial and add the remaining terms together. (2x - 1)(3x 2 + y) CAUTION! If the polynomial had been written as 6x 3 3x 2-2xy + y, when you do the grouping, you have to change the sign of the last term: 6x 3 3x 2-2xy + y = (6x 3 3x 2 ) (2xy y) this sign changes because this negative sign is now a coefficient of 1: - (2xy y) = -2xy (-y) = -2xy + y Department of Mathematics, Sinclair Community College, Dayton, OH 2
3 Factoring Trinomials: x 2 + bx + c (coefficient of 1 on the x 2 ) When you multiply two binomials (using the FOIL method), the terms add up like this: (x+3)(x+5) = x 2 + 5x + 3x + 15 = x 2 + 8x + 15 Notice that the last term in the trinomial is the product of the last terms in the binomials (15 = 3 5). Now notice that the numerical part of the middle term in the trinomial is the sum of the last terms in the binomials (8 = 3 + 5). IF THE TRINOMIAL IS FACTORABLE, THIS IS ALWAYS TRUE. (Important! this is true only if the x 2 term is multiplied only by 1.) Using this information, if you have a trinomial with no common factors, you can do a trial-anderror way of factoring. Always check and take out any common factors first! Example 4: Factor x x + 16 Step 1. The last term is +16. The numerical part of the middle term is +10. List possible factors of the last term: +16 = Step 2. Test pairs of factors by adding them together = = -17 Does any set of factors add up to the middle term of +10? 2+8 = = -10 We have a winner! 4+4 = = -8 Step 3. We can now write x x + 16 as (x+2)(x+8). Step 4. Check your factoring by doing the multiplication: (x+2)(x+8) = x 2 + 8x + 2x + 16 = x x + 16 Notice that I could have gotten +16 by multiplying two positive numbers together or by multiplying two negative numbers together, but only the positive factors added up to +10. Here s some rules-of-thumb to figure out the signs in the binomial factors. Last term positive x x + 16 (x + 2)(x + 8) Middle term positive the signs in both factors are positive pos pos pos pos Last term positive x 2-10x + 16 (x - 2)(x - 8) Middle term negative the signs in both factors are negative: neg pos neg neg (-2)(-8) = = -10 Department of Mathematics, Sinclair Community College, Dayton, OH 3
4 Last term negative x 2 + 6x - 16 (x - 2)(x + 8) Middle term positive the sign in the factor with the pos neg neg pos larger number will be positive and (larger number) the sign in the other factor will be negative. Last term negative x 2-6x - 16 (x + 2)(x - 8) Middle term negative the sign in the factor with the neg neg pos neg larger number will be negative and (larger number) the sign in the other factor will be positive. Factoring Trinomials: ax 2 + bx + c (coefficient of a number other than 1 on the x 2 ) What if the x 2 term in the trinomial has a coefficient other than 1 in front of it? Remember when you FOIL two binomials: (2x + 3)(3x + 4) First term First term = First term of the trinomial 2x 3x = 6x 2 Outer term Outer term + Inner term Inner term 2x 4 + 3x 3 = 8x + 9x = 17x = Middle term of the trinomial Last term Last term = Last term of the trinomial 3 4 = 12 (2x + 3)(3x + 4) = 6x x + 12 Let s look at: 9x x + 8. Now we can t just look at the factors of the last term (8) to see if they add up to 18, because that 9 in front of the x 2 is also going to be involved in calculating the middle term. One method to resolve our dilemma is trial-and-error. Step 1. Factor both the 9 in the first term 9 8 and the 8 of the last term. Line up your factors next to each other The first column contains possible numbers of the first terms of the binomials that our trinomial will (hopefully) factor into. The second column contains possible numbers of the last terms of the binomials. Step 2. Picture the trinomial in factored form: (? +?)(? +?) Distribute the factors of the 9 to the first term in each binomial factor; distribute the factors of the 8 to the last term in each binomial factor. (1 + 1)(9 + 8) first terms last terms Department of Mathematics, Sinclair Community College, Dayton, OH 4
5 Step 3. To get the middle term of the trinomial, multiply only the outer terms and the inner terms and add the products. Do any add up to our middle term of 18? Outer Inner (1 + 1)(9 + 8) = = 17 (9 + 1)(1 + 8) = = 73 (3 + 1)(3 + 8) = = 27 (1 + 2)(9 + 4) = = 22 (3 + 2)(3 + 4) = = 18 Step 4. Use the factors that work to write the trinomial in factored form. 9x x + 8 = (3x + 2)(3x + 4) Step 5. Check by multiplying. (3x + 2)(3x + 4) = 9x x + 6x + 8 = 9x x + 8 With practice, you ll get faster at just listing the factors, doing the products and sums in your head, and discovering the right combination. And watch your signs! Another method for factoring trinomials ax 2 + bx + c is to factor by grouping. Grouping is a step-by-step method for factoring a trinomial. If you have trouble with the trialand-error method, this method may work better for you. Let s work with the following: 6x 2 15x + 6 Step 1. Multiply the coefficient on the first 6 6 = 36 term and the final constant Step 2. Factor this product. 36 = ±2 ±18 ±3 ±12 ±4 ±9 ±6 ±6 Step 3. Find the pair of factors that add up to = -15 the middle term of the trinomial (-15). Step 4. Rewrite the middle term of the 6x 2 15x + 6 = 6x 2 12x 3x + 6 trinomial as the sum of these two factors. sign change! Step 5. Group the first two and the last (6x 2 12x) (3x 6) two terms and take out common factors. = 6x(x 2) 3(x 2) Watch your signs! Step 6. Take out the common binomial (6x 3)(x 2) to finish the factoring. Check your work by multiplying. Department of Mathematics, Sinclair Community College, Dayton, OH 5
6 If Step 5 doesn t produce a common factor, try switching the middle two terms to create a different grouping. Factoring a trinomial by grouping takes more time. However, the method is also useful to check a trinomial for factorability, that is, is this trinomial prime and can t be factored? Here s how to check for primeness of the trinomial 2x 2-5x Step 1. Multiply the coefficient on the first term by the last term. 2 (-20) = -40 Step 2. Factor the product (-40) and sum the 2 + (-20) = = 18 factors of each pair. Does any sum equal 4 + (-10) = = 6 the middle term of 5? 8 + (-5) = = (-40) = = 39 No we can t get the middle term, so this trinomial is not factorable. Sample Problems Find three factorizations for the monomial Factor by grouping 1. 25x x x x 3 + x 2 + 8x + 2 Factor; check by multiplying x 3 21x 2 12x x 5 + 6x x 5 y x 3 y 3 18x 2 y 11. 3x 2 y 2 + 6x 2 y x x 5-0.6x x 2 Factor completely Factor: 12. x 3 + x 2 56x 7. x 2 (y - 3) + 5(y 3) 13. x 2 9x y(2z + 1) + (2z + 1) 14. 5x x 4-90x x x a 2 21a x 2 6xy 27y 2 Department of Mathematics, Sinclair Community College, Dayton, OH 6
7 Answers 1. 5x 5x 3, 5x 2 5x 2, 25x 3 x, 25x 2 x 2, 25x x x 3 or 9 (-5x 3 ), -9x 5x 2, -9x 2 x, -45 x 3, -45x x 2, -45x 2 x x 6, 2x 4x 5, 2x 2 4x 4, 2x 3 4x 3, 2x 4 4x 2, 2x 5 4x, 2x 6 4, 8 x 6, 8x x 5, etc 4. 2x 2 (4x 3 + 3) 5. 3x 2 y(7x 3 y + 9xy 2 6) x 2 (2x 5 + 4x 3 x + 3) 7. (x 2 + 5)(y - 3) 8. (4y + 1)(2z + 1) 9. (x 2 + 2)(4x + 1) 10. (7x 2 6)(2x 3) 11. (3x 2 1)(y 2 + 2) 12. x(x + 8)(x 7) 13. (x 6)(x 3) 14. 5x 3 (x + 9)(x 2) 15. (5x + 2)(x + 5) 16. 3(3a 4)(a 1) 17. (8x + 9y)(2x 3y) Department of Mathematics, Sinclair Community College, Dayton, OH 7
1.3 Polynomials and Factoring
 1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
Operations with Algebraic Expressions: Multiplication of Polynomials
 Operations with Algebraic Expressions: Multiplication of Polynomials The product of a monomial x monomial To multiply a monomial times a monomial, multiply the coefficients and add the on powers with the
Operations with Algebraic Expressions: Multiplication of Polynomials The product of a monomial x monomial To multiply a monomial times a monomial, multiply the coefficients and add the on powers with the
Factoring Trinomials: The ac Method
 6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c
 Tallahassee Community College 55 FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c This kind of trinomial differs from the previous kind we have factored because the coefficient of x is no longer "1".
Tallahassee Community College 55 FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c This kind of trinomial differs from the previous kind we have factored because the coefficient of x is no longer "1".
Chapter R.4 Factoring Polynomials
 Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
Factoring Trinomials of the Form x 2 bx c
 4.2 Factoring Trinomials of the Form x 2 bx c 4.2 OBJECTIVES 1. Factor a trinomial of the form x 2 bx c 2. Factor a trinomial containing a common factor NOTE The process used to factor here is frequently
4.2 Factoring Trinomials of the Form x 2 bx c 4.2 OBJECTIVES 1. Factor a trinomial of the form x 2 bx c 2. Factor a trinomial containing a common factor NOTE The process used to factor here is frequently
Using the ac Method to Factor
 4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
Factoring Quadratic Expressions
 Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
Greatest Common Factor (GCF) Factoring
 Section 4 4: Greatest Common Factor (GCF) Factoring The last chapter introduced the distributive process. The distributive process takes a product of a monomial and a polynomial and changes the multiplication
Section 4 4: Greatest Common Factor (GCF) Factoring The last chapter introduced the distributive process. The distributive process takes a product of a monomial and a polynomial and changes the multiplication
FACTORING ax 2 bx c. Factoring Trinomials with Leading Coefficient 1
 5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
expression is written horizontally. The Last terms ((2)( 4)) because they are the last terms of the two polynomials. This is called the FOIL method.
 A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
Tool 1. Greatest Common Factor (GCF)
 Chapter 4: Factoring Review Tool 1 Greatest Common Factor (GCF) This is a very important tool. You must try to factor out the GCF first in every problem. Some problems do not have a GCF but many do. When
Chapter 4: Factoring Review Tool 1 Greatest Common Factor (GCF) This is a very important tool. You must try to factor out the GCF first in every problem. Some problems do not have a GCF but many do. When
Factoring Flow Chart
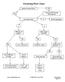 Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
In algebra, factor by rewriting a polynomial as a product of lower-degree polynomials
 Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
Name Intro to Algebra 2. Unit 1: Polynomials and Factoring
 Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
NSM100 Introduction to Algebra Chapter 5 Notes Factoring
 Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
Factoring Polynomials
 Factoring a Polynomial Expression Factoring a polynomial is expressing the polynomial as a product of two or more factors. Simply stated, it is somewhat the reverse process of multiplying. To factor polynomials,
Factoring a Polynomial Expression Factoring a polynomial is expressing the polynomial as a product of two or more factors. Simply stated, it is somewhat the reverse process of multiplying. To factor polynomials,
Factoring Special Polynomials
 6.6 Factoring Special Polynomials 6.6 OBJECTIVES 1. Factor the difference of two squares 2. Factor the sum or difference of two cubes In this section, we will look at several special polynomials. These
6.6 Factoring Special Polynomials 6.6 OBJECTIVES 1. Factor the difference of two squares 2. Factor the sum or difference of two cubes In this section, we will look at several special polynomials. These
Section 6.1 Factoring Expressions
 Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
Factoring Guidelines. Greatest Common Factor Two Terms Three Terms Four Terms. 2008 Shirley Radai
 Factoring Guidelines Greatest Common Factor Two Terms Three Terms Four Terms 008 Shirley Radai Greatest Common Factor 008 Shirley Radai Factoring by Finding the Greatest Common Factor Always check for
Factoring Guidelines Greatest Common Factor Two Terms Three Terms Four Terms 008 Shirley Radai Greatest Common Factor 008 Shirley Radai Factoring by Finding the Greatest Common Factor Always check for
Factoring Polynomials
 Factoring Polynomials Factoring Factoring is the process of writing a polynomial as the product of two or more polynomials. The factors of 6x 2 x 2 are 2x + 1 and 3x 2. In this section, we will be factoring
Factoring Polynomials Factoring Factoring is the process of writing a polynomial as the product of two or more polynomials. The factors of 6x 2 x 2 are 2x + 1 and 3x 2. In this section, we will be factoring
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0).
 This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
By reversing the rules for multiplication of binomials from Section 4.6, we get rules for factoring polynomials in certain forms.
 SECTION 5.4 Special Factoring Techniques 317 5.4 Special Factoring Techniques OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor
SECTION 5.4 Special Factoring Techniques 317 5.4 Special Factoring Techniques OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor
POLYNOMIALS and FACTORING
 POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
6.4 Special Factoring Rules
 6.4 Special Factoring Rules OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor a sum of cubes. By reversing the rules for multiplication
6.4 Special Factoring Rules OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor a sum of cubes. By reversing the rules for multiplication
Factoring and Applications
 Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
15.1 Factoring Polynomials
 LESSON 15.1 Factoring Polynomials Use the structure of an expression to identify ways to rewrite it. Also A.SSE.3? ESSENTIAL QUESTION How can you use the greatest common factor to factor polynomials? EXPLORE
LESSON 15.1 Factoring Polynomials Use the structure of an expression to identify ways to rewrite it. Also A.SSE.3? ESSENTIAL QUESTION How can you use the greatest common factor to factor polynomials? EXPLORE
6.1 The Greatest Common Factor; Factoring by Grouping
 386 CHAPTER 6 Factoring and Applications 6.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
386 CHAPTER 6 Factoring and Applications 6.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
A. Factoring out the Greatest Common Factor.
 DETAILED SOLUTIONS AND CONCEPTS - FACTORING POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to [email protected]. Thank you!
DETAILED SOLUTIONS AND CONCEPTS - FACTORING POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to [email protected]. Thank you!
( ) FACTORING. x In this polynomial the only variable in common to all is x.
 FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
7-6. Choosing a Factoring Model. Extension: Factoring Polynomials with More Than One Variable IN T RO DUC E T EACH. Standards for Mathematical Content
 7-6 Choosing a Factoring Model Extension: Factoring Polynomials with More Than One Variable Essential question: How can you factor polynomials with more than one variable? What is the connection between
7-6 Choosing a Factoring Model Extension: Factoring Polynomials with More Than One Variable Essential question: How can you factor polynomials with more than one variable? What is the connection between
Math 25 Activity 6: Factoring Advanced
 Instructor! Math 25 Activity 6: Factoring Advanced Last week we looked at greatest common factors and the basics of factoring out the GCF. In this second activity, we will discuss factoring more difficult
Instructor! Math 25 Activity 6: Factoring Advanced Last week we looked at greatest common factors and the basics of factoring out the GCF. In this second activity, we will discuss factoring more difficult
x 4-1 = (x²)² - (1)² = (x² + 1) (x² - 1) = (x² + 1) (x - 1) (x + 1)
 Factoring Polynomials EXAMPLES STEP 1 : Greatest Common Factor GCF Factor out the greatest common factor. 6x³ + 12x²y = 6x² (x + 2y) 5x - 5 = 5 (x - 1) 7x² + 2y² = 1 (7x² + 2y²) 2x (x - 3) - (x - 3) =
Factoring Polynomials EXAMPLES STEP 1 : Greatest Common Factor GCF Factor out the greatest common factor. 6x³ + 12x²y = 6x² (x + 2y) 5x - 5 = 5 (x - 1) 7x² + 2y² = 1 (7x² + 2y²) 2x (x - 3) - (x - 3) =
Factoring Polynomials and Solving Quadratic Equations
 Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder).
 Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Factoring - Grouping
 6.2 Factoring - Grouping Objective: Factor polynomials with four terms using grouping. The first thing we will always do when factoring is try to factor out a GCF. This GCF is often a monomial like in
6.2 Factoring - Grouping Objective: Factor polynomials with four terms using grouping. The first thing we will always do when factoring is try to factor out a GCF. This GCF is often a monomial like in
5 means to write it as a product something times something instead of a sum something plus something plus something.
 Intermediate algebra Class notes Factoring Introduction (section 6.1) Recall we factor 10 as 5. Factoring something means to think of it as a product! Factors versus terms: terms: things we are adding
Intermediate algebra Class notes Factoring Introduction (section 6.1) Recall we factor 10 as 5. Factoring something means to think of it as a product! Factors versus terms: terms: things we are adding
A Systematic Approach to Factoring
 A Systematic Approach to Factoring Step 1 Count the number of terms. (Remember****Knowing the number of terms will allow you to eliminate unnecessary tools.) Step 2 Is there a greatest common factor? Tool
A Systematic Approach to Factoring Step 1 Count the number of terms. (Remember****Knowing the number of terms will allow you to eliminate unnecessary tools.) Step 2 Is there a greatest common factor? Tool
1.3 Algebraic Expressions
 1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
Sect 6.1 - Greatest Common Factor and Factoring by Grouping
 Sect 6.1 - Greatest Common Factor and Factoring by Grouping Our goal in this chapter is to solve non-linear equations by breaking them down into a series of linear equations that we can solve. To do this,
Sect 6.1 - Greatest Common Factor and Factoring by Grouping Our goal in this chapter is to solve non-linear equations by breaking them down into a series of linear equations that we can solve. To do this,
Algebra 2 PreAP. Name Period
 Algebra 2 PreAP Name Period IMPORTANT INSTRUCTIONS FOR STUDENTS!!! We understand that students come to Algebra II with different strengths and needs. For this reason, students have options for completing
Algebra 2 PreAP Name Period IMPORTANT INSTRUCTIONS FOR STUDENTS!!! We understand that students come to Algebra II with different strengths and needs. For this reason, students have options for completing
The Greatest Common Factor; Factoring by Grouping
 296 CHAPTER 5 Factoring and Applications 5.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
296 CHAPTER 5 Factoring and Applications 5.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
When factoring, we look for greatest common factor of each term and reverse the distributive property and take out the GCF.
 Factoring: reversing the distributive property. The distributive property allows us to do the following: When factoring, we look for greatest common factor of each term and reverse the distributive property
Factoring: reversing the distributive property. The distributive property allows us to do the following: When factoring, we look for greatest common factor of each term and reverse the distributive property
Polynomial Expression
 DETAILED SOLUTIONS AND CONCEPTS - POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to [email protected]. Thank you! PLEASE NOTE
DETAILED SOLUTIONS AND CONCEPTS - POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to [email protected]. Thank you! PLEASE NOTE
Factor Polynomials Completely
 9.8 Factor Polynomials Completely Before You factored polynomials. Now You will factor polynomials completely. Why? So you can model the height of a projectile, as in Ex. 71. Key Vocabulary factor by grouping
9.8 Factor Polynomials Completely Before You factored polynomials. Now You will factor polynomials completely. Why? So you can model the height of a projectile, as in Ex. 71. Key Vocabulary factor by grouping
Factoring. Factoring Polynomial Equations. Special Factoring Patterns. Factoring. Special Factoring Patterns. Special Factoring Patterns
 Factoring Factoring Polynomial Equations Ms. Laster Earlier, you learned to factor several types of quadratic expressions: General trinomial - 2x 2-5x-12 = (2x + 3)(x - 4) Perfect Square Trinomial - x
Factoring Factoring Polynomial Equations Ms. Laster Earlier, you learned to factor several types of quadratic expressions: General trinomial - 2x 2-5x-12 = (2x + 3)(x - 4) Perfect Square Trinomial - x
6.3 FACTORING ax 2 bx c WITH a 1
 290 (6 14) Chapter 6 Factoring e) What is the approximate maximum revenue? f) Use the accompanying graph to estimate the price at which the revenue is zero. y Revenue (thousands of dollars) 300 200 100
290 (6 14) Chapter 6 Factoring e) What is the approximate maximum revenue? f) Use the accompanying graph to estimate the price at which the revenue is zero. y Revenue (thousands of dollars) 300 200 100
SPECIAL PRODUCTS AND FACTORS
 CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
4.4 Factoring ax 2 + bx + c
 4.4 Factoring ax 2 + bx + c From the last section, we now know a trinomial should factor as two binomials. With this in mind, we need to look at how to factor a trinomial when the leading coefficient is
4.4 Factoring ax 2 + bx + c From the last section, we now know a trinomial should factor as two binomials. With this in mind, we need to look at how to factor a trinomial when the leading coefficient is
CHAPTER 7: FACTORING POLYNOMIALS
 CHAPTER 7: FACTORING POLYNOMIALS FACTOR (noun) An of two or more quantities which form a product when multiplied together. 1 can be rewritten as 3*, where 3 and are FACTORS of 1. FACTOR (verb) - To factor
CHAPTER 7: FACTORING POLYNOMIALS FACTOR (noun) An of two or more quantities which form a product when multiplied together. 1 can be rewritten as 3*, where 3 and are FACTORS of 1. FACTOR (verb) - To factor
Factoring a Difference of Two Squares. Factoring a Difference of Two Squares
 284 (6 8) Chapter 6 Factoring 87. Tomato soup. The amount of metal S (in square inches) that it takes to make a can for tomato soup is a function of the radius r and height h: S 2 r 2 2 rh a) Rewrite this
284 (6 8) Chapter 6 Factoring 87. Tomato soup. The amount of metal S (in square inches) that it takes to make a can for tomato soup is a function of the radius r and height h: S 2 r 2 2 rh a) Rewrite this
Algebra 1 Chapter 08 review
 Name: Class: Date: ID: A Algebra 1 Chapter 08 review Multiple Choice Identify the choice that best completes the statement or answers the question. Simplify the difference. 1. (4w 2 4w 8) (2w 2 + 3w 6)
Name: Class: Date: ID: A Algebra 1 Chapter 08 review Multiple Choice Identify the choice that best completes the statement or answers the question. Simplify the difference. 1. (4w 2 4w 8) (2w 2 + 3w 6)
Polynomials and Factoring
 7.6 Polynomials and Factoring Basic Terminology A term, or monomial, is defined to be a number, a variable, or a product of numbers and variables. A polynomial is a term or a finite sum or difference of
7.6 Polynomials and Factoring Basic Terminology A term, or monomial, is defined to be a number, a variable, or a product of numbers and variables. A polynomial is a term or a finite sum or difference of
Factoring Algebra- Chapter 8B Assignment Sheet
 Name: Factoring Algebra- Chapter 8B Assignment Sheet Date Section Learning Targets Assignment Tues 2/17 Find the prime factorization of an integer Find the greatest common factor (GCF) for a set of monomials.
Name: Factoring Algebra- Chapter 8B Assignment Sheet Date Section Learning Targets Assignment Tues 2/17 Find the prime factorization of an integer Find the greatest common factor (GCF) for a set of monomials.
FACTORING OUT COMMON FACTORS
 278 (6 2) Chapter 6 Factoring 6.1 FACTORING OUT COMMON FACTORS In this section Prime Factorization of Integers Greatest Common Factor Finding the Greatest Common Factor for Monomials Factoring Out the
278 (6 2) Chapter 6 Factoring 6.1 FACTORING OUT COMMON FACTORS In this section Prime Factorization of Integers Greatest Common Factor Finding the Greatest Common Factor for Monomials Factoring Out the
MATH 90 CHAPTER 6 Name:.
 MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
Factors and Products
 CHAPTER 3 Factors and Products What You ll Learn use different strategies to find factors and multiples of whole numbers identify prime factors and write the prime factorization of a number find square
CHAPTER 3 Factors and Products What You ll Learn use different strategies to find factors and multiples of whole numbers identify prime factors and write the prime factorization of a number find square
Factoring Trinomials of the Form
 Section 4 6B: Factoring Trinomials of the Form A x 2 + Bx + C where A > 1 by The AC and Factor By Grouping Method Easy Trinomials: 1 x 2 + Bx + C The last section covered the topic of factoring second
Section 4 6B: Factoring Trinomials of the Form A x 2 + Bx + C where A > 1 by The AC and Factor By Grouping Method Easy Trinomials: 1 x 2 + Bx + C The last section covered the topic of factoring second
Factoring Trinomials using Algebra Tiles Student Activity
 Factoring Trinomials using Algebra Tiles Student Activity Materials: Algebra Tiles (student set) Worksheet: Factoring Trinomials using Algebra Tiles Algebra Tiles: Each algebra tile kits should contain
Factoring Trinomials using Algebra Tiles Student Activity Materials: Algebra Tiles (student set) Worksheet: Factoring Trinomials using Algebra Tiles Algebra Tiles: Each algebra tile kits should contain
Pre-Calculus II Factoring and Operations on Polynomials
 Factoring... 1 Polynomials...1 Addition of Polynomials... 1 Subtraction of Polynomials...1 Multiplication of Polynomials... Multiplying a monomial by a monomial... Multiplying a monomial by a polynomial...
Factoring... 1 Polynomials...1 Addition of Polynomials... 1 Subtraction of Polynomials...1 Multiplication of Polynomials... Multiplying a monomial by a monomial... Multiplying a monomial by a polynomial...
FACTORING ax 2 bx c WITH a 1
 296 (6 20) Chapter 6 Factoring 6.4 FACTORING a 2 b c WITH a 1 In this section The ac Method Trial and Error Factoring Completely In Section 6.3 we factored trinomials with a leading coefficient of 1. In
296 (6 20) Chapter 6 Factoring 6.4 FACTORING a 2 b c WITH a 1 In this section The ac Method Trial and Error Factoring Completely In Section 6.3 we factored trinomials with a leading coefficient of 1. In
SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS
 (Section 0.6: Polynomial, Rational, and Algebraic Expressions) 0.6.1 SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS LEARNING OBJECTIVES Be able to identify polynomial, rational, and algebraic
(Section 0.6: Polynomial, Rational, and Algebraic Expressions) 0.6.1 SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS LEARNING OBJECTIVES Be able to identify polynomial, rational, and algebraic
How To Factor By Gcf In Algebra 1.5
 7-2 Factoring by GCF Warm Up Lesson Presentation Lesson Quiz Algebra 1 Warm Up Simplify. 1. 2(w + 1) 2. 3x(x 2 4) 2w + 2 3x 3 12x Find the GCF of each pair of monomials. 3. 4h 2 and 6h 2h 4. 13p and 26p
7-2 Factoring by GCF Warm Up Lesson Presentation Lesson Quiz Algebra 1 Warm Up Simplify. 1. 2(w + 1) 2. 3x(x 2 4) 2w + 2 3x 3 12x Find the GCF of each pair of monomials. 3. 4h 2 and 6h 2h 4. 13p and 26p
Factoring Polynomials
 UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
6.1 Add & Subtract Polynomial Expression & Functions
 6.1 Add & Subtract Polynomial Expression & Functions Objectives 1. Know the meaning of the words term, monomial, binomial, trinomial, polynomial, degree, coefficient, like terms, polynomial funciton, quardrtic
6.1 Add & Subtract Polynomial Expression & Functions Objectives 1. Know the meaning of the words term, monomial, binomial, trinomial, polynomial, degree, coefficient, like terms, polynomial funciton, quardrtic
FACTORING POLYNOMIALS
 296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
1.4. Arithmetic of Algebraic Fractions. Introduction. Prerequisites. Learning Outcomes
 Arithmetic of Algebraic Fractions 1.4 Introduction Just as one whole number divided by another is called a numerical fraction, so one algebraic expression divided by another is known as an algebraic fraction.
Arithmetic of Algebraic Fractions 1.4 Introduction Just as one whole number divided by another is called a numerical fraction, so one algebraic expression divided by another is known as an algebraic fraction.
CAHSEE on Target UC Davis, School and University Partnerships
 UC Davis, School and University Partnerships CAHSEE on Target Mathematics Curriculum Published by The University of California, Davis, School/University Partnerships Program 006 Director Sarah R. Martinez,
UC Davis, School and University Partnerships CAHSEE on Target Mathematics Curriculum Published by The University of California, Davis, School/University Partnerships Program 006 Director Sarah R. Martinez,
Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III
 Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III Name Date Adding and Subtracting Polynomials Algebra Standard 10.0 A polynomial is a sum of one ore more monomials. Polynomial
Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III Name Date Adding and Subtracting Polynomials Algebra Standard 10.0 A polynomial is a sum of one ore more monomials. Polynomial
1.5. Factorisation. Introduction. Prerequisites. Learning Outcomes. Learning Style
 Factorisation 1.5 Introduction In Block 4 we showed the way in which brackets were removed from algebraic expressions. Factorisation, which can be considered as the reverse of this process, is dealt with
Factorisation 1.5 Introduction In Block 4 we showed the way in which brackets were removed from algebraic expressions. Factorisation, which can be considered as the reverse of this process, is dealt with
Factoring Methods. Example 1: 2x + 2 2 * x + 2 * 1 2(x + 1)
 Factoring Methods When you are trying to factor a polynomial, there are three general steps you want to follow: 1. See if there is a Greatest Common Factor 2. See if you can Factor by Grouping 3. See if
Factoring Methods When you are trying to factor a polynomial, there are three general steps you want to follow: 1. See if there is a Greatest Common Factor 2. See if you can Factor by Grouping 3. See if
Veterans Upward Bound Algebra I Concepts - Honors
 Veterans Upward Bound Algebra I Concepts - Honors Brenda Meery Kaitlyn Spong Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org Chapter 6. Factoring CHAPTER
Veterans Upward Bound Algebra I Concepts - Honors Brenda Meery Kaitlyn Spong Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org Chapter 6. Factoring CHAPTER
Math 10C. Course: Polynomial Products and Factors. Unit of Study: Step 1: Identify the Outcomes to Address. Guiding Questions:
 Course: Unit of Study: Math 10C Polynomial Products and Factors Step 1: Identify the Outcomes to Address Guiding Questions: What do I want my students to learn? What can they currently understand and do?
Course: Unit of Study: Math 10C Polynomial Products and Factors Step 1: Identify the Outcomes to Address Guiding Questions: What do I want my students to learn? What can they currently understand and do?
Radicals - Multiply and Divide Radicals
 8. Radicals - Multiply and Divide Radicals Objective: Multiply and divide radicals using the product and quotient rules of radicals. Multiplying radicals is very simple if the index on all the radicals
8. Radicals - Multiply and Divide Radicals Objective: Multiply and divide radicals using the product and quotient rules of radicals. Multiplying radicals is very simple if the index on all the radicals
Introduction Assignment
 PRE-CALCULUS 11 Introduction Assignment Welcome to PREC 11! This assignment will help you review some topics from a previous math course and introduce you to some of the topics that you ll be studying
PRE-CALCULUS 11 Introduction Assignment Welcome to PREC 11! This assignment will help you review some topics from a previous math course and introduce you to some of the topics that you ll be studying
AIP Factoring Practice/Help
 The following pages include many problems to practice factoring skills. There are also several activities with examples to help you with factoring if you feel like you are not proficient with it. There
The following pages include many problems to practice factoring skills. There are also several activities with examples to help you with factoring if you feel like you are not proficient with it. There
ESSENTIAL QUESTION How can you factor expressions of the form ax 2 + bx + c?
 LESSON 15.3 Factoring ax 2 + bx + c A.SSE.2 Use the structure of an expression to identify ways to rewrite it. Also A.SSE.3? ESSENTIAL QUESTION How can you factor expressions of the form ax 2 + bx + c?
LESSON 15.3 Factoring ax 2 + bx + c A.SSE.2 Use the structure of an expression to identify ways to rewrite it. Also A.SSE.3? ESSENTIAL QUESTION How can you factor expressions of the form ax 2 + bx + c?
MATH 10034 Fundamental Mathematics IV
 MATH 0034 Fundamental Mathematics IV http://www.math.kent.edu/ebooks/0034/funmath4.pdf Department of Mathematical Sciences Kent State University January 2, 2009 ii Contents To the Instructor v Polynomials.
MATH 0034 Fundamental Mathematics IV http://www.math.kent.edu/ebooks/0034/funmath4.pdf Department of Mathematical Sciences Kent State University January 2, 2009 ii Contents To the Instructor v Polynomials.
6.6 Factoring Strategy
 456 CHAPTER 6. FACTORING 6.6 Factoring Strategy When you are concentrating on factoring problems of a single type, after doing a few you tend to get into a rhythm, and the remainder of the exercises, because
456 CHAPTER 6. FACTORING 6.6 Factoring Strategy When you are concentrating on factoring problems of a single type, after doing a few you tend to get into a rhythm, and the remainder of the exercises, because
Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any.
 Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
Factoring (pp. 1 of 4)
 Factoring (pp. 1 of 4) Algebra Review Try these items from middle school math. A) What numbers are the factors of 4? B) Write down the prime factorization of 7. C) 6 Simplify 48 using the greatest common
Factoring (pp. 1 of 4) Algebra Review Try these items from middle school math. A) What numbers are the factors of 4? B) Write down the prime factorization of 7. C) 6 Simplify 48 using the greatest common
5.1 FACTORING OUT COMMON FACTORS
 C H A P T E R 5 Factoring he sport of skydiving was born in the 1930s soon after the military began using parachutes as a means of deploying troops. T Today, skydiving is a popular sport around the world.
C H A P T E R 5 Factoring he sport of skydiving was born in the 1930s soon after the military began using parachutes as a means of deploying troops. T Today, skydiving is a popular sport around the world.
Factoring A Quadratic Polynomial
 Factoring A Quadratic Polynomial If we multiply two binomials together, the result is a quadratic polynomial: This multiplication is pretty straightforward, using the distributive property of multiplication
Factoring A Quadratic Polynomial If we multiply two binomials together, the result is a quadratic polynomial: This multiplication is pretty straightforward, using the distributive property of multiplication
A.3. Polynomials and Factoring. Polynomials. What you should learn. Definition of a Polynomial in x. Why you should learn it
 Appendi A.3 Polynomials and Factoring A23 A.3 Polynomials and Factoring What you should learn Write polynomials in standard form. Add,subtract,and multiply polynomials. Use special products to multiply
Appendi A.3 Polynomials and Factoring A23 A.3 Polynomials and Factoring What you should learn Write polynomials in standard form. Add,subtract,and multiply polynomials. Use special products to multiply
ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form
 ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form Goal Graph quadratic functions. VOCABULARY Quadratic function A function that can be written in the standard form y = ax 2 + bx+ c where a 0 Parabola
ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form Goal Graph quadratic functions. VOCABULARY Quadratic function A function that can be written in the standard form y = ax 2 + bx+ c where a 0 Parabola
3.1. RATIONAL EXPRESSIONS
 3.1. RATIONAL EXPRESSIONS RATIONAL NUMBERS In previous courses you have learned how to operate (do addition, subtraction, multiplication, and division) on rational numbers (fractions). Rational numbers
3.1. RATIONAL EXPRESSIONS RATIONAL NUMBERS In previous courses you have learned how to operate (do addition, subtraction, multiplication, and division) on rational numbers (fractions). Rational numbers
Mathematics Placement
 Mathematics Placement The ACT COMPASS math test is a self-adaptive test, which potentially tests students within four different levels of math including pre-algebra, algebra, college algebra, and trigonometry.
Mathematics Placement The ACT COMPASS math test is a self-adaptive test, which potentially tests students within four different levels of math including pre-algebra, algebra, college algebra, and trigonometry.
BEGINNING ALGEBRA ACKNOWLEDMENTS
 BEGINNING ALGEBRA The Nursing Department of Labouré College requested the Department of Academic Planning and Support Services to help with mathematics preparatory materials for its Bachelor of Science
BEGINNING ALGEBRA The Nursing Department of Labouré College requested the Department of Academic Planning and Support Services to help with mathematics preparatory materials for its Bachelor of Science
Polynomials. Key Terms. quadratic equation parabola conjugates trinomial. polynomial coefficient degree monomial binomial GCF
 Polynomials 5 5.1 Addition and Subtraction of Polynomials and Polynomial Functions 5.2 Multiplication of Polynomials 5.3 Division of Polynomials Problem Recognition Exercises Operations on Polynomials
Polynomials 5 5.1 Addition and Subtraction of Polynomials and Polynomial Functions 5.2 Multiplication of Polynomials 5.3 Division of Polynomials Problem Recognition Exercises Operations on Polynomials
In the above, the number 19 is an example of a number because its only positive factors are one and itself.
 Math 100 Greatest Common Factor and Factoring by Grouping (Review) Factoring Definition: A factor is a number, variable, monomial, or polynomial which is multiplied by another number, variable, monomial,
Math 100 Greatest Common Factor and Factoring by Grouping (Review) Factoring Definition: A factor is a number, variable, monomial, or polynomial which is multiplied by another number, variable, monomial,
Gouvernement du Québec Ministère de l Éducation, 2004 04-00813 ISBN 2-550-43545-1
 Gouvernement du Québec Ministère de l Éducation, 004 04-00813 ISBN -550-43545-1 Legal deposit Bibliothèque nationale du Québec, 004 1. INTRODUCTION This Definition of the Domain for Summative Evaluation
Gouvernement du Québec Ministère de l Éducation, 004 04-00813 ISBN -550-43545-1 Legal deposit Bibliothèque nationale du Québec, 004 1. INTRODUCTION This Definition of the Domain for Summative Evaluation
SUNY ECC. ACCUPLACER Preparation Workshop. Algebra Skills
 SUNY ECC ACCUPLACER Preparation Workshop Algebra Skills Gail A. Butler Ph.D. Evaluating Algebraic Epressions Substitute the value (#) in place of the letter (variable). Follow order of operations!!! E)
SUNY ECC ACCUPLACER Preparation Workshop Algebra Skills Gail A. Butler Ph.D. Evaluating Algebraic Epressions Substitute the value (#) in place of the letter (variable). Follow order of operations!!! E)
Polynomial Equations and Factoring
 7 Polynomial Equations and Factoring 7.1 Adding and Subtracting Polynomials 7.2 Multiplying Polynomials 7.3 Special Products of Polynomials 7.4 Dividing Polynomials 7.5 Solving Polynomial Equations in
7 Polynomial Equations and Factoring 7.1 Adding and Subtracting Polynomials 7.2 Multiplying Polynomials 7.3 Special Products of Polynomials 7.4 Dividing Polynomials 7.5 Solving Polynomial Equations in
Factoring ax 2 + bx + c - Teacher Notes
 Southern Nevada Regional Professi onal D evel opment Program VOLUME 1, ISSUE 8 MAY 009 A N ewsletter from the Sec ondary Mathematic s Team Factoring ax + bx + c - Teacher Notes Here we look at sample teacher
Southern Nevada Regional Professi onal D evel opment Program VOLUME 1, ISSUE 8 MAY 009 A N ewsletter from the Sec ondary Mathematic s Team Factoring ax + bx + c - Teacher Notes Here we look at sample teacher
A Concrete Introduction. to the Abstract Concepts. of Integers and Algebra using Algebra Tiles
 A Concrete Introduction to the Abstract Concepts of Integers and Algebra using Algebra Tiles Table of Contents Introduction... 1 page Integers 1: Introduction to Integers... 3 2: Working with Algebra Tiles...
A Concrete Introduction to the Abstract Concepts of Integers and Algebra using Algebra Tiles Table of Contents Introduction... 1 page Integers 1: Introduction to Integers... 3 2: Working with Algebra Tiles...
