SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS
|
|
|
- Clinton Barnett
- 10 years ago
- Views:
Transcription
1 (Section 0.6: Polynomial, Rational, and Algebraic Expressions) SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS LEARNING OBJECTIVES Be able to identify polynomial, rational, and algebraic expressions. Understand terminology and notation for polynomials. PART A: DISCUSSION In Chapters 1 and 2, we will discuss polynomial, rational, and algebraic functions, as well as their graphs. PART B: POLYNOMIALS Let n be a nonnegative integer. An n th -degree polynomial in x, written in descending powers of x, has the following general form: a n x n + a n 1 x n a 1 x + a 0, ( a n 0) The coefficients, denoted by a 1, a 2,, a n, are typically assumed to be real numbers, though some theorems will require integers or rational numbers. a n, the leading coefficient, must be nonzero, although any of the other coefficients could be zero (i.e., their corresponding terms could be missing ). a n x n is the leading term. a 0 is the constant term. It can be thought of as a 0 x 0, where x 0 1. Because n is a nonnegative integer, all of the exponents on x indicated above must be nonnegative integers, as well. Each exponent is the degree of its corresponding term.
2 Example 1 (A Polynomial) (Section 0.6: Polynomial, Rational, and Algebraic Expressions) x x2 + 1 is a 3 rd -degree polynomial in x with leading coefficient 4, leading term 4x 3, and constant term 1. The same would be true even if the terms were reordered: x2 + 4x 3. The polynomial 4x x2 + 1 fits the form a n x n + a n 1 x n a 1 x + a 0, with degree n 3. It can be rewritten as: 4x x2 + 0x + 1, which fits the form a 3 x 3 + a 2 x 2 + a 1 x + a 0, where the coefficients are: a 3 4 a a 1 0 a 0 1 ( leading coefficient) ( constant term) Example Set 2 (Constant Polynomials) 7 is a 0 th -degree polynomial. It can be thought of as 7x 0. 0 is a polynomial with no degree.
3 (Section 0.6: Polynomial, Rational, and Algebraic Expressions) PART C: CATEGORIZING POLYNOMIALS BY DEGREE Degree Type Examples 0 [Nonzero] Constant 7 1 Linear 3x Quadratic 5x 2 x Cubic x 3 + 4x 4 Quartic x 4 5 Quintic x 5 PART D: CATEGORIZING POLYNOMIALS BY NUMBER OF TERMS Number of Terms Type Examples 1 Monomial x 5 2 Binomial x 3 + 4x 3 Trinomial 5x 2 x + 1 PART E: SQUARING BINOMIALS Formulas for Squaring Binomials ( a + b) 2 a 2 + 2ab + b 2 ( a b) 2 a 2 2ab + b 2 WARNING 1: When squaring binomials, don t forget the middle term of the resulting Perfect Square Trinomial (PST). 2 x 2 + 6x + 9. Observe that 6x is twice the product of the For example, x + 3 terms x and 3: 6x 2( x) ( 3). The figure below implies that x + y 2 x 2 + 2xy + y 2 for x > 0 and y > 0.
4 (Section 0.6: Polynomial, Rational, and Algebraic Expressions) PART F: RATIONAL AND ALGEBRAIC EXPRESSIONS A rational expression in x can be expressed in the form: polynomial in x nonzero polynomial in x Example Set 3 (Rational Expressions) Examples of rational expressions include: a) 1 x. 5x 3 1 b). Irrational coefficients such as 2 are permissible x 2 + 7x 2 as coefficients of either polynomial. c) x 7 + x which equals x7 + x 1. In fact, all polynomials are rational expressions. An algebraic expression in x is also permitted to contain non-integer rational powers of variable expressions (and their equivalents in radical form). Example Set 4 (Algebraic Expressions) Examples of algebraic expressions include: a) x 1/2, or x. b) x 3 + 7x 5/7 3 x x (See Footnote 1.) All rational expressions are algebraic.
5 (Section 0.6: Polynomial, Rational, and Algebraic Expressions) The Venn diagram below is for expressions in x that correspond to functions (see Chapter 1): FOOTNOTES 1. Algebraic expressions. Some sources forbid the presence of in an algebraic expression, since is a transcendental (i.e., non-algebraic) number. That means that is not a zero of any polynomial with integer coefficients, as, say, 2 is.
6 (Section 0.7: Factoring Polynomials) SECTION 0.7: FACTORING POLYNOMIALS LEARNING OBJECTIVES Know techniques and formulas for factoring polynomials. Know the Test for Factorability for factoring quadratic trinomials. Recognize polynomials in quadratic form and be able to factor them. PART A: DISCUSSION Factoring is a very commonly used technique in precalculus and calculus. Factoring helps us simplify expressions, find zeros, solve equations and inequalities, and find partial fraction decompositions (see Section 7.3). Rewriting a sum of terms as a product of factors helps us perform sign analyses, as we will see in Sections 2.4 and PART B: FACTORING OUT GCFs For now, when we factor a polynomial, we factor it completely over the integers, meaning that the factors cannot be broken down further using only integer coefficients. That is, the factors must be prime (or irreducible) over the integers. In Chapter 2, we will factor over other sets, such as,, or. TIP 1: The Greatest Common Factor (GCF), if it is not 1, should typically be factored out first, although it can be factored out piece-by-piece for more complicated expressions. (Unfortunately, there is no simple, standard definition for the GCF.) Example 1 (Factoring out a GCF) We factor 8x + 6 as 2( 4x + 3), because 2 is the GCF. 2 is the greatest common divisor of 8 and 6. Example 2 (Factoring out a GCF) We factor x 5 + x 3 as x 3 ( x 2 + 1), because x 3 is the GCF. x 3 is the power of x with the least exponent.
7 (Section 0.7: Factoring Polynomials) TIP 2: Sometimes, it is helpful to factor out 1, particularly when a polynomial has a negative leading coefficient. Example 3 (Factoring out -1 First) Solution Factor 8x 5 6x 3. 8x 5 6x 3 8x 5 + 6x 3 2x 3 4x WARNING 1: Sometimes, people confuse signs if they try to factor out 2x 3 immediately. WARNING 2: Be careful when factoring the base of a power. Make sure to apply the exponent to all factors. Example 4 (Factoring out of a Power) ( x 3 + x) 5 is not equivalent to x x The following is correct: 5. ( x 3 + x) 5 x x x 5 x Each factor of the base must be raised to the exponent, 5. See Section 0.5, Law 4: xy n x n y n. 5
8 (Section 0.7: Factoring Polynomials) PART C: FACTORING FORMULAS Factoring Formulas Factoring a Perfect Square Trinomial (PST) Sum of Two Squares Difference of Two Squares Sum of Two Cubes Difference of Two Cubes Formula 2 a 2 + 2ab + b 2 a + b a 2 2ab + b 2 ( a b) 2 (A rule will be provided for a 2 + b 2 when we discuss imaginary numbers in Section 2.1. As is, it is prime for now.) a 2 b 2 a + b a 3 + b 3 a + b a 3 b 3 a b ( a b) a 2 ab + b 2 a 2 + ab + b 2 WARNING 3: Many math students forgot or never learned the last two formulas. WARNING 4: In the last two formulas, there is no 2 or 2 coefficient on the ab term of the trinomial factor. If a and b have no common factors (aside from 1 and 1), the trinomial factors are typically prime. Sometimes, people confuse these trinomials with Perfect Square Trinomials (PSTs), which we introduced in Section 0.6, Part E. TIP 3: In the last two formulas, observe that the binomial factor is as expected : ( a + b) for a 3 + b 3, and ( a b) for a 3 b 3. The visible signs on the right-hand sides follow the pattern: same, different, and +.
9 (Section 0.7: Factoring Polynomials) PART D: TEST FOR FACTORABILITY and PRACTICE EXAMPLES Test for Factorability This test applies to any quadratic trinomial of the form ax 2 + bx + c, where a, b, and c are nonzero, integer coefficients. (Assume the GCF is 1 or 1; if it is not, factor it out.) The discriminant of the trinomial is b 2 4ac. If the discriminant is a perfect square (such as 0, 1, 4, 9, etc.; these are squares of integers), then the trinomial can be factored over the integers. For example, x 2 + 3x + 2 has discriminant 1 and can be factored as ( x + 2) ( x + 1). In fact, if the discriminant is 0, then the trinomial is a perfect square trinomial (PST) and can be factored as the square of a binomial with integer coefficients. For example, x 2 6x + 9 has discriminant 0 and can be factored as x 3 2. If the discriminant is not a perfect square, then the trinomial is prime over the integers. This test may be applied in Example Set 5, a) through g), which serve as review exercises for the reader. The discriminant is denoted by (uppercase delta), though that symbol is also used for other purposes. It is seen in the Quadratic Formula in Section We will discuss a method for factoring quadratic trinomials using the Quadratic Formula in Chapter 2.
10 (Section 0.7: Factoring Polynomials) Example Set 5 (Factoring Polynomials) Factor the following polynomials over the integers. a) x 2 + 9x + 20 b) x 2 20x (Hint: This is a Perfect Square Trinomial (PST).) c) x 2 4x 12 d) 3x 2 20x 7 e) 4x x + 6 f) 2x x + 5 g) 3x 2 + 6x 3 h) x 4 16 i) a 3 3a + 2a 2 b 6b (Hint: Use Factoring by Grouping. This is when we group terms and factor each group locally before we factor the entire expression globally by factoring out the GCF.) j) 4x 2 + 9y 2 k) x y 3 l) x 3 125y 3
11 Solution a) ax 2 + bx + c x 2 + 9x + 20 ( x + 5) ( x + 4) b) x 2 ( x) 2 (Section 0.7: Factoring Polynomials) We want 5 and 4, because they have product c 20 and (since this is the a 1 case) sum b 9. We can rearrange the factors: ( x + 4) ( x + 5). 20x ( 10) 2 Guess that this is a PST for now. x 10 Check: 2( x) ( 10) 20x c) x 2 4x 12 ( x 6) ( x + 2) How do we know we need 6 and + 2? 2, or ( x 10) ( x 10) ( x 10) 2 The constant term, c, is negative, so use opposite signs: one "+" and one "." The middle coefficient, b, is negative, so the negative number must be higher in absolute value than the positive number; it carries more weight. 2-factorizations of 12 (which is c) Think: What? What?? , +1 6, +2 4, +3 d) F + ( O + I )+ L 3x 2 20x 7 ( 3x + 1) ( x 7) Sum b 4? ( a 1 case) No Yes Can stop No F First product (product of the First terms) O Outer product (product of the Outer terms) I Inner product (product of the Inner terms) L Last product (product of the Last terms) ( 3x )( x ) F 3x 2 ; factors must be 3x and x Need L Makes O + I 20x. We need O + I to be 20x, which is the middle term of the trinomial. We're only off by a sign, so we change both signs Makes O + I 20x. This works Also, b 20, a "very negative" coefficient, so we are inclined to pair up the 3x and the 7 to form the outer product, since they form 21x.
12 (Section 0.7: Factoring Polynomials) e) 4x x + 6 ( 4x + 3) ( x + 2) Method 1: Trial-and-Error ("Guess") Method 4x 2x x 2x Method 2: Factoring by Grouping F 4x 2 L 6; need both " + " because of + 11x 4 and 6 are neither prime nor 1, so we may prefer this method. We want two integers whose product is ac (4)(6) 24 and whose sum is b 11. We want 8 and 3; split the middle term accordingly. 4x x + 6 4x 2 + 8x + 3x + 6 OK to switch ( 4x 2 + 8x)+ 3x + 6 4x( x + 2)+ 3 x + 2 4x + 3 Group terms "Local factoring" ( x + 2) "Global factoring" f) 2x x + 5 is prime or irreducible over the integers (i.e., it cannot be broken down further using integer coefficients). None of these combinations work: ( 2x )( x ) F 2x 2 ; factors must be 2x and x Need L 5; need both " + " because of + 10x g) We could also apply the Test for Factorability. The discriminant b 2 4ac ( 10) 2 4( 2) ( 5) , which is not a perfect square, and the GCF 1, so the polynomial is prime. 3x 2 + 6x 3 3 x 2 2x + 1 GCF a PST You should usually factor out the GCF first. 3( x 1) 2
13 h) Apply the Difference of Two Squares formula a 2 b 2 a + b x 4 16 ( x 2 ) 2 ( 4) 2 ( x2 + 4 ) x2 4 prime ( x) 2 ( 2) 2 ( x + 2) ( x 2) x i) Use Factoring by Grouping: a 3 3a + 2a 2 b 6b ( a 3 3a)+ 2a 2 b 6b aa ( 2 3)+ 2b( a 2 3) ( a 2 3) a + 2b (Section 0.7: Factoring Polynomials) [ ( a b) ] twice: j) 4x 2 + 9y 2 is prime. The GCF 1, and we have no formula for the Sum of Two Squares (for now ; this will change when we discuss imaginary numbers in Section 2.1). k) Apply the Sum of Two Cubes formula a 3 + b 3 a + b x y3 ( x) 3 5y 3 ( x + 5y) ( x 2 5xy + 25y ) 2 a2 ab + b2 "Expected NOT factor" 2ab The visible signs follow the pattern: same, different, "+" l) Apply the Difference of Two Cubes formula a 3 b 3 a b a2 + ab + b2 "Expected NOT factor" +2ab The visible signs follow the pattern: same, different, "+" : : x 3 125y3 ( x) 3 5y 3 ( x 5y) ( x 2 + 5xy + 25y 2 ).
14 (Section 0.7: Factoring Polynomials) PART E: FACTORING EXPRESSIONS IN QUADRATIC FORM An expression is in quadratic form It can be expressed as au 2 + bu + c after performing a u substitution, where a 0, and a, b, and c are real coefficients. The term quadratic form is defined differently in higher math; that definition requires each term to have degree 2. Example 6 (Factoring an Expression in Quadratic Form) Solution Factor 2x 6 x 3 1 over the integers. The trinomial 2x 6 x 3 1 is in quadratic form, because the exponent on x in the first term is twice that in the second term (6 is twice 3), and the third term is a constant. We will use the substitution u x 3, the power of x in the middle term. Then, u 2 x 3 2 x 6. 2x 6 x 3 1 2u 2 u 1 Now, factor as usual. 2u + 1 ( u 1) Substitute back. Replace u with x 3. ( x 3 1) 2x With practice, the substitution process can be avoided. Either way, we are not done yet! It is true that 2x will help us verify that. However, x 3 1 apply the Difference of Two Cubes formula. is prime over the integers; Chapter 2 is not prime, because we can ( 2x 3 + 1) ( x 3 1) ( 2x 3 + 1) ( x 1) ( x 2 + x + 1) This is factored completely over the integers. The Test for Factorability can be used to show that the trinomial factor x 2 + x + 1 is prime, as expected.
15 (Section 0.8: Factoring Rational and Algebraic Expressions) SECTION 0.8: FACTORING RATIONAL AND ALGEBRAIC EXPRESSIONS LEARNING OBJECTIVES Know techniques for factoring rational and algebraic expressions. PART A: DISCUSSION In this section, we will extend techniques for factoring polynomials to other rational and algebraic expressions, including those with negative and fractional exponents. Prior to a precalculus course, most students have no experience factoring such expressions. PART B: FACTORING OUT GCFs When we factor x 5 + x 3 as x 3 ( x 2 + 1), we factor out x 3, the power of x with the least exponent; x 3 is the GCF. We then divide each term of x 5 + x 3 by x 3 to obtain the other factor, ( x 2 + 1). When we divide x 5 by x 3, we subtract the exponents in that order and get x 2. TIP 1: Think: We re factoring x 3 out of x 5. 5 takeaway 3 is 2. These techniques apply even when the exponents involved are negative and/or fractional.
16 (Section 0.8: Factoring Rational and Algebraic Expressions) Example 1 (Factoring with Negative Exponents) Solution Factor x 7 + x 4 2x 1 over the integers. Observe that 7 is the least exponent on x. Our GCF is x 7, so we will factor it out and subtract 7 from each of the exponents. x 7 + x 4 2x 1 x ( 7 1+ x 4 ( 7) 2x 1 ( 7) ) x 7 1+ x x 1+ 7 x 7 1+ x 3 2x 6 TIP 2: Observe that this last trinomial has no negative exponents on x. This is a sign that we have factored out the GCF correctly. WARNING 1: We usually try to avoid negative exponents in final answers, so we will rewrite the expression as a fraction. 1+ x3 2x 6 x 7 We are not done yet! We can factor the numerator further over the integers. TIP 3: We will first factor out 1 so that the new leading coefficient is positive. This tends to make factoring easier. ( 1 x3 + 2x 6 ) x 7 The indicated 1 factor can be moved in front of the fraction with no other sign changes. WARNING 2: This is because it is a factor of the entire numerator. 1 x3 + 2x 6 x 7
17 (Section 0.8: Factoring Rational and Algebraic Expressions) TIP 4: We will now rewrite the numerator in descending powers of x. This tends to make factoring easier. 2x6 x 3 1 x 7 Fortunately, we have already factored the numerator in Section 0.7, Example 6. ( x 3 1) 2x x3 + 1 x 7 x 1 x 2 + x + 1 x 7 Example 2 (Factoring with Negative and Fractional Exponents) Solution Factor ( x 3 + 2) 1/3 + ( x 3 + 2) 5/3 over the integers. WARNING 3: Exponents do not typically distribute over sums. WARNING 4: Likewise, the root of a sum is not typically equal to the sum of the roots. WARNING 5: All negative exponents are less than all positive exponents. Observe that 5 3 is the least exponent on ( x3 + 2). Our GCF is ( x 3 + 2) 5/3, so we will factor it out and subtract 5 3 from each of the exponents on ( x 3 + 2).
18 (Section 0.8: Factoring Rational and Algebraic Expressions) ( x 3 + 2) 1/3 + ( x 3 + 2) 5/3 ( x 3 + 2) 5/3 ( x 3 + 2) 1 3 x /3 ( x 3 + 2) ( 5/3 x 3 + 2) x ( x 3 + 2) 5/3 x 6 + 4x ( x 3 + 2) 5/3 x 6 + 4x x6 + 4x ( x 3 + 2) 5/3 Although x 6 + 4x is in quadratic form, it is prime over the integers.
19 (Section 0.9: Simplifying Algebraic Expressions) SECTION 0.9: SIMPLIFYING ALGEBRAIC EXPRESSIONS LEARNING OBJECTIVES Be able to use factoring and canceling (i.e., division) to simplify algebraic expressions. Be able to rationalize the numerator or the denominator of a fraction containing radical(s). Be aware of common errors when rewriting and simplifying expressions. PART A: DISCUSSION The factoring techniques from Sections 0.7 and 0.8 will help us simplify fractions by canceling (i.e., dividing out) common factors. We can also re-express or simplify a fraction by rationalizing the numerator or the denominator. PART B: CANCELING COMMON FACTORS IN A FRACTION We are typically required to provide answers in simplified form. While there are different opinions as to what that means, there is common agreement that factors (other than 1 and 1) that are common to both the numerator and the denominator of a fraction must be canceled (i.e., divided out). WARNING 1: Some instructors object to the term canceling, because students often abuse the idea by inappropriately and carelessly deleting matching expressions. Remember to rely on mathematical rules, not merely wishful thinking! Canceling Rule for Fractions As we simplify a fraction, we can cancel : a nonzero factor of the entire numerator with an equivalent factor of the entire denominator. That is, we can divide the entire numerator and the entire denominator by equivalent nonzero factors.
20 (Section 0.9: Simplifying Algebraic Expressions) For example, we can divide the numerator and the denominator of by x and obtain 1 x x+ 4. We have canceled a pair of x factors: x 2 x () 1 x ( x + 4) 1 x x+ 4 WARNING 2: We cannot cancel a pair of x factors in not shown as a factor of the entire denominator. x x 2 x + 4 x, because x is x Canceling and Restrictions When canceling, if a factor is eliminated from the denominator of a fraction, check to see if any restrictions have been hidden. Such restrictions must be written out separately. It is usually acceptable to wait until the end to write such restrictions. For example, x 2 2 x x ( x + 4) x x+ 4 () 1 ( x) x ( x + 4 x 0 ) ( x 0)
21 PART C: CANCELING OPPOSITE FACTORS (Section 0.9: Simplifying Algebraic Expressions) ( a b) and ( b a) are opposites. Canceling Opposite Factors The quotient of nonzero, opposite factors is 1. Example 1 (Canceling Opposite Factors) Simplify 9 x2 x 3. Solution Method 1 9 x 2 x 3 3+ x ( 3 x) ( x 3) WARNING 3: It is incorrect to factor 9 x 2 as ( x + 3) ( x 3), which is the factorization of x 2 9. ( 3 x) and x 3 order is 1. ( 1) ( 3+ x) 3 x ( x 3) () 1 are opposites, so their quotient in either ( x 3) TIP 1: The parentheses around the 1 remind us that it is a factor of the numerator, not a term. ( 3 + x) ( x 3), or 3 x x 3 The choice between ( 3 + x) and 3 x may depend on context.
22 Solution Method 2 9 x 2 x 3 x 2 9 x 3 x2 9 x 3 ( x + 3) x 3 ( x 3) () 1 ( x + 3) ( x 3), or (Section 0.9: Simplifying Algebraic Expressions) () 1 x 3 x 3 ( x 3) PART D: SIMPLIFYING ALGEBRAIC EXPRESSIONS Example 2 (Simplifying an Algebraic Expression) Simplify ( 4x + 7) 1/3 ( 2x) x x + 7 ( 2/3 4). ( 4x + 7) 2/3 Do not leave nonpositive exponents in the final expression. Solution In calculus, the given expression is obtained by applying the Quotient Rule for Differentiation to 3 x 2. 4x + 7 We begin by cleaning up the numerator. ( 4x + 7) 1/3 ( 2x) x x + 7 4x + 7 2/3 2/3 4 2x( 4x + 7) 1/3 4 ( 3 x2 4x + 7) 2/3 ( 4x + 7) 2/3
23 Method 1 (Factor the Numerator) (Section 0.9: Simplifying Algebraic Expressions) We will factor out the GCF of the numerator, which is x( 4x + 7) 2/3. TIP 2: It may be easier to factor out x in one step and then ( 4x + 7) 2/3 in another step. The GCF does not have to be factored out in one step. TIP 3: It may be easier to substitute u 4x + 7 and obtain 2xu 1/3 4 3 x2 u 2/3 u 2/3. Make sure to substitute back later. 2x( 4x + 7) 1/3 4 ( 3 x2 4x + 7) 2/3 or ( 4x + 7) 2/3 2/3 2( 4x + 7) x 4x + 7 x 4x + 7 4x + 7 2/3 2 4x x 2/3 or 4 3 x 4x + 7 2/3 or 2xu 1/3 4 3 x2 u 2/3 xu 2/3 xu 2/3 u 2/3 1 2u u 2/3 2u 4 3 x u 2/3 4 3 x We now divide 4x + 7 If we let u 4x + 7 : 2/3 by ( 4x + 7) 2/3. ( 4x + 7) 2/3 u ( 4x + 7) 2/3 2/3 u 2/3 u u u 1 4/3 4x + 7 4/3 The division yields ( 4x + 7) 4/3 in the denominator. x 2( 4x + 7) 4 3 x ( 4x + 7) 4/3 x 8x x ( 4x + 7) 4/3
24 (Section 0.9: Simplifying Algebraic Expressions) WARNING 4: Compound fractions are typically unacceptable in a simplified expression. We will multiply the numerator and the denominator by 3. 3x 8x x 34x + 7 4/3 24x2 + 42x 4x 2 34x + 7 4/3 20x2 + 42x 34x + 7, or 2x 10x /3 34x + 7 4/3 WARNING 5: We should factor the numerator and see if there are any common factors with the denominator, aside from 1 and 1. Such factors must be canceled (divided out). WARNING 6: Do not distribute the 3 in the denominator. The 4/3 exponent forbids that. No restrictions need to be written. The only restriction on the given expression was x 7 4, and it is implied by the final expression. Method 2 (Rewrite as a Compound Fraction First) Because of the negative exponent 2, the expressions in blue below can be 3 rewritten as fractions containing positive exponents. Again, the substitution u 4x + 7 may help. 2x( 4x + 7) 1/3 4 ( 3 x2 4x + 7) 2/3 or ( 4x + 7) 2/3 4x 2 2x( 4x + 7) 1/3 34x ( + 7) 2/3 or ( 4x + 7) 2/3 2xu 1/3 4 3 x2 u 2/3 u 2/3 2xu 1/3 4x2 3u 2/3 u 2/3
25 (Section 0.9: Simplifying Algebraic Expressions) We will multiply the numerator and the denominator by the Least Common Denominator (LCD), 34x + 7 2/3, or 3u 2/3. 34x ( + 7) 2/3 2x ( 4x 2 4x + 7 )1/3 34x x ( + 7) 2/3 ( 4x + 7) 2/3 or 3u 2/3 2xu 1/3 4x2 3u 2/3 u 2/3 3u 2/3 2/3 WARNING 7: Do not cancel the expressions above in red. We must apply the Distributive Property. If it helps, write the following step; with experience, you can skip it. 2/3 34x + 7 or 1/3 2x 4x + 7 2/3 34x + 7 2/3 34x + 7 2/3 4x + 7 4x 2 3u 2/3 2xu 1/3 3u 2/3 3u 2/3 u 2/3 3u 2/3 4x 2 2/3 34x + 7 6xu 4x2 3u 4/3 6x( 4x + 7) 4x2 4/3 34x x2 + 42x 4x 2 34x + 7 4/3 20x2 + 42x 34x + 7, or 2x 10x /3 34x + 7 4/3
26 (Section 0.9: Simplifying Algebraic Expressions) PART E: RATIONALIZING DENOMINATORS AND NUMERATORS When we rationalize the denominator of a fraction, we eliminate radicals and non-integer exponents in the denominator but possibly introduce them in the numerator. For example, 1 2 is unacceptable in a simplified expression, so we rewrite it: For more complicated expressions, there 2 are different opinions as to when denominators need to be rationalized. (See Footnote 1) When we rationalize the numerator of a fraction, we eliminate radicals and non-integer exponents in the numerator but possibly introduce them in the denominator. Example 3 (Rationalizing a Numerator) Solution Re-express x + h h x by rationalizing the numerator. This expression is an example of a difference quotient (see Section 1.10). Rationalizing the numerator will help us find a derivative (see Section 1.11). We will multiply the numerator and the denominator by x + h + x, the conjugate of x + h x. x + h h x ( x + h x ) ( x + h + x ) h ( x + h + x ) To multiply out the numerator, we use the rule: ( a b) ( a + b) a 2 b 2.
27 (Section 0.9: Simplifying Algebraic Expressions) ( x + h) 2 x 2 h x+ h + x WARNING 8: Do not forget the radical expression in the denominator. ( x + h) x h x+ h + x x + h x h x+ h + x h h x+ h + x h 1 () We now cancel the h factors and note the restriction h 0. () 1 h ( x + h + x ) 1 x + h + x ( h 0) ( h 0)
28 PART F: COMMON ERRORS (Section 0.9: Simplifying Algebraic Expressions) Beware of the following errors when rewriting or simplifying an expression. Errors involving Radicals and Exponents Error (crossed out) Related Correct Formulas Comments a 2 a, if a < 0 a + b a + b a b a b ( a + b) 1/2 a 1/2 + b 1/2 ( a b) 1/2 a 1/2 b 1/2 ab + ac a b+ c ( ab + ac) 1/2 ab+ ( c) 1/2 a 2 a 3 a 3 a ( a ) 2 a, if a 0 ab a b, if a 0 and b 0. a b a b, if a 0 and b > 0. ab + ac ab+ ( c) a b + c, if a 0 and b + c 0. ( ab + ac) 1/2 ab+ c 1/2 1/2, a 1/2 b + c if a 0 and b + c 0. The formula a 2 a is often forgotten. Do not apply radicals or exponents term-by-term. There is no general formula for the square root of a sum (or a difference), as there is for a product or a quotient. When factoring a radicand or the base of a power, make sure to apply the appropriate radical or exponent to all factors.
29 (Section 0.9: Simplifying Algebraic Expressions) Errors involving Fractions Error (crossed out) Related Correct Formulas Comments ( x) ( 1) x x 2 ( x) x a + 1 b 1 a + b a d b + c d a b + c d x 2 2 x x ( x + 4) x x+ 4 () 1 x ( x + 4 x 0 ) a 1 + b 1 a + b 1. ( x 0) 1 a + 1 b 1 a b b + 1 b a a b + a ab, or a + b ab. a d b + c d a ( b + c) d 1 x + x 2 x1 + x 2 1 x + 1 x 2 x1 + x 2 1 7x 1 4/3 7x4/3 7x 1 4/3 7 x4/3 ( x 0) We can cancel (nonzero, equivalent) factors of the entire numerator and the entire denominator. If we add like fractions, we add the numerators and keep the common denominator. If we add unlike fractions, we do not add the denominators. A fraction groups together its numerator (and groups together its denominator). Reciprocals cannot be taken term-by-term. The negative exponent only applies to x. FOOTNOTES 1. Rationalizing denominators. The expression 2x 10x + 21 from Example 2 is often 4/3 34x + 7 considered simplified. If we were to rationalize the denominator, we would have (nontrivial) powers of 4x + 7 as factors of the numerator and the denominator: 2x 10x x + 7 2x 10x /3 34x + 7 ( 4x + 7) 2/3 4/3 ( 4x + 7) We may be inclined to divide those powers and go back to 4x x 10x /3 34x + 7 2x ( 10x + 21 ) 34x ( + 7). 4/3 2/3
30 (Section 0.10: More Algebraic Manipulations) SECTION 0.10: MORE ALGEBRAIC MANIPULATIONS LEARNING OBJECTIVES Learn additional ways to write equivalent expressions. PART A: DISCUSSION The techniques of this section will help us rewrite expressions so that they are easier to manipulate. They will also help us fit expressions to particular forms and templates. PART B: SPLITTING A FRACTION THROUGH ITS NUMERATOR Example 1 (Splitting a Fraction Through its Numerator) Fill in the boxes below with appropriate, simplified numbers: 7x x x + x Solution 4 We begin by rewriting x as x 1/4, because the template on the right-hand side suggests a preference for exponential form over radical form. 7x x 7x + 3 x 1/4 We will rewrite this as a sum by splitting it through its numerator. 7x1 x + 3 1/4 x 1/4 7x 3/4 + 3x 1/4
31 (Section 0.10: More Algebraic Manipulations) Answer: 7x x 7 x x 1 4 In calculus, the right-hand side is much easier to differentiate and integrate. WARNING 1: Do not split a fraction in this way through its denominator. 1 For example, x + y is not equivalent to 1 x + 1 y. PART C: MAKING COMPOUND FRACTIONS When we divide by a nonzero number, we multiply by its reciprocal. When we multiply by a nonzero number, we divide by its reciprocal. Example 2 (Making Compound Fractions) Fill in the boxes below with appropriate, simplified numbers: 9x 2 + 3y2 4 x 2 + y 2 Solution 9x 2 + 3y x y2 WARNING 2: 3 4y is not equivalent to y2. x y2 4 3 Answer: 9x 2 + 3y2 4 x y2 4 3 This technique will be used in Chapter 10 to set up standard forms for equations of conics.
32 (Section 0.10: More Algebraic Manipulations) PART D: COMPENSATION Sometimes, we can alter an expression if we compensate for the change and maintain equivalence. Example 3 (Compensation Using Addition and Subtraction) Solution Fill in the box below with an appropriate, simplified expression: x x We know that x + 1 x ( x 1 ), so we would like to add 1 to the x numerator of. To compensate for that, we must also subtract 1 from x + 1 the numerator. WARNING 3: If we add 1 to the numerator of a fraction, we cannot compensate by adding 1 to the denominator. For example, x x + 1 x x + 1 x + 1 x x x + 1 Answer: x x x + 1 A similar compensation technique is used when Completing the Square (CTS) in Sections 0.11, 0.13, and 2.2 and Chapter 10.
33 (Section 0.10: More Algebraic Manipulations) Example 4 (Compensation Using Multiplication and Division) Fill in the box below with an appropriate, simplified number: ( 4x + 1) 5 ( 4x + 1) 5 ( 4) Solution The expression on the left-hand side has been multiplied by 4. We compensate by dividing by 4, or by multiplying by its reciprocal, 1 4. Answer: ( 4x + 1) ( 4x + 1) 5 ( 4) In calculus, this technique helps us integrate using the u-substitution method.
Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any.
 Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
NSM100 Introduction to Algebra Chapter 5 Notes Factoring
 Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
1.3 Polynomials and Factoring
 1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
SECTION 2.5: FINDING ZEROS OF POLYNOMIAL FUNCTIONS
 SECTION 2.5: FINDING ZEROS OF POLYNOMIAL FUNCTIONS Assume f ( x) is a nonconstant polynomial with real coefficients written in standard form. PART A: TECHNIQUES WE HAVE ALREADY SEEN Refer to: Notes 1.31
SECTION 2.5: FINDING ZEROS OF POLYNOMIAL FUNCTIONS Assume f ( x) is a nonconstant polynomial with real coefficients written in standard form. PART A: TECHNIQUES WE HAVE ALREADY SEEN Refer to: Notes 1.31
1.3 Algebraic Expressions
 1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
This is a square root. The number under the radical is 9. (An asterisk * means multiply.)
 Page of Review of Radical Expressions and Equations Skills involving radicals can be divided into the following groups: Evaluate square roots or higher order roots. Simplify radical expressions. Rationalize
Page of Review of Radical Expressions and Equations Skills involving radicals can be divided into the following groups: Evaluate square roots or higher order roots. Simplify radical expressions. Rationalize
Math 0980 Chapter Objectives. Chapter 1: Introduction to Algebra: The Integers.
 Math 0980 Chapter Objectives Chapter 1: Introduction to Algebra: The Integers. 1. Identify the place value of a digit. 2. Write a number in words or digits. 3. Write positive and negative numbers used
Math 0980 Chapter Objectives Chapter 1: Introduction to Algebra: The Integers. 1. Identify the place value of a digit. 2. Write a number in words or digits. 3. Write positive and negative numbers used
expression is written horizontally. The Last terms ((2)( 4)) because they are the last terms of the two polynomials. This is called the FOIL method.
 A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
Algebra 1 Course Title
 Algebra 1 Course Title Course- wide 1. What patterns and methods are being used? Course- wide 1. Students will be adept at solving and graphing linear and quadratic equations 2. Students will be adept
Algebra 1 Course Title Course- wide 1. What patterns and methods are being used? Course- wide 1. Students will be adept at solving and graphing linear and quadratic equations 2. Students will be adept
Vocabulary Words and Definitions for Algebra
 Name: Period: Vocabulary Words and s for Algebra Absolute Value Additive Inverse Algebraic Expression Ascending Order Associative Property Axis of Symmetry Base Binomial Coefficient Combine Like Terms
Name: Period: Vocabulary Words and s for Algebra Absolute Value Additive Inverse Algebraic Expression Ascending Order Associative Property Axis of Symmetry Base Binomial Coefficient Combine Like Terms
In algebra, factor by rewriting a polynomial as a product of lower-degree polynomials
 Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
Review of Intermediate Algebra Content
 Review of Intermediate Algebra Content Table of Contents Page Factoring GCF and Trinomials of the Form + b + c... Factoring Trinomials of the Form a + b + c... Factoring Perfect Square Trinomials... 6
Review of Intermediate Algebra Content Table of Contents Page Factoring GCF and Trinomials of the Form + b + c... Factoring Trinomials of the Form a + b + c... Factoring Perfect Square Trinomials... 6
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0).
 This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
Section 5.0A Factoring Part 1
 Section 5.0A Factoring Part 1 I. Work Together A. Multiply the following binomials into trinomials. (Write the final result in descending order, i.e., a + b + c ). ( 7)( + 5) ( + 7)( + ) ( + 7)( + 5) (
Section 5.0A Factoring Part 1 I. Work Together A. Multiply the following binomials into trinomials. (Write the final result in descending order, i.e., a + b + c ). ( 7)( + 5) ( + 7)( + ) ( + 7)( + 5) (
HIBBING COMMUNITY COLLEGE COURSE OUTLINE
 HIBBING COMMUNITY COLLEGE COURSE OUTLINE COURSE NUMBER & TITLE: - Beginning Algebra CREDITS: 4 (Lec 4 / Lab 0) PREREQUISITES: MATH 0920: Fundamental Mathematics with a grade of C or better, Placement Exam,
HIBBING COMMUNITY COLLEGE COURSE OUTLINE COURSE NUMBER & TITLE: - Beginning Algebra CREDITS: 4 (Lec 4 / Lab 0) PREREQUISITES: MATH 0920: Fundamental Mathematics with a grade of C or better, Placement Exam,
( ) FACTORING. x In this polynomial the only variable in common to all is x.
 FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
EAP/GWL Rev. 1/2011 Page 1 of 5. Factoring a polynomial is the process of writing it as the product of two or more polynomial factors.
 EAP/GWL Rev. 1/2011 Page 1 of 5 Factoring a polynomial is the process of writing it as the product of two or more polynomial factors. Example: Set the factors of a polynomial equation (as opposed to an
EAP/GWL Rev. 1/2011 Page 1 of 5 Factoring a polynomial is the process of writing it as the product of two or more polynomial factors. Example: Set the factors of a polynomial equation (as opposed to an
SUNY ECC. ACCUPLACER Preparation Workshop. Algebra Skills
 SUNY ECC ACCUPLACER Preparation Workshop Algebra Skills Gail A. Butler Ph.D. Evaluating Algebraic Epressions Substitute the value (#) in place of the letter (variable). Follow order of operations!!! E)
SUNY ECC ACCUPLACER Preparation Workshop Algebra Skills Gail A. Butler Ph.D. Evaluating Algebraic Epressions Substitute the value (#) in place of the letter (variable). Follow order of operations!!! E)
COLLEGE ALGEBRA. Paul Dawkins
 COLLEGE ALGEBRA Paul Dawkins Table of Contents Preface... iii Outline... iv Preliminaries... Introduction... Integer Exponents... Rational Exponents... 9 Real Exponents...5 Radicals...6 Polynomials...5
COLLEGE ALGEBRA Paul Dawkins Table of Contents Preface... iii Outline... iv Preliminaries... Introduction... Integer Exponents... Rational Exponents... 9 Real Exponents...5 Radicals...6 Polynomials...5
A. Factoring out the Greatest Common Factor.
 DETAILED SOLUTIONS AND CONCEPTS - FACTORING POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to [email protected]. Thank you!
DETAILED SOLUTIONS AND CONCEPTS - FACTORING POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to [email protected]. Thank you!
Factoring and Applications
 Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form
 ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form Goal Graph quadratic functions. VOCABULARY Quadratic function A function that can be written in the standard form y = ax 2 + bx+ c where a 0 Parabola
ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form Goal Graph quadratic functions. VOCABULARY Quadratic function A function that can be written in the standard form y = ax 2 + bx+ c where a 0 Parabola
Florida Math 0028. Correlation of the ALEKS course Florida Math 0028 to the Florida Mathematics Competencies - Upper
 Florida Math 0028 Correlation of the ALEKS course Florida Math 0028 to the Florida Mathematics Competencies - Upper Exponents & Polynomials MDECU1: Applies the order of operations to evaluate algebraic
Florida Math 0028 Correlation of the ALEKS course Florida Math 0028 to the Florida Mathematics Competencies - Upper Exponents & Polynomials MDECU1: Applies the order of operations to evaluate algebraic
Name Intro to Algebra 2. Unit 1: Polynomials and Factoring
 Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
Algebra I Vocabulary Cards
 Algebra I Vocabulary Cards Table of Contents Expressions and Operations Natural Numbers Whole Numbers Integers Rational Numbers Irrational Numbers Real Numbers Absolute Value Order of Operations Expression
Algebra I Vocabulary Cards Table of Contents Expressions and Operations Natural Numbers Whole Numbers Integers Rational Numbers Irrational Numbers Real Numbers Absolute Value Order of Operations Expression
MATH 10034 Fundamental Mathematics IV
 MATH 0034 Fundamental Mathematics IV http://www.math.kent.edu/ebooks/0034/funmath4.pdf Department of Mathematical Sciences Kent State University January 2, 2009 ii Contents To the Instructor v Polynomials.
MATH 0034 Fundamental Mathematics IV http://www.math.kent.edu/ebooks/0034/funmath4.pdf Department of Mathematical Sciences Kent State University January 2, 2009 ii Contents To the Instructor v Polynomials.
Mathematics Placement
 Mathematics Placement The ACT COMPASS math test is a self-adaptive test, which potentially tests students within four different levels of math including pre-algebra, algebra, college algebra, and trigonometry.
Mathematics Placement The ACT COMPASS math test is a self-adaptive test, which potentially tests students within four different levels of math including pre-algebra, algebra, college algebra, and trigonometry.
Factoring Polynomials
 UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
MATH 095, College Prep Mathematics: Unit Coverage Pre-algebra topics (arithmetic skills) offered through BSE (Basic Skills Education)
 MATH 095, College Prep Mathematics: Unit Coverage Pre-algebra topics (arithmetic skills) offered through BSE (Basic Skills Education) Accurately add, subtract, multiply, and divide whole numbers, integers,
MATH 095, College Prep Mathematics: Unit Coverage Pre-algebra topics (arithmetic skills) offered through BSE (Basic Skills Education) Accurately add, subtract, multiply, and divide whole numbers, integers,
Factoring Polynomials
 Factoring Polynomials Factoring Factoring is the process of writing a polynomial as the product of two or more polynomials. The factors of 6x 2 x 2 are 2x + 1 and 3x 2. In this section, we will be factoring
Factoring Polynomials Factoring Factoring is the process of writing a polynomial as the product of two or more polynomials. The factors of 6x 2 x 2 are 2x + 1 and 3x 2. In this section, we will be factoring
Unit 6: Polynomials. 1 Polynomial Functions and End Behavior. 2 Polynomials and Linear Factors. 3 Dividing Polynomials
 Date Period Unit 6: Polynomials DAY TOPIC 1 Polynomial Functions and End Behavior Polynomials and Linear Factors 3 Dividing Polynomials 4 Synthetic Division and the Remainder Theorem 5 Solving Polynomial
Date Period Unit 6: Polynomials DAY TOPIC 1 Polynomial Functions and End Behavior Polynomials and Linear Factors 3 Dividing Polynomials 4 Synthetic Division and the Remainder Theorem 5 Solving Polynomial
POLYNOMIAL FUNCTIONS
 POLYNOMIAL FUNCTIONS Polynomial Division.. 314 The Rational Zero Test.....317 Descarte s Rule of Signs... 319 The Remainder Theorem.....31 Finding all Zeros of a Polynomial Function.......33 Writing a
POLYNOMIAL FUNCTIONS Polynomial Division.. 314 The Rational Zero Test.....317 Descarte s Rule of Signs... 319 The Remainder Theorem.....31 Finding all Zeros of a Polynomial Function.......33 Writing a
Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III
 Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III Name Date Adding and Subtracting Polynomials Algebra Standard 10.0 A polynomial is a sum of one ore more monomials. Polynomial
Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III Name Date Adding and Subtracting Polynomials Algebra Standard 10.0 A polynomial is a sum of one ore more monomials. Polynomial
Determinants can be used to solve a linear system of equations using Cramer s Rule.
 2.6.2 Cramer s Rule Determinants can be used to solve a linear system of equations using Cramer s Rule. Cramer s Rule for Two Equations in Two Variables Given the system This system has the unique solution
2.6.2 Cramer s Rule Determinants can be used to solve a linear system of equations using Cramer s Rule. Cramer s Rule for Two Equations in Two Variables Given the system This system has the unique solution
Algebra and Geometry Review (61 topics, no due date)
 Course Name: Math 112 Credit Exam LA Tech University Course Code: ALEKS Course: Trigonometry Instructor: Course Dates: Course Content: 159 topics Algebra and Geometry Review (61 topics, no due date) Properties
Course Name: Math 112 Credit Exam LA Tech University Course Code: ALEKS Course: Trigonometry Instructor: Course Dates: Course Content: 159 topics Algebra and Geometry Review (61 topics, no due date) Properties
Algebraic expressions are a combination of numbers and variables. Here are examples of some basic algebraic expressions.
 Page 1 of 13 Review of Linear Expressions and Equations Skills involving linear equations can be divided into the following groups: Simplifying algebraic expressions. Linear expressions. Solving linear
Page 1 of 13 Review of Linear Expressions and Equations Skills involving linear equations can be divided into the following groups: Simplifying algebraic expressions. Linear expressions. Solving linear
Higher Education Math Placement
 Higher Education Math Placement Placement Assessment Problem Types 1. Whole Numbers, Fractions, and Decimals 1.1 Operations with Whole Numbers Addition with carry Subtraction with borrowing Multiplication
Higher Education Math Placement Placement Assessment Problem Types 1. Whole Numbers, Fractions, and Decimals 1.1 Operations with Whole Numbers Addition with carry Subtraction with borrowing Multiplication
Florida Math for College Readiness
 Core Florida Math for College Readiness Florida Math for College Readiness provides a fourth-year math curriculum focused on developing the mastery of skills identified as critical to postsecondary readiness
Core Florida Math for College Readiness Florida Math for College Readiness provides a fourth-year math curriculum focused on developing the mastery of skills identified as critical to postsecondary readiness
LAKE ELSINORE UNIFIED SCHOOL DISTRICT
 LAKE ELSINORE UNIFIED SCHOOL DISTRICT Title: PLATO Algebra 1-Semester 2 Grade Level: 10-12 Department: Mathematics Credit: 5 Prerequisite: Letter grade of F and/or N/C in Algebra 1, Semester 2 Course Description:
LAKE ELSINORE UNIFIED SCHOOL DISTRICT Title: PLATO Algebra 1-Semester 2 Grade Level: 10-12 Department: Mathematics Credit: 5 Prerequisite: Letter grade of F and/or N/C in Algebra 1, Semester 2 Course Description:
FACTORING POLYNOMIALS
 296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
What are the place values to the left of the decimal point and their associated powers of ten?
 The verbal answers to all of the following questions should be memorized before completion of algebra. Answers that are not memorized will hinder your ability to succeed in geometry and algebra. (Everything
The verbal answers to all of the following questions should be memorized before completion of algebra. Answers that are not memorized will hinder your ability to succeed in geometry and algebra. (Everything
Section 6.1 Factoring Expressions
 Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
A.3. Polynomials and Factoring. Polynomials. What you should learn. Definition of a Polynomial in x. Why you should learn it
 Appendi A.3 Polynomials and Factoring A23 A.3 Polynomials and Factoring What you should learn Write polynomials in standard form. Add,subtract,and multiply polynomials. Use special products to multiply
Appendi A.3 Polynomials and Factoring A23 A.3 Polynomials and Factoring What you should learn Write polynomials in standard form. Add,subtract,and multiply polynomials. Use special products to multiply
MATH 21. College Algebra 1 Lecture Notes
 MATH 21 College Algebra 1 Lecture Notes MATH 21 3.6 Factoring Review College Algebra 1 Factoring and Foiling 1. (a + b) 2 = a 2 + 2ab + b 2. 2. (a b) 2 = a 2 2ab + b 2. 3. (a + b)(a b) = a 2 b 2. 4. (a
MATH 21 College Algebra 1 Lecture Notes MATH 21 3.6 Factoring Review College Algebra 1 Factoring and Foiling 1. (a + b) 2 = a 2 + 2ab + b 2. 2. (a b) 2 = a 2 2ab + b 2. 3. (a + b)(a b) = a 2 b 2. 4. (a
6.1 The Greatest Common Factor; Factoring by Grouping
 386 CHAPTER 6 Factoring and Applications 6.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
386 CHAPTER 6 Factoring and Applications 6.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
2.3. Finding polynomial functions. An Introduction:
 2.3. Finding polynomial functions. An Introduction: As is usually the case when learning a new concept in mathematics, the new concept is the reverse of the previous one. Remember how you first learned
2.3. Finding polynomial functions. An Introduction: As is usually the case when learning a new concept in mathematics, the new concept is the reverse of the previous one. Remember how you first learned
Tool 1. Greatest Common Factor (GCF)
 Chapter 4: Factoring Review Tool 1 Greatest Common Factor (GCF) This is a very important tool. You must try to factor out the GCF first in every problem. Some problems do not have a GCF but many do. When
Chapter 4: Factoring Review Tool 1 Greatest Common Factor (GCF) This is a very important tool. You must try to factor out the GCF first in every problem. Some problems do not have a GCF but many do. When
0.4 FACTORING POLYNOMIALS
 36_.qxd /3/5 :9 AM Page -9 SECTION. Factoring Polynomials -9. FACTORING POLYNOMIALS Use special products and factorization techniques to factor polynomials. Find the domains of radical expressions. Use
36_.qxd /3/5 :9 AM Page -9 SECTION. Factoring Polynomials -9. FACTORING POLYNOMIALS Use special products and factorization techniques to factor polynomials. Find the domains of radical expressions. Use
POLYNOMIALS and FACTORING
 POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
Math Review. for the Quantitative Reasoning Measure of the GRE revised General Test
 Math Review for the Quantitative Reasoning Measure of the GRE revised General Test www.ets.org Overview This Math Review will familiarize you with the mathematical skills and concepts that are important
Math Review for the Quantitative Reasoning Measure of the GRE revised General Test www.ets.org Overview This Math Review will familiarize you with the mathematical skills and concepts that are important
3.3. Solving Polynomial Equations. Introduction. Prerequisites. Learning Outcomes
 Solving Polynomial Equations 3.3 Introduction Linear and quadratic equations, dealt within Sections 3.1 and 3.2, are members of a class of equations, called polynomial equations. These have the general
Solving Polynomial Equations 3.3 Introduction Linear and quadratic equations, dealt within Sections 3.1 and 3.2, are members of a class of equations, called polynomial equations. These have the general
3.1. RATIONAL EXPRESSIONS
 3.1. RATIONAL EXPRESSIONS RATIONAL NUMBERS In previous courses you have learned how to operate (do addition, subtraction, multiplication, and division) on rational numbers (fractions). Rational numbers
3.1. RATIONAL EXPRESSIONS RATIONAL NUMBERS In previous courses you have learned how to operate (do addition, subtraction, multiplication, and division) on rational numbers (fractions). Rational numbers
AIP Factoring Practice/Help
 The following pages include many problems to practice factoring skills. There are also several activities with examples to help you with factoring if you feel like you are not proficient with it. There
The following pages include many problems to practice factoring skills. There are also several activities with examples to help you with factoring if you feel like you are not proficient with it. There
Chapter 7 - Roots, Radicals, and Complex Numbers
 Math 233 - Spring 2009 Chapter 7 - Roots, Radicals, and Complex Numbers 7.1 Roots and Radicals 7.1.1 Notation and Terminology In the expression x the is called the radical sign. The expression under the
Math 233 - Spring 2009 Chapter 7 - Roots, Radicals, and Complex Numbers 7.1 Roots and Radicals 7.1.1 Notation and Terminology In the expression x the is called the radical sign. The expression under the
Chapter R.4 Factoring Polynomials
 Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
Algebra Practice Problems for Precalculus and Calculus
 Algebra Practice Problems for Precalculus and Calculus Solve the following equations for the unknown x: 1. 5 = 7x 16 2. 2x 3 = 5 x 3. 4. 1 2 (x 3) + x = 17 + 3(4 x) 5 x = 2 x 3 Multiply the indicated polynomials
Algebra Practice Problems for Precalculus and Calculus Solve the following equations for the unknown x: 1. 5 = 7x 16 2. 2x 3 = 5 x 3. 4. 1 2 (x 3) + x = 17 + 3(4 x) 5 x = 2 x 3 Multiply the indicated polynomials
Factoring Polynomials and Solving Quadratic Equations
 Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
ACCUPLACER. Testing & Study Guide. Prepared by the Admissions Office Staff and General Education Faculty Draft: January 2011
 ACCUPLACER Testing & Study Guide Prepared by the Admissions Office Staff and General Education Faculty Draft: January 2011 Thank you to Johnston Community College staff for giving permission to revise
ACCUPLACER Testing & Study Guide Prepared by the Admissions Office Staff and General Education Faculty Draft: January 2011 Thank you to Johnston Community College staff for giving permission to revise
a 1 x + a 0 =0. (3) ax 2 + bx + c =0. (4)
 ROOTS OF POLYNOMIAL EQUATIONS In this unit we discuss polynomial equations. A polynomial in x of degree n, where n 0 is an integer, is an expression of the form P n (x) =a n x n + a n 1 x n 1 + + a 1 x
ROOTS OF POLYNOMIAL EQUATIONS In this unit we discuss polynomial equations. A polynomial in x of degree n, where n 0 is an integer, is an expression of the form P n (x) =a n x n + a n 1 x n 1 + + a 1 x
FACTORING OUT COMMON FACTORS
 278 (6 2) Chapter 6 Factoring 6.1 FACTORING OUT COMMON FACTORS In this section Prime Factorization of Integers Greatest Common Factor Finding the Greatest Common Factor for Monomials Factoring Out the
278 (6 2) Chapter 6 Factoring 6.1 FACTORING OUT COMMON FACTORS In this section Prime Factorization of Integers Greatest Common Factor Finding the Greatest Common Factor for Monomials Factoring Out the
Factoring Trinomials: The ac Method
 6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
Polynomials and Factoring
 7.6 Polynomials and Factoring Basic Terminology A term, or monomial, is defined to be a number, a variable, or a product of numbers and variables. A polynomial is a term or a finite sum or difference of
7.6 Polynomials and Factoring Basic Terminology A term, or monomial, is defined to be a number, a variable, or a product of numbers and variables. A polynomial is a term or a finite sum or difference of
0.8 Rational Expressions and Equations
 96 Prerequisites 0.8 Rational Expressions and Equations We now turn our attention to rational expressions - that is, algebraic fractions - and equations which contain them. The reader is encouraged to
96 Prerequisites 0.8 Rational Expressions and Equations We now turn our attention to rational expressions - that is, algebraic fractions - and equations which contain them. The reader is encouraged to
Lesson 9: Radicals and Conjugates
 Student Outcomes Students understand that the sum of two square roots (or two cube roots) is not equal to the square root (or cube root) of their sum. Students convert expressions to simplest radical form.
Student Outcomes Students understand that the sum of two square roots (or two cube roots) is not equal to the square root (or cube root) of their sum. Students convert expressions to simplest radical form.
6.1 Add & Subtract Polynomial Expression & Functions
 6.1 Add & Subtract Polynomial Expression & Functions Objectives 1. Know the meaning of the words term, monomial, binomial, trinomial, polynomial, degree, coefficient, like terms, polynomial funciton, quardrtic
6.1 Add & Subtract Polynomial Expression & Functions Objectives 1. Know the meaning of the words term, monomial, binomial, trinomial, polynomial, degree, coefficient, like terms, polynomial funciton, quardrtic
MATH 90 CHAPTER 6 Name:.
 MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
Indiana State Core Curriculum Standards updated 2009 Algebra I
 Indiana State Core Curriculum Standards updated 2009 Algebra I Strand Description Boardworks High School Algebra presentations Operations With Real Numbers Linear Equations and A1.1 Students simplify and
Indiana State Core Curriculum Standards updated 2009 Algebra I Strand Description Boardworks High School Algebra presentations Operations With Real Numbers Linear Equations and A1.1 Students simplify and
CORRELATED TO THE SOUTH CAROLINA COLLEGE AND CAREER-READY FOUNDATIONS IN ALGEBRA
 We Can Early Learning Curriculum PreK Grades 8 12 INSIDE ALGEBRA, GRADES 8 12 CORRELATED TO THE SOUTH CAROLINA COLLEGE AND CAREER-READY FOUNDATIONS IN ALGEBRA April 2016 www.voyagersopris.com Mathematical
We Can Early Learning Curriculum PreK Grades 8 12 INSIDE ALGEBRA, GRADES 8 12 CORRELATED TO THE SOUTH CAROLINA COLLEGE AND CAREER-READY FOUNDATIONS IN ALGEBRA April 2016 www.voyagersopris.com Mathematical
A Systematic Approach to Factoring
 A Systematic Approach to Factoring Step 1 Count the number of terms. (Remember****Knowing the number of terms will allow you to eliminate unnecessary tools.) Step 2 Is there a greatest common factor? Tool
A Systematic Approach to Factoring Step 1 Count the number of terms. (Remember****Knowing the number of terms will allow you to eliminate unnecessary tools.) Step 2 Is there a greatest common factor? Tool
The Method of Partial Fractions Math 121 Calculus II Spring 2015
 Rational functions. as The Method of Partial Fractions Math 11 Calculus II Spring 015 Recall that a rational function is a quotient of two polynomials such f(x) g(x) = 3x5 + x 3 + 16x x 60. The method
Rational functions. as The Method of Partial Fractions Math 11 Calculus II Spring 015 Recall that a rational function is a quotient of two polynomials such f(x) g(x) = 3x5 + x 3 + 16x x 60. The method
Polynomial Degree and Finite Differences
 CONDENSED LESSON 7.1 Polynomial Degree and Finite Differences In this lesson you will learn the terminology associated with polynomials use the finite differences method to determine the degree of a polynomial
CONDENSED LESSON 7.1 Polynomial Degree and Finite Differences In this lesson you will learn the terminology associated with polynomials use the finite differences method to determine the degree of a polynomial
Five 5. Rational Expressions and Equations C H A P T E R
 Five C H A P T E R Rational Epressions and Equations. Rational Epressions and Functions. Multiplication and Division of Rational Epressions. Addition and Subtraction of Rational Epressions.4 Comple Fractions.
Five C H A P T E R Rational Epressions and Equations. Rational Epressions and Functions. Multiplication and Division of Rational Epressions. Addition and Subtraction of Rational Epressions.4 Comple Fractions.
CAHSEE on Target UC Davis, School and University Partnerships
 UC Davis, School and University Partnerships CAHSEE on Target Mathematics Curriculum Published by The University of California, Davis, School/University Partnerships Program 006 Director Sarah R. Martinez,
UC Davis, School and University Partnerships CAHSEE on Target Mathematics Curriculum Published by The University of California, Davis, School/University Partnerships Program 006 Director Sarah R. Martinez,
ALGEBRA 2 CRA 2 REVIEW - Chapters 1-6 Answer Section
 ALGEBRA 2 CRA 2 REVIEW - Chapters 1-6 Answer Section MULTIPLE CHOICE 1. ANS: C 2. ANS: A 3. ANS: A OBJ: 5-3.1 Using Vertex Form SHORT ANSWER 4. ANS: (x + 6)(x 2 6x + 36) OBJ: 6-4.2 Solving Equations by
ALGEBRA 2 CRA 2 REVIEW - Chapters 1-6 Answer Section MULTIPLE CHOICE 1. ANS: C 2. ANS: A 3. ANS: A OBJ: 5-3.1 Using Vertex Form SHORT ANSWER 4. ANS: (x + 6)(x 2 6x + 36) OBJ: 6-4.2 Solving Equations by
SECTION P.5 Factoring Polynomials
 BLITMCPB.QXP.0599_48-74 /0/0 0:4 AM Page 48 48 Chapter P Prerequisites: Fundamental Concepts of Algebra Technology Eercises Critical Thinking Eercises 98. The common cold is caused by a rhinovirus. The
BLITMCPB.QXP.0599_48-74 /0/0 0:4 AM Page 48 48 Chapter P Prerequisites: Fundamental Concepts of Algebra Technology Eercises Critical Thinking Eercises 98. The common cold is caused by a rhinovirus. The
Polynomial Operations and Factoring
 Algebra 1, Quarter 4, Unit 4.1 Polynomial Operations and Factoring Overview Number of instructional days: 15 (1 day = 45 60 minutes) Content to be learned Identify terms, coefficients, and degree of polynomials.
Algebra 1, Quarter 4, Unit 4.1 Polynomial Operations and Factoring Overview Number of instructional days: 15 (1 day = 45 60 minutes) Content to be learned Identify terms, coefficients, and degree of polynomials.
Factoring Quadratic Expressions
 Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
Algebra 2 Year-at-a-Glance Leander ISD 2007-08. 1st Six Weeks 2nd Six Weeks 3rd Six Weeks 4th Six Weeks 5th Six Weeks 6th Six Weeks
 Algebra 2 Year-at-a-Glance Leander ISD 2007-08 1st Six Weeks 2nd Six Weeks 3rd Six Weeks 4th Six Weeks 5th Six Weeks 6th Six Weeks Essential Unit of Study 6 weeks 3 weeks 3 weeks 6 weeks 3 weeks 3 weeks
Algebra 2 Year-at-a-Glance Leander ISD 2007-08 1st Six Weeks 2nd Six Weeks 3rd Six Weeks 4th Six Weeks 5th Six Weeks 6th Six Weeks Essential Unit of Study 6 weeks 3 weeks 3 weeks 6 weeks 3 weeks 3 weeks
Veterans Upward Bound Algebra I Concepts - Honors
 Veterans Upward Bound Algebra I Concepts - Honors Brenda Meery Kaitlyn Spong Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org Chapter 6. Factoring CHAPTER
Veterans Upward Bound Algebra I Concepts - Honors Brenda Meery Kaitlyn Spong Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org Chapter 6. Factoring CHAPTER
Greatest Common Factor (GCF) Factoring
 Section 4 4: Greatest Common Factor (GCF) Factoring The last chapter introduced the distributive process. The distributive process takes a product of a monomial and a polynomial and changes the multiplication
Section 4 4: Greatest Common Factor (GCF) Factoring The last chapter introduced the distributive process. The distributive process takes a product of a monomial and a polynomial and changes the multiplication
5.1 Radical Notation and Rational Exponents
 Section 5.1 Radical Notation and Rational Exponents 1 5.1 Radical Notation and Rational Exponents We now review how exponents can be used to describe not only powers (such as 5 2 and 2 3 ), but also roots
Section 5.1 Radical Notation and Rational Exponents 1 5.1 Radical Notation and Rational Exponents We now review how exponents can be used to describe not only powers (such as 5 2 and 2 3 ), but also roots
Factoring Flow Chart
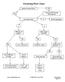 Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Math 10C. Course: Polynomial Products and Factors. Unit of Study: Step 1: Identify the Outcomes to Address. Guiding Questions:
 Course: Unit of Study: Math 10C Polynomial Products and Factors Step 1: Identify the Outcomes to Address Guiding Questions: What do I want my students to learn? What can they currently understand and do?
Course: Unit of Study: Math 10C Polynomial Products and Factors Step 1: Identify the Outcomes to Address Guiding Questions: What do I want my students to learn? What can they currently understand and do?
Answers to Basic Algebra Review
 Answers to Basic Algebra Review 1. -1.1 Follow the sign rules when adding and subtracting: If the numbers have the same sign, add them together and keep the sign. If the numbers have different signs, subtract
Answers to Basic Algebra Review 1. -1.1 Follow the sign rules when adding and subtracting: If the numbers have the same sign, add them together and keep the sign. If the numbers have different signs, subtract
Welcome to Math 19500 Video Lessons. Stanley Ocken. Department of Mathematics The City College of New York Fall 2013
 Welcome to Math 19500 Video Lessons Prof. Department of Mathematics The City College of New York Fall 2013 An important feature of the following Beamer slide presentations is that you, the reader, move
Welcome to Math 19500 Video Lessons Prof. Department of Mathematics The City College of New York Fall 2013 An important feature of the following Beamer slide presentations is that you, the reader, move
MATH 60 NOTEBOOK CERTIFICATIONS
 MATH 60 NOTEBOOK CERTIFICATIONS Chapter #1: Integers and Real Numbers 1.1a 1.1b 1.2 1.3 1.4 1.8 Chapter #2: Algebraic Expressions, Linear Equations, and Applications 2.1a 2.1b 2.1c 2.2 2.3a 2.3b 2.4 2.5
MATH 60 NOTEBOOK CERTIFICATIONS Chapter #1: Integers and Real Numbers 1.1a 1.1b 1.2 1.3 1.4 1.8 Chapter #2: Algebraic Expressions, Linear Equations, and Applications 2.1a 2.1b 2.1c 2.2 2.3a 2.3b 2.4 2.5
Algebra 1. Curriculum Map
 Algebra 1 Curriculum Map Table of Contents Unit 1: Expressions and Unit 2: Linear Unit 3: Representing Linear Unit 4: Linear Inequalities Unit 5: Systems of Linear Unit 6: Polynomials Unit 7: Factoring
Algebra 1 Curriculum Map Table of Contents Unit 1: Expressions and Unit 2: Linear Unit 3: Representing Linear Unit 4: Linear Inequalities Unit 5: Systems of Linear Unit 6: Polynomials Unit 7: Factoring
6 EXTENDING ALGEBRA. 6.0 Introduction. 6.1 The cubic equation. Objectives
 6 EXTENDING ALGEBRA Chapter 6 Extending Algebra Objectives After studying this chapter you should understand techniques whereby equations of cubic degree and higher can be solved; be able to factorise
6 EXTENDING ALGEBRA Chapter 6 Extending Algebra Objectives After studying this chapter you should understand techniques whereby equations of cubic degree and higher can be solved; be able to factorise
Factoring (pp. 1 of 4)
 Factoring (pp. 1 of 4) Algebra Review Try these items from middle school math. A) What numbers are the factors of 4? B) Write down the prime factorization of 7. C) 6 Simplify 48 using the greatest common
Factoring (pp. 1 of 4) Algebra Review Try these items from middle school math. A) What numbers are the factors of 4? B) Write down the prime factorization of 7. C) 6 Simplify 48 using the greatest common
The majority of college students hold credit cards. According to the Nellie May
 CHAPTER 6 Factoring Polynomials 6.1 The Greatest Common Factor and Factoring by Grouping 6. Factoring Trinomials of the Form b c 6.3 Factoring Trinomials of the Form a b c and Perfect Square Trinomials
CHAPTER 6 Factoring Polynomials 6.1 The Greatest Common Factor and Factoring by Grouping 6. Factoring Trinomials of the Form b c 6.3 Factoring Trinomials of the Form a b c and Perfect Square Trinomials
Big Bend Community College. Beginning Algebra MPC 095. Lab Notebook
 Big Bend Community College Beginning Algebra MPC 095 Lab Notebook Beginning Algebra Lab Notebook by Tyler Wallace is licensed under a Creative Commons Attribution 3.0 Unported License. Permissions beyond
Big Bend Community College Beginning Algebra MPC 095 Lab Notebook Beginning Algebra Lab Notebook by Tyler Wallace is licensed under a Creative Commons Attribution 3.0 Unported License. Permissions beyond
Students will be able to simplify and evaluate numerical and variable expressions using appropriate properties and order of operations.
 Outcome 1: (Introduction to Algebra) Skills/Content 1. Simplify numerical expressions: a). Use order of operations b). Use exponents Students will be able to simplify and evaluate numerical and variable
Outcome 1: (Introduction to Algebra) Skills/Content 1. Simplify numerical expressions: a). Use order of operations b). Use exponents Students will be able to simplify and evaluate numerical and variable
Math 25 Activity 6: Factoring Advanced
 Instructor! Math 25 Activity 6: Factoring Advanced Last week we looked at greatest common factors and the basics of factoring out the GCF. In this second activity, we will discuss factoring more difficult
Instructor! Math 25 Activity 6: Factoring Advanced Last week we looked at greatest common factors and the basics of factoring out the GCF. In this second activity, we will discuss factoring more difficult
Pre-Calculus II Factoring and Operations on Polynomials
 Factoring... 1 Polynomials...1 Addition of Polynomials... 1 Subtraction of Polynomials...1 Multiplication of Polynomials... Multiplying a monomial by a monomial... Multiplying a monomial by a polynomial...
Factoring... 1 Polynomials...1 Addition of Polynomials... 1 Subtraction of Polynomials...1 Multiplication of Polynomials... Multiplying a monomial by a monomial... Multiplying a monomial by a polynomial...
Lagrange Interpolation is a method of fitting an equation to a set of points that functions well when there are few points given.
 Polynomials (Ch.1) Study Guide by BS, JL, AZ, CC, SH, HL Lagrange Interpolation is a method of fitting an equation to a set of points that functions well when there are few points given. Sasha s method
Polynomials (Ch.1) Study Guide by BS, JL, AZ, CC, SH, HL Lagrange Interpolation is a method of fitting an equation to a set of points that functions well when there are few points given. Sasha s method
Answer Key for California State Standards: Algebra I
 Algebra I: Symbolic reasoning and calculations with symbols are central in algebra. Through the study of algebra, a student develops an understanding of the symbolic language of mathematics and the sciences.
Algebra I: Symbolic reasoning and calculations with symbols are central in algebra. Through the study of algebra, a student develops an understanding of the symbolic language of mathematics and the sciences.
SPECIAL PRODUCTS AND FACTORS
 CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
Some Polynomial Theorems. John Kennedy Mathematics Department Santa Monica College 1900 Pico Blvd. Santa Monica, CA 90405 [email protected].
 Some Polynomial Theorems by John Kennedy Mathematics Department Santa Monica College 1900 Pico Blvd. Santa Monica, CA 90405 [email protected] This paper contains a collection of 31 theorems, lemmas,
Some Polynomial Theorems by John Kennedy Mathematics Department Santa Monica College 1900 Pico Blvd. Santa Monica, CA 90405 [email protected] This paper contains a collection of 31 theorems, lemmas,
