Math 10C. Course: Polynomial Products and Factors. Unit of Study: Step 1: Identify the Outcomes to Address. Guiding Questions:
|
|
|
- Isabel Baldwin
- 7 years ago
- Views:
Transcription
1 Course: Unit of Study: Math 10C Polynomial Products and Factors Step 1: Identify the Outcomes to Address Guiding Questions: What do I want my students to learn? What can they currently understand and do? What do I want my students to be able to understand and do based on the big ideas and specific outcomes in the program of studies? Outcome(s) from the Program of Studies: Algebra and Number (S01 students must have complete the real numbers unit prior to this unit of study so that SO1 will be covered already) SO1. Demonstrate an understanding of factors of whole numbers by determining the: prime factors greatest common factor least common multiple square root cube root. [CN, ME, R] SO4. Demonstrate an understanding of the multiplication of polynomial expressions (limited to monomials, binomials and trinomials), concretely, pictorially and symbolically. [CN, R, V] SO5. Demonstrate an understanding of common factors and trinomial factoring, concretely, pictorially and symbolically. [C, CN, R, V] 1 M10C CH Products & Factors Lesson Plans.docx
2 Step : Learning Trajectory Prior Learning Current Learning Future Learning Grade 5 Number Strand 4. Apply mental mathematics strategies for multiplication, such as: annexing then adding zero halving and doubling using the distributive property. [C, CN, ME, R, V] Grade 7 Patterns and Relations (variables and Equations) S.O. #4. Explain the difference between an expression and an equation. [C, CN] Grade 9: Patterns and Relations (variables and Equations) S.O. #5 Demonstrate an understanding of polynomials (limited to polynomials of a degree less than or equal to ) SO. #6 Model, record and explain the operations of addition and subtraction of polynomial expressions, concretely, pictorially and symbolically (limited to polynomials of degree less than or equal to ). S.O. #7. Model, record and explain the operations of multiplication and division of polynomial expressions (limited to polynomials of degree less than or equal to ) by monomials, concretely, pictorially and symbolically. [C, CN, R, V] Grade 9 Number Strand Algebra and Number SO1. Demonstrate an understanding of factors of whole numbers by determining the: prime factors greatest common factor least common multiple square root cube root. [CN, ME, R] SO4. Demonstrate an understanding of the multiplication of polynomial expressions (limited to monomials, binomials and trinomials), concretely, pictorially and symbolically. [CN, R, V] SO5. Demonstrate an understanding of common factors and trinomial factoring, concretely, pictorially and symbolically. [C, CN, R, V] 0 1 Algebra and Number S.O 4. Determine equivalent forms of rational expressions (limited to numerators and denominators that are monomials, binomials or trinomials). [C, ME, R] 5. Perform operations on rational expressions (limited to numerators and denominators that are monomials, binomials or trinomials). [CN, ME, R] 6. Solve problems that involve rational equations (limited to numerators and denominators that are monomials, binomials or trinomials). [C, PS, R] 0 1 Relations and Functions 1. Factor polynomial expressions of the form: ax+bx+c,a 0 ax by,a 0,b 0 ( ( )) ( ( )) a f x +b f x +c,a 0 ( ( )) ( ( )) a f x bg y,a 0,b 0 where a, b and c are rational numbers. [CN, ME, R] 0 1 Relations and Functions S.O. #4. Analyze quadratic functions of the form y=a +bx+cto identify characteristics of the corresponding graph, including: x vertex domain and range direction of opening axis of symmetry x and y intercepts and to solve problems. [CN, PS, R, T, V] [ICT: C6 4.1, C6 4.] S.O. 5. Solve problems that involve M10C CH Products & Factors Lesson Plans.docx
3 S.O. #1 Demonstrate an understanding of powers with integral bases (excluding base 0) and whole number exponents by: representing repeated multiplication, using powers using patterns to show that a power with an exponent of zero is equal to one solving problems involving powers. [C, CN, PS, R]. Demonstrate an understanding of operations on powers with integral bases (excluding base 0) and whole number exponents: (am)(an)=am+n am an=am n,m>n (am)n =amn (ab)m= ambm, 0. n n n a b a b b = [C, CN, PS, R, T] [ICT: P.4] S.O. #5. Determine the square root of positive rational numbers that are perfect squares. [C, CN, PS, R, T] S.O. 5. Determine the square root of positive rational numbers that are perfect squares. [C, CN, PS, R, T] [ICT: P.4] Grade 8 Number Strand S.O. #1. Demonstrate an understanding of perfect squares and square roots, concretely, pictorially and symbolically (limited to whole numbers). [C, CN, R, V] quadratic equations. [C, CN, PS, R, T, V] [ICT: C6 4.1] S.O. #6. Solve, algebraically and graphically, problems that involve systems of linear quadratic and quadratic quadratic equations in two variables. [CN, PS, R, T, V] [ICT: C6 4.1, C6 4.4] 0 1 Trigonometry S.O.# 5. Solve, algebraically and graphically, first and second degree trigonometric equations with the domain expressed in degrees and radians. [CN, PS, R, T, V] [ICT: C6 4.1, C6 4.4] S.O. #6. Prove trigonometric identities, using: reciprocal identities quotient identities Pythagorean identities sum or difference identities (restricted to sine, cosine and tangent) double angle identities (restricted to sine, cosine and tangent). [R, T, V] [ICT: C6 4.1, C6 4.4] Relations and Functions S.O. # 10. Solve problems that involve exponential and logarithmic equations. [C, CN, PS, R] S.O. # 11. Demonstrate an understanding of factoring polynomials of degree greater than (limited to polynomials of degree 5 with integral coefficients). [C, CN, ME] S.O. #1. Graph and analyze polynomial functions (limited to polynomial functions of degree 5 ). [C, CN, T, V] [ICT: C6 4., C6 4.4] M10C CH Products & Factors Lesson Plans.docx
4 Grade 10C Algebra and Number. Demonstrate an understanding of powers with integral and rational exponents. [C, CN, PS, R] 0 Patterns and Relations. Solve problems that involve quadratic equations. [C, CN, PS, R, T, V] [ICT: C6 4.1, C6 4.] 0 Relations and Functions 1. Determine equivalent forms of rational expressions (limited to numerators and denominators that are monomials and binomials). [C, ME, R]. Perform operations on rational expressions (limited to numerators and denominators that are monomials and binomials). [CN, ME, R]. Solve problems that involve rational equations (limited to numerators and denominators that are monomials and binomials). [C, CN, PS, R] 7. Represent data, using polynomial functions (of degree ), to solve problems. [C, CN, PS, T, V] [ICT: C6 4.1, C6 4., C6 4.4] 4 M10C CH Products & Factors Lesson Plans.docx
5 Step : Necessary Pre Requisites Pre Requisite Knowledge and Skills - Collecting like terms - Finding perfect squares - Distributive property - Add/ subtract polynomials - multiply / divide monomials - Algebra tiles - Expanding and simplifying Pre Requisite Vocabulary - Like terms - Perfect squares - Distributive law - Expression vs Equation - Polynomial - Monomial, Binomial, Trinomial polynomial - Constant term - Variable - Degree - Coefficient - Simplify - Factors - Multiples 5 M10C CH Products & Factors Lesson Plans.docx
6 Step 4: Learning Development Developing Knowledge and Skills - Binomial multiplication - Factorization (common factoring, difference of squares, trinomial, perfect square trinomials) - Where does this apply to real life situations? - Seeing factors as length/ width of a rectangle? Square? Etc? - Using factors to create area - Using algebra tiles to factor and expand. Developing Vocabulary - All prerequisite vocabulary (from Jr High) - Like terms - Perfect squares - Distributive law - Expression vs Equation - Polynomial - Monomial, Binomial, Trinomial polynomial - Constant term - Variable - Degree - Coefficient - Simplify - Factors - Multiples - GCF - Prime factorization - LCM - Perfect cube/ perfect root - Radicand/ radical/ index (from previous unit likely) - Decomposition Predictable Misunderstandings and Errors Adding/ Subtracting polynomials (collecting like terms) vs multiplying and dividing polynomials (using the powers laws). Students will want to change the exponent when adding and subtracting rather than just add/subtract the coefficient. 6 M10C CH Products & Factors Lesson Plans.docx
7 Step 5: The Big Picture Essential Understanding: - Tiles can be used to represent factors and multiples - Factors can be used in a variety of real life situations such as: area, volume, construction, design, modeling. Big Ideas: - Multiplication and Division are inverses of each other - A rectangle diagram can be used to represent area and factors - Factors and multiples can be used for polynomials - Expressions can be written in various equivalent forms (factored or expanded) Essential Question: - How could the understandings from this unit be used in construction and design? Consider the perspectives of potential: Architect? Carpenter? Plumber? Landscape engineers? Etc. 7 M10C CH Products & Factors Lesson Plans.docx
8 Day 1 1. Polynomial an expression consisting of variables and real numbers. The exponents of the variables must be whole numbers. Ex: x + 11, x +, x, 7x x y, ( rd and 5 th are not polynomials). y. Coefficient the number immediately preceding a variable in a term (i.e. in 4x + 7x, the coefficients are 4 and 7).. Degree of a term The sum of the exponents of the variables in the term. Ex: 9x 4 + x + 7 Degree = Degree of a polynomial. Degree of a polynomial is determined by the term with the highest degree. Ex: 4y 10 6y 7 + y 4 Degree of this polynomial is 10. Degree = Constant term. The term which has no variable. Ex: a. x + 7x 6 (constant term is 6) b. 7x 5 (constant term is 0) 8 M10C CH Products & Factors Lesson Plans.docx
9 6. Classifying polynomials according to the number of terms. See for examples of mono, bi and trinomials. Number of terms Name 1 monomial binomial trinomial 4 or more polynomial 7. Classifying polynomials according to the degree of the polynomial. Degree Name Examples 0 constant 11 1 linear 7x + quadratic x 7x + cubic 5x + 8x 9x 6 Questions Number of terms Degree Name of polynomial according to Number of terms Degree x. x x 5x x x x x x x Number of terms Degree Name of polynomial according to Number of terms Degree Answers monomial constant. 7x 1 1 monomial linear. x binomial linear 4. x 5x 6 trinomial quadratic 5. 5x x x 10 4 polynomial cubic 6. x x x trinomial cubic 9 M10C CH Products & Factors Lesson Plans.docx
10 II. Addition and subtraction of polynomials. add/subtract like terms (terms that have the same variable(s) and exponent(s)). Ex: 1. (x + 4x ) + (x 6x + 9) = x x + 7. (4y y + ) (y + 5y ) = y 7y + 5 Try: 1. (6a ab + 4) (7a + 4ab ). (x + y ) + (x y) (5x 5y + y ) Assignment: M10C CH Poly Intro.docx Contains Blackline Master.1c 10 M10C CH Products & Factors Lesson Plans.docx
11 Day Polynomial Multiplication and Division Grade 9 Review of Laws or properties of exponents. 1. Product law: x a. x b = x a + b i.e. 4 7 m m = m See for further explanations. Quotient law: x x a b a b = x i.e. m 9 7 m = m See for further explanations. Power laws: See x m a. ( ) n mn = x b. ( x a y b ) c x ac y bc = c. a c x b = y x y ac bc i.e. ( ) 4 1 m = m i.e. ( m n ) 5 = m n i.e m m = n n 4 0 Multiplication Monomial by Monomial. YouTube explanation of mono X mono. Ex: 1. (x )(x ) = 6x 5. ( 4a b )(ab) = 8a b 4. (8x y 1 ) xy = 4 4x y 4. ( 4x y )(xy )( xy) = 16x 5 y 6 Division of Monomial by Monomial. Ex: 1. 50x 10x = 5. 0x 5x = 4x. 0x y 5x y 4 4xy 4. (x y )(5xy) xy = 5x y YouTube explanation of mono divided by a mono 11 M10C CH Products & Factors Lesson Plans.docx
12 Division of Polynomial by Monomial Rule: Take each term in the numerator (top) and divide it by the term in the denominator (bottom) 4t + 8t Ex: 1. = t +, t 0 4t 4t 4t = t 8t 4t = Thus, t +. 10m + 5m + 15m 5m = m + m +, m 0 10m 5m = m 5m 5m = m 15m 5m = Thus, m + m +. 6r r + 9r r 4 = r r +, r 0 4 6r r = r r r = r 9r r = 4. 8x + 16x = x + x + 8x 8 = x 16x 8 = x 4 8 = Distributive Property (Monomial multiplied by a Binomial/Trinomial. Ex: 1. x (x 7y + ). (x 7) + x(x + 5) (8x + 5x 7) = 6x 1x y + 6x = 6x 1+ x + 5x 8x 5x + 7 = (x + 5) = 9 6x 10 = 6x 1 1 M10C CH Products & Factors Lesson Plans.docx
13 4. 4a(a + ) + a(a 1) a(a + 4) a a a a a a 4a + 6 a 5. x [ + 4(x + 6)] [ + (x + 1)] Hard Question! [ ] [ ] = x + 8x x + Distribute the 4 and the. = x 6 16x 48 x Distribute the and the. = 16x 59 Clean up. Assignment M10C CH Poly Multiply & Divide.docx 1 M10C CH Products & Factors Lesson Plans.docx
14 Day Binomial x Binomial (Also known as FOIL) Multiply ( x + y)( a + b) Two different binomials. a. ( x + )( y + 1) Method 1 Algebra Tiles Step 1 Draw (x + ) on the vertical axis and (y + 1) on the horizontal axis. Step Multiply the vertical and horizontal values and fill in the rectangle. Step Determine your final product. There is 1 xy, 1 x, y's and one's. So, the answer is xy + x + y + 14 M10C CH Products & Factors Lesson Plans.docx
15 Method Area model Step 1 Create a square grid with (x + ) on the vertical axis and (y + 1) on the horizontal axis. x y 1 Step Fill in the grid y 1 x xy x y Step Determine your final product. There is 1 xy, 1 x, y's and a. So, the answer is xy + x + y + Method FOIL (First, Outer, Inner, Last) The most "mathematical" method. ( x + )( y + 1) ( x )( y 1) + + First x times y = xy ( x )( y 1) + + Outer x times 1 = x ( x )( y 1) + + Inner times y = y ( x )( y 1) + + Last times 1 = You now collect your terms. There is 1 xy, 1 x, y's and a. So, the answer is xy + x + y + 15 M10C CH Products & Factors Lesson Plans.docx
16 b. ( x )( y ) + Negatives are grey. Algebra Tiles 1 y y y y y y 1 1 x xy xy x x x xy xy x x y y 1 1 Determine your final product. 4 xy's, 4 x's, 6 y's and 6 1's = 4xy 4x + 6 y 6 Area model Step 1 Create a square grid with (x + ) on the vertical axis and (y ) on the horizontal axis. x y Step Fill in the grid y x 4xy 4x 6y 6 Step Determine your final product. There are 4 xy's, 4 x's, 6 y's and 6 1's = 4xy 4x + 6 y 6 16 M10C CH Products & Factors Lesson Plans.docx
17 FOIL (First, Outer, Inner, Last) ( x + )( y ) ( x )( y ) + First x times y = 4xy ( x )( y ) + Outer x times = 4x ( x )( y ) + Inner times y = 6y ( x )( y ) + Last times = 6 You now collect your terms. There are 4 xy's, 4 x's, 6 y's and 6 1's = 4xy 4x + 6 y 6 YouTube explanation of FOIL M10C CH Products & Factors Lesson Plans.docx
18 Multiply ( x + y)( x y) Two binomials that "are the same" but different signs. a. ( a b)( a b) + Notice how the a and b exist in both, but one is + and the other. FOIL (First, Outer, Inner, Last) ( a b)( a + b) ( a b)( a b) + First a times a = 4a ( a b)( a b) + Outer a times b = 6ab ( a b)( a b) + Inner b times a = 6ab ( a b)( a b) + Last b times b = -9b You now collect your terms. There is a 4a, a 6ab, a 6ab and a 9b = 4a 9b Notice how the Outer and the Inner cancel each other out? This is always true for ( x + y)( x y) So, a general rule when multiplying binomials of the type ( x + y)( x y) is not FOIL, but FL. First and Last. 18 M10C CH Products & Factors Lesson Plans.docx
19 b. ( 5x + 4 y)( 5x 4y) First, let's try FOIL (First, Outer, Inner, Last) ( 5x + 4 y)( 5x 4y) ( 5x 4 y)( 5x 4y) + First 5x times 5x = 6 5x ( 5x 4 y)( 5x 4y) + Outer 5x times 4y = 0x y ( 5x 4 y)( 5x 4y) + Inner 4y times 5x = 0x y ( 5x 4 y)( 5x 4y) + Last 4y times 4y = 16y Collect our like terms = 5x 16 y 6 Now, let's try FL (First, Last) ( 5x + 4 y)( 5x 4y) ( 5x 4 y)( 5x 4y) + First 5x times 5x = 6 5x ( 5x 4 y)( 5x 4y) + Last 4y times 4y = 16y Collect our like terms = 5x 16 y 6 Thus, when dealing with conjugates (that's what ( x + y)( x y) are called), you can FOIL or you can FL. 19 M10C CH Products & Factors Lesson Plans.docx
20 Multiply ( x ) + y Squaring a binomial. YouTube video and explanation of ( ) a. ( m + 5n) a + b. Let's realize that ( m + 5n) is no different than ( m 5n)( m 5n) multiple two binomials, FOIL! FOIL (First, Outer, Inner, Last) ( m + 5n) = ( m + 5n)( m + 5n) ( m 5n)( m 5n) + + First m times m = + + and we know how to 4m ( m 5n)( m 5n) + + Outer m times 5n = 10mn ( m 5n)( m 5n) + + Inner 5n times m = 10mn ( m 5n)( m 5n) + + Last 5n times 5n = 5n You now collect your terms. 4m + 10mn + 10mn + 5n = 4m + 0mn + 5n As you can see, squaring a binomial ( x ) + y is just as easy as using FOIL. But wait! Squaring a binomial ( x ) + y has a shortcut! 0 M10C CH Products & Factors Lesson Plans.docx
21 Let's try the previous question again. a. ( m + 5n) When you are squaring a binomial, here is the shortcut... square the first, square the last, multiply the two and double it. Easy right? Let's see it in practice. Square the first m squared = Square the last 5n squared = 4m 5n Multiple the two and double it Let's collect our like terms = m times 5n is 10mn, doubled = 0mn. 4m + 0mn + 5n That's the same answer! Cool huh? 6 b. ( ) 7c 8d Square the first ( ) 7c = 49c Square the last ( ) 6 1 8d = 64d 6 Multiple the two and double it Let's collect our like terms = 6 6 7c 8d = 56c d double that gets 49c 11c d + 64d c d a b YouTube video and explanation of ( ) Assignment pg 186 #5c,e,f 6a 15ace, 18(tough) pg 194 #4 1 M10C CH Products & Factors Lesson Plans.docx
22 Day 4 Applications Find the area of the shaded region. 4x + 6 A = A Large A Small x x + 4 5x 4 = (4x + 6)(5x 4) (x + 4)(x ) = 14x + 6x 16 Multiplication and simplifying of: 1. Mono x Poly. Bin x Bin. Poly x Poly Examples 1. (x )(x + 5x 7) Put the (x ) into the trinomial The x multiplies into the trinomial and then the multiples into the trinomial. = x + x x x x = + + x 1x 1x 14. 4a(a + ) + a(a 1) a(a + 4) a a a a a a 4a + 6 a. (x 1)(x + ) (x 4)(x 5) = x + 5x x 9x + 0 = + + x 5x x 9x 0 = + x 14x M10C CH Products & Factors Lesson Plans.docx
23 4. (x + )(x + )(x 1) Foil the first binomials. Then multiple again. ( x 5x 6)( x 1) = + + = x + x + x x x = x + x + x 4 6 The first two binomials are FOILed Distribute the (x 1) into the trinomial Collect like tems. 5. (x ) (x + 5)(x 5) ( x 6x 9) ( x 5) = + Keep the negative out of the squaring of (x ) and out of FOILing (x+5)(x 5) = x + 6x 9 x + 5 Fire the negatives into the brackets = x + 6x + 16 Collect like terms 6. t ( t) + 5(t 1)(t + 1) ( ) ( ) = t 9 1t + 4t + 5 4t 1 square ( t) Watch the negative! FOIL (t 1)(t+1) = t 9 + 1t 4t + 0t 5 Distribute the negative into the trinomial and the 5 into the binomial. = 19t + 1t 14 Collect like terms. 7. (a + )(a ) + (a + ) ( a ) ( a a ) = FOIL (a+)(a ) and square (a+) = a 18 + a + 1a + 1 Distribute the and the = 5a + 1a 6 Collect like terms M10C CH Products & Factors Lesson Plans.docx
24 8. (x 4 y) Isn`t this the same as (x 4 y)(x 4 y)(x 4 y) Yes it is! We can do this! It is no different than question 4. FOIL the first two binomials an then distribute the third binomial into the trinomial. = (x 4 y)(x 4 y)(x 4 y) ( 9x 4xy 16y )( x 4y) = + = 7x 7x y + 48xy 6x y + 96xy 64y = 7x 108x y + 144xy 64y Thus, if you ever need to cube a binomial, write it out as the multiplication of binomials and follow proper math : ) 9. ( x + y z)( x y + 4z) Area Model Here we have a trinomial times a trinomial. We can look at it in a couple of ways. x y 4z x x 4xy 8xz y xy 6y 1yz z xz yz 4z Collect like terms = x xy + 7xz 6y + 14yz 4z 4 M10C CH Products & Factors Lesson Plans.docx
25 Distributive Property Distribute the x, y and the z into the trinomial ( x y + 4z) ( x y z)( x y 4z) + + = x ( x y z)( x y 4z) + + = 4xy ( x y z)( x y 4z) + + = 8xz ( x y z)( x y 4z) + + = xy ( x y z)( x y 4z) + + = 6y ( x y z)( x y 4z) + + = 1yz ( x y z)( x y 4z) + + = xz ( x y z)( x y 4z) + + = yz ( x y z)( x y 4z) + + = Assignment 4z Collect like terms = Page 177 #8 Page 186 #4,7, 8, 11, 1, 14, 19ace, 1ace x xy + 7xz 6y + 14yz 4z 5 M10C CH Products & Factors Lesson Plans.docx
26 Day 5 Common Factors (Prime factorization, GCF, LCM and GCF of a polynomial) Prime Number - a whole number that has exactly two factors, itself and 1. i.e.,, 5, 7, 11, etc. Why aren't 0 or 1 prime numbers? Class discussion. Prime Factorization - writing a number as a product of its prime factors. 1. Write the prime factorization of the following numbers. a. 6 b But wait, is 10 a prime number? No! Keep going. 5 = 5 either is acceptable c. 60 What number goes into 60? Many, but I'll use What goes into 5? = 5 1 d. 55 Let's use a factor tree x x 5 x 1 5 x 5 x x 7 = 5 7 Question What is common between the words rake and cat? They both have an a. The a would be considered a factor in mathematics. Question What is the greatest common factor for these numbers? Note: the GCF (greatest common factor) is the largest number common in the set. a. 6 and 9 b. 15, 40, 55 c. 9, 7, 45 GCF = GCF = 5 GCF = 9 (yes a GCF can be one of the numbers) 6 M10C CH Products & Factors Lesson Plans.docx
27 d. 6a and 9a e. x and x f x y and 1xy GCF = a GCF = 6x GCF = 4xy Thus, when dealing with polynomials, always look to see if there is a GCF for the polynomial. Question Factor using GCF. Note: Always look for GCF! Always! 1. 5x + 10x. x + 7x x. 8a b + 16a b + a bc = 5 x( x + ) = x x + x ( 7 ) = a b + b + c 8 (1 4 ) 4. x(a + b) + 7(a + b) 5. 7a(x 1) + (x 1) ( a b)( x 7) = + + = ( x 1)(7a + ) 6. x (y + 5) + x(y + 5) 7. x(5 x) 9(5 x) + 8y(5 x) = y + x + x ( 5)( ) = x(5 x) 9(5 x) + 8 y(5 x) = (5 x)(x y) Least Common Multiple or Lowest Common Multiple - the lowest number that a set of numbers are all factors of. Question Find the LCM for the given set of numbers. a., 4 and 6 One way to do this is to write out all the multiples of each number LCM = 1, 6, 9, 1 4, 8, 1 6, 1 b. 4, 6, 9 4, 8, 1, 16, 0, 4, 8,, 6 6, 1, 18, 4, 0, 6 LCM = 6 9, 18, 7, 6 7 M10C CH Products & Factors Lesson Plans.docx
28 Real Life Example Mr. Boychuk has tiles that measure 14 inches by 16 inches that he wishes to make into a square mosaic. What is the smallest square that Mr. Boychuk can create using his 14x16 inch tiles? Option 1: Draw a diagram Keep adding 14x16 rectangles until the square is created. Option : List the factors of 14 and 16 to determine the LCM. 14, 8, 4, 56, 70, 84, 98, 11 16,, 48, 64, 80, 96, 11 Thus, a square 11 inches by 11 inches will fit the 14x16 tiles. Assignment Pg 140 #5 ace, 6ace, 7, 10 ace, 11 ac, 1, Pg (ace in each), 1a, 14ac, 16ace, 18 8 M10C CH Products & Factors Lesson Plans.docx
29 Day 6 Factoring Difference of Square and Perfect Squares I. Factoring a difference of squares. YouTube video on Difference of Squares Let's go back to Day and multiply the following ( x y)( x y) could FOIL, or we need on FL. You need only FL because ( x y)( x y) +. If we remember, we + are called conjugate binomials. This means the binomials are identical except one has addition while the other has subtraction. ( x y)( x y) + = 9x + 6xy 6xy 4y = 9x 4y This was Day so very easy :-) Let's notice something about the answer and more specifically, what always occurs when you multiply conjugate binomials. ( x y)( x y) ( x y ) + = There are three things to notice about the answer: 1. The answer is a binomial. The answer has subtraction. Both terms are perfect squares. So, if we can multiply binomials, why can't we take the answer and factor it into the original binomials? We can! Remember, if you notice the three things mentioned above, you have what's called A Difference of Squares. Let's Factor Ex: 1. x 16. x 5y. 49x 64 = ( x 4)( x + 4) ( x 5y)( x 5y) = + = ( 7x 8)( 7x + 8) Notice how in questions 1-, they were all binomials, they were all subtraction and each term was a perfect square? Hence, we knew we had A Difference of Squares. 9 M10C CH Products & Factors Lesson Plans.docx
30 4. x 4 81 ( x 9)( x 9) ( x )( x )( x 9) = + = + + The ( 9) x is another difference of squares. 5. x y y (GCF) Wait! I see a binomial, I see subtraction, but each term is not a perfect square. What do we do? Notice the Greatest Common Factor! Always factor the GCF out first. ( 1) = y x y Now the binomial is a perfect square. ( 1)( xy 1) = y xy + 6. y 6 1d 6 = ( y 4 d ) Factor out the GCF,. = ( y d )( y + d ) The binomial was A Difference of Squares. 7. x 0 16 = (x ) (x 10 4) Are we done? No! (x 10 4) can be factored. = (x )(x 5 + )(x 5 ) Assignment Pg 194 #6, 10aceg, 1ac, 1ace 0 M10C CH Products & Factors Lesson Plans.docx
31 II. Factoring Perfect squares. Recall from Day that (a + ) = a + 6a + 9 We learned that we could FOIL the binomial, or we could square the first term, square the last term, multiply the two terms and double the product. a + b = a + ab + b Thus, in general ( ) So, when we have a trinomial of the form a + ab + b, it is called a Perfect Square Trinomial and can easily be factored back to a single binomial squared. Ex: 1. a + 8a + 16 = (a + 4). 9a + 10a = (a + 0). 81a 7ab + 16b 6 = (9a 4b ) Notice in the first three questions how the first and last terms were perfect squares. That's a requirement for Perfect Square Trinomials. 4. 8a + 8a + 7 Wait! these aren't perfect squares. What to do? GCF, pull out the 7. = 7(4a + 4a + 1) 4 and 1, those are perfect squares. = 7(a + 1) 5. 15ax + 90ax + 15a = 15a( x + 6x + 9) = 15(x + ) 1 M10C CH Products & Factors Lesson Plans.docx
32 a + a This question can be left as is and factored or rearranged in descending order of x, then factored. Option 1 - Leave as is. Option - Rewrite 1 1a + 6a 6a 1a + 1 = ( 1 6a) = ( 6a 1) These two answers appear different yet they are the same. One answer is negative while the other answer is positive. Think about it, 6 = 6 and 6. Thus, if your answer is squared, then the number being squared could be positive or negative. Assignment Pg 194 #7a, 8, 1acd, 1bd M10C CH Products & Factors Lesson Plans.docx
33 Day 7 Trinomial Factorization ( ax + bx + c ) I. Factoring trinomials (ax + bx + c, a = 1) Recall: (x + 4)(x + ) = x + 7x + 1 The middle term is the sum of the last terms of each binomial. The end term is the product of the last terms of each binomial. Ex: 1. x + 8x + 16 = ( x + 4)( x + 4) Hey, this is a perfect square!. = ( x + 4) x + 5x + 6 ( x?)( x?) = + + We know if must break down to two binomials each with an x. The latter two numbers need to multiply to 6 and add to 5. Since the 6 and 5 are both positive, we know the? numbers both need to be positive. ( x )( x ) = + +. x 4 8x + 15 ( x?)( x?) = + + We know if must break down to two binomials each with an x. The latter two numbers need to multiply to 15 and add to 8. Since the 15 is positive and the 8 is negative, we know the? numbers both need to be negative. ( x )( x 5) = 4. x 10 + x ( x?)( x?) = + + We know if must break down to two 5 binomials each with an x. The later two numbers need to multiply to 8 and add to. Since the 8 is negative we know the? numbers need to be opposite signs, one positive and one negative. So what numbers multiply to 8 and add to? 7 and 4. Note: it can't be 7 and 4. ( x 7)( x 4) = + M10C CH Products & Factors Lesson Plans.docx
34 5. x 10xy + 1y ( x? y)( x? y) = + + Since the last term has a y, there needs to be a y in each binomial. We now need two numbers that multiply to 1 and add to 10. To multiply out positive but add up negative, both numbers must be negative! = ( x y)( x 7 y) 6. x 10 7x 5 y 0y 6 = ( x? y )( x? y ) 10 x breaks down to 5 x and 6 y breaks down to y What numbers multiply to 0 and add to 7? = ( x 10 y )( x y ) GCF 7. x + 10x 8 Whoa! What's going on? Think, what is common? The is common! Factor a out. = ( x + 5x 14) Now find two numbers that multiply to 14 = ( x + 7)( x ) and add to 5. GCF 8. x x y 8xy 4 What's common? The x. Factor it out. Optional Hints: 4 = x( x xy 8 y ) Now find two numbers that multiply to 8 = x x y x + y ( 4 )( ) and add to. 1. Both terms positive (middle and last), then both parts are positive. x + 1x + = (x +8)(x + 4). Last term positive, middle term negative, then both parts are negative. x 1x + = (x 8)(x 4). Last term is negative, then one part is negative and the other is positive. x 4x = (x 8)(x + 4) x + 4x = (x + 8)(x 4) 4. The middle term contains the variables that are found in the first and last terms. The exponents are half of what they are in the first and last terms. 4 M10C CH Products & Factors Lesson Plans.docx
35 II. Factoring trinomials (ax + bx + c, a 1) 1. x + 1x + 15 Here, there is no GCF. So, what are the factors of ( x?)( x?) = + + Now we need two numbers that multiply to 15. x? The 1 in the middle is not too important as the will influence it. Two factors of 15 are 5 and. Let's put the 5 and into the?, but which goes where? We'll try both. = ( x + 5)( x + ) = ( x + )( x + 5) We must FOIL both out to see which is correct. = x + 11x + 15 This is NOT correct. Thus, when the a value in the question = + + This is correct. x 1x 15 ax + bx + c is not 1, there is extra work to be done.. 5x 16x + + Again, no GCF so find the factors of ( 5 x?)( x?) 5x. = + + Now we need the factors of. and 1 are good. But again, which goes where? Try both. = ( 5x + 1)( x + ) = ( 5x + )( x + 1) We must FOIL both out to see which is correct. = + + This is correct. 5x 16x = 5x + 8x + This is NOT correct.. 1x 4 16x + 5 This is a tough question. We need the factors of ( 6x 5)( x 1) 4 1x. We know that x will be in both binomials, but the factors of 1 are &6, &4 and 1&1. Which pair is it? There is no easy answer and sadly we must try them all. A good rule of thumb, start in the middle (&4) and work out. = This is the correct answer. You can FOIL to verify. 5 M10C CH Products & Factors Lesson Plans.docx
36 4. 8x + 10xy y = ( ax + by)( cx dy) We know that 0 x breaks down as 10 x and y breaks down as y. The factors of 8 are (1&8) and (&4). The factors of are (&-1) and ( &1). We must now test our options. ( x 10 y)( 4x 10 y) = + This is the correct answer. You can FOIL to verify x 44xy 0y GCF. Factor a out. =(5x x 15y ) = ( ax + by)( cx dy) Find the factors of 5 and 15. =(5x + y)(x 5y) This is the correct answer. You can FOIL to verify. Extra Questions if needed: 6. x + 11x m + 1m 5 = ( x + )( x + 4) = ( m 1)( m + 5) 8. 4x 5xy 6y 9. 6x 5x 4 = ( 4x + y)( x y) = ( x 4)( x + 1) Assignment Pg 166 #11aceg, 14aceg, 15ac, 17 a = 1 Pg 177 # 1aceg, 15aceg, 17, 19aceg a 1 6 M10C CH Products & Factors Lesson Plans.docx
37 Day 8 Square Roots and Cube Roots Square Root - a number, when raise to the power of results in a given number. 9 = ± A Square Root always gives two answers. = 9 = 9 Cube Root - a number, when raised to the power of results in a given number. 64 = 4 A cube root only produces one answer = 64 To get a cube root on a TI calculator, hit MATH then 4. Square - a dimensional object where all sides are equal. Area = length x width = s Cube - a dimension object where all sides are equal. example - a 6 sided die. Volume = length x width x height = s Examples 1. Find the sides of the square if the area is 89 km. A = s 89 = s 89 = s = 17km s The negative answer is not applicable so we disregard it.. Find the sides of a cube if the area volume is 1167 cm. V = s 1167 = s 1167 = s = cm s 7 M10C CH Products & Factors Lesson Plans.docx
38 Creating Factorable Trinomials. We know that when we factor and add up to b. ( )( ) x x x x ax + bx + c, if a = 1 then we need two numbers that multiply to c = times 6 = 0 and 5+6 = 11 Question: a. x + x + 6 Fill in the box to create factorable trinomials. We need two numbers that multiply to 6. (1&6) or (&) If we use 1&6, then our answer is If we use &, then our answer is x x + 7x x + 6 But wait! Doesn't 1 6 = 6? Or = 6? Yes! So... we also have... If we use -1&-6, then our answer is If we use -&-, then our answer is x x 7x + 6 5x + 6 Final Answer could be, 7 or 5 or -7 or -5. Any of the four will make the trinomial factorable. b. x + x 14 We need two numbers that multiply to 6. (1&-14) or (-1&14) or (,-7) or (-&7) If we use 1&-14, then our answer is x If we use -1&14, then our answer is x If we use &-7, then our answer is x If we use -&7, then our answer is x 1x x 14 5x x 14 Final Answer could be, 1 or 5 or -1 or -5. Any of the four will make the trinomial factorable. 8 M10C CH Products & Factors Lesson Plans.docx
39 c. x + 4x + Now we need two numbers that add to 4. So choose a pair. Let's try 1 and. ( 1+ )( + )( 1+ 5)( + 6 )... There are an infinite number! ( )( ) x + 1 x + = x + 4x + Or we could try 1 and 5. ( )( ) x 1 x + 5 = x + 4x + 4 So choose a pair of numbers that add to 4 and FOIL away! d. x 5x + Now we need two numbers that add to 5. Again, infinite possibilities. Let's try 8 and. ( )( ) x 8 x + = x 5x 4 Some Tricky Factorization Factor the following: 1. 4 x 81 A difference of squares question. =( 9 )( 9 x + x ) The ( 9) x can be factored again! =( x 9)( x )( x ) + + Rule = factor until you can factor no more.. x x 1 Need two numbers that multiply to 1 and add to 1 4 =( x 4 )( x ) + First binomial is a difference of squares. =( x )( x + )( x + ). x 10x 11 Need two numbers that multiply to 1 and add to 1 4 =( x 1)( x 11) + Second binomial is a difference of squares. =( x + 1)( x 11)( x + 11) 9 M10C CH Products & Factors Lesson Plans.docx
40 Assignment Page 147 #7, 8 Page 187 #0a Page 156 #17 Page 167 #19, 0 Page 195 #0 Square and Cube Roots Volume of Cube Neat Factoring Question Determining b and c values to make trinomials factorable Two step factorization 40 M10C CH Products & Factors Lesson Plans.docx
41 Day 9 Practicing all types of Factoring. YouTube video of what to look for when factoring. I. All types of factoring. Ex: 1. x 7x 18. 6m + 19mn + 10n = ( x 9)( x + ) = (m + n)(m + 5 n). x 8 4. x 4x + 4x = ( x 4) = ( x )( x + ) = x x + ( 4x 4) = x( x ) 5. x(m ) 4(m ) 6. ab 9ab + 6a b = ( m )( x 4) = ab(1 b + a) 7. y 7 y x 7x y + 1y 4 4 = ( y 1)( y + 4) = ( x 4y )( x y ) ( x y)( x y)( x y ) = + Assignment M10C W CH Factoring.doc 41 M10C CH Products & Factors Lesson Plans.docx
42 Textbook Review Questions The textbook has very good questions that can be used for review. You will notice that each set of questions indicated what section of the text it covers. If you need help with a question, you may refer to the section in the text. Page 198 Questions Section #1-.1 Prime Factors, Lowest Common Multiple & Greatest Common Factor #6-10. Square Roots and Cube Roots # Factoring Binomials and Trinomials #18, 19, 0a, 1.5 FOIL and Factoring #, FOIL and Factoring #7-0.7 Binomials multiplied by Trinomials and Tri times Tri #-5.8 Factoring Difference of Squares, Perfect Squares and Applications 4 M10C CH Products & Factors Lesson Plans.docx
Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any.
 Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
1.3 Algebraic Expressions
 1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
expression is written horizontally. The Last terms ((2)( 4)) because they are the last terms of the two polynomials. This is called the FOIL method.
 A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
Higher Education Math Placement
 Higher Education Math Placement Placement Assessment Problem Types 1. Whole Numbers, Fractions, and Decimals 1.1 Operations with Whole Numbers Addition with carry Subtraction with borrowing Multiplication
Higher Education Math Placement Placement Assessment Problem Types 1. Whole Numbers, Fractions, and Decimals 1.1 Operations with Whole Numbers Addition with carry Subtraction with borrowing Multiplication
1.3 Polynomials and Factoring
 1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
Algebra and Geometry Review (61 topics, no due date)
 Course Name: Math 112 Credit Exam LA Tech University Course Code: ALEKS Course: Trigonometry Instructor: Course Dates: Course Content: 159 topics Algebra and Geometry Review (61 topics, no due date) Properties
Course Name: Math 112 Credit Exam LA Tech University Course Code: ALEKS Course: Trigonometry Instructor: Course Dates: Course Content: 159 topics Algebra and Geometry Review (61 topics, no due date) Properties
SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS
 (Section 0.6: Polynomial, Rational, and Algebraic Expressions) 0.6.1 SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS LEARNING OBJECTIVES Be able to identify polynomial, rational, and algebraic
(Section 0.6: Polynomial, Rational, and Algebraic Expressions) 0.6.1 SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS LEARNING OBJECTIVES Be able to identify polynomial, rational, and algebraic
ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form
 ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form Goal Graph quadratic functions. VOCABULARY Quadratic function A function that can be written in the standard form y = ax 2 + bx+ c where a 0 Parabola
ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form Goal Graph quadratic functions. VOCABULARY Quadratic function A function that can be written in the standard form y = ax 2 + bx+ c where a 0 Parabola
MATH 10034 Fundamental Mathematics IV
 MATH 0034 Fundamental Mathematics IV http://www.math.kent.edu/ebooks/0034/funmath4.pdf Department of Mathematical Sciences Kent State University January 2, 2009 ii Contents To the Instructor v Polynomials.
MATH 0034 Fundamental Mathematics IV http://www.math.kent.edu/ebooks/0034/funmath4.pdf Department of Mathematical Sciences Kent State University January 2, 2009 ii Contents To the Instructor v Polynomials.
3.1. RATIONAL EXPRESSIONS
 3.1. RATIONAL EXPRESSIONS RATIONAL NUMBERS In previous courses you have learned how to operate (do addition, subtraction, multiplication, and division) on rational numbers (fractions). Rational numbers
3.1. RATIONAL EXPRESSIONS RATIONAL NUMBERS In previous courses you have learned how to operate (do addition, subtraction, multiplication, and division) on rational numbers (fractions). Rational numbers
Name Intro to Algebra 2. Unit 1: Polynomials and Factoring
 Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
Algebra I Vocabulary Cards
 Algebra I Vocabulary Cards Table of Contents Expressions and Operations Natural Numbers Whole Numbers Integers Rational Numbers Irrational Numbers Real Numbers Absolute Value Order of Operations Expression
Algebra I Vocabulary Cards Table of Contents Expressions and Operations Natural Numbers Whole Numbers Integers Rational Numbers Irrational Numbers Real Numbers Absolute Value Order of Operations Expression
PRE-CALCULUS GRADE 12
 PRE-CALCULUS GRADE 12 [C] Communication Trigonometry General Outcome: Develop trigonometric reasoning. A1. Demonstrate an understanding of angles in standard position, expressed in degrees and radians.
PRE-CALCULUS GRADE 12 [C] Communication Trigonometry General Outcome: Develop trigonometric reasoning. A1. Demonstrate an understanding of angles in standard position, expressed in degrees and radians.
Mathematics Placement
 Mathematics Placement The ACT COMPASS math test is a self-adaptive test, which potentially tests students within four different levels of math including pre-algebra, algebra, college algebra, and trigonometry.
Mathematics Placement The ACT COMPASS math test is a self-adaptive test, which potentially tests students within four different levels of math including pre-algebra, algebra, college algebra, and trigonometry.
Radicals - Multiply and Divide Radicals
 8. Radicals - Multiply and Divide Radicals Objective: Multiply and divide radicals using the product and quotient rules of radicals. Multiplying radicals is very simple if the index on all the radicals
8. Radicals - Multiply and Divide Radicals Objective: Multiply and divide radicals using the product and quotient rules of radicals. Multiplying radicals is very simple if the index on all the radicals
Tool 1. Greatest Common Factor (GCF)
 Chapter 4: Factoring Review Tool 1 Greatest Common Factor (GCF) This is a very important tool. You must try to factor out the GCF first in every problem. Some problems do not have a GCF but many do. When
Chapter 4: Factoring Review Tool 1 Greatest Common Factor (GCF) This is a very important tool. You must try to factor out the GCF first in every problem. Some problems do not have a GCF but many do. When
Operations with Algebraic Expressions: Multiplication of Polynomials
 Operations with Algebraic Expressions: Multiplication of Polynomials The product of a monomial x monomial To multiply a monomial times a monomial, multiply the coefficients and add the on powers with the
Operations with Algebraic Expressions: Multiplication of Polynomials The product of a monomial x monomial To multiply a monomial times a monomial, multiply the coefficients and add the on powers with the
6.1 Add & Subtract Polynomial Expression & Functions
 6.1 Add & Subtract Polynomial Expression & Functions Objectives 1. Know the meaning of the words term, monomial, binomial, trinomial, polynomial, degree, coefficient, like terms, polynomial funciton, quardrtic
6.1 Add & Subtract Polynomial Expression & Functions Objectives 1. Know the meaning of the words term, monomial, binomial, trinomial, polynomial, degree, coefficient, like terms, polynomial funciton, quardrtic
15.1 Factoring Polynomials
 LESSON 15.1 Factoring Polynomials Use the structure of an expression to identify ways to rewrite it. Also A.SSE.3? ESSENTIAL QUESTION How can you use the greatest common factor to factor polynomials? EXPLORE
LESSON 15.1 Factoring Polynomials Use the structure of an expression to identify ways to rewrite it. Also A.SSE.3? ESSENTIAL QUESTION How can you use the greatest common factor to factor polynomials? EXPLORE
This is a square root. The number under the radical is 9. (An asterisk * means multiply.)
 Page of Review of Radical Expressions and Equations Skills involving radicals can be divided into the following groups: Evaluate square roots or higher order roots. Simplify radical expressions. Rationalize
Page of Review of Radical Expressions and Equations Skills involving radicals can be divided into the following groups: Evaluate square roots or higher order roots. Simplify radical expressions. Rationalize
Factoring Polynomials
 UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
MATH 90 CHAPTER 6 Name:.
 MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
NSM100 Introduction to Algebra Chapter 5 Notes Factoring
 Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
Factors and Products
 CHAPTER 3 Factors and Products What You ll Learn use different strategies to find factors and multiples of whole numbers identify prime factors and write the prime factorization of a number find square
CHAPTER 3 Factors and Products What You ll Learn use different strategies to find factors and multiples of whole numbers identify prime factors and write the prime factorization of a number find square
Review of Intermediate Algebra Content
 Review of Intermediate Algebra Content Table of Contents Page Factoring GCF and Trinomials of the Form + b + c... Factoring Trinomials of the Form a + b + c... Factoring Perfect Square Trinomials... 6
Review of Intermediate Algebra Content Table of Contents Page Factoring GCF and Trinomials of the Form + b + c... Factoring Trinomials of the Form a + b + c... Factoring Perfect Square Trinomials... 6
Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III
 Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III Name Date Adding and Subtracting Polynomials Algebra Standard 10.0 A polynomial is a sum of one ore more monomials. Polynomial
Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III Name Date Adding and Subtracting Polynomials Algebra Standard 10.0 A polynomial is a sum of one ore more monomials. Polynomial
SPECIAL PRODUCTS AND FACTORS
 CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
CAHSEE on Target UC Davis, School and University Partnerships
 UC Davis, School and University Partnerships CAHSEE on Target Mathematics Curriculum Published by The University of California, Davis, School/University Partnerships Program 006 Director Sarah R. Martinez,
UC Davis, School and University Partnerships CAHSEE on Target Mathematics Curriculum Published by The University of California, Davis, School/University Partnerships Program 006 Director Sarah R. Martinez,
Introduction Assignment
 PRE-CALCULUS 11 Introduction Assignment Welcome to PREC 11! This assignment will help you review some topics from a previous math course and introduce you to some of the topics that you ll be studying
PRE-CALCULUS 11 Introduction Assignment Welcome to PREC 11! This assignment will help you review some topics from a previous math course and introduce you to some of the topics that you ll be studying
Factoring Trinomials: The ac Method
 6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
POLYNOMIALS and FACTORING
 POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
Veterans Upward Bound Algebra I Concepts - Honors
 Veterans Upward Bound Algebra I Concepts - Honors Brenda Meery Kaitlyn Spong Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org Chapter 6. Factoring CHAPTER
Veterans Upward Bound Algebra I Concepts - Honors Brenda Meery Kaitlyn Spong Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org Chapter 6. Factoring CHAPTER
Florida Math 0028. Correlation of the ALEKS course Florida Math 0028 to the Florida Mathematics Competencies - Upper
 Florida Math 0028 Correlation of the ALEKS course Florida Math 0028 to the Florida Mathematics Competencies - Upper Exponents & Polynomials MDECU1: Applies the order of operations to evaluate algebraic
Florida Math 0028 Correlation of the ALEKS course Florida Math 0028 to the Florida Mathematics Competencies - Upper Exponents & Polynomials MDECU1: Applies the order of operations to evaluate algebraic
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0).
 This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
Math 0980 Chapter Objectives. Chapter 1: Introduction to Algebra: The Integers.
 Math 0980 Chapter Objectives Chapter 1: Introduction to Algebra: The Integers. 1. Identify the place value of a digit. 2. Write a number in words or digits. 3. Write positive and negative numbers used
Math 0980 Chapter Objectives Chapter 1: Introduction to Algebra: The Integers. 1. Identify the place value of a digit. 2. Write a number in words or digits. 3. Write positive and negative numbers used
Factoring and Applications
 Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
Vocabulary Words and Definitions for Algebra
 Name: Period: Vocabulary Words and s for Algebra Absolute Value Additive Inverse Algebraic Expression Ascending Order Associative Property Axis of Symmetry Base Binomial Coefficient Combine Like Terms
Name: Period: Vocabulary Words and s for Algebra Absolute Value Additive Inverse Algebraic Expression Ascending Order Associative Property Axis of Symmetry Base Binomial Coefficient Combine Like Terms
FACTORING POLYNOMIALS
 296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
FACTORING OUT COMMON FACTORS
 278 (6 2) Chapter 6 Factoring 6.1 FACTORING OUT COMMON FACTORS In this section Prime Factorization of Integers Greatest Common Factor Finding the Greatest Common Factor for Monomials Factoring Out the
278 (6 2) Chapter 6 Factoring 6.1 FACTORING OUT COMMON FACTORS In this section Prime Factorization of Integers Greatest Common Factor Finding the Greatest Common Factor for Monomials Factoring Out the
Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder).
 Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
ALGEBRA REVIEW LEARNING SKILLS CENTER. Exponents & Radicals
 ALGEBRA REVIEW LEARNING SKILLS CENTER The "Review Series in Algebra" is taught at the beginning of each quarter by the staff of the Learning Skills Center at UC Davis. This workshop is intended to be an
ALGEBRA REVIEW LEARNING SKILLS CENTER The "Review Series in Algebra" is taught at the beginning of each quarter by the staff of the Learning Skills Center at UC Davis. This workshop is intended to be an
Polynomials. Key Terms. quadratic equation parabola conjugates trinomial. polynomial coefficient degree monomial binomial GCF
 Polynomials 5 5.1 Addition and Subtraction of Polynomials and Polynomial Functions 5.2 Multiplication of Polynomials 5.3 Division of Polynomials Problem Recognition Exercises Operations on Polynomials
Polynomials 5 5.1 Addition and Subtraction of Polynomials and Polynomial Functions 5.2 Multiplication of Polynomials 5.3 Division of Polynomials Problem Recognition Exercises Operations on Polynomials
MATH 095, College Prep Mathematics: Unit Coverage Pre-algebra topics (arithmetic skills) offered through BSE (Basic Skills Education)
 MATH 095, College Prep Mathematics: Unit Coverage Pre-algebra topics (arithmetic skills) offered through BSE (Basic Skills Education) Accurately add, subtract, multiply, and divide whole numbers, integers,
MATH 095, College Prep Mathematics: Unit Coverage Pre-algebra topics (arithmetic skills) offered through BSE (Basic Skills Education) Accurately add, subtract, multiply, and divide whole numbers, integers,
A Systematic Approach to Factoring
 A Systematic Approach to Factoring Step 1 Count the number of terms. (Remember****Knowing the number of terms will allow you to eliminate unnecessary tools.) Step 2 Is there a greatest common factor? Tool
A Systematic Approach to Factoring Step 1 Count the number of terms. (Remember****Knowing the number of terms will allow you to eliminate unnecessary tools.) Step 2 Is there a greatest common factor? Tool
Algebra Cheat Sheets
 Sheets Algebra Cheat Sheets provide you with a tool for teaching your students note-taking, problem-solving, and organizational skills in the context of algebra lessons. These sheets teach the concepts
Sheets Algebra Cheat Sheets provide you with a tool for teaching your students note-taking, problem-solving, and organizational skills in the context of algebra lessons. These sheets teach the concepts
How To Factor By Gcf In Algebra 1.5
 7-2 Factoring by GCF Warm Up Lesson Presentation Lesson Quiz Algebra 1 Warm Up Simplify. 1. 2(w + 1) 2. 3x(x 2 4) 2w + 2 3x 3 12x Find the GCF of each pair of monomials. 3. 4h 2 and 6h 2h 4. 13p and 26p
7-2 Factoring by GCF Warm Up Lesson Presentation Lesson Quiz Algebra 1 Warm Up Simplify. 1. 2(w + 1) 2. 3x(x 2 4) 2w + 2 3x 3 12x Find the GCF of each pair of monomials. 3. 4h 2 and 6h 2h 4. 13p and 26p
Factor Polynomials Completely
 9.8 Factor Polynomials Completely Before You factored polynomials. Now You will factor polynomials completely. Why? So you can model the height of a projectile, as in Ex. 71. Key Vocabulary factor by grouping
9.8 Factor Polynomials Completely Before You factored polynomials. Now You will factor polynomials completely. Why? So you can model the height of a projectile, as in Ex. 71. Key Vocabulary factor by grouping
POLYNOMIAL FUNCTIONS
 POLYNOMIAL FUNCTIONS Polynomial Division.. 314 The Rational Zero Test.....317 Descarte s Rule of Signs... 319 The Remainder Theorem.....31 Finding all Zeros of a Polynomial Function.......33 Writing a
POLYNOMIAL FUNCTIONS Polynomial Division.. 314 The Rational Zero Test.....317 Descarte s Rule of Signs... 319 The Remainder Theorem.....31 Finding all Zeros of a Polynomial Function.......33 Writing a
Prentice Hall Mathematics: Algebra 2 2007 Correlated to: Utah Core Curriculum for Math, Intermediate Algebra (Secondary)
 Core Standards of the Course Standard 1 Students will acquire number sense and perform operations with real and complex numbers. Objective 1.1 Compute fluently and make reasonable estimates. 1. Simplify
Core Standards of the Course Standard 1 Students will acquire number sense and perform operations with real and complex numbers. Objective 1.1 Compute fluently and make reasonable estimates. 1. Simplify
Factoring Quadratic Expressions
 Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
MATH 60 NOTEBOOK CERTIFICATIONS
 MATH 60 NOTEBOOK CERTIFICATIONS Chapter #1: Integers and Real Numbers 1.1a 1.1b 1.2 1.3 1.4 1.8 Chapter #2: Algebraic Expressions, Linear Equations, and Applications 2.1a 2.1b 2.1c 2.2 2.3a 2.3b 2.4 2.5
MATH 60 NOTEBOOK CERTIFICATIONS Chapter #1: Integers and Real Numbers 1.1a 1.1b 1.2 1.3 1.4 1.8 Chapter #2: Algebraic Expressions, Linear Equations, and Applications 2.1a 2.1b 2.1c 2.2 2.3a 2.3b 2.4 2.5
Factoring Algebra- Chapter 8B Assignment Sheet
 Name: Factoring Algebra- Chapter 8B Assignment Sheet Date Section Learning Targets Assignment Tues 2/17 Find the prime factorization of an integer Find the greatest common factor (GCF) for a set of monomials.
Name: Factoring Algebra- Chapter 8B Assignment Sheet Date Section Learning Targets Assignment Tues 2/17 Find the prime factorization of an integer Find the greatest common factor (GCF) for a set of monomials.
6.3 FACTORING ax 2 bx c WITH a 1
 290 (6 14) Chapter 6 Factoring e) What is the approximate maximum revenue? f) Use the accompanying graph to estimate the price at which the revenue is zero. y Revenue (thousands of dollars) 300 200 100
290 (6 14) Chapter 6 Factoring e) What is the approximate maximum revenue? f) Use the accompanying graph to estimate the price at which the revenue is zero. y Revenue (thousands of dollars) 300 200 100
Solving Quadratic Equations
 9.3 Solving Quadratic Equations by Using the Quadratic Formula 9.3 OBJECTIVES 1. Solve a quadratic equation by using the quadratic formula 2. Determine the nature of the solutions of a quadratic equation
9.3 Solving Quadratic Equations by Using the Quadratic Formula 9.3 OBJECTIVES 1. Solve a quadratic equation by using the quadratic formula 2. Determine the nature of the solutions of a quadratic equation
Chapter R.4 Factoring Polynomials
 Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
Chapter 7 - Roots, Radicals, and Complex Numbers
 Math 233 - Spring 2009 Chapter 7 - Roots, Radicals, and Complex Numbers 7.1 Roots and Radicals 7.1.1 Notation and Terminology In the expression x the is called the radical sign. The expression under the
Math 233 - Spring 2009 Chapter 7 - Roots, Radicals, and Complex Numbers 7.1 Roots and Radicals 7.1.1 Notation and Terminology In the expression x the is called the radical sign. The expression under the
Algebra 1 Course Title
 Algebra 1 Course Title Course- wide 1. What patterns and methods are being used? Course- wide 1. Students will be adept at solving and graphing linear and quadratic equations 2. Students will be adept
Algebra 1 Course Title Course- wide 1. What patterns and methods are being used? Course- wide 1. Students will be adept at solving and graphing linear and quadratic equations 2. Students will be adept
Exponents and Radicals
 Exponents and Radicals (a + b) 10 Exponents are a very important part of algebra. An exponent is just a convenient way of writing repeated multiplications of the same number. Radicals involve the use of
Exponents and Radicals (a + b) 10 Exponents are a very important part of algebra. An exponent is just a convenient way of writing repeated multiplications of the same number. Radicals involve the use of
LAKE ELSINORE UNIFIED SCHOOL DISTRICT
 LAKE ELSINORE UNIFIED SCHOOL DISTRICT Title: PLATO Algebra 1-Semester 2 Grade Level: 10-12 Department: Mathematics Credit: 5 Prerequisite: Letter grade of F and/or N/C in Algebra 1, Semester 2 Course Description:
LAKE ELSINORE UNIFIED SCHOOL DISTRICT Title: PLATO Algebra 1-Semester 2 Grade Level: 10-12 Department: Mathematics Credit: 5 Prerequisite: Letter grade of F and/or N/C in Algebra 1, Semester 2 Course Description:
South Carolina College- and Career-Ready (SCCCR) Pre-Calculus
 South Carolina College- and Career-Ready (SCCCR) Pre-Calculus Key Concepts Arithmetic with Polynomials and Rational Expressions PC.AAPR.2 PC.AAPR.3 PC.AAPR.4 PC.AAPR.5 PC.AAPR.6 PC.AAPR.7 Standards Know
South Carolina College- and Career-Ready (SCCCR) Pre-Calculus Key Concepts Arithmetic with Polynomials and Rational Expressions PC.AAPR.2 PC.AAPR.3 PC.AAPR.4 PC.AAPR.5 PC.AAPR.6 PC.AAPR.7 Standards Know
Factoring. Factoring Monomials Monomials can often be factored in more than one way.
 Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
Students will be able to simplify and evaluate numerical and variable expressions using appropriate properties and order of operations.
 Outcome 1: (Introduction to Algebra) Skills/Content 1. Simplify numerical expressions: a). Use order of operations b). Use exponents Students will be able to simplify and evaluate numerical and variable
Outcome 1: (Introduction to Algebra) Skills/Content 1. Simplify numerical expressions: a). Use order of operations b). Use exponents Students will be able to simplify and evaluate numerical and variable
Chapter 3 Section 6 Lesson Polynomials
 Chapter Section 6 Lesson Polynomials Introduction This lesson introduces polynomials and like terms. As we learned earlier, a monomial is a constant, a variable, or the product of constants and variables.
Chapter Section 6 Lesson Polynomials Introduction This lesson introduces polynomials and like terms. As we learned earlier, a monomial is a constant, a variable, or the product of constants and variables.
Expression. Variable Equation Polynomial Monomial Add. Area. Volume Surface Space Length Width. Probability. Chance Random Likely Possibility Odds
 Isosceles Triangle Congruent Leg Side Expression Equation Polynomial Monomial Radical Square Root Check Times Itself Function Relation One Domain Range Area Volume Surface Space Length Width Quantitative
Isosceles Triangle Congruent Leg Side Expression Equation Polynomial Monomial Radical Square Root Check Times Itself Function Relation One Domain Range Area Volume Surface Space Length Width Quantitative
Unit 7 Quadratic Relations of the Form y = ax 2 + bx + c
 Unit 7 Quadratic Relations of the Form y = ax 2 + bx + c Lesson Outline BIG PICTURE Students will: manipulate algebraic expressions, as needed to understand quadratic relations; identify characteristics
Unit 7 Quadratic Relations of the Form y = ax 2 + bx + c Lesson Outline BIG PICTURE Students will: manipulate algebraic expressions, as needed to understand quadratic relations; identify characteristics
In this section, you will develop a method to change a quadratic equation written as a sum into its product form (also called its factored form).
 CHAPTER 8 In Chapter 4, you used a web to organize the connections you found between each of the different representations of lines. These connections enabled you to use any representation (such as a graph,
CHAPTER 8 In Chapter 4, you used a web to organize the connections you found between each of the different representations of lines. These connections enabled you to use any representation (such as a graph,
Answer Key for California State Standards: Algebra I
 Algebra I: Symbolic reasoning and calculations with symbols are central in algebra. Through the study of algebra, a student develops an understanding of the symbolic language of mathematics and the sciences.
Algebra I: Symbolic reasoning and calculations with symbols are central in algebra. Through the study of algebra, a student develops an understanding of the symbolic language of mathematics and the sciences.
Algebra 2 PreAP. Name Period
 Algebra 2 PreAP Name Period IMPORTANT INSTRUCTIONS FOR STUDENTS!!! We understand that students come to Algebra II with different strengths and needs. For this reason, students have options for completing
Algebra 2 PreAP Name Period IMPORTANT INSTRUCTIONS FOR STUDENTS!!! We understand that students come to Algebra II with different strengths and needs. For this reason, students have options for completing
CORRELATED TO THE SOUTH CAROLINA COLLEGE AND CAREER-READY FOUNDATIONS IN ALGEBRA
 We Can Early Learning Curriculum PreK Grades 8 12 INSIDE ALGEBRA, GRADES 8 12 CORRELATED TO THE SOUTH CAROLINA COLLEGE AND CAREER-READY FOUNDATIONS IN ALGEBRA April 2016 www.voyagersopris.com Mathematical
We Can Early Learning Curriculum PreK Grades 8 12 INSIDE ALGEBRA, GRADES 8 12 CORRELATED TO THE SOUTH CAROLINA COLLEGE AND CAREER-READY FOUNDATIONS IN ALGEBRA April 2016 www.voyagersopris.com Mathematical
6706_PM10SB_C4_CO_pp192-193.qxd 5/8/09 9:53 AM Page 192 192 NEL
 92 NEL Chapter 4 Factoring Algebraic Epressions GOALS You will be able to Determine the greatest common factor in an algebraic epression and use it to write the epression as a product Recognize different
92 NEL Chapter 4 Factoring Algebraic Epressions GOALS You will be able to Determine the greatest common factor in an algebraic epression and use it to write the epression as a product Recognize different
Polynomials and Factoring
 7.6 Polynomials and Factoring Basic Terminology A term, or monomial, is defined to be a number, a variable, or a product of numbers and variables. A polynomial is a term or a finite sum or difference of
7.6 Polynomials and Factoring Basic Terminology A term, or monomial, is defined to be a number, a variable, or a product of numbers and variables. A polynomial is a term or a finite sum or difference of
FACTORING ax 2 bx c. Factoring Trinomials with Leading Coefficient 1
 5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
Big Bend Community College. Beginning Algebra MPC 095. Lab Notebook
 Big Bend Community College Beginning Algebra MPC 095 Lab Notebook Beginning Algebra Lab Notebook by Tyler Wallace is licensed under a Creative Commons Attribution 3.0 Unported License. Permissions beyond
Big Bend Community College Beginning Algebra MPC 095 Lab Notebook Beginning Algebra Lab Notebook by Tyler Wallace is licensed under a Creative Commons Attribution 3.0 Unported License. Permissions beyond
Algebra 2 Year-at-a-Glance Leander ISD 2007-08. 1st Six Weeks 2nd Six Weeks 3rd Six Weeks 4th Six Weeks 5th Six Weeks 6th Six Weeks
 Algebra 2 Year-at-a-Glance Leander ISD 2007-08 1st Six Weeks 2nd Six Weeks 3rd Six Weeks 4th Six Weeks 5th Six Weeks 6th Six Weeks Essential Unit of Study 6 weeks 3 weeks 3 weeks 6 weeks 3 weeks 3 weeks
Algebra 2 Year-at-a-Glance Leander ISD 2007-08 1st Six Weeks 2nd Six Weeks 3rd Six Weeks 4th Six Weeks 5th Six Weeks 6th Six Weeks Essential Unit of Study 6 weeks 3 weeks 3 weeks 6 weeks 3 weeks 3 weeks
In algebra, factor by rewriting a polynomial as a product of lower-degree polynomials
 Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
Polynomial Operations and Factoring
 Algebra 1, Quarter 4, Unit 4.1 Polynomial Operations and Factoring Overview Number of instructional days: 15 (1 day = 45 60 minutes) Content to be learned Identify terms, coefficients, and degree of polynomials.
Algebra 1, Quarter 4, Unit 4.1 Polynomial Operations and Factoring Overview Number of instructional days: 15 (1 day = 45 60 minutes) Content to be learned Identify terms, coefficients, and degree of polynomials.
Radicals - Rationalize Denominators
 8. Radicals - Rationalize Denominators Objective: Rationalize the denominators of radical expressions. It is considered bad practice to have a radical in the denominator of a fraction. When this happens
8. Radicals - Rationalize Denominators Objective: Rationalize the denominators of radical expressions. It is considered bad practice to have a radical in the denominator of a fraction. When this happens
Unit 7: Radical Functions & Rational Exponents
 Date Period Unit 7: Radical Functions & Rational Exponents DAY 0 TOPIC Roots and Radical Expressions Multiplying and Dividing Radical Expressions Binomial Radical Expressions Rational Exponents 4 Solving
Date Period Unit 7: Radical Functions & Rational Exponents DAY 0 TOPIC Roots and Radical Expressions Multiplying and Dividing Radical Expressions Binomial Radical Expressions Rational Exponents 4 Solving
Section 5.0A Factoring Part 1
 Section 5.0A Factoring Part 1 I. Work Together A. Multiply the following binomials into trinomials. (Write the final result in descending order, i.e., a + b + c ). ( 7)( + 5) ( + 7)( + ) ( + 7)( + 5) (
Section 5.0A Factoring Part 1 I. Work Together A. Multiply the following binomials into trinomials. (Write the final result in descending order, i.e., a + b + c ). ( 7)( + 5) ( + 7)( + ) ( + 7)( + 5) (
Sect 6.7 - Solving Equations Using the Zero Product Rule
 Sect 6.7 - Solving Equations Using the Zero Product Rule 116 Concept #1: Definition of a Quadratic Equation A quadratic equation is an equation that can be written in the form ax 2 + bx + c = 0 (referred
Sect 6.7 - Solving Equations Using the Zero Product Rule 116 Concept #1: Definition of a Quadratic Equation A quadratic equation is an equation that can be written in the form ax 2 + bx + c = 0 (referred
Greatest Common Factor (GCF) Factoring
 Section 4 4: Greatest Common Factor (GCF) Factoring The last chapter introduced the distributive process. The distributive process takes a product of a monomial and a polynomial and changes the multiplication
Section 4 4: Greatest Common Factor (GCF) Factoring The last chapter introduced the distributive process. The distributive process takes a product of a monomial and a polynomial and changes the multiplication
Calculate Highest Common Factors(HCFs) & Least Common Multiples(LCMs) NA1
 Calculate Highest Common Factors(HCFs) & Least Common Multiples(LCMs) NA1 What are the multiples of 5? The multiples are in the five times table What are the factors of 90? Each of these is a pair of factors.
Calculate Highest Common Factors(HCFs) & Least Common Multiples(LCMs) NA1 What are the multiples of 5? The multiples are in the five times table What are the factors of 90? Each of these is a pair of factors.
MATH 21. College Algebra 1 Lecture Notes
 MATH 21 College Algebra 1 Lecture Notes MATH 21 3.6 Factoring Review College Algebra 1 Factoring and Foiling 1. (a + b) 2 = a 2 + 2ab + b 2. 2. (a b) 2 = a 2 2ab + b 2. 3. (a + b)(a b) = a 2 b 2. 4. (a
MATH 21 College Algebra 1 Lecture Notes MATH 21 3.6 Factoring Review College Algebra 1 Factoring and Foiling 1. (a + b) 2 = a 2 + 2ab + b 2. 2. (a b) 2 = a 2 2ab + b 2. 3. (a + b)(a b) = a 2 b 2. 4. (a
CRLS Mathematics Department Algebra I Curriculum Map/Pacing Guide
 Curriculum Map/Pacing Guide page 1 of 14 Quarter I start (CP & HN) 170 96 Unit 1: Number Sense and Operations 24 11 Totals Always Include 2 blocks for Review & Test Operating with Real Numbers: How are
Curriculum Map/Pacing Guide page 1 of 14 Quarter I start (CP & HN) 170 96 Unit 1: Number Sense and Operations 24 11 Totals Always Include 2 blocks for Review & Test Operating with Real Numbers: How are
SUNY ECC. ACCUPLACER Preparation Workshop. Algebra Skills
 SUNY ECC ACCUPLACER Preparation Workshop Algebra Skills Gail A. Butler Ph.D. Evaluating Algebraic Epressions Substitute the value (#) in place of the letter (variable). Follow order of operations!!! E)
SUNY ECC ACCUPLACER Preparation Workshop Algebra Skills Gail A. Butler Ph.D. Evaluating Algebraic Epressions Substitute the value (#) in place of the letter (variable). Follow order of operations!!! E)
The Greatest Common Factor; Factoring by Grouping
 296 CHAPTER 5 Factoring and Applications 5.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
296 CHAPTER 5 Factoring and Applications 5.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
ALGEBRA I (Created 2014) Amherst County Public Schools
 ALGEBRA I (Created 2014) Amherst County Public Schools The 2009 Mathematics Standards of Learning Curriculum Framework is a companion document to the 2009 Mathematics Standards of Learning and amplifies
ALGEBRA I (Created 2014) Amherst County Public Schools The 2009 Mathematics Standards of Learning Curriculum Framework is a companion document to the 2009 Mathematics Standards of Learning and amplifies
Learning Objectives 9.2. Media Run Times 9.3
 Unit 9 Table of Contents Unit 9: Factoring Video Overview Learning Objectives 9.2 Media Run Times 9.3 Instructor Notes 9.4 The Mathematics of Factoring Polynomials Teaching Tips: Conceptual Challenges
Unit 9 Table of Contents Unit 9: Factoring Video Overview Learning Objectives 9.2 Media Run Times 9.3 Instructor Notes 9.4 The Mathematics of Factoring Polynomials Teaching Tips: Conceptual Challenges
Factoring Flow Chart
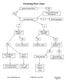 Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Factoring a Difference of Two Squares. Factoring a Difference of Two Squares
 284 (6 8) Chapter 6 Factoring 87. Tomato soup. The amount of metal S (in square inches) that it takes to make a can for tomato soup is a function of the radius r and height h: S 2 r 2 2 rh a) Rewrite this
284 (6 8) Chapter 6 Factoring 87. Tomato soup. The amount of metal S (in square inches) that it takes to make a can for tomato soup is a function of the radius r and height h: S 2 r 2 2 rh a) Rewrite this
2.3. Finding polynomial functions. An Introduction:
 2.3. Finding polynomial functions. An Introduction: As is usually the case when learning a new concept in mathematics, the new concept is the reverse of the previous one. Remember how you first learned
2.3. Finding polynomial functions. An Introduction: As is usually the case when learning a new concept in mathematics, the new concept is the reverse of the previous one. Remember how you first learned
How To Understand And Solve Algebraic Equations
 College Algebra Course Text Barnett, Raymond A., Michael R. Ziegler, and Karl E. Byleen. College Algebra, 8th edition, McGraw-Hill, 2008, ISBN: 978-0-07-286738-1 Course Description This course provides
College Algebra Course Text Barnett, Raymond A., Michael R. Ziegler, and Karl E. Byleen. College Algebra, 8th edition, McGraw-Hill, 2008, ISBN: 978-0-07-286738-1 Course Description This course provides
Thnkwell s Homeschool Precalculus Course Lesson Plan: 36 weeks
 Thnkwell s Homeschool Precalculus Course Lesson Plan: 36 weeks Welcome to Thinkwell s Homeschool Precalculus! We re thrilled that you ve decided to make us part of your homeschool curriculum. This lesson
Thnkwell s Homeschool Precalculus Course Lesson Plan: 36 weeks Welcome to Thinkwell s Homeschool Precalculus! We re thrilled that you ve decided to make us part of your homeschool curriculum. This lesson
Mathematics, Basic Math and Algebra
 NONRESIDENT TRAINING COURSE Mathematics, Basic Math and Algebra NAVEDTRA 14139 DISTRIBUTION STATEMENT A: Approved for public release; distribution is unlimited. PREFACE About this course: This is a self-study
NONRESIDENT TRAINING COURSE Mathematics, Basic Math and Algebra NAVEDTRA 14139 DISTRIBUTION STATEMENT A: Approved for public release; distribution is unlimited. PREFACE About this course: This is a self-study
Factoring (pp. 1 of 4)
 Factoring (pp. 1 of 4) Algebra Review Try these items from middle school math. A) What numbers are the factors of 4? B) Write down the prime factorization of 7. C) 6 Simplify 48 using the greatest common
Factoring (pp. 1 of 4) Algebra Review Try these items from middle school math. A) What numbers are the factors of 4? B) Write down the prime factorization of 7. C) 6 Simplify 48 using the greatest common
Using the ac Method to Factor
 4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
Lesson 9.1 Solving Quadratic Equations
 Lesson 9.1 Solving Quadratic Equations 1. Sketch the graph of a quadratic equation with a. One -intercept and all nonnegative y-values. b. The verte in the third quadrant and no -intercepts. c. The verte
Lesson 9.1 Solving Quadratic Equations 1. Sketch the graph of a quadratic equation with a. One -intercept and all nonnegative y-values. b. The verte in the third quadrant and no -intercepts. c. The verte
Algebra 2 Chapter 1 Vocabulary. identity - A statement that equates two equivalent expressions.
 Chapter 1 Vocabulary identity - A statement that equates two equivalent expressions. verbal model- A word equation that represents a real-life problem. algebraic expression - An expression with variables.
Chapter 1 Vocabulary identity - A statement that equates two equivalent expressions. verbal model- A word equation that represents a real-life problem. algebraic expression - An expression with variables.
Factoring Special Polynomials
 6.6 Factoring Special Polynomials 6.6 OBJECTIVES 1. Factor the difference of two squares 2. Factor the sum or difference of two cubes In this section, we will look at several special polynomials. These
6.6 Factoring Special Polynomials 6.6 OBJECTIVES 1. Factor the difference of two squares 2. Factor the sum or difference of two cubes In this section, we will look at several special polynomials. These
