Math 53 Worksheet Solutions- Minmax and Lagrange
|
|
|
- Emery West
- 8 years ago
- Views:
Transcription
1 Math 5 Worksheet Solutions- Minmax and Lagrange. Find the local maximum and minimum values as well as the saddle point(s) of the function f(x, y) = e y (y x ). Solution. First we calculate the partial derivatives and set them equal to zero. f x (x, y) = xe y = 0, f y (x, y) = e y (y x ) + ye y = 0. For the first equation, e y 0, so we have x = 0. Plugging this in to the second equation, we have e y [y + y] = 0, and since again e y 0, we have y = 0 and y =. So our two critical points are (0, 0) and (0, ). We now must check what kind of critical points these are. To do this we need the second and mixed partials, f xx (x, y) = e y, f yy (x, y) = e y (y x + y) + e y (y + ), f xy (x, y) = xe y. At the point (0, 0), we have and so f xx (0, 0) =, f yy (0, 0) =, f xy (0, 0) = 0, D = f xx (0, 0)f yy (0, 0) [f xy (0, 0)] = 4 < 0, and since f xx (0, 0) < 0, we know that f has a local maximum at (0,0) by the second derivative test. At the point (0, ), we have and so f xx (0, ) = e, f yy (0, ) = e, f xy (0, ) = 0, so f has a saddle point at (0, ). D = f xx (0, )f yy (0, ) [f xy (0, )] = 4 > 0,. Find the absolute maximum and minimum values of f(x, y) = x + y 4 on the set D = {(x, y) x + y }. Solution. Recall the method for find absolute maxima and minima:. Find the critical points of f. No second derivative test is needed.. Find the values of f at the function s critical points.. Find the extreme values of f on the boundary of the region in question. (Don t forget endpoints!) 4. The largest value from () and () is the maximum; the smallest is the minimum.
2 With these in mind, we re ready to attack the problem. So let s find the critical points by taking partials. f x (x, y) = 6x = 0, f y (x, y) = 4y = 0, so (x, y) = (0, 0) is the only critical point. And note that f(0, 0) = 0. Now we must look at the boundary, the circle x + y =. On this circle, y = x, so define g(x) = f(x, y) = x + ( x ), and we will now find the extra of g(x) as in traditional one-variable calculus. First calculate the derivative and set equal to zero. g (x) = 6x 4x( x ) = 0 = x[x + x ] = 0, and so we have solutions x = 0 and x = ± =,, but we can ignore the solution x = as we seek to find the extrema of g(x) on the interval [, ]. So we have g(0) =, g( ) = 6. But we still need to check the endpoints of g, since we re finding its extrema on a closed interval! Note that g( ) =, g() =. Looking back at all the values of f(x, y), it turns out that the maximum occurs at (, 0) and the minimum at (, 0). (Remember that g( ) = f(, 0) and g() = f(, 0).). Use Lagrange multipliers to find the maximum and minimum values of the function f(x, y) = x y z subject to the constraint x + y + z =. Solution. The function we re finding extrema of is f(x, y, z) = x y z and the constraint is g(x, y, z) = x + y + z = 0. Then f(x, y, z) = xy z, yx z, zx y, g(x, y, z) = x, y, z, and so we must solve f = λ g. This equation is actually the three equations, xy z = xλ, yx z = yλ, zx y = xλ, along with the constraint equation. Observe that if any one of x, y, z is zero. Then f(x, y, z) = 0, according to the equation for f(x, y, z). If none of the variables is equal to zero, then the equations become λ = y z = x z = x y,
3 and because x, y, z 0, this indicates that x = y = z. The constraint is then x = 0, or x =. In this case, f (,, ) ( ) 6 = = 7. So the maximum occurs at (x, y, z) = (,, ) and the minimum occurs at any point (x, y, z) where one of the variables is zero. The maximum value is and the 7 minimum value is The plane x + y + z = intersects the paraboloid z = x + y in an ellipse. Find the points on this ellipse that are nearest to and farthest from the origin. Solution. The key here is that we needn t worry about the equation of the ellipse formed by the intersection; instead, we regard the two surfaces as constraints and seek to minimize the distance from the origin. More precisely, we ll minimize f(x, y, z) = x + y + z, the distance squared, since this is minimized precisely when the distance is, and this function is a lot easier to work with. You should remember this trick. The constraints then are We must now solve So we calculate, g(x, y, z) = x + y + z = 0, h(x, y, z) = x + y z = 0. f = λ g + µ h. f = x, y, z, g =,,, h = x, y,. And the equation we must solve becomes three equations, in addition to the two constraints. x = λ + xµ, y = λ + yµ, z = λ µ. Solving five equations for five unknowns can get tricky, to say the least. One idea is to observe that the first two equations above are quite similar. In fact, we can write x xµ = λ = y yµ = (x y)( µ) = 0. And so either µ = or x = y. First consider the case where µ =. Then from the first equation above, λ = 0. Then z =. But then x + y =, and there are clearly no solutions in this case. So now assume x = y. At this point, we can dispense with solving for λ and µ entirely. (Remember, nothing about the problem insists we find their values!) So, going back to the original constraints, we have x + z =, x = z.
4 These are much simpler! From the first equation, we get z = x, so the second then shows x + x = 0, and this factors as (x )(x + ) = 0, so x = and x = are solutions. So the two critical points are (,, ) and (,, ). Now we just calculate that ( f,, ) =, f(,, ) = 6, 4 and these are the minimum and maximum values, respectively. (Where minimum means the point closest to the origin and maximum is the point furthest.) 5. If the length of the diagonal of a rectangular box must be L, what is the largest possible volume? Solution. It s not hard to see that if the side lengths are x, y, and z, then the length of the diagonal L and the volume V satisfy L = x + y + z, V = xyz. Now, we could use Lagrange multipliers to solve this problem, but let s do it first without such an advanced technique. To implement the constraint, we solve for z in the first equation and get z = L x y, so that we can write V (x, y) = xy L x y. And now we just need to maximize V with the constraints x, y > 0 and x + y L. So, first we find the critical points. V x (x, y) = y x y L x y L x y, Setting the components equal to zero gives L x y [ L x y ] y = 0, V y(x, y) = x xy L x y L x y. and L x y [ L x y ] x = 0. Now x, y 0, as noted above, so we must have L x y = 0, L x y = 0. Write the first equation as y = L x and substitute into the second. We then have L x (L x ) = 0, = x = L, and so x = L. Substituting this into the first equation, it follows that y = L. So the maximum volume is obtained when x = y = z = L, 4
5 and the volume then is ( ) L V = = L. The problem is indeed easier with Lagrange. Here f(x, y, z) = xyz and g(x, y, z) = x + y + z L = 0. Then f(x, y, z) = yz, xz, xy, g(x, y, z) = x, y, z, and the equations are yz = xλ, xz = yλ, xy = zλ. Then xyz = x λ = y λ = z λ, which we obtain by multiplying each equation by x, y, and z respectively. Thus either λ = 0 or x = y = z, since x, y, z > 0. If λ = 0, then at least one of x, y, z is zero, which cannot happen. So we must have x = y = z and, from the constraint equation, this means we must have x = y = z = L. Then, again, we find that ( ) L V = = L. 5
(a) We have x = 3 + 2t, y = 2 t, z = 6 so solving for t we get the symmetric equations. x 3 2. = 2 y, z = 6. t 2 2t + 1 = 0,
 Name: Solutions to Practice Final. Consider the line r(t) = 3 + t, t, 6. (a) Find symmetric equations for this line. (b) Find the point where the first line r(t) intersects the surface z = x + y. (a) We
Name: Solutions to Practice Final. Consider the line r(t) = 3 + t, t, 6. (a) Find symmetric equations for this line. (b) Find the point where the first line r(t) intersects the surface z = x + y. (a) We
1 3 4 = 8i + 20j 13k. x + w. y + w
 ) Find the point of intersection of the lines x = t +, y = 3t + 4, z = 4t + 5, and x = 6s + 3, y = 5s +, z = 4s + 9, and then find the plane containing these two lines. Solution. Solve the system of equations
) Find the point of intersection of the lines x = t +, y = 3t + 4, z = 4t + 5, and x = 6s + 3, y = 5s +, z = 4s + 9, and then find the plane containing these two lines. Solution. Solve the system of equations
SOLUTIONS. f x = 6x 2 6xy 24x, f y = 3x 2 6y. To find the critical points, we solve
 SOLUTIONS Problem. Find the critical points of the function f(x, y = 2x 3 3x 2 y 2x 2 3y 2 and determine their type i.e. local min/local max/saddle point. Are there any global min/max? Partial derivatives
SOLUTIONS Problem. Find the critical points of the function f(x, y = 2x 3 3x 2 y 2x 2 3y 2 and determine their type i.e. local min/local max/saddle point. Are there any global min/max? Partial derivatives
( 1)2 + 2 2 + 2 2 = 9 = 3 We would like to make the length 6. The only vectors in the same direction as v are those
 1.(6pts) Which of the following vectors has the same direction as v 1,, but has length 6? (a), 4, 4 (b),, (c) 4,, 4 (d), 4, 4 (e) 0, 6, 0 The length of v is given by ( 1) + + 9 3 We would like to make
1.(6pts) Which of the following vectors has the same direction as v 1,, but has length 6? (a), 4, 4 (b),, (c) 4,, 4 (d), 4, 4 (e) 0, 6, 0 The length of v is given by ( 1) + + 9 3 We would like to make
Solutions for Review Problems
 olutions for Review Problems 1. Let be the triangle with vertices A (,, ), B (4,, 1) and C (,, 1). (a) Find the cosine of the angle BAC at vertex A. (b) Find the area of the triangle ABC. (c) Find a vector
olutions for Review Problems 1. Let be the triangle with vertices A (,, ), B (4,, 1) and C (,, 1). (a) Find the cosine of the angle BAC at vertex A. (b) Find the area of the triangle ABC. (c) Find a vector
Section 12.6: Directional Derivatives and the Gradient Vector
 Section 26: Directional Derivatives and the Gradient Vector Recall that if f is a differentiable function of x and y and z = f(x, y), then the partial derivatives f x (x, y) and f y (x, y) give the rate
Section 26: Directional Derivatives and the Gradient Vector Recall that if f is a differentiable function of x and y and z = f(x, y), then the partial derivatives f x (x, y) and f y (x, y) give the rate
Linear and quadratic Taylor polynomials for functions of several variables.
 ams/econ 11b supplementary notes ucsc Linear quadratic Taylor polynomials for functions of several variables. c 010, Yonatan Katznelson Finding the extreme (minimum or maximum) values of a function, is
ams/econ 11b supplementary notes ucsc Linear quadratic Taylor polynomials for functions of several variables. c 010, Yonatan Katznelson Finding the extreme (minimum or maximum) values of a function, is
SECOND DERIVATIVE TEST FOR CONSTRAINED EXTREMA
 SECOND DERIVATIVE TEST FOR CONSTRAINED EXTREMA This handout presents the second derivative test for a local extrema of a Lagrange multiplier problem. The Section 1 presents a geometric motivation for the
SECOND DERIVATIVE TEST FOR CONSTRAINED EXTREMA This handout presents the second derivative test for a local extrema of a Lagrange multiplier problem. The Section 1 presents a geometric motivation for the
5.7 Maximum and Minimum Values
 5.7 Maximum and Minimum Values Objectives Icandefinecriticalpoints. I know the di erence between local and absolute minimums/maximums. I can find local maximum(s), minimum(s), and saddle points for a given
5.7 Maximum and Minimum Values Objectives Icandefinecriticalpoints. I know the di erence between local and absolute minimums/maximums. I can find local maximum(s), minimum(s), and saddle points for a given
Name: ID: Discussion Section:
 Math 28 Midterm 3 Spring 2009 Name: ID: Discussion Section: This exam consists of 6 questions: 4 multiple choice questions worth 5 points each 2 hand-graded questions worth a total of 30 points. INSTRUCTIONS:
Math 28 Midterm 3 Spring 2009 Name: ID: Discussion Section: This exam consists of 6 questions: 4 multiple choice questions worth 5 points each 2 hand-graded questions worth a total of 30 points. INSTRUCTIONS:
Adding vectors We can do arithmetic with vectors. We ll start with vector addition and related operations. Suppose you have two vectors
 1 Chapter 13. VECTORS IN THREE DIMENSIONAL SPACE Let s begin with some names and notation for things: R is the set (collection) of real numbers. We write x R to mean that x is a real number. A real number
1 Chapter 13. VECTORS IN THREE DIMENSIONAL SPACE Let s begin with some names and notation for things: R is the set (collection) of real numbers. We write x R to mean that x is a real number. A real number
Math 265 (Butler) Practice Midterm II B (Solutions)
 Math 265 (Butler) Practice Midterm II B (Solutions) 1. Find (x 0, y 0 ) so that the plane tangent to the surface z f(x, y) x 2 + 3xy y 2 at ( x 0, y 0, f(x 0, y 0 ) ) is parallel to the plane 16x 2y 2z
Math 265 (Butler) Practice Midterm II B (Solutions) 1. Find (x 0, y 0 ) so that the plane tangent to the surface z f(x, y) x 2 + 3xy y 2 at ( x 0, y 0, f(x 0, y 0 ) ) is parallel to the plane 16x 2y 2z
42 CHAPTER 1. VECTORS AND THE GEOMETRY OF SPACE. Figure 1.18: Parabola y = 2x 2. 1.6.1 Brief review of Conic Sections
 2 CHAPTER 1. VECTORS AND THE GEOMETRY OF SPACE Figure 1.18: Parabola y = 2 1.6 Quadric Surfaces 1.6.1 Brief review of Conic Sections You may need to review conic sections for this to make more sense. You
2 CHAPTER 1. VECTORS AND THE GEOMETRY OF SPACE Figure 1.18: Parabola y = 2 1.6 Quadric Surfaces 1.6.1 Brief review of Conic Sections You may need to review conic sections for this to make more sense. You
Section 1. Finding Common Terms
 Worksheet 2.1 Factors of Algebraic Expressions Section 1 Finding Common Terms In worksheet 1.2 we talked about factors of whole numbers. Remember, if a b = ab then a is a factor of ab and b is a factor
Worksheet 2.1 Factors of Algebraic Expressions Section 1 Finding Common Terms In worksheet 1.2 we talked about factors of whole numbers. Remember, if a b = ab then a is a factor of ab and b is a factor
This makes sense. t 2 1 + 1/t 2 dt = 1. t t 2 + 1dt = 2 du = 1 3 u3/2 u=5
 1. (Line integrals Using parametrization. Two types and the flux integral) Formulas: ds = x (t) dt, d x = x (t)dt and d x = T ds since T = x (t)/ x (t). Another one is Nds = T ds ẑ = (dx, dy) ẑ = (dy,
1. (Line integrals Using parametrization. Two types and the flux integral) Formulas: ds = x (t) dt, d x = x (t)dt and d x = T ds since T = x (t)/ x (t). Another one is Nds = T ds ẑ = (dx, dy) ẑ = (dy,
FINAL EXAM SOLUTIONS Math 21a, Spring 03
 INAL EXAM SOLUIONS Math 21a, Spring 3 Name: Start by printing your name in the above box and check your section in the box to the left. MW1 Ken Chung MW1 Weiyang Qiu MW11 Oliver Knill h1 Mark Lucianovic
INAL EXAM SOLUIONS Math 21a, Spring 3 Name: Start by printing your name in the above box and check your section in the box to the left. MW1 Ken Chung MW1 Weiyang Qiu MW11 Oliver Knill h1 Mark Lucianovic
Review Sheet for Test 1
 Review Sheet for Test 1 Math 261-00 2 6 2004 These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And
Review Sheet for Test 1 Math 261-00 2 6 2004 These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And
COLLEGE ALGEBRA. Paul Dawkins
 COLLEGE ALGEBRA Paul Dawkins Table of Contents Preface... iii Outline... iv Preliminaries... Introduction... Integer Exponents... Rational Exponents... 9 Real Exponents...5 Radicals...6 Polynomials...5
COLLEGE ALGEBRA Paul Dawkins Table of Contents Preface... iii Outline... iv Preliminaries... Introduction... Integer Exponents... Rational Exponents... 9 Real Exponents...5 Radicals...6 Polynomials...5
Maximizing volume given a surface area constraint
 Maximizing volume given a surface area constraint Math 8 Department of Mathematics Dartmouth College Maximizing volume given a surface area constraint p.1/9 Maximizing wih a constraint We wish to solve
Maximizing volume given a surface area constraint Math 8 Department of Mathematics Dartmouth College Maximizing volume given a surface area constraint p.1/9 Maximizing wih a constraint We wish to solve
2 Integrating Both Sides
 2 Integrating Both Sides So far, the only general method we have for solving differential equations involves equations of the form y = f(x), where f(x) is any function of x. The solution to such an equation
2 Integrating Both Sides So far, the only general method we have for solving differential equations involves equations of the form y = f(x), where f(x) is any function of x. The solution to such an equation
Practice Final Math 122 Spring 12 Instructor: Jeff Lang
 Practice Final Math Spring Instructor: Jeff Lang. Find the limit of the sequence a n = ln (n 5) ln (3n + 8). A) ln ( ) 3 B) ln C) ln ( ) 3 D) does not exist. Find the limit of the sequence a n = (ln n)6
Practice Final Math Spring Instructor: Jeff Lang. Find the limit of the sequence a n = ln (n 5) ln (3n + 8). A) ln ( ) 3 B) ln C) ln ( ) 3 D) does not exist. Find the limit of the sequence a n = (ln n)6
Solutions to Homework 10
 Solutions to Homework 1 Section 7., exercise # 1 (b,d): (b) Compute the value of R f dv, where f(x, y) = y/x and R = [1, 3] [, 4]. Solution: Since f is continuous over R, f is integrable over R. Let x
Solutions to Homework 1 Section 7., exercise # 1 (b,d): (b) Compute the value of R f dv, where f(x, y) = y/x and R = [1, 3] [, 4]. Solution: Since f is continuous over R, f is integrable over R. Let x
Math 120 Final Exam Practice Problems, Form: A
 Math 120 Final Exam Practice Problems, Form: A Name: While every attempt was made to be complete in the types of problems given below, we make no guarantees about the completeness of the problems. Specifically,
Math 120 Final Exam Practice Problems, Form: A Name: While every attempt was made to be complete in the types of problems given below, we make no guarantees about the completeness of the problems. Specifically,
1.5. Factorisation. Introduction. Prerequisites. Learning Outcomes. Learning Style
 Factorisation 1.5 Introduction In Block 4 we showed the way in which brackets were removed from algebraic expressions. Factorisation, which can be considered as the reverse of this process, is dealt with
Factorisation 1.5 Introduction In Block 4 we showed the way in which brackets were removed from algebraic expressions. Factorisation, which can be considered as the reverse of this process, is dealt with
1.7 Graphs of Functions
 64 Relations and Functions 1.7 Graphs of Functions In Section 1.4 we defined a function as a special type of relation; one in which each x-coordinate was matched with only one y-coordinate. We spent most
64 Relations and Functions 1.7 Graphs of Functions In Section 1.4 we defined a function as a special type of relation; one in which each x-coordinate was matched with only one y-coordinate. We spent most
Practice with Proofs
 Practice with Proofs October 6, 2014 Recall the following Definition 0.1. A function f is increasing if for every x, y in the domain of f, x < y = f(x) < f(y) 1. Prove that h(x) = x 3 is increasing, using
Practice with Proofs October 6, 2014 Recall the following Definition 0.1. A function f is increasing if for every x, y in the domain of f, x < y = f(x) < f(y) 1. Prove that h(x) = x 3 is increasing, using
To give it a definition, an implicit function of x and y is simply any relationship that takes the form:
 2 Implicit function theorems and applications 21 Implicit functions The implicit function theorem is one of the most useful single tools you ll meet this year After a while, it will be second nature to
2 Implicit function theorems and applications 21 Implicit functions The implicit function theorem is one of the most useful single tools you ll meet this year After a while, it will be second nature to
Limits and Continuity
 Math 20C Multivariable Calculus Lecture Limits and Continuity Slide Review of Limit. Side limits and squeeze theorem. Continuous functions of 2,3 variables. Review: Limits Slide 2 Definition Given a function
Math 20C Multivariable Calculus Lecture Limits and Continuity Slide Review of Limit. Side limits and squeeze theorem. Continuous functions of 2,3 variables. Review: Limits Slide 2 Definition Given a function
Exam 1 Sample Question SOLUTIONS. y = 2x
 Exam Sample Question SOLUTIONS. Eliminate the parameter to find a Cartesian equation for the curve: x e t, y e t. SOLUTION: You might look at the coordinates and notice that If you don t see it, we can
Exam Sample Question SOLUTIONS. Eliminate the parameter to find a Cartesian equation for the curve: x e t, y e t. SOLUTION: You might look at the coordinates and notice that If you don t see it, we can
L 2 : x = s + 1, y = s, z = 4s + 4. 3. Suppose that C has coordinates (x, y, z). Then from the vector equality AC = BD, one has
 The line L through the points A and B is parallel to the vector AB = 3, 2, and has parametric equations x = 3t + 2, y = 2t +, z = t Therefore, the intersection point of the line with the plane should satisfy:
The line L through the points A and B is parallel to the vector AB = 3, 2, and has parametric equations x = 3t + 2, y = 2t +, z = t Therefore, the intersection point of the line with the plane should satisfy:
Constrained optimization.
 ams/econ 11b supplementary notes ucsc Constrained optimization. c 2010, Yonatan Katznelson 1. Constraints In many of the optimization problems that arise in economics, there are restrictions on the values
ams/econ 11b supplementary notes ucsc Constrained optimization. c 2010, Yonatan Katznelson 1. Constraints In many of the optimization problems that arise in economics, there are restrictions on the values
correct-choice plot f(x) and draw an approximate tangent line at x = a and use geometry to estimate its slope comment The choices were:
 Topic 1 2.1 mode MultipleSelection text How can we approximate the slope of the tangent line to f(x) at a point x = a? This is a Multiple selection question, so you need to check all of the answers that
Topic 1 2.1 mode MultipleSelection text How can we approximate the slope of the tangent line to f(x) at a point x = a? This is a Multiple selection question, so you need to check all of the answers that
constraint. Let us penalize ourselves for making the constraint too big. We end up with a
 Chapter 4 Constrained Optimization 4.1 Equality Constraints (Lagrangians) Suppose we have a problem: Maximize 5, (x 1, 2) 2, 2(x 2, 1) 2 subject to x 1 +4x 2 =3 If we ignore the constraint, we get the
Chapter 4 Constrained Optimization 4.1 Equality Constraints (Lagrangians) Suppose we have a problem: Maximize 5, (x 1, 2) 2, 2(x 2, 1) 2 subject to x 1 +4x 2 =3 If we ignore the constraint, we get the
Equations Involving Lines and Planes Standard equations for lines in space
 Equations Involving Lines and Planes In this section we will collect various important formulas regarding equations of lines and planes in three dimensional space Reminder regarding notation: any quantity
Equations Involving Lines and Planes In this section we will collect various important formulas regarding equations of lines and planes in three dimensional space Reminder regarding notation: any quantity
1 Lecture: Integration of rational functions by decomposition
 Lecture: Integration of rational functions by decomposition into partial fractions Recognize and integrate basic rational functions, except when the denominator is a power of an irreducible quadratic.
Lecture: Integration of rational functions by decomposition into partial fractions Recognize and integrate basic rational functions, except when the denominator is a power of an irreducible quadratic.
Solving DEs by Separation of Variables.
 Solving DEs by Separation of Variables. Introduction and procedure Separation of variables allows us to solve differential equations of the form The steps to solving such DEs are as follows: dx = gx).
Solving DEs by Separation of Variables. Introduction and procedure Separation of variables allows us to solve differential equations of the form The steps to solving such DEs are as follows: dx = gx).
APPLICATIONS. are symmetric, but. are not.
 CHAPTER III APPLICATIONS Real Symmetric Matrices The most common matrices we meet in applications are symmetric, that is, they are square matrices which are equal to their transposes In symbols, A t =
CHAPTER III APPLICATIONS Real Symmetric Matrices The most common matrices we meet in applications are symmetric, that is, they are square matrices which are equal to their transposes In symbols, A t =
Solutions to Homework 5
 Solutions to Homework 5 1. Let z = f(x, y) be a twice continously differentiable function of x and y. Let x = r cos θ and y = r sin θ be the equations which transform polar coordinates into rectangular
Solutions to Homework 5 1. Let z = f(x, y) be a twice continously differentiable function of x and y. Let x = r cos θ and y = r sin θ be the equations which transform polar coordinates into rectangular
MATH 21. College Algebra 1 Lecture Notes
 MATH 21 College Algebra 1 Lecture Notes MATH 21 3.6 Factoring Review College Algebra 1 Factoring and Foiling 1. (a + b) 2 = a 2 + 2ab + b 2. 2. (a b) 2 = a 2 2ab + b 2. 3. (a + b)(a b) = a 2 b 2. 4. (a
MATH 21 College Algebra 1 Lecture Notes MATH 21 3.6 Factoring Review College Algebra 1 Factoring and Foiling 1. (a + b) 2 = a 2 + 2ab + b 2. 2. (a b) 2 = a 2 2ab + b 2. 3. (a + b)(a b) = a 2 b 2. 4. (a
+ 4θ 4. We want to minimize this function, and we know that local minima occur when the derivative equals zero. Then consider
 Math Xb Applications of Trig Derivatives 1. A woman at point A on the shore of a circular lake with radius 2 miles wants to arrive at the point C diametrically opposite A on the other side of the lake
Math Xb Applications of Trig Derivatives 1. A woman at point A on the shore of a circular lake with radius 2 miles wants to arrive at the point C diametrically opposite A on the other side of the lake
Factoring - Greatest Common Factor
 6.1 Factoring - Greatest Common Factor Objective: Find the greatest common factor of a polynomial and factor it out of the expression. The opposite of multiplying polynomials together is factoring polynomials.
6.1 Factoring - Greatest Common Factor Objective: Find the greatest common factor of a polynomial and factor it out of the expression. The opposite of multiplying polynomials together is factoring polynomials.
Factoring Flow Chart
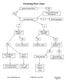 Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Solutions to Practice Problems for Test 4
 olutions to Practice Problems for Test 4 1. Let be the line segmentfrom the point (, 1, 1) to the point (,, 3). Evaluate the line integral y ds. Answer: First, we parametrize the line segment from (, 1,
olutions to Practice Problems for Test 4 1. Let be the line segmentfrom the point (, 1, 1) to the point (,, 3). Evaluate the line integral y ds. Answer: First, we parametrize the line segment from (, 1,
SOLUTIONS TO HOMEWORK ASSIGNMENT #4, MATH 253
 SOLUTIONS TO HOMEWORK ASSIGNMENT #4, MATH 253 1. Prove that the following differential equations are satisfied by the given functions: (a) 2 u + 2 u 2 y + 2 u 2 z =0,whereu 2 =(x2 + y 2 + z 2 ) 1/2. (b)
SOLUTIONS TO HOMEWORK ASSIGNMENT #4, MATH 253 1. Prove that the following differential equations are satisfied by the given functions: (a) 2 u + 2 u 2 y + 2 u 2 z =0,whereu 2 =(x2 + y 2 + z 2 ) 1/2. (b)
Name Intro to Algebra 2. Unit 1: Polynomials and Factoring
 Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
In this section, we will consider techniques for solving problems of this type.
 Constrained optimisation roblems in economics typically involve maximising some quantity, such as utility or profit, subject to a constraint for example income. We shall therefore need techniques for solving
Constrained optimisation roblems in economics typically involve maximising some quantity, such as utility or profit, subject to a constraint for example income. We shall therefore need techniques for solving
Module 1 : Conduction. Lecture 5 : 1D conduction example problems. 2D conduction
 Module 1 : Conduction Lecture 5 : 1D conduction example problems. 2D conduction Objectives In this class: An example of optimization for insulation thickness is solved. The 1D conduction is considered
Module 1 : Conduction Lecture 5 : 1D conduction example problems. 2D conduction Objectives In this class: An example of optimization for insulation thickness is solved. The 1D conduction is considered
CHAPTER 8, GEOMETRY. 4. A circular cylinder has a circumference of 33 in. Use 22 as the approximate value of π and find the radius of this cylinder.
 TEST A CHAPTER 8, GEOMETRY 1. A rectangular plot of ground is to be enclosed with 180 yd of fencing. If the plot is twice as long as it is wide, what are its dimensions? 2. A 4 cm by 6 cm rectangle has
TEST A CHAPTER 8, GEOMETRY 1. A rectangular plot of ground is to be enclosed with 180 yd of fencing. If the plot is twice as long as it is wide, what are its dimensions? 2. A 4 cm by 6 cm rectangle has
299ReviewProblemSolutions.nb 1. Review Problems. Final Exam: Wednesday, 12/16/2009 1:30PM. Mathematica 6.0 Initializations
 99ReviewProblemSolutions.nb Review Problems Final Exam: Wednesday, /6/009 :30PM Mathematica 6.0 Initializations R.) Put x@td = t - and y@td = t -. Sketch on the axes below the curve traced out by 8x@tD,
99ReviewProblemSolutions.nb Review Problems Final Exam: Wednesday, /6/009 :30PM Mathematica 6.0 Initializations R.) Put x@td = t - and y@td = t -. Sketch on the axes below the curve traced out by 8x@tD,
Basic Properties of Rational Expressions
 Basic Properties of Rational Expressions A fraction is not defined when the denominator is zero! Examples: Simplify and use Mathematics Writing Style. a) x + 8 b) x 9 x 3 Solution: a) x + 8 (x + 4) x +
Basic Properties of Rational Expressions A fraction is not defined when the denominator is zero! Examples: Simplify and use Mathematics Writing Style. a) x + 8 b) x 9 x 3 Solution: a) x + 8 (x + 4) x +
Factor Polynomials Completely
 9.8 Factor Polynomials Completely Before You factored polynomials. Now You will factor polynomials completely. Why? So you can model the height of a projectile, as in Ex. 71. Key Vocabulary factor by grouping
9.8 Factor Polynomials Completely Before You factored polynomials. Now You will factor polynomials completely. Why? So you can model the height of a projectile, as in Ex. 71. Key Vocabulary factor by grouping
Math 241, Exam 1 Information.
 Math 241, Exam 1 Information. 9/24/12, LC 310, 11:15-12:05. Exam 1 will be based on: Sections 12.1-12.5, 14.1-14.3. The corresponding assigned homework problems (see http://www.math.sc.edu/ boylan/sccourses/241fa12/241.html)
Math 241, Exam 1 Information. 9/24/12, LC 310, 11:15-12:05. Exam 1 will be based on: Sections 12.1-12.5, 14.1-14.3. The corresponding assigned homework problems (see http://www.math.sc.edu/ boylan/sccourses/241fa12/241.html)
Mathematics Placement
 Mathematics Placement The ACT COMPASS math test is a self-adaptive test, which potentially tests students within four different levels of math including pre-algebra, algebra, college algebra, and trigonometry.
Mathematics Placement The ACT COMPASS math test is a self-adaptive test, which potentially tests students within four different levels of math including pre-algebra, algebra, college algebra, and trigonometry.
Derive 5: The Easiest... Just Got Better!
 Liverpool John Moores University, 1-15 July 000 Derive 5: The Easiest... Just Got Better! Michel Beaudin École de Technologie Supérieure, Canada Email; mbeaudin@seg.etsmtl.ca 1. Introduction Engineering
Liverpool John Moores University, 1-15 July 000 Derive 5: The Easiest... Just Got Better! Michel Beaudin École de Technologie Supérieure, Canada Email; mbeaudin@seg.etsmtl.ca 1. Introduction Engineering
ALGEBRA I (Common Core)
 The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION ALGEBRA I (Common Core) Wednesday, June 17, 2015 1:15 to 4:15 p.m. MODEL RESPONSE SET Table of Contents Question 25..................
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION ALGEBRA I (Common Core) Wednesday, June 17, 2015 1:15 to 4:15 p.m. MODEL RESPONSE SET Table of Contents Question 25..................
Determine whether the following lines intersect, are parallel, or skew. L 1 : x = 6t y = 1 + 9t z = 3t. x = 1 + 2s y = 4 3s z = s
 Homework Solutions 5/20 10.5.17 Determine whether the following lines intersect, are parallel, or skew. L 1 : L 2 : x = 6t y = 1 + 9t z = 3t x = 1 + 2s y = 4 3s z = s A vector parallel to L 1 is 6, 9,
Homework Solutions 5/20 10.5.17 Determine whether the following lines intersect, are parallel, or skew. L 1 : L 2 : x = 6t y = 1 + 9t z = 3t x = 1 + 2s y = 4 3s z = s A vector parallel to L 1 is 6, 9,
Solutions - Homework sections 17.7-17.9
 olutions - Homework sections 7.7-7.9 7.7 6. valuate xy d, where is the triangle with vertices (,, ), (,, ), and (,, ). The three points - and therefore the triangle between them - are on the plane x +
olutions - Homework sections 7.7-7.9 7.7 6. valuate xy d, where is the triangle with vertices (,, ), (,, ), and (,, ). The three points - and therefore the triangle between them - are on the plane x +
FACTORING ax 2 bx c. Factoring Trinomials with Leading Coefficient 1
 5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
Unit 1 Equations, Inequalities, Functions
 Unit 1 Equations, Inequalities, Functions Algebra 2, Pages 1-100 Overview: This unit models real-world situations by using one- and two-variable linear equations. This unit will further expand upon pervious
Unit 1 Equations, Inequalities, Functions Algebra 2, Pages 1-100 Overview: This unit models real-world situations by using one- and two-variable linear equations. This unit will further expand upon pervious
Section 9: Applied Optimization
 Chapter The Derivative Applied Calculus 148 Section 9: Applied Optimization We have used derivatives to help find the maximums and minimums of some functions given by equations, but it is very unlikely
Chapter The Derivative Applied Calculus 148 Section 9: Applied Optimization We have used derivatives to help find the maximums and minimums of some functions given by equations, but it is very unlikely
CAHSEE on Target UC Davis, School and University Partnerships
 UC Davis, School and University Partnerships CAHSEE on Target Mathematics Curriculum Published by The University of California, Davis, School/University Partnerships Program 006 Director Sarah R. Martinez,
UC Davis, School and University Partnerships CAHSEE on Target Mathematics Curriculum Published by The University of California, Davis, School/University Partnerships Program 006 Director Sarah R. Martinez,
Lecture L26-3D Rigid Body Dynamics: The Inertia Tensor
 J. Peraire, S. Widnall 16.07 Dynaics Fall 008 Lecture L6-3D Rigid Body Dynaics: The Inertia Tensor Version.1 In this lecture, we will derive an expression for the angular oentu of a 3D rigid body. We shall
J. Peraire, S. Widnall 16.07 Dynaics Fall 008 Lecture L6-3D Rigid Body Dynaics: The Inertia Tensor Version.1 In this lecture, we will derive an expression for the angular oentu of a 3D rigid body. We shall
SAT Math Facts & Formulas Review Quiz
 Test your knowledge of SAT math facts, formulas, and vocabulary with the following quiz. Some questions are more challenging, just like a few of the questions that you ll encounter on the SAT; these questions
Test your knowledge of SAT math facts, formulas, and vocabulary with the following quiz. Some questions are more challenging, just like a few of the questions that you ll encounter on the SAT; these questions
If Σ is an oriented surface bounded by a curve C, then the orientation of Σ induces an orientation for C, based on the Right-Hand-Rule.
 Oriented Surfaces and Flux Integrals Let be a surface that has a tangent plane at each of its nonboundary points. At such a point on the surface two unit normal vectors exist, and they have opposite directions.
Oriented Surfaces and Flux Integrals Let be a surface that has a tangent plane at each of its nonboundary points. At such a point on the surface two unit normal vectors exist, and they have opposite directions.
Constrained Optimization: The Method of Lagrange Multipliers:
 Constrained Optimization: The Method of Lagrange Multipliers: Suppose the equation p(x,) x 60x 7 00 models profit when x represents the number of handmade chairs and is the number of handmade rockers produced
Constrained Optimization: The Method of Lagrange Multipliers: Suppose the equation p(x,) x 60x 7 00 models profit when x represents the number of handmade chairs and is the number of handmade rockers produced
Lagrange Interpolation is a method of fitting an equation to a set of points that functions well when there are few points given.
 Polynomials (Ch.1) Study Guide by BS, JL, AZ, CC, SH, HL Lagrange Interpolation is a method of fitting an equation to a set of points that functions well when there are few points given. Sasha s method
Polynomials (Ch.1) Study Guide by BS, JL, AZ, CC, SH, HL Lagrange Interpolation is a method of fitting an equation to a set of points that functions well when there are few points given. Sasha s method
Solutions to old Exam 1 problems
 Solutions to old Exam 1 problems Hi students! I am putting this old version of my review for the first midterm review, place and time to be announced. Check for updates on the web site as to which sections
Solutions to old Exam 1 problems Hi students! I am putting this old version of my review for the first midterm review, place and time to be announced. Check for updates on the web site as to which sections
Finding the Measure of Segments Examples
 Finding the Measure of Segments Examples 1. In geometry, the distance between two points is used to define the measure of a segment. Segments can be defined by using the idea of betweenness. In the figure
Finding the Measure of Segments Examples 1. In geometry, the distance between two points is used to define the measure of a segment. Segments can be defined by using the idea of betweenness. In the figure
Prot Maximization and Cost Minimization
 Simon Fraser University Prof. Karaivanov Department of Economics Econ 0 COST MINIMIZATION Prot Maximization and Cost Minimization Remember that the rm's problem is maximizing prots by choosing the optimal
Simon Fraser University Prof. Karaivanov Department of Economics Econ 0 COST MINIMIZATION Prot Maximization and Cost Minimization Remember that the rm's problem is maximizing prots by choosing the optimal
5 Systems of Equations
 Systems of Equations Concepts: Solutions to Systems of Equations-Graphically and Algebraically Solving Systems - Substitution Method Solving Systems - Elimination Method Using -Dimensional Graphs to Approximate
Systems of Equations Concepts: Solutions to Systems of Equations-Graphically and Algebraically Solving Systems - Substitution Method Solving Systems - Elimination Method Using -Dimensional Graphs to Approximate
Two vectors are equal if they have the same length and direction. They do not
 Vectors define vectors Some physical quantities, such as temperature, length, and mass, can be specified by a single number called a scalar. Other physical quantities, such as force and velocity, must
Vectors define vectors Some physical quantities, such as temperature, length, and mass, can be specified by a single number called a scalar. Other physical quantities, such as force and velocity, must
2.3. Finding polynomial functions. An Introduction:
 2.3. Finding polynomial functions. An Introduction: As is usually the case when learning a new concept in mathematics, the new concept is the reverse of the previous one. Remember how you first learned
2.3. Finding polynomial functions. An Introduction: As is usually the case when learning a new concept in mathematics, the new concept is the reverse of the previous one. Remember how you first learned
The Fourth International DERIVE-TI92/89 Conference Liverpool, U.K., 12-15 July 2000. Derive 5: The Easiest... Just Got Better!
 The Fourth International DERIVE-TI9/89 Conference Liverpool, U.K., -5 July 000 Derive 5: The Easiest... Just Got Better! Michel Beaudin École de technologie supérieure 00, rue Notre-Dame Ouest Montréal
The Fourth International DERIVE-TI9/89 Conference Liverpool, U.K., -5 July 000 Derive 5: The Easiest... Just Got Better! Michel Beaudin École de technologie supérieure 00, rue Notre-Dame Ouest Montréal
~ EQUIVALENT FORMS ~
 ~ EQUIVALENT FORMS ~ Critical to understanding mathematics is the concept of equivalent forms. Equivalent forms are used throughout this course. Throughout mathematics one encounters equivalent forms of
~ EQUIVALENT FORMS ~ Critical to understanding mathematics is the concept of equivalent forms. Equivalent forms are used throughout this course. Throughout mathematics one encounters equivalent forms of
Factoring Polynomials
 UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
Click on the links below to jump directly to the relevant section
 Click on the links below to jump directly to the relevant section What is algebra? Operations with algebraic terms Mathematical properties of real numbers Order of operations What is Algebra? Algebra is
Click on the links below to jump directly to the relevant section What is algebra? Operations with algebraic terms Mathematical properties of real numbers Order of operations What is Algebra? Algebra is
1.1 Practice Worksheet
 Math 1 MPS Instructor: Cheryl Jaeger Balm 1 1.1 Practice Worksheet 1. Write each English phrase as a mathematical expression. (a) Three less than twice a number (b) Four more than half of a number (c)
Math 1 MPS Instructor: Cheryl Jaeger Balm 1 1.1 Practice Worksheet 1. Write each English phrase as a mathematical expression. (a) Three less than twice a number (b) Four more than half of a number (c)
REVIEW EXERCISES DAVID J LOWRY
 REVIEW EXERCISES DAVID J LOWRY Contents 1. Introduction 1 2. Elementary Functions 1 2.1. Factoring and Solving Quadratics 1 2.2. Polynomial Inequalities 3 2.3. Rational Functions 4 2.4. Exponentials and
REVIEW EXERCISES DAVID J LOWRY Contents 1. Introduction 1 2. Elementary Functions 1 2.1. Factoring and Solving Quadratics 1 2.2. Polynomial Inequalities 3 2.3. Rational Functions 4 2.4. Exponentials and
Increasing for all. Convex for all. ( ) Increasing for all (remember that the log function is only defined for ). ( ) Concave for all.
 1. Differentiation The first derivative of a function measures by how much changes in reaction to an infinitesimal shift in its argument. The largest the derivative (in absolute value), the faster is evolving.
1. Differentiation The first derivative of a function measures by how much changes in reaction to an infinitesimal shift in its argument. The largest the derivative (in absolute value), the faster is evolving.
Line and surface integrals: Solutions
 hapter 5 Line and surface integrals: olutions Example 5.1 Find the work done by the force F(x, y) x 2 i xyj in moving a particle along the curve which runs from (1, ) to (, 1) along the unit circle and
hapter 5 Line and surface integrals: olutions Example 5.1 Find the work done by the force F(x, y) x 2 i xyj in moving a particle along the curve which runs from (1, ) to (, 1) along the unit circle and
Simplify the rational expression. Find all numbers that must be excluded from the domain of the simplified rational expression.
 MAC 1105 Final Review Simplify the rational expression. Find all numbers that must be excluded from the domain of the simplified rational expression. 1) 8x 2-49x + 6 x - 6 A) 1, x 6 B) 8x - 1, x 6 x -
MAC 1105 Final Review Simplify the rational expression. Find all numbers that must be excluded from the domain of the simplified rational expression. 1) 8x 2-49x + 6 x - 6 A) 1, x 6 B) 8x - 1, x 6 x -
Polynomials. Key Terms. quadratic equation parabola conjugates trinomial. polynomial coefficient degree monomial binomial GCF
 Polynomials 5 5.1 Addition and Subtraction of Polynomials and Polynomial Functions 5.2 Multiplication of Polynomials 5.3 Division of Polynomials Problem Recognition Exercises Operations on Polynomials
Polynomials 5 5.1 Addition and Subtraction of Polynomials and Polynomial Functions 5.2 Multiplication of Polynomials 5.3 Division of Polynomials Problem Recognition Exercises Operations on Polynomials
How To Solve Factoring Problems
 05-W4801-AM1.qxd 8/19/08 8:45 PM Page 241 Factoring, Solving Equations, and Problem Solving 5 5.1 Factoring by Using the Distributive Property 5.2 Factoring the Difference of Two Squares 5.3 Factoring
05-W4801-AM1.qxd 8/19/08 8:45 PM Page 241 Factoring, Solving Equations, and Problem Solving 5 5.1 Factoring by Using the Distributive Property 5.2 Factoring the Difference of Two Squares 5.3 Factoring
3. Solve the equation containing only one variable for that variable.
 Question : How do you solve a system of linear equations? There are two basic strategies for solving a system of two linear equations and two variables. In each strategy, one of the variables is eliminated
Question : How do you solve a system of linear equations? There are two basic strategies for solving a system of two linear equations and two variables. In each strategy, one of the variables is eliminated
0.8 Rational Expressions and Equations
 96 Prerequisites 0.8 Rational Expressions and Equations We now turn our attention to rational expressions - that is, algebraic fractions - and equations which contain them. The reader is encouraged to
96 Prerequisites 0.8 Rational Expressions and Equations We now turn our attention to rational expressions - that is, algebraic fractions - and equations which contain them. The reader is encouraged to
5 Double Integrals over Rectangular Regions
 Chapter 7 Section 5 Doule Integrals over Rectangular Regions 569 5 Doule Integrals over Rectangular Regions In Prolems 5 through 53, use the method of Lagrange multipliers to find the indicated maximum
Chapter 7 Section 5 Doule Integrals over Rectangular Regions 569 5 Doule Integrals over Rectangular Regions In Prolems 5 through 53, use the method of Lagrange multipliers to find the indicated maximum
Factoring Trinomials of the Form x 2 bx c
 4.2 Factoring Trinomials of the Form x 2 bx c 4.2 OBJECTIVES 1. Factor a trinomial of the form x 2 bx c 2. Factor a trinomial containing a common factor NOTE The process used to factor here is frequently
4.2 Factoring Trinomials of the Form x 2 bx c 4.2 OBJECTIVES 1. Factor a trinomial of the form x 2 bx c 2. Factor a trinomial containing a common factor NOTE The process used to factor here is frequently
Negative Integer Exponents
 7.7 Negative Integer Exponents 7.7 OBJECTIVES. Define the zero exponent 2. Use the definition of a negative exponent to simplify an expression 3. Use the properties of exponents to simplify expressions
7.7 Negative Integer Exponents 7.7 OBJECTIVES. Define the zero exponent 2. Use the definition of a negative exponent to simplify an expression 3. Use the properties of exponents to simplify expressions
FACTORING POLYNOMIALS
 296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
Understanding Basic Calculus
 Understanding Basic Calculus S.K. Chung Dedicated to all the people who have helped me in my life. i Preface This book is a revised and expanded version of the lecture notes for Basic Calculus and other
Understanding Basic Calculus S.K. Chung Dedicated to all the people who have helped me in my life. i Preface This book is a revised and expanded version of the lecture notes for Basic Calculus and other
https://williamshartunionca.springboardonline.org/ebook/book/27e8f1b87a1c4555a1212b...
 of 19 9/2/2014 12:09 PM Answers Teacher Copy Plan Pacing: 1 class period Chunking the Lesson Example A #1 Example B Example C #2 Check Your Understanding Lesson Practice Teach Bell-Ringer Activity Students
of 19 9/2/2014 12:09 PM Answers Teacher Copy Plan Pacing: 1 class period Chunking the Lesson Example A #1 Example B Example C #2 Check Your Understanding Lesson Practice Teach Bell-Ringer Activity Students
Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder).
 Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Math 432 HW 2.5 Solutions
 Math 432 HW 2.5 Solutions Assigned: 1-10, 12, 13, and 14. Selected for Grading: 1 (for five points), 6 (also for five), 9, 12 Solutions: 1. (2y 3 + 2y 2 ) dx + (3y 2 x + 2xy) dy = 0. M/ y = 6y 2 + 4y N/
Math 432 HW 2.5 Solutions Assigned: 1-10, 12, 13, and 14. Selected for Grading: 1 (for five points), 6 (also for five), 9, 12 Solutions: 1. (2y 3 + 2y 2 ) dx + (3y 2 x + 2xy) dy = 0. M/ y = 6y 2 + 4y N/
Recognizing Types of First Order Differential Equations E. L. Lady
 Recognizing Types of First Order Differential Equations E. L. Lady Every first order differential equation to be considered here can be written can be written in the form P (x, y)+q(x, y)y =0. This means
Recognizing Types of First Order Differential Equations E. L. Lady Every first order differential equation to be considered here can be written can be written in the form P (x, y)+q(x, y)y =0. This means
Math Review. for the Quantitative Reasoning Measure of the GRE revised General Test
 Math Review for the Quantitative Reasoning Measure of the GRE revised General Test www.ets.org Overview This Math Review will familiarize you with the mathematical skills and concepts that are important
Math Review for the Quantitative Reasoning Measure of the GRE revised General Test www.ets.org Overview This Math Review will familiarize you with the mathematical skills and concepts that are important
CNC Applications. Introduction to Machining Centers
 CNC Applications Introduction to Machining Centers Machining Centers A machining center is simply a CNC milling machine with an automatic tool changer and an enclosure. There are a number of different
CNC Applications Introduction to Machining Centers Machining Centers A machining center is simply a CNC milling machine with an automatic tool changer and an enclosure. There are a number of different
The Theory and Practice of Using a Sine Bar, version 2
 The Theory and Practice of Using a Sine Bar, version 2 By R. G. Sparber Copyleft protects this document. 1 The Quick Answer If you just want to set an angle with a sine bar and stack of blocks, then take
The Theory and Practice of Using a Sine Bar, version 2 By R. G. Sparber Copyleft protects this document. 1 The Quick Answer If you just want to set an angle with a sine bar and stack of blocks, then take
8 Polynomials Worksheet
 8 Polynomials Worksheet Concepts: Quadratic Functions The Definition of a Quadratic Function Graphs of Quadratic Functions - Parabolas Vertex Absolute Maximum or Absolute Minimum Transforming the Graph
8 Polynomials Worksheet Concepts: Quadratic Functions The Definition of a Quadratic Function Graphs of Quadratic Functions - Parabolas Vertex Absolute Maximum or Absolute Minimum Transforming the Graph
SPECIAL PRODUCTS AND FACTORS
 CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
Chapter 7 - Roots, Radicals, and Complex Numbers
 Math 233 - Spring 2009 Chapter 7 - Roots, Radicals, and Complex Numbers 7.1 Roots and Radicals 7.1.1 Notation and Terminology In the expression x the is called the radical sign. The expression under the
Math 233 - Spring 2009 Chapter 7 - Roots, Radicals, and Complex Numbers 7.1 Roots and Radicals 7.1.1 Notation and Terminology In the expression x the is called the radical sign. The expression under the
