Factoring ax 2 + bx + c - Teacher Notes
|
|
|
- Arline McLaughlin
- 8 years ago
- Views:
Transcription
1 Southern Nevada Regional Professi onal D evel opment Program VOLUME 1, ISSUE 8 MAY 009 A N ewsletter from the Sec ondary Mathematic s Team Factoring ax + bx + c - Teacher Notes Here we look at sample teacher notes to develop instruction on how to factor the dreaded quadratic expression or equation after having taught multiplication of binomials. Sometimes this method is referred to as splitting the middle term. Teachers should supplement with more examples as needed. Page 4 provides additional practice examples. Page 5 gives lyrics for a rap, song, or poem to learn the ac method. Pages 6-8 of this newsletter provide background for the X-Games that can be used to reinforce the concept of looking for factors of a number that add to another number when working with quadratics in the form x + bx + c. OR x(+3) allows us to com- Do you remember when we introduced the distributive property? We may have explained that x + 3x could be written as 5x, because (+3)x bine like terms (in this case constants), and 3. Math Resources And, in the reverse order, that 5x could also be written as x+3x. It didn t seem like earth-shattering news for such simple examples, but sometimes students missed the concept completely. Maybe because it was too easy. Later, we used the distributive property for factoring. For example, x + x became x(x+), 6x+1 factored to 6(x+), 3x+6 to 3(x ), and so on. It s interesting that one of the first steps we teach in factoring is to check for common factors, but that step often gets missed by students when we teach factoring quadratics Example 1: x + x + 3x + 6 x + x + 3x + 6 can be grouped, (x + x) + (3x + 6) and then factored using the distributive property on each piece, as x(x+) + 3(x+). Hopefully we notice that there is still a common factor, (x+) that can be factored out. In this issue: Factoring quadratics 1-3 Practice examples... 4 Factor Rap... 5 X-games... 6 Patterns - Multiply... 7 Patterns - Factor... 8 So, x + x + 3x + 6 = (x + x) + (3x + 6) = = x(x+) + 3(x+) OR (x+3)(x+). Example : x + 3x + 4x + 1 Review the patterns to combine the like terms or write them differently. The middle term 7x can be split into two terms. This reinforces the link with the inverse operation of adding or combining like terms. We then factor by grouping. Yes, teachers ALWAYS do problems showing how to combine like terms, but do we develop possible ways to combine terms to achieve a given sum and product? x + 3x + 4x + 1 can be written as x + 7x + 1; AND x + 7x + 1 can be written in place of x + 3x + 4x Example 3: x + 5x + 4x + 0 Notice that this example is written as x + 5x + 4x + 0 instead of x + 9x + 0. Why do this? We know that when we teach factoring and it is seen as x + 9x + 0, we ALWAYS say, we are looking for factors of 0 whose sum is 9. Then we often jump to trial and error and list binomial factors (x + )(x + ). Maybe we list all factors and try 1 and 0, or and 10, or 4 and 5. If we are lucky enough to choose 5 and 4, we place them in the parentheses in the correct place and check by multiplying the binomials. We see with multiplication that (x + 5 )(x + 4 ) = x + 5x + 4x + 0 and simplify or combine like terms to get x + 9x + 0. It s pretty interesting that when the correct factors are chosen AND written into the expression as x + 5x + 4x + 0, the middle term has been split into two parts that add to 9x and the coefficients multiply to 0. Now, to finish the example, x + 5x + 4x + 0 is grouped as underlined, or placed in parentheses (x + 5x) + (4x + 0), then factored using the distributive property again, x(x+5) + 4(x+5). AND, factoring out the common factor (x+5) we get (x+5)(x+4). Yeh!!!
2 Page Factoring ax + bx + c - Teacher Notes continued What about the student who mixes up the 4 and the 5 and writes x + 4x + 5x + 0? This results in x(x+4) + 5(x+4), then, finally the same two factors, (x+4)(x+5). Interesting, huh? Will this always work? When you can split the middle term in such a way that the product of the two like term coefficients is the last term (constant), the trinomial IS factorable. What s more, if the middle term can not be split it in such a way that the product of the two like term coefficients is the last term (constant), the trinomial is NOT factorable. (This also works for difference of squares.) Examples 4 7: These examples show importance of signs. x + 8x +1 x x 1 x + 10x 4 x 10x +4 x + 6x +x +1 x +3x 4x -1 x + 1x x 4 x 6x 4x +4 Yes, students can often just do it, but keep following the connections to see patterns and practice the skill development. Try factoring each of these examples. Be careful with the signs. Example 8: x + 11x +1 OR ax + bx + c How about x + 11x +1? What s different? Let s look at the method sometimes referred to as the ac method, which is just an extension of the method describe above, splitting the middle term. Looking back at the simple examples, when a = 1, we factored c. Everyone knows that ac=c, when a=1. After identifying a and c we multiply a times c. Now we factor ac, or in this case (1) or 4, and look for factors of 4 that add to 11. It is easy to show that = 11, so 3x + 8x = 11x. We can write x + 11x +1 as x + 3x + 8x +1, then group (associate) x + 3x + 8x +1. Factor each group x(x+3) + 4(x+3) by factoring out the common factor (x+3). The factors are (x+4)(x+3). So, x + 11x +1 = (x+4)(x+3). Check by FOIL and multiplication of means-extremes. More examples? Variations? Example 9: 1x - 11x -15 a ( c) = 1 ( 15) = 180 Factors of 180 that differ by & 0, specifically 9 and 0 So, 1x 11x 15 can be written as 1x 0x + 9x 15 OR 1x + 9x 0x 15. Take your pick! Group 1x 0x + 9x 15 OR 1x + 9x 0x 15 (1x 0x) + (9x 15) (1x + 9x) + ( 0x +15) 4x(3x 5) + 3(3x 5) 3x(4x+3) 5(4x+3) (4x+3)(3x 5) OR (3x 5)(4x+3) Therefore, 1x 11x -15 = (4x+3)(3x 5). Check by multiplication. Let s try another example with a slight variation. Example 10: 4x + 4x 4 Note that there is a common factor that could/should be factored out of each term first. 4x + 4x 4 can be written as 4(x + x 6), and it fits into our plan for factoring without the big numbers. Keep the 4 as a factor. Then, splitting the middle term, since +x = 3x x, 4[x + 3x x 6] which, when grouped looks like 4[(x + 3x) (x + 6)] and 4[x(x + 3) (x + 3)]. So 4x + 4x 4 = 4[(x + 3) (x )]
3 Page 3 Factoring ax + bx + c - Teacher Notes continued Example 11: 6x + x 0 Again, there is a common factor, so it becomes (3x + x 10). Use a = 3 and c = 10, ac = 3 ( 10) = 30 and we keep the factor throughout the problem. Factors of 30 that combine to & 6, because ( = 1) So, (3x + x 10) can be written as (3x + 6x 5x 10) OR (3x 5x + 6x 10). Take your pick! Group (3x + 6x 5x 10) OR (3x 5x + 6x 10) And factor out the common factors [3x(x+) 5(x + )] [x(3x 5) + (3x 5)] So, 6x + x 0 = (3x 5)(x + ) OR (x + )(3x 5) Can it be used to identify trinomials that do not factor? Example 1: Does 3x 0x + 7 factor? ac = 3(7) = +1 Factors of +1 are 1, 1; 1, 1; 3, 7; or 3, 7 Since factors must be the same sign to give a product of positive 1, there are no factors of 1 with the same sign that combine to be 0. Therefore, 3x 0x + 7 is not factorable. (You might show that 3x 0x 7 is factorable. Why?) How about difference of squares? Trinomial squares? Example 13: x 64. Same plan: factor 64 so the factors combine to 0. (8 and 8) It is easily shown that x + 8x 8x 64 factors to x(x+8) 8(x+8) and then (x 8)(x+8). x 64 = (x 8)(x+8) Summary: The connections and linkage to previous instruction are numerous. Throughout this technique, teachers can refer to concepts such as factoring integers, distributive property and factoring, sum of factors, and product of factors. The method has benefits that link writing math expressions for the words we use to teach factoring - factors that multiply to be the constant and combine to the middle term. The method may save time from trial and error; it finds use/practice for the distributive property that is important in future math applications; it stresses the connection to sum and product of roots, listing factors in a factor tree, and it aids in determining if a trinomial is factorable. There are also links to factoring with multiplying the means and extremes of binomials to get the middle term. Factoring quadratics in the form x + bx + c can be accomplished by a method referred to as splitting the middle term. This method can also be extended for quadratics in the form ax + bx + c by using the ac method. The algorithm for the ac method is as follows: 1. Form the product ac.. Find a pair of numbers b 1 and b whose product is also ac and whose sum is b (if such integers don t exist, it can t be factored using rational numbers). 3. Split the middle term using b 1 and b ; that is, express the term bx as b 1 x + b x. 4. Now you have 4 terms and you will be factoring by grouping pairs of terms. 5. Factor out the common factor in each pair of terms. The common factor at this point should be a binomial. Check by multiplying. Notice the means-extremes products should be your split.
4 Page 4 Factoring ax + bx + c - Example Problems ExampleProblems Use split the middle term or ac method Factor each example, if possible! Write not-factorable if it can t be factored. 1 x 5x x 10 x 7x 6 3 x 8x x 4x 5 10x 13x 3 6 8x 1x 3 7 x x 15 8 x 1x 36 Fill in the blank with a number that makes the trinomial factorable. How many ways can it be done? 9 x 11x x x x 11x 4 0 Be careful 13 8x x x 9x 1 0 Be careful
5 Page 5 The Factor Rap Example The Factor Rap (song, poem, ditty ) ax bx c First line: said enthusiastically. x 11x 1 I use * *3 because x 8x 3x To factor quadratic trinomials, find a times c Then factor out the product so the sum is b We write the thing again so the middle term is split (x 8 x) (3x 1) Then we pair the terms we see to make groups out of it x( x 4) 3( x 4) Factor common factors with distributive property (x 3)( x 4) Now we do the same again.. It s as easy as can be. Finale... But wait, if the sum of the factors can never equal b The trinomial doesn t factor, it s as easy as can be!
6 Page 6 This activity can be used from the beginning of the school year to get students more familiar and comfortable with patterns. It provides very good practice to review material you want to make sure students remember or to preview something they will see later on. It should be a short (time) activity that stimulates student engagement. X-Games show patterns for multiplying, then extend the patterns to factoring and looking for specific factors. Getting started: Begin by drawing an X on the board. Refer to the openings as top, bottom, right, and left. Write numbers in the right and left and ask students to guess what goes in top and bottom. To teach the game, place the sum of right and left in the top opening. The bottom will be the product of right and left. Although it is not critical whether the product is placed in the top or bottom of the X, it is important to maintain consistency throughout the year. However, you need not tell the students these rules. In the beginning you want them to feel free to guess and not to feel like they are expected to know the right answers. Try to find a positive way to respond to each wrong answer. Provide examples and give hints, as needed, until students come up with the right answers. Write those answers in the appropriate places. Some students will begin to see the pattern very quickly. Once the students seem to have discovered the pattern, have a student explain it to the class. Then start varying the given information by filling in top and right, bottom and left, top and bottom, etc. Also, now that students know the pattern, you can also start using negatives, decimals, fractions, variable expressions, or any other expressions that you want to review or preview in a non-threatening, fun way. As a variation, you may also decide to change the way the top and bottom numbers are determined. For example, top might be the result of squaring the number in the left and adding the right number, while bottom might be found by doubling the number in the left and adding the right number. This would demonstrate contrast between squaring and doubling Example: There is a special pattern for multiplying and/or factoring trinomials. For example, to multiply (x+3)(x+4) put the 3 in the right (or left) and the 4 in the left (or right). Then fill in the top and bottom. The top will be the sum and bottom will be the product. The product would be pulled from the X as (x+3)(x+4) The product is x + 7x + 1. X-Games, X-Patterns, X-Factors, Diamonds To factor x + 7x + 1, do the reverse. That is, put the 7 at top, 1 at bottom, then find the two numbers whose sum is 7 and whose product is 1. You get (x+3)(x+4). Again, the X-Games can be used for other math practice. Practice using the X concept with fractions, integers, radicals, absolute value, opposites, factorials, squares, cubes, double and add, and vocabulary. 3 sum 7 1 product 4
7 Page 7 X-Games, X-Patterns, X-Factors, Diamonds - for x + bx + c [Same signs] (x + )(x + 3) = (x 4)(x 5) = Patterns for Multiplying Binomials (x 6)(x ) = [Different signs] (x )(x + 3) = (x + 4)(x 5) = (x 6)(x + ) = [Conjugates] (x + 4)(x 4) = (x + 6)(x 6) = (x 5)(x + 5) = [Binomial squared] (x + 3) = (x 4) = (x + 7) = You can get through a lot of examples quickly with the X-Factor. The pattern is adding to get the middle term and multiplying to get the last term, every time. Note: This is not to replace instruction, just to provide quick mental connections. ALWAYS bring them back to the actual multiplication methods utilizing the distributive property. Now: What if we UNDO the multiplication process (factor)? NEXT: It is interesting to note that (x + )(x + 3) =x + x + 3x + 6 = x + 5x + 6 Notice that, going backwards, 5x is split up into x + 3x Does this always work for these kinds of problems?
8 Page 8 X-Games, X-Patterns, X-Factors, Diamonds - for x + bx + c [Same signs] (x + )(x + ) = Patterns for Factoring Trinomials x + 5x +6 x 9x +0 x 8x +1 (x )(x ) = (x )(x ) = [Different signs] (x )(x + ) = (x + )(x ) = x + x 6 x x 0 x 4x (x )(x ) = [Conjugates] (x + )(x ) = x 16 x 36 x 5 (x )(x + ) = (x )(x ) = [Binomial squared] (x + ) = x + 6x +9 x 8x +16 x + 14x +49 (x - ) = (x ) = After the pattern is well developed, discuss with students what they could use for the other three numbers if only the top number was provided. You can get through a lot of examples quickly with the X-Factor. The pattern is figuring out what to add to get the middle term and also multiply to get the last term. Note: This is not to replace instruction, just to provide quick mental connections. ALWAYS bring them back to the actual multiplication methods utilizing the distributive property and the inverse of factoring.
NSM100 Introduction to Algebra Chapter 5 Notes Factoring
 Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
expression is written horizontally. The Last terms ((2)( 4)) because they are the last terms of the two polynomials. This is called the FOIL method.
 A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
Factoring Trinomials: The ac Method
 6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
Section 6.1 Factoring Expressions
 Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
Factoring and Applications
 Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
1.3 Algebraic Expressions
 1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
MATH 90 CHAPTER 6 Name:.
 MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
Factoring Quadratic Expressions
 Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
In algebra, factor by rewriting a polynomial as a product of lower-degree polynomials
 Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
FACTORING ax 2 bx c. Factoring Trinomials with Leading Coefficient 1
 5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
Factoring Flow Chart
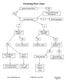 Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
SOLVING QUADRATIC EQUATIONS BY THE NEW TRANSFORMING METHOD (By Nghi H Nguyen Updated Oct 28, 2014))
 SOLVING QUADRATIC EQUATIONS BY THE NEW TRANSFORMING METHOD (By Nghi H Nguyen Updated Oct 28, 2014)) There are so far 8 most common methods to solve quadratic equations in standard form ax² + bx + c = 0.
SOLVING QUADRATIC EQUATIONS BY THE NEW TRANSFORMING METHOD (By Nghi H Nguyen Updated Oct 28, 2014)) There are so far 8 most common methods to solve quadratic equations in standard form ax² + bx + c = 0.
Using the ac Method to Factor
 4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any.
 Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
Chapter R.4 Factoring Polynomials
 Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
Factoring A Quadratic Polynomial
 Factoring A Quadratic Polynomial If we multiply two binomials together, the result is a quadratic polynomial: This multiplication is pretty straightforward, using the distributive property of multiplication
Factoring A Quadratic Polynomial If we multiply two binomials together, the result is a quadratic polynomial: This multiplication is pretty straightforward, using the distributive property of multiplication
A. Factoring out the Greatest Common Factor.
 DETAILED SOLUTIONS AND CONCEPTS - FACTORING POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to ingrid.stewart@csn.edu. Thank you!
DETAILED SOLUTIONS AND CONCEPTS - FACTORING POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to ingrid.stewart@csn.edu. Thank you!
Factoring Guidelines. Greatest Common Factor Two Terms Three Terms Four Terms. 2008 Shirley Radai
 Factoring Guidelines Greatest Common Factor Two Terms Three Terms Four Terms 008 Shirley Radai Greatest Common Factor 008 Shirley Radai Factoring by Finding the Greatest Common Factor Always check for
Factoring Guidelines Greatest Common Factor Two Terms Three Terms Four Terms 008 Shirley Radai Greatest Common Factor 008 Shirley Radai Factoring by Finding the Greatest Common Factor Always check for
FACTORING QUADRATICS 8.1.1 and 8.1.2
 FACTORING QUADRATICS 8.1.1 and 8.1.2 Chapter 8 introduces students to quadratic equations. These equations can be written in the form of y = ax 2 + bx + c and, when graphed, produce a curve called a parabola.
FACTORING QUADRATICS 8.1.1 and 8.1.2 Chapter 8 introduces students to quadratic equations. These equations can be written in the form of y = ax 2 + bx + c and, when graphed, produce a curve called a parabola.
SOLVING QUADRATIC EQUATIONS - COMPARE THE FACTORING ac METHOD AND THE NEW DIAGONAL SUM METHOD By Nghi H. Nguyen
 SOLVING QUADRATIC EQUATIONS - COMPARE THE FACTORING ac METHOD AND THE NEW DIAGONAL SUM METHOD By Nghi H. Nguyen A. GENERALITIES. When a given quadratic equation can be factored, there are 2 best methods
SOLVING QUADRATIC EQUATIONS - COMPARE THE FACTORING ac METHOD AND THE NEW DIAGONAL SUM METHOD By Nghi H. Nguyen A. GENERALITIES. When a given quadratic equation can be factored, there are 2 best methods
Factoring Polynomials and Solving Quadratic Equations
 Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
Factoring. Factoring Monomials Monomials can often be factored in more than one way.
 Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
Math 25 Activity 6: Factoring Advanced
 Instructor! Math 25 Activity 6: Factoring Advanced Last week we looked at greatest common factors and the basics of factoring out the GCF. In this second activity, we will discuss factoring more difficult
Instructor! Math 25 Activity 6: Factoring Advanced Last week we looked at greatest common factors and the basics of factoring out the GCF. In this second activity, we will discuss factoring more difficult
Factoring Polynomials
 Factoring Polynomials Factoring Factoring is the process of writing a polynomial as the product of two or more polynomials. The factors of 6x 2 x 2 are 2x + 1 and 3x 2. In this section, we will be factoring
Factoring Polynomials Factoring Factoring is the process of writing a polynomial as the product of two or more polynomials. The factors of 6x 2 x 2 are 2x + 1 and 3x 2. In this section, we will be factoring
By reversing the rules for multiplication of binomials from Section 4.6, we get rules for factoring polynomials in certain forms.
 SECTION 5.4 Special Factoring Techniques 317 5.4 Special Factoring Techniques OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor
SECTION 5.4 Special Factoring Techniques 317 5.4 Special Factoring Techniques OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor
In this section, you will develop a method to change a quadratic equation written as a sum into its product form (also called its factored form).
 CHAPTER 8 In Chapter 4, you used a web to organize the connections you found between each of the different representations of lines. These connections enabled you to use any representation (such as a graph,
CHAPTER 8 In Chapter 4, you used a web to organize the connections you found between each of the different representations of lines. These connections enabled you to use any representation (such as a graph,
FOIL FACTORING. Factoring is merely undoing the FOIL method. Let s look at an example: Take the polynomial x²+4x+4.
 FOIL FACTORING Factoring is merely undoing the FOIL method. Let s look at an example: Take the polynomial x²+4x+4. First we take the 3 rd term (in this case 4) and find the factors of it. 4=1x4 4=2x2 Now
FOIL FACTORING Factoring is merely undoing the FOIL method. Let s look at an example: Take the polynomial x²+4x+4. First we take the 3 rd term (in this case 4) and find the factors of it. 4=1x4 4=2x2 Now
( ) FACTORING. x In this polynomial the only variable in common to all is x.
 FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
CAHSEE on Target UC Davis, School and University Partnerships
 UC Davis, School and University Partnerships CAHSEE on Target Mathematics Curriculum Published by The University of California, Davis, School/University Partnerships Program 006 Director Sarah R. Martinez,
UC Davis, School and University Partnerships CAHSEE on Target Mathematics Curriculum Published by The University of California, Davis, School/University Partnerships Program 006 Director Sarah R. Martinez,
1.3 Polynomials and Factoring
 1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
Tool 1. Greatest Common Factor (GCF)
 Chapter 4: Factoring Review Tool 1 Greatest Common Factor (GCF) This is a very important tool. You must try to factor out the GCF first in every problem. Some problems do not have a GCF but many do. When
Chapter 4: Factoring Review Tool 1 Greatest Common Factor (GCF) This is a very important tool. You must try to factor out the GCF first in every problem. Some problems do not have a GCF but many do. When
FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c
 Tallahassee Community College 55 FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c This kind of trinomial differs from the previous kind we have factored because the coefficient of x is no longer "1".
Tallahassee Community College 55 FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c This kind of trinomial differs from the previous kind we have factored because the coefficient of x is no longer "1".
SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS
 (Section 0.6: Polynomial, Rational, and Algebraic Expressions) 0.6.1 SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS LEARNING OBJECTIVES Be able to identify polynomial, rational, and algebraic
(Section 0.6: Polynomial, Rational, and Algebraic Expressions) 0.6.1 SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS LEARNING OBJECTIVES Be able to identify polynomial, rational, and algebraic
AIP Factoring Practice/Help
 The following pages include many problems to practice factoring skills. There are also several activities with examples to help you with factoring if you feel like you are not proficient with it. There
The following pages include many problems to practice factoring skills. There are also several activities with examples to help you with factoring if you feel like you are not proficient with it. There
Math 0980 Chapter Objectives. Chapter 1: Introduction to Algebra: The Integers.
 Math 0980 Chapter Objectives Chapter 1: Introduction to Algebra: The Integers. 1. Identify the place value of a digit. 2. Write a number in words or digits. 3. Write positive and negative numbers used
Math 0980 Chapter Objectives Chapter 1: Introduction to Algebra: The Integers. 1. Identify the place value of a digit. 2. Write a number in words or digits. 3. Write positive and negative numbers used
A Quick Algebra Review
 1. Simplifying Epressions. Solving Equations 3. Problem Solving 4. Inequalities 5. Absolute Values 6. Linear Equations 7. Systems of Equations 8. Laws of Eponents 9. Quadratics 10. Rationals 11. Radicals
1. Simplifying Epressions. Solving Equations 3. Problem Solving 4. Inequalities 5. Absolute Values 6. Linear Equations 7. Systems of Equations 8. Laws of Eponents 9. Quadratics 10. Rationals 11. Radicals
SOLVING QUADRATIC EQUATIONS - COMPARE THE FACTORING AC METHOD AND THE NEW TRANSFORMING METHOD (By Nghi H. Nguyen - Jan 18, 2015)
 SOLVING QUADRATIC EQUATIONS - COMPARE THE FACTORING AC METHOD AND THE NEW TRANSFORMING METHOD (By Nghi H. Nguyen - Jan 18, 2015) GENERALITIES. When a given quadratic equation can be factored, there are
SOLVING QUADRATIC EQUATIONS - COMPARE THE FACTORING AC METHOD AND THE NEW TRANSFORMING METHOD (By Nghi H. Nguyen - Jan 18, 2015) GENERALITIES. When a given quadratic equation can be factored, there are
Name Intro to Algebra 2. Unit 1: Polynomials and Factoring
 Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
Greatest Common Factor (GCF) Factoring
 Section 4 4: Greatest Common Factor (GCF) Factoring The last chapter introduced the distributive process. The distributive process takes a product of a monomial and a polynomial and changes the multiplication
Section 4 4: Greatest Common Factor (GCF) Factoring The last chapter introduced the distributive process. The distributive process takes a product of a monomial and a polynomial and changes the multiplication
Polynomials and Factoring. Unit Lesson Plan
 Polynomials and Factoring Unit Lesson Plan By: David Harris University of North Carolina Chapel Hill Math 410 Dr. Thomas, M D. 2 Abstract This paper will discuss, and give, lesson plans for all the topics
Polynomials and Factoring Unit Lesson Plan By: David Harris University of North Carolina Chapel Hill Math 410 Dr. Thomas, M D. 2 Abstract This paper will discuss, and give, lesson plans for all the topics
Factoring Polynomials
 Factoring a Polynomial Expression Factoring a polynomial is expressing the polynomial as a product of two or more factors. Simply stated, it is somewhat the reverse process of multiplying. To factor polynomials,
Factoring a Polynomial Expression Factoring a polynomial is expressing the polynomial as a product of two or more factors. Simply stated, it is somewhat the reverse process of multiplying. To factor polynomials,
A Concrete Introduction. to the Abstract Concepts. of Integers and Algebra using Algebra Tiles
 A Concrete Introduction to the Abstract Concepts of Integers and Algebra using Algebra Tiles Table of Contents Introduction... 1 page Integers 1: Introduction to Integers... 3 2: Working with Algebra Tiles...
A Concrete Introduction to the Abstract Concepts of Integers and Algebra using Algebra Tiles Table of Contents Introduction... 1 page Integers 1: Introduction to Integers... 3 2: Working with Algebra Tiles...
HIBBING COMMUNITY COLLEGE COURSE OUTLINE
 HIBBING COMMUNITY COLLEGE COURSE OUTLINE COURSE NUMBER & TITLE: - Beginning Algebra CREDITS: 4 (Lec 4 / Lab 0) PREREQUISITES: MATH 0920: Fundamental Mathematics with a grade of C or better, Placement Exam,
HIBBING COMMUNITY COLLEGE COURSE OUTLINE COURSE NUMBER & TITLE: - Beginning Algebra CREDITS: 4 (Lec 4 / Lab 0) PREREQUISITES: MATH 0920: Fundamental Mathematics with a grade of C or better, Placement Exam,
Factoring Trinomials of the Form x 2 bx c
 4.2 Factoring Trinomials of the Form x 2 bx c 4.2 OBJECTIVES 1. Factor a trinomial of the form x 2 bx c 2. Factor a trinomial containing a common factor NOTE The process used to factor here is frequently
4.2 Factoring Trinomials of the Form x 2 bx c 4.2 OBJECTIVES 1. Factor a trinomial of the form x 2 bx c 2. Factor a trinomial containing a common factor NOTE The process used to factor here is frequently
Successful completion of Math 7 or Algebra Readiness along with teacher recommendation.
 MODESTO CITY SCHOOLS COURSE OUTLINE COURSE TITLE:... Basic Algebra COURSE NUMBER:... RECOMMENDED GRADE LEVEL:... 8-11 ABILITY LEVEL:... Basic DURATION:... 1 year CREDIT:... 5.0 per semester MEETS GRADUATION
MODESTO CITY SCHOOLS COURSE OUTLINE COURSE TITLE:... Basic Algebra COURSE NUMBER:... RECOMMENDED GRADE LEVEL:... 8-11 ABILITY LEVEL:... Basic DURATION:... 1 year CREDIT:... 5.0 per semester MEETS GRADUATION
Factors and Products
 CHAPTER 3 Factors and Products What You ll Learn use different strategies to find factors and multiples of whole numbers identify prime factors and write the prime factorization of a number find square
CHAPTER 3 Factors and Products What You ll Learn use different strategies to find factors and multiples of whole numbers identify prime factors and write the prime factorization of a number find square
4.1. COMPLEX NUMBERS
 4.1. COMPLEX NUMBERS What You Should Learn Use the imaginary unit i to write complex numbers. Add, subtract, and multiply complex numbers. Use complex conjugates to write the quotient of two complex numbers
4.1. COMPLEX NUMBERS What You Should Learn Use the imaginary unit i to write complex numbers. Add, subtract, and multiply complex numbers. Use complex conjugates to write the quotient of two complex numbers
ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form
 ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form Goal Graph quadratic functions. VOCABULARY Quadratic function A function that can be written in the standard form y = ax 2 + bx+ c where a 0 Parabola
ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form Goal Graph quadratic functions. VOCABULARY Quadratic function A function that can be written in the standard form y = ax 2 + bx+ c where a 0 Parabola
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0).
 This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
Radicals - Multiply and Divide Radicals
 8. Radicals - Multiply and Divide Radicals Objective: Multiply and divide radicals using the product and quotient rules of radicals. Multiplying radicals is very simple if the index on all the radicals
8. Radicals - Multiply and Divide Radicals Objective: Multiply and divide radicals using the product and quotient rules of radicals. Multiplying radicals is very simple if the index on all the radicals
Contents. How You May Use This Resource Guide
 Contents How You May Use This Resource Guide ii 7 Factoring and Algebraic Fractions 1 Worksheet 7.1: The Box Problem......................... 4 Worksheet 7.2: Multiplying and Factoring Polynomials with
Contents How You May Use This Resource Guide ii 7 Factoring and Algebraic Fractions 1 Worksheet 7.1: The Box Problem......................... 4 Worksheet 7.2: Multiplying and Factoring Polynomials with
Multiplying and Factoring Notes
 Multiplying/Factoring 3 Multiplying and Factoring Notes I. Content: This lesson is going to focus on wrapping up and solidifying concepts that we have been discovering and working with. The students have
Multiplying/Factoring 3 Multiplying and Factoring Notes I. Content: This lesson is going to focus on wrapping up and solidifying concepts that we have been discovering and working with. The students have
POLYNOMIALS and FACTORING
 POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
MATH 108 REVIEW TOPIC 10 Quadratic Equations. B. Solving Quadratics by Completing the Square
 Math 108 T10-Review Topic 10 Page 1 MATH 108 REVIEW TOPIC 10 Quadratic Equations I. Finding Roots of a Quadratic Equation A. Factoring B. Quadratic Formula C. Taking Roots II. III. Guidelines for Finding
Math 108 T10-Review Topic 10 Page 1 MATH 108 REVIEW TOPIC 10 Quadratic Equations I. Finding Roots of a Quadratic Equation A. Factoring B. Quadratic Formula C. Taking Roots II. III. Guidelines for Finding
What are the place values to the left of the decimal point and their associated powers of ten?
 The verbal answers to all of the following questions should be memorized before completion of algebra. Answers that are not memorized will hinder your ability to succeed in geometry and algebra. (Everything
The verbal answers to all of the following questions should be memorized before completion of algebra. Answers that are not memorized will hinder your ability to succeed in geometry and algebra. (Everything
Unit 12: Introduction to Factoring. Learning Objectives 12.2
 Unit 1 Table of Contents Unit 1: Introduction to Factoring Learning Objectives 1. Instructor Notes The Mathematics of Factoring Teaching Tips: Challenges and Approaches Additional Resources Instructor
Unit 1 Table of Contents Unit 1: Introduction to Factoring Learning Objectives 1. Instructor Notes The Mathematics of Factoring Teaching Tips: Challenges and Approaches Additional Resources Instructor
A Systematic Approach to Factoring
 A Systematic Approach to Factoring Step 1 Count the number of terms. (Remember****Knowing the number of terms will allow you to eliminate unnecessary tools.) Step 2 Is there a greatest common factor? Tool
A Systematic Approach to Factoring Step 1 Count the number of terms. (Remember****Knowing the number of terms will allow you to eliminate unnecessary tools.) Step 2 Is there a greatest common factor? Tool
7-6. Choosing a Factoring Model. Extension: Factoring Polynomials with More Than One Variable IN T RO DUC E T EACH. Standards for Mathematical Content
 7-6 Choosing a Factoring Model Extension: Factoring Polynomials with More Than One Variable Essential question: How can you factor polynomials with more than one variable? What is the connection between
7-6 Choosing a Factoring Model Extension: Factoring Polynomials with More Than One Variable Essential question: How can you factor polynomials with more than one variable? What is the connection between
Square Roots and Other Radicals
 Radicals - Definition Radicals, or roots, are the opposite operation of applying exponents. A power can be undone with a radical and a radical can be undone with a power. For example, if you square 2,
Radicals - Definition Radicals, or roots, are the opposite operation of applying exponents. A power can be undone with a radical and a radical can be undone with a power. For example, if you square 2,
Using the Area Model to Teach Multiplying, Factoring and Division of Polynomials
 visit us at www.cpm.org Using the Area Model to Teach Multiplying, Factoring and Division of Polynomials For more information about the materials presented, contact Chris Mikles mikles@cpm.org From CCA
visit us at www.cpm.org Using the Area Model to Teach Multiplying, Factoring and Division of Polynomials For more information about the materials presented, contact Chris Mikles mikles@cpm.org From CCA
EAP/GWL Rev. 1/2011 Page 1 of 5. Factoring a polynomial is the process of writing it as the product of two or more polynomial factors.
 EAP/GWL Rev. 1/2011 Page 1 of 5 Factoring a polynomial is the process of writing it as the product of two or more polynomial factors. Example: Set the factors of a polynomial equation (as opposed to an
EAP/GWL Rev. 1/2011 Page 1 of 5 Factoring a polynomial is the process of writing it as the product of two or more polynomial factors. Example: Set the factors of a polynomial equation (as opposed to an
Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder).
 Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
6.4 Special Factoring Rules
 6.4 Special Factoring Rules OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor a sum of cubes. By reversing the rules for multiplication
6.4 Special Factoring Rules OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor a sum of cubes. By reversing the rules for multiplication
Partial Fractions. (x 1)(x 2 + 1)
 Partial Fractions Adding rational functions involves finding a common denominator, rewriting each fraction so that it has that denominator, then adding. For example, 3x x 1 3x(x 1) (x + 1)(x 1) + 1(x +
Partial Fractions Adding rational functions involves finding a common denominator, rewriting each fraction so that it has that denominator, then adding. For example, 3x x 1 3x(x 1) (x + 1)(x 1) + 1(x +
2.3. Finding polynomial functions. An Introduction:
 2.3. Finding polynomial functions. An Introduction: As is usually the case when learning a new concept in mathematics, the new concept is the reverse of the previous one. Remember how you first learned
2.3. Finding polynomial functions. An Introduction: As is usually the case when learning a new concept in mathematics, the new concept is the reverse of the previous one. Remember how you first learned
Algebra 1 Course Title
 Algebra 1 Course Title Course- wide 1. What patterns and methods are being used? Course- wide 1. Students will be adept at solving and graphing linear and quadratic equations 2. Students will be adept
Algebra 1 Course Title Course- wide 1. What patterns and methods are being used? Course- wide 1. Students will be adept at solving and graphing linear and quadratic equations 2. Students will be adept
Academic Success Centre
 250) 960-6367 Factoring Polynomials Sometimes when we try to solve or simplify an equation or expression involving polynomials the way that it looks can hinder our progress in finding a solution. Factorization
250) 960-6367 Factoring Polynomials Sometimes when we try to solve or simplify an equation or expression involving polynomials the way that it looks can hinder our progress in finding a solution. Factorization
Factorising quadratics
 Factorising quadratics An essential skill in many applications is the ability to factorise quadratic expressions. In this unit you will see that this can be thought of as reversing the process used to
Factorising quadratics An essential skill in many applications is the ability to factorise quadratic expressions. In this unit you will see that this can be thought of as reversing the process used to
Factoring Polynomials
 UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
Exponents and Radicals
 Exponents and Radicals (a + b) 10 Exponents are a very important part of algebra. An exponent is just a convenient way of writing repeated multiplications of the same number. Radicals involve the use of
Exponents and Radicals (a + b) 10 Exponents are a very important part of algebra. An exponent is just a convenient way of writing repeated multiplications of the same number. Radicals involve the use of
The majority of college students hold credit cards. According to the Nellie May
 CHAPTER 6 Factoring Polynomials 6.1 The Greatest Common Factor and Factoring by Grouping 6. Factoring Trinomials of the Form b c 6.3 Factoring Trinomials of the Form a b c and Perfect Square Trinomials
CHAPTER 6 Factoring Polynomials 6.1 The Greatest Common Factor and Factoring by Grouping 6. Factoring Trinomials of the Form b c 6.3 Factoring Trinomials of the Form a b c and Perfect Square Trinomials
Vocabulary Words and Definitions for Algebra
 Name: Period: Vocabulary Words and s for Algebra Absolute Value Additive Inverse Algebraic Expression Ascending Order Associative Property Axis of Symmetry Base Binomial Coefficient Combine Like Terms
Name: Period: Vocabulary Words and s for Algebra Absolute Value Additive Inverse Algebraic Expression Ascending Order Associative Property Axis of Symmetry Base Binomial Coefficient Combine Like Terms
Factoring Polynomials
 Factoring Polynomials Hoste, Miller, Murieka September 12, 2011 1 Factoring In the previous section, we discussed how to determine the product of two or more terms. Consider, for instance, the equations
Factoring Polynomials Hoste, Miller, Murieka September 12, 2011 1 Factoring In the previous section, we discussed how to determine the product of two or more terms. Consider, for instance, the equations
MATH 10034 Fundamental Mathematics IV
 MATH 0034 Fundamental Mathematics IV http://www.math.kent.edu/ebooks/0034/funmath4.pdf Department of Mathematical Sciences Kent State University January 2, 2009 ii Contents To the Instructor v Polynomials.
MATH 0034 Fundamental Mathematics IV http://www.math.kent.edu/ebooks/0034/funmath4.pdf Department of Mathematical Sciences Kent State University January 2, 2009 ii Contents To the Instructor v Polynomials.
Unit 3: Day 2: Factoring Polynomial Expressions
 Unit 3: Day : Factoring Polynomial Expressions Minds On: 0 Action: 45 Consolidate:10 Total =75 min Learning Goals: Extend knowledge of factoring to factor cubic and quartic expressions that can be factored
Unit 3: Day : Factoring Polynomial Expressions Minds On: 0 Action: 45 Consolidate:10 Total =75 min Learning Goals: Extend knowledge of factoring to factor cubic and quartic expressions that can be factored
Florida Math 0028. Correlation of the ALEKS course Florida Math 0028 to the Florida Mathematics Competencies - Upper
 Florida Math 0028 Correlation of the ALEKS course Florida Math 0028 to the Florida Mathematics Competencies - Upper Exponents & Polynomials MDECU1: Applies the order of operations to evaluate algebraic
Florida Math 0028 Correlation of the ALEKS course Florida Math 0028 to the Florida Mathematics Competencies - Upper Exponents & Polynomials MDECU1: Applies the order of operations to evaluate algebraic
Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III
 Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III Name Date Adding and Subtracting Polynomials Algebra Standard 10.0 A polynomial is a sum of one ore more monomials. Polynomial
Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III Name Date Adding and Subtracting Polynomials Algebra Standard 10.0 A polynomial is a sum of one ore more monomials. Polynomial
4.4 Factoring ax 2 + bx + c
 4.4 Factoring ax 2 + bx + c From the last section, we now know a trinomial should factor as two binomials. With this in mind, we need to look at how to factor a trinomial when the leading coefficient is
4.4 Factoring ax 2 + bx + c From the last section, we now know a trinomial should factor as two binomials. With this in mind, we need to look at how to factor a trinomial when the leading coefficient is
Veterans Upward Bound Algebra I Concepts - Honors
 Veterans Upward Bound Algebra I Concepts - Honors Brenda Meery Kaitlyn Spong Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org Chapter 6. Factoring CHAPTER
Veterans Upward Bound Algebra I Concepts - Honors Brenda Meery Kaitlyn Spong Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org Chapter 6. Factoring CHAPTER
15.1 Factoring Polynomials
 LESSON 15.1 Factoring Polynomials Use the structure of an expression to identify ways to rewrite it. Also A.SSE.3? ESSENTIAL QUESTION How can you use the greatest common factor to factor polynomials? EXPLORE
LESSON 15.1 Factoring Polynomials Use the structure of an expression to identify ways to rewrite it. Also A.SSE.3? ESSENTIAL QUESTION How can you use the greatest common factor to factor polynomials? EXPLORE
Polynomials and Quadratics
 Polynomials and Quadratics Want to be an environmental scientist? Better be ready to get your hands dirty!.1 Controlling the Population Adding and Subtracting Polynomials............703.2 They re Multiplying
Polynomials and Quadratics Want to be an environmental scientist? Better be ready to get your hands dirty!.1 Controlling the Population Adding and Subtracting Polynomials............703.2 They re Multiplying
The program also provides supplemental modules on topics in geometry and probability and statistics.
 Algebra 1 Course Overview Students develop algebraic fluency by learning the skills needed to solve equations and perform important manipulations with numbers, variables, equations, and inequalities. Students
Algebra 1 Course Overview Students develop algebraic fluency by learning the skills needed to solve equations and perform important manipulations with numbers, variables, equations, and inequalities. Students
Introduction Assignment
 PRE-CALCULUS 11 Introduction Assignment Welcome to PREC 11! This assignment will help you review some topics from a previous math course and introduce you to some of the topics that you ll be studying
PRE-CALCULUS 11 Introduction Assignment Welcome to PREC 11! This assignment will help you review some topics from a previous math course and introduce you to some of the topics that you ll be studying
Mathematics Placement
 Mathematics Placement The ACT COMPASS math test is a self-adaptive test, which potentially tests students within four different levels of math including pre-algebra, algebra, college algebra, and trigonometry.
Mathematics Placement The ACT COMPASS math test is a self-adaptive test, which potentially tests students within four different levels of math including pre-algebra, algebra, college algebra, and trigonometry.
MATH 095, College Prep Mathematics: Unit Coverage Pre-algebra topics (arithmetic skills) offered through BSE (Basic Skills Education)
 MATH 095, College Prep Mathematics: Unit Coverage Pre-algebra topics (arithmetic skills) offered through BSE (Basic Skills Education) Accurately add, subtract, multiply, and divide whole numbers, integers,
MATH 095, College Prep Mathematics: Unit Coverage Pre-algebra topics (arithmetic skills) offered through BSE (Basic Skills Education) Accurately add, subtract, multiply, and divide whole numbers, integers,
Algebra and Geometry Review (61 topics, no due date)
 Course Name: Math 112 Credit Exam LA Tech University Course Code: ALEKS Course: Trigonometry Instructor: Course Dates: Course Content: 159 topics Algebra and Geometry Review (61 topics, no due date) Properties
Course Name: Math 112 Credit Exam LA Tech University Course Code: ALEKS Course: Trigonometry Instructor: Course Dates: Course Content: 159 topics Algebra and Geometry Review (61 topics, no due date) Properties
Quadratics - Build Quadratics From Roots
 9.5 Quadratics - Build Quadratics From Roots Objective: Find a quadratic equation that has given roots using reverse factoring and reverse completing the square. Up to this point we have found the solutions
9.5 Quadratics - Build Quadratics From Roots Objective: Find a quadratic equation that has given roots using reverse factoring and reverse completing the square. Up to this point we have found the solutions
Learning Objectives 9.2. Media Run Times 9.3
 Unit 9 Table of Contents Unit 9: Factoring Video Overview Learning Objectives 9.2 Media Run Times 9.3 Instructor Notes 9.4 The Mathematics of Factoring Polynomials Teaching Tips: Conceptual Challenges
Unit 9 Table of Contents Unit 9: Factoring Video Overview Learning Objectives 9.2 Media Run Times 9.3 Instructor Notes 9.4 The Mathematics of Factoring Polynomials Teaching Tips: Conceptual Challenges
SOLVING QUADRATIC EQUATIONS BY THE DIAGONAL SUM METHOD
 SOLVING QUADRATIC EQUATIONS BY THE DIAGONAL SUM METHOD A quadratic equation in one variable has as standard form: ax^2 + bx + c = 0. Solving it means finding the values of x that make the equation true.
SOLVING QUADRATIC EQUATIONS BY THE DIAGONAL SUM METHOD A quadratic equation in one variable has as standard form: ax^2 + bx + c = 0. Solving it means finding the values of x that make the equation true.
ALGEBRA I (Created 2014) Amherst County Public Schools
 ALGEBRA I (Created 2014) Amherst County Public Schools The 2009 Mathematics Standards of Learning Curriculum Framework is a companion document to the 2009 Mathematics Standards of Learning and amplifies
ALGEBRA I (Created 2014) Amherst County Public Schools The 2009 Mathematics Standards of Learning Curriculum Framework is a companion document to the 2009 Mathematics Standards of Learning and amplifies
A.3. Polynomials and Factoring. Polynomials. What you should learn. Definition of a Polynomial in x. Why you should learn it
 Appendi A.3 Polynomials and Factoring A23 A.3 Polynomials and Factoring What you should learn Write polynomials in standard form. Add,subtract,and multiply polynomials. Use special products to multiply
Appendi A.3 Polynomials and Factoring A23 A.3 Polynomials and Factoring What you should learn Write polynomials in standard form. Add,subtract,and multiply polynomials. Use special products to multiply
Factoring Methods. Example 1: 2x + 2 2 * x + 2 * 1 2(x + 1)
 Factoring Methods When you are trying to factor a polynomial, there are three general steps you want to follow: 1. See if there is a Greatest Common Factor 2. See if you can Factor by Grouping 3. See if
Factoring Methods When you are trying to factor a polynomial, there are three general steps you want to follow: 1. See if there is a Greatest Common Factor 2. See if you can Factor by Grouping 3. See if
Polynomials and Factoring
 7.6 Polynomials and Factoring Basic Terminology A term, or monomial, is defined to be a number, a variable, or a product of numbers and variables. A polynomial is a term or a finite sum or difference of
7.6 Polynomials and Factoring Basic Terminology A term, or monomial, is defined to be a number, a variable, or a product of numbers and variables. A polynomial is a term or a finite sum or difference of
Solving Quadratic Equations by Factoring
 4.7 Solving Quadratic Equations by Factoring 4.7 OBJECTIVE 1. Solve quadratic equations by factoring The factoring techniques you have learned provide us with tools for solving equations that can be written
4.7 Solving Quadratic Equations by Factoring 4.7 OBJECTIVE 1. Solve quadratic equations by factoring The factoring techniques you have learned provide us with tools for solving equations that can be written
ACCUPLACER. Testing & Study Guide. Prepared by the Admissions Office Staff and General Education Faculty Draft: January 2011
 ACCUPLACER Testing & Study Guide Prepared by the Admissions Office Staff and General Education Faculty Draft: January 2011 Thank you to Johnston Community College staff for giving permission to revise
ACCUPLACER Testing & Study Guide Prepared by the Admissions Office Staff and General Education Faculty Draft: January 2011 Thank you to Johnston Community College staff for giving permission to revise
SPECIAL PRODUCTS AND FACTORS
 CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
Section 5.0A Factoring Part 1
 Section 5.0A Factoring Part 1 I. Work Together A. Multiply the following binomials into trinomials. (Write the final result in descending order, i.e., a + b + c ). ( 7)( + 5) ( + 7)( + ) ( + 7)( + 5) (
Section 5.0A Factoring Part 1 I. Work Together A. Multiply the following binomials into trinomials. (Write the final result in descending order, i.e., a + b + c ). ( 7)( + 5) ( + 7)( + ) ( + 7)( + 5) (
POLYNOMIAL FUNCTIONS
 POLYNOMIAL FUNCTIONS Polynomial Division.. 314 The Rational Zero Test.....317 Descarte s Rule of Signs... 319 The Remainder Theorem.....31 Finding all Zeros of a Polynomial Function.......33 Writing a
POLYNOMIAL FUNCTIONS Polynomial Division.. 314 The Rational Zero Test.....317 Descarte s Rule of Signs... 319 The Remainder Theorem.....31 Finding all Zeros of a Polynomial Function.......33 Writing a
