Recap Clipping Culling Hidden surface removal. Graphics 2011/2012, 4th quarter. Lecture 08: graphics pipeline (clipping and culling)
|
|
|
- Shana Price
- 7 years ago
- Views:
Transcription
1 Lecture 8 Graphics pipeline (clipping and culling)
2 Graphics pipeline - part 1 (recap) Graphics pipeline (part 1) Linear transformations Affine transformations Projective transformations Perspective projection by matrix multiplication: x pixel y pixel z canonical 1 x = M vpm per M cam y z 1 This is an important part of the graphics pipeline.
3 Graphics pipeline - part 1 (recap) Graphics pipeline (part 1) Linear transformations Affine transformations Projective transformations View frustum Specify camera position and view frustum Camera transformation Move from world space to camera space Orthographic view volume Transform view frustum to axis-parallel box Canonical view volumn Transform orthographic view volume to 2x2x2 cube around the origin Windowing transformation Orthographic projection and transformation to screen space
4 Extending homogeneous coordinates Graphics pipeline (part 1) Linear transformations Affine transformations Projective transformations Linear transformations: Points represented by vectors (x, y, z) x x = ax + by + cz
5 Extending homogeneous coordinates Graphics pipeline (part 1) Linear transformations Affine transformations Projective transformations Linear transformations: Points represented by vectors (x, y, z) x x = ax + by + cz Affine transformations: (x, y, z, 1) represents point (x, y, z) x x = ax + by + cz + d
6 Geometric interpretation (in 2D) Graphics pipeline (part 1) Linear transformations Affine transformations Projective transformations
7 Extending homogeneous coordinates Graphics pipeline (part 1) Linear transformations Affine transformations Projective transformations Linear transformations: Points represented by vectors (x, y, z) x x = ax + by + cz Affine transformations: (x, y, z, 1) represents point (x, y, z) x x = ax + by + cz + d Projective transformations: ( x, ỹ, z, w) represents ( x/w, ỹ/w, z/w, 1) which in turn represents ( x/w, ỹ/w, z/w) which in turn represents point (x, y, z). x x = ax+by+cz+d ex+fy+gz+h
8 Geometric interpretation (in 1D) Graphics pipeline (part 1) Linear transformations Affine transformations Projective transformations
9 Extending homogeneous coordinates Graphics pipeline (part 1) Linear transformations Affine transformations Projective transformations Matrix multiplication: x a 1 b 1 c 1 d 1 x a 1 x + b 1 y + c 1 z + d 1 ỹ z = a 2 b 2 c 2 d 2 y a 3 b 3 c 3 d 3 z = a 2 x + b 2 y + c 2 z + d 2 a 3 x + b 3 y + c 3 z + d 3 w e f g h 1 ex + fy + gz + h Homogenization: a 1 x + b 1 y + c 1 z + d 1 a 2 x + b 2 y + c 2 z + d 2 a 3 x + b 3 y + c 3 z + d 3 homogenize ex + fy + gz + h a 1x+b 1y+c 1z+d 1 ex+fy+gz+h a 2x+b 2y+c 2z+d 2 ex+fy+gz+h a 3x+b 3y+c 3z+d 3 ex+fy+gz+h 1
10 Extending homogeneous coordinates Matrix multiplication: Graphics pipeline (part 1) Linear transformations Affine transformations Projective transformations x a 1 b 1 c 1 d 1 x c(a 1 x + b 1 y + c 1 z + d 1 ) ỹ z = c a 2 b 2 c 2 d 2 y a 3 b 3 c 3 d 3 z = c(a 2 x + b 2 y + c 2 z + d 2 ) c(a 3 x + b 3 y + c 3 z + d 3 ) w e f g h 1 c(ex + fy + gz + h) Homogenization: c(a 1 x + b 1 y + c 1 z + d 1 ) c(a 2 x + b 2 y + c 2 z + d 2 ) c(a 3 x + b 3 y + c 3 z + d 3 ) homogenize c(ex + fy + gz + h) c(a 1x+b 1y+c 1z+d 1) c(ex+fy+gz+h) c(a 2x+b 2y+c 2z+d 2) c(ex+fy+gz+h) c(a 3x+b 3y+c 3z+d 3) c(ex+fy+gz+h) 1
11 Extending homogeneous coordinates Graphics pipeline (part 1) Linear transformations Affine transformations Projective transformations Hence, both of these two matrices can be used as perspective matrix: n n n + f fn and n+f 0 0 n f and n 0
12 Graphics pipeline (part 1) Linear transformations Affine transformations Projective transformations Other stages in the graphics pipeline (recap) Triangles that lie (partly) outside the view frustum need not be projected, and are clipped. The remaining triangles are projected if they are front facing. Projected triangles have to be shaded and/or textured.
13 Recap How to clip triangles Where to clip? arbitrary polygons In general, we cannot expect all triangles to lie within the view frustum. Triangles that lie partly outside the view frustum must be clipped. We must... 1 verify if a triangle intersects with a hyperplane 2 create new triangle(s)
14 Implicit equations revisited How to clip triangles Where to clip? arbitrary polygons Remember the implicit equation of a plane: f( p) = n( p p 0 ) = 0 or f( p) = n p + d = 0 We already learned that f( p) splits our space into a positive and a negative subspace for which f( p) > 0 and f( p) < 0, respectively.
15 Finding candidates for clipping How to clip triangles Where to clip? arbitrary polygons In tutorial 1 and 2, we have proven that the normal always points to the positive side. Hence, if the normals of the clipping planes point outward: p is inside the plane if f( p) < 0 p is outside the plane if f( p) > 0
16 Finding intersection points How to clip triangles Where to clip? arbitrary polygons If two points a and b are on different sides of a hyperplane, we first determine the parametric equation of the line through the points: p(t) = a + t( b a) Substituting this into the hyperplane equation yields t n a + d = n ( a b)
17 Creating clipped triangles How to clip triangles Where to clip? arbitrary polygons Given the intersection points, we can clip the triangle against the hyperplane as follows: If two vertices are on the positive side, we get one new triangle. If one vertex is on the positive side of the hyperplane, we get two new triangles.
18 against a hyperplane How to clip triangles Where to clip? arbitrary polygons But what do we do if a triangle is intersected by two clipping planes?
19 against a hyperplane How to clip triangles Where to clip? arbitrary polygons We have to deal with such situations one clipping plane at a time. We first clip the initial triangle against one of the clipping planes...
20 against a hyperplane How to clip triangles Where to clip? arbitrary polygons... and clip the remaining triangle(s) against the other clipping plane.
21 against a hyperplane How to clip triangles Where to clip? arbitrary polygons Similarly, we can deal with situations where a triangle is intersected by three clipping planes.
22 Where should we do the clipping? How to clip triangles Where to clip? arbitrary polygons
23 after the perspective divide How to clip triangles Where to clip? arbitrary polygons Advantage: equations for these hyperplanes are quite simple: x + l = 0 x r = 0 y + b = 0 y t = 0 z + n = 0 z f = 0 But: there s a problem at the XY -plane...
24 after the perspective divide How to clip triangles Where to clip? arbitrary polygons after the perspective divide may lead to incorrect results if line segments cross the XY -plane, since a division by z is involved: z = n + f fn z
25 How to clip triangles Where to clip? arbitrary polygons before the perspective divide It is possible to clip against the six clipping planes right before the perspective divide. The eight corners of the view frustum are easily found by the inverse transformation M 1 per. From these, we can derive the plane equations for the view frustum.
26 How to clip triangles Where to clip? arbitrary polygons in homogeneous coordinates Surprisingly, it turns out to be easiest to clip in homogeneous coordinates, which means that we clip in four dimensions against three-dimensional clipping hyperplanes. The equations for these hyperplanes are quite simple: x + lw = 0 x rw = 0 y + bw = 0 y tw = 0 z + nw = 0 z fw = 0
27 How to clip triangles Where to clip? arbitrary polygons in homogeneous coordinates (x, y, z, 1) Hyperplanes in homogeneous coordinates: x + lw = 0 x rw = 0 y + bw = 0 y tw = 0 z + nw = 0 z fw = 0 matrix multiplication (x, y, z, w ) homogeneous divide rasterize ( x w, y w, z w, 1)
28 arbitrary polygons How to clip triangles Where to clip? arbitrary polygons p 1 p 2 Some rendering engines deal with arbitrary polygons rather than with triangles. Also, in drawing programs we often need to clip arbitrary polygons. i 0 i 1 p 6 p 5 p 0 i 2 p 4 p 3
29 The Sutherland-Hodgman algorithm How to clip triangles Where to clip? arbitrary polygons p 1 p 2 The Sutherland-Hodgman clipping algorithm is straightforward: Clip the polygon subsequently against every clipping hyperplane. i 0 i 1 p 6 p 5 p 0 i 2 p 4 p 3
30 The Sutherland-Hodgman algorithm How to clip triangles Where to clip? arbitrary polygons Extend upper side of rectangle across 2D space Start at one vertex of the polygone and follow its path Create new vertex where path crosses clipping line Repeat till we are back at starting vertex Create new polygon from sets over vertices on or beneath clipping line Repeat for every clipping line p 1 p 2 i 0 i 1 p 6 p 0 p 5 i 2 p 4 p 3
31 The Sutherland-Hodgman algorithm How to clip triangles Where to clip? arbitrary polygons p 1 p 2 However, sometimes the Sutherland-Hodgman algorithm results in degenerate polygons. p 8 p 7 r 1 r 2 i 0 i 1 p 5 i 2 p p6 0 For example, the resulting polygon on the right has vertices p 0, i 0, r 2, i 3, p 4, p 5, i 2, r 2, and i 1, consecutively. r 0 p 4 i 3 r 3 p 3
32 The Weiler-Atherton algorithm How to clip triangles Where to clip? arbitrary polygons Basic idea: create a graph with nodes for all vertices of the polygone, corners of the view frustum, and intersection points and edges that allow us to easily extract the clipped polygones. p 0 p 1 p 2 p 1 p 2 i 0 r 0 p 8 r 1 r 2 i 0 i 1 p 7 p 3 p 4 i 3 r 1 p 0 p 5 i 2 p6 p 5 p 6 i 2 r 2 r 0 p 4 i 3 r 3 p 3 p 7 i 1 r 3 p 8
33 The Weiler-Atherton algorithm How to clip triangles Where to clip? arbitrary polygons Building the graph: Make a graph with three groups of vertices: polygon vertices, clipping region vertices, and intersection vertices. Insert edges by walking along the boundary of the polygon, including the intersection vertices. Distinguish outgoing intersections (colored red in the image) and incoming intersections (colored pink). Insert edges by walking along the boundary of the clipping region, including the intersection vertices.
34 The Weiler-Atherton algorithm How to clip triangles Where to clip? arbitrary polygons p 1 p 2 p 8 r 1 r 2 i 0 i 1 p 7 p 0 p 5 i 2 p6 r 0 p 4 i 3 r 3 p 3
35 The Weiler-Atherton algorithm How to clip triangles Where to clip? arbitrary polygons Using the graph: Start at an outgoing intersection vertex, and walk along the boundary of the clipping region (black edges in image), reporting every vertex along the way. Upon encountering an incoming intersection vertex, continue along the boundary of the polygon (red edges in image). Continue, changing from polygon boundary to clipping region boundary and the other way around at outgoing and incoming intersection vertices, respectively, until we reach the starting vertex. Start at the next unvisited outgoing intersection vertex to output the next clipped polygon, etc, until no unvisited outgoing intersection vertices are left.
36 The Weiler-Atherton algorithm How to clip triangles Where to clip? arbitrary polygons p 0 p 1 p 2 p 1 p 2 i 0 r 0 p 8 r 1 r 2 i 0 i 1 p 7 p 3 p 4 i 3 r 1 p 0 p 5 i 2 p6 p 5 i 2 r 2 r 0 p 4 i 3 r 3 p 3 p 6 p 7 i 1 r 3 p 8
37 triangles Recap View frustum culling Backface culling When a triangle lies entirely outside the view frustum, it can be culled, i.e., removed from the graphics pipeline. Testing individual triangles is expensive, however.
38 bounding volumes View frustum culling Backface culling bounding volumes of complicated objects (consisting of many triangles) will generally improve the performance of the graphics pipeline. If a bounding volume is outside of the frustum, then so are the enclosed triangles. This is called a conservative test. (Why?)
39 bounding volumes View frustum culling Backface culling Often spheres are used as bounding volumes. If the plane is defined by ( p a) n = 0 and the bounding sphere has center c and radius r, then we have to check if ( c a) n n > r
40 bounding volumes View frustum culling Backface culling ( c a) n n = cos θ c a n n = cos θ c a Remember that the projection p v of a vector v onto another vector is cos θ v with θ being the angle between both vectors. Hence, cos θ = p c a c a and thus cos θ c a = p c a
41 Other forms of culling View frustum culling Backface culling frustum culling culling of triangles outside of the view frustum occlusion culling culling of triangles withing the frustum that are occluded by others backface culling culling of triangles facing away from the camera
42 Backface culling Recap View frustum culling Backface culling frustum culling culling of triangles outside of the view frustum occlusion culling culling of triangles withing the frustum that are occluded by others backface culling culling of triangles facing away from the camera
43 Backface culling Recap View frustum culling Backface culling Surfaces of polyhedral objects are often modeled with connected, outward facing triangles. How many triangles do we need to model a cube? What is the maximum number of these triangles that is visible from any given viewing direction?
44 Backface culling Recap View frustum culling Backface culling Obviously, if a camera faces the backside of a triangle, there is no need to draw it. But how do we know which side we are looking at?
45 Backface culling Recap View frustum culling Backface culling If our models have outward facing normals, we can again use the implicit representation to verify if the camera e is on the positive or negative side of the plane / triangle: If f( e) > 0, we draw the triangle If f( e) < 0, we apply backface culling
46 Painter s algorithm Recap Painter s algorithm Z-buffer If we draw triangles that are further away before triangles that are closer to the viewing point, we end up with a correct image:
47 Painter s algorithm Recap Painter s algorithm Z-buffer If we draw triangles that are further away before triangles that are closer to the viewing point, we end up with a correct image:
48 Painter s algorithm Recap Painter s algorithm Z-buffer If we draw triangles that are further away before triangles that are closer to the viewing point, we end up with a correct image:
49 Cyclic overlap Recap Painter s algorithm Z-buffer However, not every arrangement of triangles admits a back-to-front ordering: And how about intersecting triangles?
50 Z-Buffer Recap Painter s algorithm Z-buffer Most common approach for hidden surface removal: Z-buffer (or depth buffer) Uses additional storage for depth information (mostly hardware, but implementations in software exist as well)
51 Z-buffer algorithm: basic idea Painter s algorithm Z-buffer Apart from the frame buffer, which contains the pixels of the image, also maintain a Z-buffer of the same width and height, to store depth information for the projected triangles.
52 Z-buffer algorithm: basic idea Painter s algorithm Z-buffer Initialize all Z-buffer entries to z max If a pixel is to be drawn at position [i, j], first test if its corresponding z-value p z is smaller then Z-buffer[i, j] If this is the case, draw the pixel, and update Z-buffer[i, j] to p z Otherwise, do not draw the pixel z-values for projected vertices: calculated; for remaining pixels: interpolated
53 Precision issues Recap Painter s algorithm Z-buffer For speed: z-values stored as non-negative integers, i.e. B values {0, 1,..., B 1} Hence, the z-values are mapped to intervals of size z = (f n)/b Points on near plane z = n mapped to 0 Points on far plane z = f mapped to B 1 Remember: z is reciprocal to z!
54 Precision issues Recap Painter s algorithm Z-buffer This results in higher precision close to the eye lower precision in the distance If we have b bits for our z-buffer, then B = 2 b and the size of our intervals is z = (f n)/2 b Hence, we can influence the precision by increasing b pushing n further away moving f closer
55 Painter s algorithm Z-buffer Other stages in the graphics pipeline (recap) Triangles that lie (partly) outside the view frustum need not be projected, and are clipped. The remaining triangles are projected if they are front facing. Projected triangles have to be shaded and/or textured.
Image Processing and Computer Graphics. Rendering Pipeline. Matthias Teschner. Computer Science Department University of Freiburg
 Image Processing and Computer Graphics Rendering Pipeline Matthias Teschner Computer Science Department University of Freiburg Outline introduction rendering pipeline vertex processing primitive processing
Image Processing and Computer Graphics Rendering Pipeline Matthias Teschner Computer Science Department University of Freiburg Outline introduction rendering pipeline vertex processing primitive processing
INTRODUCTION TO RENDERING TECHNIQUES
 INTRODUCTION TO RENDERING TECHNIQUES 22 Mar. 212 Yanir Kleiman What is 3D Graphics? Why 3D? Draw one frame at a time Model only once X 24 frames per second Color / texture only once 15, frames for a feature
INTRODUCTION TO RENDERING TECHNIQUES 22 Mar. 212 Yanir Kleiman What is 3D Graphics? Why 3D? Draw one frame at a time Model only once X 24 frames per second Color / texture only once 15, frames for a feature
A Short Introduction to Computer Graphics
 A Short Introduction to Computer Graphics Frédo Durand MIT Laboratory for Computer Science 1 Introduction Chapter I: Basics Although computer graphics is a vast field that encompasses almost any graphical
A Short Introduction to Computer Graphics Frédo Durand MIT Laboratory for Computer Science 1 Introduction Chapter I: Basics Although computer graphics is a vast field that encompasses almost any graphical
Monash University Clayton s School of Information Technology CSE3313 Computer Graphics Sample Exam Questions 2007
 Monash University Clayton s School of Information Technology CSE3313 Computer Graphics Questions 2007 INSTRUCTIONS: Answer all questions. Spend approximately 1 minute per mark. Question 1 30 Marks Total
Monash University Clayton s School of Information Technology CSE3313 Computer Graphics Questions 2007 INSTRUCTIONS: Answer all questions. Spend approximately 1 minute per mark. Question 1 30 Marks Total
Scan-Line Fill. Scan-Line Algorithm. Sort by scan line Fill each span vertex order generated by vertex list
 Scan-Line Fill Can also fill by maintaining a data structure of all intersections of polygons with scan lines Sort by scan line Fill each span vertex order generated by vertex list desired order Scan-Line
Scan-Line Fill Can also fill by maintaining a data structure of all intersections of polygons with scan lines Sort by scan line Fill each span vertex order generated by vertex list desired order Scan-Line
CS 4204 Computer Graphics
 CS 4204 Computer Graphics 3D views and projection Adapted from notes by Yong Cao 1 Overview of 3D rendering Modeling: *Define object in local coordinates *Place object in world coordinates (modeling transformation)
CS 4204 Computer Graphics 3D views and projection Adapted from notes by Yong Cao 1 Overview of 3D rendering Modeling: *Define object in local coordinates *Place object in world coordinates (modeling transformation)
Realtime 3D Computer Graphics Virtual Reality
 Realtime 3D Computer Graphics Virtual Realit Viewing and projection Classical and General Viewing Transformation Pipeline CPU Pol. DL Pixel Per Vertex Texture Raster Frag FB object ee clip normalized device
Realtime 3D Computer Graphics Virtual Realit Viewing and projection Classical and General Viewing Transformation Pipeline CPU Pol. DL Pixel Per Vertex Texture Raster Frag FB object ee clip normalized device
Arrangements And Duality
 Arrangements And Duality 3.1 Introduction 3 Point configurations are tbe most basic structure we study in computational geometry. But what about configurations of more complicated shapes? For example,
Arrangements And Duality 3.1 Introduction 3 Point configurations are tbe most basic structure we study in computational geometry. But what about configurations of more complicated shapes? For example,
Largest Fixed-Aspect, Axis-Aligned Rectangle
 Largest Fixed-Aspect, Axis-Aligned Rectangle David Eberly Geometric Tools, LLC http://www.geometrictools.com/ Copyright c 1998-2016. All Rights Reserved. Created: February 21, 2004 Last Modified: February
Largest Fixed-Aspect, Axis-Aligned Rectangle David Eberly Geometric Tools, LLC http://www.geometrictools.com/ Copyright c 1998-2016. All Rights Reserved. Created: February 21, 2004 Last Modified: February
Section 1.4. Lines, Planes, and Hyperplanes. The Calculus of Functions of Several Variables
 The Calculus of Functions of Several Variables Section 1.4 Lines, Planes, Hyperplanes In this section we will add to our basic geometric understing of R n by studying lines planes. If we do this carefully,
The Calculus of Functions of Several Variables Section 1.4 Lines, Planes, Hyperplanes In this section we will add to our basic geometric understing of R n by studying lines planes. If we do this carefully,
Introduction to Computer Graphics
 Introduction to Computer Graphics Torsten Möller TASC 8021 778-782-2215 torsten@sfu.ca www.cs.sfu.ca/~torsten Today What is computer graphics? Contents of this course Syllabus Overview of course topics
Introduction to Computer Graphics Torsten Möller TASC 8021 778-782-2215 torsten@sfu.ca www.cs.sfu.ca/~torsten Today What is computer graphics? Contents of this course Syllabus Overview of course topics
Chapter 9. Systems of Linear Equations
 Chapter 9. Systems of Linear Equations 9.1. Solve Systems of Linear Equations by Graphing KYOTE Standards: CR 21; CA 13 In this section we discuss how to solve systems of two linear equations in two variables
Chapter 9. Systems of Linear Equations 9.1. Solve Systems of Linear Equations by Graphing KYOTE Standards: CR 21; CA 13 In this section we discuss how to solve systems of two linear equations in two variables
Triangle Scan Conversion using 2D Homogeneous Coordinates
 Triangle Scan Conversion using 2D Homogeneous Coordinates Marc Olano 1 Trey Greer 2 University of North Carolina Hewlett-Packard ABSTRACT We present a new triangle scan conversion algorithm that works
Triangle Scan Conversion using 2D Homogeneous Coordinates Marc Olano 1 Trey Greer 2 University of North Carolina Hewlett-Packard ABSTRACT We present a new triangle scan conversion algorithm that works
Transformations in the pipeline
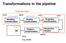 Transformations in the pipeline gltranslatef() Modeling transformation ModelView Matrix OCS WCS glulookat() VCS CCS Viewing transformation Projection transformation DCS Viewport transformation (e.g. pixels)
Transformations in the pipeline gltranslatef() Modeling transformation ModelView Matrix OCS WCS glulookat() VCS CCS Viewing transformation Projection transformation DCS Viewport transformation (e.g. pixels)
Computer Graphics. Introduction. Computer graphics. What is computer graphics? Yung-Yu Chuang
 Introduction Computer Graphics Instructor: Yung-Yu Chuang ( 莊 永 裕 ) E-mail: c@csie.ntu.edu.tw Office: CSIE 527 Grading: a MatchMove project Computer Science ce & Information o Technolog og Yung-Yu Chuang
Introduction Computer Graphics Instructor: Yung-Yu Chuang ( 莊 永 裕 ) E-mail: c@csie.ntu.edu.tw Office: CSIE 527 Grading: a MatchMove project Computer Science ce & Information o Technolog og Yung-Yu Chuang
Introduction to 2D and 3D Computer Graphics Mastering 2D & 3D Computer Graphics Pipelines
 Introduction to 2D and 3D Computer Graphics Mastering 2D & 3D Computer Graphics Pipelines CS447 3-1 Mastering 2D & 3D Graphics Overview of 2D & 3D Pipelines What are pipelines? What are the fundamental
Introduction to 2D and 3D Computer Graphics Mastering 2D & 3D Computer Graphics Pipelines CS447 3-1 Mastering 2D & 3D Graphics Overview of 2D & 3D Pipelines What are pipelines? What are the fundamental
Section 1.1. Introduction to R n
 The Calculus of Functions of Several Variables Section. Introduction to R n Calculus is the study of functional relationships and how related quantities change with each other. In your first exposure to
The Calculus of Functions of Several Variables Section. Introduction to R n Calculus is the study of functional relationships and how related quantities change with each other. In your first exposure to
12.5 Equations of Lines and Planes
 Instructor: Longfei Li Math 43 Lecture Notes.5 Equations of Lines and Planes What do we need to determine a line? D: a point on the line: P 0 (x 0, y 0 ) direction (slope): k 3D: a point on the line: P
Instructor: Longfei Li Math 43 Lecture Notes.5 Equations of Lines and Planes What do we need to determine a line? D: a point on the line: P 0 (x 0, y 0 ) direction (slope): k 3D: a point on the line: P
H.Calculating Normal Vectors
 Appendix H H.Calculating Normal Vectors This appendix describes how to calculate normal vectors for surfaces. You need to define normals to use the OpenGL lighting facility, which is described in Chapter
Appendix H H.Calculating Normal Vectors This appendix describes how to calculate normal vectors for surfaces. You need to define normals to use the OpenGL lighting facility, which is described in Chapter
Geometry of Vectors. 1 Cartesian Coordinates. Carlo Tomasi
 Geometry of Vectors Carlo Tomasi This note explores the geometric meaning of norm, inner product, orthogonality, and projection for vectors. For vectors in three-dimensional space, we also examine the
Geometry of Vectors Carlo Tomasi This note explores the geometric meaning of norm, inner product, orthogonality, and projection for vectors. For vectors in three-dimensional space, we also examine the
Adding vectors We can do arithmetic with vectors. We ll start with vector addition and related operations. Suppose you have two vectors
 1 Chapter 13. VECTORS IN THREE DIMENSIONAL SPACE Let s begin with some names and notation for things: R is the set (collection) of real numbers. We write x R to mean that x is a real number. A real number
1 Chapter 13. VECTORS IN THREE DIMENSIONAL SPACE Let s begin with some names and notation for things: R is the set (collection) of real numbers. We write x R to mean that x is a real number. A real number
Geometric Camera Parameters
 Geometric Camera Parameters What assumptions have we made so far? -All equations we have derived for far are written in the camera reference frames. -These equations are valid only when: () all distances
Geometric Camera Parameters What assumptions have we made so far? -All equations we have derived for far are written in the camera reference frames. -These equations are valid only when: () all distances
521493S Computer Graphics. Exercise 2 & course schedule change
 521493S Computer Graphics Exercise 2 & course schedule change Course Schedule Change Lecture from Wednesday 31th of March is moved to Tuesday 30th of March at 16-18 in TS128 Question 2.1 Given two nonparallel,
521493S Computer Graphics Exercise 2 & course schedule change Course Schedule Change Lecture from Wednesday 31th of March is moved to Tuesday 30th of March at 16-18 in TS128 Question 2.1 Given two nonparallel,
Visualization of 2D Domains
 Visualization of 2D Domains This part of the visualization package is intended to supply a simple graphical interface for 2- dimensional finite element data structures. Furthermore, it is used as the low
Visualization of 2D Domains This part of the visualization package is intended to supply a simple graphical interface for 2- dimensional finite element data structures. Furthermore, it is used as the low
Computational Geometry. Lecture 1: Introduction and Convex Hulls
 Lecture 1: Introduction and convex hulls 1 Geometry: points, lines,... Plane (two-dimensional), R 2 Space (three-dimensional), R 3 Space (higher-dimensional), R d A point in the plane, 3-dimensional space,
Lecture 1: Introduction and convex hulls 1 Geometry: points, lines,... Plane (two-dimensional), R 2 Space (three-dimensional), R 3 Space (higher-dimensional), R d A point in the plane, 3-dimensional space,
Geometric Transformation CS 211A
 Geometric Transformation CS 211A What is transformation? Moving points (x,y) moves to (x+t, y+t) Can be in any dimension 2D Image warps 3D 3D Graphics and Vision Can also be considered as a movement to
Geometric Transformation CS 211A What is transformation? Moving points (x,y) moves to (x+t, y+t) Can be in any dimension 2D Image warps 3D 3D Graphics and Vision Can also be considered as a movement to
Lecture 2: Homogeneous Coordinates, Lines and Conics
 Lecture 2: Homogeneous Coordinates, Lines and Conics 1 Homogeneous Coordinates In Lecture 1 we derived the camera equations λx = P X, (1) where x = (x 1, x 2, 1), X = (X 1, X 2, X 3, 1) and P is a 3 4
Lecture 2: Homogeneous Coordinates, Lines and Conics 1 Homogeneous Coordinates In Lecture 1 we derived the camera equations λx = P X, (1) where x = (x 1, x 2, 1), X = (X 1, X 2, X 3, 1) and P is a 3 4
EdExcel Decision Mathematics 1
 EdExcel Decision Mathematics 1 Linear Programming Section 1: Formulating and solving graphically Notes and Examples These notes contain subsections on: Formulating LP problems Solving LP problems Minimisation
EdExcel Decision Mathematics 1 Linear Programming Section 1: Formulating and solving graphically Notes and Examples These notes contain subsections on: Formulating LP problems Solving LP problems Minimisation
3.1 Solving Systems Using Tables and Graphs
 Algebra 2 Chapter 3 3.1 Solve Systems Using Tables & Graphs 3.1 Solving Systems Using Tables and Graphs A solution to a system of linear equations is an that makes all of the equations. To solve a system
Algebra 2 Chapter 3 3.1 Solve Systems Using Tables & Graphs 3.1 Solving Systems Using Tables and Graphs A solution to a system of linear equations is an that makes all of the equations. To solve a system
Algebra 2 Chapter 1 Vocabulary. identity - A statement that equates two equivalent expressions.
 Chapter 1 Vocabulary identity - A statement that equates two equivalent expressions. verbal model- A word equation that represents a real-life problem. algebraic expression - An expression with variables.
Chapter 1 Vocabulary identity - A statement that equates two equivalent expressions. verbal model- A word equation that represents a real-life problem. algebraic expression - An expression with variables.
B2.53-R3: COMPUTER GRAPHICS. NOTE: 1. There are TWO PARTS in this Module/Paper. PART ONE contains FOUR questions and PART TWO contains FIVE questions.
 B2.53-R3: COMPUTER GRAPHICS NOTE: 1. There are TWO PARTS in this Module/Paper. PART ONE contains FOUR questions and PART TWO contains FIVE questions. 2. PART ONE is to be answered in the TEAR-OFF ANSWER
B2.53-R3: COMPUTER GRAPHICS NOTE: 1. There are TWO PARTS in this Module/Paper. PART ONE contains FOUR questions and PART TWO contains FIVE questions. 2. PART ONE is to be answered in the TEAR-OFF ANSWER
Computer Graphics CS 543 Lecture 12 (Part 1) Curves. Prof Emmanuel Agu. Computer Science Dept. Worcester Polytechnic Institute (WPI)
 Computer Graphics CS 54 Lecture 1 (Part 1) Curves Prof Emmanuel Agu Computer Science Dept. Worcester Polytechnic Institute (WPI) So Far Dealt with straight lines and flat surfaces Real world objects include
Computer Graphics CS 54 Lecture 1 (Part 1) Curves Prof Emmanuel Agu Computer Science Dept. Worcester Polytechnic Institute (WPI) So Far Dealt with straight lines and flat surfaces Real world objects include
Copyright 2011 Casa Software Ltd. www.casaxps.com. Centre of Mass
 Centre of Mass A central theme in mathematical modelling is that of reducing complex problems to simpler, and hopefully, equivalent problems for which mathematical analysis is possible. The concept of
Centre of Mass A central theme in mathematical modelling is that of reducing complex problems to simpler, and hopefully, equivalent problems for which mathematical analysis is possible. The concept of
2.3 WINDOW-TO-VIEWPORT COORDINATE TRANSFORMATION
 2.3 WINDOW-TO-VIEWPORT COORDINATE TRANSFORMATION A world-coordinate area selected for display is called a window. An area on a display device to which a window is mapped is called a viewport. The window
2.3 WINDOW-TO-VIEWPORT COORDINATE TRANSFORMATION A world-coordinate area selected for display is called a window. An area on a display device to which a window is mapped is called a viewport. The window
Investigating Area Under a Curve
 Mathematics Investigating Area Under a Curve About this Lesson This lesson is an introduction to areas bounded by functions and the x-axis on a given interval. Since the functions in the beginning of the
Mathematics Investigating Area Under a Curve About this Lesson This lesson is an introduction to areas bounded by functions and the x-axis on a given interval. Since the functions in the beginning of the
Freehand Sketching. Sections
 3 Freehand Sketching Sections 3.1 Why Freehand Sketches? 3.2 Freehand Sketching Fundamentals 3.3 Basic Freehand Sketching 3.4 Advanced Freehand Sketching Key Terms Objectives Explain why freehand sketching
3 Freehand Sketching Sections 3.1 Why Freehand Sketches? 3.2 Freehand Sketching Fundamentals 3.3 Basic Freehand Sketching 3.4 Advanced Freehand Sketching Key Terms Objectives Explain why freehand sketching
Face detection is a process of localizing and extracting the face region from the
 Chapter 4 FACE NORMALIZATION 4.1 INTRODUCTION Face detection is a process of localizing and extracting the face region from the background. The detected face varies in rotation, brightness, size, etc.
Chapter 4 FACE NORMALIZATION 4.1 INTRODUCTION Face detection is a process of localizing and extracting the face region from the background. The detected face varies in rotation, brightness, size, etc.
L 2 : x = s + 1, y = s, z = 4s + 4. 3. Suppose that C has coordinates (x, y, z). Then from the vector equality AC = BD, one has
 The line L through the points A and B is parallel to the vector AB = 3, 2, and has parametric equations x = 3t + 2, y = 2t +, z = t Therefore, the intersection point of the line with the plane should satisfy:
The line L through the points A and B is parallel to the vector AB = 3, 2, and has parametric equations x = 3t + 2, y = 2t +, z = t Therefore, the intersection point of the line with the plane should satisfy:
Reflection and Refraction
 Equipment Reflection and Refraction Acrylic block set, plane-concave-convex universal mirror, cork board, cork board stand, pins, flashlight, protractor, ruler, mirror worksheet, rectangular block worksheet,
Equipment Reflection and Refraction Acrylic block set, plane-concave-convex universal mirror, cork board, cork board stand, pins, flashlight, protractor, ruler, mirror worksheet, rectangular block worksheet,
SketchUp Instructions
 SketchUp Instructions Every architect needs to know how to use SketchUp! SketchUp is free from Google just Google it and download to your computer. You can do just about anything with it, but it is especially
SketchUp Instructions Every architect needs to know how to use SketchUp! SketchUp is free from Google just Google it and download to your computer. You can do just about anything with it, but it is especially
Solving Simultaneous Equations and Matrices
 Solving Simultaneous Equations and Matrices The following represents a systematic investigation for the steps used to solve two simultaneous linear equations in two unknowns. The motivation for considering
Solving Simultaneous Equations and Matrices The following represents a systematic investigation for the steps used to solve two simultaneous linear equations in two unknowns. The motivation for considering
Angle - a figure formed by two rays or two line segments with a common endpoint called the vertex of the angle; angles are measured in degrees
 Angle - a figure formed by two rays or two line segments with a common endpoint called the vertex of the angle; angles are measured in degrees Apex in a pyramid or cone, the vertex opposite the base; in
Angle - a figure formed by two rays or two line segments with a common endpoint called the vertex of the angle; angles are measured in degrees Apex in a pyramid or cone, the vertex opposite the base; in
Figure 1.1 Vector A and Vector F
 CHAPTER I VECTOR QUANTITIES Quantities are anything which can be measured, and stated with number. Quantities in physics are divided into two types; scalar and vector quantities. Scalar quantities have
CHAPTER I VECTOR QUANTITIES Quantities are anything which can be measured, and stated with number. Quantities in physics are divided into two types; scalar and vector quantities. Scalar quantities have
Section 13.5 Equations of Lines and Planes
 Section 13.5 Equations of Lines and Planes Generalizing Linear Equations One of the main aspects of single variable calculus was approximating graphs of functions by lines - specifically, tangent lines.
Section 13.5 Equations of Lines and Planes Generalizing Linear Equations One of the main aspects of single variable calculus was approximating graphs of functions by lines - specifically, tangent lines.
Essential Mathematics for Computer Graphics fast
 John Vince Essential Mathematics for Computer Graphics fast Springer Contents 1. MATHEMATICS 1 Is mathematics difficult? 3 Who should read this book? 4 Aims and objectives of this book 4 Assumptions made
John Vince Essential Mathematics for Computer Graphics fast Springer Contents 1. MATHEMATICS 1 Is mathematics difficult? 3 Who should read this book? 4 Aims and objectives of this book 4 Assumptions made
Solutions to Practice Problems
 Higher Geometry Final Exam Tues Dec 11, 5-7:30 pm Practice Problems (1) Know the following definitions, statements of theorems, properties from the notes: congruent, triangle, quadrilateral, isosceles
Higher Geometry Final Exam Tues Dec 11, 5-7:30 pm Practice Problems (1) Know the following definitions, statements of theorems, properties from the notes: congruent, triangle, quadrilateral, isosceles
Equations Involving Lines and Planes Standard equations for lines in space
 Equations Involving Lines and Planes In this section we will collect various important formulas regarding equations of lines and planes in three dimensional space Reminder regarding notation: any quantity
Equations Involving Lines and Planes In this section we will collect various important formulas regarding equations of lines and planes in three dimensional space Reminder regarding notation: any quantity
3D Viewing. Chapter 7. Projections. 3D clipping. OpenGL viewing functions and clipping planes
 3D Viewing Chapter 7 Projections 3D clipping OpenGL viewing functions and clipping planes 1 Projections Parallel Perspective Coordinates are transformed along parallel lines Relative sizes are preserved
3D Viewing Chapter 7 Projections 3D clipping OpenGL viewing functions and clipping planes 1 Projections Parallel Perspective Coordinates are transformed along parallel lines Relative sizes are preserved
Unified Lecture # 4 Vectors
 Fall 2005 Unified Lecture # 4 Vectors These notes were written by J. Peraire as a review of vectors for Dynamics 16.07. They have been adapted for Unified Engineering by R. Radovitzky. References [1] Feynmann,
Fall 2005 Unified Lecture # 4 Vectors These notes were written by J. Peraire as a review of vectors for Dynamics 16.07. They have been adapted for Unified Engineering by R. Radovitzky. References [1] Feynmann,
Solving Geometric Problems with the Rotating Calipers *
 Solving Geometric Problems with the Rotating Calipers * Godfried Toussaint School of Computer Science McGill University Montreal, Quebec, Canada ABSTRACT Shamos [1] recently showed that the diameter of
Solving Geometric Problems with the Rotating Calipers * Godfried Toussaint School of Computer Science McGill University Montreal, Quebec, Canada ABSTRACT Shamos [1] recently showed that the diameter of
Lesson 26: Reflection & Mirror Diagrams
 Lesson 26: Reflection & Mirror Diagrams The Law of Reflection There is nothing really mysterious about reflection, but some people try to make it more difficult than it really is. All EMR will reflect
Lesson 26: Reflection & Mirror Diagrams The Law of Reflection There is nothing really mysterious about reflection, but some people try to make it more difficult than it really is. All EMR will reflect
Geometry Notes PERIMETER AND AREA
 Perimeter and Area Page 1 of 57 PERIMETER AND AREA Objectives: After completing this section, you should be able to do the following: Calculate the area of given geometric figures. Calculate the perimeter
Perimeter and Area Page 1 of 57 PERIMETER AND AREA Objectives: After completing this section, you should be able to do the following: Calculate the area of given geometric figures. Calculate the perimeter
1 Determinants and the Solvability of Linear Systems
 1 Determinants and the Solvability of Linear Systems In the last section we learned how to use Gaussian elimination to solve linear systems of n equations in n unknowns The section completely side-stepped
1 Determinants and the Solvability of Linear Systems In the last section we learned how to use Gaussian elimination to solve linear systems of n equations in n unknowns The section completely side-stepped
9.4. The Scalar Product. Introduction. Prerequisites. Learning Style. Learning Outcomes
 The Scalar Product 9.4 Introduction There are two kinds of multiplication involving vectors. The first is known as the scalar product or dot product. This is so-called because when the scalar product of
The Scalar Product 9.4 Introduction There are two kinds of multiplication involving vectors. The first is known as the scalar product or dot product. This is so-called because when the scalar product of
3D Scanner using Line Laser. 1. Introduction. 2. Theory
 . Introduction 3D Scanner using Line Laser Di Lu Electrical, Computer, and Systems Engineering Rensselaer Polytechnic Institute The goal of 3D reconstruction is to recover the 3D properties of a geometric
. Introduction 3D Scanner using Line Laser Di Lu Electrical, Computer, and Systems Engineering Rensselaer Polytechnic Institute The goal of 3D reconstruction is to recover the 3D properties of a geometric
The Graphical Method: An Example
 The Graphical Method: An Example Consider the following linear program: Maximize 4x 1 +3x 2 Subject to: 2x 1 +3x 2 6 (1) 3x 1 +2x 2 3 (2) 2x 2 5 (3) 2x 1 +x 2 4 (4) x 1, x 2 0, where, for ease of reference,
The Graphical Method: An Example Consider the following linear program: Maximize 4x 1 +3x 2 Subject to: 2x 1 +3x 2 6 (1) 3x 1 +2x 2 3 (2) 2x 2 5 (3) 2x 1 +x 2 4 (4) x 1, x 2 0, where, for ease of reference,
Vector storage and access; algorithms in GIS. This is lecture 6
 Vector storage and access; algorithms in GIS This is lecture 6 Vector data storage and access Vectors are built from points, line and areas. (x,y) Surface: (x,y,z) Vector data access Access to vector
Vector storage and access; algorithms in GIS This is lecture 6 Vector data storage and access Vectors are built from points, line and areas. (x,y) Surface: (x,y,z) Vector data access Access to vector
Lines & Planes. Packages: linalg, plots. Commands: evalm, spacecurve, plot3d, display, solve, implicitplot, dotprod, seq, implicitplot3d.
 Lines & Planes Introduction and Goals: This lab is simply to give you some practice with plotting straight lines and planes and how to do some basic problem solving with them. So the exercises will be
Lines & Planes Introduction and Goals: This lab is simply to give you some practice with plotting straight lines and planes and how to do some basic problem solving with them. So the exercises will be
Section 1: How will you be tested? This section will give you information about the different types of examination papers that are available.
 REVISION CHECKLIST for IGCSE Mathematics 0580 A guide for students How to use this guide This guide describes what topics and skills you need to know for your IGCSE Mathematics examination. It will help
REVISION CHECKLIST for IGCSE Mathematics 0580 A guide for students How to use this guide This guide describes what topics and skills you need to know for your IGCSE Mathematics examination. It will help
SolidWorks Implementation Guides. Sketching Concepts
 SolidWorks Implementation Guides Sketching Concepts Sketching in SolidWorks is the basis for creating features. Features are the basis for creating parts, which can be put together into assemblies. Sketch
SolidWorks Implementation Guides Sketching Concepts Sketching in SolidWorks is the basis for creating features. Features are the basis for creating parts, which can be put together into assemblies. Sketch
Lecture 3: Coordinate Systems and Transformations
 Lecture 3: Coordinate Systems and Transformations Topics: 1. Coordinate systems and frames 2. Change of frames 3. Affine transformations 4. Rotation, translation, scaling, and shear 5. Rotation about an
Lecture 3: Coordinate Systems and Transformations Topics: 1. Coordinate systems and frames 2. Change of frames 3. Affine transformations 4. Rotation, translation, scaling, and shear 5. Rotation about an
Lecture Notes, CEng 477
 Computer Graphics Hardware and Software Lecture Notes, CEng 477 What is Computer Graphics? Different things in different contexts: pictures, scenes that are generated by a computer. tools used to make
Computer Graphics Hardware and Software Lecture Notes, CEng 477 What is Computer Graphics? Different things in different contexts: pictures, scenes that are generated by a computer. tools used to make
Content. Chapter 4 Functions 61 4.1 Basic concepts on real functions 62. Credits 11
 Content Credits 11 Chapter 1 Arithmetic Refresher 13 1.1 Algebra 14 Real Numbers 14 Real Polynomials 19 1.2 Equations in one variable 21 Linear Equations 21 Quadratic Equations 22 1.3 Exercises 28 Chapter
Content Credits 11 Chapter 1 Arithmetic Refresher 13 1.1 Algebra 14 Real Numbers 14 Real Polynomials 19 1.2 Equations in one variable 21 Linear Equations 21 Quadratic Equations 22 1.3 Exercises 28 Chapter
THREE DIMENSIONAL GEOMETRY
 Chapter 8 THREE DIMENSIONAL GEOMETRY 8.1 Introduction In this chapter we present a vector algebra approach to three dimensional geometry. The aim is to present standard properties of lines and planes,
Chapter 8 THREE DIMENSIONAL GEOMETRY 8.1 Introduction In this chapter we present a vector algebra approach to three dimensional geometry. The aim is to present standard properties of lines and planes,
Biggar High School Mathematics Department. National 5 Learning Intentions & Success Criteria: Assessing My Progress
 Biggar High School Mathematics Department National 5 Learning Intentions & Success Criteria: Assessing My Progress Expressions & Formulae Topic Learning Intention Success Criteria I understand this Approximation
Biggar High School Mathematics Department National 5 Learning Intentions & Success Criteria: Assessing My Progress Expressions & Formulae Topic Learning Intention Success Criteria I understand this Approximation
Intersection of Convex Objects: The Method of Separating Axes
 Intersection of Convex Objects: The Method of Separating Axes David Eberly Geometric Tools, LLC http://www.geometrictools.com/ Copyright c 1998-2016. All Rights Reserved. Created: January 28, 2001 Last
Intersection of Convex Objects: The Method of Separating Axes David Eberly Geometric Tools, LLC http://www.geometrictools.com/ Copyright c 1998-2016. All Rights Reserved. Created: January 28, 2001 Last
Math 2443, Section 16.3
 Math 44, Section 6. Review These notes will supplement not replace) the lectures based on Section 6. Section 6. i) ouble integrals over general regions: We defined double integrals over rectangles in the
Math 44, Section 6. Review These notes will supplement not replace) the lectures based on Section 6. Section 6. i) ouble integrals over general regions: We defined double integrals over rectangles in the
Section 2.4: Equations of Lines and Planes
 Section.4: Equations of Lines and Planes An equation of three variable F (x, y, z) 0 is called an equation of a surface S if For instance, (x 1, y 1, z 1 ) S if and only if F (x 1, y 1, z 1 ) 0. x + y
Section.4: Equations of Lines and Planes An equation of three variable F (x, y, z) 0 is called an equation of a surface S if For instance, (x 1, y 1, z 1 ) S if and only if F (x 1, y 1, z 1 ) 0. x + y
The Essentials of CAGD
 The Essentials of CAGD Chapter 2: Lines and Planes Gerald Farin & Dianne Hansford CRC Press, Taylor & Francis Group, An A K Peters Book www.farinhansford.com/books/essentials-cagd c 2000 Farin & Hansford
The Essentials of CAGD Chapter 2: Lines and Planes Gerald Farin & Dianne Hansford CRC Press, Taylor & Francis Group, An A K Peters Book www.farinhansford.com/books/essentials-cagd c 2000 Farin & Hansford
Math 1B, lecture 5: area and volume
 Math B, lecture 5: area and volume Nathan Pflueger 6 September 2 Introduction This lecture and the next will be concerned with the computation of areas of regions in the plane, and volumes of regions in
Math B, lecture 5: area and volume Nathan Pflueger 6 September 2 Introduction This lecture and the next will be concerned with the computation of areas of regions in the plane, and volumes of regions in
Geometry Chapter 1. 1.1 Point (pt) 1.1 Coplanar (1.1) 1.1 Space (1.1) 1.2 Line Segment (seg) 1.2 Measure of a Segment
 Geometry Chapter 1 Section Term 1.1 Point (pt) Definition A location. It is drawn as a dot, and named with a capital letter. It has no shape or size. undefined term 1.1 Line A line is made up of points
Geometry Chapter 1 Section Term 1.1 Point (pt) Definition A location. It is drawn as a dot, and named with a capital letter. It has no shape or size. undefined term 1.1 Line A line is made up of points
Geometry and Measurement
 The student will be able to: Geometry and Measurement 1. Demonstrate an understanding of the principles of geometry and measurement and operations using measurements Use the US system of measurement for
The student will be able to: Geometry and Measurement 1. Demonstrate an understanding of the principles of geometry and measurement and operations using measurements Use the US system of measurement for
TWO-DIMENSIONAL TRANSFORMATION
 CHAPTER 2 TWO-DIMENSIONAL TRANSFORMATION 2.1 Introduction As stated earlier, Computer Aided Design consists of three components, namely, Design (Geometric Modeling), Analysis (FEA, etc), and Visualization
CHAPTER 2 TWO-DIMENSIONAL TRANSFORMATION 2.1 Introduction As stated earlier, Computer Aided Design consists of three components, namely, Design (Geometric Modeling), Analysis (FEA, etc), and Visualization
Linear Programming. Solving LP Models Using MS Excel, 18
 SUPPLEMENT TO CHAPTER SIX Linear Programming SUPPLEMENT OUTLINE Introduction, 2 Linear Programming Models, 2 Model Formulation, 4 Graphical Linear Programming, 5 Outline of Graphical Procedure, 5 Plotting
SUPPLEMENT TO CHAPTER SIX Linear Programming SUPPLEMENT OUTLINE Introduction, 2 Linear Programming Models, 2 Model Formulation, 4 Graphical Linear Programming, 5 Outline of Graphical Procedure, 5 Plotting
Computer Graphics Hardware An Overview
 Computer Graphics Hardware An Overview Graphics System Monitor Input devices CPU/Memory GPU Raster Graphics System Raster: An array of picture elements Based on raster-scan TV technology The screen (and
Computer Graphics Hardware An Overview Graphics System Monitor Input devices CPU/Memory GPU Raster Graphics System Raster: An array of picture elements Based on raster-scan TV technology The screen (and
LINEAR INEQUALITIES. Mathematics is the art of saying many things in many different ways. MAXWELL
 Chapter 6 LINEAR INEQUALITIES 6.1 Introduction Mathematics is the art of saying many things in many different ways. MAXWELL In earlier classes, we have studied equations in one variable and two variables
Chapter 6 LINEAR INEQUALITIES 6.1 Introduction Mathematics is the art of saying many things in many different ways. MAXWELL In earlier classes, we have studied equations in one variable and two variables
In mathematics, there are four attainment targets: using and applying mathematics; number and algebra; shape, space and measures, and handling data.
 MATHEMATICS: THE LEVEL DESCRIPTIONS In mathematics, there are four attainment targets: using and applying mathematics; number and algebra; shape, space and measures, and handling data. Attainment target
MATHEMATICS: THE LEVEL DESCRIPTIONS In mathematics, there are four attainment targets: using and applying mathematics; number and algebra; shape, space and measures, and handling data. Attainment target
ALGEBRA. sequence, term, nth term, consecutive, rule, relationship, generate, predict, continue increase, decrease finite, infinite
 ALGEBRA Pupils should be taught to: Generate and describe sequences As outcomes, Year 7 pupils should, for example: Use, read and write, spelling correctly: sequence, term, nth term, consecutive, rule,
ALGEBRA Pupils should be taught to: Generate and describe sequences As outcomes, Year 7 pupils should, for example: Use, read and write, spelling correctly: sequence, term, nth term, consecutive, rule,
Planar Curve Intersection
 Chapter 7 Planar Curve Intersection Curve intersection involves finding the points at which two planar curves intersect. If the two curves are parametric, the solution also identifies the parameter values
Chapter 7 Planar Curve Intersection Curve intersection involves finding the points at which two planar curves intersect. If the two curves are parametric, the solution also identifies the parameter values
Chapter 19. General Matrices. An n m matrix is an array. a 11 a 12 a 1m a 21 a 22 a 2m A = a n1 a n2 a nm. The matrix A has n row vectors
 Chapter 9. General Matrices An n m matrix is an array a a a m a a a m... = [a ij]. a n a n a nm The matrix A has n row vectors and m column vectors row i (A) = [a i, a i,..., a im ] R m a j a j a nj col
Chapter 9. General Matrices An n m matrix is an array a a a m a a a m... = [a ij]. a n a n a nm The matrix A has n row vectors and m column vectors row i (A) = [a i, a i,..., a im ] R m a j a j a nj col
We can display an object on a monitor screen in three different computer-model forms: Wireframe model Surface Model Solid model
 CHAPTER 4 CURVES 4.1 Introduction In order to understand the significance of curves, we should look into the types of model representations that are used in geometric modeling. Curves play a very significant
CHAPTER 4 CURVES 4.1 Introduction In order to understand the significance of curves, we should look into the types of model representations that are used in geometric modeling. Curves play a very significant
Solutions to Homework 10
 Solutions to Homework 1 Section 7., exercise # 1 (b,d): (b) Compute the value of R f dv, where f(x, y) = y/x and R = [1, 3] [, 4]. Solution: Since f is continuous over R, f is integrable over R. Let x
Solutions to Homework 1 Section 7., exercise # 1 (b,d): (b) Compute the value of R f dv, where f(x, y) = y/x and R = [1, 3] [, 4]. Solution: Since f is continuous over R, f is integrable over R. Let x
Cabri Geometry Application User Guide
 Cabri Geometry Application User Guide Preview of Geometry... 2 Learning the Basics... 3 Managing File Operations... 12 Setting Application Preferences... 14 Selecting and Moving Objects... 17 Deleting
Cabri Geometry Application User Guide Preview of Geometry... 2 Learning the Basics... 3 Managing File Operations... 12 Setting Application Preferences... 14 Selecting and Moving Objects... 17 Deleting
Math 181 Handout 16. Rich Schwartz. March 9, 2010
 Math 8 Handout 6 Rich Schwartz March 9, 200 The purpose of this handout is to describe continued fractions and their connection to hyperbolic geometry. The Gauss Map Given any x (0, ) we define γ(x) =
Math 8 Handout 6 Rich Schwartz March 9, 200 The purpose of this handout is to describe continued fractions and their connection to hyperbolic geometry. The Gauss Map Given any x (0, ) we define γ(x) =
CIRCLE COORDINATE GEOMETRY
 CIRCLE COORDINATE GEOMETRY (EXAM QUESTIONS) Question 1 (**) A circle has equation x + y = 2x + 8 Determine the radius and the coordinates of the centre of the circle. r = 3, ( 1,0 ) Question 2 (**) A circle
CIRCLE COORDINATE GEOMETRY (EXAM QUESTIONS) Question 1 (**) A circle has equation x + y = 2x + 8 Determine the radius and the coordinates of the centre of the circle. r = 3, ( 1,0 ) Question 2 (**) A circle
MA 323 Geometric Modelling Course Notes: Day 02 Model Construction Problem
 MA 323 Geometric Modelling Course Notes: Day 02 Model Construction Problem David L. Finn November 30th, 2004 In the next few days, we will introduce some of the basic problems in geometric modelling, and
MA 323 Geometric Modelling Course Notes: Day 02 Model Construction Problem David L. Finn November 30th, 2004 In the next few days, we will introduce some of the basic problems in geometric modelling, and
The Dot and Cross Products
 The Dot and Cross Products Two common operations involving vectors are the dot product and the cross product. Let two vectors =,, and =,, be given. The Dot Product The dot product of and is written and
The Dot and Cross Products Two common operations involving vectors are the dot product and the cross product. Let two vectors =,, and =,, be given. The Dot Product The dot product of and is written and
4. How many integers between 2004 and 4002 are perfect squares?
 5 is 0% of what number? What is the value of + 3 4 + 99 00? (alternating signs) 3 A frog is at the bottom of a well 0 feet deep It climbs up 3 feet every day, but slides back feet each night If it started
5 is 0% of what number? What is the value of + 3 4 + 99 00? (alternating signs) 3 A frog is at the bottom of a well 0 feet deep It climbs up 3 feet every day, but slides back feet each night If it started
MA107 Precalculus Algebra Exam 2 Review Solutions
 MA107 Precalculus Algebra Exam 2 Review Solutions February 24, 2008 1. The following demand equation models the number of units sold, x, of a product as a function of price, p. x = 4p + 200 a. Please write
MA107 Precalculus Algebra Exam 2 Review Solutions February 24, 2008 1. The following demand equation models the number of units sold, x, of a product as a function of price, p. x = 4p + 200 a. Please write
Basic Problem: Map a 3D object to a 2D display surface. Analogy - Taking a snapshot with a camera
 3D Viewing Basic Problem: Map a 3D object to a 2D display surface Analogy - Taking a snapshot with a camera Synthetic camera virtual camera we can move to any location & orient in any way then create a
3D Viewing Basic Problem: Map a 3D object to a 2D display surface Analogy - Taking a snapshot with a camera Synthetic camera virtual camera we can move to any location & orient in any way then create a
Closest Pair Problem
 Closest Pair Problem Given n points in d-dimensions, find two whose mutual distance is smallest. Fundamental problem in many applications as well as a key step in many algorithms. p q A naive algorithm
Closest Pair Problem Given n points in d-dimensions, find two whose mutual distance is smallest. Fundamental problem in many applications as well as a key step in many algorithms. p q A naive algorithm
LINES AND PLANES CHRIS JOHNSON
 LINES AND PLANES CHRIS JOHNSON Abstract. In this lecture we derive the equations for lines and planes living in 3-space, as well as define the angle between two non-parallel planes, and determine the distance
LINES AND PLANES CHRIS JOHNSON Abstract. In this lecture we derive the equations for lines and planes living in 3-space, as well as define the angle between two non-parallel planes, and determine the distance
Computer Graphics. Anders Hast
 Computer Graphics Anders Hast Who am I?! 5 years in Industry after graduation, 2 years as high school teacher.! 1996 Teacher, University of Gävle! 2004 PhD, Computerised Image Processing " Computer Graphics!
Computer Graphics Anders Hast Who am I?! 5 years in Industry after graduation, 2 years as high school teacher.! 1996 Teacher, University of Gävle! 2004 PhD, Computerised Image Processing " Computer Graphics!
Section 1.1 Linear Equations: Slope and Equations of Lines
 Section. Linear Equations: Slope and Equations of Lines Slope The measure of the steepness of a line is called the slope of the line. It is the amount of change in y, the rise, divided by the amount of
Section. Linear Equations: Slope and Equations of Lines Slope The measure of the steepness of a line is called the slope of the line. It is the amount of change in y, the rise, divided by the amount of
11.1. Objectives. Component Form of a Vector. Component Form of a Vector. Component Form of a Vector. Vectors and the Geometry of Space
 11 Vectors and the Geometry of Space 11.1 Vectors in the Plane Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. 2 Objectives! Write the component form of
11 Vectors and the Geometry of Space 11.1 Vectors in the Plane Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. 2 Objectives! Write the component form of
ME 111: Engineering Drawing
 ME 111: Engineering Drawing Lecture # 14 (10/10/2011) Development of Surfaces http://www.iitg.ernet.in/arindam.dey/me111.htm http://www.iitg.ernet.in/rkbc/me111.htm http://shilloi.iitg.ernet.in/~psr/ Indian
ME 111: Engineering Drawing Lecture # 14 (10/10/2011) Development of Surfaces http://www.iitg.ernet.in/arindam.dey/me111.htm http://www.iitg.ernet.in/rkbc/me111.htm http://shilloi.iitg.ernet.in/~psr/ Indian
Solutions to Math 51 First Exam January 29, 2015
 Solutions to Math 5 First Exam January 29, 25. ( points) (a) Complete the following sentence: A set of vectors {v,..., v k } is defined to be linearly dependent if (2 points) there exist c,... c k R, not
Solutions to Math 5 First Exam January 29, 25. ( points) (a) Complete the following sentence: A set of vectors {v,..., v k } is defined to be linearly dependent if (2 points) there exist c,... c k R, not
Contents. 2 Lines and Circles 3 2.1 Cartesian Coordinates... 3 2.2 Distance and Midpoint Formulas... 3 2.3 Lines... 3 2.4 Circles...
 Contents Lines and Circles 3.1 Cartesian Coordinates.......................... 3. Distance and Midpoint Formulas.................... 3.3 Lines.................................. 3.4 Circles..................................
Contents Lines and Circles 3.1 Cartesian Coordinates.......................... 3. Distance and Midpoint Formulas.................... 3.3 Lines.................................. 3.4 Circles..................................
MATH2210 Notebook 1 Fall Semester 2016/2017. 1 MATH2210 Notebook 1 3. 1.1 Solving Systems of Linear Equations... 3
 MATH0 Notebook Fall Semester 06/07 prepared by Professor Jenny Baglivo c Copyright 009 07 by Jenny A. Baglivo. All Rights Reserved. Contents MATH0 Notebook 3. Solving Systems of Linear Equations........................
MATH0 Notebook Fall Semester 06/07 prepared by Professor Jenny Baglivo c Copyright 009 07 by Jenny A. Baglivo. All Rights Reserved. Contents MATH0 Notebook 3. Solving Systems of Linear Equations........................
Activity Set 4. Trainer Guide
 Geometry and Measurement of Solid Figures Activity Set 4 Trainer Guide Mid_SGe_04_TG Copyright by the McGraw-Hill Companies McGraw-Hill Professional Development GEOMETRY AND MEASUREMENT OF SOLID FIGURES
Geometry and Measurement of Solid Figures Activity Set 4 Trainer Guide Mid_SGe_04_TG Copyright by the McGraw-Hill Companies McGraw-Hill Professional Development GEOMETRY AND MEASUREMENT OF SOLID FIGURES
