Projections and Transformations in OpenGL
|
|
|
- Jacob Young
- 7 years ago
- Views:
Transcription
1 Image Processing and Computer Graphics Projections and Transformations in OpenGL Matthias Teschner Computer Science Department University of Freiburg
2 Motivation for the rendering of objects in 3D space, a planar view has to be generated 3D space is projected onto a 2D plane considering external and internal camera parameters position, orientation, focal length in homogeneous notation, 3D projections can be represented with a 4x4 transformation matrix University of Freiburg Computer Science Department Computer Graphics - 2
3 Examples left images 3D scene with a view volume right images projections onto the viewplane top-right parallel projection top-bottom perspective projection [Song Ho Ahn] University of Freiburg Computer Science Department Computer Graphics - 3
4 Outline 2D projection 3D projection OpenGL projection matrix OpenGL transformation matrices University of Freiburg Computer Science Department Computer Graphics - 4
5 Projection in 2D a 2D projection from v onto l maps a point p onto p' p' is the intersection of the line through p and v with line l v is the viewpoint, center of perspectivity l is the viewline the line through p and v is a projector v is not on the line l, p v University of Freiburg Computer Science Department Computer Graphics - 5
6 Projection in 2D if the homogeneous component of the viewpoint v is not equal to zero, we have a perspective projection projectors are not parallel if v is at infinity, we have a parallel projection projectors are parallel perspective projection parallel projection University of Freiburg Computer Science Department Computer Graphics - 6
7 Classification location of viewpoint and orientation of the viewline determine the type of projection parallel (viewpoint at infinity, parallel projectors) orthographic (viewline orthogonal to the projectors) oblique (viewline not orthogonal to the projectors) perspective (non-parallel projectors) one-point (viewline intersects one principal axis, i.e. viewline is parallel to a principal axis, one vanishing point) two-point (viewline intersects two principal axis, two vanishing points) University of Freiburg Computer Science Department Computer Graphics - 7
8 General Case a 2D projection is represented by matrix University of Freiburg Computer Science Department Computer Graphics - 8
9 Example e.g. d=-1, (1,2) T is mapped to (0,1) T University of Freiburg Computer Science Department Computer Graphics - 9
10 Discussion matrices M and M represent the same transformation therefore, and represent the same transformation x is mapped to zero, y is scaled depending on x moving d to infinity results in parallel projection University of Freiburg Computer Science Department Computer Graphics - 10
11 Discussion parallel projection University of Freiburg Computer Science Department Computer Graphics - 11
12 Discussion maps p to p' x = 0 maps p to p' y = -d p y maps p with p w =1 to p' w = p x - d University of Freiburg Computer Science Department Computer Graphics - 12
13 Discussion 2D transformation in homogeneous form w x and w y map the homogeneous component w of a point to a value w' that depends on x and y therefore, the scaling of a point depends on x and / or y in perspective 3D projections, this is generally employed to scale the x- and y- component with respect to z, its distance to the viewer University of Freiburg Computer Science Department Computer Graphics - 13
14 Outline 2D projection 3D projection OpenGL projection matrix OpenGL transformation matrices University of Freiburg Computer Science Department Computer Graphics - 14
15 Projection in 3D a 3D projection from v onto n maps a point p onto p' p' is the intersection of the line through p and v with plane n v is the viewpoint, center of perspectivity n is the viewplane the line through p and v is a projector v is not on the plane n, p v University of Freiburg Computer Science Department Computer Graphics - 15
16 General Case a 3D projection is represented by a matrix University of Freiburg Computer Science Department Computer Graphics - 16
17 Example e.g. d=-1, (1,2,0) T is mapped to (0,1,0) T University of Freiburg Computer Science Department Computer Graphics - 17
18 Example parallel projection onto the plane z = 0 with viewpoint / viewing direction v = (0,0,1,0) T x- and y-component are unchanged, z is mapped to zero remember that M and M with, e. g., =-1 represent the same transformation University of Freiburg Computer Science Department Computer Graphics - 18
19 Outline 2D projection 3D projection OpenGL projection matrix perspective projection parallel projection OpenGL transformation matrices University of Freiburg Computer Science Department Computer Graphics - 19
20 View Volume in OpenGL, the projection transformation maps a view volume to the canonical view volume the view volume is specified by its boundary left, right, bottom, top, near far the canonical view volume is a cube from (-1,-1,-1) to (1,1,1) (l, t, f) (x, y, f) [Song Ho Ahn] this transformation implements this transformation implements orthographic projection perspective projection University of Freiburg Computer Science Department Computer Graphics - 20
21 OpenGL Projection Transform the projection transform maps from eye coordinates to clip coordinates (w-component is not necessarily one) to normalized device coordinates NDC (x and y are normalized with respect to w, w is preserved for further processing) the projection transform maps the x-component of a point from (left, right) to (-1, 1) the y-component of a point from (bottom, top) to (-1, 1) the z-component of a point from (near, far) to (-1, 1) in OpenGL, near and far are negative, so the mapping incorporates a reflection (change of right-handed to left-handed) however, in OpenGL functions, usually the negative of near and far is specified which is positive University of Freiburg Computer Science Department Computer Graphics - 21
22 Perspective Projection to obtain x- and y-component of a projected point, the point is first projected onto the near plane (viewplane) [Song Ho Ahn] note that n and f denote the negative near and far values University of Freiburg Computer Science Department Computer Graphics - 22
23 Mapping of x p and y p to (-1, 1) [Song Ho Ahn] University of Freiburg Computer Science Department Computer Graphics - 23
24 Projection Matrix from we get clip coordinates with normalized device coordinates University of Freiburg Computer Science Department Computer Graphics - 24
25 Mapping of z e to (-1, 1) z e is mapped from (near, far) or (-n, -f) to (-1, 1) the transform does not depend on x e and y e so, we have to solve for A and B in University of Freiburg Computer Science Department Computer Graphics - 25
26 Mapping of z e to (-1, 1) z e =-n with w e =1 is mapped to z n =-1 z e =-f with w e =1 is mapped to z f =1 the complete matrix is University of Freiburg Computer Science Department Computer Graphics - 26
27 Perspective Projection Matrix the matrix transforms the view volume, the pyramidal frustum to the canonical view volume pyramidal frustum [Song Ho Ahn] University of Freiburg Computer Science Department Computer Graphics - 27
28 Perspective Projection Matrix projection matrix for negated values for n and f (OpenGL) projection matrix for actual values for n and f University of Freiburg Computer Science Department Computer Graphics - 28
29 Symmetric Setting the matrix simplifies for r = -l and t = -b University of Freiburg Computer Science Department Computer Graphics - 29
30 Near Plane nonlinear mapping of z e : varying resolution / accuracy due to fix-point representation of depth values in the depth buffer z n z n z n z e z e z e do not move the near plane too close to zero University of Freiburg Computer Science Department Computer Graphics - 30
31 Far Plane setting the far plane to infinity is not too critical z n z e University of Freiburg Computer Science Department Computer Graphics - 31
32 Outline 2D projection 3D projection OpenGL projection matrix perspective projection parallel projection OpenGL transformation matrices University of Freiburg Computer Science Department Computer Graphics - 32
33 Parallel Projection the view volume is represented by a cuboid left, right, bottom, top, near, far [Song Ho Ahn] the projection transform maps the cuboid to the canonical view volume University of Freiburg Computer Science Department Computer Graphics - 33
34 Mapping of x e, y e, z e to (-1,1) all components of a point in eye coordinates are linearly mapped to the range of (-1,1) [Song Ho Ahn] linear in x e, y e, z e combination of scale and translation University of Freiburg Computer Science Department Computer Graphics - 34
35 Orthographic Projection Matrix general form simplified form for a symmetric view volume University of Freiburg Computer Science Department Computer Graphics - 35
36 Outline 2D projection 3D projection OpenGL projection matrix OpenGL transformation matrices University of Freiburg Computer Science Department Computer Graphics - 36
37 OpenGL Matrices objects are transformed from object to eye space with the GL_MODELVIEW matrix objects are transformed from eye space to clip space with the GL_PROJECTION matrix colors are transformed with the color matrix GL_COLOR texture coordinates are transformed with the texture matrix GL_TEXTURE University of Freiburg Computer Science Department Computer Graphics - 37
38 Matrix Stack each matrix type has a stack the matrix on top of the stack is used glmatrixmode(gl_projection); choose a matrix stack glloadidentity(); glfrustum(left, right, bottom, top, near, far); the top element is replaced with I 4 projection matrix P is generated the top element on the stack is multiplied with P resulting in I 4 P University of Freiburg Computer Science Department Computer Graphics - 38
39 Matrix Stack glmatrixmode(gl_modelview); glloadidentity(); gltranslatef(x,y,z); glrotatef(alpha,1,0,0); choose a matrix stack the top element is replaced with I 4 translation matrix T is generated the top element on the stack is multiplied with T resulting in I 4 T rotation matrix R is generated the top element on the stack is multiplied with R resulting in I 4 T R note that objects are rotated by R, followed by the translation T University of Freiburg Computer Science Department Computer Graphics - 39
40 Matrix Stack glmatrixmode(gl_modelview); glloadidentity(); gltranslatef(x,y,z); glrotatef(alpha,1,0,0); glpush(); gltranslatef(x,y,z); glpop(); choose a matrix stack the top element is replaced with I 4 the top element is I 4 T the top element is I 4 T R the top element I 4 T R is pushed into the stack the newly generated top element is initialized with I 4 T R the top element is I 4 T R T the top element is replaced by the previously stored element I 4 T R University of Freiburg Computer Science Department Computer Graphics - 40
41 OpenGL Matrix Functions glpushmatrix(): push the current matrix into the current matrix stack. glpopmatrix(): pop the current matrix from the current matrix stack. glloadidentity(): set the current matrix to the identity matrix. glloadmatrix{fd}(m): replace the current matrix with the matrix m. glloadtransposematrix{fd}(m) : replace the current matrix with the rowmajor ordered matrix m. glmultmatrix{fd}(m): multiply the current matrix by the matrix m, and update the result to the current matrix. glmulttransposematrix{fd}(m): multiply the current matrix by the row-major ordered matrix m, and update the result to the current matrix. glgetfloatv(gl_modelview_matrix, m): return 16 values of GL_MODELVIEW matrix to m. note that OpenGL functions expect column-major matrices in contrast to commonly used row-major matrices University of Freiburg Computer Science Department Computer Graphics - 41
42 Modelview Example objects are transformed with V -1 M V=T v R v the camera is oriented and then translated M 1..4 =T 1..4 R 1..4 implementation choose the GL_MODELVIEW stack initialize with I 4 rotate with R v -1 translate with T v -1 push translate with T 1 rotate with R 1 render object M 1 pop objects are oriented and then translated I 4 R v -1 R v -1 T v -1 = V -1 R v -1 T v -1 R v -1 T v -1 T 1 R v -1 T v -1 T 1 R 1 R v -1 T v -1 M 1 M 3 M 2 University of Freiburg Computer Science Department Computer Graphics - 42 V M 4 [Akenine-Moeller et al.: Real-time Rendering]
43 Summary 2D projection 3D projection OpenGL projection matrix perspective projection parallel projection OpenGL transformation matrices University of Freiburg Computer Science Department Computer Graphics - 43
44 References Duncan Marsh: "Applied Geometry for Computer Graphics and CAD", Springer Verlag, Berlin, Song Ho Ahn: "OpenGL", University of Freiburg Computer Science Department Computer Graphics - 44
Image Processing and Computer Graphics. Rendering Pipeline. Matthias Teschner. Computer Science Department University of Freiburg
 Image Processing and Computer Graphics Rendering Pipeline Matthias Teschner Computer Science Department University of Freiburg Outline introduction rendering pipeline vertex processing primitive processing
Image Processing and Computer Graphics Rendering Pipeline Matthias Teschner Computer Science Department University of Freiburg Outline introduction rendering pipeline vertex processing primitive processing
Realtime 3D Computer Graphics Virtual Reality
 Realtime 3D Computer Graphics Virtual Realit Viewing and projection Classical and General Viewing Transformation Pipeline CPU Pol. DL Pixel Per Vertex Texture Raster Frag FB object ee clip normalized device
Realtime 3D Computer Graphics Virtual Realit Viewing and projection Classical and General Viewing Transformation Pipeline CPU Pol. DL Pixel Per Vertex Texture Raster Frag FB object ee clip normalized device
CS 4204 Computer Graphics
 CS 4204 Computer Graphics 2D and 3D Transformations Doug Bowman Adapted from notes by Yong Cao Virginia Tech 1 Transformations What are they? changing something to something else via rules mathematics:
CS 4204 Computer Graphics 2D and 3D Transformations Doug Bowman Adapted from notes by Yong Cao Virginia Tech 1 Transformations What are they? changing something to something else via rules mathematics:
CS 4204 Computer Graphics
 CS 4204 Computer Graphics 3D views and projection Adapted from notes by Yong Cao 1 Overview of 3D rendering Modeling: *Define object in local coordinates *Place object in world coordinates (modeling transformation)
CS 4204 Computer Graphics 3D views and projection Adapted from notes by Yong Cao 1 Overview of 3D rendering Modeling: *Define object in local coordinates *Place object in world coordinates (modeling transformation)
4BA6 - Topic 4 Dr. Steven Collins. Chap. 5 3D Viewing and Projections
 4BA6 - Topic 4 Dr. Steven Collins Chap. 5 3D Viewing and Projections References Computer graphics: principles & practice, Fole, vandam, Feiner, Hughes, S-LEN 5.644 M23*;-6 (has a good appendix on linear
4BA6 - Topic 4 Dr. Steven Collins Chap. 5 3D Viewing and Projections References Computer graphics: principles & practice, Fole, vandam, Feiner, Hughes, S-LEN 5.644 M23*;-6 (has a good appendix on linear
521493S Computer Graphics. Exercise 2 & course schedule change
 521493S Computer Graphics Exercise 2 & course schedule change Course Schedule Change Lecture from Wednesday 31th of March is moved to Tuesday 30th of March at 16-18 in TS128 Question 2.1 Given two nonparallel,
521493S Computer Graphics Exercise 2 & course schedule change Course Schedule Change Lecture from Wednesday 31th of March is moved to Tuesday 30th of March at 16-18 in TS128 Question 2.1 Given two nonparallel,
Geometry for Computer Graphics
 Computer Graphics and Visualisation Geometry for Computer Graphics Student Notes Developed by F Lin K Wyrwas J Irwin C Lilley W T Hewitt T L J Howard Computer Graphics Unit Manchester Computing Centre
Computer Graphics and Visualisation Geometry for Computer Graphics Student Notes Developed by F Lin K Wyrwas J Irwin C Lilley W T Hewitt T L J Howard Computer Graphics Unit Manchester Computing Centre
Transformations in the pipeline
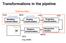 Transformations in the pipeline gltranslatef() Modeling transformation ModelView Matrix OCS WCS glulookat() VCS CCS Viewing transformation Projection transformation DCS Viewport transformation (e.g. pixels)
Transformations in the pipeline gltranslatef() Modeling transformation ModelView Matrix OCS WCS glulookat() VCS CCS Viewing transformation Projection transformation DCS Viewport transformation (e.g. pixels)
INTRODUCTION TO RENDERING TECHNIQUES
 INTRODUCTION TO RENDERING TECHNIQUES 22 Mar. 212 Yanir Kleiman What is 3D Graphics? Why 3D? Draw one frame at a time Model only once X 24 frames per second Color / texture only once 15, frames for a feature
INTRODUCTION TO RENDERING TECHNIQUES 22 Mar. 212 Yanir Kleiman What is 3D Graphics? Why 3D? Draw one frame at a time Model only once X 24 frames per second Color / texture only once 15, frames for a feature
Monash University Clayton s School of Information Technology CSE3313 Computer Graphics Sample Exam Questions 2007
 Monash University Clayton s School of Information Technology CSE3313 Computer Graphics Questions 2007 INSTRUCTIONS: Answer all questions. Spend approximately 1 minute per mark. Question 1 30 Marks Total
Monash University Clayton s School of Information Technology CSE3313 Computer Graphics Questions 2007 INSTRUCTIONS: Answer all questions. Spend approximately 1 minute per mark. Question 1 30 Marks Total
Given a point cloud, polygon, or sampled parametric curve, we can use transformations for several purposes:
 3 3.1 2D Given a point cloud, polygon, or sampled parametric curve, we can use transformations for several purposes: 1. Change coordinate frames (world, window, viewport, device, etc). 2. Compose objects
3 3.1 2D Given a point cloud, polygon, or sampled parametric curve, we can use transformations for several purposes: 1. Change coordinate frames (world, window, viewport, device, etc). 2. Compose objects
3D Viewing. Chapter 7. Projections. 3D clipping. OpenGL viewing functions and clipping planes
 3D Viewing Chapter 7 Projections 3D clipping OpenGL viewing functions and clipping planes 1 Projections Parallel Perspective Coordinates are transformed along parallel lines Relative sizes are preserved
3D Viewing Chapter 7 Projections 3D clipping OpenGL viewing functions and clipping planes 1 Projections Parallel Perspective Coordinates are transformed along parallel lines Relative sizes are preserved
Basic Problem: Map a 3D object to a 2D display surface. Analogy - Taking a snapshot with a camera
 3D Viewing Basic Problem: Map a 3D object to a 2D display surface Analogy - Taking a snapshot with a camera Synthetic camera virtual camera we can move to any location & orient in any way then create a
3D Viewing Basic Problem: Map a 3D object to a 2D display surface Analogy - Taking a snapshot with a camera Synthetic camera virtual camera we can move to any location & orient in any way then create a
Aston University. School of Engineering & Applied Science
 CS2150 Aston University School of Engineering & Applied Science CS2150: Computer Graphics January Examinations 2010 Date: XXX Time: XXX Instructions to Candidates: 1. Answer Question ONE and any other
CS2150 Aston University School of Engineering & Applied Science CS2150: Computer Graphics January Examinations 2010 Date: XXX Time: XXX Instructions to Candidates: 1. Answer Question ONE and any other
Lecture 3: Coordinate Systems and Transformations
 Lecture 3: Coordinate Systems and Transformations Topics: 1. Coordinate systems and frames 2. Change of frames 3. Affine transformations 4. Rotation, translation, scaling, and shear 5. Rotation about an
Lecture 3: Coordinate Systems and Transformations Topics: 1. Coordinate systems and frames 2. Change of frames 3. Affine transformations 4. Rotation, translation, scaling, and shear 5. Rotation about an
The Geometry of Perspective Projection
 The Geometry o Perspective Projection Pinhole camera and perspective projection - This is the simplest imaging device which, however, captures accurately the geometry o perspective projection. -Rays o
The Geometry o Perspective Projection Pinhole camera and perspective projection - This is the simplest imaging device which, however, captures accurately the geometry o perspective projection. -Rays o
Computer Graphics Labs
 Computer Graphics Labs Abel J. P. Gomes LAB. 2 Department of Computer Science and Engineering University of Beira Interior Portugal 2011 Copyright 2009-2011 All rights reserved. LAB. 2 1. Learning goals
Computer Graphics Labs Abel J. P. Gomes LAB. 2 Department of Computer Science and Engineering University of Beira Interior Portugal 2011 Copyright 2009-2011 All rights reserved. LAB. 2 1. Learning goals
Geometric Camera Parameters
 Geometric Camera Parameters What assumptions have we made so far? -All equations we have derived for far are written in the camera reference frames. -These equations are valid only when: () all distances
Geometric Camera Parameters What assumptions have we made so far? -All equations we have derived for far are written in the camera reference frames. -These equations are valid only when: () all distances
Essential Mathematics for Computer Graphics fast
 John Vince Essential Mathematics for Computer Graphics fast Springer Contents 1. MATHEMATICS 1 Is mathematics difficult? 3 Who should read this book? 4 Aims and objectives of this book 4 Assumptions made
John Vince Essential Mathematics for Computer Graphics fast Springer Contents 1. MATHEMATICS 1 Is mathematics difficult? 3 Who should read this book? 4 Aims and objectives of this book 4 Assumptions made
Lecture Notes. Fundamentals of Computer Graphics. Prof. Michael Langer School of Computer Science McGill University
 COMP 557 Winter 2015 Lecture Notes Fundamentals of Computer Graphics Prof. Michael Langer School of Computer Science McGill University NOTE: These lecture notes are dynamic. The initial version of the
COMP 557 Winter 2015 Lecture Notes Fundamentals of Computer Graphics Prof. Michael Langer School of Computer Science McGill University NOTE: These lecture notes are dynamic. The initial version of the
Graphics Pipeline in a Nutshell
 Graphics Pipeline in a Nutshell How do we create a rendering such as this? CS334 Spring 2008 Design the scene (technical drawing in wireframe ) Apply perspective transformations to the scene geometry for
Graphics Pipeline in a Nutshell How do we create a rendering such as this? CS334 Spring 2008 Design the scene (technical drawing in wireframe ) Apply perspective transformations to the scene geometry for
LINES AND PLANES CHRIS JOHNSON
 LINES AND PLANES CHRIS JOHNSON Abstract. In this lecture we derive the equations for lines and planes living in 3-space, as well as define the angle between two non-parallel planes, and determine the distance
LINES AND PLANES CHRIS JOHNSON Abstract. In this lecture we derive the equations for lines and planes living in 3-space, as well as define the angle between two non-parallel planes, and determine the distance
Introduction to Computer Graphics
 Introduction to Computer Graphics Torsten Möller TASC 8021 778-782-2215 torsten@sfu.ca www.cs.sfu.ca/~torsten Today What is computer graphics? Contents of this course Syllabus Overview of course topics
Introduction to Computer Graphics Torsten Möller TASC 8021 778-782-2215 torsten@sfu.ca www.cs.sfu.ca/~torsten Today What is computer graphics? Contents of this course Syllabus Overview of course topics
Proseminar Graphikprogrammierung
 Proseminar Graphikprogrammierung Matthias Teschner Computer Science Department University of Freiburg Contact Matthias Teschner 052 / 01-005 teschner@informatik.uni-freiburg.de http://cg.informatik.unifreiburg.de/teaching.htm
Proseminar Graphikprogrammierung Matthias Teschner Computer Science Department University of Freiburg Contact Matthias Teschner 052 / 01-005 teschner@informatik.uni-freiburg.de http://cg.informatik.unifreiburg.de/teaching.htm
Solving Simultaneous Equations and Matrices
 Solving Simultaneous Equations and Matrices The following represents a systematic investigation for the steps used to solve two simultaneous linear equations in two unknowns. The motivation for considering
Solving Simultaneous Equations and Matrices The following represents a systematic investigation for the steps used to solve two simultaneous linear equations in two unknowns. The motivation for considering
Lecture 2: Homogeneous Coordinates, Lines and Conics
 Lecture 2: Homogeneous Coordinates, Lines and Conics 1 Homogeneous Coordinates In Lecture 1 we derived the camera equations λx = P X, (1) where x = (x 1, x 2, 1), X = (X 1, X 2, X 3, 1) and P is a 3 4
Lecture 2: Homogeneous Coordinates, Lines and Conics 1 Homogeneous Coordinates In Lecture 1 we derived the camera equations λx = P X, (1) where x = (x 1, x 2, 1), X = (X 1, X 2, X 3, 1) and P is a 3 4
Pro/ENGINEER Wildfire 4.0 Basic Design
 Introduction Datum features are non-solid features used during the construction of other features. The most common datum features include planes, axes, coordinate systems, and curves. Datum features do
Introduction Datum features are non-solid features used during the construction of other features. The most common datum features include planes, axes, coordinate systems, and curves. Datum features do
Android and OpenGL. Android Smartphone Programming. Matthias Keil. University of Freiburg
 Android and OpenGL Android Smartphone Programming Matthias Keil Institute for Computer Science Faculty of Engineering 16. Dezember 2013 Outline 1 OpenGL Introduction 2 Displaying Graphics 3 Interaction
Android and OpenGL Android Smartphone Programming Matthias Keil Institute for Computer Science Faculty of Engineering 16. Dezember 2013 Outline 1 OpenGL Introduction 2 Displaying Graphics 3 Interaction
Q27.1 When a charged particle moves near a bar magnet, the magnetic force on the particle at a certain point depends
 Q27.1 When a charged particle moves near a bar magnet, the magnetic force on the particle at a certain point depends A. on the direction of the magnetic field at that point only. B. on the magnetic field
Q27.1 When a charged particle moves near a bar magnet, the magnetic force on the particle at a certain point depends A. on the direction of the magnetic field at that point only. B. on the magnetic field
α = u v. In other words, Orthogonal Projection
 Orthogonal Projection Given any nonzero vector v, it is possible to decompose an arbitrary vector u into a component that points in the direction of v and one that points in a direction orthogonal to v
Orthogonal Projection Given any nonzero vector v, it is possible to decompose an arbitrary vector u into a component that points in the direction of v and one that points in a direction orthogonal to v
Orthogonal Projections
 Orthogonal Projections and Reflections (with exercises) by D. Klain Version.. Corrections and comments are welcome! Orthogonal Projections Let X,..., X k be a family of linearly independent (column) vectors
Orthogonal Projections and Reflections (with exercises) by D. Klain Version.. Corrections and comments are welcome! Orthogonal Projections Let X,..., X k be a family of linearly independent (column) vectors
Geometric Transformation CS 211A
 Geometric Transformation CS 211A What is transformation? Moving points (x,y) moves to (x+t, y+t) Can be in any dimension 2D Image warps 3D 3D Graphics and Vision Can also be considered as a movement to
Geometric Transformation CS 211A What is transformation? Moving points (x,y) moves to (x+t, y+t) Can be in any dimension 2D Image warps 3D 3D Graphics and Vision Can also be considered as a movement to
From 3D to 2D: Orthographic and Perspective Projection Part 1
 From 3D to 2D: Orthographic and Perspective Projection Part 1 History Geometrical Constructions Types of Projection Projection in Computer Graphics Andries van Dam September 13, 2001 3D Viewing I 1/34
From 3D to 2D: Orthographic and Perspective Projection Part 1 History Geometrical Constructions Types of Projection Projection in Computer Graphics Andries van Dam September 13, 2001 3D Viewing I 1/34
3D Math Overview and 3D Graphics Foundations
 Freescale Semiconductor Application Note Document Number: AN4132 Rev. 0, 05/2010 3D Math Overview and 3D Graphics Foundations by Multimedia Applications Division Freescale Semiconductor, Inc. Austin, TX
Freescale Semiconductor Application Note Document Number: AN4132 Rev. 0, 05/2010 3D Math Overview and 3D Graphics Foundations by Multimedia Applications Division Freescale Semiconductor, Inc. Austin, TX
3 Orthogonal Vectors and Matrices
 3 Orthogonal Vectors and Matrices The linear algebra portion of this course focuses on three matrix factorizations: QR factorization, singular valued decomposition (SVD), and LU factorization The first
3 Orthogonal Vectors and Matrices The linear algebra portion of this course focuses on three matrix factorizations: QR factorization, singular valued decomposition (SVD), and LU factorization The first
B2.53-R3: COMPUTER GRAPHICS. NOTE: 1. There are TWO PARTS in this Module/Paper. PART ONE contains FOUR questions and PART TWO contains FIVE questions.
 B2.53-R3: COMPUTER GRAPHICS NOTE: 1. There are TWO PARTS in this Module/Paper. PART ONE contains FOUR questions and PART TWO contains FIVE questions. 2. PART ONE is to be answered in the TEAR-OFF ANSWER
B2.53-R3: COMPUTER GRAPHICS NOTE: 1. There are TWO PARTS in this Module/Paper. PART ONE contains FOUR questions and PART TWO contains FIVE questions. 2. PART ONE is to be answered in the TEAR-OFF ANSWER
Adding vectors We can do arithmetic with vectors. We ll start with vector addition and related operations. Suppose you have two vectors
 1 Chapter 13. VECTORS IN THREE DIMENSIONAL SPACE Let s begin with some names and notation for things: R is the set (collection) of real numbers. We write x R to mean that x is a real number. A real number
1 Chapter 13. VECTORS IN THREE DIMENSIONAL SPACE Let s begin with some names and notation for things: R is the set (collection) of real numbers. We write x R to mean that x is a real number. A real number
Least-Squares Intersection of Lines
 Least-Squares Intersection of Lines Johannes Traa - UIUC 2013 This write-up derives the least-squares solution for the intersection of lines. In the general case, a set of lines will not intersect at a
Least-Squares Intersection of Lines Johannes Traa - UIUC 2013 This write-up derives the least-squares solution for the intersection of lines. In the general case, a set of lines will not intersect at a
Geometric Constraints
 Simulation in Computer Graphics Geometric Constraints Matthias Teschner Computer Science Department University of Freiburg Outline introduction penalty method Lagrange multipliers local constraints University
Simulation in Computer Graphics Geometric Constraints Matthias Teschner Computer Science Department University of Freiburg Outline introduction penalty method Lagrange multipliers local constraints University
B4 Computational Geometry
 3CG 2006 / B4 Computational Geometry David Murray david.murray@eng.o.ac.uk www.robots.o.ac.uk/ dwm/courses/3cg Michaelmas 2006 3CG 2006 2 / Overview Computational geometry is concerned with the derivation
3CG 2006 / B4 Computational Geometry David Murray david.murray@eng.o.ac.uk www.robots.o.ac.uk/ dwm/courses/3cg Michaelmas 2006 3CG 2006 2 / Overview Computational geometry is concerned with the derivation
GUI GRAPHICS AND USER INTERFACES. Welcome to GUI! Mechanics. Mihail Gaianu 26/02/2014 1
 Welcome to GUI! Mechanics 26/02/2014 1 Requirements Info If you don t know C++, you CAN take this class additional time investment required early on GUI Java to C++ transition tutorial on course website
Welcome to GUI! Mechanics 26/02/2014 1 Requirements Info If you don t know C++, you CAN take this class additional time investment required early on GUI Java to C++ transition tutorial on course website
Projective Geometry: A Short Introduction. Lecture Notes Edmond Boyer
 Projective Geometry: A Short Introduction Lecture Notes Edmond Boyer Contents 1 Introduction 2 11 Objective 2 12 Historical Background 3 13 Bibliography 4 2 Projective Spaces 5 21 Definitions 5 22 Properties
Projective Geometry: A Short Introduction Lecture Notes Edmond Boyer Contents 1 Introduction 2 11 Objective 2 12 Historical Background 3 13 Bibliography 4 2 Projective Spaces 5 21 Definitions 5 22 Properties
SketchUp Instructions
 SketchUp Instructions Every architect needs to know how to use SketchUp! SketchUp is free from Google just Google it and download to your computer. You can do just about anything with it, but it is especially
SketchUp Instructions Every architect needs to know how to use SketchUp! SketchUp is free from Google just Google it and download to your computer. You can do just about anything with it, but it is especially
Mechanics lecture 7 Moment of a force, torque, equilibrium of a body
 G.1 EE1.el3 (EEE1023): Electronics III Mechanics lecture 7 Moment of a force, torque, equilibrium of a body Dr Philip Jackson http://www.ee.surrey.ac.uk/teaching/courses/ee1.el3/ G.2 Moments, torque and
G.1 EE1.el3 (EEE1023): Electronics III Mechanics lecture 7 Moment of a force, torque, equilibrium of a body Dr Philip Jackson http://www.ee.surrey.ac.uk/teaching/courses/ee1.el3/ G.2 Moments, torque and
Relating Vanishing Points to Catadioptric Camera Calibration
 Relating Vanishing Points to Catadioptric Camera Calibration Wenting Duan* a, Hui Zhang b, Nigel M. Allinson a a Laboratory of Vision Engineering, University of Lincoln, Brayford Pool, Lincoln, U.K. LN6
Relating Vanishing Points to Catadioptric Camera Calibration Wenting Duan* a, Hui Zhang b, Nigel M. Allinson a a Laboratory of Vision Engineering, University of Lincoln, Brayford Pool, Lincoln, U.K. LN6
Solution Guide III-C. 3D Vision. Building Vision for Business. MVTec Software GmbH
 Solution Guide III-C 3D Vision MVTec Software GmbH Building Vision for Business Machine vision in 3D world coordinates, Version 10.0.4 All rights reserved. No part of this publication may be reproduced,
Solution Guide III-C 3D Vision MVTec Software GmbH Building Vision for Business Machine vision in 3D world coordinates, Version 10.0.4 All rights reserved. No part of this publication may be reproduced,
KEANSBURG SCHOOL DISTRICT KEANSBURG HIGH SCHOOL Mathematics Department. HSPA 10 Curriculum. September 2007
 KEANSBURG HIGH SCHOOL Mathematics Department HSPA 10 Curriculum September 2007 Written by: Karen Egan Mathematics Supervisor: Ann Gagliardi 7 days Sample and Display Data (Chapter 1 pp. 4-47) Surveys and
KEANSBURG HIGH SCHOOL Mathematics Department HSPA 10 Curriculum September 2007 Written by: Karen Egan Mathematics Supervisor: Ann Gagliardi 7 days Sample and Display Data (Chapter 1 pp. 4-47) Surveys and
Notes on Orthogonal and Symmetric Matrices MENU, Winter 2013
 Notes on Orthogonal and Symmetric Matrices MENU, Winter 201 These notes summarize the main properties and uses of orthogonal and symmetric matrices. We covered quite a bit of material regarding these topics,
Notes on Orthogonal and Symmetric Matrices MENU, Winter 201 These notes summarize the main properties and uses of orthogonal and symmetric matrices. We covered quite a bit of material regarding these topics,
Chapter 2 - Graphics Programming with JOGL
 Chapter 2 - Graphics Programming with JOGL Graphics Software: Classification and History JOGL Hello World Program 2D Coordinate Systems in JOGL Dealing with Window Reshaping 3D Coordinate Systems in JOGL
Chapter 2 - Graphics Programming with JOGL Graphics Software: Classification and History JOGL Hello World Program 2D Coordinate Systems in JOGL Dealing with Window Reshaping 3D Coordinate Systems in JOGL
Jan Köhnlein and Helmut Weberpals 01.12.99
 1 Graphics Primitives Graphics Primitives 3-dimensional point class Point3d 3-dimensional (directional) vector class Vector3d Class of 3-dimensional line segments LineArray 2 Modeling of 3D Objects Modeling
1 Graphics Primitives Graphics Primitives 3-dimensional point class Point3d 3-dimensional (directional) vector class Vector3d Class of 3-dimensional line segments LineArray 2 Modeling of 3D Objects Modeling
Introduction to 2D and 3D Computer Graphics Mastering 2D & 3D Computer Graphics Pipelines
 Introduction to 2D and 3D Computer Graphics Mastering 2D & 3D Computer Graphics Pipelines CS447 3-1 Mastering 2D & 3D Graphics Overview of 2D & 3D Pipelines What are pipelines? What are the fundamental
Introduction to 2D and 3D Computer Graphics Mastering 2D & 3D Computer Graphics Pipelines CS447 3-1 Mastering 2D & 3D Graphics Overview of 2D & 3D Pipelines What are pipelines? What are the fundamental
w = COI EYE view direction vector u = w ( 010,, ) cross product with y-axis v = w u up vector
 . w COI EYE view direction vector u w ( 00,, ) cross product with -ais v w u up vector (EQ ) Computer Animation: Algorithms and Techniques 29 up vector view vector observer center of interest 30 Computer
. w COI EYE view direction vector u w ( 00,, ) cross product with -ais v w u up vector (EQ ) Computer Animation: Algorithms and Techniques 29 up vector view vector observer center of interest 30 Computer
How To Draw A Billiards Ball In Gta 3D With Texture Mapping (Gta 3) On A Computer Or 2D Or Gta 2D (Gt) On Your Computer Or Computer Or Your Computer (Or Your Computer)
 Pool Billiard An OpenGL-based billiard simulation Stefan HUBER Kamran SAFDAR Andreas SCHRÖCKER Fachbereich Computerwissenschaften Universität Salzburg June 10, 2009 S. Huber, K. Safdar, A. Schröcker: Pool
Pool Billiard An OpenGL-based billiard simulation Stefan HUBER Kamran SAFDAR Andreas SCHRÖCKER Fachbereich Computerwissenschaften Universität Salzburg June 10, 2009 S. Huber, K. Safdar, A. Schröcker: Pool
TWO-DIMENSIONAL TRANSFORMATION
 CHAPTER 2 TWO-DIMENSIONAL TRANSFORMATION 2.1 Introduction As stated earlier, Computer Aided Design consists of three components, namely, Design (Geometric Modeling), Analysis (FEA, etc), and Visualization
CHAPTER 2 TWO-DIMENSIONAL TRANSFORMATION 2.1 Introduction As stated earlier, Computer Aided Design consists of three components, namely, Design (Geometric Modeling), Analysis (FEA, etc), and Visualization
Essay 5 Tutorial for a Three-Dimensional Heat Conduction Problem Using ANSYS Workbench
 Essay 5 Tutorial for a Three-Dimensional Heat Conduction Problem Using ANSYS Workbench 5.1 Introduction The problem selected to illustrate the use of ANSYS software for a three-dimensional steadystate
Essay 5 Tutorial for a Three-Dimensional Heat Conduction Problem Using ANSYS Workbench 5.1 Introduction The problem selected to illustrate the use of ANSYS software for a three-dimensional steadystate
Mediated Reality using Computer Graphics Hardware for Computer Vision
 Mediated Reality using Computer Graphics Hardware for Computer Vision James Fung, Felix Tang and Steve Mann University of Toronto, Dept. of Electrical and Computer Engineering 10 King s College Road, Toronto,
Mediated Reality using Computer Graphics Hardware for Computer Vision James Fung, Felix Tang and Steve Mann University of Toronto, Dept. of Electrical and Computer Engineering 10 King s College Road, Toronto,
A Short Introduction to Computer Graphics
 A Short Introduction to Computer Graphics Frédo Durand MIT Laboratory for Computer Science 1 Introduction Chapter I: Basics Although computer graphics is a vast field that encompasses almost any graphical
A Short Introduction to Computer Graphics Frédo Durand MIT Laboratory for Computer Science 1 Introduction Chapter I: Basics Although computer graphics is a vast field that encompasses almost any graphical
Vector Math Computer Graphics Scott D. Anderson
 Vector Math Computer Graphics Scott D. Anderson 1 Dot Product The notation v w means the dot product or scalar product or inner product of two vectors, v and w. In abstract mathematics, we can talk about
Vector Math Computer Graphics Scott D. Anderson 1 Dot Product The notation v w means the dot product or scalar product or inner product of two vectors, v and w. In abstract mathematics, we can talk about
Number Sense and Operations
 Number Sense and Operations representing as they: 6.N.1 6.N.2 6.N.3 6.N.4 6.N.5 6.N.6 6.N.7 6.N.8 6.N.9 6.N.10 6.N.11 6.N.12 6.N.13. 6.N.14 6.N.15 Demonstrate an understanding of positive integer exponents
Number Sense and Operations representing as they: 6.N.1 6.N.2 6.N.3 6.N.4 6.N.5 6.N.6 6.N.7 6.N.8 6.N.9 6.N.10 6.N.11 6.N.12 6.N.13. 6.N.14 6.N.15 Demonstrate an understanding of positive integer exponents
2x + y = 3. Since the second equation is precisely the same as the first equation, it is enough to find x and y satisfying the system
 1. Systems of linear equations We are interested in the solutions to systems of linear equations. A linear equation is of the form 3x 5y + 2z + w = 3. The key thing is that we don t multiply the variables
1. Systems of linear equations We are interested in the solutions to systems of linear equations. A linear equation is of the form 3x 5y + 2z + w = 3. The key thing is that we don t multiply the variables
SYNTHESIZING FREE-VIEWPOINT IMAGES FROM MULTIPLE VIEW VIDEOS IN SOCCER STADIUM
 SYNTHESIZING FREE-VIEWPOINT IMAGES FROM MULTIPLE VIEW VIDEOS IN SOCCER STADIUM Kunihiko Hayashi, Hideo Saito Department of Information and Computer Science, Keio University {hayashi,saito}@ozawa.ics.keio.ac.jp
SYNTHESIZING FREE-VIEWPOINT IMAGES FROM MULTIPLE VIEW VIDEOS IN SOCCER STADIUM Kunihiko Hayashi, Hideo Saito Department of Information and Computer Science, Keio University {hayashi,saito}@ozawa.ics.keio.ac.jp
2D Geometric Transformations
 2D Geometric Transformations (Chapter 5 in FVD) 2D Geometric Transformations Question: How do we represent a geometric object in the plane? Answer: For now, assume that objects consist of points and lines.
2D Geometric Transformations (Chapter 5 in FVD) 2D Geometric Transformations Question: How do we represent a geometric object in the plane? Answer: For now, assume that objects consist of points and lines.
is in plane V. However, it may be more convenient to introduce a plane coordinate system in V.
 .4 COORDINATES EXAMPLE Let V be the plane in R with equation x +2x 2 +x 0, a two-dimensional subspace of R. We can describe a vector in this plane by its spatial (D)coordinates; for example, vector x 5
.4 COORDINATES EXAMPLE Let V be the plane in R with equation x +2x 2 +x 0, a two-dimensional subspace of R. We can describe a vector in this plane by its spatial (D)coordinates; for example, vector x 5
1 Symmetries of regular polyhedra
 1230, notes 5 1 Symmetries of regular polyhedra Symmetry groups Recall: Group axioms: Suppose that (G, ) is a group and a, b, c are elements of G. Then (i) a b G (ii) (a b) c = a (b c) (iii) There is an
1230, notes 5 1 Symmetries of regular polyhedra Symmetry groups Recall: Group axioms: Suppose that (G, ) is a group and a, b, c are elements of G. Then (i) a b G (ii) (a b) c = a (b c) (iii) There is an
Fractions and Linear Equations
 Fractions and Linear Equations Fraction Operations While you can perform operations on fractions using the calculator, for this worksheet you must perform the operations by hand. You must show all steps
Fractions and Linear Equations Fraction Operations While you can perform operations on fractions using the calculator, for this worksheet you must perform the operations by hand. You must show all steps
Section 1.7 22 Continued
 Section 1.5 23 A homogeneous equation is always consistent. TRUE - The trivial solution is always a solution. The equation Ax = 0 gives an explicit descriptions of its solution set. FALSE - The equation
Section 1.5 23 A homogeneous equation is always consistent. TRUE - The trivial solution is always a solution. The equation Ax = 0 gives an explicit descriptions of its solution set. FALSE - The equation
Solutions to Math 51 First Exam January 29, 2015
 Solutions to Math 5 First Exam January 29, 25. ( points) (a) Complete the following sentence: A set of vectors {v,..., v k } is defined to be linearly dependent if (2 points) there exist c,... c k R, not
Solutions to Math 5 First Exam January 29, 25. ( points) (a) Complete the following sentence: A set of vectors {v,..., v k } is defined to be linearly dependent if (2 points) there exist c,... c k R, not
The Car Tutorial Part 1 Creating a Racing Game for Unity
 The Car Tutorial Part 1 Creating a Racing Game for Unity Introduction 3 We will show 3 Prerequisites 3 We will not show 4 Part 1: Assembling the Car 5 Adding Collision 6 Shadow settings for the car model
The Car Tutorial Part 1 Creating a Racing Game for Unity Introduction 3 We will show 3 Prerequisites 3 We will not show 4 Part 1: Assembling the Car 5 Adding Collision 6 Shadow settings for the car model
MATH 551 - APPLIED MATRIX THEORY
 MATH 55 - APPLIED MATRIX THEORY FINAL TEST: SAMPLE with SOLUTIONS (25 points NAME: PROBLEM (3 points A web of 5 pages is described by a directed graph whose matrix is given by A Do the following ( points
MATH 55 - APPLIED MATRIX THEORY FINAL TEST: SAMPLE with SOLUTIONS (25 points NAME: PROBLEM (3 points A web of 5 pages is described by a directed graph whose matrix is given by A Do the following ( points
We can display an object on a monitor screen in three different computer-model forms: Wireframe model Surface Model Solid model
 CHAPTER 4 CURVES 4.1 Introduction In order to understand the significance of curves, we should look into the types of model representations that are used in geometric modeling. Curves play a very significant
CHAPTER 4 CURVES 4.1 Introduction In order to understand the significance of curves, we should look into the types of model representations that are used in geometric modeling. Curves play a very significant
COMP175: Computer Graphics. Lecture 1 Introduction and Display Technologies
 COMP175: Computer Graphics Lecture 1 Introduction and Display Technologies Course mechanics Number: COMP 175-01, Fall 2009 Meetings: TR 1:30-2:45pm Instructor: Sara Su (sarasu@cs.tufts.edu) TA: Matt Menke
COMP175: Computer Graphics Lecture 1 Introduction and Display Technologies Course mechanics Number: COMP 175-01, Fall 2009 Meetings: TR 1:30-2:45pm Instructor: Sara Su (sarasu@cs.tufts.edu) TA: Matt Menke
Anamorphic Projection Photographic Techniques for setting up 3D Chalk Paintings
 Anamorphic Projection Photographic Techniques for setting up 3D Chalk Paintings By Wayne and Cheryl Renshaw. Although it is centuries old, the art of street painting has been going through a resurgence.
Anamorphic Projection Photographic Techniques for setting up 3D Chalk Paintings By Wayne and Cheryl Renshaw. Although it is centuries old, the art of street painting has been going through a resurgence.
GRADES 7, 8, AND 9 BIG IDEAS
 Table 1: Strand A: BIG IDEAS: MATH: NUMBER Introduce perfect squares, square roots, and all applications Introduce rational numbers (positive and negative) Introduce the meaning of negative exponents for
Table 1: Strand A: BIG IDEAS: MATH: NUMBER Introduce perfect squares, square roots, and all applications Introduce rational numbers (positive and negative) Introduce the meaning of negative exponents for
Cross product and determinants (Sect. 12.4) Two main ways to introduce the cross product
 Cross product and determinants (Sect. 12.4) Two main ways to introduce the cross product Geometrical definition Properties Expression in components. Definition in components Properties Geometrical expression.
Cross product and determinants (Sect. 12.4) Two main ways to introduce the cross product Geometrical definition Properties Expression in components. Definition in components Properties Geometrical expression.
Rotation Matrices and Homogeneous Transformations
 Rotation Matrices and Homogeneous Transformations A coordinate frame in an n-dimensional space is defined by n mutually orthogonal unit vectors. In particular, for a two-dimensional (2D) space, i.e., n
Rotation Matrices and Homogeneous Transformations A coordinate frame in an n-dimensional space is defined by n mutually orthogonal unit vectors. In particular, for a two-dimensional (2D) space, i.e., n
11.1. Objectives. Component Form of a Vector. Component Form of a Vector. Component Form of a Vector. Vectors and the Geometry of Space
 11 Vectors and the Geometry of Space 11.1 Vectors in the Plane Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. 2 Objectives! Write the component form of
11 Vectors and the Geometry of Space 11.1 Vectors in the Plane Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. 2 Objectives! Write the component form of
Vector Notation: AB represents the vector from point A to point B on a graph. The vector can be computed by B A.
 1 Linear Transformations Prepared by: Robin Michelle King A transformation of an object is a change in position or dimension (or both) of the object. The resulting object after the transformation is called
1 Linear Transformations Prepared by: Robin Michelle King A transformation of an object is a change in position or dimension (or both) of the object. The resulting object after the transformation is called
CATIA: Navigating the CATIA V5 environment. D. CHABLAT / S. CARO Damien.Chablat@irccyn.ec-nantes.fr
 CATIA: Navigating the CATIA V5 environment D. CHABLAT / S. CARO Damien.Chablat@irccyn.ec-nantes.fr Standard Screen Layout 5 4 6 7 1 2 3 8 9 10 11 12 13 14 15 D. Chablat / S. Caro -- Institut de Recherche
CATIA: Navigating the CATIA V5 environment D. CHABLAT / S. CARO Damien.Chablat@irccyn.ec-nantes.fr Standard Screen Layout 5 4 6 7 1 2 3 8 9 10 11 12 13 14 15 D. Chablat / S. Caro -- Institut de Recherche
Orthogonal Diagonalization of Symmetric Matrices
 MATH10212 Linear Algebra Brief lecture notes 57 Gram Schmidt Process enables us to find an orthogonal basis of a subspace. Let u 1,..., u k be a basis of a subspace V of R n. We begin the process of finding
MATH10212 Linear Algebra Brief lecture notes 57 Gram Schmidt Process enables us to find an orthogonal basis of a subspace. Let u 1,..., u k be a basis of a subspace V of R n. We begin the process of finding
What is Visualization? Information Visualization An Overview. Information Visualization. Definitions
 What is Visualization? Information Visualization An Overview Jonathan I. Maletic, Ph.D. Computer Science Kent State University Visualize/Visualization: To form a mental image or vision of [some
What is Visualization? Information Visualization An Overview Jonathan I. Maletic, Ph.D. Computer Science Kent State University Visualize/Visualization: To form a mental image or vision of [some
LEAVING CERT DCG SCHEME OF WORK
 2010-11 LEAVING CERT DCG SCHEME OF WORK ST OLIVER S COMMUNITY COLLEGE Mission statement The technology department aspires to provide a safe, stimulating environment where all students can develop their
2010-11 LEAVING CERT DCG SCHEME OF WORK ST OLIVER S COMMUNITY COLLEGE Mission statement The technology department aspires to provide a safe, stimulating environment where all students can develop their
EQUATIONS and INEQUALITIES
 EQUATIONS and INEQUALITIES Linear Equations and Slope 1. Slope a. Calculate the slope of a line given two points b. Calculate the slope of a line parallel to a given line. c. Calculate the slope of a line
EQUATIONS and INEQUALITIES Linear Equations and Slope 1. Slope a. Calculate the slope of a line given two points b. Calculate the slope of a line parallel to a given line. c. Calculate the slope of a line
The Essentials of CAGD
 The Essentials of CAGD Chapter 2: Lines and Planes Gerald Farin & Dianne Hansford CRC Press, Taylor & Francis Group, An A K Peters Book www.farinhansford.com/books/essentials-cagd c 2000 Farin & Hansford
The Essentials of CAGD Chapter 2: Lines and Planes Gerald Farin & Dianne Hansford CRC Press, Taylor & Francis Group, An A K Peters Book www.farinhansford.com/books/essentials-cagd c 2000 Farin & Hansford
MATHS LEVEL DESCRIPTORS
 MATHS LEVEL DESCRIPTORS Number Level 3 Understand the place value of numbers up to thousands. Order numbers up to 9999. Round numbers to the nearest 10 or 100. Understand the number line below zero, and
MATHS LEVEL DESCRIPTORS Number Level 3 Understand the place value of numbers up to thousands. Order numbers up to 9999. Round numbers to the nearest 10 or 100. Understand the number line below zero, and
2. SPATIAL TRANSFORMATIONS
 Digitales Video 1 2. SPATIAL TRANSFORMATIONS This chapter describes common spatial transformations derived for digital image warping applications in computer vision and computer graphics. A spatial transformation
Digitales Video 1 2. SPATIAL TRANSFORMATIONS This chapter describes common spatial transformations derived for digital image warping applications in computer vision and computer graphics. A spatial transformation
A Novel Multitouch Interface for 3D Object Manipulation
 A Novel Multitouch Interface for 3D Object Manipulation Oscar Kin-Chung Au School of Creative Media City University of Hong Kong kincau@cityu.edu.hk Chiew-Lan Tai Department of Computer Science & Engineering
A Novel Multitouch Interface for 3D Object Manipulation Oscar Kin-Chung Au School of Creative Media City University of Hong Kong kincau@cityu.edu.hk Chiew-Lan Tai Department of Computer Science & Engineering
Linear Equations. Find the domain and the range of the following set. {(4,5), (7,8), (-1,3), (3,3), (2,-3)}
 Linear Equations Domain and Range Domain refers to the set of possible values of the x-component of a point in the form (x,y). Range refers to the set of possible values of the y-component of a point in
Linear Equations Domain and Range Domain refers to the set of possible values of the x-component of a point in the form (x,y). Range refers to the set of possible values of the y-component of a point in
Vector has a magnitude and a direction. Scalar has a magnitude
 Vector has a magnitude and a direction Scalar has a magnitude Vector has a magnitude and a direction Scalar has a magnitude a brick on a table Vector has a magnitude and a direction Scalar has a magnitude
Vector has a magnitude and a direction Scalar has a magnitude Vector has a magnitude and a direction Scalar has a magnitude a brick on a table Vector has a magnitude and a direction Scalar has a magnitude
What is Linear Programming?
 Chapter 1 What is Linear Programming? An optimization problem usually has three essential ingredients: a variable vector x consisting of a set of unknowns to be determined, an objective function of x to
Chapter 1 What is Linear Programming? An optimization problem usually has three essential ingredients: a variable vector x consisting of a set of unknowns to be determined, an objective function of x to
Thin Lenses Drawing Ray Diagrams
 Drawing Ray Diagrams Fig. 1a Fig. 1b In this activity we explore how light refracts as it passes through a thin lens. Eyeglasses have been in use since the 13 th century. In 1610 Galileo used two lenses
Drawing Ray Diagrams Fig. 1a Fig. 1b In this activity we explore how light refracts as it passes through a thin lens. Eyeglasses have been in use since the 13 th century. In 1610 Galileo used two lenses
13 MATH FACTS 101. 2 a = 1. 7. The elements of a vector have a graphical interpretation, which is particularly easy to see in two or three dimensions.
 3 MATH FACTS 0 3 MATH FACTS 3. Vectors 3.. Definition We use the overhead arrow to denote a column vector, i.e., a linear segment with a direction. For example, in three-space, we write a vector in terms
3 MATH FACTS 0 3 MATH FACTS 3. Vectors 3.. Definition We use the overhead arrow to denote a column vector, i.e., a linear segment with a direction. For example, in three-space, we write a vector in terms
Geometry of Vectors. 1 Cartesian Coordinates. Carlo Tomasi
 Geometry of Vectors Carlo Tomasi This note explores the geometric meaning of norm, inner product, orthogonality, and projection for vectors. For vectors in three-dimensional space, we also examine the
Geometry of Vectors Carlo Tomasi This note explores the geometric meaning of norm, inner product, orthogonality, and projection for vectors. For vectors in three-dimensional space, we also examine the
The process components and related data characteristics addressed in this document are:
 TM Tech Notes Certainty 3D November 1, 2012 To: General Release From: Ted Knaak Certainty 3D, LLC Re: Structural Wall Monitoring (#1017) rev: A Introduction TopoDOT offers several tools designed specifically
TM Tech Notes Certainty 3D November 1, 2012 To: General Release From: Ted Knaak Certainty 3D, LLC Re: Structural Wall Monitoring (#1017) rev: A Introduction TopoDOT offers several tools designed specifically
Equations Involving Lines and Planes Standard equations for lines in space
 Equations Involving Lines and Planes In this section we will collect various important formulas regarding equations of lines and planes in three dimensional space Reminder regarding notation: any quantity
Equations Involving Lines and Planes In this section we will collect various important formulas regarding equations of lines and planes in three dimensional space Reminder regarding notation: any quantity
Algebra 1 Course Title
 Algebra 1 Course Title Course- wide 1. What patterns and methods are being used? Course- wide 1. Students will be adept at solving and graphing linear and quadratic equations 2. Students will be adept
Algebra 1 Course Title Course- wide 1. What patterns and methods are being used? Course- wide 1. Students will be adept at solving and graphing linear and quadratic equations 2. Students will be adept
Math 241, Exam 1 Information.
 Math 241, Exam 1 Information. 9/24/12, LC 310, 11:15-12:05. Exam 1 will be based on: Sections 12.1-12.5, 14.1-14.3. The corresponding assigned homework problems (see http://www.math.sc.edu/ boylan/sccourses/241fa12/241.html)
Math 241, Exam 1 Information. 9/24/12, LC 310, 11:15-12:05. Exam 1 will be based on: Sections 12.1-12.5, 14.1-14.3. The corresponding assigned homework problems (see http://www.math.sc.edu/ boylan/sccourses/241fa12/241.html)
Technical Drawing Specifications Resource A guide to support VCE Visual Communication Design study design 2013-17
 A guide to support VCE Visual Communication Design study design 2013-17 1 Contents INTRODUCTION The Australian Standards (AS) Key knowledge and skills THREE-DIMENSIONAL DRAWING PARALINE DRAWING Isometric
A guide to support VCE Visual Communication Design study design 2013-17 1 Contents INTRODUCTION The Australian Standards (AS) Key knowledge and skills THREE-DIMENSIONAL DRAWING PARALINE DRAWING Isometric
Cortona3D Viewer. User's Guide. Copyright 1999-2011 ParallelGraphics
 Cortona3D Viewer User's Guide Copyright 1999-2011 ParallelGraphics Table of contents Introduction 1 The Cortona3D Viewer Window 1 Navigating in Cortona3D Viewer 1 Using Viewpoints 1 Moving around: Walk,
Cortona3D Viewer User's Guide Copyright 1999-2011 ParallelGraphics Table of contents Introduction 1 The Cortona3D Viewer Window 1 Navigating in Cortona3D Viewer 1 Using Viewpoints 1 Moving around: Walk,
Metrics on SO(3) and Inverse Kinematics
 Mathematical Foundations of Computer Graphics and Vision Metrics on SO(3) and Inverse Kinematics Luca Ballan Institute of Visual Computing Optimization on Manifolds Descent approach d is a ascent direction
Mathematical Foundations of Computer Graphics and Vision Metrics on SO(3) and Inverse Kinematics Luca Ballan Institute of Visual Computing Optimization on Manifolds Descent approach d is a ascent direction
Taking Inverse Graphics Seriously
 CSC2535: 2013 Advanced Machine Learning Taking Inverse Graphics Seriously Geoffrey Hinton Department of Computer Science University of Toronto The representation used by the neural nets that work best
CSC2535: 2013 Advanced Machine Learning Taking Inverse Graphics Seriously Geoffrey Hinton Department of Computer Science University of Toronto The representation used by the neural nets that work best
