CSEE 3827: Fundamentals of Computer Systems. Standard Forms and Simplification with Karnaugh Maps
|
|
|
- Ferdinand McDaniel
- 7 years ago
- Views:
Transcription
1 CSEE 3827: Fundamentals of Computer Systems Standard Forms and Simplification with Karnaugh Maps
2 Agenda (M&K ) Standard Forms Product-of-Sums (PoS) Sum-of-Products (SoP) converting between Min-terms and Max-terms Simplification via Karnaugh Maps (K-maps) 2, 3, and 4 variable Implicants, Prime Implicants, Essential Prime Implicants Using K-maps to reduce PoS form Don t Care Conditions 2
3 Standard Forms There are many ways to express a boolean expression F = XYZ + XYZ + XZ = XY(Z + Z) + XZ = XY + XZ It is useful to have a standard or canonical way Derived from truth table Generally not the simplest form
4 Two principle standard forms Sum-of-products (SOP) Product-of-sums (POS)
5 Product and sum terms Product term: logical AND of literals (e.g., XYZ) Sum term: logical OR of literals (e.g., A + B + C) 5
6 PoS & SoP Sum of products (SoP): OR of ANDs e.g., F = Y + XYZ + XY Product of sums (PoS): AND of ORs e.g., G = X(Y + Z)(X + Y + Z) 6
7 Converting from PoS (or any form) to SoP Just multiply through and simplify, e.g., G = X(Y + Z)(X + Y + Z) = XYX + XYY + XYZ + XZX + XZY + XZZ = XY + XY + XYZ + XZ + XZY + XZ = XY + XZ 7
8 Converting from SoP to PoS Complement, multiply through, complement via DeMorgan, e.g., Note: X = X F = Y Z + XY Z + XYZ F' = (Y+Z)(X +Y+Z )(X +Y +Z) = YZ + X Y + X Z (after lots of simplification) F = (Y +Z )(X+Y )(X+Z ) 8
9 Minterms e.g., Minterms for 3 variables A,B,C A B C minterm m0 ABC m1 ABC m2 ABC m3 ABC m4 ABC m5 ABC m6 ABC m7 ABC A product term in which all variables appear once, either complemented or uncomplemented (i.e., an entry in the truth table). Each minterm evaluates to 1 for exactly one variable assignment, 0 for all others. Denoted by mx where X corresponds to the variable assignment for which mx = 1. 9
10 Minterms to describe a function sometimes also called a minterm expansion or disjunctive normal form (DNF) This term is TRUE when A=0,B=1,C=0 A B C F F F = ABC + ABC + ABC + ABC + ABC F = ABC + ABC + ABC
11 Sum of minterms form The logical OR of all minterms for which F = 1. A B C minterm F m0 ABC m1 ABC m2 ABC m3 ABC m4 ABC 0 F = ABC + ABC + ABC = m1 + m2 + m3 = m(1,2,3) m5 ABC m6 ABC m7 ABC 0 11
12 Minterm form cont d (variables appear once in each minterm) A B C F F minterm m0 ABC m1 ABC m2 ABC m3 ABC m4 ABC m5 ABC m6 ABC m7 ABC F = ABC + ABC + ABC + ABC + ABC 0 m0 + m1 + m2 + m4 + m5 0 m(0,1,2,4,5) F = ABC + ABC + ABC 0 m3 + m6 + m7 0 m(3,6,7)
13 Minterms as a circuit A B C F = ABC + ABC + ABC + ABC + ABC 0 m0 + m1 + m2 + m4 + m5 0 m(1,0,2,4,5) F Standard form is not minimal form!
14 Maxterms A B C maxterm M0 A+B+C M1 A+B+C M2 A+B+C M3 A+B+C M4 A+B+C M5 A+B+C M6 A+B+C M7 A+B+C A sum term in which all variables appear once, either complemented or uncomplemented. Each maxterm evaluates to 0 for exactly one variable assignment, 1 for all others. Denoted by MX where X corresponds to the variable assignment for which MX = 0. 14
15 Maxterm description of a function sometimes also called a maxterm expansion or conjunctive normal form (CNF) This term is FALSE when A=1,B=1,C=0 A B C F F F = (A+B+C) (A+B+C) (A+B+C) Force to 0
16 Product of maxterms form The logical AND of all maxterms for which F = 0. A B C maxterm F M0 A+B+C M1 A+B+C M2 A+B+C M3 A+B+C M4 A+B+C 0 F = (A+B+C) (A+B+C) (A+B+C) (A+B+C) (A+B+C) = (M0) (M4) (M5) (M6) (M7) = M(0,4,5,6,7) M5 A+B+C M6 A+B+C M7 A+B+C 0 16
17 One final example A B C F F F F Minterms (SOP) Maxterms (POS)
18 Summary of Minterms and Maxterms F F Minterms (SOP) Maxterms (POS) m(f = 1) m(f = 0) M(F = 0) M(F = 1)
19 Relations between standard forms sum of products product of sums F DeMorgan s F sum of minterms product of maxterms all boolean expressions 19
20 Simplification with Karnaugh Maps
21 Cost criteria Literal cost: the number of literals in an expression Gate-input cost: the literal cost + all terms with more than one literal + (optionally) the number of distinct, complemented single literals Roughly proportional to the number of transistors and wires in an AND/OR/NOT circuits. Does not apply, to more complex gates, for example XOR. Literal cost Gate-input cost G = ABCD + ABCD (4) G = (A+B)(B+C)(C+D)(D+A) (4) 21
22 Karnaugh maps (a.k.a., K-maps) All functions can be expressed with a map There is one square in the map for each minterm in a function s truth table X Y F 0 0 m0 0 1 m1 1 0 m2 1 1 m3 X Y m0 XY m2 XY m1 XY m3 XY 22
23 Karnaugh maps express functions Fill out table with value of a function X Y F X Y
24 Simplification using a k-map Whenever two squares share an edge and both are 1, those two terms can be combined to form a single term with one less variable X Y X Y X Y F = Y + XY F = XY + XY + XY X Y F = X + Y F = X + XY 24
25 Simplification using a k-map (2) Circle contiguous groups of 1s (circle sizes must be a power of 2) There is a correspondence between circles on a k-map and terms in a function expression The bigger the circle, the simpler the term Add circles (and terms) until all 1s on the k-map are circled X Y F = X + Y 25
26 3-variable Karnaugh maps Use gray ordering on edges with multiple variables Gray encoding: order of values such that only one bit changes at a time Two minterms are considered adjacent if they differ in only one variable (this means maps wrap ) X Y Z Y= m0 XYZ m1 XYZ m3 XYZ m2 XYZ X=1 1 m4 XYZ m5 XYZ Z=1 m7 XYZ m6 XYZ 26
27 4-variable Karnaugh maps Extension of 3-variable maps WX Y Z Y WXYZ or W+X+Y+Z 0 0 m0 m1 m3 m2 W 0 1 m4 m5 m7 m6 1 1 m12 m13 m15 m m8 m9 m11 m10 Z X 27
28 Implicants Implicant: a product term, which, viewed in a K-Map is a 2 i x 2 j size rectangle (possibly wrapping around) where i=0,1,2, j=0,1,2 WX Y Z Y WX Y Z Y m0 m1 m3 m2 0 0 m0 m1 m3 m2 W 0 1 m4 m5 m7 m6 1 1 m12 m13 m15 m m8 m9 m11 m10 X W 0 1 m4 m5 m7 m6 1 1 m12 m13 m15 m m8 m9 m11 m10 X Z Z 28
29 Implicants Implicant: a product term, which, viewed in a K-Map is a 2 i x 2 j size rectangle (possibly wrapping around) where i=0,1,2, j=0,1,2 WX Y Z Y WX Y Z Y W 0 0 m0 m1 m3 m2 0 1 m4 m5 m7 m6 1 1 m12 m13 m15 m14 WZ WY WXY 1 0 m8 m9 m11 m10 X WXYZ W 0 0 m0 m1 m3 m2 W 0 1 m4 m5 m7 m6 WX 1 1 m12 m13 m15 m m8 m9 m11 m10 X Z Z WXZ Note: bigger rectangles = fewer literals 29
30 4-variable Karnaugh map example W X Y Z F WX Y Z Y W X Z
31 Implicant terminology implicant: a product term, which, viewed in a K-Map is a 2 i x 2 j size rectangle (possibly wrapping around) where i=0,1,2, j=0,1,2 prime implicant: An implicant not contained within another implicant. essential prime implicant: a prime implicant that is the only prime implicant to cover some minterm. 31
32 4-variable Karnaugh maps (3) List all all of the prime implicants for this function Is any of them an essential prime implicant? What is a simplified expression for this function? WX Y Z Y W Z X 32
33 Using K-maps to build simplified circuits Step 1: Identify all PIs and essential PIs Step 2: Include all Essential PIs in the circuit (Why?) Step 3: If any 1-valued minterms are uncovered by EPIs, choose PIs that are big and do a good job covering
34 Design example : 2-bit multiplier a1 a0 b1 b0 z3 z2 z1 z two 2-bit # s multiplied together to give a 4-bit solution e.g., a1a0 = 10, b1b0 = 11, z3z2z1z0 =
35 K-Maps: Complements, PoS, don t care conditions
36 Finding F Find prime implicants corresponding to the 0s on a k-map Y Z Y Z WX WX F = Y + XZ + WZ F = YZ + WXY 36
37 PoS expressions from a k-map Find F as SoP and then apply DeMorgan s WX Y Z F = YZ + XZ + YX DeMorgan s F = (Y+Z)(Z+X)(Y+X) 37
38 Don t care conditions There are circumstances in which the value of an output doesn t matter For example, in that 2-bit multiplier, what if we are told that a and b will be non-0? We don t care what the output looks like for the input cases that should not occur Don t care situations are denoted by an X in a truth table and in Karnaugh maps. a1 a0 b1 b0 z3 z2 z1 z X X X X X X X X X X X X X X X X X X X X Can also be expressed in minterm form: During minimization can be treated as either a 1 or a 0 z2 = m(10,11,14) d2 = m(0,1,2,3,4,8,12) X X X X X X X X
39 2-bit multiplier non-0 multiplier a1 a0 b1 b0 z3 z2 z1 z X X X X X X X X X X X X X X X X X X X X X X X X X X X X a1 b0 X X X X X X X s must be covered 0 s must not be covered X s are optionally covered b1 a0 a1 z3 = z2 = b0 X X X X X X X b1 a0 39
40 2-bit multiplier non-0 multiplier (2) a1 a0 b1 b0 z3 z2 z1 z X X X X X X X X X X X X X X X X X X X X X X X X X X X X a1 z1 = b0 X X X X X X X b1 a0 a1 b0 X X X X X X X z0 = b1 a0 40
41 Final thoughts on Don t care conditions Sometimes don t cares greatly simplify circuitry A D 1 X X X X 1 X X X 0 0 X 1 C B ABCD + ABCD + ABCD + ABCD vs. A + C 41
Karnaugh Maps. Circuit-wise, this leads to a minimal two-level implementation
 Karnaugh Maps Applications of Boolean logic to circuit design The basic Boolean operations are AND, OR and NOT These operations can be combined to form complex expressions, which can also be directly translated
Karnaugh Maps Applications of Boolean logic to circuit design The basic Boolean operations are AND, OR and NOT These operations can be combined to form complex expressions, which can also be directly translated
Karnaugh Maps & Combinational Logic Design. ECE 152A Winter 2012
 Karnaugh Maps & Combinational Logic Design ECE 52A Winter 22 Reading Assignment Brown and Vranesic 4 Optimized Implementation of Logic Functions 4. Karnaugh Map 4.2 Strategy for Minimization 4.2. Terminology
Karnaugh Maps & Combinational Logic Design ECE 52A Winter 22 Reading Assignment Brown and Vranesic 4 Optimized Implementation of Logic Functions 4. Karnaugh Map 4.2 Strategy for Minimization 4.2. Terminology
BOOLEAN ALGEBRA & LOGIC GATES
 BOOLEAN ALGEBRA & LOGIC GATES Logic gates are electronic circuits that can be used to implement the most elementary logic expressions, also known as Boolean expressions. The logic gate is the most basic
BOOLEAN ALGEBRA & LOGIC GATES Logic gates are electronic circuits that can be used to implement the most elementary logic expressions, also known as Boolean expressions. The logic gate is the most basic
Simplifying Logic Circuits with Karnaugh Maps
 Simplifying Logic Circuits with Karnaugh Maps The circuit at the top right is the logic equivalent of the Boolean expression: f = abc + abc + abc Now, as we have seen, this expression can be simplified
Simplifying Logic Circuits with Karnaugh Maps The circuit at the top right is the logic equivalent of the Boolean expression: f = abc + abc + abc Now, as we have seen, this expression can be simplified
Boolean Algebra Part 1
 Boolean Algebra Part 1 Page 1 Boolean Algebra Objectives Understand Basic Boolean Algebra Relate Boolean Algebra to Logic Networks Prove Laws using Truth Tables Understand and Use First Basic Theorems
Boolean Algebra Part 1 Page 1 Boolean Algebra Objectives Understand Basic Boolean Algebra Relate Boolean Algebra to Logic Networks Prove Laws using Truth Tables Understand and Use First Basic Theorems
CSE140: Components and Design Techniques for Digital Systems
 CSE4: Components and Design Techniques for Digital Systems Tajana Simunic Rosing What we covered thus far: Number representations Logic gates Boolean algebra Introduction to CMOS HW#2 due, HW#3 assigned
CSE4: Components and Design Techniques for Digital Systems Tajana Simunic Rosing What we covered thus far: Number representations Logic gates Boolean algebra Introduction to CMOS HW#2 due, HW#3 assigned
Logic in Computer Science: Logic Gates
 Logic in Computer Science: Logic Gates Lila Kari The University of Western Ontario Logic in Computer Science: Logic Gates CS2209, Applied Logic for Computer Science 1 / 49 Logic and bit operations Computers
Logic in Computer Science: Logic Gates Lila Kari The University of Western Ontario Logic in Computer Science: Logic Gates CS2209, Applied Logic for Computer Science 1 / 49 Logic and bit operations Computers
CHAPTER 3 Boolean Algebra and Digital Logic
 CHAPTER 3 Boolean Algebra and Digital Logic 3.1 Introduction 121 3.2 Boolean Algebra 122 3.2.1 Boolean Expressions 123 3.2.2 Boolean Identities 124 3.2.3 Simplification of Boolean Expressions 126 3.2.4
CHAPTER 3 Boolean Algebra and Digital Logic 3.1 Introduction 121 3.2 Boolean Algebra 122 3.2.1 Boolean Expressions 123 3.2.2 Boolean Identities 124 3.2.3 Simplification of Boolean Expressions 126 3.2.4
CSE140: Midterm 1 Solution and Rubric
 CSE140: Midterm 1 Solution and Rubric April 23, 2014 1 Short Answers 1.1 True or (6pts) 1. A maxterm must include all input variables (1pt) True 2. A canonical product of sums is a product of minterms
CSE140: Midterm 1 Solution and Rubric April 23, 2014 1 Short Answers 1.1 True or (6pts) 1. A maxterm must include all input variables (1pt) True 2. A canonical product of sums is a product of minterms
CH3 Boolean Algebra (cont d)
 CH3 Boolean Algebra (cont d) Lecturer: 吳 安 宇 Date:2005/10/7 ACCESS IC LAB v Today, you ll know: Introduction 1. Guidelines for multiplying out/factoring expressions 2. Exclusive-OR and Equivalence operations
CH3 Boolean Algebra (cont d) Lecturer: 吳 安 宇 Date:2005/10/7 ACCESS IC LAB v Today, you ll know: Introduction 1. Guidelines for multiplying out/factoring expressions 2. Exclusive-OR and Equivalence operations
Unit 3 Boolean Algebra (Continued)
 Unit 3 Boolean Algebra (Continued) 1. Exclusive-OR Operation 2. Consensus Theorem Department of Communication Engineering, NCTU 1 3.1 Multiplying Out and Factoring Expressions Department of Communication
Unit 3 Boolean Algebra (Continued) 1. Exclusive-OR Operation 2. Consensus Theorem Department of Communication Engineering, NCTU 1 3.1 Multiplying Out and Factoring Expressions Department of Communication
Boolean Algebra (cont d) UNIT 3 BOOLEAN ALGEBRA (CONT D) Guidelines for Multiplying Out and Factoring. Objectives. Iris Hui-Ru Jiang Spring 2010
 Boolean Algebra (cont d) 2 Contents Multiplying out and factoring expressions Exclusive-OR and Exclusive-NOR operations The consensus theorem Summary of algebraic simplification Proving validity of an
Boolean Algebra (cont d) 2 Contents Multiplying out and factoring expressions Exclusive-OR and Exclusive-NOR operations The consensus theorem Summary of algebraic simplification Proving validity of an
Digital Logic Design. Basics Combinational Circuits Sequential Circuits. Pu-Jen Cheng
 Digital Logic Design Basics Combinational Circuits Sequential Circuits Pu-Jen Cheng Adapted from the slides prepared by S. Dandamudi for the book, Fundamentals of Computer Organization and Design. Introduction
Digital Logic Design Basics Combinational Circuits Sequential Circuits Pu-Jen Cheng Adapted from the slides prepared by S. Dandamudi for the book, Fundamentals of Computer Organization and Design. Introduction
Switching Algebra and Logic Gates
 Chapter 2 Switching Algebra and Logic Gates The word algebra in the title of this chapter should alert you that more mathematics is coming. No doubt, some of you are itching to get on with digital design
Chapter 2 Switching Algebra and Logic Gates The word algebra in the title of this chapter should alert you that more mathematics is coming. No doubt, some of you are itching to get on with digital design
United States Naval Academy Electrical and Computer Engineering Department. EC262 Exam 1
 United States Naval Academy Electrical and Computer Engineering Department EC262 Exam 29 September 2. Do a page check now. You should have pages (cover & questions). 2. Read all problems in their entirety.
United States Naval Academy Electrical and Computer Engineering Department EC262 Exam 29 September 2. Do a page check now. You should have pages (cover & questions). 2. Read all problems in their entirety.
Karnaugh Maps (K-map) Alternate representation of a truth table
 Karnaugh Maps (K-map) lternate representation of a truth table Red decimal = minterm value Note that is the MS for this minterm numbering djacent squares have distance = 1 Valuable tool for logic minimization
Karnaugh Maps (K-map) lternate representation of a truth table Red decimal = minterm value Note that is the MS for this minterm numbering djacent squares have distance = 1 Valuable tool for logic minimization
Binary Adders: Half Adders and Full Adders
 Binary Adders: Half Adders and Full Adders In this set of slides, we present the two basic types of adders: 1. Half adders, and 2. Full adders. Each type of adder functions to add two binary bits. In order
Binary Adders: Half Adders and Full Adders In this set of slides, we present the two basic types of adders: 1. Half adders, and 2. Full adders. Each type of adder functions to add two binary bits. In order
Logic Reference Guide
 Logic eference Guide Advanced Micro evices INTOUCTION Throughout this data book and design guide we have assumed that you have a good working knowledge of logic. Unfortunately, there always comes a time
Logic eference Guide Advanced Micro evices INTOUCTION Throughout this data book and design guide we have assumed that you have a good working knowledge of logic. Unfortunately, there always comes a time
Take-Home Exercise. z y x. Erik Jonsson School of Engineering and Computer Science. The University of Texas at Dallas
 Take-Home Exercise Assume you want the counter below to count mod-6 backward. That is, it would count 0-5-4-3-2-1-0, etc. Assume it is reset on startup, and design the wiring to make the counter count
Take-Home Exercise Assume you want the counter below to count mod-6 backward. That is, it would count 0-5-4-3-2-1-0, etc. Assume it is reset on startup, and design the wiring to make the counter count
Boolean Algebra. Boolean Algebra. Boolean Algebra. Boolean Algebra
 2 Ver..4 George Boole was an English mathematician of XIX century can operate on logic (or Boolean) variables that can assume just 2 values: /, true/false, on/off, closed/open Usually value is associated
2 Ver..4 George Boole was an English mathematician of XIX century can operate on logic (or Boolean) variables that can assume just 2 values: /, true/false, on/off, closed/open Usually value is associated
DESIGN OF GATE NETWORKS
 DESIGN OF GATE NETWORKS DESIGN OF TWO-LEVEL NETWORKS: and-or and or-and NETWORKS MINIMAL TWO-LEVEL NETWORKS KARNAUGH MAPS MINIMIZATION PROCEDURE AND TOOLS LIMITATIONS OF TWO-LEVEL NETWORKS DESIGN OF TWO-LEVEL
DESIGN OF GATE NETWORKS DESIGN OF TWO-LEVEL NETWORKS: and-or and or-and NETWORKS MINIMAL TWO-LEVEL NETWORKS KARNAUGH MAPS MINIMIZATION PROCEDURE AND TOOLS LIMITATIONS OF TWO-LEVEL NETWORKS DESIGN OF TWO-LEVEL
CDA 3200 Digital Systems. Instructor: Dr. Janusz Zalewski Developed by: Dr. Dahai Guo Spring 2012
 CDA 3200 Digital Systems Instructor: Dr. Janusz Zalewski Developed by: Dr. Dahai Guo Spring 2012 Outline Multi-Level Gate Circuits NAND and NOR Gates Design of Two-Level Circuits Using NAND and NOR Gates
CDA 3200 Digital Systems Instructor: Dr. Janusz Zalewski Developed by: Dr. Dahai Guo Spring 2012 Outline Multi-Level Gate Circuits NAND and NOR Gates Design of Two-Level Circuits Using NAND and NOR Gates
C H A P T E R. Logic Circuits
 C H A P T E R Logic Circuits Many important functions are naturally computed with straight-line programs, programs without loops or branches. Such computations are conveniently described with circuits,
C H A P T E R Logic Circuits Many important functions are naturally computed with straight-line programs, programs without loops or branches. Such computations are conveniently described with circuits,
2.0 Chapter Overview. 2.1 Boolean Algebra
 Thi d t t d ith F M k 4 0 2 Boolean Algebra Chapter Two Logic circuits are the basis for modern digital computer systems. To appreciate how computer systems operate you will need to understand digital
Thi d t t d ith F M k 4 0 2 Boolean Algebra Chapter Two Logic circuits are the basis for modern digital computer systems. To appreciate how computer systems operate you will need to understand digital
Chapter 2: Boolean Algebra and Logic Gates. Boolean Algebra
 The Universit Of Alabama in Huntsville Computer Science Chapter 2: Boolean Algebra and Logic Gates The Universit Of Alabama in Huntsville Computer Science Boolean Algebra The algebraic sstem usuall used
The Universit Of Alabama in Huntsville Computer Science Chapter 2: Boolean Algebra and Logic Gates The Universit Of Alabama in Huntsville Computer Science Boolean Algebra The algebraic sstem usuall used
Two-level logic using NAND gates
 CSE140: Components and Design Techniques for Digital Systems Two and Multilevel logic implementation Tajana Simunic Rosing 1 Two-level logic using NND gates Replace minterm ND gates with NND gates Place
CSE140: Components and Design Techniques for Digital Systems Two and Multilevel logic implementation Tajana Simunic Rosing 1 Two-level logic using NND gates Replace minterm ND gates with NND gates Place
Introduction. The Quine-McCluskey Method Handout 5 January 21, 2016. CSEE E6861y Prof. Steven Nowick
 CSEE E6861y Prof. Steven Nowick The Quine-McCluskey Method Handout 5 January 21, 2016 Introduction The Quine-McCluskey method is an exact algorithm which finds a minimum-cost sum-of-products implementation
CSEE E6861y Prof. Steven Nowick The Quine-McCluskey Method Handout 5 January 21, 2016 Introduction The Quine-McCluskey method is an exact algorithm which finds a minimum-cost sum-of-products implementation
Combinational circuits
 Combinational circuits Combinational circuits are stateless The outputs are functions only of the inputs Inputs Combinational circuit Outputs 3 Thursday, September 2, 3 Enabler Circuit (High-level view)
Combinational circuits Combinational circuits are stateless The outputs are functions only of the inputs Inputs Combinational circuit Outputs 3 Thursday, September 2, 3 Enabler Circuit (High-level view)
Digital Electronics Part I Combinational and Sequential Logic. Dr. I. J. Wassell
 Digital Electronics Part I Combinational and Sequential Logic Dr. I. J. Wassell Introduction Aims To familiarise students with Combinational logic circuits Sequential logic circuits How digital logic gates
Digital Electronics Part I Combinational and Sequential Logic Dr. I. J. Wassell Introduction Aims To familiarise students with Combinational logic circuits Sequential logic circuits How digital logic gates
Basic Logic Gates Richard E. Haskell
 BASIC LOGIC GATES 1 E Basic Logic Gates Richard E. Haskell All digital systems are made from a few basic digital circuits that we call logic gates. These circuits perform the basic logic functions that
BASIC LOGIC GATES 1 E Basic Logic Gates Richard E. Haskell All digital systems are made from a few basic digital circuits that we call logic gates. These circuits perform the basic logic functions that
1. True or False? A voltage level in the range 0 to 2 volts is interpreted as a binary 1.
 File: chap04, Chapter 04 1. True or False? A voltage level in the range 0 to 2 volts is interpreted as a binary 1. 2. True or False? A gate is a device that accepts a single input signal and produces one
File: chap04, Chapter 04 1. True or False? A voltage level in the range 0 to 2 volts is interpreted as a binary 1. 2. True or False? A gate is a device that accepts a single input signal and produces one
FINDING THE LEAST COMMON DENOMINATOR
 0 (7 18) Chapter 7 Rational Expressions GETTING MORE INVOLVED 7. Discussion. Evaluate each expression. a) One-half of 1 b) One-third of c) One-half of x d) One-half of x 7. Exploration. Let R 6 x x 0 x
0 (7 18) Chapter 7 Rational Expressions GETTING MORE INVOLVED 7. Discussion. Evaluate each expression. a) One-half of 1 b) One-third of c) One-half of x d) One-half of x 7. Exploration. Let R 6 x x 0 x
A Course Material on DIGITAL PRINCIPLES AND SYSTEM DESIGN
 A Course Material on By MS.G.MANJULA ASSISTANT PROFESSOR DEPARTMENT OF ELECTRONICS AND COMMUNICATION ENGINEERING SASURIE COLLEGE OF ENGINEERING VIJAYAMANGALAM 638 56 QUALITY CERTIFICATE This is to certify
A Course Material on By MS.G.MANJULA ASSISTANT PROFESSOR DEPARTMENT OF ELECTRONICS AND COMMUNICATION ENGINEERING SASURIE COLLEGE OF ENGINEERING VIJAYAMANGALAM 638 56 QUALITY CERTIFICATE This is to certify
Digital circuits make up all computers and computer systems. The operation of digital circuits is based on
 Digital Logic Circuits Digital circuits make up all computers and computer systems. The operation of digital circuits is based on Boolean algebra, the mathematics of binary numbers. Boolean algebra is
Digital Logic Circuits Digital circuits make up all computers and computer systems. The operation of digital circuits is based on Boolean algebra, the mathematics of binary numbers. Boolean algebra is
Class One: Degree Sequences
 Class One: Degree Sequences For our purposes a graph is a just a bunch of points, called vertices, together with lines or curves, called edges, joining certain pairs of vertices. Three small examples of
Class One: Degree Sequences For our purposes a graph is a just a bunch of points, called vertices, together with lines or curves, called edges, joining certain pairs of vertices. Three small examples of
Sum-of-Products and Product-of-Sums expressions
 Sum-of-Products and Product-of-Sums expressions This worksheet and all related files are licensed under the reative ommons ttribution License, version.. To view a copy of this license, visit http://creativecommons.org/licenses/by/./,
Sum-of-Products and Product-of-Sums expressions This worksheet and all related files are licensed under the reative ommons ttribution License, version.. To view a copy of this license, visit http://creativecommons.org/licenses/by/./,
Gates & Boolean Algebra. Boolean Operators. Combinational Logic. Introduction
 Introduction Gates & Boolean lgebra Boolean algebra: named after mathematician George Boole (85 864). 2-valued algebra. digital circuit can have one of 2 values. Signal between and volt =, between 4 and
Introduction Gates & Boolean lgebra Boolean algebra: named after mathematician George Boole (85 864). 2-valued algebra. digital circuit can have one of 2 values. Signal between and volt =, between 4 and
Combinational Logic Design Process
 Combinational Logic Design Process Create truth table from specification Generate K-maps & obtain logic equations Draw logic diagram (sharing common gates) Simulate circuit for design verification Debug
Combinational Logic Design Process Create truth table from specification Generate K-maps & obtain logic equations Draw logic diagram (sharing common gates) Simulate circuit for design verification Debug
Understanding Logic Design
 Understanding Logic Design ppendix of your Textbook does not have the needed background information. This document supplements it. When you write add DD R0, R1, R2, you imagine something like this: R1
Understanding Logic Design ppendix of your Textbook does not have the needed background information. This document supplements it. When you write add DD R0, R1, R2, you imagine something like this: R1
Digital Logic Design
 Digital Logic Design Version 4.6 printed on February 2016 First published on August 2006 Background and Acknowledgements This material has been developed for the first course in Digital Logic Design. The
Digital Logic Design Version 4.6 printed on February 2016 First published on August 2006 Background and Acknowledgements This material has been developed for the first course in Digital Logic Design. The
Digital Electronics Detailed Outline
 Digital Electronics Detailed Outline Unit 1: Fundamentals of Analog and Digital Electronics (32 Total Days) Lesson 1.1: Foundations and the Board Game Counter (9 days) 1. Safety is an important concept
Digital Electronics Detailed Outline Unit 1: Fundamentals of Analog and Digital Electronics (32 Total Days) Lesson 1.1: Foundations and the Board Game Counter (9 days) 1. Safety is an important concept
Lecture 12: More on Registers, Multiplexers, Decoders, Comparators and Wot- Nots
 Lecture 12: More on Registers, Multiplexers, Decoders, Comparators and Wot- Nots Registers As you probably know (if you don t then you should consider changing your course), data processing is usually
Lecture 12: More on Registers, Multiplexers, Decoders, Comparators and Wot- Nots Registers As you probably know (if you don t then you should consider changing your course), data processing is usually
FORDHAM UNIVERSITY CISC 3593. Dept. of Computer and Info. Science Spring, 2011. The Binary Adder
 FORDHAM UNIVERITY CIC 3593 Fordham College Lincoln Center Computer Organization Dept. of Computer and Info. cience pring, 2011 1 Introduction The Binar Adder The binar adder circuit is an important building
FORDHAM UNIVERITY CIC 3593 Fordham College Lincoln Center Computer Organization Dept. of Computer and Info. cience pring, 2011 1 Introduction The Binar Adder The binar adder circuit is an important building
Section 1. Finding Common Terms
 Worksheet 2.1 Factors of Algebraic Expressions Section 1 Finding Common Terms In worksheet 1.2 we talked about factors of whole numbers. Remember, if a b = ab then a is a factor of ab and b is a factor
Worksheet 2.1 Factors of Algebraic Expressions Section 1 Finding Common Terms In worksheet 1.2 we talked about factors of whole numbers. Remember, if a b = ab then a is a factor of ab and b is a factor
SIMPLIFYING SQUARE ROOTS
 40 (8-8) Chapter 8 Powers and Roots 8. SIMPLIFYING SQUARE ROOTS In this section Using the Product Rule Rationalizing the Denominator Simplified Form of a Square Root In Section 8. you learned to simplify
40 (8-8) Chapter 8 Powers and Roots 8. SIMPLIFYING SQUARE ROOTS In this section Using the Product Rule Rationalizing the Denominator Simplified Form of a Square Root In Section 8. you learned to simplify
Simplification of Radical Expressions
 8. Simplification of Radical Expressions 8. OBJECTIVES 1. Simplify a radical expression by using the product property. Simplify a radical expression by using the quotient property NOTE A precise set of
8. Simplification of Radical Expressions 8. OBJECTIVES 1. Simplify a radical expression by using the product property. Simplify a radical expression by using the quotient property NOTE A precise set of
3.Basic Gate Combinations
 3.Basic Gate Combinations 3.1 TTL NAND Gate In logic circuits transistors play the role of switches. For those in the TTL gate the conducting state (on) occurs when the baseemmiter signal is high, and
3.Basic Gate Combinations 3.1 TTL NAND Gate In logic circuits transistors play the role of switches. For those in the TTL gate the conducting state (on) occurs when the baseemmiter signal is high, and
Combinational Logic Design
 Chapter 4 Combinational Logic Design The foundations for the design of digital logic circuits were established in the preceding chapters. The elements of Boolean algebra (two-element switching algebra
Chapter 4 Combinational Logic Design The foundations for the design of digital logic circuits were established in the preceding chapters. The elements of Boolean algebra (two-element switching algebra
CHAPTER 8, GEOMETRY. 4. A circular cylinder has a circumference of 33 in. Use 22 as the approximate value of π and find the radius of this cylinder.
 TEST A CHAPTER 8, GEOMETRY 1. A rectangular plot of ground is to be enclosed with 180 yd of fencing. If the plot is twice as long as it is wide, what are its dimensions? 2. A 4 cm by 6 cm rectangle has
TEST A CHAPTER 8, GEOMETRY 1. A rectangular plot of ground is to be enclosed with 180 yd of fencing. If the plot is twice as long as it is wide, what are its dimensions? 2. A 4 cm by 6 cm rectangle has
FACTORING ax 2 bx c. Factoring Trinomials with Leading Coefficient 1
 5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
NAND and NOR Implementation
 University of Wisconsin - Madison EE/omp ci 352 Digital ystems Fundamentals harles R. Kime ection 2 Fall 200 hapter 2 ombinational Logic ircuits Part 7 harles Kime & Thomas Kaminski NND and NOR Implementation
University of Wisconsin - Madison EE/omp ci 352 Digital ystems Fundamentals harles R. Kime ection 2 Fall 200 hapter 2 ombinational Logic ircuits Part 7 harles Kime & Thomas Kaminski NND and NOR Implementation
Resolution. Informatics 1 School of Informatics, University of Edinburgh
 Resolution In this lecture you will see how to convert the natural proof system of previous lectures into one with fewer operators and only one proof rule. You will see how this proof system can be used
Resolution In this lecture you will see how to convert the natural proof system of previous lectures into one with fewer operators and only one proof rule. You will see how this proof system can be used
earlier in the semester: The Full adder above adds two bits and the output is at the end. So if we do this eight times, we would have an 8-bit adder.
 The circuit created is an 8-bit adder. The 8-bit adder adds two 8-bit binary inputs and the result is produced in the output. In order to create a Full 8-bit adder, I could use eight Full -bit adders and
The circuit created is an 8-bit adder. The 8-bit adder adds two 8-bit binary inputs and the result is produced in the output. In order to create a Full 8-bit adder, I could use eight Full -bit adders and
Sect 6.1 - Greatest Common Factor and Factoring by Grouping
 Sect 6.1 - Greatest Common Factor and Factoring by Grouping Our goal in this chapter is to solve non-linear equations by breaking them down into a series of linear equations that we can solve. To do this,
Sect 6.1 - Greatest Common Factor and Factoring by Grouping Our goal in this chapter is to solve non-linear equations by breaking them down into a series of linear equations that we can solve. To do this,
COMPUTER SCIENCE. Paper 1 (THEORY)
 COMPUTER SCIENCE Paper 1 (THEORY) (Three hours) Maximum Marks: 70 (Candidates are allowed additional 15 minutes for only reading the paper. They must NOT start writing during this time) -----------------------------------------------------------------------------------------------------------------------
COMPUTER SCIENCE Paper 1 (THEORY) (Three hours) Maximum Marks: 70 (Candidates are allowed additional 15 minutes for only reading the paper. They must NOT start writing during this time) -----------------------------------------------------------------------------------------------------------------------
exclusive-or and Binary Adder R eouven Elbaz reouven@uwaterloo.ca Office room: DC3576
 exclusive-or and Binary Adder R eouven Elbaz reouven@uwaterloo.ca Office room: DC3576 Outline exclusive OR gate (XOR) Definition Properties Examples of Applications Odd Function Parity Generation and Checking
exclusive-or and Binary Adder R eouven Elbaz reouven@uwaterloo.ca Office room: DC3576 Outline exclusive OR gate (XOR) Definition Properties Examples of Applications Odd Function Parity Generation and Checking
ELEC 2210 - EXPERIMENT 1 Basic Digital Logic Circuits
 Objectives ELEC - EXPERIMENT Basic Digital Logic Circuits The experiments in this laboratory exercise will provide an introduction to digital electronic circuits. You will learn how to use the IDL-00 Bit
Objectives ELEC - EXPERIMENT Basic Digital Logic Circuits The experiments in this laboratory exercise will provide an introduction to digital electronic circuits. You will learn how to use the IDL-00 Bit
Lecture 5: Gate Logic Logic Optimization
 Lecture 5: Gate Logic Logic Optimization MAH, AEN EE271 Lecture 5 1 Overview Reading McCluskey, Logic Design Principles- or any text in boolean algebra Introduction We could design at the level of irsim
Lecture 5: Gate Logic Logic Optimization MAH, AEN EE271 Lecture 5 1 Overview Reading McCluskey, Logic Design Principles- or any text in boolean algebra Introduction We could design at the level of irsim
Gates, Circuits, and Boolean Algebra
 Gates, Circuits, and Boolean Algebra Computers and Electricity A gate is a device that performs a basic operation on electrical signals Gates are combined into circuits to perform more complicated tasks
Gates, Circuits, and Boolean Algebra Computers and Electricity A gate is a device that performs a basic operation on electrical signals Gates are combined into circuits to perform more complicated tasks
Elementary Logic Gates
 Elementary Logic Gates Name Symbol Inverter (NOT Gate) ND Gate OR Gate Truth Table Logic Equation = = = = = + C. E. Stroud Combinational Logic Design (/6) Other Elementary Logic Gates NND Gate NOR Gate
Elementary Logic Gates Name Symbol Inverter (NOT Gate) ND Gate OR Gate Truth Table Logic Equation = = = = = + C. E. Stroud Combinational Logic Design (/6) Other Elementary Logic Gates NND Gate NOR Gate
Figure 8-1 Four Possible Results of Adding Two Bits
 CHPTER EIGHT Combinational Logic pplications Thus far, our discussion has focused on the theoretical design issues of computer systems. We have not yet addressed any of the actual hardware you might find
CHPTER EIGHT Combinational Logic pplications Thus far, our discussion has focused on the theoretical design issues of computer systems. We have not yet addressed any of the actual hardware you might find
FACTORING OUT COMMON FACTORS
 278 (6 2) Chapter 6 Factoring 6.1 FACTORING OUT COMMON FACTORS In this section Prime Factorization of Integers Greatest Common Factor Finding the Greatest Common Factor for Monomials Factoring Out the
278 (6 2) Chapter 6 Factoring 6.1 FACTORING OUT COMMON FACTORS In this section Prime Factorization of Integers Greatest Common Factor Finding the Greatest Common Factor for Monomials Factoring Out the
Computer Engineering 290. Digital Design: I. Lecture Notes Summer 2002
 Computer Engineering 290 Digital Design: I Lecture Notes Summer 2002 W.D. Little Dept. of Electrical and Computer Engineering University of Victoria 1 Preface These lecture notes complement the material
Computer Engineering 290 Digital Design: I Lecture Notes Summer 2002 W.D. Little Dept. of Electrical and Computer Engineering University of Victoria 1 Preface These lecture notes complement the material
FORDHAM UNIVERSITY CISC 3593. Dept. of Computer and Info. Science Spring, 2011. Lab 2. The Full-Adder
 FORDHAM UNIVERSITY CISC 3593 Fordham College Lincoln Center Computer Organization Dept. of Computer and Info. Science Spring, 2011 Lab 2 The Full-Adder 1 Introduction In this lab, the student will construct
FORDHAM UNIVERSITY CISC 3593 Fordham College Lincoln Center Computer Organization Dept. of Computer and Info. Science Spring, 2011 Lab 2 The Full-Adder 1 Introduction In this lab, the student will construct
Factoring (pp. 1 of 4)
 Factoring (pp. 1 of 4) Algebra Review Try these items from middle school math. A) What numbers are the factors of 4? B) Write down the prime factorization of 7. C) 6 Simplify 48 using the greatest common
Factoring (pp. 1 of 4) Algebra Review Try these items from middle school math. A) What numbers are the factors of 4? B) Write down the prime factorization of 7. C) 6 Simplify 48 using the greatest common
Scilab Textbook Companion for Digital Electronics: An Introduction To Theory And Practice by W. H. Gothmann 1
 Scilab Textbook Companion for Digital Electronics: An Introduction To Theory And Practice by W. H. Gothmann 1 Created by Aritra Ray B.Tech Electronics Engineering NIT-DURGAPUR College Teacher Prof. Sabyasachi
Scilab Textbook Companion for Digital Electronics: An Introduction To Theory And Practice by W. H. Gothmann 1 Created by Aritra Ray B.Tech Electronics Engineering NIT-DURGAPUR College Teacher Prof. Sabyasachi
Click on the links below to jump directly to the relevant section
 Click on the links below to jump directly to the relevant section What is algebra? Operations with algebraic terms Mathematical properties of real numbers Order of operations What is Algebra? Algebra is
Click on the links below to jump directly to the relevant section What is algebra? Operations with algebraic terms Mathematical properties of real numbers Order of operations What is Algebra? Algebra is
Counters and Decoders
 Physics 3330 Experiment #10 Fall 1999 Purpose Counters and Decoders In this experiment, you will design and construct a 4-bit ripple-through decade counter with a decimal read-out display. Such a counter
Physics 3330 Experiment #10 Fall 1999 Purpose Counters and Decoders In this experiment, you will design and construct a 4-bit ripple-through decade counter with a decimal read-out display. Such a counter
High School Geometry Test Sampler Math Common Core Sampler Test
 High School Geometry Test Sampler Math Common Core Sampler Test Our High School Geometry sampler covers the twenty most common questions that we see targeted for this level. For complete tests and break
High School Geometry Test Sampler Math Common Core Sampler Test Our High School Geometry sampler covers the twenty most common questions that we see targeted for this level. For complete tests and break
Binary full adder. 2-bit ripple-carry adder. CSE 370 Spring 2006 Introduction to Digital Design Lecture 12: Adders
 SE 370 Spring 2006 Introduction to Digital Design Lecture 12: dders Last Lecture Ls and Ls Today dders inary full 1-bit full omputes sum, carry-out arry-in allows cascaded s = xor xor = + + 32 ND2 11 ND2
SE 370 Spring 2006 Introduction to Digital Design Lecture 12: dders Last Lecture Ls and Ls Today dders inary full 1-bit full omputes sum, carry-out arry-in allows cascaded s = xor xor = + + 32 ND2 11 ND2
Lecture 8: Synchronous Digital Systems
 Lecture 8: Synchronous Digital Systems The distinguishing feature of a synchronous digital system is that the circuit only changes in response to a system clock. For example, consider the edge triggered
Lecture 8: Synchronous Digital Systems The distinguishing feature of a synchronous digital system is that the circuit only changes in response to a system clock. For example, consider the edge triggered
Read-only memory Implementing logic with ROM Programmable logic devices Implementing logic with PLDs Static hazards
 Points ddressed in this Lecture Lecture 8: ROM Programmable Logic Devices Professor Peter Cheung Department of EEE, Imperial College London Read-only memory Implementing logic with ROM Programmable logic
Points ddressed in this Lecture Lecture 8: ROM Programmable Logic Devices Professor Peter Cheung Department of EEE, Imperial College London Read-only memory Implementing logic with ROM Programmable logic
Factoring Flow Chart
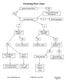 Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
DEPARTMENT OF INFORMATION TECHNLOGY
 DRONACHARYA GROUP OF INSTITUTIONS, GREATER NOIDA Affiliated to Mahamaya Technical University, Noida Approved by AICTE DEPARTMENT OF INFORMATION TECHNLOGY Lab Manual for Computer Organization Lab ECS-453
DRONACHARYA GROUP OF INSTITUTIONS, GREATER NOIDA Affiliated to Mahamaya Technical University, Noida Approved by AICTE DEPARTMENT OF INFORMATION TECHNLOGY Lab Manual for Computer Organization Lab ECS-453
Using Logic to Design Computer Components
 CHAPTER 13 Using Logic to Design Computer Components Parallel and sequential operation In this chapter we shall see that the propositional logic studied in the previous chapter can be used to design digital
CHAPTER 13 Using Logic to Design Computer Components Parallel and sequential operation In this chapter we shall see that the propositional logic studied in the previous chapter can be used to design digital
1.3 Polynomials and Factoring
 1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
Course Requirements & Evaluation Methods
 Course Title: Logic Circuits Course Prefix: ELEG Course No.: 3063 Sections: 01 & 02 Department of Electrical and Computer Engineering College of Engineering Instructor Name: Justin Foreman Office Location:
Course Title: Logic Circuits Course Prefix: ELEG Course No.: 3063 Sections: 01 & 02 Department of Electrical and Computer Engineering College of Engineering Instructor Name: Justin Foreman Office Location:
Introduction to Digital Logic with Laboratory Exercises
 Introduction to Digital Logic with Laboratory Exercises Introduction to Digital Logic with Laboratory Exercises James Feher Copyright 29 James Feher Editor-In-Chief: James Feher Associate Editor: Marisa
Introduction to Digital Logic with Laboratory Exercises Introduction to Digital Logic with Laboratory Exercises James Feher Copyright 29 James Feher Editor-In-Chief: James Feher Associate Editor: Marisa
IAEA Training Course on Safety Assessment of NPPs to Assist Decision Making. System Analysis. Lecturer. Workshop Information IAEA Workshop
 IAEA Training Course on Safety Assessment of NPPs to Assist Decision Making System Analysis Lecturer Lesson Lesson IV IV 3_2.3 3_2.3 Workshop Information IAEA Workshop City, XX XX - City -XX, Country Month,
IAEA Training Course on Safety Assessment of NPPs to Assist Decision Making System Analysis Lecturer Lesson Lesson IV IV 3_2.3 3_2.3 Workshop Information IAEA Workshop City, XX XX - City -XX, Country Month,
COMBINATIONAL CIRCUITS
 COMBINATIONAL CIRCUITS http://www.tutorialspoint.com/computer_logical_organization/combinational_circuits.htm Copyright tutorialspoint.com Combinational circuit is a circuit in which we combine the different
COMBINATIONAL CIRCUITS http://www.tutorialspoint.com/computer_logical_organization/combinational_circuits.htm Copyright tutorialspoint.com Combinational circuit is a circuit in which we combine the different
EE360: Digital Design I Course Syllabus
 : Course Syllabus Dr. Mohammad H. Awedh Fall 2008 Course Description This course introduces students to the basic concepts of digital systems, including analysis and design. Both combinational and sequential
: Course Syllabus Dr. Mohammad H. Awedh Fall 2008 Course Description This course introduces students to the basic concepts of digital systems, including analysis and design. Both combinational and sequential
Determine If An Equation Represents a Function
 Question : What is a linear function? The term linear function consists of two parts: linear and function. To understand what these terms mean together, we must first understand what a function is. The
Question : What is a linear function? The term linear function consists of two parts: linear and function. To understand what these terms mean together, we must first understand what a function is. The
www.mohandesyar.com SOLUTIONS MANUAL DIGITAL DESIGN FOURTH EDITION M. MORRIS MANO California State University, Los Angeles MICHAEL D.
 27 Pearson Education, Inc., Upper Saddle River, NJ. ll rights reserved. This publication is protected by opyright and written permission should be obtained or likewise. For information regarding permission(s),
27 Pearson Education, Inc., Upper Saddle River, NJ. ll rights reserved. This publication is protected by opyright and written permission should be obtained or likewise. For information regarding permission(s),
A single register, called the accumulator, stores the. operand before the operation, and stores the result. Add y # add y from memory to the acc
 Other architectures Example. Accumulator-based machines A single register, called the accumulator, stores the operand before the operation, and stores the result after the operation. Load x # into acc
Other architectures Example. Accumulator-based machines A single register, called the accumulator, stores the operand before the operation, and stores the result after the operation. Load x # into acc
Formal Languages and Automata Theory - Regular Expressions and Finite Automata -
 Formal Languages and Automata Theory - Regular Expressions and Finite Automata - Samarjit Chakraborty Computer Engineering and Networks Laboratory Swiss Federal Institute of Technology (ETH) Zürich March
Formal Languages and Automata Theory - Regular Expressions and Finite Automata - Samarjit Chakraborty Computer Engineering and Networks Laboratory Swiss Federal Institute of Technology (ETH) Zürich March
SAT Math Strategies Quiz
 When you are stumped on an SAT or ACT math question, there are two very useful strategies that may help you to get the correct answer: 1) work with the answers; and 2) plug in real numbers. This review
When you are stumped on an SAT or ACT math question, there are two very useful strategies that may help you to get the correct answer: 1) work with the answers; and 2) plug in real numbers. This review
Design and Development of Virtual Instrument (VI) Modules for an Introductory Digital Logic Course
 Session ENG 206-6 Design and Development of Virtual Instrument (VI) Modules for an Introductory Digital Logic Course Nikunja Swain, Ph.D., PE South Carolina State University swain@scsu.edu Raghu Korrapati,
Session ENG 206-6 Design and Development of Virtual Instrument (VI) Modules for an Introductory Digital Logic Course Nikunja Swain, Ph.D., PE South Carolina State University swain@scsu.edu Raghu Korrapati,
5.1 FACTORING OUT COMMON FACTORS
 C H A P T E R 5 Factoring he sport of skydiving was born in the 1930s soon after the military began using parachutes as a means of deploying troops. T Today, skydiving is a popular sport around the world.
C H A P T E R 5 Factoring he sport of skydiving was born in the 1930s soon after the military began using parachutes as a means of deploying troops. T Today, skydiving is a popular sport around the world.
Math Review. for the Quantitative Reasoning Measure of the GRE revised General Test
 Math Review for the Quantitative Reasoning Measure of the GRE revised General Test www.ets.org Overview This Math Review will familiarize you with the mathematical skills and concepts that are important
Math Review for the Quantitative Reasoning Measure of the GRE revised General Test www.ets.org Overview This Math Review will familiarize you with the mathematical skills and concepts that are important
Sistemas Digitais I LESI - 2º ano
 Sistemas Digitais I LESI - 2º ano Lesson 6 - Combinational Design Practices Prof. João Miguel Fernandes (miguel@di.uminho.pt) Dept. Informática UNIVERSIDADE DO MINHO ESCOLA DE ENGENHARIA - PLDs (1) - The
Sistemas Digitais I LESI - 2º ano Lesson 6 - Combinational Design Practices Prof. João Miguel Fernandes (miguel@di.uminho.pt) Dept. Informática UNIVERSIDADE DO MINHO ESCOLA DE ENGENHARIA - PLDs (1) - The
RUTGERS UNIVERSITY Department of Electrical and Computer Engineering 14:332:233 DIGITAL LOGIC DESIGN LABORATORY
 RUTGERS UNIVERSITY Department of Electrical and Computer Engineering 14:332:233 DIGITAL LOGIC DESIGN LABORATORY Fall 2012 Contents 1 LABORATORY No 1 3 11 Equipment 3 12 Protoboard 4 13 The Input-Control/Output-Display
RUTGERS UNIVERSITY Department of Electrical and Computer Engineering 14:332:233 DIGITAL LOGIC DESIGN LABORATORY Fall 2012 Contents 1 LABORATORY No 1 3 11 Equipment 3 12 Protoboard 4 13 The Input-Control/Output-Display
6.4 Special Factoring Rules
 6.4 Special Factoring Rules OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor a sum of cubes. By reversing the rules for multiplication
6.4 Special Factoring Rules OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor a sum of cubes. By reversing the rules for multiplication
6. BOOLEAN LOGIC DESIGN
 6. OOLEN LOGI DESIGN 89 Topics: oolean algebra onverting between oolean algebra and logic gates and ladder logic Logic examples Objectives: e able to simplify designs with oolean algebra 6. INTRODUTION
6. OOLEN LOGI DESIGN 89 Topics: oolean algebra onverting between oolean algebra and logic gates and ladder logic Logic examples Objectives: e able to simplify designs with oolean algebra 6. INTRODUTION
Radicals - Square Roots
 8.1 Radicals - Square Roots Objective: Simplify expressions with square roots. Square roots are the most common type of radical used. A square root unsquares a number. For example, because 5 2 = 25 we
8.1 Radicals - Square Roots Objective: Simplify expressions with square roots. Square roots are the most common type of radical used. A square root unsquares a number. For example, because 5 2 = 25 we
SAT Math Facts & Formulas Review Quiz
 Test your knowledge of SAT math facts, formulas, and vocabulary with the following quiz. Some questions are more challenging, just like a few of the questions that you ll encounter on the SAT; these questions
Test your knowledge of SAT math facts, formulas, and vocabulary with the following quiz. Some questions are more challenging, just like a few of the questions that you ll encounter on the SAT; these questions
Digital Circuit Design
 Test and Diagnosis of of ICs Fault coverage (%) 95 9 85 8 75 7 65 97.92 SSL 4,246 Shawn Blanton Professor Department of ECE Center for Silicon System Implementation CMU Laboratory for Integrated Systems
Test and Diagnosis of of ICs Fault coverage (%) 95 9 85 8 75 7 65 97.92 SSL 4,246 Shawn Blanton Professor Department of ECE Center for Silicon System Implementation CMU Laboratory for Integrated Systems
Lecture 4: Binary. CS442: Great Insights in Computer Science Michael L. Littman, Spring 2006. I-Before-E, Continued
 Lecture 4: Binary CS442: Great Insights in Computer Science Michael L. Littman, Spring 26 I-Before-E, Continued There are two ideas from last time that I d like to flesh out a bit more. This time, let
Lecture 4: Binary CS442: Great Insights in Computer Science Michael L. Littman, Spring 26 I-Before-E, Continued There are two ideas from last time that I d like to flesh out a bit more. This time, let
COLLEGE ALGEBRA. Paul Dawkins
 COLLEGE ALGEBRA Paul Dawkins Table of Contents Preface... iii Outline... iv Preliminaries... Introduction... Integer Exponents... Rational Exponents... 9 Real Exponents...5 Radicals...6 Polynomials...5
COLLEGE ALGEBRA Paul Dawkins Table of Contents Preface... iii Outline... iv Preliminaries... Introduction... Integer Exponents... Rational Exponents... 9 Real Exponents...5 Radicals...6 Polynomials...5
FACTORING POLYNOMIALS
 296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
Math 53 Worksheet Solutions- Minmax and Lagrange
 Math 5 Worksheet Solutions- Minmax and Lagrange. Find the local maximum and minimum values as well as the saddle point(s) of the function f(x, y) = e y (y x ). Solution. First we calculate the partial
Math 5 Worksheet Solutions- Minmax and Lagrange. Find the local maximum and minimum values as well as the saddle point(s) of the function f(x, y) = e y (y x ). Solution. First we calculate the partial
