Decomposing Rational Functions into Partial Fractions:
|
|
|
- Laurence Robinson
- 9 years ago
- Views:
Transcription
1 Prof. Keely's Math Online Lessons University of Phoenix Online & Clark College, Vancouver WA Copyright 2003 Sally J. Keely. All Rights Reserved. COLLEGE ALGEBRA Hi! Today's topic is highly structured and algebraically interesting ;-) We are going to rewrite a large rational function as a sum of smaller fractions. This is the act of "decomposing" rational functions into "partial fractions" and it is really useful in Integral Calculus! Topics of Importance: Decompose proper rational functions into partial fractions (including linear factors, quadratic factors, repeated factors) Decompose improper rational functions into partial fractions Decomposing Rational Functions into Partial Fractions: The best way to learn decomposition into partial fractions is to work through lots of examples, so let's get right to it. Example 1. Linear factors. Decompose Always start by factoring the denominator completely. We want to rewrite this rational function as a sum of smaller fractions. The denominators of those fractions will be the factors in the denominator of the original rational expression. The numerator of each smaller fraction will be a number (at least for now), but we don't know what they are, so we'll use A and B to represent them. Thus, the rational function can be expanded into partial fraction form as: "expanded" form
2 Next, multiply both sides of this equation by the LCD (x+2)(x-1) to eliminate the denominators leaving, 2x-11 = A(x-1) + B(x+2) We need to solve for A and B. One way to do this is to pick "nifty x's" that would make either the A or the B disappear. For instance, if we let x=1 and substitute it in for x throughout the equation we get, 2(1)-11 = A(1-1) + B(1+2) 2-11 = 0A + 3B -9 = 3B B = -3 See how the A disappears and we are able to solve for B? Now do this again picking a different "nifty x"... this time one that would make the B disappear. Yes, let x=-2 to get, 2(-2)-11 = A(-2-1) + B(-2+2) = -3A + 0B -15 = -3A A = 5 Cool! Substituting these values back into the expanded form of the rational function gives our final decomposed form: final "decomposed" form There, we have written the original rational function as a sum/difference of two smaller fractions, thus we have decomposed the original rational function If you want to check this answer, combine 5/(x+2)-3/(x-1) by building them up to each have the LCD and simplifying to see if you get the original rational expression.
3 Example 2. Linear Factors. Decompose First factor the denominator completely, Then expand into partial fraction form, Multiply through by the LCD x(x-2)(x+2) to get, 3x 2 +7x-2 = A(x-2)(x+2) + Bx(x+2) + Cx(x-2) Pick "nifty x's", substitute them in, and solve for A, B, and C: Let x=2... 3(2) 2 +7(2)-2 = A(0)(4) + B(2)(4) + C(2)(0) 24 = 8B B = 3 Let x= (-2) 2 +7(-2)-2 = A(-4)(0) + B(-2)(0) + C(-2)(-4) -4 = 8C C = -½ Let x=0... 3(0) 2 +7(0)-2 = A(-2)(2) + B(0)(2) + C(0)(-2) -2 = -4A A = ½ Finally, substitute A, B, and C back into the expanded form. Here we may want to simplify to avoid leaving compound fractions in the final answer. Example 3. Repeated linear factors. Decompose The denominator is already factored, but notice that it has repeated factors. When expanding repeated factors into partial fractions, we must include a fraction with each power of the factor. In this case it is ( ) 3 so we need a fraction with ( ) 1 in the denominator, a fraction with ( ) 2 in the denominator, and a fraction with ( ) 3 in the denominator. Here then is the expansion: Multiplying through by the LCD (x-2) 3 gives, 2x 2-9x = A(x-2) 2 + B(x-2) + C
4 Pick 2 as our "nifty x", substitute it in, and solve: Let x=2... 2(2) 2-9(2) = A(0) 2 + B(0) + C C = -10 Uh oh, that is the only possible "nifty x". Now what? How can we solve for A and B? We need a second method for finding these constants. Return to, 2x 2-9x = A(x-2) 2 + B(x-2) + C FOIL and simplify on the right hand side: 2x 2-9x = A(x-2)(x-2) + B(x-2) + C 2x 2-9x = A(x 2-4x+4) + B(x-2) + C 2x 2-9x = Ax 2-4Ax+4A + Bx-2B + C 2x 2-9x = Ax 2 + (-4A+B)x + (4A-2B+C) Now, here is a neat trick. If the polynomial on the left is equal to the polynomial on the right, then the coefficient of the x 2 -term on the left must equal the coefficient of the x 2 - term on the right; the coefficient of the x-term on the left must equal the coefficient of the x-term on the right, and the constant term on the left must equal the constant term on the right. So, equate them! coefficients of x 2 -terms 2 = A coefficients of x-terms -9 = -4A+B -9 = -4(2)+B B = -1 constant terms 0 = 4A-2B+C (But we needn't solve this equation because at this point in this problem, we have already found the A, B, and C.) So, our final answer is, Thus, if the "nifty x" method doesn't produce all the constants, resort to the "equating coefficients" method. With practice, you really won't need to do the FOIL and simplify step in most cases. For instance, in example 3 we had 2x 2-9x = A(x-2) 2 + B(x-2) + C. You can easily look at this and tell that the only x 2 term on the right will be Ax 2 (so right away we have A=2). It is also easy to see without FOILing that the constant terms on the right will be 4A-2B+C. Given that we had already found C=-10 and A=2, we can plug these into the equation obtained by equating constant terms from both sides of the equation to get 0=4A-2B+C 0=4(2)-2B+(-10) B=-1. Usually working with just the highest degree term and/or the constant term will enable you to complete the identification of all the unknown letters.
5 Example 4. Quadratic factors. Decompose Start by factoring the denominator, Next we need to write the expansion. But, this expansion will be a bit different since we have a quadratic factor (well, quadratic irreducible in the eals). The term in the numerator of each fraction in the expansion is actually one degree less than the factor in the denominator. When we had only linear factors, one degree less gave us constants in the numerators. But when you have a quadratic factor, one degree less means we need a linear term in the numerator. So above the x 2 +1 quadratic factor we need the linear factor Bx+C as shown in the expansion: Multiplying through by the LCD (x+3)(x 2 +1) gives, 4x 2 +x-3 = A(x 2 +1) + (Bx+C)(x+3) Pick -3 as our "nifty x", substitute it in, and solve: Let x= (-3) 2 +(-3)-3 = A((-3) 2 +1) + (B(-3)+C)(-3+3) 30 = 10A A = 3 Since there is no eal number that can be substituted in for x to make x 2 +1 zero out, we must resort to the "equate coefficients" method for finding B and C. Looking at 4x 2 +x-3 = A(x 2 +1) + (Bx+C)(x+3) we can equate coefficients of the leading term and equate constants (those two terms are the easiest to "see" without having to FOIL and simplify first). x 2 -terms 4 = A+B 4 = 3+B B = 1 constant terms -3 = A+3C -3 = 3+3C C = -2 Substituting these values in for A, B, and C gives the final decomposed form, A bit more on this "one degree less" in the numerator rule. Suppose we had had a fourth-degree factor (irreducible in ) in the denominator such as x 4 +16, then its numerator in the expansion would have to have been one degree less, i.e. a cubic such as Ax 3 +Bx 2 +Cx+D. Does that make sense?
6 Also, look back at example 3. One of the fractions in the expansion was C/(x-2) 3... but shouldn't we have used a quadratic term in the numerator since the denominator was (if FOILed out) cubic? No! CAUTION: The rule is to use an expression in the numerator that is one degree less than the factor in the denominator, not the simplified expression in the denominator. So, you use an expression that is one degree less than the inside of the ( ) in the denominator. Example 5. Quadratic factors.decompose As always, factor the denominator first, Which (remembering to use linear expressions in the numerators of the quadratic factors) expands to, Multiplying through by the LCD (x 2 +4)(x 2 +1) gives, 5x 3 -x 2 +14x-1 = (Ax+B)(x 2 +1) + (Cx+D)(x 2 +4) Since both factors only have non- eal roots, we can't use the "nifty x" method at all (why not?) and must resort to the "equate coefficients" method. x 3 -terms 5 = A+C x 2 -terms -1 = B+D x-terms 14 = A+4C constant terms -1 = B+4D Essentially what we have now is a 4x4 linear system. We can solve it algebraically, but if you have a calculator handy that has a linear system solver, take advantage of it! (See my MOL Calculator Guide: Linear Systems at for information about how to a TI calculator's linear solver.) To solve electronically the system will likely need to be rewritten as: 1A + 0B + 1C + 0D = 5 0A + 1B + 0C + 1D = -1 1A + 0B + 4C + 0D = 14 0A + 1B + 0C + 4D = -1
7 The solution should yield A=2, B=-1, C=3, D=0. Plugging those into the expansion gives the final answer, Example 6. Repeated quadratic factors. Write expanded into general partial fraction form. You do not need to perform the full decomposition. The denominator is factored completely, so we are ready to expand. Hmmm, why does the x 2 term not have a numerator of Bx+C? Because x 2 should really be thought of as (x) 2 thus the stuff inside the parentheses is a linear factor so we only need a constant in its numerator. Similarly the x 3 term is really (x) 3 so again we have a linear factor inside the parentheses requiring only a constant in its numerator. CAUTION! LQ Try this Lesson Question! Discuss the solution with others :) Is there a way to predict how many fractions the partial fraction expansion is going to have? Is there a way to predict how many letters will be needed in the partial fraction expansion? Look for patterns in example 6 to discover the answers to these questions :) Decomposing Improper Rational Functions into Partial Fractions: So far all of our examples have been proper fractions, but if the original rational function is an improper fraction (meaning that the degree of the numerator is greater than or equal to the degree of the denominator) then you must perform long division before attempting the partial fraction decomposition.
8 Example 7. Improper fraction. Decompose Since the degree of the numerator is greater than or equal to the degree of the denominator we must start by performing long division. Thus the original fraction can be rewritten as, The fraction obtained from the remainder is the only part that needs to be decomposed x+2 = A(2x+1) + Bx Let x=-½... -½+2 = A(0) + B(-½) 3/2 = -½B B = -3 Let x= = A(2*0+1) + B(0) A = 2 Thus the final answer is, I hope you have enjoyed these examples and had fun with the algebra. You will find partial fraction decomposition quite handy in Integral Calculus. It is FAR easier to integrate the partial fractions than to integrate the original big old fraction. I bet you can't wait to get there!! So much fun awaits you in Calculus :) Additional Resources:
Partial Fractions. (x 1)(x 2 + 1)
 Partial Fractions Adding rational functions involves finding a common denominator, rewriting each fraction so that it has that denominator, then adding. For example, 3x x 1 3x(x 1) (x + 1)(x 1) + 1(x +
Partial Fractions Adding rational functions involves finding a common denominator, rewriting each fraction so that it has that denominator, then adding. For example, 3x x 1 3x(x 1) (x + 1)(x 1) + 1(x +
Partial Fractions. Combining fractions over a common denominator is a familiar operation from algebra:
 Partial Fractions Combining fractions over a common denominator is a familiar operation from algebra: From the standpoint of integration, the left side of Equation 1 would be much easier to work with than
Partial Fractions Combining fractions over a common denominator is a familiar operation from algebra: From the standpoint of integration, the left side of Equation 1 would be much easier to work with than
1.3 Algebraic Expressions
 1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
The Method of Partial Fractions Math 121 Calculus II Spring 2015
 Rational functions. as The Method of Partial Fractions Math 11 Calculus II Spring 015 Recall that a rational function is a quotient of two polynomials such f(x) g(x) = 3x5 + x 3 + 16x x 60. The method
Rational functions. as The Method of Partial Fractions Math 11 Calculus II Spring 015 Recall that a rational function is a quotient of two polynomials such f(x) g(x) = 3x5 + x 3 + 16x x 60. The method
Integrals of Rational Functions
 Integrals of Rational Functions Scott R. Fulton Overview A rational function has the form where p and q are polynomials. For example, r(x) = p(x) q(x) f(x) = x2 3 x 4 + 3, g(t) = t6 + 4t 2 3, 7t 5 + 3t
Integrals of Rational Functions Scott R. Fulton Overview A rational function has the form where p and q are polynomials. For example, r(x) = p(x) q(x) f(x) = x2 3 x 4 + 3, g(t) = t6 + 4t 2 3, 7t 5 + 3t
Partial Fractions Examples
 Partial Fractions Examples Partial fractions is the name given to a technique of integration that may be used to integrate any ratio of polynomials. A ratio of polynomials is called a rational function.
Partial Fractions Examples Partial fractions is the name given to a technique of integration that may be used to integrate any ratio of polynomials. A ratio of polynomials is called a rational function.
1 Lecture: Integration of rational functions by decomposition
 Lecture: Integration of rational functions by decomposition into partial fractions Recognize and integrate basic rational functions, except when the denominator is a power of an irreducible quadratic.
Lecture: Integration of rational functions by decomposition into partial fractions Recognize and integrate basic rational functions, except when the denominator is a power of an irreducible quadratic.
1.7. Partial Fractions. 1.7.1. Rational Functions and Partial Fractions. A rational function is a quotient of two polynomials: R(x) = P (x) Q(x).
 .7. PRTIL FRCTIONS 3.7. Partial Fractions.7.. Rational Functions and Partial Fractions. rational function is a quotient of two polynomials: R(x) = P (x) Q(x). Here we discuss how to integrate rational
.7. PRTIL FRCTIONS 3.7. Partial Fractions.7.. Rational Functions and Partial Fractions. rational function is a quotient of two polynomials: R(x) = P (x) Q(x). Here we discuss how to integrate rational
is identically equal to x 2 +3x +2
 Partial fractions 3.6 Introduction It is often helpful to break down a complicated algebraic fraction into a sum of simpler fractions. 4x+7 For example it can be shown that has the same value as 1 + 3
Partial fractions 3.6 Introduction It is often helpful to break down a complicated algebraic fraction into a sum of simpler fractions. 4x+7 For example it can be shown that has the same value as 1 + 3
expression is written horizontally. The Last terms ((2)( 4)) because they are the last terms of the two polynomials. This is called the FOIL method.
 A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
a 1 x + a 0 =0. (3) ax 2 + bx + c =0. (4)
 ROOTS OF POLYNOMIAL EQUATIONS In this unit we discuss polynomial equations. A polynomial in x of degree n, where n 0 is an integer, is an expression of the form P n (x) =a n x n + a n 1 x n 1 + + a 1 x
ROOTS OF POLYNOMIAL EQUATIONS In this unit we discuss polynomial equations. A polynomial in x of degree n, where n 0 is an integer, is an expression of the form P n (x) =a n x n + a n 1 x n 1 + + a 1 x
SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS
 (Section 0.6: Polynomial, Rational, and Algebraic Expressions) 0.6.1 SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS LEARNING OBJECTIVES Be able to identify polynomial, rational, and algebraic
(Section 0.6: Polynomial, Rational, and Algebraic Expressions) 0.6.1 SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS LEARNING OBJECTIVES Be able to identify polynomial, rational, and algebraic
Factoring Quadratic Expressions
 Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
1.4. Arithmetic of Algebraic Fractions. Introduction. Prerequisites. Learning Outcomes
 Arithmetic of Algebraic Fractions 1.4 Introduction Just as one whole number divided by another is called a numerical fraction, so one algebraic expression divided by another is known as an algebraic fraction.
Arithmetic of Algebraic Fractions 1.4 Introduction Just as one whole number divided by another is called a numerical fraction, so one algebraic expression divided by another is known as an algebraic fraction.
3.6. Partial Fractions. Introduction. Prerequisites. Learning Outcomes
 Partial Fractions 3.6 Introduction It is often helpful to break down a complicated algebraic fraction into a sum of simpler fractions. For 4x + 7 example it can be shown that x 2 + 3x + 2 has the same
Partial Fractions 3.6 Introduction It is often helpful to break down a complicated algebraic fraction into a sum of simpler fractions. For 4x + 7 example it can be shown that x 2 + 3x + 2 has the same
Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any.
 Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
FOIL FACTORING. Factoring is merely undoing the FOIL method. Let s look at an example: Take the polynomial x²+4x+4.
 FOIL FACTORING Factoring is merely undoing the FOIL method. Let s look at an example: Take the polynomial x²+4x+4. First we take the 3 rd term (in this case 4) and find the factors of it. 4=1x4 4=2x2 Now
FOIL FACTORING Factoring is merely undoing the FOIL method. Let s look at an example: Take the polynomial x²+4x+4. First we take the 3 rd term (in this case 4) and find the factors of it. 4=1x4 4=2x2 Now
Partial Fractions. p(x) q(x)
 Partial Fractions Introduction to Partial Fractions Given a rational function of the form p(x) q(x) where the degree of p(x) is less than the degree of q(x), the method of partial fractions seeks to break
Partial Fractions Introduction to Partial Fractions Given a rational function of the form p(x) q(x) where the degree of p(x) is less than the degree of q(x), the method of partial fractions seeks to break
0.4 FACTORING POLYNOMIALS
 36_.qxd /3/5 :9 AM Page -9 SECTION. Factoring Polynomials -9. FACTORING POLYNOMIALS Use special products and factorization techniques to factor polynomials. Find the domains of radical expressions. Use
36_.qxd /3/5 :9 AM Page -9 SECTION. Factoring Polynomials -9. FACTORING POLYNOMIALS Use special products and factorization techniques to factor polynomials. Find the domains of radical expressions. Use
CM2202: Scientific Computing and Multimedia Applications General Maths: 2. Algebra - Factorisation
 CM2202: Scientific Computing and Multimedia Applications General Maths: 2. Algebra - Factorisation Prof. David Marshall School of Computer Science & Informatics Factorisation Factorisation is a way of
CM2202: Scientific Computing and Multimedia Applications General Maths: 2. Algebra - Factorisation Prof. David Marshall School of Computer Science & Informatics Factorisation Factorisation is a way of
CAHSEE on Target UC Davis, School and University Partnerships
 UC Davis, School and University Partnerships CAHSEE on Target Mathematics Curriculum Published by The University of California, Davis, School/University Partnerships Program 006 Director Sarah R. Martinez,
UC Davis, School and University Partnerships CAHSEE on Target Mathematics Curriculum Published by The University of California, Davis, School/University Partnerships Program 006 Director Sarah R. Martinez,
NSM100 Introduction to Algebra Chapter 5 Notes Factoring
 Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
3.3. Solving Polynomial Equations. Introduction. Prerequisites. Learning Outcomes
 Solving Polynomial Equations 3.3 Introduction Linear and quadratic equations, dealt within Sections 3.1 and 3.2, are members of a class of equations, called polynomial equations. These have the general
Solving Polynomial Equations 3.3 Introduction Linear and quadratic equations, dealt within Sections 3.1 and 3.2, are members of a class of equations, called polynomial equations. These have the general
FACTORING QUADRATICS 8.1.1 and 8.1.2
 FACTORING QUADRATICS 8.1.1 and 8.1.2 Chapter 8 introduces students to quadratic equations. These equations can be written in the form of y = ax 2 + bx + c and, when graphed, produce a curve called a parabola.
FACTORING QUADRATICS 8.1.1 and 8.1.2 Chapter 8 introduces students to quadratic equations. These equations can be written in the form of y = ax 2 + bx + c and, when graphed, produce a curve called a parabola.
JUST THE MATHS UNIT NUMBER 1.8. ALGEBRA 8 (Polynomials) A.J.Hobson
 JUST THE MATHS UNIT NUMBER 1.8 ALGEBRA 8 (Polynomials) by A.J.Hobson 1.8.1 The factor theorem 1.8.2 Application to quadratic and cubic expressions 1.8.3 Cubic equations 1.8.4 Long division of polynomials
JUST THE MATHS UNIT NUMBER 1.8 ALGEBRA 8 (Polynomials) by A.J.Hobson 1.8.1 The factor theorem 1.8.2 Application to quadratic and cubic expressions 1.8.3 Cubic equations 1.8.4 Long division of polynomials
is identically equal to x 2 +3x +2
 Partial fractions.6 Introduction It is often helpful to break down a complicated algebraic fraction into a sum of simpler fractions. 4x+7 For example it can be shown that has the same value as + for any
Partial fractions.6 Introduction It is often helpful to break down a complicated algebraic fraction into a sum of simpler fractions. 4x+7 For example it can be shown that has the same value as + for any
Factoring Polynomials and Solving Quadratic Equations
 Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
Factoring Flow Chart
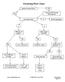 Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Algebra Practice Problems for Precalculus and Calculus
 Algebra Practice Problems for Precalculus and Calculus Solve the following equations for the unknown x: 1. 5 = 7x 16 2. 2x 3 = 5 x 3. 4. 1 2 (x 3) + x = 17 + 3(4 x) 5 x = 2 x 3 Multiply the indicated polynomials
Algebra Practice Problems for Precalculus and Calculus Solve the following equations for the unknown x: 1. 5 = 7x 16 2. 2x 3 = 5 x 3. 4. 1 2 (x 3) + x = 17 + 3(4 x) 5 x = 2 x 3 Multiply the indicated polynomials
To add fractions we rewrite the fractions with a common denominator then add the numerators. = +
 Partial Fractions Adding fractions To add fractions we rewrite the fractions with a common denominator then add the numerators. Example Find the sum of 3 x 5 The common denominator of 3 and x 5 is 3 x
Partial Fractions Adding fractions To add fractions we rewrite the fractions with a common denominator then add the numerators. Example Find the sum of 3 x 5 The common denominator of 3 and x 5 is 3 x
SOLVING POLYNOMIAL EQUATIONS
 C SOLVING POLYNOMIAL EQUATIONS We will assume in this appendix that you know how to divide polynomials using long division and synthetic division. If you need to review those techniques, refer to an algebra
C SOLVING POLYNOMIAL EQUATIONS We will assume in this appendix that you know how to divide polynomials using long division and synthetic division. If you need to review those techniques, refer to an algebra
Partial Fractions Decomposition
 Partial Fractions Decomposition Dr. Philippe B. Laval Kennesaw State University August 6, 008 Abstract This handout describes partial fractions decomposition and how it can be used when integrating rational
Partial Fractions Decomposition Dr. Philippe B. Laval Kennesaw State University August 6, 008 Abstract This handout describes partial fractions decomposition and how it can be used when integrating rational
Answers to Basic Algebra Review
 Answers to Basic Algebra Review 1. -1.1 Follow the sign rules when adding and subtracting: If the numbers have the same sign, add them together and keep the sign. If the numbers have different signs, subtract
Answers to Basic Algebra Review 1. -1.1 Follow the sign rules when adding and subtracting: If the numbers have the same sign, add them together and keep the sign. If the numbers have different signs, subtract
2.3. Finding polynomial functions. An Introduction:
 2.3. Finding polynomial functions. An Introduction: As is usually the case when learning a new concept in mathematics, the new concept is the reverse of the previous one. Remember how you first learned
2.3. Finding polynomial functions. An Introduction: As is usually the case when learning a new concept in mathematics, the new concept is the reverse of the previous one. Remember how you first learned
Lagrange Interpolation is a method of fitting an equation to a set of points that functions well when there are few points given.
 Polynomials (Ch.1) Study Guide by BS, JL, AZ, CC, SH, HL Lagrange Interpolation is a method of fitting an equation to a set of points that functions well when there are few points given. Sasha s method
Polynomials (Ch.1) Study Guide by BS, JL, AZ, CC, SH, HL Lagrange Interpolation is a method of fitting an equation to a set of points that functions well when there are few points given. Sasha s method
FACTORISATION YEARS. A guide for teachers - Years 9 10 June 2011. The Improving Mathematics Education in Schools (TIMES) Project
 9 10 YEARS The Improving Mathematics Education in Schools (TIMES) Project FACTORISATION NUMBER AND ALGEBRA Module 33 A guide for teachers - Years 9 10 June 2011 Factorisation (Number and Algebra : Module
9 10 YEARS The Improving Mathematics Education in Schools (TIMES) Project FACTORISATION NUMBER AND ALGEBRA Module 33 A guide for teachers - Years 9 10 June 2011 Factorisation (Number and Algebra : Module
Sample Problems. Practice Problems
 Lecture Notes Partial Fractions page Sample Problems Compute each of the following integrals.. x dx. x + x (x + ) (x ) (x ) dx 8. x x dx... x (x + ) (x + ) dx x + x x dx x + x x + 6x x dx + x 6. 7. x (x
Lecture Notes Partial Fractions page Sample Problems Compute each of the following integrals.. x dx. x + x (x + ) (x ) (x ) dx 8. x x dx... x (x + ) (x + ) dx x + x x dx x + x x + 6x x dx + x 6. 7. x (x
Name Intro to Algebra 2. Unit 1: Polynomials and Factoring
 Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
ALGEBRA REVIEW LEARNING SKILLS CENTER. Exponents & Radicals
 ALGEBRA REVIEW LEARNING SKILLS CENTER The "Review Series in Algebra" is taught at the beginning of each quarter by the staff of the Learning Skills Center at UC Davis. This workshop is intended to be an
ALGEBRA REVIEW LEARNING SKILLS CENTER The "Review Series in Algebra" is taught at the beginning of each quarter by the staff of the Learning Skills Center at UC Davis. This workshop is intended to be an
4.1. COMPLEX NUMBERS
 4.1. COMPLEX NUMBERS What You Should Learn Use the imaginary unit i to write complex numbers. Add, subtract, and multiply complex numbers. Use complex conjugates to write the quotient of two complex numbers
4.1. COMPLEX NUMBERS What You Should Learn Use the imaginary unit i to write complex numbers. Add, subtract, and multiply complex numbers. Use complex conjugates to write the quotient of two complex numbers
6 EXTENDING ALGEBRA. 6.0 Introduction. 6.1 The cubic equation. Objectives
 6 EXTENDING ALGEBRA Chapter 6 Extending Algebra Objectives After studying this chapter you should understand techniques whereby equations of cubic degree and higher can be solved; be able to factorise
6 EXTENDING ALGEBRA Chapter 6 Extending Algebra Objectives After studying this chapter you should understand techniques whereby equations of cubic degree and higher can be solved; be able to factorise
Partial Fractions: Undetermined Coefficients
 1. Introduction Partial Fractions: Undetermined Coefficients Not every F(s) we encounter is in the Laplace table. Partial fractions is a method for re-writing F(s) in a form suitable for the use of the
1. Introduction Partial Fractions: Undetermined Coefficients Not every F(s) we encounter is in the Laplace table. Partial fractions is a method for re-writing F(s) in a form suitable for the use of the
A Quick Algebra Review
 1. Simplifying Epressions. Solving Equations 3. Problem Solving 4. Inequalities 5. Absolute Values 6. Linear Equations 7. Systems of Equations 8. Laws of Eponents 9. Quadratics 10. Rationals 11. Radicals
1. Simplifying Epressions. Solving Equations 3. Problem Solving 4. Inequalities 5. Absolute Values 6. Linear Equations 7. Systems of Equations 8. Laws of Eponents 9. Quadratics 10. Rationals 11. Radicals
Zeros of Polynomial Functions
 Review: Synthetic Division Find (x 2-5x - 5x 3 + x 4 ) (5 + x). Factor Theorem Solve 2x 3-5x 2 + x + 2 =0 given that 2 is a zero of f(x) = 2x 3-5x 2 + x + 2. Zeros of Polynomial Functions Introduction
Review: Synthetic Division Find (x 2-5x - 5x 3 + x 4 ) (5 + x). Factor Theorem Solve 2x 3-5x 2 + x + 2 =0 given that 2 is a zero of f(x) = 2x 3-5x 2 + x + 2. Zeros of Polynomial Functions Introduction
Algebraic expressions are a combination of numbers and variables. Here are examples of some basic algebraic expressions.
 Page 1 of 13 Review of Linear Expressions and Equations Skills involving linear equations can be divided into the following groups: Simplifying algebraic expressions. Linear expressions. Solving linear
Page 1 of 13 Review of Linear Expressions and Equations Skills involving linear equations can be divided into the following groups: Simplifying algebraic expressions. Linear expressions. Solving linear
9. POLYNOMIALS. Example 1: The expression a(x) = x 3 4x 2 + 7x 11 is a polynomial in x. The coefficients of a(x) are the numbers 1, 4, 7, 11.
 9. POLYNOMIALS 9.1. Definition of a Polynomial A polynomial is an expression of the form: a(x) = a n x n + a n-1 x n-1 +... + a 1 x + a 0. The symbol x is called an indeterminate and simply plays the role
9. POLYNOMIALS 9.1. Definition of a Polynomial A polynomial is an expression of the form: a(x) = a n x n + a n-1 x n-1 +... + a 1 x + a 0. The symbol x is called an indeterminate and simply plays the role
COLLEGE ALGEBRA 10 TH EDITION LIAL HORNSBY SCHNEIDER 1.1-1
 10 TH EDITION COLLEGE ALGEBRA LIAL HORNSBY SCHNEIDER 1.1-1 1.1 Linear Equations Basic Terminology of Equations Solving Linear Equations Identities 1.1-2 Equations An equation is a statement that two expressions
10 TH EDITION COLLEGE ALGEBRA LIAL HORNSBY SCHNEIDER 1.1-1 1.1 Linear Equations Basic Terminology of Equations Solving Linear Equations Identities 1.1-2 Equations An equation is a statement that two expressions
This is a square root. The number under the radical is 9. (An asterisk * means multiply.)
 Page of Review of Radical Expressions and Equations Skills involving radicals can be divided into the following groups: Evaluate square roots or higher order roots. Simplify radical expressions. Rationalize
Page of Review of Radical Expressions and Equations Skills involving radicals can be divided into the following groups: Evaluate square roots or higher order roots. Simplify radical expressions. Rationalize
Five 5. Rational Expressions and Equations C H A P T E R
 Five C H A P T E R Rational Epressions and Equations. Rational Epressions and Functions. Multiplication and Division of Rational Epressions. Addition and Subtraction of Rational Epressions.4 Comple Fractions.
Five C H A P T E R Rational Epressions and Equations. Rational Epressions and Functions. Multiplication and Division of Rational Epressions. Addition and Subtraction of Rational Epressions.4 Comple Fractions.
Zeros of a Polynomial Function
 Zeros of a Polynomial Function An important consequence of the Factor Theorem is that finding the zeros of a polynomial is really the same thing as factoring it into linear factors. In this section we
Zeros of a Polynomial Function An important consequence of the Factor Theorem is that finding the zeros of a polynomial is really the same thing as factoring it into linear factors. In this section we
Zeros of Polynomial Functions
 Zeros of Polynomial Functions Objectives: 1.Use the Fundamental Theorem of Algebra to determine the number of zeros of polynomial functions 2.Find rational zeros of polynomial functions 3.Find conjugate
Zeros of Polynomial Functions Objectives: 1.Use the Fundamental Theorem of Algebra to determine the number of zeros of polynomial functions 2.Find rational zeros of polynomial functions 3.Find conjugate
Equations, Inequalities & Partial Fractions
 Contents Equations, Inequalities & Partial Fractions.1 Solving Linear Equations 2.2 Solving Quadratic Equations 1. Solving Polynomial Equations 1.4 Solving Simultaneous Linear Equations 42.5 Solving Inequalities
Contents Equations, Inequalities & Partial Fractions.1 Solving Linear Equations 2.2 Solving Quadratic Equations 1. Solving Polynomial Equations 1.4 Solving Simultaneous Linear Equations 42.5 Solving Inequalities
Algebra 1 If you are okay with that placement then you have no further action to take Algebra 1 Portion of the Math Placement Test
 Dear Parents, Based on the results of the High School Placement Test (HSPT), your child should forecast to take Algebra 1 this fall. If you are okay with that placement then you have no further action
Dear Parents, Based on the results of the High School Placement Test (HSPT), your child should forecast to take Algebra 1 this fall. If you are okay with that placement then you have no further action
Polynomial Expression
 DETAILED SOLUTIONS AND CONCEPTS - POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to [email protected]. Thank you! PLEASE NOTE
DETAILED SOLUTIONS AND CONCEPTS - POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to [email protected]. Thank you! PLEASE NOTE
MATH 21. College Algebra 1 Lecture Notes
 MATH 21 College Algebra 1 Lecture Notes MATH 21 3.6 Factoring Review College Algebra 1 Factoring and Foiling 1. (a + b) 2 = a 2 + 2ab + b 2. 2. (a b) 2 = a 2 2ab + b 2. 3. (a + b)(a b) = a 2 b 2. 4. (a
MATH 21 College Algebra 1 Lecture Notes MATH 21 3.6 Factoring Review College Algebra 1 Factoring and Foiling 1. (a + b) 2 = a 2 + 2ab + b 2. 2. (a b) 2 = a 2 2ab + b 2. 3. (a + b)(a b) = a 2 b 2. 4. (a
Math 10C. Course: Polynomial Products and Factors. Unit of Study: Step 1: Identify the Outcomes to Address. Guiding Questions:
 Course: Unit of Study: Math 10C Polynomial Products and Factors Step 1: Identify the Outcomes to Address Guiding Questions: What do I want my students to learn? What can they currently understand and do?
Course: Unit of Study: Math 10C Polynomial Products and Factors Step 1: Identify the Outcomes to Address Guiding Questions: What do I want my students to learn? What can they currently understand and do?
Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III
 Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III Name Date Adding and Subtracting Polynomials Algebra Standard 10.0 A polynomial is a sum of one ore more monomials. Polynomial
Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III Name Date Adding and Subtracting Polynomials Algebra Standard 10.0 A polynomial is a sum of one ore more monomials. Polynomial
1.5. Factorisation. Introduction. Prerequisites. Learning Outcomes. Learning Style
 Factorisation 1.5 Introduction In Block 4 we showed the way in which brackets were removed from algebraic expressions. Factorisation, which can be considered as the reverse of this process, is dealt with
Factorisation 1.5 Introduction In Block 4 we showed the way in which brackets were removed from algebraic expressions. Factorisation, which can be considered as the reverse of this process, is dealt with
Algebra 2 PreAP. Name Period
 Algebra 2 PreAP Name Period IMPORTANT INSTRUCTIONS FOR STUDENTS!!! We understand that students come to Algebra II with different strengths and needs. For this reason, students have options for completing
Algebra 2 PreAP Name Period IMPORTANT INSTRUCTIONS FOR STUDENTS!!! We understand that students come to Algebra II with different strengths and needs. For this reason, students have options for completing
ACCUPLACER. Testing & Study Guide. Prepared by the Admissions Office Staff and General Education Faculty Draft: January 2011
 ACCUPLACER Testing & Study Guide Prepared by the Admissions Office Staff and General Education Faculty Draft: January 2011 Thank you to Johnston Community College staff for giving permission to revise
ACCUPLACER Testing & Study Guide Prepared by the Admissions Office Staff and General Education Faculty Draft: January 2011 Thank you to Johnston Community College staff for giving permission to revise
Unit 3: Day 2: Factoring Polynomial Expressions
 Unit 3: Day : Factoring Polynomial Expressions Minds On: 0 Action: 45 Consolidate:10 Total =75 min Learning Goals: Extend knowledge of factoring to factor cubic and quartic expressions that can be factored
Unit 3: Day : Factoring Polynomial Expressions Minds On: 0 Action: 45 Consolidate:10 Total =75 min Learning Goals: Extend knowledge of factoring to factor cubic and quartic expressions that can be factored
A. Factoring out the Greatest Common Factor.
 DETAILED SOLUTIONS AND CONCEPTS - FACTORING POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to [email protected]. Thank you!
DETAILED SOLUTIONS AND CONCEPTS - FACTORING POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to [email protected]. Thank you!
Radicals - Rationalize Denominators
 8. Radicals - Rationalize Denominators Objective: Rationalize the denominators of radical expressions. It is considered bad practice to have a radical in the denominator of a fraction. When this happens
8. Radicals - Rationalize Denominators Objective: Rationalize the denominators of radical expressions. It is considered bad practice to have a radical in the denominator of a fraction. When this happens
Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder).
 Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Solving Quadratic & Higher Degree Inequalities
 Ch. 8 Solving Quadratic & Higher Degree Inequalities We solve quadratic and higher degree inequalities very much like we solve quadratic and higher degree equations. One method we often use to solve quadratic
Ch. 8 Solving Quadratic & Higher Degree Inequalities We solve quadratic and higher degree inequalities very much like we solve quadratic and higher degree equations. One method we often use to solve quadratic
minimal polyonomial Example
 Minimal Polynomials Definition Let α be an element in GF(p e ). We call the monic polynomial of smallest degree which has coefficients in GF(p) and α as a root, the minimal polyonomial of α. Example: We
Minimal Polynomials Definition Let α be an element in GF(p e ). We call the monic polynomial of smallest degree which has coefficients in GF(p) and α as a root, the minimal polyonomial of α. Example: We
Polynomial and Synthetic Division. Long Division of Polynomials. Example 1. 6x 2 7x 2 x 2) 19x 2 16x 4 6x3 12x 2 7x 2 16x 7x 2 14x. 2x 4.
 _.qd /7/5 9: AM Page 5 Section.. Polynomial and Synthetic Division 5 Polynomial and Synthetic Division What you should learn Use long division to divide polynomials by other polynomials. Use synthetic
_.qd /7/5 9: AM Page 5 Section.. Polynomial and Synthetic Division 5 Polynomial and Synthetic Division What you should learn Use long division to divide polynomials by other polynomials. Use synthetic
Tim Kerins. Leaving Certificate Honours Maths - Algebra. Tim Kerins. the date
 Leaving Certificate Honours Maths - Algebra the date Chapter 1 Algebra This is an important portion of the course. As well as generally accounting for 2 3 questions in examination it is the basis for many
Leaving Certificate Honours Maths - Algebra the date Chapter 1 Algebra This is an important portion of the course. As well as generally accounting for 2 3 questions in examination it is the basis for many
COLLEGE ALGEBRA. Paul Dawkins
 COLLEGE ALGEBRA Paul Dawkins Table of Contents Preface... iii Outline... iv Preliminaries... Introduction... Integer Exponents... Rational Exponents... 9 Real Exponents...5 Radicals...6 Polynomials...5
COLLEGE ALGEBRA Paul Dawkins Table of Contents Preface... iii Outline... iv Preliminaries... Introduction... Integer Exponents... Rational Exponents... 9 Real Exponents...5 Radicals...6 Polynomials...5
A Concrete Introduction. to the Abstract Concepts. of Integers and Algebra using Algebra Tiles
 A Concrete Introduction to the Abstract Concepts of Integers and Algebra using Algebra Tiles Table of Contents Introduction... 1 page Integers 1: Introduction to Integers... 3 2: Working with Algebra Tiles...
A Concrete Introduction to the Abstract Concepts of Integers and Algebra using Algebra Tiles Table of Contents Introduction... 1 page Integers 1: Introduction to Integers... 3 2: Working with Algebra Tiles...
2.5 ZEROS OF POLYNOMIAL FUNCTIONS. Copyright Cengage Learning. All rights reserved.
 2.5 ZEROS OF POLYNOMIAL FUNCTIONS Copyright Cengage Learning. All rights reserved. What You Should Learn Use the Fundamental Theorem of Algebra to determine the number of zeros of polynomial functions.
2.5 ZEROS OF POLYNOMIAL FUNCTIONS Copyright Cengage Learning. All rights reserved. What You Should Learn Use the Fundamental Theorem of Algebra to determine the number of zeros of polynomial functions.
1.3 Polynomials and Factoring
 1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
calculating the result modulo 3, as follows: p(0) = 0 3 + 0 + 1 = 1 0,
 Homework #02, due 1/27/10 = 9.4.1, 9.4.2, 9.4.5, 9.4.6, 9.4.7. Additional problems recommended for study: (9.4.3), 9.4.4, 9.4.9, 9.4.11, 9.4.13, (9.4.14), 9.4.17 9.4.1 Determine whether the following polynomials
Homework #02, due 1/27/10 = 9.4.1, 9.4.2, 9.4.5, 9.4.6, 9.4.7. Additional problems recommended for study: (9.4.3), 9.4.4, 9.4.9, 9.4.11, 9.4.13, (9.4.14), 9.4.17 9.4.1 Determine whether the following polynomials
Integrating algebraic fractions
 Integrating algebraic fractions Sometimes the integral of an algebraic fraction can be found by first epressing the algebraic fraction as the sum of its partial fractions. In this unit we will illustrate
Integrating algebraic fractions Sometimes the integral of an algebraic fraction can be found by first epressing the algebraic fraction as the sum of its partial fractions. In this unit we will illustrate
Click on the links below to jump directly to the relevant section
 Click on the links below to jump directly to the relevant section What is algebra? Operations with algebraic terms Mathematical properties of real numbers Order of operations What is Algebra? Algebra is
Click on the links below to jump directly to the relevant section What is algebra? Operations with algebraic terms Mathematical properties of real numbers Order of operations What is Algebra? Algebra is
Veterans Upward Bound Algebra I Concepts - Honors
 Veterans Upward Bound Algebra I Concepts - Honors Brenda Meery Kaitlyn Spong Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org Chapter 6. Factoring CHAPTER
Veterans Upward Bound Algebra I Concepts - Honors Brenda Meery Kaitlyn Spong Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org Chapter 6. Factoring CHAPTER
3.1. RATIONAL EXPRESSIONS
 3.1. RATIONAL EXPRESSIONS RATIONAL NUMBERS In previous courses you have learned how to operate (do addition, subtraction, multiplication, and division) on rational numbers (fractions). Rational numbers
3.1. RATIONAL EXPRESSIONS RATIONAL NUMBERS In previous courses you have learned how to operate (do addition, subtraction, multiplication, and division) on rational numbers (fractions). Rational numbers
FACTORING ax 2 bx c. Factoring Trinomials with Leading Coefficient 1
 5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
EAP/GWL Rev. 1/2011 Page 1 of 5. Factoring a polynomial is the process of writing it as the product of two or more polynomial factors.
 EAP/GWL Rev. 1/2011 Page 1 of 5 Factoring a polynomial is the process of writing it as the product of two or more polynomial factors. Example: Set the factors of a polynomial equation (as opposed to an
EAP/GWL Rev. 1/2011 Page 1 of 5 Factoring a polynomial is the process of writing it as the product of two or more polynomial factors. Example: Set the factors of a polynomial equation (as opposed to an
Equations Involving Fractions
 . Equations Involving Fractions. OBJECTIVES. Determine the ecluded values for the variables of an algebraic fraction. Solve a fractional equation. Solve a proportion for an unknown NOTE The resulting equation
. Equations Involving Fractions. OBJECTIVES. Determine the ecluded values for the variables of an algebraic fraction. Solve a fractional equation. Solve a proportion for an unknown NOTE The resulting equation
2.3 Solving Equations Containing Fractions and Decimals
 2. Solving Equations Containing Fractions and Decimals Objectives In this section, you will learn to: To successfully complete this section, you need to understand: Solve equations containing fractions
2. Solving Equations Containing Fractions and Decimals Objectives In this section, you will learn to: To successfully complete this section, you need to understand: Solve equations containing fractions
Factoring Guidelines. Greatest Common Factor Two Terms Three Terms Four Terms. 2008 Shirley Radai
 Factoring Guidelines Greatest Common Factor Two Terms Three Terms Four Terms 008 Shirley Radai Greatest Common Factor 008 Shirley Radai Factoring by Finding the Greatest Common Factor Always check for
Factoring Guidelines Greatest Common Factor Two Terms Three Terms Four Terms 008 Shirley Radai Greatest Common Factor 008 Shirley Radai Factoring by Finding the Greatest Common Factor Always check for
3.6. The factor theorem
 3.6. The factor theorem Example 1. At the right we have drawn the graph of the polynomial y = x 4 9x 3 + 8x 36x + 16. Your problem is to write the polynomial in factored form. Does the geometry of the
3.6. The factor theorem Example 1. At the right we have drawn the graph of the polynomial y = x 4 9x 3 + 8x 36x + 16. Your problem is to write the polynomial in factored form. Does the geometry of the
Section 6.1 Factoring Expressions
 Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
MATH 108 REVIEW TOPIC 10 Quadratic Equations. B. Solving Quadratics by Completing the Square
 Math 108 T10-Review Topic 10 Page 1 MATH 108 REVIEW TOPIC 10 Quadratic Equations I. Finding Roots of a Quadratic Equation A. Factoring B. Quadratic Formula C. Taking Roots II. III. Guidelines for Finding
Math 108 T10-Review Topic 10 Page 1 MATH 108 REVIEW TOPIC 10 Quadratic Equations I. Finding Roots of a Quadratic Equation A. Factoring B. Quadratic Formula C. Taking Roots II. III. Guidelines for Finding
Introduction Assignment
 PRE-CALCULUS 11 Introduction Assignment Welcome to PREC 11! This assignment will help you review some topics from a previous math course and introduce you to some of the topics that you ll be studying
PRE-CALCULUS 11 Introduction Assignment Welcome to PREC 11! This assignment will help you review some topics from a previous math course and introduce you to some of the topics that you ll be studying
Multiplying Fractions
 . Multiplying Fractions. OBJECTIVES 1. Multiply two fractions. Multiply two mixed numbers. Simplify before multiplying fractions 4. Estimate products by rounding Multiplication is the easiest of the four
. Multiplying Fractions. OBJECTIVES 1. Multiply two fractions. Multiply two mixed numbers. Simplify before multiplying fractions 4. Estimate products by rounding Multiplication is the easiest of the four
Factoring and Applications
 Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
In algebra, factor by rewriting a polynomial as a product of lower-degree polynomials
 Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form
 ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form Goal Graph quadratic functions. VOCABULARY Quadratic function A function that can be written in the standard form y = ax 2 + bx+ c where a 0 Parabola
ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form Goal Graph quadratic functions. VOCABULARY Quadratic function A function that can be written in the standard form y = ax 2 + bx+ c where a 0 Parabola
Factoring Trinomials: The ac Method
 6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
Factoring. Factoring Monomials Monomials can often be factored in more than one way.
 Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
In this section, you will develop a method to change a quadratic equation written as a sum into its product form (also called its factored form).
 CHAPTER 8 In Chapter 4, you used a web to organize the connections you found between each of the different representations of lines. These connections enabled you to use any representation (such as a graph,
CHAPTER 8 In Chapter 4, you used a web to organize the connections you found between each of the different representations of lines. These connections enabled you to use any representation (such as a graph,
Math 0980 Chapter Objectives. Chapter 1: Introduction to Algebra: The Integers.
 Math 0980 Chapter Objectives Chapter 1: Introduction to Algebra: The Integers. 1. Identify the place value of a digit. 2. Write a number in words or digits. 3. Write positive and negative numbers used
Math 0980 Chapter Objectives Chapter 1: Introduction to Algebra: The Integers. 1. Identify the place value of a digit. 2. Write a number in words or digits. 3. Write positive and negative numbers used
A Systematic Approach to Factoring
 A Systematic Approach to Factoring Step 1 Count the number of terms. (Remember****Knowing the number of terms will allow you to eliminate unnecessary tools.) Step 2 Is there a greatest common factor? Tool
A Systematic Approach to Factoring Step 1 Count the number of terms. (Remember****Knowing the number of terms will allow you to eliminate unnecessary tools.) Step 2 Is there a greatest common factor? Tool
Florida Math 0028. Correlation of the ALEKS course Florida Math 0028 to the Florida Mathematics Competencies - Upper
 Florida Math 0028 Correlation of the ALEKS course Florida Math 0028 to the Florida Mathematics Competencies - Upper Exponents & Polynomials MDECU1: Applies the order of operations to evaluate algebraic
Florida Math 0028 Correlation of the ALEKS course Florida Math 0028 to the Florida Mathematics Competencies - Upper Exponents & Polynomials MDECU1: Applies the order of operations to evaluate algebraic
Vieta s Formulas and the Identity Theorem
 Vieta s Formulas and the Identity Theorem This worksheet will work through the material from our class on 3/21/2013 with some examples that should help you with the homework The topic of our discussion
Vieta s Formulas and the Identity Theorem This worksheet will work through the material from our class on 3/21/2013 with some examples that should help you with the homework The topic of our discussion
Solving Rational Equations
 Lesson M Lesson : Student Outcomes Students solve rational equations, monitoring for the creation of extraneous solutions. Lesson Notes In the preceding lessons, students learned to add, subtract, multiply,
Lesson M Lesson : Student Outcomes Students solve rational equations, monitoring for the creation of extraneous solutions. Lesson Notes In the preceding lessons, students learned to add, subtract, multiply,
