Unit 3: Day 2: Factoring Polynomial Expressions
|
|
|
- Blanche O’Brien’
- 8 years ago
- Views:
Transcription
1 Unit 3: Day : Factoring Polynomial Expressions Minds On: 0 Action: 45 Consolidate:10 Total =75 min Learning Goals: Extend knowledge of factoring to factor cubic and quartic expressions that can be factored using common factoring, difference of squares, trinomial factoring and grouping. Minds On Groups of 4 Placemat Activity Students complete BLM 3..1 using their prior knowledge to write everything that they know about factoring. They should consider the following. 1. Defining the terms factors and factoring.. Providing examples of different methods of factoring and if possible, provide the names of those methods. 3. Indicating when factoring is useful. After students have completed their space on the placemat, groups will discuss their ideas and agree upon a response to be shared with the class, which is recorded in the centre box on the placemat. Curriculum Expectations/Observation/Mental Note Observe student responses and listen to student dialogue during the placemat activity. Assess student understanding of the curriculum expectations addressed to this point in the unit. Whole Class Discussion One member of each group will be called upon to share their group s response with the whole class. Students should create a summary note from the discussion. If desired, the placemats can be posted in the classroom. MCT 4C Assessment Opportunities Materials BLM LCD projector or overhead projector (optional) This activity will give a good overview of what the students remember about factoring, indicating the depth to which factoring needs to be reviewed as a class. More information about Placemats can be found in Think Literacy! Action! Consolidate Debrief Concept Practice Mathematical Process Focus: Reflecting - Reflect on prior knowledge of factoring Connecting - Connect prior factoring knowledge to factoring higher order polynomials Whole Class Discussion Have students identify the thinking process involved in the factoring process. Students should identify the factoring strategies utilized and the characteristics of the polynomial that provide insight into the appropriate choice of strategies. BLM 3.. provides an example of one way to organize this thinking process for your reference. Introduce factoring by grouping. Explain that sometimes questions involve more than one strategy in order to be fully factored. (There are examples of this in BLM 3..3, #6.) Small Groups Activity Students practice these strategies as they complete BLM Partners Activity Using BLM 3..4, students match up edges of the small squares so that each polynomial is placed with its factored form in order to create a 4 by 4 square, using all of the small squares. The solution is given in BLM Home Activity or Further Classroom Consolidation Complete BLM BLM 3..4 will have to be cut. 1
2 3..1: Factoring: You must remember this!
3 3..: Factoring Strategies (Teacher Notes) Factoring is the process where a polynomial expression is written as a product of other algebraic expressions. Factoring Question Is there a common factor? Yes Factor out the common factor No How many terms are there? 3 4 Could be a difference of squares Is a >1 (ax + bx + c )? Could be a factoring by grouping No Yes This is a simple trinomial. Factor using method of choice. This is a complex trinomial. Factor using method of choice. Factoring is used to solve polynomial equations and to graph polynomial functions. Factoring will be used in this unit to accomplish these tasks. 3
4 3..3: Let s Practice Factoring 1. Factor by common factoring a) a b + ab b) 5x! 30x + 35x c) 7x(x + ) - 5(x + ). Factor as a simple trinomial. a) t + 3t! 10 b) x! 10x! 4 c) x! 8x + 16 d) x 4 + 6x Factor. a) 3m! m! 30 b) 8m! 5m! 3 c) 7x + x! 8 4
5 3..3: Let s Practice Factoring (continued) 4. Factor as a difference of squares. a) y! 81 b) 9m! 1 c) 169x! 144z 5. Factor by grouping. 4 3 a) a! a + ad! d b) x! 3x + x! 6 3 c) y + y + y + 6. Factor fully. It might be necessary to use more than one factoring strategy in order to fully factor these polynomial expressions. a) x 3 3x 4! + x b) x! 18x 3 c) x! x! 4x + 4 5
6 3..4: Factoring Game 3 + 4x - 15x (3 5x)(1 + 3x) 15x + 3x - 1 3(5x 4)(x + 1) 15x 3-30x + 10x 3x(5x 4)(x + 1) x + 13x + 15 (x + 3)(x + 5) x + 1x - 45 (x + 15)(x 3) x + 3x - 8 (x + 7)(x 4) 16x 36 5xy x x + 3x x - 6x + 1 4(x + 3)(x 3) x(5y ) (x + 8)(x 5) (3x - 1) 15x + 3x - 1 3(5x 4)(x + 1) x 3 + 5x + 6x x(x + 3)(x + ) x - 6x + (x 3x + 1) 10x + x - 3 5xy y x - 3x x + 6x + 1 (5x + 3)(x 1) y(5x ) (x - 8)(x + 5) (3x + 1) 10x - x x - 7 x + 13x x - 1 (5x - 3)(x + 1) 5x 10x 5x(x ) (5x 6)(5x + 6) x 4-81 (x + 9)(x + 3)(x 3) (x + 8)(x + 5) x x x x (x + 8)(x + 5) (3x - 1)(3x + 1) 6
7 3..5: Factoring Fun Determine which type of factoring is needed in each problem and then factor each expression. Remember that an expression might require more than one factoring strategy in order to be fully factored! 1. x 3 x. x 3 + 3x x x 3 9x 4. 3x 3 + x 5. -x 3 + x + x x 3 6x 7. x 4 3x 3 8. x 4-5x x 4 x 3 3x + 3x 10. -x 4 + x 3 + 4x 4x 11. -x 4 + 4x 1. -x 4 +5x 4 7
8 Unit 3: Day 3: Cubic and Quartic Equations Minds On: 0 Action: 5 Consolidate:30 Learning Goal: Solve equations, of degree no higher than four, and verify the solutions using technology. Solve cubic and quartic equations in standard form that can only be factored using common factoring, difference of squares, trinomial factoring and/or the quadratic formula. MCT 4C Materials PPT PPT 3.3. BLM LCD projector Graphing calculators Total=75 min Minds On Pairs Discussion Compare answers from the homework activity 3..5 from the previous lesson. Action! Whole Class Discussion Discuss any questions that pairs were not able to answer. Whole Class Presentation/Investigation Present PPT and work through the investigation together. Stress the point that to find when the height is zero, we would want to make h = 0. Discuss strategies employed in the past to solve for zeros (solving directly for linear equations; factoring; quadratic formula). Highlight the goal of this lesson which is to develop a strategy to solve equations of degree greater than two. Whole Class Presentation Observe, using PPT 3.3., the connection between factoring expressions and solving equations. By using graphing calculators during the presentation, the connection between solving for the roots and what they represent will be established. Assessment Opportunities The teacher may want to a have a copy of BLM 3..5 on the overhead projector. Note: The connection between the roots or solutions to an equation and the zeros of a function should have been introduced in the first lesson of Unit 3. Students will still need a graphing calculator for this portion of the lesson. Consolidate Debrief Exploration Application Mathematical Process Focus: Connecting Students connect prior knowledge of factoring to solving for the roots of cubic and quartic functions in standard form. Students connect with the understanding that roots are x-intercepts. Individual Activity Complete BLM Curriculum Expectations/Performance Task/Checklist Collect BLM and assess student understanding. This information can inform planning for Day 4. Home Activity or Further Classroom Consolidation Decide how to solve the following equations: x 3 = 0 x 4 16 = 0 x = 0 Try your strategy and solve for the roots, if possible. Portions of BLM can be assessed for student learning. 8
9 3.3.1: Solve & Graph it! 1. Solve. a) x 3 x x = 0 b) 0 = x 4 x 3 5x + 6x c) 0 = x 4 1 d) 0 = 3x + 1x + 1 e) 0 = -x 3 + x + 4x 8 f) -x 4 4x 3 4x = 0 g) x 3 9x + 9x 7 = 0 h) 0 = x 4 5x 3 + 6x + 4x 8 9
10 3.3.1: Solve & Graph it! (Continued). Use your graphing calculator to sketch a graph of the functions below. Compare the roots from #1 with the sketches to determine if these roots and x-intercepts match. a) y = x 3 x x b) y = x 4 x 3 5x + 6x c) y = x 4 1 d) y = 3x + 1x + 1 e) y = -x 3 + x + 4x 8 f) y = -x 4 4x 3 4x g) y = x 3 9x + 9x 7 h) y = x 4 5x 3 + 6x + 4x 8 10
11 3.3.1: Solve & Graph it! (Continued) 3. Solve. Factor and use the quadratic formula where needed. a) x 4 + 4x 3 + 5x = 0 b) 0 = x 4 + x c) -4x x x = 0 11
Unit 7 Quadratic Relations of the Form y = ax 2 + bx + c
 Unit 7 Quadratic Relations of the Form y = ax 2 + bx + c Lesson Outline BIG PICTURE Students will: manipulate algebraic expressions, as needed to understand quadratic relations; identify characteristics
Unit 7 Quadratic Relations of the Form y = ax 2 + bx + c Lesson Outline BIG PICTURE Students will: manipulate algebraic expressions, as needed to understand quadratic relations; identify characteristics
expression is written horizontally. The Last terms ((2)( 4)) because they are the last terms of the two polynomials. This is called the FOIL method.
 A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
NSM100 Introduction to Algebra Chapter 5 Notes Factoring
 Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
Section 6.1 Factoring Expressions
 Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
Factoring Quadratic Expressions
 Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
1.3 Algebraic Expressions
 1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
Factoring Trinomials: The ac Method
 6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
Examples of Tasks from CCSS Edition Course 3, Unit 5
 Examples of Tasks from CCSS Edition Course 3, Unit 5 Getting Started The tasks below are selected with the intent of presenting key ideas and skills. Not every answer is complete, so that teachers can
Examples of Tasks from CCSS Edition Course 3, Unit 5 Getting Started The tasks below are selected with the intent of presenting key ideas and skills. Not every answer is complete, so that teachers can
Algebra I. In this technological age, mathematics is more important than ever. When students
 In this technological age, mathematics is more important than ever. When students leave school, they are more and more likely to use mathematics in their work and everyday lives operating computer equipment,
In this technological age, mathematics is more important than ever. When students leave school, they are more and more likely to use mathematics in their work and everyday lives operating computer equipment,
Algebra II A Final Exam
 Algebra II A Final Exam Multiple Choice Identify the choice that best completes the statement or answers the question. Evaluate the expression for the given value of the variable(s). 1. ; x = 4 a. 34 b.
Algebra II A Final Exam Multiple Choice Identify the choice that best completes the statement or answers the question. Evaluate the expression for the given value of the variable(s). 1. ; x = 4 a. 34 b.
How To Factor Quadratic Trinomials
 Factoring Quadratic Trinomials Student Probe Factor Answer: Lesson Description This lesson uses the area model of multiplication to factor quadratic trinomials Part 1 of the lesson consists of circle puzzles
Factoring Quadratic Trinomials Student Probe Factor Answer: Lesson Description This lesson uses the area model of multiplication to factor quadratic trinomials Part 1 of the lesson consists of circle puzzles
Unit #3: Investigating Quadratics (9 days + 1 jazz day + 1 summative evaluation day) BIG Ideas:
 Unit #3: Investigating Quadratics (9 days + 1 jazz day + 1 summative evaluation day) BIG Ideas: Developing strategies for determining the zeroes of quadratic functions Making connections between the meaning
Unit #3: Investigating Quadratics (9 days + 1 jazz day + 1 summative evaluation day) BIG Ideas: Developing strategies for determining the zeroes of quadratic functions Making connections between the meaning
Factoring Polynomials and Solving Quadratic Equations
 Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
Factoring Quadratic Trinomials
 Factoring Quadratic Trinomials Student Probe Factor x x 3 10. Answer: x 5 x Lesson Description This lesson uses the area model of multiplication to factor quadratic trinomials. Part 1 of the lesson consists
Factoring Quadratic Trinomials Student Probe Factor x x 3 10. Answer: x 5 x Lesson Description This lesson uses the area model of multiplication to factor quadratic trinomials. Part 1 of the lesson consists
This unit has primarily been about quadratics, and parabolas. Answer the following questions to aid yourselves in creating your own study guide.
 COLLEGE ALGEBRA UNIT 2 WRITING ASSIGNMENT This unit has primarily been about quadratics, and parabolas. Answer the following questions to aid yourselves in creating your own study guide. 1) What is the
COLLEGE ALGEBRA UNIT 2 WRITING ASSIGNMENT This unit has primarily been about quadratics, and parabolas. Answer the following questions to aid yourselves in creating your own study guide. 1) What is the
Name Intro to Algebra 2. Unit 1: Polynomials and Factoring
 Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
Zeros of Polynomial Functions
 Review: Synthetic Division Find (x 2-5x - 5x 3 + x 4 ) (5 + x). Factor Theorem Solve 2x 3-5x 2 + x + 2 =0 given that 2 is a zero of f(x) = 2x 3-5x 2 + x + 2. Zeros of Polynomial Functions Introduction
Review: Synthetic Division Find (x 2-5x - 5x 3 + x 4 ) (5 + x). Factor Theorem Solve 2x 3-5x 2 + x + 2 =0 given that 2 is a zero of f(x) = 2x 3-5x 2 + x + 2. Zeros of Polynomial Functions Introduction
In this section, you will develop a method to change a quadratic equation written as a sum into its product form (also called its factored form).
 CHAPTER 8 In Chapter 4, you used a web to organize the connections you found between each of the different representations of lines. These connections enabled you to use any representation (such as a graph,
CHAPTER 8 In Chapter 4, you used a web to organize the connections you found between each of the different representations of lines. These connections enabled you to use any representation (such as a graph,
For each learner you will need: mini-whiteboard. For each small group of learners you will need: Card set A Factors; Card set B True/false.
 Level A11 of challenge: D A11 Mathematical goals Starting points Materials required Time needed Factorising cubics To enable learners to: associate x-intercepts with finding values of x such that f (x)
Level A11 of challenge: D A11 Mathematical goals Starting points Materials required Time needed Factorising cubics To enable learners to: associate x-intercepts with finding values of x such that f (x)
( ) FACTORING. x In this polynomial the only variable in common to all is x.
 FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
1.5. Factorisation. Introduction. Prerequisites. Learning Outcomes. Learning Style
 Factorisation 1.5 Introduction In Block 4 we showed the way in which brackets were removed from algebraic expressions. Factorisation, which can be considered as the reverse of this process, is dealt with
Factorisation 1.5 Introduction In Block 4 we showed the way in which brackets were removed from algebraic expressions. Factorisation, which can be considered as the reverse of this process, is dealt with
6.1 Add & Subtract Polynomial Expression & Functions
 6.1 Add & Subtract Polynomial Expression & Functions Objectives 1. Know the meaning of the words term, monomial, binomial, trinomial, polynomial, degree, coefficient, like terms, polynomial funciton, quardrtic
6.1 Add & Subtract Polynomial Expression & Functions Objectives 1. Know the meaning of the words term, monomial, binomial, trinomial, polynomial, degree, coefficient, like terms, polynomial funciton, quardrtic
Lagrange Interpolation is a method of fitting an equation to a set of points that functions well when there are few points given.
 Polynomials (Ch.1) Study Guide by BS, JL, AZ, CC, SH, HL Lagrange Interpolation is a method of fitting an equation to a set of points that functions well when there are few points given. Sasha s method
Polynomials (Ch.1) Study Guide by BS, JL, AZ, CC, SH, HL Lagrange Interpolation is a method of fitting an equation to a set of points that functions well when there are few points given. Sasha s method
Indiana State Core Curriculum Standards updated 2009 Algebra I
 Indiana State Core Curriculum Standards updated 2009 Algebra I Strand Description Boardworks High School Algebra presentations Operations With Real Numbers Linear Equations and A1.1 Students simplify and
Indiana State Core Curriculum Standards updated 2009 Algebra I Strand Description Boardworks High School Algebra presentations Operations With Real Numbers Linear Equations and A1.1 Students simplify and
Factor Polynomials Completely
 9.8 Factor Polynomials Completely Before You factored polynomials. Now You will factor polynomials completely. Why? So you can model the height of a projectile, as in Ex. 71. Key Vocabulary factor by grouping
9.8 Factor Polynomials Completely Before You factored polynomials. Now You will factor polynomials completely. Why? So you can model the height of a projectile, as in Ex. 71. Key Vocabulary factor by grouping
1.3 Polynomials and Factoring
 1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
is the degree of the polynomial and is the leading coefficient.
 Property: T. Hrubik-Vulanovic e-mail: thrubik@kent.edu Content (in order sections were covered from the book): Chapter 6 Higher-Degree Polynomial Functions... 1 Section 6.1 Higher-Degree Polynomial Functions...
Property: T. Hrubik-Vulanovic e-mail: thrubik@kent.edu Content (in order sections were covered from the book): Chapter 6 Higher-Degree Polynomial Functions... 1 Section 6.1 Higher-Degree Polynomial Functions...
LAKE ELSINORE UNIFIED SCHOOL DISTRICT
 LAKE ELSINORE UNIFIED SCHOOL DISTRICT Title: PLATO Algebra 1-Semester 2 Grade Level: 10-12 Department: Mathematics Credit: 5 Prerequisite: Letter grade of F and/or N/C in Algebra 1, Semester 2 Course Description:
LAKE ELSINORE UNIFIED SCHOOL DISTRICT Title: PLATO Algebra 1-Semester 2 Grade Level: 10-12 Department: Mathematics Credit: 5 Prerequisite: Letter grade of F and/or N/C in Algebra 1, Semester 2 Course Description:
POLYNOMIALS and FACTORING
 POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III
 Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III Name Date Adding and Subtracting Polynomials Algebra Standard 10.0 A polynomial is a sum of one ore more monomials. Polynomial
Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III Name Date Adding and Subtracting Polynomials Algebra Standard 10.0 A polynomial is a sum of one ore more monomials. Polynomial
FACTORISATION YEARS. A guide for teachers - Years 9 10 June 2011. The Improving Mathematics Education in Schools (TIMES) Project
 9 10 YEARS The Improving Mathematics Education in Schools (TIMES) Project FACTORISATION NUMBER AND ALGEBRA Module 33 A guide for teachers - Years 9 10 June 2011 Factorisation (Number and Algebra : Module
9 10 YEARS The Improving Mathematics Education in Schools (TIMES) Project FACTORISATION NUMBER AND ALGEBRA Module 33 A guide for teachers - Years 9 10 June 2011 Factorisation (Number and Algebra : Module
1 Shapes of Cubic Functions
 MA 1165 - Lecture 05 1 1/26/09 1 Shapes of Cubic Functions A cubic function (a.k.a. a third-degree polynomial function) is one that can be written in the form f(x) = ax 3 + bx 2 + cx + d. (1) Quadratic
MA 1165 - Lecture 05 1 1/26/09 1 Shapes of Cubic Functions A cubic function (a.k.a. a third-degree polynomial function) is one that can be written in the form f(x) = ax 3 + bx 2 + cx + d. (1) Quadratic
ALGEBRA 2 CRA 2 REVIEW - Chapters 1-6 Answer Section
 ALGEBRA 2 CRA 2 REVIEW - Chapters 1-6 Answer Section MULTIPLE CHOICE 1. ANS: C 2. ANS: A 3. ANS: A OBJ: 5-3.1 Using Vertex Form SHORT ANSWER 4. ANS: (x + 6)(x 2 6x + 36) OBJ: 6-4.2 Solving Equations by
ALGEBRA 2 CRA 2 REVIEW - Chapters 1-6 Answer Section MULTIPLE CHOICE 1. ANS: C 2. ANS: A 3. ANS: A OBJ: 5-3.1 Using Vertex Form SHORT ANSWER 4. ANS: (x + 6)(x 2 6x + 36) OBJ: 6-4.2 Solving Equations by
FACTORING ax 2 bx c. Factoring Trinomials with Leading Coefficient 1
 5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS
 (Section 0.6: Polynomial, Rational, and Algebraic Expressions) 0.6.1 SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS LEARNING OBJECTIVES Be able to identify polynomial, rational, and algebraic
(Section 0.6: Polynomial, Rational, and Algebraic Expressions) 0.6.1 SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS LEARNING OBJECTIVES Be able to identify polynomial, rational, and algebraic
AIP Factoring Practice/Help
 The following pages include many problems to practice factoring skills. There are also several activities with examples to help you with factoring if you feel like you are not proficient with it. There
The following pages include many problems to practice factoring skills. There are also several activities with examples to help you with factoring if you feel like you are not proficient with it. There
CAHSEE on Target UC Davis, School and University Partnerships
 UC Davis, School and University Partnerships CAHSEE on Target Mathematics Curriculum Published by The University of California, Davis, School/University Partnerships Program 006 Director Sarah R. Martinez,
UC Davis, School and University Partnerships CAHSEE on Target Mathematics Curriculum Published by The University of California, Davis, School/University Partnerships Program 006 Director Sarah R. Martinez,
1.2 GRAPHS OF EQUATIONS. Copyright Cengage Learning. All rights reserved.
 1.2 GRAPHS OF EQUATIONS Copyright Cengage Learning. All rights reserved. What You Should Learn Sketch graphs of equations. Find x- and y-intercepts of graphs of equations. Use symmetry to sketch graphs
1.2 GRAPHS OF EQUATIONS Copyright Cengage Learning. All rights reserved. What You Should Learn Sketch graphs of equations. Find x- and y-intercepts of graphs of equations. Use symmetry to sketch graphs
3.3. Solving Polynomial Equations. Introduction. Prerequisites. Learning Outcomes
 Solving Polynomial Equations 3.3 Introduction Linear and quadratic equations, dealt within Sections 3.1 and 3.2, are members of a class of equations, called polynomial equations. These have the general
Solving Polynomial Equations 3.3 Introduction Linear and quadratic equations, dealt within Sections 3.1 and 3.2, are members of a class of equations, called polynomial equations. These have the general
UNCORRECTED PAGE PROOFS
 number and and algebra TopIC 17 Polynomials 17.1 Overview Why learn this? Just as number is learned in stages, so too are graphs. You have been building your knowledge of graphs and functions over time.
number and and algebra TopIC 17 Polynomials 17.1 Overview Why learn this? Just as number is learned in stages, so too are graphs. You have been building your knowledge of graphs and functions over time.
Factoring Special Polynomials
 6.6 Factoring Special Polynomials 6.6 OBJECTIVES 1. Factor the difference of two squares 2. Factor the sum or difference of two cubes In this section, we will look at several special polynomials. These
6.6 Factoring Special Polynomials 6.6 OBJECTIVES 1. Factor the difference of two squares 2. Factor the sum or difference of two cubes In this section, we will look at several special polynomials. These
FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c
 Tallahassee Community College 55 FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c This kind of trinomial differs from the previous kind we have factored because the coefficient of x is no longer "1".
Tallahassee Community College 55 FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c This kind of trinomial differs from the previous kind we have factored because the coefficient of x is no longer "1".
6 EXTENDING ALGEBRA. 6.0 Introduction. 6.1 The cubic equation. Objectives
 6 EXTENDING ALGEBRA Chapter 6 Extending Algebra Objectives After studying this chapter you should understand techniques whereby equations of cubic degree and higher can be solved; be able to factorise
6 EXTENDING ALGEBRA Chapter 6 Extending Algebra Objectives After studying this chapter you should understand techniques whereby equations of cubic degree and higher can be solved; be able to factorise
Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder).
 Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
7.2 Quadratic Equations
 476 CHAPTER 7 Graphs, Equations, and Inequalities 7. Quadratic Equations Now Work the Are You Prepared? problems on page 48. OBJECTIVES 1 Solve Quadratic Equations by Factoring (p. 476) Solve Quadratic
476 CHAPTER 7 Graphs, Equations, and Inequalities 7. Quadratic Equations Now Work the Are You Prepared? problems on page 48. OBJECTIVES 1 Solve Quadratic Equations by Factoring (p. 476) Solve Quadratic
Successful completion of Math 7 or Algebra Readiness along with teacher recommendation.
 MODESTO CITY SCHOOLS COURSE OUTLINE COURSE TITLE:... Basic Algebra COURSE NUMBER:... RECOMMENDED GRADE LEVEL:... 8-11 ABILITY LEVEL:... Basic DURATION:... 1 year CREDIT:... 5.0 per semester MEETS GRADUATION
MODESTO CITY SCHOOLS COURSE OUTLINE COURSE TITLE:... Basic Algebra COURSE NUMBER:... RECOMMENDED GRADE LEVEL:... 8-11 ABILITY LEVEL:... Basic DURATION:... 1 year CREDIT:... 5.0 per semester MEETS GRADUATION
Factoring and Applications
 Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
Springfield Technical Community College School of Mathematics, Sciences & Engineering Transfer
 Springfield Technical Community College School of Mathematics, Sciences & Engineering Transfer Department: Mathematics Course Title: Algebra 2 Course Number: MAT-097 Semester: Fall 2015 Credits: 3 Non-Graduation
Springfield Technical Community College School of Mathematics, Sciences & Engineering Transfer Department: Mathematics Course Title: Algebra 2 Course Number: MAT-097 Semester: Fall 2015 Credits: 3 Non-Graduation
Mathematics Online Instructional Materials Correlation to the 2009 Algebra I Standards of Learning and Curriculum Framework
 Provider York County School Division Course Syllabus URL http://yorkcountyschools.org/virtuallearning/coursecatalog.aspx Course Title Algebra I AB Last Updated 2010 - A.1 The student will represent verbal
Provider York County School Division Course Syllabus URL http://yorkcountyschools.org/virtuallearning/coursecatalog.aspx Course Title Algebra I AB Last Updated 2010 - A.1 The student will represent verbal
Factoring Polynomials
 UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
FACTORING QUADRATICS 8.1.1 and 8.1.2
 FACTORING QUADRATICS 8.1.1 and 8.1.2 Chapter 8 introduces students to quadratic equations. These equations can be written in the form of y = ax 2 + bx + c and, when graphed, produce a curve called a parabola.
FACTORING QUADRATICS 8.1.1 and 8.1.2 Chapter 8 introduces students to quadratic equations. These equations can be written in the form of y = ax 2 + bx + c and, when graphed, produce a curve called a parabola.
Lesson 9.1 Solving Quadratic Equations
 Lesson 9.1 Solving Quadratic Equations 1. Sketch the graph of a quadratic equation with a. One -intercept and all nonnegative y-values. b. The verte in the third quadrant and no -intercepts. c. The verte
Lesson 9.1 Solving Quadratic Equations 1. Sketch the graph of a quadratic equation with a. One -intercept and all nonnegative y-values. b. The verte in the third quadrant and no -intercepts. c. The verte
a 1 x + a 0 =0. (3) ax 2 + bx + c =0. (4)
 ROOTS OF POLYNOMIAL EQUATIONS In this unit we discuss polynomial equations. A polynomial in x of degree n, where n 0 is an integer, is an expression of the form P n (x) =a n x n + a n 1 x n 1 + + a 1 x
ROOTS OF POLYNOMIAL EQUATIONS In this unit we discuss polynomial equations. A polynomial in x of degree n, where n 0 is an integer, is an expression of the form P n (x) =a n x n + a n 1 x n 1 + + a 1 x
A Systematic Approach to Factoring
 A Systematic Approach to Factoring Step 1 Count the number of terms. (Remember****Knowing the number of terms will allow you to eliminate unnecessary tools.) Step 2 Is there a greatest common factor? Tool
A Systematic Approach to Factoring Step 1 Count the number of terms. (Remember****Knowing the number of terms will allow you to eliminate unnecessary tools.) Step 2 Is there a greatest common factor? Tool
Question 1a of 14 ( 2 Identifying the roots of a polynomial and their importance 91008 )
 Quiz: Factoring by Graphing Question 1a of 14 ( 2 Identifying the roots of a polynomial and their importance 91008 ) (x-3)(x-6), (x-6)(x-3), (1x-3)(1x-6), (1x-6)(1x-3), (x-3)*(x-6), (x-6)*(x-3), (1x- 3)*(1x-6),
Quiz: Factoring by Graphing Question 1a of 14 ( 2 Identifying the roots of a polynomial and their importance 91008 ) (x-3)(x-6), (x-6)(x-3), (1x-3)(1x-6), (1x-6)(1x-3), (x-3)*(x-6), (x-6)*(x-3), (1x- 3)*(1x-6),
FACTORING POLYNOMIALS
 296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
MATH 90 CHAPTER 6 Name:.
 MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
Factors and Products
 CHAPTER 3 Factors and Products What You ll Learn use different strategies to find factors and multiples of whole numbers identify prime factors and write the prime factorization of a number find square
CHAPTER 3 Factors and Products What You ll Learn use different strategies to find factors and multiples of whole numbers identify prime factors and write the prime factorization of a number find square
Section 3.1 Quadratic Functions and Models
 Section 3.1 Quadratic Functions and Models DEFINITION: A quadratic function is a function f of the form fx) = ax 2 +bx+c where a,b, and c are real numbers and a 0. Graphing Quadratic Functions Using the
Section 3.1 Quadratic Functions and Models DEFINITION: A quadratic function is a function f of the form fx) = ax 2 +bx+c where a,b, and c are real numbers and a 0. Graphing Quadratic Functions Using the
In algebra, factor by rewriting a polynomial as a product of lower-degree polynomials
 Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form
 ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form Goal Graph quadratic functions. VOCABULARY Quadratic function A function that can be written in the standard form y = ax 2 + bx+ c where a 0 Parabola
ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form Goal Graph quadratic functions. VOCABULARY Quadratic function A function that can be written in the standard form y = ax 2 + bx+ c where a 0 Parabola
Tool 1. Greatest Common Factor (GCF)
 Chapter 4: Factoring Review Tool 1 Greatest Common Factor (GCF) This is a very important tool. You must try to factor out the GCF first in every problem. Some problems do not have a GCF but many do. When
Chapter 4: Factoring Review Tool 1 Greatest Common Factor (GCF) This is a very important tool. You must try to factor out the GCF first in every problem. Some problems do not have a GCF but many do. When
Factoring a Difference of Two Squares. Factoring a Difference of Two Squares
 284 (6 8) Chapter 6 Factoring 87. Tomato soup. The amount of metal S (in square inches) that it takes to make a can for tomato soup is a function of the radius r and height h: S 2 r 2 2 rh a) Rewrite this
284 (6 8) Chapter 6 Factoring 87. Tomato soup. The amount of metal S (in square inches) that it takes to make a can for tomato soup is a function of the radius r and height h: S 2 r 2 2 rh a) Rewrite this
Zeros of Polynomial Functions
 Zeros of Polynomial Functions The Rational Zero Theorem If f (x) = a n x n + a n-1 x n-1 + + a 1 x + a 0 has integer coefficients and p/q (where p/q is reduced) is a rational zero, then p is a factor of
Zeros of Polynomial Functions The Rational Zero Theorem If f (x) = a n x n + a n-1 x n-1 + + a 1 x + a 0 has integer coefficients and p/q (where p/q is reduced) is a rational zero, then p is a factor of
Algebra I Vocabulary Cards
 Algebra I Vocabulary Cards Table of Contents Expressions and Operations Natural Numbers Whole Numbers Integers Rational Numbers Irrational Numbers Real Numbers Absolute Value Order of Operations Expression
Algebra I Vocabulary Cards Table of Contents Expressions and Operations Natural Numbers Whole Numbers Integers Rational Numbers Irrational Numbers Real Numbers Absolute Value Order of Operations Expression
Factoring. Factoring Monomials Monomials can often be factored in more than one way.
 Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
BEST METHODS FOR SOLVING QUADRATIC INEQUALITIES.
 BEST METHODS FOR SOLVING QUADRATIC INEQUALITIES. I. GENERALITIES There are 3 common methods to solve quadratic inequalities. Therefore, students sometimes are confused to select the fastest and the best
BEST METHODS FOR SOLVING QUADRATIC INEQUALITIES. I. GENERALITIES There are 3 common methods to solve quadratic inequalities. Therefore, students sometimes are confused to select the fastest and the best
Introduction Assignment
 PRE-CALCULUS 11 Introduction Assignment Welcome to PREC 11! This assignment will help you review some topics from a previous math course and introduce you to some of the topics that you ll be studying
PRE-CALCULUS 11 Introduction Assignment Welcome to PREC 11! This assignment will help you review some topics from a previous math course and introduce you to some of the topics that you ll be studying
6.3 FACTORING ax 2 bx c WITH a 1
 290 (6 14) Chapter 6 Factoring e) What is the approximate maximum revenue? f) Use the accompanying graph to estimate the price at which the revenue is zero. y Revenue (thousands of dollars) 300 200 100
290 (6 14) Chapter 6 Factoring e) What is the approximate maximum revenue? f) Use the accompanying graph to estimate the price at which the revenue is zero. y Revenue (thousands of dollars) 300 200 100
CM2202: Scientific Computing and Multimedia Applications General Maths: 2. Algebra - Factorisation
 CM2202: Scientific Computing and Multimedia Applications General Maths: 2. Algebra - Factorisation Prof. David Marshall School of Computer Science & Informatics Factorisation Factorisation is a way of
CM2202: Scientific Computing and Multimedia Applications General Maths: 2. Algebra - Factorisation Prof. David Marshall School of Computer Science & Informatics Factorisation Factorisation is a way of
MA107 Precalculus Algebra Exam 2 Review Solutions
 MA107 Precalculus Algebra Exam 2 Review Solutions February 24, 2008 1. The following demand equation models the number of units sold, x, of a product as a function of price, p. x = 4p + 200 a. Please write
MA107 Precalculus Algebra Exam 2 Review Solutions February 24, 2008 1. The following demand equation models the number of units sold, x, of a product as a function of price, p. x = 4p + 200 a. Please write
Sect 6.7 - Solving Equations Using the Zero Product Rule
 Sect 6.7 - Solving Equations Using the Zero Product Rule 116 Concept #1: Definition of a Quadratic Equation A quadratic equation is an equation that can be written in the form ax 2 + bx + c = 0 (referred
Sect 6.7 - Solving Equations Using the Zero Product Rule 116 Concept #1: Definition of a Quadratic Equation A quadratic equation is an equation that can be written in the form ax 2 + bx + c = 0 (referred
Algebra II Unit Number 4
 Title Polynomial Functions, Expressions, and Equations Big Ideas/Enduring Understandings Applying the processes of solving equations and simplifying expressions to problems with variables of varying degrees.
Title Polynomial Functions, Expressions, and Equations Big Ideas/Enduring Understandings Applying the processes of solving equations and simplifying expressions to problems with variables of varying degrees.
6.4 Factoring Polynomials
 Name Class Date 6.4 Factoring Polynomials Essential Question: What are some ways to factor a polynomial, and how is factoring useful? Resource Locker Explore Analyzing a Visual Model for Polynomial Factorization
Name Class Date 6.4 Factoring Polynomials Essential Question: What are some ways to factor a polynomial, and how is factoring useful? Resource Locker Explore Analyzing a Visual Model for Polynomial Factorization
Factoring Guidelines. Greatest Common Factor Two Terms Three Terms Four Terms. 2008 Shirley Radai
 Factoring Guidelines Greatest Common Factor Two Terms Three Terms Four Terms 008 Shirley Radai Greatest Common Factor 008 Shirley Radai Factoring by Finding the Greatest Common Factor Always check for
Factoring Guidelines Greatest Common Factor Two Terms Three Terms Four Terms 008 Shirley Radai Greatest Common Factor 008 Shirley Radai Factoring by Finding the Greatest Common Factor Always check for
MATH 10034 Fundamental Mathematics IV
 MATH 0034 Fundamental Mathematics IV http://www.math.kent.edu/ebooks/0034/funmath4.pdf Department of Mathematical Sciences Kent State University January 2, 2009 ii Contents To the Instructor v Polynomials.
MATH 0034 Fundamental Mathematics IV http://www.math.kent.edu/ebooks/0034/funmath4.pdf Department of Mathematical Sciences Kent State University January 2, 2009 ii Contents To the Instructor v Polynomials.
Solving Rational Equations
 Lesson M Lesson : Student Outcomes Students solve rational equations, monitoring for the creation of extraneous solutions. Lesson Notes In the preceding lessons, students learned to add, subtract, multiply,
Lesson M Lesson : Student Outcomes Students solve rational equations, monitoring for the creation of extraneous solutions. Lesson Notes In the preceding lessons, students learned to add, subtract, multiply,
Academic Success Centre
 250) 960-6367 Factoring Polynomials Sometimes when we try to solve or simplify an equation or expression involving polynomials the way that it looks can hinder our progress in finding a solution. Factorization
250) 960-6367 Factoring Polynomials Sometimes when we try to solve or simplify an equation or expression involving polynomials the way that it looks can hinder our progress in finding a solution. Factorization
Veterans Upward Bound Algebra I Concepts - Honors
 Veterans Upward Bound Algebra I Concepts - Honors Brenda Meery Kaitlyn Spong Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org Chapter 6. Factoring CHAPTER
Veterans Upward Bound Algebra I Concepts - Honors Brenda Meery Kaitlyn Spong Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org Chapter 6. Factoring CHAPTER
JUST THE MATHS UNIT NUMBER 1.8. ALGEBRA 8 (Polynomials) A.J.Hobson
 JUST THE MATHS UNIT NUMBER 1.8 ALGEBRA 8 (Polynomials) by A.J.Hobson 1.8.1 The factor theorem 1.8.2 Application to quadratic and cubic expressions 1.8.3 Cubic equations 1.8.4 Long division of polynomials
JUST THE MATHS UNIT NUMBER 1.8 ALGEBRA 8 (Polynomials) by A.J.Hobson 1.8.1 The factor theorem 1.8.2 Application to quadratic and cubic expressions 1.8.3 Cubic equations 1.8.4 Long division of polynomials
SOLVING POLYNOMIAL EQUATIONS
 C SOLVING POLYNOMIAL EQUATIONS We will assume in this appendix that you know how to divide polynomials using long division and synthetic division. If you need to review those techniques, refer to an algebra
C SOLVING POLYNOMIAL EQUATIONS We will assume in this appendix that you know how to divide polynomials using long division and synthetic division. If you need to review those techniques, refer to an algebra
Brunswick High School has reinstated a summer math curriculum for students Algebra 1, Geometry, and Algebra 2 for the 2014-2015 school year.
 Brunswick High School has reinstated a summer math curriculum for students Algebra 1, Geometry, and Algebra 2 for the 2014-2015 school year. Goal The goal of the summer math program is to help students
Brunswick High School has reinstated a summer math curriculum for students Algebra 1, Geometry, and Algebra 2 for the 2014-2015 school year. Goal The goal of the summer math program is to help students
Algebra 1 If you are okay with that placement then you have no further action to take Algebra 1 Portion of the Math Placement Test
 Dear Parents, Based on the results of the High School Placement Test (HSPT), your child should forecast to take Algebra 1 this fall. If you are okay with that placement then you have no further action
Dear Parents, Based on the results of the High School Placement Test (HSPT), your child should forecast to take Algebra 1 this fall. If you are okay with that placement then you have no further action
Learning Objectives 9.2. Media Run Times 9.3
 Unit 9 Table of Contents Unit 9: Factoring Video Overview Learning Objectives 9.2 Media Run Times 9.3 Instructor Notes 9.4 The Mathematics of Factoring Polynomials Teaching Tips: Conceptual Challenges
Unit 9 Table of Contents Unit 9: Factoring Video Overview Learning Objectives 9.2 Media Run Times 9.3 Instructor Notes 9.4 The Mathematics of Factoring Polynomials Teaching Tips: Conceptual Challenges
Algebra 1 Chapter 08 review
 Name: Class: Date: ID: A Algebra 1 Chapter 08 review Multiple Choice Identify the choice that best completes the statement or answers the question. Simplify the difference. 1. (4w 2 4w 8) (2w 2 + 3w 6)
Name: Class: Date: ID: A Algebra 1 Chapter 08 review Multiple Choice Identify the choice that best completes the statement or answers the question. Simplify the difference. 1. (4w 2 4w 8) (2w 2 + 3w 6)
Mathematics as Problem Solving The students will demonstrate the ability to gather information from a graphical representation of an equation.
 Title: Another Way of Factoring Brief Overview: Students will find factors for quadratic equations with a leading coefficient of one. The students will then graph these equations using a graphing calculator
Title: Another Way of Factoring Brief Overview: Students will find factors for quadratic equations with a leading coefficient of one. The students will then graph these equations using a graphing calculator
Factoring Flow Chart
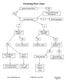 Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Chapter R.4 Factoring Polynomials
 Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
Using the ac Method to Factor
 4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
Topic: Special Products and Factors Subtopic: Rules on finding factors of polynomials
 Quarter I: Special Products and Factors and Quadratic Equations Topic: Special Products and Factors Subtopic: Rules on finding factors of polynomials Time Frame: 20 days Time Frame: 3 days Content Standard:
Quarter I: Special Products and Factors and Quadratic Equations Topic: Special Products and Factors Subtopic: Rules on finding factors of polynomials Time Frame: 20 days Time Frame: 3 days Content Standard:
6.5 Factoring Special Forms
 440 CHAPTER 6. FACTORING 6.5 Factoring Special Forms In this section we revisit two special product forms that we learned in Chapter 5, the first of which was squaring a binomial. Squaring a binomial.
440 CHAPTER 6. FACTORING 6.5 Factoring Special Forms In this section we revisit two special product forms that we learned in Chapter 5, the first of which was squaring a binomial. Squaring a binomial.
ALGEBRA I (Created 2014) Amherst County Public Schools
 ALGEBRA I (Created 2014) Amherst County Public Schools The 2009 Mathematics Standards of Learning Curriculum Framework is a companion document to the 2009 Mathematics Standards of Learning and amplifies
ALGEBRA I (Created 2014) Amherst County Public Schools The 2009 Mathematics Standards of Learning Curriculum Framework is a companion document to the 2009 Mathematics Standards of Learning and amplifies
Definition 8.1 Two inequalities are equivalent if they have the same solution set. Add or Subtract the same value on both sides of the inequality.
 8 Inequalities Concepts: Equivalent Inequalities Linear and Nonlinear Inequalities Absolute Value Inequalities (Sections 4.6 and 1.1) 8.1 Equivalent Inequalities Definition 8.1 Two inequalities are equivalent
8 Inequalities Concepts: Equivalent Inequalities Linear and Nonlinear Inequalities Absolute Value Inequalities (Sections 4.6 and 1.1) 8.1 Equivalent Inequalities Definition 8.1 Two inequalities are equivalent
Students Currently in Algebra 2 Maine East Math Placement Exam Review Problems
 Students Currently in Algebra Maine East Math Placement Eam Review Problems The actual placement eam has 100 questions 3 hours. The placement eam is free response students must solve questions and write
Students Currently in Algebra Maine East Math Placement Eam Review Problems The actual placement eam has 100 questions 3 hours. The placement eam is free response students must solve questions and write
PERFECT SQUARES AND FACTORING EXAMPLES
 PERFECT SQUARES AND FACTORING EXAMPLES 1. Ask the students what is meant by identical. Get their responses and then explain that when we have two factors that are identical, we call them perfect squares.
PERFECT SQUARES AND FACTORING EXAMPLES 1. Ask the students what is meant by identical. Get their responses and then explain that when we have two factors that are identical, we call them perfect squares.
SPECIAL PRODUCTS AND FACTORS
 CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
Factoring. Factoring Polynomial Equations. Special Factoring Patterns. Factoring. Special Factoring Patterns. Special Factoring Patterns
 Factoring Factoring Polynomial Equations Ms. Laster Earlier, you learned to factor several types of quadratic expressions: General trinomial - 2x 2-5x-12 = (2x + 3)(x - 4) Perfect Square Trinomial - x
Factoring Factoring Polynomial Equations Ms. Laster Earlier, you learned to factor several types of quadratic expressions: General trinomial - 2x 2-5x-12 = (2x + 3)(x - 4) Perfect Square Trinomial - x
Analyzing Functions Intervals of Increase & Decrease Lesson 76
 (A) Lesson Objectives a. Understand what is meant by the terms increasing/decreasing as it relates to functions b. Use graphic and algebraic methods to determine intervals of increase/decrease c. Apply
(A) Lesson Objectives a. Understand what is meant by the terms increasing/decreasing as it relates to functions b. Use graphic and algebraic methods to determine intervals of increase/decrease c. Apply
Contents. How You May Use This Resource Guide
 Contents How You May Use This Resource Guide ii 7 Factoring and Algebraic Fractions 1 Worksheet 7.1: The Box Problem......................... 4 Worksheet 7.2: Multiplying and Factoring Polynomials with
Contents How You May Use This Resource Guide ii 7 Factoring and Algebraic Fractions 1 Worksheet 7.1: The Box Problem......................... 4 Worksheet 7.2: Multiplying and Factoring Polynomials with
Operations with Algebraic Expressions: Multiplication of Polynomials
 Operations with Algebraic Expressions: Multiplication of Polynomials The product of a monomial x monomial To multiply a monomial times a monomial, multiply the coefficients and add the on powers with the
Operations with Algebraic Expressions: Multiplication of Polynomials The product of a monomial x monomial To multiply a monomial times a monomial, multiply the coefficients and add the on powers with the
