CM2202: Scientific Computing and Multimedia Applications General Maths: 2. Algebra - Factorisation
|
|
|
- Reynard McDonald
- 8 years ago
- Views:
Transcription
1 CM2202: Scientific Computing and Multimedia Applications General Maths: 2. Algebra - Factorisation Prof. David Marshall School of Computer Science & Informatics
2
3 Factorisation Factorisation is a way of simplifying algebraic expressions. As we have seen, this can be effective when finding the roots of an equation f (x) = 0. There are many other uses where factorisation can simplify the maths e.g. algebraic fractions Simple factorisation examples: 25ab 2 5a 2 b 40ab 2 24a 2 b = 5ab(5b 3a) 8ab(5b 3a) = 5 8 x 2 2x + = (x ) 2 x 2 3x + 2 = (x )(x 2) 2 / 26
4 Methods and Tools for Factorisation There are many methods and tools you can use to factorise expressions Common factors Common factors by grouping The ac method Know your algebra! - Practice makes Perfect! 3 / 26
5 Common factors The simplest form of factorisation: Extract the highest common factors (HCF) from an expression These can be variables and/or integers (coefficients). Example: 24x 2 y 2 8xy 3 The HCF of the coefficients is 6 The HCF of x is x The HCF of y is y 2 So 24x 2 y 2 8xy 3 = 6xy 2 (4x 3y) 4 / 26
6 Exercise: Common factors Factorise: 8x 4 y 3 + 6x 3 y 2 = 5a 3 b 9a 2 b 2 = 5 / 26
7 Common factors by grouping Multiple termed expressions can sometimes be factorised into binomial expressions by extracting common factors from each, e.g.: 2ac + 6bc + ad + 3bd = (2ac + 6bc) + (ad + 3bd) = 2c(a + 3b) + d(a + 3b) = (a + 3b)(2c + d) The trick here is to spot the factors! 6 / 26
8 Exercise: Common factors by grouping Factorise: x 3 + 4x 2 y xy 4y 2 = 7 / 26
9 Know your Algebra! Recap: General Rules of Algebraic Multiplication: c(a + b) = ac + bc (a + b)(c + d) = ac + ad + bc + bd (a + b) 2 = (a + b)(a + b) = aa + ba + ab + bb = a 2 + 2ab + b 2 (a b)(a+b) = aa+ab ba bb = a 2 +ab ab b 2 = a 2 b 2 8 / 26
10 Examples: Expanding/Simplifying Expressions We are quite used to expanding algebraic expressions: 3(6a + 3b c) 5(2a b + 3c) = 8a + 9b 3c 0a + 5b 5c = 8a + 4b 8c 2(3m n) + 4(m + 2n) 3(2m + 3n) = 6m 2n + 4m + 8n 6m 9n = 4m 3n (x + )(x + 6) = x 2 + x + 6x + 6 = x 2 + 7x + 6 (x + y)(m + n) = mx + nx + my + ny (x + 4) 2 = x 2 + 8x + 6 (x 3)(x + 3) = x / 26
11 Examples: Factorisation Factorisations of the following expressions are: 8x 2 2x = 4x(2x 3) 5x 2 + 5x 3 = 5x 2 ( + 3x) x 2 2x 5 = (x + 3)(x 5) x 2 + 9x + 20 = (x + 5)(x + 4) xz + 2yz 2y x = xz x + 2yz 2y = x(z ) + 2y(z ) = (z )(x + 2y) 2x 2 3x 2 = (2x + )(x 2) 0 / 26
12 The ac Method Guidance for factorising quadratics of the type ax 2 + bx + c where a 0 Obtain ac i.e. the numerical value of the product ac ignoring the sign of the product. Write down all the possible pairs of factors of ac If c is positive, we select the two factors of ac whose sum is equal to b : both of these factors have the same sign as b. If c is negative, we select the two factors of ac which differ by the value of b ; the numerically larger of these two factors has the same sign as that of b and the other has the opposite sign. In each case, denote the two factors obtained as f and f 2 Then ax 2 + bx + c is now written ax 2 + f x + f 2 x + c and this is factorised by finding common factors. / 26
13 Example:Factorising quadratics ax 2 + bx + c, a 0 Factorise: 6x 2 + x + 3 So we have a = 6, b =, c = 3 Therefore ac = 8 Factors of 8: (, 8), (2, 9), (3, 6) c is +ve therefore: f and f 2 should add up to b = Therefore the required factors are (2, 9) We therefore write: 6x 2 + x + 3 = 6x 2 + 2x + 9x + 3 = (6x 2 + 9x) + (2x + 3) = 3x(2x + 3) + (2x + 3) = (3x + )(2x + 3) 2 / 26
14 Exercise:Factorising quadratics ax 2 + bx + c, a or 0 Factorise: 3x 2 4x + 8 = 8x 2 + 8x 5 = 3 / 26
15 Factors as Algebraic Fractions Trivially: Any factors which appear in BOTH the numerator and denominator are called common factors and can simply be cancelled Simple example: 8x 2 = 3x 6x This is a useful property to similarly apply to algebraic fractions: A fraction is expressed in its simplest form by factorising the numerator and denominator and cancelling any common factors. Example: Simplify x 2 (x )(x + ) x 2 = + 3x + 2 (x + 2)(x + ) = x x / 26
16 Cubic Equations If f (x) is a cubic function ax 3 + bx 2 + cx + d then Note: the equation f (x) = 0 can have up to three real roots. The number of real roots will depend upon the values of a, b, c and d. Factors of the cubic clearly give us its roots. e.g.s: x 3 6x 2 + x 6 = 0 can be written as (x )(x 2)(x 3) = 0. Consequently, the values of x which satisfy this equation are x =, x = 2 and x = 3 5 / 26
17 Factor Theorem and Remainder Theorem () Factor theorem Definition: If for a given polynomial function f (x),f (a) = 0 then x a is a factor of the polynomial f (x). Example: Factorise 2x 3 + x 2 3x + 6 If a = then f () = (x ) is not a factor If a = then f ( ) = (x + ) is not a factor If a = 2 then f (2) = =0 (x 2) is a factor 6 / 26
18 Factor Theorem and Remainder Theorem (2) To find other factors of 2x 3 + x 2 3x + 6 we can now factor out x 2. We need to do arithmetic (long) division: 2x 2 +5x 3 x 2 )2x 3 + x 2 3x +6 2x 3 4x 2 5x 2 3x +6 5x 2 0x -3x +6-3x / 26
19 Factor Theorem and Remainder Theorem (3) It follows that 2x 2 + 5x 3 is also a factor of 2x 3 + x 2 3x + 6. Now 2x 2 + 5x 3 = (2x )(x + 3) Therefore (2x )(x + 3) are factors too So all the factors of 2x 3 + x 2 3x + 6 are: (x 2)(2x )(x + 3) 8 / 26
20 Exercise: Factor Theorem Use the factor theorem to factorise the following polynomial x 3 + 3x 2 x 3: What are the roots of the equation: x 3 + 3x 2 x 3 = 0? 9 / 26
21 Factor Theorem and Remainder Theorem (4) Remainder theorem: When f (x) is divided by (x a) remainder is f (a). Example: Find the remainder when x 3 + 6x 2 + 7x 4 is divided by x + 3 Using the remainder theorem a = 3 So f (a) = f (x = a = 3), (setting x = 3) x 3 +6x 2 +7x 4 = ( 3) 3 +6( 3) 2 +7( 3) 4 = = 2 20 / 26
22 Exercise : Remainder Theorem When the polynomial f (x) = x 3 + 8x 2 + kx + 0 is divided by x 2, there is a remainder of 84. Show that k = 7. 2 / 26
23 Exercise 2: Remainder Theorem Given that x + 3 is a factor of 2x 3 + 9x 2 + ax 6, find the value of a. Using this value of a, solve the equation 2x 3 + 9x 2 + ax 6 = / 26
24 Sum or difference of two cubes Another formula for factoring is the sum or difference of two cubes. The sum can be represented by and the difference by a 3 + b 3 = (a + b)(a 2 ab + b 2 ) a 3 b 3 = (a b)(a 2 + ab + b 2 ) 23 / 26
25 Quartic Equations Recap: A Polynomial of Order 4: f (x) = ax 4 + bx 3 + cx 2 + dx + e In principal, the solution to a Quartic uses the same tools as for a cubic and quadratic - it s just a little more long winded or more complex. The same idea, as just introduced with cubics, of using the Factor Theorem applies 24 / 26
26 4 a a a a (b 2 3ac + 2d) 3 2b 3 9abc + 27c a 2 d 72bd + 4(b 2 3ac + 2d) 3 +(2b 3 9abc + 27c a 2 d 72bd) (b 2 3ac + 2d) 3 2b 3 9abc + 27c a 2 d 72bd + 4(b 2 3ac + 2d) 3 +(2b 3 9abc + 27c a 2 d 72bd) (b 2 3ac + 2d) 3 2b 3 9abc + 27c a 2 d 72bd + 4(b 2 3ac + 2d) 3 +(2b 3 9abc + 27c a 2 d 72bd) (b 2 3ac + 2d) 3 2b 3 9abc + 27c a 2 d 72bd + 4(b 2 3ac + 2d) 3 +(2b 3 9abc + 27c a 2 d 72bd) (b 2 3ac + 2d) 3 +(2b 3 9abc + 27c a 2 d 72bd) (b 2 3ac + 2d) 3 +(2b 3 9abc + 27c a 2 d 72bd) (b 2 3ac + 2d) 3 +(2b 3 9abc + 27c a 2 d 72bd) (b 2 3ac + 2d) 3 +(2b 3 9abc + 27c a 2 d 72bd) a 2 a 2 a 2 a 2 3 (b 2 3ac + 2d) 3 2b 3 9abc + 27c a 2 d 72bd + 4(b 2 3ac + 2d) 3 +(2b 3 9abc + 27c a 2 d 72bd) (b 2 3ac + 2d) 3 2b 3 9abc + 27c a 2 d 72bd + 4(b 2 3ac + 2d) 3 +(2b 3 9abc + 27c a 2 d 72bd) (b 2 3ac + 2d) 3 2b 3 9abc + 27c a 2 d 72bd + 4(b 2 3ac + 2d) 3 +(2b 3 9abc + 27c a 2 d 72bd) (b 2 3ac + 2d) 3 2b 3 9abc + 27c a 2 d 72bd + 4(b 2 3ac + 2d) 3 +(2b 3 9abc + 27c a 2 d 72bd) 2 3 4(b 2 3ac + 2d) 3 +(2b 3 9abc + 27c a 2 d 72bd) (b 2 3ac + 2d) 3 +(2b 3 9abc + 27c a 2 d 72bd) (b 2 3ac + 2d) 3 +(2b 3 9abc + 27c a 2 d 72bd) (b 2 3ac + 2d) 3 +(2b 3 9abc + 27c a 2 d 72bd) a 2 4 a 2 4 a 2 4 a 2 a 3 +4ab 8c 2b + 3 9abc+27c 2 +27a 2 d 72bd+ 4(b 2 3ac+2d) 3 +(2b 3 9abc+27c 2 +27a 2 d 72bd) b 3 9abc+27c 2 +27a 2 d 72bd+ 4(b 2 3ac+2d) 3 +(2b 3 9abc+27c 2 +27a 2 d 72bd) a 3 +4ab 8c 2b + 3 9abc+27c 2 +27a 2 d 72bd+ 4(b 2 3ac+2d) 3 +(2b 3 9abc+27c 2 +27a 2 d 72bd) b 3 9abc+27c 2 +27a 2 d 72bd+ 4(b 2 3ac+2d) 3 +(2b 3 9abc+27c 2 +27a 2 d 72bd) a 3 +4ab 8c 2b + 3 9abc+27c 2 +27a 2 d 72bd+ 4(b 2 3ac+2d) 3 +(2b 3 9abc+27c 2 +27a 2 d 72bd) b 3 9abc+27c 2 +27a 2 d 72bd+ 4(b 2 3ac+2d) 3 +(2b 3 9abc+27c 2 +27a 2 d 72bd) a 3 +4ab 8c 2b + 3 9abc+27c 2 +27a 2 d 72bd+ 4(b 2 3ac+2d) 3 +(2b 3 9abc+27c 2 +27a 2 d 72bd) b 3 9abc+27c 2 +27a 2 d 72bd+ 4(b 2 3ac+2d) 3 +(2b 3 9abc+27c 2 +27a 2 d 72bd) Closed form Quartic Solution A closed form solution for a quartic actually does exist: The four roots r,r2,r3,r4 of a quartic polynomial equation x 4 + ax 3 + bx 2 + cx + d = 0 are given by r = a r2 = a r3 = a r4 = a 4 2b b b b b3 9abc + 27c a 2 d 72bd + 2b3 9abc + 27c a 2 d 72bd + 2b3 9abc + 27c a 2 d 72bd + 2b3 9abc + 27c a 2 d 72bd b b b b 3 2 2b3 9abc + 27c a 2 d 72bd + 2b3 9abc + 27c a 2 d 72bd + 2b3 9abc + 27c a 2 d 72bd + 2b3 9abc + 27c a 2 d 72bd + The four roots r,r2,r3,r4 of a quartic polynomial equation x First part enlarged: 4 + ax 3 + bx 2 + cx + d = 0 are given by 4 2b (b 2 3ac+2d) 4 2b (b 2 3ac+2d) 4 2b (b 2 3ac+2d) 4 2b (b 2 3ac+2d) r = a 4 a b (b 2 3ac + 2d) + 2b3 9abc + 3 2b 3 9abc + 27c a 2 d 72bd + 4(b 2 3ac + 2d) 3 +(2b 3 9abc + 27c a 2 d 72bd) 2 3 r2 = a 4 a b (b 2 3ac + 2d) + 2b3 9abc + 3 2b 3 9abc + 27c a 2 d 72bd + 4(b 2 3ac + 2d) 3 +(2b 3 9abc + 27c a 2 d 72bd) 2 3 r3 = a 4 + a b (b 2 3ac + 2d) + 2b3 9abc + 3 2b 3 9abc + 27c a 2 d 72bd + 4(b 2 3ac + 2d) 3 +(2b 3 9abc + 27c a 2 d 72bd) 2 3 However, in practice, this is too unwieldy to be used for solving quartic equations (Source r4 = a 4 + a b (b 2 3ac + 2d) + 2b3 9abc + 3 2b 3 9abc + 27c a 2 d 72bd + 4(b 2 3ac + 2d) 3 +(2b 3 9abc + 27c a 2 d 72bd) / 26
27 Matlab to the Rescue We can use MATLAB to relieve the stress of factorisation: >> syms x ; >> f = 4 x ˆ4 3 x ˆ3 2 x ˆ2 + x ; >> f a c t o r ( f ) ans = x ( x ) (4 x ˆ2 + x ) >> d o u b l e ( s o l v e ( f ) ) ans = / 26
1.4. Arithmetic of Algebraic Fractions. Introduction. Prerequisites. Learning Outcomes
 Arithmetic of Algebraic Fractions 1.4 Introduction Just as one whole number divided by another is called a numerical fraction, so one algebraic expression divided by another is known as an algebraic fraction.
Arithmetic of Algebraic Fractions 1.4 Introduction Just as one whole number divided by another is called a numerical fraction, so one algebraic expression divided by another is known as an algebraic fraction.
1.3 Polynomials and Factoring
 1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
Factoring Polynomials
 Factoring Polynomials 4-1-2014 The opposite of multiplying polynomials is factoring. Why would you want to factor a polynomial? Let p(x) be a polynomial. p(c) = 0 is equivalent to x c dividing p(x). Recall
Factoring Polynomials 4-1-2014 The opposite of multiplying polynomials is factoring. Why would you want to factor a polynomial? Let p(x) be a polynomial. p(c) = 0 is equivalent to x c dividing p(x). Recall
a 1 x + a 0 =0. (3) ax 2 + bx + c =0. (4)
 ROOTS OF POLYNOMIAL EQUATIONS In this unit we discuss polynomial equations. A polynomial in x of degree n, where n 0 is an integer, is an expression of the form P n (x) =a n x n + a n 1 x n 1 + + a 1 x
ROOTS OF POLYNOMIAL EQUATIONS In this unit we discuss polynomial equations. A polynomial in x of degree n, where n 0 is an integer, is an expression of the form P n (x) =a n x n + a n 1 x n 1 + + a 1 x
SOLVING QUADRATIC EQUATIONS - COMPARE THE FACTORING ac METHOD AND THE NEW DIAGONAL SUM METHOD By Nghi H. Nguyen
 SOLVING QUADRATIC EQUATIONS - COMPARE THE FACTORING ac METHOD AND THE NEW DIAGONAL SUM METHOD By Nghi H. Nguyen A. GENERALITIES. When a given quadratic equation can be factored, there are 2 best methods
SOLVING QUADRATIC EQUATIONS - COMPARE THE FACTORING ac METHOD AND THE NEW DIAGONAL SUM METHOD By Nghi H. Nguyen A. GENERALITIES. When a given quadratic equation can be factored, there are 2 best methods
1.3 Algebraic Expressions
 1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
NSM100 Introduction to Algebra Chapter 5 Notes Factoring
 Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
Factoring Polynomials and Solving Quadratic Equations
 Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any.
 Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
FACTORISATION YEARS. A guide for teachers - Years 9 10 June 2011. The Improving Mathematics Education in Schools (TIMES) Project
 9 10 YEARS The Improving Mathematics Education in Schools (TIMES) Project FACTORISATION NUMBER AND ALGEBRA Module 33 A guide for teachers - Years 9 10 June 2011 Factorisation (Number and Algebra : Module
9 10 YEARS The Improving Mathematics Education in Schools (TIMES) Project FACTORISATION NUMBER AND ALGEBRA Module 33 A guide for teachers - Years 9 10 June 2011 Factorisation (Number and Algebra : Module
( ) FACTORING. x In this polynomial the only variable in common to all is x.
 FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
expression is written horizontally. The Last terms ((2)( 4)) because they are the last terms of the two polynomials. This is called the FOIL method.
 A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
Factoring Polynomials
 UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
JUST THE MATHS UNIT NUMBER 1.8. ALGEBRA 8 (Polynomials) A.J.Hobson
 JUST THE MATHS UNIT NUMBER 1.8 ALGEBRA 8 (Polynomials) by A.J.Hobson 1.8.1 The factor theorem 1.8.2 Application to quadratic and cubic expressions 1.8.3 Cubic equations 1.8.4 Long division of polynomials
JUST THE MATHS UNIT NUMBER 1.8 ALGEBRA 8 (Polynomials) by A.J.Hobson 1.8.1 The factor theorem 1.8.2 Application to quadratic and cubic expressions 1.8.3 Cubic equations 1.8.4 Long division of polynomials
AIP Factoring Practice/Help
 The following pages include many problems to practice factoring skills. There are also several activities with examples to help you with factoring if you feel like you are not proficient with it. There
The following pages include many problems to practice factoring skills. There are also several activities with examples to help you with factoring if you feel like you are not proficient with it. There
Factoring Polynomials
 Factoring Polynomials Factoring Factoring is the process of writing a polynomial as the product of two or more polynomials. The factors of 6x 2 x 2 are 2x + 1 and 3x 2. In this section, we will be factoring
Factoring Polynomials Factoring Factoring is the process of writing a polynomial as the product of two or more polynomials. The factors of 6x 2 x 2 are 2x + 1 and 3x 2. In this section, we will be factoring
Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder).
 Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Factoring Quadratic Expressions
 Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
Section 6.1 Factoring Expressions
 Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
Lagrange Interpolation is a method of fitting an equation to a set of points that functions well when there are few points given.
 Polynomials (Ch.1) Study Guide by BS, JL, AZ, CC, SH, HL Lagrange Interpolation is a method of fitting an equation to a set of points that functions well when there are few points given. Sasha s method
Polynomials (Ch.1) Study Guide by BS, JL, AZ, CC, SH, HL Lagrange Interpolation is a method of fitting an equation to a set of points that functions well when there are few points given. Sasha s method
1.5. Factorisation. Introduction. Prerequisites. Learning Outcomes. Learning Style
 Factorisation 1.5 Introduction In Block 4 we showed the way in which brackets were removed from algebraic expressions. Factorisation, which can be considered as the reverse of this process, is dealt with
Factorisation 1.5 Introduction In Block 4 we showed the way in which brackets were removed from algebraic expressions. Factorisation, which can be considered as the reverse of this process, is dealt with
Tim Kerins. Leaving Certificate Honours Maths - Algebra. Tim Kerins. the date
 Leaving Certificate Honours Maths - Algebra the date Chapter 1 Algebra This is an important portion of the course. As well as generally accounting for 2 3 questions in examination it is the basis for many
Leaving Certificate Honours Maths - Algebra the date Chapter 1 Algebra This is an important portion of the course. As well as generally accounting for 2 3 questions in examination it is the basis for many
Name Intro to Algebra 2. Unit 1: Polynomials and Factoring
 Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
6 EXTENDING ALGEBRA. 6.0 Introduction. 6.1 The cubic equation. Objectives
 6 EXTENDING ALGEBRA Chapter 6 Extending Algebra Objectives After studying this chapter you should understand techniques whereby equations of cubic degree and higher can be solved; be able to factorise
6 EXTENDING ALGEBRA Chapter 6 Extending Algebra Objectives After studying this chapter you should understand techniques whereby equations of cubic degree and higher can be solved; be able to factorise
3.3. Solving Polynomial Equations. Introduction. Prerequisites. Learning Outcomes
 Solving Polynomial Equations 3.3 Introduction Linear and quadratic equations, dealt within Sections 3.1 and 3.2, are members of a class of equations, called polynomial equations. These have the general
Solving Polynomial Equations 3.3 Introduction Linear and quadratic equations, dealt within Sections 3.1 and 3.2, are members of a class of equations, called polynomial equations. These have the general
Factoring Trinomials: The ac Method
 6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
Partial Fractions Examples
 Partial Fractions Examples Partial fractions is the name given to a technique of integration that may be used to integrate any ratio of polynomials. A ratio of polynomials is called a rational function.
Partial Fractions Examples Partial fractions is the name given to a technique of integration that may be used to integrate any ratio of polynomials. A ratio of polynomials is called a rational function.
A Systematic Approach to Factoring
 A Systematic Approach to Factoring Step 1 Count the number of terms. (Remember****Knowing the number of terms will allow you to eliminate unnecessary tools.) Step 2 Is there a greatest common factor? Tool
A Systematic Approach to Factoring Step 1 Count the number of terms. (Remember****Knowing the number of terms will allow you to eliminate unnecessary tools.) Step 2 Is there a greatest common factor? Tool
BEGINNING ALGEBRA ACKNOWLEDMENTS
 BEGINNING ALGEBRA The Nursing Department of Labouré College requested the Department of Academic Planning and Support Services to help with mathematics preparatory materials for its Bachelor of Science
BEGINNING ALGEBRA The Nursing Department of Labouré College requested the Department of Academic Planning and Support Services to help with mathematics preparatory materials for its Bachelor of Science
Using the ac Method to Factor
 4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
Algebra I Vocabulary Cards
 Algebra I Vocabulary Cards Table of Contents Expressions and Operations Natural Numbers Whole Numbers Integers Rational Numbers Irrational Numbers Real Numbers Absolute Value Order of Operations Expression
Algebra I Vocabulary Cards Table of Contents Expressions and Operations Natural Numbers Whole Numbers Integers Rational Numbers Irrational Numbers Real Numbers Absolute Value Order of Operations Expression
SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS
 (Section 0.6: Polynomial, Rational, and Algebraic Expressions) 0.6.1 SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS LEARNING OBJECTIVES Be able to identify polynomial, rational, and algebraic
(Section 0.6: Polynomial, Rational, and Algebraic Expressions) 0.6.1 SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS LEARNING OBJECTIVES Be able to identify polynomial, rational, and algebraic
SOLVING POLYNOMIAL EQUATIONS
 C SOLVING POLYNOMIAL EQUATIONS We will assume in this appendix that you know how to divide polynomials using long division and synthetic division. If you need to review those techniques, refer to an algebra
C SOLVING POLYNOMIAL EQUATIONS We will assume in this appendix that you know how to divide polynomials using long division and synthetic division. If you need to review those techniques, refer to an algebra
Partial Fractions. (x 1)(x 2 + 1)
 Partial Fractions Adding rational functions involves finding a common denominator, rewriting each fraction so that it has that denominator, then adding. For example, 3x x 1 3x(x 1) (x + 1)(x 1) + 1(x +
Partial Fractions Adding rational functions involves finding a common denominator, rewriting each fraction so that it has that denominator, then adding. For example, 3x x 1 3x(x 1) (x + 1)(x 1) + 1(x +
6.1 Add & Subtract Polynomial Expression & Functions
 6.1 Add & Subtract Polynomial Expression & Functions Objectives 1. Know the meaning of the words term, monomial, binomial, trinomial, polynomial, degree, coefficient, like terms, polynomial funciton, quardrtic
6.1 Add & Subtract Polynomial Expression & Functions Objectives 1. Know the meaning of the words term, monomial, binomial, trinomial, polynomial, degree, coefficient, like terms, polynomial funciton, quardrtic
SOLVING QUADRATIC EQUATIONS BY THE DIAGONAL SUM METHOD
 SOLVING QUADRATIC EQUATIONS BY THE DIAGONAL SUM METHOD A quadratic equation in one variable has as standard form: ax^2 + bx + c = 0. Solving it means finding the values of x that make the equation true.
SOLVING QUADRATIC EQUATIONS BY THE DIAGONAL SUM METHOD A quadratic equation in one variable has as standard form: ax^2 + bx + c = 0. Solving it means finding the values of x that make the equation true.
Factoring (pp. 1 of 4)
 Factoring (pp. 1 of 4) Algebra Review Try these items from middle school math. A) What numbers are the factors of 4? B) Write down the prime factorization of 7. C) 6 Simplify 48 using the greatest common
Factoring (pp. 1 of 4) Algebra Review Try these items from middle school math. A) What numbers are the factors of 4? B) Write down the prime factorization of 7. C) 6 Simplify 48 using the greatest common
3 1. Note that all cubes solve it; therefore, there are no more
 Math 13 Problem set 5 Artin 11.4.7 Factor the following polynomials into irreducible factors in Q[x]: (a) x 3 3x (b) x 3 3x + (c) x 9 6x 6 + 9x 3 3 Solution: The first two polynomials are cubics, so if
Math 13 Problem set 5 Artin 11.4.7 Factor the following polynomials into irreducible factors in Q[x]: (a) x 3 3x (b) x 3 3x + (c) x 9 6x 6 + 9x 3 3 Solution: The first two polynomials are cubics, so if
SPECIAL PRODUCTS AND FACTORS
 CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
0.4 FACTORING POLYNOMIALS
 36_.qxd /3/5 :9 AM Page -9 SECTION. Factoring Polynomials -9. FACTORING POLYNOMIALS Use special products and factorization techniques to factor polynomials. Find the domains of radical expressions. Use
36_.qxd /3/5 :9 AM Page -9 SECTION. Factoring Polynomials -9. FACTORING POLYNOMIALS Use special products and factorization techniques to factor polynomials. Find the domains of radical expressions. Use
calculating the result modulo 3, as follows: p(0) = 0 3 + 0 + 1 = 1 0,
 Homework #02, due 1/27/10 = 9.4.1, 9.4.2, 9.4.5, 9.4.6, 9.4.7. Additional problems recommended for study: (9.4.3), 9.4.4, 9.4.9, 9.4.11, 9.4.13, (9.4.14), 9.4.17 9.4.1 Determine whether the following polynomials
Homework #02, due 1/27/10 = 9.4.1, 9.4.2, 9.4.5, 9.4.6, 9.4.7. Additional problems recommended for study: (9.4.3), 9.4.4, 9.4.9, 9.4.11, 9.4.13, (9.4.14), 9.4.17 9.4.1 Determine whether the following polynomials
PUTNAM TRAINING POLYNOMIALS. Exercises 1. Find a polynomial with integral coefficients whose zeros include 2 + 5.
 PUTNAM TRAINING POLYNOMIALS (Last updated: November 17, 2015) Remark. This is a list of exercises on polynomials. Miguel A. Lerma Exercises 1. Find a polynomial with integral coefficients whose zeros include
PUTNAM TRAINING POLYNOMIALS (Last updated: November 17, 2015) Remark. This is a list of exercises on polynomials. Miguel A. Lerma Exercises 1. Find a polynomial with integral coefficients whose zeros include
Tool 1. Greatest Common Factor (GCF)
 Chapter 4: Factoring Review Tool 1 Greatest Common Factor (GCF) This is a very important tool. You must try to factor out the GCF first in every problem. Some problems do not have a GCF but many do. When
Chapter 4: Factoring Review Tool 1 Greatest Common Factor (GCF) This is a very important tool. You must try to factor out the GCF first in every problem. Some problems do not have a GCF but many do. When
Mathematics Placement
 Mathematics Placement The ACT COMPASS math test is a self-adaptive test, which potentially tests students within four different levels of math including pre-algebra, algebra, college algebra, and trigonometry.
Mathematics Placement The ACT COMPASS math test is a self-adaptive test, which potentially tests students within four different levels of math including pre-algebra, algebra, college algebra, and trigonometry.
UNCORRECTED PAGE PROOFS
 number and and algebra TopIC 17 Polynomials 17.1 Overview Why learn this? Just as number is learned in stages, so too are graphs. You have been building your knowledge of graphs and functions over time.
number and and algebra TopIC 17 Polynomials 17.1 Overview Why learn this? Just as number is learned in stages, so too are graphs. You have been building your knowledge of graphs and functions over time.
1 Lecture: Integration of rational functions by decomposition
 Lecture: Integration of rational functions by decomposition into partial fractions Recognize and integrate basic rational functions, except when the denominator is a power of an irreducible quadratic.
Lecture: Integration of rational functions by decomposition into partial fractions Recognize and integrate basic rational functions, except when the denominator is a power of an irreducible quadratic.
FACTORING OUT COMMON FACTORS
 278 (6 2) Chapter 6 Factoring 6.1 FACTORING OUT COMMON FACTORS In this section Prime Factorization of Integers Greatest Common Factor Finding the Greatest Common Factor for Monomials Factoring Out the
278 (6 2) Chapter 6 Factoring 6.1 FACTORING OUT COMMON FACTORS In this section Prime Factorization of Integers Greatest Common Factor Finding the Greatest Common Factor for Monomials Factoring Out the
Chapter 5. Rational Expressions
 5.. Simplify Rational Expressions KYOTE Standards: CR ; CA 7 Chapter 5. Rational Expressions Definition. A rational expression is the quotient P Q of two polynomials P and Q in one or more variables, where
5.. Simplify Rational Expressions KYOTE Standards: CR ; CA 7 Chapter 5. Rational Expressions Definition. A rational expression is the quotient P Q of two polynomials P and Q in one or more variables, where
Decomposing Rational Functions into Partial Fractions:
 Prof. Keely's Math Online Lessons University of Phoenix Online & Clark College, Vancouver WA Copyright 2003 Sally J. Keely. All Rights Reserved. COLLEGE ALGEBRA Hi! Today's topic is highly structured and
Prof. Keely's Math Online Lessons University of Phoenix Online & Clark College, Vancouver WA Copyright 2003 Sally J. Keely. All Rights Reserved. COLLEGE ALGEBRA Hi! Today's topic is highly structured and
To add fractions we rewrite the fractions with a common denominator then add the numerators. = +
 Partial Fractions Adding fractions To add fractions we rewrite the fractions with a common denominator then add the numerators. Example Find the sum of 3 x 5 The common denominator of 3 and x 5 is 3 x
Partial Fractions Adding fractions To add fractions we rewrite the fractions with a common denominator then add the numerators. Example Find the sum of 3 x 5 The common denominator of 3 and x 5 is 3 x
9. POLYNOMIALS. Example 1: The expression a(x) = x 3 4x 2 + 7x 11 is a polynomial in x. The coefficients of a(x) are the numbers 1, 4, 7, 11.
 9. POLYNOMIALS 9.1. Definition of a Polynomial A polynomial is an expression of the form: a(x) = a n x n + a n-1 x n-1 +... + a 1 x + a 0. The symbol x is called an indeterminate and simply plays the role
9. POLYNOMIALS 9.1. Definition of a Polynomial A polynomial is an expression of the form: a(x) = a n x n + a n-1 x n-1 +... + a 1 x + a 0. The symbol x is called an indeterminate and simply plays the role
Veterans Upward Bound Algebra I Concepts - Honors
 Veterans Upward Bound Algebra I Concepts - Honors Brenda Meery Kaitlyn Spong Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org Chapter 6. Factoring CHAPTER
Veterans Upward Bound Algebra I Concepts - Honors Brenda Meery Kaitlyn Spong Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org Chapter 6. Factoring CHAPTER
Polynomials. Key Terms. quadratic equation parabola conjugates trinomial. polynomial coefficient degree monomial binomial GCF
 Polynomials 5 5.1 Addition and Subtraction of Polynomials and Polynomial Functions 5.2 Multiplication of Polynomials 5.3 Division of Polynomials Problem Recognition Exercises Operations on Polynomials
Polynomials 5 5.1 Addition and Subtraction of Polynomials and Polynomial Functions 5.2 Multiplication of Polynomials 5.3 Division of Polynomials Problem Recognition Exercises Operations on Polynomials
The Method of Partial Fractions Math 121 Calculus II Spring 2015
 Rational functions. as The Method of Partial Fractions Math 11 Calculus II Spring 015 Recall that a rational function is a quotient of two polynomials such f(x) g(x) = 3x5 + x 3 + 16x x 60. The method
Rational functions. as The Method of Partial Fractions Math 11 Calculus II Spring 015 Recall that a rational function is a quotient of two polynomials such f(x) g(x) = 3x5 + x 3 + 16x x 60. The method
1.7. Partial Fractions. 1.7.1. Rational Functions and Partial Fractions. A rational function is a quotient of two polynomials: R(x) = P (x) Q(x).
 .7. PRTIL FRCTIONS 3.7. Partial Fractions.7.. Rational Functions and Partial Fractions. rational function is a quotient of two polynomials: R(x) = P (x) Q(x). Here we discuss how to integrate rational
.7. PRTIL FRCTIONS 3.7. Partial Fractions.7.. Rational Functions and Partial Fractions. rational function is a quotient of two polynomials: R(x) = P (x) Q(x). Here we discuss how to integrate rational
MATH 108 REVIEW TOPIC 10 Quadratic Equations. B. Solving Quadratics by Completing the Square
 Math 108 T10-Review Topic 10 Page 1 MATH 108 REVIEW TOPIC 10 Quadratic Equations I. Finding Roots of a Quadratic Equation A. Factoring B. Quadratic Formula C. Taking Roots II. III. Guidelines for Finding
Math 108 T10-Review Topic 10 Page 1 MATH 108 REVIEW TOPIC 10 Quadratic Equations I. Finding Roots of a Quadratic Equation A. Factoring B. Quadratic Formula C. Taking Roots II. III. Guidelines for Finding
In algebra, factor by rewriting a polynomial as a product of lower-degree polynomials
 Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
Factoring Special Polynomials
 6.6 Factoring Special Polynomials 6.6 OBJECTIVES 1. Factor the difference of two squares 2. Factor the sum or difference of two cubes In this section, we will look at several special polynomials. These
6.6 Factoring Special Polynomials 6.6 OBJECTIVES 1. Factor the difference of two squares 2. Factor the sum or difference of two cubes In this section, we will look at several special polynomials. These
By reversing the rules for multiplication of binomials from Section 4.6, we get rules for factoring polynomials in certain forms.
 SECTION 5.4 Special Factoring Techniques 317 5.4 Special Factoring Techniques OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor
SECTION 5.4 Special Factoring Techniques 317 5.4 Special Factoring Techniques OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor
Sect 6.1 - Greatest Common Factor and Factoring by Grouping
 Sect 6.1 - Greatest Common Factor and Factoring by Grouping Our goal in this chapter is to solve non-linear equations by breaking them down into a series of linear equations that we can solve. To do this,
Sect 6.1 - Greatest Common Factor and Factoring by Grouping Our goal in this chapter is to solve non-linear equations by breaking them down into a series of linear equations that we can solve. To do this,
Algebra 2 PreAP. Name Period
 Algebra 2 PreAP Name Period IMPORTANT INSTRUCTIONS FOR STUDENTS!!! We understand that students come to Algebra II with different strengths and needs. For this reason, students have options for completing
Algebra 2 PreAP Name Period IMPORTANT INSTRUCTIONS FOR STUDENTS!!! We understand that students come to Algebra II with different strengths and needs. For this reason, students have options for completing
15.1 Factoring Polynomials
 LESSON 15.1 Factoring Polynomials Use the structure of an expression to identify ways to rewrite it. Also A.SSE.3? ESSENTIAL QUESTION How can you use the greatest common factor to factor polynomials? EXPLORE
LESSON 15.1 Factoring Polynomials Use the structure of an expression to identify ways to rewrite it. Also A.SSE.3? ESSENTIAL QUESTION How can you use the greatest common factor to factor polynomials? EXPLORE
Academic Success Centre
 250) 960-6367 Factoring Polynomials Sometimes when we try to solve or simplify an equation or expression involving polynomials the way that it looks can hinder our progress in finding a solution. Factorization
250) 960-6367 Factoring Polynomials Sometimes when we try to solve or simplify an equation or expression involving polynomials the way that it looks can hinder our progress in finding a solution. Factorization
FACTORING POLYNOMIALS
 296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
Algebra 1 If you are okay with that placement then you have no further action to take Algebra 1 Portion of the Math Placement Test
 Dear Parents, Based on the results of the High School Placement Test (HSPT), your child should forecast to take Algebra 1 this fall. If you are okay with that placement then you have no further action
Dear Parents, Based on the results of the High School Placement Test (HSPT), your child should forecast to take Algebra 1 this fall. If you are okay with that placement then you have no further action
FACTORING ax 2 bx c. Factoring Trinomials with Leading Coefficient 1
 5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
Factoring Flow Chart
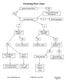 Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Florida Math 0028. Correlation of the ALEKS course Florida Math 0028 to the Florida Mathematics Competencies - Upper
 Florida Math 0028 Correlation of the ALEKS course Florida Math 0028 to the Florida Mathematics Competencies - Upper Exponents & Polynomials MDECU1: Applies the order of operations to evaluate algebraic
Florida Math 0028 Correlation of the ALEKS course Florida Math 0028 to the Florida Mathematics Competencies - Upper Exponents & Polynomials MDECU1: Applies the order of operations to evaluate algebraic
Algebra Cheat Sheets
 Sheets Algebra Cheat Sheets provide you with a tool for teaching your students note-taking, problem-solving, and organizational skills in the context of algebra lessons. These sheets teach the concepts
Sheets Algebra Cheat Sheets provide you with a tool for teaching your students note-taking, problem-solving, and organizational skills in the context of algebra lessons. These sheets teach the concepts
MATH 10034 Fundamental Mathematics IV
 MATH 0034 Fundamental Mathematics IV http://www.math.kent.edu/ebooks/0034/funmath4.pdf Department of Mathematical Sciences Kent State University January 2, 2009 ii Contents To the Instructor v Polynomials.
MATH 0034 Fundamental Mathematics IV http://www.math.kent.edu/ebooks/0034/funmath4.pdf Department of Mathematical Sciences Kent State University January 2, 2009 ii Contents To the Instructor v Polynomials.
MATH 21. College Algebra 1 Lecture Notes
 MATH 21 College Algebra 1 Lecture Notes MATH 21 3.6 Factoring Review College Algebra 1 Factoring and Foiling 1. (a + b) 2 = a 2 + 2ab + b 2. 2. (a b) 2 = a 2 2ab + b 2. 3. (a + b)(a b) = a 2 b 2. 4. (a
MATH 21 College Algebra 1 Lecture Notes MATH 21 3.6 Factoring Review College Algebra 1 Factoring and Foiling 1. (a + b) 2 = a 2 + 2ab + b 2. 2. (a b) 2 = a 2 2ab + b 2. 3. (a + b)(a b) = a 2 b 2. 4. (a
1.4. Removing Brackets. Introduction. Prerequisites. Learning Outcomes. Learning Style
 Removing Brackets 1. Introduction In order to simplify an expression which contains brackets it is often necessary to rewrite the expression in an equivalent form but without any brackets. This process
Removing Brackets 1. Introduction In order to simplify an expression which contains brackets it is often necessary to rewrite the expression in an equivalent form but without any brackets. This process
Unit 3: Day 2: Factoring Polynomial Expressions
 Unit 3: Day : Factoring Polynomial Expressions Minds On: 0 Action: 45 Consolidate:10 Total =75 min Learning Goals: Extend knowledge of factoring to factor cubic and quartic expressions that can be factored
Unit 3: Day : Factoring Polynomial Expressions Minds On: 0 Action: 45 Consolidate:10 Total =75 min Learning Goals: Extend knowledge of factoring to factor cubic and quartic expressions that can be factored
MATH 90 CHAPTER 6 Name:.
 MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
Vocabulary Words and Definitions for Algebra
 Name: Period: Vocabulary Words and s for Algebra Absolute Value Additive Inverse Algebraic Expression Ascending Order Associative Property Axis of Symmetry Base Binomial Coefficient Combine Like Terms
Name: Period: Vocabulary Words and s for Algebra Absolute Value Additive Inverse Algebraic Expression Ascending Order Associative Property Axis of Symmetry Base Binomial Coefficient Combine Like Terms
What are the place values to the left of the decimal point and their associated powers of ten?
 The verbal answers to all of the following questions should be memorized before completion of algebra. Answers that are not memorized will hinder your ability to succeed in geometry and algebra. (Everything
The verbal answers to all of the following questions should be memorized before completion of algebra. Answers that are not memorized will hinder your ability to succeed in geometry and algebra. (Everything
Math Review. for the Quantitative Reasoning Measure of the GRE revised General Test
 Math Review for the Quantitative Reasoning Measure of the GRE revised General Test www.ets.org Overview This Math Review will familiarize you with the mathematical skills and concepts that are important
Math Review for the Quantitative Reasoning Measure of the GRE revised General Test www.ets.org Overview This Math Review will familiarize you with the mathematical skills and concepts that are important
Simplification of Radical Expressions
 8. Simplification of Radical Expressions 8. OBJECTIVES 1. Simplify a radical expression by using the product property. Simplify a radical expression by using the quotient property NOTE A precise set of
8. Simplification of Radical Expressions 8. OBJECTIVES 1. Simplify a radical expression by using the product property. Simplify a radical expression by using the quotient property NOTE A precise set of
6.6 Factoring Strategy
 456 CHAPTER 6. FACTORING 6.6 Factoring Strategy When you are concentrating on factoring problems of a single type, after doing a few you tend to get into a rhythm, and the remainder of the exercises, because
456 CHAPTER 6. FACTORING 6.6 Factoring Strategy When you are concentrating on factoring problems of a single type, after doing a few you tend to get into a rhythm, and the remainder of the exercises, because
Factoring Algebra- Chapter 8B Assignment Sheet
 Name: Factoring Algebra- Chapter 8B Assignment Sheet Date Section Learning Targets Assignment Tues 2/17 Find the prime factorization of an integer Find the greatest common factor (GCF) for a set of monomials.
Name: Factoring Algebra- Chapter 8B Assignment Sheet Date Section Learning Targets Assignment Tues 2/17 Find the prime factorization of an integer Find the greatest common factor (GCF) for a set of monomials.
5.1 FACTORING OUT COMMON FACTORS
 C H A P T E R 5 Factoring he sport of skydiving was born in the 1930s soon after the military began using parachutes as a means of deploying troops. T Today, skydiving is a popular sport around the world.
C H A P T E R 5 Factoring he sport of skydiving was born in the 1930s soon after the military began using parachutes as a means of deploying troops. T Today, skydiving is a popular sport around the world.
Year 9 set 1 Mathematics notes, to accompany the 9H book.
 Part 1: Year 9 set 1 Mathematics notes, to accompany the 9H book. equations 1. (p.1), 1.6 (p. 44), 4.6 (p.196) sequences 3. (p.115) Pupils use the Elmwood Press Essential Maths book by David Raymer (9H
Part 1: Year 9 set 1 Mathematics notes, to accompany the 9H book. equations 1. (p.1), 1.6 (p. 44), 4.6 (p.196) sequences 3. (p.115) Pupils use the Elmwood Press Essential Maths book by David Raymer (9H
3.6. Partial Fractions. Introduction. Prerequisites. Learning Outcomes
 Partial Fractions 3.6 Introduction It is often helpful to break down a complicated algebraic fraction into a sum of simpler fractions. For 4x + 7 example it can be shown that x 2 + 3x + 2 has the same
Partial Fractions 3.6 Introduction It is often helpful to break down a complicated algebraic fraction into a sum of simpler fractions. For 4x + 7 example it can be shown that x 2 + 3x + 2 has the same
Factoring Guidelines. Greatest Common Factor Two Terms Three Terms Four Terms. 2008 Shirley Radai
 Factoring Guidelines Greatest Common Factor Two Terms Three Terms Four Terms 008 Shirley Radai Greatest Common Factor 008 Shirley Radai Factoring by Finding the Greatest Common Factor Always check for
Factoring Guidelines Greatest Common Factor Two Terms Three Terms Four Terms 008 Shirley Radai Greatest Common Factor 008 Shirley Radai Factoring by Finding the Greatest Common Factor Always check for
Zero: If P is a polynomial and if c is a number such that P (c) = 0 then c is a zero of P.
 MATH 11011 FINDING REAL ZEROS KSU OF A POLYNOMIAL Definitions: Polynomial: is a function of the form P (x) = a n x n + a n 1 x n 1 + + a x + a 1 x + a 0. The numbers a n, a n 1,..., a 1, a 0 are called
MATH 11011 FINDING REAL ZEROS KSU OF A POLYNOMIAL Definitions: Polynomial: is a function of the form P (x) = a n x n + a n 1 x n 1 + + a x + a 1 x + a 0. The numbers a n, a n 1,..., a 1, a 0 are called
Math 10C. Course: Polynomial Products and Factors. Unit of Study: Step 1: Identify the Outcomes to Address. Guiding Questions:
 Course: Unit of Study: Math 10C Polynomial Products and Factors Step 1: Identify the Outcomes to Address Guiding Questions: What do I want my students to learn? What can they currently understand and do?
Course: Unit of Study: Math 10C Polynomial Products and Factors Step 1: Identify the Outcomes to Address Guiding Questions: What do I want my students to learn? What can they currently understand and do?
2010 Solutions. a + b. a + b 1. (a + b)2 + (b a) 2. (b2 + a 2 ) 2 (a 2 b 2 ) 2
 00 Problem If a and b are nonzero real numbers such that a b, compute the value of the expression ( ) ( b a + a a + b b b a + b a ) ( + ) a b b a + b a +. b a a b Answer: 8. Solution: Let s simplify the
00 Problem If a and b are nonzero real numbers such that a b, compute the value of the expression ( ) ( b a + a a + b b b a + b a ) ( + ) a b b a + b a +. b a a b Answer: 8. Solution: Let s simplify the
How To Factor By Gcf In Algebra 1.5
 7-2 Factoring by GCF Warm Up Lesson Presentation Lesson Quiz Algebra 1 Warm Up Simplify. 1. 2(w + 1) 2. 3x(x 2 4) 2w + 2 3x 3 12x Find the GCF of each pair of monomials. 3. 4h 2 and 6h 2h 4. 13p and 26p
7-2 Factoring by GCF Warm Up Lesson Presentation Lesson Quiz Algebra 1 Warm Up Simplify. 1. 2(w + 1) 2. 3x(x 2 4) 2w + 2 3x 3 12x Find the GCF of each pair of monomials. 3. 4h 2 and 6h 2h 4. 13p and 26p
Operations with Algebraic Expressions: Multiplication of Polynomials
 Operations with Algebraic Expressions: Multiplication of Polynomials The product of a monomial x monomial To multiply a monomial times a monomial, multiply the coefficients and add the on powers with the
Operations with Algebraic Expressions: Multiplication of Polynomials The product of a monomial x monomial To multiply a monomial times a monomial, multiply the coefficients and add the on powers with the
SOLVING QUADRATIC EQUATIONS BY THE NEW TRANSFORMING METHOD (By Nghi H Nguyen Updated Oct 28, 2014))
 SOLVING QUADRATIC EQUATIONS BY THE NEW TRANSFORMING METHOD (By Nghi H Nguyen Updated Oct 28, 2014)) There are so far 8 most common methods to solve quadratic equations in standard form ax² + bx + c = 0.
SOLVING QUADRATIC EQUATIONS BY THE NEW TRANSFORMING METHOD (By Nghi H Nguyen Updated Oct 28, 2014)) There are so far 8 most common methods to solve quadratic equations in standard form ax² + bx + c = 0.
The Notebook Series. The solution of cubic and quartic equations. R.S. Johnson. Professor of Applied Mathematics
 The Notebook Series The solution of cubic and quartic equations by R.S. Johnson Professor of Applied Mathematics School of Mathematics & Statistics University of Newcastle upon Tyne R.S.Johnson 006 CONTENTS
The Notebook Series The solution of cubic and quartic equations by R.S. Johnson Professor of Applied Mathematics School of Mathematics & Statistics University of Newcastle upon Tyne R.S.Johnson 006 CONTENTS
MBA Jump Start Program
 MBA Jump Start Program Module 2: Mathematics Thomas Gilbert Mathematics Module Online Appendix: Basic Mathematical Concepts 2 1 The Number Spectrum Generally we depict numbers increasing from left to right
MBA Jump Start Program Module 2: Mathematics Thomas Gilbert Mathematics Module Online Appendix: Basic Mathematical Concepts 2 1 The Number Spectrum Generally we depict numbers increasing from left to right
Section 1. Finding Common Terms
 Worksheet 2.1 Factors of Algebraic Expressions Section 1 Finding Common Terms In worksheet 1.2 we talked about factors of whole numbers. Remember, if a b = ab then a is a factor of ab and b is a factor
Worksheet 2.1 Factors of Algebraic Expressions Section 1 Finding Common Terms In worksheet 1.2 we talked about factors of whole numbers. Remember, if a b = ab then a is a factor of ab and b is a factor
SOLVING QUADRATIC EQUATIONS - COMPARE THE FACTORING AC METHOD AND THE NEW TRANSFORMING METHOD (By Nghi H. Nguyen - Jan 18, 2015)
 SOLVING QUADRATIC EQUATIONS - COMPARE THE FACTORING AC METHOD AND THE NEW TRANSFORMING METHOD (By Nghi H. Nguyen - Jan 18, 2015) GENERALITIES. When a given quadratic equation can be factored, there are
SOLVING QUADRATIC EQUATIONS - COMPARE THE FACTORING AC METHOD AND THE NEW TRANSFORMING METHOD (By Nghi H. Nguyen - Jan 18, 2015) GENERALITIES. When a given quadratic equation can be factored, there are
Mathematics, Basic Math and Algebra
 NONRESIDENT TRAINING COURSE Mathematics, Basic Math and Algebra NAVEDTRA 14139 DISTRIBUTION STATEMENT A: Approved for public release; distribution is unlimited. PREFACE About this course: This is a self-study
NONRESIDENT TRAINING COURSE Mathematics, Basic Math and Algebra NAVEDTRA 14139 DISTRIBUTION STATEMENT A: Approved for public release; distribution is unlimited. PREFACE About this course: This is a self-study
Section A-3 Polynomials: Factoring APPLICATIONS. A-22 Appendix A A BASIC ALGEBRA REVIEW
 A- Appendi A A BASIC ALGEBRA REVIEW C In Problems 53 56, perform the indicated operations and simplify. 53. ( ) 3 ( ) 3( ) 4 54. ( ) 3 ( ) 3( ) 7 55. 3{[ ( )] ( )( 3)} 56. {( 3)( ) [3 ( )]} 57. Show by
A- Appendi A A BASIC ALGEBRA REVIEW C In Problems 53 56, perform the indicated operations and simplify. 53. ( ) 3 ( ) 3( ) 4 54. ( ) 3 ( ) 3( ) 7 55. 3{[ ( )] ( )( 3)} 56. {( 3)( ) [3 ( )]} 57. Show by
Factoring and Applications
 Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
EAP/GWL Rev. 1/2011 Page 1 of 5. Factoring a polynomial is the process of writing it as the product of two or more polynomial factors.
 EAP/GWL Rev. 1/2011 Page 1 of 5 Factoring a polynomial is the process of writing it as the product of two or more polynomial factors. Example: Set the factors of a polynomial equation (as opposed to an
EAP/GWL Rev. 1/2011 Page 1 of 5 Factoring a polynomial is the process of writing it as the product of two or more polynomial factors. Example: Set the factors of a polynomial equation (as opposed to an
