A. Factoring out the Greatest Common Factor.
|
|
|
- Arabella Thomas
- 10 years ago
- Views:
Transcription
1 DETAILED SOLUTIONS AND CONCEPTS - FACTORING POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to [email protected]. Thank you! PLEASE NOTE THAT YOU CANNOT USE A CALCULATOR ON THE ACCUPLACER - ELEMENTARY ALGEBRA TEST! YOU MUST BE ABLE TO DO THE FOLLOWING PROBLEMS WITHOUT A CALCULATOR! Factoring - It actually means to "divide out.". When you are asked to "factor" a polynomial expression, you are actually told to write the expression as a product of factors. Often you are asked to factor "relative to the integers." This means that your factors cannot include rational, irrational, or imaginary numbers. A. Factoring out the Greatest Common Factor. Write each number in an expression in prime factored form. List each prime number that is a factor of every number in the list. Multiply these numbers. This is our greatest common numeric factor. Note: Most of the time you can find the common numeric factor by "casual observation." Find the variable with the smallest exponent. This is our greatest common variable factor. Problem 1: Given the polynomial expression 3x 7-18x 3 + 9x 2, factor out the Greatest Common Factor. We can easily find the greatest common numeric factor by "casual observation." It is 3. The greatest common variable factor is x 2. Therefore, 3x 7-18x 3 + 9x 2 can be written as 3x 2 ( x 5-6x + 3), which is a product of two factors. One is a monomial and the other one a trinomial. Problem 2: Given the polynomial expression 15x 2-5x, factor out the Greatest Common Factor. We can easily find the greatest common numeric factor by "casual observation." It is 5. The greatest common variable factor is x. Therefore, 15x 2-5x can be written as 5x ( 3x - 1), which is a product of two factors.
2 Problem 3: Given the polynomial expression 8x 2 + 4, factor out the Greatest Common Factor. We can easily find the greatest common numeric factor by "casual observation." It is 4. There is no greatest common variable factor. Therefore, 8x can be written as 4(2x 2 + 1), which is a product of two factors. Problem 4: Given the polynomial expression 6x 3-8x 2, factor out the Greatest Common Factor. We can easily find the greatest common numeric factor by "casual observation." It is 2. The greatest common variable factor is x 2. Therefore, 6x 3-8x 2 can be written as 2x 2 (3x - 4), which is a product of two factors. Problem 5: Given the polynomial expression kx 2 - ktx + 3x - 3t, where k and t are constants, factor out the Greatest Common Factor in the two middle terms. The two middle terms -ktx and 3x do not have a greatest common numeric factor. The greatest common variable factor is x. Therefore, kx 2 - ktx + 3x - 3t can be written as follows: kx 2 - (kt - 3)x - 3t or kx 2 + (-kt + 3)x - 3t or kx 2 + (3 - kt)x - 3t Problem 6: Given the polynomial expression 2x(x - 3) - (x - 3), factor out the Greatest Common Factor. This expression has two terms and both contain the factor x - 3. This is the Greatest Common Factor and we will factor it out as follows: 2x(x - 3) - (x - 3) = (x - 3)( 2x - 1) Please note that "factoring" means to "divide out". When we divide x - 3 out of the first term, we are left with a factor of 2x; and when we divide x - 3 out of the second term we are left with a factor of -1.
3 Problem 7: Given the polynomial expression 25q 2 (m + 1) 2-15q(m + 1) 2 + 5(m + 1) 2, factor out the Greatest Common Factor. This expression has three terms and all contain the factor 5(m + 1) 2. This is the Greatest Common Factor and we will factor it out as follows.: 5(m + 1) 2 (5q 2-3q + 1) Please note that "factoring" means to "divide out". When we divide 5(m + 1) 2 out of the first term, we are left with a factor of 5q 2 ; when we divide 5(m + 1) 2 out of the second term we are left with a factor of -3q; and when we divide out of the third term we are left with a factor of 1. Problem 8: Given the polynomial expression 15x 2 (r + 3) 3-33x 2 (r + 3) 2, factor out the Greatest Common Factor. This expression has three terms and all contain the factor 3x 2 (r + 3) 2. This is the Greatest Common Factor and we will factor it out as follows.: 3x 2 (r + 3) 2 [5(r + 3) - 11] = 3x 2 (r + 3) 2 (5r ) = 3x 2 (r + 3) 2 (5r + 4) Please note that "factoring" means to "divide out". When we divide 3x 2 (r + 3) 2 out of the first term, we are left with a factor of 5(r + 3); and when we divide 3x 2 (r + 3) 2 out of the second term we are left with a factor of 11. In this case, we were even able to combine like terms in the final product! This type of factoring is often necessary in a calculus course! B. Factoring relative to the integers using the Grouping Method. Collect the terms in an expression into two groups. Factor out the greatest common factor from each group. You should end up with an identical multinomial factor in each term. If not, regroup, then factor out the greatest common factor again. If you still don't end up with an identical multinomial factor in each term, the expression is NOT factorable by grouping. Factor out the identical multinomial factor from each term. Problem 9: Try to factor the polynomial expression x 3-4x 2 + 2x - 8 relative to the integers using the Grouping Method. Let's form two groups as follows: (x 3-4x 2 )+ (2x - 8) Please note that these were the most convenient groups. It just so happens that when we factor common factors out of both, we have an identical binomial factor in each term!
4 x 2 (x - 4)+ 2(x - 4) Note that we now have an identical binomial factor in each term! Lastly, we will factor out the identical binomial factor (x - 4) as follows: (x - 4)(x 2 + 2) Therefore, x 3-4x 2 + 2x - 8 can be written as (x - 4)(x 2 + 2), which is a product of two factors. Both are binomials. Let's use FOIL to check the factoring process! NOTE: FOIL stands for First, Outer, Inner, Last and refers to how the terms in two binomials are multiplied out. FOIL is a shortcut for the Distributive Property! First: x x 2 = x 3 Outer: x 2 = 2x Inner: -4 x 2 = -4x 2 Last: -4 2 = -8 Problem 10: Using FOIL, we can indeed see that (x- 4)(x 2 +2) = x 3-4x 2 + 2x - 8. Try to factor the polynomial expression 3x 3 + 2x 2-6x + 2 relative to the integers using the Grouping Method. Let's form two groups as follows: (3x 3 + 2x 2 ) - (6x - 2) Please note that the sign between 6x and 2 changed. This is due to factoring out a minus! Now we'll factor out the greatest common factor from each group. x 2 (3x + 2) - 2(3x - 1) Note that we did not get two identical factors in each term. Before we give up, let's try a different set of groups. By rewriting 3x 3 + 2x 2-6x + 2 to 3x 3-6x + 2x we can group as follows: (3x 3-6x) + (2x 2 + 2) Again we factor out the greatest common factor from each group.
5 3x(x 2-2) + 2(x 2 + 1) Since we did not get two identical factors in each term again, we concede that we cannot use the Grouping Method to factor this polynomial relative to the integers. Please be aware that not all polynomial expressions are factorable, although, in this case we have not tried more advanced method beyond the scope of this lecture! C. Factoring the trinomial ax2 + bx + c relative to the integers. Assume a = 1. Using "educated guessing", find two integers whose product equals c and whose sum equals b. These integers are always factors of c. If this is not possible, the trinomial cannot be factored relative to the integers. Form a product using two binomials containing the variable x and each of the integers found. Problem 11: Try to factor the trinomial x 2-5x + 6 relative to the integers. Given the general trinomial ax 2 + bx + c, we find that b = -5 and c = 6. YES, actually using some educated guessing, we need to find two integers whose product equals 6 and whose sum equals -5. However, the guessing is simplified because the integers MUST be factors of c. In this case of 6. Let's write down the factors of 6: -6, -3, -2, -1, 1, 2, 3, 6 It seems that the two integers we need are -2 and -3 since -2(-3) = 6 and -2 + (-3) = -5. Therefore, x 2-5x + 6 factored relative to the integers becomes the product (x - 2)(x - 3). As a beginner you might want to use FOIL to convince yourself that you have indeed found the correct factors. Problem 12: Try to factor the trinomial x 2 + 5x + 6 relative to the integers. Given the general trinomial ax 2 + bx + c, we find that b = 5 and c = 6. Again, using some educated guessing, we need to find two integers whose product equals 6 and whose sum equals 5. Let's write down the factors of 6: -6, -3, -2, -1, 1, 2, 3, 6 The two integers we need this time are 2 and 3 since 2(3) = 6 and = 5.
6 Therefore, x 2 + 5x + 6 factored relative to the integers becomes the product (x + 2)(x + 3). As a beginner you might want to use FOIL to convince yourself that you have indeed found the correct factors. Problem 13: Try to factor the trinomial x 2-5x - 6 relative to the integers. Given the general trinomial ax 2 + bx + c, we find that b = -5 and c = -6. Let's write down the factors of -6: -6, -3, -2, -1, 1, 2, 3, 6 Remember, we need to find two integers whose product equals -6 and whose sum equals -5. The two integers we need are -6 and 1 since -6(1) = -6 and = -5. Therefore, x 2-5x - 6 factored relative to the integers becomes the product (x - 6)(x + 1). As a beginner you might want to use FOIL to convince yourself that you have indeed found the correct factors. Problem 14: Try to factor the trinomial x 2 + 5x - 6 relative to the integers. Given the general trinomial ax 2 + bx + c, we find that b = 5 and c = -6. Let's write down the factors of -6: -6, -3, -2, -1, 1, 2, 3, 6 We need to find two integers whose product equals -6 and whose sum equals 5. The two integers we need are 6 and -1 since 6(-1) = -6 and 6 + (-1) = 5. Therefore, x 2 + 5x - 6 factored relative to the integers becomes the product (x + 6)(x - 1). As a beginner you might want to use FOIL to convince yourself that you have indeed found the correct factors. Problem 15: Try to factor the trinomial x 2-10x + 25 relative to the integers. Given the general trinomial ax 2 + bx + c, we find that b = -10 and c = 25. Let's write down the factors of 25:
7 -25, -5, -1, 1, 5, 25 We need to find two integers whose product equals 25 and whose sum equals -10. The two integers we need are -5 and -5 since -5(-5) = 25 and -5 + (-5) = -10. Therefore, x 2-10x + 25 factored relative to the integers becomes the product (x - 5)(x - 5) = (x - 5) 2 This is called a Perfect Square Trinomial. Problem 16: Try to factor the trinomial x 2 + 6x + 9 relative to the integers. Given the general trinomial ax 2 + bx + c, we find that b = 6 and c = 9. Let's write down the factors of 9: -9, -3, -1, 1, 3, 9 We need to find two integers whose product equals 9 and whose sum equals 6. The two integers we need are 3 and 3 since 3(3) = 9 and = 6. Therefore, x 2 + 6x + 9 factored relative to the integers becomes the product (x + 3)(x + 3) = (x + 3) 2 This is also called a Perfect Square Trinomial. Problem 17: Try to factor the trinomial x 2 + 2x + 4 relative to the integers. Given the general trinomial ax 2 + bx + c, we find that b = 2 and c = 4. Let's write down the factors of 4: -4, -2, -1, 1, 2, 4 We need to find two integers whose product equals 4 and whose sum equals 2. This trinomial cannot be factored relative to the integers: Using 2 and 2 we get 2(2) = 4, but Using -2 and -2 we get -2(-2) = 4, but -2 + (-2) 2. Using 4 and 1 we get 4(1) = 4, but Using -4 and -1 we get -4(-1) = 4, but -4 + (-1) 2.
8 D. Factoring the Trinomial ax 2 + bx + c relative to the Integers. Assume a 1. Find two integers whose product equals ac and whose sum equals b. These integers are always factors of ac. If this is not possible, the trinomial cannot be factored relative to the integers. Replace the middle term bx in ax 2 + bx + c with the sum of the integers. Use the factoring by grouping method to find a product of two binomials. Problem 18: Try to factor the trinomial 2x 2 + 7x + 6 relative to the integers. Given the general trinomial ax 2 + bx + c, we find that a = 2, b = 7 and c = 6. We need to find two integers whose product equals 2(6) = 12 and whose sum equals 7. However, the guessing is simplified because the integers MUST be factors of ac. In this case of 12. Let's write down the factors of 12: -12, -6, -4, -3, -2, -1, 1, 2, 3, 4, 6, 12 It seems that the two integers we need are 3 and 4 since 3(4) = 12 and = 7. Now we write 2x 2 + 7x + 6 as follows: 2x 2 + 3x + 4x + 6 Next, we'll use the factoring by grouping method to get (2x 2 + 3x) + (4x + 6). Then, we factor the common factor out of both groups as follows: x(2x + 3) + 2(2x + 3) Lastly, we will factor out the identical binomial factor to get (2x + 3)(x + 2). Therefore, 2x 2 + 7x + 6 factored relative to the integers becomes the product (2x + 3)(x + 2). As a beginner you might want to use FOIL to convince yourself that you have indeed found the correct factors. Problem 19: Try to factor the trinomial 6x 2 + x - 2 relative to the integers. Given the general trinomial ax 2 + bx + c, we find that a = 6, b = 1 and c = -2. We need to find two integers whose product equals 6(-2) = -12 and whose sum equals 1.
9 However, the guessing is simplified because the integers MUST be factors of ac. In this case of 12. Let's write down the factors of -12: -12, -6, -4, -3, -2, -1, 1, 2, 3, 4, 6, 12 It seems that the two integers we need are -3 and 4 since -3(4) = -12 and = 1. Now we write 6x 2 + x - 2 as follows: 6x 2-3x + 4x - 2 Next, we'll use the factoring by grouping method to get (6x 2-3x) + (4x - 2). Then, we factor the common factor out of both groups as follows: 3x(2x - 1) + 2(2x - 1) Lastly, we will factor out the identical binomial factor to get (2x - 1)(3x + 2). Therefore, 6x 2 + x - 2 factored relative to the integers becomes the product (2x - 1)(3x + 2). As a beginner you might want to use FOIL to convince yourself that you have indeed found the correct factors. E. Factoring "special" polynomials relative to the Integers. Difference of Squares: Difference of Cubes: Sum of Cubes: Please note that a Sums of Squares cannot be factored relative to the integers. The factors of Sums of Squares are imaginary! This will be discussed at a later time! Problem 20: Factor the following "special" polynomials relative to the integers. (a) x 2-9 Using the Difference of Squares formula with a = 3, we can factor as follows: (x - 3)(x + 3)
10 (b) k 2 - m 2 Using the Difference of Squares formula with a = m, we can factor as follows: (k - m)(k + m) (c) x 3-8 Using the Difference of Cubes formula with a = 2, we can factor as follows: (x - 2)(x 2 + 2x + 4) (d) x Using the Sum of Cubes formula a = 5, we can factor as follows: (x + 5)(x 2-5x + 25) E. Factoring polynomials that are "quadratic" in form relative to the integers. Problem 21: Factor relative to the integers. Sometimes, you can encounter polynomial expressions that are "quadratic" in form. That is, one exponent is exactly twice as large as the other exponent! We can rewrite the first variable as follows using the Laws of Exponents: Please note that we could now say the following: Let and we can rewrite the given polynomial expressions as. We know that we can factor into. Therefore, we can factor the original expression as follows: We further recognize that the factor factored into. is a Difference of Squares, which can be
11 Now, the factor is a Sum of Squares. As noted above, Sums of Squares cannot be factored relative to the integers! Their factors are imaginary. This will be discussed at a later time Finally, the original expression can be written as!
Finding Solutions of Polynomial Equations
 DETAILED SOLUTIONS AND CONCEPTS - POLYNOMIAL EQUATIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to [email protected]. Thank you! PLEASE NOTE
DETAILED SOLUTIONS AND CONCEPTS - POLYNOMIAL EQUATIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to [email protected]. Thank you! PLEASE NOTE
NSM100 Introduction to Algebra Chapter 5 Notes Factoring
 Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
1.3 Polynomials and Factoring
 1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
expression is written horizontally. The Last terms ((2)( 4)) because they are the last terms of the two polynomials. This is called the FOIL method.
 A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
Polynomial Expression
 DETAILED SOLUTIONS AND CONCEPTS - POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to [email protected]. Thank you! PLEASE NOTE
DETAILED SOLUTIONS AND CONCEPTS - POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to [email protected]. Thank you! PLEASE NOTE
A Systematic Approach to Factoring
 A Systematic Approach to Factoring Step 1 Count the number of terms. (Remember****Knowing the number of terms will allow you to eliminate unnecessary tools.) Step 2 Is there a greatest common factor? Tool
A Systematic Approach to Factoring Step 1 Count the number of terms. (Remember****Knowing the number of terms will allow you to eliminate unnecessary tools.) Step 2 Is there a greatest common factor? Tool
Factoring Polynomials
 Factoring Polynomials Factoring Factoring is the process of writing a polynomial as the product of two or more polynomials. The factors of 6x 2 x 2 are 2x + 1 and 3x 2. In this section, we will be factoring
Factoring Polynomials Factoring Factoring is the process of writing a polynomial as the product of two or more polynomials. The factors of 6x 2 x 2 are 2x + 1 and 3x 2. In this section, we will be factoring
In algebra, factor by rewriting a polynomial as a product of lower-degree polynomials
 Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
Factoring Polynomials
 Factoring a Polynomial Expression Factoring a polynomial is expressing the polynomial as a product of two or more factors. Simply stated, it is somewhat the reverse process of multiplying. To factor polynomials,
Factoring a Polynomial Expression Factoring a polynomial is expressing the polynomial as a product of two or more factors. Simply stated, it is somewhat the reverse process of multiplying. To factor polynomials,
Section 6.1 Factoring Expressions
 Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
Chapter R.4 Factoring Polynomials
 Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0).
 This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
FACTORING ax 2 bx c. Factoring Trinomials with Leading Coefficient 1
 5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
Factoring Flow Chart
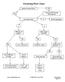 Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
( ) FACTORING. x In this polynomial the only variable in common to all is x.
 FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
MATH 90 CHAPTER 6 Name:.
 MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III
 Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III Name Date Adding and Subtracting Polynomials Algebra Standard 10.0 A polynomial is a sum of one ore more monomials. Polynomial
Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III Name Date Adding and Subtracting Polynomials Algebra Standard 10.0 A polynomial is a sum of one ore more monomials. Polynomial
Factoring Guidelines. Greatest Common Factor Two Terms Three Terms Four Terms. 2008 Shirley Radai
 Factoring Guidelines Greatest Common Factor Two Terms Three Terms Four Terms 008 Shirley Radai Greatest Common Factor 008 Shirley Radai Factoring by Finding the Greatest Common Factor Always check for
Factoring Guidelines Greatest Common Factor Two Terms Three Terms Four Terms 008 Shirley Radai Greatest Common Factor 008 Shirley Radai Factoring by Finding the Greatest Common Factor Always check for
Operations with Algebraic Expressions: Multiplication of Polynomials
 Operations with Algebraic Expressions: Multiplication of Polynomials The product of a monomial x monomial To multiply a monomial times a monomial, multiply the coefficients and add the on powers with the
Operations with Algebraic Expressions: Multiplication of Polynomials The product of a monomial x monomial To multiply a monomial times a monomial, multiply the coefficients and add the on powers with the
Name Intro to Algebra 2. Unit 1: Polynomials and Factoring
 Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
1.3 Algebraic Expressions
 1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
Factoring Trinomials: The ac Method
 6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
Factoring Quadratic Expressions
 Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
x 4-1 = (x²)² - (1)² = (x² + 1) (x² - 1) = (x² + 1) (x - 1) (x + 1)
 Factoring Polynomials EXAMPLES STEP 1 : Greatest Common Factor GCF Factor out the greatest common factor. 6x³ + 12x²y = 6x² (x + 2y) 5x - 5 = 5 (x - 1) 7x² + 2y² = 1 (7x² + 2y²) 2x (x - 3) - (x - 3) =
Factoring Polynomials EXAMPLES STEP 1 : Greatest Common Factor GCF Factor out the greatest common factor. 6x³ + 12x²y = 6x² (x + 2y) 5x - 5 = 5 (x - 1) 7x² + 2y² = 1 (7x² + 2y²) 2x (x - 3) - (x - 3) =
6.4 Special Factoring Rules
 6.4 Special Factoring Rules OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor a sum of cubes. By reversing the rules for multiplication
6.4 Special Factoring Rules OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor a sum of cubes. By reversing the rules for multiplication
Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any.
 Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
Factoring and Applications
 Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS
 (Section 0.6: Polynomial, Rational, and Algebraic Expressions) 0.6.1 SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS LEARNING OBJECTIVES Be able to identify polynomial, rational, and algebraic
(Section 0.6: Polynomial, Rational, and Algebraic Expressions) 0.6.1 SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS LEARNING OBJECTIVES Be able to identify polynomial, rational, and algebraic
Factoring Polynomials and Solving Quadratic Equations
 Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
Factoring. Factoring Monomials Monomials can often be factored in more than one way.
 Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
By reversing the rules for multiplication of binomials from Section 4.6, we get rules for factoring polynomials in certain forms.
 SECTION 5.4 Special Factoring Techniques 317 5.4 Special Factoring Techniques OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor
SECTION 5.4 Special Factoring Techniques 317 5.4 Special Factoring Techniques OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor
Factoring Special Polynomials
 6.6 Factoring Special Polynomials 6.6 OBJECTIVES 1. Factor the difference of two squares 2. Factor the sum or difference of two cubes In this section, we will look at several special polynomials. These
6.6 Factoring Special Polynomials 6.6 OBJECTIVES 1. Factor the difference of two squares 2. Factor the sum or difference of two cubes In this section, we will look at several special polynomials. These
Factoring Polynomials
 UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
Simplifying Square-Root Radicals Containing Perfect Square Factors
 DETAILED SOLUTIONS AND CONCEPTS - OPERATIONS ON IRRATIONAL NUMBERS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to [email protected]. Thank you!
DETAILED SOLUTIONS AND CONCEPTS - OPERATIONS ON IRRATIONAL NUMBERS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to [email protected]. Thank you!
Factoring Algebra- Chapter 8B Assignment Sheet
 Name: Factoring Algebra- Chapter 8B Assignment Sheet Date Section Learning Targets Assignment Tues 2/17 Find the prime factorization of an integer Find the greatest common factor (GCF) for a set of monomials.
Name: Factoring Algebra- Chapter 8B Assignment Sheet Date Section Learning Targets Assignment Tues 2/17 Find the prime factorization of an integer Find the greatest common factor (GCF) for a set of monomials.
POLYNOMIALS and FACTORING
 POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
Algebra 2 PreAP. Name Period
 Algebra 2 PreAP Name Period IMPORTANT INSTRUCTIONS FOR STUDENTS!!! We understand that students come to Algebra II with different strengths and needs. For this reason, students have options for completing
Algebra 2 PreAP Name Period IMPORTANT INSTRUCTIONS FOR STUDENTS!!! We understand that students come to Algebra II with different strengths and needs. For this reason, students have options for completing
Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder).
 Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Polynomials and Factoring
 7.6 Polynomials and Factoring Basic Terminology A term, or monomial, is defined to be a number, a variable, or a product of numbers and variables. A polynomial is a term or a finite sum or difference of
7.6 Polynomials and Factoring Basic Terminology A term, or monomial, is defined to be a number, a variable, or a product of numbers and variables. A polynomial is a term or a finite sum or difference of
ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form
 ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form Goal Graph quadratic functions. VOCABULARY Quadratic function A function that can be written in the standard form y = ax 2 + bx+ c where a 0 Parabola
ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form Goal Graph quadratic functions. VOCABULARY Quadratic function A function that can be written in the standard form y = ax 2 + bx+ c where a 0 Parabola
EAP/GWL Rev. 1/2011 Page 1 of 5. Factoring a polynomial is the process of writing it as the product of two or more polynomial factors.
 EAP/GWL Rev. 1/2011 Page 1 of 5 Factoring a polynomial is the process of writing it as the product of two or more polynomial factors. Example: Set the factors of a polynomial equation (as opposed to an
EAP/GWL Rev. 1/2011 Page 1 of 5 Factoring a polynomial is the process of writing it as the product of two or more polynomial factors. Example: Set the factors of a polynomial equation (as opposed to an
FACTORING QUADRATICS 8.1.1 and 8.1.2
 FACTORING QUADRATICS 8.1.1 and 8.1.2 Chapter 8 introduces students to quadratic equations. These equations can be written in the form of y = ax 2 + bx + c and, when graphed, produce a curve called a parabola.
FACTORING QUADRATICS 8.1.1 and 8.1.2 Chapter 8 introduces students to quadratic equations. These equations can be written in the form of y = ax 2 + bx + c and, when graphed, produce a curve called a parabola.
ALGEBRA 2 CRA 2 REVIEW - Chapters 1-6 Answer Section
 ALGEBRA 2 CRA 2 REVIEW - Chapters 1-6 Answer Section MULTIPLE CHOICE 1. ANS: C 2. ANS: A 3. ANS: A OBJ: 5-3.1 Using Vertex Form SHORT ANSWER 4. ANS: (x + 6)(x 2 6x + 36) OBJ: 6-4.2 Solving Equations by
ALGEBRA 2 CRA 2 REVIEW - Chapters 1-6 Answer Section MULTIPLE CHOICE 1. ANS: C 2. ANS: A 3. ANS: A OBJ: 5-3.1 Using Vertex Form SHORT ANSWER 4. ANS: (x + 6)(x 2 6x + 36) OBJ: 6-4.2 Solving Equations by
6.1 The Greatest Common Factor; Factoring by Grouping
 386 CHAPTER 6 Factoring and Applications 6.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
386 CHAPTER 6 Factoring and Applications 6.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
Using the ac Method to Factor
 4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
Polynomial Operations and Factoring
 Algebra 1, Quarter 4, Unit 4.1 Polynomial Operations and Factoring Overview Number of instructional days: 15 (1 day = 45 60 minutes) Content to be learned Identify terms, coefficients, and degree of polynomials.
Algebra 1, Quarter 4, Unit 4.1 Polynomial Operations and Factoring Overview Number of instructional days: 15 (1 day = 45 60 minutes) Content to be learned Identify terms, coefficients, and degree of polynomials.
Math 25 Activity 6: Factoring Advanced
 Instructor! Math 25 Activity 6: Factoring Advanced Last week we looked at greatest common factors and the basics of factoring out the GCF. In this second activity, we will discuss factoring more difficult
Instructor! Math 25 Activity 6: Factoring Advanced Last week we looked at greatest common factors and the basics of factoring out the GCF. In this second activity, we will discuss factoring more difficult
Greatest Common Factor (GCF) Factoring
 Section 4 4: Greatest Common Factor (GCF) Factoring The last chapter introduced the distributive process. The distributive process takes a product of a monomial and a polynomial and changes the multiplication
Section 4 4: Greatest Common Factor (GCF) Factoring The last chapter introduced the distributive process. The distributive process takes a product of a monomial and a polynomial and changes the multiplication
Tool 1. Greatest Common Factor (GCF)
 Chapter 4: Factoring Review Tool 1 Greatest Common Factor (GCF) This is a very important tool. You must try to factor out the GCF first in every problem. Some problems do not have a GCF but many do. When
Chapter 4: Factoring Review Tool 1 Greatest Common Factor (GCF) This is a very important tool. You must try to factor out the GCF first in every problem. Some problems do not have a GCF but many do. When
Factoring Methods. Example 1: 2x + 2 2 * x + 2 * 1 2(x + 1)
 Factoring Methods When you are trying to factor a polynomial, there are three general steps you want to follow: 1. See if there is a Greatest Common Factor 2. See if you can Factor by Grouping 3. See if
Factoring Methods When you are trying to factor a polynomial, there are three general steps you want to follow: 1. See if there is a Greatest Common Factor 2. See if you can Factor by Grouping 3. See if
Factoring Trinomials of the Form x 2 bx c
 4.2 Factoring Trinomials of the Form x 2 bx c 4.2 OBJECTIVES 1. Factor a trinomial of the form x 2 bx c 2. Factor a trinomial containing a common factor NOTE The process used to factor here is frequently
4.2 Factoring Trinomials of the Form x 2 bx c 4.2 OBJECTIVES 1. Factor a trinomial of the form x 2 bx c 2. Factor a trinomial containing a common factor NOTE The process used to factor here is frequently
5 means to write it as a product something times something instead of a sum something plus something plus something.
 Intermediate algebra Class notes Factoring Introduction (section 6.1) Recall we factor 10 as 5. Factoring something means to think of it as a product! Factors versus terms: terms: things we are adding
Intermediate algebra Class notes Factoring Introduction (section 6.1) Recall we factor 10 as 5. Factoring something means to think of it as a product! Factors versus terms: terms: things we are adding
Algebra 1 Course Title
 Algebra 1 Course Title Course- wide 1. What patterns and methods are being used? Course- wide 1. Students will be adept at solving and graphing linear and quadratic equations 2. Students will be adept
Algebra 1 Course Title Course- wide 1. What patterns and methods are being used? Course- wide 1. Students will be adept at solving and graphing linear and quadratic equations 2. Students will be adept
FACTORING POLYNOMIALS
 296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
CHAPTER 7: FACTORING POLYNOMIALS
 CHAPTER 7: FACTORING POLYNOMIALS FACTOR (noun) An of two or more quantities which form a product when multiplied together. 1 can be rewritten as 3*, where 3 and are FACTORS of 1. FACTOR (verb) - To factor
CHAPTER 7: FACTORING POLYNOMIALS FACTOR (noun) An of two or more quantities which form a product when multiplied together. 1 can be rewritten as 3*, where 3 and are FACTORS of 1. FACTOR (verb) - To factor
Vocabulary Words and Definitions for Algebra
 Name: Period: Vocabulary Words and s for Algebra Absolute Value Additive Inverse Algebraic Expression Ascending Order Associative Property Axis of Symmetry Base Binomial Coefficient Combine Like Terms
Name: Period: Vocabulary Words and s for Algebra Absolute Value Additive Inverse Algebraic Expression Ascending Order Associative Property Axis of Symmetry Base Binomial Coefficient Combine Like Terms
PROBLEMS AND SOLUTIONS - OPERATIONS ON IRRATIONAL NUMBERS
 PROBLEMS AND SOLUTIONS - OPERATIONS ON IRRATIONAL NUMBERS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to [email protected]. Thank you! PLEASE NOTE
PROBLEMS AND SOLUTIONS - OPERATIONS ON IRRATIONAL NUMBERS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to [email protected]. Thank you! PLEASE NOTE
FACTORING OUT COMMON FACTORS
 278 (6 2) Chapter 6 Factoring 6.1 FACTORING OUT COMMON FACTORS In this section Prime Factorization of Integers Greatest Common Factor Finding the Greatest Common Factor for Monomials Factoring Out the
278 (6 2) Chapter 6 Factoring 6.1 FACTORING OUT COMMON FACTORS In this section Prime Factorization of Integers Greatest Common Factor Finding the Greatest Common Factor for Monomials Factoring Out the
6.1 Add & Subtract Polynomial Expression & Functions
 6.1 Add & Subtract Polynomial Expression & Functions Objectives 1. Know the meaning of the words term, monomial, binomial, trinomial, polynomial, degree, coefficient, like terms, polynomial funciton, quardrtic
6.1 Add & Subtract Polynomial Expression & Functions Objectives 1. Know the meaning of the words term, monomial, binomial, trinomial, polynomial, degree, coefficient, like terms, polynomial funciton, quardrtic
Factoring (pp. 1 of 4)
 Factoring (pp. 1 of 4) Algebra Review Try these items from middle school math. A) What numbers are the factors of 4? B) Write down the prime factorization of 7. C) 6 Simplify 48 using the greatest common
Factoring (pp. 1 of 4) Algebra Review Try these items from middle school math. A) What numbers are the factors of 4? B) Write down the prime factorization of 7. C) 6 Simplify 48 using the greatest common
Math 0980 Chapter Objectives. Chapter 1: Introduction to Algebra: The Integers.
 Math 0980 Chapter Objectives Chapter 1: Introduction to Algebra: The Integers. 1. Identify the place value of a digit. 2. Write a number in words or digits. 3. Write positive and negative numbers used
Math 0980 Chapter Objectives Chapter 1: Introduction to Algebra: The Integers. 1. Identify the place value of a digit. 2. Write a number in words or digits. 3. Write positive and negative numbers used
Factoring a Difference of Two Squares. Factoring a Difference of Two Squares
 284 (6 8) Chapter 6 Factoring 87. Tomato soup. The amount of metal S (in square inches) that it takes to make a can for tomato soup is a function of the radius r and height h: S 2 r 2 2 rh a) Rewrite this
284 (6 8) Chapter 6 Factoring 87. Tomato soup. The amount of metal S (in square inches) that it takes to make a can for tomato soup is a function of the radius r and height h: S 2 r 2 2 rh a) Rewrite this
Factors and Products
 CHAPTER 3 Factors and Products What You ll Learn use different strategies to find factors and multiples of whole numbers identify prime factors and write the prime factorization of a number find square
CHAPTER 3 Factors and Products What You ll Learn use different strategies to find factors and multiples of whole numbers identify prime factors and write the prime factorization of a number find square
SPECIAL PRODUCTS AND FACTORS
 CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
Sect 6.7 - Solving Equations Using the Zero Product Rule
 Sect 6.7 - Solving Equations Using the Zero Product Rule 116 Concept #1: Definition of a Quadratic Equation A quadratic equation is an equation that can be written in the form ax 2 + bx + c = 0 (referred
Sect 6.7 - Solving Equations Using the Zero Product Rule 116 Concept #1: Definition of a Quadratic Equation A quadratic equation is an equation that can be written in the form ax 2 + bx + c = 0 (referred
6.3 FACTORING ax 2 bx c WITH a 1
 290 (6 14) Chapter 6 Factoring e) What is the approximate maximum revenue? f) Use the accompanying graph to estimate the price at which the revenue is zero. y Revenue (thousands of dollars) 300 200 100
290 (6 14) Chapter 6 Factoring e) What is the approximate maximum revenue? f) Use the accompanying graph to estimate the price at which the revenue is zero. y Revenue (thousands of dollars) 300 200 100
Determinants can be used to solve a linear system of equations using Cramer s Rule.
 2.6.2 Cramer s Rule Determinants can be used to solve a linear system of equations using Cramer s Rule. Cramer s Rule for Two Equations in Two Variables Given the system This system has the unique solution
2.6.2 Cramer s Rule Determinants can be used to solve a linear system of equations using Cramer s Rule. Cramer s Rule for Two Equations in Two Variables Given the system This system has the unique solution
FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c
 Tallahassee Community College 55 FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c This kind of trinomial differs from the previous kind we have factored because the coefficient of x is no longer "1".
Tallahassee Community College 55 FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c This kind of trinomial differs from the previous kind we have factored because the coefficient of x is no longer "1".
Factoring. Factoring Polynomial Equations. Special Factoring Patterns. Factoring. Special Factoring Patterns. Special Factoring Patterns
 Factoring Factoring Polynomial Equations Ms. Laster Earlier, you learned to factor several types of quadratic expressions: General trinomial - 2x 2-5x-12 = (2x + 3)(x - 4) Perfect Square Trinomial - x
Factoring Factoring Polynomial Equations Ms. Laster Earlier, you learned to factor several types of quadratic expressions: General trinomial - 2x 2-5x-12 = (2x + 3)(x - 4) Perfect Square Trinomial - x
Polynomials. Key Terms. quadratic equation parabola conjugates trinomial. polynomial coefficient degree monomial binomial GCF
 Polynomials 5 5.1 Addition and Subtraction of Polynomials and Polynomial Functions 5.2 Multiplication of Polynomials 5.3 Division of Polynomials Problem Recognition Exercises Operations on Polynomials
Polynomials 5 5.1 Addition and Subtraction of Polynomials and Polynomial Functions 5.2 Multiplication of Polynomials 5.3 Division of Polynomials Problem Recognition Exercises Operations on Polynomials
A.3. Polynomials and Factoring. Polynomials. What you should learn. Definition of a Polynomial in x. Why you should learn it
 Appendi A.3 Polynomials and Factoring A23 A.3 Polynomials and Factoring What you should learn Write polynomials in standard form. Add,subtract,and multiply polynomials. Use special products to multiply
Appendi A.3 Polynomials and Factoring A23 A.3 Polynomials and Factoring What you should learn Write polynomials in standard form. Add,subtract,and multiply polynomials. Use special products to multiply
Wentzville School District Algebra 1: Unit 8 Stage 1 Desired Results
 Wentzville School District Algebra 1: Unit 8 Stage 1 Desired Results Unit Title: Quadratic Expressions & Equations Course: Algebra I Unit 8 - Quadratic Expressions & Equations Brief Summary of Unit: At
Wentzville School District Algebra 1: Unit 8 Stage 1 Desired Results Unit Title: Quadratic Expressions & Equations Course: Algebra I Unit 8 - Quadratic Expressions & Equations Brief Summary of Unit: At
AIP Factoring Practice/Help
 The following pages include many problems to practice factoring skills. There are also several activities with examples to help you with factoring if you feel like you are not proficient with it. There
The following pages include many problems to practice factoring skills. There are also several activities with examples to help you with factoring if you feel like you are not proficient with it. There
Answers to Basic Algebra Review
 Answers to Basic Algebra Review 1. -1.1 Follow the sign rules when adding and subtracting: If the numbers have the same sign, add them together and keep the sign. If the numbers have different signs, subtract
Answers to Basic Algebra Review 1. -1.1 Follow the sign rules when adding and subtracting: If the numbers have the same sign, add them together and keep the sign. If the numbers have different signs, subtract
Algebra 1 Chapter 08 review
 Name: Class: Date: ID: A Algebra 1 Chapter 08 review Multiple Choice Identify the choice that best completes the statement or answers the question. Simplify the difference. 1. (4w 2 4w 8) (2w 2 + 3w 6)
Name: Class: Date: ID: A Algebra 1 Chapter 08 review Multiple Choice Identify the choice that best completes the statement or answers the question. Simplify the difference. 1. (4w 2 4w 8) (2w 2 + 3w 6)
What are the place values to the left of the decimal point and their associated powers of ten?
 The verbal answers to all of the following questions should be memorized before completion of algebra. Answers that are not memorized will hinder your ability to succeed in geometry and algebra. (Everything
The verbal answers to all of the following questions should be memorized before completion of algebra. Answers that are not memorized will hinder your ability to succeed in geometry and algebra. (Everything
Algebra I Vocabulary Cards
 Algebra I Vocabulary Cards Table of Contents Expressions and Operations Natural Numbers Whole Numbers Integers Rational Numbers Irrational Numbers Real Numbers Absolute Value Order of Operations Expression
Algebra I Vocabulary Cards Table of Contents Expressions and Operations Natural Numbers Whole Numbers Integers Rational Numbers Irrational Numbers Real Numbers Absolute Value Order of Operations Expression
Factor Polynomials Completely
 9.8 Factor Polynomials Completely Before You factored polynomials. Now You will factor polynomials completely. Why? So you can model the height of a projectile, as in Ex. 71. Key Vocabulary factor by grouping
9.8 Factor Polynomials Completely Before You factored polynomials. Now You will factor polynomials completely. Why? So you can model the height of a projectile, as in Ex. 71. Key Vocabulary factor by grouping
Factoring Trinomials using Algebra Tiles Student Activity
 Factoring Trinomials using Algebra Tiles Student Activity Materials: Algebra Tiles (student set) Worksheet: Factoring Trinomials using Algebra Tiles Algebra Tiles: Each algebra tile kits should contain
Factoring Trinomials using Algebra Tiles Student Activity Materials: Algebra Tiles (student set) Worksheet: Factoring Trinomials using Algebra Tiles Algebra Tiles: Each algebra tile kits should contain
HIBBING COMMUNITY COLLEGE COURSE OUTLINE
 HIBBING COMMUNITY COLLEGE COURSE OUTLINE COURSE NUMBER & TITLE: - Beginning Algebra CREDITS: 4 (Lec 4 / Lab 0) PREREQUISITES: MATH 0920: Fundamental Mathematics with a grade of C or better, Placement Exam,
HIBBING COMMUNITY COLLEGE COURSE OUTLINE COURSE NUMBER & TITLE: - Beginning Algebra CREDITS: 4 (Lec 4 / Lab 0) PREREQUISITES: MATH 0920: Fundamental Mathematics with a grade of C or better, Placement Exam,
SOLVING QUADRATIC EQUATIONS BY THE NEW TRANSFORMING METHOD (By Nghi H Nguyen Updated Oct 28, 2014))
 SOLVING QUADRATIC EQUATIONS BY THE NEW TRANSFORMING METHOD (By Nghi H Nguyen Updated Oct 28, 2014)) There are so far 8 most common methods to solve quadratic equations in standard form ax² + bx + c = 0.
SOLVING QUADRATIC EQUATIONS BY THE NEW TRANSFORMING METHOD (By Nghi H Nguyen Updated Oct 28, 2014)) There are so far 8 most common methods to solve quadratic equations in standard form ax² + bx + c = 0.
Polynomials and Quadratics
 Polynomials and Quadratics Want to be an environmental scientist? Better be ready to get your hands dirty!.1 Controlling the Population Adding and Subtracting Polynomials............703.2 They re Multiplying
Polynomials and Quadratics Want to be an environmental scientist? Better be ready to get your hands dirty!.1 Controlling the Population Adding and Subtracting Polynomials............703.2 They re Multiplying
Gouvernement du Québec Ministère de l Éducation, 2004 04-00813 ISBN 2-550-43545-1
 Gouvernement du Québec Ministère de l Éducation, 004 04-00813 ISBN -550-43545-1 Legal deposit Bibliothèque nationale du Québec, 004 1. INTRODUCTION This Definition of the Domain for Summative Evaluation
Gouvernement du Québec Ministère de l Éducation, 004 04-00813 ISBN -550-43545-1 Legal deposit Bibliothèque nationale du Québec, 004 1. INTRODUCTION This Definition of the Domain for Summative Evaluation
Mathematics Placement
 Mathematics Placement The ACT COMPASS math test is a self-adaptive test, which potentially tests students within four different levels of math including pre-algebra, algebra, college algebra, and trigonometry.
Mathematics Placement The ACT COMPASS math test is a self-adaptive test, which potentially tests students within four different levels of math including pre-algebra, algebra, college algebra, and trigonometry.
15.1 Factoring Polynomials
 LESSON 15.1 Factoring Polynomials Use the structure of an expression to identify ways to rewrite it. Also A.SSE.3? ESSENTIAL QUESTION How can you use the greatest common factor to factor polynomials? EXPLORE
LESSON 15.1 Factoring Polynomials Use the structure of an expression to identify ways to rewrite it. Also A.SSE.3? ESSENTIAL QUESTION How can you use the greatest common factor to factor polynomials? EXPLORE
Algebra Practice Problems for Precalculus and Calculus
 Algebra Practice Problems for Precalculus and Calculus Solve the following equations for the unknown x: 1. 5 = 7x 16 2. 2x 3 = 5 x 3. 4. 1 2 (x 3) + x = 17 + 3(4 x) 5 x = 2 x 3 Multiply the indicated polynomials
Algebra Practice Problems for Precalculus and Calculus Solve the following equations for the unknown x: 1. 5 = 7x 16 2. 2x 3 = 5 x 3. 4. 1 2 (x 3) + x = 17 + 3(4 x) 5 x = 2 x 3 Multiply the indicated polynomials
Florida Math for College Readiness
 Core Florida Math for College Readiness Florida Math for College Readiness provides a fourth-year math curriculum focused on developing the mastery of skills identified as critical to postsecondary readiness
Core Florida Math for College Readiness Florida Math for College Readiness provides a fourth-year math curriculum focused on developing the mastery of skills identified as critical to postsecondary readiness
Section 5.0A Factoring Part 1
 Section 5.0A Factoring Part 1 I. Work Together A. Multiply the following binomials into trinomials. (Write the final result in descending order, i.e., a + b + c ). ( 7)( + 5) ( + 7)( + ) ( + 7)( + 5) (
Section 5.0A Factoring Part 1 I. Work Together A. Multiply the following binomials into trinomials. (Write the final result in descending order, i.e., a + b + c ). ( 7)( + 5) ( + 7)( + ) ( + 7)( + 5) (
This is a square root. The number under the radical is 9. (An asterisk * means multiply.)
 Page of Review of Radical Expressions and Equations Skills involving radicals can be divided into the following groups: Evaluate square roots or higher order roots. Simplify radical expressions. Rationalize
Page of Review of Radical Expressions and Equations Skills involving radicals can be divided into the following groups: Evaluate square roots or higher order roots. Simplify radical expressions. Rationalize
ALGEBRA I (Created 2014) Amherst County Public Schools
 ALGEBRA I (Created 2014) Amherst County Public Schools The 2009 Mathematics Standards of Learning Curriculum Framework is a companion document to the 2009 Mathematics Standards of Learning and amplifies
ALGEBRA I (Created 2014) Amherst County Public Schools The 2009 Mathematics Standards of Learning Curriculum Framework is a companion document to the 2009 Mathematics Standards of Learning and amplifies
CORRELATED TO THE SOUTH CAROLINA COLLEGE AND CAREER-READY FOUNDATIONS IN ALGEBRA
 We Can Early Learning Curriculum PreK Grades 8 12 INSIDE ALGEBRA, GRADES 8 12 CORRELATED TO THE SOUTH CAROLINA COLLEGE AND CAREER-READY FOUNDATIONS IN ALGEBRA April 2016 www.voyagersopris.com Mathematical
We Can Early Learning Curriculum PreK Grades 8 12 INSIDE ALGEBRA, GRADES 8 12 CORRELATED TO THE SOUTH CAROLINA COLLEGE AND CAREER-READY FOUNDATIONS IN ALGEBRA April 2016 www.voyagersopris.com Mathematical
Polynomials and Factoring. Unit Lesson Plan
 Polynomials and Factoring Unit Lesson Plan By: David Harris University of North Carolina Chapel Hill Math 410 Dr. Thomas, M D. 2 Abstract This paper will discuss, and give, lesson plans for all the topics
Polynomials and Factoring Unit Lesson Plan By: David Harris University of North Carolina Chapel Hill Math 410 Dr. Thomas, M D. 2 Abstract This paper will discuss, and give, lesson plans for all the topics
Factoring ax 2 + bx + c - Teacher Notes
 Southern Nevada Regional Professi onal D evel opment Program VOLUME 1, ISSUE 8 MAY 009 A N ewsletter from the Sec ondary Mathematic s Team Factoring ax + bx + c - Teacher Notes Here we look at sample teacher
Southern Nevada Regional Professi onal D evel opment Program VOLUME 1, ISSUE 8 MAY 009 A N ewsletter from the Sec ondary Mathematic s Team Factoring ax + bx + c - Teacher Notes Here we look at sample teacher
Higher Education Math Placement
 Higher Education Math Placement Placement Assessment Problem Types 1. Whole Numbers, Fractions, and Decimals 1.1 Operations with Whole Numbers Addition with carry Subtraction with borrowing Multiplication
Higher Education Math Placement Placement Assessment Problem Types 1. Whole Numbers, Fractions, and Decimals 1.1 Operations with Whole Numbers Addition with carry Subtraction with borrowing Multiplication
Factoring Polynomials
 Factoring Polynomials Hoste, Miller, Murieka September 12, 2011 1 Factoring In the previous section, we discussed how to determine the product of two or more terms. Consider, for instance, the equations
Factoring Polynomials Hoste, Miller, Murieka September 12, 2011 1 Factoring In the previous section, we discussed how to determine the product of two or more terms. Consider, for instance, the equations
Big Bend Community College. Beginning Algebra MPC 095. Lab Notebook
 Big Bend Community College Beginning Algebra MPC 095 Lab Notebook Beginning Algebra Lab Notebook by Tyler Wallace is licensed under a Creative Commons Attribution 3.0 Unported License. Permissions beyond
Big Bend Community College Beginning Algebra MPC 095 Lab Notebook Beginning Algebra Lab Notebook by Tyler Wallace is licensed under a Creative Commons Attribution 3.0 Unported License. Permissions beyond
