SOLVING QUADRATIC EQUATIONS BY THE NEW TRANSFORMING METHOD (By Nghi H Nguyen Updated Oct 28, 2014))
|
|
|
- Mercy Nash
- 8 years ago
- Views:
Transcription
1 SOLVING QUADRATIC EQUATIONS BY THE NEW TRANSFORMING METHOD (By Nghi H Nguyen Updated Oct 28, 2014)) There are so far 8 most common methods to solve quadratic equations in standard form ax² + bx + c = 0. They are: graphing, completing the squares, factoring FOIL method, quadratic formula, the Bluma Method, the Diagonal Sum Method, the factoring AC Method, and the new Transforming Method that was recently introduced on Google or Yahoo Search. This new method is fast, convenient, systematic, with no guessing, and it is applicable whenever the quadratic equation can be factored. It can immediately obtain the 2 real roots without factoring by grouping, and solving the binomials. It contains in its solving process three features: - The Rule of Signs For Real Roots of a quadratic equation that shows in advance the signs (- or +) of the 2 real roots to select a better solving approach. - The Diagonal Sum Method for solving quadratic equations type x² + bx + c = 0, (a = 1). - The transformation of a given quadratic equation in standard form ax² + bx + c = 0 (1) into a simplified equation, with a = 1, for a better solving approach. (See References) RECALL THE RULE OF SIGNS FOR REAL ROOTS OF A QUADRATIC EQUATION - If a and c have opposite signs, the 2 real roots have opposite signs. Example. The equation x² - 8x 9 = 0 has 2 real roots with different signs: -1 and 9. - If a and c have same sign, the 2 real roots have same sign. If a and b have same sign, both real roots are negative Example: The equation x² + 17x + 15 = 0 has 2 real roots both negative: -1 and -15. If a and b have different signs, both real roots are positive. Example: The equation 5x² 14x + 9 = 0 has 2 real roots both positive: 1 and 9/5. SOLVING QUADRATIC EQUATIONS BY THE DIAGONAL SUM METHOD When a = 1 Solving equation type x² + bx + c = 0. In this case, solving results in finding 2 numbers knowing their sum (-b) and their product (c). Applying the Rule of Signs, the solving process using the Diagonal Sum Method (Google or Yahoo Search) is simple, fast, and doesn t require factoring by grouping and solving the 2 binomials. It proceeds by composing factor pairs of c following these 3 Tips. a. TIP 1. When roots have different signs (a and c different signs). Compose the factor pairs of c with all first numbers of the pairs being negative. Stop composing when you find the pair whose sum is equal to (b), or (-b). If you don t find it, then the equation can t be factored, and you probably should use the quadratic formula to solve it. Example 1. Solve: x² 11x 102 = 0. Page 1 of 6
2 Solution. The Rule of Signs indicates roots have different signs. First, compose factor pairs of c = -102 with all first numbers being negative. Proceeding: (-1, 102),(-2, 51),(-3, 34),(-6, 17). OK.. This last sum is 17 6 = 11 = -b. Consequently, the 2 real roots are -6 and 17. There is no need to factor by grouping and to solve the 2 binomials for x. Note. If we compose the factors of c = -102 differently, the results will be the same. Proceeding: (1, -102),(2, -51),(3, -34),(6, -17). This last sum is 6 17 = -11 = b. According to the Diagonal Sum Rule, when the diagonal sum equals to (b) the answers are the opposite. Then, the 2 real roots are -6 and 17. b. TIP 2. When both roots are positive, compose factors of c with all positive numbers. Page 2 of 6
3 Example 2. Solve: x² 28x + 96 = 0. Solution. Both real roots are positive. Compose factors of c = 96 with all positive numbers. Proceeding: (1, 96),(2, 48),(3, 32),(4, 24). This last sum is: = 28 = -b. Then, the 2 real roots are 4 and 28. Note. If we compose the factors of c = 96 differently, the outcome is still the same. Proceeding: (-1, -96),(-2,-48),(-3, -32),(-4, -24). This last sum is (-4 24) = -28 = b. The real roots make the negative of this pair. Then, the real roots are 4 and 24. c. TIP 3. When both roots are negative, compose factor pairs of c with all negative numbers. Example 3. Solve: x² + 39x = 0. Solution. Both real roots are negative. Compose factors of c = 108 with all numbers negative. Proceeding: (-1, -108),(-2, -54),(-3, -36). OK. The last sum is = -39 = -b. Then, the 2 real roots are -3 and -36. Page 3 of 6
4 SOLVING QUADRATIC EQUATIONS BY THE NEW TRANSFORMING METHOD This new method proceeds through 3 steps: Step 1. Transform the given quadratic equation in standard form ax² + bx + c = 0 (1) into a simplified equation with a = 1 and with the new constant C = a*c. The new equation has the form: x² + bx + a*c = 0 (2). Step 2. Solve this transformed equation (2) by the Diagonal Sum Method that immediately obtains the 2 real roots without factoring by grouping or solving binomials. Suppose the 2 found real roots of the equation (2) are: y1 and y2. Step 3. Divide both y1 and y2 by the coefficient a to get the 2 real roots x1 and x2 of the original equation (1): x1 = y1/a, and x2 = y2/a. Important Notes. 1. When composing factor pairs of a*c, always start from the first factor (-1, c), or (1, c), or (-1, -c), then gradually go up the chain. Stop composing when you find the factor pair whose sum is equal to (b), or (-b). If you can t find this pair, then the given quadratic equation can t be factored, and consequently you probably should use the quadratic formula to solve it. 2. To save time when composing the long chain of factor pairs of a*c, that is a very large number, take into consideration the relative values of b as compared to a*c. a. If b is relatively as large as a*c, start the factor chain from the beginning. Example 4: Solve: 5x² - 18x - 8 = 0. Compose factor pairs of a*c = -40 from the beginning. Proceeding: (-1, 40),(-2, 20). OK. b. If b is very small as compared to a*c, start the factor chain from the middle. Example 5. Solve: 15x² 53x + 16 = 0. Since b = 5 is small number as compared to a*c = 15*16 = 240, start composing factor pairs from the middle of the chain. Proceeding: (3, 80),(4, 60),(5, 48).. EXAMPLES OF SOLVING BY THE NEW TRANSFORMING METHOD Example 6. Solve: 8x² 22x 13 = 0. (1) (a*c = 8*-13 = -104) Solution. Solve the transformed equation: x² 22x 104 = 0 (2), by the Diagonal Sum Method. Roots have different signs. Compose factors of a*c = -104 with all first numbers being negative. Proceeding: (-1, 104)(-2, 52)(-4, 26). This last sum is 26 4 = 22 = -b. The 2 real roots of the transformed equation (2) are: y1 = -4, and y2 = 26. Consequently, the 2 real roots of (1) are: x1 = y1/8 = -4/8 = -1/2, and x2 = y2/8 = 26/8 = 13/4. Page 4 of 6
5 Example 7. Solve: 16x² 62x + 21 = 0 (1) (a*c = 16* 21 = 336) Solution. Solve the transformed equation: x² 62x = 0 (2). Both real roots are positive. Compose factors of a*c = 336 with all numbers being positive. Proceeding: (1, 336) (2, 168)(4, 82)(6, 56). This last sum is = 62 = -b. Then, the 2 real roots are: y1 = 56, and y2 = 6. Back to the original equation (1), the 2 real roots are: x1 = 56/16 = 7/2, and x2 = 6/16 = 3/8. Example 8. Solve: 12x² + 46 x + 20 = 0. (1). (a*c = 12*20 = 240) Solution. Solve the transformed equation: x² + 46x (2), by the Diagonal Sum Method Both roots are negative. Compose factor pairs of a*c = 240 with all negative numbers. Proceeding: (-1, -240)(-2, -120)(-3, -80)(-4, -60)(-5, -48)(-6, -40). This last sum is (-46) = -b. The 2 real roots of (2) are: y1 = -6, and y2 = -40. Then, the 2 real roots of the original equation (1) are: x1 = -6/12 = -1/2, and x2 = -40/12 = -10/3. Page 5 of 6
6 More examples on solving quadratic equations by the Transforming Method. Example 9. Solve: 6x² + 17x 14 = 0 (1) (a*c = 6*-14 = -84) Solution. Solve the transformed equation: x² + 17x 84 = 0 (2). Roots have opposite signs. Compose factor pairs of a*c = Proceeding: (-1, 84)(-2, 42)(-3, 28)(-4, 21). This last sum is 21 4 = 17 = b. Then, the 2 real roots are: 4 and -21 (Rule of Signs). Back to equation (1), the 2 real roots are: x1 = 4/6 = 2/3; and x2 = -21/6 = -7/2. Example 10. Solve: 45x² - 74x + 24 = 0 (1) (a*c = 45*24 = 1080) Solution. Solve the transformed equation: x² - 74x = 0 (2). Both roots are positive. Compose factor pairs of a*c = 1080 with all positive numbers. Proceeding: (2, 540)(3, 360). (15, 72)(18, 60)(20, 54). This last sum is 74 = -b. Then the 2 real roots of (2) are: 20 and 54. Back to the equation (1), the 2 real roots are: x1 = 20/45 = 4/9; and x2 = 54/45 = 6/5. Example 11. Solve: 24x² + 59x + 36 = 0 (1) (a*c = 24*36 = 864) Solution. Solve the transformed equation: x² + 59x = 0 (2). Both roots are negative. Compose factor pairs of a*c = 864 with all negative numbers. Proceeding: (-18, - 48)(-24, - 36)(-27, -32). This last sum is: = -59 = -b. The 2 real roots of (2) are: -27. And -32. Back to the original equation (1), the 3 real roots are: x1 = -27/24 = -9/8, and x2 = -32/-24 = -4/3 CONCLUSION The main strong points of the new Transforming Method are: simple, fast, systematic, no guessing, no factoring by grouping, and no solving binomials. References: - The Diagonal Sum Method was publicly presented in math articles titled: Solving quadratic equations by the Diagonal Sum Method (Google or Yahoo Search). - The transformation of an equation in standard form ax² + bx + c = 0 into an equation in simplified form x² + bx + a*c = 0 was publicly presented in 3 math articles (Google or Yahoo Search): 1. AC Method for factoring- Regent Exam Prep Center at 2. A different way to solve Quadratic The Bluma Method. 3. Factoring trinomials Simplified AC Method at: 2000clicks.com/mathhelp (This math article was written by Nghi H Nguyen, author of the math article: Solving trigonometric inequalities Concept, Methods, and Steps (Google, Yahoo, or Bing Search) - Updated on Oct. 28, 2014)) Page 6 of 6
SOLVING QUADRATIC EQUATIONS - COMPARE THE FACTORING AC METHOD AND THE NEW TRANSFORMING METHOD (By Nghi H. Nguyen - Jan 18, 2015)
 SOLVING QUADRATIC EQUATIONS - COMPARE THE FACTORING AC METHOD AND THE NEW TRANSFORMING METHOD (By Nghi H. Nguyen - Jan 18, 2015) GENERALITIES. When a given quadratic equation can be factored, there are
SOLVING QUADRATIC EQUATIONS - COMPARE THE FACTORING AC METHOD AND THE NEW TRANSFORMING METHOD (By Nghi H. Nguyen - Jan 18, 2015) GENERALITIES. When a given quadratic equation can be factored, there are
SOLVING QUADRATIC EQUATIONS - COMPARE THE FACTORING ac METHOD AND THE NEW DIAGONAL SUM METHOD By Nghi H. Nguyen
 SOLVING QUADRATIC EQUATIONS - COMPARE THE FACTORING ac METHOD AND THE NEW DIAGONAL SUM METHOD By Nghi H. Nguyen A. GENERALITIES. When a given quadratic equation can be factored, there are 2 best methods
SOLVING QUADRATIC EQUATIONS - COMPARE THE FACTORING ac METHOD AND THE NEW DIAGONAL SUM METHOD By Nghi H. Nguyen A. GENERALITIES. When a given quadratic equation can be factored, there are 2 best methods
SOLVING QUADRATIC EQUATIONS BY THE DIAGONAL SUM METHOD
 SOLVING QUADRATIC EQUATIONS BY THE DIAGONAL SUM METHOD A quadratic equation in one variable has as standard form: ax^2 + bx + c = 0. Solving it means finding the values of x that make the equation true.
SOLVING QUADRATIC EQUATIONS BY THE DIAGONAL SUM METHOD A quadratic equation in one variable has as standard form: ax^2 + bx + c = 0. Solving it means finding the values of x that make the equation true.
BEST METHODS FOR SOLVING QUADRATIC INEQUALITIES.
 BEST METHODS FOR SOLVING QUADRATIC INEQUALITIES. I. GENERALITIES There are 3 common methods to solve quadratic inequalities. Therefore, students sometimes are confused to select the fastest and the best
BEST METHODS FOR SOLVING QUADRATIC INEQUALITIES. I. GENERALITIES There are 3 common methods to solve quadratic inequalities. Therefore, students sometimes are confused to select the fastest and the best
Factoring Polynomials and Solving Quadratic Equations
 Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
Chapter R.4 Factoring Polynomials
 Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
NSM100 Introduction to Algebra Chapter 5 Notes Factoring
 Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
expression is written horizontally. The Last terms ((2)( 4)) because they are the last terms of the two polynomials. This is called the FOIL method.
 A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
FACTORING QUADRATICS 8.1.1 and 8.1.2
 FACTORING QUADRATICS 8.1.1 and 8.1.2 Chapter 8 introduces students to quadratic equations. These equations can be written in the form of y = ax 2 + bx + c and, when graphed, produce a curve called a parabola.
FACTORING QUADRATICS 8.1.1 and 8.1.2 Chapter 8 introduces students to quadratic equations. These equations can be written in the form of y = ax 2 + bx + c and, when graphed, produce a curve called a parabola.
1.3 Algebraic Expressions
 1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
( ) FACTORING. x In this polynomial the only variable in common to all is x.
 FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
Factoring Trinomials: The ac Method
 6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
Using the ac Method to Factor
 4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
HIBBING COMMUNITY COLLEGE COURSE OUTLINE
 HIBBING COMMUNITY COLLEGE COURSE OUTLINE COURSE NUMBER & TITLE: - Beginning Algebra CREDITS: 4 (Lec 4 / Lab 0) PREREQUISITES: MATH 0920: Fundamental Mathematics with a grade of C or better, Placement Exam,
HIBBING COMMUNITY COLLEGE COURSE OUTLINE COURSE NUMBER & TITLE: - Beginning Algebra CREDITS: 4 (Lec 4 / Lab 0) PREREQUISITES: MATH 0920: Fundamental Mathematics with a grade of C or better, Placement Exam,
FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c
 Tallahassee Community College 55 FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c This kind of trinomial differs from the previous kind we have factored because the coefficient of x is no longer "1".
Tallahassee Community College 55 FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c This kind of trinomial differs from the previous kind we have factored because the coefficient of x is no longer "1".
1.3 Polynomials and Factoring
 1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
Factoring and Applications
 Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
CONVERT QUADRATIC FUNCTIONS FROM ONE FORM TO ANOTHER (Standard Form <==> Intercept Form <==> Vertex Form) (By Nghi H Nguyen Dec 08, 2014)
 CONVERT QUADRATIC FUNCTIONS FROM ONE FORM TO ANOTHER (Standard Form Intercept Form Vertex Form) (By Nghi H Nguyen Dec 08, 2014) 1. THE QUADRATIC FUNCTION IN INTERCEPT FORM The graph of the quadratic
CONVERT QUADRATIC FUNCTIONS FROM ONE FORM TO ANOTHER (Standard Form Intercept Form Vertex Form) (By Nghi H Nguyen Dec 08, 2014) 1. THE QUADRATIC FUNCTION IN INTERCEPT FORM The graph of the quadratic
Factoring Quadratic Expressions
 Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
A. Factoring out the Greatest Common Factor.
 DETAILED SOLUTIONS AND CONCEPTS - FACTORING POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to ingrid.stewart@csn.edu. Thank you!
DETAILED SOLUTIONS AND CONCEPTS - FACTORING POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to ingrid.stewart@csn.edu. Thank you!
Math 25 Activity 6: Factoring Advanced
 Instructor! Math 25 Activity 6: Factoring Advanced Last week we looked at greatest common factors and the basics of factoring out the GCF. In this second activity, we will discuss factoring more difficult
Instructor! Math 25 Activity 6: Factoring Advanced Last week we looked at greatest common factors and the basics of factoring out the GCF. In this second activity, we will discuss factoring more difficult
ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form
 ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form Goal Graph quadratic functions. VOCABULARY Quadratic function A function that can be written in the standard form y = ax 2 + bx+ c where a 0 Parabola
ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form Goal Graph quadratic functions. VOCABULARY Quadratic function A function that can be written in the standard form y = ax 2 + bx+ c where a 0 Parabola
Algebra 2: Q1 & Q2 Review
 Name: Class: Date: ID: A Algebra 2: Q1 & Q2 Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Which is the graph of y = 2(x 2) 2 4? a. c. b. d. Short
Name: Class: Date: ID: A Algebra 2: Q1 & Q2 Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Which is the graph of y = 2(x 2) 2 4? a. c. b. d. Short
A Systematic Approach to Factoring
 A Systematic Approach to Factoring Step 1 Count the number of terms. (Remember****Knowing the number of terms will allow you to eliminate unnecessary tools.) Step 2 Is there a greatest common factor? Tool
A Systematic Approach to Factoring Step 1 Count the number of terms. (Remember****Knowing the number of terms will allow you to eliminate unnecessary tools.) Step 2 Is there a greatest common factor? Tool
Factoring ax 2 + bx + c - Teacher Notes
 Southern Nevada Regional Professi onal D evel opment Program VOLUME 1, ISSUE 8 MAY 009 A N ewsletter from the Sec ondary Mathematic s Team Factoring ax + bx + c - Teacher Notes Here we look at sample teacher
Southern Nevada Regional Professi onal D evel opment Program VOLUME 1, ISSUE 8 MAY 009 A N ewsletter from the Sec ondary Mathematic s Team Factoring ax + bx + c - Teacher Notes Here we look at sample teacher
Wentzville School District Algebra 1: Unit 8 Stage 1 Desired Results
 Wentzville School District Algebra 1: Unit 8 Stage 1 Desired Results Unit Title: Quadratic Expressions & Equations Course: Algebra I Unit 8 - Quadratic Expressions & Equations Brief Summary of Unit: At
Wentzville School District Algebra 1: Unit 8 Stage 1 Desired Results Unit Title: Quadratic Expressions & Equations Course: Algebra I Unit 8 - Quadratic Expressions & Equations Brief Summary of Unit: At
Factoring Guidelines. Greatest Common Factor Two Terms Three Terms Four Terms. 2008 Shirley Radai
 Factoring Guidelines Greatest Common Factor Two Terms Three Terms Four Terms 008 Shirley Radai Greatest Common Factor 008 Shirley Radai Factoring by Finding the Greatest Common Factor Always check for
Factoring Guidelines Greatest Common Factor Two Terms Three Terms Four Terms 008 Shirley Radai Greatest Common Factor 008 Shirley Radai Factoring by Finding the Greatest Common Factor Always check for
Academic Success Centre
 250) 960-6367 Factoring Polynomials Sometimes when we try to solve or simplify an equation or expression involving polynomials the way that it looks can hinder our progress in finding a solution. Factorization
250) 960-6367 Factoring Polynomials Sometimes when we try to solve or simplify an equation or expression involving polynomials the way that it looks can hinder our progress in finding a solution. Factorization
Name Intro to Algebra 2. Unit 1: Polynomials and Factoring
 Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
Factoring Polynomials
 Factoring Polynomials Factoring Factoring is the process of writing a polynomial as the product of two or more polynomials. The factors of 6x 2 x 2 are 2x + 1 and 3x 2. In this section, we will be factoring
Factoring Polynomials Factoring Factoring is the process of writing a polynomial as the product of two or more polynomials. The factors of 6x 2 x 2 are 2x + 1 and 3x 2. In this section, we will be factoring
AIP Factoring Practice/Help
 The following pages include many problems to practice factoring skills. There are also several activities with examples to help you with factoring if you feel like you are not proficient with it. There
The following pages include many problems to practice factoring skills. There are also several activities with examples to help you with factoring if you feel like you are not proficient with it. There
Determinants can be used to solve a linear system of equations using Cramer s Rule.
 2.6.2 Cramer s Rule Determinants can be used to solve a linear system of equations using Cramer s Rule. Cramer s Rule for Two Equations in Two Variables Given the system This system has the unique solution
2.6.2 Cramer s Rule Determinants can be used to solve a linear system of equations using Cramer s Rule. Cramer s Rule for Two Equations in Two Variables Given the system This system has the unique solution
SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS
 (Section 0.6: Polynomial, Rational, and Algebraic Expressions) 0.6.1 SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS LEARNING OBJECTIVES Be able to identify polynomial, rational, and algebraic
(Section 0.6: Polynomial, Rational, and Algebraic Expressions) 0.6.1 SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS LEARNING OBJECTIVES Be able to identify polynomial, rational, and algebraic
MATH 90 CHAPTER 6 Name:.
 MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
Section 6.1 Factoring Expressions
 Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
FACTORING ax 2 bx c. Factoring Trinomials with Leading Coefficient 1
 5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
POLYNOMIALS and FACTORING
 POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder).
 Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Factoring Flow Chart
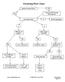 Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Algebra and Geometry Review (61 topics, no due date)
 Course Name: Math 112 Credit Exam LA Tech University Course Code: ALEKS Course: Trigonometry Instructor: Course Dates: Course Content: 159 topics Algebra and Geometry Review (61 topics, no due date) Properties
Course Name: Math 112 Credit Exam LA Tech University Course Code: ALEKS Course: Trigonometry Instructor: Course Dates: Course Content: 159 topics Algebra and Geometry Review (61 topics, no due date) Properties
Factoring Algebra- Chapter 8B Assignment Sheet
 Name: Factoring Algebra- Chapter 8B Assignment Sheet Date Section Learning Targets Assignment Tues 2/17 Find the prime factorization of an integer Find the greatest common factor (GCF) for a set of monomials.
Name: Factoring Algebra- Chapter 8B Assignment Sheet Date Section Learning Targets Assignment Tues 2/17 Find the prime factorization of an integer Find the greatest common factor (GCF) for a set of monomials.
3.3. Solving Polynomial Equations. Introduction. Prerequisites. Learning Outcomes
 Solving Polynomial Equations 3.3 Introduction Linear and quadratic equations, dealt within Sections 3.1 and 3.2, are members of a class of equations, called polynomial equations. These have the general
Solving Polynomial Equations 3.3 Introduction Linear and quadratic equations, dealt within Sections 3.1 and 3.2, are members of a class of equations, called polynomial equations. These have the general
EAP/GWL Rev. 1/2011 Page 1 of 5. Factoring a polynomial is the process of writing it as the product of two or more polynomial factors.
 EAP/GWL Rev. 1/2011 Page 1 of 5 Factoring a polynomial is the process of writing it as the product of two or more polynomial factors. Example: Set the factors of a polynomial equation (as opposed to an
EAP/GWL Rev. 1/2011 Page 1 of 5 Factoring a polynomial is the process of writing it as the product of two or more polynomial factors. Example: Set the factors of a polynomial equation (as opposed to an
Math 0980 Chapter Objectives. Chapter 1: Introduction to Algebra: The Integers.
 Math 0980 Chapter Objectives Chapter 1: Introduction to Algebra: The Integers. 1. Identify the place value of a digit. 2. Write a number in words or digits. 3. Write positive and negative numbers used
Math 0980 Chapter Objectives Chapter 1: Introduction to Algebra: The Integers. 1. Identify the place value of a digit. 2. Write a number in words or digits. 3. Write positive and negative numbers used
The Method of Partial Fractions Math 121 Calculus II Spring 2015
 Rational functions. as The Method of Partial Fractions Math 11 Calculus II Spring 015 Recall that a rational function is a quotient of two polynomials such f(x) g(x) = 3x5 + x 3 + 16x x 60. The method
Rational functions. as The Method of Partial Fractions Math 11 Calculus II Spring 015 Recall that a rational function is a quotient of two polynomials such f(x) g(x) = 3x5 + x 3 + 16x x 60. The method
FACTORING QUADRATIC EQUATIONS
 FACTORING QUADRATIC EQUATIONS Summary 1. Difference of squares... 1 2. Mise en évidence simple... 2 3. compounded factorization... 3 4. Exercises... 7 The goal of this section is to summarize the methods
FACTORING QUADRATIC EQUATIONS Summary 1. Difference of squares... 1 2. Mise en évidence simple... 2 3. compounded factorization... 3 4. Exercises... 7 The goal of this section is to summarize the methods
Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III
 Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III Name Date Adding and Subtracting Polynomials Algebra Standard 10.0 A polynomial is a sum of one ore more monomials. Polynomial
Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III Name Date Adding and Subtracting Polynomials Algebra Standard 10.0 A polynomial is a sum of one ore more monomials. Polynomial
Unit 12: Introduction to Factoring. Learning Objectives 12.2
 Unit 1 Table of Contents Unit 1: Introduction to Factoring Learning Objectives 1. Instructor Notes The Mathematics of Factoring Teaching Tips: Challenges and Approaches Additional Resources Instructor
Unit 1 Table of Contents Unit 1: Introduction to Factoring Learning Objectives 1. Instructor Notes The Mathematics of Factoring Teaching Tips: Challenges and Approaches Additional Resources Instructor
Tool 1. Greatest Common Factor (GCF)
 Chapter 4: Factoring Review Tool 1 Greatest Common Factor (GCF) This is a very important tool. You must try to factor out the GCF first in every problem. Some problems do not have a GCF but many do. When
Chapter 4: Factoring Review Tool 1 Greatest Common Factor (GCF) This is a very important tool. You must try to factor out the GCF first in every problem. Some problems do not have a GCF but many do. When
Springfield Technical Community College School of Mathematics, Sciences & Engineering Transfer
 Springfield Technical Community College School of Mathematics, Sciences & Engineering Transfer Department: Mathematics Course Title: Algebra 2 Course Number: MAT-097 Semester: Fall 2015 Credits: 3 Non-Graduation
Springfield Technical Community College School of Mathematics, Sciences & Engineering Transfer Department: Mathematics Course Title: Algebra 2 Course Number: MAT-097 Semester: Fall 2015 Credits: 3 Non-Graduation
FACTORING ax 2 bx c WITH a 1
 296 (6 20) Chapter 6 Factoring 6.4 FACTORING a 2 b c WITH a 1 In this section The ac Method Trial and Error Factoring Completely In Section 6.3 we factored trinomials with a leading coefficient of 1. In
296 (6 20) Chapter 6 Factoring 6.4 FACTORING a 2 b c WITH a 1 In this section The ac Method Trial and Error Factoring Completely In Section 6.3 we factored trinomials with a leading coefficient of 1. In
Brunswick High School has reinstated a summer math curriculum for students Algebra 1, Geometry, and Algebra 2 for the 2014-2015 school year.
 Brunswick High School has reinstated a summer math curriculum for students Algebra 1, Geometry, and Algebra 2 for the 2014-2015 school year. Goal The goal of the summer math program is to help students
Brunswick High School has reinstated a summer math curriculum for students Algebra 1, Geometry, and Algebra 2 for the 2014-2015 school year. Goal The goal of the summer math program is to help students
Lagrange Interpolation is a method of fitting an equation to a set of points that functions well when there are few points given.
 Polynomials (Ch.1) Study Guide by BS, JL, AZ, CC, SH, HL Lagrange Interpolation is a method of fitting an equation to a set of points that functions well when there are few points given. Sasha s method
Polynomials (Ch.1) Study Guide by BS, JL, AZ, CC, SH, HL Lagrange Interpolation is a method of fitting an equation to a set of points that functions well when there are few points given. Sasha s method
Zero: If P is a polynomial and if c is a number such that P (c) = 0 then c is a zero of P.
 MATH 11011 FINDING REAL ZEROS KSU OF A POLYNOMIAL Definitions: Polynomial: is a function of the form P (x) = a n x n + a n 1 x n 1 + + a x + a 1 x + a 0. The numbers a n, a n 1,..., a 1, a 0 are called
MATH 11011 FINDING REAL ZEROS KSU OF A POLYNOMIAL Definitions: Polynomial: is a function of the form P (x) = a n x n + a n 1 x n 1 + + a x + a 1 x + a 0. The numbers a n, a n 1,..., a 1, a 0 are called
MATH 108 REVIEW TOPIC 10 Quadratic Equations. B. Solving Quadratics by Completing the Square
 Math 108 T10-Review Topic 10 Page 1 MATH 108 REVIEW TOPIC 10 Quadratic Equations I. Finding Roots of a Quadratic Equation A. Factoring B. Quadratic Formula C. Taking Roots II. III. Guidelines for Finding
Math 108 T10-Review Topic 10 Page 1 MATH 108 REVIEW TOPIC 10 Quadratic Equations I. Finding Roots of a Quadratic Equation A. Factoring B. Quadratic Formula C. Taking Roots II. III. Guidelines for Finding
Section 5.0A Factoring Part 1
 Section 5.0A Factoring Part 1 I. Work Together A. Multiply the following binomials into trinomials. (Write the final result in descending order, i.e., a + b + c ). ( 7)( + 5) ( + 7)( + ) ( + 7)( + 5) (
Section 5.0A Factoring Part 1 I. Work Together A. Multiply the following binomials into trinomials. (Write the final result in descending order, i.e., a + b + c ). ( 7)( + 5) ( + 7)( + ) ( + 7)( + 5) (
IOWA End-of-Course Assessment Programs. Released Items ALGEBRA I. Copyright 2010 by The University of Iowa.
 IOWA End-of-Course Assessment Programs Released Items Copyright 2010 by The University of Iowa. ALGEBRA I 1 Sally works as a car salesperson and earns a monthly salary of $2,000. She also earns $500 for
IOWA End-of-Course Assessment Programs Released Items Copyright 2010 by The University of Iowa. ALGEBRA I 1 Sally works as a car salesperson and earns a monthly salary of $2,000. She also earns $500 for
Florida Math for College Readiness
 Core Florida Math for College Readiness Florida Math for College Readiness provides a fourth-year math curriculum focused on developing the mastery of skills identified as critical to postsecondary readiness
Core Florida Math for College Readiness Florida Math for College Readiness provides a fourth-year math curriculum focused on developing the mastery of skills identified as critical to postsecondary readiness
Algebra 2 PreAP. Name Period
 Algebra 2 PreAP Name Period IMPORTANT INSTRUCTIONS FOR STUDENTS!!! We understand that students come to Algebra II with different strengths and needs. For this reason, students have options for completing
Algebra 2 PreAP Name Period IMPORTANT INSTRUCTIONS FOR STUDENTS!!! We understand that students come to Algebra II with different strengths and needs. For this reason, students have options for completing
MATH 095, College Prep Mathematics: Unit Coverage Pre-algebra topics (arithmetic skills) offered through BSE (Basic Skills Education)
 MATH 095, College Prep Mathematics: Unit Coverage Pre-algebra topics (arithmetic skills) offered through BSE (Basic Skills Education) Accurately add, subtract, multiply, and divide whole numbers, integers,
MATH 095, College Prep Mathematics: Unit Coverage Pre-algebra topics (arithmetic skills) offered through BSE (Basic Skills Education) Accurately add, subtract, multiply, and divide whole numbers, integers,
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0).
 This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
Introduction Assignment
 PRE-CALCULUS 11 Introduction Assignment Welcome to PREC 11! This assignment will help you review some topics from a previous math course and introduce you to some of the topics that you ll be studying
PRE-CALCULUS 11 Introduction Assignment Welcome to PREC 11! This assignment will help you review some topics from a previous math course and introduce you to some of the topics that you ll be studying
4.1. COMPLEX NUMBERS
 4.1. COMPLEX NUMBERS What You Should Learn Use the imaginary unit i to write complex numbers. Add, subtract, and multiply complex numbers. Use complex conjugates to write the quotient of two complex numbers
4.1. COMPLEX NUMBERS What You Should Learn Use the imaginary unit i to write complex numbers. Add, subtract, and multiply complex numbers. Use complex conjugates to write the quotient of two complex numbers
Warm-Up Oct. 22. Daily Agenda:
 Evaluate y = 2x 3x + 5 when x = 1, 0, and 2. Daily Agenda: Grade Assignment Go over Ch 3 Test; Retakes must be done by next Tuesday 5.1 notes / assignment Graphing Quadratic Functions 5.2 notes / assignment
Evaluate y = 2x 3x + 5 when x = 1, 0, and 2. Daily Agenda: Grade Assignment Go over Ch 3 Test; Retakes must be done by next Tuesday 5.1 notes / assignment Graphing Quadratic Functions 5.2 notes / assignment
MATH 21. College Algebra 1 Lecture Notes
 MATH 21 College Algebra 1 Lecture Notes MATH 21 3.6 Factoring Review College Algebra 1 Factoring and Foiling 1. (a + b) 2 = a 2 + 2ab + b 2. 2. (a b) 2 = a 2 2ab + b 2. 3. (a + b)(a b) = a 2 b 2. 4. (a
MATH 21 College Algebra 1 Lecture Notes MATH 21 3.6 Factoring Review College Algebra 1 Factoring and Foiling 1. (a + b) 2 = a 2 + 2ab + b 2. 2. (a b) 2 = a 2 2ab + b 2. 3. (a + b)(a b) = a 2 b 2. 4. (a
Florida Math 0028. Correlation of the ALEKS course Florida Math 0028 to the Florida Mathematics Competencies - Upper
 Florida Math 0028 Correlation of the ALEKS course Florida Math 0028 to the Florida Mathematics Competencies - Upper Exponents & Polynomials MDECU1: Applies the order of operations to evaluate algebraic
Florida Math 0028 Correlation of the ALEKS course Florida Math 0028 to the Florida Mathematics Competencies - Upper Exponents & Polynomials MDECU1: Applies the order of operations to evaluate algebraic
Algebra 1 If you are okay with that placement then you have no further action to take Algebra 1 Portion of the Math Placement Test
 Dear Parents, Based on the results of the High School Placement Test (HSPT), your child should forecast to take Algebra 1 this fall. If you are okay with that placement then you have no further action
Dear Parents, Based on the results of the High School Placement Test (HSPT), your child should forecast to take Algebra 1 this fall. If you are okay with that placement then you have no further action
SOLVING TRIGONOMETRIC INEQUALITIES (CONCEPT, METHODS, AND STEPS) By Nghi H. Nguyen
 SOLVING TRIGONOMETRIC INEQUALITIES (CONCEPT, METHODS, AND STEPS) By Nghi H. Nguyen DEFINITION. A trig inequality is an inequality in standard form: R(x) > 0 (or < 0) that contains one or a few trig functions
SOLVING TRIGONOMETRIC INEQUALITIES (CONCEPT, METHODS, AND STEPS) By Nghi H. Nguyen DEFINITION. A trig inequality is an inequality in standard form: R(x) > 0 (or < 0) that contains one or a few trig functions
Factoring Polynomials
 Factoring Polynomials 4-1-2014 The opposite of multiplying polynomials is factoring. Why would you want to factor a polynomial? Let p(x) be a polynomial. p(c) = 0 is equivalent to x c dividing p(x). Recall
Factoring Polynomials 4-1-2014 The opposite of multiplying polynomials is factoring. Why would you want to factor a polynomial? Let p(x) be a polynomial. p(c) = 0 is equivalent to x c dividing p(x). Recall
CM2202: Scientific Computing and Multimedia Applications General Maths: 2. Algebra - Factorisation
 CM2202: Scientific Computing and Multimedia Applications General Maths: 2. Algebra - Factorisation Prof. David Marshall School of Computer Science & Informatics Factorisation Factorisation is a way of
CM2202: Scientific Computing and Multimedia Applications General Maths: 2. Algebra - Factorisation Prof. David Marshall School of Computer Science & Informatics Factorisation Factorisation is a way of
CAHSEE on Target UC Davis, School and University Partnerships
 UC Davis, School and University Partnerships CAHSEE on Target Mathematics Curriculum Published by The University of California, Davis, School/University Partnerships Program 006 Director Sarah R. Martinez,
UC Davis, School and University Partnerships CAHSEE on Target Mathematics Curriculum Published by The University of California, Davis, School/University Partnerships Program 006 Director Sarah R. Martinez,
Systems of Equations Involving Circles and Lines
 Name: Systems of Equations Involving Circles and Lines Date: In this lesson, we will be solving two new types of Systems of Equations. Systems of Equations Involving a Circle and a Line Solving a system
Name: Systems of Equations Involving Circles and Lines Date: In this lesson, we will be solving two new types of Systems of Equations. Systems of Equations Involving a Circle and a Line Solving a system
Algebra 1 Course Title
 Algebra 1 Course Title Course- wide 1. What patterns and methods are being used? Course- wide 1. Students will be adept at solving and graphing linear and quadratic equations 2. Students will be adept
Algebra 1 Course Title Course- wide 1. What patterns and methods are being used? Course- wide 1. Students will be adept at solving and graphing linear and quadratic equations 2. Students will be adept
Algebra 2/Trig Unit 2 Notes Packet Period: Quadratic Equations
 Algebra 2/Trig Unit 2 Notes Packet Name: Date: Period: # Quadratic Equations (1) Page 253 #4 6 **Check on Graphing Calculator (GC)** (2) Page 253 254 #20, 26, 32**Check on GC** (3) Page 253 254 #10 12,
Algebra 2/Trig Unit 2 Notes Packet Name: Date: Period: # Quadratic Equations (1) Page 253 #4 6 **Check on Graphing Calculator (GC)** (2) Page 253 254 #20, 26, 32**Check on GC** (3) Page 253 254 #10 12,
JUST THE MATHS UNIT NUMBER 1.8. ALGEBRA 8 (Polynomials) A.J.Hobson
 JUST THE MATHS UNIT NUMBER 1.8 ALGEBRA 8 (Polynomials) by A.J.Hobson 1.8.1 The factor theorem 1.8.2 Application to quadratic and cubic expressions 1.8.3 Cubic equations 1.8.4 Long division of polynomials
JUST THE MATHS UNIT NUMBER 1.8 ALGEBRA 8 (Polynomials) by A.J.Hobson 1.8.1 The factor theorem 1.8.2 Application to quadratic and cubic expressions 1.8.3 Cubic equations 1.8.4 Long division of polynomials
Polynomials and Factoring
 7.6 Polynomials and Factoring Basic Terminology A term, or monomial, is defined to be a number, a variable, or a product of numbers and variables. A polynomial is a term or a finite sum or difference of
7.6 Polynomials and Factoring Basic Terminology A term, or monomial, is defined to be a number, a variable, or a product of numbers and variables. A polynomial is a term or a finite sum or difference of
In algebra, factor by rewriting a polynomial as a product of lower-degree polynomials
 Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
Sect 6.7 - Solving Equations Using the Zero Product Rule
 Sect 6.7 - Solving Equations Using the Zero Product Rule 116 Concept #1: Definition of a Quadratic Equation A quadratic equation is an equation that can be written in the form ax 2 + bx + c = 0 (referred
Sect 6.7 - Solving Equations Using the Zero Product Rule 116 Concept #1: Definition of a Quadratic Equation A quadratic equation is an equation that can be written in the form ax 2 + bx + c = 0 (referred
0.4 FACTORING POLYNOMIALS
 36_.qxd /3/5 :9 AM Page -9 SECTION. Factoring Polynomials -9. FACTORING POLYNOMIALS Use special products and factorization techniques to factor polynomials. Find the domains of radical expressions. Use
36_.qxd /3/5 :9 AM Page -9 SECTION. Factoring Polynomials -9. FACTORING POLYNOMIALS Use special products and factorization techniques to factor polynomials. Find the domains of radical expressions. Use
6.4 Special Factoring Rules
 6.4 Special Factoring Rules OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor a sum of cubes. By reversing the rules for multiplication
6.4 Special Factoring Rules OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor a sum of cubes. By reversing the rules for multiplication
Solving Quadratic Equations
 9.3 Solving Quadratic Equations by Using the Quadratic Formula 9.3 OBJECTIVES 1. Solve a quadratic equation by using the quadratic formula 2. Determine the nature of the solutions of a quadratic equation
9.3 Solving Quadratic Equations by Using the Quadratic Formula 9.3 OBJECTIVES 1. Solve a quadratic equation by using the quadratic formula 2. Determine the nature of the solutions of a quadratic equation
Higher Education Math Placement
 Higher Education Math Placement Placement Assessment Problem Types 1. Whole Numbers, Fractions, and Decimals 1.1 Operations with Whole Numbers Addition with carry Subtraction with borrowing Multiplication
Higher Education Math Placement Placement Assessment Problem Types 1. Whole Numbers, Fractions, and Decimals 1.1 Operations with Whole Numbers Addition with carry Subtraction with borrowing Multiplication
Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any.
 Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
Algebra II A Final Exam
 Algebra II A Final Exam Multiple Choice Identify the choice that best completes the statement or answers the question. Evaluate the expression for the given value of the variable(s). 1. ; x = 4 a. 34 b.
Algebra II A Final Exam Multiple Choice Identify the choice that best completes the statement or answers the question. Evaluate the expression for the given value of the variable(s). 1. ; x = 4 a. 34 b.
Algebra Practice Problems for Precalculus and Calculus
 Algebra Practice Problems for Precalculus and Calculus Solve the following equations for the unknown x: 1. 5 = 7x 16 2. 2x 3 = 5 x 3. 4. 1 2 (x 3) + x = 17 + 3(4 x) 5 x = 2 x 3 Multiply the indicated polynomials
Algebra Practice Problems for Precalculus and Calculus Solve the following equations for the unknown x: 1. 5 = 7x 16 2. 2x 3 = 5 x 3. 4. 1 2 (x 3) + x = 17 + 3(4 x) 5 x = 2 x 3 Multiply the indicated polynomials
Factoring Polynomials
 UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
Polynomial Operations and Factoring
 Algebra 1, Quarter 4, Unit 4.1 Polynomial Operations and Factoring Overview Number of instructional days: 15 (1 day = 45 60 minutes) Content to be learned Identify terms, coefficients, and degree of polynomials.
Algebra 1, Quarter 4, Unit 4.1 Polynomial Operations and Factoring Overview Number of instructional days: 15 (1 day = 45 60 minutes) Content to be learned Identify terms, coefficients, and degree of polynomials.
What are the place values to the left of the decimal point and their associated powers of ten?
 The verbal answers to all of the following questions should be memorized before completion of algebra. Answers that are not memorized will hinder your ability to succeed in geometry and algebra. (Everything
The verbal answers to all of the following questions should be memorized before completion of algebra. Answers that are not memorized will hinder your ability to succeed in geometry and algebra. (Everything
ALGEBRA 2 CRA 2 REVIEW - Chapters 1-6 Answer Section
 ALGEBRA 2 CRA 2 REVIEW - Chapters 1-6 Answer Section MULTIPLE CHOICE 1. ANS: C 2. ANS: A 3. ANS: A OBJ: 5-3.1 Using Vertex Form SHORT ANSWER 4. ANS: (x + 6)(x 2 6x + 36) OBJ: 6-4.2 Solving Equations by
ALGEBRA 2 CRA 2 REVIEW - Chapters 1-6 Answer Section MULTIPLE CHOICE 1. ANS: C 2. ANS: A 3. ANS: A OBJ: 5-3.1 Using Vertex Form SHORT ANSWER 4. ANS: (x + 6)(x 2 6x + 36) OBJ: 6-4.2 Solving Equations by
Successful completion of Math 7 or Algebra Readiness along with teacher recommendation.
 MODESTO CITY SCHOOLS COURSE OUTLINE COURSE TITLE:... Basic Algebra COURSE NUMBER:... RECOMMENDED GRADE LEVEL:... 8-11 ABILITY LEVEL:... Basic DURATION:... 1 year CREDIT:... 5.0 per semester MEETS GRADUATION
MODESTO CITY SCHOOLS COURSE OUTLINE COURSE TITLE:... Basic Algebra COURSE NUMBER:... RECOMMENDED GRADE LEVEL:... 8-11 ABILITY LEVEL:... Basic DURATION:... 1 year CREDIT:... 5.0 per semester MEETS GRADUATION
Factoring. Factoring Monomials Monomials can often be factored in more than one way.
 Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
15.1 Factoring Polynomials
 LESSON 15.1 Factoring Polynomials Use the structure of an expression to identify ways to rewrite it. Also A.SSE.3? ESSENTIAL QUESTION How can you use the greatest common factor to factor polynomials? EXPLORE
LESSON 15.1 Factoring Polynomials Use the structure of an expression to identify ways to rewrite it. Also A.SSE.3? ESSENTIAL QUESTION How can you use the greatest common factor to factor polynomials? EXPLORE
FOIL FACTORING. Factoring is merely undoing the FOIL method. Let s look at an example: Take the polynomial x²+4x+4.
 FOIL FACTORING Factoring is merely undoing the FOIL method. Let s look at an example: Take the polynomial x²+4x+4. First we take the 3 rd term (in this case 4) and find the factors of it. 4=1x4 4=2x2 Now
FOIL FACTORING Factoring is merely undoing the FOIL method. Let s look at an example: Take the polynomial x²+4x+4. First we take the 3 rd term (in this case 4) and find the factors of it. 4=1x4 4=2x2 Now
Factoring Trinomials of the Form x 2 bx c
 4.2 Factoring Trinomials of the Form x 2 bx c 4.2 OBJECTIVES 1. Factor a trinomial of the form x 2 bx c 2. Factor a trinomial containing a common factor NOTE The process used to factor here is frequently
4.2 Factoring Trinomials of the Form x 2 bx c 4.2 OBJECTIVES 1. Factor a trinomial of the form x 2 bx c 2. Factor a trinomial containing a common factor NOTE The process used to factor here is frequently
Factoring Polynomials
 Factoring a Polynomial Expression Factoring a polynomial is expressing the polynomial as a product of two or more factors. Simply stated, it is somewhat the reverse process of multiplying. To factor polynomials,
Factoring a Polynomial Expression Factoring a polynomial is expressing the polynomial as a product of two or more factors. Simply stated, it is somewhat the reverse process of multiplying. To factor polynomials,
6706_PM10SB_C4_CO_pp192-193.qxd 5/8/09 9:53 AM Page 192 192 NEL
 92 NEL Chapter 4 Factoring Algebraic Epressions GOALS You will be able to Determine the greatest common factor in an algebraic epression and use it to write the epression as a product Recognize different
92 NEL Chapter 4 Factoring Algebraic Epressions GOALS You will be able to Determine the greatest common factor in an algebraic epression and use it to write the epression as a product Recognize different
In this section, you will develop a method to change a quadratic equation written as a sum into its product form (also called its factored form).
 CHAPTER 8 In Chapter 4, you used a web to organize the connections you found between each of the different representations of lines. These connections enabled you to use any representation (such as a graph,
CHAPTER 8 In Chapter 4, you used a web to organize the connections you found between each of the different representations of lines. These connections enabled you to use any representation (such as a graph,
PERT Mathematics Test Review
 PERT Mathematics Test Review Prof. Miguel A. Montañez ESL/Math Seminar Math Test? NO!!!!!!! I am not good at Math! I cannot graduate because of Math! I hate Math! Helpful Sites Math Dept Web Site Wolfson
PERT Mathematics Test Review Prof. Miguel A. Montañez ESL/Math Seminar Math Test? NO!!!!!!! I am not good at Math! I cannot graduate because of Math! I hate Math! Helpful Sites Math Dept Web Site Wolfson
Factoring Trinomials of the Form
 Section 4 6B: Factoring Trinomials of the Form A x 2 + Bx + C where A > 1 by The AC and Factor By Grouping Method Easy Trinomials: 1 x 2 + Bx + C The last section covered the topic of factoring second
Section 4 6B: Factoring Trinomials of the Form A x 2 + Bx + C where A > 1 by The AC and Factor By Grouping Method Easy Trinomials: 1 x 2 + Bx + C The last section covered the topic of factoring second
