How To Fator
|
|
|
- Godwin Henderson
- 3 years ago
- Views:
Transcription
1 CHAPTER hapter 4 > Make the Connetion 4 INTRODUCTION Developing seret odes is big business beause of the widespread use of omputers and the Internet. Corporations all over the world sell enryption systems that are supposed to keep data seure and safe. In 1977, three professors from the Massahusetts Institute of Tehnology developed an enryption system they alled RSA, a name derived from the first letters of their last names. Their seurity ode was based on a number that has 129 digits. They alled the ode RSA-129. For the ode to be broken, the 129-digit number must be fatored into two prime numbers. A data seurity ompany says that people who are using their system are safe beause as yet no truly effiient algorithm for finding prime fators of massive numbers has been found, although one may someday exist. This ompany, hoping to test its enrypting system, now sponsors ontests hallenging people to fator more very large numbers into two prime numbers. RSA-576 up to RSA-2048 are being worked on now. The U.S. government does not allow any odes to be used for whih it does not have the key. The software firms laim that this prohibition is osting them about $60 billion in lost sales beause many ompanies will not buy an enryption system knowing they an be monitored by the U.S. government. Fatoring CHAPTER 4 OUTLINE Chapter 4 :: Pretest An Introdution to Fatoring Fatoring Trinomials of the Form x 2 bx Fatoring Trinomials of the Form ax 2 bx Differene of Squares and Perfet Square Trinomials Strategies in Fatoring Solving Quadrati Equations by Fatoring 433 Chapter 4 :: Summary / Summary Exerises / Self-Test / Cumulative Review :: Chapters
2 4 pretest CHAPTER 4 Name Setion Date This pretest provides a preview of the types of exerises you will enounter in eah setion of this hapter. The answers for these exerises an be found in the bak of the text. If you are working on your own, or ahead of the lass, this pretest an help you identify the setions in whih you should fous more of your time. Answers Fator eah of the following polynomials q 4 20q x 2 12x d 2 21d 14d Fator eah of the following trinomials b 2 2b x 2 10x x 2 14x a 2 7ab 12b 2 Fator eah of the following trinomials ompletely y 2 5y w 2 23w x 2 5xy 21y x 3 7x 2 15x Fator eah of the following polynomials ompletely b p 2 q x 2 12xy 4y xy 2 48x 3 Solve eah of the following equations x 2 11x x 2 5x x 2 7x p 2 18p 0 374
3 4.1 An Introdution to Fatoring < 4.1 Objetives > 1 > Fator out the greatest ommon fator (GCF) 2 > Fator out a binomial GCF 3 > Fator a polynomial by grouping terms Overoming Math Anxiety Hint #5 Working Together How many of your lassmates do you know? Whether you are by nature gregarious or shy, you have muh to gain by getting to know your lassmates. 1. It is important to have someone to all when you miss lass or are unlear on an assignment. 2. Working with another person is almost always benefiial to both people. If you don t understand something, it helps to have someone to ask about it. If you do understand something, nothing ements that understanding more than explaining the idea to another person. 3. Sometimes we need to ommiserate. If an assignment is partiularly frustrating, it is reassuring to find that it is also frustrating for other students. 4. Have you ever thought you had the right answer, but it doesn t math the answer in the text? Frequently the answers are equivalent, but that s not always easy to see. A different perspetive an help you see that. Oasionally there is an error in a textbook (here we are talking about other textbooks). In suh ases it is wonderfully reassuring to find that someone else has the same answer you do. In Chapter 3 you were given fators and asked to find a produt. We are now going to reverse the proess. You will be given a polynomial and asked to find its fators. This is alled fatoring. We start with an example from arithmeti. To multiply 5 7, you write To fator 35, you would write Fatoring is the reverse of multipliation. Now let s look at fatoring in algebra. You have used the distributive property as a(b ) ab a 375
4 376 CHAPTER 4 Fatoring NOTE 3 and x 5are the fators of 3x 15. For instane, 3(x 5) 3x 15 To use the distributive property in fatoring, we reverse that property as ab a a(b ) The property lets us fator out the ommon fator a from the terms of ab a. To use this in fatoring, the first step is to see whether eah term of the polynomial has a ommon monomial fator. In our earlier example, 3x 15 3 x 3 5 Common fator NOTES Again, fatoring is the reverse of multipliation. So, by the distributive property, 3x 15 3(x 5) The original terms are eah divided by the greatest ommon fator to determine the terms in parentheses. To hek this, multiply 3(x 5). Multiplying Fatoring out the GCF is the first method to try in any of the fatoring problems we will disuss. Definition Greatest Common Fator < Objetive 1 > Example 1 3(x 5) 3x 15 Fatoring The first step in fatoring is to identify the greatest ommon fator (GCF) of a set of terms. This fator is the produt of the largest ommon numerial oeffiient and the largest ommon fator of eah variable. The greatest ommon fator (GCF) of a polynomial is the fator that is the produt of the largest ommon numerial oeffiient fator of the polynomial and eah variable with the smallest exponent in any term. Finding the GCF Find the GCF for eah set of terms. (a) 9 and 12 The largest number that is a fator of both is 3. (b) 10, 25, 150 The GCF is 5. () x 4 and x 7 x 4 x x x x x 7 x x x x x x x The largest power that divides both terms is x 4. (d) 12a 3 and 18a 2 12a a a a 18a a a The GCF is 6a 2.
5 An Introdution to Fatoring SECTION Chek Yourself 1 Find the GCF for eah set of terms. (a) 14, 24 (b) 9, 27, 81 () a 9, a 5 (d) 10x 5, 35x 4 Step by Step To Fator a Monomial from a Polynomial Step 1 Step 2 Step 3 Find the GCF for all the terms. Use the GCF to fator eah term and then apply the distributive property. Mentally hek your fatoring by multipliation. Cheking your answer is always important and perhaps is never easier than after you have fatored. Example 2 Finding the GCF of a Binomial NOTE It is also true that 6a 4 ( 18a 2 ) 3a(2a 3 ( 6a)). However, this is not ompletely fatored. Do you see why? You want to find the ommon monomial fator with the largest possible oeffiient and the largest exponent, in this ase 6a 2. (a) Fator 8x 2 12x. The largest ommon numerial fator of 8 and 12 is 4, and x is the ommon variable fator with the largest power. So 4x is the GCF. Write 8x 2 12x 4x 2x 4x 3 Chek Yourself 2 GCF Now, by the distributive property, we have 8x 2 12x 4x(2x 3) It is always a good idea to hek your answer by multiplying to make sure that you get the original polynomial. Try it here. Multiply 4x by 2x 3. (b) Fator 6a 4 18a 2. The GCF in this ase is 6a 2. Write 6a 4 ( 18a 2 ) 6a 2 a 2 6a 2 ( 3) GCF Again, using the distributive property yields 6a 4 18a 2 6a 2 (a 2 3) You should hek this by multiplying. Fator eah of the following polynomials. (a) 5x 20 (b) 6x 2 24x () 10a 3 15a 2
6 378 CHAPTER 4 Fatoring The proess is exatly the same for polynomials with more than two terms. Consider Example 3. Example 3 Finding the GCF of a Polynomial (a) Fator 5x 2 10x 15. NOTES The GCF is 5. 5x 2 10x 15 5 x 2 5 2x 5 3 5(x 2 2x 3) (b) Fator 6ab 9ab 2 15a 2. 6ab 9ab 2 15a 2 3a 2b 3a 3b 2 3a 5a GCF The GCF is 3a. 3a(2b 3b 2 5a) () Fator 4a 4 12a 3 20a 2. 4a 4 12a 3 20a 2 4a 2 a 2 4a 2 3a 4a 2 5 GCF The GCF is 4a 2. In eah of these examples, you should hek the result by multiplying the fators. < Objetive 2 > NOTE Example 4 Beause of the ommutative property, the fators an be written in either order. 4a 2 (a 2 3a 5) (d) Fator 6a 2 b 9ab 2 3ab. Mentally note that 3, a, and b are fators of eah term, so 6a 2 b 9ab 2 3ab 3ab(2a 3b 1) Chek Yourself 3 We an have two or more terms that have a binomial fator in ommon, as is the ase in Example 4. GCF Fator eah of the following polynomials. (a) 8b 2 16b 32 (b) 4xy 8x 2 y 12x 3 () 7x 4 14x 3 21x 2 (d) 5x 2 y 2 10xy 2 15x 2 y Finding a Common Fator (a) Fator 3x(x y) 2(x y). We see that the binomial x y is a ommon fator and an be removed. 3x(x y) 2(x y) (x y) 3x (x y) 2 (x y)(3x 2) (b) Fator 3x 2 (x y) 6x(x y) 9(x y).
7 An Introdution to Fatoring SECTION We note that here the GCF is 3(x y). Fatoring as before, we have 3(x y)(x 2 2x 3). Chek Yourself 4 Completely fator eah of the polynomials. (a) 7a(a 2b) 3(a 2b) (b) 4x 2 (x y) 8x(x y) 16(x y) Some polynomials an be fatored by grouping the terms and finding ommon fators within eah group. Suh a proess is alled fatoring by grouping and will be explored now. In Example 4, we looked at the expression 3x(x y) 2(x y) and found that we ould fator out the ommon binomial, (x y), giving us (x y)(3x 2) That tehnique will be used in Example 5. < Objetive 3 > NOTE Example 5 Note that our example has four terms. That is a lue for trying the fatoring by grouping method. Fatoring by Grouping Terms Suppose we want to fator the polynomial ax ay bx by As you an see, the polynomial has no ommon fators. However, look at what happens if we separate the polynomial into two groups of two terms. ax ay bx by ax ay bx by (1) (2) Now eah group has a ommon fator, and we an write the polynomial as a(x y) b(x y) In this form, we an see that x y is the GCF. Fatoring out x y, we get a(x y) b(x y) (x y)(a b) Chek Yourself 5 Use the fatoring by grouping method. x 2 2xy 3x 6y Be partiularly areful of your treatment of algebrai signs when applying the fatoring by grouping method. Consider Example 6.
8 380 CHAPTER 4 Fatoring Example 6 Fatoring by Grouping Terms Fator 2x 3 3x 2 6x 9. We group the polynomial as follows. NOTE 2x 3 3x 2 6x 9 (1) (2) Fator out the ommon fator of 3 from the seond two terms. 9 ( 3)( 3) x 2 (2x 3) 3(2x 3) (2x 3)(x 2 3) Chek Yourself 6 Fator by grouping. 3y 3 2y 2 6y 4 It may also be neessary to hange the order of the terms as they are grouped. Look at Example 7. Example 7 Fatoring by Grouping Terms Fator x 2 6yz 2xy 3xz. Grouping the terms as before, we have x 2 6yz 2xy 3xz (1) (2) Do you see that we have aomplished nothing beause there are no ommon fators in the first group? We an, however, rearrange the terms to write the original polynomial as x 2 2xy 3xz 6yz (1) (2) x(x 2y) 3z(x 2y) (x 2y)(x 3z) We an now fator out the ommon fator of x 2y in group (1) and group (2). Note: It is often true that the grouping an be done in more than one way. The fatored form will be the same. Chek Yourself 7 We an write the polynomial of Example 7 as x 2 3xz 2xy 6yz Fator and verify that the fatored form is the same in either ase.
9 An Introdution to Fatoring SECTION Chek Yourself ANSWERS 1. (a) 2; (b) 9; () a 5 ; (d) 5x 4 2. (a) 5(x 4); (b) 6x(x 4); () 5a 2 (2a 3) 3. (a) 8(b 2 2b 4); (b) 4x( y 2xy 3x 2 ); () 7x 2 (x 2 2x 3); (d) 5xy(xy 2y 3x) 4. (a) (a 2b)(7a 3); (b) 4(x y)(x 2 2x 4) 5. (x 2y)(x 3) 6. (3y 2)( y 2 2) 7. (x 3z)(x 2y) Reading Your Text The following fill-in-the-blank exerises are designed to ensure that you understand some of the key voabulary used in this setion. SECTION 4.1 (a) The GCF of a polynomial is the fator that is the produt of the numerial oeffiient fator of the polynomial and eah variable with the smallest exponent in any term. b (b) To fator a monomial from a polynomial, first find the GCF for all of the. () Some polynomials an be fatored by grouping the terms and finding ommon within eah group. (d) It is often true that grouping an be done in more than one way. The fatored form will be the.
10 4.1 exerises Basi Skills Advaned Skills Voational-Tehnial Appliations Calulator/Computer Above and Beyond Getting Ready < Objetive 1 > Find the greatest ommon fator for eah of the following sets of terms. Boost your grade at mathzone.om! > Pratie Problems > NetTutor > Self-Tests > e-professors > Videos 1. 10, , , 32, , 33, 132 Name Setion Date 5. x 2, x 5 6. y 7, y 9 7. a 3, a 6, a 9 8. b 4, b 6, b 8 Answers x 4, 10x y 9, 24y a 4, 6a 6, 10a b 3, 6b 5, 12b x 2 y, 12xy 2, 15x 2 y a 3 b 2, 18a 2 b 3, 6a 4 b ab 3, 10a 2 b, 25b x 2, 3xy 3, 6y a 2 b 2, 9ab 2 2, 6a 2 b x 3 y 2 z 3, 27x 4 y 2 z 3, 81xy 2 z > Videos 19. (x y) 2, (x y) (a b) 4, 4(a b) 3 Fator eah of the following polynomials a x m 32n 24. 7p 21q m n s 2 5s y 2 6y 382 SECTION 4.1
11 4.1 exerises x 2 12x b 2 14b Answers a 3 25a b 4 24b pq 18p 2 q 34. 8ab 24ab x 2 18x a 2 21a a 3 6a 2 12a 38. 5x 3 15x 2 25x m 9mn 12mn s 6st 14st r 3 s 2 25r 2 s 2 15r 2 s x 2 y 3 35x 2 y 2 42x 3 y > Videos a 5 15a 4 21a 3 27a 44. 8p 6 40p 4 24p 3 16p 2 Basi Skills Advaned Skills Voational-Tehnial Appliations Calulator/Computer Above and Beyond Getting Ready Complete eah of the following statements with never, sometimes, or always. 45. The GCF for two numbers is a prime number. 46. The GCF of a polynomial inludes variables. 47. Multiplying the result of fatoring will result in the original polynomial. 48. Fatoring a negative number from a negative term will result in a negative term. < Objetive 2 > Fator out the binomial in eah expression. 49. a(a 2) 3(a 2) 50. b(b 5) 2(b 5) 51. x(x 2) 3(x 2) > Videos 52. y( y 5) 3( y 5) SECTION
12 4.1 exerises Answers < Objetive 3 > Fator eah polynomial by grouping the first two terms and the last two terms. 53. x 3 4x 2 3x x 3 6x 2 2x a 3 3a 2 5a x 3 2x 2 9x x 3 5x 2 2x x 5 x 3 2x x 4 2x 3 3x 6 > Videos 60. x 3 4x 2 2x 8 Fator eah polynomial ompletely by fatoring out any ommon fators and then fator by grouping. Do not ombine like terms x 6 xy 2y 62. 2x 10 xy 5y 63. ab a b 2 b > Videos 64. ax 2a bx 2b x 2 2xy 3x 2y 66. xy 5y 2 x 5y 67. 5s 2 15st 2st 6t a 3 3ab 2 2a 2 b 2b x 3 6x 2 y x 2 y 2xy p 4 3p 3 q 2p 3 q 3p 2 q 2 > Videos Basi Skills Advaned Skills Voational-Tehnial Appliations Calulator/Computer Above and Beyond Getting Ready 71. ALLIED HEALTH A patient s protein seretion amount, in milligrams per day, is reorded over several days. Based on these observations, lab tehniians determine that the polynomial t 3 6t 2 11t 66 provides a good approximation of the patient s protein seretion amounts t days after testing begins. Fator this polynomial. g 72. ALLIED HEALTH The onentration, in mirograms per milliliter of the ml antibioti hlorampheniol is given by 8t 2 2t 3, in whih t is the number of hours after the drug is taken. Fator this polynomial. 73. MANUFACTURING TECHNOLOGY Polymer pellets need to be as perfetly round as possible. In order to avoid flat spots from forming during the hardening proess, the pellets are kept off a surfae by blasts of air. The height of a pellet above the surfae t seonds after a blast is given by v 0 t 4.9t 2. Fator this expression. 384 SECTION 4.1
13 4.1 exerises 74. INFORMATION TECHNOLOGY The total time to transmit a paket is given by the expression d 2p, in whih d is the quotient of the distane and the propagation veloity and p is the quotient of the size of the paket and the information transfer rate. How long will it take to transmit a 1,500-byte paket 10 meters on an Ethernet if the information transfer rate is 100 MB per seond and the propagation veloity is m/s? Answers Basi Skills Advaned Skills Voational-Tehnial Appliations Calulator/Computer Above and Beyond Getting Ready 75. The GCF of 2x 6 is 2. The GCF of 5x 10 is 5. Find the GCF of the produt (2x 6)(5x 10) The GCF of 3z 12 is 3. The GCF of 4z 8 is 4. Find the GCF of the produt (3z 12)(4z 8) The GCF of 2x 3 4x is 2x. The GCF of 3x 6 is 3. Find the GCF of the produt (2x 3 4x)(3x 6) State, in a sentene, the rule that exerises 75 to 77 illustrated. Find the GCF of eah produt. 79. (2a 8)(3a 6) 80. (5b 10)(2b 4) 81. (2x 2 5x)(7x 14) 82. (6y 2 3y)( y 7) 83. GEOMETRY The area of a retangle with width t is given by 33t t 2. Fator the expression and determine the length of the retangle in terms of t. 84. GEOMETRY The area of a retangle of length x is given by 3x 2 5x. Find the width of the retangle. 85. NUMBER PROBLEM For enturies, mathematiians have found fatoring numbers into prime fators a fasinating subjet. A prime number is a number that annot be written as a produt of any numbers but 1 and itself. The list of primes begins with 2 beause 1 is not onsidered a prime number and then goes on: 3, 5, 7, 11,... What are the first 10 primes? What are the primes less than 100? If you list the numbers from 1 to 100 and then ross out all numbers that are multiples of 2, 3, 5, and 7, what is left? Are all the numbers not rossed out prime? Write a paragraph to explain why this might be so. You might want to investigate the Sieve of Eratosthenes, a system from 230 B.C.E. for finding prime numbers SECTION
14 4.1 exerises Answers (a) (b) 86. NUMBER PROBLEM If we ould make a list of all the prime numbers, what number would be at the end of the list? Beause there are an infinite number of prime numbers, there is no largest prime number. But is there some formula that will give us all the primes? Here are some formulas proposed over the enturies: n 2 n 17 2n 2 29 n 2 n 11 In all these expressions, n 1, 2, 3, 4,..., that is, a positive integer beginning with 1. Investigate these expressions with a partner. Do the expressions give prime numbers when they are evaluated for these values of n? Do the expressions give every prime in the range of resulting numbers? Can you put in any positive number for n? () (d) (e) 87. NUMBER PROBLEM How are primes used in oding messages and for seurity? Work together to deode the messages. The messages are oded using this ode: After the numbers are fatored into prime fators, the power of 2 gives the number of the letter in the alphabet. This ode would be easy for a ode breaker to figure out. Can you make up ode that would be more diffiult to break? hapter 4 > Make the Connetion (f) (a) , , , 1760, 460, , 336 (b) , 286, 4608, , 1344, 98304, , 352, , () Code a message using this rule. Exhange your message with a partner to deode it. Basi Skills Advaned Skills Voational-Tehnial Appliations Calulator/Computer Above and Beyond Getting Ready Multiply. (a) (a 1)(a 4) (b) (x 1)(x 3) () (x 3)(x 3) (d) ( y 11)( y 3) (e) (x 5)(x 7) (f) ( y 1)( y 13) Answers x 2 7. a x a xy 15. 5b 17. 3ab (x y) (2a 1) 23. 8(3m 4n) 25. 4(3m 2) 27. 5s(2s 1) x(x 1) 31. 5a 2 (3a 5) 33. 6pq(1 3p) 35. 6(x 2 3x 5) 37. 3a(a 2 2a 4) 39. 3m(2 3n 4n 2 ) 41. 5r 2 s 2 (2r 5 3s) 43. 3a(3a 4 5a 3 7a 2 9) 45. sometimes 47. always 49. (a 3)(a 2) 51. (x 3)(x 2) 53. (x 4)(x 2 3) 55. (a 3)(a 2 5) 57. (2x 1)(5x 2 1) 59. (x 2)(x 3 3) 61. (x 2)(3 y) 63. (b )(a b) 65. (x 1)(3x 2y) 67. (s 3t)(5s 2t) 69. x(x 2y)(3x y) 71. (t 6)( t 2 11) 73. t(v 0 4.9t) x x 83. t(33 t); 33 t 85. Above and Beyond 87. Above and Beyond (a) a 2 3a 4 (b) x 2 2x 3 () x 2 6x 9 (d) y 2 8y 33 (e) x 2 12x 35 (f) y 2 12y SECTION 4.1
15 4.2 Fatoring Trinomials of the Form x 2 bx < 4.2 Objetives > 1 > Fator a trinomial of the form x 2 bx 2 > Fator a trinomial ontaining a ommon fator NOTE The proess used to fator here is frequently alled the trial-and-error method. You ll see the reason for the name as you work through this setion. You learned how to find the produt of any two binomials by using the FOIL method in Setion 3.4. Beause fatoring is the reverse of multipliation, we now want to use that pattern to find the fators of ertain trinomials. Reall that when we multiply the binomials x 2 and x 3, our result is (x 2)(x 3) x 2 5x 6 > CAUTION Not every trinomial an be written as the produt of two binomials. The produt The sum of The produt of the first the produts of the last terms (x x). of the outer terms (2 3). and inner terms (3x and 2x). Suppose now that you are given x 2 5x 6 and want to find its fators. First, you know that the fators of a trinomial may be two binomials. So write x 2 5x 6 ( )( ) Beause the first term of the trinomial is x 2, the first terms of the binomial fators must be x and x. We now have x 2 5x 6 (x )(x ) The produt of the last terms must be 6. Beause 6 is positive, the fators must have like signs. Here are the possibilities: ( 1)( 6) ( 2)( 3) This means that the possible fators of the trinomial are (x 1)(x 6) (x 2)(x 3) (x 1)(x 6) (x 2)(x 3) 387
16 388 CHAPTER 4 Fatoring How do we tell whih is the orret pair? From the FOIL pattern we know that the sum of the outer and inner produts must equal the middle term of the trinomial, in this ase 5x. This is the ruial step! Possible Fatorizations Middle Terms (x 1)(x 6) 7x (x 2)(x 3) 5x (x 1)(x 6) 7x (x 2)(x 3) 5x The orret middle term! So we know that the orret fatorization is x 2 5x 6 (x 2)(x 3) Are there any lues so far that will make this proess quiker? Yes, there is an important one that you may have spotted. We started with a trinomial that had a positive middle term and a positive last term. The negative pairs of fators for 6 led to negative middle terms. So you don t need to bother with the negative fators if the middle term and the last term of the trinomial are both positive. < Objetive 1 > NOTE Example 1 If you are wondering why we didn t list (x 8)(x 1) as a possibility, remember that multipliation is ommutative. The order doesn t matter! NOTE The fator-pairs of 20 are Fatoring a Trinomial (a) Fator x 2 9x 8. Beause the middle term and the last term of the trinomial are both positive, onsider only the positive fators of 8, that is, or Possible Fatorizations (x 1)(x 8) 9x (x 2)(x 4) 6x Middle Terms Beause the first pair gives the orret middle term, x 2 9x 8 (x 1)(x 8) (b) Fator x 2 12x 20. Possible Fatorizations (x 1)(x 20) 21x (x 2)(x 10) 12x (x 4)(x 5) 9x So x 2 12x 20 (x 2)(x 10) Middle Terms
17 Fatoring Trinomials of the Form x 2 bx SECTION Chek Yourself 1 Fator. (a) x 2 6x 5 (b) x 2 10x 16 What if the middle term of the trinomial is negative but the first and last terms are still positive? Consider Positive Positive x 2 11x 18 Negative Beause we want a negative middle term ( 11x) and a positive last term, we use two negative fators for 18. Reall that the produt of two negative numbers is positive. Example 2 Fatoring a Trinomial NOTE The negative fators of 18 are 18 ( 1)( 18) ( 2)( 9) ( 3)( 6) NOTE The negative fators of 12 are 12 ( 1)( 12) ( 2)( 6) ( 3)( 4) (a) Fator x 2 11x 18. Possible Fatorizations (x 1)(x 18) 19x (x 2)(x 9) 11x (x 3)(x 6) 9x So x 2 11x 18 (x 2)(x 9) (b) Fator x 2 13x 12. Possible Fatorizations (x 1)(x 12) 13x (x 2)(x 6) 8x (x 3)(x 4) 7x Middle Terms Middle Terms So x 2 13x 12 (x 1)(x 12) A few more lues: We have listed all the possible fators in the above examples. It really isn t neessary. Just work until you find the right pair. Also, with pratie muh of this work an be done mentally.
18 390 CHAPTER 4 Fatoring Chek Yourself 2 Fator. (a) x 2 10x 9 (b) x 2 10x 21 Now let s look at the proess of fatoring a trinomial whose last term is negative. For instane, to fator x 2 2x 15, we an start as before: x 2 2x 15 (x?)(x?) Note that the produt of the last terms must be negative ( 15 here). So we must hoose fators that have different signs. What are our hoies for the fators of 15? 15 (1)( 15) ( 1)(15) (3)( 5) ( 3)(5) NOTE Another lue: Some students prefer to look at the list of numerial fators rather than looking at the atual algebrai fators. Here you want the pair whose sum is 2, the oeffiient of the middle term of the trinomial. That pair is 3 and 5, whih leads us to the orret fators. NOTE Example 3 You may be able to pik the fators diretly from this list. You want the pair whose sum is 5 (the oeffiient of the middle term). This means that the possible fators and the resulting middle terms are Possible Fatorizations (x 1)(x 15) 14x (x 1)(x 15) 14x (x 3)(x 5) 2x (x 3)(x 5) 2x Middle Terms So x 2 2x 15 (x 3)(x 5). Let s work through some examples in whih the onstant term is negative. Fatoring a Trinomial (a) Fator x 2 5x 6. First, list the fators of 6. Of ourse, one fator will be positive, and one will be negative. 6 (1)( 6) ( 1)(6) (2)( 3) ( 2)(3)
19 Fatoring Trinomials of the Form x 2 bx SECTION For the trinomial, then, we have Possible Fatorizations Middle Terms (x 1)(x 6) 5x (x 1)(x 6) 5x (x 2)(x 3) x (x 2)(x 3) x So x 2 5x 6 (x 1)(x 6). (b) Fator x 2 8xy 9y 2. The proess is similar if two variables are involved in the trinomial. Start with x 2 8xy 9y 2 (x?)(x?). 9y 2 ( y)(9y) ( y)( 9y) (3y)( 3y) The produt of the last terms must be 9y 2. < Objetive 2 > Example 4 Possible Fatorizations (x y)(x 9y) 8xy (x y)(x 9y) 8xy (x 3y)(x 3y) 0 So x 2 8xy 9y 2 (x y)(x 9y). Chek Yourself 3 Fator. Middle Terms (a) x 2 7x 30 (b) x 2 3xy 10y 2 As we pointed out in Setion 4.1, any time that there is a ommon fator, that fator should be fatored out before we try any other fatoring tehnique. Consider Example 4. Fatoring a Trinomial (a) Fator 3x 2 21x 18. 3x 2 21x 18 3(x 2 7x 6) Fator out the ommon fator of 3.
20 392 CHAPTER 4 Fatoring We now fator the remaining trinomial. For x 2 7x 6: Possible Fatorizations Middle Terms > CAUTION (x 1)(x 6) 7x (x 2)(x 3) 5x The orret middle term A ommon mistake is to forget to write the 3 that was fatored out as the first step. So 3x 2 21x 18 3(x 1)(x 6). (b) Fator 2x 3 16x 2 40x. 2x 3 16x 2 40x 2x(x 2 8x 20) Fator out the ommon fator of 2x. To fator the remaining trinomial, whih is x 2 8x 20, we have NOTE Possible Fatorizations Middle Terms One we have found the desired middle term, there is no need to ontinue. (x 2)(x 10) 8x (x 2)(x 10) 8x The orret middle term So 2x 3 16x 2 40x 2x(x 2)(x 10). Chek Yourself 4 Fator. (a) 3x 2 3x 36 (b) 4x 3 24x 2 32x One further omment: Have you wondered whether all trinomials are fatorable? Look at the trinomial x 2 2x 6 The only possible fators are (x 1)(x 6) and (x 2)(x 3). Neither pair is orret (you should hek the middle terms), and so this trinomial does not have fators with integer oeffiients. Of ourse, there are many other trinomials that annot be fatored. Can you find one? Chek Yourself ANSWERS 1. (a) (x 1)(x 5); (b) (x 2)(x 8) 2. (a) (x 9)(x 1); (b) (x 3)(x 7) 3. (a) (x 10)(x 3); (b) (x 2y)(x 5y) 4. (a) 3(x 4)(x 3); (b) 4x(x 2)(x 4)
21 Fatoring Trinomials of the Form x 2 bx SECTION Reading Your Text The following fill-in-the-blank exerises are designed to ensure that you understand some of the key voabulary used in this setion. SECTION 4.2 (a) Fatoring is the reverse of. (b) From the FOIL pattern, we know that the sum of the inner and outer produts must equal the term of the trinomial. () The produt of two negative fators is always. b (d) Some trinomials do not have with integer oeffiients.
22 4.2 exerises Basi Skills Advaned Skills Voational-Tehnial Appliations Calulator/Computer Above and Beyond Getting Ready < Objetive 1 > Complete eah of the following statements. Boost your grade at mathzone.om! > Pratie Problems > NetTutor > Self-Tests > e-professors > Videos 1. x 2 8x 15 (x 3)( ) 2. y 2 3y 18 (y 6)( ) 3. m 2 8m 12 (m 2)( ) 4. x 2 10x 24 (x 6)( ) Name Setion Date 5. p 2 8p 20 ( p 2)( ) 6. a 2 9a 36 (a 12)( ) Answers 7. x 2 16x 64 (x 8)( ) 8. w 2 12w 45 (w 3)( ) x 2 7xy 10y 2 (x 2y)( ) > Videos a 2 18ab 81b 2 (a 9b)( ) Fator eah of the following trinomials ompletely. 11. x 2 8x x 2 11x x 2 11x y 2 y s 2 13s b 2 14b a 2 2a x 2 17x x 2 8x x 2 7x m 2 3m 28 > Videos 22. a 2 10a x 2 6x x 2 11x SECTION 4.2
23 4.2 exerises 25. x 2 14x s 2 4s 32 Answers 27. p 2 10p x 2 11x x 2 5x a 2 2a t 2 4t x 2 7xy 10y x 2 8xy 12y a 2 ab 42b m 2 8mn 16n 2 > Videos 37. x 2 13xy 40y r 2 9rs 36s x 2 2xy 8y u 2 6uv 55v m 2 10mn n m 2 16mn n 2 Basi Skills Advaned Skills Voational-Tehnial Appliations Calulator/Computer Above and Beyond Getting Ready Determine whether eah of the following statements is true or false. 43. Fatoring is the reverse of division. 44. From the FOIL pattern, we know that the sum of the inner and outer produts must equal the middle term of the trinomial. 45. The sum of two negative fators is always negative. 46. Every trinomial has integer oeffiients. < Objetive 2 > Fator eah of the following trinomials ompletely a 2 3a r 3 7r 2 18r 50. m 3 5m 2 14m SECTION
24 4.2 exerises 51. 2x 3 20x 2 48x 52. 3p 3 48p 2 108p Answers x 2 y 9xy 2 36y 3 > Videos 54. 4s 4 20s 3 t 96s 2 t m 3 29m 2 n 120mn a 3 52a 2 b 96ab Basi Skills Advaned Skills Voational-Tehnial Appliations Calulator/Computer Above and Beyond Getting Ready MANUFACTURING TECHNOLOGY The shape of a beam loaded with a single onentrated load is desribed by the expression Fator the numerator, x (x 2 64) (a) (b) () (d) (e) (f) (g) (h) 58. ALLIED HEALTH The onentration, in mirograms per milliliter (mg/ml), of Vanoin, an antibioti used to treat peritonitis, is given by the negative of the polynomial t 2 8t 20, where t is the number of hours sine the drug was administered via intravenous injetion. Write this given polynomial in fatored form. Basi Skills Advaned Skills Voational-Tehnial Appliations Calulator/Computer Above and Beyond Getting Ready Find all positive values for k for whih eah of the following an be fatored. 59. x 2 kx x 2 kx 17 > Videos 61. x 2 kx x 2 kx x 2 3x k 64. x 2 5x k 65. x 2 2x k 66. x 2 x k Basi Skills Advaned Skills Voational-Tehnial Appliations Calulator/Computer Above and Beyond Getting Ready Multiply. (a) (2x 1)(2x 3) (b) (3a 1)(a 4) () (x 4)(2x 3) (d) (2w 11)(w 2) (e) (y 5)(2y 9) (f) (2x 1)(x 12) (g) ( p 9)(2p 5) (h) (3a 5)(2a 4) 396 SECTION 4.2
25 4.2 exerises Answers 1. x 5 3. m 6 5. p x 8 9. x 5y 11. (x 3)(x 5) 13. (x 4)(x 7) 15. (s 3)(s 10) 17. (a 8)(a 6) 19. (x 1)(x 7) 21. (m 7)(m 4) 23. (x 4)(x 10) 25. (x 7)(x 7) 27. ( p 12)( p 2) 29. (x 11)(x 6) 31. ( 4)( 15) 33. (x 2y)(x 5y) 35. (a 6b)(a 7b) 37. (x 5y)(x 8y) 39. (x 2y)(x 4y) 41. (5m n)(5m n) 43. False 45. True 47. 3(a 6)(a 7) 49. r(r 2)(r 9) 51. 2x(x 12)(x 2) 53. y(x 3y)(x 12y) 55. m(m 5n)(m 24n) 57. (x 8)(x 8) 59. 8, 10, or , 8, 15, 24,... (a) 4x 2 4x 3 (b) 3a 2 11a 4 () 2x 2 11x 12 (d) 2w 2 7w 22 (e) 2y 2 19y 45 (f) 2x 2 23x 12 (g) 2p 2 23p 45 (h) 6a 2 2a 20 SECTION
26 4.3 Fatoring Trinomials of the Form ax 2 bx < 4.3 Objetives > 1 > Fator a trinomial of the form ax 2 bx 2 > Completely fator a trinomial 3 > Use the a test to determine fatorability 4 > Use the results of the a test to fator a trinomial Fatoring trinomials is more time-onsuming when the oeffiient of the first term is not 1. Look at the following multipliation. (5x 2)(2x 3) 10x 2 19x 6 Property Sign Patterns for Fatoring Trinomials < Objetive 1 > Example 1 Fators Fators of 10x 2 of 6 Do you see the additional problem? We must onsider all possible fators of the first oeffiient (10 in our example) as well as those of the third term (6 in our example). There is no easy way out! You need to form all possible ombinations of fators and then hek the middle term until the proper pair is found. If this seems a bit like guesswork, it is. In fat, some all this proess fatoring by trial and error. We an simplify the work a bit by reviewing the sign patterns found in Setion If all terms of a trinomial are positive, the signs between the terms in the binomial fators are both plus signs. 2. If the third term of the trinomial is positive and the middle term is negative, the signs between the terms in the binomial fators are both minus signs. 3. If the third term of the trinomial is negative, the signs between the terms in the binomial fators are opposite (one is and one is ). Fatoring a Trinomial Fator 3x 2 14x 15. First, list the possible fators of 3, the oeffiient of the first term Now list the fators of 15, the last term
27 Fatoring Trinomials of the Form ax 2 bx SECTION Beause the signs of the trinomial are all positive, we know any fators will have the form (_x _)(_x _) The produt of the numbers in the last blanks must be 15. The produt of the numbers in the first blanks must be 3. So the following are the possible fators and the orresponding middle terms: Possible Fatorizations Middle Terms NOTE Take the time to multiply the binomial fators. This habit will ensure that you have an expression equivalent to the original problem. (x 1)(3x 15) 18x (x 15)(3x 1) 46x (3x 3)(x 5) 18x (3x 5)(x 3) 14x The orret middle term So 3x 2 14x 15 (3x 5)(x 3) Example 2 Chek Yourself 1 Fator. (a) 5x 2 14x 8 (b) 3x 2 20x 12 Fatoring a Trinomial Fator 4x 2 11x 6. Beause only the middle term is negative, we know the fators have the form (_x _)(_x _) Both signs are negative. Now look at the fators of the first oeffiient and the last term This gives us the possible fators: Possible Fatorizations Middle Terms (x 1)(4x 6) 10x (x 6)(4x 1) 25x (x 2)(4x 3) 11x The orret middle term
28 400 CHAPTER 4 Fatoring RECALL Again, at least mentally, hek your work by multiplying the fators. Note that, in this example, we stopped as soon as the orret pair of fators was found. So 4x 2 11x 6 (x 2)(4x 3) Chek Yourself 2 Fator. (a) 2x 2 9x 9 (b) 6x 2 17x 10 Next, we will fator a trinomial whose last term is negative. Example 3 Fatoring a Trinomial Fator 5x 2 6x 8. Beause the last term is negative, the fators have the form (_x _)(_x _) Consider the fators of the first oeffiient and the last term. Example 4 5 = = 1 8 = 2 4 The possible fators are then Possible Fatorizations (x 1)(5x 8) 3x (x 8)(5x 1) 39x (5x 1)(x 8) 39x (5x 8)(x 1) 3x (x 2)(5x 4) 6x Middle Terms Again we stop as soon as the orret pair of fators is found. 5x 2 6x 8 (x 2)(5x 4) Chek Yourself 3 Fator 4x 2 5x 6. The same proess is used to fator a trinomial with more than one variable. Fatoring a Trinomial Fator 6x 2 7xy 10y 2.
29 Fatoring Trinomials of the Form ax 2 bx SECTION The form of the fators must be (_x _ y)(_x _ y) The signs are opposite beause the last term is negative. The produt of the first terms is an x 2 term. The produt of the seond terms is a y 2 term. Again look at the fators of the first and last oeffiients NOTE Be ertain that you have a pattern that mathes up every possible pair of oeffiients. Possible Fatorizations (x y)(6x 10y) 4xy (x 10y)(6x y) 59xy (6x y)(x 10y) 59xy (6x 10y)(x y) 4xy (x 2y)(6x 5y) 7xy Middle Terms Example 5 One more, we stop as soon as the orret fators are found. 6x 2 7xy 10y 2 (x 2y)(6x 5y) Chek Yourself 4 Fator 15x 2 4xy 4y 2. Example 5 illustrates a speial kind of trinomial alled a perfet square trinomial. Fatoring a Trinomial Fator 9x 2 12xy 4y 2. Beause all terms are positive, the form of the fators must be (_x _y)(_x _y) Consider the fators of the first and last oeffiients Possible Fatorizations (x y)(9x 4y) 13xy (x 4y)(9x y) 37xy (3x 2y)(3x 2y) 12xy Middle Terms
30 402 CHAPTER 4 Fatoring NOTE Perfet square trinomials an be fatored by using previous methods. Reognizing the speial pattern simply saves time. So 9x 2 12xy 4y 2 (3x 2y)(3x 2y) (3x 2y) 2 Square 2(3x)(2y) Square of 3x of 2y This trinomial is the result of squaring a binomial, thus the speial name of perfet square trinomial. Chek Yourself 5 Fator. (a) 4x 2 28x 49 (b) 16x 2 40xy 25y 2 Before looking at Example 6, review one important point from Setion 4.2. Reall that when you fator trinomials, you should not forget to look for a ommon fator as the first step. If there is a ommon fator, fator it out and then fator the remaining trinomial as before. < Objetive 2 > NOTE Example 6 If you don t see why this is true, use your penil to work it out before you move on! Example 7 Fatoring a Trinomial Fator 18x 2 18x 4. First look for a ommon fator in all three terms. Here that fator is 2, so write 18x 2 18x 4 2(9x 2 9x 2) By our earlier methods, we an fator the remaining trinomial as 9x 2 9x 2 (3x 1)(3x 2) So 18x 2 18x 4 2(3x 1)(3x 2) Fator Chek Yourself 6 Fator 16x 2 44x 12. Don t forget the 2 that was fatored out! Now look at an example in whih the ommon fator inludes a variable. Fatoring a Trinomial 6x 3 10x 2 4x The ommon fator is 2x.
31 Fatoring Trinomials of the Form ax 2 bx SECTION So 6x 3 10x 2 4x 2x(3x 2 5x 2) RECALL Be ertain to inlude the monomial fator. Beause 3x 2 5x 2 (3x 1)(x 2) we have 6x 3 10x 2 4x 2x(3x 1)(x 2) Chek Yourself 7 Fator 6x 3 27x 2 30x. You have now had a hane to work with a variety of fatoring tehniques. Your suess in fatoring polynomials depends on your ability to reognize when to use whih tehnique. Here are some guidelines to help you apply the fatoring methods you have studied in this hapter. Step by Step Fatoring Polynomials NOTE Example 8 m 2 4 annot be fatored any further. Step 1 Step 2 Look for a greatest ommon fator other than 1. If suh a fator exists, fator out the GCF. If the polynomial that remains is a trinomial, try to fator the trinomial by the trial-and-error methods of Setions 4.2 and 4.3. Example 8 illustrates the use of this strategy. Fatoring a Trinomial (a) Fator 5m 2 n 20n. First, we see that the GCF is 5n. Fatoring it out gives 5m 2 n 20n 5n(m 2 4) (b) Fator 3x 3 24x 2 48x. First, we see that the GCF is 3x. Fatoring out 3x yields 3x 3 24x 2 48x 3x(x 2 8x 16) 3x(x 4)(x 4) or 3x(x 4) 2 () Fator 8r 2 s 20rs 2 12s 3. First, the GCF is 4s, and we an write the original polynomial as 8r 2 s 20rs 2 12s 3 4s(2r 2 5rs 3s 2 ) Beause the remaining polynomial is a trinomial, we an use the trial-and-error method to omplete the fatoring. 8r 2 s 20rs 2 12s 3 4s(2r s)(r 3s)
32 404 CHAPTER 4 Fatoring Chek Yourself 8 Fator the following polynomials. (a) 8a 3 32a 2 b 32ab 2 (b) 7x 3 7x 2 y 42xy 2 () 5m 4 15m 3 5m 2 To this point we have used the trial-and-error method to fator trinomials. We have also learned that not all trinomials an be fatored. In the remainder of this setion we will look at the same kinds of trinomials, but in a slightly different ontext. We first determine whether a trinomial is fatorable. We then use the results of that analysis to fator the trinomial. Some students prefer the trial-and-error method for fatoring beause it is generally faster and more intuitive. Other students prefer the method used in the remainder of this setion (alled the a method) beause it yields the answer in a systemati way. We let you determine whih method you prefer. We begin by looking at some fatored trinomials. Example 9 Mathing Trinomials and Their Fators Determine whih of the following are true statements. (a) x 2 2x 8 (x 4)(x 2) This is a true statement. Using the FOIL method, we see that (x 4)(x 2) x 2 2x 4x 8 x 2 2x 8 (b) x 2 6x 5 (x 2)(x 3) This is not a true statement. (x 2)(x 3) x 2 3x 2x 6 x 2 5x 6 () x 2 5x 14 (x 2)(x 7) This is true: (x 2)(x 7) x 2 7x 2x 14 x 2 5x 14 (d) x 2 8x 15 (x 5)(x 3) This is false: (x 5)(x 3) x 2 3x 5x 15 x 2 8x 15 Chek Yourself 9 Determine whih of the following are true statements. (a) 2x 2 2x 3 (2x 3)(x 1) (b) 3x 2 11x 4 (3x 1)(x 4) () 2x 2 7x 3 (x 3)(2x 1) The first step in learning to fator a trinomial is to identify its oeffiients. So that we are onsistent, we first write the trinomial in standard form, ax 2 bx, and then label the three oeffiients as a, b, and.
33 Fatoring Trinomials of the Form ax 2 bx SECTION Example 10 Identifying the Coeffiients of ax 2 bx NOTE The negative sign is attahed to the oeffiient. First, when neessary, rewrite the trinomial in ax 2 bx form. Then give the values for a, b, and, in whih a is the oeffiient of the x 2 term, b is the oeffiient of the x term, and is the onstant. (a) x 2 3x 18 a 1 b 3 18 (b) x 2 24x 23 a 1 b () x x First rewrite the trinomial in desending-exponent order: x 2 11x 8 a 1 b 11 8 Chek Yourself 10 Definition The a Test < Objetive 3 > Example 11 First, when neessary, rewrite the trinomials in ax 2 bx form. Then label a, b, and, in whih a is the oeffiient of the x 2 term, b is the oeffiient of the x term, and is the onstant. (a) x 2 5x 14 (b) x 2 18x 17 () x 6 2x 2 Not all trinomials an be fatored. To disover whether a trinomial is fatorable, we try the a test. A trinomial of the form ax 2 bx is fatorable if (and only if) there are two integers, m and n, suh that a mn and b m n In Example 11 we will look for m and n to determine whether eah trinomial is fatorable. Using the a Test Use the a test to determine whih of the following trinomials an be fatored. Find the values of m and n for eah trinomial that an be fatored. (a) x 2 3x 18 First, we find the values of a, b, and, so that we an find a. a 1 b 3 18 a 1( 18) 18 and b 3
34 406 CHAPTER 4 Fatoring Then, we look for two numbers, m and n, suh that their produt is a and their sum is b. In this ase, that means mn 18 and m n 3 We now look at all pairs of integers with a produt of 18. We then look at the sum of eah pair of integers, looking for a sum of 3. mn m n 1( 18) 18 1 ( 18) 17 2( 9) 18 2 ( 9) 7 3( 6) 18 3 ( 6) 3 6( 3) 18 9( 2) 18 18( 1) 18 We need to look no further than 3 and 6. NOTE We ould have hosen m 6 and n 3 as well. 3 and 6 are the two integers with a produt of a and a sum of b. We an say that m 3 and n 6 Beause we found values for m and n, we know that x 2 3x 18 is fatorable. (b) x 2 24x 23 We find that a 1 b a 1(23) 23 and b 24 So mn 23 and m n 24 We now alulate integer pairs, looking for two numbers with a produt of 23 and a sum of 24. mn m n 1(23) ( 23) 23 1 ( 23) 24 m 1 and n 23 So, x 2 24x 23 is fatorable. () x 2 11x 8 We find that a 1, b 11, and 8. Therefore, a 8 and b 11. Thus mn 8 and m n 11. We alulate integer pairs: mn m n 1(8) (4) ( 8) 8 1 ( 8) 9 2( 4) 8 2 ( 4) 6
35 Fatoring Trinomials of the Form ax 2 bx SECTION There are no other pairs of integers with a produt of 8, and none of these pairs has a sum of 11. The trinomial x 2 11x 8 is not fatorable. (d) 2x 2 7x 15 We find that a 2, b 7, and 15. Therefore, a 2( 15) 30 and b 7. Thus mn 30 and m n 7. We alulate integer pairs: mn m n 1( 30) 30 1 ( 30) 29 2( 15) 30 2 ( 15) 13 3( 10) 30 3 ( 10) 7 5( 6) 30 5 ( 6) 1 6( 5) 30 6 ( 5) 1 10( 3) ( 3) 7 There is no need to go any further. We see that 10 and 3 have a produt of 30 and a sum of 7, so m 10 and n 3 Therefore, 2x 2 7x 15 is fatorable. Chek Yourself 11 < Objetive 4 > Example 12 Use the a test to determine whih of the following trinomials an be fatored. Find the values of m and n for eah trinomial that an be fatored. (a) x 2 7x 12 (b) x 2 5x 14 () 3x 2 6x 7 (d) 2x 2 x 6 It is not always neessary to evaluate all the produts and sums to determine whether a trinomial is fatorable. You may have notied patterns and shortuts that make it easier to find m and n. By all means, use them to help you find m and n. This is essential in mathematial thinking. You are taught a mathematial proess that will always work for solving a problem. Suh a proess is alled an algorithm. It is very easy to teah a omputer to use an algorithm. It is very diffiult (some would say impossible) for a omputer to have insight. Shortuts that you disover are insights. They may be the most important part of your mathematial eduation. So far we have used the results of the a test to determine whether a trinomial is fatorable. The results an also be used to help fator the trinomial. Using the Results of the a Test to Fator Rewrite the middle term as the sum of two terms and then fator by grouping. (a) x 2 3x 18 We find that a 1, b 3, and 18, so a 18 and b 3. We are looking for two numbers, m and n,where mn 18 and m n 3. In Example 11, part (a), we looked at every pair of integers whose produt (mn) was 18, to find a pair that had a sum (m n) of 3. We found the two integers to be 3 and 6,
36 408 CHAPTER 4 Fatoring beause 3( 6) 18 and 3 ( 6) 3, so m 3 and n 6. We now use that result to rewrite the middle term as the sum of 3x and 6x. x 2 3x 6x 18 We then fator by grouping: (x 2 3x) (6x 18) x 2 3x 6x 18 x(x 3) 6(x 3) (x 3)(x 6) (b) x 2 24x 23 We use the results from Example 11, part (b), in whih we found m 1 and n 23, to rewrite the middle term of the equation. x 2 24x 23 x 2 x 23x 23 Then we fator by grouping: x 2 x 23x 23 (x 2 x) (23x 23) x(x 1) 23(x 1) (x 1)(x 23) () 2x 2 7x 15 From Example 11, part (d), we know that this trinomial is fatorable, and m 10 and n 3. We use that result to rewrite the middle term of the trinomial. 2x 2 7x 15 2x 2 10x 3x 15 (2x 2 10x) (3x 15) 2x(x 5) 3(x 5) (x 5)(2x 3) Example 13 Note that we did not fator the trinomial in Example 11, part (), x 2 11x 8. Reall that, by the a method, we determined that this trinomial is not fatorable. Chek Yourself 12 Use the results of Chek Yourself 11 to rewrite the middle term as the sum of two terms and then fator by grouping. (a) x 2 7x 12 (b) x 2 5x 14 () 2x 2 x 6 Next, we look at some examples that require us to first find m and n and then fator the trinomial. Rewriting Middle Terms to Fator Rewrite the middle term as the sum of two terms and then fator by grouping. (a) 2x 2 13x 7 We find a 2, b 13, and 7, so mn a 14 and m n b 13. Therefore, mn 1( 14) 14 m n 1 ( 14) 13
37 Fatoring Trinomials of the Form ax 2 bx SECTION So, m 1 and n 14. We rewrite the middle term of the trinomial as follows: 2x 2 13x 7 2x 2 x 14x 7 (2x 2 x) (14x 7) x(2x 1) 7(2x 1) (2x 1)(x 7) (b) 6x 2 5x 6 We find that a 6, b 5, and 6, so mn a 36 and m n b 5. mn 1( 36) 36 2( 18) 36 3( 12) 36 4( 9) 36 m n 1 ( 36) 35 2 ( 18) 16 3 ( 12) 9 4 ( 9) 5 So, m 4 and n 9. We rewrite the middle term of the trinomial: Example 14 6x 2 5x 6 6x 2 4x 9x 6 (6x 2 4x) (9x 6) 2x(3x 2) 3(3x 2) (3x 2)(2x 3) Chek Yourself 13 Rewrite the middle term as the sum of two terms and then fator by grouping. (a) 2x 2 7x 15 (b) 6x 2 5x 4 Be ertain to hek trinomials and binomial fators for any ommon monomial fator. (There is no ommon fator in the binomial unless it is also a ommon fator in the original trinomial.) Example 14 shows the fatoring out of monomial fators. Fatoring Out Common Fators Completely fator the trinomial. 3x 2 12x 15 We ould first fator out the ommon fator of 3: 3x 2 12x 15 3(x 2 4x 5) Finding m and n for the trinomial x 2 4x 5 yields mn 5 and m n 4. mn m n 1( 5) 5 1 ( 5) 4 5( 1) 5 1 (5) 4
38 410 CHAPTER 4 Fatoring So, m 5 and n 1. This gives us 3x 2 12x 15 3(x 2 4x 5) 3(x 2 5x x 5) 3[(x 2 5x) (x 5)] 3[x(x 5) (x 5)] 3[(x 5)(x 1)] 3(x 5)(x 1) Chek Yourself 14 Completely fator the trinomial. 6x 3 3x 2 18x Not all possible produt pairs need to be tried to find m and n. A look at the sign pattern of the trinomial will eliminate many of the possibilities. Assuming the leading oeffiient is positive, there are four possible sign patterns. Pattern Example Conlusion 1. b and are both positive. 2x 2 13x 15 m and n must both be positive. 2. b is negative and is positive. x 2 7x 12 m and n must both be negative. 3. b is positive and is negative. x 2 3x 10 m and n are of opposite signs. (The value with the larger absolute value is positive.) 4. b and are both negative. x 2 3x 10 m and n are of opposite signs. (The value with the larger absolute value is negative.) Chek Yourself ANSWERS 1. (a) (5x 4)(x 2); (b) (3x 2)(x 6) 2. (a) (2x 3)(x 3); (b) (6x 5)(x 2) 3. (4x 3)(x 2) 4. (3x 2y)(5x 2y) 5. (a) (2x 7) 2 ; (b) (4x 5y) (4x 1)(x 3) 7. 3x(2x 5)(x 2) 8. (a) 8a(a 2b)(a 2b); (b) 7x(x 3y)(x 2y); () 5m 2 (m 2 3m 1) 9. (a) False; (b) true; () true 10. (a) a 1, b 5, 14; (b) a 1, b 18, 17; () a 2, b 1, (a) Fatorable, m 3, n 4; (b) fatorable, m 7, n 2; () not fatorable; (d) fatorable, m 4, n (a) x 2 3x 4x 12 (x 3)(x 4); (b) x 2 7x 2x 14 (x 7)(x 2); () 2x 2 4x 3x 6 (x 2)(2x 3) 13. (a) 2x 2 10x 3x 15 (x 5)(2x 3); (b) 6x 2 8x 3x 4 (3x 4)(2x 1) 14. 3x(2x 3)(x 2)
39 Fatoring Trinomials of the Form ax 2 bx SECTION Reading Your Text The following fill-in-the-blank exerises are designed to ensure that you understand some of the key voabulary used in this setion. SECTION 4.3 (a) If all the terms of a trinomial are positive, the signs between the terms in the binomial fators are both signs. (b) If the third term of a trinomial is negative, the signs between the terms in the binomial fators are. () The first step in fatoring a polynomial is to fator out the. (d) A mathematial proess that will always work for solving a problem is alled an. b
40 4.3 exerises Basi Skills Advaned Skills Voational-Tehnial Appliations Calulator/Computer Above and Beyond Getting Ready < Objetive 1 > Complete eah of the following statements. Boost your grade at mathzone.om! > Pratie Problems > NetTutor > Self-Tests > e-professors > Videos 1. 4x 2 4x 3 (2x 1)( ) 2. 3w 2 11w 4 (w 4)( ) Name 3. 6a 2 13a 6 (2a 3)( ) Setion Date 4. 25y 2 10y 1 (5y 1)( ) Answers 5. 15x 2 16x 4 (3x 2)( ) m 2 5m 4 (3m 4)( ) a 2 8ab b 2 (4a b)( ) x 2 5xy 4y 2 (3x 4y)( ) 9. 4m 2 5mn 6n 2 (m 2n)( ) p 2 pq 3q 2 (5p 3q)( ) State whether eah of the following is true or false. 11. x 2 2x 3 (x 3)(x 1) 12. y 2 3y 18 ( y 6)( y 3) 13. x 2 10x 24 (x 6)(x 4) 14. a 2 9a 36 (a 12)(a 4) 15. x 2 16x 64 (x 8)(x 8) 16. w 2 12w 45 (w 9)(w 5) y 2 10y 1 (5y 1)(5y 1) > Videos > Videos 412 SECTION 4.3
Factoring Trinomials of the Form x 2 bx c
 4.2 Factoring Trinomials of the Form x 2 bx c 4.2 OBJECTIVES 1. Factor a trinomial of the form x 2 bx c 2. Factor a trinomial containing a common factor NOTE The process used to factor here is frequently
4.2 Factoring Trinomials of the Form x 2 bx c 4.2 OBJECTIVES 1. Factor a trinomial of the form x 2 bx c 2. Factor a trinomial containing a common factor NOTE The process used to factor here is frequently
Using the ac Method to Factor
 4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
FACTORING ax 2 bx c. Factoring Trinomials with Leading Coefficient 1
 5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
1.3 Complex Numbers; Quadratic Equations in the Complex Number System*
 04 CHAPTER Equations and Inequalities Explaining Conepts: Disussion and Writing 7. Whih of the following pairs of equations are equivalent? Explain. x 2 9; x 3 (b) x 29; x 3 () x - 2x - 22 x - 2 2 ; x
04 CHAPTER Equations and Inequalities Explaining Conepts: Disussion and Writing 7. Whih of the following pairs of equations are equivalent? Explain. x 2 9; x 3 (b) x 29; x 3 () x - 2x - 22 x - 2 2 ; x
1.3 Polynomials and Factoring
 1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
FACTORING POLYNOMIALS
 296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
By reversing the rules for multiplication of binomials from Section 4.6, we get rules for factoring polynomials in certain forms.
 SECTION 5.4 Special Factoring Techniques 317 5.4 Special Factoring Techniques OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor
SECTION 5.4 Special Factoring Techniques 317 5.4 Special Factoring Techniques OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor
Factoring Trinomials: The ac Method
 6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
FACTORING OUT COMMON FACTORS
 278 (6 2) Chapter 6 Factoring 6.1 FACTORING OUT COMMON FACTORS In this section Prime Factorization of Integers Greatest Common Factor Finding the Greatest Common Factor for Monomials Factoring Out the
278 (6 2) Chapter 6 Factoring 6.1 FACTORING OUT COMMON FACTORS In this section Prime Factorization of Integers Greatest Common Factor Finding the Greatest Common Factor for Monomials Factoring Out the
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0).
 This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
6.1 The Greatest Common Factor; Factoring by Grouping
 386 CHAPTER 6 Factoring and Applications 6.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
386 CHAPTER 6 Factoring and Applications 6.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
Factoring Special Polynomials
 6.6 Factoring Special Polynomials 6.6 OBJECTIVES 1. Factor the difference of two squares 2. Factor the sum or difference of two cubes In this section, we will look at several special polynomials. These
6.6 Factoring Special Polynomials 6.6 OBJECTIVES 1. Factor the difference of two squares 2. Factor the sum or difference of two cubes In this section, we will look at several special polynomials. These
The Greatest Common Factor; Factoring by Grouping
 296 CHAPTER 5 Factoring and Applications 5.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
296 CHAPTER 5 Factoring and Applications 5.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
5.1 FACTORING OUT COMMON FACTORS
 C H A P T E R 5 Factoring he sport of skydiving was born in the 1930s soon after the military began using parachutes as a means of deploying troops. T Today, skydiving is a popular sport around the world.
C H A P T E R 5 Factoring he sport of skydiving was born in the 1930s soon after the military began using parachutes as a means of deploying troops. T Today, skydiving is a popular sport around the world.
Polynomials. Key Terms. quadratic equation parabola conjugates trinomial. polynomial coefficient degree monomial binomial GCF
 Polynomials 5 5.1 Addition and Subtraction of Polynomials and Polynomial Functions 5.2 Multiplication of Polynomials 5.3 Division of Polynomials Problem Recognition Exercises Operations on Polynomials
Polynomials 5 5.1 Addition and Subtraction of Polynomials and Polynomial Functions 5.2 Multiplication of Polynomials 5.3 Division of Polynomials Problem Recognition Exercises Operations on Polynomials
Factoring Flow Chart
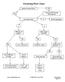 Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
How To Factor By Gcf In Algebra 1.5
 7-2 Factoring by GCF Warm Up Lesson Presentation Lesson Quiz Algebra 1 Warm Up Simplify. 1. 2(w + 1) 2. 3x(x 2 4) 2w + 2 3x 3 12x Find the GCF of each pair of monomials. 3. 4h 2 and 6h 2h 4. 13p and 26p
7-2 Factoring by GCF Warm Up Lesson Presentation Lesson Quiz Algebra 1 Warm Up Simplify. 1. 2(w + 1) 2. 3x(x 2 4) 2w + 2 3x 3 12x Find the GCF of each pair of monomials. 3. 4h 2 and 6h 2h 4. 13p and 26p
Factoring Methods. Example 1: 2x + 2 2 * x + 2 * 1 2(x + 1)
 Factoring Methods When you are trying to factor a polynomial, there are three general steps you want to follow: 1. See if there is a Greatest Common Factor 2. See if you can Factor by Grouping 3. See if
Factoring Methods When you are trying to factor a polynomial, there are three general steps you want to follow: 1. See if there is a Greatest Common Factor 2. See if you can Factor by Grouping 3. See if
Factoring. Factoring Monomials Monomials can often be factored in more than one way.
 Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
NSM100 Introduction to Algebra Chapter 5 Notes Factoring
 Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
In algebra, factor by rewriting a polynomial as a product of lower-degree polynomials
 Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
Factoring and Applications
 Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
expression is written horizontally. The Last terms ((2)( 4)) because they are the last terms of the two polynomials. This is called the FOIL method.
 A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
The majority of college students hold credit cards. According to the Nellie May
 CHAPTER 6 Factoring Polynomials 6.1 The Greatest Common Factor and Factoring by Grouping 6. Factoring Trinomials of the Form b c 6.3 Factoring Trinomials of the Form a b c and Perfect Square Trinomials
CHAPTER 6 Factoring Polynomials 6.1 The Greatest Common Factor and Factoring by Grouping 6. Factoring Trinomials of the Form b c 6.3 Factoring Trinomials of the Form a b c and Perfect Square Trinomials
SPECIAL PRODUCTS AND FACTORS
 CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
Operations with Algebraic Expressions: Multiplication of Polynomials
 Operations with Algebraic Expressions: Multiplication of Polynomials The product of a monomial x monomial To multiply a monomial times a monomial, multiply the coefficients and add the on powers with the
Operations with Algebraic Expressions: Multiplication of Polynomials The product of a monomial x monomial To multiply a monomial times a monomial, multiply the coefficients and add the on powers with the
Section 6.1 Factoring Expressions
 Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
Factoring Polynomials
 UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
6.4 Special Factoring Rules
 6.4 Special Factoring Rules OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor a sum of cubes. By reversing the rules for multiplication
6.4 Special Factoring Rules OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor a sum of cubes. By reversing the rules for multiplication
Math 25 Activity 6: Factoring Advanced
 Instructor! Math 25 Activity 6: Factoring Advanced Last week we looked at greatest common factors and the basics of factoring out the GCF. In this second activity, we will discuss factoring more difficult
Instructor! Math 25 Activity 6: Factoring Advanced Last week we looked at greatest common factors and the basics of factoring out the GCF. In this second activity, we will discuss factoring more difficult
Chapter R.4 Factoring Polynomials
 Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
( ) FACTORING. x In this polynomial the only variable in common to all is x.
 FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder).
 Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
7-6. Choosing a Factoring Model. Extension: Factoring Polynomials with More Than One Variable IN T RO DUC E T EACH. Standards for Mathematical Content
 7-6 Choosing a Factoring Model Extension: Factoring Polynomials with More Than One Variable Essential question: How can you factor polynomials with more than one variable? What is the connection between
7-6 Choosing a Factoring Model Extension: Factoring Polynomials with More Than One Variable Essential question: How can you factor polynomials with more than one variable? What is the connection between
15.1 Factoring Polynomials
 LESSON 15.1 Factoring Polynomials Use the structure of an expression to identify ways to rewrite it. Also A.SSE.3? ESSENTIAL QUESTION How can you use the greatest common factor to factor polynomials? EXPLORE
LESSON 15.1 Factoring Polynomials Use the structure of an expression to identify ways to rewrite it. Also A.SSE.3? ESSENTIAL QUESTION How can you use the greatest common factor to factor polynomials? EXPLORE
6.3 FACTORING ax 2 bx c WITH a 1
 290 (6 14) Chapter 6 Factoring e) What is the approximate maximum revenue? f) Use the accompanying graph to estimate the price at which the revenue is zero. y Revenue (thousands of dollars) 300 200 100
290 (6 14) Chapter 6 Factoring e) What is the approximate maximum revenue? f) Use the accompanying graph to estimate the price at which the revenue is zero. y Revenue (thousands of dollars) 300 200 100
POLYNOMIALS and FACTORING
 POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
Name Intro to Algebra 2. Unit 1: Polynomials and Factoring
 Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
How To Solve Factoring Problems
 05-W4801-AM1.qxd 8/19/08 8:45 PM Page 241 Factoring, Solving Equations, and Problem Solving 5 5.1 Factoring by Using the Distributive Property 5.2 Factoring the Difference of Two Squares 5.3 Factoring
05-W4801-AM1.qxd 8/19/08 8:45 PM Page 241 Factoring, Solving Equations, and Problem Solving 5 5.1 Factoring by Using the Distributive Property 5.2 Factoring the Difference of Two Squares 5.3 Factoring
Algebra 2 PreAP. Name Period
 Algebra 2 PreAP Name Period IMPORTANT INSTRUCTIONS FOR STUDENTS!!! We understand that students come to Algebra II with different strengths and needs. For this reason, students have options for completing
Algebra 2 PreAP Name Period IMPORTANT INSTRUCTIONS FOR STUDENTS!!! We understand that students come to Algebra II with different strengths and needs. For this reason, students have options for completing
FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c
 Tallahassee Community College 55 FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c This kind of trinomial differs from the previous kind we have factored because the coefficient of x is no longer "1".
Tallahassee Community College 55 FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c This kind of trinomial differs from the previous kind we have factored because the coefficient of x is no longer "1".
A. Factoring out the Greatest Common Factor.
 DETAILED SOLUTIONS AND CONCEPTS - FACTORING POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to ingrid.stewart@csn.edu. Thank you!
DETAILED SOLUTIONS AND CONCEPTS - FACTORING POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to ingrid.stewart@csn.edu. Thank you!
Factoring Algebra- Chapter 8B Assignment Sheet
 Name: Factoring Algebra- Chapter 8B Assignment Sheet Date Section Learning Targets Assignment Tues 2/17 Find the prime factorization of an integer Find the greatest common factor (GCF) for a set of monomials.
Name: Factoring Algebra- Chapter 8B Assignment Sheet Date Section Learning Targets Assignment Tues 2/17 Find the prime factorization of an integer Find the greatest common factor (GCF) for a set of monomials.
Chapter 1 Microeconomics of Consumer Theory
 Chapter 1 Miroeonomis of Consumer Theory The two broad ategories of deision-makers in an eonomy are onsumers and firms. Eah individual in eah of these groups makes its deisions in order to ahieve some
Chapter 1 Miroeonomis of Consumer Theory The two broad ategories of deision-makers in an eonomy are onsumers and firms. Eah individual in eah of these groups makes its deisions in order to ahieve some
MATH 90 CHAPTER 6 Name:.
 MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
5.2 The Master Theorem
 170 CHAPTER 5. RECURSION AND RECURRENCES 5.2 The Master Theorem Master Theorem In the last setion, we saw three different kinds of behavior for reurrenes of the form at (n/2) + n These behaviors depended
170 CHAPTER 5. RECURSION AND RECURRENCES 5.2 The Master Theorem Master Theorem In the last setion, we saw three different kinds of behavior for reurrenes of the form at (n/2) + n These behaviors depended
Factoring Polynomials
 Factoring a Polynomial Expression Factoring a polynomial is expressing the polynomial as a product of two or more factors. Simply stated, it is somewhat the reverse process of multiplying. To factor polynomials,
Factoring a Polynomial Expression Factoring a polynomial is expressing the polynomial as a product of two or more factors. Simply stated, it is somewhat the reverse process of multiplying. To factor polynomials,
Factoring - Grouping
 6.2 Factoring - Grouping Objective: Factor polynomials with four terms using grouping. The first thing we will always do when factoring is try to factor out a GCF. This GCF is often a monomial like in
6.2 Factoring - Grouping Objective: Factor polynomials with four terms using grouping. The first thing we will always do when factoring is try to factor out a GCF. This GCF is often a monomial like in
Factoring Polynomials
 Factoring Polynomials Factoring Factoring is the process of writing a polynomial as the product of two or more polynomials. The factors of 6x 2 x 2 are 2x + 1 and 3x 2. In this section, we will be factoring
Factoring Polynomials Factoring Factoring is the process of writing a polynomial as the product of two or more polynomials. The factors of 6x 2 x 2 are 2x + 1 and 3x 2. In this section, we will be factoring
SUNY ECC. ACCUPLACER Preparation Workshop. Algebra Skills
 SUNY ECC ACCUPLACER Preparation Workshop Algebra Skills Gail A. Butler Ph.D. Evaluating Algebraic Epressions Substitute the value (#) in place of the letter (variable). Follow order of operations!!! E)
SUNY ECC ACCUPLACER Preparation Workshop Algebra Skills Gail A. Butler Ph.D. Evaluating Algebraic Epressions Substitute the value (#) in place of the letter (variable). Follow order of operations!!! E)
Greatest Common Factor (GCF) Factoring
 Section 4 4: Greatest Common Factor (GCF) Factoring The last chapter introduced the distributive process. The distributive process takes a product of a monomial and a polynomial and changes the multiplication
Section 4 4: Greatest Common Factor (GCF) Factoring The last chapter introduced the distributive process. The distributive process takes a product of a monomial and a polynomial and changes the multiplication
Factoring a Difference of Two Squares. Factoring a Difference of Two Squares
 284 (6 8) Chapter 6 Factoring 87. Tomato soup. The amount of metal S (in square inches) that it takes to make a can for tomato soup is a function of the radius r and height h: S 2 r 2 2 rh a) Rewrite this
284 (6 8) Chapter 6 Factoring 87. Tomato soup. The amount of metal S (in square inches) that it takes to make a can for tomato soup is a function of the radius r and height h: S 2 r 2 2 rh a) Rewrite this
SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS
 (Section 0.6: Polynomial, Rational, and Algebraic Expressions) 0.6.1 SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS LEARNING OBJECTIVES Be able to identify polynomial, rational, and algebraic
(Section 0.6: Polynomial, Rational, and Algebraic Expressions) 0.6.1 SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS LEARNING OBJECTIVES Be able to identify polynomial, rational, and algebraic
Factoring (pp. 1 of 4)
 Factoring (pp. 1 of 4) Algebra Review Try these items from middle school math. A) What numbers are the factors of 4? B) Write down the prime factorization of 7. C) 6 Simplify 48 using the greatest common
Factoring (pp. 1 of 4) Algebra Review Try these items from middle school math. A) What numbers are the factors of 4? B) Write down the prime factorization of 7. C) 6 Simplify 48 using the greatest common
Veterans Upward Bound Algebra I Concepts - Honors
 Veterans Upward Bound Algebra I Concepts - Honors Brenda Meery Kaitlyn Spong Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org Chapter 6. Factoring CHAPTER
Veterans Upward Bound Algebra I Concepts - Honors Brenda Meery Kaitlyn Spong Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org Chapter 6. Factoring CHAPTER
A Systematic Approach to Factoring
 A Systematic Approach to Factoring Step 1 Count the number of terms. (Remember****Knowing the number of terms will allow you to eliminate unnecessary tools.) Step 2 Is there a greatest common factor? Tool
A Systematic Approach to Factoring Step 1 Count the number of terms. (Remember****Knowing the number of terms will allow you to eliminate unnecessary tools.) Step 2 Is there a greatest common factor? Tool
MATH 10034 Fundamental Mathematics IV
 MATH 0034 Fundamental Mathematics IV http://www.math.kent.edu/ebooks/0034/funmath4.pdf Department of Mathematical Sciences Kent State University January 2, 2009 ii Contents To the Instructor v Polynomials.
MATH 0034 Fundamental Mathematics IV http://www.math.kent.edu/ebooks/0034/funmath4.pdf Department of Mathematical Sciences Kent State University January 2, 2009 ii Contents To the Instructor v Polynomials.
5 means to write it as a product something times something instead of a sum something plus something plus something.
 Intermediate algebra Class notes Factoring Introduction (section 6.1) Recall we factor 10 as 5. Factoring something means to think of it as a product! Factors versus terms: terms: things we are adding
Intermediate algebra Class notes Factoring Introduction (section 6.1) Recall we factor 10 as 5. Factoring something means to think of it as a product! Factors versus terms: terms: things we are adding
AIP Factoring Practice/Help
 The following pages include many problems to practice factoring skills. There are also several activities with examples to help you with factoring if you feel like you are not proficient with it. There
The following pages include many problems to practice factoring skills. There are also several activities with examples to help you with factoring if you feel like you are not proficient with it. There
Academic Success Centre
 250) 960-6367 Factoring Polynomials Sometimes when we try to solve or simplify an equation or expression involving polynomials the way that it looks can hinder our progress in finding a solution. Factorization
250) 960-6367 Factoring Polynomials Sometimes when we try to solve or simplify an equation or expression involving polynomials the way that it looks can hinder our progress in finding a solution. Factorization
Factoring - Greatest Common Factor
 6.1 Factoring - Greatest Common Factor Objective: Find the greatest common factor of a polynomial and factor it out of the expression. The opposite of multiplying polynomials together is factoring polynomials.
6.1 Factoring - Greatest Common Factor Objective: Find the greatest common factor of a polynomial and factor it out of the expression. The opposite of multiplying polynomials together is factoring polynomials.
Polynomials and Factoring
 7.6 Polynomials and Factoring Basic Terminology A term, or monomial, is defined to be a number, a variable, or a product of numbers and variables. A polynomial is a term or a finite sum or difference of
7.6 Polynomials and Factoring Basic Terminology A term, or monomial, is defined to be a number, a variable, or a product of numbers and variables. A polynomial is a term or a finite sum or difference of
Factor Polynomials Completely
 9.8 Factor Polynomials Completely Before You factored polynomials. Now You will factor polynomials completely. Why? So you can model the height of a projectile, as in Ex. 71. Key Vocabulary factor by grouping
9.8 Factor Polynomials Completely Before You factored polynomials. Now You will factor polynomials completely. Why? So you can model the height of a projectile, as in Ex. 71. Key Vocabulary factor by grouping
 Chapter 6 A N ovel Solution Of Linear Congruenes Proeedings NCUR IX. (1995), Vol. II, pp. 708{712 Jerey F. Gold Department of Mathematis, Department of Physis University of Utah Salt Lake City, Utah 84112
Chapter 6 A N ovel Solution Of Linear Congruenes Proeedings NCUR IX. (1995), Vol. II, pp. 708{712 Jerey F. Gold Department of Mathematis, Department of Physis University of Utah Salt Lake City, Utah 84112
BEGINNING ALGEBRA ACKNOWLEDMENTS
 BEGINNING ALGEBRA The Nursing Department of Labouré College requested the Department of Academic Planning and Support Services to help with mathematics preparatory materials for its Bachelor of Science
BEGINNING ALGEBRA The Nursing Department of Labouré College requested the Department of Academic Planning and Support Services to help with mathematics preparatory materials for its Bachelor of Science
Sect 6.1 - Greatest Common Factor and Factoring by Grouping
 Sect 6.1 - Greatest Common Factor and Factoring by Grouping Our goal in this chapter is to solve non-linear equations by breaking them down into a series of linear equations that we can solve. To do this,
Sect 6.1 - Greatest Common Factor and Factoring by Grouping Our goal in this chapter is to solve non-linear equations by breaking them down into a series of linear equations that we can solve. To do this,
Electrician'sMathand BasicElectricalFormulas
 Eletriian'sMathand BasiEletrialFormulas MikeHoltEnterprises,In. 1.888.NEC.CODE www.mikeholt.om Introdution Introdution This PDF is a free resoure from Mike Holt Enterprises, In. It s Unit 1 from the Eletrial
Eletriian'sMathand BasiEletrialFormulas MikeHoltEnterprises,In. 1.888.NEC.CODE www.mikeholt.om Introdution Introdution This PDF is a free resoure from Mike Holt Enterprises, In. It s Unit 1 from the Eletrial
Math 10C. Course: Polynomial Products and Factors. Unit of Study: Step 1: Identify the Outcomes to Address. Guiding Questions:
 Course: Unit of Study: Math 10C Polynomial Products and Factors Step 1: Identify the Outcomes to Address Guiding Questions: What do I want my students to learn? What can they currently understand and do?
Course: Unit of Study: Math 10C Polynomial Products and Factors Step 1: Identify the Outcomes to Address Guiding Questions: What do I want my students to learn? What can they currently understand and do?
Mathematics Placement
 Mathematics Placement The ACT COMPASS math test is a self-adaptive test, which potentially tests students within four different levels of math including pre-algebra, algebra, college algebra, and trigonometry.
Mathematics Placement The ACT COMPASS math test is a self-adaptive test, which potentially tests students within four different levels of math including pre-algebra, algebra, college algebra, and trigonometry.
Factoring Quadratic Expressions
 Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
6.6 Factoring Strategy
 456 CHAPTER 6. FACTORING 6.6 Factoring Strategy When you are concentrating on factoring problems of a single type, after doing a few you tend to get into a rhythm, and the remainder of the exercises, because
456 CHAPTER 6. FACTORING 6.6 Factoring Strategy When you are concentrating on factoring problems of a single type, after doing a few you tend to get into a rhythm, and the remainder of the exercises, because
COLLEGE ALGEBRA. Paul Dawkins
 COLLEGE ALGEBRA Paul Dawkins Table of Contents Preface... iii Outline... iv Preliminaries... Introduction... Integer Exponents... Rational Exponents... 9 Real Exponents...5 Radicals...6 Polynomials...5
COLLEGE ALGEBRA Paul Dawkins Table of Contents Preface... iii Outline... iv Preliminaries... Introduction... Integer Exponents... Rational Exponents... 9 Real Exponents...5 Radicals...6 Polynomials...5
A.3. Polynomials and Factoring. Polynomials. What you should learn. Definition of a Polynomial in x. Why you should learn it
 Appendi A.3 Polynomials and Factoring A23 A.3 Polynomials and Factoring What you should learn Write polynomials in standard form. Add,subtract,and multiply polynomials. Use special products to multiply
Appendi A.3 Polynomials and Factoring A23 A.3 Polynomials and Factoring What you should learn Write polynomials in standard form. Add,subtract,and multiply polynomials. Use special products to multiply
a. You can t do the simple trick of finding two integers that multiply to give 6 and add to give 5 because the a (a = 4) is not equal to one.
 FACTORING TRINOMIALS USING THE AC METHOD. Factoring trinomial epressions in one unknown is an important skill necessary to eventually solve quadratic equations. Trinomial epressions are of the form a 2
FACTORING TRINOMIALS USING THE AC METHOD. Factoring trinomial epressions in one unknown is an important skill necessary to eventually solve quadratic equations. Trinomial epressions are of the form a 2
FACTORING ax 2 bx c WITH a 1
 296 (6 20) Chapter 6 Factoring 6.4 FACTORING a 2 b c WITH a 1 In this section The ac Method Trial and Error Factoring Completely In Section 6.3 we factored trinomials with a leading coefficient of 1. In
296 (6 20) Chapter 6 Factoring 6.4 FACTORING a 2 b c WITH a 1 In this section The ac Method Trial and Error Factoring Completely In Section 6.3 we factored trinomials with a leading coefficient of 1. In
Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any.
 Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
Polynomial Equations and Factoring
 7 Polynomial Equations and Factoring 7.1 Adding and Subtracting Polynomials 7.2 Multiplying Polynomials 7.3 Special Products of Polynomials 7.4 Dividing Polynomials 7.5 Solving Polynomial Equations in
7 Polynomial Equations and Factoring 7.1 Adding and Subtracting Polynomials 7.2 Multiplying Polynomials 7.3 Special Products of Polynomials 7.4 Dividing Polynomials 7.5 Solving Polynomial Equations in
1.3 Algebraic Expressions
 1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
SECTION P.5 Factoring Polynomials
 BLITMCPB.QXP.0599_48-74 /0/0 0:4 AM Page 48 48 Chapter P Prerequisites: Fundamental Concepts of Algebra Technology Eercises Critical Thinking Eercises 98. The common cold is caused by a rhinovirus. The
BLITMCPB.QXP.0599_48-74 /0/0 0:4 AM Page 48 48 Chapter P Prerequisites: Fundamental Concepts of Algebra Technology Eercises Critical Thinking Eercises 98. The common cold is caused by a rhinovirus. The
Factors and Products
 CHAPTER 3 Factors and Products What You ll Learn use different strategies to find factors and multiples of whole numbers identify prime factors and write the prime factorization of a number find square
CHAPTER 3 Factors and Products What You ll Learn use different strategies to find factors and multiples of whole numbers identify prime factors and write the prime factorization of a number find square
Factoring Polynomials and Solving Quadratic Equations
 Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
6.1 Add & Subtract Polynomial Expression & Functions
 6.1 Add & Subtract Polynomial Expression & Functions Objectives 1. Know the meaning of the words term, monomial, binomial, trinomial, polynomial, degree, coefficient, like terms, polynomial funciton, quardrtic
6.1 Add & Subtract Polynomial Expression & Functions Objectives 1. Know the meaning of the words term, monomial, binomial, trinomial, polynomial, degree, coefficient, like terms, polynomial funciton, quardrtic
Fixed-income Securities Lecture 2: Basic Terminology and Concepts. Present value (fixed interest rate) Present value (fixed interest rate): the arb
 Fixed-inome Seurities Leture 2: Basi Terminology and Conepts Philip H. Dybvig Washington University in Saint Louis Various interest rates Present value (PV) and arbitrage Forward and spot interest rates
Fixed-inome Seurities Leture 2: Basi Terminology and Conepts Philip H. Dybvig Washington University in Saint Louis Various interest rates Present value (PV) and arbitrage Forward and spot interest rates
1.5. Factorisation. Introduction. Prerequisites. Learning Outcomes. Learning Style
 Factorisation 1.5 Introduction In Block 4 we showed the way in which brackets were removed from algebraic expressions. Factorisation, which can be considered as the reverse of this process, is dealt with
Factorisation 1.5 Introduction In Block 4 we showed the way in which brackets were removed from algebraic expressions. Factorisation, which can be considered as the reverse of this process, is dealt with
Factoring Guidelines. Greatest Common Factor Two Terms Three Terms Four Terms. 2008 Shirley Radai
 Factoring Guidelines Greatest Common Factor Two Terms Three Terms Four Terms 008 Shirley Radai Greatest Common Factor 008 Shirley Radai Factoring by Finding the Greatest Common Factor Always check for
Factoring Guidelines Greatest Common Factor Two Terms Three Terms Four Terms 008 Shirley Radai Greatest Common Factor 008 Shirley Radai Factoring by Finding the Greatest Common Factor Always check for
A Holistic Method for Selecting Web Services in Design of Composite Applications
 A Holisti Method for Seleting Web Servies in Design of Composite Appliations Mārtiņš Bonders, Jānis Grabis Institute of Information Tehnology, Riga Tehnial University, 1 Kalu Street, Riga, LV 1658, Latvia,
A Holisti Method for Seleting Web Servies in Design of Composite Appliations Mārtiņš Bonders, Jānis Grabis Institute of Information Tehnology, Riga Tehnial University, 1 Kalu Street, Riga, LV 1658, Latvia,
In the above, the number 19 is an example of a number because its only positive factors are one and itself.
 Math 100 Greatest Common Factor and Factoring by Grouping (Review) Factoring Definition: A factor is a number, variable, monomial, or polynomial which is multiplied by another number, variable, monomial,
Math 100 Greatest Common Factor and Factoring by Grouping (Review) Factoring Definition: A factor is a number, variable, monomial, or polynomial which is multiplied by another number, variable, monomial,
Math 0980 Chapter Objectives. Chapter 1: Introduction to Algebra: The Integers.
 Math 0980 Chapter Objectives Chapter 1: Introduction to Algebra: The Integers. 1. Identify the place value of a digit. 2. Write a number in words or digits. 3. Write positive and negative numbers used
Math 0980 Chapter Objectives Chapter 1: Introduction to Algebra: The Integers. 1. Identify the place value of a digit. 2. Write a number in words or digits. 3. Write positive and negative numbers used
Algebra 1 Chapter 08 review
 Name: Class: Date: ID: A Algebra 1 Chapter 08 review Multiple Choice Identify the choice that best completes the statement or answers the question. Simplify the difference. 1. (4w 2 4w 8) (2w 2 + 3w 6)
Name: Class: Date: ID: A Algebra 1 Chapter 08 review Multiple Choice Identify the choice that best completes the statement or answers the question. Simplify the difference. 1. (4w 2 4w 8) (2w 2 + 3w 6)
EAP/GWL Rev. 1/2011 Page 1 of 5. Factoring a polynomial is the process of writing it as the product of two or more polynomial factors.
 EAP/GWL Rev. 1/2011 Page 1 of 5 Factoring a polynomial is the process of writing it as the product of two or more polynomial factors. Example: Set the factors of a polynomial equation (as opposed to an
EAP/GWL Rev. 1/2011 Page 1 of 5 Factoring a polynomial is the process of writing it as the product of two or more polynomial factors. Example: Set the factors of a polynomial equation (as opposed to an
4.4 Factoring ax 2 + bx + c
 4.4 Factoring ax 2 + bx + c From the last section, we now know a trinomial should factor as two binomials. With this in mind, we need to look at how to factor a trinomial when the leading coefficient is
4.4 Factoring ax 2 + bx + c From the last section, we now know a trinomial should factor as two binomials. With this in mind, we need to look at how to factor a trinomial when the leading coefficient is
SOLVING QUADRATIC EQUATIONS - COMPARE THE FACTORING ac METHOD AND THE NEW DIAGONAL SUM METHOD By Nghi H. Nguyen
 SOLVING QUADRATIC EQUATIONS - COMPARE THE FACTORING ac METHOD AND THE NEW DIAGONAL SUM METHOD By Nghi H. Nguyen A. GENERALITIES. When a given quadratic equation can be factored, there are 2 best methods
SOLVING QUADRATIC EQUATIONS - COMPARE THE FACTORING ac METHOD AND THE NEW DIAGONAL SUM METHOD By Nghi H. Nguyen A. GENERALITIES. When a given quadratic equation can be factored, there are 2 best methods
Retirement Option Election Form with Partial Lump Sum Payment
 Offie of the New York State Comptroller New York State and Loal Retirement System Employees Retirement System Polie and Fire Retirement System 110 State Street, Albany, New York 12244-0001 Retirement Option
Offie of the New York State Comptroller New York State and Loal Retirement System Employees Retirement System Polie and Fire Retirement System 110 State Street, Albany, New York 12244-0001 Retirement Option
3 Game Theory: Basic Concepts
 3 Game Theory: Basi Conepts Eah disipline of the soial sienes rules omfortably ithin its on hosen domain: : : so long as it stays largely oblivious of the others. Edard O. Wilson (1998):191 3.1 and and
3 Game Theory: Basi Conepts Eah disipline of the soial sienes rules omfortably ithin its on hosen domain: : : so long as it stays largely oblivious of the others. Edard O. Wilson (1998):191 3.1 and and
FINDING THE LEAST COMMON DENOMINATOR
 0 (7 18) Chapter 7 Rational Expressions GETTING MORE INVOLVED 7. Discussion. Evaluate each expression. a) One-half of 1 b) One-third of c) One-half of x d) One-half of x 7. Exploration. Let R 6 x x 0 x
0 (7 18) Chapter 7 Rational Expressions GETTING MORE INVOLVED 7. Discussion. Evaluate each expression. a) One-half of 1 b) One-third of c) One-half of x d) One-half of x 7. Exploration. Let R 6 x x 0 x
Algebra Cheat Sheets
 Sheets Algebra Cheat Sheets provide you with a tool for teaching your students note-taking, problem-solving, and organizational skills in the context of algebra lessons. These sheets teach the concepts
Sheets Algebra Cheat Sheets provide you with a tool for teaching your students note-taking, problem-solving, and organizational skills in the context of algebra lessons. These sheets teach the concepts
Computer Networks Framing
 Computer Networks Framing Saad Mneimneh Computer Siene Hunter College of CUNY New York Introdution Who framed Roger rabbit? A detetive, a woman, and a rabbit in a network of trouble We will skip the physial
Computer Networks Framing Saad Mneimneh Computer Siene Hunter College of CUNY New York Introdution Who framed Roger rabbit? A detetive, a woman, and a rabbit in a network of trouble We will skip the physial
