DRAFT. University of Pennsylvania Moore School of Electrical Engineering ESE319 Electronic Circuits - Modeling and Measurement Techniques
|
|
|
- Amanda Hoover
- 8 years ago
- Views:
Transcription
1 University of Pennsylvania Moore School of Electrical Engineering ESE319 Electronic Circuits - Modeling and Measurement Techniques 1. Introduction. Students are often frustrated in their attempts to execute laboratory experiments in electronics courses. Their experimental results often do not bear much resemblance to what they expect to see based on the theory they learn in lecture and from their textbooks. Most of the difficulties they encounter exist because conventional texts and classroom discussions assume the ideal behavior of typical circuits. These instructional sources do not mention several important considerations that have a striking effect on the outcome of any attempted experimental procedure. Physical phenomena that tend to corrupt experimental results include: Circuit loading characteristics of laboratory instruments, parasitic circuit elements inserted in the ideal circuit,. The principal cause is the non-ideal behavior of the convenient ProtoBoard interconnect system, and noise generated by external sources and induced in the circuit wiring. If we were able to satisfy the following conditions: input devices - function generators, for example - have zero output impedance, output measuring instruments - oscilloscopes, voltmeters, etc. - have infinite input impedance, connecting wires are of zero length, and all sources of electrical energy production and consumption - radio transmitters, fluorescent lighting fixtures, electric motors, etc., are turned off during the course of our experiments, our experimental results consistently would agree much better with textbook predictions. Unfortunately, such is not the case and we must conduct experiments in a less than ideal real-world environment. Many, but not all, of these problems can be eliminated by following some simple "rules of thumb" when constructing a circuit, but much experience and insight into circuit behavior is required to make high performance circuits work properly. Circuit design engineers - particularly analog designers - spend years learning how to deal intelligently with these idiosyncrasies of circuit design and layout. Although one cannot hope to capture the knowledge of an experienced designer in a few pages, the following material hopefully will assist students in completing electronics laboratory experiments with a high degree of success. 2. Organization. The following sections will address the physical limitations of electronics experimental setups in the following order: Copyright 2001,
2 First, we will examine techniques for modeling circuit interconnect wiring and the basic passive circuit components: resistors, capacitors, and inductors. Each length of wire, including the leads on resistors, inductors, and capacitors, has parasitic (undesired) inductance and resistance. These parasitic effects may be negligible or significant, depending on the impedance level of the rest of the circuit and on the circuit's operating frequency. Additional parasitic effects exist as capacitance or mutual inductance between adjacent wires, or as a capacitance between a wire and a conducting ground plane. Next, we will discuss the modeling of coaxial cable. Coax is used generally to connect signal sources, such as function generators, and measuring instruments - multimeters and oscilloscopes - to the circuit being built and tested. Then we will cover circuit models for typical function generators and oscilloscopes and discuss how these instruments interact with the circuit under test. Next, we will show several ways in which noise signals can enter the circuit under test and corrupt circuit performance. Finally, we will illustrate how to derive detailed models for several simple circuits, illustrating how certain parasitic effects may have negligible effect on the circuit under test in some instances and have significant effect in others. 2. Circuit models for the laboratory. 2.1 Interconnect wiring. Resistance describes the relationship between voltage across and current through an electrical conductor. Inductance, on the other hand, is a measure of the relationship between current flow and the magnetic flux resulting from that current. Every current-carrying wire has resistance and inductance and, as a consequence, every wire exhibits a certain amount of frequency-dependent impedance to current flow. Since interconnecting wires in a circuit ideally are assumed to be impedance-free, the undesired circuit elements - resistance and inductance - are called parasitics. R lead L lead Fig. 2.1 Interconnect lead model Accurate formulas for computing the inductance of a conductor are complex, but one sufficiently exact for our purposes is given as: L(µH ).002 l 2.5 log 10 4 l d 0.75 (2.1) Where l is the length in cm. of a straight piece of wire and d is its diameter in cm (2.54 cm. 1 inch). Copyright 2001,
3 Table 2.1 illustrates the inductance in microhenries of one foot and one meter of wire for several common wire gauges used for circuit interconnect. The resistance of the wire also is tabulated. Wire Wire Wire Inductance Inductance Resistance Resistance gauge diameter diameter per foot per meter per foot per meter AWG mils cm. uh. uh. Ohms Ohms Table 2.1 Copper wire inductance and resistance. Interconnect wiring resistance usually can be ignored since its impedance usually is much less than other impedances in series with the wire. Parasitic inductance is another matter, however, and its effect cannot be neglected at higher frequencies. The inductive reactance ( jωl r ) of a one meter length of 18 gauge wire is tabulated in Table 2.2. The reader easily can calculate the reactance of other wire gauges and of other lengths using proportionality and linearity arguments. As a rough estimate, all of the common wire gauges can be considered to have the same inductance per unit length as 18 gauge wire. All inductive reactance estimates can be obtained by multiplying the reactance of a 1 meter length by the actual length of the wire in meters (or fractions thereof). Frequency Frequency Reactance KHz. Kradians/sec. Ohms Table 2.2 Inductive reactance of 1 meter of 18 gauge wire. 2.2 Resistors. Ideal resistors exhibit only resistance. Physical resistors, however, have associated parasitic inductance, since they require a finite length current-conducting path. A good high frequency resistor model also should include a parasitic capacitor across the resistor body. At a high enough frequency, this seemingly small capacitor will have a smaller reactance than the resistance of the resistor and most current flow will be through the terminal-to-terminal capacitance of the resistor, rather than through its resistive material. This capacitance typically is about 0.5 picofarad, which corresponds to a capacitive reactance of about 31.8 kilohms at 10 megahertz and 318 megohms at 1 kilohertz. We shall not have to consider this parasitic capacitance unless the capacitive reactance is less than 10 times the resistance of our physical resistor at the highest operating frequency of our Copyright 2001,
4 circuit. The shunting (parallel) capacitance of a 1 kilohm resistor operating at 10 megahertz, for example, can be ignored, but not that of a 10 kilohm one used at 10 megahertz. A resistor's lead inductance is quite small and usually can be neglected, since the leads will generally be less than an inch in length. Only at very high frequencies - RF frequencies - will we need to consider resistor lead inductance. A detailed circuit model for a resistor is shown in Fig We will discuss some useful "rules-of-thumb" for circuit simplifications of this type later in this document C r R L r Fig. 2.2 High frequency resistor model. 2.3 Capacitors. Ideal capacitors are purely reactive - conduction occurs via a displacement current across the capacitor dielectric. As is the case for resistors, however, capacitors have parasitics: series resistance and series inductance. Inductance and resistance exist because of the finite conducting path. Additional resistance effects due to energy losses in the capacitor dielectric also must be considered in some cases. All capacitors also have a small amount of leakage current - conductive current that flows directly through its less-than-perfectly insulating dielectric. A detailed model for a physical capacitor is shown in Fig R cs C L c R cp Fig. 2.3 High frequency capacitor model. Perhaps the most serious problem occurring with capacitors is the interaction between the capacitor's capacitance and its series inductance. If we neglect the large leakage resistance, R cp, the complex impedance of a physical capacitor is Z C R cs + j ωl c 1 (2.2) ωc This element combination will series resonate at the frequency where: Copyright 2001,
5 ωl c 1 ωc (2.3) and the capacitor impedance will attain a minimum value equal to its small series resistance. Above its resonant frequency, the capacitor impedance will increase - it is now behaving like an inductor! In most of our applications, capacitors are used either to block dc or to provide a low impedance path for signal currents. In any case, they are supposed to have negligible impedance at all frequencies of interest. If, however, one tries for "overkill" and uses a much larger value capacitor in a circuit than necessary, series resonance may occur and the super size capacitor chosen for its super low impedance may actually have a rather high impedance at higher operating frequencies. For example, if we decide to use a 100 microfarad capacitor in a situation where we want an effective an "short," and the capacitor's lead inductance is 0.01 microhenry, a self resonance will occur at about 160 kilohertz and the impedance of the "capacitor" will increase above that frequency since the inductive reactance of the leads will be greater than the capacitive reactance of the capacitor. 2.4 Inductors. It is difficult to construct physical inductors that do not have significant associated parasitics. Series resistance and shunt capacitance effects are the most common. It is even more difficult to obtain a circuit model that will be accurate over a wide frequency range. Fortunately, the only inductance we usually will have to deal is the parasitic inductance of circuit leads, resistors, or capacitors. 3. Coaxial cable. Coaxial cable ("coax") usually is used to connect test instruments to a circuit under test. When properly used, coax has the ability to minimize noise pickup from external sources and to prevent the test leads themselves from radiating undesired signals into our test environment. Coax consists of an inner conducting wire surrounded by an outside metallic sheath. The sheath forms the return path for the current flowing down the inner wire (Fig. 3.1). An insulating material chosen for its dielectric properties separates the two conductors. If equal currents flow in opposite directions on the inner conductor and on the outer shell, i.e., if the line currents are balanced, the electromagnetic fields caused by the current are confined within the coax. Insulating jacket Outer conducting shell Dielectric Inner conductor Fig. 3.1 Coaxial cable cross-section. Since coax is composed of current-carrying conductors, it has a well-defined inductance per unit length. The cable conductors are held in close proximity by the dielectric, thus coax also has a well- Copyright 2001,
6 defined capacitance per unit length. The line inductance and capacitance are intermingled - distributed - along the length of the line and a precise treatment of the behavior of the line needs to take the distributed nature of the line parameters into account. Coax is classified as a transmission line and its properties are described by its characteristic impedance. The characteristic impedance of coax is defined as the geometric mean (square root) of the product of its per-unit-length inductive reactance and its pre-unit-length capacitive reactance. Z o ωl ωc L C (3.1) The most common value for Z o is 50 ohms and a typical coax capacitance is 30 pf per foot. It then follows that this "fifty-ohm" coax has a per-unit inductance of: L CZ o µH per foot (3.2) The cable also has resistance, but this resistance usually is small enough to be ignored. Fro our purposes, we can assume that coax is a "lossless" (resistance-less) transmission line. A theoretical treatment of the behavior of transmission lines is beyond the scope of this discussion, but we will make several observations about their properties: If a transmission line is terminated in its characteristic impedance, the impedance across its input terminals will equal its characteristic impedance, regardless of the length of the line, even though it be many wavelengths long. In a properly terminated line, the signal at the line termination will "look like" the signal at its input, delayed by a time interval proportional to the length of the line. If coax is terminated in other than its characteristic impedance, standing waves will appear across the line and the impedance at the input terminals of the coax will not equal its terminating impedance, but will vary, depending on the length of the line in electrical wavelengths. As an extreme example, a line whose termination is an open circuit will have an input impedance that varies periodically from infinity to zero, depending on the length of the line and on its excitation frequency. A short-circuited line will have an input impedance that also varies periodically from zero to infinity as its excitation frequency, or its length, changes. A transmission line connected to two circuit nodes on one end and open or short-circuited on the other is called a stub. By selecting a proper stub length, we theoretically can obtain any desired circuit impedance at any desired frequency at the line input nodes. We can make a transmission line stub look like a capacitor or an inductor with reactance of any value we want. Unfortunately, stubs are useful only at radio frequencies with their short wavelengths. The stub lengths required for use in the kilohertz signal range would be far too long to be practical. For our purposes, any length of coax we use in the lab will be "short" - a small fraction of a wavelength of the signal applied to it. If the coax is terminated in a "large" impedance, such as an oscilloscope input, we can approximate the piece of coax as a capacitor whose capacitance is equal to Copyright 2001,
7 the length of the coax times its per-unit length capacitance. If the coax is terminated in a "small" valued impedance- seldom the case - we can approximate it as an inductor whose inductance equals the length of the coax times its per length inductance. The inductance is split between the inner and the outer conductors. 4. Function generator characteristics. A function generator is generally a well-behaved instrument in most laboratory setups. Typically, it has a switch-selectable choice of sine, square wave, or triangular output waveshape and the generator frequency and output amplitude can be varied over a wide range. A circuit model for a generic function generator consists of an ideal voltage source representing the output waveshape at the desired voltage and a series resistance representing the non-zero output impedance of the generator. The function generator output impedance typically is 50 or 600 ohms for low frequency generators and 50 ohms (to match coaxial cable) for radio frequency and microwave generators. A model for the generic function generator is shown in Fig Coax connector V g R g Earth Power line ground Fig Function generator circuit model The output terminals of the generator are usually brought to a coaxial cable connector and the generator is connected to the circuit using a length of 50 ohm coaxial cable. Note that the function generator "low" terminal is connected to earth over the lab power line wiring. As we will soon see, this ground connection - necessary for safety reasons - can cause problems, introducing noise into our circuit measurements through "ground loop" effects. If we assume that the input impedance of the circuit to which the generator is connected is considerably higher than 50 ohms, the coax can be represented as a capacitor connected across the function generator terminals. A one meter length of coax has capacitance of about 100 picofarads therefore its reactance at 1 megahertz is: X C π π 1592 ohms (4.1) and at 10 megahertz it is ohms. The coax impedance exerts a significant load on the function generator at higher frequencies and its effect must be compensated. This frequency-dependent Copyright 2001,
8 loading is not a problem if the function generator is producing pure sine waves - a 'scope probe could be connected across the circuit connection points of the function generator and the generator amplitude adjusted for the correct voltage at the probe. For best accuracy, the probe should be kept connected for the duration of the measurement, since its high frequency input impedance may be low enough to load the function generator and its removal may cause a significant change in the voltage applied to the circuit under test. Problems occur if we try to drive our circuit with a high frequency square wave or triangular wave. Recall from Fourier series theory that these waveforms can be represented as a sum of harmonicallyrelated sinusoids. Unfortunately, the load on the function generator is frequency-dependent so the harmonic content of a square wave, for example, will not be preserved and the waveform presented to the circuit will be distorted. A simple way to handle this is to terminate the coax with a 47 or 51 ohm resistor - resistance values suitably close to the characteristic impedance of the coax - and connect the coax- resistor junction to the circuit under test (Fig. 4.2). recall from the discussion of the properties of coaxial cable that if the coax termination matches its characteristic impedance, the impedance across its input terminals - those connected to the function generator will equal the characteristic impedance at all frequencies. Loading thus is the same at all frequencies and the signal waveshape at the circuit will be the same as that generated by the function generator, but delayed in time. Also, a function generator with 50 ohm output impedance at the end of the terminated coax will look like a voltage source of 1/2 the open-circuit source value with a 25 ohm Thevinen equivalent output impedance. Since the circuit input impedance also is connected across the coax, this model will hold only if it is much greater than 50 ohms at all frequencies of interest. Function generator 50 Ohm Coax Circuit input V g R g Coax connector 47 Ohms Circuit ground Earth Power line ground Fig. 4.2 Termination for frequency independent coax loading. 5. Oscilloscope characteristics. The most important measuring instrument that you will use in electronics is the oscilloscope. Often the only way that you can observe the performance of your circuit is to display the time waveforms existing at different layout nodes. Connecting an instrument to your circuit, however, is equivalent to connecting more circuit elements across the measurement points. A schematic of the input terminals of a typical oscilloscope is shown in Fig. 5.1 Copyright 2001,
9 Coax Connector R 1 Mohm C 20 pf Scope power cable ground wire To other circuits on this line Power system ground Earth Fig. 5.1 Oscilloscope input circuit There are two important features to note about the oscilloscope input connection: The 'scope input impedance has a maximum value of 1 megohm at dc and decreases with increasing frequency since the reactance of the parallel capacitor decreases with frequency. Decreasing input impedance means that the load that the oscilloscope places on the circuit under test increases as the circuit operating frequency increases. Because of oscilloscope loading, what may be an accurate measurement at 1 kilohertz may be a very poor one at 10 megahertz! The shell of the 'scope connector is tied to earth through the 'scope power line connection. This path to earth is shared with any other electrical device that happens to be connected to the same circuit. Ground paths shared with operating electrical devices - fluorescent lights, for example - are a common source of the noise that appears in an experimental circuit. 5.a. Oscilloscope input interface. We need to connect our oscilloscope to the nodes that we wish to observe. This connection requires that a conductor run between the 'scope input and the node. The usual approach is to use a piece of coaxial cable with a coaxial connector on one end and clip leads on the other. One clip is connected to the coax shield, which is connected to earth. The other is connected to the coax center connector. The voltage we will observe is that between the center connector lead and the grounded lead, which should be connected to the common ("ground") node of the circuit under test. Unfortunately, this connecting cable introduces additional capacitance in parallel with the input capacitance of the oscilloscope. Coaxial cable of this type typically has a capacitance of about 30 pf per foot, so a three foot cable would increase the effective capacitance connected across the measurement points to over 100 pf. Table 5.1 gives some idea of the oscilloscope input impedance variation with frequency using this type of connection, assuming100 pf total capacitance. Copyright 2001,
10 Frequency Frequency Input Input Impedance Rad/sec Hz reactance resistance magnitude E E E E E E E E E+06 1, E E E+05 10, , E E E , , E E E+04 1,000, , E E E+04 10,000, ,591, E E E+03 Table 5.1. Oscilloscope input impedance variation with frequency. Note that for frequencies below about 1,000 radians per second, or 159 Hz. the input impedance can be approximated reasonably as a resistance of 1 megohm. Above about 100,000 radians per second, KHz., the input connection to the 'scope can be approximated closely as purely capacitive and the 'scope input impedance decreases rapidly with frequency. 5.b Attenuating oscilloscope probes. The common approach taken to reduce oscilloscope loading is to use special probes to connect the 'scope input to the circuit nodes. Fig. 5.2 represents a "10x probe" attached to a oscilloscope input connector. A 10x probe attenuates the input voltage at the probe tip by a factor of 10 at the 'scope input connector. Thus, the voltage seen at the 'scope input is only 1/10 of the input voltage. Why intentionally attenuate the voltage we wish to observe? Because it increases the impedance across the test nodes by a factor of 10! Probe Body C p 12 pf Coax Oscilloscope Input Probe Tip R p 9 Mohm C c 1 Mohm C s 20 pf Ground Clip Cable Capacitance 80 pf Fig x probe connected to oscilloscope input. Modeling of the probe action is based on the voltage divider action of the series combination of two impedances, each consisting of a capacitor and resistor in parallel. The first parallel circuit consists of the 'scope input resistance and a parallel combination of the cable capacitance and the 'scope input capacitance. We have a 100 pf equivalent capacitance in parallel with a 1 megohm resistor: Z s+ c 1 + sc s+ c 1 sc s+ c s C s +c +1 (5.1) Copyright 2001,
11 We define the time constant of the probe-plus-cable combination as: τ s +c C s +c (5.2) The probe contains a comparable parallel circuit consisting of the probe resistor and an adjustable capacitor. The impedance of the probe is: Z p R p 1 sc p R p + 1 sc p R p sr p C p +1 (5.3) and the probe time constant is: τ p R p C p (5.4) The parallel impedance pairs form a simple voltage divider leading to a 'scope voltage of: or: V scope Z s + c Z s +c + Z p V in (5.5) sτ V scope s +c +1 sτ s +c +1 + R V in (5.6) p sτ p +1 If the probe capacitor is adjusted properly: and R p C p C s+ c τ p τ s+ c (5.7) (5.8) With this time constant match and the resultant cancellation of the sτ +1 terms in Eq. (5.6), the voltage divider ratio becomes: Since V scope R p C p C s+ c + R p V in R p V in V in 1 10 V in (5.9) (5.10) we have: Copyright 2001,
12 R p C s+ c C p (5.11) If we then substitute for the resistance ratio in Eq. (5.9), we obtain an equivalent expression for the voltage divider: V scope C V C p in V s +c C p + C in (5.12) s +c C p The voltage divider output is equal to one-tenth of the probe input voltage and is independent of the frequency of the input signal. This type of circuit is called an allpass filter, since its output voltage magnitude is independent of frequency. Another important characteristic of the probe is its effect on the 'scope input impedance. The input impedance is formed by a series combination of two parallel RC circuits with equal time constants: Z in sτ s+ c +1 + R p sτ p +1 R + p sτ +1 (5.13) Note that the common time constant is the same as the time constant we had obtained previously for the 'scope connected directly to the test points via a piece of coaxial cable. We leave it to the reader to verify that an equivalent expression for the input impedance time constant is: C τ ( + R p ) p C s+ c (R C p + C s + R p )C ser (5.14) s+ c As far as the input impedance is concerned, the probe appears as a combination of two series resistors connected in parallel with two series capacitors. The "real" mid-point connection of the resistors and capacitors is effectively "opened" since the mid-point voltage drop across the resistors equals that across the capacitors at all frequencies and no current flows through the md-point connection. The probe equivalent series resistance is 10 megohms and its equivalent series capacitance is: C ser τ + R p C s +c + R p 1 10 C s+ c (5.15) Thus, the input resistance is ten times the basic oscilloscope input resistance, the equivalent capacitance is one-tenth the oscilloscope plus coax input capacitance, and the probe increases the measurement input impedance by an order of magnitude. Unfortunately, the oscilloscope still may have insufficient input impedance for circuit measurements at high frequencies. Table 5.2 shows the input impedance variation with frequency of this typical 10x probe. Copyright 2001,
13 Frequency Frequency Input Input Impedance Rad/sec Hz reactance resistance magnitude E E E E E E E E E+07 1, E E E+06 10, , E E E , , E E E+05 1,000, , E E E+05 10,000, ,591, E E E+04 Table x probe input impedance. Although the measurement input impedance has increased by a factor of 10, it can be seen that the input capacitance still dominates at frequencies above about 1 KHz. At 15 Khz, the input of the 'scope looks like a capacitor to the rest of the circuit! This phenomenon makes oscilloscope measurements difficult to make at high frequencies. If we wish to measure the output of an amplifier at 10 MHz., for example, we need to contend with the fact that connecting our 'scope to the test points is equivalent to placing a 10 pf capacitor across those nodes. This capacitor will have a reactance of 1591 ohms - a value sufficient to cause significant measurement error if the capacitor is placed across a resistor whose value is much greater than about 100 ohms! The situation, however, would be much worse if we did not use the probe. 5.3 Oscilloscope grounding. An oscilloscope's "low" terminal is connected to earth through its power line connection. Oscilloscope input Function generator Sneak ground current path (ground loop) Earth connection 115v ac RMS power Arc-type electrical device Fig. 5.3 Illustrating undesired current flow in our circuit. If any other device in a circuit under test is also connected to ground, an undesired path through our circuit is provided for currents from outside sources which use earth connections for their conducting Copyright 2001,
14 paths. Usually, a line-powered function generator is part of our circuit and this generator is also connected to earth through its power line connector. A simple circuit illustrating a potential problem source is shown in Fig The loop created by this connection also creates an opportunity for other sources to couple magnetically with our circuit. Ground loops are common sources of 60 Hz. power line noise in our measurements. Ground loops also act as radio antennas and will pick up quite strong RF signals from nearby radio transmitters. The best way to minimize ground loop effects is minimize the length of the path between the instrument power line ground and circuit measurement ground connections: Connect the 'scope probe ground clip to the circuit node closest to the function generator input "low" terminal and plug both instruments into the same ac outlet (Fig. 5.4). Oscilloscope input Function generator Shorten path to minimize impedance to noise current Earth connection Minimize noise voltage drop 115v ac RMS power Arc-type electrical device Fig. 5.4 Illustrating ground loop effect minimization. Actually, it's good form, where possible, to connect all off-ground power supply voltage leads to one point on the circuit board and all power and circuit "ground" leads to another single point. All ground lead paths should be as short as possible and connections are made to the 'scope, the function generator, and the power supply ground terminal at this point. All powered devices, should have their off-ground power supply potential points also run to a common point from which a connection is made to the power supply. This approach minimizes the possibility that signal currents flowing through power leads from different parts of the circuit will, through impedance drops in the leads, interact with other parts of the circuit. It also minimizes the size of the ground loop around our experimental circuit. Copyright 2001,
EMI and t Layout Fundamentals for Switched-Mode Circuits
 v sg (t) (t) DT s V pp = n - 1 2 V pp V g n V T s t EE core insulation primary return secondary return Supplementary notes on EMI and t Layout Fundamentals for Switched-Mode Circuits secondary primary
v sg (t) (t) DT s V pp = n - 1 2 V pp V g n V T s t EE core insulation primary return secondary return Supplementary notes on EMI and t Layout Fundamentals for Switched-Mode Circuits secondary primary
Impedance Matching and Matching Networks. Valentin Todorow, December, 2009
 Impedance Matching and Matching Networks Valentin Todorow, December, 2009 RF for Plasma Processing - Definition of RF What is RF? The IEEE Standard Dictionary of Electrical and Electronics Terms defines
Impedance Matching and Matching Networks Valentin Todorow, December, 2009 RF for Plasma Processing - Definition of RF What is RF? The IEEE Standard Dictionary of Electrical and Electronics Terms defines
A wave lab inside a coaxial cable
 INSTITUTE OF PHYSICS PUBLISHING Eur. J. Phys. 25 (2004) 581 591 EUROPEAN JOURNAL OF PHYSICS PII: S0143-0807(04)76273-X A wave lab inside a coaxial cable JoãoMSerra,MiguelCBrito,JMaiaAlves and A M Vallera
INSTITUTE OF PHYSICS PUBLISHING Eur. J. Phys. 25 (2004) 581 591 EUROPEAN JOURNAL OF PHYSICS PII: S0143-0807(04)76273-X A wave lab inside a coaxial cable JoãoMSerra,MiguelCBrito,JMaiaAlves and A M Vallera
The W5JCK Guide to the Mathematic Equations Required for the Amateur Extra Class Exam
 The W5JCK Guide to the Mathematic Equations Required for the Amateur Extra Class Exam This document contains every question from the Extra Class (Element 4) Question Pool* that requires one or more mathematical
The W5JCK Guide to the Mathematic Equations Required for the Amateur Extra Class Exam This document contains every question from the Extra Class (Element 4) Question Pool* that requires one or more mathematical
Application Note AN:005. FPA Printed Circuit Board Layout Guidelines. Introduction Contents. The Importance of Board Layout
 FPA Printed Circuit Board Layout Guidelines By Paul Yeaman Principal Product Line Engineer V I Chip Strategic Accounts Introduction Contents Page Introduction 1 The Importance of 1 Board Layout Low DC
FPA Printed Circuit Board Layout Guidelines By Paul Yeaman Principal Product Line Engineer V I Chip Strategic Accounts Introduction Contents Page Introduction 1 The Importance of 1 Board Layout Low DC
RLC Resonant Circuits
 C esonant Circuits Andrew McHutchon April 20, 203 Capacitors and Inductors There is a lot of inconsistency when it comes to dealing with reactances of complex components. The format followed in this document
C esonant Circuits Andrew McHutchon April 20, 203 Capacitors and Inductors There is a lot of inconsistency when it comes to dealing with reactances of complex components. The format followed in this document
Engineering Sciences 151. Electromagnetic Communication Laboratory Assignment 3 Fall Term 1998-99
 Engineering Sciences 151 Electromagnetic Communication Laboratory Assignment 3 Fall Term 1998-99 WAVE PROPAGATION II: HIGH FREQUENCY SLOTTED LINE AND REFLECTOMETER MEASUREMENTS OBJECTIVES: To build greater
Engineering Sciences 151 Electromagnetic Communication Laboratory Assignment 3 Fall Term 1998-99 WAVE PROPAGATION II: HIGH FREQUENCY SLOTTED LINE AND REFLECTOMETER MEASUREMENTS OBJECTIVES: To build greater
Current Probes, More Useful Than You Think
 Current Probes, More Useful Than You Think Training and design help in most areas of Electrical Engineering Copyright 1998 Institute of Electrical and Electronics Engineers. Reprinted from the IEEE 1998
Current Probes, More Useful Than You Think Training and design help in most areas of Electrical Engineering Copyright 1998 Institute of Electrical and Electronics Engineers. Reprinted from the IEEE 1998
Balanced vs. Unbalanced Audio Interconnections
 Revised 7/2/08 Balanced vs. Unbalanced Audio Interconnections In discussing the characteristics and performance of various interconnect systems; two points should be kept in mind. Balance is defined in
Revised 7/2/08 Balanced vs. Unbalanced Audio Interconnections In discussing the characteristics and performance of various interconnect systems; two points should be kept in mind. Balance is defined in
Current Probes. User Manual
 Current Probes User Manual ETS-Lindgren L.P. reserves the right to make changes to any product described herein in order to improve function, design, or for any other reason. Nothing contained herein shall
Current Probes User Manual ETS-Lindgren L.P. reserves the right to make changes to any product described herein in order to improve function, design, or for any other reason. Nothing contained herein shall
Since any real component also has loss due to the resistive component, the average power dissipated is 2 2R
 Quality factor, Q Reactive components such as capacitors and inductors are often described with a figure of merit called Q. While it can be defined in many ways, it s most fundamental description is: Q
Quality factor, Q Reactive components such as capacitors and inductors are often described with a figure of merit called Q. While it can be defined in many ways, it s most fundamental description is: Q
Physics 6C, Summer 2006 Homework 2 Solutions
 Physics 6C, Summer 006 Homework Solutions All problems are from the nd edition of Walker. Numerical values are different for each student. Chapter 3 Problems. Figure 3-30 below shows a circuit containing
Physics 6C, Summer 006 Homework Solutions All problems are from the nd edition of Walker. Numerical values are different for each student. Chapter 3 Problems. Figure 3-30 below shows a circuit containing
Physics 3330 Experiment #2 Fall 1999. DC techniques, dividers, and bridges R 2 =(1-S)R P R 1 =SR P. R P =10kΩ 10-turn pot.
 Physics 3330 Experiment #2 Fall 1999 DC techniques, dividers, and bridges Purpose You will gain a familiarity with the circuit board and work with a variety of DC techniques, including voltage dividers,
Physics 3330 Experiment #2 Fall 1999 DC techniques, dividers, and bridges Purpose You will gain a familiarity with the circuit board and work with a variety of DC techniques, including voltage dividers,
Measurement of Capacitance
 Measurement of Capacitance Pre-Lab Questions Page Name: Class: Roster Number: Instructor:. A capacitor is used to store. 2. What is the SI unit for capacitance? 3. A capacitor basically consists of two
Measurement of Capacitance Pre-Lab Questions Page Name: Class: Roster Number: Instructor:. A capacitor is used to store. 2. What is the SI unit for capacitance? 3. A capacitor basically consists of two
ε: Voltage output of Signal Generator (also called the Source voltage or Applied
 Experiment #10: LR & RC Circuits Frequency Response EQUIPMENT NEEDED Science Workshop Interface Power Amplifier (2) Voltage Sensor graph paper (optional) (3) Patch Cords Decade resistor, capacitor, and
Experiment #10: LR & RC Circuits Frequency Response EQUIPMENT NEEDED Science Workshop Interface Power Amplifier (2) Voltage Sensor graph paper (optional) (3) Patch Cords Decade resistor, capacitor, and
E. K. A. ADVANCED PHYSICS LABORATORY PHYSICS 3081, 4051 NUCLEAR MAGNETIC RESONANCE
 E. K. A. ADVANCED PHYSICS LABORATORY PHYSICS 3081, 4051 NUCLEAR MAGNETIC RESONANCE References for Nuclear Magnetic Resonance 1. Slichter, Principles of Magnetic Resonance, Harper and Row, 1963. chapter
E. K. A. ADVANCED PHYSICS LABORATORY PHYSICS 3081, 4051 NUCLEAR MAGNETIC RESONANCE References for Nuclear Magnetic Resonance 1. Slichter, Principles of Magnetic Resonance, Harper and Row, 1963. chapter
An equivalent circuit of a loop antenna.
 3.2.1. Circuit Modeling: Loop Impedance A loop antenna can be represented by a lumped circuit when its dimension is small with respect to a wavelength. In this representation, the circuit parameters (generally
3.2.1. Circuit Modeling: Loop Impedance A loop antenna can be represented by a lumped circuit when its dimension is small with respect to a wavelength. In this representation, the circuit parameters (generally
Keysight Technologies Understanding the Fundamental Principles of Vector Network Analysis. Application Note
 Keysight Technologies Understanding the Fundamental Principles of Vector Network Analysis Application Note Introduction Network analysis is the process by which designers and manufacturers measure the
Keysight Technologies Understanding the Fundamental Principles of Vector Network Analysis Application Note Introduction Network analysis is the process by which designers and manufacturers measure the
An Overview of Practical Capacitance Bridge Functioning. by Paul Moses
 An Overview of Practical Capacitance Bridge Functioning by Paul Moses INTRODUCTION The laboratory has a variety of bridges, both automatic and manual which can be used to measure the capacitance and dielectric
An Overview of Practical Capacitance Bridge Functioning by Paul Moses INTRODUCTION The laboratory has a variety of bridges, both automatic and manual which can be used to measure the capacitance and dielectric
Reading: HH Sections 4.11 4.13, 4.19 4.20 (pgs. 189-212, 222 224)
 6 OP AMPS II 6 Op Amps II In the previous lab, you explored several applications of op amps. In this exercise, you will look at some of their limitations. You will also examine the op amp integrator and
6 OP AMPS II 6 Op Amps II In the previous lab, you explored several applications of op amps. In this exercise, you will look at some of their limitations. You will also examine the op amp integrator and
DRIVING LOOOONG CABLES
 DRIVING LOOOONG CABLES INTRODUCTION Microphone or line level cables may appear to be foolproof compared to loudspeaker cables. However, they are not. In particular you can easily encounter high frequency
DRIVING LOOOONG CABLES INTRODUCTION Microphone or line level cables may appear to be foolproof compared to loudspeaker cables. However, they are not. In particular you can easily encounter high frequency
Application Note. So You Need to Measure Some Inductors?
 So You Need to Measure Some nductors? Take a look at the 1910 nductance Analyzer. Although specifically designed for production testing of inductors and coils, in addition to measuring inductance (L),
So You Need to Measure Some nductors? Take a look at the 1910 nductance Analyzer. Although specifically designed for production testing of inductors and coils, in addition to measuring inductance (L),
Harmonics and Noise in Photovoltaic (PV) Inverter and the Mitigation Strategies
 Soonwook Hong, Ph. D. Michael Zuercher Martinson Harmonics and Noise in Photovoltaic (PV) Inverter and the Mitigation Strategies 1. Introduction PV inverters use semiconductor devices to transform the
Soonwook Hong, Ph. D. Michael Zuercher Martinson Harmonics and Noise in Photovoltaic (PV) Inverter and the Mitigation Strategies 1. Introduction PV inverters use semiconductor devices to transform the
Signal Integrity: Tips and Tricks
 White Paper: Virtex-II, Virtex-4, Virtex-5, and Spartan-3 FPGAs R WP323 (v1.0) March 28, 2008 Signal Integrity: Tips and Tricks By: Austin Lesea Signal integrity (SI) engineering has become a necessary
White Paper: Virtex-II, Virtex-4, Virtex-5, and Spartan-3 FPGAs R WP323 (v1.0) March 28, 2008 Signal Integrity: Tips and Tricks By: Austin Lesea Signal integrity (SI) engineering has become a necessary
2. A conductor of length 2m moves at 4m/s at 30 to a uniform magnetic field of 0.1T. Which one of the following gives the e.m.f. generated?
 Extra Questions - 2 1. A straight length of wire moves through a uniform magnetic field. The e.m.f. produced across the ends of the wire will be maximum if it moves: a) along the lines of magnetic flux
Extra Questions - 2 1. A straight length of wire moves through a uniform magnetic field. The e.m.f. produced across the ends of the wire will be maximum if it moves: a) along the lines of magnetic flux
Understanding SWR by Example
 Understanding SWR by Example Take the mystery and mystique out of standing wave ratio. Darrin Walraven, K5DVW It sometimes seems that one of the most mysterious creatures in the world of Amateur Radio
Understanding SWR by Example Take the mystery and mystique out of standing wave ratio. Darrin Walraven, K5DVW It sometimes seems that one of the most mysterious creatures in the world of Amateur Radio
SERIES-PARALLEL DC CIRCUITS
 Name: Date: Course and Section: Instructor: EXPERIMENT 1 SERIES-PARALLEL DC CIRCUITS OBJECTIVES 1. Test the theoretical analysis of series-parallel networks through direct measurements. 2. Improve skills
Name: Date: Course and Section: Instructor: EXPERIMENT 1 SERIES-PARALLEL DC CIRCUITS OBJECTIVES 1. Test the theoretical analysis of series-parallel networks through direct measurements. 2. Improve skills
Measuring Impedance and Frequency Response of Guitar Pickups
 Measuring Impedance and Frequency Response of Guitar Pickups Peter D. Hiscocks Syscomp Electronic Design Limited phiscock@ee.ryerson.ca www.syscompdesign.com April 30, 2011 Introduction The CircuitGear
Measuring Impedance and Frequency Response of Guitar Pickups Peter D. Hiscocks Syscomp Electronic Design Limited phiscock@ee.ryerson.ca www.syscompdesign.com April 30, 2011 Introduction The CircuitGear
Measuring Parasitic Capacitance and Inductance Using TDR
 Measuring Parasitic apacitance and Inductance Using TDR Time-domain reflectometry (TDR) is commonly used as a convenient method of determining the characteristic impedance of a transmission line or quantifying
Measuring Parasitic apacitance and Inductance Using TDR Time-domain reflectometry (TDR) is commonly used as a convenient method of determining the characteristic impedance of a transmission line or quantifying
MEASUREMENT SET-UP FOR TRAPS
 Completed on 26th of June, 2012 MEASUREMENT SET-UP FOR TRAPS AUTHOR: IW2FND Attolini Lucio Via XXV Aprile, 52/B 26037 San Giovanni in Croce (CR) - Italy iw2fnd@gmail.com Trappole_01_EN 1 1 DESCRIPTION...3
Completed on 26th of June, 2012 MEASUREMENT SET-UP FOR TRAPS AUTHOR: IW2FND Attolini Lucio Via XXV Aprile, 52/B 26037 San Giovanni in Croce (CR) - Italy iw2fnd@gmail.com Trappole_01_EN 1 1 DESCRIPTION...3
Three phase circuits
 Three phase circuits THREE PHASE CIRCUITS THREE-PHASE ADVANTAGES 1. The horsepower rating of three-phase motors and the kva rating of three-phase transformers are 150% greater than single-phase motors
Three phase circuits THREE PHASE CIRCUITS THREE-PHASE ADVANTAGES 1. The horsepower rating of three-phase motors and the kva rating of three-phase transformers are 150% greater than single-phase motors
Constructing a precision SWR meter and antenna analyzer. Mike Brink HNF, Design Technologist.
 Constructing a precision SWR meter and antenna analyzer. Mike Brink HNF, Design Technologist. Abstract. I have been asked to put together a detailed article on a SWR meter. In this article I will deal
Constructing a precision SWR meter and antenna analyzer. Mike Brink HNF, Design Technologist. Abstract. I have been asked to put together a detailed article on a SWR meter. In this article I will deal
A Simple Current-Sense Technique Eliminating a Sense Resistor
 INFINITY Application Note AN-7 A Simple Current-Sense Technique Eliminating a Sense Resistor Copyright 998 A SIMPE CURRENT-SENSE TECHNIQUE EIMINATING A SENSE RESISTOR INTRODUCTION A sense resistor R S,
INFINITY Application Note AN-7 A Simple Current-Sense Technique Eliminating a Sense Resistor Copyright 998 A SIMPE CURRENT-SENSE TECHNIQUE EIMINATING A SENSE RESISTOR INTRODUCTION A sense resistor R S,
GenTech Practice Questions
 GenTech Practice Questions Basic Electronics Test: This test will assess your knowledge of and ability to apply the principles of Basic Electronics. This test is comprised of 90 questions in the following
GenTech Practice Questions Basic Electronics Test: This test will assess your knowledge of and ability to apply the principles of Basic Electronics. This test is comprised of 90 questions in the following
Understanding Power Impedance Supply for Optimum Decoupling
 Introduction Noise in power supplies is not only caused by the power supply itself, but also the load s interaction with the power supply (i.e. dynamic loads, switching, etc.). To lower load induced noise,
Introduction Noise in power supplies is not only caused by the power supply itself, but also the load s interaction with the power supply (i.e. dynamic loads, switching, etc.). To lower load induced noise,
The Effects Of Cable On Signal Quality
 The Effects Of Cable On Signal Quality By Jim Brown Audio Systems Group, Inc. jim@audiosystemgroup.com System designs often require output amplifier stages of microphones and line-level devices to drive
The Effects Of Cable On Signal Quality By Jim Brown Audio Systems Group, Inc. jim@audiosystemgroup.com System designs often require output amplifier stages of microphones and line-level devices to drive
Troubleshooting accelerometer installations
 Troubleshooting accelerometer installations Accelerometer based monitoring systems can be tested to verify proper installation and operation. Testing ensures data integrity and can identify most problems.
Troubleshooting accelerometer installations Accelerometer based monitoring systems can be tested to verify proper installation and operation. Testing ensures data integrity and can identify most problems.
EDEXCEL NATIONAL CERTIFICATE/DIPLOMA UNIT 5 - ELECTRICAL AND ELECTRONIC PRINCIPLES NQF LEVEL 3 OUTCOME 4 - ALTERNATING CURRENT
 EDEXCEL NATIONAL CERTIFICATE/DIPLOMA UNIT 5 - ELECTRICAL AND ELECTRONIC PRINCIPLES NQF LEVEL 3 OUTCOME 4 - ALTERNATING CURRENT 4 Understand single-phase alternating current (ac) theory Single phase AC
EDEXCEL NATIONAL CERTIFICATE/DIPLOMA UNIT 5 - ELECTRICAL AND ELECTRONIC PRINCIPLES NQF LEVEL 3 OUTCOME 4 - ALTERNATING CURRENT 4 Understand single-phase alternating current (ac) theory Single phase AC
DIODE CIRCUITS LABORATORY. Fig. 8.1a Fig 8.1b
 DIODE CIRCUITS LABORATORY A solid state diode consists of a junction of either dissimilar semiconductors (pn junction diode) or a metal and a semiconductor (Schottky barrier diode). Regardless of the type,
DIODE CIRCUITS LABORATORY A solid state diode consists of a junction of either dissimilar semiconductors (pn junction diode) or a metal and a semiconductor (Schottky barrier diode). Regardless of the type,
Grounding Demystified
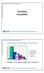 Grounding Demystified 3-1 Importance Of Grounding Techniques 45 40 35 30 25 20 15 10 5 0 Grounding 42% Case 22% Cable 18% Percent Used Filter 12% PCB 6% Grounding 42% Case Shield 22% Cable Shielding 18%
Grounding Demystified 3-1 Importance Of Grounding Techniques 45 40 35 30 25 20 15 10 5 0 Grounding 42% Case 22% Cable 18% Percent Used Filter 12% PCB 6% Grounding 42% Case Shield 22% Cable Shielding 18%
WHY DIFFERENTIAL? instruments connected to the circuit under test and results in V COMMON.
 WHY DIFFERENTIAL? Voltage, The Difference Whether aware of it or not, a person using an oscilloscope to make any voltage measurement is actually making a differential voltage measurement. By definition,
WHY DIFFERENTIAL? Voltage, The Difference Whether aware of it or not, a person using an oscilloscope to make any voltage measurement is actually making a differential voltage measurement. By definition,
Lab E1: Introduction to Circuits
 E1.1 Lab E1: Introduction to Circuits The purpose of the this lab is to introduce you to some basic instrumentation used in electrical circuits. You will learn to use a DC power supply, a digital multimeter
E1.1 Lab E1: Introduction to Circuits The purpose of the this lab is to introduce you to some basic instrumentation used in electrical circuits. You will learn to use a DC power supply, a digital multimeter
AN-837 APPLICATION NOTE
 APPLICATION NOTE One Technology Way P.O. Box 916 Norwood, MA 262-916, U.S.A. Tel: 781.329.47 Fax: 781.461.3113 www.analog.com DDS-Based Clock Jitter Performance vs. DAC Reconstruction Filter Performance
APPLICATION NOTE One Technology Way P.O. Box 916 Norwood, MA 262-916, U.S.A. Tel: 781.329.47 Fax: 781.461.3113 www.analog.com DDS-Based Clock Jitter Performance vs. DAC Reconstruction Filter Performance
UNDERSTANDING AND CONTROLLING COMMON-MODE EMISSIONS IN HIGH-POWER ELECTRONICS
 Page 1 UNDERSTANDING AND CONTROLLING COMMON-MODE EMISSIONS IN HIGH-POWER ELECTRONICS By Henry Ott Consultants Livingston, NJ 07039 (973) 992-1793 www.hottconsultants.com hott@ieee.org Page 2 THE BASIC
Page 1 UNDERSTANDING AND CONTROLLING COMMON-MODE EMISSIONS IN HIGH-POWER ELECTRONICS By Henry Ott Consultants Livingston, NJ 07039 (973) 992-1793 www.hottconsultants.com hott@ieee.org Page 2 THE BASIC
T = 1 f. Phase. Measure of relative position in time within a single period of a signal For a periodic signal f(t), phase is fractional part t p
 Data Transmission Concepts and terminology Transmission terminology Transmission from transmitter to receiver goes over some transmission medium using electromagnetic waves Guided media. Waves are guided
Data Transmission Concepts and terminology Transmission terminology Transmission from transmitter to receiver goes over some transmission medium using electromagnetic waves Guided media. Waves are guided
Line Reactors and AC Drives
 Line Reactors and AC Drives Rockwell Automation Mequon Wisconsin Quite often, line and load reactors are installed on AC drives without a solid understanding of why or what the positive and negative consequences
Line Reactors and AC Drives Rockwell Automation Mequon Wisconsin Quite often, line and load reactors are installed on AC drives without a solid understanding of why or what the positive and negative consequences
Selecting Receiving Antennas for Radio Tracking
 Selecting Receiving Antennas for Radio Tracking Larry B Kuechle, Advanced Telemetry Systems, Inc. Isanti, Minnesota 55040 lkuechle@atstrack.com The receiving antenna is an integral part of any radio location
Selecting Receiving Antennas for Radio Tracking Larry B Kuechle, Advanced Telemetry Systems, Inc. Isanti, Minnesota 55040 lkuechle@atstrack.com The receiving antenna is an integral part of any radio location
Fundamentals of radio communication
 Fundamentals of radio communication This worksheet and all related files are licensed under the Creative Commons Attribution License, version 1.0. To view a copy of this license, visit http://creativecommons.org/licenses/by/1.0/,
Fundamentals of radio communication This worksheet and all related files are licensed under the Creative Commons Attribution License, version 1.0. To view a copy of this license, visit http://creativecommons.org/licenses/by/1.0/,
Capacitor Self-Resonance
 Capacitor Self-Resonance By: Dr. Mike Blewett University of Surrey United Kingdom Objective This Experiment will demonstrate some of the limitations of capacitors when used in Radio Frequency circuits.
Capacitor Self-Resonance By: Dr. Mike Blewett University of Surrey United Kingdom Objective This Experiment will demonstrate some of the limitations of capacitors when used in Radio Frequency circuits.
Measuring Insulation Resistance of Capacitors
 Application Note Measuring Insulation Resistance of Capacitors A common use of high resistance measuring instruments (often called megohmmeters or insulation resistance testers) is measuring the insulation
Application Note Measuring Insulation Resistance of Capacitors A common use of high resistance measuring instruments (often called megohmmeters or insulation resistance testers) is measuring the insulation
Pulsed Power Engineering Diagnostics
 Pulsed Power Engineering Diagnostics January 12-16, 2009 Craig Burkhart, PhD Power Conversion Department SLAC National Accelerator Laboratory Diagnostic Techniques and Considerations in Pulsed Power Systems
Pulsed Power Engineering Diagnostics January 12-16, 2009 Craig Burkhart, PhD Power Conversion Department SLAC National Accelerator Laboratory Diagnostic Techniques and Considerations in Pulsed Power Systems
Step Response of RC Circuits
 Step Response of RC Circuits 1. OBJECTIVES...2 2. REFERENCE...2 3. CIRCUITS...2 4. COMPONENTS AND SPECIFICATIONS...3 QUANTITY...3 DESCRIPTION...3 COMMENTS...3 5. DISCUSSION...3 5.1 SOURCE RESISTANCE...3
Step Response of RC Circuits 1. OBJECTIVES...2 2. REFERENCE...2 3. CIRCUITS...2 4. COMPONENTS AND SPECIFICATIONS...3 QUANTITY...3 DESCRIPTION...3 COMMENTS...3 5. DISCUSSION...3 5.1 SOURCE RESISTANCE...3
Introduction. Harmonics and IEEE 519 Page 1 of 19
 Introduction In an ideal power system, the voltage supplied to customer equipment, and the resulting load current are perfect sine waves. In practice, however, conditions are never ideal, so these waveforms
Introduction In an ideal power system, the voltage supplied to customer equipment, and the resulting load current are perfect sine waves. In practice, however, conditions are never ideal, so these waveforms
Transmission Line Transformers
 Radio Frequency Circuit Design. W. Alan Davis, Krishna Agarwal Copyright 2001 John Wiley & Sons, Inc. Print ISBN 0-471-35052-4 Electronic ISBN 0-471-20068-9 CHAPTER SIX Transmission Line Transformers 6.1
Radio Frequency Circuit Design. W. Alan Davis, Krishna Agarwal Copyright 2001 John Wiley & Sons, Inc. Print ISBN 0-471-35052-4 Electronic ISBN 0-471-20068-9 CHAPTER SIX Transmission Line Transformers 6.1
Circuits with inductors and alternating currents. Chapter 20 #45, 46, 47, 49
 Circuits with inductors and alternating currents Chapter 20 #45, 46, 47, 49 RL circuits Ch. 20 (last section) Symbol for inductor looks like a spring. An inductor is a circuit element that has a large
Circuits with inductors and alternating currents Chapter 20 #45, 46, 47, 49 RL circuits Ch. 20 (last section) Symbol for inductor looks like a spring. An inductor is a circuit element that has a large
LR Phono Preamps. Pete Millett ETF.13. pmillett@hotmail.com
 LR Phono Preamps Pete Millett ETF.13 pmillett@hotmail.com Agenda A bit about me Part 1: What is, and why use, RIAA? Grooves on records The RIAA standard Implementations of RIAA EQ networks and preamps
LR Phono Preamps Pete Millett ETF.13 pmillett@hotmail.com Agenda A bit about me Part 1: What is, and why use, RIAA? Grooves on records The RIAA standard Implementations of RIAA EQ networks and preamps
Germanium Diode AM Radio
 Germanium Diode AM Radio LAB 3 3.1 Introduction In this laboratory exercise you will build a germanium diode based AM (Medium Wave) radio. Earliest radios used simple diode detector circuits. The diodes
Germanium Diode AM Radio LAB 3 3.1 Introduction In this laboratory exercise you will build a germanium diode based AM (Medium Wave) radio. Earliest radios used simple diode detector circuits. The diodes
BSNL TTA Question Paper-Instruments and Measurement Specialization 2007
 BSNL TTA Question Paper-Instruments and Measurement Specialization 2007 (1) Instrument is a device for determining (a) the magnitude of a quantity (b) the physics of a variable (c) either of the above
BSNL TTA Question Paper-Instruments and Measurement Specialization 2007 (1) Instrument is a device for determining (a) the magnitude of a quantity (b) the physics of a variable (c) either of the above
When designing. Inductors at UHF: EM Simulation Guides Vector Network Analyzer. measurement. EM SIMULATION. There are times when it is
 Inductors at UHF: EM Simulation Guides Vector Network Analyzer Measurements John B. Call Thales Communications Inc., USA When designing There are times when it is circuits for necessary to measure a operation
Inductors at UHF: EM Simulation Guides Vector Network Analyzer Measurements John B. Call Thales Communications Inc., USA When designing There are times when it is circuits for necessary to measure a operation
PHY3128 / PHYM203 (Electronics / Instrumentation) Transmission Lines. Repeated n times I L
 Transmission Lines Introduction A transmission line guides energy from one place to another. Optical fibres, waveguides, telephone lines and power cables are all electromagnetic transmission lines. are
Transmission Lines Introduction A transmission line guides energy from one place to another. Optical fibres, waveguides, telephone lines and power cables are all electromagnetic transmission lines. are
RLC Series Resonance
 RLC Series Resonance 11EM Object: The purpose of this laboratory activity is to study resonance in a resistor-inductor-capacitor (RLC) circuit by examining the current through the circuit as a function
RLC Series Resonance 11EM Object: The purpose of this laboratory activity is to study resonance in a resistor-inductor-capacitor (RLC) circuit by examining the current through the circuit as a function
An Ethernet Cable Discharge Event (CDE) Test and Measurement System
 An Ethernet Cable Discharge Event (CDE) Test and Measurement System Wei Huang, Jerry Tichenor ESDEMC Technology LLC Rolla, MO, USA whuang@esdemc.com Abstract A Cable Discharge Event (CDE) is an electrostatic
An Ethernet Cable Discharge Event (CDE) Test and Measurement System Wei Huang, Jerry Tichenor ESDEMC Technology LLC Rolla, MO, USA whuang@esdemc.com Abstract A Cable Discharge Event (CDE) is an electrostatic
Chapter 14: Inductor design
 Chapter 14 Inductor Design 14.1 Filter inductor design constraints 14.2 A step-by-step design procedure 14.3 Multiple-winding magnetics design using the K g method 14.4 Examples 14.5 Summary of key points
Chapter 14 Inductor Design 14.1 Filter inductor design constraints 14.2 A step-by-step design procedure 14.3 Multiple-winding magnetics design using the K g method 14.4 Examples 14.5 Summary of key points
Frequency Response of Filters
 School of Engineering Department of Electrical and Computer Engineering 332:224 Principles of Electrical Engineering II Laboratory Experiment 2 Frequency Response of Filters 1 Introduction Objectives To
School of Engineering Department of Electrical and Computer Engineering 332:224 Principles of Electrical Engineering II Laboratory Experiment 2 Frequency Response of Filters 1 Introduction Objectives To
G019.A (4/99) UNDERSTANDING COMMON MODE NOISE
 UNDERSTANDING COMMON MODE NOISE PAGE 2 OF 7 TABLE OF CONTENTS 1 INTRODUCTION 2 DIFFERENTIAL MODE AND COMMON MODE SIGNALS 2.1 Differential Mode signals 2.2 Common Mode signals 3 DIFFERENTIAL AND COMMON
UNDERSTANDING COMMON MODE NOISE PAGE 2 OF 7 TABLE OF CONTENTS 1 INTRODUCTION 2 DIFFERENTIAL MODE AND COMMON MODE SIGNALS 2.1 Differential Mode signals 2.2 Common Mode signals 3 DIFFERENTIAL AND COMMON
Inductors in AC Circuits
 Inductors in AC Circuits Name Section Resistors, inductors, and capacitors all have the effect of modifying the size of the current in an AC circuit and the time at which the current reaches its maximum
Inductors in AC Circuits Name Section Resistors, inductors, and capacitors all have the effect of modifying the size of the current in an AC circuit and the time at which the current reaches its maximum
Digital Systems Ribbon Cables I CMPE 650. Ribbon Cables A ribbon cable is any cable having multiple conductors bound together in a flat, wide strip.
 Ribbon Cables A ribbon cable is any cable having multiple conductors bound together in a flat, wide strip. Each dielectric configuration has different high-frequency characteristics. All configurations
Ribbon Cables A ribbon cable is any cable having multiple conductors bound together in a flat, wide strip. Each dielectric configuration has different high-frequency characteristics. All configurations
Eðlisfræði 2, vor 2007
 [ Assignment View ] [ Print ] Eðlisfræði 2, vor 2007 30. Inductance Assignment is due at 2:00am on Wednesday, March 14, 2007 Credit for problems submitted late will decrease to 0% after the deadline has
[ Assignment View ] [ Print ] Eðlisfræði 2, vor 2007 30. Inductance Assignment is due at 2:00am on Wednesday, March 14, 2007 Credit for problems submitted late will decrease to 0% after the deadline has
LVDS Technology Solves Typical EMI Problems Associated with Cell Phone Cameras and Displays
 AN-5059 Fairchild Semiconductor Application Note May 2005 Revised May 2005 LVDS Technology Solves Typical EMI Problems Associated with Cell Phone Cameras and Displays Differential technologies such as
AN-5059 Fairchild Semiconductor Application Note May 2005 Revised May 2005 LVDS Technology Solves Typical EMI Problems Associated with Cell Phone Cameras and Displays Differential technologies such as
1. Oscilloscope is basically a graph-displaying device-it draws a graph of an electrical signal.
 CHAPTER 3: OSCILLOSCOPE AND SIGNAL GENERATOR 3.1 Introduction to oscilloscope 1. Oscilloscope is basically a graph-displaying device-it draws a graph of an electrical signal. 2. The graph show signal change
CHAPTER 3: OSCILLOSCOPE AND SIGNAL GENERATOR 3.1 Introduction to oscilloscope 1. Oscilloscope is basically a graph-displaying device-it draws a graph of an electrical signal. 2. The graph show signal change
AN2866 Application note
 Application note How to design a 13.56 MHz customized tag antenna Introduction RFID (radio-frequency identification) tags extract all of their power from the reader s field. The tags and reader s antennas
Application note How to design a 13.56 MHz customized tag antenna Introduction RFID (radio-frequency identification) tags extract all of their power from the reader s field. The tags and reader s antennas
Fundamentals of Signature Analysis
 Fundamentals of Signature Analysis An In-depth Overview of Power-off Testing Using Analog Signature Analysis www.huntron.com 1 www.huntron.com 2 Table of Contents SECTION 1. INTRODUCTION... 7 PURPOSE...
Fundamentals of Signature Analysis An In-depth Overview of Power-off Testing Using Analog Signature Analysis www.huntron.com 1 www.huntron.com 2 Table of Contents SECTION 1. INTRODUCTION... 7 PURPOSE...
WAVEGUIDE-COAXIAL LINE TRANSITIONS
 WAVEGUIDE-COAXIAL LINE TRANSITIONS 1. Overview Equipment at microwave frequencies is usually based on a combination of PCB and waveguide components. Filters and antennas often use waveguide techniques,
WAVEGUIDE-COAXIAL LINE TRANSITIONS 1. Overview Equipment at microwave frequencies is usually based on a combination of PCB and waveguide components. Filters and antennas often use waveguide techniques,
White Paper: Electrical Ground Rules
 Acromag, Incorporated 30765 S Wixom Rd, Wixom, MI 48393 USA Tel: 248-295-0880 Fax: 248-624-9234 www.acromag.com White Paper: Electrical Ground Rules Best Practices for Grounding Your Electrical Equipment
Acromag, Incorporated 30765 S Wixom Rd, Wixom, MI 48393 USA Tel: 248-295-0880 Fax: 248-624-9234 www.acromag.com White Paper: Electrical Ground Rules Best Practices for Grounding Your Electrical Equipment
Shielding Effectiveness Test Method. Harbour s LL, SB, and SS Coaxial Cables. Designs for Improved Shielding Effectiveness
 Shielding Effectiveness Test Method Harbour s LL, SB, and SS Coaxial Cables Designs for Improved Shielding Effectiveness Harbour Industries 4744 Shelburne Road Shelburne Vermont 05482 USA 802-985-3311
Shielding Effectiveness Test Method Harbour s LL, SB, and SS Coaxial Cables Designs for Improved Shielding Effectiveness Harbour Industries 4744 Shelburne Road Shelburne Vermont 05482 USA 802-985-3311
HARMONIC DISTORTION IN THE ELECTRIC SUPPLY SYSTEM
 Technical Note No.3 March 2000 HARMONIC DISTORTION IN THE ELECTRIC SUPPLY SYSTEM This Technical Note discusses harmonic distortion, its causes and adverse effects, what levels are unacceptable and how
Technical Note No.3 March 2000 HARMONIC DISTORTION IN THE ELECTRIC SUPPLY SYSTEM This Technical Note discusses harmonic distortion, its causes and adverse effects, what levels are unacceptable and how
EB215E Printed Circuit Board Layout for Improved Electromagnetic Compatibility
 Printed Circuit Board Layout for Improved Author: Eilhard Haseloff Date: 10.07.96 Rev: * The electromagnetic compatibility (EMC) of electronic circuits and systems has recently become of increasing significance.
Printed Circuit Board Layout for Improved Author: Eilhard Haseloff Date: 10.07.96 Rev: * The electromagnetic compatibility (EMC) of electronic circuits and systems has recently become of increasing significance.
RX-AM4SF Receiver. Pin-out. Connections
 RX-AM4SF Receiver The super-heterodyne receiver RX-AM4SF can provide a RSSI output indicating the amplitude of the received signal: this output can be used to create a field-strength meter capable to indicate
RX-AM4SF Receiver The super-heterodyne receiver RX-AM4SF can provide a RSSI output indicating the amplitude of the received signal: this output can be used to create a field-strength meter capable to indicate
LS RS. Figure 1: Assumed inductor model
 Characterizing Inductors at HF and VHF Inductors are a key component in RF circuits. Their performance makes a great difference in the operation of amplifiers, oscillators, and other circuit blocks --
Characterizing Inductors at HF and VHF Inductors are a key component in RF circuits. Their performance makes a great difference in the operation of amplifiers, oscillators, and other circuit blocks --
Basic Electrical Technology Dr. L. Umanand Department of Electrical Engineering Indian Institute of Science, Bangalore. Lecture - 33 3 phase System 4
 Basic Electrical Technology Dr. L. Umanand Department of Electrical Engineering Indian Institute of Science, Bangalore Lecture - 33 3 phase System 4 Hello everybody. So, in the last class we have been
Basic Electrical Technology Dr. L. Umanand Department of Electrical Engineering Indian Institute of Science, Bangalore Lecture - 33 3 phase System 4 Hello everybody. So, in the last class we have been
The Importance of the X/R Ratio in Low-Voltage Short Circuit Studies
 The Importance of the X/R Ratio in Low-Voltage Short Circuit Studies DATE: November 17, 1999 REVISION: AUTHOR: John Merrell Introduction In some short circuit studies, the X/R ratio is ignored when comparing
The Importance of the X/R Ratio in Low-Voltage Short Circuit Studies DATE: November 17, 1999 REVISION: AUTHOR: John Merrell Introduction In some short circuit studies, the X/R ratio is ignored when comparing
Understanding the Fundamental Principles of Vector Network Analysis. Application Note 1287-1. Table of Contents. Page
 Understanding the Fundamental Principles of Vector Network Analysis Application Note 1287-1 Table of Contents Page Introduction 2 Measurements in Communications Systems 2 Importance of Vector Measurements
Understanding the Fundamental Principles of Vector Network Analysis Application Note 1287-1 Table of Contents Page Introduction 2 Measurements in Communications Systems 2 Importance of Vector Measurements
Module 11: Conducted Emissions
 Module 11: Conducted Emissions 11.1 Overview The term conducted emissions refers to the mechanism that enables electromagnetic energy to be created in an electronic device and coupled to its AC power cord.
Module 11: Conducted Emissions 11.1 Overview The term conducted emissions refers to the mechanism that enables electromagnetic energy to be created in an electronic device and coupled to its AC power cord.
On Cables and Connections A discussion by Dr. J. Kramer
 KRAMER ELECTRONICS LTD. On Cables and Connections A discussion by Dr. J. Kramer We are frequently asked - "what length of cable can I use for a specific application?" Seemingly a simple question, but the
KRAMER ELECTRONICS LTD. On Cables and Connections A discussion by Dr. J. Kramer We are frequently asked - "what length of cable can I use for a specific application?" Seemingly a simple question, but the
Understanding Power Splitters
 Understanding Power Splitters how they work, what parameters are critical, and how to select the best value for your application. Basically, a 0 splitter is a passive device which accepts an input signal
Understanding Power Splitters how they work, what parameters are critical, and how to select the best value for your application. Basically, a 0 splitter is a passive device which accepts an input signal
Application Note AN- 1095
 Application Note AN- 1095 Design of the Inverter Output Filter for Motor Drives with IRAMS Power Modules Cesare Bocchiola Table of Contents Page Section 1: Introduction...2 Section 2 : Output Filter Design
Application Note AN- 1095 Design of the Inverter Output Filter for Motor Drives with IRAMS Power Modules Cesare Bocchiola Table of Contents Page Section 1: Introduction...2 Section 2 : Output Filter Design
Magnetic Field of a Circular Coil Lab 12
 HB 11-26-07 Magnetic Field of a Circular Coil Lab 12 1 Magnetic Field of a Circular Coil Lab 12 Equipment- coil apparatus, BK Precision 2120B oscilloscope, Fluke multimeter, Wavetek FG3C function generator,
HB 11-26-07 Magnetic Field of a Circular Coil Lab 12 1 Magnetic Field of a Circular Coil Lab 12 Equipment- coil apparatus, BK Precision 2120B oscilloscope, Fluke multimeter, Wavetek FG3C function generator,
FILTERS - IN RADIO COMMUNICATIONS
 Reading 32 Ron Bertrand VK2DQ http://www.radioelectronicschool.com FILTERS - IN RADIO COMMUNICATIONS RADIO SIGNALS In radio communications we talk a lot about radio signals. A radio signal is a very broad
Reading 32 Ron Bertrand VK2DQ http://www.radioelectronicschool.com FILTERS - IN RADIO COMMUNICATIONS RADIO SIGNALS In radio communications we talk a lot about radio signals. A radio signal is a very broad
Aircraft Electrical System
 Chapter 9 Aircraft Electrical System Introduction The satisfactory performance of any modern aircraft depends to a very great degree on the continuing reliability of electrical systems and subsystems.
Chapter 9 Aircraft Electrical System Introduction The satisfactory performance of any modern aircraft depends to a very great degree on the continuing reliability of electrical systems and subsystems.
Antenna Properties and their impact on Wireless System Performance. Dr. Steven R. Best. Cushcraft Corporation 48 Perimeter Road Manchester, NH 03013
 Antenna Properties and their impact on Wireless System Performance Dr. Steven R. Best Cushcraft Corporation 48 Perimeter Road Manchester, NH 03013 Phone (603) 627-7877 FAX: (603) 627-1764 Email: sbest@cushcraft.com
Antenna Properties and their impact on Wireless System Performance Dr. Steven R. Best Cushcraft Corporation 48 Perimeter Road Manchester, NH 03013 Phone (603) 627-7877 FAX: (603) 627-1764 Email: sbest@cushcraft.com
Eatman Associates 2014 Rockwall TX 800-388-4036 rev. October 1, 2014. Striplines and Microstrips (PCB Transmission Lines)
 Eatman Associates 2014 Rockwall TX 800-388-4036 rev. October 1, 2014 Striplines and Microstrips (PCB Transmission Lines) Disclaimer: This presentation is merely a compilation of information from public
Eatman Associates 2014 Rockwall TX 800-388-4036 rev. October 1, 2014 Striplines and Microstrips (PCB Transmission Lines) Disclaimer: This presentation is merely a compilation of information from public
RigExpert AA-30 Antenna Analyzer (0.1 to 30 MHz) AA-54 Antenna Analyzer (0.1 to 54 MHz) User s manual
 RigExpert AA-30 Antenna Analyzer (0.1 to 30 MHz) AA-54 Antenna Analyzer (0.1 to 54 MHz) User s manual Table of contents 1. Description... 3 2. Specifications... 4 3. Precautions... 5 4. Operation... 6
RigExpert AA-30 Antenna Analyzer (0.1 to 30 MHz) AA-54 Antenna Analyzer (0.1 to 54 MHz) User s manual Table of contents 1. Description... 3 2. Specifications... 4 3. Precautions... 5 4. Operation... 6
DEPARTMENT OF DEFENSE TEST METHOD STANDARD METHOD OF INSERTION LOSS MEASUREMENT
 INCH-POUND MIL-STD-220C 14 May 2009 SUPERSEDING MIL-STD-220B 24 January 2000 DEPARTMENT OF DEFENSE TEST METHOD STANDARD METHOD OF INSERTION LOSS MEASUREMENT AMSC N/A FSC EMCS FOREWORD 1. This standard
INCH-POUND MIL-STD-220C 14 May 2009 SUPERSEDING MIL-STD-220B 24 January 2000 DEPARTMENT OF DEFENSE TEST METHOD STANDARD METHOD OF INSERTION LOSS MEASUREMENT AMSC N/A FSC EMCS FOREWORD 1. This standard
75 Ω Transmission System
 NRAO NTC-DSL Laboratory Report Dynamic Spectroscopy Laboratory Report Series Report 03 September, 2006 75 Ω Transmission System Chaitali R. Parashare Department of Electrical and Computer Engineering,
NRAO NTC-DSL Laboratory Report Dynamic Spectroscopy Laboratory Report Series Report 03 September, 2006 75 Ω Transmission System Chaitali R. Parashare Department of Electrical and Computer Engineering,
Printed-Circuit-Board Layout for Improved Electromagnetic Compatibility
 Printed-Circuit-Board Layout for Improved Electromagnetic Compatibility SDYA011 October 1996 1 IMPORTANT NOTICE Texas Instruments (TI) reserves the right to make changes to its products or to discontinue
Printed-Circuit-Board Layout for Improved Electromagnetic Compatibility SDYA011 October 1996 1 IMPORTANT NOTICE Texas Instruments (TI) reserves the right to make changes to its products or to discontinue
Transmission Lines in Communication Systems FACET
 Computer-Based Electronics Training System Transmission Lines in Communication Systems FACET 36970- Order no.: 36970-00 First Edition Revision level: 02/2015 By the staff of Festo Didactic Festo Didactic
Computer-Based Electronics Training System Transmission Lines in Communication Systems FACET 36970- Order no.: 36970-00 First Edition Revision level: 02/2015 By the staff of Festo Didactic Festo Didactic
Cable Solutions for Servo and Variable Frequency Drives (VFD)
 Cable Solutions for Servo and Variable Frequency Drives (VFD) Electric drive systems with continuous torque and speed control are widespread today. They allow an optimal adjustment of the drive with respect
Cable Solutions for Servo and Variable Frequency Drives (VFD) Electric drive systems with continuous torque and speed control are widespread today. They allow an optimal adjustment of the drive with respect
Laboratory 4: Feedback and Compensation
 Laboratory 4: Feedback and Compensation To be performed during Week 9 (Oct. 20-24) and Week 10 (Oct. 27-31) Due Week 11 (Nov. 3-7) 1 Pre-Lab This Pre-Lab should be completed before attending your regular
Laboratory 4: Feedback and Compensation To be performed during Week 9 (Oct. 20-24) and Week 10 (Oct. 27-31) Due Week 11 (Nov. 3-7) 1 Pre-Lab This Pre-Lab should be completed before attending your regular
application note The Measurement and Suppression of RF Interference from TDMA Phones GSM Cellular Introduction
 APPLICATION NOTE AN-3 The Measurement and Suppression of RF Interference from TDMA Phones Introduction While the recent explosion of mobile telephone usage has improved the quality of life for many in
APPLICATION NOTE AN-3 The Measurement and Suppression of RF Interference from TDMA Phones Introduction While the recent explosion of mobile telephone usage has improved the quality of life for many in
Critical thin-film processes such as deposition and etching take place in a vacuum
 WHITEPAPER INTRODUCING POWER SUPPLIES AND PLASMA Critical thin-film processes such as deposition and etching take place in a vacuum SYSTEMS chamber in the presence of a plasma. A plasma is an electrically
WHITEPAPER INTRODUCING POWER SUPPLIES AND PLASMA Critical thin-film processes such as deposition and etching take place in a vacuum SYSTEMS chamber in the presence of a plasma. A plasma is an electrically
