How To Prove That The Zero Locus Is Not A Zero Loci
|
|
|
- Александр Даудов
- 3 years ago
- Views:
Transcription
1 оповiдi НАЦIОНАЛЬНОЇ АКАДЕМIЇ НАУК УКРАЇНИ Науково-теоретичний журнал Президiї Нацiональної академiї наук України Заснований у 1939 р. Виходить щомiсяця РЕДАКЦIЙНА КОЛЕГIЯ ЖУРНАЛУ А. Г. Наумовець (головний редактор), П. I. Андон, Я. Б. Блюм, В. Л. Богданов (заст. головного редактора з наук. питань), А.Ф. Булат, Г.М. Гавричкова (заст. головного редактора), П. Ф. Гожик, В. П. Горбулiн, В. Т. Грiнченко, Г. В. Єльська, А. Г. Загороднiй, М. Ю. Iльченко, М. Т. Картель, О. В. Кириленко, С.В. Комiсаренко, В.Г. Кошечко, В.П. Кухар, Л.М. Лобанов, В. М. Локтєв, В. В. Моргун, О. М. Пономаренко, А. М. Самойленко, В. I. Старостенко, Є. Я. Хруслов, В. Ф. Чехун, М. Ф. Шульга, Я. С. Яцкiв Нацiональна академiя наук України, 2015
2 Редактори роздiлiв Л.М. Литвинова, Л.I. Пузанкова, Т. I. Хоменко Оформлення художника В. Г. Самсонова Комп ютерна верстка В. I. Бойко, Г. В. Попович Видавничий дiм «Академперiодика» НАН України Свiдоцтво про внесення до Держреєстру суб єкта видавничої справи серiї ДК 544 вiд , Київ, вул. Терещенкiвська, 4 Пiдписано до друку Формат /16. Ум. друк. арк. 16,8. Обл.-вид. арк. 16,36. Тираж 184 прим. Зам Цiна 40 грн. Видавець Видавничий дiм «Академперiодика» НАН України , Київ, вул. Терещенкiвська, 4
3 Змiст Математика Баранник Т. А. Класифiкацiя галiлеєво-iнварiантних систем нелiнiйних рiвнянь реакцiї-дифузiї Сердюк А.С., Степанюк Т.А. Оцiнки найкращих ортогональних тригонометричних наближень класiв згорток перiодичних функцiй невеликої гладкостi Чепурухiна I.С. Напiводнорiдна елiптична задача з додатковими невiдомими функцiями в крайових умовах Pokrovskii A.V. A simple proof of the Radó and Král theorems on removability of the zero locus for analytic and harmonic functions Iнформатика та кiбернетика Механiка Фiзика Ляшко С.I., Грищенко О.Ю., Федорова В.С., Загородня Г.О. Про один скiнченнорiзницевий алгоритм моделювання процесiв кiнетики адсорбцiї Багно А.М. О волнах Лэмба в системе слой идеальной жидкости упругий слой Кубенко В.Д. О нестационарном деформировании упругого слоя при смешанных граничных условиях Лоза И.А. Кинематический анализ распространения осесимметричных электроупругих волн в полом слоистом цилиндре при механическом способе возбуждения Селiванов М.Ф. Модель трiщини з зоною зчеплення при змiшаному режимi руйнування Савкiна Р.К., Смiрнов О.Б. Ефект наноструктурування Si та GaAs шляхом кавiтацiйної обробки в рiдкому азотi Енергетика Бiлецький В. С., Круть О. А. Оцiнка властивостей водовугiльної суспензiї у гiдродинамiчних умовах Науки про Землю Хiмiя Гордиенко В.В., Гордиенко И.В., Завгородняя О.В. Современная активизация и тепловое поле Южно-Украинской моноклинали и Скифской плиты Кушнiр С.В. Причини барботажного хiмiчного ефекту i диференцiацiї iонiв при утвореннi морських аерозолiв (фiзико-хiмiчний аналiз) Усенко О.В. Эволюция мантийных расплавов и флюидов в докембрии Шевчук О.А. Трахеїди з юрських вiдкладiв України Булавко Г.В., Ищенко А.А. Природа аниона и фотовольтаические свойства катионных полиметиновых красителей
4 Бiологiя Бiохiмiя Ткаченко И.М., Кобзарь Я.Л., Шекера О.В., Шевченко В. В. Синтез 4,4 -бис(нонафторобифенил-4-оксифенил)-бис(трифторометил)метана и на его основе лестничного полиэфира, содержащего спиробисиндановые фрагменты Гулевский А.К., Ахатова Ю.С. Стимулирующее влияние низкомолекулярной фракции (до 5 кда) кордовой крови на гликогенолиз в нейтрофилах лейкоконцентрата донорской крови человека Драговоз I.В., Леонова Н.О., Зелена Л.Б., Ребрiєв А.В., Авдєєва Л.В. Iдентифiкацiя екзометаболiтiв штаму Bacillus amyloliquefaciens subsp. plantarum IМВ В-7404 з антифунгальною активнiстю Плоховская C.Г., Заславский В.А., Емец А.И., Блюм Я.Б. Участие актиновых филаментов в ответе клеток корня Arabidopsis thaliana на действие низкой температуры Медицина Екологiя Пiлiнська М.А., Дибський С.С., Дибська О.Б., Швайко Л.I., Сушко В.О. Тривалiсть зберiгання прихованої хромосомної нестабiльностi в лiмфоцитах периферичної кровi людини при професiйному контактi з iонiзуючою радiацiєю Семiнська О.О., Кучерук Д.Д., Балакiна М.М., Гончарук В.В. Використання зворотного осмосу та нанофiльтрацiї в очищеннi стiчних вод вiд фосфатiв
5 Contents Mathematics Barannyk T.A. The classification of the Galilei-invariant systems of nonlinear reactiondiffusion equations Serdyuk A.S., Stepaniuk T.A. Estimates of the best orthogonal trigonometric approximations of the classes of convolutions of periodic functions of not high smoothness.. 13 Chepurukhina I.S. A semihomogeneous elliptic problem with additional unknown functions in boundary conditions Pokrovskii A.V. A simple proof of the Radó and Král theorems on removability of the zero locus for analytic and harmonic functions Information Science and Cybernetics Mechanics Energetics Physics Lyashko S.I., Gryshchenko O.Yu., Fedorova V.S., Zagorodnya G.O. About a finitedifference algorithm of modeling the adsorption kinetic processes Bahno O.M. On Lamb waves in the system: an ideal fluid layer an elastic layer Kubenko V.D. On the nonstationary deforming of an elastic layer under mixed boundary conditions Loza I.A. Kinematic analysis of the propagation of axisymmetric elastoelectric waves in a hollow layered cylinder under a mechanical mode of excitation Selivanov M. F. A model of crack with cohesive zone for a mixed mode of fracture Bilecky V.S., Krut O.A. The evaluation of properties of coal water slurries under hydrodynamic conditions Savkina R.K., Smirnov A.B. Nanostructurization of Si and GaAs by acoustic cavitation in liquid nitrogen Geosciences Chemistry Gordienko V.V., Gordienko I.V., Zavgorodnjaja O.V. Recent activization and heat field of the South-Ukrainian monocline and the Scyphian plate Kuschnir S.V. Reasons for the bubbling chemical effect and differentiation of ions in the formation of marine aerosols (physico-chemical analysis) Usenko O.V. Evolution of mantle melts and fluids at the Precambrian Shevchuk O.V. Tracheids of the Jurassic sediments of Ukraine Bulavko G.V., Ishchenko A.A. The nature of counterion and photovoltaic properties of cationic polymethine dyes Tkachenko I.M., Kobzar Ya.L., Shekera O.V., Shevchenko V.V. Synthesis of 4,4- bis(nonafluorobiphenyl-4-oxyphenyl)-bis(trifluoromethyl)methane and a ladder polyether with spirobisindane fragments on its base
6 Biology Gulevskyy O.K., Akhatova Yu.S. Stimulating effect of a low-molecular fraction (below 5 kda) from cord blood on glycogenolysis in neutrophils of human donor blood leukoconcentrate Biochemistry Medicine Ecology Dragovoz I.V., Leonova N.O., Zelena L.V., Rebriyev A.V., Avdeeva L.V. Identification of Bacillus amyloliquefaciens subsp. plantarum IMV B-7404 strain exometabolites with antifungal activity Plohovska S.G., Zaslavsky V.A., Yemets A.I., Blume Ya.B. Participation of actin filaments in the response of Arabidopsis thaliana root cells to low-temperature action Pilinskaya M. A., Dibskiy S. S., Dibskaya Ye. B., Shvayko L. I., Sushko V. A. Duration of the hidden chromosome instability persistence in peripheral blood lymphocytes of persons occupationally exposed to ionizing radiation Seminska O.O., Kucheruk D.D., Balakina M.M., Goncharuk V.V. The use of reverse osmosis and nanofiltration in wastewater purification from phosphates
7 оповiдi НАЦIОНАЛЬНОЇ АКАДЕМIЇ НАУК УКРАЇНИ МАТЕМАТИКА УДК 517.9: Т.А. Баранник Класифiкацiя галiлеєво-iнварiантних систем нелiнiйних рiвнянь реакцiї-дифузiї (Представлено членом-кореспондентом НАН України А.Г. Нiкiтiним) Наведено повний опис галiлеєво-iнварiантних систем нелiнiйних рiвнянь реакцiї-дифузiї у випадку, коли коренi характеристичного рiвняння матрицi дифузiї є дiйсними числами. Ключовi слова: рiвняння реакцiї-дифузiї, перетворення Галiлея, симетрiя. 1. Принцип вiдносностi Галiлея є одним iз фундаментальних постулатiв, який повиннi задовольняти фiзичнi, хiмiчнi, бiологiчнi та iншi системи. Математичною мовою це означає, що математичнi моделi цих систем повиннi бути iнварiантними вiдносно груп Галiлея. У данiй роботi пропонується опис систем нелiнiйних рiвнянь реакцiї-дифузiї, iнварiантних вiдносно груп Галiлея, якi мають вигляд u m t A 2 u x 2 i=1 i = f(u), (1) де u = стовпець(u 1,u 2,...,u n ) є вектор-функцiєю вiд t, x 1,...,x m, f(u) = стовпець (f 1,f 2,...,f n ) є вектор-функцiєю вiд u, A невироджена квадратна матриця порядку n. Такi системи знаходять широке застосування в теорiї тепломасоперенесення, а також в математичнiй бiологiї та хiмiї. Тому симетрiйний аналiз системи рiвнянь (1) має прикладне значення i може бути використаний, наприклад, для побудови точних розв язкiв широкого класу фiзичних i бiологiчних систем. Перша спроба класифiкувати систему (1) у випадку n = 2 належить Ю. А. Данiлову [1], який обмежився випадком дiагональної матрицi A. Дослiдження лiївських симетрiй системи (1) для n = 2 з дiагональною матрицею A було проведено в роботах [2 4], а з матрицею дифузiї A загального вигляду у роботах [5, 6]. Завершеного вигляду ця класифiкацiя досягла в роботi [7]. А. Г. Нiкiтiн i Р. Вiльтшире [5, 6] запропонували ефективний пiдхiд до дослiдження класичної i умовної симетрiй, який може бути застосований до рiвняння (1) з довiльними n i m. Т.А. Баранник, 2015 ISSN Доповiдi НАН України, 2015, 7 7
8 2. За допомогою методу С. Лi неважко переконатися, що система рiвнянь (1) iнварiантна вiдносно операторiв Галiлея G a = t +x a x a n i,j=1 b ij u j u i (2) тодi i тiльки тодi, коли B = (b ij ) = 1/2A 1, а функцiя f(u) задовольняє систему рiвнянь (A 1 ) kb f b = (A 1 ) ab u b fk u a. (3) Отже, класифiкацiя систем (1), iнварiантних вiдносно перетворень Галiлея, зводиться до знаходження розв язкiв системи рiвнянь (3). Характер розв язкiв системи (3) суттєво залежить вiд типу матрицi A 1. З точнiстю до перетворень подiбностi матриця A 1 може бути зведена до однiєї з трьох канонiчних форм залежно вiд значень коренiв характеристичного рiвняння [8, c ]. a) Коренi характеристичного рiвняння матрицi A 1 дiйснi. Матриця A 1 в цьому випадку подiбна до матрицi J m1,λ 1 + +J ms,λ s = J m1,λ J ms,λ s де J mi,λ i є клiткою Жордана порядку m i для i = 1,2,...,s: λ i J mi,λ i = 1 λ i λ i, (4) b) Коренi характеристичного рiвняння матрицi A 1 комплекснi. Матриця A 1 в цьому випадку подiбна до матрицi J m 1 b 1,d 1 + +J m k b k,d k, d i 0 для i = 1,2,...,k, де Jb,d m узагальнена клiтка Жордана, тобто матриця порядку 2m такого вигляду: b d 1 0 d b 0 1 Jb,d m = b d d b O O b d d b. У випадку m i = 1 для i = 1,2,...,k матриця A 1 подiбна до матрицi J 1 b 1,d 1 + +J 1 b k,d k. (5) 8 ISSN Dopov. Nac. akad. nauk Ukr., 2015, 7
9 c) Характеристичне рiвняння матрицi A 1 має s дiйсних коренiв i t комплексних коренiв з врахуванням їх кратностi. Матриця A 1 в даному випадку подiбна до матрицi J m1,λ 1 + +J mk,λ k +J n 1 b 1,d 1 + +J n l b l,d l, де m 1 + +m k = s, 2n n l = t. Зокрема, якщо n 1 = = n l = 1, то матриця A 1 подiбна до матрицi J m1,λ 1 + +J mk,λ k +J 1 b 1,d 1 + +J 1 b l,d l. (6) 3. Опис систем рiвнянь (1), якi допускають перетворення Галiлея, зводиться до iнтегрування системи звичайних диференцiальних рiвнянь (3). Далi наведено розв язки цiєї системи для випадкiв, коли матриця A 1 має вигляд (4), (5), (6). Нехай матриця A 1 є клiткою Жордана J n,λ. Для визначення всiх можливих нелiнiйних форм компонент вектор-функцiї f(u) введемо нову змiнну τ, яка визначається iз спiввiдношення u a τ = (A 1 ) ab u b. Лема. Першими iнтегралами системи (7) є функцiї (7) C k = k ( 1) p 1 λ p p! p=0 u k+1 p u 1 ln p u 1, k = 1,...,n 1. (8) Теорема 1. Якщо матриця A 1 є клiткою Жордана J n,λ, то загальний розв язок системи (3) утворюють функцiї k 1 1 f k = u 1 λ p p! ϕ k pln p u 1, k = 1,...,n, (9) p=0 де ϕ 1,...,ϕ n є довiльними функцiями вiд перших iнтегралiв (8) системи рiвнянь (7). Доведення. Введемо нову змiнну τ, яка визначається системою (7). Використовуючи змiнну τ, рiвняння (3) запишемо у виглядi f a τ = (A 1 ) ab f b. Проiнтегрувавши ситему (10), знаходимо її загальний розв язок (10) k 1 f k = e λτ p=0 C k p τ p p!, k = 1,...,n, де C 1,..., C n довiльнi сталi. Враховуючи, щоu 1 = e λτ, отримуємо на пiдставi леми загальний розв язок системи рiвнянь (3), який визначається формулами (9). Теорема доведена. У теоремах, що сформульованi нижче, для компактного запису компонент вектор-функцiї f = стовпець(f 1,f 2,...,f n ) i u = стовпець(u 1,u 2,...,u n ) використано такi позначення: f (1) k = f k для k = 1,...,m 1 ; ISSN Доповiдi НАН України, 2015, 7 9
10 f (i) k = f m1 + +m i 1 +k для k = 1,...,m i, якщо i > 1; u (1) k = u k для k = 1,...,m 1 ; u (i) k = u m 1 + +m i 1 +k для k = 1,...,m i, якщо i > 1. Теорема 2. Нехай обернена матриця дифузiї A 1 має вигляд (4). Вiдповiдна система рiвнянь реакцiї-дифузiї (1) iнварiантна вiдносно перетворень Галiлея, якщо нелiнiйностi f 1, f 2,...,f n мають такий вигляд: f (i) k = u (i) k 1 1 p=0 1 λ p i p!ϕ(i) де ϕ (i) 1,...,ϕ(i) m i є довiльними функцiями вiд (i) k ( 1) p 1 u λ p i p! p=0 k+1 p u (i) 1 [u (j) 1 ]λ 1 [u (1) 1 ] λ j, j = 2,...,s. k p lnp u (i) 1, k = 1,...,m i, i = 1,...,s, (11) ln p u (i) 1, k = 1,...,m i 1, i = 1,...,s; Теорема 3. Нехай обернена матриця дифузiї A 1 має вигляд (5). Вiдповiдна система рiвнянь реакцiї-дифузiї (1) iнварiантна вiдносно перетворень Галiлея, якщо нелiнiйностi f 1,f 2,...,f n мають такий вигляд: f (i) 1 = ϕ (i) 1 u(i) 2 +ϕ(i) 2 u(i) 1, f (i) 2 = ϕ (i) 1 u(i) 1 +ϕ(i) 2 u(i) 2, i = 1,...,k, де ϕ (i) 1 i ϕ (i) 2 є довiльними функцiями вiд ( R i exp b ) i arctan u(i) 2, R b j 1 d R b 1 j, j = 2,...,k, де Ri 2 = [u (i) 1 ]2 +[u (i) 2 ]2. i u (i) 1 Теорема 4. Нехай обернена матриця дифузiї A 1 має вигляд (6). Вiдповiдна система рiвнянь реакцiї-дифузiї (1) iнварiантна вiдносно перетворень Галiлея, якщо нелiнiйностi f 1, f 2,...,f n мають такий вигляд: f (i) k = u (i) k 1 1 p=0 1 λ p i p!ϕ(i) f (j) 1 = ϕ (j) 1 u(j) 2 +ϕ (j) 2 u(j) 1, f (j) 2 = ϕ (j) 1 u(j) 1 +ϕ (j) k p lnp u (i) 1, k = 1,...,m i; i = 1,...,r; 2 u(j) 2, j = r +1,...,r +l, де ϕ (i) 1,...,ϕ(i) m i, ϕ (j) 1, ϕ(j) 2 є довiльними функцiями вiд (i) k ( 1) p 1 u λ p i p! p=0 k+1 p u (i) 1 ln p u (i) 1, k = 1,...,m i; i = 1,...,r; 10 ISSN Dopov. Nac. akad. nauk Ukr., 2015, 7
11 ( R j exp b j r arctan u(j) 2 d j r [u (r+1) 1 ] 2 +[u (r+1) 2 ] 2 u (j) 1 [u (1) 1 ]2b 1 λ 1, R 2 j = [u(j) Цитована лiтература ), R b 1 r+1 R b j r j, j = r +2,...,r +l, 1 ]2 +[u (j) 2 ]2. 1. Данилов Ю.А. Групповой анализ системы Тьюринга и ее аналогов. Москва, с. (Препр. / АН СССР. Ин-т атомной энергии им. И.В. Курчатова; 3287/1). 2. Cherniha R., King J. R. Lie symmetries of nonlinear multidimensional reaction-diffusion systems: I // J. Phys. A: Math. Gen P Cherniha R., King J. R. Lie symmetries of nonlinear multidimensional reaction-diffusion systems: I. Addendum // J. Phys. A: Math. Gen P Cherniha R., King J. R. Lie symmetries of nonlinear multidimensional reaction-diffusion systems: II // J. Phys. A: Math. Gen P Nikitin A. G., Wiltshire R. J. Symmetries of systems of nonlinear reaction-diffusion equations // Proc. Institute of Mathematics of the NAS of Ukraine , Pt. 1. P Nikitin A. G., Wiltshire R. J. Systems of reaction-diffusion equations and their symmetry properties // J. Math. Phys , No 4. P Nikitin A. G. Group classification of systems of nonlinear reaction-diffusion equations // Укр. мат. вiсник , No 1. P Мальцев А.И. Основы линейной алгебры. Москва: Наука, с. References 1. Danilov Yu. A. Group analysis of the Turing systems and of its analogues. Preprint, Kurchatov Institute of Atomic Energy, IAE 3287/1, Moscow, 1980 (in Russian). 2. Cherniha R., King J.R. J. Phys. A: Math. Gen., 2000, 33: Cherniha R., King J.R. J. Phys. A: Math. Gen., 2000, 33: Cherniha R., King J.R. J. Phys. A: Math. Gen., 2002, 36: Nikitin A.G., Wiltshire R. Proceeding of Institute of Mathematics of the NAS of Ukraine, 2000, 30, Pt. 1: Nikitin A.G., Wiltshire R.J. J. Math. Phys., 2001, 42, No 4: Nikitin A.G. Ukr. math. visnyk, 2005, 2, No 1: Malcev A.I. Foundations of linear algebra, Moscow: Nauka, 1970 (in Russian). Полтавський нацiональний педагогiчний унiверситет iм. В. Г. Короленка Надiйшло до редакцiї Т. А. Баранник Классификация галилеево-инвариантных систем нелинейных уравнений реакции-диффузии Полтавский национальный педагогический университет им. В. Г. Короленко Приведено полное описание галилеево-инвариантных систем нелинейных уравнений реакции-диффузии в случае, когда корни характеристического уравнения матрицы диффузии являются действительными числами. Ключевые слова: уравнение реакции-диффузии, преобразование Галилея, симметрия. ISSN Доповiдi НАН України, 2015, 7 11
12 T.A. Barannyk The classification of the Galilei-invariant systems of nonlinear reaction-diffusion equations V. G. Korolenko Poltava National Pedagogical University The full description of the Galilei-invariant systems of nonlinear reaction-diffusion equations is presented in the case where the roots of the characteristic equation of the diffusion matrix are real numbers. Keywords: reaction-diffusion equation, Galilei transformation, symmetry. 12 ISSN Dopov. Nac. akad. nauk Ukr., 2015, 7
13 УДК А.С. Сердюк, Т.А. Степанюк Оцiнки найкращих ортогональних тригонометричних наближень класiв згорток перiодичних функцiй невеликої гладкостi (Представлено членом-кореспондентом НАН України М.Л. Горбачуком) Отримано порядковi оцiнки для найкращих рiвномiрних ортогональних тригонометричних наближень на класах 2π-перiодичних функцiй таких, що їх (ψ, β)-похiднi належать одиничним кулям просторiв L p, 1 p <, у випадку, коли послiдовнiсть ψ така, що добуток ψ(n)n 1/p може прямувати до нуля повiльнiше за довiльну степеневу функцiю i ψ p (k)k p 2 < при 1 < p <, 1/p+1/p = 1 або ψ(k) < при p = 1. Аналогiчнi k=1 k=1 оцiнки отримано для наближень в L p -метриках класiв (ψ,β)-диференцiйовних функцiй таких, що f ψ β 1 1. Ключовi слова: найкращi ортогональнi тригонометричнi наближення, класи згорток, класи (ψ, β)-диференцiйовних функцiй. Нехай L p, 1 p <, простiр 2π-перiодичних сумовних в p-му степенi на [0,2π) функцiй f: R C з нормою f p := ( 2π 0 f(t) p dt) 1/p, L простiр 2π-перiодичних вимiрних i суттєво обмежених функцiй f: R C з нормою f := esssup f(t). t Через L ψ β,p, 1 p, позначимо множину функцiй f: R R iз L 1, якi зображуються у виглядi згорток f(x) = a π π π з фiксованим твiрним ядром Ψ β вигляду Ψ β (t) = 1 2 Z/{0} Ψ β (x t)ϕ(t)dt, a 0 R, ϕ 1, ϕ 1, (1) ψ( k )e i(kt+βπ 2 signk) = k=1 ( ψ(k) cos kt βπ ). (2) 2 Функцiю ϕ в рiвностi (1) називають (див., наприклад, [1, с. 132, 136]) (ψ, β)-похiдною функцiї f i позначають через f ψ β. А.С. Сердюк, Т.А. Степанюк, 2015 ISSN Доповiдi НАН України, 2015, 7 13
14 У випадку коли ψ(k) = k r, r > 0, класи L ψ β,p, 1 p, β R, є вiдомими класами Вейля Надя Wβ,p r. Якщо послiдовнiсть ψ(k) монотонно спадає i ψ q (k)k q 2 <, 1 < q <, k=1 то, згiдно з лемою монографiї [2, с. 193], має мiсце включення Ψ β L q, 1/q+1/q = 1. З твердження iз [1, с. 137] i твердження з [3, с. 43] випливає, що при ψ(k) 0, ψ p (k)k p 2 <, 1 < p <, k=1 1 p + 1 p = 1, справедливi вкладення L ψ β,p L, L ψ β,1 L p, а з твердження iз [1, с. 137] випливає, що при ψ(k) > 0 i ψ(k) < виконується вкладення L ψ β,1 L. k=1 Будемо вважати, що послiдовностi ψ(k), k N, якi задають класи L ψ β,p, є звуженнями на множину натуральних чисел деяких додатних, неперервних, опуклих донизу функцiй ψ(t), заданих на [1, ), що задовольняють умову lim ψ(t) = 0. Множину всiх таких функцiй ψ t позначатимемо через M. Для класифiкацiї функцiй ψ iз M за їх швидкiстю спадання до нуля важливу роль вiдiграє характеристика α(ψ;t) := ψ(t) t ψ (t), ψ (t) := ψ (t+0). (3) За її допомогою з множини M видiляють такi пiдмножини (див., наприклад, [1, с ]): M 0 := {ψ M: K > 0 t 1 0 < K α(ψ;t)}, (4) M C := {ψ M: K 1,K 2 > 0 t 1 K 1 α(ψ;t) K 2 < }. (5) В (4) i (5) величини K, K 1, K 2 можуть залежати вiд ψ. Очевидно, що M C M 0. Нехай m N. Величину e m(l ψ β,p ) s = sup inf f(x) f(k)e ikx s, 1 p,s, (6) f L ψ γ m β,p k γ m 1 де γ m довiльнi набори iз m цiлих чисел, f(k) := 2π π π f(t)e ikt dt коефiцiєнти Фур є функцiї f, називають найкращим ортогональним тригонометричним наближенням класу L ψ β,p в метрицi простору L s. Метою даної роботи є знаходження точних порядкових оцiнок величин e n (Lψ β,p ) p, i e n (Lψ β,1 ) p при 1 p <, 1/p + 1/p = 1. Для класiв Вейля Надя Wβ,p r порядковi оцiнки величин (6) дослiджувалися в роботах Е.С. Белiнського [4] та А.С. Романюка [5 7]. 14 ISSN Dopov. Nac. akad. nauk Ukr., 2015, 7
15 Для класiв L ψ β,p порядковi оцiнки величин (6) вивчалися в роботах В.В. Шкапи [8, 9] та О.С. Федоренка [10, 11]. При цьому в роботах [8, 9] порядковi рiвностi для величин e m (Lψ β,p ), 1 < p <, β R, було знайдено за умови ψ B Θ p, а для величин e m (Lψ β,1 ) p, 1 < p <, 1/p+1/p = 1, β R, за умов ψ B Θ p i опуклостi функцiї 1/ψ(t), де B множина незростаючих додатних функцiй ψ(t), t 1, для кожної з яких можна вказати додатну сталу K таку, що ψ(t)/ψ(2t) K, t 1, а Θ p множина незростаючих додатних функцiй ψ(t), для яких iснує ε > 0 таке, що послiдовнiсть ψ(k)k (1/p)+ε не зростає. При зазначених умовах iз [8, 9] випливають оцiнки e n (Lψ β,p ) e n (Lψ β,1 ) p ψ(n)n1/p, β R, 1 < p <, 1 p + 1 p = 1. (7) У данiй роботi знайдено порядковi оцiнки величин e n (Lψ β,p ) i e n (Lψ β,1 ) p, 1 p <, 1/p+1/p = 1, у випадку, коли функцiя g p (t) = ψ(t)t 1/p належить до множини M 0, i, крiм того, ψ p (k)k p 2 < при 1 < p < або ψ(k) < при p = 1. При цьому константи k=1 k=1 в отриманих оцiнках виражаються через параметри класiв в явному виглядi. Щоб сформулювати основнi результати роботи, введемо такi позначення. Для кожного 1 < s < покладемо { ( ) π 1/s ξ(s) := max 4, 14(8π) s} 1/s, (8) s 1 а для будь-якої функцiї ψ M через α n (ψ), n N, будемо позначати величини α n (ψ) := inf t n α(ψ;t), (9) де характеристика α(ψ; t) означається формулою (3). Теорема 1. Нехай 1 < p <, ψ p (k)k p 2 <, 1/p + 1/p = 1, а функцiя g p (t) = k=1 = ψ(t)t 1/p така, що g p M 0 i α 1 (g p ) = inf t 1 α(g p;t) > p. Тодi для довiльних n N i β R мають мiсце спiввiдношення ( K (1) ψ,p k=n ( 4 3 K(1) ψ,p k=n ψ p (k)k p 2 ψ p (k)k p 2 ) 1/p ( e 2n(L ψ β,p ) e 2n 1(L ψ β,p ) K (2) ψ,p ) 1/p k=n ψ p (k)k p 2 ( e 2n (Lψ β,1 ) p e 2n 1 (Lψ β,1 ) p K(2) ψ,p ψ p (k)k p 2 в яких K (1) ψ,p = 1 ( ) α1 (g p ) 1/p ) (1 p 3ξ(p) p, K (2) +α 1 (g p ) α 1 (g p ) ψ,p = 1 ( p +α π ξ(p ) 1 (g p ) α 1 (g p ) Наслiдок 1. Нехай 1 < p <, 1/p + 1/p = 1, k=n ) 1/p ) 1/p ) 1/p, (10), (11) ψ p (k)k p 2 < i g p (t) = ψ(t)t 1/p k=1 така, що α 1 (g p ) = inf t 1 α(g p;t) > p. Тодi якщо g p M 0, то ISSN Доповiдi НАН України, 2015, 7 15.
16 ( e n(l ψ β,p ) e n(l ψ β,1 ) p ψ p (k)k p 2 k=n ) 1/p якщо ж g p M C, то виконуються порядковi рiвностi (7). Зауважимо, що коли g p M 0 i, β R, (12) lim t α(g p;t) =, (13) то порядковi рiвностi (7) мiсця не мають, оскiльки в цьому випадку виконується оцiнка (( ) 1/p ) ψ(n)n 1/p = o ψ p (k)k p 2, n. k=n Прикладом функцiй ψ, якi задовольняють умови наслiдку 1 i для яких виконується умова (13), є функцiї виду ψ(t) = t 1/p ln γ (t+k), γ > 1/p, K e γp 1, 1 < p <, 1/p+1/p = 1. Дiйсно, для них, як неважко одержати з (12), справедливi порядковi оцiнки e n(l ψ β,p ) e n(l ψ β,1 ) p ψ(n)n1/p ln 1/p n, n N\{1}, β R. Теорема 2. Нехай β R, ψ(k) <, а функцiя g(t) = ψ(t)t така, що g M 0, k=1 α 1 (g) = infα(g;t) > 1. Тодi якщо cos(βπ/2) 0, то для довiльного n N t 1 1 cos βπ ( 1 1 ) 12π 2 α 1 (g) k=n а якщо cos(βπ/2) = 0, то для довiльного n N ( π α 1 (g) ψ(k) e 2n (Lψ β,1 ) e 2n 1 (Lψ β,1 ) 1 π ) ψ(n)n e 2n (Lψ β,1 ) e 2n 1 (Lψ β,1 ) ψ(k), (14) k=n ( 1+ 2 ) ψ(n)n. (15) π Теорема 3. Нехай ψ(k) < i β R. Тодi якщо функцiя g(t) = ψ(t)t така, що k=1 g M 0, то e n(l ψ β,1 ) k=n ψ(n)n, якщо ж g M C, то ψ(k), cos βπ 2 0, cos βπ 2 = 0, (16) e n (Lψ β,1 ) ψ(n)n. (17) Поклавши в теоремi 3 ψ(t) = t r, r > 1, отримаємо таке твердження. Наслiдок 2. Нехай r > 1 i β R. Тодi e n(w r β,1 ) n r ISSN Dopov. Nac. akad. nauk Ukr., 2015, 7
17 Зауважимо, що коли g M 0, g(t) = ψ(t)t i lim α(g;t) =, t (18) то в цьому випадку виконується оцiнка ( ) ψ(n)n = o ψ(k), n. k=n Прикладом функцiй ψ(t), якi задовольняють умови теореми 3 i для яких виконується умова (18), є функцiї виду ψ(t) = t 1 ln γ (t+k), γ > 1, K > 0. Для них, згiдно з (18), при β R i n N \ {1} справедливi порядковi оцiнки e n (Lψ β,1 ) ψ(n)n, ψ(n)nlnn, cos βπ 2 0, cos βπ 2 = 0. Зауважимо, що для знаходження оцiнок зверху найкращих ортогональних тригонометричних наближень вигляду (6) в теоремах 1 3 були використанi нерiвностi e 2n 1 (Lψ β,p ) s E n (L ψ β,p ) s, 1 p,s, де E n (L ψ β,p ) s := sup f L ψ β,p n 1 f( ) k= n+1 f(k)e ikx s, 1 p,s. (19) Точнi порядки величинe n (L ψ β,p ) ie n (L ψ β,1 ) p при1 p < було знайдено в роботах [12 14]. Цитована лiтература 1. Степанец А.И. Методы теории приближений: В 2 ч., Ч.I. Киев: Ин-т математики НАН Украины, с. (Працi Iнституту математики НАН України; Т. 40). 2. Зигмунд А. Тригонометрические ряды: В 2 т. Москва: Мир, Т с. 3. Корнейчук Н.П. Точные константы в теории приближения. Москва: Наука, с. 4. Белинский Э. С. Приближение плавающей системой экспонент на классах периодических функций с ограниченной смешанной производной // Исследования по теории функций многих вещественных переменных. Ярославль: Ярослав. ун-т, С Романюк А. С. Приближение классов периодических функций многих переменных // Мат. заметки , 1. P Романюк А. С. Наилучшие тригонометрические приближения классов периодических функций многих переменных в равномерной метрике // Мат. заметки , 2. С Романюк А. С. Аппроксимативные характеристики классов периодических функций многих переменных. Киев: Ин-т математики НАН Украины, с. (Працi Iнституту математики НАН України; T. 93). 8. Шкапа В.В. Найкращi ортогональнi тригонометричнi наближення функцiй iз класiв L ψ β,1 // Теорiя наближення функцiй та сумiжнi питання: Зб. праць Iн-ту математики НАН України , 3. С ISSN Доповiдi НАН України, 2015, 7 17
18 9. Шкапа В. В. Оцiнки найкращих M-членних та ортогональних тригонометричних наближень функцiй iз класiв L ψ β,p у рiвномiрнiй метрицi // Диференцiальнi рiвняння та сумiжнi питання: Зб. праць Iн-ту математики НАН України , 2. С Федоренко О. С. Про найкращi m-членнi тригонометричнi та ортогональнi тригонометричнi наближення функцiй класiв L ψ β,p // Укр. мат. журн , 12. С Федоренко О.С. Наближення (ψ,β)-диференцiйовних функцiй тригонометричними полiномами: Автореф. дис.... канд. фiз.-мат. наук / Iн-т математики НАН України. Київ, с. 12. Грабова У. З., Сердюк А. С. Порядковi оцiнки найкращих наближень i наближень сумами Фур є класiв (ψ,β)-диференцiйовних функцiй // Укр. мат. журн , 9. С Сердюк А.С., Степанюк Т.А. Порядковi оцiнки найкращих наближень та наближень сумами Фур є в рiвномiрнiй метрицi класiв згорток перiодичних функцiй невеликої гладкостi // Укр. мат. журн , 12. С Степанюк Т. А. Оцiнки найкращих наближень та наближень сумами Фур є класiв згорток перiодичних функцiй невеликої гладкостi в iнтегральних метриках // Теорiя наближення функцiй та сумiжнi питання: Зб. праць Iн-ту математики НАН України , 3. С References 1. Stepanets A. I. Methods of approximation theory. I, Pratsi Instytutu Matematyky NAN Ukrainy. Matematyka ta ii Zastosuvannya, Vol. 40, Kyiv: Instytut Matematyky NAN Ukrainy, 2002 (in Russian). 2. Zygmund A. Trigonometric Series, Vol. 2, Moscow: Mir, 1965 (in Russian). 3. Korneichuk N.P. Exact constants in approximation theory, Moscow: Nauka, 1987 (in Russian). 4. Belinsky E. S. Approximation by a floating system of exponents on the classes of periodic functions with bounded mixed derivative, Issled. po teorii func. mnog. vesch. perem., Jaroslavl : Jaroslav. un t, 1988: (in Russian). 5. Romanyuk A.S. Math. Notes, 2002, 71, No 1: Romanyuk A.S. Math. Notes, 2007, 82, No 2: Romanyuk A.S. Approximation characteristics of classes of periodic functions of several variables, Pratsi Instytutu Matematyky NAN Ukrainy. Matematyka ta ii Zastosuvannya, Vol. 93, Kyiv: Instytut Matematyky NAN Ukrainy, 2012 (in Russian). 8. Shkapa V.V. Zb. Pr. Instytutu Matematyky NAN Ukrainy, 2014, 11, No 3: (in Ukrainian). 9. Shkapa V.V. Zb. Pr. Instytutu Matematyky NAN Ukrainy, 2014, 11, No 2: (in Ukrainian). 10. Fedorenko A.S. Ukr. Math. J., 1999, 51, No 12: Fedorenko O. S. Approximation of (ψ, β)-differentiable functions by trigonometric polynomials: Autoref. diss.... cand. phys.-math. sciences, Kyiv: Insitute of Mathematics of NAS of Ukraine, 2001 (in Ukrainian). 12. Hrabova U.Z., Serdyuk A.S. Ukr. Mat. J., 2013, 65, No 9: Serdyuk A.S., Stepaniuk T.A. Ukr. Math. J., 2014, 66, No 12: (in Ukrainian). 14. Stepanyuk T.A. Zb. Pr. Instytutu Matematyky NAN Ukrainy, 2014, 11, No 3: (in Ukrainian). Iнститут математики НАН України, Київ Схiдноєвропейський нацiональний унiверситет iм. Лесi Українки, Луцьк Надiйшло до редакцiї ISSN Dopov. Nac. akad. nauk Ukr., 2015, 7
19 А.С. Сердюк, Т. А. Степанюк Оценки наилучших ортогональных тригонометрических приближений классов сверток периодических функций небольшой гладкости Институт математики НАН Украины, Киев Восточноевропейский национальный университет им. Леси Украинки, Луцк Получены порядковые оценки для наилучших равномерных ортогональных тригонометрических приближений на классах 2π-периодических функций таких, что их (ψ,β)-производные принадлежат единичным шарам пространств L p, 1 p <, в случае, когда последовательность ψ такая, что произведение ψ(n)n 1/p может стремиться к нулю медленнее, чем любая степенная функция, и ψ p (k)k p 2 < при 1 < p <, 1/p + 1/p = 1 или k=1 ψ(k) < при p = 1. Аналогичные оценки получены для приближений в L p -метриках k=1 классов (ψ,β)-дифференцируемых функций таких, что f ψ β 1 1. Ключевые слова: наилучшие ортогональные тригонометрические приближения, классы сверток, классы (ψ, β)-дифференцируемых функций. А.S. Serdyuk, Т.А. Stepaniuk Estimates of the best orthogonal trigonometric approximations of the classes of convolutions of periodic functions of not high smoothness Institute of Mathematics of the NAS of Ukraine, Kiev Lesya Ukrainka Eastern European National University, Lutsk We obtain order estimates for the best uniform orthogonal trigonometric approximations of 2π-periodic functions, whose (ψ,β)-derivatives belong to unit balls of spaces L p, 1 p <, in the case where a consequence ψ(k) is such that the product ψ(n)n 1/p can tend to zero slower than any power function, and ψ p (k)k p 2 <, when 1 < p <, 1/p + 1/p = 1 or ψ(k) <, k=1 when p = 1. We establish the analogous estimates in the L p -metric for the classes of summable (ψ,β)-differentiable functions such that f ψ β 1 1. Keywords: best orthogonal trigonometric approximations, classes of convolutions, classes of(ψ, β)- differentiable functions. k=1 ISSN Доповiдi НАН України, 2015, 7 19
20 УДК I.С. Чепурухiна Напiводнорiдна елiптична задача з додатковими невiдомими функцiями в крайових умовах (Представлено академiком НАН України А. М. Самойленком) Дослiджено елiптичну крайову задачу для однорiдного диференцiального рiвняння, яка мiстить додатковi невiдомi функцiї у крайових умовах. Доведено, що оператор, який вiдповiдає цiй задачi, є обмеженим i нетеровим у пiдходящих парах гiльбертових просторiв Соболєва i iзотропних просторiв Хермандера, що утворюють двобiчну уточнену соболєвську шкалу. Для останнiх показниками регулярностi служать довiльнi дiйсне число i додатна функцiя, повiльно змiнна на нескiнченностi за Караматою. Доведено теореми про апрiорну оцiнку узагальнених розв язкiв задачi та їх регулярнiсть. Ключовi слова: елiптична крайова задача, повiльно змiнна функцiя, простiр Хермандера, нетерiв оператор, апрiорна оцiнка розв язкiв, регулярнiсть розв язкiв. Елiптичнi крайовi задачi з додатковими невiдомими функцiями у крайових умовах були введенi Б. Лавруком [1, 2]. Такi задачi виникають при переходi вiд загальної елiптичної крайової задачi до формально спряженої задачi (у випадку нерегулярних крайових умов). Бiльше того, клас цих задач замкнений вiдносно такого переходу. До цього класу належать рiзнi задачi теорiї пружностi i гiдродинамiки [3, 4]. Для елiптичних крайових задач з додатковими невiдомими функцiями в крайових умовах доведено теореми про нетеровiсть вiдповiдних операторiв, породженi ними iзоморфiзми, апрiорнi оцiнки розв язкiв i їх регулярнiсть у двобiчних шкалах функцiональних просторiв (див. [5, розд. 3] i [6, розд. 2]). Цi шкали складаються з просторiв, введених Я.А. Ройтбергом [7]. Останнi збiгаються з просторами Соболєва лише для достатньо великих показникiв регулярностi. Для iнших значень показникiв простори Ройтберга мiстять елементи, якi навiть не є розподiлами в евклiдовiй областi, де задана задача. Мета роботи встановити версiї цих теорем для двобiчної шкали просторiв, утворених саме розподiлами в евклiдовiй областi. Така шкала складається з гiльбертових просторiв Соболєва i деяких iзотропних просторiв Хермандера [8, п. 2.2]. Для останнiх показниками регулярностi служать довiльнi дiйсне число i додатна функцiя, повiльно змiнна на нескiнченностi за Й. Караматою [9]. Ця уточнена соболєвська шкала була видiлена i дослiджена В. А. Михайлецем i О. О. Мурачем [10], якi побудували для неї теорiю розв язностi елiптичних крайових задач [11, 12]. Проте клас елiптичних крайових задач з додатковими невiдомими функцiями в крайових умовах не був охоплений їх теорiєю. У роботi розглянуто крайовi задачi для однорiдних елiптичних рiвнянь. Оператор, який вiдповiдає такiй напiводнорiднiй задачi, коректно означений на всiй двобiчнiй уточненiй соболєвськiй шкалi, що дає можливiсть отримати завершенi результати. Для позитивної частини шкали цi задачi дослiджено в [13] для неоднорiдних елiптичних рiвнянь. 1. Постановка задачi. Нехай Ω довiльна обмежена область у евклiдовому просторi R n, деn 2. Припустимо, що її межаγ := Ω є нескiнченно гладким замкненим многовидом вимiрностin 1 (C структура наγєпороджена просторомr n ). Як звичайно,ω := Ω Γ. I. С. Чепурухiна, ISSN Dopov. Nac. akad. nauk Ukr., 2015, 7
21 Виберемо довiльно цiлi числа q 1, κ 1, m 1,...,m q+κ [0,2q 1] i r 1,...,r κ. В областi Ω розглянемо напiводнорiдну лiнiйну елiптичну крайову задачу з κ додатковими невiдомими функцiями на межi Γ: Au = 0 в Ω, B j u+ κ C j,k v k = g j на Γ, j = 1,...,q +κ. (2) k=1 Тут A := A(x,D) диференцiальний оператор на Ω парного порядку 2q, кожне B j := = B j (x,d) крайовий диференцiальний оператор на Γ порядку m j, а кожне C j,k := = C j,k (x,d τ ) дотичний диференцiальний оператор на Γ порядку ordc j,k m j + r k. Усi коефiцiєнти цих диференцiальних операторiв є нескiнченно гладкi функцiї, заданi на Ω i Γ вiдповiдно. Функцiя u на Ω i всi функцiї v 1,...,v κ на Γ є шуканi в крайовiй задачi (1), (2). У роботi всi функцiї i розподiли вважаються комплекснозначними. Нагадаємо (див. [5, п ] або [6, п. 2.2]), що крайова задача (1), (2) називається елiптичною в областi Ω, якщо диференцiальний оператор A правильно елiптичний на Ω, а система крайових умов (2) накриває A на Γ (тобто задовольняє аналог умови Шапiро Лопатинського щодо A на Γ). Позначимо черезka (Ω) множину всiх функцiйu C (Ω) таких, щоau = 0 в областiω. Пов яжемо з крайовою задачею (1), (2) лiнiйне вiдображення ( κ κ Λ : (u,v 1,...,v κ ) B 1 u+ C 1,k v k,...,b q+κ u+ C q+κ,k v k ), (3) k=1 де u K A (Ω), i v 1,...,v κ C (Γ). Дослiдимо властивостi продовження (за неперервнiстю) цього вiдображення у пiдходящих парах гiльбертових просторiв Хермандера. Для опису областi значень цього продовження нам знадобиться формула Грiна ( ) q+κ κ (Au,w) Ω + B j u+ C j,k v k,h j = j=1 j=1 k=1 ( ) 2q q+κ = (u,a + w) Ω + Dν j 1 u,k j w + Q + k,j h k Γ k=1 Γ k=1 + ( ) κ q+κ v j, C + k,j h k, правильна для довiльних функцiй u, w C (Ω) i v 1,...,v κ, h 1,...,h q+κ C (Γ) (див. [5, теорема 3.1.2]). Тут i далi через (, ) Ω i (, ) Γ позначено скалярнi добутки в просторах L 2 (Ω) i L 2 (Γ) усiх функцiй, квадратично iнтегровних на Ω i Γ вiдповiдно, а також розширення за неперервнiстю цих скалярних добуткiв. Тут також A + є диференцiальний оператор, формально спряжений до A вiдносно (, ) Ω, а C + k,j i Q+ k,j є дотичнi диференцiальнi оператори, формально спряженi вiдповiдно до C k,j i Q k,j вiдносно (, ) Γ. При цьому дотичний диференцiальний оператор Q k,j := Q k,j (x,d τ ) узято iз зображення крайового диференцiального оператора B j у виглядi 2q B j (x,d) = Q j,k (x,d τ )Dν k 1 k=1 ISSN Доповiдi НАН України, 2015, 7 21 j=1 k=1 Γ (1)
22 (якщо k > m j, то Q j,k := 0). Тут i у формулi Грiна D ν := i ν, де i уявна одиниця, а ν оператор диференцiювання вздовж внутрiшньої нормалi до межi Γ областi Ω. Крiм того, K j := K j (x,d) є деякий лiнiйний крайовий диференцiальний оператор на Γ порядку ordk j 2q j. З урахуванням формули Грiна розглянемо таку напiводнорiдну крайову задачу в областi Ω з q + κ додатковими невiдомими функцiями на межi Γ: A + w = 0 в Ω, (4) q+κ K j w+ Q + k,j h k = χ j на Γ, j = 1,...,2q, (5) q+κ k=1 C + k,j h k = χ 2q+j на Γ, j = 1,...,κ. (6) k=1 Ця задача є формально спряженою до задачi (1), (2) вiдносно вказаної формули Грiна. Вiдмiтимо, що задача (1), (2) елiптична в областi Ω тодi i тiльки тодi, коли там елiптична формально спряжена задача (4) (6) (див. [5, теорема 3.1.2]). 2. Уточнена соболєвська шкала. Розглянемо гiльбертовi функцiональнi простори, в яких буде дослiджена крайова задача (1), (2). Вони утворюють уточнену соболєвську шкалу {H s,ϕ : s R,ϕ M}, введену в [10]. Тут i надалi M множина всiх вимiрних за Борелем функцiй ϕ: [1, ) (0, ), якi обмеженi й вiдокремленi вiд нуля на кожному компактi i повiльно змiнюються на нескiнченностi за Й. Караматою [9], тобто ϕ(λt)/ϕ(t) 1 при t для кожного λ > 0. Повiльно змiннi функцiї добре вивченi i мають рiзноманiтнi застосування [14]. Їх характерним прикладом є функцiя ϕ(t) := (lnt) r 1 (lnlnt) r2 (ln...lnt) r k, t 1, де k N i r 1,...,r k R. Нехай s R i ϕ M. Означимо простiр H s,ϕ спочатку на R n, де n 1, а потiм на Ω i Γ. Будемо додержуватись монографiї [12, пп. 1.3, 2.1, 3.2]. За означенням, комплексний лiнiйний простiр H s,ϕ (R n ) складається з усiх повiльно зростаючих розподiлiв w на R n таких, що їх перетворення Фур є ŵ є локально сумовним за Лебегом на R n i задовольняє умову w 2 H s,ϕ (R n ) := R n ξ 2s ϕ 2 ( ξ ) ŵ(ξ) 2 dξ <, де ξ := (1+ ξ 2 ) 1/2. Простiр H s,ϕ (R n ) гiльбертiв вiдносно норми w H s,ϕ (R n ). Простiр H s,ϕ (R n ) є iзотропний випадок гiльбертових просторiв B 2,µ, введених i дослiджених Л. Хермандером [8, п. 2.2] i також Л.Р. Волевичем, Б.П. Панеяхом [15, 2]. Для цих просторiв показником регулярностi служить вагова функцiя µ: R n (0, ). У нас µ(ξ) = ξ s ϕ( ξ ) є радiальною функцiєю аргументу ξ R n. У випадку, коли ϕ 1, простiр H s,ϕ (R n ) стає гiльбертовим простором Соболєва H s (R n ) порядку s. Взагалi, виконуються неперервнi i щiльнi вкладення H s+ε (R n ) H s,ϕ (R n ) H s ε (R n ) для кожного ε > 0. (7) 22 ISSN Dopov. Nac. akad. nauk Ukr., 2015, 7
23 З них видно, що у класi просторiв {H s,ϕ (R n ): s R,ϕ M} числовий параметр s задає основну регулярнiсть, а функцiональний параметр ϕ додаткову регулярнiсть, пiдпорядковану основнiй. Коротко кажучи, ϕ уточнює основну регулярнiсть s. Тому цей клас названо уточненою соболєвською шкалою на R n. Її аналоги для Ω i Γ означаються таким чином. Лiнiйний простiр H s,ϕ (Ω) складається, за означенням, зi звужень на область Ω усiх розподiлiв w H s,ϕ (R n ). У ньому введена норма за формулою u H s,ϕ (Ω) := inf{ w H s,ϕ (R n ): w H s,ϕ (R n ), w = u в Ω}, де u H s,ϕ (Ω). Цей простiр гiльбертiв i сепарабельний вiдносно введеної норми, а множина C (Ω) щiльна в ньому. Лiнiйний простiр H s,ϕ (Γ) складається, коротко кажучи, з усiх розподiлiв на Γ, якi в локальних координатах належать до H s,ϕ (R n 1 ). Дамо детальне означення. Iз C -структури на многовидi Γ виберемо який-небудь скiнченний атлас, утворений локальними картами α j : R n 1 Γ j, де j = 1,...,λ. Тут вiдкритi множини Γ 1,...,Γ λ складають покриття многовиду Γ. Крiм того, довiльно виберемо функцiї χ j C (Γ), де j = 1,...,λ, якi утворюють розбиття одиницi на Γ, що задовольняє умову suppχ j Γ j. Тодi, за означенням, простiр H s,ϕ (Γ) складається з усiх розподiлiв h на Γ таких, що (χ j h) α j H s,ϕ (R n 1 ) для кожного номера j {1,...,λ}. Тут (χ j h) α j є зображенням розподiлу χ j h у локальнiй картi α j. Норма в просторi H s,ϕ (Γ) означена за формулою ( λ 1/2 h H s,ϕ (Γ) := (χ j h) α j 2 H s,ϕ (R )). n 1 j=1 Цей простiр гiльбертiв i сепарабельний. Вiн з точнiстю до еквiвалентностi норм не залежить вiд зробленого вибору атласу i розбиття одиницi [12, теорема 2.3]. Множина C (Γ) щiльна в просторi H s,ϕ (Γ). Цi гiльбертовi функцiональнi простори утворюють уточненi соболєвськi шкали {H s,ϕ (Ω): s R,ϕ M} i {H s,ϕ (Γ): s R,ϕ M} (8) наωiγвiдповiдно. Вони мiстять гiльбертовi соболєвськi шкали: якщоϕ(t) 1, тоh s,ϕ (Ω) = =: H s (Ω) i H s,ϕ (Γ) =: H s (Γ) є простори Соболєва порядку s R. Для шкал (8) виконуються компактнi i щiльнi вкладення (7), якщо у формулi (7) замiнити R n на Ω або Γ вiдповiдно. 3. Результати. Сформулюємо результати роботи про властивостi напiводнорiдної елiптичної крайової задачi (1), (2) в уточнених соболєвських шкалах (8). Iз задачею (1), (2) i формально спряженою задачею (4) (6) пов яжемо лiнiйнi простори N i N + нескiнченно гладких розв язкiв цих задач у випадку однорiдних крайових умов. А саме: N складається з усiх розв язкiв (u,v 1,...,v κ ) C (Ω) (C (Γ)) κ задачi (1), (2) у випадку, коли всi g j = 0 на Γ, а N + складається з усiх розв язкiв (w,h 1,...,h q+κ ) C (Ω) (C (Γ)) q+κ задачi (4) (6) у випадку, коли всi χ j = 0 i всi χ 2q+j = 0 на Γ. Оскiльки цi задачi елiптичнi в Ω, простори N i N + скiнченновимiрнi [5, лема 3.4.2]. Позначимо через N 1 + скiнченновимiрний простiр усiх векторiв (h 1,...,h q+κ ) (C (Γ)) q+κ таких, що (w,h 1,...,h q+κ ) N + для деякого w C (Ω). Покладемо K s,ϕ A (Ω) := {u Hs,ϕ (Ω): Au = 0 в Ω} для довiльних s R i ϕ M. Тут образ Au розумiємо в сенсi теорiї розподiлiв, а K s,ϕ A (Ω) розглядаємо як (замкнений) ISSN Доповiдi НАН України, 2015, 7 23
24 пiдпростiр гiльбертового простору H s,ϕ (Ω). Згiдно з [12, теорема 3.11] множина KA (Ω) щiльна в K s,ϕ A (Ω). Введемо гiльбертовi простори κ K s,ϕ A (Ω,Γ) := Ks,ϕ A (Ω) H s+rk 1/2,ϕ (Γ), H s,ϕ (Γ) := H s mj 1/2,ϕ (Γ). k=1 Теорема 1. Для довiльних s R i ϕ M вiдображення (3) продовжується єдиним чином (за неперервнiстю) до обмеженого оператора Λ : K s,ϕ A (Ω,Γ) H s,ϕ(γ). (9) Цей оператор нетерiв. Його ядро збiгається з N, а область значень складається з усiх векторiв (g 1,...,g q+κ ) H s,ϕ (Γ) таких, що (g 1,h 1 ) Γ +...+(g q+κ,h q+κ ) Γ = 0 для кожного (h 1,...,h q+κ ) N + 1. (10) Iндекс оператора (9) дорiвнює dimn dimn 1 + i не залежить вiд s та ϕ. З огляду на цю теорему нагадаємо, що лiнiйний обмежений оператор T : E 1 E 2, що дiє у парi банахових просторiв E 1 i E 2, називають нетеровим, якщо його ядро kert i коядро E 2 /T(E 1 ) скiнченновимiрнi. Якщо оператор нетерiв, то його область значень T(E 1 ) замкнена в E 2, а iндекс indt := dimkert dim(e 2 /T(E 1 )) скiнченний. Якщо N = {0} i N 1 + = {0}, то оператор (9) є iзоморфiзмом за теоремою 1. У загальнiй ситуацiї цей оператор породжує iзоморфiзм мiж деякими пiдпросторами, що мають скiнченну ковимiрнiсть. У цьому зв язку розглянемо такi розклади просторiв, в яких дiє оператор (9), у виглядi прямих сум пiдпросторiв { K s,ϕ A (Ω,Γ) = N (u,u (0) ) Ω + (u,v 1,...,v κ ) K s,ϕ A (Ω,Γ): } κ (v k,v (0) k ) Γ = 0 для всiх (u (0),v (0) 1,...,v(0) κ ) N, (11) k=1 H s,ϕ (Γ) = N + 1 {(g 1,...,g q+κ ) H s,ϕ (Γ): виконується (10)}. (12) Позначимо через P i P 1 + вiдповiдно проектори просторiв K s,ϕ A (Ω,Γ) i H s,ϕ(γ) на другий доданок у сумах (11) i (12) паралельно першому доданку. Цi проектори не залежать (як вiдображення) вiд s i ϕ. Теорема 2. Для довiльних s R i ϕ M звуження оператора (9) на пiдпростiр P(K s,ϕ A (Ω,Γ)) є iзоморфiзмом Λ : P(K s,ϕ A (Ω,Γ)) P+ 1 (H s,ϕ(γ)). (13) Перейдемо до властивостей узагальнених розв язкiв елiптичної крайової задачi (1), (2). Попередньо дамо означення такого розв язку. Позначимо через KA (Ω,Γ) об єднання усiх просторiв Ks,ϕ A (Ω,Γ), де s R i ϕ M. За теоремою 1 для кожного вектора (u,v) := (u,v 1,...,v κ ) K A (Ω,Γ) (14) 24 ISSN Dopov. Nac. akad. nauk Ukr., 2015, 7 q+κ j=1
25 коректно означенi за замиканням правi частини елiптичної крайової задачi (1), (2). Його називаємо (сильним) узагальненим розв язком цiєї задачi. Вiн задовольняє таку апрiорну оцiнку. Теорема 3. Нехай s R, ϕ M i число σ > 0. Тодi iснує число c > 0 таке, що (u,v) K s,ϕ A (Ω,Γ) c( Λ (u,v) Hs,ϕ(Γ) + (u,v) K s σ,ϕ A (Ω,Γ) ) (15) для довiльного вектора (u,v) K s,ϕ A (Ω,Γ). Тут c = c(s,ϕ,σ) не залежить вiд (u,v). Дослiдимо регулярнiсть узагальненого розв язку. Теорема 4. Нехай вектор (14) є узагальненим розв язком елiптичної крайової задачi (1), (2), правi частини якої задовольняють умову g := (g 1,...,g q+κ ) H s,ϕ (Γ) для деяких параметрiв s R i ϕ M. Тодi (u,v) K s,ϕ A (Ω,Γ). Покладемо m := max{m 1,...,m q+κ }. З огляду на вкладення K s,ϕ A (Ω) C (Ω) узагальнений розв язок (14) крайової задачi (1), (2) називається класичним, якщо u C m (Ω) i v k C m+r k (Γ) для кожного k {1,...,κ}. Тодi лiвi частини рiвнянь (2) обчислюються за допомогою класичних похiдних i є неперервними функцiями. Теорема 5. Припустимо, що вектор (14) є узагальненим розв язком елiптичної крайової задачi (1), (2), правi частини якої задовольняють умову g H m+n/2,ϕ (Γ) для деякого параметра ϕ M такого, що 1 dt tϕ 2 (t) <. Тодi цей розв язок класичний. Зауважимо, що в теоремi 5 умова (16) не лише достатня для класичностi розв язку (14), але й необхiдна на класi всiх розглянутих узагальнених розв язкiв. Вiдмiтимо, що теореми 1 4 є новими i для соболєвських просторiв, тобто коли ϕ Обгрунтування результатiв. Теорема 1 у соболєвському випадку, коли s Z i ϕ 1, випливає з [5, теорема 3.4.1]. Це доводиться за допомогою мiркувань, подiбних до тих, що наведенi в [12, п ] (доведення теореми 4.25). Для довiльних s R i ϕ M теорема 1 виводиться iз соболєвського випадку методом iнтерполяцiї з функцiональним параметром пар гiльбертових просторiв (її означення i властивостi викладенi в [12, п. 1.1]). А саме: виберемо додатнi числа ε i δ такi, що s ε i s+δ є цiлими числами. Маємо обмеженi i нетеровi оператори Λ : K s ε A (Ω,Γ) H s ε(γ) i Λ : K s+δ A (Ω,Γ) H s+δ(γ), що дiють у парах просторiв Соболєва. (У випадку ϕ 1 пропускаємо iндекс ϕ у позначеннях просторiв.) Означимо iнтерполяцiйний параметр ψ за формулами ψ(t) := t ε/(ε+δ) ϕ(t 1/(ε+δ) ) при t 1 i ψ(t) := ϕ(1) при 0 < t < 1. Застосувавши iнтерполяцiю з параметром ψ, отримаємо обмежений оператор Λ : [K s ε A (Ω,Γ),Ks+δ A (Ω,Γ)] ψ [H s ε (Γ),H s+δ (Γ)] ψ. Згiдно з [12, теорема 1.7] нетеровiсть цього оператора й iншi його властивостi, сформульованi в теоремi 1, є наслiдком нетеровостi зазначених вище операторiв, якi дiють у просторах Соболєва та мають спiльне ядро i однаковий iндекс. Залишається використати iнтерполяцiйнi формули [K s ε A (Ω,Γ),Ks+δ A (Ω,Γ)] ψ = K s,ϕ A (Ω,Γ), [H s ε(γ),h s+δ (Γ)] ψ = H s,ϕ (Γ). (17) ISSN Доповiдi НАН України, 2015, 7 25 (16)
26 Вони є наслiдками теорем 1.5 i 2.2 з [12] i рiвностi [K s ε A (Ω),Ks+δ A (Ω)] ψ = K s,ϕ A (Ω). Остання випливає з другої рiвностi в (17) для κ = 0 на пiдставi теореми 3.11 з [12]. Теорема 2 випливає з теореми 1. Справдi, за теоремою 1 N ядро, а P 1 + (H s,ϕ(γ)) область значень обмеженого оператора (9). Тому обмежений оператор (13) є бiєкцiєю i за теоремою Банаха про обернений оператор є iзоморфiзмом. Перейдемо до теореми 3. Для довiльного вектора (u,v) K s,ϕ A (Ω,Γ) потрiбна оцiнка (15) випливає з нерiвностей P(u,v) K s,ϕ A (Ω,Γ) c 1 Λ (u,v) Hs,ϕ(Γ), (1 P)(u,v) K s,ϕ A (Ω,Γ) c 2 (u,v) K s σ,ϕ A (Ω,Γ). Тут c 1 є норма оператора, оберненого до iзоморфiзму (13), а c 2 є норма оператора 1 P : K s σ,ϕ A (Ω,Γ) N, де N розглядається як скiнченновимiрний пiдпростiр в K s,ϕ A (Ω,Γ). Обгрунтуємо теорему 4. Нехай вектори (u, v) i g задовольняють її умову. Оскiльки g P 1 + (H s,ϕ(γ)), то за теоремою 2 iснує розв язок (u,v ) K s,ϕ A (Ω,Γ) крайової задачi Λ (u,v ) = g. Звiдси (u u,v v ) N i тому (u,v) K s,ϕ A (Ω,Γ). Теорема 5 випливає з теореми 4 i версiй [12, теореми 2.8, 3.4] теореми вкладення Хермандера [8, теорема 2.2.7] для шкал просторiв (8). Справдi, з умови g H m+n/2,ϕ (Γ) випливає включення (u,v) K m+n/2,ϕ A (Ω,Γ) за теоремою 4. Тодi u H m+n/2,ϕ (Ω) C m (Ω) i v k H m+n/2+rk 1/2,ϕ (Γ) C m+r k (Γ) для кожного номера k {1,...,κ} на пiдставi цих версiй i умови (16). Отже, розв язок (u, v) класичний. Автор висловлює вдячнiсть О. О. Мурачу за керiвництво роботою. Цитована лiтература 1. Лаврук Б. О параметрических граничных задачах для эллиптических систем линейных дифференциальных уравнений. I. Построение сопряженных задач // Bull. Acad. Polon. Sci. Sér. Sci. Math. Astronom. Phys , No 5. С Лаврук Б. О параметрических граничных задачах для эллиптических систем линейных дифференциальных уравнений. II. Граничная задача для полупространства // Bull. Acad. Polon. Sci. Sér. Sci. Math. Astronom. Phys , 5. С Ciarlet P. G. Plates and junctions in elastic multi-structures. An asymptotic analysis. Paris: Masson, p. 4. Nazarov S., Pileckas K. On noncompact free boundary problems for the plane stationary Navier Stokes equations // J. Reine Angew. Math P Kozlov V.A., Maz ya V.G., Rossmann J. Elliptic boundary value problems in domains with point singularities. Providence: Amer. Math. Soc., p. 6. Roitberg Ya. A. Elliptic boundary value problems in the spaces of distributions. Dordrecht: Kluwer, p. 7. Ройтберг Я. А. Эллиптические задачи с неоднородными граничными условиями и локальное повышение гладкости вплоть до границы обобщенных решений // Докл. АН СССР , 4. С Хермандер Л. Линейные дифференциальные операторы с частными производными. Москва: Мир, с. 9. Karamata J. Sur certains Tauberian theorems de M. M. Hardy et Littlewood // Mathematica (Cluj) P Михайлец В. А., Мурач А. А. Уточненные шкалы пространств и эллиптические краевые задачи. II // Укр. мат. журн , 3. С Mikhailets V. A., Murach A. A. The refined Sobolev scale, interpolation, and elliptic problems // Banach J. Math. Anal , No 2. P Mikhailets V. A., Murach A. A. Hörmander spaces, interpolation, and elliptic problems. Berlin; Boston: De Gruyter, p. (Русское издание книги доступно как arxiv: ). 26 ISSN Dopov. Nac. akad. nauk Ukr., 2015, 7
Problem A. Nanoassembly
 Problem A. Nanoassembly 2.5 seconds One of the problems of creating elements of nanostructures is the colossal time necessary for the construction of nano-parts from separate atoms. Transporting each of
Problem A. Nanoassembly 2.5 seconds One of the problems of creating elements of nanostructures is the colossal time necessary for the construction of nano-parts from separate atoms. Transporting each of
Programming the Microchip Pic 16f84a Microcontroller As a Signal Generator Frequencies in Railway Automation
 988 Programming the Microchip Pic 16f84a Microcontroller As a Signal Generator Frequencies in Railway Automation High School of Transport "Todor Kableshkov" 1574 Sofia, 158 Geo Milev str. Ivan Velev Abstract
988 Programming the Microchip Pic 16f84a Microcontroller As a Signal Generator Frequencies in Railway Automation High School of Transport "Todor Kableshkov" 1574 Sofia, 158 Geo Milev str. Ivan Velev Abstract
Some remarks on Phragmén-Lindelöf theorems for weak solutions of the stationary Schrödinger operator
 Wan Boundary Value Problems (2015) 2015:239 DOI 10.1186/s13661-015-0508-0 R E S E A R C H Open Access Some remarks on Phragmén-Lindelöf theorems for weak solutions of the stationary Schrödinger operator
Wan Boundary Value Problems (2015) 2015:239 DOI 10.1186/s13661-015-0508-0 R E S E A R C H Open Access Some remarks on Phragmén-Lindelöf theorems for weak solutions of the stationary Schrödinger operator
Russian Introductory Course
 Russian Introductory Course Natasha Bershadski Learn another language the way you learnt your own Succeed with the and learn another language the way you learnt your own Developed over 50 years, the amazing
Russian Introductory Course Natasha Bershadski Learn another language the way you learnt your own Succeed with the and learn another language the way you learnt your own Developed over 50 years, the amazing
IС A A RT 2013. Proceedings Volume 2. 5th International Conference on Agents and Artificial Intelligence. Barcelona, Spain 15-18 February, 2013
 «'.''«ИЧИЧГШ ИШ М Ш * /////>. л ъ и г ш я ш и ъ в т ъ т ', : 4 р * т Ъ ъ ^ Х 'Ш У Л *а * 1 ЛЧй==:й?й!^'ййй IС A A RT 2013. *»ф«ч>»д* 'И И в Я в З Г З г И Ж /а 1 * icw-ia & «:*>if E M e i i i i y. x '-
«'.''«ИЧИЧГШ ИШ М Ш * /////>. л ъ и г ш я ш и ъ в т ъ т ', : 4 р * т Ъ ъ ^ Х 'Ш У Л *а * 1 ЛЧй==:й?й!^'ййй IС A A RT 2013. *»ф«ч>»д* 'И И в Я в З Г З г И Ж /а 1 * icw-ia & «:*>if E M e i i i i y. x '-
The European Ombudsman
 Overview The European Ombudsman Е в р о п е й с к и о м б у д с м а н E l D e f e n s o r d e l P u e b l o E u r o p e o E v r o p s k ý v e ř e j n ý o c h r á n c e p r á v D e n E u r o p æ i s k e
Overview The European Ombudsman Е в р о п е й с к и о м б у д с м а н E l D e f e n s o r d e l P u e b l o E u r o p e o E v r o p s k ý v e ř e j n ý o c h r á n c e p r á v D e n E u r o p æ i s k e
THE REGULAR OPEN CONTINUOUS IMAGES OF COMPLETE METRIC SPACES
 PACIFIC JOURNAL OF MATHEMATICS Vol 23 No 3, 1967 THE REGULAR OPEN CONTINUOUS IMAGES OF COMPLETE METRIC SPACES HOWARD H WICKE This article characterizes the regular T o open continuous images of complete
PACIFIC JOURNAL OF MATHEMATICS Vol 23 No 3, 1967 THE REGULAR OPEN CONTINUOUS IMAGES OF COMPLETE METRIC SPACES HOWARD H WICKE This article characterizes the regular T o open continuous images of complete
UNDERGRADUATE STUDY SKILLS GUIDE 2014-15
 SCHOOL OF SLAVONIC AND EAST EUROPEAN STUDIES UNDERGRADUATE STUDY SKILLS GUIDE 2014-15 ECONOMICS AND BUSINESS HISTORY LANGUAGES AND CULTURE POLITICS AND SOCIOLOGY 1 1. AN INTRODUCTION TO STUDY SKILLS 5
SCHOOL OF SLAVONIC AND EAST EUROPEAN STUDIES UNDERGRADUATE STUDY SKILLS GUIDE 2014-15 ECONOMICS AND BUSINESS HISTORY LANGUAGES AND CULTURE POLITICS AND SOCIOLOGY 1 1. AN INTRODUCTION TO STUDY SKILLS 5
1. Oblast rozvoj spolků a SU UK 1.1. Zvyšování kvalifikace Školení Zapojení do projektů Poradenství 1.2. Financování 1.2.1.
 1. O b l a s t r o z v o j s p o l k a S U U K 1. 1. Z v y š o v á n í k v a l i f i k a c e Š k o l e n í o S t u d e n t s k á u n i e U n i v e r z i t y K a r l o v y ( d á l e j e n S U U K ) z í
1. O b l a s t r o z v o j s p o l k a S U U K 1. 1. Z v y š o v á n í k v a l i f i k a c e Š k o l e n í o S t u d e n t s k á u n i e U n i v e r z i t y K a r l o v y ( d á l e j e n S U U K ) z í
Stochastic processes crossing from ballistic to fractional diffusion with memory: exact results
 Condensed Matter Physics, Vol. 3, No, 3: 8 http://www.icmp.lviv.ua/journal Stochastic processes crossing from ballistic to fractional diffusion with memory: exact results V. Ilyin, I. Procaccia, A. Zagorodny
Condensed Matter Physics, Vol. 3, No, 3: 8 http://www.icmp.lviv.ua/journal Stochastic processes crossing from ballistic to fractional diffusion with memory: exact results V. Ilyin, I. Procaccia, A. Zagorodny
1 Introduction, Notation and Statement of the main results
 XX Congreso de Ecuaciones Diferenciales y Aplicaciones X Congreso de Matemática Aplicada Sevilla, 24-28 septiembre 2007 (pp. 1 6) Skew-product maps with base having closed set of periodic points. Juan
XX Congreso de Ecuaciones Diferenciales y Aplicaciones X Congreso de Matemática Aplicada Sevilla, 24-28 septiembre 2007 (pp. 1 6) Skew-product maps with base having closed set of periodic points. Juan
Football fever: self-affirmation model for goal distributions
 Condensed Matter Physics 2009, Vol. 12, No 4, pp. 739 752 Football fever: self-affirmation model for goal distributions W. Janke 1, E. Bittner 1, A. Nußbaumer 1, M. Weigel 2,3 1 Institut für Theoretische
Condensed Matter Physics 2009, Vol. 12, No 4, pp. 739 752 Football fever: self-affirmation model for goal distributions W. Janke 1, E. Bittner 1, A. Nußbaumer 1, M. Weigel 2,3 1 Institut für Theoretische
ISSN 0975-413X CODEN (USA): PCHHAX. The study of dissolution kinetics of drugs with riboxinum (inosine)
 Available online at www.derpharmachemica.com ISSN 0975-413X CODEN (USA): PCHHAX Der Pharma Chemica, 2016, 8(1):412-416 (http://derpharmachemica.com/archive.html) The study of dissolution kinetics of drugs
Available online at www.derpharmachemica.com ISSN 0975-413X CODEN (USA): PCHHAX Der Pharma Chemica, 2016, 8(1):412-416 (http://derpharmachemica.com/archive.html) The study of dissolution kinetics of drugs
MARI-ENGLISH DICTIONARY
 MARI-ENGLISH DICTIONARY This project was funded by the Austrian Science Fund (FWF) 1, grant P22786-G20, and carried out at the Department of Finno-Ugric Studies 2 at the University of Vienna 3. Editors:
MARI-ENGLISH DICTIONARY This project was funded by the Austrian Science Fund (FWF) 1, grant P22786-G20, and carried out at the Department of Finno-Ugric Studies 2 at the University of Vienna 3. Editors:
CONCEPT OF STATE SOVEREIGNTY: MODERN ATTITUDES. Karen Gevorgyan 1
 CONCEPT OF STATE SOVEREIGNTY: MODERN ATTITUDES Karen Gevorgyan 1 For decades, international law and public law aspects of the concept of sovereignty were in the center of attention of the representatives
CONCEPT OF STATE SOVEREIGNTY: MODERN ATTITUDES Karen Gevorgyan 1 For decades, international law and public law aspects of the concept of sovereignty were in the center of attention of the representatives
Some Problems of Second-Order Rational Difference Equations with Quadratic Terms
 International Journal of Difference Equations ISSN 0973-6069, Volume 9, Number 1, pp. 11 21 (2014) http://campus.mst.edu/ijde Some Problems of Second-Order Rational Difference Equations with Quadratic
International Journal of Difference Equations ISSN 0973-6069, Volume 9, Number 1, pp. 11 21 (2014) http://campus.mst.edu/ijde Some Problems of Second-Order Rational Difference Equations with Quadratic
Publikationsliste. 1 Referierte Zeitschriftenartikel
 Publikationsliste 1 Referierte Zeitschriftenartikel [1 ] An estimate for the maximum of solutions of parabolic equations with the Venttsel condition, Vestnik Leningrad. Univ. (Ser. Mat. Mekh. Astronom.,
Publikationsliste 1 Referierte Zeitschriftenartikel [1 ] An estimate for the maximum of solutions of parabolic equations with the Venttsel condition, Vestnik Leningrad. Univ. (Ser. Mat. Mekh. Astronom.,
UNCERTAINTY TREATMENT IN STOCK MARKET MODELING
 UNCERTAINTY TREATMENT IN STOCK MARKET MODELING Stanislaw Raczynski Universidad Panamericana Augusto Rodin 498, 03910 Mexico City, Mexico e-mail: stanracz@netservice.com.mx Abstract A model of stock market
UNCERTAINTY TREATMENT IN STOCK MARKET MODELING Stanislaw Raczynski Universidad Panamericana Augusto Rodin 498, 03910 Mexico City, Mexico e-mail: stanracz@netservice.com.mx Abstract A model of stock market
Finite speed of propagation in porous media. by mass transportation methods
 Finite speed of propagation in porous media by mass transportation methods José Antonio Carrillo a, Maria Pia Gualdani b, Giuseppe Toscani c a Departament de Matemàtiques - ICREA, Universitat Autònoma
Finite speed of propagation in porous media by mass transportation methods José Antonio Carrillo a, Maria Pia Gualdani b, Giuseppe Toscani c a Departament de Matemàtiques - ICREA, Universitat Autònoma
Victims Compensation Claim Status of All Pending Claims and Claims Decided Within the Last Three Years
 Claim#:021914-174 Initials: J.T. Last4SSN: 6996 DOB: 5/3/1970 Crime Date: 4/30/2013 Status: Claim is currently under review. Decision expected within 7 days Claim#:041715-334 Initials: M.S. Last4SSN: 2957
Claim#:021914-174 Initials: J.T. Last4SSN: 6996 DOB: 5/3/1970 Crime Date: 4/30/2013 Status: Claim is currently under review. Decision expected within 7 days Claim#:041715-334 Initials: M.S. Last4SSN: 2957
ON SUPERCYCLICITY CRITERIA. Nuha H. Hamada Business Administration College Al Ain University of Science and Technology 5-th st, Abu Dhabi, 112612, UAE
 International Journal of Pure and Applied Mathematics Volume 101 No. 3 2015, 401-405 ISSN: 1311-8080 (printed version); ISSN: 1314-3395 (on-line version) url: http://www.ijpam.eu doi: http://dx.doi.org/10.12732/ijpam.v101i3.7
International Journal of Pure and Applied Mathematics Volume 101 No. 3 2015, 401-405 ISSN: 1311-8080 (printed version); ISSN: 1314-3395 (on-line version) url: http://www.ijpam.eu doi: http://dx.doi.org/10.12732/ijpam.v101i3.7
ON THE EMBEDDING OF BIRKHOFF-WITT RINGS IN QUOTIENT FIELDS
 ON THE EMBEDDING OF BIRKHOFF-WITT RINGS IN QUOTIENT FIELDS DOV TAMARI 1. Introduction and general idea. In this note a natural problem arising in connection with so-called Birkhoff-Witt algebras of Lie
ON THE EMBEDDING OF BIRKHOFF-WITT RINGS IN QUOTIENT FIELDS DOV TAMARI 1. Introduction and general idea. In this note a natural problem arising in connection with so-called Birkhoff-Witt algebras of Lie
SOLVING LINEAR SYSTEMS
 SOLVING LINEAR SYSTEMS Linear systems Ax = b occur widely in applied mathematics They occur as direct formulations of real world problems; but more often, they occur as a part of the numerical analysis
SOLVING LINEAR SYSTEMS Linear systems Ax = b occur widely in applied mathematics They occur as direct formulations of real world problems; but more often, they occur as a part of the numerical analysis
Lipschitz classes of A-harmonic functions in Carnot groups
 Lipschitz classes of A-harmonic functions in Carnot groups Craig A. Nolder Department of Mathematics Florida State University Tallahassee, FL 32306-4510, USA nolder@math.fsu.edu 30 October 2005 Abstract
Lipschitz classes of A-harmonic functions in Carnot groups Craig A. Nolder Department of Mathematics Florida State University Tallahassee, FL 32306-4510, USA nolder@math.fsu.edu 30 October 2005 Abstract
( ) ( ) [2],[3],[4],[5],[6],[7]
![( ) ( ) [2],[3],[4],[5],[6],[7] ( ) ( ) [2],[3],[4],[5],[6],[7]](/thumbs/39/20163578.jpg) ( ) ( ) Lebesgue Takagi, - []., [2],[3],[4],[5],[6],[7].,. [] M. Hata and M. Yamaguti, The Takagi function and its generalization, Japan J. Appl. Math., (984), 83 99. [2] T. Sekiguchi and Y. Shiota, A
( ) ( ) Lebesgue Takagi, - []., [2],[3],[4],[5],[6],[7].,. [] M. Hata and M. Yamaguti, The Takagi function and its generalization, Japan J. Appl. Math., (984), 83 99. [2] T. Sekiguchi and Y. Shiota, A
Notes on Symmetric Matrices
 CPSC 536N: Randomized Algorithms 2011-12 Term 2 Notes on Symmetric Matrices Prof. Nick Harvey University of British Columbia 1 Symmetric Matrices We review some basic results concerning symmetric matrices.
CPSC 536N: Randomized Algorithms 2011-12 Term 2 Notes on Symmetric Matrices Prof. Nick Harvey University of British Columbia 1 Symmetric Matrices We review some basic results concerning symmetric matrices.
Viscous flow through pipes of various cross-sections
 IOP PUBLISHING Eur. J. Phys. 28 (2007 521 527 EUROPEAN JOURNAL OF PHYSICS doi:10.1088/0143-0807/28/3/014 Viscous flow through pipes of various cross-sections John Lekner School of Chemical and Physical
IOP PUBLISHING Eur. J. Phys. 28 (2007 521 527 EUROPEAN JOURNAL OF PHYSICS doi:10.1088/0143-0807/28/3/014 Viscous flow through pipes of various cross-sections John Lekner School of Chemical and Physical
Heat Exchangers - Introduction
 Heat Exchangers - Introduction Concentric Pipe Heat Exchange T h1 T c1 T c2 T h1 Energy Balance on Cold Stream (differential) dq C = wc p C dt C = C C dt C Energy Balance on Hot Stream (differential) dq
Heat Exchangers - Introduction Concentric Pipe Heat Exchange T h1 T c1 T c2 T h1 Energy Balance on Cold Stream (differential) dq C = wc p C dt C = C C dt C Energy Balance on Hot Stream (differential) dq
1.- L a m e j o r o p c ió n e s c l o na r e l d i s co ( s e e x p li c a r á d es p u é s ).
 PROCEDIMIENTO DE RECUPERACION Y COPIAS DE SEGURIDAD DEL CORTAFUEGOS LINUX P ar a p od e r re c u p e ra r nu e s t r o c o rt a f u e go s an t e un d es a s t r e ( r ot u r a d e l di s c o o d e l a
PROCEDIMIENTO DE RECUPERACION Y COPIAS DE SEGURIDAD DEL CORTAFUEGOS LINUX P ar a p od e r re c u p e ra r nu e s t r o c o rt a f u e go s an t e un d es a s t r e ( r ot u r a d e l di s c o o d e l a
ON THE K-WINNERS-TAKE-ALL NETWORK
 634 ON THE K-WINNERS-TAKE-ALL NETWORK E. Majani Jet Propulsion Laboratory California Institute of Technology R. Erlanson, Y. Abu-Mostafa Department of Electrical Engineering California Institute of Technology
634 ON THE K-WINNERS-TAKE-ALL NETWORK E. Majani Jet Propulsion Laboratory California Institute of Technology R. Erlanson, Y. Abu-Mostafa Department of Electrical Engineering California Institute of Technology
 Rev. Mat. Iberoam, 17 (1), 49{419 Dynamical instability of symmetric vortices Lus Almeida and Yan Guo Abstract. Using the Maxwell-Higgs model, we prove that linearly unstable symmetric vortices in the
Rev. Mat. Iberoam, 17 (1), 49{419 Dynamical instability of symmetric vortices Lus Almeida and Yan Guo Abstract. Using the Maxwell-Higgs model, we prove that linearly unstable symmetric vortices in the
STATISTICAL FIELD THEORY FOR A MULTICOMPONENT FLUID: THE COLLECTIVE VARIABLES APPROACH
 ЖУРНАЛ ФIЗИЧНИХ ДОСЛIДЖЕНЬ т., (007) с. 33 4 JOURNAL OF PHYSICAL STUDIES v., No. (007) p. 33 4 STATISTICAL FIELD THEORY FOR A MULTICOMPONENT FLUID: THE COLLECTIVE VARIABLES APPROACH O. Patsahan, I. Mryglod,
ЖУРНАЛ ФIЗИЧНИХ ДОСЛIДЖЕНЬ т., (007) с. 33 4 JOURNAL OF PHYSICAL STUDIES v., No. (007) p. 33 4 STATISTICAL FIELD THEORY FOR A MULTICOMPONENT FLUID: THE COLLECTIVE VARIABLES APPROACH O. Patsahan, I. Mryglod,
Properties of BMO functions whose reciprocals are also BMO
 Properties of BMO functions whose reciprocals are also BMO R. L. Johnson and C. J. Neugebauer The main result says that a non-negative BMO-function w, whose reciprocal is also in BMO, belongs to p> A p,and
Properties of BMO functions whose reciprocals are also BMO R. L. Johnson and C. J. Neugebauer The main result says that a non-negative BMO-function w, whose reciprocal is also in BMO, belongs to p> A p,and
7 Gaussian Elimination and LU Factorization
 7 Gaussian Elimination and LU Factorization In this final section on matrix factorization methods for solving Ax = b we want to take a closer look at Gaussian elimination (probably the best known method
7 Gaussian Elimination and LU Factorization In this final section on matrix factorization methods for solving Ax = b we want to take a closer look at Gaussian elimination (probably the best known method
ANALYTICITY OF SETS ASSOCIATED TO LELONG NUMBERS AND THE EXTENSION OF MEROMORPHIC MAPS 1
 BULLETIN OF THE AMERICAN MATHEMATICAL SOCIETY Volume 79, Number 6, November 1973 ANALYTICITY OF SETS ASSOCIATED TO LELONG NUMBERS AND THE EXTENSION OF MEROMORPHIC MAPS 1 BY YUM-TONG SIU 2 Communicated
BULLETIN OF THE AMERICAN MATHEMATICAL SOCIETY Volume 79, Number 6, November 1973 ANALYTICITY OF SETS ASSOCIATED TO LELONG NUMBERS AND THE EXTENSION OF MEROMORPHIC MAPS 1 BY YUM-TONG SIU 2 Communicated
Two classes of ternary codes and their weight distributions
 Two classes of ternary codes and their weight distributions Cunsheng Ding, Torleiv Kløve, and Francesco Sica Abstract In this paper we describe two classes of ternary codes, determine their minimum weight
Two classes of ternary codes and their weight distributions Cunsheng Ding, Torleiv Kløve, and Francesco Sica Abstract In this paper we describe two classes of ternary codes, determine their minimum weight
MIKAEL LINDSTRÖM LIST OF PUBLICATIONS 10.4.2014. Articles in international peer-reviewed journals
 MIKAEL LINDSTRÖM LIST OF PUBLICATIONS 10.4.2014 Articles in international peer-reviewed journals 2. Mikael Lindström: On Schwartz convergence vector spaces, Math. Nachr. 117, 37-49, 1984. 3. Mikael Lindström:
MIKAEL LINDSTRÖM LIST OF PUBLICATIONS 10.4.2014 Articles in international peer-reviewed journals 2. Mikael Lindström: On Schwartz convergence vector spaces, Math. Nachr. 117, 37-49, 1984. 3. Mikael Lindström:
PETER HÄSTÖ, RIKU KLÉN, SWADESH KUMAR SAHOO, AND MATTI VUORINEN
 GEOMETRIC PROPERTIES OF ϕ-uniform DOMAINS PETER HÄSTÖ, RIKU KLÉN, SWADESH KUMAR SAHOO, AND MATTI VUORINEN Abstract. We consider proper subdomains G of R n and their images G = f(g) under quasiconformal
GEOMETRIC PROPERTIES OF ϕ-uniform DOMAINS PETER HÄSTÖ, RIKU KLÉN, SWADESH KUMAR SAHOO, AND MATTI VUORINEN Abstract. We consider proper subdomains G of R n and their images G = f(g) under quasiconformal
ก (048044 04804422 22) Principles of Plant Physiology
 ก ก ก (048044 04804422 22) Principles of Plant Physiology. 1. (Introduction to plant physiology) 2. ก (Plant Plant-water relation) 3. (Plant mineral nutrition) 4. (Metabolism)
ก ก ก (048044 04804422 22) Principles of Plant Physiology. 1. (Introduction to plant physiology) 2. ก (Plant Plant-water relation) 3. (Plant mineral nutrition) 4. (Metabolism)
Opis przedmiotu zamówienia - zakres czynności Usługi sprzątania obiektów Gdyńskiego Centrum Sportu
 O p i s p r z e d m i o t u z a m ó w i e n i a - z a k r e s c z y n n o c i f U s ł u i s p r z» t a n i a o b i e k t ó w G d y s k i e C eo n t r u m S p o r t us I S t a d i o n p i ł k a r s k i
O p i s p r z e d m i o t u z a m ó w i e n i a - z a k r e s c z y n n o c i f U s ł u i s p r z» t a n i a o b i e k t ó w G d y s k i e C eo n t r u m S p o r t us I S t a d i o n p i ł k a r s k i
COMPLIANCE OF MANAGEMENT ACCOUNTING WHEN USING INFORMATION TECHNOLOGIES
 Margaryta I. Skrypnyk, Mykola M. Matiukha COMPLIANCE OF MANAGEMENT ACCOUNTING WHEN USING INFORMATION TECHNOLOGIES The article studies the correspondence of management accounting structure when using of
Margaryta I. Skrypnyk, Mykola M. Matiukha COMPLIANCE OF MANAGEMENT ACCOUNTING WHEN USING INFORMATION TECHNOLOGIES The article studies the correspondence of management accounting structure when using of
Killer Te categors of Subspace in CpNN
 Three observations regarding Schatten p classes Gideon Schechtman Abstract The paper contains three results, the common feature of which is that they deal with the Schatten p class. The first is a presentation
Three observations regarding Schatten p classes Gideon Schechtman Abstract The paper contains three results, the common feature of which is that they deal with the Schatten p class. The first is a presentation
1. Prove that the empty set is a subset of every set.
 1. Prove that the empty set is a subset of every set. Basic Topology Written by Men-Gen Tsai email: b89902089@ntu.edu.tw Proof: For any element x of the empty set, x is also an element of every set since
1. Prove that the empty set is a subset of every set. Basic Topology Written by Men-Gen Tsai email: b89902089@ntu.edu.tw Proof: For any element x of the empty set, x is also an element of every set since
Rate of convergence towards Hartree dynamics
 Rate of convergence towards Hartree dynamics Benjamin Schlein, LMU München and University of Cambridge Universitá di Milano Bicocca, October 22, 2007 Joint work with I. Rodnianski 1. Introduction boson
Rate of convergence towards Hartree dynamics Benjamin Schlein, LMU München and University of Cambridge Universitá di Milano Bicocca, October 22, 2007 Joint work with I. Rodnianski 1. Introduction boson
8. Linear least-squares
 8. Linear least-squares EE13 (Fall 211-12) definition examples and applications solution of a least-squares problem, normal equations 8-1 Definition overdetermined linear equations if b range(a), cannot
8. Linear least-squares EE13 (Fall 211-12) definition examples and applications solution of a least-squares problem, normal equations 8-1 Definition overdetermined linear equations if b range(a), cannot
9 More on differentiation
 Tel Aviv University, 2013 Measure and category 75 9 More on differentiation 9a Finite Taylor expansion............... 75 9b Continuous and nowhere differentiable..... 78 9c Differentiable and nowhere monotone......
Tel Aviv University, 2013 Measure and category 75 9 More on differentiation 9a Finite Taylor expansion............... 75 9b Continuous and nowhere differentiable..... 78 9c Differentiable and nowhere monotone......
The Method of Partial Fractions Math 121 Calculus II Spring 2015
 Rational functions. as The Method of Partial Fractions Math 11 Calculus II Spring 015 Recall that a rational function is a quotient of two polynomials such f(x) g(x) = 3x5 + x 3 + 16x x 60. The method
Rational functions. as The Method of Partial Fractions Math 11 Calculus II Spring 015 Recall that a rational function is a quotient of two polynomials such f(x) g(x) = 3x5 + x 3 + 16x x 60. The method
TERMINOLOGY OF KOGNITIVE LINGUISTICS: CONCEPTUAL SYSTEM AND CONCEPTUAL PICTURE OF THE WORLD
 UDC 811.161.1' 1(082) M. V. PIMENOVA (Kemerovo, Russia) TERMINOLOGY OF KOGNITIVE LINGUISTICS: CONCEPTUAL SYSTEM AND CONCEPTUAL PICTURE OF THE WORLD The article deals with the determination of the terms
UDC 811.161.1' 1(082) M. V. PIMENOVA (Kemerovo, Russia) TERMINOLOGY OF KOGNITIVE LINGUISTICS: CONCEPTUAL SYSTEM AND CONCEPTUAL PICTURE OF THE WORLD The article deals with the determination of the terms
Nonlinear Algebraic Equations Example
 Nonlinear Algebraic Equations Example Continuous Stirred Tank Reactor (CSTR). Look for steady state concentrations & temperature. s r (in) p,i (in) i In: N spieces with concentrations c, heat capacities
Nonlinear Algebraic Equations Example Continuous Stirred Tank Reactor (CSTR). Look for steady state concentrations & temperature. s r (in) p,i (in) i In: N spieces with concentrations c, heat capacities
 C o a t i a n P u b l i c D e b tm a n a g e m e n t a n d C h a l l e n g e s o f M a k e t D e v e l o p m e n t Z a g e bo 8 t h A p i l 2 0 1 1 h t t pdd w w wp i j fp h D p u b l i c2 d e b td S t
C o a t i a n P u b l i c D e b tm a n a g e m e n t a n d C h a l l e n g e s o f M a k e t D e v e l o p m e n t Z a g e bo 8 t h A p i l 2 0 1 1 h t t pdd w w wp i j fp h D p u b l i c2 d e b td S t
EFFICIENCY OF INTERACTION OF INTERSTITIAL CARBON WITH OXYGEN, TIN, AND SUBSTITUTION CARBON IN IRRADIATED SILICON
 M.I. GRITSENKO, O.O. KOBZAR, Yu.V. POMOZOV et al. EFFICIENCY OF INTERACTION OF INTERSTITIAL CARBON WITH OXYGEN, TIN, AND SUBSTITUTION CARBON IN IRRADIATED SILICON M.I. GRITSENKO, 1 O.O. KOBZAR, 1 YU.V.
M.I. GRITSENKO, O.O. KOBZAR, Yu.V. POMOZOV et al. EFFICIENCY OF INTERACTION OF INTERSTITIAL CARBON WITH OXYGEN, TIN, AND SUBSTITUTION CARBON IN IRRADIATED SILICON M.I. GRITSENKO, 1 O.O. KOBZAR, 1 YU.V.
Systems with Persistent Memory: the Observation Inequality Problems and Solutions
 Chapter 6 Systems with Persistent Memory: the Observation Inequality Problems and Solutions Facts that are recalled in the problems wt) = ut) + 1 c A 1 s ] R c t s)) hws) + Ks r)wr)dr ds. 6.1) w = w +
Chapter 6 Systems with Persistent Memory: the Observation Inequality Problems and Solutions Facts that are recalled in the problems wt) = ut) + 1 c A 1 s ] R c t s)) hws) + Ks r)wr)dr ds. 6.1) w = w +
Name: Section Registered In:
 Name: Section Registered In: Math 125 Exam 3 Version 1 April 24, 2006 60 total points possible 1. (5pts) Use Cramer s Rule to solve 3x + 4y = 30 x 2y = 8. Be sure to show enough detail that shows you are
Name: Section Registered In: Math 125 Exam 3 Version 1 April 24, 2006 60 total points possible 1. (5pts) Use Cramer s Rule to solve 3x + 4y = 30 x 2y = 8. Be sure to show enough detail that shows you are
RINGS WITH A POLYNOMIAL IDENTITY
 RINGS WITH A POLYNOMIAL IDENTITY IRVING KAPLANSKY 1. Introduction. In connection with his investigation of projective planes, M. Hall [2, Theorem 6.2]* proved the following theorem: a division ring D in
RINGS WITH A POLYNOMIAL IDENTITY IRVING KAPLANSKY 1. Introduction. In connection with his investigation of projective planes, M. Hall [2, Theorem 6.2]* proved the following theorem: a division ring D in
( ) = ( ) = {,,, } β ( ), < 1 ( ) + ( ) = ( ) + ( )
 { } ( ) = ( ) = {,,, } ( ) β ( ), < 1 ( ) + ( ) = ( ) + ( ) max, ( ) [ ( )] + ( ) [ ( )], [ ( )] [ ( )] = =, ( ) = ( ) = 0 ( ) = ( ) ( ) ( ) =, ( ), ( ) =, ( ), ( ). ln ( ) = ln ( ). + 1 ( ) = ( ) Ω[ (
{ } ( ) = ( ) = {,,, } ( ) β ( ), < 1 ( ) + ( ) = ( ) + ( ) max, ( ) [ ( )] + ( ) [ ( )], [ ( )] [ ( )] = =, ( ) = ( ) = 0 ( ) = ( ) ( ) ( ) =, ( ), ( ) =, ( ), ( ). ln ( ) = ln ( ). + 1 ( ) = ( ) Ω[ (
A survey on multivalued integration 1
 Atti Sem. Mat. Fis. Univ. Modena Vol. L (2002) 53-63 A survey on multivalued integration 1 Anna Rita SAMBUCINI Dipartimento di Matematica e Informatica 1, Via Vanvitelli - 06123 Perugia (ITALY) Abstract
Atti Sem. Mat. Fis. Univ. Modena Vol. L (2002) 53-63 A survey on multivalued integration 1 Anna Rita SAMBUCINI Dipartimento di Matematica e Informatica 1, Via Vanvitelli - 06123 Perugia (ITALY) Abstract
A sufficient and necessary condition for the convergence of the sequence of successive approximations to a unique fixed point II
 Suzuki and Alamri Fixed Point Theory and Applications (2015) 2015:59 DOI 10.1186/s13663-015-0302-9 RESEARCH Open Access A sufficient and necessary condition for the convergence of the sequence of successive
Suzuki and Alamri Fixed Point Theory and Applications (2015) 2015:59 DOI 10.1186/s13663-015-0302-9 RESEARCH Open Access A sufficient and necessary condition for the convergence of the sequence of successive
A PRIORI ESTIMATES FOR SEMISTABLE SOLUTIONS OF SEMILINEAR ELLIPTIC EQUATIONS. In memory of Rou-Huai Wang
 A PRIORI ESTIMATES FOR SEMISTABLE SOLUTIONS OF SEMILINEAR ELLIPTIC EQUATIONS XAVIER CABRÉ, MANEL SANCHÓN, AND JOEL SPRUCK In memory of Rou-Huai Wang 1. Introduction In this note we consider semistable
A PRIORI ESTIMATES FOR SEMISTABLE SOLUTIONS OF SEMILINEAR ELLIPTIC EQUATIONS XAVIER CABRÉ, MANEL SANCHÓN, AND JOEL SPRUCK In memory of Rou-Huai Wang 1. Introduction In this note we consider semistable
Earthquake Hazard Zones: The relative risk of damage to Canadian buildings
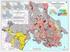 Earthquake Hazard Zones: The relative risk of damage to Canadian buildings by Paul Kovacs Executive Director, Institute for Catastrophic Loss Reduction Adjunct Research Professor, Economics, Univ. of Western
Earthquake Hazard Zones: The relative risk of damage to Canadian buildings by Paul Kovacs Executive Director, Institute for Catastrophic Loss Reduction Adjunct Research Professor, Economics, Univ. of Western
FUNCTIONS OF THE MODAL VERBS IN ENGLISH (MODAL VERBS ANALOGIES IN THE RUSSIAN LANGUAGE) Сompiled by G.V. Kuzmina
 FUNCTIONS OF THE MODAL VERBS IN ENGLISH (MODAL VERBS ANALOGIES IN THE RUSSIAN LANGUAGE) Сompiled by G.V. Kuzmina Москва Издательство Российского университета дружбы народов 2002 FUNCTIONS OF THE MODAL
FUNCTIONS OF THE MODAL VERBS IN ENGLISH (MODAL VERBS ANALOGIES IN THE RUSSIAN LANGUAGE) Сompiled by G.V. Kuzmina Москва Издательство Российского университета дружбы народов 2002 FUNCTIONS OF THE MODAL
Finding the Measure of Segments Examples
 Finding the Measure of Segments Examples 1. In geometry, the distance between two points is used to define the measure of a segment. Segments can be defined by using the idea of betweenness. In the figure
Finding the Measure of Segments Examples 1. In geometry, the distance between two points is used to define the measure of a segment. Segments can be defined by using the idea of betweenness. In the figure
The course of understanding British and American prose and poetry by future managers
 4. Полат Е. С. Новые педагогические и информационные технологии в системе образования. М.: Просвещение, 2000. 5. Гальцова Н. П., Мезенцева Т. И., Швадленко И. А. Использование электронных информационно-образовательных
4. Полат Е. С. Новые педагогические и информационные технологии в системе образования. М.: Просвещение, 2000. 5. Гальцова Н. П., Мезенцева Т. И., Швадленко И. А. Использование электронных информационно-образовательных
n k=1 k=0 1/k! = e. Example 6.4. The series 1/k 2 converges in R. Indeed, if s n = n then k=1 1/k, then s 2n s n = 1 n + 1 +...
 6 Series We call a normed space (X, ) a Banach space provided that every Cauchy sequence (x n ) in X converges. For example, R with the norm = is an example of Banach space. Now let (x n ) be a sequence
6 Series We call a normed space (X, ) a Banach space provided that every Cauchy sequence (x n ) in X converges. For example, R with the norm = is an example of Banach space. Now let (x n ) be a sequence
Inner Product Spaces and Orthogonality
 Inner Product Spaces and Orthogonality week 3-4 Fall 2006 Dot product of R n The inner product or dot product of R n is a function, defined by u, v a b + a 2 b 2 + + a n b n for u a, a 2,, a n T, v b,
Inner Product Spaces and Orthogonality week 3-4 Fall 2006 Dot product of R n The inner product or dot product of R n is a function, defined by u, v a b + a 2 b 2 + + a n b n for u a, a 2,, a n T, v b,
On duality of modular G-Riesz bases and G-Riesz bases in Hilbert C*-modules
 Journal of Linear and Topological Algebra Vol. 04, No. 02, 2015, 53-63 On duality of modular G-Riesz bases and G-Riesz bases in Hilbert C*-modules M. Rashidi-Kouchi Young Researchers and Elite Club Kahnooj
Journal of Linear and Topological Algebra Vol. 04, No. 02, 2015, 53-63 On duality of modular G-Riesz bases and G-Riesz bases in Hilbert C*-modules M. Rashidi-Kouchi Young Researchers and Elite Club Kahnooj
EXISTENCE AND NON-EXISTENCE RESULTS FOR A NONLINEAR HEAT EQUATION
 Sixth Mississippi State Conference on Differential Equations and Computational Simulations, Electronic Journal of Differential Equations, Conference 5 (7), pp. 5 65. ISSN: 7-669. UL: http://ejde.math.txstate.edu
Sixth Mississippi State Conference on Differential Equations and Computational Simulations, Electronic Journal of Differential Equations, Conference 5 (7), pp. 5 65. ISSN: 7-669. UL: http://ejde.math.txstate.edu
4)(x) du(x) = n-' E?(zi(x)) du(x),
 PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 98, Number 1, September 1986 ORTHOGONALITY AND THE HAUSDORFF DIMENSION OF THE MAXIMAL MEASURE ARTUR OSCAR LOPES ABSTRACT. In this paper the orthogonality
PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 98, Number 1, September 1986 ORTHOGONALITY AND THE HAUSDORFF DIMENSION OF THE MAXIMAL MEASURE ARTUR OSCAR LOPES ABSTRACT. In this paper the orthogonality
Chapter 7. Continuity
 Chapter 7 Continuity There are many processes and eects that depends on certain set of variables in such a way that a small change in these variables acts as small change in the process. Changes of this
Chapter 7 Continuity There are many processes and eects that depends on certain set of variables in such a way that a small change in these variables acts as small change in the process. Changes of this
4. Introduction to Heat & Mass Transfer
 4. Introduction to Heat & Mass Transfer This section will cover the following concepts: A rudimentary introduction to mass transfer. Mass transfer from a molecular point of view. Fundamental similarity
4. Introduction to Heat & Mass Transfer This section will cover the following concepts: A rudimentary introduction to mass transfer. Mass transfer from a molecular point of view. Fundamental similarity
Dist INDEX OF PLANS CML-6204(114) STATE OF CALIFORNIA MODOC SISKIYOU LOCATIONS OF CONSTRUCTION 5-16 PROJECT PLANS FOR CONSTRUCTION ON
 ist X F -0() F F 0, 8.0/5.0, 0.0/3. 77 K F 5 - F - J 7 - J F 37 - Q G G, F, Q G V F Q 7 & 77 G F G 78-8 G, Q 00 F 87-0 - G,, Q / p K lv G wy wy 3-3 V, 35-35K 38 30 t 57 5 G kwy v t 70 lv : F F F. 3 t 0
ist X F -0() F F 0, 8.0/5.0, 0.0/3. 77 K F 5 - F - J 7 - J F 37 - Q G G, F, Q G V F Q 7 & 77 G F G 78-8 G, Q 00 F 87-0 - G,, Q / p K lv G wy wy 3-3 V, 35-35K 38 30 t 57 5 G kwy v t 70 lv : F F F. 3 t 0
SIA EVENT CODE LIBRARY
 CODE CODE NAME DESCRIPTION Address field AR AC restoral AC power has been restored unused AT AC trouble AC power has been failed unused BA Burglary alarm Burglary zone has been violated while armed zone
CODE CODE NAME DESCRIPTION Address field AR AC restoral AC power has been restored unused AT AC trouble AC power has been failed unused BA Burglary alarm Burglary zone has been violated while armed zone
An optimal transportation problem with import/export taxes on the boundary
 An optimal transportation problem with import/export taxes on the boundary Julián Toledo Workshop International sur les Mathématiques et l Environnement Essaouira, November 2012..................... Joint
An optimal transportation problem with import/export taxes on the boundary Julián Toledo Workshop International sur les Mathématiques et l Environnement Essaouira, November 2012..................... Joint
Geometrical Characterization of RN-operators between Locally Convex Vector Spaces
 Geometrical Characterization of RN-operators between Locally Convex Vector Spaces OLEG REINOV St. Petersburg State University Dept. of Mathematics and Mechanics Universitetskii pr. 28, 198504 St, Petersburg
Geometrical Characterization of RN-operators between Locally Convex Vector Spaces OLEG REINOV St. Petersburg State University Dept. of Mathematics and Mechanics Universitetskii pr. 28, 198504 St, Petersburg
CONSTANT-SIGN SOLUTIONS FOR A NONLINEAR NEUMANN PROBLEM INVOLVING THE DISCRETE p-laplacian. Pasquale Candito and Giuseppina D Aguí
 Opuscula Math. 34 no. 4 2014 683 690 http://dx.doi.org/10.7494/opmath.2014.34.4.683 Opuscula Mathematica CONSTANT-SIGN SOLUTIONS FOR A NONLINEAR NEUMANN PROBLEM INVOLVING THE DISCRETE p-laplacian Pasquale
Opuscula Math. 34 no. 4 2014 683 690 http://dx.doi.org/10.7494/opmath.2014.34.4.683 Opuscula Mathematica CONSTANT-SIGN SOLUTIONS FOR A NONLINEAR NEUMANN PROBLEM INVOLVING THE DISCRETE p-laplacian Pasquale
ON NONNEGATIVE SOLUTIONS OF NONLINEAR TWO-POINT BOUNDARY VALUE PROBLEMS FOR TWO-DIMENSIONAL DIFFERENTIAL SYSTEMS WITH ADVANCED ARGUMENTS
 ON NONNEGATIVE SOLUTIONS OF NONLINEAR TWO-POINT BOUNDARY VALUE PROBLEMS FOR TWO-DIMENSIONAL DIFFERENTIAL SYSTEMS WITH ADVANCED ARGUMENTS I. KIGURADZE AND N. PARTSVANIA A. Razmadze Mathematical Institute
ON NONNEGATIVE SOLUTIONS OF NONLINEAR TWO-POINT BOUNDARY VALUE PROBLEMS FOR TWO-DIMENSIONAL DIFFERENTIAL SYSTEMS WITH ADVANCED ARGUMENTS I. KIGURADZE AND N. PARTSVANIA A. Razmadze Mathematical Institute
The Gaussian Surface Area and Noise Sensitivity of Degree-d Polynomial Threshold Functions. Daniel M. Kane
 The Gaussian Surface Area and Noise Sensitivity of Degree-d Polynomial Threshold Functions Daniel M. Kane Outline Definitions and Motivation Previous Work Statements of Theorems Proof of the Noise Sensitivity
The Gaussian Surface Area and Noise Sensitivity of Degree-d Polynomial Threshold Functions Daniel M. Kane Outline Definitions and Motivation Previous Work Statements of Theorems Proof of the Noise Sensitivity
NOTES ON LINEAR TRANSFORMATIONS
 NOTES ON LINEAR TRANSFORMATIONS Definition 1. Let V and W be vector spaces. A function T : V W is a linear transformation from V to W if the following two properties hold. i T v + v = T v + T v for all
NOTES ON LINEAR TRANSFORMATIONS Definition 1. Let V and W be vector spaces. A function T : V W is a linear transformation from V to W if the following two properties hold. i T v + v = T v + T v for all
 W Cisco Kompetanse eek end 2 0 0 8 SMB = Store Mu ll ii gg hh eter! Nina Gullerud ng ulleru@ c is c o. c o m 1 Vår E n t e r p r i s e e r f a r i n g... 2 S m å o g M e llo m s t o r e B e d r i f t e
W Cisco Kompetanse eek end 2 0 0 8 SMB = Store Mu ll ii gg hh eter! Nina Gullerud ng ulleru@ c is c o. c o m 1 Vår E n t e r p r i s e e r f a r i n g... 2 S m å o g M e llo m s t o r e B e d r i f t e
The Australian Journal of Mathematical Analysis and Applications
 The Australian Journal of Mathematical Analysis and Applications Volume 7, Issue, Article 11, pp. 1-14, 011 SOME HOMOGENEOUS CYCLIC INEQUALITIES OF THREE VARIABLES OF DEGREE THREE AND FOUR TETSUYA ANDO
The Australian Journal of Mathematical Analysis and Applications Volume 7, Issue, Article 11, pp. 1-14, 011 SOME HOMOGENEOUS CYCLIC INEQUALITIES OF THREE VARIABLES OF DEGREE THREE AND FOUR TETSUYA ANDO
RECURSIVE ENUMERATION OF PYTHAGOREAN TRIPLES
 RECURSIVE ENUMERATION OF PYTHAGOREAN TRIPLES DARRYL MCCULLOUGH AND ELIZABETH WADE In [9], P. W. Wade and W. R. Wade (no relation to the second author gave a recursion formula that produces Pythagorean
RECURSIVE ENUMERATION OF PYTHAGOREAN TRIPLES DARRYL MCCULLOUGH AND ELIZABETH WADE In [9], P. W. Wade and W. R. Wade (no relation to the second author gave a recursion formula that produces Pythagorean
PÓLYA URN MODELS UNDER GENERAL REPLACEMENT SCHEMES
 J. Japan Statist. Soc. Vol. 31 No. 2 2001 193 205 PÓLYA URN MODELS UNDER GENERAL REPLACEMENT SCHEMES Kiyoshi Inoue* and Sigeo Aki* In this paper, we consider a Pólya urn model containing balls of m different
J. Japan Statist. Soc. Vol. 31 No. 2 2001 193 205 PÓLYA URN MODELS UNDER GENERAL REPLACEMENT SCHEMES Kiyoshi Inoue* and Sigeo Aki* In this paper, we consider a Pólya urn model containing balls of m different
 G d y n i a U s ł u g a r e j e s t r a c j i i p o m i a r u c z a s u u c z e s t n i k ó w i m p r e z s p o r t o w y c h G d y s k i e g o O r o d k a S p o r t u i R e k r e a c j i w r o k u 2 0
G d y n i a U s ł u g a r e j e s t r a c j i i p o m i a r u c z a s u u c z e s t n i k ó w i m p r e z s p o r t o w y c h G d y s k i e g o O r o d k a S p o r t u i R e k r e a c j i w r o k u 2 0
ON SOME ANALOGUE OF THE GENERALIZED ALLOCATION SCHEME
 ON SOME ANALOGUE OF THE GENERALIZED ALLOCATION SCHEME Alexey Chuprunov Kazan State University, Russia István Fazekas University of Debrecen, Hungary 2012 Kolchin s generalized allocation scheme A law of
ON SOME ANALOGUE OF THE GENERALIZED ALLOCATION SCHEME Alexey Chuprunov Kazan State University, Russia István Fazekas University of Debrecen, Hungary 2012 Kolchin s generalized allocation scheme A law of
Pain-Free Injections
 T N S Bk P-F Ij I P Bk DV Dv Iv D D - I 8 8 9 1 D v C U C Y N D j I W U v v I k I W j k T k z D M I v 965 1 M Tk C P 1 2 v T I C G v j V T D v v A I W S DD G v v S D @ v DV M I USA! j DV - v - j I v v
T N S Bk P-F Ij I P Bk DV Dv Iv D D - I 8 8 9 1 D v C U C Y N D j I W U v v I k I W j k T k z D M I v 965 1 M Tk C P 1 2 v T I C G v j V T D v v A I W S DD G v v S D @ v DV M I USA! j DV - v - j I v v
Operator-valued version of conditionally free product
 STUDIA MATHEMATICA 153 (1) (2002) Operator-valued version of conditionally free product by Wojciech Młotkowski (Wrocław) Abstract. We present an operator-valued version of the conditionally free product
STUDIA MATHEMATICA 153 (1) (2002) Operator-valued version of conditionally free product by Wojciech Młotkowski (Wrocław) Abstract. We present an operator-valued version of the conditionally free product
SKEW-PRODUCTS WITH SIMPLE APPROXIMATIONS
 proceedings of the american mathematical society Volume 72, Number 3, December 1978 SKEW-PRODUCTS WITH SIMPLE APPROXIMATIONS P. N. WHITMAN Abstract. Conditions are given in order that the cartesian product
proceedings of the american mathematical society Volume 72, Number 3, December 1978 SKEW-PRODUCTS WITH SIMPLE APPROXIMATIONS P. N. WHITMAN Abstract. Conditions are given in order that the cartesian product
On an anti-ramsey type result
 On an anti-ramsey type result Noga Alon, Hanno Lefmann and Vojtĕch Rödl Abstract We consider anti-ramsey type results. For a given coloring of the k-element subsets of an n-element set X, where two k-element
On an anti-ramsey type result Noga Alon, Hanno Lefmann and Vojtĕch Rödl Abstract We consider anti-ramsey type results. For a given coloring of the k-element subsets of an n-element set X, where two k-element
MATHEMATICS BONUS FILES for faculty and students http://www2.onu.edu/~mcaragiu1/bonus_files.html
 MATHEMATICS BONUS FILES for faculty and students http://www2onuedu/~mcaragiu1/bonus_fileshtml RECEIVED: November 1 2007 PUBLISHED: November 7 2007 Solving integrals by differentiation with respect to a
MATHEMATICS BONUS FILES for faculty and students http://www2onuedu/~mcaragiu1/bonus_fileshtml RECEIVED: November 1 2007 PUBLISHED: November 7 2007 Solving integrals by differentiation with respect to a
Summer course on Convex Optimization. Fifth Lecture Interior-Point Methods (1) Michel Baes, K.U.Leuven Bharath Rangarajan, U.
 Summer course on Convex Optimization Fifth Lecture Interior-Point Methods (1) Michel Baes, K.U.Leuven Bharath Rangarajan, U.Minnesota Interior-Point Methods: the rebirth of an old idea Suppose that f is
Summer course on Convex Optimization Fifth Lecture Interior-Point Methods (1) Michel Baes, K.U.Leuven Bharath Rangarajan, U.Minnesota Interior-Point Methods: the rebirth of an old idea Suppose that f is
Numerical Methods for Solving Systems of Nonlinear Equations
 Numerical Methods for Solving Systems of Nonlinear Equations by Courtney Remani A project submitted to the Department of Mathematical Sciences in conformity with the requirements for Math 4301 Honour s
Numerical Methods for Solving Systems of Nonlinear Equations by Courtney Remani A project submitted to the Department of Mathematical Sciences in conformity with the requirements for Math 4301 Honour s
Factorization Theorems
 Chapter 7 Factorization Theorems This chapter highlights a few of the many factorization theorems for matrices While some factorization results are relatively direct, others are iterative While some factorization
Chapter 7 Factorization Theorems This chapter highlights a few of the many factorization theorems for matrices While some factorization results are relatively direct, others are iterative While some factorization
Influences in low-degree polynomials
 Influences in low-degree polynomials Artūrs Bačkurs December 12, 2012 1 Introduction In 3] it is conjectured that every bounded real polynomial has a highly influential variable The conjecture is known
Influences in low-degree polynomials Artūrs Bačkurs December 12, 2012 1 Introduction In 3] it is conjectured that every bounded real polynomial has a highly influential variable The conjecture is known
Sumit Chandok and T. D. Narang INVARIANT POINTS OF BEST APPROXIMATION AND BEST SIMULTANEOUS APPROXIMATION
 F A S C I C U L I M A T H E M A T I C I Nr 51 2013 Sumit Chandok and T. D. Narang INVARIANT POINTS OF BEST APPROXIMATION AND BEST SIMULTANEOUS APPROXIMATION Abstract. In this paper we generalize and extend
F A S C I C U L I M A T H E M A T I C I Nr 51 2013 Sumit Chandok and T. D. Narang INVARIANT POINTS OF BEST APPROXIMATION AND BEST SIMULTANEOUS APPROXIMATION Abstract. In this paper we generalize and extend
December 4, 2013 MATH 171 BASIC LINEAR ALGEBRA B. KITCHENS
 December 4, 2013 MATH 171 BASIC LINEAR ALGEBRA B KITCHENS The equation 1 Lines in two-dimensional space (1) 2x y = 3 describes a line in two-dimensional space The coefficients of x and y in the equation
December 4, 2013 MATH 171 BASIC LINEAR ALGEBRA B KITCHENS The equation 1 Lines in two-dimensional space (1) 2x y = 3 describes a line in two-dimensional space The coefficients of x and y in the equation
Linear Maps. Isaiah Lankham, Bruno Nachtergaele, Anne Schilling (February 5, 2007)
 MAT067 University of California, Davis Winter 2007 Linear Maps Isaiah Lankham, Bruno Nachtergaele, Anne Schilling (February 5, 2007) As we have discussed in the lecture on What is Linear Algebra? one of
MAT067 University of California, Davis Winter 2007 Linear Maps Isaiah Lankham, Bruno Nachtergaele, Anne Schilling (February 5, 2007) As we have discussed in the lecture on What is Linear Algebra? one of
Multiplicative Relaxation with respect to Thompson s Metric
 Revista Colombiana de Matemáticas Volumen 48(2042, páginas 2-27 Multiplicative Relaxation with respect to Thompson s Metric Relajamiento multiplicativo con respecto a la métrica de Thompson Gerd Herzog
Revista Colombiana de Matemáticas Volumen 48(2042, páginas 2-27 Multiplicative Relaxation with respect to Thompson s Metric Relajamiento multiplicativo con respecto a la métrica de Thompson Gerd Herzog
n(n + 1) 2 1 + 2 + + n = 1 r (iii) infinite geometric series: if r < 1 then 1 + 2r + 3r 2 1 e x = 1 + x + x2 3! + for x < 1 ln(1 + x) = x x2 2 + x3 3
 ACTS 4308 FORMULA SUMMARY Section 1: Calculus review and effective rates of interest and discount 1 Some useful finite and infinite series: (i) sum of the first n positive integers: (ii) finite geometric
ACTS 4308 FORMULA SUMMARY Section 1: Calculus review and effective rates of interest and discount 1 Some useful finite and infinite series: (i) sum of the first n positive integers: (ii) finite geometric
On the Relationship between Classes P and NP
 Journal of Computer Science 8 (7): 1036-1040, 2012 ISSN 1549-3636 2012 Science Publications On the Relationship between Classes P and NP Anatoly D. Plotnikov Department of Computer Systems and Networks,
Journal of Computer Science 8 (7): 1036-1040, 2012 ISSN 1549-3636 2012 Science Publications On the Relationship between Classes P and NP Anatoly D. Plotnikov Department of Computer Systems and Networks,
Universal Algorithm for Trading in Stock Market Based on the Method of Calibration
 Universal Algorithm for Trading in Stock Market Based on the Method of Calibration Vladimir V yugin Institute for Information Transmission Problems, Russian Academy of Sciences, Bol shoi Karetnyi per.
Universal Algorithm for Trading in Stock Market Based on the Method of Calibration Vladimir V yugin Institute for Information Transmission Problems, Russian Academy of Sciences, Bol shoi Karetnyi per.
Notes for AA214, Chapter 7. T. H. Pulliam Stanford University
 Notes for AA214, Chapter 7 T. H. Pulliam Stanford University 1 Stability of Linear Systems Stability will be defined in terms of ODE s and O E s ODE: Couples System O E : Matrix form from applying Eq.
Notes for AA214, Chapter 7 T. H. Pulliam Stanford University 1 Stability of Linear Systems Stability will be defined in terms of ODE s and O E s ODE: Couples System O E : Matrix form from applying Eq.
