Lesson 3: RLC circuits & resonance
|
|
|
- Jeffrey Osborne Mason
- 9 years ago
- Views:
Transcription
1 P. Piot, PHYS 375 Spring 008 esson 3: RC circuits & resonance nductor, nductance Comparison of nductance and Capacitance nductance in an AC signals R circuits C circuits: the electric pendulum RC series & parallel circuits Resonance
2 Start with Maxwell s equation ntegrate over a surface S (bounded by contour C) and use Stoke s theorem: The voltage is thus S V r r r E. da emf S C Φ t nductor r r E. dl r r r B E t S r B r. da t d V dt V Z i ω Φ t Magnetic flux in Weber P. Piot, PHYS 375 Spring 008 Wihelm Weber (804-89)
3 P. Piot, PHYS 375 Spring 008 nductor Now need to find a relation between magnetic field generated by a loop and current flowing through the loop s wire. Used Biot and Savart s law: ntegrate over a surface S the magnetic flux is going to be of the form The voltage is thus r µ r r db 0 dl ˆ 4π r Φ B nductance measured in Henri (symbol H) Φ V t d Joseph Henri ( )
4 P. Piot, PHYS 375 Spring 008 nductor Case of loop made with an infinitely thin wire µ B l. 4π δ f the inductor is composed of n loop per meter then total B-field is So inductance is Φ BA B µ 4π µ An 4π Area of the loop n µ An 4π ncrease magnetic permeability (e.g. use metallic core instead of air) ncrease number of wire per unit length increase
5 P. Piot, PHYS 375 Spring 008 nductor in an AC Circuit d V dt V Z V T V iω ntroduce reactance for an inductor: X ω V V P
6 P. Piot, PHYS 375 Spring 008 nductor, Capacitor, Resistor Resistance friction against motion of electrons Reactance inertia that opposes motion of electrons X ω Z X C ωc X mpedance is a generally complex number: R Z R + Note also one introduces the Admittance: Y G + ib Z conductance ix susceptance
7 P. Piot, PHYS 375 Spring 008 nductor versus Capacitor CAPACTOR NDUCTOR
8 P. Piot, PHYS 375 Spring 008 R series Circuits d V T V R+ V R + ( R + iω ) Z R + iω R + ix V T V V T For the above circuit we can compute a numerical value for the impedance: V R Z ( i) Ω Z , Θ 37.0
9 P. Piot, PHYS 375 Spring 008 R parallel Circuits V R+ + V ( + ) V Z R + R R iω ( iω ) V For the above circuit we can compute a numerical value for the impedance: Z (.8+.40i) Ω Z 3.0, Θ 5.98
10 P. Piot, PHYS 375 Spring 008 nductor: Technical aspects nductors are made a conductor wired around air or a ferromagnetic core Unit of inductance is Henri, symbol is H Real inductors also have a resistance (in series with inductance)
11 RC series/parallel Circuits P. Piot, PHYS 375 Spring 008
12 P. Piot, PHYS 375 Spring 008 RC series/parallel Circuits: an example Compute impedance of the circuit below Step : consider C in series with Z Step : consider Z in parallel with R Z Step 3: consider Z in series with C et s do this: Z i ω i Z i Cω + i Z R Z3 Z i Cω Current in the circuit is V i ma, Z 3 And then one can get the voltage across any components
13 C circuit: An electrical pendulum P. Piot, PHYS 375 Spring 008
14 P. Piot, PHYS 375 Spring 008 C circuit: An electrical pendulum Mechanical pendulum: oscillation between potential and kinetic energy Electrical pendulum: oscillation between magnetic (/ ) and electrostatic (/CV ) energy n practice, the C circuit showed has some resistance, i.e. some energy is dissipated and therefore the oscillation amplitude is damped. The oscillation frequency keeps unchanged. C circuit are sometime called tank circuit and oscillate (resonate)
15 P. Piot, PHYS 375 Spring 008 Example of a simple tank (C) circuit ODE governing this circuit? dv C+ C + V d C d V + V d V + C V d Equation of a simple harmonic oscillator with pulsation: ω C Or one can state that system oscillate if impedance associated to C and are equal, i.e.: ω Cω
16 P. Piot, PHYS 375 Spring 008 Example of a simple tank (C) circuit What is the total impedance of the circuits? i Z iω i( ω ω) 0 Cω Z So the tank circuit behaves as an open circuit at resonance! n a very similar way one can show that a series C circuit behaves as a short circuit when driven on resonance i.e., Z 0
17 P. Piot, PHYS 375 Spring 008 RC series circuit nd order ODE: d Q R + + V C dq with ; Q CU d U ( t ) du ( t ) C + RC + Resonant frequency still Voltage across capacitor U ( t ) V ( t ) U(t) et s define the parameter Then the ODE rewrites d U + du ζ + ω0u V
18 P. Piot, PHYS 375 Spring 008 RC series circuit: regimes of operation () et s consider V(t) to be a dirac-like impulsion (not physical ) at t0. Then for t>0, V(t)0 and the previous equation simplifies to d U du + ζ + ω0u 0 With solutions U( t) Ae λ+ t + Be λ t Where the λ are solutions of the characteristics polynomial is The discriminant is And the solutions are R C 4C λ± ζ ( ± )
19 P. Piot, PHYS 375 Spring 008 RC series circuit: regimes of operation () f <0 that is if Under damped λ ± R ± U(t) is of the form R < C R C / δ ± δ ω 0 U ( t ) e δt δ ω t Ae + 0 Be 0 δ ω t A and B are found from initial conditions. f 0 critical damping U( t) Ae δt
20 P. Piot, PHYS 375 Spring 008 RC series circuit: regimes of operation (3) R > C / R R λ± ± i δ ± i C f >0 that is if Strong damping U(t) is of the form U ( t ) e δt i ω t Ae + 0 δ Be i ω δ 0 0 ω δ t A and B are found from initial conditions. Which can be rewritten U( t) De sin ( ) ω δ t + φ δt 0
21 P. Piot, PHYS 375 Spring 008 RC series circuit: regimes of operation (4) Over-damped Critical damping Under-damped For under-damped regime, the solutions are exponentially decaying sinusoidal signals. The time requires for these oscillation to die out is /Q where the quality factor is defined as: Q R C
22 P. Piot, PHYS 375 Spring 008 RC series circuit: mpedance () nd order ODE: d V VR + V + VC R + + C d R d dv + + C. Resonant frequency still et s define the parameter Then the ODE rewrites d d + ζ + ω0 dv
23 P. Piot, PHYS 375 Spring 008 Take back (but could also jut compute the impedance of the system) Explicit in its complex form and deduce the current: ntroducing xω/ω 0 we have RC series circuit: mpedance () dv d d ω ζ ω ω ζω ω ω ω ω ω ζω ω C R Y i i V Y V i i + x x Q R Y
24 P. Piot, PHYS 375 Spring 008 RC series circuit: resonance Values of Q
25 P. Piot, PHYS 375 Spring 008 RC parallel circuit : resonance The same formalism as before can be applied to parallel RC circuits. The difference with serial circuit is: at resonance the impedance has a maximum (and not the admittance as in a serial circuit)
Chapter 30 Inductance
 Chapter 30 Inductance - Mutual Inductance - Self-Inductance and Inductors - Magnetic-Field Energy - The R- Circuit - The -C Circuit - The -R-C Series Circuit . Mutual Inductance - A changing current in
Chapter 30 Inductance - Mutual Inductance - Self-Inductance and Inductors - Magnetic-Field Energy - The R- Circuit - The -C Circuit - The -R-C Series Circuit . Mutual Inductance - A changing current in
Slide 1 / 26. Inductance. 2011 by Bryan Pflueger
 Slide 1 / 26 Inductance 2011 by Bryan Pflueger Slide 2 / 26 Mutual Inductance If two coils of wire are placed near each other and have a current passing through them, they will each induce an emf on one
Slide 1 / 26 Inductance 2011 by Bryan Pflueger Slide 2 / 26 Mutual Inductance If two coils of wire are placed near each other and have a current passing through them, they will each induce an emf on one
Application Note. So You Need to Measure Some Inductors?
 So You Need to Measure Some nductors? Take a look at the 1910 nductance Analyzer. Although specifically designed for production testing of inductors and coils, in addition to measuring inductance (L),
So You Need to Measure Some nductors? Take a look at the 1910 nductance Analyzer. Although specifically designed for production testing of inductors and coils, in addition to measuring inductance (L),
DEGREE: Bachelor's Degree in Industrial Electronics and Automation COURSE: 1º TERM: 2º WEEKLY PLANNING
 SESSION WEEK COURSE: Physics II DEGREE: Bachelor's Degree in Industrial Electronics and Automation COURSE: 1º TERM: 2º WEEKLY PLANNING DESCRIPTION GROUPS (mark ) Indicate YES/NO If the session needs 2
SESSION WEEK COURSE: Physics II DEGREE: Bachelor's Degree in Industrial Electronics and Automation COURSE: 1º TERM: 2º WEEKLY PLANNING DESCRIPTION GROUPS (mark ) Indicate YES/NO If the session needs 2
Chapter 35 Alternating Current Circuits
 hapter 35 Alternating urrent ircuits ac-ircuits Phasor Diagrams Resistors, apacitors and nductors in ac-ircuits R ac-ircuits ac-ircuit power. Resonance Transformers ac ircuits Alternating currents and
hapter 35 Alternating urrent ircuits ac-ircuits Phasor Diagrams Resistors, apacitors and nductors in ac-ircuits R ac-ircuits ac-ircuit power. Resonance Transformers ac ircuits Alternating currents and
Circuits with inductors and alternating currents. Chapter 20 #45, 46, 47, 49
 Circuits with inductors and alternating currents Chapter 20 #45, 46, 47, 49 RL circuits Ch. 20 (last section) Symbol for inductor looks like a spring. An inductor is a circuit element that has a large
Circuits with inductors and alternating currents Chapter 20 #45, 46, 47, 49 RL circuits Ch. 20 (last section) Symbol for inductor looks like a spring. An inductor is a circuit element that has a large
Physics 6C, Summer 2006 Homework 2 Solutions
 Physics 6C, Summer 006 Homework Solutions All problems are from the nd edition of Walker. Numerical values are different for each student. Chapter 3 Problems. Figure 3-30 below shows a circuit containing
Physics 6C, Summer 006 Homework Solutions All problems are from the nd edition of Walker. Numerical values are different for each student. Chapter 3 Problems. Figure 3-30 below shows a circuit containing
Inductors in AC Circuits
 Inductors in AC Circuits Name Section Resistors, inductors, and capacitors all have the effect of modifying the size of the current in an AC circuit and the time at which the current reaches its maximum
Inductors in AC Circuits Name Section Resistors, inductors, and capacitors all have the effect of modifying the size of the current in an AC circuit and the time at which the current reaches its maximum
Induced voltages and Inductance Faraday s Law
 Induced voltages and Inductance Faraday s Law concept #1, 4, 5, 8, 13 Problem # 1, 3, 4, 5, 6, 9, 10, 13, 15, 24, 23, 25, 31, 32a, 34, 37, 41, 43, 51, 61 Last chapter we saw that a current produces a magnetic
Induced voltages and Inductance Faraday s Law concept #1, 4, 5, 8, 13 Problem # 1, 3, 4, 5, 6, 9, 10, 13, 15, 24, 23, 25, 31, 32a, 34, 37, 41, 43, 51, 61 Last chapter we saw that a current produces a magnetic
First Order Circuits. EENG223 Circuit Theory I
 First Order Circuits EENG223 Circuit Theory I First Order Circuits A first-order circuit can only contain one energy storage element (a capacitor or an inductor). The circuit will also contain resistance.
First Order Circuits EENG223 Circuit Theory I First Order Circuits A first-order circuit can only contain one energy storage element (a capacitor or an inductor). The circuit will also contain resistance.
W03 Analysis of DC Circuits. Yrd. Doç. Dr. Aytaç Gören
 W03 Analysis of DC Circuits Yrd. Doç. Dr. Aytaç Gören ELK 2018 - Contents W01 Basic Concepts in Electronics W02 AC to DC Conversion W03 Analysis of DC Circuits (self and condenser) W04 Transistors and
W03 Analysis of DC Circuits Yrd. Doç. Dr. Aytaç Gören ELK 2018 - Contents W01 Basic Concepts in Electronics W02 AC to DC Conversion W03 Analysis of DC Circuits (self and condenser) W04 Transistors and
Let s examine the response of the circuit shown on Figure 1. The form of the source voltage Vs is shown on Figure 2. R. Figure 1.
 Examples of Transient and RL Circuits. The Series RLC Circuit Impulse response of Circuit. Let s examine the response of the circuit shown on Figure 1. The form of the source voltage Vs is shown on Figure.
Examples of Transient and RL Circuits. The Series RLC Circuit Impulse response of Circuit. Let s examine the response of the circuit shown on Figure 1. The form of the source voltage Vs is shown on Figure.
Diodes have an arrow showing the direction of the flow.
 The Big Idea Modern circuitry depends on much more than just resistors and capacitors. The circuits in your computer, cell phone, Ipod depend on circuit elements called diodes, inductors, transistors,
The Big Idea Modern circuitry depends on much more than just resistors and capacitors. The circuits in your computer, cell phone, Ipod depend on circuit elements called diodes, inductors, transistors,
Last time : energy storage elements capacitor.
 Last time : energy storage elements capacitor. Charge on plates Energy stored in the form of electric field Passive sign convention Vlt Voltage drop across real capacitor can not change abruptly because
Last time : energy storage elements capacitor. Charge on plates Energy stored in the form of electric field Passive sign convention Vlt Voltage drop across real capacitor can not change abruptly because
RLC Resonant Circuits
 C esonant Circuits Andrew McHutchon April 20, 203 Capacitors and Inductors There is a lot of inconsistency when it comes to dealing with reactances of complex components. The format followed in this document
C esonant Circuits Andrew McHutchon April 20, 203 Capacitors and Inductors There is a lot of inconsistency when it comes to dealing with reactances of complex components. The format followed in this document
ES250: Electrical Science. HW7: Energy Storage Elements
 ES250: Electrical Science HW7: Energy Storage Elements Introduction This chapter introduces two more circuit elements, the capacitor and the inductor whose elements laws involve integration or differentiation;
ES250: Electrical Science HW7: Energy Storage Elements Introduction This chapter introduces two more circuit elements, the capacitor and the inductor whose elements laws involve integration or differentiation;
Eðlisfræði 2, vor 2007
 [ Assignment View ] [ Print ] Eðlisfræði 2, vor 2007 30. Inductance Assignment is due at 2:00am on Wednesday, March 14, 2007 Credit for problems submitted late will decrease to 0% after the deadline has
[ Assignment View ] [ Print ] Eðlisfræði 2, vor 2007 30. Inductance Assignment is due at 2:00am on Wednesday, March 14, 2007 Credit for problems submitted late will decrease to 0% after the deadline has
Homework #11 203-1-1721 Physics 2 for Students of Mechanical Engineering
 Homework #11 203-1-1721 Physics 2 for Students of Mechanical Engineering 2. A circular coil has a 10.3 cm radius and consists of 34 closely wound turns of wire. An externally produced magnetic field of
Homework #11 203-1-1721 Physics 2 for Students of Mechanical Engineering 2. A circular coil has a 10.3 cm radius and consists of 34 closely wound turns of wire. An externally produced magnetic field of
Physics 2102 Lecture 19. Physics 2102
 Physics 2102 Jonathan Dowling Physics 2102 Lecture 19 Ch 30: Inductors and RL Circuits Nikolai Tesla What are we going to learn? A road map Electric charge Electric force on other electric charges Electric
Physics 2102 Jonathan Dowling Physics 2102 Lecture 19 Ch 30: Inductors and RL Circuits Nikolai Tesla What are we going to learn? A road map Electric charge Electric force on other electric charges Electric
Solution Derivations for Capa #11
 Solution Derivations for Capa #11 Caution: The symbol E is used interchangeably for energy and EMF. 1) DATA: V b = 5.0 V, = 155 Ω, L = 8.400 10 2 H. In the diagram above, what is the voltage across the
Solution Derivations for Capa #11 Caution: The symbol E is used interchangeably for energy and EMF. 1) DATA: V b = 5.0 V, = 155 Ω, L = 8.400 10 2 H. In the diagram above, what is the voltage across the
EE301 Lesson 14 Reading: 10.1-10.4, 10.11-10.12, 11.1-11.4 and 11.11-11.13
 CAPACITORS AND INDUCTORS Learning Objectives EE301 Lesson 14 a. Define capacitance and state its symbol and unit of measurement. b. Predict the capacitance of a parallel plate capacitor. c. Analyze how
CAPACITORS AND INDUCTORS Learning Objectives EE301 Lesson 14 a. Define capacitance and state its symbol and unit of measurement. b. Predict the capacitance of a parallel plate capacitor. c. Analyze how
2. A conductor of length 2m moves at 4m/s at 30 to a uniform magnetic field of 0.1T. Which one of the following gives the e.m.f. generated?
 Extra Questions - 2 1. A straight length of wire moves through a uniform magnetic field. The e.m.f. produced across the ends of the wire will be maximum if it moves: a) along the lines of magnetic flux
Extra Questions - 2 1. A straight length of wire moves through a uniform magnetic field. The e.m.f. produced across the ends of the wire will be maximum if it moves: a) along the lines of magnetic flux
Chapter 29 Alternating-Current Circuits
 hapter 9 Alternating-urrent ircuits onceptual Problems A coil in an ac generator rotates at 6 Hz. How much time elapses between successive emf values of the coil? Determine the oncept Successive s are
hapter 9 Alternating-urrent ircuits onceptual Problems A coil in an ac generator rotates at 6 Hz. How much time elapses between successive emf values of the coil? Determine the oncept Successive s are
12.4 UNDRIVEN, PARALLEL RLC CIRCUIT*
 + v C C R L - v i L FIGURE 12.24 The parallel second-order RLC circuit shown in Figure 2.14a. 12.4 UNDRIVEN, PARALLEL RLC CIRCUIT* We will now analyze the undriven parallel RLC circuit shown in Figure
+ v C C R L - v i L FIGURE 12.24 The parallel second-order RLC circuit shown in Figure 2.14a. 12.4 UNDRIVEN, PARALLEL RLC CIRCUIT* We will now analyze the undriven parallel RLC circuit shown in Figure
Direction of Induced Current
 Direction of Induced Current Bar magnet moves through coil Current induced in coil A S N v Reverse pole Induced current changes sign B N S v v Coil moves past fixed bar magnet Current induced in coil as
Direction of Induced Current Bar magnet moves through coil Current induced in coil A S N v Reverse pole Induced current changes sign B N S v v Coil moves past fixed bar magnet Current induced in coil as
Chapter 10. RC Circuits ISU EE. C.Y. Lee
 Chapter 10 RC Circuits Objectives Describe the relationship between current and voltage in an RC circuit Determine impedance and phase angle in a series RC circuit Analyze a series RC circuit Determine
Chapter 10 RC Circuits Objectives Describe the relationship between current and voltage in an RC circuit Determine impedance and phase angle in a series RC circuit Analyze a series RC circuit Determine
45. The peak value of an alternating current in a 1500-W device is 5.4 A. What is the rms voltage across?
 PHYS Practice Problems hapters 8- hapter 8. 45. The peak value of an alternating current in a 5-W device is 5.4 A. What is the rms voltage across? The power and current can be used to find the peak voltage,
PHYS Practice Problems hapters 8- hapter 8. 45. The peak value of an alternating current in a 5-W device is 5.4 A. What is the rms voltage across? The power and current can be used to find the peak voltage,
Chapter 11. Inductors ISU EE. C.Y. Lee
 Chapter 11 Inductors Objectives Describe the basic structure and characteristics of an inductor Discuss various types of inductors Analyze series inductors Analyze parallel inductors Analyze inductive
Chapter 11 Inductors Objectives Describe the basic structure and characteristics of an inductor Discuss various types of inductors Analyze series inductors Analyze parallel inductors Analyze inductive
Problem Solving 8: RC and LR Circuits
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Physics Problem Solving 8: RC and LR Circuits Section Table and Group (e.g. L04 3C ) Names Hand in one copy per group at the end of the Friday Problem
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Physics Problem Solving 8: RC and LR Circuits Section Table and Group (e.g. L04 3C ) Names Hand in one copy per group at the end of the Friday Problem
Frequency response: Resonance, Bandwidth, Q factor
 Frequency response: esonance, Bandwidth, Q factor esonance. Let s continue the exploration of the frequency response of circuits by investigating the series circuit shown on Figure. C + V - Figure The
Frequency response: esonance, Bandwidth, Q factor esonance. Let s continue the exploration of the frequency response of circuits by investigating the series circuit shown on Figure. C + V - Figure The
Experiment 8: Undriven & Driven RLC Circuits
 Experiment 8: Undriven & Driven RLC Circuits Answer these questions on a separate sheet of paper and turn them in before the lab 1. RLC Circuits Consider the circuit at left, consisting of an AC function
Experiment 8: Undriven & Driven RLC Circuits Answer these questions on a separate sheet of paper and turn them in before the lab 1. RLC Circuits Consider the circuit at left, consisting of an AC function
Inductors & Inductance. Electronic Components
 Electronic Components Induction In 1824, Oersted discovered that current passing though a coil created a magnetic field capable of shifting a compass needle. Seven years later, Faraday and Henry discovered
Electronic Components Induction In 1824, Oersted discovered that current passing though a coil created a magnetic field capable of shifting a compass needle. Seven years later, Faraday and Henry discovered
Chapter 12 Driven RLC Circuits
 hapter Driven ircuits. A Sources... -. A ircuits with a Source and One ircuit Element... -3.. Purely esistive oad... -3.. Purely Inductive oad... -6..3 Purely apacitive oad... -8.3 The Series ircuit...
hapter Driven ircuits. A Sources... -. A ircuits with a Source and One ircuit Element... -3.. Purely esistive oad... -3.. Purely Inductive oad... -6..3 Purely apacitive oad... -8.3 The Series ircuit...
EE 1202 Experiment #4 Capacitors, Inductors, and Transient Circuits
 EE 1202 Experiment #4 Capacitors, Inductors, and Transient Circuits 1. Introduction and Goal: Exploring transient behavior due to inductors and capacitors in DC circuits; gaining experience with lab instruments.
EE 1202 Experiment #4 Capacitors, Inductors, and Transient Circuits 1. Introduction and Goal: Exploring transient behavior due to inductors and capacitors in DC circuits; gaining experience with lab instruments.
Alternating-Current Circuits
 hapter 1 Alternating-urrent ircuits 1.1 A Sources... 1-1. Simple A circuits... 1-3 1..1 Purely esistive load... 1-3 1.. Purely Inductive oad... 1-5 1..3 Purely apacitive oad... 1-7 1.3 The Series ircuit...
hapter 1 Alternating-urrent ircuits 1.1 A Sources... 1-1. Simple A circuits... 1-3 1..1 Purely esistive load... 1-3 1.. Purely Inductive oad... 1-5 1..3 Purely apacitive oad... 1-7 1.3 The Series ircuit...
CHAPTER 28 ELECTRIC CIRCUITS
 CHAPTER 8 ELECTRIC CIRCUITS 1. Sketch a circuit diagram for a circuit that includes a resistor R 1 connected to the positive terminal of a battery, a pair of parallel resistors R and R connected to the
CHAPTER 8 ELECTRIC CIRCUITS 1. Sketch a circuit diagram for a circuit that includes a resistor R 1 connected to the positive terminal of a battery, a pair of parallel resistors R and R connected to the
Since any real component also has loss due to the resistive component, the average power dissipated is 2 2R
 Quality factor, Q Reactive components such as capacitors and inductors are often described with a figure of merit called Q. While it can be defined in many ways, it s most fundamental description is: Q
Quality factor, Q Reactive components such as capacitors and inductors are often described with a figure of merit called Q. While it can be defined in many ways, it s most fundamental description is: Q
Edmund Li. Where is defined as the mutual inductance between and and has the SI units of Henries (H).
 INDUCTANCE MUTUAL INDUCTANCE If we consider two neighbouring closed loops and with bounding surfaces respectively then a current through will create a magnetic field which will link with as the flux passes
INDUCTANCE MUTUAL INDUCTANCE If we consider two neighbouring closed loops and with bounding surfaces respectively then a current through will create a magnetic field which will link with as the flux passes
L and C connected together. To be able: To analyse some basic circuits.
 circuits: Sinusoidal Voltages and urrents Aims: To appreciate: Similarities between oscillation in circuit and mechanical pendulum. Role of energy loss mechanisms in damping. Why we study sinusoidal signals
circuits: Sinusoidal Voltages and urrents Aims: To appreciate: Similarities between oscillation in circuit and mechanical pendulum. Role of energy loss mechanisms in damping. Why we study sinusoidal signals
580.439 Course Notes: Linear circuit theory and differential equations
 58.439 ourse Notes: Linear circuit theory and differential equations eading: Koch, h. ; any text on linear signal and system theory can be consulted for more details. These notes will review the basics
58.439 ourse Notes: Linear circuit theory and differential equations eading: Koch, h. ; any text on linear signal and system theory can be consulted for more details. These notes will review the basics
Experiment #11: LRC Circuit (Power Amplifier, Voltage Sensor)
 Experiment #11: LRC Circuit (Power Amplifier, Voltage Sensor) Concept: circuits Time: 30 m SW Interface: 750 Windows file: RLC.SWS EQUIPMENT NEEDED Science Workshop Interface Power Amplifier (2) Voltage
Experiment #11: LRC Circuit (Power Amplifier, Voltage Sensor) Concept: circuits Time: 30 m SW Interface: 750 Windows file: RLC.SWS EQUIPMENT NEEDED Science Workshop Interface Power Amplifier (2) Voltage
Chapter 30 Inductance, Electromagnetic Oscillations, and AC Circuits. Copyright 2009 Pearson Education, Inc.
 Chapter 30 Inductance, Electromagnetic Oscillations, and AC Circuits 30-1 Mutual Inductance Mutual inductance: a changing current in one coil will induce a current in a second coil: Coil 1 produces a flux
Chapter 30 Inductance, Electromagnetic Oscillations, and AC Circuits 30-1 Mutual Inductance Mutual inductance: a changing current in one coil will induce a current in a second coil: Coil 1 produces a flux
CHAPTER 30: Inductance, Electromagnetic Oscillations, and AC Circuits
 HAPTE 3: Inductance, Electromagnetic Oscillations, and A ircuits esponses to Questions. (a) For the maximum value of the mutual inductance, place the coils close together, face to face, on the same axis.
HAPTE 3: Inductance, Electromagnetic Oscillations, and A ircuits esponses to Questions. (a) For the maximum value of the mutual inductance, place the coils close together, face to face, on the same axis.
Critical thin-film processes such as deposition and etching take place in a vacuum
 WHITEPAPER INTRODUCING POWER SUPPLIES AND PLASMA Critical thin-film processes such as deposition and etching take place in a vacuum SYSTEMS chamber in the presence of a plasma. A plasma is an electrically
WHITEPAPER INTRODUCING POWER SUPPLIES AND PLASMA Critical thin-film processes such as deposition and etching take place in a vacuum SYSTEMS chamber in the presence of a plasma. A plasma is an electrically
SCHWEITZER ENGINEERING LABORATORIES, COMERCIAL LTDA.
 Pocket book of Electrical Engineering Formulas Content 1. Elementary Algebra and Geometry 1. Fundamental Properties (real numbers) 1 2. Exponents 2 3. Fractional Exponents 2 4. Irrational Exponents 2 5.
Pocket book of Electrical Engineering Formulas Content 1. Elementary Algebra and Geometry 1. Fundamental Properties (real numbers) 1 2. Exponents 2 3. Fractional Exponents 2 4. Irrational Exponents 2 5.
First Year (Electrical & Electronics Engineering)
 Z PRACTICAL WORK BOOK For The Course EE-113 Basic Electrical Engineering For First Year (Electrical & Electronics Engineering) Name of Student: Class: Batch : Discipline: Class Roll No.: Examination Seat
Z PRACTICAL WORK BOOK For The Course EE-113 Basic Electrical Engineering For First Year (Electrical & Electronics Engineering) Name of Student: Class: Batch : Discipline: Class Roll No.: Examination Seat
Applications of Second-Order Differential Equations
 Applications of Second-Order Differential Equations Second-order linear differential equations have a variety of applications in science and engineering. In this section we explore two of them: the vibration
Applications of Second-Order Differential Equations Second-order linear differential equations have a variety of applications in science and engineering. In this section we explore two of them: the vibration
5. Measurement of a magnetic field
 H 5. Measurement of a magnetic field 5.1 Introduction Magnetic fields play an important role in physics and engineering. In this experiment, three different methods are examined for the measurement of
H 5. Measurement of a magnetic field 5.1 Introduction Magnetic fields play an important role in physics and engineering. In this experiment, three different methods are examined for the measurement of
A wave lab inside a coaxial cable
 INSTITUTE OF PHYSICS PUBLISHING Eur. J. Phys. 25 (2004) 581 591 EUROPEAN JOURNAL OF PHYSICS PII: S0143-0807(04)76273-X A wave lab inside a coaxial cable JoãoMSerra,MiguelCBrito,JMaiaAlves and A M Vallera
INSTITUTE OF PHYSICS PUBLISHING Eur. J. Phys. 25 (2004) 581 591 EUROPEAN JOURNAL OF PHYSICS PII: S0143-0807(04)76273-X A wave lab inside a coaxial cable JoãoMSerra,MiguelCBrito,JMaiaAlves and A M Vallera
CURRENT ELECTRICITY INTRODUCTION TO RESISTANCE, CAPACITANCE AND INDUCTANCE
 CURRENT ELECTRICITY INTRODUCTION TO RESI STANCE, CAPACITANCE AND INDUCTANCE P R E A M B L E This problem is adapted from an on-line knowledge enhancement module for a PGCE programme. It is used to cover
CURRENT ELECTRICITY INTRODUCTION TO RESI STANCE, CAPACITANCE AND INDUCTANCE P R E A M B L E This problem is adapted from an on-line knowledge enhancement module for a PGCE programme. It is used to cover
Using the Impedance Method
 Using the Impedance Method The impedance method allows us to completely eliminate the differential equation approach for the determination of the response of circuits. In fact the impedance method even
Using the Impedance Method The impedance method allows us to completely eliminate the differential equation approach for the determination of the response of circuits. In fact the impedance method even
Properties of electrical signals
 DC Voltage Component (Average voltage) Properties of electrical signals v(t) = V DC + v ac (t) V DC is the voltage value displayed on a DC voltmeter Triangular waveform DC component Half-wave rectifier
DC Voltage Component (Average voltage) Properties of electrical signals v(t) = V DC + v ac (t) V DC is the voltage value displayed on a DC voltmeter Triangular waveform DC component Half-wave rectifier
Inductance. Motors. Generators
 Inductance Motors Generators Self-inductance Self-inductance occurs when the changing flux through a circuit arises from the circuit itself. As the current increases, the magnetic flux through a loop due
Inductance Motors Generators Self-inductance Self-inductance occurs when the changing flux through a circuit arises from the circuit itself. As the current increases, the magnetic flux through a loop due
Slide 10.1. Basic system Models
 Slide 10.1 Basic system Models Objectives: Devise Models from basic building blocks of mechanical, electrical, fluid and thermal systems Recognize analogies between mechanical, electrical, fluid and thermal
Slide 10.1 Basic system Models Objectives: Devise Models from basic building blocks of mechanical, electrical, fluid and thermal systems Recognize analogies between mechanical, electrical, fluid and thermal
BASIC ELECTRONICS AC CIRCUIT ANALYSIS. December 2011
 AM 5-202 BASIC ELECTRONICS AC CIRCUIT ANALYSIS December 2011 DISTRIBUTION RESTRICTION: Approved for Pubic Release. Distribution is unlimited. DEPARTMENT OF THE ARMY MILITARY AUXILIARY RADIO SYSTEM FORT
AM 5-202 BASIC ELECTRONICS AC CIRCUIT ANALYSIS December 2011 DISTRIBUTION RESTRICTION: Approved for Pubic Release. Distribution is unlimited. DEPARTMENT OF THE ARMY MILITARY AUXILIARY RADIO SYSTEM FORT
How To Understand And Understand The Theory Of Electricity
 DIRECT CURRENT AND ALTERNATING CURRENT SYSTEMS N. Rajkumar, Research Fellow, Energy Systems Group, City University Northampton Square, London EC1V 0HB, UK Keywords: Electrical energy, direct current, alternating
DIRECT CURRENT AND ALTERNATING CURRENT SYSTEMS N. Rajkumar, Research Fellow, Energy Systems Group, City University Northampton Square, London EC1V 0HB, UK Keywords: Electrical energy, direct current, alternating
Reading assignment: All students should read the Appendix about using oscilloscopes.
 10. A ircuits* Objective: To learn how to analyze current and voltage relationships in alternating current (a.c.) circuits. You will use the method of phasors, or the vector addition of rotating vectors
10. A ircuits* Objective: To learn how to analyze current and voltage relationships in alternating current (a.c.) circuits. You will use the method of phasors, or the vector addition of rotating vectors
Fundamentals of radio communication
 Fundamentals of radio communication This worksheet and all related files are licensed under the Creative Commons Attribution License, version 1.0. To view a copy of this license, visit http://creativecommons.org/licenses/by/1.0/,
Fundamentals of radio communication This worksheet and all related files are licensed under the Creative Commons Attribution License, version 1.0. To view a copy of this license, visit http://creativecommons.org/licenses/by/1.0/,
Line Reactors and AC Drives
 Line Reactors and AC Drives Rockwell Automation Mequon Wisconsin Quite often, line and load reactors are installed on AC drives without a solid understanding of why or what the positive and negative consequences
Line Reactors and AC Drives Rockwell Automation Mequon Wisconsin Quite often, line and load reactors are installed on AC drives without a solid understanding of why or what the positive and negative consequences
EDEXCEL NATIONAL CERTIFICATE/DIPLOMA UNIT 5 - ELECTRICAL AND ELECTRONIC PRINCIPLES NQF LEVEL 3 OUTCOME 4 - ALTERNATING CURRENT
 EDEXCEL NATIONAL CERTIFICATE/DIPLOMA UNIT 5 - ELECTRICAL AND ELECTRONIC PRINCIPLES NQF LEVEL 3 OUTCOME 4 - ALTERNATING CURRENT 4 Understand single-phase alternating current (ac) theory Single phase AC
EDEXCEL NATIONAL CERTIFICATE/DIPLOMA UNIT 5 - ELECTRICAL AND ELECTRONIC PRINCIPLES NQF LEVEL 3 OUTCOME 4 - ALTERNATING CURRENT 4 Understand single-phase alternating current (ac) theory Single phase AC
April 1. Physics 272. Spring 2014 http://www.phys.hawaii.edu/~philipvd/pvd_14_spring_272_uhm.html. Prof. Philip von Doetinchem philipvd@hawaii.
 Physics 272 April 1 Spring 2014 http://www.phys.hawaii.edu/~philipvd/pvd_14_spring_272_uhm.html Prof. Philip von Doetinchem [email protected] Phys272 - Spring 14 - von Doetinchem - 164 Summary Gauss's
Physics 272 April 1 Spring 2014 http://www.phys.hawaii.edu/~philipvd/pvd_14_spring_272_uhm.html Prof. Philip von Doetinchem [email protected] Phys272 - Spring 14 - von Doetinchem - 164 Summary Gauss's
BSNL TTA Question Paper-Instruments and Measurement Specialization 2007
 BSNL TTA Question Paper-Instruments and Measurement Specialization 2007 (1) Instrument is a device for determining (a) the magnitude of a quantity (b) the physics of a variable (c) either of the above
BSNL TTA Question Paper-Instruments and Measurement Specialization 2007 (1) Instrument is a device for determining (a) the magnitude of a quantity (b) the physics of a variable (c) either of the above
EXPERIMENT NUMBER 8 CAPACITOR CURRENT-VOLTAGE RELATIONSHIP
 1 EXPERIMENT NUMBER 8 CAPACITOR CURRENT-VOLTAGE RELATIONSHIP Purpose: To demonstrate the relationship between the voltage and current of a capacitor. Theory: A capacitor is a linear circuit element whose
1 EXPERIMENT NUMBER 8 CAPACITOR CURRENT-VOLTAGE RELATIONSHIP Purpose: To demonstrate the relationship between the voltage and current of a capacitor. Theory: A capacitor is a linear circuit element whose
Inductors. Resources and methods for learning about these subjects (list a few here, in preparation for your research):
 Inductors This worksheet and all related files are licensed under the Creative Commons Attribution License, version 1.0. To view a copy of this license, visit http://creativecommons.org/licenses/by/1.0/,
Inductors This worksheet and all related files are licensed under the Creative Commons Attribution License, version 1.0. To view a copy of this license, visit http://creativecommons.org/licenses/by/1.0/,
Inductance and Magnetic Energy
 Chapter 11 Inductance and Magnetic Energy 11.1 Mutual Inductance... 11-3 Example 11.1 Mutual Inductance of Two Concentric Coplanar Loops... 11-5 11. Self-Inductance... 11-5 Example 11. Self-Inductance
Chapter 11 Inductance and Magnetic Energy 11.1 Mutual Inductance... 11-3 Example 11.1 Mutual Inductance of Two Concentric Coplanar Loops... 11-5 11. Self-Inductance... 11-5 Example 11. Self-Inductance
CHAPTER - 1. Chapter ONE: WAVES CHAPTER - 2. Chapter TWO: RAY OPTICS AND OPTICAL INSTRUMENTS. CHAPTER - 3 Chapter THREE: WAVE OPTICS PERIODS PERIODS
 BOARD OF INTERMEDIATE EDUCATION, A.P., HYDERABAD REVISION OF SYLLABUS Subject PHYSICS-II (w.e.f 2013-14) Chapter ONE: WAVES CHAPTER - 1 1.1 INTRODUCTION 1.2 Transverse and longitudinal waves 1.3 Displacement
BOARD OF INTERMEDIATE EDUCATION, A.P., HYDERABAD REVISION OF SYLLABUS Subject PHYSICS-II (w.e.f 2013-14) Chapter ONE: WAVES CHAPTER - 1 1.1 INTRODUCTION 1.2 Transverse and longitudinal waves 1.3 Displacement
Series and Parallel Circuits
 Direct Current (DC) Direct current (DC) is the unidirectional flow of electric charge. The term DC is used to refer to power systems that use refer to the constant (not changing with time), mean (average)
Direct Current (DC) Direct current (DC) is the unidirectional flow of electric charge. The term DC is used to refer to power systems that use refer to the constant (not changing with time), mean (average)
Common Mode and Differential Mode Noise Filtering
 Summary Introduction This application note gives a practical explanation of differential mode and common mode noise along with the traditional filtering approaches. In addition, an alternative method of
Summary Introduction This application note gives a practical explanation of differential mode and common mode noise along with the traditional filtering approaches. In addition, an alternative method of
Module 22: Inductance and Magnetic Field Energy
 Module 22: Inductance and Magnetic Field Energy 1 Module 22: Outline Self Inductance Energy in Inductors Circuits with Inductors: RL Circuit 2 Faraday s Law of Induction dφ = B dt Changing magnetic flux
Module 22: Inductance and Magnetic Field Energy 1 Module 22: Outline Self Inductance Energy in Inductors Circuits with Inductors: RL Circuit 2 Faraday s Law of Induction dφ = B dt Changing magnetic flux
Effect of Frequency on Inductive Reactance
 TUNED CIRCUITS Effect of Frequency on Inductive Reactance Resonance The ideal series-resonant circuit How the Parallel-LC Circuit Stores Energy Parallel resonance Resonant circuits as filter circuits Pulsed
TUNED CIRCUITS Effect of Frequency on Inductive Reactance Resonance The ideal series-resonant circuit How the Parallel-LC Circuit Stores Energy Parallel resonance Resonant circuits as filter circuits Pulsed
Aircraft Electrical System
 Chapter 9 Aircraft Electrical System Introduction The satisfactory performance of any modern aircraft depends to a very great degree on the continuing reliability of electrical systems and subsystems.
Chapter 9 Aircraft Electrical System Introduction The satisfactory performance of any modern aircraft depends to a very great degree on the continuing reliability of electrical systems and subsystems.
Circuits. The light bulbs in the circuits below are identical. Which configuration produces more light? (a) circuit I (b) circuit II (c) both the same
 Circuits The light bulbs in the circuits below are identical. Which configuration produces more light? (a) circuit I (b) circuit II (c) both the same Circuit II has ½ current of each branch of circuit
Circuits The light bulbs in the circuits below are identical. Which configuration produces more light? (a) circuit I (b) circuit II (c) both the same Circuit II has ½ current of each branch of circuit
Scott Hughes 7 April 2005. Massachusetts Institute of Technology Department of Physics 8.022 Spring 2005. Lecture 15: Mutual and Self Inductance.
 Scott Hughes 7 April 2005 151 Using induction Massachusetts nstitute of Technology Department of Physics 8022 Spring 2005 Lecture 15: Mutual and Self nductance nduction is a fantastic way to create EMF;
Scott Hughes 7 April 2005 151 Using induction Massachusetts nstitute of Technology Department of Physics 8022 Spring 2005 Lecture 15: Mutual and Self nductance nduction is a fantastic way to create EMF;
Your Comments. This was a very confusing prelecture. Do you think you could go over thoroughly how the LC circuits work qualitatively?
 Your omments I am not feeling great about this mierm...some of this stuff is really confusing still and I don't know if I can shove everything into my brain in time, especially after spring break. an you
Your omments I am not feeling great about this mierm...some of this stuff is really confusing still and I don't know if I can shove everything into my brain in time, especially after spring break. an you
Introduction to Electricity & Magnetism. Dr Lisa Jardine-Wright Cavendish Laboratory
 Introduction to Electricity & Magnetism Dr Lisa Jardine-Wright Cavendish Laboratory Examples of uses of electricity Christmas lights Cars Electronic devices Human body Electricity? Electricity is the presence
Introduction to Electricity & Magnetism Dr Lisa Jardine-Wright Cavendish Laboratory Examples of uses of electricity Christmas lights Cars Electronic devices Human body Electricity? Electricity is the presence
Grounding Demystified
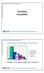 Grounding Demystified 3-1 Importance Of Grounding Techniques 45 40 35 30 25 20 15 10 5 0 Grounding 42% Case 22% Cable 18% Percent Used Filter 12% PCB 6% Grounding 42% Case Shield 22% Cable Shielding 18%
Grounding Demystified 3-1 Importance Of Grounding Techniques 45 40 35 30 25 20 15 10 5 0 Grounding 42% Case 22% Cable 18% Percent Used Filter 12% PCB 6% Grounding 42% Case Shield 22% Cable Shielding 18%
PHYSICAL METHODS, INSTRUMENTS AND MEASUREMENTS - Measurements Of Electrical Quantities - Ján Šaliga MEASUREMENTS OF ELECTRICAL QUANTITIES
 MEASUREMENTS OF ELECTRICAL QUANTITIES Ján Šaliga Department of Electronics and Multimedia Telecommunication, Technical University of Košice, Košice, Slovak Republic Keywords: basic electrical quantities,
MEASUREMENTS OF ELECTRICAL QUANTITIES Ján Šaliga Department of Electronics and Multimedia Telecommunication, Technical University of Košice, Košice, Slovak Republic Keywords: basic electrical quantities,
ε: Voltage output of Signal Generator (also called the Source voltage or Applied
 Experiment #10: LR & RC Circuits Frequency Response EQUIPMENT NEEDED Science Workshop Interface Power Amplifier (2) Voltage Sensor graph paper (optional) (3) Patch Cords Decade resistor, capacitor, and
Experiment #10: LR & RC Circuits Frequency Response EQUIPMENT NEEDED Science Workshop Interface Power Amplifier (2) Voltage Sensor graph paper (optional) (3) Patch Cords Decade resistor, capacitor, and
Impedance Matching and Matching Networks. Valentin Todorow, December, 2009
 Impedance Matching and Matching Networks Valentin Todorow, December, 2009 RF for Plasma Processing - Definition of RF What is RF? The IEEE Standard Dictionary of Electrical and Electronics Terms defines
Impedance Matching and Matching Networks Valentin Todorow, December, 2009 RF for Plasma Processing - Definition of RF What is RF? The IEEE Standard Dictionary of Electrical and Electronics Terms defines
Positive Feedback and Oscillators
 Physics 3330 Experiment #6 Fall 1999 Positive Feedback and Oscillators Purpose In this experiment we will study how spontaneous oscillations may be caused by positive feedback. You will construct an active
Physics 3330 Experiment #6 Fall 1999 Positive Feedback and Oscillators Purpose In this experiment we will study how spontaneous oscillations may be caused by positive feedback. You will construct an active
Candidate Number. General Certificate of Education Advanced Level Examination June 2014
 entre Number andidate Number Surname Other Names andidate Signature General ertificate of Education dvanced Level Examination June 214 Physics PHY4/1 Unit 4 Fields and Further Mechanics Section Wednesday
entre Number andidate Number Surname Other Names andidate Signature General ertificate of Education dvanced Level Examination June 214 Physics PHY4/1 Unit 4 Fields and Further Mechanics Section Wednesday
RUPHYS2272015 ( RUPHY227F2015 ) My Courses Course Settings University Physics with Modern Physics, 14e Young/Freedman
 Signed in as Jolie Cizewski, Instructor Help Sign Out RUPHYS2272015 ( RUPHY227F2015 ) My Courses Course Settings University Physics with Modern Physics, 14e Young/Freedman Course Home Assignments Roster
Signed in as Jolie Cizewski, Instructor Help Sign Out RUPHYS2272015 ( RUPHY227F2015 ) My Courses Course Settings University Physics with Modern Physics, 14e Young/Freedman Course Home Assignments Roster
Lecture 7 Circuit analysis via Laplace transform
 S. Boyd EE12 Lecture 7 Circuit analysis via Laplace transform analysis of general LRC circuits impedance and admittance descriptions natural and forced response circuit analysis with impedances natural
S. Boyd EE12 Lecture 7 Circuit analysis via Laplace transform analysis of general LRC circuits impedance and admittance descriptions natural and forced response circuit analysis with impedances natural
Chapter 12: Three Phase Circuits
 Chapter 12: Three Phase Circuits 12.1 What Is a Three Phase Circuit? 12.2 Balance Three Phase Voltages 12.3 Balance Three Phase Y to Y Connection 12.4 Other Balance Three Phase Connections 12.5 Power in
Chapter 12: Three Phase Circuits 12.1 What Is a Three Phase Circuit? 12.2 Balance Three Phase Voltages 12.3 Balance Three Phase Y to Y Connection 12.4 Other Balance Three Phase Connections 12.5 Power in
Objectives. Capacitors 262 CHAPTER 5 ENERGY
 Objectives Describe a capacitor. Explain how a capacitor stores energy. Define capacitance. Calculate the electrical energy stored in a capacitor. Describe an inductor. Explain how an inductor stores energy.
Objectives Describe a capacitor. Explain how a capacitor stores energy. Define capacitance. Calculate the electrical energy stored in a capacitor. Describe an inductor. Explain how an inductor stores energy.
Assessment Plan for Learning Outcomes for BA/BS in Physics
 Department of Physics and Astronomy Goals and Learning Outcomes 1. Students know basic physics principles [BS, BA, MS] 1.1 Students can demonstrate an understanding of Newton s laws 1.2 Students can demonstrate
Department of Physics and Astronomy Goals and Learning Outcomes 1. Students know basic physics principles [BS, BA, MS] 1.1 Students can demonstrate an understanding of Newton s laws 1.2 Students can demonstrate
ElectroMagnetic Induction. AP Physics B
 ElectroMagnetic Induction AP Physics B What is E/M Induction? Electromagnetic Induction is the process of using magnetic fields to produce voltage, and in a complete circuit, a current. Michael Faraday
ElectroMagnetic Induction AP Physics B What is E/M Induction? Electromagnetic Induction is the process of using magnetic fields to produce voltage, and in a complete circuit, a current. Michael Faraday
Faraday s Law of Induction
 Chapter 10 Faraday s Law of Induction 10.1 Faraday s Law of Induction...10-10.1.1 Magnetic Flux...10-3 10.1. Lenz s Law...10-5 10. Motional EMF...10-7 10.3 Induced Electric Field...10-10 10.4 Generators...10-1
Chapter 10 Faraday s Law of Induction 10.1 Faraday s Law of Induction...10-10.1.1 Magnetic Flux...10-3 10.1. Lenz s Law...10-5 10. Motional EMF...10-7 10.3 Induced Electric Field...10-10 10.4 Generators...10-1
Electrochemical Impedance Spectroscopy (EIS): A Powerful and Cost- Effective Tool for Fuel Cell Diagnostics
 Electrochemical Impedance Spectroscopy (EIS): A Powerful and Cost- Effective Tool for Fuel Cell Diagnostics Electrochemical Impedance Spectroscopy (EIS) is a powerful diagnostic tool that you can use to
Electrochemical Impedance Spectroscopy (EIS): A Powerful and Cost- Effective Tool for Fuel Cell Diagnostics Electrochemical Impedance Spectroscopy (EIS) is a powerful diagnostic tool that you can use to
Magnetic Circuits. Outline. Ampere s Law Revisited Review of Last Time: Magnetic Materials Magnetic Circuits Examples
 Magnetic Circuits Outline Ampere s Law Revisited Review of Last Time: Magnetic Materials Magnetic Circuits Examples 1 Electric Fields Magnetic Fields S ɛ o E da = ρdv B V = Q enclosed S da =0 GAUSS GAUSS
Magnetic Circuits Outline Ampere s Law Revisited Review of Last Time: Magnetic Materials Magnetic Circuits Examples 1 Electric Fields Magnetic Fields S ɛ o E da = ρdv B V = Q enclosed S da =0 GAUSS GAUSS
Current, Resistance and Electromotive Force. Young and Freedman Chapter 25
 Current, Resistance and Electromotive Force Young and Freedman Chapter 25 Electric Current: Analogy, water flowing in a pipe H 2 0 gallons/minute Flow Rate is the NET amount of water passing through a
Current, Resistance and Electromotive Force Young and Freedman Chapter 25 Electric Current: Analogy, water flowing in a pipe H 2 0 gallons/minute Flow Rate is the NET amount of water passing through a
Sinusoidal. Oscillators
 364 4 Principles of Electronics Sinusoidal Oscillators 4. Sinusoidal Oscillator 4.2 Types of Sinusoidal Oscillations 4.3 Oscillatory Circuit 4.4 Undamped Oscillations from Tank Circuit 4.5 Positive Feedback
364 4 Principles of Electronics Sinusoidal Oscillators 4. Sinusoidal Oscillator 4.2 Types of Sinusoidal Oscillations 4.3 Oscillatory Circuit 4.4 Undamped Oscillations from Tank Circuit 4.5 Positive Feedback
d di Flux (B) Current (H)
 Comparison of Inductance Calculation Techniques Tony Morcos Magnequench Technology Center Research Triangle Park, North Carolina 1 VCM Baseline: Geometry Axially-magnetized MQ3-F 42 NdFeB disk Br = 131kG
Comparison of Inductance Calculation Techniques Tony Morcos Magnequench Technology Center Research Triangle Park, North Carolina 1 VCM Baseline: Geometry Axially-magnetized MQ3-F 42 NdFeB disk Br = 131kG
Chapter 7. DC Circuits
 Chapter 7 DC Circuits 7.1 Introduction... 7-3 Example 7.1.1: Junctions, branches and loops... 7-4 7.2 Electromotive Force... 7-5 7.3 Electrical Energy and Power... 7-9 7.4 Resistors in Series and in Parallel...
Chapter 7 DC Circuits 7.1 Introduction... 7-3 Example 7.1.1: Junctions, branches and loops... 7-4 7.2 Electromotive Force... 7-5 7.3 Electrical Energy and Power... 7-9 7.4 Resistors in Series and in Parallel...
DRAFT. University of Pennsylvania Moore School of Electrical Engineering ESE319 Electronic Circuits - Modeling and Measurement Techniques
 University of Pennsylvania Moore School of Electrical Engineering ESE319 Electronic Circuits - Modeling and Measurement Techniques 1. Introduction. Students are often frustrated in their attempts to execute
University of Pennsylvania Moore School of Electrical Engineering ESE319 Electronic Circuits - Modeling and Measurement Techniques 1. Introduction. Students are often frustrated in their attempts to execute
Three phase circuits
 Three phase circuits THREE PHASE CIRCUITS THREE-PHASE ADVANTAGES 1. The horsepower rating of three-phase motors and the kva rating of three-phase transformers are 150% greater than single-phase motors
Three phase circuits THREE PHASE CIRCUITS THREE-PHASE ADVANTAGES 1. The horsepower rating of three-phase motors and the kva rating of three-phase transformers are 150% greater than single-phase motors
Lecture 22. Inductance. Magnetic Field Energy. Outline:
 Lecture 22. Inductance. Magnetic Field Energy. Outline: Self-induction and self-inductance. Inductance of a solenoid. The energy of a magnetic field. Alternative definition of inductance. Mutual Inductance.
Lecture 22. Inductance. Magnetic Field Energy. Outline: Self-induction and self-inductance. Inductance of a solenoid. The energy of a magnetic field. Alternative definition of inductance. Mutual Inductance.
Physics 102: Lecture 13 RLC circuits & Resonance
 Physics 102: Lecture 13 L circuits & esonance L Physics 102: Lecture 13, Slide 1 I = I max sin(2pft) V = I max sin(2pft) V in phase with I eview: A ircuit L V = I max X sin(2pft p/2) V lags I IE I V t
Physics 102: Lecture 13 L circuits & esonance L Physics 102: Lecture 13, Slide 1 I = I max sin(2pft) V = I max sin(2pft) V in phase with I eview: A ircuit L V = I max X sin(2pft p/2) V lags I IE I V t
