Batteries in general: Batteries. Anode/cathode in rechargeable batteries. Rechargeable batteries
|
|
|
- Marshall Clarke
- 7 years ago
- Views:
Transcription
1 Bttris i grl: Bttris How -bsd bttris work A rducig (gtiv) lctrod A oxidizig (positiv) lctrod A - th ioic coductor Rchrgbl bttris Rctios ust b rvrsibl Not too y irrvrsibl sid rctios Aod/cthod i rchrgbl bttris Th lctrods i rchrgbl bttris will chg btw big od d cthod dpdig o if th bttry is chrgd or dischrgd Th trs positiv d gtiv lctrod y b usd istd 1
2 Elctrods Elctrods Ngtiv lctrod I bttry, th positiv lctrod withdrws Positiv lctros fro th gtiv. lctrod (ii this cs fro Ngtiv lctrod I bttry, th positiv lctrod withdrws Positiv lctros fro th gtiv. lctrod I this cs fro Elctro trsport Elctro trsport + - Ngtiv lctrod Th lctros c ot ov Positiv through th, lctrod oly through th xtrl circuit - Ngtiv lctrod Th lctros c ot ov Positiv through th, lctrod oly through th xtrl circuit 2
3 Elctro trsport Elctro trsport - - Ngtiv lctrod Th lctros c ot ov Positiv through th, lctrod oly through th xtrl circuit Ngtiv lctrod Th lctros c ot ov Positiv through th, lctrod oly through th xtrl circuit Elctro trsport - Elctro trsport - Ngtiv lctrod Th lctros c ot ov Positiv through th, lctrod oly through th xtrl circuit Ngtiv lctrod Th lctros c ot ov Positiv through th, lctrod oly through th xtrl circuit 3
4 Elctro trsport Io trsport Ngtiv lctrod - Th lctros c ot ov Positiv through th, lctrod oly through th xtrl circuit If ios do ot follow fro - th gtiv to th positiv Ngtiv Positiv lctrod, th cll rctio lctrod lctrod will stop. Io trsport Two kids of chrg trsport Ngtiv lctrod If ios do ot follow fro - th gtiv to th positiv Positiv lctrod, th cll rctio Ngtiv Positiv Th trs positiv d lctrod will stop. lctrod lctrod gtiv lctrod y b isldig. (Frdy) 4
5 Two kids of chrg trsport Two kids of chrg trsport Ngtiv lctrod To bgi with, both Positiv lctrods r lctriclly lctrod utrl. (Thy hv qul outs of positiv d gtiv prticls) Ngtiv lctrod Th tr positiv lctrod s tht this lctrod Positiv cotis sothig tht lctrod ttrcts lctros. Two such xpls r Cu 2+ r Co 4+ Two kids of chrg trsport Two kids of chrg trsport Ngtiv lctrod Wh lctros r pulld - ovr, th lctrods will b Positiv chrgd i wy tht stops lctrod y furthr rctio Ngtiv lctrod (O y sy tht th - positiv lctrod gts Positiv gtiv chrg, d th lctrod gtiv lctrod gts positiv chrg) 5
6 Two kids of chrg trsport Two kids of chrg trsport Ngtiv lctrod - Th io trsport qulizs Positiv th chrg d llows th lctrod rctio to go o. Ngtiv lctrod - Th io trsport qulizs Positiv th chrg d llows th lctrod rctio to go o. Ngtiv lctrod Two kids of chrg trsport Positiv lctrod s i grl hv - low coductivity, d should b thi, with lrg surfc (ot log d rrow) -bsd bttris Oxidtio (gtiv lctrod): + - Rductio (positiv lctrod): Cosists of copouds cotiig trsitio tls with or th o oxidtio stt. E.g. coblt: Co Co 3+ 6
7 Uchrgd bttry Chrgig - Ngtiv lctrod d of grphit Positiv lctrod d of CoO2 + - CoO2 cotis d Co 3+ ios Wh th bttry is chrgd, lctros d -ios r «pupd» ovr to th grphit lctrod d ks -tl Siultously, Co 3+ is oxidizd to Co 4+ Chrgig - Chrgig Wh th bttry is chrgd, lctros d -ios r «pupd» ovr to th grphit lctrod d ks -tl Siultously, Co 3+ is oxidizd to Co 4+ Wh th bttry is chrgd, lctros d -ios r «pupd» ovr to th grphit lctrod d ks -tl Siultously, Co 3+ is oxidizd to Co 4+ 7
8 Chrgig - Dischrg Wh th bttry is chrgd, lctros d -ios r «pupd» ovr to th grphit lctrod d ks -tl Siultously, Co 3+ is oxidizd to Co 4+ Co 4+ is strog oxidtio gt (ttrcts lctros powrfully), d is sily oxidizd. This givs -coblt bttris high voltg (Norlly bout 3,7 V) Dischrg - Dischrg / Chrg Co 4+ is strog oxidtio gt (withdrws lctros powrfully), d is sily oxidizd. This givs -coblt bttris high voltg (Norlly bout 3,7 V) Ths bttris c b chrgd d dischrgd y tis, d is sotis clld Rockig chir bttris 8
9 Dischrg / Chrg - Dischrg / Chrg Ths bttris c b chrgd d dischrgd y tis, d is sotis clld Rockig chir bttris Ths bttris c b chrgd d dischrgd y tis, d is sotis clld Rockig chir bttris Dischrg / Chrg - Dischrg / Chrg Ths bttris c b chrgd d dischrgd y tis, d is sotis clld Rockig chir bttris Ths bttris c b chrgd d dischrgd y tis, d is sotis clld Rockig chir bttris 9
10 Dischrg / Chrg - Dischrg / Chrg Ths bttris c b chrgd d dischrgd y tis, d is sotis clld Rockig chir bttris Ths bttris c b chrgd d dischrgd y tis, d is sotis clld Rockig chir bttris Dischrg / Chrg - Dischrg / Chrg Ths bttris c b chrgd d dischrgd y tis, d is sotis clld Rockig chir bttris Ths bttris c b chrgd d dischrgd y tis, d is sotis clld Rockig chir bttris 10
11 Dischrg / Chrg - Dischrg / Chrg Ths bttris c b chrgd d dischrgd y tis, d is sotis clld Rockig chir bttris Ths bttris c b chrgd d dischrgd y tis, d is sotis clld Rockig chir bttris Dischrg / Chrg - Dischrg / Chrg Ths bttris c b chrgd d dischrgd y tis, d is sotis clld Rockig chir bttris Ths bttris c b chrgd d dischrgd y tis, d is sotis clld Rockig chir bttris 11
12 Dischrg / Chrg - Dischrg / Chrg Ths bttris c b chrgd d dischrgd y tis, d is sotis clld Rockig chir bttris Ths bttris c b chrgd d dischrgd y tis, d is sotis clld Rockig chir bttris Dischrg / Chrg - Dischrg / Chrg Ths bttris c b chrgd d dischrgd y tis, d is sotis clld Rockig chir bttris Ths bttris c b chrgd d dischrgd y tis, d is sotis clld Rockig chir bttris 12
13 -bsd bttris Ngtiv lctrod Thir copots: tiu is vry rctiv (rducig gt), but wh solvd (itrcltd) i grphit, it c b usd sfly i bttris. Elctros d c sily ov ito d out fro th grphit lctrod Nt rctio: + - All bttris ust hv with good ioic coductivity, but o lctroic coductivity I old-fshiod bttris, this could b ppr oistd with slt solutio Sic rcts strogly with wtr, th s i -bsd bttris r ithr solid, or solutio of copoud i orgic solvt. Positiv lctrod Th positiv lctrod cotis trsitio tl bl to switch btw two oxidtio stts (Co,,F, Ni, V...) It ust b coductor, d hv th bility to solv (itrclt). CoO2 is coo lctrod tril with t rctio:
14 odr bttris r d i y shps d sizs Iprovig -bsd bttris Wht r th probls? f ti -bsd bttris oly lst for fw yrs bcus of: Irrvrsibl rctios durig chrgig d durig hvy dischrgig - d t high tprturs Prforc High powr c giv irrvrsibl dg liits th us i.g. lctric vhicls s should hv high coductc d rsist high tprturs 14
15 Rchrg ti supply High powr d tprturs giv irrvrsibl dg Rsultig i log rchrg ti Th worlds supply of is liitd Altrtivs r tstd (.g. K, g, Al og N) Dsig To chiv bttr proprtis, lctrods, s d bttry dsig ust b optiizd o trils y b usd to solv so of ths probls Itrcltio i grphit Grphit is crbo with lyrd structur I btw ths lyrs, thr is ough spc for.g. - or K-ios to ov i d out This is clld itrcltio, d is iportt ftur i bttry lctrods O to c b itrcltd for vry 6th crbo to: C C6 15
16 C C6 Itrcltio i lithiu coblt oxid thiu coblt oxid s forul is CoO2 ios r itrcltd btw lyrs of coblt oxid Fro bov Sid viw O O Co CoO2 ios btw lyrs of coblt oxid Itrcltio i lithiu coblt oxid High voltg y forc lctros d ios out fro this structur Siilrly, coblt ios r oxidizd fro Co 3+ to Co 4+ 16
17 thiu-bsd bttris Rpidly dvlopig tchology O of svrl proisig bttry tchologis 17
Higher. Exponentials and Logarithms 160
hsn uknt Highr Mthmtics UNIT UTCME Eponntils nd Logrithms Contnts Eponntils nd Logrithms 6 Eponntils 6 Logrithms 6 Lws of Logrithms 6 Eponntils nd Logrithms to th Bs 65 5 Eponntil nd Logrithmic Equtions
Lecture 27. Rectangular Metal Waveguides
Lctu 7 Rctgul Mtl Wvguids I this lctu u will l: Rctgul tl wvguids T d TM guidd ds i ctgul tl wvguids C 303 Fll 006 Fh R Cll Uivsit Plll Plt Mtl Wvguids d 1 T Mds: Dispsi lti: ( ) si { 1,, d d d 1 TM Mds:
We will begin this chapter with a quick refresher of what an exponent is.
.1 Exoets We will egi this chter with quick refresher of wht exoet is. Recll: So, exoet is how we rereset reeted ultilictio. We wt to tke closer look t the exoet. We will egi with wht the roerties re for
Problem Set 6 Solutions
6.04/18.06J Mathmatics for Computr Scic March 15, 005 Srii Dvadas ad Eric Lhma Problm St 6 Solutios Du: Moday, March 8 at 9 PM Problm 1. Sammy th Shar is a fiacial srvic providr who offrs loas o th followig
Power Means Calculus Product Calculus, Harmonic Mean Calculus, and Quadratic Mean Calculus
Gug Istitut Jourl, Volum 4, No 4, Novmbr 008 H. Vic Do Powr Ms Clculus Product Clculus, Hrmoic M Clculus, d Qudrtic M Clculus H. Vic Do vick@dc.com Mrch, 008 Gug Istitut Jourl, Volum 4, No 4, Novmbr 008
NerveCenter Protocol and Perl Metrics. November 2014 NCSD-PPM-01
rvcntr Procol nd Prl Mtrics ovbr 2014 CSD-PPM-01 Procol nd Prl Mtrics Strting in rvcntr 6.1 Bld28, th nccd cond lin utility supports gnrting trics for rvcntr Srvr s procol lyr nd Prl intrprtrs. Cling upon
THE EFFECT OF GROUND SETTLEMENTS ON THE AXIAL RESPONSE OF PILES: SOME CLOSED FORM SOLUTIONS CUED/D-SOILS/TR 341 (Aug 2005) By A. Klar and K.
THE EFFECT OF GROUND SETTEMENTS ON THE AXIA RESPONSE OF PIES: SOME COSED FORM SOUTIONS CUED/D-SOIS/TR 4 Aug 5 By A. Klr d K. Sog Klr d Sog "Th Effct of Groud Displcmt o Axil Rspos of Pils: Som Closd Form
Chapter 3 Chemical Equations and Stoichiometry
Chptr Chmicl Equtions nd Stoichiomtry Homwork (This is VERY importnt chptr) Chptr 27, 29, 1, 9, 5, 7, 9, 55, 57, 65, 71, 75, 77, 81, 87, 91, 95, 99, 101, 111, 117, 121 1 2 Introduction Up until now w hv
Student Satisfaction Survey
Stut Stiftio Survy REPORT Dprtt of Ititutiol Rrh KIMEP UNIVERSITY 2013 KEY MESSAGE Th rgulr Stut Stiftio Survy, urig th lvl of tut tiftio with thir xpri t KIMEP, w out urig Mrh 15 April 7. Th totl ubr
Application Note: Cisco A S A - Ce r t if ica t e T o S S L V P N Con n e ct ion P r of il e Overview: T h i s a p p l i ca ti o n n o te e x p l a i n s h o w to co n f i g u r e th e A S A to a cco m
BASIC DEFINITIONS AND TERMINOLOGY OF SOILS
1 BASIC DEFINITIONS AND TERMINOLOGY OF SOILS Soil i a thr pha atrial hich coit of olid particl hich ak up th oil klto ad void hich ay b full of atr if th oil i aturatd, ay b full of air if th oil i dry,
AC Circuits Three-Phase Circuits
AC Circuits Thr-Phs Circuits Contnts Wht is Thr-Phs Circuit? Blnc Thr-Phs oltgs Blnc Thr-Phs Connction Powr in Blncd Systm Unblncd Thr-Phs Systms Aliction Rsidntil Wiring Sinusoidl voltg sourcs A siml
Instruction: Solving Exponential Equations without Logarithms. This lecture uses a four-step process to solve exponential equations:
49 Instuction: Solving Eponntil Equtions without Logithms This lctu uss fou-stp pocss to solv ponntil qutions: Isolt th bs. Wit both sids of th qution s ponntil pssions with lik bss. St th ponnts qul to
Question 3: How do you find the relative extrema of a function?
ustion 3: How do you find th rlativ trma of a function? Th stratgy for tracking th sign of th drivativ is usful for mor than dtrmining whr a function is incrasing or dcrasing. It is also usful for locating
Fundamentals of Tensor Analysis
MCEN 503/ASEN 50 Chptr Fundmntls of Tnsor Anlysis Fll, 006 Fundmntls of Tnsor Anlysis Concpts of Sclr, Vctor, nd Tnsor Sclr α Vctor A physicl quntity tht cn compltly dscrid y rl numr. Exmpl: Tmprtur; Mss;
1.- L a m e j o r o p c ió n e s c l o na r e l d i s co ( s e e x p li c a r á d es p u é s ).
PROCEDIMIENTO DE RECUPERACION Y COPIAS DE SEGURIDAD DEL CORTAFUEGOS LINUX P ar a p od e r re c u p e ra r nu e s t r o c o rt a f u e go s an t e un d es a s t r e ( r ot u r a d e l di s c o o d e l a
Zuordnung dimensionelle Messgeräte zu Prüf- und Kalibriernormalen
Zuordu disioll Mssrät zu Prüf- ud Klibrirorl This tbultd syosis cotis currtly vilbl rtfcts wh y b usd s stdrds d wh r suitbl for th clibrtio of stylus or oticl istruts d SPMs. Stdrds r listd i rbitrry
Budgeting. Here are five easy ways to keep your budget. Keeping up with all the INS and OUTS POSITIVE. Budget Quick Start. Go Green!
Bgig K lif G h igh l f chl Mbil, li, v g bkig h w chck cc c i blc M bk l ff li bkig, which i g w k ll f ic i chck Lk f chckig vig cc h icl li bkig l v bil bkig, c k chck bg i G G! G f l li lik li bill
SINUS SURGERY. A Patient Guide to the Sinuses and Nose. William A. Portuese, M.D. Ballard Ear, Nose & Throat and Allergy Clinic
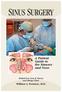SINUS SURGERY A Pin Guid o h Sinuss nd Nos Bllrd Er, Nos & Thro nd Allrgy Clinic Willim A Porus, MD SIGNS & SYMPTOMS OF CHRONIC SINUSITIS Fcil Hdchs Fcil Prssur / Pin Allrgis nd Hyfvr Rpiiv Sinus infcions
Uses for Binary Trees -- Binary Search Trees
CS122 Algorithms n Dt Struturs MW 11:00 m 12:15 pm, MSEC 101 Instrutor: Xio Qin Ltur 10: Binry Srh Trs n Binry Exprssion Trs Uss or Binry Trs Binry Srh Trs n Us or storing n rtriving inormtion n Insrt,
Oracle PL/SQL Programming Advanced
Orl PL/SQL Progrmming Avn In orr to lrn whih qustions hv n nswr orrtly: 1. Print ths pgs. 2. Answr th qustions. 3. Sn this ssssmnt with th nswrs vi:. FAX to (212) 967-3498. Or. Mil th nswrs to th following
A Note on Approximating. the Normal Distribution Function
Applid Mathmatical Scincs, Vol, 00, no 9, 45-49 A Not on Approimating th Normal Distribution Function K M Aludaat and M T Alodat Dpartmnt of Statistics Yarmouk Univrsity, Jordan Aludaatkm@hotmailcom and
GRANT ADMINISTRATION: How Do I Close Out An Expired Grant or Award?
GRANT AMINISTRATION PROCEURES - Scio 6.5 GRANT AMINISTRATION: ow o I Clos Ou A Expird Gr or Awrd? Iroducio Th Niol Isius of lh ( NI ) hs sblishd h followig rquirs for fdrl gr or wrd o b closd ou by isiuios
Heat (or Diffusion) equation in 1D*
Heat (or Diffusio) equatio i D* Derivatio of the D heat equatio Separatio of variables (refresher) Worked eamples *Kreysig, 8 th Ed, Sectios.4b Physical assumptios We cosider temperature i a log thi wire
Numerical and Experimental Study on Nugget Formation in Resistance Spot Welding for High Strength Steel Sheets in Automobile Bodies
rasactios of JWRI, ol.38 (9), No. rasactios of JWRI, ol.38 (9), No. Numrical ad Exprimtal Study o Nuggt Formatio i Rsistac Spot Wldig for High Strgth Stl Shts i Automobil Bodis MA Nishu* ad MURAKAWA Hidkazu**
SYSTEMS & SERVICES VENDOR PROGRAMS SPECIALTY MARKET PROGRAMS BE A SPECIALIST OR REFER A SPECIALIST
SYSS & SVICS CNUY 21 is th xclusiv sponso in th l stt ctgoy, nd is th only l stt ogniztion tht cn off I ILS wd ils. Poud suppot of st Sls sinc 1979. In 2008, CNUY 21 Cnd ctd th Kids to Cp pog wh vy $2,100
Reading. Minimum Spanning Trees. Outline. A File Sharing Problem. A Kevin Bacon Problem. Spanning Trees. Section 9.6
Rin Stion 9.6 Minimum Spnnin Trs Outlin Minimum Spnnin Trs Prim s Alorithm Kruskl s Alorithm Extr:Distriut Shortst-Pth Alorithms A Fil Shrin Prolm Sy unh o usrs wnt to istriut il monst thmslvs. Btwn h
WAVEGUIDES (& CAVITY RESONATORS)
CAPTR 3 WAVGUIDS & CAVIT RSONATORS AND DILCTRIC WAVGUIDS OPTICAL FIBRS 導 波 管 & 共 振 腔 與 介 質 導 波 管 光 纖 W t rqu is t irowv rg >4 G? t losss o wv i two-odutor trsissio li du to iprt odutor d loss diltri o
Last time Interprocedural analysis Dimensions of precision (flow- and context-sensitivity) Flow-Sensitive Pointer Analysis
Flow-Insnsitiv Pointr Anlysis Lst tim Intrprocurl nlysis Dimnsions of prcision (flow- n contxt-snsitivity) Flow-Snsitiv Pointr Anlysis Toy Flow-Insnsitiv Pointr Anlysis CIS 570 Lctur 12 Flow-Insnsitiv
What parents or other loved ones have to say
i s i l i Fm io t i i S N TRA A ut h o Y s s of Tr t r for P d i u G c Rsour Estblishd i 1983, Prid & Prjudic ws th first progrm to offr cousllig d support to lsbi, gy, bisxul, trssxul d trsgdr (LGBTT)
Week 11 - Inductance
Week - Inductnce November 6, 202 Exercise.: Discussion Questions ) A trnsformer consists bsiclly of two coils in close proximity but not in electricl contct. A current in one coil mgneticlly induces n
Magic Message Maker Amaze your customers with this Gift of Caring communication piece
Magic Mssag Makr maz your customrs with this Gift of aring communication pic Girls larn th powr and impact of crativ markting with this attntion grabbing communication pic that will hlp thm o a World of
Schedule C. Notice in terms of Rule 5(10) of the Capital Gains Rules, 1993
(Rul 5(10)) Shul C Noti in trms o Rul 5(10) o th Cpitl Gins Ruls, 1993 Sttmnt to sumitt y trnsror o shrs whr thr is trnsr o ontrolling intrst Prt 1 - Dtils o Trnsror Nm Arss ROC No (ompnis only) Inom Tx
G ri d m on i tori n g w i th N A G I O S (*) (*) Work in collaboration with P. Lo Re, G. S av a and G. T ortone WP3-I CHEP 2000, N F N 10.02.2000 M e e t i n g, N a p l e s, 29.1 1.20 0 2 R o b e r 1
What Is Required? You need to find the final temperature of an iron ring heated by burning alcohol. 4.95 g
Calculatig Theral Eergy i a Bob Calorieter (Studet textbook page 309) 31. Predict the fial teperature of a 5.00 10 2 g iro rig that is iitially at 25.0 C ad is heated by cobustig 4.95 g of ethaol, C 2
n Using the formula we get a confidence interval of 80±1.64
9.52 The professor of sttistics oticed tht the rks i his course re orlly distributed. He hs lso oticed tht his orig clss verge is 73% with stdrd devitio of 12% o their fil exs. His fteroo clsses verge
Words Symbols Diagram. abcde. a + b + c + d + e
Logi Gtes nd Properties We will e using logil opertions to uild mhines tht n do rithmeti lultions. It s useful to think of these opertions s si omponents tht n e hooked together into omplex networks. To
TIME VALUE OF MONEY: APPLICATION AND RATIONALITY- AN APPROACH USING DIFFERENTIAL EQUATIONS AND DEFINITE INTEGRALS
MPRA Muich Prsoal RPEc Archiv TIME VALUE OF MONEY: APPLICATION AND RATIONALITY- AN APPROACH USING DIFFERENTIAL EQUATIONS AND DEFINITE INTEGRALS Mahbub Parvz Daffodil Itratioal Uivrsy 6. Dcmbr 26 Oli at
Repeated multiplication is represented using exponential notation, for example:
Appedix A: The Lws of Expoets Expoets re short-hd ottio used to represet my fctors multiplied together All of the rules for mipultig expoets my be deduced from the lws of multiplictio d divisio tht you
LanguageScript EasyScript speedwriting ComputerScript software MiniScript shorthand EnglishScript REGULAR TEXT
LanguageScript is a short form of the language that can improve reading, writing, typing and transcription skills. It is based on the English grammar and language structure utilizing its basic components
The Casino Experience. Let us entertain you
The Csio Expeiee Let us eteti you The Csio Expeiee If you e lookig fo get ight out, Csio Expeiee is just fo you. 10 The Stight Flush Expeiee 25 pe peso This is get itodutio to gmig tht sves you moey Kik
3 The Utility Maximization Problem
3 The Utility Mxiiztion Proble We hve now discussed how to describe preferences in ters of utility functions nd how to forulte siple budget sets. The rtionl choice ssuption, tht consuers pick the best
PRIMER TESTIMONIO. -F o l i o n ú m e r o 1 2 0. ḋḋḋḋḋḋḋḋḋḋḋḋḋḋḋḋḋḋḋḋḋḋḋḋḋḋḋḋḋḋḋḋḋḋḋḋḋ ESC RITU RA NU MERO TREINTA.- E n l a c i u d a d d e B u e n os A i r e s, c a p i t a l d e l a R e p ú b l i c
Factorials! Stirling s formula
Author s not: This articl may us idas you havn t larnd yt, and might sm ovrly complicatd. It is not. Undrstanding Stirling s formula is not for th faint of hart, and rquirs concntrating on a sustaind mathmatical
December Homework- Week 1
Dcmbr Hmwrk- Wk 1 Mth Cmmn Cr Stndrds: K.CC.A.1 - Cunt t 100 by ns nd by tns. K.CC.A.2 - Cunt frwrd bginning frm givn numbr within th knwn squnc (instd f hving t bgin t 1). K.CC.B.4.A - Whn cunting bjcts,
L a h ip e r t e n s ió n a r t e r ia l s e d e f in e c o m o u n n iv e l d e p r e s ió n a r t e r ia l s is t ó lic a ( P A S ) m a y o r o
V e r s i ó n P á g i n a 1 G U I A D E M A N E J O D E H I P E R T E N S I O N E S C E N C I A L 1. D E F I N I C I O N. L a h ip e r t e n s ió n a r t e r ia l s e d e f in e c o m o u n n iv e l d
Physics 106 Lecture 12. Oscillations II. Recap: SHM using phasors (uniform circular motion) music structural and mechanical engineering waves
Physics 6 Lctur Oscillations II SJ 7 th Ed.: Chap 5.4, Rad only 5.6 & 5.7 Rcap: SHM using phasors (unifor circular otion) Physical pndulu xapl apd haronic oscillations Forcd oscillations and rsonanc. Rsonanc
Distributed Systems Principles and Paradigms. Chapter 11: Distributed File Systems. Distributed File Systems. Example: NFS Architecture
Distriut Systms Prinipls n Prigms Mrtn vn Stn VU mstrm, Dpt. Computr Sin stn@s.vu.nl Chptr 11: Vrsion: Dmr 10, 2012 1 / 14 Gnrl gol Try to mk fil systm trnsprntly vill to rmot lints. 1. Fil mov to lint
Jesus Performed Miracles
F Jonl P Ju Pr Mircl ch f lo Al n fri r b f Li blo n of ick li on Po k r u yi li br o n o y o on y r v y o r b f ch rfriror n -ll cr r p r o y k li Tor n of o ll y r u o kn on r ch n L ch p Ju Hl Officil
Usability Test Checklist
Crtifi Profssionl for Usility n Usr Exprin Usility Tsting (CPUX-UT) Vrsion.0, Jun 0 Pulishr: UXQB. V. Contt: info@uxq.org www.uxq.org Autorn: R. Molih, T. Gis, B. Rumml, O. Klug, K. Polkhn Contnt Lgn...
M Mobile Based Clinical Decision Support System Bhudeb Chakravarti & Dr. Suman Bhusan Bhattacharyya Provider & Public Health Group, VBU-HL P S aty am C om puter S ervices L im ited Bhudeb_ C hak ravarti@
from the desk of the ceo
SUMMIT NEWS July 2014 VOL 14. Iu 3 Ii thi iu 3 6 10 Sptlight Wrmth Cumr-irct cr ifrmti i Rit try - Hm wy frm hm frm th k f th c Th w ficil yr brig w chg t th tir g cr ctr. I thi iti f SummitNw w highlight
BLADE 12th Generation. Rafał Olszewski. Łukasz Matras
BLADE 12th Generation Rafał Olszewski Łukasz Matras Jugowice, 15-11-2012 Gl o b a l M a r k e t i n g Dell PowerEdge M-Series Blade Server Portfolio M-Series Blades couple powerful computing capabilities
H ig h L e v e l O v e r v iew. S te p h a n M a rt in. S e n io r S y s te m A rc h i te ct
H ig h L e v e l O v e r v iew S te p h a n M a rt in S e n io r S y s te m A rc h i te ct OPEN XCHANGE Architecture Overview A ge nda D es ig n G o als A rc h i te ct u re O ve rv i ew S c a l a b ili
at 10 knots to avoid the hurricane, what could be the maximum CPA? 59 miles - 54 nm STEP 1 Ship s Speed Radius (e-r) 10 k - 1.0 nm every 6 minutes
:1 Navigatio :1 Gal 1 1 1 Rf: P, Huica You a udway o cous T ad you axiu spd is 1 kots. Th y of a huica bas 1 T, ils fo you positio. Th huica is ovig towads T at 1 kots. If you auv at 1 kots to avoid th
e Videobewaking ov er I P Marty K n o p e rt 1 A l l m z u l l b t g r u m a k h w k h w k z a l z r E p r m a r k t t c m a r k t Video vision: e vor en va n video en in de na ij e oek om st eb ik en
5.4 Exponential Functions: Differentiation and Integration TOOTLIFTST:
.4 Eponntial Functions: Diffrntiation an Intgration TOOTLIFTST: Eponntial functions ar of th form f ( ) Ab. W will, in this sction, look at a spcific typ of ponntial function whr th bas, b, is.78.... This
Cruisin with Carina Motorcycle and Car Tour Guide
Ifi Tchlgy Slui Wh Swdih hpiliy V, ully. Cuii wih Ci Mcycl d C Tu Guid Ikp: Ci Th 290 Ru 100 W Dv, V 05356 800-745-3615 802-464-2474 L h g ll! Th d i ck, c, i d l x. My 17h, 18h, & 19h W ivi yu c cui h
Outline. Binary Tree
Outlin Similrity Srh Th Nikolus Augstn Fr Univrsity of Bozn-Bolzno Fulty of Computr Sin DIS 1 Binry Rprsnttion of Tr Binry Brnhs Lowr Boun for th Eit Distn Unit 10 My 17, 2012 Nikolus Augstn (DIS) Similrity
CLOUD COMPUTING BUSINESS MODELS
da MODLS Atlir d l iova CLOUD COMPUTING MODLS Chair coomi d l iova - Mourad Zroukhi C d chrch Écoomi t Maagmt Uivrsité d Chair coomi d l iova - da MODLS AGNDA Cloud Computig : What is it? Cloud Dploymt
Tutorial on How to Create Electric Machine Models
PSIM Sotwre Tutoril on How to Crete Electric Mchine Models Powersi Inc. Septber 2009 www.powersitech.co Tutoril on Creting Electric Mchine Models Users cn crete electric chine odels using the bsic unction
Using Predictive Modeling to Reduce Claims Losses in Auto Physical Damage
Using Predictive Modeling to Reduce Claims Losses in Auto Physical Damage CAS Loss Reserve Seminar 23 Session 3 Private Passenger Automobile Insurance Frank Cacchione Carlos Ariza September 8, 23 Today
G S e r v i c i o C i s c o S m a r t C a r e u ي a d e l L a b o r a t o r i o d e D e m o s t r a c i n R ل p i d a V e r s i n d e l S e r v i c i o C i s c o S m a r t C a r e : 1 4 ع l t i m a A c
Frequently Asked Questions Registrant Site Testing. Q: How do I access the testing and what is my login?
Frquly Akd Qui Rgir Si Tig Q: Hw d I cc h ig d wh i my lgi? A: T r dmiird hrugh crl i hp://rgir.qflippr.cm/ Yu mu b rgird wih h i fr cc. Fr m ud, cc i grd hrugh rgiri lik mild wih yur cur mril. Hwvr, m
SOME IMPORTANT MATHEMATICAL FORMULAE
SOME IMPORTANT MATHEMATICAL FORMULAE Circle : Are = π r ; Circuferece = π r Squre : Are = ; Perieter = 4 Rectgle: Are = y ; Perieter = (+y) Trigle : Are = (bse)(height) ; Perieter = +b+c Are of equilterl
5.6 POSITIVE INTEGRAL EXPONENTS
54 (5 ) Chpter 5 Polynoils nd Eponents 5.6 POSITIVE INTEGRAL EXPONENTS In this section The product rule for positive integrl eponents ws presented in Section 5., nd the quotient rule ws presented in Section
PIN #1 ID FIDUCIAL LOCATED IN THIS AREA TOP VIEW. ccc C SIDE VIEW
Packag iagrams ruary 20 all W Packag Option : i0 P imnsions in illimtrs ata ht r PI # I IUI OT I TI R (X) 2 OTTO VIW. X Ø s TOP VIW Ø.0 Ø.0 I VIW OT:. IIO TOR PR Y. 99. 2. IIO R I IITR. IIO I UR T T XIU
Campus Sustainability Assessment and Related Literature
Campus Sustainability Assessment and Related Literature An Annotated Bibliography and Resource Guide Andrew Nixon February 2002 Campus Sustainability Assessment Review Project Telephone: (616) 387-5626
AIRCRAFT RESCUE AND FIRE FIGHTING CHART
IRCRFT RSCU ND FIR FIGHTING CHRT NOT THIS CHRT GIVS TH GNRL LYOUT OF TH 380-800 STNDRD VRSI TH NUMBR ND RRNGMNT OF TH INDIVIDUL ITMS VRY WITH TH CUSTOMRS. ISSUD BY : IRBUS S..S. CUSTOMR SRVICS TCHNICL
Effect of Design Parameter on the Performance of Lithium Ion Battery
Aadil Ahmad, Mohd. Parvz / Intrnational Journal of Enginring Rarch and Application Vol. 3, Iu 4, Jul-Aug 2013, pp.1196-1201 Effct of Dign Paramtr on th Prformanc of Lithium Ion Battry Aadil Ahmad 1, Mohd.
CV-measurement basics
V-measuremet basics M-capacitor V measuremet measuremet of differetial by small ac modulatio of the bias voltage (dc d d G G M j G M ω M j ω Y M G M G M M ualitative poit of view ad diagram i geeral (here
Microanalyses of Ferroelectric Properties of BaTiO 3
Micronly of Frrolctric Proprti of BTiO io i Liu Domin Grin boundry Micronly of Frrolctric Proprti of BTiO Im Fchbrich Elktrotchnik und Informtiontchnik dr Brgichn Univrität-Gmthochchul Wupprtl Zur Erlngn
The Binomial Multi- Section Transformer
4/15/21 The Bioial Multisectio Matchig Trasforer.doc 1/17 The Bioial Multi- Sectio Trasforer Recall that a ulti-sectio atchig etwork ca be described usig the theory of sall reflectios as: where: Γ ( ω
int Ron t Marc ier rise e la Impasse du u Liv oue re M lin Berthel ry roix Fleu m Clos inot s int V urg S Faub Rue Rue du C rc de l ' Etuv e Stuart
. Big i N éi N Cil l l Néi l N i C lli C i é Néi i i I. N -D z Ei if ig Vll Bl ig Vig l'o l S Bg i i g l Ci Qi i Blf Si ig l i i 1945 g li gg ég Ni l Bl l i H Si J iz Eg S i Villi I l Bl i i i H Bliz Dli
UNDERSTANDING FLOW PROCESSING WITHIN THE CISCO ACE M ODULE Application de liv e r y pr odu cts can distr ib u te tr af f ic to applications and w e b se r v ice s u sing v ar y ing le v e ls of application
SINCLAIR COMMUNITY COLLEGE DAYTON, OHIO DEPARTMENT SYLLABUS FOR COURSE IN MAT 1355 - INTERMEDIATE ALGEBRA I (3 CREDIT HOURS)
SINCLAIR COMMUNITY COLLEGE DAYTON OHIO DEPARTMENT SYLLABUS FOR COURSE IN MAT 1355 - INTERMEDIATE ALGEBRA I (3 CREDIT HOURS) 1. COURSE DESCRIPTION: Ftorig; opertios with polyoils d rtiol expressios; solvig
Present. and. RFA No79/2OO5
IN TE IG OURT OF KARNATAKA IRUIT BEN AT DARWAD Dted this the Q7th Dy of Mch 211 Pesent TE BLE MRJUSTIE KLMANJUNAT nd TE BLE MRJUSTIE NNAGAMOAN DAS BETWEEN: RFA No7/2OO5 Shi Adiveppgoud S/o MllngoudRyngoud,
Physics 43 Homework Set 9 Chapter 40 Key
Physics 43 Homework Set 9 Chpter 4 Key. The wve function for n electron tht is confined to x nm is. Find the normliztion constnt. b. Wht is the probbility of finding the electron in. nm-wide region t x
OFFSHORE INTERNATIONAL MARINE PERSONNEL SERVICES, INC. EMPLOYMENT APPLICATION
OFFSHORE INTERNATIONAL MARINE PERSONNEL SERVICES, INC. 3802 W. Nvy Bvd Po, FL 32507 Tho: (850) 455-2995 Tx: (850) 455-3033 www.oho-.om EMPLOYMENT APPLICATION Poo Ay Fo Nm: F L SS# - - Add Cy/S Z Pho: Hom
ProfileXT, CheckPoint 360, & Profiles Sales Assessment
lt H urc I ig fctur u M t rvic l Et S R g i urc Outo l i & t g ffi R St c i rv S gy holo c T vic t Sr D uctio Ed rig gi E l ci i F r lthc H E S CA DY U T S r g imgi l op p t g Stffi ig urc o t u do omp
The objectives for this meeting are:
Trsitis: Hdl With Cr Sttwid Mtig: Sssi 2 f 3 Nvmbr 14, 2013 9:00.m. 3:30 p.m. Turf Vlly Rsrt d Cfrc Ctr 2700 Turf Vlly Rd, Ellictt City, MD 21042 Tdy s mtig is wrkig mtig, prvidig tim fr yu d yur crss-ctiuum
Mathematics. Mathematics 3. hsn.uk.net. Higher HSN23000
hsn uknt Highr Mathmatics UNIT Mathmatics HSN000 This documnt was producd spcially for th HSNuknt wbsit, and w rquir that any copis or drivativ works attribut th work to Highr Still Nots For mor dtails
1 Analysis of heat transfer in a single-phase transformer
Assignent -7 Analysis of heat transr in a single-phase transforer The goal of the first assignent is to study the ipleentation of equivalent circuit ethod (ECM) and finite eleent ethod (FEM) for an electroagnetic
How To Get A Pension In Chile
Bc Accou fo A cocul m bw lo d d l h h v h h l h h h o o u u cfc oy, owd by by h h lo, fo fo cfd od m m u fo fo uld, d d lly odc, ch ch ym ().. Ch 21 Coc m m Rl Rl ym Excuoy Co Co Rco cclbl Ely Ely mo Dful
For personal use only
ASX RELEASE: 28 th February 2014 ROSTER ELF PRESENTATION Applabs Technologies Ltd (ASX: ALA, Applabs) is pleased to release a copy of presentation to be made by magement of Roster Elf Pty Ltd ( Roster
LG has introduced the NeON 2, with newly developed Cello Technology which improves performance and reliability. Up to 320W 300W
Cllo Tchnology LG has introducd th NON 2, with nwly dvlopd Cllo Tchnology which improvs prformanc and rliability. Up to 320W 300W Cllo Tchnology Cll Connction Elctrically Low Loss Low Strss Optical Absorption
Electronic Thesis and Dissertations UC Berkeley
Eltoi Thsis d Dissttios UC Bkly P Rviwd Titl: Essys o th iil Bod kt tho: Wilkoff, S ikl t Dt: 1 Sis: UC Bkly Eltoi Thss d Dissttios Dg: Ph.D., Bsiss dmiisttio, Ph.D. PogmUC Bkly dviso(s): ff, Dwight Committ:
DEPARTMENT OF ACTUARIAL STUDIES RESEARCH PAPER SERIES
DEPARTMENT OF ACTUARIAL STUDIES RESEARCH PAPER SERIES The ulti-bioil odel d pplictios by Ti Kyg Reserch Pper No. 005/03 July 005 Divisio of Ecooic d Ficil Studies Mcqurie Uiversity Sydey NSW 09 Austrli
Traffic Flow Analysis (2)
Traffic Flow Analysis () Statistical Proprtis. Flow rat distributions. Hadway distributions. Spd distributions by Dr. Gang-Ln Chang, Profssor Dirctor of Traffic safty and Oprations Lab. Univrsity of Maryland,
Standard Conditions for Street Traders The Royal Borough of Kensington and Chelsea. Revised standard conditions for street trading
Stnr Conitions or Strt Trrs Th Royl Borough o Knsington n Chls Rvis stnr onitions or strt tring Th Royl Borough o Knsington n Chls strt tring linss stnr onitions 2006 1 Dinitions Th ollowing xprssions
EXECUTIVE SUMMARY. Survey Objective. How to Use This Report. Methodology
O M N NA ONAL AL N N MA K NG C OMP ANYW B C M OF WA AL O GAN Z A ON D C AL F O C NON D C AL F O C D B U O 2 0 1 2 l dm k g P c c u y F d g f d p h u yp d gp MM d m mb w hc mp h d l dm k g g z l u c u d
Implementationof CLLD 2014-2020
Implementationof CLLD 2014-2020 - State of play, monitoring and evaluation 1 Have you submitted an official proposal for the Rural Development Programme to the Commission? Yes: FI, LV, EE, DK, SE No: We
Example 27.1 Draw a Venn diagram to show the relationship between counting numbers, whole numbers, integers, and rational numbers.
2 Rtionl Numbers Integers such s 5 were importnt when solving the eqution x+5 = 0. In similr wy, frctions re importnt for solving equtions like 2x = 1. Wht bout equtions like 2x + 1 = 0? Equtions of this
v T R x m Version PREVIEW Practice 7 carroll (11108) 1
Version PEVIEW Prctice 7 crroll (08) his print-out should he 5 questions. Multiple-choice questions y continue on the next colun or pge find ll choices before nswering. Atwood Mchine 05 00 0.0 points A
A Cyclical Nurse Schedule Using Goal Programming
ITB J. Sci., Vol. 43 A, No. 3, 2011, 151-164 151 A Cyclical Nurse Schedule Usig Goal Prograig Ruzzaiah Jeal 1,*, Wa Rosaira Isail 2, Liog Choog Yeu 3 & Ahed Oughalie 4 1 School of Iforatio Techology, Faculty
Projections - 3D Viewing. Overview Lecture 4. Projection - 3D viewing. Projections. Projections Parallel Perspective
Ovrviw Lctur 4 Projctions - 3D Viwing Projctions Paralll Prspctiv 3D Viw Volum 3D Viwing Transformation Camra Modl - Assignmnt 2 OFF fils 3D mor compl than 2D On mor dimnsion Displa dvic still 2D Analog
Wireless Communication for Hatchery Alarm and Monitoring Systems
Wireless Communication for Hatchery larm and Monitoring Systems Setting up a wireless network Things we need to know: What are you trying to monitor? iscrete or analog data? How do want to use the data?
11 + Non-verbal Reasoning
Prti Tst + Non-vrl Rsoning R th instrutions rfully. Do not gin th tst or opn th ooklt until tol to o so. Work s quikly n s rfully s you n. Cirl th orrt lttr from th options givn to nswr h qustion. You
Scheduling and Rostering. Marco Kuhlmann & Guido Tack Lecture 7
Schduling and Rostring Marco Kuhlann & Guido Tack Lctur Th story so ar Modlling in Gcod/J Foral rawork or constraint prograing Propagation, global constraints Sarch Th story so ar Modlling in Gcod/J Foral