Короткий довiдник з математики. Оформив: Виспянський Iгор ( Версiя 1.00, Веб-сайт:
|
|
|
- Надежда Домашнева
- 7 years ago
- Views:
Transcription
1 Короткий довiдник з математики Оформив: Виспянський Iгор ( Версiя 1.00, Веб-сайт:
2 Змiст 1 Властивостi степеня Многочлени 3 3 Властивостi арифметичних коренiв 3 4 Тотожнi перетворення тригонометричних виразiв Формули додавання Формули подвiйного аргументу Формули половинного аргументу Формули перетворення суми в добуток Формули перетворення добутку в суму Спiввiдношення мiж sin x, cos x i tg x Формули зведення Прогресiї Арифметична прогресiя Геометрична прогресiя Комбiнаторика i бiном Ньютона 6 7 Логарифми. Показниковi i логарифмiчнi рiвняння 7 8 Тригонометричнi рiвняння 8 9 Трикутник Довiльний трикутник Прямокутний трикутник Рiвностороннiй трикутник Чотирикутник Паралелограм Ромб Прямокутник Квадрат Трапецiя Многокутник Описаний многокутник Правильний многокутник Коло, круг Додатковi спiввiдношення мiж елементами фiгур 11 1
3 14 Многогранники Довiльна призма Пряма призма Прямокутний паралелепiпед Довiльна пiрамiда Куб Правильна пiрамiда Довiльна зрiзана пiрамiда Правильна зрiзана пiрамiда Тiла обертання Цилiндр Конус Куля, сфера Кульовий сегмент Кульовий сектор Зрiзаний конус Деякi спiввiдношення мiж елементами фiгур Формули диференцiювання Первiснi Прямокутна декартова система координат Прямокутна декартова система координат на площинi Прямокутна декартова система координат у просторi Властивостi степеня a 0 = 1 a x a y = a x+y a x a y = ax y (a x ) y = a x y (a b) x = a x b x ( a b ) x = ax b x a x = 1 a x
4 Многочлени де x 1 i x коренi рiвняння a b = (a b)(a + b) (a + b) = a + ab + b (a b) = a ab + b (a + b) 3 = a 3 + 3a b + 3ab + b 3 (a + b) 3 = a 3 + b 3 + 3ab(a + b) (a b) 3 = a 3 3a b + 3ab b 3 (a b) 3 = a 3 b 3 + 3ab(a b) a 3 + b 3 = (a + b)(a ab + b ) a 3 b 3 = (a b)(a + ab + b ) ax + bx + c = a(x x 1 )(x x ), ax + bx + c = 0 3 Властивостi арифметичних коренiв n ab = n a n b n a n a b = n, (b 0) b ( n a) k = n a k n k a = kn a n a = nk a k ( n a) n = a, (a 0) n a < n b, якщо 0 a < b a = a = { a, при a 0, a, при a < 0 n a n = a n+1 a = n+1 a, a 0 3
5 4 Тотожнi перетворення тригонометричних виразiв 4.1 Формули додавання sin x + cos x = 1 tg x = sin x cos x, x π (n + 1), n Z ctg x = cos x sin x, x πk, k Z tg x ctg x = 1, x πn, n Z 1 + tg x = 1 cos x, x π (n + 1) 1 + ctg x = 1 sin x, x πn) sin(x + y) = sin x cos y + cos x sin y sin(x y) = sin x cos y cos x sin y cos(x + y) = cos x cos y sin x sin y cos(x y) = cos x cos y + sin x sin y tg(x + y) = tg(x y) = tg x + tg y 1 tg x tg y tg x tg y 1 + tg x tg y, x, y, x y π + πn, n Z 4. Формули подвiйного аргументу sin x = sin x cos x cos x = cos x sin x = cos x 1 = 1 sin x tg x = tg x 1 tg x x π 4 + π k, k Z, x π + πn, n Z 4.3 Формули половинного аргументу tg x = sin x = 1 cos x cos x = 1 + cos x sin x 1 + cos x = 1 cos x sin x, x π + πn, n Z 4
6 4.4 Формули перетворення суми в добуток sin x + sin y = sin x + y sin x sin y = cos x + y cos x + cos y = cos x + y cos x cos y = sin x + y tg x tg y = tg x + tg y = sin(x + y) cos x cos y cos x y sin x y cos x y sin x y sin(x y) cos x cos y, x, y π + πn, n Z 4.5 Формули перетворення добутку в суму sin x sin y = 1 (cos(x y) cos(x + y)) cos x cos y = 1 (cos(x y) cos(x + y)) sin x cos y = 1 (sin(x y) sin(x + y)) 4.6 Спiввiдношення мiж sin x, cos x i tg x 4.7 Формули зведення sin x = tg x 1 + tg x, x (n + 1)π cos x = 1 tg x 1 + tg x, x (n + 1)π π u + α π + α 3π + α α π α π α 3π α sin u cos α sin α cos α sin α cos α sin α cos α cos u sin α cos α sin α cos α sin α cos α sin α tg u ctg α tg α ctg α tg α ctg α tg α ctg α ctg u tg α ctg α tg α ctg α tg α ctg α tg α 5
7 5 Прогресiї 5.1 Арифметична прогресiя S n = a 1 + a n a n = a 1 + d(n 1) n = a 1 + d(n 1) n a k = a k 1 + a k+1, k =, 3,..., n 1 a k + a m = a p + a q, де k + m = p + q a 1 - перший член; d - рiзниця; n - число членiв; a n - n-й член; S n - сума n перших членiв. 5. Геометрична прогресiя b n = b 1 q n 1 b 1 - перший член, q - знаменник (q 0), n - число членiв, b n - n-й член, S n - сума n перших членiв. S n = b 1(1 q n ), q 1 1 q b k = b k 1 b k+1, k =, 3,..., (n 1) b k b m = b p b q, де k + m = p + q S = b 1, де q < 1 1 q S - сума нескiнченної геометричної прогресiї. 6 Комбiнаторика i бiном Ньютона P n = 1... (n 1) n = n! Cn m n! = m!(n m)!, C0 n = 1 Cn m = Cn n m = Cn m + Cn m+1 = Cn+1 m+1 A m n = P n Cn m n! = (n m)! (a + b) n = C 0 na n + C 1 na n 1 b C k na n k b k C n nb n (a + b) n = a n + na n 1 n(n 1)... (n k + 1) b a n k b k b n k! Cna k n k b k = T k+1 - (k + 1)-й член у розкладi бiнома (k = 0, 1,,..., n) C 0 n + C 1 n C n n = n 6
8 7 Логарифми. Показниковi i логарифмiчнi рiвняння y = a x, a > 0, a 1 y = log a x x > 0, x = a log a x log a a = 1 log a 1 = 0 log a (bc) = log a b + log a c log a b c = log a b log a c log a x p = p log a x log a x = log b x log b a log a b = 1 log b a log b b log b a = 1 log a b = log a p b p = p log a p b a log a b = b log c a log a b = log c b log a α b β = β α log a b a log c b = b log c a log a α b = log a b log a a α = 1 α log a b log c a log c b = log c b log c a log c b log c a = log c a log c b a f(x) = b g(x) f(x) log c a = g(x) log c b 7
9 8 Тригонометричнi рiвняння 9 Трикутник 9.1 Довiльний трикутник sin x = 0, x = πn, n Z sin x = 1, x = π + πn sin x = 1, x = π + πn cos x = 0, x = π + πn cos x = 1, x = πn cos x = 1, x = π + πn tg x = 0, x = πn ctg x = 0, x = π + πn sin x = a, x = ( 1) n arcsin a + πn cos x = a, x = ± arccos a + πn tg x = a, x = arctg a + πn ctg x = a, x = arcctg a + πn S = S = 1 ah a S = 1 bc sin α p(p a)(p b)(p c) r = S p R = abc 4S a = b + c bc cos α (теорема косинусiв) a sin α = b sin β = c sin γ = R (теорема синусiв) 8
10 9. Прямокутний трикутник S = 1 ab S = 1 ch c r = a + b c R = c a + b = c (теорема Пiфагора) a c h c = h c a c a = a c b c b = b c a c, b c - проекцiї катетiв на гiпотенузу. a = c sin α = c cos β = b tg α = b ctg β 9.3 Рiвностороннiй трикутник 10 Чотирикутник b c S = a 3 4 r = a 3 6 R = a 3 3 S = 1 d 1d sin ϕ 10.1 Паралелограм S = ah a = ab sin α = 1 d 1d sin ϕ 10. Ромб S = ah a = a sin α = 1 d 1d 9
11 10.3 Прямокутник S = ab = 1 d 1d sin ϕ 10.4 Квадрат S = a = d 10.5 Трапецiя S = a + b h = lh, де l = a + b 11 Многокутник 11.1 Описаний многокутник S = pr 11. Правильний многокутник 1 Коло, круг a 3 = R 3 a 4 = R a 6 = R S = na nr c = πr S = πr Сектор (l- довжина дуги, яка обмежує сектор, α- радiанна мiра центрального кута, n - градусна мiра центрального кута). l = πrn 180 = rα S = πr n 360 = 1 r α 10
12 13 Додатковi спiввiдношення мiж елементами фiгур три медiани трикутника перетинаються в однiй точцi, яка дiлить кожну медiану у вiдношенннi : 1, починаючи вiд вершини трикутника медiана трикутника обчислюється за формулою m a = 1 (b + c ) a сторона трикутника обчислюється за формулою a = 3 де m a, m b, m c медiани (m b + m c) m a, бiсектриса дiлить сторону трикутника на вiдрiзки, пропорцiйнi двом iншим його сторонам бiсектриса трикутника обчислюється за формулою l c = ab a 1 b 1 бiсектриса трикутника визначається через його сторони a, b i c за формулою ab(a + b + c)(a + b c) l c = a + b для всякого трикутника залежнiсть мiж висотами h a, h b, h c i радiусом r вписаного кола визначається за формулою 1 h a + 1 h b + 1 h c = 1 r площа S рiвнобiчної трапецiї, дiагоналi якої взаємно перпендикулярнi, дорiвнює квадрату її висоти, тобто S = h висота рiвнобiчної трапецiї, в яку можна вписати коло, є середнiм геометричним її основ h = ab a + b = c (c бiчне ребро) 11
13 14 Многогранники 14.1 Довiльна призма S бiч = Pпер l Pпер периметр перпендикулярного перерiзу. V = S H 14. Пряма призма S бiч = P l 14.3 Прямокутний паралелепiпед S бiч = P H V = a b c 14.4 Довiльна пiрамiда V = 1 3 S H 14.5 Куб V = a 3 d = a Правильна пiрамiда S бiч = 1 P l V = 1 3 S H 14.7 Довiльна зрiзана пiрамiда V = 1 3 h (S 1 + S + S 1 S ) 14.8 Правильна зрiзана пiрамiда S бiч = 1 (P 1 + P ) l 1
14 15 Тiла обертання 15.1 Цилiндр S бiч = π R H V = π R H = S H 15. Конус S бiч = π R l V = 1 3 π R H = 1 3 S H 15.3 Куля, сфера S = 4π R V = 4 3 π R Кульовий сегмент S = π R h V = π h (R 1 3 h) 15.5 Кульовий сектор V = 3 π R h 15.6 Зрiзаний конус V = 1 3 π h (R 1 + R 1 R + R) S = π(r 1 + R )l 16 Деякi спiввiдношення мiж елементами фiгур площу паралелограма можна обчислити за такими формулами D C A B S = AC BD 4 tg A 13
15 S = AB AD tg AOD справджуються такi спiввiдношення мiж елементами сфери i вписаного в неї конуса l = R sin α l = RH α - кут мiж твiрною i площиною основи, l - довжина твiрної конуса. 17 Формули диференцiювання c = 0 (x) = 1 (x α ) = αx α 1 (sin x) = cos x (cos x) = sin x (tg x) = 1 cos x (ctg x) = 1 sin x (e x ) = e x (a x ) = a x ln a (ln x) = 1 x (log a x) = 1 x ln a ( x) = 1 x (f 1 (x) ± f (x)) = f 1(x) ± f (x) (f 1 (x) f (x)) = f 1(x) f (x) + f 1 (x) f (x) (c f(x)) = c f (x) (f(kx + b)) = k f (kx + b) ( ) f1 (x) = f 1 (x)f (x) f 1 (x)f (x) f (x) f (x) (f(u(x))) = f u(u) u (x) 14
16 Формула Ньютона-Лейбнiца має вигляд b a Площа криволiнiйної трапецiї S = f(x)dx = F (b) F (a) b a f(x)dx Рiвняння дотичної до графiка ф-цiї y = f(x) має вигляд y y 0 = f (x 0 )(x x 0 ) 18 Первiснi x α dx = xα+1 α C sin xdx = cos x + C cos xdx = sin x + C 1 cos dx = tg x + C x 1 sin dx = ctg x + C x 1 dx = ln x + C x e x dx = e x + C a x dx = ax ln a + C f(ax + b)dx = 1 f(ax + b) + C a 15
17 19 Прямокутна декартова система координат 19.1 Прямокутна декартова система координат на площинi Вiдстань мiж точками A 1 (x 1 ; y 1 ) i A (x ; y ) визначається за ф-лою A 1 A = Координати середини вiдрiзка (x x 1 ) + (y y 1 ) x = x 1 + x ; y = y 1 + y Рiвняння прямої з кутовим коефiцiєнтом i початковою ординатою має вигляд y = kx + q k = tg α, q значення ординати точки перетину прямої з вiссю O y. Загальне рiвняння прямої ax + by + c = 0 Рiвняння прямих, паралельних вiдповiдно осям O y i O x, мають вигляд x = a; y = b Умови паралельностi i перпендикулярностi прямих y 1 = kx 1 + q 1 i y = kx + q вiдповiдно мають вигляд k 1 = k ; k 1 k = 1. (x x 0 ) + (y y 0 ) = R рiвняння кiл з радiусом R i з центром вiдповiдно в точках O(0; 0) i C(x 0 ; y 0 ). Для y = ax + bx + c xв = b a 19. Прямокутна декартова система координат у просторi ā = a 1 + a + a 3 (a 1 ; a ; a 3 ) + (b 1 ; b ; b 3 ) = (a 1 + b 1 ; a + b ; a 3 + b 3 ) ā 0 = ā ā одиничний вектор. λ(a 1 ; a ; a 3 ) = (λa 1 ; λa ; λa 3 ) āb = ā b cos ϕ 16
18 Скалярний добуток векторiв ā(a 1 ; a ; a 3 ) i b(b 1 ; b ; b 3 ) cos ϕ = Умова перпендикулярностi або āb = a 1 b 1 + a b + a 3 b 3. ā = āā = ā, ā = a a 1 b 1 + a b + a 3 b 3 a 1 + a + a 3 āb = 0 a 1 b 1 + a b + a 3 b 3 = 0 b 1 + b + b 3 Загальне рiвняння площини, перпендикулярної до вектора n(a; b; c) має вигляд ax + by + cz + d = 0 Рiвняння площини, перпендикулярної до вектора n(a; b; c), яка проходить через точку (x 0 ; y 0 ; z 0 ) має вигляд a(x x 0 ) + b(y y 0 ) + c(z z 0 ) = 0 17
CM2202: Scientific Computing and Multimedia Applications General Maths: 2. Algebra - Factorisation
 CM2202: Scientific Computing and Multimedia Applications General Maths: 2. Algebra - Factorisation Prof. David Marshall School of Computer Science & Informatics Factorisation Factorisation is a way of
CM2202: Scientific Computing and Multimedia Applications General Maths: 2. Algebra - Factorisation Prof. David Marshall School of Computer Science & Informatics Factorisation Factorisation is a way of
Online EFFECTIVE AS OF JANUARY 2013
 2013 A and C Session Start Dates (A-B Quarter Sequence*) 2013 B and D Session Start Dates (B-A Quarter Sequence*) Quarter 5 2012 1205A&C Begins November 5, 2012 1205A Ends December 9, 2012 Session Break
2013 A and C Session Start Dates (A-B Quarter Sequence*) 2013 B and D Session Start Dates (B-A Quarter Sequence*) Quarter 5 2012 1205A&C Begins November 5, 2012 1205A Ends December 9, 2012 Session Break
1.4. Removing Brackets. Introduction. Prerequisites. Learning Outcomes. Learning Style
 Removing Brackets 1. Introduction In order to simplify an expression which contains brackets it is often necessary to rewrite the expression in an equivalent form but without any brackets. This process
Removing Brackets 1. Introduction In order to simplify an expression which contains brackets it is often necessary to rewrite the expression in an equivalent form but without any brackets. This process
SUBSTITUTION I.. f(ax + b)
 Integrtion SUBSTITUTION I.. f(x + b) Grhm S McDonld nd Silvi C Dll A Tutoril Module for prctising the integrtion of expressions of the form f(x + b) Tble of contents Begin Tutoril c 004 g.s.mcdonld@slford.c.uk
Integrtion SUBSTITUTION I.. f(x + b) Grhm S McDonld nd Silvi C Dll A Tutoril Module for prctising the integrtion of expressions of the form f(x + b) Tble of contents Begin Tutoril c 004 g.s.mcdonld@slford.c.uk
To differentiate logarithmic functions with bases other than e, use
 To ifferentiate logarithmic functions with bases other than e, use 1 1 To ifferentiate logarithmic functions with bases other than e, use log b m = ln m ln b 1 To ifferentiate logarithmic functions with
To ifferentiate logarithmic functions with bases other than e, use 1 1 To ifferentiate logarithmic functions with bases other than e, use log b m = ln m ln b 1 To ifferentiate logarithmic functions with
Exercise Set 3. Similar triangles. Parallel lines
 Exercise Set 3. Similar triangles Parallel lines Note: The exercises marked with are more difficult and go beyond the course/examination requirements. (1) Let ABC be a triangle with AB = AC. Let D be an
Exercise Set 3. Similar triangles Parallel lines Note: The exercises marked with are more difficult and go beyond the course/examination requirements. (1) Let ABC be a triangle with AB = AC. Let D be an
Find all of the real numbers x that satisfy the algebraic equation:
 Appendix C: Factoring Algebraic Expressions Factoring algebraic equations is the reverse of expanding algebraic expressions discussed in Appendix B. Factoring algebraic equations can be a great help when
Appendix C: Factoring Algebraic Expressions Factoring algebraic equations is the reverse of expanding algebraic expressions discussed in Appendix B. Factoring algebraic equations can be a great help when
CHAPTER 1. LINES AND PLANES IN SPACE
 CHAPTER 1. LINES AND PLANES IN SPACE 1. Angles and distances between skew lines 1.1. Given cube ABCDA 1 B 1 C 1 D 1 with side a. Find the angle and the distance between lines A 1 B and AC 1. 1.2. Given
CHAPTER 1. LINES AND PLANES IN SPACE 1. Angles and distances between skew lines 1.1. Given cube ABCDA 1 B 1 C 1 D 1 with side a. Find the angle and the distance between lines A 1 B and AC 1. 1.2. Given
Using the ac Method to Factor
 4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
Nonhomogeneous Linear Equations
 Nonhomogeneous Linear Equations In this section we learn how to solve second-order nonhomogeneous linear differential equations with constant coefficients, that is, equations of the form ay by cy G x where
Nonhomogeneous Linear Equations In this section we learn how to solve second-order nonhomogeneous linear differential equations with constant coefficients, that is, equations of the form ay by cy G x where
www.sakshieducation.com
 LENGTH OF THE PERPENDICULAR FROM A POINT TO A STRAIGHT LINE AND DISTANCE BETWEEN TWO PAPALLEL LINES THEOREM The perpendicular distance from a point P(x 1, y 1 ) to the line ax + by + c 0 is ax1+ by1+ c
LENGTH OF THE PERPENDICULAR FROM A POINT TO A STRAIGHT LINE AND DISTANCE BETWEEN TWO PAPALLEL LINES THEOREM The perpendicular distance from a point P(x 1, y 1 ) to the line ax + by + c 0 is ax1+ by1+ c
CS 261 Fall 2011 Solutions to Assignment #4
 CS 61 Fall 011 Solutions to Assignment #4 The following four algorithms are used to implement the bisection method, Newton s method, the secant method, and the method of false position, respectively. In
CS 61 Fall 011 Solutions to Assignment #4 The following four algorithms are used to implement the bisection method, Newton s method, the secant method, and the method of false position, respectively. In
How To Understand The Theory Of Algebraic Functions
 Homework 4 3.4,. Show that x x cos x x holds for x 0. Solution: Since cos x, multiply all three parts by x > 0, we get: x x cos x x, and since x 0 x x 0 ( x ) = 0, then by Sandwich theorem, we get: x 0
Homework 4 3.4,. Show that x x cos x x holds for x 0. Solution: Since cos x, multiply all three parts by x > 0, we get: x x cos x x, and since x 0 x x 0 ( x ) = 0, then by Sandwich theorem, we get: x 0
Factoring Methods. Example 1: 2x + 2 2 * x + 2 * 1 2(x + 1)
 Factoring Methods When you are trying to factor a polynomial, there are three general steps you want to follow: 1. See if there is a Greatest Common Factor 2. See if you can Factor by Grouping 3. See if
Factoring Methods When you are trying to factor a polynomial, there are three general steps you want to follow: 1. See if there is a Greatest Common Factor 2. See if you can Factor by Grouping 3. See if
1.4. Arithmetic of Algebraic Fractions. Introduction. Prerequisites. Learning Outcomes
 Arithmetic of Algebraic Fractions 1.4 Introduction Just as one whole number divided by another is called a numerical fraction, so one algebraic expression divided by another is known as an algebraic fraction.
Arithmetic of Algebraic Fractions 1.4 Introduction Just as one whole number divided by another is called a numerical fraction, so one algebraic expression divided by another is known as an algebraic fraction.
L 2 : x = s + 1, y = s, z = 4s + 4. 3. Suppose that C has coordinates (x, y, z). Then from the vector equality AC = BD, one has
 The line L through the points A and B is parallel to the vector AB = 3, 2, and has parametric equations x = 3t + 2, y = 2t +, z = t Therefore, the intersection point of the line with the plane should satisfy:
The line L through the points A and B is parallel to the vector AB = 3, 2, and has parametric equations x = 3t + 2, y = 2t +, z = t Therefore, the intersection point of the line with the plane should satisfy:
Section 3.7. Rolle s Theorem and the Mean Value Theorem. Difference Equations to Differential Equations
 Difference Equations to Differential Equations Section.7 Rolle s Theorem and the Mean Value Theorem The two theorems which are at the heart of this section draw connections between the instantaneous rate
Difference Equations to Differential Equations Section.7 Rolle s Theorem and the Mean Value Theorem The two theorems which are at the heart of this section draw connections between the instantaneous rate
On Triangles with Vertices on the Angle Bisectors
 Forum Geometricorum Volume 6 (2006) 247 253. FORUM GEOM SSN 1534-1178 On Triangles with Vertices on the ngle isectors Eric Danneels bstract. We study interesting properties of triangles whose vertices
Forum Geometricorum Volume 6 (2006) 247 253. FORUM GEOM SSN 1534-1178 On Triangles with Vertices on the ngle isectors Eric Danneels bstract. We study interesting properties of triangles whose vertices
Acceptance Page 2. Revision History 3. Introduction 14. Control Categories 15. Scope 15. General Requirements 15
 Acceptance Page 2 Revision History 3 Introduction 14 Control Categories 15 Scope 15 General Requirements 15 Control Category: 0.0 Information Security Management Program 17 Objective Name: 0.01 Information
Acceptance Page 2 Revision History 3 Introduction 14 Control Categories 15 Scope 15 General Requirements 15 Control Category: 0.0 Information Security Management Program 17 Objective Name: 0.01 Information
DHL EXPRESS CANADA E-BILL STANDARD SPECIFICATIONS
 DHL EXPRESS CANADA E-BILL STANDARD SPECIFICATIONS 1 E-Bill Standard Layout A B C D E F G Field/ DHL Account Number Billing Customer Name Billing Customer Address Billing Customer City Billing Customer
DHL EXPRESS CANADA E-BILL STANDARD SPECIFICATIONS 1 E-Bill Standard Layout A B C D E F G Field/ DHL Account Number Billing Customer Name Billing Customer Address Billing Customer City Billing Customer
Factoring Trinomials: The ac Method
 6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
Solutions Manual for How to Read and Do Proofs
 Solutions Manual for How to Read and Do Proofs An Introduction to Mathematical Thought Processes Sixth Edition Daniel Solow Department of Operations Weatherhead School of Management Case Western Reserve
Solutions Manual for How to Read and Do Proofs An Introduction to Mathematical Thought Processes Sixth Edition Daniel Solow Department of Operations Weatherhead School of Management Case Western Reserve
Factoring - Factoring Special Products
 6.5 Factoring - Factoring Special Products Objective: Identify and factor special products including a difference of squares, perfect squares, and sum and difference of cubes. When factoring there are
6.5 Factoring - Factoring Special Products Objective: Identify and factor special products including a difference of squares, perfect squares, and sum and difference of cubes. When factoring there are
SPECIAL PRODUCTS AND FACTORS
 CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
14.1. Basic Concepts of Integration. Introduction. Prerequisites. Learning Outcomes. Learning Style
 Basic Concepts of Integration 14.1 Introduction When a function f(x) is known we can differentiate it to obtain its derivative df. The reverse dx process is to obtain the function f(x) from knowledge of
Basic Concepts of Integration 14.1 Introduction When a function f(x) is known we can differentiate it to obtain its derivative df. The reverse dx process is to obtain the function f(x) from knowledge of
Transient Voltage Suppressor SMBJ5.0 - SMBJ440CA
 Features: Glass passivated junction Low incremental surge resistance, excellent clamping capability 600W peak pulse power capability with a 10/1,000μs waveform, repetition rate (duty cycle): 0.01% Very
Features: Glass passivated junction Low incremental surge resistance, excellent clamping capability 600W peak pulse power capability with a 10/1,000μs waveform, repetition rate (duty cycle): 0.01% Very
1.5. Factorisation. Introduction. Prerequisites. Learning Outcomes. Learning Style
 Factorisation 1.5 Introduction In Block 4 we showed the way in which brackets were removed from algebraic expressions. Factorisation, which can be considered as the reverse of this process, is dealt with
Factorisation 1.5 Introduction In Block 4 we showed the way in which brackets were removed from algebraic expressions. Factorisation, which can be considered as the reverse of this process, is dealt with
Warm-up Theorems about triangles. Geometry. Theorems about triangles. Misha Lavrov. ARML Practice 12/15/2013
 ARML Practice 12/15/2013 Problem Solution Warm-up problem Lunes of Hippocrates In the diagram below, the blue triangle is a right triangle with side lengths 3, 4, and 5. What is the total area of the green
ARML Practice 12/15/2013 Problem Solution Warm-up problem Lunes of Hippocrates In the diagram below, the blue triangle is a right triangle with side lengths 3, 4, and 5. What is the total area of the green
Future Trends in Airline Pricing, Yield. March 13, 2013
 Future Trends in Airline Pricing, Yield Management, &AncillaryFees March 13, 2013 THE OPPORTUNITY IS NOW FOR CORPORATE TRAVEL MANAGEMENT BUT FIRST: YOU HAVE TO KNOCK DOWN BARRIERS! but it won t hurt much!
Future Trends in Airline Pricing, Yield Management, &AncillaryFees March 13, 2013 THE OPPORTUNITY IS NOW FOR CORPORATE TRAVEL MANAGEMENT BUT FIRST: YOU HAVE TO KNOCK DOWN BARRIERS! but it won t hurt much!
Chapter. Numerical Calculations
 Chapter 3 Numerical Calculations 3-1 Before Performing a Calculation 3-2 Differential Calculations 3-3 Quadratic Differential Calculations 3-4 Integration Calculations 3-5 Maximum/Minimum Value Calculations
Chapter 3 Numerical Calculations 3-1 Before Performing a Calculation 3-2 Differential Calculations 3-3 Quadratic Differential Calculations 3-4 Integration Calculations 3-5 Maximum/Minimum Value Calculations
INTEGRATING FACTOR METHOD
 Differential Equations INTEGRATING FACTOR METHOD Graham S McDonald A Tutorial Module for learning to solve 1st order linear differential equations Table of contents Begin Tutorial c 2004 g.s.mcdonald@salford.ac.uk
Differential Equations INTEGRATING FACTOR METHOD Graham S McDonald A Tutorial Module for learning to solve 1st order linear differential equations Table of contents Begin Tutorial c 2004 g.s.mcdonald@salford.ac.uk
calculating the result modulo 3, as follows: p(0) = 0 3 + 0 + 1 = 1 0,
 Homework #02, due 1/27/10 = 9.4.1, 9.4.2, 9.4.5, 9.4.6, 9.4.7. Additional problems recommended for study: (9.4.3), 9.4.4, 9.4.9, 9.4.11, 9.4.13, (9.4.14), 9.4.17 9.4.1 Determine whether the following polynomials
Homework #02, due 1/27/10 = 9.4.1, 9.4.2, 9.4.5, 9.4.6, 9.4.7. Additional problems recommended for study: (9.4.3), 9.4.4, 9.4.9, 9.4.11, 9.4.13, (9.4.14), 9.4.17 9.4.1 Determine whether the following polynomials
Factoring Polynomials: Factoring by Grouping
 OpenStax-CNX module: m21901 1 Factoring Polynomials: Factoring by Grouping Wade Ellis Denny Burzynski This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 3.0
OpenStax-CNX module: m21901 1 Factoring Polynomials: Factoring by Grouping Wade Ellis Denny Burzynski This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 3.0
Sequences and Series
 Sequences and Series Consider the following sum: 2 + 4 + 8 + 6 + + 2 i + The dots at the end indicate that the sum goes on forever. Does this make sense? Can we assign a numerical value to an infinite
Sequences and Series Consider the following sum: 2 + 4 + 8 + 6 + + 2 i + The dots at the end indicate that the sum goes on forever. Does this make sense? Can we assign a numerical value to an infinite
Lecture 3: Derivatives and extremes of functions
 Lecture 3: Derivatives and extremes of functions Lejla Batina Institute for Computing and Information Sciences Digital Security Version: spring 2011 Lejla Batina Version: spring 2011 Wiskunde 1 1 / 16
Lecture 3: Derivatives and extremes of functions Lejla Batina Institute for Computing and Information Sciences Digital Security Version: spring 2011 Lejla Batina Version: spring 2011 Wiskunde 1 1 / 16
Factoring a Difference of Two Squares. Factoring a Difference of Two Squares
 284 (6 8) Chapter 6 Factoring 87. Tomato soup. The amount of metal S (in square inches) that it takes to make a can for tomato soup is a function of the radius r and height h: S 2 r 2 2 rh a) Rewrite this
284 (6 8) Chapter 6 Factoring 87. Tomato soup. The amount of metal S (in square inches) that it takes to make a can for tomato soup is a function of the radius r and height h: S 2 r 2 2 rh a) Rewrite this
Techniques of Integration
 8 Techniques of Integration Over the next few sections we examine some techniques that are frequently successful when seeking antiderivatives of functions. Sometimes this is a simple problem, since it
8 Techniques of Integration Over the next few sections we examine some techniques that are frequently successful when seeking antiderivatives of functions. Sometimes this is a simple problem, since it
San Jose Math Circle April 25 - May 2, 2009 ANGLE BISECTORS
 San Jose Math Circle April 25 - May 2, 2009 ANGLE BISECTORS Recall that the bisector of an angle is the ray that divides the angle into two congruent angles. The most important results about angle bisectors
San Jose Math Circle April 25 - May 2, 2009 ANGLE BISECTORS Recall that the bisector of an angle is the ray that divides the angle into two congruent angles. The most important results about angle bisectors
Solutions to old Exam 1 problems
 Solutions to old Exam 1 problems Hi students! I am putting this old version of my review for the first midterm review, place and time to be announced. Check for updates on the web site as to which sections
Solutions to old Exam 1 problems Hi students! I am putting this old version of my review for the first midterm review, place and time to be announced. Check for updates on the web site as to which sections
Algebra I Vocabulary Cards
 Algebra I Vocabulary Cards Table of Contents Expressions and Operations Natural Numbers Whole Numbers Integers Rational Numbers Irrational Numbers Real Numbers Absolute Value Order of Operations Expression
Algebra I Vocabulary Cards Table of Contents Expressions and Operations Natural Numbers Whole Numbers Integers Rational Numbers Irrational Numbers Real Numbers Absolute Value Order of Operations Expression
tegrals as General & Particular Solutions
 tegrals as General & Particular Solutions dy dx = f(x) General Solution: y(x) = f(x) dx + C Particular Solution: dy dx = f(x), y(x 0) = y 0 Examples: 1) dy dx = (x 2)2 ;y(2) = 1; 2) dy ;y(0) = 0; 3) dx
tegrals as General & Particular Solutions dy dx = f(x) General Solution: y(x) = f(x) dx + C Particular Solution: dy dx = f(x), y(x 0) = y 0 Examples: 1) dy dx = (x 2)2 ;y(2) = 1; 2) dy ;y(0) = 0; 3) dx
2 Integrating Both Sides
 2 Integrating Both Sides So far, the only general method we have for solving differential equations involves equations of the form y = f(x), where f(x) is any function of x. The solution to such an equation
2 Integrating Both Sides So far, the only general method we have for solving differential equations involves equations of the form y = f(x), where f(x) is any function of x. The solution to such an equation
PUTNAM TRAINING POLYNOMIALS. Exercises 1. Find a polynomial with integral coefficients whose zeros include 2 + 5.
 PUTNAM TRAINING POLYNOMIALS (Last updated: November 17, 2015) Remark. This is a list of exercises on polynomials. Miguel A. Lerma Exercises 1. Find a polynomial with integral coefficients whose zeros include
PUTNAM TRAINING POLYNOMIALS (Last updated: November 17, 2015) Remark. This is a list of exercises on polynomials. Miguel A. Lerma Exercises 1. Find a polynomial with integral coefficients whose zeros include
Homework # 3 Solutions
 Homework # 3 Solutions February, 200 Solution (2.3.5). Noting that and ( + 3 x) x 8 = + 3 x) by Equation (2.3.) x 8 x 8 = + 3 8 by Equations (2.3.7) and (2.3.0) =3 x 8 6x2 + x 3 ) = 2 + 6x 2 + x 3 x 8
Homework # 3 Solutions February, 200 Solution (2.3.5). Noting that and ( + 3 x) x 8 = + 3 x) by Equation (2.3.) x 8 x 8 = + 3 8 by Equations (2.3.7) and (2.3.0) =3 x 8 6x2 + x 3 ) = 2 + 6x 2 + x 3 x 8
Vehicle Identification Numbering System 00.03
 Vehicle Identification Numbering System 00.03 IMPORTANT: See Subject 050 for the vehicle identification numbering system for vehicles built before May 1, 2000. Federal Motor Vehicle Safety Standard 115
Vehicle Identification Numbering System 00.03 IMPORTANT: See Subject 050 for the vehicle identification numbering system for vehicles built before May 1, 2000. Federal Motor Vehicle Safety Standard 115
Chapter 11 Balanced Three-Phase Circuits
 Chapter 11 Balanced Three-Phase Circuits 11.1-2 Three-Phase Systems 11.3 Analysis of the Y-Y Circuit 11.4 Analysis of the Y- Circuit 11.5 Power Calculations in Balanced Three-Phase Circuits 11.6 Measuring
Chapter 11 Balanced Three-Phase Circuits 11.1-2 Three-Phase Systems 11.3 Analysis of the Y-Y Circuit 11.4 Analysis of the Y- Circuit 11.5 Power Calculations in Balanced Three-Phase Circuits 11.6 Measuring
Calculus 1: Sample Questions, Final Exam, Solutions
 Calculus : Sample Questions, Final Exam, Solutions. Short answer. Put your answer in the blank. NO PARTIAL CREDIT! (a) (b) (c) (d) (e) e 3 e Evaluate dx. Your answer should be in the x form of an integer.
Calculus : Sample Questions, Final Exam, Solutions. Short answer. Put your answer in the blank. NO PARTIAL CREDIT! (a) (b) (c) (d) (e) e 3 e Evaluate dx. Your answer should be in the x form of an integer.
The Greatest Common Factor; Factoring by Grouping
 296 CHAPTER 5 Factoring and Applications 5.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
296 CHAPTER 5 Factoring and Applications 5.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
BALANCED THREE-PHASE AC CIRCUIT
 BAANCED THREE-PHASE AC CRCUT Balanced Three-Phase oltage Sources Delta Connection Star Connection Balanced 3-hase oad Delta Connection Star Connection Power in a Balanced Phase Circuit ntroduction Three
BAANCED THREE-PHASE AC CRCUT Balanced Three-Phase oltage Sources Delta Connection Star Connection Balanced 3-hase oad Delta Connection Star Connection Power in a Balanced Phase Circuit ntroduction Three
MATH 381 HOMEWORK 2 SOLUTIONS
 MATH 38 HOMEWORK SOLUTIONS Question (p.86 #8). If g(x)[e y e y ] is harmonic, g() =,g () =, find g(x). Let f(x, y) = g(x)[e y e y ].Then Since f(x, y) is harmonic, f + f = and we require x y f x = g (x)[e
MATH 38 HOMEWORK SOLUTIONS Question (p.86 #8). If g(x)[e y e y ] is harmonic, g() =,g () =, find g(x). Let f(x, y) = g(x)[e y e y ].Then Since f(x, y) is harmonic, f + f = and we require x y f x = g (x)[e
Math 312 Homework 1 Solutions
 Math 31 Homework 1 Solutions Last modified: July 15, 01 This homework is due on Thursday, July 1th, 01 at 1:10pm Please turn it in during class, or in my mailbox in the main math office (next to 4W1) Please
Math 31 Homework 1 Solutions Last modified: July 15, 01 This homework is due on Thursday, July 1th, 01 at 1:10pm Please turn it in during class, or in my mailbox in the main math office (next to 4W1) Please
Section 2.7 One-to-One Functions and Their Inverses
 Section. One-to-One Functions and Their Inverses One-to-One Functions HORIZONTAL LINE TEST: A function is one-to-one if and only if no horizontal line intersects its graph more than once. EXAMPLES: 1.
Section. One-to-One Functions and Their Inverses One-to-One Functions HORIZONTAL LINE TEST: A function is one-to-one if and only if no horizontal line intersects its graph more than once. EXAMPLES: 1.
u dx + y = 0 z x z x = x + y + 2 + 2 = 0 6) 2
 DIFFERENTIAL EQUATIONS 6 Many physical problems, when formulated in mathematical forms, lead to differential equations. Differential equations enter naturally as models for many phenomena in economics,
DIFFERENTIAL EQUATIONS 6 Many physical problems, when formulated in mathematical forms, lead to differential equations. Differential equations enter naturally as models for many phenomena in economics,
Inverse Functions and Logarithms
 Section 3. Inverse Functions and Logarithms 1 Kiryl Tsishchanka Inverse Functions and Logarithms DEFINITION: A function f is called a one-to-one function if it never takes on the same value twice; that
Section 3. Inverse Functions and Logarithms 1 Kiryl Tsishchanka Inverse Functions and Logarithms DEFINITION: A function f is called a one-to-one function if it never takes on the same value twice; that
19.6. Finding a Particular Integral. Introduction. Prerequisites. Learning Outcomes. Learning Style
 Finding a Particular Integral 19.6 Introduction We stated in Block 19.5 that the general solution of an inhomogeneous equation is the sum of the complementary function and a particular integral. We have
Finding a Particular Integral 19.6 Introduction We stated in Block 19.5 that the general solution of an inhomogeneous equation is the sum of the complementary function and a particular integral. We have
Using a table of derivatives
 Using a table of derivatives In this unit we construct a Table of Derivatives of commonly occurring functions. This is done using the knowledge gained in previous units on differentiation from first principles.
Using a table of derivatives In this unit we construct a Table of Derivatives of commonly occurring functions. This is done using the knowledge gained in previous units on differentiation from first principles.
2. Let H and K be subgroups of a group G. Show that H K G if and only if H K or K H.
 Math 307 Abstract Algebra Sample final examination questions with solutions 1. Suppose that H is a proper subgroup of Z under addition and H contains 18, 30 and 40, Determine H. Solution. Since gcd(18,
Math 307 Abstract Algebra Sample final examination questions with solutions 1. Suppose that H is a proper subgroup of Z under addition and H contains 18, 30 and 40, Determine H. Solution. Since gcd(18,
Function Name Algebra. Parent Function. Characteristics. Harold s Parent Functions Cheat Sheet 28 December 2015
 Harold s s Cheat Sheet 8 December 05 Algebra Constant Linear Identity f(x) c f(x) x Range: [c, c] Undefined (asymptote) Restrictions: c is a real number Ay + B 0 g(x) x Restrictions: m 0 General Fms: Ax
Harold s s Cheat Sheet 8 December 05 Algebra Constant Linear Identity f(x) c f(x) x Range: [c, c] Undefined (asymptote) Restrictions: c is a real number Ay + B 0 g(x) x Restrictions: m 0 General Fms: Ax
3. INNER PRODUCT SPACES
 . INNER PRODUCT SPACES.. Definition So far we have studied abstract vector spaces. These are a generalisation of the geometric spaces R and R. But these have more structure than just that of a vector space.
. INNER PRODUCT SPACES.. Definition So far we have studied abstract vector spaces. These are a generalisation of the geometric spaces R and R. But these have more structure than just that of a vector space.
Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder).
 Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Taylor and Maclaurin Series
 Taylor and Maclaurin Series In the preceding section we were able to find power series representations for a certain restricted class of functions. Here we investigate more general problems: Which functions
Taylor and Maclaurin Series In the preceding section we were able to find power series representations for a certain restricted class of functions. Here we investigate more general problems: Which functions
Exam 1 Sample Question SOLUTIONS. y = 2x
 Exam Sample Question SOLUTIONS. Eliminate the parameter to find a Cartesian equation for the curve: x e t, y e t. SOLUTION: You might look at the coordinates and notice that If you don t see it, we can
Exam Sample Question SOLUTIONS. Eliminate the parameter to find a Cartesian equation for the curve: x e t, y e t. SOLUTION: You might look at the coordinates and notice that If you don t see it, we can
Partial Fractions Examples
 Partial Fractions Examples Partial fractions is the name given to a technique of integration that may be used to integrate any ratio of polynomials. A ratio of polynomials is called a rational function.
Partial Fractions Examples Partial fractions is the name given to a technique of integration that may be used to integrate any ratio of polynomials. A ratio of polynomials is called a rational function.
6 Commutators and the derived series. [x,y] = xyx 1 y 1.
![6 Commutators and the derived series. [x,y] = xyx 1 y 1. 6 Commutators and the derived series. [x,y] = xyx 1 y 1.](/thumbs/19/254057.jpg) 6 Commutators and the derived series Definition. Let G be a group, and let x,y G. The commutator of x and y is [x,y] = xyx 1 y 1. Note that [x,y] = e if and only if xy = yx (since x 1 y 1 = (yx) 1 ). Proposition
6 Commutators and the derived series Definition. Let G be a group, and let x,y G. The commutator of x and y is [x,y] = xyx 1 y 1. Note that [x,y] = e if and only if xy = yx (since x 1 y 1 = (yx) 1 ). Proposition
TOPPER Sample Paper - I. Class : XI MATHEMATICS. Questions. Time Allowed : 3 Hrs Maximum Marks: 100
 TOPPER Sample Paper - I Class : XI MATHEMATICS Questions Time Allowed : 3 Hrs Maximum Marks: 100 1. All questions are compulsory.. The question paper consist of 9 questions divided into three sections
TOPPER Sample Paper - I Class : XI MATHEMATICS Questions Time Allowed : 3 Hrs Maximum Marks: 100 1. All questions are compulsory.. The question paper consist of 9 questions divided into three sections
Algebra (Expansion and Factorisation)
 Chapter10 Algebra (Expansion and Factorisation) Contents: A B C D E F The distributive law Siplifying algebraic expressions Brackets with negative coefficients The product (a + b)(c + d) Geoetric applications
Chapter10 Algebra (Expansion and Factorisation) Contents: A B C D E F The distributive law Siplifying algebraic expressions Brackets with negative coefficients The product (a + b)(c + d) Geoetric applications
Factoring Special Polynomials
 6.6 Factoring Special Polynomials 6.6 OBJECTIVES 1. Factor the difference of two squares 2. Factor the sum or difference of two cubes In this section, we will look at several special polynomials. These
6.6 Factoring Special Polynomials 6.6 OBJECTIVES 1. Factor the difference of two squares 2. Factor the sum or difference of two cubes In this section, we will look at several special polynomials. These
Tim Kerins. Leaving Certificate Honours Maths - Algebra. Tim Kerins. the date
 Leaving Certificate Honours Maths - Algebra the date Chapter 1 Algebra This is an important portion of the course. As well as generally accounting for 2 3 questions in examination it is the basis for many
Leaving Certificate Honours Maths - Algebra the date Chapter 1 Algebra This is an important portion of the course. As well as generally accounting for 2 3 questions in examination it is the basis for many
SAT Subject Test Practice Test II: Math Level II Time 60 minutes, 50 Questions
 SAT Subject Test Practice Test II: Math Level II Time 60 minutes, 50 Questions All questions in the Math Level 1 and Math Level Tests are multiple-choice questions in which you are asked to choose the
SAT Subject Test Practice Test II: Math Level II Time 60 minutes, 50 Questions All questions in the Math Level 1 and Math Level Tests are multiple-choice questions in which you are asked to choose the
SOLUTIONS. f x = 6x 2 6xy 24x, f y = 3x 2 6y. To find the critical points, we solve
 SOLUTIONS Problem. Find the critical points of the function f(x, y = 2x 3 3x 2 y 2x 2 3y 2 and determine their type i.e. local min/local max/saddle point. Are there any global min/max? Partial derivatives
SOLUTIONS Problem. Find the critical points of the function f(x, y = 2x 3 3x 2 y 2x 2 3y 2 and determine their type i.e. local min/local max/saddle point. Are there any global min/max? Partial derivatives
ALGEBRA REVIEW LEARNING SKILLS CENTER. Exponents & Radicals
 ALGEBRA REVIEW LEARNING SKILLS CENTER The "Review Series in Algebra" is taught at the beginning of each quarter by the staff of the Learning Skills Center at UC Davis. This workshop is intended to be an
ALGEBRA REVIEW LEARNING SKILLS CENTER The "Review Series in Algebra" is taught at the beginning of each quarter by the staff of the Learning Skills Center at UC Davis. This workshop is intended to be an
0.4 FACTORING POLYNOMIALS
 36_.qxd /3/5 :9 AM Page -9 SECTION. Factoring Polynomials -9. FACTORING POLYNOMIALS Use special products and factorization techniques to factor polynomials. Find the domains of radical expressions. Use
36_.qxd /3/5 :9 AM Page -9 SECTION. Factoring Polynomials -9. FACTORING POLYNOMIALS Use special products and factorization techniques to factor polynomials. Find the domains of radical expressions. Use
Intermediate Value Theorem, Rolle s Theorem and Mean Value Theorem
 Intermediate Value Theorem, Rolle s Theorem and Mean Value Theorem February 21, 214 In many problems, you are asked to show that something exists, but are not required to give a specific example or formula
Intermediate Value Theorem, Rolle s Theorem and Mean Value Theorem February 21, 214 In many problems, you are asked to show that something exists, but are not required to give a specific example or formula
www.pioneermathematics.com
 Problems and Solutions: INMO-2012 1. Let ABCD be a quadrilateral inscribed in a circle. Suppose AB = 2+ 2 and AB subtends 135 at the centre of the circle. Find the maximum possible area of ABCD. Solution:
Problems and Solutions: INMO-2012 1. Let ABCD be a quadrilateral inscribed in a circle. Suppose AB = 2+ 2 and AB subtends 135 at the centre of the circle. Find the maximum possible area of ABCD. Solution:
4. Binomial Expansions
 4. Binomial Expansions 4.. Pascal's Triangle The expansion of (a + x) 2 is (a + x) 2 = a 2 + 2ax + x 2 Hence, (a + x) 3 = (a + x)(a + x) 2 = (a + x)(a 2 + 2ax + x 2 ) = a 3 + ( + 2)a 2 x + (2 + )ax 2 +
4. Binomial Expansions 4.. Pascal's Triangle The expansion of (a + x) 2 is (a + x) 2 = a 2 + 2ax + x 2 Hence, (a + x) 3 = (a + x)(a + x) 2 = (a + x)(a 2 + 2ax + x 2 ) = a 3 + ( + 2)a 2 x + (2 + )ax 2 +
Polynomials. Key Terms. quadratic equation parabola conjugates trinomial. polynomial coefficient degree monomial binomial GCF
 Polynomials 5 5.1 Addition and Subtraction of Polynomials and Polynomial Functions 5.2 Multiplication of Polynomials 5.3 Division of Polynomials Problem Recognition Exercises Operations on Polynomials
Polynomials 5 5.1 Addition and Subtraction of Polynomials and Polynomial Functions 5.2 Multiplication of Polynomials 5.3 Division of Polynomials Problem Recognition Exercises Operations on Polynomials
Factoring Polynomials
 UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
Solutions for Review Problems
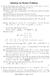 olutions for Review Problems 1. Let be the triangle with vertices A (,, ), B (4,, 1) and C (,, 1). (a) Find the cosine of the angle BAC at vertex A. (b) Find the area of the triangle ABC. (c) Find a vector
olutions for Review Problems 1. Let be the triangle with vertices A (,, ), B (4,, 1) and C (,, 1). (a) Find the cosine of the angle BAC at vertex A. (b) Find the area of the triangle ABC. (c) Find a vector
a 1 x + a 0 =0. (3) ax 2 + bx + c =0. (4)
 ROOTS OF POLYNOMIAL EQUATIONS In this unit we discuss polynomial equations. A polynomial in x of degree n, where n 0 is an integer, is an expression of the form P n (x) =a n x n + a n 1 x n 1 + + a 1 x
ROOTS OF POLYNOMIAL EQUATIONS In this unit we discuss polynomial equations. A polynomial in x of degree n, where n 0 is an integer, is an expression of the form P n (x) =a n x n + a n 1 x n 1 + + a 1 x
T ( a i x i ) = a i T (x i ).
 Chapter 2 Defn 1. (p. 65) Let V and W be vector spaces (over F ). We call a function T : V W a linear transformation form V to W if, for all x, y V and c F, we have (a) T (x + y) = T (x) + T (y) and (b)
Chapter 2 Defn 1. (p. 65) Let V and W be vector spaces (over F ). We call a function T : V W a linear transformation form V to W if, for all x, y V and c F, we have (a) T (x + y) = T (x) + T (y) and (b)
100. In general, we can define this as if b x = a then x = log b
 Exponents and Logarithms Review 1. Solving exponential equations: Solve : a)8 x = 4! x! 3 b)3 x+1 + 9 x = 18 c)3x 3 = 1 3. Recall: Terminology of Logarithms If 10 x = 100 then of course, x =. However,
Exponents and Logarithms Review 1. Solving exponential equations: Solve : a)8 x = 4! x! 3 b)3 x+1 + 9 x = 18 c)3x 3 = 1 3. Recall: Terminology of Logarithms If 10 x = 100 then of course, x =. However,
RESULTANT AND DISCRIMINANT OF POLYNOMIALS
 RESULTANT AND DISCRIMINANT OF POLYNOMIALS SVANTE JANSON Abstract. This is a collection of classical results about resultants and discriminants for polynomials, compiled mainly for my own use. All results
RESULTANT AND DISCRIMINANT OF POLYNOMIALS SVANTE JANSON Abstract. This is a collection of classical results about resultants and discriminants for polynomials, compiled mainly for my own use. All results
Solutions to TOPICS IN ALGEBRA I.N. HERSTEIN. Part II: Group Theory
 Solutions to TOPICS IN ALGEBRA I.N. HERSTEIN Part II: Group Theory No rights reserved. Any part of this work can be reproduced or transmitted in any form or by any means. Version: 1.1 Release: Jan 2013
Solutions to TOPICS IN ALGEBRA I.N. HERSTEIN Part II: Group Theory No rights reserved. Any part of this work can be reproduced or transmitted in any form or by any means. Version: 1.1 Release: Jan 2013
Solving DEs by Separation of Variables.
 Solving DEs by Separation of Variables. Introduction and procedure Separation of variables allows us to solve differential equations of the form The steps to solving such DEs are as follows: dx = gx).
Solving DEs by Separation of Variables. Introduction and procedure Separation of variables allows us to solve differential equations of the form The steps to solving such DEs are as follows: dx = gx).
Chapter 7. Matrices. Definition. An m n matrix is an array of numbers set out in m rows and n columns. Examples. ( 1 1 5 2 0 6
 Chapter 7 Matrices Definition An m n matrix is an array of numbers set out in m rows and n columns Examples (i ( 1 1 5 2 0 6 has 2 rows and 3 columns and so it is a 2 3 matrix (ii 1 0 7 1 2 3 3 1 is a
Chapter 7 Matrices Definition An m n matrix is an array of numbers set out in m rows and n columns Examples (i ( 1 1 5 2 0 6 has 2 rows and 3 columns and so it is a 2 3 matrix (ii 1 0 7 1 2 3 3 1 is a
AP Calculus BC Exam. The Calculus BC Exam. At a Glance. Section I. SECTION I: Multiple-Choice Questions. Instructions. About Guessing.
 The Calculus BC Exam AP Calculus BC Exam SECTION I: Multiple-Choice Questions At a Glance Total Time 1 hour, 45 minutes Number of Questions 45 Percent of Total Grade 50% Writing Instrument Pencil required
The Calculus BC Exam AP Calculus BC Exam SECTION I: Multiple-Choice Questions At a Glance Total Time 1 hour, 45 minutes Number of Questions 45 Percent of Total Grade 50% Writing Instrument Pencil required
Baltic Way 1995. Västerås (Sweden), November 12, 1995. Problems and solutions
 Baltic Way 995 Västerås (Sweden), November, 995 Problems and solutions. Find all triples (x, y, z) of positive integers satisfying the system of equations { x = (y + z) x 6 = y 6 + z 6 + 3(y + z ). Solution.
Baltic Way 995 Västerås (Sweden), November, 995 Problems and solutions. Find all triples (x, y, z) of positive integers satisfying the system of equations { x = (y + z) x 6 = y 6 + z 6 + 3(y + z ). Solution.
SMT 2014 Algebra Test Solutions February 15, 2014
 1. Alice and Bob are painting a house. If Alice and Bob do not take any breaks, they will finish painting the house in 20 hours. If, however, Bob stops painting once the house is half-finished, then the
1. Alice and Bob are painting a house. If Alice and Bob do not take any breaks, they will finish painting the house in 20 hours. If, however, Bob stops painting once the house is half-finished, then the
4.3 Lagrange Approximation
 206 CHAP. 4 INTERPOLATION AND POLYNOMIAL APPROXIMATION Lagrange Polynomial Approximation 4.3 Lagrange Approximation Interpolation means to estimate a missing function value by taking a weighted average
206 CHAP. 4 INTERPOLATION AND POLYNOMIAL APPROXIMATION Lagrange Polynomial Approximation 4.3 Lagrange Approximation Interpolation means to estimate a missing function value by taking a weighted average
correct-choice plot f(x) and draw an approximate tangent line at x = a and use geometry to estimate its slope comment The choices were:
 Topic 1 2.1 mode MultipleSelection text How can we approximate the slope of the tangent line to f(x) at a point x = a? This is a Multiple selection question, so you need to check all of the answers that
Topic 1 2.1 mode MultipleSelection text How can we approximate the slope of the tangent line to f(x) at a point x = a? This is a Multiple selection question, so you need to check all of the answers that
Operations with Algebraic Expressions: Multiplication of Polynomials
 Operations with Algebraic Expressions: Multiplication of Polynomials The product of a monomial x monomial To multiply a monomial times a monomial, multiply the coefficients and add the on powers with the
Operations with Algebraic Expressions: Multiplication of Polynomials The product of a monomial x monomial To multiply a monomial times a monomial, multiply the coefficients and add the on powers with the
Paper Reference. Ruler graduated in centimetres and millimetres, protractor, compasses, pen, HB pencil, eraser. Tracing paper may be used.
 Centre No. Candidate No. Paper Reference 1 3 8 0 3 H Paper Reference(s) 1380/3H Edexcel GCSE Mathematics (Linear) 1380 Paper 3 (Non-Calculator) Higher Tier Monday 18 May 2009 Afternoon Time: 1 hour 45
Centre No. Candidate No. Paper Reference 1 3 8 0 3 H Paper Reference(s) 1380/3H Edexcel GCSE Mathematics (Linear) 1380 Paper 3 (Non-Calculator) Higher Tier Monday 18 May 2009 Afternoon Time: 1 hour 45
1. First-order Ordinary Differential Equations
 Advanced Engineering Mathematics 1. First-order ODEs 1 1. First-order Ordinary Differential Equations 1.1 Basic concept and ideas 1.2 Geometrical meaning of direction fields 1.3 Separable differential
Advanced Engineering Mathematics 1. First-order ODEs 1 1. First-order Ordinary Differential Equations 1.1 Basic concept and ideas 1.2 Geometrical meaning of direction fields 1.3 Separable differential
LINEAR MAPS, THE TOTAL DERIVATIVE AND THE CHAIN RULE. Contents
 LINEAR MAPS, THE TOTAL DERIVATIVE AND THE CHAIN RULE ROBERT LIPSHITZ Abstract We will discuss the notion of linear maps and introduce the total derivative of a function f : R n R m as a linear map We will
LINEAR MAPS, THE TOTAL DERIVATIVE AND THE CHAIN RULE ROBERT LIPSHITZ Abstract We will discuss the notion of linear maps and introduce the total derivative of a function f : R n R m as a linear map We will
Factoring Polynomials
 Factoring Polynomials 4-1-2014 The opposite of multiplying polynomials is factoring. Why would you want to factor a polynomial? Let p(x) be a polynomial. p(c) = 0 is equivalent to x c dividing p(x). Recall
Factoring Polynomials 4-1-2014 The opposite of multiplying polynomials is factoring. Why would you want to factor a polynomial? Let p(x) be a polynomial. p(c) = 0 is equivalent to x c dividing p(x). Recall
BEGINNING ALGEBRA ACKNOWLEDMENTS
 BEGINNING ALGEBRA The Nursing Department of Labouré College requested the Department of Academic Planning and Support Services to help with mathematics preparatory materials for its Bachelor of Science
BEGINNING ALGEBRA The Nursing Department of Labouré College requested the Department of Academic Planning and Support Services to help with mathematics preparatory materials for its Bachelor of Science
PROBLEM SET 6: POLYNOMIALS
 PROBLEM SET 6: POLYNOMIALS 1. introduction In this problem set we will consider polynomials with coefficients in K, where K is the real numbers R, the complex numbers C, the rational numbers Q or any other
PROBLEM SET 6: POLYNOMIALS 1. introduction In this problem set we will consider polynomials with coefficients in K, where K is the real numbers R, the complex numbers C, the rational numbers Q or any other
Approximating functions by Taylor Polynomials.
 Chapter 4 Approximating functions by Taylor Polynomials. 4.1 Linear Approximations We have already seen how to approximate a function using its tangent line. This was the key idea in Euler s method. If
Chapter 4 Approximating functions by Taylor Polynomials. 4.1 Linear Approximations We have already seen how to approximate a function using its tangent line. This was the key idea in Euler s method. If
POINT OF INTERSECTION OF TWO STRAIGHT LINES
 POINT OF INTERSECTION OF TWO STRAIGHT LINES THEOREM The point of intersection of the two non parallel lines bc bc ca ca a x + b y + c = 0, a x + b y + c = 0 is,. ab ab ab ab Proof: The lines are not parallel
POINT OF INTERSECTION OF TWO STRAIGHT LINES THEOREM The point of intersection of the two non parallel lines bc bc ca ca a x + b y + c = 0, a x + b y + c = 0 is,. ab ab ab ab Proof: The lines are not parallel

