Two-Dimensional Motion and Vectors
|
|
|
- Pauline Norman
- 7 years ago
- Views:
Transcription
1 CHAPTER 3 Planning Guide OBJECTIVES LABS, DEMONSTRATIONS, AND ACTIVITIES TECHNOLOGY RESOURCES PACING 45 min pp ANC Discovery Lab Vector Treasure Hunt* b CD Visual Concepts, Chapter 3 b Chapter Opener PACING 45 min pp Section 1 Introduction to Vectors Distinguish between a scalar and a vector. Add and subtract vectors by using the graphical method. Multiply and divide vectors by scalars. PACING 45 min pp Section 2 Vector Operations Identify appropriate coordinate systems for solving problems with vectors. Apply the Pythagorean theorem and tangent function to calculate the magnitude and direction of a resultant vector. Resolve vectors into components using the sine and cosine functions. Add vectors that are not perpendicular. PACING 135 min pp Section 3 Projectile Motion Recognize examples of projectile motion. Describe the path of a projectile as a parabola. Resolve vectors into their components and apply the kinematic equations to solve problems involving projectile motion. Two-Dimensional Motion and Vectors TE Demonstration Vector Addition, p. 83 g TE Demonstration Air Resistance, p. 96 g SE Quick Lab Projectile Motion, p. 97 g SE Inquiry Lab Velocity of a Projectile, pp ANC Datasheet Inquiry Lab, Velocity of a Projectile* g ANC Datasheet Skills Practice Lab, Velocity of a Projectile* ANC Invention Lab The Path of a Human Cannonball* ANC CBL TM Experiment Projectile Motion* a OSP Lesson Plans TR 6 Graphical Method of Vector Addition TR 14A Commutative Property of Vectors OSP Lesson Plans TR 15A The Pythagorean Theorem and the Tangent Function TR 16A Adding Vectors That Are Not Perpendicular TR 17A Adding Vectors Algebraically OSP Lesson Plans TR 7 Vertical Motion of a Projectile PACING 45 min pp Advanced Level OSP Lesson Plans Section 4 Relative Motion TR 8 Frames of Reference Describe situations in terms of frame of reference. Solve problems involving relative velocity. Compression Guide To shorten instruction because of time limitations, omit the opener and Section 4 and abbreviate the review. PACING 90 min CHAPTER REVIEW, ASSESSMENT, AND STANDARDIZED TEST PREPARATION SE Chapter Highlights, p. 107 SE Chapter Review, pp SE Graphing Calculator Practice, p. 113 g SE Alternative Assessment, p. 113 a SE Standardized Test Prep, pp g SE Appendix D: Equations, pp SE Appendix I: Additional Problems, pp ANC Study Guide Worksheet Mixed Review* g ANC Chapter Test A* g ANC Chapter Test B* a OSP Test Generator Online and Technology Resources Visit go.hrw.com to find a variety of online resources. To access this chapter s extensions, enter the keyword HF6TDMXT and click the go button. Click Holt Online Learning for an online edition of this textbook, and other interactive resources. This DVD package includes: Holt Calendar Planner Customizable Lesson Plans Editable Worksheets ExamView Version 6 Assessment Suite Interactive Teacher s Edition Holt PuzzlePro Holt PowerPoint Resources MindPoint Quiz Show 80A Chapter 3 Two-Dimensional Motion and Vectors
2 KEY SE Student Edition TE Teacher Edition ANC Ancillary Worksheet OSP One-Stop Planner CD CD or CD-ROM TR Teaching Transparencies EXT Online Extension * Also on One-Stop Planner Requires advance prep SKILLS DEVELOPMENT RESOURCES REVIEW AND ASSESSMENT CORRELATIONS National Science Education Standards SE Section Review, p. 85 g ANC Study Guide Worksheet Section 1* g ANC Quiz Section 1* b UCP 2, 3 SAI 1, 2 SE Sample Set A Finding Resultant Magnitude, pp g TE Classroom Practice, p. 88 g ANC Problem Workbook* and OSP Problem Bank Sample Set A g SE Sample Set B Resolving Vectors, pp g TE Classroom Practice, p. 91 g ANC Problem Workbook* and OSP Problem Bank Sample Set B g SE Sample Set C Adding Vectors Algebraically, pp g TE Classroom Practice, p. 93 g ANC Problem Workbook* and OSP Problem Bank Sample Set C g SE Sample Set D Projectiles Launched Horizontally, pp g TE Classroom Practice, p. 98 g ANC Problem Workbook* and OSP Problem Bank Sample Set D g SE Sample Set E Projectiles Launched at an Angle, pp g TE Classroom Practice, p. 100 g ANC Problem Workbook* and OSP Problem Bank Sample Set E g SE Section Review, p. 94 g ANC Study Guide Worksheet Section 2* g ANC Quiz Section 2* b SE Section Review, p. 101 g ANC Study Guide Worksheet Section 3* g ANC Quiz Section 3* b UCP 2, 3 UCP 2, 3 SAI 1, 2 SE Conceptual Challenge, p. 103 a SE Sample Set F Relative Velocity, pp g TE Classroom Practice, p. 104 g ANC Problem Workbook* and OSP Problem Bank Sample Set F g SE Appendix J: Advanced Topics Special Relativity and Velocities, pp a SE Section Review, p. 105 a ANC Study Guide Worksheet Section 4* g ANC Quiz Section 4* g UCP 2, 3 Maintained by the National Science Teachers Association. Topic: Vectors SciLinks Code: HF61597 Topic: Projectile Motion SciLinks Code: HF61223 Classroom CD-ROMs Guided Reading Audio Program Student One Stop Virtual Investigations Visual Concepts Search for any lab by topic, standard, difficulty level, or time. Edit any lab to fit your needs, or create your own labs. Use the Lab Materials QuickList software to customize your lab materials list. Chapter 3 Planning Guide 80B
3 CHAPTER X 3 CHAPTER Overview Section 1 discusses scalar and vector quantities and graphical vector addition. Section 2 explains the use of the Pythagorean theorem and trigonometric functions to find resultant vectors and vector components. Section 3 explores projectile motion, neglecting air resistance. Section 4 describes relative motion in terms of vector operations. About the Illustration This fountain is located in Bayfront Park in Sarasota, Florida. Point out that each drop of water emerging from the fountain moves as a projectile and obeys the rules for projectile motion described in this chapter. Likewise, the dolphins move as projectiles as they sail through the air. 80
4 CHAPTER 3 vx vx Two-Dimensional Motion and Vectors vx vx vy vy vx vy vx vy vy Without air resistance, any object that is thrown or launched into the air and that is subject to gravitational force will follow a parabolic path. The water droplets in this fountain are one example. The velocity of any object in twodimensional motion such as one of these water droplets can be separated into horizontal and vertical components, as shown in the diagram. WHAT TO EXPECT In this chapter, you will use vectors to analyze two-dimensional motion and to solve problems in which objects are projected into the air. Why It Matters Tapping Prior Knowledge Knowledge to Review Displacement is a change in location relative to a reference point. Velocity includes speed and direction. Acceleration is the rate of change of velocity with respect to time. It has both magnitude and direction. Items to Probe Displacement versus distance: Have students decide displacement and distance values for scenarios listed on the board, such as round trips versus one-way trips, or by walking from one place to another in the Why classroom. Acceleration and velocity: Ask students to describe the effects of the four possible combinations of acceleration and velocity in one dimension: a > 0, v > 0; a < 0, v > 0; a > 0, v < 0; a < 0, v < 0. After you know how to analyze two-dimensional motion, you can predict where a falling object will land based on its initial velocity and position. CHAPTER PREVIEW 1 Introduction to Vectors Scalars and Vectors Properties of Vectors 2 Vector Operations Coordinate Systems in Two Dimensions Determining Resultant Magnitude and Direction Resolving Vectors into Components Adding Vectors That Are Not Perpendicular 3 Projectile Motion Two-Dimensional Motion 4 Relative Motion Frames of Reference Relative Velocity 81 81
5 SECTION 1 General Level SECTION 1 Introduction to Vectors Teaching Tip Carry an arrow with you to class, and use it often to describe the direction of the vector. The Language of Physics Establish a convention for distinguishing vectors from scalars for use in your classroom. Using an arrow above the variable is a good substitute for bold type, which would be hard to reproduce on a chalkboard. Make sure to be consistent when using this convention. For instance, when you use an arrow above the symbol to designate a vector, be sure to signify the direction of the vector as well as its magnitude and units. Visual Strategy Figure 1 Tell students that the arrows in the figure represent velocity, that is, both speed and direction. Why do we consider velocity Q instead of speed in order to decide which player reaches the ball first? Direction is important A because a player may run very fast but not toward the ball. SECTION OBJECTIVES Distinguish between a scalar and a vector. Add and subtract vectors by using the graphical method. Multiply and divide vectors by scalars. scalar a physical quantity that has magnitude but no direction vector a physical quantity that has both magnitude and direction Figure 1 The lengths of the vector arrows represent the magnitudes of these two soccer players velocities. SCALARS AND VECTORS In the chapter Motion in One Dimension, our discussion of motion was limited to two directions, forward and backward. Mathematically, we described these directions of motion with a positive or negative sign. That method works only for motion in a straight line. This chapter explains a method of describing the motion of objects that do not travel along a straight line. Vectors indicate direction; scalars do not Each of the physical quantities encountered in this book can be categorized as either a scalar quantity or a vector quantity. A scalar is a quantity that has magnitude but no direction. Examples of scalar quantities are speed, volume, and the number of pages in this textbook. A vector is a physical quantity that has both direction and magnitude. As we look back to the chapter Motion in One Dimension, we can see that displacement is an example of a vector quantity. An airline pilot planning a trip must know exactly how far and which way to fly. Velocity is also a vector quantity. If we wish to describe the velocity of a bird, we must specify both its speed (say, 3.5 m/s) and the direction in which the bird is flying (say, northeast). Another example of a vector quantity is acceleration. Vectors are represented by boldface symbols In physics, quantities are often represented by symbols, such as t for time. To help you keep track of which symbols represent vector quantities and which are used to indicate scalar quantities, this book will use boldface type to indicate vector quantities. Scalar quantities will be in italics. For example, the speed of a bird is written as v = 3.5 m/s. But a velocity, which includes a direction, is written as v = 3.5 m/s to the northeast. When writing a vector on your paper, you can distinguish it from a scalar by drawing an arrow above the abbreviation for a quantity, such as v = 3.5 m/s to the northeast. One way to keep track of vectors and their directions is to use diagrams. In diagrams, vectors are shown as arrows that point in the direction of the vector. The length of a vector arrow in a diagram is proportional to the vector s magnitude. For example, in Figure 1 the arrows represent the velocities of the two soccer players running toward the soccer ball Chapter 3
6 A resultant vector represents the sum of two or more vectors When adding vectors, you must make certain that they have the same units and describe similar quantities. For example, it would be meaningless to add a velocity vector to a displacement vector because they describe different physical quantities. Similarly, it would be meaningless, as well as incorrect, to add two displacement vectors that are not expressed in the same units. For example, you cannot add meters and feet together. Section 1 of the chapter Motion in One Dimension covered vector addition and subtraction in one dimension. Think back to the example of the gecko that ran up a tree from a 20 cm marker to an 80 cm marker. Then the gecko reversed direction and ran back to the 50 cm marker. Because the two parts of this displacement are opposite, they can be added together to give a total displacement of 30 cm. The answer found by adding two vectors in this way is called the resultant. Vectors can be added graphically Consider a student walking 1600 m to a friend s house and then 1600 m to school, as shown in Figure 2. The student s total displacement during his walk to school is in a direction from his house to the school, as shown by the dotted line. This direct path is the vector sum of the student s displacement from his house to his friend s house and his displacement from the friend s house to school. How can this resultant displacement be found? One way to find the magnitude and direction of the student s total displacement is to draw the situation to scale on paper. Use a reasonable scale, such as 50 m on land equals 1 cm on paper. First draw the vector representing the student s displacement from his house to his friend s house, giving the proper direction and scaled magnitude. Then draw the vector representing his walk to the school, starting with the tail at the head of the first vector. Again give its scaled magnitude and the right direction. The magnitude of the resultant vector can then be determined by using a ruler. Measure the length of the vector pointing from the tail of the first vector to the head of the second vector. The length of that vector can then be multiplied by 50 (or whatever scale you have chosen) to get the actual magnitude of the student s total displacement in meters. The direction of the resultant vector may be determined by using a protractor to measure the angle between the resultant and the first vector or between the resultant and any chosen reference line. (c) Did you know? The word vector is also used by airline pilots and navigators. In this context, a vector is the particular path followed or to be followed, given as a compass heading. resultant a vector that represents the sum of two or more vectors Figure 2 A student walks from his house to his friend s house (a), then from his friend s house to the school (b). The student s resultant displacement (c) can be found by using a ruler and a protractor. (b) (a) SECTION 1 Demonstration Vector Addition GENERAL Purpose Preview force as a vector quantity to demonstrate vector addition. Materials large, empty box Procedure Ask for a student volunteer. Explain to the class that you will push the box in one direction while the student will push the box in a second, perpendicular direction at the same time. Ask students to predict the motion of the box. Have the student volunteer take a practice push alone, and emphasize that the box moves in the direction of the push. Take a practice push by yourself on the box, and again emphasize that the box moves in the direction of the push. Return the box to its original location, and both you and the student push the box perpendicular to each other at the count of three. Ask a student to explain why the box moved along the diagonal. (The box moved in a direction between the directions of the two pushes.) Show the vector addition for the demonstration qualitatively on the chalkboard. This should lay the groundwork for a discussion of why vector addition is a valuable activity. Two-Dimensional Motion and Vectors 83 83
7 SECTION 1 Misconception STOP Alert Students may have difficulty visualizing the movement of the toy car on the walkway. Illustrate the situation on the board, and emphasize that the motion represented in Figure 3 is drawn as viewed by a stationary observer above the walkway. Frame of reference will be covered in Section 4. The Language of Physics The triangle method of vector addition is also called the polygon method, the head-to-tail method, or the tip-to-tail method. Teaching Tip Students will better understand the commutative property of GENERAL vector addition if they work several examples on paper with a ruler and protractor. Visual Strategy Figure 4 Reinforce students understanding of the difference between distance and displacement by pointing out that if the runner starts and ends at the positions shown in Figure 4, the runner s displacement will be the same regardless of the path the runner chooses to follow. How can the runner increase Q distance but begin and end at the same points? The runner can take a different, longer path but will have A to double back somewhere along the path to end up at the same point. vcar = 0.80 m/s Car (b) v walkway = 1.5 m/s (c) (a) v resultant Figure 3 The resultant velocity (a) of a toy car moving at a velocity of 0.80 m/s (b) across a moving walkway with a velocity of 1.5 m/s (c) can be found using a ruler and a protractor. d d (a) (b) Figure 4 A marathon runner s displacement, d, will be the same regardless of whether the runner takes path (a) or (b) because the vectors can be added in any order. PROPERTIES OF VECTORS Now consider a case in which two or more vectors act at the same point. When this occurs, it is possible to find a resultant vector that has the same net effect as the combination of the individual vectors. Imagine looking down from the second level of an airport at a toy car moving at 0.80 m/s across a walkway that moves at 1.5 m/s. How can you determine what the car s resultant velocity will look like from your view point? Vectors can be moved parallel to themselves in a diagram Note that the car s resultant velocity while moving from one side of the walkway to the other will be the combination of two independent motions. Thus, the moving car can be thought of as traveling first at 0.80 m/s across the walkway and then at 1.5 m/s down the walkway. In this way, we can draw a given vector anywhere in the diagram as long as the vector is parallel to its previous alignment (so that it still points in the same direction). Thus, you can draw one vector with its tail starting at the tip of the other as long as the size and direction of each vector do not change. This process is illustrated in Figure 3. Although both vectors act on the car at the same point, the horizontal vector has been moved up so that its tail begins at the tip of the vertical vector. The resultant vector can then be drawn from the tail of the first vector to the tip of the last vector. This method is known as the triangle (or polygon) method of addition. Again, the magnitude of the resultant vector can be measured using a ruler, and the angle can be measured with a protractor. In the next section, we will develop a technique for adding vectors that is less time-consuming because it involves a calculator instead of a ruler and protractor. Vectors can be added in any order When two or more vectors are added, the sum is independent of the order of the addition. This idea is demonstrated by a runner practicing for a marathon along city streets, as represented in Figure 4. The runner executes the same four displacements in each case, but the order is different. Regardless of which path the runner takes, the runner will have the same total displacement, expressed as d. Similarly, the vector sum of two or more vectors is the same regardless of the order in which the vectors are added, provided that the magnitude and direction of each vector remain the same. To subtract a vector, add its opposite Vector subtraction makes use of the definition of the negative of a vector. The negative of a vector is defined as a vector with the same magnitude as the original vector but opposite in direction. For instance, the negative of the velocity of a car traveling 30 m/s to the west is 30 m/s to the west, or +30 m/s to the east. Thus, adding a vector to its negative vector gives zero Chapter 3
8 When subtracting vectors in two dimensions, first draw the negative of the vector to be subtracted. Then add that negative vector to the other vector by using the triangle method of addition. Multiplying or dividing vectors by scalars results in vectors There are mathematical operations in which vectors can multiply other vectors, but they are not needed in this book. This book does, however, make use of vectors multiplied by scalars, with a vector as the result. For example, if a cab driver obeys a customer who tells him to go twice as fast, that cab s original velocity vector, v cab, is multiplied by the scalar number 2. The result, written 2v cab, is a vector with a magnitude twice that of the original vector and pointing in the same direction. On the other hand, if another cab driver is told to go twice as fast in the opposite direction, this is the same as multiplying by the scalar number 2. The result is a vector with a magnitude two times the initial velocity but pointing in the opposite direction, written as 2v cab. Topic: Vectors Code: HF61597 SECTION 1 Teaching Tip Some students may need further explanation and visual examples of the negative of a vector. Give several examples of vectors in different directions, and then show their negative vectors. SECTION REVIEW SECTION REVIEW ANSWERS 1. Which of the following quantities are scalars, and which are vectors? a. the acceleration of a plane as it takes off b. the number of passengers on the plane c. the duration of the flight d. the displacement of the flight e. the amount of fuel required for the flight 2. A roller coaster moves 85 m horizontally, then travels 45 m at an angle of 30.0 above the horizontal. What is its displacement from its starting point? Use graphical techniques. 1. a. vector b. scalar c. scalar d. vector e. scalar m at ( ) above the horizontal km/h at 75 north of east km/h at 54 north of east 5. zero 3. A novice pilot sets a plane s controls, thinking the plane will fly at km/h to the north. If the wind blows at 75 km/h toward the southeast, what is the plane s resultant velocity? Use graphical techniques. 4. While flying over the Grand Canyon, the pilot slows the plane down to one-half the velocity in item 3. If the wind s velocity is still 75 km/h toward the southeast, what will the plane s new resultant velocity be? Use graphical techniques. 5. Critical Thinking The water used in many fountains is recycled. For instance, a single water particle in a fountain travels through an 85 m system and then returns to the same point. What is the displacement of this water particle during one cycle? Two-Dimensional Motion and Vectors 85 85
9 SECTION 2 General Level SECTION 2 Vector Operations Teaching Tip Review the sign conventions for coordinate systems that were established in the chapter Motion in One Dimension. Movements to the right along the x-axis and upward along the y- axis are considered positive, and movements to the left along the x-axis and downward along the y-axis are considered negative. Visual Strategy GENERAL Figure 6 Point out the two very different choices for coordinate axes. Which set of axes will give the Q correct answer? Either set of axes must give A the same results. SECTION OBJECTIVES Identify appropriate coordinate systems for solving problems with vectors. Apply the Pythagorean theorem and tangent function to calculate the magnitude and direction of a resultant vector. Resolve vectors into components using the sine and cosine functions. Add vectors that are not perpendicular. y Δy COORDINATE SYSTEMS IN TWO DIMENSIONS In the chapter Motion in One Dimension, the motion of a gecko climbing a tree was described as motion along the y-axis. The direction of the displacement of the gecko was denoted by a positive or negative sign. The displacement of the gecko can now be described by an arrow pointing along the y-axis, as shown in Figure 5. A more versatile system for diagraming the motion of an object, however, employs vectors and the use of both the x- and y-axes simultaneously. The addition of another axis not only helps describe motion in two dimensions but also simplifies analysis of motion in one dimension. For example, two methods can be used to describe the motion of a jet moving at 300 m/s to the northeast. In one approach, the coordinate system can be turned so that the plane is depicted as moving along the y-axis, as in Figure 6(a). The jet s motion also can be depicted on a two-dimensional coordinate system whose axes point north and east, as shown in Figure 6(b). One problem with the first method is that the axis must be turned again if the direction of the plane changes. Another problem is that the first method provides no way to deal with a second airplane that is not traveling in the same direction as the first airplane. Thus, axes are often designated using fixed directions. For example, in Figure 6(b), the positive y-axis points north and the positive x-axis points east. Similarly, when you analyze the motion of objects thrown into the air, orienting the y-axis parallel to the vertical direction simplifies problem solving. N y y Figure 5 A gecko s displacement while climbing a tree can be represented by an arrow pointing along the y-axis. W S E v = 300 m/s at 45 v = 300 m/s northeast x (a) (b) Figure 6 A plane traveling northeast at a velocity of 300 m/s can be represented as either (a) moving along a y-axis chosen to point to the northeast or (b) moving at an angle of 45 to both the x- and y-axes, which line up with west-east and south-north, respectively Chapter 3
10 There are no firm rules for applying coordinate systems to situations involving vectors. As long as you are consistent, the final answer will be correct regardless of the system you choose. Perhaps your best choice for orienting axes is the approach that makes solving the problem easiest for you. DETERMINING RESULTANT MAGNITUDE AND DIRECTION In Section 1, the magnitude and direction of a resultant were found graphically. However, this approach is time consuming, and the accuracy of the answer depends on how carefully the diagram is drawn and measured. A simpler method uses the Pythagorean theorem and the tangent function. Use the Pythagorean theorem to find the magnitude of the resultant Imagine a tourist climbing a pyramid in Egypt. The tourist knows the height and width of the pyramid and would like to know the distance covered in a climb from the bottom to the top of the pyramid. Assume that the tourist climbs directly up the middle of one face. As can be seen in Figure 7, the magnitude of the tourist s vertical displacement, Δy, is the height of the pyramid. The magnitude of the horizontal displacement, Δx, equals the distance from one edge of the pyramid to the middle, or half the pyramid s width. Notice that these two vectors are perpendicular and form a right triangle with the displacement, d. As shown in Figure 8(a), the Pythagorean theorem states that for any right triangle, the square of the hypotenuse the side opposite the right angle equals the sum of the squares of the other two sides, or legs. PYTHAGOREAN THEOREM FOR RIGHT TRIANGLES c 2 = a 2 + b 2 (length of hypotenuse) 2 = (length of one leg) 2 + (length of other leg) 2 In Figure 8(b), the Pythagorean theorem is applied to find the tourist s displacement. The square of the displacement is equal to the sum of the square of the horizontal displacement and the square of the vertical displacement. In this way, you can find out the magnitude of the displacement, d. Δx d Δy 2Δx Figure 7 Because the base and height of a pyramid are perpendicular, we can find a tourist s total displacement, d, if we know the height, Δy, and width, 2Δx, of the pyramid. SECTION 2 STOP Misconception Alert Students often try to apply the Pythagorean theorem to triangles that do not contain a right angle. Point out that the Pythagorean theorem can be used only with a right triangle. Some students may know the Law of Cosines, which applies to all triangles. This law states that c 2 = a 2 + b 2 2ab cosq.the Law of Cosines can be used to calculate one side of any triangle when the opposite angle and the lengths of the other two sides are known. In this expression, c is the unknown side, q is the angle opposite c, and a and b are the two known sides. Some students may attempt to use the Law of Cosines to add nonperpendicular vectors. This approach will give the correct answer, but it entails more computation and is more prone to student error when more than two vectors are to be added. Teaching Tip GENERAL Point out that finding the resultant for the pyramid is fairly simple because the height, halfwidth, and hypotenuse form a right triangle. It is important to mention at this point that right triangles will also allow students to find the x and y components that are important for vector addition. (a) d Δy c a b (b) Δx c 2 = a 2 + b 2 d 2 = Δx 2 + Δy 2 Figure 8 (a) The Pythagorean theorem can be applied to any right triangle. (b) It can also be applied to find the magnitude of a resultant displacement. Two-Dimensional Motion and Vectors 87 87
11 SECTION 2 Finding Resultant Magnitude and Direction A plane travels from Houston, Texas, to Washington, D.C., which is 1540 km east and 1160 km north of Houston. What is the total displacement of the plane? Answer 1930 km at 37.0 north of east A camper travels 4.5 km northeast and 4.5 km northwest. What is the camper s total displacement? Answer 6.4 km north Hypotenuse (a) θ Adjacent tan θ = opp adj d Δy θ (b) Δx tan θ = Δy Δx θ = tan 1 Δy ( Δx) Opposite Figure 9 (a) The tangent function can be applied to any right triangle, and (b) it can also be used to find the direction of a resultant displacement. Use the tangent function to find the direction of the resultant In order to completely describe the tourist s displacement, you must also know the direction of the tourist s motion. Because Δx, Δy, and d form a right triangle, as shown in Figure 9(b), the inverse tangent function can be used to find the angle q, which denotes the direction of the tourist s displacement. For any right triangle, the tangent of an angle is defined as the ratio of the opposite and adjacent legs with respect to a specified acute angle of a right triangle, as shown in Figure 9(a). As shown below, the magnitude of the opposite leg divided by the magnitude of the adjacent leg equals the tangent of the angle. DEFINITION OF THE TANGENT FUNCTION FOR RIGHT TRIANGLES tan q = o pp adj tangent of angle = o pposite leg adjacentleg The inverse of the tangent function, which is shown below, gives the angle. q = tan 1 o pp adj Focus on the Standards Teaching Physics 1j* to Mastery Students know how to resolve two-dimensional vectors into their components and calculate the magnitude and direction of a vector from its components. Activity Give students directions for a treasure hunt with movements that are all perpendicular to one another (i.e. move front/back and right/left). Have a student follow the directions to find a treasure. Now have the class do the problem by resolving the directions into two components and then calculate the resultant vector. Have a student use this to go directly from the start position to the treasure. SAMPLE PROBLEM A Finding Resultant Magnitude and Direction PROBLEM SOLUTION 1. DEFINE 2. PLAN An archaeologist climbs the Great Pyramid in Giza, Egypt. The pyramid s height is 136 m and its width is m. What is the magnitude and the direction of the displacement of the archaeologist after she has climbed from the bottom of the pyramid to the top? Given: Δy = 136 m Δx = 1 2 (width) = 115 m Unknown: d =? q =? Diagram: Choose the archaeologist s starting position as the origin of the coordinate system. Choose an equation or situation: The Pythagorean theorem can be used to find the magnitude of the archaeologist s displacement. The direction of the displacement can be found by using the tangent function. d 2 =Δx 2 +Δy 2 Δy tan q = Δ x y θ d Δx = 115 m Δy =136 m x Chapter 3
12 3. CALCULATE 4. EVALUATE PRACTICE A Rearrange the equations to isolate the unknowns: d = Δ x 2 + Δ y 2 q = tan 1 Δy Δx Substitute the values into the equations and solve: d = (1 15 m ) 2 + ( 13 6 m ) 2 d = 178 m q = tan m 115 m q = 49.8 Because d is the hypotenuse, the archaeologist s displacement should be less than the sum of the height and half of the width. The angle is expected to be more than 45 because the height is greater than half of the width. Finding Resultant Magnitude and Direction 1. A truck driver is attempting to deliver some furniture. First, he travels 8 km east, and then he turns around and travels 3 km west. Finally, he turns again and travels 12 km east to his destination. a. What distance has the driver traveled? b. What is the driver s total displacement? 2. While following the directions on a treasure map, a pirate walks 45.0 m north and then turns and walks 7.5 m east. What single straight-line displacement could the pirate have taken to reach the treasure? 3. Emily passes a soccer ball 6.0 m directly across the field to Kara. Kara then kicks the ball 14.5 m directly down the field to Luisa. What is the ball s total displacement as it travels between Emily and Luisa? 4. A hummingbird, 3.4 m above the ground, flies 1.2 m along a straight path. Upon spotting a flower below, the hummingbird drops directly downward 1.4 m to hover in front of the flower. What is the hummingbird s total displacement? Be sure your calculator is set to calculate angles measured in degrees. Some calculators have a button labeled DRG that, when pressed, toggles between degrees, radians, and grads. SECTION 2 Alternative Problem- Solving Approach The angle may be calculated using any trigonometric function, such as the following. q = sin 1 Δ y d = 49.8 PROBLEM GUIDE A Use this guide to assign problems. SE = Student Edition Textbook PW = Problem Workbook PB = Problem Bank on the One-Stop Planner (OSP) Solving for: re- SE Sample, 1 4; sultant Ch. Rvw , 23* PW 2, 4 5, 7* PB Sample, 1 5 com- PW Sample, 1, 3*, ponent 6* PB 6 10 *Challenging Problem Consult the printed Solutions Manual or the OSP for detailed solutions. ANSWERS Practice A 1. a. 23 km b. 17 km to the east m at 9.5 east of north m at 22 to the side of downfield m at 49 below the horizontal Two-Dimensional Motion and Vectors 89 89
13 SECTION 2 Teaching Tip In mathematics, the components of a vector are called projections. The x component is the projection of the vector along the x-axis, and the y component is the projection of the vector along the y-axis. STOP Misconception Alert GENERAL Because of the prominence of angles measured from the x-axis, students may develop the misconception that the x component of a vector is always calculated using the cosine function. This misconception may be corrected by using examples on the board in which the angles are measured from the y-axis. Teaching Tip Students who need a refresher on trigonometry should be directed to Appendix A, which includes a more detailed discussion of the sine, cosine, and tangent functions, as well as the Pythagorean theorem. components of a vector the projections of a vector along the axes of a coordinate system 20 v plane v t ruck Figure 10 A truck carrying a film crew must be driven at the correct velocity to enable the crew to film the underside of a biplane. The plane flies at 95 km/h at an angle of 20 relative to the ground. RESOLVING VECTORS INTO COMPONENTS In the pyramid example, the horizontal and vertical parts that add up to give the tourist s actual displacement are called components. The x component is parallel to the x-axis. The y component is parallel to the y-axis. Any vector can be completely described by a set of perpendicular components. In this textbook, components of vectors are shown as outlined, open arrows. Components have arrowheads to indicate their direction. Components are scalars (numbers), but they are signed numbers, and the direction is important to determine their sign in a particular coordinate system. You can often describe an object s motion more conveniently by breaking a single vector into two components, or resolving the vector. Resolving a vector allows you to analyze the motion in each direction. This point may be illustrated by examining a scene on the set of a new action movie. For this scene, a biplane travels at 95 km/h at an angle of 20 relative to the ground. Attempting to film the plane from below, a camera team travels in a truck that is directly beneath the plane at all times, as shown in Figure 10. To find the velocity that the truck must maintain to stay beneath the plane, we must know the horizontal component of the plane s velocity. Once more, the key to solving the problem is to recognize that a right triangle can be drawn using the plane s velocity and its x and y components. The situation can then be analyzed using trigonometry. The sine and cosine functions are defined in terms of the lengths of the sides of such right triangles. The sine of an angle is the ratio of the leg opposite that angle to the hypotenuse. DEFINITION OF THE SINE FUNCTION FOR RIGHT TRIANGLES sin q = o pp hyp sine of an angle = o pposite leg hypotenuse v plane = 95 km/h 20 v x v y Figure 11 To stay beneath the biplane, the truck must be driven with a velocity equal to the x component (v x )of the biplane s velocity. In Figure 11, the leg opposite the 20 angle represents the y component, v y, which describes the vertical speed of the airplane. The hypotenuse, v plane, is the resultant vector that describes the airplane s total velocity. The cosine of an angle is the ratio between the leg adjacent to that angle and the hypotenuse. DEFINITION OF THE COSINE FUNCTION FOR RIGHT TRIANGLES adj cos q = h yp cosine of an angle = a djacent leg hypotenuse In Figure 11, the adjacent leg represents the x component, v x, which describes the airplane s horizontal speed. This x component equals the speed that the truck must maintain to stay beneath the plane. Thus, the truck must maintain a speed of v x = (cos 20 )(95 km/h) = 90 km/h Chapter 3
14 SAMPLE PROBLEM B SECTION 2 Resolving Vectors PROBLEM SOLUTION 1. DEFINE 2. PLAN 3. CALCULATE 4. EVALUATE Find the components of the velocity of a helicopter traveling 95 km/h at an angle of 35 to the ground. Given: v = 95 km/h q = 35 Unknown: v x =? v y =? Diagram: The most convenient coordinate system is one with the x-axis directed along the ground and the y-axis directed vertically. Choose an equation or situation: Because the axes are perpendicular, the sine and cosine functions can be used to find the components. sin q = v y v cos q = v x v Rearrange the equations to isolate the unknowns: v y = v sin q v x = v cos q Substitute the values into the equations and solve: v y = (95 km/h)(sin 35 ) v y = 54 km/h v x = (95 km/h)(cos 35 ) v x = 78 km/h Because the components of the velocity form a right triangle with the helicopter s actual velocity, the components must satisfy the Pythagorean theorem. v 2 = v x 2 + vy 2 (95) 2 = (78) 2 + (54) The slight difference is due to rounding. y v = 95 km/h 35 v x Don t assume that the cosine function can always be used for the x-component and the sine function can always be used for the y-component. The correct choice of function depends on where the given angle is located. Instead, always check to see which component is adjacent and which component is opposite to the given angle. v y x Resolving Vectors An arrow is shot from a bow at an angle of 25 above the horizontal with an initial speed of 45 m/s. Find the horizontal and vertical components of the arrow s initial velocity. Answer 41 m/s, 19 m/s The arrow strikes the target with a speed of 45 m/s at an angle of 25 with respect to the horizontal. Calculate the horizontal and vertical components of the arrow s final velocity. Answer 41 m/s, 19 m/s PROBLEM GUIDE B Use this guide to assign problems. SE = Student Edition Textbook PW = Problem Workbook PB = Problem Bank on the One-Stop Planner (OSP) Solving for: one SE 1 2 com- PW Sample, 1, 3 ponent PB 1 4 both SE Sample, 3 4; com- Ch. Rvw ponents PW 2 8 PB Sample, 5 10 *Challenging Problem Consult the printed Solutions Manual or the OSP for detailed solutions. Two-Dimensional Motion and Vectors 91 91
15 SECTION 2 ANSWERS Practice B km/h km/h m/s, 5.7 m/s 4. 0 m, 5 m Teaching Tip GENERAL Problems involving vectors that are not perpendicular use both vector addition and vector resolution. Because they act as a nice summary to the concepts of this section, you may want to do several examples involving this type of problem. These problems require a methodical approach to problem solving, which should prove helpful to students while studying more-difficult subjects, such as inclined-plane problems and equilibrium problems. Teaching Tip Be sure students distinguish between the components of d 1 and d 2 in Figure 12. Ask students to draw each vector and its components separately. Then, have them sum the components in each direction and add the summed components together to find d. Repeat with additional examples to help prepare students for Sample Problem C on the next page. PRACTICE B Resolving Vectors 1. How fast must a truck travel to stay beneath an airplane that is moving 105 km/h at an angle of 25 to the ground? 2. What is the magnitude of the vertical component of the velocity of the plane in item 1? 3. A truck drives up a hill with a 15 incline. If the truck has a constant speed of 22 m/s, what are the horizontal and vertical components of the truck s velocity? 4. What are the horizontal and vertical components of a cat s displacement when the cat has climbed 5 m directly up a tree? ADDING VECTORS THAT ARE NOT PERPENDICULAR Until this point, the vector-addition problems concerned vectors that are perpendicular to one another. However, many objects move in one direction and then turn at an angle before continuing their motion. Suppose that a plane initially travels 5 km at an angle of 35 to the ground, then climbs at only 10 relative to the ground for 22 km. How can you determine the magnitude and direction for the vector denoting the total displacement of the plane? Because the original displacement vectors do not form a right triangle, you can not apply the tangent function or the Pythagorean theorem when adding the original two vectors. Determining the magnitude and the direction of the resultant can be achieved by resolving each of the plane s displacement vectors into its x and y components. Then the components along each axis can be added together. As shown in Figure 12, these sums will be the two perpendicular components of the resultant, d. The resultant s magnitude can then be found by using the Pythagorean theorem, and its direction can be found by using the inverse tangent function. d 2 Δy 2 Figure 12 d 1 Δx 1 d Δx 2 Δy 1 Add the components of the original displacement vectors to find two components that form a right triangle with the resultant vector Chapter 3
16 SAMPLE PROBLEM C SECTION 2 STRATEGY Adding Vectors Algebraically PROBLEM SOLUTION A hiker walks 27.0 km from her base camp at 35 south of east. The next day, she walks 41.0 km in a direction 65 north of east and discovers a forest ranger s tower. Find the magnitude and direction of her resultant displacement between the base camp and the tower. Select a coordinate system. Then sketch and label each vector. Given: d 1 = 27.0 km q 1 = 35 d 2 = 41.0 km q 2 = 65 Unknown: d =? q =? q 1 is negative, because clockwise angles from the positive x-axis are conventionally considered to be negative. Find the x and y components of all vectors. Make a separate sketch of the displacements for each day. Use the cosine and sine functions to find the displacement components. cos q = Δ x sin q = Δ y d d (a) For day 1: Δx 1 = d 1 cos q 1 = (27.0 km) [cos ( 35 )] = 22 km Δy 1 = d 1 sin q 1 = (27.0 km) [sin ( 35 )] = 15 km y Base camp d θ 1 d 1 Δx 1 θ Ranger s tower θ 2 θ 1 = 35 d 1 = 27.0 km d 2 Δy 1 x x Adding Vectors Algebraically A camper walks 4.5 km at 45 north of east then 4.5 km due south. Find the camper s total displacement. Answer 3.4 km at 22 south of east A plane flies 118 km at 15.0 south of east and then flies 118 km at 35.0 west of north. Find the magnitude and direction of the total displacement of the plane. Answer 81 km at 55 north of east (b) For day 2: Δx 2 = d 2 cos q 2 = (41.0 km) (cos 65 ) = 17 km (a) Δy 2 = d 2 sin q 2 = (41.0 km) (sin 65 ) = 37 km Find the x and y components of the total displacement. Δx tot =Δx 1 +Δx 2 = 22 km + 17 km = 39 km Δy tot =Δy 1 +Δy 2 = 15 km + 37 km = 22 km Use the Pythagorean theorem to find the magnitude of the resultant vector. d 2 = (Δx tot ) 2 + (Δy tot ) 2 d = (Δ x tot ) 2 + ( Δ y tot Use a suitable trigonometric function to find the angle. ) 2 = (3 9 km ) 2 + ( 22 k m ) 2 = y d 2 = 41.0 km θ 2 = 65 Δx 2 45 km Δy 2 x (b) PROBLEM GUIDE C Use this guide to assign problems. SE = Student Edition Textbook PW = Problem Workbook PB = Problem Bank on the One-Stop Planner (OSP) Solving for: vector SE Sample, 1 3, 4*; sum Ch. Rvw. 26, 53* PW Sample, 1 5 PB Sample, 1 10 q = tan 1 Δy t ot Δxtot = tan km 9 km = 29 north of east *Challenging Problem Consult the printed Solutions Manual or the OSP for detailed solutions. Two-Dimensional Motion and Vectors 93 93
17 SECTION 2 Interactive Problem- ANSWERS Practice C m at 7.3 to the right of downfield km at 26 above the horizontal m at 57 north of east km at 34 east of north PRACTICE C Adding Vectors Algebraically 1. A football player runs directly down the field for 35 m before turning to the right at an angle of 25 from his original direction and running an additional 15 m before getting tackled. What is the magnitude and direction of the runner s total displacement? 2. A plane travels 2.5 km at an angle of 35 to the ground and then changes direction and travels 5.2 km at an angle of 22 to the ground. What is the magnitude and direction of the plane s total displacement? 3. During a rodeo, a clown runs 8.0 m north, turns 55 north of east, and runs 3.5 m. Then, after waiting for the bull to come near, the clown turns due east and runs 5.0 m to exit the arena. What is the clown s total displacement? 4. An airplane flying parallel to the ground undergoes two consecutive displacements. The first is 75 km 30.0 west of north, and the second is 155 km 60.0 east of north. What is the total displacement of the airplane? SECTION REVIEW ANSWERS 1. a. x-axis: forward and backward on sidewalk y-axis: left and right on sidewalk b. x-axis: forward and backward on rope y-axis: up and down c. x-axis: horizontal at water level y-axis: up and down 2. a. 5.8 m/s at 59 downriver from its intended path b. 6.1 m/s at 9.5 from the direction the wave is traveling 3. a km north, 7.07 km east b. 1.6 m/s 2 horizontal, 1.1 m/s 2 vertical 4. because the Pythagorean theorem and the tangent function can be applied only to right triangles SECTION REVIEW 1. Identify a convenient coordinate system for analyzing each of the following situations: a. a dog walking along a sidewalk b. an acrobat walking along a high wire c. a submarine submerging at an angle of 30 to the horizontal 2. Find the magnitude and direction of the resultant velocity vector for the following perpendicular velocities: a. a fish swimming at 3.0 m/s relative to the water across a river that moves at 5.0 m/s b. a surfer traveling at 1.0 m/s relative to the water across a wave that is traveling at 6.0 m/s 3. Find the vector components along the directions noted in parentheses. a. a car displaced 45 north of east by 10.0 km (north and east) b. a duck accelerating away from a hunter at 2.0 m/s 2 at an angle of 35 to the ground (horizontal and vertical) 4. Critical Thinking Why do nonperpendicular vectors need to be resolved into components before you can add the vectors together? Chapter 3
18 Projectile Motion SECTION 3 SECTION 3 General Level TWO-DIMENSIONAL MOTION In the last section, quantities such as displacement and velocity were shown to be vectors that can be resolved into components. In this section, these components will be used to understand and predict the motion of objects thrown into the air. Use of components avoids vector multiplication How can you know the displacement, velocity, and acceleration of a ball at any point in time during its flight? All of the kinematic equations could be rewritten in terms of vector quantities. However, when an object is propelled into the air in a direction other than straight up or down, the velocity, acceleration, and displacement of the object do not all point in the same direction. This makes the vector forms of the equations difficult to solve. One way to deal with these situations is to avoid using the complicated vector forms of the equations altogether. Instead, apply the technique of resolving vectors into components. Then you can apply the simpler one-dimensional forms of the equations for each component. Finally, you can recombine the components to determine the resultant. Components simplify projectile motion When a long jumper approaches his jump, he runs along a straight line, which can be called the x-axis. When he jumps, as shown in Figure 13, his velocity has both horizontal and vertical components. Movement in this plane can be depicted by using both the x- and y-axes. Note that in Figure 14(b), a jumper s velocity vector is resolved into its two vector components. This way, the jumper s motion can be analyzed using the kinematic equations applied to one direction at a time. SECTION OBJECTIVES Recognize examples of projectile motion. Describe the path of a projectile as a parabola. Resolve vectors into their components and apply the kinematic equations to solve problems involving projectile motion. Figure 13 When the long jumper is in the air, his velocity has both a horizontal and a vertical component. GENERAL Teaching Tip On the chalkboard, show examples of vector components and the kinematic equations. Show the simplification of the x-direction equations when the x component of acceleration is zero. Visual Strategy Figure 13 Tell students that the long jumper builds up speed in the x direction and jumps, so there is also a component of speed in the y direction. Does the angle of takeoff Q matter to the jumper? Consider the difference between a very small angle (near 0 ) and a larger angle (near 45 ). The angle matters because it A affects how long the jumper stays off the ground and how far he goes horizontally while in the air. v (a) v y v x (b) Figure 14 (a) A long jumper s velocity while sprinting along the runway can be represented by a horizontal vector. (b) Once the jumper is airborne, the jumper s velocity at any instant can be described by the components of the velocity. Two-Dimensional Motion and Vectors 95 95
3. KINEMATICS IN TWO DIMENSIONS; VECTORS.
 3. KINEMATICS IN TWO DIMENSIONS; VECTORS. Key words: Motion in Two Dimensions, Scalars, Vectors, Addition of Vectors by Graphical Methods, Tail to Tip Method, Parallelogram Method, Negative Vector, Vector
3. KINEMATICS IN TWO DIMENSIONS; VECTORS. Key words: Motion in Two Dimensions, Scalars, Vectors, Addition of Vectors by Graphical Methods, Tail to Tip Method, Parallelogram Method, Negative Vector, Vector
PHYSICS 151 Notes for Online Lecture #6
 PHYSICS 151 Notes for Online Lecture #6 Vectors - A vector is basically an arrow. The length of the arrow represents the magnitude (value) and the arrow points in the direction. Many different quantities
PHYSICS 151 Notes for Online Lecture #6 Vectors - A vector is basically an arrow. The length of the arrow represents the magnitude (value) and the arrow points in the direction. Many different quantities
Chapter 3 Practice Test
 Chapter 3 Practice Test Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Which of the following is a physical quantity that has both magnitude and direction?
Chapter 3 Practice Test Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Which of the following is a physical quantity that has both magnitude and direction?
Difference between a vector and a scalar quantity. N or 90 o. S or 270 o
 Vectors Vectors and Scalars Distinguish between vector and scalar quantities, and give examples of each. method. A vector is represented in print by a bold italicized symbol, for example, F. A vector has
Vectors Vectors and Scalars Distinguish between vector and scalar quantities, and give examples of each. method. A vector is represented in print by a bold italicized symbol, for example, F. A vector has
6. Vectors. 1 2009-2016 Scott Surgent (surgent@asu.edu)
 6. Vectors For purposes of applications in calculus and physics, a vector has both a direction and a magnitude (length), and is usually represented as an arrow. The start of the arrow is the vector s foot,
6. Vectors For purposes of applications in calculus and physics, a vector has both a direction and a magnitude (length), and is usually represented as an arrow. The start of the arrow is the vector s foot,
Figure 1.1 Vector A and Vector F
 CHAPTER I VECTOR QUANTITIES Quantities are anything which can be measured, and stated with number. Quantities in physics are divided into two types; scalar and vector quantities. Scalar quantities have
CHAPTER I VECTOR QUANTITIES Quantities are anything which can be measured, and stated with number. Quantities in physics are divided into two types; scalar and vector quantities. Scalar quantities have
Solving Simultaneous Equations and Matrices
 Solving Simultaneous Equations and Matrices The following represents a systematic investigation for the steps used to solve two simultaneous linear equations in two unknowns. The motivation for considering
Solving Simultaneous Equations and Matrices The following represents a systematic investigation for the steps used to solve two simultaneous linear equations in two unknowns. The motivation for considering
In order to describe motion you need to describe the following properties.
 Chapter 2 One Dimensional Kinematics How would you describe the following motion? Ex: random 1-D path speeding up and slowing down In order to describe motion you need to describe the following properties.
Chapter 2 One Dimensional Kinematics How would you describe the following motion? Ex: random 1-D path speeding up and slowing down In order to describe motion you need to describe the following properties.
Parallel and Perpendicular. We show a small box in one of the angles to show that the lines are perpendicular.
 CONDENSED L E S S O N. Parallel and Perpendicular In this lesson you will learn the meaning of parallel and perpendicular discover how the slopes of parallel and perpendicular lines are related use slopes
CONDENSED L E S S O N. Parallel and Perpendicular In this lesson you will learn the meaning of parallel and perpendicular discover how the slopes of parallel and perpendicular lines are related use slopes
Examples of Scalar and Vector Quantities 1. Candidates should be able to : QUANTITY VECTOR SCALAR
 Candidates should be able to : Examples of Scalar and Vector Quantities 1 QUANTITY VECTOR SCALAR Define scalar and vector quantities and give examples. Draw and use a vector triangle to determine the resultant
Candidates should be able to : Examples of Scalar and Vector Quantities 1 QUANTITY VECTOR SCALAR Define scalar and vector quantities and give examples. Draw and use a vector triangle to determine the resultant
Physics: Principles and Applications, 6e Giancoli Chapter 2 Describing Motion: Kinematics in One Dimension
 Physics: Principles and Applications, 6e Giancoli Chapter 2 Describing Motion: Kinematics in One Dimension Conceptual Questions 1) Suppose that an object travels from one point in space to another. Make
Physics: Principles and Applications, 6e Giancoli Chapter 2 Describing Motion: Kinematics in One Dimension Conceptual Questions 1) Suppose that an object travels from one point in space to another. Make
Exam 1 Review Questions PHY 2425 - Exam 1
 Exam 1 Review Questions PHY 2425 - Exam 1 Exam 1H Rev Ques.doc - 1 - Section: 1 7 Topic: General Properties of Vectors Type: Conceptual 1 Given vector A, the vector 3 A A) has a magnitude 3 times that
Exam 1 Review Questions PHY 2425 - Exam 1 Exam 1H Rev Ques.doc - 1 - Section: 1 7 Topic: General Properties of Vectors Type: Conceptual 1 Given vector A, the vector 3 A A) has a magnitude 3 times that
2-1 Position, Displacement, and Distance
 2-1 Position, Displacement, and Distance In describing an object s motion, we should first talk about position where is the object? A position is a vector because it has both a magnitude and a direction:
2-1 Position, Displacement, and Distance In describing an object s motion, we should first talk about position where is the object? A position is a vector because it has both a magnitude and a direction:
1 of 7 9/5/2009 6:12 PM
 1 of 7 9/5/2009 6:12 PM Chapter 2 Homework Due: 9:00am on Tuesday, September 8, 2009 Note: To understand how points are awarded, read your instructor's Grading Policy. [Return to Standard Assignment View]
1 of 7 9/5/2009 6:12 PM Chapter 2 Homework Due: 9:00am on Tuesday, September 8, 2009 Note: To understand how points are awarded, read your instructor's Grading Policy. [Return to Standard Assignment View]
Physics 590 Homework, Week 6 Week 6, Homework 1
 Physics 590 Homework, Week 6 Week 6, Homework 1 Prob. 6.1.1 A descent vehicle landing on the moon has a vertical velocity toward the surface of the moon of 35 m/s. At the same time it has a horizontal
Physics 590 Homework, Week 6 Week 6, Homework 1 Prob. 6.1.1 A descent vehicle landing on the moon has a vertical velocity toward the surface of the moon of 35 m/s. At the same time it has a horizontal
Worksheet to Review Vector and Scalar Properties
 Worksheet to Review Vector and Scalar Properties 1. Differentiate between vectors and scalar quantities 2. Know what is being requested when the question asks for the magnitude of a quantity 3. Define
Worksheet to Review Vector and Scalar Properties 1. Differentiate between vectors and scalar quantities 2. Know what is being requested when the question asks for the magnitude of a quantity 3. Define
Introduction and Mathematical Concepts
 CHAPTER 1 Introduction and Mathematical Concepts PREVIEW In this chapter you will be introduced to the physical units most frequently encountered in physics. After completion of the chapter you will be
CHAPTER 1 Introduction and Mathematical Concepts PREVIEW In this chapter you will be introduced to the physical units most frequently encountered in physics. After completion of the chapter you will be
Projectile Motion 1:Horizontally Launched Projectiles
 A cannon shoots a clown directly upward with a speed of 20 m/s. What height will the clown reach? How much time will the clown spend in the air? Projectile Motion 1:Horizontally Launched Projectiles Two
A cannon shoots a clown directly upward with a speed of 20 m/s. What height will the clown reach? How much time will the clown spend in the air? Projectile Motion 1:Horizontally Launched Projectiles Two
How To Solve The Pythagorean Triangle
 Name Period CHAPTER 9 Right Triangles and Trigonometry Section 9.1 Similar right Triangles Objectives: Solve problems involving similar right triangles. Use a geometric mean to solve problems. Ex. 1 Use
Name Period CHAPTER 9 Right Triangles and Trigonometry Section 9.1 Similar right Triangles Objectives: Solve problems involving similar right triangles. Use a geometric mean to solve problems. Ex. 1 Use
Solving Quadratic Equations
 9.3 Solving Quadratic Equations by Using the Quadratic Formula 9.3 OBJECTIVES 1. Solve a quadratic equation by using the quadratic formula 2. Determine the nature of the solutions of a quadratic equation
9.3 Solving Quadratic Equations by Using the Quadratic Formula 9.3 OBJECTIVES 1. Solve a quadratic equation by using the quadratic formula 2. Determine the nature of the solutions of a quadratic equation
Web review - Ch 3 motion in two dimensions practice test
 Name: Class: _ Date: _ Web review - Ch 3 motion in two dimensions practice test Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Which type of quantity
Name: Class: _ Date: _ Web review - Ch 3 motion in two dimensions practice test Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Which type of quantity
Lab 2: Vector Analysis
 Lab 2: Vector Analysis Objectives: to practice using graphical and analytical methods to add vectors in two dimensions Equipment: Meter stick Ruler Protractor Force table Ring Pulleys with attachments
Lab 2: Vector Analysis Objectives: to practice using graphical and analytical methods to add vectors in two dimensions Equipment: Meter stick Ruler Protractor Force table Ring Pulleys with attachments
Physics Midterm Review Packet January 2010
 Physics Midterm Review Packet January 2010 This Packet is a Study Guide, not a replacement for studying from your notes, tests, quizzes, and textbook. Midterm Date: Thursday, January 28 th 8:15-10:15 Room:
Physics Midterm Review Packet January 2010 This Packet is a Study Guide, not a replacement for studying from your notes, tests, quizzes, and textbook. Midterm Date: Thursday, January 28 th 8:15-10:15 Room:
2 Session Two - Complex Numbers and Vectors
 PH2011 Physics 2A Maths Revision - Session 2: Complex Numbers and Vectors 1 2 Session Two - Complex Numbers and Vectors 2.1 What is a Complex Number? The material on complex numbers should be familiar
PH2011 Physics 2A Maths Revision - Session 2: Complex Numbers and Vectors 1 2 Session Two - Complex Numbers and Vectors 2.1 What is a Complex Number? The material on complex numbers should be familiar
Physics Kinematics Model
 Physics Kinematics Model I. Overview Active Physics introduces the concept of average velocity and average acceleration. This unit supplements Active Physics by addressing the concept of instantaneous
Physics Kinematics Model I. Overview Active Physics introduces the concept of average velocity and average acceleration. This unit supplements Active Physics by addressing the concept of instantaneous
Uniformly Accelerated Motion
 Uniformly Accelerated Motion Under special circumstances, we can use a series of three equations to describe or predict movement V f = V i + at d = V i t + 1/2at 2 V f2 = V i2 + 2ad Most often, these equations
Uniformly Accelerated Motion Under special circumstances, we can use a series of three equations to describe or predict movement V f = V i + at d = V i t + 1/2at 2 V f2 = V i2 + 2ad Most often, these equations
Unified Lecture # 4 Vectors
 Fall 2005 Unified Lecture # 4 Vectors These notes were written by J. Peraire as a review of vectors for Dynamics 16.07. They have been adapted for Unified Engineering by R. Radovitzky. References [1] Feynmann,
Fall 2005 Unified Lecture # 4 Vectors These notes were written by J. Peraire as a review of vectors for Dynamics 16.07. They have been adapted for Unified Engineering by R. Radovitzky. References [1] Feynmann,
AP PHYSICS C Mechanics - SUMMER ASSIGNMENT FOR 2016-2017
 AP PHYSICS C Mechanics - SUMMER ASSIGNMENT FOR 2016-2017 Dear Student: The AP physics course you have signed up for is designed to prepare you for a superior performance on the AP test. To complete material
AP PHYSICS C Mechanics - SUMMER ASSIGNMENT FOR 2016-2017 Dear Student: The AP physics course you have signed up for is designed to prepare you for a superior performance on the AP test. To complete material
v v ax v a x a v a v = = = Since F = ma, it follows that a = F/m. The mass of the arrow is unchanged, and ( )
 Week 3 homework IMPORTANT NOTE ABOUT WEBASSIGN: In the WebAssign versions of these problems, various details have been changed, so that the answers will come out differently. The method to find the solution
Week 3 homework IMPORTANT NOTE ABOUT WEBASSIGN: In the WebAssign versions of these problems, various details have been changed, so that the answers will come out differently. The method to find the solution
Trigonometry. An easy way to remember trigonometric properties is:
 Trigonometry It is possible to solve many force and velocity problems by drawing vector diagrams. However, the degree of accuracy is dependent upon the exactness of the person doing the drawing and measuring.
Trigonometry It is possible to solve many force and velocity problems by drawing vector diagrams. However, the degree of accuracy is dependent upon the exactness of the person doing the drawing and measuring.
Chapter 6 Work and Energy
 Chapter 6 WORK AND ENERGY PREVIEW Work is the scalar product of the force acting on an object and the displacement through which it acts. When work is done on or by a system, the energy of that system
Chapter 6 WORK AND ENERGY PREVIEW Work is the scalar product of the force acting on an object and the displacement through which it acts. When work is done on or by a system, the energy of that system
One advantage of this algebraic approach is that we can write down
 . Vectors and the dot product A vector v in R 3 is an arrow. It has a direction and a length (aka the magnitude), but the position is not important. Given a coordinate axis, where the x-axis points out
. Vectors and the dot product A vector v in R 3 is an arrow. It has a direction and a length (aka the magnitude), but the position is not important. Given a coordinate axis, where the x-axis points out
CHAPTER 6 WORK AND ENERGY
 CHAPTER 6 WORK AND ENERGY CONCEPTUAL QUESTIONS. REASONING AND SOLUTION The work done by F in moving the box through a displacement s is W = ( F cos 0 ) s= Fs. The work done by F is W = ( F cos θ). s From
CHAPTER 6 WORK AND ENERGY CONCEPTUAL QUESTIONS. REASONING AND SOLUTION The work done by F in moving the box through a displacement s is W = ( F cos 0 ) s= Fs. The work done by F is W = ( F cos θ). s From
Unit 11 Additional Topics in Trigonometry - Classwork
 Unit 11 Additional Topics in Trigonometry - Classwork In geometry and physics, concepts such as temperature, mass, time, length, area, and volume can be quantified with a single real number. These are
Unit 11 Additional Topics in Trigonometry - Classwork In geometry and physics, concepts such as temperature, mass, time, length, area, and volume can be quantified with a single real number. These are
Vectors and Scalars. AP Physics B
 Vectors and Scalars P Physics Scalar SCLR is NY quantity in physics that has MGNITUDE, but NOT a direction associated with it. Magnitude numerical value with units. Scalar Example Speed Distance ge Magnitude
Vectors and Scalars P Physics Scalar SCLR is NY quantity in physics that has MGNITUDE, but NOT a direction associated with it. Magnitude numerical value with units. Scalar Example Speed Distance ge Magnitude
SPEED, VELOCITY, AND ACCELERATION
 reflect Look at the picture of people running across a field. What words come to mind? Maybe you think about the word speed to describe how fast the people are running. You might think of the word acceleration
reflect Look at the picture of people running across a field. What words come to mind? Maybe you think about the word speed to describe how fast the people are running. You might think of the word acceleration
Definition: A vector is a directed line segment that has and. Each vector has an initial point and a terminal point.
 6.1 Vectors in the Plane PreCalculus 6.1 VECTORS IN THE PLANE Learning Targets: 1. Find the component form and the magnitude of a vector.. Perform addition and scalar multiplication of two vectors. 3.
6.1 Vectors in the Plane PreCalculus 6.1 VECTORS IN THE PLANE Learning Targets: 1. Find the component form and the magnitude of a vector.. Perform addition and scalar multiplication of two vectors. 3.
Biggar High School Mathematics Department. National 5 Learning Intentions & Success Criteria: Assessing My Progress
 Biggar High School Mathematics Department National 5 Learning Intentions & Success Criteria: Assessing My Progress Expressions & Formulae Topic Learning Intention Success Criteria I understand this Approximation
Biggar High School Mathematics Department National 5 Learning Intentions & Success Criteria: Assessing My Progress Expressions & Formulae Topic Learning Intention Success Criteria I understand this Approximation
Pythagorean Theorem: 9. x 2 2
 Geometry Chapter 8 - Right Triangles.7 Notes on Right s Given: any 3 sides of a Prove: the is acute, obtuse, or right (hint: use the converse of Pythagorean Theorem) If the (longest side) 2 > (side) 2
Geometry Chapter 8 - Right Triangles.7 Notes on Right s Given: any 3 sides of a Prove: the is acute, obtuse, or right (hint: use the converse of Pythagorean Theorem) If the (longest side) 2 > (side) 2
The Dot and Cross Products
 The Dot and Cross Products Two common operations involving vectors are the dot product and the cross product. Let two vectors =,, and =,, be given. The Dot Product The dot product of and is written and
The Dot and Cross Products Two common operations involving vectors are the dot product and the cross product. Let two vectors =,, and =,, be given. The Dot Product The dot product of and is written and
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. 1) Vector A has length 4 units and directed to the north. Vector B has length 9 units and is directed
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. 1) Vector A has length 4 units and directed to the north. Vector B has length 9 units and is directed
Extra Credit Assignment Lesson plan. The following assignment is optional and can be completed to receive up to 5 points on a previously taken exam.
 Extra Credit Assignment Lesson plan The following assignment is optional and can be completed to receive up to 5 points on a previously taken exam. The extra credit assignment is to create a typed up lesson
Extra Credit Assignment Lesson plan The following assignment is optional and can be completed to receive up to 5 points on a previously taken exam. The extra credit assignment is to create a typed up lesson
The Force Table Introduction: Theory:
 1 The Force Table Introduction: "The Force Table" is a simple tool for demonstrating Newton s First Law and the vector nature of forces. This tool is based on the principle of equilibrium. An object is
1 The Force Table Introduction: "The Force Table" is a simple tool for demonstrating Newton s First Law and the vector nature of forces. This tool is based on the principle of equilibrium. An object is
Trigonometry for AC circuits
 Trigonometry for AC circuits This worksheet and all related files are licensed under the Creative Commons Attribution License, version 1.0. To view a copy of this license, visit http://creativecommons.org/licenses/by/1.0/,
Trigonometry for AC circuits This worksheet and all related files are licensed under the Creative Commons Attribution License, version 1.0. To view a copy of this license, visit http://creativecommons.org/licenses/by/1.0/,
Projectile motion simulator. http://www.walter-fendt.de/ph11e/projectile.htm
 More Chapter 3 Projectile motion simulator http://www.walter-fendt.de/ph11e/projectile.htm The equations of motion for constant acceleration from chapter 2 are valid separately for both motion in the x
More Chapter 3 Projectile motion simulator http://www.walter-fendt.de/ph11e/projectile.htm The equations of motion for constant acceleration from chapter 2 are valid separately for both motion in the x
Plotting and Adjusting Your Course: Using Vectors and Trigonometry in Navigation
 Plotting and Adjusting Your Course: Using Vectors and Trigonometry in Navigation ED 5661 Mathematics & Navigation Teacher Institute August 2011 By Serena Gay Target: Precalculus (grades 11 or 12) Lesson
Plotting and Adjusting Your Course: Using Vectors and Trigonometry in Navigation ED 5661 Mathematics & Navigation Teacher Institute August 2011 By Serena Gay Target: Precalculus (grades 11 or 12) Lesson
Experiment 2 Free Fall and Projectile Motion
 Name Partner(s): Experiment 2 Free Fall and Projectile Motion Objectives Preparation Pre-Lab Learn how to solve projectile motion problems. Understand that the acceleration due to gravity is constant (9.8
Name Partner(s): Experiment 2 Free Fall and Projectile Motion Objectives Preparation Pre-Lab Learn how to solve projectile motion problems. Understand that the acceleration due to gravity is constant (9.8
Chapter 3 Vectors. m = m1 + m2 = 3 kg + 4 kg = 7 kg (3.1)
 COROLLARY I. A body, acted on by two forces simultaneously, will describe the diagonal of a parallelogram in the same time as it would describe the sides by those forces separately. Isaac Newton - Principia
COROLLARY I. A body, acted on by two forces simultaneously, will describe the diagonal of a parallelogram in the same time as it would describe the sides by those forces separately. Isaac Newton - Principia
2After completing this chapter you should be able to
 After completing this chapter you should be able to solve problems involving motion in a straight line with constant acceleration model an object moving vertically under gravity understand distance time
After completing this chapter you should be able to solve problems involving motion in a straight line with constant acceleration model an object moving vertically under gravity understand distance time
Section 10.4 Vectors
 Section 10.4 Vectors A vector is represented by using a ray, or arrow, that starts at an initial point and ends at a terminal point. Your textbook will always use a bold letter to indicate a vector (such
Section 10.4 Vectors A vector is represented by using a ray, or arrow, that starts at an initial point and ends at a terminal point. Your textbook will always use a bold letter to indicate a vector (such
Geometry Notes RIGHT TRIANGLE TRIGONOMETRY
 Right Triangle Trigonometry Page 1 of 15 RIGHT TRIANGLE TRIGONOMETRY Objectives: After completing this section, you should be able to do the following: Calculate the lengths of sides and angles of a right
Right Triangle Trigonometry Page 1 of 15 RIGHT TRIANGLE TRIGONOMETRY Objectives: After completing this section, you should be able to do the following: Calculate the lengths of sides and angles of a right
Vector Math Computer Graphics Scott D. Anderson
 Vector Math Computer Graphics Scott D. Anderson 1 Dot Product The notation v w means the dot product or scalar product or inner product of two vectors, v and w. In abstract mathematics, we can talk about
Vector Math Computer Graphics Scott D. Anderson 1 Dot Product The notation v w means the dot product or scalar product or inner product of two vectors, v and w. In abstract mathematics, we can talk about
III. Applications of Force and Motion Concepts. Concept Review. Conflicting Contentions. 1. Airplane Drop 2. Moving Ball Toss 3. Galileo s Argument
 III. Applications of Force and Motion Concepts Concept Review Conflicting Contentions 1. Airplane Drop 2. Moving Ball Toss 3. Galileo s Argument Qualitative Reasoning 1. Dropping Balls 2. Spinning Bug
III. Applications of Force and Motion Concepts Concept Review Conflicting Contentions 1. Airplane Drop 2. Moving Ball Toss 3. Galileo s Argument Qualitative Reasoning 1. Dropping Balls 2. Spinning Bug
Chapter 3B - Vectors. A PowerPoint Presentation by Paul E. Tippens, Professor of Physics Southern Polytechnic State University
 Chapter 3B - Vectors A PowerPoint Presentation by Paul E. Tippens, Professor of Physics Southern Polytechnic State University 2007 Vectors Surveyors use accurate measures of magnitudes and directions to
Chapter 3B - Vectors A PowerPoint Presentation by Paul E. Tippens, Professor of Physics Southern Polytechnic State University 2007 Vectors Surveyors use accurate measures of magnitudes and directions to
Lecture L3 - Vectors, Matrices and Coordinate Transformations
 S. Widnall 16.07 Dynamics Fall 2009 Lecture notes based on J. Peraire Version 2.0 Lecture L3 - Vectors, Matrices and Coordinate Transformations By using vectors and defining appropriate operations between
S. Widnall 16.07 Dynamics Fall 2009 Lecture notes based on J. Peraire Version 2.0 Lecture L3 - Vectors, Matrices and Coordinate Transformations By using vectors and defining appropriate operations between
FRICTION, WORK, AND THE INCLINED PLANE
 FRICTION, WORK, AND THE INCLINED PLANE Objective: To measure the coefficient of static and inetic friction between a bloc and an inclined plane and to examine the relationship between the plane s angle
FRICTION, WORK, AND THE INCLINED PLANE Objective: To measure the coefficient of static and inetic friction between a bloc and an inclined plane and to examine the relationship between the plane s angle
Angles and Quadrants. Angle Relationships and Degree Measurement. Chapter 7: Trigonometry
 Chapter 7: Trigonometry Trigonometry is the study of angles and how they can be used as a means of indirect measurement, that is, the measurement of a distance where it is not practical or even possible
Chapter 7: Trigonometry Trigonometry is the study of angles and how they can be used as a means of indirect measurement, that is, the measurement of a distance where it is not practical or even possible
Geometry Notes PERIMETER AND AREA
 Perimeter and Area Page 1 of 57 PERIMETER AND AREA Objectives: After completing this section, you should be able to do the following: Calculate the area of given geometric figures. Calculate the perimeter
Perimeter and Area Page 1 of 57 PERIMETER AND AREA Objectives: After completing this section, you should be able to do the following: Calculate the area of given geometric figures. Calculate the perimeter
Math, Trigonometry and Vectors. Geometry. Trig Definitions. sin(θ) = opp hyp. cos(θ) = adj hyp. tan(θ) = opp adj. Here's a familiar image.
 Math, Trigonometr and Vectors Geometr Trig Definitions Here's a familiar image. To make predictive models of the phsical world, we'll need to make visualizations, which we can then turn into analtical
Math, Trigonometr and Vectors Geometr Trig Definitions Here's a familiar image. To make predictive models of the phsical world, we'll need to make visualizations, which we can then turn into analtical
Right Triangles A right triangle, as the one shown in Figure 5, is a triangle that has one angle measuring
 Page 1 9 Trigonometry of Right Triangles Right Triangles A right triangle, as the one shown in Figure 5, is a triangle that has one angle measuring 90. The side opposite to the right angle is the longest
Page 1 9 Trigonometry of Right Triangles Right Triangles A right triangle, as the one shown in Figure 5, is a triangle that has one angle measuring 90. The side opposite to the right angle is the longest
Right Triangles 4 A = 144 A = 16 12 5 A = 64
 Right Triangles If I looked at enough right triangles and experimented a little, I might eventually begin to notice a relationship developing if I were to construct squares formed by the legs of a right
Right Triangles If I looked at enough right triangles and experimented a little, I might eventually begin to notice a relationship developing if I were to construct squares formed by the legs of a right
TRIGONOMETRY Compound & Double angle formulae
 TRIGONOMETRY Compound & Double angle formulae In order to master this section you must first learn the formulae, even though they will be given to you on the matric formula sheet. We call these formulae
TRIGONOMETRY Compound & Double angle formulae In order to master this section you must first learn the formulae, even though they will be given to you on the matric formula sheet. We call these formulae
ANALYTICAL METHODS FOR ENGINEERS
 UNIT 1: Unit code: QCF Level: 4 Credit value: 15 ANALYTICAL METHODS FOR ENGINEERS A/601/1401 OUTCOME - TRIGONOMETRIC METHODS TUTORIAL 1 SINUSOIDAL FUNCTION Be able to analyse and model engineering situations
UNIT 1: Unit code: QCF Level: 4 Credit value: 15 ANALYTICAL METHODS FOR ENGINEERS A/601/1401 OUTCOME - TRIGONOMETRIC METHODS TUTORIAL 1 SINUSOIDAL FUNCTION Be able to analyse and model engineering situations
8-3 Dot Products and Vector Projections
 8-3 Dot Products and Vector Projections Find the dot product of u and v Then determine if u and v are orthogonal 1u =, u and v are not orthogonal 2u = 3u =, u and v are not orthogonal 6u = 11i + 7j; v
8-3 Dot Products and Vector Projections Find the dot product of u and v Then determine if u and v are orthogonal 1u =, u and v are not orthogonal 2u = 3u =, u and v are not orthogonal 6u = 11i + 7j; v
9.4. The Scalar Product. Introduction. Prerequisites. Learning Style. Learning Outcomes
 The Scalar Product 9.4 Introduction There are two kinds of multiplication involving vectors. The first is known as the scalar product or dot product. This is so-called because when the scalar product of
The Scalar Product 9.4 Introduction There are two kinds of multiplication involving vectors. The first is known as the scalar product or dot product. This is so-called because when the scalar product of
Chapter 07 Test A. Name: Class: Date: Multiple Choice Identify the choice that best completes the statement or answers the question.
 Class: Date: Chapter 07 Test A Multiple Choice Identify the choice that best completes the statement or answers the question. 1. An example of a vector quantity is: a. temperature. b. length. c. velocity.
Class: Date: Chapter 07 Test A Multiple Choice Identify the choice that best completes the statement or answers the question. 1. An example of a vector quantity is: a. temperature. b. length. c. velocity.
Triangle Trigonometry and Circles
 Math Objectives Students will understand that trigonometric functions of an angle do not depend on the size of the triangle within which the angle is contained, but rather on the ratios of the sides of
Math Objectives Students will understand that trigonometric functions of an angle do not depend on the size of the triangle within which the angle is contained, but rather on the ratios of the sides of
Lesson 33: Example 1 (5 minutes)
 Student Outcomes Students understand that the Law of Sines can be used to find missing side lengths in a triangle when you know the measures of the angles and one side length. Students understand that
Student Outcomes Students understand that the Law of Sines can be used to find missing side lengths in a triangle when you know the measures of the angles and one side length. Students understand that
Chapter 10: Linear Kinematics of Human Movement
 Chapter 10: Linear Kinematics of Human Movement Basic Biomechanics, 4 th edition Susan J. Hall Presentation Created by TK Koesterer, Ph.D., ATC Humboldt State University Objectives Discuss the interrelationship
Chapter 10: Linear Kinematics of Human Movement Basic Biomechanics, 4 th edition Susan J. Hall Presentation Created by TK Koesterer, Ph.D., ATC Humboldt State University Objectives Discuss the interrelationship
Work-Energy Bar Charts
 Name: Work-Energy Bar Charts Read from Lesson 2 of the Work, Energy and Power chapter at The Physics Classroom: http://www.physicsclassroom.com/class/energy/u5l2c.html MOP Connection: Work and Energy:
Name: Work-Energy Bar Charts Read from Lesson 2 of the Work, Energy and Power chapter at The Physics Classroom: http://www.physicsclassroom.com/class/energy/u5l2c.html MOP Connection: Work and Energy:
sin(θ) = opp hyp cos(θ) = adj hyp tan(θ) = opp adj
 Math, Trigonometr and Vectors Geometr 33º What is the angle equal to? a) α = 7 b) α = 57 c) α = 33 d) α = 90 e) α cannot be determined α Trig Definitions Here's a familiar image. To make predictive models
Math, Trigonometr and Vectors Geometr 33º What is the angle equal to? a) α = 7 b) α = 57 c) α = 33 d) α = 90 e) α cannot be determined α Trig Definitions Here's a familiar image. To make predictive models
Force on Moving Charges in a Magnetic Field
 [ Assignment View ] [ Eðlisfræði 2, vor 2007 27. Magnetic Field and Magnetic Forces Assignment is due at 2:00am on Wednesday, February 28, 2007 Credit for problems submitted late will decrease to 0% after
[ Assignment View ] [ Eðlisfræði 2, vor 2007 27. Magnetic Field and Magnetic Forces Assignment is due at 2:00am on Wednesday, February 28, 2007 Credit for problems submitted late will decrease to 0% after
Copyright 2011 Casa Software Ltd. www.casaxps.com. Centre of Mass
 Centre of Mass A central theme in mathematical modelling is that of reducing complex problems to simpler, and hopefully, equivalent problems for which mathematical analysis is possible. The concept of
Centre of Mass A central theme in mathematical modelling is that of reducing complex problems to simpler, and hopefully, equivalent problems for which mathematical analysis is possible. The concept of
TIME OF COMPLETION DEPARTMENT OF NATURAL SCIENCES. PHYS 1111, Exam 2 Section 1 Version 1 October 30, 2002 Total Weight: 100 points
 TIME OF COMPLETION NAME DEPARTMENT OF NATURAL SCIENCES PHYS 1111, Exam 2 Section 1 Version 1 October 30, 2002 Total Weight: 100 points 1. Check your examination for completeness prior to starting. There
TIME OF COMPLETION NAME DEPARTMENT OF NATURAL SCIENCES PHYS 1111, Exam 2 Section 1 Version 1 October 30, 2002 Total Weight: 100 points 1. Check your examination for completeness prior to starting. There
What You ll Learn Why It s Important Rock Climbing Think About This physicspp.com 118
 What You ll Learn You will represent vector quantities both graphically and algebraically. You will use Newton s laws to analyze motion when friction is involved. You will use Newton s laws and your knowledge
What You ll Learn You will represent vector quantities both graphically and algebraically. You will use Newton s laws to analyze motion when friction is involved. You will use Newton s laws and your knowledge
Physics Section 3.2 Free Fall
 Physics Section 3.2 Free Fall Aristotle Aristotle taught that the substances making up the Earth were different from the substance making up the heavens. He also taught that dynamics (the branch of physics
Physics Section 3.2 Free Fall Aristotle Aristotle taught that the substances making up the Earth were different from the substance making up the heavens. He also taught that dynamics (the branch of physics
Physical Quantities and Units
 Physical Quantities and Units 1 Revision Objectives This chapter will explain the SI system of units used for measuring physical quantities and will distinguish between vector and scalar quantities. You
Physical Quantities and Units 1 Revision Objectives This chapter will explain the SI system of units used for measuring physical quantities and will distinguish between vector and scalar quantities. You
Football Learning Guide for Parents and Educators. Overview
 Overview Did you know that when Victor Cruz catches a game winning touchdown, the prolate spheroid he s holding helped the quarterback to throw a perfect spiral? Wait, what? Well, the shape of a football
Overview Did you know that when Victor Cruz catches a game winning touchdown, the prolate spheroid he s holding helped the quarterback to throw a perfect spiral? Wait, what? Well, the shape of a football
6. LECTURE 6. Objectives
 6. LECTURE 6 Objectives I understand how to use vectors to understand displacement. I can find the magnitude of a vector. I can sketch a vector. I can add and subtract vector. I can multiply a vector by
6. LECTURE 6 Objectives I understand how to use vectors to understand displacement. I can find the magnitude of a vector. I can sketch a vector. I can add and subtract vector. I can multiply a vector by
Pre-Calculus Unit Plan: Vectors and their Applications. Dr. Mohr-Schroeder. Fall 2012. University of Kentucky. Jessica Doering.
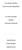 Pre-Calculus Unit Plan: Vectors and their Applications Dr. Mohr-Schroeder Fall 2012 University of Kentucky Jessica Doering Andrea Meadors Stephen Powers Table of Contents Narrative and Overview of Unit
Pre-Calculus Unit Plan: Vectors and their Applications Dr. Mohr-Schroeder Fall 2012 University of Kentucky Jessica Doering Andrea Meadors Stephen Powers Table of Contents Narrative and Overview of Unit
Vectors. Objectives. Assessment. Assessment. Equations. Physics terms 5/15/14. State the definition and give examples of vector and scalar variables.
 Vectors Objectives State the definition and give examples of vector and scalar variables. Analyze and describe position and movement in two dimensions using graphs and Cartesian coordinates. Organize and
Vectors Objectives State the definition and give examples of vector and scalar variables. Analyze and describe position and movement in two dimensions using graphs and Cartesian coordinates. Organize and
Dear Accelerated Pre-Calculus Student:
 Dear Accelerated Pre-Calculus Student: I am very excited that you have decided to take this course in the upcoming school year! This is a fastpaced, college-preparatory mathematics course that will also
Dear Accelerated Pre-Calculus Student: I am very excited that you have decided to take this course in the upcoming school year! This is a fastpaced, college-preparatory mathematics course that will also
SCALAR VS. VECTOR QUANTITIES
 SCIENCE 1206 MOTION - Unit 3 Slideshow 2 SPEED CALCULATIONS NAME: TOPICS OUTLINE SCALAR VS. VECTOR SCALAR QUANTITIES DISTANCE TYPES OF SPEED SPEED CALCULATIONS DISTANCE-TIME GRAPHS SPEED-TIME GRAPHS SCALAR
SCIENCE 1206 MOTION - Unit 3 Slideshow 2 SPEED CALCULATIONS NAME: TOPICS OUTLINE SCALAR VS. VECTOR SCALAR QUANTITIES DISTANCE TYPES OF SPEED SPEED CALCULATIONS DISTANCE-TIME GRAPHS SPEED-TIME GRAPHS SCALAR
Solutions to old Exam 1 problems
 Solutions to old Exam 1 problems Hi students! I am putting this old version of my review for the first midterm review, place and time to be announced. Check for updates on the web site as to which sections
Solutions to old Exam 1 problems Hi students! I am putting this old version of my review for the first midterm review, place and time to be announced. Check for updates on the web site as to which sections
Work, Energy & Momentum Homework Packet Worksheet 1: This is a lot of work!
 Work, Energy & Momentum Homework Packet Worksheet 1: This is a lot of work! 1. A student holds her 1.5-kg psychology textbook out of a second floor classroom window until her arm is tired; then she releases
Work, Energy & Momentum Homework Packet Worksheet 1: This is a lot of work! 1. A student holds her 1.5-kg psychology textbook out of a second floor classroom window until her arm is tired; then she releases
Physics 2A, Sec B00: Mechanics -- Winter 2011 Instructor: B. Grinstein Final Exam
 Physics 2A, Sec B00: Mechanics -- Winter 2011 Instructor: B. Grinstein Final Exam INSTRUCTIONS: Use a pencil #2 to fill your scantron. Write your code number and bubble it in under "EXAM NUMBER;" an entry
Physics 2A, Sec B00: Mechanics -- Winter 2011 Instructor: B. Grinstein Final Exam INSTRUCTIONS: Use a pencil #2 to fill your scantron. Write your code number and bubble it in under "EXAM NUMBER;" an entry
TEACHER ANSWER KEY November 12, 2003. Phys - Vectors 11-13-2003
 Phys - Vectors 11-13-2003 TEACHER ANSWER KEY November 12, 2003 5 1. A 1.5-kilogram lab cart is accelerated uniformly from rest to a speed of 2.0 meters per second in 0.50 second. What is the magnitude
Phys - Vectors 11-13-2003 TEACHER ANSWER KEY November 12, 2003 5 1. A 1.5-kilogram lab cart is accelerated uniformly from rest to a speed of 2.0 meters per second in 0.50 second. What is the magnitude
force (mass)(acceleration) or F ma The unbalanced force is called the net force, or resultant of all the forces acting on the system.
 4 Forces 4-1 Forces and Acceleration Vocabulary Force: A push or a pull. When an unbalanced force is exerted on an object, the object accelerates in the direction of the force. The acceleration is proportional
4 Forces 4-1 Forces and Acceleration Vocabulary Force: A push or a pull. When an unbalanced force is exerted on an object, the object accelerates in the direction of the force. The acceleration is proportional
One- and Two-dimensional Motion
 PHYS-101 LAB-02 One- and Two-dimensional Motion 1. Objective The objectives of this experiment are: to measure the acceleration of gravity using one-dimensional motion to demonstrate the independence of
PHYS-101 LAB-02 One- and Two-dimensional Motion 1. Objective The objectives of this experiment are: to measure the acceleration of gravity using one-dimensional motion to demonstrate the independence of
1. Units of a magnetic field might be: A. C m/s B. C s/m C. C/kg D. kg/c s E. N/C m ans: D
 Chapter 28: MAGNETIC FIELDS 1 Units of a magnetic field might be: A C m/s B C s/m C C/kg D kg/c s E N/C m 2 In the formula F = q v B: A F must be perpendicular to v but not necessarily to B B F must be
Chapter 28: MAGNETIC FIELDS 1 Units of a magnetic field might be: A C m/s B C s/m C C/kg D kg/c s E N/C m 2 In the formula F = q v B: A F must be perpendicular to v but not necessarily to B B F must be
The Force Table Vector Addition and Resolution
 Name School Date The Force Table Vector Addition and Resolution Vectors? I don't have any vectors, I'm just a kid. From Flight of the Navigator Explore the Apparatus/Theory We ll use the Force Table Apparatus
Name School Date The Force Table Vector Addition and Resolution Vectors? I don't have any vectors, I'm just a kid. From Flight of the Navigator Explore the Apparatus/Theory We ll use the Force Table Apparatus
Physics Notes Class 11 CHAPTER 3 MOTION IN A STRAIGHT LINE
 1 P a g e Motion Physics Notes Class 11 CHAPTER 3 MOTION IN A STRAIGHT LINE If an object changes its position with respect to its surroundings with time, then it is called in motion. Rest If an object
1 P a g e Motion Physics Notes Class 11 CHAPTER 3 MOTION IN A STRAIGHT LINE If an object changes its position with respect to its surroundings with time, then it is called in motion. Rest If an object
PHY121 #8 Midterm I 3.06.2013
 PHY11 #8 Midterm I 3.06.013 AP Physics- Newton s Laws AP Exam Multiple Choice Questions #1 #4 1. When the frictionless system shown above is accelerated by an applied force of magnitude F, the tension
PHY11 #8 Midterm I 3.06.013 AP Physics- Newton s Laws AP Exam Multiple Choice Questions #1 #4 1. When the frictionless system shown above is accelerated by an applied force of magnitude F, the tension
2008 FXA DERIVING THE EQUATIONS OF MOTION 1. Candidates should be able to :
 Candidates should be able to : Derive the equations of motion for constant acceleration in a straight line from a velocity-time graph. Select and use the equations of motion for constant acceleration in
Candidates should be able to : Derive the equations of motion for constant acceleration in a straight line from a velocity-time graph. Select and use the equations of motion for constant acceleration in
WEIGHTLESS WONDER Reduced Gravity Flight
 WEIGHTLESS WONDER Reduced Gravity Flight Instructional Objectives Students will use trigonometric ratios to find vertical and horizontal components of a velocity vector; derive a formula describing height
WEIGHTLESS WONDER Reduced Gravity Flight Instructional Objectives Students will use trigonometric ratios to find vertical and horizontal components of a velocity vector; derive a formula describing height
Newton s Laws. Physics 1425 lecture 6. Michael Fowler, UVa.
 Newton s Laws Physics 1425 lecture 6 Michael Fowler, UVa. Newton Extended Galileo s Picture of Galileo said: Motion to Include Forces Natural horizontal motion is at constant velocity unless a force acts:
Newton s Laws Physics 1425 lecture 6 Michael Fowler, UVa. Newton Extended Galileo s Picture of Galileo said: Motion to Include Forces Natural horizontal motion is at constant velocity unless a force acts:
Graphing Motion. Every Picture Tells A Story
 Graphing Motion Every Picture Tells A Story Read and interpret motion graphs Construct and draw motion graphs Determine speed, velocity and accleration from motion graphs If you make a graph by hand it
Graphing Motion Every Picture Tells A Story Read and interpret motion graphs Construct and draw motion graphs Determine speed, velocity and accleration from motion graphs If you make a graph by hand it
Section V.3: Dot Product
 Section V.3: Dot Product Introduction So far we have looked at operations on a single vector. There are a number of ways to combine two vectors. Vector addition and subtraction will not be covered here,
Section V.3: Dot Product Introduction So far we have looked at operations on a single vector. There are a number of ways to combine two vectors. Vector addition and subtraction will not be covered here,
MODERN APPLICATIONS OF PYTHAGORAS S THEOREM
 UNIT SIX MODERN APPLICATIONS OF PYTHAGORAS S THEOREM Coordinate Systems 124 Distance Formula 127 Midpoint Formula 131 SUMMARY 134 Exercises 135 UNIT SIX: 124 COORDINATE GEOMETRY Geometry, as presented
UNIT SIX MODERN APPLICATIONS OF PYTHAGORAS S THEOREM Coordinate Systems 124 Distance Formula 127 Midpoint Formula 131 SUMMARY 134 Exercises 135 UNIT SIX: 124 COORDINATE GEOMETRY Geometry, as presented
Geometry 1. Unit 3: Perpendicular and Parallel Lines
 Geometry 1 Unit 3: Perpendicular and Parallel Lines Geometry 1 Unit 3 3.1 Lines and Angles Lines and Angles Parallel Lines Parallel lines are lines that are coplanar and do not intersect. Some examples
Geometry 1 Unit 3: Perpendicular and Parallel Lines Geometry 1 Unit 3 3.1 Lines and Angles Lines and Angles Parallel Lines Parallel lines are lines that are coplanar and do not intersect. Some examples
