Chapter 17. For the most part, we have limited our consideration so COMPRESSIBLE FLOW. Objectives
|
|
|
- Merryl Freeman
- 8 years ago
- Views:
Transcription
1 Chapter 17 COMPRESSIBLE FLOW For the most part, we have limited our consideration so far to flows for which density variations and thus compressibility effects are negligible. In this chapter we lift this limitation and consider flows that involve significant changes in density. Such flows are called compressible flows, and they are frequently encountered in devices that involve the flow of gases at very high velocities. Compressible flow combines fluid dynamics and thermodynamics in that both are necessary to the development of the required theoretical background. In this chapter, we develop the general relations associated with one-dimensional compressible flows for an ideal gas with constant specific heats. We start this chapter by introducing the concepts of stagnation state, speed of sound, and Mach number for compressible flows. The relationships between the static and stagnation fluid properties are developed for isentropic flows of ideal gases, and they are expressed as functions of specificheat ratios and the Mach number. The effects of area changes for one-dimensional isentropic subsonic and supersonic flows are discussed. These effects are illustrated by considering the isentropic flow through converging and converging diverging nozzles. The concept of shock waves and the variation of flow properties across normal and oblique shocks are discussed. Finally, we consider the effects of heat transfer on compressible flows and examine steam nozzles. Objectives The objectives of Chapter 17 are to: Develop the general relations for compressible flows encountered when gases flow at high speeds. Introduce the concepts of stagnation state, speed of sound, and Mach number for a compressible fluid. Develop the relationships between the static and stagnation fluid properties for isentropic flows of ideal gases. Derive the relationships between the static and stagnation fluid properties as functions of specific-heat ratios and Mach number. Derive the effects of area changes for one-dimensional isentropic subsonic and supersonic flows. Solve problems of isentropic flow through converging and converging diverging nozzles. Discuss the shock wave and the variation of flow properties across the shock wave. Develop the concept of duct flow with heat transfer and negligible friction known as Rayleigh flow. Examine the operation of steam nozzles commonly used in steam turbines. 849
2 850 Thermodynamics FIGURE 17 1 Aircraft and jet engines involve high speeds, and thus the kinetic energy term should always be considered when analyzing them. (a) Photo courtesy of NASA, jpeg, and (b) Figure courtesy of Pratt and Whitney. Used by permission. h 1 h V Control 1 V volume h 01 h 0 = h 01 FIGURE 17 Steady flow of a fluid through an adiabatic duct STAGNATION PROPERTIES When analyzing control volumes, we find it very convenient to combine the internal energy and the flow energy of a fluid into a single term, enthalpy, defined per unit mass as h u Pv. Whenever the kinetic and potential energies of the fluid are negligible, as is often the case, the enthalpy represents the total energy of a fluid. For high-speed flows, such as those encountered in jet engines (Fig. 17 1), the potential energy of the fluid is still negligible, but the kinetic energy is not. In such cases, it is convenient to combine the enthalpy and the kinetic energy of the fluid into a single term called stagnation (or total) enthalpy h 0, defined per unit mass as (17 1) When the potential energy of the fluid is negligible, the stagnation enthalpy represents the total energy of a flowing fluid stream per unit mass. Thus it simplifies the thermodynamic analysis of high-speed flows. Throughout this chapter the ordinary enthalpy h is referred to as the static enthalpy, whenever necessary, to distinguish it from the stagnation enthalpy. Notice that the stagnation enthalpy is a combination property of a fluid, just like the static enthalpy, and these two enthalpies become identical when the kinetic energy of the fluid is negligible. Consider the steady flow of a fluid through a duct such as a nozzle, diffuser, or some other flow passage where the flow takes place adiabatically and with no shaft or electrical work, as shown in Fig. 17. Assuming the fluid experiences little or no change in its elevation and its potential energy, the energy balance relation (E. in E. out ) for this single-stream steady-flow system reduces to or h 0 h V 1kJ>kg h 1 V 1 h V (17 ) h 01 h 0 (17 3) That is, in the absence of any heat and work interactions and any changes in potential energy, the stagnation enthalpy of a fluid remains constant during a steady-flow process. Flows through nozzles and diffusers usually satisfy these conditions, and any increase in fluid velocity in these devices creates an equivalent decrease in the static enthalpy of the fluid. If the fluid were brought to a complete stop, then the velocity at state would be zero and Eq. 17 would become h 1 V 1 h h 0 Thus the stagnation enthalpy represents the enthalpy of a fluid when it is brought to rest adiabatically. During a stagnation process, the kinetic energy of a fluid is converted to enthalpy (internal energy flow energy), which results in an increase in the fluid temperature and pressure (Fig. 17 3). The properties of a fluid at the stagnation state are called stagnation properties (stagnation temperature,
3 stagnation pressure, stagnation density, etc.). The stagnation state and the stagnation properties are indicated by the subscript 0. The stagnation state is called the isentropic stagnation state when the stagnation process is reversible as well as adiabatic (i.e., isentropic). The entropy of a fluid remains constant during an isentropic stagnation process. The actual (irreversible) and isentropic stagnation processes are shown on the h-s diagram in Fig Notice that the stagnation enthalpy of the fluid (and the stagnation temperature if the fluid is an ideal gas) is the same for both cases. However, the actual stagnation pressure is lower than the isentropic stagnation pressure since entropy increases during the actual stagnation process as a result of fluid friction. The stagnation processes are often approximated to be isentropic, and the isentropic stagnation properties are simply referred to as stagnation properties. When the fluid is approximated as an ideal gas with constant specific heats, its enthalpy can be replaced by c p T and Eq can be expressed as or c p T 0 c p T V T 0 T V (17 4) Here T 0 is called the stagnation (or total) temperature, and it represents the temperature an ideal gas attains when it is brought to rest adiabatically. The term V /c p corresponds to the temperature rise during such a process and is called the dynamic temperature. For example, the dynamic temperature of air flowing at 100 m/s is (100 m/s) /( kj/kg K) 5.0 K. Therefore, when air at 300 K and 100 m/s is brought to rest adiabatically (at the tip of a temperature probe, for example), its temperature rises to the stagnation value of 305 K (Fig. 17 5). Note that for low-speed flows, the stagnation and static (or ordinary) temperatures are practically the same. But for high-speed flows, the temperature measured by a stationary probe placed in the fluid (the stagnation temperature) may be significantly higher than the static temperature of the fluid. The pressure a fluid attains when brought to rest isentropically is called the stagnation pressure P 0. For ideal gases with constant specific heats, P 0 is related to the static pressure of the fluid by P 0 P a T 0 T b k>1k 1 (17 5) By noting that r 1/v and using the isentropic relation Pv k P 0 v 0 k, the ratio of the stagnation density to static density can be expressed as r 0 r a T 0 T b 1>1k 1 (17 6) When stagnation enthalpies are used, there is no need to refer explicitly to kinetic energy. Then the energy balance E # in E # out for a single-stream, steady-flow device can be expressed as c p q in w in 1h 01 gz 1 q out w out 1h 0 gz (17 7) Chapter FIGURE 17 3 Kinetic energy is converted to enthalpy during a stagnation process. Reprinted with special permission of King Features Syndicate. h h0 h Isentropic stagnation state V P 0 P 0,act Actual stagnation state P Actual state FIGURE 17 4 The actual state, actual stagnation state, and isentropic stagnation state of a fluid on an h-s diagram. s
4 85 Thermodynamics Temperature rise during stagnation AIR 100 m/s 305 K 300 K FIGURE 17 5 The temperature of an ideal gas flowing at a velocity V rises by V /c p when it is brought to a complete stop. T 1 = 55.7 K P 1 = kpa V 1 = 50 m/s Diffuser FIGURE 17 6 Schematic for Example Compressor Aircraft engine where h 01 and h 0 are the stagnation enthalpies at states 1 and, respectively. When the fluid is an ideal gas with constant specific heats, Eq becomes 1q in q out 1w in w out c p 1T 0 T 01 g 1z z 1 (17 8) where T 01 and T 0 are the stagnation temperatures. Notice that kinetic energy terms do not explicitly appear in Eqs and 17 8, but the stagnation enthalpy terms account for their contribution. EXAMPLE 17 1 Compression of High-Speed Air in an Aircraft An aircraft is flying at a cruising speed of 50 m/s at an altitude of 5000 m where the atmospheric pressure is kpa and the ambient air temperature is 55.7 K. The ambient air is first decelerated in a diffuser before it enters the compressor (Fig. 17 6). Assuming both the diffuser and the compressor to be isentropic, determine (a) the stagnation pressure at the compressor inlet and (b) the required compressor work per unit mass if the stagnation pressure ratio of the compressor is 8. Solution High-speed air enters the diffuser and the compressor of an aircraft. The stagnation pressure of air and the compressor work input are to be determined. Assumptions 1 Both the diffuser and the compressor are isentropic. Air is an ideal gas with constant specific heats at room temperature. Properties The constant-pressure specific heat c p and the specific heat ratio k of air at room temperature are (Table A a) Analysis (a) Under isentropic conditions, the stagnation pressure at the compressor inlet (diffuser exit) can be determined from Eq However, first we need to find the stagnation temperature T 01 at the compressor inlet. Under the stated assumptions, T 01 can be determined from Eq to be 86.8 K Then from Eq. 17 5, c p kj>kg # K and k 1.4 T 01 T 1 V 1 c p 55.7 K P 01 P 1 a T k>1k 1 01 b kpa a 86.8 K 1.4> T K b kpa 150 m>s kj>kg # K a 1 kj>kg 1000 m >s b That is, the temperature of air would increase by 31.1 C and the pressure by 6.7 kpa as air is decelerated from 50 m/s to zero velocity. These increases in the temperature and pressure of air are due to the conversion of the kinetic energy into enthalpy. (b) To determine the compressor work, we need to know the stagnation temperature of air at the compressor exit T 0. The stagnation pressure ratio across the compressor P 0 /P 01 is specified to be 8. Since the compression process is assumed to be isentropic, T 0 can be determined from the idealgas isentropic relation (Eq. 17 5): T 0 T 01 a P 1k 1>k 0 b K > K P 01
5 Chapter Disregarding potential energy changes and heat transfer, the compressor work per unit mass of air is determined from Eq. 17 8: w in c p 1T 0 T kj>kg # K K 86.8 K 33.9 kj/kg Thus the work supplied to the compressor is 33.9 kj/kg. Discussion Notice that using stagnation properties automatically accounts for any changes in the kinetic energy of a fluid stream. 17 SPEED OF SOUND AND MACH NUMBER An important parameter in the study of compressible flow is the speed of sound (or the sonic speed), which is the speed at which an infinitesimally small pressure wave travels through a medium. The pressure wave may be caused by a small disturbance, which creates a slight rise in local pressure. To obtain a relation for the speed of sound in a medium, consider a pipe that is filled with a fluid at rest, as shown in Fig A piston fitted in the pipe is now moved to the right with a constant incremental velocity dv, creating a sonic wave. The wave front moves to the right through the fluid at the speed of sound c and separates the moving fluid adjacent to the piston from the fluid still at rest. The fluid to the left of the wave front experiences an incremental change in its thermodynamic properties, while the fluid on the right of the wave front maintains its original thermodynamic properties, as shown in Fig To simplify the analysis, consider a control volume that encloses the wave front and moves with it, as shown in Fig To an observer traveling with the wave front, the fluid to the right will appear to be moving toward the wave front with a speed of c and the fluid to the left to be moving away from the wave front with a speed of c dv. Of course, the observer will think the control volume that encloses the wave front (and herself or himself) is stationary, and the observer will be witnessing a steady-flow process. The mass balance for this single-stream, steady-flow process can be expressed as or rac 1r dra 1c dv By canceling the cross-sectional (or flow) area A and neglecting the higherorder terms, this equation reduces to No heat or work crosses the boundaries of the control volume during this steady-flow process, and the potential energy change, if any, can be neglected. Then the steady-flow energy balance e in e out becomes h c m # right m # left c dr r dv 0 h dh 1c dv (a) V 0 P Piston dv h + dh P + dp c h P r + dr r dv P + dp Moving wave front Stationary fluid FIGURE 17 7 Propagation of a small pressure wave along a duct. Control volume traveling with the wave front h + dh c dv c h P + dp P r + dr r FIGURE 17 8 Control volume moving with the small pressure wave along a duct. P x x
6 854 Thermodynamics which yields dh c dv 0 where we have neglected the second-order term dv. The amplitude of the ordinary sonic wave is very small and does not cause any appreciable change in the pressure and temperature of the fluid. Therefore, the propagation of a sonic wave is not only adiabatic but also very nearly isentropic. Then the second Tdsrelation developed in Chapter 7 reduces to T ds 0 dh dp r (b) or dh dp r (c) Combining Eqs. a, b, and c yields the desired expression for the speed of sound as c dp at s constant dr or c a 0P (17 9) 0r b s It is left as an exercise for the reader to show, by using thermodynamic property relations (see Chap. 1) that Eq can also be written as c k a 0P 0r b T (17 10) where k is the specific heat ratio of the fluid. Note that the speed of sound in a fluid is a function of the thermodynamic properties of that fluid. When the fluid is an ideal gas (P rrt), the differentiation in Eq can easily be performed to yield AIR HELIUM or c k a 0P 0r b k c 0 1rRT d krt T 0r T 84 m/s 347 m/s 634 m/s 00 K 300 K 1000 K 83 m/s 1019 m/s 1861 m/s c krt (17 11) Noting that the gas constant R has a fixed value for a specified ideal gas and the specific heat ratio k of an ideal gas is, at most, a function of temperature, we see that the speed of sound in a specified ideal gas is a function of temperature alone (Fig. 17 9). A second important parameter in the analysis of compressible fluid flow is the Mach number Ma, named after the Austrian physicist Ernst Mach ( ). It is the ratio of the actual velocity of the fluid (or an object in still air) to the speed of sound in the same fluid at the same state: FIGURE 17 9 The speed of sound changes with temperature and varies with the fluid. Ma V c (17 1) Note that the Mach number depends on the speed of sound, which depends on the state of the fluid. Therefore, the Mach number of an aircraft cruising
7 at constant velocity in still air may be different at different locations (Fig ). Fluid flow regimes are often described in terms of the flow Mach number. The flow is called sonic when Ma 1, subsonic when Ma 1, supersonic when Ma 1, hypersonic when Ma 1, and transonic when Ma 1. EXAMPLE 17 Mach Number of Air Entering a Diffuser Air enters a diffuser shown in Fig with a velocity of 00 m/s. Determine (a) the speed of sound and (b) the Mach number at the diffuser inlet when the air temperature is 30 C. Solution Air enters a diffuser with a high velocity. The speed of sound and the Mach number are to be determined at the diffuser inlet. Assumptions Air at specified conditions behaves as an ideal gas. Properties The gas constant of air is R 0.87 kj/kg K, and its specific heat ratio at 30 C is 1.4 (Table A a). Analysis We note that the speed of sound in a gas varies with temperature, which is given to be 30 C. (a) The speed of sound in air at 30 C is determined from Eq to be c krt B kj>kg # K1303 Ka 1000 m >s (b) Then the Mach number becomes Ma V c 00 m>s 349 m>s kj>kg b 349 m /s Discussion The flow at the diffuser inlet is subsonic since Ma 1. AIR 00 K AIR 300 K Chapter V = 30 m/s Ma = 1.13 V = 30 m/s Ma = 0.9 FIGURE The Mach number can be different at different temperatures even if the velocity is the same. AIR V = 00 m/s T = 30 C Diffuser FIGURE Schematic for Example ONE-DIMENSIONAL ISENTROPIC FLOW During fluid flow through many devices such as nozzles, diffusers, and turbine blade passages, flow quantities vary primarily in the flow direction only, and the flow can be approximated as one-dimensional isentropic flow with good accuracy. Therefore, it merits special consideration. Before presenting a formal discussion of one-dimensional isentropic flow, we illustrate some important aspects of it with an example. EXAMPLE 17 3 Gas Flow through a Converging Diverging Duct Carbon dioxide flows steadily through a varying cross-sectional-area duct such as a nozzle shown in Fig at a mass flow rate of 3 kg/s. The carbon dioxide enters the duct at a pressure of 1400 kpa and 00 C with a low velocity, and it expands in the nozzle to a pressure of 00 kpa. The duct is designed so that the flow can be approximated as isentropic. Determine the density, velocity, flow area, and Mach number at each location along the duct that corresponds to a pressure drop of 00 kpa. Solution Carbon dioxide enters a varying cross-sectional-area duct at specified conditions. The flow properties are to be determined along the duct. Stagnation region: 1400 kpa 00 C CO m kg/s P, kpa FIGURE 17 1 Schematic for Example 17 3.
8 856 Thermodynamics Assumptions 1 Carbon dioxide is an ideal gas with constant specific heats at room temperature. Flow through the duct is steady, one-dimensional, and isentropic. Properties For simplicity we use c p kj/kg K and k 1.89 throughout the calculations, which are the constant-pressure specific heat and specific heat ratio values of carbon dioxide at room temperature. The gas constant of carbon dioxide is R kj/kg K (Table A a). Analysis We note that the inlet temperature is nearly equal to the stagnation temperature since the inlet velocity is small. The flow is isentropic, and thus the stagnation temperature and pressure throughout the duct remain constant. Therefore, and To illustrate the solution procedure, we calculate the desired properties at the location where the pressure is 100 kpa, the first location that corresponds to a pressure drop of 00 kpa. From Eq. 17 5, From Eq. 17 4, From the ideal-gas relation, From the mass flow rate relation, From Eqs and 17 1, 1000 m c krt kj>kg # >s K1457 K a b m>s B 1 kj>kg Ma V c T T 0 a P 1k 1>k b P 0 V c p 1T 0 T A m# rv B kj>kg # K1473 K 457 K a 1000 m >s 3 1 kj>kg b m/s r P RT 3 kg>s kg>m m>s m 13.1 cm m>s m>s T 0 T 1 00 C 473 K P 0 P kpa > kpa 1473 Ka 1400 kpa b 457 K 100 kpa kpa # m 3 >kg # K1457 K 13.9 kg/m 3 The results for the other pressure steps are summarized in Table 17 1 and are plotted in Fig Discussion Note that as the pressure decreases, the temperature and speed of sound decrease while the fluid velocity and Mach number increase in the flow direction. The density decreases slowly at first and rapidly later as the fluid velocity increases.
9 Chapter TABLE 17 1 Variation of fluid properties in flow direction in duct described in Example 17 3 for m. 3 kg/s constant P, kpa T, K V, m/s r, kg/m 3 c, m/s A, cm Ma * * 767 kpa is the critical pressure where the local Mach number is unity. Flow direction A A, Ma, r, T, V T r Ma 1400 V P, kpa FIGURE Variation of normalized fluid properties and cross-sectional area along a duct as the pressure drops from 1400 to 00 kpa. We note from Example 17 3 that the flow area decreases with decreasing pressure up to a critical-pressure value where the Mach number is unity, and then it begins to increase with further reductions in pressure. The Mach number is unity at the location of smallest flow area, called the throat (Fig ). Note that the velocity of the fluid keeps increasing after passing the throat although the flow area increases rapidly in that region. This increase in velocity past the throat is due to the rapid decrease in the fluid density. The flow area of the duct considered in this example first decreases and then increases. Such ducts are called converging diverging nozzles. These nozzles are used to accelerate gases to supersonic speeds and should not be confused with Venturi nozzles, which are used strictly for incompressible flow. The first use of such a nozzle occurred in 1893 in a steam turbine
10 858 Thermodynamics Fluid Fluid Throat Converging nozzle Throat Converging diverging nozzle FIGURE The cross section of a nozzle at the smallest flow area is called the throat. designed by a Swedish engineer, Carl G. B. de Laval ( ), and therefore converging diverging nozzles are often called Laval nozzles. Variation of Fluid Velocity with Flow Area It is clear from Example 17 3 that the couplings among the velocity, density, and flow areas for isentropic duct flow are rather complex. In the remainder of this section we investigate these couplings more thoroughly, and we develop relations for the variation of static-to-stagnation property ratios with the Mach number for pressure, temperature, and density. We begin our investigation by seeking relationships among the pressure, temperature, density, velocity, flow area, and Mach number for onedimensional isentropic flow. Consider the mass balance for a steady-flow process: m # rav constant Differentiating and dividing the resultant equation by the mass flow rate, we obtain dr r da A dv V 0 (17 13) CONSERVATION OF ENERGY (steady flow, w = 0, q = 0, Δpe = 0) h 1 + V 1 = h + V or h + V = constant Differentiate, dh + V dv = 0 Also, 0 (isentropic) T ds = dh v dp dh = v dp = r 1 dp Substitute, dp r + V dv = 0 FIGURE Derivation of the differential form of the energy equation for steady isentropic flow. Neglecting the potential energy, the energy balance for an isentropic flow with no work interactions can be expressed in the differential form as (Fig ) dp r V dv 0 (17 14) This relation is also the differential form of Bernoulli s equation when changes in potential energy are negligible, which is a form of the conservation of momentum principle for steady-flow control volumes. Combining Eqs and gives da A dp r a 1 V dr dp b (17 15) Rearranging Eq as ( r/ P) s 1/c and substituting into Eq yield da A dp rv 11 Ma (17 16) This is an important relation for isentropic flow in ducts since it describes the variation of pressure with flow area. We note that A, r, and V are positive quantities. For subsonic flow (Ma 1), the term 1 Ma is positive; and thus da and dp must have the same sign. That is, the pressure of the fluid must increase as the flow area of the duct increases and must decrease as the flow area of the duct decreases. Thus, at subsonic velocities, the pressure decreases in converging ducts (subsonic nozzles) and increases in diverging ducts (subsonic diffusers). In supersonic flow (Ma 1), the term 1 Ma is negative, and thus da and dp must have opposite signs. That is, the pressure of the fluid must
11 increase as the flow area of the duct decreases and must decrease as the flow area of the duct increases. Thus, at supersonic velocities, the pressure decreases in diverging ducts (supersonic nozzles) and increases in converging ducts (supersonic diffusers). Another important relation for the isentropic flow of a fluid is obtained by substituting rv dp/dv from Eq into Eq : Chapter da A dv V 11 Ma (17 17) This equation governs the shape of a nozzle or a diffuser in subsonic or supersonic isentropic flow. Noting that A and V are positive quantities, we conclude the following: For subsonic flow 1Ma 6 1, For supersonic flow 1Ma 7 1, For sonic flow 1Ma 1, da dv 6 0 da dv 7 0 da dv 0 Thus the proper shape of a nozzle depends on the highest velocity desired relative to the sonic velocity. To accelerate a fluid, we must use a converging nozzle at subsonic velocities and a diverging nozzle at supersonic velocities. The velocities encountered in most familiar applications are well below the sonic velocity, and thus it is natural that we visualize a nozzle as a converging duct. However, the highest velocity we can achieve by a converging nozzle is the sonic velocity, which occurs at the exit of the nozzle. If we extend the converging nozzle by further decreasing the flow area, in hopes of accelerating the fluid to supersonic velocities, as shown in Fig , we are up for disappointment. Now the sonic velocity will occur at the exit of the converging extension, instead of the exit of the original nozzle, and the mass flow rate through the nozzle will decrease because of the reduced exit area. Based on Eq , which is an expression of the conservation of mass and energy principles, we must add a diverging section to a converging nozzle to accelerate a fluid to supersonic velocities. The result is a converging diverging nozzle. The fluid first passes through a subsonic (converging) section, where the Mach number increases as the flow area of the nozzle decreases, and then reaches the value of unity at the nozzle throat. The fluid continues to accelerate as it passes through a supersonic (diverging) section. Noting that ṁ rav for steady flow, we see that the large decrease in density makes acceleration in the diverging section possible. An example of this type of flow is the flow of hot combustion gases through a nozzle in a gas turbine. The opposite process occurs in the engine inlet of a supersonic aircraft. The fluid is decelerated by passing it first through a supersonic diffuser, which has a flow area that decreases in the flow direction. Ideally, the flow reaches a Mach number of unity at the diffuser throat. The fluid is further P 0, T 0 Converging MaA = 1 nozzle (sonic) P 0, T 0 Converging nozzle A A Ma A < 1 B Attachment MaB = 1 (sonic) FIGURE We cannot obtain supersonic velocities by attaching a converging section to a converging nozzle. Doing so will only move the sonic cross section farther downstream and decrease the mass flow rate.
12 860 Thermodynamics Ma < 1 P decreases V increases Ma increases T decreases r decreases Ma < 1 P increases V decreases Ma decreases T increases r increases Subsonic nozzle Subsonic diffuser (a) Subsonic flow FIGURE Variation of flow properties in subsonic and supersonic nozzles and diffusers. Ma > 1 P decreases V increases Ma increases T decreases r decreases Supersonic nozzle Ma > 1 (b) Supersonic flow P increases V decreases Ma decreases T increases r increases Supersonic diffuser decelerated in a subsonic diffuser, which has a flow area that increases in the flow direction, as shown in Fig Property Relations for Isentropic Flow of Ideal Gases Next we develop relations between the static properties and stagnation properties of an ideal gas in terms of the specific heat ratio k and the Mach number Ma. We assume the flow is isentropic and the gas has constant specific heats. The temperature T of an ideal gas anywhere in the flow is related to the stagnation temperature T 0 through Eq. 17 4: or Noting that c p kr/(k 1), c krt, and Ma V/c, we see that Substituting yields T 0 T V c p T 0 T 1 V c p T V c p T V 3kR>1k 14T a k 1 b V c a k 1 b Ma which is the desired relation between T 0 and T. T 0 T 1 a k 1 b Ma (17 18)
13 The ratio of the stagnation to static pressure is obtained by substituting Eq into Eq. 17 5: P 0 P c 1 a k 1 k>1k 1 b Ma d (17 19) The ratio of the stagnation to static density is obtained by substituting Eq into Eq. 17 6: T t Pt rt Chapter Subsonic nozzle Throat T * P * r * (if Ma t = 1) r 0 r c 1 a k 1 (17 0) Numerical values of T/T 0, P/P 0, and r/r 0 are listed versus the Mach number in Table A 3 for k 1.4, which are very useful for practical compressible flow calculations involving air. The properties of a fluid at a location where the Mach number is unity (the throat) are called critical properties, and the ratios in Eqs. (17 18) through (17 0) are called critical ratios (Fig ). It is common practice in the analysis of compressible flow to let the superscript asterisk (*) represent the critical values. Setting Ma 1 in Eqs through 17 0 yields T* T 0 k 1 1>1k 1 b Ma d k>1k 1 P* a P 0 k 1 b 1>1k 1 r* a r 0 k 1 b (17 1) (17 ) (17 3) These ratios are evaluated for various values of k and are listed in Table 17. The critical properties of compressible flow should not be confused with the properties of substances at the critical point (such as the critical temperature T c and critical pressure P c ). T o P ro o Throat T *, P *, r * (Ma t = 1) Supersonic nozzle FIGURE When Ma t 1, the properties at the nozzle throat become the critical properties. TABLE 17 The critical-pressure, critical-temperature, and critical-density ratios for isentropic flow of some ideal gases Superheated Hot products Monatomic steam, of combustion, Air, gases, k 1.3 k 1.33 k 1.4 k P* P 0 T* T 0 r* r
14 86 Thermodynamics EXAMPLE 17 4 Critical Temperature and Pressure in Gas Flow P 0 = 1.4 MPa T 0 = 473 K P * T * CO FIGURE Schematic for Example Calculate the critical pressure and temperature of carbon dioxide for the flow conditions described in Example 17 3 (Fig ). Solution For the flow discussed in Example 17 3, the critical pressure and temperature are to be calculated. Assumptions 1 The flow is steady, adiabatic, and one-dimensional. Carbon dioxide is an ideal gas with constant specific heats. Properties The specific heat ratio of carbon dioxide at room temperature is k 1.89 (Table A a). Analysis The ratios of critical to stagnation temperature and pressure are determined to be T* T 0 k k>1k > P* a P 0 k 1 b a b Noting that the stagnation temperature and pressure are, from Example 17 3, T K and P kpa, we see that the critical temperature and pressure in this case are T* T K 413 K P* P kpa 767 kpa Discussion Note that these values agree with those listed in Table 17 1, as expected. Also, property values other than these at the throat would indicate that the flow is not critical, and the Mach number is not unity. Reservoir P r = P 0 P e T r = T 0 V r = 0 P/P 0 1 x 1 P b (Back pressure) P b = P 0 P b > P* 17 4 ISENTROPIC FLOW THROUGH NOZZLES Converging or converging diverging nozzles are found in many engineering applications including steam and gas turbines, aircraft and spacecraft propulsion systems, and even industrial blasting nozzles and torch nozzles. In this section we consider the effects of back pressure (i.e., the pressure applied at the nozzle discharge region) on the exit velocity, the mass flow rate, and the pressure distribution along the nozzle. P* P 0 0 Lowest exit pressure FIGURE 17 0 The effect of back pressure on the pressure distribution along a converging nozzle P b =P* P b < P* P b =0 x Converging Nozzles Consider the subsonic flow through a converging nozzle as shown in Fig The nozzle inlet is attached to a reservoir at pressure P r and temperature T r. The reservoir is sufficiently large so that the nozzle inlet velocity is negligible. Since the fluid velocity in the reservoir is zero and the flow through the nozzle is approximated as isentropic, the stagnation pressure and stagnation temperature of the fluid at any cross section through the nozzle are equal to the reservoir pressure and temperature, respectively.
15 Now we begin to reduce the back pressure and observe the resulting effects on the pressure distribution along the length of the nozzle, as shown in Fig If the back pressure P b is equal to P 1, which is equal to P r, there is no flow and the pressure distribution is uniform along the nozzle. When the back pressure is reduced to P, the exit plane pressure P e also drops to P. This causes the pressure along the nozzle to decrease in the flow direction. When the back pressure is reduced to P 3 ( P*, which is the pressure required to increase the fluid velocity to the speed of sound at the exit plane or throat), the mass flow reaches a maximum value and the flow is said to be choked. Further reduction of the back pressure to level P 4 or below does not result in additional changes in the pressure distribution, or anything else along the nozzle length. Under steady-flow conditions, the mass flow rate through the nozzle is constant and can be expressed as Chapter m # rav a P RT b A 1MakRT PAMa k B RT Solving for T from Eq and for P from Eq and substituting, m # AMaP 0 k>1rt k 1Ma >4 1k 1>31k 14 (17 4) Thus the mass flow rate of a particular fluid through a nozzle is a function of the stagnation properties of the fluid, the flow area, and the Mach number. Equation 17 4 is valid at any cross section, and thus ṁ can be evaluated at any location along the length of the nozzle. For a specified flow area A and stagnation properties T 0 and P 0, the maximum mass flow rate can be determined by differentiating Eq with respect to Ma and setting the result equal to zero. It yields Ma 1. Since the only location in a nozzle where the Mach number can be unity is the location of minimum flow area (the throat), the mass flow rate through a nozzle is a maximum when Ma 1 at the throat. Denoting this area by A*, we obtain an expression for the maximum mass flow rate by substituting Ma 1 in Eq. 17 4: m m max P e /P P* P P b P 0 m # 1k 1> 31k 14 k max A*P 0 a B RT 0 k 1 b (17 5) Thus, for a particular ideal gas, the maximum mass flow rate through a nozzle with a given throat area is fixed by the stagnation pressure and temperature of the inlet flow. The flow rate can be controlled by changing the stagnation pressure or temperature, and thus a converging nozzle can be used as a flowmeter. The flow rate can also be controlled, of course, by varying the throat area. This principle is vitally important for chemical processes, medical devices, flowmeters, and anywhere the mass flux of a gas must be known and controlled. A plot of ṁ versus P b /P 0 for a converging nozzle is shown in Fig Notice that the mass flow rate increases with decreasing P b /P 0, reaches a maximum at P b P*, and remains constant for P b /P 0 values less than this P* P 0 0 P* P P b P 0 FIGURE 17 1 The effect of back pressure P b on the mass flow rate m # and the exit pressure P e of a converging nozzle.
16 864 Thermodynamics critical ratio. Also illustrated on this figure is the effect of back pressure on the nozzle exit pressure P e. We observe that P e e P b for P b P* P* for P b 6 P* To summarize, for all back pressures lower than the critical pressure P*, the pressure at the exit plane of the converging nozzle P e is equal to P*, the Mach number at the exit plane is unity, and the mass flow rate is the maximum (or choked) flow rate. Because the velocity of the flow is sonic at the throat for the maximum flow rate, a back pressure lower than the critical pressure cannot be sensed in the nozzle upstream flow and does not affect the flow rate. The effects of the stagnation temperature T 0 and stagnation pressure P 0 on the mass flow rate through a converging nozzle are illustrated in Fig. 17 where the mass flow rate is plotted against the static-to-stagnation pressure ratio at the throat P t /P 0. An increase in P 0 (or a decrease in T 0 ) will increase the mass flow rate through the converging nozzle; a decrease in P 0 (or an increase in T 0 ) will decrease it. We could also conclude this by carefully observing Eqs and A relation for the variation of flow area A through the nozzle relative to throat area A* can be obtained by combining Eqs and 17 5 for the same mass flow rate and stagnation properties of a particular fluid. This yields A A* 1 Ma ca k 1 ba1 k 1 1k 1> 31k 14 Ma bd (17 6) Table A 3 gives values of A/A* as a function of the Mach number for air (k 1.4). There is one value of A/A* for each value of the Mach number, but there are two possible values of the Mach number for each value of A/A* one for subsonic flow and another for supersonic flow. m Ma t = 1 Ma t < 1 Increase in P 0, decrease in T 0, or both P 0, T 0 Decrease in P 0, increase in T 0, or both FIGURE 17 The variation of the mass flow rate through a nozzle with inlet stagnation properties. 0 P* P P t P 0
17 Another parameter sometimes used in the analysis of one-dimensional isentropic flow of ideal gases is Ma*, which is the ratio of the local velocity to the speed of sound at the throat: Chapter Ma* V c* (17 7) It can also be expressed as Ma* V c c c* Mac c* MakRT krt* Ma T B T* where Ma is the local Mach number, T is the local temperature, and T* is the critical temperature. Solving for T from Eq and for T* from Eq and substituting, we get Ma* Ma B k 1 1k 1Ma (17 8) Values of Ma* are also listed in Table A 3 versus the Mach number for k 1.4 (Fig. 17 3). Note that the parameter Ma* differs from the Mach number Ma in that Ma* is the local velocity nondimensionalized with respect to the sonic velocity at the throat, whereas Ma is the local velocity nondimensionalized with respect to the local sonic velocity. (Recall that the sonic velocity in a nozzle varies with temperature and thus with location.) Ma Ma * A P r T A * P0 r0 T FIGURE 17 3 Various property ratios for isentropic flow through nozzles and diffusers are listed in Table A 3 for k 1.4 for convenience. EXAMPLE 17 5 Effect of Back Pressure on Mass Flow Rate Air at 1 MPa and 600 C enters a converging nozzle, shown in Fig. 17 4, with a velocity of 150 m/s. Determine the mass flow rate through the nozzle for a nozzle throat area of 50 cm when the back pressure is (a) 0.7 MPa and (b) 0.4 MPa. Solution Air enters a converging nozzle. The mass flow rate of air through the nozzle is to be determined for different back pressures. Assumptions 1 Air is an ideal gas with constant specific heats at room temperature. Flow through the nozzle is steady, one-dimensional, and isentropic. Properties The constant-pressure specific heat and the specific heat ratio of air are c p kj/kg K and k 1.4, respectively (Table A a). Analysis We use the subscripts i and t to represent the properties at the nozzle inlet and the throat, respectively. The stagnation temperature and pressure at the nozzle inlet are determined from Eqs and 17 5: T 0i T i V i 1150 m>s 873 K c p kj>kg # a 1 kj>kg K 1000 m >s b 884 K P 0i P i a T k>1k 1 0i b 11 MPa a 884 K 1.4> T i 873 K b MPa These stagnation temperature and pressure values remain constant throughout the nozzle since the flow is assumed to be isentropic. That is, T 0 T 0i 884 K and P 0 P 0i MPa AIR P i = 1 MPa T i = 600 C V i = 150 m/s Converging nozzle FIGURE 17 4 Schematic for Example P b A t = 50 cm
18 866 Thermodynamics The critical-pressure ratio is determined from Table 17 (or Eq. 17 ) to be P*/P (a) The back pressure ratio for this case is which is greater than the critical-pressure ratio, Thus the exit plane pressure (or throat pressure P t ) is equal to the back pressure in this case. That is, P t P b 0.7 MPa, and P t /P Therefore, the flow is not choked. From Table A 3 at P t /P , we read Ma t and T t /T The mass flow rate through the nozzle can be calculated from Eq But it can also be determined in a step-by-step manner as follows: Thus, r t P t RT t V t Ma t c t Ma t krt t m # r t A t V t kg>m m m>s 6.77 kg/s (b) The back pressure ratio for this case is which is less than the critical-pressure ratio, Therefore, sonic conditions exist at the exit plane (throat) of the nozzle, and Ma 1. The flow is choked in this case, and the mass flow rate through the nozzle can be calculated from Eq. 17 5: m # 1k 1>31k 14 k A*P 0 a B RT 0 k 1 b.4> m kpa B kj>kg # a K1884 K b 7.10 kg/s B kj>kg # K Ka 1000 m >s 1 kj>kg b m>s P b 0.7 MPa P MPa T t 0.89T K K 700 kpa kpa # m 3 >kg # K K kg>m 3 P b 0.4 MPa P MPa since kpa # m > kj>kg 1000 kg>s. Discussion This is the maximum mass flow rate through the nozzle for the specified inlet conditions and nozzle throat area. EXAMPLE 17 6 Gas Flow through a Converging Nozzle Nitrogen enters a duct with varying flow area at T K, P kpa, and Ma Assuming steady isentropic flow, determine T, P, and Ma at a location where the flow area has been reduced by 0 percent.
19 Chapter Solution Nitrogen gas enters a converging nozzle. The properties at the nozzle exit are to be determined. Assumptions 1 Nitrogen is an ideal gas with k 1.4. Flow through the nozzle is steady, one-dimensional, and isentropic. Analysis The schematic of the duct is shown in Fig For isentropic flow through a duct, the area ratio A/A* (the flow area over the area of the throat where Ma 1) is also listed in Table A 3. At the initial Mach number of Ma 1 0.3, we read A 1 A*.0351 T 1 T P 1 P With a 0 percent reduction in flow area, A 0.8A 1, and T 1 = 400 K P 1 = 100 kpa Ma 1 = 0.3 A 1 N Nozzle T P Ma A = 0.8A 1 FIGURE 17 5 Schematic for Example 17 6 (not to scale). A A* A A A 1 A* For this value of A /A* from Table A 3, we read T T P P Ma Here we chose the subsonic Mach number for the calculated A /A* instead of the supersonic one because the duct is converging in the flow direction and the initial flow is subsonic. Since the stagnation properties are constant for isentropic flow, we can write T T 1 T >T 0 T 1 >T 0 S T T 1 a T >T 0 T 1 >T 0 b 1400 K a b 395 K P P >P 0 S P P 1 P 1 >P P 1 a P >P 0 b 1100 kpaa b 95.7 kpa 0 P 1 >P which are the temperature and pressure at the desired location. Discussion Note that the temperature and pressure drop as the fluid accelerates in a converging nozzle. Converging Diverging Nozzles When we think of nozzles, we ordinarily think of flow passages whose cross-sectional area decreases in the flow direction. However, the highest velocity to which a fluid can be accelerated in a converging nozzle is limited to the sonic velocity (Ma 1), which occurs at the exit plane (throat) of the nozzle. Accelerating a fluid to supersonic velocities (Ma 1) can be accomplished only by attaching a diverging flow section to the subsonic nozzle at the throat. The resulting combined flow section is a converging diverging nozzle, which is standard equipment in supersonic aircraft and rocket propulsion (Fig. 17 6). Forcing a fluid through a converging diverging nozzle is no guarantee that the fluid will be accelerated to a supersonic velocity. In fact, the fluid may find itself decelerating in the diverging section instead of accelerating if the back pressure is not in the right range. The state of the nozzle flow is determined by the overall pressure ratio P b /P 0. Therefore, for given inlet conditions, the flow through a converging diverging nozzle is governed by the back pressure P b, as will be explained.
20 868 Thermodynamics FIGURE 17 6 Converging diverging nozzles are commonly used in rocket engines to provide high thrust. Courtesy of Pratt and Whitney, Used by permission. Consider the converging diverging nozzle shown in Fig A fluid enters the nozzle with a low velocity at stagnation pressure P 0. When P b P 0 (case A), there will be no flow through the nozzle. This is expected since the flow in a nozzle is driven by the pressure difference between the nozzle inlet and the exit. Now let us examine what happens as the back pressure is lowered. 1. When P 0 P b P C, the flow remains subsonic throughout the nozzle, and the mass flow is less than that for choked flow. The fluid velocity increases in the first (converging) section and reaches a maximum at the throat (but Ma 1). However, most of the gain in velocity is lost in the second (diverging) section of the nozzle, which acts as a diffuser. The pressure decreases in the converging section, reaches a minimum at the throat, and increases at the expense of velocity in the diverging section.. When P b P C, the throat pressure becomes P* and the fluid achieves sonic velocity at the throat. But the diverging section of the nozzle still acts as a diffuser, slowing the fluid to subsonic velocities. The mass flow rate that was increasing with decreasing P b also reaches its maximum value. Recall that P* is the lowest pressure that can be obtained at the throat, and the sonic velocity is the highest velocity that can be achieved with a converging nozzle. Thus, lowering P b further has no influence on the fluid flow in the converging part of the nozzle or the
21 Chapter P 0 V i 0 Throat P e P b x P P 0 P* Ma 0 Inlet 1 0 Inlet Sonic flow at throat Sonic flow at throat Throat Throat Shock in nozzle Shock in nozzle E, F, G A B C D E, F, G Exit D C P b B A Exit P A P B P C P D P E P F P G } } } } } } Subsonic flow at nozzle exit (no shock) Subsonic flow at nozzle exit (shock in nozzle) Supersonic flow at nozzle exit (no shock in nozzle) x Supersonic flow at nozzle exit (no shock in nozzle) Subsonic flow at nozzle exit (shock in nozzle) Subsonic flow at nozzle exit (no shock) x FIGURE 17 7 The effects of back pressure on the flow through a converging diverging nozzle. mass flow rate through the nozzle. However, it does influence the character of the flow in the diverging section. 3. When P C P b P E, the fluid that achieved a sonic velocity at the throat continues accelerating to supersonic velocities in the diverging section as the pressure decreases. This acceleration comes to a sudden stop, however, as a normal shock develops at a section between the throat and the exit plane, which causes a sudden drop in velocity to subsonic levels and a sudden increase in pressure. The fluid then continues to decelerate further in the remaining part of the converging diverging nozzle. Flow through the shock is highly irreversible, and thus it cannot be approximated as isentropic. The normal shock moves downstream away from the throat as P b is decreased, and it approaches the nozzle exit plane as P b approaches P E. When P b P E, the normal shock forms at the exit plane of the nozzle. The flow is supersonic through the entire diverging section in this case, and it can be approximated as isentropic. However, the fluid velocity drops to subsonic levels just before leaving the nozzle as it
22 870 Thermodynamics crosses the normal shock. Normal shock waves are discussed in Section When P E P b 0, the flow in the diverging section is supersonic, and the fluid expands to P F at the nozzle exit with no normal shock forming within the nozzle. Thus, the flow through the nozzle can be approximated as isentropic. When P b P F, no shocks occur within or outside the nozzle. When P b P F, irreversible mixing and expansion waves occur downstream of the exit plane of the nozzle. When P b P F, however, the pressure of the fluid increases from P F to P b irreversibly in the wake of the nozzle exit, creating what are called oblique shocks. T 0 = 800 K P 0 = 1.0 MPa V i 0 A t = 0 cm Ma e = EXAMPLE 17 7 Airflow through a Converging Diverging Nozzle Air enters a converging diverging nozzle, shown in Fig. 17 8, at 1.0 MPa and 800 K with a negligible velocity. The flow is steady, one-dimensional, and isentropic with k 1.4. For an exit Mach number of Ma and a throat area of 0 cm, determine (a) the throat conditions, (b) the exit plane conditions, including the exit area, and (c) the mass flow rate through the nozzle. FIGURE 17 8 Schematic for Example Solution Air flows through a converging diverging nozzle. The throat and the exit conditions and the mass flow rate are to be determined. Assumptions 1 Air is an ideal gas with constant specific heats at room temperature. Flow through the nozzle is steady, one-dimensional, and isentropic. Properties The specific heat ratio of air is given to be k 1.4. The gas constant of air is 0.87 kj/kg K. Analysis The exit Mach number is given to be. Therefore, the flow must be sonic at the throat and supersonic in the diverging section of the nozzle. Since the inlet velocity is negligible, the stagnation pressure and stagnation temperature are the same as the inlet temperature and pressure, P MPa and T K. The stagnation density is r 0 P 0 RT kpa kpa # m 3 >kg # K1800 K kg>m 3 (a) At the throat of the nozzle Ma 1, and from Table A 3 we read Thus, Also, P* 0.583P MPa MPa T* T K K r* r kg>m kg/m 3 V* c* krt* B kj>kg # K K a 1000 m >s 1 kj>kg b m/s P* P T* T r* r
CO 2 41.2 MPa (abs) 20 C
 comp_02 A CO 2 cartridge is used to propel a small rocket cart. Compressed CO 2, stored at a pressure of 41.2 MPa (abs) and a temperature of 20 C, is expanded through a smoothly contoured converging nozzle
comp_02 A CO 2 cartridge is used to propel a small rocket cart. Compressed CO 2, stored at a pressure of 41.2 MPa (abs) and a temperature of 20 C, is expanded through a smoothly contoured converging nozzle
High Speed Aerodynamics Prof. K. P. Sinhamahapatra Department of Aerospace Engineering Indian Institute of Technology, Kharagpur
 High Speed Aerodynamics Prof. K. P. Sinhamahapatra Department of Aerospace Engineering Indian Institute of Technology, Kharagpur Module No. # 01 Lecture No. # 06 One-dimensional Gas Dynamics (Contd.) We
High Speed Aerodynamics Prof. K. P. Sinhamahapatra Department of Aerospace Engineering Indian Institute of Technology, Kharagpur Module No. # 01 Lecture No. # 06 One-dimensional Gas Dynamics (Contd.) We
Fluid Mechanics Prof. S. K. Som Department of Mechanical Engineering Indian Institute of Technology, Kharagpur
 Fluid Mechanics Prof. S. K. Som Department of Mechanical Engineering Indian Institute of Technology, Kharagpur Lecture - 20 Conservation Equations in Fluid Flow Part VIII Good morning. I welcome you all
Fluid Mechanics Prof. S. K. Som Department of Mechanical Engineering Indian Institute of Technology, Kharagpur Lecture - 20 Conservation Equations in Fluid Flow Part VIII Good morning. I welcome you all
AOE 3104 Aircraft Performance Problem Sheet 2 (ans) Find the Pressure ratio in a constant temperature atmosphere:
 AOE 3104 Aircraft Performance Problem Sheet 2 (ans) 6. The atmosphere of Jupiter is essentially made up of hydrogen, H 2. For Hydrogen, the specific gas constant is 4157 Joules/(kg)(K). The acceleration
AOE 3104 Aircraft Performance Problem Sheet 2 (ans) 6. The atmosphere of Jupiter is essentially made up of hydrogen, H 2. For Hydrogen, the specific gas constant is 4157 Joules/(kg)(K). The acceleration
Sheet 5:Chapter 5 5 1C Name four physical quantities that are conserved and two quantities that are not conserved during a process.
 Thermo 1 (MEP 261) Thermodynamics An Engineering Approach Yunus A. Cengel & Michael A. Boles 7 th Edition, McGraw-Hill Companies, ISBN-978-0-07-352932-5, 2008 Sheet 5:Chapter 5 5 1C Name four physical
Thermo 1 (MEP 261) Thermodynamics An Engineering Approach Yunus A. Cengel & Michael A. Boles 7 th Edition, McGraw-Hill Companies, ISBN-978-0-07-352932-5, 2008 Sheet 5:Chapter 5 5 1C Name four physical
This chapter deals with three equations commonly used in fluid mechanics:
 MASS, BERNOULLI, AND ENERGY EQUATIONS CHAPTER 5 This chapter deals with three equations commonly used in fluid mechanics: the mass, Bernoulli, and energy equations. The mass equation is an expression of
MASS, BERNOULLI, AND ENERGY EQUATIONS CHAPTER 5 This chapter deals with three equations commonly used in fluid mechanics: the mass, Bernoulli, and energy equations. The mass equation is an expression of
INTRODUCTION TO FLUID MECHANICS
 INTRODUCTION TO FLUID MECHANICS SIXTH EDITION ROBERT W. FOX Purdue University ALAN T. MCDONALD Purdue University PHILIP J. PRITCHARD Manhattan College JOHN WILEY & SONS, INC. CONTENTS CHAPTER 1 INTRODUCTION
INTRODUCTION TO FLUID MECHANICS SIXTH EDITION ROBERT W. FOX Purdue University ALAN T. MCDONALD Purdue University PHILIP J. PRITCHARD Manhattan College JOHN WILEY & SONS, INC. CONTENTS CHAPTER 1 INTRODUCTION
Chapter 5 MASS, BERNOULLI AND ENERGY EQUATIONS
 Fluid Mechanics: Fundamentals and Applications, 2nd Edition Yunus A. Cengel, John M. Cimbala McGraw-Hill, 2010 Chapter 5 MASS, BERNOULLI AND ENERGY EQUATIONS Lecture slides by Hasan Hacışevki Copyright
Fluid Mechanics: Fundamentals and Applications, 2nd Edition Yunus A. Cengel, John M. Cimbala McGraw-Hill, 2010 Chapter 5 MASS, BERNOULLI AND ENERGY EQUATIONS Lecture slides by Hasan Hacışevki Copyright
FUNDAMENTALS OF ENGINEERING THERMODYNAMICS
 FUNDAMENTALS OF ENGINEERING THERMODYNAMICS System: Quantity of matter (constant mass) or region in space (constant volume) chosen for study. Closed system: Can exchange energy but not mass; mass is constant
FUNDAMENTALS OF ENGINEERING THERMODYNAMICS System: Quantity of matter (constant mass) or region in space (constant volume) chosen for study. Closed system: Can exchange energy but not mass; mass is constant
APPLIED THERMODYNAMICS TUTORIAL 1 REVISION OF ISENTROPIC EFFICIENCY ADVANCED STEAM CYCLES
 APPLIED THERMODYNAMICS TUTORIAL 1 REVISION OF ISENTROPIC EFFICIENCY ADVANCED STEAM CYCLES INTRODUCTION This tutorial is designed for students wishing to extend their knowledge of thermodynamics to a more
APPLIED THERMODYNAMICS TUTORIAL 1 REVISION OF ISENTROPIC EFFICIENCY ADVANCED STEAM CYCLES INTRODUCTION This tutorial is designed for students wishing to extend their knowledge of thermodynamics to a more
1 Foundations of Pyrodynamics
 1 1 Foundations of Pyrodynamics Pyrodynamics describes the process of energy conversion from chemical energy to mechanical energy through combustion phenomena, including thermodynamic and fluid dynamic
1 1 Foundations of Pyrodynamics Pyrodynamics describes the process of energy conversion from chemical energy to mechanical energy through combustion phenomena, including thermodynamic and fluid dynamic
du u U 0 U dy y b 0 b
 BASIC CONCEPTS/DEFINITIONS OF FLUID MECHANICS (by Marios M. Fyrillas) 1. Density (πυκνότητα) Symbol: 3 Units of measure: kg / m Equation: m ( m mass, V volume) V. Pressure (πίεση) Alternative definition:
BASIC CONCEPTS/DEFINITIONS OF FLUID MECHANICS (by Marios M. Fyrillas) 1. Density (πυκνότητα) Symbol: 3 Units of measure: kg / m Equation: m ( m mass, V volume) V. Pressure (πίεση) Alternative definition:
INLET AND EXAUST NOZZLES Chap. 10 AIAA AIRCRAFT ENGINE DESIGN R01-07/11/2011
 MASTER OF SCIENCE IN AEROSPACE ENGINEERING PROPULSION AND COMBUSTION INLET AND EXAUST NOZZLES Chap. 10 AIAA AIRCRAFT ENGINE DESIGN R01-07/11/2011 LECTURE NOTES AVAILABLE ON https://www.ingegneriaindustriale.unisalento.it/scheda_docente/-/people/antonio.ficarella/materiale
MASTER OF SCIENCE IN AEROSPACE ENGINEERING PROPULSION AND COMBUSTION INLET AND EXAUST NOZZLES Chap. 10 AIAA AIRCRAFT ENGINE DESIGN R01-07/11/2011 LECTURE NOTES AVAILABLE ON https://www.ingegneriaindustriale.unisalento.it/scheda_docente/-/people/antonio.ficarella/materiale
Chapter 10. Flow Rate. Flow Rate. Flow Measurements. The velocity of the flow is described at any
 Chapter 10 Flow Measurements Material from Theory and Design for Mechanical Measurements; Figliola, Third Edition Flow Rate Flow rate can be expressed in terms of volume flow rate (volume/time) or mass
Chapter 10 Flow Measurements Material from Theory and Design for Mechanical Measurements; Figliola, Third Edition Flow Rate Flow rate can be expressed in terms of volume flow rate (volume/time) or mass
ME 239: Rocket Propulsion. Over- and Under-expanded Nozzles and Nozzle Configurations. J. M. Meyers, PhD
 ME 239: Rocket Propulsion Over- and Under-expanded Nozzles and Nozzle Configurations J. M. Meyers, PhD 1 Over- and Underexpanded Nozzles Underexpanded Nozzle Discharges fluid at an exit pressure greater
ME 239: Rocket Propulsion Over- and Under-expanded Nozzles and Nozzle Configurations J. M. Meyers, PhD 1 Over- and Underexpanded Nozzles Underexpanded Nozzle Discharges fluid at an exit pressure greater
Fundamentals of Pulse Detonation Engine (PDE) and Related Propulsion Technology
 Fundamentals of Pulse Detonation Engine (PDE) and Related Propulsion Technology Dora E. Musielak, Ph.D. Aerospace Engineering Consulting Arlington, TX All rights reserved. No part of this publication may
Fundamentals of Pulse Detonation Engine (PDE) and Related Propulsion Technology Dora E. Musielak, Ph.D. Aerospace Engineering Consulting Arlington, TX All rights reserved. No part of this publication may
APPLIED THERMODYNAMICS. TUTORIAL No.3 GAS TURBINE POWER CYCLES. Revise gas expansions in turbines. Study the Joule cycle with friction.
 APPLIED HERMODYNAMICS UORIAL No. GAS URBINE POWER CYCLES In this tutorial you will do the following. Revise gas expansions in turbines. Revise the Joule cycle. Study the Joule cycle with friction. Extend
APPLIED HERMODYNAMICS UORIAL No. GAS URBINE POWER CYCLES In this tutorial you will do the following. Revise gas expansions in turbines. Revise the Joule cycle. Study the Joule cycle with friction. Extend
Theory of turbo machinery / Turbomaskinernas teori. Chapter 4
 Theory of turbo machinery / Turbomaskinernas teori Chapter 4 Axial-Flow Turbines: Mean-Line Analyses and Design Power is more certainly retained by wary measures than by daring counsels. (Tacitius, Annals)
Theory of turbo machinery / Turbomaskinernas teori Chapter 4 Axial-Flow Turbines: Mean-Line Analyses and Design Power is more certainly retained by wary measures than by daring counsels. (Tacitius, Annals)
Exergy: the quality of energy N. Woudstra
 Exergy: the quality of energy N. Woudstra Introduction Characteristic for our society is a massive consumption of goods and energy. Continuation of this way of life in the long term is only possible if
Exergy: the quality of energy N. Woudstra Introduction Characteristic for our society is a massive consumption of goods and energy. Continuation of this way of life in the long term is only possible if
FLUID MECHANICS. TUTORIAL No.7 FLUID FORCES. When you have completed this tutorial you should be able to. Solve forces due to pressure difference.
 FLUID MECHANICS TUTORIAL No.7 FLUID FORCES When you have completed this tutorial you should be able to Solve forces due to pressure difference. Solve problems due to momentum changes. Solve problems involving
FLUID MECHANICS TUTORIAL No.7 FLUID FORCES When you have completed this tutorial you should be able to Solve forces due to pressure difference. Solve problems due to momentum changes. Solve problems involving
Distinguished Professor George Washington University. Graw Hill
 Mechanics of Fluids Fourth Edition Irving H. Shames Distinguished Professor George Washington University Graw Hill Boston Burr Ridge, IL Dubuque, IA Madison, Wl New York San Francisco St. Louis Bangkok
Mechanics of Fluids Fourth Edition Irving H. Shames Distinguished Professor George Washington University Graw Hill Boston Burr Ridge, IL Dubuque, IA Madison, Wl New York San Francisco St. Louis Bangkok
Thermodynamics - Example Problems Problems and Solutions
 Thermodynamics - Example Problems Problems and Solutions 1 Examining a Power Plant Consider a power plant. At point 1 the working gas has a temperature of T = 25 C. The pressure is 1bar and the mass flow
Thermodynamics - Example Problems Problems and Solutions 1 Examining a Power Plant Consider a power plant. At point 1 the working gas has a temperature of T = 25 C. The pressure is 1bar and the mass flow
Chapter 6 The first law and reversibility
 Chapter 6 The first law and reversibility 6.1 The first law for processes in closed systems We have discussed the properties of equilibrium states and the relationship between the thermodynamic parameters
Chapter 6 The first law and reversibility 6.1 The first law for processes in closed systems We have discussed the properties of equilibrium states and the relationship between the thermodynamic parameters
ME 201 Thermodynamics
 ME 0 Thermodynamics Second Law Practice Problems. Ideally, which fluid can do more work: air at 600 psia and 600 F or steam at 600 psia and 600 F The maximum work a substance can do is given by its availablity.
ME 0 Thermodynamics Second Law Practice Problems. Ideally, which fluid can do more work: air at 600 psia and 600 F or steam at 600 psia and 600 F The maximum work a substance can do is given by its availablity.
REAL AND IDEAL GAS THERMODYNAMIC ANALYSIS OF SINGLE RESERVOIR FILLING PROCESS OF NATURAL GAS VEHICLE CYLINDERS
 Journal of Theoretical and Applied Mechanics, Sofia, 2011, vol. 41, No. 2, pp. 21 36 REAL AND IDEAL GAS THERMODYNAMIC ANALYSIS OF SINGLE RESERVOIR FILLING PROCESS OF NATURAL GAS VEHICLE CYLINDERS Mahmood
Journal of Theoretical and Applied Mechanics, Sofia, 2011, vol. 41, No. 2, pp. 21 36 REAL AND IDEAL GAS THERMODYNAMIC ANALYSIS OF SINGLE RESERVOIR FILLING PROCESS OF NATURAL GAS VEHICLE CYLINDERS Mahmood
Lesson. 11 Vapour Compression Refrigeration Systems: Performance Aspects And Cycle Modifications. Version 1 ME, IIT Kharagpur 1
 Lesson Vapour Compression Refrigeration Systems: Performance Aspects And Cycle Modifications Version ME, IIT Kharagpur The objectives of this lecture are to discuss. Performance aspects of SSS cycle and
Lesson Vapour Compression Refrigeration Systems: Performance Aspects And Cycle Modifications Version ME, IIT Kharagpur The objectives of this lecture are to discuss. Performance aspects of SSS cycle and
Compressible Fluids. Faith A. Morrison Associate Professor of Chemical Engineering Michigan Technological University November 4, 2004
 94 c 2004 Faith A. Morrison, all rights reserved. Compressible Fluids Faith A. Morrison Associate Professor of Chemical Engineering Michigan Technological University November 4, 2004 Chemical engineering
94 c 2004 Faith A. Morrison, all rights reserved. Compressible Fluids Faith A. Morrison Associate Professor of Chemical Engineering Michigan Technological University November 4, 2004 Chemical engineering
FLOW MEASUREMENT 2001 INTERNATIONAL CONFERENCE DERIVATION OF AN EXPANSIBILITY FACTOR FOR THE V-CONE METER
 FLOW MEASUREMENT 200 INTERNATIONAL CONFERENCE DERIVATION OF AN EXPANSIBILITY FACTOR FOR THE V-CONE METER Dr D G Stewart, NEL Dr M Reader-Harris, NEL Dr R J W Peters, McCrometer Inc INTRODUCTION The V-Cone
FLOW MEASUREMENT 200 INTERNATIONAL CONFERENCE DERIVATION OF AN EXPANSIBILITY FACTOR FOR THE V-CONE METER Dr D G Stewart, NEL Dr M Reader-Harris, NEL Dr R J W Peters, McCrometer Inc INTRODUCTION The V-Cone
Problem Set 1 3.20 MIT Professor Gerbrand Ceder Fall 2003
 LEVEL 1 PROBLEMS Problem Set 1 3.0 MIT Professor Gerbrand Ceder Fall 003 Problem 1.1 The internal energy per kg for a certain gas is given by U = 0. 17 T + C where U is in kj/kg, T is in Kelvin, and C
LEVEL 1 PROBLEMS Problem Set 1 3.0 MIT Professor Gerbrand Ceder Fall 003 Problem 1.1 The internal energy per kg for a certain gas is given by U = 0. 17 T + C where U is in kj/kg, T is in Kelvin, and C
Forces on the Rocket. Rocket Dynamics. Equation of Motion: F = Ma
 Rocket Dynamics orces on the Rockets - Drag Rocket Stability Rocket Equation Specific Impulse Rocket otors Thrust orces on the Rocket Equation of otion: = a orces at through the Center of ass Center of
Rocket Dynamics orces on the Rockets - Drag Rocket Stability Rocket Equation Specific Impulse Rocket otors Thrust orces on the Rocket Equation of otion: = a orces at through the Center of ass Center of
The Second Law of Thermodynamics
 The Second aw of Thermodynamics The second law of thermodynamics asserts that processes occur in a certain direction and that the energy has quality as well as quantity. The first law places no restriction
The Second aw of Thermodynamics The second law of thermodynamics asserts that processes occur in a certain direction and that the energy has quality as well as quantity. The first law places no restriction
Isentropic flow. Wikepedia
 Isentropic flow Wikepedia In thermodynamics, an isentropic process or isoentropic process (ισον = "equal" (Greek); εντροπία entropy = "disorder"(greek)) is one in which for purposes of engineering analysis
Isentropic flow Wikepedia In thermodynamics, an isentropic process or isoentropic process (ισον = "equal" (Greek); εντροπία entropy = "disorder"(greek)) is one in which for purposes of engineering analysis
Problem Set 4 Solutions
 Chemistry 360 Dr Jean M Standard Problem Set 4 Solutions 1 Two moles of an ideal gas are compressed isothermally and reversibly at 98 K from 1 atm to 00 atm Calculate q, w, ΔU, and ΔH For an isothermal
Chemistry 360 Dr Jean M Standard Problem Set 4 Solutions 1 Two moles of an ideal gas are compressed isothermally and reversibly at 98 K from 1 atm to 00 atm Calculate q, w, ΔU, and ΔH For an isothermal
where V is the velocity of the system relative to the environment.
 Exergy Exergy is the theoretical limit for the wor potential that can be obtaed from a source or a system at a given state when teractg with a reference (environment) at a constant condition. A system
Exergy Exergy is the theoretical limit for the wor potential that can be obtaed from a source or a system at a given state when teractg with a reference (environment) at a constant condition. A system
RITTER Multiple Sonic Nozzle Calibration System
 RITTER Multiple Sonic Nozzle Calibration System »Wouldn t it be great to eliminate doubtful measurement results by using proven measurement technology? Providing the most precise results ensures and increases
RITTER Multiple Sonic Nozzle Calibration System »Wouldn t it be great to eliminate doubtful measurement results by using proven measurement technology? Providing the most precise results ensures and increases
Gas Dynamics Prof. T. M. Muruganandam Department of Aerospace Engineering Indian Institute of Technology, Madras. Module No - 12 Lecture No - 25
 (Refer Slide Time: 00:22) Gas Dynamics Prof. T. M. Muruganandam Department of Aerospace Engineering Indian Institute of Technology, Madras Module No - 12 Lecture No - 25 Prandtl-Meyer Function, Numerical
(Refer Slide Time: 00:22) Gas Dynamics Prof. T. M. Muruganandam Department of Aerospace Engineering Indian Institute of Technology, Madras Module No - 12 Lecture No - 25 Prandtl-Meyer Function, Numerical
Engineering Problem Solving as Model Building
 Engineering Problem Solving as Model Building Part 1. How professors think about problem solving. Part 2. Mech2 and Brain-Full Crisis Part 1 How experts think about problem solving When we solve a problem
Engineering Problem Solving as Model Building Part 1. How professors think about problem solving. Part 2. Mech2 and Brain-Full Crisis Part 1 How experts think about problem solving When we solve a problem
Sound. References: L.D. Landau & E.M. Lifshitz: Fluid Mechanics, Chapter VIII F. Shu: The Physics of Astrophysics, Vol. 2, Gas Dynamics, Chapter 8
 References: Sound L.D. Landau & E.M. Lifshitz: Fluid Mechanics, Chapter VIII F. Shu: The Physics of Astrophysics, Vol., Gas Dynamics, Chapter 8 1 Speed of sound The phenomenon of sound waves is one that
References: Sound L.D. Landau & E.M. Lifshitz: Fluid Mechanics, Chapter VIII F. Shu: The Physics of Astrophysics, Vol., Gas Dynamics, Chapter 8 1 Speed of sound The phenomenon of sound waves is one that
Chapter 8: Flow in Pipes
 Objectives 1. Have a deeper understanding of laminar and turbulent flow in pipes and the analysis of fully developed flow 2. Calculate the major and minor losses associated with pipe flow in piping networks
Objectives 1. Have a deeper understanding of laminar and turbulent flow in pipes and the analysis of fully developed flow 2. Calculate the major and minor losses associated with pipe flow in piping networks
Differential Relations for Fluid Flow. Acceleration field of a fluid. The differential equation of mass conservation
 Differential Relations for Fluid Flow In this approach, we apply our four basic conservation laws to an infinitesimally small control volume. The differential approach provides point by point details of
Differential Relations for Fluid Flow In this approach, we apply our four basic conservation laws to an infinitesimally small control volume. The differential approach provides point by point details of
Jet Propulsion. Lecture-2. Ujjwal K Saha, Ph.D. Department of Mechanical Engineering Indian Institute of Technology Guwahati 1
 Lecture-2 Prepared under QIP-CD Cell Project Jet Propulsion Ujjwal K Saha, Ph.D. Department of Mechanical Engineering Indian Institute of Technology Guwahati 1 Simple Gas Turbine Cycle A gas turbine that
Lecture-2 Prepared under QIP-CD Cell Project Jet Propulsion Ujjwal K Saha, Ph.D. Department of Mechanical Engineering Indian Institute of Technology Guwahati 1 Simple Gas Turbine Cycle A gas turbine that
a) Use the following equation from the lecture notes: = ( 8.314 J K 1 mol 1) ( ) 10 L
 hermodynamics: Examples for chapter 4. 1. One mole of nitrogen gas is allowed to expand from 0.5 to 10 L reversible and isothermal process at 300 K. Calculate the change in molar entropy using a the ideal
hermodynamics: Examples for chapter 4. 1. One mole of nitrogen gas is allowed to expand from 0.5 to 10 L reversible and isothermal process at 300 K. Calculate the change in molar entropy using a the ideal
Textbook: Introduction to Fluid Mechanics by Philip J. Pritchard. John Wiley & Sons, 8th Edition, ISBN-13 9780470547557, -10 0470547553
 Semester: Spring 2016 Course: MEC 393, Advanced Fluid Mechanics Instructor: Professor Juldeh Sesay, 226 Heavy Engineering Bldg., (631)632-8493 Email: Juldeh.sessay@stonybrook.edu Office hours: Mondays
Semester: Spring 2016 Course: MEC 393, Advanced Fluid Mechanics Instructor: Professor Juldeh Sesay, 226 Heavy Engineering Bldg., (631)632-8493 Email: Juldeh.sessay@stonybrook.edu Office hours: Mondays
Chapter 7 Energy and Energy Balances
 CBE14, Levicky Chapter 7 Energy and Energy Balances The concept of energy conservation as expressed by an energy balance equation is central to chemical engineering calculations. Similar to mass balances
CBE14, Levicky Chapter 7 Energy and Energy Balances The concept of energy conservation as expressed by an energy balance equation is central to chemical engineering calculations. Similar to mass balances
Michael Montgomery Marketing Product Manager Rosemount Inc. Russ Evans Manager of Engineering and Design Rosemount Inc.
 ASGMT / Averaging Pitot Tube Flow Measurement Michael Montgomery Marketing Product Manager Rosemount Inc. Russ Evans Manager of Engineering and Design Rosemount Inc. Averaging Pitot Tube Meters Introduction
ASGMT / Averaging Pitot Tube Flow Measurement Michael Montgomery Marketing Product Manager Rosemount Inc. Russ Evans Manager of Engineering and Design Rosemount Inc. Averaging Pitot Tube Meters Introduction
C H A P T E R F I V E GAS TURBINES AND JET ENGINES
 169 C H A P T E R F I V E GAS TURBINES AND JET ENGINES 5.1 Introduction History records over a century and a half of interest in and work on the gas turbine. However, the history of the gas turbine as
169 C H A P T E R F I V E GAS TURBINES AND JET ENGINES 5.1 Introduction History records over a century and a half of interest in and work on the gas turbine. However, the history of the gas turbine as
The Use of Control Valve Sizing Equations with Simulation Based Process Data
 The Use of Control Valve Sizing Equations with Simulation Based Process Data Marc L. Riveland Director, Advanced Technologies Fisher Valves, Emerson Process Management Keywords: Control Valve, Thermodynamics,
The Use of Control Valve Sizing Equations with Simulation Based Process Data Marc L. Riveland Director, Advanced Technologies Fisher Valves, Emerson Process Management Keywords: Control Valve, Thermodynamics,
Chapter 8 Maxwell relations and measurable properties
 Chapter 8 Maxwell relations and measurable properties 8.1 Maxwell relations Other thermodynamic potentials emerging from Legendre transforms allow us to switch independent variables and give rise to alternate
Chapter 8 Maxwell relations and measurable properties 8.1 Maxwell relations Other thermodynamic potentials emerging from Legendre transforms allow us to switch independent variables and give rise to alternate
CFD Analysis of Supersonic Exhaust Diffuser System for Higher Altitude Simulation
 Page1 CFD Analysis of Supersonic Exhaust Diffuser System for Higher Altitude Simulation ABSTRACT Alan Vincent E V P G Scholar, Nehru Institute of Engineering and Technology, Coimbatore Tamil Nadu A high
Page1 CFD Analysis of Supersonic Exhaust Diffuser System for Higher Altitude Simulation ABSTRACT Alan Vincent E V P G Scholar, Nehru Institute of Engineering and Technology, Coimbatore Tamil Nadu A high
Lecture 3 Fluid Dynamics and Balance Equa6ons for Reac6ng Flows
 Lecture 3 Fluid Dynamics and Balance Equa6ons for Reac6ng Flows 3.- 1 Basics: equations of continuum mechanics - balance equations for mass and momentum - balance equations for the energy and the chemical
Lecture 3 Fluid Dynamics and Balance Equa6ons for Reac6ng Flows 3.- 1 Basics: equations of continuum mechanics - balance equations for mass and momentum - balance equations for the energy and the chemical
Air Flow Optimization via a Venturi Type Air Restrictor
 , July 3-5, 013, London, U.K. Air Flow Optimization via a Venturi Type Air Restrictor Anshul Singhal, Mallika Parveen, Member, IAENG Abstract The aim of this project is to create a flow restriction device
, July 3-5, 013, London, U.K. Air Flow Optimization via a Venturi Type Air Restrictor Anshul Singhal, Mallika Parveen, Member, IAENG Abstract The aim of this project is to create a flow restriction device
A drop forms when liquid is forced out of a small tube. The shape of the drop is determined by a balance of pressure, gravity, and surface tension
 A drop forms when liquid is forced out of a small tube. The shape of the drop is determined by a balance of pressure, gravity, and surface tension forces. 2 Objectives Have a working knowledge of the basic
A drop forms when liquid is forced out of a small tube. The shape of the drop is determined by a balance of pressure, gravity, and surface tension forces. 2 Objectives Have a working knowledge of the basic
Head Loss in Pipe Flow ME 123: Mechanical Engineering Laboratory II: Fluids
 Head Loss in Pipe Flow ME 123: Mechanical Engineering Laboratory II: Fluids Dr. J. M. Meyers Dr. D. G. Fletcher Dr. Y. Dubief 1. Introduction Last lab you investigated flow loss in a pipe due to the roughness
Head Loss in Pipe Flow ME 123: Mechanical Engineering Laboratory II: Fluids Dr. J. M. Meyers Dr. D. G. Fletcher Dr. Y. Dubief 1. Introduction Last lab you investigated flow loss in a pipe due to the roughness
When the fluid velocity is zero, called the hydrostatic condition, the pressure variation is due only to the weight of the fluid.
 Fluid Statics When the fluid velocity is zero, called the hydrostatic condition, the pressure variation is due only to the weight of the fluid. Consider a small wedge of fluid at rest of size Δx, Δz, Δs
Fluid Statics When the fluid velocity is zero, called the hydrostatic condition, the pressure variation is due only to the weight of the fluid. Consider a small wedge of fluid at rest of size Δx, Δz, Δs
Condensers & Evaporator Chapter 5
 Condensers & Evaporator Chapter 5 This raises the condenser temperature and the corresponding pressure thereby reducing the COP. Page 134 of 263 Condensers & Evaporator Chapter 5 OBJECTIVE QUESTIONS (GATE,
Condensers & Evaporator Chapter 5 This raises the condenser temperature and the corresponding pressure thereby reducing the COP. Page 134 of 263 Condensers & Evaporator Chapter 5 OBJECTIVE QUESTIONS (GATE,
FEASIBILITY OF A BRAYTON CYCLE AUTOMOTIVE AIR CONDITIONING SYSTEM
 FEASIBILITY OF A BRAYTON CYCLE AUTOMOTIVE AIR CONDITIONING SYSTEM L. H. M. Beatrice a, and F. A. S. Fiorelli a a Universidade de São Paulo Escola Politécnica Departamento de Engenharia Mecânica Av. Prof.
FEASIBILITY OF A BRAYTON CYCLE AUTOMOTIVE AIR CONDITIONING SYSTEM L. H. M. Beatrice a, and F. A. S. Fiorelli a a Universidade de São Paulo Escola Politécnica Departamento de Engenharia Mecânica Av. Prof.
Transient Performance Prediction for Turbocharging Systems Incorporating Variable-geometry Turbochargers
 22 Special Issue Turbocharging Technologies Research Report Transient Performance Prediction for Turbocharging Systems Incorporating Variable-geometry Turbochargers Hiroshi Uchida Abstract Turbocharging
22 Special Issue Turbocharging Technologies Research Report Transient Performance Prediction for Turbocharging Systems Incorporating Variable-geometry Turbochargers Hiroshi Uchida Abstract Turbocharging
Dimensional analysis is a method for reducing the number and complexity of experimental variables that affect a given physical phenomena.
 Dimensional Analysis and Similarity Dimensional analysis is very useful for planning, presentation, and interpretation of experimental data. As discussed previously, most practical fluid mechanics problems
Dimensional Analysis and Similarity Dimensional analysis is very useful for planning, presentation, and interpretation of experimental data. As discussed previously, most practical fluid mechanics problems
HOW TO SIZE A PRESSURE REGULATOR
 CHOOSING THE CORRECT REGULATOR HOW TO SIZE A PRESSURE REGULATOR In order to choose the correct regulator the following information is needed: - Function: Pressure reducing or backpressure control? - Pressure:
CHOOSING THE CORRECT REGULATOR HOW TO SIZE A PRESSURE REGULATOR In order to choose the correct regulator the following information is needed: - Function: Pressure reducing or backpressure control? - Pressure:
An analysis of a thermal power plant working on a Rankine cycle: A theoretical investigation
 An analysis of a thermal power plant working on a Rankine cycle: A theoretical investigation R K Kapooria Department of Mechanical Engineering, BRCM College of Engineering & Technology, Bahal (Haryana)
An analysis of a thermal power plant working on a Rankine cycle: A theoretical investigation R K Kapooria Department of Mechanical Engineering, BRCM College of Engineering & Technology, Bahal (Haryana)
Chapter23. Two important areas of application for thermodynamics POWER AND REFRIGERATION CYCLES. Objectives
 Two important areas of application for thermodynamics are power generation and refrigeration. Both power generation and refrigeration are usually accomplished by systems that operate on a thermodynamic
Two important areas of application for thermodynamics are power generation and refrigeration. Both power generation and refrigeration are usually accomplished by systems that operate on a thermodynamic
Modelling and Simulation of Supersonic Nozzle Using Computational Fluid Dynamics
 Modelling and Simulation of Supersonic Nozzle Using Computational Fluid Dynamics 1 Venkatesh.V, 2 C Jaya pal Reddy Department of Aeronautical Engineering, MLR Institute of Technology and Management, Hyderabad
Modelling and Simulation of Supersonic Nozzle Using Computational Fluid Dynamics 1 Venkatesh.V, 2 C Jaya pal Reddy Department of Aeronautical Engineering, MLR Institute of Technology and Management, Hyderabad
Air Flow Measurements
 ME-EM 30 ENERGY LABORATORY Air Flow Measurements Pitot Static Tube A slender tube aligned with the flow can measure local velocity by means of pressure differences. It has sidewall holes to measure the
ME-EM 30 ENERGY LABORATORY Air Flow Measurements Pitot Static Tube A slender tube aligned with the flow can measure local velocity by means of pressure differences. It has sidewall holes to measure the
Diesel Cycle Analysis
 Engineering Software P.O. Box 1180, Germantown, MD 20875 Phone: (301) 540-3605 FAX: (301) 540-3605 E-Mail: info@engineering-4e.com Web Site: http://www.engineering-4e.com Diesel Cycle Analysis Diesel Cycle
Engineering Software P.O. Box 1180, Germantown, MD 20875 Phone: (301) 540-3605 FAX: (301) 540-3605 E-Mail: info@engineering-4e.com Web Site: http://www.engineering-4e.com Diesel Cycle Analysis Diesel Cycle
Lecture 6 - Boundary Conditions. Applied Computational Fluid Dynamics
 Lecture 6 - Boundary Conditions Applied Computational Fluid Dynamics Instructor: André Bakker http://www.bakker.org André Bakker (2002-2006) Fluent Inc. (2002) 1 Outline Overview. Inlet and outlet boundaries.
Lecture 6 - Boundary Conditions Applied Computational Fluid Dynamics Instructor: André Bakker http://www.bakker.org André Bakker (2002-2006) Fluent Inc. (2002) 1 Outline Overview. Inlet and outlet boundaries.
The Behaviour Of Vertical Jet Fires Under Sonic And Subsonic Regimes
 The Behaviour Of Vertical Jet Fires Under Sonic And Subsonic Regimes Palacios A. and Casal J. Centre for Technological Risk Studies (CERTEC), Department of Chemical Engineering, Universitat Politècnica
The Behaviour Of Vertical Jet Fires Under Sonic And Subsonic Regimes Palacios A. and Casal J. Centre for Technological Risk Studies (CERTEC), Department of Chemical Engineering, Universitat Politècnica
State Newton's second law of motion for a particle, defining carefully each term used.
 5 Question 1. [Marks 20] An unmarked police car P is, travelling at the legal speed limit, v P, on a straight section of highway. At time t = 0, the police car is overtaken by a car C, which is speeding
5 Question 1. [Marks 20] An unmarked police car P is, travelling at the legal speed limit, v P, on a straight section of highway. At time t = 0, the police car is overtaken by a car C, which is speeding
Boiler Calculations. Helsinki University of Technology Department of Mechanical Engineering. Sebastian Teir, Antto Kulla
 Helsinki University of Technology Department of Mechanical Engineering Energy Engineering and Environmental Protection Publications Steam Boiler Technology ebook Espoo 2002 Boiler Calculations Sebastian
Helsinki University of Technology Department of Mechanical Engineering Energy Engineering and Environmental Protection Publications Steam Boiler Technology ebook Espoo 2002 Boiler Calculations Sebastian
Fundamentals of Fluid Mechanics
 Sixth Edition. Fundamentals of Fluid Mechanics International Student Version BRUCE R. MUNSON DONALD F. YOUNG Department of Aerospace Engineering and Engineering Mechanics THEODORE H. OKIISHI Department
Sixth Edition. Fundamentals of Fluid Mechanics International Student Version BRUCE R. MUNSON DONALD F. YOUNG Department of Aerospace Engineering and Engineering Mechanics THEODORE H. OKIISHI Department
REFRIGERATION (& HEAT PUMPS)
 REFRIGERATION (& HEAT PUMPS) Refrigeration is the 'artificial' extraction of heat from a substance in order to lower its temperature to below that of its surroundings Primarily, heat is extracted from
REFRIGERATION (& HEAT PUMPS) Refrigeration is the 'artificial' extraction of heat from a substance in order to lower its temperature to below that of its surroundings Primarily, heat is extracted from
FUNDAMENTALS OF GAS TURBINE ENGINES
 FUNDAMENTALS OF GAS TURBINE ENGINES INTRODUCTION The gas turbine is an internal combustion engine that uses air as the working fluid. The engine extracts chemical energy from fuel and converts it to mechanical
FUNDAMENTALS OF GAS TURBINE ENGINES INTRODUCTION The gas turbine is an internal combustion engine that uses air as the working fluid. The engine extracts chemical energy from fuel and converts it to mechanical
Answer, Key Homework 6 David McIntyre 1
 Answer, Key Homework 6 David McIntyre 1 This print-out should have 0 questions, check that it is complete. Multiple-choice questions may continue on the next column or page: find all choices before making
Answer, Key Homework 6 David McIntyre 1 This print-out should have 0 questions, check that it is complete. Multiple-choice questions may continue on the next column or page: find all choices before making
NUMERICAL ANALYSIS OF THE EFFECTS OF WIND ON BUILDING STRUCTURES
 Vol. XX 2012 No. 4 28 34 J. ŠIMIČEK O. HUBOVÁ NUMERICAL ANALYSIS OF THE EFFECTS OF WIND ON BUILDING STRUCTURES Jozef ŠIMIČEK email: jozef.simicek@stuba.sk Research field: Statics and Dynamics Fluids mechanics
Vol. XX 2012 No. 4 28 34 J. ŠIMIČEK O. HUBOVÁ NUMERICAL ANALYSIS OF THE EFFECTS OF WIND ON BUILDING STRUCTURES Jozef ŠIMIČEK email: jozef.simicek@stuba.sk Research field: Statics and Dynamics Fluids mechanics
HEAT UNIT 1.1 KINETIC THEORY OF GASES. 1.1.1 Introduction. 1.1.2 Postulates of Kinetic Theory of Gases
 UNIT HEAT. KINETIC THEORY OF GASES.. Introduction Molecules have a diameter of the order of Å and the distance between them in a gas is 0 Å while the interaction distance in solids is very small. R. Clausius
UNIT HEAT. KINETIC THEORY OF GASES.. Introduction Molecules have a diameter of the order of Å and the distance between them in a gas is 0 Å while the interaction distance in solids is very small. R. Clausius
Axial Flow Compressor Mean Line Design
 Axial Flow Compressor Mean Line Design Niclas Falck February 2008 Master Thesis Division of Thermal Power Engineering Department of Energy Sciences Lund University, Sweden Niclas Falck 2008 ISSN 0282-1990
Axial Flow Compressor Mean Line Design Niclas Falck February 2008 Master Thesis Division of Thermal Power Engineering Department of Energy Sciences Lund University, Sweden Niclas Falck 2008 ISSN 0282-1990
Response of common flowmeters to unsteady flow
 Response of common flowmeters to unsteady flow By Fredrik Laurantzon, Ramis Örlü, Nils Tillmark and P. Henrik Alfredsson CCGEx, KTH Mechanics, SE-1 44 Stockholm, Sweden Technical Report This report gives
Response of common flowmeters to unsteady flow By Fredrik Laurantzon, Ramis Örlü, Nils Tillmark and P. Henrik Alfredsson CCGEx, KTH Mechanics, SE-1 44 Stockholm, Sweden Technical Report This report gives
LECTURE 28 to 29 ACCUMULATORS FREQUENTLY ASKED QUESTIONS
 LECTURE 28 to 29 ACCUMULATORS FREQUENTLY ASKED QUESTIONS 1. Define an accumulator and explain its function A hydraulic accumulator is a device that stores the potential energy of an incompressible fluid
LECTURE 28 to 29 ACCUMULATORS FREQUENTLY ASKED QUESTIONS 1. Define an accumulator and explain its function A hydraulic accumulator is a device that stores the potential energy of an incompressible fluid
A comparison of heterogenous and homogenous models of two-phase transonic compressible
 Home Search Collections Journals About Contact us My IOPscience A comparison of heterogenous and homogenous models of two-phase transonic compressible CO 2 flow through a heat pump ejector This content
Home Search Collections Journals About Contact us My IOPscience A comparison of heterogenous and homogenous models of two-phase transonic compressible CO 2 flow through a heat pump ejector This content
WEEKLY SCHEDULE. GROUPS (mark X) SPECIAL ROOM FOR SESSION (Computer class room, audio-visual class room)
 SESSION WEEK COURSE: THERMAL ENGINEERING DEGREE: Aerospace Engineering YEAR: 2nd TERM: 2nd The course has 29 sessions distributed in 14 weeks. The laboratory sessions are included in these sessions. The
SESSION WEEK COURSE: THERMAL ENGINEERING DEGREE: Aerospace Engineering YEAR: 2nd TERM: 2nd The course has 29 sessions distributed in 14 weeks. The laboratory sessions are included in these sessions. The
STEAM TURBINE 1 CONTENT. Chapter Description Page. V. Steam Process in Steam Turbine 6. VI. Exhaust Steam Conditions, Extraction and Admission 7
 STEAM TURBINE 1 CONTENT Chapter Description Page I Purpose 2 II Steam Turbine Types 2 2.1. Impulse Turbine 2 2.2. Reaction Turbine 2 III Steam Turbine Operating Range 2 3.1. Curtis 2 3.2. Rateau 2 3.3.
STEAM TURBINE 1 CONTENT Chapter Description Page I Purpose 2 II Steam Turbine Types 2 2.1. Impulse Turbine 2 2.2. Reaction Turbine 2 III Steam Turbine Operating Range 2 3.1. Curtis 2 3.2. Rateau 2 3.3.
Thermodynamics. Chapter 13 Phase Diagrams. NC State University
 Thermodynamics Chapter 13 Phase Diagrams NC State University Pressure (atm) Definition of a phase diagram A phase diagram is a representation of the states of matter, solid, liquid, or gas as a function
Thermodynamics Chapter 13 Phase Diagrams NC State University Pressure (atm) Definition of a phase diagram A phase diagram is a representation of the states of matter, solid, liquid, or gas as a function
= 800 kg/m 3 (note that old units cancel out) 4.184 J 1000 g = 4184 J/kg o C
 Units and Dimensions Basic properties such as length, mass, time and temperature that can be measured are called dimensions. Any quantity that can be measured has a value and a unit associated with it.
Units and Dimensions Basic properties such as length, mass, time and temperature that can be measured are called dimensions. Any quantity that can be measured has a value and a unit associated with it.
Chapter 28 Fluid Dynamics
 Chapter 28 Fluid Dynamics 28.1 Ideal Fluids... 1 28.2 Velocity Vector Field... 1 28.3 Mass Continuity Equation... 3 28.4 Bernoulli s Principle... 4 28.5 Worked Examples: Bernoulli s Equation... 7 Example
Chapter 28 Fluid Dynamics 28.1 Ideal Fluids... 1 28.2 Velocity Vector Field... 1 28.3 Mass Continuity Equation... 3 28.4 Bernoulli s Principle... 4 28.5 Worked Examples: Bernoulli s Equation... 7 Example
THE KINETIC THEORY OF GASES
 Chapter 19: THE KINETIC THEORY OF GASES 1. Evidence that a gas consists mostly of empty space is the fact that: A. the density of a gas becomes much greater when it is liquefied B. gases exert pressure
Chapter 19: THE KINETIC THEORY OF GASES 1. Evidence that a gas consists mostly of empty space is the fact that: A. the density of a gas becomes much greater when it is liquefied B. gases exert pressure
A LAMINAR FLOW ELEMENT WITH A LINEAR PRESSURE DROP VERSUS VOLUMETRIC FLOW. 1998 ASME Fluids Engineering Division Summer Meeting
 TELEDYNE HASTINGS TECHNICAL PAPERS INSTRUMENTS A LAMINAR FLOW ELEMENT WITH A LINEAR PRESSURE DROP VERSUS VOLUMETRIC FLOW Proceedings of FEDSM 98: June -5, 998, Washington, DC FEDSM98 49 ABSTRACT The pressure
TELEDYNE HASTINGS TECHNICAL PAPERS INSTRUMENTS A LAMINAR FLOW ELEMENT WITH A LINEAR PRESSURE DROP VERSUS VOLUMETRIC FLOW Proceedings of FEDSM 98: June -5, 998, Washington, DC FEDSM98 49 ABSTRACT The pressure
JET ENGINE PERFORMANCE. Charles Robert O Neill. School of Mechanical and Aerospace Engineering. Oklahoma State University. Stillwater, OK 74078
 JET ENGINE PERFORMANCE Charles Robert O Neill School of Mechanical and Aerospace Engineering Oklahoma State University Stillwater, OK 74078 Honors Project in ENGSC 3233 Fluid Mechanics December 1998 JET
JET ENGINE PERFORMANCE Charles Robert O Neill School of Mechanical and Aerospace Engineering Oklahoma State University Stillwater, OK 74078 Honors Project in ENGSC 3233 Fluid Mechanics December 1998 JET
PART 1 THE SECOND LAW OF THERMODYNAMICS
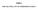 PART 1 THE SECOND LAW OF THERMODYNAMICS PART 1 - THE SECOND LAW OF THERMODYNAMICS 1.A. Background to the Second Law of Thermodynamics [IAW 23-31 (see IAW for detailed VWB&S references); VN Chapters 2,
PART 1 THE SECOND LAW OF THERMODYNAMICS PART 1 - THE SECOND LAW OF THERMODYNAMICS 1.A. Background to the Second Law of Thermodynamics [IAW 23-31 (see IAW for detailed VWB&S references); VN Chapters 2,
Statistical Mechanics, Kinetic Theory Ideal Gas. 8.01t Nov 22, 2004
 Statistical Mechanics, Kinetic Theory Ideal Gas 8.01t Nov 22, 2004 Statistical Mechanics and Thermodynamics Thermodynamics Old & Fundamental Understanding of Heat (I.e. Steam) Engines Part of Physics Einstein
Statistical Mechanics, Kinetic Theory Ideal Gas 8.01t Nov 22, 2004 Statistical Mechanics and Thermodynamics Thermodynamics Old & Fundamental Understanding of Heat (I.e. Steam) Engines Part of Physics Einstein
pressure inside the valve just before the final release of air. in pipeline systems resulting from 2p 1 p a m C D A o
 BY SRINIVASA LINGIREDDY, DON J. WOOD, AND NAFTALI ZLOZOWER It is a common practice to locate air valves at high elevations along water transmission mains. Improper sizing of an air valve could lead to
BY SRINIVASA LINGIREDDY, DON J. WOOD, AND NAFTALI ZLOZOWER It is a common practice to locate air valves at high elevations along water transmission mains. Improper sizing of an air valve could lead to
2. Parallel pump system Q(pump) = 300 gpm, h p = 270 ft for each of the two pumps
 Pumping Systems: Parallel and Series Configurations For some piping system designs, it may be desirable to consider a multiple pump system to meet the design requirements. Two typical options include parallel
Pumping Systems: Parallel and Series Configurations For some piping system designs, it may be desirable to consider a multiple pump system to meet the design requirements. Two typical options include parallel
4. Introduction to Heat & Mass Transfer
 4. Introduction to Heat & Mass Transfer This section will cover the following concepts: A rudimentary introduction to mass transfer. Mass transfer from a molecular point of view. Fundamental similarity
4. Introduction to Heat & Mass Transfer This section will cover the following concepts: A rudimentary introduction to mass transfer. Mass transfer from a molecular point of view. Fundamental similarity
INTERNAL COMBUSTION (IC) ENGINES
 INTERNAL COMBUSTION (IC) ENGINES An IC engine is one in which the heat transfer to the working fluid occurs within the engine itself, usually by the combustion of fuel with the oxygen of air. In external
INTERNAL COMBUSTION (IC) ENGINES An IC engine is one in which the heat transfer to the working fluid occurs within the engine itself, usually by the combustion of fuel with the oxygen of air. In external
Lecture 4 Classification of Flows. Applied Computational Fluid Dynamics
 Lecture 4 Classification of Flows Applied Computational Fluid Dynamics Instructor: André Bakker http://www.bakker.org André Bakker (00-006) Fluent Inc. (00) 1 Classification: fluid flow vs. granular flow
Lecture 4 Classification of Flows Applied Computational Fluid Dynamics Instructor: André Bakker http://www.bakker.org André Bakker (00-006) Fluent Inc. (00) 1 Classification: fluid flow vs. granular flow
A basic introduction to steam
 A basic introduction to steam FOR HOT, COLD, MOIST AND DRY, FOUR CHAMPIONS FIERCE. STRIVE HERE FOR MASTERY Milton 1666 Steam Wonderful Steam Very high heat content Recyclable Clean, non toxic Biodegradable
A basic introduction to steam FOR HOT, COLD, MOIST AND DRY, FOUR CHAMPIONS FIERCE. STRIVE HERE FOR MASTERY Milton 1666 Steam Wonderful Steam Very high heat content Recyclable Clean, non toxic Biodegradable
Mohan Chandrasekharan #1
 International Journal of Students Research in Technology & Management Exergy Analysis of Vapor Compression Refrigeration System Using R12 and R134a as Refrigerants Mohan Chandrasekharan #1 # Department
International Journal of Students Research in Technology & Management Exergy Analysis of Vapor Compression Refrigeration System Using R12 and R134a as Refrigerants Mohan Chandrasekharan #1 # Department
Fan Performance By: Mark Stevens AMCA International Deputy Executive Director Technical Affairs
 Fan Performance By: Mark Stevens AMCA International Deputy Executive Director Technical Affairs Fan Performance (Paper I.D. 021) Mark Stevens Air Movement and Control Association International Abstract
Fan Performance By: Mark Stevens AMCA International Deputy Executive Director Technical Affairs Fan Performance (Paper I.D. 021) Mark Stevens Air Movement and Control Association International Abstract
Lesson 11. Luis Anchordoqui. Physics 168. Tuesday, December 8, 15
 Lesson 11 Physics 168 1 Oscillations and Waves 2 Simple harmonic motion If an object vibrates or oscillates back and forth over same path each cycle taking same amount of time motion is called periodic
Lesson 11 Physics 168 1 Oscillations and Waves 2 Simple harmonic motion If an object vibrates or oscillates back and forth over same path each cycle taking same amount of time motion is called periodic
FLUID FLOW Introduction General Description
 FLUID FLOW Introduction Fluid flow is an important part of many processes, including transporting materials from one point to another, mixing of materials, and chemical reactions. In this experiment, you
FLUID FLOW Introduction Fluid flow is an important part of many processes, including transporting materials from one point to another, mixing of materials, and chemical reactions. In this experiment, you
