Steady-State Power System Security Analysis with PowerWorld Simulator
|
|
|
- Lorena Porter
- 10 years ago
- Views:
Transcription
1 Steady-State Power System Security Analysis with PowerWorld Simulator S: Power System Modeling Methods and Equations 00 South First Street Champaign, Illinois (7) [email protected]
2 Topics in the Section Nominal Voltage Levels Per Unit Values Admittance and Impedance Y-Bus Matri Buses Transmission Branches Loads Switched Shunts Generators Power Flow Equations PV, PQ, Slack buses Newton's Method Multiple Solutions -Bus Power Flow PV and QV Curves Maimum Loadability S: Power System Modeling 04 PowerWorld Corporation
3 Transmission System: Nominal Voltage Levels Why do transmission systems operate at many different voltage levels? Power Voltage * Current Thus for a given power, if you use a higher voltage, then the current will be lower Why do we care? Transmission Losses Losses Resistance * (Current) Eample: What if we want to transmit 460 MW? At 30 kv, that means,000 Amps At 5 kv, that means 4,000 Amps Because current is Twice as high for 5 kv, that means the losses would be 4 times higher Thus Higher Voltage is better, but more epensive, thus there is a trade-off Means voltages vary depending on the situation S: Power System Modeling 04 PowerWorld Corporation 3
4 Transmission System: Nominal Voltage Levels Varying Nominal Voltage Harder for a human to compare the voltage levels Harder to handle in the equations used in power systems You d have to include turns-ratio multipliers all over the place This leads the industry to use a normalization method 38 kv 345 kv 38 kv 69 kv 345 kv 345 kv 38 kv 69 kv S: Power System Modeling 04 PowerWorld Corporation 4
5 Transmission Voltage Normalization using Per-Unit Values Per unit values are used in power systems to avoid worrying about various voltage level transitions created by transformers They also allow us to compare voltages using a percentagelike number All buses in the power system are assigned a Nominal Voltage. Normally this is corresponds the physical voltage rating of devices connected to this bus and voltages are epected to be close to this This means.00 per unit voltage is usually normal But strictly speaking it doesn t have to be. It s just a number used to normalize the various parameters in the power system model. Eample: In Western United States, there is a lot of 500 kv transmission, but it generally operates at about 55 kv S: Power System Modeling 04 PowerWorld Corporation 5
6 Base Values Define a Power Base (SBase ) for the entire system Transmission system SBase 00 MVA The Voltage Base (VBase) for each part of the system is equal to the nominal voltage From these determine the Impedance Base (ZBase) and Current Base (IBase) ZBase (VBase) SBase IBase SBase 3 VBase S: Power System Modeling 04 PowerWorld Corporation 6
7 Current Base Calculation: Line to Line Voltage Nominal Voltages are specified as the Line to Line voltage by tradition This is the voltage magnitude difference between the A-B phase, B-C phase, and C-A phase V line-to-ground V linetoline 38 kv 80 kv Line-Ground Current applies to only one phase, but the Power is the sum across all three phases, thus S 3I V S 3IV line-to-ground linetoline 3 S MVARating I I Rating 3 3NomVoltage V line toline A B Ground C S: Power System Modeling 04 PowerWorld Corporation 7
8 Voltage Base Zones 345 kv 345 kv VBase 345 kv 38 kv 345 kv 38 kv VBase 38 kv 38 kv 69 kv 69 kv VBase 69 kv NOTE: Zones are separated by transformers S: Power System Modeling 04 PowerWorld Corporation 8
9 Determining a Per-Unit Value To determine a per-unit value, simply divide the actual number by the base For eample Z 0 + j50 ohms SBase 00 MVA ZBase S: Power System Modeling (38,000) 00,000, PowerWorld Corporation 38 kv Base Ohms Z 0 + j50 Ohms Zpu ZBase Ohms j0.65 9
10 The Transmission System - Model of the Wires Y-Bus (Admittance Matri ) Will review the various parts of the transmission system How we model transmission system How these models are entered into software S: Power System Modeling 04 PowerWorld Corporation 0
11 Impedance (Z) and Admittance (Y) and related terms R, X, B, and G The comple number for Impedance is represented by the letter Z Z R + jx R Resistance X Reactance Admittance is the numeric inverse of Impedance and represented by the letter Y Y G + jb G Conductance B Susceptance S: Power System Modeling 04 PowerWorld Corporation
12 Conversion Between Impedance (Z) and Admittance (Y) Impedance and Admittance are comple numbers and are inverses of each other y z r + j r + r + g - j r + b g r r + b r + S: Power System Modeling 04 PowerWorld Corporation
13 Y-Bus Matri (the Admittance Matri) Used to model ALL of the transmission lines, transformers, capacitors, etc. These are all the passive elements This part of the model does not change for different solution states Represents only constant impedances The Y-Bus is an N X N matri N is the number of buses in the system A software package will calculate the Y-Bus from the data provided by the user regarding the passive elements of the system Transmission Lines Line Shunts Switched Shunts (Capacitors/Reactors) Bus Shunts S: Power System Modeling 04 PowerWorld Corporation 3
14 Power System Bus (or node) Nominal Voltage (in kv) B Shunt, G Shunt (in Nominal Mvar) Voltage Magnitude in per unit (calculated) Used as initial guess in power flow solution Voltage Angle in degrees (calculated) Used as initial guess in power flow solution S: Power System Modeling 04 PowerWorld Corporation 4
15 Converting Nominal MW/Mvar into a per unit admittance G Shunt and B Shunt are given as MW or Mvar at Nominal Voltage ( GShuntMW and BShuntMVar ) They represent constant admittance G + jb Writing this in actual units Converting to Per Unit Values B pu + BShunt SBase MVar Similar derivation for G BShunt B MVar V nom BShunt SBase V nom V nom B MVar pu BShunt SBase MVar S: Power System Modeling 04 PowerWorld Corporation 5
16 Bus Shunts (B and G) Values epressed in MW/Mvar at nominal voltage Represent a constant impedance/admittance at bus B Shunt : represents an impedance Mvar injection G Shunt : represents an impedance MW absorption S: Power System Modeling Sign of B and G are opposite for historical reasons G represented a load term B represented a capacitor term Y-Bus is affected only on diagonal On Bus Dialog Bus K Bus K 04 PowerWorld Corporation GShunt SBase MW BShunt + j SBase MVar 6
17 Transmission Branch (Line or Transformer) Impedance Parameters Series Resistance (R) in per unit Series Reactance (X) in per unit Shunt Charging (B) in per unit Shunt Conductance (G) in per unit On Branch Dialog Bus K R + jx Bus M jb G jb G S: Power System Modeling Note: This model is modified when including tap-ratios or phase-shifts for variable transformers 04 PowerWorld Corporation 7
18 Transmission Branch affect on the Y-Bus To make the Y-Bus, we epress all the impedances of the model as an admittance g series r r + b series + Then add several terms to the Y-Bus as a result of the transmission line (or transformer) BusK BusM g BusK series + G jbseries + + ( g jb ) series series B j BusM g series r ( g jb ) + series series G jbseries + + B j S: Power System Modeling 04 PowerWorld Corporation 8
19 Switched Shunts (Capacitor and Reactor Banks) Input the nominal MVAR, the MVAR supplied by the capacitor at nominal voltage It represents a constant impedance Use same conversion as with the Bus Shunts Y-Bus is thus affected only on diagonal terms Bus K On Switched Shunt Dialog Bus K + j QMVar SBase Bus K jb S: Power System Modeling 04 PowerWorld Corporation 9
20 What does Y-Bus look like? Graphic represents a 8 Bus System Sparse or Mostly Zeros Incident Symmetric Each dot represents a non-zero entry in the Y-Bus S: Power System Modeling 04 PowerWorld Corporation 0
21 Loads (ZIP model) Loads are modeled as constant impedance (Z), current (I), power (P), or a combination of the three For each of these values you specify a real power and a reactive power (P spec + jq spec ) Constant Power - the most commonly used On Load Dialog S Lk P + spec jq spec S: Power System Modeling 04 PowerWorld Corporation
22 Constant Current Load P+jQ specified are what the load would be at nominal voltage of.0 per unit Go back to the equations for comple power and derive epression for S S VI * I * S V P + jqspec Pspec + jq S V θ v.0 θv. 0 θv spec Load becomes a linear function of voltage magnitude On Load Dialog spec S V + Lk ( P jq spec spec ) S: Power System Modeling 04 PowerWorld Corporation
23 Constant Impedance Load P+jQ specified are what the load would be at nominal voltage of.0 per unit Go back to the equations for comple power load * spec * (.0) + jq spec * V Load becomes a quadratic function of voltage magnitude S S S VI P V V Z V Lk V + V Z Z * (P spec ( Pspec jqspec V S + ) jq P spec spec ) (.0) + jq On Load Dialog spec S: Power System Modeling 04 PowerWorld Corporation 3
24 Generators Model them as a source of Real and Reactive Power - MW, MVAR output Control features of generators AVR (Automatic Voltage Regulation) Controls the reactive power output (Q) to maintain a specified voltage level at a regulated bus (doesn t have to be the bus to which it is connected) AGC (Automatic Generation Control) Modifies the real power output (P) S: Power System Modeling 04 PowerWorld Corporation 4
25 Generator MW Power Control Input MW Output Minimum and Maimum MW Output Available for AGC Enforce Limits Participation Factor Used when on participation factor control On Generator Dialog S: Power System Modeling 04 PowerWorld Corporation 5
26 Generator Voltage Control Features Mvar Output Minimum and Maimum MVAR output Or can Use Capability Curve More detailed, but more data Voltage Setpoint in per unit Available for AVR Remote Regulation % Used when more than one generator is controlling the same bus voltage S: Power System Modeling On Generator Dialog (AVR) 04 PowerWorld Corporation Q out Must Stay inside shaded region during operation P out 6
27 The Power Flow Equations This is the heart of all power system analysis Kirchoff s Laws for a power system: Sum of the Currents at every Node Equals Zero S: Power System Modeling 04 PowerWorld Corporation 7
28 Why the Power Flow? Many loads (like heaters) are just big resistors which should be just an impedance, so why solve the power flow? Because our input data is MW and MVAR values. This is because The eperience of utilities for more than 00 years shows that consumers behave similar to constant power over the long-run If the voltage drops on a heater, the power consumption also decreases, but eventually some people get cold and turn up the heat Actually the built in thermostat and control system probably do this automatically S: Power System Modeling 04 PowerWorld Corporation 8
29 Deriving the Power Flow Equations Using the Y-Bus, write Kirchoff s Current Law at every bus as a matri equation YV I I 0 generators + loads We are studying POWER systems, so we like to talk about power not current, so S VI * * [V](V Y * [V](V Y * ) -S * generators ) -[V]I + S loads * generators etc. These are N- comple number equations (where N the number of buses in the system) 0 + [V]I * loads 0 S: Power System Modeling 04 PowerWorld Corporation 9
30 The Power Flow Equations These N- comple number equations can then be written as *(N-) real number equations as below P k 0 V N k m [ V [ g cos( δ δ ) + b sin( δ δ ) ] m km k m km k m P Gk + P Lk Transmission lines, transformers, capacitors Generators Loads Q k 0 V N k m [ Vm[ gkm sin( δ k δ m ) bkm cos( δ k δ m ) ] QGk + QLk S: Power System Modeling Elements of the Y-Bus Note: The variables g km and b km are the real and imaginary parts of the Y-Bus. ( Y G + jb or y km g km + jb km ) 04 PowerWorld Corporation 30
31 The Power Flow Equation Variables Four parameters describe the bus Voltage magnitude (V) Voltage angle (δ or θ) Real Power Injection (P P gen - P load ) Reactive Power Injection (Q Q gen - Q load ) The objective of the Power Flow algorithm is to determine all four of these values S: Power System Modeling 04 PowerWorld Corporation 3
32 Three Types of Buses In the Power Flow we are given two of these values at each bus and then solve for the other two Generally, there are three types of buses in a Power Flow Type of Bus Slack Bus (Vδ-Bus) (only one of these) PV-Bus (generator on AVR control) PQ-Bus (load or generator not on AVR control) Voltage Mag. (V) Voltage Angle (δ) Power Injection (P P gen P load ) Reactive Power Injection (Q Q gen Q load ) GIVEN GIVEN SOLVE FOR SOLVE FOR GIVEN SOLVE GIVEN SOLVE FOR FOR SOLVE SOLVE GIVEN GIVEN FOR FOR S: Power System Modeling 04 PowerWorld Corporation 3
33 How does the Power Flow work? The power flow equations are non-linear, which means they can not be directly solved Linear: , so 7 Non-linear: 5 sin(), so??? To solve non-linear equations, an iterative technique must be used To solve the Power Flow, Newton s Method is normally the best technique Simulator uses this by default. S: Power System Modeling 04 PowerWorld Corporation 33
34 Solving Non-Linear Equations Power Flow Equations are NON-LINEAR equations. There are cos(*) and sin(*) terms which make the equations non-linear This means that finding a direct solution to them is impossible Thus we must use iterative numerical schemes to determine their solution For power flow equations, variations on Newton s Method has been found to be the best technique S: Power System Modeling 04 PowerWorld Corporation 34
35 35 04 PowerWorld Corporation S: Power System Modeling Discussed in Calculus courses Consider a simple scalar equation f() You can write f() as a Taylor Series Newton s Method... ) ( ) ( ) ( ) ( h o t f f f f + + +
36 36 04 PowerWorld Corporation S: Power System Modeling Now, approimate this Taylor Series by ignoring all but the first two terms We are trying to find where f() 0 (the power flow equations sum to zero), therefore we can approimate and estimate Newton s Method for Scalar Functions ) ( ) ( ) ( f f f + [ ] [ ] ) ( ) ( f f f [ ] ( 0 ) 0 0 f f
37 Newton s Method This is called an iterative method because you take a guess at 0 and use the Newton-step to a new guess called. Then you use to find, etc. Consider f() -. We find Thus f S: Power System Modeling k k ( ) k k k and + + ( k + k k k k k 04 PowerWorld Corporation ) 37
38 Newton s Method Now take and initial guess, say 0, and iterate the previous equation k k f( k ) k Done Error decreases quite quickly Quadratic convergence f( k ) is known as the mismatch The problem is solved when the mismatch is zero S: Power System Modeling 04 PowerWorld Corporation 38
39 Non-Linear Equations can have Multiple Solutions Consider the previous eample. There are two solutions. and In an iterative scheme, the initial guess determines which solutions you converge to. Consider starting at 0 -. k k f( k ) k Done S: Power System Modeling 04 PowerWorld Corporation S-39 39
40 Non-Linear Equations can have No Real Solution Consider the equation - λ 0, where λ is an independent parameter The number of real solutions depends on the value of λ. For λ > 0, there are two real solutions For λ 0, there is one real solution at 0 For λ <0, there are NO real solutions Parameter variation can change the number of solutions of nonlinear systems S: Power System Modeling 04 PowerWorld Corporation 40
41 Newton-Rhapson Convergence Characteristics Global convergence characteristics of the N-R algorithm are not easy to characterize The N-R algorithm converges quite quickly provided the initial guess is close enough to the solution However the algorithm doesn t always converge to the closest solution Some initial guesses are just plain bad. For eample, if f is near zero ( illconditioned ), the process may diverge S: Power System Modeling 04 PowerWorld Corporation 4
42 Etending Scalar to Vectors and Matrices Newton s method may also be used when you are trying to find a solution where many functions are equal to zero Let f() be a n-dimensional function and let be an n-dimensional vector f ( ) f f n ( ) ( ) n S: Power System Modeling 04 PowerWorld Corporation 4
43 43 04 PowerWorld Corporation S: Power System Modeling Now, the Newton-step is still defined as But is now a matri, called the Jacobian Newton s Method for Multiple Equations ) ( k k k k f f k + n n n n f f f f f f f f f
44 Solving the Power Flow Equations Power Flow Equations are NON-LINEAR equations The cos(*) and sin(*) terms make them non-linear This means we have to use an iterative technique to solve them Define f to be the real and reactive power balance equations at every bus Define to be the vector of voltages and angles at every bus (ecept the slack bus) S: Power System Modeling 04 PowerWorld Corporation 44
45 45 04 PowerWorld Corporation S: Power System Modeling Recall Thus, Setting up the Power Flow Solution ( ) ( ) [ ] [ ] ( ) ( ) [ ] [ ] Lk Gk N m m k km m k km m k Lk Gk N m m k km m k km m k Q Q b g V V Q P P b g V V P k k cos sin sin cos δ δ δ δ δ δ δ δ and ) ( n n n n V V V Q P Q P Q P δ δ δ f n n n n n n n n n n n n n n n n V Q Q V Q Q V P P V P P V Q Q V P P V Q Q V Q Q V Q Q V P P V P P V P P δ δ δ δ δ δ δ δ δ δ δ δ f Note: There are n buses, with bus n being the slack bus
46 Power Flow Solutions The power flow equations ehibit the same behavior as other non-linear equations In theory there are up to n - solutions to the power flow equations Of these, ALL or NONE may be real number solutions In power system analysis, we are normally interested only in the solution that is the high voltage solution for every bus S: Power System Modeling 04 PowerWorld Corporation S-46 46
47 Eample Two-Bus Power System Consider this lossless (R0) eample system Bus (Slack) R+jX j0.00 Bus P + j Q L L Variable Definitions Power balance equations : θ Voltage Angle at Bus V Voltage Magnitude at Bus 0. B 0 r PMismatch P QMismatch Q L L BV sin( θ ) + BV cos( θ ) BV S: Power System Modeling 04 PowerWorld Corporation 47
48 How do power flow solutions vary as load is changed? Solution: Calculate a series of power flow solutions for various load levels First determine the following f J( θ, V ) BV BV cos( θ ) sin( θ ) Bsin( θ ) B cos( θ ) BV k θ V ; f ( ) Q L L + P BV sin( θ ) BV cos( θ ) BV S: Power System Modeling 04 PowerWorld Corporation 48
49 Eample Power Flow Solution Now for each load level, iterate from an initial guess until the solution (hopefully) converges [ f ( 0 )] Consider a per unit load of P L pu and Q L 0 pu A 00 MW load since SBase 00 MVA 0 f Then consider a flat start for the initial guess: V 0 ; θ 0 0. Also consider a start of V ; θ S: Power System Modeling 04 PowerWorld Corporation S-49 49
50 Power Flow Two Bus.ls Simple -Bus Power Flow in Ecel Open Microsoft Ecel \S0_SystemModeling\Power Flow Two Bus.ls Gray Shaded cells are user inputs (initial guess, load and network parameters) S: Power System Modeling 04 PowerWorld Corporation 50
51 Iteration Results for Power Flow Solution Power Flow Two Bus.ls Change Initial Voltage to V 0 ; θ 0 0 Cell B5.0 Cell C5 0.0 Change Initial Voltage to V ; θ 0 - Cell B5 0.5 Cell C5 -.0 S: Power System Modeling k V k θ k (radians) High Voltage Solution k V k θ k (radians) Low Voltage Solution 04 PowerWorld Corporation 5
52 Region of Convergence Initial guess of Bus angle is plotted on -ais, voltage magnitude on y-ais, for load 00 MW, 00 Mvar; 0. pu Initial guesses in the red region converge to the high voltage solution, while those in the yellow region converge to the low voltage solution S: Power System Modeling 04 PowerWorld Corporation 5
53 PV-Curves A PV-Curve is generated by plotting these two solutions as the real power load is varied with the reactive load and impedance constant Eperiment with parameters in cells O-O4 Higher transmission impedance usually decreases the system capacity (maimum load) Per unit voltage magnitude High voltage solutions Low voltage solutions Real power load (MW) S: Power System Modeling 04 PowerWorld Corporation Note: load values below 500 have two solutions, those above 500 have no solution For a critical value (i.e. the nose point ) there is only one solution 53
54 QV-Curves A QV-Curve is generated by plotting these two solutions as the reactive power load is varied with the real load and impedance constant Per unit voltage magnitude High voltage solutions 0. Low voltage solutions Reactive power load (Mvar) S: Power System Modeling 04 PowerWorld Corporation Again: load values below 50 have two solutions, while those above 50 have no solution For a critical value (i.e. the nose point ) there is only one solution 54
55 Maimum Loadability The nose points on the PV and QV curves are critical values They correspond to points of maimum loadability from a static point of view Note: this only considers the static equations. Other problems can occur long before the power system reaches this points: lines overheating or system dynamic problems The critical values depend on the relative allocation between real and reactive power S: Power System Modeling 04 PowerWorld Corporation 55
56 Mathematical Characteristics of the Critical Value At the critical value, the power flow Jacobian will be singular A singular matri is one that has a zero determinant (a generalization of scalar case when df/d 0) A singular matri CANNOT be inverted Thus the Newton power flow does not work well near this point because it requires us to invert the Jacobian matri S: Power System Modeling k f + k 04 PowerWorld Corporation f ( k k k ) 56
Weighted-Least-Square(WLS) State Estimation
 Weighted-Least-Square(WLS) State Estimation Yousu Chen PNNL December 18, 2015 This document is a description of how to formulate the weighted-least squares (WLS) state estimation problem. Most of the formulation
Weighted-Least-Square(WLS) State Estimation Yousu Chen PNNL December 18, 2015 This document is a description of how to formulate the weighted-least squares (WLS) state estimation problem. Most of the formulation
Introduction to PowerWorld Simulator: Interface and Common Tools
 Introduction to PowerWorld Simulator: Interface and Common Tools 2001 South First Street Champaign, Illinois 61820 +1 (217) 384.6330 [email protected] http://www.powerworld.com Fault Analysis Analysis
Introduction to PowerWorld Simulator: Interface and Common Tools 2001 South First Street Champaign, Illinois 61820 +1 (217) 384.6330 [email protected] http://www.powerworld.com Fault Analysis Analysis
SAMPLE OF THE STUDY MATERIAL PART OF CHAPTER 3. Symmetrical Components & Faults Calculations
 SAMPLE OF THE STUDY MATERIAL PART OF CHAPTER 3 3.0 Introduction Fortescue's work proves that an unbalanced system of 'n' related phasors can be resolved into 'n' systems of balanced phasors called the
SAMPLE OF THE STUDY MATERIAL PART OF CHAPTER 3 3.0 Introduction Fortescue's work proves that an unbalanced system of 'n' related phasors can be resolved into 'n' systems of balanced phasors called the
Power System Simulation for Engineers (PSS/E version 33)
 Power System Simulation for Engineers (PSS/E version 33) Here are instructions for accessing and using the PSS/E-33 software. On-campus students should access this software at any of the computers in the
Power System Simulation for Engineers (PSS/E version 33) Here are instructions for accessing and using the PSS/E-33 software. On-campus students should access this software at any of the computers in the
A Direct Numerical Method for Observability Analysis
 IEEE TRANSACTIONS ON POWER SYSTEMS, VOL 15, NO 2, MAY 2000 625 A Direct Numerical Method for Observability Analysis Bei Gou and Ali Abur, Senior Member, IEEE Abstract This paper presents an algebraic method
IEEE TRANSACTIONS ON POWER SYSTEMS, VOL 15, NO 2, MAY 2000 625 A Direct Numerical Method for Observability Analysis Bei Gou and Ali Abur, Senior Member, IEEE Abstract This paper presents an algebraic method
Roots of equation fx are the values of x which satisfy the above expression. Also referred to as the zeros of an equation
 LECTURE 20 SOLVING FOR ROOTS OF NONLINEAR EQUATIONS Consider the equation f = 0 Roots of equation f are the values of which satisfy the above epression. Also referred to as the zeros of an equation f()
LECTURE 20 SOLVING FOR ROOTS OF NONLINEAR EQUATIONS Consider the equation f = 0 Roots of equation f are the values of which satisfy the above epression. Also referred to as the zeros of an equation f()
LAB1 INTRODUCTION TO PSS/E EE 461 Power Systems Colorado State University
 LAB1 INTRODUCTION TO PSS/E EE 461 Power Systems Colorado State University PURPOSE: The purpose of this lab is to introduce PSS/E. This lab will introduce the following aspects of PSS/E: Introduction to
LAB1 INTRODUCTION TO PSS/E EE 461 Power Systems Colorado State University PURPOSE: The purpose of this lab is to introduce PSS/E. This lab will introduce the following aspects of PSS/E: Introduction to
Fault Analysis I13-1. 2008 PowerWorld Corporation
 Fault Analysis Analysis of power system parameters resulting from a ground or line to line fault somewhere in the system Simulator contains a tool for analyzing faults in an automatic fashion Can perform
Fault Analysis Analysis of power system parameters resulting from a ground or line to line fault somewhere in the system Simulator contains a tool for analyzing faults in an automatic fashion Can perform
OPTIMAL DISPATCH OF POWER GENERATION SOFTWARE PACKAGE USING MATLAB
 OPTIMAL DISPATCH OF POWER GENERATION SOFTWARE PACKAGE USING MATLAB MUHAMAD FIRDAUS BIN RAMLI UNIVERSITI MALAYSIA PAHANG v ABSTRACT In the reality practical power system, power plants are not at the same
OPTIMAL DISPATCH OF POWER GENERATION SOFTWARE PACKAGE USING MATLAB MUHAMAD FIRDAUS BIN RAMLI UNIVERSITI MALAYSIA PAHANG v ABSTRACT In the reality practical power system, power plants are not at the same
Power System Simulation for Engineers (PSS/E): Fault Analysis
 Power System Simulation for Engineers (PSS/E): Fault Analysis Table of contents: A. GENERAL INSTRUCTIONS 1 B. REQUIRED DATA 2 C. READING AN EXISTING CASE 2 D. SAVING A CASE 4 E. CREATING A NEW CASE 4 F.
Power System Simulation for Engineers (PSS/E): Fault Analysis Table of contents: A. GENERAL INSTRUCTIONS 1 B. REQUIRED DATA 2 C. READING AN EXISTING CASE 2 D. SAVING A CASE 4 E. CREATING A NEW CASE 4 F.
A New Method for Estimating Maximum Power Transfer and Voltage Stability Margins to Mitigate the Risk of Voltage Collapse
 A New Method for Estimating Maximum Power Transfer and Voltage Stability Margins to Mitigate the Risk of Voltage Collapse Bernie Lesieutre Dan Molzahn University of Wisconsin-Madison PSERC Webinar, October
A New Method for Estimating Maximum Power Transfer and Voltage Stability Margins to Mitigate the Risk of Voltage Collapse Bernie Lesieutre Dan Molzahn University of Wisconsin-Madison PSERC Webinar, October
PowerWorld Simulator
 PowerWorld Simulator Quick Start Guide 2001 South First Street Champaign, Illinois 61820 +1 (217) 384.6330 [email protected] http://www.powerworld.com Purpose This quick start guide is intended to
PowerWorld Simulator Quick Start Guide 2001 South First Street Champaign, Illinois 61820 +1 (217) 384.6330 [email protected] http://www.powerworld.com Purpose This quick start guide is intended to
IMPROVED NETWORK PARAMETER ERROR IDENTIFICATION USING MULTIPLE MEASUREMENT SCANS
 IMPROVED NETWORK PARAMETER ERROR IDENTIFICATION USING MULTIPLE MEASUREMENT SCANS Liuxi Zhang and Ali Abur Department of Electrical and Computer Engineering Northeastern University Boston, MA, USA [email protected]
IMPROVED NETWORK PARAMETER ERROR IDENTIFICATION USING MULTIPLE MEASUREMENT SCANS Liuxi Zhang and Ali Abur Department of Electrical and Computer Engineering Northeastern University Boston, MA, USA [email protected]
Contouring and Advanced Visualization
 Contouring and Advanced Visualization Contouring Underlay your oneline with an image Geographic Data Views Auto-created geographic data visualization Emphasis of Display Objects Make specific objects standout
Contouring and Advanced Visualization Contouring Underlay your oneline with an image Geographic Data Views Auto-created geographic data visualization Emphasis of Display Objects Make specific objects standout
Static Analysis of Power Systems. Lennart Söder and Mehrdad Ghandhari
 Static Analysis of Power Systems Lennart Söder and Mehrdad Ghandhari Electric Power Systems Royal Institute of Technology August 200 ii Contents Introduction 2 Power system design 3 2. The development
Static Analysis of Power Systems Lennart Söder and Mehrdad Ghandhari Electric Power Systems Royal Institute of Technology August 200 ii Contents Introduction 2 Power system design 3 2. The development
Power System review W I L L I A M V. T O R R E A P R I L 1 0, 2 0 1 3
 Power System review W I L L I A M V. T O R R E A P R I L 1 0, 2 0 1 3 Basics of Power systems Network topology Transmission and Distribution Load and Resource Balance Economic Dispatch Steady State System
Power System review W I L L I A M V. T O R R E A P R I L 1 0, 2 0 1 3 Basics of Power systems Network topology Transmission and Distribution Load and Resource Balance Economic Dispatch Steady State System
Power Technology Issue 104. Modeling of Two-Winding Voltage Regulating Transformers for Positive Sequence Load Flow Analysis in PSS E
 SIEMENS Siemens Energy, Inc. Power Technology Issue 104 Modeling of TwoWinding Voltage Regulating Transformers for Positive Sequence Load Flow Analysis in PSS E Carlos GrandeMoran, Ph.D. Principal Consultant
SIEMENS Siemens Energy, Inc. Power Technology Issue 104 Modeling of TwoWinding Voltage Regulating Transformers for Positive Sequence Load Flow Analysis in PSS E Carlos GrandeMoran, Ph.D. Principal Consultant
Radial Distribution Test Feeders
 Radial Distribution Test Feeders Distribution System Analysis Subcommittee Report Abstract: Many computer programs are available for the analysis of radial distribution feeders. In 1992 a paper was published
Radial Distribution Test Feeders Distribution System Analysis Subcommittee Report Abstract: Many computer programs are available for the analysis of radial distribution feeders. In 1992 a paper was published
Chapter 9 Balanced Faults
 Chapter 9 alanced Faults 9.1 Introduction The most common types of fault are (in order) single-line-to-ground fault, line-to-line fault, and double-line-to-ground fault. All of these are unbalanced faults.
Chapter 9 alanced Faults 9.1 Introduction The most common types of fault are (in order) single-line-to-ground fault, line-to-line fault, and double-line-to-ground fault. All of these are unbalanced faults.
Transient Stability Analysis with PowerWorld Simulator
 Transient Stability Analysis with PowerWorld Simulator T6: Storage of Transient Stability Results 2001 South First Street Champaign, Illinois 61820 +1 (217) 384.6330 [email protected] http://www.powerworld.com
Transient Stability Analysis with PowerWorld Simulator T6: Storage of Transient Stability Results 2001 South First Street Champaign, Illinois 61820 +1 (217) 384.6330 [email protected] http://www.powerworld.com
Keysight Technologies Understanding the Fundamental Principles of Vector Network Analysis. Application Note
 Keysight Technologies Understanding the Fundamental Principles of Vector Network Analysis Application Note Introduction Network analysis is the process by which designers and manufacturers measure the
Keysight Technologies Understanding the Fundamental Principles of Vector Network Analysis Application Note Introduction Network analysis is the process by which designers and manufacturers measure the
Voltage Stability Improvement using Static Var Compensator in Power Systems
 Leonardo Journal of Sciences ISSN 1583-0233 Issue 14, January-June 2009 p. 167-172 Voltage Stability Improvement using Static Var Compensator in Power Systems Department of Electrical/Computer Engineering,
Leonardo Journal of Sciences ISSN 1583-0233 Issue 14, January-June 2009 p. 167-172 Voltage Stability Improvement using Static Var Compensator in Power Systems Department of Electrical/Computer Engineering,
Distributed Flexible AC Transmission System (D FACTS) Jamie Weber. [email protected], 217 384 6330 ext. 13
 Distributed Flexible AC Transmission System (D FACTS) Jamie Weber [email protected], 217 384 6330 ext. 13 Slide Preparation: Kate Rogers Davis [email protected], 217 384 6330, Ext 14 2001 South First
Distributed Flexible AC Transmission System (D FACTS) Jamie Weber [email protected], 217 384 6330 ext. 13 Slide Preparation: Kate Rogers Davis [email protected], 217 384 6330, Ext 14 2001 South First
Estimating Line-Flow Limits
 Estimating Line-Flow Limits University of Wisconsin-Madison May 1, 2013 Specifying reasonable line-flow limits requires two quantities: the surge impedance loading for the line and an estimate of the line
Estimating Line-Flow Limits University of Wisconsin-Madison May 1, 2013 Specifying reasonable line-flow limits requires two quantities: the surge impedance loading for the line and an estimate of the line
Voltage regulation in distribution systems - Tap changer and Wind Power
 CODEN:LUTEDX/(TEIE-5270)/1-59/(2010) Industrial Electrical Engineering and Automation Voltage regulation in distribution systems - Tap changer and Wind Power David Sáez Romero D of Industrial Electrical
CODEN:LUTEDX/(TEIE-5270)/1-59/(2010) Industrial Electrical Engineering and Automation Voltage regulation in distribution systems - Tap changer and Wind Power David Sáez Romero D of Industrial Electrical
Transmission Lines. Smith Chart
 Smith Chart The Smith chart is one of the most useful graphical tools for high frequency circuit applications. The chart provides a clever way to visualize complex functions and it continues to endure
Smith Chart The Smith chart is one of the most useful graphical tools for high frequency circuit applications. The chart provides a clever way to visualize complex functions and it continues to endure
Equipment: Power Supply, DAI, Variable resistance (8311), Variable inductance (8321)
 Lab 4: 3-phase circuits. Objective: to study voltage-current relationships in 3-phase circuits; to learn to make delta and Y connections; to calculate and measure real, apparent, and reactive powers. Equipment:
Lab 4: 3-phase circuits. Objective: to study voltage-current relationships in 3-phase circuits; to learn to make delta and Y connections; to calculate and measure real, apparent, and reactive powers. Equipment:
Lecture Notes ELE A6
 ecture Notes EE A6 Ramadan El-Shatshat Three Phase circuits 9/12/2006 EE A6 Three-phase Circuits 1 Three-phase Circuits 9/12/2006 EE A6 Three-phase Circuits 2 Advantages of Three-phase Circuits Smooth
ecture Notes EE A6 Ramadan El-Shatshat Three Phase circuits 9/12/2006 EE A6 Three-phase Circuits 1 Three-phase Circuits 9/12/2006 EE A6 Three-phase Circuits 2 Advantages of Three-phase Circuits Smooth
Chapter 24. Three-Phase Voltage Generation
 Chapter 24 Three-Phase Systems Three-Phase Voltage Generation Three-phase generators Three sets of windings and produce three ac voltages Windings are placed 120 apart Voltages are three identical sinusoidal
Chapter 24 Three-Phase Systems Three-Phase Voltage Generation Three-phase generators Three sets of windings and produce three ac voltages Windings are placed 120 apart Voltages are three identical sinusoidal
2.1 Introduction. 2.2 Terms and definitions
 .1 Introduction An important step in the procedure for solving any circuit problem consists first in selecting a number of independent branch currents as (known as loop currents or mesh currents) variables,
.1 Introduction An important step in the procedure for solving any circuit problem consists first in selecting a number of independent branch currents as (known as loop currents or mesh currents) variables,
Understanding Power Factor and How it Affects Your Electric Bill. Presented by Scott Peele PE
 Understanding Power Factor and How it Affects Your Electric Bill Presented by Scott Peele PE Understanding Power Factor Definitions kva, kvar, kw, Apparent Power vs. True Power Calculations Measurements
Understanding Power Factor and How it Affects Your Electric Bill Presented by Scott Peele PE Understanding Power Factor Definitions kva, kvar, kw, Apparent Power vs. True Power Calculations Measurements
Using Microsoft Excel Built-in Functions and Matrix Operations. EGN 1006 Introduction to the Engineering Profession
 Using Microsoft Ecel Built-in Functions and Matri Operations EGN 006 Introduction to the Engineering Profession Ecel Embedded Functions Ecel has a wide variety of Built-in Functions: Mathematical Financial
Using Microsoft Ecel Built-in Functions and Matri Operations EGN 006 Introduction to the Engineering Profession Ecel Embedded Functions Ecel has a wide variety of Built-in Functions: Mathematical Financial
Power Technology Issue 106. Modeling of Three-Winding Voltage Regulating Transformers for Positive Sequence Load Flow Analysis in PSS E
 SIEMENS Siemens Energy, Inc. Power Technology Issue 106 Modeling of Three-Winding Voltage Regulating Transformers for Positive Sequence Load Flow Analysis in PSS E Carlos Grande-Moran, Ph.D. Principal
SIEMENS Siemens Energy, Inc. Power Technology Issue 106 Modeling of Three-Winding Voltage Regulating Transformers for Positive Sequence Load Flow Analysis in PSS E Carlos Grande-Moran, Ph.D. Principal
Record Specification and File Format for Specifying Contingency Definitions and Remedial Actions Schemes
 Record Specification and File Format for Specifying Contingency Definitions and Remedial Actions Schemes Date : October 22, 2013 December 6, 2013 January 21, 2015 August 28, 2015 November 6, 2015, November
Record Specification and File Format for Specifying Contingency Definitions and Remedial Actions Schemes Date : October 22, 2013 December 6, 2013 January 21, 2015 August 28, 2015 November 6, 2015, November
штш User Manual 1.2.7 beta www.inorxl.com
 штш User Manual 1.2.7 beta www.inorxl.com 2 TABLE OF CONTENTS What is InorXL?... 3 How to quickstart?... 3 What can you do with InorXL?... 3 What integration with Excel gives?... 4 What is system requirements?...
штш User Manual 1.2.7 beta www.inorxl.com 2 TABLE OF CONTENTS What is InorXL?... 3 How to quickstart?... 3 What can you do with InorXL?... 3 What integration with Excel gives?... 4 What is system requirements?...
S-Parameters and Related Quantities Sam Wetterlin 10/20/09
 S-Parameters and Related Quantities Sam Wetterlin 10/20/09 Basic Concept of S-Parameters S-Parameters are a type of network parameter, based on the concept of scattering. The more familiar network parameters
S-Parameters and Related Quantities Sam Wetterlin 10/20/09 Basic Concept of S-Parameters S-Parameters are a type of network parameter, based on the concept of scattering. The more familiar network parameters
A progressive method to solve large-scale AC Optimal Power Flow with discrete variables and control of the feasibility
 A progressive method to solve large-scale AC Optimal Power Flow with discrete variables and control of the feasibility Manuel Ruiz, Jean Maeght, Alexandre Marié, Patrick Panciatici and Arnaud Renaud [email protected]
A progressive method to solve large-scale AC Optimal Power Flow with discrete variables and control of the feasibility Manuel Ruiz, Jean Maeght, Alexandre Marié, Patrick Panciatici and Arnaud Renaud [email protected]
Three-phase analysis of unbalanced systems
 Exercises of course ELEC0029 - Electric power systems analysis and operation Three-phase analysis of unbalanced systems Thierry Van Cutsem [email protected] www.montefiore.ulg.ac.be/~vct March 205
Exercises of course ELEC0029 - Electric power systems analysis and operation Three-phase analysis of unbalanced systems Thierry Van Cutsem [email protected] www.montefiore.ulg.ac.be/~vct March 205
Three phase circuits
 Three phase circuits THREE PHASE CIRCUITS THREE-PHASE ADVANTAGES 1. The horsepower rating of three-phase motors and the kva rating of three-phase transformers are 150% greater than single-phase motors
Three phase circuits THREE PHASE CIRCUITS THREE-PHASE ADVANTAGES 1. The horsepower rating of three-phase motors and the kva rating of three-phase transformers are 150% greater than single-phase motors
Ver 3537 E1.1 Analysis of Circuits (2014) E1.1 Circuit Analysis. Problem Sheet 1 (Lectures 1 & 2)
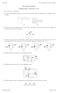 Ver 3537 E. Analysis of Circuits () Key: [A]= easy... [E]=hard E. Circuit Analysis Problem Sheet (Lectures & ). [A] One of the following circuits is a series circuit and the other is a parallel circuit.
Ver 3537 E. Analysis of Circuits () Key: [A]= easy... [E]=hard E. Circuit Analysis Problem Sheet (Lectures & ). [A] One of the following circuits is a series circuit and the other is a parallel circuit.
Matpower 4.1 User s Manual
 Matpower 4.1 User s Manual Ray D. Zimmerman Carlos E. Murillo-Sánchez December 14, 2011 2010, 2011 Power Systems Engineering Research Center (Pserc) All Rights Reserved Contents 1 Introduction 7 1.1 Background................................
Matpower 4.1 User s Manual Ray D. Zimmerman Carlos E. Murillo-Sánchez December 14, 2011 2010, 2011 Power Systems Engineering Research Center (Pserc) All Rights Reserved Contents 1 Introduction 7 1.1 Background................................
Power Factor Correction for Power Systems First Semester Report Spring Semester 2007
 Power Factor Correction for Power Systems First Semester Report Spring Semester 2007 by Pamela Ackerman Prepared to partially fulfill the requirements for EE401 Department of Electrical and Computer Engineering
Power Factor Correction for Power Systems First Semester Report Spring Semester 2007 by Pamela Ackerman Prepared to partially fulfill the requirements for EE401 Department of Electrical and Computer Engineering
Chapter 12: Three Phase Circuits
 Chapter 12: Three Phase Circuits 12.1 What Is a Three Phase Circuit? 12.2 Balance Three Phase Voltages 12.3 Balance Three Phase Y to Y Connection 12.4 Other Balance Three Phase Connections 12.5 Power in
Chapter 12: Three Phase Circuits 12.1 What Is a Three Phase Circuit? 12.2 Balance Three Phase Voltages 12.3 Balance Three Phase Y to Y Connection 12.4 Other Balance Three Phase Connections 12.5 Power in
Circuits with inductors and alternating currents. Chapter 20 #45, 46, 47, 49
 Circuits with inductors and alternating currents Chapter 20 #45, 46, 47, 49 RL circuits Ch. 20 (last section) Symbol for inductor looks like a spring. An inductor is a circuit element that has a large
Circuits with inductors and alternating currents Chapter 20 #45, 46, 47, 49 RL circuits Ch. 20 (last section) Symbol for inductor looks like a spring. An inductor is a circuit element that has a large
Basic Laws Circuit Theorems Methods of Network Analysis Non-Linear Devices and Simulation Models
 EE Modul 1: Electric Circuits Theory Basic Laws Circuit Theorems Methods of Network Analysis Non-Linear Devices and Simulation Models EE Modul 1: Electric Circuits Theory Current, Voltage, Impedance Ohm
EE Modul 1: Electric Circuits Theory Basic Laws Circuit Theorems Methods of Network Analysis Non-Linear Devices and Simulation Models EE Modul 1: Electric Circuits Theory Current, Voltage, Impedance Ohm
Polynomial Degree and Finite Differences
 CONDENSED LESSON 7.1 Polynomial Degree and Finite Differences In this lesson you will learn the terminology associated with polynomials use the finite differences method to determine the degree of a polynomial
CONDENSED LESSON 7.1 Polynomial Degree and Finite Differences In this lesson you will learn the terminology associated with polynomials use the finite differences method to determine the degree of a polynomial
Lecture 2 Linear functions and examples
 EE263 Autumn 2007-08 Stephen Boyd Lecture 2 Linear functions and examples linear equations and functions engineering examples interpretations 2 1 Linear equations consider system of linear equations y
EE263 Autumn 2007-08 Stephen Boyd Lecture 2 Linear functions and examples linear equations and functions engineering examples interpretations 2 1 Linear equations consider system of linear equations y
Understanding the Fundamental Principles of Vector Network Analysis. Application Note 1287-1. Table of Contents. Page
 Understanding the Fundamental Principles of Vector Network Analysis Application Note 1287-1 Table of Contents Page Introduction 2 Measurements in Communications Systems 2 Importance of Vector Measurements
Understanding the Fundamental Principles of Vector Network Analysis Application Note 1287-1 Table of Contents Page Introduction 2 Measurements in Communications Systems 2 Importance of Vector Measurements
A COMPARISON ON PERFORMANCE OF TCSC/SSSC FOR A RADIAL SYSTEM
 IMPACT: International Journal of Research in Engineering & Technology (IMPACT: IJRET) ISSN(E): 31-8843; ISSN(P): 347-4599 Vol. 3, Issue 9, Sep 015, 7-18 Impact Journals A COMPARISON ON PERFORMANCE OF TCSC/SSSC
IMPACT: International Journal of Research in Engineering & Technology (IMPACT: IJRET) ISSN(E): 31-8843; ISSN(P): 347-4599 Vol. 3, Issue 9, Sep 015, 7-18 Impact Journals A COMPARISON ON PERFORMANCE OF TCSC/SSSC
PowerWorld Transmission Line Parameter Calculator
 PowerWorld Transmission Line Parameter Calculator Introduction The PowerWorld Transmission Line Parameter Calculator is a tool designed to compute characteristic line parameters given the type of the conductor
PowerWorld Transmission Line Parameter Calculator Introduction The PowerWorld Transmission Line Parameter Calculator is a tool designed to compute characteristic line parameters given the type of the conductor
Critical thin-film processes such as deposition and etching take place in a vacuum
 WHITEPAPER INTRODUCING POWER SUPPLIES AND PLASMA Critical thin-film processes such as deposition and etching take place in a vacuum SYSTEMS chamber in the presence of a plasma. A plasma is an electrically
WHITEPAPER INTRODUCING POWER SUPPLIES AND PLASMA Critical thin-film processes such as deposition and etching take place in a vacuum SYSTEMS chamber in the presence of a plasma. A plasma is an electrically
Basic Electrical Technology Dr. L. Umanand Department of Electrical Engineering Indian Institute of Science, Bangalore. Lecture - 33 3 phase System 4
 Basic Electrical Technology Dr. L. Umanand Department of Electrical Engineering Indian Institute of Science, Bangalore Lecture - 33 3 phase System 4 Hello everybody. So, in the last class we have been
Basic Electrical Technology Dr. L. Umanand Department of Electrical Engineering Indian Institute of Science, Bangalore Lecture - 33 3 phase System 4 Hello everybody. So, in the last class we have been
Section 5.0A Factoring Part 1
 Section 5.0A Factoring Part 1 I. Work Together A. Multiply the following binomials into trinomials. (Write the final result in descending order, i.e., a + b + c ). ( 7)( + 5) ( + 7)( + ) ( + 7)( + 5) (
Section 5.0A Factoring Part 1 I. Work Together A. Multiply the following binomials into trinomials. (Write the final result in descending order, i.e., a + b + c ). ( 7)( + 5) ( + 7)( + ) ( + 7)( + 5) (
Students Manual for the Exam. General Engineering and Electrical Civil Engineering Discipline
 Students Manual for the Exam General Engineering and Electrical Civil Engineering Discipline -- October March 2014 2013 -- COPYRIGHT NOTICE COPYRIGHTS 2013 NATIONAL CENTER FOR ASSESSMENT IN HIGHER EDUCATION
Students Manual for the Exam General Engineering and Electrical Civil Engineering Discipline -- October March 2014 2013 -- COPYRIGHT NOTICE COPYRIGHTS 2013 NATIONAL CENTER FOR ASSESSMENT IN HIGHER EDUCATION
RLC Resonant Circuits
 C esonant Circuits Andrew McHutchon April 20, 203 Capacitors and Inductors There is a lot of inconsistency when it comes to dealing with reactances of complex components. The format followed in this document
C esonant Circuits Andrew McHutchon April 20, 203 Capacitors and Inductors There is a lot of inconsistency when it comes to dealing with reactances of complex components. The format followed in this document
NETWORK RECONFIGURATION FOR LOSS REDUCTION IN THREE-PHASE POWER DISTRIBUTION SYSTEMS
 NETWORK RECONFIGURATION FOR LOSS REDUCTION IN THREE-PHASE POWER DISTRIBUTION SYSTEMS A Thesis Presented to the Faculty of the Graduate School of Cornell University in Partial Fulfillment of the Requirements
NETWORK RECONFIGURATION FOR LOSS REDUCTION IN THREE-PHASE POWER DISTRIBUTION SYSTEMS A Thesis Presented to the Faculty of the Graduate School of Cornell University in Partial Fulfillment of the Requirements
1 Introduction. 2 Power Flow. J.L. Kirtley Jr.
 Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.061 Introduction to Power Systems Class Notes Chapter 5 Introduction To Load Flow J.L. Kirtley Jr. 1 Introduction
Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.061 Introduction to Power Systems Class Notes Chapter 5 Introduction To Load Flow J.L. Kirtley Jr. 1 Introduction
Application of GA for Optimal Location of FACTS Devices for Steady State Voltage Stability Enhancement of Power System
 I.J. Intelligent Systems and Applications, 2014, 03, 69-75 Published Online February 2014 in MECS (http://www.mecs-press.org/) DOI: 10.5815/ijisa.2014.03.07 Application of GA for Optimal Location of Devices
I.J. Intelligent Systems and Applications, 2014, 03, 69-75 Published Online February 2014 in MECS (http://www.mecs-press.org/) DOI: 10.5815/ijisa.2014.03.07 Application of GA for Optimal Location of Devices
Genetic Algorithm approach to find excitation capacitances for 3- phase smseig operating single phase loads
 Genetic Algorithm approach to find excitation capacitances for 3- phase smseig operating single phase loads Authors & Affiliation: V.Ravi Kiran, V.Manoj and P.Praveen Kumar Asst. Professor, EEE Dept GMRIT,
Genetic Algorithm approach to find excitation capacitances for 3- phase smseig operating single phase loads Authors & Affiliation: V.Ravi Kiran, V.Manoj and P.Praveen Kumar Asst. Professor, EEE Dept GMRIT,
COMPREHENSIVE DISTRIBUTION POWER FLOW: MODELING, FORMULATION, SOLUTION ALGORITHMS AND ANALYSIS
 COMPREHENSIVE DISTRIBUTION POWER FLOW: MODELING, FORMULATION, SOLUTION ALGORITHMS AND ANALYSIS A Dissertation Presented to the Faculty of the Graduate School of Cornell University in Partial Fulfillment
COMPREHENSIVE DISTRIBUTION POWER FLOW: MODELING, FORMULATION, SOLUTION ALGORITHMS AND ANALYSIS A Dissertation Presented to the Faculty of the Graduate School of Cornell University in Partial Fulfillment
ACADEMIC INTERGRITY POLICY
 Western Michigan University, Electrical and Computer Engineering Department ECE 4300/5300 Electric Power Systems (3-0), Spring 2016 Course Information and Policies CRN: 11647-100/14042-100 9:30-10:20 a.m.
Western Michigan University, Electrical and Computer Engineering Department ECE 4300/5300 Electric Power Systems (3-0), Spring 2016 Course Information and Policies CRN: 11647-100/14042-100 9:30-10:20 a.m.
EEL303: Power Engineering I - Tutorial 4
 1. Determine the voltage at the generating station and the efficiency of the following system (Figure 1): Both transformers have ratio of 2kV/11kV. The resistance on LV side of both Figure 1: transformers
1. Determine the voltage at the generating station and the efficiency of the following system (Figure 1): Both transformers have ratio of 2kV/11kV. The resistance on LV side of both Figure 1: transformers
The Importance of the X/R Ratio in Low-Voltage Short Circuit Studies
 The Importance of the X/R Ratio in Low-Voltage Short Circuit Studies DATE: November 17, 1999 REVISION: AUTHOR: John Merrell Introduction In some short circuit studies, the X/R ratio is ignored when comparing
The Importance of the X/R Ratio in Low-Voltage Short Circuit Studies DATE: November 17, 1999 REVISION: AUTHOR: John Merrell Introduction In some short circuit studies, the X/R ratio is ignored when comparing
N-1-1 Contingency Analysis using PowerWorld Simulator
 N-1-1 Contingency nalysis using PowerWorld Simulator uthor: PowerWorld Corporation Scott R. Dahman, P.E. Date: March 24, 2010 October 25, 2012 (revised) Table of Contents Background and Objective... 2
N-1-1 Contingency nalysis using PowerWorld Simulator uthor: PowerWorld Corporation Scott R. Dahman, P.E. Date: March 24, 2010 October 25, 2012 (revised) Table of Contents Background and Objective... 2
sin(θ) = opp hyp cos(θ) = adj hyp tan(θ) = opp adj
 Math, Trigonometr and Vectors Geometr 33º What is the angle equal to? a) α = 7 b) α = 57 c) α = 33 d) α = 90 e) α cannot be determined α Trig Definitions Here's a familiar image. To make predictive models
Math, Trigonometr and Vectors Geometr 33º What is the angle equal to? a) α = 7 b) α = 57 c) α = 33 d) α = 90 e) α cannot be determined α Trig Definitions Here's a familiar image. To make predictive models
= (0.400 A) (4.80 V) = 1.92 W = (0.400 A) (7.20 V) = 2.88 W
 Physics 2220 Module 06 Homework 0. What are the magnitude and direction of the current in the 8 Ω resister in the figure? Assume the current is moving clockwise. Then use Kirchhoff's second rule: 3.00
Physics 2220 Module 06 Homework 0. What are the magnitude and direction of the current in the 8 Ω resister in the figure? Assume the current is moving clockwise. Then use Kirchhoff's second rule: 3.00
Section 1.1. Introduction to R n
 The Calculus of Functions of Several Variables Section. Introduction to R n Calculus is the study of functional relationships and how related quantities change with each other. In your first exposure to
The Calculus of Functions of Several Variables Section. Introduction to R n Calculus is the study of functional relationships and how related quantities change with each other. In your first exposure to
Chapter 3 AUTOMATIC VOLTAGE CONTROL
 Chapter 3 AUTOMATIC VOLTAGE CONTROL . INTRODUCTION TO EXCITATION SYSTEM The basic function of an excitation system is to provide necessary direct current to the field winding of the synchronous generator.
Chapter 3 AUTOMATIC VOLTAGE CONTROL . INTRODUCTION TO EXCITATION SYSTEM The basic function of an excitation system is to provide necessary direct current to the field winding of the synchronous generator.
Load Flow Analysis on IEEE 30 bus System
 International Journal of Scientific and Research Publications, Volume 2, Issue 11, November 2012 1 Load Flow Analysis on IEEE 30 bus System Dharamjit *, D.K.Tanti ** * Department of Electrical Engineering,
International Journal of Scientific and Research Publications, Volume 2, Issue 11, November 2012 1 Load Flow Analysis on IEEE 30 bus System Dharamjit *, D.K.Tanti ** * Department of Electrical Engineering,
Impedance Matching and Matching Networks. Valentin Todorow, December, 2009
 Impedance Matching and Matching Networks Valentin Todorow, December, 2009 RF for Plasma Processing - Definition of RF What is RF? The IEEE Standard Dictionary of Electrical and Electronics Terms defines
Impedance Matching and Matching Networks Valentin Todorow, December, 2009 RF for Plasma Processing - Definition of RF What is RF? The IEEE Standard Dictionary of Electrical and Electronics Terms defines
G.A. Pavliotis. Department of Mathematics. Imperial College London
 EE1 MATHEMATICS NUMERICAL METHODS G.A. Pavliotis Department of Mathematics Imperial College London 1. Numerical solution of nonlinear equations (iterative processes). 2. Numerical evaluation of integrals.
EE1 MATHEMATICS NUMERICAL METHODS G.A. Pavliotis Department of Mathematics Imperial College London 1. Numerical solution of nonlinear equations (iterative processes). 2. Numerical evaluation of integrals.
1 Introduction. 2 The Symmetrical Component Transformation. J.L. Kirtley Jr.
 Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.06 Introduction to Power Systems Class Notes Chapter 4 Introduction To Symmetrical Components J.L. Kirtley
Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.06 Introduction to Power Systems Class Notes Chapter 4 Introduction To Symmetrical Components J.L. Kirtley
3. Solve the equation containing only one variable for that variable.
 Question : How do you solve a system of linear equations? There are two basic strategies for solving a system of two linear equations and two variables. In each strategy, one of the variables is eliminated
Question : How do you solve a system of linear equations? There are two basic strategies for solving a system of two linear equations and two variables. In each strategy, one of the variables is eliminated
Analysis of the Effect of Tap Changing Transformer on Performance of SVC
 Analysis of the Effect of Tap Changing Transformer on Performance of SVC Dipesh A. Patel 1, Nirav P. Patani 2, Prabhat Kumar 3 1 Senior Lecturer, Electrical Engineering Department, M.L.I.D.S. Bhandu, Gujarat.
Analysis of the Effect of Tap Changing Transformer on Performance of SVC Dipesh A. Patel 1, Nirav P. Patani 2, Prabhat Kumar 3 1 Senior Lecturer, Electrical Engineering Department, M.L.I.D.S. Bhandu, Gujarat.
Bill is the author of 15 papers and lectures on transmission lines and other power system topics.
 Transmission Lines Electricity s Highway This talk starts with an explanation of Surge Impedance Loading and demonstrates how it is used for transmission line work. The St. Clair Curve widely used in transmission
Transmission Lines Electricity s Highway This talk starts with an explanation of Surge Impedance Loading and demonstrates how it is used for transmission line work. The St. Clair Curve widely used in transmission
Power measurement in balanced 3 phase circuits and power factor improvement. 1 Power in Single Phase Circuits. Experiment no 1
 Experiment no 1 Power measurement in balanced 3 phase circuits and power factor improvement 1 Power in Single Phase Circuits Let v = m cos(ωt) = cos(ωt) is the voltage applied to a R-L circuit and i =
Experiment no 1 Power measurement in balanced 3 phase circuits and power factor improvement 1 Power in Single Phase Circuits Let v = m cos(ωt) = cos(ωt) is the voltage applied to a R-L circuit and i =
Nonlinear Systems of Ordinary Differential Equations
 Differential Equations Massoud Malek Nonlinear Systems of Ordinary Differential Equations Dynamical System. A dynamical system has a state determined by a collection of real numbers, or more generally
Differential Equations Massoud Malek Nonlinear Systems of Ordinary Differential Equations Dynamical System. A dynamical system has a state determined by a collection of real numbers, or more generally
Roots of Equations (Chapters 5 and 6)
 Roots of Equations (Chapters 5 and 6) Problem: given f() = 0, find. In general, f() can be any function. For some forms of f(), analytical solutions are available. However, for other functions, we have
Roots of Equations (Chapters 5 and 6) Problem: given f() = 0, find. In general, f() can be any function. For some forms of f(), analytical solutions are available. However, for other functions, we have
Agilent AN 154 S-Parameter Design Application Note
 Agilent AN 154 S-Parameter Design Application Note Introduction The need for new high-frequency, solid-state circuit design techniques has been recognized both by microwave engineers and circuit designers.
Agilent AN 154 S-Parameter Design Application Note Introduction The need for new high-frequency, solid-state circuit design techniques has been recognized both by microwave engineers and circuit designers.
Students Currently in Algebra 2 Maine East Math Placement Exam Review Problems
 Students Currently in Algebra Maine East Math Placement Eam Review Problems The actual placement eam has 100 questions 3 hours. The placement eam is free response students must solve questions and write
Students Currently in Algebra Maine East Math Placement Eam Review Problems The actual placement eam has 100 questions 3 hours. The placement eam is free response students must solve questions and write
Impedance Matching. Using transformers Using matching networks
 Impedance Matching The plasma industry uses process power over a wide range of frequencies: from DC to several gigahertz. A variety of methods are used to couple the process power into the plasma load,
Impedance Matching The plasma industry uses process power over a wide range of frequencies: from DC to several gigahertz. A variety of methods are used to couple the process power into the plasma load,
Nonlinear Iterative Partial Least Squares Method
 Numerical Methods for Determining Principal Component Analysis Abstract Factors Béchu, S., Richard-Plouet, M., Fernandez, V., Walton, J., and Fairley, N. (2016) Developments in numerical treatments for
Numerical Methods for Determining Principal Component Analysis Abstract Factors Béchu, S., Richard-Plouet, M., Fernandez, V., Walton, J., and Fairley, N. (2016) Developments in numerical treatments for
SECTION 7-4 Algebraic Vectors
 7-4 lgebraic Vectors 531 SECTIN 7-4 lgebraic Vectors From Geometric Vectors to lgebraic Vectors Vector ddition and Scalar Multiplication Unit Vectors lgebraic Properties Static Equilibrium Geometric vectors
7-4 lgebraic Vectors 531 SECTIN 7-4 lgebraic Vectors From Geometric Vectors to lgebraic Vectors Vector ddition and Scalar Multiplication Unit Vectors lgebraic Properties Static Equilibrium Geometric vectors
Introduction to the Smith Chart for the MSA Sam Wetterlin 10/12/09 Z +
 Introduction to the Smith Chart for the MSA Sam Wetterlin 10/12/09 Quick Review of Reflection Coefficient The Smith chart is a method of graphing reflection coefficients and impedance, and is often useful
Introduction to the Smith Chart for the MSA Sam Wetterlin 10/12/09 Quick Review of Reflection Coefficient The Smith chart is a method of graphing reflection coefficients and impedance, and is often useful
Math, Trigonometry and Vectors. Geometry. Trig Definitions. sin(θ) = opp hyp. cos(θ) = adj hyp. tan(θ) = opp adj. Here's a familiar image.
 Math, Trigonometr and Vectors Geometr Trig Definitions Here's a familiar image. To make predictive models of the phsical world, we'll need to make visualizations, which we can then turn into analtical
Math, Trigonometr and Vectors Geometr Trig Definitions Here's a familiar image. To make predictive models of the phsical world, we'll need to make visualizations, which we can then turn into analtical
ENERGY TRANSFER SYSTEMS AND THEIR DYNAMIC ANALYSIS
 ENERGY TRANSFER SYSTEMS AND THEIR DYNAMIC ANALYSIS Many mechanical energy systems are devoted to transfer of energy between two points: the source or prime mover (input) and the load (output). For chemical
ENERGY TRANSFER SYSTEMS AND THEIR DYNAMIC ANALYSIS Many mechanical energy systems are devoted to transfer of energy between two points: the source or prime mover (input) and the load (output). For chemical
SYNCHRONOUS MACHINES
 SYNCHRONOUS MACHINES The geometry of a synchronous machine is quite similar to that of the induction machine. The stator core and windings of a three-phase synchronous machine are practically identical
SYNCHRONOUS MACHINES The geometry of a synchronous machine is quite similar to that of the induction machine. The stator core and windings of a three-phase synchronous machine are practically identical
BALANCED THREE-PHASE CIRCUITS
 BALANCED THREE-PHASE CIRCUITS The voltages in the three-phase power system are produced by a synchronous generator (Chapter 6). In a balanced system, each of the three instantaneous voltages have equal
BALANCED THREE-PHASE CIRCUITS The voltages in the three-phase power system are produced by a synchronous generator (Chapter 6). In a balanced system, each of the three instantaneous voltages have equal
Multiplying and Dividing Algebraic Fractions
 . Multiplying and Dividing Algebraic Fractions. OBJECTIVES. Write the product of two algebraic fractions in simplest form. Write the quotient of two algebraic fractions in simplest form. Simplify a comple
. Multiplying and Dividing Algebraic Fractions. OBJECTIVES. Write the product of two algebraic fractions in simplest form. Write the quotient of two algebraic fractions in simplest form. Simplify a comple
Eigenvalues and Eigenvectors
 Chapter 6 Eigenvalues and Eigenvectors 6. Introduction to Eigenvalues Linear equations Ax D b come from steady state problems. Eigenvalues have their greatest importance in dynamic problems. The solution
Chapter 6 Eigenvalues and Eigenvectors 6. Introduction to Eigenvalues Linear equations Ax D b come from steady state problems. Eigenvalues have their greatest importance in dynamic problems. The solution
Agilent De-embedding and Embedding S-Parameter Networks Using a Vector Network Analyzer. Application Note 1364-1
 Agilent De-embedding and Embedding S-Parameter Networks Using a Vector Network Analyzer Application Note 1364-1 Introduction Traditionally RF and microwave components have been designed in packages with
Agilent De-embedding and Embedding S-Parameter Networks Using a Vector Network Analyzer Application Note 1364-1 Introduction Traditionally RF and microwave components have been designed in packages with
(Quasi-)Newton methods
 (Quasi-)Newton methods 1 Introduction 1.1 Newton method Newton method is a method to find the zeros of a differentiable non-linear function g, x such that g(x) = 0, where g : R n R n. Given a starting
(Quasi-)Newton methods 1 Introduction 1.1 Newton method Newton method is a method to find the zeros of a differentiable non-linear function g, x such that g(x) = 0, where g : R n R n. Given a starting
8 Speed control of Induction Machines
 8 Speed control of Induction Machines We have seen the speed torque characteristic of the machine. In the stable region of operation in the motoring mode, the curve is rather steep and goes from zero torque
8 Speed control of Induction Machines We have seen the speed torque characteristic of the machine. In the stable region of operation in the motoring mode, the curve is rather steep and goes from zero torque
The design and performance of Static Var Compensators for particle accelerators
 CERN-ACC-2015-0104 [email protected] The design and performance of Static Var Compensators for particle accelerators Karsten Kahle, Francisco R. Blánquez, Charles-Mathieu Genton CERN, Geneva, Switzerland,
CERN-ACC-2015-0104 [email protected] The design and performance of Static Var Compensators for particle accelerators Karsten Kahle, Francisco R. Blánquez, Charles-Mathieu Genton CERN, Geneva, Switzerland,
7.7 Solving Rational Equations
 Section 7.7 Solving Rational Equations 7 7.7 Solving Rational Equations When simplifying comple fractions in the previous section, we saw that multiplying both numerator and denominator by the appropriate
Section 7.7 Solving Rational Equations 7 7.7 Solving Rational Equations When simplifying comple fractions in the previous section, we saw that multiplying both numerator and denominator by the appropriate
Implicit Differentiation
 Revision Notes 2 Calculus 1270 Fall 2007 INSTRUCTOR: Peter Roper OFFICE: LCB 313 [EMAIL: [email protected]] Standard Disclaimer These notes are not a complete review of the course thus far, and some
Revision Notes 2 Calculus 1270 Fall 2007 INSTRUCTOR: Peter Roper OFFICE: LCB 313 [EMAIL: [email protected]] Standard Disclaimer These notes are not a complete review of the course thus far, and some
Two vectors are equal if they have the same length and direction. They do not
 Vectors define vectors Some physical quantities, such as temperature, length, and mass, can be specified by a single number called a scalar. Other physical quantities, such as force and velocity, must
Vectors define vectors Some physical quantities, such as temperature, length, and mass, can be specified by a single number called a scalar. Other physical quantities, such as force and velocity, must
6 J - vector electric current density (A/m2 )
 Determination of Antenna Radiation Fields Using Potential Functions Sources of Antenna Radiation Fields 6 J - vector electric current density (A/m2 ) M - vector magnetic current density (V/m 2 ) Some problems
Determination of Antenna Radiation Fields Using Potential Functions Sources of Antenna Radiation Fields 6 J - vector electric current density (A/m2 ) M - vector magnetic current density (V/m 2 ) Some problems
Fundamentals of Microelectronics
 Fundamentals of Microelectronics CH1 Why Microelectronics? CH2 Basic Physics of Semiconductors CH3 Diode Circuits CH4 Physics of Bipolar Transistors CH5 Bipolar Amplifiers CH6 Physics of MOS Transistors
Fundamentals of Microelectronics CH1 Why Microelectronics? CH2 Basic Physics of Semiconductors CH3 Diode Circuits CH4 Physics of Bipolar Transistors CH5 Bipolar Amplifiers CH6 Physics of MOS Transistors
