State-Variable Analysis
|
|
|
- Laureen Benson
- 7 years ago
- Views:
Transcription
1 C h a p t e r 19 State-Variable Analysis Specific goals and objectives of this chapter include: Introducing the concept of state variables and normal-form equations Learning how to write a complete set of normal-form equations for a given circuit Matrix-based solution of the circuit equations Development of a general technique applicable to higher-order problems 19.1 Introduction Up to this point, we have seen several different methods by which circuits might be analyzed. The resistive circuit came first, and for it we wrote a set of algebraic equations, often cast in the form of nodal or mesh equations. However, in Appendix 1 we learn that we can choose other, more convenient voltage or current variables after drawing an appropriate tree for the network. The tree sprouts up again in this chapter, in the selection of circuit variables. We next added inductors and capacitors to our networks, and this produced equations containing derivatives and integrals with respect to time. Except for simple first- and second-order systems that either were source-free or contained only dc sources, we did not attempt solving these equations. The results we obtained were found by time-domain methods. Subsequently, we explored the use of phasors to determine the sinusoidal steady-state response of such circuits, and a little later on we were introduced to the concept of complex frequency and the Laplace transform method. In this last chapter, we return to the time domain and introduce the use of state variables. Once again we will not obtain many explicit solutions for circuits of even moderate complexity, but we will write sets of equations compatible with numerical analysis techniques. 19-1
2 19-2 CHAPTER 19 State-Variable Analysis Figure 19.1 L v C1 v C2 A four-node RLC circuit. C 1 Here we are using a prime symbol to denote a derivative with respect to time. C 2 R i s 19.2 State Variables and Normal-Form Equations State-variable analysis, or state-space analysis, as it is sometimes called, is a procedure that can be applied both to linear and, with some modifications, to nonlinear circuits, as well as to circuits containing time-varying parameters, such as the capacitance C = 50 cos 20t pf. Our attention, however, will be restricted to time-invariant linear circuits. We introduce some of the ideas underlying state variables by looking at a general RLC circuit drawn in Fig When we write equations for this circuit, we could use nodal analysis, the two dependent variables being the node voltages at the central and right nodes. We could also opt for mesh analysis and use two currents as the variables, or, alternatively, we could draw a tree first and then select a set of tree-branch voltages or link currents as the dependent variables. It is possible that each approach could lead to a different number of variables, although two seems to be the most likely number for this circuit. The set of variables we will select in state-variable analysis is a hybrid set that may include both currents and voltages. They are the inductor currents and the capacitor voltages. Each of these quantities may be used directly to express the energy stored in the inductor or capacitor at any instant of time. That is, they collectively describe the energy state of the system, and for that reason, they are called the state variables. Let us try to write a set of equations for the circuit of Fig in terms of the state variables, v C1, and v C2,asdefined on the circuit diagram. The method we use will be outlined more formally in the following section, but for the present let us try to use KVL once for each inductor, and KCL once for each capacitor. Beginning with the inductor, we set the sum of voltages around the lower left mesh equal to zero: Li L v C2 = 0 [1] We presume that the source voltage and the source current i s are known, and we therefore have one equation in terms of our chosen state variables. Next, we consider the capacitor C 1. Since the left terminal of C 1 is also one terminal of a voltage source, it will become part of a supernode. Therefore, we select the right terminal of C 1 as the node to which we apply KCL. The current through the capacitor branch is C 1 v C1, the upward source current is i s, and the current in R is obtained by noting that the voltage across R, positive reference on the left, is (v C2 v C1 ) and, therefore, the current to the right in R is (v C2 v C1 )/R. Thus, C 1 v C1 1 R (v C2 v C1 ) i s = 0 [2] Again we have been able to write an equation without introducing any new variables, although we might not have been able to express the current through R directly in terms of the state variables if the circuit had been any more complicated.
3 SECTION 19.2 State Variables and Normal-Form Equations 19-3 Finally, we apply KCL to the upper terminal of C 2 : C 2 v C2 1 R (v C2 v C1 ) = 0 [3] Equations [1] to [3] are written solely in terms of the three state variables, the known element values, and the two known forcing functions. They are not, however, written in the standardized form which state-variable analysis demands. The state equations are said to be in normal form when the derivative of each state variable is expressed as a linear combination of all the state variables and forcing functions. The ordering of the equations defining the derivatives and the order in which the state variables appear in every equation must be the same. Let us arbitrarily select the order, v C1, v C2, and rewrite Eq. [1] as = 1 L v C2 1 L [4] Then Eq. [2] is rewritten as v C1 = 1 v C1 1 v C2 1 1 i s [5] RC 1 RC 1 RC 1 C 1 while Eq. [3] becomes v C2 = 1 C 2 1 RC 2 v C1 1 RC 2 v C2 1 RC 2 [6] Note that these equations define, in order, i L, v C1, and v C2, with a corresponding order of variables on the right sides,, v C1, and v C2. The forcing functions come last and may be written in any convenient order. As another example of the determination of a set of normal-form equations, we look at the circuit shown in Fig. 19.2a. Since the circuit has one capacitor and one inductor, we expect two state variables, the capacitor voltage and the inductor current. To facilitate writing the normal-form equations, let us construct a tree for this circuit which follows all the rules for tree construction discussed in Appendix 1 and in addition requires all capacitors to be located in the tree and all inductors in the cotree. This is usually possible and it leads to a normal tree. In those few exceptional cases where it is not possible to draw a normal tree, we use a slightly different method which will be considered at the end of Sec Here, we are able to place C in the tree and L and i s in the cotree, as shown in Fig. 19.2b. This is the only normal tree possible for this circuit. The source quantities and the state variables are indicated on the tree and cotree. Next, we determine the current in every link and the voltage across each tree branch in terms of the state variables. For a simple circuit such as this, it is possible to do so by beginning with any resistor for which either the current or the voltage is obvious. The results are shown on the tree in Fig. 19.2c. We may now write the normal-form equations by invoking KCL at the upper terminal of the capacitor: 0.4v C 0.2v C i s = 0 Figure F 5 i s 2 H v C v C v C 5 (a) (b) 7 (c) (a) An RLC circuit requiring two state variables. (b) A normal tree showing the state variables v C and. (c) The current in every link and the voltage across every tree branch is expressed in terms of the state variables. i s i s
4 19-4 CHAPTER 19 State-Variable Analysis or, in normal form, Around the outer loop, we have or v C = 0.5v C i s [7] 2i L v C 7 = 0 i L = 0.5v C 3.5 [8] Equations [7] and [8] are the desired normal-form equations. Their solution will yield all the information necessary for a complete analysis of the given circuit. Of course, explicit expressions for the state variables can be obtained only if a specific function is given for i s (t). For example, it will be shown later that if i s (t) = e 2t u(t) A [9] then and v C (t) = 35 (10e t 12e 2t 2e 3t )u(t) V [10] (t) = 5 (2e t 4e 2t 2e 3t )u(t) A [11] The solutions, however, are far from obvious, and we will develop the technique for obtaining them from the normal-form equations in Sec Practice Write a set of normal-form equations for the circuit shown in Fig Order the state variables as 1, 2, and v C. Figure H v C 0.1 F 2 = 2 cos 10t u(t) V 4 2 H Ans: i L1 = v C 0.2 ; i L2 = ; v C = Writing a Set of Normal-Form Equations In the two examples considered in the previous section, the methods whereby we obtained a set of normal-form equations may have seemed to be more of an art than a science. In order to bring a little order into our chaos, let s try to follow the procedure used when we were studying nodal analysis, mesh analysis, and the use of trees in general loop and general nodal analysis. We
5 SECTION 19.3 Writing a Set of Normal-Form Equations 19-5 seek a set of guidelines that will systematize the procedure. Then we will apply these rules to three new examples, each a little more involved than the preceding one. Here are the six steps that we have been following: 1. Establish a normal tree. Place capacitors and voltage sources in the tree, and inductors and current sources in the cotree; place control voltages in the tree and control currents in the cotree if possible. More than one normal tree may be possible. Certain types of networks do not permit any normal tree to be drawn; these exceptions are considered at the end of this section. 2. Assign voltage and current variables. Assign a voltage (with polarity reference) to every capacitor and a current (with arrow) to every inductor; these voltages and currents are the state variables. Indicate the voltage across every tree branch and the current through every link in terms of the source voltages, the source currents, and the state variables, if possible; otherwise, assign a new voltage or current variable to that resistive tree branch or link. 3. Write the C equations. Use KCL to write one equation for each capacitor. Set Cv C equal to the sum of link currents obtained by considering the node (or supernode) at either end of the capacitor. The supernode is identified as the set of all tree branches connected to that terminal of the capacitor. Do not introduce any new variables. 4. Write the L equations. Use KVL to write one equation for each inductor. Set Li L equal to the sum of tree-branch voltages obtained by considering the single closed path consisting of the link in which L lies and a convenient set of tree branches. Do not introduce any new variables. 5. Write the R equations (if necessary). If any new voltage variables were assigned to resistors in step 2, use KCL to set v R /R equal to a sum of link currents. If any new current variables were assigned to resistors in step 2, use KVL to set i R R equal to a sum of tree-branch voltages. Solve these resistor equations simultaneously to obtain explicit expressions for each v R and i R in terms of the state variables and source quantities. 6. Write the normal-form equations. Substitute the expressions for each v R and i R into the equations obtained in steps 3 and 4, thus eliminating all resistor variables. Put the resultant equations in normal form. Obtain the normal-form equations for the circuit of Fig. 19.4a, a four-node circuit containing two capacitors, one inductor, and two independent sources. Following step 1, we draw a normal tree. Note that only one such tree is possible here, as shown in Fig. 19.4b, since the two capacitors and the voltage source must be in the tree and the inductor and the current source must be in the cotree. We next define the voltage across the 1 6 -F capacitor as v C1, the voltage across the 1 7 -F capacitor as v C2, and the current through the inductor as. The source voltage EXAMPLE 19.1
6 19-6 CHAPTER 19 State-Variable Analysis Figure F 3 Ω 1 5 H (t) 1 6 F i s (t) (a) v C2 1 (v 3 C1 ) v C1 i s (b) (a) A given circuit for which normal-form equations are to be written. (b) Only one normal tree is possible. (c) Tree-branch voltages and link currents are assigned. (c) is indicated across its tree branch, the source current is marked on its link, and only the resistor link remains without an assigned variable. The current directed to the left through that link is the voltage v C1 divided by 3, and we thus find it unnecessary to introduce any additional variables. These tree-branch voltages and link currents are shown in Fig. 19.4c. Two equations must be written for step 3. For the 1 -F capacitor, we apply KCL to 6 the central node: v C (v C1 ) = 0 while the right-hand node is most convenient for the 1 -F capacitor: 7 v C2 7 i s = 0 Moving on to step 4, KVL is applied to the inductor link and the entire tree in this case: i L 5 v C2 v C1 = 0 Since there were no new variables assigned to the resistor, we skip step 5 and simply rearrange the three preceding equations to obtain the desired normal-form equations, v C1 = 2v C1 6 2 [12] v C2 = 7 7i s [13] i L = 5v C1 5v C2 5 [14]
7 SECTION 19.3 Writing a Set of Normal-Form Equations 19-7 The state variables have arbitrarily been ordered as v C1, v C2, and. If the order, v C1, v C2 had been selected instead, the three normal-form equations would be i L = 5v C1 5v C2 5 v C1 = 6 2v C1 2 v C2 = 7 7i s Note that the ordering of the terms on the right-hand sides of the equations has been changed to agree with the ordering of the equations. Write a set of normal-form equations for the circuit of Fig. 19.5a. EXAMPLE 19.2 Figure F 2 9 H i s 2 (a) v C v C i s v R i R v R v C 6 i s 2 (b) (c) (a) The given circuit. (b) One of many possible normal trees. (c) The assigned voltages and currents. The circuit contains several resistors, and this time it will be necessary to introduce resistor variables. Many different normal trees can be constructed for this network, and it is often worthwhile to sketch several possible trees to see whether resistor voltage and current variables can be avoided by a judicious selection. The tree we shall use is shown in Fig. 19.5b. The state variables v C and and the forcing functions and i s are indicated on the graph. Although we might study this circuit and the tree for a few minutes and arrive at a method to avoid the introduction of any new variables, let us plead temporary stupidity and assign the tree-branch voltage v R and link current i R for the 1- and 3- branches, respectively. The voltage across the 2- resistor is easily expressed as 2, while the downward current through the 6- resistor becomes (v R v C )/6. All the link currents and tree-branch voltages are marked on Fig. 19.5c. The capacitor equation may now be written v C 9 = i R i s v R v C 6 [15]
8 19-8 CHAPTER 19 State-Variable Analysis and that for the inductor is 2 9 i L = v C v R 2 [16] We begin step 5 with the 1- resistor. Since it is in the tree, we must equate its current to a sum of link currents. Both terminals of the capacitor collapse into a supernode, and we have v R 1 = i s i R v R v C 6 The 3- resistor is next, and its voltage may be written as 3i R = v C v R These last two equations must now be solved simultaneously for v R and i R in terms of, v C, and the two forcing functions. Doing so, we find that v R = v C i s 2 9 i R = 2 9 v C i s 7 27 Finally, these results are substituted in Eqs. [15] and [16], and the normal-form equations for Fig are obtained: v C = 3v C 6 2 6i s [17] i L = 3v C 12 3i s [18] Up to now we have discussed only those circuits in which the voltage and current sources were independent sources. At this time we will look at a circuit containing a dependent source. EXAMPLE 19.3 Find the set of normal-form equations for the circuit of Fig The only possible normal tree is that shown in Fig. 19.6b, and it might be noted that it was not possible to place the controlling current i x in a link. The tree-branch voltages and link currents are shown on the linear graph, and they are unchanged from the earlier example except for the additional source voltage, 18i x. For the 1 -F capacitor, we again find that 6 v C (v C1 ) = 0 [19] Letting the dependent voltage source shrink into a supernode, we also find the relationship unchanged for the 1 -F capacitor, 7 v C2 7 i s = 0 [20] Our previous result for the inductor changes, however, because there is an added branch in the tree: i L 5 18i x v C2 v C1 = 0
9 SECTION 19.3 Writing a Set of Normal-Form Equations 19-9 Figure F 3 18i x v C2 18i x 1 (v C1 ) i 3 L 1 6 F i x 1 5 H i s v C1 i s (a) (b) (a) A circuit containing a dependent voltage source. (b) The normal tree for this circuit with tree-branch voltages and link currents assigned. Finally, we must write a control equation that expresses i x in terms of our tree-branch voltages and link currents. It is and thus the inductor equation becomes i x = v C1 3 i L v C1 6 v C2 v C1 = 0 [21] When Eqs. [19] to [21] are written in normal form, we have v C1 = 2v C1 6 2 [22] v C2 = 7 7i s [23] i L = 35v C1 5v C [24] Our equation-writing process must be modified slightly if we cannot construct a normal tree for the circuit, and there are two types of networks for which this occurs. One contains a loop in which every element is a capacitor or voltage source, thus making it impossible to place them all in the tree. The other occurs if there is a node or supernode that is connected to the remainder of the circuit only by inductors and current sources. When either of these events occurs, we meet the challenge by leaving a capacitor out of the tree in one case and omitting an inductor from the cotree in the other. We then are faced with a capacitor in a link for which we must specify a current, or an inductor, in the tree which requires a voltage. The capacitor current may be expressed as the capacitance times the time derivative of the voltage across it, as defined by a sequence of treebranch voltages; and the inductor voltage is given by the inductance times the derivative of the current entering or leaving the node or supernode at either terminal of the inductor. Remember, a tree, by definition, contains no closed paths (loops), and every node must have at least one tree branch connected to it.
10 19-10 CHAPTER 19 State-Variable Analysis EXAMPLE 19.4 Write a set of normal-form equations for the network shown in Fig. 19.7a. Figure 19.7 i H 0.3 H 2t 2 u(t) V 3e t 2 A 4 2t 2 u(t) 3e t 2 (a) (a) A circuit for which a normal tree cannot be drawn. (b) A tree is constructed in which one inductor must be a tree branch. (b) The only elements connected to the upper central node are the two inductors and the current source, and we therefore must place one inductor in the tree, as illustrated by Fig. 19.7b. The two forcing functions and the single state variable, the current i 1, are shown on the graph. Note that the current in the upper right-hand inductor is known in terms of i 1 and 3e t2 A. Thus we could not specify the energy states of the two inductors independently of each other, and this system requires only the single state variable i 1. Of course, if we had placed the 0.1-H inductor in the tree (instead of the 0.3-H inductor), the current in the right-hand inductor would have ended up as the single state variable. We must still assign voltages to the remaining two tree branches in Fig. 19.7b. Since the current directed to the right in the 0.3-H inductor is i 1 3e t2, the voltages appearing across the inductor and the 4- resistor are 0.3 d(i 1 3e t2 )/dt = 0.3i 1 1.8te t2 and 4i 1 12e t2, respectively. The single normal-form equation is obtained in step 4 of our procedure: or 0.1i 1 0.3i 1 1.8te t2 4i 1 12e t2 2t 2 u(t) = 0 i 1 = 10i 1 e t2 (4.5t 30) 5t 2 u(t) [25] Note that one of the terms on the right-hand side of the equation is proportional to the derivative of one of the source functions. Figure H 2t 2 u(t) V 0.3 H 3e t 2 A The circuit of Fig. 19.7a is redrawn in such a way as to cause the supernode containing the voltage source to be connected to the remainder of the network only through the two inductors and the current source. 4 Ω In this example, the two inductors and the current source were all connected to a common node. With circuits containing more branches and more nodes, the connection may be to a supernode. As an indication of such a network, Fig shows a slight rearrangement of two elements appearing in Fig. 19.7a. Note that, once again, the energy states of the two inductors cannot be specified independently; with one specified, and the source current given, the other is then specified also. The method of obtaining the normal-form equation is the same. The exception created by a loop of capacitors and voltage sources is treated by a similar (dual) procedure, and the wary student should have only the most minor troubles.
11 SECTION 19.4 The Use of Matrix Notation Write normal-form equations for the circuit of Fig. 19.9a. Figure 19.9 Practice cos 2t u(t)v 20 1 mh 50 5 mh 1 mf mf v 1 v 2 10 v 5 5 mf 5 (a) (b) Write the normal-form equations for the circuit of Fig. 19.9b using the statevariable order v 1, v 2, v Find the normal-form equation for the circuit shown in Fig using the state variable: (a) v C1 ; (b) v C2. Figure F Ans: 19.2: i 1 = 20,000i 1 20,000i cos 2t u(t); i 5 = 4000i 1 14,000i cos 2t u(t) [using i 1 and i 5 ]. 19.3: v 1 = 160v 1 100v 2 60v ; v 2 = 50v 1 125v 2 75v 5 75 ; v 5 = 12v 1 30v 2 42v : v C1 = 6.67v C ; v C2 = 6.67v C v C1 5 k v C2 10 F 19.4 The Use of Matrix Notation In the examples that we studied in the previous two sections, the state variables selected were the capacitor voltages and the inductor currents, except for the final case, where it was not possible to draw a normal tree and only one inductor current could be selected as a state variable. As the number of inductors and capacitors in a network increases, it is apparent that the number of state variables will increase. More complicated circuits thus require a greater number of state equations, each of which contains a greater array of state variables on the right-hand side. Not only does the solution of such a set of equations require computer assistance, 1 but also the sheer effort of writing down all the equations can easily lead to writer s cramp. In this section we will establish a useful symbolic notation that minimizes the equation-writing effort. Let us introduce this method by recalling the normal-form equations that we obtained for the circuit of Fig. 19.6, which contained two independent sources, and i s. The results were given as Eqs. [22] to [24] of Sec. 19.3: v C1 = 2v C1 6 2 v C2 = 7 7i s i L = 35v C1 5v C [22] [23] [24] 1 Although SPICE can be used to analyze any of the circuits we meet in this chapter, other computer programs are used specifically to solve normal-form equations.
12 19-12 CHAPTER 19 State-Variable Analysis Two of our state variables are voltages, one is a current, one source function is a voltage, one is a current, and the units associated with the constants on the right-hand sides of these equations have the dimensions of ohms, or siemens, or they are dimensionless. To avoid notational problems in a more generalized treatment, we will use the letter q to denote a state variable, a to indicate a constant multiplier of q, and f to represent the entire forcing function appearing on the right-hand side of an equation. Thus, Eqs. [22] to [24] become q 1 = a 11q 1 a 12 q 2 a 13 q 3 f 1 [26] q 2 = a 21q 1 a 22 q 2 a 23 q 3 f 2 [27] q 3 = a 31q 1 a 32 q 2 a 33 q 3 f 3 [28] where For a review of matrices and matrix notation refer to Appendix 2. q 1 = v C1 a 11 = 2 a 12 = 0 a 13 = 6 f 1 = 2 q 2 = v C2 a 21 = 0 a 22 = 0 a 23 = 7 f 2 = 7i s q 3 = a 31 = 35 a 32 = 5 a 33 = 90 f 3 = 35 We now turn to the use of matrices and linear algebra to simplify our equations and further generalize the methods. We first define a matrix q which we call the state vector: q 1 (t) q 2 (t) q(t) =. q n (t) [29] The derivative of a matrix is obtained by taking the derivative of each element of the matrix. Thus, q 1 (t) q q (t) = 2 (t). q n (t) We shall represent all matrices and vectors in this chapter by lowercase boldface letters, such as q or q(t), with the single exception of the identity matrix I,tobedefined in Sec The elements of any matrix are scalars, and they are symbolized by lowercase italic letters, such as q 1 or q 1 (t). We also define the set of forcing functions, f 1, f 2,...,f n, as a matrix f and call it the forcing-function matrix: f(t) = f 1 (t) f 2 (t). f n (t) [30] Now let us turn our attention to the coefficients a ij, which represent elements in the (n n) square matrix a, a 11 a 12 a 1n a = a 21 a 22 a 2n [31] a n1 a n2 a nn The matrix a is termed the system matrix.
13 SECTION 19.4 The Use of Matrix Notation Using the matrices we have defined in the preceding paragraphs, we can combine these results to obtain a concise, compact representation of the state equations, q = aq f [32] The matrices q and f, and the matrix product aq, are all (n 1) column matrices. The advantages of this representation are obvious, because a system of 100 equations in 100 state variables has exactly the same form as one equation in one state variable. For the example of Eqs. [22] to [24], the four matrices in Eq. [32] may be written out explicitly as v C1 v C2 i L = v C1 v C2 2 7i s 35 [33] Everyone except full-blooded matrix experts should take a few minutes off to expand Eq. [33] and then check the results with Eqs. [22] to [24]; three identical equations should result. What now is our status with respect to state-variable analysis? Given a circuit, we should be able to construct a normal tree, specify a set of state variables, order them as the state vector, write a set of normal-form equations, and finally specify the system matrix and the forcing-function vector from the equations. The next problem facing us is to obtain the explicit functions of time that the state variables represent. [ ] (a) Using the state vector q = iv, determine the system matrix and the forcing-function [ ] vector for the circuit of Fig (b) Repeat for the state v vector q =. i Practice Figure v 0.1 F 20u(t) V 0.5 H 10 3u(t) A i [ Ans: ] [, 43.3u(t) 8.33u(t) ] [ ; ] [ 8.33u(t), 43.3u(t) ]
14 19-14 CHAPTER 19 State-Variable Analysis 19.5 Solution of the First-Order Equation The matrix equation representing the set of normal-form equations for a general nth-order system was obtained as Eq. [32] in the previous section, and it is repeated here for convenience as Eq. [34]: q = aq f [34] The (n n) system matrix a is composed of constant elements for our timeinvariant circuits, and q, q, and f are all (n 1) column matrices. We need to solve this matrix equation for q, whose elements are q 1, q 2,...,q n. Each must be found as a function of time. Remember that these are the state variables, the collection of which enables us to specify every voltage and current in the given circuit. Probably the simplest way of approaching this problem is to recall the method by which we solved the corresponding first-order (scalar) equation back in Sec We will quickly repeat that process, but, as we do so, we should keep in mind the fact that we are next going to extend the procedure to a matrix equation. If each matrix in Eq. [34] has only one row and one column, then we may write the matrix equation as [q 1 (t)] =[a 11][q 1 (t)][f 1 (t)] =[a 11 q 1 (t)][f 1 (t)] =[a 11 q 1 (t) f 1 (t)] and therefore, we have the first-order equation q 1 (t) = a 11q 1 (t) f 1 (t) [35] or q 1 (t) a 11q 1 (t) = f 1 (t) [36] Equation [36] has the same form as Eq. [12] of Sec. 8.8, and we therefore proceed with a similar method of solution by multiplying each side of the equation by the integrating factor e ta 11 : e ta 11 q 1 (t) e ta 11 q 1 (t) = e ta 11 f 1 (t) The left-hand side of this equation is again an exact derivative, and so we have d dt [e ta 11 q 1 (t)] =e ta 11 f 1 (t) [37] The order in which the various factors in Eq. [37] have been written may seem a little strange, because a term which is the product of a constant and a time function is usually written with the constant appearing first and the time function following it. In scalar equations, multiplication is commutative, and so the order in which the factors appear is of no consequence. But in the matrix equations which we will be considering next, the corresponding
15 SECTION 19.5 Solution of the First-Order Equation factors will be matrices, and matrix multiplication is not commutative. That is, we know that [ ][ ] [ ] 2 4 a b (2a 4c) (2b 4d) = 6 8 c d (6a 8c) (6b 8d) while [ a b c d ][ ] [ ] (2a 6b) (4a 8b) = (2c 6d) (4c 8d) Different results are obtained, and we therefore need to be careful later about the order in which we write matrix factors. Continuing with Eq. [37], let us integrate each side with respect to time from to a general time t: e ta 11 q 1 (t) = t e za 11 f 1 (z) dz [38] where z is simply a dummy variable of integration, and where we have assumed that e ta 11 q 1 (t) approaches zero as t approaches. We now multiply (premultiply, if this were a matrix equation) each side of Eq. [38] by the exponential factor e ta 11, obtaining q 1 (t) = e ta 11 t e za 11 f 1 (z) dz [39] which is the desired expression for the single unknown state variable. In many circuits, however, particularly those in which switches are present and the circuit is reconfigured at some instant of time (often t = 0), we do not know the forcing function or the normal-form equation prior to that instant. We therefore incorporate all of the past history in an integral from to that instant, here assumed to be t = 0, by letting t = 0 in Eq. [39]: q 1 (0) = 0 e za 11 f 1 (z) dz We then use this initial value in the general solution for q 1 (t): q 1 (t) = e ta 11 q 1 (0) e ta 11 t 0 e za 11 f 1 (z) dz [40] This last expression shows that the state-variable time function may be interpreted as the sum of two terms. The first is the response that would arise if the forcing function were zero [f 1 (t) = 0], and in the language of statevariable analysis it is called the zero-input response. It has the form of the natural response, although it may not have the same amplitude as the term we have been calling the natural response. The zero-input response also is the solution to the homogeneous normal-form equation, obtained by letting f 1 (t) = 0 in Eq. [36]. The second part of the solution would represent the complete response if q 1 (0) were zero, and it is termed the zero-state response. We will see in a following example that what we have termed the forced response appears as a part of the zero-state response.
16 19-16 CHAPTER 19 State-Variable Analysis EXAMPLE 19.5 Find v C (t) for the circuit of Fig Figure cos 10t u(t) V v 0.1 F C A first-order circuit for which v C (t) is to be found through the methods of state-variable analysis. The normal-form equation is easily found to be v C = 5v C 250 cos 10t u(t) Thus, a 11 = 5, f 1 (t) = 250 cos 10t ut(t), and we may substitute directly in Eq. [39] to obtain the solution: t v C (t) = e 5t e 5z 250 cos 10z u(z) dz The unit-step function inside the integral may be replaced by u(t) outside the integral if the lower limit is changed to zero: Integrating, we have v C (t) = e 5t u(t) t 0 e 5z 250 cos 10zdz or [ ] 250e v C (t) = e 5t 5z t u(t) (5 cos 10z 10 sin 10z) v C (t) =[ 10e 5t 10(cos 10t 2 sin 10t)]u(t) [41] The same result may be obtained through the use of Eq. [40]. Since v C (0) = 0, we have t v C (t) = e 5t (0) e 5t e 5z 250 cos 10z u(z) dz t = e 5t u(t) e 5z 250 cos 10zdz 0 and this leads to the same solution as before, of course. However, we also see that the entire solution for v C (t) is the zero-state response, and there is no zero-input response. It is interesting to note that, if we had solved this problem by the methods of Chap. 8, we would have set up a natural response, 0 v C,n (t) = Ae 5t and computed the forced response by frequency-domain methods, V C,f = 50 ( j1) = 10 j20 2 j1
17 SECTION 19.5 Solution of the First-Order Equation so that v C,f (t) = 10 cos 10t 20 sin 10t Thus, v C (t) = Ae 5t 10(cos 10t 2 sin 10t) (t > 0) and the application of the initial condition, v C (0) = 0, leads to A = 10 and an expression identical to Eq. [41] once again. Looking at the partial responses obtained in the two methods, we therefore find that v C,zero input = 0 v C,zero state =[ 10e 5t 10(cos 10t 2 sin 10t)]u(t) v C,n = 10e 5t u(t) v C,f = 10(cos 10t 2 sin 10t)u(t) The switch in the circuit of Fig is thrown at t = 0, and the form of the circuit changes at that instant. Find (t) for t>0. EXAMPLE 19.6 Figure t = 0 12 V 0.5 H 60 V A first-order example in which the form of the circuit changes at t = 0. We represent everything before t = 0 by the statement that (0) = 4 A, and we obtain the normal-form equation for the circuit in the configuration it has after t = 0. It is i L (t) = 4(t) 24 This time, we must use Eq. [40], since we do not have a single normal-form equation that is valid for all time. The result is t (t) = e 4t (4) e 4t e 4z ( 24)dz or (t) = 4e 4t 6(1 e 4t ) (t > 0) The several components of the response are now identified:, zero-input = 4e 4t (t > 0), zero-state = 6(1 e 4t ) (t > 0) while our earlier analytical methods would have led to,n = 10e 4t (t > 0),f = 6 (t > 0) 0
18 19-18 CHAPTER 19 State-Variable Analysis These first-order networks certainly do not require the use of state variables for their analyses. However, the method by which we solved the single normal-form equation does offer a few clues to how the nth-order solution might be obtained. We follow this exciting trail in the next section. Practice (a) Write the normal-form equation for the circuit of Fig Find v C (t) for t>0by(b) Eq. [39]; (c) Eq. [40]. Figure v C 5u(t) A mf 15 2 A Ans: v C = 4v C u(t); 20 50e 4t V; 20 50e 4t V The Solution of the Matrix Equation The general matrix equation for the nth-order system that we now wish to solve is given as Eq. [34] in Sec. 19.4, q = aq f [34] where a is an (n n) square matrix of constants and the other three matrices are all (n 1) column matrices whose elements are, in general, time functions. In the most general case, all the matrices would be composed of time functions. In this section we obtain the matrix solution for this equation. In the following section we will interpret our results and indicate how we might obtain a useful solution for q. We begin by subtracting the matrix product aq from each side of Eq. [34]: q aq = f [42] Recalling our case of the integrating factor e ta 11 in the first-order case, let us premultiply each side of Eq. [42] by e ta : e ta q e ta aq = e ta f [43]
19 SECTION 19.6 The Solution of the Matrix Equation Although the presence of a matrix as an exponent may seem to be somewhat strange, the function e ta may be defined in terms of its infinite power series expansion in t, e ta = I ta t 2 2! (a)2 t 3 3! (a)3 [44] We identify I as the (n n) identity matrix, I = such that Ia = ai = a The products (a) 2, (a) 3, and so forth in Eq. [44] may be obtained by repeated multiplication of the matrix a by itself, and therefore each term in the expansion is again an (n n) matrix. Thus, it is apparent that e ta is also an (n n) square matrix, but its elements are all functions of time in general. Again following the first-order procedure, we would now like to show that the left-hand side of Eq. [43] is equal to the time derivative of e ta q. Since this is a product of two functions of time, we have d dt (e ta q) = e ta d [ ] d dt (q) dt (e ta ) q The derivative of e ta is obtained by again considering the infinite series of Eq. [44], and we find that it is given by ae ta. The series expansion can also be used to show that ae ta = e ta a. Thus d dt (e ta q) = e ta q e ta aq and Eq. [43] helps to simplify this expression into the form d dt (e ta q) = e ta f Multiplying by dt and integrating from to t,wehave e ta q = t e za f(z) dz [45] To solve for q, we must premultiply the left-hand side of Eq. [45] by the matrix inverse of e ta. That is, any square matrix b has an inverse b 1 such that b 1 b = bb 1 = I. In this case, another power series expansion shows that the inverse of e ta is e ta,or e ta e ta q = Iq = q and we may therefore write our solution as t q = e ta e za f(z) dz [46]
20 19-20 CHAPTER 19 State-Variable Analysis In terms of the initial value of the state vector, t q = e ta q(0) e ta e za f(z) dz [47] The function e ta is a very important quantity in state-space analysis. It is called the state-transition matrix, for it describes how the state of the system changes from its zero state to its state at time t. Equations [46] and [47] are the nth-order matrix equations that correspond to the first-order results we numbered [39] and [40]. Although these expressions represent the solutions for q, the fact that we express e ta and e ta only as infinite series is a serious deterrent to our making any effective use of these results. We would have infinite power series in t for each q i (t), and while a computer might find this procedure compatible with its memory and computational speed, we would probably have other, more pressing chores to handle than carrying out the summation by ourselves. 0 Practice [ Let a = ] and t = 0.1 s. Use the power series expansion to find the (a) matrix e ta ; (b) matrix e ta ; (c) value of the determinant of e ta ; (d) value of the determinant of e ta ; (e) product of the last two results. [ Ans: ] [ ; ] ; ; ; A Further Look at the State-Transition Matrix In this section we seek a more satisfactory representation for e ta and e ta.if the system matrix a is an (n n) square matrix, then each of these exponentials is an (n n) square matrix of time functions, and one of the consequences of a theorem developed in linear algebra, known as the Cayley-Hamilton theorem, shows that such a matrix may be expressed as an (n 1)st-degree polynomial in the matrix a. That is, e ta = u 0 I u 1 a u 2 (a) 2 u n 1 (a) n 1 [48] where each of the u i is a scalar function of time that is still to be determined; the a i are constant (n n) matrices. The theorem also states that Eq. [48] remains an equality if I is replaced by unity and a is replaced by any one of the scalar roots s i of the nth-degree scalar equation, det(a si) = 0 [49] The expression det(a si) indicates the determinant of the matrix (a si). This determinant is an nth-degree polynomial in s. We assume that the n roots are all different. Equation [49] is called the characteristic equation of the matrix a, and the values of s which are the roots of the equation are known as the eigenvalues of a. These values of s are identical with the natural frequencies that we dealt with in Chap. 15 as poles of an appropriate transfer function. That is, if our
21 SECTION 19.7 A Further Look at the State-Transition Matrix state variable is v C1 (t), then the poles of H(s) = V C1 (s)/i s or of V C1 (s)/v s are also the eigenvalues of the characteristic equation. Thus, this is the procedure we shall follow to obtain a simpler form for e ta : 1. Given a, form the matrix (a si). 2. Set the determinant of this square matrix equal to zero. 3. Solve the resultant nth-degree polynomial for its n roots, s 1, s 2,...,s n. 4. Write the n scalar equations of the form e ts i = u 0 u 1 s i u n 1 s n 1 i [50] 5. Solve for the n time functions u 0, u 1,...,u n Substitute these time functions in Eq. [48] to obtain the (n n) matrix e ta. To illustrate this procedure, let us use the system matrix that corresponds to Eqs. [7] and [8] of Sec and to the circuit shown in Fig. 19.2a. [ ] a = Therefore, [ ] [ ] (a si) = s [ ] ( 0.5 s) 2.5 = 0.5 ( 3.5 s) and the expansion of the corresponding (2 2) determinant gives [ ] ( 0.5 s) 2.5 ( 0.5 s) 2.5 det = 0.5 ( 3.5 s) 0.5 ( 3.5 s) so that det(a si) = s 2 4s 3 = ( 0.5 s)( 3.5 s) 1.25 The roots of this polynomial are s 1 = 1 and s 2 = 3, and we substitute each of these values in Eq. [50], obtaining the two equations Subtracting, we find that and, therefore, e t = u 0 u 1 and e 3t = u 0 3u 1 u 1 = 0.5e t 0.5e 3t u 0 = 1.5e t 0.5e 3t Note that each u i has the general form of the natural response.
22 19-22 CHAPTER 19 State-Variable Analysis When these two functions are installed in Eq. [48], so that [ ] e ta = (1.5e t 0.5e 3t )I (0.5e t 0.5e 3t ) we may carry out the indicated operations to find [ (1.25e t 0.25e 3t ) ( 1.25e t 1.25e 3t ) e ta = (0.25e t 0.25e 3t ) ( 0.25e t 1.25e 3t ) ] [51] Having e ta, we form e ta by replacing each t in Eq. [51] by t. To complete this example, we may identify q and f from Eqs. [7], [8], and [9]: [ ] vc q = f = [ 30 8e 2t u(t) 0 ] [52] Since part of the forcing-function vector is present for t < 0, we may as well use Eq. [46] to solve for the state vector: q = e ta t e za f(z) dz [46] The matrix product e za f(z) is next formed by replacing t by z in Eq. [51] and then postmultiplying by Eq. [52] with z replacing t. With only moderate labor, we find that [ ] 37.5e z e za 7.5e 3z (10e z 2e z )u(z) f = 7.5e z 7.5e 3z (2e z 2e z )u(z) Integrating the first two terms of each element from to t and the last two terms from 0 to t, wehave [ ] t 35.5e t e za 2.5e 3t 10e t 12 f dz = 5.5e t 2.5e 3t 2e t (t > 0) 4 Finally, we must premultiply this matrix by Eq. [51] and this matrix multiplication involves a large number of scalar multiplications and algebraic additions of like time functions. The result is the desired state vector [ ] 35 10e t 12e 2t 2e 3t q = 5 2e t 4e 2t 2e 3t (t > 0) These are the expressions that were given offhandedly in Eqs. [10] and [11] at the end of Sec We now have a general technique that we could apply to higher-order problems. Such a procedure is theoretically possible, but the labor involved soon becomes monumental. Instead, we utilize computer programs that work directly from the normal-form equations and the initial values of the state
23 SECTION 19.8 Summary and Review variables. Knowing q(0), we compute f(0) and solve the equations for q (0). Then q( t) may be approximated from the initial value and its derivative: q( t) =. q(0)q (0) t. With this value for q( t), the normal-form equations are used to determine a value for q ( t), and the process moves along by time increments of t. Smaller values for t lead to greater accuracy for q(t) at any time t>0, but with attendant penalties in computational time and computer storage requirements. We accomplished several things in this chapter. First, and perhaps most important, we have learned some of the terms and ideas of this branch of system analysis, and this should make future study of this field more meaningful and pleasurable. Another accomplishment is the general solution for the first-order case in matrix form. We have also obtained the matrix solution for the general case. This introduction to the use of matrices in circuit and system analysis is a tool which becomes increasingly necessary in more advanced work in these areas. Finally, we have indicated how a numerical solution might be obtained using numerical methods, hopefully by a digital computer Given q = [ vc ] [ 0 27, a = ] [ 243u(t), f = 40u(t) ] [ 150, and q(0) = 5 use a t of s and calculate: (a) v C (0.001); (b) (0.001); (c) v C (0.001); (d) i L (0.001); (e) v C(0.002); (f ) (0.002). ], Practice Ans: V; 5.04 A; V/s; A/s; V; A Summary and Review The term state variable in circuit analysis refers to either an inductor current or a capacitor voltage, as they can be used to describe the energy state of a system (i.e., a circuit). The six steps for constructing a set of equations for state-variable analysis are: 1. Establish a normal tree. 2. Assign voltage and current variables. 3. Write the C equations. 4. Write the L equations. 5. Write the R equations (if necessary). 6. Write the normal-form equations. The state vector is a matrix which contains the state variables q i. The forcing-function matrix is a matrix which contains the set of forcing functions f i. The system matrix a contains the coefficients a ij of the state equations.
24 19-24 CHAPTER 19 State-Variable Analysis If we write the first-order matrix equation representation of the set of normal-form state variable equations as q = aq f, the single unknown state variable q 1 (t) is given as the sum of the zero-input response e ta 11 q 1 (0) and the zero-state response e ta 11 t 0 e za 11 f 1 (z) dz. The general solution to the matrix equation, expressed in terms of the state-transition matrix e ta,isq = e ta t e za f(z) dz. Exercises 19.2 State Variables and Normal-Form Equations 1. Using the order i 1, i 2, i 3, write the following equations as a set of normal-form equations: 2i 1 6i 3 = 52 cos 10t 3i 12i 2,4i 2 = 0.05i i i 3, i 2 = 2i 1 5i t 0 (i 1 i 3 )dt Given the two linear differential equations x y = x y 1 and x 2y = 2x y 1: (a) write the two normal-form equations, using the order x, y; (b) obtain a single differential equation involving only x(t) and its derivatives. (c) If x(0) = 2 and y(0) = 5, find x (0), x (0), and x (0). 3. Write the following equations in normal form, using the order x, y, z: x 2y 3z = f 1 (t), 2x 5z = 3, z 2y x = If x = 2x 3y 4 and y = 5x 6y 7, let x(0) = 2 and y(0) = 1 3, and find: (a) x (0); (b) y (0); (c) y (0) Writing a Set of Normal-Form Equations 5. If = 100 cos 120πt V, write a set of normal-form equations for the circuit shown in Fig Use and v C as the state variables. Figure v x 0.2 H 60 5 F v C 0.04v x 6. (a) Draw a normal tree for the circuit of Fig and assign the necessary state variables (for uniformity, put references at the top or left side of an element, and direct arrows down or to the right). (b) Specify every link current and tree-branch voltage in terms of the sources, element values, and state variables. (c) Write the normal-form equations using the order, v x, v 2F. Figure v x 3 F 5 H 4 8u(t) V 2 F 2v x 6
25 Exercises Write a set of normal-form equations for each circuit shown in Fig Use the state-variable order given below the circuit. Figure i s 50 i A 0.2 mf v C 2 mh 15 3i A F v F v F v 3, v C (a) v 1, v 2, v 3 (b) 8. A resistor is placed in series with the 0.2-mF capacitor in the circuit of Fig a. Using one current and one voltage, in that order, write a set of normal-form equations for this circuit. 9. (a) Write normal-form equations in the state variables v 1, v 2, i 1, and i 2 for Fig (b) Repeat if the current source is replaced with a 3- resistor. Figure i H 0.1 F 0.2 F v 1 v Write a set of normal-form equations in the order, v C for each circuit shown in Fig i s 0.05 H i 2 Figure F v C 2 Ω 0.5 H i s 20 Ω 0.2 H v C 0.2 F 5 Ω (a) (b) 11. Write a set of normal-form equations for the circuit shown in Fig Use the variable order v, i. Figure Figure F 0.1 F 0.05 F v i i x i s 20 Ω 0.2 H 5 Ω 5 Ω 20 Ω 4i x 12. If = 5 sin 2t u(t) V, write a set of normal-form equations for the circuit of Fig
26 19-26 CHAPTER 19 State-Variable Analysis Figure The Use of Matrix Notation 13. (a) Given q = 1 2 v C, a = , and f = 2t 3t 2 1 t, write [ ] [ ] il 0 6 out the three normal-form equations. (b) If q =, a =, and v C 4 0 [ ] 1 f =, show the state variables and the elements (with their values) on the 0 skeleton circuit diagram of Fig Replace the capacitors in the circuit of Fig b by 0.1-H, 0.2-H, and 0.5-H inductors and find a and f if 1, 2, and 3 are the state variables Given the state vector q =, let the system matrix a =, v C1 v C2 and the forcing function vector f = circuit appear in the vector w = v o1 v o2 i R1 i R Other voltages and currents in the, and they are related to the state vector by w = bq d, where b = and d = 2 2. Write out the set of equations giving v o1, v o2, i R1, and i R2 as functions of the state variables. 16. Let q = q 1 q 2 q , a = , and d = determine q(0) and q (0) if y(0) =, f = cos 2πt sin 2πt 0, y = y 1 y 2 y 3 y 3, b =. Then if q = aq f and q = by d, Solution of the First-Order Equation [ vc 17. Find a and f for the circuit shown in Fig if q = ]. Figure i s Figure t = 0 18 Ω 2 H 6 Ω 3 Ω 4 F v C 9 Ω 10 Ω 50 Ω i 30 V 2 H 18. For the circuit shown in Fig : (a) write the normal-form equation for i, t>0; (b) solve this equation for i; (c) identify the zero-state and zero-input responses; (d) find i by the methods of Chap. 8 and specify the natural and forced responses.
27 Exercises Let = 2tu(t) V in the circuit shown in Fig Find i 2 (t). Figure Ω i 2 50 F 200 Ω Figure u(t) A 100 V 5 Ω 10 Ω 0.3 H 20. (a) Use state-variable methods to find (t) for all t in the circuit shown in Fig (b) Identify the zero-input, zero-state, natural, and forced responses. 21. Let = 100[u(t) u(t 0.5)] cos πt V in Fig Find v C for t> (a) Write the normal-form equation for the circuit shown in Fig (b) Find v(t) for t<0and t>0. (c) Identify the forced response, the natural response, the zero-state response, and the zero-input response. Figure Ω 200 Ω 0.01 F v C Figure u(t) A 100 V 20 Ω 5 Ω v 25 mf 23. Let = 90e t [u(t) u(t 0.5)] V in the circuit of Fig Find (t). Figure Ω 90 Ω 15 H 19.6 The Solution of the Matrix Equation [ ] Given the system matrix a =, let t = 10 ms and use the infinite power series for the exponential to find (a) e ta ; (b) e ta ; (c) e ta e ta A Further Look at the State-Transition Matrix 25. (a) If q = x y z, f = u(t) cos t u(t), and a = set of normal-form equations. (b) If q(0) = t = 0.1. (c) Repeat for t = , write the, estimate q(0.1) using
First Order Circuits. EENG223 Circuit Theory I
 First Order Circuits EENG223 Circuit Theory I First Order Circuits A first-order circuit can only contain one energy storage element (a capacitor or an inductor). The circuit will also contain resistance.
First Order Circuits EENG223 Circuit Theory I First Order Circuits A first-order circuit can only contain one energy storage element (a capacitor or an inductor). The circuit will also contain resistance.
2.1 Introduction. 2.2 Terms and definitions
 .1 Introduction An important step in the procedure for solving any circuit problem consists first in selecting a number of independent branch currents as (known as loop currents or mesh currents) variables,
.1 Introduction An important step in the procedure for solving any circuit problem consists first in selecting a number of independent branch currents as (known as loop currents or mesh currents) variables,
MATRIX ALGEBRA AND SYSTEMS OF EQUATIONS
 MATRIX ALGEBRA AND SYSTEMS OF EQUATIONS Systems of Equations and Matrices Representation of a linear system The general system of m equations in n unknowns can be written a x + a 2 x 2 + + a n x n b a
MATRIX ALGEBRA AND SYSTEMS OF EQUATIONS Systems of Equations and Matrices Representation of a linear system The general system of m equations in n unknowns can be written a x + a 2 x 2 + + a n x n b a
Circuits 1 M H Miller
 Introduction to Graph Theory Introduction These notes are primarily a digression to provide general background remarks. The subject is an efficient procedure for the determination of voltages and currents
Introduction to Graph Theory Introduction These notes are primarily a digression to provide general background remarks. The subject is an efficient procedure for the determination of voltages and currents
ES250: Electrical Science. HW7: Energy Storage Elements
 ES250: Electrical Science HW7: Energy Storage Elements Introduction This chapter introduces two more circuit elements, the capacitor and the inductor whose elements laws involve integration or differentiation;
ES250: Electrical Science HW7: Energy Storage Elements Introduction This chapter introduces two more circuit elements, the capacitor and the inductor whose elements laws involve integration or differentiation;
Circuit Analysis using the Node and Mesh Methods
 Circuit Analysis using the Node and Mesh Methods We have seen that using Kirchhoff s laws and Ohm s law we can analyze any circuit to determine the operating conditions (the currents and voltages). The
Circuit Analysis using the Node and Mesh Methods We have seen that using Kirchhoff s laws and Ohm s law we can analyze any circuit to determine the operating conditions (the currents and voltages). The
Lecture 7 Circuit analysis via Laplace transform
 S. Boyd EE12 Lecture 7 Circuit analysis via Laplace transform analysis of general LRC circuits impedance and admittance descriptions natural and forced response circuit analysis with impedances natural
S. Boyd EE12 Lecture 7 Circuit analysis via Laplace transform analysis of general LRC circuits impedance and admittance descriptions natural and forced response circuit analysis with impedances natural
CHAPTER 28 ELECTRIC CIRCUITS
 CHAPTER 8 ELECTRIC CIRCUITS 1. Sketch a circuit diagram for a circuit that includes a resistor R 1 connected to the positive terminal of a battery, a pair of parallel resistors R and R connected to the
CHAPTER 8 ELECTRIC CIRCUITS 1. Sketch a circuit diagram for a circuit that includes a resistor R 1 connected to the positive terminal of a battery, a pair of parallel resistors R and R connected to the
MATRIX ALGEBRA AND SYSTEMS OF EQUATIONS. + + x 2. x n. a 11 a 12 a 1n b 1 a 21 a 22 a 2n b 2 a 31 a 32 a 3n b 3. a m1 a m2 a mn b m
 MATRIX ALGEBRA AND SYSTEMS OF EQUATIONS 1. SYSTEMS OF EQUATIONS AND MATRICES 1.1. Representation of a linear system. The general system of m equations in n unknowns can be written a 11 x 1 + a 12 x 2 +
MATRIX ALGEBRA AND SYSTEMS OF EQUATIONS 1. SYSTEMS OF EQUATIONS AND MATRICES 1.1. Representation of a linear system. The general system of m equations in n unknowns can be written a 11 x 1 + a 12 x 2 +
W03 Analysis of DC Circuits. Yrd. Doç. Dr. Aytaç Gören
 W03 Analysis of DC Circuits Yrd. Doç. Dr. Aytaç Gören ELK 2018 - Contents W01 Basic Concepts in Electronics W02 AC to DC Conversion W03 Analysis of DC Circuits (self and condenser) W04 Transistors and
W03 Analysis of DC Circuits Yrd. Doç. Dr. Aytaç Gören ELK 2018 - Contents W01 Basic Concepts in Electronics W02 AC to DC Conversion W03 Analysis of DC Circuits (self and condenser) W04 Transistors and
Notes on Determinant
 ENGG2012B Advanced Engineering Mathematics Notes on Determinant Lecturer: Kenneth Shum Lecture 9-18/02/2013 The determinant of a system of linear equations determines whether the solution is unique, without
ENGG2012B Advanced Engineering Mathematics Notes on Determinant Lecturer: Kenneth Shum Lecture 9-18/02/2013 The determinant of a system of linear equations determines whether the solution is unique, without
Introduction to Matrix Algebra
 Psychology 7291: Multivariate Statistics (Carey) 8/27/98 Matrix Algebra - 1 Introduction to Matrix Algebra Definitions: A matrix is a collection of numbers ordered by rows and columns. It is customary
Psychology 7291: Multivariate Statistics (Carey) 8/27/98 Matrix Algebra - 1 Introduction to Matrix Algebra Definitions: A matrix is a collection of numbers ordered by rows and columns. It is customary
LS.6 Solution Matrices
 LS.6 Solution Matrices In the literature, solutions to linear systems often are expressed using square matrices rather than vectors. You need to get used to the terminology. As before, we state the definitions
LS.6 Solution Matrices In the literature, solutions to linear systems often are expressed using square matrices rather than vectors. You need to get used to the terminology. As before, we state the definitions
8.2. Solution by Inverse Matrix Method. Introduction. Prerequisites. Learning Outcomes
 Solution by Inverse Matrix Method 8.2 Introduction The power of matrix algebra is seen in the representation of a system of simultaneous linear equations as a matrix equation. Matrix algebra allows us
Solution by Inverse Matrix Method 8.2 Introduction The power of matrix algebra is seen in the representation of a system of simultaneous linear equations as a matrix equation. Matrix algebra allows us
Basic numerical skills: EQUATIONS AND HOW TO SOLVE THEM. x + 5 = 7 2 + 5-2 = 7-2 5 + (2-2) = 7-2 5 = 5. x + 5-5 = 7-5. x + 0 = 20.
 Basic numerical skills: EQUATIONS AND HOW TO SOLVE THEM 1. Introduction (really easy) An equation represents the equivalence between two quantities. The two sides of the equation are in balance, and solving
Basic numerical skills: EQUATIONS AND HOW TO SOLVE THEM 1. Introduction (really easy) An equation represents the equivalence between two quantities. The two sides of the equation are in balance, and solving
Nodal and Loop Analysis
 Nodal and Loop Analysis The process of analyzing circuits can sometimes be a difficult task to do. Examining a circuit with the node or loop methods can reduce the amount of time required to get important
Nodal and Loop Analysis The process of analyzing circuits can sometimes be a difficult task to do. Examining a circuit with the node or loop methods can reduce the amount of time required to get important
Basic Laws Circuit Theorems Methods of Network Analysis Non-Linear Devices and Simulation Models
 EE Modul 1: Electric Circuits Theory Basic Laws Circuit Theorems Methods of Network Analysis Non-Linear Devices and Simulation Models EE Modul 1: Electric Circuits Theory Current, Voltage, Impedance Ohm
EE Modul 1: Electric Circuits Theory Basic Laws Circuit Theorems Methods of Network Analysis Non-Linear Devices and Simulation Models EE Modul 1: Electric Circuits Theory Current, Voltage, Impedance Ohm
Lecture Notes: ECS 203 Basic Electrical Engineering Semester 1/2010. Dr.Prapun Suksompong 1 June 16, 2010
 Sirindhorn International Institute of Technology Thammasat University School of Information, Computer and Communication Technology Lecture Notes: ECS 203 Basic Electrical Engineering Semester 1/2010 Dr.Prapun
Sirindhorn International Institute of Technology Thammasat University School of Information, Computer and Communication Technology Lecture Notes: ECS 203 Basic Electrical Engineering Semester 1/2010 Dr.Prapun
6 Series Parallel Circuits
 6 Series Parallel Circuits This work is licensed under the Creative Commons Attribution 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by/3.0/. Air Washington
6 Series Parallel Circuits This work is licensed under the Creative Commons Attribution 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by/3.0/. Air Washington
The Characteristic Polynomial
 Physics 116A Winter 2011 The Characteristic Polynomial 1 Coefficients of the characteristic polynomial Consider the eigenvalue problem for an n n matrix A, A v = λ v, v 0 (1) The solution to this problem
Physics 116A Winter 2011 The Characteristic Polynomial 1 Coefficients of the characteristic polynomial Consider the eigenvalue problem for an n n matrix A, A v = λ v, v 0 (1) The solution to this problem
Second Order Linear Nonhomogeneous Differential Equations; Method of Undetermined Coefficients. y + p(t) y + q(t) y = g(t), g(t) 0.
 Second Order Linear Nonhomogeneous Differential Equations; Method of Undetermined Coefficients We will now turn our attention to nonhomogeneous second order linear equations, equations with the standard
Second Order Linear Nonhomogeneous Differential Equations; Method of Undetermined Coefficients We will now turn our attention to nonhomogeneous second order linear equations, equations with the standard
Series and Parallel Resistive Circuits
 Series and Parallel Resistive Circuits The configuration of circuit elements clearly affects the behaviour of a circuit. Resistors connected in series or in parallel are very common in a circuit and act
Series and Parallel Resistive Circuits The configuration of circuit elements clearly affects the behaviour of a circuit. Resistors connected in series or in parallel are very common in a circuit and act
CONTROLLABILITY. Chapter 2. 2.1 Reachable Set and Controllability. Suppose we have a linear system described by the state equation
 Chapter 2 CONTROLLABILITY 2 Reachable Set and Controllability Suppose we have a linear system described by the state equation ẋ Ax + Bu (2) x() x Consider the following problem For a given vector x in
Chapter 2 CONTROLLABILITY 2 Reachable Set and Controllability Suppose we have a linear system described by the state equation ẋ Ax + Bu (2) x() x Consider the following problem For a given vector x in
1 Determinants and the Solvability of Linear Systems
 1 Determinants and the Solvability of Linear Systems In the last section we learned how to use Gaussian elimination to solve linear systems of n equations in n unknowns The section completely side-stepped
1 Determinants and the Solvability of Linear Systems In the last section we learned how to use Gaussian elimination to solve linear systems of n equations in n unknowns The section completely side-stepped
SERIES-PARALLEL DC CIRCUITS
 Name: Date: Course and Section: Instructor: EXPERIMENT 1 SERIES-PARALLEL DC CIRCUITS OBJECTIVES 1. Test the theoretical analysis of series-parallel networks through direct measurements. 2. Improve skills
Name: Date: Course and Section: Instructor: EXPERIMENT 1 SERIES-PARALLEL DC CIRCUITS OBJECTIVES 1. Test the theoretical analysis of series-parallel networks through direct measurements. 2. Improve skills
Linearly Independent Sets and Linearly Dependent Sets
 These notes closely follow the presentation of the material given in David C. Lay s textbook Linear Algebra and its Applications (3rd edition). These notes are intended primarily for in-class presentation
These notes closely follow the presentation of the material given in David C. Lay s textbook Linear Algebra and its Applications (3rd edition). These notes are intended primarily for in-class presentation
Phasors. Phasors. by Prof. Dr. Osman SEVAİOĞLU Electrical and Electronics Engineering Department. ^ V cos (wt + θ) ^ V sin (wt + θ)
 V cos (wt θ) V sin (wt θ) by Prof. Dr. Osman SEVAİOĞLU Electrical and Electronics Engineering Department EE 209 Fundamentals of Electrical and Electronics Engineering, Prof. Dr. O. SEVAİOĞLU, Page 1 Vector
V cos (wt θ) V sin (wt θ) by Prof. Dr. Osman SEVAİOĞLU Electrical and Electronics Engineering Department EE 209 Fundamentals of Electrical and Electronics Engineering, Prof. Dr. O. SEVAİOĞLU, Page 1 Vector
2.161 Signal Processing: Continuous and Discrete Fall 2008
 MT OpenCourseWare http://ocw.mit.edu.6 Signal Processing: Continuous and Discrete Fall 00 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSETTS
MT OpenCourseWare http://ocw.mit.edu.6 Signal Processing: Continuous and Discrete Fall 00 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSETTS
12.4 UNDRIVEN, PARALLEL RLC CIRCUIT*
 + v C C R L - v i L FIGURE 12.24 The parallel second-order RLC circuit shown in Figure 2.14a. 12.4 UNDRIVEN, PARALLEL RLC CIRCUIT* We will now analyze the undriven parallel RLC circuit shown in Figure
+ v C C R L - v i L FIGURE 12.24 The parallel second-order RLC circuit shown in Figure 2.14a. 12.4 UNDRIVEN, PARALLEL RLC CIRCUIT* We will now analyze the undriven parallel RLC circuit shown in Figure
SYSTEMS OF EQUATIONS AND MATRICES WITH THE TI-89. by Joseph Collison
 SYSTEMS OF EQUATIONS AND MATRICES WITH THE TI-89 by Joseph Collison Copyright 2000 by Joseph Collison All rights reserved Reproduction or translation of any part of this work beyond that permitted by Sections
SYSTEMS OF EQUATIONS AND MATRICES WITH THE TI-89 by Joseph Collison Copyright 2000 by Joseph Collison All rights reserved Reproduction or translation of any part of this work beyond that permitted by Sections
Chapter 2 Determinants, and Linear Independence
 Chapter 2 Determinants, and Linear Independence 2.1 Introduction to Determinants and Systems of Equations Determinants can be defined and studied independently of matrices, though when square matrices
Chapter 2 Determinants, and Linear Independence 2.1 Introduction to Determinants and Systems of Equations Determinants can be defined and studied independently of matrices, though when square matrices
Mechanics 1: Conservation of Energy and Momentum
 Mechanics : Conservation of Energy and Momentum If a certain quantity associated with a system does not change in time. We say that it is conserved, and the system possesses a conservation law. Conservation
Mechanics : Conservation of Energy and Momentum If a certain quantity associated with a system does not change in time. We say that it is conserved, and the system possesses a conservation law. Conservation
PHASOR DIAGRAMS HANDS-ON RELAY SCHOOL WSU PULLMAN, WA. RON ALEXANDER - BPA
 PHASOR DIAGRAMS HANDS-ON RELAY SCHOOL WSU PULLMAN, WA. RON ALEXANDER - BPA What are phasors??? In normal practice, the phasor represents the rms maximum value of the positive half cycle of the sinusoid
PHASOR DIAGRAMS HANDS-ON RELAY SCHOOL WSU PULLMAN, WA. RON ALEXANDER - BPA What are phasors??? In normal practice, the phasor represents the rms maximum value of the positive half cycle of the sinusoid
Integrals of Rational Functions
 Integrals of Rational Functions Scott R. Fulton Overview A rational function has the form where p and q are polynomials. For example, r(x) = p(x) q(x) f(x) = x2 3 x 4 + 3, g(t) = t6 + 4t 2 3, 7t 5 + 3t
Integrals of Rational Functions Scott R. Fulton Overview A rational function has the form where p and q are polynomials. For example, r(x) = p(x) q(x) f(x) = x2 3 x 4 + 3, g(t) = t6 + 4t 2 3, 7t 5 + 3t
The Membrane Equation
 The Membrane Equation Professor David Heeger September 5, 2000 RC Circuits Figure 1A shows an RC (resistor, capacitor) equivalent circuit model for a patch of passive neural membrane. The capacitor represents
The Membrane Equation Professor David Heeger September 5, 2000 RC Circuits Figure 1A shows an RC (resistor, capacitor) equivalent circuit model for a patch of passive neural membrane. The capacitor represents
EDEXCEL NATIONAL CERTIFICATE/DIPLOMA UNIT 5 - ELECTRICAL AND ELECTRONIC PRINCIPLES NQF LEVEL 3 OUTCOME 4 - ALTERNATING CURRENT
 EDEXCEL NATIONAL CERTIFICATE/DIPLOMA UNIT 5 - ELECTRICAL AND ELECTRONIC PRINCIPLES NQF LEVEL 3 OUTCOME 4 - ALTERNATING CURRENT 4 Understand single-phase alternating current (ac) theory Single phase AC
EDEXCEL NATIONAL CERTIFICATE/DIPLOMA UNIT 5 - ELECTRICAL AND ELECTRONIC PRINCIPLES NQF LEVEL 3 OUTCOME 4 - ALTERNATING CURRENT 4 Understand single-phase alternating current (ac) theory Single phase AC
Eðlisfræði 2, vor 2007
 [ Assignment View ] [ Print ] Eðlisfræði 2, vor 2007 30. Inductance Assignment is due at 2:00am on Wednesday, March 14, 2007 Credit for problems submitted late will decrease to 0% after the deadline has
[ Assignment View ] [ Print ] Eðlisfræði 2, vor 2007 30. Inductance Assignment is due at 2:00am on Wednesday, March 14, 2007 Credit for problems submitted late will decrease to 0% after the deadline has
Linear Programming. March 14, 2014
 Linear Programming March 1, 01 Parts of this introduction to linear programming were adapted from Chapter 9 of Introduction to Algorithms, Second Edition, by Cormen, Leiserson, Rivest and Stein [1]. 1
Linear Programming March 1, 01 Parts of this introduction to linear programming were adapted from Chapter 9 of Introduction to Algorithms, Second Edition, by Cormen, Leiserson, Rivest and Stein [1]. 1
Department of Electrical and Electronic Engineering, California State University, Sacramento
 Department of Electrical and Electronic Engineering, California State University, Sacramento Engr 17 Introductory Circuit Analysis, graded, 3 units Instructor: Tatro - Spring 2016 Section 2, Call No. 30289,
Department of Electrical and Electronic Engineering, California State University, Sacramento Engr 17 Introductory Circuit Analysis, graded, 3 units Instructor: Tatro - Spring 2016 Section 2, Call No. 30289,
Circuits with inductors and alternating currents. Chapter 20 #45, 46, 47, 49
 Circuits with inductors and alternating currents Chapter 20 #45, 46, 47, 49 RL circuits Ch. 20 (last section) Symbol for inductor looks like a spring. An inductor is a circuit element that has a large
Circuits with inductors and alternating currents Chapter 20 #45, 46, 47, 49 RL circuits Ch. 20 (last section) Symbol for inductor looks like a spring. An inductor is a circuit element that has a large
Solving Systems of Linear Equations Using Matrices
 Solving Systems of Linear Equations Using Matrices What is a Matrix? A matrix is a compact grid or array of numbers. It can be created from a system of equations and used to solve the system of equations.
Solving Systems of Linear Equations Using Matrices What is a Matrix? A matrix is a compact grid or array of numbers. It can be created from a system of equations and used to solve the system of equations.
Let s examine the response of the circuit shown on Figure 1. The form of the source voltage Vs is shown on Figure 2. R. Figure 1.
 Examples of Transient and RL Circuits. The Series RLC Circuit Impulse response of Circuit. Let s examine the response of the circuit shown on Figure 1. The form of the source voltage Vs is shown on Figure.
Examples of Transient and RL Circuits. The Series RLC Circuit Impulse response of Circuit. Let s examine the response of the circuit shown on Figure 1. The form of the source voltage Vs is shown on Figure.
POLYNOMIAL FUNCTIONS
 POLYNOMIAL FUNCTIONS Polynomial Division.. 314 The Rational Zero Test.....317 Descarte s Rule of Signs... 319 The Remainder Theorem.....31 Finding all Zeros of a Polynomial Function.......33 Writing a
POLYNOMIAL FUNCTIONS Polynomial Division.. 314 The Rational Zero Test.....317 Descarte s Rule of Signs... 319 The Remainder Theorem.....31 Finding all Zeros of a Polynomial Function.......33 Writing a
13 MATH FACTS 101. 2 a = 1. 7. The elements of a vector have a graphical interpretation, which is particularly easy to see in two or three dimensions.
 3 MATH FACTS 0 3 MATH FACTS 3. Vectors 3.. Definition We use the overhead arrow to denote a column vector, i.e., a linear segment with a direction. For example, in three-space, we write a vector in terms
3 MATH FACTS 0 3 MATH FACTS 3. Vectors 3.. Definition We use the overhead arrow to denote a column vector, i.e., a linear segment with a direction. For example, in three-space, we write a vector in terms
Section 10.4 Vectors
 Section 10.4 Vectors A vector is represented by using a ray, or arrow, that starts at an initial point and ends at a terminal point. Your textbook will always use a bold letter to indicate a vector (such
Section 10.4 Vectors A vector is represented by using a ray, or arrow, that starts at an initial point and ends at a terminal point. Your textbook will always use a bold letter to indicate a vector (such
Figure 1.1 Vector A and Vector F
 CHAPTER I VECTOR QUANTITIES Quantities are anything which can be measured, and stated with number. Quantities in physics are divided into two types; scalar and vector quantities. Scalar quantities have
CHAPTER I VECTOR QUANTITIES Quantities are anything which can be measured, and stated with number. Quantities in physics are divided into two types; scalar and vector quantities. Scalar quantities have
December 4, 2013 MATH 171 BASIC LINEAR ALGEBRA B. KITCHENS
 December 4, 2013 MATH 171 BASIC LINEAR ALGEBRA B KITCHENS The equation 1 Lines in two-dimensional space (1) 2x y = 3 describes a line in two-dimensional space The coefficients of x and y in the equation
December 4, 2013 MATH 171 BASIC LINEAR ALGEBRA B KITCHENS The equation 1 Lines in two-dimensional space (1) 2x y = 3 describes a line in two-dimensional space The coefficients of x and y in the equation
Using the Impedance Method
 Using the Impedance Method The impedance method allows us to completely eliminate the differential equation approach for the determination of the response of circuits. In fact the impedance method even
Using the Impedance Method The impedance method allows us to completely eliminate the differential equation approach for the determination of the response of circuits. In fact the impedance method even
TECHNIQUES OF. C.T. Pan 1. C.T. Pan
 TECHNIQUES OF CIRCUIT ANALYSIS C.T. Pan 1 4.1 Introduction 4.2 The Node-Voltage Method ( Nodal Analysis ) 4.3 The Mesh-Current Method ( Mesh Analysis ) 4.4 Fundamental Loop Analysis 4.5 Fundamental Cutset
TECHNIQUES OF CIRCUIT ANALYSIS C.T. Pan 1 4.1 Introduction 4.2 The Node-Voltage Method ( Nodal Analysis ) 4.3 The Mesh-Current Method ( Mesh Analysis ) 4.4 Fundamental Loop Analysis 4.5 Fundamental Cutset
Matrix Differentiation
 1 Introduction Matrix Differentiation ( and some other stuff ) Randal J. Barnes Department of Civil Engineering, University of Minnesota Minneapolis, Minnesota, USA Throughout this presentation I have
1 Introduction Matrix Differentiation ( and some other stuff ) Randal J. Barnes Department of Civil Engineering, University of Minnesota Minneapolis, Minnesota, USA Throughout this presentation I have
Introduction to Matrices for Engineers
 Introduction to Matrices for Engineers C.T.J. Dodson, School of Mathematics, Manchester Universit 1 What is a Matrix? A matrix is a rectangular arra of elements, usuall numbers, e.g. 1 0-8 4 0-1 1 0 11
Introduction to Matrices for Engineers C.T.J. Dodson, School of Mathematics, Manchester Universit 1 What is a Matrix? A matrix is a rectangular arra of elements, usuall numbers, e.g. 1 0-8 4 0-1 1 0 11
DC mesh current analysis
 DC mesh current analysis This worksheet and all related files are licensed under the Creative Commons Attribution License, version 1.0. To view a copy of this license, visit http://creativecommons.org/licenses/by/1.0/,
DC mesh current analysis This worksheet and all related files are licensed under the Creative Commons Attribution License, version 1.0. To view a copy of this license, visit http://creativecommons.org/licenses/by/1.0/,
Lecture L3 - Vectors, Matrices and Coordinate Transformations
 S. Widnall 16.07 Dynamics Fall 2009 Lecture notes based on J. Peraire Version 2.0 Lecture L3 - Vectors, Matrices and Coordinate Transformations By using vectors and defining appropriate operations between
S. Widnall 16.07 Dynamics Fall 2009 Lecture notes based on J. Peraire Version 2.0 Lecture L3 - Vectors, Matrices and Coordinate Transformations By using vectors and defining appropriate operations between
2.3. Finding polynomial functions. An Introduction:
 2.3. Finding polynomial functions. An Introduction: As is usually the case when learning a new concept in mathematics, the new concept is the reverse of the previous one. Remember how you first learned
2.3. Finding polynomial functions. An Introduction: As is usually the case when learning a new concept in mathematics, the new concept is the reverse of the previous one. Remember how you first learned
The Time Constant of an RC Circuit
 The Time Constant of an RC Circuit 1 Objectives 1. To determine the time constant of an RC Circuit, and 2. To determine the capacitance of an unknown capacitor. 2 Introduction What the heck is a capacitor?
The Time Constant of an RC Circuit 1 Objectives 1. To determine the time constant of an RC Circuit, and 2. To determine the capacitance of an unknown capacitor. 2 Introduction What the heck is a capacitor?
Chapter 12 Modal Decomposition of State-Space Models 12.1 Introduction The solutions obtained in previous chapters, whether in time domain or transfor
 Lectures on Dynamic Systems and Control Mohammed Dahleh Munther A. Dahleh George Verghese Department of Electrical Engineering and Computer Science Massachuasetts Institute of Technology 1 1 c Chapter
Lectures on Dynamic Systems and Control Mohammed Dahleh Munther A. Dahleh George Verghese Department of Electrical Engineering and Computer Science Massachuasetts Institute of Technology 1 1 c Chapter
Equations, Inequalities & Partial Fractions
 Contents Equations, Inequalities & Partial Fractions.1 Solving Linear Equations 2.2 Solving Quadratic Equations 1. Solving Polynomial Equations 1.4 Solving Simultaneous Linear Equations 42.5 Solving Inequalities
Contents Equations, Inequalities & Partial Fractions.1 Solving Linear Equations 2.2 Solving Quadratic Equations 1. Solving Polynomial Equations 1.4 Solving Simultaneous Linear Equations 42.5 Solving Inequalities
Click on the links below to jump directly to the relevant section
 Click on the links below to jump directly to the relevant section What is algebra? Operations with algebraic terms Mathematical properties of real numbers Order of operations What is Algebra? Algebra is
Click on the links below to jump directly to the relevant section What is algebra? Operations with algebraic terms Mathematical properties of real numbers Order of operations What is Algebra? Algebra is
4.3 Lagrange Approximation
 206 CHAP. 4 INTERPOLATION AND POLYNOMIAL APPROXIMATION Lagrange Polynomial Approximation 4.3 Lagrange Approximation Interpolation means to estimate a missing function value by taking a weighted average
206 CHAP. 4 INTERPOLATION AND POLYNOMIAL APPROXIMATION Lagrange Polynomial Approximation 4.3 Lagrange Approximation Interpolation means to estimate a missing function value by taking a weighted average
Ver 3537 E1.1 Analysis of Circuits (2014) E1.1 Circuit Analysis. Problem Sheet 1 (Lectures 1 & 2)
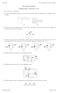 Ver 3537 E. Analysis of Circuits () Key: [A]= easy... [E]=hard E. Circuit Analysis Problem Sheet (Lectures & ). [A] One of the following circuits is a series circuit and the other is a parallel circuit.
Ver 3537 E. Analysis of Circuits () Key: [A]= easy... [E]=hard E. Circuit Analysis Problem Sheet (Lectures & ). [A] One of the following circuits is a series circuit and the other is a parallel circuit.
a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a 2n x n = b 2.
 Chapter 1 LINEAR EQUATIONS 1.1 Introduction to linear equations A linear equation in n unknowns x 1, x,, x n is an equation of the form a 1 x 1 + a x + + a n x n = b, where a 1, a,..., a n, b are given
Chapter 1 LINEAR EQUATIONS 1.1 Introduction to linear equations A linear equation in n unknowns x 1, x,, x n is an equation of the form a 1 x 1 + a x + + a n x n = b, where a 1, a,..., a n, b are given
The Matrix Elements of a 3 3 Orthogonal Matrix Revisited
 Physics 116A Winter 2011 The Matrix Elements of a 3 3 Orthogonal Matrix Revisited 1. Introduction In a class handout entitled, Three-Dimensional Proper and Improper Rotation Matrices, I provided a derivation
Physics 116A Winter 2011 The Matrix Elements of a 3 3 Orthogonal Matrix Revisited 1. Introduction In a class handout entitled, Three-Dimensional Proper and Improper Rotation Matrices, I provided a derivation
MATH10212 Linear Algebra. Systems of Linear Equations. Definition. An n-dimensional vector is a row or a column of n numbers (or letters): a 1.
 MATH10212 Linear Algebra Textbook: D. Poole, Linear Algebra: A Modern Introduction. Thompson, 2006. ISBN 0-534-40596-7. Systems of Linear Equations Definition. An n-dimensional vector is a row or a column
MATH10212 Linear Algebra Textbook: D. Poole, Linear Algebra: A Modern Introduction. Thompson, 2006. ISBN 0-534-40596-7. Systems of Linear Equations Definition. An n-dimensional vector is a row or a column
South Carolina College- and Career-Ready (SCCCR) Pre-Calculus
 South Carolina College- and Career-Ready (SCCCR) Pre-Calculus Key Concepts Arithmetic with Polynomials and Rational Expressions PC.AAPR.2 PC.AAPR.3 PC.AAPR.4 PC.AAPR.5 PC.AAPR.6 PC.AAPR.7 Standards Know
South Carolina College- and Career-Ready (SCCCR) Pre-Calculus Key Concepts Arithmetic with Polynomials and Rational Expressions PC.AAPR.2 PC.AAPR.3 PC.AAPR.4 PC.AAPR.5 PC.AAPR.6 PC.AAPR.7 Standards Know
Algebra Unpacked Content For the new Common Core standards that will be effective in all North Carolina schools in the 2012-13 school year.
 This document is designed to help North Carolina educators teach the Common Core (Standard Course of Study). NCDPI staff are continually updating and improving these tools to better serve teachers. Algebra
This document is designed to help North Carolina educators teach the Common Core (Standard Course of Study). NCDPI staff are continually updating and improving these tools to better serve teachers. Algebra
J.L. Kirtley Jr. Electric network theory deals with two primitive quantities, which we will refer to as: 1. Potential (or voltage), and
 Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.061 Introduction to Power Systems Class Notes Chapter 1: eiew of Network Theory J.L. Kirtley Jr. 1 Introduction
Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.061 Introduction to Power Systems Class Notes Chapter 1: eiew of Network Theory J.L. Kirtley Jr. 1 Introduction
Solving Simultaneous Equations and Matrices
 Solving Simultaneous Equations and Matrices The following represents a systematic investigation for the steps used to solve two simultaneous linear equations in two unknowns. The motivation for considering
Solving Simultaneous Equations and Matrices The following represents a systematic investigation for the steps used to solve two simultaneous linear equations in two unknowns. The motivation for considering
CORRELATED TO THE SOUTH CAROLINA COLLEGE AND CAREER-READY FOUNDATIONS IN ALGEBRA
 We Can Early Learning Curriculum PreK Grades 8 12 INSIDE ALGEBRA, GRADES 8 12 CORRELATED TO THE SOUTH CAROLINA COLLEGE AND CAREER-READY FOUNDATIONS IN ALGEBRA April 2016 www.voyagersopris.com Mathematical
We Can Early Learning Curriculum PreK Grades 8 12 INSIDE ALGEBRA, GRADES 8 12 CORRELATED TO THE SOUTH CAROLINA COLLEGE AND CAREER-READY FOUNDATIONS IN ALGEBRA April 2016 www.voyagersopris.com Mathematical
Vector has a magnitude and a direction. Scalar has a magnitude
 Vector has a magnitude and a direction Scalar has a magnitude Vector has a magnitude and a direction Scalar has a magnitude a brick on a table Vector has a magnitude and a direction Scalar has a magnitude
Vector has a magnitude and a direction Scalar has a magnitude Vector has a magnitude and a direction Scalar has a magnitude a brick on a table Vector has a magnitude and a direction Scalar has a magnitude
Positive Feedback and Oscillators
 Physics 3330 Experiment #6 Fall 1999 Positive Feedback and Oscillators Purpose In this experiment we will study how spontaneous oscillations may be caused by positive feedback. You will construct an active
Physics 3330 Experiment #6 Fall 1999 Positive Feedback and Oscillators Purpose In this experiment we will study how spontaneous oscillations may be caused by positive feedback. You will construct an active
5.5. Solving linear systems by the elimination method
 55 Solving linear systems by the elimination method Equivalent systems The major technique of solving systems of equations is changing the original problem into another one which is of an easier to solve
55 Solving linear systems by the elimination method Equivalent systems The major technique of solving systems of equations is changing the original problem into another one which is of an easier to solve
Chapter 7 Direct-Current Circuits
 Chapter 7 Direct-Current Circuits 7. Introduction...7-7. Electromotive Force...7-3 7.3 Resistors in Series and in Parallel...7-5 7.4 Kirchhoff s Circuit Rules...7-7 7.5 Voltage-Current Measurements...7-9
Chapter 7 Direct-Current Circuits 7. Introduction...7-7. Electromotive Force...7-3 7.3 Resistors in Series and in Parallel...7-5 7.4 Kirchhoff s Circuit Rules...7-7 7.5 Voltage-Current Measurements...7-9
Mesh-Current Method (Loop Analysis)
 Mesh-Current Method (Loop Analysis) Nodal analysis was developed by applying KCL at each non-reference node. Mesh-Current method is developed by applying KVL around meshes in the circuit. A mesh is a loop
Mesh-Current Method (Loop Analysis) Nodal analysis was developed by applying KCL at each non-reference node. Mesh-Current method is developed by applying KVL around meshes in the circuit. A mesh is a loop
Dependent Sources: Introduction and analysis of circuits containing dependent sources.
 Dependent Sources: Introduction and analysis of circuits containing dependent sources. So far we have explored timeindependent (resistive) elements that are also linear. We have seen that two terminal
Dependent Sources: Introduction and analysis of circuits containing dependent sources. So far we have explored timeindependent (resistive) elements that are also linear. We have seen that two terminal
3.1. Solving linear equations. Introduction. Prerequisites. Learning Outcomes. Learning Style
 Solving linear equations 3.1 Introduction Many problems in engineering reduce to the solution of an equation or a set of equations. An equation is a type of mathematical expression which contains one or
Solving linear equations 3.1 Introduction Many problems in engineering reduce to the solution of an equation or a set of equations. An equation is a type of mathematical expression which contains one or
Similarity and Diagonalization. Similar Matrices
 MATH022 Linear Algebra Brief lecture notes 48 Similarity and Diagonalization Similar Matrices Let A and B be n n matrices. We say that A is similar to B if there is an invertible n n matrix P such that
MATH022 Linear Algebra Brief lecture notes 48 Similarity and Diagonalization Similar Matrices Let A and B be n n matrices. We say that A is similar to B if there is an invertible n n matrix P such that
Dynamic Eigenvalues for Scalar Linear Time-Varying Systems
 Dynamic Eigenvalues for Scalar Linear Time-Varying Systems P. van der Kloet and F.L. Neerhoff Department of Electrical Engineering Delft University of Technology Mekelweg 4 2628 CD Delft The Netherlands
Dynamic Eigenvalues for Scalar Linear Time-Varying Systems P. van der Kloet and F.L. Neerhoff Department of Electrical Engineering Delft University of Technology Mekelweg 4 2628 CD Delft The Netherlands
Introduction to Complex Numbers in Physics/Engineering
 Introduction to Complex Numbers in Physics/Engineering ference: Mary L. Boas, Mathematical Methods in the Physical Sciences Chapter 2 & 14 George Arfken, Mathematical Methods for Physicists Chapter 6 The
Introduction to Complex Numbers in Physics/Engineering ference: Mary L. Boas, Mathematical Methods in the Physical Sciences Chapter 2 & 14 George Arfken, Mathematical Methods for Physicists Chapter 6 The
Lecture 1: Systems of Linear Equations
 MTH Elementary Matrix Algebra Professor Chao Huang Department of Mathematics and Statistics Wright State University Lecture 1 Systems of Linear Equations ² Systems of two linear equations with two variables
MTH Elementary Matrix Algebra Professor Chao Huang Department of Mathematics and Statistics Wright State University Lecture 1 Systems of Linear Equations ² Systems of two linear equations with two variables
S-Parameters and Related Quantities Sam Wetterlin 10/20/09
 S-Parameters and Related Quantities Sam Wetterlin 10/20/09 Basic Concept of S-Parameters S-Parameters are a type of network parameter, based on the concept of scattering. The more familiar network parameters
S-Parameters and Related Quantities Sam Wetterlin 10/20/09 Basic Concept of S-Parameters S-Parameters are a type of network parameter, based on the concept of scattering. The more familiar network parameters
EXAMPLE 8: An Electrical System (Mechanical-Electrical Analogy)
 EXAMPLE 8: An Electrical System (Mechanical-Electrical Analogy) A completely analogous procedure can be used to find the state equations of electrical systems (and, ultimately, electro-mechanical systems
EXAMPLE 8: An Electrical System (Mechanical-Electrical Analogy) A completely analogous procedure can be used to find the state equations of electrical systems (and, ultimately, electro-mechanical systems
Example: Determine the power supplied by each of the sources, independent and dependent, in this circuit:
 Example: Determine the power supplied by each of the sources, independent and dependent, in this circuit: Solution: We ll begin by choosing the bottom node to be the reference node. Next we ll label the
Example: Determine the power supplied by each of the sources, independent and dependent, in this circuit: Solution: We ll begin by choosing the bottom node to be the reference node. Next we ll label the
Understanding Poles and Zeros
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY DEPARTMENT OF MECHANICAL ENGINEERING 2.14 Analysis and Design of Feedback Control Systems Understanding Poles and Zeros 1 System Poles and Zeros The transfer function
MASSACHUSETTS INSTITUTE OF TECHNOLOGY DEPARTMENT OF MECHANICAL ENGINEERING 2.14 Analysis and Design of Feedback Control Systems Understanding Poles and Zeros 1 System Poles and Zeros The transfer function
3.6. Partial Fractions. Introduction. Prerequisites. Learning Outcomes
 Partial Fractions 3.6 Introduction It is often helpful to break down a complicated algebraic fraction into a sum of simpler fractions. For 4x + 7 example it can be shown that x 2 + 3x + 2 has the same
Partial Fractions 3.6 Introduction It is often helpful to break down a complicated algebraic fraction into a sum of simpler fractions. For 4x + 7 example it can be shown that x 2 + 3x + 2 has the same
School of Engineering Department of Electrical and Computer Engineering
 1 School of Engineering Department of Electrical and Computer Engineering 332:223 Principles of Electrical Engineering I Laboratory Experiment #4 Title: Operational Amplifiers 1 Introduction Objectives
1 School of Engineering Department of Electrical and Computer Engineering 332:223 Principles of Electrical Engineering I Laboratory Experiment #4 Title: Operational Amplifiers 1 Introduction Objectives
Step response of an RLC series circuit
 School of Engineering Department of Electrical and Computer Engineering 332:224 Principles of Electrical Engineering II Laboratory Experiment 5 Step response of an RLC series circuit 1 Introduction Objectives
School of Engineering Department of Electrical and Computer Engineering 332:224 Principles of Electrical Engineering II Laboratory Experiment 5 Step response of an RLC series circuit 1 Introduction Objectives
Solution of Linear Systems
 Chapter 3 Solution of Linear Systems In this chapter we study algorithms for possibly the most commonly occurring problem in scientific computing, the solution of linear systems of equations. We start
Chapter 3 Solution of Linear Systems In this chapter we study algorithms for possibly the most commonly occurring problem in scientific computing, the solution of linear systems of equations. We start
is identically equal to x 2 +3x +2
 Partial fractions 3.6 Introduction It is often helpful to break down a complicated algebraic fraction into a sum of simpler fractions. 4x+7 For example it can be shown that has the same value as 1 + 3
Partial fractions 3.6 Introduction It is often helpful to break down a complicated algebraic fraction into a sum of simpler fractions. 4x+7 For example it can be shown that has the same value as 1 + 3
Name: Section Registered In:
 Name: Section Registered In: Math 125 Exam 3 Version 1 April 24, 2006 60 total points possible 1. (5pts) Use Cramer s Rule to solve 3x + 4y = 30 x 2y = 8. Be sure to show enough detail that shows you are
Name: Section Registered In: Math 125 Exam 3 Version 1 April 24, 2006 60 total points possible 1. (5pts) Use Cramer s Rule to solve 3x + 4y = 30 x 2y = 8. Be sure to show enough detail that shows you are
Linear Algebra Notes for Marsden and Tromba Vector Calculus
 Linear Algebra Notes for Marsden and Tromba Vector Calculus n-dimensional Euclidean Space and Matrices Definition of n space As was learned in Math b, a point in Euclidean three space can be thought of
Linear Algebra Notes for Marsden and Tromba Vector Calculus n-dimensional Euclidean Space and Matrices Definition of n space As was learned in Math b, a point in Euclidean three space can be thought of
1 Sets and Set Notation.
 LINEAR ALGEBRA MATH 27.6 SPRING 23 (COHEN) LECTURE NOTES Sets and Set Notation. Definition (Naive Definition of a Set). A set is any collection of objects, called the elements of that set. We will most
LINEAR ALGEBRA MATH 27.6 SPRING 23 (COHEN) LECTURE NOTES Sets and Set Notation. Definition (Naive Definition of a Set). A set is any collection of objects, called the elements of that set. We will most
AC CIRCUITS - CAPACITORS AND INDUCTORS
 EXPRIMENT#8 AC CIRCUITS - CAPACITORS AND INDUCTORS NOTE: Two weeks are allocated for this experiment. Before performing this experiment, review the Proper Oscilloscope Use section of Experiment #7. Objective
EXPRIMENT#8 AC CIRCUITS - CAPACITORS AND INDUCTORS NOTE: Two weeks are allocated for this experiment. Before performing this experiment, review the Proper Oscilloscope Use section of Experiment #7. Objective
Equivalent Circuits and Transfer Functions
 R eq isc Equialent Circuits and Transfer Functions Samantha R Summerson 14 September, 009 1 Equialent Circuits eq ± Figure 1: Théenin equialent circuit. i sc R eq oc Figure : Mayer-Norton equialent circuit.
R eq isc Equialent Circuits and Transfer Functions Samantha R Summerson 14 September, 009 1 Equialent Circuits eq ± Figure 1: Théenin equialent circuit. i sc R eq oc Figure : Mayer-Norton equialent circuit.
Question 2: How do you solve a matrix equation using the matrix inverse?
 Question : How do you solve a matrix equation using the matrix inverse? In the previous question, we wrote systems of equations as a matrix equation AX B. In this format, the matrix A contains the coefficients
Question : How do you solve a matrix equation using the matrix inverse? In the previous question, we wrote systems of equations as a matrix equation AX B. In this format, the matrix A contains the coefficients
CIRCUITS LABORATORY EXPERIMENT 3. AC Circuit Analysis
 CIRCUITS LABORATORY EXPERIMENT 3 AC Circuit Analysis 3.1 Introduction The steady-state behavior of circuits energized by sinusoidal sources is an important area of study for several reasons. First, the
CIRCUITS LABORATORY EXPERIMENT 3 AC Circuit Analysis 3.1 Introduction The steady-state behavior of circuits energized by sinusoidal sources is an important area of study for several reasons. First, the
How To Find The Current Of A Circuit
 The node voltage method Equivalent resistance Voltage / current dividers Source transformations Node voltages Mesh currents Superposition Not every circuit lends itself to short-cut methods. Sometimes
The node voltage method Equivalent resistance Voltage / current dividers Source transformations Node voltages Mesh currents Superposition Not every circuit lends itself to short-cut methods. Sometimes
ε: Voltage output of Signal Generator (also called the Source voltage or Applied
 Experiment #10: LR & RC Circuits Frequency Response EQUIPMENT NEEDED Science Workshop Interface Power Amplifier (2) Voltage Sensor graph paper (optional) (3) Patch Cords Decade resistor, capacitor, and
Experiment #10: LR & RC Circuits Frequency Response EQUIPMENT NEEDED Science Workshop Interface Power Amplifier (2) Voltage Sensor graph paper (optional) (3) Patch Cords Decade resistor, capacitor, and
Outline. Systems and Signals 214 / 244 & Energy Systems 244 / 344. Ideal Inductor. Ideal Inductor (cont... )
 Outline Systems and Signals 214 / 244 & Energy Systems 244 / 344 Inductance, Leakage Inductance, Mutual Inductance & Transformers 1 Inductor revision Ideal Inductor Non-Ideal Inductor Dr. P.J. Randewijk
Outline Systems and Signals 214 / 244 & Energy Systems 244 / 344 Inductance, Leakage Inductance, Mutual Inductance & Transformers 1 Inductor revision Ideal Inductor Non-Ideal Inductor Dr. P.J. Randewijk
The Method of Partial Fractions Math 121 Calculus II Spring 2015
 Rational functions. as The Method of Partial Fractions Math 11 Calculus II Spring 015 Recall that a rational function is a quotient of two polynomials such f(x) g(x) = 3x5 + x 3 + 16x x 60. The method
Rational functions. as The Method of Partial Fractions Math 11 Calculus II Spring 015 Recall that a rational function is a quotient of two polynomials such f(x) g(x) = 3x5 + x 3 + 16x x 60. The method
Indiana State Core Curriculum Standards updated 2009 Algebra I
 Indiana State Core Curriculum Standards updated 2009 Algebra I Strand Description Boardworks High School Algebra presentations Operations With Real Numbers Linear Equations and A1.1 Students simplify and
Indiana State Core Curriculum Standards updated 2009 Algebra I Strand Description Boardworks High School Algebra presentations Operations With Real Numbers Linear Equations and A1.1 Students simplify and
