Linear Regression and Correlation
|
|
|
- Jack Andrews
- 7 years ago
- Views:
Transcription
1 Chapter 12 Linear Regression and Correlation 12.1 Linear Regression and Correlation Student Learning Objectives By the end of this chapter, the student should be able to: Discuss basic ideas of linear regression and correlation. Create and interpret a line of best fit. Calculate and interpret the correlation coefficient. Calculate and interpret outliers Introduction Professionals often want to know how two or more variables are related. For example, is there a relationship between the grade on the second math exam a student takes and the grade on the final exam? If there is a relationship, what is it and how strong is the relationship? In another example, your income may be determined by your education, your profession, your years of experience, and your ability. The amount you pay a repair person for labor is often determined by an initial amount plus an hourly fee. These are all examples in which regression can be used. The type of data described in the examples is bivariate data - "bi" for two variables. In reality, statisticians use multivariate data, meaning many variables. In this chapter, you will be studying the simplest form of regression, "linear regression" with one independent variable (x). This involves data that fits a line in two dimensions. You will also study correlation which measures how strong the relationship is Linear Equations 2 Linear regression for two variables is based on a linear equation with one independent variable. It has the form: 1 This content is available online at < 2 This content is available online at < y = a + bx (12.1) 475
2 476 CHAPTER 12. LINEAR REGRESSION AND CORRELATION where a and b are constant numbers. x is the independent variable, and y is the dependent variable. Typically, you choose a value to substitute for the independent variable and then solve for the dependent variable. Example 12.1 The following examples are linear equations. y = 3 + 2x (12.2) y = x (12.3) The graph of a linear equation of the form y = a + bx is a straight line. Any line that is not vertical can be described by this equation. Example 12.2 Figure 12.1: Graph of the equation y = 1 + 2x. Linear equations of this form occur in applications of life sciences, social sciences, psychology, business, economics, physical sciences, mathematics, and other areas. Example 12.3 Aaron s Word Processing Service (AWPS) does word processing. Its rate is $32 per hour plus a $31.50 one-time charge. The total cost to a customer depends on the number of hours it takes to do the word processing job. Problem Find the equation that expresses the total cost in terms of the number of hours required to finish the word processing job. Solution Let x = the number of hours it takes to get the job done. Let y = the total cost to the customer. The $31.50 is a fixed cost. If it takes x hours to complete the job, then (32) (x) is the cost of the word processing only. The total cost is:
3 477 y = x 12.3 Slope and Y-Intercept of a Linear Equation 3 For the linear equation y = a + bx, b = slope and a = y-intercept. From algebra recall that the slope is a number that describes the steepness of a line and the y-intercept is the y coordinate of the point (0, a) where the line crosses the y-axis. (a) (b) (c) Figure 12.2: Three possible graphs of y = a + bx. (a) If b > 0, the line slopes upward to the right. (b) If b = 0, the line is horizontal. (c) If b < 0, the line slopes downward to the right. Example 12.4 Svetlana tutors to make extra money for college. For each tutoring session, she charges a one time fee of $25 plus $15 per hour of tutoring. A linear equation that expresses the total amount of money Svetlana earns for each session she tutors is y = x. Problem What are the independent and dependent variables? What is the y-intercept and what is the slope? Interpret them using complete sentences. Solution The independent variable (x) is the number of hours Svetlana tutors each session. The dependent variable (y) is the amount, in dollars, Svetlana earns for each session. The y-intercept is 25 (a = 25). At the start of the tutoring session, Svetlana charges a one-time fee of $25 (this is when x = 0). The slope is 15 (b = 15). For each session, Svetlana earns $15 for each hour she tutors Scatter Plots 4 Before we take up the discussion of linear regression and correlation, we need to examine a way to display the relation between two variables x and y. The most common and easiest way is a scatter plot. The following example illustrates a scatter plot. 3 This content is available online at < 4 This content is available online at <
4 478 CHAPTER 12. LINEAR REGRESSION AND CORRELATION Example 12.5 From an article in the Wall Street Journal: In Europe and Asia, m-commerce is becoming more popular. M-commerce users have special mobile phones that work like electronic wallets as well as provide phone and Internet services. Users can do everything from paying for parking to buying a TV set or soda from a machine to banking to checking sports scores on the Internet. In the next few years, will there be a relationship between the year and the number of m-commerce users? Construct a scatter plot. Let x = the year and let y = the number of m-commerce users, in millions. x (year) (a) y (# of users) (b) Figure 12.3: (a) Table showing the number of m-commerce users (in millions) by year. (b) Scatter plot showing the number of m-commerce users (in millions) by year. A scatter plot shows the direction and strength of a relationship between the variables. A clear direction happens when there is either: High values of one variable occurring with high values of the other variable or low values of one variable occurring with low values of the other variable. High values of one variable occurring with low values of the other variable. You can determine the strength of the relationship by looking at the scatter plot and seeing how close the points are to a line, a power function, an exponential function, or to some other type of function. When you look at a scatterplot, you want to notice the overall pattern and any deviations from the pattern. The following scatterplot examples illustrate these concepts.
5 479 (a) Positive Linear Pattern (Strong) (b) Linear Pattern w/ One Deviation Figure 12.4 (a) Negative Linear Pattern (Strong) (b) Negative Linear Pattern (Weak) Figure 12.5 (a) Exponential Growth Pattern (b) No Pattern Figure 12.6 In this chapter, we are interested in scatter plots that show a linear pattern. Linear patterns are quite common. The linear relationship is strong if the points are close to a straight line. If we think that the points show a linear relationship, we would like to draw a line on the scatter plot. This line can be calculated through a process called linear regression. However, we only calculate a regression line if one of the variables helps to explain or predict the other variable. If x is the independent variable and y the dependent variable, then we can use a regression line to predict y for a given value of x.
6 480 CHAPTER 12. LINEAR REGRESSION AND CORRELATION 12.5 The Regression Equation 5 Data rarely fit a straight line exactly. Usually, you must be satisfied with rough predictions. Typically, you have a set of data whose scatter plot appears to "fit" a straight line. This is called a Line of Best Fit or Least Squares Line Optional Collaborative Classroom Activity If you know a person s pinky (smallest) finger length, do you think you could predict that person s height? Collect data from your class (pinky finger length, in inches). The independent variable, x, is pinky finger length and the dependent variable, y, is height. For each set of data, plot the points on graph paper. Make your graph big enough and use a ruler. Then "by eye" draw a line that appears to "fit" the data. For your line, pick two convenient points and use them to find the slope of the line. Find the y-intercept of the line by extending your lines so they cross the y-axis. Using the slopes and the y-intercepts, write your equation of "best fit". Do you think everyone will have the same equation? Why or why not? Using your equation, what is the predicted height for a pinky length of 2.5 inches? Example 12.6 A random sample of 11 statistics students produced the following data where x is the third exam score, out of 80, and y is the final exam score, out of 200. Can you predict the final exam score of a random student if you know the third exam score? 5 This content is available online at <
7 481 x (third exam score) (a) y (final exam score) (b) Figure 12.7: (a) Table showing the scores on the final exam based on scores from the third exam. (b) Scatter plot showing the scores on the final exam based on scores from the third exam. The third exam score, x, is the independent variable and the final exam score, y, is the dependent variable. We will plot a regression line that best "fits" the data. If each of you were to fit a line "by eye", you would draw different lines. We can use what is called a least-squares regression line to obtain the best fit line. Consider the following diagram. Each point of data is of ( the ) the form (x, y)and each point of the line of best fit using least-squares linear regression has the form x, ^y. The ^y is read "y hat" and is the estimated value of y. It is the value of y obtained using the regression line. It is not generally equal to y from data.
8 482 CHAPTER 12. LINEAR REGRESSION AND CORRELATION Figure 12.8 The term y 0 ^y 0 = ɛ 0 is called the "error" or residual. It is not an error in the sense of a mistake, but measures the vertical distance between the actual value of y and the estimated value of y. ɛ = the Greek letter epsilon For each data point, you can calculate, y i ^y i = ɛ i for i = 1, 2, 3,..., 11. Each ɛ is a vertical distance. For the example about the third exam scores and the final exam scores for the 11 statistics students, there are 11 data points. Therefore, there are 11 ɛ values. If you square each ɛ and add, you get (ɛ 1 ) 2 + (ɛ 2 ) (ɛ 11 ) 2 = 11 Σ i = 1 ɛ 2 This is called the Sum of Squared Errors (SSE). Using calculus, you can determine the values of a and b that make the SSE a minimum. When you make the SSE a minimum, you have determined the points that are on the line of best fit. It turns out that the line of best fit has the equation: ^y= a + bx (12.4) where a = y b x and b = Σ(x x) (y y) 2 Σ(x x). x and y are the averages of the x values and the y values, respectively. The best fit line always passes through the point (x, y). ( ) sy The slope b can be written as b = r s x where s y = the standard deviation of the y values and s x = the standard deviation of the x values. r is the correlation coefficient which is discussed in the next section.
9 483 NOTE: Many calculators or any linear regression and correlation computer program can calculate the best fit line. The calculations tend to be tedious if done by hand. In the technology section, there are instructions for calculating the best fit line. The graph of the line of best fit for the third exam/final exam example is shown below: Figure 12.9 Remember, the best fit line is called the least squares regression line (it is sometimes referred to as the LSL which is an acronym for least squares line). The best fit line for the third exam/final exam example has the equation: ^y= x (12.5) The idea behind finding the best fit line is based on the assumption that the data are actually scattered about a straight line. Remember, it is always important to plot a scatter diagram first (which many calculators and computer programs can do) to see if it is worth calculating the line of best fit. The slope of the line is 4.83 (b = 4.83). We can interpret the slope as follows: As the third exam score increases by one point, the final exam score increases by 4.83 points. NOTE: If the scatter plot indicates that there is a linear relationship between the variables, then it is reasonable to use a best fit line to make predictions for y given x within the domain of x-values in the sample data, but not necessarily for x-values outside that domain The Correlation Coefficient 6 Besides looking at the scatter plot and seeing that a line seems reasonable, how can you tell if the line is a good predictor? Use the correlation coefficient as another indicator (besides the scatterplot) of the strength of the relationship between x and y. The correlation coefficient, r, is defined as: 6 This content is available online at <
10 484 CHAPTER 12. LINEAR REGRESSION AND CORRELATION r = n Σx y (Σx) (Σy) [n Σx 2 (Σx) 2 ] [n Σy 2 (Σy) 2 ] where n = the number of data points. If you suspect a linear relationship between x and y, then r can measure how strong the linear relationship is. One property of r is that 1 r 1. If r = 1, there is perfect positive correlation. If r = 1, there is perfect negative correlation. In both these cases, the original data points lie on a straight line. Of course, in the real world, this will not generally happen. The formula for r looks formidable. However, many calculators and any regression and correlation computer program can calculate r. The sign of r is the same as the slope, b, of the best fit line Facts About the Correlation Coefficient for Linear Regression 7 A positive r means that when x increases, y increases and when x decreases, y decreases (positive correlation). A negative r means that when x increases, y decreases and when x decreases, y increases (negative correlation). An r of zero means there is absolutely no linear relationship between x and y (no correlation). High correlation does not suggest that x causes y or y causes x. We say "correlation does not imply causation." For example, every person who learned math in the 17th century is dead. However, learning math does not necessarily cause death! (a) Positive Correlation (b) Negative Correlation (c) Zero Correlation Figure 12.10: (a) A scatter plot showing data with a positive correlation. (b) A scatter plot showing data with a negative correlation. (c) A scatter plot showing data with zero correlation. The 95% Critical Values of the Sample Correlation Coefficient Table (Section 12.10) at the end of this chapter (before the Summary (Section 12.11)) may be used to give you a good idea of whether the computed value of r is significant or not. Compare r to the appropriate critical value in the table. If r is significant, then you may want to use the line for prediction. Example 12.7 Suppose you computed r = using n = 10 data points. df = n 2 = 10 2 = 8. The critical values associated with df = 8 are and If r< negative critical value or r > 7 This content is available online at <
11 485 positive critical value, then r is significant. Since r = and > 0.632, r is significant and the line may be used for prediction. If you view this example on a number line, it will help you. Figure 12.11: r is not significant between and r = > Therefore, r is significant. Example 12.8 Suppose you computed r = with 14 data points. df = 14 2 = 12. The critical values are and Since 0.624< 0.532, r is significant and the line may be used for prediction Figure 12.12: r = 0.624< Therefore, r is significant. Example 12.9 Suppose you computed r = and n = 6. df = 6 2 = 4. The critical values are and Since 0.811< < 0.811, r is not significant and the line should not be used for prediction. Figure 12.13: 0.811<r = 0.776< Therefore, r is not significant. If r = 1 or r = +1, then all the data points lie exactly on a straight line. If the line is significant, then within the range of the x-values, the line can be used to predict a y value. As an illustration, consider the third exam/final exam example. The line of best fit is: ^y= x with r = Can the line be used for prediction? Given a third exam score (x value), can we successfully predict the final exam score (predicted y value). Test r = with its appropriate critical value. Using the table with df = 11 2 = 9, the critical values are and Since > 0.602, r is significant. Because r is significant and the scatter plot shows a reasonable linear trend, the line can be used to predict final exam scores.
12 486 CHAPTER 12. LINEAR REGRESSION AND CORRELATION Example Suppose you computed the following correlation coefficients. Using the table at the end of the chapter, determine if r is significant and the line of best fit associated with each r can be used to predict a y value. If it helps, draw a number line. r = and the sample size, n, is 19. The df = n 2 = 17. The critical value is < so r is significant. r = and the sample size, n, is 9. The df = n 2 = 7. The critical value is > so r is significant. r = and the sample size, n, is 14. The df = 14 2 = 12. The critical value is is between and so r is not significant. r = 0 and the sample size, n, is 5. No matter what the dfs are, r = 0 is between the two critical values so r is not significant Prediction 8 The exam scores (x-values) range from 65 to 75. Suppose you want to know the final exam score of statistics students who received 73 on the third exam. Since 73 is between the x-values 65 and 75, substitute x = 73 into the equation. Then: ^y= (73) = (12.7) We predict that a statistics student who receives a 73 on the third exam will receive on the final exam. Remember, do not use the regression equation to predict values outside the domain of x. Example Recall the third exam/final exam example. Problem 1 What would you predict the final exam score to be for a student who scored a 66 on the third exam? Solution Problem 2 (Solution on p. 520.) What would you predict the final exam score to be for a student who scored a 78 on the third exam? 12.9 Outliers 9 In some data sets, there are values (points) called outliers. Outliers are points that are far from the least squares line. They have large "errors." Outliers need to be examined closely. Sometimes, for some reason or another, they should not be included in the analysis of the data. It is possible that an outlier is a result of erroneous data. Other times, an outlier may hold valuable information about the population under study. The key is to carefully examine what causes a data point to be an outlier. 8 This content is available online at < 9 This content is available online at <
13 487 Example In the third exam/final exam example, you can determine if there is an outlier or not. If there is one, as an exercise, delete it and fit the remaining data to a new line. For this example, the new line ought to fit the remaining data better. This means the SSE should be smaller and the correlation coefficient ought to be closer to 1 or -1. Solution Computers and many calculators can determine outliers from the data. However, as an exercise, we will go through the steps that are needed to calculate an outlier. In the table below, the first two columns are the third exam and the final exam data. The third column shows the y-hat values calculated from the line of best fit. x y ^y Table 12.1 A Residual is the Actual y value predicted y value = y ^y Calculate the absolute value of each residual. Calculate each y ^y :
14 488 CHAPTER 12. LINEAR REGRESSION AND CORRELATION x y ^y y ^y = = = = = = = = = = = 1 Table 12.2 Square each y ^y : 35 2 ; 17 2 ; 16 2 ; 6 2 ; 19 2 ; 9 2 ; 3 2 ; 1 2 ; 10 2 ; 9 2 ; 1 2 Then, add (sum) all the y ^y squared terms: ( 11 Σ y ^y ) 2 = 11 Σ i = 1 i = 1 ɛ2 (Recall that y i ^y i = ɛ i.) = = 2440 = SSE Next, calculate s, the standard deviation of all the y ^y = ɛ values where n = the total number of data points. (Calculate the standard deviation of 35; 17; 16; 6; 19; 9; 3; 1; 10; 9; 1.) s = SSE n For the third exam/final exam problem, s = 11 2 = Next, multiply s by 1.9 and get (1.9) (16.47) = (the value is almost 2 standard deviations away from the mean of the y ^y values.) NOTE: The number 1.9s is equal to 1.9 standard deviations. It is a measure that is almost 2 standard deviations. If we were to measure the vertical distance from any data point to the corresponding point on the line of best fit and that distance was equal to 1.9s or greater, then we would consider the data point to be "too far" from the line of best fit. We would call that point a potential outlier.
15 489 For the example, if any of the y ^y values are at least 31.29, the corresponding (x, y) point (data point) is a potential outlier. Mathematically, we say that if y ^y (1.9) (s), then the corresponding point is an outlier. For the third exam/final exam problem, all the y ^y s are less than except for the first one which is > That is, y ^y (1.9) (s) The point which corresponds to y ^y = 35 is (65, 175). Therefore, the point (65, 175) is an outlier. For this example, we will delete it. (Remember, we do not always delete an outlier.) The next step is to compute a new best-fit line using the 10 remaining points. The new line of best fit and the correlation coefficient are: ^y= x and r = If you compare r = to its critical value 0.632, > Therefore, r is significant. In fact, r = is a better r than the original (0.6631) because r = is closer to 1. This means that the 10 points fit the line better. The line can better predict the final exam score given the third exam score. Example Using the new line of best fit (calculated with 10 points), what would a student who receives a 73 on the third exam expect to receive on the final exam? Example (From The Consumer Price Indexes Web site) The Consumer Price Index (CPI) measures the average change over time in the prices paid by urban consumers for consumer goods and services. The CPI affects nearly all Americans because of the many ways it is used. One of its biggest uses is as a measure of inflation. By providing information about price changes in the Nation s economy to government, business, and labor, the CPI helps them to make economic decisions. The President, Congress, and the Federal Reserve Board use the CPI s trends to formulate monetary and fiscal policies. In the following table, x is the year and y is the CPI.
16 490 CHAPTER 12. LINEAR REGRESSION AND CORRELATION Data: Problem Make a scatterplot of the data. x y Table 12.3 Calculate the least squares line. Write the equation in the form ^y= a + bx. Draw the line on the scatterplot. Find the correlation coefficient. Is it significant? What is the average CPI for the year 1990? Solution Scatter plot and line of best fit. ^y= x is the equation of the line of best fit. r = The number of data points is n = 14. Use the 95% Critical Values of the Sample Correlation Coefficient table at the end of Chapter 12. n 2 = 12. The corresponding critical value is Since > 0.532, r is significant. ^y= (1990) = CPI
17 491 Figure % Critical Values of the Sample Correlation Coefficient Table 10 Degrees of Freedom: n 2 Critical Values: (+ and ) continued on next page 10 This content is available online at <
18 492 CHAPTER 12. LINEAR REGRESSION AND CORRELATION and over Table 12.4
19 Summary 11 Bivariate Data: Each data point has two values. The form is (x, y). Line of Best Fit or Least Squares Line (LSL): ^y= a + bx x = independent variable; y = dependent variable Residual: Actual y value predicted y value = y ^y Correlation Coefficient r: 1. Used to determine whether a line of best fit is good for prediction. 2. Between -1 and 1 inclusive. The closer r is to 1 or -1, the closer the original points are to a straight line. 3. If r is negative, the slope is negative. If r is positive, the slope is positive. 4. If r = 0, then the line is horizontal. Sum of Squared Errors (SSE): The smaller the SSE, the better the original set of points fits the line of best fit. Outlier: A point that does not seem to fit the rest of the data. 11 This content is available online at <
20 494 CHAPTER 12. LINEAR REGRESSION AND CORRELATION Practice: Linear Regression Student Learning Outcomes The student will explore the properties of linear regression Given The data below are real. Keep in mind that these are only reported figures. (Source: Centers for Disease Control and Prevention, National Center for HIV, STD, and TB Prevention, October 24, 2003) Adults and Adolescents only, United States Year # AIDS cases diagnosed # AIDS deaths Pre , ,076 1, ,240 3, ,776 6, ,032 11, ,564 16, ,447 20, ,674 27, ,634 31, ,660 36, ,530 41, ,834 44, ,874 49, ,505 49, ,347 38, ,149 20, ,393 19, ,174 18, ,522 17, ,643 17, ,464 16,371 Total 802, ,093 Table This content is available online at <
21 495 NOTE: We will use the columns year and # AIDS cases diagnosed for all questions unless otherwise stated Graphing Graph year vs. # AIDS cases diagnosed. Plot the points on the graph located below in the section titled "Plot". Do not include pre Label both axes with words. Scale both axes Data Exercise Enter your data into your calculator or computer. The pre-1981 data should not be included. Why is that so? Linear Equation Write the linear equation below, rounding to 4 decimal places: Exercise (Solution on p. 520.) Calculate the following: a. a = b. b = c. corr. = d. n =(# of pairs) Exercise (Solution on p. 520.) equation: ^y= Solve Exercise (Solution on p. 520.) Solve. a. When x = 1985, ^y= b. When x = 1990, ^y= Plot Plot the 2 above points on the graph below. Then, connect the 2 points to form the regression line.
22 496 CHAPTER 12. LINEAR REGRESSION AND CORRELATION Obtain the graph on your calculator or computer Discussion Questions Look at the graph above. Exercise Does the line seem to fit the data? Why or why not? Exercise Do you think a linear fit is best? Why or why not? Exercise Hand draw a smooth curve on the graph above that shows the flow of the data. Exercise What does the correlation imply about the relationship between time (years) and the number of diagnosed AIDS cases reported in the U.S.? Exercise Why is year the independent variable and # AIDS cases diagnosed. the dependent variable (instead of the reverse)? Exercise (Solution on p. 520.) Solve. a. When x = 1970, ^y=: b. Why doesn t this answer make sense?
23 Homework 13 Exercise (Solution on p. 520.) For each situation below, state the independent variable and the dependent variable. a. A study is done to determine if elderly drivers are involved in more motor vehicle fatalities than all other drivers. The number of fatalities per 100,000 drivers is compared to the age of drivers. b. A study is done to determine if the weekly grocery bill changes based on the number of family members. c. Insurance companies base life insurance premiums partially on the age of the applicant. d. Utility bills vary according to power consumption. e. A study is done to determine if a higher education reduces the crime rate in a population. Exercise In 1990 the number of driver deaths per 100,000 for the different age groups was as follows (Source: The National Highway Traffic Safety Administration s National Center for Statistics and Analysis): Age Number of Driver Deaths per 100, Table 12.6 a. For each age group, pick the midpoint of the interval for the x value. (For the 80+ group, use 85.) b. Using ages as the independent variable and Number of driver deaths per 100,000 as the dependent variable, make a scatter plot of the data. c. Calculate the least squares (best fit) line. Put the equation in the form of: ^y= a + bx d. Find the correlation coefficient. Is it significant? e. Pick two ages and find the estimated fatality rates. f. Use the two points in (e) to plot the least squares line on your graph from (b). g. Based on the above data, is there a linear relationship between age of a driver and driver fatality rate? h. What is the slope of the least squares (best-fit) line? Interpret the slope. Exercise (Solution on p. 520.) The average number of people in a family that received welfare for various years is given below. (Source: House Ways and Means Committee, Health and Human Services Department) 13 This content is available online at <
24 498 CHAPTER 12. LINEAR REGRESSION AND CORRELATION Year Welfare family size Table 12.7 a. Using year as the independent variable and welfare family size as the dependent variable, make a scatter plot of the data. b. Calculate the least squares line. Put the equation in the form of: ^y= a + bx c. Find the correlation coefficient. Is it significant? d. Pick two years between 1969 and 1991 and find the estimated welfare family sizes. e. Use the two points in (d) to plot the least squares line on your graph from (b). f. Based on the above data, is there a linear relationship between the year and the average number of people in a welfare family? g. Using the least squares line, estimate the welfare family sizes for 1960 and Does the least squares line give an accurate estimate for those years? Explain why or why not. h. Are there any outliers in the above data? i. What is the estimated average welfare family size for 1986? Does the least squares line give an accurate estimate for that year? Explain why or why not. j. What is the slope of the least squares (best-fit) line? Interpret the slope. Exercise Use the AIDS data from the practice for this section (Section : Given), but this time use the columns year # and # new AIDS deaths in U.S. Answer all of the questions from the practice again, using the new columns. Exercise (Solution on p. 520.) The height (sidewalk to roof) of notable tall buildings in America is compared to the number of stories of the building (beginning at street level). (Source: Microsoft Bookshelf)
25 499 Height (in feet) Stories Table 12.8 a. Using stories as the independent variable and height as the dependent variable, make a scatter plot of the data. b. Does it appear from inspection that there is a relationship between the variables? c. Calculate the least squares line. Put the equation in the form of: ^y= a + bx d. Find the correlation coefficient. Is it significant? e. Find the estimated heights for 32 stories and for 94 stories. f. Use the two points in (e) to plot the least squares line on your graph from (b). g. Based on the above data, is there a linear relationship between the number of stories in tall buildings and the height of the buildings? h. Are there any outliers in the above data? If so, which point(s)? i. What is the estimated height of a building with 6 stories? Does the least squares line give an accurate estimate of height? Explain why or why not. j. Based on the least squares line, adding an extra story adds about how many feet to a building? k. What is the slope of the least squares (best-fit) line? Interpret the slope.
26 500 CHAPTER 12. LINEAR REGRESSION AND CORRELATION Exercise Below is the life expectancy for an individual born in the United States in certain years. (Source: National Center for Health Statistics) Year of Birth Life Expectancy Table 12.9 a. Decide which variable should be the independent variable and which should be the dependent variable. b. Draw a scatter plot of the ordered pairs. c. Calculate the least squares line. Put the equation in the form of: ^y= a + bx d. Find the correlation coefficient. Is it significant? e. Find the estimated life expectancy for an individual born in 1950 and for one born in f. Why aren t the answers to part (e) the values on the above chart that correspond to those years? g. Use the two points in (e) to plot the least squares line on your graph from (b). h. Based on the above data, is there a linear relationship between the year of birth and life expectancy? i. Are there any outliers in the above data? j. Using the least squares line, find the estimated life expectancy for an individual born in Does the least squares line give an accurate estimate for that year? Explain why or why not. k. What is the slope of the least squares (best-fit) line? Interpret the slope. Exercise (Solution on p. 521.) The percent of female wage and salary workers who are paid hourly rates is given below for the years (Source: Bureau of Labor Statistics, U.S. Dept. of Labor)
27 501 Year Percent of workers paid hourly rates Table a. Using year as the independent variable and percent as the dependent variable, make a scatter plot of the data. b. Does it appear from inspection that there is a relationship between the variables? Why or why not? c. Calculate the least squares line. Put the equation in the form of: ^y= a + bx d. Find the correlation coefficient. Is it significant? e. Find the estimated percents for 1991 and f. Use the two points in (e) to plot the least squares line on your graph from (b). g. Based on the above data, is there a linear relationship between the year and the percent of female wage and salary earners who are paid hourly rates? h. Are there any outliers in the above data? i. What is the estimated percent for the year 2050? Does the least squares line give an accurate estimate for that year? Explain why or why not? j. What is the slope of the least squares (best-fit) line? Interpret the slope. Exercise The maximum discount value of the Entertainment card for the Fine Dining section, Edition 10, for various pages is given below.
28 502 CHAPTER 12. LINEAR REGRESSION AND CORRELATION Page number Maximum value ($) Table a. Decide which variable should be the independent variable and which should be the dependent variable. b. Draw a scatter plot of the ordered pairs. c. Calculate the least squares line. Put the equation in the form of: ^y= a + bx d. Find the correlation coefficient. Is it significant? e. Find the estimated maximum values for the restaurants on page 10 and on page 70. f. Use the two points in (e) to plot the least squares line on your graph from (b). g. Does it appear that the restaurants giving the maximum value are placed in the beginning of the Fine Dining section? How did you arrive at your answer? h. Suppose that there were 200 pages of restaurants. What do you estimate to be the maximum value for a restaurant listed on page 200? i. Is the least squares line valid for page 200? Why or why not? j. What is the slope of the least squares (best-fit) line? Interpret the slope. The next two questions refer to the following data: The cost of a leading liquid laundry detergent in different sizes is given below. Size (ounces) Cost ($) Cost per ounce Table Exercise (Solution on p. 521.) a. Using size as the independent variable and cost as the dependent variable, make a scatter plot. b. Does it appear from inspection that there is a relationship between the variables? Why or why not?
29 503 c. Calculate the least squares line. Put the equation in the form of: ^y= a + bx d. Find the correlation coefficient. Is it significant? e. If the laundry detergent were sold in a 40 ounce size, find the estimated cost. f. If the laundry detergent were sold in a 90 ounce size, find the estimated cost. g. Use the two points in (e) and (f) to plot the least squares line on your graph from (a). h. Does it appear that a line is the best way to fit the data? Why or why not? i. Are there any outliers in the above data? j. Is the least squares line valid for predicting what a 300 ounce size of the laundry detergent would cost? Why or why not? k. What is the slope of the least squares (best-fit) line? Interpret the slope. Exercise a. Complete the above table for the cost per ounce of the different sizes. b. Using Size as the independent variable and Cost per ounce as the dependent variable, make a scatter plot of the data. c. Does it appear from inspection that there is a relationship between the variables? Why or why not? d. Calculate the least squares line. Put the equation in the form of: ^y= a + bx e. Find the correlation coefficient. Is it significant? f. If the laundry detergent were sold in a 40 ounce size, find the estimated cost per ounce. g. If the laundry detergent were sold in a 90 ounce size, find the estimated cost per ounce. h. Use the two points in (f) and (g) to plot the least squares line on your graph from (b). i. Does it appear that a line is the best way to fit the data? Why or why not? j. Are there any outliers in the above data? k. Is the least squares line valid for predicting what a 300 ounce size of the laundry detergent would cost per ounce? Why or why not? l. What is the slope of the least squares (best-fit) line? Interpret the slope. Exercise (Solution on p. 521.) According to flyer by a Prudential Insurance Company representative, the costs of approximate probate fees and taxes for selected net taxable estates are as follows: Net Taxable Estate ($) Approximate Probate Fees and Taxes ($) 600,000 30, ,000 92,500 1,000, ,000 1,500, ,000 2,000, ,000 2,500,000 1,037,000 3,000,000 1,350,000 Table a. Decide which variable should be the independent variable and which should be the dependent variable. b. Make a scatter plot of the data.
30 504 CHAPTER 12. LINEAR REGRESSION AND CORRELATION c. Does it appear from inspection that there is a relationship between the variables? Why or why not? d. Calculate the least squares line. Put the equation in the form of: ^y= a + bx e. Find the correlation coefficient. Is it significant? f. Find the estimated total cost for a net taxable estate of $1,000,000. Find the cost for $2,500,000. g. Use the two points in (f) to plot the least squares line on your graph from (b). h. Does it appear that a line is the best way to fit the data? Why or why not? i. Are there any outliers in the above data? j. Based on the above, what would be the probate fees and taxes for an estate that does not have any assets? k. What is the slope of the least squares (best-fit) line? Interpret the slope. Exercise The following are advertised sale prices of color televisions at Anderson s. Size (inches) Sale Price ($) Table a. Decide which variable should be the independent variable and which should be the dependent variable. b. Make a scatter plot of the data. c. Does it appear from inspection that there is a relationship between the variables? Why or why not? d. Calculate the least squares line. Put the equation in the form of: ^y= a + bx e. Find the correlation coefficient. Is it significant? f. Find the estimated sale price for a 32 inch television. Find the cost for a 50 inch television. g. Use the two points in (f) to plot the least squares line on your graph from (b). h. Does it appear that a line is the best way to fit the data? Why or why not? i. Are there any outliers in the above data? j. What is the slope of the least squares (best-fit) line? Interpret the slope. Exercise (Solution on p. 521.) Below are the average heights for American boys. (Source: Physician s Handbook, 1990)
31 505 Age (years) Height (cm) birth Table a. Decide which variable should be the independent variable and which should be the dependent variable. b. Make a scatter plot of the data. c. Does it appear from inspection that there is a relationship between the variables? Why or why not? d. Calculate the least squares line. Put the equation in the form of: ^y= a + bx e. Find the correlation coefficient. Is it significant? f. Find the estimated average height for a one year old. Find the estimated average height for an eleven year old. g. Use the two points in (f) to plot the least squares line on your graph from (b). h. Does it appear that a line is the best way to fit the data? Why or why not? i. Are there any outliers in the above data? j. Use the least squares line to estimate the average height for a sixty two year old man. Do you think that your answer is reasonable? Why or why not? k. What is the slope of the least squares (best-fit) line? Interpret the slope. Exercise The following chart gives the gold medal times for every other Summer Olympics for the women s 100 meter freestyle (swimming). Year Time (seconds) Table 12.16
32 506 CHAPTER 12. LINEAR REGRESSION AND CORRELATION a. Decide which variable should be the independent variable and which should be the dependent variable. b. Make a scatter plot of the data. c. Does it appear from inspection that there is a relationship between the variables? Why or why not? d. Calculate the least squares line. Put the equation in the form of: ^y= a + bx e. Find the correlation coefficient. Is the decrease in times significant? f. Find the estimated gold medal time for Find the estimated time for g. Why are the answers from (f) different from the chart values? h. Use the two points in (f) to plot the least squares line on your graph from (b). i. Does it appear that a line is the best way to fit the data? Why or why not? j. Use the least squares line to estimate the gold medal time for the next Summer Olympics. Do you think that your answer is reasonable? Why or why not? The next three questions use the following state information. State # letters in name Year entered the Union Rank for entering the Union Area miles) Alabama ,423 Colorado ,100 Hawaii ,932 Iowa ,276 Maryland ,407 Missouri ,709 New Jersey ,722 Ohio ,828 South Carolina ,008 Utah ,904 Wisconsin ,499 (square Table Exercise (Solution on p. 521.) We are interested in whether or not the number of letters in a state name depends upon the year the state entered the Union. a. Decide which variable should be the independent variable and which should be the dependent variable. b. Make a scatter plot of the data. c. Does it appear from inspection that there is a relationship between the variables? Why or why not? d. Calculate the least squares line. Put the equation in the form of: ^y= a + bx e. Find the correlation coefficient. What does it imply about the significance of the relationship? f. Find the estimated number of letters (to the nearest integer) a state would have if it entered the Union in Find the estimated number of letters a state would have if it entered the Union in 1940.
33 507 g. Use the two points in (f) to plot the least squares line on your graph from (b). h. Does it appear that a line is the best way to fit the data? Why or why not? i. Use the least squares line to estimate the number of letters a new state that enters the Union this year would have. Can the least squares line be used to predict it? Why or why not? Exercise We are interested in whether there is a relationship between the ranking of a state and the area of the state. a. Let rank be the independent variable and area be the dependent variable. b. What do you think the scatter plot will look like? Make a scatter plot of the data. c. Does it appear from inspection that there is a relationship between the variables? Why or why not? d. Calculate the least squares line. Put the equation in the form of: ^y= a + bx e. Find the correlation coefficient. What does it imply about the significance of the relationship? f. Find the estimated areas for Alabama and for Colorado. Are they close to the actual areas? g. Use the two points in (f) to plot the least squares line on your graph from (b). h. Does it appear that a line is the best way to fit the data? Why or why not? i. Are there any outliers? j. Use the least squares line to estimate the area of a new state that enters the Union. Can the least squares line be used to predict it? Why or why not? k. Delete Hawaii and substitute Alaska for it. Alaska is the fortieth state with an area of 656,424 square miles. l. Calculate the new least squares line. m. Find the estimated area for Alabama. Is it closer to the actual area with this new least squares line or with the previous one that included Hawaii? Why do you think that s the case? n. Do you think that, in general, newer states are larger than the original states? Exercise (Solution on p. 522.) We are interested in whether there is a relationship between the rank of a state and the year it entered the Union. a. Let year be the independent variable and rank be the dependent variable. b. What do you think the scatter plot will look like? Make a scatter plot of the data. c. Why must the relationship be positive between the variables? d. Calculate the least squares line. Put the equation in the form of: ^y= a + bx e. Find the correlation coefficient. What does it imply about the significance of the relationship? f. Let s say a fifty-first state entered the union. Based upon the least squares line, when should that have occurred? g. Using the least squares line, how many states do we currently have? h. Why isn t the least squares line a good estimator for this year? Exercise Below are the percents of the U.S. labor force (excluding self-employed and unemployed ) that are members of a union. We are interested in whether the decrease is significant. (Source: Bureau of Labor Statistics, U.S. Dept. of Labor)
34 508 CHAPTER 12. LINEAR REGRESSION AND CORRELATION Year Percent Table a. Let year be the independent variable and percent be the dependent variable. b. What do you think the scatter plot will look like? Make a scatter plot of the data. c. Why will the relationship between the variables be negative? d. Calculate the least squares line. Put the equation in the form of: ^y= a + bx e. Find the correlation coefficient. What does it imply about the significance of the relationship? f. Based on your answer to (e), do you think that the relationship can be said to be decreasing? g. If the trend continues, when will there no longer be any union members? Do you think that will happen? The next two questions refer to the following information: The data below reflects the Reunion Class Giving. (Source: SUNY Albany alumni magazine) Class Year Average Gift Total Giving , , , , , , , , , , ,590 Table Exercise (Solution on p. 522.) We will use the columns class year and total giving for all questions, unless otherwise stated.
35 509 a. What do you think the scatter plot will look like? Make a scatter plot of the data. b. Calculate the least squares line. Put the equation in the form of: ^y= a + bx c. Find the correlation coefficient. What does it imply about the significance of the relationship? d. For the class of 1930, predict the total class gift. e. For the class of 1964, predict the total class gift. f. For the class of 1850, predict the total class gift. Why doesn t this value make any sense? Exercise We will use the columns class year and average gift for all questions, unless otherwise stated. a. What do you think the scatter plot will look like? Make a scatter plot of the data. b. Calculate the least squares line. Put the equation in the form of: ^y= a + bx c. Find the correlation coefficient. What does it imply about the significance of the relationship? d. For the class of 1930, predict the average class gift. e. For the class of 1964, predict the average class gift. f. For the class of 2010, predict the average class gift. Why doesn t this value make any sense? Try these multiple choice questions Exercise (Solution on p. 522.) A correlation coefficient of means there is a between the two variables. A. Strong positive correlation B. Weak negative correlation C. Strong negative correlation D. No Correlation Exercise (Solution on p. 522.) According to the data reported by the New York State Department of Health regarding West Nile Virus for the years , the least squares line equation for the number of reported dead birds (x) versus the number of human West Nile virus cases (y) is ^y= x. If the number of dead birds reported in a year is 732, how many human cases of West Nile virus can be expected? A B C D The next three questions refer to the following data: (showing the number of hurricanes by category to directly strike the mainland U.S. each decade) obtained from 14 A major hurricane is one with a strength rating of 3, 4 or
Chapter 10. Key Ideas Correlation, Correlation Coefficient (r),
 Chapter 0 Key Ideas Correlation, Correlation Coefficient (r), Section 0-: Overview We have already explored the basics of describing single variable data sets. However, when two quantitative variables
Chapter 0 Key Ideas Correlation, Correlation Coefficient (r), Section 0-: Overview We have already explored the basics of describing single variable data sets. However, when two quantitative variables
Session 7 Bivariate Data and Analysis
 Session 7 Bivariate Data and Analysis Key Terms for This Session Previously Introduced mean standard deviation New in This Session association bivariate analysis contingency table co-variation least squares
Session 7 Bivariate Data and Analysis Key Terms for This Session Previously Introduced mean standard deviation New in This Session association bivariate analysis contingency table co-variation least squares
Correlation key concepts:
 CORRELATION Correlation key concepts: Types of correlation Methods of studying correlation a) Scatter diagram b) Karl pearson s coefficient of correlation c) Spearman s Rank correlation coefficient d)
CORRELATION Correlation key concepts: Types of correlation Methods of studying correlation a) Scatter diagram b) Karl pearson s coefficient of correlation c) Spearman s Rank correlation coefficient d)
Example: Boats and Manatees
 Figure 9-6 Example: Boats and Manatees Slide 1 Given the sample data in Table 9-1, find the value of the linear correlation coefficient r, then refer to Table A-6 to determine whether there is a significant
Figure 9-6 Example: Boats and Manatees Slide 1 Given the sample data in Table 9-1, find the value of the linear correlation coefficient r, then refer to Table A-6 to determine whether there is a significant
Correlation Coefficient The correlation coefficient is a summary statistic that describes the linear relationship between two numerical variables 2
 Lesson 4 Part 1 Relationships between two numerical variables 1 Correlation Coefficient The correlation coefficient is a summary statistic that describes the linear relationship between two numerical variables
Lesson 4 Part 1 Relationships between two numerical variables 1 Correlation Coefficient The correlation coefficient is a summary statistic that describes the linear relationship between two numerical variables
Exercise 1.12 (Pg. 22-23)
 Individuals: The objects that are described by a set of data. They may be people, animals, things, etc. (Also referred to as Cases or Records) Variables: The characteristics recorded about each individual.
Individuals: The objects that are described by a set of data. They may be people, animals, things, etc. (Also referred to as Cases or Records) Variables: The characteristics recorded about each individual.
Section 14 Simple Linear Regression: Introduction to Least Squares Regression
 Slide 1 Section 14 Simple Linear Regression: Introduction to Least Squares Regression There are several different measures of statistical association used for understanding the quantitative relationship
Slide 1 Section 14 Simple Linear Regression: Introduction to Least Squares Regression There are several different measures of statistical association used for understanding the quantitative relationship
Chapter 7: Simple linear regression Learning Objectives
 Chapter 7: Simple linear regression Learning Objectives Reading: Section 7.1 of OpenIntro Statistics Video: Correlation vs. causation, YouTube (2:19) Video: Intro to Linear Regression, YouTube (5:18) -
Chapter 7: Simple linear regression Learning Objectives Reading: Section 7.1 of OpenIntro Statistics Video: Correlation vs. causation, YouTube (2:19) Video: Intro to Linear Regression, YouTube (5:18) -
Module 3: Correlation and Covariance
 Using Statistical Data to Make Decisions Module 3: Correlation and Covariance Tom Ilvento Dr. Mugdim Pašiƒ University of Delaware Sarajevo Graduate School of Business O ften our interest in data analysis
Using Statistical Data to Make Decisions Module 3: Correlation and Covariance Tom Ilvento Dr. Mugdim Pašiƒ University of Delaware Sarajevo Graduate School of Business O ften our interest in data analysis
Lecture 11: Chapter 5, Section 3 Relationships between Two Quantitative Variables; Correlation
 Lecture 11: Chapter 5, Section 3 Relationships between Two Quantitative Variables; Correlation Display and Summarize Correlation for Direction and Strength Properties of Correlation Regression Line Cengage
Lecture 11: Chapter 5, Section 3 Relationships between Two Quantitative Variables; Correlation Display and Summarize Correlation for Direction and Strength Properties of Correlation Regression Line Cengage
Elasticity. I. What is Elasticity?
 Elasticity I. What is Elasticity? The purpose of this section is to develop some general rules about elasticity, which may them be applied to the four different specific types of elasticity discussed in
Elasticity I. What is Elasticity? The purpose of this section is to develop some general rules about elasticity, which may them be applied to the four different specific types of elasticity discussed in
Plot the following two points on a graph and draw the line that passes through those two points. Find the rise, run and slope of that line.
 Objective # 6 Finding the slope of a line Material: page 117 to 121 Homework: worksheet NOTE: When we say line... we mean straight line! Slope of a line: It is a number that represents the slant of a line
Objective # 6 Finding the slope of a line Material: page 117 to 121 Homework: worksheet NOTE: When we say line... we mean straight line! Slope of a line: It is a number that represents the slant of a line
Relationships Between Two Variables: Scatterplots and Correlation
 Relationships Between Two Variables: Scatterplots and Correlation Example: Consider the population of cars manufactured in the U.S. What is the relationship (1) between engine size and horsepower? (2)
Relationships Between Two Variables: Scatterplots and Correlation Example: Consider the population of cars manufactured in the U.S. What is the relationship (1) between engine size and horsepower? (2)
1.3 LINEAR EQUATIONS IN TWO VARIABLES. Copyright Cengage Learning. All rights reserved.
 1.3 LINEAR EQUATIONS IN TWO VARIABLES Copyright Cengage Learning. All rights reserved. What You Should Learn Use slope to graph linear equations in two variables. Find the slope of a line given two points
1.3 LINEAR EQUATIONS IN TWO VARIABLES Copyright Cengage Learning. All rights reserved. What You Should Learn Use slope to graph linear equations in two variables. Find the slope of a line given two points
Correlation and Regression
 Correlation and Regression Scatterplots Correlation Explanatory and response variables Simple linear regression General Principles of Data Analysis First plot the data, then add numerical summaries Look
Correlation and Regression Scatterplots Correlation Explanatory and response variables Simple linear regression General Principles of Data Analysis First plot the data, then add numerical summaries Look
Review of Fundamental Mathematics
 Review of Fundamental Mathematics As explained in the Preface and in Chapter 1 of your textbook, managerial economics applies microeconomic theory to business decision making. The decision-making tools
Review of Fundamental Mathematics As explained in the Preface and in Chapter 1 of your textbook, managerial economics applies microeconomic theory to business decision making. The decision-making tools
Unit 31 A Hypothesis Test about Correlation and Slope in a Simple Linear Regression
 Unit 31 A Hypothesis Test about Correlation and Slope in a Simple Linear Regression Objectives: To perform a hypothesis test concerning the slope of a least squares line To recognize that testing for a
Unit 31 A Hypothesis Test about Correlation and Slope in a Simple Linear Regression Objectives: To perform a hypothesis test concerning the slope of a least squares line To recognize that testing for a
Solving Quadratic Equations
 9.3 Solving Quadratic Equations by Using the Quadratic Formula 9.3 OBJECTIVES 1. Solve a quadratic equation by using the quadratic formula 2. Determine the nature of the solutions of a quadratic equation
9.3 Solving Quadratic Equations by Using the Quadratic Formula 9.3 OBJECTIVES 1. Solve a quadratic equation by using the quadratic formula 2. Determine the nature of the solutions of a quadratic equation
Section 3 Part 1. Relationships between two numerical variables
 Section 3 Part 1 Relationships between two numerical variables 1 Relationship between two variables The summary statistics covered in the previous lessons are appropriate for describing a single variable.
Section 3 Part 1 Relationships between two numerical variables 1 Relationship between two variables The summary statistics covered in the previous lessons are appropriate for describing a single variable.
Linear Regression. Chapter 5. Prediction via Regression Line Number of new birds and Percent returning. Least Squares
 Linear Regression Chapter 5 Regression Objective: To quantify the linear relationship between an explanatory variable (x) and response variable (y). We can then predict the average response for all subjects
Linear Regression Chapter 5 Regression Objective: To quantify the linear relationship between an explanatory variable (x) and response variable (y). We can then predict the average response for all subjects
What does the number m in y = mx + b measure? To find out, suppose (x 1, y 1 ) and (x 2, y 2 ) are two points on the graph of y = mx + b.
 PRIMARY CONTENT MODULE Algebra - Linear Equations & Inequalities T-37/H-37 What does the number m in y = mx + b measure? To find out, suppose (x 1, y 1 ) and (x 2, y 2 ) are two points on the graph of
PRIMARY CONTENT MODULE Algebra - Linear Equations & Inequalities T-37/H-37 What does the number m in y = mx + b measure? To find out, suppose (x 1, y 1 ) and (x 2, y 2 ) are two points on the graph of
6.4 Normal Distribution
 Contents 6.4 Normal Distribution....................... 381 6.4.1 Characteristics of the Normal Distribution....... 381 6.4.2 The Standardized Normal Distribution......... 385 6.4.3 Meaning of Areas under
Contents 6.4 Normal Distribution....................... 381 6.4.1 Characteristics of the Normal Distribution....... 381 6.4.2 The Standardized Normal Distribution......... 385 6.4.3 Meaning of Areas under
EQUATIONS and INEQUALITIES
 EQUATIONS and INEQUALITIES Linear Equations and Slope 1. Slope a. Calculate the slope of a line given two points b. Calculate the slope of a line parallel to a given line. c. Calculate the slope of a line
EQUATIONS and INEQUALITIES Linear Equations and Slope 1. Slope a. Calculate the slope of a line given two points b. Calculate the slope of a line parallel to a given line. c. Calculate the slope of a line
CHAPTER 13 SIMPLE LINEAR REGRESSION. Opening Example. Simple Regression. Linear Regression
 Opening Example CHAPTER 13 SIMPLE LINEAR REGREION SIMPLE LINEAR REGREION! Simple Regression! Linear Regression Simple Regression Definition A regression model is a mathematical equation that descries the
Opening Example CHAPTER 13 SIMPLE LINEAR REGREION SIMPLE LINEAR REGREION! Simple Regression! Linear Regression Simple Regression Definition A regression model is a mathematical equation that descries the
ALGEBRA I (Common Core) Thursday, January 28, 2016 1:15 to 4:15 p.m., only
 ALGEBRA I (COMMON CORE) The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION ALGEBRA I (Common Core) Thursday, January 28, 2016 1:15 to 4:15 p.m., only Student Name: School Name: The
ALGEBRA I (COMMON CORE) The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION ALGEBRA I (Common Core) Thursday, January 28, 2016 1:15 to 4:15 p.m., only Student Name: School Name: The
Simple Regression Theory II 2010 Samuel L. Baker
 SIMPLE REGRESSION THEORY II 1 Simple Regression Theory II 2010 Samuel L. Baker Assessing how good the regression equation is likely to be Assignment 1A gets into drawing inferences about how close the
SIMPLE REGRESSION THEORY II 1 Simple Regression Theory II 2010 Samuel L. Baker Assessing how good the regression equation is likely to be Assignment 1A gets into drawing inferences about how close the
Updates to Graphing with Excel
 Updates to Graphing with Excel NCC has recently upgraded to a new version of the Microsoft Office suite of programs. As such, many of the directions in the Biology Student Handbook for how to graph with
Updates to Graphing with Excel NCC has recently upgraded to a new version of the Microsoft Office suite of programs. As such, many of the directions in the Biology Student Handbook for how to graph with
PLOTTING DATA AND INTERPRETING GRAPHS
 PLOTTING DATA AND INTERPRETING GRAPHS Fundamentals of Graphing One of the most important sets of skills in science and mathematics is the ability to construct graphs and to interpret the information they
PLOTTING DATA AND INTERPRETING GRAPHS Fundamentals of Graphing One of the most important sets of skills in science and mathematics is the ability to construct graphs and to interpret the information they
AP Physics 1 and 2 Lab Investigations
 AP Physics 1 and 2 Lab Investigations Student Guide to Data Analysis New York, NY. College Board, Advanced Placement, Advanced Placement Program, AP, AP Central, and the acorn logo are registered trademarks
AP Physics 1 and 2 Lab Investigations Student Guide to Data Analysis New York, NY. College Board, Advanced Placement, Advanced Placement Program, AP, AP Central, and the acorn logo are registered trademarks
CALCULATIONS & STATISTICS
 CALCULATIONS & STATISTICS CALCULATION OF SCORES Conversion of 1-5 scale to 0-100 scores When you look at your report, you will notice that the scores are reported on a 0-100 scale, even though respondents
CALCULATIONS & STATISTICS CALCULATION OF SCORES Conversion of 1-5 scale to 0-100 scores When you look at your report, you will notice that the scores are reported on a 0-100 scale, even though respondents
. 58 58 60 62 64 66 68 70 72 74 76 78 Father s height (inches)
 PEARSON S FATHER-SON DATA The following scatter diagram shows the heights of 1,0 fathers and their full-grown sons, in England, circa 1900 There is one dot for each father-son pair Heights of fathers and
PEARSON S FATHER-SON DATA The following scatter diagram shows the heights of 1,0 fathers and their full-grown sons, in England, circa 1900 There is one dot for each father-son pair Heights of fathers and
1. The parameters to be estimated in the simple linear regression model Y=α+βx+ε ε~n(0,σ) are: a) α, β, σ b) α, β, ε c) a, b, s d) ε, 0, σ
 STA 3024 Practice Problems Exam 2 NOTE: These are just Practice Problems. This is NOT meant to look just like the test, and it is NOT the only thing that you should study. Make sure you know all the material
STA 3024 Practice Problems Exam 2 NOTE: These are just Practice Problems. This is NOT meant to look just like the test, and it is NOT the only thing that you should study. Make sure you know all the material
F.IF.7b: Graph Root, Piecewise, Step, & Absolute Value Functions
 F.IF.7b: Graph Root, Piecewise, Step, & Absolute Value Functions F.IF.7b: Graph Root, Piecewise, Step, & Absolute Value Functions Analyze functions using different representations. 7. Graph functions expressed
F.IF.7b: Graph Root, Piecewise, Step, & Absolute Value Functions F.IF.7b: Graph Root, Piecewise, Step, & Absolute Value Functions Analyze functions using different representations. 7. Graph functions expressed
CURVE FITTING LEAST SQUARES APPROXIMATION
 CURVE FITTING LEAST SQUARES APPROXIMATION Data analysis and curve fitting: Imagine that we are studying a physical system involving two quantities: x and y Also suppose that we expect a linear relationship
CURVE FITTING LEAST SQUARES APPROXIMATION Data analysis and curve fitting: Imagine that we are studying a physical system involving two quantities: x and y Also suppose that we expect a linear relationship
MATH 60 NOTEBOOK CERTIFICATIONS
 MATH 60 NOTEBOOK CERTIFICATIONS Chapter #1: Integers and Real Numbers 1.1a 1.1b 1.2 1.3 1.4 1.8 Chapter #2: Algebraic Expressions, Linear Equations, and Applications 2.1a 2.1b 2.1c 2.2 2.3a 2.3b 2.4 2.5
MATH 60 NOTEBOOK CERTIFICATIONS Chapter #1: Integers and Real Numbers 1.1a 1.1b 1.2 1.3 1.4 1.8 Chapter #2: Algebraic Expressions, Linear Equations, and Applications 2.1a 2.1b 2.1c 2.2 2.3a 2.3b 2.4 2.5
Homework 11. Part 1. Name: Score: / null
 Name: Score: / Homework 11 Part 1 null 1 For which of the following correlations would the data points be clustered most closely around a straight line? A. r = 0.50 B. r = -0.80 C. r = 0.10 D. There is
Name: Score: / Homework 11 Part 1 null 1 For which of the following correlations would the data points be clustered most closely around a straight line? A. r = 0.50 B. r = -0.80 C. r = 0.10 D. There is
Section 1.1 Linear Equations: Slope and Equations of Lines
 Section. Linear Equations: Slope and Equations of Lines Slope The measure of the steepness of a line is called the slope of the line. It is the amount of change in y, the rise, divided by the amount of
Section. Linear Equations: Slope and Equations of Lines Slope The measure of the steepness of a line is called the slope of the line. It is the amount of change in y, the rise, divided by the amount of
https://williamshartunionca.springboardonline.org/ebook/book/27e8f1b87a1c4555a1212b...
 of 19 9/2/2014 12:09 PM Answers Teacher Copy Plan Pacing: 1 class period Chunking the Lesson Example A #1 Example B Example C #2 Check Your Understanding Lesson Practice Teach Bell-Ringer Activity Students
of 19 9/2/2014 12:09 PM Answers Teacher Copy Plan Pacing: 1 class period Chunking the Lesson Example A #1 Example B Example C #2 Check Your Understanding Lesson Practice Teach Bell-Ringer Activity Students
Chapter 1: Looking at Data Section 1.1: Displaying Distributions with Graphs
 Types of Variables Chapter 1: Looking at Data Section 1.1: Displaying Distributions with Graphs Quantitative (numerical)variables: take numerical values for which arithmetic operations make sense (addition/averaging)
Types of Variables Chapter 1: Looking at Data Section 1.1: Displaying Distributions with Graphs Quantitative (numerical)variables: take numerical values for which arithmetic operations make sense (addition/averaging)
Elements of a graph. Click on the links below to jump directly to the relevant section
 Click on the links below to jump directly to the relevant section Elements of a graph Linear equations and their graphs What is slope? Slope and y-intercept in the equation of a line Comparing lines on
Click on the links below to jump directly to the relevant section Elements of a graph Linear equations and their graphs What is slope? Slope and y-intercept in the equation of a line Comparing lines on
2. Simple Linear Regression
 Research methods - II 3 2. Simple Linear Regression Simple linear regression is a technique in parametric statistics that is commonly used for analyzing mean response of a variable Y which changes according
Research methods - II 3 2. Simple Linear Regression Simple linear regression is a technique in parametric statistics that is commonly used for analyzing mean response of a variable Y which changes according
" Y. Notation and Equations for Regression Lecture 11/4. Notation:
 Notation: Notation and Equations for Regression Lecture 11/4 m: The number of predictor variables in a regression Xi: One of multiple predictor variables. The subscript i represents any number from 1 through
Notation: Notation and Equations for Regression Lecture 11/4 m: The number of predictor variables in a regression Xi: One of multiple predictor variables. The subscript i represents any number from 1 through
Homework 8 Solutions
 Math 17, Section 2 Spring 2011 Homework 8 Solutions Assignment Chapter 7: 7.36, 7.40 Chapter 8: 8.14, 8.16, 8.28, 8.36 (a-d), 8.38, 8.62 Chapter 9: 9.4, 9.14 Chapter 7 7.36] a) A scatterplot is given below.
Math 17, Section 2 Spring 2011 Homework 8 Solutions Assignment Chapter 7: 7.36, 7.40 Chapter 8: 8.14, 8.16, 8.28, 8.36 (a-d), 8.38, 8.62 Chapter 9: 9.4, 9.14 Chapter 7 7.36] a) A scatterplot is given below.
Econometrics Simple Linear Regression
 Econometrics Simple Linear Regression Burcu Eke UC3M Linear equations with one variable Recall what a linear equation is: y = b 0 + b 1 x is a linear equation with one variable, or equivalently, a straight
Econometrics Simple Linear Regression Burcu Eke UC3M Linear equations with one variable Recall what a linear equation is: y = b 0 + b 1 x is a linear equation with one variable, or equivalently, a straight
Simple linear regression
 Simple linear regression Introduction Simple linear regression is a statistical method for obtaining a formula to predict values of one variable from another where there is a causal relationship between
Simple linear regression Introduction Simple linear regression is a statistical method for obtaining a formula to predict values of one variable from another where there is a causal relationship between
17. SIMPLE LINEAR REGRESSION II
 17. SIMPLE LINEAR REGRESSION II The Model In linear regression analysis, we assume that the relationship between X and Y is linear. This does not mean, however, that Y can be perfectly predicted from X.
17. SIMPLE LINEAR REGRESSION II The Model In linear regression analysis, we assume that the relationship between X and Y is linear. This does not mean, however, that Y can be perfectly predicted from X.
G r a d e 1 0 I n t r o d u c t i o n t o A p p l i e d a n d P r e - C a l c u l u s M a t h e m a t i c s ( 2 0 S ) Final Practice Exam
 G r a d e 1 0 I n t r o d u c t i o n t o A p p l i e d a n d P r e - C a l c u l u s M a t h e m a t i c s ( 2 0 S ) Final Practice Exam G r a d e 1 0 I n t r o d u c t i o n t o A p p l i e d a n d
G r a d e 1 0 I n t r o d u c t i o n t o A p p l i e d a n d P r e - C a l c u l u s M a t h e m a t i c s ( 2 0 S ) Final Practice Exam G r a d e 1 0 I n t r o d u c t i o n t o A p p l i e d a n d
Bar Graphs and Dot Plots
 CONDENSED L E S S O N 1.1 Bar Graphs and Dot Plots In this lesson you will interpret and create a variety of graphs find some summary values for a data set draw conclusions about a data set based on graphs
CONDENSED L E S S O N 1.1 Bar Graphs and Dot Plots In this lesson you will interpret and create a variety of graphs find some summary values for a data set draw conclusions about a data set based on graphs
Section 1.5 Linear Models
 Section 1.5 Linear Models Some real-life problems can be modeled using linear equations. Now that we know how to find the slope of a line, the equation of a line, and the point of intersection of two lines,
Section 1.5 Linear Models Some real-life problems can be modeled using linear equations. Now that we know how to find the slope of a line, the equation of a line, and the point of intersection of two lines,
Math 120 Final Exam Practice Problems, Form: A
 Math 120 Final Exam Practice Problems, Form: A Name: While every attempt was made to be complete in the types of problems given below, we make no guarantees about the completeness of the problems. Specifically,
Math 120 Final Exam Practice Problems, Form: A Name: While every attempt was made to be complete in the types of problems given below, we make no guarantees about the completeness of the problems. Specifically,
Answer: C. The strength of a correlation does not change if units change by a linear transformation such as: Fahrenheit = 32 + (5/9) * Centigrade
 Statistics Quiz Correlation and Regression -- ANSWERS 1. Temperature and air pollution are known to be correlated. We collect data from two laboratories, in Boston and Montreal. Boston makes their measurements
Statistics Quiz Correlation and Regression -- ANSWERS 1. Temperature and air pollution are known to be correlated. We collect data from two laboratories, in Boston and Montreal. Boston makes their measurements
1. Which of the 12 parent functions we know from chapter 1 are power functions? List their equations and names.
 Pre Calculus Worksheet. 1. Which of the 1 parent functions we know from chapter 1 are power functions? List their equations and names.. Analyze each power function using the terminology from lesson 1-.
Pre Calculus Worksheet. 1. Which of the 1 parent functions we know from chapter 1 are power functions? List their equations and names.. Analyze each power function using the terminology from lesson 1-.
1) Write the following as an algebraic expression using x as the variable: Triple a number subtracted from the number
 1) Write the following as an algebraic expression using x as the variable: Triple a number subtracted from the number A. 3(x - x) B. x 3 x C. 3x - x D. x - 3x 2) Write the following as an algebraic expression
1) Write the following as an algebraic expression using x as the variable: Triple a number subtracted from the number A. 3(x - x) B. x 3 x C. 3x - x D. x - 3x 2) Write the following as an algebraic expression
A Determination of g, the Acceleration Due to Gravity, from Newton's Laws of Motion
 A Determination of g, the Acceleration Due to Gravity, from Newton's Laws of Motion Objective In the experiment you will determine the cart acceleration, a, and the friction force, f, experimentally for
A Determination of g, the Acceleration Due to Gravity, from Newton's Laws of Motion Objective In the experiment you will determine the cart acceleration, a, and the friction force, f, experimentally for
Temperature Scales. The metric system that we are now using includes a unit that is specific for the representation of measured temperatures.
 Temperature Scales INTRODUCTION The metric system that we are now using includes a unit that is specific for the representation of measured temperatures. The unit of temperature in the metric system is
Temperature Scales INTRODUCTION The metric system that we are now using includes a unit that is specific for the representation of measured temperatures. The unit of temperature in the metric system is
Week 1: Functions and Equations
 Week 1: Functions and Equations Goals: Review functions Introduce modeling using linear and quadratic functions Solving equations and systems Suggested Textbook Readings: Chapter 2: 2.1-2.2, and Chapter
Week 1: Functions and Equations Goals: Review functions Introduce modeling using linear and quadratic functions Solving equations and systems Suggested Textbook Readings: Chapter 2: 2.1-2.2, and Chapter
II. DISTRIBUTIONS distribution normal distribution. standard scores
 Appendix D Basic Measurement And Statistics The following information was developed by Steven Rothke, PhD, Department of Psychology, Rehabilitation Institute of Chicago (RIC) and expanded by Mary F. Schmidt,
Appendix D Basic Measurement And Statistics The following information was developed by Steven Rothke, PhD, Department of Psychology, Rehabilitation Institute of Chicago (RIC) and expanded by Mary F. Schmidt,
Dealing with Data in Excel 2010
 Dealing with Data in Excel 2010 Excel provides the ability to do computations and graphing of data. Here we provide the basics and some advanced capabilities available in Excel that are useful for dealing
Dealing with Data in Excel 2010 Excel provides the ability to do computations and graphing of data. Here we provide the basics and some advanced capabilities available in Excel that are useful for dealing
MATH 10034 Fundamental Mathematics IV
 MATH 0034 Fundamental Mathematics IV http://www.math.kent.edu/ebooks/0034/funmath4.pdf Department of Mathematical Sciences Kent State University January 2, 2009 ii Contents To the Instructor v Polynomials.
MATH 0034 Fundamental Mathematics IV http://www.math.kent.edu/ebooks/0034/funmath4.pdf Department of Mathematical Sciences Kent State University January 2, 2009 ii Contents To the Instructor v Polynomials.
Algebra II End of Course Exam Answer Key Segment I. Scientific Calculator Only
 Algebra II End of Course Exam Answer Key Segment I Scientific Calculator Only Question 1 Reporting Category: Algebraic Concepts & Procedures Common Core Standard: A-APR.3: Identify zeros of polynomials
Algebra II End of Course Exam Answer Key Segment I Scientific Calculator Only Question 1 Reporting Category: Algebraic Concepts & Procedures Common Core Standard: A-APR.3: Identify zeros of polynomials
Unit 1 Equations, Inequalities, Functions
 Unit 1 Equations, Inequalities, Functions Algebra 2, Pages 1-100 Overview: This unit models real-world situations by using one- and two-variable linear equations. This unit will further expand upon pervious
Unit 1 Equations, Inequalities, Functions Algebra 2, Pages 1-100 Overview: This unit models real-world situations by using one- and two-variable linear equations. This unit will further expand upon pervious
Linear Equations. Find the domain and the range of the following set. {(4,5), (7,8), (-1,3), (3,3), (2,-3)}
 Linear Equations Domain and Range Domain refers to the set of possible values of the x-component of a point in the form (x,y). Range refers to the set of possible values of the y-component of a point in
Linear Equations Domain and Range Domain refers to the set of possible values of the x-component of a point in the form (x,y). Range refers to the set of possible values of the y-component of a point in
1.6. Solve Linear Inequalities E XAMPLE 1 E XAMPLE 2. Graph simple inequalities. Graph compound inequalities
 .6 Solve Linear Inequalities Before You solved linear equations. Now You will solve linear inequalities. Why? So you can describe temperature ranges, as in Ex. 54. Key Vocabulary linear inequality compound
.6 Solve Linear Inequalities Before You solved linear equations. Now You will solve linear inequalities. Why? So you can describe temperature ranges, as in Ex. 54. Key Vocabulary linear inequality compound
Part 1 Expressions, Equations, and Inequalities: Simplifying and Solving
 Section 7 Algebraic Manipulations and Solving Part 1 Expressions, Equations, and Inequalities: Simplifying and Solving Before launching into the mathematics, let s take a moment to talk about the words
Section 7 Algebraic Manipulations and Solving Part 1 Expressions, Equations, and Inequalities: Simplifying and Solving Before launching into the mathematics, let s take a moment to talk about the words
HISTOGRAMS, CUMULATIVE FREQUENCY AND BOX PLOTS
 Mathematics Revision Guides Histograms, Cumulative Frequency and Box Plots Page 1 of 25 M.K. HOME TUITION Mathematics Revision Guides Level: GCSE Higher Tier HISTOGRAMS, CUMULATIVE FREQUENCY AND BOX PLOTS
Mathematics Revision Guides Histograms, Cumulative Frequency and Box Plots Page 1 of 25 M.K. HOME TUITION Mathematics Revision Guides Level: GCSE Higher Tier HISTOGRAMS, CUMULATIVE FREQUENCY AND BOX PLOTS
Introduction to Quadratic Functions
 Introduction to Quadratic Functions The St. Louis Gateway Arch was constructed from 1963 to 1965. It cost 13 million dollars to build..1 Up and Down or Down and Up Exploring Quadratic Functions...617.2
Introduction to Quadratic Functions The St. Louis Gateway Arch was constructed from 1963 to 1965. It cost 13 million dollars to build..1 Up and Down or Down and Up Exploring Quadratic Functions...617.2
Straightening Data in a Scatterplot Selecting a Good Re-Expression Model
 Straightening Data in a Scatterplot Selecting a Good Re-Expression What Is All This Stuff? Here s what is included: Page 3: Graphs of the three main patterns of data points that the student is likely to
Straightening Data in a Scatterplot Selecting a Good Re-Expression What Is All This Stuff? Here s what is included: Page 3: Graphs of the three main patterns of data points that the student is likely to
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Module 7 Test Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. You are given information about a straight line. Use two points to graph the equation.
Module 7 Test Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. You are given information about a straight line. Use two points to graph the equation.
Unit 9 Describing Relationships in Scatter Plots and Line Graphs
 Unit 9 Describing Relationships in Scatter Plots and Line Graphs Objectives: To construct and interpret a scatter plot or line graph for two quantitative variables To recognize linear relationships, non-linear
Unit 9 Describing Relationships in Scatter Plots and Line Graphs Objectives: To construct and interpret a scatter plot or line graph for two quantitative variables To recognize linear relationships, non-linear
We are often interested in the relationship between two variables. Do people with more years of full-time education earn higher salaries?
 Statistics: Correlation Richard Buxton. 2008. 1 Introduction We are often interested in the relationship between two variables. Do people with more years of full-time education earn higher salaries? Do
Statistics: Correlation Richard Buxton. 2008. 1 Introduction We are often interested in the relationship between two variables. Do people with more years of full-time education earn higher salaries? Do
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION INTEGRATED ALGEBRA. Thursday, August 16, 2012 8:30 to 11:30 a.m.
 INTEGRATED ALGEBRA The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION INTEGRATED ALGEBRA Thursday, August 16, 2012 8:30 to 11:30 a.m., only Student Name: School Name: Print your name
INTEGRATED ALGEBRA The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION INTEGRATED ALGEBRA Thursday, August 16, 2012 8:30 to 11:30 a.m., only Student Name: School Name: Print your name
Florida Math for College Readiness
 Core Florida Math for College Readiness Florida Math for College Readiness provides a fourth-year math curriculum focused on developing the mastery of skills identified as critical to postsecondary readiness
Core Florida Math for College Readiness Florida Math for College Readiness provides a fourth-year math curriculum focused on developing the mastery of skills identified as critical to postsecondary readiness
3.2. Solving quadratic equations. Introduction. Prerequisites. Learning Outcomes. Learning Style
 Solving quadratic equations 3.2 Introduction A quadratic equation is one which can be written in the form ax 2 + bx + c = 0 where a, b and c are numbers and x is the unknown whose value(s) we wish to find.
Solving quadratic equations 3.2 Introduction A quadratic equation is one which can be written in the form ax 2 + bx + c = 0 where a, b and c are numbers and x is the unknown whose value(s) we wish to find.
The importance of graphing the data: Anscombe s regression examples
 The importance of graphing the data: Anscombe s regression examples Bruce Weaver Northern Health Research Conference Nipissing University, North Bay May 30-31, 2008 B. Weaver, NHRC 2008 1 The Objective
The importance of graphing the data: Anscombe s regression examples Bruce Weaver Northern Health Research Conference Nipissing University, North Bay May 30-31, 2008 B. Weaver, NHRC 2008 1 The Objective
Lecture 13/Chapter 10 Relationships between Measurement (Quantitative) Variables
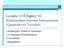 Lecture 13/Chapter 10 Relationships between Measurement (Quantitative) Variables Scatterplot; Roles of Variables 3 Features of Relationship Correlation Regression Definition Scatterplot displays relationship
Lecture 13/Chapter 10 Relationships between Measurement (Quantitative) Variables Scatterplot; Roles of Variables 3 Features of Relationship Correlation Regression Definition Scatterplot displays relationship
COWLEY COUNTY COMMUNITY COLLEGE REVIEW GUIDE Compass Algebra Level 2
 COWLEY COUNTY COMMUNITY COLLEGE REVIEW GUIDE Compass Algebra Level This study guide is for students trying to test into College Algebra. There are three levels of math study guides. 1. If x and y 1, what
COWLEY COUNTY COMMUNITY COLLEGE REVIEW GUIDE Compass Algebra Level This study guide is for students trying to test into College Algebra. There are three levels of math study guides. 1. If x and y 1, what
ALGEBRA I (Common Core) Wednesday, August 13, 2014 8:30 to 11:30 a.m., only
 ALGEBRA I (COMMON CORE) The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION ALGEBRA I (Common Core) Wednesday, August 13, 2014 8:30 to 11:30 a.m., only Student Name: School Name: The
ALGEBRA I (COMMON CORE) The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION ALGEBRA I (Common Core) Wednesday, August 13, 2014 8:30 to 11:30 a.m., only Student Name: School Name: The
ALGEBRA I (Common Core) Thursday, June 16, 2016 9:15 a.m. to 12:15 p.m., only
 ALGEBRA I (COMMON CORE) The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION ALGEBRA I (Common Core) Thursday, June 16, 2016 9:15 a.m. to 12:15 p.m., only Student Name: School Name:
ALGEBRA I (COMMON CORE) The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION ALGEBRA I (Common Core) Thursday, June 16, 2016 9:15 a.m. to 12:15 p.m., only Student Name: School Name:
Polynomial and Rational Functions
 Polynomial and Rational Functions Quadratic Functions Overview of Objectives, students should be able to: 1. Recognize the characteristics of parabolas. 2. Find the intercepts a. x intercepts by solving
Polynomial and Rational Functions Quadratic Functions Overview of Objectives, students should be able to: 1. Recognize the characteristics of parabolas. 2. Find the intercepts a. x intercepts by solving
MATH 103/GRACEY PRACTICE EXAM/CHAPTERS 2-3. MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 MATH 3/GRACEY PRACTICE EXAM/CHAPTERS 2-3 Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Provide an appropriate response. 1) The frequency distribution
MATH 3/GRACEY PRACTICE EXAM/CHAPTERS 2-3 Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Provide an appropriate response. 1) The frequency distribution
Chapter 3 Review Math 1030
 Section A.1: Three Ways of Using Percentages Using percentages We can use percentages in three different ways: To express a fraction of something. For example, A total of 10, 000 newspaper employees, 2.6%
Section A.1: Three Ways of Using Percentages Using percentages We can use percentages in three different ways: To express a fraction of something. For example, A total of 10, 000 newspaper employees, 2.6%
Algebra I Vocabulary Cards
 Algebra I Vocabulary Cards Table of Contents Expressions and Operations Natural Numbers Whole Numbers Integers Rational Numbers Irrational Numbers Real Numbers Absolute Value Order of Operations Expression
Algebra I Vocabulary Cards Table of Contents Expressions and Operations Natural Numbers Whole Numbers Integers Rational Numbers Irrational Numbers Real Numbers Absolute Value Order of Operations Expression
EdExcel Decision Mathematics 1
 EdExcel Decision Mathematics 1 Linear Programming Section 1: Formulating and solving graphically Notes and Examples These notes contain subsections on: Formulating LP problems Solving LP problems Minimisation
EdExcel Decision Mathematics 1 Linear Programming Section 1: Formulating and solving graphically Notes and Examples These notes contain subsections on: Formulating LP problems Solving LP problems Minimisation
Algebra 1 Course Information
 Course Information Course Description: Students will study patterns, relations, and functions, and focus on the use of mathematical models to understand and analyze quantitative relationships. Through
Course Information Course Description: Students will study patterns, relations, and functions, and focus on the use of mathematical models to understand and analyze quantitative relationships. Through
7.1 Graphs of Quadratic Functions in Vertex Form
 7.1 Graphs of Quadratic Functions in Vertex Form Quadratic Function in Vertex Form A quadratic function in vertex form is a function that can be written in the form f (x) = a(x! h) 2 + k where a is called
7.1 Graphs of Quadratic Functions in Vertex Form Quadratic Function in Vertex Form A quadratic function in vertex form is a function that can be written in the form f (x) = a(x! h) 2 + k where a is called
FREE FALL. Introduction. Reference Young and Freedman, University Physics, 12 th Edition: Chapter 2, section 2.5
 Physics 161 FREE FALL Introduction This experiment is designed to study the motion of an object that is accelerated by the force of gravity. It also serves as an introduction to the data analysis capabilities
Physics 161 FREE FALL Introduction This experiment is designed to study the motion of an object that is accelerated by the force of gravity. It also serves as an introduction to the data analysis capabilities
Chapter 13 Introduction to Linear Regression and Correlation Analysis
 Chapter 3 Student Lecture Notes 3- Chapter 3 Introduction to Linear Regression and Correlation Analsis Fall 2006 Fundamentals of Business Statistics Chapter Goals To understand the methods for displaing
Chapter 3 Student Lecture Notes 3- Chapter 3 Introduction to Linear Regression and Correlation Analsis Fall 2006 Fundamentals of Business Statistics Chapter Goals To understand the methods for displaing
The correlation coefficient
 The correlation coefficient Clinical Biostatistics The correlation coefficient Martin Bland Correlation coefficients are used to measure the of the relationship or association between two quantitative
The correlation coefficient Clinical Biostatistics The correlation coefficient Martin Bland Correlation coefficients are used to measure the of the relationship or association between two quantitative
DESCRIPTIVE STATISTICS. The purpose of statistics is to condense raw data to make it easier to answer specific questions; test hypotheses.
 DESCRIPTIVE STATISTICS The purpose of statistics is to condense raw data to make it easier to answer specific questions; test hypotheses. DESCRIPTIVE VS. INFERENTIAL STATISTICS Descriptive To organize,
DESCRIPTIVE STATISTICS The purpose of statistics is to condense raw data to make it easier to answer specific questions; test hypotheses. DESCRIPTIVE VS. INFERENTIAL STATISTICS Descriptive To organize,
2.1 Increasing, Decreasing, and Piecewise Functions; Applications
 2.1 Increasing, Decreasing, and Piecewise Functions; Applications Graph functions, looking for intervals on which the function is increasing, decreasing, or constant, and estimate relative maxima and minima.
2.1 Increasing, Decreasing, and Piecewise Functions; Applications Graph functions, looking for intervals on which the function is increasing, decreasing, or constant, and estimate relative maxima and minima.
Unit 26 Estimation with Confidence Intervals
 Unit 26 Estimation with Confidence Intervals Objectives: To see how confidence intervals are used to estimate a population proportion, a population mean, a difference in population proportions, or a difference
Unit 26 Estimation with Confidence Intervals Objectives: To see how confidence intervals are used to estimate a population proportion, a population mean, a difference in population proportions, or a difference
Statistics E100 Fall 2013 Practice Midterm I - A Solutions
 STATISTICS E100 FALL 2013 PRACTICE MIDTERM I - A SOLUTIONS PAGE 1 OF 5 Statistics E100 Fall 2013 Practice Midterm I - A Solutions 1. (16 points total) Below is the histogram for the number of medals won
STATISTICS E100 FALL 2013 PRACTICE MIDTERM I - A SOLUTIONS PAGE 1 OF 5 Statistics E100 Fall 2013 Practice Midterm I - A Solutions 1. (16 points total) Below is the histogram for the number of medals won
Lesson 4: Solving and Graphing Linear Equations
 Lesson 4: Solving and Graphing Linear Equations Selected Content Standards Benchmarks Addressed: A-2-M Modeling and developing methods for solving equations and inequalities (e.g., using charts, graphs,
Lesson 4: Solving and Graphing Linear Equations Selected Content Standards Benchmarks Addressed: A-2-M Modeling and developing methods for solving equations and inequalities (e.g., using charts, graphs,
The Dummy s Guide to Data Analysis Using SPSS
 The Dummy s Guide to Data Analysis Using SPSS Mathematics 57 Scripps College Amy Gamble April, 2001 Amy Gamble 4/30/01 All Rights Rerserved TABLE OF CONTENTS PAGE Helpful Hints for All Tests...1 Tests
The Dummy s Guide to Data Analysis Using SPSS Mathematics 57 Scripps College Amy Gamble April, 2001 Amy Gamble 4/30/01 All Rights Rerserved TABLE OF CONTENTS PAGE Helpful Hints for All Tests...1 Tests
POLYNOMIAL FUNCTIONS
 POLYNOMIAL FUNCTIONS Polynomial Division.. 314 The Rational Zero Test.....317 Descarte s Rule of Signs... 319 The Remainder Theorem.....31 Finding all Zeros of a Polynomial Function.......33 Writing a
POLYNOMIAL FUNCTIONS Polynomial Division.. 314 The Rational Zero Test.....317 Descarte s Rule of Signs... 319 The Remainder Theorem.....31 Finding all Zeros of a Polynomial Function.......33 Writing a
Graphing Quadratic Functions
 Problem 1 The Parabola Examine the data in L 1 and L to the right. Let L 1 be the x- value and L be the y-values for a graph. 1. How are the x and y-values related? What pattern do you see? To enter the
Problem 1 The Parabola Examine the data in L 1 and L to the right. Let L 1 be the x- value and L be the y-values for a graph. 1. How are the x and y-values related? What pattern do you see? To enter the
Univariate Regression
 Univariate Regression Correlation and Regression The regression line summarizes the linear relationship between 2 variables Correlation coefficient, r, measures strength of relationship: the closer r is
Univariate Regression Correlation and Regression The regression line summarizes the linear relationship between 2 variables Correlation coefficient, r, measures strength of relationship: the closer r is
Expression. Variable Equation Polynomial Monomial Add. Area. Volume Surface Space Length Width. Probability. Chance Random Likely Possibility Odds
 Isosceles Triangle Congruent Leg Side Expression Equation Polynomial Monomial Radical Square Root Check Times Itself Function Relation One Domain Range Area Volume Surface Space Length Width Quantitative
Isosceles Triangle Congruent Leg Side Expression Equation Polynomial Monomial Radical Square Root Check Times Itself Function Relation One Domain Range Area Volume Surface Space Length Width Quantitative
Foundations for Functions
 Activity: TEKS: Overview: Materials: Grouping: Time: Crime Scene Investigation (A.2) Foundations for functions. The student uses the properties and attributes of functions. The student is expected to:
Activity: TEKS: Overview: Materials: Grouping: Time: Crime Scene Investigation (A.2) Foundations for functions. The student uses the properties and attributes of functions. The student is expected to:
What are the place values to the left of the decimal point and their associated powers of ten?
 The verbal answers to all of the following questions should be memorized before completion of algebra. Answers that are not memorized will hinder your ability to succeed in geometry and algebra. (Everything
The verbal answers to all of the following questions should be memorized before completion of algebra. Answers that are not memorized will hinder your ability to succeed in geometry and algebra. (Everything
