SERIES-PARALLEL DC CIRCUITS
|
|
|
- Quentin Rodgers
- 10 years ago
- Views:
Transcription
1 Name: Date: Course and Section: Instructor: EXPERIMENT 1 SERIES-PARALLEL DC CIRCUITS OBJECTIVES 1. Test the theoretical analysis of series-parallel networks through direct measurements. 2. Improve skills of identifying series or parallel elements. 3. Measure properly the voltages and currents of a series-parallel network. 4. Practice applying Kirchhoff s voltage and current laws, the current divider rule, and the voltage divider rule. LAB EQUIPMENT AND COMPONENTS Resistors: 1 kω, 2.2 kω, 3.3 kω, 4.7 kω
2 PROCEDURE Part 1 (a) Construct the series-parallel network of Fig Insert the measured value of the resistors in the space provided. R T R 1 measured = R 2 measured = R 3 measured = Fig.1.1 (b) Calculate the total resistance R T using the measured resistance values. R T (calculated) = (c) Use the ohmmeter section of the multimeter to measure R T. R T (measured) = (d) Determine the magnitude of the percent difference between the calculated and measured values of parts 1(b) and 1(c) using the following equation: % Difference = Calculated Measured Calculated X 100 % (1.1) Use Eq. (1.1) for all percent difference calculations in this laboratory experiment. % Difference =
3 (e) If 12 V were applied, as shown in Fig.1.2, calculate the currents I s, I 1, I 2, and I 3 using the measured resistor values. Fig.1.2 I s = I 1 = I 2 = I 3 = (f) Apply 12 V and measure the currents I 1, I 2, and I 3 using the milliammeter section of your multimeter. Be sure the meter is in series with the resistor through which the current is to be measured. Calculate the magnitude of the percent difference between calculated and measured values using Eq. (1.1). I 1 = I 2 = I 3 = % Difference (I 1 ) = % Difference (I 2 ) =
4 % Difference (I 3 ) = How are the currents I 1 and I s related? Why? Insert the level of I s (measured) here: I s = (g) Using the results of part 1(e), calculate the voltages V 1, V 2, and V 3 using measured values. V 1 = V 2 = V 3 = (h) Measure the voltages V 1, V 2, and V 3. Determine the magnitude of the percent difference between the calculated and measured values. V 1 = V 2 = V 3 = % Difference (V 1 ) = % Difference (V 2 ) = % Difference (V 3 ) = How are the voltages V 2 and V 3 related? Why? (i) Referring to Fig. 1.2, does E = V 1 + V 2, as required by Kirchhoff s voltage law? Use the measured values of part 1(h) to check this equality.
5 Part 2 (a) Construct the series-parallel network of Fig Insert the measured value of each resistor. R 1 measured = R 2 measured = R 3 measured = (b) Calculate the total resistance R T using measured resistor values. Fig.1.3 R T (calculated) = (c) Use the ohmmeter section of your multimeter to measure the total resistance R T. R T (measured) = Calculate the magnitude of the percent difference between the calculated value of part 2(b) and the measured value of part 2(c). % Difference = (d) If 12 V were applied to the network, as shown in Fig. 1.4, calculate the currents I s, I 1, I 2, and I 3 using measured resistor values. Fig.1.4
6 I s = I 1 = I 2 = I 3 = (e) Apply 12 V and measure the currents I s, I 1, I 2, and I 3. I s = I 1 = I 2 = I 3 = Calculate the magnitude of the percent difference between the calculated and measured values for each current. % Difference (I s ) = % Difference (I 1 ) = % Difference (I 2 ) = % Difference (I 3 ) = How are the currents I 2 and I 3 related? Why? (f) Referring to Fig. 1.4, does I s = I 1 + I 2, as required by Kirchhoff s current law? Use the measured values of part 2(e) to check this equality. (g) Using the results of part 2(d) and measured resistor values calculate the voltages V 1, V 2, and V 3. V 1 = V 2 = V 3 =
7 (h) Measure the voltages V 1, V 2, and V 3. V 1 = V 2 = V 3 = Calculate the magnitude of the percent difference between the calculated and measured values for each voltage. Part 3 % Difference (V 1 ) = % Difference (V 2 ) = % Difference (V 3 ) = (i) How are the voltages E, V 1, and the sum of V 2 and V 3 related? Use the measured values of part 2(h) to determine the sum of V 2 and V 3. (a) Construct the series-parallel network of Fig. 1.5 and insert the measured value of each resistor. Fig.1.5 (b) How is the total voltage across the two series elements R 1 and R 2 related to the applied voltage E? Why? How is the total voltage across the two series elements R 3 and R 4 related to the applied voltage E? Why?
8 (c) Using the conclusions of part 3(b), calculate the voltages V 2 and V 4 using the voltage divider rule and measured resistor values. V2 = V4 = (d) Measure the voltages V2 and V4. V2 = V4 = Calculate the magnitude of the percent difference between calculated and measured values. % Difference (V 2 ) = % Difference (V 4 ) = (e) Using the results part 3(c), calculate the voltage V ab using Kirchhoff s voltage law. V ab = (f) Measure the voltage V ab and determine the magnitude of the percent difference between the calculated and measured values. V ab = % Difference = (g) Is the voltage V ab also equal to V 3 - V 1? Why? (h) Calculate the current I s using any method you prefer. Use measured resistor values. I s =
9 (i) Measure the current I s and calculate the magnitude of the percent difference between calculated and measured values. I s = % Difference = Part 4 (a) Construct the network of Fig Insert the measured value of each resistor. R T R 1 measured = R 2 measured = R 3 measured = R 4 measured = Fig.1.6 (b) Calculate the voltage V 4 using the measured resistor values. V 4 (calculated) = (c) Measure the voltage V 4 and calculate the magnitude of the percent difference between calculated and measured values. V 4 (measured) = % Difference =
10 (d) Measure the current I s and calculate the total input resistance from R T = E / I s. I s = R T = (e) Disconnect the power supply and measure R T using the ohmmeter section of the DMM. Then calculate the magnitude of the percent difference between the calculated and measured values. R T = % Difference =
11 PROBLEMS 1. For the series-parallel network of Fig. 1.7, determine V 1, R 1, and R 2 using the information provided. Show all work! Assume R internal = 0 Ω for all meters. V 1 = R 1 = R 2 = Fig For the series-parallel network of Fig. 1.8, determine V 1, R 2, and R 3 using the information provided. Show all work! Assume R internal = 0 Ω for all meters. V 1 = R 2 = R 3 = Fig.1.8
12 Name: Date: Course and Section: Instructor: EXPERIMENT 2 METHODS OF ANALYSIS OBJECTIVES 1. Validate the branch-current analysis technique through experimental measurements. 2. Test the mesh- (loop-) analysis approach with experimental measurements. 3. Demonstrate the validity of the nodal-analysis technique through experimental measurements. LAB EQUIPMENT AND COMPONENTS Resistors 1.0 kω, 1.2 kω, 2.2 kω, 3.3 kω.
13 RESUME OF THEORY Read Chapter 8 Methods of Analysis and Selected Topics (dc) (page 227) (Boylestad). PROCEDURE Part 1 Branch-current Analysis (a) Construct the network of Fig. 2.1 and insert the measured values of the resistors in the spaces provided. R 1 measured = R 2 measured = R 3 measured = Fig.2.1 Caution: Be sure dc supplies are hooked up as shown (common ground) before turning the power on. (b) Using branch-current analysis, calculate the current through each branch of the network of Fig. 2.1 and insert in Table 2.2. Use the measured resistor values and assume the current directions shown in the figure. Show all your calculations in the space provided and be neat! Table 2.2 Current Calculated Measured % Difference I 1 I 2 I 3
14 (c) Measure the voltages V 1, V 2, and V 3 and enter below with a minus sign for any polarity that is opposite to that in Fig V 1 = V 2 = V 3 = Calculate the I 1, I 2, and I3 using the measured resistor values and insert in Table 2.2 as the measured values. Be sure to include a minus sign if the current direction is opposite to that appearing in Fig Show all work. How do the calculated and measured results compare? Determine the percent difference for each current in Table 2.2 using the equation: % Difference = Calculated Measured Calculated X 100 % (2.1) Part 2 Mesh Analysis (a) Construct the network of Fig. 2.2 and insert the measured values of resistors in the spaces provided. R 1 measured = R 2 measured = R 3 measured = Fig.2.2
15 Caution: Be sure dc supplies are hooked up as shown (common ground) before turning the power on. (b) Using mesh analysis, calculate the mesh currents I 1 and I 2 of the network. Use the measured resistor values and the indicated directions for the mesh currents. Then determine the current through each resistor and insert in Table 2.3 in the Calculated column. Include all your calculations and organize your work. Mesh currents (calculated): I 1 = I 2 = Table 2.3 Current Calculated Measured % Difference I 1 I 2 I 3 (c) Measure the voltages V 1, V 2, and V 3 and enter here with a minus sign for any polarity that is opposite to that in Fig V 1 = V 2 = V 3 = Calculate the currents I R1, I R2, and I R3 using the measured voltage and resistor values and insert in Table 2.3 as the measured values. Be sure to include a minus sign if the current direction is opposite to that defined by the polarity of the voltage across the resistor.
16 How do the calculated and measured results compare? Determine the percent difference for each current of Table 2.3. Part 3 Nodal Analysis (a) Construct the network of Fig. 2.3 and insert the measured resistor values. R 1 measured = R 2 measured = R 3 measured = Fig. 2.3 Caution: Be sure dc supplies are hooked up as shown (common ground) before turning the power on. Calculations: (b) Using measured resistor values, determine V a using nodal analysis. Show all work and be neat! V a (calculated) =
17 (c) Using Va, calculate the current I R1 and I R3 using measured resistor values and insert in Table 2.4. Table 2.4 Current Calculated Measured % Difference I R1 I R3 Measurements: (d) Energize the network and measure the voltage Va. Compare with the result of part 3(b). V a (measured) = (e) Using V a (measured), calculate the current I R1 and I R3 using measured resistor values and insert in Table 2.4 as the measured results. (f) How do the calculated and measured results for I R1 and I R3 compare? Determine the percent differences for each current in Table 2.4.
18 Part 4 Bridge Network (a) Construct the network of Fig Insert the measured resistor values. R 1 measured = R 2 measured = R 3 measured = R 4 measured = R 5 measured = Fig. 2.4 (b) Using any of the three techniques examined in this experiment, calculate the voltage V 5 and current I 5. Use the measured resistor values. V 5 (calculated) = I 5 (calculated) = (c) Measure the voltage V 5 and insert below with a minus sign if the polarity is different from that appearing in Fig V 5 (measured) = (d) Calculate the percent difference between the two values of V 5. % Difference =
19 (e) Calculate the current I 5 using the measured value of V 5 and the measured value of the resistor R 5. I 5 (measured) = How does the measured value of I 5 compare with the calculated value of part 4(b)? Determine the percent difference. % Difference = QUESTION Many times one is faced with the question of which method to use in a particular problem. The laboratory activity does not prepare one to make such choices but only shows that the methods work and are solid. From your experience in this activity, summarize in your own words which method you prefer and why you chose the method you did for the analysis of part 4.
20 Name: Date: Course and Section: Instructor: EXPERIMENT 3 SUPERPOSITION THEOREM (DC) OBJECTIVES 1. Validate the superposition theorem. 2. Demonstrate that the superposition theorem can be applied to both current and voltage levels. 3. Demonstrate that the superposition theorem can not be applied to nonlinear functions. LAB EQUIPMENT AND COMPONENTS Resistors: 1.2 kω, 2.2 kω, 3.3 kω, 4.7 kω, 6.8 kω.
21 RESUME OF THEORY Read Chapter 9 Network Theorem, 9.2 Superposition Theorem (page 287) PROCEDURE Part 1 Superposition Theorem (Applied to Current Levels) The first configuration to be analyzed using the superposition theorem appears in Fig The currents I 1, I 2 and I 3 will be determined by considering the effects of E 1 and E 2 and then adding the resulting levels algebraically. Caution: Be sure the dc supplies have common ground. Fig. 3.1 (a) Determining the effects of E 1 : Construct the network of Fig. 3.2 and insert the measured value of each resistor. Note that the supply E 2 has been replaced by a short-circuit equivalent. This does not mean that one should place a short-circuit across the terminals of the supply. Simply remove the supply from the network and replace it by a direction to ground, as shown in Fig Keep this in mind for all similar operations throughout the laboratory session. Calculate the currents I 1, I2 and I 3 using the measured resistor values.
22 R 1 measured = R 2 measured = R 3 measured = Fig. 3.2 I 1 =.., I 2 =.., I 3 =.. Turn on the supply E 1 and measure the currents I 1, I 2 and I 3. Check your measurements by noting whether Kirchhoff s current law (I 1 =I 2 +I 3 ) is satisfied. I 1 =.., I 2 =.., I 3 =.. How do the calculated and measured values of I 1, I 2 and I 3 compare? (b) Determining the effects of E 2 : Construct the network of Fig. 3.3 and insert the measured value of each resistor. Calculate the currents I 1, I 2 and I 3 using the measured resistor values. R 1 measured = R 2 measured = R 3 measured = Fig. 3.3
23 I 1 =.., I 2 =.., I 3 =.. Turn on the supply E 2 and measure the currents I 1, I 2 and I 3. Check your measurements by noting whether Kirchhoff s current law (I 1 =I 2 +I 3 ) is satisfied. I 1 =.., I 2 =.., I 3 =.. How do the calculated and measured values of I 1, I 2 and I 3 compare? (c) Determining the total effects of E 1 and E 2 : Construct the network of Fig. 3.1 and insert the measured value of each resistor. Using the calculated results of parts 1(a) and 1(b), calculate the currents I 1, I 2 and I 3, being very aware of their directions in Figs. 3.2 and 3.3. Next to each result, indicate the direction of the resulting current through each resistor. I 1T =.., I 2T =.., I 3T =.. Turn on both supplies and measure the currents I 1, I 2 and I 3. Determine the direction of each current from the meter connections and insert next to the measured value. I 1T =.., I 2T =.., I 3T =..
24 How do the calculated and measured levels compare? Has the superposition theorem been validated? (d) Power levels: Using the measured current levels of part 1(a), calculate the power delivered to each resistor. Show all work! P 1 =..., P 2 =..., P 3 =... Using the measured current levels of part 1(b), calculate the power delivered to each resistor. P 1 =..., P 2 =..., P 3 =... Using the measured levels of part 1(c), calculate the power delivered to each resistor. P 1 =..., P 2 =..., P 3 =... For each resistor, compare the power delivered with both supplies present to the sum of the power levels resulting from each supply. P 1 (a+b) =..., P 1 (c) =...
25 P 2 (a+b) =..., P 2 (c) =... P 3 (a+b) =..., P 3 (c) =... Based on these results, is the superposition theorem applicable to power effects? Explain your answer. Part 2 Superposition Theorem (Applied to Voltage Levels) The second configuration to be analyzed using the superposition theorem appears in Fig The voltages V 1, V 2 and V 3 will be determined by considering the effects of E 1 and E 2 and then adding the resulting levels algebraically. Fig. 3.4 (a) Determining the effects of E 1 : Calculate the voltages V 1, V 2 and V 3 for the network of Fig. 3.5 using measured resistor values. Insert the measured resistor values in the space provided.
26 R 1 measured = R 2 measured = R 3 measured = Fig. 3.5 V 1 =..., V 2 =..., V 3 =... Construct the network of Fig. 3.5, turn on the supply E 1, and measure the voltages V 1, V 2 and V 3. V 1 =..., V 2 =..., V 3 =... How do the calculated and measured values of V 1, V 2 and V 3 compare? (b) Determining the effect of E 2 : Calculate the voltages V 1, V 2 and V 3 for the network of Fig. 3.6 using the measured resistor values.
27 Fig. 3.6 V 1 =..., V 2 =..., V 3 =... Construct the network of Fig. 3.6 turn on the supply, and measure the voltages V 1, V 2 and V 3. V 1 =..., V 2 =..., V 3 =... How do the calculated and measured values of V 1, V 2 and V 3 compare? (c) Determining the total effects of E 1 and E 2 : Using the calculated results of parts 2(a) and 2(b), calculate the net voltages V 1, V 2 and V 3. Be very aware of their polarities in Figs. 3.5 and 3.6. Next to each result indicate the polarity of the voltage across each resistor on Fig. 3.4.
28 V 1 =..., V 2 =..., V 3 =... Construct the network of Fig. 3.4, turn on the supply, and measure the voltages V 1, V 2 and V 3. Be sure to note the polarity of each reading on the schematic. V 1 =..., V 2 =..., V 3 =... How do the calculated and measured levels compare? Has the superposition theorem been validated for voltage levels? Part 3 A Third Configuration (For this part you must have supplies with isolated ground connections. If not available, do not complete this part.) (a) Construct the network of Fig. 3.7, taking special note of the fact that the positive side of E 2 is connected to ground potential. Using the measured resistor values, calculate the voltages V 1, V 2 and V 3 using superposition. Show your work in the space provided. Indicate the resulting polarities for each voltage next to each result. R 1 measured = R 2 measured = R 3 measured = Fig. 3.7 V 1 =..., V 2 =..., V 3 =...
29 (b) Construct and energize the network of Fig. 3.7 and measure the voltages V 1, V 2 and V 3. Is the superposition theorem verified? V 1 =..., V 2 =..., V 3 =... PROBLEMS 1. For the network of Fig. 3.8: Fig. 3.8 (a) By inspection (meaning no calculation whatsoever) using the superposition theorem, which source (I 1, I 2, or E) would appear to have the most impact on the current, I? (b) Determine the current, I, using superposition and note whether your conclusion in part (a) was correct. I =...
30 2. Using superposition, determine the current, I, for the network of Fig Fig. 3.9
31 Name: Date: Course and Section: Instructor: EXPERIMENT 4 THEVENIN S THEOREM AND MAXIMUM POWER TRANSFER OBJECTIVES 1. Validate Thevenin s theorem through experimental measurements. 2. Become aware of an experimental procedure to determine E Th and R Th. 3. Demonstrate that maximum power transfer to a load is defined by the condition R L = R Th. LAB EQUIPMENT AND COMPONENTS Resistors: 91Ω, 220Ω, 330Ω, 470Ω, 1kΩ, 2.2 kω, 3.3 kω 1 kω, 10 kω potentiometer.
32 RESUME OF THEORY Read Chapter 9 Network Theorems, 9.3 Thevenin s Theorem (page 294) and 9.5 Maximum Power Transfer Theorem (page 308) PROCEDURE Part 1 Thevenin s Theorem Calculations: (a) Construct the network of Fig Calculate the Thevenin voltage and resistance for the network to the left of points a-a using measured resistor values. Show all your work! R 1measured = R 2measured = R 3measured = R Lmeasured = Fig. 4.1 E Th = R Th = Enter these values in column 1 of Table 4.1. Table 4.1 Calculated Values of E th and R th [Part 1(a)] Measured Values of E th and Rth [Parts 1(e)and 1(f)] E th = E th = (part 1(f)) R th = R th = (part 1(e)) % Difference
33 (b) Insert the values of E Th and R Th in Fig. 4.2 and calculate I L. Fig. 4.2 I L = (c) Calculate the current I L in the original network of Fig. 4.1 using series-parallel techniques (use measured resistor values). Show all your work! I L = How does this calculated value of I L compare to the value of part 1(b)? Measurements: (d) Turn on the 12-V supply of Fig. 4.1 and measure the voltage V L. Using the measured value of R L, calculate the current I L. V L (measured) = I L (calculated from V L ) = How does this measured value of I L compare with the calculated levels of parts 1(b) and 1(c)?
34 Determining R Th : (e) Determine R Th by constructing the network of Fig. 4.3 and measuring the resistance between a-a with R L removed. Ω Fig. 4.3 R Th = Enter this value in column 2.of table 4.1. Determining E Th : (f) Determine E Th by constructing the network of Fig. 4.4 and measuring the open-circuit between points a-a. Fig. 4.4 E Th (measured) = Enter this value in column 2 of Table 4.1.
35 Thevenin Network: (g) Construct the network of Fig. 4.5 and set the values obtained for the measured values of E th and R th in parts 1(e) and 1(f), respectively. Use the ohmmeter section of your meter to set the potentiometer properly. Then measured the voltage V L and current I L using the measured value of R L. Fig. 4.5 V L (measured) = I L (calculated from V L ) = How does the value of I L compare with the calculated level of part 1(b)? How do the calculated and the measured values E Th and R Th compare? Insert the magnitude of the percent difference in the third column of Table 4.1 using the equations: % Difference = Calculated Measured Calculated X 100 % (4.1) Noting the overall results of Table 4.1, has Thevenin s theorem been verified?
36 Part 2 Maximum Power Transfer (Validating the Condition R L = R Th ) (a) Construct the network of Fig. 4.6 and set the potentiometer to 50Ω. Measure the voltage across RL as you vary R L through the following values: 50, 100, 200, 300, 330, 400, 600, and 1000Ω. Be sure to set the resistance with the ohmmeter section of your meter before each reading. Remember to turn off the dc supply and disconnect one terminal of the potentiometer when setting the resistance level. Complete Table 4.2 and plot P L versus, R L on graph 4.1. Fig. 4.6 Table 4.2 R L (Ω) V L (V) R 1 measured = VL P= ( mw ) RL
37 (b) Theoretically, for the network of Fig. 4.6, what value of R L should result in maximum power to R L? R L = Referring to the plot of graph 4.1, what value of R L resulted in maximum power transfer to R L? R L = How do the theoretical and measured values of R L compare? (c) Under maximum power transfer conditions, how are the voltages V L and E related? Why? Based on the preceding conclusion, determine V L for maximum power transfer to R L. V L = Graph P (mw) R (kω)
38 Set the potentiometer to the resistance R L that resulted in maximum power transfer on graph 4.1 and measure the resulting voltage across R L. V L = How does the measured value compare to the expected theoretical level? Part 3 Maximum Power Transfer (Experimental Approach) (a) Construct the network of Fig Insert the measured value of each resistor. R 1measured = R 2measured = R 3measured = R 4measured = Fig. 4.7 (b) The Thevenin equivalent circuit will now be determined for the network to the left of the terminals a-b without disturbing the structure of the network. All the measurements. Will be made at the terminals a-b.
39 E Th : Determine E Th by turning on the supply and measuring the opencircuit voltage V ab. E Th = V ab = R Th : Introduce the 1-kΩ potentiometer to the network of Fig. 4.7, as shown in Fig Fig. 4.8 Turn on the supply and adjust the potentiometer until the voltage V L is E Th / 2, a condition that must exist if R L = R Th.Then turn off the supply and remove the potentiometer from the network without disturbing the position of the wiper arm. Measure the resistance between the two terminals connected to a-b and record as R Th. R Th = R L = (c) Now we need to check our measured results against a theoretical solution. Calculate R Th and E Th for the network to the left of terminals a-b of Fig Use measured resistor values. R Th = E Th = How do the calculated and measured values compare?
40 (d) Let us now plot P L and V L versus R L to confirm once more that the conditions for maximum power transfer to a load are that R L = R Th and V L = E Th / 2. Leave the potentiometer as connected in Fig. 4.8 and measure V L for all the values of R L appearing in Table 4.3*. Then calculate the resulting power to the load and complete the Table. Finally, plot both P L and V L versus R L on graphs 4.1 and 4.2, respectively. Table 4.3 R L (Ω) V L (V) measured 2 VL P= ( mw ) (calculated) RL * Be sure to remove the potentiometer from the network when setting each value of R L. At the very least disconnect one side of the potentiometer when making the setting.
41 Graph P L (mw) R L (kω) Reviewing graph 4.1, did maximum power transfer to the load occur when R L = R Th? What conclusion can be drawn from the results?
42 Graph V L (Volts) R L (kω) Noting graph 4.2, does V L = E Th / 2 when R L = R Th? Comment accordingly.
43 PROBLEMS For the network of Fig. 4.9: (a) Determine R Th and E Th for the network external to the 2-kΩ resistor. Fig. 4.9 R Th = E Th = (b) Determine the power delivered to the 2-kΩ resistor using the Thevenin equivalent circuit. (c) Is the power determined in part (b) the maximum power that could be delivered to a resistor between terminals a and b? If not, what is the maximum power?
44 Name: Date: Course and Section: Instructor: EXPERIMENT 5 CAPACITORS OBJECTIVES 1. Validate conclusions regarding the behavior of capacitors in a steady-state dc network. 2. Plot the exponential curve for the voltage across a charging capacitor. 3. Verify the basic equations for determining the total capacitance for capacitors in series and parallel. 4. Demonstrate the usefulness of Thevenin s theorem for networks not having the basic series R-C form. LAB EQUIPMENT AND COMPONENTS Resistors: 1.2 kω, 3.3 kω, 47 kω, 100 kω. Capacitors: 100 µf, 220 µf (electrolytic)
45 RESUME OF THEORY Read Chapter 10 Capacitors (page 341) PROCEDURE Part 1 Basic Series R-C Circuit (a) Construct the network of Fig Insert the measured resistor value. Be sure to note polarity on electrolytic capacitors as shown in figure. R measured = FIG. 5.1 (b) Calculate the steady-state value (defined by a period of time greater than five time constant) of the current I and the voltages V 1 and V 2. I =..., V 1 =..., V 2 =... (c) Measure the voltages V 1 and V 2 and calculate the current I from Ohm s law. Compare with the results of part 1(b). V 1 =..., V 2 =... I =... (d) Calculate the energy stored by the capacitor.
46 W =... (e) Carefully disconnect the supply and quickly measure the voltage across the disconnected capacitor. Is there a reading? Why? V C =... (f) Short the capacitor terminals with a lead and then measure V C again. Why was it necessary to perform this step? Part 2 Parallel R-C dc Network (a) Construct the network of Fig Insert the measured resistor values. R 1measured = R 2measured = FIG. 5.2 (b) Using the measured values, calculate the theoretical steady-state levels (time greater than five time constants) of the following quantities. I 1 =..., I 2 =..., I 3 =... V 1 =..., V 2 =..., V 3 =...
47 (c) Energize the system and measure the voltages V 1, V 2 and V 3. Calculate the currents I 1 and I 2 from Ohm s law and the current I 3 from Kirchhoff s current law. Compare the results with those of part 2(b). V 1 =..., V 2 =..., V 3 =... I 1 =..., I 2 =..., I 3 =... Part 3 Series-Parallel R-C dc Network (a) Construct the network Fig Insert the measured resistor values. R 1measured = R 2measured = FIG. 5.3 (b) Assuming ideal capacitors and using measured resistor values, calculate the theoretical steady-state levels of the following quantities: I 1 =..., I 2 =..., I 3 =..., I 4 =..., V 1 =..., V 2 =..., V 3 =..., V 4 =...,
48 (c) Energize the system and measure the voltages V 1, V 2, V 3 and V 4. Compare the results with those in part 3(b). V 1 =..., V 2 =..., V 3 =..., V 4 =..., Part 4 Determining C (Actual Value) This part of the experiment will determine the actual capacitance of the capacitor. In most cases the actual value will be more than the nameplate value. (a) Construct the network of Fig Insert the measured resistance value. R measured = FIG. 5.4 (b) Calculate the time constant determined by the measured resistance value and the nameplate value. τ (theoretical) =... (c) Before turning on the power supply or closing the switch be sure to discharge the capacitor by placing a lead across its terminals. Then energize the source, close the switch, and note how many seconds pass before the voltage V C reaches 63.2% of its final value or (0.632)(10V) = 6.32 V. Recall from the Resume of Theory that the voltage V C should reach 63.2% of its final steady-state value in one time constant. τ (measured) =... (d) The actual capacitance (measured value) is then defined by C measured = τ (measured) / R (measured)
49 Determine C measured for the capacitor of Fig C measured =... For the rest of this experiment, use the measured value for each capacitance. How do the measured and nameplate values of C compare? What does the difference suggest about the actual versus nameplate levels of capacitance? Part 5 Charging Network (Parallel Capacitors) (a) Construct the network of Fig Insert the measured resistance and capacitance values. R measured = C 1measured = C 2measured = FIG. 5.5 (b) Calculate the total capacitance for the network using the measured capacitance levels. C T =... (c) Determine the time constant for the network. τ =... (d) Calculate the charging time (5τ) for the voltage across the capacitor, C T. 5τ =...
50 (e) Using a watch, record (to the best of your ability) the voltage across the capacitor at the time intervals appearing in Table 5.1 after the switch is closed. You may want to make a test run before recording the actual levels. Complete the table using the fact that V R = E- V C. Be sure to discharge the capacitor between each run. Table 5.1 t (s) V C V R 0 V 12 V t (s) V C V R (f) Plot the curves of V C and V R versus time on Graph 5.1. Label each curve and indicate the intervals 1τ through 5τ on the horizontal axis. (g) What is the level of V C after one time constant (from the graph)? V C (1τ) =... Is this level 63.2% of the final steady-state level, as dictated by the Resume of Theory? (h) What is the level of V C after five time constants? V C (5τ) =... Does the level of V C suggest that the major portion of the transient phase has passed after five time constants? (i) Write the mathematical expression for the voltage V C during the charging phase. V C =... Determine the voltage V C = at t = 25s by substituting the time into the preceding mathematical expression and performing the required mathematical computations.
51 V C (at t = 25s) =... Determine V C at t = 25s from the V C curve of Graph 5.1. V C (at t = 25s) =... How do the calculated and the measured levels of V C at t = 25s compare? Part 6 Charging Network (Series Capacitors) (a) Construct the network of Fig Insert the measured resistance and capacitance values. R 1measured = R 2measured = C 1measured = C 2measured = FIG. 5.6 (b) Determine the total resistance and capacitance for the network. R T =..., C T =... (c) Calculate the time constant for the network. τ =... (d) Calculate the charging time (5τ) for the voltage across the capacitor, C T. 5τ =...
52 (e) Using a watch, record (to the best of your ability) the voltage across the series capacitors at the time intervals appearing in Table 5.2 after the switch is closed. You may want to make a test run before recording the actual levels. Complete the table using the fact that V R = E- V C. Again, be sure to discharge the capacitor between each run. Table 5.2 t (s) V C V R 0 V 12 V t (s) V C V R (f) Plot the curves of V C and V R versus time on Graph 5.2. Label each curve and indicate the intervals 1τ through 5τ on the horizontal axis. Be sure to include the t = 0s levels as determined theoretically. (g) What is the level of V C after one time constant (from the graph)? V C (1τ) =... Is this level 63.2% of the final steady-state level, as dictated by the Resume of Theory? (h) What is the level of V C after five time constants? V C (5τ) =... Does the level of V C suggest that the major portion of the transient phase has passed after five time constants? (i) Write the mathematical expression for the voltage V R during the charging phase. V R =...
53 Using the preceding mathematical expression, determine the time t when the voltage V R has dropped to 50% of the value at t =0 s. t =... Using the plot of V R on Graph 5.2, determine the time t at which V R dropped to 50% of the value at t =0s. How does it compare to the theoretical value just determined? t =... Part 7 Applying Thevenin s Theorem (a) Construct the network of Fig Insert the measured values of the resistors and the capacitor. FIG. 5.7 (b) Using Thevenin s theorem calculate the Thevenin resistance for the network to the left of the capacitor (between terminals a and b). R Th =... Using Thevenin s theorem, calculate the open circuit Thevenin voltage between terminals a and b for the network to the left of the capacitor.
54 E Th =... (c) Redraw the network of Fig. 5.8 (in the space below) with the equivalent Thevenin circuit in the place to the left of the switch and capacitor. (d) Calculate the resulting time constant (τ) and charging time (5τ) for the voltage across the capacitor C after the switch is closed. 1τ =... 5τ =... (e) Write the mathematical expression for the charging voltage V C and determine the voltage V C after one time constant. V C =... V C (1τ) =... (f) Close the switch for the network of Fig. 5.8 and record the level of V C after one time constant. V C (1τ) =... How does the value of V C after one time constant compare with the calculated value of part 6(d)? (g) Are the results of parts 6(c) and 6(f) sufficiently close to validate the Thevenin equivalent circuit?
55 PROBLEMS 1. The voltage V C for the network of Fig. 5.8 has risen to 16V 5s after the switch was closed. Determine the value of C in microfarads. FIG. 5.8 C = Determine the mathematical expression for the voltage V C of Fig. 5.9 following the closing of the switch. FIG. 5.9 V C =...
56 V (volts) GRAPH t (s)
57 V (volts) GRAPH t (s)
58 Name: Date: Course and Section: Instructor: EXPERIMENT 6 THE OSCILLOSCOPE OBJECTIVES 1. Become familiar with the construction, components and fundamental operation of an oscilloscope. 2. Learn how to set the amplitude and frequency of a function generator. 3. Understand how to use an oscilloscope to measure both dc and ac voltage levels. 4. Understand the impact of the AC/DC/GND switch on the displayed waveform. LAB EQUIPMENT AND COMPONENTS Instruments: DMM Oscilloscope Audio oscillator or function generator Frequency counter (if available)
59 RESUME OF THEORY Read chapters related to the oscilloscope. dc Levels: How to make measurements? (a) Voltage Measurements: To use the scope to measure dc levels, first place the DC/AC/GND switch in the GND position to establish the ground (0 V) level on the screen. Then switch the DC/AC/GND switch to the dc position to measure the dc level. In the ac mode, a capacitor blocks the dc from the screen. Then place the scope leads across the unknown dc level and use the following equation to determine the dc level: ac Levels: dc Level (V) = Deflection (div.) X Vertical Sensitivity (V/div.) After re-establishing the ground level, place the DC/AC/GND switch in the ac mode and connect the scope leads across the unknown voltage. The peak-to-peak value can then be determined from: V p-p (V) = Deflection Peak to Peak (div.) X Vertical Sensitivity (V/div.) (b) Frequency Measurements: The oscilloscope can be used to set the frequency of an audio oscillator or function generator using the horizontal sensitivity in the following manner. Determine the period of the desired waveform and then calculate the number of divisions required to display the waveform on the horizontal axis using the provided µs/div., ms/div., s/div. on the horizontal sensitivity control. Then adjust the audio oscillator or function generator to provide the proper horizontal deflection for the desired frequency. Of course, the reverse of the above procedure will determine the frequency of an unknown signal.
60 PROCEDURE Part 1 Introduction (a) Your instructor will introduce the basic operation of the oscilloscope and audio oscillator or function generator. (b) Turn on the oscilloscope and establish a horizontal line centered on the face of the screen. There are no connections to the vertical input sections of the scope for this part. (c) Adjust the controls listed in Table 6.1 and comment on the effects. TABLE 6.1 Control Focus Intensity Y-position X-position Observed Effect Part 2 dc Voltage Measurements (a) Set the DC/AC/GND switch to GND position and adjust the Y-position control until the 0-V reference is a line centered vertically on the screen. (b) Once the 0-V level is established, move the DC/AC/GND switch to the dc position and set the vertical sensitivity to 1 V/div. and connect one channel of the scope across the 1.5-V battery as shown in Fig FIG.6.1
61 Record the vertical shift below. Vertical Shift = (divisions) Determine the dc voltage that established the shift by multiplying by the vertical sensitivity. That is, dc Voltage = (Vertical Shift)( Vertical Sensitivity) =( ) ( ) = V Change the sensitivity to 0.5 V/div. and note the effect on the vertical shift. Recalculate the dc voltage with this new shift. dc Voltage = (Vertical Shift)( Vertical Sensitivity) =( ) ( ) = V How do the two measurements compare? Which is more accurate? Why? (c) Disconnect the 1.5 V battery and re-establish the 0-V reference line. Then connect the vertical input section of the scope as shown in Fig. 6.2 with the vertical sensitivity set at 1 V/div. FIG.6.2
62 What was the direction of the shift? Why? Based on the above can a scope determine the polarity of a voltage? How? Calculate the magnitude (no sign) of the measured voltage as follows: dc Voltage = (Vertical Shift)( Vertical Sensitivity) =( ) ( ) = V Measure the total voltage across the two series batteries with DMM and compare with the level determined using the oscilloscope. dc Voltage (DMM) = V Part 3 Sinusoidal Waveforms Magnitude In this part of the experiment, we will learn how to set the magnitude of a sinusoidal signal using an oscilloscope or DMM (or VOM). The frequency will remain fixed at 500 Hz. Oscilloscope: (a) Connect the output of the oscillator or generator directly to one channel of the scope as shown in Fig If it is available, hook up the frequency counter. Vertical Channel 1 FIG.6.3
63 (b) Set the output frequency of the oscillator or generator at 500 Hz using the dial and appropriate multiplier. Turn the amplitude knob all the way to the left for minimum output. (c) Set the vertical sensitivity of the scope to 1 V/div. and the horizontal sensitivity to 0.5 ms/div. and turn on both the scope and the oscillator or generator. (d) Set the DC/AC/GND switch to GND position to establish the 0-V reference level (also the vertical center of a sinusoidal waveform) and then return the switch to the ac position. (e) Now adjust the amplitude control of the oscillator or generator until the signal has a 6-V peak-to-peak swing. The resulting waveform has the following mathematical formulation: v = V m sin 2πft = 3 sin 2π500t (f) Switch to the dc position and comment below on any change in location or appearance of the waveform. (g) Make the necessary adjustments to display the following waveforms on the screen. Sketch both patterns in Figs. 6.4 and 6.5, showing the number of divisions (in centimeters) for the vertical and horizontal distances, and the vertical and horizontal sensitivities. Use a sharp pencil for the sketch. Be neat and accurate! 1. v = 0.2 sin 2π500t Vertical Sensitivity = Horizontal Sensitivity = FIG.6.4
64 2. v = 8 sin 2π500t Vertical Sensitivity = Horizontal Sensitivity = DMM: FIG.6.5 (h) The sinusoidal signal 3 sin 2π500t has an effective value determined by V eff = V m = 0.707(3 V) = V Connect the DMM directly across the oscillator in the ac rms mode and adjust the oscillator output until V eff = V Then connect the output of the oscillator directly to the scope and note the total peak-to-peak swing. Is the waveform the same as that obtained in part 3(e)? (i) Use the DMM to set the following sinusoidal output from the oscillator: v = 0.5 sin 2π500t Veff = V Set V e ff with the DMM by adjusting the output of the oscillator, and place the signal on the screen. Calculate the peak-to-peak voltage as follows: Vp-p = (vertical distance peak to peak)(vertical sensitivity) = ( )( ) = V
65 How does the above compare with the desired 1-V peak-topeak voltage? Part 4 Sinusoidal Waveforms Frequency This section will demonstrate how the oscilloscope can be used to set the frequency output of an oscillator or generator. In other words, the scope can be used to make fine adjustments on the frequency set by the dials of the oscillator or generator. For a signal such as 2 sin2π500t, the frequency is 500 Hz and the period is 1/500 = 2 ms. With a horizontal sensitivity of 0.5 ms/div., the waveform should appear in exactly four horizontal divisions. If it does not, the fine-adjust control on the frequency of the oscillator or generator can be adjusted until it is exactly 4 divisions. The scope has then set the output frequency of the oscillator. Make the necessary adjustments to place the following waveforms on the scope. Sketch the waveforms on the scope patterns in Figs. 6.6 and 6.7, indicating the number of vertical and horizontal deflections and the sensitivity of each. Use a frequency counter if it is available. 1. v = 0.4 sin t f= Hz, T= s FIG.6.6
66 Vertical Deflection (peak value) = divisions Vertical Sensitivity = Horizontal Deflection (for one period of waveform) = Horizontal Sensitivity = divisions 2. v = 5 sin 377t f= Hz, T= s FIG.6.7 Vertical Deflection (peak value) = divisions Vertical Sensitivity = Horizontal Deflection (for one period of waveform) = Horizontal Sensitivity = divisions
67 Part 5 Sinusoidal Waveforms on a dc Level (a) Set the oscillator or generator to an output of 1 sin2π500t using a vertical sensitivity of 1 V/div. on the scope with a horizontal sensitivity of 0.5 ms/div. (b) Measure the dc voltage of one of the D cells and insert in Fig E = V (c) Construct the series combination of supplies as shown in Fig. 6.8 and connect the scope as indicated. FIG.6.8 (d) The input signal now has a dc level equal to the dc voltage of the D cell. Set the DC/AC/GND switch to the GND position and adjust the zero line to the center of the screen. (e) Switch to the AC mode and sketch the waveform on Fig FIG.6.9
68 (f) Now switch to the DC mode and sketch the waveform on the same scope pattern as part 5(e). (g) What was the effect of switching from the AC to the DC mode? Did the shape of the sinusoidal pattern change at all? How does the vertical shift compare to the dc level of the battery? (h) Switch to the GND mode and describe what happened to the waveform. In general, what is the effect of switching to the GND position, no matter where the leads of the scope are connected? PROBLEMS 1. Write the sinusoidal expression for the waveform appearing in Fig v = Vertical Sensitivity: 4V/div Horizontal Sensitivity: 5µs/div FIG.6.10
69 2. Sketch the waveform defined by V= Sin 2π(20*10 3 )t on the scope pattern of Fig.6.11 include the vertical and horizontal sensitivities. FIG.6.11 Vertical Sensitivity: Horizontal Sensitivity:
70 Name: Date: Course and Section: Instructor: EXPERIMENT 7 Frequency Response of R, L, and C Components OBJECTIVES 1. Verify that the resistance of a resistor is independent of frequency for frequencies in the audio range. 2. Note that the reactance of an inductor increases linearly with increase in frequency. 3. Confirm that the reactance of a capacitor decreases nonlinearly with in crease in frequency. LAB EQUIPMENT AND COMPONENTS Instruments: 1 DMM 1 Oscilloscope 1 Audio oscillator (or function generator) 1 Frequency counter (if available)
71 RESUME OF THEORY The resistance of a carbon resistor is unaffected by frequency, except for extremely high frequencies. This rule is also true for the total resistance of resistors in series or parallel. The reactance of an inductor is linearly dependent on the frequency applied. That is, if we double the frequency, we double the reactance, as determined by X L = 2πfL. For very low frequencies, the reactance is correspondingly very small, whereas for increasing frequencies, the reactance will increase to a very large value. For dc conditions, we find that X L = 2π(0)L is 0 Ω, corresponding with the short-circuit representation we used in our analysis of dc circuits. For very high frequencies, X L is so high that we can often use an open-circuit approximation. At low frequencies the reactance of a coil is quite low, whereas for a capacitor the reactance is quite high at low frequencies, often permitting the use of an open-circuit equivalent. At higher frequencies the reactance of a coil increases rapidly in a linear fashion, but the reactance of a capacitor decreases in a nonlinear manner. In fact, it drops off more rapidly than the reactance of a coil increases. At very high frequencies the capacitor can be approximated by a short-circuit equivalency. PROCEDURE Part 1 Resistors Construct the circuit of Fig Insert the measured value of R. Hook up the frequency counter if available. Oscilloscope Vertical input 4 V(p-p) Black FIG. 7.1 In this part of the experiment, the voltage across the resistor will be held constant at 4 V (p-p) while only the frequency is varied. If the resistance is frequency independent, the current through the circuit should not change as a function of frequency. Therefore, by keeping the voltage V R constant and changing the frequency while monitoring the current I, we can verify if, indeed, resistance is frequency independent. Set the voltage V R across the 1 -kω resistor to 4 V (p-p) using the oscilloscope. Note that the first frequency of Table 7.2 is 50 Hz. In addition, note that it is the voltage across the resistor that is set to 4 V (p-p), not the supply voltage. For each frequency of Table 7.2, be sure V R is maintained at 4 V (p-p) as the rms level of the current is measured using the DMM.
72 TABLE 7.2 Frequency V R(p-p) V R (rms)=0.707 (V R(p-p) / 2) Measurement I rms Calculation R = V R (rms)/ Irms 50 Hz 4V 1.414V 100 Hz 4V 1.414V 200 Hz 4V V 500 Hz 4V V 1000 Hz 4V 1.414V Calculate the level of R at each frequency using Ohm's law and complete Table 7.2. Use the following space for your calculations. Based on the results of Table 7.2, is the resistance of the resistor independent of frequency for the tested range? Part 2 Inductors (a) Construct the circuit of Fig The dc resistance of the coil (R L ) will be ignored for this experiment, because X L» R L. Insert the measured value of R s, and hook up the frequency counter if available. FIG. 7.2 In this part, the resistor of part 1 is replaced by the inductor. Here again, the voltage across the inductor will be kept constant while we vary the frequency of that voltage and monitor the current in the circuit. Set the frequency of the function generator to 1 khz and adjust E s until the voltage across the coil (V L ) is 4 V (p-p). Then turn off the supply without touching its controls and interchange the positions of the sensing resistor R s and the inductor. The purpose of this maneuver is to ensure a common ground between the oscilloscope and the supply. Turn on the supply and measure the peak-to-peak voltage V Rs across the sensing resistor. Use Ohm's law to determine the peak-to-peak value of the current through the series circuit and insert in Table 7.3. Repeat the above for each frequency appearing in Table 7.3.
73 Table 7.3 Frequency V L(p-p) V Rs(p-p) I p-p = V Rs(p-p) / Rs(mea.) X L (mea.)=v L (p-p) / I(p-p) X L(cal.) =2πfL 1 khz 4V 3 khz 4V 5 khz 4V 7 khz 4V 10 khz 4V The DMM was not used to measure the current in this part of the experiment because many commercial units are limited to frequencies of 1 khz or less. (a) Calculate the reactance X L (magnitude only) at each frequency and insert the values in Table 7.3 under the heading "X L (measured)." (b) Calculate the reactance at each frequency of Table 7.3 using the nameplate value of inductance (10 mh), and complete the table. (c) How do the measured and calculated values of X L compare? (d) Plot the measured value of X L versus frequency on Graph 7.1. Label the curve and plot the points accurately. Include the plot point of f=0hz and X L = 0 Ω as determined by X L = 2πfL=2π(0 Hz)L = 0 Ω. (e) Is the resulting plot a straight line? Should it be? Why?
74 GRAPH X L (kω) f(khz) (f) Determine the inductance at 1.5 khz using the plot of part 2(d). That is, determine X L from the graph at f= 1.5 khz and calculate L from L = X L /2πf. Compare with the nameplate value. X L (at 1.5 khz) = L cal.= L nameplate =
75 Part 3 Capacitors (a) Construct the circuit of Fig FIG. 7.3 The 100Ω sensing resistor will be used to "sense" the current level in the network. With the generator set at 100 Hz, adjust the output of supply until a 4-V peak-to-peak signal is obtained across the capacitor. Then repeat the procedure as outlined in part 2(a) to determine I p-p for each frequency appearing in Table 7.4. Table 7.4 Frequency Vc(p-p) V Rs(p-p) Ip-p Xc(cal) = Vc(p-p) / Ip-p Xc(cal)=1/2πfC 100 Hz 4V 200 Hz 4V 300 Hz 4V 400 Hz 4V 500 Hz 4V 800 Hz 4V 1000 Hz 4V 2000 Hz 4V
76 (b) Calculate X c from the measured values at each frequency and insert in the X c (measured) column of Table 7.4, since both V c and I are measured values. (c) Calculate X c using the nameplate capacitance level of 0.1 µf at each frequency and insert in the X c(calculated) column. (d) How do the results in the X c (measured) column compare with those in the X c(calculated) column? (e) Plot X c (measured) versus frequency on Graph 7.2. Extend the curve below the lowest measured frequency level using a calculated or estimated level of X c. Label the curve and clearly show all the data points. GRAPH Xc(kΩ) f(khz) In what frequency range does the greatest chance in Xc occur? Is the grapg linear or nonlinear? How would you compare the curve of Xc versus frequency to that of X L versus frequency from part2?
77 (f) Determine X c at a frequency of 650 Hz from the curve just plotted. X c = At this frequency, determine the equivalent capacitance level using the fact that C = 1/ 2πfX c as defined by X c = 1/2πfC C= How does this level compare with the nameplate level of 0.1 µf? PROBLEMS 1. In the experiment, the effect of an increase in capacitance on the Xc curve was investigated. Let us now note the effect of an increase in inductance on the X L curve. Increase the inductance of Fig. 7.2 to 20 mh and plot the curve of X L versus frequency on Graph 7.1 for a frequency range of 0 Hz to 10 khz. Be sure to label the curve and clearly indicate the plot points chosen. What was the effect on the X L curve due to an increase in inductance? 2. Determine the level of C to establish the voltage levels of Fig Show all calculations and organize your work µF 7.2V (p-p) - Fig. 7.4
78 3. Determine the level of L to establish the voltage levels of Fig Again, show all required calculations and organize your work V(p-p) - Fig. 7.5
79 Name: Date: Course and Section: Instructor: EXPERIMENT 8 The Oscilloscope and Phase Measurements OBJECTIVES 1. Use the dual trace (two vertical channels) to determine the phase angle between two sinusoidal waveforms. 2. Become aware of the use of Lissajous patterns to determine the phase angle between two sinusoidal waveforms. 3. Become aware of the effect of increasing levels of resistance on the phase angles of a series R-C circuit. LAB EQUIPMENT AND COMPONENTS Resistors: 1kΩ,3.3 kω,6.8 kω Capacitors: 0.47µ Instruments: 1 DMM 1 Oscilloscope 1 Audio oscillator (or function generator) 1 Frequency counter (if available)
80 RESUME OF THEORY The phase angle between two signals of the same frequency can be determined using the oscilloscope. There are two methods available. 1. Dual-trace comparison with the calibrated time base 2. Lissajous pattern Dual-Trace Method of Phase Measurement The dual-trace method of phase measurement, aside from providing a high degree of accuracy, can compare two signals of different amplitudes and, in fact, different wave shapes. The method can be applied directly to oscilloscopes equipped with two vertical channels or to a conventional single-trace oscilloscope with an external electronic switch, as shown in Fig The electronic switch will switch between inputs at a very high speed, so both patterns will appear on the screen. Fig 8.1 Regardless of which oscilloscope is available, the procedure essentially consists of displaying both traces on the screen simultaneously, and measuring the distance (in scale divisions) between two identical points on the two traces (Fig. 8.2). Fig 8.2 One signal will be chosen as a reference, that is, zero-phase angle. In the comparison, therefore, we can assume that the signal being compared is leading (+θ) if it is to the left of the reference and lagging ( θ) if it is to the right of the reference. To use the dual-trace phase measurement method, therefore, proceed as follows:
81 1. Connect the two signals to the two vertical channels, making sure to observe proper grounding. For clarity, adjust the vertical sensitivity of each waveform until both signals have the same relative size. 2. Select the mode of operation "Alternate" or "Chop." For frequencies less than 50 khz, use Chop. For frequencies greater than 50 khz, use Alternate. 3. Once the traces are on the screen, use the GND switch to set both patterns in the vertical center of the screen. 4. Measure the number of horizontal divisions (D 1 in Fig. 8.2) required for one full cycle of either waveform (they both have the same frequency). 5. Measure the number of horizontal divisions in the phase shift (D2), as shown in Fig Because D1 is associated with a full cycle of 360 and D2 is associated with the phase angle θ, we can set up the following ratio and solve for θ: D 1 = 360 D 2 θ (8.1) For the case of Fig. 8.2, D θ = 2 * 360 D 1 2div. θ = * 360 = 72 10div. (8.2) Lissajous-Pattern Phase Measurement The Lissajous-pattern method is also called the X-Y phase measurement. To use this method, proceed as follows: 1. Connect one signal to a vertical channel and the other to the horizontal input (often de noted X-Y). 2. A display known as a Lissajous pattern will appear on the screen. The type of pattern will reveal the phase relationship, and in fact the pattern can be used to calculate the phase angle. It will define the angle by which the horizontal input leads the vertical input. The patterns shown in Fig. 8.3 indicate the phase relationship appearing with each figure.
82 Fig 8.3 The patterns shown in Fig. 8.4 can be used to calculate the phase angle (θ), as indicated below the figures. Fig 8.4 (8.3) (8.4) EXAMPLE Assume that the patterns in Figs. 8.5 and 8.6 appear on an oscilloscope screen. Calculate the phase angle θ in each case. Fig 8.5
83 PROCEDURE Part 1 Fig 8.6 The phase relationship between E and V R of Fig. 8.7 will be determined in this part using the dual-trace capability of the oscilloscope. Fig 8.7 Since E is defined as having an angle of 0, it will appear as shown in Fig In an R-C circuit, the current I will lead the applied voltage as shown in the phasor diagram. The voltage V R is in phase with I, and the voltage Vc will lag the voltage E. Fig 8.8 Note that θ + = 90 and that the vector sum of V R and Vc equals the applied voltage E. 1 θ 2 (a) Construct the network of Fig. 8.9, designed to place the source voltage E on channel 1 of the scope and V R on channel 2. The oscillator or function generator is set to 200 Hz with an amplitude of 8 V (p-p). Set the vertical and horizontal sensitivities as indicated on Fig. 8.9.
84 Fig 8.9 (b) Enter the measured value of R in Table 8.1. Then calculate the reactance of the capacitor or a frequency of 200 Hz and enter in column 2 of Table 8.1. TABLE 8.1 (c) Assuming E = 8 V (p-p) <0, calculate the peak-to-peak value of V R and the angle (θ 1 ) associated with V R and insert in Table 8.1. Show all work! Be precise. (d) Energize the network of Fig. 8.9 and determine the peak-to-peak value of V R. Insert in the measured column of Table 8.1. (e) Determine the number of horizontal divisions for one full cycle of E or V R. D 1 =.. divisions Determine the number of horizontal divisions representing the phase shift between waveforms. D 2 =.. divisions Determine the phase shift in degrees using Eq. (8.2). θ 1 =..
85 Insert the measured value of θ 1 in Table 8.1. (f) How do the calculated and measured values for V R and θ 1 compare? (g) Replace the 1-kΩ resistor with a 3.3- kω resistor and repeat the above calculations and measurements. Show all calculations below and insert the results in Table 8.2. Be neat. TABLE 8.2 (h) Replace the 3.3-kΩ resistor with a 6.8-kΩ resistor and repeat the above calculations and measurements. Show all calculations below and insert the results in Table 8.3. Be neat. TABLE 8.3 (i) Are you satisfied with the results of parts (g) and (h)? Comment accordingly. (j) The vector E = E <θ = 8 V <0 has been placed on each phasor diagram of Graph 8.1. Note that the voltage has been scaled to match the 2-V/div. scale of the horizontal and vertical axes. Using the measured values of V R(p-p) and θ 1, insert the phasor V R for each value of R. Clearly indicate the angle θ 1 and the magnitude of V R(p-p).
86 Graph 8.1 Part 2 The phase relationship between E and Vc of the same network as Fig. 8.7 will now be determined by interchanging the resistor R and capacitor C, as shown in Fig Fig 8.10 The elements must exchange positions to avoid a "shorting out" of the resistor R of Fig. 8.7 if the oscilloscope were simply placed across the capacitor of Fig The grounds of the scope and supply would establish a 0-V drop across R and possibly high currents in the remaining network since Xc is the only impedance to limit the current level. (a) The connections are now made as shown in Fig Note that E remains on channel 1 and Vc is placed on channel 2. The phase angle θ 2 between E and Vc can therefore be determined from the display.
87 Fig 8.11 (b) Enter the measured value of R in Table 8.4. Then enter the reactance at 200 Hz from Table 8.1. TABLE 8.4 (c) Assuming E = 8 V (p-p) <0, calculate the peak-to-peak value of Vc and the angle (θ 2 ) associated with Vc and insert in Table 8.4. Show all work! Be neat. (d) Energize the network of Fig and determine the peak-to-peak value of Vc.Insert in the measured column of Table 8.4. (e) Determine the phase shift in the same manner as described for part 1. D 1 =.. divisions, D 2 =.. divisions θ 2 =.. Insert the measured value in Table 8.4. (f) How do the calculated and measured values for Vc and θ 2 compare?
88 (g) Replace the 1-kΩ resistor by a 3.3-kΩ resistor and repeat the above calculations and measurements. Show all calculations below and insert the results in Table 8.5. Be neat. TABLE 8.5 (h) Replace the 3.3- kω resistor with a 6.8- kω resistor and repeat the above calculations and measurements. Show all calculations below and insert the results in Table 8.6. Be neat! TABLE 8.6 (i) Are you satisfied with the results of parts (g) and (h)? Comment accordingly. (j) Complete the phasor diagrams of Graph 8.1 with the insertion of the phasor Vc for each resistance level using peak-to peak values for the voltages. Label each vector. (k) It was noted in Fig. 8.7 that θ + = 90. For each resistance level, add 1 θ 2 the two measured values and determine the magnitude of the percent difference using the equation
89 90 θt % Difference = *100% 90 Record the values in Table 8.7. TABLE 8.7 Part 3 In this part, the phase angle will be determined from the Lissajous pattern. (a) Construct the network of Fig. 8.12, which is exactly the same as Fig except now V R is connected to the horizontal input. Fig 8.12 The resulting Lissajous patterns will determine the phase angle between E and V R for various values of R as described in the Resume of Theory. (b) Change the value of R as indicated in Table 8.7 and measure the y-intercept (y o ) and the y-maximum (y m ) from the Lissajous pattern. Record in Table 8.8.
90 TABLE 8.8 (c) Then compare the measured values of θ 1 obtained in Tables 8.1, 8.2, and 8.3 with those in Table 8.8 by completing Table 8.9, where % Difference = TABLE 8.9 θ1( Tables8.1,8.2,8.3) θ1( Table8.8) θ ( Tables8.1,8.2,8.3) 1 *100% (Tables 8.1, 8.2, 8.3) (Table 8.8) (d) Which method do you believe provided the higher degree of accuracy for determining θ 1? With which are you more comfortable? Why?
91 PROBLEMS 1. Determine the phase shift between the two sinusoidal voltages of Fig Fig 8.13 θ =. 2. Determine the phase shift between two sinusoidal waveforms that established the Lissajous pattern of Fig Fig 8.14 θ =.
92 Name: Date: Course and Section: Instructor: EXPERIMENT 9 Series Resonant Circuits OBJECTIVES 1. Validate the basic equation for the resonant frequency of a series resonant circuit. 2. Plot the various voltages and current for a series resonant circuit versus frequency. 3. Verify that the input impedance is a minimum at the resonant frequency. 4. Demonstrate the relationship between the Q of a series resonant circuit and the resulting bandwidth. LAB EQUIPMENT AND COMPONENTS Resistors 1-33Ω, 220-Ω Inductors 1-10 mh Capacitors µF, 1-µF Instruments 1 DMM 1 Audio oscillator or function generator 1 Frequency counter (strongly recommended)
93 RESUME OF THEORY In a series R-L-C circuit, there exists one frequency at which X L = X C or wl = 1/wC. At this frequency the circuit is in resonance, and the input voltage and current are in phase. At resonance, the circuit is resistive in nature and has a minimum value of impedance or a maximum value of current. The resonant radian frequency w s = 1/LC and frequency f s = 1/ 2 πlc. The Q of the circuit is defined as w s L/R and affects the selectivity of the circuit through BW = f s IQ. High-Q circuits are very selective. At resonance, V c = QE input. The half-power frequencies f 1 and f 2 are defined as those frequencies at which the power dissipated is one-half the power dissipated at resonance. In addition, the current is (or 1/V2) times the current at resonance. The bandwidth BW = f 2 f 1. The smaller the bandwidth, the more selective the circuit is. In Fig. 9.1, note that increasing R results in a less selective circuit. Figure 9.2 shows the voltages across the three elements versus the frequency. The voltage across the resistor, V R, has exactly the same shape as the current, since it differs by the constant R. V R is a maximum at resonance. V c and V L are equal at resonance (f s ) since X L = X c, but note that they are not maximum at the resonant frequency. At frequencies below fs, V c > V L ; at frequencies above fs, V L > V o as indicated in Fig Fig 9.1
94 Fig 9.2 PROCEDURE Part 1 Low- Q Circuit (a) Construct the circuit of Fig Insert the measured resistance values. In this experiment the dc resistance of the coil (R,) must be included. If available, the frequency counter should be employed. Fig 9.3 (b) Using the nameplate values (L = 10 mh, C = 0.1 µf), compute the radian frequency w s and the frequency f s at resonance. Show all your work in the following space. Organize the presentation and be neat! Insert the calculated level of f s in Table 9.2 and calculate the two additional frequency levels that are a function of f s.
95 (c) Energize the circuit and set the oscillator to the frequencies indicated in Table 9.1. At each frequency, reset the input to 8 V (p-p) with the oscilloscope and measure the peak-to-peak values of the voltage V c with the oscilloscope. Take all the readings for V c and then interchange the positions of the capacitor and inductor and take all the V L readings of Table 9.1. Be sure to take the additional readings near the peak value. Finally, interchange the positions of the inductor and resistor and take the V R readings. This procedure must be followed to ensure a common ground between the source and measured voltage. Take a few extra readings near the resonant frequency. Use the dual-trace feature of the oscilloscope to measure the desired voltage and maintain E at 8 V (p-p) for each reading. If necessary, change scales to obtain the most accurate reading possible (d) Calculate the peak-to-peak value of the current at each frequency using Ohm's law and insert in Table 9.1. (e) Calculate the input impedance at each frequency and complete Table 9.1. (f) Plot Z i, versus frequency on Graph 9.1. Clearly indicate each plot point and label the curve and the resonant frequency. Table 9.1
96 Graph 9.1 (g) At resonance, compare the input impedance Z i, to the total resistance of the circuit R T = R + R l. (h) Describe in a few sentences how the input impedance of a series resonant circuit varies with frequency. Which element has the most influence on the input impedance at the low and high ends of the frequency spectrum? (i) If the input impedance is a minimum at the resonant frequency, what would you expect to be true about the current at resonance?
97 Plot I p. p versus frequency on Graph 9.2 and comment on whether the preceding conclusion was verified. How does the maximum current compare to the value determined by I p. p = E p _ p / R T = E p. p / (R + R l )? Graph 9.2 (j) Plot V R(p-p) versus frequency on Graph 9.3. Clearly indicate each point and label the curve. Use peak-to-peak values.
98 Graph 9.3 (k) Plot V L (p-p) and W c(p-p) versus frequency on Graph 9.4. Clearly indicate each plot point and label the curves. Use peak-to-peak values. At what frequency are V R, V L and V c a maximum? Did V c peak before f s and V L below f s, as noted in the Resume of Theory? Does the maximum value of V R occur at the same frequency noted for the current I? If so, why? (l) On Graph 9.2 indicate the resonant and half-power frequencies. Then define the bandwidth and record the levels below:
99 Graph 9.4 Using measured resistor values, calculate the quality factor using the equation Qs = X L IR T. Then determine Q s using the resonant frequency and bandwidth from Graph 9.2 and the equation Q s = f s /BW and compare to the previous result. Have the equations been verified? If not, why not?
100 (m)after placing R in the position of C in Fig 9.3, place E and V R on a dual-trace oscilloscope. Vary the frequency applied from 0 to 10 khz and note when E and V R are in phase. At what frequency are the two in phase? When they are in phase, what does it reveal about the input impedance of the circuit at resonance? Part 2 Higher- Q Circuit We will now repeat the preceding analysis for a higher-g (more selective) series resonant circuit by replacing the 220-Ωresistor with a 33-Ω resistor and note the effect on the various plots. (a) Measure the resistance of the 33-Ω resistor and record below. Repeat parts 1 (a) through 1(e) after replacing the 220-Ω resistor with a 33-Ω resistor and enter the results below and in Table 9.3. For readings near the maximum, you may have to use a 10:1 probe or set the GND line at the bottom of the display and multiply the resulting positive excursion by 2 to obtain the peakto-peak value. Be sure to take a reading at the resonant frequency and the frequencies defined by f s. Table 9.2
101 (b) Plot Z i versus frequency on Graph 9.1. Clearly indicate each plot point and label the curve to distinguish it from the other curve. How has the shape of the curve changed? Is the resonant frequency the same even though the resistance was changed? Is the minimum value still equal to R T = R + R l. (c) Plot I p-p versus frequency on Graph 9.2. How has the shape of the curve changed with an increased Q value? Is the maximum current the same, or has it changed? Calculate the new maximum using the circuit values and compare to the measured graph value. (d) Plot V R(P - P) versus frequency on Graph 9.3. Clearly indicate each plot point and label the curve. Use peak-to-peak values. Does the maximum value of V R continue to occur at the same frequency noted for the current /? If so, why? (e) Plot V L(p-p ) and V C ( p-p ) versus frequency on Graph 9.4. Clearly indicate each plot point and label the curves. Use peak-to-peak values. At what frequency are V R, V L and V c a maximum? Are the frequencies at which V L and V c reached their maximums closer to the resonant frequency than they were for the low-q network? A theoretical analysis will reveal that the higher the Q of the network, the closer the maximums of V L and V c are to the resonant frequency (f) On Graph 9.2 indicate the half-power frequencies and the bandwidth. Record Using measured resistor values, calculate the quality factor using the equation Q S = X L /RT. Then calculate Q s using the resonant frequency and bandwidth from Graph 9.2 and the equation Q s = f s / BW and compare to the preceding result.
102 Have the equations been verified? If not, why not? PROBLEMS 1) Design a series resonant circuit with the following specifications: L = 10 mh, R1 = 4 Ω, / max = 200 ma, f s = 10 khz, Q s = 20 That is, determine the required R, C, and supply voltage E. For R and C, use the closest standard values. Consult any catalog in the laboratory area for standard values. 2) Redesign the network of Problem 1 to have a Q s of 10. All the other specifications remain the same.
Unit/Standard Number. High School Graduation Years 2010, 2011 and 2012
 1 Secondary Task List 100 SAFETY 101 Demonstrate an understanding of State and School safety regulations. 102 Practice safety techniques for electronics work. 103 Demonstrate an understanding of proper
1 Secondary Task List 100 SAFETY 101 Demonstrate an understanding of State and School safety regulations. 102 Practice safety techniques for electronics work. 103 Demonstrate an understanding of proper
CIRCUITS LABORATORY EXPERIMENT 3. AC Circuit Analysis
 CIRCUITS LABORATORY EXPERIMENT 3 AC Circuit Analysis 3.1 Introduction The steady-state behavior of circuits energized by sinusoidal sources is an important area of study for several reasons. First, the
CIRCUITS LABORATORY EXPERIMENT 3 AC Circuit Analysis 3.1 Introduction The steady-state behavior of circuits energized by sinusoidal sources is an important area of study for several reasons. First, the
First Year (Electrical & Electronics Engineering)
 Z PRACTICAL WORK BOOK For The Course EE-113 Basic Electrical Engineering For First Year (Electrical & Electronics Engineering) Name of Student: Class: Batch : Discipline: Class Roll No.: Examination Seat
Z PRACTICAL WORK BOOK For The Course EE-113 Basic Electrical Engineering For First Year (Electrical & Electronics Engineering) Name of Student: Class: Batch : Discipline: Class Roll No.: Examination Seat
Electrical Resonance
 Electrical Resonance (R-L-C series circuit) APPARATUS 1. R-L-C Circuit board 2. Signal generator 3. Oscilloscope Tektronix TDS1002 with two sets of leads (see Introduction to the Oscilloscope ) INTRODUCTION
Electrical Resonance (R-L-C series circuit) APPARATUS 1. R-L-C Circuit board 2. Signal generator 3. Oscilloscope Tektronix TDS1002 with two sets of leads (see Introduction to the Oscilloscope ) INTRODUCTION
EE 1202 Experiment #4 Capacitors, Inductors, and Transient Circuits
 EE 1202 Experiment #4 Capacitors, Inductors, and Transient Circuits 1. Introduction and Goal: Exploring transient behavior due to inductors and capacitors in DC circuits; gaining experience with lab instruments.
EE 1202 Experiment #4 Capacitors, Inductors, and Transient Circuits 1. Introduction and Goal: Exploring transient behavior due to inductors and capacitors in DC circuits; gaining experience with lab instruments.
RLC Series Resonance
 RLC Series Resonance 11EM Object: The purpose of this laboratory activity is to study resonance in a resistor-inductor-capacitor (RLC) circuit by examining the current through the circuit as a function
RLC Series Resonance 11EM Object: The purpose of this laboratory activity is to study resonance in a resistor-inductor-capacitor (RLC) circuit by examining the current through the circuit as a function
Basic Laws Circuit Theorems Methods of Network Analysis Non-Linear Devices and Simulation Models
 EE Modul 1: Electric Circuits Theory Basic Laws Circuit Theorems Methods of Network Analysis Non-Linear Devices and Simulation Models EE Modul 1: Electric Circuits Theory Current, Voltage, Impedance Ohm
EE Modul 1: Electric Circuits Theory Basic Laws Circuit Theorems Methods of Network Analysis Non-Linear Devices and Simulation Models EE Modul 1: Electric Circuits Theory Current, Voltage, Impedance Ohm
Lab E1: Introduction to Circuits
 E1.1 Lab E1: Introduction to Circuits The purpose of the this lab is to introduce you to some basic instrumentation used in electrical circuits. You will learn to use a DC power supply, a digital multimeter
E1.1 Lab E1: Introduction to Circuits The purpose of the this lab is to introduce you to some basic instrumentation used in electrical circuits. You will learn to use a DC power supply, a digital multimeter
Inductors in AC Circuits
 Inductors in AC Circuits Name Section Resistors, inductors, and capacitors all have the effect of modifying the size of the current in an AC circuit and the time at which the current reaches its maximum
Inductors in AC Circuits Name Section Resistors, inductors, and capacitors all have the effect of modifying the size of the current in an AC circuit and the time at which the current reaches its maximum
The Time Constant of an RC Circuit
 The Time Constant of an RC Circuit 1 Objectives 1. To determine the time constant of an RC Circuit, and 2. To determine the capacitance of an unknown capacitor. 2 Introduction What the heck is a capacitor?
The Time Constant of an RC Circuit 1 Objectives 1. To determine the time constant of an RC Circuit, and 2. To determine the capacitance of an unknown capacitor. 2 Introduction What the heck is a capacitor?
W03 Analysis of DC Circuits. Yrd. Doç. Dr. Aytaç Gören
 W03 Analysis of DC Circuits Yrd. Doç. Dr. Aytaç Gören ELK 2018 - Contents W01 Basic Concepts in Electronics W02 AC to DC Conversion W03 Analysis of DC Circuits (self and condenser) W04 Transistors and
W03 Analysis of DC Circuits Yrd. Doç. Dr. Aytaç Gören ELK 2018 - Contents W01 Basic Concepts in Electronics W02 AC to DC Conversion W03 Analysis of DC Circuits (self and condenser) W04 Transistors and
RC Circuits and The Oscilloscope Physics Lab X
 Objective RC Circuits and The Oscilloscope Physics Lab X In this series of experiments, the time constant of an RC circuit will be measured experimentally and compared with the theoretical expression for
Objective RC Circuits and The Oscilloscope Physics Lab X In this series of experiments, the time constant of an RC circuit will be measured experimentally and compared with the theoretical expression for
Lab 3 Rectifier Circuits
 ECET 242 Electronic Circuits Lab 3 Rectifier Circuits Page 1 of 5 Name: Objective: Students successfully completing this lab exercise will accomplish the following objectives: 1. Learn how to construct
ECET 242 Electronic Circuits Lab 3 Rectifier Circuits Page 1 of 5 Name: Objective: Students successfully completing this lab exercise will accomplish the following objectives: 1. Learn how to construct
PROCEDURE: 1. Measure and record the actual values of the four resistors listed in Table 10-1.
 The answer to two questions will help you identify a series or parallel connection: (1) Will the identical current go through both components? f the answer is yes, the components are in series. (2) Are
The answer to two questions will help you identify a series or parallel connection: (1) Will the identical current go through both components? f the answer is yes, the components are in series. (2) Are
DIODE CIRCUITS LABORATORY. Fig. 8.1a Fig 8.1b
 DIODE CIRCUITS LABORATORY A solid state diode consists of a junction of either dissimilar semiconductors (pn junction diode) or a metal and a semiconductor (Schottky barrier diode). Regardless of the type,
DIODE CIRCUITS LABORATORY A solid state diode consists of a junction of either dissimilar semiconductors (pn junction diode) or a metal and a semiconductor (Schottky barrier diode). Regardless of the type,
ε: Voltage output of Signal Generator (also called the Source voltage or Applied
 Experiment #10: LR & RC Circuits Frequency Response EQUIPMENT NEEDED Science Workshop Interface Power Amplifier (2) Voltage Sensor graph paper (optional) (3) Patch Cords Decade resistor, capacitor, and
Experiment #10: LR & RC Circuits Frequency Response EQUIPMENT NEEDED Science Workshop Interface Power Amplifier (2) Voltage Sensor graph paper (optional) (3) Patch Cords Decade resistor, capacitor, and
MATERIALS. Multisim screen shots sent to TA.
 Page 1/8 Revision 0 9-Jun-10 OBJECTIVES Learn new Multisim components and instruments. Conduct a Multisim transient analysis. Gain proficiency in the function generator and oscilloscope. MATERIALS Multisim
Page 1/8 Revision 0 9-Jun-10 OBJECTIVES Learn new Multisim components and instruments. Conduct a Multisim transient analysis. Gain proficiency in the function generator and oscilloscope. MATERIALS Multisim
Laboratory Manual for AC Electrical Circuits
 AC Electrical Circuits Laboratory Manual James M. Fiore 2 Laboratory Manual for AC Electrical Circuits Laboratory Manual for AC Electrical Circuits by James M. Fiore Version 1.3.1, 01 March 2016 Laboratory
AC Electrical Circuits Laboratory Manual James M. Fiore 2 Laboratory Manual for AC Electrical Circuits Laboratory Manual for AC Electrical Circuits by James M. Fiore Version 1.3.1, 01 March 2016 Laboratory
See Horenstein 4.3 and 4.4
 EE 462: Laboratory # 4 DC Power Supply Circuits Using Diodes by Drs. A.V. Radun and K.D. Donohue (2/14/07) Department of Electrical and Computer Engineering University of Kentucky Lexington, KY 40506 Updated
EE 462: Laboratory # 4 DC Power Supply Circuits Using Diodes by Drs. A.V. Radun and K.D. Donohue (2/14/07) Department of Electrical and Computer Engineering University of Kentucky Lexington, KY 40506 Updated
Solution Derivations for Capa #11
 Solution Derivations for Capa #11 Caution: The symbol E is used interchangeably for energy and EMF. 1) DATA: V b = 5.0 V, = 155 Ω, L = 8.400 10 2 H. In the diagram above, what is the voltage across the
Solution Derivations for Capa #11 Caution: The symbol E is used interchangeably for energy and EMF. 1) DATA: V b = 5.0 V, = 155 Ω, L = 8.400 10 2 H. In the diagram above, what is the voltage across the
Lab #4 Thevenin s Theorem
 In this experiment you will become familiar with one of the most important theorems in circuit analysis, Thevenin s Theorem. Thevenin s Theorem can be used for two purposes: 1. To calculate the current
In this experiment you will become familiar with one of the most important theorems in circuit analysis, Thevenin s Theorem. Thevenin s Theorem can be used for two purposes: 1. To calculate the current
= V peak 2 = 0.707V peak
 BASIC ELECTRONICS - RECTIFICATION AND FILTERING PURPOSE Suppose that you wanted to build a simple DC electronic power supply, which operated off of an AC input (e.g., something you might plug into a standard
BASIC ELECTRONICS - RECTIFICATION AND FILTERING PURPOSE Suppose that you wanted to build a simple DC electronic power supply, which operated off of an AC input (e.g., something you might plug into a standard
Basic Electrical Technology Dr. L. Umanand Department of Electrical Engineering Indian Institute of Science, Bangalore. Lecture - 33 3 phase System 4
 Basic Electrical Technology Dr. L. Umanand Department of Electrical Engineering Indian Institute of Science, Bangalore Lecture - 33 3 phase System 4 Hello everybody. So, in the last class we have been
Basic Electrical Technology Dr. L. Umanand Department of Electrical Engineering Indian Institute of Science, Bangalore Lecture - 33 3 phase System 4 Hello everybody. So, in the last class we have been
Fig. 1 Analogue Multimeter Fig.2 Digital Multimeter
 ELECTRICAL INSTRUMENT AND MEASUREMENT Electrical measuring instruments are devices used to measure electrical quantities such as electric current, voltage, resistance, electrical power and energy. MULTIMETERS
ELECTRICAL INSTRUMENT AND MEASUREMENT Electrical measuring instruments are devices used to measure electrical quantities such as electric current, voltage, resistance, electrical power and energy. MULTIMETERS
PHYSICS 111 LABORATORY Experiment #3 Current, Voltage and Resistance in Series and Parallel Circuits
 PHYSCS 111 LABORATORY Experiment #3 Current, Voltage and Resistance in Series and Parallel Circuits This experiment is designed to investigate the relationship between current and potential in simple series
PHYSCS 111 LABORATORY Experiment #3 Current, Voltage and Resistance in Series and Parallel Circuits This experiment is designed to investigate the relationship between current and potential in simple series
Step response of an RLC series circuit
 School of Engineering Department of Electrical and Computer Engineering 332:224 Principles of Electrical Engineering II Laboratory Experiment 5 Step response of an RLC series circuit 1 Introduction Objectives
School of Engineering Department of Electrical and Computer Engineering 332:224 Principles of Electrical Engineering II Laboratory Experiment 5 Step response of an RLC series circuit 1 Introduction Objectives
EXPERIMENT NUMBER 8 CAPACITOR CURRENT-VOLTAGE RELATIONSHIP
 1 EXPERIMENT NUMBER 8 CAPACITOR CURRENT-VOLTAGE RELATIONSHIP Purpose: To demonstrate the relationship between the voltage and current of a capacitor. Theory: A capacitor is a linear circuit element whose
1 EXPERIMENT NUMBER 8 CAPACITOR CURRENT-VOLTAGE RELATIONSHIP Purpose: To demonstrate the relationship between the voltage and current of a capacitor. Theory: A capacitor is a linear circuit element whose
LAB 7 MOSFET CHARACTERISTICS AND APPLICATIONS
 LAB 7 MOSFET CHARACTERISTICS AND APPLICATIONS Objective In this experiment you will study the i-v characteristics of an MOS transistor. You will use the MOSFET as a variable resistor and as a switch. BACKGROUND
LAB 7 MOSFET CHARACTERISTICS AND APPLICATIONS Objective In this experiment you will study the i-v characteristics of an MOS transistor. You will use the MOSFET as a variable resistor and as a switch. BACKGROUND
Parallel Plate Capacitor
 Parallel Plate Capacitor Capacitor Charge, Plate Separation, and Voltage A capacitor is used to store electric charge. The more voltage (electrical pressure) you apply to the capacitor, the more charge
Parallel Plate Capacitor Capacitor Charge, Plate Separation, and Voltage A capacitor is used to store electric charge. The more voltage (electrical pressure) you apply to the capacitor, the more charge
= (0.400 A) (4.80 V) = 1.92 W = (0.400 A) (7.20 V) = 2.88 W
 Physics 2220 Module 06 Homework 0. What are the magnitude and direction of the current in the 8 Ω resister in the figure? Assume the current is moving clockwise. Then use Kirchhoff's second rule: 3.00
Physics 2220 Module 06 Homework 0. What are the magnitude and direction of the current in the 8 Ω resister in the figure? Assume the current is moving clockwise. Then use Kirchhoff's second rule: 3.00
Laboratory 4: Feedback and Compensation
 Laboratory 4: Feedback and Compensation To be performed during Week 9 (Oct. 20-24) and Week 10 (Oct. 27-31) Due Week 11 (Nov. 3-7) 1 Pre-Lab This Pre-Lab should be completed before attending your regular
Laboratory 4: Feedback and Compensation To be performed during Week 9 (Oct. 20-24) and Week 10 (Oct. 27-31) Due Week 11 (Nov. 3-7) 1 Pre-Lab This Pre-Lab should be completed before attending your regular
Experiment1: Introduction to laboratory equipment and basic components.
 Experiment1: Introduction to laboratory equipment and basic components. 1 OBJECTIVES. This experiment will provide exposure to the various test equipment to be used in subsequent experiments. A primary
Experiment1: Introduction to laboratory equipment and basic components. 1 OBJECTIVES. This experiment will provide exposure to the various test equipment to be used in subsequent experiments. A primary
Lab #9: AC Steady State Analysis
 Theory & Introduction Lab #9: AC Steady State Analysis Goals for Lab #9 The main goal for lab 9 is to make the students familar with AC steady state analysis, db scale and the NI ELVIS frequency analyzer.
Theory & Introduction Lab #9: AC Steady State Analysis Goals for Lab #9 The main goal for lab 9 is to make the students familar with AC steady state analysis, db scale and the NI ELVIS frequency analyzer.
Lab 3 - DC Circuits and Ohm s Law
 Lab 3 DC Circuits and Ohm s Law L3-1 Name Date Partners Lab 3 - DC Circuits and Ohm s Law OBJECTIES To learn to apply the concept of potential difference (voltage) to explain the action of a battery in
Lab 3 DC Circuits and Ohm s Law L3-1 Name Date Partners Lab 3 - DC Circuits and Ohm s Law OBJECTIES To learn to apply the concept of potential difference (voltage) to explain the action of a battery in
RLC Resonant Circuits
 C esonant Circuits Andrew McHutchon April 20, 203 Capacitors and Inductors There is a lot of inconsistency when it comes to dealing with reactances of complex components. The format followed in this document
C esonant Circuits Andrew McHutchon April 20, 203 Capacitors and Inductors There is a lot of inconsistency when it comes to dealing with reactances of complex components. The format followed in this document
AC CIRCUITS - CAPACITORS AND INDUCTORS
 EXPRIMENT#8 AC CIRCUITS - CAPACITORS AND INDUCTORS NOTE: Two weeks are allocated for this experiment. Before performing this experiment, review the Proper Oscilloscope Use section of Experiment #7. Objective
EXPRIMENT#8 AC CIRCUITS - CAPACITORS AND INDUCTORS NOTE: Two weeks are allocated for this experiment. Before performing this experiment, review the Proper Oscilloscope Use section of Experiment #7. Objective
EDEXCEL NATIONAL CERTIFICATE/DIPLOMA UNIT 5 - ELECTRICAL AND ELECTRONIC PRINCIPLES NQF LEVEL 3 OUTCOME 4 - ALTERNATING CURRENT
 EDEXCEL NATIONAL CERTIFICATE/DIPLOMA UNIT 5 - ELECTRICAL AND ELECTRONIC PRINCIPLES NQF LEVEL 3 OUTCOME 4 - ALTERNATING CURRENT 4 Understand single-phase alternating current (ac) theory Single phase AC
EDEXCEL NATIONAL CERTIFICATE/DIPLOMA UNIT 5 - ELECTRICAL AND ELECTRONIC PRINCIPLES NQF LEVEL 3 OUTCOME 4 - ALTERNATING CURRENT 4 Understand single-phase alternating current (ac) theory Single phase AC
Ver 3537 E1.1 Analysis of Circuits (2014) E1.1 Circuit Analysis. Problem Sheet 1 (Lectures 1 & 2)
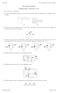 Ver 3537 E. Analysis of Circuits () Key: [A]= easy... [E]=hard E. Circuit Analysis Problem Sheet (Lectures & ). [A] One of the following circuits is a series circuit and the other is a parallel circuit.
Ver 3537 E. Analysis of Circuits () Key: [A]= easy... [E]=hard E. Circuit Analysis Problem Sheet (Lectures & ). [A] One of the following circuits is a series circuit and the other is a parallel circuit.
DEGREE: Bachelor in Biomedical Engineering YEAR: 2 TERM: 2 WEEKLY PLANNING
 SESSION WEEK COURSE: Electronic Technology in Biomedicine DEGREE: Bachelor in Biomedical Engineering YEAR: 2 TERM: 2 WEEKLY PLANNING DESCRIPTION GROUPS (mark X) SPECIAL ROOM FOR SESSION (Computer class
SESSION WEEK COURSE: Electronic Technology in Biomedicine DEGREE: Bachelor in Biomedical Engineering YEAR: 2 TERM: 2 WEEKLY PLANNING DESCRIPTION GROUPS (mark X) SPECIAL ROOM FOR SESSION (Computer class
ES250: Electrical Science. HW7: Energy Storage Elements
 ES250: Electrical Science HW7: Energy Storage Elements Introduction This chapter introduces two more circuit elements, the capacitor and the inductor whose elements laws involve integration or differentiation;
ES250: Electrical Science HW7: Energy Storage Elements Introduction This chapter introduces two more circuit elements, the capacitor and the inductor whose elements laws involve integration or differentiation;
Fundamentals of Signature Analysis
 Fundamentals of Signature Analysis An In-depth Overview of Power-off Testing Using Analog Signature Analysis www.huntron.com 1 www.huntron.com 2 Table of Contents SECTION 1. INTRODUCTION... 7 PURPOSE...
Fundamentals of Signature Analysis An In-depth Overview of Power-off Testing Using Analog Signature Analysis www.huntron.com 1 www.huntron.com 2 Table of Contents SECTION 1. INTRODUCTION... 7 PURPOSE...
Experiment 8 Series-Parallel Circuits
 Experiment 8 Series-Parallel Circuits EL 111 - DC Fundamentals By: Walter Banzhaf, E.K. Smith, and Winfield Young University of Hartford Ward College of Technology Objectives: 1. For the student to measure
Experiment 8 Series-Parallel Circuits EL 111 - DC Fundamentals By: Walter Banzhaf, E.K. Smith, and Winfield Young University of Hartford Ward College of Technology Objectives: 1. For the student to measure
Experiment #11: LRC Circuit (Power Amplifier, Voltage Sensor)
 Experiment #11: LRC Circuit (Power Amplifier, Voltage Sensor) Concept: circuits Time: 30 m SW Interface: 750 Windows file: RLC.SWS EQUIPMENT NEEDED Science Workshop Interface Power Amplifier (2) Voltage
Experiment #11: LRC Circuit (Power Amplifier, Voltage Sensor) Concept: circuits Time: 30 m SW Interface: 750 Windows file: RLC.SWS EQUIPMENT NEEDED Science Workshop Interface Power Amplifier (2) Voltage
Step Response of RC Circuits
 Step Response of RC Circuits 1. OBJECTIVES...2 2. REFERENCE...2 3. CIRCUITS...2 4. COMPONENTS AND SPECIFICATIONS...3 QUANTITY...3 DESCRIPTION...3 COMMENTS...3 5. DISCUSSION...3 5.1 SOURCE RESISTANCE...3
Step Response of RC Circuits 1. OBJECTIVES...2 2. REFERENCE...2 3. CIRCUITS...2 4. COMPONENTS AND SPECIFICATIONS...3 QUANTITY...3 DESCRIPTION...3 COMMENTS...3 5. DISCUSSION...3 5.1 SOURCE RESISTANCE...3
Eðlisfræði 2, vor 2007
 [ Assignment View ] [ Print ] Eðlisfræði 2, vor 2007 30. Inductance Assignment is due at 2:00am on Wednesday, March 14, 2007 Credit for problems submitted late will decrease to 0% after the deadline has
[ Assignment View ] [ Print ] Eðlisfræði 2, vor 2007 30. Inductance Assignment is due at 2:00am on Wednesday, March 14, 2007 Credit for problems submitted late will decrease to 0% after the deadline has
ELECTRICAL ENGINEERING AND ELECTRONICS. GUIDE TO LABORATORY EXERCISES
 TOMSK POLYTECHNIС UNIVERSITY F.Yu. Kanev and G.V. Nosov ELECTRICAL ENGINEERING AND ELECTRONICS. GUIDE TO LABORATORY EXERCISES Recommended for publishing as a guide to laboratory exercises by the Editorial
TOMSK POLYTECHNIС UNIVERSITY F.Yu. Kanev and G.V. Nosov ELECTRICAL ENGINEERING AND ELECTRONICS. GUIDE TO LABORATORY EXERCISES Recommended for publishing as a guide to laboratory exercises by the Editorial
DOE FUNDAMENTALS HANDBOOK ELECTRICAL SCIENCE Volume 3 of 4
 DOE-HDBK-1011/3-92 JUNE 1992 DOE FUNDAMENTALS HANDBOOK ELECTRICAL SCIENCE Volume 3 of 4 U.S. Department of Energy Washington, D.C. 20585 FSC-6910 Distribution Statement A. Approved for public release;
DOE-HDBK-1011/3-92 JUNE 1992 DOE FUNDAMENTALS HANDBOOK ELECTRICAL SCIENCE Volume 3 of 4 U.S. Department of Energy Washington, D.C. 20585 FSC-6910 Distribution Statement A. Approved for public release;
Three phase circuits
 Three phase circuits THREE PHASE CIRCUITS THREE-PHASE ADVANTAGES 1. The horsepower rating of three-phase motors and the kva rating of three-phase transformers are 150% greater than single-phase motors
Three phase circuits THREE PHASE CIRCUITS THREE-PHASE ADVANTAGES 1. The horsepower rating of three-phase motors and the kva rating of three-phase transformers are 150% greater than single-phase motors
Oscilloscope, Function Generator, and Voltage Division
 1. Introduction Oscilloscope, Function Generator, and Voltage Division In this lab the student will learn to use the oscilloscope and function generator. The student will also verify the concept of voltage
1. Introduction Oscilloscope, Function Generator, and Voltage Division In this lab the student will learn to use the oscilloscope and function generator. The student will also verify the concept of voltage
Measurement of Capacitance
 Measurement of Capacitance Pre-Lab Questions Page Name: Class: Roster Number: Instructor:. A capacitor is used to store. 2. What is the SI unit for capacitance? 3. A capacitor basically consists of two
Measurement of Capacitance Pre-Lab Questions Page Name: Class: Roster Number: Instructor:. A capacitor is used to store. 2. What is the SI unit for capacitance? 3. A capacitor basically consists of two
Series-Parallel Circuits. Objectives
 Series-Parallel Circuits Objectives Identify series-parallel configuration Analyze series-parallel circuits Apply KVL and KCL to the series-parallel circuits Analyze loaded voltage dividers Determine the
Series-Parallel Circuits Objectives Identify series-parallel configuration Analyze series-parallel circuits Apply KVL and KCL to the series-parallel circuits Analyze loaded voltage dividers Determine the
Experiment #5, Series and Parallel Circuits, Kirchhoff s Laws
 Physics 182 Summer 2013 Experiment #5 1 Experiment #5, Series and Parallel Circuits, Kirchhoff s Laws 1 Purpose Our purpose is to explore and validate Kirchhoff s laws as a way to better understanding
Physics 182 Summer 2013 Experiment #5 1 Experiment #5, Series and Parallel Circuits, Kirchhoff s Laws 1 Purpose Our purpose is to explore and validate Kirchhoff s laws as a way to better understanding
Circuits with inductors and alternating currents. Chapter 20 #45, 46, 47, 49
 Circuits with inductors and alternating currents Chapter 20 #45, 46, 47, 49 RL circuits Ch. 20 (last section) Symbol for inductor looks like a spring. An inductor is a circuit element that has a large
Circuits with inductors and alternating currents Chapter 20 #45, 46, 47, 49 RL circuits Ch. 20 (last section) Symbol for inductor looks like a spring. An inductor is a circuit element that has a large
Chapter 29 Alternating-Current Circuits
 hapter 9 Alternating-urrent ircuits onceptual Problems A coil in an ac generator rotates at 6 Hz. How much time elapses between successive emf values of the coil? Determine the oncept Successive s are
hapter 9 Alternating-urrent ircuits onceptual Problems A coil in an ac generator rotates at 6 Hz. How much time elapses between successive emf values of the coil? Determine the oncept Successive s are
LABORATORY 10 TIME AVERAGES, RMS VALUES AND THE BRIDGE RECTIFIER. Bridge Rectifier
 LABORATORY 10 TIME AVERAGES, RMS VALUES AND THE BRIDGE RECTIFIER Full-wave Rectification: Bridge Rectifier For many electronic circuits, DC supply voltages are required but only AC voltages are available.
LABORATORY 10 TIME AVERAGES, RMS VALUES AND THE BRIDGE RECTIFIER Full-wave Rectification: Bridge Rectifier For many electronic circuits, DC supply voltages are required but only AC voltages are available.
PHYSICS 360 - LAB #2 Passive Low-pass and High-pass Filter Circuits and Integrator and Differentiator Circuits
 PHYSICS 360 - LAB #2 Passie Low-pass and High-pass Filter Circuits and Integrator and Differentiator Circuits Objectie: Study the behaior of low-pass and high-pass filters. Study the differentiator and
PHYSICS 360 - LAB #2 Passie Low-pass and High-pass Filter Circuits and Integrator and Differentiator Circuits Objectie: Study the behaior of low-pass and high-pass filters. Study the differentiator and
GenTech Practice Questions
 GenTech Practice Questions Basic Electronics Test: This test will assess your knowledge of and ability to apply the principles of Basic Electronics. This test is comprised of 90 questions in the following
GenTech Practice Questions Basic Electronics Test: This test will assess your knowledge of and ability to apply the principles of Basic Electronics. This test is comprised of 90 questions in the following
Experiment 4 ~ Resistors in Series & Parallel
 Experiment 4 ~ Resistors in Series & Parallel Objective: In this experiment you will set up three circuits: one with resistors in series, one with resistors in parallel, and one with some of each. You
Experiment 4 ~ Resistors in Series & Parallel Objective: In this experiment you will set up three circuits: one with resistors in series, one with resistors in parallel, and one with some of each. You
Designing Stable Compensation Networks for Single Phase Voltage Mode Buck Regulators
 Designing Stable Compensation Networks for Single Phase Voltage Mode Buck Regulators Technical Brief December 3 TB47. Author: Doug Mattingly Assumptions This Technical Brief makes the following assumptions:.
Designing Stable Compensation Networks for Single Phase Voltage Mode Buck Regulators Technical Brief December 3 TB47. Author: Doug Mattingly Assumptions This Technical Brief makes the following assumptions:.
Transistor Amplifiers
 Physics 3330 Experiment #7 Fall 1999 Transistor Amplifiers Purpose The aim of this experiment is to develop a bipolar transistor amplifier with a voltage gain of minus 25. The amplifier must accept input
Physics 3330 Experiment #7 Fall 1999 Transistor Amplifiers Purpose The aim of this experiment is to develop a bipolar transistor amplifier with a voltage gain of minus 25. The amplifier must accept input
BASIC ELECTRONICS AC CIRCUIT ANALYSIS. December 2011
 AM 5-202 BASIC ELECTRONICS AC CIRCUIT ANALYSIS December 2011 DISTRIBUTION RESTRICTION: Approved for Pubic Release. Distribution is unlimited. DEPARTMENT OF THE ARMY MILITARY AUXILIARY RADIO SYSTEM FORT
AM 5-202 BASIC ELECTRONICS AC CIRCUIT ANALYSIS December 2011 DISTRIBUTION RESTRICTION: Approved for Pubic Release. Distribution is unlimited. DEPARTMENT OF THE ARMY MILITARY AUXILIARY RADIO SYSTEM FORT
BSNL TTA Question Paper-Instruments and Measurement Specialization 2007
 BSNL TTA Question Paper-Instruments and Measurement Specialization 2007 (1) Instrument is a device for determining (a) the magnitude of a quantity (b) the physics of a variable (c) either of the above
BSNL TTA Question Paper-Instruments and Measurement Specialization 2007 (1) Instrument is a device for determining (a) the magnitude of a quantity (b) the physics of a variable (c) either of the above
Aircraft Electrical System
 Chapter 9 Aircraft Electrical System Introduction The satisfactory performance of any modern aircraft depends to a very great degree on the continuing reliability of electrical systems and subsystems.
Chapter 9 Aircraft Electrical System Introduction The satisfactory performance of any modern aircraft depends to a very great degree on the continuing reliability of electrical systems and subsystems.
Q1. The graph below shows how a sinusoidal alternating voltage varies with time when connected across a resistor, R.
 Q1. The graph below shows how a sinusoidal alternating voltage varies with time when connected across a resistor, R. (a) (i) State the peak-to-peak voltage. peak-to-peak voltage...v (1) (ii) State the
Q1. The graph below shows how a sinusoidal alternating voltage varies with time when connected across a resistor, R. (a) (i) State the peak-to-peak voltage. peak-to-peak voltage...v (1) (ii) State the
Power Supplies. 1.0 Power Supply Basics. www.learnabout-electronics.org. Module
 Module 1 www.learnabout-electronics.org Power Supplies 1.0 Power Supply Basics What you ll learn in Module 1 Section 1.0 Power Supply Basics. Basic functions of a power supply. Safety aspects of working
Module 1 www.learnabout-electronics.org Power Supplies 1.0 Power Supply Basics What you ll learn in Module 1 Section 1.0 Power Supply Basics. Basic functions of a power supply. Safety aspects of working
First Order Circuits. EENG223 Circuit Theory I
 First Order Circuits EENG223 Circuit Theory I First Order Circuits A first-order circuit can only contain one energy storage element (a capacitor or an inductor). The circuit will also contain resistance.
First Order Circuits EENG223 Circuit Theory I First Order Circuits A first-order circuit can only contain one energy storage element (a capacitor or an inductor). The circuit will also contain resistance.
Bipolar Transistor Amplifiers
 Physics 3330 Experiment #7 Fall 2005 Bipolar Transistor Amplifiers Purpose The aim of this experiment is to construct a bipolar transistor amplifier with a voltage gain of minus 25. The amplifier must
Physics 3330 Experiment #7 Fall 2005 Bipolar Transistor Amplifiers Purpose The aim of this experiment is to construct a bipolar transistor amplifier with a voltage gain of minus 25. The amplifier must
EXPERIMENT NUMBER 5 BASIC OSCILLOSCOPE OPERATIONS
 1 EXPERIMENT NUMBER 5 BASIC OSCILLOSCOPE OPERATIONS The oscilloscope is the most versatile and most important tool in this lab and is probably the best tool an electrical engineer uses. This outline guides
1 EXPERIMENT NUMBER 5 BASIC OSCILLOSCOPE OPERATIONS The oscilloscope is the most versatile and most important tool in this lab and is probably the best tool an electrical engineer uses. This outline guides
CHAPTER 28 ELECTRIC CIRCUITS
 CHAPTER 8 ELECTRIC CIRCUITS 1. Sketch a circuit diagram for a circuit that includes a resistor R 1 connected to the positive terminal of a battery, a pair of parallel resistors R and R connected to the
CHAPTER 8 ELECTRIC CIRCUITS 1. Sketch a circuit diagram for a circuit that includes a resistor R 1 connected to the positive terminal of a battery, a pair of parallel resistors R and R connected to the
45. The peak value of an alternating current in a 1500-W device is 5.4 A. What is the rms voltage across?
 PHYS Practice Problems hapters 8- hapter 8. 45. The peak value of an alternating current in a 5-W device is 5.4 A. What is the rms voltage across? The power and current can be used to find the peak voltage,
PHYS Practice Problems hapters 8- hapter 8. 45. The peak value of an alternating current in a 5-W device is 5.4 A. What is the rms voltage across? The power and current can be used to find the peak voltage,
Diodes have an arrow showing the direction of the flow.
 The Big Idea Modern circuitry depends on much more than just resistors and capacitors. The circuits in your computer, cell phone, Ipod depend on circuit elements called diodes, inductors, transistors,
The Big Idea Modern circuitry depends on much more than just resistors and capacitors. The circuits in your computer, cell phone, Ipod depend on circuit elements called diodes, inductors, transistors,
Understanding Power Impedance Supply for Optimum Decoupling
 Introduction Noise in power supplies is not only caused by the power supply itself, but also the load s interaction with the power supply (i.e. dynamic loads, switching, etc.). To lower load induced noise,
Introduction Noise in power supplies is not only caused by the power supply itself, but also the load s interaction with the power supply (i.e. dynamic loads, switching, etc.). To lower load induced noise,
FREQUENCY RESPONSE OF AN AUDIO AMPLIFIER
 2014 Amplifier - 1 FREQUENCY RESPONSE OF AN AUDIO AMPLIFIER The objectives of this experiment are: To understand the concept of HI-FI audio equipment To generate a frequency response curve for an audio
2014 Amplifier - 1 FREQUENCY RESPONSE OF AN AUDIO AMPLIFIER The objectives of this experiment are: To understand the concept of HI-FI audio equipment To generate a frequency response curve for an audio
Experiment 2 Diode Applications: Rectifiers
 ECE 3550 - Practicum Fall 2007 Experiment 2 Diode Applications: Rectifiers Objectives 1. To investigate the characteristics of half-wave and full-wave rectifier circuits. 2. To recognize the usefulness
ECE 3550 - Practicum Fall 2007 Experiment 2 Diode Applications: Rectifiers Objectives 1. To investigate the characteristics of half-wave and full-wave rectifier circuits. 2. To recognize the usefulness
What is a multimeter?
 What is a multimeter? A multimeter is a devise used to measure voltage, resistance and current in electronics & electrical equipment It is also used to test continuity between to 2 points to verify if
What is a multimeter? A multimeter is a devise used to measure voltage, resistance and current in electronics & electrical equipment It is also used to test continuity between to 2 points to verify if
Electronics. Discrete assembly of an operational amplifier as a transistor circuit. LD Physics Leaflets P4.2.1.1
 Electronics Operational Amplifier Internal design of an operational amplifier LD Physics Leaflets Discrete assembly of an operational amplifier as a transistor circuit P4.2.1.1 Objects of the experiment
Electronics Operational Amplifier Internal design of an operational amplifier LD Physics Leaflets Discrete assembly of an operational amplifier as a transistor circuit P4.2.1.1 Objects of the experiment
Measuring Impedance and Frequency Response of Guitar Pickups
 Measuring Impedance and Frequency Response of Guitar Pickups Peter D. Hiscocks Syscomp Electronic Design Limited [email protected] www.syscompdesign.com April 30, 2011 Introduction The CircuitGear
Measuring Impedance and Frequency Response of Guitar Pickups Peter D. Hiscocks Syscomp Electronic Design Limited [email protected] www.syscompdesign.com April 30, 2011 Introduction The CircuitGear
LM 358 Op Amp. If you have small signals and need a more useful reading we could amplify it using the op amp, this is commonly used in sensors.
 LM 358 Op Amp S k i l l L e v e l : I n t e r m e d i a t e OVERVIEW The LM 358 is a duel single supply operational amplifier. As it is a single supply it eliminates the need for a duel power supply, thus
LM 358 Op Amp S k i l l L e v e l : I n t e r m e d i a t e OVERVIEW The LM 358 is a duel single supply operational amplifier. As it is a single supply it eliminates the need for a duel power supply, thus
The full wave rectifier consists of two diodes and a resister as shown in Figure
 The Full-Wave Rectifier The full wave rectifier consists of two diodes and a resister as shown in Figure The transformer has a centre-tapped secondary winding. This secondary winding has a lead attached
The Full-Wave Rectifier The full wave rectifier consists of two diodes and a resister as shown in Figure The transformer has a centre-tapped secondary winding. This secondary winding has a lead attached
Impedance Matching and Matching Networks. Valentin Todorow, December, 2009
 Impedance Matching and Matching Networks Valentin Todorow, December, 2009 RF for Plasma Processing - Definition of RF What is RF? The IEEE Standard Dictionary of Electrical and Electronics Terms defines
Impedance Matching and Matching Networks Valentin Todorow, December, 2009 RF for Plasma Processing - Definition of RF What is RF? The IEEE Standard Dictionary of Electrical and Electronics Terms defines
Lab 8: DC generators: shunt, series, and compounded.
 Lab 8: DC generators: shunt, series, and compounded. Objective: to study the properties of DC generators under no-load and full-load conditions; to learn how to connect these generators; to obtain their
Lab 8: DC generators: shunt, series, and compounded. Objective: to study the properties of DC generators under no-load and full-load conditions; to learn how to connect these generators; to obtain their
Lecture Notes: ECS 203 Basic Electrical Engineering Semester 1/2010. Dr.Prapun Suksompong 1 June 16, 2010
 Sirindhorn International Institute of Technology Thammasat University School of Information, Computer and Communication Technology Lecture Notes: ECS 203 Basic Electrical Engineering Semester 1/2010 Dr.Prapun
Sirindhorn International Institute of Technology Thammasat University School of Information, Computer and Communication Technology Lecture Notes: ECS 203 Basic Electrical Engineering Semester 1/2010 Dr.Prapun
EXPERIMENT 7 OHM S LAW, RESISTORS IN SERIES AND PARALLEL
 260 7- I. THEOY EXPEIMENT 7 OHM S LAW, ESISTOS IN SEIES AND PAALLEL The purposes of this experiment are to test Ohm's Law, to study resistors in series and parallel, and to learn the correct use of ammeters
260 7- I. THEOY EXPEIMENT 7 OHM S LAW, ESISTOS IN SEIES AND PAALLEL The purposes of this experiment are to test Ohm's Law, to study resistors in series and parallel, and to learn the correct use of ammeters
Episode 126: Capacitance and the equation C =Q/V
 Episode 126: Capacitance and the equation C =Q/V Having established that there is charge on each capacitor plate, the next stage is to establish the relationship between charge and potential difference
Episode 126: Capacitance and the equation C =Q/V Having established that there is charge on each capacitor plate, the next stage is to establish the relationship between charge and potential difference
Physics 6C, Summer 2006 Homework 2 Solutions
 Physics 6C, Summer 006 Homework Solutions All problems are from the nd edition of Walker. Numerical values are different for each student. Chapter 3 Problems. Figure 3-30 below shows a circuit containing
Physics 6C, Summer 006 Homework Solutions All problems are from the nd edition of Walker. Numerical values are different for each student. Chapter 3 Problems. Figure 3-30 below shows a circuit containing
Dependent Sources: Introduction and analysis of circuits containing dependent sources.
 Dependent Sources: Introduction and analysis of circuits containing dependent sources. So far we have explored timeindependent (resistive) elements that are also linear. We have seen that two terminal
Dependent Sources: Introduction and analysis of circuits containing dependent sources. So far we have explored timeindependent (resistive) elements that are also linear. We have seen that two terminal
Basic Op Amp Circuits
 Basic Op Amp ircuits Manuel Toledo INEL 5205 Instrumentation August 3, 2008 Introduction The operational amplifier (op amp or OA for short) is perhaps the most important building block for the design of
Basic Op Amp ircuits Manuel Toledo INEL 5205 Instrumentation August 3, 2008 Introduction The operational amplifier (op amp or OA for short) is perhaps the most important building block for the design of
Line Reactors and AC Drives
 Line Reactors and AC Drives Rockwell Automation Mequon Wisconsin Quite often, line and load reactors are installed on AC drives without a solid understanding of why or what the positive and negative consequences
Line Reactors and AC Drives Rockwell Automation Mequon Wisconsin Quite often, line and load reactors are installed on AC drives without a solid understanding of why or what the positive and negative consequences
RC & RL Transient Response
 EE 2006 University of Minnesota Duluth ab 8 1. Introduction R & R Transient Response The student will analyze series R and R circuits. A step input will excite these respective circuits, producing a transient
EE 2006 University of Minnesota Duluth ab 8 1. Introduction R & R Transient Response The student will analyze series R and R circuits. A step input will excite these respective circuits, producing a transient
The W5JCK Guide to the Mathematic Equations Required for the Amateur Extra Class Exam
 The W5JCK Guide to the Mathematic Equations Required for the Amateur Extra Class Exam This document contains every question from the Extra Class (Element 4) Question Pool* that requires one or more mathematical
The W5JCK Guide to the Mathematic Equations Required for the Amateur Extra Class Exam This document contains every question from the Extra Class (Element 4) Question Pool* that requires one or more mathematical
ANALYTICAL METHODS FOR ENGINEERS
 UNIT 1: Unit code: QCF Level: 4 Credit value: 15 ANALYTICAL METHODS FOR ENGINEERS A/601/1401 OUTCOME - TRIGONOMETRIC METHODS TUTORIAL 1 SINUSOIDAL FUNCTION Be able to analyse and model engineering situations
UNIT 1: Unit code: QCF Level: 4 Credit value: 15 ANALYTICAL METHODS FOR ENGINEERS A/601/1401 OUTCOME - TRIGONOMETRIC METHODS TUTORIAL 1 SINUSOIDAL FUNCTION Be able to analyse and model engineering situations
Chapter 22 Further Electronics
 hapter 22 Further Electronics washing machine has a delay on the door opening after a cycle of washing. Part of this circuit is shown below. s the cycle ends, switch S closes. t this stage the capacitor
hapter 22 Further Electronics washing machine has a delay on the door opening after a cycle of washing. Part of this circuit is shown below. s the cycle ends, switch S closes. t this stage the capacitor
Objectives The purpose of this lab is build and analyze Differential amplifiers based on NPN transistors (or NMOS transistors).
 1 Lab 03: Differential Amplifiers (BJT) (20 points) NOTE: 1) Please use the basic current mirror from Lab01 for the second part of the lab (Fig. 3). 2) You can use the same chip as the basic current mirror;
1 Lab 03: Differential Amplifiers (BJT) (20 points) NOTE: 1) Please use the basic current mirror from Lab01 for the second part of the lab (Fig. 3). 2) You can use the same chip as the basic current mirror;
Electricity & Electronics 5: Alternating Current and Voltage
 Electricity & Electronics 5: lternating Current and Voltage lternating Current and Voltage IM This unit looks at several aspects of alternating current and voltage including measurement of frequency and
Electricity & Electronics 5: lternating Current and Voltage lternating Current and Voltage IM This unit looks at several aspects of alternating current and voltage including measurement of frequency and
Reading assignment: All students should read the Appendix about using oscilloscopes.
 10. A ircuits* Objective: To learn how to analyze current and voltage relationships in alternating current (a.c.) circuits. You will use the method of phasors, or the vector addition of rotating vectors
10. A ircuits* Objective: To learn how to analyze current and voltage relationships in alternating current (a.c.) circuits. You will use the method of phasors, or the vector addition of rotating vectors
Measuring Biased Inductors with the GenRad Digibridge
 534 Main Street, Westbury NY 11590 www.ietlabs.com [email protected] P: 5163345959, 8008998438 pplication Note Measuring Biased Inductors with the GenRad Digibridge This note is intended for those who
534 Main Street, Westbury NY 11590 www.ietlabs.com [email protected] P: 5163345959, 8008998438 pplication Note Measuring Biased Inductors with the GenRad Digibridge This note is intended for those who
EE362L, Power Electronics Triac Light Dimmer
 1 EE362L, Power Electronics Triac Light Dimmer Rochelle Stortz and Brian Taraba, Team 277 2/2/05 Abstract - This document presents the construction of a light dimmer circuit that utilizes the current-regulating
1 EE362L, Power Electronics Triac Light Dimmer Rochelle Stortz and Brian Taraba, Team 277 2/2/05 Abstract - This document presents the construction of a light dimmer circuit that utilizes the current-regulating
Frequency Response of Filters
 School of Engineering Department of Electrical and Computer Engineering 332:224 Principles of Electrical Engineering II Laboratory Experiment 2 Frequency Response of Filters 1 Introduction Objectives To
School of Engineering Department of Electrical and Computer Engineering 332:224 Principles of Electrical Engineering II Laboratory Experiment 2 Frequency Response of Filters 1 Introduction Objectives To
Lesson 3 DIRECT AND ALTERNATING CURRENTS. Task. The skills and knowledge taught in this lesson are common to all missile repairer tasks.
 Lesson 3 DIRECT AND ALTERNATING CURRENTS Task. The skills and knowledge taught in this lesson are common to all missile repairer tasks. Objectives. When you have completed this lesson, you should be able
Lesson 3 DIRECT AND ALTERNATING CURRENTS Task. The skills and knowledge taught in this lesson are common to all missile repairer tasks. Objectives. When you have completed this lesson, you should be able
OPERATIONAL AMPLIFIERS
 INTRODUCTION OPERATIONAL AMPLIFIERS The student will be introduced to the application and analysis of operational amplifiers in this laboratory experiment. The student will apply circuit analysis techniques
INTRODUCTION OPERATIONAL AMPLIFIERS The student will be introduced to the application and analysis of operational amplifiers in this laboratory experiment. The student will apply circuit analysis techniques
