Translation Guide. Not both P and Q ~(P Q) Not either P or Q (neither/nor)
|
|
|
- Jared French
- 10 years ago
- Views:
Transcription
1 Translation Guide If P, then Q (P Q) P, if Q (Q P) What follows if is the antecedent of a conditional. P, provided that Q (Q P) Provided that means if. Assuming that, given that, etc., work the same way. Since they all mean if, what follows them is the antecedent of a conditional. P only if Q (P Q) This says that P is true only if Q is true. So, if P is true, so is Q. Unlike iff, it doesn t tell us that P is false only when Q is false. So, What follows only if is the consequent of a conditional. P if and only ( iff ) Q (P Q) Note that this is equivalent to the conjunction of P if Q --i.e., (Q P), and P only if Q --i.e., (P Q). P unless Q (P v Q) or (~Q P) Think: P is true, unless Q is, i.e., P is true if Q isn t, i.e., (~Q P). But (~Q P) is logically equivalent to (P v Q). While either answer is correct, it is simpler to remember that unless just means or. P just if Q (P Q) My ear tells me just if is more like only if than if and only if. But this is how the author wants it translated, and this is what is expected in Logicola. I won t put examples of just if on the test. P is sufficient for Q ( enough ) (P Q) P is necessary for Q (Q P) or (~P ~ Q) Since P is necessary for Q, Q can t be true unless P is. So, if Q is true, then it must be that P is also. Hence, P is necessary for Q means If Q, then P. You might also think: without P, no Q, i.e., (~P ~ Q). These are equivalent. P is necessary and sufficient for Q (P Q) P but Q (P. Q) P or Q, but not both ((P v Q) ~(P Q)) or ~(P Q) Not both P and Q ~(P Q) Not either P or Q (neither/nor) ~(P v Q
2 Quantified Logic All As are Bs. (Every A is a B.) Everything is A. Some As are Bs. (At least one A is a B.) Something is A. Nothing is A. (Not even one thing is A.) --Everything is non-a. No As are Bs. (Not even one A is B.) Not all As are Bs. --Some As are not Bs (are non-bs). a has property Q. (a is a Q; a Qs) the so-and-so (this names an object) (x)(ax Bx) (x)ax ( x)(ax Bx) ( x)ax ~( x)ax log. equiv. to (x)~ax ~( x)(ax Bx) log. equiv. to (x)~ (Ax Bx) ~(x)(ax Bx) log. equiv. to ( x)(ax ~Bx) Qa t (a constant) Something/everything is either A or/and B. ( x)(ax Bx) ( x)(ax Bx) (x)(ax Bx) (x) (Ax Bx) --Note that these are quantified statements. But, Both/Either something/everything is A and/or something/everything is B. (( x)ax v ( x)bx) (( x)ax ( x)bx) ((x) Ax v ( x)bx) ((x)ax ( x)bx) --Note that these are not quantified statements, but disjunctions or conjunctions (the left column are disjunction, the right column conjunctions). In general: Quantified statements begin with (x) or ( x). (You can apply drop quantifier rules only to quantified statements.) Negated quantified statements begin with ~(x) or ~( x). (You can apply reverse squiggle rules only to negated quantified statements.) If the statement begins with anything else, you cannot apply drop universal or reverse squiggle rules to it!
3 Quantified Translations With Identity a is identical to (the same things as) b. a=b or b=a (In general, the order in identity statements doesn t matter.) a isn t identical to b. Bob is a dentist. ( Being a dentist is a property Bob has.) Bob is the dentist. ( The dentist is a thing that is identical to Bob.) Someone other than Bob is a dentist. Someone in addition to Bob is a dentist. Bob alone is a dentist. (No else besides Bob is a dentist.) ~a=b or ~b=a Db b=d ( x)(dx ~x=b) (Db ( x)(dx ~x=b)) (Db ~( x)(dx ~x=b)) There is at least one dentist. ( x)dx (At least one is means something is, but says nothing about whether or not anything else is ) There is exactly one dentist. ( x)(dx ~( y)(~x=y Dx)) There is something such that it is a dentist and such that there is nothing else (i.e., other than the first thing) that is a dentist. There is something, call it x, such that it is a dentist and such that it is not the case that there is something, call it y, where x isn t identical to y and y is a dentist. Or ( x)(dx (y)(dy y=x)) There is an x such x is a dentist and is such that for all y, if y is dentist, then y is identical to x. There are at least two dentists. ( x)( y)((dx Dy) ~x=y)) (At least two are means something is and something not identical to it is, but says nothing about whether or not anything further is ) There are exactly two dentists. ( x)( y)(((dx Dy) ~x=y) ~( z)(dz (~z=x ~z=y))) There are an x and y such that x and y are dentists, are not identical to one another, and such that there is no z that is a dentist and isn t identical to either x or y. Or --similar to exactly one
4 Quantified Translations, with Identity and other relations Romeo loves Juliet. Lrj Juliet loves Romeo. Ljr (the order matters!) Romeo gave the flowers to Juliet. Grfj Someone loves Romeo. ( x)lxr Romeo loves someone. ( x)lrx Everyone loves Romeo. (x)lxr Romeo loves everyone. (x)lrx No one loves Romeo. ~( x)lxr or (x)~lxr Romeo loves no one. ~( x)lrx or (x)~lrx All logicians admire Gensler. (x)(lx Axg) Some logicians admire Gensler. ( x)(lx Axg) No logician admires Gensler. (Sorry, Harry!) ~( x)(lx Axg) Gensler admires all logicians. (x)(lx Agx) Gensler admires some logicians. ( x)(lx Agx) Gensler admires no logicians. ~( x)(lx Lgx) Some logicians besides Baldner admire Gensler. ( x)((lx ~x=b) Axg) There are logicians who aren t Baldner that admire Gensler. Some logicians in addition to Baldner admire Gensler (Abg ( x)((lx ~x=b) Axg)) No logicians except Baldner admire Gensler. (Abg ~( x)((lx ~x=b) Axg)) Note on the previous three examples: Do we need to add that Baldner is a logician (thus adding Lb somewhere) to the above? This is like the is a boastful druggist in the previous chapter. It all depends on the context of the argument. Is there anything in the argument as a whole that depends upon the explicit claim that Baldner is a logician? If we wanted to add this clause to the last example, it would come out: ((Lb Abg) ~( x)((lx ~x=b) Axg)) On the test I will either, like last time, make it clear how I want it translated, or I will accept either (correct!) answer.
5 And With Multiple Relations and Mixed Quantifiers! Someone loves someone. Someone loves everyone. ( x)( y)lxy ( x)(y)lxy Everyone loves everyone. (x)(y)axy Everyone loves someone. Note: This might be understood in two distinct ways: Everyone loves someone or other, this is generally what is meant versus There is some specific person that everyone loves. These are not equivalent. Thus: Everyone loves someone or other. (x)( y)lxy Everyone is such that there is someone they love. For everyone, there is someone they love. There is some specific person who everyone loves. ( x)(y)lyx There is someone such that everyone loves that person. There is someone that is loved by everyone. Pay attention to the difference in the order of x and y in the above examples! All dentists love one another. Every banker loves some dentist. Some banker loves every dentist. (x)(y)((dx Dy) Lxy) (x)(bx ( y)(dx Lxy)) ( x)(bx (y)(dy Lxy)) Jones is a lover. ( x)ljx In the text, the author understands x is a lover as there is someone that x loves. There is an unloved lover. ( x)(~( y)lyx ( y)lxy) There is someone such that no one loves that person, but there is someone that person loves. For some x, it is false that there is a y such that y loves x and it is true that there is a y such that x loves y. Everyone loves a lover. (x)(( y)lxy (y)lyx) Everyone loves anybody who loves somebody. Everyone is such that, if there is someone they love, then they are loved by everyone. For all x, if there is a y that x loves, then, for all y, y loves x. Everybody doesn t love something, but nobody doesn t love Sara Lee. (an ad slogan from before your time!) ((x)( y)~lxy). ~( x)~lxs) It is true both that for all x there is some y such that x doesn t love y, and there is no x such that x doesn t love Sara Lee.
Invalidity in Predicate Logic
 Invalidity in Predicate Logic So far we ve got a method for establishing that a predicate logic argument is valid: do a derivation. But we ve got no method for establishing invalidity. In propositional
Invalidity in Predicate Logic So far we ve got a method for establishing that a predicate logic argument is valid: do a derivation. But we ve got no method for establishing invalidity. In propositional
FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c
 Tallahassee Community College 55 FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c This kind of trinomial differs from the previous kind we have factored because the coefficient of x is no longer "1".
Tallahassee Community College 55 FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c This kind of trinomial differs from the previous kind we have factored because the coefficient of x is no longer "1".
1.2 Forms and Validity
 1.2 Forms and Validity Deductive Logic is the study of methods for determining whether or not an argument is valid. In this section we identify some famous valid argument forms. Argument Forms Consider
1.2 Forms and Validity Deductive Logic is the study of methods for determining whether or not an argument is valid. In this section we identify some famous valid argument forms. Argument Forms Consider
If an English sentence is ambiguous, it may allow for more than one adequate transcription.
 Transcription from English to Predicate Logic General Principles of Transcription In transcribing an English sentence into Predicate Logic, some general principles apply. A transcription guide must be
Transcription from English to Predicate Logic General Principles of Transcription In transcribing an English sentence into Predicate Logic, some general principles apply. A transcription guide must be
Predicate Logic Review
 Predicate Logic Review UC Berkeley, Philosophy 142, Spring 2016 John MacFarlane 1 Grammar A term is an individual constant or a variable. An individual constant is a lowercase letter from the beginning
Predicate Logic Review UC Berkeley, Philosophy 142, Spring 2016 John MacFarlane 1 Grammar A term is an individual constant or a variable. An individual constant is a lowercase letter from the beginning
Boolean Algebra Part 1
 Boolean Algebra Part 1 Page 1 Boolean Algebra Objectives Understand Basic Boolean Algebra Relate Boolean Algebra to Logic Networks Prove Laws using Truth Tables Understand and Use First Basic Theorems
Boolean Algebra Part 1 Page 1 Boolean Algebra Objectives Understand Basic Boolean Algebra Relate Boolean Algebra to Logic Networks Prove Laws using Truth Tables Understand and Use First Basic Theorems
1.4. Removing Brackets. Introduction. Prerequisites. Learning Outcomes. Learning Style
 Removing Brackets 1. Introduction In order to simplify an expression which contains brackets it is often necessary to rewrite the expression in an equivalent form but without any brackets. This process
Removing Brackets 1. Introduction In order to simplify an expression which contains brackets it is often necessary to rewrite the expression in an equivalent form but without any brackets. This process
1.5. Factorisation. Introduction. Prerequisites. Learning Outcomes. Learning Style
 Factorisation 1.5 Introduction In Block 4 we showed the way in which brackets were removed from algebraic expressions. Factorisation, which can be considered as the reverse of this process, is dealt with
Factorisation 1.5 Introduction In Block 4 we showed the way in which brackets were removed from algebraic expressions. Factorisation, which can be considered as the reverse of this process, is dealt with
1.4. Arithmetic of Algebraic Fractions. Introduction. Prerequisites. Learning Outcomes
 Arithmetic of Algebraic Fractions 1.4 Introduction Just as one whole number divided by another is called a numerical fraction, so one algebraic expression divided by another is known as an algebraic fraction.
Arithmetic of Algebraic Fractions 1.4 Introduction Just as one whole number divided by another is called a numerical fraction, so one algebraic expression divided by another is known as an algebraic fraction.
Factoring a Difference of Two Squares. Factoring a Difference of Two Squares
 284 (6 8) Chapter 6 Factoring 87. Tomato soup. The amount of metal S (in square inches) that it takes to make a can for tomato soup is a function of the radius r and height h: S 2 r 2 2 rh a) Rewrite this
284 (6 8) Chapter 6 Factoring 87. Tomato soup. The amount of metal S (in square inches) that it takes to make a can for tomato soup is a function of the radius r and height h: S 2 r 2 2 rh a) Rewrite this
POLYNOMIALS and FACTORING
 POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
Math 432 HW 2.5 Solutions
 Math 432 HW 2.5 Solutions Assigned: 1-10, 12, 13, and 14. Selected for Grading: 1 (for five points), 6 (also for five), 9, 12 Solutions: 1. (2y 3 + 2y 2 ) dx + (3y 2 x + 2xy) dy = 0. M/ y = 6y 2 + 4y N/
Math 432 HW 2.5 Solutions Assigned: 1-10, 12, 13, and 14. Selected for Grading: 1 (for five points), 6 (also for five), 9, 12 Solutions: 1. (2y 3 + 2y 2 ) dx + (3y 2 x + 2xy) dy = 0. M/ y = 6y 2 + 4y N/
TERMS. Parts of Speech
 TERMS Parts of Speech Noun: a word that names a person, place, thing, quality, or idea (examples: Maggie, Alabama, clarinet, satisfaction, socialism). Pronoun: a word used in place of a noun (examples:
TERMS Parts of Speech Noun: a word that names a person, place, thing, quality, or idea (examples: Maggie, Alabama, clarinet, satisfaction, socialism). Pronoun: a word used in place of a noun (examples:
Factoring Trinomials of the Form x 2 bx c
 4.2 Factoring Trinomials of the Form x 2 bx c 4.2 OBJECTIVES 1. Factor a trinomial of the form x 2 bx c 2. Factor a trinomial containing a common factor NOTE The process used to factor here is frequently
4.2 Factoring Trinomials of the Form x 2 bx c 4.2 OBJECTIVES 1. Factor a trinomial of the form x 2 bx c 2. Factor a trinomial containing a common factor NOTE The process used to factor here is frequently
UNDERSTANDING YOUR ONLINE FOOTPRINTS: HOW TO PROTECT YOUR PERSONAL INFORMATION ON THE INTERNET
 UNDERSTANDING YOUR ONLINE FOOTPRINTS: HOW TO PROTECT YOUR PERSONAL INFORMATION ON THE INTERNET SPEAKING NOTES FOR GRADES 4 TO 6 PRESENTATION SLIDE (1) Title Slide SLIDE (2) Key Points It can be really
UNDERSTANDING YOUR ONLINE FOOTPRINTS: HOW TO PROTECT YOUR PERSONAL INFORMATION ON THE INTERNET SPEAKING NOTES FOR GRADES 4 TO 6 PRESENTATION SLIDE (1) Title Slide SLIDE (2) Key Points It can be really
Operations with Algebraic Expressions: Multiplication of Polynomials
 Operations with Algebraic Expressions: Multiplication of Polynomials The product of a monomial x monomial To multiply a monomial times a monomial, multiply the coefficients and add the on powers with the
Operations with Algebraic Expressions: Multiplication of Polynomials The product of a monomial x monomial To multiply a monomial times a monomial, multiply the coefficients and add the on powers with the
Exam 1 Sample Question SOLUTIONS. y = 2x
 Exam Sample Question SOLUTIONS. Eliminate the parameter to find a Cartesian equation for the curve: x e t, y e t. SOLUTION: You might look at the coordinates and notice that If you don t see it, we can
Exam Sample Question SOLUTIONS. Eliminate the parameter to find a Cartesian equation for the curve: x e t, y e t. SOLUTION: You might look at the coordinates and notice that If you don t see it, we can
Factoring - Grouping
 6.2 Factoring - Grouping Objective: Factor polynomials with four terms using grouping. The first thing we will always do when factoring is try to factor out a GCF. This GCF is often a monomial like in
6.2 Factoring - Grouping Objective: Factor polynomials with four terms using grouping. The first thing we will always do when factoring is try to factor out a GCF. This GCF is often a monomial like in
A Short Course in Logic Example 8
 A Short ourse in Logic xample 8 I) Recognizing Arguments III) valuating Arguments II) Analyzing Arguments valuating Arguments with More than one Line of Reasoning valuating If then Premises Independent
A Short ourse in Logic xample 8 I) Recognizing Arguments III) valuating Arguments II) Analyzing Arguments valuating Arguments with More than one Line of Reasoning valuating If then Premises Independent
The Handshake Problem
 The Handshake Problem Tamisha is in a Geometry class with 5 students. On the first day of class her teacher asks everyone to shake hands and introduce themselves to each other. Tamisha wants to know how
The Handshake Problem Tamisha is in a Geometry class with 5 students. On the first day of class her teacher asks everyone to shake hands and introduce themselves to each other. Tamisha wants to know how
Section 6.1 Joint Distribution Functions
 Section 6.1 Joint Distribution Functions We often care about more than one random variable at a time. DEFINITION: For any two random variables X and Y the joint cumulative probability distribution function
Section 6.1 Joint Distribution Functions We often care about more than one random variable at a time. DEFINITION: For any two random variables X and Y the joint cumulative probability distribution function
CSL105: Discrete Mathematical Structures. Ragesh Jaiswal, CSE, IIT Delhi
 Propositional Logic: logical operators Negation ( ) Conjunction ( ) Disjunction ( ). Exclusive or ( ) Conditional statement ( ) Bi-conditional statement ( ): Let p and q be propositions. The biconditional
Propositional Logic: logical operators Negation ( ) Conjunction ( ) Disjunction ( ). Exclusive or ( ) Conditional statement ( ) Bi-conditional statement ( ): Let p and q be propositions. The biconditional
Module 6: How to Write the Book
 Module 6: How to Write the Book Okay, guys. Katrina Starzhynskaya here, and lesson 6, how to actually write the book: time frame, where to get your ideas from, and how to get inspired. Let s begin. Time
Module 6: How to Write the Book Okay, guys. Katrina Starzhynskaya here, and lesson 6, how to actually write the book: time frame, where to get your ideas from, and how to get inspired. Let s begin. Time
Mathematics Review for MS Finance Students
 Mathematics Review for MS Finance Students Anthony M. Marino Department of Finance and Business Economics Marshall School of Business Lecture 1: Introductory Material Sets The Real Number System Functions,
Mathematics Review for MS Finance Students Anthony M. Marino Department of Finance and Business Economics Marshall School of Business Lecture 1: Introductory Material Sets The Real Number System Functions,
Factoring Polynomials and Solving Quadratic Equations
 Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
Grammar Unit: Pronouns
 Name: Miss Phillips Period: Grammar Unit: Pronouns Unit Objectives: 1. Students will identify personal, indefinite, and possessive pronouns and recognize antecedents of pronouns. 2. Students will demonstrate
Name: Miss Phillips Period: Grammar Unit: Pronouns Unit Objectives: 1. Students will identify personal, indefinite, and possessive pronouns and recognize antecedents of pronouns. 2. Students will demonstrate
Chapter 9. Systems of Linear Equations
 Chapter 9. Systems of Linear Equations 9.1. Solve Systems of Linear Equations by Graphing KYOTE Standards: CR 21; CA 13 In this section we discuss how to solve systems of two linear equations in two variables
Chapter 9. Systems of Linear Equations 9.1. Solve Systems of Linear Equations by Graphing KYOTE Standards: CR 21; CA 13 In this section we discuss how to solve systems of two linear equations in two variables
Handout #1: Mathematical Reasoning
 Math 101 Rumbos Spring 2010 1 Handout #1: Mathematical Reasoning 1 Propositional Logic A proposition is a mathematical statement that it is either true or false; that is, a statement whose certainty or
Math 101 Rumbos Spring 2010 1 Handout #1: Mathematical Reasoning 1 Propositional Logic A proposition is a mathematical statement that it is either true or false; that is, a statement whose certainty or
Factoring. Factoring Monomials Monomials can often be factored in more than one way.
 Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
Being a Guarantor. Financial Series. in Alberta. What is a Guarantor? June 2011. Has someone you know asked you to be a Guarantor?
 Financial Series June 2011 Being a Guarantor in Alberta Has someone you know asked you to be a Guarantor? Are you already a Guarantor and worried about what comes next, or what is already occurring? This
Financial Series June 2011 Being a Guarantor in Alberta Has someone you know asked you to be a Guarantor? Are you already a Guarantor and worried about what comes next, or what is already occurring? This
SCRIPT FOR PROVIDER/ACO PHONE INQUIRIES. What is an ACO?
 SCRIPT FOR PROVIDER/ACO PHONE INQUIRIES What is an ACO? An Accountable Care Organization (ACO) is a group of doctors and other healthcare providers who agree to work together with Medicare to give you
SCRIPT FOR PROVIDER/ACO PHONE INQUIRIES What is an ACO? An Accountable Care Organization (ACO) is a group of doctors and other healthcare providers who agree to work together with Medicare to give you
10.4 Traditional Subject Predicate Propositions
 M10_COPI1396_13_SE_C10.QXD 10/22/07 8:42 AM Page 445 10.4 Traditional Subject Predicate Propositions 445 Continuing to assume the existence of at least one individual, we can say, referring to this square,
M10_COPI1396_13_SE_C10.QXD 10/22/07 8:42 AM Page 445 10.4 Traditional Subject Predicate Propositions 445 Continuing to assume the existence of at least one individual, we can say, referring to this square,
Your child s lawyer. Court-appointed lawyer for the child in cases deciding on care of children
 Your child s lawyer Court-appointed lawyer for the child in cases deciding on care of children When disputes about the care of your children are at the Family Court, the court often appoints an independent
Your child s lawyer Court-appointed lawyer for the child in cases deciding on care of children When disputes about the care of your children are at the Family Court, the court often appoints an independent
www.arden Fumigation.com (408) 279-2040 1
 1 FREE REPORT 5 Crucial Things You Should Know Before Choosing a Pest Control Service 2 We all know how difficult it is when we need to get rid of pests in our house. It is even more difficult to do it
1 FREE REPORT 5 Crucial Things You Should Know Before Choosing a Pest Control Service 2 We all know how difficult it is when we need to get rid of pests in our house. It is even more difficult to do it
CHAPTER 7 ARGUMENTS WITH DEFIITIONAL AND MISSING PREMISES
 CHAPTER 7 ARGUMENTS WITH DEFIITIONAL AND MISSING PREMISES What You ll Learn in this Chapter In Chapters -5, we developed a skill set that s sufficient for the recognition, analysis, evaluation and construction
CHAPTER 7 ARGUMENTS WITH DEFIITIONAL AND MISSING PREMISES What You ll Learn in this Chapter In Chapters -5, we developed a skill set that s sufficient for the recognition, analysis, evaluation and construction
CROSS EXAMINATION OF AN EXPERT WITNESS IN A CHILD SEXUAL ABUSE CASE. Mark Montgomery
 CROSS EXAMINATION OF AN EXPERT WITNESS IN A CHILD SEXUAL ABUSE CASE Mark Montgomery Post Office Box 161 Durham, NC 27702 (919) 680-6249 [email protected] Opinion Testimony by a Pediatrician/Nurse/Counselor/Social
CROSS EXAMINATION OF AN EXPERT WITNESS IN A CHILD SEXUAL ABUSE CASE Mark Montgomery Post Office Box 161 Durham, NC 27702 (919) 680-6249 [email protected] Opinion Testimony by a Pediatrician/Nurse/Counselor/Social
NSM100 Introduction to Algebra Chapter 5 Notes Factoring
 Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
COLLEGE ALGEBRA. Paul Dawkins
 COLLEGE ALGEBRA Paul Dawkins Table of Contents Preface... iii Outline... iv Preliminaries... Introduction... Integer Exponents... Rational Exponents... 9 Real Exponents...5 Radicals...6 Polynomials...5
COLLEGE ALGEBRA Paul Dawkins Table of Contents Preface... iii Outline... iv Preliminaries... Introduction... Integer Exponents... Rational Exponents... 9 Real Exponents...5 Radicals...6 Polynomials...5
THERE ARE SEVERAL KINDS OF PRONOUNS:
 PRONOUNS WHAT IS A PRONOUN? A Pronoun is a word used in place of a noun or of more than one noun. Example: The high school graduate accepted the diploma proudly. She had worked hard for it. The pronoun
PRONOUNS WHAT IS A PRONOUN? A Pronoun is a word used in place of a noun or of more than one noun. Example: The high school graduate accepted the diploma proudly. She had worked hard for it. The pronoun
How To Understand The Theory Of Hyperreals
 Ultraproducts and Applications I Brent Cody Virginia Commonwealth University September 2, 2013 Outline Background of the Hyperreals Filters and Ultrafilters Construction of the Hyperreals The Transfer
Ultraproducts and Applications I Brent Cody Virginia Commonwealth University September 2, 2013 Outline Background of the Hyperreals Filters and Ultrafilters Construction of the Hyperreals The Transfer
Kickass Offline Profits Imran Naseem http://www.imrannaseem.com
 Kickass Offline Profits Imran Naseem http://www.imrannaseem.com Let s get right into with this report. Everyone knows that there is a TON of money to be made in the offline niche. I am also going to assume
Kickass Offline Profits Imran Naseem http://www.imrannaseem.com Let s get right into with this report. Everyone knows that there is a TON of money to be made in the offline niche. I am also going to assume
The Classes P and NP
 The Classes P and NP We now shift gears slightly and restrict our attention to the examination of two families of problems which are very important to computer scientists. These families constitute the
The Classes P and NP We now shift gears slightly and restrict our attention to the examination of two families of problems which are very important to computer scientists. These families constitute the
Law firms and the 7 Ps. Why is there no real legal marketing?
 . Why is there no real legal marketing? The past. I first joined a law firm in 2006. At that point most law firm marketing & business development teams comprised marketing generalists. In the eyes of the
. Why is there no real legal marketing? The past. I first joined a law firm in 2006. At that point most law firm marketing & business development teams comprised marketing generalists. In the eyes of the
Business Loan. This document sets out your loan s terms and conditions. Contents of these terms and conditions. Terms and Conditions
 Business Loan Terms and Conditions This document sets out your loan s terms and conditions In this document we ve explained the terms and conditions applying to your ANZ Business Loan. It includes key
Business Loan Terms and Conditions This document sets out your loan s terms and conditions In this document we ve explained the terms and conditions applying to your ANZ Business Loan. It includes key
Your guide to. Communicating with people with a learning disability
 Your guide to Communicating with people with a learning disability About this guide This guide is designed to provide a brief introduction to communication, and the problems faced by someone with a learning
Your guide to Communicating with people with a learning disability About this guide This guide is designed to provide a brief introduction to communication, and the problems faced by someone with a learning
Reducing Customer Churn
 Reducing Customer Churn A Love Story smarter customer contact Breaking up is hard to do The old adage that it s cheaper (and better) to hold onto an existing customer than to acquire a new one isn t just
Reducing Customer Churn A Love Story smarter customer contact Breaking up is hard to do The old adage that it s cheaper (and better) to hold onto an existing customer than to acquire a new one isn t just
Rotation Matrices and Homogeneous Transformations
 Rotation Matrices and Homogeneous Transformations A coordinate frame in an n-dimensional space is defined by n mutually orthogonal unit vectors. In particular, for a two-dimensional (2D) space, i.e., n
Rotation Matrices and Homogeneous Transformations A coordinate frame in an n-dimensional space is defined by n mutually orthogonal unit vectors. In particular, for a two-dimensional (2D) space, i.e., n
How To Plan At A Tribe Of People
 ONE Don t Mark My Paper, Help Me Get an A Garry Ridge AS I SHARE with you how we successfully implemented our Don t Mark My Paper, Help Me Get an A philosophy into our performance review system, we ll
ONE Don t Mark My Paper, Help Me Get an A Garry Ridge AS I SHARE with you how we successfully implemented our Don t Mark My Paper, Help Me Get an A philosophy into our performance review system, we ll
In the above, the number 19 is an example of a number because its only positive factors are one and itself.
 Math 100 Greatest Common Factor and Factoring by Grouping (Review) Factoring Definition: A factor is a number, variable, monomial, or polynomial which is multiplied by another number, variable, monomial,
Math 100 Greatest Common Factor and Factoring by Grouping (Review) Factoring Definition: A factor is a number, variable, monomial, or polynomial which is multiplied by another number, variable, monomial,
Particular Solutions. y = Ae 4x and y = 3 at x = 0 3 = Ae 4 0 3 = A y = 3e 4x
 Particular Solutions If the differential equation is actually modeling something (like the cost of milk as a function of time) it is likely that you will know a specific value (like the fact that milk
Particular Solutions If the differential equation is actually modeling something (like the cost of milk as a function of time) it is likely that you will know a specific value (like the fact that milk
Kant s deontological ethics
 Michael Lacewing Kant s deontological ethics DEONTOLOGY Deontologists believe that morality is a matter of duty. We have moral duties to do things which it is right to do and moral duties not to do things
Michael Lacewing Kant s deontological ethics DEONTOLOGY Deontologists believe that morality is a matter of duty. We have moral duties to do things which it is right to do and moral duties not to do things
First-Order Logics and Truth Degrees
 First-Order Logics and Truth Degrees George Metcalfe Mathematics Institute University of Bern LATD 2014, Vienna Summer of Logic, 15-19 July 2014 George Metcalfe (University of Bern) First-Order Logics
First-Order Logics and Truth Degrees George Metcalfe Mathematics Institute University of Bern LATD 2014, Vienna Summer of Logic, 15-19 July 2014 George Metcalfe (University of Bern) First-Order Logics
Kim: Thank you Todd, I m delighted to be here today and totally looking forward to our conversation.
 Filename: P4P 019 The Facts of Life Insurance Todd: [0:00:18] Hey everybody, welcome to another edition of The Prosperity Podcast, this is No BS Money Guy Todd Strobel. Once again, we re lucky enough to
Filename: P4P 019 The Facts of Life Insurance Todd: [0:00:18] Hey everybody, welcome to another edition of The Prosperity Podcast, this is No BS Money Guy Todd Strobel. Once again, we re lucky enough to
7-6. Choosing a Factoring Model. Extension: Factoring Polynomials with More Than One Variable IN T RO DUC E T EACH. Standards for Mathematical Content
 7-6 Choosing a Factoring Model Extension: Factoring Polynomials with More Than One Variable Essential question: How can you factor polynomials with more than one variable? What is the connection between
7-6 Choosing a Factoring Model Extension: Factoring Polynomials with More Than One Variable Essential question: How can you factor polynomials with more than one variable? What is the connection between
STRING TELEPHONES. Education Development Center, Inc. DESIGN IT! ENGINEERING IN AFTER SCHOOL PROGRAMS. KELVIN Stock #651817
 STRING TELEPHONES KELVIN Stock #6587 DESIGN IT! ENGINEERING IN AFTER SCHOOL PROGRAMS Education Development Center, Inc. DESIGN IT! Engineering in After School Programs Table of Contents Overview...3...
STRING TELEPHONES KELVIN Stock #6587 DESIGN IT! ENGINEERING IN AFTER SCHOOL PROGRAMS Education Development Center, Inc. DESIGN IT! Engineering in After School Programs Table of Contents Overview...3...
Combined Business Loan
 Combined Business Loan Terms and Conditions This document sets out your loan or facility s terms and conditions In this document we ve explained the terms and conditions applying to your ANZ Business Loan
Combined Business Loan Terms and Conditions This document sets out your loan or facility s terms and conditions In this document we ve explained the terms and conditions applying to your ANZ Business Loan
Factoring Quadratic Expressions
 Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
Debt collector response template
 Debt collector response template You re saying: This is not my debt. Use the sample letter on the next page if you want to tell a debt collector that you aren t responsible for this debt, and that you
Debt collector response template You re saying: This is not my debt. Use the sample letter on the next page if you want to tell a debt collector that you aren t responsible for this debt, and that you
expression is written horizontally. The Last terms ((2)( 4)) because they are the last terms of the two polynomials. This is called the FOIL method.
 A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
Relations: their uses in programming and computational specifications
 PEPS Relations, 15 December 2008 1/27 Relations: their uses in programming and computational specifications Dale Miller INRIA - Saclay & LIX, Ecole Polytechnique 1. Logic and computation Outline 2. Comparing
PEPS Relations, 15 December 2008 1/27 Relations: their uses in programming and computational specifications Dale Miller INRIA - Saclay & LIX, Ecole Polytechnique 1. Logic and computation Outline 2. Comparing
Where's Gone? LEAD GENERATION PRINTABLE WORKBOOK
 Have you ever stopped to think why you are in business? Good question, isn t it? But before we take a closer look at this, spend a few moments now thinking about what you believe your reasons to be. Jot
Have you ever stopped to think why you are in business? Good question, isn t it? But before we take a closer look at this, spend a few moments now thinking about what you believe your reasons to be. Jot
1.3 Polynomials and Factoring
 1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
Mathematical Induction
 Mathematical Induction In logic, we often want to prove that every member of an infinite set has some feature. E.g., we would like to show: N 1 : is a number 1 : has the feature Φ ( x)(n 1 x! 1 x) How
Mathematical Induction In logic, we often want to prove that every member of an infinite set has some feature. E.g., we would like to show: N 1 : is a number 1 : has the feature Φ ( x)(n 1 x! 1 x) How
Three Attributes of Every Successful Merchant Services Program-20140604 1602-1
 Three Attributes of Every Successful Merchant Services Program-20140604 1602-1 [Start of recorded material] [Starts Mid Sentence] thank everyone that s joined the call today. I know everybody is busy with
Three Attributes of Every Successful Merchant Services Program-20140604 1602-1 [Start of recorded material] [Starts Mid Sentence] thank everyone that s joined the call today. I know everybody is busy with
Creating and Managing Shared Folders
 Creating and Managing Shared Folders Microsoft threw all sorts of new services, features, and functions into Windows 2000 Server, but at the heart of it all was still the requirement to be a good file
Creating and Managing Shared Folders Microsoft threw all sorts of new services, features, and functions into Windows 2000 Server, but at the heart of it all was still the requirement to be a good file
Student Outcomes. Lesson Notes. Classwork. Discussion (10 minutes)
 NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 5 8 Student Outcomes Students know the definition of a number raised to a negative exponent. Students simplify and write equivalent expressions that contain
NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 5 8 Student Outcomes Students know the definition of a number raised to a negative exponent. Students simplify and write equivalent expressions that contain
Double-Entry Bookkeeping: Assets and Liabilities
 Double-Entry Bookkeeping: Assets and Liabilities The purpose of this chapter is to introduce the fundamentals of double-entry bookkeeping and its role in accounting for business. The objectives of accounting
Double-Entry Bookkeeping: Assets and Liabilities The purpose of this chapter is to introduce the fundamentals of double-entry bookkeeping and its role in accounting for business. The objectives of accounting
Introduction to Python
 WEEK ONE Introduction to Python Python is such a simple language to learn that we can throw away the manual and start with an example. Traditionally, the first program to write in any programming language
WEEK ONE Introduction to Python Python is such a simple language to learn that we can throw away the manual and start with an example. Traditionally, the first program to write in any programming language
A Short Course in Logic Zeno s Paradox
 1 Grappling with Good Arguments A Short Course in Logic Zeno s Paradox We ve seen that if we decide that an argument is good then we should be inclined to believe that the ultimate conclusion is true.
1 Grappling with Good Arguments A Short Course in Logic Zeno s Paradox We ve seen that if we decide that an argument is good then we should be inclined to believe that the ultimate conclusion is true.
The Adventures of Leo Rahula Leads The Way
 The Adventures of Leo Rahula Leads The Way by S. Dhammika & Susan Harmer [Screen Quality] E-mail: [email protected] Web site: www.buddhanet.net Buddha Dharma Education Association Inc. Copyright Buddha
The Adventures of Leo Rahula Leads The Way by S. Dhammika & Susan Harmer [Screen Quality] E-mail: [email protected] Web site: www.buddhanet.net Buddha Dharma Education Association Inc. Copyright Buddha
6.4 Special Factoring Rules
 6.4 Special Factoring Rules OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor a sum of cubes. By reversing the rules for multiplication
6.4 Special Factoring Rules OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor a sum of cubes. By reversing the rules for multiplication
Standard Life Active Retirement For accessing your pension money
 Standard Life Active Retirement For accessing your pension money Standard Life Active Retirement our ready-made investment solution that allows you to access your pension savings while still giving your
Standard Life Active Retirement For accessing your pension money Standard Life Active Retirement our ready-made investment solution that allows you to access your pension savings while still giving your
We will learn the Python programming language. Why? Because it is easy to learn and many people write programs in Python so we can share.
 LING115 Lecture Note Session #4 Python (1) 1. Introduction As we have seen in previous sessions, we can use Linux shell commands to do simple text processing. We now know, for example, how to count words.
LING115 Lecture Note Session #4 Python (1) 1. Introduction As we have seen in previous sessions, we can use Linux shell commands to do simple text processing. We now know, for example, how to count words.
5 Group Policy Management Capabilities You re Missing
 5 Group Policy Management Capabilities You re Missing Don Jones 1. 8 0 0. 8 1 3. 6 4 1 5 w w w. s c r i p t l o g i c. c o m / s m b I T 2011 ScriptLogic Corporation ALL RIGHTS RESERVED. ScriptLogic, the
5 Group Policy Management Capabilities You re Missing Don Jones 1. 8 0 0. 8 1 3. 6 4 1 5 w w w. s c r i p t l o g i c. c o m / s m b I T 2011 ScriptLogic Corporation ALL RIGHTS RESERVED. ScriptLogic, the
Using the ac Method to Factor
 4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
THE GREAT DEBATE: Is GPS Tracking Really Beneficial for Fleets? Fear of Employee Pushback. Fleet Intelligence for Your Business GPS INSIGHT
 THE GREAT DEBATE: Is GPS Tracking Really Beneficial for Fleets? Since GPS tracking was first introduced to the fleet industry, there has been a debate whether this technology is really beneficial for fleets
THE GREAT DEBATE: Is GPS Tracking Really Beneficial for Fleets? Since GPS tracking was first introduced to the fleet industry, there has been a debate whether this technology is really beneficial for fleets
CHAPTER 3. Methods of Proofs. 1. Logical Arguments and Formal Proofs
 CHAPTER 3 Methods of Proofs 1. Logical Arguments and Formal Proofs 1.1. Basic Terminology. An axiom is a statement that is given to be true. A rule of inference is a logical rule that is used to deduce
CHAPTER 3 Methods of Proofs 1. Logical Arguments and Formal Proofs 1.1. Basic Terminology. An axiom is a statement that is given to be true. A rule of inference is a logical rule that is used to deduce
LIFETIME MORTGAGE LUMP SUM
 LIFETIME MORTGAGE LUMP SUM Terms and Conditions (version 5) This is an important document. Please keep it in a safe place. LV= Lifetime Mortgage lump sum Terms and Conditions Welcome to LV=, and thank
LIFETIME MORTGAGE LUMP SUM Terms and Conditions (version 5) This is an important document. Please keep it in a safe place. LV= Lifetime Mortgage lump sum Terms and Conditions Welcome to LV=, and thank
Material for Peers: Portfolios
 TOPSIDE Training Opportunities for Peer Supporters with Intellectual Disabilities in Europe Material for Peers: Portfolios Inclusion Europe www.peer-training.eu Authors: TOPSIDE partners Hugh Savage, ENABLE
TOPSIDE Training Opportunities for Peer Supporters with Intellectual Disabilities in Europe Material for Peers: Portfolios Inclusion Europe www.peer-training.eu Authors: TOPSIDE partners Hugh Savage, ENABLE
Last time we had arrived at the following provisional interpretation of Aquinas second way:
 Aquinas Third Way Last time we had arrived at the following provisional interpretation of Aquinas second way: 1. 2. 3. 4. At least one thing has an efficient cause. Every causal chain must either be circular,
Aquinas Third Way Last time we had arrived at the following provisional interpretation of Aquinas second way: 1. 2. 3. 4. At least one thing has an efficient cause. Every causal chain must either be circular,
Factoring Guidelines. Greatest Common Factor Two Terms Three Terms Four Terms. 2008 Shirley Radai
 Factoring Guidelines Greatest Common Factor Two Terms Three Terms Four Terms 008 Shirley Radai Greatest Common Factor 008 Shirley Radai Factoring by Finding the Greatest Common Factor Always check for
Factoring Guidelines Greatest Common Factor Two Terms Three Terms Four Terms 008 Shirley Radai Greatest Common Factor 008 Shirley Radai Factoring by Finding the Greatest Common Factor Always check for
How to Outsource Without Being a Ninnyhammer
 How to Outsource Without Being a Ninnyhammer 5 mistakes people make when outsourcing for profit By Jason Fladlien 2 Introduction The way everyone does outsourcing is patently wrong, and this report is
How to Outsource Without Being a Ninnyhammer 5 mistakes people make when outsourcing for profit By Jason Fladlien 2 Introduction The way everyone does outsourcing is patently wrong, and this report is
0:00:18 Todd: 0:00:30 Kim: 0:01:15 Todd: 0:02:10 Kim: 0:04:10 Todd:
 0:00:18 Todd: Hey everybody, welcome to another edition of The Prosperity Podcast, this is No BS Money Guy Todd Strobel. Once again, we have my cohost and bestselling financial author Kim Butler with us,
0:00:18 Todd: Hey everybody, welcome to another edition of The Prosperity Podcast, this is No BS Money Guy Todd Strobel. Once again, we have my cohost and bestselling financial author Kim Butler with us,
To give it a definition, an implicit function of x and y is simply any relationship that takes the form:
 2 Implicit function theorems and applications 21 Implicit functions The implicit function theorem is one of the most useful single tools you ll meet this year After a while, it will be second nature to
2 Implicit function theorems and applications 21 Implicit functions The implicit function theorem is one of the most useful single tools you ll meet this year After a while, it will be second nature to
SOLVING QUADRATIC EQUATIONS - COMPARE THE FACTORING ac METHOD AND THE NEW DIAGONAL SUM METHOD By Nghi H. Nguyen
 SOLVING QUADRATIC EQUATIONS - COMPARE THE FACTORING ac METHOD AND THE NEW DIAGONAL SUM METHOD By Nghi H. Nguyen A. GENERALITIES. When a given quadratic equation can be factored, there are 2 best methods
SOLVING QUADRATIC EQUATIONS - COMPARE THE FACTORING ac METHOD AND THE NEW DIAGONAL SUM METHOD By Nghi H. Nguyen A. GENERALITIES. When a given quadratic equation can be factored, there are 2 best methods
Parenting. Coping with DEATH. For children aged 6 to 12
 Parenting Positively Coping with DEATH For children aged 6 to 12 This booklet will help you to understand more about death and the feelings we all have when someone we care about, like a parent, a brother
Parenting Positively Coping with DEATH For children aged 6 to 12 This booklet will help you to understand more about death and the feelings we all have when someone we care about, like a parent, a brother
How To Create a Short Animated Story
 How To Create a Short Animated Story Written by Sven Nilsen The Ingredients There are three ingredients in a story that makes it exciting, entertaining and funny: A character that the viewer sympethises
How To Create a Short Animated Story Written by Sven Nilsen The Ingredients There are three ingredients in a story that makes it exciting, entertaining and funny: A character that the viewer sympethises
FACTORING ax 2 bx c. Factoring Trinomials with Leading Coefficient 1
 5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
Critical analysis. Be more critical! More analysis needed! That s what my tutors say about my essays. I m not really sure what they mean.
 Critical analysis Be more critical! More analysis needed! That s what my tutors say about my essays. I m not really sure what they mean. I thought I had written a really good assignment this time. I did
Critical analysis Be more critical! More analysis needed! That s what my tutors say about my essays. I m not really sure what they mean. I thought I had written a really good assignment this time. I did
Filename: P4P 016 Todd: Kim: Todd: Kim:
 Filename: P4P 016 Todd: [0:00:18] Hey everybody, welcome to another edition of The Prosperity Podcast, this is No BS Money Guy Todd Strobel. Once again, we have my cohost, bestselling financial author
Filename: P4P 016 Todd: [0:00:18] Hey everybody, welcome to another edition of The Prosperity Podcast, this is No BS Money Guy Todd Strobel. Once again, we have my cohost, bestselling financial author
DEPARTMENT OF PUBLIC WORKS - It's Not What You Think
 DEPARTMENT OF PUBLIC WORKS, BUREAU OF ENGINEERING LACC EXPANSION - Public Meeting 1/15/15 Public Comments Received Jan 15 th Jan 30th Transcription of the Comment/Question Session (after the Presentation)
DEPARTMENT OF PUBLIC WORKS, BUREAU OF ENGINEERING LACC EXPANSION - Public Meeting 1/15/15 Public Comments Received Jan 15 th Jan 30th Transcription of the Comment/Question Session (after the Presentation)
Factoring Flow Chart
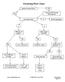 Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Dedekind s forgotten axiom and why we should teach it (and why we shouldn t teach mathematical induction in our calculus classes)
 Dedekind s forgotten axiom and why we should teach it (and why we shouldn t teach mathematical induction in our calculus classes) by Jim Propp (UMass Lowell) March 14, 2010 1 / 29 Completeness Three common
Dedekind s forgotten axiom and why we should teach it (and why we shouldn t teach mathematical induction in our calculus classes) by Jim Propp (UMass Lowell) March 14, 2010 1 / 29 Completeness Three common
Todd: Kim: Todd: Kim: Todd: Kim:
 Todd: [0:00:18] Hey everybody, welcome to another edition of The Prosperity Podcast, this is No BS Money Guy Todd Strobel. Once again, we have my cohost, bestselling financial author Kim Butler with us,
Todd: [0:00:18] Hey everybody, welcome to another edition of The Prosperity Podcast, this is No BS Money Guy Todd Strobel. Once again, we have my cohost, bestselling financial author Kim Butler with us,
