Matter Waves. Home Work Solutions
|
|
|
- Coleen Houston
- 9 years ago
- Views:
Transcription
1 Chapter 5 Matter Waves. Home Work s 5.1 Problem 5.10 (In the text book) An electron has a de Broglie wavelength equal to the diameter of the hydrogen atom. What is the kinetic energy of the electron? How does this energy compare with the ground-state energy of the hydrogen atom? The radius of the hydrogen atom can be taken as the radius of the first orbit or, Bohr radius a m. The de Broglie wave length of the given electron is: λ 2a m Using p h/λ, where p is the momentum of the electron, the kinetic energy K of the electron is: K p2 2m e h 2 c 2 2m e c 2 λ 2 ( ev m) (ev ) ( m) ev The energy of the ground state of the hydrogen atom is 13.6 ev, so the kinetic energy of the given electron is about times the energy of the ground state of the hydrogen atom.
2 2 CHAPTER 5. MATTER WAVES. HOME WORK SOLUTIONS 5.2 Problem 5.14 (In the text book) (a) Show that the formula for low-energy electron diffraction (LEED), when electrons are incident perpendicular to a crystal surface, may be written as sin φ nhc d 2m e c 2 K where n is the order of the maximum, d is the atomic spacing, m e is the electron mass, K is the electron s kinetic energy, and φ is the angle between the incident and diffracted beams. (b) Calculate the atomic spacing in a crystal that has consecutive diffraction maxima at φ 24.1 and φ 54.9 for 100-eV electrons. (a) For a maximum in electron diffraction from crystal planes we have: nλ d sin φ sin φ nλ d where λ is the de Broglie wave length of the electron, and λ h/p, where p is the electrons momentum. The kinetic energy of the electron K p 2 /2m e, we th get: sin φ n h d p n ( ) h d 2Kme ( ) nhc d 2Km e c 2
3 5.2. PROBLEM 5.14 (IN THE TEXT BOOK) 3 (b) The atomic spacing is; d nhc sin φ 2Km e c 2 For φ 24.1 the atomic spacing d 1 is: d 1 n (ev m) sin(24.1) (ev ) 100(eV ) m 3.00n A For φ 54.9 the atomic spacing d 1 is: d 2 (n + 1) (ev m) sin(54.9) (ev ) 100(eV ) 3.00(n + 1) m 3.00(n + 1) A for the same spacing we should have: d 1 d n 1.50(n + 1) n 1 which means the 24.1 corresponds to n 1 maximum and 54.9 corresponds to n 2 maximum.
4 4 CHAPTER 5. MATTER WAVES. HOME WORK SOLUTIONS 5.3 Problem 5.20 (In the text book) We wish to measure simultaneously the wavelength and position of a photon. Assume that the wavelength measurement gives λ 6000 A with an accuracy of one part in a million, that is, λ/λ What is the minimum uncertainty in the position of the photon? The momentum p of the photon is given by: we then get: p h λ p λ dp dλ Since, h λ 2 p h λ λ 2 p x 1 2 ( p x) min 1 2 x min 2 p 2(hδλ/λ 2 ) hλ 4π(h λ/λ) λ 4π( λ/λ) 6000 A A m
5 5.4. PROBLEM 5.30 (IN THE TEXT BOOK) Problem 5.30 (In the text book) Robert Hofistadter won the 1961 Nobel prize in physics for his pioneering work in scattering 20-GeV electrons from nuclei. (a) What is the γ factor for a 20-GeV electron, where γ (1 v 2 /c 2 ) 1 2? What is the momentum of the electron in kg m/s? (b) What is the wavelength of a 20-GeV electron and how does it compare with the size of a nucleus? (a) Using the relativistic definition of the total energy we get: E γm e c 2 γ E m e c (MeV ) 0.511(MeV ) Since the energy of the electron is very high, then, m e c 2 pc, and using the relativistic definition of the total energy, in terms of the momentum, we get: E 2 (pc) 2 + m 2 ec 4 p E c (MeV ) (J/MeV ) m/s kg m/s (b) The de Broglie wavelength of the 20 GeV electron is:
6 6 CHAPTER 5. MATTER WAVES. HOME WORK SOLUTIONS λ h p (J s) kg m/s m the size of the nucleus is about m, so the wavelength of the 20 GeV electron is about 1000 times smaller than the nucleus.
7 5.5. PROBLEM 5.34 (IN THE TEXT BOOK) Problem 5.34 (In the text book) Figure 5.1: (a) Find and sketch the spectral content of the rectangular pulse of width 2τ- shown in Figure (5.1). (b) Show that a reciprocity relation ω t π holds in this case. Take t τ and define ω similarly. (c) What range of frequencies is required to compose a pulse of width 2τ 1 µs? A pulse of width 2τ 1 ns? (a) Using Fourier integrals: g(ω) 1 2π 1 2π V (t) e iωt dt V (t) (cos ωt i sin ωt) dt V (t) sin ωt is an odd function in t so its integral vanishes, we then get: g(ω) 1 2π V (t) cos ωt dt
8 h π terest 2π ( s)( ev)( J ev) J s 8 CHAPTER 5. MATTER WAVES. HOME WORK SOLUTIONS 5 12 from Figure (5.1), V (t) V when τ < t < τ and V (t) 0 everywhere else. Also, V (t) is symmetric around t 0: V()( t cosωt isinωt) dt, V( t) sinω t is an odd function 2 τ g(ω) V cos ωt dt 2π 0 τ [ ] 12 τ ω 2 2π 2 sin ωt π V cosω ω π V sin ωτ ω sinωτ g V0 tdt V 0. π ω ( 2 ) shes leaving ( ) ( ) n below. A plot of g(ω) is shown in Figure (5.2). 12 g(ω) 2 π V, t 0 ω 2π τ π τ π τ 2π τ Figure 5.2: (b) Since the major contribution to the pulse comes from π/τ < t < +π/τ, we take ω as π/τ and since t τ, we then get: ω t π τ τ π (c) The frequency range required to compose a pulse of width 2τ 1 µs, 2 f is:
9 5.5. PROBLEM 5.34 (IN THE TEXT BOOK) 9 and for a 1 ns pulse: ω 2πf ω 2π f ω t π 2 f ω π π π t 1 t Hz 2 f 1 t Hz Notice that to make the pulse sorter, i.e. localized in a smaller time range you need a much larger frequency range.
Physics 111 Homework Solutions Week #9 - Tuesday
 Physics 111 Homework Solutions Week #9 - Tuesday Friday, February 25, 2011 Chapter 22 Questions - None Multiple-Choice 223 A 224 C 225 B 226 B 227 B 229 D Problems 227 In this double slit experiment we
Physics 111 Homework Solutions Week #9 - Tuesday Friday, February 25, 2011 Chapter 22 Questions - None Multiple-Choice 223 A 224 C 225 B 226 B 227 B 229 D Problems 227 In this double slit experiment we
How To Understand Light And Color
 PRACTICE EXAM IV P202 SPRING 2004 1. In two separate double slit experiments, an interference pattern is observed on a screen. In the first experiment, violet light (λ = 754 nm) is used and a second-order
PRACTICE EXAM IV P202 SPRING 2004 1. In two separate double slit experiments, an interference pattern is observed on a screen. In the first experiment, violet light (λ = 754 nm) is used and a second-order
Chapter 15, example problems:
 Chapter, example problems: (.0) Ultrasound imaging. (Frequenc > 0,000 Hz) v = 00 m/s. λ 00 m/s /.0 mm =.0 0 6 Hz. (Smaller wave length implies larger frequenc, since their product,
Chapter, example problems: (.0) Ultrasound imaging. (Frequenc > 0,000 Hz) v = 00 m/s. λ 00 m/s /.0 mm =.0 0 6 Hz. (Smaller wave length implies larger frequenc, since their product,
TIME OF COMPLETION NAME SOLUTION DEPARTMENT OF NATURAL SCIENCES. PHYS 3650, Exam 2 Section 1 Version 1 October 31, 2005 Total Weight: 100 points
 TIME OF COMPLETION NAME SOLUTION DEPARTMENT OF NATURAL SCIENCES PHYS 3650, Exam 2 Section 1 Version 1 October 31, 2005 Total Weight: 100 points 1. Check your examination for completeness prior to starting.
TIME OF COMPLETION NAME SOLUTION DEPARTMENT OF NATURAL SCIENCES PHYS 3650, Exam 2 Section 1 Version 1 October 31, 2005 Total Weight: 100 points 1. Check your examination for completeness prior to starting.
Monday 11 June 2012 Afternoon
 Monday 11 June 2012 Afternoon A2 GCE PHYSICS B (ADVANCING PHYSICS) G495 Field and Particle Pictures *G412090612* Candidates answer on the Question Paper. OCR supplied materials: Data, Formulae and Relationships
Monday 11 June 2012 Afternoon A2 GCE PHYSICS B (ADVANCING PHYSICS) G495 Field and Particle Pictures *G412090612* Candidates answer on the Question Paper. OCR supplied materials: Data, Formulae and Relationships
Chapters 21-29. Magnetic Force. for a moving charge. F=BQvsinΘ. F=BIlsinΘ. for a current
 Chapters 21-29 Chapter 21:45,63 Chapter 22:25,49 Chapter 23:35,38,53,55,58,59 Chapter 24:17,18,20,42,43,44,50,52,53.59,63 Chapter 26:27,33,34,39,54 Chapter 27:17,18,34,43,50,51,53,56 Chapter 28: 10,11,28,47,52
Chapters 21-29 Chapter 21:45,63 Chapter 22:25,49 Chapter 23:35,38,53,55,58,59 Chapter 24:17,18,20,42,43,44,50,52,53.59,63 Chapter 26:27,33,34,39,54 Chapter 27:17,18,34,43,50,51,53,56 Chapter 28: 10,11,28,47,52
Solutions to Problems in Goldstein, Classical Mechanics, Second Edition. Chapter 7
 Solutions to Problems in Goldstein, Classical Mechanics, Second Edition Homer Reid April 21, 2002 Chapter 7 Problem 7.2 Obtain the Lorentz transformation in which the velocity is at an infinitesimal angle
Solutions to Problems in Goldstein, Classical Mechanics, Second Edition Homer Reid April 21, 2002 Chapter 7 Problem 7.2 Obtain the Lorentz transformation in which the velocity is at an infinitesimal angle
Examples of Uniform EM Plane Waves
 Examples of Uniform EM Plane Waves Outline Reminder of Wave Equation Reminder of Relation Between E & H Energy Transported by EM Waves (Poynting Vector) Examples of Energy Transport by EM Waves 1 Coupling
Examples of Uniform EM Plane Waves Outline Reminder of Wave Equation Reminder of Relation Between E & H Energy Transported by EM Waves (Poynting Vector) Examples of Energy Transport by EM Waves 1 Coupling
Solution: F = kx is Hooke s law for a mass and spring system. Angular frequency of this system is: k m therefore, k
 Physics 1C Midterm 1 Summer Session II, 2011 Solutions 1. If F = kx, then k m is (a) A (b) ω (c) ω 2 (d) Aω (e) A 2 ω Solution: F = kx is Hooke s law for a mass and spring system. Angular frequency of
Physics 1C Midterm 1 Summer Session II, 2011 Solutions 1. If F = kx, then k m is (a) A (b) ω (c) ω 2 (d) Aω (e) A 2 ω Solution: F = kx is Hooke s law for a mass and spring system. Angular frequency of
Does Quantum Mechanics Make Sense? Size
 Does Quantum Mechanics Make Sense? Some relatively simple concepts show why the answer is yes. Size Classical Mechanics Quantum Mechanics Relative Absolute What does relative vs. absolute size mean? Why
Does Quantum Mechanics Make Sense? Some relatively simple concepts show why the answer is yes. Size Classical Mechanics Quantum Mechanics Relative Absolute What does relative vs. absolute size mean? Why
Chapter 18: The Structure of the Atom
 Chapter 18: The Structure of the Atom 1. For most elements, an atom has A. no neutrons in the nucleus. B. more protons than electrons. C. less neutrons than electrons. D. just as many electrons as protons.
Chapter 18: The Structure of the Atom 1. For most elements, an atom has A. no neutrons in the nucleus. B. more protons than electrons. C. less neutrons than electrons. D. just as many electrons as protons.
Oscillations. Vern Lindberg. June 10, 2010
 Oscillations Vern Lindberg June 10, 2010 You have discussed oscillations in Vibs and Waves: we will therefore touch lightly on Chapter 3, mainly trying to refresh your memory and extend the concepts. 1
Oscillations Vern Lindberg June 10, 2010 You have discussed oscillations in Vibs and Waves: we will therefore touch lightly on Chapter 3, mainly trying to refresh your memory and extend the concepts. 1
PHOTOELECTRIC EFFECT AND DUAL NATURE OF MATTER AND RADIATIONS
 PHOTOELECTRIC EFFECT AND DUAL NATURE OF MATTER AND RADIATIONS 1. Photons 2. Photoelectric Effect 3. Experimental Set-up to study Photoelectric Effect 4. Effect of Intensity, Frequency, Potential on P.E.
PHOTOELECTRIC EFFECT AND DUAL NATURE OF MATTER AND RADIATIONS 1. Photons 2. Photoelectric Effect 3. Experimental Set-up to study Photoelectric Effect 4. Effect of Intensity, Frequency, Potential on P.E.
13- What is the maximum number of electrons that can occupy the subshell 3d? a) 1 b) 3 c) 5 d) 2
 Assignment 06 A 1- What is the energy in joules of an electron undergoing a transition from n = 3 to n = 5 in a Bohr hydrogen atom? a) -3.48 x 10-17 J b) 2.18 x 10-19 J c) 1.55 x 10-19 J d) -2.56 x 10-19
Assignment 06 A 1- What is the energy in joules of an electron undergoing a transition from n = 3 to n = 5 in a Bohr hydrogen atom? a) -3.48 x 10-17 J b) 2.18 x 10-19 J c) 1.55 x 10-19 J d) -2.56 x 10-19
6) How wide must a narrow slit be if the first diffraction minimum occurs at ±12 with laser light of 633 nm?
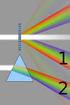 Test IV Name 1) In a single slit diffraction experiment, the width of the slit is 3.1 10-5 m and the distance from the slit to the screen is 2.2 m. If the beam of light of wavelength 600 nm passes through
Test IV Name 1) In a single slit diffraction experiment, the width of the slit is 3.1 10-5 m and the distance from the slit to the screen is 2.2 m. If the beam of light of wavelength 600 nm passes through
Second Order Systems
 Second Order Systems Second Order Equations Standard Form G () s = τ s K + ζτs + 1 K = Gain τ = Natural Period of Oscillation ζ = Damping Factor (zeta) Note: this has to be 1.0!!! Corresponding Differential
Second Order Systems Second Order Equations Standard Form G () s = τ s K + ζτs + 1 K = Gain τ = Natural Period of Oscillation ζ = Damping Factor (zeta) Note: this has to be 1.0!!! Corresponding Differential
The Phenomenon of Photoelectric Emission:
 The Photoelectric Effect. The Wave particle duality of light Light, like any other E.M.R (electromagnetic radiation) has got a dual nature. That is there are experiments that prove that it is made up of
The Photoelectric Effect. The Wave particle duality of light Light, like any other E.M.R (electromagnetic radiation) has got a dual nature. That is there are experiments that prove that it is made up of
British Physics Olympiad
 1 British Physics Olympiad Paper 3. 2005 Monday 28 February 2005. Time allowed 3hrs plus 15 minutes reading time. All questions should be attempted. Question 1 carries 40 marks, the other questions 20
1 British Physics Olympiad Paper 3. 2005 Monday 28 February 2005. Time allowed 3hrs plus 15 minutes reading time. All questions should be attempted. Question 1 carries 40 marks, the other questions 20
F en = mω 0 2 x. We should regard this as a model of the response of an atom, rather than a classical model of the atom itself.
 The Electron Oscillator/Lorentz Atom Consider a simple model of a classical atom, in which the electron is harmonically bound to the nucleus n x e F en = mω 0 2 x origin resonance frequency Note: We should
The Electron Oscillator/Lorentz Atom Consider a simple model of a classical atom, in which the electron is harmonically bound to the nucleus n x e F en = mω 0 2 x origin resonance frequency Note: We should
Masses in Atomic Units
 Nuclear Composition - the forces binding protons and neutrons in the nucleus are much stronger (binding energy of MeV) than the forces binding electrons to the atom (binding energy of ev) - the constituents
Nuclear Composition - the forces binding protons and neutrons in the nucleus are much stronger (binding energy of MeV) than the forces binding electrons to the atom (binding energy of ev) - the constituents
Atomic Structure: Chapter Problems
 Atomic Structure: Chapter Problems Bohr Model Class Work 1. Describe the nuclear model of the atom. 2. Explain the problems with the nuclear model of the atom. 3. According to Niels Bohr, what does n stand
Atomic Structure: Chapter Problems Bohr Model Class Work 1. Describe the nuclear model of the atom. 2. Explain the problems with the nuclear model of the atom. 3. According to Niels Bohr, what does n stand
Review for Test 3. Polarized light. Action of a Polarizer. Polarized light. Light Intensity after a Polarizer. Review for Test 3.
 Review for Test 3 Polarized light No equation provided! Polarized light In linearly polarized light, the electric field vectors all lie in one single direction. Action of a Polarizer Transmission axis
Review for Test 3 Polarized light No equation provided! Polarized light In linearly polarized light, the electric field vectors all lie in one single direction. Action of a Polarizer Transmission axis
Calculating particle properties of a wave
 Calculating particle properties of a wave A light wave consists of particles (photons): The energy E of the particle is calculated from the frequency f of the wave via Planck: E = h f (1) A particle can
Calculating particle properties of a wave A light wave consists of particles (photons): The energy E of the particle is calculated from the frequency f of the wave via Planck: E = h f (1) A particle can
Experiment #12: The Bohr Atom. Equipment: Spectroscope Hydrogen and Helium Gas Discharge Tubes, Holder, and Variac Flashlight
 Experiment #12: The Bohr Atom Purpose: To observe the visible spectrum of hydrogen and helium and verify the Bohr model of the hydrogen atom. Equipment: Spectroscope Hydrogen and Helium Gas Discharge Tubes,
Experiment #12: The Bohr Atom Purpose: To observe the visible spectrum of hydrogen and helium and verify the Bohr model of the hydrogen atom. Equipment: Spectroscope Hydrogen and Helium Gas Discharge Tubes,
Suggested solutions, FYS 500 Classical Mechanics and Field Theory 2014 fall
 UNIVERSITETET I STAVANGER Institutt for matematikk og naturvitenskap Suggested solutions, FYS 500 Classical Mecanics and Field Teory 014 fall Set 11 for 17/18. November 014 Problem 59: Te Lagrangian for
UNIVERSITETET I STAVANGER Institutt for matematikk og naturvitenskap Suggested solutions, FYS 500 Classical Mecanics and Field Teory 014 fall Set 11 for 17/18. November 014 Problem 59: Te Lagrangian for
O6: The Diffraction Grating Spectrometer
 2B30: PRACTICAL ASTROPHYSICS FORMAL REPORT: O6: The Diffraction Grating Spectrometer Adam Hill Lab partner: G. Evans Tutor: Dr. Peter Storey 1 Abstract The calibration of a diffraction grating spectrometer
2B30: PRACTICAL ASTROPHYSICS FORMAL REPORT: O6: The Diffraction Grating Spectrometer Adam Hill Lab partner: G. Evans Tutor: Dr. Peter Storey 1 Abstract The calibration of a diffraction grating spectrometer
Nanoelectronics. Chapter 2 Classical Particles, Classical Waves, and Quantum Particles. [email protected]@2015.3
 Nanoelectronics Chapter 2 Classical Particles, Classical Waves, and Quantum Particles [email protected]@2015.3 1 Electron Double-Slit Experiment [email protected]@2015.3 2 2.1 Comparison of Classical and
Nanoelectronics Chapter 2 Classical Particles, Classical Waves, and Quantum Particles [email protected]@2015.3 1 Electron Double-Slit Experiment [email protected]@2015.3 2 2.1 Comparison of Classical and
Development of Optical Wave Microphone Measuring Sound Waves with No Diaphragm
 Progress In Electromagnetics Research Symposium Proceedings, Taipei, March 5 8, 3 359 Development of Optical Wave Microphone Measuring Sound Waves with No Diaphragm Yoshito Sonoda, Takashi Samatsu, and
Progress In Electromagnetics Research Symposium Proceedings, Taipei, March 5 8, 3 359 Development of Optical Wave Microphone Measuring Sound Waves with No Diaphragm Yoshito Sonoda, Takashi Samatsu, and
Wave Function, ψ. Chapter 28 Atomic Physics. The Heisenberg Uncertainty Principle. Line Spectrum
 Wave Function, ψ Chapter 28 Atomic Physics The Hydrogen Atom The Bohr Model Electron Waves in the Atom The value of Ψ 2 for a particular object at a certain place and time is proportional to the probability
Wave Function, ψ Chapter 28 Atomic Physics The Hydrogen Atom The Bohr Model Electron Waves in the Atom The value of Ψ 2 for a particular object at a certain place and time is proportional to the probability
Main properties of atoms and nucleus
 Main properties of atoms and nucleus. Atom Structure.... Structure of Nuclei... 3. Definition of Isotopes... 4. Energy Characteristics of Nuclei... 5. Laws of Radioactive Nuclei Transformation... 3. Atom
Main properties of atoms and nucleus. Atom Structure.... Structure of Nuclei... 3. Definition of Isotopes... 4. Energy Characteristics of Nuclei... 5. Laws of Radioactive Nuclei Transformation... 3. Atom
Acousto-optic modulator
 1 of 3 Acousto-optic modulator F An acousto-optic modulator (AOM), also called a Bragg cell, uses the acousto-optic effect to diffract and shift the frequency of light using sound waves (usually at radio-frequency).
1 of 3 Acousto-optic modulator F An acousto-optic modulator (AOM), also called a Bragg cell, uses the acousto-optic effect to diffract and shift the frequency of light using sound waves (usually at radio-frequency).
Bohr's Theory of the Hydrogen Atom
 OpenStax-CNX module: m42596 1 Bohr's Theory of the Hydrogen Atom OpenStax College This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 4.0 Abstract Describe
OpenStax-CNX module: m42596 1 Bohr's Theory of the Hydrogen Atom OpenStax College This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 4.0 Abstract Describe
CHEM 1411 Chapter 5 Homework Answers
 1 CHEM 1411 Chapter 5 Homework Answers 1. Which statement regarding the gold foil experiment is false? (a) It was performed by Rutherford and his research group early in the 20 th century. (b) Most of
1 CHEM 1411 Chapter 5 Homework Answers 1. Which statement regarding the gold foil experiment is false? (a) It was performed by Rutherford and his research group early in the 20 th century. (b) Most of
Columbia University Department of Physics QUALIFYING EXAMINATION
 Columbia University Department of Physics QUALIFYING EXAMINATION Monday, January 13, 2014 1:00PM to 3:00PM Classical Physics Section 1. Classical Mechanics Two hours are permitted for the completion of
Columbia University Department of Physics QUALIFYING EXAMINATION Monday, January 13, 2014 1:00PM to 3:00PM Classical Physics Section 1. Classical Mechanics Two hours are permitted for the completion of
Arrangement of Electrons in Atoms
 CHAPTER 4 PRE-TEST Arrangement of Electrons in Atoms In the space provided, write the letter of the term that best completes each sentence or best answers each question. 1. Which of the following orbital
CHAPTER 4 PRE-TEST Arrangement of Electrons in Atoms In the space provided, write the letter of the term that best completes each sentence or best answers each question. 1. Which of the following orbital
EQUATION OF STATE. e (E µ)/kt ± 1 h 3 dp,
 EQUATION OF STATE Consider elementary cell in a phase space with a volume x y z p x p y p z = h 3, (st.1) where h = 6.63 1 7 erg s is the Planck constant, x y z is volume in ordinary space measured in
EQUATION OF STATE Consider elementary cell in a phase space with a volume x y z p x p y p z = h 3, (st.1) where h = 6.63 1 7 erg s is the Planck constant, x y z is volume in ordinary space measured in
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION PHYSICAL SETTING PHYSICS. Wednesday, June 17, 2015 1:15 to 4:15 p.m.
 P.S./PHYSICS The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION PHYSICAL SETTING PHYSICS Wednesday, June 17, 2015 1:15 to 4:15 p.m., only The possession or use of any communications
P.S./PHYSICS The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION PHYSICAL SETTING PHYSICS Wednesday, June 17, 2015 1:15 to 4:15 p.m., only The possession or use of any communications
ANALYTICAL METHODS FOR ENGINEERS
 UNIT 1: Unit code: QCF Level: 4 Credit value: 15 ANALYTICAL METHODS FOR ENGINEERS A/601/1401 OUTCOME - TRIGONOMETRIC METHODS TUTORIAL 1 SINUSOIDAL FUNCTION Be able to analyse and model engineering situations
UNIT 1: Unit code: QCF Level: 4 Credit value: 15 ANALYTICAL METHODS FOR ENGINEERS A/601/1401 OUTCOME - TRIGONOMETRIC METHODS TUTORIAL 1 SINUSOIDAL FUNCTION Be able to analyse and model engineering situations
Physics 30 Worksheet # 14: Michelson Experiment
 Physics 30 Worksheet # 14: Michelson Experiment 1. The speed of light found by a Michelson experiment was found to be 2.90 x 10 8 m/s. If the two hills were 20.0 km apart, what was the frequency of the
Physics 30 Worksheet # 14: Michelson Experiment 1. The speed of light found by a Michelson experiment was found to be 2.90 x 10 8 m/s. If the two hills were 20.0 km apart, what was the frequency of the
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Exam in: FYS 310 Classical Mechanics and Electrodynamics Day of exam: Tuesday June 4, 013 Exam hours: 4 hours, beginning at 14:30 This examination
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Exam in: FYS 310 Classical Mechanics and Electrodynamics Day of exam: Tuesday June 4, 013 Exam hours: 4 hours, beginning at 14:30 This examination
Homework #10 (749508)
 Homework #10 (749508) Current Score: 0 out of 100 Description Homework on quantum physics and radioactivity Instructions Answer all the questions as best you can. 1. Hewitt10 32.E.001. [481697] 0/5 points
Homework #10 (749508) Current Score: 0 out of 100 Description Homework on quantum physics and radioactivity Instructions Answer all the questions as best you can. 1. Hewitt10 32.E.001. [481697] 0/5 points
Blackbody radiation. Main Laws. Brightness temperature. 1. Concepts of a blackbody and thermodynamical equilibrium.
 Lecture 4 lackbody radiation. Main Laws. rightness temperature. Objectives: 1. Concepts of a blackbody, thermodynamical equilibrium, and local thermodynamical equilibrium.. Main laws: lackbody emission:
Lecture 4 lackbody radiation. Main Laws. rightness temperature. Objectives: 1. Concepts of a blackbody, thermodynamical equilibrium, and local thermodynamical equilibrium.. Main laws: lackbody emission:
Alternating-Current Circuits
 hapter 1 Alternating-urrent ircuits 1.1 A Sources... 1-1. Simple A circuits... 1-3 1..1 Purely esistive load... 1-3 1.. Purely Inductive oad... 1-5 1..3 Purely apacitive oad... 1-7 1.3 The Series ircuit...
hapter 1 Alternating-urrent ircuits 1.1 A Sources... 1-1. Simple A circuits... 1-3 1..1 Purely esistive load... 1-3 1.. Purely Inductive oad... 1-5 1..3 Purely apacitive oad... 1-7 1.3 The Series ircuit...
Answer, Key Homework 3 David McIntyre 1
 Answer, Key Homewor 3 Daid McIntyre 1 This print-out should hae 26 questions, chec that it is complete Multiple-choice questions may continue on the next column or page: find all choices before maing your
Answer, Key Homewor 3 Daid McIntyre 1 This print-out should hae 26 questions, chec that it is complete Multiple-choice questions may continue on the next column or page: find all choices before maing your
Lab 9: The Acousto-Optic Effect
 Lab 9: The Acousto-Optic Effect Incoming Laser Beam Travelling Acoustic Wave (longitudinal wave) O A 1st order diffracted laser beam A 1 Introduction qb d O 2qb rarefractions compressions Refer to Appendix
Lab 9: The Acousto-Optic Effect Incoming Laser Beam Travelling Acoustic Wave (longitudinal wave) O A 1st order diffracted laser beam A 1 Introduction qb d O 2qb rarefractions compressions Refer to Appendix
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION PHYSICAL SETTING PHYSICS
 PS/PHYSICS The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION PHYSICAL SETTING PHYSICS Wednesday, June 24, 2009 9:15 a.m. to 12:15 p.m., only The answer sheet for Part A and Part B
PS/PHYSICS The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION PHYSICAL SETTING PHYSICS Wednesday, June 24, 2009 9:15 a.m. to 12:15 p.m., only The answer sheet for Part A and Part B
HOOKE S LAW AND SIMPLE HARMONIC MOTION
 HOOKE S LAW AND SIMPLE HARMONIC MOTION Alexander Sapozhnikov, Brooklyn College CUNY, New York, [email protected] Objectives Study Hooke s Law and measure the spring constant. Study Simple Harmonic
HOOKE S LAW AND SIMPLE HARMONIC MOTION Alexander Sapozhnikov, Brooklyn College CUNY, New York, [email protected] Objectives Study Hooke s Law and measure the spring constant. Study Simple Harmonic
Experiment: Crystal Structure Analysis in Engineering Materials
 Experiment: Crystal Structure Analysis in Engineering Materials Objective The purpose of this experiment is to introduce students to the use of X-ray diffraction techniques for investigating various types
Experiment: Crystal Structure Analysis in Engineering Materials Objective The purpose of this experiment is to introduce students to the use of X-ray diffraction techniques for investigating various types
Free Electron Fermi Gas (Kittel Ch. 6)
 Free Electron Fermi Gas (Kittel Ch. 6) Role of Electrons in Solids Electrons are responsible for binding of crystals -- they are the glue that hold the nuclei together Types of binding (see next slide)
Free Electron Fermi Gas (Kittel Ch. 6) Role of Electrons in Solids Electrons are responsible for binding of crystals -- they are the glue that hold the nuclei together Types of binding (see next slide)
Photons. ConcepTest 27.1. 1) red light 2) yellow light 3) green light 4) blue light 5) all have the same energy. Which has more energy, a photon of:
 ConcepTest 27.1 Photons Which has more energy, a photon of: 1) red light 2) yellow light 3) green light 4) blue light 5) all have the same energy 400 nm 500 nm 600 nm 700 nm ConcepTest 27.1 Photons Which
ConcepTest 27.1 Photons Which has more energy, a photon of: 1) red light 2) yellow light 3) green light 4) blue light 5) all have the same energy 400 nm 500 nm 600 nm 700 nm ConcepTest 27.1 Photons Which
ATOMIC SPECTRA. Apparatus: Optical spectrometer, spectral tubes, power supply, incandescent lamp, bottles of dyed water, elevating jack or block.
 1 ATOMIC SPECTRA Objective: To measure the wavelengths of visible light emitted by atomic hydrogen and verify the measured wavelengths against those predicted by quantum theory. To identify an unknown
1 ATOMIC SPECTRA Objective: To measure the wavelengths of visible light emitted by atomic hydrogen and verify the measured wavelengths against those predicted by quantum theory. To identify an unknown
Fraunhofer Diffraction
 Physics 334 Spring 1 Purpose Fraunhofer Diffraction The experiment will test the theory of Fraunhofer diffraction at a single slit by comparing a careful measurement of the angular dependence of intensity
Physics 334 Spring 1 Purpose Fraunhofer Diffraction The experiment will test the theory of Fraunhofer diffraction at a single slit by comparing a careful measurement of the angular dependence of intensity
Sample Exercise 6.1 Concepts of Wavelength and Frequency
 Sample Exercise 6.1 Concepts of Wavelength and Frequency Two electromagnetic waves are represented in the margin. (a) Which wave has the higher frequency? (b) If one wave represents visible light and the
Sample Exercise 6.1 Concepts of Wavelength and Frequency Two electromagnetic waves are represented in the margin. (a) Which wave has the higher frequency? (b) If one wave represents visible light and the
Unit 2: Chemical Bonding and Organic Chemistry
 Chemistry AP Unit : Chemical Bonding and Organic Chemistry Unit : Chemical Bonding and Organic Chemistry Chapter 7: Atomic Structure and Periodicity 7.1: Electromagnetic Radiation Electromagnetic (EM)
Chemistry AP Unit : Chemical Bonding and Organic Chemistry Unit : Chemical Bonding and Organic Chemistry Chapter 7: Atomic Structure and Periodicity 7.1: Electromagnetic Radiation Electromagnetic (EM)
AS COMPETITION PAPER 2008
 AS COMPETITION PAPER 28 Name School Town & County Total Mark/5 Time Allowed: One hour Attempt as many questions as you can. Write your answers on this question paper. Marks allocated for each question
AS COMPETITION PAPER 28 Name School Town & County Total Mark/5 Time Allowed: One hour Attempt as many questions as you can. Write your answers on this question paper. Marks allocated for each question
THE BOHR QUANTUM MODEL
 THE BOHR QUANTUM MODEL INTRODUCTION When light from a low-pressure gas is subject to an electric discharge, a discrete line spectrum is emitted. When light from such a low-pressure gas is examined with
THE BOHR QUANTUM MODEL INTRODUCTION When light from a low-pressure gas is subject to an electric discharge, a discrete line spectrum is emitted. When light from such a low-pressure gas is examined with
Nuclear Physics and Radioactivity
 Nuclear Physics and Radioactivity 1. The number of electrons in an atom of atomic number Z and mass number A is 1) A 2) Z 3) A+Z 4) A-Z 2. The repulsive force between the positively charged protons does
Nuclear Physics and Radioactivity 1. The number of electrons in an atom of atomic number Z and mass number A is 1) A 2) Z 3) A+Z 4) A-Z 2. The repulsive force between the positively charged protons does
Basic Nuclear Concepts
 Section 7: In this section, we present a basic description of atomic nuclei, the stored energy contained within them, their occurrence and stability Basic Nuclear Concepts EARLY DISCOVERIES [see also Section
Section 7: In this section, we present a basic description of atomic nuclei, the stored energy contained within them, their occurrence and stability Basic Nuclear Concepts EARLY DISCOVERIES [see also Section
PHYSICS PAPER 1 (THEORY)
 PHYSICS PAPER 1 (THEORY) (Three hours) (Candidates are allowed additional 15 minutes for only reading the paper. They must NOT start writing during this time.) ---------------------------------------------------------------------------------------------------------------------
PHYSICS PAPER 1 (THEORY) (Three hours) (Candidates are allowed additional 15 minutes for only reading the paper. They must NOT start writing during this time.) ---------------------------------------------------------------------------------------------------------------------
Friday 18 January 2013 Morning
 Friday 18 January 2013 Morning AS GCE PHYSICS B (ADVANCING PHYSICS) G492/01 Understanding Processes / Experimentation and Data Handling *G411640113* Candidates answer on the Question Paper. OCR supplied
Friday 18 January 2013 Morning AS GCE PHYSICS B (ADVANCING PHYSICS) G492/01 Understanding Processes / Experimentation and Data Handling *G411640113* Candidates answer on the Question Paper. OCR supplied
GRID AND PRISM SPECTROMETERS
 FYSA230/2 GRID AND PRISM SPECTROMETERS 1. Introduction Electromagnetic radiation (e.g. visible light) experiences reflection, refraction, interference and diffraction phenomena when entering and passing
FYSA230/2 GRID AND PRISM SPECTROMETERS 1. Introduction Electromagnetic radiation (e.g. visible light) experiences reflection, refraction, interference and diffraction phenomena when entering and passing
Solved Problems in Special Relativity
 Solved Problems in Special Relativity Charles Asman, Adam Monahan and Malcolm McMillan Department of Physics and Astronomy University of British Columbia, Vancouver, British Columbia, Canada Fall 1999;
Solved Problems in Special Relativity Charles Asman, Adam Monahan and Malcolm McMillan Department of Physics and Astronomy University of British Columbia, Vancouver, British Columbia, Canada Fall 1999;
Introduction to Powder X-Ray Diffraction History Basic Principles
 Introduction to Powder X-Ray Diffraction History Basic Principles Folie.1 History: Wilhelm Conrad Röntgen Wilhelm Conrad Röntgen discovered 1895 the X-rays. 1901 he was honoured by the Noble prize for
Introduction to Powder X-Ray Diffraction History Basic Principles Folie.1 History: Wilhelm Conrad Röntgen Wilhelm Conrad Röntgen discovered 1895 the X-rays. 1901 he was honoured by the Noble prize for
L and C connected together. To be able: To analyse some basic circuits.
 circuits: Sinusoidal Voltages and urrents Aims: To appreciate: Similarities between oscillation in circuit and mechanical pendulum. Role of energy loss mechanisms in damping. Why we study sinusoidal signals
circuits: Sinusoidal Voltages and urrents Aims: To appreciate: Similarities between oscillation in circuit and mechanical pendulum. Role of energy loss mechanisms in damping. Why we study sinusoidal signals
arxiv:1111.4354v2 [physics.acc-ph] 27 Oct 2014
![arxiv:1111.4354v2 [physics.acc-ph] 27 Oct 2014 arxiv:1111.4354v2 [physics.acc-ph] 27 Oct 2014](/thumbs/39/19151390.jpg) Theory of Electromagnetic Fields Andrzej Wolski University of Liverpool, and the Cockcroft Institute, UK arxiv:1111.4354v2 [physics.acc-ph] 27 Oct 2014 Abstract We discuss the theory of electromagnetic
Theory of Electromagnetic Fields Andrzej Wolski University of Liverpool, and the Cockcroft Institute, UK arxiv:1111.4354v2 [physics.acc-ph] 27 Oct 2014 Abstract We discuss the theory of electromagnetic
PHYA5/1. General Certificate of Education Advanced Level Examination June 2012. Unit 5 Nuclear and Thermal Physics Section A
 Centre Number Surname Candidate Number For Examinerʼs Use Other Names Candidate Signature Examinerʼs Initials General Certificate of Education Advanced Level Examination June 2012 Question 1 2 Mark Physics
Centre Number Surname Candidate Number For Examinerʼs Use Other Names Candidate Signature Examinerʼs Initials General Certificate of Education Advanced Level Examination June 2012 Question 1 2 Mark Physics
Notes: Most of the material in this chapter is taken from Young and Freedman, Chap. 13.
 Chapter 5. Gravitation Notes: Most of the material in this chapter is taken from Young and Freedman, Chap. 13. 5.1 Newton s Law of Gravitation We have already studied the effects of gravity through the
Chapter 5. Gravitation Notes: Most of the material in this chapter is taken from Young and Freedman, Chap. 13. 5.1 Newton s Law of Gravitation We have already studied the effects of gravity through the
3.5.4.2 One example: Michelson interferometer
 3.5.4.2 One example: Michelson interferometer mirror 1 mirror 2 light source 1 2 3 beam splitter 4 object (n object ) interference pattern we either observe fringes of same thickness (parallel light) or
3.5.4.2 One example: Michelson interferometer mirror 1 mirror 2 light source 1 2 3 beam splitter 4 object (n object ) interference pattern we either observe fringes of same thickness (parallel light) or
............... [2] At the time of purchase of a Strontium-90 source, the activity is 3.7 10 6 Bq.
![............... [2] At the time of purchase of a Strontium-90 source, the activity is 3.7 10 6 Bq. ............... [2] At the time of purchase of a Strontium-90 source, the activity is 3.7 10 6 Bq.](/thumbs/40/21837699.jpg) 1 Strontium-90 decays with the emission of a β-particle to form Yttrium-90. The reaction is represented by the equation 90 38 The decay constant is 0.025 year 1. 90 39 0 1 Sr Y + e + 0.55 MeV. (a) Suggest,
1 Strontium-90 decays with the emission of a β-particle to form Yttrium-90. The reaction is represented by the equation 90 38 The decay constant is 0.025 year 1. 90 39 0 1 Sr Y + e + 0.55 MeV. (a) Suggest,
Chapter 21. Magnetic Forces and Magnetic Fields
 Chapter 21 Magnetic Forces and Magnetic Fields 21.1 Magnetic Fields The needle of a compass is permanent magnet that has a north magnetic pole (N) at one end and a south magnetic pole (S) at the other.
Chapter 21 Magnetic Forces and Magnetic Fields 21.1 Magnetic Fields The needle of a compass is permanent magnet that has a north magnetic pole (N) at one end and a south magnetic pole (S) at the other.
Candidate Number. General Certificate of Education Advanced Level Examination June 2012
 entre Number andidate Number Surname Other Names andidate Signature General ertificate of Education dvanced Level Examination June 212 Physics PHY4/1 Unit 4 Fields and Further Mechanics Section Monday
entre Number andidate Number Surname Other Names andidate Signature General ertificate of Education dvanced Level Examination June 212 Physics PHY4/1 Unit 4 Fields and Further Mechanics Section Monday
104 Practice Exam 2-3/21/02
 104 Practice Exam 2-3/21/02 1. Two electrons are located in a region of space where the magnetic field is zero. Electron A is at rest; and electron B is moving westward with a constant velocity. A non-zero
104 Practice Exam 2-3/21/02 1. Two electrons are located in a region of space where the magnetic field is zero. Electron A is at rest; and electron B is moving westward with a constant velocity. A non-zero
The rate of change of velocity with respect to time. The average rate of change of distance/displacement with respect to time.
 H2 PHYSICS DEFINITIONS LIST Scalar Vector Term Displacement, s Speed Velocity, v Acceleration, a Average speed/velocity Instantaneous Velocity Newton s First Law Newton s Second Law Newton s Third Law
H2 PHYSICS DEFINITIONS LIST Scalar Vector Term Displacement, s Speed Velocity, v Acceleration, a Average speed/velocity Instantaneous Velocity Newton s First Law Newton s Second Law Newton s Third Law
Lecture 3: Optical Properties of Bulk and Nano. 5 nm
 Lecture 3: Optical Properties of Bulk and Nano 5 nm The Previous Lecture Origin frequency dependence of χ in real materials Lorentz model (harmonic oscillator model) 0 e - n( ) n' n '' n ' = 1 + Nucleus
Lecture 3: Optical Properties of Bulk and Nano 5 nm The Previous Lecture Origin frequency dependence of χ in real materials Lorentz model (harmonic oscillator model) 0 e - n( ) n' n '' n ' = 1 + Nucleus
A Guide to Acousto-Optic Modulators
 A Guide to Acousto-Optic Modulators D. J. McCarron December 7, 2007 1 Introduction Acousto-optic modulators (AOMs) are useful devices which allow the frequency, intensity and direction of a laser beam
A Guide to Acousto-Optic Modulators D. J. McCarron December 7, 2007 1 Introduction Acousto-optic modulators (AOMs) are useful devices which allow the frequency, intensity and direction of a laser beam
1. Degenerate Pressure
 . Degenerate Pressure We next consider a Fermion gas in quite a different context: the interior of a white dwarf star. Like other stars, white dwarfs have fully ionized plasma interiors. The positively
. Degenerate Pressure We next consider a Fermion gas in quite a different context: the interior of a white dwarf star. Like other stars, white dwarfs have fully ionized plasma interiors. The positively
PHYSICAL QUANTITIES AND UNITS
 1 PHYSICAL QUANTITIES AND UNITS Introduction Physics is the study of matter, its motion and the interaction between matter. Physics involves analysis of physical quantities, the interaction between them
1 PHYSICAL QUANTITIES AND UNITS Introduction Physics is the study of matter, its motion and the interaction between matter. Physics involves analysis of physical quantities, the interaction between them
Nuclear Physics. Nuclear Physics comprises the study of:
 Nuclear Physics Nuclear Physics comprises the study of: The general properties of nuclei The particles contained in the nucleus The interaction between these particles Radioactivity and nuclear reactions
Nuclear Physics Nuclear Physics comprises the study of: The general properties of nuclei The particles contained in the nucleus The interaction between these particles Radioactivity and nuclear reactions
Review of the isotope effect in the hydrogen spectrum
 Review of the isotope effect in the hydrogen spectrum 1 Balmer and Rydberg Formulas By the middle of the 19th century it was well established that atoms emitted light at discrete wavelengths. This is in
Review of the isotope effect in the hydrogen spectrum 1 Balmer and Rydberg Formulas By the middle of the 19th century it was well established that atoms emitted light at discrete wavelengths. This is in
Interference and Diffraction
 Chapter 14 nterference and Diffraction 14.1 Superposition of Waves... 14-14. Young s Double-Slit Experiment... 14-4 Example 14.1: Double-Slit Experiment... 14-7 14.3 ntensity Distribution... 14-8 Example
Chapter 14 nterference and Diffraction 14.1 Superposition of Waves... 14-14. Young s Double-Slit Experiment... 14-4 Example 14.1: Double-Slit Experiment... 14-7 14.3 ntensity Distribution... 14-8 Example
Name Date Class ELECTRONS IN ATOMS. Standard Curriculum Core content Extension topics
 13 ELECTRONS IN ATOMS Conceptual Curriculum Concrete concepts More abstract concepts or math/problem-solving Standard Curriculum Core content Extension topics Honors Curriculum Core honors content Options
13 ELECTRONS IN ATOMS Conceptual Curriculum Concrete concepts More abstract concepts or math/problem-solving Standard Curriculum Core content Extension topics Honors Curriculum Core honors content Options
Heisenberg Uncertainty
 Heisenberg Uncertainty Outline - Heisenberg Microscope - Measurement Uncertainty - Example: Hydrogen Atom - Example: Single Slit Diffraction - Example: Quantum Dots 1 TRUE / FALSE A photon (quantum of
Heisenberg Uncertainty Outline - Heisenberg Microscope - Measurement Uncertainty - Example: Hydrogen Atom - Example: Single Slit Diffraction - Example: Quantum Dots 1 TRUE / FALSE A photon (quantum of
GCE Physics A. Mark Scheme for June 2014. Unit G485: Fields, Particles and Frontiers of Physics. Advanced GCE. Oxford Cambridge and RSA Examinations
 GCE Physics A Unit G485: Fields, Particles and Frontiers of Physics Advanced GCE Mark Scheme for June 014 Oxford Cambridge and RSA Examinations OCR (Oxford Cambridge and RSA) is a leading UK awarding body,
GCE Physics A Unit G485: Fields, Particles and Frontiers of Physics Advanced GCE Mark Scheme for June 014 Oxford Cambridge and RSA Examinations OCR (Oxford Cambridge and RSA) is a leading UK awarding body,
v = fλ PROGRESSIVE WAVES 1 Candidates should be able to :
 PROGRESSIVE WAVES 1 Candidates should be able to : Describe and distinguish between progressive longitudinal and transverse waves. With the exception of electromagnetic waves, which do not need a material
PROGRESSIVE WAVES 1 Candidates should be able to : Describe and distinguish between progressive longitudinal and transverse waves. With the exception of electromagnetic waves, which do not need a material
Spectroscopy and Regions of the Spectrum
 Basics 9 Spectroscopy and Regions of the Spectrum Different regions of the spectrum probe different types of energy levels of an atomic or molecular system. It is not uncommon to refer to a spectroscopic
Basics 9 Spectroscopy and Regions of the Spectrum Different regions of the spectrum probe different types of energy levels of an atomic or molecular system. It is not uncommon to refer to a spectroscopic
Understanding Poles and Zeros
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY DEPARTMENT OF MECHANICAL ENGINEERING 2.14 Analysis and Design of Feedback Control Systems Understanding Poles and Zeros 1 System Poles and Zeros The transfer function
MASSACHUSETTS INSTITUTE OF TECHNOLOGY DEPARTMENT OF MECHANICAL ENGINEERING 2.14 Analysis and Design of Feedback Control Systems Understanding Poles and Zeros 1 System Poles and Zeros The transfer function
Katharina Lückerath (AG Dr. Martin Zörnig) adapted from Dr. Jörg Hildmann BD Biosciences,Customer Service
 Introduction into Flow Cytometry Katharina Lückerath (AG Dr. Martin Zörnig) adapted from Dr. Jörg Hildmann BD Biosciences,Customer Service How does a FACS look like? FACSCalibur FACScan What is Flow Cytometry?
Introduction into Flow Cytometry Katharina Lückerath (AG Dr. Martin Zörnig) adapted from Dr. Jörg Hildmann BD Biosciences,Customer Service How does a FACS look like? FACSCalibur FACScan What is Flow Cytometry?
Code number given on the right hand side of the question paper should be written on the title page of the answerbook by the candidate.
 Series ONS SET-1 Roll No. Candiates must write code on the title page of the answer book Please check that this question paper contains 16 printed pages. Code number given on the right hand side of the
Series ONS SET-1 Roll No. Candiates must write code on the title page of the answer book Please check that this question paper contains 16 printed pages. Code number given on the right hand side of the
Physical Quantities, Symbols and Units
 Table 1 below indicates the physical quantities required for numerical calculations that are included in the Access 3 Physics units and the Intermediate 1 Physics units and course together with the SI
Table 1 below indicates the physical quantities required for numerical calculations that are included in the Access 3 Physics units and the Intermediate 1 Physics units and course together with the SI
PHY2061 Enriched Physics 2 Lecture Notes Relativity 4. Relativity 4
 PHY6 Enriched Physics Lectre Notes Relativity 4 Relativity 4 Disclaimer: These lectre notes are not meant to replace the corse textbook. The content may be incomplete. Some topics may be nclear. These
PHY6 Enriched Physics Lectre Notes Relativity 4 Relativity 4 Disclaimer: These lectre notes are not meant to replace the corse textbook. The content may be incomplete. Some topics may be nclear. These
X-Ray Free Electron Lasers
 X-Ray Free Electron Lasers Lecture 5. Self-amplified spontaneous emission. FLASH and the European XFEL in Hamburg Igor Zagorodnov Deutsches Elektronen Synchrotron TU Darmstadt, Fachbereich 18 2. June 2014
X-Ray Free Electron Lasers Lecture 5. Self-amplified spontaneous emission. FLASH and the European XFEL in Hamburg Igor Zagorodnov Deutsches Elektronen Synchrotron TU Darmstadt, Fachbereich 18 2. June 2014
AP* Atomic Structure & Periodicity Free Response Questions KEY page 1
 AP* Atomic Structure & Periodicity ree Response Questions KEY page 1 1980 a) points 1s s p 6 3s 3p 6 4s 3d 10 4p 3 b) points for the two electrons in the 4s: 4, 0, 0, +1/ and 4, 0, 0, - 1/ for the three
AP* Atomic Structure & Periodicity ree Response Questions KEY page 1 1980 a) points 1s s p 6 3s 3p 6 4s 3d 10 4p 3 b) points for the two electrons in the 4s: 4, 0, 0, +1/ and 4, 0, 0, - 1/ for the three
Matter Waves. In the previous chapter we discussed some important discoveries and theoretical. Chapter Outline
 5 Matter Waves Chapter Outline 5.1 The Pilot Waves of de Broglie De Broglie s Explanation of Quantization in the Bohr Model 5.2 The Davisson Germer Experiment The Electron Microscope 5.3 Wave Groups and
5 Matter Waves Chapter Outline 5.1 The Pilot Waves of de Broglie De Broglie s Explanation of Quantization in the Bohr Model 5.2 The Davisson Germer Experiment The Electron Microscope 5.3 Wave Groups and
Chapter 5. Second Edition ( 2001 McGraw-Hill) 5.6 Doped GaAs. Solution
 Chapter 5 5.6 Doped GaAs Consider the GaAs crystal at 300 K. a. Calculate the intrinsic conductivity and resistivity. Second Edition ( 2001 McGraw-Hill) b. In a sample containing only 10 15 cm -3 ionized
Chapter 5 5.6 Doped GaAs Consider the GaAs crystal at 300 K. a. Calculate the intrinsic conductivity and resistivity. Second Edition ( 2001 McGraw-Hill) b. In a sample containing only 10 15 cm -3 ionized
Light as a Wave. The Nature of Light. EM Radiation Spectrum. EM Radiation Spectrum. Electromagnetic Radiation
 The Nature of Light Light and other forms of radiation carry information to us from distance astronomical objects Visible light is a subset of a huge spectrum of electromagnetic radiation Maxwell pioneered
The Nature of Light Light and other forms of radiation carry information to us from distance astronomical objects Visible light is a subset of a huge spectrum of electromagnetic radiation Maxwell pioneered
