X-Ray Free Electron Lasers
|
|
|
- Antonia Ryan
- 9 years ago
- Views:
Transcription
1 X-Ray Free Electron Lasers Lecture 5. Self-amplified spontaneous emission. FLASH and the European XFEL in Hamburg Igor Zagorodnov Deutsches Elektronen Synchrotron TU Darmstadt, Fachbereich June 2014
2 Contents Motivation Shot noise in electron beam Current modulation from shot noise FEL start up from shot noise Statistical properties of SASE radiation FEL facilities Outlook PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 2
3 Motivation How to obtain a useful external field? SASE Electrons produce spontaneous undulators radiation A. Kondratenko, E. Saldin, Part. Accelerators 10, 207 (1980) R.Bonifacio et al, Opt. Comm.50, 373 (1984) PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 3
4 Motivation Low-energy undulator test line (LEUTL), USA 530 nm PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 4
5 Motivation TESLA Test Facility (TTF), Hamburg PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 5
6 Shot-noise in electron beam Fluctuations of the electron beam current density serve as the input signal in the SAS EFEL P( t ) Laser pulse P( ω) Spectrum ω ~ ρω t[ a. u] ω ω PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 6
7 Shot-noise in electron beam The electron beam current (at the undulator entrance) consists from electrons randomly arriving at time t k N I ( t) = e δ ( t tk ) k= 1 The electron beam averaged over an ensemble of bunches I ( t) enf( t) The electron beam profile function can be, for example, 1 Fg ( t) = e 2πσ T 2 t 2σ 2 T χ 1 F ( t) = ( t) T χ r [0, T ] [0, T ] 1, 0 t T, ( t) = 0, otherwise PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 7
8 Shot-noise in electron beam In frequency domain N N i ω t i ω t i t k k= 1 k= 1 I ( ω) = I ( t) e dω = e e δ ( t t ) dω = e e ω k It follows from central limit theorem that the real and imaginary parts are normally distributed x 2σ p ( x) = e x, x = Re I ( ω), or x = Im I ( ω) 2πσ x The probability density distribution of spectral power x 1 p ( x) = e λ, λ = x, x = I ( ω) λ 2 PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 8
9 Shot-noise in electron beam First-order correlation function * 2 N N i ω t i ω ' t I ( ω) I ( ω ') = e e k n = N k= 1n= 1 N i ω ω t iωt iω ' t 2 ( ') 2 = e e + e e e k= 1 k n k k n iωt 1 iωt iωt F( ω) = F( t) e dω = δ ( t t ) k k e dω = e N N k= 1 * 2 2 * I ( ω) I ( ω ') = e NF( ω ω ') + e N ( N 1) F( ω) F ( ω ') PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 9
10 Shot-noise in electron beam First-order correlation function * 2 2 * I ( ω) I ( ω ') = e NF( ω ω ') + e N( N 1) F( ω) F ( ω ') Fg ( ω) 2 2 T ω σ 2 = e F ( ω) = sinc( 0.5ωT ) = * r NF( ω) F ( ω ') << 1, forωσ >> 1 sin 0.5ωT ( ) 0.5ωT ( ) Averaged spectral current density ( white noise ) T * 2 I ( ω) I ( ω ') e NF( ω ω ') I ( ω) 2 2 e N PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 10
11 Current modulation from shot-noise We consider a rectangular averaged current 1 Fr ( t) ( ) T χ I ( t) = enf ( t) χ = [0, T ] t [0, T ] r ( t) 1, 0 t T, = 0, otherwise F r ( ω) = sinc 0.5ωT ( ) I ( ω) = enf ( ω) = ensinc 0.5ωT r ( ) PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 11
12 Current modulation from shot-noise Spectral power density of averaged current S( ω) dω = I ( t) dt = I ( ω) dω = T T π = 1 1 T π 0 F r ( ω) T 2 Parseval's theorem dω 2 I ( ω) ( ) 2 S ω = ~ sinc ( 0.5ωT ) 0, for Tω >> 1 πt PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 12
13 Current modulation from shot-noise We are interested in an averaged spectral power density of shot noise, which by analogy can be written as S shot ( ω) I ( ω) 2 2 e N ei = = 0 πt πt π The amplification takes place in bandwidth ω and we can replace the power of the current in this bandwidth by power of the equivalent current with fluctuations at ω at amplitude I 2 rms ɶj ( ω ) = S ( ω ) ω 1 shot 1 I ω S ( ω ) ω I ( ω) e ω rms ( 1 ) shot 1 1,shot = = j0 A 0 b Ab I π 2 2 e N PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 13
14 FEL start up from shot-noise High-gain FEL model with space-charge d n 2 ku n, n 1,2,... N dz ψ = η = dη ek[ JJ ] n iψ == R( Eɶ n ) z n xe 2 e γ r γ r e µ ck[ JJ ] ee ( ψ ) dz m c m c d E ɶ 0 x( z ) = ɶ j z1 dz 4γ r N 2 i m z1 = z0 N ψ m= 1 N jz0 z ( ψ n) = π sgn ψ n ψ m ψ n ψ m Nωε 0 m= 1 ɶj j e E ( ) ( ) ( ) PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 14
15 FEL start up from shot-noise Eɶ x Eɶ 2 2 ˆ x E iη ɶ + + ˆ η x ieɶ x = Γ Γ Γ η ˆ η = ρ 3 ɶ j ( ) z x( η, ) = 0 0 j ( η) η = γ j= 1 0 2ω0 E z c e α η γ γ ω ω c 1 Eɶ x(0) α1 α2 α3 c2 = Eɶ x (0) α c 1 α2 α3 3 Eɶ x (0) c Eɶ (0) 1 x 1 c2 = A Eɶ x (0) c 3 Eɶ x (0) PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 15
16 FEL start up from shot-noise µ ck[ JJ ] ɶ 0 x (0) = ɶ 0 jz1(0) Ex = 4γ r E ɶ µ ck[ JJ ] (0) ɶj z 1(0) 4γ d ɶj j e 2 k, n 1, 2,... N N 2 i n z1 = z0 N ψ n u n n= 1 dz ψ = η = N N ɶ 2 iψ 2 n iψ j n z = ij z e ψ n = kuij z0 e ηn N n= 1 N n= 1 r ηn(0) η, n = 1, 2,... N ɶj (0) = i2 k ηɶj (0) z1 u z1 ck[ JJ ] Eɶ µ (0) i2 k ɶj (0) 0 x = uη z1 4γ r PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 16
17 FEL start up from shot-noise Start up from current modulation c (0) 1 Eɶ x µ 0cK[ JJ ] c2 = A Eɶ x (0) = A 1 ɶ jz1(0) 4γ r c 3 E (0) i2k x uη ɶ Start up from seed field c1 c 2 c 3 Eɶ x (0) Ein 1 1 = A Eɶ x (0) = A 0 Eɶ (0) 0 x PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 17
18 FEL start up from shot-noise On resonance energy γ γ Eɶ η = r x 0 ieɶ = 0 3 x Γ γ r ɶ z x = Ae α α 3 = iγ 3 E ( i ) α 1 = + 3 Γ 2 ( i ) α 2 α 2 = 3 Γ 2 Imα α 1 Reα Γ α 3 = iγ Eɶ x 3 = j= 1 c e α j j z A * α α α = A = α1 α2 α3 * PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 18
19 FEL start up from shot-noise Start up from seed field Start up from current modulation c1 c 2 c 3 Ein 1 1 Ein = A 0 = * c1 0 α1 1 µ 0cK[ JJ ] 1 µ 0cK[ JJ ] * c2 1 jz1(0) jz1(0) α2 = A ɶ = ɶ 4γ r 3 4γ r c * 3 0 α3 µ ck[ JJ ] ck[ JJ ] e E ɶ µ ω j j γ γ π 0 0 in, shot = z1, shot (0) = rγ rγ I ω 2ρω 1 PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 19
20 FEL start up from shot-noise PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 20
21 Statistical properties of SASE radiation Interference Coherence Coherence is a property of waves that enables interference. Temporal coherence is the measure of correlation between the wave and itself delayed. it characterizes how well a wave can interfere with itself at a different time. The delay over which the phase or amplitude wanders by a significant amount is defined as the coherence time PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 21
22 Statistical properties of SASE radiation Coherence time The time-averaged intensity (blue) detected at the output of an interferometer plotted as a function of delay. The interference envelope gives the degree of coherence τ coh 1 1 ~ ~ ω ω ρ PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 22 1
23 Statistical properties of SASE radiation Coherence length Typical length of one spike l coh N = c τ = c l c coh ~ I ce c ρω 1 Number of cooperative electrons Number of spikes (longitudinal modes) P [GW] l coh Laserpuls s[µm] Lb 1 1 M = = : l τ T coh c b PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 23
24 Statistical properties of SASE radiation Spikes in spectrum S( ω ) Spectrum ( ) S ω M = 6 M = 2.6 λ ~ 2ρλ 1 long bunch (~100fs) V. Ayvazyan et al, Eur. Phys.Journ. D 20, 149 (2002) short bunch (~40fs) PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 24
25 Statistical properties of SASE radiation Fluctuations of SASE pulse energy PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 25
26 Statistical properties of SASE radiation Fluctuations of SASE pulse energy (linear regime) M M 1 M u pm ( u) = e Γ( M ) Mu u = U U rad rad Γ = z 1 t ( z) t e dt 0 PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 26
27 Statistical properties of SASE radiation Fluctuations of SASE pulse energy (after saturation, 13 nm, FLASH) PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 27
28 Statistical properties of SASE radiation Saturation length (SASE) P ρw b SASE with N c L sat L g = ln N c L electrons on coherence length z g PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 28
29 Statistical properties of SASE radiation Coherence Longitudinal profile with large statical fluctuations radiation electrons Transverse profile is coherent PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 29
30 FEL facilities TESLA Test Facility ( until 2002) PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 30
31 FEL facilities TESLA Test Facility ( until 2002) Three undulator modules. Total length 15m PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 31
32 FEL facilities TESLA Test Facility ( until 2002) PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 32
33 FEL facilities TESLA Test Facility ( until 2002) PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 33
34 FEL facilities TESLA Test Facility II ( ) From 2003 on, TTF1 was expanded to TTF2, an FEL user facility for the spectral range of soft x-rays, including a new tunnel and a new experimental hall (in the foreground). In April 2006, the facility was renamed FLASH: FEL in Hamburg PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 34
35 FEL facilities FLASH ( from 2006) PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 35
36 FEL facilities FLASH ( from 2005) PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 36
37 FEL facilities FLASH ( from 2005) PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 37
38 Phase space linearization rollover compression vs. linearized compression Q=0.5 nc ~ 1.5 ka Q=1 nc ~2.5 ka PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 38
39 Phase space linearization FLASH In accelerator modules the energy of the electrons is increased from 5 MeV (gun) to 1200 MeV (undulator). PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 39
40 Phase space linearization FLASH In compressors the peak current I is increased from A (gun) to 2500 A (undulator). PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 40
41 Phase space linearization FLASH FEL radiation parameters Wavelength Range nm Average Single Pulse Energy µj Pulse Duration (FWHM) Peak Power (from av.) Average Power (5000 pulses/sec) fs 1-3 GW 400 mw Spectral Width (FWHM) % Average Brilliance 10^17-10^21 photons/s/mrad2/mm2/0.1%bw PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 41
42 FEL facilities FLASH 2 ( from 2013) PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 42
43 FEL facilities FLASH 2 ( from 2013) PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 43
44 FEL facilities FLASH 2 Photon Beam HHG SASE Wavelength range (fundamental) Average single pulse energy Pulse duration (FWHM) Peak power (from av.) Spectral width (FWHM) Peak Brilliance*10-40 nm nm 4-80 nm 1 50 µj µj <15 fs fs 1 5 GW 1 5 GW % % PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 44
45 FEL facilities LCLS E= GeV Intensity distrubution for λ= 0.14 nm radiation power ~ GW pulse length ~30 fs G.Gutt et al, PRL, 108, (2012) PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 45
46 FEL facilities LCLS λ=1.4 P. Emma et al, Nature Photon. 4, 641(2010) radiation power ~ GW Pulse length ~30 fs G.Gutt et al, PRL, 108, (2012) PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 46
47 FEL facilities European XFEL - kürzeste Wellenlänge - größte Brillanz PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 47
48 FEL facilities European XFEL PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 48
49 FEL facilities European XFEL PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 49
50 FEL facilities European XFEL PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 50
51 FEL facilities European XFEL PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 51
52 FEL facilities European XFEL PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 52
53 FEL facilities European XFEL PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 53
54 FEL facilities European XFEL Parameter Value SASE 1 SASE 2 SASE 3 photon energy [kev] wavelength [nm] peak power [GW] average power [W] photon beam size (FWHM) [µm] photon beam divergence (FWHM) [µrad] bandwidth (FWHM) [%] coherence time [fs] pulse duration (FWHM) [fs] average brillance [x10^25, photons/(s mrad^2 mm^2 0.1% bandwidth)] PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 54
55 FEL facilities Linac Coherent Light Source (LCLS) Spring-8 Angstrom Compact Laser (SACLA) European XFEL Standort USA Japan Deutschland Start der Inbetriebnahme Beschleuniger Technologie Anzahl der Lichtblitze pro Sekunde Minimale Wellenlänge normalleitend normalleitend supraleitend nm 0.1 nm 0.05 nm Länge 1500 m 750 m 3400 m PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 55
56 Outlook Methods for improving of coherence self- seeding Monochromator high harmonics of laser light PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 56
57 Outlook Table-Top-FEL λ=740 nm spontaneous undulator radiation with a laser plasma accelerator H.-P. Schlenvoigt et al, Nature Physics 4, 130 (2008) λ=17 nm M.Fuchs et al, Nature Physics 5, 826(2009) PD Dr. Igor Zagorodnov X-Ray Free Electron Lasers. Lecture 5 2. June 2014 Seite 57
X-Ray Free Electron Lasers
 X-Ray Free Electron Lasers Lecture 1. Introduction. Acceleration of charged particles Igor Zagorodnov Deutsches Elektronen Synchrotron TU Darmstadt, Fachbereich 18 0. April 015 General information Lecture:
X-Ray Free Electron Lasers Lecture 1. Introduction. Acceleration of charged particles Igor Zagorodnov Deutsches Elektronen Synchrotron TU Darmstadt, Fachbereich 18 0. April 015 General information Lecture:
Status of the FERMI@Elettra Free Electron Laser
 Status of the FERMI@Elettra Free Electron Laser E. Allaria on behalf of the FERMI team Work partially supported by the Italian Ministry of University and Research under grants FIRB-RBAP045JF2 and FIRB-RBAP06AWK3
Status of the FERMI@Elettra Free Electron Laser E. Allaria on behalf of the FERMI team Work partially supported by the Italian Ministry of University and Research under grants FIRB-RBAP045JF2 and FIRB-RBAP06AWK3
ULTRAFAST LASERS: Free electron lasers thrive from synergy with ultrafast laser systems
 Page 1 of 6 ULTRAFAST LASERS: Free electron lasers thrive from synergy with ultrafast laser systems Free electron lasers support unique time-resolved experiments over a wide range of x-ray wavelengths,
Page 1 of 6 ULTRAFAST LASERS: Free electron lasers thrive from synergy with ultrafast laser systems Free electron lasers support unique time-resolved experiments over a wide range of x-ray wavelengths,
F en = mω 0 2 x. We should regard this as a model of the response of an atom, rather than a classical model of the atom itself.
 The Electron Oscillator/Lorentz Atom Consider a simple model of a classical atom, in which the electron is harmonically bound to the nucleus n x e F en = mω 0 2 x origin resonance frequency Note: We should
The Electron Oscillator/Lorentz Atom Consider a simple model of a classical atom, in which the electron is harmonically bound to the nucleus n x e F en = mω 0 2 x origin resonance frequency Note: We should
Matter Waves. Home Work Solutions
 Chapter 5 Matter Waves. Home Work s 5.1 Problem 5.10 (In the text book) An electron has a de Broglie wavelength equal to the diameter of the hydrogen atom. What is the kinetic energy of the electron? How
Chapter 5 Matter Waves. Home Work s 5.1 Problem 5.10 (In the text book) An electron has a de Broglie wavelength equal to the diameter of the hydrogen atom. What is the kinetic energy of the electron? How
Examples of Uniform EM Plane Waves
 Examples of Uniform EM Plane Waves Outline Reminder of Wave Equation Reminder of Relation Between E & H Energy Transported by EM Waves (Poynting Vector) Examples of Energy Transport by EM Waves 1 Coupling
Examples of Uniform EM Plane Waves Outline Reminder of Wave Equation Reminder of Relation Between E & H Energy Transported by EM Waves (Poynting Vector) Examples of Energy Transport by EM Waves 1 Coupling
Wake Field Calculations at DESY
 Wake Field Calculations at DESY Impedance Budget for the European XFEL Igor Zagorodnov Collaboration Meeting at PAL Pohang, Korea 2-6. September 213 Overview Numerical Methods for Wake Filed Calculations
Wake Field Calculations at DESY Impedance Budget for the European XFEL Igor Zagorodnov Collaboration Meeting at PAL Pohang, Korea 2-6. September 213 Overview Numerical Methods for Wake Filed Calculations
Limiting factors in fiber optic transmissions
 Limiting factors in fiber optic transmissions Sergiusz Patela, Dr Sc Room I/48, Th. 13:00-16:20, Fri. 9:20-10:50 [email protected] eportal.pwr.wroc.pl Copying and processing permitted for noncommercial
Limiting factors in fiber optic transmissions Sergiusz Patela, Dr Sc Room I/48, Th. 13:00-16:20, Fri. 9:20-10:50 [email protected] eportal.pwr.wroc.pl Copying and processing permitted for noncommercial
Comb beam for particle-driven plasma-based accelerators
 A. Mostacci, on behalf of the SPARC team Comb beams are sub-picosecond, high-brightness electron bunch trains generated via the velocity bunching technique. Such bunch trains can be used to drive tunable
A. Mostacci, on behalf of the SPARC team Comb beams are sub-picosecond, high-brightness electron bunch trains generated via the velocity bunching technique. Such bunch trains can be used to drive tunable
Damping Wigglers in PETRA III
 Damping Wigglers in PETRA III WIGGLE2005, Frascati 21-22.2.2005 Winni Decking, DESY-MPY Introduction Damping Wiggler Parameters Nonlinear Dynamics with DW Operational Aspects Summary DESY and its Accelerators
Damping Wigglers in PETRA III WIGGLE2005, Frascati 21-22.2.2005 Winni Decking, DESY-MPY Introduction Damping Wiggler Parameters Nonlinear Dynamics with DW Operational Aspects Summary DESY and its Accelerators
A Quick primer on synchrotron radiation: How would an MBA source change my x-ray beam. Jonathan Lang Advanced Photon Source
 A Quick primer on synchrotron radiation: How would an MBA source change my x-ray beam Jonathan Lang Advanced Photon Source APS Upgrade - MBA Lattice ε ο = 3100 pm ε ο = 80 pm What is emi7ance? I don t
A Quick primer on synchrotron radiation: How would an MBA source change my x-ray beam Jonathan Lang Advanced Photon Source APS Upgrade - MBA Lattice ε ο = 3100 pm ε ο = 80 pm What is emi7ance? I don t
LUNEX5: Toward an advanced FEL project
 UVX 2012, 01009 (2013) DOI: 10.1051/uvx/201301009 C Owned by the authors, published by EDP Sciences, 2013 LUNEX5: Toward an advanced FEL project M.E. Couprie 1, C. Benabderrahmane 1,P. Betinelli 1, F.
UVX 2012, 01009 (2013) DOI: 10.1051/uvx/201301009 C Owned by the authors, published by EDP Sciences, 2013 LUNEX5: Toward an advanced FEL project M.E. Couprie 1, C. Benabderrahmane 1,P. Betinelli 1, F.
- thus, the total number of atoms per second that absorb a photon is
 Stimulated Emission of Radiation - stimulated emission is referring to the emission of radiation (a photon) from one quantum system at its transition frequency induced by the presence of other photons
Stimulated Emission of Radiation - stimulated emission is referring to the emission of radiation (a photon) from one quantum system at its transition frequency induced by the presence of other photons
Activitity (of a radioisotope): The number of nuclei in a sample undergoing radioactive decay in each second. It is commonly expressed in curies
 Activitity (of a radioisotope): The number of nuclei in a sample undergoing radioactive decay in each second. It is commonly expressed in curies (Ci), where 1 Ci = 3.7x10 10 disintegrations per second.
Activitity (of a radioisotope): The number of nuclei in a sample undergoing radioactive decay in each second. It is commonly expressed in curies (Ci), where 1 Ci = 3.7x10 10 disintegrations per second.
Interferometric Measurement of Dispersion in Optical Components
 Interferometric Measurement of Dispersion in Optical Components Mark Froggatt, Eric Moore, and Matthew Wolfe Luna Technologies, Incorporated, 293-A Commerce Street, Blacksburg, Virginia 246 [email protected].
Interferometric Measurement of Dispersion in Optical Components Mark Froggatt, Eric Moore, and Matthew Wolfe Luna Technologies, Incorporated, 293-A Commerce Street, Blacksburg, Virginia 246 [email protected].
Class Notes from: Geotechnical Earthquake Engineering By Steven Kramer, Prentice-Hall. Ground motion parameters
 These notes have been prepared by Mr. Liangcai He, 4 Class Notes from: Geotechnical Earthquake Engineering By Steven Kramer, Prentice-Hall Ground motion parameters Ground motion parameters are important
These notes have been prepared by Mr. Liangcai He, 4 Class Notes from: Geotechnical Earthquake Engineering By Steven Kramer, Prentice-Hall Ground motion parameters Ground motion parameters are important
The European X-ray Free-Electron Laser Facility European XFEL Massimo Altarelli. www.xfel.eu
 The European X-ray Free-Electron Laser Facility European XFEL Massimo Altarelli European X-ray Free-Electron Laser Facility 22607 Hamburg, Germany www.xfel.eu The European XFEL 2 Undulator Tunnels First
The European X-ray Free-Electron Laser Facility European XFEL Massimo Altarelli European X-ray Free-Electron Laser Facility 22607 Hamburg, Germany www.xfel.eu The European XFEL 2 Undulator Tunnels First
Towards large dynamic range beam diagnostics and beam dynamics studies. Pavel Evtushenko
 Towards large dynamic range beam diagnostics and beam dynamics studies Pavel Evtushenko Motivation Linacs with average current 1-2 ma and energy 1-2.5 GeV are envisioned as drivers for next generation
Towards large dynamic range beam diagnostics and beam dynamics studies Pavel Evtushenko Motivation Linacs with average current 1-2 ma and energy 1-2.5 GeV are envisioned as drivers for next generation
Acousto-optic modulator
 1 of 3 Acousto-optic modulator F An acousto-optic modulator (AOM), also called a Bragg cell, uses the acousto-optic effect to diffract and shift the frequency of light using sound waves (usually at radio-frequency).
1 of 3 Acousto-optic modulator F An acousto-optic modulator (AOM), also called a Bragg cell, uses the acousto-optic effect to diffract and shift the frequency of light using sound waves (usually at radio-frequency).
Institute of Accelerator Technologies of Ankara University and TARLA Facility
 Institute of Accelerator Technologies of Ankara University and TARLA Facility Avni Aksoy Ankara University [email protected] On behalf of IAT & TARLA Team Contents Brief history of TAC project Institute
Institute of Accelerator Technologies of Ankara University and TARLA Facility Avni Aksoy Ankara University [email protected] On behalf of IAT & TARLA Team Contents Brief history of TAC project Institute
Optical Fibres. Introduction. Safety precautions. For your safety. For the safety of the apparatus
 Please do not remove this manual from from the lab. It is available at www.cm.ph.bham.ac.uk/y2lab Optics Introduction Optical fibres are widely used for transmitting data at high speeds. In this experiment,
Please do not remove this manual from from the lab. It is available at www.cm.ph.bham.ac.uk/y2lab Optics Introduction Optical fibres are widely used for transmitting data at high speeds. In this experiment,
Les Accélérateurs Laser Plasma
 Les Accélérateurs Laser Plasma Victor Malka Laboratoire d Optique Appliquée ENSTA ParisTech Ecole Polytechnique CNRS PALAISEAU, France [email protected] Accelerators : One century of exploration of
Les Accélérateurs Laser Plasma Victor Malka Laboratoire d Optique Appliquée ENSTA ParisTech Ecole Polytechnique CNRS PALAISEAU, France [email protected] Accelerators : One century of exploration of
Instrumenter til E-XFEL. Martin Meedom Nielsen Section for Neutrons and X-rays for Materials Physics
 Instrumenter til E-XFEL Martin Meedom Nielsen Section for Neutrons and X-rays for Materials Physics Enlightening Science European XFEL a leading new research facility 2 The European XFEL (X-Ray Free-Electron
Instrumenter til E-XFEL Martin Meedom Nielsen Section for Neutrons and X-rays for Materials Physics Enlightening Science European XFEL a leading new research facility 2 The European XFEL (X-Ray Free-Electron
The coherence length of black-body radiation
 Eur. J. Phys. 19 (1998) 245 249. Printed in the UK PII: S143-87(98)86653-1 The coherence length of black-body radiation Axel Donges Fachhochschule und Berufskollegs NTA Prof. Dr Grübler, Seidenstrasse
Eur. J. Phys. 19 (1998) 245 249. Printed in the UK PII: S143-87(98)86653-1 The coherence length of black-body radiation Axel Donges Fachhochschule und Berufskollegs NTA Prof. Dr Grübler, Seidenstrasse
11th International Computational Accelerator Physics Conference (ICAP) August 19 24, 2012, Rostock-Warnemünde (Germany)
 Numerical Modeling of RF Electron Sources for FEL-Accelerators Erion Gjonaj Computational Electromagetics Laboratory (TEMF), Technische Universität Darmstadt, Germany 11th International Computational Accelerator
Numerical Modeling of RF Electron Sources for FEL-Accelerators Erion Gjonaj Computational Electromagetics Laboratory (TEMF), Technische Universität Darmstadt, Germany 11th International Computational Accelerator
3.5.4.2 One example: Michelson interferometer
 3.5.4.2 One example: Michelson interferometer mirror 1 mirror 2 light source 1 2 3 beam splitter 4 object (n object ) interference pattern we either observe fringes of same thickness (parallel light) or
3.5.4.2 One example: Michelson interferometer mirror 1 mirror 2 light source 1 2 3 beam splitter 4 object (n object ) interference pattern we either observe fringes of same thickness (parallel light) or
The IR FEL at the Fritz Haber Institute Berlin: A Tool for IR Spectroscopy of Molecules, Clusters, and Solids
 The IR FEL at the Fritz Haber Institute Berlin: A Tool for IR Spectroscopy of Molecules, Clusters, and Solids Wieland Schöllkopf Fritz-Haber-Institut der Max-Planck-Gesellschaft, Berlin Outline 1. Design
The IR FEL at the Fritz Haber Institute Berlin: A Tool for IR Spectroscopy of Molecules, Clusters, and Solids Wieland Schöllkopf Fritz-Haber-Institut der Max-Planck-Gesellschaft, Berlin Outline 1. Design
Frequency-domain and stochastic model for an articulated wave power device
 Frequency-domain stochastic model for an articulated wave power device J. Cândido P.A.P. Justino Department of Renewable Energies, Instituto Nacional de Engenharia, Tecnologia e Inovação Estrada do Paço
Frequency-domain stochastic model for an articulated wave power device J. Cândido P.A.P. Justino Department of Renewable Energies, Instituto Nacional de Engenharia, Tecnologia e Inovação Estrada do Paço
Self-Mixing Laser Diode Vibrometer with Wide Dynamic Range
 Self-Mixing Laser Diode Vibrometer with Wide Dynamic Range G. Giuliani,, S. Donati, L. Monti -, Italy Outline Conventional Laser vibrometry (LDV) Self-mixing interferometry Self-mixing vibrometer Principle:
Self-Mixing Laser Diode Vibrometer with Wide Dynamic Range G. Giuliani,, S. Donati, L. Monti -, Italy Outline Conventional Laser vibrometry (LDV) Self-mixing interferometry Self-mixing vibrometer Principle:
Chapter 15, example problems:
 Chapter, example problems: (.0) Ultrasound imaging. (Frequenc > 0,000 Hz) v = 00 m/s. λ 00 m/s /.0 mm =.0 0 6 Hz. (Smaller wave length implies larger frequenc, since their product,
Chapter, example problems: (.0) Ultrasound imaging. (Frequenc > 0,000 Hz) v = 00 m/s. λ 00 m/s /.0 mm =.0 0 6 Hz. (Smaller wave length implies larger frequenc, since their product,
6) How wide must a narrow slit be if the first diffraction minimum occurs at ±12 with laser light of 633 nm?
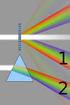 Test IV Name 1) In a single slit diffraction experiment, the width of the slit is 3.1 10-5 m and the distance from the slit to the screen is 2.2 m. If the beam of light of wavelength 600 nm passes through
Test IV Name 1) In a single slit diffraction experiment, the width of the slit is 3.1 10-5 m and the distance from the slit to the screen is 2.2 m. If the beam of light of wavelength 600 nm passes through
Controller Design in Frequency Domain
 ECSE 4440 Control System Engineering Fall 2001 Project 3 Controller Design in Frequency Domain TA 1. Abstract 2. Introduction 3. Controller design in Frequency domain 4. Experiment 5. Colclusion 1. Abstract
ECSE 4440 Control System Engineering Fall 2001 Project 3 Controller Design in Frequency Domain TA 1. Abstract 2. Introduction 3. Controller design in Frequency domain 4. Experiment 5. Colclusion 1. Abstract
Calculation of Eigenmodes in Superconducting Cavities
 Calculation of Eigenmodes in Superconducting Cavities W. Ackermann, C. Liu, W.F.O. Müller, T. Weiland Institut für Theorie Elektromagnetischer Felder, Technische Universität Darmstadt Status Meeting December
Calculation of Eigenmodes in Superconducting Cavities W. Ackermann, C. Liu, W.F.O. Müller, T. Weiland Institut für Theorie Elektromagnetischer Felder, Technische Universität Darmstadt Status Meeting December
VCO Phase noise. Characterizing Phase Noise
 VCO Phase noise Characterizing Phase Noise The term phase noise is widely used for describing short term random frequency fluctuations of a signal. Frequency stability is a measure of the degree to which
VCO Phase noise Characterizing Phase Noise The term phase noise is widely used for describing short term random frequency fluctuations of a signal. Frequency stability is a measure of the degree to which
Time domain modeling
 Time domain modeling Equationof motion of a WEC Frequency domain: Ok if all effects/forces are linear M+ A ω X && % ω = F% ω K + K X% ω B ω + B X% & ω ( ) H PTO PTO + others Time domain: Must be linear
Time domain modeling Equationof motion of a WEC Frequency domain: Ok if all effects/forces are linear M+ A ω X && % ω = F% ω K + K X% ω B ω + B X% & ω ( ) H PTO PTO + others Time domain: Must be linear
Advanced Micro Ring Resonator Filter Technology
 Advanced Micro Ring Resonator Filter Technology G. Lenz and C. K. Madsen Lucent Technologies, Bell Labs Report Documentation Page Form Approved OMB No. 0704-0188 Public reporting burden for the collection
Advanced Micro Ring Resonator Filter Technology G. Lenz and C. K. Madsen Lucent Technologies, Bell Labs Report Documentation Page Form Approved OMB No. 0704-0188 Public reporting burden for the collection
Slice Emittance Measurements at the SLAC Gun Test Facility*
 SLAC-PUB-954 September Slice Emittance Measurements at the SLAC Gun Test Facility* D. H. Dowell, P. R. Bolton, J.E. Clendenin, P. Emma, S.M. Gierman, C.G. Limborg, B.F. Murphy, J.F. Schmerge Stanford Linear
SLAC-PUB-954 September Slice Emittance Measurements at the SLAC Gun Test Facility* D. H. Dowell, P. R. Bolton, J.E. Clendenin, P. Emma, S.M. Gierman, C.G. Limborg, B.F. Murphy, J.F. Schmerge Stanford Linear
7. DYNAMIC LIGHT SCATTERING 7.1 First order temporal autocorrelation function.
 7. DYNAMIC LIGHT SCATTERING 7. First order temporal autocorrelation function. Dynamic light scattering (DLS) studies the properties of inhomogeneous and dynamic media. A generic situation is illustrated
7. DYNAMIC LIGHT SCATTERING 7. First order temporal autocorrelation function. Dynamic light scattering (DLS) studies the properties of inhomogeneous and dynamic media. A generic situation is illustrated
University of Maryland Fraternity & Sorority Life Spring 2015 Academic Report
 University of Maryland Fraternity & Sorority Life Academic Report Academic and Population Statistics Population: # of Students: # of New Members: Avg. Size: Avg. GPA: % of the Undergraduate Population
University of Maryland Fraternity & Sorority Life Academic Report Academic and Population Statistics Population: # of Students: # of New Members: Avg. Size: Avg. GPA: % of the Undergraduate Population
Concept 2. A. Description of light-matter interaction B. Quantitatities in spectroscopy
 Concept 2 A. Description of light-matter interaction B. Quantitatities in spectroscopy Dipole approximation Rabi oscillations Einstein kinetics in two-level system B. Absorption: quantitative description
Concept 2 A. Description of light-matter interaction B. Quantitatities in spectroscopy Dipole approximation Rabi oscillations Einstein kinetics in two-level system B. Absorption: quantitative description
Lab 9: The Acousto-Optic Effect
 Lab 9: The Acousto-Optic Effect Incoming Laser Beam Travelling Acoustic Wave (longitudinal wave) O A 1st order diffracted laser beam A 1 Introduction qb d O 2qb rarefractions compressions Refer to Appendix
Lab 9: The Acousto-Optic Effect Incoming Laser Beam Travelling Acoustic Wave (longitudinal wave) O A 1st order diffracted laser beam A 1 Introduction qb d O 2qb rarefractions compressions Refer to Appendix
Synthetic Aperture Radar (SAR)
 asic Concept of SAR: Consider fied array Synthetic Aperture Radar (SAR) L Angular resolution θ λ /L v(t i ) Σ Claim Equivalent to Moving Antenna: θ Assumes phase coherence in oscillator during each image
asic Concept of SAR: Consider fied array Synthetic Aperture Radar (SAR) L Angular resolution θ λ /L v(t i ) Σ Claim Equivalent to Moving Antenna: θ Assumes phase coherence in oscillator during each image
PHYS 331: Junior Physics Laboratory I Notes on Noise Reduction
 PHYS 331: Junior Physics Laboratory I Notes on Noise Reduction When setting out to make a measurement one often finds that the signal, the quantity we want to see, is masked by noise, which is anything
PHYS 331: Junior Physics Laboratory I Notes on Noise Reduction When setting out to make a measurement one often finds that the signal, the quantity we want to see, is masked by noise, which is anything
7. Beats. sin( + λ) + sin( λ) = 2 cos(λ) sin( )
 34 7. Beats 7.1. What beats are. Musicians tune their instruments using beats. Beats occur when two very nearby pitches are sounded simultaneously. We ll make a mathematical study of this effect, using
34 7. Beats 7.1. What beats are. Musicians tune their instruments using beats. Beats occur when two very nearby pitches are sounded simultaneously. We ll make a mathematical study of this effect, using
Appendix D Digital Modulation and GMSK
 D1 Appendix D Digital Modulation and GMSK A brief introduction to digital modulation schemes is given, showing the logical development of GMSK from simpler schemes. GMSK is of interest since it is used
D1 Appendix D Digital Modulation and GMSK A brief introduction to digital modulation schemes is given, showing the logical development of GMSK from simpler schemes. GMSK is of interest since it is used
054414 PROCESS CONTROL SYSTEM DESIGN. 054414 Process Control System Design LECTURE 2: FREQUENCY DOMAIN ANALYSIS
 05444 PROCESS CONTROL SYSTEM DESIGN 05444 Process Control System Design LECTURE : FREQUENCY DOMAIN ANALYSIS Daniel R. Lewin Department of Chemical Engineering Technion, Haifa, Israel - Objectives On completing
05444 PROCESS CONTROL SYSTEM DESIGN 05444 Process Control System Design LECTURE : FREQUENCY DOMAIN ANALYSIS Daniel R. Lewin Department of Chemical Engineering Technion, Haifa, Israel - Objectives On completing
How To Understand The Physics Of Quantum Chemistry
 Ultrakurze Röntgenimpulse am PSI: vom FEMTO-Projekt zum SwissFEL Paul Beaud Swiss Light Source, Paul Scherrer Institut, Villigen, Switzerland SwissFEL SLS Warum ultrakurze Röntgenpulse? Raum mm ns μm ps
Ultrakurze Röntgenimpulse am PSI: vom FEMTO-Projekt zum SwissFEL Paul Beaud Swiss Light Source, Paul Scherrer Institut, Villigen, Switzerland SwissFEL SLS Warum ultrakurze Röntgenpulse? Raum mm ns μm ps
An octave bandwidth dipole antenna
 An octave bandwidth dipole antenna Abstract: Achieving wideband performance from resonant structures is challenging because their radiation properties and impedance characteristics are usually sensitive
An octave bandwidth dipole antenna Abstract: Achieving wideband performance from resonant structures is challenging because their radiation properties and impedance characteristics are usually sensitive
Testing thermo-acoustic sound generation in water with proton and laser beams
 International ARENA Workshop DESY, Zeuthen 17th 19th of May 25 Testing thermo-acoustic sound generation in water with proton and laser beams Kay Graf Universität Erlangen-Nürnberg Physikalisches Institut
International ARENA Workshop DESY, Zeuthen 17th 19th of May 25 Testing thermo-acoustic sound generation in water with proton and laser beams Kay Graf Universität Erlangen-Nürnberg Physikalisches Institut
Scalable Frequency Generation from Single Optical Wave
 Scalable Frequency Generation from Single Optical Wave S. Radic Jacobs School Of Engineering Qualcomm Institute University of California San Diego - Motivation - Bandwidth Engineering - Noise Inhibition
Scalable Frequency Generation from Single Optical Wave S. Radic Jacobs School Of Engineering Qualcomm Institute University of California San Diego - Motivation - Bandwidth Engineering - Noise Inhibition
Short overview of TEUFEL-project
 Short overview of TEUFEL-project ELAN-meeting may 2004 Frascati (I) Contents Overview of TEUFEL project at Twente Photo cathode research Recent experience Outlook Overview FEL Drive laser Photo cathode
Short overview of TEUFEL-project ELAN-meeting may 2004 Frascati (I) Contents Overview of TEUFEL project at Twente Photo cathode research Recent experience Outlook Overview FEL Drive laser Photo cathode
THE TESLA TEST FACILITY AS A PROTOTYPE FOR THE GLOBAL ACCELERATOR NETWORK
 THE TESLA TEST FACILITY AS A PROTOTYPE FOR THE GLOBAL ACCELERATOR NETWORK K. Rehlich, DESY, Hamburg, Germany Abstract The next generation of large accelerators facilities will be produced and operated
THE TESLA TEST FACILITY AS A PROTOTYPE FOR THE GLOBAL ACCELERATOR NETWORK K. Rehlich, DESY, Hamburg, Germany Abstract The next generation of large accelerators facilities will be produced and operated
Installation, Commissioning and Operation of the Master Laser Oscillator at FLASH
 Installation, Commissioning and Operation of the Master Laser Oscillator at FLASH Patrick Geßler DESY II Timing & Synchronization Workshop, ICTP, Trieste 09.03.2009 V. Arsov, B. Bayer, M. K. Bock, M. Felber,
Installation, Commissioning and Operation of the Master Laser Oscillator at FLASH Patrick Geßler DESY II Timing & Synchronization Workshop, ICTP, Trieste 09.03.2009 V. Arsov, B. Bayer, M. K. Bock, M. Felber,
Self-Guided Intense Laser Pulse Propagation in Air
 Nonlinear Analysis: Modelling and Control, 2000, v.6, No, 2-26 Self-Guided Intense Laser Pulse Propagation in Air R. Danielius, D. Mikalauskas, A. Dubietis and A. Piskarskas Department of Quantum Electronics,
Nonlinear Analysis: Modelling and Control, 2000, v.6, No, 2-26 Self-Guided Intense Laser Pulse Propagation in Air R. Danielius, D. Mikalauskas, A. Dubietis and A. Piskarskas Department of Quantum Electronics,
Wir schaffen Wissen heute für morgen
 Diffractive optics for photon beam diagnostics at hard XFELs Wir schaffen Wissen heute für morgen PSI: SLAC: ESRF: SOLEIL: APS: SACLA: EuroXFEL C. David, S. Rutishauser, P. Karvinen, Y. Kayser, U. Flechsig,
Diffractive optics for photon beam diagnostics at hard XFELs Wir schaffen Wissen heute für morgen PSI: SLAC: ESRF: SOLEIL: APS: SACLA: EuroXFEL C. David, S. Rutishauser, P. Karvinen, Y. Kayser, U. Flechsig,
Perfect Fluids: From Nano to Tera
 Perfect Fluids: From Nano to Tera Thomas Schaefer North Carolina State University 1 2 Perfect Fluids sqgp (T=180 MeV) Neutron Matter (T=1 MeV) Trapped Atoms (T=0.1 nev) 3 Hydrodynamics Long-wavelength,
Perfect Fluids: From Nano to Tera Thomas Schaefer North Carolina State University 1 2 Perfect Fluids sqgp (T=180 MeV) Neutron Matter (T=1 MeV) Trapped Atoms (T=0.1 nev) 3 Hydrodynamics Long-wavelength,
Solution: F = kx is Hooke s law for a mass and spring system. Angular frequency of this system is: k m therefore, k
 Physics 1C Midterm 1 Summer Session II, 2011 Solutions 1. If F = kx, then k m is (a) A (b) ω (c) ω 2 (d) Aω (e) A 2 ω Solution: F = kx is Hooke s law for a mass and spring system. Angular frequency of
Physics 1C Midterm 1 Summer Session II, 2011 Solutions 1. If F = kx, then k m is (a) A (b) ω (c) ω 2 (d) Aω (e) A 2 ω Solution: F = kx is Hooke s law for a mass and spring system. Angular frequency of
Introduction to Optical Link Design
 University of Cyprus Πανεπιστήµιο Κύπρου 1 Introduction to Optical Link Design Stavros Iezekiel Department of Electrical and Computer Engineering University of Cyprus HMY 445 Lecture 08 Fall Semester 2014
University of Cyprus Πανεπιστήµιο Κύπρου 1 Introduction to Optical Link Design Stavros Iezekiel Department of Electrical and Computer Engineering University of Cyprus HMY 445 Lecture 08 Fall Semester 2014
Oscillations. Vern Lindberg. June 10, 2010
 Oscillations Vern Lindberg June 10, 2010 You have discussed oscillations in Vibs and Waves: we will therefore touch lightly on Chapter 3, mainly trying to refresh your memory and extend the concepts. 1
Oscillations Vern Lindberg June 10, 2010 You have discussed oscillations in Vibs and Waves: we will therefore touch lightly on Chapter 3, mainly trying to refresh your memory and extend the concepts. 1
Study of electron cloud at MI and slip stacking process simulation
 Study of electron cloud at MI and slip stacking process simulation Alexandr S. Valkovich Purpose 1.Understand the slip stacking process which happens in the Main Injector. 2. Calculation of bunch distortion
Study of electron cloud at MI and slip stacking process simulation Alexandr S. Valkovich Purpose 1.Understand the slip stacking process which happens in the Main Injector. 2. Calculation of bunch distortion
Lecture 3: Optical Properties of Bulk and Nano. 5 nm
 Lecture 3: Optical Properties of Bulk and Nano 5 nm The Previous Lecture Origin frequency dependence of χ in real materials Lorentz model (harmonic oscillator model) 0 e - n( ) n' n '' n ' = 1 + Nucleus
Lecture 3: Optical Properties of Bulk and Nano 5 nm The Previous Lecture Origin frequency dependence of χ in real materials Lorentz model (harmonic oscillator model) 0 e - n( ) n' n '' n ' = 1 + Nucleus
Advanced Photon Source. RF Beam Position Monitor Upgrade Robert M. Lill
 Advanced Photon Source RF Beam Position Monitor Upgrade Robert M. Lill Filter Comparator (original design) to ATT LPF A+B ATT BPF S bo ATT ATT LPF 180 A-B 180 ATT BPF D x ti ATT LPF C+D ATT BPF D y 180
Advanced Photon Source RF Beam Position Monitor Upgrade Robert M. Lill Filter Comparator (original design) to ATT LPF A+B ATT BPF S bo ATT ATT LPF 180 A-B 180 ATT BPF D x ti ATT LPF C+D ATT BPF D y 180
DIODE PUMPED CRYSTALASER
 DIODE PUMPED CRYSTALASER Ultra-compact CW & Pulsed Turnkey Systems UV Visible to IR High Reliability High Stability High Efficiency TEMoo & SLM Low Noise Low Cost ULTRA-COMPACT DIODE-PUMPED CRYSTAL LASER
DIODE PUMPED CRYSTALASER Ultra-compact CW & Pulsed Turnkey Systems UV Visible to IR High Reliability High Stability High Efficiency TEMoo & SLM Low Noise Low Cost ULTRA-COMPACT DIODE-PUMPED CRYSTAL LASER
Scanning Near Field Optical Microscopy: Principle, Instrumentation and Applications
 Scanning Near Field Optical Microscopy: Principle, Instrumentation and Applications Saulius Marcinkevičius Optics, ICT, KTH 1 Outline Optical near field. Principle of scanning near field optical microscope
Scanning Near Field Optical Microscopy: Principle, Instrumentation and Applications Saulius Marcinkevičius Optics, ICT, KTH 1 Outline Optical near field. Principle of scanning near field optical microscope
SpectraTec II. Polarized Multi-Laser Source BLUE SKY RESEARCH WAVELENGTHS. The SpectraTec II
 BLUE SKY RESEARCH The SpectraTec II, two wavelength laser module is a highly integrated system comprised of two lasers, individual driving and temperature control electronics, wavelength combining, and
BLUE SKY RESEARCH The SpectraTec II, two wavelength laser module is a highly integrated system comprised of two lasers, individual driving and temperature control electronics, wavelength combining, and
Broadband THz Generation from Photoconductive Antenna
 Progress In Electromagnetics Research Symposium 2005, Hangzhou, China, August 22-26 331 Broadband THz Generation from Photoconductive Antenna Qing Chang 1, Dongxiao Yang 1,2, and Liang Wang 1 1 Zhejiang
Progress In Electromagnetics Research Symposium 2005, Hangzhou, China, August 22-26 331 Broadband THz Generation from Photoconductive Antenna Qing Chang 1, Dongxiao Yang 1,2, and Liang Wang 1 1 Zhejiang
5. Scanning Near-Field Optical Microscopy 5.1. Resolution of conventional optical microscopy
 5. Scanning Near-Field Optical Microscopy 5.1. Resolution of conventional optical microscopy Resolution of optical microscope is limited by diffraction. Light going through an aperture makes diffraction
5. Scanning Near-Field Optical Microscopy 5.1. Resolution of conventional optical microscopy Resolution of optical microscope is limited by diffraction. Light going through an aperture makes diffraction
Broadband microwave conductance across the T=0 superconductor-resistive magnetic field tuned transition in InO x!
 Broadband microwave conductance across the T=0 superconductor-resistive magnetic field tuned transition in InO x! N. Peter Armitage! Dept. of Physics and Astronomy! The Johns Hopkins University! Lidong
Broadband microwave conductance across the T=0 superconductor-resistive magnetic field tuned transition in InO x! N. Peter Armitage! Dept. of Physics and Astronomy! The Johns Hopkins University! Lidong
SASE X-Ray Free Electron Laser in DESY --The 4th Generation Light Source. 1. Introduction
 Journal of the GCPD e.v. 6 December 2000-5 - SASE X-Ray Free Electron Laser in DESY --The 4th Generation Light Source Wenlong SHI Deutsches Elektronen-Synchrotron DESY 22603 Hamburg, Germany ABSTRACT The
Journal of the GCPD e.v. 6 December 2000-5 - SASE X-Ray Free Electron Laser in DESY --The 4th Generation Light Source Wenlong SHI Deutsches Elektronen-Synchrotron DESY 22603 Hamburg, Germany ABSTRACT The
Fraunhofer Diffraction
 Physics 334 Spring 1 Purpose Fraunhofer Diffraction The experiment will test the theory of Fraunhofer diffraction at a single slit by comparing a careful measurement of the angular dependence of intensity
Physics 334 Spring 1 Purpose Fraunhofer Diffraction The experiment will test the theory of Fraunhofer diffraction at a single slit by comparing a careful measurement of the angular dependence of intensity
Simulation of Electron Cloud Effects in the PETRA Positron Storage Ring
 DESY M 3-2 December 23 Simulation of Electron Cloud Effects in the PETRA Positron Storage Ring R. Wanzenberg DESY, Notkestr. 85, 2263 Hamburg, Germany December 1, 23 Abstract In positron storage rings
DESY M 3-2 December 23 Simulation of Electron Cloud Effects in the PETRA Positron Storage Ring R. Wanzenberg DESY, Notkestr. 85, 2263 Hamburg, Germany December 1, 23 Abstract In positron storage rings
Specifying Plasma Deposited Hard Coated Optical Thin Film Filters. Alluxa Engineering Staff
 Specifying Plasma Deposited Hard Coated Optical Thin Film Filters. Alluxa Engineering Staff December 2012 Specifying Advanced Plasma Deposited Hard Coated Optical Bandpass and Dichroic Filters. Introduction
Specifying Plasma Deposited Hard Coated Optical Thin Film Filters. Alluxa Engineering Staff December 2012 Specifying Advanced Plasma Deposited Hard Coated Optical Bandpass and Dichroic Filters. Introduction
Calorimetry in particle physics experiments
 Calorimetry in particle physics experiments Unit n. 8 Calibration techniques Roberta Arcidiacono Lecture overview Introduction Hardware Calibration Test Beam Calibration In-situ Calibration (EM calorimeters)
Calorimetry in particle physics experiments Unit n. 8 Calibration techniques Roberta Arcidiacono Lecture overview Introduction Hardware Calibration Test Beam Calibration In-situ Calibration (EM calorimeters)
Quasi-Continuous Wave (CW) UV Laser Xcyte Series
 COMMERCIAL LASERS Quasi-Continuous Wave (CW) UV Laser Xcyte Series Key Features 355 nm outputs available Quasi-CW UV output Field-proven Direct-Coupled Pump (DCP ) TEM00 mode quality Light-regulated output
COMMERCIAL LASERS Quasi-Continuous Wave (CW) UV Laser Xcyte Series Key Features 355 nm outputs available Quasi-CW UV output Field-proven Direct-Coupled Pump (DCP ) TEM00 mode quality Light-regulated output
ELECTROMAGNETIC ANALYSIS AND COLD TEST OF A DISTRIBUTED WINDOW FOR A HIGH POWER GYROTRON
 ELECTROMAGNETIC ANALYSIS AND COLD TEST OF A DISTRIBUTED WINDOW FOR A HIGH POWER GYROTRON M.A.Shapiro, C.P.Moeller, and R.J.Temkin Plasma Science and Fusion Ceer, Massachusetts Institute of Technology,
ELECTROMAGNETIC ANALYSIS AND COLD TEST OF A DISTRIBUTED WINDOW FOR A HIGH POWER GYROTRON M.A.Shapiro, C.P.Moeller, and R.J.Temkin Plasma Science and Fusion Ceer, Massachusetts Institute of Technology,
Nuclear Physics Lab I: Geiger-Müller Counter and Nuclear Counting Statistics
 Nuclear Physics Lab I: Geiger-Müller Counter and Nuclear Counting Statistics PART I Geiger Tube: Optimal Operating Voltage and Resolving Time Objective: To become acquainted with the operation and characteristics
Nuclear Physics Lab I: Geiger-Müller Counter and Nuclear Counting Statistics PART I Geiger Tube: Optimal Operating Voltage and Resolving Time Objective: To become acquainted with the operation and characteristics
Digital Modulation. David Tipper. Department of Information Science and Telecommunications University of Pittsburgh. Typical Communication System
 Digital Modulation David Tipper Associate Professor Department of Information Science and Telecommunications University of Pittsburgh http://www.tele.pitt.edu/tipper.html Typical Communication System Source
Digital Modulation David Tipper Associate Professor Department of Information Science and Telecommunications University of Pittsburgh http://www.tele.pitt.edu/tipper.html Typical Communication System Source
Realization and characterization of a phase locked laser system for coherent spectroscopy of fiber-coupled cesium atoms
 Johannes Gutenberg-Universität Mainz - Institut für Physik Realization and characterization of a phase locked laser system for coherent spectroscopy of fiber-coupled cesium atoms Diplomarbeit von Melanie
Johannes Gutenberg-Universität Mainz - Institut für Physik Realization and characterization of a phase locked laser system for coherent spectroscopy of fiber-coupled cesium atoms Diplomarbeit von Melanie
HP 70950B OPTICAL SPECTRUM ANALYZER
 HP 71450B, 71451B, and 71452B Optical Spectrum Analyzers Technical Specifications Spectral Measurements from 600 to 1700 nm HP 70950B OPTICAL SPECTRUM ANALYZER OPTICAL INPUT The HP 71450B, 71451B, and
HP 71450B, 71451B, and 71452B Optical Spectrum Analyzers Technical Specifications Spectral Measurements from 600 to 1700 nm HP 70950B OPTICAL SPECTRUM ANALYZER OPTICAL INPUT The HP 71450B, 71451B, and
SOFTWARE FOR GENERATION OF SPECTRUM COMPATIBLE TIME HISTORY
 3 th World Conference on Earthquake Engineering Vancouver, B.C., Canada August -6, 24 Paper No. 296 SOFTWARE FOR GENERATION OF SPECTRUM COMPATIBLE TIME HISTORY ASHOK KUMAR SUMMARY One of the important
3 th World Conference on Earthquake Engineering Vancouver, B.C., Canada August -6, 24 Paper No. 296 SOFTWARE FOR GENERATION OF SPECTRUM COMPATIBLE TIME HISTORY ASHOK KUMAR SUMMARY One of the important
Aliasing, Image Sampling and Reconstruction
 Aliasing, Image Sampling and Reconstruction Recall: a pixel is a point It is NOT a box, disc or teeny wee light It has no dimension It occupies no area It can have a coordinate More than a point, it is
Aliasing, Image Sampling and Reconstruction Recall: a pixel is a point It is NOT a box, disc or teeny wee light It has no dimension It occupies no area It can have a coordinate More than a point, it is
Laser plasma wakefield acceleration and ICAN
 Laser plasma wakefield acceleration and ICAN Laura Corner John Adams Institute, University of Oxford Special thanks to S.M. Hooker ICAN workshop, Paris, April 28 th 2014 Outline The basic idea. Experimental
Laser plasma wakefield acceleration and ICAN Laura Corner John Adams Institute, University of Oxford Special thanks to S.M. Hooker ICAN workshop, Paris, April 28 th 2014 Outline The basic idea. Experimental
Data-analysis scheme and infrastructure at the X-ray free electron laser facility, SACLA
 Data-analysis scheme and infrastructure at the X-ray free electron laser facility, SACLA T. Sugimoto, T. Abe, Y. Joti, T. Kameshima, K. Okada, M. Yamaga, R. Tanaka (Japan Synchrotron Radiation Research
Data-analysis scheme and infrastructure at the X-ray free electron laser facility, SACLA T. Sugimoto, T. Abe, Y. Joti, T. Kameshima, K. Okada, M. Yamaga, R. Tanaka (Japan Synchrotron Radiation Research
Fourier Analysis. u m, a n u n = am um, u m
 Fourier Analysis Fourier series allow you to expand a function on a finite interval as an infinite series of trigonometric functions. What if the interval is infinite? That s the subject of this chapter.
Fourier Analysis Fourier series allow you to expand a function on a finite interval as an infinite series of trigonometric functions. What if the interval is infinite? That s the subject of this chapter.
Two-photon FCS Tutorial. Berland Lab Department of Physics Emory University
 Two-photon FCS Tutorial Berland Lab Department of Physics Emory University What is FCS? FCS : Fluorescence Correlation Spectroscopy FCS is a technique for acquiring dynamical information from spontaneous
Two-photon FCS Tutorial Berland Lab Department of Physics Emory University What is FCS? FCS : Fluorescence Correlation Spectroscopy FCS is a technique for acquiring dynamical information from spontaneous
Antenna A mean for radiating and receiving radio waves Transitional structure between free-space and a guiding device. Application: Radiation
 Antenna A mean for radiating and receiving radio waves Transitional structure between free-space and a guiding device Application: adiation Introduction An antenna is designed to radiate or receive electromagnetic
Antenna A mean for radiating and receiving radio waves Transitional structure between free-space and a guiding device Application: adiation Introduction An antenna is designed to radiate or receive electromagnetic
OPTICAL RADIATION SAFETY INFORMATION Application Note
 OPTICAL RADIATION SAFETY INFORMATION Application Note General Direct viewing the intensive optical radiation from the laser diode (LD) may cause damage to the eye. The potential optical hazard depends
OPTICAL RADIATION SAFETY INFORMATION Application Note General Direct viewing the intensive optical radiation from the laser diode (LD) may cause damage to the eye. The potential optical hazard depends
16th International Toki Conference on Advanced Imaging and Plasma Diagnostics
 16th International Toki Conference on Advanced Imaging and Plasma Diagnostics Temperature Diagnostics for Field-Reversed Configuration Plasmas on the Pulsed High Density (PHD) Experiment Hiroshi Gota,
16th International Toki Conference on Advanced Imaging and Plasma Diagnostics Temperature Diagnostics for Field-Reversed Configuration Plasmas on the Pulsed High Density (PHD) Experiment Hiroshi Gota,
