A stochastic individual-based model for immunotherapy of cancer
|
|
|
- Clemence Gwen Boone
- 8 years ago
- Views:
Transcription
1 A stochastic individual-based model for immunotherapy of cancer Loren Coquille - Joint work with Martina Baar, Anton Bovier, Hannah Mayer (IAM Bonn) Michael Hölzel, Meri Rogava, Thomas Tüting (UniKlinik Bonn) Institute for Applied Mathematics Bonn CIRM, Marseille - June 15, 2015 Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
2 Plan 1 Biological motivations 2 Adaptative dynamics The model State of the art 3 Only switches : Relapse caused by stochastic fluctuations Therapy with 1 type of T-cell Biological parameters Therapy with 2 types of T-cells 4 Only mutations : Early mutation induced by the therapy 5 Mutations and switches : Polymorphic Evolution Sequence 6 Conclusion Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
3 Biological motivations Plan 1 Biological motivations 2 Adaptative dynamics The model State of the art 3 Only switches : Relapse caused by stochastic fluctuations Therapy with 1 type of T-cell Biological parameters Therapy with 2 types of T-cells 4 Only mutations : Early mutation induced by the therapy 5 Mutations and switches : Polymorphic Evolution Sequence 6 Conclusion Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
4 Biological motivations Experiment on melanoma (UniKlinik Bonn) Injection of T-cells able to kill a specific type of melanoma. The treatment induces an inflammation, to which the melanoma react by changing their phenotype (markers disappear on their surface, "switch"). The T-cells cannot kill them any more, the tumor continues to grow. Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
5 Biological motivations Without therapy : exponential growth of the tumor. With therapy : relapse after 140 days. With therapy and restimulation : late relapse. Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
6 Adaptative dynamics Plan 1 Biological motivations 2 Adaptative dynamics The model State of the art 3 Only switches : Relapse caused by stochastic fluctuations Therapy with 1 type of T-cell Biological parameters Therapy with 2 types of T-cells 4 Only mutations : Early mutation induced by the therapy 5 Mutations and switches : Polymorphic Evolution Sequence 6 Conclusion Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
7 Adaptative dynamics The model Individual-based model Cancer cells (melanoma): each cell is characterized by a genotype and a phenotype. Each can reproduce, die, mutate (repr. with genotypic change) or switch (change its phenotype) at prescribed rates. Immune cells (T-cells): Each cell can reproduce, die, or kill a cancer cell of prescribed type (which produces a chemical messenger) at prescribed rates. Chemical messenger (TNF α): Each particle can die at a prescribed rate. Its presence influences the ability of a fixed type of cancer cell to switch. Trait space and measure : X = G P Z W = {g 1,..., g G } {p 1,..., p P } {z 1,..., z Z } w n = (n (g1,p 1 ),..., n (g G,p P ), n z1,..., n z Z, n w ) Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
8 Adaptative dynamics The model Example for 2 types of melanoma and 1 type of T-cell The stochastic model converges, in the limit of large populations, towards the solution this dynamical system with logistic, predator-prey, switch: ( ) ṅ x = n x b x d x c xx n x c xy n y + s n y s w n w n x t xz n zx n x ( ) ṅ y = n y b y d y c yy n y c yx n x s n y + s w n w n x ṅ zx ṅ w = d zx n zx + b zx n zx n x = d w n w + l x t xz n x n zx Event Rates for x Rates for y for z for w (Re)production b x b y b zx n x Natural death d x + c xx n x + c xy n y d y + c yy n x + c yx n y d zx d w Therapy death t xz n zx 0 Switch s w n w s Deterministically, a number l w of TNF-α particles are produced when z kills x. Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
9 Adaptative dynamics State of the art State of the art for the BPDL model In general X continuous. Measure ν t = N t i=1 δ x i. Markov process on the space of positive measures. Event Clonal reproduction Reproduction with mutation Death Rate (1 p(x)) b(x) m(x, dy) p(x) b(x) d(x) + X c(x, y)ν(dy) Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
10 Adaptative dynamics State of the art State of the art for the BPDL model In general X continuous. Measure ν t = 1 K Nt i=1 δ x i. Markov process on the space of positive measures. Event Clonal reproduction Reproduction with mutation Death Rate (1 µp(x)) b(x) m(x, dy) µp(x) b(x) d(x) + X c(x,y) K ν(dy) Limit of large populations and rare mutations K µ 0 Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
11 Adaptative dynamics State of the art Scalings and time scales K, µ fixed, T < : Law of large numbers, deterministic limit [Fournier, Méléard, 2004] K, µ 0, T < : Law of large numbers, deterministic limit without mutations. K, µ 0, T log(1/µ) : Deterministic jump process [Bovier, Wang, 2012] 1 1 (K, µ) (, 0) t.q. µk log K, T µk : Random jump process [Champagnat, Méléard, 2009, 2010] Trait Substitution Sequence Polymorphic Evolution Sequence Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
12 Adaptative dynamics State of the art Scalings and time scales K, µ fixed, T < : Law of large numbers, deterministic limit [Fournier, Méléard, 2004] limit dynamical systems (with switch) are not classified K, µ 0, T < : Law of large numbers, deterministic limit without mutations. K, µ 0, T log(1/µ) : Deterministic jump process [Bovier, Wang, 2012] 1 1 (K, µ) (, 0) t.q. µk log K, T µk : Random jump process [Champagnat, Méléard, 2009, 2010] Trait Substitution Sequence Polymorphic Evolution Sequence Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
13 Only switches : Relapse caused by stochastic fluctuations Plan 1 Biological motivations 2 Adaptative dynamics The model State of the art 3 Only switches : Relapse caused by stochastic fluctuations Therapy with 1 type of T-cell Biological parameters Therapy with 2 types of T-cells 4 Only mutations : Early mutation induced by the therapy 5 Mutations and switches : Polymorphic Evolution Sequence 6 Conclusion Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
14 Only switches : Relapse caused by stochastic fluctuations Therapy with 1 type of T-cell Solution of the determinisitic system Legend : Melanoma x, melanoma y, T-cells, TNF-α Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
15 Only switches : Relapse caused by stochastic fluctuations Therapy with 1 type of T-cell 4 fixed points in the positive quadrant With reasonable parameters we have : 4 y 3 Pxyz Pxy 0 P000 (Px00) x Pxyz is stable. Pxy0 is stable on the invariant sub-space {n z = 0}. Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
16 Only switches : Relapse caused by stochastic fluctuations Therapy with 1 type of T-cell Relapse towards Pxyz, (K = 200) Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
17 Only switches : Relapse caused by stochastic fluctuations Therapy with 1 type of T-cell Relapse towards Pxy0 due to the death of z Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
18 Only switches : Relapse caused by stochastic fluctuations Biological parameters Adjustment of parameters : data Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
19 Only switches : Relapse caused by stochastic fluctuations Biological parameters Adjustment of parameters : simulations (K = 10 5 ) Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
20 Only switches : Relapse caused by stochastic fluctuations Therapy with 2 types of T-cells Therapy with 1 types of T-cells ( ) ṅ x = n x b x d x c xx n x c xy n y t xz n zx n x + s n y s w n w n x ( ) ṅ y = n y b y d y c yy n y c yx n x s n y + s w n w n x ṅ zx = d zx n zx + b zx n zx n x ṅ w = d w n w + l x t xz n x n zx Event Rates for x Rates for y Reproduction b x b y Natural death d x + c xx n x + c xy n y d y + c yy n x + c yx n y Death due to therapy t xz n zx 0 Switch s w n w s Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
21 Only switches : Relapse caused by stochastic fluctuations Therapy with 2 types of T-cells Therapy with 2 types of T-cells ( ) ṅ x = n x b x d x c xx n x c xy n y t xz n zx n x + s n y s w n w n x ( ) ṅ y = n y b y d y c yy n y c yx n x t yz n zy n y s n y + s w n w n x ṅ zx ṅ zy ṅ w = d zx n zx + b zx n zx n x = d zy n zy + b zy n zy n y = d w n w + l x t xz n x n zx + l y t yz n y n zy Event Rates for x Rates for y Reproduction b x b y Natural death d x + c xx n x + c xy n y d y + c yy n x + c yx n y Death due to therapy t xz n zx t yz n zy Switch s w n w s Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
22 Only switches : Relapse caused by stochastic fluctuations Therapy with 2 types of T-cells Solution of the deterministic limit Legend : Melanoma x, melanoma y, T-cell z x, T-cell z y,tnf-α Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
23 Only switches : Relapse caused by stochastic fluctuations Therapy with 2 types of T-cells 6 fixed points in the positive quadrant 4 y Pxyz x 0 Pxyz x z y P0000 Pxy00 Pxy0z y (Px000) x Pxyz x z y is stable. Pxyz x 0 is stable in the invariant subspace {n zy = 0} Pxy0z y is stable in the invariant subspace {n zx = 0} Pxy00 is stable in the invariant subspace {n zx = 0} {n zy = 0} Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
24 Only switches : Relapse caused by stochastic fluctuations Therapy with 2 types of T-cells Branching between several possible relapses z x = 0 P xy0z y P xyz x z y z y = 0 P xy00 P xyz x 0 Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
25 Only switches : Relapse caused by stochastic fluctuations Therapy with 2 types of T-cells Stochastic system close to the deterministic system Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
26 Only switches : Relapse caused by stochastic fluctuations Therapy with 2 types of T-cells Relapse towards Pxyz x 0 caused by the death of z y Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
27 Only switches : Relapse caused by stochastic fluctuations Therapy with 2 types of T-cells Relapse towards Pxy0z y caused by the death of z x Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
28 Only switches : Relapse caused by stochastic fluctuations Therapy with 2 types of T-cells Relapse towards Pxy00 caused by the death of z x and z y Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
29 Only switches : Relapse caused by stochastic fluctuations Therapy with 2 types of T-cells Cure! (P0000) Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
30 Only mutations : Early mutation induced by the therapy Plan 1 Biological motivations 2 Adaptative dynamics The model State of the art 3 Only switches : Relapse caused by stochastic fluctuations Therapy with 1 type of T-cell Biological parameters Therapy with 2 types of T-cells 4 Only mutations : Early mutation induced by the therapy 5 Mutations and switches : Polymorphic Evolution Sequence 6 Conclusion Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
31 Only mutations : Early mutation induced by the therapy Example for 2 types of melanoma and 1 type of T-cell BPDL + therapy with usual competition Event Clonal reproduction Mutation towards y Natural death Death due to therapy Rates for x (1 µ)b(x) µb(x) d(x) + c(x, x)n x + c(x, y)n y t(z, x)n z Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
32 Only mutations : Early mutation induced by the therapy Example for 2 types of melanoma and 1 type of T-cell BPDL + therapy with birth-reducing competition Event Rates for x Clonal reproduction (1 µ) b(x) c(x, x)n x c(x, y)n y + Mutation towards y µ b(x) c(x, x)n x c(x, y)n y + Natural death d(x) + b(x) c(x, x)n x c(x, y)n y Death due to therapy t(z, x)n z Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
33 Only mutations : Early mutation induced by the therapy Example for 2 types of melanoma and 1 type of T-cell BPDL + therapy with birth-reducing competition Event Rates for y Clonal reproduction b(y) c(y, y)n y c(y, x)n x + Mutation towards x 0 Natural death d(y) + b(y) c(y, y)n y c(y, x)n x Death due to therapy 0 Event Reproduction Death Rates for z b(z, x)n x d(z) No switch The chemical messenger (TNF-α) has a trivial role : ṅ w = 0 Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
34 Only mutations : Early mutation induced by the therapy Limiting determinisitic system When (K, µ) (, 0) such that µ K α > 0 then µ disappears from the deterministic system on the time scale T <. ( ) ṅ x = n x b x d x c xx n x c xy n y t xz n zx n x ( ) ṅ y = n y b y d y c yy n y c yx n x ṅ zx = d zx n zx + b zx n zx n x The deterministic system doesn t "see" the difference between death enhancing and birth-reducing competiton. Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
35 Only mutations : Early mutation induced by the therapy With birth-reducing competition Let n(0) = (n x (0), 0, 0), then the initial mutation rate is quadratic in the population n x : m(n x ) µ bx2 4c xx m(n x ) := µ b x c xx n x + n x 0 d x c xx b x 2c xx bx dx n x := c xx is the equilibrium of the initial x population. A smaller population can have a higher mutation rate. Note m(n x ) = O(µK). n x b x c xx n x Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
36 Only mutations : Early mutation induced by the therapy Without treatment and n x (0) n x Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
37 Only mutations : Early mutation induced by the therapy Without treatment and n x (0) small Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
38 Only mutations : Early mutation induced by the therapy With treatment Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
39 Mutations and switches : Polymorphic Evolution Sequence Plan 1 Biological motivations 2 Adaptative dynamics The model State of the art 3 Only switches : Relapse caused by stochastic fluctuations Therapy with 1 type of T-cell Biological parameters Therapy with 2 types of T-cells 4 Only mutations : Early mutation induced by the therapy 5 Mutations and switches : Polymorphic Evolution Sequence 6 Conclusion Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
40 Mutations and switches : Polymorphic Evolution Sequence Two time scales Rares mutations in the genotype space G : (K, µ) (, 0) such that Fast switches in the phenotype space P : s((g, p), (g, p )) = O(1) 1 µk log K p, p P Step 1 : branching approx, O(log(K)) Step 2 : approx with det.syst., O(1) Step 3 : branching approx, O(log(K)) < 1 >< 2 >< 3 > Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
41 Mutations and switches : Polymorphic Evolution Sequence Invasion fitness? For the BPDL model : f (x, M) = b(x) d(x) y M c(x, y) n y. is the growth rate of a single individual with trait x M in the presence of the equilibrium population n on M. f (x, M) > 0 : positive probability for the mutant (uniformly in K) to grow to a population of size O(K); f (x, M) < 0 : the mutant population dies out with probability tending to one (as K ) before this happens. We need to generalize this notion to the case when fast phenotypic switches are present. Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
42 Mutations and switches : Polymorphic Evolution Sequence Consider an initial population of genotype g (associated with l different phenotypes p 1,..., p l ) which is able to mutate at rate µ to another genotype g, associated with k different phenotypes p 1,..., p k. Consider as initial condition n(0) = (n (g,p1 )(0),..., n (g,pl )(0)) a stable fixed point, n, of the following system: l l l ṅ (g,pi ) = n (g,pi ) b i d i c ij n (g,pj ) s ij + s ji n (g,pj ). j=1 As long as the mutant population has less than ɛk individuals (with ɛ 1), the mutant population (g, p 1 ),..., (g, p k ) is well approximated by a k-type branching process with rates: p i p i p i with rate b i p i with rate d i + l l=1 c il n l for i, j {1,..., k}. p i p j with rate s ij j=1 j=1 Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
43 Mutations and switches : Polymorphic Evolution Sequence Multi-type branching processes have been analysed by Kesten/Stigum and Atreya/Ney. Their behavior are classified in terms of the matrix A, given by f 1 s s 1k A = s 21 f s k1... f k where f i := b i d i l c il n l l=1 The multi-type process is super-critical, if and only if the largest eigenvalue, λ 1 = λ 1 (A) > 0. It is thus the appropriate generalization of the invasion fitness: F (g, g) := λ 1 (A). k j=1 s ij. Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
44 Mutations and switches : Polymorphic Evolution Sequence Example : Resonance s 12 = s 21 = 2 f 1 = f 2 = 1 F (g, g) = λ 1 = 1 F (g, g ) = 1 Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
45 Conclusion Plan 1 Biological motivations 2 Adaptative dynamics The model State of the art 3 Only switches : Relapse caused by stochastic fluctuations Therapy with 1 type of T-cell Biological parameters Therapy with 2 types of T-cells 4 Only mutations : Early mutation induced by the therapy 5 Mutations and switches : Polymorphic Evolution Sequence 6 Conclusion Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
46 Conclusion Still a lot to understand... Biologically : measure precise parameters appearing in the model check predictions (e.g. therapy with 2 types of T-cells) etc. Mathematically : How do the transition probabilities between different relapses scale with K? What happens if the deterministic system has limit cycles? How does the birth-reducing competition affect the mutation probability in presence of treatment? etc. Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
47 Conclusion Thanks! Loren Coquille (IAM-Bonn) CIRM - June 15, / 43
1.5. Factorisation. Introduction. Prerequisites. Learning Outcomes. Learning Style
Factorisation 1.5 Introduction In Block 4 we showed the way in which brackets were removed from algebraic expressions. Factorisation, which can be considered as the reverse of this process, is dealt with
MATH 304 Linear Algebra Lecture 20: Inner product spaces. Orthogonal sets.
MATH 304 Linear Algebra Lecture 20: Inner product spaces. Orthogonal sets. Norm The notion of norm generalizes the notion of length of a vector in R n. Definition. Let V be a vector space. A function α
SECOND DERIVATIVE TEST FOR CONSTRAINED EXTREMA
SECOND DERIVATIVE TEST FOR CONSTRAINED EXTREMA This handout presents the second derivative test for a local extrema of a Lagrange multiplier problem. The Section 1 presents a geometric motivation for the
1 The basic equations of fluid dynamics
1 The basic equations of fluid dynamics The main task in fluid dynamics is to find the velocity field describing the flow in a given domain. To do this, one uses the basic equations of fluid flow, which
Reaction diffusion systems and pattern formation
Chapter 5 Reaction diffusion systems and pattern formation 5.1 Reaction diffusion systems from biology In ecological problems, different species interact with each other, and in chemical reactions, different
Math 432 HW 2.5 Solutions
Math 432 HW 2.5 Solutions Assigned: 1-10, 12, 13, and 14. Selected for Grading: 1 (for five points), 6 (also for five), 9, 12 Solutions: 1. (2y 3 + 2y 2 ) dx + (3y 2 x + 2xy) dy = 0. M/ y = 6y 2 + 4y N/
Online Appendix to Stochastic Imitative Game Dynamics with Committed Agents
Online Appendix to Stochastic Imitative Game Dynamics with Committed Agents William H. Sandholm January 6, 22 O.. Imitative protocols, mean dynamics, and equilibrium selection In this section, we consider
A Local Stability of Mathematical Models for Cancer Treatment by Using Gene Therapy
International Journal of Modeling Optimization, Vol 5, No 3, June 2015 A Local Stability of Mathematical Models for Cancer Treatment by Using Gene Therapy Dwi Lestari Ratnasari Dwi Ambarwati Abstract This
Random access protocols for channel access. Markov chains and their stability. Laurent Massoulié.
Random access protocols for channel access Markov chains and their stability laurent.massoulie@inria.fr Aloha: the first random access protocol for channel access [Abramson, Hawaii 70] Goal: allow machines
A characterization of trace zero symmetric nonnegative 5x5 matrices
A characterization of trace zero symmetric nonnegative 5x5 matrices Oren Spector June 1, 009 Abstract The problem of determining necessary and sufficient conditions for a set of real numbers to be the
Factoring Quadratic Expressions
Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
Linear and quadratic Taylor polynomials for functions of several variables.
ams/econ 11b supplementary notes ucsc Linear quadratic Taylor polynomials for functions of several variables. c 010, Yonatan Katznelson Finding the extreme (minimum or maximum) values of a function, is
Høgskolen i Narvik Sivilingeniørutdanningen
Høgskolen i Narvik Sivilingeniørutdanningen Eksamen i Faget STE66 ELASTISITETSTEORI Klasse: 4.ID Dato: 7.0.009 Tid: Kl. 09.00 1.00 Tillatte hjelpemidler under eksamen: Kalkulator Kopi av Boken Mechanics
BEGINNING ALGEBRA ACKNOWLEDMENTS
BEGINNING ALGEBRA The Nursing Department of Labouré College requested the Department of Academic Planning and Support Services to help with mathematics preparatory materials for its Bachelor of Science
FACTORING ax 2 bx c. Factoring Trinomials with Leading Coefficient 1
5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
Adding vectors We can do arithmetic with vectors. We ll start with vector addition and related operations. Suppose you have two vectors
1 Chapter 13. VECTORS IN THREE DIMENSIONAL SPACE Let s begin with some names and notation for things: R is the set (collection) of real numbers. We write x R to mean that x is a real number. A real number
Solutions for Review Problems
olutions for Review Problems 1. Let be the triangle with vertices A (,, ), B (4,, 1) and C (,, 1). (a) Find the cosine of the angle BAC at vertex A. (b) Find the area of the triangle ABC. (c) Find a vector
Rotation Matrices and Homogeneous Transformations
Rotation Matrices and Homogeneous Transformations A coordinate frame in an n-dimensional space is defined by n mutually orthogonal unit vectors. In particular, for a two-dimensional (2D) space, i.e., n
On the mathematical theory of splitting and Russian roulette
On the mathematical theory of splitting and Russian roulette techniques St.Petersburg State University, Russia 1. Introduction Splitting is an universal and potentially very powerful technique for increasing
UNIT I: RANDOM VARIABLES PART- A -TWO MARKS
UNIT I: RANDOM VARIABLES PART- A -TWO MARKS 1. Given the probability density function of a continuous random variable X as follows f(x) = 6x (1-x) 0
Mechanical Properties - Stresses & Strains
Mechanical Properties - Stresses & Strains Types of Deformation : Elasic Plastic Anelastic Elastic deformation is defined as instantaneous recoverable deformation Hooke's law : For tensile loading, σ =
EXIT TIME PROBLEMS AND ESCAPE FROM A POTENTIAL WELL
EXIT TIME PROBLEMS AND ESCAPE FROM A POTENTIAL WELL Exit Time problems and Escape from a Potential Well Escape From a Potential Well There are many systems in physics, chemistry and biology that exist
Envelope Theorem. Kevin Wainwright. Mar 22, 2004
Envelope Theorem Kevin Wainwright Mar 22, 2004 1 Maximum Value Functions A maximum (or minimum) value function is an objective function where the choice variables have been assigned their optimal values.
RAJALAKSHMI ENGINEERING COLLEGE MA 2161 UNIT I - ORDINARY DIFFERENTIAL EQUATIONS PART A
RAJALAKSHMI ENGINEERING COLLEGE MA 26 UNIT I - ORDINARY DIFFERENTIAL EQUATIONS. Solve (D 2 + D 2)y = 0. 2. Solve (D 2 + 6D + 9)y = 0. PART A 3. Solve (D 4 + 4)x = 0 where D = d dt 4. Find Particular Integral:
LECTURE 4. Last time: Lecture outline
LECTURE 4 Last time: Types of convergence Weak Law of Large Numbers Strong Law of Large Numbers Asymptotic Equipartition Property Lecture outline Stochastic processes Markov chains Entropy rate Random
Two Topics in Parametric Integration Applied to Stochastic Simulation in Industrial Engineering
Two Topics in Parametric Integration Applied to Stochastic Simulation in Industrial Engineering Department of Industrial Engineering and Management Sciences Northwestern University September 15th, 2014
Section 1. Finding Common Terms
Worksheet 2.1 Factors of Algebraic Expressions Section 1 Finding Common Terms In worksheet 1.2 we talked about factors of whole numbers. Remember, if a b = ab then a is a factor of ab and b is a factor
Math 53 Worksheet Solutions- Minmax and Lagrange
Math 5 Worksheet Solutions- Minmax and Lagrange. Find the local maximum and minimum values as well as the saddle point(s) of the function f(x, y) = e y (y x ). Solution. First we calculate the partial
Line and surface integrals: Solutions
hapter 5 Line and surface integrals: olutions Example 5.1 Find the work done by the force F(x, y) x 2 i xyj in moving a particle along the curve which runs from (1, ) to (, 1) along the unit circle and
Factoring Polynomials
UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
THE DYING FIBONACCI TREE. 1. Introduction. Consider a tree with two types of nodes, say A and B, and the following properties:
THE DYING FIBONACCI TREE BERNHARD GITTENBERGER 1. Introduction Consider a tree with two types of nodes, say A and B, and the following properties: 1. Let the root be of type A.. Each node of type A produces
1. First-order Ordinary Differential Equations
Advanced Engineering Mathematics 1. First-order ODEs 1 1. First-order Ordinary Differential Equations 1.1 Basic concept and ideas 1.2 Geometrical meaning of direction fields 1.3 Separable differential
Notes on metric spaces
Notes on metric spaces 1 Introduction The purpose of these notes is to quickly review some of the basic concepts from Real Analysis, Metric Spaces and some related results that will be used in this course.
Portfolio Distribution Modelling and Computation. Harry Zheng Department of Mathematics Imperial College h.zheng@imperial.ac.uk
Portfolio Distribution Modelling and Computation Harry Zheng Department of Mathematics Imperial College h.zheng@imperial.ac.uk Workshop on Fast Financial Algorithms Tanaka Business School Imperial College
Modern Optimization Methods for Big Data Problems MATH11146 The University of Edinburgh
Modern Optimization Methods for Big Data Problems MATH11146 The University of Edinburgh Peter Richtárik Week 3 Randomized Coordinate Descent With Arbitrary Sampling January 27, 2016 1 / 30 The Problem
Stochastic Gene Expression in Prokaryotes: A Point Process Approach
Stochastic Gene Expression in Prokaryotes: A Point Process Approach Emanuele LEONCINI INRIA Rocquencourt - INRA Jouy-en-Josas ASMDA Mataró June 28 th 2013 Emanuele LEONCINI (INRIA) Stochastic Gene Expression
tegrals as General & Particular Solutions
tegrals as General & Particular Solutions dy dx = f(x) General Solution: y(x) = f(x) dx + C Particular Solution: dy dx = f(x), y(x 0) = y 0 Examples: 1) dy dx = (x 2)2 ;y(2) = 1; 2) dy ;y(0) = 0; 3) dx
Two-Stage Stochastic Linear Programs
Two-Stage Stochastic Linear Programs Operations Research Anthony Papavasiliou 1 / 27 Two-Stage Stochastic Linear Programs 1 Short Reviews Probability Spaces and Random Variables Convex Analysis 2 Deterministic
Markov Chains And Existtime Stabilization
50 15. MARKOV CHAINS: DEFINITIONS AND EXAMPLES Along with the discussion of martingales, we have introduced the concept of a discrete-time stochastic process. In this chapter we will study a particular
Laminar to Turbulent Transition in Cylindrical Pipes
Course I: Fluid Mechanics & Energy Conversion Laminar to Turbulent Transition in Cylindrical Pipes By, Sai Sandeep Tallam IIT Roorkee Mentors: Dr- Ing. Buelent Unsal Ms. Mina Nishi Indo German Winter Academy
Optimal order placement in a limit order book. Adrien de Larrard and Xin Guo. Laboratoire de Probabilités, Univ Paris VI & UC Berkeley
Optimal order placement in a limit order book Laboratoire de Probabilités, Univ Paris VI & UC Berkeley Outline 1 Background: Algorithm trading in different time scales 2 Some note on optimal execution
Machine Learning and Pattern Recognition Logistic Regression
Machine Learning and Pattern Recognition Logistic Regression Course Lecturer:Amos J Storkey Institute for Adaptive and Neural Computation School of Informatics University of Edinburgh Crichton Street,
ECE 842 Report Implementation of Elliptic Curve Cryptography
ECE 842 Report Implementation of Elliptic Curve Cryptography Wei-Yang Lin December 15, 2004 Abstract The aim of this report is to illustrate the issues in implementing a practical elliptic curve cryptographic
On closed-form solutions to a class of ordinary differential equations
International Journal of Advanced Mathematical Sciences, 2 (1 (2014 57-70 c Science Publishing Corporation www.sciencepubco.com/index.php/ijams doi: 10.14419/ijams.v2i1.1556 Research Paper On closed-form
Sect 6.1 - Greatest Common Factor and Factoring by Grouping
Sect 6.1 - Greatest Common Factor and Factoring by Grouping Our goal in this chapter is to solve non-linear equations by breaking them down into a series of linear equations that we can solve. To do this,
Differential Operators and their Adjoint Operators
Differential Operators and their Adjoint Operators Differential Operators inear functions from E n to E m may be described, once bases have been selected in both spaces ordinarily one uses the standard
A Uniform Asymptotic Estimate for Discounted Aggregate Claims with Subexponential Tails
12th International Congress on Insurance: Mathematics and Economics July 16-18, 2008 A Uniform Asymptotic Estimate for Discounted Aggregate Claims with Subexponential Tails XUEMIAO HAO (Based on a joint
How To Solve A Sequential Mca Problem
Monte Carlo-based statistical methods (MASM11/FMS091) Jimmy Olsson Centre for Mathematical Sciences Lund University, Sweden Lecture 6 Sequential Monte Carlo methods II February 3, 2012 Changes in HA1 Problem
Factoring Flow Chart
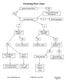Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Elliptical copulae. Dorota Kurowicka, Jolanta Misiewicz, Roger Cooke
Elliptical copulae Dorota Kurowicka, Jolanta Misiewicz, Roger Cooke Abstract: In this paper we construct a copula, that is, a distribution with uniform marginals. This copula is continuous and can realize
The two dimensional heat equation
The two dimensional heat equation Ryan C. Trinity University Partial Differential Equations March 6, 2012 Physical motivation Consider a thin rectangular plate made of some thermally conductive material.
The Effects of Cycling on Drug Resistance HIV
The Effects of Cycling on Drug Resistance HIV Aaron Abromowitz 1, Andre Robinson 2 Walter Chambliss 3, Emmanuel J. Morales-Butler 4, Anuj Mubayi 5, Xiaohong Wang 5, Abdessemad Tridane 5 1 Department of
Probability Generating Functions
page 39 Chapter 3 Probability Generating Functions 3 Preamble: Generating Functions Generating functions are widely used in mathematics, and play an important role in probability theory Consider a sequence
Homework set 4 - Solutions
Homework set 4 - Solutions Math 495 Renato Feres Problems R for continuous time Markov chains The sequence of random variables of a Markov chain may represent the states of a random system recorded at
Vector and Matrix Norms
Chapter 1 Vector and Matrix Norms 11 Vector Spaces Let F be a field (such as the real numbers, R, or complex numbers, C) with elements called scalars A Vector Space, V, over the field F is a non-empty
15. Symmetric polynomials
15. Symmetric polynomials 15.1 The theorem 15.2 First examples 15.3 A variant: discriminants 1. The theorem Let S n be the group of permutations of {1,, n}, also called the symmetric group on n things.
Factoring - Grouping
6.2 Factoring - Grouping Objective: Factor polynomials with four terms using grouping. The first thing we will always do when factoring is try to factor out a GCF. This GCF is often a monomial like in
VERTICES OF GIVEN DEGREE IN SERIES-PARALLEL GRAPHS
VERTICES OF GIVEN DEGREE IN SERIES-PARALLEL GRAPHS MICHAEL DRMOTA, OMER GIMENEZ, AND MARC NOY Abstract. We show that the number of vertices of a given degree k in several kinds of series-parallel labelled
National Sun Yat-Sen University CSE Course: Information Theory. Gambling And Entropy
Gambling And Entropy 1 Outline There is a strong relationship between the growth rate of investment in a horse race and the entropy of the horse race. The value of side information is related to the mutual
x o R n a π(a, x o ) A R n π(a, x o ) π(a, x o ) A R n a a x o x o x n X R n δ(x n, x o ) d(a, x n ) d(, ) δ(, ) R n x n X d(a, x n ) δ(x n, x o ) a = a A π(a, xo ) a a A = X = R π(a, x o ) = (x o + ρ)
10 Evolutionarily Stable Strategies
10 Evolutionarily Stable Strategies There is but a step between the sublime and the ridiculous. Leo Tolstoy In 1973 the biologist John Maynard Smith and the mathematician G. R. Price wrote an article in
Vector and Tensor Algebra (including Column and Matrix Notation)
Vector and Tensor Algebra (including Column and Matrix Notation) 2 Vectors and tensors In mechanics and other fields of physics, quantities are represented by vectors and tensors. Essential manipulations
Estimating the Degree of Activity of jumps in High Frequency Financial Data. joint with Yacine Aït-Sahalia
Estimating the Degree of Activity of jumps in High Frequency Financial Data joint with Yacine Aït-Sahalia Aim and setting An underlying process X = (X t ) t 0, observed at equally spaced discrete times
1 3 4 = 8i + 20j 13k. x + w. y + w
) Find the point of intersection of the lines x = t +, y = 3t + 4, z = 4t + 5, and x = 6s + 3, y = 5s +, z = 4s + 9, and then find the plane containing these two lines. Solution. Solve the system of equations
Tutorial: Stochastic Modeling in Biology Applications of Discrete- Time Markov Chains. NIMBioS Knoxville, Tennessee March 16-18, 2011
Tutorial: Stochastic Modeling in Biology Applications of Discrete- Time Markov Chains Linda J. S. Allen Texas Tech University Lubbock, Texas U.S.A. NIMBioS Knoxville, Tennessee March 16-18, 2011 OUTLINE
3. Regression & Exponential Smoothing
3. Regression & Exponential Smoothing 3.1 Forecasting a Single Time Series Two main approaches are traditionally used to model a single time series z 1, z 2,..., z n 1. Models the observation z t as a
Stochastic Gene Expression in Prokaryotes: A Point Process Approach
Stochastic Gene Expression in Prokaryotes: A Point Process Approach Emanuele LEONCINI INRIA Rocquencourt - INRA Jouy-en-Josas Mathematical Modeling in Cell Biology March 27 th 2013 Emanuele LEONCINI (INRIA)
Lectures on Stochastic Processes. William G. Faris
Lectures on Stochastic Processes William G. Faris November 8, 2001 2 Contents 1 Random walk 7 1.1 Symmetric simple random walk................... 7 1.2 Simple random walk......................... 9 1.3
Joint Exam 1/P Sample Exam 1
Joint Exam 1/P Sample Exam 1 Take this practice exam under strict exam conditions: Set a timer for 3 hours; Do not stop the timer for restroom breaks; Do not look at your notes. If you believe a question
1 Completeness of a Set of Eigenfunctions. Lecturer: Naoki Saito Scribe: Alexander Sheynis/Allen Xue. May 3, 2007. 1.1 The Neumann Boundary Condition
MAT 280: Laplacian Eigenfunctions: Theory, Applications, and Computations Lecture 11: Laplacian Eigenvalue Problems for General Domains III. Completeness of a Set of Eigenfunctions and the Justification
Generating Random Numbers Variance Reduction Quasi-Monte Carlo. Simulation Methods. Leonid Kogan. MIT, Sloan. 15.450, Fall 2010
Simulation Methods Leonid Kogan MIT, Sloan 15.450, Fall 2010 c Leonid Kogan ( MIT, Sloan ) Simulation Methods 15.450, Fall 2010 1 / 35 Outline 1 Generating Random Numbers 2 Variance Reduction 3 Quasi-Monte
6 Scalar, Stochastic, Discrete Dynamic Systems
47 6 Scalar, Stochastic, Discrete Dynamic Systems Consider modeling a population of sand-hill cranes in year n by the first-order, deterministic recurrence equation y(n + 1) = Ry(n) where R = 1 + r = 1
27.3. Introduction. Prerequisites. Learning Outcomes
olume Integrals 27. Introduction In the previous two sections, surface integrals (or double integrals) were introduced i.e. functions were integrated with respect to one variable and then with respect
BRANCHING RANDOM WALKS AND MULTI-TYPE CONTACT-PROCESSES ON THE PERCOLATION CLUSTER OF Z d
BRANCHING RANDOM WALKS AND MULTI-TYPE CONTACT-PROCESSES ON THE PERCOLATION CLUSTER OF Z d DANIELA BERTACCHI AND FABIO ZUCCA Abstract. In this paper we prove that under the assumption of quasi-transitivity,
M/M/1 and M/M/m Queueing Systems
M/M/ and M/M/m Queueing Systems M. Veeraraghavan; March 20, 2004. Preliminaries. Kendall s notation: G/G/n/k queue G: General - can be any distribution. First letter: Arrival process; M: memoryless - exponential
NONASSOCIATIVE ALGEBRAS SATISFYING IDENTITIES OF DEGREE THREE(i)
NONASSOCIATIVE ALGEBRAS SATISFYING IDENTITIES OF DEGREE THREE(i) BY FRANK ROSIER AND J. MARSHALL OSBORN A number of different authors have studied classes of nonassociative algebras or rings satisfying
Lecture 8 - Turbulence. Applied Computational Fluid Dynamics
Lecture 8 - Turbulence Applied Computational Fluid Dynamics Instructor: André Bakker http://www.bakker.org André Bakker (2002-2006) Fluent Inc. (2002) 1 Turbulence What is turbulence? Effect of turbulence
Linear algebra and the geometry of quadratic equations. Similarity transformations and orthogonal matrices
MATH 30 Differential Equations Spring 006 Linear algebra and the geometry of quadratic equations Similarity transformations and orthogonal matrices First, some things to recall from linear algebra Two
1.4. Removing Brackets. Introduction. Prerequisites. Learning Outcomes. Learning Style
Removing Brackets 1. Introduction In order to simplify an expression which contains brackets it is often necessary to rewrite the expression in an equivalent form but without any brackets. This process
Monte Carlo-based statistical methods (MASM11/FMS091)
Monte Carlo-based statistical methods (MASM11/FMS091) Magnus Wiktorsson Centre for Mathematical Sciences Lund University, Sweden Lecture 6 Sequential Monte Carlo methods II February 7, 2014 M. Wiktorsson
MATH PROBLEMS, WITH SOLUTIONS
MATH PROBLEMS, WITH SOLUTIONS OVIDIU MUNTEANU These are free online notes that I wrote to assist students that wish to test their math skills with some problems that go beyond the usual curriculum. These
Biology 1406 - Notes for exam 5 - Population genetics Ch 13, 14, 15
Biology 1406 - Notes for exam 5 - Population genetics Ch 13, 14, 15 Species - group of individuals that are capable of interbreeding and producing fertile offspring; genetically similar 13.7, 14.2 Population
SOME PROPERTIES OF SYMBOL ALGEBRAS OF DEGREE THREE
SOME PROPERTIES OF SYMBOL ALGEBRAS OF DEGREE THREE CRISTINA FLAUT and DIANA SAVIN Communicated by the former editorial board In this paper, we study some properties of the matrix representations of the
LESSON 3.5 WORKBOOK. How do cancer cells evolve? Workbook Lesson 3.5
LESSON 3.5 WORKBOOK How do cancer cells evolve? In this unit we have learned how normal cells can be transformed so that they stop behaving as part of a tissue community and become unresponsive to regulation.
3. Let A and B be two n n orthogonal matrices. Then prove that AB and BA are both orthogonal matrices. Prove a similar result for unitary matrices.
Exercise 1 1. Let A be an n n orthogonal matrix. Then prove that (a) the rows of A form an orthonormal basis of R n. (b) the columns of A form an orthonormal basis of R n. (c) for any two vectors x,y R
UNIFORM ASYMPTOTICS FOR DISCOUNTED AGGREGATE CLAIMS IN DEPENDENT RISK MODELS
Applied Probability Trust 2 October 2013 UNIFORM ASYMPTOTICS FOR DISCOUNTED AGGREGATE CLAIMS IN DEPENDENT RISK MODELS YANG YANG, Nanjing Audit University, and Southeast University KAIYONG WANG, Southeast
Bayesian coalescent inference of population size history
Bayesian coalescent inference of population size history Alexei Drummond University of Auckland Workshop on Population and Speciation Genomics, 2016 1st February 2016 1 / 39 BEAST tutorials Population
Lecture 11: 0-1 Quadratic Program and Lower Bounds
Lecture : - Quadratic Program and Lower Bounds (3 units) Outline Problem formulations Reformulation: Linearization & continuous relaxation Branch & Bound Method framework Simple bounds, LP bound and semidefinite
BANACH AND HILBERT SPACE REVIEW
BANACH AND HILBET SPACE EVIEW CHISTOPHE HEIL These notes will briefly review some basic concepts related to the theory of Banach and Hilbert spaces. We are not trying to give a complete development, but
Department of Mathematics, Indian Institute of Technology, Kharagpur Assignment 2-3, Probability and Statistics, March 2015. Due:-March 25, 2015.
Department of Mathematics, Indian Institute of Technology, Kharagpur Assignment -3, Probability and Statistics, March 05. Due:-March 5, 05.. Show that the function 0 for x < x+ F (x) = 4 for x < for x
Monte Carlo and Empirical Methods for Stochastic Inference (MASM11/FMS091)
Monte Carlo and Empirical Methods for Stochastic Inference (MASM11/FMS091) Magnus Wiktorsson Centre for Mathematical Sciences Lund University, Sweden Lecture 5 Sequential Monte Carlo methods I February
Introduction to Topology
Introduction to Topology Tomoo Matsumura November 30, 2010 Contents 1 Topological spaces 3 1.1 Basis of a Topology......................................... 3 1.2 Comparing Topologies.......................................
Mathematical Methods of Engineering Analysis
Mathematical Methods of Engineering Analysis Erhan Çinlar Robert J. Vanderbei February 2, 2000 Contents Sets and Functions 1 1 Sets................................... 1 Subsets.............................
Structure Preserving Model Reduction for Logistic Networks
Structure Preserving Model Reduction for Logistic Networks Fabian Wirth Institute of Mathematics University of Würzburg Workshop on Stochastic Models of Manufacturing Systems Einhoven, June 24 25, 2010.
FastTest. You ve read the book... ... now test yourself
FastTest You ve read the book...... now test yourself To ensure you have learned the key points that will improve your patient care, read the authors questions below. Please refer back to relevant sections
Hedging Options In The Incomplete Market With Stochastic Volatility. Rituparna Sen Sunday, Nov 15
Hedging Options In The Incomplete Market With Stochastic Volatility Rituparna Sen Sunday, Nov 15 1. Motivation This is a pure jump model and hence avoids the theoretical drawbacks of continuous path models.
Why discuss CLL? Common: 40% of US leukaemia. approx 100 pa in SJH / MWHB 3 inpatients in SJH at any time
Why discuss CLL? Common: 40% of US leukaemia approx 100 pa in SJH / MWHB 3 inpatients in SJH at any time Median age of dx is 65 (30s. Incurable, survival 2-202 20 years Require ongoing supportive care
discuss how to describe points, lines and planes in 3 space.
Chapter 2 3 Space: lines and planes In this chapter we discuss how to describe points, lines and planes in 3 space. introduce the language of vectors. discuss various matters concerning the relative position
CM2202: Scientific Computing and Multimedia Applications General Maths: 2. Algebra - Factorisation
CM2202: Scientific Computing and Multimedia Applications General Maths: 2. Algebra - Factorisation Prof. David Marshall School of Computer Science & Informatics Factorisation Factorisation is a way of
Student name: Earlham College. Fall 2011 December 15, 2011
Student name: Earlham College MATH 320: Differential Equations Final exam - In class part Fall 2011 December 15, 2011 Instructions: This is a regular closed-book test, and is to be taken without the use