Fundamentals of Electromagnetic Fields and Waves: I
|
|
|
- Jack Fox
- 10 years ago
- Views:
Transcription
1 Fundamentals of Electromagnetic Fields and Waves: I Fall 2007, EE 30348, Electrical Engineering, University of Notre Dame Mid Term II: Solutions Please show your steps clearly and sketch figures wherever necessary. Points will be awarded for correct steps shown in the solutions. Necessary formulae and values of constants are given in the end of this document. There are THREE problems in this exam. Answer all. Problem 1 (4 Points) Answer the following short questions (1 point each): (a) Which three parameters describe the behavior of electric and magnetic fields and the propagation of electromagnetic waves inside material medium? Solution: The three parameters are the electrical conductivity (σ), the relative dielectric constant (ɛ r ), and the relative magnetic permeability (µ r ). (b) Of the three material parameters in part (a), only one leads to energy (or power) loss when an EM wave propagates. Which one? Why? Solution: The electrical conductivity σ is the only parameter that contributes to energy (or power) loss. Energy can be stored and retrieved from the parts that go into the electric and magnetic dipoles (via ɛ r and µ r ), but not from the conduction current I 2 R loss since this energy is converted to mechanical vibrations or heat, which is not an electromagnetic wave. (c) In order to gather information about outer space, why is it necessary to send out satellites and space telescopes outside the earth s atmosphere? Solution: Since the earth s atmosphere contains various gases with varying degrees of conductivity (for example the ionosphere is very conductive), weak signals in the form of EM waves from outer space get attenuated strongly by the time they reach the earth s surface. To prevent this from happening, satellites and space telescopes are sent out of the atmosphere where they can collect much stronger signals and beam them back to the earth. (d) What is the only property of an EM wave that does not change when it crosses from one medium to another? Find the change in the wavelength when an EM wave that had λ = 500 nm in air enters water with ɛ r 81 and µ r = 1. Solution: The frequency f = ω/2π of an EM wave remains constant when it crosses from one material medium to another. For an EM wave in any medium, f = v/λ is constant, where v is 1
2 the speed of the wave and λ is the wavelength. Also, in a material medium, v = c/ ɛ r µ r, where c = m/s is the speed of light in vacuum. Therefore the wavelength in water is λ water = ( v water )λ air = = 500/9 56nm. (1) c 81 Problem 2 (6 Points) An infinitely long straight wire is carrying a current given by I(t) = I 0 cos ωt. A small conducting loop of area S = S ˆn and resistance R 0 placed at a very large distance ρ 0 from the wire. Find (a) The current flowing through this loop as a function of the angle θ the normal to the surface ˆn makes with the axis of the infinite wire, and Solution: The magnetic field due to the infinite wire at the location of the small loop is given by B = µ 0I 0 cos ωt a φ (2) If the surface vector ˆn of the small loop makes an angle θ with the axis of the wire which is along a z, then a φ ˆn = sin θ. In that case, the total magnetic flux passing through the small loop is given by φ m = and the emf generated in the loop is then given by s B ds B S cos θ = µ 0I 0 S cos ωt sin θ, (3) V (t) = dφ m dt = ωµ 0I 0 S sin ωt sin θ, (4) and since the resistance of the loop is R 0, the current that flows through it is I(t) = V (t) R 0 = ωµ 0I 0 S sin ωt R 0 sin θ. (5) We can check that the units do work out to Amps. (b) The power (in Watts) picked up by the loop as a function of the angle. Can we connect the small loop to light up a bulb (in principle)? At what angle θ will the bulb glow the brightest if it does? Solution: The power generated in the loop at any time t is given by I(t)V (t) = I(t) 2 R 0 = V (t) 2 /R 0 in Watts. Clearly, this is given by power(t) = [ ωµ 0I 0 S sin ωt sin θ] 2 2 R 0. (6)
3 This is clearly ac power, and just like ordinary light bulbs that run on Hz ac power, sure, it will light up. The loop has to be aligned in a way to maximize the magnetic flux crossing it for obtaining the highest power. This is achieved when the θ = π/2, or the surface is perpendicular to the magnetic flux lines. Problem 3 (10 Points) An electromagnetic plane wave moves from air (ɛ r1, µ r1 ) into a wafer of silicon (ɛ r2, µ r2 ) at normal incidence (Poynting vector along the interface normal), as shown in Figure 1. E i, H i, and P i as shown in the figure stand for the electric field, magnetic field intensity, and the Poynting vector of the incident EM wave respectively. The incident electric and magnetic field vectors are parallel to the Silicon-air interface, as shown. Just like for any wave incident on a material medium, a part of it will be transmitted and part of it will be reflected. As shown in the figure, the subscript t stands for the transmitted components, and r stands for the reflected components. Answer the following questions - P t Silicon Air z x y E t E i H t P i H i Er z = 0 H r P r Figure 1: An electromagnetic plane wave moving from air into a silicon wafer. (a) Call the wave impedance of air as η 1. Find the wave impedance η 2 in Silicon. (0.5 Point) Solution: η 1 = η 0 µr1 ɛ r1, and η 2 = η 0 µr2 ɛ r2, where η 0 377Ω is the wave impedance of vacuum. (b) The Poynting vector indicates the direction of wave propagation, as well as the movement of energy. Clearly, the reflected wave carries part of the energy back towards z (shown in Fig 1). Using this fact, and assuming that the reflected electric field points in the direction indicated, find the direction of the magnetic field of the reflected wave. (0.5 Point) Solution: P r is in the z direction, and E r is along +x. Since P r = E r H r, H r has to point in the y direction by the right hand rule. (c) Now that all directions of the vectors are fixed, lets find the relationships between the fields in air and in Silicon. We can write the incident electric field in the phasor notation as Ê i = E mi e jβz a x where E mi is the amplitude of the incident electric field. Assume that there are no charges or currents on the surface of Silicon, and that the wafer is insulating. Using boundary conditions for the total electric field, find a relation between E mi, E mt, and E mr. Call this equation (1). (2 Points) 3
4 Solution: Since the tangential component of the electric field is continuous across the air-silicon interface, the relation is E mi + E mr = E mt. (7) (d) We know that the amplitudes of H and E are related by the wave impedance of the material medium. Write the incident magnetic field amplitude H mi in terms of E mi, H mt in terms of E mt, and H mr in terms of E mr. Make sure you keep track of the directions of the vectors before writing the scalar equation. (2 Points) Solution: Since the magnetic field intensity and the electric field of an EM wave are related by the local wave impedance, H mi = E mi /η 1, H mr = E mr /η 1, and H mt = E mt /η 2. (e) Using boundary conditions for the total magnetic field intensity, find a new relation between E mi, E mt, and E mr from part (d). Call this equation (2). (2 Points) Solution: Since the tangential component of the magnetic field intensity is also continuous, we have E mi η 1 E mr η 1 = E mt η 2. (8) Note that the negative sign is to keep track of the direction of the reflected component of the magnetic field intensity. (f) Use Equations (1) and (2) from above to find the ratios T = E mt /E mi and R = E mr /E mi in terms of the impedances of air (η 1 ) and Silicon (η 2 ). Explain why T and R are related to the transmitted and reflected parts of the EM wave. What values do they take when η 1 = η 2? What does this signify? (3 Points) Solution: Solving Eqs (7 & 8) above, we have and T = 2η 2 η 1 + η 2, (9) R = η 2 η 1 η 1 + η 2. (10) Since T is the ratio of the amplitudes of the electric fields of the transmitted and the incident waves, it represents the part of the EM wave that is transmitted, and similarly, since R is the ratio of the reflected EM wave amplitude and the incident amplitude, it represents the part that is reflected. When η 1 = η 2, clearly T = 1 and R = 0, meaning that the EM wave is transmitted entirely (no reflection) if there is no impedance mismatch at the interface. This can only happen if there is no mismatch in the material properties (ɛ r, µ r ) across the interface, i.e., we have the same material on both sides. End 4
5 Formulae A) Fundamental constants Permittivity of vacuum: ɛ π 10 9 F/m, Permeability of vacuum: µ 0 = 4π 10 7 H/m. Speed of light in free space: c = 1/ ɛ 0 µ m/s. Speed of light in non-conductive media: v = c/ ɛ r µ r. B) Maxwell s Equations: [Integral Form], [Differential Form] Gauss s Law for Electric Fields : [ s D ds = v ρ vdv = Q encl ], [ D = ρ v ] Gauss s Law for Magnetic Fields : [ s B ds = 0], [ B = 0] Faraday s Law : [ c E dl = d dt ( db s B ds)], [ E = dt ] Ampere s Law : [ c H dl = s J ds + d dt ( s D ds)], [ H = J + dd dt ] Charge continuity equation: J + ρv t = 0. In all of the above, D = ɛ 0 ɛ r E and B = µ 0 µ r H, where ɛ r is the relative dielectric constant and µ r is the relative permeability of the material medium. C) Wave propagation characteristics in material medium The conduction current density that adds to Ampere s law above is given by J c = σe, where σ is the conductivity of the material medium. In addition to Maxwell s equations above in (B), the boundary conditions are - For electric fields, n (D 1 D 2 ) = ρ s, and n (E 1 E 2 ) = 0. For magnetic fields, n (B 1 B 2 ) = 0 and n (H 1 H 2 ) = J s. In a generic material medium characterized by the parameters (ɛ r, µ r, σ), the phasor notation of the electric field component of an EM wave moving in the +z direction can be written as Ê = E ˆ m e ˆγz, where ˆγ = α + jβ, α = ω µɛ µɛ 2 [ 1 + ( σ ωɛ )2 1] 1/2, β = ω 2 [ 1 + ( σ ωɛ )2 + 1] 1/2, and the corresponding Ĥ is related to the electric field component by the complex impedance Ĥ = Ê/ˆη, where ˆη = µ µ (ɛ j σ ɛ ) = ɛ e j 1 [1+( σ ωɛ )2 ] 1/4 2 tan 1 ( σ ωɛ ). The skin depth of a conductive medium is δ = 1/α. The total power stored in the electric field is 1 v 2 ɛ E 2 dv and in the magnetic field is 1 v 2 µ H 2 dv. Power is transported by an EM wave, and the Poynting vector is defined as P = E H. The time-averaged power transported by an EM wave propagating in the +z direction is given by P av = E ˆ m 2 2η 0 a z in vacuum or air, and by P av = E ˆ m 2 2ˆη e 2αz cos θa z, where θ = 1 2 tan 1 ( σ ωɛ ) in a conductive medium. D) Line, Surface, and Volume vector differential elements Rectangular: (Unit Vectors: a x, a x, a x ) dl = dxa x + dya y + dza z, ds x = dydza x, ds y = dxdza y, ds z = dxdya z, dv = dxdydz. 5
6 Cylindrical: (Unit Vectors: a ρ, a φ, a z ) dl = dρa ρ + ρdφdya φ + dza z, ds ρ = ρdφdza ρ, ds φ = dρdza φ, ds z = ρdρdφa z, dv = ρdρdφdz. Spherical: (Unit Vectors: a r, a θ, a φ ) dl = dra r + rdθa θ + r sin θdφa φ, ds r = r 2 sin θdθdφa r, ds θ = r sin θdrdφa θ, ds φ = rdrdθa φ, dv = r 2 sin θdrdθdφ. E) div, grad, & curl expressions in various coordinate systems Use the metric coefficients from the Table below. For a vector field A = A 1 a 1 + A 2 a 2 + A 3 a 3, grad Φ = Φ = 1 h 1 Φ u 1 a h 1 Φ u 2 a h 3 Φ u 3 a 3, div A = 1 h 1 h 2 h 3 [ (A 1h 2 h 3 ) u 1 + (A 2h 1 h 3 ) u 2 + (A 3h 1 h 2 ) u 3 ], and a 1 a 2 a 3 h 2 h 3 h 1 h 3 h 1 h 2 curl(a) = u 1 u 2 u 3 h 1 A 1 h 2 A 2 h 3 A. 3 Cartesian Cylindrical Spherical Independent Variables (u 1, u 2, u 3 ) x, y, x ρ, φ, z r, θ, φ Vector components (A 1, A 2, A 3 ) A x, A y, A z A ρ, A φ, A z A r, A θ, A φ Unit Vectors (a 1, a 2, a 3 ) a x, a x, a x a ρ, a φ, a z a r, a θ, a φ Metric Coefficients (h 1, h 2, h 3 ) 1, 1, 1 1, ρ, 1 1, r, r sin θ 6
Antenna A mean for radiating and receiving radio waves Transitional structure between free-space and a guiding device. Application: Radiation
 Antenna A mean for radiating and receiving radio waves Transitional structure between free-space and a guiding device Application: adiation Introduction An antenna is designed to radiate or receive electromagnetic
Antenna A mean for radiating and receiving radio waves Transitional structure between free-space and a guiding device Application: adiation Introduction An antenna is designed to radiate or receive electromagnetic
arxiv:1111.4354v2 [physics.acc-ph] 27 Oct 2014
![arxiv:1111.4354v2 [physics.acc-ph] 27 Oct 2014 arxiv:1111.4354v2 [physics.acc-ph] 27 Oct 2014](/thumbs/39/19151390.jpg) Theory of Electromagnetic Fields Andrzej Wolski University of Liverpool, and the Cockcroft Institute, UK arxiv:1111.4354v2 [physics.acc-ph] 27 Oct 2014 Abstract We discuss the theory of electromagnetic
Theory of Electromagnetic Fields Andrzej Wolski University of Liverpool, and the Cockcroft Institute, UK arxiv:1111.4354v2 [physics.acc-ph] 27 Oct 2014 Abstract We discuss the theory of electromagnetic
Examples of Uniform EM Plane Waves
 Examples of Uniform EM Plane Waves Outline Reminder of Wave Equation Reminder of Relation Between E & H Energy Transported by EM Waves (Poynting Vector) Examples of Energy Transport by EM Waves 1 Coupling
Examples of Uniform EM Plane Waves Outline Reminder of Wave Equation Reminder of Relation Between E & H Energy Transported by EM Waves (Poynting Vector) Examples of Energy Transport by EM Waves 1 Coupling
Physics 6C, Summer 2006 Homework 2 Solutions
 Physics 6C, Summer 006 Homework Solutions All problems are from the nd edition of Walker. Numerical values are different for each student. Chapter 3 Problems. Figure 3-30 below shows a circuit containing
Physics 6C, Summer 006 Homework Solutions All problems are from the nd edition of Walker. Numerical values are different for each student. Chapter 3 Problems. Figure 3-30 below shows a circuit containing
An equivalent circuit of a loop antenna.
 3.2.1. Circuit Modeling: Loop Impedance A loop antenna can be represented by a lumped circuit when its dimension is small with respect to a wavelength. In this representation, the circuit parameters (generally
3.2.1. Circuit Modeling: Loop Impedance A loop antenna can be represented by a lumped circuit when its dimension is small with respect to a wavelength. In this representation, the circuit parameters (generally
PHY114 S11 Term Exam 3
 PHY4 S Term Exam S. G. Rajeev Mar 2 20 2:0 pm to :45 pm PLEASE write your workshop number and your workshop leader s name at the top of your book, so that you can collect your graded exams at the workshop.
PHY4 S Term Exam S. G. Rajeev Mar 2 20 2:0 pm to :45 pm PLEASE write your workshop number and your workshop leader s name at the top of your book, so that you can collect your graded exams at the workshop.
Electromagnetism Laws and Equations
 Electromagnetism Laws and Equations Andrew McHutchon Michaelmas 203 Contents Electrostatics. Electric E- and D-fields............................................. Electrostatic Force............................................2
Electromagnetism Laws and Equations Andrew McHutchon Michaelmas 203 Contents Electrostatics. Electric E- and D-fields............................................. Electrostatic Force............................................2
Physics 25 Exam 3 November 3, 2009
 1. A long, straight wire carries a current I. If the magnetic field at a distance d from the wire has magnitude B, what would be the the magnitude of the magnetic field at a distance d/3 from the wire,
1. A long, straight wire carries a current I. If the magnetic field at a distance d from the wire has magnitude B, what would be the the magnitude of the magnetic field at a distance d/3 from the wire,
Chapter 4. Electrostatic Fields in Matter
 Chapter 4. Electrostatic Fields in Matter 4.1. Polarization A neutral atom, placed in an external electric field, will experience no net force. However, even though the atom as a whole is neutral, the
Chapter 4. Electrostatic Fields in Matter 4.1. Polarization A neutral atom, placed in an external electric field, will experience no net force. However, even though the atom as a whole is neutral, the
Electromagnetic waves
 Chapter 8 lectromagnetic waves David Morin, [email protected] The waves we ve dealt with so far in this book have been fairly easy to visualize. Waves involving springs/masses, strings, and air
Chapter 8 lectromagnetic waves David Morin, [email protected] The waves we ve dealt with so far in this book have been fairly easy to visualize. Waves involving springs/masses, strings, and air
6 J - vector electric current density (A/m2 )
 Determination of Antenna Radiation Fields Using Potential Functions Sources of Antenna Radiation Fields 6 J - vector electric current density (A/m2 ) M - vector magnetic current density (V/m 2 ) Some problems
Determination of Antenna Radiation Fields Using Potential Functions Sources of Antenna Radiation Fields 6 J - vector electric current density (A/m2 ) M - vector magnetic current density (V/m 2 ) Some problems
Physics 202 Problems - Week 8 Worked Problems Chapter 25: 7, 23, 36, 62, 72
 Physics 202 Problems - Week 8 Worked Problems Chapter 25: 7, 23, 36, 62, 72 Problem 25.7) A light beam traveling in the negative z direction has a magnetic field B = (2.32 10 9 T )ˆx + ( 4.02 10 9 T )ŷ
Physics 202 Problems - Week 8 Worked Problems Chapter 25: 7, 23, 36, 62, 72 Problem 25.7) A light beam traveling in the negative z direction has a magnetic field B = (2.32 10 9 T )ˆx + ( 4.02 10 9 T )ŷ
Electromagnetism - Lecture 2. Electric Fields
 Electromagnetism - Lecture 2 Electric Fields Review of Vector Calculus Differential form of Gauss s Law Poisson s and Laplace s Equations Solutions of Poisson s Equation Methods of Calculating Electric
Electromagnetism - Lecture 2 Electric Fields Review of Vector Calculus Differential form of Gauss s Law Poisson s and Laplace s Equations Solutions of Poisson s Equation Methods of Calculating Electric
A wave lab inside a coaxial cable
 INSTITUTE OF PHYSICS PUBLISHING Eur. J. Phys. 25 (2004) 581 591 EUROPEAN JOURNAL OF PHYSICS PII: S0143-0807(04)76273-X A wave lab inside a coaxial cable JoãoMSerra,MiguelCBrito,JMaiaAlves and A M Vallera
INSTITUTE OF PHYSICS PUBLISHING Eur. J. Phys. 25 (2004) 581 591 EUROPEAN JOURNAL OF PHYSICS PII: S0143-0807(04)76273-X A wave lab inside a coaxial cable JoãoMSerra,MiguelCBrito,JMaiaAlves and A M Vallera
Edmund Li. Where is defined as the mutual inductance between and and has the SI units of Henries (H).
 INDUCTANCE MUTUAL INDUCTANCE If we consider two neighbouring closed loops and with bounding surfaces respectively then a current through will create a magnetic field which will link with as the flux passes
INDUCTANCE MUTUAL INDUCTANCE If we consider two neighbouring closed loops and with bounding surfaces respectively then a current through will create a magnetic field which will link with as the flux passes
Physics 235 Chapter 1. Chapter 1 Matrices, Vectors, and Vector Calculus
 Chapter 1 Matrices, Vectors, and Vector Calculus In this chapter, we will focus on the mathematical tools required for the course. The main concepts that will be covered are: Coordinate transformations
Chapter 1 Matrices, Vectors, and Vector Calculus In this chapter, we will focus on the mathematical tools required for the course. The main concepts that will be covered are: Coordinate transformations
Amplification of the Radiation from Two Collocated Cellular System Antennas by the Ground Wave of an AM Broadcast Station
 Amplification of the Radiation from Two Collocated Cellular System Antennas by the Ground Wave of an AM Broadcast Station Dr. Bill P. Curry EMSciTek Consulting Co., W101 McCarron Road Glen Ellyn, IL 60137,
Amplification of the Radiation from Two Collocated Cellular System Antennas by the Ground Wave of an AM Broadcast Station Dr. Bill P. Curry EMSciTek Consulting Co., W101 McCarron Road Glen Ellyn, IL 60137,
Code number given on the right hand side of the question paper should be written on the title page of the answerbook by the candidate.
 Series ONS SET-1 Roll No. Candiates must write code on the title page of the answer book Please check that this question paper contains 16 printed pages. Code number given on the right hand side of the
Series ONS SET-1 Roll No. Candiates must write code on the title page of the answer book Please check that this question paper contains 16 printed pages. Code number given on the right hand side of the
104 Practice Exam 2-3/21/02
 104 Practice Exam 2-3/21/02 1. Two electrons are located in a region of space where the magnetic field is zero. Electron A is at rest; and electron B is moving westward with a constant velocity. A non-zero
104 Practice Exam 2-3/21/02 1. Two electrons are located in a region of space where the magnetic field is zero. Electron A is at rest; and electron B is moving westward with a constant velocity. A non-zero
Vector surface area Differentials in an OCS
 Calculus and Coordinate systems EE 311 - Lecture 17 1. Calculus and coordinate systems 2. Cartesian system 3. Cylindrical system 4. Spherical system In electromagnetics, we will often need to perform integrals
Calculus and Coordinate systems EE 311 - Lecture 17 1. Calculus and coordinate systems 2. Cartesian system 3. Cylindrical system 4. Spherical system In electromagnetics, we will often need to perform integrals
Antennas. Antennas are transducers that transfer electromagnetic energy between a transmission line and free space. Electromagnetic Wave
 Antennas Transmitter I Transmitting Antenna Transmission Line Electromagnetic Wave I Receiver I Receiving Antenna Transmission Line Electromagnetic Wave I Antennas are transducers that transfer electromagnetic
Antennas Transmitter I Transmitting Antenna Transmission Line Electromagnetic Wave I Receiver I Receiving Antenna Transmission Line Electromagnetic Wave I Antennas are transducers that transfer electromagnetic
PHYS 222 Spring 2012 Final Exam. Closed books, notes, etc. No electronic device except a calculator.
 PHYS 222 Spring 2012 Final Exam Closed books, notes, etc. No electronic device except a calculator. NAME: (all questions with equal weight) 1. If the distance between two point charges is tripled, the
PHYS 222 Spring 2012 Final Exam Closed books, notes, etc. No electronic device except a calculator. NAME: (all questions with equal weight) 1. If the distance between two point charges is tripled, the
physics 112N magnetic fields and forces
 physics 112N magnetic fields and forces bar magnet & iron filings physics 112N 2 bar magnets physics 112N 3 the Earth s magnetic field physics 112N 4 electro -magnetism! is there a connection between electricity
physics 112N magnetic fields and forces bar magnet & iron filings physics 112N 2 bar magnets physics 112N 3 the Earth s magnetic field physics 112N 4 electro -magnetism! is there a connection between electricity
potential in the centre of the sphere with respect to infinity.
 Umeå Universitet, Fysik 1 Vitaly Bychkov Prov i fysik, Electricity and Waves, 2006-09-27, kl 16.00-22.00 Hjälpmedel: Students can use any book. Define the notations you are using properly. Present your
Umeå Universitet, Fysik 1 Vitaly Bychkov Prov i fysik, Electricity and Waves, 2006-09-27, kl 16.00-22.00 Hjälpmedel: Students can use any book. Define the notations you are using properly. Present your
The performance improvement by ferrite loading means - increasing, - increasing of ratio, implicitly related to the input impedance.
 3.2.3. Ferrite Loading Magnetic ferrite loading can enhance a transmitting signal as high as 2 to 10 db for MHz [Devore and Bohley, 1977]. There is an optimum frequency range where ferrite loading is beneficial.
3.2.3. Ferrite Loading Magnetic ferrite loading can enhance a transmitting signal as high as 2 to 10 db for MHz [Devore and Bohley, 1977]. There is an optimum frequency range where ferrite loading is beneficial.
Chapter 22: Electric Flux and Gauss s Law
 22.1 ntroduction We have seen in chapter 21 that determining the electric field of a continuous charge distribution can become very complicated for some charge distributions. t would be desirable if we
22.1 ntroduction We have seen in chapter 21 that determining the electric field of a continuous charge distribution can become very complicated for some charge distributions. t would be desirable if we
Solution Derivations for Capa #11
 Solution Derivations for Capa #11 Caution: The symbol E is used interchangeably for energy and EMF. 1) DATA: V b = 5.0 V, = 155 Ω, L = 8.400 10 2 H. In the diagram above, what is the voltage across the
Solution Derivations for Capa #11 Caution: The symbol E is used interchangeably for energy and EMF. 1) DATA: V b = 5.0 V, = 155 Ω, L = 8.400 10 2 H. In the diagram above, what is the voltage across the
Antenna Properties and their impact on Wireless System Performance. Dr. Steven R. Best. Cushcraft Corporation 48 Perimeter Road Manchester, NH 03013
 Antenna Properties and their impact on Wireless System Performance Dr. Steven R. Best Cushcraft Corporation 48 Perimeter Road Manchester, NH 03013 Phone (603) 627-7877 FAX: (603) 627-1764 Email: [email protected]
Antenna Properties and their impact on Wireless System Performance Dr. Steven R. Best Cushcraft Corporation 48 Perimeter Road Manchester, NH 03013 Phone (603) 627-7877 FAX: (603) 627-1764 Email: [email protected]
CHAPTER - 1. Chapter ONE: WAVES CHAPTER - 2. Chapter TWO: RAY OPTICS AND OPTICAL INSTRUMENTS. CHAPTER - 3 Chapter THREE: WAVE OPTICS PERIODS PERIODS
 BOARD OF INTERMEDIATE EDUCATION, A.P., HYDERABAD REVISION OF SYLLABUS Subject PHYSICS-II (w.e.f 2013-14) Chapter ONE: WAVES CHAPTER - 1 1.1 INTRODUCTION 1.2 Transverse and longitudinal waves 1.3 Displacement
BOARD OF INTERMEDIATE EDUCATION, A.P., HYDERABAD REVISION OF SYLLABUS Subject PHYSICS-II (w.e.f 2013-14) Chapter ONE: WAVES CHAPTER - 1 1.1 INTRODUCTION 1.2 Transverse and longitudinal waves 1.3 Displacement
45. The peak value of an alternating current in a 1500-W device is 5.4 A. What is the rms voltage across?
 PHYS Practice Problems hapters 8- hapter 8. 45. The peak value of an alternating current in a 5-W device is 5.4 A. What is the rms voltage across? The power and current can be used to find the peak voltage,
PHYS Practice Problems hapters 8- hapter 8. 45. The peak value of an alternating current in a 5-W device is 5.4 A. What is the rms voltage across? The power and current can be used to find the peak voltage,
Consideration of a high-capacity foil cable:
 Consideration of a high-capacity foil cable: Newly discovered ancient knowledge. The old RF-developers already knew the benefits of longplanar lines and have been used (electronic) Eonen (times) thin flat
Consideration of a high-capacity foil cable: Newly discovered ancient knowledge. The old RF-developers already knew the benefits of longplanar lines and have been used (electronic) Eonen (times) thin flat
Interference. Physics 102 Workshop #3. General Instructions
 Interference Physics 102 Workshop #3 Name: Lab Partner(s): Instructor: Time of Workshop: General Instructions Workshop exercises are to be carried out in groups of three. One report per group is due by
Interference Physics 102 Workshop #3 Name: Lab Partner(s): Instructor: Time of Workshop: General Instructions Workshop exercises are to be carried out in groups of three. One report per group is due by
Problem 1 (25 points)
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Physics 8.02 Spring 2012 Exam Three Solutions Problem 1 (25 points) Question 1 (5 points) Consider two circular rings of radius R, each perpendicular
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Physics 8.02 Spring 2012 Exam Three Solutions Problem 1 (25 points) Question 1 (5 points) Consider two circular rings of radius R, each perpendicular
Magnetic Field of a Circular Coil Lab 12
 HB 11-26-07 Magnetic Field of a Circular Coil Lab 12 1 Magnetic Field of a Circular Coil Lab 12 Equipment- coil apparatus, BK Precision 2120B oscilloscope, Fluke multimeter, Wavetek FG3C function generator,
HB 11-26-07 Magnetic Field of a Circular Coil Lab 12 1 Magnetic Field of a Circular Coil Lab 12 Equipment- coil apparatus, BK Precision 2120B oscilloscope, Fluke multimeter, Wavetek FG3C function generator,
JUST THE MATHS UNIT NUMBER 8.5. VECTORS 5 (Vector equations of straight lines) A.J.Hobson
 JUST THE MATHS UNIT NUMBER 8.5 VECTORS 5 (Vector equations of straight lines) by A.J.Hobson 8.5.1 Introduction 8.5. The straight line passing through a given point and parallel to a given vector 8.5.3
JUST THE MATHS UNIT NUMBER 8.5 VECTORS 5 (Vector equations of straight lines) by A.J.Hobson 8.5.1 Introduction 8.5. The straight line passing through a given point and parallel to a given vector 8.5.3
Chapter 33. The Magnetic Field
 Chapter 33. The Magnetic Field Digital information is stored on a hard disk as microscopic patches of magnetism. Just what is magnetism? How are magnetic fields created? What are their properties? These
Chapter 33. The Magnetic Field Digital information is stored on a hard disk as microscopic patches of magnetism. Just what is magnetism? How are magnetic fields created? What are their properties? These
5. Measurement of a magnetic field
 H 5. Measurement of a magnetic field 5.1 Introduction Magnetic fields play an important role in physics and engineering. In this experiment, three different methods are examined for the measurement of
H 5. Measurement of a magnetic field 5.1 Introduction Magnetic fields play an important role in physics and engineering. In this experiment, three different methods are examined for the measurement of
How To Understand And Understand The Theory Of Electricity
 DIRECT CURRENT AND ALTERNATING CURRENT SYSTEMS N. Rajkumar, Research Fellow, Energy Systems Group, City University Northampton Square, London EC1V 0HB, UK Keywords: Electrical energy, direct current, alternating
DIRECT CURRENT AND ALTERNATING CURRENT SYSTEMS N. Rajkumar, Research Fellow, Energy Systems Group, City University Northampton Square, London EC1V 0HB, UK Keywords: Electrical energy, direct current, alternating
Physics 210 Q1 2012 ( PHYSICS210BRIDGE ) My Courses Course Settings
 1 of 11 9/7/2012 1:06 PM Logged in as Julie Alexander, Instructor Help Log Out Physics 210 Q1 2012 ( PHYSICS210BRIDGE ) My Courses Course Settings Course Home Assignments Roster Gradebook Item Library
1 of 11 9/7/2012 1:06 PM Logged in as Julie Alexander, Instructor Help Log Out Physics 210 Q1 2012 ( PHYSICS210BRIDGE ) My Courses Course Settings Course Home Assignments Roster Gradebook Item Library
Eðlisfræði 2, vor 2007
 [ Assignment View ] [ Pri Eðlisfræði 2, vor 2007 28. Sources of Magnetic Field Assignment is due at 2:00am on Wednesday, March 7, 2007 Credit for problems submitted late will decrease to 0% after the deadline
[ Assignment View ] [ Pri Eðlisfræði 2, vor 2007 28. Sources of Magnetic Field Assignment is due at 2:00am on Wednesday, March 7, 2007 Credit for problems submitted late will decrease to 0% after the deadline
Analysis of Electromagnetic Propulsion on a Two-Electric-Dipole System
 Electronics and Communications in Japan, Part 2, Vol. 83, No. 4, 2000 Translated from Denshi Joho Tsushin Gakkai Ronbunshi, Vol. J82-C-I, No. 6, June 1999, pp. 310 317 Analysis of Electromagnetic Propulsion
Electronics and Communications in Japan, Part 2, Vol. 83, No. 4, 2000 Translated from Denshi Joho Tsushin Gakkai Ronbunshi, Vol. J82-C-I, No. 6, June 1999, pp. 310 317 Analysis of Electromagnetic Propulsion
DEGREE: Bachelor's Degree in Industrial Electronics and Automation COURSE: 1º TERM: 2º WEEKLY PLANNING
 SESSION WEEK COURSE: Physics II DEGREE: Bachelor's Degree in Industrial Electronics and Automation COURSE: 1º TERM: 2º WEEKLY PLANNING DESCRIPTION GROUPS (mark ) Indicate YES/NO If the session needs 2
SESSION WEEK COURSE: Physics II DEGREE: Bachelor's Degree in Industrial Electronics and Automation COURSE: 1º TERM: 2º WEEKLY PLANNING DESCRIPTION GROUPS (mark ) Indicate YES/NO If the session needs 2
Induced voltages and Inductance Faraday s Law
 Induced voltages and Inductance Faraday s Law concept #1, 4, 5, 8, 13 Problem # 1, 3, 4, 5, 6, 9, 10, 13, 15, 24, 23, 25, 31, 32a, 34, 37, 41, 43, 51, 61 Last chapter we saw that a current produces a magnetic
Induced voltages and Inductance Faraday s Law concept #1, 4, 5, 8, 13 Problem # 1, 3, 4, 5, 6, 9, 10, 13, 15, 24, 23, 25, 31, 32a, 34, 37, 41, 43, 51, 61 Last chapter we saw that a current produces a magnetic
SCHWEITZER ENGINEERING LABORATORIES, COMERCIAL LTDA.
 Pocket book of Electrical Engineering Formulas Content 1. Elementary Algebra and Geometry 1. Fundamental Properties (real numbers) 1 2. Exponents 2 3. Fractional Exponents 2 4. Irrational Exponents 2 5.
Pocket book of Electrical Engineering Formulas Content 1. Elementary Algebra and Geometry 1. Fundamental Properties (real numbers) 1 2. Exponents 2 3. Fractional Exponents 2 4. Irrational Exponents 2 5.
Mode Patterns of Parallel plates &Rectangular wave guides Mr.K.Chandrashekhar, Dr.Girish V Attimarad
 International Journal of Scientific & Engineering Research Volume 3, Issue 8, August-2012 1 Mode Patterns of Parallel plates &Rectangular wave guides Mr.K.Chandrashekhar, Dr.Girish V Attimarad Abstract-Parallel
International Journal of Scientific & Engineering Research Volume 3, Issue 8, August-2012 1 Mode Patterns of Parallel plates &Rectangular wave guides Mr.K.Chandrashekhar, Dr.Girish V Attimarad Abstract-Parallel
Faraday s Law of Induction
 Chapter 10 Faraday s Law of Induction 10.1 Faraday s Law of Induction...10-10.1.1 Magnetic Flux...10-3 10.1. Lenz s Law...10-5 10. Motional EMF...10-7 10.3 Induced Electric Field...10-10 10.4 Generators...10-1
Chapter 10 Faraday s Law of Induction 10.1 Faraday s Law of Induction...10-10.1.1 Magnetic Flux...10-3 10.1. Lenz s Law...10-5 10. Motional EMF...10-7 10.3 Induced Electric Field...10-10 10.4 Generators...10-1
Polarization of Light
 Polarization of Light References Halliday/Resnick/Walker Fundamentals of Physics, Chapter 33, 7 th ed. Wiley 005 PASCO EX997A and EX999 guide sheets (written by Ann Hanks) weight Exercises and weights
Polarization of Light References Halliday/Resnick/Walker Fundamentals of Physics, Chapter 33, 7 th ed. Wiley 005 PASCO EX997A and EX999 guide sheets (written by Ann Hanks) weight Exercises and weights
FURTHER VECTORS (MEI)
 Mathematics Revision Guides Further Vectors (MEI) (column notation) Page of MK HOME TUITION Mathematics Revision Guides Level: AS / A Level - MEI OCR MEI: C FURTHER VECTORS (MEI) Version : Date: -9-7 Mathematics
Mathematics Revision Guides Further Vectors (MEI) (column notation) Page of MK HOME TUITION Mathematics Revision Guides Level: AS / A Level - MEI OCR MEI: C FURTHER VECTORS (MEI) Version : Date: -9-7 Mathematics
Experimental results for the focal waveform and beam width in the focusing lens with a 100 ps filter
 EM Implosion Memos Memo 51 July, 2010 Experimental results for the focal waveform and beam width in the focusing lens with a 100 ps filter Prashanth Kumar, Carl E. Baum, Serhat Altunc, Christos G. Christodoulou
EM Implosion Memos Memo 51 July, 2010 Experimental results for the focal waveform and beam width in the focusing lens with a 100 ps filter Prashanth Kumar, Carl E. Baum, Serhat Altunc, Christos G. Christodoulou
Teaching Electromagnetic Field Theory Using Differential Forms
 IEEE TRANSACTIONS ON EDUCATION, VOL. 40, NO. 1, FEBRUARY 1997 53 Teaching Electromagnetic Field Theory Using Differential Forms Karl F. Warnick, Richard H. Selfridge, Member, IEEE, and David V. Arnold
IEEE TRANSACTIONS ON EDUCATION, VOL. 40, NO. 1, FEBRUARY 1997 53 Teaching Electromagnetic Field Theory Using Differential Forms Karl F. Warnick, Richard H. Selfridge, Member, IEEE, and David V. Arnold
Selected Radio Frequency Exposure Limits
 ENVIRONMENT, SAFETY & HEALTH DIVISION Chapter 50: Non-ionizing Radiation Selected Radio Frequency Exposure Limits Product ID: 94 Revision ID: 1736 Date published: 30 June 2015 Date effective: 30 June 2015
ENVIRONMENT, SAFETY & HEALTH DIVISION Chapter 50: Non-ionizing Radiation Selected Radio Frequency Exposure Limits Product ID: 94 Revision ID: 1736 Date published: 30 June 2015 Date effective: 30 June 2015
GPR Polarization Simulation with 3D HO FDTD
 Progress In Electromagnetics Research Symposium Proceedings, Xi an, China, March 6, 00 999 GPR Polarization Simulation with 3D HO FDTD Jing Li, Zhao-Fa Zeng,, Ling Huang, and Fengshan Liu College of Geoexploration
Progress In Electromagnetics Research Symposium Proceedings, Xi an, China, March 6, 00 999 GPR Polarization Simulation with 3D HO FDTD Jing Li, Zhao-Fa Zeng,, Ling Huang, and Fengshan Liu College of Geoexploration
Grounding Demystified
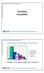 Grounding Demystified 3-1 Importance Of Grounding Techniques 45 40 35 30 25 20 15 10 5 0 Grounding 42% Case 22% Cable 18% Percent Used Filter 12% PCB 6% Grounding 42% Case Shield 22% Cable Shielding 18%
Grounding Demystified 3-1 Importance Of Grounding Techniques 45 40 35 30 25 20 15 10 5 0 Grounding 42% Case 22% Cable 18% Percent Used Filter 12% PCB 6% Grounding 42% Case Shield 22% Cable Shielding 18%
PHYSICAL QUANTITIES AND UNITS
 1 PHYSICAL QUANTITIES AND UNITS Introduction Physics is the study of matter, its motion and the interaction between matter. Physics involves analysis of physical quantities, the interaction between them
1 PHYSICAL QUANTITIES AND UNITS Introduction Physics is the study of matter, its motion and the interaction between matter. Physics involves analysis of physical quantities, the interaction between them
Frequency-dependent underground cable model for electromagnetic transient simulation
 Frequency-dependent underground cable model for electromagnetic transient simulation Vasco José Realista Medeiros Soeiro Abstract A computation method for transients in a three-phase underground power-transmission
Frequency-dependent underground cable model for electromagnetic transient simulation Vasco José Realista Medeiros Soeiro Abstract A computation method for transients in a three-phase underground power-transmission
ElectroMagnetic Induction. AP Physics B
 ElectroMagnetic Induction AP Physics B What is E/M Induction? Electromagnetic Induction is the process of using magnetic fields to produce voltage, and in a complete circuit, a current. Michael Faraday
ElectroMagnetic Induction AP Physics B What is E/M Induction? Electromagnetic Induction is the process of using magnetic fields to produce voltage, and in a complete circuit, a current. Michael Faraday
Physics 9e/Cutnell. correlated to the. College Board AP Physics 1 Course Objectives
 Physics 9e/Cutnell correlated to the College Board AP Physics 1 Course Objectives Big Idea 1: Objects and systems have properties such as mass and charge. Systems may have internal structure. Enduring
Physics 9e/Cutnell correlated to the College Board AP Physics 1 Course Objectives Big Idea 1: Objects and systems have properties such as mass and charge. Systems may have internal structure. Enduring
( )( 10!12 ( 0.01) 2 2 = 624 ( ) Exam 1 Solutions. Phy 2049 Fall 2011
 Phy 49 Fall 11 Solutions 1. Three charges form an equilateral triangle of side length d = 1 cm. The top charge is q = - 4 μc, while the bottom two are q1 = q = +1 μc. What is the magnitude of the net force
Phy 49 Fall 11 Solutions 1. Three charges form an equilateral triangle of side length d = 1 cm. The top charge is q = - 4 μc, while the bottom two are q1 = q = +1 μc. What is the magnitude of the net force
DOING PHYSICS WITH MATLAB COMPUTATIONAL OPTICS RAYLEIGH-SOMMERFELD DIFFRACTION INTEGRAL OF THE FIRST KIND
 DOING PHYSICS WITH MATLAB COMPUTATIONAL OPTICS RAYLEIGH-SOMMERFELD DIFFRACTION INTEGRAL OF THE FIRST KIND THE THREE-DIMENSIONAL DISTRIBUTION OF THE RADIANT FLUX DENSITY AT THE FOCUS OF A CONVERGENCE BEAM
DOING PHYSICS WITH MATLAB COMPUTATIONAL OPTICS RAYLEIGH-SOMMERFELD DIFFRACTION INTEGRAL OF THE FIRST KIND THE THREE-DIMENSIONAL DISTRIBUTION OF THE RADIANT FLUX DENSITY AT THE FOCUS OF A CONVERGENCE BEAM
Practice Final Math 122 Spring 12 Instructor: Jeff Lang
 Practice Final Math Spring Instructor: Jeff Lang. Find the limit of the sequence a n = ln (n 5) ln (3n + 8). A) ln ( ) 3 B) ln C) ln ( ) 3 D) does not exist. Find the limit of the sequence a n = (ln n)6
Practice Final Math Spring Instructor: Jeff Lang. Find the limit of the sequence a n = ln (n 5) ln (3n + 8). A) ln ( ) 3 B) ln C) ln ( ) 3 D) does not exist. Find the limit of the sequence a n = (ln n)6
 CHAPTER TEN Shielding This chapter addresses the concept of shielding of electronic circuits. The term shield usually refers to a metallic enclosure that completely encloses an electronic product or a
CHAPTER TEN Shielding This chapter addresses the concept of shielding of electronic circuits. The term shield usually refers to a metallic enclosure that completely encloses an electronic product or a
COLLATED QUESTIONS: ELECTROMAGNETIC RADIATION
 COLLATED QUESTIONS: ELECTROMAGNETIC RADIATION 2011(2): WAVES Doppler radar can determine the speed and direction of a moving car. Pulses of extremely high frequency radio waves are sent out in a narrow
COLLATED QUESTIONS: ELECTROMAGNETIC RADIATION 2011(2): WAVES Doppler radar can determine the speed and direction of a moving car. Pulses of extremely high frequency radio waves are sent out in a narrow
Electromagnetic (EM) waves. Electric and Magnetic Fields. L 30 Electricity and Magnetism [7] James Clerk Maxwell (1831-1879)
![Electromagnetic (EM) waves. Electric and Magnetic Fields. L 30 Electricity and Magnetism [7] James Clerk Maxwell (1831-1879) Electromagnetic (EM) waves. Electric and Magnetic Fields. L 30 Electricity and Magnetism [7] James Clerk Maxwell (1831-1879)](/thumbs/40/20813653.jpg) L 30 Electricity and Magnetism [7] ELECTROMAGNETIC WAVES Faraday laid the groundwork with his discovery of electromagnetic induction Maxwell added the last piece of the puzzle Heinrich Hertz made the experimental
L 30 Electricity and Magnetism [7] ELECTROMAGNETIC WAVES Faraday laid the groundwork with his discovery of electromagnetic induction Maxwell added the last piece of the puzzle Heinrich Hertz made the experimental
Proposal for a Slot Pair Array Having an Invariant Main Beam Direction with a Cosecant Radiation Pattern Using a Post-Wall Waveguide
 176 IEICE TRANS. ELECTRON., VOL.E86 C, NO.2 FEBRUARY 2003 PAPER Special Issue on Circuit and Device Technology for High-Speed Wireless Communication Proposal for a Slot Pair Array Having an Invariant Main
176 IEICE TRANS. ELECTRON., VOL.E86 C, NO.2 FEBRUARY 2003 PAPER Special Issue on Circuit and Device Technology for High-Speed Wireless Communication Proposal for a Slot Pair Array Having an Invariant Main
Human Exposure to Outdoor PLC System
 1602 PIERS Proceedings, Marrakesh, MOROCCO, March 20 23, 2011 Human Exposure to Outdoor PLC System Vicko Doric 1, Dragan Poljak 1, and Khalil El Khamlichi Drissi 2 1 University of Split, Croatia 2 Blaise
1602 PIERS Proceedings, Marrakesh, MOROCCO, March 20 23, 2011 Human Exposure to Outdoor PLC System Vicko Doric 1, Dragan Poljak 1, and Khalil El Khamlichi Drissi 2 1 University of Split, Croatia 2 Blaise
i( t) L i( t) 56mH 1.1A t = τ ln 1 = ln 1 ln 1 6.67ms
 Exam III PHY 49 Summer C July 16, 8 1. In the circuit shown, L = 56 mh, R = 4.6 Ω an V = 1. V. The switch S has been open for a long time then is suenly close at t =. At what value of t (in msec) will
Exam III PHY 49 Summer C July 16, 8 1. In the circuit shown, L = 56 mh, R = 4.6 Ω an V = 1. V. The switch S has been open for a long time then is suenly close at t =. At what value of t (in msec) will
Review of Vector Analysis in Cartesian Coordinates
 R. evicky, CBE 6333 Review of Vector Analysis in Cartesian Coordinates Scalar: A quantity that has magnitude, but no direction. Examples are mass, temperature, pressure, time, distance, and real numbers.
R. evicky, CBE 6333 Review of Vector Analysis in Cartesian Coordinates Scalar: A quantity that has magnitude, but no direction. Examples are mass, temperature, pressure, time, distance, and real numbers.
1) Define the term 'Mobility' of charge carriers in a conductor. Write its S.I. unit.
 1 1) Define the term 'Mobility' of charge carriers in a conductor. Write its S.I. unit. SOL: Mobility: Mobility of a charge carrier is defined as the drift velocity of the charge carrier per unit electric
1 1) Define the term 'Mobility' of charge carriers in a conductor. Write its S.I. unit. SOL: Mobility: Mobility of a charge carrier is defined as the drift velocity of the charge carrier per unit electric
Name Class. Date Section. Test Form A Chapter 11. Chapter 11 Test Bank 155
 Chapter Test Bank 55 Test Form A Chapter Name Class Date Section. Find a unit vector in the direction of v if v is the vector from P,, 3 to Q,, 0. (a) 3i 3j 3k (b) i j k 3 i 3 j 3 k 3 i 3 j 3 k. Calculate
Chapter Test Bank 55 Test Form A Chapter Name Class Date Section. Find a unit vector in the direction of v if v is the vector from P,, 3 to Q,, 0. (a) 3i 3j 3k (b) i j k 3 i 3 j 3 k 3 i 3 j 3 k. Calculate
PHY3128 / PHYM203 (Electronics / Instrumentation) Transmission Lines. Repeated n times I L
 Transmission Lines Introduction A transmission line guides energy from one place to another. Optical fibres, waveguides, telephone lines and power cables are all electromagnetic transmission lines. are
Transmission Lines Introduction A transmission line guides energy from one place to another. Optical fibres, waveguides, telephone lines and power cables are all electromagnetic transmission lines. are
v = fλ PROGRESSIVE WAVES 1 Candidates should be able to :
 PROGRESSIVE WAVES 1 Candidates should be able to : Describe and distinguish between progressive longitudinal and transverse waves. With the exception of electromagnetic waves, which do not need a material
PROGRESSIVE WAVES 1 Candidates should be able to : Describe and distinguish between progressive longitudinal and transverse waves. With the exception of electromagnetic waves, which do not need a material
Power measurement in balanced 3 phase circuits and power factor improvement. 1 Power in Single Phase Circuits. Experiment no 1
 Experiment no 1 Power measurement in balanced 3 phase circuits and power factor improvement 1 Power in Single Phase Circuits Let v = m cos(ωt) = cos(ωt) is the voltage applied to a R-L circuit and i =
Experiment no 1 Power measurement in balanced 3 phase circuits and power factor improvement 1 Power in Single Phase Circuits Let v = m cos(ωt) = cos(ωt) is the voltage applied to a R-L circuit and i =
E/M Experiment: Electrons in a Magnetic Field.
 E/M Experiment: Electrons in a Magnetic Field. PRE-LAB You will be doing this experiment before we cover the relevant material in class. But there are only two fundamental concepts that you need to understand.
E/M Experiment: Electrons in a Magnetic Field. PRE-LAB You will be doing this experiment before we cover the relevant material in class. But there are only two fundamental concepts that you need to understand.
AB2.5: Surfaces and Surface Integrals. Divergence Theorem of Gauss
 AB2.5: urfaces and urface Integrals. Divergence heorem of Gauss epresentations of surfaces or epresentation of a surface as projections on the xy- and xz-planes, etc. are For example, z = f(x, y), x =
AB2.5: urfaces and urface Integrals. Divergence heorem of Gauss epresentations of surfaces or epresentation of a surface as projections on the xy- and xz-planes, etc. are For example, z = f(x, y), x =
EEE1001/PHY1002. Magnetic Circuits. The circuit is of length l=2πr. B andφ circulate
 1 Magnetic Circuits Just as we view electric circuits as related to the flow of charge, we can also view magnetic flux flowing around a magnetic circuit. The sum of fluxes entering a point must sum to
1 Magnetic Circuits Just as we view electric circuits as related to the flow of charge, we can also view magnetic flux flowing around a magnetic circuit. The sum of fluxes entering a point must sum to
EE301 Lesson 14 Reading: 10.1-10.4, 10.11-10.12, 11.1-11.4 and 11.11-11.13
 CAPACITORS AND INDUCTORS Learning Objectives EE301 Lesson 14 a. Define capacitance and state its symbol and unit of measurement. b. Predict the capacitance of a parallel plate capacitor. c. Analyze how
CAPACITORS AND INDUCTORS Learning Objectives EE301 Lesson 14 a. Define capacitance and state its symbol and unit of measurement. b. Predict the capacitance of a parallel plate capacitor. c. Analyze how
Circuits with inductors and alternating currents. Chapter 20 #45, 46, 47, 49
 Circuits with inductors and alternating currents Chapter 20 #45, 46, 47, 49 RL circuits Ch. 20 (last section) Symbol for inductor looks like a spring. An inductor is a circuit element that has a large
Circuits with inductors and alternating currents Chapter 20 #45, 46, 47, 49 RL circuits Ch. 20 (last section) Symbol for inductor looks like a spring. An inductor is a circuit element that has a large
Homework #11 203-1-1721 Physics 2 for Students of Mechanical Engineering
 Homework #11 203-1-1721 Physics 2 for Students of Mechanical Engineering 2. A circular coil has a 10.3 cm radius and consists of 34 closely wound turns of wire. An externally produced magnetic field of
Homework #11 203-1-1721 Physics 2 for Students of Mechanical Engineering 2. A circular coil has a 10.3 cm radius and consists of 34 closely wound turns of wire. An externally produced magnetic field of
Physical Science Study Guide Unit 7 Wave properties and behaviors, electromagnetic spectrum, Doppler Effect
 Objectives: PS-7.1 Physical Science Study Guide Unit 7 Wave properties and behaviors, electromagnetic spectrum, Doppler Effect Illustrate ways that the energy of waves is transferred by interaction with
Objectives: PS-7.1 Physical Science Study Guide Unit 7 Wave properties and behaviors, electromagnetic spectrum, Doppler Effect Illustrate ways that the energy of waves is transferred by interaction with
This makes sense. t 2 1 + 1/t 2 dt = 1. t t 2 + 1dt = 2 du = 1 3 u3/2 u=5
 1. (Line integrals Using parametrization. Two types and the flux integral) Formulas: ds = x (t) dt, d x = x (t)dt and d x = T ds since T = x (t)/ x (t). Another one is Nds = T ds ẑ = (dx, dy) ẑ = (dy,
1. (Line integrals Using parametrization. Two types and the flux integral) Formulas: ds = x (t) dt, d x = x (t)dt and d x = T ds since T = x (t)/ x (t). Another one is Nds = T ds ẑ = (dx, dy) ẑ = (dy,
Physics 116. Nov 4, 2011. Session 22 Review: ray optics. R. J. Wilkes Email: [email protected]
 Physics 116 Session 22 Review: ray optics Nov 4, 2011 R. J. Wilkes Email: [email protected] ! Exam 2 is Monday!! All multiple choice, similar to HW problems, same format as Exam 1!!! Announcements
Physics 116 Session 22 Review: ray optics Nov 4, 2011 R. J. Wilkes Email: [email protected] ! Exam 2 is Monday!! All multiple choice, similar to HW problems, same format as Exam 1!!! Announcements
Review Questions PHYS 2426 Exam 2
 Review Questions PHYS 2426 Exam 2 1. If 4.7 x 10 16 electrons pass a particular point in a wire every second, what is the current in the wire? A) 4.7 ma B) 7.5 A C) 2.9 A D) 7.5 ma E) 0.29 A Ans: D 2.
Review Questions PHYS 2426 Exam 2 1. If 4.7 x 10 16 electrons pass a particular point in a wire every second, what is the current in the wire? A) 4.7 ma B) 7.5 A C) 2.9 A D) 7.5 ma E) 0.29 A Ans: D 2.
PHYSICS PAPER 1 (THEORY)
 PHYSICS PAPER 1 (THEORY) (Three hours) (Candidates are allowed additional 15 minutes for only reading the paper. They must NOT start writing during this time.) ---------------------------------------------------------------------------------------------------------------------
PHYSICS PAPER 1 (THEORY) (Three hours) (Candidates are allowed additional 15 minutes for only reading the paper. They must NOT start writing during this time.) ---------------------------------------------------------------------------------------------------------------------
L 2 : x = s + 1, y = s, z = 4s + 4. 3. Suppose that C has coordinates (x, y, z). Then from the vector equality AC = BD, one has
 The line L through the points A and B is parallel to the vector AB = 3, 2, and has parametric equations x = 3t + 2, y = 2t +, z = t Therefore, the intersection point of the line with the plane should satisfy:
The line L through the points A and B is parallel to the vector AB = 3, 2, and has parametric equations x = 3t + 2, y = 2t +, z = t Therefore, the intersection point of the line with the plane should satisfy:
Chapter 27 Magnetic Field and Magnetic Forces
 Chapter 27 Magnetic Field and Magnetic Forces - Magnetism - Magnetic Field - Magnetic Field Lines and Magnetic Flux - Motion of Charged Particles in a Magnetic Field - Applications of Motion of Charged
Chapter 27 Magnetic Field and Magnetic Forces - Magnetism - Magnetic Field - Magnetic Field Lines and Magnetic Flux - Motion of Charged Particles in a Magnetic Field - Applications of Motion of Charged
Phasors. Phasors. by Prof. Dr. Osman SEVAİOĞLU Electrical and Electronics Engineering Department. ^ V cos (wt + θ) ^ V sin (wt + θ)
 V cos (wt θ) V sin (wt θ) by Prof. Dr. Osman SEVAİOĞLU Electrical and Electronics Engineering Department EE 209 Fundamentals of Electrical and Electronics Engineering, Prof. Dr. O. SEVAİOĞLU, Page 1 Vector
V cos (wt θ) V sin (wt θ) by Prof. Dr. Osman SEVAİOĞLU Electrical and Electronics Engineering Department EE 209 Fundamentals of Electrical and Electronics Engineering, Prof. Dr. O. SEVAİOĞLU, Page 1 Vector
1. The diagram below represents magnetic lines of force within a region of space.
 1. The diagram below represents magnetic lines of force within a region of space. 4. In which diagram below is the magnetic flux density at point P greatest? (1) (3) (2) (4) The magnetic field is strongest
1. The diagram below represents magnetic lines of force within a region of space. 4. In which diagram below is the magnetic flux density at point P greatest? (1) (3) (2) (4) The magnetic field is strongest
Force on a square loop of current in a uniform B-field.
 Force on a square loop of current in a uniform B-field. F top = 0 θ = 0; sinθ = 0; so F B = 0 F bottom = 0 F left = I a B (out of page) F right = I a B (into page) Assume loop is on a frictionless axis
Force on a square loop of current in a uniform B-field. F top = 0 θ = 0; sinθ = 0; so F B = 0 F bottom = 0 F left = I a B (out of page) F right = I a B (into page) Assume loop is on a frictionless axis
Lecture 5. Electric Flux and Flux Density, Gauss Law in Integral Form
 Lecture 5 Electric Flux and Flux ensity, Gauss Law in Integral Form ections: 3.1, 3., 3.3 Homework: ee homework file LECTURE 5 slide 1 Faraday s Experiment (1837), Flux charge transfer from inner to outer
Lecture 5 Electric Flux and Flux ensity, Gauss Law in Integral Form ections: 3.1, 3., 3.3 Homework: ee homework file LECTURE 5 slide 1 Faraday s Experiment (1837), Flux charge transfer from inner to outer
The waveguide adapter consists of a rectangular part smoothly transcending into an elliptical part as seen in Figure 1.
 Waveguide Adapter Introduction This is a model of an adapter for microwave propagation in the transition between a rectangular and an elliptical waveguide. Such waveguide adapters are designed to keep
Waveguide Adapter Introduction This is a model of an adapter for microwave propagation in the transition between a rectangular and an elliptical waveguide. Such waveguide adapters are designed to keep
Two primary advantages of radars: all-weather and day /night imaging
 Lecture 0 Principles of active remote sensing: Radars. Objectives: 1. Radar basics. Main types of radars.. Basic antenna parameters. Required reading: G: 8.1, p.401-40 dditional/advanced reading: Online
Lecture 0 Principles of active remote sensing: Radars. Objectives: 1. Radar basics. Main types of radars.. Basic antenna parameters. Required reading: G: 8.1, p.401-40 dditional/advanced reading: Online
Lecture 22. Inductance. Magnetic Field Energy. Outline:
 Lecture 22. Inductance. Magnetic Field Energy. Outline: Self-induction and self-inductance. Inductance of a solenoid. The energy of a magnetic field. Alternative definition of inductance. Mutual Inductance.
Lecture 22. Inductance. Magnetic Field Energy. Outline: Self-induction and self-inductance. Inductance of a solenoid. The energy of a magnetic field. Alternative definition of inductance. Mutual Inductance.
1 Basic Optics (1.2) Since. ε 0 = 8.854 10 12 C 2 N 1 m 2 and μ 0 = 4π 10 7 Ns 2 C 2 (1.3) Krishna Thyagarajan and Ajoy Ghatak. 1.
 1 1 Basic Optics Krishna Thyagarajan and Ajoy Ghatak 1.1 Introduction This chapter on optics provides the reader with the basic understanding of light rays and light waves, image formation and aberrations,
1 1 Basic Optics Krishna Thyagarajan and Ajoy Ghatak 1.1 Introduction This chapter on optics provides the reader with the basic understanding of light rays and light waves, image formation and aberrations,
Keysight Technologies Understanding the Fundamental Principles of Vector Network Analysis. Application Note
 Keysight Technologies Understanding the Fundamental Principles of Vector Network Analysis Application Note Introduction Network analysis is the process by which designers and manufacturers measure the
Keysight Technologies Understanding the Fundamental Principles of Vector Network Analysis Application Note Introduction Network analysis is the process by which designers and manufacturers measure the
Tesla Wireless Energy Transfer at CCC
 Tesla Wireless Energy Transfer at CCC Davor Jadrijević December 10, 2009 Abstract Tesla s Long Distance High-Power and High-Efficiency Wireless Energy Transfer System is still a mystery to our technology.
Tesla Wireless Energy Transfer at CCC Davor Jadrijević December 10, 2009 Abstract Tesla s Long Distance High-Power and High-Efficiency Wireless Energy Transfer System is still a mystery to our technology.
Physics 221 Experiment 5: Magnetic Fields
 Physics 221 Experiment 5: Magnetic Fields August 25, 2007 ntroduction This experiment will examine the properties of magnetic fields. Magnetic fields can be created in a variety of ways, and are also found
Physics 221 Experiment 5: Magnetic Fields August 25, 2007 ntroduction This experiment will examine the properties of magnetic fields. Magnetic fields can be created in a variety of ways, and are also found
Chapter 35 Alternating Current Circuits
 hapter 35 Alternating urrent ircuits ac-ircuits Phasor Diagrams Resistors, apacitors and nductors in ac-ircuits R ac-ircuits ac-ircuit power. Resonance Transformers ac ircuits Alternating currents and
hapter 35 Alternating urrent ircuits ac-ircuits Phasor Diagrams Resistors, apacitors and nductors in ac-ircuits R ac-ircuits ac-ircuit power. Resonance Transformers ac ircuits Alternating currents and
12. The current in an inductor is changing at the rate of 100 A/s, and the inductor emf is 40 V. What is its self-inductance?
 12. The current in an inductor is changing at the rate of 100 A/s, and the inductor emf is 40 V. What is its self-inductance? From Equation 32-5, L = -E=(dI =dt) = 40 V=(100 A/s) = 0.4 H. 15. A cardboard
12. The current in an inductor is changing at the rate of 100 A/s, and the inductor emf is 40 V. What is its self-inductance? From Equation 32-5, L = -E=(dI =dt) = 40 V=(100 A/s) = 0.4 H. 15. A cardboard
