Frequency-dependent underground cable model for electromagnetic transient simulation
|
|
|
- Anne Greer
- 10 years ago
- Views:
Transcription
1 Frequency-dependent underground cable model for electromagnetic transient simulation Vasco José Realista Medeiros Soeiro Abstract A computation method for transients in a three-phase underground power-transmission system is presented in this paper. Two methods will be used for this purpose: The first using the Fourier Transform, allowing the transient analysis in linear time-invariant systems. The second is an equivalent network with lumped parameters whose behaviour, within a given frequency band, is similar to the transmission line itself. Transient waveforms are evaluated using a software for mathematical applications, MATLAB, and in particular one of its tools, SIMULINK. The main interest in the use of a method to make a time analysis is the introduction possibility of nonlinear elements in the network. Nomenclature transmission systems, researches on the viability of the underground cable models became necessary. The magnetic field based on Maxwell s equations is calculated for the underground cable model system. The general solution for the magnetic field on the soil is developed using arbitrary boundary conditions in a cylindrical surface, at a finite depth under the plane earth/air surface. The general Polaczek solution is developed. Finally the system constitutive parameters are evaluated. Two methods for the electromagnetic transient simulation on underground cable systems are studied in this paper. The first is the Fourier Transform that will be implemented using the Fast Fourier Transform (FFT) and the Inverse Fast Fourier Transform (IFFT). The second is the equivalent network with lumped parameters. Transient regimes obtained by both methods are compared showing an excellent result accuracy. Voltage vector Current vector Impedance matrix Admittance matrix Bessel Function Bessel functions H Hankel function Radius Radius of central conductor Radius over main insulation Radius over conducting sheath Outer radius cable Angular frequency Resistivity or charge density Conductivity Permitivity Permeability Soil penetration I Introduction The social and economic development that occurred in the past years led to an urban and industrial centre growth, increasing the electrical power demand and leading to the use of relatively long cable circuits operating at high voltage. In these conditions it is expected to overcome transient overvoltages induced in the conductors of the underground system. For the stated reasons and the recent interest in underground II Magnetic field in underground powertransmission systems The problem of an infinitely long cylindrical conductor can be treated as a 2D problem which is easier to analyze. When the conductors are displayed with an axial symmetry the field also satisfies this symmetry and the solution becomes considerably easier. The calculation of the magnetic field due to an underground cable of finite radius with cylindrical boundary will be made taking into account several assumptions: 1. The earth is a semi-infinite surface where the Earth / Air is a plane. 2. The geometry is considered infinitely long in the z coordinate (axial). 3. The cable is cylindrical and it is buried at a constant depth. 4. Earth and air are considered homogeneous, the air with a permeability and earth with a permeability and conductivity. 5. The hypothesis of a quasi-static regime is considered, neglecting the capacitive effects, which for the case of the earth is an adequate approximation for frequencies up to 1 MHz. 1
2 Fa is a function to be determined by the boundary conditions of the problem. The solution is written in Fourier series: A R re (6) Considering the Bessel functions we obtain: (7) Figure 1. Underground cylindrical surface of finite radius. The formulation of the electromagnetic field in a power transmission system is based on the magnetic vector potential,, which satisfies in the frequency domain:, (1) 0, Where η represents the voltage drop per unit of axial length. Magnetic vector potential inside earth The general solution for the magnetic field in the soil is developed satisfying arbitrary boundary conditions in a cylindrical surface buried at a finite depth under a plain Earth/Air surface. It is considered a generalization of the Pollaczec solution for cylindrical underground cables with circular sheath and finite radius, taking into account the proximity of the magnetic field. The corrections for the longitudinal impedance due to the return path of the earth are determined at the expense of an approximation equivalent to the solution of Pollaczek. The solution of the field in the soil can be made by the linear combination of two linearly independent terms. The first,, to consider the boundary conditions on the earth / air surface, Sa. The second,, in turn, allows the boundary conditions to be considered on the surface. The solution can then be written in Cartesian coordinates (x, y): Where A x, y Na, ye da (2) Na, y Fae da, y 0 (3) Rea q 0 (4) Or: (8) Where is a Bessel function of the first kind of order m and argument. is a Bessel function of the second kind of order m and argument. and are the Hankel functions of the first and second kind respectively of order m and argument. For a hollow conductor, the case in study, it is used the Hankel equation of the second kind that is regular for. (9) Thus, the term A can be written in cylindrical coordinates r, φ around by:,, (10) Where is the Hankel function of the second kind and order m with argument and, 0, 1, 2, are coefficients to be determined. In order to impose boundary conditions on the surface is convenient to write 12 in Cartesian coordinates. Since the Hankel function of the second type is defined by [2]: (11) Considering the integration paths defined in [3] we obtain for the case study: Where: (12), (13) q, δ (5) µ 2
3 Thus the solution of the vector potential is:,,, 0 With:, 2 2 (14) 2 2 (15) Under certain conditions it is possible to use the Pollaczec solution where: 0,, 0 valid for 1, and 1., (24) In the surface of the conductor and taking in consideration the boundaries:, (25) Potential vector of the magnetic field in air Assuming that the solution is:, (16) Boundary conditions on the surface cable/earth Due to the geometric shape of the surface of the cable, the solution is written in cylindrical coordinates. And,, 0 (17) Where,, 0 (18) The following result in:,, 0 (19) Boundary conditions on the earth/air surface The boundary conditions are:,,, 0, 0 (20) In the earth, taking into account the earth/air and earth/conductor boundaries: (21) (22) Magnetic vector potential in the air, taking into account the two boundary conditions:, (23) Figure 2. Representation of the earth/cable surface, with indication of the cable axis and the exterior radius Given the Pollaczec approximation:, (26) Now taking into account the boundary conditions at (earth/conductor):,,,, (27) Inside the cable sheath with dielectric characteristics, being the radius shown in Figure 3:, (28) Then,, (29) 3
4 , / (30) and is the outer sheath internal impedance given from the voltage drop along the outer surface of the sheath [4]. (35) Where 0,0 (31) 1 1 0,0 and are complex current amplitudes that flow in the phase conductor and the conducting sheath of the cable. III Constitutive parameters of underground power-transmission systems The three phase underground cables can be monopolar or tripolar. The conductors are isolated and surrounded by a sheath, with mechanical and chemical protection function, connected to the earth. Each cable has two metallic conductors, one is the central conductor and the other the conductor sheath. This is the basic configuration normally used for high voltage cables. In this work it was considered monopolar cables. (36) 1 qr q With: r qr 1 qr qr (37) 1 qr 1 q r 1 q r 1 q r (40) The mutual impedance between the cable and the sheath is: (38) is the sheath mutual impedance given by [4]: q s The impedance of the conductor itself is given by: (39) (40) is the internal impedance of the inner conductor, the impedance due to the time-varying magnetic field in the inner insulation and is the inner sheath internal impedance calculated from the voltage drop on the inner surface of the sheath [4]. (41) Figure 3. Cross section of an underground cable. Longitudinal Impedance Assuming a three-phase system consisting of three equal cables: (32) J qr r q J qr 1 1 qr 2 0 q (42) r b 1 0 q r 2 1 qr be qr (43) In the calculation of the impedance for elements outside the diagonal, the provision of the different cables must be taken into account. In this case the cables are in flat configuration. The matrices of the diagonal are then: (33) The impedance of the sheath itself is then: (34) Where is the impedance related to the earth, is due to the variation of the flux in the outer insulation, Figure 4. Geometry of the system. Cables in line. 4
5 Thus the impedance between cable and is given by: (44) is the impedance between the phase conductor of cable and the phase conductor of cable. is the impedance between the sheath of cable and the sheath of cable. (45) The field outside the cable is taken into account for the calculation of. For the mutual impedance between the cable sheath and the conductor, the cable is seen as driven by a conductor running in a homogeneous soil. may be evaluated by using a closed form with appropriate Bessel and Henkel functions: q x ij q x ij, (46) In matrix form: (52) Finally resulting in the longitudinal admittance matrix, inverting the matrix in order to obtain Frequency domain propagation (60) According to the linearity problem, the propagation problem is entirely formulated in the frequency domain. So the following systems can be written: Longitudinal Admittance The complex amplitude and are now just function of the longitudinal coordinate. Capacity coefficients matrix (47) The capacitance matrix allows the conductor to hold the potential throughout the insulation. In order for this matrix to be determined, it is considered its inverse, the potential coefficients matrix. It is only considered the potential vector inside the cables, being the non diagonal elements,, null. For the main diagonal elements,, we have: With (48) (49) (50) (53) (54) The product can be transformed in a diagonal matrix using the transformation matrix. The transformation matrix can transform the product in a diagonal matrix. Matrix is obtained by the eigenvectors of and matrix by the eigenvectors of. The diagonal matrix of the eigenvalues of is and is obtained by: (55) (56) Can be decomposed into a product of two diagonal matrices and by: (57) For the calculation of the matrix, it is necessary to build a matrix so it verifies the equation, then: (51) 5
6 (58) Introducing and to the system and applying the necessary simplifications: (59) There is now a system of equations, which can be written in the following matrix form: (60),, and are column vectors for modal quantities. For the voltage the expression is: Γ Γ (61) And for the current: Assuming: ΓΓ ΓΓ (62) Γ Γ Γ Γ (68) Where: Γ Γ 1 Note that Γ is a non-diagonal matrix. IV-Transient analysis of underground power-transmission systems (63) The tools used in this work are the Fast Fourier Transform (FFT) and the Inverse Fast Fourier Transform (IFFT). These are fast algorithms for implementing a number of samples where the input signal is transformed in the same number of frequency points. The calculations performed by these algorithms are multiplications and additions for 2 samples [7]. Equations of the line ended with a three-phase load Considering a three-phase generator and the frequency propagation equations: Where: 0 0 (64) 0 - Column vector of complex amplitude voltages at the beginning of the line, 0. - Column vector of complex amplitude voltages for the three-phase generator 3x3 matrix with each element being an impedance 0 - Column vector of complex amplitude currents at the beginning of the line, 0. Now considering the three-phase load at the end of the line: Where: (65) - Column vector of complex amplitude voltages at the end of the line,. 3x3 matrix with each element being an impedance - Column vector of complex amplitude currents at the end of the line,. It will be established matrix transfer functions in order to relate the voltage and current complex amplitudes on a determined place of the line. The generator is considered to be of 230 amplitude. Transfer Functions For 0 and : 0 0 Γ Γ Γ Γ Γ Γ Γ Γ (66) Where: (67) (68) And the transfer functions that allow the calculation of voltages and currents at a generic point : Γ Γ Γ Γ Γ (69) 6
7 With: Γ EΓ Γ E Γ EΓ Γ (70) Γ Γ E Γ E (71) Frequency domain Figure 6. Phase Voltage at z=5km. To analyze the electromagnetic transient in a power-transmission system, it is necessary to pass the time domain voltages of the generator to the frequency domain. The FFT algorithm was used, the real part is represented in blue with the imaginary in red. Figure 7. Sheath current at z=5km. The other voltages and currents are not represented because the results gave a null amplitude. Figure 5. Fourier transform of the phase generator voltages. Transient analysis of a three-phase line with load To study the electromagnetic transients it is necessary to know the parameters of the three-phase line: Short-Circuit Load Phase impedance 0Ω, sheath impedance 0Ω. The generator phases are in short-circuit and the sheaths with a 1 Ω impedance. The system is 5km in length. Real part is represented in blue with the imaginary in red. Figure 8. Phase current at z=5km. Table 1. Parameters of the system. The permittivity and permeability represented in the above table refers to the insulating layer surrounding the phase conductor and conducting sheath. No Load Phase impedance, sheath impedance 0Ω. The generator phases are in short-circuit and the sheaths with a 1 Ω impedance. The system is 5km in length. Real part is represented in blue with the imaginary in red. Figure 9. Sheath current at z=5km. 7
8 The other voltages and currents are not represented because the results gave a null amplitude. Adapted Load Phase impedance 66.4Ω, 63.14Ω, sheath impedance 0Ω. The generator phases are in short-circuit and the sheaths with a 1 Ω impedance. The system is 5km in length. Real part is represented in blue with the imaginary in red. Propagation mode parameters From the equivalent quadripole of a mono-phase line section: 0 0 (72) Where and are the longitudinal modal impedance and transversal modal admittance: 2 (73) Figure 10. Phase voltage at z=5km. Figure 11. Phase current at z=5km. If and: 1, then, (74) Where is the k mode longitudinal impedance in modal coordinates. and are the diagonal elements of and. In order to simplify the problem is is considered that the sheaths are connected to the earth, this way only the phases are considered (75) (76) (77) Transformation matrix is the eigenvectors matrix that diagonalizes the product. Transformation matrix is: (78) Figure 12. Sheath current at z=5km. The other voltages and currents are not represented because the results gave a null amplitude. Modal impedance matrix is obtained by: (79) V Equivalent network with lumped parameters An equivalent network with lumped parameters is a system that is close to the behavior of a power transmission line in a determined frequency band. In this work the conducting sheaths are connected to the earth. This allows the reduction of the matrix dimensions from 6x6 to 3x3, obtaining three independent modes. Figure 13. Real part of the longitudinal impedance. 8
9 Transformation matrices of voltages and currents It is implemented in this section a circuit with the objective to simulate the behavior of an underground system with a equivalent network. With the 20 section circuit there exist two adaptation nets, one at the generator and the other at the load that transform modal magnitudes into real ones and vice-versa. It is considered the normalized and matrices, and their inverse. No frequency variation is considered. Figure 14. Imaginary part of the longitudinal impedance No Load Longitudinal impedance synthesis Each element of will be approximate by the 5 parallel branches of the circuit impedance. 1 Z 1 1 (80) For n frequencies (86) represents a system of n equations. It is resolved by the following interactive process: Z ii, (81) The process is initiated with and values that correspond to 5 times the longitudinal impedance. This values are changed at each interaction, and it is applied to all. The process is repeated until there is no significant change in the parameters values. The adjustment frequencies where chosen in geometric progression so no negative elements would occur. The following figures represent the results for 3 propagation modes at a frequency band, the equivalent system is represented by lines and the equivalent network by dots. The line has 5 divided by 20 sections 250 each. Figure 17. Current by the Fourier Transform for z=0km Figure 18. Current by the equivalent network for z=0km Figure 15. Comparison of the longitudinal impedance at 50Hz. Figure 19. Voltage by the Fourier Transform for z=5km Figure 16. Comparison of the longitudinal impedance at 100kHz. Figure 20. Voltage by the equivalent network for z=5km 9
10 Short-Circuit Load Figure 21. Current by the Fourier Transform for z=0km VI Conclusions The equivalent network with lumped parameters is a more complete method for the system analysis, but requires more memory and processor capacity. After applying some simplifications, such as the sheath connection to the earth, the phase modes have similar attenuations, converging at high frequencies. The modal method and the longitudinal impedance synthesis converge at both low and high frequencies. The results are similar, obtaining a small difference in the oscillations of the transients for both voltage and current. For a possible investigation topic in this subject, it is recommended a development of a program able to solve the set of differential equations to treat this transmission system, as well as the problem of the complete set of six modes. VII References Figure 22. Current by the equivalent network for z=0km [1] Simonyi, K Foundations of Electrical Engineering. Pergamon Press. [2] Sommerfeld, A Partial Differential Equations in Physics. Academic Press [3] Machado, V. Maló & da Silva, J. F. Borges Series-Impedance of Underground Transmission Systems, in IEEE Transactions on Power Delivery, Vol. 3, No.2, pp [4] Wedepohl, L. M. & Wilcox, D. J Transient analysis of underground power-transmission systems: System model and wave propagation characteristics, Proceedings Inst. Elec. Eng., vol. 120, pp [5] Guerreiro Neves, M. V Cálculo de Transitórios em Linhas de Transmissão de Energia Baseado no Emprego dum Esquema Equivalente por Troços Comparação com o Método da Transformada de Laplace, Departamento de Engenharia Electrotécnica e de Computadores do Instituto Superior Tecnico, Universidade Técnica de Lisboa. [6] Da Silva, J. F. Borges Electrotecnia Teórica, Departamento de Engenharia Electrotécnica e de Computadores do Instituto Superior Técnico, Universidade Técnica de Lisboa. [7] Shenkman, Arieh L Transient Analysis of Electric Power Circuits Handbook. Holon Academic Institute of Technology. Figure 23. Voltage by the Fourier Transform for z=5km Figure 24. Voltage by the equivalent network for z=5km 10
A wave lab inside a coaxial cable
 INSTITUTE OF PHYSICS PUBLISHING Eur. J. Phys. 25 (2004) 581 591 EUROPEAN JOURNAL OF PHYSICS PII: S0143-0807(04)76273-X A wave lab inside a coaxial cable JoãoMSerra,MiguelCBrito,JMaiaAlves and A M Vallera
INSTITUTE OF PHYSICS PUBLISHING Eur. J. Phys. 25 (2004) 581 591 EUROPEAN JOURNAL OF PHYSICS PII: S0143-0807(04)76273-X A wave lab inside a coaxial cable JoãoMSerra,MiguelCBrito,JMaiaAlves and A M Vallera
zcable Model for Frequency Dependent Modelling of Cable Transmission Systems
 zcable Model for Frequency Dependent Modelling of Cable Transmission Systems T. C. Yu Dept. of Electrical and Computer Engineering The University of British Columbia 356 Main Mall, Vancouver, B.C., Canada
zcable Model for Frequency Dependent Modelling of Cable Transmission Systems T. C. Yu Dept. of Electrical and Computer Engineering The University of British Columbia 356 Main Mall, Vancouver, B.C., Canada
An equivalent circuit of a loop antenna.
 3.2.1. Circuit Modeling: Loop Impedance A loop antenna can be represented by a lumped circuit when its dimension is small with respect to a wavelength. In this representation, the circuit parameters (generally
3.2.1. Circuit Modeling: Loop Impedance A loop antenna can be represented by a lumped circuit when its dimension is small with respect to a wavelength. In this representation, the circuit parameters (generally
Edmund Li. Where is defined as the mutual inductance between and and has the SI units of Henries (H).
 INDUCTANCE MUTUAL INDUCTANCE If we consider two neighbouring closed loops and with bounding surfaces respectively then a current through will create a magnetic field which will link with as the flux passes
INDUCTANCE MUTUAL INDUCTANCE If we consider two neighbouring closed loops and with bounding surfaces respectively then a current through will create a magnetic field which will link with as the flux passes
INTEGRAL METHODS IN LOW-FREQUENCY ELECTROMAGNETICS
 INTEGRAL METHODS IN LOW-FREQUENCY ELECTROMAGNETICS I. Dolezel Czech Technical University, Praha, Czech Republic P. Karban University of West Bohemia, Plzeft, Czech Republic P. Solin University of Nevada,
INTEGRAL METHODS IN LOW-FREQUENCY ELECTROMAGNETICS I. Dolezel Czech Technical University, Praha, Czech Republic P. Karban University of West Bohemia, Plzeft, Czech Republic P. Solin University of Nevada,
6 J - vector electric current density (A/m2 )
 Determination of Antenna Radiation Fields Using Potential Functions Sources of Antenna Radiation Fields 6 J - vector electric current density (A/m2 ) M - vector magnetic current density (V/m 2 ) Some problems
Determination of Antenna Radiation Fields Using Potential Functions Sources of Antenna Radiation Fields 6 J - vector electric current density (A/m2 ) M - vector magnetic current density (V/m 2 ) Some problems
potential in the centre of the sphere with respect to infinity.
 Umeå Universitet, Fysik 1 Vitaly Bychkov Prov i fysik, Electricity and Waves, 2006-09-27, kl 16.00-22.00 Hjälpmedel: Students can use any book. Define the notations you are using properly. Present your
Umeå Universitet, Fysik 1 Vitaly Bychkov Prov i fysik, Electricity and Waves, 2006-09-27, kl 16.00-22.00 Hjälpmedel: Students can use any book. Define the notations you are using properly. Present your
High Voltage Transient Analysis
 High Voltage Transient Analysis 4. Surges on Transmission Lines Due to a variety of reasons, such as a direct stroke of lightning on the line, or by indirect strokes, or by switching operations or by faults,
High Voltage Transient Analysis 4. Surges on Transmission Lines Due to a variety of reasons, such as a direct stroke of lightning on the line, or by indirect strokes, or by switching operations or by faults,
Comparison of Power Título Transmission Line Models with Finite Elements
 CEPEL Comparison of Power Título Transmission do trabalho Line Models with Finite Elements Carlos K. C. Arruda, Anny A. Silveira, Fernando C. Dart Autor/apresentador Área Departamento de Linhas e Estações
CEPEL Comparison of Power Título Transmission do trabalho Line Models with Finite Elements Carlos K. C. Arruda, Anny A. Silveira, Fernando C. Dart Autor/apresentador Área Departamento de Linhas e Estações
Effects of Cell Phone Radiation on the Head. BEE 4530 Computer-Aided Engineering: Applications to Biomedical Processes
 Effects of Cell Phone Radiation on the Head BEE 4530 Computer-Aided Engineering: Applications to Biomedical Processes Group 3 Angela Cai Youjin Cho Mytien Nguyen Praveen Polamraju Table of Contents I.
Effects of Cell Phone Radiation on the Head BEE 4530 Computer-Aided Engineering: Applications to Biomedical Processes Group 3 Angela Cai Youjin Cho Mytien Nguyen Praveen Polamraju Table of Contents I.
www.integratedsoft.com Electromagnetic Sensor Design: Key Considerations when selecting CAE Software
 www.integratedsoft.com Electromagnetic Sensor Design: Key Considerations when selecting CAE Software Content Executive Summary... 3 Characteristics of Electromagnetic Sensor Systems... 3 Basic Selection
www.integratedsoft.com Electromagnetic Sensor Design: Key Considerations when selecting CAE Software Content Executive Summary... 3 Characteristics of Electromagnetic Sensor Systems... 3 Basic Selection
PHY3128 / PHYM203 (Electronics / Instrumentation) Transmission Lines. Repeated n times I L
 Transmission Lines Introduction A transmission line guides energy from one place to another. Optical fibres, waveguides, telephone lines and power cables are all electromagnetic transmission lines. are
Transmission Lines Introduction A transmission line guides energy from one place to another. Optical fibres, waveguides, telephone lines and power cables are all electromagnetic transmission lines. are
STUDY OF DAM-RESERVOIR DYNAMIC INTERACTION USING VIBRATION TESTS ON A PHYSICAL MODEL
 STUDY OF DAM-RESERVOIR DYNAMIC INTERACTION USING VIBRATION TESTS ON A PHYSICAL MODEL Paulo Mendes, Instituto Superior de Engenharia de Lisboa, Portugal Sérgio Oliveira, Laboratório Nacional de Engenharia
STUDY OF DAM-RESERVOIR DYNAMIC INTERACTION USING VIBRATION TESTS ON A PHYSICAL MODEL Paulo Mendes, Instituto Superior de Engenharia de Lisboa, Portugal Sérgio Oliveira, Laboratório Nacional de Engenharia
Mode Patterns of Parallel plates &Rectangular wave guides Mr.K.Chandrashekhar, Dr.Girish V Attimarad
 International Journal of Scientific & Engineering Research Volume 3, Issue 8, August-2012 1 Mode Patterns of Parallel plates &Rectangular wave guides Mr.K.Chandrashekhar, Dr.Girish V Attimarad Abstract-Parallel
International Journal of Scientific & Engineering Research Volume 3, Issue 8, August-2012 1 Mode Patterns of Parallel plates &Rectangular wave guides Mr.K.Chandrashekhar, Dr.Girish V Attimarad Abstract-Parallel
Motor-CAD Software for Thermal Analysis of Electrical Motors - Links to Electromagnetic and Drive Simulation Models
 Motor-CAD Software for Thermal Analysis of Electrical Motors - Links to Electromagnetic and Drive Simulation Models Dave Staton, Douglas Hawkins and Mircea Popescu Motor Design Ltd., Ellesmere, Shropshire,
Motor-CAD Software for Thermal Analysis of Electrical Motors - Links to Electromagnetic and Drive Simulation Models Dave Staton, Douglas Hawkins and Mircea Popescu Motor Design Ltd., Ellesmere, Shropshire,
Coupling Impedance of SIS18 and SIS100 beampipe CERN-GSI-Webmeeting
 Coupling Impedance of SIS18 and SIS100 beampipe CERN-GSI-Webmeeting 23 October 2011 TU Darmstadt Fachbereich 18 Institut Theorie Elektromagnetischer Felder Uwe Niedermayer 1 Contents Motivation / Overview
Coupling Impedance of SIS18 and SIS100 beampipe CERN-GSI-Webmeeting 23 October 2011 TU Darmstadt Fachbereich 18 Institut Theorie Elektromagnetischer Felder Uwe Niedermayer 1 Contents Motivation / Overview
Copyright 2000 IEEE. Reprinted from IEEE MTT-S International Microwave Symposium 2000
 Copyright 2000 IEEE Reprinted from IEEE MTT-S International Microwave Symposium 2000 This material is posted here with permission of the IEEE. Such permission of the IEEE does not in any way imply IEEE
Copyright 2000 IEEE Reprinted from IEEE MTT-S International Microwave Symposium 2000 This material is posted here with permission of the IEEE. Such permission of the IEEE does not in any way imply IEEE
Assessment Plan for Learning Outcomes for BA/BS in Physics
 Department of Physics and Astronomy Goals and Learning Outcomes 1. Students know basic physics principles [BS, BA, MS] 1.1 Students can demonstrate an understanding of Newton s laws 1.2 Students can demonstrate
Department of Physics and Astronomy Goals and Learning Outcomes 1. Students know basic physics principles [BS, BA, MS] 1.1 Students can demonstrate an understanding of Newton s laws 1.2 Students can demonstrate
Fundamentals of Electromagnetic Fields and Waves: I
 Fundamentals of Electromagnetic Fields and Waves: I Fall 2007, EE 30348, Electrical Engineering, University of Notre Dame Mid Term II: Solutions Please show your steps clearly and sketch figures wherever
Fundamentals of Electromagnetic Fields and Waves: I Fall 2007, EE 30348, Electrical Engineering, University of Notre Dame Mid Term II: Solutions Please show your steps clearly and sketch figures wherever
State of Stress at Point
 State of Stress at Point Einstein Notation The basic idea of Einstein notation is that a covector and a vector can form a scalar: This is typically written as an explicit sum: According to this convention,
State of Stress at Point Einstein Notation The basic idea of Einstein notation is that a covector and a vector can form a scalar: This is typically written as an explicit sum: According to this convention,
C;Ri.N. (<b &>o3s8: Université Louis Pasteur de Strasbourg. Institut National de Physique Nucléaire et de Physique des Particules t...
 (o3s8: C;Ri.N CWMB 7»-fi CO i\ ANGULAR ASSÏMBTRIBS IN A SHIELDED -^ PAIR LINE CO CJ H.-FANMarri, C.A. GMCIA CANAL «nd H. VUCETICH o \. CHRKE DE «CH.1RCHES KKXEAIRES UHIVERSITB LOUIS PASTEUR STRASBOURG
(o3s8: C;Ri.N CWMB 7»-fi CO i\ ANGULAR ASSÏMBTRIBS IN A SHIELDED -^ PAIR LINE CO CJ H.-FANMarri, C.A. GMCIA CANAL «nd H. VUCETICH o \. CHRKE DE «CH.1RCHES KKXEAIRES UHIVERSITB LOUIS PASTEUR STRASBOURG
Physics 9e/Cutnell. correlated to the. College Board AP Physics 1 Course Objectives
 Physics 9e/Cutnell correlated to the College Board AP Physics 1 Course Objectives Big Idea 1: Objects and systems have properties such as mass and charge. Systems may have internal structure. Enduring
Physics 9e/Cutnell correlated to the College Board AP Physics 1 Course Objectives Big Idea 1: Objects and systems have properties such as mass and charge. Systems may have internal structure. Enduring
Introduction to acoustic imaging
 Introduction to acoustic imaging Contents 1 Propagation of acoustic waves 3 1.1 Wave types.......................................... 3 1.2 Mathematical formulation.................................. 4 1.3
Introduction to acoustic imaging Contents 1 Propagation of acoustic waves 3 1.1 Wave types.......................................... 3 1.2 Mathematical formulation.................................. 4 1.3
GPR Polarization Simulation with 3D HO FDTD
 Progress In Electromagnetics Research Symposium Proceedings, Xi an, China, March 6, 00 999 GPR Polarization Simulation with 3D HO FDTD Jing Li, Zhao-Fa Zeng,, Ling Huang, and Fengshan Liu College of Geoexploration
Progress In Electromagnetics Research Symposium Proceedings, Xi an, China, March 6, 00 999 GPR Polarization Simulation with 3D HO FDTD Jing Li, Zhao-Fa Zeng,, Ling Huang, and Fengshan Liu College of Geoexploration
Introduction to Engineering System Dynamics
 CHAPTER 0 Introduction to Engineering System Dynamics 0.1 INTRODUCTION The objective of an engineering analysis of a dynamic system is prediction of its behaviour or performance. Real dynamic systems are
CHAPTER 0 Introduction to Engineering System Dynamics 0.1 INTRODUCTION The objective of an engineering analysis of a dynamic system is prediction of its behaviour or performance. Real dynamic systems are
WAVES AND FIELDS IN INHOMOGENEOUS MEDIA
 WAVES AND FIELDS IN INHOMOGENEOUS MEDIA WENG CHO CHEW UNIVERSITY OF ILLINOIS URBANA-CHAMPAIGN IEEE PRESS Series on Electromagnetic Waves Donald G. Dudley, Series Editor IEEE Antennas and Propagation Society,
WAVES AND FIELDS IN INHOMOGENEOUS MEDIA WENG CHO CHEW UNIVERSITY OF ILLINOIS URBANA-CHAMPAIGN IEEE PRESS Series on Electromagnetic Waves Donald G. Dudley, Series Editor IEEE Antennas and Propagation Society,
COMPUTATION OF THREE-DIMENSIONAL ELECTRIC FIELD PROBLEMS BY A BOUNDARY INTEGRAL METHOD AND ITS APPLICATION TO INSULATION DESIGN
 PERIODICA POLYTECHNICA SER. EL. ENG. VOL. 38, NO. ~, PP. 381-393 (199~) COMPUTATION OF THREE-DIMENSIONAL ELECTRIC FIELD PROBLEMS BY A BOUNDARY INTEGRAL METHOD AND ITS APPLICATION TO INSULATION DESIGN H.
PERIODICA POLYTECHNICA SER. EL. ENG. VOL. 38, NO. ~, PP. 381-393 (199~) COMPUTATION OF THREE-DIMENSIONAL ELECTRIC FIELD PROBLEMS BY A BOUNDARY INTEGRAL METHOD AND ITS APPLICATION TO INSULATION DESIGN H.
SCHWEITZER ENGINEERING LABORATORIES, COMERCIAL LTDA.
 Pocket book of Electrical Engineering Formulas Content 1. Elementary Algebra and Geometry 1. Fundamental Properties (real numbers) 1 2. Exponents 2 3. Fractional Exponents 2 4. Irrational Exponents 2 5.
Pocket book of Electrical Engineering Formulas Content 1. Elementary Algebra and Geometry 1. Fundamental Properties (real numbers) 1 2. Exponents 2 3. Fractional Exponents 2 4. Irrational Exponents 2 5.
Electromagnetism Laws and Equations
 Electromagnetism Laws and Equations Andrew McHutchon Michaelmas 203 Contents Electrostatics. Electric E- and D-fields............................................. Electrostatic Force............................................2
Electromagnetism Laws and Equations Andrew McHutchon Michaelmas 203 Contents Electrostatics. Electric E- and D-fields............................................. Electrostatic Force............................................2
Fault location on power cables. Fault location on power cables
 Fault location on power cables Fault location on power cables Contents: 1. Introduction 2. Construction of power cables 3. Cable faults 01. Introduction Fault location on communication and power cables
Fault location on power cables Fault location on power cables Contents: 1. Introduction 2. Construction of power cables 3. Cable faults 01. Introduction Fault location on communication and power cables
The waveguide adapter consists of a rectangular part smoothly transcending into an elliptical part as seen in Figure 1.
 Waveguide Adapter Introduction This is a model of an adapter for microwave propagation in the transition between a rectangular and an elliptical waveguide. Such waveguide adapters are designed to keep
Waveguide Adapter Introduction This is a model of an adapter for microwave propagation in the transition between a rectangular and an elliptical waveguide. Such waveguide adapters are designed to keep
Co-simulation of Microwave Networks. Sanghoon Shin, Ph.D. RS Microwave
 Co-simulation of Microwave Networks Sanghoon Shin, Ph.D. RS Microwave Outline Brief review of EM solvers 2D and 3D EM simulators Technical Tips for EM solvers Co-simulated Examples of RF filters and Diplexer
Co-simulation of Microwave Networks Sanghoon Shin, Ph.D. RS Microwave Outline Brief review of EM solvers 2D and 3D EM simulators Technical Tips for EM solvers Co-simulated Examples of RF filters and Diplexer
Dynamic Process Modeling. Process Dynamics and Control
 Dynamic Process Modeling Process Dynamics and Control 1 Description of process dynamics Classes of models What do we need for control? Modeling for control Mechanical Systems Modeling Electrical circuits
Dynamic Process Modeling Process Dynamics and Control 1 Description of process dynamics Classes of models What do we need for control? Modeling for control Mechanical Systems Modeling Electrical circuits
IEEE TRANSACTIONS ON POWER DELIVERY, VOL. 22, NO. 4, OCTOBER 2007 2489 0885-8977/$25.00 2007 IEEE
 IEEE TRANSACTIONS ON POWER DELIVERY, VOL. 22, NO. 4, OCTOBER 2007 2489 Analysis of Harmonics in Subsea Power Transmission Cables Used in VSC HVDC Transmission Systems Operating Under Steady-State Conditions
IEEE TRANSACTIONS ON POWER DELIVERY, VOL. 22, NO. 4, OCTOBER 2007 2489 Analysis of Harmonics in Subsea Power Transmission Cables Used in VSC HVDC Transmission Systems Operating Under Steady-State Conditions
MODULE VII LARGE BODY WAVE DIFFRACTION
 MODULE VII LARGE BODY WAVE DIFFRACTION 1.0 INTRODUCTION In the wave-structure interaction problems, it is classical to divide into two major classification: slender body interaction and large body interaction.
MODULE VII LARGE BODY WAVE DIFFRACTION 1.0 INTRODUCTION In the wave-structure interaction problems, it is classical to divide into two major classification: slender body interaction and large body interaction.
TRANSFORMER MODELING BASED ON STANDARD FREQUENCY RESPONSE MEASUREMENTS
 TRANSFORMER MODELING BASED ON STANDARD FREQUENCY RESPONSE MEASUREMENTS M. Heindl 1*, S. Tenbohlen 1 and R. Wimmer 2 1 University of Stuttgart, Pfaffenwaldring 47, 70569 Stuttgart, Germany 2 Siemens AG,
TRANSFORMER MODELING BASED ON STANDARD FREQUENCY RESPONSE MEASUREMENTS M. Heindl 1*, S. Tenbohlen 1 and R. Wimmer 2 1 University of Stuttgart, Pfaffenwaldring 47, 70569 Stuttgart, Germany 2 Siemens AG,
Minimizing crosstalk in a high-speed cable-connector assembly.
 Minimizing crosstalk in a high-speed cable-connector assembly. Evans, B.J. Calvo Giraldo, E. Motos Lopez, T. CERN, 1211 Geneva 23, Switzerland [email protected] [email protected] [email protected]
Minimizing crosstalk in a high-speed cable-connector assembly. Evans, B.J. Calvo Giraldo, E. Motos Lopez, T. CERN, 1211 Geneva 23, Switzerland [email protected] [email protected] [email protected]
METHODOLOGICAL CONSIDERATIONS OF DRIVE SYSTEM SIMULATION, WHEN COUPLING FINITE ELEMENT MACHINE MODELS WITH THE CIRCUIT SIMULATOR MODELS OF CONVERTERS.
 SEDM 24 June 16th - 18th, CPRI (Italy) METHODOLOGICL CONSIDERTIONS OF DRIVE SYSTEM SIMULTION, WHEN COUPLING FINITE ELEMENT MCHINE MODELS WITH THE CIRCUIT SIMULTOR MODELS OF CONVERTERS. Áron Szûcs BB Electrical
SEDM 24 June 16th - 18th, CPRI (Italy) METHODOLOGICL CONSIDERTIONS OF DRIVE SYSTEM SIMULTION, WHEN COUPLING FINITE ELEMENT MCHINE MODELS WITH THE CIRCUIT SIMULTOR MODELS OF CONVERTERS. Áron Szûcs BB Electrical
2. Permanent Magnet (De-) Magnetization 2.1 Methodology
 Permanent Magnet (De-) Magnetization and Soft Iron Hysteresis Effects: A comparison of FE analysis techniques A.M. Michaelides, J. Simkin, P. Kirby and C.P. Riley Cobham Technical Services Vector Fields
Permanent Magnet (De-) Magnetization and Soft Iron Hysteresis Effects: A comparison of FE analysis techniques A.M. Michaelides, J. Simkin, P. Kirby and C.P. Riley Cobham Technical Services Vector Fields
INVESTIGATION OF ELECTRIC FIELD INTENSITY AND DEGREE OF UNIFORMITY BETWEEN ELECTRODES UNDER HIGH VOLTAGE BY CHARGE SIMULATIO METHOD
 INVESTIGATION OF ELECTRIC FIELD INTENSITY AND DEGREE OF UNIFORMITY BETWEEN ELECTRODES UNDER HIGH VOLTAGE BY CHARGE SIMULATIO METHOD Md. Ahsan Habib, Muhammad Abdul Goffar Khan, Md. Khaled Hossain, Shafaet
INVESTIGATION OF ELECTRIC FIELD INTENSITY AND DEGREE OF UNIFORMITY BETWEEN ELECTRODES UNDER HIGH VOLTAGE BY CHARGE SIMULATIO METHOD Md. Ahsan Habib, Muhammad Abdul Goffar Khan, Md. Khaled Hossain, Shafaet
Wireless Power Transfer System Design. Julius Saitz ANSYS
 Wireless Power Transfer System Design Julius Saitz ANSYS 1 WPT System 2 Wireless Power Transfer (WPT) Near-Field (Inductive coupling, resonant) Do not rely on propagating EM waves Operate at distances
Wireless Power Transfer System Design Julius Saitz ANSYS 1 WPT System 2 Wireless Power Transfer (WPT) Near-Field (Inductive coupling, resonant) Do not rely on propagating EM waves Operate at distances
DRAFT. University of Pennsylvania Moore School of Electrical Engineering ESE319 Electronic Circuits - Modeling and Measurement Techniques
 University of Pennsylvania Moore School of Electrical Engineering ESE319 Electronic Circuits - Modeling and Measurement Techniques 1. Introduction. Students are often frustrated in their attempts to execute
University of Pennsylvania Moore School of Electrical Engineering ESE319 Electronic Circuits - Modeling and Measurement Techniques 1. Introduction. Students are often frustrated in their attempts to execute
Digital Systems Ribbon Cables I CMPE 650. Ribbon Cables A ribbon cable is any cable having multiple conductors bound together in a flat, wide strip.
 Ribbon Cables A ribbon cable is any cable having multiple conductors bound together in a flat, wide strip. Each dielectric configuration has different high-frequency characteristics. All configurations
Ribbon Cables A ribbon cable is any cable having multiple conductors bound together in a flat, wide strip. Each dielectric configuration has different high-frequency characteristics. All configurations
Agilent De-embedding and Embedding S-Parameter Networks Using a Vector Network Analyzer. Application Note 1364-1
 Agilent De-embedding and Embedding S-Parameter Networks Using a Vector Network Analyzer Application Note 1364-1 Introduction Traditionally RF and microwave components have been designed in packages with
Agilent De-embedding and Embedding S-Parameter Networks Using a Vector Network Analyzer Application Note 1364-1 Introduction Traditionally RF and microwave components have been designed in packages with
Consideration of a high-capacity foil cable:
 Consideration of a high-capacity foil cable: Newly discovered ancient knowledge. The old RF-developers already knew the benefits of longplanar lines and have been used (electronic) Eonen (times) thin flat
Consideration of a high-capacity foil cable: Newly discovered ancient knowledge. The old RF-developers already knew the benefits of longplanar lines and have been used (electronic) Eonen (times) thin flat
CONCEPT-II. Overview of demo examples
 CONCEPT-II CONCEPT-II is a frequency domain method of moment (MoM) code, under development at the Institute of Electromagnetic Theory at the Technische Universität Hamburg-Harburg (www.tet.tuhh.de). Overview
CONCEPT-II CONCEPT-II is a frequency domain method of moment (MoM) code, under development at the Institute of Electromagnetic Theory at the Technische Universität Hamburg-Harburg (www.tet.tuhh.de). Overview
Chapter 22: Electric Flux and Gauss s Law
 22.1 ntroduction We have seen in chapter 21 that determining the electric field of a continuous charge distribution can become very complicated for some charge distributions. t would be desirable if we
22.1 ntroduction We have seen in chapter 21 that determining the electric field of a continuous charge distribution can become very complicated for some charge distributions. t would be desirable if we
Selecting Receiving Antennas for Radio Tracking
 Selecting Receiving Antennas for Radio Tracking Larry B Kuechle, Advanced Telemetry Systems, Inc. Isanti, Minnesota 55040 [email protected] The receiving antenna is an integral part of any radio location
Selecting Receiving Antennas for Radio Tracking Larry B Kuechle, Advanced Telemetry Systems, Inc. Isanti, Minnesota 55040 [email protected] The receiving antenna is an integral part of any radio location
Human Exposure to Outdoor PLC System
 1602 PIERS Proceedings, Marrakesh, MOROCCO, March 20 23, 2011 Human Exposure to Outdoor PLC System Vicko Doric 1, Dragan Poljak 1, and Khalil El Khamlichi Drissi 2 1 University of Split, Croatia 2 Blaise
1602 PIERS Proceedings, Marrakesh, MOROCCO, March 20 23, 2011 Human Exposure to Outdoor PLC System Vicko Doric 1, Dragan Poljak 1, and Khalil El Khamlichi Drissi 2 1 University of Split, Croatia 2 Blaise
Standex-Meder Electronics. Custom Engineered Solutions for Tomorrow
 Standex-Meder Electronics Custom Engineered Solutions for Tomorrow RF Reed Relays Part II Product Training Copyright 2013 Standex-Meder Electronics. All rights reserved. Introduction Purpose Designing
Standex-Meder Electronics Custom Engineered Solutions for Tomorrow RF Reed Relays Part II Product Training Copyright 2013 Standex-Meder Electronics. All rights reserved. Introduction Purpose Designing
Department of Electrical and Computer Engineering Ben-Gurion University of the Negev. LAB 1 - Introduction to USRP
 Department of Electrical and Computer Engineering Ben-Gurion University of the Negev LAB 1 - Introduction to USRP - 1-1 Introduction In this lab you will use software reconfigurable RF hardware from National
Department of Electrical and Computer Engineering Ben-Gurion University of the Negev LAB 1 - Introduction to USRP - 1-1 Introduction In this lab you will use software reconfigurable RF hardware from National
Current Probes, More Useful Than You Think
 Current Probes, More Useful Than You Think Training and design help in most areas of Electrical Engineering Copyright 1998 Institute of Electrical and Electronics Engineers. Reprinted from the IEEE 1998
Current Probes, More Useful Than You Think Training and design help in most areas of Electrical Engineering Copyright 1998 Institute of Electrical and Electronics Engineers. Reprinted from the IEEE 1998
Crosstalk on Printed Circuit Boards
 Crosstalk on Printed Circuit Boards Jan Carlsson Second Edition Abstract This document treats the crosstalk between parallel conductors. The conductors can represent either conductors in a multiconductor
Crosstalk on Printed Circuit Boards Jan Carlsson Second Edition Abstract This document treats the crosstalk between parallel conductors. The conductors can represent either conductors in a multiconductor
The performance improvement by ferrite loading means - increasing, - increasing of ratio, implicitly related to the input impedance.
 3.2.3. Ferrite Loading Magnetic ferrite loading can enhance a transmitting signal as high as 2 to 10 db for MHz [Devore and Bohley, 1977]. There is an optimum frequency range where ferrite loading is beneficial.
3.2.3. Ferrite Loading Magnetic ferrite loading can enhance a transmitting signal as high as 2 to 10 db for MHz [Devore and Bohley, 1977]. There is an optimum frequency range where ferrite loading is beneficial.
ANALYSIS AND VERIFICATION OF A PROPOSED ANTENNA DESIGN FOR AN IMPLANTABLE. RFID TAG AT 915 MHz RAHUL BAKORE
 ANALYSIS AND VERIFICATION OF A PROPOSED ANTENNA DESIGN FOR AN IMPLANTABLE RFID TAG AT 915 MHz By RAHUL BAKORE Bachelor of Engineering in Electronics and Communication University Of Rajasthan Jaipur, Rajasthan,
ANALYSIS AND VERIFICATION OF A PROPOSED ANTENNA DESIGN FOR AN IMPLANTABLE RFID TAG AT 915 MHz By RAHUL BAKORE Bachelor of Engineering in Electronics and Communication University Of Rajasthan Jaipur, Rajasthan,
High-fidelity electromagnetic modeling of large multi-scale naval structures
 High-fidelity electromagnetic modeling of large multi-scale naval structures F. Vipiana, M. A. Francavilla, S. Arianos, and G. Vecchi (LACE), and Politecnico di Torino 1 Outline ISMB and Antenna/EMC Lab
High-fidelity electromagnetic modeling of large multi-scale naval structures F. Vipiana, M. A. Francavilla, S. Arianos, and G. Vecchi (LACE), and Politecnico di Torino 1 Outline ISMB and Antenna/EMC Lab
Impedance 50 (75 connectors via adapters)
 VECTOR NETWORK ANALYZER PLANAR TR1300/1 DATA SHEET Frequency range: 300 khz to 1.3 GHz Measured parameters: S11, S21 Dynamic range of transmission measurement magnitude: 130 db Measurement time per point:
VECTOR NETWORK ANALYZER PLANAR TR1300/1 DATA SHEET Frequency range: 300 khz to 1.3 GHz Measured parameters: S11, S21 Dynamic range of transmission measurement magnitude: 130 db Measurement time per point:
EM Noise Mitigation in Circuit Boards and Cavities
 EM Noise Mitigation in Circuit Boards and Cavities Faculty (UMD): Omar M. Ramahi, Neil Goldsman and John Rodgers Visiting Professors (Finland): Fad Seydou Graduate Students (UMD): Xin Wu, Lin Li, Baharak
EM Noise Mitigation in Circuit Boards and Cavities Faculty (UMD): Omar M. Ramahi, Neil Goldsman and John Rodgers Visiting Professors (Finland): Fad Seydou Graduate Students (UMD): Xin Wu, Lin Li, Baharak
Coupling Effect in Substation Ground Measurements
 SERBIAN JOURNAL OF ELECTRICAL ENGINEERING Vol. 9, No. 3, October 2012, 315-324 UDK: 621.316.13.011.2 DOI: 10.2298/SJEE1203315F Coupling Effect in Substation Ground Measurements Alex Farber 1, Boris Katz
SERBIAN JOURNAL OF ELECTRICAL ENGINEERING Vol. 9, No. 3, October 2012, 315-324 UDK: 621.316.13.011.2 DOI: 10.2298/SJEE1203315F Coupling Effect in Substation Ground Measurements Alex Farber 1, Boris Katz
Grounding Demystified
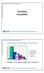 Grounding Demystified 3-1 Importance Of Grounding Techniques 45 40 35 30 25 20 15 10 5 0 Grounding 42% Case 22% Cable 18% Percent Used Filter 12% PCB 6% Grounding 42% Case Shield 22% Cable Shielding 18%
Grounding Demystified 3-1 Importance Of Grounding Techniques 45 40 35 30 25 20 15 10 5 0 Grounding 42% Case 22% Cable 18% Percent Used Filter 12% PCB 6% Grounding 42% Case Shield 22% Cable Shielding 18%
Application Note. So You Need to Measure Some Inductors?
 So You Need to Measure Some nductors? Take a look at the 1910 nductance Analyzer. Although specifically designed for production testing of inductors and coils, in addition to measuring inductance (L),
So You Need to Measure Some nductors? Take a look at the 1910 nductance Analyzer. Although specifically designed for production testing of inductors and coils, in addition to measuring inductance (L),
When designing. Inductors at UHF: EM Simulation Guides Vector Network Analyzer. measurement. EM SIMULATION. There are times when it is
 Inductors at UHF: EM Simulation Guides Vector Network Analyzer Measurements John B. Call Thales Communications Inc., USA When designing There are times when it is circuits for necessary to measure a operation
Inductors at UHF: EM Simulation Guides Vector Network Analyzer Measurements John B. Call Thales Communications Inc., USA When designing There are times when it is circuits for necessary to measure a operation
Instrument Transformers Application Guide
 Instrument Transformers Application Guide Edited by ABB AB High Voltage Products Department: Marketing & Sales Text: Knut Sjövall, ABB Layout, 3D and images: Mats Findell, ABB SE-771 80 LUDVIKA, Sweden
Instrument Transformers Application Guide Edited by ABB AB High Voltage Products Department: Marketing & Sales Text: Knut Sjövall, ABB Layout, 3D and images: Mats Findell, ABB SE-771 80 LUDVIKA, Sweden
Project 1: Rectangular Waveguide (HFSS)
 Project 1: Rectangular Waveguide (HFSS) b ε r a a = 0.9 (2.286cm) b = 0.4 (1.016cm) ε r = 1.0 Objective Getting Started with HFSS (a tutorial) Using HFSS, simulate an air-filled WR-90 waveguide shown above.
Project 1: Rectangular Waveguide (HFSS) b ε r a a = 0.9 (2.286cm) b = 0.4 (1.016cm) ε r = 1.0 Objective Getting Started with HFSS (a tutorial) Using HFSS, simulate an air-filled WR-90 waveguide shown above.
Chapter 9 Balanced Faults
 Chapter 9 alanced Faults 9.1 Introduction The most common types of fault are (in order) single-line-to-ground fault, line-to-line fault, and double-line-to-ground fault. All of these are unbalanced faults.
Chapter 9 alanced Faults 9.1 Introduction The most common types of fault are (in order) single-line-to-ground fault, line-to-line fault, and double-line-to-ground fault. All of these are unbalanced faults.
G019.A (4/99) UNDERSTANDING COMMON MODE NOISE
 UNDERSTANDING COMMON MODE NOISE PAGE 2 OF 7 TABLE OF CONTENTS 1 INTRODUCTION 2 DIFFERENTIAL MODE AND COMMON MODE SIGNALS 2.1 Differential Mode signals 2.2 Common Mode signals 3 DIFFERENTIAL AND COMMON
UNDERSTANDING COMMON MODE NOISE PAGE 2 OF 7 TABLE OF CONTENTS 1 INTRODUCTION 2 DIFFERENTIAL MODE AND COMMON MODE SIGNALS 2.1 Differential Mode signals 2.2 Common Mode signals 3 DIFFERENTIAL AND COMMON
Eðlisfræði 2, vor 2007
 [ Assignment View ] [ Pri Eðlisfræði 2, vor 2007 28. Sources of Magnetic Field Assignment is due at 2:00am on Wednesday, March 7, 2007 Credit for problems submitted late will decrease to 0% after the deadline
[ Assignment View ] [ Pri Eðlisfræði 2, vor 2007 28. Sources of Magnetic Field Assignment is due at 2:00am on Wednesday, March 7, 2007 Credit for problems submitted late will decrease to 0% after the deadline
DDX 7000 & 8003. Digital Partial Discharge Detectors FEATURES APPLICATIONS
 DDX 7000 & 8003 Digital Partial Discharge Detectors The HAEFELY HIPOTRONICS DDX Digital Partial Discharge Detector offers the high accuracy and flexibility of digital technology, plus the real-time display
DDX 7000 & 8003 Digital Partial Discharge Detectors The HAEFELY HIPOTRONICS DDX Digital Partial Discharge Detector offers the high accuracy and flexibility of digital technology, plus the real-time display
Dynamics at the Horsetooth, Volume 2A, Focussed Issue: Asymptotics and Perturbations
 Dynamics at the Horsetooth, Volume A, Focussed Issue: Asymptotics and Perturbations Asymptotic Expansion of Bessel Functions; Applications to Electromagnetics Department of Electrical Engineering Colorado
Dynamics at the Horsetooth, Volume A, Focussed Issue: Asymptotics and Perturbations Asymptotic Expansion of Bessel Functions; Applications to Electromagnetics Department of Electrical Engineering Colorado
4.4 WAVE CHARACTERISTICS 4.5 WAVE PROPERTIES HW/Study Packet
 4.4 WAVE CHARACTERISTICS 4.5 WAVE PROPERTIES HW/Study Packet Required: READ Hamper pp 115-134 SL/HL Supplemental: Cutnell and Johnson, pp 473-477, 507-513 Tsokos, pp 216-242 REMEMBER TO. Work through all
4.4 WAVE CHARACTERISTICS 4.5 WAVE PROPERTIES HW/Study Packet Required: READ Hamper pp 115-134 SL/HL Supplemental: Cutnell and Johnson, pp 473-477, 507-513 Tsokos, pp 216-242 REMEMBER TO. Work through all
How To Counter Noise Noise From A Low Voltage Differential Signaling Circuit
 TDK EMC Technology Practice Section EMC Countermeasures of Low Voltage Differential Signaling Circuits TDK Corporation Magnetics Business Group Toshio Tomonari 1 Introduction Low Voltage Differential Signaling
TDK EMC Technology Practice Section EMC Countermeasures of Low Voltage Differential Signaling Circuits TDK Corporation Magnetics Business Group Toshio Tomonari 1 Introduction Low Voltage Differential Signaling
Dispersion diagrams of a water-loaded cylindrical shell obtained from the structural and acoustic responses of the sensor array along the shell
 Dispersion diagrams of a water-loaded cylindrical shell obtained from the structural and acoustic responses of the sensor array along the shell B.K. Jung ; J. Ryue ; C.S. Hong 3 ; W.B. Jeong ; K.K. Shin
Dispersion diagrams of a water-loaded cylindrical shell obtained from the structural and acoustic responses of the sensor array along the shell B.K. Jung ; J. Ryue ; C.S. Hong 3 ; W.B. Jeong ; K.K. Shin
DOING PHYSICS WITH MATLAB COMPUTATIONAL OPTICS RAYLEIGH-SOMMERFELD DIFFRACTION INTEGRAL OF THE FIRST KIND
 DOING PHYSICS WITH MATLAB COMPUTATIONAL OPTICS RAYLEIGH-SOMMERFELD DIFFRACTION INTEGRAL OF THE FIRST KIND THE THREE-DIMENSIONAL DISTRIBUTION OF THE RADIANT FLUX DENSITY AT THE FOCUS OF A CONVERGENCE BEAM
DOING PHYSICS WITH MATLAB COMPUTATIONAL OPTICS RAYLEIGH-SOMMERFELD DIFFRACTION INTEGRAL OF THE FIRST KIND THE THREE-DIMENSIONAL DISTRIBUTION OF THE RADIANT FLUX DENSITY AT THE FOCUS OF A CONVERGENCE BEAM
Harmonics and Noise in Photovoltaic (PV) Inverter and the Mitigation Strategies
 Soonwook Hong, Ph. D. Michael Zuercher Martinson Harmonics and Noise in Photovoltaic (PV) Inverter and the Mitigation Strategies 1. Introduction PV inverters use semiconductor devices to transform the
Soonwook Hong, Ph. D. Michael Zuercher Martinson Harmonics and Noise in Photovoltaic (PV) Inverter and the Mitigation Strategies 1. Introduction PV inverters use semiconductor devices to transform the
EMI in Electric Vehicles
 EMI in Electric Vehicles S. Guttowski, S. Weber, E. Hoene, W. John, H. Reichl Fraunhofer Institute for Reliability and Microintegration Gustav-Meyer-Allee 25, 13355 Berlin, Germany Phone: ++49(0)3046403144,
EMI in Electric Vehicles S. Guttowski, S. Weber, E. Hoene, W. John, H. Reichl Fraunhofer Institute for Reliability and Microintegration Gustav-Meyer-Allee 25, 13355 Berlin, Germany Phone: ++49(0)3046403144,
Today s handsets have to meet tough ELECTROMAGNETIC SIMULATION OF MOBILE PHONE ANTENNA PERFORMANCE
 ELECTROMAGNETIC SIMULATION OF MOBILE PHONE ANTENNA PERFORMANCE The telecommunications sector is making great advances aimed at delivering an even stream of high-tech devices, covering the significant consumer
ELECTROMAGNETIC SIMULATION OF MOBILE PHONE ANTENNA PERFORMANCE The telecommunications sector is making great advances aimed at delivering an even stream of high-tech devices, covering the significant consumer
2. THE TEORRETICAL OF GROUND PENETRATING RADAR:
 Sixteenth International Water Technology Conference, IWTC 16 2012, Istanbul, Turkey 1 THE USE OF GROUND PENETRATING RADAR WITH A FREQUENCY 1GHZ TO DETECT WATER LEAKS FROM PIPELINES Alaa Ezzat Hasan Ministry
Sixteenth International Water Technology Conference, IWTC 16 2012, Istanbul, Turkey 1 THE USE OF GROUND PENETRATING RADAR WITH A FREQUENCY 1GHZ TO DETECT WATER LEAKS FROM PIPELINES Alaa Ezzat Hasan Ministry
Software for Design NMR Probes Using the Shielded Split Ring and the Shielded Symmetrical Band Resonators
 Software for Design NMR Probes Using the Shielded Split Ring and the Shielded Symmetrical Band Resonators Nasreddine Benahmed University of Tlemcen, Algeria ABSTRACT This article presents a software (NMR
Software for Design NMR Probes Using the Shielded Split Ring and the Shielded Symmetrical Band Resonators Nasreddine Benahmed University of Tlemcen, Algeria ABSTRACT This article presents a software (NMR
Designing the NEWCARD Connector Interface to Extend PCI Express Serial Architecture to the PC Card Modular Form Factor
 Designing the NEWCARD Connector Interface to Extend PCI Express Serial Architecture to the PC Card Modular Form Factor Abstract This paper provides information about the NEWCARD connector and board design
Designing the NEWCARD Connector Interface to Extend PCI Express Serial Architecture to the PC Card Modular Form Factor Abstract This paper provides information about the NEWCARD connector and board design
Bandwidth analysis of multimode fiber passive optical networks (PONs)
 Optica Applicata, Vol. XXXIX, No. 2, 2009 Bandwidth analysis of multimode fiber passive optical networks (PONs) GRZEGORZ STEPNIAK *, LUKASZ MAKSYMIUK, JERZY SIUZDAK Institute of Telecommunications, Warsaw
Optica Applicata, Vol. XXXIX, No. 2, 2009 Bandwidth analysis of multimode fiber passive optical networks (PONs) GRZEGORZ STEPNIAK *, LUKASZ MAKSYMIUK, JERZY SIUZDAK Institute of Telecommunications, Warsaw
Overview. also give you an idea of ANSYS capabilities. In this chapter, we will define Finite Element Analysis and. Topics covered: B.
 2. FEA and ANSYS FEA and ANSYS Overview In this chapter, we will define Finite Element Analysis and also give you an idea of ANSYS capabilities. Topics covered: A. What is FEA? B. About ANSYS FEA and ANSYS
2. FEA and ANSYS FEA and ANSYS Overview In this chapter, we will define Finite Element Analysis and also give you an idea of ANSYS capabilities. Topics covered: A. What is FEA? B. About ANSYS FEA and ANSYS
PHY114 S11 Term Exam 3
 PHY4 S Term Exam S. G. Rajeev Mar 2 20 2:0 pm to :45 pm PLEASE write your workshop number and your workshop leader s name at the top of your book, so that you can collect your graded exams at the workshop.
PHY4 S Term Exam S. G. Rajeev Mar 2 20 2:0 pm to :45 pm PLEASE write your workshop number and your workshop leader s name at the top of your book, so that you can collect your graded exams at the workshop.
Time and Frequency Domain Analysis for Right Angle Corners on Printed Circuit Board Traces
 Time and Frequency Domain Analysis for Right Angle Corners on Printed Circuit Board Traces Mark I. Montrose Montrose Compliance Services 2353 Mission Glen Dr. Santa Clara, CA 95051-1214 Abstract: For years,
Time and Frequency Domain Analysis for Right Angle Corners on Printed Circuit Board Traces Mark I. Montrose Montrose Compliance Services 2353 Mission Glen Dr. Santa Clara, CA 95051-1214 Abstract: For years,
Amplification of the Radiation from Two Collocated Cellular System Antennas by the Ground Wave of an AM Broadcast Station
 Amplification of the Radiation from Two Collocated Cellular System Antennas by the Ground Wave of an AM Broadcast Station Dr. Bill P. Curry EMSciTek Consulting Co., W101 McCarron Road Glen Ellyn, IL 60137,
Amplification of the Radiation from Two Collocated Cellular System Antennas by the Ground Wave of an AM Broadcast Station Dr. Bill P. Curry EMSciTek Consulting Co., W101 McCarron Road Glen Ellyn, IL 60137,
Cable Analysis and Fault Detection using the Bode 100
 Cable Analysis and Fault Detection using the Bode 100 By Stephan Synkule 2014 by OMICRON Lab V1.3 Visit www.omicron-lab.com for more information. Contact [email protected] for technical support.
Cable Analysis and Fault Detection using the Bode 100 By Stephan Synkule 2014 by OMICRON Lab V1.3 Visit www.omicron-lab.com for more information. Contact [email protected] for technical support.
VBA Macro for construction of an EM 3D model of a tyre and part of the vehicle
 VBA Macro for construction of an EM 3D model of a tyre and part of the vehicle Guillermo Vietti, Gianluca Dassano, Mario Orefice LACE, Politecnico di Torino, Turin, Italy. [email protected] Work
VBA Macro for construction of an EM 3D model of a tyre and part of the vehicle Guillermo Vietti, Gianluca Dassano, Mario Orefice LACE, Politecnico di Torino, Turin, Italy. [email protected] Work
SYNCHRONOUS MACHINES
 SYNCHRONOUS MACHINES The geometry of a synchronous machine is quite similar to that of the induction machine. The stator core and windings of a three-phase synchronous machine are practically identical
SYNCHRONOUS MACHINES The geometry of a synchronous machine is quite similar to that of the induction machine. The stator core and windings of a three-phase synchronous machine are practically identical
FEASIBILITY OF ELECTRICAL SEPARATION OF PROXIMATE GROUNDING SYSTEMS AS A FUNCTION OF SOIL STRUCTURE
 FEASIBILITY OF ELECTRICAL SEPARATION OF PROXIMATE GROUNDING SYSTEMS AS A FUNCTION OF SOIL STRUCTURE Sharon Tee and Farid P. Dawalibi Safe Engineering Services & technologies ltd. 1544 Viel, Montreal, Quebec,
FEASIBILITY OF ELECTRICAL SEPARATION OF PROXIMATE GROUNDING SYSTEMS AS A FUNCTION OF SOIL STRUCTURE Sharon Tee and Farid P. Dawalibi Safe Engineering Services & technologies ltd. 1544 Viel, Montreal, Quebec,
Physics 210 Q1 2012 ( PHYSICS210BRIDGE ) My Courses Course Settings
 1 of 11 9/7/2012 1:06 PM Logged in as Julie Alexander, Instructor Help Log Out Physics 210 Q1 2012 ( PHYSICS210BRIDGE ) My Courses Course Settings Course Home Assignments Roster Gradebook Item Library
1 of 11 9/7/2012 1:06 PM Logged in as Julie Alexander, Instructor Help Log Out Physics 210 Q1 2012 ( PHYSICS210BRIDGE ) My Courses Course Settings Course Home Assignments Roster Gradebook Item Library
BSEE Degree Plan Bachelor of Science in Electrical Engineering: 2015-16
 BSEE Degree Plan Bachelor of Science in Electrical Engineering: 2015-16 Freshman Year ENG 1003 Composition I 3 ENG 1013 Composition II 3 ENGR 1402 Concepts of Engineering 2 PHYS 2034 University Physics
BSEE Degree Plan Bachelor of Science in Electrical Engineering: 2015-16 Freshman Year ENG 1003 Composition I 3 ENG 1013 Composition II 3 ENGR 1402 Concepts of Engineering 2 PHYS 2034 University Physics
ADVANCED APPLICATIONS OF ELECTRICAL ENGINEERING
 Development of a Software Tool for Performance Evaluation of MIMO OFDM Alamouti using a didactical Approach as a Educational and Research support in Wireless Communications JOSE CORDOVA, REBECA ESTRADA
Development of a Software Tool for Performance Evaluation of MIMO OFDM Alamouti using a didactical Approach as a Educational and Research support in Wireless Communications JOSE CORDOVA, REBECA ESTRADA
Transmission Lines in Communication Systems FACET
 Computer-Based Electronics Training System Transmission Lines in Communication Systems FACET 36970- Order no.: 36970-00 First Edition Revision level: 02/2015 By the staff of Festo Didactic Festo Didactic
Computer-Based Electronics Training System Transmission Lines in Communication Systems FACET 36970- Order no.: 36970-00 First Edition Revision level: 02/2015 By the staff of Festo Didactic Festo Didactic
Mathematics (MAT) MAT 061 Basic Euclidean Geometry 3 Hours. MAT 051 Pre-Algebra 4 Hours
 MAT 051 Pre-Algebra Mathematics (MAT) MAT 051 is designed as a review of the basic operations of arithmetic and an introduction to algebra. The student must earn a grade of C or in order to enroll in MAT
MAT 051 Pre-Algebra Mathematics (MAT) MAT 051 is designed as a review of the basic operations of arithmetic and an introduction to algebra. The student must earn a grade of C or in order to enroll in MAT
DEGREE: Bachelor's Degree in Industrial Electronics and Automation COURSE: 1º TERM: 2º WEEKLY PLANNING
 SESSION WEEK COURSE: Physics II DEGREE: Bachelor's Degree in Industrial Electronics and Automation COURSE: 1º TERM: 2º WEEKLY PLANNING DESCRIPTION GROUPS (mark ) Indicate YES/NO If the session needs 2
SESSION WEEK COURSE: Physics II DEGREE: Bachelor's Degree in Industrial Electronics and Automation COURSE: 1º TERM: 2º WEEKLY PLANNING DESCRIPTION GROUPS (mark ) Indicate YES/NO If the session needs 2
Chapter 7: Polarization
 Chapter 7: Polarization Joaquín Bernal Méndez Group 4 1 Index Introduction Polarization Vector The Electric Displacement Vector Constitutive Laws: Linear Dielectrics Energy in Dielectric Systems Forces
Chapter 7: Polarization Joaquín Bernal Méndez Group 4 1 Index Introduction Polarization Vector The Electric Displacement Vector Constitutive Laws: Linear Dielectrics Energy in Dielectric Systems Forces
