A wave lab inside a coaxial cable
|
|
|
- Gilbert Hunter
- 10 years ago
- Views:
Transcription
1 INSTITUTE OF PHYSICS PUBLISHING Eur. J. Phys. 25 (2004) EUROPEAN JOURNAL OF PHYSICS PII: S (04)76273-X A wave lab inside a coaxial cable JoãoMSerra,MiguelCBrito,JMaiaAlves and A M Vallera Departamento Física, CFMC, Faculdade de Ciências Universidade de Lisboa, Edificio C8, Campo Grande, Lisboa, Portugal [email protected] Received 16 February 2004 Published 10 June 2004 Online at stacks.iop.org/ejp/25/581 doi: / /25/5/001 Abstract The study of electromagnetic wave propagation in a coaxial cable can be a powerful approach to the study of waves at an undergraduate level. This study can explore different experimental situations, going from those where the finite velocity of propagation must be considered (distributed or transmission line behaviour), to those where this velocity may be considered infinite (lumped behaviour). We believe that the student observation of the existence of these two regimes can be important for the understanding of wave phenomena in general. In this work we show that this can be achieved using low-cost equipment and a set of quite simple experiments, such as the measurement of wave propagation velocity or the study of standing waves and resonance. The results obtained in a coherent set of selected experiments are discussed. 1. Introduction Experimental activities aimed at the exploration of the distributed or transmission line behaviour of a coaxial cable are usually undertaken using very expensive pulse generators and high speed oscilloscopes [1 4]. Moreover, these experimental activities are not designed to show that in the limit of very large pulse widths (compared with transit time in the transmission line) the physics of the coaxial cable can be well understood in the framework of circuit theory and how both descriptions become equivalent. For these reasons, we have planned a coherent set of simple experiments to explore both limits (propagation time higher than pulse width and pulse width much larger than propagation time) and designed a low-cost kit specially suited for this purpose (this can be easily done if long cables are used). We shall start by making a quick review of some well-known fundamental properties of a coaxial cable, that can be found in almost any course on electromagnetism [5]. A coaxial cable can be described as a transmission line with cylindrical geometry, composed of a central conductor, with diameter r i, and an external tube-shaped conductor, with diameter r e. The space between these two conductors is filled with a dielectric /04/ $30.00 c 2004 IOP Publishing Ltd Printed in the UK 581
2 582 JMSerraet al Electromagnetic waves will propagate in the direction of cable length and the associated fields will have nonzero values mainly in the dielectric, being shielded from the exterior by the external conductor. Considering this geometry, and assuming that the boundary conditions of the dielectric are imposed by perfectly conducting walls (the conductor surfaces), the field lines are quite simple to predict: the electric field must be normal to these walls and will thus have radial field lines, while the magnetic field must be tangential to the conductor surfaces, which means that magnetic field lines are essentially circular. Using Gauss theorem and Ampere s law, the capacitance and the self-inductance of this transmission line, per unit length, are easily calculated to be C l = 2πε ln r L e l = µ r i 2π ln r e (1) r i where ε represents the dielectric constant and µ is the magnetic permeability of the dielectric (which will be considered equal to the magnetic permeability of vacuum, µ 0 ). Since the electric (E E ) and magnetic energy (E M ) densities are equal we can write E E = 1 2 C lv 2 = E M = 1 2 L li 2 (2) where V and I represent the potential and electric current at the same point, respectively. The ratio V/I is thus a constant that depends only on the dielectric constant, the magnetic permeability of the medium and the geometry of the cable. This constant is usually called its characteristic impedance, Z 0. Combining equations (1) and (2) we obtain Z 0 = V I = L l = 1 C l 2π µ0 ε ln r e r i. (3) The velocity of propagation of the electromagnetic waves is given by c = 1 = c 0 (4) εµ0 n where c 0 stands for the light velocity in vacuum and n = ε rel represents the refractive index of the dielectric. If the line is terminated with a purely resistive load of impedance R then waves will be reflected at the end of the line. The reflection coefficient R depends on the boundary conditions according to R= R Z 0 R + Z 0. (5) 2. Experimental setup The kit, shown in figure 1, consists of a specially built pulse generator, one (or more) 50 m long RG58 coaxial cable(s) and coupling boxes to adjust the impedance of the cable ends and set the desired length. The pulse generator was designed to meet the following requirements: low cost and simple to build, adjustable pulse width capability, and repetition rate compatible with the use of a low-cost 20 MHz oscilloscope. Figure 2 shows the electric schematics of the pulse generator developed according to these requirements. The main specifications of the pulse generator are 15 V output in open circuit conditions, 50 output impedance, pulse width adjustable from 35 ns to 10 µs with a fall time of 10 ns, and a repetition rate that can be adjusted from 3 to 50 khz. A pre-pulse signal for synchronizing the oscilloscope is also available at the front panel of the unit. In figure 3 we
3 A wave lab inside a coaxial cable 583 Figure 1. Experimental setup: the coaxial cable wave propagation kit. Figure 2. Schematics of the pulse generator. (a) (b) Figure 3. The coupling box can be used to (a) set the terminating impedance of the coaxial cable or (b) as a coupling circuit. show a picture of one of the coupling boxes that can be used to insert a variable terminating impedance for the coaxial cable (figure 3(a)) or to couple two cables together (figure 3(b)).
4 584 JMSerraet al Any of these two functions can easily be selected by the user by simply inserting a (variable) resistor or a copper conductor in the appropriate position. 3. Experimental activities 3.1. Wave propagation velocity and reflection coefficient We shall start with a classic experimental situation that clearly shows the distributed or transmission line behaviour of a coaxial cable. This will happen if the time of propagation of an electrical pulse in the transmission line (l/c) has at least the same order of magnitude as the pulse width. In this limit, the coaxial cable can be described as an extended network where electromagnetic wave propagation must be taken into account. In figure 4 we show photographs of the signals that can be measured with a 20 MHz oscilloscope when a voltage pulse is introduced in a 100 m long coaxial cable. Each of the three insets corresponds to what is measured at the beginning and end of the cable for different boundary conditions at the end of the cable (open, 50 resistor and short circuit). Students should be alerted to the fact that, since we are exploring the transmission line behaviour of the coaxial cable, the conductors are not in general equipotentials and for that reason the ground connection must be made in the end of the cable in which measurements are being made. The discussion of these signals can be interesting for the student since it will show the exact meaning of having a reflection coefficient R=±1 (open or short circuited end) and R=0 when the purely resistive cable termination has an impedance that equals the characteristic cable impedance. Comparing the signals measured at the end of the cable with the echoes received at the origin will help students to understand the mirror wave concept [7] (R =±1) and the energy absorption that occurs when the wave enters a purely resistive medium with the same characteristic impedance (R =0) [7]. Note that this is precisely what happens at the beginning of the cable because the pulse generator output impedance is adjusted to 50. If a variable resistor is inserted at the cable end coupling box, students will be able to continuously change the reflection coefficient from 1 to close to +1 and observe the evolution of the different signals. When the terminating resistance R is larger than Z 0 the reflected impulse has the same polarity as the incident one. If R exactly matches Z 0 there is no reflected signal. If R is smaller than Z 0 the reflected pulse has the opposite polarity of the incident one. The characteristic impedance Z 0 of the cable can thus be determined by adjusting a variable resistor at the end of the cable in order to eliminate the reflected impulse. Using the falling edges of two pulses to measure the pulse transit time and knowing the corresponding travelled length, one can calculate the velocity of electromagnetic waves in the transmission line. In particular, from figures 4(a) and (c) the time transit corresponding to a 200 m distance is about 1 µs. The velocity of electromagnetic waves in this transmission line is therefore roughly c = 2l / t ms 1 = ms c 0. This experimental value is to be compared with the value ms 1 that can be computed using equation (3) and the tabulated properties for the cable RG-58 [6], namely, ε = Fm 1. If one compares the amplitude and shape of the pulses as they travel longer distances in the transmission line it becomes quite clear (figure 4) that high frequency Fourier components of the pulse are preferentially attenuated, since the echoes look much less sharper than the
5 A wave lab inside a coaxial cable 585 (a) (b) (c) Figure 4. Signals measured at the beginning (top) and end (bottom) of the cable corresponding to different boundary conditions at the end of the cable: (a) open end; (b) 50 resistor end; (c) short-circuited end. The cable length is 100 m. original pulses. This is what is to be expected in a dispersive medium where the propagation velocity depends on the frequency.
6 586 JMSerraet al 10 Amplitude/ V y = -0,0064x + 6, Distance/m Figure 5. Pulse losses in the transmission line. (a) (b) Figure 6. Multiple reflections in the coaxial cavity configuration corresponding to (a) open end and (b) short circuited end. In figure 5 we represent the amplitude of the pulse as a function of travelled distance. The amplitude decays exponentially with distance and from the best line fit coefficient adjusted to the results we can obtain a pulse loss coefficient (analogous to an absorption coefficient that can be rigorously defined for a single frequency) which we find to be about db m Multiple reflections If we introduce a resistor with an impedance greater than the characteristic impedance of the cable (for instance 1 k ) at the input of the transmission line (i.e. between the pulse generator and the cable), we will have a reflected wave at the beginning of the cable, just as we have at the end (since the impedance seen by the echo is no longer the output impedance of the pulse generator). This can be done simply by using a small coaxial cable connecting the pulse generator to a coupling box whose other terminal is connected to the transmission line, and inserting the resistor in place of the copper wire that is used to connect cables (figure 3(b)). In this case the cable will act as a cavity for the electromagnetic waves. Successive echoes, with decreasing amplitude due to attenuation along the length of the cable, will travel back and forward in the transmission line. Figure 6 shows a photograph of the signal as measured
7 A wave lab inside a coaxial cable Voltage [V] Time [µs] Figure 7. Measured signal at the input of the transmission line for increasing pulse widths. The solid dark line shows the fit to the experimental data using RC circuit theory. at the input of the coaxial cable. The two lines correspond to different boundary conditions at the cable end: (a) open end; (b) short-circuited end Multiple reflections in the limit of long pulse width Now, if one increases the pulse width, the successive pulses start adding up, since the reflected pulse arrives before the end of the input pulse. In the limit situation, when the pulses can be well described by Heaviside-type functions (meaning that they last until the amplitude of the reflected echoes is almost zero) the coaxial cable can be described as a capacitor, since all points of the cable are at the same potential. Figure 7 shows the signal measured with the oscilloscope at the beginning of the cable for increasing pulse widths. The measured signal is clearly approaching the typical capacitance charge curve seen for RC circuits. So, in this limit of slowly varying potentials, circuit theory comes in. Assuming that we use a resistor R to create the electromagnetic cavity and that the output of the pulse generator is a pulse with amplitude V 0, the resulting pulse on the cable will have an amplitude given by V 0 [Z 0 /(R + Z 0 )]. If the cable end is open (reflection coefficient at this end equal to unity) the voltage at the beginning of the coaxial cable after n reflections will then be [ ] 2Z 0 V n = V 0 [1 + R + R R n ] (6) (R + Z 0 ) where R represents the reflection coefficient at the beginning of the transmission line for waves propagating from the end to the beginning of the cable. In the limit when n goes to infinity the geometric series converges and we will have [ ][ 2Z 0 1 V = V 0 (R + Z 0 ) (1 R) ]. (7) Using the definition of R (equation (5)), it can be easily seen that the voltage measured at the beginning of the cable will go to V 0 for large n, as it should be if the cable can be well represented by a capacitor in this limit.
8 588 JMSerraet al The ratio V n+1 /V n can be written as V(t n+1 ) = 1 R(n+1) where t V(t n ) 1 R n (n+1) = t n + 2l c. (8) From circuit theory we know that if we apply a Heaviside pulse of amplitude V 0 in a cable with a capacitance C, connected to the pulse generator through a resistor R, the voltage V c (t) is given by ( ) V c (t) = V 0 1 e t τ (9) where the time constant τ is equal to the RC time constant. From the circuit theory point of view, equation (8) should then be written as V(t n+1 ) V(t n ) = 1 e (n+1) 2l cτ 2l n 1 e cτ Comparing equations (8) and (10) we must conclude that. (10) 2l n e cτ =R n τ = 2l c ln(r). (11) For R close to unity (R Z 0 ) we can expand ln(r) in series retaining only the first term. Equation (11) will then be approximated by [ ] = l c τ 2l 1 (R + Z 0 ). (12) c (R 1) Z 0 Once again using the fact that R is close to unity, we can make another approximation taking (R + Z 0 ) R. Under these circumstances, and using equation (4), we can rewrite equation (12) in the form τ l c R = l εµ0 R. (13) Z 0 Z 0 Since from circuit theory τ = RC we conclude that the quantity (l εµ 0 )/Z 0 must be the capacitance of the transmission line, C TL, that we can use to model our transmission line as a lumped network in the limit of large pulse widths. Using equations (3) and (13) we can write C TL in the form C TL = l 2πε ln ( r e ) (14) r i which is consistent with the capacitance per unit length expressed by equation (1). The solid dark line shown in figure 7 yields a time constant of 5.22 µs. Since a 1 k resistor was used to create the electromagnetic cavity this means that the measured capacitance of the cable is about F, corresponding to a capacitance of about 99 pf m 1 (the cable is 50 m long). This value is in good agreement with what is obtained from equation (1): pf m Resonances in the electromagnetic cavity If we now introduce a sinusoidal signal in the electromagnetic cavity (using a common signal generator instead of our pulse generator), wave theory tells us that standing waves will appear, since waves travelling in opposite directions will interfere with each other. For a discrete set of frequencies (that depend on the boundary conditions) we will have a resonance in the cavity. If the end of the cable is left open (R =+1) this set is composed of frequencies such that the cable length is an integer multiple of λ/2. If the cable end is short circuited (R =0) we will have a resonance when the cable length is an odd multiple of λ/4.
9 A wave lab inside a coaxial cable 589 (a) (b) (c) Figure 8. Standing waves inside a coaxial cable with both ends open. The insets show signals measured at the beginning (a), halfway (b) and end of the cable (c) for the first three resonance frequencies. In figure 8 we show the signals measured at the two ends and in the middle of the coaxial cable for the first three resonance frequencies (304 khz, 612 khz and 925 khz) with the cable end open. In fact the origin of the cable is not entirely open because this cable end is closed through a 1 k resistor. For the top inset, the wavelength is twice the cable length, and the node occurs at the middle. Note the 180 phase difference between ends. The next resonance frequency is shown in the middle inset. Here the wavelength is equal to the cable length, and the nodes occur now at l/4 and 3l/4. As expected the signal in the middle is at 180 with the end signals. When we reach the next resonance frequency (wavelength equal to 2l/3) we again have a node at the middle of the cable. However, the phase relationship of the potential between ends has now changed from 0 to 180. It should be noted that we never have an exact zero in the middle of the cable as should be expected since waves are attenuated as they
10 590 JMSerraet al (a) (b) (c) Figure 9. Standing waves inside a coaxial cable with one end open and one end shorted. The insets show signals measured at the beginning (a), halfway (b) and at the end of the cable (c) for the first three resonance frequencies. propagate in the transmission line and the reflection coefficient near the signal generator is smaller than 1. In figure 9 we show equivalent signals for the first three resonant frequencies (146 khz, 460 khz and 781 khz) with the cable end shorted. Once again the phase relationship between the signals is in good agreement with what is to be expected as can be seen by comparison with the schemes close to the images. Using all the measured frequencies we can compute the propagation velocity c. The mean value obtained by this calculation is ms 1, showing once again the internal consistency of all the results. When pulse attenuation was discussed it was argued that progressive pulse rounding as they travel in the transmission line could be a consequence of an attenuation increase with frequency. That this is the case, can be seen in figure 10 where the maximum amplitude of the resonance is represented as a function of frequency (results obtained with a 350 m cable
11 A wave lab inside a coaxial cable Voltage [V] Frequency [KHz] Figure 10. Amplitude of resonance as a function of frequency. using always the same input amplitude for the sine wave). The resonance amplitude clearly decreases with frequency showing qualitatively that we have in fact an increase in attenuation at higher frequencies. 4. Conclusions We have presented a low-cost kit for the study of electromagnetic wave propagation using a coaxial cable. Different levels of experiments can be carried out, illustrating several concepts of wave propagation such as boundary conditions, standing waves and dispersive effects. Also, a cross bridge from wave theory to circuit theory is extremely simple to illustrate using this equipment. We must emphasize the good internal coherency of all the results that can be obtained using this equipment. References [1] dodds/files231/expt04.pdf [2] coan/4211/cable.ps [3] www2.physics.umd.edu/ gcchang/courses/phys375/common/lab2.ps [4] pulse.pdf [5] Lorrain P and Corson D 1970 Electromagnetic Fields and Waves 2nd edn (New York: Freeman) [6] [7] phys15c/lectures/lect09.ppt
PHY3128 / PHYM203 (Electronics / Instrumentation) Transmission Lines. Repeated n times I L
 Transmission Lines Introduction A transmission line guides energy from one place to another. Optical fibres, waveguides, telephone lines and power cables are all electromagnetic transmission lines. are
Transmission Lines Introduction A transmission line guides energy from one place to another. Optical fibres, waveguides, telephone lines and power cables are all electromagnetic transmission lines. are
Transmission Lines in Communication Systems FACET
 Computer-Based Electronics Training System Transmission Lines in Communication Systems FACET 36970- Order no.: 36970-00 First Edition Revision level: 02/2015 By the staff of Festo Didactic Festo Didactic
Computer-Based Electronics Training System Transmission Lines in Communication Systems FACET 36970- Order no.: 36970-00 First Edition Revision level: 02/2015 By the staff of Festo Didactic Festo Didactic
T = 1 f. Phase. Measure of relative position in time within a single period of a signal For a periodic signal f(t), phase is fractional part t p
 Data Transmission Concepts and terminology Transmission terminology Transmission from transmitter to receiver goes over some transmission medium using electromagnetic waves Guided media. Waves are guided
Data Transmission Concepts and terminology Transmission terminology Transmission from transmitter to receiver goes over some transmission medium using electromagnetic waves Guided media. Waves are guided
DRAFT. University of Pennsylvania Moore School of Electrical Engineering ESE319 Electronic Circuits - Modeling and Measurement Techniques
 University of Pennsylvania Moore School of Electrical Engineering ESE319 Electronic Circuits - Modeling and Measurement Techniques 1. Introduction. Students are often frustrated in their attempts to execute
University of Pennsylvania Moore School of Electrical Engineering ESE319 Electronic Circuits - Modeling and Measurement Techniques 1. Introduction. Students are often frustrated in their attempts to execute
Grounding Demystified
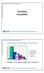 Grounding Demystified 3-1 Importance Of Grounding Techniques 45 40 35 30 25 20 15 10 5 0 Grounding 42% Case 22% Cable 18% Percent Used Filter 12% PCB 6% Grounding 42% Case Shield 22% Cable Shielding 18%
Grounding Demystified 3-1 Importance Of Grounding Techniques 45 40 35 30 25 20 15 10 5 0 Grounding 42% Case 22% Cable 18% Percent Used Filter 12% PCB 6% Grounding 42% Case Shield 22% Cable Shielding 18%
Digital Systems Ribbon Cables I CMPE 650. Ribbon Cables A ribbon cable is any cable having multiple conductors bound together in a flat, wide strip.
 Ribbon Cables A ribbon cable is any cable having multiple conductors bound together in a flat, wide strip. Each dielectric configuration has different high-frequency characteristics. All configurations
Ribbon Cables A ribbon cable is any cable having multiple conductors bound together in a flat, wide strip. Each dielectric configuration has different high-frequency characteristics. All configurations
SECTION 2 Transmission Line Theory
 SEMICONDUCTOR DESIGN GUIDE Transmission Line Theory SECTION 2 Transmission Line Theory Introduction The ECLinPS family has pushed the world of ECL into the realm of picoseconds. When output transitions
SEMICONDUCTOR DESIGN GUIDE Transmission Line Theory SECTION 2 Transmission Line Theory Introduction The ECLinPS family has pushed the world of ECL into the realm of picoseconds. When output transitions
An equivalent circuit of a loop antenna.
 3.2.1. Circuit Modeling: Loop Impedance A loop antenna can be represented by a lumped circuit when its dimension is small with respect to a wavelength. In this representation, the circuit parameters (generally
3.2.1. Circuit Modeling: Loop Impedance A loop antenna can be represented by a lumped circuit when its dimension is small with respect to a wavelength. In this representation, the circuit parameters (generally
Application Note. So You Need to Measure Some Inductors?
 So You Need to Measure Some nductors? Take a look at the 1910 nductance Analyzer. Although specifically designed for production testing of inductors and coils, in addition to measuring inductance (L),
So You Need to Measure Some nductors? Take a look at the 1910 nductance Analyzer. Although specifically designed for production testing of inductors and coils, in addition to measuring inductance (L),
LOW COST MOTOR PROTECTION FILTERS FOR PWM DRIVE APPLICATIONS STOPS MOTOR DAMAGE
 LOW COST MOTOR PROTECTION FILTERS FOR PWM DRIVE APPLICATIONS STOPS MOTOR DAMAGE Karl M. Hink, Executive Vice President Originally presented at the Power Quality 99 Conference ABSTRACT Motor protection
LOW COST MOTOR PROTECTION FILTERS FOR PWM DRIVE APPLICATIONS STOPS MOTOR DAMAGE Karl M. Hink, Executive Vice President Originally presented at the Power Quality 99 Conference ABSTRACT Motor protection
Experimental results for the focal waveform and beam width in the focusing lens with a 100 ps filter
 EM Implosion Memos Memo 51 July, 2010 Experimental results for the focal waveform and beam width in the focusing lens with a 100 ps filter Prashanth Kumar, Carl E. Baum, Serhat Altunc, Christos G. Christodoulou
EM Implosion Memos Memo 51 July, 2010 Experimental results for the focal waveform and beam width in the focusing lens with a 100 ps filter Prashanth Kumar, Carl E. Baum, Serhat Altunc, Christos G. Christodoulou
Edmund Li. Where is defined as the mutual inductance between and and has the SI units of Henries (H).
 INDUCTANCE MUTUAL INDUCTANCE If we consider two neighbouring closed loops and with bounding surfaces respectively then a current through will create a magnetic field which will link with as the flux passes
INDUCTANCE MUTUAL INDUCTANCE If we consider two neighbouring closed loops and with bounding surfaces respectively then a current through will create a magnetic field which will link with as the flux passes
potential in the centre of the sphere with respect to infinity.
 Umeå Universitet, Fysik 1 Vitaly Bychkov Prov i fysik, Electricity and Waves, 2006-09-27, kl 16.00-22.00 Hjälpmedel: Students can use any book. Define the notations you are using properly. Present your
Umeå Universitet, Fysik 1 Vitaly Bychkov Prov i fysik, Electricity and Waves, 2006-09-27, kl 16.00-22.00 Hjälpmedel: Students can use any book. Define the notations you are using properly. Present your
Standex-Meder Electronics. Custom Engineered Solutions for Tomorrow
 Standex-Meder Electronics Custom Engineered Solutions for Tomorrow RF Reed Relays Part II Product Training Copyright 2013 Standex-Meder Electronics. All rights reserved. Introduction Purpose Designing
Standex-Meder Electronics Custom Engineered Solutions for Tomorrow RF Reed Relays Part II Product Training Copyright 2013 Standex-Meder Electronics. All rights reserved. Introduction Purpose Designing
Introduction to acoustic imaging
 Introduction to acoustic imaging Contents 1 Propagation of acoustic waves 3 1.1 Wave types.......................................... 3 1.2 Mathematical formulation.................................. 4 1.3
Introduction to acoustic imaging Contents 1 Propagation of acoustic waves 3 1.1 Wave types.......................................... 3 1.2 Mathematical formulation.................................. 4 1.3
PHY114 S11 Term Exam 3
 PHY4 S Term Exam S. G. Rajeev Mar 2 20 2:0 pm to :45 pm PLEASE write your workshop number and your workshop leader s name at the top of your book, so that you can collect your graded exams at the workshop.
PHY4 S Term Exam S. G. Rajeev Mar 2 20 2:0 pm to :45 pm PLEASE write your workshop number and your workshop leader s name at the top of your book, so that you can collect your graded exams at the workshop.
Crosstalk effects of shielded twisted pairs
 This article deals with the modeling and simulation of shielded twisted pairs with CST CABLE STUDIO. The quality of braided shields is investigated with respect to perfect solid shields. Crosstalk effects
This article deals with the modeling and simulation of shielded twisted pairs with CST CABLE STUDIO. The quality of braided shields is investigated with respect to perfect solid shields. Crosstalk effects
Measuring Parasitic Capacitance and Inductance Using TDR
 Measuring Parasitic apacitance and Inductance Using TDR Time-domain reflectometry (TDR) is commonly used as a convenient method of determining the characteristic impedance of a transmission line or quantifying
Measuring Parasitic apacitance and Inductance Using TDR Time-domain reflectometry (TDR) is commonly used as a convenient method of determining the characteristic impedance of a transmission line or quantifying
Introduction to the Smith Chart for the MSA Sam Wetterlin 10/12/09 Z +
 Introduction to the Smith Chart for the MSA Sam Wetterlin 10/12/09 Quick Review of Reflection Coefficient The Smith chart is a method of graphing reflection coefficients and impedance, and is often useful
Introduction to the Smith Chart for the MSA Sam Wetterlin 10/12/09 Quick Review of Reflection Coefficient The Smith chart is a method of graphing reflection coefficients and impedance, and is often useful
Physics 9e/Cutnell. correlated to the. College Board AP Physics 1 Course Objectives
 Physics 9e/Cutnell correlated to the College Board AP Physics 1 Course Objectives Big Idea 1: Objects and systems have properties such as mass and charge. Systems may have internal structure. Enduring
Physics 9e/Cutnell correlated to the College Board AP Physics 1 Course Objectives Big Idea 1: Objects and systems have properties such as mass and charge. Systems may have internal structure. Enduring
Engineering Sciences 151. Electromagnetic Communication Laboratory Assignment 3 Fall Term 1998-99
 Engineering Sciences 151 Electromagnetic Communication Laboratory Assignment 3 Fall Term 1998-99 WAVE PROPAGATION II: HIGH FREQUENCY SLOTTED LINE AND REFLECTOMETER MEASUREMENTS OBJECTIVES: To build greater
Engineering Sciences 151 Electromagnetic Communication Laboratory Assignment 3 Fall Term 1998-99 WAVE PROPAGATION II: HIGH FREQUENCY SLOTTED LINE AND REFLECTOMETER MEASUREMENTS OBJECTIVES: To build greater
Understanding SWR by Example
 Understanding SWR by Example Take the mystery and mystique out of standing wave ratio. Darrin Walraven, K5DVW It sometimes seems that one of the most mysterious creatures in the world of Amateur Radio
Understanding SWR by Example Take the mystery and mystique out of standing wave ratio. Darrin Walraven, K5DVW It sometimes seems that one of the most mysterious creatures in the world of Amateur Radio
MEASUREMENT SET-UP FOR TRAPS
 Completed on 26th of June, 2012 MEASUREMENT SET-UP FOR TRAPS AUTHOR: IW2FND Attolini Lucio Via XXV Aprile, 52/B 26037 San Giovanni in Croce (CR) - Italy [email protected] Trappole_01_EN 1 1 DESCRIPTION...3
Completed on 26th of June, 2012 MEASUREMENT SET-UP FOR TRAPS AUTHOR: IW2FND Attolini Lucio Via XXV Aprile, 52/B 26037 San Giovanni in Croce (CR) - Italy [email protected] Trappole_01_EN 1 1 DESCRIPTION...3
Oscar E. Morel UtilX Corporation
 Oscar E. Morel UtilX Corporation Time Domain Reflectometry (TDR) has been the preferred technique to assess: Cable length Splice number and spatial location, and Metallic neutral condition Tests for neutral
Oscar E. Morel UtilX Corporation Time Domain Reflectometry (TDR) has been the preferred technique to assess: Cable length Splice number and spatial location, and Metallic neutral condition Tests for neutral
Rock Bolt Condition Monitoring Using Ultrasonic Guided Waves
 Rock Bolt Condition Monitoring Using Ultrasonic Guided Waves Bennie Buys Department of Mechanical and Aeronautical Engineering University of Pretoria Introduction Rock Bolts and their associated problems
Rock Bolt Condition Monitoring Using Ultrasonic Guided Waves Bennie Buys Department of Mechanical and Aeronautical Engineering University of Pretoria Introduction Rock Bolts and their associated problems
ELECTRON SPIN RESONANCE Last Revised: July 2007
 QUESTION TO BE INVESTIGATED ELECTRON SPIN RESONANCE Last Revised: July 2007 How can we measure the Landé g factor for the free electron in DPPH as predicted by quantum mechanics? INTRODUCTION Electron
QUESTION TO BE INVESTIGATED ELECTRON SPIN RESONANCE Last Revised: July 2007 How can we measure the Landé g factor for the free electron in DPPH as predicted by quantum mechanics? INTRODUCTION Electron
Impedance Matching and Matching Networks. Valentin Todorow, December, 2009
 Impedance Matching and Matching Networks Valentin Todorow, December, 2009 RF for Plasma Processing - Definition of RF What is RF? The IEEE Standard Dictionary of Electrical and Electronics Terms defines
Impedance Matching and Matching Networks Valentin Todorow, December, 2009 RF for Plasma Processing - Definition of RF What is RF? The IEEE Standard Dictionary of Electrical and Electronics Terms defines
AVX EMI SOLUTIONS Ron Demcko, Fellow of AVX Corporation Chris Mello, Principal Engineer, AVX Corporation Brian Ward, Business Manager, AVX Corporation
 AVX EMI SOLUTIONS Ron Demcko, Fellow of AVX Corporation Chris Mello, Principal Engineer, AVX Corporation Brian Ward, Business Manager, AVX Corporation Abstract EMC compatibility is becoming a key design
AVX EMI SOLUTIONS Ron Demcko, Fellow of AVX Corporation Chris Mello, Principal Engineer, AVX Corporation Brian Ward, Business Manager, AVX Corporation Abstract EMC compatibility is becoming a key design
Step Response of RC Circuits
 Step Response of RC Circuits 1. OBJECTIVES...2 2. REFERENCE...2 3. CIRCUITS...2 4. COMPONENTS AND SPECIFICATIONS...3 QUANTITY...3 DESCRIPTION...3 COMMENTS...3 5. DISCUSSION...3 5.1 SOURCE RESISTANCE...3
Step Response of RC Circuits 1. OBJECTIVES...2 2. REFERENCE...2 3. CIRCUITS...2 4. COMPONENTS AND SPECIFICATIONS...3 QUANTITY...3 DESCRIPTION...3 COMMENTS...3 5. DISCUSSION...3 5.1 SOURCE RESISTANCE...3
Transistor Amplifiers
 Physics 3330 Experiment #7 Fall 1999 Transistor Amplifiers Purpose The aim of this experiment is to develop a bipolar transistor amplifier with a voltage gain of minus 25. The amplifier must accept input
Physics 3330 Experiment #7 Fall 1999 Transistor Amplifiers Purpose The aim of this experiment is to develop a bipolar transistor amplifier with a voltage gain of minus 25. The amplifier must accept input
Eatman Associates 2014 Rockwall TX 800-388-4036 rev. October 1, 2014. Striplines and Microstrips (PCB Transmission Lines)
 Eatman Associates 2014 Rockwall TX 800-388-4036 rev. October 1, 2014 Striplines and Microstrips (PCB Transmission Lines) Disclaimer: This presentation is merely a compilation of information from public
Eatman Associates 2014 Rockwall TX 800-388-4036 rev. October 1, 2014 Striplines and Microstrips (PCB Transmission Lines) Disclaimer: This presentation is merely a compilation of information from public
TIMING SIGNALS, IRIG-B AND PULSES
 TIMING SIGNALS, IRIG-B AND PULSES Document No. PD0043200B July 2013 Arbiter Systems, Inc. 1324 Vendels Circle, Suite 121 Paso Robles, CA 93446 U.S.A. (805) 237-3831, (800) 321-3831 http://www.arbiter.com
TIMING SIGNALS, IRIG-B AND PULSES Document No. PD0043200B July 2013 Arbiter Systems, Inc. 1324 Vendels Circle, Suite 121 Paso Robles, CA 93446 U.S.A. (805) 237-3831, (800) 321-3831 http://www.arbiter.com
EMC STANDARDS STANDARDS AND STANDARD MAKING BODIES. International. International Electrotechnical Commission (IEC) http://www.iec.
 EMC STANDARDS The EMC standards that a particular electronic product must meet depend on the product application (commercial or military) and the country in which the product is to be used. These EMC regulatory
EMC STANDARDS The EMC standards that a particular electronic product must meet depend on the product application (commercial or military) and the country in which the product is to be used. These EMC regulatory
Physics 25 Exam 3 November 3, 2009
 1. A long, straight wire carries a current I. If the magnetic field at a distance d from the wire has magnitude B, what would be the the magnitude of the magnetic field at a distance d/3 from the wire,
1. A long, straight wire carries a current I. If the magnetic field at a distance d from the wire has magnitude B, what would be the the magnitude of the magnetic field at a distance d/3 from the wire,
Vector Network Analyzer Techniques to Measure WR340 Waveguide Windows
 LS-296 Vector Network Analyzer Techniques to Measure WR340 Waveguide Windows T. L. Smith ASD / RF Group Advanced Photon Source Argonne National Laboratory June 26, 2002 Table of Contents 1) Introduction
LS-296 Vector Network Analyzer Techniques to Measure WR340 Waveguide Windows T. L. Smith ASD / RF Group Advanced Photon Source Argonne National Laboratory June 26, 2002 Table of Contents 1) Introduction
5. Measurement of a magnetic field
 H 5. Measurement of a magnetic field 5.1 Introduction Magnetic fields play an important role in physics and engineering. In this experiment, three different methods are examined for the measurement of
H 5. Measurement of a magnetic field 5.1 Introduction Magnetic fields play an important role in physics and engineering. In this experiment, three different methods are examined for the measurement of
HOW TO SELECT VARISTORS
 HOW TO SELECT VARISTORS We have three alternatives: - selection of the varistors suitable for the operating voltage of the application - calculating the surge current, energy absorption and average power
HOW TO SELECT VARISTORS We have three alternatives: - selection of the varistors suitable for the operating voltage of the application - calculating the surge current, energy absorption and average power
Chapter 4: Passive Analog Signal Processing
 hapter 4: Passive Analog Signal Processing In this chapter we introduce filters and signal transmission theory. Filters are essential components of most analog circuits and are used to remove unwanted
hapter 4: Passive Analog Signal Processing In this chapter we introduce filters and signal transmission theory. Filters are essential components of most analog circuits and are used to remove unwanted
Shielding Effectiveness Test Method. Harbour s LL, SB, and SS Coaxial Cables. Designs for Improved Shielding Effectiveness
 Shielding Effectiveness Test Method Harbour s LL, SB, and SS Coaxial Cables Designs for Improved Shielding Effectiveness Harbour Industries 4744 Shelburne Road Shelburne Vermont 05482 USA 802-985-3311
Shielding Effectiveness Test Method Harbour s LL, SB, and SS Coaxial Cables Designs for Improved Shielding Effectiveness Harbour Industries 4744 Shelburne Road Shelburne Vermont 05482 USA 802-985-3311
Experiment 7: Familiarization with the Network Analyzer
 Experiment 7: Familiarization with the Network Analyzer Measurements to characterize networks at high frequencies (RF and microwave frequencies) are usually done in terms of scattering parameters (S parameters).
Experiment 7: Familiarization with the Network Analyzer Measurements to characterize networks at high frequencies (RF and microwave frequencies) are usually done in terms of scattering parameters (S parameters).
Reading: HH Sections 4.11 4.13, 4.19 4.20 (pgs. 189-212, 222 224)
 6 OP AMPS II 6 Op Amps II In the previous lab, you explored several applications of op amps. In this exercise, you will look at some of their limitations. You will also examine the op amp integrator and
6 OP AMPS II 6 Op Amps II In the previous lab, you explored several applications of op amps. In this exercise, you will look at some of their limitations. You will also examine the op amp integrator and
E. K. A. ADVANCED PHYSICS LABORATORY PHYSICS 3081, 4051 NUCLEAR MAGNETIC RESONANCE
 E. K. A. ADVANCED PHYSICS LABORATORY PHYSICS 3081, 4051 NUCLEAR MAGNETIC RESONANCE References for Nuclear Magnetic Resonance 1. Slichter, Principles of Magnetic Resonance, Harper and Row, 1963. chapter
E. K. A. ADVANCED PHYSICS LABORATORY PHYSICS 3081, 4051 NUCLEAR MAGNETIC RESONANCE References for Nuclear Magnetic Resonance 1. Slichter, Principles of Magnetic Resonance, Harper and Row, 1963. chapter
Harmonics and Noise in Photovoltaic (PV) Inverter and the Mitigation Strategies
 Soonwook Hong, Ph. D. Michael Zuercher Martinson Harmonics and Noise in Photovoltaic (PV) Inverter and the Mitigation Strategies 1. Introduction PV inverters use semiconductor devices to transform the
Soonwook Hong, Ph. D. Michael Zuercher Martinson Harmonics and Noise in Photovoltaic (PV) Inverter and the Mitigation Strategies 1. Introduction PV inverters use semiconductor devices to transform the
Data Transmission. Data Communications Model. CSE 3461 / 5461: Computer Networking & Internet Technologies. Presentation B
 CSE 3461 / 5461: Computer Networking & Internet Technologies Data Transmission Presentation B Kannan Srinivasan 08/30/2012 Data Communications Model Figure 1.2 Studying Assignment: 3.1-3.4, 4.1 Presentation
CSE 3461 / 5461: Computer Networking & Internet Technologies Data Transmission Presentation B Kannan Srinivasan 08/30/2012 Data Communications Model Figure 1.2 Studying Assignment: 3.1-3.4, 4.1 Presentation
Germanium Diode AM Radio
 Germanium Diode AM Radio LAB 3 3.1 Introduction In this laboratory exercise you will build a germanium diode based AM (Medium Wave) radio. Earliest radios used simple diode detector circuits. The diodes
Germanium Diode AM Radio LAB 3 3.1 Introduction In this laboratory exercise you will build a germanium diode based AM (Medium Wave) radio. Earliest radios used simple diode detector circuits. The diodes
Subject: Glenair MIL-PRF 24758 Conduit Surface Transfer Impedance Test
 Lothar O. Hoeft, Ph.D. Consultant, Electromagnetic Effects 5012 San Pedro Ct., NE Albuquerque, New Mexico 87109-2515 Phone: (505)-889-9705 E-mail: [email protected] 1 February 24, 2006 Subject: Glenair
Lothar O. Hoeft, Ph.D. Consultant, Electromagnetic Effects 5012 San Pedro Ct., NE Albuquerque, New Mexico 87109-2515 Phone: (505)-889-9705 E-mail: [email protected] 1 February 24, 2006 Subject: Glenair
EXPERIMENT NUMBER 8 CAPACITOR CURRENT-VOLTAGE RELATIONSHIP
 1 EXPERIMENT NUMBER 8 CAPACITOR CURRENT-VOLTAGE RELATIONSHIP Purpose: To demonstrate the relationship between the voltage and current of a capacitor. Theory: A capacitor is a linear circuit element whose
1 EXPERIMENT NUMBER 8 CAPACITOR CURRENT-VOLTAGE RELATIONSHIP Purpose: To demonstrate the relationship between the voltage and current of a capacitor. Theory: A capacitor is a linear circuit element whose
Frequency Response of Filters
 School of Engineering Department of Electrical and Computer Engineering 332:224 Principles of Electrical Engineering II Laboratory Experiment 2 Frequency Response of Filters 1 Introduction Objectives To
School of Engineering Department of Electrical and Computer Engineering 332:224 Principles of Electrical Engineering II Laboratory Experiment 2 Frequency Response of Filters 1 Introduction Objectives To
Section 5.0 : Horn Physics. By Martin J. King, 6/29/08 Copyright 2008 by Martin J. King. All Rights Reserved.
 Section 5. : Horn Physics Section 5. : Horn Physics By Martin J. King, 6/29/8 Copyright 28 by Martin J. King. All Rights Reserved. Before discussing the design of a horn loaded loudspeaker system, it is
Section 5. : Horn Physics Section 5. : Horn Physics By Martin J. King, 6/29/8 Copyright 28 by Martin J. King. All Rights Reserved. Before discussing the design of a horn loaded loudspeaker system, it is
An octave bandwidth dipole antenna
 An octave bandwidth dipole antenna Abstract: Achieving wideband performance from resonant structures is challenging because their radiation properties and impedance characteristics are usually sensitive
An octave bandwidth dipole antenna Abstract: Achieving wideband performance from resonant structures is challenging because their radiation properties and impedance characteristics are usually sensitive
Lab E1: Introduction to Circuits
 E1.1 Lab E1: Introduction to Circuits The purpose of the this lab is to introduce you to some basic instrumentation used in electrical circuits. You will learn to use a DC power supply, a digital multimeter
E1.1 Lab E1: Introduction to Circuits The purpose of the this lab is to introduce you to some basic instrumentation used in electrical circuits. You will learn to use a DC power supply, a digital multimeter
RLC Resonant Circuits
 C esonant Circuits Andrew McHutchon April 20, 203 Capacitors and Inductors There is a lot of inconsistency when it comes to dealing with reactances of complex components. The format followed in this document
C esonant Circuits Andrew McHutchon April 20, 203 Capacitors and Inductors There is a lot of inconsistency when it comes to dealing with reactances of complex components. The format followed in this document
OPTICAL FIBERS INTRODUCTION
 OPTICAL FIBERS References: J. Hecht: Understanding Fiber Optics, Ch. 1-3, Prentice Hall N.J. 1999 D. R. Goff: Fiber Optic Reference Guide (2 nd ed.) Focal Press 1999 Projects in Fiber Optics (Applications
OPTICAL FIBERS References: J. Hecht: Understanding Fiber Optics, Ch. 1-3, Prentice Hall N.J. 1999 D. R. Goff: Fiber Optic Reference Guide (2 nd ed.) Focal Press 1999 Projects in Fiber Optics (Applications
Mutual Inductance and Transformers F3 3. r L = ω o
 utual Inductance and Transformers F3 1 utual Inductance & Transformers If a current, i 1, flows in a coil or circuit then it produces a magnetic field. Some of the magnetic flux may link a second coil
utual Inductance and Transformers F3 1 utual Inductance & Transformers If a current, i 1, flows in a coil or circuit then it produces a magnetic field. Some of the magnetic flux may link a second coil
Electronics. Discrete assembly of an operational amplifier as a transistor circuit. LD Physics Leaflets P4.2.1.1
 Electronics Operational Amplifier Internal design of an operational amplifier LD Physics Leaflets Discrete assembly of an operational amplifier as a transistor circuit P4.2.1.1 Objects of the experiment
Electronics Operational Amplifier Internal design of an operational amplifier LD Physics Leaflets Discrete assembly of an operational amplifier as a transistor circuit P4.2.1.1 Objects of the experiment
Bipolar Transistor Amplifiers
 Physics 3330 Experiment #7 Fall 2005 Bipolar Transistor Amplifiers Purpose The aim of this experiment is to construct a bipolar transistor amplifier with a voltage gain of minus 25. The amplifier must
Physics 3330 Experiment #7 Fall 2005 Bipolar Transistor Amplifiers Purpose The aim of this experiment is to construct a bipolar transistor amplifier with a voltage gain of minus 25. The amplifier must
Measuring Impedance and Frequency Response of Guitar Pickups
 Measuring Impedance and Frequency Response of Guitar Pickups Peter D. Hiscocks Syscomp Electronic Design Limited [email protected] www.syscompdesign.com April 30, 2011 Introduction The CircuitGear
Measuring Impedance and Frequency Response of Guitar Pickups Peter D. Hiscocks Syscomp Electronic Design Limited [email protected] www.syscompdesign.com April 30, 2011 Introduction The CircuitGear
POWER SYSTEM HARMONICS. A Reference Guide to Causes, Effects and Corrective Measures AN ALLEN-BRADLEY SERIES OF ISSUES AND ANSWERS
 A Reference Guide to Causes, Effects and Corrective Measures AN ALLEN-BRADLEY SERIES OF ISSUES AND ANSWERS By: Robert G. Ellis, P. Eng., Rockwell Automation Medium Voltage Business CONTENTS INTRODUCTION...
A Reference Guide to Causes, Effects and Corrective Measures AN ALLEN-BRADLEY SERIES OF ISSUES AND ANSWERS By: Robert G. Ellis, P. Eng., Rockwell Automation Medium Voltage Business CONTENTS INTRODUCTION...
Frequency-dependent underground cable model for electromagnetic transient simulation
 Frequency-dependent underground cable model for electromagnetic transient simulation Vasco José Realista Medeiros Soeiro Abstract A computation method for transients in a three-phase underground power-transmission
Frequency-dependent underground cable model for electromagnetic transient simulation Vasco José Realista Medeiros Soeiro Abstract A computation method for transients in a three-phase underground power-transmission
Cable Analysis and Fault Detection using the Bode 100
 Cable Analysis and Fault Detection using the Bode 100 By Stephan Synkule 2014 by OMICRON Lab V1.3 Visit www.omicron-lab.com for more information. Contact [email protected] for technical support.
Cable Analysis and Fault Detection using the Bode 100 By Stephan Synkule 2014 by OMICRON Lab V1.3 Visit www.omicron-lab.com for more information. Contact [email protected] for technical support.
CHAPTER 26 ELECTROSTATIC ENERGY AND CAPACITORS
 CHAPTER 6 ELECTROSTATIC ENERGY AND CAPACITORS. Three point charges, each of +q, are moved from infinity to the vertices of an equilateral triangle of side l. How much work is required? The sentence preceding
CHAPTER 6 ELECTROSTATIC ENERGY AND CAPACITORS. Three point charges, each of +q, are moved from infinity to the vertices of an equilateral triangle of side l. How much work is required? The sentence preceding
Antenna Properties and their impact on Wireless System Performance. Dr. Steven R. Best. Cushcraft Corporation 48 Perimeter Road Manchester, NH 03013
 Antenna Properties and their impact on Wireless System Performance Dr. Steven R. Best Cushcraft Corporation 48 Perimeter Road Manchester, NH 03013 Phone (603) 627-7877 FAX: (603) 627-1764 Email: [email protected]
Antenna Properties and their impact on Wireless System Performance Dr. Steven R. Best Cushcraft Corporation 48 Perimeter Road Manchester, NH 03013 Phone (603) 627-7877 FAX: (603) 627-1764 Email: [email protected]
The Critical Length of a Transmission Line
 Page 1 of 9 The Critical Length of a Transmission Line Dr. Eric Bogatin President, Bogatin Enterprises Oct 1, 2004 Abstract A transmission line is always a transmission line. However, if it is physically
Page 1 of 9 The Critical Length of a Transmission Line Dr. Eric Bogatin President, Bogatin Enterprises Oct 1, 2004 Abstract A transmission line is always a transmission line. However, if it is physically
104 Practice Exam 2-3/21/02
 104 Practice Exam 2-3/21/02 1. Two electrons are located in a region of space where the magnetic field is zero. Electron A is at rest; and electron B is moving westward with a constant velocity. A non-zero
104 Practice Exam 2-3/21/02 1. Two electrons are located in a region of space where the magnetic field is zero. Electron A is at rest; and electron B is moving westward with a constant velocity. A non-zero
Broadband Slotted Coaxial Broadcast Antenna Technology
 Broadband Slotted Coaxial Broadcast Antenna Technology Summary Slotted coaxial antennas have many advantages over traditional broadband panel antennas including much smaller size and wind load, higher
Broadband Slotted Coaxial Broadcast Antenna Technology Summary Slotted coaxial antennas have many advantages over traditional broadband panel antennas including much smaller size and wind load, higher
Antennas & Propagation. CS 6710 Spring 2010 Rajmohan Rajaraman
 Antennas & Propagation CS 6710 Spring 2010 Rajmohan Rajaraman Introduction An antenna is an electrical conductor or system of conductors o Transmission - radiates electromagnetic energy into space o Reception
Antennas & Propagation CS 6710 Spring 2010 Rajmohan Rajaraman Introduction An antenna is an electrical conductor or system of conductors o Transmission - radiates electromagnetic energy into space o Reception
Transmission Line Transformers
 Radio Frequency Circuit Design. W. Alan Davis, Krishna Agarwal Copyright 2001 John Wiley & Sons, Inc. Print ISBN 0-471-35052-4 Electronic ISBN 0-471-20068-9 CHAPTER SIX Transmission Line Transformers 6.1
Radio Frequency Circuit Design. W. Alan Davis, Krishna Agarwal Copyright 2001 John Wiley & Sons, Inc. Print ISBN 0-471-35052-4 Electronic ISBN 0-471-20068-9 CHAPTER SIX Transmission Line Transformers 6.1
Development and optimization of a hybrid passive/active liner for flow duct applications
 Development and optimization of a hybrid passive/active liner for flow duct applications 1 INTRODUCTION Design of an acoustic liner effective throughout the entire frequency range inherent in aeronautic
Development and optimization of a hybrid passive/active liner for flow duct applications 1 INTRODUCTION Design of an acoustic liner effective throughout the entire frequency range inherent in aeronautic
Fundamentals of Electromagnetic Fields and Waves: I
 Fundamentals of Electromagnetic Fields and Waves: I Fall 2007, EE 30348, Electrical Engineering, University of Notre Dame Mid Term II: Solutions Please show your steps clearly and sketch figures wherever
Fundamentals of Electromagnetic Fields and Waves: I Fall 2007, EE 30348, Electrical Engineering, University of Notre Dame Mid Term II: Solutions Please show your steps clearly and sketch figures wherever
2/20/2009 3 Transmission Lines and Waveguides.doc 1/3. and Waveguides. Transmission Line A two conductor structure that can support a TEM wave.
 2/20/2009 3 Transmission Lines and Waveguides.doc 1/3 Chapter 3 Transmission Lines and Waveguides First, some definitions: Transmission Line A two conductor structure that can support a TEM wave. Waveguide
2/20/2009 3 Transmission Lines and Waveguides.doc 1/3 Chapter 3 Transmission Lines and Waveguides First, some definitions: Transmission Line A two conductor structure that can support a TEM wave. Waveguide
Current Probes. User Manual
 Current Probes User Manual ETS-Lindgren L.P. reserves the right to make changes to any product described herein in order to improve function, design, or for any other reason. Nothing contained herein shall
Current Probes User Manual ETS-Lindgren L.P. reserves the right to make changes to any product described herein in order to improve function, design, or for any other reason. Nothing contained herein shall
Transmission-Line Essentials for Digital Electronics
 Transmission-Line Essentials for Digital Electronics Prof. Tzong-Lin Wu EMC Laboratory Department of Electrical Engineering National Taiwan University EM II / Prof. Tzong-Lin Wu 1 Introduction 6.1 Transmission
Transmission-Line Essentials for Digital Electronics Prof. Tzong-Lin Wu EMC Laboratory Department of Electrical Engineering National Taiwan University EM II / Prof. Tzong-Lin Wu 1 Introduction 6.1 Transmission
Laboratory 4: Feedback and Compensation
 Laboratory 4: Feedback and Compensation To be performed during Week 9 (Oct. 20-24) and Week 10 (Oct. 27-31) Due Week 11 (Nov. 3-7) 1 Pre-Lab This Pre-Lab should be completed before attending your regular
Laboratory 4: Feedback and Compensation To be performed during Week 9 (Oct. 20-24) and Week 10 (Oct. 27-31) Due Week 11 (Nov. 3-7) 1 Pre-Lab This Pre-Lab should be completed before attending your regular
Selecting IHLP Composite Inductors for Non-Isolated Converters Utilizing Vishay s Application Sheet
 VISHAY DALE www.vishay.com Magnetics Selecting IHLP Composite Inductors for Non-Isolated Converters INTRODUCTION This application note will provide information to assist in the specification of IHLP composite
VISHAY DALE www.vishay.com Magnetics Selecting IHLP Composite Inductors for Non-Isolated Converters INTRODUCTION This application note will provide information to assist in the specification of IHLP composite
CHAPTER - 1. Chapter ONE: WAVES CHAPTER - 2. Chapter TWO: RAY OPTICS AND OPTICAL INSTRUMENTS. CHAPTER - 3 Chapter THREE: WAVE OPTICS PERIODS PERIODS
 BOARD OF INTERMEDIATE EDUCATION, A.P., HYDERABAD REVISION OF SYLLABUS Subject PHYSICS-II (w.e.f 2013-14) Chapter ONE: WAVES CHAPTER - 1 1.1 INTRODUCTION 1.2 Transverse and longitudinal waves 1.3 Displacement
BOARD OF INTERMEDIATE EDUCATION, A.P., HYDERABAD REVISION OF SYLLABUS Subject PHYSICS-II (w.e.f 2013-14) Chapter ONE: WAVES CHAPTER - 1 1.1 INTRODUCTION 1.2 Transverse and longitudinal waves 1.3 Displacement
Agilent Time Domain Analysis Using a Network Analyzer
 Agilent Time Domain Analysis Using a Network Analyzer Application Note 1287-12 0.0 0.045 0.6 0.035 Cable S(1,1) 0.4 0.2 Cable S(1,1) 0.025 0.015 0.005 0.0 1.0 1.5 2.0 2.5 3.0 3.5 4.0 Frequency (GHz) 0.005
Agilent Time Domain Analysis Using a Network Analyzer Application Note 1287-12 0.0 0.045 0.6 0.035 Cable S(1,1) 0.4 0.2 Cable S(1,1) 0.025 0.015 0.005 0.0 1.0 1.5 2.0 2.5 3.0 3.5 4.0 Frequency (GHz) 0.005
Experiment 8: Undriven & Driven RLC Circuits
 Experiment 8: Undriven & Driven RLC Circuits Answer these questions on a separate sheet of paper and turn them in before the lab 1. RLC Circuits Consider the circuit at left, consisting of an AC function
Experiment 8: Undriven & Driven RLC Circuits Answer these questions on a separate sheet of paper and turn them in before the lab 1. RLC Circuits Consider the circuit at left, consisting of an AC function
Physics 202 Problems - Week 8 Worked Problems Chapter 25: 7, 23, 36, 62, 72
 Physics 202 Problems - Week 8 Worked Problems Chapter 25: 7, 23, 36, 62, 72 Problem 25.7) A light beam traveling in the negative z direction has a magnetic field B = (2.32 10 9 T )ˆx + ( 4.02 10 9 T )ŷ
Physics 202 Problems - Week 8 Worked Problems Chapter 25: 7, 23, 36, 62, 72 Problem 25.7) A light beam traveling in the negative z direction has a magnetic field B = (2.32 10 9 T )ˆx + ( 4.02 10 9 T )ŷ
Chapter 11. Inductors ISU EE. C.Y. Lee
 Chapter 11 Inductors Objectives Describe the basic structure and characteristics of an inductor Discuss various types of inductors Analyze series inductors Analyze parallel inductors Analyze inductive
Chapter 11 Inductors Objectives Describe the basic structure and characteristics of an inductor Discuss various types of inductors Analyze series inductors Analyze parallel inductors Analyze inductive
Transmission Line and Back Loaded Horn Physics
 Introduction By Martin J. King, 3/29/3 Copyright 23 by Martin J. King. All Rights Reserved. In order to differentiate between a transmission line and a back loaded horn, it is really important to understand
Introduction By Martin J. King, 3/29/3 Copyright 23 by Martin J. King. All Rights Reserved. In order to differentiate between a transmission line and a back loaded horn, it is really important to understand
RFID Receiver Antenna Project for 13.56 Mhz Band
 RFID Receiver Antenna Project for 13.56 Mhz Band Fatih Eken TE 401 Microwave Course Term Project, Fall 2004 Supervised by Asst. Prof. İbrahim Tekin Telecommunication Program in Faculty of Engineering and
RFID Receiver Antenna Project for 13.56 Mhz Band Fatih Eken TE 401 Microwave Course Term Project, Fall 2004 Supervised by Asst. Prof. İbrahim Tekin Telecommunication Program in Faculty of Engineering and
TESTS OF 1 MHZ SIGNAL SOURCE FOR SPECTRUM ANALYZER CALIBRATION 7/8/08 Sam Wetterlin
 TESTS OF 1 MHZ SIGNAL SOURCE FOR SPECTRUM ANALYZER CALIBRATION 7/8/08 Sam Wetterlin (Updated 7/19/08 to delete sine wave output) I constructed the 1 MHz square wave generator shown in the Appendix. This
TESTS OF 1 MHZ SIGNAL SOURCE FOR SPECTRUM ANALYZER CALIBRATION 7/8/08 Sam Wetterlin (Updated 7/19/08 to delete sine wave output) I constructed the 1 MHz square wave generator shown in the Appendix. This
AN-837 APPLICATION NOTE
 APPLICATION NOTE One Technology Way P.O. Box 916 Norwood, MA 262-916, U.S.A. Tel: 781.329.47 Fax: 781.461.3113 www.analog.com DDS-Based Clock Jitter Performance vs. DAC Reconstruction Filter Performance
APPLICATION NOTE One Technology Way P.O. Box 916 Norwood, MA 262-916, U.S.A. Tel: 781.329.47 Fax: 781.461.3113 www.analog.com DDS-Based Clock Jitter Performance vs. DAC Reconstruction Filter Performance
Cable Impedance and Structural Return Loss Measurement Methodologies
 Cable Impedance and Structural Return Loss Measurement Methodologies Introduction Joe Rowell Joel Dunsmore and Les Brabetz Hewlett Packard Company Santa Rosa, California Two critical electrical specifications
Cable Impedance and Structural Return Loss Measurement Methodologies Introduction Joe Rowell Joel Dunsmore and Les Brabetz Hewlett Packard Company Santa Rosa, California Two critical electrical specifications
The performance improvement by ferrite loading means - increasing, - increasing of ratio, implicitly related to the input impedance.
 3.2.3. Ferrite Loading Magnetic ferrite loading can enhance a transmitting signal as high as 2 to 10 db for MHz [Devore and Bohley, 1977]. There is an optimum frequency range where ferrite loading is beneficial.
3.2.3. Ferrite Loading Magnetic ferrite loading can enhance a transmitting signal as high as 2 to 10 db for MHz [Devore and Bohley, 1977]. There is an optimum frequency range where ferrite loading is beneficial.
Keysight Technologies Understanding the Fundamental Principles of Vector Network Analysis. Application Note
 Keysight Technologies Understanding the Fundamental Principles of Vector Network Analysis Application Note Introduction Network analysis is the process by which designers and manufacturers measure the
Keysight Technologies Understanding the Fundamental Principles of Vector Network Analysis Application Note Introduction Network analysis is the process by which designers and manufacturers measure the
Exercises on Voltage, Capacitance and Circuits. A d = (8.85 10 12 ) π(0.05)2 = 6.95 10 11 F
 Exercises on Voltage, Capacitance and Circuits Exercise 1.1 Instead of buying a capacitor, you decide to make one. Your capacitor consists of two circular metal plates, each with a radius of 5 cm. The
Exercises on Voltage, Capacitance and Circuits Exercise 1.1 Instead of buying a capacitor, you decide to make one. Your capacitor consists of two circular metal plates, each with a radius of 5 cm. The
Connectivity in a Wireless World. Cables Connectors 2014. A Special Supplement to
 Connectivity in a Wireless World Cables Connectors 204 A Special Supplement to Signal Launch Methods for RF/Microwave PCBs John Coonrod Rogers Corp., Chandler, AZ COAX CABLE MICROSTRIP TRANSMISSION LINE
Connectivity in a Wireless World Cables Connectors 204 A Special Supplement to Signal Launch Methods for RF/Microwave PCBs John Coonrod Rogers Corp., Chandler, AZ COAX CABLE MICROSTRIP TRANSMISSION LINE
Computer Networks and Internets, 5e Chapter 6 Information Sources and Signals. Introduction
 Computer Networks and Internets, 5e Chapter 6 Information Sources and Signals Modified from the lecture slides of Lami Kaya ([email protected]) for use CECS 474, Fall 2008. 2009 Pearson Education Inc., Upper
Computer Networks and Internets, 5e Chapter 6 Information Sources and Signals Modified from the lecture slides of Lami Kaya ([email protected]) for use CECS 474, Fall 2008. 2009 Pearson Education Inc., Upper
S-Parameters and Related Quantities Sam Wetterlin 10/20/09
 S-Parameters and Related Quantities Sam Wetterlin 10/20/09 Basic Concept of S-Parameters S-Parameters are a type of network parameter, based on the concept of scattering. The more familiar network parameters
S-Parameters and Related Quantities Sam Wetterlin 10/20/09 Basic Concept of S-Parameters S-Parameters are a type of network parameter, based on the concept of scattering. The more familiar network parameters
Lab #9: AC Steady State Analysis
 Theory & Introduction Lab #9: AC Steady State Analysis Goals for Lab #9 The main goal for lab 9 is to make the students familar with AC steady state analysis, db scale and the NI ELVIS frequency analyzer.
Theory & Introduction Lab #9: AC Steady State Analysis Goals for Lab #9 The main goal for lab 9 is to make the students familar with AC steady state analysis, db scale and the NI ELVIS frequency analyzer.
AN2866 Application note
 Application note How to design a 13.56 MHz customized tag antenna Introduction RFID (radio-frequency identification) tags extract all of their power from the reader s field. The tags and reader s antennas
Application note How to design a 13.56 MHz customized tag antenna Introduction RFID (radio-frequency identification) tags extract all of their power from the reader s field. The tags and reader s antennas
EECC694 - Shaaban. Transmission Channel
 The Physical Layer: Data Transmission Basics Encode data as energy at the data (information) source and transmit the encoded energy using transmitter hardware: Possible Energy Forms: Electrical, light,
The Physical Layer: Data Transmission Basics Encode data as energy at the data (information) source and transmit the encoded energy using transmitter hardware: Possible Energy Forms: Electrical, light,
Lecture 22. Inductance. Magnetic Field Energy. Outline:
 Lecture 22. Inductance. Magnetic Field Energy. Outline: Self-induction and self-inductance. Inductance of a solenoid. The energy of a magnetic field. Alternative definition of inductance. Mutual Inductance.
Lecture 22. Inductance. Magnetic Field Energy. Outline: Self-induction and self-inductance. Inductance of a solenoid. The energy of a magnetic field. Alternative definition of inductance. Mutual Inductance.
INTERFERENCE OF SOUND WAVES
 1/2016 Sound 1/8 INTERFERENCE OF SOUND WAVES PURPOSE: To measure the wavelength, frequency, and propagation speed of ultrasonic sound waves and to observe interference phenomena with ultrasonic sound waves.
1/2016 Sound 1/8 INTERFERENCE OF SOUND WAVES PURPOSE: To measure the wavelength, frequency, and propagation speed of ultrasonic sound waves and to observe interference phenomena with ultrasonic sound waves.
Software for Design NMR Probes Using the Shielded Split Ring and the Shielded Symmetrical Band Resonators
 Software for Design NMR Probes Using the Shielded Split Ring and the Shielded Symmetrical Band Resonators Nasreddine Benahmed University of Tlemcen, Algeria ABSTRACT This article presents a software (NMR
Software for Design NMR Probes Using the Shielded Split Ring and the Shielded Symmetrical Band Resonators Nasreddine Benahmed University of Tlemcen, Algeria ABSTRACT This article presents a software (NMR
Pre-Compliance Test Method for Radiated Emissions of Automotive Components Using Scattering Parameter Transfer Functions
 PreCompliance Test Method for Radiated Emissions of Automotive Components Using Scattering Parameter Transfer Functions D. Schneider 1*, S. Tenbohlen 1, W. Köhler 1 1 Institute of Power Transmission and
PreCompliance Test Method for Radiated Emissions of Automotive Components Using Scattering Parameter Transfer Functions D. Schneider 1*, S. Tenbohlen 1, W. Köhler 1 1 Institute of Power Transmission and
Lab Exercise 1: Acoustic Waves
 Lab Exercise 1: Acoustic Waves Contents 1-1 PRE-LAB ASSIGNMENT................. 2 1-3.1 Spreading Factor: Spherical Waves........ 2 1-3.2 Interference In 3-D................. 3 1-4 EQUIPMENT........................
Lab Exercise 1: Acoustic Waves Contents 1-1 PRE-LAB ASSIGNMENT................. 2 1-3.1 Spreading Factor: Spherical Waves........ 2 1-3.2 Interference In 3-D................. 3 1-4 EQUIPMENT........................
Selecting Receiving Antennas for Radio Tracking
 Selecting Receiving Antennas for Radio Tracking Larry B Kuechle, Advanced Telemetry Systems, Inc. Isanti, Minnesota 55040 [email protected] The receiving antenna is an integral part of any radio location
Selecting Receiving Antennas for Radio Tracking Larry B Kuechle, Advanced Telemetry Systems, Inc. Isanti, Minnesota 55040 [email protected] The receiving antenna is an integral part of any radio location
Eðlisfræði 2, vor 2007
 [ Assignment View ] [ Print ] Eðlisfræði 2, vor 2007 30. Inductance Assignment is due at 2:00am on Wednesday, March 14, 2007 Credit for problems submitted late will decrease to 0% after the deadline has
[ Assignment View ] [ Print ] Eðlisfræði 2, vor 2007 30. Inductance Assignment is due at 2:00am on Wednesday, March 14, 2007 Credit for problems submitted late will decrease to 0% after the deadline has
