BROCK UNIVERSITY MATHEMATICS MODULES
|
|
|
- Earl Dickerson
- 7 years ago
- Views:
Transcription
1 BROCK UNIVERSITY MATHEMATICS MODULES 11A2.2 Introduction to Factoring a Polynomial Author: Darcy Berry WWW What it is: Expressing a polynomial as a product of polynomials of smaller degree. Why you need it: Factoring a polynomial aids in analyzing its behaviour, including analyzing its graph. Factoring a polynomial also helps in solving equations involving polynomial expressions. When to use it: Use factoring as a first attempt when analyzing polynomial functions and solving equations involving polynomials. PREREQUISITES Before you tackle this module, make sure you have completed these modules: Expanding Polynomials ***, Common Factoring *** WARMUP Before you tackle this module, make sure you can solve the following exercises. If you have difficulties, please review the appropriate prerequisite modules. (Answers below.) 1. Factor each expression. (a) 8m 3 4m 2 (b) 20a 4 40a 5 (c) 5x 2 y x 3 y 2 10x 3 y 2 (d) 2a 4 b 2 c 5 10a 3 b 3 c 5 d (e) 7a 2 b ab a 3 b 3 (f) 12s 3 t 6 u 4 v 2 36s 4 t 5 u 5 (g) 3xy 12xy 2 z + 21x 2 yz 2 (h) m 3 n 2 p 5 q 4 3m 2 p 3 q 5 + 4p 3 q 3 Answers: 1. (a) 4m 2 (2m 1) (b) 20a 4 (1 2a) (c) 5x 2 y 2 (1+x) (d) 2a 3 b 2 c 5 (a 5bd) (e) 7ab 3 (ab+2b 2 +3a 2 ) (f) 12s 3 t 5 u 4 (tv 2 3su) (g) 3xy(1 4yz + 7xz 2 ) (h) p 3 q 3 (m 3 n 2 p 2 q 3m 2 q 2 + 4) Introduction In this module, you will learn how to factor a variety of polynomial expressions, with a primary focus on trinomials. Factoring is used as a means of simplifying an expression into a product of its simplest parts. Factored form assists in the analysis of the behaviour of a polynomial function, including analyzing its graph. Factoring is also helpful when determining the coördinates of specific points on a polynomial function s graph (for example, maximum or minimum points), as well as solving equations involving polynomial expressions. 1
2 You will learn in subsequent modules that factoring applies particularly to finding important x-values of a function known as zeros, which are a key component in graphing and function analysis. Before we start let s consider a geometric interpretation to present an alternative, visual representation of the factoring algorithm. Expanding a product of binomials can be expressed geometrically using an area model of multiplication. So, consider a kitchen floor with an array of tiles. Each floor tile is square and measures 1 unit by 1 unit and as such has an area of 1 square unit. If you have an area of tiles that measures 7 units long by 5 units wide, then the number of tiles is 35, which is also the area of the tiled part of the floor. Similarly, if you have a floor measuring (4 + 3) tiles wide by (4 + 1) tiles long, the area would once again be 35. Now, if we draw a horizontal line and a vertical line, we can break up the same floor into four rectangular pieces, the first measuring 4 by 4, the second 4 by 1, the third 3 by 4 and the fourth 3 by 1. Now let s consider a similar diagram, but this time rather than measuring (4+3) by (4+1) let s assign the dimensions (x + 3) and (x + 1) to the width and length respectively. We can create the same four rectangular pieces, measuring x 2, x(1), (3)x, and (3)(1) respectively. Therefore, we can see that when we expand a factored expression we get four terms and as such (x + 3)(x + 1) does not equal x 2 + (3)(1) but rather x 2 + x(1) + (3)x + (3)(1), which when simplified equals x 2 + 4x + 3. The algebraic analogue of this geometric observation is that when you expand (x+3)(x+1), the coefficient of x is 3 + 1, and the constant coefficient is (3)(1). This observation can be generalized and expressed from a factoring perspective as follows: KEY IDEA A quadratic expression of the form x 2 + bx + c can be factored in the form (x + s)(x + t) if the following two conditions are satisfied: 1. s + t = b 2. st = c Thus, if you wish to factor an expression of the form x 2 + bx + c, seek two numbers that add to give b and that multiply to give c. Keeping this key idea in mind, let s look at the following example. 2
3 EXAMPLE 1 Factor the trinomial x x Given the trinomial x x + 18 (i.e. b = 11 and c = 18) we must find two numbers that multiply to give 18 and add to give 11. Let s hope the two numbers are both integers, which would make our task easier. (If they are not integers, we might have to resort to the quadratic formula, which is discussed in Module 11A2.8.) Because 18 > 0, either the two numbers are both positive or both negative. However, the two numbers must add to give 11, so they must both be positive. Steps: 1. First consider those positive integers that multiply to give 18 (i.e., c): 1 18, 2 9, and Now, determine whether the sum of any of these pairs of numbers equals 11 (i.e., b) = = = 9 3. Checking the list in the previous step, we notice that there is a pair of whole numbers, namely 2 and 9, that satisfy both conditions: = 11, and 2 9 = 18. Therefore, x x + 18 = (x + 2)(x + 9). 4. Finally you can check your work by expanding (x + 2)(x + 9) and verifying that it really does equal x x Let s consider a few more examples. EXAMPLE 2 Factor the trinomial x 2 + 8x We need to find two numbers that when multiplied give 12 and when added give 8. So we look at the pairs 1 & 12, 2 & 6, and 3 & 4, which are the positive factors of 12. (We don t bother with the negative factors of 12, because we know that the factors must either be both positive or both negative; however we can rule out the negative possibilities, because the sum of the factors is 8, which is positive.) Notice that , , but = 8. This means that the numbers that satisfy both conditions are 2 and 6, because = 8 and 2 6 = 12. Therefore, the solution is x 2 + 8x + 12 = (x + 2)(x + 6). As usual, you can check your work by expanding the right side of the previous equation and verifying that it really does equal the left side. 3
4 EXAMPLE 3 Factor the trinomial y 2 3y 28. We need to find two numbers that multiply to give 28 and add to give 3. This means that one of the numbers must be positive and the other must be negative. The integers factors of 28 are 28 and 1, 14 and 2, 7 and 4, 4 and 7, 2 and 14, and finally, 1 and 28. By adding each pair of numbers together, we find that there is one pair that adds to 3, namely 7 and 4. The solution is thus y 2 3y 28 = (y + 4)(y 7). Check by expanding the right side! EXAMPLE 4 Factor the trinomial x 2 12x Given the trinomial x 2 12x + 20 we require two numbers with a product of 20 and a sum of 12. We find that the two numbers that satisfy both conditions are 2 and 10. Thus, the solution is x 2 12x + 20 = (x 2)(x 10). Check by expanding the right side! The previous examples allow us to note the following key ideas. KEY IDEA If x 2 + bx + c can be factored as (x + s)(x + t), then: When c is positive, then the product of s and t is positive. This means that s and t are either both positive or both negative. When c is negative, then the product of s and t is negative. This means that s and t have opposite signs. Therefore if s is positive, t is negative, and vice versa. Now it s your turn! Try these problems out on your own. PRACTICE (Answers below.) 1. Factor each trinomial. (a) a 2 13a + 42 (b) t 2 + 8t + 16 (c) a a + 24 (d) d 2 7d + 12 (e) y 2 2y 8 (f) k 2 k 6 Answers: 1.(a) (a 7)(a 6) (b) (t + 4)(t + 4) = (t + 4) 2 (c) (a + 12)(a + 2) (d) (d 4)(d 3) (e) (y + 2)(y 4) (f) (k + 2)(k 3) 4
5 Trinomials are not always quadratic in nature, having powers greater than 2, and sometimes they involve more than one variable. However, in certain cases we can use the same steps as learned above to factor these special trinomials. We ll strive to follow the same steps and process as outlined above to the subsequent examples. It may help you to recall that when terms with the same base are multiplied, the base remains the same and the exponents are added. Let s consider a few examples to illustrate this concept. EXAMPLE 5 Factor the trinomial x 2 + 7xy + 12y 2. Consider the trinomial x 2 + 7x Using the methods discussed earlier in this module, we can factor this trinomial to obtain x 2 + 7x + 12 = (x + 3)(x + 4). This trinomial is similar to the one we are asked to factor, which makes us wonder whether we could just tinker with the factors we just obtained to guess factors for the trinomial x 2 + 7xy + 12y 2. First guess: x 2 + 7xy + 12y 2 = (x + 3y 2 )(x + 4). Maybe by including a y 2 in the first factor this will work. Expanding the right side shows that this does not work: (x + 3y 2 )(x + 4) = x 2 + 4x + 3xy y 2. The first and fourth terms are correct, but the middle two terms are incorrect. Second guess: x 2 + 7xy + 12y 2 = (x + 3)(x + 4y 2 ). This does not work for a similar reason as the first guess: (x + 3)(x + 4y 2 ) = x 2 + 4xy 2 + 3x + 12y 2. The first and fourth terms are correct, but the middle two terms are incorrect. Third guess: We need a y 2 term; another way to achieve this is to include a factor of y in each of the parentheses in the factored form. So our third guess is: x 2 +7xy+12y 2 = (x+3y)(x+4y). This does work, as you can see by expanding the parentheses: (x+3y)(x+4y) = x 2 +4xy+3xy+12y 2 = x 2 + 7xy + 12y 2. What we ve learned from this example is that it is possible to factor trinomials in two variables using the same method as factoring a trinomial in one variable, as long as the trinomial has the right form. EXAMPLE 6 Factor the trinomial w uw + 40u 2. The form of the trinomial is the same as in the previous example. So let s proceed using the same method, searching for two numbers that add to 14 and multiply to give 40. After some thought, you will see that the two needed numbers are 4 and 10. Thus, Check the result by exanding the right side. w uw + 40u 2 = (w + 4u)(w + 10u) 5
6 EXAMPLE 7 Factor the trinomial x 2 y 2 10xy This is somewhat similar in form to the previous examples, but it is a little different. If we search for two numbers that add to give 10 and multiply to give 24, we will be successful: 6 and 4. This gives us the confidence to try a few guesses: First guess: One way to produce the x 2 y 2 term is to include an x 2 term in the first parenthesis and a y 2 term in the second parenethesis, like this: x 2 y 2 10xy +24 = (x 2 6)(y 2 4). Checking the guess by expanding, we see that it does not work: (x 2 6)(y 2 4) = x 2 y 2 4x 2 6y The first and fourth terms are correct, but the middle two terms are not correct. Second guess: Another way to produce the x 2 y 2 term is to include an xy term in each parenthesis, like this: x 2 y 2 10xy + 24 = (xy 6)(xy 4). Checking the guess by expanding, we see that it does work: (xy 6)(xy 4) = x 2 y 2 4xy 6xy + 24 = x 2 y 2 10xy Let s now look at a trinomial for which the degree is greater than 2. EXAMPLE 8 Factor the trinomial x 4 8x 2 y 2 20y 4. If we attempt to use a method similar to the one used in the previous examples, we seek two numbers that add to give 8 and multiply to give 20. After some searching, we find that the two numbers are 10 and 2. What expressions should go inside the two parentheses? As a first guess, we could try x 2 in each of the two parentheses, because their product is x 4, and then perhaps 10y 2 in one parenthesis and 2y 2 in the other, because their product is 20y 4. Putting this all together, our guess is x 4 8x 2 y 2 20y 4 = (x 2 10y 2 )(x 2 + 2y 2 ) Expanding the right side, we see that the guess works! (Check it for yourself!) Now let s see if you can apply everything you ve learned so far to the following exercises. PRACTICE (Answers below.) 2. Factor each trinomial. (a) m 2 + 9mn + 18n 2 (b) s st + 36t 2 (c) c 2 d cd 100 (d) x 4 29x 2 y y 4 (e) y 4 5y 2 36 (f) p 2 q pq + 80 Answers: (a) (m + 6n)(m + 3n) (b) (s + 18t)(s + 2t) (c) (cd + 25)(cd 4) (d) (x 2 25y 2 )(x 2 4y 2 ) (e) (y 2 9)(y 2 + 4) (f) (pq + 8)(pq + 10) 6
7 So far we ve only looked at trinomials where the x 2 term has a coefficient of 1. However, generally trinomials are of the form y = ax 2 + bx + c where a, the coefficient of the x 2 term, is not necessarily equal to 1. This leads to the following observation. KEY IDEA A quadratic, trinomial expression of the form y = ax 2 + bx + c can be factored in the form y = (qx + s)(rx + t), if the following three conditions are satisfied: 1. qr = a 2. st = c 3. qt + rs = b Note that when compared to the conditions that must be satisfied for factoring simple trinomials, the second condition is the same as before, and the new condition 1 is similar, but the third condition is a little more complicated. This complication makes such trinomials tricky and hence more difficult to factor if we rely on pattern recognition. We will present two methods for factoring tricky trinomials. Select and use whichever one is easiest for you to understand and works best for you. Method 1: Trial and Error Method At first this will require you to simply guess and check, however with time you ll find that guessing becomes less of a factor and it will become more intuitive. Also, despite the perceived abstractness of the method, you ll find that the guess is not as random as one would think, but rather requires pattern recognition and deduction. Steps: 1. Check for a common factor first. You may find that after common factoring, the trinomial is not actually tricky but rather simple in nature. 2. Choose two factors that multiply to produce the correct first coefficient (i.e. a). These numbers will take the place of q and r in the factored form outlined in the key-idea box. For example, consider 5z z 3. One could guess that two factors that multiply to give the coefficient of a are (5)(1) = 5. (Of course, one could also guess that the factors are ( 5)( 1) = 5, but let s try the first guess first.) 3. Choose two factors that multiply to produce the correct constant coefficient (i.e. c). These numbers will take the place of s and t in the factored form outlined in the key-idea box. For instance, we could choose (3)( 1) = Check that the factors that you have selected can be arranged so that they give the correct coefficient of the linear term (i.e. b). In our example, let s try (5)( 1) + (1)(3) = = 2 b, which does not work. A second try is (5)(3) + (1)( 1) = 15 1 = 14 = b, which does work. Therefore, the solution is 5z z 3 = (5z 1)(z + 3). Check that this is valid by expanding the right side. Method 2: Common Factor Method This is a systematic procedure that does not require any guessing. Steps: 7
8 1. Multiply the first and third coefficients together (i.e. a and c) let s call the resulting number d. For example, once again consider 5z 2 +14z 3. Multiplying the first and third coefficients together results in d = 5( 3) = Determine two factors of d that when added give b. After some thought, you will come up with 15 and 1, because b = 14 = Now write the expression again, this time replacing the linear term by two terms corresponding to the numbers obtained in Step 2. For our example, this means 5z 2 +14z 3 = 5z 2 +15z z Group the first two terms together, and group the third and fourth terms together. Common factor, if possible, within each group. Note that the remaining terms will have a common factor. In our example, 5z z z 3 = 5z(z + 3) (z + 3). 5. Common factor once more to obtain the final result. For our example, 5z(z + 3) (z + 3) = (5z 1)(z + 3). Thus, the final result is 5z z 3 = (5z 1)(z + 3). Notice that the result of each method is the same, as you can check by expanding. As the thought process behind Method 1 is unique to every individual, and is thus difficult to document, let s consider a few more examples using Method 2. EXAMPLE 9 Factor 3x 2 10x + 8. Notice that a = 3, b = 10, and c = 8. Multiplying a and c together, we observe that d = (3)(8) = 24. Now if we look for two factors of d = 24 such that their sum gives b = 10, we discover that the necessary numbers are 6 and 4, because ( 6)( 4) = 24 = d and 6 + ( 4) = 10 = b. Rewriting our expression, replacing the linear term by two terms that correspond to the numbers 6 and 4, we get 3x 2 6x 4x + 8. Grouping and common factoring, this results in 3x(x 2) 4(x 2). Common factoring once more, we find the solution to be 3x 2 10x + 8 = (x 2)(3x 4). Check the final result by expanding. EXAMPLE 10 Factor 2y 2 5y 12. Note that a = 2, b = 5 and c = 12. Then d = ac = (2)( 12) = 24. Considering divisors of 24, we can deduce that 3 and 8 are the required numbers, because (3)( 8) = 24 and 3 + ( 8) = 5. Rewriting our expression, we get 2y 2 5y 12 = 2y 2 + 3y 8y 12. Grouping and common factoring results in 2y 2 + 3y 8y 12 = y(2y + 3) 4(2y + 3). Common factoring once more we get the solution 2y 2 5y 12 = (2y + 3)(y 4). Check the final result by expanding. 8
9 EXAMPLE 11 Factor 9x x + 4. Note that a = 9, b = 12, and c = 4. Then d = ac = (9)(4) = 36. From the value of d we can deduce that the factors that satisfy the required conditions are 6 and 6, because (6)(6) = 36 = d and = 12 = b. The rewritten expression yields 9x 2 + 6x + 6x + 4 and after grouping and common factoring results in 3x(3x + 2) + 2(3x + 2). After common factoring one last time, we find the solution to be 9x 2 +12x+4 = (3x+2)(3x+2) = (3x + 2) 2. Check by expanding! Now it s time for you to practice! Remember to use whichever method you prefer and makes the most sense to you. PRACTICE (Answers below.) 3. Factor each trinomial. (a) 2x 2 + 5x + 3 (b) 6a 2 + 7a + 2 (c) 21c c + 4 (d) 10s s 5 (e) 3q 2 5q 2 (f) 6p 2 p 12 Answers: (a) (2x+3)(x+1) (b) (3x+2)(2x+1) (c) (7x+2)(3x+2) (d) (5x 1)(2x+5) (e) (3q +1)(q 2) (f) (3p + 4)(2p 3) KEY IDEA Though we didn t see any examples of this above, as mentioned with Step 1 of the first method, it s important to always look for common factors first. This may make what appears to be a tricky trinomial into a simple trinomial, or reduce the size of the coefficients and thus simplify the task of factoring the expression. To illustrate this point try the following exercises. PRACTICE (Answers below.) 4. Factor each trinomial. (a) 3x 2 12xy 96y 2 (b) 4x 2 28x + 48 (c) 2x 2 y + 4xy 48y (d) 4a 2 b 2 12ab 40 Answers: (a) 3(x 8y)(x + 4y) (b) 4(x 4)(x 3) (c) 2y(x 4)(x + 6) (d) 4(ab 5)(ab + 2) We will now examine one last factoring pattern known as the difference of squares factoring pattern. In the title we see the word square, a geometric shape that we know to have sides of 9
10 equal length. The algebraic analogue of this is a number that is the product of two equal numbers. Note this concept is not limited merely to numbers, as it includes quantities as well. For example, x 2 can be written as (x)(x), and as such is also a square. Recall that the whole square numbers are 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225,.... Consider quadratic expressions of the form x 2 k 2. You may have noticed already that this differs slightly from the general form y = x 2 + bx + c, as in this case b = 0 and as such there is no linear term. We re left simply with a binomial expression. We re also writing c as k 2 to guide us to think about a difference of squares. Thinking back to our kitchen floor tiles, for a to equal 0, our factors s and t must have the same absolute values, but with opposite signs so that when the factored expression is expanded the x-terms will cancel, leaving only the x 2 -term and constant term. To illustrate this, observe that when we expand the factored expression (x 3)(x + 3), we get (x)(x) + (x)(3) (3)(x) (3)(3), and after collecting like terms, the simplified expression yields x 2 + 3x 3x 9 = x 2 9. KEY IDEA A quadratic expression of the form y = x 2 k 2 can be factored in the form (x k)(x + k). Consider these examples to help solidify the concept. EXAMPLE 12 Factor 100 y 2. Looking at the expression 100 y 2 note that 100 = (10)(10) = (10) 2, so the expression is in the form of a difference of squares. Therefore, we can deduce that 100 y 2 = (10 y)(10 + y). Check by expanding, and notice how the linear terms cancel so that there is no linear term in the final expanded expression. EXAMPLE 13 Factor y 2 81x 4. We recognize the first term as a square, but the second term is a little more complicated. By recognizing that 81 = 9 2 and x 4 = (x 2 ) 2, we can write (81)(x 4 ) as (9) 2 (x 2 ) 2 or equivalently as ((9)(x 2 )) 2. Therefore, using the difference-of-squares factoring pattern, we can write y 2 81x 4 = (y 9x 2 )(y + 9x 2 ) 10
11 EXAMPLE 14 Factor 16x 2 y 2 25b 2. We can recognize the first term as a square by writing it as 16x 2 y 2 25b 2 = 4 2 x 2 y b 2 = (4xy) 2 (5b) 2. Therefore, using the difference-of-squares factoring pattern, we can write Therefore, the solution is 16x 2 y 2 25b 2 = (4xy 5b)(4xy + 5b) EXAMPLE 15 Factor (2x + 5) 2 81x 2. This expression has the structure of a difference of squares; that is, it is in the form a 2 b 2, where a 2 = (2x + 5) 2, and therefore a = (2x + 5), and b 2 = 81x 2 = (9x) 2, and therefore b = 9x. Thus, according to the difference of squares pattern, (2x + 5) 2 81x 2 = (2x + 5) 2 (9x) 2 = a 2 b 2 = (a b)(a + b) = (2x + 5 9x) (2x x) = ( 7x + 5) (11x + 5) Now you give it a try! PRACTICE (Answers below.) 5. Factor each expression. (a) x 2 49 (b) t 2 (c) 49c 2 d b2 (d) 144x 4 1 (e) (2x y) 2 (6x 2y) 2 (f) p 2 q 2 81 (g) 4x 16xy 2 (h) 27xy 75a 2 xy Answers: (a) (x 7)(x + 7) (b) (11 6t)(11 + 6t) (c) (7cd 9 5 b)(7cd b) (d) (12x2 1)(12x 2 + 1) (e) ( 4x + y)(8x 3y) (f) (pq 9)(pq + 9) (g) 4x(1 2y)(1 + 2y) (h) 3xy(3 5a)(3 + 5a) 11
12 KEY IDEA It s important to note that more than one factoring step may be needed to fully factor a polynomial expression. This may require a combination of the methods discussed throughout the lesson. Consider the following example: Suppose we wish to factor x 4 29x 2 y y 4. The first step is always to look for any common factors. As none exist, we proceed by treating this expression as a simple trinomial and factoring accordingly. This gives x 4 29x 2 y y 4 = (x 2 4y 2 )(x 2 25y 2 ). Note that each of the factors is a difference of squares, and therefore each factor can be factored further. Using the difference of squares pattern for each factor, we get the final result x 4 29x 2 y y 4 = (x + 2y)(x 2y)(x + 5y)(x 5y). RECAP: Steps for factoring a trinomial 1. First check for common factors. 2. If there are two terms, check to see whether the expression fits the difference of squares pattern. If so, factor using this pattern. 3. If there are three terms, attempt to factor according to one of the trinomial patterns learned in this module. 4. Check to see if any of the newly found factors can be factored further. 5. Check your final result by expanding and comparing with the original expression. 6. Learn more factoring patterns, in case none of the ones used here works! 7. It s possible that your expression cannot be factored, or at least cannot be factored easily. Once again, learning some advanced mathematics will be helpful! WWW What we did: We learned how to factor simple, special, and tricky trinomials as well as how to use the difference of squares method to factor specific binomials. Why we did it: Factoring polynomial expressions is helpful in solving certain equations, and in analyzing and plotting certain graphs. What s next: We can build on what we have learned here to solve polynomial equations, and to help us determine zeros of polynomial functions. EXERCISES 1. Factor each expression. (a) 15y 3 35y 2 (b) 4 81x 2 (c) x 2 + 5x 66 (d) 18a 2 50 (e) 5x 2 17x + 6 (f) 30x x 2 15x 12
Using the ac Method to Factor
 4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
Factoring Trinomials: The ac Method
 6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
Factoring Trinomials of the Form x 2 bx c
 4.2 Factoring Trinomials of the Form x 2 bx c 4.2 OBJECTIVES 1. Factor a trinomial of the form x 2 bx c 2. Factor a trinomial containing a common factor NOTE The process used to factor here is frequently
4.2 Factoring Trinomials of the Form x 2 bx c 4.2 OBJECTIVES 1. Factor a trinomial of the form x 2 bx c 2. Factor a trinomial containing a common factor NOTE The process used to factor here is frequently
FACTORING ax 2 bx c. Factoring Trinomials with Leading Coefficient 1
 5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
MATH 10034 Fundamental Mathematics IV
 MATH 0034 Fundamental Mathematics IV http://www.math.kent.edu/ebooks/0034/funmath4.pdf Department of Mathematical Sciences Kent State University January 2, 2009 ii Contents To the Instructor v Polynomials.
MATH 0034 Fundamental Mathematics IV http://www.math.kent.edu/ebooks/0034/funmath4.pdf Department of Mathematical Sciences Kent State University January 2, 2009 ii Contents To the Instructor v Polynomials.
NSM100 Introduction to Algebra Chapter 5 Notes Factoring
 Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
Factoring Polynomials
 UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
FACTORING POLYNOMIALS
 296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
By reversing the rules for multiplication of binomials from Section 4.6, we get rules for factoring polynomials in certain forms.
 SECTION 5.4 Special Factoring Techniques 317 5.4 Special Factoring Techniques OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor
SECTION 5.4 Special Factoring Techniques 317 5.4 Special Factoring Techniques OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor
Factoring Polynomials and Solving Quadratic Equations
 Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
( ) FACTORING. x In this polynomial the only variable in common to all is x.
 FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
Factoring Quadratic Expressions
 Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
Polynomials. Key Terms. quadratic equation parabola conjugates trinomial. polynomial coefficient degree monomial binomial GCF
 Polynomials 5 5.1 Addition and Subtraction of Polynomials and Polynomial Functions 5.2 Multiplication of Polynomials 5.3 Division of Polynomials Problem Recognition Exercises Operations on Polynomials
Polynomials 5 5.1 Addition and Subtraction of Polynomials and Polynomial Functions 5.2 Multiplication of Polynomials 5.3 Division of Polynomials Problem Recognition Exercises Operations on Polynomials
Negative Integer Exponents
 7.7 Negative Integer Exponents 7.7 OBJECTIVES. Define the zero exponent 2. Use the definition of a negative exponent to simplify an expression 3. Use the properties of exponents to simplify expressions
7.7 Negative Integer Exponents 7.7 OBJECTIVES. Define the zero exponent 2. Use the definition of a negative exponent to simplify an expression 3. Use the properties of exponents to simplify expressions
1.3 Polynomials and Factoring
 1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
Factoring Polynomials
 Factoring Polynomials 4-1-2014 The opposite of multiplying polynomials is factoring. Why would you want to factor a polynomial? Let p(x) be a polynomial. p(c) = 0 is equivalent to x c dividing p(x). Recall
Factoring Polynomials 4-1-2014 The opposite of multiplying polynomials is factoring. Why would you want to factor a polynomial? Let p(x) be a polynomial. p(c) = 0 is equivalent to x c dividing p(x). Recall
Click on the links below to jump directly to the relevant section
 Click on the links below to jump directly to the relevant section What is algebra? Operations with algebraic terms Mathematical properties of real numbers Order of operations What is Algebra? Algebra is
Click on the links below to jump directly to the relevant section What is algebra? Operations with algebraic terms Mathematical properties of real numbers Order of operations What is Algebra? Algebra is
3.2. Solving quadratic equations. Introduction. Prerequisites. Learning Outcomes. Learning Style
 Solving quadratic equations 3.2 Introduction A quadratic equation is one which can be written in the form ax 2 + bx + c = 0 where a, b and c are numbers and x is the unknown whose value(s) we wish to find.
Solving quadratic equations 3.2 Introduction A quadratic equation is one which can be written in the form ax 2 + bx + c = 0 where a, b and c are numbers and x is the unknown whose value(s) we wish to find.
Solving Quadratic Equations
 9.3 Solving Quadratic Equations by Using the Quadratic Formula 9.3 OBJECTIVES 1. Solve a quadratic equation by using the quadratic formula 2. Determine the nature of the solutions of a quadratic equation
9.3 Solving Quadratic Equations by Using the Quadratic Formula 9.3 OBJECTIVES 1. Solve a quadratic equation by using the quadratic formula 2. Determine the nature of the solutions of a quadratic equation
0.8 Rational Expressions and Equations
 96 Prerequisites 0.8 Rational Expressions and Equations We now turn our attention to rational expressions - that is, algebraic fractions - and equations which contain them. The reader is encouraged to
96 Prerequisites 0.8 Rational Expressions and Equations We now turn our attention to rational expressions - that is, algebraic fractions - and equations which contain them. The reader is encouraged to
POLYNOMIALS and FACTORING
 POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
Rational Exponents. Squaring both sides of the equation yields. and to be consistent, we must have
 8.6 Rational Exponents 8.6 OBJECTIVES 1. Define rational exponents 2. Simplify expressions containing rational exponents 3. Use a calculator to estimate the value of an expression containing rational exponents
8.6 Rational Exponents 8.6 OBJECTIVES 1. Define rational exponents 2. Simplify expressions containing rational exponents 3. Use a calculator to estimate the value of an expression containing rational exponents
expression is written horizontally. The Last terms ((2)( 4)) because they are the last terms of the two polynomials. This is called the FOIL method.
 A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
Factoring Special Polynomials
 6.6 Factoring Special Polynomials 6.6 OBJECTIVES 1. Factor the difference of two squares 2. Factor the sum or difference of two cubes In this section, we will look at several special polynomials. These
6.6 Factoring Special Polynomials 6.6 OBJECTIVES 1. Factor the difference of two squares 2. Factor the sum or difference of two cubes In this section, we will look at several special polynomials. These
Academic Success Centre
 250) 960-6367 Factoring Polynomials Sometimes when we try to solve or simplify an equation or expression involving polynomials the way that it looks can hinder our progress in finding a solution. Factorization
250) 960-6367 Factoring Polynomials Sometimes when we try to solve or simplify an equation or expression involving polynomials the way that it looks can hinder our progress in finding a solution. Factorization
6.3 FACTORING ax 2 bx c WITH a 1
 290 (6 14) Chapter 6 Factoring e) What is the approximate maximum revenue? f) Use the accompanying graph to estimate the price at which the revenue is zero. y Revenue (thousands of dollars) 300 200 100
290 (6 14) Chapter 6 Factoring e) What is the approximate maximum revenue? f) Use the accompanying graph to estimate the price at which the revenue is zero. y Revenue (thousands of dollars) 300 200 100
1.4. Arithmetic of Algebraic Fractions. Introduction. Prerequisites. Learning Outcomes
 Arithmetic of Algebraic Fractions 1.4 Introduction Just as one whole number divided by another is called a numerical fraction, so one algebraic expression divided by another is known as an algebraic fraction.
Arithmetic of Algebraic Fractions 1.4 Introduction Just as one whole number divided by another is called a numerical fraction, so one algebraic expression divided by another is known as an algebraic fraction.
1.5. Factorisation. Introduction. Prerequisites. Learning Outcomes. Learning Style
 Factorisation 1.5 Introduction In Block 4 we showed the way in which brackets were removed from algebraic expressions. Factorisation, which can be considered as the reverse of this process, is dealt with
Factorisation 1.5 Introduction In Block 4 we showed the way in which brackets were removed from algebraic expressions. Factorisation, which can be considered as the reverse of this process, is dealt with
In algebra, factor by rewriting a polynomial as a product of lower-degree polynomials
 Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
Mathematics Placement
 Mathematics Placement The ACT COMPASS math test is a self-adaptive test, which potentially tests students within four different levels of math including pre-algebra, algebra, college algebra, and trigonometry.
Mathematics Placement The ACT COMPASS math test is a self-adaptive test, which potentially tests students within four different levels of math including pre-algebra, algebra, college algebra, and trigonometry.
How To Factor By Gcf In Algebra 1.5
 7-2 Factoring by GCF Warm Up Lesson Presentation Lesson Quiz Algebra 1 Warm Up Simplify. 1. 2(w + 1) 2. 3x(x 2 4) 2w + 2 3x 3 12x Find the GCF of each pair of monomials. 3. 4h 2 and 6h 2h 4. 13p and 26p
7-2 Factoring by GCF Warm Up Lesson Presentation Lesson Quiz Algebra 1 Warm Up Simplify. 1. 2(w + 1) 2. 3x(x 2 4) 2w + 2 3x 3 12x Find the GCF of each pair of monomials. 3. 4h 2 and 6h 2h 4. 13p and 26p
1.3 Algebraic Expressions
 1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
6.1 Add & Subtract Polynomial Expression & Functions
 6.1 Add & Subtract Polynomial Expression & Functions Objectives 1. Know the meaning of the words term, monomial, binomial, trinomial, polynomial, degree, coefficient, like terms, polynomial funciton, quardrtic
6.1 Add & Subtract Polynomial Expression & Functions Objectives 1. Know the meaning of the words term, monomial, binomial, trinomial, polynomial, degree, coefficient, like terms, polynomial funciton, quardrtic
Veterans Upward Bound Algebra I Concepts - Honors
 Veterans Upward Bound Algebra I Concepts - Honors Brenda Meery Kaitlyn Spong Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org Chapter 6. Factoring CHAPTER
Veterans Upward Bound Algebra I Concepts - Honors Brenda Meery Kaitlyn Spong Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org Chapter 6. Factoring CHAPTER
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0).
 This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
6 EXTENDING ALGEBRA. 6.0 Introduction. 6.1 The cubic equation. Objectives
 6 EXTENDING ALGEBRA Chapter 6 Extending Algebra Objectives After studying this chapter you should understand techniques whereby equations of cubic degree and higher can be solved; be able to factorise
6 EXTENDING ALGEBRA Chapter 6 Extending Algebra Objectives After studying this chapter you should understand techniques whereby equations of cubic degree and higher can be solved; be able to factorise
Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder).
 Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
3.1. RATIONAL EXPRESSIONS
 3.1. RATIONAL EXPRESSIONS RATIONAL NUMBERS In previous courses you have learned how to operate (do addition, subtraction, multiplication, and division) on rational numbers (fractions). Rational numbers
3.1. RATIONAL EXPRESSIONS RATIONAL NUMBERS In previous courses you have learned how to operate (do addition, subtraction, multiplication, and division) on rational numbers (fractions). Rational numbers
7-6. Choosing a Factoring Model. Extension: Factoring Polynomials with More Than One Variable IN T RO DUC E T EACH. Standards for Mathematical Content
 7-6 Choosing a Factoring Model Extension: Factoring Polynomials with More Than One Variable Essential question: How can you factor polynomials with more than one variable? What is the connection between
7-6 Choosing a Factoring Model Extension: Factoring Polynomials with More Than One Variable Essential question: How can you factor polynomials with more than one variable? What is the connection between
Math 25 Activity 6: Factoring Advanced
 Instructor! Math 25 Activity 6: Factoring Advanced Last week we looked at greatest common factors and the basics of factoring out the GCF. In this second activity, we will discuss factoring more difficult
Instructor! Math 25 Activity 6: Factoring Advanced Last week we looked at greatest common factors and the basics of factoring out the GCF. In this second activity, we will discuss factoring more difficult
Exponents and Radicals
 Exponents and Radicals (a + b) 10 Exponents are a very important part of algebra. An exponent is just a convenient way of writing repeated multiplications of the same number. Radicals involve the use of
Exponents and Radicals (a + b) 10 Exponents are a very important part of algebra. An exponent is just a convenient way of writing repeated multiplications of the same number. Radicals involve the use of
Factoring. Factoring Monomials Monomials can often be factored in more than one way.
 Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS
 (Section 0.6: Polynomial, Rational, and Algebraic Expressions) 0.6.1 SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS LEARNING OBJECTIVES Be able to identify polynomial, rational, and algebraic
(Section 0.6: Polynomial, Rational, and Algebraic Expressions) 0.6.1 SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS LEARNING OBJECTIVES Be able to identify polynomial, rational, and algebraic
COLLEGE ALGEBRA. Paul Dawkins
 COLLEGE ALGEBRA Paul Dawkins Table of Contents Preface... iii Outline... iv Preliminaries... Introduction... Integer Exponents... Rational Exponents... 9 Real Exponents...5 Radicals...6 Polynomials...5
COLLEGE ALGEBRA Paul Dawkins Table of Contents Preface... iii Outline... iv Preliminaries... Introduction... Integer Exponents... Rational Exponents... 9 Real Exponents...5 Radicals...6 Polynomials...5
BEGINNING ALGEBRA ACKNOWLEDMENTS
 BEGINNING ALGEBRA The Nursing Department of Labouré College requested the Department of Academic Planning and Support Services to help with mathematics preparatory materials for its Bachelor of Science
BEGINNING ALGEBRA The Nursing Department of Labouré College requested the Department of Academic Planning and Support Services to help with mathematics preparatory materials for its Bachelor of Science
Chapter R.4 Factoring Polynomials
 Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
Algebraic expressions are a combination of numbers and variables. Here are examples of some basic algebraic expressions.
 Page 1 of 13 Review of Linear Expressions and Equations Skills involving linear equations can be divided into the following groups: Simplifying algebraic expressions. Linear expressions. Solving linear
Page 1 of 13 Review of Linear Expressions and Equations Skills involving linear equations can be divided into the following groups: Simplifying algebraic expressions. Linear expressions. Solving linear
A Concrete Introduction. to the Abstract Concepts. of Integers and Algebra using Algebra Tiles
 A Concrete Introduction to the Abstract Concepts of Integers and Algebra using Algebra Tiles Table of Contents Introduction... 1 page Integers 1: Introduction to Integers... 3 2: Working with Algebra Tiles...
A Concrete Introduction to the Abstract Concepts of Integers and Algebra using Algebra Tiles Table of Contents Introduction... 1 page Integers 1: Introduction to Integers... 3 2: Working with Algebra Tiles...
Factoring Flow Chart
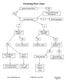 Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
POLYNOMIAL FUNCTIONS
 POLYNOMIAL FUNCTIONS Polynomial Division.. 314 The Rational Zero Test.....317 Descarte s Rule of Signs... 319 The Remainder Theorem.....31 Finding all Zeros of a Polynomial Function.......33 Writing a
POLYNOMIAL FUNCTIONS Polynomial Division.. 314 The Rational Zero Test.....317 Descarte s Rule of Signs... 319 The Remainder Theorem.....31 Finding all Zeros of a Polynomial Function.......33 Writing a
Math 10C. Course: Polynomial Products and Factors. Unit of Study: Step 1: Identify the Outcomes to Address. Guiding Questions:
 Course: Unit of Study: Math 10C Polynomial Products and Factors Step 1: Identify the Outcomes to Address Guiding Questions: What do I want my students to learn? What can they currently understand and do?
Course: Unit of Study: Math 10C Polynomial Products and Factors Step 1: Identify the Outcomes to Address Guiding Questions: What do I want my students to learn? What can they currently understand and do?
Algebra Cheat Sheets
 Sheets Algebra Cheat Sheets provide you with a tool for teaching your students note-taking, problem-solving, and organizational skills in the context of algebra lessons. These sheets teach the concepts
Sheets Algebra Cheat Sheets provide you with a tool for teaching your students note-taking, problem-solving, and organizational skills in the context of algebra lessons. These sheets teach the concepts
A Systematic Approach to Factoring
 A Systematic Approach to Factoring Step 1 Count the number of terms. (Remember****Knowing the number of terms will allow you to eliminate unnecessary tools.) Step 2 Is there a greatest common factor? Tool
A Systematic Approach to Factoring Step 1 Count the number of terms. (Remember****Knowing the number of terms will allow you to eliminate unnecessary tools.) Step 2 Is there a greatest common factor? Tool
6.1 The Greatest Common Factor; Factoring by Grouping
 386 CHAPTER 6 Factoring and Applications 6.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
386 CHAPTER 6 Factoring and Applications 6.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
Section 6.1 Factoring Expressions
 Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
The Greatest Common Factor; Factoring by Grouping
 296 CHAPTER 5 Factoring and Applications 5.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
296 CHAPTER 5 Factoring and Applications 5.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
ALGEBRA REVIEW LEARNING SKILLS CENTER. Exponents & Radicals
 ALGEBRA REVIEW LEARNING SKILLS CENTER The "Review Series in Algebra" is taught at the beginning of each quarter by the staff of the Learning Skills Center at UC Davis. This workshop is intended to be an
ALGEBRA REVIEW LEARNING SKILLS CENTER The "Review Series in Algebra" is taught at the beginning of each quarter by the staff of the Learning Skills Center at UC Davis. This workshop is intended to be an
This is a square root. The number under the radical is 9. (An asterisk * means multiply.)
 Page of Review of Radical Expressions and Equations Skills involving radicals can be divided into the following groups: Evaluate square roots or higher order roots. Simplify radical expressions. Rationalize
Page of Review of Radical Expressions and Equations Skills involving radicals can be divided into the following groups: Evaluate square roots or higher order roots. Simplify radical expressions. Rationalize
Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any.
 Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
Factoring and Applications
 Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
What does the number m in y = mx + b measure? To find out, suppose (x 1, y 1 ) and (x 2, y 2 ) are two points on the graph of y = mx + b.
 PRIMARY CONTENT MODULE Algebra - Linear Equations & Inequalities T-37/H-37 What does the number m in y = mx + b measure? To find out, suppose (x 1, y 1 ) and (x 2, y 2 ) are two points on the graph of
PRIMARY CONTENT MODULE Algebra - Linear Equations & Inequalities T-37/H-37 What does the number m in y = mx + b measure? To find out, suppose (x 1, y 1 ) and (x 2, y 2 ) are two points on the graph of
Vieta s Formulas and the Identity Theorem
 Vieta s Formulas and the Identity Theorem This worksheet will work through the material from our class on 3/21/2013 with some examples that should help you with the homework The topic of our discussion
Vieta s Formulas and the Identity Theorem This worksheet will work through the material from our class on 3/21/2013 with some examples that should help you with the homework The topic of our discussion
Factor Polynomials Completely
 9.8 Factor Polynomials Completely Before You factored polynomials. Now You will factor polynomials completely. Why? So you can model the height of a projectile, as in Ex. 71. Key Vocabulary factor by grouping
9.8 Factor Polynomials Completely Before You factored polynomials. Now You will factor polynomials completely. Why? So you can model the height of a projectile, as in Ex. 71. Key Vocabulary factor by grouping
Definition 8.1 Two inequalities are equivalent if they have the same solution set. Add or Subtract the same value on both sides of the inequality.
 8 Inequalities Concepts: Equivalent Inequalities Linear and Nonlinear Inequalities Absolute Value Inequalities (Sections 4.6 and 1.1) 8.1 Equivalent Inequalities Definition 8.1 Two inequalities are equivalent
8 Inequalities Concepts: Equivalent Inequalities Linear and Nonlinear Inequalities Absolute Value Inequalities (Sections 4.6 and 1.1) 8.1 Equivalent Inequalities Definition 8.1 Two inequalities are equivalent
MATH 60 NOTEBOOK CERTIFICATIONS
 MATH 60 NOTEBOOK CERTIFICATIONS Chapter #1: Integers and Real Numbers 1.1a 1.1b 1.2 1.3 1.4 1.8 Chapter #2: Algebraic Expressions, Linear Equations, and Applications 2.1a 2.1b 2.1c 2.2 2.3a 2.3b 2.4 2.5
MATH 60 NOTEBOOK CERTIFICATIONS Chapter #1: Integers and Real Numbers 1.1a 1.1b 1.2 1.3 1.4 1.8 Chapter #2: Algebraic Expressions, Linear Equations, and Applications 2.1a 2.1b 2.1c 2.2 2.3a 2.3b 2.4 2.5
Systems of Equations Involving Circles and Lines
 Name: Systems of Equations Involving Circles and Lines Date: In this lesson, we will be solving two new types of Systems of Equations. Systems of Equations Involving a Circle and a Line Solving a system
Name: Systems of Equations Involving Circles and Lines Date: In this lesson, we will be solving two new types of Systems of Equations. Systems of Equations Involving a Circle and a Line Solving a system
AIP Factoring Practice/Help
 The following pages include many problems to practice factoring skills. There are also several activities with examples to help you with factoring if you feel like you are not proficient with it. There
The following pages include many problems to practice factoring skills. There are also several activities with examples to help you with factoring if you feel like you are not proficient with it. There
6.4 Special Factoring Rules
 6.4 Special Factoring Rules OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor a sum of cubes. By reversing the rules for multiplication
6.4 Special Factoring Rules OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor a sum of cubes. By reversing the rules for multiplication
CAHSEE on Target UC Davis, School and University Partnerships
 UC Davis, School and University Partnerships CAHSEE on Target Mathematics Curriculum Published by The University of California, Davis, School/University Partnerships Program 006 Director Sarah R. Martinez,
UC Davis, School and University Partnerships CAHSEE on Target Mathematics Curriculum Published by The University of California, Davis, School/University Partnerships Program 006 Director Sarah R. Martinez,
CM2202: Scientific Computing and Multimedia Applications General Maths: 2. Algebra - Factorisation
 CM2202: Scientific Computing and Multimedia Applications General Maths: 2. Algebra - Factorisation Prof. David Marshall School of Computer Science & Informatics Factorisation Factorisation is a way of
CM2202: Scientific Computing and Multimedia Applications General Maths: 2. Algebra - Factorisation Prof. David Marshall School of Computer Science & Informatics Factorisation Factorisation is a way of
Radicals - Multiply and Divide Radicals
 8. Radicals - Multiply and Divide Radicals Objective: Multiply and divide radicals using the product and quotient rules of radicals. Multiplying radicals is very simple if the index on all the radicals
8. Radicals - Multiply and Divide Radicals Objective: Multiply and divide radicals using the product and quotient rules of radicals. Multiplying radicals is very simple if the index on all the radicals
Integrals of Rational Functions
 Integrals of Rational Functions Scott R. Fulton Overview A rational function has the form where p and q are polynomials. For example, r(x) = p(x) q(x) f(x) = x2 3 x 4 + 3, g(t) = t6 + 4t 2 3, 7t 5 + 3t
Integrals of Rational Functions Scott R. Fulton Overview A rational function has the form where p and q are polynomials. For example, r(x) = p(x) q(x) f(x) = x2 3 x 4 + 3, g(t) = t6 + 4t 2 3, 7t 5 + 3t
2.6 Exponents and Order of Operations
 2.6 Exponents and Order of Operations We begin this section with exponents applied to negative numbers. The idea of applying an exponent to a negative number is identical to that of a positive number (repeated
2.6 Exponents and Order of Operations We begin this section with exponents applied to negative numbers. The idea of applying an exponent to a negative number is identical to that of a positive number (repeated
Factoring Methods. Example 1: 2x + 2 2 * x + 2 * 1 2(x + 1)
 Factoring Methods When you are trying to factor a polynomial, there are three general steps you want to follow: 1. See if there is a Greatest Common Factor 2. See if you can Factor by Grouping 3. See if
Factoring Methods When you are trying to factor a polynomial, there are three general steps you want to follow: 1. See if there is a Greatest Common Factor 2. See if you can Factor by Grouping 3. See if
Polynomials and Factoring
 7.6 Polynomials and Factoring Basic Terminology A term, or monomial, is defined to be a number, a variable, or a product of numbers and variables. A polynomial is a term or a finite sum or difference of
7.6 Polynomials and Factoring Basic Terminology A term, or monomial, is defined to be a number, a variable, or a product of numbers and variables. A polynomial is a term or a finite sum or difference of
Operations with Algebraic Expressions: Multiplication of Polynomials
 Operations with Algebraic Expressions: Multiplication of Polynomials The product of a monomial x monomial To multiply a monomial times a monomial, multiply the coefficients and add the on powers with the
Operations with Algebraic Expressions: Multiplication of Polynomials The product of a monomial x monomial To multiply a monomial times a monomial, multiply the coefficients and add the on powers with the
Solving Rational Equations
 Lesson M Lesson : Student Outcomes Students solve rational equations, monitoring for the creation of extraneous solutions. Lesson Notes In the preceding lessons, students learned to add, subtract, multiply,
Lesson M Lesson : Student Outcomes Students solve rational equations, monitoring for the creation of extraneous solutions. Lesson Notes In the preceding lessons, students learned to add, subtract, multiply,
5.1 Radical Notation and Rational Exponents
 Section 5.1 Radical Notation and Rational Exponents 1 5.1 Radical Notation and Rational Exponents We now review how exponents can be used to describe not only powers (such as 5 2 and 2 3 ), but also roots
Section 5.1 Radical Notation and Rational Exponents 1 5.1 Radical Notation and Rational Exponents We now review how exponents can be used to describe not only powers (such as 5 2 and 2 3 ), but also roots
MATH 90 CHAPTER 6 Name:.
 MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
5.1 FACTORING OUT COMMON FACTORS
 C H A P T E R 5 Factoring he sport of skydiving was born in the 1930s soon after the military began using parachutes as a means of deploying troops. T Today, skydiving is a popular sport around the world.
C H A P T E R 5 Factoring he sport of skydiving was born in the 1930s soon after the military began using parachutes as a means of deploying troops. T Today, skydiving is a popular sport around the world.
The Point-Slope Form
 7. The Point-Slope Form 7. OBJECTIVES 1. Given a point and a slope, find the graph of a line. Given a point and the slope, find the equation of a line. Given two points, find the equation of a line y Slope
7. The Point-Slope Form 7. OBJECTIVES 1. Given a point and a slope, find the graph of a line. Given a point and the slope, find the equation of a line. Given two points, find the equation of a line y Slope
Tool 1. Greatest Common Factor (GCF)
 Chapter 4: Factoring Review Tool 1 Greatest Common Factor (GCF) This is a very important tool. You must try to factor out the GCF first in every problem. Some problems do not have a GCF but many do. When
Chapter 4: Factoring Review Tool 1 Greatest Common Factor (GCF) This is a very important tool. You must try to factor out the GCF first in every problem. Some problems do not have a GCF but many do. When
Name Intro to Algebra 2. Unit 1: Polynomials and Factoring
 Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
10.1. Solving Quadratic Equations. Investigation: Rocket Science CONDENSED
 CONDENSED L E S S O N 10.1 Solving Quadratic Equations In this lesson you will look at quadratic functions that model projectile motion use tables and graphs to approimate solutions to quadratic equations
CONDENSED L E S S O N 10.1 Solving Quadratic Equations In this lesson you will look at quadratic functions that model projectile motion use tables and graphs to approimate solutions to quadratic equations
SPECIAL PRODUCTS AND FACTORS
 CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
FACTORING OUT COMMON FACTORS
 278 (6 2) Chapter 6 Factoring 6.1 FACTORING OUT COMMON FACTORS In this section Prime Factorization of Integers Greatest Common Factor Finding the Greatest Common Factor for Monomials Factoring Out the
278 (6 2) Chapter 6 Factoring 6.1 FACTORING OUT COMMON FACTORS In this section Prime Factorization of Integers Greatest Common Factor Finding the Greatest Common Factor for Monomials Factoring Out the
2.3. Finding polynomial functions. An Introduction:
 2.3. Finding polynomial functions. An Introduction: As is usually the case when learning a new concept in mathematics, the new concept is the reverse of the previous one. Remember how you first learned
2.3. Finding polynomial functions. An Introduction: As is usually the case when learning a new concept in mathematics, the new concept is the reverse of the previous one. Remember how you first learned
3.3. Solving Polynomial Equations. Introduction. Prerequisites. Learning Outcomes
 Solving Polynomial Equations 3.3 Introduction Linear and quadratic equations, dealt within Sections 3.1 and 3.2, are members of a class of equations, called polynomial equations. These have the general
Solving Polynomial Equations 3.3 Introduction Linear and quadratic equations, dealt within Sections 3.1 and 3.2, are members of a class of equations, called polynomial equations. These have the general
In this section, you will develop a method to change a quadratic equation written as a sum into its product form (also called its factored form).
 CHAPTER 8 In Chapter 4, you used a web to organize the connections you found between each of the different representations of lines. These connections enabled you to use any representation (such as a graph,
CHAPTER 8 In Chapter 4, you used a web to organize the connections you found between each of the different representations of lines. These connections enabled you to use any representation (such as a graph,
Simplifying Algebraic Fractions
 5. Simplifying Algebraic Fractions 5. OBJECTIVES. Find the GCF for two monomials and simplify a fraction 2. Find the GCF for two polynomials and simplify a fraction Much of our work with algebraic fractions
5. Simplifying Algebraic Fractions 5. OBJECTIVES. Find the GCF for two monomials and simplify a fraction 2. Find the GCF for two polynomials and simplify a fraction Much of our work with algebraic fractions
6706_PM10SB_C4_CO_pp192-193.qxd 5/8/09 9:53 AM Page 192 192 NEL
 92 NEL Chapter 4 Factoring Algebraic Epressions GOALS You will be able to Determine the greatest common factor in an algebraic epression and use it to write the epression as a product Recognize different
92 NEL Chapter 4 Factoring Algebraic Epressions GOALS You will be able to Determine the greatest common factor in an algebraic epression and use it to write the epression as a product Recognize different
Factoring Algebra- Chapter 8B Assignment Sheet
 Name: Factoring Algebra- Chapter 8B Assignment Sheet Date Section Learning Targets Assignment Tues 2/17 Find the prime factorization of an integer Find the greatest common factor (GCF) for a set of monomials.
Name: Factoring Algebra- Chapter 8B Assignment Sheet Date Section Learning Targets Assignment Tues 2/17 Find the prime factorization of an integer Find the greatest common factor (GCF) for a set of monomials.
Answer Key for California State Standards: Algebra I
 Algebra I: Symbolic reasoning and calculations with symbols are central in algebra. Through the study of algebra, a student develops an understanding of the symbolic language of mathematics and the sciences.
Algebra I: Symbolic reasoning and calculations with symbols are central in algebra. Through the study of algebra, a student develops an understanding of the symbolic language of mathematics and the sciences.
How To Solve Factoring Problems
 05-W4801-AM1.qxd 8/19/08 8:45 PM Page 241 Factoring, Solving Equations, and Problem Solving 5 5.1 Factoring by Using the Distributive Property 5.2 Factoring the Difference of Two Squares 5.3 Factoring
05-W4801-AM1.qxd 8/19/08 8:45 PM Page 241 Factoring, Solving Equations, and Problem Solving 5 5.1 Factoring by Using the Distributive Property 5.2 Factoring the Difference of Two Squares 5.3 Factoring
x 2 + y 2 = 1 y 1 = x 2 + 2x y = x 2 + 2x + 1
 Implicit Functions Defining Implicit Functions Up until now in this course, we have only talked about functions, which assign to every real number x in their domain exactly one real number f(x). The graphs
Implicit Functions Defining Implicit Functions Up until now in this course, we have only talked about functions, which assign to every real number x in their domain exactly one real number f(x). The graphs
Topic: Special Products and Factors Subtopic: Rules on finding factors of polynomials
 Quarter I: Special Products and Factors and Quadratic Equations Topic: Special Products and Factors Subtopic: Rules on finding factors of polynomials Time Frame: 20 days Time Frame: 3 days Content Standard:
Quarter I: Special Products and Factors and Quadratic Equations Topic: Special Products and Factors Subtopic: Rules on finding factors of polynomials Time Frame: 20 days Time Frame: 3 days Content Standard:
Quotient Rings and Field Extensions
 Chapter 5 Quotient Rings and Field Extensions In this chapter we describe a method for producing field extension of a given field. If F is a field, then a field extension is a field K that contains F.
Chapter 5 Quotient Rings and Field Extensions In this chapter we describe a method for producing field extension of a given field. If F is a field, then a field extension is a field K that contains F.
1.6 The Order of Operations
 1.6 The Order of Operations Contents: Operations Grouping Symbols The Order of Operations Exponents and Negative Numbers Negative Square Roots Square Root of a Negative Number Order of Operations and Negative
1.6 The Order of Operations Contents: Operations Grouping Symbols The Order of Operations Exponents and Negative Numbers Negative Square Roots Square Root of a Negative Number Order of Operations and Negative
