FLIGHT AND MAINTENANCE PLANNING OF MILITARY AIRCRAFT FOR MAXIMUM FLEET AVAILABILITY: A BIOBJECTIVE MODEL
|
|
|
- Ethel Holmes
- 7 years ago
- Views:
Transcription
1 CD 2006, Chania, Greece, June 9-23, 2006 FLIGHT AND AINTENANCE PLANNING OF ILITARY AIRCRAFT FOR AXIU FLEET AVAILABILITY: A BIOBJECTIVE ODEL George Kozanidis and Athanasios Skipis Systems Optimization Laboratory Dept. of echanical & Industrial Engineering University of Thessaly Pedion Areos, Volos, Greece {gkoz; atskipis}@uth.gr Keywords: fleet availability, flight and maintenance planning, mixed integer linear program, biobjective model, military application Summary: Every aircraft, military or civilian, must be grounded for maintenance after it has completed a certain number of flight hours since its last maintenance check. Flight and maintenance planning of military aircraft addresses the problem of deciding which available aircraft to fly and for how long, and which grounded aircraft to perform maintenance operations on, in a set of aircraft that comprise a combat unit. The objective is to achieve maximum availability of the unit over the planning horizon. In this work, we develop a biobjective optimization model of the flight and maintenance planning problem, and we illustrate its application and solution on a real life instance drawn from the Hellenic Air Force. We formulate the flight and maintenance planning problem as a mixed integer linear program, with two objectives: total number of available aircraft and total residual flight time. The residual flight time of an available aircraft is defined as the total remaining time that this aircraft can fly, until it has to be grounded for maintenance check. For the solution of the problem we apply the weighted sums approach and lexicographic optimization. By comparing and analyzing the solutions obtained, we get insight into the behavior of the model. We conclude with a discussion based on these results and suggestions on how the model can be extended in the future.. Introduction Flight and maintenance planning (FP) of military aircraft addresses the problem of deciding which available aircraft to fly and for how long and which grounded aircraft to perform maintenance operations on, in a set of aircraft that comprise a combat unit. The objective is to achieve maximum availability of the unit over the planning horizon. The large number of parameters involved increases the complexity of the problem and the time required to reach an optimal solution. In this work, we develop a biobjective optimization model for the FP problem and we illustrate its application on a real life instance drawn from the Hellenic Air Force (HAF). We formulate the FP problem as a mixed integer linear program with two objectives, both of which depict the readiness of the unit to respond to external threats. We apply several approaches for the solution of the problem which enable us to explore the behavior of the model. Even though this is a military application, the model can be applied to several non-military ones, such as planning for fire-fighting aircraft, rescue choppers, etc. George Kozanidis is a recipient of a research grant from the State Scholarships Foundation, which partially supported this work
2 A significant part of the total operational budget of a fleet is spent for maintaining the aircraft that belong to it. The safety standards used by the Air Force in different countries are usually similar, since these standards are often determined by the aircraft manufacturer. Each aircraft has to undergo a regular maintenance check as soon as it completes a certain number of flight hours since its last maintenance check. There are also restrictions regarding the calendar time and number of takeoffs, but these are rarely used in practice, because the flight time restrictions usually apply sooner. The HAF, which provided the application that motivated this study, is supported by a three level maintenance program as follows: st level maintenance (organizational level): This maintenance check is performed on site and includes inspection, repair and parts replacement. 2nd level maintenance (intermediate level): This check is performed on site and includes more thorough inspection, repair, and parts replacement than the st level maintenance. 3rd level maintenance - anufacturer s maintenance (depot level): This check is performed in special facilities by specially trained professionals. It includes more thorough repair and parts replacement than the other two levels. Several aircraft planning and scheduling problems have been investigated in the past, although the vast majority of the published works are on scheduling rather than planning. Additionally, several authors have presented reviews of models and methods for airline operations related problems. Arguello et al. (997) studied models and methods for dynamic management of airline operations in case of irregular situations. Gopalan and Talluri (998) surveyed models and solution techniques for various airline problems that include fleet assignment and maintenance routing decisions. Barnhart et al. (2003) presented an overview of several important areas of operations research applications in the air transport industry as well as a brief summary of the state of the art. Even though the literature dealing with airline operations is quite rich, none of the published works deals with the type of problem that we address in this paper. To the best of our knowledge, no such work has been published to date, perhaps because most of the publicly reported research in this area has been directed towards problems in the commercial airline industry, which have different objectives and requirements than problems in the Air Force. We believe that the FP problem is an important practical problem that demands special attention, due to the significance of the related issues and the serious impact that the involved decisions can have on national security. The remainder of this paper is structured as follows. In Section 2, we describe in detail the FP problem, and we present the mathematical model that was developed for its solution. In Section 3, we illustrate the application of the model on a real-life instance drawn from the HAF and we present a discussion that provides insight into the model. Finally, in Section 4 we conclude this work, by summarizing the results obtained and proposing possible future extensions. 2. odel Development 2. Problem Description The problem that we study arose as an operations management problem in a typical Combat Wing of the HAF. This wing consists of three squadrons, each of which serves as the base for several aircraft of various types. In what follows, we use the term "wing" to refer to all the squadrons considered together. At the beginning of each planning horizon, the wing command issues the flight requirements for each squadron and period combination. These requirements determine the total time that all the aircraft in each squadron should fly during each time period of the horizon. Separate requirements are issued for each aircraft type, because different aircraft types have different flight capabilities and maintenance needs. For this reason, the model introduced in this paper was developed for use on a specific aircraft type. Of course, the same model can be applied repeatedly until all plans have been issued, if more than one 2
3 aircraft types are involved. The requirements issued by the wing command contain target values from which only small deviations are permitted. For each specific aircraft, we define its residual flight time as the total remaining time that this aircraft can fly until it has to undergo a maintenance check. The residual flight time of an aircraft is positive if and only if this aircraft is available to fly. At any time, the total residual flight time of a squadron is equal to the sum of the residual flight times of all the aircraft that belong to this squadron. The total residual flight time of the wing is equal to the sum of the residual flight times of all squadrons. Clearly, there exist many possible combinations of individual aircraft residual flight times that can result in the same total squadron or wing residual flight time. Similarly, we define the residual maintenance time of a nonavailable aircraft as the total remaining time that this aircraft needs in order to complete its maintenance check. The residual maintenance time of an aircraft is positive if and only if this aircraft is undergoing a maintenance check (and is therefore not available to fly). For the maintenance needs of the wing, there exists a maintenance station, responsible for providing maintenance services to the aircraft of the wing. This station has certain space and time capacity capabilities. Given the flight requirements for each squadron and period combination, and the physical constraints that stem from the capacity of the maintenance station, the objective is to issue a flight and maintenance plan for each individual aircraft in each squadron of the wing so that some appropriate measure of effectiveness is optimized. As already mentioned, maximizing the readiness to respond to external threats is the most appropriate measure of effectiveness for this application. This readiness depends on the total number of available aircraft, and on the total residual flight time of all available aircraft. Therefore, the two objectives of the model depict aircraft and residual flight time availability, respectively. Consider the 2-dimensional graph shown in Figure. The vertical axis represents residual flight time measured in some appropriate units, and the horizontal axis represents the indices of the available aircraft in increasing order of their residual flight times, being the index of the aircraft with the smallest and N being the index of the aircraft with the largest residual time (N is the total number of available aircraft). Consider also the line segment connecting the origin and the point with coordinates (N, Y), where Y is the maximum time that an aircraft can fly between two consecutive maintenance checks. By mapping each aircraft on this graph, we can visualize the total availability of the squadron or of the wing, whichever of the two the graph refers to. To describe the smoothness of the distribution of the total residual flight time of all aircraft, we use a "total deviation index". This index is equal to the sum of the vertical distances (deviations) of each point mapping a single aircraft from the line segment that connects the origin with point (N, Y). The smaller this sum is, the smoother the distribution of the total residual flight time. Ideally, the total deviation index is equal to zero, in which case all points lie on this line segment. When issuing the individual aircraft plans, the intention is to keep each point close to this line segment, in order to keep the value of the total deviation index as small as possible. To date, this technique has been used to issue the flight and maintenance plans of individual aircraft in the Combat Wing that we studied. The intuition behind the utilization of the graph described above is straightforward. By providing a wide range of different residual flight times, we establish a smooth sequence that determines the order in which the aircraft should visit the maintenance station. This in turn prevents bottlenecks in the maintenance station and ensures a smooth utilization of the maintenance station. ore importantly, it ensures a fairly constant level of aircraft availability. 3
4 Y residual flight times N A/F Figure : Visual representation of aircraft residual flight times 2.2 Problem Formulation In this section, we present the mathematical model that we developed for the FP problem described above. We use the following notation: Sets: : set of squadrons, indexed by m, : set of aircraft in squadron m, indexed by n, T : length of the planning horizon, indexed by t. Decision Variables: z : minimum total number of available aircraft over all periods, z 2 : minimum total residual flight time over all periods, a mnt : binary decision variable that takes the value if aircraft n of squadron m is available in period t, and 0 otherwise, y mnt : residual flight time of aircraft n of squadron m at the beginning of period t, x mnt : flight time of aircraft n of squadron m during period t, g mnt : residual maintenance time of aircraft n of squadron m at the beginning of period t, h mnt : maintenance time of aircraft n of squadron m during period t, d mnt : binary decision variable that takes the value if aircraft n of squadron m exits the maintenance station at the beginning of period t, and 0 otherwise, f mnt : binary decision variable that takes the value if aircraft n of squadron m enters the maintenance station at the beginning of period t, and 0 otherwise, q t, p mnt, r mnt : auxiliary binary decision variables. Parameters: S mt : required flight time of squadron m during period t, B t : time capacity of the maintenance station during period t, G : residual maintenance time of an aircraft immediately after it enters the maintenance station, Y : residual flight time of an aircraft immediately after it exits the maintenance station, C : maximum number of aircraft that the maintenance station can handle simultaneously, A mn : state of aircraft n of squadron m at the first period of the planning horizon (= a mn ), Y mn : residual flight time of aircraft n of squadron m at the first period of the planning horizon (= y mn ), G mn : residual maintenance time of aircraft n of squadron m at the first period of the planning horizon (= g mn ), X max : maximum time that an aircraft can fly during a single time period, Y min : minimum residual flight time of an available aircraft, 4
5 G min : minimum residual maintenance time of a non-available aircraft, L, U : real numbers denoting the maximum deviation from the value of S mt that can be tolerated, K : a sufficiently large number. Based on the above notation, we present next the formulation of the FP problem. In order to make easier the comprehension of this formulation, each time we introduce a set of constraints we include a description that explains its purpose. ax z () ax z 2 (2) s.t. z amnt, t = 2,..., T + (3) m= n= mnt m= n= z2 y, t = 2,..., T + (4) The objective function () maximizes z, which, by constraint set (3), denotes the minimum total number of available aircraft over all periods. Similarly, the objective function (2) maximizes z 2, which, by constraint set (4), denotes the minimum total residual flight time over all periods. The availability of the first period is fixed; therefore it is not included in these objective functions. In order to account for a smooth continuity of the model over the next horizon, the expressions for z and z 2 are also extended to the first period of that horizon, i.e. period T +. This is necessary in other constraints of the model too. y mnt+ = y mnt x mnt + d mnt+ Y, m =,,, n =,,, t =,..,T (5) d mnt+ > a mnt+ a mnt, m =,,, n =,,, t =,..,T (6) a mnt+ a mnt +.( d mnt+ ) > 0., m =,,, n =,,, t =,..,T (7) g mnt+ = g mnt h mnt + f mnt+ G, m =,,, n =,,, t =,..,T (8) f mnt+ > a mnt a mnt+, m =,,, n =,,, t =,..,T (9) a mnt a mnt+ +.( f mnt+ ) > 0., m =,,, n =,,, t =,..,T (0) Constraint set (5) is used to update the residual flight time of each aircraft at the beginning of the next period, based on its residual flight time at the beginning of the previous period and the time that it flew during that period. Binary variable d takes the value only when the corresponding aircraft exits the maintenance station. This way, an aircraft that exits the maintenance station is available to fly again with the maximum residual flight time, Y. Similarly, constraint set (8) is used to update the residual maintenance time of each aircraft at the beginning of the next period, based on its residual maintenance time at the beginning of the previous period and the time that it received maintenance during that period. Binary variable f takes the value only when the corresponding aircraft enters the maintenance station for service. This way, an aircraft that enters the maintenance station is ready to receive maintenance with the maximum residual maintenance time, G. 5
6 Constraint sets (6), (7), (9) and (0) ensure that variables d and f take correct values, based on the values of variables a. Consider the n th aircraft of the m th squadron. Then, (a mnt,a mnt+ ) can take any of the values (0,), (0,0), (,0) and (,) and the difference (a mnt+ - a mnt ) is equal to, 0, - and 0, respectively. Variable d mnt+ should take the value when (a mnt,a mnt+ ) = (0,) and this is ensured by constraint set (6). In any other case, d mnt+ should be 0 and this is ensured by constraint set (7). Similarly, variable f mnt+ should take the value when (a mnt,a mnt+ ) = (,0) and this is ensured by constraint set (9). In any other case, f mnt+ should be 0 and this is ensured by constraint set (0). LS x US, m =,...,, t =,..., T () mt mnt mt n= m= n= hmnt Bt, t =,..., T (2) m= n= ( amnt ) C, t = 2,..., T + (3) B h + K( q ), t =,..., T (4) t mnt t m= n= N m m g h + Kq, t =,..., T (5) mnt mnt t m= n= m= n= N Constraint set () ensures that the flight requirements for each squadron and period combination are met. Variables L and U define an interval [LS mt, US mt ], in which the actual squadron flight time for the associated period should lie. For example, when L = 0.95 and U =.05, a maximum deviation of 5% from the target values of the flight requirements is permitted. Constraint sets (2) and (3) ensure that the time and space capacity constraints of the maintenance station are not violated in any period. Constraint sets (4) and (5) are introduced to ensure that the maintenance will not idle whenever there is at least one aircraft waiting for service. With the introduction of the auxiliary binary variable q t, it is ensured that the total maintenance time provided by the station in period t will either be equal to the total time capacity of the station during this period or to the total maintenance requirements of this period, whichever of these two is smaller. y mnt + K p mnt < K, m =,,, n =,,, t =,..,T (6) a mnt+ (y mnt x mnt )K + K p mnt, m =,,, n =,,, t =,..,T (7) g mnt + K r mnt < K, m =,,, n =,,, t =,..,T (8) -a mnt+ (g mnt h mnt )K + K r mnt, m =,,, n =,,, t =,..,T (9) Constraint sets (6) and (7) are introduced to ensure that an aircraft s availability terminates as soon as its residual flight time drops to zero. If y mnt > 0, the auxiliary binary decision variable p mnt in constraint (6) is forced to zero. In this case, constraint (7) forces a mnt+ to zero if y mnt = x mnt, since this means that the residual flight time of this aircraft drops to zero during period t. Similarly, constraint sets (8) and (9) ensure that an aircraft becomes available as soon as its residual maintenance time drops to zero. If g mnt > 0, the auxiliary decision variable r mnt in constraint (8) is forced to zero. In this case, constraint (9) forces a mnt+ to if g mnt = h mnt, since this means that the residual maintenance time of this aircraft drops to zero during period t. 6
7 y mnt a mnt Y, m =,,, n =,,, t = 2,...,T + (20) g mnt (-a mnt )G, m =,,, n =,,, t = 2,...,T + (2) x mnt a mnt X max, m =,,, n =,,, t =,..,T (22) y mnt a mnt Y min, m =,,, n =,,, t = 2,...,T + (23) g mnt ( a mnt )G min, m =,,, n =,,, t = 2,...,T + (24) x mnt y mnt, m =,,, n =,,, t =,..,T (25) h mnt g mnt, m =,,, n =,,, t =,..,T (26) Constraint set (20) states that the residual flight time of an aircraft cannot exceed the maximum value, Y, and ensures that it will be zero whenever this aircraft is not available. Similarly, constraint set (2) states that the residual maintenance time of an aircraft cannot exceed the maximum value, G, and ensures that it will be zero whenever this aircraft is available. Constraint set (22) imposes an upper bound on the maximum time that an aircraft can fly during a single time period. Such a restriction is usually present due to technical reasons. Constraint sets (23) and (24) impose lower bounds on the residual flight and maintenance time of each aircraft. They are introduced to eliminate the situation in which an aircraft has a negligible residual flight or maintenance time. Constraint set (25) ensures that the total time that an aircraft flies during a single period does not exceed its residual flight time at the beginning of the same period. Similarly, constraint set (26) ensures that the total time that the maintenance crew works on a particular aircraft during a single period does not exceed the residual maintenance time of this aircraft at the beginning of the same period. a mn = A mn, m =,,, n =,, (27) y mn =Y mn, m =,,, n =,, (28) g mn = G mn, m =,,, n =,, (29) Finally, constraint sets (27), (28) and (29) are used to initialize the state of the system at the first period of the planning horizon. When an aircraft exits or enters the maintenance station at the first period of the planning horizon, its residual flight or maintenance time is directly updated; therefore variables d mn and f mn are never used. 3. Application of the odel In this section we illustrate the application of the model in a problem instance drawn from a Combat Wing of the HAF with 3 squadrons and 8 aircraft in each squadron. The planning horizon is 6 monthly periods. At the beginning of the planning horizon there are 3 aircraft at the maintenance station, one from each squadron. Their residual maintenance times are g 3 = 320, g 22 = 200 and g 33 = 00 hours, respectively. Table presents the required flight times for each squadron and period combination, Table 2 presents the time capacity of the maintenance station for each time period, and Table 3 presents the 7
8 residual flight times of the aircraft in the first period of the planning horizon. The time capacity of the maintenance station may vary from period to period, due to personnel vacations, holidays, etc. The values of the other problem parameters are G = 320 hours, Y = 300 hours, C = 3, X max = 50 hours, Y min = 0. hours, G min = 0. hours, L = 0.9 and U =.. m Table : Required flight times (S mt ) in hours t Table 2: Time capacity of the maintenance station in hours t B t Table 3: Aircraft residual flight times at the beginning of the planning horizon (y mn ) in hours n m The first method that we apply for the solution of the problem is the weighted sums approach (see Steuer, 986). We consider strictly positive weights w and w 2 such that w + w 2 =. After multiplying the first objective with 50 in order to scale it, we transform the problem into a single criterion one with objective ax 50w z + w 2 z 2. Table 4 presents the solutions obtained for values of w and w 2 that vary between 0.05 and 0.95, with a step of 0.5. Table 4: Solutions obtained using the weighted sums approach w w 2 z z The seven solutions shown in Table 4 are distinct, although they provide us with only two possible choices for the values of the two objectives, (z, z 2 ) = (22, 2800) and (z, z 2 ) = (23, 23). This is a main characteristic of the problem, since a slight change of the optimal flight and maintenance plan can produce a different solution with same objective function values. After comparing the solutions for which (z, z 2 ) = (22, 2800), we select the one with w = 0.2, because it gives better results for the minimum availability of each squadron over all periods. For the same reason, out of the two solutions for which (z, z 2 ) = (23, 23), we select the one with w = In order to make our final decision, we perform a side by side comparison between these two solutions. The results are shown in Table 5. The upper half of this table shows how the number of available aircraft of the wing and of each squadron separately varies from period to period according to these two solutions, and the lower half shows similar results for the residual flight time. 8
9 Table 5: Comparison of the solutions with w = 0.2 and w = 0.95 w = 0.2 w = 0.95 t m = m = 2 m = 3 wing m = m = 2 m = 3 wing We observe in Table 5 that, with respect to z, the solution with w = 0.95 gives better results in five out of the six periods of the planning horizon, i.e. in periods 2-6. Note that the availability of the first period of the planning horizon is fixed; therefore it was not included in the objective functions. On the other hand, while the residual flight time availability of the wing in period 2 is the same in both solutions, in the solution with w = 0.2 it is higher by approximately 300 hours in periods 3-5 and by approximately 500 hours in periods 6 and 7. oreover, with very few exceptions, the residual flight time availability of each squadron in each time period is significantly higher in the solution with w = 0.2. Therefore, we conclude by selecting that solution over the one with w = The maximum possible values for z and z 2 are 23 and 2800, respectively. These values are obtained when the problem is solved with a single objective, z or z 2. Table 6 presents the two solutions obtained when lexicographic optimization (see Steuer, 986) is applied for the solution of the problem. When z 2 is maximized subject to the constraint that z is no less than 23, the optimal solution is 23. When z is maximized subject to the constraint that z 2 is no less than 2800, the optimal solution is 22. Of course, both these solutions are efficient (see Steuer, 986). Interesting is the fact that this pair of solutions looks very similar to the pair of solutions that were compared in the final step of the weighted sums approach (i.e., in Table 5). Using a similar reasoning as above, between the two solutions compared in Table 6, we promote the one with z = 22 and z 2 = Although there do not exist many differences between this solution and the one selected using the weighted sums approach, we select that one over the one obtained using lexicographic optimization, mainly because it exhibits a more constant level of availability. The above analysis motivated us to consider a four-objective version of the model, which besides the minimum availability of the wing, maximizes the minimum availability of each squadron too. Hence, we considered two additional objective functions, z 3 and z 4, expressed as follows: ax z 3 (30) ax z 4 (3) 9
10 s.t. z3 amnt, m=,...,, t = 2,..., T + (32) n= n= z4 ymnt, m=,...,, t = 2,..., T + (33) Table 6: The two solutions obtained using lexicographic optimization z = 23, z 2 = 23 z = 22, z 2 = 2800 t m = m = 2 m = 3 wing m = m = 2 m = 3 wing In these expressions, z 3 denotes the minimum number of available aircraft of any squadron over all periods, and z 4 denotes the minimum residual flight time of any squadron over all periods. For the solution of this problem, we considered the weighted sums approach, with various combinations of the weights, in which w = w 2 and w 3 = w 4. For scaling purposes, we multiplied the first objective with 50, the third objective with 3(50) = 450, and the fourth objective with 3. This way, the single objective that was obtained was ax 50w z + w 2 z w 3 z 3 + 3w 4 z 4. The results are shown in Table 7. We observe in this table that all solutions obtained give the same exact values for the four objectives. oreover, while the values of z, z 2 and z 3 are the same with those of the solution selected for the biobjective version of the problem, the value of z 4 is improved (79 over 58). Table 7: Solutions obtained for the four criteria problem with the weighted sums approach w w 2 w 3 w 4 z z 2 z 3 z The model of the FP problem that we introduced is a mixed integer linear program, and the computational effort needed to reach an optimal solution depends strongly on the size and the parameters of the specific problem instance. In many cases, the large number of constraints may lead to the optimal solution very fast, due to the fact that the feasible region determined by these constraints is small. In other cases, this may not occur, due to the fact that a larger feasible region exists and many different combinations of the decision variables have to be compared. For this reason, the size of the problem 0
11 alone is not indicative of the time needed to reach an optimal solution. Of course, an increase in the size of the problem results in general in greater computational effort, since the number of decision variables and constraints increases significantly. The time needed to solve each of the problems presented above was typically less than half a minute on a Pentium IV/2.5 GHz processor, using version 9. of APL (see Fourer et al. 2002) as the mixed integer optimization software, with solver CPLEX and default values. Various experiments that were conducted showed that besides the size of the problem, the total computational effort also depends on the range in which the problem parameters take their values. For the solution of larger problems, one can either implement the heuristic discussed shortly in Section 2., or break the planning horizon into smaller ones and apply the model repeatedly. This latter option however does not always produce solutions of high quality. 4. Conclusions In this work, we introduced a mixed integer biobjective optimization model for military aircraft flight and maintenance planning, and illustrated its application on a real instance drawn from the Hellenic Air Force. The two objectives of the model maximize the readiness of a combat unit to respond to external threats. The model can be easily extended to include additional aspects of the problem that may arise in different situations, such as the rotation of the aircraft that are used to satisfy the flight requirements, the incorporation of special maintenance checks and parts removal, the observance of the daily schedule of the pilots, etc. We believe that future research should be more intensively directed towards finding analytical tools for similar problems, due to the importance of the related issues and the serious impact that the involved decisions can have on national security. References Arguello,.F., Bard, J.F. and Yu, G. (997) odels and methods for managing airline irregular operations aircraft routing Operations Research in the Airline Industry ed. G. Yu, pp Kluwer Academic Publishers, Boston. Barnhart, C., Belobaba, P. and Odoni, A.R. (2003) Applications of operations research in the air transport industry Transportation Science, 37(4), Fourer, R., Gay, D.. and Kernighan, B.W. (2002) APL: A odeling Language for athematical Programming, Duxbury Press. Gopalan, R. and Talluri, K.T. (998) athematical models in airline schedule planning: A survey Annals of Operations Research, 76, Steuer, R. E. (986) ultiple Criteria Optimization: theory, computation and application, New York: Wiley.
Airline Schedule Development
 Airline Schedule Development 16.75J/1.234J Airline Management Dr. Peter Belobaba February 22, 2006 Airline Schedule Development 1. Schedule Development Process Airline supply terminology Sequential approach
Airline Schedule Development 16.75J/1.234J Airline Management Dr. Peter Belobaba February 22, 2006 Airline Schedule Development 1. Schedule Development Process Airline supply terminology Sequential approach
Instituto de Engenharia de Sistemas e Computadores de Coimbra Institute of Systems Engineering and Computers INESC Coimbra
 Instituto de Engenharia de Sistemas e Computadores de Coimbra Institute of Systems Engineering and Computers INESC Coimbra João Clímaco and Marta Pascoal A new method to detere unsupported non-doated solutions
Instituto de Engenharia de Sistemas e Computadores de Coimbra Institute of Systems Engineering and Computers INESC Coimbra João Clímaco and Marta Pascoal A new method to detere unsupported non-doated solutions
A Reference Point Method to Triple-Objective Assignment of Supporting Services in a Healthcare Institution. Bartosz Sawik
 Decision Making in Manufacturing and Services Vol. 4 2010 No. 1 2 pp. 37 46 A Reference Point Method to Triple-Objective Assignment of Supporting Services in a Healthcare Institution Bartosz Sawik Abstract.
Decision Making in Manufacturing and Services Vol. 4 2010 No. 1 2 pp. 37 46 A Reference Point Method to Triple-Objective Assignment of Supporting Services in a Healthcare Institution Bartosz Sawik Abstract.
Branch-and-Price Approach to the Vehicle Routing Problem with Time Windows
 TECHNISCHE UNIVERSITEIT EINDHOVEN Branch-and-Price Approach to the Vehicle Routing Problem with Time Windows Lloyd A. Fasting May 2014 Supervisors: dr. M. Firat dr.ir. M.A.A. Boon J. van Twist MSc. Contents
TECHNISCHE UNIVERSITEIT EINDHOVEN Branch-and-Price Approach to the Vehicle Routing Problem with Time Windows Lloyd A. Fasting May 2014 Supervisors: dr. M. Firat dr.ir. M.A.A. Boon J. van Twist MSc. Contents
Sensitivity Analysis 3.1 AN EXAMPLE FOR ANALYSIS
 Sensitivity Analysis 3 We have already been introduced to sensitivity analysis in Chapter via the geometry of a simple example. We saw that the values of the decision variables and those of the slack and
Sensitivity Analysis 3 We have already been introduced to sensitivity analysis in Chapter via the geometry of a simple example. We saw that the values of the decision variables and those of the slack and
Fast Sequential Summation Algorithms Using Augmented Data Structures
 Fast Sequential Summation Algorithms Using Augmented Data Structures Vadim Stadnik vadim.stadnik@gmail.com Abstract This paper provides an introduction to the design of augmented data structures that offer
Fast Sequential Summation Algorithms Using Augmented Data Structures Vadim Stadnik vadim.stadnik@gmail.com Abstract This paper provides an introduction to the design of augmented data structures that offer
Linear Programming. Solving LP Models Using MS Excel, 18
 SUPPLEMENT TO CHAPTER SIX Linear Programming SUPPLEMENT OUTLINE Introduction, 2 Linear Programming Models, 2 Model Formulation, 4 Graphical Linear Programming, 5 Outline of Graphical Procedure, 5 Plotting
SUPPLEMENT TO CHAPTER SIX Linear Programming SUPPLEMENT OUTLINE Introduction, 2 Linear Programming Models, 2 Model Formulation, 4 Graphical Linear Programming, 5 Outline of Graphical Procedure, 5 Plotting
R u t c o r Research R e p o r t. A Method to Schedule Both Transportation and Production at the Same Time in a Special FMS.
 R u t c o r Research R e p o r t A Method to Schedule Both Transportation and Production at the Same Time in a Special FMS Navid Hashemian a Béla Vizvári b RRR 3-2011, February 21, 2011 RUTCOR Rutgers
R u t c o r Research R e p o r t A Method to Schedule Both Transportation and Production at the Same Time in a Special FMS Navid Hashemian a Béla Vizvári b RRR 3-2011, February 21, 2011 RUTCOR Rutgers
An optimization model for aircraft maintenance scheduling and re-assignment
 Transportation Research Part A 37 (2003) 29 48 www.elsevier.com/locate/tra An optimization model for aircraft maintenance scheduling and re-assignment Chellappan Sriram 1, Ali Haghani * Department of Civil
Transportation Research Part A 37 (2003) 29 48 www.elsevier.com/locate/tra An optimization model for aircraft maintenance scheduling and re-assignment Chellappan Sriram 1, Ali Haghani * Department of Civil
6.4 Normal Distribution
 Contents 6.4 Normal Distribution....................... 381 6.4.1 Characteristics of the Normal Distribution....... 381 6.4.2 The Standardized Normal Distribution......... 385 6.4.3 Meaning of Areas under
Contents 6.4 Normal Distribution....................... 381 6.4.1 Characteristics of the Normal Distribution....... 381 6.4.2 The Standardized Normal Distribution......... 385 6.4.3 Meaning of Areas under
Algebra 2 Chapter 1 Vocabulary. identity - A statement that equates two equivalent expressions.
 Chapter 1 Vocabulary identity - A statement that equates two equivalent expressions. verbal model- A word equation that represents a real-life problem. algebraic expression - An expression with variables.
Chapter 1 Vocabulary identity - A statement that equates two equivalent expressions. verbal model- A word equation that represents a real-life problem. algebraic expression - An expression with variables.
Linear Programming Notes V Problem Transformations
 Linear Programming Notes V Problem Transformations 1 Introduction Any linear programming problem can be rewritten in either of two standard forms. In the first form, the objective is to maximize, the material
Linear Programming Notes V Problem Transformations 1 Introduction Any linear programming problem can be rewritten in either of two standard forms. In the first form, the objective is to maximize, the material
The Point-Slope Form
 7. The Point-Slope Form 7. OBJECTIVES 1. Given a point and a slope, find the graph of a line. Given a point and the slope, find the equation of a line. Given two points, find the equation of a line y Slope
7. The Point-Slope Form 7. OBJECTIVES 1. Given a point and a slope, find the graph of a line. Given a point and the slope, find the equation of a line. Given two points, find the equation of a line y Slope
Linear Programming for Optimization. Mark A. Schulze, Ph.D. Perceptive Scientific Instruments, Inc.
 1. Introduction Linear Programming for Optimization Mark A. Schulze, Ph.D. Perceptive Scientific Instruments, Inc. 1.1 Definition Linear programming is the name of a branch of applied mathematics that
1. Introduction Linear Programming for Optimization Mark A. Schulze, Ph.D. Perceptive Scientific Instruments, Inc. 1.1 Definition Linear programming is the name of a branch of applied mathematics that
LECTURE - 3 RESOURCE AND WORKFORCE SCHEDULING IN SERVICES
 LECTURE - 3 RESOURCE AND WORKFORCE SCHEDULING IN SERVICES Learning objective To explain various work shift scheduling methods for service sector. 8.9 Workforce Management Workforce management deals in
LECTURE - 3 RESOURCE AND WORKFORCE SCHEDULING IN SERVICES Learning objective To explain various work shift scheduling methods for service sector. 8.9 Workforce Management Workforce management deals in
LINEAR INEQUALITIES. Mathematics is the art of saying many things in many different ways. MAXWELL
 Chapter 6 LINEAR INEQUALITIES 6.1 Introduction Mathematics is the art of saying many things in many different ways. MAXWELL In earlier classes, we have studied equations in one variable and two variables
Chapter 6 LINEAR INEQUALITIES 6.1 Introduction Mathematics is the art of saying many things in many different ways. MAXWELL In earlier classes, we have studied equations in one variable and two variables
TEACHER NOTES MATH NSPIRED
 Math Objectives Students will understand that normal distributions can be used to approximate binomial distributions whenever both np and n(1 p) are sufficiently large. Students will understand that when
Math Objectives Students will understand that normal distributions can be used to approximate binomial distributions whenever both np and n(1 p) are sufficiently large. Students will understand that when
n 2 + 4n + 3. The answer in decimal form (for the Blitz): 0, 75. Solution. (n + 1)(n + 3) = n + 3 2 lim m 2 1
 . Calculate the sum of the series Answer: 3 4. n 2 + 4n + 3. The answer in decimal form (for the Blitz):, 75. Solution. n 2 + 4n + 3 = (n + )(n + 3) = (n + 3) (n + ) = 2 (n + )(n + 3) ( 2 n + ) = m ( n
. Calculate the sum of the series Answer: 3 4. n 2 + 4n + 3. The answer in decimal form (for the Blitz):, 75. Solution. n 2 + 4n + 3 = (n + )(n + 3) = (n + 3) (n + ) = 2 (n + )(n + 3) ( 2 n + ) = m ( n
Research Article Batch Scheduling on Two-Machine Flowshop with Machine-Dependent Setup Times
 Hindawi Publishing Corporation Advances in Operations Research Volume 2009, Article ID 153910, 10 pages doi:10.1155/2009/153910 Research Article Batch Scheduling on Two-Machine Flowshop with Machine-Dependent
Hindawi Publishing Corporation Advances in Operations Research Volume 2009, Article ID 153910, 10 pages doi:10.1155/2009/153910 Research Article Batch Scheduling on Two-Machine Flowshop with Machine-Dependent
Resource Allocation Modeling Techniques Applied to Air Force Crew Scheduling Problem
 Kepler Research, Inc. Proprietary Resource Allocation Modeling Techniques Applied to Air Force Crew Scheduling Problem Submitted by: Kepler Research, Inc. February 2012 1. Introduction and Background The
Kepler Research, Inc. Proprietary Resource Allocation Modeling Techniques Applied to Air Force Crew Scheduling Problem Submitted by: Kepler Research, Inc. February 2012 1. Introduction and Background The
1 if 1 x 0 1 if 0 x 1
 Chapter 3 Continuity In this chapter we begin by defining the fundamental notion of continuity for real valued functions of a single real variable. When trying to decide whether a given function is or
Chapter 3 Continuity In this chapter we begin by defining the fundamental notion of continuity for real valued functions of a single real variable. When trying to decide whether a given function is or
Formulation of simple workforce skill constraints in assembly line balancing models
 Ŕ periodica polytechnica Social and Management Sciences 19/1 (2011) 43 50 doi: 10.3311/pp.so.2011-1.06 web: http:// www.pp.bme.hu/ so c Periodica Polytechnica 2011 Formulation of simple workforce skill
Ŕ periodica polytechnica Social and Management Sciences 19/1 (2011) 43 50 doi: 10.3311/pp.so.2011-1.06 web: http:// www.pp.bme.hu/ so c Periodica Polytechnica 2011 Formulation of simple workforce skill
The Goldberg Rao Algorithm for the Maximum Flow Problem
 The Goldberg Rao Algorithm for the Maximum Flow Problem COS 528 class notes October 18, 2006 Scribe: Dávid Papp Main idea: use of the blocking flow paradigm to achieve essentially O(min{m 2/3, n 1/2 }
The Goldberg Rao Algorithm for the Maximum Flow Problem COS 528 class notes October 18, 2006 Scribe: Dávid Papp Main idea: use of the blocking flow paradigm to achieve essentially O(min{m 2/3, n 1/2 }
Lecture 2. Marginal Functions, Average Functions, Elasticity, the Marginal Principle, and Constrained Optimization
 Lecture 2. Marginal Functions, Average Functions, Elasticity, the Marginal Principle, and Constrained Optimization 2.1. Introduction Suppose that an economic relationship can be described by a real-valued
Lecture 2. Marginal Functions, Average Functions, Elasticity, the Marginal Principle, and Constrained Optimization 2.1. Introduction Suppose that an economic relationship can be described by a real-valued
Cumulative Diagrams: An Example
 Cumulative Diagrams: An Example Consider Figure 1 in which the functions (t) and (t) denote, respectively, the demand rate and the service rate (or capacity ) over time at the runway system of an airport
Cumulative Diagrams: An Example Consider Figure 1 in which the functions (t) and (t) denote, respectively, the demand rate and the service rate (or capacity ) over time at the runway system of an airport
TIME BETWEEN AIRCRAFT OVERHAULS OPTIMIZATION BY MAXIMIZING FLEET TOTAL FLYING HOURS
 1 st Logistics International Conference Belgrade, Serbia 28-30 November 2013 TIME BETWEEN AIRCRAFT OVERHAULS OPTIMIZATION BY MAXIMIZING FLEET TOTAL FLYING HOURS Ivan Djokic State University of Novi Pazar,
1 st Logistics International Conference Belgrade, Serbia 28-30 November 2013 TIME BETWEEN AIRCRAFT OVERHAULS OPTIMIZATION BY MAXIMIZING FLEET TOTAL FLYING HOURS Ivan Djokic State University of Novi Pazar,
INTEGER PROGRAMMING. Integer Programming. Prototype example. BIP model. BIP models
 Integer Programming INTEGER PROGRAMMING In many problems the decision variables must have integer values. Example: assign people, machines, and vehicles to activities in integer quantities. If this is
Integer Programming INTEGER PROGRAMMING In many problems the decision variables must have integer values. Example: assign people, machines, and vehicles to activities in integer quantities. If this is
COMP 250 Fall 2012 lecture 2 binary representations Sept. 11, 2012
 Binary numbers The reason humans represent numbers using decimal (the ten digits from 0,1,... 9) is that we have ten fingers. There is no other reason than that. There is nothing special otherwise about
Binary numbers The reason humans represent numbers using decimal (the ten digits from 0,1,... 9) is that we have ten fingers. There is no other reason than that. There is nothing special otherwise about
Chapter 10. Key Ideas Correlation, Correlation Coefficient (r),
 Chapter 0 Key Ideas Correlation, Correlation Coefficient (r), Section 0-: Overview We have already explored the basics of describing single variable data sets. However, when two quantitative variables
Chapter 0 Key Ideas Correlation, Correlation Coefficient (r), Section 0-: Overview We have already explored the basics of describing single variable data sets. However, when two quantitative variables
Overview of Violations of the Basic Assumptions in the Classical Normal Linear Regression Model
 Overview of Violations of the Basic Assumptions in the Classical Normal Linear Regression Model 1 September 004 A. Introduction and assumptions The classical normal linear regression model can be written
Overview of Violations of the Basic Assumptions in the Classical Normal Linear Regression Model 1 September 004 A. Introduction and assumptions The classical normal linear regression model can be written
What is Linear Programming?
 Chapter 1 What is Linear Programming? An optimization problem usually has three essential ingredients: a variable vector x consisting of a set of unknowns to be determined, an objective function of x to
Chapter 1 What is Linear Programming? An optimization problem usually has three essential ingredients: a variable vector x consisting of a set of unknowns to be determined, an objective function of x to
A Weighted-Sum Mixed Integer Program for Bi-Objective Dynamic Portfolio Optimization
 AUTOMATYKA 2009 Tom 3 Zeszyt 2 Bartosz Sawik* A Weighted-Sum Mixed Integer Program for Bi-Objective Dynamic Portfolio Optimization. Introduction The optimal security selection is a classical portfolio
AUTOMATYKA 2009 Tom 3 Zeszyt 2 Bartosz Sawik* A Weighted-Sum Mixed Integer Program for Bi-Objective Dynamic Portfolio Optimization. Introduction The optimal security selection is a classical portfolio
Scheduling Jobs and Preventive Maintenance Activities on Parallel Machines
 Scheduling Jobs and Preventive Maintenance Activities on Parallel Machines Maher Rebai University of Technology of Troyes Department of Industrial Systems 12 rue Marie Curie, 10000 Troyes France maher.rebai@utt.fr
Scheduling Jobs and Preventive Maintenance Activities on Parallel Machines Maher Rebai University of Technology of Troyes Department of Industrial Systems 12 rue Marie Curie, 10000 Troyes France maher.rebai@utt.fr
Linear Programming. March 14, 2014
 Linear Programming March 1, 01 Parts of this introduction to linear programming were adapted from Chapter 9 of Introduction to Algorithms, Second Edition, by Cormen, Leiserson, Rivest and Stein [1]. 1
Linear Programming March 1, 01 Parts of this introduction to linear programming were adapted from Chapter 9 of Introduction to Algorithms, Second Edition, by Cormen, Leiserson, Rivest and Stein [1]. 1
TU e. Advanced Algorithms: experimentation project. The problem: load balancing with bounded look-ahead. Input: integer m 2: number of machines
 The problem: load balancing with bounded look-ahead Input: integer m 2: number of machines integer k 0: the look-ahead numbers t 1,..., t n : the job sizes Problem: assign jobs to machines machine to which
The problem: load balancing with bounded look-ahead Input: integer m 2: number of machines integer k 0: the look-ahead numbers t 1,..., t n : the job sizes Problem: assign jobs to machines machine to which
Chapter 5: Working with contours
 Introduction Contoured topographic maps contain a vast amount of information about the three-dimensional geometry of the land surface and the purpose of this chapter is to consider some of the ways in
Introduction Contoured topographic maps contain a vast amount of information about the three-dimensional geometry of the land surface and the purpose of this chapter is to consider some of the ways in
Lecture 10 Scheduling 1
 Lecture 10 Scheduling 1 Transportation Models -1- large variety of models due to the many modes of transportation roads railroad shipping airlines as a consequence different type of equipment and resources
Lecture 10 Scheduling 1 Transportation Models -1- large variety of models due to the many modes of transportation roads railroad shipping airlines as a consequence different type of equipment and resources
Session 7 Bivariate Data and Analysis
 Session 7 Bivariate Data and Analysis Key Terms for This Session Previously Introduced mean standard deviation New in This Session association bivariate analysis contingency table co-variation least squares
Session 7 Bivariate Data and Analysis Key Terms for This Session Previously Introduced mean standard deviation New in This Session association bivariate analysis contingency table co-variation least squares
Coordination in vehicle routing
 Coordination in vehicle routing Catherine Rivers Mathematics Massey University New Zealand 00.@compuserve.com Abstract A coordination point is a place that exists in space and time for the transfer of
Coordination in vehicle routing Catherine Rivers Mathematics Massey University New Zealand 00.@compuserve.com Abstract A coordination point is a place that exists in space and time for the transfer of
Clustering and scheduling maintenance tasks over time
 Clustering and scheduling maintenance tasks over time Per Kreuger 2008-04-29 SICS Technical Report T2008:09 Abstract We report results on a maintenance scheduling problem. The problem consists of allocating
Clustering and scheduling maintenance tasks over time Per Kreuger 2008-04-29 SICS Technical Report T2008:09 Abstract We report results on a maintenance scheduling problem. The problem consists of allocating
Appendix: Simple Methods for Shift Scheduling in Multi-Skill Call Centers
 MSOM.1070.0172 Appendix: Simple Methods for Shift Scheduling in Multi-Skill Call Centers In Bhulai et al. (2006) we presented a method for computing optimal schedules, separately, after the optimal staffing
MSOM.1070.0172 Appendix: Simple Methods for Shift Scheduling in Multi-Skill Call Centers In Bhulai et al. (2006) we presented a method for computing optimal schedules, separately, after the optimal staffing
Integrated maintenance scheduling for semiconductor manufacturing
 Integrated maintenance scheduling for semiconductor manufacturing Andrew Davenport davenport@us.ibm.com Department of Business Analytics and Mathematical Science, IBM T. J. Watson Research Center, P.O.
Integrated maintenance scheduling for semiconductor manufacturing Andrew Davenport davenport@us.ibm.com Department of Business Analytics and Mathematical Science, IBM T. J. Watson Research Center, P.O.
Special Situations in the Simplex Algorithm
 Special Situations in the Simplex Algorithm Degeneracy Consider the linear program: Maximize 2x 1 +x 2 Subject to: 4x 1 +3x 2 12 (1) 4x 1 +x 2 8 (2) 4x 1 +2x 2 8 (3) x 1, x 2 0. We will first apply the
Special Situations in the Simplex Algorithm Degeneracy Consider the linear program: Maximize 2x 1 +x 2 Subject to: 4x 1 +3x 2 12 (1) 4x 1 +x 2 8 (2) 4x 1 +2x 2 8 (3) x 1, x 2 0. We will first apply the
Section 1.1 Linear Equations: Slope and Equations of Lines
 Section. Linear Equations: Slope and Equations of Lines Slope The measure of the steepness of a line is called the slope of the line. It is the amount of change in y, the rise, divided by the amount of
Section. Linear Equations: Slope and Equations of Lines Slope The measure of the steepness of a line is called the slope of the line. It is the amount of change in y, the rise, divided by the amount of
EdExcel Decision Mathematics 1
 EdExcel Decision Mathematics 1 Linear Programming Section 1: Formulating and solving graphically Notes and Examples These notes contain subsections on: Formulating LP problems Solving LP problems Minimisation
EdExcel Decision Mathematics 1 Linear Programming Section 1: Formulating and solving graphically Notes and Examples These notes contain subsections on: Formulating LP problems Solving LP problems Minimisation
Random Map Generator v1.0 User s Guide
 Random Map Generator v1.0 User s Guide Jonathan Teutenberg 2003 1 Map Generation Overview...4 1.1 Command Line...4 1.2 Operation Flow...4 2 Map Initialisation...5 2.1 Initialisation Parameters...5 -w xxxxxxx...5
Random Map Generator v1.0 User s Guide Jonathan Teutenberg 2003 1 Map Generation Overview...4 1.1 Command Line...4 1.2 Operation Flow...4 2 Map Initialisation...5 2.1 Initialisation Parameters...5 -w xxxxxxx...5
10.2 Series and Convergence
 10.2 Series and Convergence Write sums using sigma notation Find the partial sums of series and determine convergence or divergence of infinite series Find the N th partial sums of geometric series and
10.2 Series and Convergence Write sums using sigma notation Find the partial sums of series and determine convergence or divergence of infinite series Find the N th partial sums of geometric series and
Review of Fundamental Mathematics
 Review of Fundamental Mathematics As explained in the Preface and in Chapter 1 of your textbook, managerial economics applies microeconomic theory to business decision making. The decision-making tools
Review of Fundamental Mathematics As explained in the Preface and in Chapter 1 of your textbook, managerial economics applies microeconomic theory to business decision making. The decision-making tools
Section 1.3 P 1 = 1 2. = 1 4 2 8. P n = 1 P 3 = Continuing in this fashion, it should seem reasonable that, for any n = 1, 2, 3,..., = 1 2 4.
 Difference Equations to Differential Equations Section. The Sum of a Sequence This section considers the problem of adding together the terms of a sequence. Of course, this is a problem only if more than
Difference Equations to Differential Equations Section. The Sum of a Sequence This section considers the problem of adding together the terms of a sequence. Of course, this is a problem only if more than
Fairness in Routing and Load Balancing
 Fairness in Routing and Load Balancing Jon Kleinberg Yuval Rabani Éva Tardos Abstract We consider the issue of network routing subject to explicit fairness conditions. The optimization of fairness criteria
Fairness in Routing and Load Balancing Jon Kleinberg Yuval Rabani Éva Tardos Abstract We consider the issue of network routing subject to explicit fairness conditions. The optimization of fairness criteria
Optimal Scheduling for Dependent Details Processing Using MS Excel Solver
 BULGARIAN ACADEMY OF SCIENCES CYBERNETICS AND INFORMATION TECHNOLOGIES Volume 8, No 2 Sofia 2008 Optimal Scheduling for Dependent Details Processing Using MS Excel Solver Daniela Borissova Institute of
BULGARIAN ACADEMY OF SCIENCES CYBERNETICS AND INFORMATION TECHNOLOGIES Volume 8, No 2 Sofia 2008 Optimal Scheduling for Dependent Details Processing Using MS Excel Solver Daniela Borissova Institute of
A Quantitative Decision Support Framework for Optimal Railway Capacity Planning
 A Quantitative Decision Support Framework for Optimal Railway Capacity Planning Y.C. Lai, C.P.L. Barkan University of Illinois at Urbana-Champaign, Urbana, USA Abstract Railways around the world are facing
A Quantitative Decision Support Framework for Optimal Railway Capacity Planning Y.C. Lai, C.P.L. Barkan University of Illinois at Urbana-Champaign, Urbana, USA Abstract Railways around the world are facing
In this chapter, you will learn improvement curve concepts and their application to cost and price analysis.
 7.0 - Chapter Introduction In this chapter, you will learn improvement curve concepts and their application to cost and price analysis. Basic Improvement Curve Concept. You may have learned about improvement
7.0 - Chapter Introduction In this chapter, you will learn improvement curve concepts and their application to cost and price analysis. Basic Improvement Curve Concept. You may have learned about improvement
Solving Linear Programs
 Solving Linear Programs 2 In this chapter, we present a systematic procedure for solving linear programs. This procedure, called the simplex method, proceeds by moving from one feasible solution to another,
Solving Linear Programs 2 In this chapter, we present a systematic procedure for solving linear programs. This procedure, called the simplex method, proceeds by moving from one feasible solution to another,
9.4. The Scalar Product. Introduction. Prerequisites. Learning Style. Learning Outcomes
 The Scalar Product 9.4 Introduction There are two kinds of multiplication involving vectors. The first is known as the scalar product or dot product. This is so-called because when the scalar product of
The Scalar Product 9.4 Introduction There are two kinds of multiplication involving vectors. The first is known as the scalar product or dot product. This is so-called because when the scalar product of
1 Solving LPs: The Simplex Algorithm of George Dantzig
 Solving LPs: The Simplex Algorithm of George Dantzig. Simplex Pivoting: Dictionary Format We illustrate a general solution procedure, called the simplex algorithm, by implementing it on a very simple example.
Solving LPs: The Simplex Algorithm of George Dantzig. Simplex Pivoting: Dictionary Format We illustrate a general solution procedure, called the simplex algorithm, by implementing it on a very simple example.
Revenue Management for Transportation Problems
 Revenue Management for Transportation Problems Francesca Guerriero Giovanna Miglionico Filomena Olivito Department of Electronic Informatics and Systems, University of Calabria Via P. Bucci, 87036 Rende
Revenue Management for Transportation Problems Francesca Guerriero Giovanna Miglionico Filomena Olivito Department of Electronic Informatics and Systems, University of Calabria Via P. Bucci, 87036 Rende
The Rolling Stock Recovery Problem. Literature review. Julie Jespersen Groth *α, Jesper Larsen β and Jens Clausen *γ
 The Rolling Stock Recovery Problem Julie Jespersen Groth *α, Jesper Larsen β and Jens Clausen *γ DTU Management Engineering, The Technical University of Denmark, Produktionstorvet, DTU Building 424, 2800
The Rolling Stock Recovery Problem Julie Jespersen Groth *α, Jesper Larsen β and Jens Clausen *γ DTU Management Engineering, The Technical University of Denmark, Produktionstorvet, DTU Building 424, 2800
This paper introduces a new method for shift scheduling in multiskill call centers. The method consists of
 MANUFACTURING & SERVICE OPERATIONS MANAGEMENT Vol. 10, No. 3, Summer 2008, pp. 411 420 issn 1523-4614 eissn 1526-5498 08 1003 0411 informs doi 10.1287/msom.1070.0172 2008 INFORMS Simple Methods for Shift
MANUFACTURING & SERVICE OPERATIONS MANAGEMENT Vol. 10, No. 3, Summer 2008, pp. 411 420 issn 1523-4614 eissn 1526-5498 08 1003 0411 informs doi 10.1287/msom.1070.0172 2008 INFORMS Simple Methods for Shift
HYBRID GENETIC ALGORITHMS FOR SCHEDULING ADVERTISEMENTS ON A WEB PAGE
 HYBRID GENETIC ALGORITHMS FOR SCHEDULING ADVERTISEMENTS ON A WEB PAGE Subodha Kumar University of Washington subodha@u.washington.edu Varghese S. Jacob University of Texas at Dallas vjacob@utdallas.edu
HYBRID GENETIC ALGORITHMS FOR SCHEDULING ADVERTISEMENTS ON A WEB PAGE Subodha Kumar University of Washington subodha@u.washington.edu Varghese S. Jacob University of Texas at Dallas vjacob@utdallas.edu
MIP-Based Approaches for Solving Scheduling Problems with Batch Processing Machines
 The Eighth International Symposium on Operations Research and Its Applications (ISORA 09) Zhangjiajie, China, September 20 22, 2009 Copyright 2009 ORSC & APORC, pp. 132 139 MIP-Based Approaches for Solving
The Eighth International Symposium on Operations Research and Its Applications (ISORA 09) Zhangjiajie, China, September 20 22, 2009 Copyright 2009 ORSC & APORC, pp. 132 139 MIP-Based Approaches for Solving
Randomization Approaches for Network Revenue Management with Customer Choice Behavior
 Randomization Approaches for Network Revenue Management with Customer Choice Behavior Sumit Kunnumkal Indian School of Business, Gachibowli, Hyderabad, 500032, India sumit kunnumkal@isb.edu March 9, 2011
Randomization Approaches for Network Revenue Management with Customer Choice Behavior Sumit Kunnumkal Indian School of Business, Gachibowli, Hyderabad, 500032, India sumit kunnumkal@isb.edu March 9, 2011
Nan Kong, Andrew J. Schaefer. Department of Industrial Engineering, Univeristy of Pittsburgh, PA 15261, USA
 A Factor 1 2 Approximation Algorithm for Two-Stage Stochastic Matching Problems Nan Kong, Andrew J. Schaefer Department of Industrial Engineering, Univeristy of Pittsburgh, PA 15261, USA Abstract We introduce
A Factor 1 2 Approximation Algorithm for Two-Stage Stochastic Matching Problems Nan Kong, Andrew J. Schaefer Department of Industrial Engineering, Univeristy of Pittsburgh, PA 15261, USA Abstract We introduce
Project Scheduling: PERT/CPM
 Project Scheduling: PERT/CPM CHAPTER 8 LEARNING OBJECTIVES After completing this chapter, you should be able to: 1. Describe the role and application of PERT/CPM for project scheduling. 2. Define a project
Project Scheduling: PERT/CPM CHAPTER 8 LEARNING OBJECTIVES After completing this chapter, you should be able to: 1. Describe the role and application of PERT/CPM for project scheduling. 2. Define a project
Approximation Algorithms
 Approximation Algorithms or: How I Learned to Stop Worrying and Deal with NP-Completeness Ong Jit Sheng, Jonathan (A0073924B) March, 2012 Overview Key Results (I) General techniques: Greedy algorithms
Approximation Algorithms or: How I Learned to Stop Worrying and Deal with NP-Completeness Ong Jit Sheng, Jonathan (A0073924B) March, 2012 Overview Key Results (I) General techniques: Greedy algorithms
Data Review and Analysis Program (DRAP) Flight Data Visualization Program for Enhancement of FOQA
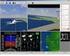 86 Data Review and Analysis Program (DRAP) Flight Data Visualization Program for Enhancement of FOQA Koji MURAOKA and Noriaki OKADA, Flight Systems Research Center, E-mail: muraoka@nal.go.jp Keywords:
86 Data Review and Analysis Program (DRAP) Flight Data Visualization Program for Enhancement of FOQA Koji MURAOKA and Noriaki OKADA, Flight Systems Research Center, E-mail: muraoka@nal.go.jp Keywords:
How To Check For Differences In The One Way Anova
 MINITAB ASSISTANT WHITE PAPER This paper explains the research conducted by Minitab statisticians to develop the methods and data checks used in the Assistant in Minitab 17 Statistical Software. One-Way
MINITAB ASSISTANT WHITE PAPER This paper explains the research conducted by Minitab statisticians to develop the methods and data checks used in the Assistant in Minitab 17 Statistical Software. One-Way
Dynamic Programming 11.1 AN ELEMENTARY EXAMPLE
 Dynamic Programming Dynamic programming is an optimization approach that transforms a complex problem into a sequence of simpler problems; its essential characteristic is the multistage nature of the optimization
Dynamic Programming Dynamic programming is an optimization approach that transforms a complex problem into a sequence of simpler problems; its essential characteristic is the multistage nature of the optimization
Numerical Matrix Analysis
 Numerical Matrix Analysis Lecture Notes #10 Conditioning and / Peter Blomgren, blomgren.peter@gmail.com Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research
Numerical Matrix Analysis Lecture Notes #10 Conditioning and / Peter Blomgren, blomgren.peter@gmail.com Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research
The Effects of Start Prices on the Performance of the Certainty Equivalent Pricing Policy
 BMI Paper The Effects of Start Prices on the Performance of the Certainty Equivalent Pricing Policy Faculty of Sciences VU University Amsterdam De Boelelaan 1081 1081 HV Amsterdam Netherlands Author: R.D.R.
BMI Paper The Effects of Start Prices on the Performance of the Certainty Equivalent Pricing Policy Faculty of Sciences VU University Amsterdam De Boelelaan 1081 1081 HV Amsterdam Netherlands Author: R.D.R.
Models in Transportation. Tim Nieberg
 Models in Transportation Tim Nieberg Transportation Models large variety of models due to the many modes of transportation roads railroad shipping airlines as a consequence different type of equipment
Models in Transportation Tim Nieberg Transportation Models large variety of models due to the many modes of transportation roads railroad shipping airlines as a consequence different type of equipment
Two objective functions for a real life Split Delivery Vehicle Routing Problem
 International Conference on Industrial Engineering and Systems Management IESM 2011 May 25 - May 27 METZ - FRANCE Two objective functions for a real life Split Delivery Vehicle Routing Problem Marc Uldry
International Conference on Industrial Engineering and Systems Management IESM 2011 May 25 - May 27 METZ - FRANCE Two objective functions for a real life Split Delivery Vehicle Routing Problem Marc Uldry
Module1. x 1000. y 800.
 Module1 1 Welcome to the first module of the course. It is indeed an exciting event to share with you the subject that has lot to offer both from theoretical side and practical aspects. To begin with,
Module1 1 Welcome to the first module of the course. It is indeed an exciting event to share with you the subject that has lot to offer both from theoretical side and practical aspects. To begin with,
On Lexicographic (Dictionary) Preference
 MICROECONOMICS LECTURE SUPPLEMENTS Hajime Miyazaki File Name: lexico95.usc/lexico99.dok DEPARTMENT OF ECONOMICS OHIO STATE UNIVERSITY Fall 993/994/995 Miyazaki.@osu.edu On Lexicographic (Dictionary) Preference
MICROECONOMICS LECTURE SUPPLEMENTS Hajime Miyazaki File Name: lexico95.usc/lexico99.dok DEPARTMENT OF ECONOMICS OHIO STATE UNIVERSITY Fall 993/994/995 Miyazaki.@osu.edu On Lexicographic (Dictionary) Preference
Section 1.1. Introduction to R n
 The Calculus of Functions of Several Variables Section. Introduction to R n Calculus is the study of functional relationships and how related quantities change with each other. In your first exposure to
The Calculus of Functions of Several Variables Section. Introduction to R n Calculus is the study of functional relationships and how related quantities change with each other. In your first exposure to
Locating and Decoding EAN-13 Barcodes from Images Captured by Digital Cameras
 Locating and Decoding EAN-13 Barcodes from Images Captured by Digital Cameras W3A.5 Douglas Chai and Florian Hock Visual Information Processing Research Group School of Engineering and Mathematics Edith
Locating and Decoding EAN-13 Barcodes from Images Captured by Digital Cameras W3A.5 Douglas Chai and Florian Hock Visual Information Processing Research Group School of Engineering and Mathematics Edith
TIME SERIES ANALYSIS. A time series is essentially composed of the following four components:
 TIME SERIES ANALYSIS A time series is a sequence of data indexed by time, often comprising uniformly spaced observations. It is formed by collecting data over a long range of time at a regular time interval
TIME SERIES ANALYSIS A time series is a sequence of data indexed by time, often comprising uniformly spaced observations. It is formed by collecting data over a long range of time at a regular time interval
Batch Production Scheduling in the Process Industries. By Prashanthi Ravi
 Batch Production Scheduling in the Process Industries By Prashanthi Ravi INTRODUCTION Batch production - where a batch means a task together with the quantity produced. The processing of a batch is called
Batch Production Scheduling in the Process Industries By Prashanthi Ravi INTRODUCTION Batch production - where a batch means a task together with the quantity produced. The processing of a batch is called
Re-optimization of Rolling Stock Rotations
 Konrad-Zuse-Zentrum für Informationstechnik Berlin Takustraße 7 D-14195 Berlin-Dahlem Germany RALF BORNDÖRFER 1, JULIKA MEHRGARDT 1, MARKUS REUTHER 1, THOMAS SCHLECHTE 1, KERSTIN WAAS 2 Re-optimization
Konrad-Zuse-Zentrum für Informationstechnik Berlin Takustraße 7 D-14195 Berlin-Dahlem Germany RALF BORNDÖRFER 1, JULIKA MEHRGARDT 1, MARKUS REUTHER 1, THOMAS SCHLECHTE 1, KERSTIN WAAS 2 Re-optimization
So let us begin our quest to find the holy grail of real analysis.
 1 Section 5.2 The Complete Ordered Field: Purpose of Section We present an axiomatic description of the real numbers as a complete ordered field. The axioms which describe the arithmetic of the real numbers
1 Section 5.2 The Complete Ordered Field: Purpose of Section We present an axiomatic description of the real numbers as a complete ordered field. The axioms which describe the arithmetic of the real numbers
Normal distribution. ) 2 /2σ. 2π σ
 Normal distribution The normal distribution is the most widely known and used of all distributions. Because the normal distribution approximates many natural phenomena so well, it has developed into a
Normal distribution The normal distribution is the most widely known and used of all distributions. Because the normal distribution approximates many natural phenomena so well, it has developed into a
Factoring Trinomials: The ac Method
 6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
(Refer Slide Time: 01.26)
 Discrete Mathematical Structures Dr. Kamala Krithivasan Department of Computer Science and Engineering Indian Institute of Technology, Madras Lecture # 27 Pigeonhole Principle In the next few lectures
Discrete Mathematical Structures Dr. Kamala Krithivasan Department of Computer Science and Engineering Indian Institute of Technology, Madras Lecture # 27 Pigeonhole Principle In the next few lectures
Unraveling versus Unraveling: A Memo on Competitive Equilibriums and Trade in Insurance Markets
 Unraveling versus Unraveling: A Memo on Competitive Equilibriums and Trade in Insurance Markets Nathaniel Hendren January, 2014 Abstract Both Akerlof (1970) and Rothschild and Stiglitz (1976) show that
Unraveling versus Unraveling: A Memo on Competitive Equilibriums and Trade in Insurance Markets Nathaniel Hendren January, 2014 Abstract Both Akerlof (1970) and Rothschild and Stiglitz (1976) show that
4. Continuous Random Variables, the Pareto and Normal Distributions
 4. Continuous Random Variables, the Pareto and Normal Distributions A continuous random variable X can take any value in a given range (e.g. height, weight, age). The distribution of a continuous random
4. Continuous Random Variables, the Pareto and Normal Distributions A continuous random variable X can take any value in a given range (e.g. height, weight, age). The distribution of a continuous random
Chapter 3 RANDOM VARIATE GENERATION
 Chapter 3 RANDOM VARIATE GENERATION In order to do a Monte Carlo simulation either by hand or by computer, techniques must be developed for generating values of random variables having known distributions.
Chapter 3 RANDOM VARIATE GENERATION In order to do a Monte Carlo simulation either by hand or by computer, techniques must be developed for generating values of random variables having known distributions.
! Solve problem to optimality. ! Solve problem in poly-time. ! Solve arbitrary instances of the problem. !-approximation algorithm.
 Approximation Algorithms Chapter Approximation Algorithms Q Suppose I need to solve an NP-hard problem What should I do? A Theory says you're unlikely to find a poly-time algorithm Must sacrifice one of
Approximation Algorithms Chapter Approximation Algorithms Q Suppose I need to solve an NP-hard problem What should I do? A Theory says you're unlikely to find a poly-time algorithm Must sacrifice one of
Duality in Linear Programming
 Duality in Linear Programming 4 In the preceding chapter on sensitivity analysis, we saw that the shadow-price interpretation of the optimal simplex multipliers is a very useful concept. First, these shadow
Duality in Linear Programming 4 In the preceding chapter on sensitivity analysis, we saw that the shadow-price interpretation of the optimal simplex multipliers is a very useful concept. First, these shadow
LINEAR EQUATIONS IN TWO VARIABLES
 66 MATHEMATICS CHAPTER 4 LINEAR EQUATIONS IN TWO VARIABLES The principal use of the Analytic Art is to bring Mathematical Problems to Equations and to exhibit those Equations in the most simple terms that
66 MATHEMATICS CHAPTER 4 LINEAR EQUATIONS IN TWO VARIABLES The principal use of the Analytic Art is to bring Mathematical Problems to Equations and to exhibit those Equations in the most simple terms that
Linear Programming Supplement E
 Linear Programming Supplement E Linear Programming Linear programming: A technique that is useful for allocating scarce resources among competing demands. Objective function: An expression in linear programming
Linear Programming Supplement E Linear Programming Linear programming: A technique that is useful for allocating scarce resources among competing demands. Objective function: An expression in linear programming
2x + y = 3. Since the second equation is precisely the same as the first equation, it is enough to find x and y satisfying the system
 1. Systems of linear equations We are interested in the solutions to systems of linear equations. A linear equation is of the form 3x 5y + 2z + w = 3. The key thing is that we don t multiply the variables
1. Systems of linear equations We are interested in the solutions to systems of linear equations. A linear equation is of the form 3x 5y + 2z + w = 3. The key thing is that we don t multiply the variables
Let s explore the content and skills assessed by Heart of Algebra questions.
 Chapter 9 Heart of Algebra Heart of Algebra focuses on the mastery of linear equations, systems of linear equations, and linear functions. The ability to analyze and create linear equations, inequalities,
Chapter 9 Heart of Algebra Heart of Algebra focuses on the mastery of linear equations, systems of linear equations, and linear functions. The ability to analyze and create linear equations, inequalities,
DEVELOPMENT OF A VULNERABILITY ASSESSMENT CODE FOR A PHYSICAL PROTECTION SYSTEM: SYSTEMATIC ANALYSIS OF PHYSICAL PROTECTION EFFECTIVENESS (SAPE)
 DEVELOPMENT OF A VULNERABILITY ASSESSMENT CODE FOR A PHYSICAL PROTECTION SYSTEM: SYSTEMATIC ANALYSIS OF PHYSICAL PROTECTION EFFECTIVENESS (SAPE) SUNG SOON JANG *, SUNG-WOO KWAK, HOSIK YOO, JUNG-SOO KIM
DEVELOPMENT OF A VULNERABILITY ASSESSMENT CODE FOR A PHYSICAL PROTECTION SYSTEM: SYSTEMATIC ANALYSIS OF PHYSICAL PROTECTION EFFECTIVENESS (SAPE) SUNG SOON JANG *, SUNG-WOO KWAK, HOSIK YOO, JUNG-SOO KIM
7.7 Solving Rational Equations
 Section 7.7 Solving Rational Equations 7 7.7 Solving Rational Equations When simplifying comple fractions in the previous section, we saw that multiplying both numerator and denominator by the appropriate
Section 7.7 Solving Rational Equations 7 7.7 Solving Rational Equations When simplifying comple fractions in the previous section, we saw that multiplying both numerator and denominator by the appropriate
Chapter 4. Polynomial and Rational Functions. 4.1 Polynomial Functions and Their Graphs
 Chapter 4. Polynomial and Rational Functions 4.1 Polynomial Functions and Their Graphs A polynomial function of degree n is a function of the form P = a n n + a n 1 n 1 + + a 2 2 + a 1 + a 0 Where a s
Chapter 4. Polynomial and Rational Functions 4.1 Polynomial Functions and Their Graphs A polynomial function of degree n is a function of the form P = a n n + a n 1 n 1 + + a 2 2 + a 1 + a 0 Where a s
The correlation coefficient
 The correlation coefficient Clinical Biostatistics The correlation coefficient Martin Bland Correlation coefficients are used to measure the of the relationship or association between two quantitative
The correlation coefficient Clinical Biostatistics The correlation coefficient Martin Bland Correlation coefficients are used to measure the of the relationship or association between two quantitative
Graphical Integration Exercises Part Four: Reverse Graphical Integration
 D-4603 1 Graphical Integration Exercises Part Four: Reverse Graphical Integration Prepared for the MIT System Dynamics in Education Project Under the Supervision of Dr. Jay W. Forrester by Laughton Stanley
D-4603 1 Graphical Integration Exercises Part Four: Reverse Graphical Integration Prepared for the MIT System Dynamics in Education Project Under the Supervision of Dr. Jay W. Forrester by Laughton Stanley
Describing, Exploring, and Comparing Data
 24 Chapter 2. Describing, Exploring, and Comparing Data Chapter 2. Describing, Exploring, and Comparing Data There are many tools used in Statistics to visualize, summarize, and describe data. This chapter
24 Chapter 2. Describing, Exploring, and Comparing Data Chapter 2. Describing, Exploring, and Comparing Data There are many tools used in Statistics to visualize, summarize, and describe data. This chapter
Locating and sizing bank-branches by opening, closing or maintaining facilities
 Locating and sizing bank-branches by opening, closing or maintaining facilities Marta S. Rodrigues Monteiro 1,2 and Dalila B. M. M. Fontes 2 1 DMCT - Universidade do Minho Campus de Azurém, 4800 Guimarães,
Locating and sizing bank-branches by opening, closing or maintaining facilities Marta S. Rodrigues Monteiro 1,2 and Dalila B. M. M. Fontes 2 1 DMCT - Universidade do Minho Campus de Azurém, 4800 Guimarães,
A Branch and Bound Algorithm for Solving the Binary Bi-level Linear Programming Problem
 A Branch and Bound Algorithm for Solving the Binary Bi-level Linear Programming Problem John Karlof and Peter Hocking Mathematics and Statistics Department University of North Carolina Wilmington Wilmington,
A Branch and Bound Algorithm for Solving the Binary Bi-level Linear Programming Problem John Karlof and Peter Hocking Mathematics and Statistics Department University of North Carolina Wilmington Wilmington,
