TRANSFORM AND ITS APPLICATION
|
|
|
- Anastasia Richards
- 7 years ago
- Views:
Transcription
1 LAPLACE TRANSFORM AND ITS APPLICATION IN CIRCUIT ANALYSIS C.T. Pan. Definition of the Laplace Tranform. Ueful Laplace Tranform Pair.3 Circuit Analyi in S Domain.4 The Tranfer Function and the Convolution Integral C.T. Pan
2 .5 The Tranfer Function and the Steady tate Sinuoidal Repone.6 The Impule Function in Circuit Analyi C.T. Pan 3. Definition of the Laplace Tranform Pierre Simon Laplace (749-87) : A French atronomer and mathematician Firt preented the Laplace tranform and it application to differential equation in 979. C.T. Pan 4
3 . Definition of the Laplace Tranform Definition: [ ] = = 0 t L f() t F () f() te dt = σ jω a complex variable The Laplace tranform i an integral tranformation of a function f(t) from the time domain into the complex frequency domain, F(). C.T. Pan 5. Definition of the Laplace Tranform One-ided (unilateral) Laplace tranform Two-ided (bilateral) Laplace tranform [ ] = = π j j σ ω σ jω L F () f() t Fe () d t Look-up table,an eaier way for circuit application f() t F () C.T. Pan 6
4 . Definition of the Laplace Tranform Similar to the application of phaor tranform to olve the teady tate AC circuit, Laplace tranform can be ued to tranform the time domain circuit into S domain circuit to implify the olution of integral differential equation to the manipulation of a et of algebraic equation. C.T. Pan 7. Ueful Laplace Tranform Pair Function f(t), t> F() impule tep ramp exponential δ () t ut () t 0 S S at e S a ine inωt S ω ω C.T. Pan 8
5 . Ueful Laplace Tranform Pair Function f(t), t> F() 0 coine damped ramp damped ine e S S ω ( S a) coωt at te at inωt ω ( ) S a ω damped coine e at coωt S a ( ) S a ω C.T. Pan 9. Ueful Laplace Tranform Pair d L f ( t) = F ( ) f (0 ) dt t F ( ) L f ( ) d = - τ τ 0 S L f ( t a ) u ( t a ) = a e F ( ), a > 0 [ ] at L e f ( t) = F ( a ) L [ f ( at) ] = F ( ), a > 0 a a f ( t) = F ( ) lim t 0 lim [ ] [ ] lim lim f ( t) = F ( ) t 0 C.T. Pan 0
6 . Ueful Laplace Tranform Pair Example Ue the Laplace tranform to olve the differential equation. dv dv 6 8v= ut () dt dt v(0) = v '(0) = Take Laplace tranfrom [ ] V() v(0) v'(0) 6 V() v(0) 8 V() = C.T. Pan. Ueful Laplace Tranform Pair [ ] V() v(0) v'(0) 6 V() v(0) 8 V() = ( 6 8) V() = V() = = ( 6 8) ( )( 4) t 4t vt () = ( e e ) ut () 4 C.T. Pan
![dv dv 6 8v= ut () dt dt v(0) = v '(0) = Take Laplace tranfrom [ ] V() v(0) v'(0) 6 V()](/docs-images/46/21455160/images/page_6.jpg "v(0) 8 V() = C.T. Pan.")
7 .3 Circuit Analyi in S Domain () KCL, i () t = 0, for any node. n k Take Laplace Tranform n I k () = 0, for any node. () KVL, v () t = 0, for any loop. m k Take Laplace Tranform Vk () = 0, for any loop. m C.T. Pan 3.3 Circuit Analyi in S Domain (3) Circuit Component Model reitor v () t = Ri () t R R V () = RI () R R I () = GV () R R C.T. Pan 4
8 .3 Circuit Analyi in S Domain inductor dil vl() t = L dt t il() t = il(0 ) v ( ) 0 L d L τ τ Li L (0 ) V () = LI () Li (0 ) L L L VL() il(0 ) I () = L i L (0) C.T. Pan 5.3 Circuit Analyi in S Domain capacitor dvc ic = C dt t vc() t = vc(0 ) i ( ) 0 C d C τ τ C v C (0 ) I () = CV () Cv (0 ) C C c vc(0 ) VC() = IC() C C Cv C (0 ) C.T. Pan 6
9 .3 Circuit Analyi in S Domain Coupling inductor i M i v L L v - - d i = L M dt d i = M L dt d i dt d i dt V ()=L SI ()-L i (0)MSI ()-Mi (0) V ()= MSI ()- Mi (0)L SI ()-L i (0) v v C.T. Pan 7.3 Circuit Analyi in S Domain For zero initial condition V() = Z () IS ( ) IS ( ) = Y() = V() Z () V() = ZI () () ohm' lawindomain C.T. Pan 8
10 .3 Circuit Analyi in S Domain The elegance of uing the Laplace tranform in circuit analyi lie in the automatic incluion of the initial condition in the tranformation proce, thu providing a complete (tranient and teady tate) olution. C.T. Pan 9.3 Circuit Analyi in S Domain Circuit analyi in domain Step : Tranform the time domain circuit into -domain circuit. Step : Solve the -domain circuit. e.g. Nodal analyi or meh analyi. Step 3 : Tranform the olution back into time domain. C.T. Pan 0
11 .3 Circuit Analyi in S Domain Example Find v o (t) given v o (0)=5V S-domain equivalent circuit 0 0 C.T. Pan.3 Circuit Analyi in S Domain 0 0 Nodal analyi 0 Vo () Vo() Vo() 0.5 = 0 0 0/ Vo() = = ( )( ) t t v () t = (0e 5 e ) ut () V o C.T. Pan
12 .4 The Tranfer Function and the Convolution Integral Given a linear circuit N in domain a hown below Tranfer function H() i defined a H () = Y() X() C.T. Pan 3.4 The Tranfer Function and the Convolution Integral If Y() = V (), X() = V() ; then H() = voltage gain o i If Y() = I (), X() = I () ; then H() = current gain o i If Y() = V(), X() = I () ; then H() = impedance If Y() = I (), X() = V() ; then H() = admittance C.T. Pan 4
13 .4 The Tranfer Function and the Convolution Integral Given the tranfer funtion H() and input X(), then Y()=H()X() If the input i δ(t), then X()= and Y()=H() Hence, the phyical meaning of H() i in fact the Laplace tranform of the impule repone of the correponding circuit. C.T. Pan 5.4 The Tranfer Function and the Convolution Integral Y()=H()X(), in -domain yt () = ht ( τ) x( τ) ht () xt () in time domain Geometrical interpretation of finding the convolution integral value at t=t k i baed on : C.T. Pan 6
14 .4 The Tranfer Function and the Convolution Integral ()Approximating the input function by uing a erie of impule function. ()Shifting property of linear ytem input x(t) outputy(t) x(t-τ) output y(t- τ) (3)Superpoition theorem for linear ytem (4)Definition of integral : finding the area C.T. Pan 7.4 The Tranfer Function and the Convolution Integral ()Input x(τ) i approximated uing impule function, x(τ)=0, for τ<0 x( τ ) x(0) 0 x() τ 0 τ τ τ τ 3 4 τ5 τ τ intant τ, x( τ ) value, area 0 τ = Vτ, x( τ ), x( τ ) Vτ τ = Vτ, x( τ ), x( τ ) Vτ τ = 3 Vτ, x( τ ), x( τ ) Vτ C.T. Pan 8 k k τ = 0, x(0), x(0) Vτ x( τ) f δτ ( ) fδτ ( τ ) f δτ ( τ ) L xk ( Vτ) Vτδ( τ kvτ) k= 0
15 .4 The Tranfer Function and the Convolution Integral () Ue the linearity property input output( repone) x(0) Vτδ( τ) x(0) Vτh( τ) x( τ ) Vτδ( τ τ ) x( τ ) Vτh( τ τ ) x( τ ) Vτδ( τ τ ) x( τ ) Vτh( τ τ ) M M up to τ =t k C.T. Pan 9.4 The Tranfer Function and the Convolution Integral (3) Ue uperpoition theorem to find the total approximate repone $ yt ( k) = xk ( Vτ) Vτ ht ( k kvτ) k= 0 tk n= integer[ ] Vτ n C.T. Pan 30
16 .4 The Tranfer Function and the Convolution Integral (4) Take the limit, Δτ dτ, $ yt ( ) yt ( ) k k yt ( k) = x( τ) ht ( k τ) dτ Due to cauality principle, h(t-τ)=0 for t t k and x(τ)=0 for τ<0 t k = ht ( k τ) x ( τ) d τ 0 C.T. Pan 3.4 The Tranfer Function and the Convolution Integral Example: t Given xt () = ut (), ht () = e ut (), find y(4), yt () = ht ( τ) x( τ) dτ y(4) = h(4 τ) x( τ) dτ C.T. Pan 3
17 .4 The Tranfer Function and the Convolution Integral Step. xx ( τ ) h ( τ ).0 τ C.T. Pan τ.4 The Tranfer Function and the Convolution Integral Step. Shift to t k =4 h (4 4τ ) C.T. Pan 34 τ
18 .4 The Tranfer Function and the Convolution Integral Step3. Find the product h(4-τ)x(τ) C.T. Pan 35.4 The Tranfer Function and the Convolution Integral Step4. Find the integral (area) 4 4 (4 τ) 4 τ 4 τ 4 y(4) = e dτ = e edτ= e e Step5. Check 0 0 e e = e = ( ) ( ) Y () = HX () () = = a a a a t yt () = ( e ), a= a 4 y(4) = ( e ) C.T. Pan 36 0
19 .5 The Tranfer Function and the Steady State Sinuoidal Repone From definition of tranfer function H() = Y() X() Y() = H() X() Aume input X(t)=Aco(wtФ) and H() i given, then one can get the teady tate olution without needing a eparate phaor analyi. C.T. Pan 37.5 The Tranfer Function and the Steady State Sinuoidal Repone proof : X() t = AcoφcoωtAinφin ωt A(coφin φω) X() = ω Y() = H() X() * K K = jω jω other term dueto pole under teady tate : * K K Y () = jω jω HA () ( coφωin φ) K = jω =ω j = H( jω) Ae C.T. Pan 38 jφ
20 .5 The Tranfer Function and the Steady State Sinuoidal Repone Let H( jω ) = H( jω) e jθ( ω) and takeinvere Laplacetranform Then y () t = A H( jω) co[ ω t φ θ( ω)] ie.. PXt ( ()) = A φ then Py ( ()) t = A H( jω) φ θ( ω) C.T. Pan 39.5 The Tranfer Function and the Steady State Sinuoidal Repone Example : The tranfer function H() of the circuit given below i known. Find the teady tate olution of V o (t) for the given V g (t). C.T. Pan 40
21 .5 The Tranfer Function and the Steady State Sinuoidal Repone 000( 5000) H() = Vg( t) = 0co(5000t 30 ) V C.T. Pan 4.5 The Tranfer Function and the Steady State Sinuoidal Repone Solution: Let = jω= j ( j ) Evaluate H(5000) j = 5 0 j5000(6000) 5 0 = Then Vo () t = 0 co(5000t ) 6 = 0 co(5000t5 ) V C.T. Pan 4
22 .5 The Tranfer Function and the Steady State Sinuoidal Repone In theory, the relationhip between H() and H(jw) provide a link between the time domain and the frequency domain. In ome cae, we can determine H(jw) experimentally and then contruct H() from the data. C.T. Pan 43.5 The Tranfer Function and the Steady State Sinuoidal Repone Example: Find the impule repone of the following circuit. v in _ R C v o _ C.T. Pan 44
23 .5 The Tranfer Function and the Steady State Sinuoidal Repone (a) Time domain olution dvo RC vo = δ () t dt At t = 0, v (0 ) = 0 o t δ () t At t = 0, vo (0 ) = dt C 0 R = V RC δ () t v () t o C.T. Pan 45.5 The Tranfer Function and the Steady State Sinuoidal Repone For t > 0, δ() t = 0 R C vo () t, v(0 ) = _ RC dv RC dt o v = 0 t RC vo () t = e ut () RC o C.T. Pan 46
24 .5 The Tranfer Function and the Steady State Sinuoidal Repone (b) -domain olution Find the tranfer function Vo() H() = V () in zero IC.. Tranform into -domain circuit V () in R C V () o _ C.T. Pan 47.5 The Tranfer Function and the Steady State Sinuoidal Repone Vo() H() = = C = V () in R RC C - ht () = L [ H()] V () in R C V () o _ = e RC t RC ut () Same anwer. C.T. Pan 48
25 .6 The Impule Function in Circuit Analyi Example : Impule voltage ource excitation it () V δ () t O i(0 ) = 0 C.T. Pan 49.6 The Impule Function in Circuit Analyi (a) Time domain olution At t = 0, i(0 ) = 0 t i(0 ) = V ( ) 0 Oδ x dx L VO = ( A) L V Oδ () t i(0 ) The impule voltage ource ha tored energy, L( ) i(0 ), in the inductor a an initial current in an infiniteimal moment. C.T. Pan 50
26 .6 The Impule Function in Circuit Analyi For t > 0, δ() t = 0 di L Ri = 0, natural repone dt VO i(0 ) = A L V L L R O t / τ it () = e ut (), τ = it () Note that the impule ource jut build up an initial inductor current but doe not contribute to any forced repone. C.T. Pan 5.6 The Impule Function in Circuit Analyi (b) -domain olution VO VO / L I () = = R L R L VO t/ τ it () = e ut () L V O Same anwer but much eaier. R I () L C.T. Pan 5
27 .6 The Impule Function in Circuit Analyi Example : Impule current ource excitation I δ () t o R C vt (), v(0 ) = 0 _ C.T. Pan 53.6 The Impule Function in Circuit Analyi (a) Time domain olution At t = 0, v(0 ) = 0 v(0) = 0, hort circuit I δ () t t v(0 ) = I ( ) 0 o x dx C δ Io = C The impule current ource ha tored energy, o C( ) v(0 ) R, in the capacitor a an initial voltage in an infiniteimal moment. C.T. Pan 54
28 .6 The Impule Function in Circuit Analyi For t > 0, δ () t = 0, open circuit dv v C = 0, natural repone dt R Io v(0 ) = C t I o τ vt () = e ut (), τ = RC C vt () Note that the impule current jut build up an initial capacitor voltage but doe not contribute to any forced repone. C.T. Pan 55.6 The Impule Function in Circuit Analyi (b) -domain olution Tranform into -domain circuit I o R C C.T. Pan 56 V _ () R Io/ C V( ) = I C o = R C RC t I o τ vt () = e ut () C Same anwer but much eaier.
29 .6 The Impule Function in Circuit Analyi Example 3: Impule caued by witching operation The witch i cloed at t=0 in the following circuit. Notethat v(0 ) v (0 ) C.T. Pan 57.6 The Impule Function in Circuit Analyi Tranform into -domain Vo I () Vo Ce C C C C V C V C Ce= V = = C C C C C v t o e o, () it () = VC o eδ() t C () = V C C C.T. Pan 58 o
30 .6 The Impule Function in Circuit Analyi At t=0, a finite charge of C i tranferred to C intantaneouly. Note that, a the witch i cloed, the voltage acro C doe not jump to V o of C but to it final value of the two paralleled capacitor. C.T. Pan 59.6 The Impule Function in Circuit Analyi C C = =, > 0 C C C = =, > 0 C C =, > 0 Note Q C V Vo t Q C V Vo t Q Q C Vo t Alo att = Q = CV Q =, 0, o, 0 Q Q CV o = Conervationof charge. C.T. Pan 60
31 .6 The Impule Function in Circuit Analyi If we conider charged capacitor a voltage ource, then we hould not connect two capacitor with unequal voltage in parallel. Due to violation of KVL, an impule will occur which may damage the component. C.T. Pan 6.6 The Impule Function in Circuit Analyi Example 4: Impule caued by witching operation The witch i opened at t = 0 in the following circuit. 00V 0Ω 3H i L t = 0 i L 5Ω H vo _ At t = 0, teady tate olution 00V i (0 ) = = 0 A 0Ω i (0 ) = 0 A C.T. Pan 6
32 .6 The Impule Function in Circuit Analyi For t > 0, the S-domain S circuit i 00 0Ω 3 I () L 30 L 5Ω V () o (00/ ) 30 4 I () = = Vo () = I () ( 5) = 5 it = e ut A 5t () (4 ) ()...( ) vt () = δ () t (60 0 e ) ut ()...( B) 5t C.T. Pan 63.6 The Impule Function in Circuit Analyi 0Ω I () L L 5Ω V () o Note t = 0, i (0 ) = 0 A, i (0 ) = 0 A L L t = 0, from ( A), i (0 ) = 6 A, i (0 ) = 6 A L L Alo, from ( B), there exit δ() t at v (). t o C.T. Pan 64
33 .6 The Impule Function in Circuit Analyi Thu, if we conider an inductor current a a current ource, then two inductor with unequal current hould not be connected in erie. Due to violation of KCL, it will reult in impule voltage which may damage the component. 00 C.T. Pan 65 0Ω 3 I() L 30 L 5Ω V () o SUMMARY Objective : Know the component model in -domain. Objective : Be able to tranform a time domain circuit into the -domain circuit. Objective 3 : Know how to analyze the -domain circuit and tranform the olution back to time domain. C.T. Pan 66
34 SUMMARY Objective 4 : Undertand the ignificance of tranfer function and be able to calculate the tranfer function from the -domain circuit. Objective 5 : Know the geometrical interpretation of convolution integral and be able to calculate the integral. C.T. Pan 67 SUMMARY Objective 6 : Know the relation between the phaor olution technique for finding inuoidal teady tate olution and the -domain olution technique. Objective 7 : Know how to ue -domain olution technique to olve a circuit containing impule ource or a witching circuit which may reult in impule function. C.T. Pan 68
35 SUMMARY Chapter problem : C.T. Pan 69
Lecture 7 Circuit analysis via Laplace transform
S. Boyd EE12 Lecture 7 Circuit analysis via Laplace transform analysis of general LRC circuits impedance and admittance descriptions natural and forced response circuit analysis with impedances natural
Math 22B, Homework #8 1. y 5y + 6y = 2e t
Math 22B, Homework #8 3.7 Problem # We find a particular olution of the ODE y 5y + 6y 2e t uing the method of variation of parameter and then verify the olution uing the method of undetermined coefficient.
Using the Impedance Method
Using the Impedance Method The impedance method allows us to completely eliminate the differential equation approach for the determination of the response of circuits. In fact the impedance method even
Solutions to Sample Problems for Test 3
22 Differential Equation Intructor: Petronela Radu November 8 25 Solution to Sample Problem for Tet 3 For each of the linear ytem below find an interval in which the general olution i defined (a) x = x
Ohm s Law. Ohmic relationship V=IR. Electric Power. Non Ohmic devises. Schematic representation. Electric Power
Ohm Law Ohmic relationhip V=IR Ohm law tate that current through the conductor i directly proportional to the voltage acro it if temperature and other phyical condition do not change. In many material,
Introduction to Complex Numbers in Physics/Engineering
Introduction to Complex Numbers in Physics/Engineering ference: Mary L. Boas, Mathematical Methods in the Physical Sciences Chapter 2 & 14 George Arfken, Mathematical Methods for Physicists Chapter 6 The
12.4 UNDRIVEN, PARALLEL RLC CIRCUIT*
+ v C C R L - v i L FIGURE 12.24 The parallel second-order RLC circuit shown in Figure 2.14a. 12.4 UNDRIVEN, PARALLEL RLC CIRCUIT* We will now analyze the undriven parallel RLC circuit shown in Figure
Solution of the Heat Equation for transient conduction by LaPlace Transform
Solution of the Heat Equation for tranient conduction by LaPlace Tranform Thi notebook ha been written in Mathematica by Mark J. McCready Profeor and Chair of Chemical Engineering Univerity of Notre Dame
Mixed Method of Model Reduction for Uncertain Systems
SERBIAN JOURNAL OF ELECTRICAL ENGINEERING Vol 4 No June Mixed Method of Model Reduction for Uncertain Sytem N Selvaganean Abtract: A mixed method for reducing a higher order uncertain ytem to a table reduced
Part IB Paper 6: Information Engineering LINEAR SYSTEMS AND CONTROL Dr Glenn Vinnicombe HANDOUT 3. Stability and pole locations.
Part IB Paper 6: Information Engineering LINEAR SYSTEMS AND CONTROL Dr Glenn Vinnicombe HANDOUT 3 Stability and pole locations asymptotically stable marginally stable unstable Imag(s) repeated poles +
CHAPTER 5 BROADBAND CLASS-E AMPLIFIER
CHAPTER 5 BROADBAND CLASS-E AMPLIFIER 5.0 Introduction Cla-E amplifier wa firt preented by Sokal in 1975. The application of cla- E amplifier were limited to the VHF band. At thi range of frequency, cla-e
Design of The Feedback Controller (PID Controller) for The Buck Boost Converter
Deign of The Feedback Controller (PID Controller) for The Buck Boot Converter )Sattar Jaber Al-Iawi ) Ehan A. Abd Al-Nabi Department of Electromechanical Eng. The High Intitute for Indutry-Libya-Mirata
Let s examine the response of the circuit shown on Figure 1. The form of the source voltage Vs is shown on Figure 2. R. Figure 1.
Examples of Transient and RL Circuits. The Series RLC Circuit Impulse response of Circuit. Let s examine the response of the circuit shown on Figure 1. The form of the source voltage Vs is shown on Figure.
First Order Circuits. EENG223 Circuit Theory I
First Order Circuits EENG223 Circuit Theory I First Order Circuits A first-order circuit can only contain one energy storage element (a capacitor or an inductor). The circuit will also contain resistance.
v = x t = x 2 x 1 t 2 t 1 The average speed of the particle is absolute value of the average velocity and is given Distance travelled t
Chapter 2 Motion in One Dimenion 2.1 The Important Stuff 2.1.1 Poition, Time and Diplacement We begin our tudy of motion by conidering object which are very mall in comparion to the ize of their movement
580.439 Course Notes: Linear circuit theory and differential equations
58.439 ourse Notes: Linear circuit theory and differential equations eading: Koch, h. ; any text on linear signal and system theory can be consulted for more details. These notes will review the basics
Figure 2.1. a. Block diagram representation of a system; b. block diagram representation of an interconnection of subsystems
Figure. a. Block diagram repreentation o a ytem; b. block diagram repreentation o an interconnection o ubytem REVIEW OF THE LAPLACE TRANSFORM Table. Laplace tranorm table Table. Laplace tranorm theorem
MECH 2110 - Statics & Dynamics
Chapter D Problem 3 Solution 1/7/8 1:8 PM MECH 11 - Static & Dynamic Chapter D Problem 3 Solution Page 7, Engineering Mechanic - Dynamic, 4th Edition, Meriam and Kraige Given: Particle moving along a traight
On Reference RIAA Networks by Jim Hagerman
On eference IAA Network by Jim Hagerman You d think there would be nothing left to ay. Everything you need to know about IAA network ha already been publihed. However, a few year back I came acro an intereting
J.L. Kirtley Jr. Electric network theory deals with two primitive quantities, which we will refer to as: 1. Potential (or voltage), and
Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.061 Introduction to Power Systems Class Notes Chapter 1: eiew of Network Theory J.L. Kirtley Jr. 1 Introduction
ES250: Electrical Science. HW7: Energy Storage Elements
ES250: Electrical Science HW7: Energy Storage Elements Introduction This chapter introduces two more circuit elements, the capacitor and the inductor whose elements laws involve integration or differentiation;
Optical Illusion. Sara Bolouki, Roger Grosse, Honglak Lee, Andrew Ng
Optical Illuion Sara Bolouki, Roger Groe, Honglak Lee, Andrew Ng. Introduction The goal of thi proect i to explain ome of the illuory phenomena uing pare coding and whitening model. Intead of the pare
Chapter 20 Quasi-Resonant Converters
Chapter 0 Quasi-Resonant Converters Introduction 0.1 The zero-current-switching quasi-resonant switch cell 0.1.1 Waveforms of the half-wave ZCS quasi-resonant switch cell 0.1. The average terminal waveforms
MATH 425, PRACTICE FINAL EXAM SOLUTIONS.
MATH 45, PRACTICE FINAL EXAM SOLUTIONS. Exercise. a Is the operator L defined on smooth functions of x, y by L u := u xx + cosu linear? b Does the answer change if we replace the operator L by the operator
Delft. Matlab and Simulink for Modeling and Control. Robert Babuška and Stefano Stramigioli. November 1999
Matlab and Simulink for Modeling and Control Robert Babuška and Stefano Stramigioli November 999 Delft Delft Univerity of Technology Control Laboratory Faculty of Information Technology and Sytem Delft
Chapter 11 Current Programmed Control
Chapter 11 Current Programmed Control Buck converter v g i s Q 1 D 1 L i L C v R The peak transistor current replaces the duty cycle as the converter control input. Measure switch current R f i s Clock
2. METHOD DATA COLLECTION
Key to learning in pecific ubject area of engineering education an example from electrical engineering Anna-Karin Cartenen,, and Jonte Bernhard, School of Engineering, Jönköping Univerity, S- Jönköping,
Understanding Poles and Zeros
MASSACHUSETTS INSTITUTE OF TECHNOLOGY DEPARTMENT OF MECHANICAL ENGINEERING 2.14 Analysis and Design of Feedback Control Systems Understanding Poles and Zeros 1 System Poles and Zeros The transfer function
CIRCUITS LABORATORY EXPERIMENT 3. AC Circuit Analysis
CIRCUITS LABORATORY EXPERIMENT 3 AC Circuit Analysis 3.1 Introduction The steady-state behavior of circuits energized by sinusoidal sources is an important area of study for several reasons. First, the
W03 Analysis of DC Circuits. Yrd. Doç. Dr. Aytaç Gören
W03 Analysis of DC Circuits Yrd. Doç. Dr. Aytaç Gören ELK 2018 - Contents W01 Basic Concepts in Electronics W02 AC to DC Conversion W03 Analysis of DC Circuits (self and condenser) W04 Transistors and
Two Dimensional FEM Simulation of Ultrasonic Wave Propagation in Isotropic Solid Media using COMSOL
Excerpt from the Proceeding of the COMSO Conference 0 India Two Dimenional FEM Simulation of Ultraonic Wave Propagation in Iotropic Solid Media uing COMSO Bikah Ghoe *, Krihnan Balaubramaniam *, C V Krihnamurthy
S. Boyd EE102. Lecture 1 Signals. notation and meaning. common signals. size of a signal. qualitative properties of signals.
S. Boyd EE102 Lecture 1 Signals notation and meaning common signals size of a signal qualitative properties of signals impulsive signals 1 1 Signals a signal is a function of time, e.g., f is the force
1 Introduction. 2 Complex Exponential Notation. J.L. Kirtley Jr.
Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.06 Introduction to Power Systems Class Notes Chapter AC Power Flow in Linear Networks J.L. Kirtley Jr.
Phasors. Phasors. by Prof. Dr. Osman SEVAİOĞLU Electrical and Electronics Engineering Department. ^ V cos (wt + θ) ^ V sin (wt + θ)
V cos (wt θ) V sin (wt θ) by Prof. Dr. Osman SEVAİOĞLU Electrical and Electronics Engineering Department EE 209 Fundamentals of Electrical and Electronics Engineering, Prof. Dr. O. SEVAİOĞLU, Page 1 Vector
Get Here Jeffrey M. Kurtz Client Feedback Evaluation Implementation Extenion/Termination Solution Development Analyi Data Collection Problem Definition Entry & Contracting CORE to all Problem Solving Equilibrium
s-domain Circuit Analysis
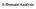S-Doman naly -Doman rcut naly Tme doman t doman near rcut aplace Tranform omplex frequency doman doman Tranformed rcut Dfferental equaton lacal technque epone waveform aplace Tranform nvere Tranform -
Direction of Induced Current
Direction of Induced Current Bar magnet moves through coil Current induced in coil A S N v Reverse pole Induced current changes sign B N S v v Coil moves past fixed bar magnet Current induced in coil as
Bode Diagrams of Transfer Functions and Impedances ECEN 2260 Supplementary Notes R. W. Erickson
Bode Diagrams of Transfer Functions and Impedances ECEN 2260 Supplementary Notes. W. Erickson In the design of a signal processing network, control system, or other analog system, it is usually necessary
FUNDAMENTALS OF ENGINEERING (FE) EXAMINATION REVIEW
FE: Electric Circuits C.A. Gross EE1-1 FUNDAMENTALS OF ENGINEERING (FE) EXAMINATION REIEW ELECTRICAL ENGINEERING Charles A. Gross, Professor Emeritus Electrical and Comp Engineering Auburn University Broun
Lecture 14: Transformers. Ideal Transformers
White, EE 3 Lecture 14 Page 1 of 9 Lecture 14: Tranforer. deal Tranforer n general, a tranforer i a ultiort ac device that convert voltage, current and iedance fro one value to another. Thi device only
Curcuits and Differential Equaitons
Objective: Curcuits and Differential Equaitons Given a circuit, find the differential equation which describes that circuit. Solve that differential equation numerically (with SPICE, MATAB, or ISSIM) Ciruits
Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science
aachuett Intitute of Technology Department of Electrical Engineering and Computer Science 6.685 Electric achinery Cla Note 10: Induction achine Control and Simulation c 2003 Jame L. Kirtley Jr. 1 Introduction
Nonlinear Systems and Control Lecture # 15 Positive Real Transfer Functions & Connection with Lyapunov Stability. p. 1/?
Nonlinear Systems and Control Lecture # 15 Positive Real Transfer Functions & Connection with Lyapunov Stability p. 1/? p. 2/? Definition: A p p proper rational transfer function matrix G(s) is positive
Equivalent Circuits and Transfer Functions
R eq isc Equialent Circuits and Transfer Functions Samantha R Summerson 14 September, 009 1 Equialent Circuits eq ± Figure 1: Théenin equialent circuit. i sc R eq oc Figure : Mayer-Norton equialent circuit.
Three Phase Theory - Professor J R Lucas
Three Phae Theory - Profeor J Luca A you are aware, to tranit power with ingle phae alternating current, we need two wire live wire and neutral. However you would have een that ditribution line uually
2.161 Signal Processing: Continuous and Discrete Fall 2008
MT OpenCourseWare http://ocw.mit.edu.6 Signal Processing: Continuous and Discrete Fall 00 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSETTS
Review of First- and Second-Order System Response 1
MASSACHUSETTS INSTITUTE OF TECHNOLOGY DEPARTMENT OF MECHANICAL ENGINEERING 2.151 Advanced System Dynamics and Control Review of First- and Second-Order System Response 1 1 First-Order Linear System Transient
Applications of Second-Order Differential Equations
Applications of Second-Order Differential Equations Second-order linear differential equations have a variety of applications in science and engineering. In this section we explore two of them: the vibration
Application of network analyzer in measuring the performance functions of power supply
J Indian Inst Sci, July Aug 2006, 86, 315 325 Indian Institute of Science Application of network analyzer in measuring the performance functions of power supply B SWAMINATHAN* AND V RAMANARAYANAN Power
Frequency response: Resonance, Bandwidth, Q factor
Frequency response: esonance, Bandwidth, Q factor esonance. Let s continue the exploration of the frequency response of circuits by investigating the series circuit shown on Figure. C + V - Figure The
Mesh-Current Method (Loop Analysis)
Mesh-Current Method (Loop Analysis) Nodal analysis was developed by applying KCL at each non-reference node. Mesh-Current method is developed by applying KVL around meshes in the circuit. A mesh is a loop
Simulation of Power Systems Dynamics using Dynamic Phasor Models. Power Systems Laboratory. ETH Zürich Switzerland
X SEPOPE 2 a 25 de maio de 26 May 2 rt to 25 th 26 FLORIANÓPOLIS (SC) BRASIL X SIMPÓSIO DE ESPECIALISTAS EM PLANEJAMENTO DA OPERAÇÃO E EXPANSÃO ELÉTRICA X SYMPOSIUM OF SPECIALISTS IN ELECTRIC OPERATIONAL
19.7. Applications of Differential Equations. Introduction. Prerequisites. Learning Outcomes. Learning Style
Applications of Differential Equations 19.7 Introduction Blocks 19.2 to 19.6 have introduced several techniques for solving commonly-occurring firstorder and second-order ordinary differential equations.
Basic Laws Circuit Theorems Methods of Network Analysis Non-Linear Devices and Simulation Models
EE Modul 1: Electric Circuits Theory Basic Laws Circuit Theorems Methods of Network Analysis Non-Linear Devices and Simulation Models EE Modul 1: Electric Circuits Theory Current, Voltage, Impedance Ohm
Mutual Inductance and Transformers F3 3. r L = ω o
utual Inductance and Transformers F3 1 utual Inductance & Transformers If a current, i 1, flows in a coil or circuit then it produces a magnetic field. Some of the magnetic flux may link a second coil
Chapter 10. RC Circuits ISU EE. C.Y. Lee
Chapter 10 RC Circuits Objectives Describe the relationship between current and voltage in an RC circuit Determine impedance and phase angle in a series RC circuit Analyze a series RC circuit Determine
IMPORTANT: Read page 2 ASAP. *Please feel free to email (longo.physics@gmail.com) me at any time if you have questions or concerns.
rev. 05/4/16 AP Phyic C: Mechanic Summer Aignment 016-017 Mr. Longo Foret Park HS longo.phyic@gmail.com longodb@pwc.edu Welcome to AP Phyic C: Mechanic. The purpoe of thi ummer aignment i to give you a
6. Friction, Experiment and Theory
6. Friction, Experiment and Theory The lab thi wee invetigate the rictional orce and the phyical interpretation o the coeicient o riction. We will mae ue o the concept o the orce o gravity, the normal
EXAMPLE 8: An Electrical System (Mechanical-Electrical Analogy)
EXAMPLE 8: An Electrical System (Mechanical-Electrical Analogy) A completely analogous procedure can be used to find the state equations of electrical systems (and, ultimately, electro-mechanical systems
Step Response of RC Circuits
Step Response of RC Circuits 1. OBJECTIVES...2 2. REFERENCE...2 3. CIRCUITS...2 4. COMPONENTS AND SPECIFICATIONS...3 QUANTITY...3 DESCRIPTION...3 COMMENTS...3 5. DISCUSSION...3 5.1 SOURCE RESISTANCE...3
Laplace Transform. f(t)e st dt,
Chapter 7 Laplace Tranform The Laplace tranform can be ued to olve differential equation. Beide being a different and efficient alternative to variation of parameter and undetermined coefficient, the Laplace
2.1 Introduction. 2.2 Terms and definitions
.1 Introduction An important step in the procedure for solving any circuit problem consists first in selecting a number of independent branch currents as (known as loop currents or mesh currents) variables,
FEDERATION OF ARAB SCIENTIFIC RESEARCH COUNCILS
Aignment Report RP/98-983/5/0./03 Etablihment of cientific and technological information ervice for economic and ocial development FOR INTERNAL UE NOT FOR GENERAL DITRIBUTION FEDERATION OF ARAB CIENTIFIC
OUTPUT STREAM OF BINDING NEURON WITH DELAYED FEEDBACK
binding neuron, biological and medical cybernetic, interpike interval ditribution, complex ytem, cognition and ytem Alexander VIDYBIDA OUTPUT STREAM OF BINDING NEURON WITH DELAYED FEEDBACK A binding neuron
Scalar Valued Functions of Several Variables; the Gradient Vector
Scalar Valued Functions of Several Variables; the Gradient Vector Scalar Valued Functions vector valued function of n variables: Let us consider a scalar (i.e., numerical, rather than y = φ(x = φ(x 1,
SIMULATIONS OF PARALLEL RESONANT CIRCUIT POWER ELECTRONICS COLORADO STATE UNIVERSITY
SIMULATIONS OF PARALLEL RESONANT CIRCUIT POWER ELECTRONICS COLORADO STATE UNIVERSITY Page 1 of 25 PURPOSE: The purpose of this lab is to simulate the LCC circuit using MATLAB and ORCAD Capture CIS to better
Fundamentals of Electrical Engineering 2 Grundlagen der Elektrotechnik 2
Fundamentals of Electrical Engineering 2 Grundlagen der Elektrotechnik 2 Chapter: Sinusoidal Steady State Analysis / Netzwerkanalyse bei harmonischer Erregung Michael E. Auer Source of figures: Alexander/Sadiku:
UNIVERSITY OF CALIFORNIA, SAN DIEGO Electrical & Computer Engineering Department ECE 101 - Fall 2010 Linear Systems Fundamentals
UNIVERSITY OF CALIFORNIA, SAN DIEGO Electrical & Computer Engineering Department ECE 101 - Fall 2010 Linear Systems Fundamentals FINAL EXAM WITH SOLUTIONS (YOURS!) You are allowed one 2-sided sheet of
HADNOUT E.13 - EXAMPLES ON TRANSFER FUNCTIONS, POLES AND ZEROS
Paraura Leture 3 Augut HADNOUT E3 - EXAMPLES ON TRANSFER FUNCTIONS POLES AND ZEROS Exaple Deterine the tranfer funtion of the a-pring-daper yte The governing differential equation of a a-pring-daper yte
MSc Financial Economics: International Finance. Bubbles in the Foreign Exchange Market. Anne Sibert. Revised Spring 2013. Contents
MSc Financial Economic: International Finance Bubble in the Foreign Exchange Market Anne Sibert Revied Spring 203 Content Introduction................................................. 2 The Mone Market.............................................
1 2 3 1 1 2 x = + x 2 + x 4 1 0 1
(d) If the vector b is the sum of the four columns of A, write down the complete solution to Ax = b. 1 2 3 1 1 2 x = + x 2 + x 4 1 0 0 1 0 1 2. (11 points) This problem finds the curve y = C + D 2 t which
HOMOTOPY PERTURBATION METHOD FOR SOLVING A MODEL FOR HIV INFECTION OF CD4 + T CELLS
İtanbul icaret Üniveritei Fen Bilimleri Dergii Yıl: 6 Sayı: Güz 7/. 9-5 HOMOOPY PERURBAION MEHOD FOR SOLVING A MODEL FOR HIV INFECION OF CD4 + CELLS Mehmet MERDAN ABSRAC In thi article, homotopy perturbation
A note on profit maximization and monotonicity for inbound call centers
A note on profit maximization and monotonicity for inbound call center Ger Koole & Aue Pot Department of Mathematic, Vrije Univeriteit Amterdam, The Netherland 23rd December 2005 Abtract We conider an
Report 4668-1b 30.10.2010. Measurement report. Sylomer - field test
Report 4668-1b Meaurement report Sylomer - field tet Report 4668-1b 2(16) Contet 1 Introduction... 3 1.1 Cutomer... 3 1.2 The ite and purpoe of the meaurement... 3 2 Meaurement... 6 2.1 Attenuation of
Homework Assignment 03
Question 1 (2 points each unless noted otherwise) Homework Assignment 03 1. A 9-V dc power supply generates 10 W in a resistor. What peak-to-peak amplitude should an ac source have to generate the same
3.4 - BJT DIFFERENTIAL AMPLIFIERS
BJT Differential Amplifiers (6/4/00) Page 1 3.4 BJT DIFFERENTIAL AMPLIFIERS INTRODUCTION Objective The objective of this presentation is: 1.) Define and characterize the differential amplifier.) Show the
Partial optimal labeling search for a NP-hard subclass of (max,+) problems
Partial optimal labeling earch for a NP-hard ubcla of (max,+) problem Ivan Kovtun International Reearch and Training Center of Information Technologie and Sytem, Kiev, Uraine, ovtun@image.iev.ua Dreden
TECHNIQUES OF. C.T. Pan 1. C.T. Pan
TECHNIQUES OF CIRCUIT ANALYSIS C.T. Pan 1 4.1 Introduction 4.2 The Node-Voltage Method ( Nodal Analysis ) 4.3 The Mesh-Current Method ( Mesh Analysis ) 4.4 Fundamental Loop Analysis 4.5 Fundamental Cutset
Physics 111. Exam #1. January 24, 2014
Phyic 111 Exam #1 January 24, 2014 Name Pleae read and follow thee intruction carefully: Read all problem carefully before attempting to olve them. Your work mut be legible, and the organization clear.
Ver 3537 E1.1 Analysis of Circuits (2014) E1.1 Circuit Analysis. Problem Sheet 1 (Lectures 1 & 2)
Ver 3537 E. Analysis of Circuits () Key: [A]= easy... [E]=hard E. Circuit Analysis Problem Sheet (Lectures & ). [A] One of the following circuits is a series circuit and the other is a parallel circuit.
EXPERIMENT NUMBER 8 CAPACITOR CURRENT-VOLTAGE RELATIONSHIP
1 EXPERIMENT NUMBER 8 CAPACITOR CURRENT-VOLTAGE RELATIONSHIP Purpose: To demonstrate the relationship between the voltage and current of a capacitor. Theory: A capacitor is a linear circuit element whose
Homework #1 Solutions
MAT 303 Spring 203 Homework # Solutions Problems Section.:, 4, 6, 34, 40 Section.2:, 4, 8, 30, 42 Section.4:, 2, 3, 4, 8, 22, 24, 46... Verify that y = x 3 + 7 is a solution to y = 3x 2. Solution: From
Linear energy-preserving integrators for Poisson systems
BIT manucript No. (will be inerted by the editor Linear energy-preerving integrator for Poion ytem David Cohen Ernt Hairer Received: date / Accepted: date Abtract For Hamiltonian ytem with non-canonical
1.5 / 1 -- Communication Networks II (Görg) -- www.comnets.uni-bremen.de. 1.5 Transforms
.5 / -- Communication Networks II (Görg) -- www.comnets.uni-bremen.de.5 Transforms Using different summation and integral transformations pmf, pdf and cdf/ccdf can be transformed in such a way, that even
Unit2: Resistor/Capacitor-Filters
Unit2: Resistor/Capacitor-Filters Physics335 Student October 3, 27 Physics 335-Section Professor J. Hobbs Partner: Physics335 Student2 Abstract Basic RC-filters were constructed and properties such as
Chapter 2. Parameterized Curves in R 3
Chapter 2. Parameterized Curves in R 3 Def. A smooth curve in R 3 is a smooth map σ : (a, b) R 3. For each t (a, b), σ(t) R 3. As t increases from a to b, σ(t) traces out a curve in R 3. In terms of components,
Network Theory Question Bank
Network Theory Question Bank Unit-I JNTU SYLLABUS: Three Phase Circuits Three phase circuits: Phase sequence Star and delta connection Relation between line and phase voltages and currents in balanced
Simple Modular Half-Bridge
Simple Modular HalfBridge Shane Colton Email: colton@mit.edu Maachuett Intitute of Technology Rev.1.1 13 March, 2009 Simple Modular HalfBridge Module Overview V i V i Iolated DCDC Supply: Supplied by 12V
Chapter 3 AUTOMATIC VOLTAGE CONTROL
Chapter 3 AUTOMATIC VOLTAGE CONTROL . INTRODUCTION TO EXCITATION SYSTEM The basic function of an excitation system is to provide necessary direct current to the field winding of the synchronous generator.
Convolution, Correlation, & Fourier Transforms. James R. Graham 10/25/2005
Convolution, Correlation, & Fourier Transforms James R. Graham 10/25/2005 Introduction A large class of signal processing techniques fall under the category of Fourier transform methods These methods fall
10.450 Process Dynamics, Operations, and Control Lecture Notes - 11 Lesson 11. Frequency response of dynamic systems.
Lesson. Frequency response of dynamic systems..0 Context We have worked with step, pulse, and sine disturbances. Of course, there are many sine disturbances, because the applied frequency may vary. Surely
Step response of an RLC series circuit
School of Engineering Department of Electrical and Computer Engineering 332:224 Principles of Electrical Engineering II Laboratory Experiment 5 Step response of an RLC series circuit 1 Introduction Objectives
Analysis of Variable Frequency Three Phase Induction Motor Drive
World Academy of Science, ngineering and Technology 4 008 Analyi of Variable Frequency Three Phae Induction Motor Drive Thida Win, Nang Sabai, and Hnin Nandar Maung Abtract AC motor drive are widely ued
Bob York. Simple FET DC Bias Circuits
Bob York Simple FET DC Bia Circuit Loa-Line an Q-point Conier the effect of a rain reitor in the comnon-ource configuration: Smaller + g D out KL: Thi i the equation of a line that can be uperimpoe on
Research Article An (s, S) Production Inventory Controlled Self-Service Queuing System
Probability and Statitic Volume 5, Article ID 558, 8 page http://dxdoiorg/55/5/558 Reearch Article An (, S) Production Inventory Controlled Self-Service Queuing Sytem Anoop N Nair and M J Jacob Department
Passive control. Carles Batlle. II EURON/GEOPLEX Summer School on Modeling and Control of Complex Dynamical Systems Bertinoro, Italy, July 18-22 2005
Passive control theory I Carles Batlle II EURON/GEOPLEX Summer School on Modeling and Control of Complex Dynamical Systems Bertinoro, Italy, July 18-22 25 Contents of this lecture Change of paradigm in
The continuous and discrete Fourier transforms
FYSA21 Mathematical Tools in Science The continuous and discrete Fourier transforms Lennart Lindegren Lund Observatory (Department of Astronomy, Lund University) 1 The continuous Fourier transform 1.1
1 Norms and Vector Spaces
008.10.07.01 1 Norms and Vector Spaces Suppose we have a complex vector space V. A norm is a function f : V R which satisfies (i) f(x) 0 for all x V (ii) f(x + y) f(x) + f(y) for all x,y V (iii) f(λx)