Measures of distance between samples: Euclidean

Transcription

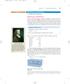
1 4- Chapter 4 Measures of istance between samples: Eucliean We will be talking a lot about istances in this book. The concept of istance between two samples or between two variables is funamental in multivariate analysis almost everything we o has a relation with this measure. If we talk about a single variable we take this concept for grante. If one sample has a ph of 6. an another a ph of 7.5, the istance between them is.4: but we woul usually call this the absolute ifference. But on the ph line, the values 6. an 7.5 are at a istance apart of.4 units, an this is how we want to start thinking about ata: points on a line, points in a plane, even points in a tenimensional space! So, given samples with not one measurement on them but several, how o we efine istance between them. There are a multitue of answers to this question, an we evote three chapters to this topic. In the present chapter we consier what are calle Eucliean istances, which coincie with our most basic physical iea of istance, but generalize to multiimensional points. Contents Pythagoras theorem Eucliean istance Stanarize Eucliean istance Weighte Eucliean istance Distances for count ata Chi-square istance Distances for categorical ata Pythagoras theorem The photo shows Michael in July 008 in the town of Pythagorion, Samos islan, Greece, paying homage to the one who is repute to have mae almost all the content of this book possible: ΠΥΘΑΓΟΡΑΣ Ο ΣΑΜΙΟΣ, Pythagoras the Samian. The illustrative geometric proof of Pythagoras theorem stans carve on the marble base of the statue it is this theorem that is at the heart of most of the multivariate analysis presente in this book, an particularly the graphical approach to ata analysis that we are strongly promoting. When you see the wor square mentione in a statistical text (for example, chi square or least squares), you can be almost sure that the corresponing theory has some relation to this theorem. We first show the theorem in its simplest an most familiar two-imensional form, before showing how easy it is to generalize it to multiimensional space. In a right-

2 4- angle triangle, the square on the hypotenuse (the sie enote by A in Exhibit 4.) is equal to the sum of the squares on the other two sies (B an C); that is, A = B + C. Exhibit 4. Pythagoras theorem in the familiar right-angle triangle, an the monument to this triangle in the port of Pythagorion, Samos islan, Greece, with Pythagoras himself forming one of the sies. A = B + C B A C Eucliean istance The immeiate consequence of this is that the square length of a vector x = [ x x ] is the sum of the squares of its coorinates (see triangle OPA in Exhibit 4., or triangle OPB OP enotes the square length of x, that is the istance between point O an P); an the Exhibit 4. Pythagoras theorem applie to istances in two-imensional space. Axis OP = x + x PQ = ( x y) + ( x y ) B x P x = [ x x ] x y y D Q y = [ y y ] O A x y Axis x y

3 4-3 square istance between two vectors x = [ x x ] an y = [ y y ] is the sum of square ifferences in their coorinates (see triangle PQD in Exhibit 4.; PQ enotes the square istance between points P an Q). To enote the istance between vectors x an y we can use the notation so that this last result can be written as: x, y = (x x,y y ) + (x y ) (4.) that is, the istance itself is the square root, y = ( x y) + ( x y x ) (4.) What we calle the square length of x, the istance between points P an O in Exhibit 4., is the istance between the vector x = [ x x ] an the zero vector 0 = [ 0 0 ] with coorinates all zero:, 0 = x x x + (4.3) which we coul ust enote by x. The zero vector is calle the origin of the space. Exhibit 4.3 Pythagoras theorem extene into three imensional space Axis 3 C x 3 x = [ x x x 3 ] P OP = x + x + x 3 O x B Axis x A S Axis

4 4-4 We move immeiately to a three-imensional point x = [ x x x 3 ], shown in Exhibit 4.3. This figure has to be imagine in a room where the origin O is at the corner to reinforce this iea floor tiles have been rawn on the plane of axes an, which is the floor of the room. The three coorinates are at points A, B an C along the axes, an the angles AOB, AOC an COB are all 90 as well as the angle OSP at S, where the point P (epicting vector x) is proecte onto the floor. Using Pythagoras theorem twice we have: an so OP = OS + PS (because of right-angle at S) OS = OA + AS (because of right-angle at A) OP = OA + AS + PS that is, the square length of x is the sum of its three square coorinates an so + x x3 = x + x It is also clear that placing a point Q in Exhibit 4.3 to epict another vector y an going through the motions to calculate the istance between x an y will lea to, y = ( x y) + ( x y ) + ( x3 y3 x ) (4.4) Furthermore, we can carry on like this into 4 or more imensions, in general J imensions, where J is the number of variables. Although we cannot raw the geometry any more, we can express the istance between two J-imensional vectors x an y as: J x, y = ( x y ) (4.5) = This well-known istance measure, which generalizes our notion of physical istance in two- or three-imensional space to multiimensional space, is calle the Eucliean istance (but often referre to as the Pythagorean istance as well). Stanarize Eucliean istance Let us consier measuring the istances between our 30 samples in Exhibit., using ust the three continuous variables pollution, epth an temperature. What woul happen if we applie formula (4.4) to measure istance between the last two samples, s9 an s30, for example? Here is the calculation: s9,s30 = (6.0.9) + (5 99) + (3.0.9) = = =

5 4-5 The contribution of the secon variable epth to this calculation is huge one coul say that the istance is practically ust the absolute ifference in the epth values (equal to 5-99 = 48) with only tiny aitional contributions from pollution an temperature. This is the problem of stanarization iscusse in Chapter 3 the three variables are on completely ifferent scales of measurement an the larger epth values have larger intersample ifferences, so they will ominate in the calculation of Eucliean istances. Some form of stanarization is necessary to balance out the contributions, an the conventional way to o this is to transform the variables so they all have the same variance of. At the same time we centre the variables at their means this centring is not necessary for calculating istance, but it makes the variables all have mean zero an thus easier to compare. The transformation commonly calle stanarization is thus as follows: stanarize value = (original value mean) / stanar eviation (4.5) The means an stanar eviations of the three variables are: Pollution Depth Temperature mean s leaing to the table of stanarize values given in Exhibit 4.4. These values are now on Exhibit 4.4 Stanarize values of the three continuous variables of Exhibit. SITE ENVIRONMENTAL VARIABLES NO. Pollution Depth Temperature s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s

6 4-6 comparable stanarize scales, in units of stanar eviation units with respect to the mean. For example, the value woul signify stanar eviations above the mean, an. woul signify. stanar eviations below the mean. The istance calculation thus aggregates square ifferences in stanar eviation units of each variable. As an example, the istance between the last two sites of Table is: s9,s30 = [ (.)] + [ ] + [ 0.0 (.557)] = = 3.43 = Pollution an temperature have higher contributions than before but epth still plays the largest role in this particular example, even after stanarization. But this contribution is ustifie now, since it oes show the biggest stanarize ifference between the samples. We call this the stanarize Eucliean istance, meaning that it is the Eucliean istance calculate on stanarize ata. It will be assume that stanarization refers to the form efine by (4.5), unless specifie otherwise. We can repeat this calculation for all pairs of samples. Since the istance between sample A an sample B will be the same as between sample B an sample A, we can report these istances in a triangular matrix Exhibit 4.5 shows part of this istance matrix, which contains a total of ½ 30 9 = 435 istances. Exhibit 4.5 Stanarize Eucliean istances between the 30 samples, base on the three continuous environmental variables, showing part of the triangular istance matrix. s 3.68 s s s3 s4 s5 s6 s4 s5 s6 s7 s8 s9 s s s s s s s s s s s

7 4-7 Reaers might ask how all this has helpe them why convert a ata table with 90 numbers to one that has 435, almost five times more? Were the histograms an scatterplots in Exhibits. an.4 not enough to unerstan these three variables? This is a goo question, but we shall have to leave the answer to the Part 3 of the book, from Chapter 7 onwars, when we escribe actual analyses of these istance matrices. At this early stage in the book, we can only ask reaers to be patient try to unerstan fully the concept of istance which will be the main threa to all the analytical methos to come. Weighte Eucliean istance The stanarize Eucliean istance between two J-imensional vectors can be written as: J x y, = ) x y ( (4.6) s s = where s is the sample stanar eviation of the -th variable. Notice that we nee not subtract the -th mean from x an y because they will ust cancel out in the ifferencing. Now (4.6) can be rewritten in the following equivalent way: x, y = = J = J = s ( x y ) w ( x y ) (4.7) where w = / s is the inverse of the -th variance. We think of w as a weight attache to the -th variable: in other wors, we compute the usual square ifferences between the variables on their original scales, as we i in the (unstanarize) Eucliean istance, but then multiply these square ifferences by their corresponing weights. Notice in this case how the weight of a variable with high variance is low, while the weight of a variable with low variance is high, which is another way of thinking about the compensatory effect prouce by stanarization. The weights of the three variables in our example are (to 4 significant figures) 0.8, an.64 respectively, showing how much the epth variable is ownweighte an the temperature variable upweighte: epth has over 3000 times the variance of temperature, so each square ifference in (4.7) is ownweighte relatively by that much. We call (4.7) weighte Eucliean istance. Distances for count ata So far we have looke at the istances between samples base on continuous ata, now we consier istances on count ata, for example the abunance ata for the five taxa labelle a, b, c, an e in Exhibit.. First, notice that these five variables apparently o not have the problem of ifferent measurement scales that we ha for the continuous

8 4-8 environmental variables all variables are counts. There are, however, ifferent average frequencies of counts, an as we mentione in Chapter 3, variances of count variables can be positively relate to their means. The means an variances of these five variables are as follows: a b c e mean variance Variable a with the highest mean also has the highest variance, while e with the lowest mean has the lowest variance. Only is out of line with the others, having smaller variance than b an c but a higher mean. Because this variance mean relationship is a natural phenomenon for count variables, not one that is ust particular any given example, some form of compensation of the variances nees to be performe, as before. It is not usual for count ata to be stanarize in the style of mean 0, variance, as was the case for continuous variables in (4.5). The most common ways of balancing the contributions are: a power transformation: usually square root n /, but also ouble square root (i.e.,fourth root n /4 ) when the variance increases faster than the mean (this situation is calle overispersion in the literature); a shifte log transformation: because of the many zeros in ecological count ata, a positive number, usually, has to be ae to the ata before log-transforming; that is, log(+n); chi-square istance: this is a weighte Eucliean istance of the form (4.7) which we iscuss now. The chi-square istance is special because it is at the heart of corresponence analysis, extensively use in ecological research. The first premise of this istance function is that it is calculate on relative counts, an not on the original ones, an the secon is that it stanarizes by the mean an not by the variance. In our example, the count ata are first converte into relative counts by iviing out the rows by their row totals so that each row contains relative proportions that a up to. These sets of proportions are calle profiles, site profiles in this example see Exhibit 4.6. The extra row at the en of Exhibit 4.6 gives the set of proportions calle the average profile. These are the proportions calculate on the set of column totals, which are equal to 404, 6, 5, 37 an 89 respectively, with gran total 334. Hence, 404/334 = 0.303, 6/334 = 0.96, etc. Chi-square istances are then calculate between the profiles, in a weighte Eucliean fashion, using the inverse of the average proportions as weights. Suppose c enotes the -th element of the average profile, that is the abunance proportion of the -th species in the whole ata set. Then the chi-square istance, enote by χ, between two sites with profiles x = [ x x x J ] an y = [ y y y J ] is efine as: J χ = x, y ( x y ) (4.8) c = From the efinition of this istance function it woul have been better to call it the chi istance function, because it is not square, as in the chi-square statistic! But the chi-square epithet persists in the literature, so when we talk of its square we say the square chi-square istance.

9 4-9 Exhibit 4.6 Profiles of the sites, obtaine by iviing the rows of counts in Exhibit. by their respective row totals. The last row is the average profile, compute in the same way, as proportions of the column totals of the original table of counts. SITE SPECIES PROPORTIONS NO. a b c e s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s ave Exhibit 4.7 shows part of the triangular matrix of chi-square istances. Once again, this is a large matrix with more numbers (435) than the original table of counts (50), an we shall see the benefit of calculating these istances from Part 3 onwars. For the moment, think of Exhibit 4.5 as a way of measuring similarities an ifferences between the 30 samples base on the (continuous) environmental ata, while Exhibit 4.7 is the similar iea but base on the count ata. But notice that the scale of istances in Exhibit 4.5 is not comparable to that of Exhibit 4.7, but the orering of the values oes have some meaning: for example, in Exhibit 4.5 the smallest stanarize Eucliean istance (amongst those that we report there) is 0.38, between sites s30 an s5. In Exhibit 4.7 these two sites have one of the smallest chi-square istances as well. This means that these two sites are relatively similar in their environmental variables an also in their biological compositions. This might be something interesting, but we nee to stuy all the pairwise istances, an not ust an isolate one, in orer to see if there is any connection between the biological abunances an the environmental variables (this will come later).

10 4-0 Exhibit 4.7 Chi-square istances between the 30 samples, base on the biological count ata, showing part of the triangular istance matrix. s.39 s s s3 s4 s5 s6 s4 s5 s6 s7 s8 s9 s s s s s s s s s s s Distances for categorical ata In our introuctory example we have only one categorical variable (seiment), so the question of computing istance is fairly trivial: if two samples have the same seiment then their istance is 0, an if its ifferent it is. But what if there were several categorical variables, say K of them? There are several possibilities, one of the simplest being to simply exten the matching iea an count how many matches an mismatches there are between samples, with optional averaging over variables. For example, suppose that there are five categorical variables, C to C5, each with three categories, which we enote by a/b/c an that there are two samples with the following characteristics: C C C3 C4 C5 sample a c c b a sample b c b a a : Then the number of matches is an the number of mismatches is 3, hence the istance between the two samples is 3 ivie by 5, the number of variables, that is 0.6. This is calle the simple matching coefficient. Sometimes this coefficient is expresse in terms of similarity, not issimilarity, in which case it woul be equal to 0.4, the relative number of matches make sure you know which way it is being efine. Here we stick to istances, in other wors issimilarities or mismatches. Note that this coefficient is irectly proportional to the square Eucliean istance calculate between these ata in ummy variable form, where each category efines a zero-one variable:

11 4- Ca Cb Cc Ca Cb Cc C3a C3b C3c C4a C4b C4c C5a C5b C5c sample sample The square Eucliean istance sums the square ifferences between these two vectors: if there is an agreement (there are two matches in this example) there is zero sum of square ifferences, but if there is a iscrepancy there are two ifferences, + an, which give a sum of squares of. So the sum of square ifferences here is 6, an if this is expresse relative to the maximum iscrepancy that can be achieve, namely 0 when there are no matches in the 5 variables, then this gives exactly the same value 0.6 as before. There are several variations on the theme of the matching coefficient, an one of them is the chi-square istance for multivariate categorical ata, which introuces a weighting of each category inverse to its mean value, as for profile ata base on counts. Suppose that there are J categories in total (in the above example J = 5) an that the total occurrences of each category are enote by n,, n J, with total n = Σ n (since the totals for each variable equal the sample size, n will be the sample size times the number of variables). Then efine c as follows: c = n /n an use /c as weights in a weighte Eucliean istance between the samples coe in ummy variable form. The iea here is, as before, that the rarity of a category shoul count more than in the istance than a frequent category. Just like the chi-square istance function is at the heart of corresponence analysis of abunance ata, so this form of the chi-square for multivariate categorical ata is at the heart of multiple corresponence analysis. We o not treat multiple corresponence analysis specifically in this book, as it is more common in the social sciences where almost all the ata are categorical, for example in questionnaire research. SUMMARY: Measures of istance between samples: Eucliean. Pythagoras theorem extens to vectors in multiimensional space: the square length of a vector is the sum of squares of its coorinates.. As a consequence, square istances between two vectors in multiimensional space are the sum of square ifferences in their coorinates. This multiimensional istance is calle the Eucliean istance, an is the natural generalization of our threeimensional notion of physical istance to more imensions. 3. When variables are on ifferent measurement scales, stanarization is necessary to balance the contributions of the variables in the computation of istance. The Eucliean istance compute on stanarize variables is calle the stanarize Eucliean istance. 4. Stanarization in the calculation of istances is equivalently thought of as weighting the variables this leas to the notion of Eucliean istances with any choice of weights, calle weighte Eucliean istance. 5. A particular weighte Eucliean istance applicable to count ata is the chi-square istance, which is calculate between the relative counts for each sample, calle profiles, an weights each variable by the inverse of the variable s overall mean count.