Using the Quadrant. Protractor. Eye Piece. You can measure angles of incline from 0º ( horizontal ) to 90º (vertical ). Ignore measurements >90º.
|
|
|
- Terence Fletcher
- 8 years ago
- Views:
Transcription
1 Using the Quadrant Eye Piece Protractor Handle You can measure angles of incline from 0º ( horizontal ) to 90º (vertical ). Ignore measurements 90º. Plumb Bob ø <----Read angle of incline (ø) here. Eye ø
2 Using the Quadrant To Make a Similar Triangle. Use the quadrant to measure the height of tall objects in an indirect manner. First, locate yourself on a piece of ground that is level with the object to be measured. The object's base and your feet should be on the same horizontal plane. Measure the distance from your feet to the base of the object and record it on the diagram. Choose a multiple of ten feet (or other linear unit ) for this distance to simplify calculation. Second, walk to the object and mark it with a piece of marking tape at your eye level.. The quadrant should read 0º when you aim it at the eye level tape mark. Measure this height and record it on the diagram. Object to be measured Next, aim the quadrant at the top of the object to be measured. Aim the quadrant at the top of the object. - Have your partner read the quadrant's protractor as you hold it steady. The angle of incline should be between 0º and 90º. After that, record your angle of incline on the diagram. Finally, use these measurements to determine the object's height using the graph paper worksheet. Angle of incline: What is your eye level height? Sight a level line and mark the object at that height. Marking tape Make sure that you add your eye height to your height calculation. What is the distance to the object? Measure this distance accurately with a tape measure. < Level ground- - -
3 Using the Quadrant To Determine the Opposite Side Using Tangent. Use the quadrant to measure the height of tall objects in an indirect manner. First, locate yourself on a piece of ground that is level with the object to be measured. The object's base and your feet should be on the same horizontal plane. Measure the distance from your feet to the base of the object and record it on the diagram. Choose a multiple of ten feet (or other linear unit ) for this distance to simplify calculation. Second, walk to the object and mark it with a piece of marking tape at your eye level. Measure this height and record it on the diagram. Third, aim the quadrant at the object to be measured. The quadrant should read 0º when you aim it at the eye level tape mark. - Have your partner read the quadrant's protractor as you hold it steady. Aim the quadrant at the top of the object. Have your partner read the quadrant as you hold it steady. The angle of incline should be between 0º and 90º. Record your angle of incline on the diagram. Object to be measured Finally, Substitute measured values for variables on the following tangent worksheet.. Angle of incline: What is your eye level height? Sight a level line and mark the object at that height. Marking tape Make sure that you add your eye height to your height calculation. Measure this distance accurately with a tape measure. < Level ground- - -
4 Using the Quadrant To Find The Height of an Object Using the Tangent Function. Side opposite Ø Object ( Ø Use the Quadrant to find this angle(ø ). Measured side adjacent to Ø = What is Ø? What is Tan Ø? (Find this on your calculator, or from a Tangent table.) How long is the side adjacent Ø? The side opposite to Ø = "H" Tan Ø = So... Tan Ø ( Side Adjacent ) = Side Opposite Substitute measured values, then evaluate: ( ) = H
5 Make a similar triangle to measure indirectly. Using the Quadrant Mark the angle of incline on the protractor. Vertical scale = horizontal scale. 90º 80º 70º 60º 50º 40º 30º 20º 10º v For estimation purposes only.
6 Make a similar triangle to measure indirectly. Using the Quadrant Mark the angle of incline on the protractor. Mark the distance to the object on the horizontal scale. Draw a vertical line at that point. Connect the protractor's vertex mark "V" with the angle you marked, then extend this line to the vertical line you drew. This intersection marks the object's height from your eye level. Read this vertical distance from the scale on the right. 60 feet 50 feet 40 feet 30 feet 90º 80º 70º 60º 50º 40º 20 feet 30º 20º 10º 10 feet v For estimation purposes only. 30 feet 40 feet 50 feet 60 feet 70 feet 80 feet 90 feet 100 feet
7 Make a similar triangle to measure indirectly. Using the Quadrant Mark the angle of incline on the protractor. Mark the distance to the object on the horizontal scale. Draw a vertical line at that point. Connect the protractor's vertex mark "V" with the angle you marked, then extend this line to the vertical line you drew. This intersection marks the object's height from your eye level. Read this vertical distance from the scale on the right. 120 feet 100 feet 80 feet 60 feet 90º 80º 70º 60º 50º 40º 40 feet 30º 20º 10º 20 feet v For estimation purposes only. 60 feet 80 feet 100 feet 120 feet 140 feet 160 feet 180 feet 200 feet
The Primary Trigonometric Ratios Word Problems
 The Primary Trigonometric Ratios Word Problems. etermining the measures of the sides and angles of right triangles using the primary ratios When we want to measure the height of an inaccessible object
The Primary Trigonometric Ratios Word Problems. etermining the measures of the sides and angles of right triangles using the primary ratios When we want to measure the height of an inaccessible object
Lines. We have learned that the graph of a linear equation. y = mx +b
 Section 0. Lines We have learne that the graph of a linear equation = m +b is a nonvertical line with slope m an -intercept (0, b). We can also look at the angle that such a line makes with the -ais. This
Section 0. Lines We have learne that the graph of a linear equation = m +b is a nonvertical line with slope m an -intercept (0, b). We can also look at the angle that such a line makes with the -ais. This
Geometry 1. Unit 3: Perpendicular and Parallel Lines
 Geometry 1 Unit 3: Perpendicular and Parallel Lines Geometry 1 Unit 3 3.1 Lines and Angles Lines and Angles Parallel Lines Parallel lines are lines that are coplanar and do not intersect. Some examples
Geometry 1 Unit 3: Perpendicular and Parallel Lines Geometry 1 Unit 3 3.1 Lines and Angles Lines and Angles Parallel Lines Parallel lines are lines that are coplanar and do not intersect. Some examples
Chapter 3.1 Angles. Geometry. Objectives: Define what an angle is. Define the parts of an angle.
 Chapter 3.1 Angles Define what an angle is. Define the parts of an angle. Recall our definition for a ray. A ray is a line segment with a definite starting point and extends into infinity in only one direction.
Chapter 3.1 Angles Define what an angle is. Define the parts of an angle. Recall our definition for a ray. A ray is a line segment with a definite starting point and extends into infinity in only one direction.
Geometry and Measurement
 The student will be able to: Geometry and Measurement 1. Demonstrate an understanding of the principles of geometry and measurement and operations using measurements Use the US system of measurement for
The student will be able to: Geometry and Measurement 1. Demonstrate an understanding of the principles of geometry and measurement and operations using measurements Use the US system of measurement for
Solutions to Exercises, Section 5.1
 Instructor s Solutions Manual, Section 5.1 Exercise 1 Solutions to Exercises, Section 5.1 1. Find all numbers t such that ( 1 3,t) is a point on the unit circle. For ( 1 3,t)to be a point on the unit circle
Instructor s Solutions Manual, Section 5.1 Exercise 1 Solutions to Exercises, Section 5.1 1. Find all numbers t such that ( 1 3,t) is a point on the unit circle. For ( 1 3,t)to be a point on the unit circle
TIgeometry.com. Geometry. Angle Bisectors in a Triangle
 Angle Bisectors in a Triangle ID: 8892 Time required 40 minutes Topic: Triangles and Their Centers Use inductive reasoning to postulate a relationship between an angle bisector and the arms of the angle.
Angle Bisectors in a Triangle ID: 8892 Time required 40 minutes Topic: Triangles and Their Centers Use inductive reasoning to postulate a relationship between an angle bisector and the arms of the angle.
Extra Credit Assignment Lesson plan. The following assignment is optional and can be completed to receive up to 5 points on a previously taken exam.
 Extra Credit Assignment Lesson plan The following assignment is optional and can be completed to receive up to 5 points on a previously taken exam. The extra credit assignment is to create a typed up lesson
Extra Credit Assignment Lesson plan The following assignment is optional and can be completed to receive up to 5 points on a previously taken exam. The extra credit assignment is to create a typed up lesson
1. A student followed the given steps below to complete a construction. Which type of construction is best represented by the steps given above?
 1. A student followed the given steps below to complete a construction. Step 1: Place the compass on one endpoint of the line segment. Step 2: Extend the compass from the chosen endpoint so that the width
1. A student followed the given steps below to complete a construction. Step 1: Place the compass on one endpoint of the line segment. Step 2: Extend the compass from the chosen endpoint so that the width
Algebra Geometry Glossary. 90 angle
 lgebra Geometry Glossary 1) acute angle an angle less than 90 acute angle 90 angle 2) acute triangle a triangle where all angles are less than 90 3) adjacent angles angles that share a common leg Example:
lgebra Geometry Glossary 1) acute angle an angle less than 90 acute angle 90 angle 2) acute triangle a triangle where all angles are less than 90 3) adjacent angles angles that share a common leg Example:
What s Your Angle? (Measurement)
 The Middle School Math Project What s Your Angle? (Measurement) Objective Using inductive reasoning, students will devise procedures for using a protractor to measure the number of degrees in an angle.
The Middle School Math Project What s Your Angle? (Measurement) Objective Using inductive reasoning, students will devise procedures for using a protractor to measure the number of degrees in an angle.
Postulate 17 The area of a square is the square of the length of a. Postulate 18 If two figures are congruent, then they have the same.
 Chapter 11: Areas of Plane Figures (page 422) 11-1: Areas of Rectangles (page 423) Rectangle Rectangular Region Area is measured in units. Postulate 17 The area of a square is the square of the length
Chapter 11: Areas of Plane Figures (page 422) 11-1: Areas of Rectangles (page 423) Rectangle Rectangular Region Area is measured in units. Postulate 17 The area of a square is the square of the length
Indirect Measurement Technique: Using Trigonometric Ratios Grade Nine
 Ohio Standards Connections Measurement Benchmark D Use proportional reasoning and apply indirect measurement techniques, including right triangle trigonometry and properties of similar triangles, to solve
Ohio Standards Connections Measurement Benchmark D Use proportional reasoning and apply indirect measurement techniques, including right triangle trigonometry and properties of similar triangles, to solve
Common Core Unit Summary Grades 6 to 8
 Common Core Unit Summary Grades 6 to 8 Grade 8: Unit 1: Congruence and Similarity- 8G1-8G5 rotations reflections and translations,( RRT=congruence) understand congruence of 2 d figures after RRT Dilations
Common Core Unit Summary Grades 6 to 8 Grade 8: Unit 1: Congruence and Similarity- 8G1-8G5 rotations reflections and translations,( RRT=congruence) understand congruence of 2 d figures after RRT Dilations
8-3 Dot Products and Vector Projections
 8-3 Dot Products and Vector Projections Find the dot product of u and v Then determine if u and v are orthogonal 1u =, u and v are not orthogonal 2u = 3u =, u and v are not orthogonal 6u = 11i + 7j; v
8-3 Dot Products and Vector Projections Find the dot product of u and v Then determine if u and v are orthogonal 1u =, u and v are not orthogonal 2u = 3u =, u and v are not orthogonal 6u = 11i + 7j; v
Examples of Scalar and Vector Quantities 1. Candidates should be able to : QUANTITY VECTOR SCALAR
 Candidates should be able to : Examples of Scalar and Vector Quantities 1 QUANTITY VECTOR SCALAR Define scalar and vector quantities and give examples. Draw and use a vector triangle to determine the resultant
Candidates should be able to : Examples of Scalar and Vector Quantities 1 QUANTITY VECTOR SCALAR Define scalar and vector quantities and give examples. Draw and use a vector triangle to determine the resultant
3.1 Solving Systems Using Tables and Graphs
 Algebra 2 Chapter 3 3.1 Solve Systems Using Tables & Graphs 3.1 Solving Systems Using Tables and Graphs A solution to a system of linear equations is an that makes all of the equations. To solve a system
Algebra 2 Chapter 3 3.1 Solve Systems Using Tables & Graphs 3.1 Solving Systems Using Tables and Graphs A solution to a system of linear equations is an that makes all of the equations. To solve a system
Worksheet to Review Vector and Scalar Properties
 Worksheet to Review Vector and Scalar Properties 1. Differentiate between vectors and scalar quantities 2. Know what is being requested when the question asks for the magnitude of a quantity 3. Define
Worksheet to Review Vector and Scalar Properties 1. Differentiate between vectors and scalar quantities 2. Know what is being requested when the question asks for the magnitude of a quantity 3. Define
http://www.castlelearning.com/review/teacher/assignmentprinting.aspx 5. 2 6. 2 1. 10 3. 70 2. 55 4. 180 7. 2 8. 4
 of 9 1/28/2013 8:32 PM Teacher: Mr. Sime Name: 2 What is the slope of the graph of the equation y = 2x? 5. 2 If the ratio of the measures of corresponding sides of two similar triangles is 4:9, then the
of 9 1/28/2013 8:32 PM Teacher: Mr. Sime Name: 2 What is the slope of the graph of the equation y = 2x? 5. 2 If the ratio of the measures of corresponding sides of two similar triangles is 4:9, then the
Angles and Quadrants. Angle Relationships and Degree Measurement. Chapter 7: Trigonometry
 Chapter 7: Trigonometry Trigonometry is the study of angles and how they can be used as a means of indirect measurement, that is, the measurement of a distance where it is not practical or even possible
Chapter 7: Trigonometry Trigonometry is the study of angles and how they can be used as a means of indirect measurement, that is, the measurement of a distance where it is not practical or even possible
Heron s Formula. Key Words: Triangle, area, Heron s formula, angle bisectors, incenter
 Heron s Formula Lesson Summary: Students will investigate the Heron s formula for finding the area of a triangle. The lab has students find the area using three different methods: Heron s, the basic formula,
Heron s Formula Lesson Summary: Students will investigate the Heron s formula for finding the area of a triangle. The lab has students find the area using three different methods: Heron s, the basic formula,
Writing the Equation of a Line in Slope-Intercept Form
 Writing the Equation of a Line in Slope-Intercept Form Slope-Intercept Form y = mx + b Example 1: Give the equation of the line in slope-intercept form a. With y-intercept (0, 2) and slope -9 b. Passing
Writing the Equation of a Line in Slope-Intercept Form Slope-Intercept Form y = mx + b Example 1: Give the equation of the line in slope-intercept form a. With y-intercept (0, 2) and slope -9 b. Passing
RIGHT TRIANGLE TRIGONOMETRY
 RIGHT TRIANGLE TRIGONOMETRY The word Trigonometry can be broken into the parts Tri, gon, and metry, which means Three angle measurement, or equivalently Triangle measurement. Throughout this unit, we will
RIGHT TRIANGLE TRIGONOMETRY The word Trigonometry can be broken into the parts Tri, gon, and metry, which means Three angle measurement, or equivalently Triangle measurement. Throughout this unit, we will
Name Class. Date Section. Test Form A Chapter 11. Chapter 11 Test Bank 155
 Chapter Test Bank 55 Test Form A Chapter Name Class Date Section. Find a unit vector in the direction of v if v is the vector from P,, 3 to Q,, 0. (a) 3i 3j 3k (b) i j k 3 i 3 j 3 k 3 i 3 j 3 k. Calculate
Chapter Test Bank 55 Test Form A Chapter Name Class Date Section. Find a unit vector in the direction of v if v is the vector from P,, 3 to Q,, 0. (a) 3i 3j 3k (b) i j k 3 i 3 j 3 k 3 i 3 j 3 k. Calculate
GEOMETRIC DESIGN CIVL 3161
 GEOMETRIC DESIGN CIVL 3161 Reading Assignment: p. 45-72 (4 th ed.) p.45-75 (previous ed.) in Mannering textbook. Geometric design of highway facilities deals with the proportion of physical elements of
GEOMETRIC DESIGN CIVL 3161 Reading Assignment: p. 45-72 (4 th ed.) p.45-75 (previous ed.) in Mannering textbook. Geometric design of highway facilities deals with the proportion of physical elements of
Objective: To distinguish between degree and radian measure, and to solve problems using both.
 CHAPTER 3 LESSON 1 Teacher s Guide Radian Measure AW 3.2 MP 4.1 Objective: To distinguish between degree and radian measure, and to solve problems using both. Prerequisites Define the following concepts.
CHAPTER 3 LESSON 1 Teacher s Guide Radian Measure AW 3.2 MP 4.1 Objective: To distinguish between degree and radian measure, and to solve problems using both. Prerequisites Define the following concepts.
of surface, 569-571, 576-577, 578-581 of triangle, 548 Associative Property of addition, 12, 331 of multiplication, 18, 433
 Absolute Value and arithmetic, 730-733 defined, 730 Acute angle, 477 Acute triangle, 497 Addend, 12 Addition associative property of, (see Commutative Property) carrying in, 11, 92 commutative property
Absolute Value and arithmetic, 730-733 defined, 730 Acute angle, 477 Acute triangle, 497 Addend, 12 Addition associative property of, (see Commutative Property) carrying in, 11, 92 commutative property
Chapter 8 Geometry We will discuss following concepts in this chapter.
 Mat College Mathematics Updated on Nov 5, 009 Chapter 8 Geometry We will discuss following concepts in this chapter. Two Dimensional Geometry: Straight lines (parallel and perpendicular), Rays, Angles
Mat College Mathematics Updated on Nov 5, 009 Chapter 8 Geometry We will discuss following concepts in this chapter. Two Dimensional Geometry: Straight lines (parallel and perpendicular), Rays, Angles
Parallel and Perpendicular. We show a small box in one of the angles to show that the lines are perpendicular.
 CONDENSED L E S S O N. Parallel and Perpendicular In this lesson you will learn the meaning of parallel and perpendicular discover how the slopes of parallel and perpendicular lines are related use slopes
CONDENSED L E S S O N. Parallel and Perpendicular In this lesson you will learn the meaning of parallel and perpendicular discover how the slopes of parallel and perpendicular lines are related use slopes
Lesson 1: Exploring Trigonometric Ratios
 Lesson 1: Exploring Trigonometric Ratios Common Core Georgia Performance Standards MCC9 12.G.SRT.6 MCC9 12.G.SRT.7 Essential Questions 1. How are the properties of similar triangles used to create trigonometric
Lesson 1: Exploring Trigonometric Ratios Common Core Georgia Performance Standards MCC9 12.G.SRT.6 MCC9 12.G.SRT.7 Essential Questions 1. How are the properties of similar triangles used to create trigonometric
2006 Geometry Form A Page 1
 2006 Geometry Form Page 1 1. he hypotenuse of a right triangle is 12" long, and one of the acute angles measures 30 degrees. he length of the shorter leg must be: () 4 3 inches () 6 3 inches () 5 inches
2006 Geometry Form Page 1 1. he hypotenuse of a right triangle is 12" long, and one of the acute angles measures 30 degrees. he length of the shorter leg must be: () 4 3 inches () 6 3 inches () 5 inches
Warm-Up y. What type of triangle is formed by the points A(4,2), B(6, 1), and C( 1, 3)? A. right B. equilateral C. isosceles D.
 CST/CAHSEE: Warm-Up Review: Grade What tpe of triangle is formed b the points A(4,), B(6, 1), and C( 1, 3)? A. right B. equilateral C. isosceles D. scalene Find the distance between the points (, 5) and
CST/CAHSEE: Warm-Up Review: Grade What tpe of triangle is formed b the points A(4,), B(6, 1), and C( 1, 3)? A. right B. equilateral C. isosceles D. scalene Find the distance between the points (, 5) and
Solutions to old Exam 1 problems
 Solutions to old Exam 1 problems Hi students! I am putting this old version of my review for the first midterm review, place and time to be announced. Check for updates on the web site as to which sections
Solutions to old Exam 1 problems Hi students! I am putting this old version of my review for the first midterm review, place and time to be announced. Check for updates on the web site as to which sections
Solving Simultaneous Equations and Matrices
 Solving Simultaneous Equations and Matrices The following represents a systematic investigation for the steps used to solve two simultaneous linear equations in two unknowns. The motivation for considering
Solving Simultaneous Equations and Matrices The following represents a systematic investigation for the steps used to solve two simultaneous linear equations in two unknowns. The motivation for considering
13. Write the decimal approximation of 9,000,001 9,000,000, rounded to three significant
 æ If 3 + 4 = x, then x = 2 gold bar is a rectangular solid measuring 2 3 4 It is melted down, and three equal cubes are constructed from this gold What is the length of a side of each cube? 3 What is the
æ If 3 + 4 = x, then x = 2 gold bar is a rectangular solid measuring 2 3 4 It is melted down, and three equal cubes are constructed from this gold What is the length of a side of each cube? 3 What is the
Pythagorean Theorem: 9. x 2 2
 Geometry Chapter 8 - Right Triangles.7 Notes on Right s Given: any 3 sides of a Prove: the is acute, obtuse, or right (hint: use the converse of Pythagorean Theorem) If the (longest side) 2 > (side) 2
Geometry Chapter 8 - Right Triangles.7 Notes on Right s Given: any 3 sides of a Prove: the is acute, obtuse, or right (hint: use the converse of Pythagorean Theorem) If the (longest side) 2 > (side) 2
Right Triangles 4 A = 144 A = 16 12 5 A = 64
 Right Triangles If I looked at enough right triangles and experimented a little, I might eventually begin to notice a relationship developing if I were to construct squares formed by the legs of a right
Right Triangles If I looked at enough right triangles and experimented a little, I might eventually begin to notice a relationship developing if I were to construct squares formed by the legs of a right
MEMORANDUM. All students taking the CLC Math Placement Exam PLACEMENT INTO CALCULUS AND ANALYTIC GEOMETRY I, MTH 145:
 MEMORANDUM To: All students taking the CLC Math Placement Eam From: CLC Mathematics Department Subject: What to epect on the Placement Eam Date: April 0 Placement into MTH 45 Solutions This memo is an
MEMORANDUM To: All students taking the CLC Math Placement Eam From: CLC Mathematics Department Subject: What to epect on the Placement Eam Date: April 0 Placement into MTH 45 Solutions This memo is an
Number Sense and Operations
 Number Sense and Operations representing as they: 6.N.1 6.N.2 6.N.3 6.N.4 6.N.5 6.N.6 6.N.7 6.N.8 6.N.9 6.N.10 6.N.11 6.N.12 6.N.13. 6.N.14 6.N.15 Demonstrate an understanding of positive integer exponents
Number Sense and Operations representing as they: 6.N.1 6.N.2 6.N.3 6.N.4 6.N.5 6.N.6 6.N.7 6.N.8 6.N.9 6.N.10 6.N.11 6.N.12 6.N.13. 6.N.14 6.N.15 Demonstrate an understanding of positive integer exponents
CRLS Mathematics Department Algebra I Curriculum Map/Pacing Guide
 Curriculum Map/Pacing Guide page 1 of 14 Quarter I start (CP & HN) 170 96 Unit 1: Number Sense and Operations 24 11 Totals Always Include 2 blocks for Review & Test Operating with Real Numbers: How are
Curriculum Map/Pacing Guide page 1 of 14 Quarter I start (CP & HN) 170 96 Unit 1: Number Sense and Operations 24 11 Totals Always Include 2 blocks for Review & Test Operating with Real Numbers: How are
Introduction Assignment
 PRE-CALCULUS 11 Introduction Assignment Welcome to PREC 11! This assignment will help you review some topics from a previous math course and introduce you to some of the topics that you ll be studying
PRE-CALCULUS 11 Introduction Assignment Welcome to PREC 11! This assignment will help you review some topics from a previous math course and introduce you to some of the topics that you ll be studying
Difference between a vector and a scalar quantity. N or 90 o. S or 270 o
 Vectors Vectors and Scalars Distinguish between vector and scalar quantities, and give examples of each. method. A vector is represented in print by a bold italicized symbol, for example, F. A vector has
Vectors Vectors and Scalars Distinguish between vector and scalar quantities, and give examples of each. method. A vector is represented in print by a bold italicized symbol, for example, F. A vector has
DETERMINING SOLAR ALTITUDE USING THE GNOMON. How does the altitude change during the day or from day to day?
 Name Partner(s) Section Date DETERMINING SOLAR ALTITUDE USING THE GNOMON Does the Sun ever occur directly overhead in Maryland? If it does, how would you determine or know it was directly overhead? How
Name Partner(s) Section Date DETERMINING SOLAR ALTITUDE USING THE GNOMON Does the Sun ever occur directly overhead in Maryland? If it does, how would you determine or know it was directly overhead? How
2312 test 2 Fall 2010 Form B
 2312 test 2 Fall 2010 Form B 1. Write the slope-intercept form of the equation of the line through the given point perpendicular to the given lin point: ( 7, 8) line: 9x 45y = 9 2. Evaluate the function
2312 test 2 Fall 2010 Form B 1. Write the slope-intercept form of the equation of the line through the given point perpendicular to the given lin point: ( 7, 8) line: 9x 45y = 9 2. Evaluate the function
How To Solve The Pythagorean Triangle
 Name Period CHAPTER 9 Right Triangles and Trigonometry Section 9.1 Similar right Triangles Objectives: Solve problems involving similar right triangles. Use a geometric mean to solve problems. Ex. 1 Use
Name Period CHAPTER 9 Right Triangles and Trigonometry Section 9.1 Similar right Triangles Objectives: Solve problems involving similar right triangles. Use a geometric mean to solve problems. Ex. 1 Use
Semester 2, Unit 4: Activity 21
 Resources: SpringBoard- PreCalculus Online Resources: PreCalculus Springboard Text Unit 4 Vocabulary: Identity Pythagorean Identity Trigonometric Identity Cofunction Identity Sum and Difference Identities
Resources: SpringBoard- PreCalculus Online Resources: PreCalculus Springboard Text Unit 4 Vocabulary: Identity Pythagorean Identity Trigonometric Identity Cofunction Identity Sum and Difference Identities
Introduction and Mathematical Concepts
 CHAPTER 1 Introduction and Mathematical Concepts PREVIEW In this chapter you will be introduced to the physical units most frequently encountered in physics. After completion of the chapter you will be
CHAPTER 1 Introduction and Mathematical Concepts PREVIEW In this chapter you will be introduced to the physical units most frequently encountered in physics. After completion of the chapter you will be
Trigonometry. An easy way to remember trigonometric properties is:
 Trigonometry It is possible to solve many force and velocity problems by drawing vector diagrams. However, the degree of accuracy is dependent upon the exactness of the person doing the drawing and measuring.
Trigonometry It is possible to solve many force and velocity problems by drawing vector diagrams. However, the degree of accuracy is dependent upon the exactness of the person doing the drawing and measuring.
Final Review Geometry A Fall Semester
 Final Review Geometry Fall Semester Multiple Response Identify one or more choices that best complete the statement or answer the question. 1. Which graph shows a triangle and its reflection image over
Final Review Geometry Fall Semester Multiple Response Identify one or more choices that best complete the statement or answer the question. 1. Which graph shows a triangle and its reflection image over
D.3. Angles and Degree Measure. Review of Trigonometric Functions
 APPENDIX D Precalculus Review D7 SECTION D. Review of Trigonometric Functions Angles and Degree Measure Radian Measure The Trigonometric Functions Evaluating Trigonometric Functions Solving Trigonometric
APPENDIX D Precalculus Review D7 SECTION D. Review of Trigonometric Functions Angles and Degree Measure Radian Measure The Trigonometric Functions Evaluating Trigonometric Functions Solving Trigonometric
TRIGONOMETRY Compound & Double angle formulae
 TRIGONOMETRY Compound & Double angle formulae In order to master this section you must first learn the formulae, even though they will be given to you on the matric formula sheet. We call these formulae
TRIGONOMETRY Compound & Double angle formulae In order to master this section you must first learn the formulae, even though they will be given to you on the matric formula sheet. We call these formulae
Algebra II A Final Exam
 Algebra II A Final Exam Multiple Choice Identify the choice that best completes the statement or answers the question. Evaluate the expression for the given value of the variable(s). 1. ; x = 4 a. 34 b.
Algebra II A Final Exam Multiple Choice Identify the choice that best completes the statement or answers the question. Evaluate the expression for the given value of the variable(s). 1. ; x = 4 a. 34 b.
Physics 2048 Test 1 Solution (solutions to problems 2-5 are from student papers) Problem 1 (Short Answer: 20 points)
 Physics 248 Test 1 Solution (solutions to problems 25 are from student papers) Problem 1 (Short Answer: 2 points) An object's motion is restricted to one dimension along the distance axis. Answer each
Physics 248 Test 1 Solution (solutions to problems 25 are from student papers) Problem 1 (Short Answer: 2 points) An object's motion is restricted to one dimension along the distance axis. Answer each
Algebra 1 2008. Academic Content Standards Grade Eight and Grade Nine Ohio. Grade Eight. Number, Number Sense and Operations Standard
 Academic Content Standards Grade Eight and Grade Nine Ohio Algebra 1 2008 Grade Eight STANDARDS Number, Number Sense and Operations Standard Number and Number Systems 1. Use scientific notation to express
Academic Content Standards Grade Eight and Grade Nine Ohio Algebra 1 2008 Grade Eight STANDARDS Number, Number Sense and Operations Standard Number and Number Systems 1. Use scientific notation to express
Session 5 Indirect Measurement and Trigonometry
 Session 5 Indirect Measurement and Trigonometry Key Terms in This Session Previously Introduced ratio scale factor New in This Session proportion similar triangles tangent Introduction How do people determine
Session 5 Indirect Measurement and Trigonometry Key Terms in This Session Previously Introduced ratio scale factor New in This Session proportion similar triangles tangent Introduction How do people determine
13.4 THE CROSS PRODUCT
 710 Chapter Thirteen A FUNDAMENTAL TOOL: VECTORS 62. Use the following steps and the results of Problems 59 60 to show (without trigonometry) that the geometric and algebraic definitions of the dot product
710 Chapter Thirteen A FUNDAMENTAL TOOL: VECTORS 62. Use the following steps and the results of Problems 59 60 to show (without trigonometry) that the geometric and algebraic definitions of the dot product
2009 Chicago Area All-Star Math Team Tryouts Solutions
 1. 2009 Chicago Area All-Star Math Team Tryouts Solutions If a car sells for q 1000 and the salesman earns q% = q/100, he earns 10q 2. He earns an additional 100 per car, and he sells p cars, so his total
1. 2009 Chicago Area All-Star Math Team Tryouts Solutions If a car sells for q 1000 and the salesman earns q% = q/100, he earns 10q 2. He earns an additional 100 per car, and he sells p cars, so his total
The Triangle and its Properties
 THE TRINGLE ND ITS PROPERTIES 113 The Triangle and its Properties Chapter 6 6.1 INTRODUCTION triangle, you have seen, is a simple closed curve made of three line segments. It has three vertices, three
THE TRINGLE ND ITS PROPERTIES 113 The Triangle and its Properties Chapter 6 6.1 INTRODUCTION triangle, you have seen, is a simple closed curve made of three line segments. It has three vertices, three
4. How many integers between 2004 and 4002 are perfect squares?
 5 is 0% of what number? What is the value of + 3 4 + 99 00? (alternating signs) 3 A frog is at the bottom of a well 0 feet deep It climbs up 3 feet every day, but slides back feet each night If it started
5 is 0% of what number? What is the value of + 3 4 + 99 00? (alternating signs) 3 A frog is at the bottom of a well 0 feet deep It climbs up 3 feet every day, but slides back feet each night If it started
Geometry Module 4 Unit 2 Practice Exam
 Name: Class: Date: ID: A Geometry Module 4 Unit 2 Practice Exam Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Which diagram shows the most useful positioning
Name: Class: Date: ID: A Geometry Module 4 Unit 2 Practice Exam Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Which diagram shows the most useful positioning
POINT OF INTERSECTION OF TWO STRAIGHT LINES
 POINT OF INTERSECTION OF TWO STRAIGHT LINES THEOREM The point of intersection of the two non parallel lines bc bc ca ca a x + b y + c = 0, a x + b y + c = 0 is,. ab ab ab ab Proof: The lines are not parallel
POINT OF INTERSECTION OF TWO STRAIGHT LINES THEOREM The point of intersection of the two non parallel lines bc bc ca ca a x + b y + c = 0, a x + b y + c = 0 is,. ab ab ab ab Proof: The lines are not parallel
9 Right Triangle Trigonometry
 www.ck12.org CHAPTER 9 Right Triangle Trigonometry Chapter Outline 9.1 THE PYTHAGOREAN THEOREM 9.2 CONVERSE OF THE PYTHAGOREAN THEOREM 9.3 USING SIMILAR RIGHT TRIANGLES 9.4 SPECIAL RIGHT TRIANGLES 9.5
www.ck12.org CHAPTER 9 Right Triangle Trigonometry Chapter Outline 9.1 THE PYTHAGOREAN THEOREM 9.2 CONVERSE OF THE PYTHAGOREAN THEOREM 9.3 USING SIMILAR RIGHT TRIANGLES 9.4 SPECIAL RIGHT TRIANGLES 9.5
cos Newington College HSC Mathematics Ext 1 Trial Examination 2011 QUESTION ONE (12 Marks) (b) Find the exact value of if. 2 . 3
 1 QUESTION ONE (12 Marks) Marks (a) Find tan x e 1 2 cos dx x (b) Find the exact value of if. 2 (c) Solve 5 3 2x 1. 3 (d) If are the roots of the equation 2 find the value of. (e) Use the substitution
1 QUESTION ONE (12 Marks) Marks (a) Find tan x e 1 2 cos dx x (b) Find the exact value of if. 2 (c) Solve 5 3 2x 1. 3 (d) If are the roots of the equation 2 find the value of. (e) Use the substitution
L 2 : x = s + 1, y = s, z = 4s + 4. 3. Suppose that C has coordinates (x, y, z). Then from the vector equality AC = BD, one has
 The line L through the points A and B is parallel to the vector AB = 3, 2, and has parametric equations x = 3t + 2, y = 2t +, z = t Therefore, the intersection point of the line with the plane should satisfy:
The line L through the points A and B is parallel to the vector AB = 3, 2, and has parametric equations x = 3t + 2, y = 2t +, z = t Therefore, the intersection point of the line with the plane should satisfy:
Physics 590 Homework, Week 6 Week 6, Homework 1
 Physics 590 Homework, Week 6 Week 6, Homework 1 Prob. 6.1.1 A descent vehicle landing on the moon has a vertical velocity toward the surface of the moon of 35 m/s. At the same time it has a horizontal
Physics 590 Homework, Week 6 Week 6, Homework 1 Prob. 6.1.1 A descent vehicle landing on the moon has a vertical velocity toward the surface of the moon of 35 m/s. At the same time it has a horizontal
3.1. Angle Pairs. What s Your Angle? Angle Pairs. ACTIVITY 3.1 Investigative. Activity Focus Measuring angles Angle pairs
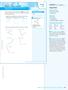 SUGGESTED LEARNING STRATEGIES: Think/Pair/Share, Use Manipulatives Two rays with a common endpoint form an angle. The common endpoint is called the vertex. You can use a protractor to draw and measure
SUGGESTED LEARNING STRATEGIES: Think/Pair/Share, Use Manipulatives Two rays with a common endpoint form an angle. The common endpoint is called the vertex. You can use a protractor to draw and measure
CHAPTER 7 TRAVERSE Section I. SELECTION OF TRAVERSE DEFINITION
 CHAPTER 7 TRAVERSE Section I. SELECTION OF TRAVERSE DEFINITION A traverse is a series of straight lines called traverse legs. The surveyor uses them to connect a series of selected points called traverse
CHAPTER 7 TRAVERSE Section I. SELECTION OF TRAVERSE DEFINITION A traverse is a series of straight lines called traverse legs. The surveyor uses them to connect a series of selected points called traverse
Chapter 5 Resource Masters
 Chapter Resource Masters New York, New York Columbus, Ohio Woodland Hills, California Peoria, Illinois StudentWorks TM This CD-ROM includes the entire Student Edition along with the Study Guide, Practice,
Chapter Resource Masters New York, New York Columbus, Ohio Woodland Hills, California Peoria, Illinois StudentWorks TM This CD-ROM includes the entire Student Edition along with the Study Guide, Practice,
Duplicating Segments and Angles
 CONDENSED LESSON 3.1 Duplicating Segments and ngles In this lesson, you Learn what it means to create a geometric construction Duplicate a segment by using a straightedge and a compass and by using patty
CONDENSED LESSON 3.1 Duplicating Segments and ngles In this lesson, you Learn what it means to create a geometric construction Duplicate a segment by using a straightedge and a compass and by using patty
Higher Education Math Placement
 Higher Education Math Placement Placement Assessment Problem Types 1. Whole Numbers, Fractions, and Decimals 1.1 Operations with Whole Numbers Addition with carry Subtraction with borrowing Multiplication
Higher Education Math Placement Placement Assessment Problem Types 1. Whole Numbers, Fractions, and Decimals 1.1 Operations with Whole Numbers Addition with carry Subtraction with borrowing Multiplication
39 Symmetry of Plane Figures
 39 Symmetry of Plane Figures In this section, we are interested in the symmetric properties of plane figures. By a symmetry of a plane figure we mean a motion of the plane that moves the figure so that
39 Symmetry of Plane Figures In this section, we are interested in the symmetric properties of plane figures. By a symmetry of a plane figure we mean a motion of the plane that moves the figure so that
GeoGebra. 10 lessons. Gerrit Stols
 GeoGebra in 10 lessons Gerrit Stols Acknowledgements GeoGebra is dynamic mathematics open source (free) software for learning and teaching mathematics in schools. It was developed by Markus Hohenwarter
GeoGebra in 10 lessons Gerrit Stols Acknowledgements GeoGebra is dynamic mathematics open source (free) software for learning and teaching mathematics in schools. It was developed by Markus Hohenwarter
This is a tentative schedule, date may change. Please be sure to write down homework assignments daily.
 Mon Tue Wed Thu Fri Aug 26 Aug 27 Aug 28 Aug 29 Aug 30 Introductions, Expectations, Course Outline and Carnegie Review summer packet Topic: (1-1) Points, Lines, & Planes Topic: (1-2) Segment Measure Quiz
Mon Tue Wed Thu Fri Aug 26 Aug 27 Aug 28 Aug 29 Aug 30 Introductions, Expectations, Course Outline and Carnegie Review summer packet Topic: (1-1) Points, Lines, & Planes Topic: (1-2) Segment Measure Quiz
MODERN APPLICATIONS OF PYTHAGORAS S THEOREM
 UNIT SIX MODERN APPLICATIONS OF PYTHAGORAS S THEOREM Coordinate Systems 124 Distance Formula 127 Midpoint Formula 131 SUMMARY 134 Exercises 135 UNIT SIX: 124 COORDINATE GEOMETRY Geometry, as presented
UNIT SIX MODERN APPLICATIONS OF PYTHAGORAS S THEOREM Coordinate Systems 124 Distance Formula 127 Midpoint Formula 131 SUMMARY 134 Exercises 135 UNIT SIX: 124 COORDINATE GEOMETRY Geometry, as presented
Tangent Properties. Line m is a tangent to circle O. Point T is the point of tangency.
 CONDENSED LESSON 6.1 Tangent Properties In this lesson you will Review terms associated with circles Discover how a tangent to a circle and the radius to the point of tangency are related Make a conjecture
CONDENSED LESSON 6.1 Tangent Properties In this lesson you will Review terms associated with circles Discover how a tangent to a circle and the radius to the point of tangency are related Make a conjecture
ACTIVITY: Finding a Formula Experimentally. Work with a partner. Use a paper cup that is shaped like a cone.
 8. Volumes of Cones How can you find the volume of a cone? You already know how the volume of a pyramid relates to the volume of a prism. In this activity, you will discover how the volume of a cone relates
8. Volumes of Cones How can you find the volume of a cone? You already know how the volume of a pyramid relates to the volume of a prism. In this activity, you will discover how the volume of a cone relates
Copyright 2011 Casa Software Ltd. www.casaxps.com. Centre of Mass
 Centre of Mass A central theme in mathematical modelling is that of reducing complex problems to simpler, and hopefully, equivalent problems for which mathematical analysis is possible. The concept of
Centre of Mass A central theme in mathematical modelling is that of reducing complex problems to simpler, and hopefully, equivalent problems for which mathematical analysis is possible. The concept of
Transformations Worksheet. How many units and in which direction were the x-coordinates of parallelogram ABCD moved? C. D.
 Name: ate: 1. Parallelogram ABC was translated to parallelogram A B C. 2. A shape is shown below. Which shows this shape transformed by a flip? A. B. How many units and in which direction were the x-coordinates
Name: ate: 1. Parallelogram ABC was translated to parallelogram A B C. 2. A shape is shown below. Which shows this shape transformed by a flip? A. B. How many units and in which direction were the x-coordinates
5.1 Midsegment Theorem and Coordinate Proof
 5.1 Midsegment Theorem and Coordinate Proof Obj.: Use properties of midsegments and write coordinate proofs. Key Vocabulary Midsegment of a triangle - A midsegment of a triangle is a segment that connects
5.1 Midsegment Theorem and Coordinate Proof Obj.: Use properties of midsegments and write coordinate proofs. Key Vocabulary Midsegment of a triangle - A midsegment of a triangle is a segment that connects
Name: Class: Date: Multiple Choice Identify the choice that best completes the statement or answers the question.
 Name: Class: Date: ID: A Q3 Geometry Review Multiple Choice Identify the choice that best completes the statement or answers the question. Graph the image of each figure under a translation by the given
Name: Class: Date: ID: A Q3 Geometry Review Multiple Choice Identify the choice that best completes the statement or answers the question. Graph the image of each figure under a translation by the given
Section V.2: Magnitudes, Directions, and Components of Vectors
 Section V.: Magnitudes, Directions, and Components of Vectors Vectors in the plane If we graph a vector in the coordinate plane instead of just a grid, there are a few things to note. Firstl, directions
Section V.: Magnitudes, Directions, and Components of Vectors Vectors in the plane If we graph a vector in the coordinate plane instead of just a grid, there are a few things to note. Firstl, directions
Pre-Algebra 2008. Academic Content Standards Grade Eight Ohio. Number, Number Sense and Operations Standard. Number and Number Systems
 Academic Content Standards Grade Eight Ohio Pre-Algebra 2008 STANDARDS Number, Number Sense and Operations Standard Number and Number Systems 1. Use scientific notation to express large numbers and small
Academic Content Standards Grade Eight Ohio Pre-Algebra 2008 STANDARDS Number, Number Sense and Operations Standard Number and Number Systems 1. Use scientific notation to express large numbers and small
Version 005 Exam Review Practice Problems NOT FOR A GRADE alexander (55715) 1. Hence
 Version 005 Eam Review Practice Problems NOT FOR A GRADE aleander 5575 This print-out should have 47 questions Multiple-choice questions may continue on the net column or page find all choices before answering
Version 005 Eam Review Practice Problems NOT FOR A GRADE aleander 5575 This print-out should have 47 questions Multiple-choice questions may continue on the net column or page find all choices before answering
Definitions, Postulates and Theorems
 Definitions, s and s Name: Definitions Complementary Angles Two angles whose measures have a sum of 90 o Supplementary Angles Two angles whose measures have a sum of 180 o A statement that can be proven
Definitions, s and s Name: Definitions Complementary Angles Two angles whose measures have a sum of 90 o Supplementary Angles Two angles whose measures have a sum of 180 o A statement that can be proven
1.1 Practice Worksheet
 Math 1 MPS Instructor: Cheryl Jaeger Balm 1 1.1 Practice Worksheet 1. Write each English phrase as a mathematical expression. (a) Three less than twice a number (b) Four more than half of a number (c)
Math 1 MPS Instructor: Cheryl Jaeger Balm 1 1.1 Practice Worksheet 1. Write each English phrase as a mathematical expression. (a) Three less than twice a number (b) Four more than half of a number (c)
Circle Name: Radius: Diameter: Chord: Secant:
 12.1: Tangent Lines Congruent Circles: circles that have the same radius length Diagram of Examples Center of Circle: Circle Name: Radius: Diameter: Chord: Secant: Tangent to A Circle: a line in the plane
12.1: Tangent Lines Congruent Circles: circles that have the same radius length Diagram of Examples Center of Circle: Circle Name: Radius: Diameter: Chord: Secant: Tangent to A Circle: a line in the plane
Section 6-3 Double-Angle and Half-Angle Identities
 6-3 Double-Angle and Half-Angle Identities 47 Section 6-3 Double-Angle and Half-Angle Identities Double-Angle Identities Half-Angle Identities This section develops another important set of identities
6-3 Double-Angle and Half-Angle Identities 47 Section 6-3 Double-Angle and Half-Angle Identities Double-Angle Identities Half-Angle Identities This section develops another important set of identities
Find the length of the arc on a circle of radius r intercepted by a central angle θ. Round to two decimal places.
 SECTION.1 Simplify. 1. 7π π. 5π 6 + π Find the measure of the angle in degrees between the hour hand and the minute hand of a clock at the time shown. Measure the angle in the clockwise direction.. 1:0.
SECTION.1 Simplify. 1. 7π π. 5π 6 + π Find the measure of the angle in degrees between the hour hand and the minute hand of a clock at the time shown. Measure the angle in the clockwise direction.. 1:0.
Circle Theorems. This circle shown is described an OT. As always, when we introduce a new topic we have to define the things we wish to talk about.
 Circle s circle is a set of points in a plane that are a given distance from a given point, called the center. The center is often used to name the circle. T This circle shown is described an OT. s always,
Circle s circle is a set of points in a plane that are a given distance from a given point, called the center. The center is often used to name the circle. T This circle shown is described an OT. s always,
Ratios and Proportional Relationships Set 1: Ratio, Proportion, and Scale... 1 Set 2: Proportional Relationships... 8
 Table of Contents Introduction...v Standards Correlations... viii Materials List... x... 1 Set 2: Proportional Relationships... 8 The Number System Set 1: Integers and Absolute Value... 15 Set 2: Comparing
Table of Contents Introduction...v Standards Correlations... viii Materials List... x... 1 Set 2: Proportional Relationships... 8 The Number System Set 1: Integers and Absolute Value... 15 Set 2: Comparing
Review of Intermediate Algebra Content
 Review of Intermediate Algebra Content Table of Contents Page Factoring GCF and Trinomials of the Form + b + c... Factoring Trinomials of the Form a + b + c... Factoring Perfect Square Trinomials... 6
Review of Intermediate Algebra Content Table of Contents Page Factoring GCF and Trinomials of the Form + b + c... Factoring Trinomials of the Form a + b + c... Factoring Perfect Square Trinomials... 6
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION INTEGRATED ALGEBRA. Thursday, August 16, 2012 8:30 to 11:30 a.m.
 INTEGRATED ALGEBRA The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION INTEGRATED ALGEBRA Thursday, August 16, 2012 8:30 to 11:30 a.m., only Student Name: School Name: Print your name
INTEGRATED ALGEBRA The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION INTEGRATED ALGEBRA Thursday, August 16, 2012 8:30 to 11:30 a.m., only Student Name: School Name: Print your name
Lesson 2: Circles, Chords, Diameters, and Their Relationships
 Circles, Chords, Diameters, and Their Relationships Student Outcomes Identify the relationships between the diameters of a circle and other chords of the circle. Lesson Notes Students are asked to construct
Circles, Chords, Diameters, and Their Relationships Student Outcomes Identify the relationships between the diameters of a circle and other chords of the circle. Lesson Notes Students are asked to construct
Integers (pages 294 298)
 A Integers (pages 294 298) An integer is any number from this set of the whole numbers and their opposites: { 3, 2,, 0,, 2, 3, }. Integers that are greater than zero are positive integers. You can write
A Integers (pages 294 298) An integer is any number from this set of the whole numbers and their opposites: { 3, 2,, 0,, 2, 3, }. Integers that are greater than zero are positive integers. You can write
Anamorphic Projection Photographic Techniques for setting up 3D Chalk Paintings
 Anamorphic Projection Photographic Techniques for setting up 3D Chalk Paintings By Wayne and Cheryl Renshaw. Although it is centuries old, the art of street painting has been going through a resurgence.
Anamorphic Projection Photographic Techniques for setting up 3D Chalk Paintings By Wayne and Cheryl Renshaw. Although it is centuries old, the art of street painting has been going through a resurgence.
Name Date Class. Lines and Segments That Intersect Circles. AB and CD are chords. Tangent Circles. Theorem Hypothesis Conclusion
 Section. Lines That Intersect Circles Lines and Segments That Intersect Circles A chord is a segment whose endpoints lie on a circle. A secant is a line that intersects a circle at two points. A tangent
Section. Lines That Intersect Circles Lines and Segments That Intersect Circles A chord is a segment whose endpoints lie on a circle. A secant is a line that intersects a circle at two points. A tangent
Solving Equations Involving Parallel and Perpendicular Lines Examples
 Solving Equations Involving Parallel and Perpendicular Lines Examples. The graphs of y = x, y = x, and y = x + are lines that have the same slope. They are parallel lines. Definition of Parallel Lines
Solving Equations Involving Parallel and Perpendicular Lines Examples. The graphs of y = x, y = x, and y = x + are lines that have the same slope. They are parallel lines. Definition of Parallel Lines
Technical Note T -5 Elementary Mathematics of Model Rocket Flight
 Technical Note T -5 Elementary Mathematics of Model Rocket Flight By Robert L. Cannon Updated and edited by Ann Grimm EstesEducator.com educator@estesrockets.com 800.80.00 01 Estes-Cox Corp. This publication
Technical Note T -5 Elementary Mathematics of Model Rocket Flight By Robert L. Cannon Updated and edited by Ann Grimm EstesEducator.com educator@estesrockets.com 800.80.00 01 Estes-Cox Corp. This publication
Geometry Notes PERIMETER AND AREA
 Perimeter and Area Page 1 of 57 PERIMETER AND AREA Objectives: After completing this section, you should be able to do the following: Calculate the area of given geometric figures. Calculate the perimeter
Perimeter and Area Page 1 of 57 PERIMETER AND AREA Objectives: After completing this section, you should be able to do the following: Calculate the area of given geometric figures. Calculate the perimeter
Lesson 26: Reflection & Mirror Diagrams
 Lesson 26: Reflection & Mirror Diagrams The Law of Reflection There is nothing really mysterious about reflection, but some people try to make it more difficult than it really is. All EMR will reflect
Lesson 26: Reflection & Mirror Diagrams The Law of Reflection There is nothing really mysterious about reflection, but some people try to make it more difficult than it really is. All EMR will reflect
