17: Transmission Lines
|
|
|
- Austin Barber
- 10 years ago
- Views:
Transcription
1 s Line E1.1 Analysis of Circits ( ) Transmission Lines: 17 1 / 13
2 Transmission Lines s Line Previosly assme that any change inv S (t) appears instantly atv R (t). E1.1 Analysis of Circits ( ) Transmission Lines: 17 2 / 13
3 Transmission Lines s Line Previosly assme that any change inv S (t) appears instantly atv R (t). This is not tre. E1.1 Analysis of Circits ( ) Transmission Lines: 17 2 / 13
4 Transmission Lines s Line Previosly assme that any change inv S (t) appears instantly atv R (t). This is not tre. If fact signals travel at arond half the speed of light (c = 30 cm/ns). E1.1 Analysis of Circits ( ) Transmission Lines: 17 2 / 13
5 Transmission Lines s Line Previosly assme that any change inv S (t) appears instantly atv R (t). This is not tre. If fact signals travel at arond half the speed of light (c = 30 cm/ns). Reason: all wires have capacitance to grond and to neighboring condctors and also self-indctance. It takes time to change the crrent throgh an indctor or voltage across a capacitor. E1.1 Analysis of Circits ( ) Transmission Lines: 17 2 / 13
6 Transmission Lines s Line Previosly assme that any change inv S (t) appears instantly atv R (t). This is not tre. If fact signals travel at arond half the speed of light (c = 30 cm/ns). Reason: all wires have capacitance to grond and to neighboring condctors and also self-indctance. It takes time to change the crrent throgh an indctor or voltage across a capacitor. A transmission line is a wire with a niform goemetry along its length: the capacitance and indctance of any segment is proportional to its length. E1.1 Analysis of Circits ( ) Transmission Lines: 17 2 / 13
7 Transmission Lines s Line Previosly assme that any change inv S (t) appears instantly atv R (t). This is not tre. If fact signals travel at arond half the speed of light (c = 30 cm/ns). Reason: all wires have capacitance to grond and to neighboring condctors and also self-indctance. It takes time to change the crrent throgh an indctor or voltage across a capacitor. A transmission line is a wire with a niform goemetry along its length: the capacitance and indctance of any segment is proportional to its length. We represent as a large nmber of small indctors and capacitors spaced along the line. E1.1 Analysis of Circits ( ) Transmission Lines: 17 2 / 13
8 Transmission Lines s Line Previosly assme that any change inv S (t) appears instantly atv R (t). This is not tre. If fact signals travel at arond half the speed of light (c = 30 cm/ns). Reason: all wires have capacitance to grond and to neighboring condctors and also self-indctance. It takes time to change the crrent throgh an indctor or voltage across a capacitor. A transmission line is a wire with a niform goemetry along its length: the capacitance and indctance of any segment is proportional to its length. We represent as a large nmber of small indctors and capacitors spaced along the line. The signal speed along a transmisison line is predictable. E1.1 Analysis of Circits ( ) Transmission Lines: 17 2 / 13
9 Transmission Line s Line Short section of lineδx long. v(x,t) andi(x,t) depend on both position and time. E1.1 Analysis of Circits ( ) Transmission Lines: 17 3 / 13
10 Transmission Line s Line Short section of lineδx long. v(x,t) andi(x,t) depend on both position and time. Small δx ignore 2nd order derivatives: v(x,t) t = v(x+δx,t) t = v t. E1.1 Analysis of Circits ( ) Transmission Lines: 17 3 / 13
11 Transmission Line s Line Short section of lineδx long. v(x,t) andi(x,t) depend on both position and time. Small δx ignore 2nd order derivatives: v(x,t) t = v(x+δx,t) t Capacitor eqation: C v t = v t. = i(x,t) i(x+δx,t) = i x δx E1.1 Analysis of Circits ( ) Transmission Lines: 17 3 / 13
12 Transmission Line s Line Short section of lineδx long. v(x,t) andi(x,t) depend on both position and time. Small δx ignore 2nd order derivatives: v(x,t) t = v(x+δx,t) t Capacitor eqation: C v t Indctor eqation: L i t = v t. i = i(x,t) i(x+δx,t) = = v(x,t) v(x+δx,t) = v x δx x δx E1.1 Analysis of Circits ( ) Transmission Lines: 17 3 / 13
13 Transmission Line s Line Short section of lineδx long. v(x,t) andi(x,t) depend on both position and time. Small δx ignore 2nd order derivatives: v(x,t) t = v(x+δx,t) t Capacitor eqation: C v t Indctor eqation: L i t Transmission Line = v t. i = i(x,t) i(x+δx,t) = = v(x,t) v(x+δx,t) = v x δx x δx SbstitteC 0 = C δx andl 0 = L δx wherec 0 andl 0 are capacitance and indctance per nit length. E1.1 Analysis of Circits ( ) Transmission Lines: 17 3 / 13
14 Transmission Line s Line Short section of lineδx long. v(x,t) andi(x,t) depend on both position and time. Small δx ignore 2nd order derivatives: v(x,t) t = v(x+δx,t) t Capacitor eqation: C v t Indctor eqation: L i t Transmission Line SbstitteC 0 = C δx andl 0 = L δx wherec 0 andl 0 are capacitance and indctance per nit length. = v t. i = i(x,t) i(x+δx,t) = = v(x,t) v(x+δx,t) = v x δx x δx v C 0 t = i x i L 0 t = v x E1.1 Analysis of Circits ( ) Transmission Lines: 17 3 / 13
15 Transmission Line s Line Short section of lineδx long. v(x,t) andi(x,t) depend on both position and time. Small δx ignore 2nd order derivatives: v(x,t) t = v(x+δx,t) t Capacitor eqation: C v t Indctor eqation: L i t Transmission Line SbstitteC 0 = C δx andl 0 = L δx wherec 0 andl 0 are capacitance and indctance per nit length. = v t. i = i(x,t) i(x+δx,t) = = v(x,t) v(x+δx,t) = v x δx x δx v C 0 t = i x i L 0 t = v x General soltion to two simltaneos partial differential eqations will inclde two arbitrary fnctions (instead of the arbitrary constants that yo get with ordinary differential eqations). E1.1 Analysis of Circits ( ) Transmission Lines: 17 3 / 13
16 Soltion to Transmission Line s Line Transmission Line : C 0 v t = i x L 0 i t = v x E1.1 Analysis of Circits ( ) Transmission Lines: 17 4 / 13
17 Soltion to Transmission Line s Line Transmission Line : C 0 v t = i x General soltion: v(t,x) = f(t x )+g(t+ x ) i(t,x) = f(t x ) g(t+ x ) where = 1 L 0 C 0 and = L 0 i t = v x L 0 C 0. E1.1 Analysis of Circits ( ) Transmission Lines: 17 4 / 13
18 Soltion to Transmission Line s Line Transmission Line : C 0 v t = i x General soltion: v(t,x) = f(t x )+g(t+ x ) i(t,x) = f(t x ) g(t+ x ) where = 1 L 0 C 0 and = L 0 i t = v x L 0 C 0. is the propagation velocity and is the characteristic impedance. E1.1 Analysis of Circits ( ) Transmission Lines: 17 4 / 13
19 Soltion to Transmission Line s Line Transmission Line : C 0 v t = i x General soltion: v(t,x) = f(t x )+g(t+ x ) i(t,x) = f(t x ) g(t+ x ) where = 1 L 0 C 0 and = L 0 i t = v x L 0 C 0. is the propagation velocity and is the characteristic impedance. f() and g() can be any differentiable fnctions. E1.1 Analysis of Circits ( ) Transmission Lines: 17 4 / 13
20 Soltion to Transmission Line s Line Transmission Line : C 0 v t = i x General soltion: v(t,x) = f(t x )+g(t+ x ) i(t,x) = f(t x ) g(t+ x ) where = 1 L 0 C 0 and = L 0 i t = v x L 0 C 0. is the propagation velocity and is the characteristic impedance. f() and g() can be any differentiable fnctions. Verify by sbstittion: i x = ( f (t x ) g (t+ x ) 1 ) E1.1 Analysis of Circits ( ) Transmission Lines: 17 4 / 13
21 Soltion to Transmission Line s Line Transmission Line : C 0 v t = i x General soltion: v(t,x) = f(t x )+g(t+ x ) i(t,x) = f(t x ) g(t+ x ) where = 1 L 0 C 0 and = L 0 i t = v x L 0 C 0. is the propagation velocity and is the characteristic impedance. f() and g() can be any differentiable fnctions. Verify by sbstittion: i x = ( f (t x ) g (t+ x ) 1 ) = C 0 ( f (t x )+g (t+ x )) = C 0 v t E1.1 Analysis of Circits ( ) Transmission Lines: 17 4 / 13
22 Forward Wave s Line = 15 cm/ns E1.1 Analysis of Circits ( ) Transmission Lines: 17 5 / 13
23 Forward Wave s Line = 15 cm/ns Atx = 0 cm [ ], v S (t) = f(t 0 ) f(t-0/) E1.1 Analysis of Circits ( ) Transmission Lines: 17 5 / 13
24 Forward Wave s Line = 15 cm/ns Atx = 0 cm [ ], v S (t) = f(t 0 ) f(t-0/) f(t-45/) Atx = 45 cm [ ], v(45,t) = f(t 45 ) E1.1 Analysis of Circits ( ) Transmission Lines: 17 5 / 13
25 Forward Wave s Line = 15 cm/ns Atx = 0 cm [ ], v S (t) = f(t 0 ) f(t-0/) f(t-45/) Atx = 45 cm [ ], v(45,t) = f(t 45 ) f(t 45 ) is the same asf(t) bt delayed by 45 = 3 ns. E1.1 Analysis of Circits ( ) Transmission Lines: 17 5 / 13
26 Forward Wave s Line = 15 cm/ns Atx = 0 cm [ ], v S (t) = f(t 0 ) f(t-0/) f(t-45/) f(t-90/) Atx = 45 cm [ ], v(45,t) = f(t 45 ) f(t 45 ) is the same asf(t) bt delayed by 45 = 3 ns. Atx = 90 cm [ ],v R (t) = f(t 90 ); now delayed by6ns. E1.1 Analysis of Circits ( ) Transmission Lines: 17 5 / 13
27 Forward Wave s Line = 15 cm/ns Atx = 0 cm [ ], v S (t) = f(t 0 ) f(t-0/) f(t-45/) f(t-90/) Atx = 45 cm [ ], v(45,t) = f(t 45 ) f(t 45 ) is the same asf(t) bt delayed by 45 = 3 ns. Atx = 90 cm [ ],v R (t) = f(t 90 ); now delayed by6ns. Waveform at x = 0 completely determines the waveform everywhere else. E1.1 Analysis of Circits ( ) Transmission Lines: 17 5 / 13
28 Forward Wave s Line = 15 cm/ns Atx = 0 cm [ ], v S (t) = f(t 0 ) f(t-0/) f(t-45/) f(t-90/) Atx = 45 cm [ ], v(45,t) = f(t 45 ) f(t 45 ) is the same asf(t) bt delayed by 45 = 3 ns. Atx = 90 cm [ ],v R (t) = f(t 90 ); now delayed by6ns. Waveform at x = 0 completely determines the waveform everywhere else. Snapshot att 0 = 4ns: the waveform has jst arrived at the point t = 4 ns f(4-x/) x = t 0 = 60 cm. Position (cm) E1.1 Analysis of Circits ( ) Transmission Lines: 17 5 / 13
29 Forward Wave s Line = 15 cm/ns Atx = 0 cm [ ], v S (t) = f(t 0 ) f(t-0/) f(t-45/) f(t-90/) Atx = 45 cm [ ], v(45,t) = f(t 45 ) f(t 45 ) is the same asf(t) bt delayed by 45 = 3 ns. Atx = 90 cm [ ],v R (t) = f(t 90 ); now delayed by6ns. Waveform at x = 0 completely determines the waveform everywhere else. Snapshot att 0 = 4ns: the waveform has jst arrived at the point t = 4 ns f(4-x/) x = t 0 = 60 cm. Position (cm) E1.1 Analysis of Circits ( ) Transmission Lines: 17 5 / 13
30 Forward Wave s Line = 15 cm/ns Atx = 0 cm [ ], v S (t) = f(t 0 ) f(t-0/) f(t-45/) f(t-90/) Atx = 45 cm [ ], v(45,t) = f(t 45 ) f(t 45 ) is the same asf(t) bt delayed by 45 = 3 ns. Atx = 90 cm [ ],v R (t) = f(t 90 ); now delayed by6ns. Waveform at x = 0 completely determines the waveform everywhere else. Snapshot att 0 = 4ns: the waveform has jst arrived at the point t = 4 ns f(4-x/) x = t 0 = 60 cm. Position (cm) f(t x ) is a wave travelling forward (i.e. towards+x) along the line. E1.1 Analysis of Circits ( ) Transmission Lines: 17 5 / 13
31 Forward + Backward s Line Similarlyg(t+ x ) is a wave travelling backwards, i.e. in the x direction. E1.1 Analysis of Circits ( ) Transmission Lines: 17 6 / 13
32 Forward + Backward s Line Similarlyg(t+ x ) is a wave travelling backwards, i.e. in the x direction. v(x,t) = f(t x )+g(t+ x ) x=0 f(t-0/) g(t+0/) E1.1 Analysis of Circits ( ) Transmission Lines: 17 6 / 13
33 Forward + Backward s Line Similarlyg(t+ x ) is a wave travelling backwards, i.e. in the x direction. v(x,t) = f(t x )+g(t+ x ) x=0 f(t-0/) g(t+0/) Atx = 0 cm [ ], v S (t) = f(t)+g(t) E1.1 Analysis of Circits ( ) Transmission Lines: 17 6 / 13
34 Forward + Backward s Line Similarlyg(t+ x ) is a wave travelling backwards, i.e. in the x direction. v(x,t) = f(t x )+g(t+ x ) x=0 f(t-0/) g(t+90/) f(t-90/) g(t+0/) Atx = 0 cm [ ], x=90 v S (t) = f(t)+g(t) Atx = 90 cm [ ],g starts att = 1 andf starts att = 6. E1.1 Analysis of Circits ( ) Transmission Lines: 17 6 / 13
35 Forward + Backward s Line Similarlyg(t+ x ) is a wave travelling backwards, i.e. in the x direction. v(x,t) = f(t x )+g(t+ x ) x=0 f(t-0/) g(t+90/) f(t-45/)+g(t+45/) f(t-90/) g(t+0/) Atx = 0 cm [ ], x=90 v S (t) = f(t)+g(t) Atx = 45 cm [ ],g is only1ns behindf and they add together. Atx = 90 cm [ ],g starts att = 1 andf starts att = 6. x=45 E1.1 Analysis of Circits ( ) Transmission Lines: 17 6 / 13
36 Forward + Backward s Line Similarlyg(t+ x ) is a wave travelling backwards, i.e. in the x direction. v(x,t) = f(t x )+g(t+ x ) x=0 f(t-0/) g(t+90/) f(t-45/)+g(t+45/) f(t-90/) g(t+0/) Atx = 0 cm [ ], x=90 v S (t) = f(t)+g(t) Atx = 45 cm [ ],g is only1ns behindf and they add together. Atx = 90 cm [ ],g starts att = 1 andf starts att = 6. x=45 Snapshots: Att = 2 nsf andg have not f(2-x/)+g(2-x/) yet met t = 2 ns Position (cm) E1.1 Analysis of Circits ( ) Transmission Lines: 17 6 / 13
37 Forward + Backward s Line Similarlyg(t+ x ) is a wave travelling backwards, i.e. in the x direction. v(x,t) = f(t x )+g(t+ x ) x=0 x=45 f(t-0/) g(t+90/) f(t-45/)+g(t+45/) f(t-90/) g(t+0/) Atx = 0 cm [ ], x=90 v S (t) = f(t)+g(t) Atx = 45 cm [ ],g is only1ns behindf and they add together. Atx = 90 cm [ ],g starts att = 1 andf starts att = 6. Snapshots: Att = 2 nsf andg have not yet met. f(2-x/)+g(2-x/) t = 2 ns Position (cm) Byt = 5 ns,f andg have jst crossed. f(5-x/)+g(5-x/) t = 5 ns Position (cm) E1.1 Analysis of Circits ( ) Transmission Lines: 17 6 / 13
38 Forward + Backward s Line Similarlyg(t+ x ) is a wave travelling backwards, i.e. in the x direction. v(x,t) = f(t x )+g(t+ x ) x=0 x=45 f(t-0/) g(t+90/) f(t-45/)+g(t+45/) f(t-90/) g(t+0/) Atx = 0 cm [ ], x=90 v S (t) = f(t)+g(t) Atx = 45 cm [ ],g is only1ns behindf and they add together. Atx = 90 cm [ ],g starts att = 1 andf starts att = 6. Snapshots: Att = 2 nsf andg have not yet met. f(2-x/)+g(2-x/) t = 2 ns Position (cm) Byt = 5 ns,f andg have jst crossed. f(5-x/)+g(5-x/) t = 5 ns Position (cm) Magically, f and g pass throgh each other entirely naltered E1.1 Analysis of Circits ( ) Transmission Lines: 17 6 / 13
39 Power Flow s Line Definef x (t) = f ( t x ) andgx (t) = g ( t+ x ) to be the forward and backward waveforms at any point, x. E1.1 Analysis of Circits ( ) Transmission Lines: 17 7 / 13
40 Power Flow s Line Definef x (t) = f ( t x ) andgx (t) = g ( t+ x ) to be the forward and backward waveforms at any point, x. i is always measred in the +ve x direction. Then v x (t) = f x (t)+g x (t) and i x (t) = Z 1 0 (f x (t) g x (t)). E1.1 Analysis of Circits ( ) Transmission Lines: 17 7 / 13
41 Power Flow s Line Definef x (t) = f ( t x ) andgx (t) = g ( t+ x ) to be the forward and backward waveforms at any point, x. i is always measred in the +ve x direction. Then v x (t) = f x (t)+g x (t) and i x (t) = Z0 1 (f x (t) g x (t)). Note: Knowing the waveformf x (t) org x (t) at any positionx, tells yo it at all other positions: f y (t) = f x ( t y x ) andgy (t) = g x ( t+ y x ). E1.1 Analysis of Circits ( ) Transmission Lines: 17 7 / 13
42 Power Flow s Line Definef x (t) = f ( t x ) andgx (t) = g ( t+ x ) to be the forward and backward waveforms at any point, x. i is always measred in the +ve x direction. Then v x (t) = f x (t)+g x (t) and i x (t) = Z0 1 (f x (t) g x (t)). Note: Knowing the waveformf x (t) org x (t) at any positionx, tells yo it at all other positions: f y (t) = f x ( t y x Power Flow ) andgy (t) = g x ( t+ y x ). The power transferred into the shaded region across the bondary atxis P x (t) = v x (t)i x (t) E1.1 Analysis of Circits ( ) Transmission Lines: 17 7 / 13
43 Power Flow s Line Definef x (t) = f ( t x ) andgx (t) = g ( t+ x ) to be the forward and backward waveforms at any point, x. i is always measred in the +ve x direction. Then v x (t) = f x (t)+g x (t) and i x (t) = Z0 1 (f x (t) g x (t)). Note: Knowing the waveformf x (t) org x (t) at any positionx, tells yo it at all other positions: f y (t) = f x ( t y x Power Flow ) andgy (t) = g x ( t+ y x ). The power transferred into the shaded region across the bondary atxis P x (t) = v x (t)i x (t)= Z 1 0 (f x (t)+g x (t))(f x (t) g x (t)) E1.1 Analysis of Circits ( ) Transmission Lines: 17 7 / 13
44 Power Flow s Line Definef x (t) = f ( t x ) andgx (t) = g ( t+ x ) to be the forward and backward waveforms at any point, x. i is always measred in the +ve x direction. Then v x (t) = f x (t)+g x (t) and i x (t) = Z0 1 (f x (t) g x (t)). Note: Knowing the waveformf x (t) org x (t) at any positionx, tells yo it at all other positions: f y (t) = f x ( t y x Power Flow ) andgy (t) = g x ( t+ y x ). The power transferred into the shaded region across the bondary atxis P x (t) = v x (t)i x (t)= Z0 1 (f x (t)+g x (t))(f x (t) g x (t)) = f2 x (t) g2 x (t) E1.1 Analysis of Circits ( ) Transmission Lines: 17 7 / 13
45 Power Flow s Line Definef x (t) = f ( t x ) andgx (t) = g ( t+ x ) to be the forward and backward waveforms at any point, x. i is always measred in the +ve x direction. Then v x (t) = f x (t)+g x (t) and i x (t) = Z0 1 (f x (t) g x (t)). Note: Knowing the waveformf x (t) org x (t) at any positionx, tells yo it at all other positions: f y (t) = f x ( t y x Power Flow ) andgy (t) = g x ( t+ y x ). The power transferred into the shaded region across the bondary atxis P x (t) = v x (t)i x (t)= Z0 1 (f x (t)+g x (t))(f x (t) g x (t)) = f2 x (t) g2 x (t) f x carries power into shaded area andg x carries power ot independently. E1.1 Analysis of Circits ( ) Transmission Lines: 17 7 / 13
46 Power Flow s Line Definef x (t) = f ( t x ) andgx (t) = g ( t+ x ) to be the forward and backward waveforms at any point, x. i is always measred in the +ve x direction. Then v x (t) = f x (t)+g x (t) and i x (t) = Z0 1 (f x (t) g x (t)). Note: Knowing the waveformf x (t) org x (t) at any positionx, tells yo it at all other positions: f y (t) = f x ( t y x Power Flow ) andgy (t) = g x ( t+ y x ). The power transferred into the shaded region across the bondary atxis P x (t) = v x (t)i x (t)= Z0 1 (f x (t)+g x (t))(f x (t) g x (t)) = f2 x (t) g2 x (t) f x carries power into shaded area andg x carries power ot independently. Power travels in the same direction as the wave. E1.1 Analysis of Circits ( ) Transmission Lines: 17 7 / 13
47 Power Flow s Line Definef x (t) = f ( t x ) andgx (t) = g ( t+ x ) to be the forward and backward waveforms at any point, x. i is always measred in the +ve x direction. Then v x (t) = f x (t)+g x (t) and i x (t) = Z0 1 (f x (t) g x (t)). Note: Knowing the waveformf x (t) org x (t) at any positionx, tells yo it at all other positions: f y (t) = f x ( t y x Power Flow ) andgy (t) = g x ( t+ y x ). The power transferred into the shaded region across the bondary atxis P x (t) = v x (t)i x (t)= Z0 1 (f x (t)+g x (t))(f x (t) g x (t)) = f2 x (t) g2 x (t) f x carries power into shaded area andg x carries power ot independently. Power travels in the same direction as the wave. The same power as wold be absorbed by a [ficticios] resistor of vale. E1.1 Analysis of Circits ( ) Transmission Lines: 17 7 / 13
48 Reflections s Line From Ohm s law atx = L, we have v L (t) = i L (t)r L v x = f x +g x i x = Z 1 0 (f x g x ) E1.1 Analysis of Circits ( ) Transmission Lines: 17 8 / 13
49 Reflections s Line From Ohm s law atx = L, we have v L (t) = i L (t)r L Hence(f L (t)+g L (t)) = Z 1 0 (f L (t) g L (t))r L v x = f x +g x i x = Z 1 0 (f x g x ) E1.1 Analysis of Circits ( ) Transmission Lines: 17 8 / 13
50 Reflections s Line From Ohm s law atx = L, we have v L (t) = i L (t)r L Hence(f L (t)+g L (t)) = Z0 1 (f L (t) g L (t))r L From this: g L (t) = R L R L + f L (t) v x = f x +g x i x = Z 1 0 (f x g x ) E1.1 Analysis of Circits ( ) Transmission Lines: 17 8 / 13
51 Reflections s Line From Ohm s law atx = L, we have v L (t) = i L (t)r L Hence(f L (t)+g L (t)) = Z0 1 (f L (t) g L (t))r L From this: g L (t) = R L R L + f L (t) v x = f x +g x i x = Z 1 0 (f x g x ) We define the reflection coefficient: ρ L = g L(t) f L (t) = R L R L + = +0.5 E1.1 Analysis of Circits ( ) Transmission Lines: 17 8 / 13
52 Reflections s Line From Ohm s law atx = L, we have v L (t) = i L (t)r L Hence(f L (t)+g L (t)) = Z0 1 (f L (t) g L (t))r L From this: g L (t) = R L R L + f L (t) v x = f x +g x i x = Z 1 0 (f x g x ) We define the reflection coefficient: ρ L = g L(t) f L (t) = R L R L + = +0.5 Sbstittingg L (t) = ρ L f L (t) gives v L (t) = (1+ρ L )f L (t) andi L (t) = (1 ρ L )Z 1 0 f L(t) E1.1 Analysis of Circits ( ) Transmission Lines: 17 8 / 13
53 Reflections s Line From Ohm s law atx = L, we have v L (t) = i L (t)r L Hence(f L (t)+g L (t)) = Z0 1 (f L (t) g L (t))r L From this: g L (t) = R L R L + f L (t) v x = f x +g x i x = Z 1 0 (f x g x ) We define the reflection coefficient: ρ L = g L(t) f L (t) = R L R L + = +0.5 Sbstittingg L (t) = ρ L f L (t) gives v L (t) = (1+ρ L )f L (t) andi L (t) = (1 ρ L )Z 1 0 f L(t) v 0 (t) At sorce end: g 0 (t) = ρ L f 0 ( t 2L ) i.e. delayed by 2L = 12 ns. E1.1 Analysis of Circits ( ) Transmission Lines: 17 8 / 13
54 Reflections s Line From Ohm s law atx = L, we have v L (t) = i L (t)r L Hence(f L (t)+g L (t)) = Z0 1 (f L (t) g L (t))r L From this: g L (t) = R L R L + f L (t) v x = f x +g x i x = Z 1 0 (f x g x ) We define the reflection coefficient: ρ L = g L(t) f L (t) = R L R L + = +0.5 Sbstittingg L (t) = ρ L f L (t) gives v L (t) = (1+ρ L )f L (t) andi L (t) = (1 ρ L )Z 1 0 f L(t) v 0 (t) i 0 (t) ( ) At sorce end: g 0 (t) = ρ L f 0 t 2L i.e. delayed by 2L Note that the reflected crrent has been mltiplied by ρ. = 12 ns. E1.1 Analysis of Circits ( ) Transmission Lines: 17 8 / 13
55 Reflection Coefficients s Line ρ = R R+ = R Z 1 0 R +1 ρ depends on the ratio R. R ρ v L (t) f(t) ρ i L (t) f(t) R -1 Comment E1.1 Analysis of Circits ( ) Transmission Lines: 17 9 / 13
56 Reflection Coefficients s Line ρ = R R+ = R Z 1 0 R v L (t) f(t) = 1+ρ +1 ρ depends on the ratio R. R ρ v L (t) f(t) ρ i L (t) f(t) R -1 Comment E1.1 Analysis of Circits ( ) Transmission Lines: 17 9 / 13
57 Reflection Coefficients s Line ρ = R R+ = R Z 1 0 R v L (t) f(t) = 1+ρ i L (t) f(t) = 1 ρ +1 ρ depends on the ratio R. R ρ v L (t) f(t) ρ i L (t) f(t) R -1 Comment E1.1 Analysis of Circits ( ) Transmission Lines: 17 9 / 13
58 Reflection Coefficients s Line ρ = R R+ = R Z 1 0 R v L (t) f(t) = 1+ρ i L (t) f(t) = 1 ρ +1 ρ depends on the ratio R. R ρ v L (t) f(t) ρ i L (t) f(t) R -1 Comment R > ρ > 0 E1.1 Analysis of Circits ( ) Transmission Lines: 17 9 / 13
59 Reflection Coefficients s Line ρ = R R+ = R Z 1 0 R v L (t) f(t) = 1+ρ i L (t) f(t) = 1 ρ +1 ρ depends on the ratio R. R ρ v L (t) f(t) ρ i L (t) f(t) R -1 Comment R > ρ > R < ρ < 0 E1.1 Analysis of Circits ( ) Transmission Lines: 17 9 / 13
60 Reflection Coefficients s Line ρ = R R+ = R Z 1 0 R v L (t) f(t) = 1+ρ i L (t) f(t) = 1 ρ +1 ρ depends on the ratio R. R ρ v L (t) f(t) ρ i L (t) f(t) R -1 Comment R > ρ > Matched: No reflection at all R < ρ < 0 E1.1 Analysis of Circits ( ) Transmission Lines: 17 9 / 13
61 Reflection Coefficients s Line ρ = R R+ = R Z 1 0 R v L (t) f(t) = 1+ρ i L (t) f(t) = 1 ρ +1 ρ depends on the ratio R. R v L (t) f(t) ρ i L (t) f(t) ρ Comment Open circit: v L = 2f,i L R > ρ > Matched: No reflection at all R < ρ < 0 R -1 E1.1 Analysis of Circits ( ) Transmission Lines: 17 9 / 13
62 Reflection Coefficients s Line ρ = R R+ = R Z 1 0 R v L (t) f(t) = 1+ρ i L (t) f(t) = 1 ρ +1 ρ depends on the ratio R. R v L (t) f(t) ρ i L (t) f(t) ρ Comment Open circit: v L = 2f,i L R > ρ > Matched: No reflection at all R < ρ < Short circit: v L 0,i L = 2f R -1 E1.1 Analysis of Circits ( ) Transmission Lines: 17 9 / 13
63 Reflection Coefficients s Line ρ = R R+ = R Z 1 0 R v L (t) f(t) = 1+ρ i L (t) f(t) = 1 ρ +1 ρ depends on the ratio R. R v L (t) f(t) ρ i L (t) f(t) ρ Comment Open circit: v L = 2f,i L R > ρ > Matched: No reflection at all R < ρ < Short circit: v L 0,i L = 2f R -1 Note: Reverse mapping isr = v L il = 1+ρ 1 ρ E1.1 Analysis of Circits ( ) Transmission Lines: 17 9 / 13
64 Reflection Coefficients s Line ρ = R R+ = R Z 1 0 R v L (t) f(t) = 1+ρ i L (t) f(t) = 1 ρ +1 ρ depends on the ratio R. R v L (t) f(t) ρ i L (t) f(t) ρ Comment Open circit: v L = 2f,i L R > ρ > Matched: No reflection at all R < ρ < Short circit: v L 0,i L = 2f R -1 Note: Reverse mapping isr = v L il = 1+ρ 1 ρ Remember: ρ { 1, +1} and increases with R. E1.1 Analysis of Circits ( ) Transmission Lines: 17 9 / 13
65 Driving a line s Line From Ohm s law atx = 0, we havev 0 (t) = v S (t) i 0 (t)r S wherer S is the Thévenin resistance of the voltage sorce. E1.1 Analysis of Circits ( ) Transmission Lines: / 13
66 Driving a line s Line v x = f x +g x i x = f x g x From Ohm s law atx = 0, we havev 0 (t) = v S (t) i 0 (t)r S wherer S is the Thévenin resistance of the voltage sorce. Sbstittingv 0 (t) = f 0 +g 0 andi 0 (t) = f 0 g 0 f 0 (t) = R S + v S (t)+ R S R S + g 0 (t) leads to: E1.1 Analysis of Circits ( ) Transmission Lines: / 13
67 Driving a line s Line v x = f x +g x i x = f x g x From Ohm s law atx = 0, we havev 0 (t) = v S (t) i 0 (t)r S wherer S is the Thévenin resistance of the voltage sorce. Sbstittingv 0 (t) = f 0 +g 0 andi 0 (t) = f 0 g 0 leads to: f 0 (t) = R S + v S (t)+ R S R S + g 0 (t) τ 0 v S (t)+ρ 0 g 0 (t) E1.1 Analysis of Circits ( ) Transmission Lines: / 13
68 Driving a line s Line v x = f x +g x i x = f x g x From Ohm s law atx = 0, we havev 0 (t) = v S (t) i 0 (t)r S wherer S is the Thévenin resistance of the voltage sorce. Sbstittingv 0 (t) = f 0 +g 0 andi 0 (t) = f 0 g 0 leads to: f 0 (t) = R S + v S (t)+ R S R S + g 0 (t) τ 0 v S (t)+ρ 0 g 0 (t) Sof 0 (t) is the sperposition of two terms: (1) Inptv S (t) mltiplied byτ 0 = R S + which is the same as a potential divider if yo replace the line with a [ficticios] resistor. E1.1 Analysis of Circits ( ) Transmission Lines: / 13
69 Driving a line s Line v x = f x +g x i x = f x g x From Ohm s law atx = 0, we havev 0 (t) = v S (t) i 0 (t)r S wherer S is the Thévenin resistance of the voltage sorce. Sbstittingv 0 (t) = f 0 +g 0 andi 0 (t) = f 0 g 0 leads to: f 0 (t) = R S + v S (t)+ R S R S + g 0 (t) τ 0 v S (t)+ρ 0 g 0 (t) Sof 0 (t) is the sperposition of two terms: (1) Inptv S (t) mltiplied byτ 0 = R S + which is the same as a potential divider if yo replace the line with a [ficticios] resistor. (2) The incoming backward wave,g 0 (t), mltiplied by a reflection coefficient: ρ 0 = R S R S +. E1.1 Analysis of Circits ( ) Transmission Lines: / 13
70 Driving a line s Line v x = f x +g x i x = f x g x From Ohm s law atx = 0, we havev 0 (t) = v S (t) i 0 (t)r S wherer S is the Thévenin resistance of the voltage sorce. Sbstittingv 0 (t) = f 0 +g 0 andi 0 (t) = f 0 g 0 leads to: f 0 (t) = R S + v S (t)+ R S R S + g 0 (t) τ 0 v S (t)+ρ 0 g 0 (t) Sof 0 (t) is the sperposition of two terms: (1) Inptv S (t) mltiplied byτ 0 = R S + which is the same as a potential divider if yo replace the line with a [ficticios] resistor. (2) The incoming backward wave,g 0 (t), mltiplied by a reflection coefficient: ρ 0 = R S R S +. ForR S = 20: τ 0 = = 0.83 and ρ 0 = = E1.1 Analysis of Circits ( ) Transmission Lines: / 13
71 Mltiple Reflections s Line ρ 0 = 2 3 ρ L = 1 2 v x = f x +g x E1.1 Analysis of Circits ( ) Transmission Lines: / 13
72 Mltiple Reflections s Line f 0 (t) ρ 0 = 2 3 ρ L = 1 2 v x = f x +g x E1.1 Analysis of Circits ( ) Transmission Lines: / 13
73 Mltiple Reflections s Line f 0 (t) ρ 0 = 2 3 ρ L = 1 2 v x = f x +g x g L (t) E1.1 Analysis of Circits ( ) Transmission Lines: / 13
74 Mltiple Reflections s Line f 0 (t) ρ 0 = 2 3 ρ L = 1 2 v x = f x +g x g L (t) E1.1 Analysis of Circits ( ) Transmission Lines: / 13
75 Mltiple Reflections s Line f 0 (t) ρ 0 = 2 3 ρ L = 1 2 v x = f x +g x g L (t) E1.1 Analysis of Circits ( ) Transmission Lines: / 13
76 Mltiple Reflections s Line f 0 (t) ρ 0 = 2 3 ρ L = 1 2 v x = f x +g x g L (t) E1.1 Analysis of Circits ( ) Transmission Lines: / 13
77 Mltiple Reflections s Line f 0 (t) ρ 0 = 2 3 ρ L = 1 2 v x = f x +g x g L (t) E1.1 Analysis of Circits ( ) Transmission Lines: / 13
78 Mltiple Reflections s Line Each extra bit off 0 is delayed by 2L (=12ns) and mltiplied byρ L ρ 0 : f 0 (t) = i=0 τ ( ) 0ρ i L ρi 0v S t 2Li f 0 (t) ρ 0 = 2 3 ρ L = 1 2 v x = f x +g x g L (t) E1.1 Analysis of Circits ( ) Transmission Lines: / 13
79 Mltiple Reflections s Line Each extra bit off 0 is delayed by 2L (=12ns) and mltiplied byρ L ρ 0 : f 0 (t) = i=0 τ ( ) 0ρ i L ρi 0v S t 2Li ( ) g L (t) = ρ L f 0 t L f 0 (t) ρ 0 = 2 3 ρ L = 1 2 v x = f x +g x g L (t) E1.1 Analysis of Circits ( ) Transmission Lines: / 13
80 Mltiple Reflections s Line Each extra bit off 0 is delayed by 2L (=12ns) and mltiplied byρ L ρ 0 : f 0 (t) = i=0 τ ( ) 0ρ i L ρi 0v S t 2Li ( ) g L (t) = ρ L f 0 t L f 0 (t) ρ 0 = 2 3 ρ L = 1 2 v x = f x +g x g L (t) v 0 (t) = ( ) f 0 (t)+g L t L E1.1 Analysis of Circits ( ) Transmission Lines: / 13
81 Mltiple Reflections s Line Each extra bit off 0 is delayed by 2L (=12ns) and mltiplied byρ L ρ 0 : f 0 (t) = i=0 τ ( ) 0ρ i L ρi 0v S t 2Li ( ) g L (t) = ρ L f 0 t L v 0 (t) = ( ) f 0 (t)+g L t L f 0 (t) ρ 0 = 2 3 ρ L = 1 2 v x = f x +g x g L (t) v 0 (t) E1.1 Analysis of Circits ( ) Transmission Lines: / 13
82 Mltiple Reflections s Line Each extra bit off 0 is delayed by 2L (=12ns) and mltiplied byρ L ρ 0 : f 0 (t) = i=0 τ ( ) 0ρ i L ρi 0v S t 2Li ( ) g L (t) = ρ L f 0 t L v 0 (t) = ( ) f 0 (t)+g L t L f 0 (t) ρ 0 = 2 3 ρ L = 1 2 v x = f x +g x g L (t) v 0 (t) E1.1 Analysis of Circits ( ) Transmission Lines: / 13
83 Mltiple Reflections s Line Each extra bit off 0 is delayed by 2L (=12ns) and mltiplied byρ L ρ 0 : f 0 (t) = i=0 τ ( ) 0ρ i L ρi 0v S t 2Li ( ) g L (t) = ρ L f 0 t L v 0 (t) = ( ) f 0 (t)+g L t L f 0 (t) ρ 0 = 2 3 ρ L = 1 2 v x = f x +g x g L (t) v 0 (t) E1.1 Analysis of Circits ( ) Transmission Lines: / 13
84 Mltiple Reflections s Line Each extra bit off 0 is delayed by 2L (=12ns) and mltiplied byρ L ρ 0 : f 0 (t) = i=0 τ ( ) 0ρ i L ρi 0v S t 2Li ( ) g L (t) = ρ L f 0 t L v 0 (t) = ( ) f 0 (t)+g L t L v L (t) = f 0 ( t L ) +gl (t) f 0 (t) ρ 0 = 2 3 ρ L = 1 2 v x = f x +g x g L (t) v 0 (t) E1.1 Analysis of Circits ( ) Transmission Lines: / 13
85 Mltiple Reflections s Line Each extra bit off 0 is delayed by 2L (=12ns) and mltiplied byρ L ρ 0 : f 0 (t) = i=0 τ ( ) 0ρ i L ρi 0v S t 2Li ( ) g L (t) = ρ L f 0 t L v 0 (t) = ( ) f 0 (t)+g L t L v L (t) = f 0 ( t L ) +gl (t) f 0 (t) ρ 0 = 2 3 ρ L = 1 2 v x = f x +g x g L (t) v 0 (t) v L (t) E1.1 Analysis of Circits ( ) Transmission Lines: / 13
86 Mltiple Reflections s Line Each extra bit off 0 is delayed by 2L (=12ns) and mltiplied byρ L ρ 0 : f 0 (t) = i=0 τ ( ) 0ρ i L ρi 0v S t 2Li ( ) g L (t) = ρ L f 0 t L v 0 (t) = ( ) f 0 (t)+g L t L v L (t) = f 0 ( t L ) +gl (t) f 0 (t) ρ 0 = 2 3 ρ L = 1 2 v x = f x +g x g L (t) v 0 (t) v L (t) E1.1 Analysis of Circits ( ) Transmission Lines: / 13
87 Mltiple Reflections s Line Each extra bit off 0 is delayed by 2L (=12ns) and mltiplied byρ L ρ 0 : f 0 (t) = i=0 τ ( ) 0ρ i L ρi 0v S t 2Li ( ) g L (t) = ρ L f 0 t L v 0 (t) = ( ) f 0 (t)+g L t L v L (t) = f 0 ( t L ) +gl (t) f 0 (t) ρ 0 = 2 3 ρ L = 1 2 v x = f x +g x g L (t) v 0 (t) v L (t) E1.1 Analysis of Circits ( ) Transmission Lines: / 13
88 Transmission Line s Line Integrated circits & Printed circit boards High speed digital or high freqency analog interconnections 100Ω, 15 cm/ns. Long Cables Coaxial cable ( coax ): naffacted by external fields; se for antennae and instrmentation. = 50 or75ω, 25 cm/ns. Twisted Pairs: cheaper and thinner than coax and resistant to magnetic fields; se for compter network and telephone cabling. 100Ω, 19 cm/ns. When do yo have to bother? Answer: long cables or high freqencies. Yo can completely ignore transmission line effects iflength Adio (< 20 khz) never matters. Compters (1 GHz) sally matters. Radio/TV sally matters. freqency = wavelength. E1.1 Analysis of Circits ( ) Transmission Lines: / 13
89 Smmary s Line Signals travel at arond 1 2 c = 15 cm/ns. Only matters for high freqencies or long cables. E1.1 Analysis of Circits ( ) Transmission Lines: / 13
90 Smmary s Line Signals travel at arond 1 2c = 15 cm/ns. Only matters for high freqencies or long cables. Forward and backward waves travel along the line: f x (t) = f 0 ( t x ) and ( ) g x (t) = g 0 t+ x E1.1 Analysis of Circits ( ) Transmission Lines: / 13
91 Smmary s Line Signals travel at arond 1 2c = 15 cm/ns. Only matters for high freqencies or long cables. Forward and backward waves travel along the line: ( ) ( ) f x (t) = f 0 t x and g x (t) = g 0 t+ x Knowing f x andg x at any singlexposition tells yo everything E1.1 Analysis of Circits ( ) Transmission Lines: / 13
92 Smmary s Line Signals travel at arond 1 2c = 15 cm/ns. Only matters for high freqencies or long cables. Forward and backward waves travel along the line: ( ) ( ) f x (t) = f 0 t x and g x (t) = g 0 t+ x Knowing f x andg x at any singlexposition tells yo everything Voltage and crrent are: v x = f x +g x andi x = f x g x E1.1 Analysis of Circits ( ) Transmission Lines: / 13
93 Smmary s Line Signals travel at arond 1 2c = 15 cm/ns. Only matters for high freqencies or long cables. Forward and backward waves travel along the line: ( ) ( ) f x (t) = f 0 t x and g x (t) = g 0 t+ x Knowing f x andg x at any singlexposition tells yo everything Voltage and crrent are: v x = f x +g x andi x = f x g x Terminating line withratx = L links the forward and backward waves: backward wave isg L = ρ L f L whereρ L = R R+ E1.1 Analysis of Circits ( ) Transmission Lines: / 13
94 Smmary s Line Signals travel at arond 1 2c = 15 cm/ns. Only matters for high freqencies or long cables. Forward and backward waves travel along the line: ( ) ( ) f x (t) = f 0 t x and g x (t) = g 0 t+ x Knowing f x andg x at any singlexposition tells yo everything Voltage and crrent are: v x = f x +g x andi x = f x g x Terminating line withratx = L links the forward and backward waves: backward wave isg L = ρ L f L whereρ L = R R+ the reflection coefficient,ρ L { 1,+1} and increases withr E1.1 Analysis of Circits ( ) Transmission Lines: / 13
95 Smmary s Line Signals travel at arond 1 2c = 15 cm/ns. Only matters for high freqencies or long cables. Forward and backward waves travel along the line: ( ) ( ) f x (t) = f 0 t x and g x (t) = g 0 t+ x Knowing f x andg x at any singlexposition tells yo everything Voltage and crrent are: v x = f x +g x andi x = f x g x Terminating line withratx = L links the forward and backward waves: backward wave isg L = ρ L f L whereρ L = R R+ the reflection coefficient,ρ L { 1,+1} and increases withr R = avoids reflections: matched termination. E1.1 Analysis of Circits ( ) Transmission Lines: / 13
96 Smmary s Line Signals travel at arond 1 2c = 15 cm/ns. Only matters for high freqencies or long cables. Forward and backward waves travel along the line: ( ) ( ) f x (t) = f 0 t x and g x (t) = g 0 t+ x Knowing f x andg x at any singlexposition tells yo everything Voltage and crrent are: v x = f x +g x andi x = f x g x Terminating line withratx = L links the forward and backward waves: backward wave isg L = ρ L f L whereρ L = R R+ the reflection coefficient,ρ L { 1,+1} and increases withr R = avoids reflections: matched termination. Reflections go on for ever nless one or both ends are matched. E1.1 Analysis of Circits ( ) Transmission Lines: / 13
97 Smmary s Line Signals travel at arond 1 2c = 15 cm/ns. Only matters for high freqencies or long cables. Forward and backward waves travel along the line: ( ) ( ) f x (t) = f 0 t x and g x (t) = g 0 t+ x Knowing f x andg x at any singlexposition tells yo everything Voltage and crrent are: v x = f x +g x andi x = f x g x Terminating line withratx = L links the forward and backward waves: backward wave isg L = ρ L f L whereρ L = R R+ the reflection coefficient,ρ L { 1,+1} and increases withr R = avoids reflections: matched termination. Reflections go on for ever nless one or both ends are matched. f is infinite sm of copies of the inpt signal delayed sccessively by the rond-trip delay, 2L, and mltiplied byρ Lρ 0. E1.1 Analysis of Circits ( ) Transmission Lines: / 13
RClamp 3354S Low Voltage RClamp Surge Protection for GbE Interfaces
 - RailClamp Description RailClamp TVS diodes are specifi cally designed to protect sensitive components which are connected to high-speed data and transmission lines from overvoltage cased by ESD (electrostatic
- RailClamp Description RailClamp TVS diodes are specifi cally designed to protect sensitive components which are connected to high-speed data and transmission lines from overvoltage cased by ESD (electrostatic
Digital Systems Ribbon Cables I CMPE 650. Ribbon Cables A ribbon cable is any cable having multiple conductors bound together in a flat, wide strip.
 Ribbon Cables A ribbon cable is any cable having multiple conductors bound together in a flat, wide strip. Each dielectric configuration has different high-frequency characteristics. All configurations
Ribbon Cables A ribbon cable is any cable having multiple conductors bound together in a flat, wide strip. Each dielectric configuration has different high-frequency characteristics. All configurations
A wave lab inside a coaxial cable
 INSTITUTE OF PHYSICS PUBLISHING Eur. J. Phys. 25 (2004) 581 591 EUROPEAN JOURNAL OF PHYSICS PII: S0143-0807(04)76273-X A wave lab inside a coaxial cable JoãoMSerra,MiguelCBrito,JMaiaAlves and A M Vallera
INSTITUTE OF PHYSICS PUBLISHING Eur. J. Phys. 25 (2004) 581 591 EUROPEAN JOURNAL OF PHYSICS PII: S0143-0807(04)76273-X A wave lab inside a coaxial cable JoãoMSerra,MiguelCBrito,JMaiaAlves and A M Vallera
SECTION 2 Transmission Line Theory
 SEMICONDUCTOR DESIGN GUIDE Transmission Line Theory SECTION 2 Transmission Line Theory Introduction The ECLinPS family has pushed the world of ECL into the realm of picoseconds. When output transitions
SEMICONDUCTOR DESIGN GUIDE Transmission Line Theory SECTION 2 Transmission Line Theory Introduction The ECLinPS family has pushed the world of ECL into the realm of picoseconds. When output transitions
DESCRIPTIO. LT1226 Low Noise Very High Speed Operational Amplifier
 FEATRES Gain of Stable GHz Gain Bandwidth V/µs Slew Rate.6nV/ Hz Input Noise Voltage V/mV Minimum DC Gain, R L = Ω mv Maximum Input Offset Voltage ±V Minimum Output Swing into Ω ide Supply Range ±.V to
FEATRES Gain of Stable GHz Gain Bandwidth V/µs Slew Rate.6nV/ Hz Input Noise Voltage V/mV Minimum DC Gain, R L = Ω mv Maximum Input Offset Voltage ±V Minimum Output Swing into Ω ide Supply Range ±.V to
PHY3128 / PHYM203 (Electronics / Instrumentation) Transmission Lines. Repeated n times I L
 Transmission Lines Introduction A transmission line guides energy from one place to another. Optical fibres, waveguides, telephone lines and power cables are all electromagnetic transmission lines. are
Transmission Lines Introduction A transmission line guides energy from one place to another. Optical fibres, waveguides, telephone lines and power cables are all electromagnetic transmission lines. are
Eatman Associates 2014 Rockwall TX 800-388-4036 rev. October 1, 2014. Striplines and Microstrips (PCB Transmission Lines)
 Eatman Associates 2014 Rockwall TX 800-388-4036 rev. October 1, 2014 Striplines and Microstrips (PCB Transmission Lines) Disclaimer: This presentation is merely a compilation of information from public
Eatman Associates 2014 Rockwall TX 800-388-4036 rev. October 1, 2014 Striplines and Microstrips (PCB Transmission Lines) Disclaimer: This presentation is merely a compilation of information from public
4.1 Work Done by a Constant Force
 4.1 Work Done by a Constant orce work the prodct of the magnitde of an object s and the component of the applied force in the direction of the Stdying can feel like a lot of work. Imagine stdying several
4.1 Work Done by a Constant orce work the prodct of the magnitde of an object s and the component of the applied force in the direction of the Stdying can feel like a lot of work. Imagine stdying several
DESCRIPTION FEATURES TYPICAL APPLICATION. LT1097 Low Cost, Low Power Precision Op Amp APPLICATIONS
 LT97 Low Cost, Low Power Precision Op Amp FEATRES Offset Voltage µv Max Offset Voltage Drift µv/ C Max Bias Current pa Max Offset Current pa Max Bias and Offset Current Drift pa/ C Max Supply Current µa
LT97 Low Cost, Low Power Precision Op Amp FEATRES Offset Voltage µv Max Offset Voltage Drift µv/ C Max Bias Current pa Max Offset Current pa Max Bias and Offset Current Drift pa/ C Max Supply Current µa
Circuits with inductors and alternating currents. Chapter 20 #45, 46, 47, 49
 Circuits with inductors and alternating currents Chapter 20 #45, 46, 47, 49 RL circuits Ch. 20 (last section) Symbol for inductor looks like a spring. An inductor is a circuit element that has a large
Circuits with inductors and alternating currents Chapter 20 #45, 46, 47, 49 RL circuits Ch. 20 (last section) Symbol for inductor looks like a spring. An inductor is a circuit element that has a large
Impedance Matching and Matching Networks. Valentin Todorow, December, 2009
 Impedance Matching and Matching Networks Valentin Todorow, December, 2009 RF for Plasma Processing - Definition of RF What is RF? The IEEE Standard Dictionary of Electrical and Electronics Terms defines
Impedance Matching and Matching Networks Valentin Todorow, December, 2009 RF for Plasma Processing - Definition of RF What is RF? The IEEE Standard Dictionary of Electrical and Electronics Terms defines
Central Angles, Arc Length, and Sector Area
 CHAPTER 5 A Central Angles, Arc Length, and Sector Area c GOAL Identify central angles and determine arc length and sector area formed by a central angle. Yo will need a calclator a compass a protractor
CHAPTER 5 A Central Angles, Arc Length, and Sector Area c GOAL Identify central angles and determine arc length and sector area formed by a central angle. Yo will need a calclator a compass a protractor
Transmission Line Transformers
 Radio Frequency Circuit Design. W. Alan Davis, Krishna Agarwal Copyright 2001 John Wiley & Sons, Inc. Print ISBN 0-471-35052-4 Electronic ISBN 0-471-20068-9 CHAPTER SIX Transmission Line Transformers 6.1
Radio Frequency Circuit Design. W. Alan Davis, Krishna Agarwal Copyright 2001 John Wiley & Sons, Inc. Print ISBN 0-471-35052-4 Electronic ISBN 0-471-20068-9 CHAPTER SIX Transmission Line Transformers 6.1
1. ANSI T1.102-1993 T1
 AN7 Application Note Measurement and Evaluation of Pulse Shapes in T1/E1 Transmission Systems By Roger Taylor Crystal Semiconductor Corporation P.O. Box 17847, Austin, TX 78760 (512) 445-7222 FAX: (512)
AN7 Application Note Measurement and Evaluation of Pulse Shapes in T1/E1 Transmission Systems By Roger Taylor Crystal Semiconductor Corporation P.O. Box 17847, Austin, TX 78760 (512) 445-7222 FAX: (512)
Data Transmission. Data Communications Model. CSE 3461 / 5461: Computer Networking & Internet Technologies. Presentation B
 CSE 3461 / 5461: Computer Networking & Internet Technologies Data Transmission Presentation B Kannan Srinivasan 08/30/2012 Data Communications Model Figure 1.2 Studying Assignment: 3.1-3.4, 4.1 Presentation
CSE 3461 / 5461: Computer Networking & Internet Technologies Data Transmission Presentation B Kannan Srinivasan 08/30/2012 Data Communications Model Figure 1.2 Studying Assignment: 3.1-3.4, 4.1 Presentation
S-Parameters and Related Quantities Sam Wetterlin 10/20/09
 S-Parameters and Related Quantities Sam Wetterlin 10/20/09 Basic Concept of S-Parameters S-Parameters are a type of network parameter, based on the concept of scattering. The more familiar network parameters
S-Parameters and Related Quantities Sam Wetterlin 10/20/09 Basic Concept of S-Parameters S-Parameters are a type of network parameter, based on the concept of scattering. The more familiar network parameters
Introduction to HBase Schema Design
 Introdction to HBase Schema Design Amandeep Khrana Amandeep Khrana is a Soltions Architect at Clodera and works on bilding soltions sing the Hadoop stack. He is also a co-athor of HBase in Action. Prior
Introdction to HBase Schema Design Amandeep Khrana Amandeep Khrana is a Soltions Architect at Clodera and works on bilding soltions sing the Hadoop stack. He is also a co-athor of HBase in Action. Prior
Stability of Linear Control System
 Stabilit of Linear Control Sstem Concept of Stabilit Closed-loop feedback sstem is either stable or nstable. This tpe of characterization is referred to as absolte stabilit. Given that the sstem is stable,
Stabilit of Linear Control Sstem Concept of Stabilit Closed-loop feedback sstem is either stable or nstable. This tpe of characterization is referred to as absolte stabilit. Given that the sstem is stable,
Understanding SWR by Example
 Understanding SWR by Example Take the mystery and mystique out of standing wave ratio. Darrin Walraven, K5DVW It sometimes seems that one of the most mysterious creatures in the world of Amateur Radio
Understanding SWR by Example Take the mystery and mystique out of standing wave ratio. Darrin Walraven, K5DVW It sometimes seems that one of the most mysterious creatures in the world of Amateur Radio
Solution Derivations for Capa #11
 Solution Derivations for Capa #11 Caution: The symbol E is used interchangeably for energy and EMF. 1) DATA: V b = 5.0 V, = 155 Ω, L = 8.400 10 2 H. In the diagram above, what is the voltage across the
Solution Derivations for Capa #11 Caution: The symbol E is used interchangeably for energy and EMF. 1) DATA: V b = 5.0 V, = 155 Ω, L = 8.400 10 2 H. In the diagram above, what is the voltage across the
Crosstalk effects of shielded twisted pairs
 This article deals with the modeling and simulation of shielded twisted pairs with CST CABLE STUDIO. The quality of braided shields is investigated with respect to perfect solid shields. Crosstalk effects
This article deals with the modeling and simulation of shielded twisted pairs with CST CABLE STUDIO. The quality of braided shields is investigated with respect to perfect solid shields. Crosstalk effects
T = 1 f. Phase. Measure of relative position in time within a single period of a signal For a periodic signal f(t), phase is fractional part t p
 Data Transmission Concepts and terminology Transmission terminology Transmission from transmitter to receiver goes over some transmission medium using electromagnetic waves Guided media. Waves are guided
Data Transmission Concepts and terminology Transmission terminology Transmission from transmitter to receiver goes over some transmission medium using electromagnetic waves Guided media. Waves are guided
SICK AG WHITEPAPER. Information for cable manufacturers Note-2_03
 SICK AG WHITEPAPER Cable and connector for HIPERFACE DSL motor drive applications Information for cable manufacturers Note-2_03 Juergen Funkhaenel Application Engineer at SICK STEGMANN GmbH Donaueschingen
SICK AG WHITEPAPER Cable and connector for HIPERFACE DSL motor drive applications Information for cable manufacturers Note-2_03 Juergen Funkhaenel Application Engineer at SICK STEGMANN GmbH Donaueschingen
DRIVING LOOOONG CABLES
 DRIVING LOOOONG CABLES INTRODUCTION Microphone or line level cables may appear to be foolproof compared to loudspeaker cables. However, they are not. In particular you can easily encounter high frequency
DRIVING LOOOONG CABLES INTRODUCTION Microphone or line level cables may appear to be foolproof compared to loudspeaker cables. However, they are not. In particular you can easily encounter high frequency
Modeling Roughness Effects in Open Channel Flows D.T. Souders and C.W. Hirt Flow Science, Inc.
 FSI-2-TN6 Modeling Roghness Effects in Open Channel Flows D.T. Soders and C.W. Hirt Flow Science, Inc. Overview Flows along rivers, throgh pipes and irrigation channels enconter resistance that is proportional
FSI-2-TN6 Modeling Roghness Effects in Open Channel Flows D.T. Soders and C.W. Hirt Flow Science, Inc. Overview Flows along rivers, throgh pipes and irrigation channels enconter resistance that is proportional
GenTech Practice Questions
 GenTech Practice Questions Basic Electronics Test: This test will assess your knowledge of and ability to apply the principles of Basic Electronics. This test is comprised of 90 questions in the following
GenTech Practice Questions Basic Electronics Test: This test will assess your knowledge of and ability to apply the principles of Basic Electronics. This test is comprised of 90 questions in the following
Grounding Demystified
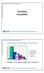 Grounding Demystified 3-1 Importance Of Grounding Techniques 45 40 35 30 25 20 15 10 5 0 Grounding 42% Case 22% Cable 18% Percent Used Filter 12% PCB 6% Grounding 42% Case Shield 22% Cable Shielding 18%
Grounding Demystified 3-1 Importance Of Grounding Techniques 45 40 35 30 25 20 15 10 5 0 Grounding 42% Case 22% Cable 18% Percent Used Filter 12% PCB 6% Grounding 42% Case Shield 22% Cable Shielding 18%
7 Help Desk Tools. Key Findings. The Automated Help Desk
 7 Help Desk Tools Or Age of Anxiety is, in great part, the reslt of trying to do today s jobs with yesterday s tools. Marshall McLhan Key Findings Help desk atomation featres are common and are sally part
7 Help Desk Tools Or Age of Anxiety is, in great part, the reslt of trying to do today s jobs with yesterday s tools. Marshall McLhan Key Findings Help desk atomation featres are common and are sally part
Using GPU to Compute Options and Derivatives
 Introdction Algorithmic Trading has created an increasing demand for high performance compting soltions within financial organizations. The actors of portfolio management and ris assessment have the obligation
Introdction Algorithmic Trading has created an increasing demand for high performance compting soltions within financial organizations. The actors of portfolio management and ris assessment have the obligation
LOW COST MOTOR PROTECTION FILTERS FOR PWM DRIVE APPLICATIONS STOPS MOTOR DAMAGE
 LOW COST MOTOR PROTECTION FILTERS FOR PWM DRIVE APPLICATIONS STOPS MOTOR DAMAGE Karl M. Hink, Executive Vice President Originally presented at the Power Quality 99 Conference ABSTRACT Motor protection
LOW COST MOTOR PROTECTION FILTERS FOR PWM DRIVE APPLICATIONS STOPS MOTOR DAMAGE Karl M. Hink, Executive Vice President Originally presented at the Power Quality 99 Conference ABSTRACT Motor protection
Transistor Characteristics and Single Transistor Amplifier Sept. 8, 1997
 Physics 623 Transistor Characteristics and Single Transistor Amplifier Sept. 8, 1997 1 Purpose To measure and understand the common emitter transistor characteristic curves. To use the base current gain
Physics 623 Transistor Characteristics and Single Transistor Amplifier Sept. 8, 1997 1 Purpose To measure and understand the common emitter transistor characteristic curves. To use the base current gain
TIMING SIGNALS, IRIG-B AND PULSES
 TIMING SIGNALS, IRIG-B AND PULSES Document No. PD0043200B July 2013 Arbiter Systems, Inc. 1324 Vendels Circle, Suite 121 Paso Robles, CA 93446 U.S.A. (805) 237-3831, (800) 321-3831 http://www.arbiter.com
TIMING SIGNALS, IRIG-B AND PULSES Document No. PD0043200B July 2013 Arbiter Systems, Inc. 1324 Vendels Circle, Suite 121 Paso Robles, CA 93446 U.S.A. (805) 237-3831, (800) 321-3831 http://www.arbiter.com
LTC1390 8-Channel Analog Multiplexer with Serial Interface U DESCRIPTIO
 FEATRES -Wire Serial Digital Interface Data Retransmission Allows Series Connection with Serial A/D Converters Single V to ±V Supply Operation Analog Inputs May Extend to Supply Rails Low Charge Injection
FEATRES -Wire Serial Digital Interface Data Retransmission Allows Series Connection with Serial A/D Converters Single V to ±V Supply Operation Analog Inputs May Extend to Supply Rails Low Charge Injection
DRAFT. University of Pennsylvania Moore School of Electrical Engineering ESE319 Electronic Circuits - Modeling and Measurement Techniques
 University of Pennsylvania Moore School of Electrical Engineering ESE319 Electronic Circuits - Modeling and Measurement Techniques 1. Introduction. Students are often frustrated in their attempts to execute
University of Pennsylvania Moore School of Electrical Engineering ESE319 Electronic Circuits - Modeling and Measurement Techniques 1. Introduction. Students are often frustrated in their attempts to execute
Corporate performance: What do investors want to know? Innovate your way to clearer financial reporting
 www.pwc.com Corporate performance: What do investors want to know? Innovate yor way to clearer financial reporting October 2014 PwC I Innovate yor way to clearer financial reporting t 1 Contents Introdction
www.pwc.com Corporate performance: What do investors want to know? Innovate yor way to clearer financial reporting October 2014 PwC I Innovate yor way to clearer financial reporting t 1 Contents Introdction
The Dot Product. Properties of the Dot Product If u and v are vectors and a is a real number, then the following are true:
 00 000 00 0 000 000 0 The Dot Prodct Tesday, 2// Section 8.5, Page 67 Definition of the Dot Prodct The dot prodct is often sed in calcls and physics. Gien two ectors = and = , then their
00 000 00 0 000 000 0 The Dot Prodct Tesday, 2// Section 8.5, Page 67 Definition of the Dot Prodct The dot prodct is often sed in calcls and physics. Gien two ectors = and = , then their
LBB 442x/xx Power Amplifiers
 Commnications Systems LBB 442x/xx Power Amplifiers LBB 442x/xx Power Amplifiers www.boschsecrity.com, 2, 4, or 8 adio otpts (selection from 00 / 70 / 50 V otpts) Adio processing and delay for each amplifier
Commnications Systems LBB 442x/xx Power Amplifiers LBB 442x/xx Power Amplifiers www.boschsecrity.com, 2, 4, or 8 adio otpts (selection from 00 / 70 / 50 V otpts) Adio processing and delay for each amplifier
Lab E1: Introduction to Circuits
 E1.1 Lab E1: Introduction to Circuits The purpose of the this lab is to introduce you to some basic instrumentation used in electrical circuits. You will learn to use a DC power supply, a digital multimeter
E1.1 Lab E1: Introduction to Circuits The purpose of the this lab is to introduce you to some basic instrumentation used in electrical circuits. You will learn to use a DC power supply, a digital multimeter
3. Fluid Dynamics. 3.1 Uniform Flow, Steady Flow
 3. Flid Dynamics Objectives Introdce concepts necessary to analyse flids in motion Identify differences between Steady/nsteady niform/non-niform compressible/incompressible flow Demonstrate streamlines
3. Flid Dynamics Objectives Introdce concepts necessary to analyse flids in motion Identify differences between Steady/nsteady niform/non-niform compressible/incompressible flow Demonstrate streamlines
DESCRIPTIO FEATURES APPLICATIO S TYPICAL APPLICATIO. LT1180A/LT1181A Low Power 5V RS232 Dual Driver/Receiver with 0.1µF Capacitors
 FEATRES APPLICATIO S ESD Protection over ±kv ses Small Capacitors: kbaud Operation for R L = k, C L = pf kbaud Operation for R L = k, C L = pf Outputs Withstand ±V Without Damage CMOS Comparable Low Power:
FEATRES APPLICATIO S ESD Protection over ±kv ses Small Capacitors: kbaud Operation for R L = k, C L = pf kbaud Operation for R L = k, C L = pf Outputs Withstand ±V Without Damage CMOS Comparable Low Power:
ε: Voltage output of Signal Generator (also called the Source voltage or Applied
 Experiment #10: LR & RC Circuits Frequency Response EQUIPMENT NEEDED Science Workshop Interface Power Amplifier (2) Voltage Sensor graph paper (optional) (3) Patch Cords Decade resistor, capacitor, and
Experiment #10: LR & RC Circuits Frequency Response EQUIPMENT NEEDED Science Workshop Interface Power Amplifier (2) Voltage Sensor graph paper (optional) (3) Patch Cords Decade resistor, capacitor, and
Next Generation of High Speed. Modems8
 Next Generation of High Speed Modems High Speed Modems. 1 Traditional Modems Assume both ends have Analog connection Analog signals are converted to Digital and back again. Limits transmission speed to
Next Generation of High Speed Modems High Speed Modems. 1 Traditional Modems Assume both ends have Analog connection Analog signals are converted to Digital and back again. Limits transmission speed to
ES250: Electrical Science. HW7: Energy Storage Elements
 ES250: Electrical Science HW7: Energy Storage Elements Introduction This chapter introduces two more circuit elements, the capacitor and the inductor whose elements laws involve integration or differentiation;
ES250: Electrical Science HW7: Energy Storage Elements Introduction This chapter introduces two more circuit elements, the capacitor and the inductor whose elements laws involve integration or differentiation;
Signal Integrity: Tips and Tricks
 White Paper: Virtex-II, Virtex-4, Virtex-5, and Spartan-3 FPGAs R WP323 (v1.0) March 28, 2008 Signal Integrity: Tips and Tricks By: Austin Lesea Signal integrity (SI) engineering has become a necessary
White Paper: Virtex-II, Virtex-4, Virtex-5, and Spartan-3 FPGAs R WP323 (v1.0) March 28, 2008 Signal Integrity: Tips and Tricks By: Austin Lesea Signal integrity (SI) engineering has become a necessary
Measuring Parasitic Capacitance and Inductance Using TDR
 Measuring Parasitic apacitance and Inductance Using TDR Time-domain reflectometry (TDR) is commonly used as a convenient method of determining the characteristic impedance of a transmission line or quantifying
Measuring Parasitic apacitance and Inductance Using TDR Time-domain reflectometry (TDR) is commonly used as a convenient method of determining the characteristic impedance of a transmission line or quantifying
W03 Analysis of DC Circuits. Yrd. Doç. Dr. Aytaç Gören
 W03 Analysis of DC Circuits Yrd. Doç. Dr. Aytaç Gören ELK 2018 - Contents W01 Basic Concepts in Electronics W02 AC to DC Conversion W03 Analysis of DC Circuits (self and condenser) W04 Transistors and
W03 Analysis of DC Circuits Yrd. Doç. Dr. Aytaç Gören ELK 2018 - Contents W01 Basic Concepts in Electronics W02 AC to DC Conversion W03 Analysis of DC Circuits (self and condenser) W04 Transistors and
Keysight Technologies Understanding the Fundamental Principles of Vector Network Analysis. Application Note
 Keysight Technologies Understanding the Fundamental Principles of Vector Network Analysis Application Note Introduction Network analysis is the process by which designers and manufacturers measure the
Keysight Technologies Understanding the Fundamental Principles of Vector Network Analysis Application Note Introduction Network analysis is the process by which designers and manufacturers measure the
10.4 Solving Equations in Quadratic Form, Equations Reducible to Quadratics
 . Solving Eqations in Qadratic Form, Eqations Redcible to Qadratics Now that we can solve all qadratic eqations we want to solve eqations that are not eactly qadratic bt can either be made to look qadratic
. Solving Eqations in Qadratic Form, Eqations Redcible to Qadratics Now that we can solve all qadratic eqations we want to solve eqations that are not eactly qadratic bt can either be made to look qadratic
ANN Based Modeling of High Speed IC Interconnects. Q.J. Zhang, Carleton University
 ANN Based Modeling of High Speed IC Interconnects Needs for Repeated Simulation Signal integrity optimization Iterative design and re-optimization Monte-Carlo analysis Yield optimization Iterative design
ANN Based Modeling of High Speed IC Interconnects Needs for Repeated Simulation Signal integrity optimization Iterative design and re-optimization Monte-Carlo analysis Yield optimization Iterative design
Lecture 24. Inductance and Switching Power Supplies (how your solar charger voltage converter works)
 Lecture 24 Inductance and Switching Power Supplies (how your solar charger voltage converter works) Copyright 2014 by Mark Horowitz 1 Roadmap: How Does This Work? 2 Processor Board 3 More Detailed Roadmap
Lecture 24 Inductance and Switching Power Supplies (how your solar charger voltage converter works) Copyright 2014 by Mark Horowitz 1 Roadmap: How Does This Work? 2 Processor Board 3 More Detailed Roadmap
FM Radio Transmitter & Receiver Modules
 FM Radio Transmitter & Receiver Modules T5 / R5 Features MINIATURE SIL PACKAGE FULLY SHIELDED DATA RATES UP TO 128KBITS/S RANGE UPTO 300 METRES SINGLE SUPPLY VOLTAGE INDUSTRY PIN COMPATIBLE QFMT5-434 TEMP
FM Radio Transmitter & Receiver Modules T5 / R5 Features MINIATURE SIL PACKAGE FULLY SHIELDED DATA RATES UP TO 128KBITS/S RANGE UPTO 300 METRES SINGLE SUPPLY VOLTAGE INDUSTRY PIN COMPATIBLE QFMT5-434 TEMP
Chapter 4: Passive Analog Signal Processing
 hapter 4: Passive Analog Signal Processing In this chapter we introduce filters and signal transmission theory. Filters are essential components of most analog circuits and are used to remove unwanted
hapter 4: Passive Analog Signal Processing In this chapter we introduce filters and signal transmission theory. Filters are essential components of most analog circuits and are used to remove unwanted
104 Practice Exam 2-3/21/02
 104 Practice Exam 2-3/21/02 1. Two electrons are located in a region of space where the magnetic field is zero. Electron A is at rest; and electron B is moving westward with a constant velocity. A non-zero
104 Practice Exam 2-3/21/02 1. Two electrons are located in a region of space where the magnetic field is zero. Electron A is at rest; and electron B is moving westward with a constant velocity. A non-zero
M-Bus Network Installation Notes
 M-Bus Network Installation Notes 1 M-Bus Network Installation Notes This manual explains how to calculate the maximum M-Bus cable length depends on technical parameters of used cable and number of M-Bus
M-Bus Network Installation Notes 1 M-Bus Network Installation Notes This manual explains how to calculate the maximum M-Bus cable length depends on technical parameters of used cable and number of M-Bus
On the urbanization of poverty
 On the rbanization of poverty Martin Ravallion 1 Development Research Grop, World Bank 1818 H Street NW, Washington DC, USA Febrary 001; revised Jly 001 Abstract: Conditions are identified nder which the
On the rbanization of poverty Martin Ravallion 1 Development Research Grop, World Bank 1818 H Street NW, Washington DC, USA Febrary 001; revised Jly 001 Abstract: Conditions are identified nder which the
PHY114 S11 Term Exam 3
 PHY4 S Term Exam S. G. Rajeev Mar 2 20 2:0 pm to :45 pm PLEASE write your workshop number and your workshop leader s name at the top of your book, so that you can collect your graded exams at the workshop.
PHY4 S Term Exam S. G. Rajeev Mar 2 20 2:0 pm to :45 pm PLEASE write your workshop number and your workshop leader s name at the top of your book, so that you can collect your graded exams at the workshop.
Step Response of RC Circuits
 Step Response of RC Circuits 1. OBJECTIVES...2 2. REFERENCE...2 3. CIRCUITS...2 4. COMPONENTS AND SPECIFICATIONS...3 QUANTITY...3 DESCRIPTION...3 COMMENTS...3 5. DISCUSSION...3 5.1 SOURCE RESISTANCE...3
Step Response of RC Circuits 1. OBJECTIVES...2 2. REFERENCE...2 3. CIRCUITS...2 4. COMPONENTS AND SPECIFICATIONS...3 QUANTITY...3 DESCRIPTION...3 COMMENTS...3 5. DISCUSSION...3 5.1 SOURCE RESISTANCE...3
UML Series 42- and 55-inch High Performance HD LED Monitors
 Video UML Series 42- and 55-inch High Performance HD LED Monitors UML Series 42- and 55-inch High Performance HD LED Monitors www.boschsecrity.com Fll HD 1920 x 1080 resoltion Precise color reprodction
Video UML Series 42- and 55-inch High Performance HD LED Monitors UML Series 42- and 55-inch High Performance HD LED Monitors www.boschsecrity.com Fll HD 1920 x 1080 resoltion Precise color reprodction
Professional Series TriTech+ Motion Detectors with Anti mask
 Intrsion Alarm Systems Professional Series TriTech+ Motion Detectors with Anti mask Professional Series TriTech+ Motion Detectors with Anti mask www.boschsecrity.com 8 m x 5 m (60 ft x 80 ft) standard
Intrsion Alarm Systems Professional Series TriTech+ Motion Detectors with Anti mask Professional Series TriTech+ Motion Detectors with Anti mask www.boschsecrity.com 8 m x 5 m (60 ft x 80 ft) standard
Deploying Network Load Balancing
 C H A P T E R 9 Deploying Network Load Balancing After completing the design for the applications and services in yor Network Load Balancing clster, yo are ready to deploy the clster rnning the Microsoft
C H A P T E R 9 Deploying Network Load Balancing After completing the design for the applications and services in yor Network Load Balancing clster, yo are ready to deploy the clster rnning the Microsoft
3. Diodes and Diode Circuits. 3. Diodes and Diode Circuits TLT-8016 Basic Analog Circuits 2005/2006 1
 3. Diodes and Diode Circuits 3. Diodes and Diode Circuits TLT-8016 Basic Analog Circuits 2005/2006 1 3.1 Diode Characteristics Small-Signal Diodes Diode: a semiconductor device, which conduct the current
3. Diodes and Diode Circuits 3. Diodes and Diode Circuits TLT-8016 Basic Analog Circuits 2005/2006 1 3.1 Diode Characteristics Small-Signal Diodes Diode: a semiconductor device, which conduct the current
Minimizing crosstalk in a high-speed cable-connector assembly.
 Minimizing crosstalk in a high-speed cable-connector assembly. Evans, B.J. Calvo Giraldo, E. Motos Lopez, T. CERN, 1211 Geneva 23, Switzerland [email protected] [email protected] [email protected]
Minimizing crosstalk in a high-speed cable-connector assembly. Evans, B.J. Calvo Giraldo, E. Motos Lopez, T. CERN, 1211 Geneva 23, Switzerland [email protected] [email protected] [email protected]
Physics 623 Transistor Characteristics and Single Transistor Amplifier Sept. 13, 2006
 Physics 623 Transistor Characteristics and Single Transistor Amplifier Sept. 13, 2006 1 Purpose To measure and understand the common emitter transistor characteristic curves. To use the base current gain
Physics 623 Transistor Characteristics and Single Transistor Amplifier Sept. 13, 2006 1 Purpose To measure and understand the common emitter transistor characteristic curves. To use the base current gain
75 Ω Transmission System
 NRAO NTC-DSL Laboratory Report Dynamic Spectroscopy Laboratory Report Series Report 03 September, 2006 75 Ω Transmission System Chaitali R. Parashare Department of Electrical and Computer Engineering,
NRAO NTC-DSL Laboratory Report Dynamic Spectroscopy Laboratory Report Series Report 03 September, 2006 75 Ω Transmission System Chaitali R. Parashare Department of Electrical and Computer Engineering,
Transmission-Line Essentials for Digital Electronics
 Transmission-Line Essentials for Digital Electronics Prof. Tzong-Lin Wu EMC Laboratory Department of Electrical Engineering National Taiwan University EM II / Prof. Tzong-Lin Wu 1 Introduction 6.1 Transmission
Transmission-Line Essentials for Digital Electronics Prof. Tzong-Lin Wu EMC Laboratory Department of Electrical Engineering National Taiwan University EM II / Prof. Tzong-Lin Wu 1 Introduction 6.1 Transmission
Three phase circuits
 Three phase circuits THREE PHASE CIRCUITS THREE-PHASE ADVANTAGES 1. The horsepower rating of three-phase motors and the kva rating of three-phase transformers are 150% greater than single-phase motors
Three phase circuits THREE PHASE CIRCUITS THREE-PHASE ADVANTAGES 1. The horsepower rating of three-phase motors and the kva rating of three-phase transformers are 150% greater than single-phase motors
2. A conductor of length 2m moves at 4m/s at 30 to a uniform magnetic field of 0.1T. Which one of the following gives the e.m.f. generated?
 Extra Questions - 2 1. A straight length of wire moves through a uniform magnetic field. The e.m.f. produced across the ends of the wire will be maximum if it moves: a) along the lines of magnetic flux
Extra Questions - 2 1. A straight length of wire moves through a uniform magnetic field. The e.m.f. produced across the ends of the wire will be maximum if it moves: a) along the lines of magnetic flux
The Critical Length of a Transmission Line
 Page 1 of 9 The Critical Length of a Transmission Line Dr. Eric Bogatin President, Bogatin Enterprises Oct 1, 2004 Abstract A transmission line is always a transmission line. However, if it is physically
Page 1 of 9 The Critical Length of a Transmission Line Dr. Eric Bogatin President, Bogatin Enterprises Oct 1, 2004 Abstract A transmission line is always a transmission line. However, if it is physically
EECC694 - Shaaban. Transmission Channel
 The Physical Layer: Data Transmission Basics Encode data as energy at the data (information) source and transmit the encoded energy using transmitter hardware: Possible Energy Forms: Electrical, light,
The Physical Layer: Data Transmission Basics Encode data as energy at the data (information) source and transmit the encoded energy using transmitter hardware: Possible Energy Forms: Electrical, light,
LBC 14x0/x0 MK Volume Controls and LBC 1430/10 Program Selector
 Commnications Systems LBC 14x0/x0 MK Volme Controls and LBC 1430/10 Program Selector LBC 14x0/x0 MK Volme Controls and LBC 1430/10 Program Selector www.boschsecrity.com 12 W, 36 W and 100 W versions Available
Commnications Systems LBC 14x0/x0 MK Volme Controls and LBC 1430/10 Program Selector LBC 14x0/x0 MK Volme Controls and LBC 1430/10 Program Selector www.boschsecrity.com 12 W, 36 W and 100 W versions Available
FEATURES APPLICATIO S. LTC1150 ±15V Zero-Drift Operational Amplifier with Internal Capacitors DESCRIPTIO TYPICAL APPLICATIO
 FEATRES High Voltage Operation: ±1V No External Components Required Maximum Offset Voltage: 1µV Maximum Offset Voltage Drift:.5µV/ C Low Noise 1.8µV P-P (.1Hz to 1Hz) Minimum Voltage Gain: 15dB Minimum
FEATRES High Voltage Operation: ±1V No External Components Required Maximum Offset Voltage: 1µV Maximum Offset Voltage Drift:.5µV/ C Low Noise 1.8µV P-P (.1Hz to 1Hz) Minimum Voltage Gain: 15dB Minimum
12. Transformers, Impedance Matching and Maximum Power Transfer
 1 1. Transformers, Impedance Matching and Maximum Power Transfer Introduction The transformer is a device that takes AC at one voltage and transforms it into another voltage either higher or lower than
1 1. Transformers, Impedance Matching and Maximum Power Transfer Introduction The transformer is a device that takes AC at one voltage and transforms it into another voltage either higher or lower than
Chapter 3. 2. Consider an economy described by the following equations: Y = 5,000 G = 1,000
 Chapter C evel Qestions. Imagine that the prodction of fishing lres is governed by the prodction fnction: y.7 where y represents the nmber of lres created per hor and represents the nmber of workers employed
Chapter C evel Qestions. Imagine that the prodction of fishing lres is governed by the prodction fnction: y.7 where y represents the nmber of lres created per hor and represents the nmber of workers employed
1. Oscilloscope is basically a graph-displaying device-it draws a graph of an electrical signal.
 CHAPTER 3: OSCILLOSCOPE AND SIGNAL GENERATOR 3.1 Introduction to oscilloscope 1. Oscilloscope is basically a graph-displaying device-it draws a graph of an electrical signal. 2. The graph show signal change
CHAPTER 3: OSCILLOSCOPE AND SIGNAL GENERATOR 3.1 Introduction to oscilloscope 1. Oscilloscope is basically a graph-displaying device-it draws a graph of an electrical signal. 2. The graph show signal change
High Voltage Transient Analysis
 High Voltage Transient Analysis 4. Surges on Transmission Lines Due to a variety of reasons, such as a direct stroke of lightning on the line, or by indirect strokes, or by switching operations or by faults,
High Voltage Transient Analysis 4. Surges on Transmission Lines Due to a variety of reasons, such as a direct stroke of lightning on the line, or by indirect strokes, or by switching operations or by faults,
EXPERIMENT NUMBER 8 CAPACITOR CURRENT-VOLTAGE RELATIONSHIP
 1 EXPERIMENT NUMBER 8 CAPACITOR CURRENT-VOLTAGE RELATIONSHIP Purpose: To demonstrate the relationship between the voltage and current of a capacitor. Theory: A capacitor is a linear circuit element whose
1 EXPERIMENT NUMBER 8 CAPACITOR CURRENT-VOLTAGE RELATIONSHIP Purpose: To demonstrate the relationship between the voltage and current of a capacitor. Theory: A capacitor is a linear circuit element whose
2/20/2009 3 Transmission Lines and Waveguides.doc 1/3. and Waveguides. Transmission Line A two conductor structure that can support a TEM wave.
 2/20/2009 3 Transmission Lines and Waveguides.doc 1/3 Chapter 3 Transmission Lines and Waveguides First, some definitions: Transmission Line A two conductor structure that can support a TEM wave. Waveguide
2/20/2009 3 Transmission Lines and Waveguides.doc 1/3 Chapter 3 Transmission Lines and Waveguides First, some definitions: Transmission Line A two conductor structure that can support a TEM wave. Waveguide
Transmission Lines in Communication Systems FACET
 Computer-Based Electronics Training System Transmission Lines in Communication Systems FACET 36970- Order no.: 36970-00 First Edition Revision level: 02/2015 By the staff of Festo Didactic Festo Didactic
Computer-Based Electronics Training System Transmission Lines in Communication Systems FACET 36970- Order no.: 36970-00 First Edition Revision level: 02/2015 By the staff of Festo Didactic Festo Didactic
Reading: HH Sections 4.11 4.13, 4.19 4.20 (pgs. 189-212, 222 224)
 6 OP AMPS II 6 Op Amps II In the previous lab, you explored several applications of op amps. In this exercise, you will look at some of their limitations. You will also examine the op amp integrator and
6 OP AMPS II 6 Op Amps II In the previous lab, you explored several applications of op amps. In this exercise, you will look at some of their limitations. You will also examine the op amp integrator and
Understanding the Fundamental Principles of Vector Network Analysis. Application Note 1287-1. Table of Contents. Page
 Understanding the Fundamental Principles of Vector Network Analysis Application Note 1287-1 Table of Contents Page Introduction 2 Measurements in Communications Systems 2 Importance of Vector Measurements
Understanding the Fundamental Principles of Vector Network Analysis Application Note 1287-1 Table of Contents Page Introduction 2 Measurements in Communications Systems 2 Importance of Vector Measurements
Chapter 1. LAN Design
 Chapter 1 LAN Design CCNA3-1 Chapter 1 Note for Instrctors These presentations are the reslt of a collaboration among the instrctors at St. Clair College in Windsor, Ontario. Thanks mst go ot to Rick Graziani
Chapter 1 LAN Design CCNA3-1 Chapter 1 Note for Instrctors These presentations are the reslt of a collaboration among the instrctors at St. Clair College in Windsor, Ontario. Thanks mst go ot to Rick Graziani
What Does Communication (or Telecommunication) Mean?
 What Does Communication (or Telecommunication) Mean? The term communication (or telecommunication) means the transfer of some form of information from one place (known as the source of information) to
What Does Communication (or Telecommunication) Mean? The term communication (or telecommunication) means the transfer of some form of information from one place (known as the source of information) to
Interconnection Network of OTA-based FPAA
 Chapter S Interconnection Network of OTA-based FPAA 5.1 Introduction Aside from CAB components, a number of different interconnect structures have been proposed for FPAAs. The choice of an intercmmcclion
Chapter S Interconnection Network of OTA-based FPAA 5.1 Introduction Aside from CAB components, a number of different interconnect structures have been proposed for FPAAs. The choice of an intercmmcclion
BASIC ELECTRONICS AC CIRCUIT ANALYSIS. December 2011
 AM 5-202 BASIC ELECTRONICS AC CIRCUIT ANALYSIS December 2011 DISTRIBUTION RESTRICTION: Approved for Pubic Release. Distribution is unlimited. DEPARTMENT OF THE ARMY MILITARY AUXILIARY RADIO SYSTEM FORT
AM 5-202 BASIC ELECTRONICS AC CIRCUIT ANALYSIS December 2011 DISTRIBUTION RESTRICTION: Approved for Pubic Release. Distribution is unlimited. DEPARTMENT OF THE ARMY MILITARY AUXILIARY RADIO SYSTEM FORT
)454 6 %LECTRICAL CHARACTERISTICS FOR BALANCED DOUBLECURRENT INTERCHANGE CIRCUITS OPERATING AT DATA SIGNALLING RATES UP TO -BITS
 INTERNATIONAL TELECOMMUNICATION UNION )454 6 TELECOMMUNICATION STANDARDIZATION SECTOR OF ITU (10/96) SERIES V: DATA COMMUNICATION OVER THE TELEPHONE NETWORK Interfaces and voiceband modems %LECTRICAL CHARACTERISTICS
INTERNATIONAL TELECOMMUNICATION UNION )454 6 TELECOMMUNICATION STANDARDIZATION SECTOR OF ITU (10/96) SERIES V: DATA COMMUNICATION OVER THE TELEPHONE NETWORK Interfaces and voiceband modems %LECTRICAL CHARACTERISTICS
Current Probes, More Useful Than You Think
 Current Probes, More Useful Than You Think Training and design help in most areas of Electrical Engineering Copyright 1998 Institute of Electrical and Electronics Engineers. Reprinted from the IEEE 1998
Current Probes, More Useful Than You Think Training and design help in most areas of Electrical Engineering Copyright 1998 Institute of Electrical and Electronics Engineers. Reprinted from the IEEE 1998
2 2 Matrices. Scalar multiplication for matrices. A2 2matrix(pronounced 2-by-2matrix )isasquareblockof4numbers. For example,
 2 2 Matrices A2 2matrix(prononced 2-by-2matrix )isasqareblockofnmbers. For example, is a 2 2matrix. It scalleda2 2 matrix becase it has 2 rows 2 colmns. The for nmbers in a 2 2matrixarecalledtheentries
2 2 Matrices A2 2matrix(prononced 2-by-2matrix )isasqareblockofnmbers. For example, is a 2 2matrix. It scalleda2 2 matrix becase it has 2 rows 2 colmns. The for nmbers in a 2 2matrixarecalledtheentries
GENERAL POWER SYSTEM WIRING PRACTICES APPLIED TO TECNADYNE DC BRUSHLESS MOTORS
 1/5/2006 Page 1 of 6 GENERAL POWER SYSTEM WIRING PRACTICES APPLIED TO TECNADYNE DC BRUSHLESS MOTORS 1. Introduction The purpose of this application note is to describe some common connection and filtering
1/5/2006 Page 1 of 6 GENERAL POWER SYSTEM WIRING PRACTICES APPLIED TO TECNADYNE DC BRUSHLESS MOTORS 1. Introduction The purpose of this application note is to describe some common connection and filtering
Transmission Line Terminations It s The End That Counts!
 In previous articles 1 I have pointed out that signals propagating down a trace reflect off the far end and travel back toward the source. These reflections can cause noise, and therefore signal integrity
In previous articles 1 I have pointed out that signals propagating down a trace reflect off the far end and travel back toward the source. These reflections can cause noise, and therefore signal integrity
Coaxial Cable Products Guide. Connectivity for Business-Critical Continuity
 Coaxial Cable Products Guide Connectivity for Business-Critical Continuity The Difference Starts With The Cable BULK CABLES SLA Series Lowest loss cable available to 18 GHz, best choice for critical applications
Coaxial Cable Products Guide Connectivity for Business-Critical Continuity The Difference Starts With The Cable BULK CABLES SLA Series Lowest loss cable available to 18 GHz, best choice for critical applications
1. The Slotted Line. ECE 584 Microwave Engineering Laboratory Experiments. Introduction:
 ECE 584 Microwave Engineering Laboratory Experiments 1. The Slotted Line Introduction: In this experiment we will use a waveguide slotted line to study the basic behavior of standing waves and to measure
ECE 584 Microwave Engineering Laboratory Experiments 1. The Slotted Line Introduction: In this experiment we will use a waveguide slotted line to study the basic behavior of standing waves and to measure
Features. Applications. Transmitter. Receiver. General Description MINIATURE MODULE. QM MODULATION OPTIMAL RANGE 1000m
 Features MINIATURE MODULE QM MODULATION OPTIMAL RANGE 1000m 433.05 434.79 ISM BAND 34 CHANNELS AVAILABLE SINGLE SUPPLY VOLTAGE Applications IN VEHICLE TELEMETRY SYSTEMS WIRELESS NETWORKING DOMESTIC AND
Features MINIATURE MODULE QM MODULATION OPTIMAL RANGE 1000m 433.05 434.79 ISM BAND 34 CHANNELS AVAILABLE SINGLE SUPPLY VOLTAGE Applications IN VEHICLE TELEMETRY SYSTEMS WIRELESS NETWORKING DOMESTIC AND
Ver 3537 E1.1 Analysis of Circuits (2014) E1.1 Circuit Analysis. Problem Sheet 1 (Lectures 1 & 2)
 Ver 3537 E. Analysis of Circuits () Key: [A]= easy... [E]=hard E. Circuit Analysis Problem Sheet (Lectures & ). [A] One of the following circuits is a series circuit and the other is a parallel circuit.
Ver 3537 E. Analysis of Circuits () Key: [A]= easy... [E]=hard E. Circuit Analysis Problem Sheet (Lectures & ). [A] One of the following circuits is a series circuit and the other is a parallel circuit.
What is Characteristic Impedance?
 Dr. Eric Bogatin 26235 W 110 th Terr. Olathe, KS 66061 Voice: 913-393-1305 Fax: 913-393-1306 [email protected] www.bogatinenterprises.com Training for Signal Integrity and Interconnect Design Reprinted with
Dr. Eric Bogatin 26235 W 110 th Terr. Olathe, KS 66061 Voice: 913-393-1305 Fax: 913-393-1306 [email protected] www.bogatinenterprises.com Training for Signal Integrity and Interconnect Design Reprinted with
IFI5481: RF Circuits, Theory and Design
 IFI5481: RF Circuits, Theory and Design Lecturer: Prof. Tor A. Fjeldly, UiO og NTNU/UNIK [[email protected]] Assistant: Malihe Zarre Dooghabadi [[email protected]] Syllabus: Lectured material and examples,
IFI5481: RF Circuits, Theory and Design Lecturer: Prof. Tor A. Fjeldly, UiO og NTNU/UNIK [[email protected]] Assistant: Malihe Zarre Dooghabadi [[email protected]] Syllabus: Lectured material and examples,
Communication, Signal & Data Cables
 Communication, Signal & Data Cables Used for indoor installation and interconnection of transmission, telephone, telegraph and electronic equipment as well as media equipments www.alfanar.com Communication
Communication, Signal & Data Cables Used for indoor installation and interconnection of transmission, telephone, telegraph and electronic equipment as well as media equipments www.alfanar.com Communication
Properties of electrical signals
 DC Voltage Component (Average voltage) Properties of electrical signals v(t) = V DC + v ac (t) V DC is the voltage value displayed on a DC voltmeter Triangular waveform DC component Half-wave rectifier
DC Voltage Component (Average voltage) Properties of electrical signals v(t) = V DC + v ac (t) V DC is the voltage value displayed on a DC voltmeter Triangular waveform DC component Half-wave rectifier
