UNIT I LESSON - 1 CONTENTS
|
|
|
- Terence Long
- 10 years ago
- Views:
Transcription
1 Page UNIT I LESSON - CONTENTS. Aims and Ojectives.. Convex and Concave Lenses.a. Reraction through a thin lens.. Equivalent Focal Length o Two Thin Lenses Separated y a distance.. Aerrations in Lenses.. Introduction... Spherical aerration:...chromatic Aerration in a Lens:..3. Condition or Achromatism o Two Thin Lenses placed in contact..4.condition or Achromatism o Two Thin Lenses separated y a inite distance.3.coma.3..astigmatism and its minimization.3..4 Let us sum up.5 Check your Progress.6 Lesson end Activities.7 Points or Discussion.8 Reerences. Aims and Ojectives From this lesson you will understand aout the principle employed in convex and concave lenses and study aout dierent types o deects and to minimize them... Convex and Concave Lenses A convex lens is a transparent reracting medium ounded y two spherical suraces. The line joining the centres o curvature o the two suraces is called the principal axis. A section o the lens through its principal axis is called its principal section.
2 Page Principal Focus and Focal Planes AB represents the principal axis o a lens (Fig. ). Fig First Principal Focus (F ) : It is that point on the principal axis o the lens, the rays starting rom which (convex lens) or appear to converge at which (concave lens) ecome parallel to principal axis ater reraction rom the lens. The plane passing through F and perpendicular to the principal axis is called irst ocal plane. Second Principal Focus (F ) :Second principal ocus is that point on the principal axis at which the rays parallel to principal axis converge (convex lens) or appear to diverge (concave lens) ater reraction rom the lens. The plan passing through F, and normal to the principal axis is called the second ocal plane. The points F, and F, are called ocal points.
3 Page 3.a. Reraction through a thin lens Consider a thin lens o reractive index n placed in a medium o reractive index n l (Fig...) Let R, and R e the radii o the irst and second suraces respectively. Consider a point oject O placed on the principal axis. Let I' e the position o the image ormed y reraction at the irst surace. Fig.. Let V e the distance o image I' and u the distance o the oject rom the irst surace. Then ' R n n u n V n () Now I' acts as the virtual oject or the second surace. The inal image I is ormed at a distance V rom the second surace. Since the rays now pass rom a medium o reractive index n into a medium o reractive index n we have R n n R n n V n V n () Adding (I) and (), R R n n u n V n Dividing throughout y n R R n u V or R R n n u V (3) here n n n is the reractive index o the material o the lens w.r.t air.
4 Page 4 First and second principal Foci: The irst principal ocus (F ) is the position o an oject on the principal axis or which the image is at ininity. The distance o the irst ocus rom the lens is the irst ocal length ƒ (Fig..a). I V =, then u= ƒ and sustituting in Eq. (3), we get, n ( n ) R R R R (4) The second principal ocus (F ) is the position o the image on the principal axis or which the oject is al ininity (u =). The distance o the second ocus rom the lens is the second ocal length, ƒ [Fig..]. V = ƒ, when u =. Sustituting in Eq. (3), n ( n ) R R R R (5) Thus the irst and second ocal lengths o a lens are numerically equal when the lens is placed in a uniorm medium. The general convention is to call the second principal ocal length as the ocal length ƒ o the lens. u n R R This ormula is known as Lens makers ormula. (6) Power o a lens: Power o a lens is its aility to converge or diverge the rays o light. The power o a lens is measured y the reciprocal o its ocal length, P = l/ƒ. The unit o power is dioptre. One dioptre is the power o a lens whose ocal length is metre. Convex lenses have positive power and concave lenses, negative power. Focal length o comination o two thin lenses in contact: When two thin lenses o ocal lengths ƒ, and ƒ are placed in contact with each other, then the ocal length o the comination is given y Power o the comination = P = P + P.. Equivalent Focal Length o Two Thin Lenses Separated y a distance: Let L, and L, e two thin lenses o ocal lengths ƒ, and ƒ placed in air coaxially a distance a apart. Consider a ray PA incident on L parallel to the axis at a height h, aove the axis
5 Page 5 [Fig..]. This ray ater reraction through the irst lens is directed towards D which is the second principal ocus o L l. Fig.. Then, deviation produced y irst lens = h The emergent ray rom the irst lens strikes the lens L, at a height h,. The lens L deviates it urther through an angle. Finally the ray meets the axis at F which is the second principal ocus o the lens system. Deviation produced y the second lens = h PA and,f B are produced to cut at E. Then a single convex lens placed in the position E P and having ocal length P F is equivalent to the leas system. Thus P F = ƒ is the equivalent local length. Then, Deviation produced y the equivalent lens = h Now = + h h () h Now ah a h O B OK BK h a h h h Sustituting the value o h in Eq(), h h a
6 Page 6 or a () a (3) Here, a is known as the optical separation or optical interval etween the two lenses. Let us ind the position o the equivalent lens, i.e., the distance O P. The triangles BF,O, and E F P are similar. a h h a P F h h F oro P F F O h h Now, a a F O F P P O a a a a Let O P =-(P lies to the let o the lens L ). a a a (4) Similarly, consider a ray parallel to the axis incident rom the right hand side [Fig..(c)]. Then we can ind the position o F, the point where the ray intersects the principal axis ater reraction through the lens system. E P is the irst principal plane. P is the irst principal point o the lens system. The distance o the irst principal point rom the irst lens is =O P. Fig.(c)
7 Page 7 O P a a a The irst principal ocus F, is situated at a distance ƒ towards the let o the point P. I P and P are the powers o the component lenses and P the power o the comination, then, P=P +P -ap P. ABERRATIONS IN LENSES:.. Introduction: The deviations in the size, shape, position and colour in the actual images produced y a lens in comparison to the oject are called aerrations produced y a lens. Chromatic aerrations are distortions o the image due to the dispersion o light in the lenses o an optical system when white light is used. The deect o coloured image ormed y a lens with white light is called chromatic aerration. I monochromatic light is used, then such deects are automatically removed. Besides these deects, there are deects which are present even when monochromatic light is used. Such deects are called monochromatic aerrations. These aerrations are the result o (i) the large aperture o the optical system, (ii) the large angle sutended y the rays with the principal axis and (iii) the large size o the oject. As a result o these aerrations, (i) a point is not imaged as a point, (ii) a plane is not imaged as a plane and (iii) equidistant points are not imaged as equidistant points. Following are the monochromatic aerrations: (i) Spherical aerration, (ii) Astigmatism, (iii) Coma, (iv) Curvature o ield and (v) Distortion. Spherical Aerration in a Lens : This aerration is due to large aperture o the lenses. The lens o large aperture may e thought to e made up o lanes. Fig...
8 Page 8 The marginal and paraxial rays orm the images at dierent places. Fig..3. shows that a monochromatic point source S on the axis is imaged as S P, and S m. Here, S P, and S m are the images ormed y marginal and paraxial rays respectively. Thus the point oject is not imaged as a point. Similarly the ocus o marginal and paraxial rays do not coincide. The distance S P S m on the axis measures longitudinal spherical aerration.... Spherical aerration: The ailure o a lens to orm a point image o a point oject on the axis is called spherical aerration. Fig...(a) Fig...() For rays parallel to principal axis, the distance etween the oci o marginal and paraxial rays gives the extent o longitudinal spherical aerration. In Fig...(a) Fp and Fm are the ocii or the paraxial and the marginal rays respectively. Spherical aerration o a convergent lens is taken to e positive as the distance (ƒp ƒm), measured along the axis. The spherical aerration o a diverging lens is negative (Fig... ). Methods o minimizing Spherical Aerration:
9 Page 9 The ollowing methods are used to reduce spherical aerration. (i) By using stops: By using stops, we can reduce the lens aperture. We can use either paraxial or marginal rays. Here, circular discs, called the stops, are used to cut o the unwanted rays. It eliminates marginal rays or paraxial rays. But the use o stops reduce the intensity o the image and the resolving power o the instrument. (ii) By using the two lenses separated y a distance: When two convex lenses separated y a inite distance are used the spherical aerration is minimum when the distance etween the lenses is equal to the dierence in their ocal lengths. In this arrangement, the total deviation is equally shared y the two lenses, Hence the spherical aerration is minimum. (iii)by using a crossed lens: The radii o curvature R, R o a thin lens satisy the ollowing relation: n R R It, there ore, shows that, spherical aerration depends upon (i) the reractive index o the lens medium (n) and (ii) the shape actor, which is determined y the ratio =R /R. I the reractive index o material o the lens is.5, the spherical aerration will e minimum when=r /R = - /6, A convex lens whose radii o curvatures ear the said ratio is called as a crossed lens. It is essential to divide the deviation on two suraces equally. The axial and marginal rays o light come to ocus with minimum o spherical aerration. Condition or Minimum Spherical Aerration o Two Thin Lenses- Separated y a distance: Spherical aerration may e minimized y using, two Plano-Convex lenses separated y a distance equal to the dierence in their ocal lengths. Let two plano convex lenses L and L o ocal lengths ƒ and ƒ e placed coaxially separated y a distance a (Fig..3.(c)). Consider a ray OA, parallel to principal axis, incident on lens L at height h aove the principal axis.
10 Page Fig...(c) The deviation produced y the lens L is given y, h () The reracted ray AB is incident at B at a height h rom the axis on lens L. The deviation produced y the lens L is given y, h () The ray AB produced meets the axis at F which is the principal ocus o lens L. Hence CF =ƒ. For minimum spherical aerration, the deviation produced y oth the lenses should e equal, i.e., = h h h or h (3) From similar triangles ACF and BDF we get AC BD CF DF CF h or CF CD h a (4) Comparing Eqs (3) and (4), we get
11 Page or a a This is the condition or minimum spherical aerration or two lenses separated y a distance...3.chromatic Aerration in a Lens: The ocal length o a lens is given y n R R Since n changes with the colour o light, ƒ must e dierent or dierent colours. This change o ocal length with colour is responsile or chromatic aerration. It is classiied into two types: (a) Longitudinal chromatic aerration, () Lateral chromatic aerration. a) Longitudinal chromatic aerration: A eam o white light is incident on a convex lens parallel to the principal axis (Fig..3.). The dispersion o colours takes place due to prismatic action o the lens. Violet is deviated most and red the least. Red rays are rought to ocus at a point arther than the violet rays. Evidently ƒ r > ƒ v. The dierence ƒ r - ƒ v is a measure o the axial chromatic aerration o a lens or parallel rays. Fig...3 Expression or Longitudinal chromatic aerration The ocal length o a lens is given y n R R Let ƒ v, ƒ r and ƒ y e the ocal lengths o the lens or violet, red and yellow colours respectively. Also let n v, n r,and n y, e the respective reractive indices. Then
12 Page R R n v v..() R R n r r () R R n y y (3) sutracting Eq.() rom Eq.(), R R n n r v r v or R R n n n n y y r v r v v r Now y r v n n n =dispersive power o the material o the lens; y r v y v r (4) () Lateral chromatic aerration: Fig...3(a) shows a convex lens and an oject AB placed in ront o the lens. The lens orms the image o white oject AB as B v A v and B r A r in violet and red colours respectively. The images o other colours lie in etween the two. Evidently, the size o red image is greater than the size o violet image (B r A r > B v A v ). The dierence (B r A r - B v A v ) is a measure o lateral or transverse chromatic aerration. Fig..3(a)
13 Page 3 Chromatic aerration is eliminated y : (i) keeping two lenses in contact with each other and (ii) keeping two lenses out o contact. Achromatic Comination o Lenses: When two or more lenses are comined together in such a way that the comination is ree rom chromatic aerration, then such a comination is called achromatic comination o lenses. The minimization or removal o chromatic aerration is called achromatisation. Chromatic aerration cannot e removed completely. Usually, achromatism is achieved or two prominent colours...4. Condition or Achromatism o Two Thin Lenses placed in contact : The ocal length o a thin lens is given y n R R () Here, ƒ is the ocal length, n the reractive index, R and R are radii o curvature o the two suraces o the lens. Now we know that ƒvaries with n. Thereore, dierentiating Eq. (), d dn R R dn dn n n R R n d dn or n Here ω is the dispersive power o the material o the lens. () Let ƒ and ƒ e the ocal lengths o the two lenses in contact and ω and ω w their dispersive powers. I ƒ is the ocal length o the comination, then
14 Page 4 Dierentiating Eq.(3) d d d d d ut and d d d (3) I the comination is to e achromatic, ƒ should e the same or all colours or dƒ=. or.(4) In order, thereore, to design an achromatic doulet o ocal length ƒ, the ocal lengths o the constituent lenses must satisy Eq. (3) and Eq. (4). Knowing ω, ω and ƒ, the magnitudes o ƒ and ƒ can e ound y solving Eqs. (3) and (4). Since ω, and ω are positive, ƒ and ƒ must e o opposite signs. That is, i one lens is convex, the other should e concave. Since the achromatic doulet is to ehave as a converging lens, ƒ must e less than ƒ. Consequently, ω, < ω. The converging lens is, thereore, made o crown glass (smaller dispersive power) and the diverging lens, o lint glass (larger dispersive power).( Fig...4) Fig...4.
15 Page Condition or Achromatism o Two Thin Lenses separated y a inite distance: Let us consider two convex lenses o ocal lengths ƒ,ƒ separated y a distance a (Fig...5). Fig...5 The ocal length o the comination is a () Dierentiating Eq.(), d d a d d d Now d and d a d Since oth the lenses are or the same material ω =ω a d For an achromatic comination, the ocal length ƒ should not change with colour. :.dƒ=. Hence, a or a
16 Page 6 a () That is, the distance etween the two coaxial lenses must e equal to hal the sum o their ocal lengths..3.coma : When a lens is corrected or spherical aerration, it orms a point image o a point oject situated on the axis. But i the point oject is situated o the principal axis, the lens, even corrected or spherical aerration, orms a comet-like image in place o point image. This deect in the image is called coma. Consider an o axis point A in the oject (Fig..3) The rays leaving A and passing through the dierent zones o the lens such as,,33 are rought to ocus at dierent points B,B,B 3, gradually nearer to the lens. The radius o these circles go on increasing with increase in radius o zone. Thus the resultant image is comet like. Fig..3. Removal o coma. The comatic aerration may e eliminated as ollows:. By using a stop eore the lens and so making the outer zones ineective.. By properly choosing the radii o curvature or the lens suraces. For example, or an oject situated at ininity, the comatic aerration may e minimized y taking a lens o n =.5 and R k R 9 3. Ae sine condition. Ae showed that coma may e eliminated i each zone o the lens satisies the Ae sine condition
17 Page 7 n h sinθ = n h sin θ, Here, n and n are reractive indices o the oject and image regions respectively. h and h are the heights o the oject and the image. θ and θ are the angles which the incident and the conjugate emergent rays make with the axis. (Fig.l.4a) Fig.3a I this condition is satisied, the lateral magniication h n sin h n sin will e same or all the rays o light, irrespective o the angles θ and θ. Thereore, coma will e eliminated..3..astigmatism and its minimization: Consider a point B situated o the axis in a line oject which is vertically elow the axis o the lens. When the cone o rays rom B alls on ull circumerence o the lens, then ater reraction all the rays do not meet at a single point ( Fig.4.) a) The rays lying in the vertical plane BMN (called meridional plane) orm the image as a horizontal line P. () The rays lying in the horizontal plane BRS (called sagittal plane) orm the image as a vertical line S. The circle o least conusion C lies in etween P and S. The est image or the oject point is otained here. This deect is called astigmatism. The distance etween P and S is a measure o astigmatism and is called the astigmatic dierence.
18 Page 8 Fig.3. The astigmatic dierence in the concave lens is in opposite direction to that produced y a convex lens. Hence astigmatism may e reduced y suitale comination o concave and convex lenses. Such a comination o lenses is called anastigmatic comination. It is used in the construction o ojective lens in a photographic camera..4 Let us sum up In this lesson you learned aout the principle employed in convex and concave lenses and studied aout the dierent types o deects and how to minimize them..5 Check your Progress ) What is meant y principal ocus and ocal planes in convex and concave lenses ) Deine spherical and chromatic aerrations in lenses 3) What is ae sine condition in a convex lens 4) What is coma and astigmatism
19 Page 9.6 Lesson end Activities ) An achromatic telescope ojective o.5 m ocal length consists o two thin layers in contact with each other and their dispersive power are.5 and.7 respectively. Calculate their ocal lengths. ) Two thin converging lenses o ocal lengths, cm and cm are separated y a distance a. Calculate the eective ocal length o the comination..7 Points or Discussion. What do you mean y spherical and chromatic aerration o a lens? Explain how they are caused. How would you correct chromatic aerration in the case o lens system in contact?. Otain an expression or the dispersive power o a lens in the condition or or achromatism o a comination o two thin coaxial lenses (i) when in contact and (ii) when separated y a dierence..8 Reerences ) Optics and spectroscopy - A. Murugesan ) Geometrical optics Brijlal and Suramanyam
20 Page LESSON CONTENTS. Aims and Ojectives. Eye-pieces.. Hygen s Eye-piece.. Ramsden s Eye-piece..3 Ae s Homogeneous Oil Immersion Ojective. Dispersion y A Prism.. Reraction through A Prism.. Angular and Chromatic Dispersions..3 Cauchy s Dispersion Formula..4 Dispersive Power.3 Rainow.3. Primary Rainow.3. Secondary Rainow.3.3 General Discussion.4 Let us Sum UP.5 Check your Progress.6 Lesson end Activities.7 Points or Discussion.8 Reerences. Aims and Ojectives From this lesson you will learn aout the usage o convex and concave lenses in dierent optical instruments as eye pieces. Also you will study aout the light relection through a prism and also aout the angular and chromatic dispersions. Also you will learn aout the ormation o dierent types o rainows.
21 Page. EYE-PIECES : An eye-piece is a comination o lenses designed to magniy the image already ormed y the ojective o a telescope and microscope. An eyepiece consists o two planoconvex lenses. F is called the ield lens and E the eye lens (Fig..5). The ield lens has large aperture to increase the ield o view. The eye lens mainly magniies the image. To reduce the spherical aerration, the lenses taken are plano-convex lenses. Further the ocal lengths o the two lenses and their separation are selected in such a way as to minimize the chromatic and spherical aerrations. A comination o lenses is used in an eyepiece o a simple lens magniier or the ollowing reasons: (i) The ield o view is enlarged y using two or more lenses. (ii) The aerrations can e minimized. Fig Huygens' Eye-piece: Fig... Construction: It consists o two plano- con vex lenses o ocal lengths 3ƒ(ield lens) and ƒ (eye lens), placed a distance ƒ apart [Fig..). They are arranged with their convex aces towards the incident rays. The eye-piece satisies the ollowing conditions o minimum spherical and chromatic aerrations. (i) The distance etween the two lenses or minimum spherical aerration is given y a = ƒ l ƒ. In Huygen's eyepiece, a= 3 ƒ - ƒ = ƒ. Hence this eye-piece satisies the condition o minimum spherical aerration.
22 Page (ii) For chromatic aerration to e minimum a. In Huygens' eyepiece, 3 a aerration.. Hence this eyepiece satisies the condition o minimum chromatic Fig.. Working: An eye-piece orms the inal image at ininity. Thus the ield lens orms the image I the irst Field Lens ocal plane o eye lens, i.e., at a distance ƒ to the let o eye-lens. Now the distance etween the ield lens and eye-lens is ƒ. Thereore, the image I lies at a distance to the right o ield lens. The image I ormed y the ojective o microscope or telescope acts as the virtual oject or the ield lens. Thus we treat I as the virtual oject or the ield lens, and I as the image o I due to it (Fig...a) or ν=ƒ., F=3ƒ, u=? We have u F or u 3 u 3 i.e. I should e ormed at a distance 3/ ƒ rom the ield lens. Thereore the rays coming rom the ojective which converge towards I are ocussed y the ield lens at I. The rays starting rom I emerge rom the eye-lens as a parallel eam.
23 Page 3 Fig...(a) Cardinal Points o Huygens Eyepiece The equivalent ocal length F o this eyepiece is a F F The second principal point is at a distance rom the eye lens. a a 3 The irst principal point is a distance α rom the ield lens. a a The position o the principal points P and P and the principal oci F and F are shown in Fig... Since the system is in air, the nodal points coincide with the principal points.
24 Page 4 Fig......Ramsden's Eyepiece Construction: It consists o two plano convex lenses each o ocal length ƒ. The distance etween them is (/3) ƒ [Fig...]. For achromatism, the distance etween the two lenses should e a. But here a =(/3)ƒ Fig... Thus in this eyepiece the chromatic aerration is only partly reduced. Similarly, or minimum spherical aerration, a. Hence the spherical aerration is not at all reduced. This is a demerit o this eyepiece. Working: I is the image ormed y the ojective o the microscope or telescope. It serves as an oject or eyepiece. The eyepiece is adjusted such that the image I ormed
25 Page 5 y the ield lens lies in the irst ocal plane o the eyelens [Fig...a]. Then the eyepiece orms the inal image at ininity. Since the ocal length o the eye lens is ƒ and a = (/3) ƒ, I is at a distance ƒ/3 rom the ield lens. Now, the image I due to ojective serves as the oject or ield lens. I is the image o I due to ield lens. Or,,, 3 F V to ind u we have u or u or F u V u Fig...(a) Thus the eyepiece its so adjusted that the image (I ) ormed y the ojective o telescope or microscope lies at a distance ƒ/4 towards the let o ield lens. The crosswire is placed at I. I serves as the oject or ield lens and its image is ormed at I. Cardinal points: The ocal length F o the equivalent lens is F a F 3 3 a a
26 Page 6 a 3 3 a The positions o the principal points P l and P and the principal oci F and F are shown in Fig...(). Since the system is in air, the nodal points coincide with the principal points. Fig...(). Distance o the irst principal ocus rom the ield lens o the eyepiece = F L = F P - = 3ƒ/4 - ƒ/=ƒ/4. Similarly the distance o the second principal ocus rom the eye lens is L F = P F - = 3ƒ/4 - ƒ/=ƒ/4. Comparison o Eyepieces Huygens' eyepiece Ramsden's eyepiece The image o the oject ormed y the ojective alls in etween the two lenses. Thereore, no cross wires can e used. For this reason. it is called a negative eyepiece. It satisies the condition or minimum spherical aerration. It satisies the condition or achromatism. It is generally used or iological oservations where no measurements are required. The image o the oject ormed y the ojective lies in ront o the ield lens. Thereore, cross wires can e used. For this reason, it is called a positive eyepiece. It does not satisy the condition or minimum spherical aerration. It does not satisy the condition or achromatism. It is used with instruments meant or physical measurements.
27 Page 7..3 ABBE S HOMOGENEOUS OIL IMMERSION OBJECTIVE: In a microscope the ojective is a lens system corrected or chromatic and spherical aerrations. In a microscope designed to magniy 5 times or more, the ojective alone produces a magniication o 5 or more. The microscope ojective is a hemispherical lens L o radius R with its plane surace directed towards the oject A. The plane surace is in contact with cedar wood oil having the same reractive index as that o the lens. Under such conditions no reraction can take place except at the spherical surace o the R lens L. I the oject is placed at A at a distance rom C, then the image ormed at I at a distance R rom C (Fig...3). Then the image will e ree rom spherical aerration. The magniication produced is CI R AC R Fig...3 I the second lens L has the centre o its concave surace at I then the rays emerging rom the hemispherical lens L will all on its lower concave surace normally and will pass undeviated. Then the rays all on the convex surace o L. The radius o the convex surace o the lens L is so selected that I is one o the planatic points. The rays appear to diverge rom J" which is the other a planatic point. This gives added magniication without introducing spherical aerration. This property o the lens L holds true only or rays rom the point A and not or points adjacent to it.
28 Page 8 The oject is immersed in oil such as cedar wood oil and the hemispherical lens with its plane ace is also immersed in the oil. This is known as Ae's homogeneous oil immersion ojective... DISPERSION BY A PRISM A eam o white light, when it passes through a prism is split up into constituent colours and that is called dispersion o light. The image thus ormed on a screen is called a. spectrum. Fig. The spectrum consists o visile and invisile regions. In the visile region the order o the colours is rom violet to red. The principal colours are given y the word VIBGYOR (Violet, Indigo, Blue, Green, Yellow, Orange and Red). The deviation produced or the violet rays o light is maximum and or red rays o light it is minimum. Fig.. represents the dispersion o a white ray o light y a prism in the visile region. The region o the spectrum, o wavelengths shorter than violet is called ultra-violet and the region o wavelengths longer than red is called inra-red. In the present chapter, the discussion relates only to the visile region o the spectrum. The reractive index or the material o a prism (or a lens) is dierent or dierent wavelengths (or colours). The deviation and hence the reractive index is more or lue rays o light than the corresponding values or red rays o light. The deviation and the
29 Page 9 reractive Index o the yellow constituent are taken as the mean values. I the dispersion through a prism does not ollow the order given y VIBGYOR, it is said to e anomalous dispersion....refraction THROUGH A PRISM: The reractive index o the material o a prism is given y A D sin A sin where A is the angle o the prism and D is the angle o minimum deviation. For a small angled prism where and reer to the angle o the prism and the angle minimum deviation (or small values o, the angle is also small and the sines o the angles are taken equal to the angles). Fig....represents the angles o deviation, and, produced in the lue, mean yellow and red rays o light. r
30 Page 3 Fig... The deviations, and r can e written as: ( ) or mean yellow light. ( ) or lue light and r ( r ) or red light The dierence in deviation etween two colors is called angular dispersion. ( ) ( ) r r ( r ) dividing r ( r ) ( ) ( r ) ( ) where and r are the reractive indices or the lue and red rays o light and is the r d reractive index or the mean yellow rays o light. The expression is called the dispersive power o the material o the prism. It is constant or two colours (or wavelengths] chosen end is represented y ω,
31 Page 3 r The reciprocal o ω is called the Constringence. It is also customary to represent, and r where F, D and C which correspond to the Fraunhoer lines (dark lines) in the solar spectrum. The P, D and O lines lie in the lue, yellow and red regions o the spectrum and their wavelengths are 486Å, 5893 Å and 6563 Å respectively. (l Å =l Angstrom unit= -8 cm)....angular AND CHROMATIC DISPERSIONS: The reractive index o the material o a prism is given y A sin A sin where A is the angle o the prism and θ is the angle o minimum deviation. A A sin sin A cos sin A I dθ is the dierence in the angle o deviation etween two spectral lines o wavelengths d λ and λ +d λ, then is called the angular dispersion etween the wavelengths λ and d λ +d λ. Dierentiating equation with respect to on the let hand side and θ y right hand side. dividing y d λ A cos d A sin d
32 Page 3 A cos d d d A sin d A sin d d d A cos d A sin sin d A d d is called chromatic dispersion o the material o the prism. The angular dispersion o d the material o a prism depends on the angle o the prism and reractive index o the material o the prism. Using a spectrometer and the given prism, a graph is drawn etween and λ ( along the Y-axis and λ along the X-axis). The tangent to the curve at d any point measures the chromatic dispersion d Sustituting this value o d in equation (iv), d..3. CAUCHY'S DISPERSION FORMULA: or that particular wavelength. d can he calculated. d When an electromagnetic wave is incident on an atom or a molecule, the periodic electric orce o the wave sets the ound charges into viratory motion. The requency with which these charges are orced to virate is equal to the requency o the wave. The phase o this motion as compared to the impressed electric orce will depend on the impressed requency. It will vary with the dierence etween the impressed requency and the natural requency o the charges. Dispersion can e explained with the concept o secondary waves that are produced y the induced oscillations o the ound charges. When a eam o light propagates through a transparent medium (solid or liquid), the amount o lateral scattering is extremely small. The scattered waves travelling in a lateral direction produce destructive intererence. However, the secondary waves travelling in the same direction as the incident eam superimpose on one another. The resultant viration will depend on the phase dierence
33 Page 33 etween the primary and the secondary, waves. This super-imposition, changes the phase o the primary waves and this is equivalent to a change in the wave velocity. Wave velocity is deined as the speed at which a condition o equal phases is propagated. Hence the variation in phase due to intererence, changes the velocity o the wave through the medium. The phase o the oscillations and hence that o the secondary waves depends upon the impressed requency. It is clear, thereore that the velocity o light in the medium varies with the requency o light. Also reractive index depends upon the velocity o light in the medium. Thereore the reractive index o the medium varies with the requency (wave length) o light. The relative permittivity o the medium in the case o dynamic polarizaility is given y r Ne m X e i i Here N is the numer o electrons per unit volume, e the charge and m the mass o the electron, ε permittivity o ree space, ƒ i oscillator strengths o the sustance, ω i is the angular requency o the electromagnetic spectrum o the sustance, ω is the impressed angular requency. Also i and relative permeaility in majority o sustances that transmit electromagnetic Waves is equal to. r Assuming that there is only one atomic requency ω o where ω < < ω o Ne m using the inomial expansion, Ne m
34 Page 34 m Ne m Ne As, c and c c m Ne mc Ne mc Ne Taking A mc Ne 8 And B mc Ne 4 8 B A Equation represents Cauchy's dispersion ormula. A and B are called Cauchy's constants. The values o A and B depend on the medium. From equation (vi) it is evident that the reractive index o the medium decreases with increase in wavelength o light. I a graph is plotted etween and it will he a straight line. m Ne
35 Page 35 Fig..3 The intercept OP on the Y-axis gives value A. the slope o the line PC gives the value o B (Fig...3) DISPERSIVE POWER According to Cauchy's dispersion ormula, A B Dierentiating equation d B 3 d d is the dispersive power o the medium. Thereore, dispersive power is inversely d proportional to the cue o the wavelength o light. At λ=4 Å (violet) the dispersive power is aout eight times the dispersive power at λ =8 Å (red). It. means the spectral lines are more dispersed near the violet end o the spectrum that at the red end.
36 Page RAINBOW Rainows are ormed y sunlight alling on raindrops. Sometimes two rainows are seen. The common rainow known as the primary rainow is a coloured and, having red on the outside and violet on the inner side. It is ormed due to two reractions and one relection o light alling on raindrops. The other rainow called the secondary rainow is ormed due to two reractions and two relections o the sunlight alling on the raindrops. The rainows are visile only when the altitude o the sun is less than 4. No rainows are seen when the altitude is more than 4. A complete rainow can e seen in an aeroplane lying at high altitudes..3.. PRIMARY RAINBOW Consider a ray o sunlight incident at the point B o a raindrop (Fig..3.). The ray AB ater reraction travels along BC and is relected along CD and inally comes out along DE. The deviation o the ray AB ater reraction is (i-r). The deviation o the ray BC ater reraction at C is (8-r) and the deviation o the ray CD ater reraction at D is (i-r). Thereore, total deviation = ( i-r)+(8-r) 8 i 4r For the angle o deviation to e maximum or minimum, the dierential coeicient o with respect to i must e zero. Fig..3.
37 Page 37 Dierentiating equation (i), or Also, Dierentiating, Equating cosi cosr sin i sin r sin r = sin i dr cos r cos i di or dr di cosi cosr d dr 4 di di d But di dr 4 di dr or di 4 cos or i cos i cos 4 - sin r - sin r r But sin r sin i 4 cos i - sin r 3 cos i - (sin r cos i) cosi 3 Taking reractive index o water or red light =.39, i=59.6 and = =4.8 Taking reractive index o water or violet light =.34,
38 Page 38 i=58.8 and = =4.8 These angles 4.8 and 4.8 are shown in Fig..3.(a) Fig.3.(a) It is to e rememered that sunlight strikes the raindrop at dierent angles o incidence and undergoes dierent deviations. Only those rays produce a rainow which have the angle o incidence corresponding to minimum angles o deviation. All such rays produce concentrated eect o light in the ormation o a rainow. Also, as shown in the diagram, in the primary rainow, the angle o inclination o red light is more on the eye than the violet. Thereore, the outside o the rainow appears red and the inner violet. The other spectral colours lie in etween violet and red in their order..3..secondary RAINBOW In the case o secondary rainow, there are two relections and two reractions. Suppose a ray AB rom the sun strikes the drop at B end ater reraction goes along BC. It is relected at C and D and ater reraction at E, inally emerges along EG (Fig..3.)
39 Page 39 Fig..3. The total deviation =(i-r)+(8-r)=36+i-6 The rays are concentrated around the directions o minimum deviation. Dierentiating with respect to i d dr 6 di di d But di dr 6 di dr or di 3 sin i Also, or sin r = sin i sin r
40 Page 4 Dierentiating, Equating dr cosr cosi di dr di cosi cosr cosi cosr 3 or or 9cos i ( sin r) sin cos r cos 9 r i But sin r = sin i 8cos 9cos i sin i (sin i i cos i) cos i 8 Taking o water or red light=.39, the angle o deviation =36-9.=3.8. The acute angle = 3.8-8= 5.8 (Fig..3.) Taking o water or violet light =.34, the angle o deviation = = The acute angle = = Fig..3.(a)
41 Page 4 In Fig..3.(a), it is shown that the angle o inclination or violet rays is more than or red rays..3.3.general DISCUSSION The primary rainow is ormed y light rom the sun undergoing one internal relection and two reractions and emerging at, minimum deviation. The inner violet edge sutends an angle o 4.8 and the outer red edge sutends an angle o 4.8. The secondary rainow is ormed y light rom the sun undergoing two internal relections and two reractions and also emerging at minimum deviation. This rainow is ainter than the primary one and inner red edge sutends an angle o 5.8 and the outer violet edge sutends an angle o Thereore the colours in the secondary rainow appear in the reverse order compared to those o the primary rainow. All the spectral colours are present in order etween violet and red (Fig..3.3). Between the two rainows no ows are viewed ecause or this the angle o deviation should e lese than the minimum in oth the cases, which is not possile. Fig..3.3
42 Page 4 Sometimes other ows are oserved which are near the inner edge o the primary ow or near the outer edge o the secondary ow. These are known as supernumerary ows and depend upon the size o the raindrops. These are due to diraction just similar to diraction at narrow slits..4 Let us sum up From this lesson your learned aout the usage o lenses as eyepices and also you learned aout the light relection through a prism and also aout angular and chromatic dispersions. Finally you learned aout the dierent types o Rainows..5 Check your Progress ) What are the dierences etween Huygens and Ramsden s eyepieces? ) What are cardinal points 3) Explain angular dispersion 4) State the importance o the Cauchy s dispersion ormulae 5) Deine dispersive power.6 Lesson end Activities ) The ocal length o an eyepiece is.5 m. Calculate the ocal length o the two lenses used in the Huygen s eyepiece. Also calculate the chromatic aerration. (Dispersive power is.3) ) The angle o the prism is 6 and its reractive index or green light is.5. I the green light passes through it ind the deviation..7 Points or Discussion. Give the theory o ormation o a (i) primary rainow (ii) secondary rainow. Explain in what order are the colours arranged.
43 Page 43. (i) Derive Cauchy s dispersive ormulae/ (ii) Write a note on ABBE s homogeneous oil immersion ojective. 3. With a neat diagram explain (i) Huygen s eyepiece and its cardinal points (ii) Ramsden s eyepiece and its cardinal points.8 Reerences: ) Light y Brijlal and Suramanyam ) Optics and Spectroscopy y R. Murugesan
44 Page 44 UNIT II LESSON - 3 CONTENTS 3. Aims and Ojectives 3. Introduction 3... Intererence due to relected light( Thin Film) 3.. Intererence due to Transmitted Light (Thin ilms) 3.. Wedge-Shaped Film (Air Wedge) 3... Experiment to measure the Diameter o a thin wire 3... Applications o Air Wedge 3.3. Newton s Rings Expression or the radii o the rings: 3.3..Determination o Wavelength o Sodium Light y Newton s Ring Determination o Reractive index o a Liquid y Newton's Rings 3.4 Let us sum up 3.5 Check your progress 3.6 Lesson end activities 3.7 Points or discussion 3.8 Reerences 3. Aims and Ojectives In this lesson you will study aout the principles o intererence and its characteristics in thin ilms or relected and transmitted light. Also you will learn aout the wedge shaped ilm. You will also learn aout Newton s rings and its application in determining the wavelength o sodium light and also the determination o o liquid. 3. INTRODUCTION Intererence is the phenomenon o the superimposition o one light source over the other. Due to the superimposition o any two light sources, the resultant energy is redistriuted into a position o maximum intensity and o minimum intensity. I the crest o one wave alls on the crest o the other, constructive intererence is produced. I the crest o one
45 Page 45 wave alls on the trough o the other, destructive intererence is produced. When a soap ilm or an oil ilm is viewed rom a relected light or transmitted light, it exhiits dierent colours. It is due to the intererence pattern produced in thin ilms 3... INTERFERENCE DUE TO REFLECTED LIGHT Consider a transparent ilm o thickness t with reractive index Let AB e the upper surace o the ilm and CD e its lower surace. Let a ray o light PQ e incident at an angle o incidence i on the upper surace o the ilm. Some part o the incident eam is relected y the upper surace along QR and the remaining part is transmitted through the ilm along QS. This transmitted eam undergoes relection y the lower surace o the ilm CD. SU is the relected eam and ST is the transmitted eam rom the interace CD. The ray SU undergoes relection at the interace AB. UV is the transmitted eam and UW is the relected eam rom the interace AB. (Fig 3...) Consider the rays PQR (ray I) and PQSUV (ray II). Ray II has traveled greater distance compared to ray. The path dierence etween the two rays can e determined y drawing a perpendicular line rom the point U to the line QR. UN is the normal to the line QR drawn rom the point U. The path dierence etween the two rays is given y, x = (QS+SU) QN Let r e the angle o reraction. (In Fig.,) consider the triangle QSM cos r SM QS..() similarly, rom le SMU, QS SM t cosr cosr t SU () cos r
46 Page 46 Thereore, Fig 3.. t t QS SU () cosr cosr
47 Page 47 rom le QSM, Consider the le QUN, QU QM sin r QS QM=QS sin r t QM QS sin r sin r (3) cosr QN sin i QU QN QU sin i (4) From Eqs (3) and (4), From Snell s law, sin i= sin r From Eqs (5) and (6), we get From Eqs(), () and (7), we get tsin isin r QN (5) cosr sin i...(6) sin r t sin r. sin r QN (7) cosr t t x sin cosr cosr t ( sin cosr r r) t cosr The ray QR is the relected ray and the ray UV is the transmitted ray. Due to relection, there is a phase change o degree or an additional path dierence o will e introduced. So, the total path dierence is written as, x t cosr
48 Page 48 To get the condition or right ringe, the path dierence is equated to an integral multiple o λ, (i.e., n=,,3 ) i.e., t cosr n n i.e., t cosr (8) To get the condition or dark ringe, the path dierence is equated to hal integral multiple o λ, i.e., t cosr (n ) or t cosr n (9) Equations (8) and (9) give the conditions or right and dark ringes produced y thin ilms due to intererence o light. 3.. Intererence due to Transmitted Light(Thin ilms): Consider a thin transparent ilm o thickness t and reractive index. A ray SA ater reraction goes along AB. At B it is partly relected along BC and partly reracted along BR. The ray BC ater relection at C, inally emerges along DQ. Here at B and C relection takes place at the rarer medium ( medium-air interace). Thereore, no phase change occurs. Draw BM normal to CD and DN normal to BR. The optical path dierence etween DQ and BR is given y, x ( BC CD) BN also, sin i sin r BN MD or BN MD
49 Page 49 Fig.3.. In Fig.3.. BPC=r and CP=BC=CD BC+CD=PD x ( PD) ( MD) ( PD MD) PM In the BPM. cosr PM BP or PM BP. cosr But, BP=t PM=t cos r x PM t cosr (i) For right ringes, the path dierence x n where t cos r=nλ n=,,,3, etc., (ii) For Dark ringes, the path dierence x (n ) t cosr (n ) where n=,,,3, etc.,
50 Page 5 In the case o transmitted light, the intererence ringes otained are less distinct ecause the dierence in amplitude etween BR and DQ is very large. However, when the angle o incidence is nearly 45, the ringes are more distinct Production o Colours in thin ilms: When white light is incident on a thin ilm, the light rays are relected rom the top and ottom suraces o the ilm. The condition or rightness or darkness depends upon (i), (ii) t and (iii) r. Here t and r are constants. White light contains a numer o wavelengths( colours). Condition or rightness in the relected system is t cosr (n ) The colour or which this condition is satisied will e present with maximum intensity, other colours in the neighorhood will have lesser intensity. Colours or which the condition or darkness t cosr n is satisied wil e asent. Hence the ilm will appear in colored. 3.. WEDGE-SHAPED FILM Consider a wedge-shaped ilm o reractive index enclosed y two plane suraces OP and OQ inclined at an angle θ (Fig..). The thickness o the ilm increases rom O to P. When the ilm is illuminated y a parallel eam o monochromatic light, intererence occurs etween the rays relected at the upper and lower suraces o the ilm. So equidistant alternate dark and right ringes are oserved. The ringes are parallel to the line o intersection o the two suraces. The interering rays are AB and DE, oth originating rom the same incident ray SA.
51 Page 5 Fig 3.. Expression or the ringe width : The condition or a dark ringe is nt cos r = mλ. Here or air n = I. For normal incidence cos r = cos θ =. Suppose the mth dark ringe is ormed where the thickness o the air ilm is t m,(fig 3.a). Then, t m =mλ or t m = mλ () Suppose the (m + ) th dark ringe is ormed where the thickness o the air ilm is t m+ Then, t m+ = (m + )λ () Suracting () rom (), (t m+ -t m )=λ (3) Let x m+ and x m e the distances o the (m+) th and mth dark ringes rom O. d=diameter o the wire; L=distance etween O and the wire. Then t x m m d Fig.3.a t x m m d L t ; m xm tm xm L d L sustituting these values in Eq(3), we get, d ( xm x) L But x m x -ringe width. or d L
52 Page 5 L d d, λ and L are constants. Thereore, ringe width β is constant. Similarly i we consider two consecutive right ringes, the ringe width β will e the same. 3...Experiment to measure the Diameter o a thin wire: An air wedge is ormed y inserting the wire etween two glass plates. Monochromatic light is relected vertically downwards on to the wedge y the inclined glass plate G (Fig.3..). A traveling microscope M with its axis vertical is placed aove G. The microscope is ocused to get clear dark and right ringes. The ringe width (β) is measured. The length (L) o the wedge also is measured. Knowing λ, the diameter (d) o the wire is calculated using the ormula, Fig.3.. L d Testing a surace or planeness: A wedge shaped air ilm is ormed etween an optically plane glass plate OP and the surace under test (OQ). The ringes will e straight i the surace under test is perectly plane. I the surace OQ is not perectly plane, the ringes will e irregular in shape. In practice, perectly plane suraces are
53 Page 53 produced y polishing the suraces and testing them rom time to time, until the ringes are straight. In testing or planeness, an extended source o light should e used. (Note: For Experiment Re. Annexure I)
54 Page Applications o Air Wedge (i) Testing o lat suraces The air wedge experiment is used to test the planeness o a glass plate. To test the planeness o a glass plate the given glass plate is placed over an optically plane glass plate. Then the intererence ringes are ormed. I the ringes are o equal thicknesses and o straight lines then the given glass plate is optically lat. The condition or right ringe is t cosr (n ) For normal incidence, cos r = and or air =. Hence, the aove equation ecomes t (n ) The intererence ringes are characterized or a particular value o n. For a particular value o n, the thickness o the air ilm and the latness o the given glass plate are constant. Thereore, straight ringes are otained. I the ringe otained or a constant value o n is a colored one, it represents the varying thickness o the ilm and it represents that the given glass plate is not lat. The latness o a given glass plate can e tested up to one tenth o the wavelength o the light used. ii) Thickness o a thin sheet o paper A monochromatic source o light is passed through a convex lens and is made to all on a glass plate inclined at an angle o 45 as shown in Fig The rays o light are relected in the downward direction and are used to illuminate an air wedge set up. An intererence pattern is ormed due to the superposition o the rays emerging rom the upper glass plate and the rays relected rom the ottom glass plate. Alternate right and dark ringes are viewed through the microscope. Anyone right or dark ringe is taken as the nth ringe and the readings
55 Page 55 corresponding to n, n + 5, n + n + 5 ringes are taken. From the oservation, the l value o the ringe width β is determined. Then, using the relation t, the thickness o the paper is determined. Fig Newton s Rings: A plano-convex lens o large radius o curvature is placed with its convex surace in contact with a plane glass plate. Then, an air ilm is ormed etween the lower surace o the lens AOB and the upper surace o the plate POQ (Fig..3). The thickness o the air ilm is zero at the point o contact O and gradually increases rom the point o contact outwards. I monochromatic light is allowed to all normally on this ilm, a system o alternate right and dark concentric rings is ormed in the air ilm. They are called Newton's rings. The thickness o air-ilm remains constant along a circle with its centre at O. Hence, the ringes are in the orm o concentric circles.
56 Page 56 Fig.3.3. Newton's rings are ormed as a result o intererence etween the light waves relected rom the upper and lower surace o the air ilm. and are the interering rays corresponding to an incident ray SR Expression or the radii o the rings: R is the radius o curvature o the lens and A is the centre o curvature (Fig..3.). Let there e mth dark ring at point C. The thickness o the airilm at point C is OB = t. The radius o the mth dark ring is r = BC. Let DC e the chord and DE the diameter intersecting at right angles at B. Fig.3. From the geometry o the circle, DB x BC = EB x BO r m (R t) t. In practice t <<R. so that R - t R or r m Rt. () The condition or a dark ring is nt=mλ where m=,,,3. m t () n Sustituting or t in Eq(), we get r m Rm n Rm r n m mr n (3)
57 Page 57 Thus the radii o the dark rings are proportional to the square roots o the natural numers. Bright Rings: The condition or a right ring is nt (m ) Sustituing or t in Eq(), we get or t ( m ) (4) n R( m ) (m ) R r m n n Radius o the m th ( m ) R right ring = r m (5) n Thus the radii o the right rings are proportional to the square roots o odd natural numers. The diameters o m th dark and right rings are D m 4mR Dark ring (6) n D m (m ) R Bright ring (7) n 3.3..Determination o Wavelength o Sodium Light y Newton s Ring. Experimental arrangement: Fig shows an experimental arrangement or producing Newton s rings y relected light. S is source o monochromatic light. The light rom S rendered parallel rays y a convex lens L. These horizontal parallel rays all on a glass plate G at 45, and are partly relected rom it. This relected eam alls normally on the lens L placed on the glass plate PQ. Intererence occurs etween the rays relected rom the upper and lower suraces o the ilm. The intererence rings are viewed with a microscope M ocused on the air ilm.
58 Page 58 L Fig Procedure: With the help o the traveling microscope the diameters o a numer o dark rings are measured. The position o the microscope is adjusted to get the centre o Newton's rings at the point o intersection o the cross-wires. The microscope is moved until one cross wire is tangential to the 6th dark ring. The microscope reading is taken. Then microscope is moved such that the cross-wire is successively tangential to th, 8th and 4th dark rings respectively. The readings are noted in each case. Readings corresponding to the same rings are taken on the other side o the centre. The readings are taulated as ollows: No. o Reading o Traveling Microscope Diameter o ring Ring Let (a) Rigth() D=a~ D Dm D p Average ( D ) m D p The average values o ( D For an air ilm n=. m D p ) is ound.
59 Page 59 The diameters o pth and mth dark rings are given y D p 4 pr and D m 4mR Dm Dp 4( m p) R D m D p 4( m p) R The radius o curvature R o the lower surace o the lens is ound y Boys method. Sustituting this values o R and the average value o ( D aove equation, λ is calculated. m D p ) with (m-p)=8 in the Determination o Reractive index o a Liquid y Newton's Rings The experiment is perormed with an air ilm etween the glass plate and the lens as descried aove. The diameters o pth and mth dark rings with air given y, D p 4 pr and D m 4mR D D 4( m p R () m p ) The transparent liquid o reractive index n is introduced etween the lens L and the glass plate G (Fig,.3.3). Then a plano--concave ilm o liquid is ormed etween the lens and the glass plate. The diameters o pth and mth dark rings are determined. Fig With liquid ilm, the diameters o pth and mth rings are given y
60 Page 6 D p 4 pr and n D m 4mR n 4( m p) R Dm D p n () Dm Dp Dividing () y (), n D m Dp Thus n o a liquid can e determined y measuring the diameters with and without liquid..3 Let us sum up From this lesson you learned aout the principle o intererence and its characteristics in thin ilms oth or relected and transmitted light. Also you learned aout the wedge shaped ilm. Next you studied aout the Newton s rings and its application to determine the wavelength o o liquid. 3.4 Check your Progress ) What is intererence ) What is the condition to get right and dark ringes in intererence pattern 3) Write a note on production o colours in thin ilms 4) How you would test the lat surace using air wedge 5) Write the equation or the radius o the m th dark ring in Newton s rings experiment 3.6 Lesson end Activities ) A parallel eam o sodium light with wavelength 589 x -9 m is incident on a thin glass plate (=.5) such that the angle o reraction into the plate is 6. Calculate the smallest thickness o the plate which will make it appear dark y relection. ) Light o wavelength 6nm alls normally on a thin wedge shaped ilm o reractive index.4 orming ringes that m apart. Find the angle o the wedge.
61 Page 6 3) The diameter o the m th ring changes rom. cm to cm when the air space etween the lens and the plate is replaced y a transparent liquid. Find the reractive index o the liquid. 3.7 Points or discussion. (i) Derive an expression or the intererence due to relected light in thin ilms. (ii) Discuss any two applications o Airwedge.. (i) Derive an expression or the radii o the Newton s rings. (ii) Explain how you would determine the Reractive index o a liquid y orming Newton rings 3.8 Reerences ) Optics and Spectroscopy y R. Murugesan ) Optics y K. Krishnamoorthy
62 Page 6 LESSON 4 CONTENTS 4. Aims and Ojectives 4.. Michelson's Intererometer 4... Types o Fringes 4...Uses o Michelson s Intererometer: 4. Jamin's Intererometer 4.3. Rayleigh's Reractometer 4.4 Let us sum up 4.5 Check your progress 4.6 Lesson end activities 4.7 Points or discussion 4.8 Reerences 4. Aims and Ojectives In this lesson you will learn aout the dierent optical instruments using the principle o intererence namely Michelson s and Jamin s intererometer. You will also learn aout the Rayleigh reractometer and the determination o reractive index y direct method..9. Michelson's Intererometer Principle: Here, the two interering eams are ormed y division o amplitude. The amplitude o the light eam rom an extended source is divided into two parts o equal intensity y partial relection and reraction. These eams are sent in two perpendicular directions. The two eams are inally rought together ater relection rom plane mirrors to produce intererence ringes. Apparatus: M and M are ront silvered plane mirrors (Fig.4.). The two mirrors are mounted vertically on two arms at right angles to each other. The planes o the mirrors can e slightly tilted with the ine screws at their acks. The mirror M is ixed. The mirror M can e moved parallel to itsel y means o very sensitive micrometer screw. G and G are two plane parallel glass plates o equal thickness. The plate G is semi-
63 Page 63 silvered on the ack side. G l is a eam splitter; i.e., a eam incident on G is partially relected and partially transmitted. G is inclined at an angle o 45 to the incident eam. G is called the compensating plate. S is a light source. Fig 4.. Working: Light rom the sources is rendered parallel y a lens L and alls on the glass plate G at an angle o 45. At the ack surace o G, it is partly relected along AC and partly transmitted along AB. The relected eam moves towards mirror M and alls normally on it. It is relected ack along the same path and emerges out along AT. The transmitted ray AB alls normally on the mirror M. It is relected along the same path. Ater relection at the ack surace o G, it moves along AT. The two emergent eams have een derived rom a single incident eam and are, thereore, coherent. The two eams produce intererence under suitale conditions. Function o the compensating plate G : The relected ray AC passes through G, thrice. But the transmitted ray AB passes through G, only once. That is why a second plate G o the same thickness and inclination as G is introduced. Thus the unction o the plate G is only to equalize the optical paths traversed y oth the eams Types o Fringes (i) Circular ringes: Concentric circular ringes are otained when oth the mirrors M, and M are mutually perpendicular. The image o M is at M parallel to M, (Fig. 4.4.).
64 Page 64 Hence, M and M, orm the equivalent o a parallel air ilm. The eective thickness o the air ilm is varied y moving mirror M, parallel to itsel. Let the eye or the telescope e set along a direction making an angle r with the normal to M. Then the path dierence etween the two coherent eams is t cos r. The condition or a right ring is tcos r = rnλ where m is an integer. The condition or a dark ring t cos r = (m - ) λ/. In either case, r will e constant or given values o t, n and λ. Hence the loci o maxima o intensity will e concentric circles having their centre on the perpendicular rom the eye or telescope on M. The circular ringes will e situated at ininity. Thereore they can e oserved y a telescope ocused or ininity. Thus we get circular ringes o equal inclination or Haidinger s ringes. I a dark circle appears at the centre o the pattern, the two rays interere destructively. I the mirror M is then moved y a distance o λ/4, the path dierence changes y m (twice the separation etween M and M ). The two rays will now interere constructively, giving a right circle in the middle. As M is moved an additional distance λ/4, a dark circle will appear once again. Thus, we see that successive dark and right circles are ormed each time M is moved a distance λ/4. Fig.4.4.(a) (ii) Straight ringes: I M and M are not exactly perpendicular, a wedge shaped air ilm is ormed etween M, and M. The ringes ecome practically straight (Fig..4.(a))when M, actually intersects M in the middle. The ringes are ringes o
65 Page 65 equal thickness. The ringes are localized in the airilm itsel. Hence the telescope has to e ocused on the ilm to oserve these ringes.
66 Page 66 Fig 4..(a) (iii) White light ringes: I white light is used, the central ringe will e dark and others will e colored. With white light, ringes are oserved only when the path dierence is small. These ringes are important ecause they are used to locate the position o zero path dierence. 4...Uses o Michelson s Intererometer:. Determination o wavelength o monochromatic light: (i) Using monochromatic radiation o unknown wavelength λ, the intererometer is adjusted or circular ringes. (ii) With any ring at the centre, the reading o micrometer is noted. Let it e x. (iii) Now the mirror M is moved with the help o micrometer screw. The ringes appear to sink or rise due to the change o path dierence. Let N ringes move and x e the new reading o the micrometer. When the mirror moves through a distance λ/, one ringe shits. Hence, () x x x N
67 Page 67 () ( x x ) x. Determination o dierence in wavelength etween two neighouring lines: Let the source o light emit two close wavelengths λ and λ (like sodium D lines). λ >λ. The apparatus is adjusted to orm circular rings. Each spectral line produces its own system o rings. We have to consider the superposed ringe-systems. I the right rings due to λ exactly coincide with right rings due to λ, then the rings are very distinct and well deined. This is called consonance. I, however, the right rings due to λ coincide with dark rings due to λ the ring system would disappear producing uniorm illumination. This is called dissonance. This is the position o maximum indistinctness. Circular rings are ormed y adjusting the intererometer using sodium light. The mirror M is gradually moved to otain dissonance and its position noted. The movement o M is continued in the same direction and successive positions o dissonance are noted. The mean distance x etween two successive dissonances is determined. When x is the distance moved y the mirror or two consecutive positions o maximum indistinctness, the path dierence is x. During this movement i N is the change in order o the longer wavelength λ at the centre o the ield, then (N+ I) will e the change in order o wavelength λ at the centre. Thereore, or dissonance x N ( N ) or x N and or x x x N x or x Put λ - λ =dλ and λ λ = λ where λ = mean wavelength d x From this equation dλ. can e calculated. N N 4.. Jamin's Intererometer:.
68 Page 68 Construction : The essential optical parts are shown in Fig. 4.. A and B are two identical optically plane, thick glass plates. The ack suraces o the plates are silvered. The plates are arranged with their aces slightly inclined to each other. S is an extended source o monochromatic light, placed at the ocal plane o the lens L. A parallel eam o light is incident on the plate A. It gives rise to two eams: (i) R relected rom the ront surace and (ii) R relected rom the ack surace. Both these relected eams pass through two identical glass tues T, and T. Then the two eams all on the plate B. The eam R, is relected y the ront surace. The eam R is relected rom the ack surace. The emergent eams have een otained rom the same eam y the division o amplitude. Hence the emergent eams interere. The straight intererence ringes are viewed y a telescope T. These are called Brewster s ringes. Fig.4. Measurement o reractive index: This arrangement is used to measure the reractive index o a gas at dierent pressures. The two tues T and T are irst evacuated. The centre o the cross-wires o the telescope is set on the centre o a right ringe. Then the gas is allowed to slowly enter one o the tues. The numer o ringes crossing the centre o the ield o view is counted. Let it e m. Let n = Reractive index o the gas at inal pressure l = length o each tue. The path dierence etween the two eams = (n - )l :. (n - ) l = mλ.
69 Page 69 Knowing l, λ and m, n is calculated rom the relation n = + (mλ/l) The experiment is repeated with the gas at dierent pressures. Let P e the density o the gas. It is ound that law. Since (n ) or ( n )/ is a constant. This is Gladstone and Dale's P,the pressure o the gas, ) (n. Jamin's compensator: To overcome the diiculty in counting the numer o ringes which quickly cross the ield o view, a compensator is used. It consists o two glass plates C and C o equal thickness and inclined at a small angle. The plates can e rotated aout a common horizontal axis y a calirated circular disc D. When the disc D is rotated, the interering eams passing through C and C are aected such that in one case the path increases and in the other case it decreases. The circular disc is calirated y counting ringes directly with a monochromatic light and is marked in terms o the reractive index and the numer o wavelengths. The tues T and T are evacuated. Using white light the compensator is adjusted so that the central right ringe is rought on the cross-wires o the telescope. Then the gas is introduced in one o the tues at a given pressure and temperature. The ringes will shit. The compensator is then rotated to ring the central white ringe again on the cross-wire. The reading on the calirated disc directly gives the reractive index o the gas RAYLEIGH'S REFRACTOMETER Monochromatic light rom a linear source S is made parallel y a lens L and split into two eams y a doule slit S,S (Fig.4.3). Ater passing through the two exactly similar tues(t, T ) and the compensating plates (C,.C ), the two eams pass through the lens L, Intererence ringes are oserved through the eyepiece E. Fig 4.3
70 Page 7 This instrument is mainly used (i) to ind the asolute value o reractive index o a gas and (ii) to ind the variation o reractive index o a gas with pressure and temperature. Initially oth the tues T and T is oserved in the ield o view o the eyepiece using white light. Now the gas at given temperature and pressure is introduced in one o the tues. This rings aout a change in the optical path o one interering eam. So the central white ringes shits rom the ield o view. By rotating the circular disc D and o the thus the plates C and C the central white ringes is rought ack to the centre o the ield view. The circular disc D is previously calirated in terms o reractive index. The reading on the calirated disc D gives the value o reractive index directly. 4.4 Let us sum up From this lesson you learned aout dierent optical instruments using the principle o intererence namely Michelson s and Jamin s intererometer. Also you learned aout the Rayleigh reractometer and the determination o reractive index y direct method. 4.5 Check your progress ) State the principle employed in Michelson s intererometer. ) What will happen to the ringes i the white light is used in Michelson intererometer? 3) How you would use the Michelson s intererometer to determine the wavelength o monochromatic light? 4) Write a note on Jamin s compensator 4.6 Lesson end Activities ) A shit o circular ringes is oserved when the movale mirror o Michelson s intererometer is shited y.3 mm. Calculate the wavelength o light. ) In an experiment with a Michelson s intererometer the distance traveled y the mirror or two successive positions o maximum distinctness was.95 mm. I the mean wavelength or the two components o sodium d lines is 5893 Angstrom, Calculate the dierence etween them
71 Page 7 3) In an experiment or determining the reractive index o air with Michelson s intererometer a shit o 5 ringes is oserved when all the air was removed rom the tue. I the wavelength o the light is 4 Angstrom in air and the length o the tue is cm, calculate the reractive index o air. 4.7 Points or Discussion Write in detail aout the ollowing i) Michelson s Intererometer (ii) Jamin s Intererometer (ii) Rayleigh s Reractometer. 4.8 Reerences ) Optics and Spectroscopy y R. Murugesan ) Optics y K. Krishnamoorthy
72 Page 7 Annexure I MATERIAL-AIR WEDGE Aim To determine the thickness o a given thin wire or thin sheet o paper y orming intererence ringes using an air wedge arrangement. Apparatus acquired Two optically plane rectangular glass plates; sodium vapour lamp; thin wire or thin sheet o paper; travelling microscope. Formulae The thickness o the wire l t m (E.) where λ is the wavelength o the monochromatic light used (5893 Å), β the ringe width and l the distance etween the edge o contact and the wire. Description An air wedge is ormed y keeping two optically plane glass plates in contact along one o their edges, and keeping a thin wire or paper at the other end parallel to the edges o contact o the glass plates, as shown in Fig. E.
73 Page 73 Fig.E.. Fig E.. The glass plate P should e parallel to the ed plate o the travelling microscope. With the help o an ordinary thin glass plate G inclined at 45 to the horizontal and a condensing lens L, light rom the sodium lamp S is made to all vertically on the airwedge, as shown in Fig. E.. Intererence takes place etween the light relected at the top and ottom r suraces o the thin air ilm etween the two glass plates. The thickness o (this wedge-shaped air ilm increases as the distance rom the edge o contact increases. Hence, a large numer o equally spaced alternate dark and right ringes are ormed, as shown in Fig. E., which are parallel to edge o contact o the two glass plates. The microscope is ocussed on these ringes and its vertical cross wire is made to coincide with a right or dark ringe near the edge o contact o the glass plates. This is considered as the n th ringe and the reading on the horizontal scale o the travelling microscope is noted. The microscope is then moved in the same direction with the help o the horizontal transverse screw and is made to coincide with successive 5 th ringes (5,, 5, etc.) and the corresponding readi ngs in the microscope are noted. The readings are taulated in Tale E. Tale E..l To ind the width o the ringe β Order o the Microscope Reading Fringes MSR (X - m) VSC X LC (x - m) Total Reading (x - m n n+5 n+. Width o ringes (X - m Width o ringe β (X - m
74 Page 74. n+4
75 Page 75 From these readings, the mean width o one ringe β is calculated. Using the travelling microscope, the distance l etween the edge o contact and the wire is measured. The oserved readings are taulated in Tale E., and thereore, the thickness o the wire is calculated y using Eq. (E.). Tale E. To ind the distance etween the edge o contact and thin wire Microscope Reading Width o Position MSR (X - m) VSC X LC (x - m) Total Reading (x - m ringes (X - m At the edge l R R (X - m o contact R At the wire R Thickness o the wire t= m
76 Page 76 UNIT III: LESSON 5 CONTENTS 5.. Aims and Ojectives 5.. Magnetic Induction (B) 5... Relation etween the three magnetic vectors B, Hand M 5... Magnetic susceptiility Magnetic Permeaility 5..Properties o diamagnetic materials Antierromagnetism and Ferrimagnetism The Electron Theory o Magnetism 5.3..Explanation o Diamagnetism 5.3..Explanation o Paramagnetism Explanation o Ferromagnetism 5.4. Langevin's Theory o Diamagnetism 5.5.Weiss's Theory o Ferromagnetism 5.6 Let us sum up 5.7 Check your progress 5.8 Lesson end activities 5.9 Points or discussion 5. Reerences 5. Aims and Ojectives In this lesson you will understand aout the magnetic induction (B), magnetic susceptiitliy and magnetic permeaility. Also you will learn aout dierent types o magnetic materials namely dia, para, and erromagnetic materials and their applications, properties and importance in magnetism. Dierent theories putorward y dierent scientists will also e discussed.
77 Page 77
78 Page Magnetic Induction (B) The magnetic induction is deined through its action on a moving charge. I a positive test charge q moving with velocity v through a point in a magnetic ield experiences a orce F. then the magnetic induction B at that point is deined y F=qv X B. F The Magnitude o the magnetic induction =B= qvsin Here, θ is the angle etween v and B. Unit o B is weer/m. The magnetic ield can e represented y lines o induction. The tangent to the line o induction at any point gives the direction o B. The numer o lines o induction per unit area normal to their direction is equal to the magnitude o B. Magnetisation (M). When a magnetic material is placed in a magnetic ield, the elementary current-loops in the material ecome aligned parallel to the ield. The material is then magnetized, and acquires a magnetic dipole moment. Magnetization M o the material is deined as the magnetic dipole moment induced per unit volume o the material. Unit o M is Am -. Let m e the magnetic dipole moment o a specimen o volume V, then M m v In an unmagnetized material M will e zero. In a uniormly magnetized material, each atomic magnetic dipole will point in the same direction and magnetization M win e constant throughout Relation etween the three magnetic vectors B, Hand M
79 Page 79 Consider a Rowland ring having a toroidal winding o N turns around it. When a current i is sent through the winding, the ring is magnetized along its circumerential length. The current i is the real current which rnagnetises the ring. This magnetization arises due to the alignment o the elementary current-loops (magnetic dipoles) resulting rom electronic motions in the material. Fig 5.. shows a section o the magnetized ring. The small circles represent the current-loops. These internal tiny circular electron currents tend to cancel each other due to the act that adjacent currents are in opposite directions. As such, there is no net current inside the core. The currents in the outer portion is o the outer most loops remain uncancelled. The numerous tiny localized surace currents can e replaced y single closed current i s, along the surace. Such a current is called Amperian current. Fig.5.. Let A = area o cross section and the ring = la The ring ehaves like a large dipole o magnetic moment i s A. l circumerential length o the ring. Then volume o is A is magnetization = M = magnetic moment per unit volume la l The magnetization M, thereore, is the surace current per unit length o the ring. This is commonly called magnetization current.
80 Page 8 Now, the magnetic induction B within the material o the ring arises due to the ree current i o in the winding, as well as due to the magnetization o the ring itsel which can e descried in terms o Amperian surace current. Here Ni i Ni i M s M l l l l B s Ni i is the ree current per unit length and s is the Amperian surace current l l perunit length. () B M Ni l The quantity - B M is called magnetizing ield or magnetic ield intensity H i.e., H B M or B ( H ) M in vector orm, B µ (H M) () This is the relation etween the three vectors B. H and M. H points in the same direction as that o B or M. Its unit is Am -. Ni Eq. (I) can. e written as H nl l Where n is the numer o turns per unit length. Thus the value o H depends only on the ree current and is independent o the core material. When no magnetic material is present in the core o the Rowland ring. i.e., there is vacuum in the core, M =. Thereore Eq. () ecomes B= H..(3) In vacuum, the magnetic ield strength H is related to the magnetic induction B o y the aove relation. When a magnetic material is placed in an external magnetic ield, the specimen is magnetized y producing (or reorienting) magnetic dipoles in the specimen. This will
81 Page 8 produce additional ield. Thus the resultant ield B is greater than Bo. In such a case, H is related to B y the relation. H B M 5... Magnetic susceptiility For isotropic linear para-and diamagnetic materials it is ound experimentally that the rnagnetization M is proportional to the magnetic ield intensity H. That is, M H or M H The constant m is called the magnetic susceptiility o the material. It may e deined as the ratio o the magnetization M to the magnetic ield intensity H. m m M H Thereore, the magnetic susceptiility o a material is deined as the intensity o magnetization acquired y the material or unit ield strength. We can classiy magnetic materials in terms o susceptiility m. I m is positive, the material is called paramagnet. I m is negative, the material is diamagnetic. The characteristic o erromagnetic materials is that is positive and very large. However, m in erromagnetic materials, M is not exactly proportional to H, and so m is not a constant. M may even e inite when H =. In most hand ooks on physical data m is not listed directly, ut instead is given as the mass susceptiility m, mass or the molar Susceptiility, m, molar these are deined y, m m, mass m m, molar A where and A arethe density and molecular weight o the material respectively. Here m, m, mass and m, molar respectively. are known as volume, mass and molar susceptiilities Magnetic Permeaility
82 Page 8 Consider the relation B= (H+M) = (H+ m H) = (+ m )H =H where = (+ ) is called the magnetic permeaility o the material. m B=H magnetic permeaility () o the medium is deined as ratio o magnetic induction to the intensity o the magnetising ield. or vacuum m = and = B H Hence the magnetic induction in vacuum is B = H The ratio B B is called the relative permeaility r oviously r =+ we may also classiy magnetic materials in terms o the relative permeaility r Diamagnetism: r < I (For Bi. r = -. 7) Paramagnetism: r > I (For Al, r = +.) Ferromagnetism: r > > I (For pure Fe, r =,) m 5..Properties o diamagnetic materials :. (i) For diamagnetic sustances r is slightly less than unity. (ii) The susceptiility ( m ) o a diamagnetic material has a low negative value. It is independent o temperature. (iii) In an external magnetic ield, they get magnetized in a direction opposite to the ield and so they have a tendency to move away rom the ield.
83 Page 83 (iv) I suspended reely. they set themselves r to the ield. S, Bi, Zn. Ag, Au. Ph etc.. are examples o diamagnetic materials. Properties o paramagnetic materials: (i) These sustances have r > and m + ve. The susceptiility decreases with rise in temperature. (ii) In an external magnetic ield, these sustances get magnetized in the direction o the ield. Hence they move rom weaker to stronger part o the external ield. (iii) I suspended reely, they set themselves to the ield. Platinum, aluminum, chromium, manganese, copper sulphate, liquid oxygen and solutions o salts o iron and nickel are examples o paramagnetic sustances. Properties o erromagnetic materials (i) The values o r and m o these materials are very large. (ii)they get strongly magnetized in the direction o the external ield and so they are strongly attracted y magnets. (iii) They set themselves parallel to the external ield i suspended reely. (iv) These materials exhiit the phenomenon o hysteresis. (v) As temperature increases, the value o m decreases. Aove a certain temperature, known as Curie temperature, erromagnetics ecome paramagnetics. Iron, nickel and coalt are some examples o Ferro-magnetic sustances. There exist two other types o magnetism, closely related to erromagnetism. These are antierromagnetism and errimagnetism Antierromagnetism and Ferrimagnetism. The only type o magnetic order which has een considered is erromagnetism, in which, in the ully magnetized state, all the dipoles are aligned in exactly the same direction (Fig.3..(a)). There are, however, sustances which show dierent types o magnetic or-
84 Page 84 der. In antierromagnetic materials such as Cr and MnO, the dipoles have equal moments, ut adjacent dipoles point in opposite directions (Fig.3..()). Thus the moments alance each other, resulting in a zero net magnetization. The gross magnetic eects o such materials are very small. When heated aove critical temperature, called the Neel temperature, the exchange interaction ceases to exist and these materials ecome paramagnetic. In errimagnetic materials (also called errites) such as Mn, Fe and O 4 the magnetic moments o adjacent ions are Antiparallel and o unequal strength (Fig 3...(c)). So there is a inite net magentisation. Thus results in net magnetism, which lies in etween erromagnetism and antierromagnetism. Here again, when the temperature is aove a critical value, the material ecomes paramagnetic. By suiitale choice o rare-earth ions in the errite lattices it is possile to design errimagnetic sustances with speciic magnetizations or use in electronic components. Ferrites are good insulators and have very small eddy current losses when sujected to high ields. For this reason, errites are oten used in microwave systems.
85 Page The Electron Theory o Magnetism The paramagnetic, diamagnetic and erromagnetic ehaviour o sustance can e explained in an elementary way in terms o the electron theory o mutter. Each electron is supposed to e revolving in an orit around the nucleus. Each moving electron ehaves like a tiny current loop and thereore possesses orital magnetic dipole moment. Furthermore, each electron is spinning aout an axis through itsel. This spin also gives rive to a magnetic dipole moment. In general, the resultant magnetic dipole moment o an atom is the vector sum o the orital and spin magnetic dipole moments o its electrons Explanation o Diamagnetism Diamagnetism occurs in those sustances whose atoms consist o an even numer o electrons. The electrons o such atoms are paired. The electrons in each pair have orital motions as well as spin motions in opposite sense. The resultant magnetic dipole moment o the atom is thus zero. Hence when such a sustance is placed in a magnetic ield, the ield does not tend to align the atoms (dipoles) o the sustance. The ield, however, modiies the motion o the electrons in orits which are equivalent to tiny current-loops. The electron moving in a direction so as to produce a magnetic ield in the same direction as the external ield is slowed down, while the other is accelerated (Lenz's law). The electron pair, and hence the atom, thus acquire an eective magnetic dipole moment which is opposite to the applied ield. Hence or diamagnetic materials M is opposite to H. So the susceptiility m o a diamagnetic sustance is negative and is very small Explanation o Paramagnetism In paramagnetic materials, the magnetic ields associated with the oriting and spinning electrons do not cancel out. There is a net intrinsic moment in it. The molecules in it ehave like little magnets. When such a sustance is placed in an external magnetic ield,
86 Page 86 it will turn and line up (with its axis parallel to the external ield. Thus it tends to move urther into, the ield. i.e., there is orce o attraction. The diamagnetic orce o repulsion is also present, ut it is not so strong as the attracting orce arising rom the magnetic properties o the material. Since M and B (and hence H) are in the same direction in paramagnetics, the susceptiility m is positive. When a paramagnetic sustance is heated, the thermal agitation o its atoms increases. So the alignment o the dipoles ecomes more diicult. This is why the magnetization o paramagnetic sustances decreases as the temperature o the sustance increases. m T Explanation o Ferromagnetism Ferromagnetic sustances are very strongly magnetic. The est-known examples o erromagnets are the transition metals Fe, Co, and Ni. A erromagnet has a spontaneous magnetic moment - a magnetic moment even in zero applied ield. The atoms (or molecules) o erromagnetic materials have a net intrinsic magnetic dipole moment which is primarily due to the spin o the electrons. The interaction etween the neighouring atomic magnetic dipoles is very strong. It is called spin exchange interaction and is present even in the asence o an external magnetic ield. It turns out that the energy o two neighouring atomic magnets due to this interaction is the least when their magnetic moments are parallel. The neighouring magnetic moments are, thereore, strongly constrained to take parallel orientation (Fig ). This eect o the exchange interaction to align the neighouring magnetic dipole moments parallel to one another spreads over a small inite volume o the ulk. This small ( -. mm across) volume o the ulk is called a domain (Fig ). All magnetic moments within a domain will point in the same direction, resulting in a large magnetic moment. Thus the ulk material consists o many domains. The domains are oriented in dierent directions. The total magnetic moment o a sample o the sustance is the vector sum o the magnetic moments o the component domains.
87 Page 87 Fig In an un magnetised piece o erromagnetic material, the magnetic moments o the domains themselves are not aligned. When an external ield is applied, those domains that are aligned with the ield increase in size at the expense o the others. In a very strong ield, all the domains are lined up in the direction o the ield and provide the high oserved magnetization. I a erromagnetic material is heated to a very high temperature, the thermal virations may ecome strong enough to oset the alignment within a domain. At such temperature, the material loses its erromagnetic property and ehaves like a paramagnetic material. The critical temperature aove which a erromagnetic material ecomes a paramagnetic is called the Curie temperature Langevin's Theory o Diamagnetism Consider an electron ( mass=m, charge=e) rotating aout the nucleus(charge=ze) in a circular orit o radius r. Let ω e the angular velocity o the electron. Then The magnetic moment o the electron is m =current X area = e F o m r Ze 4 r Ze or () 3 4 mr e r r.() Let a magnetic ield o induction B e now applied.(fig.5.4)
88 Page 88 Fig.5.4. An additional orce F L called Lorentz orce acts on the electron. F L =-e(v X B)=-eBrω The condition o stale motion is now given y mr Ze 4 r ebr (3) or Solving the quadratic equation in ω, eb Ze m 4 mr 3 eb eb 4 Ze 4 3 m m mr (4) eb eb (5) m m Where L( ) coth is called the Langevin unction. The variation o M with is Shown in Fig.3.4..
89 Page 89 Case (i)at low temperatures or large applied ield, L (). Hence, magnetisation M in this case will e M=mn So saturation is reached when all the atomic dipoles are parallel to B. (6) Fig 5.4. Case (ii). Under normal conditions is very small. Then. L ( ) coth 3..(7) nm H M mn 3 3kT (8) M nm C m H 3kT T (9) where C nm 3k is called the Curie Constant. Eq.(9) shows that m, which is Curie s law. T
90 Page Failure o Langevin Theory. (i) Langevin's theory was unale to explain, a more complicated dependence o susceptiility upon temperature exhiited y several paramagnetics such as highly compressed and cooled gases, very concentrated solutions o salts etc. (i) Langevin's theory could not account or the intimate relation etween para- and erromagnetism. 5.5.Weiss's Theory o Ferromagnetism Langevin's theory o paramagnetism was extended y Weiss to give a theoretical explanation o the ehaviour o erromagnetics. He made the ollowing two assumptions: (i) Weiss assumed that a erromagnetic specimen contains a numer o small regions (domains) which are spontaneously magnetized. The total spontaneous magnetization is the vector sum o the magnetic moments o the individual domains. (ii) The spontaneous magnetisation o each domain is due to the existence o an internal molecular ield. This tends to produce a parallel alignment o the atomic dipoles. Weiss also assumed that the internal molecular ield H i is proportional to the rnangnetisation M. i.e..h i =γ M where γ is a constant called Weiss constant. I now an external ield H acts on the dipole, then the eective ield H e is given y H e = H + H i = H + γ M... () According to Langevin's theory o paramagnetism, at high temperatures, nm H M 3kT Where k is Boltzmann Constant and T is asolute temperature. Weiss suggested that, the corresponding result or erromagnetics could e otained y replacing H y H e. Hence or erromagnerics, nm M 3 kt H M
91 Page 9 or M nm H () nm k T 3k 3 The Susceptiility m is, erro M H nm nm k T 3k 3 C T (3) nm Here, is called the Curie Constant. 3k nm is called the Curie temperature. 3k It is the temperature elow which the material shows erromagnetic ehavior. For values o temperature aove θ, the erromagnetic sustance ehaves like a paramagnetic sustance. Eq. (3) is called the Curie-Weiss law or erromagnetics. 5.6 Let us sum up In this lesson you have learned aout the magnetic induction, magnetic susceptiility and magnetic permeaility. Also you learned aout dierent magnetic materials such as dia, para and erro and their properties and importance in magnetism. Also you learned aout dierent theories putorth y dierent scientists. 5.7 Check your progress ) Deine magnetic induction ) Find the relation etween the three vectors B, H and M 3) Deine magnetic susceptiitliy and permeaility 4) Give the properties o dia magnetic materials 5) What is anti erromagnetism and errimagnetism 5.8 Lesson end activities ) A rod o magnetic material.5 m in length has a coil o turns over it uniormly. IF the current o amp is sent through it calculate a) the magnetic ield ) the intensity o magnetization c) Magnetic induction and d) relative permeaility o the material.
92 Page Points or Discussion. (i) Explain dia, para and erromagnetism on the asis o Electron theory (ii) Write a note on Antierromagnetism and erri magnetism.. (i) Explain Weiss theory o erromagnetism (ii) Derive an relation etween the three magnetic vectors 5. Reerences ) Electricity and magnetism y R. Murugesan LESSON - 6 CONTENTS 6.. Aims and Ojectives 6.. Hysterses 6... Experiment to draw M H curve (Horizontal model) 6... Experiment to draw B-H curve (Ballistic method) Energy loss due to hysteresis 6.. Importance o hysteresis curves 6.3. Choice o Magnetic materials 6.4. Let us sum up 6.5 Check your progress 6.6 Lesson end activities 6.7 Points or discussion 6.8 Reerences 6. Aims and Ojectives In this lesson the hystereses, energy loss due to hystereses, its importance and choice o magnetic materials are given. 6. HYSTERSES
93 Page Experiment to draw M H curve (Horizontal model) The lagging o the intensity o magnetisation M (or magnetic induction B) ehind the magnetising ield H is known as hysteresis. The variation o M with H can e studied y the ollowing experiment. A delection magnetometer can e used or drawing the M - H curve or iron in the orm o a rod. Description: Fig. 3.6 shows the experimental set up. A solenoid SS and compensating coil (C) are connected in series through a commutator to a attery, ammeter and rheostat. The solenoid is mounted horizontally in the east-west direction. The sample rod AB is placed well within the solenoid along its axis. The magnetometer M set in end-on position [Tan A ] is placed in level with the axes o SS and C. The magnetometer is adjusted to read zerozero. Fig. 6.. Working. The sample rod AB is removed rom SS. The compensating coil placed on the other side o the magnetometer in such a way that its magnetic ield is opposite to the solenoid's ield at the magnetometer. A current is passed through the solenoid. The
94 Page 94 position o the compensating coil C is adjusted until the magnetometer delection ecomes zero. The position o C is, then ixed throughout the experiment. The current is switched o. The sample rod AB is then introduced in SS. A current i is passed through it. To get the hysteresis loop we need a series o values o M and H (or θ and i). The current is gradually increased to.5 A. The readings o the two ends o the pointer o the magnetometer are noted and the average delection θ is calculated. The current through the solenoid is gradually increased in steps o.5 A noting the delections in each case upto the maximum current o 3A. Then the current is gradually decreased in steps o.5 A to zero. Now the current is reversed in its direction y changing the commutator and increased upto 3A. Then the current is rought to zero in steps o.5, reversed to the original direction and increased upto 3A. The delections are noted in each case. Thus the specimen has een taken through a complete cycle o magnetization. Theory: The magnetising ield H is calculated rom the equation H = ni where i is the current and n is the numer o turns per unit length o the solenoid. The value o M is calculated as ollows. The delection in M ' is now due to the magnetism acquired y the sample alone. Let it e measured as θ. The ield at M ' is B = B o tan θ.. () where B o is the horizontal induction o earth s ield. Let d = distance etween the centre o the rod AB and the centre o the magnetometer M ', L = length o the rod AB. m = magnetic dipole moment developed in the rod. Then, the ield at M' producing the delection θ is given y From Eqs () and () md B 4 L d ()
95 Page 95 tan 4 B L d md tan ) ( 4 B d L d m Let r e the radius o the rod. Then, Volume o the rod = V=( r ) L intensity o magnetization o the rod M=m/V tan ) ( ) ( 4 B L r d L d M Knowing B o, the intensity o magnetisation M is calculated or various delections 8 corresponding to dierent values o current i. A graph is drawn plotting H along the x-axis and M along the y-axis. The graph otained is in the orm o a loop ABCDEFA (Fig.6..(a)). The loop is called the hysteresis loop. From the graph the ollowing properties o the material can e calculated. Fig. 6..(a)
96 Page 96 (i) Retentivity. When the magnetisiug ield ecomes zero, the magnetisation does not ecome zero ut retains a value OB. This value o M is called the retentivity o the material. Retentivity=OB (ii) Coercivity. The ield DC which should e applied to the material in the direction opposite to its magnetisation, to remove its residual magnetism and make the magnetisation zero is called coercivity (or coercive orce). Coercivity=OC The chie sources o error in this method arc (i) uncertainty in the location o the poles o the magnetised rod, and (ii) insensitiveness o the delection magnetometer Experiment to draw B-H curve (Ballistic method) Circuit Description: A specimen o the given erromagnetic material is taken in the orm o a ring (Rowland ring). The experimental arrangement is shown in Fig A primary coil P is wound closely over the specimen ring. This winding is connected in series with a attery B, an ammeter A, a rheostat R and a resistance R through a reversing key K and a two-way key K.
97 Page 97 Fig.6.. A ta key K connected across R' acilitates either its inclusion or removal rom the circuit. The secondary winding S over the specimen, consists o a ew turns o closely wound wire. This winding S is connected in series with a rheostat R, a allistic galvanometer and the secondary winding S o a standard solenoid through a key K K g is the damping key across the allistic galvanometer. P is the primary winding o the standard solenoid. The two way key K connects either P or P to the attery circuit. Theory. Numer o turns o the winding P = n turns per metre Total numer o turns o the winding S =n turns Numer o turns o the winding P = n 3 turns per metre Total numer o turns o the winding S = n 4 turns Area o cross-section o the specimen = A sq. metres Area o cross-section o the standard solenoid = a sq. metres
98 Page 98 When the key K is closed to the let, a current i passes through the magnetizing coil P. The ring is magnetized. The intensity o the magnetizing ield =H=n i... () The rnagnetisation o the specimen develops a magnetic lux density B inside the ring. Then, The total lux linked with the secondary ==n BA. This is the change o lux in the secondary. It sets up an induced em in the secondary circuit. I R is the total resistance o the secondary circuit, then the charge passing through the allistic galvanometer q =n BA/R. I θ is the irst throw o the allistic galvanometer coil, then q = n BA/R = Kθ( + λ/).... () where K is the allistic constant and λ the logarithmic decrement o the allistic galvanometer. To eliminate K and λ A known current i is passed through the primary o the standard solenoid y closing the key K, to the right.. ' Magnetic lux linked with the secondary = n ian This change in the magnetic lux sends a charge galvanometer. I θ is the irst thorw in the galvanometer coil, then 3 4 Weer q n n ia 3 4 n3n4i a q K (3) R Dividing Eq.() y (3), we have, n BA n n ia 3 4 n3n4i a or B W/m (4) An R through the
99 Page 99 Eq. (4) gives the magnetic induction B induced in the specimen corresponding to the magnetic intensity H, given y Eq. (). Procedure: The key K is irst closed to the let and the resistances R and R' are decreased until on Closing the commutator K, the galvanometer gives a ull-scale delection rom the zero. The current required to do this is noted and is used as maximum current in the main experiment. The residual magnetism in the specimen is reduced to zero as ollows: The galvanometer circuit is irst roken and the resistances R l and R are reduced to the minimum. The current passing through the primary o the ring solenoid is then reversed many times y means o the commutator K, and R and R are gradually increased the current which is reversed is very small. The galvanometer is again put in the circuit y closing key K. The key K is closed and resistance R is given a value corresponding to the maximum current. The commutator K is closed to the right and the irst throw θ o the galvanometer is noted. 'The current i is also noted rom the ammeter. The values o B and H are calculated y using Eq. (4) and () respectively. The corresponding point on the B- H curve is a (Fig. 6..) Fig. 6.. The galvanometer circuit is again roken and the specimen is again demagnetized y reversing rapidly the commutator K as descried eore. The allistic galvanometer is again put in the circuit. Now R' is given a small value and K' is opened.the magnetising orce is therey decreased to H, producing a allistic throw θ in the galvanometer. This throw corresponds to a decrease in induction, B - B. The value o magnetising ield H is calculated y noting ammeter reading. The corresponding point on the graph is,denoted y the point. This process is repeated y
100 Page gradually increasing R, until current and hence H ecomes zero. The graph corresponding to these readings is ac. Ater each measurement, the specimen is returned to the state a y the reversal o maximum current. Hence point a works as the reerence point. The key K' is now closed and commutator is reversed several times and inally let to the right. R' is given a large value and galvanometer is a again put in the circuit. The commutator K is then thrown, over to the let and at the same time K' is opened, so that the current is reversed and at the same time made o small value. This gives a point on the part cd o the curve. The starting point is again a and change in magnetic induction is measured every time. The process is repeated in many steps until inally R' is zero when the point e on the curve is reached. The part ega can e drawn y symmetry or y repeating the, experiment using e as the reerence point and leaving the commutator now on the let. The two way key K is closed to the right. A known current i ' is passed through P. The corresponding throw θ' in the B.G, is noted. This auxiliary experiment is used to calculate H rom Eq. (4) Energy loss due to hysteresis According to Ewing's theory o molecular magnetism, a magnetic material even in the un magnetised condition consists o an indeinitely large numer o molecular magnets endowed with deinite polarity. When a magnetizing ield is applied, the molecular magnets align themselves in the direction o the ield. During this process, work is done y the magnetizing ield in turning the molecular magnets against the mutual attractive orces. This energy required to magnetize a specimen is not completely recovered when the magnetizing ield is turned o, since the magnetization does not ecome zero. The specimen retains some magnetization ecause some o the molecular magnets remain aligned in the new ormation due to the group orces. To tear them out completely, a coercive orce in the reverse direction has to e
101 Page applied. Thus, there is a loss o energy in taking a erromagnetic material through a cycle o magnetization. This loss o energy is called hysteresis loss and appears in the orm o heat. Consider a magnetic material having n molecular magnets per unit volume. Let m e the magnetic moment o each magnet and θ the angle which its axis makes with the direction o magnetizing ield H. The magnetic moment m o the molecular magnet can e resolved into a component m cos θ in the direction o H and m sinθ perpendicular to H. The component m cosθ alone contriutes to the magnetising ield and the component m sin a has no eect on the rnagnetisation o the specimen. I M e the intensity o rnagnetisation, then M=m cos θ Dierentiating Eq (), dm= d(m cos θ)=- m sin θ.dθ When M increases to M + dm, θ decreases to θ - d θ. The work done y the ield in decreasing θ y d θ is given y dw =C d θ Here, C= torque or unit delection = mhsin θ () (3) () dw= mhsin θ X (-d θ)=- mhsin θdθ.(4) The work done y the applied ield is dw H ( msin d = H dm (From Eq.() Thus work done y the magnetizing ield per unit volume o the material or completing a cycle is, W HdM HdM (5) Now B= (H+M). For erromagnetics, M>>H. So B= M From Eqs.(5) and (6). i.e., db= dm (6)
102 Page W HdB (7) The area o the B-H loop or times the area o the M-H loop gives the energy spent per cycle. When H is in Am - and B is in W m -, the energy is in joules per cycle per m 3 o the material. 6.. The Importance o hysteresis curves The magnetic properties o a erromagnetic sustance can he otained rom the size and shape o the hysteresis loop. Fig. 6. shows the hysteresis loops or sot iron and steel. Fig 6. (i) The retentivity o sot iron (OC) is greater than that o steel (OC ') i.e., sot iron retains more magnetism than steel, when the magnetising orce is totally removed. (ii) The coercive orce or son iron (OD) is smaller than that or steel (OD), i.e iron is more readily demagnetised than steel. (iii) The permeaility = (B/H) or sot iron is greater than that or steel. (iv) The susceptiility (=M/H) or sot iron is greater than that or steel.
103 Page 3 (v) The area o the B - H loop or steel is much larger than that or sot iron. Thus the energy loss per unit volume per cycle o magnetisation is greater or steel than that or sot iron Choice o Magnetic materials (i) Permanent Magnets. Materials used or making magnets are never taken through a cycle. So hysteresis loss is a minor consideration in these cases. These materials should have high retentivity and high coercivity. So steel is a suitale material or permanent magnets. Recently a numer o alloys, having large values o coercivity have een developed or the purpose o construction o permanent magnets. The very suitale alloy o highest coercivity is names as vicalloy (vanadium, iron and coalt). (ii) Electro-magnets. The material or the cores o electromagnets should have maximum lux density with comparatively small magnetizing ield and low hysteresis loss. Sot-iron is an ideal material or electro-magnets. (iii) Transormer cores. Materials or transormer cores, telephone diaphragms and chokes etc., (which are meant or otaining high magnetic lux) are requently sujected to many cycles o magnetisation in one second. So the material selected or the purpose must e associated with high magnetic induction and low hysteresis loss. Sot-iron is etter than steel or these purposes. By alloying sot-iron with 4% silicon, 'transormer steel' is produced. It has a higher initial permeaility and is an ideal material or cores o transormers. Alloys o iron and nickel, called permalloys have also very large initial permeailities. (iv) Ferrites. Their permeaility is very high. Ferrites are made y sintering powders consisting o a mixture o erric oxide and the oxides o other metals like lithium, nickel and manganese. Their hysteresis loop is almost rectangular [Fig. 6.3] which enales these to e used or memory circuit in computers. These have a high Fig. 6.3
104 Page 4 electrical resistivity unlike the erromagnetic materials which are very good conductors. So errites are widely used in the manuacture o components or radio and electrical communication equipments. 6.4 Let us sum up In this lesson you have studied the importance o Hysterisis and its use in selecting materials y drawing M-H and B-H curve. Also you learned aout the energy losses due to hysterises and the importance o hysterises curves. 6.5 Check your Progress ) What is hysteresis? ) What is coercivity 3) State the reason as to why energy losses taking place in hysteresis 4) Give any two importance o Hysteresis curves 5) What are errites 6.6 Lesson end Activities ) An iron rod o density 77 kg m -3 and speciic heat capacity 46 J Kg - K - is sujected to cycles o magnetization at the rate o 6c/s. I the area o B-H curve or the specimen is 5 Joules, calculate the rise in temperature per minute o the specimen. 6.7 Points or Discussion. What is Hysterises? Explain an experiment to dra M-H and B-H curve.. Write short notes on (i) Energy loss due to hysterises (ii) Discuss the choice o materials on the asis o Hysterises curve. 6.8 Reerences ) Electricity and Magnetism y Srivastava ) Electricity and Magnetism y R. Murugesan
105 Page 5 UNIT IV CONTENTS LESSON 7 7. Aims and Ojectives 7. Laws o Thermo e.m.. 7. Seeeck Eect. 7.a Measurement o Thermo EMF using Potentiometer 7.3 Peltier Eect - 7.3a Determination o the Peltier Co-eicient at a junction 7.4 Thermo dynamical consideration o Peltier Eect 7.4a Explanation o Seeack, Peltier and Thomson eects on the Electron theory 7.5 Thomson Eect 7.6 Thermodynamics o Thermocouple (Expression or Peltier and Thomson coeicients). 7.7 Let us sum up 7.8 Check your Progress 7.9 Lesson end Activities 7. Points or Discussion 7. Reerences 7. Aims and Ojectives AIM: In this less the laws o thermo em and dierent types o thermoelectric eects are discussed. These are Seeeck, Peltier and Thompson eects. Also you will come to know aout the applications o the aove eects. These eects are explained on the asis o electron theory. 7. Laws o Thermo e.m.. (i) Law o Intermediate Metals. The introduction o any additional metal into any thermoelectric circuit does not alter the thermo em provided the metal introduced is entirely at the same temperature as the point at which the metal is introduced.
106 Page 6 I a E is the em or a couple made o metals A and B, and E c that or the couple o metals B and C, then the em or couple o metals A and C is given y, ae c = a E + E c (ii) Law o Intermediate Temperatures. The thermo em E 3 o a thermocouple whose junctions are maintained at temperatures T and T 3 is equal to the sum o the ems E and E 3 when the junctions are maintained at temperatures T, T and T, T 3 respectively. Thus, E 3 = E + E 3 7. Seeeck Eect. When two dissimilar metal wires are joined together so as to orm a closed circuit and i the two junctions are maintained at dierent temperatures, an em is developed in the circuit (Fig 7.). This causes a current to low in the circuit as indicated y the delection in the galvanometer G.. This phenomenon is called the Seeeck eect. This arrangement is called a thermocouple. The em developed is called thermo em. The Fig. 7. thermo em so developed depends on the temperature dierence etween the two junctions and the metals chosen or the couple. Seeeck arranged the metals in a series as ollows:
107 Page 7 Bi, Ni, Pd, Pt, Cu, Mn, Hg, P, Sn, Au, Ag, Zn, Cd, Fe, S. When a thermocouple is ormed etween any two o them, the thermoelectric current lows through the hot junction rom the metal occurring earlier to the metal occurring later in the list. The more removed are the two metals in the list, the greater is the thermo em developed. The metals to the let o P are called thermoelectrically negative and those to its right are thermoelectrically positive. 7.a Measurement o Thermo EMF using Potentiometer Thermo ems are very small, o the order o only a ew millivolts. Such small ems are measured using a potentiometer. A ten-wire potentiometer o resistance R is connected in series with an accumulator and resistance oxes P and Q. A standard cell o em E is connected in the secondary circuit. The positive terminal o the cell is connected to the positive o Q. The negative terminal o the cell is connected to a galvanometer and through a key to the negative o Q. (Fig.7.(a)) Fig. 7.(a) A resistance o ER ohms is taken in Q. The resistance in P is adjusted so that on closing the key, there is no delection in the galvanometer. Now, the PD across ER ohms is equal to E. PD across R ohms o the potentiometer =( ERER) volt = () volt = millivolt
108 Page 8 Thus the all o potential per metre o the potentiometer wire is millivolt. So we can measure thermo em up to millivolt. Without altering resistances in P and Q, the positive o the thermocouple is connected to the positive terminal o the potentiometer and the negative o the thermocouple to a galvanometer and jockey. One junction is kept in melting ice and their other junction in an oil ath or in a sand ath. The jockey is moved till a alance is otained against the small em e o the thermocouple. Let AJ = l cm e the alancing length. Then, Thermo em e = l millivolt. Keeping the cold junction at C, the hot junction is heated to dierent temperatures. The thermo em generated is determined or dierent temperatures o the hot junction. A graph is drawn etween thermo em and the temperature o the hot junction (Fig 7.). The graph is a paraolic curve. Fig. 7.() The thermo em E varies with temperature according to E = at + t, where a and are constants. The thermo em increases as the temperature o the hot junction increases,
109 Page 9 reaches a maximum value T n, then decreases to zero at a particular temperature T i. On urther increasing the dierence o temperature, em is reversed in direction. For a given temperature o the cold junction, the temperature o the hot junction or which the thermo em ecomes maximum is called the neutral temperature (T n ) or the given thermocouple. For a given temperature o the cold junction, the temperature o the jot junction or which the thermo em ecomes zero and changes its direction is called the inversion temperature (T i ) or the given thermocouple. T n is a constant or the pair o metals. T i is as much aove the neutral temperature as the cold temperature as the cold junction is elow it. Note: For experiment reer Annexure I 7.3 Peltier Eect - Consider a copper-iron thermocouple (Fig 7.3). When a current is allowed to pass through the thermocouple in the direction o arrows (rom A to B), heat is asored at the Fig. 7.3 junction B and generated at the junction A. This asorption or evolution o heat at a junction when a current is sent through a thermocouple is called Peltier eect. The Peltier eect is a reversile phenomenon. I the direction o the current is reversed, then there will e cooling at the junction A and heating at the junction B.
110 Page When an electric current is passed through a closed circuit made up o two dierent metals, one junction is heated and the other junction is cooled. This is known as Peltier eect. The amount o heat H asored ir evolved at a junction is proportional to the charge q passing through the junction. i.e., H q or H It Or H = It Where π is a constant called Peltier coeicient. When I = A and t = s, then H = π. The energy that is lierated or asored at a junction etween two dissimilar metals due to the passage o unit quantity o electricity is called Peltier coeicient. It is expressed in joule/coulom i.e., volt. The Peltier coeicient is not constant ut depends on the temperature o the junction. The Peltier eect is dierent rom the I R Joule heating eect. The main dierences are given elow. S. No. Peltier eect Joule eect. It is reversile eect. It is an irreversile eect It takes place at the junctions only. It may e a heating or a cooling eect. Peltier eect is directly proportional to I (H = ± πit). It depends upon the direction o the current. It is oserved throughout the conductor. It is always a heating eect. Amount o heat evolved is directly proportional to the square o the current. It is independent o the direction o the current.
111 Page 7.3(a) Determination o the Peltier Co-eicient at a junction A copper-iron junction is immersed in a calorimeter containing water. The Cu-Fe junction is joined to a attery, a rheostat, ammeter and a commutator (ig 7.3a). Fig. 7.3a A current o i ampere, measured y an ammeter A, is passed or t second. The resulting rise in temperature o water in the calorimeter is noted. Let R e the resistance o the junction. I H Joules us the heat produced, then H = i Rt + π it ---() The same current is now passed or the same time in the reverse direction. The rise o temperature is again noted. Let H Joules e the heat produced. Then, H = i Rt - π it ---() From Equs. () and (), we have (H - H ) = πit
112 Page or π = (H - H ) / it calorimeter. Let M e the mass o water in calorimeter and W the thermal capacity o the Let θ and θ e the rises in temperature in the two cases respectively. Then, H = (M + W) θ and H = (M + W) θ (H - H ) = (M + W) (θ θ ) Thereore, π = (M + W) (θ θ ) / it Hence π is determined rom the aove relation. 7.4 Thermo dynamical consideration o Peltier Eect Consider a Cu-Fe thermocouple with the cold junction at the asolute temperature T and the hot junction at the asolute temperature T (ig 7.4). The thermoelectric current i lows in the direction as shown in ig 4.4. The low o this current provides the necessary condition or the Peltier eect to take place and consequently the heat is asored at the hot junction and generated at the cold junction. Let π and π e the Peltier coeicients o the cold and the hot junctions respectively. Fig. 7.4 Heat energy asored in t seconds at the hot junction = π i t. Heat energy evolved in t seconds at the cold junction = π i t. Thereore, Net energy asored = (π π ) it ---() This energy is used in setting up a thermo em E p in the circuit. The electrical energy developed in the thermocouple = E p it.
113 Page 3 Thereore, (π π ) it = E p it Or E p = (π π ) ---() The thermocouple acts like a heat engine in which an amount o heat energy π is asored rom the source at a higher temperature T and an amount π is rejected to the sink at the lower temperature T. Applying second law o thermodynamics, we have (π / T ) = (π / T ) or (π / π ) = (T / T ) or (π - π ) / π = (T - T ) / T or (π - π ) = (π / T ) (T - T ) or (π - π ) (T - T ) [Since, (π / T ) is constant] ---(3) From Equs. () and (3), we have E p α (T - T ) ---(4) Thus the em developed in the thermocouple is directly proportional to (T - T ), the temperature dierence etween the two junctions. The graph etween E p and T should e a straight line. But it has een ound experimentally that the graph etween E p and T is a paraolic curve. This shows that Peltier eect alone cannot explain the thermo-electric phenomenon in a thermocouple. This led to the discovery o Thosmson eect. Thomson said that there must e some additional source o EMF which has not een taken into
114 Page 4 account in Peltier eect. This additional EMF is due to the dierent parts o the same metal eing at dierent temperatures. The comined EMF due to the Peltier eect and Thomson eect showed agreement with the experimental results. 7.4a Explanation o Seeack, Peltier and Thomson eects on the Electron theory The concentration o electrons at the interace in the two metals is not the same as it depends upon the nature o the metal and its temperature. A potential dierence exists across the junction o two dissimilar metals, the concentration o the ree electrons in the metals on either side o the junction eing dierent. So the ree electrons diuse across the junction rom the metal where their concentration is higher to the metal where it is lower. Thereore, one metal ecomes negatively charged while the other ecomes positively charged when a state o dynamical equilirium is reached. This resulting potential dierence depends on the nature o the metals orming the junction. In the case o Cu-Fe junction, let V and V e steady potential dierences across the hot and cold junctions. When the two junctions are at the same temperature, V = V. Thereore, the resultant P.D. in the complete circuit is zero. I the temperature o one junction is greater than that o the other, V > V and resultant E.M.F. (V - V ) exists in the couple. It is this resultant E.M.F. that makes the thermo-electric current to low rom Cu to Fe at the hot junction and Fe to Cu at the cold junction. This explains Seeeck eect. Suppose a charge Q coulom is passed rom Cu to Fe at the junction where the P.D. is V. The charge goes up a gradient o potential asoring energy in the orm o heat rom the junction. The junction is cooled. At the other junction where the P.D. is V,
115 Page 5 the charge lows down a gradient o potential. Thereore, energy is lierated as heat at this junction. The junction is heated. This explains Peltier eect. In an unequally heated metal rod like copper, the hotter parts are assumed to e at a higher potential than those at a lower temperature. Thereore when a charge is passed rom the hot end to the cold end o a copper rod, the charge moves down a gradient o potential. This results in the lieration o energy as heat in the copper rod. I on the other hand, the charge is passed rom colder to hotter parts, it goes up a gradient potential and thereore asors energy rom the metal as heat. This explains the existence o Thomson eect in a metal like copper. 7.5 Thomson Eect Consider a copper ar AB heated in the middle at the point C (ig 7.5a). A current is passed rom A to B. It is oserved that heat is asored in the part AC and evolved in the part CB. This is known as Positive Thomson eect. Similar eect is oserved in metals like Ag, Zn, S and Cd. Fig. 7.5 (a) Fig. 7.5 () In the case o an iron ar AB, heat is evolved in the part AC and asored in the part CB (ig 7.5). This is known as Negative Thomson eect. Similar eect is oserved in metals like Pt, Ni, Co, and Bi.
116 Page 6 For lead, the Thomson eect is zero. The Thomson eect is reversile. In the case o copper, the hotter parts are at a higher potential than the colder ones. It is opposite in the case o iron. Heat is either asored or evolved when current passes etween two points having a dierence o potential. Thereore, the passage o electric current through a metal having temperature gradient results in an asorption or evolution o heat in the ody o the metal. When a current lows through an unequally heated metal, there is an asorption or evolution o heat throughout in the ody o the metal. This is known as Thomson eect. Thomson Coeicient. The Thomson coeicient σ o a metal is deined as the amount o heat energy asored or evolved when a charge o Coulom lows in the metal etween two points which dier in temperature y C. Thus, i a charge o q coulom lows in a metal etween two points having a temperature dierence o C, then Heat energy asored or evolved = σ q Joule. But i E volt e the Thomson em developed etween these points then this energy must e equal to Eq Joule. Thereore, σq = Eq Or σ = E.
117 Page 7 Thus the Thomson coeicient o a metal, expressed in joule per coulom per C, is numerically equal to the em in volt, developed etween two points diering in temperature y C. Hence it may also e expressed in volt per C. is not a constant or a given metal. It is a unction o temperature. Demonstration o Thomson eect. Fig. 7.5 (c) Fig 7.5c shows Starling s method o demonstrating the Thomson eect. An iron rod ABC is ent into U shape. Its ends A and C are dipped in mercury aths. C and C are connected in the opposite gaps o a metre ridge. The ridge is alanced. Then the mid-point B o the rod is strongly heated. A heavy current is passed through the rod. Then this current will e lowing up the temperature gradient in one arm and down the temperature gradient in the other arm. As a result, one o the coils will e cooled and the other will e warmed. The alance in the ridge will e upset and the galvanometer in its circuit will show a delection. I the direction o the current is reversed, the delection in the galvanometer will e reversed.
118 Page Thermodynamics o Thermocouple (Expression or Peltier and Thomson coeicients). Consider a thermocouple consisting o two metals A and B. Let T and T + dt e the temperatures o the cold and hot junctions respectively (ig 7.6). Let and + d e the Peltier coeicients or the pair at the cold and hot junctions. Let a and e the Thomson coeicients or the metals A and B respectively, oth taken as positive. When a charge lows through the thermocouple, heat will e asored and evolved at the junctions due to Peltier eect and all along the metal due to Thomson eect. Fig. 7.6 Let Coulom o charge low through the thermocouple in the direction rom A to B at the hot junction. Heat energy asored due to Peltier eect at the hot junction = (+ d) joules. Heat energy evolved due to Peletier eect at the cold junction = joules. Heat energy asored in the metal A due to Thomson eect = a dt Joules Heat energy evolved in the metal B due to Thomson eect = dt Joules Thereore, net heat energy asored in the thermocouple = ( + d - ) + ( a dt - dt) = d + ( a - ) dt This energy is used in estalishing a P.D. de in the thermocouple
119 Page 9 Thereore, de = d + ( a - ) dt ---() Since the Peltier and Thomson eects are reversile, the thermocouple acts as a reversile heat engine. Here, (i) the heat energy ( + d) Joules is asored rom the source at (T + dt) K and a dt Joule is asored in metal A at mean temperature T Kelvin. (ii) Also Joule is rejected to sink at T K and dt Joule is given out in metal B at the mean temperature T K. Applying Carnot s theorem, we have d a dt T dt T dt T T Or d ( T dt T T a ) dt Or T d T T dt T( T dt) ( a ) T dt Or d.t -.dt = ( - a ) dt (T + dt) Or d.t -.dt = ( - a ) T dt + ( - a ) dt Or d.t -.dt = ( - a ) T dt [Neglecting ( - a ) dt ] Or T [d + ( a - ) dt] = dt But d + ( a - ) dt = de [rom Eq. ()] Thereore, T de = dt Or = T. (de / dt) ---() The quantity (de / dt) is called the thermoelectric power (P).
120 Page Thermoelectric power (P) is deined as the thermo em per unit dierence o temperature etween the junctions. Peltier coeicient = Asolute temperature thermoelectric power Dierentiating Eq. (), d dt d E T dt de dt Sustituting the value o (de/dt) rom Eq. (), d T dt d E dt d ( a dt ) Or ( a - ) = -T. (d E / dt ) Or ( - a ) = T. (d E / dt ) ---(3) I the irst metal in the thermocouple is lead, then a = = T. (d E / dt ) ---(4) Thomson coeicient = asolute temperature o the cold junction irst derivative o thermoelectric power. From Eq. (3), (d E / dt ) = [( - a ) / T] Or (d / dt) (de / dt) = [( - a ) / T] Putting (de / dt) rom Eq. (), we have (d / dt) ( / T) - [( - a ) / T] = ---(5) This gives the relation etween Peltier and Thomson s coeicients. 7.7 Let us sum up In this lesson you learned aout the laws o thermo em and dierent types o thermoelectric eects namely Seeeck, Peltier and Thompson eect. Also you learned aout the applications o these eects. All these eects were explained on the asis o electron theory.
121 Page 7.8 Check your Progress ) State the laws o thermo em ) What is Seeeck eect? 3) Stat the dierences etween Peltier and Joule eect 4) What is Thompson eect? 7.9 Lesson end Activities ) When an electric current is passed through a closed circuit made o two dierent metals, one junction is heated and the other junction is cooled. This is known as. ). Is a reversile eect and is a irreversile eect. 3) Thermocouple acts as a.. 4) Thompson coeicient o a metal expressed in. 7. Points or Discussion ) What is meant y Peltier eect? How do you demonstrate it experimentally? How does it dier rom Joule s heating eect? Deine Peltier co eicient ) (i) Prove that the Peltier coeicient o a pair o metals is the product o the asolute temperature and thermo electric power (ii) Deine Thompson eect and Thompson co eicient 7. Reerences ) Electricity and Magnetism y R. Murugesan ) Electricity and Magnetism y Brijlal and Suramanyam
122 Page CONTENTS 8. Aims and Ojectives 8. Thermo-Electric diagrams LESSON (i) Determination o Total em 8.. (ii) Determination o Peltier em (iii) Determination o Thomson em 8..4 (iv) Thermo em in a general couple, neutral temperature and temperature o inversion. 8. Thermoelectric Rerigerator 8.3 Thermoelectric eect in p- and n-type semi-conductors 8.4 Let us sum up 8.5 Check your Progress 8.6 Lesson end Activities 8.7 Points or Discussion 8.8 Reerences 8. Aims and Ojectives In this lesson you learn aout the importance o thermoelectric diagrams ormed rom two metals A and B. In the diagram namely the graph, you will e ale to understand the characteristics o dierent metals y thermoelectric line or Cu-P couple and Fe-P couple having respectively positive and negative slope. Also you will learn aout the thermoelectric eect in the thermoelectric rerigerator. 8. Thermo-Electric diagrams A thermocouple is ormed rom two metals A and B. The dierence o temperature o the junctions is TK. The thermo em E is given y the equation E = At + Bt
123 Page 3 Where A and B are constants. A graph etween E and T is a paraola. (de/dt) = a + T de/dt is called thermoelectric power. A graph etween thermoelectric power (de/dt) and dierence o temperature T is a straight line. This graph is called the thermo-electric power line or the thermo-electric diagram. Thomson coeicient o lead is zero. So generally thermo-electric lines are drawn with lead as one metal o the thermo-couple. The thermoelectric line o a Cu-P couple has a positive slope while that o Fe-P couple has a negative slope. Fig 4.7 shows the power lines or a numer o metals. Fig. 4.7 Uses o Thermoelectric Diagrams 8.. (i) Determination o Total em. MN represents the thermo-electric power line o a metal like copper coupled with lead (ig 4.7.). MN has a positive slope.
124 Page 4 Fig Let A and B e two points corresponding to temperatures T K and T K respectively along the temperature-axis. Consider a small strip andc o thickness dt with junctions maintained at temperatures T and (T + dt). The em developed when the two junctions o the thermocouple dier y dt is de = dt (de/dt) = area adc Total em developed when the junctions o the couple are at temperatures T and T is E s T dt T de dt area ABDC 8.. (ii) Determination o Peltier em. Let and e the Peltier coeicients or the junctions o the couple at temperatures T and T respectively. The Peltier coeicient at the hot junction (T ) is de T dt T OB BD area OBDF Similarly, Peltier coeicient at the cold junction (T ) is de T dt T OA AC area OACE
125 Page 5 and give the Peltier ems at T and T respectively. Peltier em etween temperatures T and T is E p = - = area OBDF - area OACE = area ABDFECA (iii) Determination o Thomson em. Total em developed in a thermocouple etween temperatures T and T is thermocouple. T dt Es a T Here a and represent the Thomson coeicients o two metals constituting the I the metal A is copper and B is lead, then =. Es a dt T a T Or dt T T E Thus, the magnitude o Thomson em is given y, E th = ( - ) E = Area ABDFECA Area ABDC = Area CDFE 8..4 (iv) Thermo em in a general couple, neutral temperature and temperature o inversion. In practice, a thermocouple may consist o any two metals. One o them need not e always lead. Let us consider a thermocouple consisting o any two metals, say Cu and Fe. AB and CD are the thermo-electric power lines or Cu and Fe with respect to lead (ig 8..4). Let T and T e the temperatures o the cold and hot junctions corresponding to points P and Q.
126 Page 6 Fig Em o Cu P thermocouple = Area PQB A Em o Fe P thermocouple = Area PQD C the em o Cu Fe thermocouple is E Fe Cu Area PQD C Area PQB A Area A BDC The em Fe E Cu increases as the temperature o the hot junction is raised and ecomes maximum at the temperature T n, where the two thermoelectric power lines intersect each other. The temperature T n is called the neutral temperature, at T = T n, (de/dt) =. Suppose temperatures o the junctions, T and T, or a Cu Fe thermocouple are such that the neutral temperatures T n lies etween T and T (ig a). Fig (a) Then the thermo em will e represented y the dierence etween the areas A NC and B D N ecause these areas represent opposing em s. In the particular case when T n = (T
127 Page 7 + T )/, these areas are equal and the resultant em is zero. In this case, T is the temperature o inversion or the Cu Fe thermocouple. 8. Thermoelectric Rerigerator Peltier eect has een used to develop thermo-electric rerigerator. According to this eect we know that heat is asored at one end and lierated at the other junction o a thermocouple when a current is passed into a thermocouple having its two junctions at dierent temperature is aout millivolt/degree. Also its thermal conductivity is very much lower than that o metals. Hence a semiconduct5or can e used as an eective rerigerator using the Peltier eect. On this principle a rerigerator cu. Ft. cold ox has een designed. It consists o 8 thermocouples and reduces the temperature o air y -3C. It takes aout 5- amperes rom a attery or mains. 8.3 Thermoelectric eect in p- and n-type semi-conductors When one end o a semi-conductor is hotter than the other, electrons leave the hot end and tend to low to the cold end. The cold end soon ecomes negatively charged with respect to the hot end. The negative charge at irst increases till, owing to repulsion, the low o electrons rom the hot end is in equilirium with the return low rom the cold end. The ewer the electrons availale or the return low the higher will e the voltage at the cold end, eore equilirium is reached. It is or this reason that thermoelectric power is much greater in a semiconductor than that o metals. Also the voltage dierence etween the hot and cold ends o a semi-conductor is set up not only y the low o electrons ut also y the low o electrons ut also y the low o holes. In n-type semiconductors the hot end is positive. In p-type the cold end is positive. In oth types,
128 Page 8 however, the direction o electron low is rom the positive to the negative end. The low o current in such a comination is shown in ig 4.. Such a thermoelectric cell produces only th o a volt, and to otain higher voltage, a pile o such semi-conductors is used. Such a thermoelectric generator is now widely used in supplying power to radio transmitters in rockets and satellites. 8.4 Let us sum up In this lesson you learned aout the importance o thermoelectric diagrams ormed rom the metals A and B. In the diagram namely graph, you were ale to understand the characteristics o dierent metals y thermoelectric line or Cu-P couple and Fe-P couple having positive and negative slopes respectively. You have also studied aout the thermoelectric eect in the thermoelectric rerigerator. 8.5 Check your Progress ) What is thermoelectric diagram? ) What is neutral temperature and temperature o inversion? 3) Mention the uses o thermoelectric diagram 8.6 Lesson end Activities ) The em o a thermo couple, one junction o which is kept at o C is given y E = at +t. Determine the neutral temperature, temperature o inversion and the Peltier and Thompson coeicients. 8.7 Points or Discussion ) (i) Apply thermodynamic considerations to the working o the thermo couple show that, = T. (de / dt)
129 Page 9 and (d E / dt ) = [( - a ) / T] (ii) Explain any two uses o thermo electric diagrams ) (i) Descrie the loss o thermo em. Explain Seeeck eect (ii) Explain how you determine thermo em using potentio meter 8.8 Reerences ) Electricity and Magnetism y D. N. Vasudeva ) Electricity and Magnetism y R. Murugesan
130 Page 3 Annexure I Experiment: THERMO EMF MEASUREMENT USING POTENTIOMETER Aim: To measure thermo em using potentiometer Apparature Required: Potentiometer, jockey, V attery, copper constantan thermocouple, galvanometer, decade resistance ox (DRB), thermometer, ice, eaker, sand ath or hot water, tripod, wire gauge, Bunsen urner, meter ridge and accessories. Formulae: The potential drop per unit length ER ( R R ) L p p The thermo em ER p e l ( R R ) p l L where E is em o the atter, R p the resistance o the potentiometer wire, L the length o the potentiometer wire ( m), R the value o the resistance introduced in series and l the alancing length. I the all o potential per unit length is made as V/cm - then e = V x l (in cm) mv Experimental procedure: (i) Calculation o the value o R to make a potential drop o V/cm o the wire
131 Page 3 Measure the resistance (R p ) o the potentiometer wire using either a post oice ox or a meter ridge experiment or a multimeter. Measure the em (E) o the attery. A potentiometer has a length o m. I a potential o V is dropped in cm, then the total potential to e dropped x -6 x = - V =. V I E is em o the attery, then (E--) volt has to e dropped y a series resistance R employed. Thus, i R is the series resistance to e employed, then R R p ( E.). R ( E.) R p. By measuring the resistance o the potentiometer wire, R p and the em o the attery, the value o R is determined using the aove ormulae. (ii) Measurement o thermo em The experimental arrangements used or the determination o thermo em is shown elow. To make a potential drop o V cm -, the calculated value o resistance R is introduced in the resistance ox R. One junction o the thermocouple is kept in ice ath and the other is placed in water ath. The temperatures are measured with
132 Page 3 thermometer T and T. To egin the experiment the water is kept at room temperature and ice at o C. The alancing length is measured and taulated. The thermoem (mv) is ound out y multiplying V and the alancing length in cm. Now the water is heated. Balancing length or every o rise is noted. From the alancing length, thermo em are determined. A graph is plotted etween the temperature and the thermo em and is shown elow. From the curve the thermo electric power at T o C is given y P dv dt tan PQ QR... V / o C Results: (i) (ii) Resistance o the potentiometer wire =. Resistance to e introduce in series with a potentiometer wire, to make a potential drop o mv cm - =. (iii) Thermoelectric power at 5 o C =. V / o C - (iv) Thermo em at 5 o C =. mv
133 Page 33 UNIT V LESSON - 9 CONTENTS 9. Aims and Ojectives 9.Growth and decay o current in an inductive - resistive circuit: 9..: Decay o current in a circuit containing L and R 9. Charging and discharging o a capacitor through a resistor: 9.. Decay o charge (Discharging o a capacitance through Resistance): 9.3 Discharge o a Capacitor through an inductor and a Resistor in series: 9.4 Oscillatory Circuits Growth o charge in a circuit with Inductance, Capacitance and Resistance: 9.5 Measurement o High Resistance y Leakage: 9.6 Moving coil Ballistic Galvanometer: 9.6. Correction or Damping in Ballistic Galvanometer 9.6. Dead-eat and Ballistic Galvanometers 9.7 Let us sum up 9.8 Check your progress 9.9 Lesson end Activities 9. Points or Discussion 9. Reerences 9. Aims and Ojectives In this lesson you will learn aout transient currents in particular the growth and decay o current in an L and R circuit, charging and discharging o a capacitor through a resistor and inductor and a resistor in series. Also you will learn aout the principle o oscillatory circuits. Finally you will learn aout the theory o Ballistic galvanometer.
134 Page 34 9.Growth and decay o current in an inductive - resistive circuit: Consider a circuit having an inductance L and a resistance R connected in series to a cell o steady em E (Fig 9.). When the key K is pressed, there is a gradual growth o current in the circuit rom zero to maximum value I. Let I e the instantaneous current at any instant. Fig. 9. Then, the induced ack em L di dt di E RI L () dt When the current reaches the maximum value I, the ack em, di L dt Hence E RI () Sustituing this value or E in Eq. () or di RI RI L or R (I - I) = dt di I I Integrating, R L dt where C is the constant o integration, When t =, I =, di L dt R log ( I I ) t C (3) L log e I C Sustituting this value o C in Eq. (3), R log( I I) t log e I or log e ( I I) log e I L R L t
135 Page 35 log e ( I I I ) R t L I I ( R / L) t I ( R / L) t e or e I I ( R / L) t I I ( e ) (4) Eq. (4) gives the value o the instantaneous current in the LR circuit. The quantity (L/R) is called the time constant o the circuit. I L t, I I ( e ) I. 63 I R e Fig. 9. (a) Thus, the time constant L/R o a L-R circuit is the time taken y the current to grow rom zero to.63 times the steady maximum value o current in the circuit. Similarly, when t = L/R, 3L/R, the value o current I will e.8647,.95 o the inal maximum current when t=, I= and when t, I = I. Greater the value o L/R longer is the time (Re. Fig. 9.a) 9..: Decay o current in a circuit containing L and R When the circuit is roken, an induced em, equal to di L is again produced in dt the inductance L and it slows down the rate o decay o the current. The current in the circuit decays rom maximum value I to zero. During the decay, let I e the current at time t. In this case E =. The em equation or decay o current is di RI L (5) dt
136 Page 36 di dt Integrating, R L dt When t =, I = I, R log e I t C where C is a constant. L log e I C log e I R t log L e I, or log e I I R L t I ( R / L ) t I e ( R / L) t I I e (6) Eq. (6) represents the current at any instant t during decay. A graph etween current and time is shown in ig 5... (a) Fig. 9.. (a) Fig. 9.. () Fig. 9.. (c) When t = L/R, I = I e - = (/e) I =.365 I t = L/R, I = I e - =.35 I t = 3L/R, I = I e -3 =.5 I Thereore, the time constant L/R o a R-L circuit may e also deined as the time in which the current in the circuit alls to /e o its maximum value when external source o e.m.. is removed. The rate o decay o current is di dt R L I e ( R / L) t R L I Thus it is clear that greater the ratio R/L, or smaller the time constant L/R, the more rapid does the current die away (ig 5...()). Fig 5...(c) shows that the growth and decay curves are complementary.
137 Page Charging and discharging o a capacitor through a resistor: 9.. Growth o Charge: A capacitance C and resistance R are connected to a cell o em E through a Morse key K. When the key is pressed, a momentary current I lows through R. At any instant t, let Q e the charge on the capacitor o capacitance C. (Re. Fig. 9..) Fig. 9.. P.D. across capacitor = Q/C P.D. across resistor = RI The em equation o the circuit is E = (Q/C) + RI () E = (Q/C) + R (dq/dt) (since I = dq/dt) The capacitor continues getting charged till it attains the maximum charge Q. At that instant I = dq/dt =. The P.D. across the capacitor is E = Q /C. dq Q i.e., when, Q Q, and E dt C Q C Q C dq R dt ( Q Q) CR dq dt dq Q Q dt CR Integrating, -log e (Q - Q) = t/cr + K Where K is a constant. When t =, Q = log e ( Q Q) log e Q thereore, -log e Q = K t log e( Q Q) log e Q CR t CR ()
138 Page 38 Q Q log e Q t CR Q Q Q e t CR or Q Q e t CR t Q Q CR e (3) The term CR is called time constant o the circuit. At the end o time t = CR, Q = Q ( e - ) =.63 Q Thus, the time constant may e deined as the time taken y the capacitor to get charged to.63 times its maximum value. The growth o charge is shown in ig 9.. (a) The rate o growth o charge is Fig. 9.. (a) dq dt Q CR t CR e CR Q Q Thus it is seen that smaller the product CR, the more rapidly does the charge grow on the capacitor. The rate o growth o the charge is rapid in the eginning and it ecomes less and less as the charge approaches nearer and nearer the steady value. 9.. Decay o charge (Discharging o a capacitance through Resistance): Let the capacitor having charge Q e now discharged y realizing the Morse key (Reer Fig 9..). The charge lows out o the capacitor and this constitutes a current. In this case E =.
139 Page 39 dq Q R () dt C or Integrating, log When t =, Q = Q, dq Q CR t log e Q log e Q CR or log e dt t Q K, where K is a constant CR thereore log e Q = K Q t Q t / CR e or e Q CR Q t / CR Q Q e () This shows that the charge in the capacitor decays exponentially and ecomes zero ater ininite interval o time (Reer Fig 5.. (a)) The rate o discharge is I dq dt t Q Q CR e (3) CR CR Thus, smaller the time constant CR, the quicker is the discharge o the capacitor. In eq. (), i we put t = CR, then Q = Q e - =.368 Q. Hence time constant may also e deined as the time taken y the current to all rom maximum to.368 o its maximum value. 9.3 Discharge o a Capacitor through an inductor and a Resistor in series: Consider a circuit containing a capacitor o capacitance C, an inductance L and a Resistance R joined in series (ig 5.3). E is a cell, K is kept open. The capacitor is charged to maximum charge Q y closing the key K. On opening K and closing K, the capacitor discharges through the inductance L and resistance R. Let I e the current in the Fig. 9.3
140 Page 4 circuit and Q e the charge in the capacitor at any instant during discharge. The circuit equation then is C Q RI dt di L But, dt Q d dt di and dt dq I C Q dt dq R dt Q d L C Q dt dq L R dt Q d () Let then k LC and L R, Q k dt dq dt Q d () The general solution o this equation is t k t k B e A e Q ) ( ) ( (3) where A and B are aritrary constants. When t =, Q = Q and rom Eq. (3), A + B = Q (4) t k t k e k B e k A dt dq ) ( ) ( ) ( ) ( When, t =, dt dq ) ( ) ( k B k A ) ( ) ( B A k B A ) ( B A k Q k Q B A (5) From Eqs. (4) and (5), we get
141 Page 4 k Q B and k Q A Putting these values o A and B in Eq. (3), we get t k t k t e k e k e Q Q ) ( ) ( (6) Case : I > k, ) ( k is real and positive and the charge o the capacitor decays exponentially, ecoming zero asymptotically (curve o ig 9.3a). This discharge is known as over damped, non-oscillatory or dead-eat. Fig. 9.3(a) Case : When = k, Q = Q ( + t) e -t This represents a non-oscillatory discharge. This discharge is known as critically damped (curve o ig 9.3a). The charge decreases to zero exponentially in a short time. Case 3: I < k, ) ( k is imaginary. ) ( k = iω, where ω = ) ( k t t e Q i e e e e e Q e i e i e Q Q t t i t i t i t i t t i t i t sin cos Let ω = k sin α and = k cos α so that tan α =
142 Page 4 Q Q e t t Q e k k cos t sin t sin cos sin t Q Q e R t L R LC 4L sin LC R LC 4L t This equation represents a damped oscillatory charge as shown y the curve 3 o ig 5.3 (a). The charge oscillates aove and elow zero till it inally settles down to zero value. The requency o oscillation in the circuit is given y k R LC 4L When R =, LC The condition or oscillatory discharge is R L 4, LC or R L C Importance in Wireless Telegraphy: The discharge o a capacitor through an inductance is oscillatory i the resistance R o the circuit is less than ( L / C ). During the discharge, the energy o the charged capacitor is stored in the magnetic ield produced in the inductance coil, then again ack in the magnetic ield etween the capacitor plates, and so on. I the ields are caused to alternate rapidly, some energy escapes rom the circuit permanently in the orm o electro-magnetic waves which travel through space with the speed o light. These waves orm the asis o wireless telegraphy. Messages can e transmitted rom one place to another with the help o codes.
143 Page Oscillatory Circuits Growth o charge in a circuit with Inductance, Capacitance and Resistance: Consider a circuit containing an inductance L, capacitance C and resistance R joined in series to a cell o em E (ig 9.4). When the key K is pressed, the capacitor is charged. Let Q e the charge on the capacitor and I the current in the circuit at an instant t during charging. Then, the p.d. across the capacitor is Q/C and the sel induced em in the inductance coil is L (di/dt), oth eing opposite to the direction o E. The p.d. across the resistance R is RI. Fig. 9.4 The equation o em s is di Q L RI E () dt C But d Q L dt or d Q dt R dq L dt dq I and dt dq R dt Q C Q CE LC E R Putting and k, we have L LC d Q dt dq dt k Let x = Q CE. Then Q CE di dt d Q dt dx dq d x d Q and dt dt dt dt d x dx Eq. () ecomes, k x dt dt Hence the most general solution o Eq. (3) is () (3)
144 Page 44 t k t k B e A e x )] ( [ )] ( [ Now, CE = Q = inal steady charge on the capacitor. Thereore, x = Q CE = Q Q Hence Q Q = t k t k B e A e )] ( [ )] ( [ Or Q = Q + t k t k B e A e )] ( [ )] ( [ (4) Using initial conditions: At t =, Q = Thereore, = Q + (A + B) or A + B = - Q (5) t k t k e k B e k A dt dq )] ( [ )] ( [ )] ( [ )] ( [ At t =, dt dq = ] ) ( [ )] ( [ k B k A ) ( ] [ )] ( Q B A B A k or ) ( k Q B A (6) Solving Eqs (5) and (6), ) ( k Q A (7) ) ( k Q B (8) Sustituting the values o A and B in Eq. (4), we have t k t k t e k e k e Q Q Q ) ( ) ( ) ( ) ( (9) Case. I > k, ) ( k is real. The charge on the capacitor grows exponentially with time and attains the maximum value Q asymptotically ( curve o ig 9.4a ). The charge is known as over damped or dead eat.
145 Page 45 Fig. 9.4 (a) Case : I = k, the charge rises to the maximum value Q in a short time ( curve o ig 5.4a ). Such a charge is called critically damped. Case 3: < ) ( k is imaginary. Let ) ( k = i ω where i = and ω = ) ( k Eq. (9) may e written as t i t i t e i e i e Q Q Q i e e e e e Q Q Q t i t i t i t i t t t Q e Q Q t cos sin t t e Q Q t sin cos Let ω = k sin α and = k cos α so that tan α = ω/. t k t k e Q Q t sin cos cos sin or t ke Q Q t sin ()
146 Page 46 t L R LC L R LC LC e Q Q L Rt 4.sin 4 This equation represents a damped oscillatory charge as shown y the curve (3) o Fig. 5.4 (a). The charge oscillates aove and elow Q till it inally settles down to Q value. The requency o oscillation in the circuit is given y 4 L R LC k when R =, LC 9.5 Measurement o High Resistance y Leakage: When a capacitor o capacitance C and initial charge Q is allowed to discharge through a resistance R or a time t, the charge remaining on the capacitor is given y ) / ( log.36 log log / / Q Q C t Q Q C t R CR t Q Q e Q Q e Q Q e e CR t CR t I R is high, CR will e high and the rate o discharge o capacitor will e very slow. Thus i we determine Q /Q rom experiment, then R can e calculated. Connections are made as shown in ig 5.5. C is a capacitor o known capacitance, R is the high resistance to e measured, B.G. is a allistic galvanometer, E is a cell and K, K, K 3 are tap keys. Keeping K and K 3 open, the capacitor is charged y depressing the key K. K is then opened and at once K 3 is closed. The capacitor discharges through the galvanometer
147 Page 47 Fig. 9.5 which records a throw θ is proportional to Q. The capacitor is again charged to the maximum value keeping K and K 3 open and closing K. K is then opened and K is closed or a known time t. Some o the charge leaks through R. K is opened and at once K 3 is closed. The charge Q remaining on the capacitor then discharges through the galvanometer. The resulting throw θ is noted. Then Q α θ Q Now, Q R.36 C t log A series o values o t and θ are otained. A graph is plotted etween t and log which is a straight line. Its slope gives the mean value o the value o R can e calculated. t log ( /. As C is known, ) 9.6 Moving coil Ballistic Galvanometer: Principle: When a current is passed through a coil, suspended reely in a magnetic ield, it experiences a orce in a direction given y Fleming s let hand rule. Construction: It consists o a rectangular coil o thin copper wire wound on a nonmetallic rame o ivory (ig 9.6). It is suspended y means o a phosphor ronze wire etween the poles o a powerul horse-shoe magnet. A small circular mirror is attached
148 Page 48 Fig. 9.6 to the suspension wire. Lower end o the coil is attached to a hair-spring. The upper end o the suspension wire and the lower end o the spring are connected to terminals T and T. A cylindrical sot iron core (C) is placed symmetrically inside the coil etween the magnetic poles which are also made cylindrical in shape. This iron core concentrates the magnetic ield and helps in producing radial ield. The B.G. is used to measure electric charge. The charge has to pass through the coil as quickly as possile and eore the coil starts moving. The coil thus gets impulse and a throw is registered. To achieve this result, a coil o high moment o inertia is used so that the period o oscillation o the coil is airly large. The oscillations o the coil are practically undamped. Theory: (i) Consider a rectangular coil o N turns placed in a uniorm magnetic ield o magnetic induction B (ig 9.6a). Let e the length o the coil and its readth. Fig. 9.6 (a)
149 Page 49 Area o the coil = A = l When a current i passes through the coil, Torque on the coil = τ = NiBA () I the current passes or a short interval dt, the angular impulse produced in the coil is τ dt = NiBA dt () I current passes or t seconds, the total angular impulse given to the coil is dt NBA i dt NBAq (3) Here, i dt q total charge passing through the galvanometer coil. Let I e the moment o inertia o the coil aout the axis o suspension and ω its angular velocity. Then, Change in angular momentum o the coil = Iω (4) Thereore, Iω = NBAq (5) (ii) The kinetic energy o the moving system I is used in twisting the suspension wire through an angle θ. Let c e the restoring torque per unit twist o the suspension wire. Then, work done in twisting the suspension wire y an angle θ = or I c c I = c (6) (iii) The period o oscillation o the coil is T I C or T 4 I c T c I (7) 4
150 Page 5 Multiplying Eqs. (6) and (7), I ω c T = 4 or Equating (5) and (8), NBAq = or ct I (8) ct T q c NBAq This gives the relation etween the charge lowing and the allistic throw θ o the galvanometer. q α θ. T c NBAq is called the allistic reduction actor (K) Thereore, q = K θ () (9) Correction or Damping in Ballistic Galvanometer: We have assumed that the whole o the kinetic energy imparted to the coil is used in twisting the suspension o the coil. In actual practice, the motion o the coil is damped y air resistance and the induced current produced in the coil. The irst throw o the galvanometer is, thereore, smaller than it would have een in the asence o damping. The correct value o irst throw is however otained y applying damping correction. Let θ, θ, θ 3, θ 4,.. e the successive maximum delections rom zero position to the right and let (ig 5.6.). Then it is ound that Fig d () The constant d is called the decrement per hal viration. Let d = e so that = log e d. Here is called logarithmic decrement. For a complete viration,
151 Page 5 d e Let θ e the true irst throw in the asence o damping. 3 3 θ > θ. The irst throw θ is oserved ater the coil completes a quarter o viration. In this case, the value o the decrement would e e λ/. e / or () We can calculate λ y oserving the irst throw θ and the eleventh throw θ e or.36 log e log (3) T c q (4) NBA Dead-eat and Ballistic galvanometers: Galvanometers are classiied as (i) dead-eat or aperiodic and (ii) allistic galvanometers. A moving coil galvanometer in which the coil is wound on a metallic conducting rame is known as a dead-eat galvanometer. It is called dead-eat ecause it gives a steady delection without producing any oscillation, when a steady current is passed through the coil. Conditions or a moving coil galvanometer to dead eat: (i) Moment o inertia o the system should e small. (ii) Coil should e mounted on a conducting rame. (iii) Suspension ire should e comparatively thicker.
152 Page Let us sum up This lesson dealt with the transient currents namely the growth and decay o current in a L and R circuit, charging and discharging o a capacitor through a resistor and inductor and a resistor in series. Also it dealt with the principle o oscillatory circuits. Finally it dealt with the theory o Ballistic galvanometer. 9.8 Check your Progress ) Deine the time constant L/R o R-L Circuit. ) Write a note on the importance o oscillatory circuit in wireless telegraphy. 3) Write the equation or the maximum possile resistance o oscillatory discharge 4) Write the equation or the requency o oscillation or circuit containing L, C and R. 9.9 Lesson end Activities ) Find out whether the discharge o a capacitor through a circuit containing the ollowing elements is oscillatory. C=. micro arad, L = mh and R = 5 Ohms. ) I the charge on a capacitor o capacitance micro arad leaking through a high resistance o Megaohms is reduced to hal its maximum value. Calculate the time o leakage. 9. Points or Discussion ) (i) Discuss the growth o current in a circuit containing a resistance and inductance (ii) Find the decay current in a circuit containing L and R ) (i) Derive an expression or the growth o charge in a circuit with inductance, capacitance and resistance (iv) Explain how you would measure the high resistance y leakage 9. Reerences ) Electricity and Magnetism y R. Murugesan
153 Page 53 LESSON - CONTENTS. Aims and Ojectives. Dynamics o Charged particles.(a). Motion o Charged Particle in Uniorm Electric Field (Longitudinal):.() Motion o Charged Particle in Electric Field. Field applied perpendicular to the direction o motion o particles (Transverse electric ield):. Motion o Charged Particle in Alternating Electric Field:.3 Motion o Charged Particle in Uniorm Constant Magnetic Field:.4 Motion o Charged Particle in crossed Electric and Magnetic Fields:.5 Let us sum up.6 Check your progress.7 Lesson end activities.8 Points or discussion.9 Reerences. Aims and Ojectives In this lesson you will ale to know aout the motion o a charged particle in uniorm electric ield when it is applied perpendicular to the direction o motion o particles. In the same way the motion o charged particle in uniorm magnetic ield and inally the motion o charged particle in crossed electric and magnetic ields.. Dynamics o Charged particles.(a). Motion o Charged Particle in Uniorm Electric Field (Longitudinal): Consider a charged particle o mass m and charge q in uniorm electric ield o strength E. The orce experienced y charge q is F e = qe () The experienced in the direction o orce is d r a dt qe m ()
154 Page 54 Now, integrating Eq.(), velocity o the particle is dr dt where C is a constant. qe v. t C m Let u e the initial velocity o the particle at t =. Thereore, C =u. Sustituting this in the aove equation dr dt qe v. t u (3) m Displacement o the particle is otained y integrating Eq. (3) r qe m t ut C where C is another constant o integration. Let at t =, initial position r = r. Thus C = r qe r r ut r (4) m or displacement s qe m r r ut t (5).() Motion o Charged Particle in Electric Field. Field applied perpendicular to the direction o motion o particles (Transverse electric ield): Let the charged particle e moving with an initial uniorm velocity u in the X- direction and the constant electric ield e applied in the Y-direction (Fig.). Fig..
155 Page 55 Then at time t =, we have v x u, v v and x y z y z Also E x E z and E y E There is no acceleration along X and Z-directions (a x = a z = ). a y qe y qe () m m Here, m is the mass and q is the charge o the particle. But the particle has got an initial velocity in the X-direction. Hence, it will continue to move in the X-direction with the same velocity. qe v x u, v y. t, v z () m Integrating these equations w.r.t. time t, we get displacements along the three axes, qe x ut, y. t, z (3) m Eliminating t etween the equations o x and y, qe x y. m u x mu. y Ky qe where K is a constant. This equation represents a paraola. The transverse displacement suered y the particle during passage through the plates o length l is y qe qel at.. (5) m u mu When the particle leaves the ield, it ollows a straight line path which is tangent to the paraola. Its direction o travel ater emerging rom the ield is inclined to the original o travel (x-axis) y an angle θ given y v y qe qel l tan. t t (6) v mu mu u x This principle is used in cathode ray oscillographs and in television picture tues. (4)
156 Page 56. Motion o Charged Particle in Alternating Electric Field: Let E =E sin ωt, represents the alternating electric ield. Let it act on charged particle o charge q and mass m. But F F d r m dt qe qe dv m dt sin t mdv qe sin t () dt On integrating with the condition v = at t =, we get dr qe qe qe v cost cost () dt m m m On integrating with the condition r = at t =, we get qe r m qe qe sin t t t m m sin t (3) This gives the displacement o the particle in time t in alternating electric ield..3 Motion o Charged Particle in Uniorm Constant Magnetic Field: The magnetic ield on a particle having a charge q moving with a velocity v in a magnetic ield o magnetic induction B is given y F = q (v x B) () F qvb sin () (i) I the particle is at rest (v = ), F = (ii) I v and B are parallel or anti parallel, then F = Let us now discuss two cases: Case : When the particle enters the magnetic ield at right angles to the direction o the ield. Let v e the initial velocity o the particle normal to the direction o the magnetic ield. The orce due to magnetic ield acting on the charged particle is perpendicular to oth, the direction o motion o particle and the direction o ield. Hence, no work is done y the magnetic ield on the charged particle. Thus the particle gains no kinetic energy and hence its velocity remains unchanged.
157 Page 57 The magnetic orce acting on the charged particle gives rise to centripetal orce qvb. Hence, the path traversed y the particle will ecome a circle o radius r, as shown in ig. Fig.. Here the magnetic ield is shown perpendicular to the plane o the paper and directed into it. Let m e the mass o the particle. Then, F = qvb = mv /r (3) The radius o the path is r = mv / qb (4) The radius r is called the gyro radius or cyclotron radius. The angular velocity is ω = The requency is v qb (5) r m qb n m (6) This is called gyro requency or cyclotron requency o the charged particle. Case : When the charged particle enters the magnetic ield in any direction i.e., at an angle θ. Let the charged particle o charge q and mass m enter the magnetic ield making an angle θ with the direction o B (Fig.3).
158 Page 58 Fig..3 The velocity o the particle v may e resolved into components v cos θ and v sin θ, along and perpendicular to the direction o the applied magnetic ield. The component v cos θ remains unaected y the ield. Hence the particle continues to move along the ield with a speed o v cos θ. The velocity component v sin θ is in a plane perpendicular to the direction o the magnetic ield. Hence the ield exerts a orce F on the particle making it to move along a circle in this plane with a constant speed v sin θ. The radius o the circular path is mv sin r (7) qb Thus the charged particle possesses two concurrent motions one circular motion with a constant speed v sin θ in a plane perpendicular to the direction o magnetic ield and another linear motion with constant speed v cos θ along the direction o the ield. The resultant path o the charged particle is a helix(ig 5.9). The time taken y the particle or one revolution is given y r mv sin T v sin v sin qb (8) qb The distance traveled y the particle parallel to the magnetic ield in one revolution i.e., in time T, is the pitch o the helix p. mv cos p ( v cos ) T (9) qb
159 Page 59.4 Motion o Charged Particle in crossed Electric and Magnetic Fields: Consider a particle o charge q and mass m, emitted at the origin with zero initial velocity into a region o uniorm electric and magnetic ields. Let the electric ield aclong the Y-axis and magnetic ield along Z-axis: i.e., E = je and B = kb. Let v e the velocity o particle at any instant. v v i v x y j v z k The resultant orce (Lorentz orce) acting on the particle is F q [ E v B] = q [ je + ( ivx jv y kvz ) x kb] d m dt iv jv kv iqb j qe qbv ) x y z y ( x Thus the component acceleration along the three co-ordinate axes are dvx qb v y () dt dv dt dv and z dt y m qb qb v x (3) m m From Eq. (4) we understand that v z is a constant. I this component velocity is zero initially, the motion o the particle is completely in X-Y plane. Now we ind out v x and v y Dierentiating Eq. (3) with respect to t, we have d dt v y qb dv x m dt Sustituting or dv x / dt rom Eq. (), we get d dt v y q B m v y or d dt v y v where ω =qb / m = angular requency o particle. This is the general equation o S.H.M. Its solution is y v y A sin t (5) At t =, v y =. Hence = (4)
160 Page 6 A sin t (6) v y Sustituting this value o v y in Eq. (3), we have d qe qb A sin t v dt m m qe qb A cost v m m AqB qe qb cost v m m m x x x v x Now, v x = at t =. Hence A = E/B E Acost (7) B E E E v x cost cost (8) B B B From Eq. (6), Since v respectively. v y E sin t (9) B v z () dx dy and v y x and y can e ound y integrating Eqs (8) and (9) dt dt x, x E sin t t c B Here c is constant integration. At t =, x = thereore, c = E x t sin t () B E y cost c B Here c is constant o integration. At t =, y = c E B E y cos t () B
161 Page 6 Eqs. () and () are the equations or a cycloid. Cycloid is the curve traced out y a point on the circumerence o a circle rolling along a straight line. In present case, the radius o the rolling circle is E / (Bω). Thus the particle executes a cycloidal motion in XY plane (Fig.3). Fig..3 The maximum displacement (y max ) in the Y-direction is otained or cos ωt = - (i.e., ωt = ). E y max B (3).5 Let us sum up In this lesson you were ale to know aout the motion o a charged particle in uniorm electric ield, when it is applied perpendicular to the direction o motion o the particles. In the same way the motion o charged particles in uniorm magnetic ield and inally the motion o charged particle in crossed electric and magnetic ield is discussed..6 Check your Progress ) The principle o motion o the charged particle when electric ield is applied perpendicular is used in.. ) Write the equation or the displacement o the particle in time t in alternating electric ield
162 Page 6 3) Give the equation o cyclotron requency o the charged particle.7 Lesson end Activities 3) (i) Derive an expression or the discharge o a capacitor through an inductor and a resistor in series (iii) Give the theory o moving coil allistic galvanometer 4) Discuss the motion o the charged particle in electric ield when (i) the ield applied longitudinal (ii) the ield applied perpendicular.8 Points or Discussion ) (i) Derive an expression or the motion o charged particle in alternating electric ield (ii) Discuss the dierent cases with regard to the motion o charged particle in uniorm constant magnetic ield..9 Reerences ) Electricity and Magnetism y R. Murugesan
19 - RAY OPTICS Page 1 ( Answers at the end of all questions )
 19 - RAY OPTICS Page 1 1 ) A ish looking up through the water sees the outside world contained in a circular horizon. I the reractive index o water is 4 / 3 and the ish is 1 cm below the surace, the radius
19 - RAY OPTICS Page 1 1 ) A ish looking up through the water sees the outside world contained in a circular horizon. I the reractive index o water is 4 / 3 and the ish is 1 cm below the surace, the radius
AP Physics B Ch. 23 and Ch. 24 Geometric Optics and Wave Nature of Light
 AP Physics B Ch. 23 and Ch. 24 Geometric Optics and Wave Nature of Light Name: Period: Date: MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. 1) Reflection,
AP Physics B Ch. 23 and Ch. 24 Geometric Optics and Wave Nature of Light Name: Period: Date: MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. 1) Reflection,
Chapter 17: Light and Image Formation
 Chapter 17: Light and Image Formation 1. When light enters a medium with a higher index of refraction it is A. absorbed. B. bent away from the normal. C. bent towards from the normal. D. continues in the
Chapter 17: Light and Image Formation 1. When light enters a medium with a higher index of refraction it is A. absorbed. B. bent away from the normal. C. bent towards from the normal. D. continues in the
Image Formation. 7-year old s question. Reference. Lecture Overview. It receives light from all directions. Pinhole
 Image Formation Reerence http://en.wikipedia.org/wiki/lens_(optics) Reading: Chapter 1, Forsyth & Ponce Optional: Section 2.1, 2.3, Horn. The slides use illustrations rom these books Some o the ollowing
Image Formation Reerence http://en.wikipedia.org/wiki/lens_(optics) Reading: Chapter 1, Forsyth & Ponce Optional: Section 2.1, 2.3, Horn. The slides use illustrations rom these books Some o the ollowing
NATIONAL SENIOR CERTIFICATE GRADE 12
 NATIONAL SENI CERTIFICATE GRADE 1 PHYSICAL SCIENCES: PHYSICS (P1) NOVEMBER 010 MEMANDUM MARKS: 150 This memorandum consists o 3 pages. NOTE: Marking rule 1.5 was changed according to decisions taken at
NATIONAL SENI CERTIFICATE GRADE 1 PHYSICAL SCIENCES: PHYSICS (P1) NOVEMBER 010 MEMANDUM MARKS: 150 This memorandum consists o 3 pages. NOTE: Marking rule 1.5 was changed according to decisions taken at
Revision problem. Chapter 18 problem 37 page 612. Suppose you point a pinhole camera at a 15m tall tree that is 75m away.
 Revision problem Chapter 18 problem 37 page 612 Suppose you point a pinhole camera at a 15m tall tree that is 75m away. 1 Optical Instruments Thin lens equation Refractive power Cameras The human eye Combining
Revision problem Chapter 18 problem 37 page 612 Suppose you point a pinhole camera at a 15m tall tree that is 75m away. 1 Optical Instruments Thin lens equation Refractive power Cameras The human eye Combining
Physical Science Study Guide Unit 7 Wave properties and behaviors, electromagnetic spectrum, Doppler Effect
 Objectives: PS-7.1 Physical Science Study Guide Unit 7 Wave properties and behaviors, electromagnetic spectrum, Doppler Effect Illustrate ways that the energy of waves is transferred by interaction with
Objectives: PS-7.1 Physical Science Study Guide Unit 7 Wave properties and behaviors, electromagnetic spectrum, Doppler Effect Illustrate ways that the energy of waves is transferred by interaction with
DOING PHYSICS WITH MATLAB COMPUTATIONAL OPTICS RAYLEIGH-SOMMERFELD DIFFRACTION INTEGRAL OF THE FIRST KIND
 DOING PHYSICS WITH MATLAB COMPUTATIONAL OPTICS RAYLEIGH-SOMMERFELD DIFFRACTION INTEGRAL OF THE FIRST KIND THE THREE-DIMENSIONAL DISTRIBUTION OF THE RADIANT FLUX DENSITY AT THE FOCUS OF A CONVERGENCE BEAM
DOING PHYSICS WITH MATLAB COMPUTATIONAL OPTICS RAYLEIGH-SOMMERFELD DIFFRACTION INTEGRAL OF THE FIRST KIND THE THREE-DIMENSIONAL DISTRIBUTION OF THE RADIANT FLUX DENSITY AT THE FOCUS OF A CONVERGENCE BEAM
C) D) As object AB is moved from its present position toward the left, the size of the image produced A) decreases B) increases C) remains the same
 1. For a plane mirror, compared to the object distance, the image distance is always A) less B) greater C) the same 2. Which graph best represents the relationship between image distance (di) and object
1. For a plane mirror, compared to the object distance, the image distance is always A) less B) greater C) the same 2. Which graph best represents the relationship between image distance (di) and object
Physics 10. Lecture 29A. "There are two ways of spreading light: to be the candle or the mirror that reflects it." --Edith Wharton
 Physics 10 Lecture 29A "There are two ways of spreading light: to be the candle or the mirror that reflects it." --Edith Wharton Converging Lenses What if we wanted to use refraction to converge parallel
Physics 10 Lecture 29A "There are two ways of spreading light: to be the candle or the mirror that reflects it." --Edith Wharton Converging Lenses What if we wanted to use refraction to converge parallel
LIGHT REFLECTION AND REFRACTION
 QUESTION BANK IN SCIENCE CLASS-X (TERM-II) 10 LIGHT REFLECTION AND REFRACTION CONCEPTS To revise the laws of reflection at plane surface and the characteristics of image formed as well as the uses of reflection
QUESTION BANK IN SCIENCE CLASS-X (TERM-II) 10 LIGHT REFLECTION AND REFRACTION CONCEPTS To revise the laws of reflection at plane surface and the characteristics of image formed as well as the uses of reflection
Lecture 17. Image formation Ray tracing Calculation. Lenses Convex Concave. Mirrors Convex Concave. Optical instruments
 Lecture 17. Image formation Ray tracing Calculation Lenses Convex Concave Mirrors Convex Concave Optical instruments Image formation Laws of refraction and reflection can be used to explain how lenses
Lecture 17. Image formation Ray tracing Calculation Lenses Convex Concave Mirrors Convex Concave Optical instruments Image formation Laws of refraction and reflection can be used to explain how lenses
Interference. Physics 102 Workshop #3. General Instructions
 Interference Physics 102 Workshop #3 Name: Lab Partner(s): Instructor: Time of Workshop: General Instructions Workshop exercises are to be carried out in groups of three. One report per group is due by
Interference Physics 102 Workshop #3 Name: Lab Partner(s): Instructor: Time of Workshop: General Instructions Workshop exercises are to be carried out in groups of three. One report per group is due by
2) A convex lens is known as a diverging lens and a concave lens is known as a converging lens. Answer: FALSE Diff: 1 Var: 1 Page Ref: Sec.
 Physics for Scientists and Engineers, 4e (Giancoli) Chapter 33 Lenses and Optical Instruments 33.1 Conceptual Questions 1) State how to draw the three rays for finding the image position due to a thin
Physics for Scientists and Engineers, 4e (Giancoli) Chapter 33 Lenses and Optical Instruments 33.1 Conceptual Questions 1) State how to draw the three rays for finding the image position due to a thin
INTERFERENCE OBJECTIVES PRE-LECTURE. Aims
 53 L4 INTERFERENCE Aims OBJECTIVES When you have finished this chapter you should understand how the wave model of light can be used to explain the phenomenon of interference. You should be able to describe
53 L4 INTERFERENCE Aims OBJECTIVES When you have finished this chapter you should understand how the wave model of light can be used to explain the phenomenon of interference. You should be able to describe
Reflection and Refraction
 Equipment Reflection and Refraction Acrylic block set, plane-concave-convex universal mirror, cork board, cork board stand, pins, flashlight, protractor, ruler, mirror worksheet, rectangular block worksheet,
Equipment Reflection and Refraction Acrylic block set, plane-concave-convex universal mirror, cork board, cork board stand, pins, flashlight, protractor, ruler, mirror worksheet, rectangular block worksheet,
Study Guide for Exam on Light
 Name: Class: Date: Study Guide for Exam on Light Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Which portion of the electromagnetic spectrum is used
Name: Class: Date: Study Guide for Exam on Light Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Which portion of the electromagnetic spectrum is used
1 of 9 2/9/2010 3:38 PM
 1 of 9 2/9/2010 3:38 PM Chapter 23 Homework Due: 8:00am on Monday, February 8, 2010 Note: To understand how points are awarded, read your instructor's Grading Policy. [Return to Standard Assignment View]
1 of 9 2/9/2010 3:38 PM Chapter 23 Homework Due: 8:00am on Monday, February 8, 2010 Note: To understand how points are awarded, read your instructor's Grading Policy. [Return to Standard Assignment View]
Geometric Optics Converging Lenses and Mirrors Physics Lab IV
 Objective Geometric Optics Converging Lenses and Mirrors Physics Lab IV In this set of lab exercises, the basic properties geometric optics concerning converging lenses and mirrors will be explored. The
Objective Geometric Optics Converging Lenses and Mirrors Physics Lab IV In this set of lab exercises, the basic properties geometric optics concerning converging lenses and mirrors will be explored. The
WAVELENGTH OF LIGHT - DIFFRACTION GRATING
 PURPOSE In this experiment we will use the diffraction grating and the spectrometer to measure wavelengths in the mercury spectrum. THEORY A diffraction grating is essentially a series of parallel equidistant
PURPOSE In this experiment we will use the diffraction grating and the spectrometer to measure wavelengths in the mercury spectrum. THEORY A diffraction grating is essentially a series of parallel equidistant
waves rays Consider rays of light from an object being reflected by a plane mirror (the rays are diverging): mirror object
 PHYS1000 Optics 1 Optics Light and its interaction with lenses and mirrors. We assume that we can ignore the wave properties of light. waves rays We represent the light as rays, and ignore diffraction.
PHYS1000 Optics 1 Optics Light and its interaction with lenses and mirrors. We assume that we can ignore the wave properties of light. waves rays We represent the light as rays, and ignore diffraction.
Light and its effects
 Light and its effects Light and the speed of light Shadows Shadow films Pinhole camera (1) Pinhole camera (2) Reflection of light Image in a plane mirror An image in a plane mirror is: (i) the same size
Light and its effects Light and the speed of light Shadows Shadow films Pinhole camera (1) Pinhole camera (2) Reflection of light Image in a plane mirror An image in a plane mirror is: (i) the same size
UNIVERSITY OF SASKATCHEWAN Department of Physics and Engineering Physics
 UNIVERSITY OF SASKATCHEWAN Department of Physics and Engineering Physics Physics 111.6 MIDTERM TEST #4 March 15, 2007 Time: 90 minutes NAME: (Last) Please Print (Given) STUDENT NO.: LECTURE SECTION (please
UNIVERSITY OF SASKATCHEWAN Department of Physics and Engineering Physics Physics 111.6 MIDTERM TEST #4 March 15, 2007 Time: 90 minutes NAME: (Last) Please Print (Given) STUDENT NO.: LECTURE SECTION (please
Light Energy OBJECTIVES
 11 Light Energy Can you read a book in the dark? If you try to do so, then you will realize, how much we are dependent on light. Light is very important part of our daily life. We require light for a number
11 Light Energy Can you read a book in the dark? If you try to do so, then you will realize, how much we are dependent on light. Light is very important part of our daily life. We require light for a number
Chapter 36 - Lenses. A PowerPoint Presentation by Paul E. Tippens, Professor of Physics Southern Polytechnic State University
 Chapter 36 - Lenses A PowerPoint Presentation by Paul E. Tippens, Professor of Physics Southern Polytechnic State University 2007 Objectives: After completing this module, you should be able to: Determine
Chapter 36 - Lenses A PowerPoint Presentation by Paul E. Tippens, Professor of Physics Southern Polytechnic State University 2007 Objectives: After completing this module, you should be able to: Determine
6) How wide must a narrow slit be if the first diffraction minimum occurs at ±12 with laser light of 633 nm?
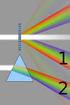 Test IV Name 1) In a single slit diffraction experiment, the width of the slit is 3.1 10-5 m and the distance from the slit to the screen is 2.2 m. If the beam of light of wavelength 600 nm passes through
Test IV Name 1) In a single slit diffraction experiment, the width of the slit is 3.1 10-5 m and the distance from the slit to the screen is 2.2 m. If the beam of light of wavelength 600 nm passes through
1051-232 Imaging Systems Laboratory II. Laboratory 4: Basic Lens Design in OSLO April 2 & 4, 2002
 05-232 Imaging Systems Laboratory II Laboratory 4: Basic Lens Design in OSLO April 2 & 4, 2002 Abstract: For designing the optics of an imaging system, one of the main types of tools used today is optical
05-232 Imaging Systems Laboratory II Laboratory 4: Basic Lens Design in OSLO April 2 & 4, 2002 Abstract: For designing the optics of an imaging system, one of the main types of tools used today is optical
The Geometry of Perspective Projection
 The Geometry o Perspective Projection Pinhole camera and perspective projection - This is the simplest imaging device which, however, captures accurately the geometry o perspective projection. -Rays o
The Geometry o Perspective Projection Pinhole camera and perspective projection - This is the simplest imaging device which, however, captures accurately the geometry o perspective projection. -Rays o
PHYSICS PAPER 1 (THEORY)
 PHYSICS PAPER 1 (THEORY) (Three hours) (Candidates are allowed additional 15 minutes for only reading the paper. They must NOT start writing during this time.) ---------------------------------------------------------------------------------------------------------------------
PHYSICS PAPER 1 (THEORY) (Three hours) (Candidates are allowed additional 15 minutes for only reading the paper. They must NOT start writing during this time.) ---------------------------------------------------------------------------------------------------------------------
ATOMIC SPECTRA. Apparatus: Optical spectrometer, spectral tubes, power supply, incandescent lamp, bottles of dyed water, elevating jack or block.
 1 ATOMIC SPECTRA Objective: To measure the wavelengths of visible light emitted by atomic hydrogen and verify the measured wavelengths against those predicted by quantum theory. To identify an unknown
1 ATOMIC SPECTRA Objective: To measure the wavelengths of visible light emitted by atomic hydrogen and verify the measured wavelengths against those predicted by quantum theory. To identify an unknown
PHYS 222 Spring 2012 Final Exam. Closed books, notes, etc. No electronic device except a calculator.
 PHYS 222 Spring 2012 Final Exam Closed books, notes, etc. No electronic device except a calculator. NAME: (all questions with equal weight) 1. If the distance between two point charges is tripled, the
PHYS 222 Spring 2012 Final Exam Closed books, notes, etc. No electronic device except a calculator. NAME: (all questions with equal weight) 1. If the distance between two point charges is tripled, the
1 Basic Optics (1.2) Since. ε 0 = 8.854 10 12 C 2 N 1 m 2 and μ 0 = 4π 10 7 Ns 2 C 2 (1.3) Krishna Thyagarajan and Ajoy Ghatak. 1.
 1 1 Basic Optics Krishna Thyagarajan and Ajoy Ghatak 1.1 Introduction This chapter on optics provides the reader with the basic understanding of light rays and light waves, image formation and aberrations,
1 1 Basic Optics Krishna Thyagarajan and Ajoy Ghatak 1.1 Introduction This chapter on optics provides the reader with the basic understanding of light rays and light waves, image formation and aberrations,
Polarization of Light
 Polarization of Light References Halliday/Resnick/Walker Fundamentals of Physics, Chapter 33, 7 th ed. Wiley 005 PASCO EX997A and EX999 guide sheets (written by Ann Hanks) weight Exercises and weights
Polarization of Light References Halliday/Resnick/Walker Fundamentals of Physics, Chapter 33, 7 th ed. Wiley 005 PASCO EX997A and EX999 guide sheets (written by Ann Hanks) weight Exercises and weights
EXPERIMENT O-6. Michelson Interferometer. Abstract. References. Pre-Lab
 EXPERIMENT O-6 Michelson Interferometer Abstract A Michelson interferometer, constructed by the student, is used to measure the wavelength of He-Ne laser light and the index of refraction of a flat transparent
EXPERIMENT O-6 Michelson Interferometer Abstract A Michelson interferometer, constructed by the student, is used to measure the wavelength of He-Ne laser light and the index of refraction of a flat transparent
Chapter 23. The Reflection of Light: Mirrors
 Chapter 23 The Reflection of Light: Mirrors Wave Fronts and Rays Defining wave fronts and rays. Consider a sound wave since it is easier to visualize. Shown is a hemispherical view of a sound wave emitted
Chapter 23 The Reflection of Light: Mirrors Wave Fronts and Rays Defining wave fronts and rays. Consider a sound wave since it is easier to visualize. Shown is a hemispherical view of a sound wave emitted
GRID AND PRISM SPECTROMETERS
 FYSA230/2 GRID AND PRISM SPECTROMETERS 1. Introduction Electromagnetic radiation (e.g. visible light) experiences reflection, refraction, interference and diffraction phenomena when entering and passing
FYSA230/2 GRID AND PRISM SPECTROMETERS 1. Introduction Electromagnetic radiation (e.g. visible light) experiences reflection, refraction, interference and diffraction phenomena when entering and passing
Size Of the Image Nature Of the Image At Infinity At the Focus Highly Diminished, Point Real and Inverted
 CHAPTER-10 LIGHT REFLECTION AND REFRACTION Light rays; are; electromagnetic in nature, and do not need material medium for Propagation Speed of light in vacuum in 3*10 8 m/s When a light ray falls on a
CHAPTER-10 LIGHT REFLECTION AND REFRACTION Light rays; are; electromagnetic in nature, and do not need material medium for Propagation Speed of light in vacuum in 3*10 8 m/s When a light ray falls on a
EXPERIMENT 6 OPTICS: FOCAL LENGTH OF A LENS
 EXPERIMENT 6 OPTICS: FOCAL LENGTH OF A LENS The following website should be accessed before coming to class. Text reference: pp189-196 Optics Bench a) For convenience of discussion we assume that the light
EXPERIMENT 6 OPTICS: FOCAL LENGTH OF A LENS The following website should be accessed before coming to class. Text reference: pp189-196 Optics Bench a) For convenience of discussion we assume that the light
Solving Newton s Second Law Problems
 Solving ewton s Second Law Problems Michael Fowler, Phys 142E Lec 8 Feb 5, 2009 Zero Acceleration Problems: Forces Add to Zero he Law is F ma : the acceleration o a given body is given by the net orce
Solving ewton s Second Law Problems Michael Fowler, Phys 142E Lec 8 Feb 5, 2009 Zero Acceleration Problems: Forces Add to Zero he Law is F ma : the acceleration o a given body is given by the net orce
Light and Sound. Pupil Booklet
 Duncanrig Secondary School East Kilbride S2 Physics Elective Light and Sound Name: Pupil Booklet Class: SCN 3-11a - By exploring the refraction of light when passed through different materials, lenses
Duncanrig Secondary School East Kilbride S2 Physics Elective Light and Sound Name: Pupil Booklet Class: SCN 3-11a - By exploring the refraction of light when passed through different materials, lenses
Physics 25 Exam 3 November 3, 2009
 1. A long, straight wire carries a current I. If the magnetic field at a distance d from the wire has magnitude B, what would be the the magnitude of the magnetic field at a distance d/3 from the wire,
1. A long, straight wire carries a current I. If the magnetic field at a distance d from the wire has magnitude B, what would be the the magnitude of the magnetic field at a distance d/3 from the wire,
Solution Derivations for Capa #14
 Solution Derivations for Capa #4 ) An image of the moon is focused onto a screen using a converging lens of focal length (f = 34.8 cm). The diameter of the moon is 3.48 0 6 m, and its mean distance from
Solution Derivations for Capa #4 ) An image of the moon is focused onto a screen using a converging lens of focal length (f = 34.8 cm). The diameter of the moon is 3.48 0 6 m, and its mean distance from
INDEX. SR NO NAME OF THE PRACTICALS Page No. Measuring the bearing of traverse lines, calculation of included angles and check.
 INDEX SR NO NAME OF THE PRACTICALS Page No 1 Measuring the bearing of traverse lines, calculation of included angles and check. 1 2 To study the essential parts of dumpy level & reduction of levels 3 To
INDEX SR NO NAME OF THE PRACTICALS Page No 1 Measuring the bearing of traverse lines, calculation of included angles and check. 1 2 To study the essential parts of dumpy level & reduction of levels 3 To
Mirrors and Lenses. Clicker Questions. Question P1.03
 3 Mirrors and Lenses Clicker Questions Question P.03 Descrition: Reasoning with geometric otics and ray-tracing. Question An object is located on the otical axis and a distance o 8 cm rom a thin converging
3 Mirrors and Lenses Clicker Questions Question P.03 Descrition: Reasoning with geometric otics and ray-tracing. Question An object is located on the otical axis and a distance o 8 cm rom a thin converging
Physics 202 Problems - Week 8 Worked Problems Chapter 25: 7, 23, 36, 62, 72
 Physics 202 Problems - Week 8 Worked Problems Chapter 25: 7, 23, 36, 62, 72 Problem 25.7) A light beam traveling in the negative z direction has a magnetic field B = (2.32 10 9 T )ˆx + ( 4.02 10 9 T )ŷ
Physics 202 Problems - Week 8 Worked Problems Chapter 25: 7, 23, 36, 62, 72 Problem 25.7) A light beam traveling in the negative z direction has a magnetic field B = (2.32 10 9 T )ˆx + ( 4.02 10 9 T )ŷ
Introduction to Optics
 Second Edition Introduction to Optics FRANK L. PEDROTTI, S.J. Marquette University Milwaukee, Wisconsin Vatican Radio, Rome LENO S. PEDROTTI Center for Occupational Research and Development Waco, Texas
Second Edition Introduction to Optics FRANK L. PEDROTTI, S.J. Marquette University Milwaukee, Wisconsin Vatican Radio, Rome LENO S. PEDROTTI Center for Occupational Research and Development Waco, Texas
First let us consider microscopes. Human eyes are sensitive to radiation having wavelengths between
 Optical Differences Between Telescopes and Microscopes Robert R. Pavlis, Girard, Kansas USA icroscopes and telescopes are optical instruments that are designed to permit observation of objects and details
Optical Differences Between Telescopes and Microscopes Robert R. Pavlis, Girard, Kansas USA icroscopes and telescopes are optical instruments that are designed to permit observation of objects and details
P R E A M B L E. Facilitated workshop problems for class discussion (1.5 hours)
 INSURANCE SCAM OPTICS - LABORATORY INVESTIGATION P R E A M B L E The original form of the problem is an Experimental Group Research Project, undertaken by students organised into small groups working as
INSURANCE SCAM OPTICS - LABORATORY INVESTIGATION P R E A M B L E The original form of the problem is an Experimental Group Research Project, undertaken by students organised into small groups working as
v = fλ PROGRESSIVE WAVES 1 Candidates should be able to :
 PROGRESSIVE WAVES 1 Candidates should be able to : Describe and distinguish between progressive longitudinal and transverse waves. With the exception of electromagnetic waves, which do not need a material
PROGRESSIVE WAVES 1 Candidates should be able to : Describe and distinguish between progressive longitudinal and transverse waves. With the exception of electromagnetic waves, which do not need a material
Science In Action 8 Unit C - Light and Optical Systems. 1.1 The Challenge of light
 1.1 The Challenge of light 1. Pythagoras' thoughts about light were proven wrong because it was impossible to see A. the light beams B. dark objects C. in the dark D. shiny objects 2. Sir Isaac Newton
1.1 The Challenge of light 1. Pythagoras' thoughts about light were proven wrong because it was impossible to see A. the light beams B. dark objects C. in the dark D. shiny objects 2. Sir Isaac Newton
Lecture Notes for Chapter 34: Images
 Lecture Notes for hapter 4: Images Disclaimer: These notes are not meant to replace the textbook. Please report any inaccuracies to the professor.. Spherical Reflecting Surfaces Bad News: This subject
Lecture Notes for hapter 4: Images Disclaimer: These notes are not meant to replace the textbook. Please report any inaccuracies to the professor.. Spherical Reflecting Surfaces Bad News: This subject
Optics. Kepler's telescope and Galileo's telescope. f 1. f 2. LD Physics Leaflets P5.1.4.2. Geometrical optics Optical instruments
 Optics Geometrical optics Optical instruments LD Physics Lealets P5.1.4.2 Kepler's telescope and Galileo's telescope Objects o the experiment g Veriying that the length o a telescope is given by the sum
Optics Geometrical optics Optical instruments LD Physics Lealets P5.1.4.2 Kepler's telescope and Galileo's telescope Objects o the experiment g Veriying that the length o a telescope is given by the sum
Basic Optics System OS-8515C
 40 50 30 60 20 70 10 80 0 90 80 10 20 70 T 30 60 40 50 50 40 60 30 C 70 20 80 10 90 90 0 80 10 70 20 60 50 40 30 Instruction Manual with Experiment Guide and Teachers Notes 012-09900B Basic Optics System
40 50 30 60 20 70 10 80 0 90 80 10 20 70 T 30 60 40 50 50 40 60 30 C 70 20 80 10 90 90 0 80 10 70 20 60 50 40 30 Instruction Manual with Experiment Guide and Teachers Notes 012-09900B Basic Optics System
Thin Lenses Drawing Ray Diagrams
 Drawing Ray Diagrams Fig. 1a Fig. 1b In this activity we explore how light refracts as it passes through a thin lens. Eyeglasses have been in use since the 13 th century. In 1610 Galileo used two lenses
Drawing Ray Diagrams Fig. 1a Fig. 1b In this activity we explore how light refracts as it passes through a thin lens. Eyeglasses have been in use since the 13 th century. In 1610 Galileo used two lenses
Physics, Chapter 38: Mirrors and Lenses
 University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln Robert Katz Publications Research Papers in Physics and Astronomy 1-1-1958 Physics, Chapter 38: Mirrors and Lenses Henry
University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln Robert Katz Publications Research Papers in Physics and Astronomy 1-1-1958 Physics, Chapter 38: Mirrors and Lenses Henry
Convex Mirrors. Ray Diagram for Convex Mirror
 Convex Mirrors Center of curvature and focal point both located behind mirror The image for a convex mirror is always virtual and upright compared to the object A convex mirror will reflect a set of parallel
Convex Mirrors Center of curvature and focal point both located behind mirror The image for a convex mirror is always virtual and upright compared to the object A convex mirror will reflect a set of parallel
Physics 30 Worksheet # 14: Michelson Experiment
 Physics 30 Worksheet # 14: Michelson Experiment 1. The speed of light found by a Michelson experiment was found to be 2.90 x 10 8 m/s. If the two hills were 20.0 km apart, what was the frequency of the
Physics 30 Worksheet # 14: Michelson Experiment 1. The speed of light found by a Michelson experiment was found to be 2.90 x 10 8 m/s. If the two hills were 20.0 km apart, what was the frequency of the
THE EFFECT OF THE SPINDLE SYSTEM ON THE POSITION OF CIRCULAR SAW TEETH A STATIC APPROACH
 TRIESKOVÉ A BEZTRIESKOVÉ OBRÁBANIE DREVA 2006 12. - 14. 10. 2006 305 THE EFFECT OF THE SPINDLE SYSTEM ON THE POSITION OF CIRCULAR SAW TEETH A STATIC APPROACH Roman Wasielewski - Kazimierz A. Orłowski Abstract
TRIESKOVÉ A BEZTRIESKOVÉ OBRÁBANIE DREVA 2006 12. - 14. 10. 2006 305 THE EFFECT OF THE SPINDLE SYSTEM ON THE POSITION OF CIRCULAR SAW TEETH A STATIC APPROACH Roman Wasielewski - Kazimierz A. Orłowski Abstract
ILLUSTRATIVE EXAMPLE: Given: A = 3 and B = 4 if we now want the value of C=? C = 3 + 4 = 9 + 16 = 25 or 2
 Forensic Spectral Anaylysis: Warm up! The study of triangles has been done since ancient times. Many of the early discoveries about triangles are still used today. We will only be concerned with the "right
Forensic Spectral Anaylysis: Warm up! The study of triangles has been done since ancient times. Many of the early discoveries about triangles are still used today. We will only be concerned with the "right
Waves Sound and Light
 Waves Sound and Light r2 c:\files\courses\1710\spr12\wavetrans.doc Ron Robertson The Nature of Waves Waves are a type of energy transmission that results from a periodic disturbance (vibration). They are
Waves Sound and Light r2 c:\files\courses\1710\spr12\wavetrans.doc Ron Robertson The Nature of Waves Waves are a type of energy transmission that results from a periodic disturbance (vibration). They are
Procedure: Geometrical Optics. Theory Refer to your Lab Manual, pages 291 294. Equipment Needed
 Theory Refer to your Lab Manual, pages 291 294. Geometrical Optics Equipment Needed Light Source Ray Table and Base Three-surface Mirror Convex Lens Ruler Optics Bench Cylindrical Lens Concave Lens Rhombus
Theory Refer to your Lab Manual, pages 291 294. Geometrical Optics Equipment Needed Light Source Ray Table and Base Three-surface Mirror Convex Lens Ruler Optics Bench Cylindrical Lens Concave Lens Rhombus
1. You stand two feet away from a plane mirror. How far is it from you to your image? a. 2.0 ft c. 4.0 ft b. 3.0 ft d. 5.0 ft
 Lenses and Mirrors 1. You stand two feet away from a plane mirror. How far is it from you to your image? a. 2.0 ft c. 4.0 ft b. 3.0 ft d. 5.0 ft 2. Which of the following best describes the image from
Lenses and Mirrors 1. You stand two feet away from a plane mirror. How far is it from you to your image? a. 2.0 ft c. 4.0 ft b. 3.0 ft d. 5.0 ft 2. Which of the following best describes the image from
Equation of a Line. Chapter H2. The Gradient of a Line. m AB = Exercise H2 1
 Chapter H2 Equation of a Line The Gradient of a Line The gradient of a line is simpl a measure of how steep the line is. It is defined as follows :- gradient = vertical horizontal horizontal A B vertical
Chapter H2 Equation of a Line The Gradient of a Line The gradient of a line is simpl a measure of how steep the line is. It is defined as follows :- gradient = vertical horizontal horizontal A B vertical
Question based on Refraction and Refractive index. Glass Slab, Lateral Shift.
 Question based on Refraction and Refractive index. Glass Slab, Lateral Shift. Q.What is refraction of light? What are the laws of refraction? Ans: Deviation of ray of light from its original path when
Question based on Refraction and Refractive index. Glass Slab, Lateral Shift. Q.What is refraction of light? What are the laws of refraction? Ans: Deviation of ray of light from its original path when
4.4 WAVE CHARACTERISTICS 4.5 WAVE PROPERTIES HW/Study Packet
 4.4 WAVE CHARACTERISTICS 4.5 WAVE PROPERTIES HW/Study Packet Required: READ Hamper pp 115-134 SL/HL Supplemental: Cutnell and Johnson, pp 473-477, 507-513 Tsokos, pp 216-242 REMEMBER TO. Work through all
4.4 WAVE CHARACTERISTICS 4.5 WAVE PROPERTIES HW/Study Packet Required: READ Hamper pp 115-134 SL/HL Supplemental: Cutnell and Johnson, pp 473-477, 507-513 Tsokos, pp 216-242 REMEMBER TO. Work through all
Solutions to old Exam 1 problems
 Solutions to old Exam 1 problems Hi students! I am putting this old version of my review for the first midterm review, place and time to be announced. Check for updates on the web site as to which sections
Solutions to old Exam 1 problems Hi students! I am putting this old version of my review for the first midterm review, place and time to be announced. Check for updates on the web site as to which sections
Click here for answers.
 CHALLENGE PROBLEMS: CHALLENGE PROBLEMS 1 CHAPTER A Click here for answers S Click here for solutions A 1 Find points P and Q on the parabola 1 so that the triangle ABC formed b the -ais and the tangent
CHALLENGE PROBLEMS: CHALLENGE PROBLEMS 1 CHAPTER A Click here for answers S Click here for solutions A 1 Find points P and Q on the parabola 1 so that the triangle ABC formed b the -ais and the tangent
Which month has larger and smaller day time?
 ACTIVITY-1 Which month has larger and smaller day time? Problem: Which month has larger and smaller day time? Aim: Finding out which month has larger and smaller duration of day in the Year 2006. Format
ACTIVITY-1 Which month has larger and smaller day time? Problem: Which month has larger and smaller day time? Aim: Finding out which month has larger and smaller duration of day in the Year 2006. Format
Optical Communications
 Optical Communications Telecommunication Engineering School of Engineering University of Rome La Sapienza Rome, Italy 2005-2006 Lecture #2, May 2 2006 The Optical Communication System BLOCK DIAGRAM OF
Optical Communications Telecommunication Engineering School of Engineering University of Rome La Sapienza Rome, Italy 2005-2006 Lecture #2, May 2 2006 The Optical Communication System BLOCK DIAGRAM OF
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Wednesday, June 20, 2012 9:15 a.m. to 12:15 p.m., only Student Name: School Name: Print your name and the name
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Wednesday, June 20, 2012 9:15 a.m. to 12:15 p.m., only Student Name: School Name: Print your name and the name
3.5.4.2 One example: Michelson interferometer
 3.5.4.2 One example: Michelson interferometer mirror 1 mirror 2 light source 1 2 3 beam splitter 4 object (n object ) interference pattern we either observe fringes of same thickness (parallel light) or
3.5.4.2 One example: Michelson interferometer mirror 1 mirror 2 light source 1 2 3 beam splitter 4 object (n object ) interference pattern we either observe fringes of same thickness (parallel light) or
3D Printing LESSON PLAN PHYSICS 8,11: OPTICS
 INVESTIGATE RATIONALE Optics is commonly taught through the use of commercial optics kits that usually include a basic set of 2-4 geometric lenses (such as double convex or double concave). These lenses
INVESTIGATE RATIONALE Optics is commonly taught through the use of commercial optics kits that usually include a basic set of 2-4 geometric lenses (such as double convex or double concave). These lenses
9/16 Optics 1 /11 GEOMETRIC OPTICS
 9/6 Optics / GEOMETRIC OPTICS PURPOSE: To review the basics of geometric optics and to observe the function of some simple and compound optical devices. APPARATUS: Optical bench, lenses, mirror, target
9/6 Optics / GEOMETRIC OPTICS PURPOSE: To review the basics of geometric optics and to observe the function of some simple and compound optical devices. APPARATUS: Optical bench, lenses, mirror, target
Experiment 3 Lenses and Images
 Experiment 3 Lenses and Images Who shall teach thee, unless it be thine own eyes? Euripides (480?-406? BC) OBJECTIVES To examine the nature and location of images formed by es. THEORY Lenses are frequently
Experiment 3 Lenses and Images Who shall teach thee, unless it be thine own eyes? Euripides (480?-406? BC) OBJECTIVES To examine the nature and location of images formed by es. THEORY Lenses are frequently
Interferometers. OBJECTIVES To examine the operation of several kinds of interferometers. d sin = n (1)
 Interferometers The true worth of an experimenter consists in his pursuing not only what he seeks in his experiment, but also what he did not seek. Claude Bernard (1813-1878) OBJECTIVES To examine the
Interferometers The true worth of an experimenter consists in his pursuing not only what he seeks in his experiment, but also what he did not seek. Claude Bernard (1813-1878) OBJECTIVES To examine the
Crystal Optics of Visible Light
 Crystal Optics of Visible Light This can be a very helpful aspect of minerals in understanding the petrographic history of a rock. The manner by which light is transferred through a mineral is a means
Crystal Optics of Visible Light This can be a very helpful aspect of minerals in understanding the petrographic history of a rock. The manner by which light is transferred through a mineral is a means
Physics 9e/Cutnell. correlated to the. College Board AP Physics 1 Course Objectives
 Physics 9e/Cutnell correlated to the College Board AP Physics 1 Course Objectives Big Idea 1: Objects and systems have properties such as mass and charge. Systems may have internal structure. Enduring
Physics 9e/Cutnell correlated to the College Board AP Physics 1 Course Objectives Big Idea 1: Objects and systems have properties such as mass and charge. Systems may have internal structure. Enduring
Code number given on the right hand side of the question paper should be written on the title page of the answerbook by the candidate.
 Series ONS SET-1 Roll No. Candiates must write code on the title page of the answer book Please check that this question paper contains 16 printed pages. Code number given on the right hand side of the
Series ONS SET-1 Roll No. Candiates must write code on the title page of the answer book Please check that this question paper contains 16 printed pages. Code number given on the right hand side of the
Teacher s Resource. 2. The student will see the images reversed left to right.
 Answer Booklet Reflection of Light With a Plane (Flat) Mirror Trace a Star Page 16 1. The individual students will complete the activity with varying degrees of difficulty. 2. The student will see the
Answer Booklet Reflection of Light With a Plane (Flat) Mirror Trace a Star Page 16 1. The individual students will complete the activity with varying degrees of difficulty. 2. The student will see the
Sandia High School Geometry Second Semester FINAL EXAM. Mark the letter to the single, correct (or most accurate) answer to each problem.
 Sandia High School Geometry Second Semester FINL EXM Name: Mark the letter to the single, correct (or most accurate) answer to each problem.. What is the value of in the triangle on the right?.. 6. D.
Sandia High School Geometry Second Semester FINL EXM Name: Mark the letter to the single, correct (or most accurate) answer to each problem.. What is the value of in the triangle on the right?.. 6. D.
How to make a Galileian Telescope
 How to make a Galileian Telescope I. THE BASICS THE PRINCIPLES OF OPTICS A Galileian telescope uses just two lenses. The objective lens is convergent (plano-convex), the ocular lens is divergent (plano-concave).
How to make a Galileian Telescope I. THE BASICS THE PRINCIPLES OF OPTICS A Galileian telescope uses just two lenses. The objective lens is convergent (plano-convex), the ocular lens is divergent (plano-concave).
Chapter 22: Electric Flux and Gauss s Law
 22.1 ntroduction We have seen in chapter 21 that determining the electric field of a continuous charge distribution can become very complicated for some charge distributions. t would be desirable if we
22.1 ntroduction We have seen in chapter 21 that determining the electric field of a continuous charge distribution can become very complicated for some charge distributions. t would be desirable if we
WEDNESDAY, 2 MAY 1.30 PM 2.25 PM. 3 Full credit will be given only where the solution contains appropriate working.
 C 500/1/01 NATIONAL QUALIFICATIONS 01 WEDNESDAY, MAY 1.0 PM.5 PM MATHEMATICS STANDARD GRADE Credit Level Paper 1 (Non-calculator) 1 You may NOT use a calculator. Answer as many questions as you can. Full
C 500/1/01 NATIONAL QUALIFICATIONS 01 WEDNESDAY, MAY 1.0 PM.5 PM MATHEMATICS STANDARD GRADE Credit Level Paper 1 (Non-calculator) 1 You may NOT use a calculator. Answer as many questions as you can. Full
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY. Wednesday, January 28, 2015 9:15 a.m. to 12:15 p.m.
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Wednesday, January 28, 2015 9:15 a.m. to 12:15 p.m., only Student Name: School Name: The possession or use of any
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Wednesday, January 28, 2015 9:15 a.m. to 12:15 p.m., only Student Name: School Name: The possession or use of any
Fraunhofer Diffraction
 Physics 334 Spring 1 Purpose Fraunhofer Diffraction The experiment will test the theory of Fraunhofer diffraction at a single slit by comparing a careful measurement of the angular dependence of intensity
Physics 334 Spring 1 Purpose Fraunhofer Diffraction The experiment will test the theory of Fraunhofer diffraction at a single slit by comparing a careful measurement of the angular dependence of intensity
SURFACE TENSION. Definition
 SURFACE TENSION Definition In the fall a fisherman s boat is often surrounded by fallen leaves that are lying on the water. The boat floats, because it is partially immersed in the water and the resulting
SURFACE TENSION Definition In the fall a fisherman s boat is often surrounded by fallen leaves that are lying on the water. The boat floats, because it is partially immersed in the water and the resulting
APPENDIX D: SOLAR RADIATION
 APPENDIX D: SOLAR RADIATION The sun is the source of most energy on the earth and is a primary factor in determining the thermal environment of a locality. It is important for engineers to have a working
APPENDIX D: SOLAR RADIATION The sun is the source of most energy on the earth and is a primary factor in determining the thermal environment of a locality. It is important for engineers to have a working
Lesson 29: Lenses. Double Concave. Double Convex. Planoconcave. Planoconvex. Convex meniscus. Concave meniscus
 Lesson 29: Lenses Remembering the basics of mirrors puts you half ways towards fully understanding lenses as well. The same sort of rules apply, just with a few modifications. Keep in mind that for an
Lesson 29: Lenses Remembering the basics of mirrors puts you half ways towards fully understanding lenses as well. The same sort of rules apply, just with a few modifications. Keep in mind that for an
O6: The Diffraction Grating Spectrometer
 2B30: PRACTICAL ASTROPHYSICS FORMAL REPORT: O6: The Diffraction Grating Spectrometer Adam Hill Lab partner: G. Evans Tutor: Dr. Peter Storey 1 Abstract The calibration of a diffraction grating spectrometer
2B30: PRACTICAL ASTROPHYSICS FORMAL REPORT: O6: The Diffraction Grating Spectrometer Adam Hill Lab partner: G. Evans Tutor: Dr. Peter Storey 1 Abstract The calibration of a diffraction grating spectrometer
CIRCLE COORDINATE GEOMETRY
 CIRCLE COORDINATE GEOMETRY (EXAM QUESTIONS) Question 1 (**) A circle has equation x + y = 2x + 8 Determine the radius and the coordinates of the centre of the circle. r = 3, ( 1,0 ) Question 2 (**) A circle
CIRCLE COORDINATE GEOMETRY (EXAM QUESTIONS) Question 1 (**) A circle has equation x + y = 2x + 8 Determine the radius and the coordinates of the centre of the circle. r = 3, ( 1,0 ) Question 2 (**) A circle
Power functions: f(x) = x n, n is a natural number The graphs of some power functions are given below. n- even n- odd
 5.1 Polynomial Functions A polynomial unctions is a unction o the orm = a n n + a n-1 n-1 + + a 1 + a 0 Eample: = 3 3 + 5 - The domain o a polynomial unction is the set o all real numbers. The -intercepts
5.1 Polynomial Functions A polynomial unctions is a unction o the orm = a n n + a n-1 n-1 + + a 1 + a 0 Eample: = 3 3 + 5 - The domain o a polynomial unction is the set o all real numbers. The -intercepts
Diffraction of Laser Light
 Diffraction of Laser Light No Prelab Introduction The laser is a unique light source because its light is coherent and monochromatic. Coherent light is made up of waves, which are all in phase. Monochromatic
Diffraction of Laser Light No Prelab Introduction The laser is a unique light source because its light is coherent and monochromatic. Coherent light is made up of waves, which are all in phase. Monochromatic
Optical Illusions Essay Angela Wall EMAT 6690
 Optical Illusions Essay Angela Wall EMAT 6690! Optical illusions are images that are visually perceived differently than how they actually appear in reality. These images can be very entertaining, but
Optical Illusions Essay Angela Wall EMAT 6690! Optical illusions are images that are visually perceived differently than how they actually appear in reality. These images can be very entertaining, but
CIRCUMFERENCE AND AREA OF A CIRCLE
 CIRCUMFERENCE AND AREA OF A CIRCLE 1. AC and BD are two perpendicular diameters of a circle with centre O. If AC = 16 cm, calculate the area and perimeter of the shaded part. (Take = 3.14) 2. In the given
CIRCUMFERENCE AND AREA OF A CIRCLE 1. AC and BD are two perpendicular diameters of a circle with centre O. If AC = 16 cm, calculate the area and perimeter of the shaded part. (Take = 3.14) 2. In the given
Experimental and modeling studies of imaging with curvilinear electronic eye cameras
 Experimental and modeling studies of imaging with curvilinear electronic eye cameras Viktor Malyarchuk, 1 Inhwa Jung, 1 John A. Rogers, 1,* Gunchul Shin, 2 and Jeong Sook Ha 2 1 Department of Materials
Experimental and modeling studies of imaging with curvilinear electronic eye cameras Viktor Malyarchuk, 1 Inhwa Jung, 1 John A. Rogers, 1,* Gunchul Shin, 2 and Jeong Sook Ha 2 1 Department of Materials
SOLID MECHANICS TUTORIAL MECHANISMS KINEMATICS - VELOCITY AND ACCELERATION DIAGRAMS
 SOLID MECHANICS TUTORIAL MECHANISMS KINEMATICS - VELOCITY AND ACCELERATION DIAGRAMS This work covers elements of the syllabus for the Engineering Council exams C105 Mechanical and Structural Engineering
SOLID MECHANICS TUTORIAL MECHANISMS KINEMATICS - VELOCITY AND ACCELERATION DIAGRAMS This work covers elements of the syllabus for the Engineering Council exams C105 Mechanical and Structural Engineering
PHYS 39a Lab 3: Microscope Optics
 PHYS 39a Lab 3: Microscope Optics Trevor Kafka December 15, 2014 Abstract In this lab task, we sought to use critical illumination and Köhler illumination techniques to view the image of a 1000 lines-per-inch
PHYS 39a Lab 3: Microscope Optics Trevor Kafka December 15, 2014 Abstract In this lab task, we sought to use critical illumination and Köhler illumination techniques to view the image of a 1000 lines-per-inch
VECTOR ALGEBRA. 10.1.1 A quantity that has magnitude as well as direction is called a vector. is given by a and is represented by a.
 VECTOR ALGEBRA Chapter 10 101 Overview 1011 A quantity that has magnitude as well as direction is called a vector 101 The unit vector in the direction of a a is given y a and is represented y a 101 Position
VECTOR ALGEBRA Chapter 10 101 Overview 1011 A quantity that has magnitude as well as direction is called a vector 101 The unit vector in the direction of a a is given y a and is represented y a 101 Position
AS COMPETITION PAPER 2008
 AS COMPETITION PAPER 28 Name School Town & County Total Mark/5 Time Allowed: One hour Attempt as many questions as you can. Write your answers on this question paper. Marks allocated for each question
AS COMPETITION PAPER 28 Name School Town & County Total Mark/5 Time Allowed: One hour Attempt as many questions as you can. Write your answers on this question paper. Marks allocated for each question
explain your reasoning
 I. A mechanical device shakes a ball-spring system vertically at its natural frequency. The ball is attached to a string, sending a harmonic wave in the positive x-direction. +x a) The ball, of mass M,
I. A mechanical device shakes a ball-spring system vertically at its natural frequency. The ball is attached to a string, sending a harmonic wave in the positive x-direction. +x a) The ball, of mass M,
