Factorising quadratics
|
|
|
- Dortha Powers
- 10 years ago
- Views:
Transcription
1 Factorising quadratics An essential skill in many applications is the ability to factorise quadratic expressions. In this unit you will see that this can be thought of as reversing the process used to remove or multiply-out brackets from an expression. You will see a number of worked examples followed by a discussion of special cases which occur frequently with which you must become familiar. In order to master the techniques explained here it is vital that you undertake plenty of practice exercises so that all this becomes second nature, and you eventually carry out the process of factorising simply by inspection. To help you to achieve this, the unit includes a substantial number of such exercises. After reading this text, and/or viewing the video tutorial on this topic, you should be able to: factorise quadratic expressions understand what is meant by, and factorise, a difference of two squares understand what is meant by, and factorise, a complete square Contents 1. Introduction 2 2. Multiplying-out brackets, and quadratic expressions 2 3. Factorising quadratics 3 4. Factorising by inspection 4 5. Expressions where the coefficient of x 2 is not Special case 1 - the difference of two squares 7 7. Special case 2 - complete squares 8 8. Special case 3 - the constant term is missing 10 1 c mathcentre August 7, 2003
2 1. Introduction In this unit you will learn how many quadratic expressions can be factorised. Essentially, this is the reverse process of removing brackets from expressions such as (x + 2)(x + 3). 2. Multiplying-out brackets, and quadratic expressions You will be familiar already with the well-known process of multiplying-out brackets. For example, you will have seen expressions like (x + 2)(x + 3) and then expanded these terms to arrive at a quadratic expression. Let us see how this works. The arrows in the figure below show how each term in the first pair of brackets multiplies each term in the second pair. (x +2)(x +3)=x 2 +3x +2x +6 = x 2 +5x + 6 Then the like-terms, 3x and 2x, are collected together to give 5x. The result of multiplying-out the brackets is the quadratic expression x 2 +5x +6. Key Point A quadratic expression has the general form ax 2 + bx + c where a, b and c are numbers. Note that in a quadratic expression the highest power of x is 2. The number a is called the coefficient of x 2, b is called the coefficient of x, and c is called the constant term. These numbers can be positive or negative. The numbers b and c can also be zero. Some examples of quadratic expressions: x 2 7x +11, 4x 2 +3x 1, x 2 +8x, 3x 2 +2 Like many processes in mathematics, it is useful to be able to go the other way. That is, starting with the quadratic expression x 2 +5x+6, can we carry out a process which will result in the form (x + 2)(x + 3)? The answer is: yes we can! This process is called factorising the quadratic expression. This would help, for example, if we wanted to solve a quadratic equation. Such an equation is formed when we set a quadratic expression equal to zero, as in x 2 +5x +6=0 This is because the equation can then be written (x + 2)(x +3)=0 and if we have two expressions multiplied together resulting in zero, then one or both of these must be zero. So, either x +2=0,orx + 3 = 0, from which we can conclude that x = 2, or x = 3. We have found the solutions of the quadratic equation x 2 +5x +6=0. c mathcentre August 7,
3 So, the ability to factorise a quadratic is a useful basic skill, which you will learn about in this unit. However, be warned, not all quadratics will factorise, but a lot do and so this is a process you have got to get to know! Exercises 1 Prepare yourself for factorising quadratic expressions by multiplying out the brackets in each of the following cases: a) (x + 1)(x +2) b) (x + 2)(x +3) c) (x + 1)(x 3) d) (x + 2)(x 4) e) (x 3)(x +7) f) x(x 7) g) (x 3)(x 2) h) (x 7)(x 7) i) (x 2)(x 2) j) (x + 2)(x 2) k) (x 3)(x +3) l) (2x + 1)(x +1) m) (x 5)(2x 1) n) (3x 1)(3x +1) o) 4x(x 2) 3. Factorising quadratics To learn how to factorise let us study again the removal of brackets from (x + 3)(x +2). (x + 3)(x +2)=x 2 +2x +3x +6=x 2 +5x +6 Clearly the number 6 in the final answer comes from multiplying the numbers 3 and 2 in the brackets. This is an important observation. The term 5x comes from adding the terms 2x and 3x. So, if we were to begin with x 2 +5x + 6 and we were going to reverse the process we need to look for two numbers which multiply to give 6 and add to give 5.?? = 6? +? = 5 What are these numbers? Well, we know that they are 3 and 2, and you will learn with practise to find these simply by inspection. Using the two numbers which add to give 5 we split the 5x term into 3x and 2x. We can set the calculation out as follows. x 2 +5x +6 = x 2 +3x +2x +6 = x(x +3)+2x + 6 by factorising the first two terms = x(x +3)+2(x + 3) by factorising the last two terms = (x + 3)(x + 2) by noting the common factor of x +3 The quadratic has been factorised. Note that you should never get these wrong, because the answer can always be checked by multiplying-out the brackets again! Suppose we want to factorise the quadratic expression x 2 7x Starting as before we look for two numbers which multiply together to give 12 and add together to give 7. Think about this for a minute and you will realise that the two numbers we seek are 3 and 4 because 4 3 = 12, and = 7 So, using the two numbers which add to give 7 we split the 7x term into 4x and 3x. We set the calculation out like this: 3 c mathcentre August 7, 2003
4 x 2 7x +12 = x 2 4x 3x +12 = x(x 4) 3x + 12 by factorising the first two terms = x(x 4) 3(x 4) by factorising the last two terms extracting a factor of 3 in order to leave x 4 = (x 4)(x 3) by noting the common factor of x 4 Once again, note that the answer can be checked by multiplying out the brackets again. Suppose we wish to factorise the quadratic expression x 2 5x 14. Starting as before we look for two numbers which multiply together to give 14 and add together to give 5. Think about this for a minute and you will realise that the two numbers we seek are 7 and 2 because 7 2 = 14, and = 5 So, using the two numbers which add to give 5 we split the 5x term into 7x and +2x. We set the calculation out like this: x 2 5x 14 = x 2 7x +2x 14 = x(x 7)+2x 14 by factorising the first two terms = x(x 7)+2(x 7) by factorising the last two terms = (x 7)(x + 2) by noting the common factor of x 7 So the factorisation of x 2 5x 14 is (x 7)(x +2). 4. Factorising by inspection Clearly, when you have some experience of this method, it is possible to avoid writing out all these stages. This is rather long-winded. What you need to do now is carry out the process by inspection. That is, simply by looking at the given expression, decide in your head which numbers need to be placed in the brackets to do the job. Look at the following two examples and see if you can do this. Suppose we want to factorise the quadratic expression x 2 9x + 20 by inspection. We write x 2 9x +20 = ( )( ) and try to place the correct quantities in brackets. Clearly we will need an x in both terms: x 2 9x +20=(x )(x ) We want two numbers which multiply to give 20 and add to give 9. With practice you will be able to do this in your head. The two numbers are 4 and 5. x 2 9x +20=(x 4)(x 5) The answer should always be checked by multiplying-out the brackets again. c mathcentre August 7,
5 Suppose we want to factorise the quadratic expression x 2 9x 22 by inspection. We write x 2 9x 22 = ( )( ) and try to place the correct quantities in brackets. Clearly we will need an x in both terms: x 2 9x 22=(x )(x ) We want two numbers which multiply to give 22 and add to give 9. The two numbers are 11 and +2. x 2 9x 22=(x 11)(x +2) The answer should always be checked by multiplying-out the brackets again. If you can t manage to do these by inspection yet do not worry. Do it the way we did it before. Your ability to do this will improve with practice and experience. All of these examples have involved quadratic expressions where the coefficient of x 2 was 1. When the coefficient is a number other than 1 the problem is more difficult. We will look at examples like this in the next section. Exercises 2. Factorise the following. a) x 2 +8x +15 b) x 2 +10x +24 c) x 2 +9x +8 d) x 2 +15x +36 e) x 2 +2x 3 f) x 2 +2x 8 g) x 2 2x 3 h) x 2 +7x 18 i) x 2 12x +35 j) x 2 11x +10 k) x 2 13x +22 l) x 2 +12x Expressions where the coefficient of x 2 is not 1. Suppose we wish to factorise the expression 3x 2 +5x 2. As we did before we look for two numbers which add to give the coefficient of x; so we seek two numbers which add to give 5. However, instead of looking for two numbers which multiply to give 2 we must look for two numbers which multiply to give 6, (that is, the coefficient of x 2 multiplied by the constant term, 3 2). This is entirely consistent with the method we applied before because in those examples the coefficient of x 2 was always 1. So??= 6? +? = 5 By inspection, or trial and error, two such numbers are 6 and = =5 We use these two numbers to split the 5x term into 6x and 1x. 3x 2 +5x 2 = 3x 2 +6x x 2 = 3x(x +2) x 2 by factorising the first two terms = 3x(x +2) (x + 2) factorising the last two terms by extracting 1 = (x + 2)(3x 1) by noting the common factor of x +2 5 c mathcentre August 7, 2003
6 Suppose we wish to factorise 2x 2 +5x 7. As we did before we look for two numbers which add to give the coefficient of x; so we seek two numbers which add to give 5. We look for two numbers which multiply to give 14, (that is, the coefficient of x 2 multiplied by the constant term, 2 7). So??= 14? +?=5 By inspection, or trial and error, two such numbers are 7 and = =5 We use these two numbers to split the 5x term into 7x and 2x. 2x 2 +5x 7 = 2x 2 +7x 2x 7 = x(2x +7) 2x 7 by factorising the first two terms = x(2x +7) (2x + 7) factorising the last two terms by extracting 1 = (2x + 7)(x 1) by noting the common factor of 2x +7 Suppose we wish to factorise 6x 2 5x 4. We look for two numbers which multiply to give 24, (that is, the coefficient of x 2 multiplied by the constant term, 6 4). We look for two numbers which add to give the coefficient of x; so we seek two numbers which add to give 5. So??= 24? +? = 5 By inspection, or trial and error, two such numbers are 8 and = = 5 We use these two numbers to split the 5x term into 3x and 8x. 6x 2 5x 4 = 6x 2 +3x 8x 4 = 3x(2x +1) 8x 4 by factorising the first two terms = 3x(2x +1) 4(2x + 1) factorising the last two terms by extracting 4 = (2x + 1)(3x 4) by noting the common factor of 2x +1 Suppose we wish to factorise 15x 2 3x 18. In this example note that the coefficients share a common factor of 3. This can be extracted: Now we are looking at factorising 5x 2 x 6. 3(5x 2 x 6) c mathcentre August 7,
7 We look for two numbers which multiply to give 30, (that is, the coefficient of x 2 multiplied by the constant term, 5 6). We look for two numbers which add to give the coefficient of x; so we seek two numbers which add to give 1. So??= 30? +? = 1 By inspection, or trial and error, two such numbers are 5 and = = 1 We use these two numbers to split the x term into 5x and 6x. 3(5x 2 x 6) = 3(5x 2 +5x 6x 6) = 3(5x(x +1) 6x 6)) by factorising the first two terms = 3(5x(x +1) 6(x + 1)) factorising the last two terms by extracting 6 = 3((x + 1)(5x 6)) by noting the common factor of x +1 Exercises 3 Factorise the following. a) 2x 2 +11x + 5 b) 3x 2 +19x + 6 c) 3x 2 +17x 6 d) 6x 2 +7x +2 e) 7x 2 6x 1 f) 12x 2 +7x + 1 g) 8x 2 +6x + 1 h) 8x 2 6x +1 6.Specialcase1-thedifferenceoftwosquares A special case concerns what is known as the difference of two squares. What does this look like? Typically, x 2 9. Note that there is no x term and that the number 9 is itself a square number. A square number is one which has resulted from squaring another number. In this case 9 is the result of squaring 3, (3 2 = 9), and so 9 is a square number. Hence x 2 9 is the difference of two squares, x When we try to factorise x 2 9 we are looking for two numbers which add to zero (because there is no term in x), and which multiply to give 9. Two such numbers are 3 and 3 because 3 3 = 9, and = 0 We use these two numbers to split the 0x term into 3x and 3x. x 2 9 = x 2 3x +3x 9 = x(x 3)+3x 9 by factorising the first two terms = x(x 3)+3(x 3) factorising the last two terms by extracting +3 = (x 3)(x + 3) by noting the common factor of x 3 So x 2 9=(x 3)(x +3) Recall that 9 is a square number, (9 = 3 2 ). So this example is a difference of two square. The result of this example is true in more general cases of the difference of two squares. It is always the case that x 2 a 2 factorises to (x a)(x + a). 7 c mathcentre August 7, 2003
8 Key Point The difference of two squares, x 2 a 2, always factorises to x 2 a 2 =(x a)(x + a) Suppose we want to factorise x Note that x 2 25 is the difference of two squares because 25 is a square number (25 = 5 2 ). So we need to factorise x We can do this by inspection using the formula above. x =(x 5)(x +5) Suppose we want to factorise 2x This time there is a common factor of 2 which can be extracted first. 2x 2 32=2(x 2 16)=2(x 4)(x +4) A slightly different form occurs if we now include a square number in front of the x 2 term. For example, suppose we wish to factorise 9x Note that 9 is a square number, and so the term 9x 2 can be written (3x) 2. So we still have a difference of two squares (3x) To factorise this we write 9x 2 16 = (3x 4)(3x +4) Exercises 4 Factorise the following. a) x b) x 2 36 c) x 2 1 d) x e) 9x 2 1 f) 16x 2 9 g) 49x 2 1 h) 25x Specialcase2-complete squares A second important special case is when we need to deal with complete squares. This happens when the answer can be written in the form ( ) 2, that is as a single term, squared. Consider the following example. c mathcentre August 7,
9 Suppose we wish to factorise x 2 +10x As before we want two numbers which multiply to give 25 and add to give 10. Two such numbers are 5 and 5 because 5 5 = 25, and = 10 We use these two numbers to split the 10x term into 5x and 5x. x 2 +10x +25 = x 2 +5x +5x +25 = x(x +5)+5x + 25 by factorising the first two terms = x(x +5)+5(x + 5) factorising the last two terms by extracting +5 = (x + 5)(x + 5) by noting the common factor of x +5 The result can be written as (x +5) 2,acomplete square. Suppose we want to factorise x 2 8x +16. We seek two numbers which add to give 8 and multiply to give 16. The two required numbers are 4 and 4 and so, by inspection, x 2 8x +16=(x 4)(x 4) The result can be written as (x 4) 2,acomplete square. More complicated examples can occur, for example when there is a number in front of the x 2. Work through the following example. Suppose we want to factorise 25x 2 20x +4. Note that 25x 2 can be written as (5x) 2, a squared term. Note also that 4 = 2 2. In this case, by inspection, 25x 2 20x +4=(5x 2)(5x 2) The result can be written as (5x 2) 2,acomplete square. Do not worry if you have difficulty with this last example. The skill will come with practice. Even if you did not recognise the complete square, you could still use the previous method: To factorise 25x 2 20x +4 As before we want two numbers which multiply to give 100 (the coefficient of x 2 multiplied by the constant term) and add to give 20. Two such numbers are 10 and 10 because = 100, and = 20 We use these two numbers to split the 20x term into 10x and 10x. 25x 2 20x +4 = 25x 2 10x 10x +4 = 5x(5x 2) 10x + 4 by factorising the first two terms = 5x(5x 2) 2(5x 2) factorising the last two terms by extracting 2 = (5x 2)(5x 2) by noting the common factor of 5x 2 So 25x 2 20x +4=(5x 2) 2 as before. 9 c mathcentre August 7, 2003
10 8.Specialcase3-theconstanttermismissing There is one more special case that you ought to be familiar with. This arises in examples where the constant term is absent, as in 3x 2 8x. How do we proceed? The way forward is to look for common factors. In the case of 3x 2 8x note that each of the two terms has a common factor of x. (Note that this is not the case when dealing with a quadratic expression containing a constant term). The common factor, x, is written outside a bracket, and the contents of the bracket are chosen by inspection so that they multiply-out to give the correct terms. 3x 2 8x = x(3x 8) Suppose we wish to factorise 10x 2 +5x. This time we note the common factor of 5x. This is extracted and we adjust the contents of the brackets accordingly: 10x 2 +5x =5x(2x +1) Exercises 5. Factorise the following. a) x 2 +18x +81 b) x 2 4x +4 c) x 2 22x d) 25x 2 +40x +16 e) 64x 2 +16x +1 f) x 2 +6x g) 3x 2 x h) 5x 2 20x Answers Exercises 1 a) x 2 +3x +2 b) x 2 +5x +6 c) x 2 2x 3 d) x 2 2x 8 e) x 2 +4x 21 f) x 2 7x g) x 2 5x +6 h) x 2 14x +49 i) x 2 4x +4 j) x 2 4 k) x 2 9 l) 2x 2 +3x +1 m) 2x 2 11x + 5 n) 9x 2 1 o) 4x 2 8x. Exercises 2 a) (x + 3)(x +5) b) (x + 4)(x +6) c) (x + 1)(x +8) d) (x + 3)(x + 12) e) (x + 3)(x 1) f) (x + 4)(x 2) g) (x 3)(x +1) h) (x + 9)(x 2) i) (x 7)(x 5) j) (x 1)(x 10) k) (x 11)(x 2) l) (x + 9)(x +3) Exercises 3 a) (2x + 1)(x +5) b) (3x + 1)(x +6) c) (3x 1)(x +6) d) (2x + 1)(3x +2) e) (7x + 1)(x 1) f) (3x + 1)(4x +1) g) (2x + 1)(4x +1) h) (2x 1)(4x 1) Exercises 4 a) (x 12)(x + 12) b) (x 6)(x +6) c) (x 1)(x +1) d) (x 11)(x + 11) e) (3x + 1)(3x 1) f) (4x + 3)(4x 3) g) (7x + 1)(7x 1) h) (5x + 4)(5x 4) Exercises 5 a) (x +9) 2 b) (x 2) 2 c) (x 11) 2 d) (5x +4) 2 e) (8x +1) 2 f) x(x +6) g) x(3x 1) h) 5x(x 4) c mathcentre August 7,
1.5. Factorisation. Introduction. Prerequisites. Learning Outcomes. Learning Style
 Factorisation 1.5 Introduction In Block 4 we showed the way in which brackets were removed from algebraic expressions. Factorisation, which can be considered as the reverse of this process, is dealt with
Factorisation 1.5 Introduction In Block 4 we showed the way in which brackets were removed from algebraic expressions. Factorisation, which can be considered as the reverse of this process, is dealt with
Section 6.1 Factoring Expressions
 Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
FACTORING QUADRATIC EQUATIONS
 FACTORING QUADRATIC EQUATIONS Summary 1. Difference of squares... 1 2. Mise en évidence simple... 2 3. compounded factorization... 3 4. Exercises... 7 The goal of this section is to summarize the methods
FACTORING QUADRATIC EQUATIONS Summary 1. Difference of squares... 1 2. Mise en évidence simple... 2 3. compounded factorization... 3 4. Exercises... 7 The goal of this section is to summarize the methods
Integrating algebraic fractions
 Integrating algebraic fractions Sometimes the integral of an algebraic fraction can be found by first epressing the algebraic fraction as the sum of its partial fractions. In this unit we will illustrate
Integrating algebraic fractions Sometimes the integral of an algebraic fraction can be found by first epressing the algebraic fraction as the sum of its partial fractions. In this unit we will illustrate
JUST THE MATHS UNIT NUMBER 1.8. ALGEBRA 8 (Polynomials) A.J.Hobson
 JUST THE MATHS UNIT NUMBER 1.8 ALGEBRA 8 (Polynomials) by A.J.Hobson 1.8.1 The factor theorem 1.8.2 Application to quadratic and cubic expressions 1.8.3 Cubic equations 1.8.4 Long division of polynomials
JUST THE MATHS UNIT NUMBER 1.8 ALGEBRA 8 (Polynomials) by A.J.Hobson 1.8.1 The factor theorem 1.8.2 Application to quadratic and cubic expressions 1.8.3 Cubic equations 1.8.4 Long division of polynomials
Factoring Quadratic Expressions
 Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
expression is written horizontally. The Last terms ((2)( 4)) because they are the last terms of the two polynomials. This is called the FOIL method.
 A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
3.2. Solving quadratic equations. Introduction. Prerequisites. Learning Outcomes. Learning Style
 Solving quadratic equations 3.2 Introduction A quadratic equation is one which can be written in the form ax 2 + bx + c = 0 where a, b and c are numbers and x is the unknown whose value(s) we wish to find.
Solving quadratic equations 3.2 Introduction A quadratic equation is one which can be written in the form ax 2 + bx + c = 0 where a, b and c are numbers and x is the unknown whose value(s) we wish to find.
is identically equal to x 2 +3x +2
 Partial fractions 3.6 Introduction It is often helpful to break down a complicated algebraic fraction into a sum of simpler fractions. 4x+7 For example it can be shown that has the same value as 1 + 3
Partial fractions 3.6 Introduction It is often helpful to break down a complicated algebraic fraction into a sum of simpler fractions. 4x+7 For example it can be shown that has the same value as 1 + 3
Completing the square
 Completing the square mc-ty-completingsquare-009-1 In this unit we consider how quadratic expressions can be written in an equivalent form using the technique known as completing the square. This technique
Completing the square mc-ty-completingsquare-009-1 In this unit we consider how quadratic expressions can be written in an equivalent form using the technique known as completing the square. This technique
NSM100 Introduction to Algebra Chapter 5 Notes Factoring
 Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
3.3. Solving Polynomial Equations. Introduction. Prerequisites. Learning Outcomes
 Solving Polynomial Equations 3.3 Introduction Linear and quadratic equations, dealt within Sections 3.1 and 3.2, are members of a class of equations, called polynomial equations. These have the general
Solving Polynomial Equations 3.3 Introduction Linear and quadratic equations, dealt within Sections 3.1 and 3.2, are members of a class of equations, called polynomial equations. These have the general
Equations, Inequalities & Partial Fractions
 Contents Equations, Inequalities & Partial Fractions.1 Solving Linear Equations 2.2 Solving Quadratic Equations 1. Solving Polynomial Equations 1.4 Solving Simultaneous Linear Equations 42.5 Solving Inequalities
Contents Equations, Inequalities & Partial Fractions.1 Solving Linear Equations 2.2 Solving Quadratic Equations 1. Solving Polynomial Equations 1.4 Solving Simultaneous Linear Equations 42.5 Solving Inequalities
3.1. Solving linear equations. Introduction. Prerequisites. Learning Outcomes. Learning Style
 Solving linear equations 3.1 Introduction Many problems in engineering reduce to the solution of an equation or a set of equations. An equation is a type of mathematical expression which contains one or
Solving linear equations 3.1 Introduction Many problems in engineering reduce to the solution of an equation or a set of equations. An equation is a type of mathematical expression which contains one or
3.6. Partial Fractions. Introduction. Prerequisites. Learning Outcomes
 Partial Fractions 3.6 Introduction It is often helpful to break down a complicated algebraic fraction into a sum of simpler fractions. For 4x + 7 example it can be shown that x 2 + 3x + 2 has the same
Partial Fractions 3.6 Introduction It is often helpful to break down a complicated algebraic fraction into a sum of simpler fractions. For 4x + 7 example it can be shown that x 2 + 3x + 2 has the same
Factoring and Applications
 Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
6 EXTENDING ALGEBRA. 6.0 Introduction. 6.1 The cubic equation. Objectives
 6 EXTENDING ALGEBRA Chapter 6 Extending Algebra Objectives After studying this chapter you should understand techniques whereby equations of cubic degree and higher can be solved; be able to factorise
6 EXTENDING ALGEBRA Chapter 6 Extending Algebra Objectives After studying this chapter you should understand techniques whereby equations of cubic degree and higher can be solved; be able to factorise
FACTORISATION YEARS. A guide for teachers - Years 9 10 June 2011. The Improving Mathematics Education in Schools (TIMES) Project
 9 10 YEARS The Improving Mathematics Education in Schools (TIMES) Project FACTORISATION NUMBER AND ALGEBRA Module 33 A guide for teachers - Years 9 10 June 2011 Factorisation (Number and Algebra : Module
9 10 YEARS The Improving Mathematics Education in Schools (TIMES) Project FACTORISATION NUMBER AND ALGEBRA Module 33 A guide for teachers - Years 9 10 June 2011 Factorisation (Number and Algebra : Module
Factoring Polynomials and Solving Quadratic Equations
 Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
MATHEMATICS FOR ENGINEERING BASIC ALGEBRA
 MATHEMATICS FOR ENGINEERING BASIC ALGEBRA TUTORIAL 3 EQUATIONS This is the one of a series of basic tutorials in mathematics aimed at beginners or anyone wanting to refresh themselves on fundamentals.
MATHEMATICS FOR ENGINEERING BASIC ALGEBRA TUTORIAL 3 EQUATIONS This is the one of a series of basic tutorials in mathematics aimed at beginners or anyone wanting to refresh themselves on fundamentals.
Factoring Polynomials
 Factoring Polynomials 4-1-2014 The opposite of multiplying polynomials is factoring. Why would you want to factor a polynomial? Let p(x) be a polynomial. p(c) = 0 is equivalent to x c dividing p(x). Recall
Factoring Polynomials 4-1-2014 The opposite of multiplying polynomials is factoring. Why would you want to factor a polynomial? Let p(x) be a polynomial. p(c) = 0 is equivalent to x c dividing p(x). Recall
For each learner you will need: mini-whiteboard. For each small group of learners you will need: Card set A Factors; Card set B True/false.
 Level A11 of challenge: D A11 Mathematical goals Starting points Materials required Time needed Factorising cubics To enable learners to: associate x-intercepts with finding values of x such that f (x)
Level A11 of challenge: D A11 Mathematical goals Starting points Materials required Time needed Factorising cubics To enable learners to: associate x-intercepts with finding values of x such that f (x)
Solving Quadratic Equations by Factoring
 4.7 Solving Quadratic Equations by Factoring 4.7 OBJECTIVE 1. Solve quadratic equations by factoring The factoring techniques you have learned provide us with tools for solving equations that can be written
4.7 Solving Quadratic Equations by Factoring 4.7 OBJECTIVE 1. Solve quadratic equations by factoring The factoring techniques you have learned provide us with tools for solving equations that can be written
Chapter R.4 Factoring Polynomials
 Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
is identically equal to x 2 +3x +2
 Partial fractions.6 Introduction It is often helpful to break down a complicated algebraic fraction into a sum of simpler fractions. 4x+7 For example it can be shown that has the same value as + for any
Partial fractions.6 Introduction It is often helpful to break down a complicated algebraic fraction into a sum of simpler fractions. 4x+7 For example it can be shown that has the same value as + for any
POLYNOMIALS and FACTORING
 POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
Factoring A Quadratic Polynomial
 Factoring A Quadratic Polynomial If we multiply two binomials together, the result is a quadratic polynomial: This multiplication is pretty straightforward, using the distributive property of multiplication
Factoring A Quadratic Polynomial If we multiply two binomials together, the result is a quadratic polynomial: This multiplication is pretty straightforward, using the distributive property of multiplication
Factoring Polynomials
 Factoring Polynomials Hoste, Miller, Murieka September 12, 2011 1 Factoring In the previous section, we discussed how to determine the product of two or more terms. Consider, for instance, the equations
Factoring Polynomials Hoste, Miller, Murieka September 12, 2011 1 Factoring In the previous section, we discussed how to determine the product of two or more terms. Consider, for instance, the equations
Factoring Polynomials
 Factoring a Polynomial Expression Factoring a polynomial is expressing the polynomial as a product of two or more factors. Simply stated, it is somewhat the reverse process of multiplying. To factor polynomials,
Factoring a Polynomial Expression Factoring a polynomial is expressing the polynomial as a product of two or more factors. Simply stated, it is somewhat the reverse process of multiplying. To factor polynomials,
A Concrete Introduction. to the Abstract Concepts. of Integers and Algebra using Algebra Tiles
 A Concrete Introduction to the Abstract Concepts of Integers and Algebra using Algebra Tiles Table of Contents Introduction... 1 page Integers 1: Introduction to Integers... 3 2: Working with Algebra Tiles...
A Concrete Introduction to the Abstract Concepts of Integers and Algebra using Algebra Tiles Table of Contents Introduction... 1 page Integers 1: Introduction to Integers... 3 2: Working with Algebra Tiles...
Sect 6.7 - Solving Equations Using the Zero Product Rule
 Sect 6.7 - Solving Equations Using the Zero Product Rule 116 Concept #1: Definition of a Quadratic Equation A quadratic equation is an equation that can be written in the form ax 2 + bx + c = 0 (referred
Sect 6.7 - Solving Equations Using the Zero Product Rule 116 Concept #1: Definition of a Quadratic Equation A quadratic equation is an equation that can be written in the form ax 2 + bx + c = 0 (referred
QUADRATIC EQUATIONS EXPECTED BACKGROUND KNOWLEDGE
 MODULE - 1 Quadratic Equations 6 QUADRATIC EQUATIONS In this lesson, you will study aout quadratic equations. You will learn to identify quadratic equations from a collection of given equations and write
MODULE - 1 Quadratic Equations 6 QUADRATIC EQUATIONS In this lesson, you will study aout quadratic equations. You will learn to identify quadratic equations from a collection of given equations and write
Factoring ax 2 + bx + c - Teacher Notes
 Southern Nevada Regional Professi onal D evel opment Program VOLUME 1, ISSUE 8 MAY 009 A N ewsletter from the Sec ondary Mathematic s Team Factoring ax + bx + c - Teacher Notes Here we look at sample teacher
Southern Nevada Regional Professi onal D evel opment Program VOLUME 1, ISSUE 8 MAY 009 A N ewsletter from the Sec ondary Mathematic s Team Factoring ax + bx + c - Teacher Notes Here we look at sample teacher
FACTORING QUADRATICS 8.1.1 and 8.1.2
 FACTORING QUADRATICS 8.1.1 and 8.1.2 Chapter 8 introduces students to quadratic equations. These equations can be written in the form of y = ax 2 + bx + c and, when graphed, produce a curve called a parabola.
FACTORING QUADRATICS 8.1.1 and 8.1.2 Chapter 8 introduces students to quadratic equations. These equations can be written in the form of y = ax 2 + bx + c and, when graphed, produce a curve called a parabola.
To add fractions we rewrite the fractions with a common denominator then add the numerators. = +
 Partial Fractions Adding fractions To add fractions we rewrite the fractions with a common denominator then add the numerators. Example Find the sum of 3 x 5 The common denominator of 3 and x 5 is 3 x
Partial Fractions Adding fractions To add fractions we rewrite the fractions with a common denominator then add the numerators. Example Find the sum of 3 x 5 The common denominator of 3 and x 5 is 3 x
APPLICATIONS AND MODELING WITH QUADRATIC EQUATIONS
 APPLICATIONS AND MODELING WITH QUADRATIC EQUATIONS Now that we are starting to feel comfortable with the factoring process, the question becomes what do we use factoring to do? There are a variety of classic
APPLICATIONS AND MODELING WITH QUADRATIC EQUATIONS Now that we are starting to feel comfortable with the factoring process, the question becomes what do we use factoring to do? There are a variety of classic
Factoring. Factoring Monomials Monomials can often be factored in more than one way.
 Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
FACTORING ax 2 bx c. Factoring Trinomials with Leading Coefficient 1
 5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
Integration by substitution
 Integration by substitution There are occasions when it is possible to perform an apparently difficult piece of integration by first making a substitution. This has the effect of changing the variable
Integration by substitution There are occasions when it is possible to perform an apparently difficult piece of integration by first making a substitution. This has the effect of changing the variable
1.4. Arithmetic of Algebraic Fractions. Introduction. Prerequisites. Learning Outcomes
 Arithmetic of Algebraic Fractions 1.4 Introduction Just as one whole number divided by another is called a numerical fraction, so one algebraic expression divided by another is known as an algebraic fraction.
Arithmetic of Algebraic Fractions 1.4 Introduction Just as one whole number divided by another is called a numerical fraction, so one algebraic expression divided by another is known as an algebraic fraction.
SOLVING QUADRATIC EQUATIONS - COMPARE THE FACTORING ac METHOD AND THE NEW DIAGONAL SUM METHOD By Nghi H. Nguyen
 SOLVING QUADRATIC EQUATIONS - COMPARE THE FACTORING ac METHOD AND THE NEW DIAGONAL SUM METHOD By Nghi H. Nguyen A. GENERALITIES. When a given quadratic equation can be factored, there are 2 best methods
SOLVING QUADRATIC EQUATIONS - COMPARE THE FACTORING ac METHOD AND THE NEW DIAGONAL SUM METHOD By Nghi H. Nguyen A. GENERALITIES. When a given quadratic equation can be factored, there are 2 best methods
Implicit Differentiation
 Implicit Differentiation Sometimes functions are given not in the form y = f(x) but in a more complicated form in which it is difficult or impossible to express y explicitly in terms of x. Such functions
Implicit Differentiation Sometimes functions are given not in the form y = f(x) but in a more complicated form in which it is difficult or impossible to express y explicitly in terms of x. Such functions
If A is divided by B the result is 2/3. If B is divided by C the result is 4/7. What is the result if A is divided by C?
 Problem 3 If A is divided by B the result is 2/3. If B is divided by C the result is 4/7. What is the result if A is divided by C? Suggested Questions to ask students about Problem 3 The key to this question
Problem 3 If A is divided by B the result is 2/3. If B is divided by C the result is 4/7. What is the result if A is divided by C? Suggested Questions to ask students about Problem 3 The key to this question
Factoring Trinomials: The ac Method
 6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
MATH 90 CHAPTER 6 Name:.
 MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
Name Intro to Algebra 2. Unit 1: Polynomials and Factoring
 Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
SOLVING QUADRATIC EQUATIONS BY THE NEW TRANSFORMING METHOD (By Nghi H Nguyen Updated Oct 28, 2014))
 SOLVING QUADRATIC EQUATIONS BY THE NEW TRANSFORMING METHOD (By Nghi H Nguyen Updated Oct 28, 2014)) There are so far 8 most common methods to solve quadratic equations in standard form ax² + bx + c = 0.
SOLVING QUADRATIC EQUATIONS BY THE NEW TRANSFORMING METHOD (By Nghi H Nguyen Updated Oct 28, 2014)) There are so far 8 most common methods to solve quadratic equations in standard form ax² + bx + c = 0.
Determinants can be used to solve a linear system of equations using Cramer s Rule.
 2.6.2 Cramer s Rule Determinants can be used to solve a linear system of equations using Cramer s Rule. Cramer s Rule for Two Equations in Two Variables Given the system This system has the unique solution
2.6.2 Cramer s Rule Determinants can be used to solve a linear system of equations using Cramer s Rule. Cramer s Rule for Two Equations in Two Variables Given the system This system has the unique solution
Year 9 set 1 Mathematics notes, to accompany the 9H book.
 Part 1: Year 9 set 1 Mathematics notes, to accompany the 9H book. equations 1. (p.1), 1.6 (p. 44), 4.6 (p.196) sequences 3. (p.115) Pupils use the Elmwood Press Essential Maths book by David Raymer (9H
Part 1: Year 9 set 1 Mathematics notes, to accompany the 9H book. equations 1. (p.1), 1.6 (p. 44), 4.6 (p.196) sequences 3. (p.115) Pupils use the Elmwood Press Essential Maths book by David Raymer (9H
Wentzville School District Algebra 1: Unit 8 Stage 1 Desired Results
 Wentzville School District Algebra 1: Unit 8 Stage 1 Desired Results Unit Title: Quadratic Expressions & Equations Course: Algebra I Unit 8 - Quadratic Expressions & Equations Brief Summary of Unit: At
Wentzville School District Algebra 1: Unit 8 Stage 1 Desired Results Unit Title: Quadratic Expressions & Equations Course: Algebra I Unit 8 - Quadratic Expressions & Equations Brief Summary of Unit: At
FOIL FACTORING. Factoring is merely undoing the FOIL method. Let s look at an example: Take the polynomial x²+4x+4.
 FOIL FACTORING Factoring is merely undoing the FOIL method. Let s look at an example: Take the polynomial x²+4x+4. First we take the 3 rd term (in this case 4) and find the factors of it. 4=1x4 4=2x2 Now
FOIL FACTORING Factoring is merely undoing the FOIL method. Let s look at an example: Take the polynomial x²+4x+4. First we take the 3 rd term (in this case 4) and find the factors of it. 4=1x4 4=2x2 Now
Algebra: Real World Applications and Problems
 Algebra: Real World Applications and Problems Algebra is boring. Right? Hopefully not. Algebra has no applications in the real world. Wrong. Absolutely wrong. I hope to show this in the following document.
Algebra: Real World Applications and Problems Algebra is boring. Right? Hopefully not. Algebra has no applications in the real world. Wrong. Absolutely wrong. I hope to show this in the following document.
2.4. Factoring Quadratic Expressions. Goal. Explore 2.4. Launch 2.4
 2.4 Factoring Quadratic Epressions Goal Use the area model and Distributive Property to rewrite an epression that is in epanded form into an equivalent epression in factored form The area of a rectangle
2.4 Factoring Quadratic Epressions Goal Use the area model and Distributive Property to rewrite an epression that is in epanded form into an equivalent epression in factored form The area of a rectangle
( ) FACTORING. x In this polynomial the only variable in common to all is x.
 FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
EVALUATING ACADEMIC READINESS FOR APPRENTICESHIP TRAINING Revised For ACCESS TO APPRENTICESHIP
 EVALUATING ACADEMIC READINESS FOR APPRENTICESHIP TRAINING For ACCESS TO APPRENTICESHIP MATHEMATICS SKILL OPERATIONS WITH INTEGERS AN ACADEMIC SKILLS MANUAL for The Precision Machining And Tooling Trades
EVALUATING ACADEMIC READINESS FOR APPRENTICESHIP TRAINING For ACCESS TO APPRENTICESHIP MATHEMATICS SKILL OPERATIONS WITH INTEGERS AN ACADEMIC SKILLS MANUAL for The Precision Machining And Tooling Trades
Find all of the real numbers x that satisfy the algebraic equation:
 Appendix C: Factoring Algebraic Expressions Factoring algebraic equations is the reverse of expanding algebraic expressions discussed in Appendix B. Factoring algebraic equations can be a great help when
Appendix C: Factoring Algebraic Expressions Factoring algebraic equations is the reverse of expanding algebraic expressions discussed in Appendix B. Factoring algebraic equations can be a great help when
FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c
 Tallahassee Community College 55 FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c This kind of trinomial differs from the previous kind we have factored because the coefficient of x is no longer "1".
Tallahassee Community College 55 FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c This kind of trinomial differs from the previous kind we have factored because the coefficient of x is no longer "1".
SOLVING QUADRATIC EQUATIONS BY THE DIAGONAL SUM METHOD
 SOLVING QUADRATIC EQUATIONS BY THE DIAGONAL SUM METHOD A quadratic equation in one variable has as standard form: ax^2 + bx + c = 0. Solving it means finding the values of x that make the equation true.
SOLVING QUADRATIC EQUATIONS BY THE DIAGONAL SUM METHOD A quadratic equation in one variable has as standard form: ax^2 + bx + c = 0. Solving it means finding the values of x that make the equation true.
Unit 3: Day 2: Factoring Polynomial Expressions
 Unit 3: Day : Factoring Polynomial Expressions Minds On: 0 Action: 45 Consolidate:10 Total =75 min Learning Goals: Extend knowledge of factoring to factor cubic and quartic expressions that can be factored
Unit 3: Day : Factoring Polynomial Expressions Minds On: 0 Action: 45 Consolidate:10 Total =75 min Learning Goals: Extend knowledge of factoring to factor cubic and quartic expressions that can be factored
Mathematics. (www.tiwariacademy.com : Focus on free Education) (Chapter 5) (Complex Numbers and Quadratic Equations) (Class XI)
 ( : Focus on free Education) Miscellaneous Exercise on chapter 5 Question 1: Evaluate: Answer 1: 1 ( : Focus on free Education) Question 2: For any two complex numbers z1 and z2, prove that Re (z1z2) =
( : Focus on free Education) Miscellaneous Exercise on chapter 5 Question 1: Evaluate: Answer 1: 1 ( : Focus on free Education) Question 2: For any two complex numbers z1 and z2, prove that Re (z1z2) =
Definition 8.1 Two inequalities are equivalent if they have the same solution set. Add or Subtract the same value on both sides of the inequality.
 8 Inequalities Concepts: Equivalent Inequalities Linear and Nonlinear Inequalities Absolute Value Inequalities (Sections 4.6 and 1.1) 8.1 Equivalent Inequalities Definition 8.1 Two inequalities are equivalent
8 Inequalities Concepts: Equivalent Inequalities Linear and Nonlinear Inequalities Absolute Value Inequalities (Sections 4.6 and 1.1) 8.1 Equivalent Inequalities Definition 8.1 Two inequalities are equivalent
Lecture 14: Section 3.3
 Lecture 14: Section 3.3 Shuanglin Shao October 23, 2013 Definition. Two nonzero vectors u and v in R n are said to be orthogonal (or perpendicular) if u v = 0. We will also agree that the zero vector in
Lecture 14: Section 3.3 Shuanglin Shao October 23, 2013 Definition. Two nonzero vectors u and v in R n are said to be orthogonal (or perpendicular) if u v = 0. We will also agree that the zero vector in
Higher. Polynomials and Quadratics 64
 hsn.uk.net Higher Mathematics UNIT OUTCOME 1 Polnomials and Quadratics Contents Polnomials and Quadratics 64 1 Quadratics 64 The Discriminant 66 3 Completing the Square 67 4 Sketching Parabolas 70 5 Determining
hsn.uk.net Higher Mathematics UNIT OUTCOME 1 Polnomials and Quadratics Contents Polnomials and Quadratics 64 1 Quadratics 64 The Discriminant 66 3 Completing the Square 67 4 Sketching Parabolas 70 5 Determining
Multiplying and Factoring Notes
 Multiplying/Factoring 3 Multiplying and Factoring Notes I. Content: This lesson is going to focus on wrapping up and solidifying concepts that we have been discovering and working with. The students have
Multiplying/Factoring 3 Multiplying and Factoring Notes I. Content: This lesson is going to focus on wrapping up and solidifying concepts that we have been discovering and working with. The students have
2.5 Zeros of a Polynomial Functions
 .5 Zeros of a Polynomial Functions Section.5 Notes Page 1 The first rule we will talk about is Descartes Rule of Signs, which can be used to determine the possible times a graph crosses the x-axis and
.5 Zeros of a Polynomial Functions Section.5 Notes Page 1 The first rule we will talk about is Descartes Rule of Signs, which can be used to determine the possible times a graph crosses the x-axis and
Factoring Special Polynomials
 6.6 Factoring Special Polynomials 6.6 OBJECTIVES 1. Factor the difference of two squares 2. Factor the sum or difference of two cubes In this section, we will look at several special polynomials. These
6.6 Factoring Special Polynomials 6.6 OBJECTIVES 1. Factor the difference of two squares 2. Factor the sum or difference of two cubes In this section, we will look at several special polynomials. These
1.3 Algebraic Expressions
 1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
In algebra, factor by rewriting a polynomial as a product of lower-degree polynomials
 Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
9. POLYNOMIALS. Example 1: The expression a(x) = x 3 4x 2 + 7x 11 is a polynomial in x. The coefficients of a(x) are the numbers 1, 4, 7, 11.
 9. POLYNOMIALS 9.1. Definition of a Polynomial A polynomial is an expression of the form: a(x) = a n x n + a n-1 x n-1 +... + a 1 x + a 0. The symbol x is called an indeterminate and simply plays the role
9. POLYNOMIALS 9.1. Definition of a Polynomial A polynomial is an expression of the form: a(x) = a n x n + a n-1 x n-1 +... + a 1 x + a 0. The symbol x is called an indeterminate and simply plays the role
High School Algebra Reasoning with Equations and Inequalities Solve equations and inequalities in one variable.
 Performance Assessment Task Quadratic (2009) Grade 9 The task challenges a student to demonstrate an understanding of quadratic functions in various forms. A student must make sense of the meaning of relations
Performance Assessment Task Quadratic (2009) Grade 9 The task challenges a student to demonstrate an understanding of quadratic functions in various forms. A student must make sense of the meaning of relations
Math Review. for the Quantitative Reasoning Measure of the GRE revised General Test
 Math Review for the Quantitative Reasoning Measure of the GRE revised General Test www.ets.org Overview This Math Review will familiarize you with the mathematical skills and concepts that are important
Math Review for the Quantitative Reasoning Measure of the GRE revised General Test www.ets.org Overview This Math Review will familiarize you with the mathematical skills and concepts that are important
Using the ac Method to Factor
 4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
Factoring - Solve by Factoring
 6.7 Factoring - Solve by Factoring Objective: Solve quadratic equation by factoring and using the zero product rule. When solving linear equations such as 2x 5 = 21 we can solve for the variable directly
6.7 Factoring - Solve by Factoring Objective: Solve quadratic equation by factoring and using the zero product rule. When solving linear equations such as 2x 5 = 21 we can solve for the variable directly
SOLVING POLYNOMIAL EQUATIONS
 C SOLVING POLYNOMIAL EQUATIONS We will assume in this appendix that you know how to divide polynomials using long division and synthetic division. If you need to review those techniques, refer to an algebra
C SOLVING POLYNOMIAL EQUATIONS We will assume in this appendix that you know how to divide polynomials using long division and synthetic division. If you need to review those techniques, refer to an algebra
2.3. Finding polynomial functions. An Introduction:
 2.3. Finding polynomial functions. An Introduction: As is usually the case when learning a new concept in mathematics, the new concept is the reverse of the previous one. Remember how you first learned
2.3. Finding polynomial functions. An Introduction: As is usually the case when learning a new concept in mathematics, the new concept is the reverse of the previous one. Remember how you first learned
The Point-Slope Form
 7. The Point-Slope Form 7. OBJECTIVES 1. Given a point and a slope, find the graph of a line. Given a point and the slope, find the equation of a line. Given two points, find the equation of a line y Slope
7. The Point-Slope Form 7. OBJECTIVES 1. Given a point and a slope, find the graph of a line. Given a point and the slope, find the equation of a line. Given two points, find the equation of a line y Slope
The Method of Partial Fractions Math 121 Calculus II Spring 2015
 Rational functions. as The Method of Partial Fractions Math 11 Calculus II Spring 015 Recall that a rational function is a quotient of two polynomials such f(x) g(x) = 3x5 + x 3 + 16x x 60. The method
Rational functions. as The Method of Partial Fractions Math 11 Calculus II Spring 015 Recall that a rational function is a quotient of two polynomials such f(x) g(x) = 3x5 + x 3 + 16x x 60. The method
GCSE MATHEMATICS. 43602H Unit 2: Number and Algebra (Higher) Report on the Examination. Specification 4360 November 2014. Version: 1.
 GCSE MATHEMATICS 43602H Unit 2: Number and Algebra (Higher) Report on the Examination Specification 4360 November 2014 Version: 1.0 Further copies of this Report are available from aqa.org.uk Copyright
GCSE MATHEMATICS 43602H Unit 2: Number and Algebra (Higher) Report on the Examination Specification 4360 November 2014 Version: 1.0 Further copies of this Report are available from aqa.org.uk Copyright
a cos x + b sin x = R cos(x α)
 a cos x + b sin x = R cos(x α) In this unit we explore how the sum of two trigonometric functions, e.g. cos x + 4 sin x, can be expressed as a single trigonometric function. Having the ability to do this
a cos x + b sin x = R cos(x α) In this unit we explore how the sum of two trigonometric functions, e.g. cos x + 4 sin x, can be expressed as a single trigonometric function. Having the ability to do this
By reversing the rules for multiplication of binomials from Section 4.6, we get rules for factoring polynomials in certain forms.
 SECTION 5.4 Special Factoring Techniques 317 5.4 Special Factoring Techniques OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor
SECTION 5.4 Special Factoring Techniques 317 5.4 Special Factoring Techniques OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor
UNCORRECTED PAGE PROOFS
 number and and algebra TopIC 17 Polynomials 17.1 Overview Why learn this? Just as number is learned in stages, so too are graphs. You have been building your knowledge of graphs and functions over time.
number and and algebra TopIC 17 Polynomials 17.1 Overview Why learn this? Just as number is learned in stages, so too are graphs. You have been building your knowledge of graphs and functions over time.
Springfield Technical Community College School of Mathematics, Sciences & Engineering Transfer
 Springfield Technical Community College School of Mathematics, Sciences & Engineering Transfer Department: Mathematics Course Title: Algebra 2 Course Number: MAT-097 Semester: Fall 2015 Credits: 3 Non-Graduation
Springfield Technical Community College School of Mathematics, Sciences & Engineering Transfer Department: Mathematics Course Title: Algebra 2 Course Number: MAT-097 Semester: Fall 2015 Credits: 3 Non-Graduation
The Notebook Series. The solution of cubic and quartic equations. R.S. Johnson. Professor of Applied Mathematics
 The Notebook Series The solution of cubic and quartic equations by R.S. Johnson Professor of Applied Mathematics School of Mathematics & Statistics University of Newcastle upon Tyne R.S.Johnson 006 CONTENTS
The Notebook Series The solution of cubic and quartic equations by R.S. Johnson Professor of Applied Mathematics School of Mathematics & Statistics University of Newcastle upon Tyne R.S.Johnson 006 CONTENTS
Zeros of Polynomial Functions
 Review: Synthetic Division Find (x 2-5x - 5x 3 + x 4 ) (5 + x). Factor Theorem Solve 2x 3-5x 2 + x + 2 =0 given that 2 is a zero of f(x) = 2x 3-5x 2 + x + 2. Zeros of Polynomial Functions Introduction
Review: Synthetic Division Find (x 2-5x - 5x 3 + x 4 ) (5 + x). Factor Theorem Solve 2x 3-5x 2 + x + 2 =0 given that 2 is a zero of f(x) = 2x 3-5x 2 + x + 2. Zeros of Polynomial Functions Introduction
Factoring Flow Chart
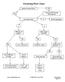 Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
19.6. Finding a Particular Integral. Introduction. Prerequisites. Learning Outcomes. Learning Style
 Finding a Particular Integral 19.6 Introduction We stated in Block 19.5 that the general solution of an inhomogeneous equation is the sum of the complementary function and a particular integral. We have
Finding a Particular Integral 19.6 Introduction We stated in Block 19.5 that the general solution of an inhomogeneous equation is the sum of the complementary function and a particular integral. We have
Unit 12: Introduction to Factoring. Learning Objectives 12.2
 Unit 1 Table of Contents Unit 1: Introduction to Factoring Learning Objectives 1. Instructor Notes The Mathematics of Factoring Teaching Tips: Challenges and Approaches Additional Resources Instructor
Unit 1 Table of Contents Unit 1: Introduction to Factoring Learning Objectives 1. Instructor Notes The Mathematics of Factoring Teaching Tips: Challenges and Approaches Additional Resources Instructor
Linear and quadratic Taylor polynomials for functions of several variables.
 ams/econ 11b supplementary notes ucsc Linear quadratic Taylor polynomials for functions of several variables. c 010, Yonatan Katznelson Finding the extreme (minimum or maximum) values of a function, is
ams/econ 11b supplementary notes ucsc Linear quadratic Taylor polynomials for functions of several variables. c 010, Yonatan Katznelson Finding the extreme (minimum or maximum) values of a function, is
MATH 108 REVIEW TOPIC 10 Quadratic Equations. B. Solving Quadratics by Completing the Square
 Math 108 T10-Review Topic 10 Page 1 MATH 108 REVIEW TOPIC 10 Quadratic Equations I. Finding Roots of a Quadratic Equation A. Factoring B. Quadratic Formula C. Taking Roots II. III. Guidelines for Finding
Math 108 T10-Review Topic 10 Page 1 MATH 108 REVIEW TOPIC 10 Quadratic Equations I. Finding Roots of a Quadratic Equation A. Factoring B. Quadratic Formula C. Taking Roots II. III. Guidelines for Finding
Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder).
 Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Numerical and Algebraic Fractions
 Numerical and Algebraic Fractions Aquinas Maths Department Preparation for AS Maths This unit covers numerical and algebraic fractions. In A level, solutions often involve fractions and one of the Core
Numerical and Algebraic Fractions Aquinas Maths Department Preparation for AS Maths This unit covers numerical and algebraic fractions. In A level, solutions often involve fractions and one of the Core
Biggar High School Mathematics Department. National 5 Learning Intentions & Success Criteria: Assessing My Progress
 Biggar High School Mathematics Department National 5 Learning Intentions & Success Criteria: Assessing My Progress Expressions & Formulae Topic Learning Intention Success Criteria I understand this Approximation
Biggar High School Mathematics Department National 5 Learning Intentions & Success Criteria: Assessing My Progress Expressions & Formulae Topic Learning Intention Success Criteria I understand this Approximation
Five 5. Rational Expressions and Equations C H A P T E R
 Five C H A P T E R Rational Epressions and Equations. Rational Epressions and Functions. Multiplication and Division of Rational Epressions. Addition and Subtraction of Rational Epressions.4 Comple Fractions.
Five C H A P T E R Rational Epressions and Equations. Rational Epressions and Functions. Multiplication and Division of Rational Epressions. Addition and Subtraction of Rational Epressions.4 Comple Fractions.
5. Factoring by the QF method
 5. Factoring by the QF method 5.0 Preliminaries 5.1 The QF view of factorability 5.2 Illustration of the QF view of factorability 5.3 The QF approach to factorization 5.4 Alternative factorization by the
5. Factoring by the QF method 5.0 Preliminaries 5.1 The QF view of factorability 5.2 Illustration of the QF view of factorability 5.3 The QF approach to factorization 5.4 Alternative factorization by the
FSMQ Additional Mathematics. OCR Report to Centres June 2015. Unit 6993: Paper 1. Free Standing Mathematics Qualification
 FSMQ Additional Mathematics Unit 6993: Paper 1 Free Standing Mathematics Qualification OCR Report to Centres June 2015 Oxford Cambridge and RSA Examinations OCR (Oxford Cambridge and RSA) is a leading
FSMQ Additional Mathematics Unit 6993: Paper 1 Free Standing Mathematics Qualification OCR Report to Centres June 2015 Oxford Cambridge and RSA Examinations OCR (Oxford Cambridge and RSA) is a leading
