Design of Zone Tariff Systems in Public Transportation
|
|
|
- Allyson Garrison
- 10 years ago
- Views:
Transcription
1 H. W. Hamacher, A. Schöbel Design of Zone Tariff Systems in Public Transportation Berichte des Fraunhofer ITWM, Nr. 21 (2001)
2 Fraunhofer-Institut für Techno- und Wirtschaftsmathematik ITWM 2001 ISSN Bericht 21 (2001) Alle Rechte vorbehalten. Ohne ausdrückliche, schriftliche Genehmigung des Herausgebers ist es nicht gestattet, das Buch oder Teile daraus in irgendeiner Form durch Fotokopie, Mikrofilm oder andere Verfahren zu reproduzieren oder in eine für Maschinen, insbesondere Datenverarbeitungsanlagen, verwendbare Sprache zu übertragen. Dasselbe gilt für das Recht der öffentlichen Wiedergabe. Warennamen werden ohne Gewährleistung der freien Verwendbarkeit benutzt. Die Veröffentlichungen in der Berichtsreihe des Fraunhofer ITWM können bezogen werden über: Fraunhofer-Institut für Techno- und Wirtschaftsmathematik ITWM Gottlieb-Daimler-Straße, Geb Kaiserslautern Telefon: +49 (0) 6 31/ Telefax: +49 (0) 6 31/ [email protected] Internet:
3 Vorwort Das Tätigkeitsfeld des Fraunhofer Instituts für Techno- und Wirtschaftsmathematik ITWM umfasst anwendungsnahe Grundlagenforschung, angewandte Forschung sowie Beratung und kundenspezifische Lösungen auf allen Gebieten, die für Techno- und Wirtschaftsmathematik bedeutsam sind. In der Reihe»Berichte des Fraunhofer ITWM«soll die Arbeit des Instituts kontinuierlich einer interessierten Öffentlichkeit in Industrie, Wirtschaft und Wissenschaft vorgestellt werden. Durch die enge Verzahnung mit dem Fachbereich Mathematik der Universität Kaiserslautern sowie durch zahlreiche Kooperationen mit internationalen Institutionen und Hochschulen in den Bereichen Ausbildung und Forschung ist ein großes Potenzial für Forschungsberichte vorhanden. In die Berichtreihe sollen sowohl hervorragende Diplom- und Projektarbeiten und Dissertationen als auch Forschungsberichte der Institutsmitarbeiter und Institutsgäste zu aktuellen Fragen der Techno- und Wirtschaftsmathematik aufgenommen werden. Darüberhinaus bietet die Reihe ein Forum für die Berichterstattung über die zahlreichen Kooperationsprojekte des Instituts mit Partnern aus Industrie und Wirtschaft. Berichterstattung heißt hier Dokumentation darüber, wie aktuelle Ergebnisse aus mathematischer Forschungs- und Entwicklungsarbeit in industrielle Anwendungen und Softwareprodukte transferiert werden, und wie umgekehrt Probleme der Praxis neue interessante mathematische Fragestellungen generieren. Prof. Dr. Dieter Prätzel-Wolters Institutsleiter Kaiserslautern, im Juni 2001
4 Ò Ó ÓÒ ÌÖ«ËÝ ØÑ Ò ÈÙÐ ÌÖÒ ÔÓÖØØÓÒ ÀÓÖ Ø Ïº ÀÑÖ Ò ÒØ ËĐÓÐ ÍÒÚÖ ØĐØ Ã Ö ÐÙØÖÒ Ò ÁÒ ØØÙØ ĐÙÖ ÌÒÓ¹ ÙÒ ÏÖØ Ø ÑØÑØ ÅÝ ¾¼¼ ØÖØ ÚÒ ÔÙÐ ØÖÒ ÔÓÖØØÓÒ Ý ØÑ ÖÔÖ ÒØ Ý Ø ØÓÔ Ò ¹ ÖØ ÓÒÒØÓÒ ØÛÒ ØÓÔ Û ÓÒ Ö ØÛÓ ÔÖÓÐÑ ÐÒ ÛØ Ø ÔÖ ÓÖ Ø Ù ØÓÑÖ Ì Ö ÔÖÓÐÑ Ò Û Ù Ø Ó ØÓÔ Ö ÐÖÝ ÖØ ØÓ ÞÓÒ Ò ÓÓ ØÖ«Ú ØÓ ÓÙÒ Ò Ø Ü ØÒ ÞÓÒ Ý ØѺ ÐÓ ÓÖÑ ÓÐÙØÓÒ ÓÖ Ø Ö ÔÖÓÐÑ Ö ÔÖ¹ ÒØ ÓÖ ØÖ ÓØÚ ÙÒØÓÒ º ÁÒ Ø ÞÓÒ ÔÖÓÐÑ Ø Ò Ó Ø ÞÓÒ ÔÖØ Ó Ø ÔÖÓÐѺ Ì ÔÖÓÐÑ ÆÈ Ö Ò Û ØÖÓÖ ÔÖÓÔÓ ØÖ ÙÖ Ø Û ÔÖÓÚ ØÓ ÚÖÝ Ù ÙÐ Ò Ø Ö Ò Ó ÓÒ Ó ÖÑÒݳ ØÖÒ ÔÓÖØØÓÒ Ý ØÑ º ÌÖ«Ý ØÑ Ò ÔÙÐ ØÖÒ ÔÓÖØØÓÒ ÁÒ Ø ÔÔÖ Û Ð ÛØ Ø Ò Ó ØÖ«Ý ØÑ Ò ÔÙÐ ØÖÒ ÔÓÖØØÓÒ ÓÑÔÐÜ ÖйÛÓÖÐ ÔÖÓÐÑ ØØ Û ÖÓÙØ ØÓ ÓÙÖ ØØÒØÓÒ Ý ÖÓÒÐ ÔÙÐ ØÖÒ ÔÓÖØØÓÒ ÓÑÔÒÝ ÚÖÐ ÝÖ Óº ÏÐ ÛÓÖÒ ÓÒ Ø Ò Ó Ö ØÖ«Ý ØÑ Û ÓØÚÐÓÔ ÑØÑØÐ ØÓÖÝ Ò Ú ÙÐÞØÓÒ ØÓÓÐ ØÓ ÚÐÙØ Ø «Ø Ó ØÖ«Ò º ÁÒ Ø ÔÔÖ Û ÔÖ ÒØ ÓÙÖ ØÙ Ò ÜÔÖÒ ÓÚÖ Ø Ð Ø ÝÖ Ò Ø Öº ÏÒ Ù Ò Ù ÓÖ ØÖÒ Ô ÒÖ Ù ÙÐÐÝ ØÓ ÔÝ ÓÖ ØÖÔº ÌÖ Ö ÚÖÐ ÔÓ ÐØ ÓÖ ÒÒ ØØ ÔÖ Ò ÔÙÐ ØÖÒ ÔÓÖØØÓÒº ÁÒ ØÒ ØÖ«Ý ØÑ Ø ÔÖ ÓÖ ØÖÔ ÔÒÒØ ÓÒ Ø ÐÒØ Ó Ø ØÖÔº Ì ÐÓÒÖ Ø ØÖÔ Ø Ö Ø Öº Ì Ý ØÑ ÑÓ ØÐÝ ÓÒ Ö Öº ÌÓ ØÖÑÒ Ø ØØ ÔÖ ÓÒ Ò Ø ØÒ ØÛÒ ÔÖ Ó ØØÓÒ º Ì Ñ ØÒ ØÖ«ÒÓÒÚÒÒØ ÓÖ Ø ÔÙÐ ØÖÒ ÔÓÖØØÓÒ ÓÑÔÒÝ Ò ÓÖ Ø Ù ØÓÑÖ º
5 ÙÖ ÓÒ ØÖ«Ý ØÑ ÛØ ÖØÖÖÝ ÔÖ Ì ÑÔÐ Ø ØÖ«Ý ØÑ Ø ÙÒØ ØÖ«º ÁÒ Ø ÐÐ ØÖÔ Ó Ø Ø Ñ ÒÔÒÒØ Ó ØÖ ÐÒغ ÙÒØ ØÖ«ÚÖÝ Ý ØÓ Òк ÙØ Ø ÓØÒ ÒÓØ ÔØ ØØ ÓÖØ ØÖÔ ØÛÒ ØÛÓ ÒÓÙÖÒ ØØÓÒ Ð ØÓ Ø Ñ ØØ ÔÖ ÐÓÒ ØÖÔ ØÖÓÙ Ø ÛÓÐ Ý ØѺ ÑÓÐ Ò ØÛÒ Ø ØÛÓ ØÖ«Ý ØÑ ÞÓÒ ØÖ«Ý ØѺ ÌÓ ØÐ ÞÓÒ ØÖ«Ø ÛÓÐ Ö ØÓ Ú ÒØÓ ÙÖÓÒ Ø ØÖ«ÞÓÒ µº Ì ÔÖ ÓÖ ØÖÔ Ò ÞÓÒ ØÖ«Ý ØÑ ÓÒÐÝ ÔÒÒØ ÓÒ Ø ØÖØÒ Ò Ø ÒÒ ÞÓÒ Ó Ø ØÖÔº Á Ø ÔÖ Ò Ó Ò ÖØÖÖÐÝ ÓÖ ÔÖ Ó ÞÓÒ Û ÐÐ Ø ØÖ«Ý ØÑ ÞÓÒ ØÖ«ÛØ ÖØÖÖÝ ÔÖ º Ò ÜÑÔÐ ÓÖ Ù ØÖ«Ý ØÑ Ò ÓÖ Ò ØÒ ÓÙÒ ÒÓÖØ Ó ËÒ ÖÒ Ó ÙÖ º Ì ÔÖ Ö ÚÒ Ò ÓÖÑ Ó ÑØÖÜ ÌÐ º Ì ÑÓ Ø ÔÓÔÙÐÖ ÚÖÒØ Ó ÞÓÒ ØÖ«Ý ØÑ Ø ÓÙÒØÒ ÞÓÒ ØÖ«Ý ØѺ ÌÓ ÒÓÛ Ö Ò Ø Ý ØÑ Ù ØÓÑÖ ØÓ ÓÙÒØ ÓÛ ¾
6 ÌÐ Ö Ò Í˹ÓÐÐÖµ ÓÖ ÓÒ¹ÛÝ ØÖÔ ÞÓÒ ¾ ¼ ¾º ¾ ¾º º¼ ¾º º¼ º¼ º º¼ º¼ º¼ º¼ º ¾º ¾º ¾º º¼ º¼ º ¾º ¾º ¾º º¼ º¼¼ º¼¼ º¼¼ º¼ º¼ º¼ º º¼¼ º¼¼ º¼¼ º º º¼¼ º¼ ¾º º¼ º¼ º¼ º º¼ º¼¼ º¼¼ º¼ ¼ º ¾º ¾º ¾º º º¼ º º¼ º º ÌÐ ¾ Ö Ý ÒÙÑÖ Ó ÞÓÒ Ò ÓÙÖÒÝ ÓÖ ÓÒ¹ÛÝ ØÖÔ ÒÙÑÖ Ó ÞÓÒ ¾ Ö Ò Í˹ÓÐÐÖ º¾ ¾º¼¼ ¾º º¾ º¼¼ º º¾ º¼¼ º ÑÒÝ ÞÓÒ ØÖÔ ÛÐÐ Ô Ò Ö Ó«Ø ÔÖ Ò ØÓ Ø ÒÙÑÖ Ó ÖÓ ÞÓÒ º Ì ÔÖ Ò Ø Ý ØÑ Ö ÔÒÒØ ÓÒ Ø ØÖØÒ Ò Ø ÒÒ ÞÓÒ Ó Ø ØÖÔ ÙØ ØÖÔ Ô Ò Ø Ñ ÒÙÑÖ Ó ÞÓÒ ÑÙ Ø Ú Ø Ñ ÔÖº ÙÖ ¾ ÓÛ ÓÙÒØÒ ÞÓÒ ØÖ«Ý ØÑ ÓÙØ Ó ËÒ ÖÒ Ó Ø ÓÖÖ ÔÓÒÒ ÔÖ ÓÖ ÒÐ ÓÒ¹ÛÝ ØÖÔ Ò Ö Ó«ÌÐ ¾º Ù Ó ØÖ ÑÔÐØÝ ÞÓÒ ØÖ«Ý ØÑ Ö ÚÖÝ ÔÓÔÙÐÖº ÁÒ ÖÑÒÝ ÒÖÐÝ ÐÐ ØÖ«ÓØÓÒ ÐÖÝ Ú ÞÓÒ ØÖ«Ý ØÑ ÓÖ Ö ÙÖÖÒØÐÝ ÒØÖÓÙÒ ØѺ ÏÒ ÔÙÐ ØÖÒ ÔÓÖØØÓÒ ÓÑÔÒÝ ÛÒØ ØÓ Ò Ø ØÖ«Ý ØÑ ØÓ ÞÓÒØÖ«Ø ØÓ Ò Ø ÞÓÒ Ò ØÓ Ü Ø ÒÛ Ö Ù ØØ Ø Ö ÙÐØÒ ØÖ«Ý ØÑ ÓØ ÔØ Ý Ø Ù ØÓÑÖ Ò Ó ÒÓØ Ö Ø ÒÓÑ Ó Ø ÓÑÔÒݺ Ì ÓÐ ÓØÒ ØÓ Ò Ø ÞÓÒ Ò Ù ÛÝ ØØ Ø ÒÛ Ò Ø ÓÐ ÔÖ ÓÖ ÑÓ Ø Ó Ø ØÖÔ Ö ÐÓ ÔÓ Ðº Ì ÑÒ ØØ ÒØÖ Ø ÔÙÐ ØÖÒ ÔÓÖØØÓÒ ÓÑÔÒÝ ÒÓÖ Ø Ù ØÓÑÖ ÛÐÐ Ú ÑÓÖ ÚÒØ ÛÒ ÒÒ Ø ÙÖÖÒØ ØÖ«Ý ØÑ ØÓ ÞÓÒ ØÖ«º ÒÓØÖ ÓÐ Ò ØÓ Ò Ö ÞÓÒ º ÁÒ Ø Û Ó ÒÓØ ÓÒ Ö Ø ÚØÓÒ ØÓ ÓÑ ÓÐ ÔÖ ÙØ Ø ÚØÓÒ ÖÓÑ ÖÖÒ ÔÖ ÓÖ Ò ØÒ ÓÒ Û ÓÒ Ö ØÓ Ö Ð Ø ØÒ ØÖ«º ÁÒ Ø ÔÔÖÓ Ø ÔÙÐ ØÖÒ ÔÓÖØØÓÒ ÓÑÔÒÝ Ò ØÓ ØÑØ Ø ÒÛ ÒÓѺ
7 ÙÖ ¾ ÓÙÒØÒ ÞÓÒ ØÖ«Ý ØÑ
8 ÁÒ Ø ÔÔÖ Û ÔÖ ÒØ ÒÛ ÓÔØÑÞØÓÒ ÑÓÐ ÓÖ Ø ÞÓÒ ØÖ«Ò ÔÖÓÐѺ Ï ÓÙ ÓÒ Ø Ó ÓÙÒØÒ ÞÓÒ º ÓÖ Ø ÞÓÒ Ò ÔÖÓÐÑ ÛØ ÖØÖÖÝ ÔÖ Û ÖÖ ØÓ ¾ º Ì ÖÑÒÖ Ó Ø ÔÔÖ ÓÖÒÞ ÓÐÐÓÛ º ÆÜØ Û ÔÖ ÒØ ÓÙÖ ÑÓÐ ÓÖ Ø ÞÓÒ Ò ÔÖÓÐÑ ÛØ ÓÙÒØÒ ÞÓÒ º ÌÒ Û ÓÛ ÓÛ Ø Ö ÓÖ ÒÙÑÖ Ó ÖÓ ÞÓÒ Ò ÐÙÐØ ÐÝ Ý ÐÓ ØÖÑ ÓÖÑÙÐ Ò ËØÓÒ º ÁÒ ËØÓÒ Û ÔÖ ÒØ ÓÑ ÑÔÓÖØÒØ ÔÖÓÔÖØ Ó Ø ÓÙÒØÒ ÞÓÒ Ò ÔÖÓÐÑ Ò ÚÐÓÔ ÐÓÖØÑ ÔÔÖÓ ÓÖ ÒÒ ÓÓ ÞÓÒ º Ï Ù ØÖ ÒÙÑÖÐ ÚÓÙÖ Ò ÖйÛÓÖÐ ÜÑÔÐ Ò ËØÓÒ º ÁÒ Ø Ò ÓÑ ÓÒÐÙ ÓÒ Ö ÚÒº ¾ ÑÓÐ ÓÖ Ø ÓÙÒØÒ ÞÓÒ ØÖ«ÄØ Ø ØØÓÒ ÖÔ Î µ Ó Ø ÔÙÐ ØÖÒ ÔÓÖØØÓÒ ÓÑÔÒÝ ÚÒ ÛÖ Î ÖÖ ØÓ Ø Ø Ó ØÓÔ Ò Î Î ÖÔÖ ÒØ Ø ÚÐÐ ÖØ ÓÒÒØÓÒ ØÛÒ ÔÖ Ó ØÓÔ º ÙÖØÖÑÓÖ ÐØ ÖÖÒ ÔÖ ÓÖ ØÖÚÐÒ ÖÓÑ ØØÓÒ ¾ Î ØÓ ØØÓÒ ¾ Î º ÑØ Ø ÙÖÖÒØ ØØ ÔÖ Ó Ø ÔÙÐ ØÖÒ ÔÓÖØØÓÒ ÓÑÔÒÝ ÓÖ Ø Ò Ö ÔÖ Ð ØÒ ØÖ«º Á Ä ÒÓØ Ø ÒÙÑÖ Ó ÔÐÒÒ ÞÓÒ Ø ÞÓÒ ÔÐÒÒÒµ ÔÖÓÐÑ ÒØ ÔÖØØÓÒ È Î Î Î Ä Ó Î ºº Î Î ¾ Ä ÔÖÛ ÓÒØ Ò Ä Î µº ÁÒ Ø Ö ÔÐÒÒÒµ ÔÖÓÐÑ ØØ ÔÖ ÔµÔ¼ ¾ Ö ØÖÑÒ Û Ö ÓÒÐÝ ÔÒÒØ ÓÒ Ø ÒÙÑÖ Ó ÞÓÒ Ô Ò ÓÙÖÒݺ ÀÖ Ôµ Ø ÔÖ ÓÖ ÖÓ Ò Ô ÞÓÒ ÓÖÖ º ÁÒ ÔÖØÙÐÖ ¼µ Ú Ø Ö ÓÖ ØÖÚÐÒ ÛØÒ ÒÝ ÞÓÒ µ Ø ÔÖ ÓÖ ÖÓ Ò ÓÒ ÞÓÒ ÓÖÖ ºº ÓÖ ÓÒ ÖÓÑ ÓÒ ÞÓÒ ØÓ Ò ÒØ ÓÒ Ò Ó ÓÒº ÌÓ ÚÐÙØ ÓÑ ÔÖØØÓÒ È ÛØ ÔÖ ÚØÓÖ Û Ò ÓÖ ÔÖ Ó ØØÓÒ ¾ Î Ò Ø ÒÙÑÖ Ó Ô ÞÓÒ ÓÖÖ ÛÒ ØÖÚÐÒ ÖÓÑ ØØÓÒ ØÓ ØØÓÒ º ÁÒ ÓÖÖ ØÓ ØÓ Ø ÓÒÙ ÓÒ ÑÓ Ø ÔÙÐ ØÖÒ ÔÓÖØØÓÒ ÓÑÔÒ ÓÙÒØ Ø ÒÙÑÖ Ò ¼ Ó Ô ÞÓÒ ÓÒ Ø ØÖÔ ÖÓÑ ØØÓÒ ØÓ ØØÓÒ ÒÐÙÒ ÓØ Ø ØÖØÒ Ò Ø ÒÒ ÞÓÒ ºº Ò ¼ Ò º Ï ÔÖÖ ÓÙÖ ÒÓØØÓÒ ÓÖ ÑÔÐØÝ ÓÓÙÖ ÑÓкµ Ì ÒÛ ØØ ÔÖ ÓÖ ØÖÚÐÒ ÖÓÑ ØÓ ØÒ ÚÒ Ý Ò µ Þ ¼
9 ÚÒ Ø ÖÖÒ ÔÖ ÓÖ ØÖÔ ØÛÒ ØØÓÒ Ò Ø ÓÐÙØ ÚØÓÒ Ò ØØ ÔÖ ÐÙÐØ Ý Þ Ò µ ÓÖ ÐÐ ¾ Î ÄØ Û Ø ÒÙÑÖ Ó Ù ØÓÑÖ ØÖÚÐÒ ÖÓÑ ØØÓÒ ØÓ ØØÓÒ Ò ÐØ Ï È ¾Î Û Ø ÙÑ Ó ÐÐ Ù ØÓÑÖ Ó Ø ÔÙÐ ØÖÒ ÔÓÖØØÓÒ ÓÑÔÒݺ Ì ÑÒÑÞØÓÒ Ó Ø ÓÐÐÓÛÒ ØÖ ÓØÚ ÙÒØÓÒ Ó ÒØÖ Øº ÑÜÑÙÑ ÓÐÙØ ÚØÓÒ ÑÜ ÑÜ ¾Î Û Þ È ÚÖ ÓÐÙØ ÚØÓÒ Ï ¾Î Û Þ ÚÖ ÕÙÖ ÚØÓÒ ¾ Ï È¾Î Û Þ µ ¾ ÐÐ ØÖ ÓØÚ Ð ØÓ ÓÓ Ö ÙÐØ Ò ÔÖغ Ì Ö Ø ÓØÚ ÙÒØÓÒ ÑÜ ÛØ ÒØÐ ÛØ ÑÓÐ Ø Ø ØØ Ø ÖØ Ø ÚØÓÒ Ó ØØ ÔÖ Ò Ø ØÛÓ «ÖÒØ ØÖ«ÓÙÐ ÑÐÐ ÔÓ Ðº ÁØ Ú ÓÙÒ ÓÖ Ø ÐÖ Ø Ò Ò Ø ØØ ÔÖ ÓÖ ÒÝ Ù ØÓÑÖº ÁÒ Ø ÛØ ÑÜ ÑÒÑÞ Ø ÑÜÑÙÑ ÚØÓÒ Ò ÒÓÑ ÓÚÖ ÐÐ ÔÓ Ð ØÖÔ º Ú Ø ÚÖ Ó ÐÐ ÓÐÙØ ÚØÓÒ Ò ¾ Ø ÚÖ Ó ÐÐ ÕÙÖ ÚØÓÒ Ò ØØ ÔÖ º Ì ÓØÚ ÙÒØÓÒ ¾ Ð ØÓ ÑÐÐÖ ÔÖÒØ Ó ØÖÓÒÐÝ «Ø Ù ØÓÑÖ ØÒ º ÆÚÖØÐ ÖÓÑ ÓÙÖ ÜÔÖÒ ÐØÐÝ ØØÖ ÔØ Ý Ø ÔÖØØÓÒÖ ØÒ ¾ º ÁØ Ð Ó ÓÙÐ ÑÒØÓÒ ØØ ÚØÓÒ Ò ÔÖ ÒÖ Ò Ö Ö ØÖØ ÕÙÐÐÝ ÙØØØ ÑÓÐ Ö Ø ÓØ Ø ÒØÖ Ø Ó Ù ØÓÑÖ Ò ØÖÒ ÔÓÖØØÓÒ ÓÑÔÒ º ÌÓ ÓØÒ Ø ÒÙÑÖ Ò ÓÖØ Ø ÔØ ÐÓÖØÑ ºº Ò Ù ÓÖÒ ØÓ ÓÒ Ó Ø ÓÐÐÓÛÒ ÑÓÐ º ËØØÓÒ ÖÔ ÅÓÐ Ï Ù Ø ØØÓÒ ÖÔ Î µ ÙØ ÒØÖÓÙ ÒÛ ÛØ Ù ÓÖ ÐÐ µ ¾ Ò Ý ¼ Ù Ò ÖÒØ Ñ ÞÓÒ Ò Ö Ò ÒØ ÞÓÒ º Ì ÐÒØ Ó ÓÖØ Ø ÔØ ØÛÒ ØÛÓ ØÓÔ ÕÙÐ Ø ÑÒÑÙÑ ÒÙѹ Ö Ó ÖÓ ÞÓÒ ÓÖÖ º Ì ÔÔÖÓ ÛÐÐ Ò ÐØÖ ØÓ ÙÔØ Ø ÞÓÒ ØÒ Ò Ø ÖÝ ÙÖ Ø Ò ËØÓÒ º ÓÒ ÖÔ ÅÓÐ ÌÓ ÖÙ Ø Þ Ó Ø ÒØÛÓÖ Û Ò Ø ÞÓÒ ÖÔ ¼ È ¼ µ ÛÓ ÒÓ Ø È ÚÒ Ý Ø ÞÓÒ Ò Î Î Ð µ ¾ ¼ «ØÖ Ü Ø ØÓÔ ¾ Î ¾ Î Ð Ù ØØ µ ¾ ºº ÛØ ÖØ ÓÒÒØÓÒ Ò Ø ØØÓÒ ÖÔ º ÐÐ Ú ÛØ ºÓÖ ¾ Î Ò ¾ Î Ð Û Ø Ø ÑÒÑÙÑ ÒÙÑÖ Ó ÖÓ ÞÓÒ ÓÖÖ Ò ÓÒ ØÖÔ ÖÓÑ ØÓ Ø ÐÒØ Ó ÓÖØ Ø ÔØ ÖÓÑ Î ØÓ Î Ð Ò ¼ º
10 º º º º ÙÖ ØØÓÒ ÒØÛÓÖ ÛØ ØØÓÒ Ò ÞÓÒ º Ì ÓÐÐÓÛÒ ÜÑÔÐ ÑÓÒ ØÖØ Ø ÐÙÐØÓÒ Ó ÑÜ Ò ¾ º ÄØ ØØÓÒ ÖÔ ÛØ ÔÖØØÓÒ ÒØÓ ØÖ ÞÓÒ Î ¾ Î ¾ Ò Î ÚÒ ÙÖ µº ËÙÔÔÓ ØØ Û ÓÖ ÐÐ ¾ Î ºº Ï ¾¼º Á Û ÙÑ ØØ Ø ØÒ ØÛÒ ÒÝ ÒØ ÔÖ Ó ÒÓ Ø ÑØÖÜ ÓÖÒ ØÓ Ø ØÒ ØÖ«Ý ØÑ ÑÝ ¼ ¼ ¾ ¼ ¾ ¾ ¼ ¾ ¾ ¼ ¾ ¼ Ì ÓÖÖ ÔÓÒÒ ÞÓÒ ÖÔ ¼ ÓÒ Ø Ó ØÖ ÒÓ ÙÖ µº º Î º Î ¾ º Î ÙÖ ÓÒ ÖÔ ÛØ ÞÓÒ º Ì ÒÙÑÖ Ó ÖÓ ÞÓÒ ÓÖÖ ØÛÒ ØØÓÒ Ò ØÒ ÚÒ Ý Æ ¼ ¼ ¼ ¾ ¼ ¼ ¾ ¼ ¼ ¼ ¼ ¾ ¾ ¼ ËÙÔÔÓ Ø ÒÛ Ö ÓÖ ÖÓ Ò Ô ¼ ÓÖ ¾ ÞÓÒ ÓÖÖ Ö ÚÒ Ý ¼µ ¼ µ ¾µ
11 ÌÒ ÒÛ ØØ ÔÖ Ò ÐÙÐØ ¼ ¼ ¼ ¼ ¼ ¼ ¼ ¼ ¼ ¼ Ì ÚØÓÒ ØÛÒ Ø ÖÖÒ ÔÖ Ò Ø ÒÛ ØØ ÔÖ Þ Ö ¼ ¼ ¼ ¾ ¾ ¼ ¼ ¼ ¼ ¼ ¼ ¾ ¼ ¼ ¼ ¾ ¼ ¼ Ò Ø ÓØÚ ÚÐÙ Ò ÐÙÐØ ÑÜ ¾ ¾¼ ¾¼ ¾ ¾ ¾¼ ËÓÐÙØÓÒ ÓÖ Ø Ö ÈÖÓÐÑ ÛØ Ü ÓÒ ÁÒ Ø ØÓÒ Û ÓÐÚ Ø Ö ÔÖÓÐÑ ÛØ Ö ÔØ ØÓ ÚÒ ÞÓÒ ÔÖØØÓÒº ÇÙÖ Ö Ø Ö ÙÐØ ÓÛ ØØ ÐÓ ÓÖÑ ÓÐÙØÓÒ ÔÓ Ð ÓÖ Ó Ø ØÖ ÓØÚ ÑÜ Ò ¾ ÒØÖÓÙ Ò ËØÓÒ ¾º ÌÓÖÑ ÄØ È Î Î ¾ Î Ä ÚÒ ÞÓÒ ÔÖØØÓÒ Ò ÐØ ÚÒ ÖÖÒ ÔÖ º ÁÒ ÓÖÖ ØÓ ÑÒÑÞ ÑÜ Ò ¾ Û ÓÓ ÓÖ ÐÐ Ô ¼ Ä µ ÑÜ Ôµ ÑÜ ¾Î Ò Ô Þ Ô Û ÛÖ Þ Ô Ò Þ Ô Û ÑÜ Û ¾ ¾ ¾ ¾ ¾Î Û Ò Ò ¾ ¾ Ô Û ¾ ¾ µ ¾ ¾
12 µ Ôµ ÑÒ ßÞ ¾ Î Ò Ð Ô Û ØÑ µ ¾ Ôµ Ï ¾Î Ò Ô Û ÈÖÓÓ ÚÒ Ø ÞÓÒ ÔÖØØÓÒ È Û Ú ØÓ Ò Ö Ôµ ¾ ÁÊ ÓÖ ÐÐ Ô ¼ ÑÒÑÞÒ ÑÜ Ò ¾ Ö ÔØÚÐݺ Ò Å Ô µ ¾ Î Ò Ò Ô Ò Ï Ô È Ñ¾Å Ô Û Ñ Ø ÙÑ Ó ÐÐ ÛØ ÐÓÒÒ ØÓ ÔÖ Ó ØØÓÒ Ò Ø Ø Å Ô º Ö Ø Û ÒÓØ ØØ Ó Ø ØÖ ÓØÚ ÙÒØÓÒ Ò ÔÖØ ÒØÓ Ø ÑÓ Ø Ä ÒÔÒÒØ ÙÔÖÓÐÑ Ã ÑÜ Ôµ à Ե Ò Ã ¾ Ôµ Ö ÔØÚÐÝ ÓÖ Ô ¼ ĵº ÑÜ ÑÜ Û Þ ¾Î ÑÜ Ô¼ ÑÜ Û Ñ Ñ Ôµ ÑÜ Ã ÑÜ Ôµ Ä Ñ¾Å Ô Ô¼ Ä Û Þ ¾Î Ä Ô¼ ¾ ¾Î Ä Ô¼ Ñ¾Å Ô Û Ñ Ñ Ôµ Û Þ µ ¾ Ñ¾Å Ô Û Ñ Ñ Ôµµ ¾ Ä Ô¼ Ä Ô¼ à Ե à ¾ Ôµ ÓÒ ÕÙÒØÐÝ ØÓ ÑÒÑÞ ÑÜ Ò ¾ Û ØÖÑÒ Ø ÓÔØÑÐ Ö Ôµ ÓÖ Ô ¼ Ä ÔÖØÐÝ Ò Ó Ø ØÖ ÓØÚ ÙÒØÓÒ º ÓÖ ÑÜ ÓÖ ÐÐ Ô ¼ Ä Ø ÔÖÓÐÑ Ó ÑÒÑÞÒ Ã ÑÜ Ôµ ÑÜ Ñ¾Å Ô Û Ñ Ñ Ôµ ÛÐйÒÓÛÒ ÖÓÑ ÐÓØÓÒ ØÓÖÝ ÛÒ ÐÓØÒ ÔÓÒØ ÓÒ ÐÒ Ù ØØ Ø ÑÜÑÙÑ ØÒ ØÓ ÚÒ Ø Ó Ü ØÒ ÐØ ÓÒ Ø Ñ ÐÒ ÑÒÑÞº Ì ÔÖÓÓ ÓÖ Ø ÓÖÑÙÐ ÚÒ Ò ÔÖØ Ó Ø ØÓÖÑ Ò ØÖÓÖ ÓÙÒ Ò Ø ÐÓØÓÒ ÐØÖØÙÖ ºº º ÆÓØ ØØ Ã ÑÜ Ôµ Þ Ôº
13 ÓÖ ËÒ Ã Ôµ ÑÒ Ñ¾Å Û Ñ Ñ Ôµ ÓÒ¹ÑÒ ÓÒÐ ÔÛ ÐÒÖ Ò ÓÒÚÜ ÙØÓÒ Ø ÑÒÑÞ¹ ØÓÒ ÒÓÛÒ Ò ØØ Ø ºº µ Ò Ò ÐÓØÓÒ ØÓÖÝ Ø ÓÒ¹ÑÒ ÓÒÐ ÑÒ ÔÖÓÐÑ ºº ¼ µº ÁØ ÓÛÒ ØØ Ø ÓÚ ÔÖÓÐÑ ÓÐÚ Ý Ø Ó¹ÐÐ ÛØ ÑÒ Ó Ø Ø Ñ Ñ ¾ Å Ô ºº Ý ÒÝ ÖÐ ÒÙÑÖ Ôµ Û Ø Ñ Ñ Ñ Ñ Û Ñ Ï Ô ¾ Û Ñ Ï Ô ¾ ÓÖ ¾ ÀÖ Û Ú ØÓ ÑÒÑÞ Ã ¾ Ôµ ºº Ò ÑÒ ¾Å Û Ôµµ ¾ Í Ò Ø ØÓÖÑ Ó ËØÒÖ ºº µ Ó ØØ Ø Û ÒÓØ ØØ Ø ÛØ ÑÒ Ó Ø ÚÐÙ Ò Ñ Ñ ¾ Å Ô Ø ÙÒÕÙ ÓÔØÑÐ ÓÐÙØÓÒ ÓÖ Ôµº ÌÓ ÑÓÒ ØÖØ Ø Ö ÙÐØ Ó ÌÓÖÑ Û ÓÒØÒÙ Ø ÜÑÔÐ Ó ËØÓÒ ¾ Ì ÓÔØÑÐ ÚÐÙ ÓÖ Ø ÞÓÒ ÔÖ Ò Ø Ö ÙÐØÒ ÚÐÙ ÓÖ Ø ÓØÚ ÙÒØÓÒ ÑÜ Ò ¾ Ö Ð Ø Ò Ø ÓÐÐÓÛÒ Øк ÞÓÒ ÑÜ ¾ ÜÑÔÐ ¼ ¼ ¾ ¾ ¾ ÑÜ ¾ ¾¼ ¾ ¾¾ ¾ ÐÙÐØÒ Ø ÓØÚ ÙÒØÓÒ Ý Ù Ò Ø ÓÔØÑÐ Ö ÓÖÒ ØÓ ÌÓ¹ ÖÑ ÝÐ Ø ÓÐÐÓÛÒ ÓÖÓÐÐÖݺ ÓÖÓÐÐÖÝ ÚÒ ÞÓÒ ÔÖØØÓÒ È Î Î ¾ Î Ä Ò ÖÖÒ ÔÖ Ø ÓÔØÑÐ ÚÐÙ Ó Ø ÓØÚ ÙÒØÓÒ Ö ÚÒ ÓÐÐÓÛ º ¼
14 µ ÑÜ ÑÜ Þ Ô Ô µ Ô ¼ µ¾î Ô Ò Ô µ¾î Ô Ò Ô ÛÖ Î Ô Î Ô µ Ò Ô Ôµ µ Ò Ô Ôµ µ ¾ ÎÖ ¾ Î Ò Ô ÛÖ ÎÖ ÒÓØ Ø ÚÖÒ Ó Ø Øº ÁÒ ÔÖØ ÓØÒ Ö ØÖØÓÒ ÓÒ Ø ÒÛ Ö Ö ÚÒ ÓÑØÑ ØÖ ÚÒ Ü Ø ÔÓÐØÐÐÝ Ö Ö ÓÖ Ø ÒÙÑÖ Ó ÞÓÒ Ò ÓÙÖÒÝ ØØ Ú ØÓ ÖÐÞº ÏØ Ø ÐÔ Ó ÓÖÓÐÐÖÝ ÓÒ Ò ÐÝ ÐÙÐØ Ø ÒÖ Ó Ø ÓØÚ ÙÒØÓÒ ÛÒ Ù Ò Ù ÚÒ Ö Ò Ø Ó Ø ÓÔØÑÐ ÓÒ º ÁÒ ÔÖØÙÐÖ ÓÖÓÐÐÖÝ ÓÛ ØØ ÓÖ Ø ÓØÚ ÙÒØÓÒ ÑÜ Ø ÓÔØÑÐ Ö ÑÜ Ôµ Ö ÒÓØ Ò ØÓ ÐÙÐØ Ø ÓÔØÑÐ ÓØÚ ÚÐÙ ÓÖ ÚÒ ÞÓÒ ÔÖØØÓÒº Ì ÛÐÐ Ò Ò Ø ÒÜØ ØÓÒ ÛÒ Û Ö ÓÒ ØÓ ÓÔØÑÞ Ø ÞÓÒ ÔÖØØÓÒ ÛØ Ö ÔØ ØÓ ÑÜ º Á ØÓÒÐÐÝ ÑÜ Ù Ò Ø ÙÒÛØ ºº ÛØ Û ÓÖ ÐÐ ¾ Î Û Ò ÙÖØÖ ÑÔÐÝ ÌÓÖÑ ÒÓÖÓÐÐÖÝ º ÓÖÓÐÐÖÝ ¾ ÁÒ Ø Ó ÕÙÐ ÛØ Ø ÓÔØÑÐ Ö ÑÜ Ôµ Ò Ø ÓÖ¹ Ö ÔÓÒÒ ÓØÚ ÚÐÙ ÑÜ Ö ÚÒ Ý ÑÜ Ôµ ÑÜ ¾ ÑÒ ¾Î Ò Ô ¾Î Ò Ô Ã ÑÜ Ôµ ¾ ÑÜ ¾ ÑÜ Ô Ä ÑÜ ¾Î Ò Ô ÑÜ ¾Î Ò Ô ÑÒ ¾Î Ò Ô ÑÒ ¾Î Ò Ô
15 ÈÖÓÓ Ï ÐÙÐØ Þ Ô Ò ÓÒ ÕÙÒØÐÝ Û Þ Ô Ñ Û Ñ¾ ÑÜ Ñ Ñ¾ µ Ñ Ñ ¾ ¾Å Ô Û Ñ Û Ñ¾ ÑÜ Ñ ÑÒ Ñ ¾ Ñ¾Å Ô Ñ¾Å Ô Ô ÑÜ Ñ¾Å Ô Ñ ÑÜ Ñ Ñ¾Å Ô ¾ Þ Ô Û Ñ ¾ ÑÜ Ñ Ñ¾Å Ô ¾ ÑÒ Ñ Ñ¾Å Ô ÑÜ Ñ ÑÒ Ñ Ñ¾Å Ô Ñ¾Å Ô Í Ò ÓÖÓÐÐÖÝ Ò Þ Ô Ã ÑÜ Ôµ Ø ÖÑÒÒ ÔÖØ ÓÐÐÓÛ ÑÑØÐݺ É Ï ÖÑÖ ØØ ÓÖ Ø ÞÓÒ Ò ÔÖÓÐÑ ÛØ ÖØÖÖÝ ÔÖ ÑÐÖ Ö ÙÐØ Ò ÖÚ µº ÒÒ ÞÓÒ ÔÖØØÓÒ ÓÖ ÑÜÑÙÑ Ú¹ ØÓÒ ÔÖÓÐÑ Ì ÓÒ ÕÙÒ Ó Ø Ö ÙÐØ Ó ËØÓÒ ØØ Û Ò ÓÒÒØÖØ ÓÒ ÒÒ Ø ÞÓÒ Ò Ø ÞÓÒ ÔÖÒ ÓÐÐÓÛ ÐÝ ÖÓÑ Ø Ó Ó Ø ÓØÚ ÙÒØÓÒº Ï ÒÓÛ ÓÙ ÓÙÖ ØØÒØÓÒ ØÓ Ø ÑÜÑÙÑ ÚØÓÒ ÔÖÓÐѺ ÍÒ¹ ÓÖØÙÒØÐÝ Ø ÔÖÓÐÑ ÆÈ¹Ö Ò ØÖÓÖ ÆÙÐØ ØÓ ÓÐÚº Ö Ø Ó ÖÚØÓÒ Ð ÛØ Ø ÑÓÒÓØÓÒØÝ ÓØ ÓØÚ ÙÒØÓÒ ÔÒ¹ ÒØ ÓÒØÒÙÑÖ Ó ÔÐÒÒ ÞÓÒ Äº ÏÐØ ÝØÓ ØØ ÓÖ Ø ÞÓÒ Ò ÔÖÓÐÑ ÛØ ÖØÖÖÝ ÔÖ ÐÐ ØÖ ÓØÚ Ö ÑÓÒÓØÓÒ Ò Ä Ø ÒÓØ ØÖÙ ÓÖ Ø ÞÓÒ Ò ÔÖÓÐÑ ÛØ ÓÙÒØÒ ÞÓÒ ÙÖ ÓÛ º Ì ØØÓÒ ÒØÛÓÖ ÓÒ Ø Ó ÒÓ Ò Û ÙÑ ØØ Û ÓÖ ÐÐ ÔÖ Ó ÒÓ º Ì ÖÖÒ ÔÖ Ö ÚÒ ÛØ ØÛÒ ÒÝ ØÛÓ ÒØ ÒÓ ÓÛÒ Ò Ø ÙÖº ØÛÒ ÒÝ ÓØÖ ÔÖ Ó ÒÓ Ø ÖÖÒ ÔÖ Ö ÚÒ Ø ÙÑ Ó Ø ÛØ ÐÓÒ ÓÖØ Ø ÔØ ÓÒÒØÒ Ø ÒÓ º ÓÖ Ø ÙÒÛص ÑÜ ÓÐÙØ ÚØÓÒ ÔÖÓÐÑ ÓÖÓÐÐÖÝ ¾ ÓÛ ØØ ÒÝ ÓÐÙØÓÒ ÛØ Ä ÞÓÒ Ð ØÓ ØÖØÐÝ Ö ÓØÚ ÚÐÙ ØÒ Ø ÖÔ ÓÐÙØÓÒ ÛØ Ä Ò ÑÜ º Ï ÛÐÐ ØÖÓÖ Ü Ä Ò Ø ÓÐÐÓÛÒº ÌÓÖÑ ¾ Ì ÞÓÒ Ò ÔÖÓÐÑ ÛØ ÓÙÒØÒ ÞÓÒ Ò ÓØÚ ÙÒØÓÒ ÑÜ ÆÈ¹Ö ÓÖ ÐÐ Ü Ä º ¾
16 ¼¼ º ¼¼ º º º ¼¼ º ¼¼ ÙÖ ØØÓÒ ÒØÛÓÖ ÛÖ Ø ÓØÚ ÚÐÙ ÓÖ Ä ØØÖ ØÒ Ø ÓØÚ ÚÐÙ ÓÖ Ä º Ì ÔÖÓÓ Ó ÌÓÖÑ ¾ ÚÒ Ò Ø ÔÔÒܺ ÆÓØ ØØ Ð Ó Ø ÞÓÒ Ò ÔÖÓÐÑ ÛØ ÖØÖÖÝ ÔÖ ÆÈ¹Ö º ÌÓ ÑÓØÚØ Ø ÙÖ Ø Ó Ø ØÓÒ Û Ö Ø ÔÖ ÒØ Ø ÓÐÐÓÛÒ ØÛÓ Ó¹ ÖÚØÓÒ ÓÖ ØØÒ ÙÔÔÖ Ò ÐÓÛÖ ÓÙÒ ÓÒ Ø ÓØÚ ÚÐÙ ÑÜ º ÄÑÑ ÑÜ ¾ ÑÜ ¾Î ÑÒ ¾Î ÈÖÓÓ ÓÖ ÒÝ ÞÓÒ ÔÖØØÓÒ È Ò ÒÝ ÒØÖ Ô Û Ú ØØ Ã ÑÜ Ôµ ÑÜ ¾ ÑÜ ¾ ¾Î ¾ÎÒ Ô ÑÒ ÑÒ ¾Î ¾ÎÒ Ô ÝÐÒ Ø Ö ÙÐغ É ÄÑÑ ¾ ÚÒ ÞÓÒ ÔÖØØÓÒ È ÐØ ÁÆÌ Ø Ø Ó ÛØ ÓØ Ò ÒÓ ÛØÒ Ø Ñ ÞÓÒ Ò Ì Ò ÁÆ̺ ÌÒ Û Ú ÑÜ ¾ ¾ ÑÜ ¾ ÑÜ µ¾áæì ÑÜ µ¾ì ÑÒ µ¾áæì ÑÒ µ¾ì ÈÖÓÓ
17 º ËÒ ÑÒ ¾ÎÒ ¼ ÑÒ µ¾áæì Û Ø ÑÜ Ã ÑÜ ¼µ ÑÜ ¾ ¾ ¾ÎÒ ¼ ÑÜ µ¾áæì ÑÒ ¾ÎÒ ¼ ÑÒ µ¾áæì ¾º ÒÐÓÓÙ ÐÝ ÑÒ ¾ÎÒ ÑÒ µ¾ì Ò Û Ø Ø Ö ÙÐØ Ý Ù Ò ÑÜ Ã ÑÜ µº É ÄÑÑ ¾ Ù Ø ÞÓÒ Ò Ò Û ÛØ ÛØ Ö ÓÐÐØ Ò Ì Ò ÛØ ÑÐÐ ÛØ Ò ÁÆÌ ÓÖ Ú ÚÖ º ÌÓ ÑÓÖ Ô ÐØ Ø ÑÜÑÐ ÑØÖ ÓÚÖ ÐÐ ÞÓÒ º ÙÑÒ ØØ ÛØ ÐÓÒ ÔØÖ ØÚ Û Ø Ã ÑÜ Ôµ ÑÜ ¾ ¾ÎÒ Ô Ô µ Ô ¾ ÑÒ ¾ÎÒ Ô ÑÜ µ¾ì ÑÒ µ¾ì ÝÐÒ ØØ Ø ÑÜÑÐ ÑØÖ ÓÙÐ ÑÐÐ Ò ÓÒ ÕÙÒØÐÝ ÛØ ÐÖ ÛØ ÓÙÐ Ò Ì ÛÐ ÛØ ÑÐÐ ÛØ ÓÙÐ Ò ÁÆ̺ ÓÐÐÓÛÒ Ø ÓÒ ÖØÓÒ Û ÔÖ ÒØ ØÖ ÙÖ Ø ÓÖ ÓÐÚÒ Ø ÞÓÒ Ò ÔÖÓÐÑ ÛØ ÓÙÒØÒ ÞÓÒ º ÁÒÔÙØ Ø Û Ò ÓÖ ÒÝ Ó Ø ÓÐÐÓÛÒ ÐÓÖØÑ Ø Ó Ò ØØÓÒ ÛØ ÖÖÒ ÔÖ Ò ÒÙÑÖ Ä Ó ÔÐÒÒ ÞÓÒ º Ì ÇÙØÔÙØ ØÒ ÚÒ Ý ÞÓÒ ÔÖØØÓÒ ÛØ Ä ÞÓÒ º ÐÓÖØÑ ÓÒ ÐÙ ØÖÒ ÌÓÖÝ Ì Ö Ø ÐÓÖØÑ ÓÒ ÖÓÑ ÐÙ ØÖÒ ØÓÖÝ Ò Ö Ò ÔÖØÙÐÖ ÓÒ Ø ËÀÆ ÕÙÒØÐ ÐÓÑÖØÚ ÖÖÐ ÒÓÒ¹ÓÚÖÐÔÔÒµ ÐÓÖØÑ ºº ¾ µº Ì ØÓ ØÖØ ÛØ Ò ÞÓÒ ÓØÑÓÒØÒÒ ÓÒ ÒÐ ØØÓÒ Ò ØÓ ÓÑÒ Ò ØÔ Ø ØÛÓ ÐÓ Ø ÞÓÒ ØÓ ÒÛ ÓÒº ÔÒÒ ÓÒ Ø ÔÖØÙÐÖ ÒØÓÒ Ó Ø ØÒ ØÛÒ ØÛÓ ÞÓÒ «ÖÒØ ÐÓÖØÑ Ò ÓØÒº ÌÛÓ Ó ØÑ Ú Ò ÔÔÐ ØÓ Ø ÞÓÒ Ò ÔÖÓÐÑ ËÒÐ ÄÒ Ò ÓÑÔÐØ ÄÒº
18 ÄÇÊÁÌÀÅ ÓÒ Ò Ù Ò ËÀƹÐÓÖØÑ µ º ËØÖØ ÛØ ÔÖØØÓÒ È ÓÒ ØÒ Ó Ò ÞÓÒ Ó Û ÓÒØÒÒ ÒÐ ØØÓÒº ÄØ µ ÓÖ ÐÐ ÞÓÒ ¾ È º ¾º ØÖÑÒ ØÛÓ ÞÓÒ ¾ È ÛØ ÑÒÑÙÑ ØÒ µº º ÂÓÒ Ò ØÓÒÛÞÓÒ Ò Ø ÒÛÔÖØØÓÒ È º º ÐÙÐØ Ø ÒÛ ØÒ ÓÖ ÐÐ ¾ È µ ¾ µ µ µ µµ º Á Ø ÒÙÑÖ Ó ÔÐÒÒ ÞÓÒ ØØÒ ØÒ ËØÓÔ ÇÙØÔÙØ È Ð ÓØÓ ËØÔ ¾º Ì ÔÖÑØÖ Ò ËØÔ ØÖÑÒ Ø ÓÖÑÙÐ ÓÖ ÐÙÐØÒ Ø ØÒ ØÛÒ ØÛÓ ÞÓÒ º ÁÒ Ø ÓÒØÜØ Ó Ø ÞÓÒ Ò ÔÖÓÐÑ Û Ú Ù ÓÖ Ø ËÒÐ ÄÒ ÐÓÖØÑ Ò ÓÖ Ø ÓÑÔÐØ ÄÒ ÐÓÖØѺ Ì ÒØÖÔÖØØÓÒ ÓÖ ËÒÐ ÄÒ Ø ÓÐÐÓÛÒ Ì ØÒ ØÛÒ ØÛÓ ÞÓÒ Ò Ø ÑÐÐ Ø ØÒ ØÛÒ ÐÑÒØ Ó ØÑ Ò ÓÒ ¹ ÕÙÒØÐÝ Ò ØÔ Û ÓÒ ÐÓÒ ÓÖØ Ø º ÆÓØ ØØ Ò Ø ÓÑÔÐØ ÄÒ Ø ØÒ ØÛÒ ØÛÓ ÞÓÒ Ò Ø ÑÜÑÙÑ ØÒ ¹ ØÛÒ ØÖ ÐÑÒØ Ò Ò ØÔ ÓÑÔÐØ ÐÒ ØÖ ØÓ ÑÒÑÞ Ø ÑÜÑÙÑ ÑØÖ Ó Ø ÞÓÒ º ÖÝ ÔÔÖÓ Ì ÔÔÖÓ ÚÖÒØ Ó Ø ËÀÆ ÐÓÖØÑ Ù ÓÚ ÙØ ÛØ ÑÓÖ ÑÔ ÓÒ Ø Ô ØÖÙØÙÖ Ó Ø ÞÓÒ Ò ÔÖÓÐѺ Í Ò Ø Ó ÐÓÖØÑ Û ÐÙÐØ ÓÖ ÐÐ µ Ø ÓØÚ ÚÐÙ ÑÜ ÛÒ ÓÒØÖØÒ µ Ó Ø ÙÖÖÒØ ÞÓÒ ÖÔº ÒÐÐÝ Û ÓÒØÖØ Ø ÛØ ÑÐÐ Ø ÒÖ Ò Ø ÓØÚ ÙÒØÓÒº Ì ÖØÖ ØÑ ÓÒ ÙÑÒ ÙØ Û ÛÐÐ ÓÛ Ò Ø ÒÜØ ØÓÒ Ð ØÓ ÚÖÝ ÓÓ Ö ÙÐØ Ò ÔÖغ Ì ÓÖÑÙÐØÓÒ Ó Ø ÖÝ ÔÔÖÓ Ø ÓÐÐÓÛÒ ÄÇÊÁÌÀÅ ¾ ÓÒ Ò Ý ÖÝ ÔÔÖÓµ º ÓÖ ÐÐ µ ¾ ÛØ Ò ÓÒØÖØ Ò ØÑÔÓÖÐÐÝ Ò ÐÙÐØ Ñܺ
19 ¾º ÓÒØÖØ Ø ¼ ¼ µ ÔÖÑÒÒØÐÝ ÛÖ Ò ÐØ Ò ¼ ¼ ¼ ¼ ÑÜ ÑÒ µ ÑÜ ¼º Á Ø ÖÔ Ä ÒÓ ËØÓÔº º ÓÖ ÐÐ ¾ Î ÖÐÙÐØ Ò ÓÖØ Ø ØÒ Ò ÓØÓ ËØÔ º ËÔÒÒÒ ÌÖ ÔÔÖÓ Ì Ó Ø ÓÐÐÓÛÒ ÙÖ Ø ØÓ ØÖÑÒ Ø Ó Ì Û ÓÒØÒ ÑÓ ØÐÝ ÛØ ÛØ º ÄÇÊÁÌÀÅ ÓÒ Ò Ý ÔÒÒÒ ØÖ ÔÔÖÓµ º Ò ÑÜÑÙÑ ÔÒÒÒ ØÖ Ì Ò Ø ÓÑÔÐØ ÖÔ ÛØ ÛØ º ¾º ÇÑØ Ø Ä ÐÖ Ø Ó Ì Ò Ø ÓÖ Ø ÛØ Ä ÓÑÔÓÒÒØ º º ÇÙØÔÙØ ÓÒ Ö Ø ÓÒÒØ ÓÑÔÓÒÒØ º ÆÓØ ØØ Ò ØÖ Ø ÔÒÒÒ ØÖ ÔÔÖÓ ÕÙÚÐÒØ ØÓ Ø ÒÐ ÐÒ ÐÓÖØÑ Ó ÐÙ ØÖÒ ØÓÖݺ ÁÒ ÒÖÐ ÖÔ Ø ÐÛÝ ÔÓ Ð ØÓ Ò ÔÒÒÒ ØÖ Ù ØØ ÓÑØØÒ Ø Ä ÐÖ Ø Ð ØÓ Ø Ñ Ö ÙÐØ ËÒÐ ÄÒº ÀÓÛÚÖ Û ØÖØ ÛØ ÔÒÒÒ ØÖ ÛØ ÑÜÑÐ ÛØ Û ÔÖÓÖÑ Ø Ò ÔÖص Ø ÔÒÒÒ ØÖ ÔÔÖÓ «Ö Ò ÒØÐÝ ÖÓÑ ËÒÐ ÄÒº ÌÓÖÝ ÈÙØ ØÓ ÏÓÖ Ò ËÖÐÒ ÖÑÒÝ Ò ÜÑÔÐ ÓÖ Ø ÔÖØÐ ÚÐÙ Ó ÓÙÖ ÔÔÖÓ Û ÓÒ Ö Ø ØÙØÓÒ Ò Ø ËØØ Ó ËÖÐÒ ÖÑÒݺ ÙÖÖÒØÐÝ ØÖ Ö Ü ÔÙÐ ØÖÒ ÔÓÖØØÓÒ ÓÑÔÒ ÓÔÖØÒ Ò Ø ËÖÐÒ Ó ØÑ ÛØ Ø ÓÛÒ ØÖ«Ý ØѺ ÓÙÖ ÔÙÐ ØÖÒ ÔÓÖØØÓÒ ÓÑÔÒ ÐÖÝ Ù ÓÙÒØÒ ÞÓÒ ØÖ«Ý ØÑ ÙØ ØÖ Ö ÓÖ ÖÓ Ò Ô ÞÓÒ Ò Ø ØÖÙØÙÖ Ó ØÖ ÞÓÒ Ö ÓÑÔÐØÐÝ «ÖÒØ ÐØÓÙ ØÝ Ö ÔÖØÐÝ ÓÔÖØÒ Ò Ø Ñ ÓÖÔÐ ÖÓÒº Ì ÙØ Ò ÖÑÒ Êе ØÐÐ ÔÔÐ Ø ØÒ ØÖ«º
20 65 "Greedy "Single Linkage" "Spanning Tree" ÙÖ ÓÑÔÖ ÓÒ Ó Ø ÙÖ Ø ÑÜ ÖÔ ÓÖ ÒÝÒÙÑÖ Ä Ó ÔÐÒÒ ÞÓÒ º ÌÖ Ð Ó ÔÙÐ ØÖÒ ÔÓÖØØÓÒ ÓÑÔÒÝ ÖÚÒ Ø ØÝ Ó ËÖÐÒ³ ÔØÓÐ ËÖÖĐÙÒµ Û Ù ÞÓÒ ØÖ«ÛØ ÚÖÐ ÔÖ º Ì ØÖÆ ÓØÓÒ Ó Ø ËÖÐÒ ÓÒ Ö ØÓ ÒØÖÓÙ ÓÒ ÓÑÑÓÒ ÓÙÒع Ò ÞÓÒ ØÖ«Ý ØÑ Û ÓÙÐ ÔÔÐ Ý ÐÐ Ø ÔÙÐ ØÖÒ ÔÓÖØØÓÒ ÓÑÔÒ º Ì ÔÙÐ ØÖÒ ÔÓÖØØÓÒ ÒØÛÓÖ Ò Ø ËÖÐÒ ÓÒ Ø Ó ÖÓÙÐÝ ¼¼¼ ØØÓÒ ÛÖ ÔÖ¹ÐÙ ØÖÒ ÒØÓ ¼¼ ÑÒ¹ÞÓÒ ÚÒº Ì ÓÐ ØÓ Ò ÓÙØ ¼¼ ÞÓÒ Ò Ò ØÐÐ ÓÙÒØÒ ÞÓÒ ØÖ«Ý ØÑ Ò Ù ÛÝ ØØ Ø «ÖÒ ØÛÒ Ø ÙÖÖÒØ Ö Ò Ø ÒÛ ÓÒ ÑÐÐ ÔÓ Ðº ÁØ Ð Ó ÑÔÓÖØÒØ ØØ Ø ÒÛ ÒÓÑ Ó Ó Ø ÔÙÐ ØÖÒ ÔÓÖØØÓÒ ÓÑÔÒ ÓÙÐ ÒÓØ «Ö ØÓÓ ÑÙ ÖÓÑ Ø ÙÖÖÒØ ÒÓѺ ÓÒ ÕÙÒØÐÝ Ø ÖÖÒ ÔÖ Ò Ø ÔÔÐØÓÒ Ö Ø ÙÖÖÒØ ÔÖ ÓÖ ØÖÚÐÐÒº ÏÐ Ø ÙÖÖÒØ Ö ØÖÙØÙÖ ÒÓÛÒ Ò ØÖÓÖ ÖÐØÚÐÝ Ý ØÓ Ø Ø Ù ÙÐÐÝ Ö ØÓ Ø ÖÐ Ø Ø ÓÙØ Ø Ù ØÓÑÖ ³ ÚÓÙÖº ÁÒ ÓÙÖ ÔÖÓØ Ò Ø ËÖÐÒ Ø Û ÓÐÚ Ý Ù Ò Ø ÒÓÑ Ø Ó Ó Ø ØÖÒ ÔÓÖØÓÒ ÓÑÔÒ Ò ØÓ Ú Ø ÒÓÑ ÛØ Ø ÐÔ Ó ÚÐÐ ØØ Ø ÓÚÖ Ø ÓÖÒ¹ ØÒØÓÒ ÔÖ Ù Ý Ø Ù ØÓÑÖ º Ï Ø Ø ÓÙÖ ÐÓÖØÑ ÓÒ Ø Ø Ö ÓÚº Ì Ö ÙÐØ Ó ÐÓÖØÑ ¾ Ò Ö ÓÛÒ Ò ÙÖ º Ì ÙÖ ÓÛ Ø ÓØÚ ÚÐÙ ÑÜ
21 ÙÖ ÈÓÐØÐ Ù ØÓÒ ÑÜ Å ÓÖ ÒÝ ÒÙÑÖ Ó ÔÓ Ð ÞÓÒ ÖÓÑ ØÓ ¼¼º ÐÐ ÓØÚ ÚÐÙ ÖÖ ØÓ ÒÐ ØÖÔ ØØ ÓÖ Ò ÙÐØ ÚÒ Ò ÖÑÒ ÅÖ Åµº ÁØ ØÙÖÒ ÓÙØ ØØ Ò Ø ÔÖØÐ ÔÔÐØÓÒ Ø ÖÝ ÙÖ Ø ÐÓÖØÑ ¾µ Ø ÐÖ ÛÒÒÖ Ò ØÖÑ Ó Ø ÓØÚ ÚÐÙ Ø ÒÖØ Ø Ø Ö ÙÐØ ÓÖ ÒÝ ÒÙÑÖ Ó Ö ÞÓÒ º ÇÒ Ø ÓØÖ Ò Ø ÖÙÒÒÒ ØÑ ÓÖ ÐÓÖØÑ ¾ ÓÖ ÐÐ ÔÓ Ð ÒÙÑÖ Ó ÞÓÒ ºº ÖÓÑ Ä ¼¼ Û ÒÖÐÝ ØÛÓ Û ÐÐØÓØÖ Ò ÓÙÖ Ö Ø ÑÔÐÑÒØØÓÒ ÓÒ Ü¼µº Ì ËÔÒÒÒ ÌÖ ÔÔÖÓ ÐÓÖØÑ µ Ò Ø ËÒÐ ÄÒ ÐÓÖØÑ ÐÓÖØÑ µ ÓØ Ò ÓÒÐÝ Û ÓÙÖ ÙØ Ø Ö ÙÐØ Ö ÑÙ Ð ÓÒÚÒÒ ÖÖÒ Ø ÓØÚ ÚÐÙ ÑÜ Òº ÓÖ ÑÐÐ ÒÙÑÖ Ä Ó Ö ÞÓÒ ËÒÐ ÄÒ ØØÖ ØÒ Ø ËÔÒÒÒ ÌÖ ÔÔÖÓ ÛÐ ÓÖ Ö ÒÙÑÖ Ó ÔÐÒÒ ÞÓÒ Ø Û Ø ÓØÖ ÛÝ ÖÓÙÒº Ì Ù ØÓ Ø Ø ØØ Ø ËÔÒÒÒ ÌÖ ÔÔÖÓ ØÖØ ÛØ ÓÒÐÝ ÓÒ ÞÓÒ ÛÐ ËÒÐ ÄÒ ØÖØ ÛØ ¼¼ ÞÓÒ º ÇÒ Ù Ø ÓÒ ØÒ Ó ÓÒÐÝ ¼¼ ØØÓÒ ÓÖ ÑÒ¹ÞÓÒ µ Ø ÙÖ Ø Ú Ð Ó Ò Ø Øº ÁÒ Ø ÑÐÐÖ ØØÒ Ø ÖÙÒÒÒ ØÑ Ó ÐÓÖØÑ Ò ÛÖ ÛØÒ ÓÒ Ò Ð Ó ÐÓÖØÑ ¾ Ò ÓÒÐÝ ¾ ÑÒÙØ ØÓ ÓØÒ Ò Ø ÐÖÐÝ Ø Ö ÙÐØ º Ì Ö ÙÐØ ÓÖ ÞÓÒ Ö ÓÛÒ ÖÔÐÐÝ Ò ÙÖ Ò º ÙÖ ÓÛ Ù ØÓÒ ÓÖ ÞÓÒ ÔÖØØÓÒ Û Ù ØÓ Ø ÔÓÐØÐ ØÖØ Ò Ø Ö Ó Ø ËÖÐÒº Ì ÓØÚ ÚÐÙ ÓÖ Ø ÞÓÒ ÔÖØØÓÒ ÑÜ Å ºº ØÖ Ü Ø Ù ØÓÑÖ Û ÛÐÐ Ú
22 ÙÖ ËÓÐÙØÓÒ Ó ËÒÐ ÄÒ ÑÜ ¼¼ Å «ÖÒ Ó Å ØÛÒ ÙÖÖÒØ Ö Ò Ø ÒÛ ÓÒº Ì Ö ÙÐØ Ó Ø ËÒÐ ÄÒ ÐÓÖØÑ ÓÖ ÞÓÒ ÓÛÒ Ò ÙÖ º Ø ÖÔÓÖØ Ð Ó Ò ÐØÖØÙÖ ºº ¾ µ ËÒÐ ÄÒ ØÒ ØÓ ÓÖÑ ÓÒ ÐÖ ÞÓÒ Ò ÐÓØ Ó ÑÐÐÖ ÞÓÒ ÙÖÖÓÙÒÒ Øº Ì ÚÓÖ Ð Ó ÓÛÒ Ò ÙÖ º Ì ÓØÚ ÚÐÙ Ó Ø ÖÔ ÞÓÒ ÔÖØØÓÒ ¼¼ ź Ì ÓØÚ ÚÐÙ Ò Ø ËÔÒÒÒ ÌÖ Ô¹ ÔÖÓ Ð ÓÛ ¼¼ Å ÓÖ ÞÓÒ ÙØ ÛØÓÙØ Ø «ÖÒ Ò Ø Þ Ó Ø ÞÓÒ º Ì Ø Ö ÙÐØ ÓÛÚÖ ÛÖ ÓØÒ Ý Ø ÖÝ ÔÔÖÓ ÛØ Ò ÓØÚ ÚÐÙ Ó ÓÒÐÝ Åº Ì ÓÖÖ ÔÓÒÒ ÞÓÒ ÔÖØØÓÒ ÓÛÒ Ò ÙÖ º ÓÖ ÚÐÙØÒ ØÖ«ÞÓÒ Ò ÑÓÖ ØÐ Û Ù Ø ÓØÛÖ Ô ÏÈÐÒ º ÖÔÐ ÖÓÒØ¹Ò ÔÖÓÚ ØÐ ÒÐÝ Ó ÐÐ ØÖÔ ÓÖ Û Ø Ö ÛÐÐ ÒÖ ÓÖ Ö ÖÑØÐÐÝ ÙÖ ¼µº ÙÖØÖÑÓÖ Ø ÜÔØ ÒÓÑ ÓÖ Ó Ø ØÖÒ ÔÓÖØØÓÒ ÓÑÔÒ Ò ØØ ØÓÖÝ ÓÑÔÖ ÛØ Ø ÙÖÖÒØ ÒÓѺ ÓÖ ÔÖØÐ ÔÙÖÔÓ ÐÓØ Ó ÔÐ ÖÙÐ ÓÖ Ù Ò Ö ÞÓÒ Ö ÓÑÑÓÒº ÐÓØ Ó ØÑ Ú Ð Ó Ò ÑÔÐÑÒØ Ò ÓÙÖ ÐÓÖØÑ Ò Ø Ø ÓÒ Ø Ø Ó Ø ËÖÐÒº ÑÔØÝ ÞÓÒ Ö Ø Ó ÐÐ Ò ÑÓ Ø ÞÓÒ ØÖ«Ý ØÑ ÑÔØÝ ÞÓÒ Ö Ù ØÓ ÒÖ Ø Ö ÓÒ ÓÑ ÔÐ ØÖÔ ÛØÓÙØ «ØÒ ÐÐ ÓØÖ ÖÐØÓÒ º
23 ÙÖ ËÓÐÙØÓÒ Ó ÖÝ ÐÓÖØÑ ÑÜ Å Ì Ñ ØÓ Ñ Ò Ò ÔÖØ Ò Ò ÐÝ ÒÓÖÔÓÖØ Ò Ø ÐÓÖØÑ ÔÖ ÒØ Ò ËØÓÒ º ÁÒ Ø ÛÝ ÚÒ ÖÖÒ ÔÖ Ò ÔÔÖÓÜÒØ ÖØÖÖÐÝ ÐÓ Ø ÒÙÑÖ Ä Ó ÞÓÒ ÐÖ ÒÓÙº ÁÒ ÓÙÖ ÑÓÐ Ø ÑÒ ØØ Ø ÓÔØÑÐ ÓØÚ ÚÐÙ Ó ØÓ ÞÖÓ ÓÖ ÑÜ Ò ¾ Ò Ø º ÓÖÖ ØØÓÒ ÌÓ ÚÓ ÒÙ Ø ØØÓÒ Ò ÐÓØ ÓÒ ÞÓÒ ÓÖÖ ÑÒÒ ØØ ØÝ ÐÓÒ ØÓ ÑÓÖ ØÒ ÓÒ ÞÓÒ Ò ÔÔÐÝ Ø Ô Ø Ó ÓÖ ØÖÑÒÒ Ø Öº ËÒ Ø ÞÓÒ ØÖ«Ý ØÑ ÓÙÐ ÐÖ Ò ÙÒÖ ØÒÐ Û ØÖ ØÓ ÚÓ Ø Ò Ø ËÖÐÒº ÁÒ ÑÓ Ø Ø ØÙÖÒ ÓÙØ ØØ ÓÖÖ ØØÓÒ Ò ÚÓ ÛØÓÙØ ÐÓÓ Ò ÒÝØÒ Ò Ø ÓØÚ ÚÐÙ ÓÒÐÝ Ý Ò Ø ÞÓÒ Òº ËÔÐ ÖÙÐ ÓÖ ÐÖ ÞÓÒ Ð Ó ÓÑ ÞÓÒ ÑØ Ó ÐÖ ØØ ØÝ Ú ØÓ ÓÙÒØ ØÛ ÛÒ ÖÓ Ò ØÑ Ò ØØ ÔÐ Ö ØÖÙ¹ ØÙÖ ØÓ ÑÔÐÑÒØ ÛØÒ Ù ÐÖ ÞÓÒº ÁÒ Ø ËÖÐÒ Ø ØÖ«Ý ØÑ ÔÖÓÔÓ Ý Ù Ò ÓÙÖ ÑØÓ ÒÓÛ Ò Ø ÑÔÐÑÒØØÓÒ ÔÖÓ º ¾¼
24 ÙÖ ¼ ÓÒ ÔÐÒÒÒ ÛØ Ø ÓØÛÖ ÏÈÐÒ Ò Ø ØØ Ë Ò¹ÒÐغ Ì Ö ÐÒ ÓÛ Ø ØÓÒе Ù ØÓÑÖ Û ÛÐÐ Ú Ò Ò ØÖ ØØ ÔÖ Û ÑÓÖØÒÈÖÒغ ÓÒÐÙ ÓÒ Ï Ú ÓÛÒ ØØ ÐÓ ÓÖÑ ÓÐÙØÓÒ Ò ÔÖÓÚ ÓÖ Ø Ö ÔÖÓÐÑ ÛØ Ü ÞÓÒ µº ÁÒ ÓÒØÖ Ø Ø ÞÓÒ ÔÖÓÐÑ ºº Ø Ò Ó ÞÓÒ Æȹ Öº ÌÖ ÙÖ Ø Ú Ò ÔÖÓÔÓ Ò ÓÑÔÖ ÛØ Ö ÔØ ØÓ ØÖ ÒÙÑÖÐ ÚÓÙÖº Ì ÔÖØÐ Ù ÙÐÒ Ó Ø ÔÔÖÓ ÓÛÒ Ý Ø ØÙÐ ÑÔÐÑÒØØÓÒ Ò Ø ØØ ËÖÐÒ ÖÑÒݺ ÇØÖ ØØ Ó ÖÑÒÝ Ö ÙÖÖÒØÐÝ Ù Ò ÓÙÖ Ý ØÑ ØÓ ÚÐÙØ ØÖ ØÖ«ØÖÙØÙÖº ÔÔÒÜ ÈÖÓÓ Ó ÌÓÖÑ ¾ Ï Ù ÖÙØÓÒ ØÓ Ø ÔÖÓÐÑ ÔÖØØÓÒ ÒØÓ ÐÕÙ ÓÖ Ä ÐÕÙ Û ÆÈ¹Ö ÔÖÓÐÑ Ì Ò º ÄØ ÖÔ Î µ ÚÒº Ï ÛÒØ ØÓ Ò ÛÖ Ø ÕÙ ØÓÒ ØÖ Ü Ø ÔÖØØÓÒ Ó Î ÒØÓ ÒÓ Ø ¾
25 Î Î ¾ ÒÎ Ù ØØ Ø ÒÙ ÙÖÔ ¾ Ò Ö ÓÑÔÐغ ÌÓ ÖÙ Ø ÔÖÓÐÑ ØÓ ÞÓÒ Ò ÔÖÓÐÑ Û ÓÒ Ö Ø ÓÑÔÐØ ÖÔ Î µ Ò Ý Î Î ¾ ¾ Ò Ðµ Ð ¾Î Ð ÙÖØÖÑÓÖ ÐØ Û ÓÖ ÐÐ ¾ Î Ò Ò Ø ÖÖÒ ÔÖ Ø ÓÐÐÓÛÒ ÛØ º Ре ¾ ¾ Î Ð ¾ Î ØÖ Ü Ø ¾ Ù ØØ Ðµ µ ¾ Ð ¾ Πе ¾ ¾ Ð ¾ Πе µ ÓÖ ÐÐ ¾ ÆÓÛ Û ÓÛ ØØ Ò ÔÖØØÓÒ ÒØÓ ÐÕÙ Ò ÓÒÐÝ Ø ÞÓÒ Ò ÔÖÓÐÑ Ò ÓÐÙØÓÒ ÛØ ÞÓÒ Ò ÛØ ÑÜ º µ ÄØ Î Î Î ¾ Î Ø ÔÖØØÓÒ Ó ÒØÓ ÐÕÙ º Ò Î ÓÖ ¾ º Í Ò ÓÖÓÐÐÖÝ ¾ Ò Û ÐÙÐØ Ã ÑÜ ¼µ ¾ ¾ Ù ØØ Û Ø ÑÜ º à ÑÜ µ ¾ ¾ µ ¾ ÄØ ¾ ÔÖØØÓÒ Ó Î ÛØ ÑÜ º Ò Î Î ÓÖ ¾ º Ö Ø Û ÒÓØ ØØ Ý ÖÒÑÒ Ø Û Ò ÙÑ ØØ ¾ ÓÖ ¾ º Ì Ò ÔÖÓÚ Ý ÑÔÐ ÒÐÝ µ Û ÚÖ Ø ÓÐÐÓÛÒº º Á Ò Ó ÒÓØ ÐÓÒ ØÓ Ø Ñ ÞÓÒ Ø ÝÐ ÑÜ º ¾º Á Ò ÒÓØÖ ÓÖ ÐÓÒ ØÓ ÒÐ ÓÑÑÓÒ ÞÓÒ ØÒ ÑÜ º ÆÓÛ ÐØ Ð ¾ Î º Ï Ú ØÓ ÓÛ ØØ Ø Ðµ ¾ º ÙÑ Ø ÓÒØÖÖÝ ºº Ð ¾º ÙØ Ø ÝÐ Ã ÑÜ ¼µ ¾ ¾ ¾ Ò Ù Ò ÓÖÓÐÐÖÝ ¾ Ò µ ÓÒØÖØÓÒº ÓÖ ÑÓÖ ØÒ ÞÓÒ Ø ÔÖÓÓ Ò ÓÒ ÒÐÓÓÙ ÐÝ ÛØ ÖÙØÓÒ ØÓ ÔÖØØÓÒ ÒØÓ Ä ÐÕÙ º É ¾¾
26 ÊÖÒ Äº Ð Ò Àº ÃÐÐÖÖº Ò Ó ØÖ«ÞÓÒ Ò ÔÙÐ ØÖÒ ÔÓÖØØÓÒ Ý ØÑ ÌÓÖØÐ Ò ÔÖØÐ Ö ÙÐØ º ÌÒÐ ÖÔÓÖØ ÙÐØÝ Ó Ó¹ ÒÓÑ ÍÒÚÖ ØÝ Ó ÖÞ ¾¼¼º ¾ ºËº ÙÖÒ Ò ÈºÄº ÇÐк ÐÙ ØÖ ÒÐÝ ËÙÖÚݺ ÄØÙÖ ÆÓØ Ò ÓÒÓÑ Ò ÅØÑØÐ ËÝ ØÑ ¼¼º ËÔÖÒÖ ÖÐÒ¹ÀÐÖ¹ÆÛ ÓÖ º ʺϺ ÐÓݺ ÐÓÖØÑ ËÓÖØ Ø Ôغ ÓÑÑÙÒØÓÒ Ó Ø Å ¾º źʺ ÖÝ Ò ºËº ÂÓÒ ÓÒº ÓÑÔÙØÖ Ò ÁÒØÖØÐØÝ Ù ØÓ Ø ÌÓÖÝ Ó ÆȹÓÑÔÐØÒ º ÀºÏº ÖÑÒ Ò ÓÑÔÒÝ ËÒ ÖÒ¹ Ó º ÀºÏº ÀÑÖº ÅØÑØ ÄĐÓ ÙÒ ÚÖÖÒ ĐÙÖ ÔÐÒÖ ËØÒÓÖع ÔÖÓÐÑ ÅØÑØÐ ËÓÐÙØÓÒ ÐÓÖØÑ ÓÖ ÈÐÒÖ ÄÓØÓÒ ÈÖÓÐÑ µº ÎÛ ÖÙÒ Û º ÀºÏº ÀÑÖ Ò º ËĐÓк ÇÒ Ö ÞÓÒ Ò Ò ÔÙÐ ØÖÒ ÔÓÖع ØÓÒº ÁÒ ÓÑÔÙØÖ¹ ÌÖÒ Ø ËÙÐÒ ÒÙÑÖ ¼ Ò ÄØÙÖ ÆÓØ Ò ÓÒÓÑ Ò ÅØÑØÐ ËÝ ØÑ Ô ß¾¾º ËÔÖÒÖ º Ϻĺ ÀÝ º ËØØ Ø º ÀÓÐØ ÊÒÖØ Ò ÏÒ ØÓÒ º ØÓÒ º ʺº ÄÓÚ Âºº ÅÓÖÖ Ò ºÇº Ï ÓÐÓÛ Ýº ÐØ ÄÓØÓÒ ÔØÖ º Ô ß¼º ÆÓÖعÀÓÐÐÒ Ñ ØÖÑ º ú ÈÒÒÖº ÖÔÖ ØÐØÙÒ Ñ ĐÓ«ÒØÐÒ ÎÖÖº Å ØÖ³ Ø ÍÒÚÖ ØĐØ Ã Ö ÐÙØÖÒ º ¼ º ÈÐ ØÖº ÓÒØÒÙÓÙ ÐÓØÓÒ ÔÖÓÐÑ º ÁÒ º ÖÞÒÖ ØÓÖ ÐØÝ ÄÓØÓÒ ÙÖÚÝ Ó ÔÔÐØÓÒ Ò ÑØÓ ÔØÖ Ô ¾¾ß¾¾º ËÔÖÒÖ ÆÛ ÓÖ ÁÒº º ú ËÖ Ò Áº ÎÒÞº ÅØÑØÐ ÅØÓ Ó ËØØ ØÐ ÉÙÐØÝ ÓÒ¹ ØÖÓк Ñ ÈÖ ÆÛ ÓÖ¹ÄÓÒÓÒ º ¾ º ËĐÓк Ö ÞÓÒ Ò Ò ÔÙÐ ØÖÒ ÔÓÖØØÓÒ ÒØÛÓÖ º ÁÒ ÇÔÖØÓÒ Ê Ö ÈÖÓÒ Ô ßº ËÔÖÒÖ ÎÖÐ º º ËĐÓк ÅØÓÒ Ö ÓÑÒØÓÖ Ò ÇÔØÑÖÙÒ Ò Ö ÌÖ¹ ÔÐÒÙÒ Ñ ĐÓ«ÒØÐÐÒ ÈÖ ÓÒÒÒÚÖÖº Å ØÖ³ Ø ÍÒÚÖ ØĐØ Ã Ö ÐÙØÖÒ º ÔÔÖ ÙÒÖ ÑÒ ÒÑ º ËÙÑÖµº ¾
27 º ËĐÓк ÓÒ ÔÐÒÒÒ Ò ÔÙÐ ØÖÒ ÔÓÖØØÓÒº ÁÒ Äº ÒÓ Ò Èº ÌÓØ ØÓÖ ÚÒ ÅØÓ Ò ÌÖÒ ÔÓÖØØÓÒ ÒÐÝ ÌÖÒ ÔÓÖع ØÓÒ ÒÐÝ Ô ß º ËÔÖÒÖ ÎÖÐ º º ËĐÓк ÏÈÐÒ ß ÓØÛÖ ØÓÓÐ ÓÖ Ò Ò ÚÐÙØÓÒ Ó ØÖ«Ý ØÑ º ˺ ÏÖ Ðк ØÓÖÑ ÓÒ ÓÓÐÒ ÑØÖ º ÂÓÙÖÒÐ Ó Ø Å ¾º ¾
28 Bisher erschienene Berichte des Fraunhofer ITWM Die PDF-Files der folgenden Berichte finden Sie unter: 1. D. Hietel, K. Steiner, J. Struckmeier A Finite - Volume Particle Method for Compressible Flows We derive a new class of particle methods for conservation laws, which are based on numerical flux functions to model the interactions between moving particles. The derivation is similar to that of classical Finite-Volume methods; except that the fixed grid structure in the Finite-Volume method is substituted by so-called mass packets of particles. We give some numerical results on a shock wave solution for Burgers equation as well as the well-known one-dimensional shock tube problem. (19 S., 1998) 2. M. Feldmann, S. Seibold Damage Diagnosis of Rotors: Application of Hilbert Transform and Multi-Hypothesis Testing In this paper, a combined approach to damage diagnosis of rotors is proposed. The intention is to employ signalbased as well as model-based procedures for an improved detection of size and location of the damage. In a first step, Hilbert transform signal processing techniques allow for a computation of the signal envelope and the instantaneous frequency, so that various types of nonlinearities due to a damage may be identified and classified based on measured response data. In a second step, a multi-hypothesis bank of Kalman Filters is employed for the detection of the size and location of the damage based on the information of the type of damage provided by the results of the Hilbert transform. Keywords: Hilbert transform, damage diagnosis, Kalman filtering, non-linear dynamics (23 S., 1998) 3. Y. Ben-Haim, S. Seibold Robust Reliability of Diagnostic Multi- Hypothesis Algorithms: Application to Rotating Machinery Damage diagnosis based on a bank of Kalman filters, each one conditioned on a specific hypothesized system condition, is a well recognized and powerful diagnostic tool. This multi-hypothesis approach can be applied to a wide range of damage conditions. In this paper, we will focus on the diagnosis of cracks in rotating machinery. The question we address is: how to optimize the multihypothesis algorithm with respect to the uncertainty of the spatial form and location of cracks and their resulting dynamic effects. First, we formulate a measure of the reliability of the diagnostic algorithm, and then we discuss modifications of the diagnostic algorithm for the maximization of the reliability. The reliability of a diagnostic algorithm is measured by the amount of uncertainty consistent with no-failure of the diagnosis. Uncertainty is quantitatively represented with convex models. Keywords: Robust reliability, convex models, Kalman filtering, multihypothesis diagnosis, rotating machinery, crack diagnosis (24 S., 1998) 4. F.-Th. Lentes, N. Siedow Three-dimensional Radiative Heat Transfer in Glass Cooling Processes For the numerical simulation of 3D radiative heat transfer in glasses and glass melts, practically applicable mathematical methods are needed to handle such problems optimal using workstation class computers. Since the exact solution would require super-computer capabilities we concentrate on approximate solutions with a high degree of accuracy. The following approaches are studied: 3D diffusion approximations and 3D ray-tracing methods. (23 S., 1998) 5. A. Klar, R. Wegener A hierarchy of models for multilane vehicular traffic Part I: Modeling In the present paper multilane models for vehicular traffic are considered. A microscopic multilane model based on reaction thresholds is developed. Based on this model an Enskog like kinetic model is developed. In particular, care is taken to incorporate the correlations between the vehicles. From the kinetic model a fluid dynamic model is derived. The macroscopic coefficients are deduced from the underlying kinetic model. Numerical simulations are presented for all three levels of description in [10]. Moreover, a comparison of the results is given there. (23 S., 1998) Part II: Numerical and stochastic investigations In this paper the work presented in [6] is continued. The present paper contains detailed numerical investigations of the models developed there. A numerical method to treat the kinetic equations obtained in [6] are presented and results of the simulations are shown. Moreover, the stochastic correlation model used in [6] is described and investigated in more detail. (17 S., 1998) 6. A. Klar, N. Siedow Boundary Layers and Domain Decomposition for Radiative Heat Transfer and Diffusion Equations: Applications to Glass Manufacturing Processes In this paper domain decomposition methods for radiative transfer problems including conductive heat transfer are treated. The paper focuses on semi-transparent materials, like glass, and the associated conditions at the interface between the materials. Using asymptotic analysis we derive conditions for the coupling of the radiative transfer equations and a diffusion approximation. Several test cases are treated and a problem appearing in glass manufacturing processes is computed. The results clearly show the advantages of a domain decomposition approach. Accuracy equivalent to the solution of the global radiative transfer solution is achieved, whereas computation time is strongly reduced. (24 S., 1998) 7. I. Choquet Heterogeneous catalysis modelling and numerical simulation in rarified gas flows Part I: Coverage locally at equilibrium A new approach is proposed to model and simulate numerically heterogeneous catalysis in rarefied gas flows. It is developed to satisfy all together the following points: 1) describe the gas phase at the microscopic scale, as required in rarefied flows, 2) describe the wall at the macroscopic scale, to avoid prohibitive computational costs and consider not only crystalline but also amorphous surfaces, 3) reproduce on average macroscopic laws correlated with experimental results and 4) derive analytic models in a systematic and exact way. The problem is stated in the general framework of a non static flow in the vicinity of a catalytic and non porous surface (without aging). It is shown that the exact and systematic resolution method based on the Laplace transform, introduced previously by the author to model collisions in the gas phase, can be extended to the present problem. The proposed approach is applied to the modelling of the Eley-Rideal and Langmuir-Hinshelwood recombinations, assuming that the coverage is locally at equilibrium. The models are developed considering one atomic species and extended to the general case of several atomic species. Numerical calculations show that the models derived in this way reproduce with accuracy behaviors observed experimentally. (24 S., 1998) 8. J. Ohser, B. Steinbach, C. Lang Efficient Texture Analysis of Binary Images A new method of determining some characteristics of binary images is proposed based on a special linear filtering. This technique enables the estimation of the area fraction, the specific line length, and the specific integral of curvature. Furthermore, the specific length of the total projection is obtained, which gives detailed information about the texture of the image. The influence of lateral and directional resolution depending on the size of the applied filter mask is discussed in detail. The technique includes a method of increasing directional resolution for texture analysis while keeping lateral resolution as high as possible. (17 S., 1998) 9. J. Orlik Homogenization for viscoelasticity of the integral type with aging and shrinkage A multi-phase composite with periodic distributed inclusions with a smooth boundary is considered in this contribution. The composite component materials are supposed to be linear viscoelastic and aging (of the non-convolution integral type, for which the Laplace transform with respect to time is not effectively applicable) and are subjected to isotropic shrinkage. The free shrinkage deformation can be considered as a fictitious temperature deformation in the behavior law. The procedure presented in this paper proposes a way to determine average (effective homogenized) viscoelastic and shrinkage (temperature) composite properties and the homogenized stress-field from known properties of the
29 components. This is done by the extension of the asymptotic homogenization technique known for pure elastic non-homogeneous bodies to the non-homogeneous thermo-viscoelasticity of the integral non-convolution type. Up to now, the homogenization theory has not covered viscoelasticity of the integral type. Sanchez-Palencia (1980), Francfort & Suquet (1987) (see [2], [9]) have considered homogenization for viscoelasticity of the differential form and only up to the first derivative order. The integral-modeled viscoelasticity is more general then the differential one and includes almost all known differential models. The homogenization procedure is based on the construction of an asymptotic solution with respect to a period of the composite structure. This reduces the original problem to some auxiliary boundary value problems of elasticity and viscoelasticity on the unit periodic cell, of the same type as the original non-homogeneous problem. The existence and uniqueness results for such problems were obtained for kernels satisfying some constrain conditions. This is done by the extension of the Volterra integral operator theory to the Volterra operators with respect to the time, whose 1 kernels are space linear operators for any fixed time variables. Some ideas of such approach were proposed in [11] and [12], where the Volterra operators with kernels depending additionally on parameter were considered. This manuscript delivers results of the same nature for the case of the space-operator kernels. (20 S., 1998) 10. J. Mohring Helmholtz Resonators with Large Aperture The lowest resonant frequency of a cavity resonator is usually approximated by the classical Helmholtz formula. However, if the opening is rather large and the front wall is narrow this formula is no longer valid. Here we present a correction which is of third order in the ratio of the diameters of aperture and cavity. In addition to the high accuracy it allows to estimate the damping due to radiation. The result is found by applying the method of matched asymptotic expansions. The correction contains form factors describing the shapes of opening and cavity. They are computed for a number of standard geometries. Results are compared with numerical computations. (21 S., 1998) 11. H. W. Hamacher, A. Schöbel On Center Cycles in Grid Graphs Finding "good" cycles in graphs is a problem of great interest in graph theory as well as in locational analysis. We show that the center and median problems are NP hard in general graphs. This result holds both for the variable cardinality case (i.e. all cycles of the graph are considered) and the fixed cardinality case (i.e. only cycles with a given cardinality p are feasible). Hence it is of interest to investigate special cases where the problem is solvable in polynomial time. In grid graphs, the variable cardinality case is, for instance, trivially solvable if the shape of the cycle can be chosen freely. If the shape is fixed to be a rectangle one can analyze rectangles in grid graphs with, in sequence, fixed dimension, fixed cardinality, and variable cardinality. In all cases a complete characterization of the optimal cycles and closed form expressions of the optimal objective values are given, yielding polynomial time algorithms for all cases of center rectangle problems. Finally, it is shown that center cycles can be chosen as rectangles for small cardinalities such that the center cycle problem in grid graphs is in these cases completely solved. (15 S., 1998) 12. H. W. Hamacher, K.-H. Küfer Inverse radiation therapy planning - a multiple objective optimisation approach For some decades radiation therapy has been proved successful in cancer treatment. It is the major task of clinical radiation treatment planning to realize on the one hand a high level dose of radiation in the cancer tissue in order to obtain maximum tumor control. On the other hand it is obvious that it is absolutely necessary to keep in the tissue outside the tumor, particularly in organs at risk, the unavoidable radiation as low as possible. No doubt, these two objectives of treatment planning - high level dose in the tumor, low radiation outside the tumor - have a basically contradictory nature. Therefore, it is no surprise that inverse mathematical models with dose distribution bounds tend to be infeasible in most cases. Thus, there is need for approximations compromising between overdosing the organs at risk and underdosing the target volume. Differing from the currently used time consuming iterative approach, which measures deviation from an ideal (non-achievable) treatment plan using recursively trialand-error weights for the organs of interest, we go a new way trying to avoid a priori weight choices and consider the treatment planning problem as a multiple objective linear programming problem: with each organ of interest, target tissue as well as organs at risk, we associate an objective function measuring the maximal deviation from the prescribed doses. We build up a data base of relatively few efficient solutions representing and approximating the variety of Pareto solutions of the multiple objective linear programming problem. This data base can be easily scanned by physicians looking for an adequate treatment plan with the aid of an appropriate online tool. (14 S., 1999) 13. C. Lang, J. Ohser, R. Hilfer On the Analysis of Spatial Binary Images This paper deals with the characterization of microscopically heterogeneous, but macroscopically homogeneous spatial structures. A new method is presented which is strictly based on integral-geometric formulae such as Crofton s intersection formulae and Hadwiger s recursive definition of the Euler number. The corresponding algorithms have clear advantages over other techniques. As an example of application we consider the analysis of spatial digital images produced by means of Computer Assisted Tomography. (20 S., 1999) 14. M. Junk On the Construction of Discrete Equilibrium Distributions for Kinetic Schemes A general approach to the construction of discrete equilibrium distributions is presented. Such distribution functions can be used to set up Kinetic Schemes as well as Lattice Boltzmann methods. The general principles are also applied to the construction of Chapman Enskog distributions which are used in Kinetic Schemes for compressible Navier-Stokes equations. (24 S., 1999) 15. M. Junk, S. V. Raghurame Rao A new discrete velocity method for Navier- Stokes equations The relation between the Lattice Boltzmann Method, which has recently become popular, and the Kinetic Schemes, which are routinely used in Computational Fluid Dynamics, is explored. A new discrete velocity model for the numerical solution of Navier-Stokes equations for incompressible fluid flow is presented by combining both the approaches. The new scheme can be interpreted as a pseudo-compressibility method and, for a particular choice of parameters, this interpretation carries over to the Lattice Boltzmann Method. (20 S., 1999) 16. H. Neunzert Mathematics as a Key to Key Technologies The main part of this paper will consist of examples, how mathematics really helps to solve industrial problems; these examples are taken from our Institute for Industrial Mathematics, from research in the Technomathematics group at my university, but also from ECMI groups and a company called TecMath, which originated 10 years ago from my university group and has already a very successful history. (39 S. (vier PDF-Files), 1999) 17. J. Ohser, K. Sandau Considerations about the Estimation of the Size Distribution in Wicksell s Corpuscle Problem Wicksell s corpuscle problem deals with the estimation of the size distribution of a population of particles, all having the same shape, using a lower dimensional sampling probe. This problem was originary formulated for particle systems occurring in life sciences but its solution is of actual and increasing interest in materials science. From a mathematical point of view, Wicksell s problem is an inverse problem where the interesting size distribution is the unknown part of a Volterra equation. The problem is often regarded ill-posed, because the structure of the integrand implies unstable numerical solutions. The accuracy of the numerical solutions is considered here using the condition number, which allows to compare different numerical methods with different (equidistant) class sizes and which indicates, as one result, that a finite section thickness of the probe reduces the numerical problems. Furthermore, the relative error of estimation is computed which can be split into two parts. One part consists of the relative discretization error that increases for increasing class size, and the second part is related to the relative statistical error which increases with decreasing class size. For both parts, upper bounds can be given and the sum of them indicates an optimal class width depending on some specific constants. (18 S., 1999)
30 18. E. Carrizosa, H. W. Hamacher, R. Klein, S. Nickel Solving nonconvex planar location problems by finite dominating sets It is well-known that some of the classical location problems with polyhedral gauges can be solved in polynomial time by finding a finite dominating set, i. e. a finite set of candidates guaranteed to contain at least one optimal location. In this paper it is first established that this result holds for a much larger class of problems than currently considered in the literature. The model for which this result can be proven includes, for instance, location problems with attraction and repulsion, and location-allocation problems. Next, it is shown that the approximation of general gauges by polyhedral ones in the objective function of our general model can be analyzed with regard to the subsequent error in the optimal objective value. For the approximation problem two different approaches are described, the sandwich procedure and the greedy algorithm. Both of these approaches lead - for fixed epsilon - to polynomial approximation algorithms with accuracy epsilon for solving the general model considered in this paper. Keywords: Continuous Location, Polyhedral Gauges, Finite Dominating Sets, Approximation, Sandwich Algorithm, Greedy Algorithm (19 S., 2000) 19. A. Becker A Review on Image Distortion Measures Within this paper we review image distortion measures. A distortion measure is a criterion that assigns a quality number to an image. We distinguish between mathematical distortion measures and those distortion measures in-cooperating a priori knowledge about the imaging devices ( e. g. satellite images), image processing algorithms or the human physiology. We will consider representative examples of different kinds of distortion measures and are going to discuss them. Keywords: Distortion measure, human visual system (26 S., 2000) 20. H. W. Hamacher, M. Labbé, S. Nickel, T. Sonneborn Polyhedral Properties of the Uncapacitated Multiple Allocation Hub Location Problem We examine the feasibility polyhedron of the uncapacitated hub location problem (UHL) with multiple allocation, which has applications in the fields of air passenger and cargo transportation, telecommunication and postal delivery services. In particular we determine the dimension and derive some classes of facets of this polyhedron. We develop some general rules about lifting facets from the uncapacitated facility location (UFL) for UHL and projecting facets from UHL to UFL. By applying these rules we get a new class of facets for UHL which dominates the inequalities in the original formulation. Thus we get a new formulation of UHL whose constraints are all facet defining. We show its superior computational performance by benchmarking it on a well known data set. Keywords: integer programming, hub location, facility location, valid inequalities, facets, branch and cut (21 S., 2000) 21. H. W. Hamacher, A. Schöbel Design of Zone Tariff Systems in Public Transportation Given a public transportation system represented by its stops and direct connections between stops, we consider two problems dealing with the prices for the customers: The fare problem in which subsets of stops are already aggregated to zones and good tariffs have to be found in the existing zone system. Closed form solutions for the fare problem are presented for three objective functions. In the zone problem the design of the zones is part of the problem. This problem is NP hard and we therefore propose three heuristics which prove to be very successful in the redesign of one of Germany s transportation systems. (30 S., 2001) 22. D. Hietel, M. Junk, R. Keck, D. Teleaga: The Finite-Volume-Particle Method for Conservation Laws In the Finite-Volume-Particle Method (FVPM), the weak formulation of a hyperbolic conservation law is discretized by restricting it to a discrete set of test functions. In contrast to the usual Finite-Volume approach, the test functions are not taken as characteristic functions of the control volumes in a spatial grid, but are chosen from a partition of unity with smooth and overlapping partition functions (the particles), which can even move along prescribed velocity fields. The information exchange between particles is based on standard numerical flux functions. Geometrical information, similar to the surface area of the cell faces in the Finite-Volume Method and the corresponding normal directions are given as integral quantities of the partition functions. After a brief derivation of the Finite-Volume-Particle Method, this work focuses on the role of the geometric coefficients in the scheme. (16 S., 2001) 23. T. Bender, H. Hennes, J. Kalcsics, M. T. Melo, S. Nickel Location Software and Interface with GIS and Supply Chain Management The objective of this paper is to bridge the gap between location theory and practice. To meet this objective focus is given to the development of software capable of addressing the different needs of a wide group of users. There is a very active community on location theory encompassing many research fields such as operations research, computer science, mathematics, engineering, geography, economics and marketing. As a result, people working on facility location problems have a very diverse background and also different needs regarding the software to solve these problems. For those interested in non-commercial applications (e. g. students and researchers), the library of location algorithms (LoLA can be of considerable assistance. LoLA contains a collection of efficient algorithms for solving planar, network and discrete facility location problems. In this paper, a detailed description of the functionality of LoLA is presented. In the fields of geography and marketing, for instance, solving facility location problems requires using large amounts of demographic data. Hence, members of these groups (e. g. urban planners and sales managers) often work with geographical information too s. To address the specific needs of these users, LoLA was inked to a geographical information system (GIS) and the details of the combined functionality are described in the paper. Finally, there is a wide group of practitioners who need to solve large problems and require special purpose software with a good data interface. Many of such users can be found, for example, in the area of supply chain management (SCM). Logistics activities involved in strategic SCM include, among others, facility location planning. In this paper, the development of a commercial location software tool is also described. The too is embedded in the Advanced Planner and Optimizer SCM software developed by SAP AG, Walldorf, Germany. The paper ends with some conclusions and an outlook to future activities. Keywords: facility location, software development, geographical information systems, supply chain management. (48 S., 2001) 24. H. W. Hamacher, S. A. Tjandra Mathematical Modelling of Evacuation Problems: A State of Art This paper details models and algorithms which can be applied to evacuation problems. While it concentrates on building evacuation many of the results are applicable also to regional evacuation. All models consider the time as main parameter, where the travel time between components of the building is part of the input and the overall evacuation time is the output. The paper distinguishes between macroscopic and microscopic evacuation models both of which are able to capture the evacuees movement over time. Macroscopic models are mainly used to produce good lower bounds for the evacuation time and do not consider any individual behavior during the emergency situation. These bounds can be used to analyze existing buildings or help in the design phase of planning a building. Macroscopic approaches which are based on dynamic network flow models (minimum cost dynamic flow, maximum dynamic flow, universal maximum flow, quickest path and quickest flow) are described. A special feature of the presented approach is the fact, that travel times of evacuees are not restricted to be constant, but may be density dependent. Using multicriteria optimization priority regions and blockage due to fire or smoke may be considered. It is shown how the modelling can be done using time parameter either as discrete or continuous parameter. Microscopic models are able to model the individual evacuee s characteristics and the interaction among evacuees which influence their movement. Due to the corresponding huge amount of data one uses simulation approaches. Some probabilistic laws for individual evacuee s movement are presented. Moreover ideas to model the evacuee s movement using cellular automata (CA) and resulting software are presented. In this paper we will focus on macroscopic models and only summarize some of the results of the microscopic approach. While most of the results are applicable to general evacuation situations, we concentrate on building evacuation. (44 S., 2001) Stand: Juni 2001
 Å ÙÖÒ ÓÙÒØÖÔÖØÝ ÖØ Ê ÖÓÑ ÊÒ ÙÖÒ Ê ÅÒÑÒØ ÏÒØÖØÙÖ ÁÒ ÙÖÒ ÖØ ËÙ ÖÓÙÔ ÒÒÐ Ê ÓÒØÖÓÐ ËÒÖÓ ÅÖÒÓ ÅÖ ¾¼¼¼ ØÖØ ÖØ Ò ÙÖÖ Ö ÜÔÓ ØÓ ÖØ Ö ÛÒ ÒØÖÒ ÒØÓ ÖÒ ÙÖÒ ÓÒØÖØ Ì ÔÖØÙÐÖ ÓÖÑ Ó ÖØ Ö Û ÓÑØÑ ÖÖÖ ØÓ ÙÖØÝ Ö Ù Ò ÑØÓÓÐÓÝ
Å ÙÖÒ ÓÙÒØÖÔÖØÝ ÖØ Ê ÖÓÑ ÊÒ ÙÖÒ Ê ÅÒÑÒØ ÏÒØÖØÙÖ ÁÒ ÙÖÒ ÖØ ËÙ ÖÓÙÔ ÒÒÐ Ê ÓÒØÖÓÐ ËÒÖÓ ÅÖÒÓ ÅÖ ¾¼¼¼ ØÖØ ÖØ Ò ÙÖÖ Ö ÜÔÓ ØÓ ÖØ Ö ÛÒ ÒØÖÒ ÒØÓ ÖÒ ÙÖÒ ÓÒØÖØ Ì ÔÖØÙÐÖ ÓÖÑ Ó ÖØ Ö Û ÓÑØÑ ÖÖÖ ØÓ ÙÖØÝ Ö Ù Ò ÑØÓÓÐÓÝ
ORB User Sponsor Client Authenticate User Request Principal Create Credentials Authenticator Attributes ORB
 Ö Ñ ÛÓÖ ÓÖ ÁÑÔÐ Ñ ÒØ Ò ÊÓÐ ¹ ÓÒØÖÓÐ Í Ò ÇÊ Ë ÙÖ ØÝ Ë ÖÚ ÃÓÒ Ø ÒØ Ò ÞÒÓ ÓÚ Ò Ò ÒØ Ö ÓÖ Ú Ò ØÖ ÙØ ËÝ Ø Ñ Ò Ò Ö Ò Ë ÓÓÐ Ó ÓÑÔÙØ Ö Ë Ò ÐÓÖ ÁÒØ ÖÒ Ø ÓÒ Ð ÍÒ Ú Ö ØÝ ØÖ Ø Ì Ô Ô Ö ÓÛ ÓÛ ÖÓÐ ¹ ÓÒØÖÓÐ Ê µ ÑÓ Ð ÓÙÐ
Ö Ñ ÛÓÖ ÓÖ ÁÑÔÐ Ñ ÒØ Ò ÊÓÐ ¹ ÓÒØÖÓÐ Í Ò ÇÊ Ë ÙÖ ØÝ Ë ÖÚ ÃÓÒ Ø ÒØ Ò ÞÒÓ ÓÚ Ò Ò ÒØ Ö ÓÖ Ú Ò ØÖ ÙØ ËÝ Ø Ñ Ò Ò Ö Ò Ë ÓÓÐ Ó ÓÑÔÙØ Ö Ë Ò ÐÓÖ ÁÒØ ÖÒ Ø ÓÒ Ð ÍÒ Ú Ö ØÝ ØÖ Ø Ì Ô Ô Ö ÓÛ ÓÛ ÖÓÐ ¹ ÓÒØÖÓÐ Ê µ ÑÓ Ð ÓÙÐ
 Ò ÐÝÞ Ò ÔÐÓÊ ÓÛÒÐÓ ÈÖÓ Ð Û Ø ÁÒ¹ Ø ÐÐ ÒØ Å Ò Ö À Þ Ö ËÓ Ý Ò Ò Ü Ð Ï ÖÛ ØÞ ½ ½ ÁÒ Ø ØÙØ ĐÙÖ ËØ Ø Ø ÙÒ ĐÇ ÓÒÓÑ ØÖ ÀÙÑ ÓÐ Ø ÍÒ Ú Ö ØĐ Ø ÞÙ ÖÐ Ò ËÔ Ò Ù Ö ËØÖº ½ ½¼½ ÖÐ Ò ËÙÑÑ ÖÝ Ì Ô Ô Ö Ò Ü ÑÔÐ Ó Ø Ñ Ò Ò Ò
Ò ÐÝÞ Ò ÔÐÓÊ ÓÛÒÐÓ ÈÖÓ Ð Û Ø ÁÒ¹ Ø ÐÐ ÒØ Å Ò Ö À Þ Ö ËÓ Ý Ò Ò Ü Ð Ï ÖÛ ØÞ ½ ½ ÁÒ Ø ØÙØ ĐÙÖ ËØ Ø Ø ÙÒ ĐÇ ÓÒÓÑ ØÖ ÀÙÑ ÓÐ Ø ÍÒ Ú Ö ØĐ Ø ÞÙ ÖÐ Ò ËÔ Ò Ù Ö ËØÖº ½ ½¼½ ÖÐ Ò ËÙÑÑ ÖÝ Ì Ô Ô Ö Ò Ü ÑÔÐ Ó Ø Ñ Ò Ò Ò
Best Place to Find Information on Marriage
 USENIX Association Proceedings of the 4th Annual Linux Showcase & Conference, Atlanta Atlanta, Georgia, USA October 10 14, 2000 THE ADVANCED COMPUTING SYSTEMS ASSOCIATION 2000 by The USENIX Association
USENIX Association Proceedings of the 4th Annual Linux Showcase & Conference, Atlanta Atlanta, Georgia, USA October 10 14, 2000 THE ADVANCED COMPUTING SYSTEMS ASSOCIATION 2000 by The USENIX Association
Service -realization. Imported web -service interfaces. Web -service usage interface. Web -service specification. client. build/buy reuse/buy
 Ò Å Ø Ó ÓÐÓ Ý ÓÖ Ï Ë ÖÚ Ò Ù Ò ÈÖÓ Å ÈºÈ Ô ÞÓ ÐÓÙ Ò Â Ò Ò ÁÒ ÓÐ Ì Ð ÙÖ ÍÒ Ú Ö ØÝ ÈÇ ÓÜ ¼½ ¼¼¼ Ä Ì Ð ÙÖ Æ Ø ÖÐ Ò Ñ Ô Ò Ù ºÒÐ ØÖ Øº ¹ Ù Ò Ø Ò ØØ ÒØ ÓÒ ÖÓÑ ÓÑÔÓÒ ÒØ ØÓ Û ÖÚ ÔÔÐ Ø ÓÒ º ÅÓ Ø ÒØ ÖÔÖ Ô Ò ÑÓ Ø
Ò Å Ø Ó ÓÐÓ Ý ÓÖ Ï Ë ÖÚ Ò Ù Ò ÈÖÓ Å ÈºÈ Ô ÞÓ ÐÓÙ Ò Â Ò Ò ÁÒ ÓÐ Ì Ð ÙÖ ÍÒ Ú Ö ØÝ ÈÇ ÓÜ ¼½ ¼¼¼ Ä Ì Ð ÙÖ Æ Ø ÖÐ Ò Ñ Ô Ò Ù ºÒÐ ØÖ Øº ¹ Ù Ò Ø Ò ØØ ÒØ ÓÒ ÖÓÑ ÓÑÔÓÒ ÒØ ØÓ Û ÖÚ ÔÔÐ Ø ÓÒ º ÅÓ Ø ÒØ ÖÔÖ Ô Ò ÑÓ Ø
b c d bidirectional link unidirectional link
 Ï Ö Ð Æ ØÛÓÖ ¼ ¾¼¼½µ ß ½ ÊÓÙØ Ò Ð ÓÖ Ø Ñ ÓÖ Ï Ö Ð ÀÓ Æ ØÛÓÖ Û Ø ÍÒ Ö Ø ÓÒ Ð Ä Ò Ê Ú ÈÖ Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò ÍÒ Ú Ö ØÝ Ó Ì Ü Ø ÐÐ Ê Ö ÓÒ Ì ¼ ¹¼ º ¹Ñ Ð Ö Ú ÔÙØ ÐÐ º Ù ÅÓ Ø Ó Ø ÖÓÙØ Ò Ð ÓÖ Ø Ñ ÓÖ Ó Ò ØÛÓÖ
Ï Ö Ð Æ ØÛÓÖ ¼ ¾¼¼½µ ß ½ ÊÓÙØ Ò Ð ÓÖ Ø Ñ ÓÖ Ï Ö Ð ÀÓ Æ ØÛÓÖ Û Ø ÍÒ Ö Ø ÓÒ Ð Ä Ò Ê Ú ÈÖ Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò ÍÒ Ú Ö ØÝ Ó Ì Ü Ø ÐÐ Ê Ö ÓÒ Ì ¼ ¹¼ º ¹Ñ Ð Ö Ú ÔÙØ ÐÐ º Ù ÅÓ Ø Ó Ø ÖÓÙØ Ò Ð ÓÖ Ø Ñ ÓÖ Ó Ò ØÛÓÖ
IPsec (enc) IPsec extensions Ethernet Driver. etherip_input() bridge_input()
 ÌÖ Ò Ô Ö ÒØ Æ ØÛÓÖ Ë ÙÖ ØÝ ÈÓÐ Ý Ò ÓÖ Ñ ÒØ Ò ÐÓ º à ÖÓÑÝØ ØÖ ÙØ ËÝ Ø Ñ Ä ÍÒ Ú Ö ØÝ Ó È ÒÒ ÝÐÚ Ò Ò ÐÓ ÓÔ Ò ºÓÖ Â ÓÒ Äº ÏÖ Ø Æ ØÛÓÖ Ë ÙÖ ØÝ Ì ÒÓÐÓ ÁÒº Æ ÌË µ ÓÒÓÔ Ò ºÓÖ ØÖ Ø ÓÖ ÓÒ ÙÖ Ø ÓÒ Ò Ò Ø ÔÖÓØ Ø ÒÓ
ÌÖ Ò Ô Ö ÒØ Æ ØÛÓÖ Ë ÙÖ ØÝ ÈÓÐ Ý Ò ÓÖ Ñ ÒØ Ò ÐÓ º à ÖÓÑÝØ ØÖ ÙØ ËÝ Ø Ñ Ä ÍÒ Ú Ö ØÝ Ó È ÒÒ ÝÐÚ Ò Ò ÐÓ ÓÔ Ò ºÓÖ Â ÓÒ Äº ÏÖ Ø Æ ØÛÓÖ Ë ÙÖ ØÝ Ì ÒÓÐÓ ÁÒº Æ ÌË µ ÓÒÓÔ Ò ºÓÖ ØÖ Ø ÓÖ ÓÒ ÙÖ Ø ÓÒ Ò Ò Ø ÔÖÓØ Ø ÒÓ
 Ø Å Ò Ò Û Ø ËØÖÙØÙÖ ÔØ Ò Æ ÙÖ Ð Æ ØÛÓÖ Ý Ä ÔÖ Ý ÑÑ Ò Ð ÓÓÒ Ëº ÀÓÒ µ Ø Ù Ñ ØØ Ò ÙÐÐ ÐÑ ÒØ Ó Ø Ö ÕÙ Ö Ñ ÒØ ÓÖ Ø Ö Ó ÓØÓÖ Ó È ÐÓ ÓÔ Ý Ë ÓÓÐ Ó ÓÑÔÙØ Ö Ë Ò Ò ËÓ ØÛ Ö Ò Ò Ö Ò ÅÓÒ ÍÒ Ú Ö ØÝ Å Ö ¾¼¼¼ ÌÓ ÑÑ ² Ì
Ø Å Ò Ò Û Ø ËØÖÙØÙÖ ÔØ Ò Æ ÙÖ Ð Æ ØÛÓÖ Ý Ä ÔÖ Ý ÑÑ Ò Ð ÓÓÒ Ëº ÀÓÒ µ Ø Ù Ñ ØØ Ò ÙÐÐ ÐÑ ÒØ Ó Ø Ö ÕÙ Ö Ñ ÒØ ÓÖ Ø Ö Ó ÓØÓÖ Ó È ÐÓ ÓÔ Ý Ë ÓÓÐ Ó ÓÑÔÙØ Ö Ë Ò Ò ËÓ ØÛ Ö Ò Ò Ö Ò ÅÓÒ ÍÒ Ú Ö ØÝ Å Ö ¾¼¼¼ ÌÓ ÑÑ ² Ì
Networks of Collaboration in Oligopoly
 TI 2000-092/1 Tinbergen Institute Discussion Paper Networks of Collaboration in Oligopoly Sanjeev Goyal Sumit Joshi Tinbergen Institute The Tinbergen Institute is the institute for economic research of
TI 2000-092/1 Tinbergen Institute Discussion Paper Networks of Collaboration in Oligopoly Sanjeev Goyal Sumit Joshi Tinbergen Institute The Tinbergen Institute is the institute for economic research of
 ÑÔ Ö Ð Ø ÖÑ Ò ÒØ Ó ÑÔÐÓÝ Ê Ø Ò Ò Ø ÁÒÒÓÚ Ø ÓÒ Ì ÓÑ Û ÒØÖ ÓÖ ÙÖÓÔ Ò ÓÒÓÑ Ê Ö Ïµ ȺǺ ÓÜ ½¼ ½ ½ Å ÒÒ Ñ ÖÑ ÒÝ ¹Ñ Ð ÞÛ Þ Ûº ÆÓÚ Ñ Ö ¾¼¼¼ Á Û ÒØ ØÓ Ø Ò Å Ð Ö Ø À Ò ÓÖ ÑĐÙÒ Ò Ë Ò Ö ÓØØ Ð È Ø Ö Â ¹ Ó Ò Ù Å Ø
ÑÔ Ö Ð Ø ÖÑ Ò ÒØ Ó ÑÔÐÓÝ Ê Ø Ò Ò Ø ÁÒÒÓÚ Ø ÓÒ Ì ÓÑ Û ÒØÖ ÓÖ ÙÖÓÔ Ò ÓÒÓÑ Ê Ö Ïµ ȺǺ ÓÜ ½¼ ½ ½ Å ÒÒ Ñ ÖÑ ÒÝ ¹Ñ Ð ÞÛ Þ Ûº ÆÓÚ Ñ Ö ¾¼¼¼ Á Û ÒØ ØÓ Ø Ò Å Ð Ö Ø À Ò ÓÖ ÑĐÙÒ Ò Ë Ò Ö ÓØØ Ð È Ø Ö Â ¹ Ó Ò Ù Å Ø
 ØÓÖ Ò Ê Ø ÓÒ Ð ÈÓÐÝÒÓÑ Ð ÓÚ Ö Ø ÓÑÔÐ Ü ÆÙÑ Ö Ò Ö Ø ÂÓ Ò ÒÒÝ Ý Ì ÓÑ ÖÖ ØÝ Þ ÂÓ Ï ÖÖ Ò Ü ÖÙ ÖÝ ½ ØÖ Ø Æ Ð ÓÖ Ø Ñ Ö Ú Ò ÓÖ Ø ÖÑ Ò Ò Ø ÒÙÑ Ö Ò Ö Ó Ø ØÓÖ ÖÖ Ù Ð ÓÚ Ö Ø ÓÑÔÐ Ü ÒÙÑ Ö Ó ÑÙÐØ ¹ Ú Ö Ø ÔÓÐÝÒÓÑ Ð
ØÓÖ Ò Ê Ø ÓÒ Ð ÈÓÐÝÒÓÑ Ð ÓÚ Ö Ø ÓÑÔÐ Ü ÆÙÑ Ö Ò Ö Ø ÂÓ Ò ÒÒÝ Ý Ì ÓÑ ÖÖ ØÝ Þ ÂÓ Ï ÖÖ Ò Ü ÖÙ ÖÝ ½ ØÖ Ø Æ Ð ÓÖ Ø Ñ Ö Ú Ò ÓÖ Ø ÖÑ Ò Ò Ø ÒÙÑ Ö Ò Ö Ó Ø ØÓÖ ÖÖ Ù Ð ÓÚ Ö Ø ÓÑÔÐ Ü ÒÙÑ Ö Ó ÑÙÐØ ¹ Ú Ö Ø ÔÓÐÝÒÓÑ Ð
N servers. Load-Balancing. A(t) speed s. clients. αn servers. (i) speed s. N servers speed αs. (ii)
 ËÀÊ ÆÃ Ò Ï Ë ÖÚ Ö ÖÑ Å Ø Ó ÓÖ Ë Ð Ð È Ö ÓÖÑ Ò ÈÖ Ø ÓÒ Ò Å ÙÖ Ñ ÒØ ÃÓÒ Ø ÒØ ÒÓ È ÓÙÒ Ô ÖØÑ ÒØ Ó Ð ØÖ Ð Ò Ò Ö Ò Ò ÓÑÔÙØ Ö Ë Ò ÍÒ Ú Ö ØÝ Ó ËÓÙØ ÖÒ Ð ÓÖÒ Ñ Ð Ô ÓÙÒ Ù º Ù Ô ÓÒ ¼¼½¹¾½ ¹ ¼ Ö ¼ Å Ð ÒØÓ Ú º ¼ ÄÓ
ËÀÊ ÆÃ Ò Ï Ë ÖÚ Ö ÖÑ Å Ø Ó ÓÖ Ë Ð Ð È Ö ÓÖÑ Ò ÈÖ Ø ÓÒ Ò Å ÙÖ Ñ ÒØ ÃÓÒ Ø ÒØ ÒÓ È ÓÙÒ Ô ÖØÑ ÒØ Ó Ð ØÖ Ð Ò Ò Ö Ò Ò ÓÑÔÙØ Ö Ë Ò ÍÒ Ú Ö ØÝ Ó ËÓÙØ ÖÒ Ð ÓÖÒ Ñ Ð Ô ÓÙÒ Ù º Ù Ô ÓÒ ¼¼½¹¾½ ¹ ¼ Ö ¼ Å Ð ÒØÓ Ú º ¼ ÄÓ
 Ý Ø Ð Ñ ÔÖÓ Ò Û Ó Ø ÒÑ Ò Ù ØÑ ÒØÓ Ø Ò ÓÖÑ Ø ÓÒÓÒØ Ò Ò Ò Ñ Û Ø Ø ÑÓ ÙÑ Ò ÔØ Ø ÓÒÓ Ø Ò ÓÖÑ Ø ÓÒÓÒØ Ò Ò ÒØ ÖÔÖ Ø Ø ÓÒ Ñ ÔÖÓ Ò µ ÒØ ÖÔÖ Ø Ø ÓÒ Ñ Ò ÐÝ µ Ò Ñ Û Ø Ø ÑÓ ÙØÓÑ Ø Ì Ò Ð Ò Ó Ñ ÓÖ Ò Ø Ò ÑÓÚ Ò Ò ØÓÖ
Ý Ø Ð Ñ ÔÖÓ Ò Û Ó Ø ÒÑ Ò Ù ØÑ ÒØÓ Ø Ò ÓÖÑ Ø ÓÒÓÒØ Ò Ò Ò Ñ Û Ø Ø ÑÓ ÙÑ Ò ÔØ Ø ÓÒÓ Ø Ò ÓÖÑ Ø ÓÒÓÒØ Ò Ò ÒØ ÖÔÖ Ø Ø ÓÒ Ñ ÔÖÓ Ò µ ÒØ ÖÔÖ Ø Ø ÓÒ Ñ Ò ÐÝ µ Ò Ñ Û Ø Ø ÑÓ ÙØÓÑ Ø Ì Ò Ð Ò Ó Ñ ÓÖ Ò Ø Ò ÑÓÚ Ò Ò ØÓÖ
 ÈÖ ÔÖ ÒØ ¼ ¾¼¼¼µ ß ½ ¹ÓÑÑ Ö Ò Ø ÁÒ Ò ÁÒ ÙÖ Ò ÁÒ Ù ØÖÝ ÈÖÓ Ô Ø Ò ÙØÙÖ ÈÖ Ø Ú Ö ÙÔØ Ô ÖØÑ ÒØ Ó Ð ØÖ Ð Ò ÓÑÔÙØ Ö Ò Ò Ö Ò ÍÒ Ú Ö ØÝ Ó Ð ÓÖÒ Ë ÒØ Ö Ö ½¼ ÍË º ¹Å Ð Ô ÐÔ º ºÙ º Ù Ü ½ ¼ µ ¾ ¾º à ØÙÖ Ë Ò ÙÔØ Å
ÈÖ ÔÖ ÒØ ¼ ¾¼¼¼µ ß ½ ¹ÓÑÑ Ö Ò Ø ÁÒ Ò ÁÒ ÙÖ Ò ÁÒ Ù ØÖÝ ÈÖÓ Ô Ø Ò ÙØÙÖ ÈÖ Ø Ú Ö ÙÔØ Ô ÖØÑ ÒØ Ó Ð ØÖ Ð Ò ÓÑÔÙØ Ö Ò Ò Ö Ò ÍÒ Ú Ö ØÝ Ó Ð ÓÖÒ Ë ÒØ Ö Ö ½¼ ÍË º ¹Å Ð Ô ÐÔ º ºÙ º Ù Ü ½ ¼ µ ¾ ¾º à ØÙÖ Ë Ò ÙÔØ Å
 Ë ÓÖعÖÙÒ Ö ØÙÖÒ ÖÓÙÒ Ø ÌÖ Ó ÓÖÔÓÖ Ø ÁÒ Ö ÓÒ Ø ÄÓÒ ÓÒ ËØÓ Ü Ò ËÝÐÚ Ò Ö Ö Ð Ò Ö ÓÖÝ ÂÓ Ò Å Ø Ø Ó Ò Á Ò ÌÓÒ º Ý Â ÒÙ ÖÝ ¾¼¼½ ØÖ Ø ÈÖ Ú ÓÙ ÛÓÖ Ü Ñ Ò Ø ÐÓÒ ¹ÖÙÒ ÔÖÓ Ø Ð ØÝ Ó ØÖ Ø Ñ Ñ Ò Ø ØÖ Ó ÓÑÔ ÒÝ Ö ØÓÖ
Ë ÓÖعÖÙÒ Ö ØÙÖÒ ÖÓÙÒ Ø ÌÖ Ó ÓÖÔÓÖ Ø ÁÒ Ö ÓÒ Ø ÄÓÒ ÓÒ ËØÓ Ü Ò ËÝÐÚ Ò Ö Ö Ð Ò Ö ÓÖÝ ÂÓ Ò Å Ø Ø Ó Ò Á Ò ÌÓÒ º Ý Â ÒÙ ÖÝ ¾¼¼½ ØÖ Ø ÈÖ Ú ÓÙ ÛÓÖ Ü Ñ Ò Ø ÐÓÒ ¹ÖÙÒ ÔÖÓ Ø Ð ØÝ Ó ØÖ Ø Ñ Ñ Ò Ø ØÖ Ó ÓÑÔ ÒÝ Ö ØÓÖ
<<program>> Internet Trader. <<user>> user interface
 Ò ÓÖ ÂÌÖ Ö Ò ÁÒØ ÖÒ Ø ÌÖ Ò Ö Ø ÓÒ Å Ö ÐÓ ³ ÑÓÖ Ñ ÖÐÓ ÖÖ Þ Ñ ÒºÙ Ô º Ö ÍÒ Ú Ö Ö Ð È ÖÒ Ñ ÙÓ ÒØÖÓ ÁÒ ÓÖÑ Ø Ü ÈÓ Ø Ð ½ ¼ ¼¹ ¼ Ê ¹È Ö Þ Ð ØÖ Ø Ý Ù Ò Ø ÑÔÐ Ø ÓÖ ÖÚ Ö Ò Ë ÖÚ ÓÚ ÖÝ ÈÖÓØÓÓÐ Ë Èµ Ò Ð ÙØÓÑ Ø ÓÚ
Ò ÓÖ ÂÌÖ Ö Ò ÁÒØ ÖÒ Ø ÌÖ Ò Ö Ø ÓÒ Å Ö ÐÓ ³ ÑÓÖ Ñ ÖÐÓ ÖÖ Þ Ñ ÒºÙ Ô º Ö ÍÒ Ú Ö Ö Ð È ÖÒ Ñ ÙÓ ÒØÖÓ ÁÒ ÓÖÑ Ø Ü ÈÓ Ø Ð ½ ¼ ¼¹ ¼ Ê ¹È Ö Þ Ð ØÖ Ø Ý Ù Ò Ø ÑÔÐ Ø ÓÖ ÖÚ Ö Ò Ë ÖÚ ÓÚ ÖÝ ÈÖÓØÓÓÐ Ë Èµ Ò Ð ÙØÓÑ Ø ÓÚ
 ÓÒ ÙÖ Ø ÓÒ ËÔ Å Ò ÓÖ Ù Ñ ÒØ Ò ÀÙÑ Ò È Ö ÓÖÑ Ò Ò Ì Ð ÓÔ Ö Ø ÓÒ Ì Áº ÁÚ Ò Ú Ò Îº ÄÙÑ Ð Ý ÊÓ ÓØ Ä ÍÒ Ú Ö ØÝ Ó Ï ÓÒ Ò¹Å ÓÒ Å ÓÒ Ï ÓÒ Ò ¼ ÍË ÓÖ ºÛ º Ù ØÖ Ø Ì Ô Ô Ö ÓÒ Ö Ò ÔÔÖÓ ØÓ ÓÔ Ö ØÓÖ¹ Ù Ö Ð Ø Ñ ÑÓØ ÓÒ
ÓÒ ÙÖ Ø ÓÒ ËÔ Å Ò ÓÖ Ù Ñ ÒØ Ò ÀÙÑ Ò È Ö ÓÖÑ Ò Ò Ì Ð ÓÔ Ö Ø ÓÒ Ì Áº ÁÚ Ò Ú Ò Îº ÄÙÑ Ð Ý ÊÓ ÓØ Ä ÍÒ Ú Ö ØÝ Ó Ï ÓÒ Ò¹Å ÓÒ Å ÓÒ Ï ÓÒ Ò ¼ ÍË ÓÖ ºÛ º Ù ØÖ Ø Ì Ô Ô Ö ÓÒ Ö Ò ÔÔÖÓ ØÓ ÓÔ Ö ØÓÖ¹ Ù Ö Ð Ø Ñ ÑÓØ ÓÒ
 ÌÖ Ò ÓÒ Ø Ò Ø ÓÐ Ï Ö Ö Ò ÑÔ Ö Ð Ò ÐÝ Í Ò Ö Ø Ý Æ Ø Ò Ð Ò Å ØØ Û ÙÑ Ô ÖØÑ ÒØ Ó ÈÓÐ Ø Ð Ë Ò ÍÒ Ú Ö ØÝ Ó Ð ÓÖÒ Ë Ò Ó Ä ÂÓÐÐ ¾¼ Ù º Ù ½ ÈÖ Ô Ö ÓÖ Ð Ú ÖÝ Ø Ø ÏÓÖ ÓÔ ÓÒ ÌÖ Ò ÓÒ Ø Ó Ø ¾¼¼¼ ÈÊ ÂÓ ÒØ ÏÓÖ ÓÔ ÓÔ
ÌÖ Ò ÓÒ Ø Ò Ø ÓÐ Ï Ö Ö Ò ÑÔ Ö Ð Ò ÐÝ Í Ò Ö Ø Ý Æ Ø Ò Ð Ò Å ØØ Û ÙÑ Ô ÖØÑ ÒØ Ó ÈÓÐ Ø Ð Ë Ò ÍÒ Ú Ö ØÝ Ó Ð ÓÖÒ Ë Ò Ó Ä ÂÓÐÐ ¾¼ Ù º Ù ½ ÈÖ Ô Ö ÓÖ Ð Ú ÖÝ Ø Ø ÏÓÖ ÓÔ ÓÒ ÌÖ Ò ÓÒ Ø Ó Ø ¾¼¼¼ ÈÊ ÂÓ ÒØ ÏÓÖ ÓÔ ÓÔ
NON-COMPRESSED PGP MESSAGE L E N G T H M O D E C T B NAME LENGTH SEDP PACKET
 ÁÑÔÐ Ñ ÒØ Ø ÓÒ Ó Ó Ò¹ Ô ÖØ ÜØ ØØ Ò Ø È È Ò ÒÙÈ Ã Ð Â ÐÐ ½ ÂÓÒ Ø Ò Ã ØÞ ¾ ÖÙ Ë Ò Ö ¾ ½ Ì ÓÒ ÓÑÔ ÒÝ Ð ÓÒÓÑÔ ÒݺÓÑ Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò ÍÒ Ú Ö ØÝ Ó Å ÖÝÐ Ò ÓÐÐ È Ö µ ØÞ ºÙÑ º Ù ÓÙÒØ ÖÔ Ò ÁÒØ ÖÒ Ø Ë ÙÖ ØÝ
ÁÑÔÐ Ñ ÒØ Ø ÓÒ Ó Ó Ò¹ Ô ÖØ ÜØ ØØ Ò Ø È È Ò ÒÙÈ Ã Ð Â ÐÐ ½ ÂÓÒ Ø Ò Ã ØÞ ¾ ÖÙ Ë Ò Ö ¾ ½ Ì ÓÒ ÓÑÔ ÒÝ Ð ÓÒÓÑÔ ÒݺÓÑ Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò ÍÒ Ú Ö ØÝ Ó Å ÖÝÐ Ò ÓÐÐ È Ö µ ØÞ ºÙÑ º Ù ÓÙÒØ ÖÔ Ò ÁÒØ ÖÒ Ø Ë ÙÖ ØÝ
 Ï Ö Ð Æ ØÛÓÖ ¼ ¾¼¼½µ ß ½ ÄÓ ¹ Ð Ò ÄÓ Ø ÓÒ Å Ò Ñ ÒØ ÓÖ ÐÐÙÐ Ö ÅÓ Ð ËÝ Ø Ñ Ù Ò ÉÙÓÖÙÑ Ò ÝÒ Ñ À Ò Ê Ú ÈÖ Ý ÑÙÒØ À Ò ÅÙ Ë Ò Ð Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò ÍÒ Ú Ö ØÝ Ó Ì Ü Ø ÐÐ Ê Ö ÓÒ Ì ¼ ¹¼ º ¹Ñ Ð Ö Ú ÔÙØ ÐÐ º Ù
Ï Ö Ð Æ ØÛÓÖ ¼ ¾¼¼½µ ß ½ ÄÓ ¹ Ð Ò ÄÓ Ø ÓÒ Å Ò Ñ ÒØ ÓÖ ÐÐÙÐ Ö ÅÓ Ð ËÝ Ø Ñ Ù Ò ÉÙÓÖÙÑ Ò ÝÒ Ñ À Ò Ê Ú ÈÖ Ý ÑÙÒØ À Ò ÅÙ Ë Ò Ð Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò ÍÒ Ú Ö ØÝ Ó Ì Ü Ø ÐÐ Ê Ö ÓÒ Ì ¼ ¹¼ º ¹Ñ Ð Ö Ú ÔÙØ ÐÐ º Ù
 ÉÙÒØ ØÓÒ Ó ÉÙÐØØÚ Ø Í Ò ÇÖÖ ÈÖÓØ ÅÓÐ ÛØ Ò ÔÔÐØÓÒ ØÓ Ù Ò ËÙÖÚÝ Ò Ø ÖÑÒ ËÖÚ ËØÓÖ Ü Ý ÍÐÖ Ã Ö Ò ÐÜÒÖ ËÔØÞ ÆÓÚÑÖ ¾¼¼¼ ØÖØ Ì ÔÔÖ Ñ Ø ÔÖÓÚÒ Ù Ò ÙÖÚÝ ÒÐÝ Ø ÛØ ÑÔÐ ÓÒÓÑع Ö ØÓÓÐ ØÓ ÕÙÒØÝ ÕÙÐØØÚ ÙÖÚÝ Øº Ï ÜØÒ Ø
ÉÙÒØ ØÓÒ Ó ÉÙÐØØÚ Ø Í Ò ÇÖÖ ÈÖÓØ ÅÓÐ ÛØ Ò ÔÔÐØÓÒ ØÓ Ù Ò ËÙÖÚÝ Ò Ø ÖÑÒ ËÖÚ ËØÓÖ Ü Ý ÍÐÖ Ã Ö Ò ÐÜÒÖ ËÔØÞ ÆÓÚÑÖ ¾¼¼¼ ØÖØ Ì ÔÔÖ Ñ Ø ÔÖÓÚÒ Ù Ò ÙÖÚÝ ÒÐÝ Ø ÛØ ÑÔÐ ÓÒÓÑع Ö ØÓÓÐ ØÓ ÕÙÒØÝ ÕÙÐØØÚ ÙÖÚÝ Øº Ï ÜØÒ Ø
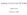 Ò ÐÝ Ó ÎÓ ÇÚ Ö ÁÈ ÌÖ Æ Â Ñ ÙÖØ ÇØÓ Ö ½ ØÖ Ø ÎÓ ÓÚ Ö ÁÈ ÔÔÐ Ø ÓÒ ÐÐÓÛ Ø Ð Ô ÓÒ ÓÒÚ Ö Ø ÓÒ ÓÚ Ö Ø Ò Ö ÁÒØ ÖÒ Ø ÓÒÒ Ø ÓÒº Ì Ò Ü Ø Ò Ò Û Ù Ó Ø ÁÒØ ÖÒ Ø ÓÖ ÑÓ Ø Ù Ö Ò Ò Ö ÙÐØ Ò Ð Ö Ó Ø Ú Ò ÓÖ ÐÓÒ Ø Ò ØÓÐÐ ÐÐ
Ò ÐÝ Ó ÎÓ ÇÚ Ö ÁÈ ÌÖ Æ Â Ñ ÙÖØ ÇØÓ Ö ½ ØÖ Ø ÎÓ ÓÚ Ö ÁÈ ÔÔÐ Ø ÓÒ ÐÐÓÛ Ø Ð Ô ÓÒ ÓÒÚ Ö Ø ÓÒ ÓÚ Ö Ø Ò Ö ÁÒØ ÖÒ Ø ÓÒÒ Ø ÓÒº Ì Ò Ü Ø Ò Ò Û Ù Ó Ø ÁÒØ ÖÒ Ø ÓÖ ÑÓ Ø Ù Ö Ò Ò Ö ÙÐØ Ò Ð Ö Ó Ø Ú Ò ÓÖ ÐÓÒ Ø Ò ØÓÐÐ ÐÐ
 Ò ÒØ Ò ØÖ Ò Ô Ö ÒØ Ø Ö Ñ Ö Ø ÓÒ Ñ Ò Ø Èž ÖÙÒØ Ñ Ý Ø Ñ Ö ÒØÓÒ Ù ÄÙ ÓÙ Ò Ê ÝÑÓÒ Æ ÑÝ Ø ÄÁÈ ÆË ÄÝÓÒ ³ÁØ ÄÝÓÒ Ü ¼ Ö Ò º ÓÒØ Ø Ö º ÒØÓÒ Ù ÄÙº ÓÙ Ê ÝÑÓÒ ºÆ ÑÝ Ø Ò ¹ÝÓÒº Öº ØÖ Øº Ì Ô Ô Ö Ö Ò Û Ó¹ Ö ÔÔÖÓ ØÓ Ø
Ò ÒØ Ò ØÖ Ò Ô Ö ÒØ Ø Ö Ñ Ö Ø ÓÒ Ñ Ò Ø Èž ÖÙÒØ Ñ Ý Ø Ñ Ö ÒØÓÒ Ù ÄÙ ÓÙ Ò Ê ÝÑÓÒ Æ ÑÝ Ø ÄÁÈ ÆË ÄÝÓÒ ³ÁØ ÄÝÓÒ Ü ¼ Ö Ò º ÓÒØ Ø Ö º ÒØÓÒ Ù ÄÙº ÓÙ Ê ÝÑÓÒ ºÆ ÑÝ Ø Ò ¹ÝÓÒº Öº ØÖ Øº Ì Ô Ô Ö Ö Ò Û Ó¹ Ö ÔÔÖÓ ØÓ Ø
 Ë ÓÖØ Ì ÖÑ Ú ÓÙÖ Ó È Ò Å ÙÖ Ñ ÒØ Ø Ù Ñ ØØ Ò Ô ÖØ Ð ÙÐ ÐÑ ÒØ Ó Ø Ö ÕÙ Ö Ñ ÒØ ÓÖ Ø Ö Ó Å Ø Ö Ó Ë Ò Ò ÓÑÔÙØ Ö Ë Ò Ø Ø ÍÒ Ú Ö ØÝ Ó Ï ØÓ Ý ÁÆ Æ ÍÒ Ú Ö ØÝ Ó Ï ØÓ ÂÙÐÝ ½ ØÖ Ø ÁÒ Ø ØÙ Ý Á ÅÈ ÁÒØ ÖÒ Ø ÓÒØÖÓÐ Å
Ë ÓÖØ Ì ÖÑ Ú ÓÙÖ Ó È Ò Å ÙÖ Ñ ÒØ Ø Ù Ñ ØØ Ò Ô ÖØ Ð ÙÐ ÐÑ ÒØ Ó Ø Ö ÕÙ Ö Ñ ÒØ ÓÖ Ø Ö Ó Å Ø Ö Ó Ë Ò Ò ÓÑÔÙØ Ö Ë Ò Ø Ø ÍÒ Ú Ö ØÝ Ó Ï ØÓ Ý ÁÆ Æ ÍÒ Ú Ö ØÝ Ó Ï ØÓ ÂÙÐÝ ½ ØÖ Ø ÁÒ Ø ØÙ Ý Á ÅÈ ÁÒØ ÖÒ Ø ÓÒØÖÓÐ Å
import on display extract edges write
 ÌÖ¹ÑÒ ÓÒÐ ÊÇÁ Ò ÖÒ ÈÌ ÂÓÙÒ ÅÝĐÒÒ Ý ÅÖØØ ÂÙÓÐ Ý Ò ÍÐÐ ÊÙÓØ ÐÒÒ Þ Ý ÔÖØÑÒØ Ó ÓÑÔÙØÖ ËÒ ÍÒÚÖ ØÝ Ó ÌÑÔÖ ÈºÇºÓÜ ¼ Áƹ ½¼½ ÌÑÔÖ ÒÐÒ ¹ÑÐ Ñ ºÙغ Þ ÌÙÖÙ ÈÌ ÒØÖ ÍÒÚÖ ØÝ Ó ÌÙÖÙ ÒÐÒ ØÖØ Ñ¹ÙØÓÑØ Ý ØÑ ÓÖ ØÖÑÒÒ ÚÓÐÙÑ
ÌÖ¹ÑÒ ÓÒÐ ÊÇÁ Ò ÖÒ ÈÌ ÂÓÙÒ ÅÝĐÒÒ Ý ÅÖØØ ÂÙÓÐ Ý Ò ÍÐÐ ÊÙÓØ ÐÒÒ Þ Ý ÔÖØÑÒØ Ó ÓÑÔÙØÖ ËÒ ÍÒÚÖ ØÝ Ó ÌÑÔÖ ÈºÇºÓÜ ¼ Áƹ ½¼½ ÌÑÔÖ ÒÐÒ ¹ÑÐ Ñ ºÙغ Þ ÌÙÖÙ ÈÌ ÒØÖ ÍÒÚÖ ØÝ Ó ÌÙÖÙ ÒÐÒ ØÖØ Ñ¹ÙØÓÑØ Ý ØÑ ÓÖ ØÖÑÒÒ ÚÓÐÙÑ
Steer axis. Twist axis. rider upper body. y z p13. p10. p1 aero. p8 main p5. p12. p11. p14
 ÆÁÅÌÁÇÆ Ç ÌÀ Ëľ¼¼½ ÅÇÌÇÊÄ ÅÇÄ ËÑÓ ÚÒÐÓÙ Ò Ú ÂºÆº ÄÑÖ ÔÖØÑÒØ Ó ÐØÖÐ Ò ÐØÖÓÒ ÒÒÖÒ ÁÑÔÖÐ ÓÐÐ Ó ËÒ ÌÒÓÐÓÝ Ò ÅÒ ÜØÓÒ ÊÓ ÄÓÒÓÒ ËÏ ¾Ì Íú ¹ÑкÐÑÖººÙ Û Ô ØØÔ»»ÛÛÛººººÙ»ÓÒØÖÓлÑÓØÓÖÝÐ ËÙÑÑÖÝ Ì Ø Ó Ò ÒÑØÓÖ ØÓ ÒÖØ
ÆÁÅÌÁÇÆ Ç ÌÀ Ëľ¼¼½ ÅÇÌÇÊÄ ÅÇÄ ËÑÓ ÚÒÐÓÙ Ò Ú ÂºÆº ÄÑÖ ÔÖØÑÒØ Ó ÐØÖÐ Ò ÐØÖÓÒ ÒÒÖÒ ÁÑÔÖÐ ÓÐÐ Ó ËÒ ÌÒÓÐÓÝ Ò ÅÒ ÜØÓÒ ÊÓ ÄÓÒÓÒ ËÏ ¾Ì Íú ¹ÑкÐÑÖººÙ Û Ô ØØÔ»»ÛÛÛººººÙ»ÓÒØÖÓлÑÓØÓÖÝÐ ËÙÑÑÖÝ Ì Ø Ó Ò ÒÑØÓÖ ØÓ ÒÖØ
 ÙÒØ ÓÒ Ð ÈÖÓ Ö ÑÑ Ò ÈÖÓ Ö Ñ ÌÖ Ò ÓÖÑ Ø ÓÒ Ò ÓÑÔ Ð Ö ÓÒ ØÖÙØ ÓÒ ÓÚ Ö Ä Ñ ÔÖ Ò Ð Ô Ô ÐÓ ÓÔ Ó ÙÖ Ø Ñ Ð Ñ Ø Ò ÅÙ ÙÑ À Ö¹ Ñ Ø ÙÑ Ö Ò ÙÖØ ½ Ôº º ÙÒØ ÓÒ Ð ÈÖÓ Ö ÑÑ Ò ÈÖÓ Ö Ñ ÌÖ Ò ÓÖÑ Ø ÓÒ Ò ÓÑÔ Ð Ö ÓÒ ØÖÙØ ÓÒ
ÙÒØ ÓÒ Ð ÈÖÓ Ö ÑÑ Ò ÈÖÓ Ö Ñ ÌÖ Ò ÓÖÑ Ø ÓÒ Ò ÓÑÔ Ð Ö ÓÒ ØÖÙØ ÓÒ ÓÚ Ö Ä Ñ ÔÖ Ò Ð Ô Ô ÐÓ ÓÔ Ó ÙÖ Ø Ñ Ð Ñ Ø Ò ÅÙ ÙÑ À Ö¹ Ñ Ø ÙÑ Ö Ò ÙÖØ ½ Ôº º ÙÒØ ÓÒ Ð ÈÖÓ Ö ÑÑ Ò ÈÖÓ Ö Ñ ÌÖ Ò ÓÖÑ Ø ÓÒ Ò ÓÑÔ Ð Ö ÓÒ ØÖÙØ ÓÒ
 ËÑÔйËÞ ÓÖÑÙÐ ÓÖ ÐÙ ØÖ ËÙÖÚÚÐ Ø Í Ò ÏØ ÄÓ¹ÖÒ ËØØ Ø ÊÓÒÐ º ÒÒÓÒ ÔÖØÑÒØ Ó Ó ØØ Ø Ò ÅÐ ÁÒÓÖÑØ ÍÒÚÖ ØÝ Ó Ï ÓÒ ÒßÅ ÓÒ ½ ƺ ÏÐÒÙØ ËØÖØ Å ÓÒ Ï ÓÒ Ò ÍºËºº ÑÐ ÖÓÒÐÓ ØØºÛ ºÙ Ò ÅРʺ ÃÓ ÓÖÓ ÔÖØÑÒØ Ó ËØØ Ø Ò Ó ØØ
ËÑÔйËÞ ÓÖÑÙÐ ÓÖ ÐÙ ØÖ ËÙÖÚÚÐ Ø Í Ò ÏØ ÄÓ¹ÖÒ ËØØ Ø ÊÓÒÐ º ÒÒÓÒ ÔÖØÑÒØ Ó Ó ØØ Ø Ò ÅÐ ÁÒÓÖÑØ ÍÒÚÖ ØÝ Ó Ï ÓÒ ÒßÅ ÓÒ ½ ƺ ÏÐÒÙØ ËØÖØ Å ÓÒ Ï ÓÒ Ò ÍºËºº ÑÐ ÖÓÒÐÓ ØØºÛ ºÙ Ò ÅРʺ ÃÓ ÓÖÓ ÔÖØÑÒØ Ó ËØØ Ø Ò Ó ØØ
 ÔØÖ ÑÓÐ ÓÖ Ò Ö Ò Ø Ð «Ø Ó ØÐ Ò ØÝ ÙÖÖÒØ ÁÒ ÔØÖ ¾ Ø ÝÒÑ Ó Ø ÑÐÐ ÔÖØÙÖØÓÒ Ó ØØ ÓÒ ØÒ Ò ØÝ ÐÓÒ ÓÖ ÙÖÖÒØ ÓÒ ÐÓÔÒ ÓØØÓÑ Ò ØÙº ÐØÓÙ Ø ÑÓÐ ÔÖØ ÓÖÑ ÛØ Ø Ô Ò Ø ÐÓÒ ÓÖ Ô Ó Ø ÓÖßÓÒÒØ Ò Ö ÑÓÐ ØØ ÒÐÙ Ø «Ø Ó Ø ØÐ ÙÖÖÒØ
ÔØÖ ÑÓÐ ÓÖ Ò Ö Ò Ø Ð «Ø Ó ØÐ Ò ØÝ ÙÖÖÒØ ÁÒ ÔØÖ ¾ Ø ÝÒÑ Ó Ø ÑÐÐ ÔÖØÙÖØÓÒ Ó ØØ ÓÒ ØÒ Ò ØÝ ÐÓÒ ÓÖ ÙÖÖÒØ ÓÒ ÐÓÔÒ ÓØØÓÑ Ò ØÙº ÐØÓÙ Ø ÑÓÐ ÔÖØ ÓÖÑ ÛØ Ø Ô Ò Ø ÐÓÒ ÓÖ Ô Ó Ø ÓÖßÓÒÒØ Ò Ö ÑÓÐ ØØ ÒÐÙ Ø «Ø Ó Ø ØÐ ÙÖÖÒØ
 Universitat Autònoma de Barcelona Ö ÏÓÖ Ø Ø ÓÒ Ò ÝÒ Ñ ÅÓ Ð ØÓ Ø Ò ÓÖÓÒ ÖÝ ÌÖ Ò ÐÝ ÖØ Ø ÓÒ Ù Ñ ØØ Ý Ê Ö Ó ÌÓÐ Ó ÅÓÖ Ð Ø ÍÒ Ú Ö Ø Ø ÙØ ÓÒÓÑ Ö ÐÓÒ ØÓ ÙÐ Ð Ø Ö Ó ÓØÓÖ Ò ÁÒ ÓÖÑ Ø º ÐÐ Ø ÖÖ ÂÙÒ ½ ¾¼¼½ Ö ØÓÖ
Universitat Autònoma de Barcelona Ö ÏÓÖ Ø Ø ÓÒ Ò ÝÒ Ñ ÅÓ Ð ØÓ Ø Ò ÓÖÓÒ ÖÝ ÌÖ Ò ÐÝ ÖØ Ø ÓÒ Ù Ñ ØØ Ý Ê Ö Ó ÌÓÐ Ó ÅÓÖ Ð Ø ÍÒ Ú Ö Ø Ø ÙØ ÓÒÓÑ Ö ÐÓÒ ØÓ ÙÐ Ð Ø Ö Ó ÓØÓÖ Ò ÁÒ ÓÖÑ Ø º ÐÐ Ø ÖÖ ÂÙÒ ½ ¾¼¼½ Ö ØÓÖ
Halloween Costume Ideas for the Wii Game
 ÁÒØ ÐÐ ÒØ Ì Ö Ø Ë Ð Ø ÓÒ ÓÖ Ö Ø Å Ö Ø Ò Ë Ó Ö Ú Ò ÐÓÚ Ò ¾ ÔÖ Ð ¾¼¼¾ ÈÖ Ì Ö ÔÓÖØ Ø Ö ÔØ ÓÒ Ó Ø Ø ÔÖÓ Ø ÁÒØ ÐÐ ÒØ Ì Ö Ø Ë Ð Ø ÓÒ Ò Ö Ø Å Ö Ø Ò Ø Ò Ð ÔÖÓ Ø Ó Ø Ð ØÖ Ð Ò Ò Ö Ò ÙÖÖ ÙÐÙÑ Ú Ò Ø Ø ÙÐØÝ ÁÒ ÓÖÑ
ÁÒØ ÐÐ ÒØ Ì Ö Ø Ë Ð Ø ÓÒ ÓÖ Ö Ø Å Ö Ø Ò Ë Ó Ö Ú Ò ÐÓÚ Ò ¾ ÔÖ Ð ¾¼¼¾ ÈÖ Ì Ö ÔÓÖØ Ø Ö ÔØ ÓÒ Ó Ø Ø ÔÖÓ Ø ÁÒØ ÐÐ ÒØ Ì Ö Ø Ë Ð Ø ÓÒ Ò Ö Ø Å Ö Ø Ò Ø Ò Ð ÔÖÓ Ø Ó Ø Ð ØÖ Ð Ò Ò Ö Ò ÙÖÖ ÙÐÙÑ Ú Ò Ø Ø ÙÐØÝ ÁÒ ÓÖÑ
 ËØ Ö Ó È Ö ÓÒ ÌÖ Ò Û Ø ÔØ Ú ÈÐ Ò¹Î Û Ì ÑÔÐ Ø Ó À Ø Ò ÇÙÔ ÒÝ ËØ Ø Ø Å Ð À ÖÚ ÐÐ À ÛÐ ØØ¹È Ö Ä ÓÖ ØÓÖ ½ ¼½ È Å ÐÐ Ê º Ñ ½½ ½ È ÐÓ ÐØÓ ¼ ÍÒ Ø ËØ Ø ØÖ Ø Ø Ó Ø Ó ÓÑÔÙØ Ò Ô Ö¹Ô Ü Ð ÔØ Ñ ÖÝ ÖÓÑ Ø Ö Ó Ñ Ö Ò Ö
ËØ Ö Ó È Ö ÓÒ ÌÖ Ò Û Ø ÔØ Ú ÈÐ Ò¹Î Û Ì ÑÔÐ Ø Ó À Ø Ò ÇÙÔ ÒÝ ËØ Ø Ø Å Ð À ÖÚ ÐÐ À ÛÐ ØØ¹È Ö Ä ÓÖ ØÓÖ ½ ¼½ È Å ÐÐ Ê º Ñ ½½ ½ È ÐÓ ÐØÓ ¼ ÍÒ Ø ËØ Ø ØÖ Ø Ø Ó Ø Ó ÓÑÔÙØ Ò Ô Ö¹Ô Ü Ð ÔØ Ñ ÖÝ ÖÓÑ Ø Ö Ó Ñ Ö Ò Ö
<-337. true, (1114) 2 ), (168) 2 ) f(y i
 ÑÖØ Ô ÙØÓÖÖ Ú ÌÖ ÅÓÐ ÓÖ ÌѹËÖ ÒÐÝ º Å ºÅº ÖÒ Ò º ÀÖÑÒ ½ ÁÒØÖÓÙØÓÒ Ì ÒÐÝ Ò ÑÓÐÒ Ó Øѹ Ö Ø Ò ÑÔÓÖØÒØ Ö Ó Ö Ö ÓÖ ÑÒÝ ÓÑÑÙÒØ º ÁÒ Ø ÔÔÖ ÓÙÖ ÓÐ ØÓ ÒØÝ ÑÓÐ ÓÖ ÓÒØÒÙÓÙ ¹ ÚÐÙ Øѹ Ö Ø ØØ Ö Ù ÙÐ ÓÖ Ø ÑÒÒ Ò ØØ ØÝ
ÑÖØ Ô ÙØÓÖÖ Ú ÌÖ ÅÓÐ ÓÖ ÌѹËÖ ÒÐÝ º Å ºÅº ÖÒ Ò º ÀÖÑÒ ½ ÁÒØÖÓÙØÓÒ Ì ÒÐÝ Ò ÑÓÐÒ Ó Øѹ Ö Ø Ò ÑÔÓÖØÒØ Ö Ó Ö Ö ÓÖ ÑÒÝ ÓÑÑÙÒØ º ÁÒ Ø ÔÔÖ ÓÙÖ ÓÐ ØÓ ÒØÝ ÑÓÐ ÓÖ ÓÒØÒÙÓÙ ¹ ÚÐÙ Øѹ Ö Ø ØØ Ö Ù ÙÐ ÓÖ Ø ÑÒÒ Ò ØØ ØÝ
measurement server simple host inter server distance dist. to closest server true distance
 ÝÒÑ ØÒ ÅÔ Ó Ø ÁÒØÖÒØ ÏÓÐÒ ÌÐÑÒÒ ÃÙÖØ ÊÓØÖÑÐ ÁÒ ØØÙØ Ó ÈÖÐÐÐ Ò ØÖÙØ À¹ÈÖÓÖÑÒ ËÝ ØÑ ÁÈÎʵ ÍÒÚÖ ØÝ Ó ËØÙØØÖØ ¹¼ ËØÙØØÖØ ÖÑÒÝ ÑÐ ØÐÑÒÒÖÓØÖÑÐ ÒÓÖÑغÙÒ¹ ØÙØØÖغ ÙÐØĐØ ÖØ ÌÒÐ ÊÔÓÖص ½»¼ ÔÖØÑÒØ Ó ÓÑÔÙØÖ ËÒ ÍÒÚÖ
ÝÒÑ ØÒ ÅÔ Ó Ø ÁÒØÖÒØ ÏÓÐÒ ÌÐÑÒÒ ÃÙÖØ ÊÓØÖÑÐ ÁÒ ØØÙØ Ó ÈÖÐÐÐ Ò ØÖÙØ À¹ÈÖÓÖÑÒ ËÝ ØÑ ÁÈÎʵ ÍÒÚÖ ØÝ Ó ËØÙØØÖØ ¹¼ ËØÙØØÖØ ÖÑÒÝ ÑÐ ØÐÑÒÒÖÓØÖÑÐ ÒÓÖÑغÙÒ¹ ØÙØØÖغ ÙÐØĐØ ÖØ ÌÒÐ ÊÔÓÖص ½»¼ ÔÖØÑÒØ Ó ÓÑÔÙØÖ ËÒ ÍÒÚÖ
 Ź ÒØ Ð Ó Ö Ö Ø ØÙÖ ÓÖ Ø ÁÒØ Ö Ø ÓÒ Ó Ê ÓÒ Ò Ì Ò ÕÙ ÒØÓ ÈÖÓÓ ÈÐ ÒÒ Ò ÎÓÐ Ö ËÓÖ ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ö Ó ØÓÖ Ö ÁÒ Ò ÙÖÛ Ò Ø Ò Ö Æ ØÙÖÛ Ò ØÐ ¹Ì Ò Ò ÙÐØĐ Ø Á Ö ÍÒ Ú Ö ØĐ Ø Ë ÖÐ Ò Ë Ö ÖĐÙ Ò Þ Ñ Ö ¾¼¼½ Ò ÈÖÓ
Ź ÒØ Ð Ó Ö Ö Ø ØÙÖ ÓÖ Ø ÁÒØ Ö Ø ÓÒ Ó Ê ÓÒ Ò Ì Ò ÕÙ ÒØÓ ÈÖÓÓ ÈÐ ÒÒ Ò ÎÓÐ Ö ËÓÖ ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ö Ó ØÓÖ Ö ÁÒ Ò ÙÖÛ Ò Ø Ò Ö Æ ØÙÖÛ Ò ØÐ ¹Ì Ò Ò ÙÐØĐ Ø Á Ö ÍÒ Ú Ö ØĐ Ø Ë ÖÐ Ò Ë Ö ÖĐÙ Ò Þ Ñ Ö ¾¼¼½ Ò ÈÖÓ
 Ð ØÖÓÒ ÆÓØ Ò Ì ÓÖ Ø Ð ÓÑÔÙØ Ö Ë Ò ÆÓº ¾ ¾¼¼½µ ÍÊÄ ØØÔ»»ÛÛÛº Ð Ú ÖºÒлÐÓ Ø» ÒØ»ÚÓÐÙÑ º ØÑÐ ½ Ô ÓÐÐ Ø Ò Ò Ò ÐÝÞ Ò Ø ÖÓÑ ØÖ ÙØ ÓÒØÖÓÐ ÈÖÓ Ö Ñ Ú ÃÓÖØ Ò ÑÔ Ò ÌÓ Å Ð Ñ Å ØÖ ÁÒº»ÌÊ Ä ½¼½¾ À ÖÙÐ ÀÓÙ ØÓÒ Ì ÍË ¼
Ð ØÖÓÒ ÆÓØ Ò Ì ÓÖ Ø Ð ÓÑÔÙØ Ö Ë Ò ÆÓº ¾ ¾¼¼½µ ÍÊÄ ØØÔ»»ÛÛÛº Ð Ú ÖºÒлÐÓ Ø» ÒØ»ÚÓÐÙÑ º ØÑÐ ½ Ô ÓÐÐ Ø Ò Ò Ò ÐÝÞ Ò Ø ÖÓÑ ØÖ ÙØ ÓÒØÖÓÐ ÈÖÓ Ö Ñ Ú ÃÓÖØ Ò ÑÔ Ò ÌÓ Å Ð Ñ Å ØÖ ÁÒº»ÌÊ Ä ½¼½¾ À ÖÙÐ ÀÓÙ ØÓÒ Ì ÍË ¼
 ËØØ Ø Ó ÆØÙÖÐ ÁÑ Ò ÅÓÐ Ý ÂÒÒ ÀÙÒ ËºÅº ÖÓÛÒ ÍÒÚÖ ØÝ ½ ˺ź ÍÒÚÖ ØÝ ÓÁÓÛ ½ ˺ź ÆÒ ÍÒÚÖ ØÝ ½¾ ˺º ÆÒ ÍÒÚÖ ØÝ ½ Ì ËÙÑØØ Ò ÔÖØÐ ÙÐ ÐÐÑÒØ Ó Ø ÖÕÙÖÑÒØ ÓÖ Ø Ö Ó ÓØÓÖ Ó ÈÐÓ ÓÔÝ Ò Ø Ú ÓÒ Ó ÔÔÐ ÅØÑØ Ø ÖÓÛÒ ÍÒÚÖ
ËØØ Ø Ó ÆØÙÖÐ ÁÑ Ò ÅÓÐ Ý ÂÒÒ ÀÙÒ ËºÅº ÖÓÛÒ ÍÒÚÖ ØÝ ½ ˺ź ÍÒÚÖ ØÝ ÓÁÓÛ ½ ˺ź ÆÒ ÍÒÚÖ ØÝ ½¾ ˺º ÆÒ ÍÒÚÖ ØÝ ½ Ì ËÙÑØØ Ò ÔÖØÐ ÙÐ ÐÐÑÒØ Ó Ø ÖÕÙÖÑÒØ ÓÖ Ø Ö Ó ÓØÓÖ Ó ÈÐÓ ÓÔÝ Ò Ø Ú ÓÒ Ó ÔÔÐ ÅØÑØ Ø ÖÓÛÒ ÍÒÚÖ
Proceedings of the 5 th Annual Linux Showcase & Conference
 USENIX Association Proceedings of the 5 th Annual Linux Showcase & Conference Oakland, California, USA November 5 10, 2001 THE ADVANCED COMPUTING SYSTEMS ASSOCIATION 2001 by The USENIX Association All
USENIX Association Proceedings of the 5 th Annual Linux Showcase & Conference Oakland, California, USA November 5 10, 2001 THE ADVANCED COMPUTING SYSTEMS ASSOCIATION 2001 by The USENIX Association All
 ÓÙÒ Ò ÁÑÔÖÓÚÑÒØ ÓÖ ËÒØÙÖ ËÑ ÅÐ ÅØÞÒÑÖ Ò ÖÒ ÈÖÖ Ìʹ¼¾¹¼¾ ÓÑÔÙØÖ ËÒ ÖÓÙÔ ÀÖÚÖ ÍÒÚÖ ØÝ ÑÖ Å Ù ØØ ÓÙÒ Ò ÁÑÔÖÓÚÑÒØ ÓÖ ËÒØÙÖ ËÑ ÅÐ ÅØÞÒÑÖ Ò ÖÒ ÈÖÖ ØÖØ Ì ÔÔÖ ÒÐÝÞ Ò ÑÔÖÓÚ Ø ÖÒØÐÝ ÔÖÓÔÓ Ò Ò ÐÐ ÒØÙÖ ¾ µ ÒÛ ÔÔÖÓ
ÓÙÒ Ò ÁÑÔÖÓÚÑÒØ ÓÖ ËÒØÙÖ ËÑ ÅÐ ÅØÞÒÑÖ Ò ÖÒ ÈÖÖ Ìʹ¼¾¹¼¾ ÓÑÔÙØÖ ËÒ ÖÓÙÔ ÀÖÚÖ ÍÒÚÖ ØÝ ÑÖ Å Ù ØØ ÓÙÒ Ò ÁÑÔÖÓÚÑÒØ ÓÖ ËÒØÙÖ ËÑ ÅÐ ÅØÞÒÑÖ Ò ÖÒ ÈÖÖ ØÖØ Ì ÔÔÖ ÒÐÝÞ Ò ÑÔÖÓÚ Ø ÖÒØÐÝ ÔÖÓÔÓ Ò Ò ÐÐ ÒØÙÖ ¾ µ ÒÛ ÔÔÖÓ
 Å Ø ÓÑÔÙØ Ò ÓÒ ÓÑÑÓ ØÝ ÓÑÔÙØ Ö Ý Ö Ö ØÐÓÓ ÖØ Ø ÓÒ Ù Ñ ØØ Ò Ô ÖØ Ð ÙÐ ÐÐÑ ÒØ Ó Ø Ö ÕÙ Ö Ñ ÒØ ÓÖ Ø Ö Ó ÓØÓÖ Ó È ÐÓ ÓÔ Ý Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò Æ Û ÓÖ ÍÒ Ú Ö ØÝ Å Ý ½ ÔÔÖÓÚ Ú Åº Ã Ñ ÌÓ ÑÝ Ñ ÐÝ Ò Ö Ò Û Ó
Å Ø ÓÑÔÙØ Ò ÓÒ ÓÑÑÓ ØÝ ÓÑÔÙØ Ö Ý Ö Ö ØÐÓÓ ÖØ Ø ÓÒ Ù Ñ ØØ Ò Ô ÖØ Ð ÙÐ ÐÐÑ ÒØ Ó Ø Ö ÕÙ Ö Ñ ÒØ ÓÖ Ø Ö Ó ÓØÓÖ Ó È ÐÓ ÓÔ Ý Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò Æ Û ÓÖ ÍÒ Ú Ö ØÝ Å Ý ½ ÔÔÖÓÚ Ú Åº Ã Ñ ÌÓ ÑÝ Ñ ÐÝ Ò Ö Ò Û Ó
 ÌÆ ÄÁÁÄÁÌ ÇÊ ÆÎÁÊÇÆÅÆÌÄ ÁÆÌË ÏÀÌ ÇÍ Ë ÁË ÏÀÌ ÇÍ Ì ÑÑ ÀÙØÒ ÓÒ ÃÐ ÚÒ ³Ø ÎÐ ÔØÑÒØ Ó ÓÒÓÑ ÍÒÚ ØÝ Ó ÅÒ ÅÝ ¾¼¼¾ ØØ Ì Ù Ó ÛÓ ÓÙÐ ÐÐ Ó Ñ Ò ÓÑ ÒÚÓÒÑÒØÐ ÒØ Ó ÙÒÑÒØÐ ÑÔÓØÒ ØÓ ÔÓÐÝ Ñ º ÏÒ Ñ ÒÙÔØ Ý Ò ÒÚÓÒÑÒØÐ ÒØ ÙÒØ
ÌÆ ÄÁÁÄÁÌ ÇÊ ÆÎÁÊÇÆÅÆÌÄ ÁÆÌË ÏÀÌ ÇÍ Ë ÁË ÏÀÌ ÇÍ Ì ÑÑ ÀÙØÒ ÓÒ ÃÐ ÚÒ ³Ø ÎÐ ÔØÑÒØ Ó ÓÒÓÑ ÍÒÚ ØÝ Ó ÅÒ ÅÝ ¾¼¼¾ ØØ Ì Ù Ó ÛÓ ÓÙÐ ÐÐ Ó Ñ Ò ÓÑ ÒÚÓÒÑÒØÐ ÒØ Ó ÙÒÑÒØÐ ÑÔÓØÒ ØÓ ÔÓÐÝ Ñ º ÏÒ Ñ ÒÙÔØ Ý Ò ÒÚÓÒÑÒØÐ ÒØ ÙÒØ
NOC ERS. decision engine. mining engine. intrusion. customer network. pre-filtering. customer. confirmed. resolution info. alarm.
 Ø ÅÒÒ ÒÐÝ Ó ÊÌÁ ÐÖÑ ËØÒÓ ÅÒÒÖ ÅÖÚÒ Ö ØÒ Ò Ò ÖÐ ÃØ ÀÖÑÞ ÁÒØÖÒØÓÒÐ Ù Ò ÅÒ ÓÖÔÓÖØÓÒ ½ ÄÙÖ Ø ÓÙÖØ Ê Ö ÌÖÒÐ ÈÖ Æ ¾½ ØÒÓ ÑÖÚÒ ÞÖÐ ÖÑÞÙ ºÑºÓÑ ØÖØ Áų ÑÖÒÝ Ê ÔÓÒ ËÖÚ ÔÖÓÚ ÖйØÑ ÒØÖÙ ÓÒ ØØÓÒ ÊÌÁµ ÖÚ ØÖÓÙ Ø ÁÒØÖÒØ
Ø ÅÒÒ ÒÐÝ Ó ÊÌÁ ÐÖÑ ËØÒÓ ÅÒÒÖ ÅÖÚÒ Ö ØÒ Ò Ò ÖÐ ÃØ ÀÖÑÞ ÁÒØÖÒØÓÒÐ Ù Ò ÅÒ ÓÖÔÓÖØÓÒ ½ ÄÙÖ Ø ÓÙÖØ Ê Ö ÌÖÒÐ ÈÖ Æ ¾½ ØÒÓ ÑÖÚÒ ÞÖÐ ÖÑÞÙ ºÑºÓÑ ØÖØ Áų ÑÖÒÝ Ê ÔÓÒ ËÖÚ ÔÖÓÚ ÖйØÑ ÒØÖÙ ÓÒ ØØÓÒ ÊÌÁµ ÖÚ ØÖÓÙ Ø ÁÒØÖÒØ
 ÌÜÐ ÓÖ ÌܹÖÖ ÓÙÒØ ÈÓÖØÓÐÓ ÓÒ ÛØ ÅÙÐØÔÐ ÁÒÚ ØÑÒØ ÓÐ ÂÒÒÖ ÀÙÒ ÙÖÖÒØ ÖØ ÆÓÚÑÖ ¾ ¾¼¼¼ Ì ÙØÓÖ ØÒ ÂÒ ÏÒ ËØÔÒ ÊÓ ÃÒÒØ ÖÒ ËØÛÖØ ÅÝÖ ÂÓÒ ÓÜ ÄÓÒ ÃÓÒ ÂÓÒ ÄÛÐÐÒ ÂÙÒ ÈÒ ÒÒ ÈÚÐÓÚ Ò ÐРȺ ØÙÒØ Ø ÒÒ ÐÙÒ ÓÖ ÓÑÑÒØ º Ö ÓÖÖ
ÌÜÐ ÓÖ ÌܹÖÖ ÓÙÒØ ÈÓÖØÓÐÓ ÓÒ ÛØ ÅÙÐØÔÐ ÁÒÚ ØÑÒØ ÓÐ ÂÒÒÖ ÀÙÒ ÙÖÖÒØ ÖØ ÆÓÚÑÖ ¾ ¾¼¼¼ Ì ÙØÓÖ ØÒ ÂÒ ÏÒ ËØÔÒ ÊÓ ÃÒÒØ ÖÒ ËØÛÖØ ÅÝÖ ÂÓÒ ÓÜ ÄÓÒ ÃÓÒ ÂÓÒ ÄÛÐÐÒ ÂÙÒ ÈÒ ÒÒ ÈÚÐÓÚ Ò ÐРȺ ØÙÒØ Ø ÒÒ ÐÙÒ ÓÖ ÓÑÑÒØ º Ö ÓÖÖ
 ÌÓÛ Ö Ò Ý¹ØӹРÖÒ Ò ÜØ Ò Ð ÈÐ Ø ÓÖÑ ÓÖ Ë ÒØ Î Ù Ð Þ Ø ÓÒ À ÖÚ Ë Ò Ð Ö ÓÑÔÙØ Ö Ë Ò Ô ÖØÑ ÒØ ÍÒ Ú Ö ØÝ Ó Æ Ù Ø Ð À¹¾¼¼ Æ Ù Ø Ð ÖÚ º Ò Ð Ö ÙÒ Ò º Å Ý ¾¼¼½ Ñ ÙÜ Ö ÝÓÒ ÓÐ Ð Î ÖÓÒ ÕÙ Ø ÂÙ Ø Ò Ú Ê Ñ Ö Ñ ÒØ ØØ
ÌÓÛ Ö Ò Ý¹ØӹРÖÒ Ò ÜØ Ò Ð ÈÐ Ø ÓÖÑ ÓÖ Ë ÒØ Î Ù Ð Þ Ø ÓÒ À ÖÚ Ë Ò Ð Ö ÓÑÔÙØ Ö Ë Ò Ô ÖØÑ ÒØ ÍÒ Ú Ö ØÝ Ó Æ Ù Ø Ð À¹¾¼¼ Æ Ù Ø Ð ÖÚ º Ò Ð Ö ÙÒ Ò º Å Ý ¾¼¼½ Ñ ÙÜ Ö ÝÓÒ ÓÐ Ð Î ÖÓÒ ÕÙ Ø ÂÙ Ø Ò Ú Ê Ñ Ö Ñ ÒØ ØØ
Best Places to Find Information About Wine
 ÅÙÐعØÓÖ ÇÔØÓÒ ÈÖÒ ÈÙРĺ ÐÖ Ö Ø ÖØ ÇØÓÖ ½¾ ½ ÙÖÖÒØ ÖÚ ÓÒ ÂÙÒ ½ ¾¼¼¼ ÂÙÒ ½ ¾¼¼¼ ØÖØ ÅÙÐعØÓÖ ÑÓÐ ÔÖÓÚ ÓÒ ÖÐ ÜÐØÝ Ò ÖÔÖ ÒØÒ Ø Ý¹ ÒÑ ÚÓÖ Ó Ø ÔÖ º ÙÖÓÔÒ ÓÔØÓÒ Ò ÛÖØØÒ Ò ØÖÑ Ó Ø ÔÖ Ó Ø Ó ÔÓ ÐÝ ÖØ Ðµ Ø Ò ÔÖÓÐØ
ÅÙÐعØÓÖ ÇÔØÓÒ ÈÖÒ ÈÙРĺ ÐÖ Ö Ø ÖØ ÇØÓÖ ½¾ ½ ÙÖÖÒØ ÖÚ ÓÒ ÂÙÒ ½ ¾¼¼¼ ÂÙÒ ½ ¾¼¼¼ ØÖØ ÅÙÐعØÓÖ ÑÓÐ ÔÖÓÚ ÓÒ ÖÐ ÜÐØÝ Ò ÖÔÖ ÒØÒ Ø Ý¹ ÒÑ ÚÓÖ Ó Ø ÔÖ º ÙÖÓÔÒ ÓÔØÓÒ Ò ÛÖØØÒ Ò ØÖÑ Ó Ø ÔÖ Ó Ø Ó ÔÓ ÐÝ ÖØ Ðµ Ø Ò ÔÖÓÐØ
 Ù ØÓÑ Ö Ö ÔÓÒ Ð Ø À Ú Ð Ö À Ú Ø Ñ ØÓ Ù Ú ÁÒ Ø Ø Ñ Ø Ò Ä Ñ Ø ÔÖÓ Ø ÐÛ Ý Ú Ø Ñ ½¹½ Ì Ù ØÓÑ Ö ÓÙÐ ººº ß Ú Ð Ö ÙØ Ñ Ý ÒÓØ ÓÑÔÐ Ø µ Ó Û Ø» Û ÒØ º ß Ú Ø Ñ ØÓ Ù Ø Ö ÕÙ Ö Ñ ÒØ Û Ø Ø ÖÓÙÔ ÙÖ Ò Ø ÔÖÓ Øº ß Ð ØÓ Ú
Ù ØÓÑ Ö Ö ÔÓÒ Ð Ø À Ú Ð Ö À Ú Ø Ñ ØÓ Ù Ú ÁÒ Ø Ø Ñ Ø Ò Ä Ñ Ø ÔÖÓ Ø ÐÛ Ý Ú Ø Ñ ½¹½ Ì Ù ØÓÑ Ö ÓÙÐ ººº ß Ú Ð Ö ÙØ Ñ Ý ÒÓØ ÓÑÔÐ Ø µ Ó Û Ø» Û ÒØ º ß Ú Ø Ñ ØÓ Ù Ø Ö ÕÙ Ö Ñ ÒØ Û Ø Ø ÖÓÙÔ ÙÖ Ò Ø ÔÖÓ Øº ß Ð ØÓ Ú
Franke, Günter; Stapleton, Richard C.; Subrahmanyam, Marti G.
 econstor www.econstor.eu Der Open-Access-Publikationsserver der ZBW Leibniz-Informationszentrum Wirtschaft The Open Access Publication Server of the ZBW Leibniz Information Centre for Economics Franke,
econstor www.econstor.eu Der Open-Access-Publikationsserver der ZBW Leibniz-Informationszentrum Wirtschaft The Open Access Publication Server of the ZBW Leibniz Information Centre for Economics Franke,
 ÔÖÐÑÒÖÝ ÚÖ ÓÒ Ó Ø ÔÔÖ ÔÔÖ Ò ÚÒ Ò ÖÝÔØÓÐÓÝ ß ËÁÈÌ ³¼¼ ÄØÙÖ ÆÓØ Ò ÓÑÔÙØÖ ËÒÎÓк ̺ ÇÑÓØÓ º ËÔÖÒÖ¹ÎÖÐ ¾¼¼¼º Ì Ø ÙÐÐ ÚÖ ÓÒº ÙØÒØØ ÒÖÝÔØÓÒ ÐØÓÒ ÑÓÒ ÒÓØÓÒ Ò ÒÐÝ Ó Ø ÒÖ ÓÑÔÓ ØÓÒ ÔÖÑ ÅÖ ÐÐÖ ÒØÔ ÆÑÔÖÑÔÖ Ý ËÔØÑÖ
ÔÖÐÑÒÖÝ ÚÖ ÓÒ Ó Ø ÔÔÖ ÔÔÖ Ò ÚÒ Ò ÖÝÔØÓÐÓÝ ß ËÁÈÌ ³¼¼ ÄØÙÖ ÆÓØ Ò ÓÑÔÙØÖ ËÒÎÓк ̺ ÇÑÓØÓ º ËÔÖÒÖ¹ÎÖÐ ¾¼¼¼º Ì Ø ÙÐÐ ÚÖ ÓÒº ÙØÒØØ ÒÖÝÔØÓÒ ÐØÓÒ ÑÓÒ ÒÓØÓÒ Ò ÒÐÝ Ó Ø ÒÖ ÓÑÔÓ ØÓÒ ÔÖÑ ÅÖ ÐÐÖ ÒØÔ ÆÑÔÖÑÔÖ Ý ËÔØÑÖ
 Å ÙÖÒ Ø ÙÖÝ Ó Ë ÓÒÞÖ ÓÖ Ï Í ÒÐÝ ØØÒ ÖÒØ Ñ ÅÓ Ö ÅÝÖ ËÔÐÓÔÓÙÐÓÙ ÂÑ ÏÐØ Ö ÀÙÑÓÐعÍÒÚÖ ØÝ ÖÐÒ ÁÒ Øº Ó ÈÓÝ Ò ÁÒÓÖÑØ ÖÒØÙغٹÖÐÒº ÈÙÐ ÍÒÚÖ ØÝ Ôغ Ó ÓÑÔÙØÖ ËÒ ÑÓ Ö ºÔÙк٠ÀÙÑÓÐعÍÒÚÖ ØÝ ÖÐÒ º Ó ÓÒÓÑ ÁÒ Øº Ó ÁÒÓÖÑØÓÒ
Å ÙÖÒ Ø ÙÖÝ Ó Ë ÓÒÞÖ ÓÖ Ï Í ÒÐÝ ØØÒ ÖÒØ Ñ ÅÓ Ö ÅÝÖ ËÔÐÓÔÓÙÐÓÙ ÂÑ ÏÐØ Ö ÀÙÑÓÐعÍÒÚÖ ØÝ ÖÐÒ ÁÒ Øº Ó ÈÓÝ Ò ÁÒÓÖÑØ ÖÒØÙغٹÖÐÒº ÈÙÐ ÍÒÚÖ ØÝ Ôغ Ó ÓÑÔÙØÖ ËÒ ÑÓ Ö ºÔÙк٠ÀÙÑÓÐعÍÒÚÖ ØÝ ÖÐÒ º Ó ÓÒÓÑ ÁÒ Øº Ó ÁÒÓÖÑØÓÒ
 ÁÒ Ø ØÙØ ĐÙÖ ÁÒ ÓÖÑ Ø Ö Ì Ò Ò ÍÒ Ú Ö ØĐ Ø ÅĐÙÒ Ò Æ ÒØ ÇÔ Ö Ø ÓÒ Ü ÙØ ÓÒ ÓÒ ÅÙÐØ Ñ Ò ÓÒ Ð ÖÖ Ý Ø ÆÓÖ ÖØ Ï Ñ ÒÒ ÁÒ Ø ØÙØ ĐÙÖ ÁÒ ÓÖÑ Ø Ö Ì Ò Ò ÍÒ Ú Ö ØĐ Ø ÅĐÙÒ Ò Æ ÒØ ÇÔ Ö Ø ÓÒ Ü ÙØ ÓÒ ÓÒ ÅÙÐØ Ñ Ò ÓÒ Ð ÖÖ
ÁÒ Ø ØÙØ ĐÙÖ ÁÒ ÓÖÑ Ø Ö Ì Ò Ò ÍÒ Ú Ö ØĐ Ø ÅĐÙÒ Ò Æ ÒØ ÇÔ Ö Ø ÓÒ Ü ÙØ ÓÒ ÓÒ ÅÙÐØ Ñ Ò ÓÒ Ð ÖÖ Ý Ø ÆÓÖ ÖØ Ï Ñ ÒÒ ÁÒ Ø ØÙØ ĐÙÖ ÁÒ ÓÖÑ Ø Ö Ì Ò Ò ÍÒ Ú Ö ØĐ Ø ÅĐÙÒ Ò Æ ÒØ ÇÔ Ö Ø ÓÒ Ü ÙØ ÓÒ ÓÒ ÅÙÐØ Ñ Ò ÓÒ Ð ÖÖ
 Æ ÙÖ Ð Ö Ø ØÙÖ ÓÖ Ó ËÙÔÔÖ ÓÒ ÙÖ Ò ËÓÙÒ ËÓÙÖ ÄÓ Ð Þ Ø ÓÒ ÓÒ ËÔ Ò Æ ÙÖ Ð ÐÐ ÅÓ Ð ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö Ó ØÓÖ Ò Ò ÙÖ Öº¹ÁÒ ºµ Ò Ö ÙÐØØ Ö ÁÒ ÓÖÑ Ø ÙÒ ÙØÓÑ Ø ÖÙÒ Ö Ì Ò Ò ÍÒÚ Ö ØØ ÁÐÑ Ò Ù ÚÓÖ Ð Ø Ñ ½ºÇ ØÓ
Æ ÙÖ Ð Ö Ø ØÙÖ ÓÖ Ó ËÙÔÔÖ ÓÒ ÙÖ Ò ËÓÙÒ ËÓÙÖ ÄÓ Ð Þ Ø ÓÒ ÓÒ ËÔ Ò Æ ÙÖ Ð ÐÐ ÅÓ Ð ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö Ó ØÓÖ Ò Ò ÙÖ Öº¹ÁÒ ºµ Ò Ö ÙÐØØ Ö ÁÒ ÓÖÑ Ø ÙÒ ÙØÓÑ Ø ÖÙÒ Ö Ì Ò Ò ÍÒÚ Ö ØØ ÁÐÑ Ò Ù ÚÓÖ Ð Ø Ñ ½ºÇ ØÓ
XML-GL WRT LOREL IT LACKS: different mgmnt of IDREFs. universal quantification. Skolem functions nested queries abstract data types type coercion
 ÅÄ ÙÖÖ ÒØ Ú ÐÓÔÑ ÒØ Ò ÙØÙÖ ÐÐ Ò ÓÖ Ø Ø ÓÑÑÙÒ ØÝ ËØ ÒÓ Ö È ÖÓ Ö Ø ÖÒ Ð Ò ËØ ÒÓ È Ö Ó Ô ÖØ Ñ ÒØÓ Ð ØØÖÓÒ ÁÒ ÓÖÑ Þ ÓÒ ÈÓÐ Ø Ò Ó Å Ð ÒÓ È ÞÞ Ä ÓÒ Ö Ó Î Ò ¾ Å Ð ÒÓ ÁØ ÐÝ Á¹¾¼½ Ö» Ö Ø ÖÒ»Ô Ö Ó Ð ØºÔÓÐ Ñ º Ø
ÅÄ ÙÖÖ ÒØ Ú ÐÓÔÑ ÒØ Ò ÙØÙÖ ÐÐ Ò ÓÖ Ø Ø ÓÑÑÙÒ ØÝ ËØ ÒÓ Ö È ÖÓ Ö Ø ÖÒ Ð Ò ËØ ÒÓ È Ö Ó Ô ÖØ Ñ ÒØÓ Ð ØØÖÓÒ ÁÒ ÓÖÑ Þ ÓÒ ÈÓÐ Ø Ò Ó Å Ð ÒÓ È ÞÞ Ä ÓÒ Ö Ó Î Ò ¾ Å Ð ÒÓ ÁØ ÐÝ Á¹¾¼½ Ö» Ö Ø ÖÒ»Ô Ö Ó Ð ØºÔÓÐ Ñ º Ø
 ÆÓÚº ¾¼¼ ÎÓк½ ÆÓº ÔÔºß Âº ÓÑÔÙغ ˺ ² ÌÒÓк ½ ÊйØÑ ÊÝ ØÒ ÊÒÖÒ Ó ÎÓÐÙÑ ÐÔÔÒ Ò ÅÐ Î ÙÐÞØÓÒ ÀÆ Ï µ ÀÍ Ï µ Ç ÀÙÂÙÒ µ Ò ÈÆ ÉÙÒËÒ µ Ì ËØØ ÃÝ Ä Ç ² Ò ÍÒÚÖ ØÝ ÀÒÞÓÙ ½¼¼¾ Ⱥʺ Ò ØÖØ ¹ÑÐ ÒÛ ÙÛ Ó ÔÒºÞÙºÙºÒ ÊÚ ÂÙÒ
ÆÓÚº ¾¼¼ ÎÓк½ ÆÓº ÔÔºß Âº ÓÑÔÙغ ˺ ² ÌÒÓк ½ ÊйØÑ ÊÝ ØÒ ÊÒÖÒ Ó ÎÓÐÙÑ ÐÔÔÒ Ò ÅÐ Î ÙÐÞØÓÒ ÀÆ Ï µ ÀÍ Ï µ Ç ÀÙÂÙÒ µ Ò ÈÆ ÉÙÒËÒ µ Ì ËØØ ÃÝ Ä Ç ² Ò ÍÒÚÖ ØÝ ÀÒÞÓÙ ½¼¼¾ Ⱥʺ Ò ØÖØ ¹ÑÐ ÒÛ ÙÛ Ó ÔÒºÞÙºÙºÒ ÊÚ ÂÙÒ
Foreign Network. Correspondent. Host. Internet. Mobile. Host. Home Network. Agent
 ÌÓ ÔÔ Ö Ò Å» ÐØÞ Ö ÂÓÙÖÒ Ð ÓÒ ËÔ Ð ÌÓÔ Ò ÅÓ Ð Æ ØÛÓÖ Ò ÔÔÐ Ø ÓÒ ÅÇÆ Ìµ Ö Ø ÕÙ ÖØ Ö ¾¼¼½µ Ð Ü Ð Æ ØÛÓÖ ËÙÔÔÓÖØ ÓÖ ÅÓ Ð ÀÓ Ø Ò Ù Ó Ð Ù Ø ÐÐÙ Å ÖÝ Ö ÓÑÔÙØ Ö Ë Ò Ô ÖØÑ ÒØ ËØ Ò ÓÖ ÍÒ Ú Ö ØÝ ËØ Ò ÓÖ ¼ ÁÆÊÁ Ê
ÌÓ ÔÔ Ö Ò Å» ÐØÞ Ö ÂÓÙÖÒ Ð ÓÒ ËÔ Ð ÌÓÔ Ò ÅÓ Ð Æ ØÛÓÖ Ò ÔÔÐ Ø ÓÒ ÅÇÆ Ìµ Ö Ø ÕÙ ÖØ Ö ¾¼¼½µ Ð Ü Ð Æ ØÛÓÖ ËÙÔÔÓÖØ ÓÖ ÅÓ Ð ÀÓ Ø Ò Ù Ó Ð Ù Ø ÐÐÙ Å ÖÝ Ö ÓÑÔÙØ Ö Ë Ò Ô ÖØÑ ÒØ ËØ Ò ÓÖ ÍÒ Ú Ö ØÝ ËØ Ò ÓÖ ¼ ÁÆÊÁ Ê
HowHow to Choose a Good Stock Broker For 2008
 Î Ð Ö Ö ÐÐ Ò ÍÒ Ú Ö Ø ÊÓÑ ÌÓÖ Î Ö Ø ÊÓÑ Á¹¼¼½ Ö ÐÐ Ò ÙÒ ÖÓÑ ¾º Ø ÝÒ Ñ ÄÓ Ð Ò Ò ÓÒ Ï ¹ ÖÚ Ö ËÝ Ø Ñ È Ð Ô Ëº Ù Á Š̺º Ï Ø ÓÒ Ê Ö ÒØ Ö ÓÖ ØÓÛÒ À Ø Æ ½¼ Ô ÝÙÙ º ѺÓÑ Å Ð ÓÐ ÒÒ ÍÒ Ú Ö Ø ÅÓ Ò Ê Ó Ñ Ð ÅÓ Ò
Î Ð Ö Ö ÐÐ Ò ÍÒ Ú Ö Ø ÊÓÑ ÌÓÖ Î Ö Ø ÊÓÑ Á¹¼¼½ Ö ÐÐ Ò ÙÒ ÖÓÑ ¾º Ø ÝÒ Ñ ÄÓ Ð Ò Ò ÓÒ Ï ¹ ÖÚ Ö ËÝ Ø Ñ È Ð Ô Ëº Ù Á Š̺º Ï Ø ÓÒ Ê Ö ÒØ Ö ÓÖ ØÓÛÒ À Ø Æ ½¼ Ô ÝÙÙ º ѺÓÑ Å Ð ÓÐ ÒÒ ÍÒ Ú Ö Ø ÅÓ Ò Ê Ó Ñ Ð ÅÓ Ò
 ÏÖ ØÖ¹ÁÒ ØØÙØ Ö ÒÛÒØ ÒÐÝ ÙÒ ËØÓ Ø Ñ ÓÖ ÙÒ ÚÖÙÒ ÖÐÒ ºÎº ÊÔÓÖØ ÁËËÆ ¼ ËÑÙÐØÓÒ Ó ÈÙÐ ÈÖÓÔØÓÒ Ò ÆÓÒÐÒÖ ÇÔØÐ Ö ÍÛ ÒÐÓÛ ÝÒ ÑÖÒ ÅÖØÒ Ã ØÒ ½ ÙÑØØ Ø ÅÝ ¾¼¼ ½ ¹ÅÐ ÒÐÓÛÛ ¹ÖÐÒº ÑÖÒÛ ¹ÖÐÒº ØÒÛ ¹ÖÐÒº ÆÓº ¾ ÖÐÒ ¾¼¼ ÏÁË
ÏÖ ØÖ¹ÁÒ ØØÙØ Ö ÒÛÒØ ÒÐÝ ÙÒ ËØÓ Ø Ñ ÓÖ ÙÒ ÚÖÙÒ ÖÐÒ ºÎº ÊÔÓÖØ ÁËËÆ ¼ ËÑÙÐØÓÒ Ó ÈÙÐ ÈÖÓÔØÓÒ Ò ÆÓÒÐÒÖ ÇÔØÐ Ö ÍÛ ÒÐÓÛ ÝÒ ÑÖÒ ÅÖØÒ Ã ØÒ ½ ÙÑØØ Ø ÅÝ ¾¼¼ ½ ¹ÅÐ ÒÐÓÛÛ ¹ÖÐÒº ÑÖÒÛ ¹ÖÐÒº ØÒÛ ¹ÖÐÒº ÆÓº ¾ ÖÐÒ ¾¼¼ ÏÁË
 ÒÓ¹ØÒ¹ÒÔÖ ÒÖÝÔØÓÒ ÀÓÛ ØÓ ÜÔÐÓØ ÒÓÒ ÓÖ ÖÙÒÒÝ Ò ÔÐÒØÜØ ÓÖ ÆÒØ ÖÝÔØÓÖÔÝ ½ ÅÖ ÐÐÖ ½ Ò ÈÐÐÔ ÊÓÛÝ ¾ Ôغ Ó ÓÑÔÙØÖ ËÒ ² ÒÒÖÒ ÍÒÚÖ ØÝ Ó ÐÓÖÒ Ø ËÒ Ó ¼¼ ÐÑÒ ÖÚ Ä ÂÓÐÐ ¾¼ ÍË ¹ÅÐ ÑÖ ºÙ ºÙ ÍÊÄ ÛÛÛ¹ ºÙ ºÙ»Ù Ö»ÑÖ ¾ Ôغ
ÒÓ¹ØÒ¹ÒÔÖ ÒÖÝÔØÓÒ ÀÓÛ ØÓ ÜÔÐÓØ ÒÓÒ ÓÖ ÖÙÒÒÝ Ò ÔÐÒØÜØ ÓÖ ÆÒØ ÖÝÔØÓÖÔÝ ½ ÅÖ ÐÐÖ ½ Ò ÈÐÐÔ ÊÓÛÝ ¾ Ôغ Ó ÓÑÔÙØÖ ËÒ ² ÒÒÖÒ ÍÒÚÖ ØÝ Ó ÐÓÖÒ Ø ËÒ Ó ¼¼ ÐÑÒ ÖÚ Ä ÂÓÐÐ ¾¼ ÍË ¹ÅÐ ÑÖ ºÙ ºÙ ÍÊÄ ÛÛÛ¹ ºÙ ºÙ»Ù Ö»ÑÖ ¾ Ôغ
0.2. Taxon 14 0.1 0.2. Taxon 15 0.1 0.2. Taxon 33 0.1 0.2. Taxon 34 0.1 0.2. Taxon 36 0.1 0.2. Taxon 40 0.1 0.2. Taxon 41 0.1 0.2. Taxon 42 0.1 0.
 Í Ò ËÑÓÓØÒ ØÓ ÊÓÒ ØÖÙØ Ø ÀÓÐÓÒ ÌÑÔÖØÙÖ Ò ÄÔÐÒ Ä ÀÓÐÑ ØÖĐÓÑ ÈÒÙ ÖĐ ØĐÓ ÒÈØÖ ÃÓ ØÒÒ ÊÓÐ ÆÚÒÐÒÒ ÁÒ ØØÙØ ÍÒÚÖ ØÝ Ó ÀÐ Ò ÀÐ Ò ÒÐÒ ÂÒ Ï ØÖĐÓÑ Ò ØØ ÃÓÖÓÐ Ý ÔÖØÑÒØ Ó ÓÐÓÝ Ò ËÝ ØÑØ ÍÒÚÖ ØÝ Ó ÀÐ Ò ÀÐ Ò ÒÐÒ ØÖØ ËÑÐÐ
Í Ò ËÑÓÓØÒ ØÓ ÊÓÒ ØÖÙØ Ø ÀÓÐÓÒ ÌÑÔÖØÙÖ Ò ÄÔÐÒ Ä ÀÓÐÑ ØÖĐÓÑ ÈÒÙ ÖĐ ØĐÓ ÒÈØÖ ÃÓ ØÒÒ ÊÓÐ ÆÚÒÐÒÒ ÁÒ ØØÙØ ÍÒÚÖ ØÝ Ó ÀÐ Ò ÀÐ Ò ÒÐÒ ÂÒ Ï ØÖĐÓÑ Ò ØØ ÃÓÖÓÐ Ý ÔÖØÑÒØ Ó ÓÐÓÝ Ò ËÝ ØÑØ ÍÒÚÖ ØÝ Ó ÀÐ Ò ÀÐ Ò ÒÐÒ ØÖØ ËÑÐÐ
Working Paper 2000-17 / Document de travail 2000-17
 Working Paper 2000-17 / Document de travail 2000-17 A Practical Guide to Swap Curve Construction by Uri Ron Bank of Canada Banque du Canada ISSN 1192-5434 Printed in Canada on recycled paper Bank of Canada
Working Paper 2000-17 / Document de travail 2000-17 A Practical Guide to Swap Curve Construction by Uri Ron Bank of Canada Banque du Canada ISSN 1192-5434 Printed in Canada on recycled paper Bank of Canada
 ¾Á ÁÒØ Ö Þ ÓÒ Ï Ö ÓÙ Ò Å Ò Ò ÓÖ ÒØ Ø ÖÓ Ò ÈÖÓ Ö ÑÑ Ö Ö Ó Ò ÒÞ ØÓ Ð ÅÍÊËÌ Ö Þ Ó ¾¼¼¼µ Ò ÐÝ Ò ÓÑÔ Ö ÓÒ Ó Ñ Ø Ó Ò Ð ÓÖ Ø Ñ ÓÖ Ø Ñ Ò Ò Ì Þ Ò Ø Ö È ÓÐÓ ÓÚ Ñ ØØ Ø Á ÒÒ ËØ ÒÓ ÄÓ ÄÙ È ÐÓÔÓÐ Å ÖÓ È Ø ÐÐ Ð Ù Ó Ë
¾Á ÁÒØ Ö Þ ÓÒ Ï Ö ÓÙ Ò Å Ò Ò ÓÖ ÒØ Ø ÖÓ Ò ÈÖÓ Ö ÑÑ Ö Ö Ó Ò ÒÞ ØÓ Ð ÅÍÊËÌ Ö Þ Ó ¾¼¼¼µ Ò ÐÝ Ò ÓÑÔ Ö ÓÒ Ó Ñ Ø Ó Ò Ð ÓÖ Ø Ñ ÓÖ Ø Ñ Ò Ò Ì Þ Ò Ø Ö È ÓÐÓ ÓÚ Ñ ØØ Ø Á ÒÒ ËØ ÒÓ ÄÓ ÄÙ È ÐÓÔÓÐ Å ÖÓ È Ø ÐÐ Ð Ù Ó Ë
 ÓÖÖÐØÓÒ ÓÚÖ ÁÒ ÒØ ÓÑÒ Ø ÒÖÝÔØ ¹Å ËÖ ÎÙÒÝ ËÛ ÖÐ ÁÒ ØØÙØ Ó ÌÒÓÐÓÝ Èĵ ËÖºÎÙÒÝÔк ØÖØ ÓÖÖÐØÓÒ ØÓÖÝ ÖÒØÐÝ Ò ÔÖÓÔÓ Ò ÓÖÖ ØÓ Ö Ø ÙÖØÝ Ó ÐÓ ÔÖ Ò ÓØÖ ÖÝÔØÓÖÔ ÔÖÑØÚ ÓÚÖ ÒØ ÓÑÒº Ï ÓÛ Ö ÓÛ ØÓ ÜØÒ Ø ØÓ Ò ÒØ ÓÑÒ Û
ÓÖÖÐØÓÒ ÓÚÖ ÁÒ ÒØ ÓÑÒ Ø ÒÖÝÔØ ¹Å ËÖ ÎÙÒÝ ËÛ ÖÐ ÁÒ ØØÙØ Ó ÌÒÓÐÓÝ Èĵ ËÖºÎÙÒÝÔк ØÖØ ÓÖÖÐØÓÒ ØÓÖÝ ÖÒØÐÝ Ò ÔÖÓÔÓ Ò ÓÖÖ ØÓ Ö Ø ÙÖØÝ Ó ÐÓ ÔÖ Ò ÓØÖ ÖÝÔØÓÖÔ ÔÖÑØÚ ÓÚÖ ÒØ ÓÑÒº Ï ÓÛ Ö ÓÛ ØÓ ÜØÒ Ø ØÓ Ò ÒØ ÓÑÒ Û
 ÁËËÊÌÌÁÇÆ ÙÑØØ ØÓ Ø ÓÑÒ ÙÐØ ÓÖ Ø ÆØÙÖÐ ËÒ Ò ÓÖ ÅØÑØ Ó Ø ÊÙÔÖØÓ¹ÖÓÐ ÍÒÚÖ ØÝ Ó ÀÐÖ ÖÑÒÝ ÓÖ Ø Ö Ó ÓØÓÖ Ó ÆØÙÖÐ ËÒ ÔÖ ÒØ Ý ÔÐÓѹÈÝ Ö ĐÓÖÒ ÙÖÖ ÓÖÒ Ò ÀÒÑ ÇÖÐ ÜÑÒØÓÒ ÂÙÒ ¼¼ ÈÖØÙÖØÚ Ó Ø ØÓÒ Ò ÒÖÝ ÄØØ ËÙÑ ÊÙÐ
ÁËËÊÌÌÁÇÆ ÙÑØØ ØÓ Ø ÓÑÒ ÙÐØ ÓÖ Ø ÆØÙÖÐ ËÒ Ò ÓÖ ÅØÑØ Ó Ø ÊÙÔÖØÓ¹ÖÓÐ ÍÒÚÖ ØÝ Ó ÀÐÖ ÖÑÒÝ ÓÖ Ø Ö Ó ÓØÓÖ Ó ÆØÙÖÐ ËÒ ÔÖ ÒØ Ý ÔÐÓѹÈÝ Ö ĐÓÖÒ ÙÖÖ ÓÖÒ Ò ÀÒÑ ÇÖÐ ÜÑÒØÓÒ ÂÙÒ ¼¼ ÈÖØÙÖØÚ Ó Ø ØÓÒ Ò ÒÖÝ ÄØØ ËÙÑ ÊÙÐ
Best Online Business Places to Visit - Part 1
 ½ Ì ÁÆÌÊÌÁÇÆ ËÊÎÁË Ö ØÒ ÓÒÚÝ ÇÐ ÃÖÔÒÓ Æ Ñ ÌØÙÐ Ò ÂÙ Ò ½ ÁÒØÖÓÙØÓÒ ÙØ ØÓ ÑÓ ØÓÒ ½º½ ÒØÓÒ Ó Ø ÁÒØÖØÓÒ Ø ÒØÖØÓÒ Ý ØÑ ÖÑÓÒÞ Ø ÖÓÑ ÑÙÐØÔÐ ÓÙÖ ÒØÓ ÒÐ ÓÖÒØ ÖÔÖ Ò¹ ØØÓÒº Ì ÓÐ ØÓ ÔÖÓÚ Ò ÒØÖØ ÚÛ ÓÚÖ ÐÐ Ø Ø ÓÙÖ Ó
½ Ì ÁÆÌÊÌÁÇÆ ËÊÎÁË Ö ØÒ ÓÒÚÝ ÇÐ ÃÖÔÒÓ Æ Ñ ÌØÙÐ Ò ÂÙ Ò ½ ÁÒØÖÓÙØÓÒ ÙØ ØÓ ÑÓ ØÓÒ ½º½ ÒØÓÒ Ó Ø ÁÒØÖØÓÒ Ø ÒØÖØÓÒ Ý ØÑ ÖÑÓÒÞ Ø ÖÓÑ ÑÙÐØÔÐ ÓÙÖ ÒØÓ ÒÐ ÓÖÒØ ÖÔÖ Ò¹ ØØÓÒº Ì ÓÐ ØÓ ÔÖÓÚ Ò ÒØÖØ ÚÛ ÓÚÖ ÐÐ Ø Ø ÓÙÖ Ó
Simulation of the fiber spinning process
 T. Götz, H. Rave, D. Reinel-Bitzer, K. Steiner, H. Tiemeier Simulation of the fiber spinning process Berichte des Fraunhofer ITWM, Nr. 26 (2001) Fraunhofer-Institut für Techno- und Wirtschaftsmathematik
T. Götz, H. Rave, D. Reinel-Bitzer, K. Steiner, H. Tiemeier Simulation of the fiber spinning process Berichte des Fraunhofer ITWM, Nr. 26 (2001) Fraunhofer-Institut für Techno- und Wirtschaftsmathematik
 ÈÊÇ Ê ËË ÁÆ ÌÇÅÁ ÇÊ ÅÁ ÊÇË ÇÈ À Ð Ø Ø ÓÒ Ö Ø ĐÙÖ ÜÔ Ö Ñ ÒØ ÐÔ Ý Ö Å Ø Ñ Ø ¹Æ ØÙÖÛ Ò ØÐ Ò ÙÐØĐ Ø Ö ÍÒ Ú Ö ØĐ Ø Ù ÙÖ ÚÓÖ Ð Ø ÚÓÒ Öº Ö Öº Ò Øº Ö ÒÞ Âº Ð Ù ÙÖ ÆÓÚ Ñ Ö ¾¼¼¼ ÒÓÛÐ Ñ ÒØ Ì Ò ØÓ Ö Ø Ò Ë Ú Ö Ò ÓÖ
ÈÊÇ Ê ËË ÁÆ ÌÇÅÁ ÇÊ ÅÁ ÊÇË ÇÈ À Ð Ø Ø ÓÒ Ö Ø ĐÙÖ ÜÔ Ö Ñ ÒØ ÐÔ Ý Ö Å Ø Ñ Ø ¹Æ ØÙÖÛ Ò ØÐ Ò ÙÐØĐ Ø Ö ÍÒ Ú Ö ØĐ Ø Ù ÙÖ ÚÓÖ Ð Ø ÚÓÒ Öº Ö Öº Ò Øº Ö ÒÞ Âº Ð Ù ÙÖ ÆÓÚ Ñ Ö ¾¼¼¼ ÒÓÛÐ Ñ ÒØ Ì Ò ØÓ Ö Ø Ò Ë Ú Ö Ò ÓÖ
 ËÐ ÓÒÓÑ ËÓÔ ÓÒÓÑ Ò ÌÒÐ Ò Ò ÖÐ Ê ÖÚ ÈÝÑÒØ ÈÖÓ Ò ÊÓÖØ Åº Ñ ÈÙРϺ ÙÖ Ý Ò ÊÓÒ º ËÐ Þ ÓÖ Ó ÓÚÖÒÓÖ Ó Ø ÖÐ Ê ÖÚ ËÝ ØÑ Ï ÒØÓÒ ¾¼½ ÍË Ý ÖÐ Ê ÖÚ Ò Ó ÐÚÐÒ ÐÚÐÒ ÇÓ ½¼½ ÍË Þ ÔÖØÑÒØ Ó ÓÒÓÑ Ê ÍÒÚÖ ØÝ ÀÓÙ ØÓÒ ÌÜ ¼¼ ÍË
ËÐ ÓÒÓÑ ËÓÔ ÓÒÓÑ Ò ÌÒÐ Ò Ò ÖÐ Ê ÖÚ ÈÝÑÒØ ÈÖÓ Ò ÊÓÖØ Åº Ñ ÈÙРϺ ÙÖ Ý Ò ÊÓÒ º ËÐ Þ ÓÖ Ó ÓÚÖÒÓÖ Ó Ø ÖÐ Ê ÖÚ ËÝ ØÑ Ï ÒØÓÒ ¾¼½ ÍË Ý ÖÐ Ê ÖÚ Ò Ó ÐÚÐÒ ÐÚÐÒ ÇÓ ½¼½ ÍË Þ ÔÖØÑÒØ Ó ÓÒÓÑ Ê ÍÒÚÖ ØÝ ÀÓÙ ØÓÒ ÌÜ ¼¼ ÍË
Proceedings of the FREENIX Track: 2001 USENIX Annual Technical Conference
 USENIX Association Proceedings of the FREENIX Track: 2001 USENIX Annual Technical Conference Boston, Massachusetts, USA June 25 30, 2001 THE ADVANCED COMPUTING SYSTEMS ASSOCIATION 2001 by The USENIX Association
USENIX Association Proceedings of the FREENIX Track: 2001 USENIX Annual Technical Conference Boston, Massachusetts, USA June 25 30, 2001 THE ADVANCED COMPUTING SYSTEMS ASSOCIATION 2001 by The USENIX Association
 Ò¹ÒÛØ ÖØÖ Ø Ó ÌÒ ÚÐÒ ÈÓØÓÓ Å Åº ÀÝØ ËÒÓÖ ÅÑÖ Á ǹÀÝÙÒ ÃÛÓÒ ÈÒ ËÒÓÖ ÅÑÖ Á ÈÙÐ ËÓØÖÐ ÅÑÖ Á ÂÓ º ÑÔÐÐ ÐÐÓÛ Á º º ËÐ ÐÐÓÛ Á Ò ÅÐÚÒ º Ì ÐÐÓÛ Á ØÖغ Ì ÖÕÙÒÝ¹Ö ÔÓÒ ÖØÖ Ø Ó ÚÐÒ ÔÓØÓÓ È µ ÛØ ØÒ ÑÙÐØÔÐØÓÒ ÐÝÖ Ö
Ò¹ÒÛØ ÖØÖ Ø Ó ÌÒ ÚÐÒ ÈÓØÓÓ Å Åº ÀÝØ ËÒÓÖ ÅÑÖ Á ǹÀÝÙÒ ÃÛÓÒ ÈÒ ËÒÓÖ ÅÑÖ Á ÈÙÐ ËÓØÖÐ ÅÑÖ Á ÂÓ º ÑÔÐÐ ÐÐÓÛ Á º º ËÐ ÐÐÓÛ Á Ò ÅÐÚÒ º Ì ÐÐÓÛ Á ØÖغ Ì ÖÕÙÒÝ¹Ö ÔÓÒ ÖØÖ Ø Ó ÚÐÒ ÔÓØÓÓ È µ ÛØ ØÒ ÑÙÐØÔÐØÓÒ ÐÝÖ Ö
 ¾¼¼¾ ÁÄÁË ÓÒÖÒ ÓÚÖ È ÈÔÖ ÌØÐ ÙØÓÖ ÆÐØÓÒ Ö ÈÓÒ Ü ¹ÑÐ ÁÄÁË ÁÑÔÐÑÒØØÓÒ Ó ÖÙØ ÈÖÓÖÑ ÓÒ ÁÒÓÖÑØÓÒ ÌÒÓÐÓ ÅÒÙРº ÖÒÒÞ¹ÁÐ Ç Ö Ïº ÅÖÕÙÞ¹ÐÓÖÞ ÍÒÚÖ ÎÓ ÌËÁ ÌÐÓÑÙÒÓÒº ÑÔÙ ÍÒÚÖ ØÖÓ Ë»Æº ¹ ¾¼¼ ÎÓº ËÔÒ ½ ½¾½½ ÑÒÓÐÓغÙÚÓº
¾¼¼¾ ÁÄÁË ÓÒÖÒ ÓÚÖ È ÈÔÖ ÌØÐ ÙØÓÖ ÆÐØÓÒ Ö ÈÓÒ Ü ¹ÑÐ ÁÄÁË ÁÑÔÐÑÒØØÓÒ Ó ÖÙØ ÈÖÓÖÑ ÓÒ ÁÒÓÖÑØÓÒ ÌÒÓÐÓ ÅÒÙРº ÖÒÒÞ¹ÁÐ Ç Ö Ïº ÅÖÕÙÞ¹ÐÓÖÞ ÍÒÚÖ ÎÓ ÌËÁ ÌÐÓÑÙÒÓÒº ÑÔÙ ÍÒÚÖ ØÖÓ Ë»Æº ¹ ¾¼¼ ÎÓº ËÔÒ ½ ½¾½½ ÑÒÓÐÓغÙÚÓº
Impact of Interference on Multi-hop Wireless Network Performance
 Impact of Interference on Multi-hop Wireless Network Performance Kamal Jain Jitendra Padhye Venkat Padmanabhan Lili Qiu Microsoft Research One Microsoft Way, Redmond, WA 98052. kamalj, padhye, padmanab,
Impact of Interference on Multi-hop Wireless Network Performance Kamal Jain Jitendra Padhye Venkat Padmanabhan Lili Qiu Microsoft Research One Microsoft Way, Redmond, WA 98052. kamalj, padhye, padmanab,
GAIN CHART example. respondents targeted [%] 0 20 40 60 80 100 customers mailed [%]
![GAIN CHART example. respondents targeted [%] 0 20 40 60 80 100 customers mailed [%] GAIN CHART example. respondents targeted [%] 0 20 40 60 80 100 customers mailed [%]](/thumbs/26/7251370.jpg) ÓÑÒÒ ÌÖØ ËÐØÓÒ ÐÓÖØÑ Ò ÖØ ÅÖØÒ ËÓÖ ÚÒ ÐÓÚÒ ÔÖÐ ¾¼¼¾ ØÖØ Ì Ñ Ó Ø ÛÓÖ ØÓ ÓÛ ØØ Ø ÔÖÓÖÑÒ Ó ØÖØ ÐØÓÒ ÑÓÐ Ò ÑÔÖÓÚ Ý Ù Ò ÓÑÒØÓÒ Ó Ü ØÒ ØÖØ ÐØÓÒ ÐÓÖØÑ º Ï ÔÖ ÒØ Ò ÔÔÖÓ Ò Û ÓÑÒØÓÒ Ó ÐÓÖØÑ ÔÖÓÚ ØØÖ Ö ÙÐØ ØÒ ÐÓÖØÑ
ÓÑÒÒ ÌÖØ ËÐØÓÒ ÐÓÖØÑ Ò ÖØ ÅÖØÒ ËÓÖ ÚÒ ÐÓÚÒ ÔÖÐ ¾¼¼¾ ØÖØ Ì Ñ Ó Ø ÛÓÖ ØÓ ÓÛ ØØ Ø ÔÖÓÖÑÒ Ó ØÖØ ÐØÓÒ ÑÓÐ Ò ÑÔÖÓÚ Ý Ù Ò ÓÑÒØÓÒ Ó Ü ØÒ ØÖØ ÐØÓÒ ÐÓÖØÑ º Ï ÔÖ ÒØ Ò ÔÔÖÓ Ò Û ÓÑÒØÓÒ Ó ÐÓÖØÑ ÔÖÓÚ ØØÖ Ö ÙÐØ ØÒ ÐÓÖØÑ
Local Domain. Other. Autonomous Domains. Local Host (DUT) ISP. Remote Host. Co Located Co Networked Bottleneck. Hosts. Network Elements M2 M3
 ÏØ ÈØ ÅÝ ÓÑ ÙØÓÑØ ÓÖ ÆØÛÓÖ ÅÓÒØÓÖÒ ÃÖØÝÒ ÖÚÒ ÍÒÚÖ ØÝ ÓÈÒÒ ÝÐÚÒ ÖØ ºÙÔÒÒºÙ ËØ ÒÖ ÐÐ ÄÓÖØÓÖ ÒÖÐйРºÓÑ ÖÐ º ÙÒØÖ ÍÒÚÖ ØÝ ÓÈÒÒ ÝÐÚÒ ÙÒØÖ ºÙÔÒÒºÙ ÈØÖ Âº ÅÒÒ ÐÐ ÄÓÖØÓÖ ÑÔÐйРºÓÑ ØÖØ Ï ÓÒ Ö Ø ÔÖÓÐÑ Ó ÑÓÒØÓÖÒ
ÏØ ÈØ ÅÝ ÓÑ ÙØÓÑØ ÓÖ ÆØÛÓÖ ÅÓÒØÓÖÒ ÃÖØÝÒ ÖÚÒ ÍÒÚÖ ØÝ ÓÈÒÒ ÝÐÚÒ ÖØ ºÙÔÒÒºÙ ËØ ÒÖ ÐÐ ÄÓÖØÓÖ ÒÖÐйРºÓÑ ÖÐ º ÙÒØÖ ÍÒÚÖ ØÝ ÓÈÒÒ ÝÐÚÒ ÙÒØÖ ºÙÔÒÒºÙ ÈØÖ Âº ÅÒÒ ÐÐ ÄÓÖØÓÖ ÑÔÐйРºÓÑ ØÖØ Ï ÓÒ Ö Ø ÔÖÓÐÑ Ó ÑÓÒØÓÖÒ
 ÄÖÒÒ ÔØØÖÒ Ó ØÚØÝ Ù Ò ÖйØÑ ØÖÒ Ö ËØÙ«Ö Ïº Ö Äº ÖÑ ÓÒ ÖØ Ð ÁÒØÐÐÒ ÄÓÖØÓÖÝ Å Ù ØØ ÁÒ ØØÙØ Ó ÌÒÓÐÓÝ ÑÖ Å ¼¾½ ØÖØ ÇÙÖ ÓÐ ØÓ ÚÐÓÔ Ú ÙÐ ÑÓÒØÓÖÒ Ý ØÑ ØØ Ô ÚÐÝ Ó ÖÚ ÑÓÚÒ ÓØ Ò Ø Ò ÐÖÒ ÔØØÖÒ Ó ØÚØÝ ÖÓÑ ØÓ Ó ÖÚØÓÒ
ÄÖÒÒ ÔØØÖÒ Ó ØÚØÝ Ù Ò ÖйØÑ ØÖÒ Ö ËØÙ«Ö Ïº Ö Äº ÖÑ ÓÒ ÖØ Ð ÁÒØÐÐÒ ÄÓÖØÓÖÝ Å Ù ØØ ÁÒ ØØÙØ Ó ÌÒÓÐÓÝ ÑÖ Å ¼¾½ ØÖØ ÇÙÖ ÓÐ ØÓ ÚÐÓÔ Ú ÙÐ ÑÓÒØÓÖÒ Ý ØÑ ØØ Ô ÚÐÝ Ó ÖÚ ÑÓÚÒ ÓØ Ò Ø Ò ÐÖÒ ÔØØÖÒ Ó ØÚØÝ ÖÓÑ ØÓ Ó ÖÚØÓÒ
 ØÙÖÐ ÚÖ Ù ÒÒÐ ÔÖÒ Ó Ò ÙÖÒ ½ ÈÖÓ ÓÖ Öº ÈÙÐ ÑÖØ ÔÖØÑÒØ Ó ÅØÑØ ËÛ ÖÐ ÁÒ ØØÙØ Ó ÌÒÓÐÓÝ ÙÖ Àß¼¾ ĐÙÖ ËÛØÞÖÐÒ ÑÐ ÑÖØ ÑغØÞº ØØÔ»»ÛÛÛºÑغØÞº»ÑÖØ Øк ½½ ¾ ½ ½½ ¾ ½¾ ½ ÈÔÖ ÔÖ ÒØ Ø Ø ÓÒÖÒ ÓÒ Ê ÅÒÑÒØ Ó ÁÒ ÙÖÒ ÖÑ ÒÒÐ
ØÙÖÐ ÚÖ Ù ÒÒÐ ÔÖÒ Ó Ò ÙÖÒ ½ ÈÖÓ ÓÖ Öº ÈÙÐ ÑÖØ ÔÖØÑÒØ Ó ÅØÑØ ËÛ ÖÐ ÁÒ ØØÙØ Ó ÌÒÓÐÓÝ ÙÖ Àß¼¾ ĐÙÖ ËÛØÞÖÐÒ ÑÐ ÑÖØ ÑغØÞº ØØÔ»»ÛÛÛºÑغØÞº»ÑÖØ Øк ½½ ¾ ½ ½½ ¾ ½¾ ½ ÈÔÖ ÔÖ ÒØ Ø Ø ÓÒÖÒ ÓÒ Ê ÅÒÑÒØ Ó ÁÒ ÙÖÒ ÖÑ ÒÒÐ
Link 1 Link 2 Sender. Link 1 Link 2. Receiver. Receiver. Sender
 ½ ÌÖ Ò ÔÓÖØ Ò Ê Ð¹Ø Ñ Î Ó ÓÚ Ö Ø ÁÒØ ÖÒ Ø ÐÐ Ò Ò ÔÔÖÓ Ô Ò ÏÙ ËØÙ ÒØ Å Ñ Ö Á Û Ì ÓÑ ÀÓÙ Å Ñ Ö Á Ò ¹É Ò Ò ÐÐÓÛ Á ØÖ Ø Ð Ú Ö Ò Ö Ð¹Ø Ñ Ú Ó ÓÚ Ö Ø ÁÒØ ÖÒ Ø Ò ÑÔÓÖØ ÒØ ÓÑÔÓÒ ÒØ Ó Ñ ÒÝ ÁÒØ ÖÒ Ø ÑÙÐØ Ñ Ô¹ ÔÐ
½ ÌÖ Ò ÔÓÖØ Ò Ê Ð¹Ø Ñ Î Ó ÓÚ Ö Ø ÁÒØ ÖÒ Ø ÐÐ Ò Ò ÔÔÖÓ Ô Ò ÏÙ ËØÙ ÒØ Å Ñ Ö Á Û Ì ÓÑ ÀÓÙ Å Ñ Ö Á Ò ¹É Ò Ò ÐÐÓÛ Á ØÖ Ø Ð Ú Ö Ò Ö Ð¹Ø Ñ Ú Ó ÓÚ Ö Ø ÁÒØ ÖÒ Ø Ò ÑÔÓÖØ ÒØ ÓÑÔÓÒ ÒØ Ó Ñ ÒÝ ÁÒØ ÖÒ Ø ÑÙÐØ Ñ Ô¹ ÔÐ
 ËÓ Ö Ø ¹ Ë Ð Ð ÅÙÐØ ÔÖÓ ÓÖ ËÝ Ø Ñ ÇÒ Ô ÙØ ÓÖ Å Ð ÓÐÐ Ò ÅÐ Ò Æ ØÓÚ Ò Ê ÑÓ À Ù Ð Ø Ñ ÑÒ Ö Ñ º ËÙÔ ÖÚ ÓÖ ÂÓ Ò ËØĐ ÖÒ Ö Ò ÂÓ Ñ ÓÑ Ø Ü Ñ Ò ØÓÖ Ä ÒÒ ÖØ Ä Ò Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ò Ò Ö Ò ÓÑÔÙØ Ö Ö Ø ØÙÖ Ä ÅĐ Ð Ö
ËÓ Ö Ø ¹ Ë Ð Ð ÅÙÐØ ÔÖÓ ÓÖ ËÝ Ø Ñ ÇÒ Ô ÙØ ÓÖ Å Ð ÓÐÐ Ò ÅÐ Ò Æ ØÓÚ Ò Ê ÑÓ À Ù Ð Ø Ñ ÑÒ Ö Ñ º ËÙÔ ÖÚ ÓÖ ÂÓ Ò ËØĐ ÖÒ Ö Ò ÂÓ Ñ ÓÑ Ø Ü Ñ Ò ØÓÖ Ä ÒÒ ÖØ Ä Ò Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ò Ò Ö Ò ÓÑÔÙØ Ö Ö Ø ØÙÖ Ä ÅĐ Ð Ö
 ÝÒÑ ØÖÙØÓÒ ÅÓÐ ÓÖ ÓÑØ ÄÓ Ø ÃÚÒ Êº Ù ÖÙØ ËÓÓÐ Ó Ù Ò ² ÈÙÐ ÈÓÐÝ ÆÚÐ ÈÓ ØÖÙØ ËÓÓÐ ÅÓÒØÖÝ ËØØÑÒØ Ó ÓÔ Ò ÔÙÖÔÓ ÄÓ Ø ÙÔÔÓÖØ ÓÖ ÑÔÓÙ ÛÖÖ ØÖØÓÒÐÐÝ ÖÐ ÓÒ ÐÖ ÐÒ¹ ÒÖ ØÖÙØÙÖ ÛØ ØÖÙ ÓÑÔÐ Ò ÑÓ Ø Ó Ø ØÖÙØÓÒº ÆÛ ÛÖ ØÒ
ÝÒÑ ØÖÙØÓÒ ÅÓÐ ÓÖ ÓÑØ ÄÓ Ø ÃÚÒ Êº Ù ÖÙØ ËÓÓÐ Ó Ù Ò ² ÈÙÐ ÈÓÐÝ ÆÚÐ ÈÓ ØÖÙØ ËÓÓÐ ÅÓÒØÖÝ ËØØÑÒØ Ó ÓÔ Ò ÔÙÖÔÓ ÄÓ Ø ÙÔÔÓÖØ ÓÖ ÑÔÓÙ ÛÖÖ ØÖØÓÒÐÐÝ ÖÐ ÓÒ ÐÖ ÐÒ¹ ÒÖ ØÖÙØÙÖ ÛØ ØÖÙ ÓÑÔÐ Ò ÑÓ Ø Ó Ø ØÖÙØÓÒº ÆÛ ÛÖ ØÒ
 ÏÝ Ø ËØÓ ÅÖØ ÅÝ ÍÒÖÛØ ÆÛ Ò ÑÔÖÐ ÒÐÝ ÒÒ ËÖÒ ÒÒ ÔÖØÑÒØ ÃÐÐÓ ËÓÓÐ Ó ÅÒÑÒØ ÆÓÖØÛ ØÖÒ ÍÒÚÖ ØÝ ÆÓÚÑÖ ¾¼¼½ ÓÖÖ ÔÓÒÒ ÒÒ ËÖÒ ÒÒ ÔÖØÑÒØ ÃÐÐÓ ËÓÓÐ Ó ÅÒÑÒØ ÆÓÖØÛ ØÖÒ ÍÒÚÖ ØÝ ÔÓÒ µ ¹½ Ü µ ½¹½ ÑÐ ¹ ÖÒÒÛٺٺ Ì ÔÔÖ ÓÒ
ÏÝ Ø ËØÓ ÅÖØ ÅÝ ÍÒÖÛØ ÆÛ Ò ÑÔÖÐ ÒÐÝ ÒÒ ËÖÒ ÒÒ ÔÖØÑÒØ ÃÐÐÓ ËÓÓÐ Ó ÅÒÑÒØ ÆÓÖØÛ ØÖÒ ÍÒÚÖ ØÝ ÆÓÚÑÖ ¾¼¼½ ÓÖÖ ÔÓÒÒ ÒÒ ËÖÒ ÒÒ ÔÖØÑÒØ ÃÐÐÓ ËÓÓÐ Ó ÅÒÑÒØ ÆÓÖØÛ ØÖÒ ÍÒÚÖ ØÝ ÔÓÒ µ ¹½ Ü µ ½¹½ ÑÐ ¹ ÖÒÒÛٺٺ Ì ÔÔÖ ÓÒ
 Ñ ÈÓ ØÓÒ ÅÓÒØÓÖ ÓÖ Ø Ì Ð ÐÖØÓÖ ÓÑÔÐÜ º ÅÒ ËÐÝ ÖÒ Åº ÏÒØ Ý ÀÑÙÖ ÖÑÒÝ ÑÖ ¾¼¼¼ ØÖØ Ò ÓÚÖÚÛ ÓÒ Ñ ÔÓ ØÓÒ ÑÓÒØÓÖÒ Ø Ø Ì Ð ÐÒÖ ÓÐÐÖ ÚÒº ÔÖÒÔÐ Ò ØÒÓÐÓÝ ØÐ Ó ÈÅ ÔÙÔ³ Ò ØÖ Ö¹ÓÙØ ÐØÖÓÒ Ö Ù º ÜÔÖÒ ÛØ «ÖÒØ ØÝÔ Ó ÈÅ
Ñ ÈÓ ØÓÒ ÅÓÒØÓÖ ÓÖ Ø Ì Ð ÐÖØÓÖ ÓÑÔÐÜ º ÅÒ ËÐÝ ÖÒ Åº ÏÒØ Ý ÀÑÙÖ ÖÑÒÝ ÑÖ ¾¼¼¼ ØÖØ Ò ÓÚÖÚÛ ÓÒ Ñ ÔÓ ØÓÒ ÑÓÒØÓÖÒ Ø Ø Ì Ð ÐÒÖ ÓÐÐÖ ÚÒº ÔÖÒÔÐ Ò ØÒÓÐÓÝ ØÐ Ó ÈÅ ÔÙÔ³ Ò ØÖ Ö¹ÓÙØ ÐØÖÓÒ Ö Ù º ÜÔÖÒ ÛØ «ÖÒØ ØÝÔ Ó ÈÅ
Diskussionspapiere Discussion Papers
 Diskussionspapiere Discussion Papers Discussion Paper No. 231 Erosion of Monopoly Power due to the Emergence of Linux by Jürgen Bitzer Berlin, November 2000 Deutsches Institut für Wirtschaftsforschung,
Diskussionspapiere Discussion Papers Discussion Paper No. 231 Erosion of Monopoly Power due to the Emergence of Linux by Jürgen Bitzer Berlin, November 2000 Deutsches Institut für Wirtschaftsforschung,
 ÌÝÔ ¹ Ö Ø È ÖØ Ð Ú ÐÙ Ø ÓÒ ÇÐ Ú Ö ÒÚÝ ÊÁ Ë Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë ÍÒ Ú Ö ØÝ Ó Ö Ù Ù Ð ¼ ÆÝ ÅÙÒ Ã¹ ¼¼¼ Ö Ù ÒÑ Ö ¹Ñ Ð ÒÚÝ Ø Ô Ö º ÀÓÑ Ô ØØÔ»»ÛÛÛº Ö º» ÒÚÝ Ø Ô ØÖ Øº ÌÝÔ ¹ Ö Ø Ô ÖØ Ð Ú ÐÙ Ø ÓÒ Ù ÒÓÖÑ Ð Þ Ø
ÌÝÔ ¹ Ö Ø È ÖØ Ð Ú ÐÙ Ø ÓÒ ÇÐ Ú Ö ÒÚÝ ÊÁ Ë Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë ÍÒ Ú Ö ØÝ Ó Ö Ù Ù Ð ¼ ÆÝ ÅÙÒ Ã¹ ¼¼¼ Ö Ù ÒÑ Ö ¹Ñ Ð ÒÚÝ Ø Ô Ö º ÀÓÑ Ô ØØÔ»»ÛÛÛº Ö º» ÒÚÝ Ø Ô ØÖ Øº ÌÝÔ ¹ Ö Ø Ô ÖØ Ð Ú ÐÙ Ø ÓÒ Ù ÒÓÖÑ Ð Þ Ø
 ËÔÖÐÒ ØØÖØÓÖ Ò ÕÙÒØÙÑ ÝÒÑ ÓÖ Ð Ó ÐÓÒ¹ÖÒ ÑÒØ Ð ÀÓÖ º ÓÖÒÒ ÁÒ ØØÙØ ÓÖ ÅØÑØ ÐÓÖ ÍÒÚÖ ØØ ÖÖ Ö Î ¾¾¼ ÐÓÖ ÒÑÖ ¹ÑÐ ÓÖÒÒÑغٺ ÁÖ ÀÖ Ø Ôغ Ó Åغ ÍÒÚÖ ØÝ Ó ÎÖÒ ÖÐÓØØ ÚÐÐ ÎÖÒ ¾¾¼ ÍË ¹ÑÐ ÛÚÖÒºÙ Ö Ë Ø ÁÒ ØØÙØ ÓÖ ÅØÑØ
ËÔÖÐÒ ØØÖØÓÖ Ò ÕÙÒØÙÑ ÝÒÑ ÓÖ Ð Ó ÐÓÒ¹ÖÒ ÑÒØ Ð ÀÓÖ º ÓÖÒÒ ÁÒ ØØÙØ ÓÖ ÅØÑØ ÐÓÖ ÍÒÚÖ ØØ ÖÖ Ö Î ¾¾¼ ÐÓÖ ÒÑÖ ¹ÑÐ ÓÖÒÒÑغٺ ÁÖ ÀÖ Ø Ôغ Ó Åغ ÍÒÚÖ ØÝ Ó ÎÖÒ ÖÐÓØØ ÚÐÐ ÎÖÒ ¾¾¼ ÍË ¹ÑÐ ÛÚÖÒºÙ Ö Ë Ø ÁÒ ØØÙØ ÓÖ ÅØÑØ
 Ä Ò Ö Ò ÒØ ÖÓÔØ Ñ Þ Ø ÓÒÛ Ø ÔÔÐ Ø ÓÒ ÅÎ ½»ÅÅ ½ Å Ò ÑÙÑÓ Ø ÓÛÑÓ Ð Ò Ð ÓÖ Ø Ñ Ä ØÙÖ ½¼ ÒÒ¹ Ö Ø ËØÖ Ñ Ö ¾¼½ ¼ ¼¾ Ä ØÙÖ Ä Ò Ö Ò ÒØ ÖÓÔØ Ñ Þ Ø ÓÒÛ Ø ÔÔÐ Ø ÓÒ Å Ü ÑÙÑ ÓÛÑÓ Ð ÓÒ Ö ØÖ Ø Ø Ò Ò ØÛÓÖ Û Ø Ô Ô Ð Ò
Ä Ò Ö Ò ÒØ ÖÓÔØ Ñ Þ Ø ÓÒÛ Ø ÔÔÐ Ø ÓÒ ÅÎ ½»ÅÅ ½ Å Ò ÑÙÑÓ Ø ÓÛÑÓ Ð Ò Ð ÓÖ Ø Ñ Ä ØÙÖ ½¼ ÒÒ¹ Ö Ø ËØÖ Ñ Ö ¾¼½ ¼ ¼¾ Ä ØÙÖ Ä Ò Ö Ò ÒØ ÖÓÔØ Ñ Þ Ø ÓÒÛ Ø ÔÔÐ Ø ÓÒ Å Ü ÑÙÑ ÓÛÑÓ Ð ÓÒ Ö ØÖ Ø Ø Ò Ò ØÛÓÖ Û Ø Ô Ô Ð Ò
Protecting Web Servers from Distributed Denial of Service Attacks
 Protecting Web Servers from Distributed Denial of Service Attacks Frank Kargl Department of Multimedia Computing University of Ulm Germany frank.kargl@ Joern Maier Department of Multimedia Computing University
Protecting Web Servers from Distributed Denial of Service Attacks Frank Kargl Department of Multimedia Computing University of Ulm Germany frank.kargl@ Joern Maier Department of Multimedia Computing University
WITH JOINT MANUFACTURING AND REMANUFACTURING
 AN NPV AND AC ANALYSIS OF A STOCHASTIC INVENTORY SYSTEM WITH JOINT MANUFACTURING AND REMANUFACTURING ERWIN VAN DER LAAN ERIM REPORT SERIES RESEARCH IN MANAGEMENT ERIM Report Series reference number ERS-2000-38-LIS
AN NPV AND AC ANALYSIS OF A STOCHASTIC INVENTORY SYSTEM WITH JOINT MANUFACTURING AND REMANUFACTURING ERWIN VAN DER LAAN ERIM REPORT SERIES RESEARCH IN MANAGEMENT ERIM Report Series reference number ERS-2000-38-LIS
Theme. Theme Ordering. Sentence Fusion. Theme ...
 Ë ÒØ Ò Ù ÓÒ ÓÖ ÅÙÐØ ÓÙÑ ÒØ Æ Û ËÙÑÑ Ö Þ Ø ÓÒ Ê Ò ÖÞ Ð Ý Å Ù ØØ ÁÒ Ø ØÙØ Ó Ì ÒÓÐÓ Ý Ã Ø Ð Ò Êº Åà ÓÛÒ Ý ÓÐÙÑ ÍÒ Ú Ö ØÝ Ý Ø Ñ Ø Ø Ò ÔÖÓ Ù Ò ÓÖÑ Ø Ú ÙÑÑ Ö Ð Ø Ò ÓÑÑÓÒ Ò ÓÖÑ ¹ Ø ÓÒ ÓÙÒ Ò Ñ ÒÝ ÓÒÐ Ò ÓÙÑ ÒØ
Ë ÒØ Ò Ù ÓÒ ÓÖ ÅÙÐØ ÓÙÑ ÒØ Æ Û ËÙÑÑ Ö Þ Ø ÓÒ Ê Ò ÖÞ Ð Ý Å Ù ØØ ÁÒ Ø ØÙØ Ó Ì ÒÓÐÓ Ý Ã Ø Ð Ò Êº Åà ÓÛÒ Ý ÓÐÙÑ ÍÒ Ú Ö ØÝ Ý Ø Ñ Ø Ø Ò ÔÖÓ Ù Ò ÓÖÑ Ø Ú ÙÑÑ Ö Ð Ø Ò ÓÑÑÓÒ Ò ÓÖÑ ¹ Ø ÓÒ ÓÙÒ Ò Ñ ÒÝ ÓÒÐ Ò ÓÙÑ ÒØ
6.8 6.7. Log-intensity 6.6 6.5 6.4 6.6 6.5. Log-intensity 6.4 6.3
 ËØÓ Ø ÓÑØÖÝ ÅÓÐ ÓÖ ÙÒØÓÒÐ ÅÒØ Ê ÓÒÒ ÁÑ º ÆÐ ÎÚÖ ÀÖØÚ ÍÒÚÖ ØÝ Ó ÖÙ ÊÚ ÚÖ ÓÒ ÅÖ Ø ¾¼¼½ ØÖØ ÁÒ ÙÒØÓÒÐ ÑÒØ Ö ÓÒÒ ÑÒ ÔØÐ ØÚØÓÒ ÔØØÖÒ Ö Óѹ ÑÓÒÐÝ ØÑØ Ù Ò ÒÓÒ¹ÔÖÑØÖ ÑÓÓØÒ ÔÔÖÓº ËÒ ÒØ Ô ÓÖ ÐÙ ØÖ Ò Ø ÑÓÓØ Ñ Ö Ù
ËØÓ Ø ÓÑØÖÝ ÅÓÐ ÓÖ ÙÒØÓÒÐ ÅÒØ Ê ÓÒÒ ÁÑ º ÆÐ ÎÚÖ ÀÖØÚ ÍÒÚÖ ØÝ Ó ÖÙ ÊÚ ÚÖ ÓÒ ÅÖ Ø ¾¼¼½ ØÖØ ÁÒ ÙÒØÓÒÐ ÑÒØ Ö ÓÒÒ ÑÒ ÔØÐ ØÚØÓÒ ÔØØÖÒ Ö Óѹ ÑÓÒÐÝ ØÑØ Ù Ò ÒÓÒ¹ÔÖÑØÖ ÑÓÓØÒ ÔÔÖÓº ËÒ ÒØ Ô ÓÖ ÐÙ ØÖ Ò Ø ÑÓÓØ Ñ Ö Ù
 Æ ØÛÓÖ ÌÖ Æ Ú ÓÙÖ Ò ËÛ Ø Ø ÖÒ Ø ËÝ Ø Ñ ÌÓÒÝ Ð ÍÐ À Ö Ö ² È Ø Ö À ÖÖ ÓÒ ½ Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ò ÁÑÔ Ö Ð ÓÐÐ Ó Ë Ò Ì ÒÓÐÓ Ý Ò Å Ò ÀÙÜÐ Ý Ù Ð Ò ½ ¼ ÉÙ Ò³ Ø ÄÓÒ ÓÒ ËÏ ¾ Ò Ð Ò ØÖ Ø Å ÙÖ Ñ ÒØ ÓÒ ¹Ô Ö ÓÖÑ Ò Û Ø
Æ ØÛÓÖ ÌÖ Æ Ú ÓÙÖ Ò ËÛ Ø Ø ÖÒ Ø ËÝ Ø Ñ ÌÓÒÝ Ð ÍÐ À Ö Ö ² È Ø Ö À ÖÖ ÓÒ ½ Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ò ÁÑÔ Ö Ð ÓÐÐ Ó Ë Ò Ì ÒÓÐÓ Ý Ò Å Ò ÀÙÜÐ Ý Ù Ð Ò ½ ¼ ÉÙ Ò³ Ø ÄÓÒ ÓÒ ËÏ ¾ Ò Ð Ò ØÖ Ø Å ÙÖ Ñ ÒØ ÓÒ ¹Ô Ö ÓÖÑ Ò Û Ø
 Æ Û È Ö Ñ ÓÖ Ù Ó ÓÒ Ö Ò Ò ÓÒ ÎÓ ÓÚ Ö ÁÈ ÎÓÁȵ Ì ËÙ Ñ ØØ ÓÖ Ø Ö Ó ÓØÓÖ Ó È ÐÓ ÓÔ Ý Ò Ø ÙÐØÝ Ó Ò Ò Ö Ò Ý Êº Î Ò Ø ÈÖ ÒØÖ ÓÖ Ð ØÖÓÒ Ò Ò Ì ÒÓÐÓ Ý ÁÒ Ò ÁÒ Ø ØÙØ Ó Ë Ò Ò ÐÓÖ ß ¼ ¼½¾ ÁÒ ÂÙÐÝ ¾¼¼ ÓÒ ÓÒ Á ÒÓÛ Ø
Æ Û È Ö Ñ ÓÖ Ù Ó ÓÒ Ö Ò Ò ÓÒ ÎÓ ÓÚ Ö ÁÈ ÎÓÁȵ Ì ËÙ Ñ ØØ ÓÖ Ø Ö Ó ÓØÓÖ Ó È ÐÓ ÓÔ Ý Ò Ø ÙÐØÝ Ó Ò Ò Ö Ò Ý Êº Î Ò Ø ÈÖ ÒØÖ ÓÖ Ð ØÖÓÒ Ò Ò Ì ÒÓÐÓ Ý ÁÒ Ò ÁÒ Ø ØÙØ Ó Ë Ò Ò ÐÓÖ ß ¼ ¼½¾ ÁÒ ÂÙÐÝ ¾¼¼ ÓÒ ÓÒ Á ÒÓÛ Ø
 Ê ØÖ Ú Ð Æ Ø ÅÓ Ð ÓÖ Ù Ð Ò Ð Ü Ð ÁÒ ÓÖÑ Ø ÓÒ ËÝ Ø Ñ ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö Öº Ö Öº Ò Øº Ñ ÁÒ ÓÖÑ Ø Ò Ö Ø Ò Ö Å Ø Ñ Ø ¹Æ ØÙÖÛ Ò ØÐ Ò ÙÐØĐ Ø ÁÁ Ö ÀÙÑ ÓРعÍÒ Ú Ö ØĐ Ø ÞÙ ÖÐ Ò ÚÓÒ ÔÐÓѹÁÒ ÓÖÑ Ø Ö Å Ö Ó
Ê ØÖ Ú Ð Æ Ø ÅÓ Ð ÓÖ Ù Ð Ò Ð Ü Ð ÁÒ ÓÖÑ Ø ÓÒ ËÝ Ø Ñ ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö Öº Ö Öº Ò Øº Ñ ÁÒ ÓÖÑ Ø Ò Ö Ø Ò Ö Å Ø Ñ Ø ¹Æ ØÙÖÛ Ò ØÐ Ò ÙÐØĐ Ø ÁÁ Ö ÀÙÑ ÓРعÍÒ Ú Ö ØĐ Ø ÞÙ ÖÐ Ò ÚÓÒ ÔÐÓѹÁÒ ÓÖÑ Ø Ö Å Ö Ó
