Graphic Algorithms and the Demographic Variations
|
|
|
- Alexandrina Sherman
- 5 years ago
- Views:
Transcription
1 DDE:AModiedDimensionExchangeMethod forloadbalancingink-aryn-cubes StateUniversityofNewYorkatBualo DepartmentofComputerScience Min-YouWuandWeiShu algorithmforthehypercubestructure.ithasbeengeneralizedtok-aryn-cubes.however,the k-aryn-cubealgorithmmusttakemanyiterationstoconvergetoabalancedstate.inthispaper, Abstract Thedimensionexchangemethod(DEM)wasinitiallyproposedasaload-balancing Bualo,NY14260 weproposeadirectmethodtomodifydem.thenewalgorithm,directdimensionexchange (DDE)method,takesloadaverageineverydimensiontoeliminateunnecessaryloadexchange.It moreaccuratelyandmuchfaster.1.introduction balancestheloaddirectlywithoutiterativelyexchangingtheload.itisabletobalancetheload sweep(logniterations),theloadisbalanced. nodepairsexchangetheirloadinformationandattempttoaveragethenumberoftasks.aftera DEMissuperiortootherschedulingmethods[7].DEMforthehypercubenetworkisasimple rithmforthehypercubestructure[5,1].itbalancestheloadforindependenttasksondistributed memorymachines.theexperimentcarriedbywillebeek-lemairandreevesconformedthat algorithm.loadbalancingisperformediterativelyineachofthelogndimensions,inwhichonly Thedimensionexchangemethod(DEM)wasinitiallyproposedasafullyload-balancingalgo- linearlyproportionaltothenumberofnodesinachain,andhencetothedimensionorderkof isnotabletoreachthebalancedstateinonesweep.thenumberofsweepsforconvergenceis network[10].becauseanodeexchangesworkloadwithonlyoneofitsneighboratatime,gde ittakesmanysweepstoconvergetothebalancedload.hosseinietal.extendeditforarbitrary structuresusingthetechniqueofedge-coloringofgraphs[3].xuandlauproposedthegeneralized dimensionexchange(gde)method[9].thegdemethodwasextendedtothek-aryn-cube Unfortunately,whenDEMappliestootherstructures,suchasthemeshorthek-aryn-cube, thek-aryn-cubestructure. 1
2 n-cube. beappliedtotwoormoredimensionstobalancetheloadforthemesh,thetorus,andthek-ary method.unlikeiterativealgorithms,thisdirectmethodcanbalancetheloadinonesweep.the orunderloadedandsubsequentlyexchangeworkloadwithothernodes.theddemethodcan beeasilyobtainedbyasumreduction.eachnodeinthechainknowswhetheritisoverloaded loadinachainisfullybalancedbyutilizinginformationofthetotalnumberoftasks,whichcan Wepresentadirectmethodforthek-aryn-cube,calledtheDirectDimensionExchange(DDE) methodiscomparedtothegdemethod.section7concludesthepaper. respectively.thealgorithmforthek-aryn-cubeispresentedinsection5.insection6,thedirect Then,thedirectmethodforthechainandtheringstructuresisdescribedinsections3and4, Thispaperisorganizedasfollows.Section2brieyreviewstheDEMandtheGDEalgorithms. Toachievethisgoal,anestimationofthetaskexecutiontimeisneeded,whichcanbedoneeither byaprogrammerorbyacompiler.sometimestheestimationcanbeapplication-specic,and sometimesitisimpossibletoobtainsuchanestimation.duetothesediculties,eachtaskis Thegoalofloadbalancingistoscheduleworkssothateachprocessorhasthesameworkload. 2.TheDEMandGDEAlgorithms presumedtorequiretheequalexecutiontimeandthegoalofthealgorithmistoscheduletasks algorithmistoredistributetaskssothatthenumberoftasksineachnodeisequal.assumethe computingnodesareconnectedbyagiventopology.eachnodeihaswitasks.ascheduling sothateachprocessorhasthesamenumberoftasks. sumofwiofallnodescanbeevenlydividedbyn.theaveragenumberoftaskswavgiscalculated Theschedulingproblemcanbedescribedasfollows.Inaparallelordistributedsystem,N wavg=pn 1 i=0wi addressesdierinonlytheleastsignicantbitbalancetheloadbetweenthemselves.next,all \integerversion"ofdemisdescribedinfigure1.allnodepairsintherstdimensionwhose andthencombinedtoformlargerdomainsuntilultimatelytheentiresystemisbalanced.the Eachnodeshouldhavewavgtasksafterscheduling. DEMwasdesignedforthehypercubestructure.InDEM,smalldomainsarebalancedrst N: nodehasbalanceditsloadwitheachofitsneighbors. nodepairsintheseconddimensionbalancetheloadbetweenthemselves,andsoforth,untileach AfterexecutionoftheDEMalgorithm,theloaddierence D=max(wi) min(wi) 2
3 DEM forl=0ton 1 wi=(d(wi+wj)=2eifwi>wj if(wj wi)>1,receiveb(wj wi)=2ctasksfromnodej if(wi wj)>1,sendb(wi wj)=2ctaskstonodej nodeiexchangeswithnodejthecurrentvaluesofwiandwj,wherej=i2l GDE b(wi+wj)=2cotherwise while(notterminate) forl=1toc foredgecoloredlconnectingnodesiandj Figure1:TheDEMalgorithmforthehypercube. wi=(d(1 )wi+wjeifwi>wj if(wj wi)>1,receiveb(wj wi)ctasksfromnodej if(wi wj)>1,sendb(wi wj)ctaskstonodej nodeiexchangeswithnodejthecurrentvaluesofwiandwj DEMalgorithmis3n[7]. isboundedbyn,thedimensionofthehypercube[3].thenumberofcommunicationstepsofthe Figure2:TheGDEalgorithmforthek-aryn-cube. b(1 )wi+wjcotherwise sweepaftercconsecutiveexchangeoperations,wherecisthenumberofcolors.ink-aryn-cubes, tasksbetweenneighboringnodesislessthanorequaltoone.theconvergenceratedependson c=2nifkisanevennumber.theterminationconditionisthatthedierenceofthenumberof Forthehypercube,theoptimal=12,andGDEisequivalenttotheoriginalDEMalgorithm.For theexchangeparameter.thevaluevariesfordierenttopologiesanddierentnetworksizes. graph.the\integerversion"ofthealgorithmisshowninfigure2.anodenishesacomplete TheGDEalgorithmoperatesoncolorgraphsderivedfromedge-coloringofthegivensystem whenthedimensionorderkincreases.thereisnocommunicationconictinthisalgorithm. topologyby\folding"themeshineachdimensiondlogmetimes[7].thismethodcouldbeapplied othertopologies,istobeoptimizedtomaximizetheconvergencerate.forthek-aryn-cube,the loaddierencebetweenanypairofnodesisboundedbynk=2.theconvergenceratedecreases Willebeek-LeMairandReevessuggestedanotherapproachtoextendDEMtoanMMmesh 3
4 pairswouldnolongerbedirectlylinkedtooneanotherandcommunicationswouldconict. tok-aryn-cubestoo.theloaddierenceisboundedbyndlogke.however,inthisapproach,node method.theworkloadinachaincanbebalanceddirectly.thebasicideaistocalculatethe totalnumberoftasksinthechainandtheaveragenumberoftaskspernode.thus,nodesinthe chaincanexchangetaskstobalancetheload. InsteadofusingtheGDEmethodwhichbalancestheloaditeratively,weproposeadirect 3.TheDDEMethodfortheChain DDE-chain Letwibethenumberoftasksinnodei,wherei=0;1;:::;k 1. 1.GlobalInformationCollection:Performthescanwithsumoperationofwi: 3.QuotaCalculation:Thequotaofeachnodeqiiscomputed: 2.AverageLoadCalculation:T=W0,wavg=bT=kc,andR=Tmodk,whereTisthe totalnumberoftasks. Wi=k 1 Xl=iwl qi=(wavg+1ifi<r 4.FlowCalculation:xi 1;i=Qi Wi,fori=1;2;:::;k 1,wherexi;jistheowon Also,anaccumulationquotaforeachnodeiscomputed: wavgotherwise edge(i;j). Qi=k 1 Figure3:TheDDEalgorithmforthechain. Xl=iql usingthescanwithsumoperationfromnodek 1tonode0,wherekisthelengthofthechain. thenodeweightwi(i=0;1;:::;k 1)andoutputsthecalculatedowxi 1;i(i=1;2;:::;k 1) foreveryedgeinthechain.therststepistoobtainthetotalnumberoftasksinthechainby oftaskspernodeatnode0.ifthenumberoftaskscannotbeevenlydividedbyk,theremaining EachnoderecordsapartialsumWi=Pk 1 TheDDEalgorithmforthechainshowninFigure3isits\integerversion."Ittakesasinput l=iwl.thesecondstepcalculatestheaveragenumber 4
5 RtasksaredistributedtotherstRnodessothattheyhaveonemoretaskthantheothers. ThevaluesofwavgandRarebroadcasttoeverynode.Inthethirdstep,eachnodecalculatesits asitsquota. theowisavailable,theworkloadisexchangedsothateachnodehasthesamenumberoftasks iscalculatedbytakingdierencebetweenqiandwi.nodeicalculatesxi 1;iandxi;i+1.When EachnodekeepsrecordsofQi,Wi,Qj,andWj,wherej=i+1.Inthefourthstep,theow quota.theaccumulationquotaqicanbecalculateddirectlyasfollows: Qi=wavg(k i)+min(0;r i): Example1: shownbelow: Then,eachnodecalculatesthevalueofQiinstep3.Thevaluesofwi,Wi,Qi,andxi 1;iareas andr: readytobescheduled.valuesofwiarecalculatedinstep1.node0calculatesthevalueofwavg AnexampleisshowninFigure4.Atthebeginningofscheduling,eachnodehaswitasks iwiwiqixi 1;i wavg=4;r=5: { i=0 94i=1 76i= i=3 11i=4 42i=5 62i=6 11 Aftertaskexchange,nodes0{4havevetaskseach,andnodes5{7havefourtaskseach. Figure4:ExampleforDDE-chain. i=7 5 toitsquota. Lemma1:AfterexecutionofDDEandtaskexchange,thenumberoftasksineachnodeisequal 5
6 Becausexi 1;i=Qi Wi;xi;i+1=Qi+1 Wi+1;Wi+1=Wi wi;andqi+1=qi qi Proof:AfterexecutionofDDEandtaskexchange,thenumberoftasksinnodeiis w0i=wi+(qi Wi) (Qi+1 Wi+1)=Qi Qi+1=qi w0i=wi+xi 1;i xi;i+1 stepsinstep4isatmostk.therefore,thetotalnumberofcommunicationstepsofthisalgorithm andapplyingthetwaalgorithmin[6].thus,thetotalnumberofcommunicationstepsofthis isnomorethan3k.thisalgorithmcanbefurtherimprovedbyselectingnodek/2astheroot algorithmcanbereducedto2k.whentisevenlydividedbyk,thisalgorithmminimizesthe Inthisalgorithm,steps1and2spend2kcommunicationsteps.Thenumberofcommunication 2 exchangealgorithms.therstone,calledreceive-before-send,isshowninfigure5. Receive-before-send totalnumberoftasktransfersandthetotalnumberofcommunications.thisalgorithmalso maximizeslocality.thatis,itminimizesthenumberoftasksthataremigratedtoothernodes. Fornodei 1.ifi>0andxi 1;i>0,waittoreceivexi 1;itasksfromnodei 1 TheworkloadisexchangedaccordingtotheowgeneratedbyDDE.Therearetwotask- 4.ifi<k 1andxi;i+1>0,sendxi;i+1taskstonodei+1 3.ifi>0andxi 1;i<0,sendjxi 1;ijtaskstonodei 1 2.ifi<k 1andxi;i+1<0,waittoreceivejxi;i+1jtasksfromnodei+1 nicationstepstonish: Usingthereceive-before-sendalgorithm,theloadexchangeinExample1takesfourcommu- (2) (1) node0tonode1,node5tonode6,node7tonode6 node1tonode2 Figure5:Taskexchange:receive-before-send. (3) (4) node2tonode3 node3tonode4 6
7 Send-before-receive Fornodei letai=xi 1;i;bi=xi;i+1 while(ai6=0orbi6=0) 1.ifi>0and(wi> ai>0)sendjaijtaskstonodei 1,andletwi=wi+ai,ai=0 2.ifi<k 1and(wi>bi>0)sendbitaskstonodei+1,andletwi=wi bi,bi=0 beforesendingoutmessages.byrelaxingthisconstraint,asend-before-receivealgorithmisshown 3.ifi>0andai>0andreceivedaitasksfromnodei 1,andletwi=wi+ai,ai=0 4.ifi<k 1andbi<0andreceivedjbijtasksfromnodei+1,andletwi=wi bi,bi=0 incomingmessage.thecommunicationtimeandprocessoridletimecanbereduced.ittakes infigure6.inthisalgorithm,anodecanstartsendingmessagesoutbeforeithasreceivedan onlytwocommunicationstepsforexample1: Inthereceive-before-sendalgorithm,eachnodemustreceiveanincomingmessage,ifany, Figure6:Taskexchange:send-before-receive. 2) 1) node5tonode6,node7tonode6 node0tonode1,node1tonode2,node3tonode4, before-sendorsend-before-receivealgorithmsisatrade-obetweencommunicationtimeand taskstoothernodes.butinthesend-before-receivealgorithm,anodemaysendlocaltasksto othernodesandthenreceivetasksfromothers.therefore,thedecisiononuseofthereceivebefore-sendalgorithm,anodecankeepthemaximumnumberoflocaltasksandsendnon-local Thesend-before-receivealgorithmmayhavesomenegativeimpactinlocality.Inthereceive- node2tonode3 locality. communicationsteps. advantageofthepipelineeectofwormholeroutingwhileavoidingchannelcontention.this oncommunicationtimecanoftenbeignored.therecursivedoublingalgorithm[2]cantake algorithmorganizesthenodesinachaintoatree.anexampleofeightnodesisshownin Figure7.ApplyingtheTWAalgorithmin[6]tothetree,theloadcanbebalancedwithin4logk Mostmassivelyparallelcomputersusewormholeroutingwithwhichtheeectofpathlength 7
8 i=0 i=6 i=4 i=5 i=2 i=3 i=1 4.TheDDEAlgorithmfortheRing Figure7:Thetreeforrecursivedoubling. i=7 tioncouldbereduced.wedescribeanalgorithmtominimizethetotalnumberoftaskstransferred. Thealgorithmisderivedfromtheminimumcostowalgorithm[4]andshowninFigure8.Inthis however,thecommunicationmaynotbeminimal.byutilizingtheend-roundedge,communica- algorithm,aninitialsolutionisobtainedbyusingdde-chainwithoutconsideringtheend-round gorithmcanbeappliedtotheringbyignoringtheend-roundedge.theloadcanbebalanced, Aringcanbeobtainedbyaddinganend-roundconnectiontoachain.TheDDE-chainal- Letnpbethenumberofedgeswithxi;j>0,nnthenumberofedgeswithxi;j<0,andnzthe numberofedgeswithxi;j=0. DDE-ring ApplyDDE-chaintotheringwithoutconsideringtheend-roundedge(k 1;0)toobtain x0;1;x1;2;:::;xk 2;k 1,wherexi;jistheowonedge(i;j).Letxk 1;0be0. Iftheowisclockwise,xi;jispositive;otherwise,itisnegative. 2.Foreachedge,xi;j=xi;j xm. 1.Ifnn+nz np<0,letxmbethemthlargestxi;jfromallxi;j>0;andifnp+nz nn<0, letxmbethemthsmallestxi;jfromallxi;j<0,wherem=dk=2e. Figure8:TheDDEalgorithmforthering. 8
9 ofdde-ring.here,weletx 1;0=xk 1;0. algorithmiso(klogk). edge.then,anaugmentationisappliedtoobtainanoptimalsolution.thecomplexityofthis Wecanuseeitherthereceive-before-sendorsend-before-receivealgorithmfortaskexchange negativecost.therefore,thenetworkowisofminimumcost[4]. numberoftaskstransferred. Lemma2:AfterexecutionofDDE-ring,thetotalnetworkowisofminimumcost. Proof:Ifnp+nz nn0andnn+nz np0,thereisnoowaugmentingcyclewith Thefollowinglemmashowsthatthisalgorithmminimizesthetotalcostofow,thatis,the Notethatn0n+n0z+n0p=k.Becauseofm=dk=2e, Then, Ifnn+nz np<0,aftermodicationofxi;j=xi;j xm,wehave n0z+n0p n0nm n0n=m (k n0z n0p)2m k n0z+n0p n0n2m k0 n0z+n0pm Then,n0n+n0z n0pk m+1 n0p=k m+1 (k n0n n0z)=1 m+n0n+n0z Wealsohave 1 m+k m+1=k 2m+2 n0n+n0zk m+1 Thus,thenetworkowisofminimumcost. costinallcases. Becauseofm=dk=2e, Thecaseofnp+nz nn<0canbeprovedsimilarly.thus,thenetworkowisofminimum n0z+n0p n0nk 2m+20 toconstructaring.applyingthedde-chainalgorithmtotheringwithoutconsideringthe AnexampleisshowninFigure9.Anend-roundedgeisaddedtothechaininFigure4 9 2
10 resultisshowninfigure9(b).thenumberoftaskstransferredisreducedto17. end-roundedge,theowisshowninfigure9(a).thenumberoftaskstransferredis19.the Becausenp+nz nn<0andthe4thsmallestxi;jis 2,everyxi;jissubtractedby 2.The augmentationisappliedtothisow:np=1;nz=2;nn=5 i=0 4i=1 6i=2 5i=3 (a) i=4 i=5 2i=6 1i=7 i=0 92i=1 74i=2 43i=3 112 Figure9:ExampleforDDE-ring. (b) i=4 42i=5 6 i=6 13i=7 5 nodes.thenodesineachringexchangetheirloadandtheneachnodeihaswl+1 n-cube.thealgorithmisshowninfigure10.initerationloftheddealgorithm,subcubeslm isdividedintokpartitionssl+1 WiththeDDE-ringalgorithm,itisnotdiculttocompositeaDDEalgorithmforthek-ary 5.TheDDEMethodforthek-aryn-cube km+bwherem=0;1;:::;kl 1andb=0;1;:::;k 1.Slmhaskn l getamesh.thisalgorithmcanbeappliedtothemeshbyperformingthedde-chainalgorithm nodesindierentdimensions.takingatorusandstripthemofalltheend-roundconnections,we orsend-before-receivealgorithm. DDE,nodeiwillhavewnitasks.Thetaskexchangestepcanuseeitherthereceive-before-send Thisalgorithmcanbeappliedtothen-dimensionaltorus,whichallowsdierentnumberof itasks.executing ofthek-aryn-cube. insteadofdde-ringineachstep. ThefollowingtheoremshowsthattheloaddierenceofDDEisboundedbyn,thedimension 10
11 DDEfork-aryn-cube Assumeak-aryn-cubeS0,thenumberofnodesiskn,andnodeihasw0itasks. forl=0ton 1 applythedde-ringalgorithmtokn 1ringsinthelthdimensionindependently, whereeveryringhasknodes(a0;a1;:::;al;:::;ak 1)andal=0;1;:::;k 1 exchangetasksaccordingtotheow eachnodeupdatesitsweightwl+1 i=wli+xi 1;i xi;i+1 Figure10:TheDDEalgorithmforthek-aryn-cube. Theorem1:AfterexecutionofDDE,theloaddierence D=max(wni) min(wni) isboundedbyn. Proof:InthelthstepofDDE,ak-ary(n l)-cubeispartitionedintokk-ary(n l 1)-cubes. Thedierenceofthenumberoftasksbetweentwopartitionsismaximalwhenineachringevery nodeinrstpartition,saysl+1 km,hasonemoretaskthanthatpossessedbythenodeintheother partitions,sl+1 Xkm+b,whereb=1;2;:::;k 1.Thus j2sl+1 kmwl+1 j=x j2sl+1 km+k 1wl+1 j+jsl+1 kmj=1 k 1(X j2slmwlj X j2sl+1 kmwl+1 j)+kn l 1 wherejsl+1 kmjdenotesthenumberofnodesinsubcubesl+1 kmwhichiskn l 1.Therefore, X j2sl+1 kmwl+1 j=1kx j2slmwlj+(k 1)kn l 2 Similarly,X j2sl+1 km+k 1wl+1 j=x j2sl+1 kmwl+1 j jsl+1 kmj=(x j2slmwlj (k 1)X j2sl+1 km+k 1wl+1 j) kn l 1 Therefore, X j2sl+1 km+k 1wl+1 j=1kx j2slmwlj kn l 2 Let Almax=max 0m<klX j2slmwlj 11
12 and Whenl=0, A0max=A0min=X Almin=min j2s0w0j=x 0m<klX j2slmwlj: Similarly, wheretisthetotalnumberoftasks.thus, Almax=(T1kAl 1 max+(k 1)kn l 1otherwise 0j<knw0j=T Thesolutiontotheaboverecurrenceisgivenby Almin=( 1kAl 1 min kn l 1otherwise T ifl=0 ifl=0 (1) Almax=Tkl+(k 1)lkn l 1 Almin=Tkl lkn l 1 (3) (4) (2) Itclearlysatises(1)and(2)forthebasis,l=0.If(3)satises(1)forl=m,then Therefore,itsatises(1)forl=m+1.Thus,byinductiononlwehaveshownthat(3)satises(1) wheneverl0.similarly,itcanbeshownthat(4)satises(2)wheneverl0. Am+1 max=t km+1+(m+1)(k 1)kn (m+1) 1=1k(T =1kA(m+1) 1 max+(k 1)kn (m+1) 1 km+(k 1)mkn m 1)+(k 1)kn (m+1) 1 BecauseD=Anmax Anmin=(k 1 atmostbyn. Letl=n Anmax=max Anmin=min k+1k)n=n,thenumberoftasksinanytwoprocessorsdiers 0j<knwnj=Tkn+k 1 0j<knwnj=Tkn 1kn; kn isshowninfigure11(c).themaximumloaddierenceis2. thatthedde-ringalgorithmappliestoeachringintherstdimension.then,dde-ringapplies toeachringintheseconddimension,asshowninfigure11(b).theresultantloaddistribution AnexampleisshowninFigure11.Thisisa4-ary2-cube(i.e.,torus44).Figure11(a)shows 2 12
13 (a) (b) Inthissection,wecompareperformanceofGDEandDDE.Weconsideratestsetofload Figure11:ExampleforDDE(4-ary2-cube). 6.ExperimentalResults (c) distributions,inwhichtheloadateachprocessorisrandomlyselectedwiththemeanequaltoa speciedvalue.inthissimulationexperiment,theaveragenumberoftasks(averageweight)per processoris1,000.eachresultistheaverageof100testcases.wetestedan88mesh,a1616 thanthatofdde. showsitsaverageindierentnetworks.here,theloaddierenceofgdeisfourtosixtimeslarger forgdeis0.723[10]. torus,an8883d-mesh,anda d-torus.forthesenetworks,theoptimalvalueof byn,whereasthatofgdeisboundedbyn(k 1)forthemeshandnk=2forthetorus.Figure12 First,wecompareloadimbalanceofGDEandDDE.TheloaddierenceofDDEisbounded 13
14 16 GDE 14 thenumberofsweepssfordierentnetworks.thevalueofsisproportionaltok[10].moreover, 12 sincreaseswiththeaverageweight.tableishowstherelationshipbetweenthenumberofsweeps andtheaveragenumberoftasks,measuredonan88mesh. DDEcompletesloadbalancinginonesweepbutGDEneedsmanysweeps.Figure13shows Figure12:Loaddierence x8 mesh 8x8x8 mesh 16x16 torus 16x16x16 torus 12 GDE 10 sweephasciterations,wherecisthenumberofcolors.forevennumberofk,c=2n.each Next,wecomparethenumberofcommunicationstepsofGDEandDDE.ForGDE,each Figure13:Thenumberofsweeps. DDE reducethenumberofcommunicationstepssignicantly.theanalysishasbeenconrmedbythe mation.loadbalancingneedsatmostk 1andk=2communicationstepsforthemeshandthe torus,respectively.therefore,2knor32kncommunicationstepsintotalarerequired.ddecan iterationhasthreecommunications,twoforexchangingloadinformationandoneforloadbalancing.therefore,thetotalnumberofcommunicationsofssweepsare3sc=6sn.fordde, therearekcommunicationstepsineachdimensionforcollectionandbroadcastingofloadinfor- 0 experiment,asshowninfigure14. 8x8 mesh 8x8x8 mesh 16x16 16x16x16 14
15 TableI:TheRelationshipBetweentheNumberofSweepsandtheAverageWeight AverageNumberofSweeps AverageNumberofTasks ,0003,00010,000 municationcostisdenedasthethetotalnumbersoftaskstransferreddividedbythetotal numberoftasks: Figure15showsthenormalizedcommunicationcostofGDEandDDE.Thenormalizedcom- Figure14:Thenumberofcommunicationsteps isabout50%largerthanthatofdde.itisduetothefactthatgdetransferstasksunnecessarily. Finally,DDEhasbetterlocalitythanGDE.Figure16showsthepercentageoflocaltasksthat whereejisthenumberoftaskstransmittedthroughtheedgej.thecommunicationcostofgde arenotmigratedtoothernodes.ddekeeps20%to50%moretasksinlocal. Piwi; Pjej x8 mesh 8x8x8 mesh 16x16 torus 16x16x16 torus GDE DDE
16 Figure15:Normalizedcommunicationcost. 8x8 mesh 8x8x8 mesh 16x16 torus 16x16x16 torus GDE DDE 60% 50% 40% 30% 20% 10% 0% Figure16:Thepercentageoflocaltasks. 16 8x8 mesh 8x8x8 mesh 16x16 torus 16x16x16 torus GDE DDE
17 n-cube,ddeisfaster,balancestheloadwell,reducescommunications,andkeepsbetterlocality. tothek-aryn-cube.comparedtothegdealgorithm,whichalsoextendeddemtothek-ary Thispaperproposedadirectmethodforloadbalancing.ItextendedtheDEMalgorithm 7.Conclusion themeshwalkingalgorithm[8].however,dderetainsitssimplicityofimplementationandcan deliverasatisedperformanceatthesametime. References DDEcanbefurtherimprovedforamorebalancedloadandlesscommunicationsbyextending [1]G.Cybenko.Dynamicloadbalancingfordistributedmemorymultiprocessors.J.ofParallel [4]E.L.Lawler.CombinatorialOptimization:NetworksandMatroids.Holt,Rinehartand [3]S.H.Hosseini,B.Litow,M.Malkawi,J.McPherson,andK.Vairavan.Analysisofagraph [2]M.Barnettetal.Broadcastingonmesheswithwormholerouting.TechnicalReportTR-93- Computing,10:160{166,1990. coloringbaseddistributedloadbalancingalgorithm.journalofparallelanddistributed 24,Univ.TexasatAustin,1993. Distrib.Comput.,7:279{301,1989. [5]S.Ranka,Y.Won,andS.Sahni.Programmingahypercubemulticomputer.IEEESoftware, [6]W.ShuandM.Y.Wu.Runtimeparallelschedulingfordistributedmemorycomputers.In Winston,1976. pages69{77,september1988. [9]C.Z.XuandF.C.M.Lau.Analysisofthegeneralizeddimensionexchangemethodfor [8]M.Y.WuandW.Shu.High-performanceincrementalschedulingonmassivelyparallelcomputers aglobalapproach.insupercomputing'95,december1995. September1993. onhighlyparallelcomputers.ieeetrans.parallelanddistributedsystem,9(4):979{993, Int'lConf.onParallelProcessing,pagesII.143{150,August1995. [7]MarcWillebeek-LeMairandAnthonyP.Reeves.Strategiesfordynamicloadbalancing [10]C.Z.XuandF.C.M.Lau.Thegeneralizeddimensionexchangemethodforloadbalancing December1992. ink-aryn-cubesandvariants.journalofparallelanddistributedcomputing,24(1):72{85, January1995. dynamicloadbalancing.journalofparallelanddistributedcomputing,16(4):385{393, 17
thek-aryn-cubestructure. 1
 DDE:AModiedDimensionExchangeMethod forloadbalancingink-aryn-cubes StateUniversityofNewYorkatBualo DepartmentofComputerScience Min-YouWuandWeiShu algorithmforthehypercubestructure.ithasbeengeneralizedtok-aryn-cubes.however,the
DDE:AModiedDimensionExchangeMethod forloadbalancingink-aryn-cubes StateUniversityofNewYorkatBualo DepartmentofComputerScience Min-YouWuandWeiShu algorithmforthehypercubestructure.ithasbeengeneralizedtok-aryn-cubes.however,the
 Ďě Ž ť č ď ť ď ú ď ť ě Ě ň Ě ě ú ň ž ú ú Ú ú ú Ě ň é é ž ú ž Ť Ť Ť ú ň Ď ú ň ď Ě ú É ž ř ú ě ň ý Ě ň ý ň ň Ť ř ď ř ň ú Ť ě ř ě ý Š Ú Ú ň ň ú Ó Ú ň Ň Ů ž ú ň Č ř ř ú É ě ň ú Ž ý ú ú Ú Ú ť ž ž ď ý ž ď ž
Ďě Ž ť č ď ť ď ú ď ť ě Ě ň Ě ě ú ň ž ú ú Ú ú ú Ě ň é é ž ú ž Ť Ť Ť ú ň Ď ú ň ď Ě ú É ž ř ú ě ň ý Ě ň ý ň ň Ť ř ď ř ň ú Ť ě ř ě ý Š Ú Ú ň ň ú Ó Ú ň Ň Ů ž ú ň Č ř ř ú É ě ň ú Ž ý ú ú Ú Ú ť ž ž ď ý ž ď ž
Chapter 2. Multiprocessors Interconnection Networks
 Chapter 2 Multiprocessors Interconnection Networks 2.1 Taxonomy Interconnection Network Static Dynamic 1-D 2-D HC Bus-based Switch-based Single Multiple SS MS Crossbar 2.2 Bus-Based Dynamic Single Bus
Chapter 2 Multiprocessors Interconnection Networks 2.1 Taxonomy Interconnection Network Static Dynamic 1-D 2-D HC Bus-based Switch-based Single Multiple SS MS Crossbar 2.2 Bus-Based Dynamic Single Bus
Mail for OS X Medical School IMAP & Exchange Email Setup Guide
 MailforOSX MedicalSchoolIMAP&ExchangeEmail SetupGuide TherearetwowaystosetupyourMedicalSchoolemailaccountusingMail.One wayisconnectingusingexchangeandtheotherisbyusingimap.thisguidewill showyouhowtosetupmailusingthesetwomethods.forbestresults,we
MailforOSX MedicalSchoolIMAP&ExchangeEmail SetupGuide TherearetwowaystosetupyourMedicalSchoolemailaccountusingMail.One wayisconnectingusingexchangeandtheotherisbyusingimap.thisguidewill showyouhowtosetupmailusingthesetwomethods.forbestresults,we
Topological Properties
 Advanced Computer Architecture Topological Properties Routing Distance: Number of links on route Node degree: Number of channels per node Network diameter: Longest minimum routing distance between any
Advanced Computer Architecture Topological Properties Routing Distance: Number of links on route Node degree: Number of channels per node Network diameter: Longest minimum routing distance between any
A. Factoring out the Greatest Common Factor.
 DETAILED SOLUTIONS AND CONCEPTS - FACTORING POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to [email protected]. Thank you!
DETAILED SOLUTIONS AND CONCEPTS - FACTORING POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to [email protected]. Thank you!
EFFICIENTANIMATIONTECHNIQUESBALANCING BOTHUSERCONTROLANDPHYSICALREALISM
 EFFICIENTANIMATIONTECHNIQUESBALANCING BOTHUSERCONTROLANDPHYSICALREALISM ADISSERTATION ZichengLiu INCANDIDACYFORTHEDEGREE PRESENTEDTOTHEFACULTY OFDOCTOROFPHILOSOPHY OFPRINCETONUNIVERSITY RECOMMENDEDFORACCEPTANCE
EFFICIENTANIMATIONTECHNIQUESBALANCING BOTHUSERCONTROLANDPHYSICALREALISM ADISSERTATION ZichengLiu INCANDIDACYFORTHEDEGREE PRESENTEDTOTHEFACULTY OFDOCTOROFPHILOSOPHY OFPRINCETONUNIVERSITY RECOMMENDEDFORACCEPTANCE
Components: Interconnect Page 1 of 18
 Components: Interconnect Page 1 of 18 PE to PE interconnect: The most expensive supercomputer component Possible implementations: FULL INTERCONNECTION: The ideal Usually not attainable Each PE has a direct
Components: Interconnect Page 1 of 18 PE to PE interconnect: The most expensive supercomputer component Possible implementations: FULL INTERCONNECTION: The ideal Usually not attainable Each PE has a direct
Hyper Node Torus: A New Interconnection Network for High Speed Packet Processors
 2011 International Symposium on Computer Networks and Distributed Systems (CNDS), February 23-24, 2011 Hyper Node Torus: A New Interconnection Network for High Speed Packet Processors Atefeh Khosravi,
2011 International Symposium on Computer Networks and Distributed Systems (CNDS), February 23-24, 2011 Hyper Node Torus: A New Interconnection Network for High Speed Packet Processors Atefeh Khosravi,
ACTS 4301 FORMULA SUMMARY Lesson 1: Probability Review. Name f(x) F (x) E[X] Var(X) Name f(x) E[X] Var(X) p x (1 p) m x mp mp(1 p)
![ACTS 4301 FORMULA SUMMARY Lesson 1: Probability Review. Name f(x) F (x) E[X] Var(X) Name f(x) E[X] Var(X) p x (1 p) m x mp mp(1 p) ACTS 4301 FORMULA SUMMARY Lesson 1: Probability Review. Name f(x) F (x) E[X] Var(X) Name f(x) E[X] Var(X) p x (1 p) m x mp mp(1 p)](/thumbs/39/20405687.jpg) ACTS 431 FORMULA SUMMARY Lesson 1: Probability Review 1. VarX)= E[X 2 ]- E[X] 2 2. V arax + by ) = a 2 V arx) + 2abCovX, Y ) + b 2 V ary ) 3. V ar X) = V arx) n 4. E X [X] = E Y [E X [X Y ]] Double expectation
ACTS 431 FORMULA SUMMARY Lesson 1: Probability Review 1. VarX)= E[X 2 ]- E[X] 2 2. V arax + by ) = a 2 V arx) + 2abCovX, Y ) + b 2 V ary ) 3. V ar X) = V arx) n 4. E X [X] = E Y [E X [X Y ]] Double expectation
Load Balancing between Computing Clusters
 Load Balancing between Computing Clusters Siu-Cheung Chau Dept. of Physics and Computing, Wilfrid Laurier University, Waterloo, Ontario, Canada, NL 3C5 e-mail: [email protected] Ada Wai-Chee Fu Dept. of Computer
Load Balancing between Computing Clusters Siu-Cheung Chau Dept. of Physics and Computing, Wilfrid Laurier University, Waterloo, Ontario, Canada, NL 3C5 e-mail: [email protected] Ada Wai-Chee Fu Dept. of Computer
Lecture 3: Models of Solutions
 Materials Science & Metallurgy Master of Philosophy, Materials Modelling, Course MP4, Thermodynamics and Phase Diagrams, H. K. D. H. Bhadeshia Lecture 3: Models of Solutions List of Symbols Symbol G M
Materials Science & Metallurgy Master of Philosophy, Materials Modelling, Course MP4, Thermodynamics and Phase Diagrams, H. K. D. H. Bhadeshia Lecture 3: Models of Solutions List of Symbols Symbol G M
Factoring Special Polynomials
 6.6 Factoring Special Polynomials 6.6 OBJECTIVES 1. Factor the difference of two squares 2. Factor the sum or difference of two cubes In this section, we will look at several special polynomials. These
6.6 Factoring Special Polynomials 6.6 OBJECTIVES 1. Factor the difference of two squares 2. Factor the sum or difference of two cubes In this section, we will look at several special polynomials. These
Lecture 4: Futures and Options Steven Skiena. http://www.cs.sunysb.edu/ skiena
 Lecture 4: Futures and Options Steven Skiena Department of Computer Science State University of New York Stony Brook, NY 11794 4400 http://www.cs.sunysb.edu/ skiena Foreign Currency Futures Assume that
Lecture 4: Futures and Options Steven Skiena Department of Computer Science State University of New York Stony Brook, NY 11794 4400 http://www.cs.sunysb.edu/ skiena Foreign Currency Futures Assume that
 Nearestneighboralgorithmsforloadbalancingin ChengzhongXu parallelcomputers DepartmentofElectricalandComputerEngg. WayneStateUniversity,Detroit,MI48202 BurkhardMonien,ReinhardLuling [email protected]
Nearestneighboralgorithmsforloadbalancingin ChengzhongXu parallelcomputers DepartmentofElectricalandComputerEngg. WayneStateUniversity,Detroit,MI48202 BurkhardMonien,ReinhardLuling [email protected]
Fast Fourier Transform: Theory and Algorithms
 Fast Fourier Transform: Theory and Algorithms Lecture Vladimir Stojanović 6.973 Communication System Design Spring 006 Massachusetts Institute of Technology Discrete Fourier Transform A review Definition
Fast Fourier Transform: Theory and Algorithms Lecture Vladimir Stojanović 6.973 Communication System Design Spring 006 Massachusetts Institute of Technology Discrete Fourier Transform A review Definition
Chapter 12: Multiprocessor Architectures. Lesson 04: Interconnect Networks
 Chapter 12: Multiprocessor Architectures Lesson 04: Interconnect Networks Objective To understand different interconnect networks To learn crossbar switch, hypercube, multistage and combining networks
Chapter 12: Multiprocessor Architectures Lesson 04: Interconnect Networks Objective To understand different interconnect networks To learn crossbar switch, hypercube, multistage and combining networks
Manual for SOA Exam MLC.
 Chapter 5 Life annuities Extract from: Arcones Manual for the SOA Exam MLC Fall 2009 Edition available at http://wwwactexmadrivercom/ 1/70 Due n year deferred annuity Definition 1 A due n year deferred
Chapter 5 Life annuities Extract from: Arcones Manual for the SOA Exam MLC Fall 2009 Edition available at http://wwwactexmadrivercom/ 1/70 Due n year deferred annuity Definition 1 A due n year deferred
Chapter 8. Shear Force and Bending Moment Diagrams for Uniformly Distributed Loads.
 hapter 8 Shear Force and ending Moment Diagrams for Uniformly Distributed Loads. 8.1 Introduction In Unit 4 we saw how to calculate moments for uniformly distributed loads. You might find it worthwhile
hapter 8 Shear Force and ending Moment Diagrams for Uniformly Distributed Loads. 8.1 Introduction In Unit 4 we saw how to calculate moments for uniformly distributed loads. You might find it worthwhile
Interconnection Network
 Interconnection Network Recap: Generic Parallel Architecture A generic modern multiprocessor Network Mem Communication assist (CA) $ P Node: processor(s), memory system, plus communication assist Network
Interconnection Network Recap: Generic Parallel Architecture A generic modern multiprocessor Network Mem Communication assist (CA) $ P Node: processor(s), memory system, plus communication assist Network
Return On Investment XpoLog Center
 Return On Investment XpoLog Center ROI Management of XpoLog Center Business white paper May 2015 In This Document: 1. ROI Metrics and Examples 2. Total Summary of ROI and TCO 3. Real Life Use Cases and
Return On Investment XpoLog Center ROI Management of XpoLog Center Business white paper May 2015 In This Document: 1. ROI Metrics and Examples 2. Total Summary of ROI and TCO 3. Real Life Use Cases and
Options, Futures, and Other Derivatives 7 th Edition, Copyright John C. Hull 2008 2
 Mechanics of Options Markets Chapter 8 Options, Futures, and Other Derivatives, 7th Edition, Copyright John C. Hull 2008 1 Review of Option Types A call is an option to buy A put is an option to sell A
Mechanics of Options Markets Chapter 8 Options, Futures, and Other Derivatives, 7th Edition, Copyright John C. Hull 2008 1 Review of Option Types A call is an option to buy A put is an option to sell A
Figure2:Themixtureoffactoranalysisgenerativemodel. j;j z
 TheEMAlgorithmforMixturesofFactorAnalyzers DepartmentofComputerScience ZoubinGhahramani GeoreyE.Hinton May21,1996(revisedFeb27,1997) TechnicalReportCRG-TR-96-1 Email:[email protected] Toronto,CanadaM5S1A4
TheEMAlgorithmforMixturesofFactorAnalyzers DepartmentofComputerScience ZoubinGhahramani GeoreyE.Hinton May21,1996(revisedFeb27,1997) TechnicalReportCRG-TR-96-1 Email:[email protected] Toronto,CanadaM5S1A4
Regression and Correlation
 Regression and Correlation Topics Covered: Dependent and independent variables. Scatter diagram. Correlation coefficient. Linear Regression line. by Dr.I.Namestnikova 1 Introduction Regression analysis
Regression and Correlation Topics Covered: Dependent and independent variables. Scatter diagram. Correlation coefficient. Linear Regression line. by Dr.I.Namestnikova 1 Introduction Regression analysis
Introduction: Overview of Kernel Methods
 Introduction: Overview of Kernel Methods Statistical Data Analysis with Positive Definite Kernels Kenji Fukumizu Institute of Statistical Mathematics, ROIS Department of Statistical Science, Graduate University
Introduction: Overview of Kernel Methods Statistical Data Analysis with Positive Definite Kernels Kenji Fukumizu Institute of Statistical Mathematics, ROIS Department of Statistical Science, Graduate University
x 3 x 4 x 2 f -7.0-9.5 4.3-4.2-9.0-8.7-3.5-5.7-8.0 3.4-6.9-8.7 9.8 3.8 5.1-2.7-6.5 0.8-3.5 7.1 6.2 9.9 7.7 0.1-7.4 Site A Site B Site C
 DistributedMultivariateRegressionUsing Wavelet-basedCollectiveDataMining SchoolofElectricalEngineeringandComputerScience DarylE.HershbergerandHillolKargupta SchoolofElectricalEngineeringandComputerScienceTechnicalReportEECS99-002
DistributedMultivariateRegressionUsing Wavelet-basedCollectiveDataMining SchoolofElectricalEngineeringandComputerScience DarylE.HershbergerandHillolKargupta SchoolofElectricalEngineeringandComputerScienceTechnicalReportEECS99-002
BERNOULLI (BETA) and INTEGER PART SEQUENCES
 BERNOULLI (BETA) and INTEGER PART SEQUENCES Rod Nillsen,Keith Tognetti and Graham Winley* School of Mathematics and Applied Statistics, (*Department of Business Systems) University of Wollongong NSW 2522
BERNOULLI (BETA) and INTEGER PART SEQUENCES Rod Nillsen,Keith Tognetti and Graham Winley* School of Mathematics and Applied Statistics, (*Department of Business Systems) University of Wollongong NSW 2522
Manual for SOA Exam MLC.
 Chapter 5 Life annuities Extract from: Arcones Manual for the SOA Exam MLC Fall 2009 Edition available at http://wwwactexmadrivercom/ 1/94 Due n year temporary annuity Definition 1 A due n year term annuity
Chapter 5 Life annuities Extract from: Arcones Manual for the SOA Exam MLC Fall 2009 Edition available at http://wwwactexmadrivercom/ 1/94 Due n year temporary annuity Definition 1 A due n year term annuity
System Interconnect Architectures. Goals and Analysis. Network Properties and Routing. Terminology - 2. Terminology - 1
 System Interconnect Architectures CSCI 8150 Advanced Computer Architecture Hwang, Chapter 2 Program and Network Properties 2.4 System Interconnect Architectures Direct networks for static connections Indirect
System Interconnect Architectures CSCI 8150 Advanced Computer Architecture Hwang, Chapter 2 Program and Network Properties 2.4 System Interconnect Architectures Direct networks for static connections Indirect
call option put option strike price/exercise price expiration date/maturity
 OPTIONS Objective This chapter introduces the readers to the concept of options which include calls and puts. All basic concepts like option buyer and seller, European and American options, and payoff
OPTIONS Objective This chapter introduces the readers to the concept of options which include calls and puts. All basic concepts like option buyer and seller, European and American options, and payoff
Online Degree Ramsey Theory
 UofL Discrete Math Workshop 2008 1 Online Degree Ramsey Theory posed by Illinois REGS (2007) problem 1 presented by Lesley Wiglesworth LATEX byadamjobson For a family of graphs F closed under subgraphs,
UofL Discrete Math Workshop 2008 1 Online Degree Ramsey Theory posed by Illinois REGS (2007) problem 1 presented by Lesley Wiglesworth LATEX byadamjobson For a family of graphs F closed under subgraphs,
RIGHT-OF-WAY ACQUISITION AND BRIDGE CONSTRUCTION BONDS 7/01/12 341150MD9 341150ND8 341150QR4
 RIGHT-OF-WAY ACQUISITION AND BRIDGE CONSTRUCTION BONDS CUSIP Numbers Maturity Date Series 2002 Dated 1/15/2002 Series 2002A New & Refunding Dated 9/01/2002 Series 2003A Dated 9/15/2003 7/01/12 341150MD9
RIGHT-OF-WAY ACQUISITION AND BRIDGE CONSTRUCTION BONDS CUSIP Numbers Maturity Date Series 2002 Dated 1/15/2002 Series 2002A New & Refunding Dated 9/01/2002 Series 2003A Dated 9/15/2003 7/01/12 341150MD9
SCHOOLOFCOMPUTERSTUDIES RESEARCHREPORTSERIES UniversityofLeeds Report95.4
 SCHOOLOFCOMPUTERSTUDIES RESEARCHREPORTSERIES UniversityofLeeds Report95.4 AcquisitionsandApplications Generic3-DShapeModel: DivisionofArticialIntelligence XShen&DCHogg by February1995 sequencesandrepresentedbythecontrolpointsofab-splinesurface.the
SCHOOLOFCOMPUTERSTUDIES RESEARCHREPORTSERIES UniversityofLeeds Report95.4 AcquisitionsandApplications Generic3-DShapeModel: DivisionofArticialIntelligence XShen&DCHogg by February1995 sequencesandrepresentedbythecontrolpointsofab-splinesurface.the
niveau : 1 ere année spécialité : mécatronique & froid et climatisation AU : 2014-2015 Programmation C Travaux pratiques
 École Supérieure Privée d Ingénieurs de Monastir niveau : 1 ere année spécialité : mécatronique & froid et climatisation AU : 2014-2015 Programmation C Travaux pratiques Correction Exercice 1 TP3 long
École Supérieure Privée d Ingénieurs de Monastir niveau : 1 ere année spécialité : mécatronique & froid et climatisation AU : 2014-2015 Programmation C Travaux pratiques Correction Exercice 1 TP3 long
Parallel Programming
 Parallel Programming Parallel Architectures Diego Fabregat-Traver and Prof. Paolo Bientinesi HPAC, RWTH Aachen [email protected] WS15/16 Parallel Architectures Acknowledgements Prof. Felix
Parallel Programming Parallel Architectures Diego Fabregat-Traver and Prof. Paolo Bientinesi HPAC, RWTH Aachen [email protected] WS15/16 Parallel Architectures Acknowledgements Prof. Felix
Transient Voltage Suppressor SMBJ5.0 - SMBJ440CA
 Features: Glass passivated junction Low incremental surge resistance, excellent clamping capability 600W peak pulse power capability with a 10/1,000μs waveform, repetition rate (duty cycle): 0.01% Very
Features: Glass passivated junction Low incremental surge resistance, excellent clamping capability 600W peak pulse power capability with a 10/1,000μs waveform, repetition rate (duty cycle): 0.01% Very
Certification of Discontinuous Composite Material Forms for Aircraft Structures
 Certification of Discontinuous Composite Material Forms for Aircraft Structures Paolo Feraboli (UWAA), Mark Tuttle (UW), Larry Ilcewicz (FAA), Bill Avery (Boeing), Bruno Boursier, Dave Barr (Hexcel) JAMS
Certification of Discontinuous Composite Material Forms for Aircraft Structures Paolo Feraboli (UWAA), Mark Tuttle (UW), Larry Ilcewicz (FAA), Bill Avery (Boeing), Bruno Boursier, Dave Barr (Hexcel) JAMS
Factoring - Factoring Special Products
 6.5 Factoring - Factoring Special Products Objective: Identify and factor special products including a difference of squares, perfect squares, and sum and difference of cubes. When factoring there are
6.5 Factoring - Factoring Special Products Objective: Identify and factor special products including a difference of squares, perfect squares, and sum and difference of cubes. When factoring there are
... Schema Integration
 DataIntegrationTechniquesbasedon MichaelGertz DataQualityAspects DepartmentofComputerScience UniversityofCalifornia,Davis IngoSchmitt [email protected] Davis,CA95616,USA OneShieldsAvenue Otto-von-Guericke-UniversitatMagdeburg
DataIntegrationTechniquesbasedon MichaelGertz DataQualityAspects DepartmentofComputerScience UniversityofCalifornia,Davis IngoSchmitt [email protected] Davis,CA95616,USA OneShieldsAvenue Otto-von-Guericke-UniversitatMagdeburg
Actuarial mathematics 2
 Actuarial mathematics 2 Life insurance contracts Edward Furman Department of Mathematics and Statistics York University January 3, 212 Edward Furman Actuarial mathematics MATH 328 1 / 45 Definition.1 (Life
Actuarial mathematics 2 Life insurance contracts Edward Furman Department of Mathematics and Statistics York University January 3, 212 Edward Furman Actuarial mathematics MATH 328 1 / 45 Definition.1 (Life
Factoring Guidelines. Greatest Common Factor Two Terms Three Terms Four Terms. 2008 Shirley Radai
 Factoring Guidelines Greatest Common Factor Two Terms Three Terms Four Terms 008 Shirley Radai Greatest Common Factor 008 Shirley Radai Factoring by Finding the Greatest Common Factor Always check for
Factoring Guidelines Greatest Common Factor Two Terms Three Terms Four Terms 008 Shirley Radai Greatest Common Factor 008 Shirley Radai Factoring by Finding the Greatest Common Factor Always check for
The Algorithms of Speech Recognition, Programming and Simulating in MATLAB
 FACULTY OF ENGINEERING AND SUSTAINABLE DEVELOPMENT. The Algorithms of Speech Recognition, Programming and Simulating in MATLAB Tingxiao Yang January 2012 Bachelor s Thesis in Electronics Bachelor s Program
FACULTY OF ENGINEERING AND SUSTAINABLE DEVELOPMENT. The Algorithms of Speech Recognition, Programming and Simulating in MATLAB Tingxiao Yang January 2012 Bachelor s Thesis in Electronics Bachelor s Program
Performance Comparison of Dynamic Load-Balancing Strategies for Distributed Computing
 Performance Comparison of Dynamic Load-Balancing Strategies for Distributed Computing A. Cortés, A. Ripoll, M.A. Senar and E. Luque Computer Architecture and Operating Systems Group Universitat Autònoma
Performance Comparison of Dynamic Load-Balancing Strategies for Distributed Computing A. Cortés, A. Ripoll, M.A. Senar and E. Luque Computer Architecture and Operating Systems Group Universitat Autònoma
Tutorial on Exploratory Data Analysis
 Tutorial on Exploratory Data Analysis Julie Josse, François Husson, Sébastien Lê julie.josse at agrocampus-ouest.fr francois.husson at agrocampus-ouest.fr Applied Mathematics Department, Agrocampus Ouest
Tutorial on Exploratory Data Analysis Julie Josse, François Husson, Sébastien Lê julie.josse at agrocampus-ouest.fr francois.husson at agrocampus-ouest.fr Applied Mathematics Department, Agrocampus Ouest
Review of Statistical Mechanics
 Review of Statistical Mechanics 3. Microcanonical, Canonical, Grand Canonical Ensembles In statistical mechanics, we deal with a situation in which even the quantum state of the system is unknown. The
Review of Statistical Mechanics 3. Microcanonical, Canonical, Grand Canonical Ensembles In statistical mechanics, we deal with a situation in which even the quantum state of the system is unknown. The
Lecture 21. The Multivariate Normal Distribution
 Lecture. The Multivariate Normal Distribution. Definitions and Comments The joint moment-generating function of X,...,X n [also called the moment-generating function of the random vector (X,...,X n )]
Lecture. The Multivariate Normal Distribution. Definitions and Comments The joint moment-generating function of X,...,X n [also called the moment-generating function of the random vector (X,...,X n )]
(1) The size of a gas particle is negligible as compared to the volume of the container in which the gas is placed.
 Gas Laws and Kinetic Molecular Theory The Gas Laws are based on experiments, and they describe how a gas behaves under certain conditions. However, Gas Laws do not attempt to explain the behavior of gases.
Gas Laws and Kinetic Molecular Theory The Gas Laws are based on experiments, and they describe how a gas behaves under certain conditions. However, Gas Laws do not attempt to explain the behavior of gases.
Factoring. Factoring Polynomial Equations. Special Factoring Patterns. Factoring. Special Factoring Patterns. Special Factoring Patterns
 Factoring Factoring Polynomial Equations Ms. Laster Earlier, you learned to factor several types of quadratic expressions: General trinomial - 2x 2-5x-12 = (2x + 3)(x - 4) Perfect Square Trinomial - x
Factoring Factoring Polynomial Equations Ms. Laster Earlier, you learned to factor several types of quadratic expressions: General trinomial - 2x 2-5x-12 = (2x + 3)(x - 4) Perfect Square Trinomial - x
Interconnection Networks
 CMPT765/408 08-1 Interconnection Networks Qianping Gu 1 Interconnection Networks The note is mainly based on Chapters 1, 2, and 4 of Interconnection Networks, An Engineering Approach by J. Duato, S. Yalamanchili,
CMPT765/408 08-1 Interconnection Networks Qianping Gu 1 Interconnection Networks The note is mainly based on Chapters 1, 2, and 4 of Interconnection Networks, An Engineering Approach by J. Duato, S. Yalamanchili,
Chapter 7. BANDIT PROBLEMS.
 Chapter 7. BANDIT PROBLEMS. Bandit problems are problems in the area of sequential selection of experiments, and they are related to stopping rule problems through the theorem of Gittins and Jones (974).
Chapter 7. BANDIT PROBLEMS. Bandit problems are problems in the area of sequential selection of experiments, and they are related to stopping rule problems through the theorem of Gittins and Jones (974).
Section 6.1 Factoring Expressions
 Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
Factors and Products
 CHAPTER 3 Factors and Products What You ll Learn use different strategies to find factors and multiples of whole numbers identify prime factors and write the prime factorization of a number find square
CHAPTER 3 Factors and Products What You ll Learn use different strategies to find factors and multiples of whole numbers identify prime factors and write the prime factorization of a number find square
Earthquake Hazard Zones: The relative risk of damage to Canadian buildings
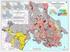 Earthquake Hazard Zones: The relative risk of damage to Canadian buildings by Paul Kovacs Executive Director, Institute for Catastrophic Loss Reduction Adjunct Research Professor, Economics, Univ. of Western
Earthquake Hazard Zones: The relative risk of damage to Canadian buildings by Paul Kovacs Executive Director, Institute for Catastrophic Loss Reduction Adjunct Research Professor, Economics, Univ. of Western
London South Bank University - United Kingdom. www.lsbu.ac.uk. Business Management
 London South Bank University - United Kingdom www.lsbu.ac.uk Business Management Level 4 Diploma in Business Management holders with at least 3 subjects passed at B or above may be eligible for entry onto
London South Bank University - United Kingdom www.lsbu.ac.uk Business Management Level 4 Diploma in Business Management holders with at least 3 subjects passed at B or above may be eligible for entry onto
Actuarial Science with
 Actuarial Science with 1. life insurance & actuarial notations Arthur Charpentier joint work with Christophe Dutang & Vincent Goulet and Giorgio Alfredo Spedicato s lifecontingencies package Meielisalp
Actuarial Science with 1. life insurance & actuarial notations Arthur Charpentier joint work with Christophe Dutang & Vincent Goulet and Giorgio Alfredo Spedicato s lifecontingencies package Meielisalp
Unit 10 Geometry Circles. NAME Period
 Unit 10 Geometry Circles NAME Period 1 Geometry Chapter 10 Circles ***In order to get full credit for your assignments they must me done on time and you must SHOW ALL WORK. *** 1. (10-1) Circles and Circumference
Unit 10 Geometry Circles NAME Period 1 Geometry Chapter 10 Circles ***In order to get full credit for your assignments they must me done on time and you must SHOW ALL WORK. *** 1. (10-1) Circles and Circumference
Repairing storm damaged roofs
 Repairing storm damaged roofs Tie-down designs for tile and sheet roofs Conforms to wind classifications of up to category N3 (previously W41N) designed to withstand a maximum gust wind speeds of 50 metres
Repairing storm damaged roofs Tie-down designs for tile and sheet roofs Conforms to wind classifications of up to category N3 (previously W41N) designed to withstand a maximum gust wind speeds of 50 metres
 StaticFrequencyAssignmentinCellular LataNarayanan Networks August,998 SunilM.Shendey tice.inthestaticfrequencyassignmentproblem,eachvertexofthegraphisa Acellularnetworkisgenerallymodeledasasubgraphofthetriangularlat-
StaticFrequencyAssignmentinCellular LataNarayanan Networks August,998 SunilM.Shendey tice.inthestaticfrequencyassignmentproblem,eachvertexofthegraphisa Acellularnetworkisgenerallymodeledasasubgraphofthetriangularlat-
Sleeve Yokes / Kayıcı Çatallar
 Sleeve Yokes / Kayıcı Çatallar 19,00 126,00 49,70 Spline / Kanal SE 1 1/16 x 16 ngle / çı 25 0 Serie 0400 MS NO SY 01 23,80 149,00 64,20 Spline / Kanal SE 1 x 10 ngle / çı 20 0 Serie 1140 MS NO SY 02 23,80
Sleeve Yokes / Kayıcı Çatallar 19,00 126,00 49,70 Spline / Kanal SE 1 1/16 x 16 ngle / çı 25 0 Serie 0400 MS NO SY 01 23,80 149,00 64,20 Spline / Kanal SE 1 x 10 ngle / çı 20 0 Serie 1140 MS NO SY 02 23,80
Issues in Information Systems Volume 14, Issue 2, pp.353-358, 2013
 A MODEL FOR SIMULTANEOUS DECISIONS ON MASTER PRODUCTION SCHEDULING, LOT SIZING, AND CAPACITY REQUIREMENTS PLANNING Harish C. Bahl, California State University-Chico, [email protected] Neelam Bahl, California
A MODEL FOR SIMULTANEOUS DECISIONS ON MASTER PRODUCTION SCHEDULING, LOT SIZING, AND CAPACITY REQUIREMENTS PLANNING Harish C. Bahl, California State University-Chico, [email protected] Neelam Bahl, California
timeout StoR!msg0 RtoS?ack0
 c1997kluweracademicpublishers,boston.manufacturedinthenetherlands. FormalMethodsinSystemDesign,,?{??(1997) SymbolicVericationofCommunication ProtocolswithInniteStateSpacesusingQDDs queues.itiswell-knownthatmostinterestingvericationproblems,suchasdeadlockdetection,
c1997kluweracademicpublishers,boston.manufacturedinthenetherlands. FormalMethodsinSystemDesign,,?{??(1997) SymbolicVericationofCommunication ProtocolswithInniteStateSpacesusingQDDs queues.itiswell-knownthatmostinterestingvericationproblems,suchasdeadlockdetection,
Lesson 9: Radicals and Conjugates
 Student Outcomes Students understand that the sum of two square roots (or two cube roots) is not equal to the square root (or cube root) of their sum. Students convert expressions to simplest radical form.
Student Outcomes Students understand that the sum of two square roots (or two cube roots) is not equal to the square root (or cube root) of their sum. Students convert expressions to simplest radical form.
Lecture 18: Interconnection Networks. CMU 15-418: Parallel Computer Architecture and Programming (Spring 2012)
 Lecture 18: Interconnection Networks CMU 15-418: Parallel Computer Architecture and Programming (Spring 2012) Announcements Project deadlines: - Mon, April 2: project proposal: 1-2 page writeup - Fri,
Lecture 18: Interconnection Networks CMU 15-418: Parallel Computer Architecture and Programming (Spring 2012) Announcements Project deadlines: - Mon, April 2: project proposal: 1-2 page writeup - Fri,
{apolin},{mcampos}@ieee.org
 {apolin},{mcampos}@ieee.org x( ) 2 x( ) x( ) = ( ) x = [ ( ) x ı x + ( ) y ( ) y ( ) z ı y + ( ) z ] T ı z 2 x ( ) = 2 ( ) x + 2 ( ) 2 y + 2 ( ) 2 z 2 2 E = 1 2 E c 2 t 2 s(x,t) 2 s x + 2 s 2 y + 2
{apolin},{mcampos}@ieee.org x( ) 2 x( ) x( ) = ( ) x = [ ( ) x ı x + ( ) y ( ) y ( ) z ı y + ( ) z ] T ı z 2 x ( ) = 2 ( ) x + 2 ( ) 2 y + 2 ( ) 2 z 2 2 E = 1 2 E c 2 t 2 s(x,t) 2 s x + 2 s 2 y + 2
Flexible Distributed Capacity Allocation and Load Redirect Algorithms for Cloud Systems
 Flexible Distributed Capacity Allocation and Load Redirect Algorithms for Cloud Systems Danilo Ardagna 1, Sara Casolari 2, Barbara Panicucci 1 1 Politecnico di Milano,, Italy 2 Universita` di Modena e
Flexible Distributed Capacity Allocation and Load Redirect Algorithms for Cloud Systems Danilo Ardagna 1, Sara Casolari 2, Barbara Panicucci 1 1 Politecnico di Milano,, Italy 2 Universita` di Modena e
THOSE WHO WAIT As recorded by Tommy Emmanuel
 ransribd by iorio Mali OSE O s rordd by ommy Emmanl (From h lbm OLY) Msi by ommy Emmanl rrand by ommy Emmanl nro r-rs = nin: DDE Dadd Fadd add Dadd rs,.. [] [] [] [] [] [] [] [] [] [] () () Fadd () add
ransribd by iorio Mali OSE O s rordd by ommy Emmanl (From h lbm OLY) Msi by ommy Emmanl rrand by ommy Emmanl nro r-rs = nin: DDE Dadd Fadd add Dadd rs,.. [] [] [] [] [] [] [] [] [] [] () () Fadd () add
Topology Optimization of Engine Mount Brackets Dr. Dirk Sprengel Ford Werke GmbH
 Topology Optimization of Engine Mount Brackets Dr. Dirk Sprengel Ford Werke GmbH Dr. D. Sprengel 6/2007 Topology Optimization of EMS Bracket 1 ( 21 ) EMS Bracket Funktion EMS: Engine Mount System Link
Topology Optimization of Engine Mount Brackets Dr. Dirk Sprengel Ford Werke GmbH Dr. D. Sprengel 6/2007 Topology Optimization of EMS Bracket 1 ( 21 ) EMS Bracket Funktion EMS: Engine Mount System Link
Tool 1. Greatest Common Factor (GCF)
 Chapter 4: Factoring Review Tool 1 Greatest Common Factor (GCF) This is a very important tool. You must try to factor out the GCF first in every problem. Some problems do not have a GCF but many do. When
Chapter 4: Factoring Review Tool 1 Greatest Common Factor (GCF) This is a very important tool. You must try to factor out the GCF first in every problem. Some problems do not have a GCF but many do. When
Home Software Hardware Benchmarks Services Store Support Forums About Us
 Pass - CPU Benchmarks - List of Benchmarked CPUs Shopping cart Search Home Software Hardware Benchmarks Services Store Support Forums About Us Home» CPU Benchmarks» CPU List CPU Benchmarks Video Card Benchmarks
Pass - CPU Benchmarks - List of Benchmarked CPUs Shopping cart Search Home Software Hardware Benchmarks Services Store Support Forums About Us Home» CPU Benchmarks» CPU List CPU Benchmarks Video Card Benchmarks
Design MEMO 60 Reinforcement design for TSS 102
 Date: 04.0.0 sss Page of 5 CONTENTS PART BASIC ASSUMTIONS... GENERAL... STANDARDS... QUALITIES... 3 DIMENSIONS... 3 LOADS... 3 PART REINFORCEMENT... 4 EQUILIBRIUM... 4 Date: 04.0.0 sss Page of 5 PART BASIC
Date: 04.0.0 sss Page of 5 CONTENTS PART BASIC ASSUMTIONS... GENERAL... STANDARDS... QUALITIES... 3 DIMENSIONS... 3 LOADS... 3 PART REINFORCEMENT... 4 EQUILIBRIUM... 4 Date: 04.0.0 sss Page of 5 PART BASIC
Asal Siviçler Basic Switches
 Asal Siviçler Asal Siviçler Asal Siviçler MN1 Serisi Mini Siviçler 03 MN2 Serisi Mini Siviçler 09 MN3 Serisi Mini Siviçler 15 MK1 Serisi Mikro Siviçler 19 BS1 Serisi Buton Siviçler 25 MA1 Serisi Mandall
Asal Siviçler Asal Siviçler Asal Siviçler MN1 Serisi Mini Siviçler 03 MN2 Serisi Mini Siviçler 09 MN3 Serisi Mini Siviçler 15 MK1 Serisi Mikro Siviçler 19 BS1 Serisi Buton Siviçler 25 MA1 Serisi Mandall
Themethodofmovingcurvesandmovingsurfacesisanew,eectivetoolfor Abstract
 OnaRelationshipbetweentheMovingLineand MovingConicCoecientMatrices DepartmentofComputerScience Houston,Texas77005 [email protected] RiceUniversity MingZhang DepartmentofInformationSystemsandComputerScience
OnaRelationshipbetweentheMovingLineand MovingConicCoecientMatrices DepartmentofComputerScience Houston,Texas77005 [email protected] RiceUniversity MingZhang DepartmentofInformationSystemsandComputerScience
OR topics in MRP-II. Mads Jepsens. OR topics in MRP-II p.1/25
 OR topics in MRP-II Mads Jepsens OR topics in MRP-II p.1/25 Overview Why bother? OR topics in MRP-II p.2/25 Why bother? Push and Pull systems Overview OR topics in MRP-II p.2/25 Overview Why bother? Push
OR topics in MRP-II Mads Jepsens OR topics in MRP-II p.1/25 Overview Why bother? OR topics in MRP-II p.2/25 Why bother? Push and Pull systems Overview OR topics in MRP-II p.2/25 Overview Why bother? Push
Development of backup power systems at Wuhan Troowin Power System
 Development of backup power systems at Wuhan Troowin Power System Zhigang Qi Workshop on Fuel Cell Backup Power for Telecommunication Base Stations Wuhan University of Technology, Wuhan, China, May 29,
Development of backup power systems at Wuhan Troowin Power System Zhigang Qi Workshop on Fuel Cell Backup Power for Telecommunication Base Stations Wuhan University of Technology, Wuhan, China, May 29,
CE 366 SETTLEMENT (Problems & Solutions)
 CE 366 SETTLEMENT (Problems & Solutions) P. 1) LOAD UNDER A RECTANGULAR AREA (1) Question: The footing shown in the figure below exerts a uniform pressure of 300 kn/m 2 to the soil. Determine vertical
CE 366 SETTLEMENT (Problems & Solutions) P. 1) LOAD UNDER A RECTANGULAR AREA (1) Question: The footing shown in the figure below exerts a uniform pressure of 300 kn/m 2 to the soil. Determine vertical
Mark Scheme (Results) November 2009
 Mark Scheme (Results) November 2009 GCSE GCSE Mathematics (Linear) - 1380 Paper: Edexcel is one of the leading examining and awarding bodies in the UK and throughout the world. We provide a wide range
Mark Scheme (Results) November 2009 GCSE GCSE Mathematics (Linear) - 1380 Paper: Edexcel is one of the leading examining and awarding bodies in the UK and throughout the world. We provide a wide range
"#$%&'((&)!*+,-./ 0+1$23!4-+5#.-)!!
 "#$%&'((&)*+,-./ 0+1$234-+5#.-) 6(75()+1-,+,-.+289(2-:7$5;"#$%&'((&) JoeWoodard,President CreativeFinancialSoftware,Inc. AdvancedCertifiedQuickBooksProAdvisor Member"IntuitSolutionProviderProgram Intuit
"#$%&'((&)*+,-./ 0+1$234-+5#.-) 6(75()+1-,+,-.+289(2-:7$5;"#$%&'((&) JoeWoodard,President CreativeFinancialSoftware,Inc. AdvancedCertifiedQuickBooksProAdvisor Member"IntuitSolutionProviderProgram Intuit
Design MEMO 54a Reinforcement design for RVK 41
 Page of 5 CONTENTS PART BASIC ASSUMTIONS... 2 GENERAL... 2 STANDARDS... 2 QUALITIES... 3 DIMENSIONS... 3 LOADS... 3 PART 2 REINFORCEMENT... 4 EQUILIBRIUM... 4 Page 2 of 5 PART BASIC ASSUMTIONS GENERAL
Page of 5 CONTENTS PART BASIC ASSUMTIONS... 2 GENERAL... 2 STANDARDS... 2 QUALITIES... 3 DIMENSIONS... 3 LOADS... 3 PART 2 REINFORCEMENT... 4 EQUILIBRIUM... 4 Page 2 of 5 PART BASIC ASSUMTIONS GENERAL
Beat the Mean Bandit
 Yisong Yue H. John Heinz III College, Carnegie Mellon University, Pittsburgh, PA, USA Thorsten Joachims Department of Computer Science, Cornell University, Ithaca, NY, USA [email protected] [email protected]
Yisong Yue H. John Heinz III College, Carnegie Mellon University, Pittsburgh, PA, USA Thorsten Joachims Department of Computer Science, Cornell University, Ithaca, NY, USA [email protected] [email protected]
How To Prove The Dirichlet Unit Theorem
 Chapter 6 The Dirichlet Unit Theorem As usual, we will be working in the ring B of algebraic integers of a number field L. Two factorizations of an element of B are regarded as essentially the same if
Chapter 6 The Dirichlet Unit Theorem As usual, we will be working in the ring B of algebraic integers of a number field L. Two factorizations of an element of B are regarded as essentially the same if
1. Prove that the empty set is a subset of every set.
 1. Prove that the empty set is a subset of every set. Basic Topology Written by Men-Gen Tsai email: [email protected] Proof: For any element x of the empty set, x is also an element of every set since
1. Prove that the empty set is a subset of every set. Basic Topology Written by Men-Gen Tsai email: [email protected] Proof: For any element x of the empty set, x is also an element of every set since
Factoring (pp. 1 of 4)
 Factoring (pp. 1 of 4) Algebra Review Try these items from middle school math. A) What numbers are the factors of 4? B) Write down the prime factorization of 7. C) 6 Simplify 48 using the greatest common
Factoring (pp. 1 of 4) Algebra Review Try these items from middle school math. A) What numbers are the factors of 4? B) Write down the prime factorization of 7. C) 6 Simplify 48 using the greatest common
